Đáp án Bài tập tự luyện số 2
Câu 1 [149223]: Biết 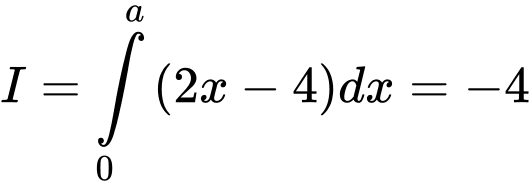 . Khi đó
. Khi đó 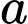 nhận giá trị bằng
nhận giá trị bằng
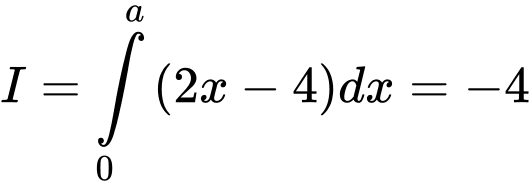 . Khi đó
. Khi đó 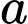 nhận giá trị bằng
nhận giá trị bằng A, 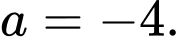
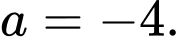
B, 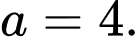
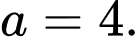
C, 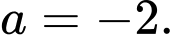
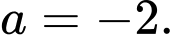
D, 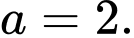
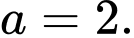
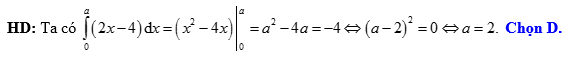 Đáp án: D
Đáp án: D
Câu 2 [149231]: Biết 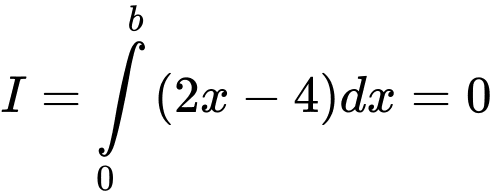 . Khi đó
. Khi đó 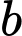 nhận giá trị bằng
nhận giá trị bằng
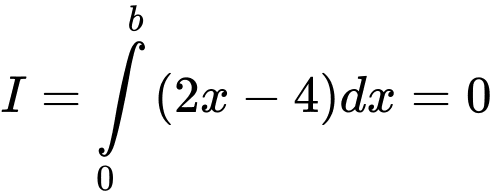 . Khi đó
. Khi đó 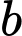 nhận giá trị bằng
nhận giá trị bằng A, 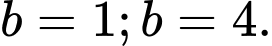
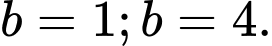
B, 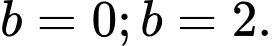
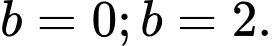
C, 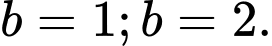
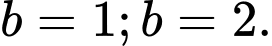
D, 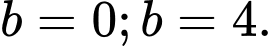
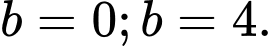
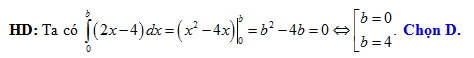 Đáp án: D
Đáp án: D
Câu 3 [149225]: Tìm số thực 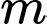 sao cho
sao cho 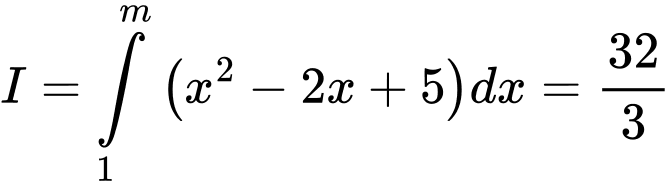 .
.
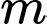 sao cho
sao cho 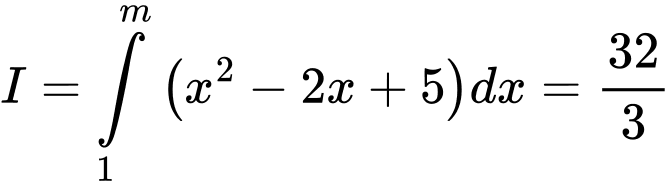 .
. A, 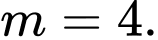
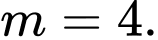
B, 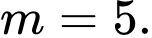
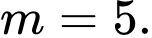
C, 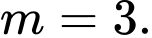
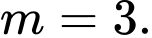
D, 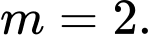
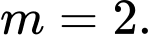
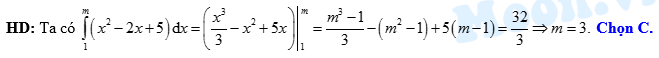 Đáp án: C
Đáp án: C
Câu 4 [149232]: Cho 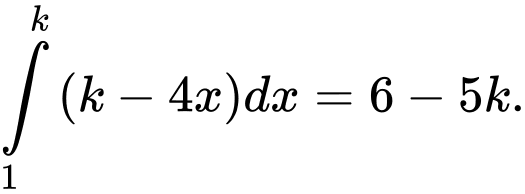 Tính giá trị của
Tính giá trị của 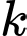 .
.
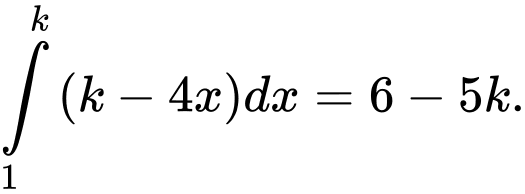 Tính giá trị của
Tính giá trị của 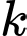 .
. A, 

B, 

C, 

D, 

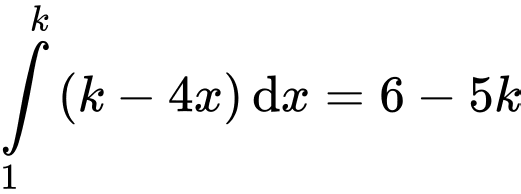
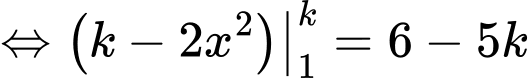
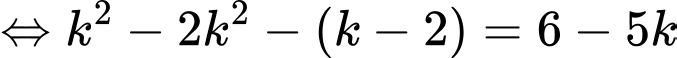
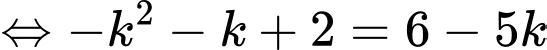
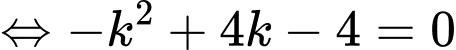
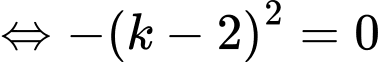
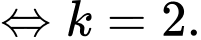
Chọn B. Đáp án: B
Câu 5 [396700]: Biết rằng 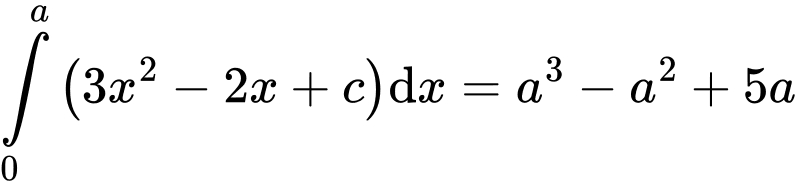 với
với 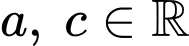 và
và 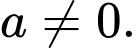 Tìm giá trị của
Tìm giá trị của 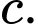
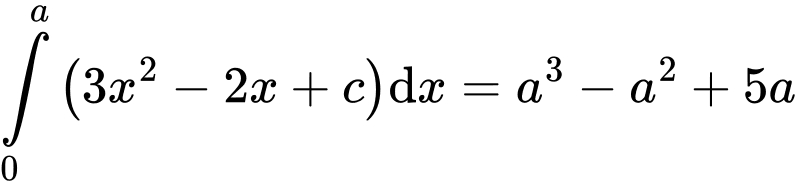 với
với 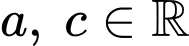 và
và 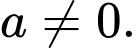 Tìm giá trị của
Tìm giá trị của 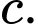
A, 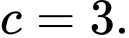
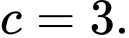
B, 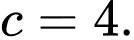
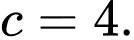
C, 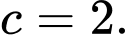
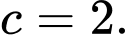
D, 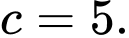
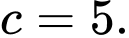
Ta có: 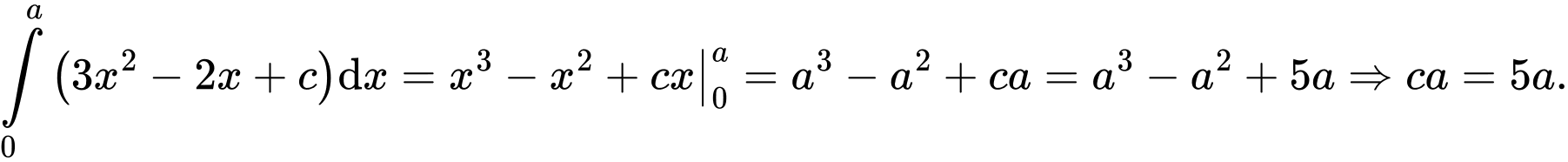
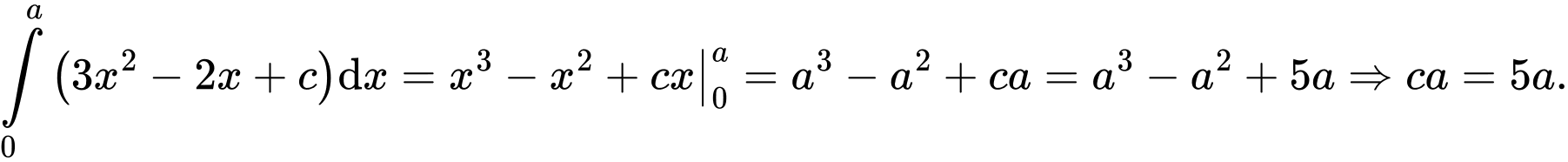
Nên suy ra 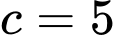 .
.
Đáp án: D 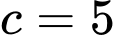 .
.
Câu 6 [396701]: Biết rằng 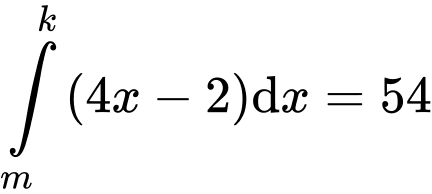 và
và 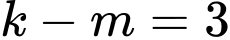 với
với 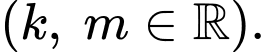 Tính
Tính 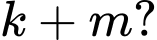
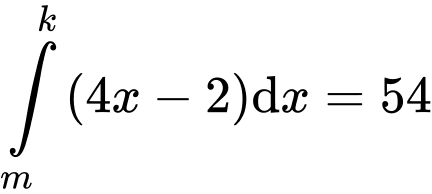 và
và 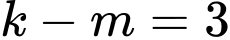 với
với 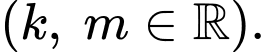 Tính
Tính 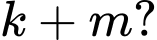
A, 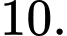
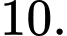
B, 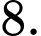
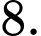
C, 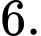
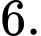
D, 
Chọn đáp án A.
Ta có:
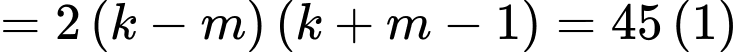
Mà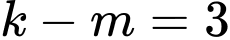 .
.
Thay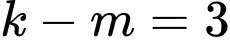 vào (1) có:
vào (1) có: 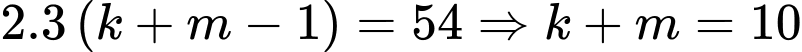 .
.
Đáp án: A
Ta có:
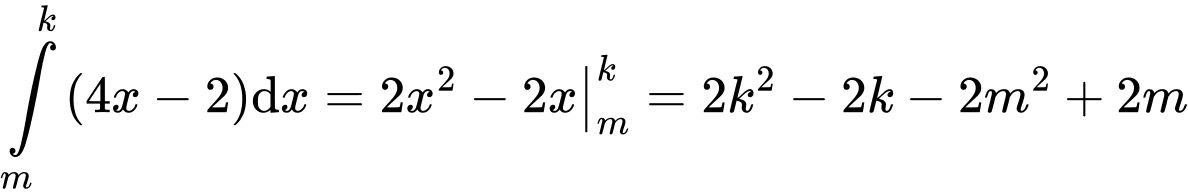
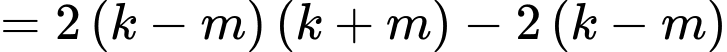
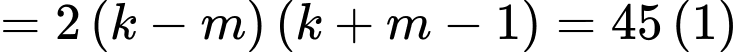
Mà
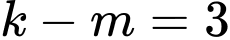 .
.Thay
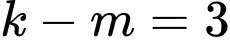 vào (1) có:
vào (1) có: 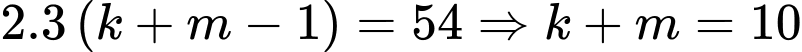 .
.Đáp án: A
Câu 7 [396702]: Biết rằng 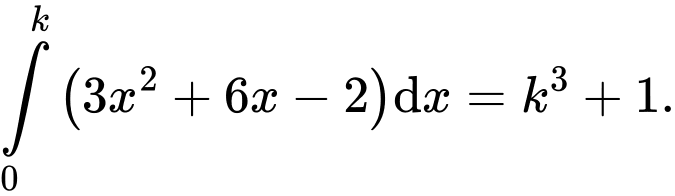 Tổng các giá trị của
Tổng các giá trị của 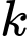 có thể nhận bằng
có thể nhận bằng
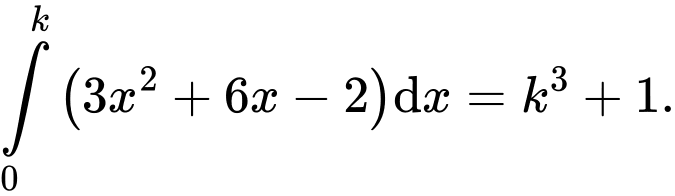 Tổng các giá trị của
Tổng các giá trị của 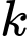 có thể nhận bằng
có thể nhận bằng A, 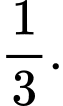
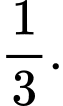
B, 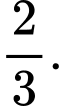
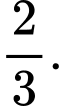
C, 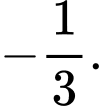
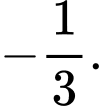
D, 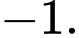
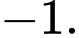
Ta có: 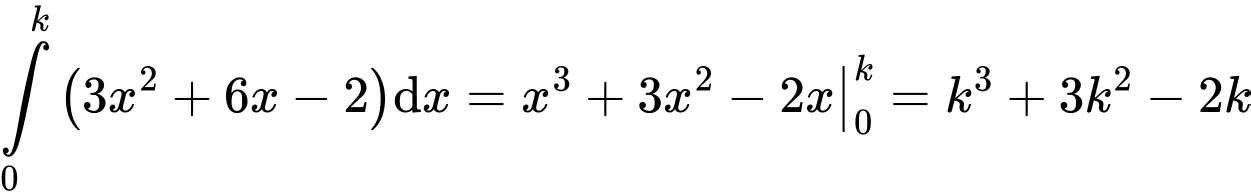
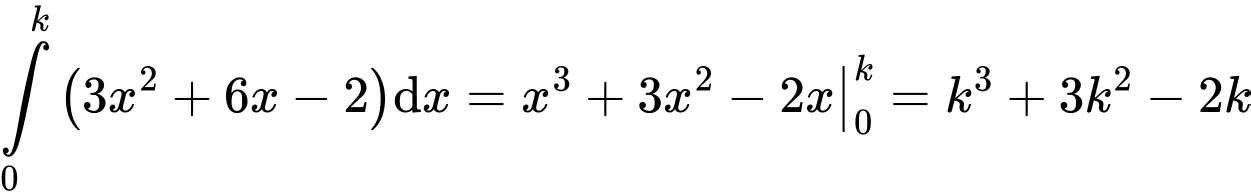
Mà 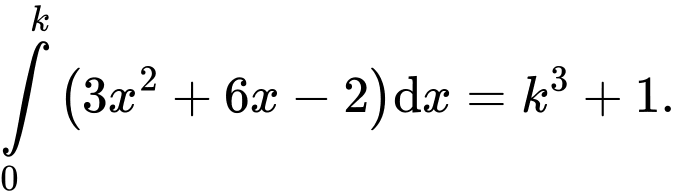
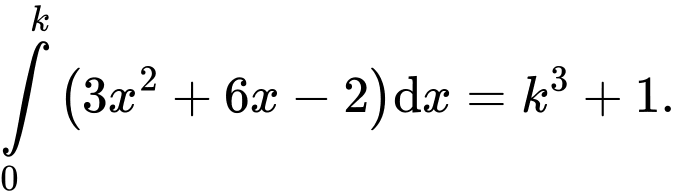
Nên có: 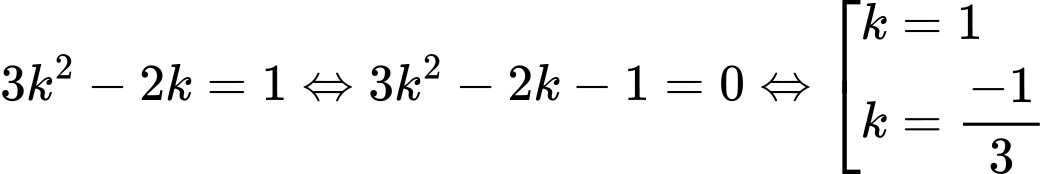
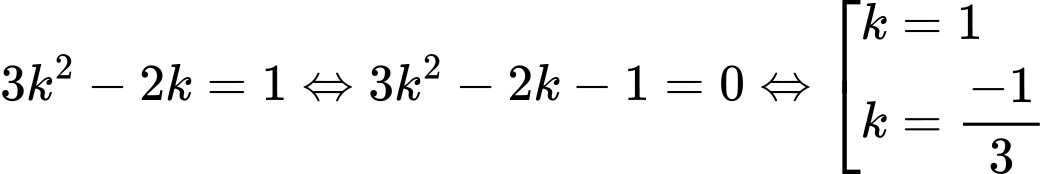
Vậy tổng các giá trị của k có thể nhận bằng 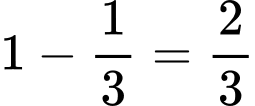 . Chọn B.
. Chọn B.
Đáp án: B 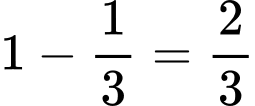 . Chọn B.
. Chọn B.
Câu 8 [149549]: Cho hàm số 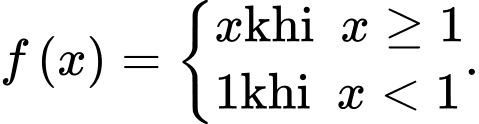 Tính tích phân
Tính tích phân
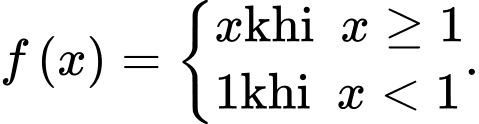 Tính tích phân
Tính tích phân
A, 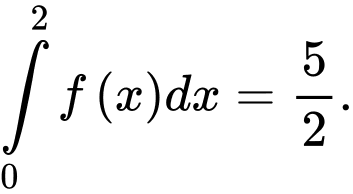
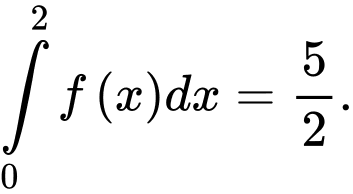
B, 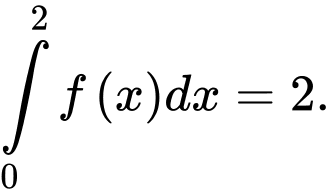
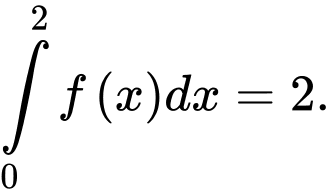
C, 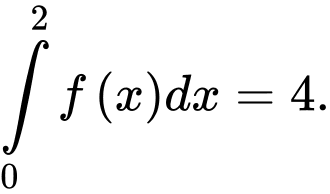
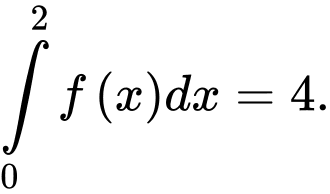
D, 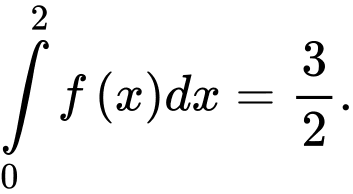
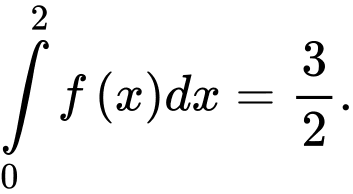
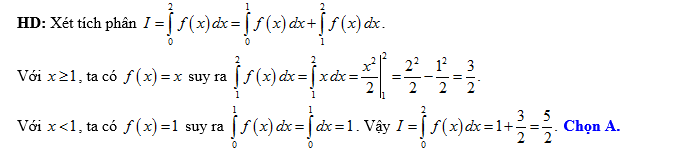 Đáp án: A
Đáp án: A
Câu 9 [904816]: Cho hàm số 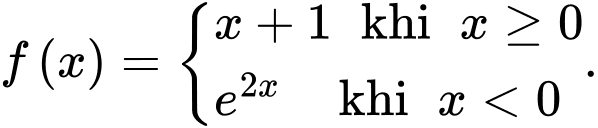 Tích phân
Tích phân 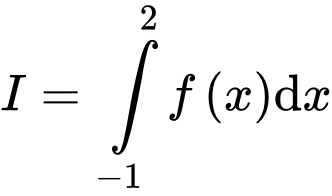 có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
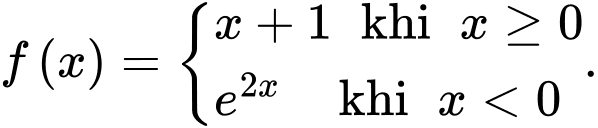 Tích phân
Tích phân 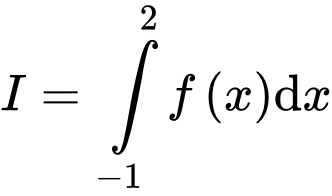 có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu? A, 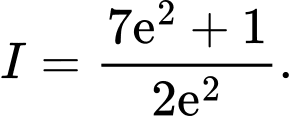
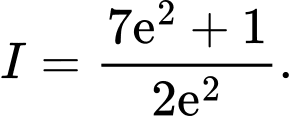
B, 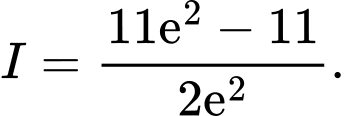
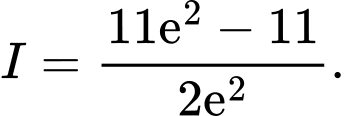
C, 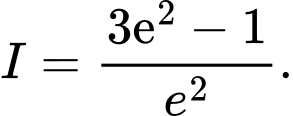
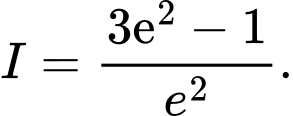
D, 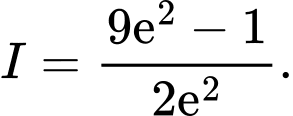
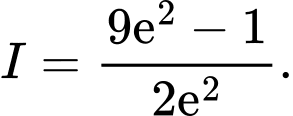
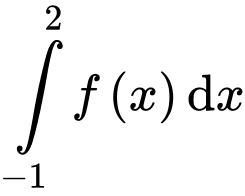
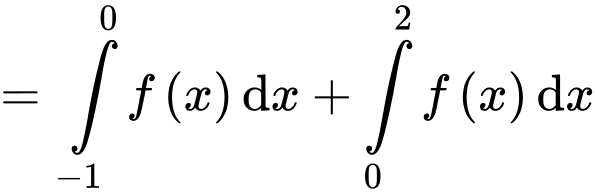
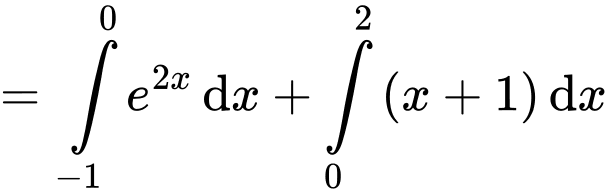
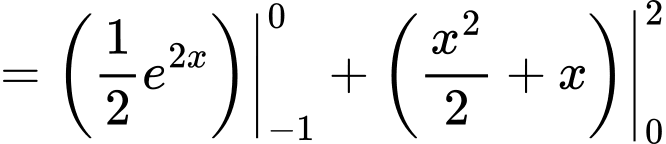
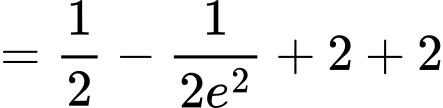
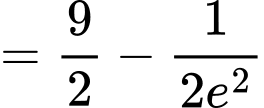
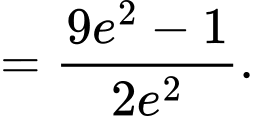
Chọn D. Đáp án: D
Câu 10 [789749]: Cho số thực 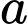 và hàm số
và hàm số 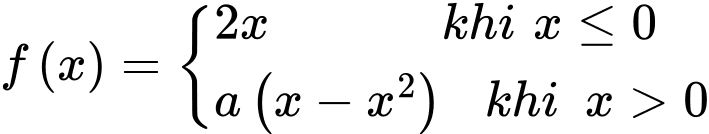 . Tính tích phân
. Tính tích phân 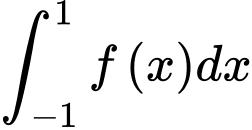 bằng
bằng
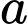 và hàm số
và hàm số 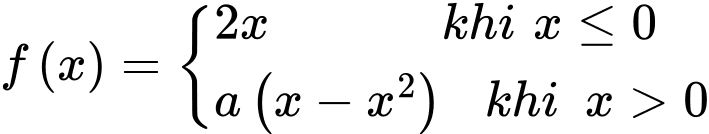 . Tính tích phân
. Tính tích phân 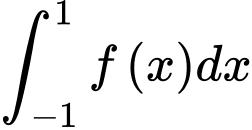 bằng
bằng A, 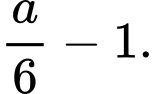
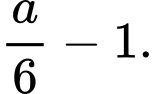
B, 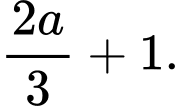
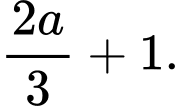
C, 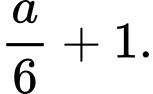
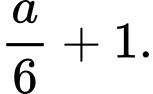
D, 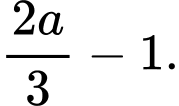
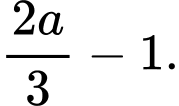
Chọn A
Ta thấy,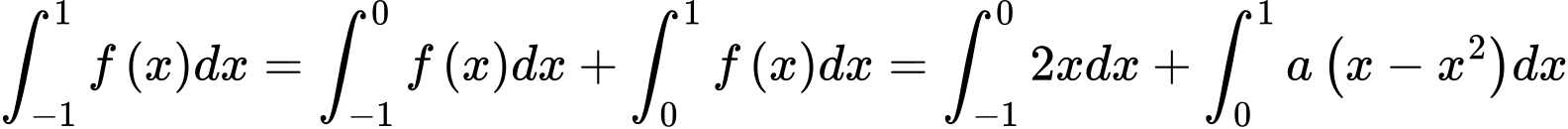
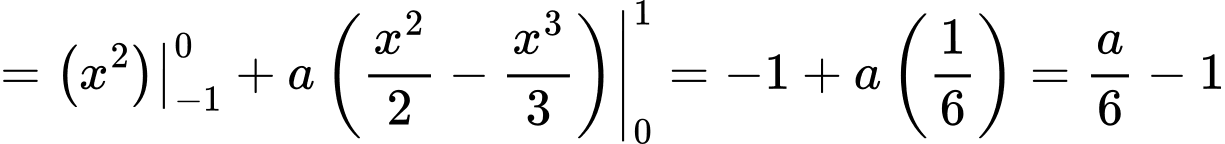 . Đáp án: A
. Đáp án: A
Ta thấy,
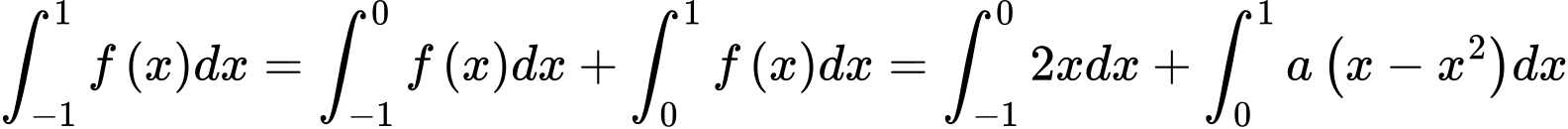
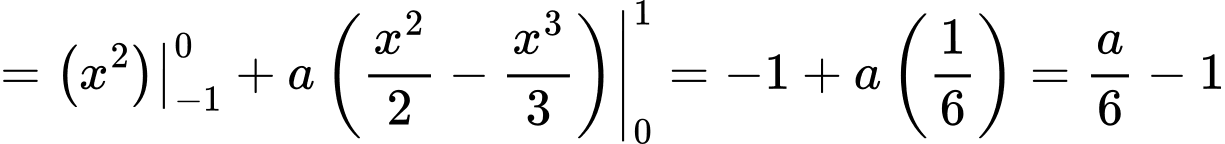 . Đáp án: A
. Đáp án: A
Câu 11 [396703]: Cho hàm số 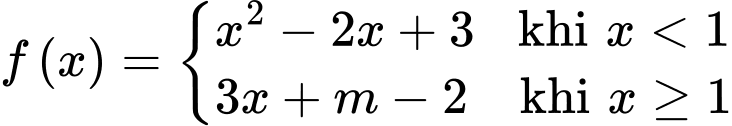 liên tục trên
liên tục trên 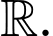 Tính tích phân
Tính tích phân 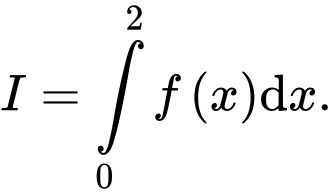
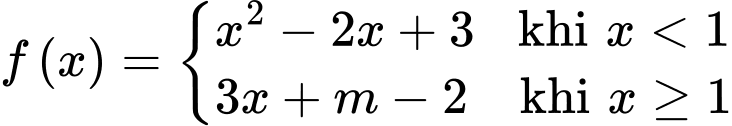 liên tục trên
liên tục trên 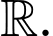 Tính tích phân
Tính tích phân 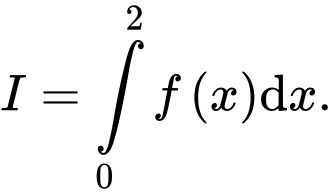
A, 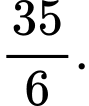
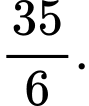
B, 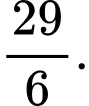
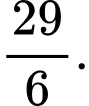
C, 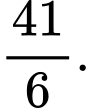
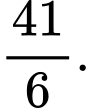
D, 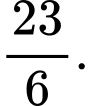
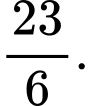
Vì hàm số liên tục trên 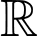 nên
nên 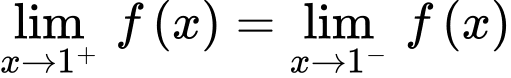
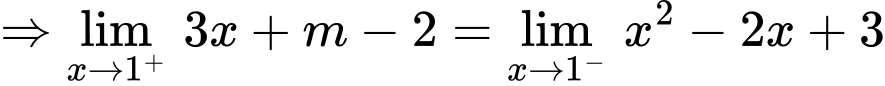
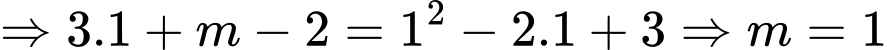
Thay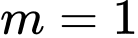 vào hàm số
vào hàm số 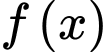 ta được
ta được 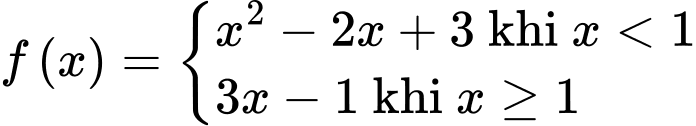
Ta có: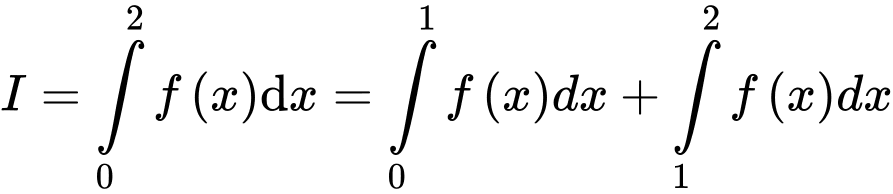
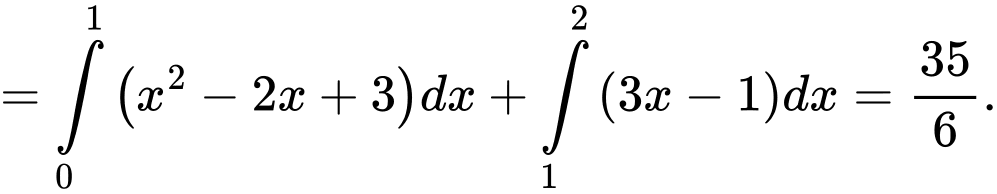 Đáp án: A
Đáp án: A
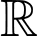 nên
nên 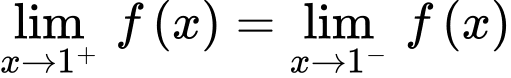
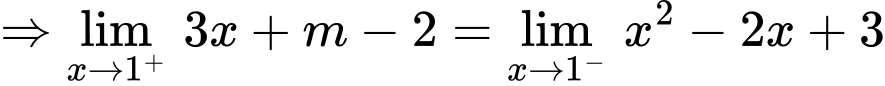
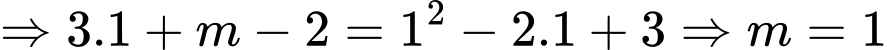
Thay
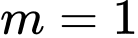 vào hàm số
vào hàm số 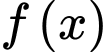 ta được
ta được 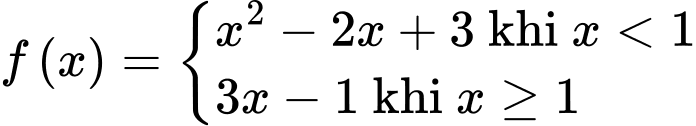
Ta có:
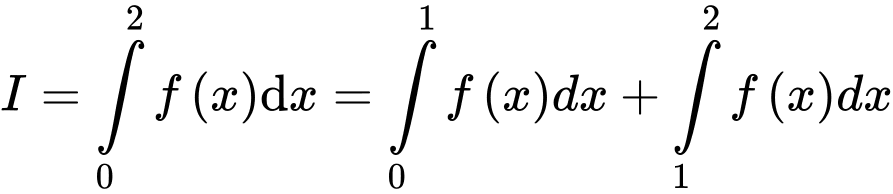
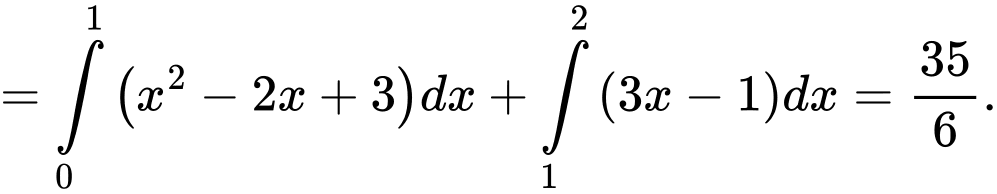 Đáp án: A
Đáp án: A
Câu 12 [396704]: Cho hàm số 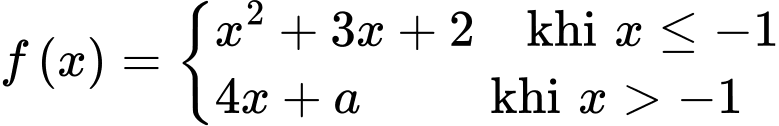 liên tục trên
liên tục trên 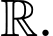 Tính tích phân
Tính tích phân 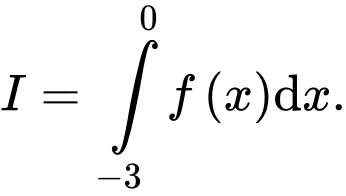
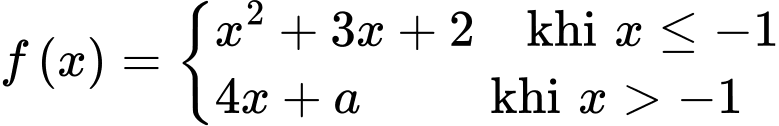 liên tục trên
liên tục trên 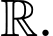 Tính tích phân
Tính tích phân 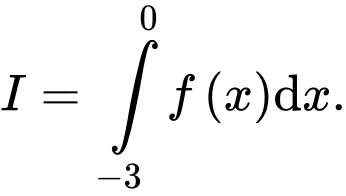
A, 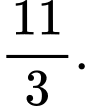
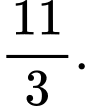
B, 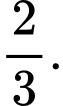
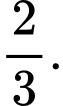
C, 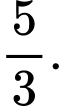
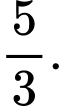
D, 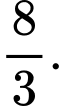
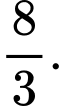
Vì hàm số liên tục trên 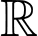 nên
nên 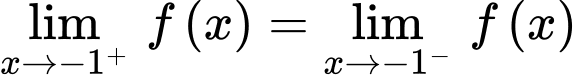
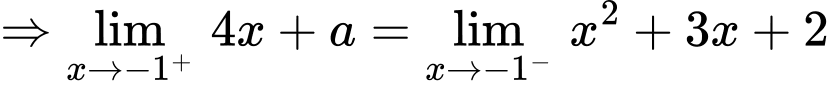
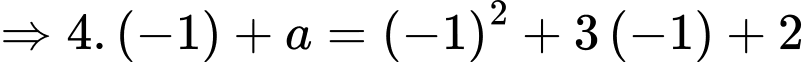
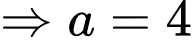
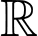 nên
nên 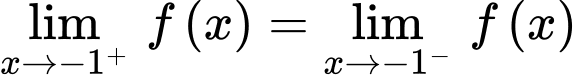
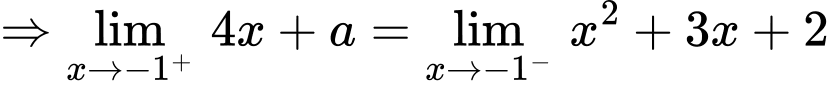
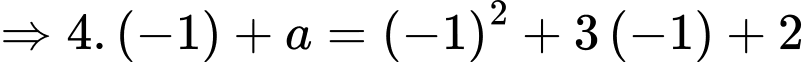
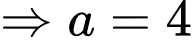
Thay  vào hàm số
vào hàm số 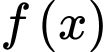 ta được
ta được 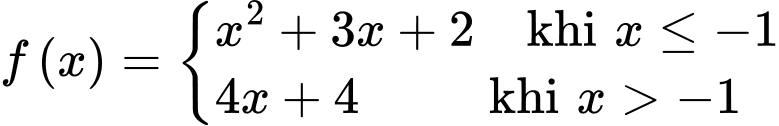
 vào hàm số
vào hàm số 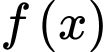 ta được
ta được 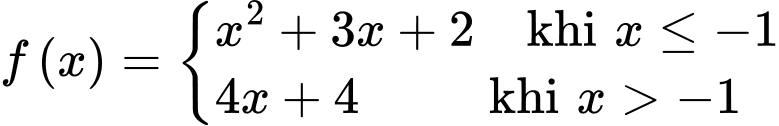
Ta có: 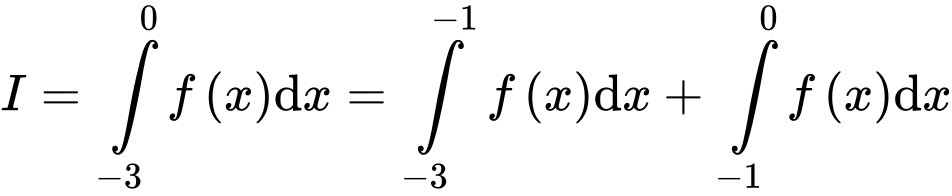
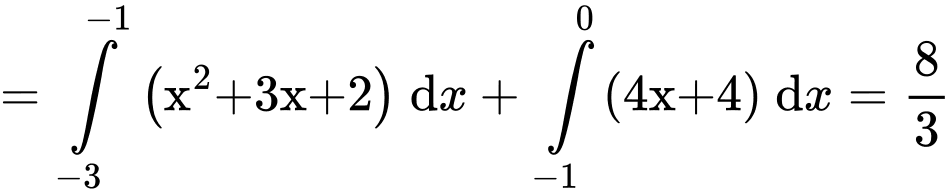
Đáp án: D 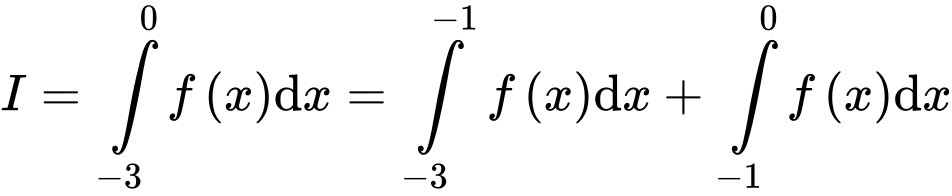
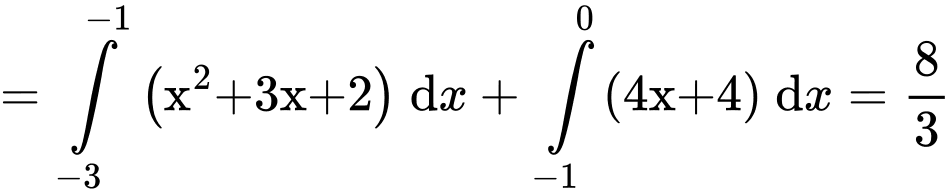
Câu 13 [149551]: Cho hàm số 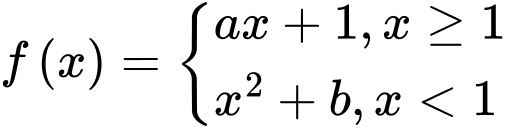 với
với 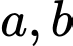 là các tham số thực. Biết rằng
là các tham số thực. Biết rằng 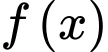 liên tục và có đạo hàm trên
liên tục và có đạo hàm trên 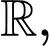 tính
tính 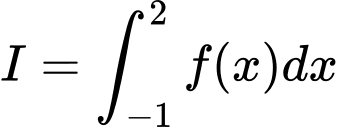 .
.
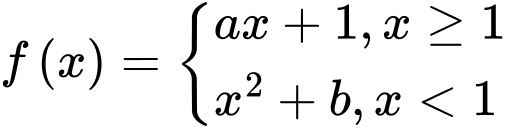 với
với 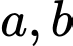 là các tham số thực. Biết rằng
là các tham số thực. Biết rằng 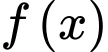 liên tục và có đạo hàm trên
liên tục và có đạo hàm trên 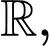 tính
tính 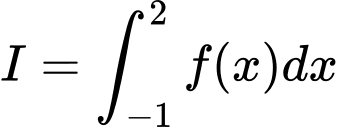 .
. A, 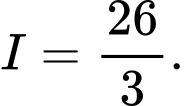
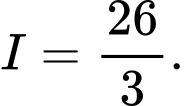
B, 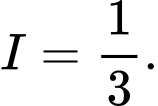
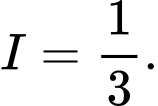
C, 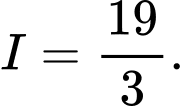
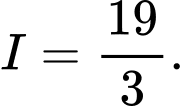
D, 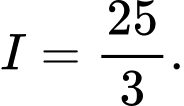
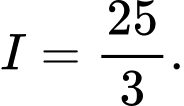
Hàm số liên tục tại điểm 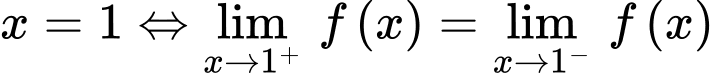
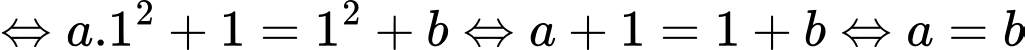
Lại có: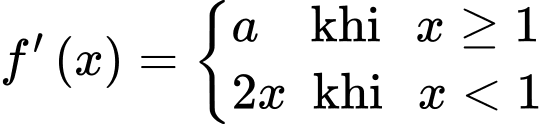
Hàm số có đạo hàm trên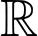 nên hàm số có đạo hàm tại điểm
nên hàm số có đạo hàm tại điểm 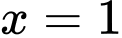
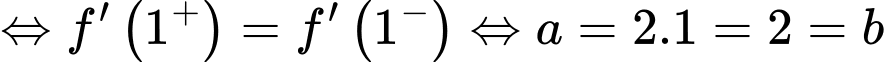
Suy ra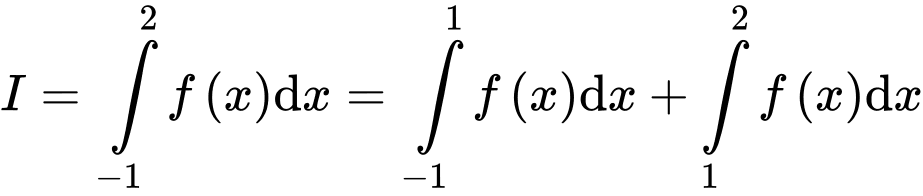
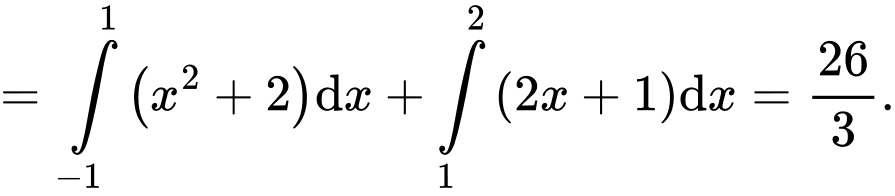
Chọn A. Đáp án: A
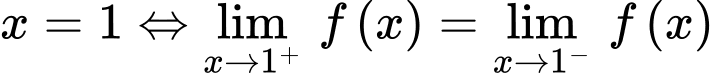
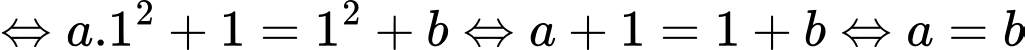
Lại có:
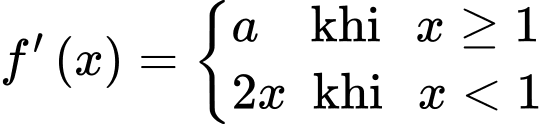
Hàm số có đạo hàm trên
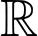 nên hàm số có đạo hàm tại điểm
nên hàm số có đạo hàm tại điểm 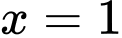
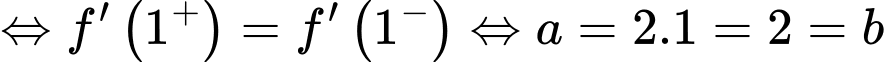
Suy ra
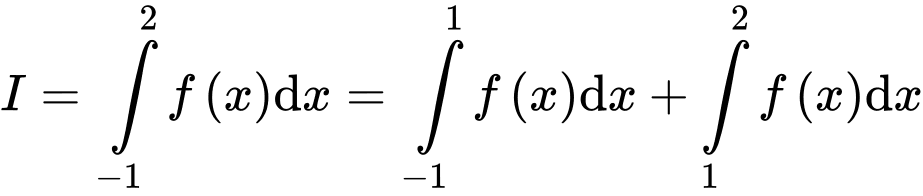
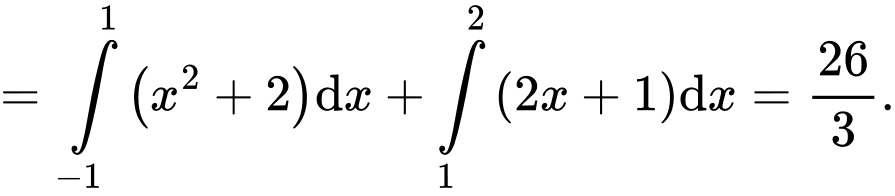
Chọn A. Đáp án: A
Câu 14 [398636]: Cho hàm số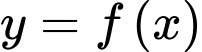 liên tục trên
liên tục trên 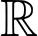 thỏa mãn
thỏa mãn 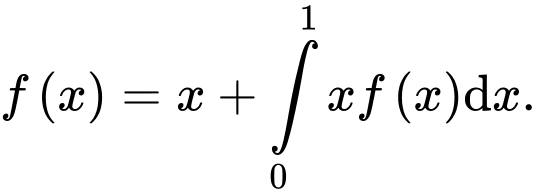 Giá trị của
Giá trị của 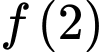 nằm trong khoảng nào sau đây?
nằm trong khoảng nào sau đây?
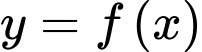 liên tục trên
liên tục trên 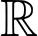 thỏa mãn
thỏa mãn 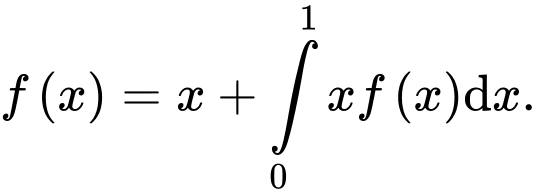 Giá trị của
Giá trị của 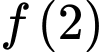 nằm trong khoảng nào sau đây?
nằm trong khoảng nào sau đây? A, 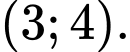
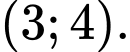
B, 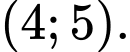
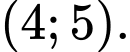
C, 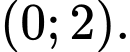
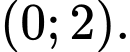
D, 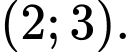
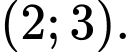
Chọn D
+)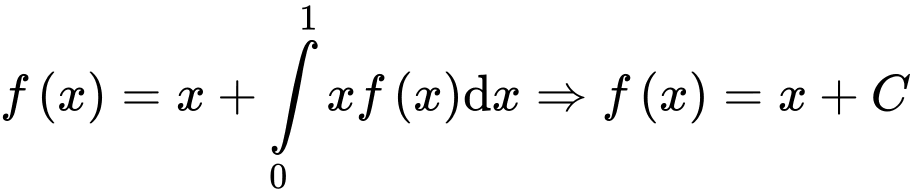 với
với 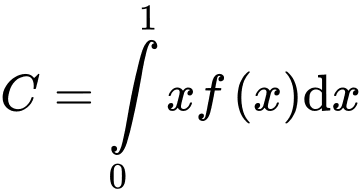
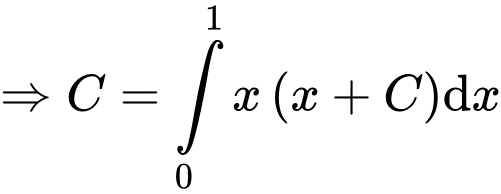
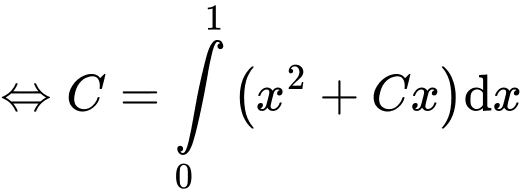
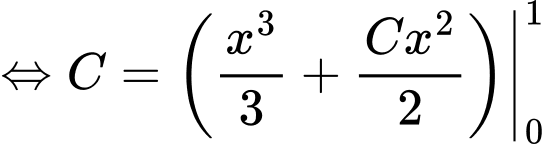
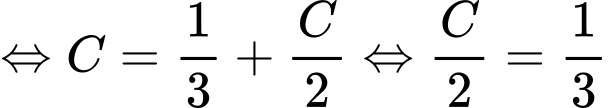
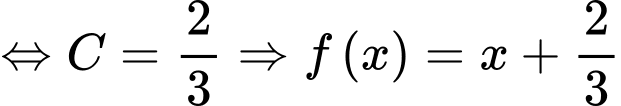
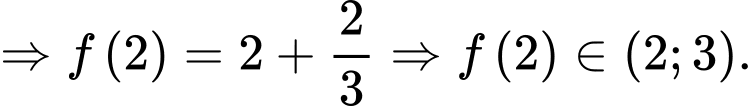 Đáp án: D
Đáp án: D
+)
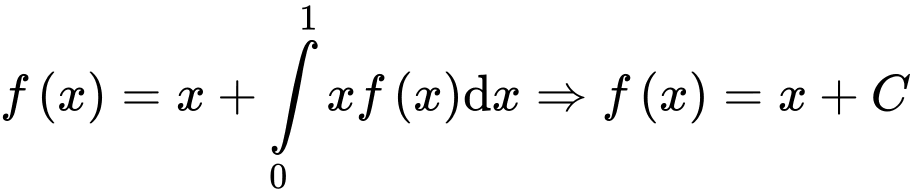 với
với 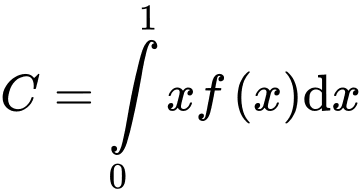
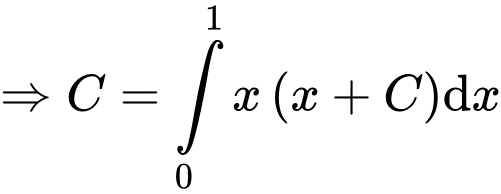
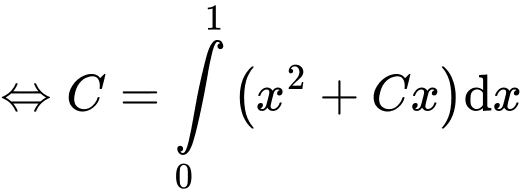
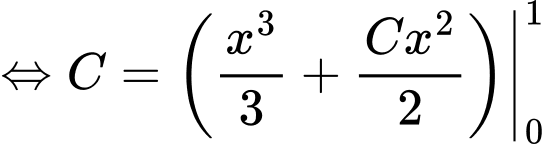
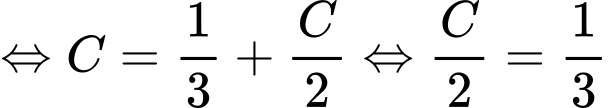
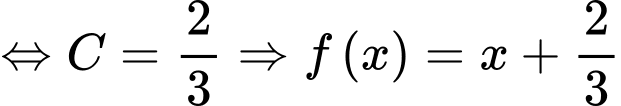
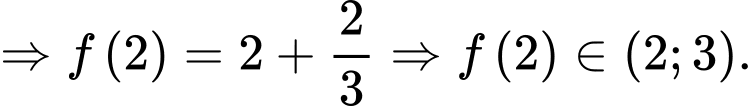 Đáp án: D
Đáp án: D
Câu 15 [161624]: Cho 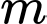 là tham số thực thỏa mãn
là tham số thực thỏa mãn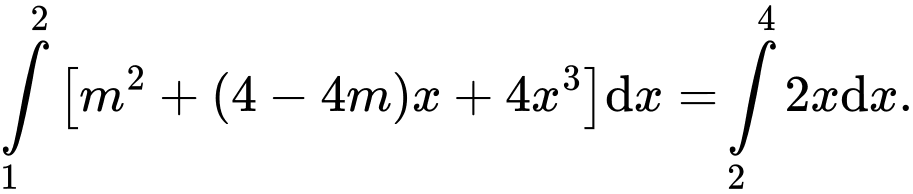 Khi đó phương trình
Khi đó phương trình 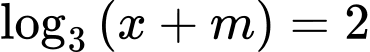 có một nghiệm duy nhất và bằng bao nhiêu?
có một nghiệm duy nhất và bằng bao nhiêu?
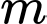 là tham số thực thỏa mãn
là tham số thực thỏa mãn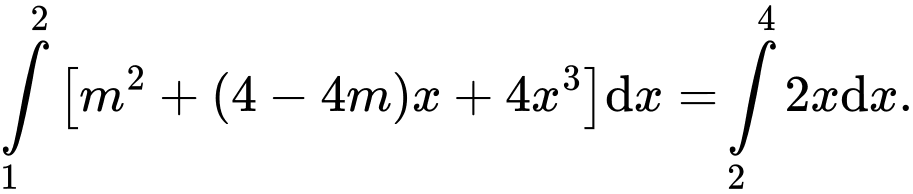 Khi đó phương trình
Khi đó phương trình 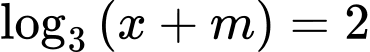 có một nghiệm duy nhất và bằng bao nhiêu?
có một nghiệm duy nhất và bằng bao nhiêu?
Ta có: 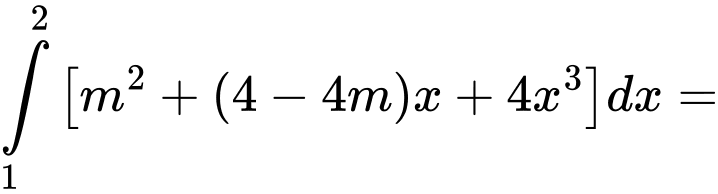
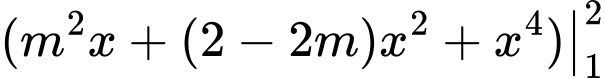
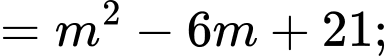
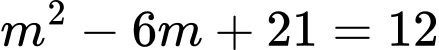
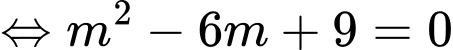
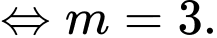 Vậy
Vậy 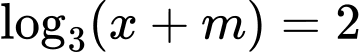
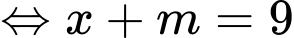
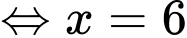
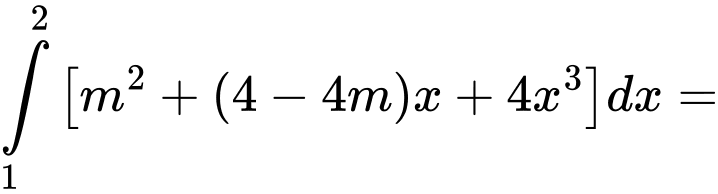
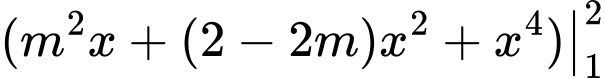
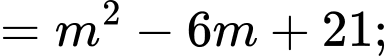
Và 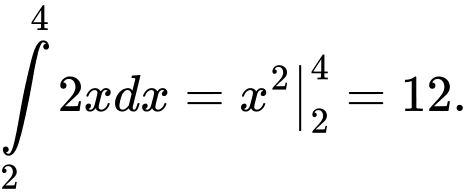
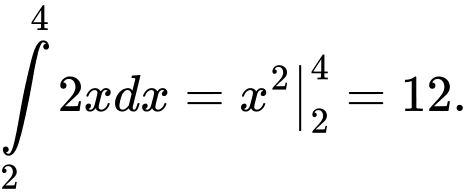
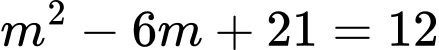
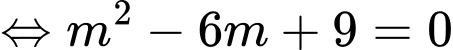
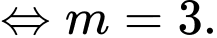 Vậy
Vậy 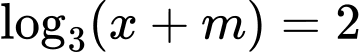
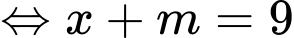
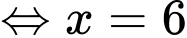
Câu 16 [386657]: Cho hàm số 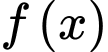 thoả mãn
thoả mãn 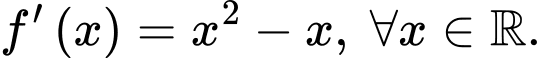 Biết
Biết 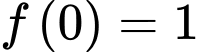 và
và 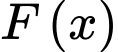 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 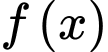 thoả mãn
thoả mãn 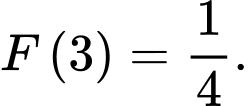 Tính
Tính 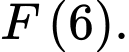 Đáp án: …………………….
Đáp án: …………………….
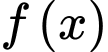 thoả mãn
thoả mãn 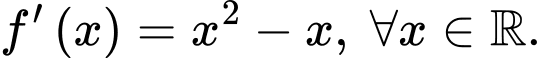 Biết
Biết 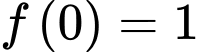 và
và 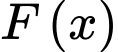 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 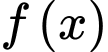 thoả mãn
thoả mãn 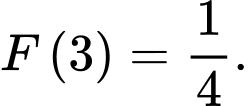 Tính
Tính 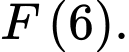 Đáp án: …………………….
Đáp án: …………………….
HD: Ta có: 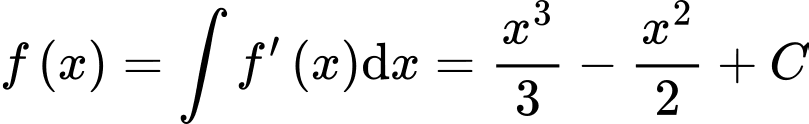 Mặt khác
Mặt khác 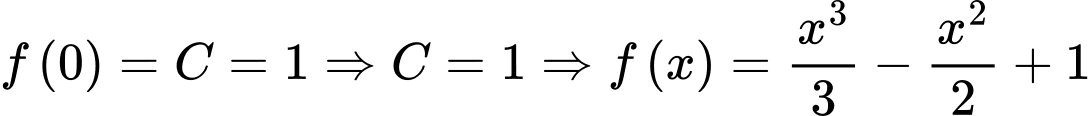 Khi đó
Khi đó 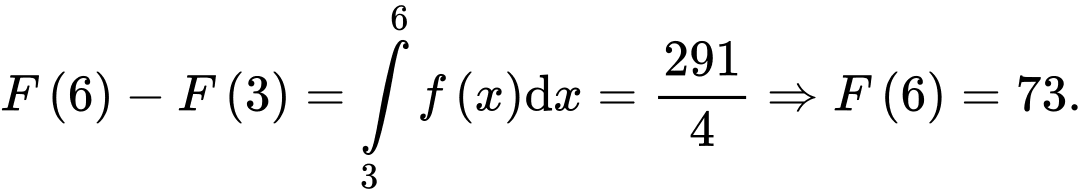
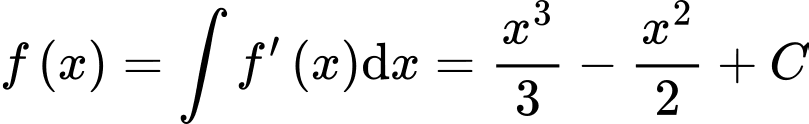 Mặt khác
Mặt khác 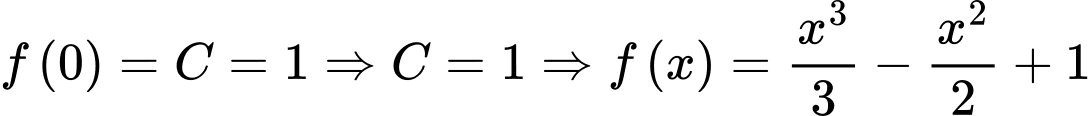 Khi đó
Khi đó 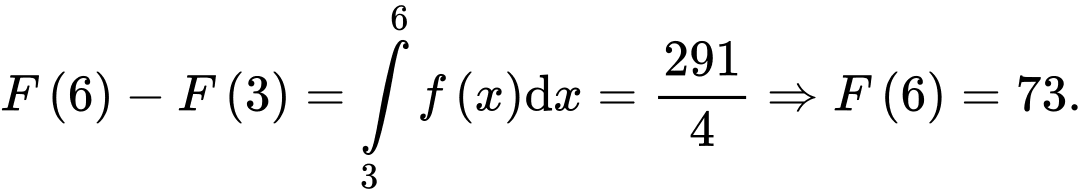
Câu 17 [386658]: Cho hàm số 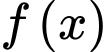 thoả mãn
thoả mãn 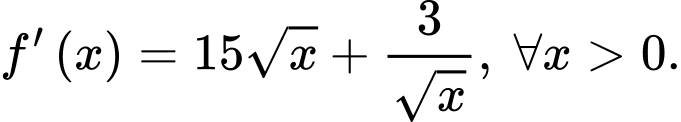 Biết
Biết 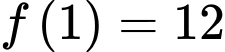 và
và 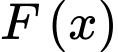 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 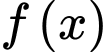 thoả mãn
thoả mãn 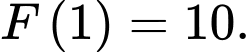 Tính
Tính 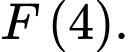 Đáp án: …………………….
Đáp án: …………………….
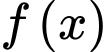 thoả mãn
thoả mãn 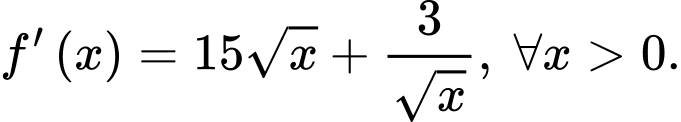 Biết
Biết 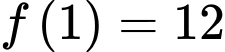 và
và 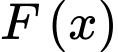 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 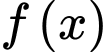 thoả mãn
thoả mãn 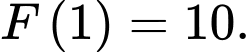 Tính
Tính 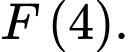 Đáp án: …………………….
Đáp án: …………………….
HD: Ta có: 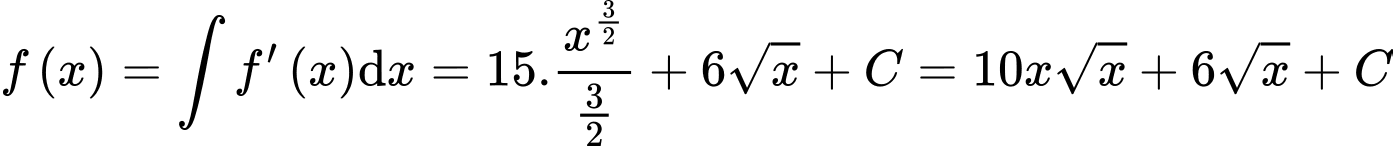 Lại có
Lại có 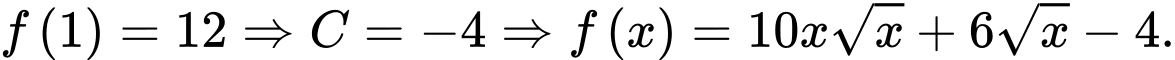 Khi đó
Khi đó 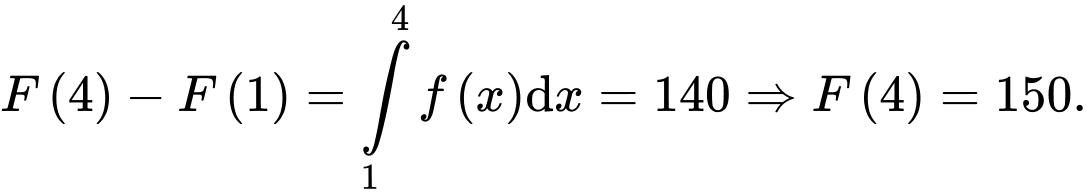
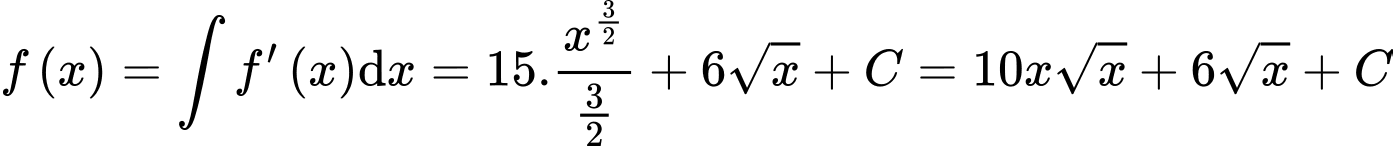 Lại có
Lại có 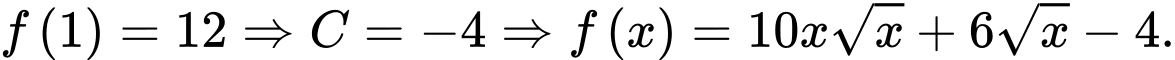 Khi đó
Khi đó 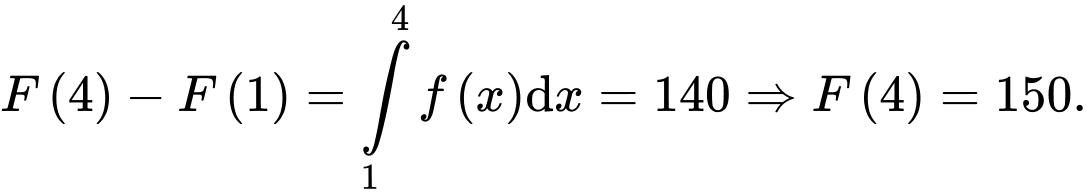
Câu 18 [396705]: Tìm giá trị của  thoả mãn
thoả mãn 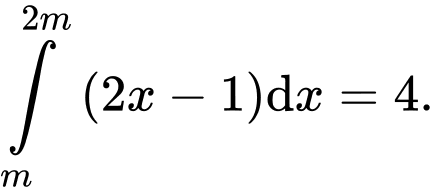
 thoả mãn
thoả mãn 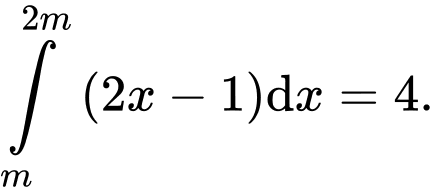
Ta có: 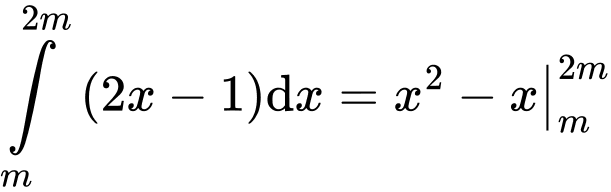
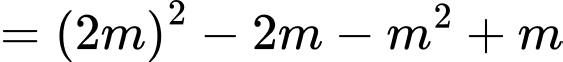
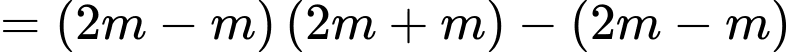
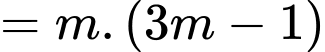
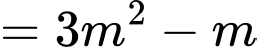
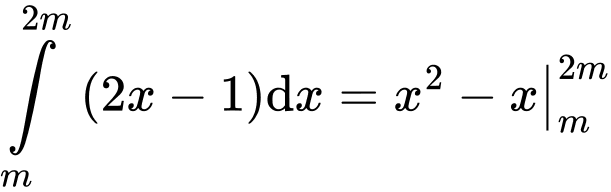
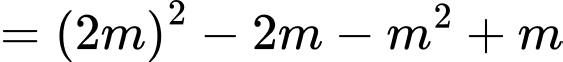
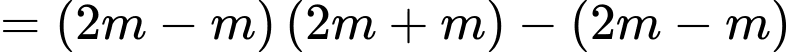
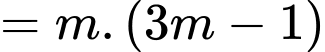
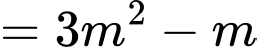
Mà 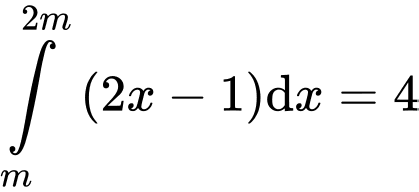
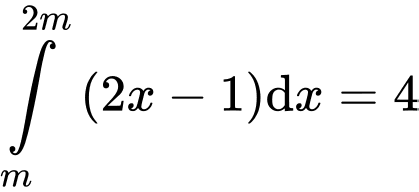
Nên 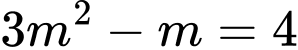
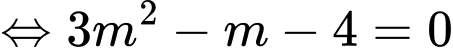
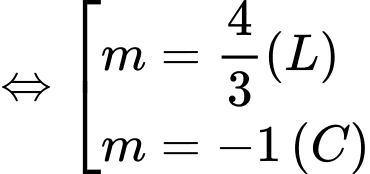
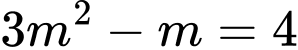
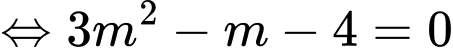
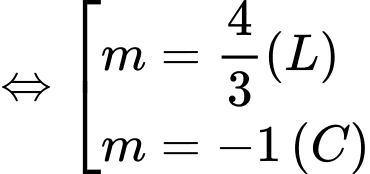
Vậy 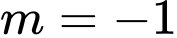
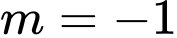
Câu 19 [396706]: Tìm 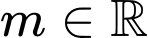 biết rằng
biết rằng 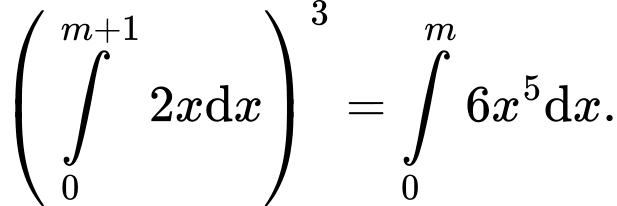
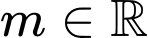 biết rằng
biết rằng 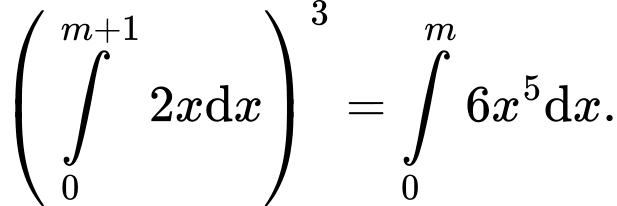
Ta có: 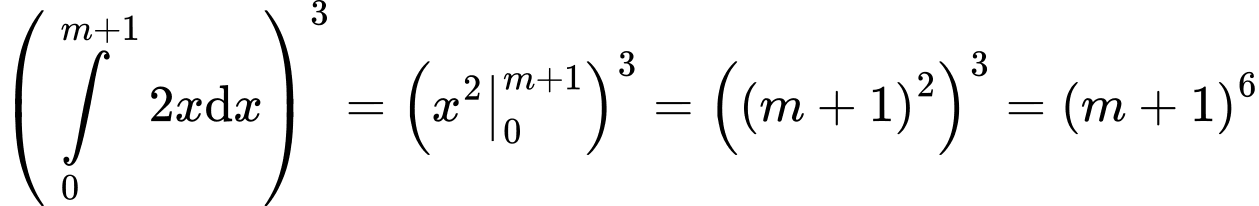
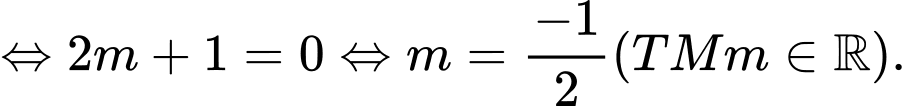
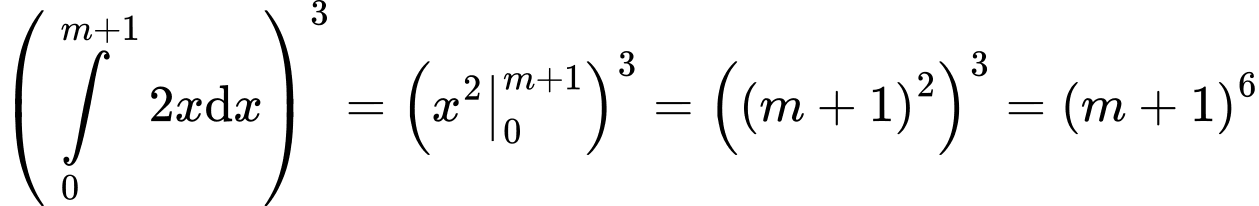
Lại có: 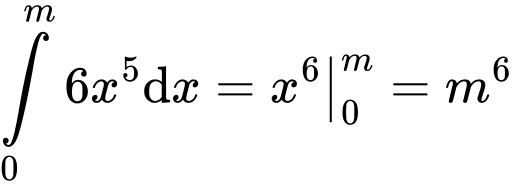
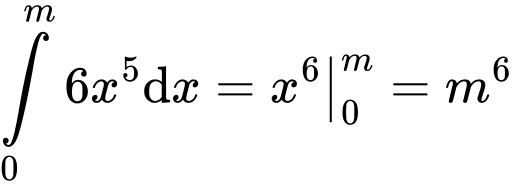
Mà 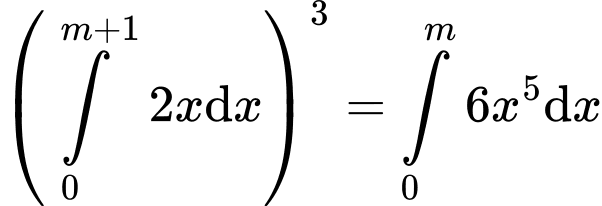 .
.
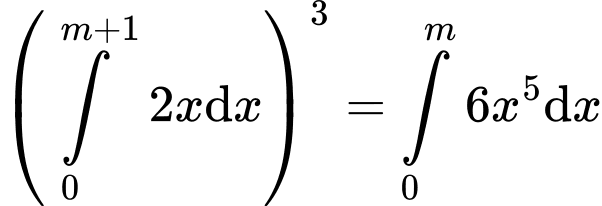 .
. Nên 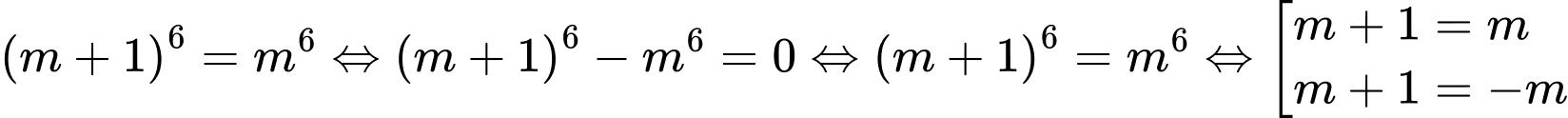
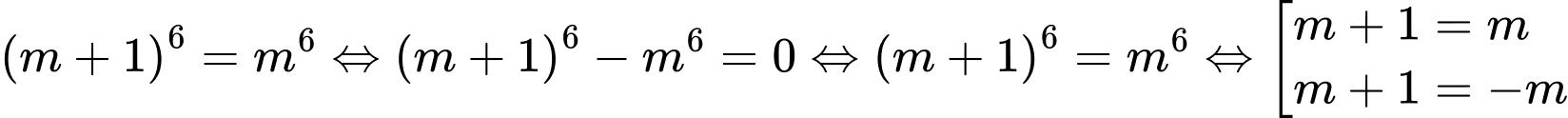
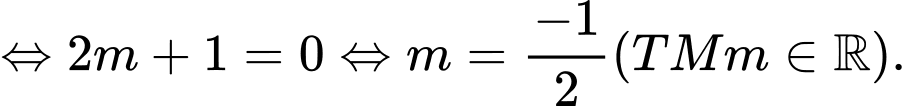
Câu 20 [396711]: Cho hàm số 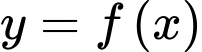 liên tục trên
liên tục trên 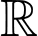 thoả mãn
thoả mãn 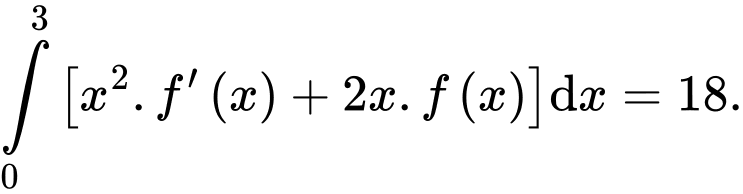 Giá trị của
Giá trị của 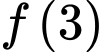 bằng
bằng
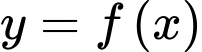 liên tục trên
liên tục trên 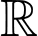 thoả mãn
thoả mãn 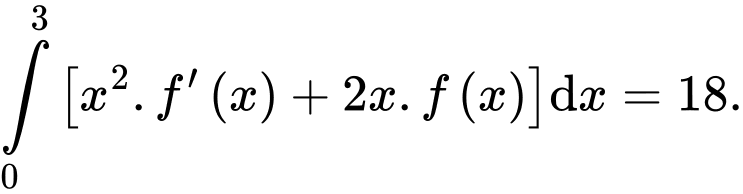 Giá trị của
Giá trị của 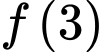 bằng
bằng
Ta có: 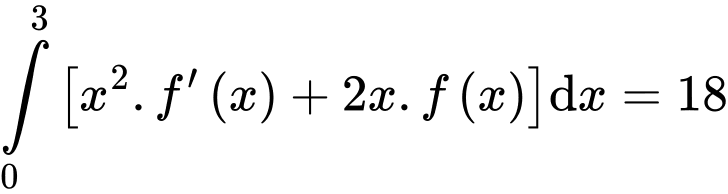
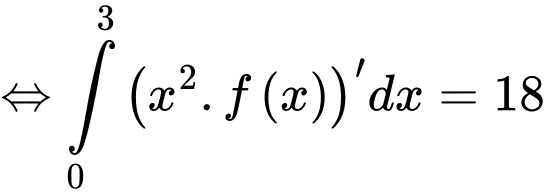
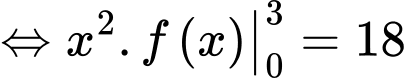
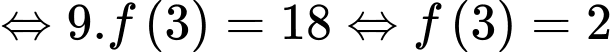
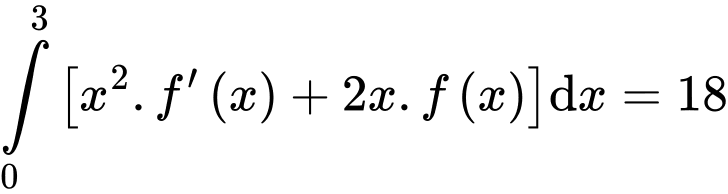
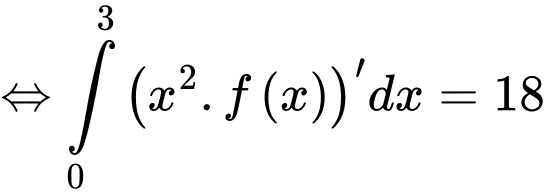
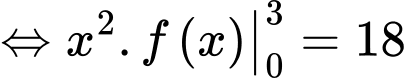
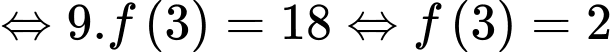
Câu 21 [396713]: Cho hàm số 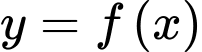 có đạo hàm đến cấp hai trên
có đạo hàm đến cấp hai trên 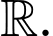 Biết hàm số
Biết hàm số 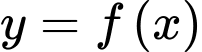 đạt cực tiểu tại
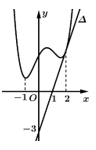
đạt cực tiểu tại 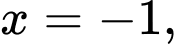 có đồ thị như hình bên và đường thẳng
có đồ thị như hình bên và đường thẳng  là tiếp tuyến của đồ thị hàm số tại điểm
là tiếp tuyến của đồ thị hàm số tại điểm 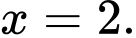 Tính
Tính 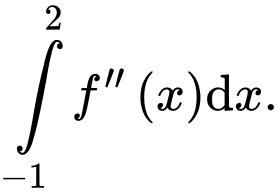
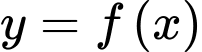 có đạo hàm đến cấp hai trên
có đạo hàm đến cấp hai trên 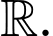 Biết hàm số
Biết hàm số 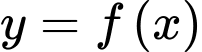 đạt cực tiểu tại
đạt cực tiểu tại 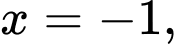 có đồ thị như hình bên và đường thẳng
có đồ thị như hình bên và đường thẳng  là tiếp tuyến của đồ thị hàm số tại điểm
là tiếp tuyến của đồ thị hàm số tại điểm 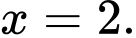 Tính
Tính 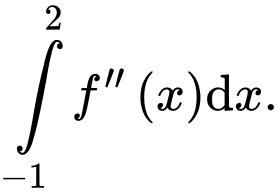

Dựa vào đồ thị hàm số ta thấy 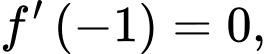
Đường thẳng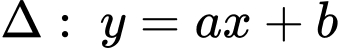 đi qua các điểm
đi qua các điểm 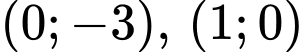 nên
nên 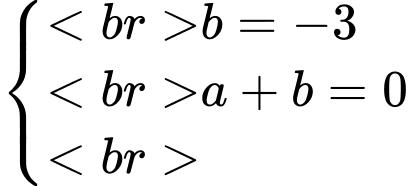
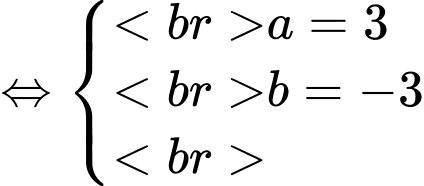
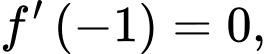
Đường thẳng
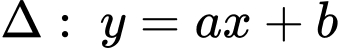 đi qua các điểm
đi qua các điểm 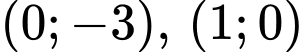 nên
nên 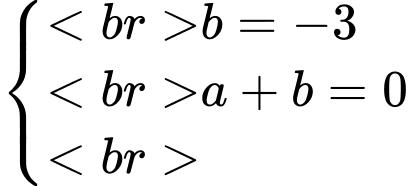
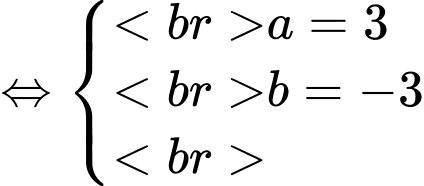
Do  là tiếp tuyến của đồ thị nên
là tiếp tuyến của đồ thị nên 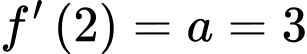
 là tiếp tuyến của đồ thị nên
là tiếp tuyến của đồ thị nên 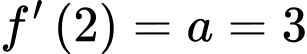
Ta có: 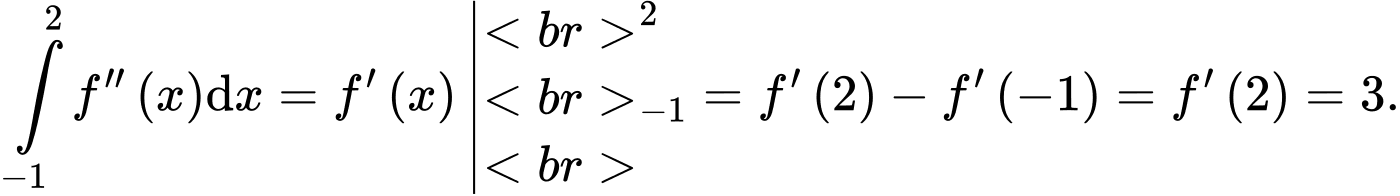
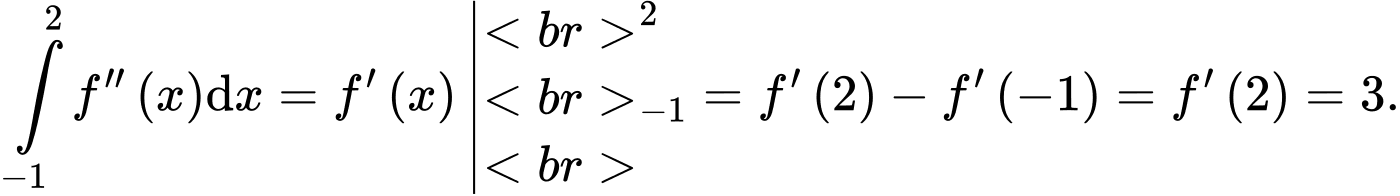
Câu 22 [396712]: Biết rằng hàm số 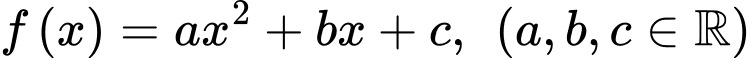 thỏa mãn
thỏa mãn 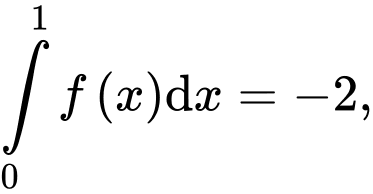
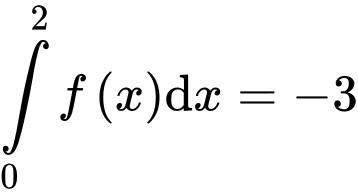 và
và 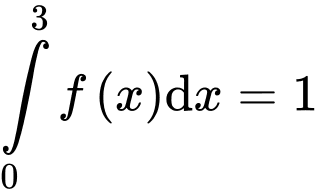 (với
(với 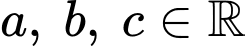 ). Tính giá trị của biểu thức
). Tính giá trị của biểu thức 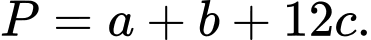
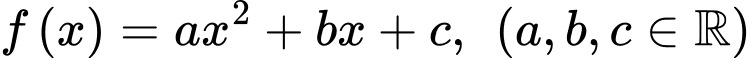 thỏa mãn
thỏa mãn 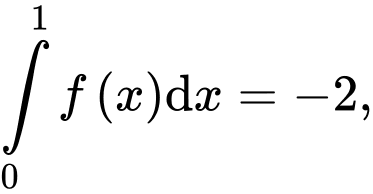
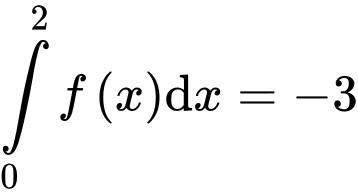 và
và 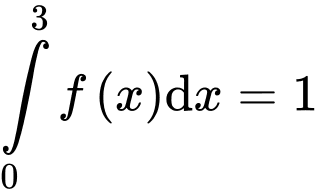 (với
(với 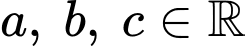 ). Tính giá trị của biểu thức
). Tính giá trị của biểu thức 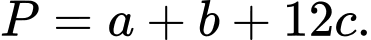
Ta có: 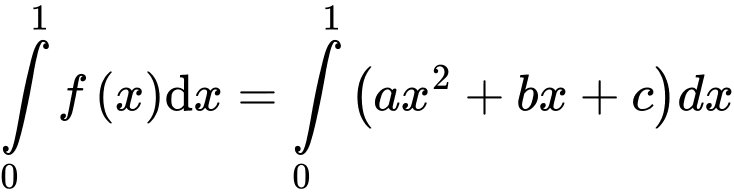
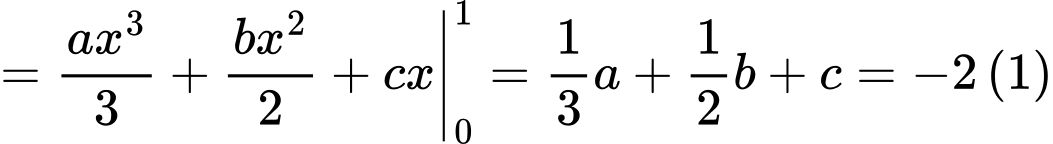
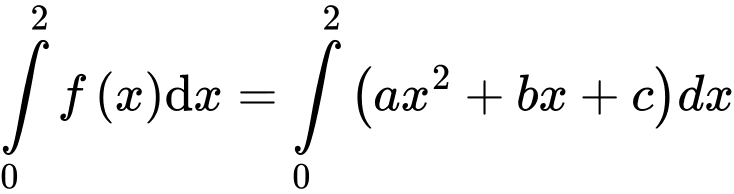
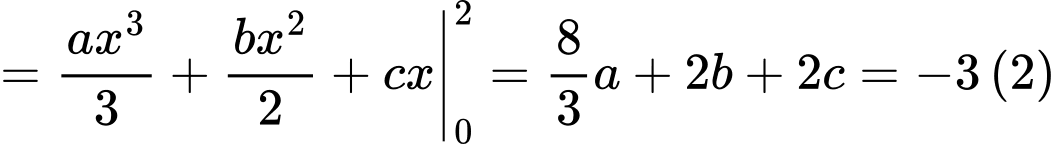
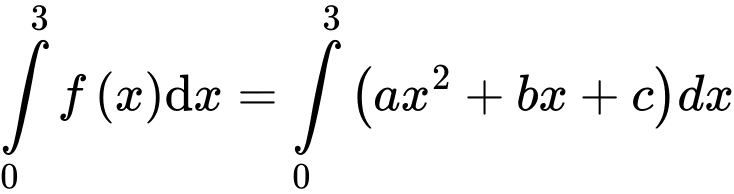
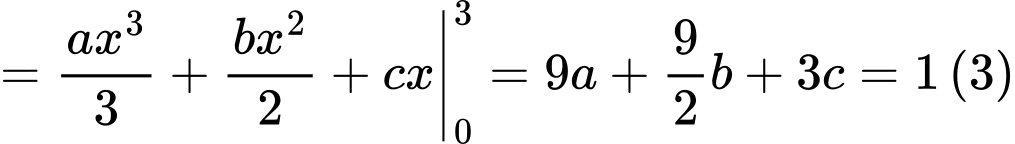
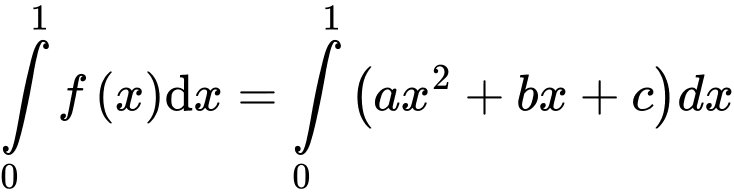
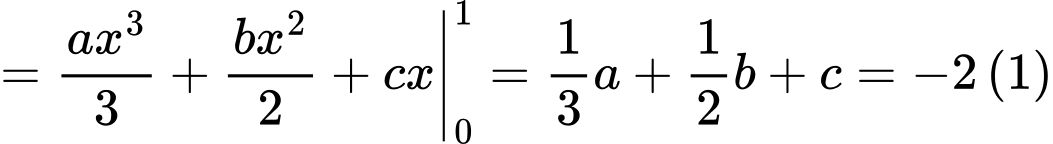
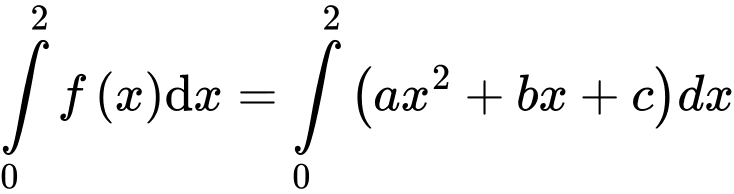
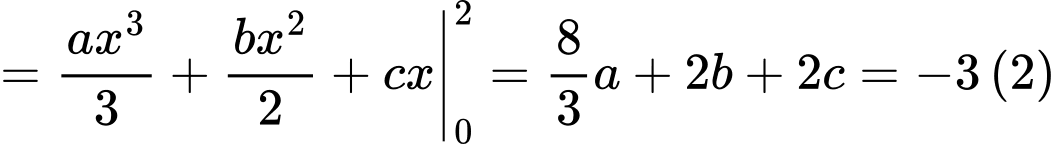
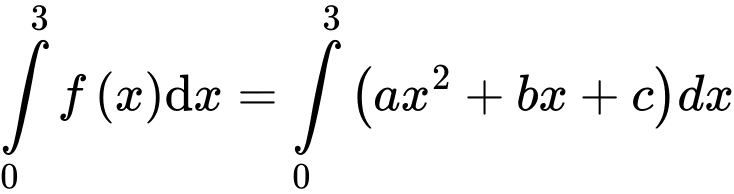
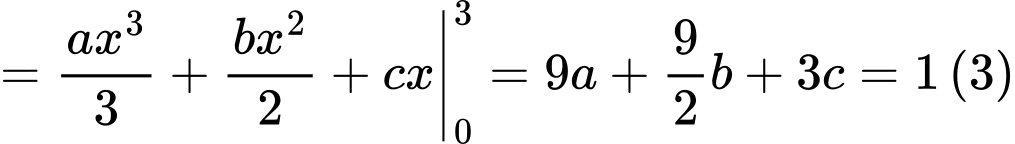
Từ (1) (2) (3) suy ra 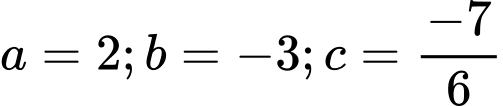
Nên
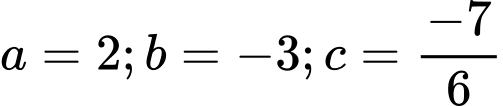
Nên

Câu 23 [396716]: Năng lượng gió trên đất liền là một trong những công nghệ năng lượng tái tạo đang được phát triển ở quy mô toàn cầu. Các turbine gió thường có ba cánh quay trên một trục ngang, lấy động năng từ quá trình di chuyển dòng không khí (gió) để chuyển đổi thành điện năng thông qua một máy phát điện được kết nối với lưới điện. Hình thang cong (tô màu đậm) trong hình dưới mô tả một phần mặt cắt đứng của cánh turbine, được giới hạn bởi các đường thẳng 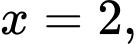
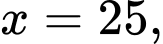 trục
trục 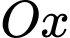 và đồ thị hàm số
và đồ thị hàm số 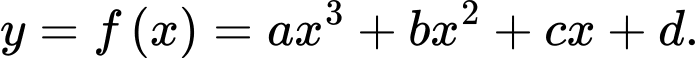 Biết rằng đồ thị hàm số
Biết rằng đồ thị hàm số 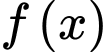 đi qua điểm
đi qua điểm 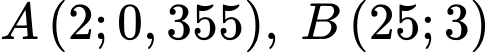 và đạt cực trị tại điểm
và đạt cực trị tại điểm 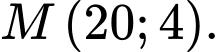 Diện tích hình thang cong đó là bao nhiêu
Diện tích hình thang cong đó là bao nhiêu 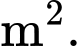 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.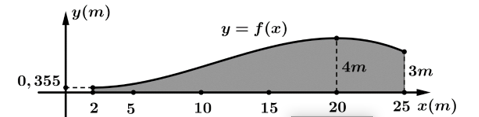
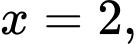
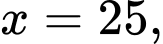 trục
trục 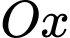 và đồ thị hàm số
và đồ thị hàm số 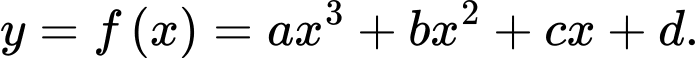 Biết rằng đồ thị hàm số
Biết rằng đồ thị hàm số 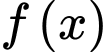 đi qua điểm
đi qua điểm 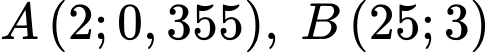 và đạt cực trị tại điểm
và đạt cực trị tại điểm 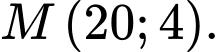 Diện tích hình thang cong đó là bao nhiêu
Diện tích hình thang cong đó là bao nhiêu 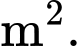 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.
Xét hàm số 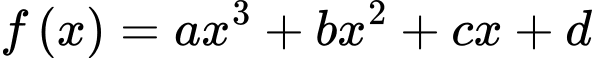
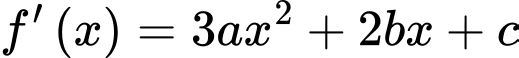
Vì hàm số đạt cực trị tại điểm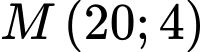 nên
nên 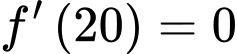
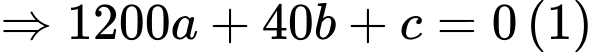
Vì đồ thị hàm số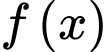 đi qua 2 điểm
đi qua 2 điểm 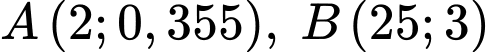 và đạt cực trị tại điểm
và đạt cực trị tại điểm 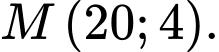
Nên thay tọa độ điểm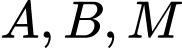 vào phương trình
vào phương trình 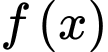 ta được
ta được
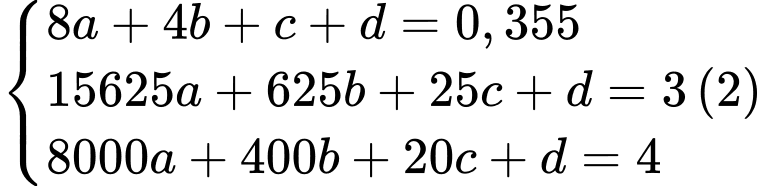
Từ (1)(2) suy ra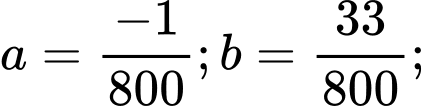
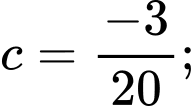
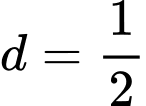
Diện tích của hình thang cong là:
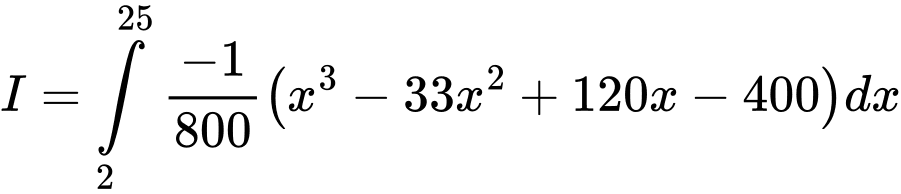
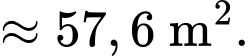
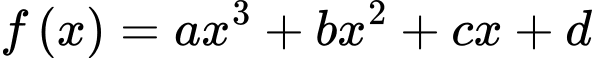
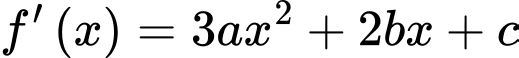
Vì hàm số đạt cực trị tại điểm
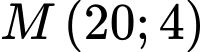 nên
nên 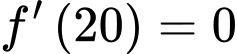
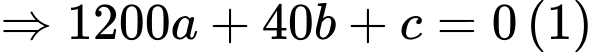
Vì đồ thị hàm số
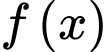 đi qua 2 điểm
đi qua 2 điểm 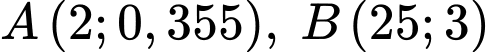 và đạt cực trị tại điểm
và đạt cực trị tại điểm 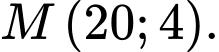
Nên thay tọa độ điểm
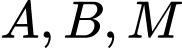 vào phương trình
vào phương trình 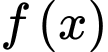 ta được
ta được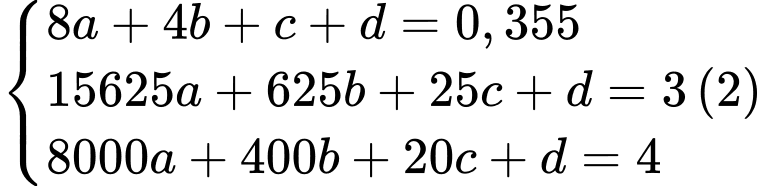
Từ (1)(2) suy ra
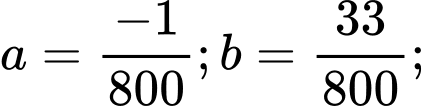
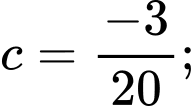
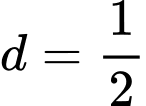
Diện tích của hình thang cong là:
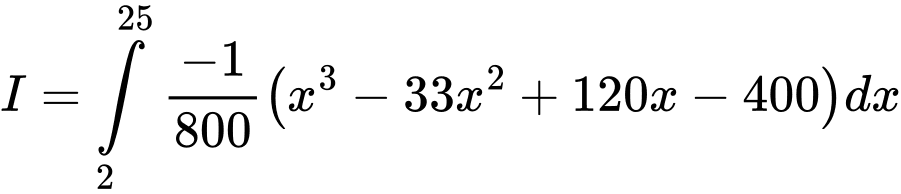
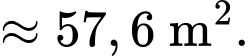
Câu 24 [396714]: Cho hàm số 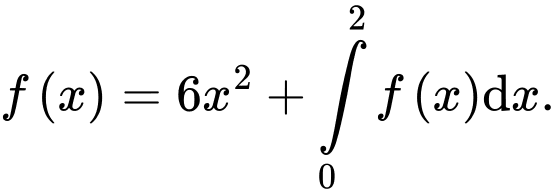 Tính giá trị của
Tính giá trị của 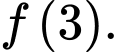
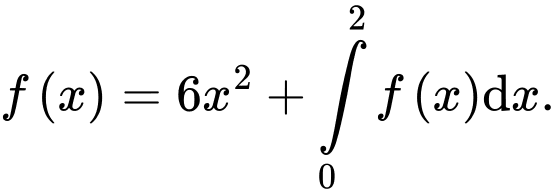 Tính giá trị của
Tính giá trị của 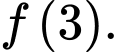
Đặt 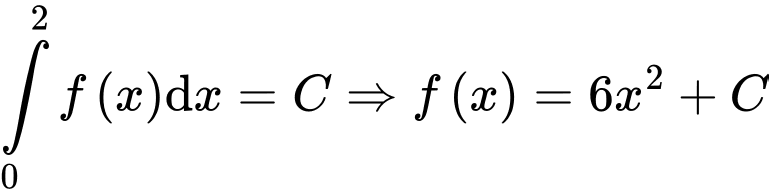 suy ra
suy ra 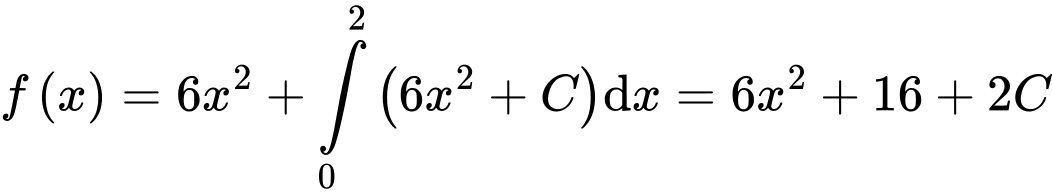
Khi đó: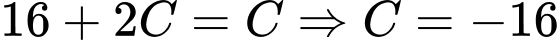 do đó
do đó 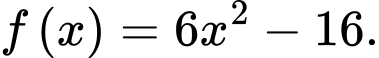
Vậy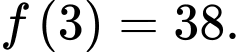
Đáp án: 38.
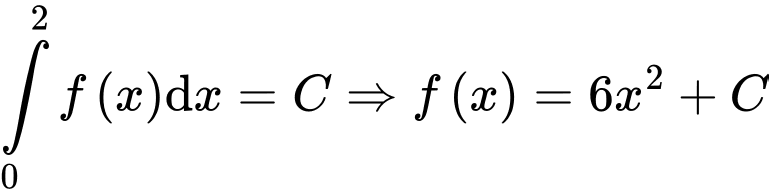 suy ra
suy ra 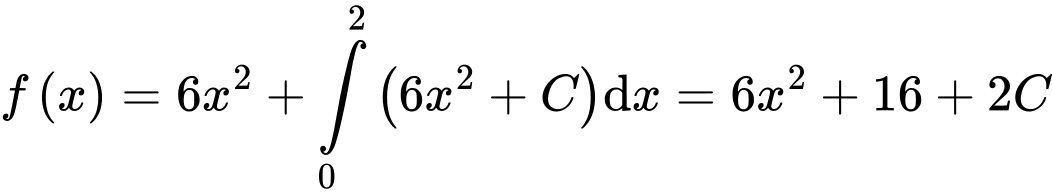
Khi đó:
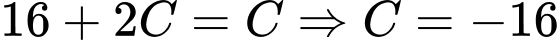 do đó
do đó 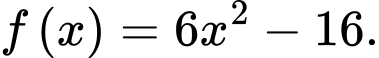
Vậy
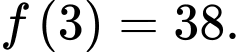
Đáp án: 38.
Câu 25 [396715]: Cho hàm số 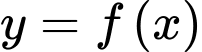 liên tục trên và thỏa mãn
liên tục trên và thỏa mãn 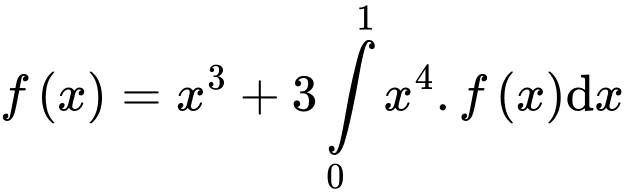 với mọi
với mọi 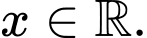 Tính
Tính 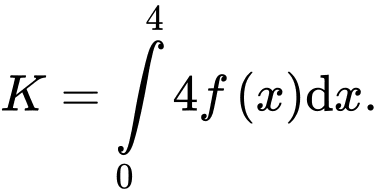
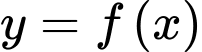 liên tục trên và thỏa mãn
liên tục trên và thỏa mãn 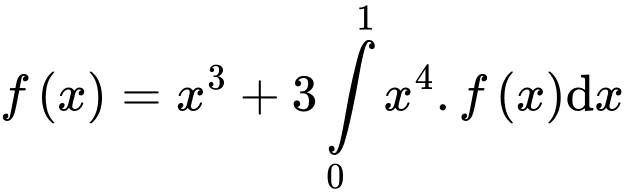 với mọi
với mọi 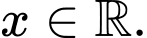 Tính
Tính 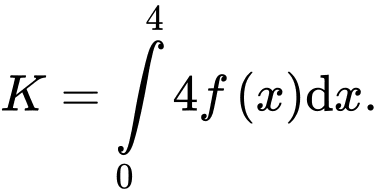
Đặt 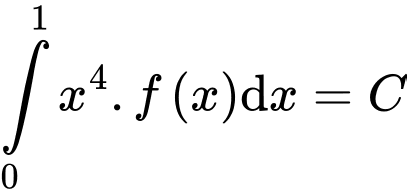 ta có:
ta có: 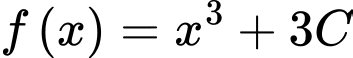
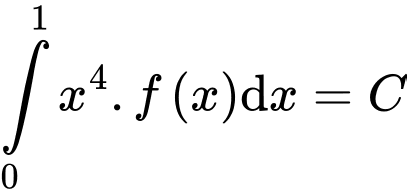 ta có:
ta có: 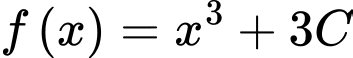
Khi đó 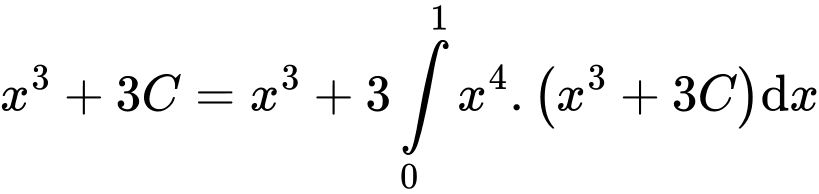
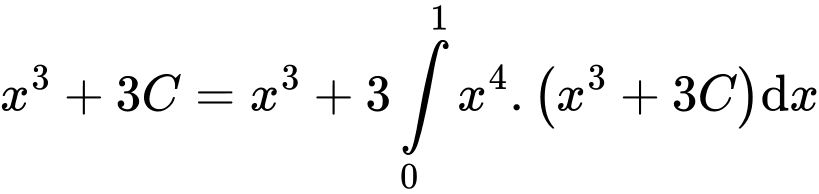
Suy ra 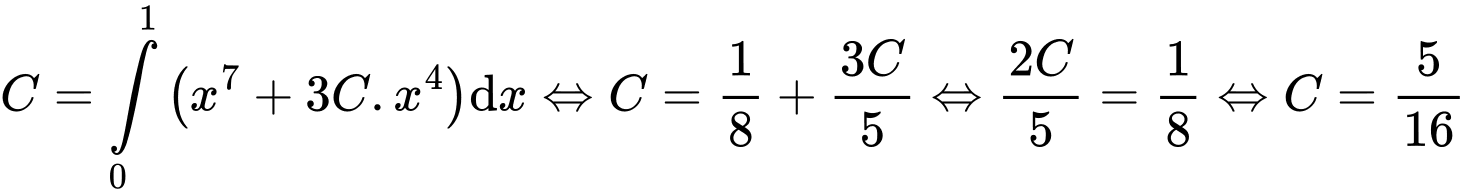
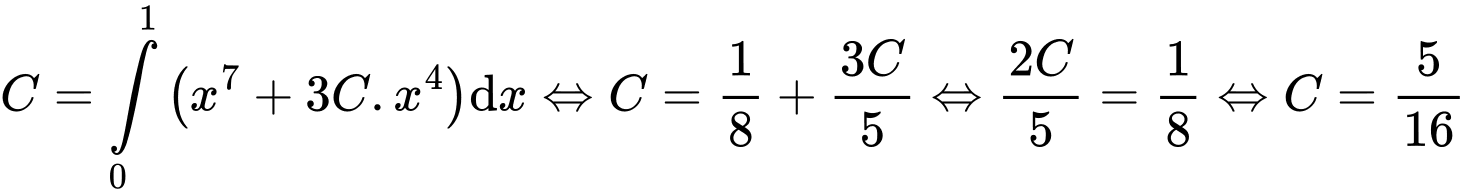
Vậy 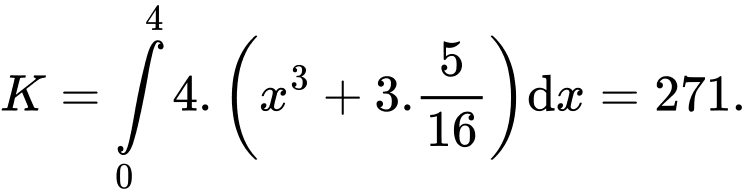
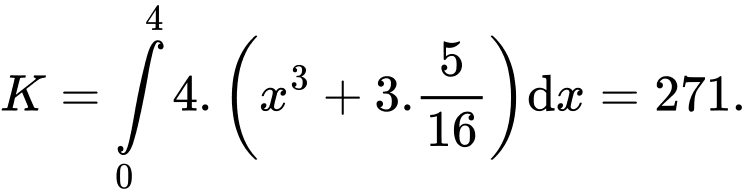
Câu 26 [396717]: [Trích SGK Cánh Diều]: Ở nhiệt độ  một phản ứng hoá học từ chất đầu
một phản ứng hoá học từ chất đầu 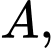 chuyển hoá thành chất sản phẩm
chuyển hoá thành chất sản phẩm 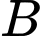 theo phương trình:
theo phương trình:  Giả sử
Giả sử  là nồng độ chất
là nồng độ chất 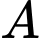 (đơn vị
(đơn vị 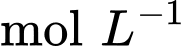 ) tại thời gian
) tại thời gian 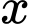 (giây),
(giây), 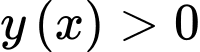 với
với 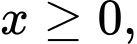 thoả mãn hệ thức:
thoả mãn hệ thức: 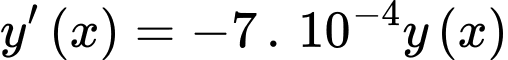 với
với  Biết rằng tại
Biết rằng tại 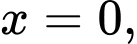 nồng độ (đầu) của
nồng độ (đầu) của 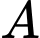 là
là  Giả sử ta tính nồng độ trung bình chất
Giả sử ta tính nồng độ trung bình chất 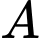 (đơn vị
(đơn vị 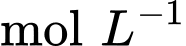 ) từ thời điểm
) từ thời điểm 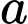 (giây) đến thời điểm
(giây) đến thời điểm 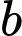 (giây) với
(giây) với 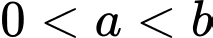 theo công thức
theo công thức 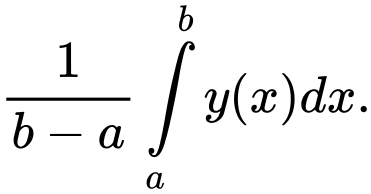 Xác định nồng độ trung bình của chất
Xác định nồng độ trung bình của chất 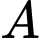 từ thời điểm 15 giây đến thời điểm 30 giây. Viết kết quả làm tròn đến phần trăm.
từ thời điểm 15 giây đến thời điểm 30 giây. Viết kết quả làm tròn đến phần trăm.
 một phản ứng hoá học từ chất đầu
một phản ứng hoá học từ chất đầu 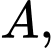 chuyển hoá thành chất sản phẩm
chuyển hoá thành chất sản phẩm 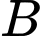 theo phương trình:
theo phương trình:  Giả sử
Giả sử  là nồng độ chất
là nồng độ chất 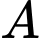 (đơn vị
(đơn vị 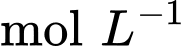 ) tại thời gian
) tại thời gian 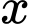 (giây),
(giây), 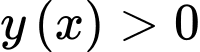 với
với 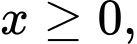 thoả mãn hệ thức:
thoả mãn hệ thức: 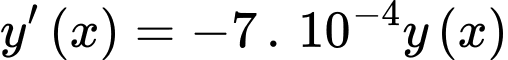 với
với  Biết rằng tại
Biết rằng tại 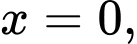 nồng độ (đầu) của
nồng độ (đầu) của 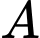 là
là  Giả sử ta tính nồng độ trung bình chất
Giả sử ta tính nồng độ trung bình chất 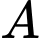 (đơn vị
(đơn vị 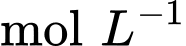 ) từ thời điểm
) từ thời điểm 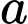 (giây) đến thời điểm
(giây) đến thời điểm 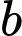 (giây) với
(giây) với 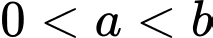 theo công thức
theo công thức 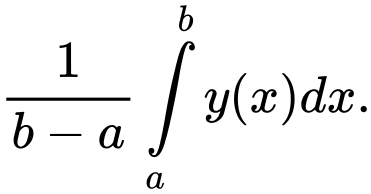 Xác định nồng độ trung bình của chất
Xác định nồng độ trung bình của chất 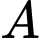 từ thời điểm 15 giây đến thời điểm 30 giây. Viết kết quả làm tròn đến phần trăm.
từ thời điểm 15 giây đến thời điểm 30 giây. Viết kết quả làm tròn đến phần trăm.
Ta có: 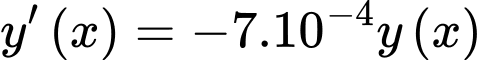
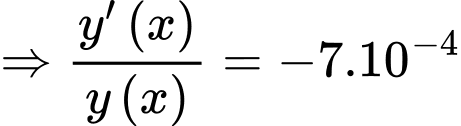
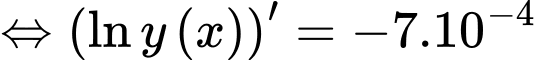
Lấy nguyên hàm hai vế ta đươc: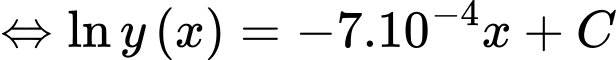
Mặt khác tại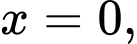 nồng độ (đầu) của
nồng độ (đầu) của 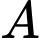 là
là  nên
nên 
Suy ra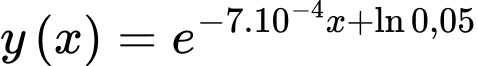 nên
nên 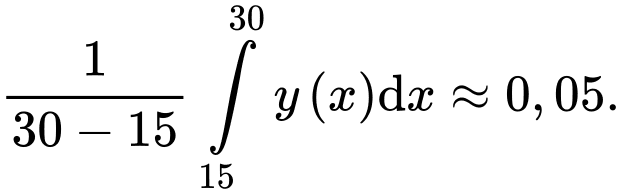
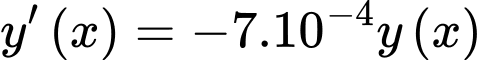
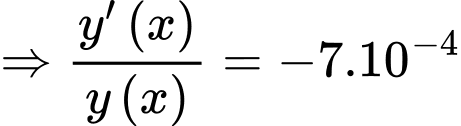
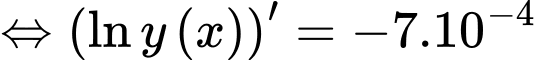
Lấy nguyên hàm hai vế ta đươc:
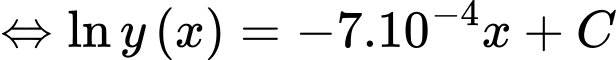
Mặt khác tại
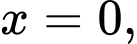 nồng độ (đầu) của
nồng độ (đầu) của 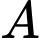 là
là  nên
nên 
Suy ra
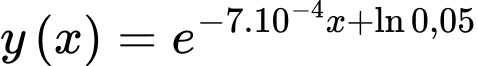 nên
nên 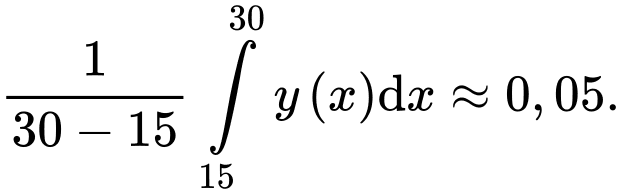
Câu 27 [971724]: [Đề thi THPT QG 2021]: Cho hàm số 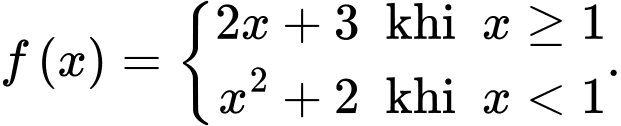 Giả sử
Giả sử 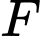 là nguyên hàm của
là nguyên hàm của 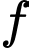 trên
trên 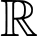 thỏa mãn
thỏa mãn 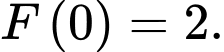 Giá trị của
Giá trị của  bằng
bằng
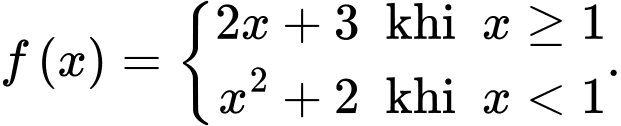 Giả sử
Giả sử 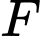 là nguyên hàm của
là nguyên hàm của 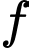 trên
trên 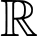 thỏa mãn
thỏa mãn 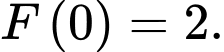 Giá trị của
Giá trị của  bằng
bằng A, 23.
B, 10.
C, 11.
D, 21.
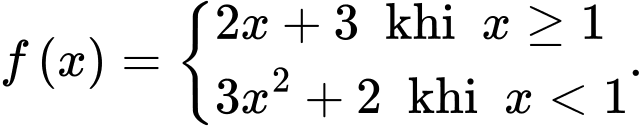
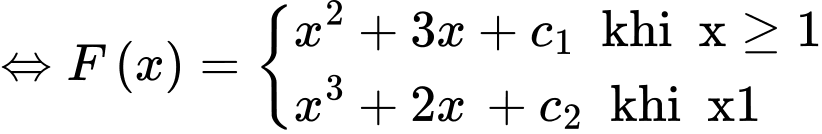
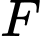 là nguyên hàm của
là nguyên hàm của 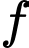 trên
trên  thỏa mãn
thỏa mãn 
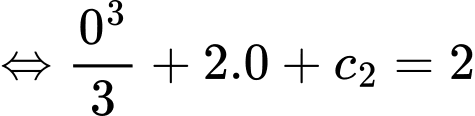
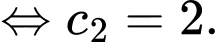
Lại có:
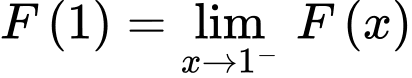
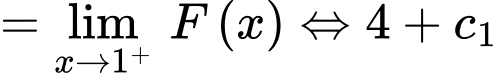
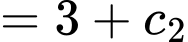
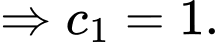
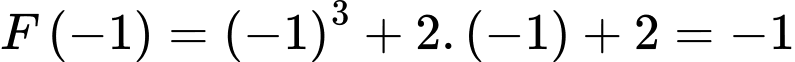
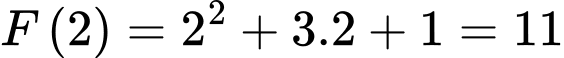
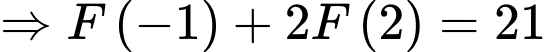
Ta chọn đáp án D Đáp án: D
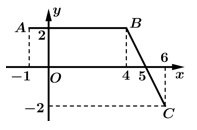
Câu 28 [971725]: [Đề thi THPT QG 2021]: Cho hàm số 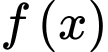 liên tục trên đoạn
liên tục trên đoạn 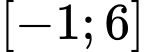 và có đồ thị hình gấp khúc
và có đồ thị hình gấp khúc 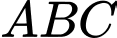 trong hình bên. Biết
trong hình bên. Biết 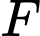 là nguyên hàm của
là nguyên hàm của 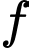 trên
trên 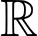 thỏa mãn
thỏa mãn 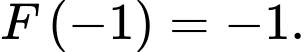 Giá trị của
Giá trị của  bằng
bằng
 liên tục trên đoạn
liên tục trên đoạn 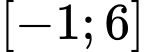 và có đồ thị hình gấp khúc
và có đồ thị hình gấp khúc 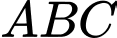 trong hình bên. Biết
trong hình bên. Biết 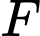 là nguyên hàm của
là nguyên hàm của 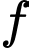 trên
trên 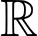 thỏa mãn
thỏa mãn 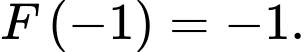 Giá trị của
Giá trị của  bằng
bằng 
A, 21.
B, 25.
C, 23.
D, 19.
Chọn đáp án D.
Dựa vào đồ thị ta có: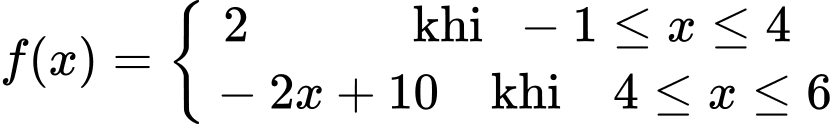
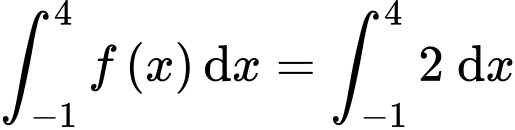
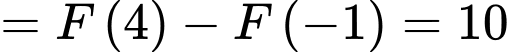
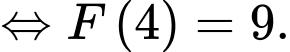
Xét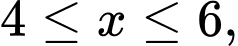 ta có:
ta có: 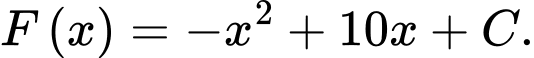
Mà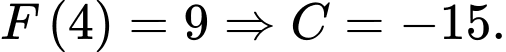
Nên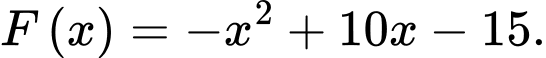
Ta có: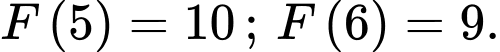
Vậy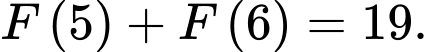 Đáp án: D
Đáp án: D
Dựa vào đồ thị ta có:
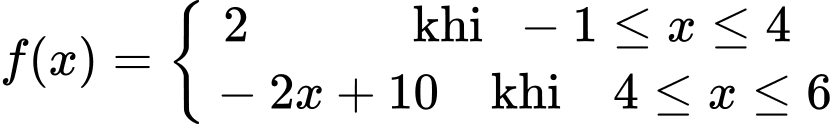
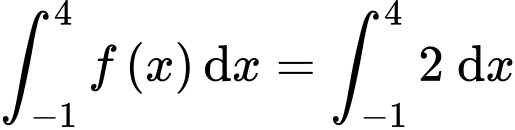
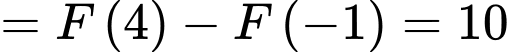
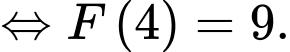
Xét
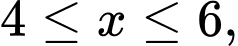 ta có:
ta có: 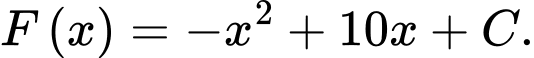
Mà
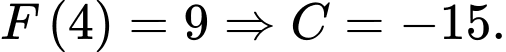
Nên
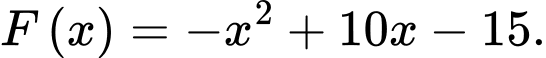
Ta có:
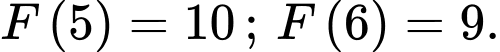
Vậy
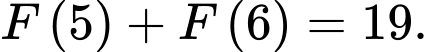 Đáp án: D
Đáp án: D
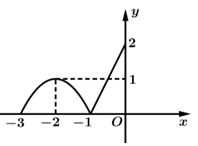
Câu 29 [396718]: Cho hàm số 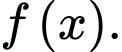 Đồ thị hàm số
Đồ thị hàm số 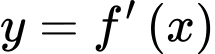 trên đoạn
trên đoạn 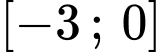 như hình vẽ sau (phần đường cong trong đồ thị là một phần của parabol
như hình vẽ sau (phần đường cong trong đồ thị là một phần của parabol 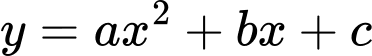 ). Biết
). Biết 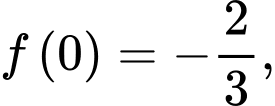 tính
tính 
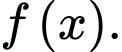 Đồ thị hàm số
Đồ thị hàm số 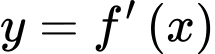 trên đoạn
trên đoạn 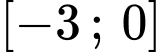 như hình vẽ sau (phần đường cong trong đồ thị là một phần của parabol
như hình vẽ sau (phần đường cong trong đồ thị là một phần của parabol 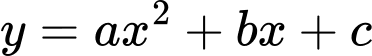 ). Biết
). Biết 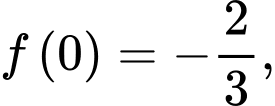 tính
tính 

Ta có: 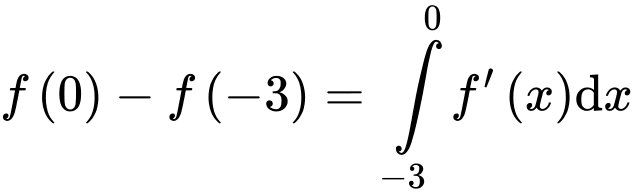
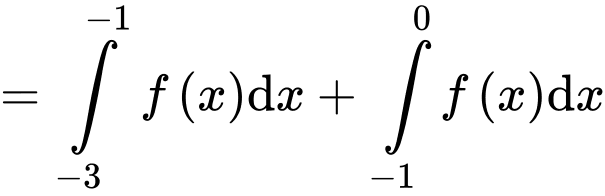
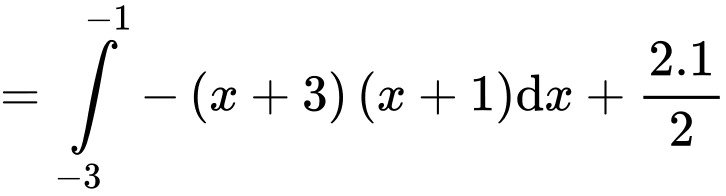
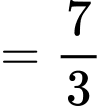
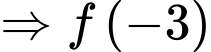
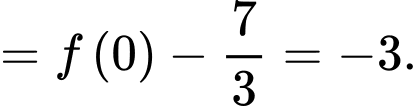
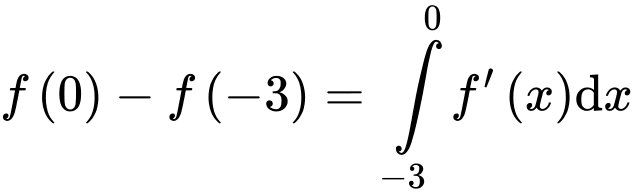
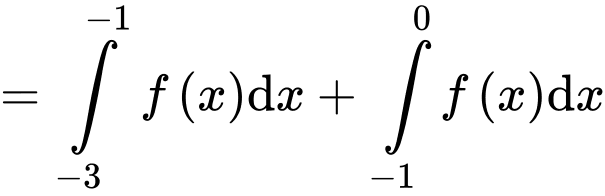
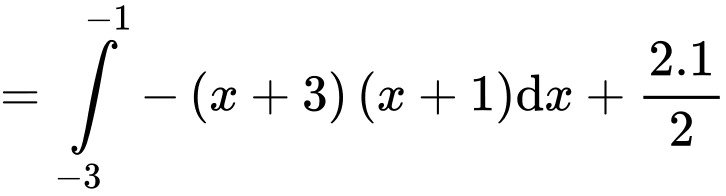
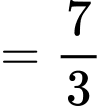
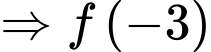
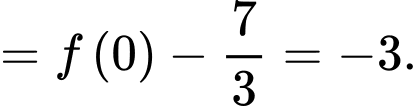
Câu 30 [175627]: [MĐ3] Cho 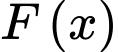 là nguyên hàm của hàm số
là nguyên hàm của hàm số 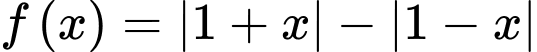 trên
trên 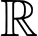 và thỏa mãn
và thỏa mãn 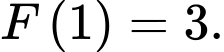 Tính tổng
Tính tổng  .
.
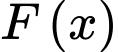 là nguyên hàm của hàm số
là nguyên hàm của hàm số 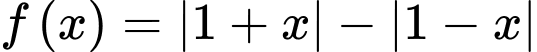 trên
trên 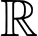 và thỏa mãn
và thỏa mãn 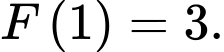 Tính tổng
Tính tổng  .
. A, 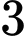 .
.
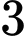 .
.B, 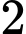 .
.
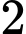 .
.C, 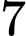 .
.
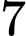 .
.D, 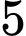 .
.
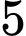 .
.
Ta có 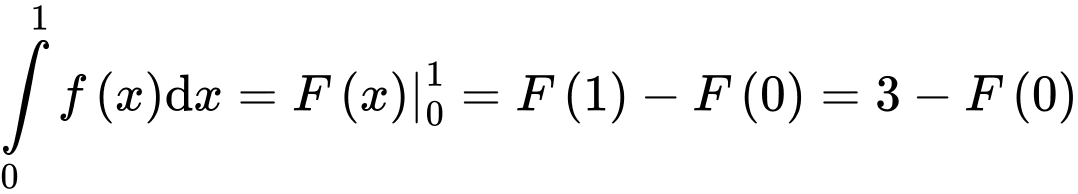 .
.
Mà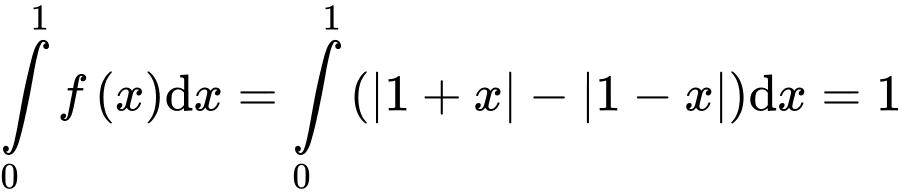 (tính tích phân bằng máy tính).
(tính tích phân bằng máy tính).
Nên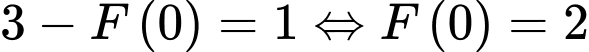 .
.
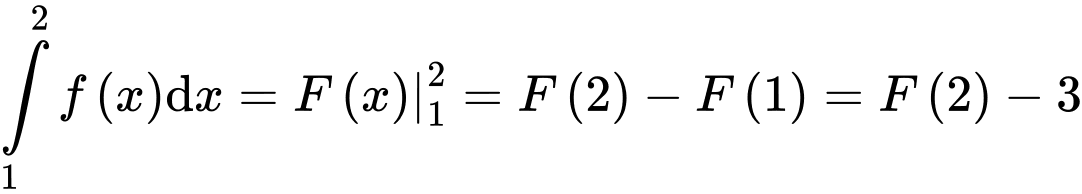 .
.
Mà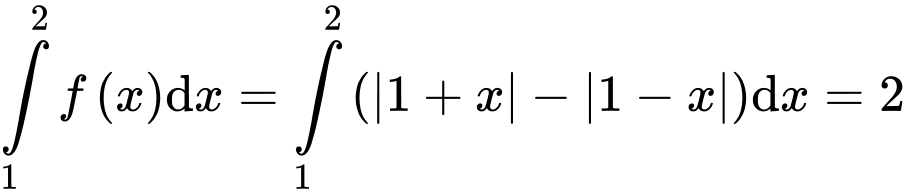 (tính tích phân bằng máy tính).
(tính tích phân bằng máy tính).
Nên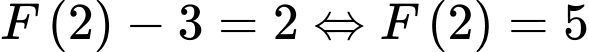 .
.
Vậy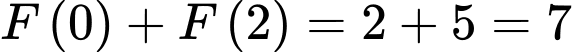 . Đáp án: C
. Đáp án: C
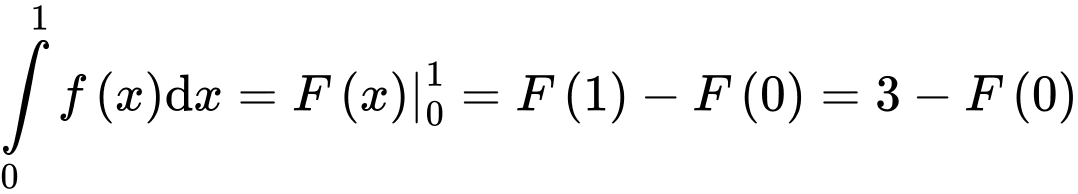 .
.
Mà
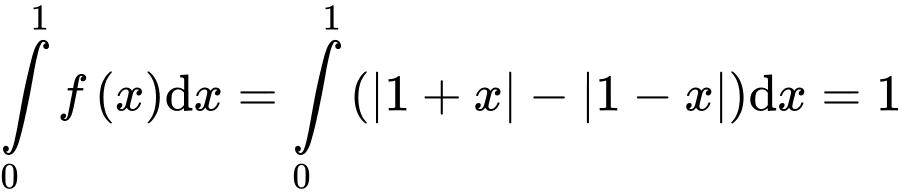 (tính tích phân bằng máy tính).
(tính tích phân bằng máy tính).
Nên
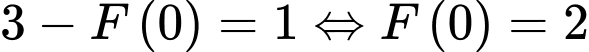 .
.
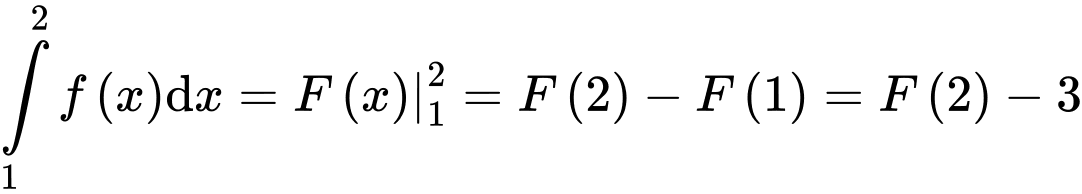 .
.
Mà
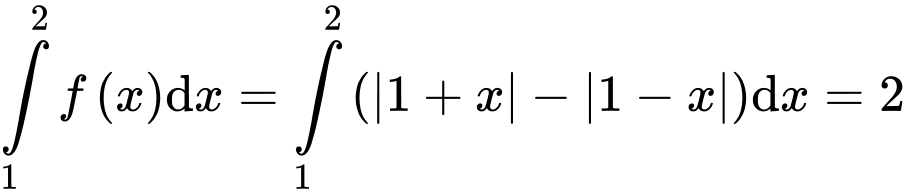 (tính tích phân bằng máy tính).
(tính tích phân bằng máy tính).
Nên
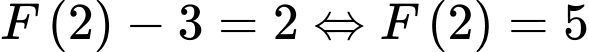 .
.
Vậy
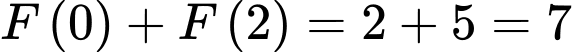 . Đáp án: C
. Đáp án: C