Đáp án Bài tập tự luyện số 2
Câu 1 [80761]: Tính thể tích  của vật thể giới hạn bởi hai mặt phẳng
của vật thể giới hạn bởi hai mặt phẳng 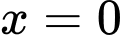 và
và 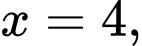 biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục 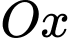 tại điểm có hoành độ
tại điểm có hoành độ 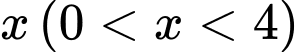 thì được thiết diện là nửa hình tròn có bán kính
thì được thiết diện là nửa hình tròn có bán kính 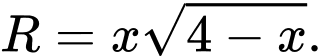
 của vật thể giới hạn bởi hai mặt phẳng
của vật thể giới hạn bởi hai mặt phẳng 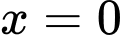 và
và 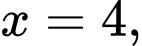 biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục 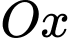 tại điểm có hoành độ
tại điểm có hoành độ 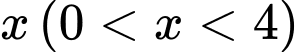 thì được thiết diện là nửa hình tròn có bán kính
thì được thiết diện là nửa hình tròn có bán kính 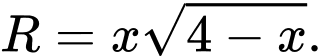
A, 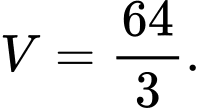
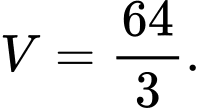
B, 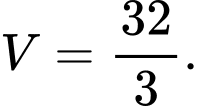
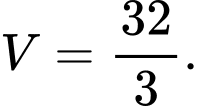
C, 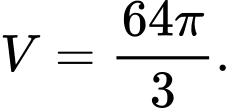
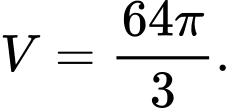
D, 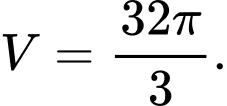
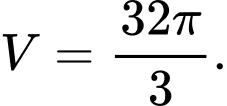
Chọn D.
Ta có 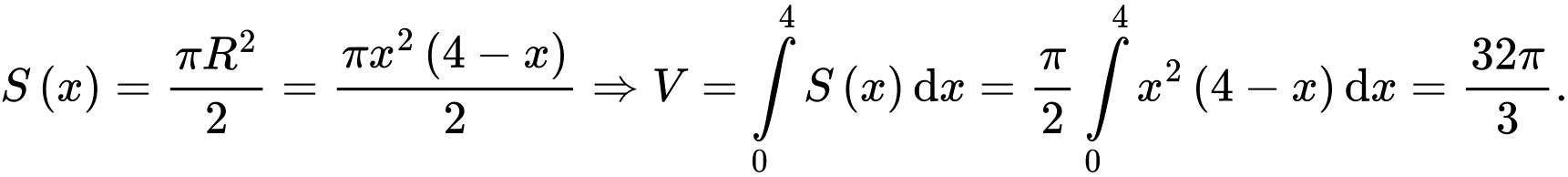
Đáp án: D 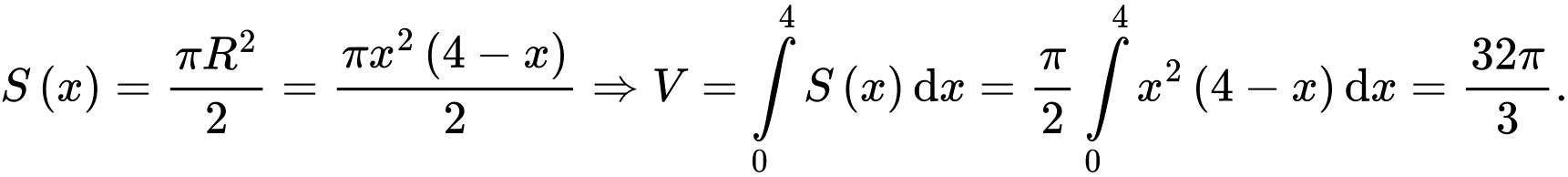
Câu 2 [151432]: Cho  là vật thể nằm giữa hai mặt phẳng
là vật thể nằm giữa hai mặt phẳng  . Tính thể tích
. Tính thể tích  của
của  biết rằng khi cắt
biết rằng khi cắt 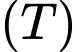 bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 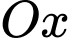 tại điểm có hoành độ bằng
tại điểm có hoành độ bằng 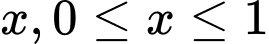 ta được thiết diện là tam giác đều cạnh bằng
ta được thiết diện là tam giác đều cạnh bằng  .
.
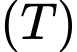 là vật thể nằm giữa hai mặt phẳng
là vật thể nằm giữa hai mặt phẳng 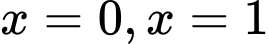 . Tính thể tích
. Tính thể tích  của
của 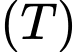 biết rằng khi cắt
biết rằng khi cắt 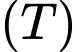 bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 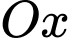 tại điểm có hoành độ bằng
tại điểm có hoành độ bằng 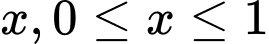 ta được thiết diện là tam giác đều cạnh bằng
ta được thiết diện là tam giác đều cạnh bằng  .
. A, 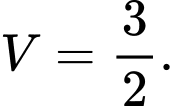
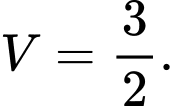
B, 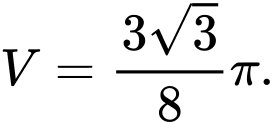
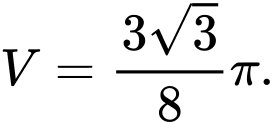
C, 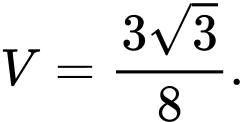
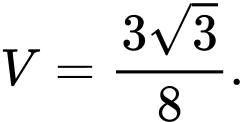
D, 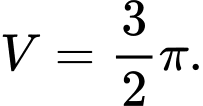
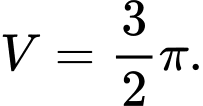
Chọn đáp án C.
Thể tích của vật thể  là
là 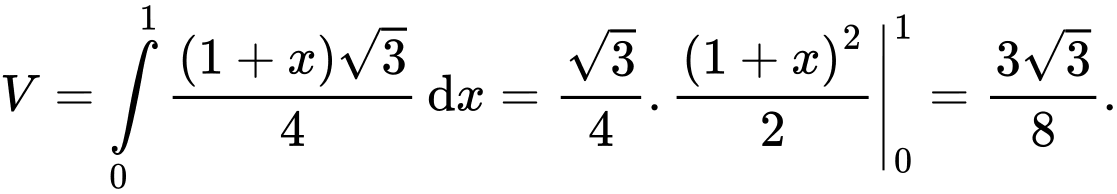
Đáp án: C  là
là 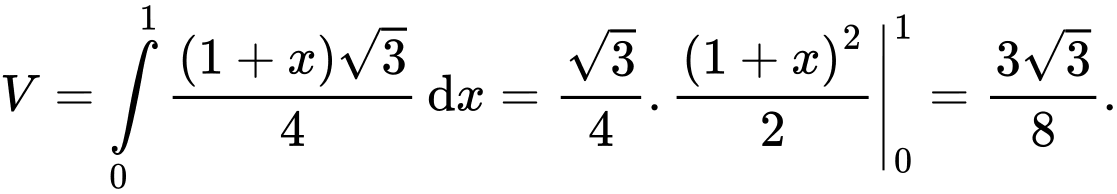
Câu 3 [140089]: Cho hình phẳng 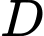 giới hạn bởi đường cong
giới hạn bởi đường cong 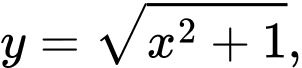 trục hoành và các đường thẳng
trục hoành và các đường thẳng 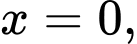
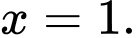 Khối tròn xoay tạo thành khi quay
Khối tròn xoay tạo thành khi quay  quanh trục hoành có thể tích
quanh trục hoành có thể tích  bằng bao nhiêu?
bằng bao nhiêu?
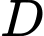 giới hạn bởi đường cong
giới hạn bởi đường cong 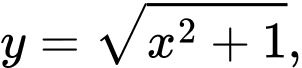 trục hoành và các đường thẳng
trục hoành và các đường thẳng 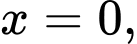
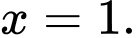 Khối tròn xoay tạo thành khi quay
Khối tròn xoay tạo thành khi quay 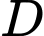 quanh trục hoành có thể tích
quanh trục hoành có thể tích  bằng bao nhiêu?
bằng bao nhiêu? A, 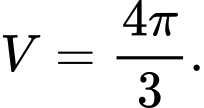
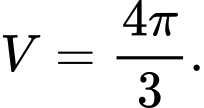
B, 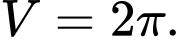
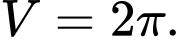
C, 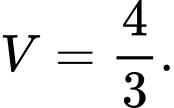
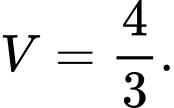
D, 

Chọn A.
Thể tích cần tính bằng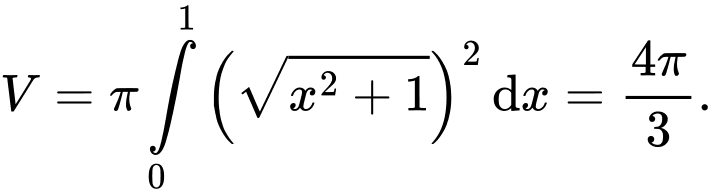 Đáp án: A
Đáp án: A
Thể tích cần tính bằng
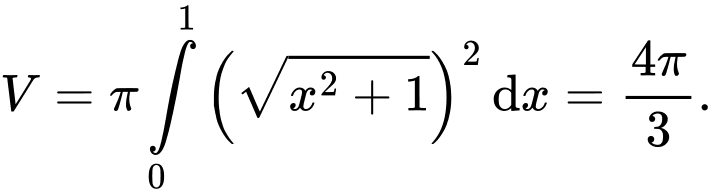 Đáp án: A
Đáp án: A
Câu 4 [151635]: Cho hình phẳng  giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 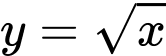 , và các đường thẳng
, và các đường thẳng 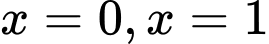 , trục hoành. Tính thể tích
, trục hoành. Tính thể tích  của khối tròn xoay sinh bởi hình
của khối tròn xoay sinh bởi hình  quay xung quanh trục
quay xung quanh trục 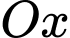 .
.
 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 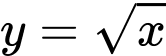 , và các đường thẳng
, và các đường thẳng 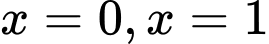 , trục hoành. Tính thể tích
, trục hoành. Tính thể tích  của khối tròn xoay sinh bởi hình
của khối tròn xoay sinh bởi hình  quay xung quanh trục
quay xung quanh trục 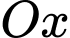 .
. A, 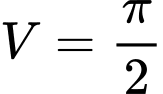 .
.
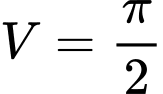 .
.B, 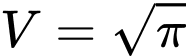 .
.
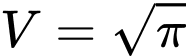 .
.C, 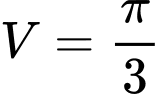 .
.
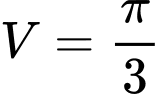 .
.D, 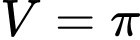 .
.
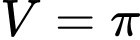 .
.
Chọn A.
Ta có 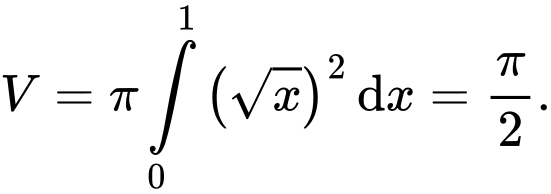
Đáp án: A 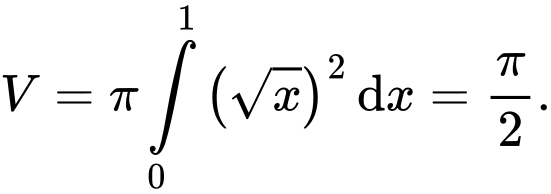
Câu 5 [151642]: Cho hình phẳng  giới hạn bởi đường cong
giới hạn bởi đường cong 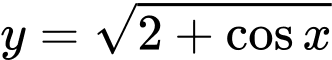 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 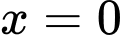 ,
, 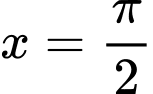 . Tính thể tích
. Tính thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 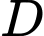 quanh trục hoành.
quanh trục hoành.
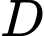 giới hạn bởi đường cong
giới hạn bởi đường cong 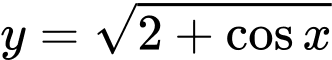 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 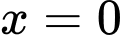 ,
, 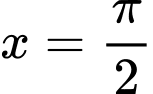 . Tính thể tích
. Tính thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay  quanh trục hoành.
quanh trục hoành. A, 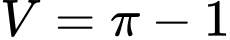 .
.
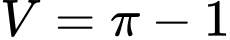 .
.B, 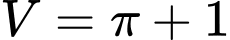 .
.
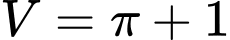 .
.C, 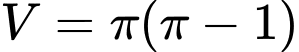 .
.
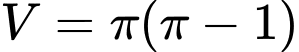 .
.D, 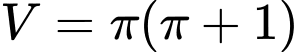 .
.
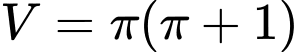 .
.
Chọn D.
Thể tích khối tròn xoay khi quay quanh trục hoành là
quanh trục hoành là 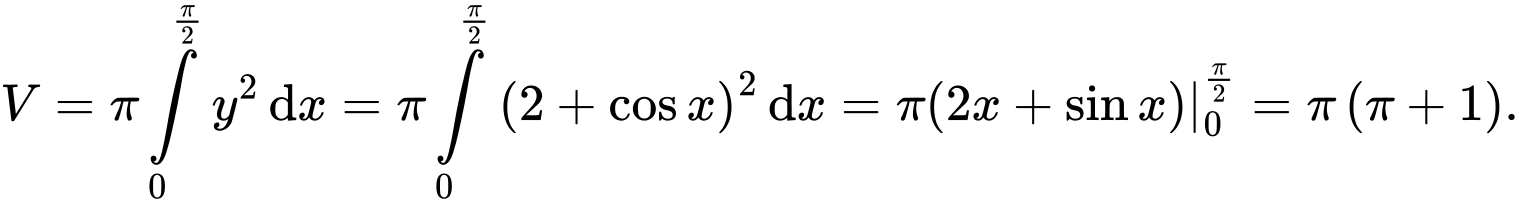 Đáp án: D
Đáp án: D
Thể tích khối tròn xoay khi quay
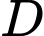 quanh trục hoành là
quanh trục hoành là 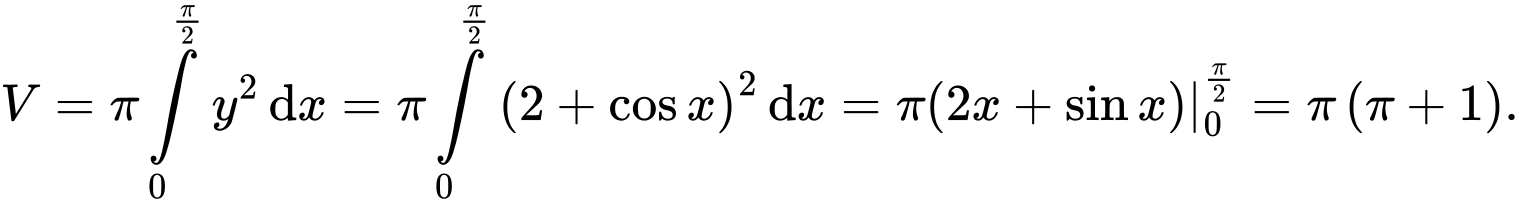 Đáp án: D
Đáp án: D
Câu 6 [151649]: Kí hiệu  là hình phẳng giới hạn bởi các đường cong
là hình phẳng giới hạn bởi các đường cong 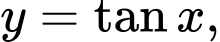 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 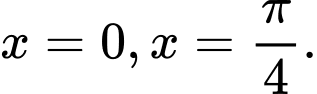 Tính thể tích
Tính thể tích  của khối tròn xoay thu được khi quay hình
của khối tròn xoay thu được khi quay hình  xung quanh trục
xung quanh trục  .
.
 là hình phẳng giới hạn bởi các đường cong
là hình phẳng giới hạn bởi các đường cong 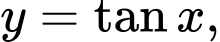 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 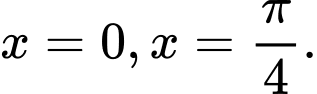 Tính thể tích
Tính thể tích  của khối tròn xoay thu được khi quay hình
của khối tròn xoay thu được khi quay hình  xung quanh trục
xung quanh trục  .
. A, 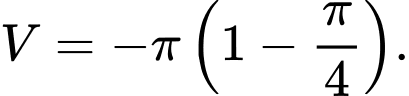
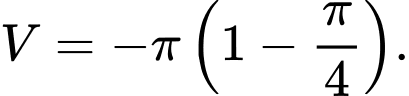
B, 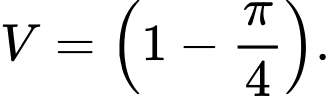
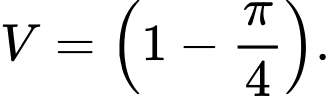
C, 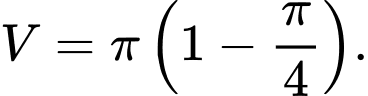
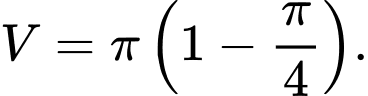
D, 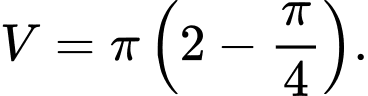
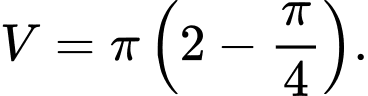
Chọn C. 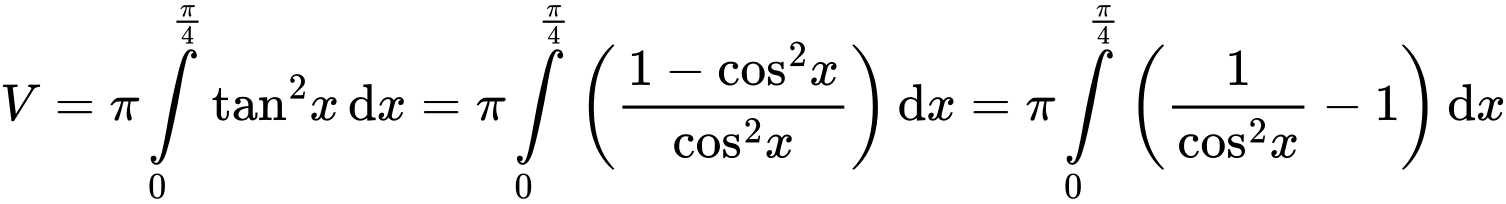
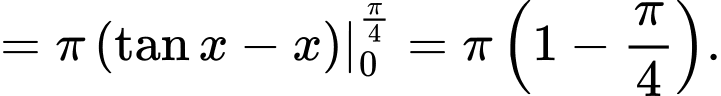 Đáp án: C
Đáp án: C
Thể tích cần tính bằng
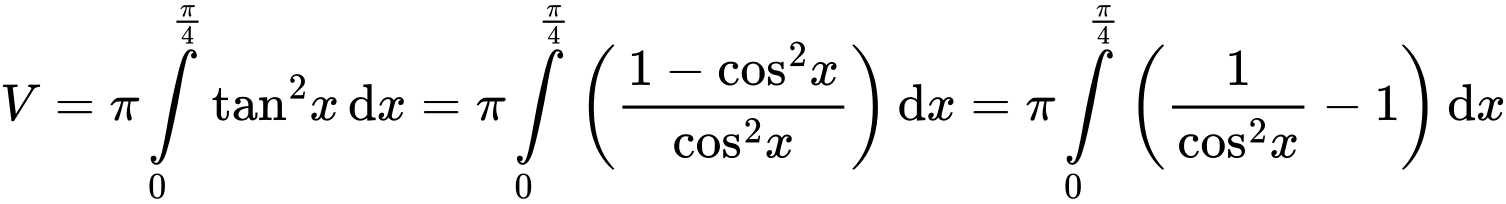
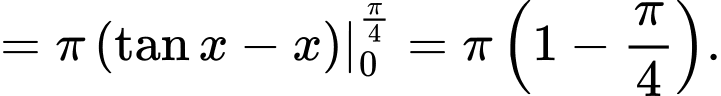
Câu 7 [151655]: Thể tích khối tròn xoay sinh ra bởi phép quay trục hoành hình phẳng giới hạn bởi đồ thị hàm số 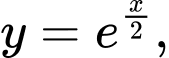 trục hoành, trục tung và đường thẳng
trục hoành, trục tung và đường thẳng 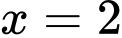 bằng
bằng
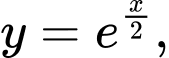 trục hoành, trục tung và đường thẳng
trục hoành, trục tung và đường thẳng 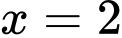 bằng
bằng A, 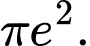
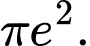
B, 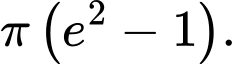
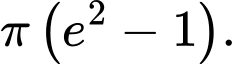
C, 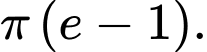
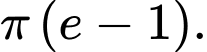
D, 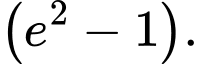
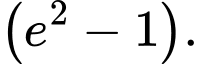
Chọn B.
Ta có 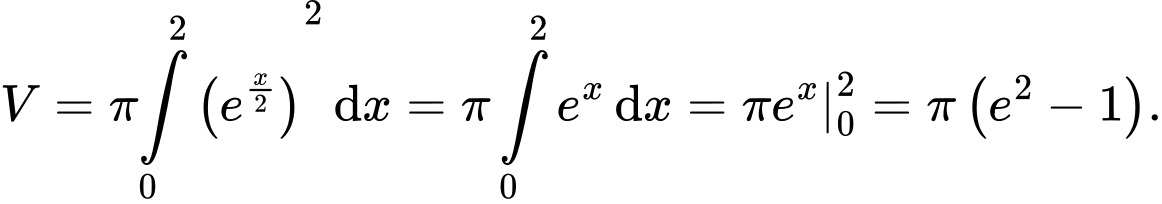
Đáp án: B 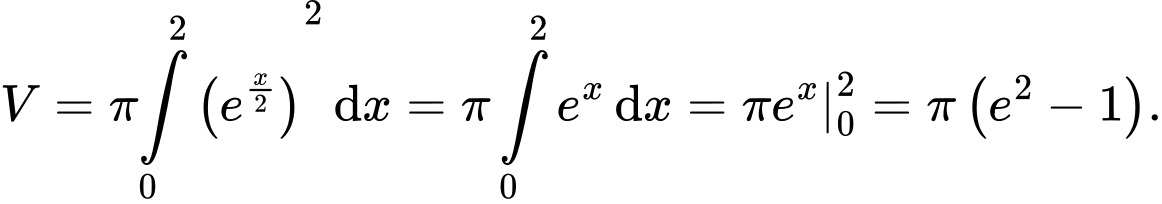
Câu 8 [151656]: Kí hiệu  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 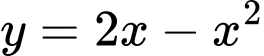 và
và 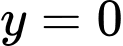 . Tính thể tích vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục
. Tính thể tích vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục 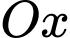 .
.
 là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 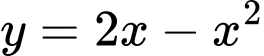 và
và 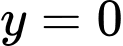 . Tính thể tích vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục
. Tính thể tích vật thể tròn xoay được sinh ra bởi hình phẳng đó khi nó quay quanh trục 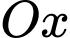 .
. A, 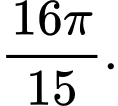
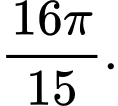
B, 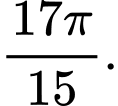
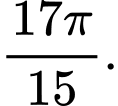
C, 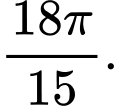
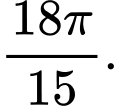
D, 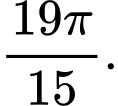
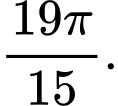
Chọn A.
Phương trình hoành độ giao điểm là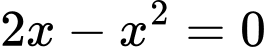
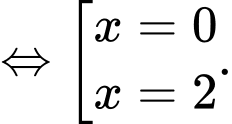
Suy ra thể tích cần tính là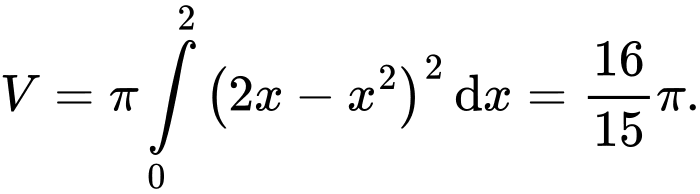 Đáp án: A
Đáp án: A
Phương trình hoành độ giao điểm là
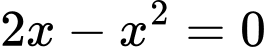
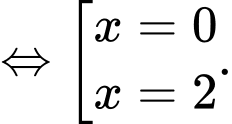
Suy ra thể tích cần tính là
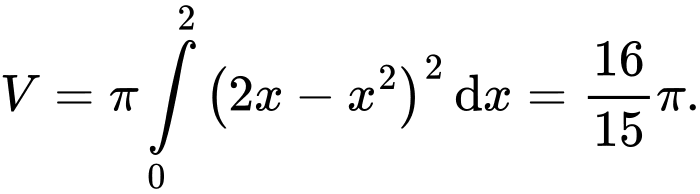 Đáp án: A
Đáp án: A
Câu 9 [146581]: Tính thể tích của vật thể tròn xoay khi quay hình  quanh
quanh 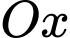 với
với  được giới hạn bởi đồ thị hàm số
được giới hạn bởi đồ thị hàm số 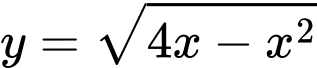 và trục hoành.
và trục hoành.
 quanh
quanh 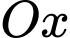 với
với  được giới hạn bởi đồ thị hàm số
được giới hạn bởi đồ thị hàm số 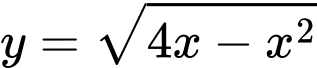 và trục hoành.
và trục hoành. A, 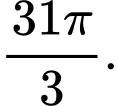
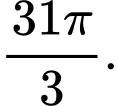
B, 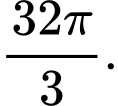
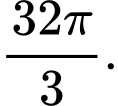
C, 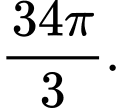
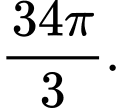
D, 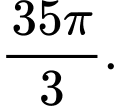
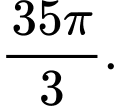
Chọn B.
Phương trình hoành độ giao điểm là 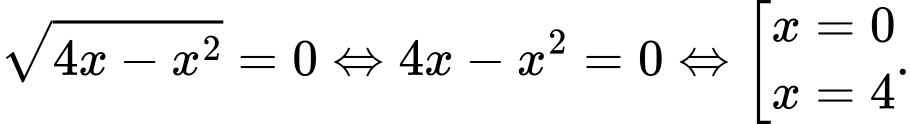
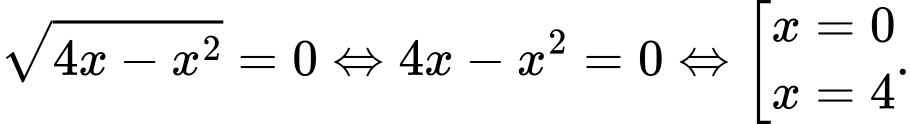
Suy ra thể tích cần tính là 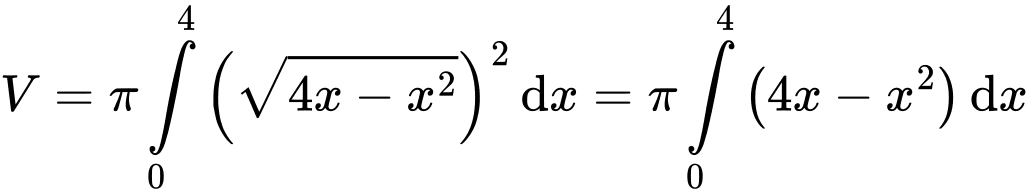
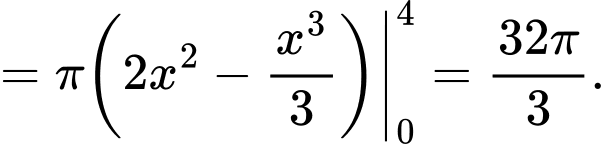
Đáp án: B 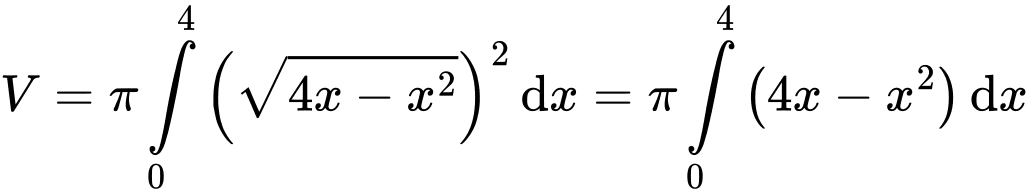
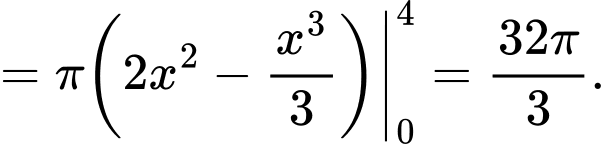
Câu 10 [397899]: [Đề mẫu ĐGNL Hà Nội]: Cho  là hình phẳng giới hạn bởi các đường thẳng
là hình phẳng giới hạn bởi các đường thẳng 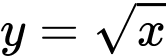 và
và 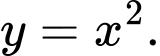 Thể tích của khối tròn xoay tạo thành khi quanh hình
Thể tích của khối tròn xoay tạo thành khi quanh hình  quanh trục
quanh trục 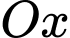 bằng
bằng
 là hình phẳng giới hạn bởi các đường thẳng
là hình phẳng giới hạn bởi các đường thẳng 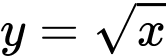 và
và 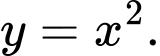 Thể tích của khối tròn xoay tạo thành khi quanh hình
Thể tích của khối tròn xoay tạo thành khi quanh hình  quanh trục
quanh trục 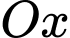 bằng
bằng A, 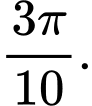
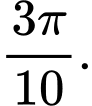
B, 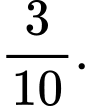
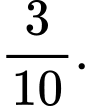
C, 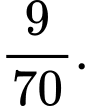
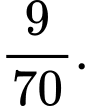
D, 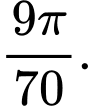
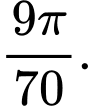
Phương trình hoành độ giao điểm là 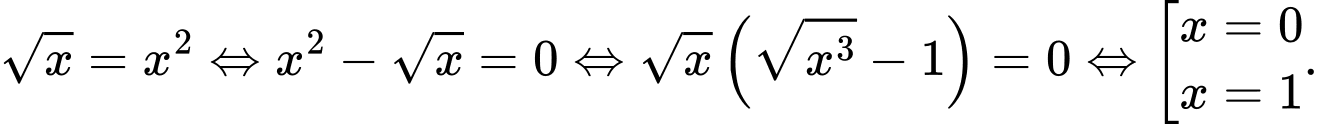
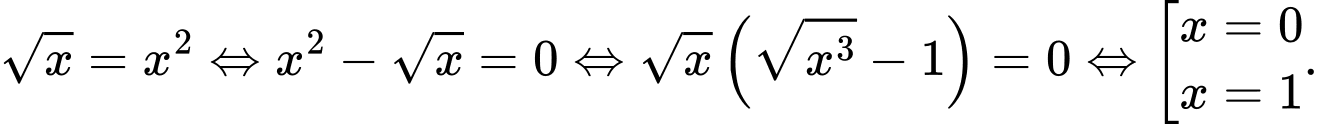
Suy ra thể tích của khối tròn xoay đó là
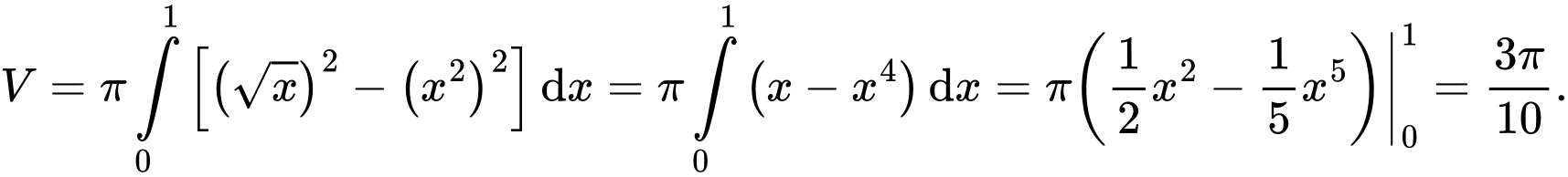
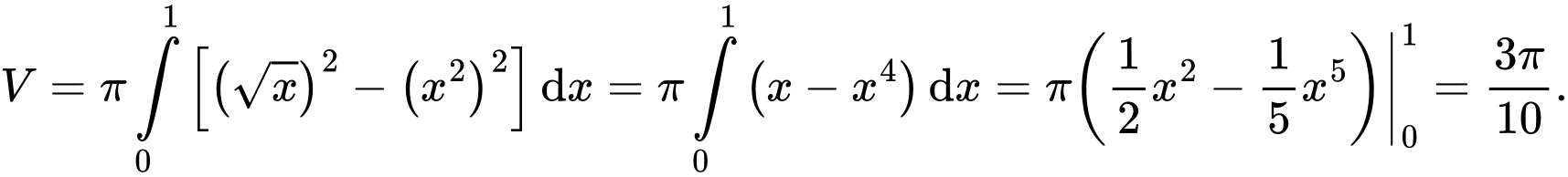
Chọn đáp án A.
Câu 11 [151661]: Gọi  là hình phẳng giới hạn bởi parabol
là hình phẳng giới hạn bởi parabol 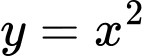 và đường thẳng
và đường thẳng 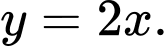 Tính thể tích
Tính thể tích  của khối tròn xoay tạo thành khi quay hình
của khối tròn xoay tạo thành khi quay hình  xung quanh trục hoành.
xung quanh trục hoành.
 là hình phẳng giới hạn bởi parabol
là hình phẳng giới hạn bởi parabol 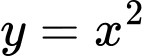 và đường thẳng
và đường thẳng 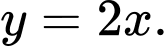 Tính thể tích
Tính thể tích  của khối tròn xoay tạo thành khi quay hình
của khối tròn xoay tạo thành khi quay hình  xung quanh trục hoành.
xung quanh trục hoành. A, 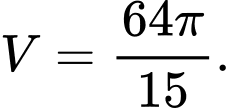
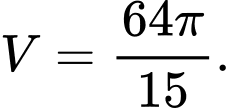
B, 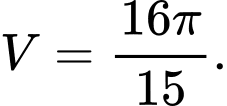
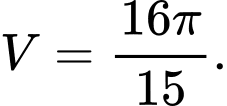
C, 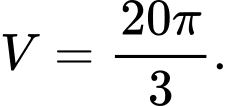
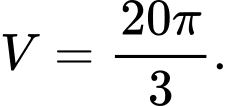
D, 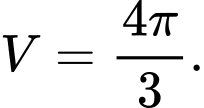
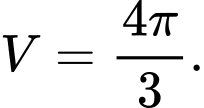
Phương trình hoành độ giao điểm là 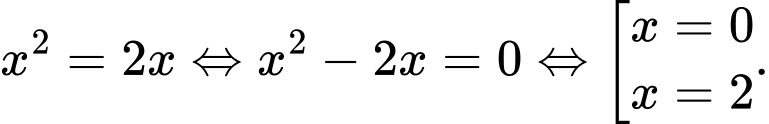
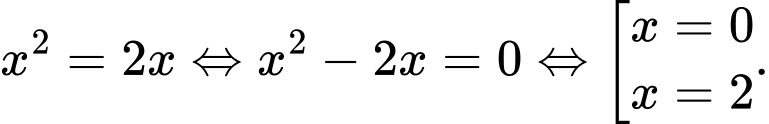
Khi đó 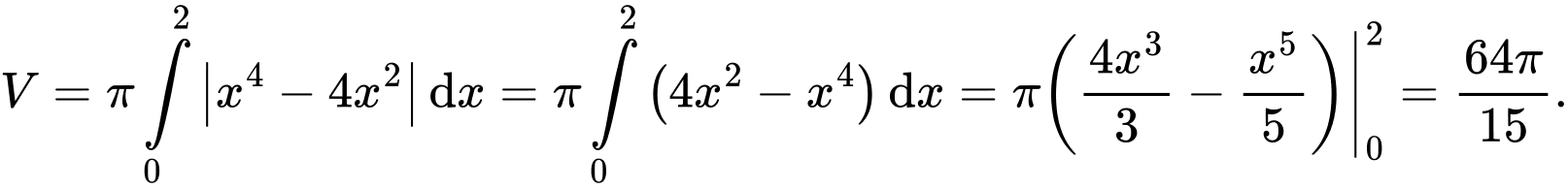
Đáp án: A 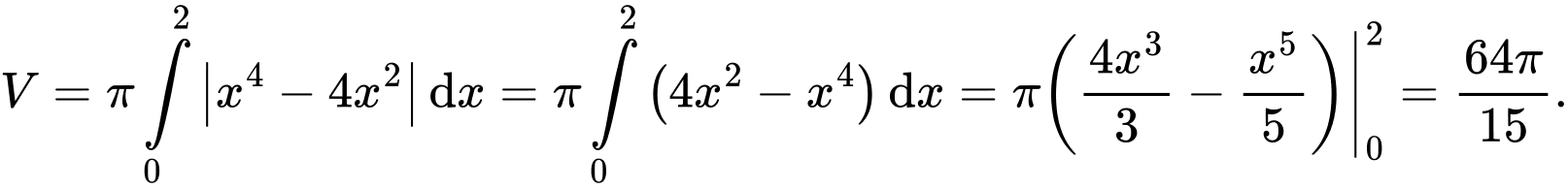
Chọn A.
Câu 12 [161580]: Cho hàm số 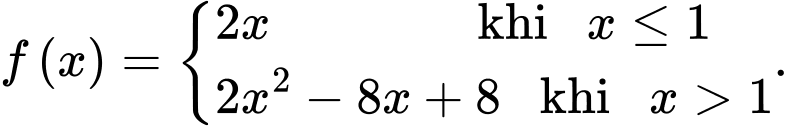 Gọi
Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số  và trục hoành. Các mệnh đề sau đúng hay sai
và trục hoành. Các mệnh đề sau đúng hay sai
a) Đồ thị hàm số cắt trục tại 2 điểm phân biệt.
tại 2 điểm phân biệt.
b)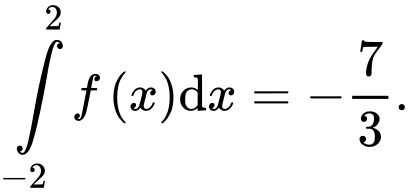
c) Diện tích hình phẳng bằng
bằng 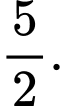
d) Thể tích khối tròn xoay thu được khi quay hình phẳng quanh trục
quanh trục 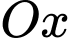 bằng
bằng 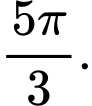
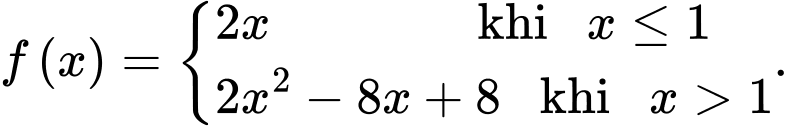 Gọi
Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 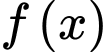 và trục hoành. Các mệnh đề sau đúng hay sai
và trục hoành. Các mệnh đề sau đúng hay saia) Đồ thị hàm số cắt trục
 tại 2 điểm phân biệt.
tại 2 điểm phân biệt.b)
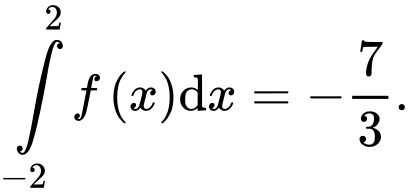
c) Diện tích hình phẳng
 bằng
bằng 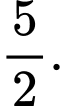
d) Thể tích khối tròn xoay thu được khi quay hình phẳng
 quanh trục
quanh trục 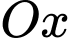 bằng
bằng 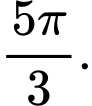
a) Đúng.
b) Đúng.
c) Sai.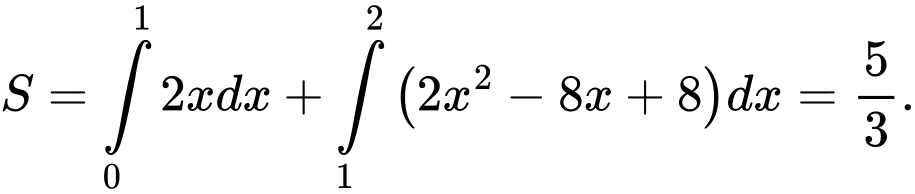
d) Sai.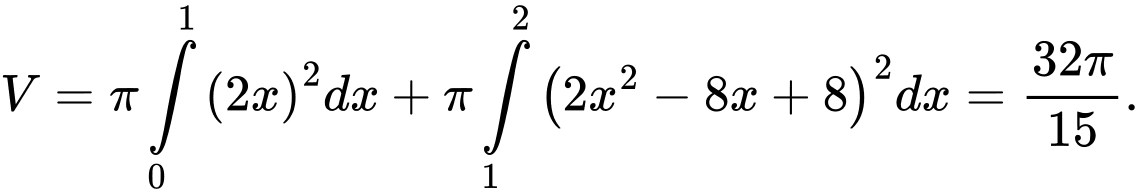
b) Đúng.
c) Sai.
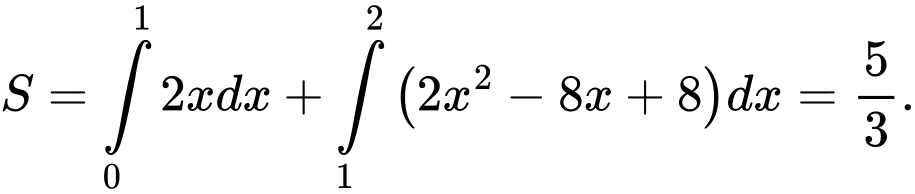
d) Sai.
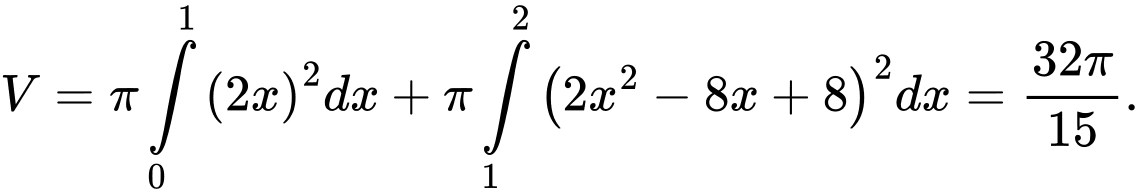
Câu 13 [371992]: Trong mặt phẳng toạ độ  cho hình thang
cho hình thang 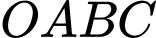 có
có 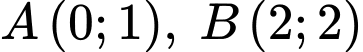 và
và 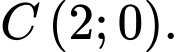 Tính thể tích khối tròn xoay tạo thành khi quay hình thang
Tính thể tích khối tròn xoay tạo thành khi quay hình thang 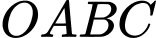 quanh trục
quanh trục 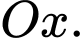 Viết kết quả làm tròn đến hàng phần chục
Viết kết quả làm tròn đến hàng phần chục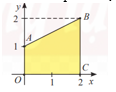
 cho hình thang
cho hình thang  có
có 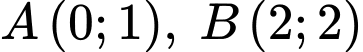 và
và 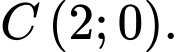 Tính thể tích khối tròn xoay tạo thành khi quay hình thang
Tính thể tích khối tròn xoay tạo thành khi quay hình thang 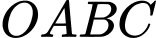 quanh trục
quanh trục 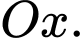 Viết kết quả làm tròn đến hàng phần chục
Viết kết quả làm tròn đến hàng phần chục
Theo giả thuyết ta có phương trình cạnh  là
là 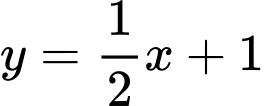 .
.
Ta có công thức tính thể tích của hình tròn xoay là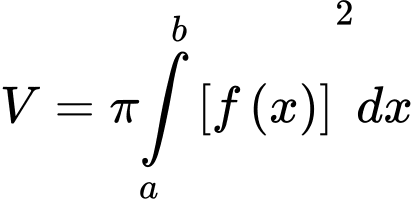
Theo yêu cầu bài toán :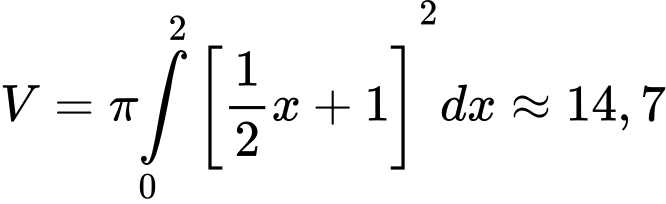
 là
là 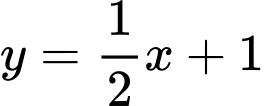 .
.Ta có công thức tính thể tích của hình tròn xoay là
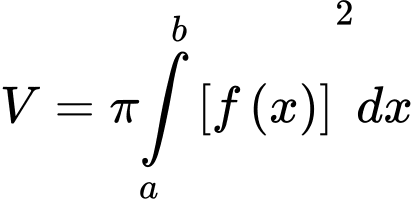
Theo yêu cầu bài toán :
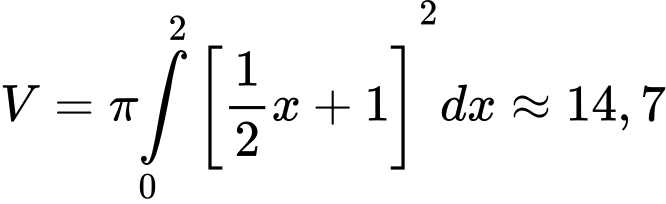
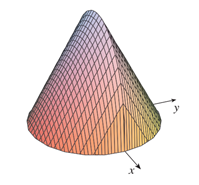
Câu 14 [151434]: Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục  tại điểm có hoành độ
tại điểm có hoành độ 
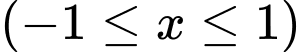 thì được thiết diện là một tam giác đều. Tính thể tích
thì được thiết diện là một tam giác đều. Tính thể tích  của vật thể đó.
của vật thể đó.
 tại điểm có hoành độ
tại điểm có hoành độ 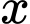
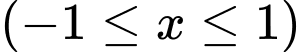 thì được thiết diện là một tam giác đều. Tính thể tích
thì được thiết diện là một tam giác đều. Tính thể tích  của vật thể đó.
của vật thể đó.
A, 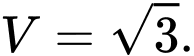
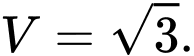
B, 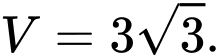
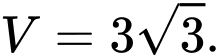
C, 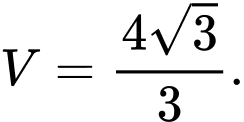
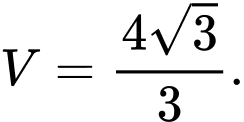
D, 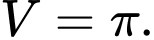
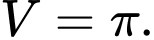
Cắt vật thể bởi mặt phẳng vuông góc với trục 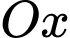 tại điểm có hoành độ
tại điểm có hoành độ 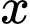 thì thiết diện là tam giác đều cạnh
thì thiết diện là tam giác đều cạnh 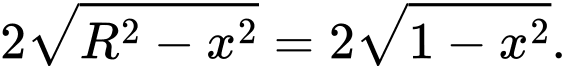
 tại điểm có hoành độ
tại điểm có hoành độ 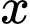 thì thiết diện là tam giác đều cạnh
thì thiết diện là tam giác đều cạnh 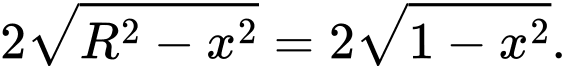
Diện tích tam giác đều cạnh 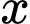 là
là 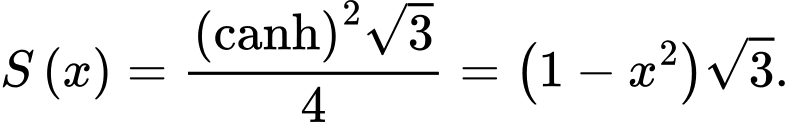
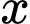 là
là 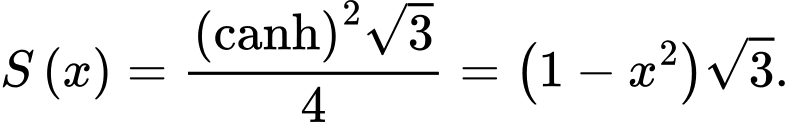
Do đó 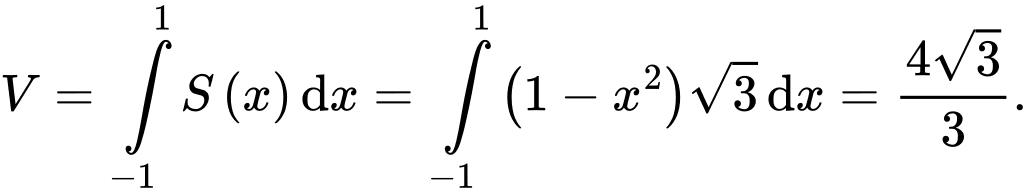
Đáp án: C 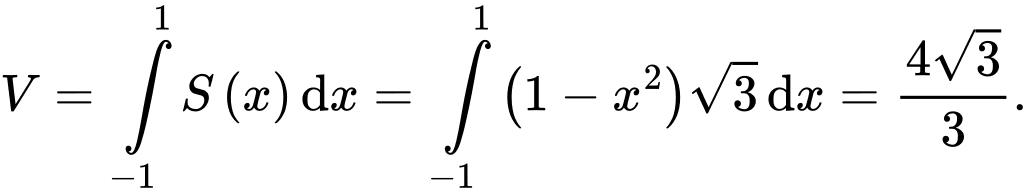
Chọn đáp án C.
Câu 15 [151678]: Một bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi các đường 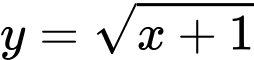 và trục
và trục  quay quanh trục
quay quanh trục  . Biết đáy lọ và miệng lọ có đường kính lần lượt là
. Biết đáy lọ và miệng lọ có đường kính lần lượt là 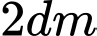 và
và 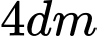 , khi đó thể tích của lọ là bao nhiêu
, khi đó thể tích của lọ là bao nhiêu 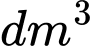 . Viết kết quả làm tròn đến hàng đơn vị
. Viết kết quả làm tròn đến hàng đơn vị
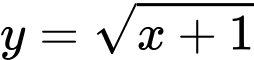 và trục
và trục 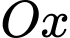 quay quanh trục
quay quanh trục 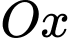 . Biết đáy lọ và miệng lọ có đường kính lần lượt là
. Biết đáy lọ và miệng lọ có đường kính lần lượt là 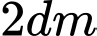 và
và 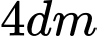 , khi đó thể tích của lọ là bao nhiêu
, khi đó thể tích của lọ là bao nhiêu 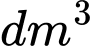 . Viết kết quả làm tròn đến hàng đơn vị
. Viết kết quả làm tròn đến hàng đơn vị A, 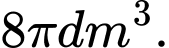
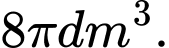
B, 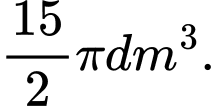
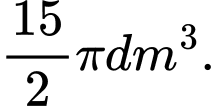
C, 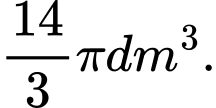
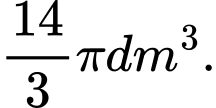
D, 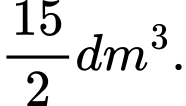
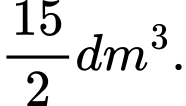
 Đáp án: B
Đáp án: B
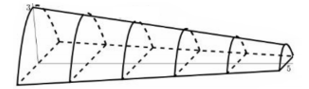
Câu 16 [789817]: (THPT Lê Quý Đôn Đà Nẵng 2019) Cho một mô hình  mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài
mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài  ; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức
; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức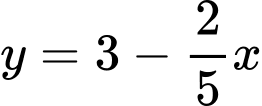
 , với
, với 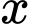
 là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị
là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị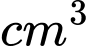 ) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị )
) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị )
 mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài
mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài  ; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức
; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức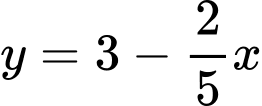
 , với
, với 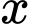
 là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị
là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị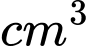 ) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị )
) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị )
A, 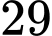 .
.
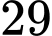 .
.B, 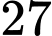 .
.
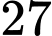 .
.C, 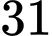 .
.
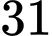 .
.D, 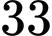 .
.
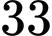 .
.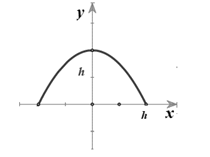
Xét một thiết diện parabol có chiều cao là
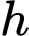 và độ dài đáy
và độ dài đáy 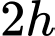 và chọn hệ trục
và chọn hệ trục 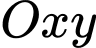 như hình vẽ trên.
như hình vẽ trên.Parabol
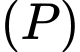 có phương trình
có phương trình 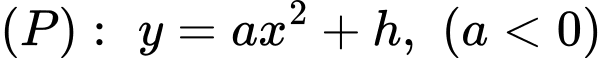
Có
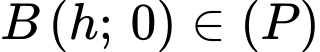
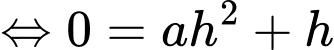
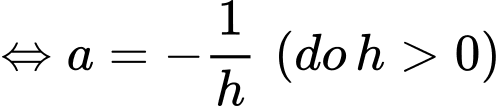
Diện tích
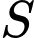 của thiết diện:
của thiết diện: 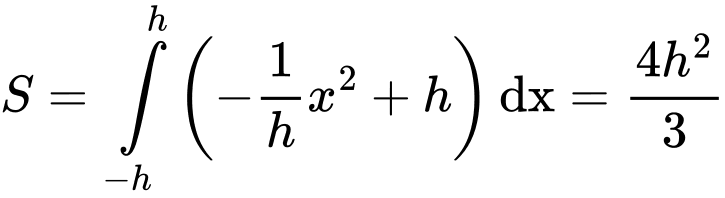 ,
, 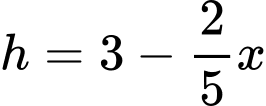
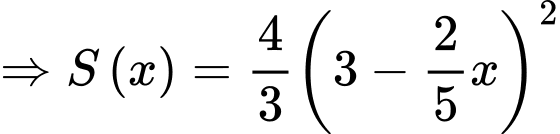
Suy ra thể tích không gian bên trong của đường hầm mô hình:
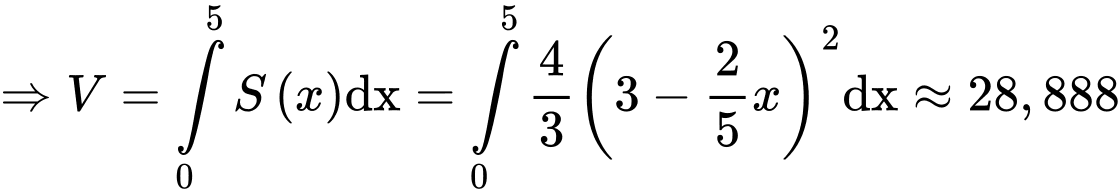
 Đáp án: A
Đáp án: A
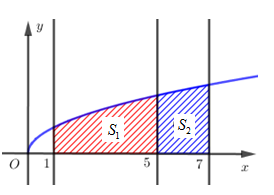
Câu 17 [140096]: Cho hình thang cong  giới hạn bởi các đường
giới hạn bởi các đường 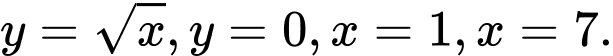 Đường thẳng
Đường thẳng 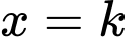 với
với 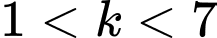 chia
chia  thành hai phần là
thành hai phần là 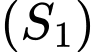 và
và 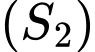 quay quanh trục
quay quanh trục 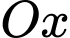 ta thu được hai khối tròn xoay có thể tích lần lượt là
ta thu được hai khối tròn xoay có thể tích lần lượt là 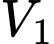 và
và 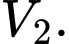 Xác định
Xác định 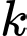 để
để 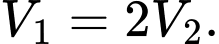
 giới hạn bởi các đường
giới hạn bởi các đường  Đường thẳng
Đường thẳng  với
với  chia
chia  thành hai phần là
thành hai phần là 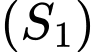 và
và 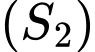 quay quanh trục
quay quanh trục 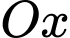 ta thu được hai khối tròn xoay có thể tích lần lượt là
ta thu được hai khối tròn xoay có thể tích lần lượt là 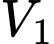 và
và 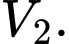 Xác định
Xác định 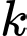 để
để 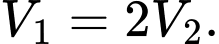

A, 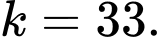
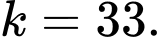
B, 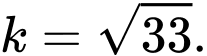
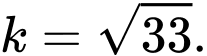
C, 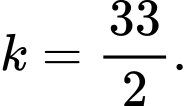
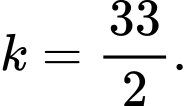
D, 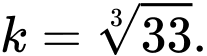
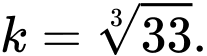
Ta có 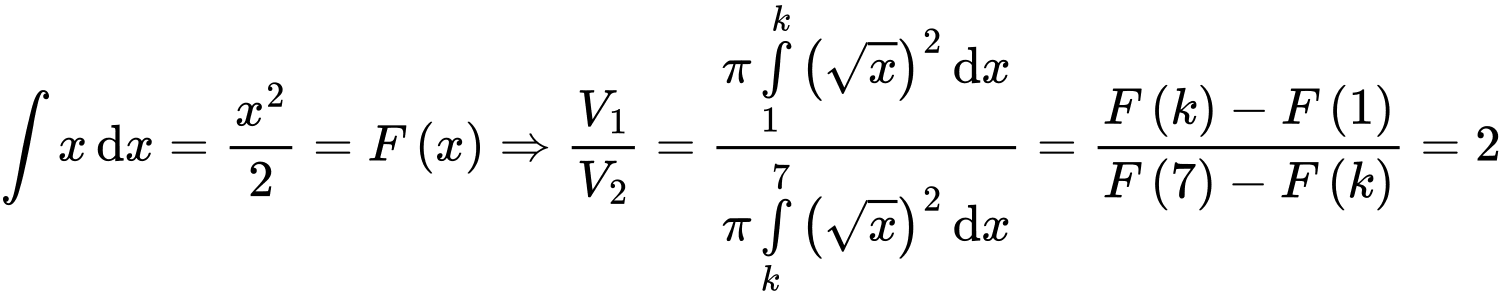
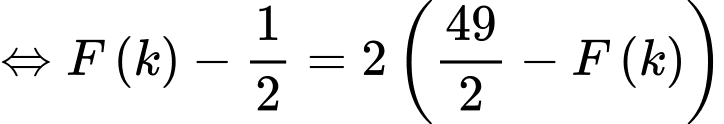
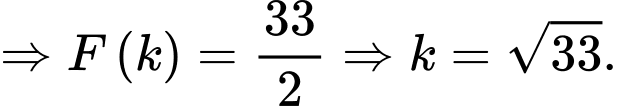 Đáp án: B
Đáp án: B
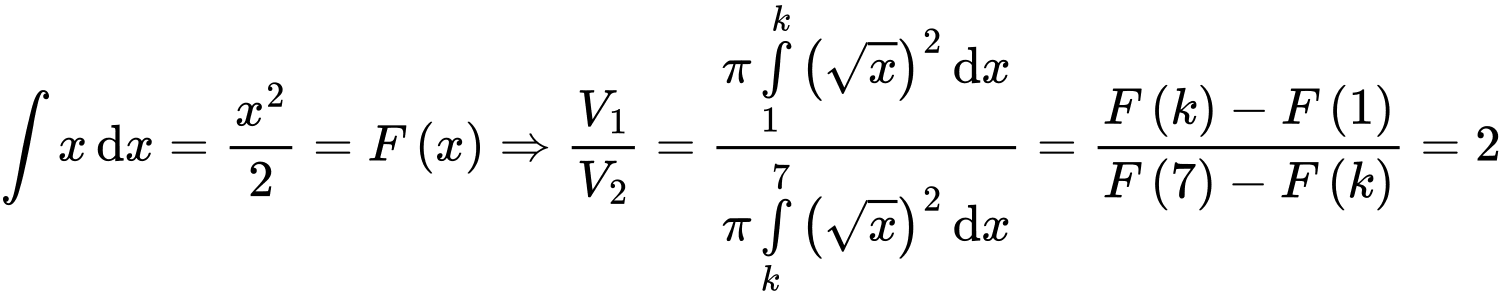
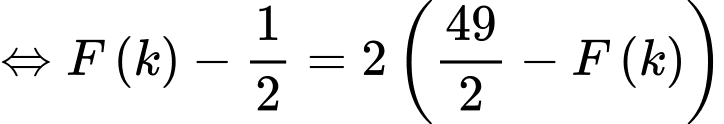
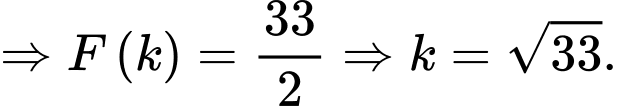
Chọn đáp án B.
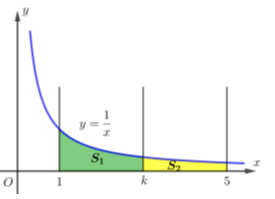
Câu 18 [151690]: Cho hình thang cong  giới hạn bởi các đường
giới hạn bởi các đường 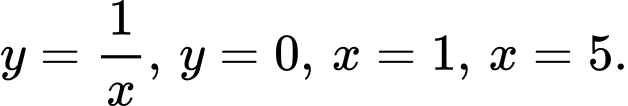 Đường thẳng
Đường thẳng 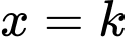 với
với 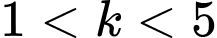 chia
chia  thành hai phần là
thành hai phần là 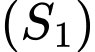 và
và 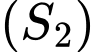 quay quanh trục
quay quanh trục 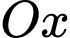 ta thu được hai khối tròn xoay có thể tích lần lượt là
ta thu được hai khối tròn xoay có thể tích lần lượt là 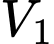 và
và 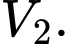 Xác định
Xác định 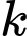 để
để 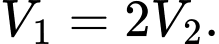
 giới hạn bởi các đường
giới hạn bởi các đường 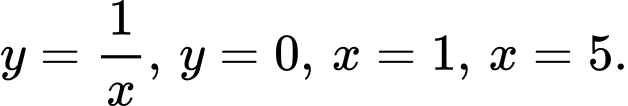 Đường thẳng
Đường thẳng 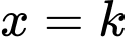 với
với 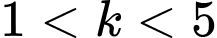 chia
chia  thành hai phần là
thành hai phần là 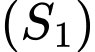 và
và 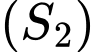 quay quanh trục
quay quanh trục 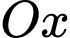 ta thu được hai khối tròn xoay có thể tích lần lượt là
ta thu được hai khối tròn xoay có thể tích lần lượt là 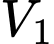 và
và 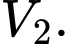 Xác định
Xác định 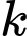 để
để 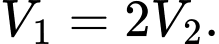

A, 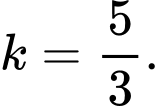
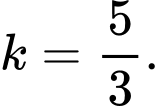
B, 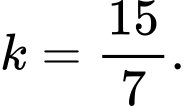
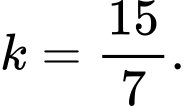
C, 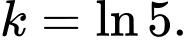
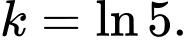
D, 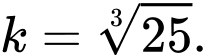
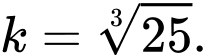
Ta có 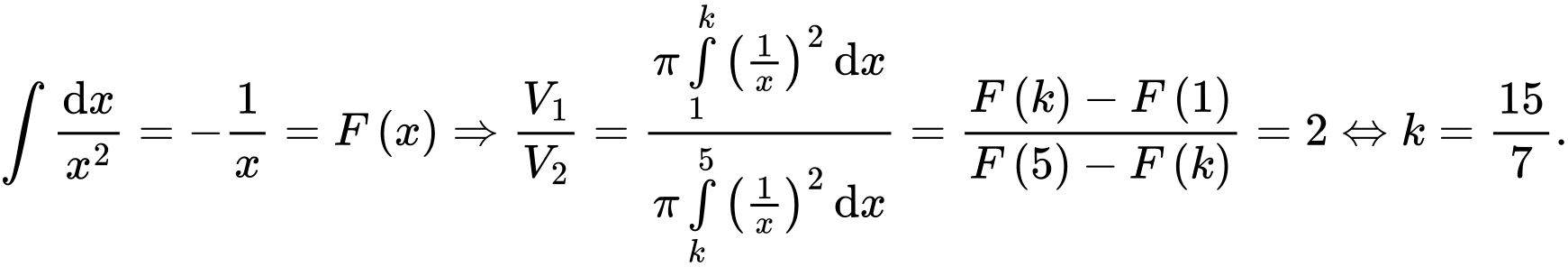
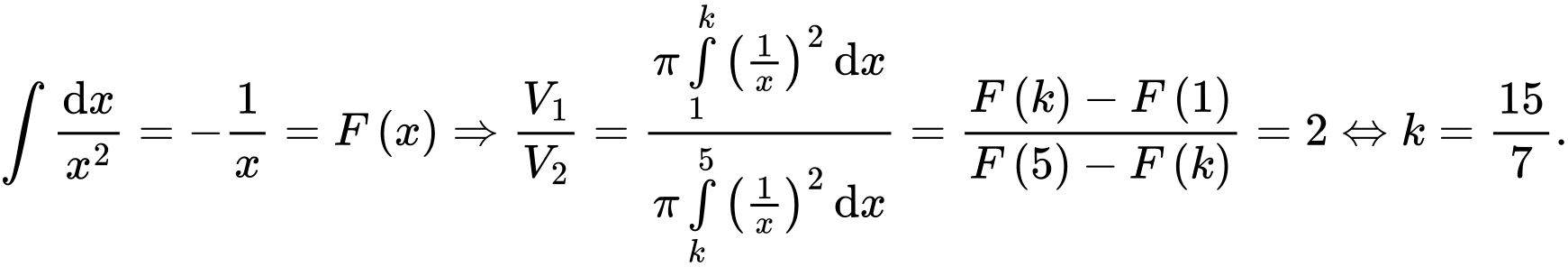
Chọn đáp án B.
Đáp án: B
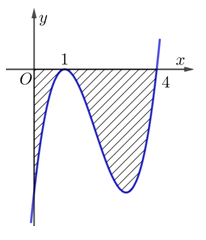
Câu 19 [146750]: Diện tích hình phẳng giới hạn bởi đồ thị hàm số bậc ba 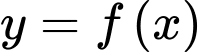 và các trục tọa độ là
và các trục tọa độ là 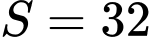 (hình vẽ bên). Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng trên quanh trục
(hình vẽ bên). Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng trên quanh trục 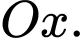
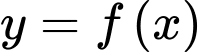 và các trục tọa độ là
và các trục tọa độ là 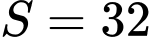 (hình vẽ bên). Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng trên quanh trục
(hình vẽ bên). Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng trên quanh trục 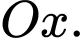

A, 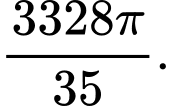
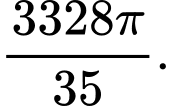
B, 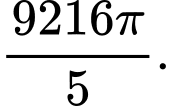
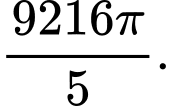
C, 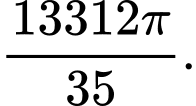
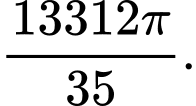
D, 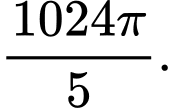
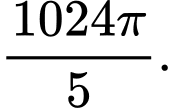
Dựa vào đồ thị hàm số suy ra 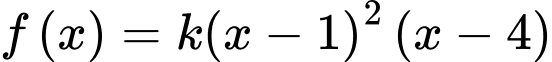 (với
(với  )
)
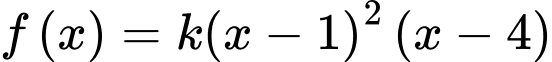 (với
(với  )
)Mặt khác 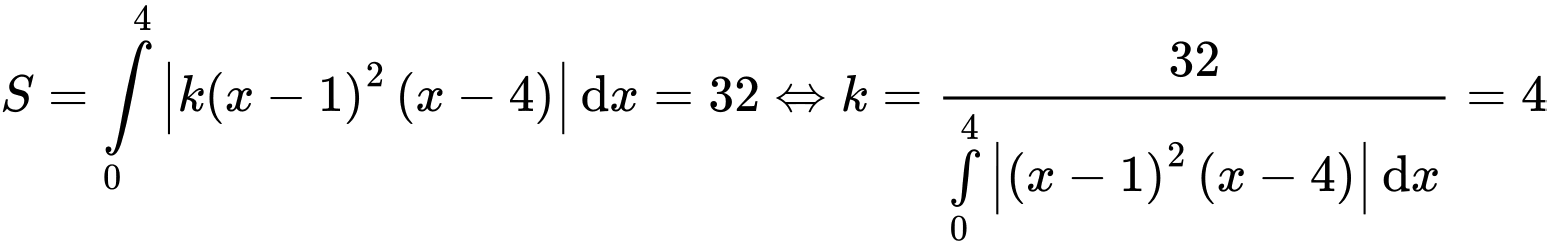
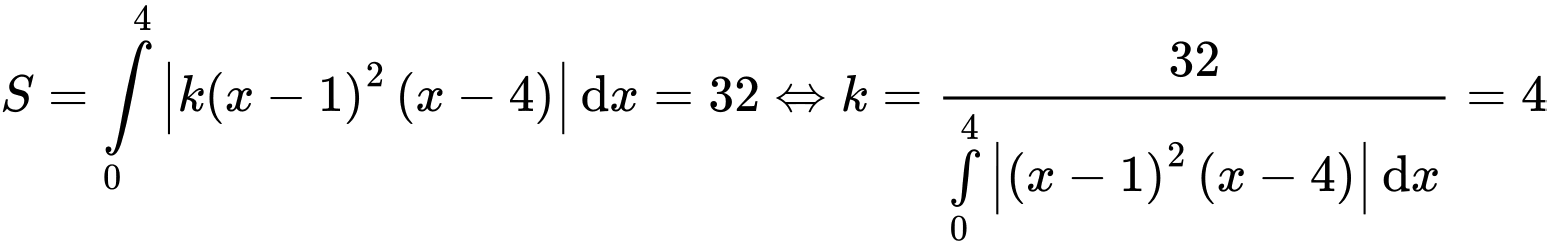
Suy ra 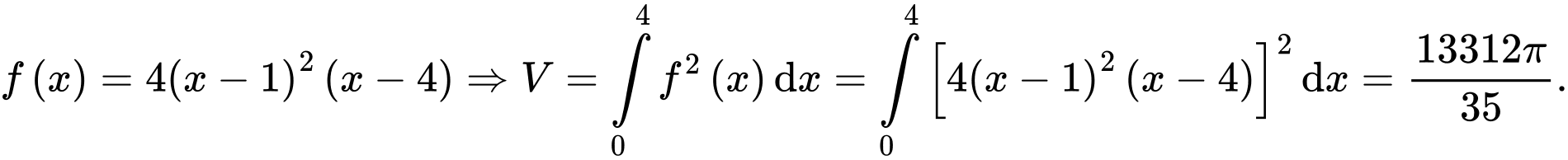
Đáp án: C 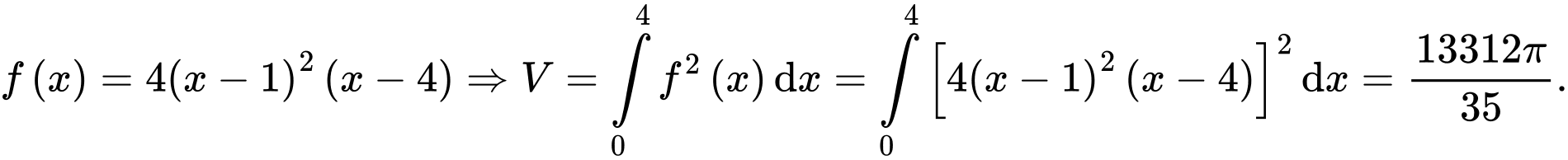
Chọn đáp án C.
Câu 20 [17694]: Cho hình vuông  có cạnh bằng 4 được chia thành hai phần bởi parabol
có cạnh bằng 4 được chia thành hai phần bởi parabol  có đỉnh
có đỉnh  . Gọi
. Gọi  là hình phẳng không bị gạch (như hình vẽ ). Tính thể tích
là hình phẳng không bị gạch (như hình vẽ ). Tính thể tích  của khối tròn xoay khi cho phần
của khối tròn xoay khi cho phần 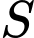 quay quanh trục
quay quanh trục 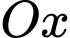 .
.
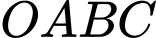 có cạnh bằng 4 được chia thành hai phần bởi parabol
có cạnh bằng 4 được chia thành hai phần bởi parabol 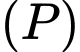 có đỉnh
có đỉnh  . Gọi
. Gọi 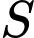 là hình phẳng không bị gạch (như hình vẽ ). Tính thể tích
là hình phẳng không bị gạch (như hình vẽ ). Tính thể tích  của khối tròn xoay khi cho phần
của khối tròn xoay khi cho phần 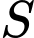 quay quanh trục
quay quanh trục 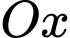 .
.
A, 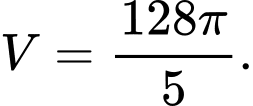
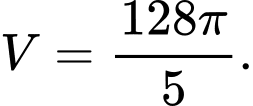
B, 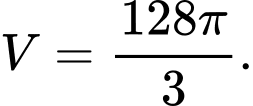
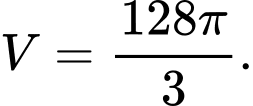
C, 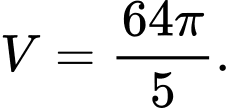
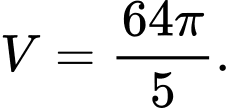
D, 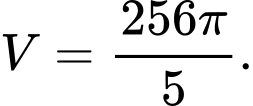
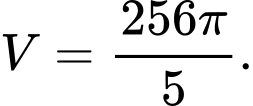
 Đáp án: D
Đáp án: D
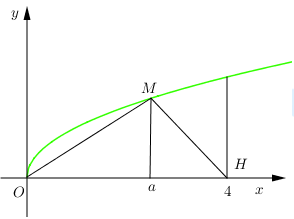
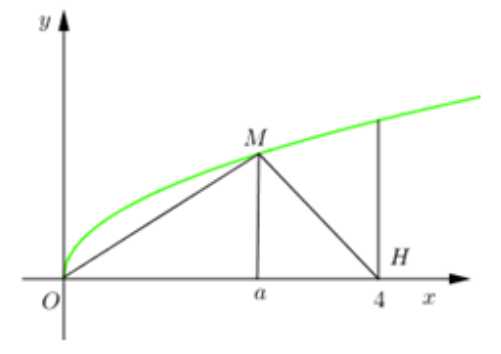
Câu 21 [151693]: Gọi  là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 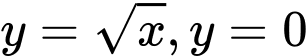 và
và  quanh trục
quanh trục  Đường thẳng
Đường thẳng 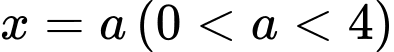 cắt đồ thị hàm số
cắt đồ thị hàm số 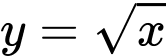 tại
tại 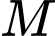 (hình vẽ bên). Gọi
(hình vẽ bên). Gọi 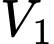 là thể tích khối tròn xoay tạo thành khi quay tam giác
là thể tích khối tròn xoay tạo thành khi quay tam giác 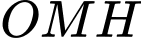 quanh trục
quanh trục 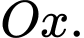 Biết rằng
Biết rằng 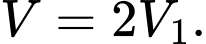 Khi đó
Khi đó  bằng bao nhiêu
bằng bao nhiêu
 là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường  và
và  quanh trục
quanh trục  Đường thẳng
Đường thẳng 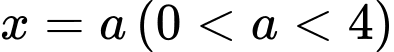 cắt đồ thị hàm số
cắt đồ thị hàm số 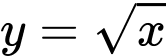 tại
tại  (hình vẽ bên). Gọi
(hình vẽ bên). Gọi 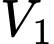 là thể tích khối tròn xoay tạo thành khi quay tam giác
là thể tích khối tròn xoay tạo thành khi quay tam giác 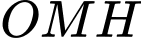 quanh trục
quanh trục 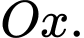 Biết rằng
Biết rằng 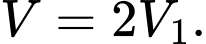 Khi đó
Khi đó 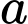 bằng bao nhiêu
bằng bao nhiêu
A, 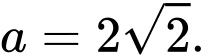
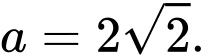
B, 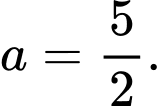
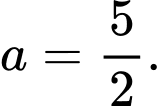
C, 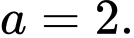
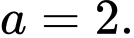
D, 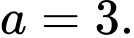
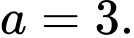
Ta có
 .
.
Gọi
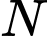 là giao điểm của đường thắng
là giao điểm của đường thắng 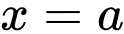 và trục hoành.
và trục hoành.
Khi đó
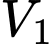 là thể tích tạo được khi xoay hai tam giác
là thể tích tạo được khi xoay hai tam giác 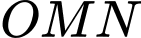 và
và 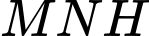 quanh trục
quanh trục 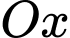 với
với 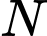 là hình chiếu của
là hình chiếu của 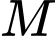 trên
trên  .
.
Ta có
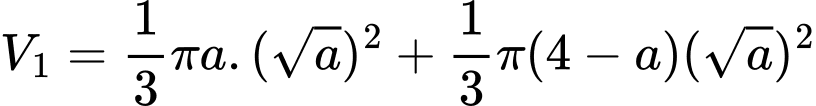
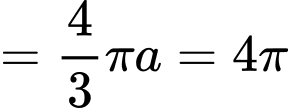
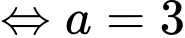 .
.
Chọn đáp án D. Đáp án: D
Câu 22 [378625]: Nghệ thuật làm gốm có lịch sử phát triển lâu đời và vẫn còn tồn tại cho đến ngày nay. Giả sử một bình gốm có mặt trong của bình là một mặt tròn xoay sinh ra khi cho phần đồ thị của hàm số 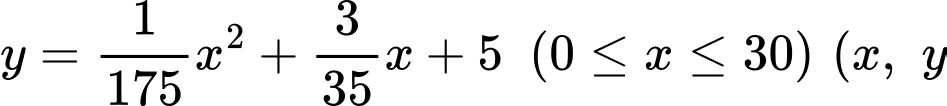 tính theo
tính theo 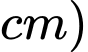 quay tròn quanh bệ gốm có trục trùng với trục hoành
quay tròn quanh bệ gốm có trục trùng với trục hoành  Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu
Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu 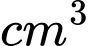 đất sét, biết rằng bình gốm đó có độ dày không đổi là
đất sét, biết rằng bình gốm đó có độ dày không đổi là 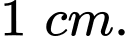
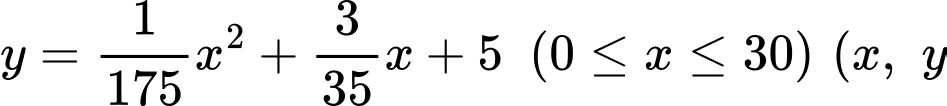 tính theo
tính theo  quay tròn quanh bệ gốm có trục trùng với trục hoành
quay tròn quanh bệ gốm có trục trùng với trục hoành  Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu
Hỏi để hoàn thành bình gốm đó ta cần sử dụng bao nhiêu 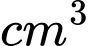 đất sét, biết rằng bình gốm đó có độ dày không đổi là
đất sét, biết rằng bình gốm đó có độ dày không đổi là 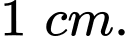
Ta có: 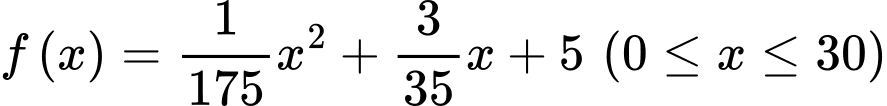
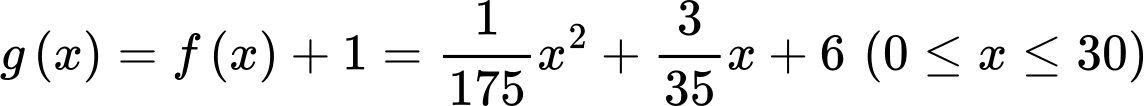
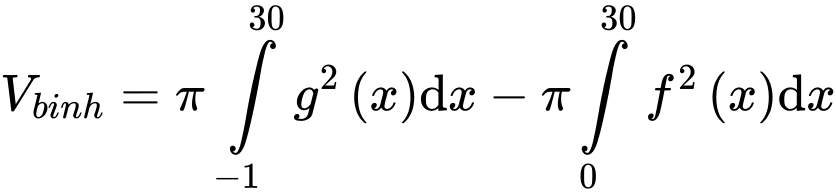
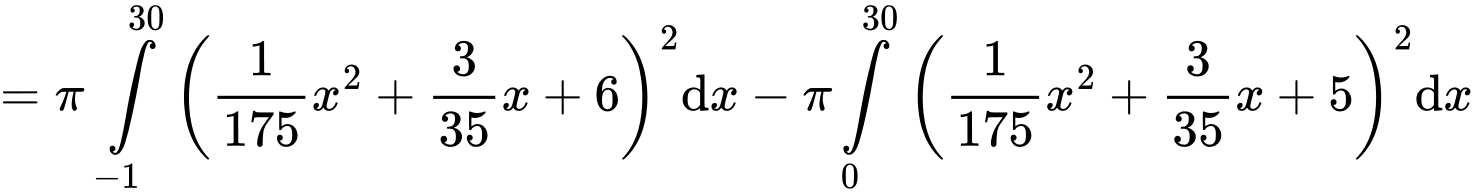
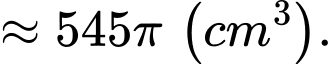
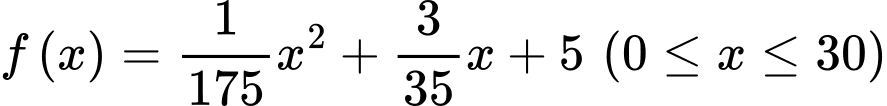
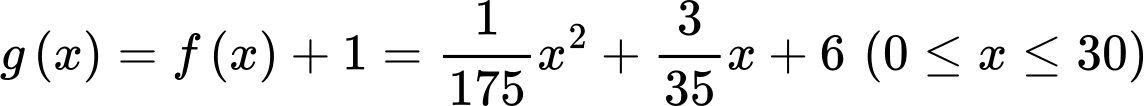
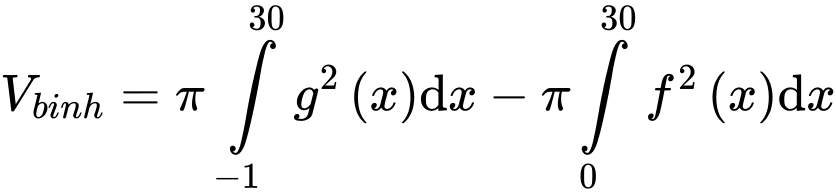
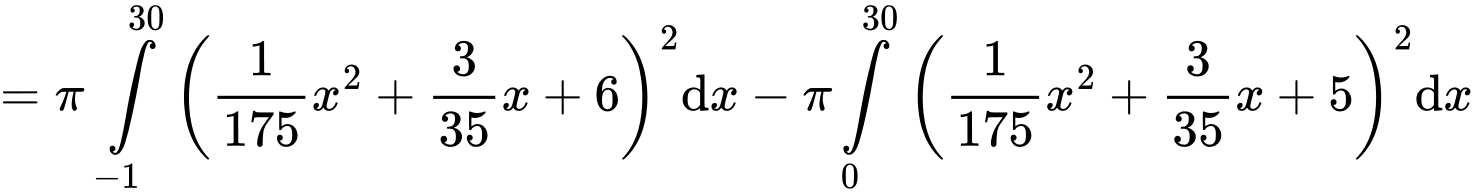
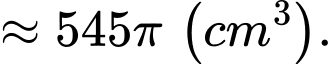
Câu 23 [38456]: Cho  là hình phẳng giới hạn bởi parabol
là hình phẳng giới hạn bởi parabol 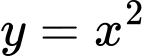 và đường tròn
và đường tròn 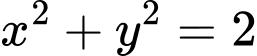 (phần tô đậm trong hình). Tính thể tích
(phần tô đậm trong hình). Tính thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay  quanh trục hoành.
quanh trục hoành.
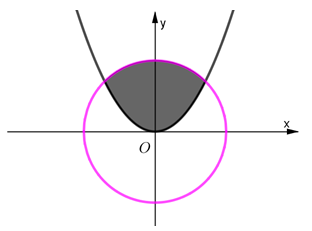
 là hình phẳng giới hạn bởi parabol
là hình phẳng giới hạn bởi parabol 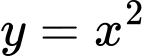 và đường tròn
và đường tròn 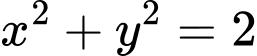 (phần tô đậm trong hình). Tính thể tích
(phần tô đậm trong hình). Tính thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay  quanh trục hoành.
quanh trục hoành.
A, 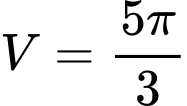 .
.
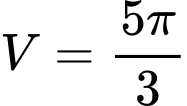 .
.B, 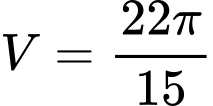 .
.
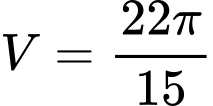 .
.C, 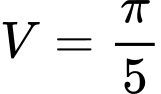 .
.
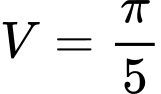 .
.D, 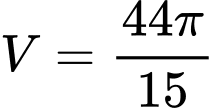 .
.
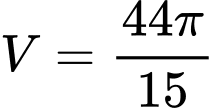 .
.