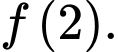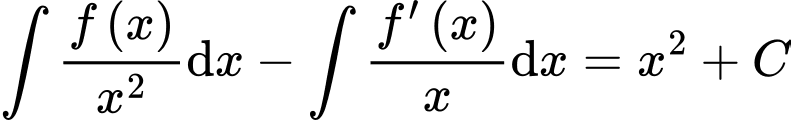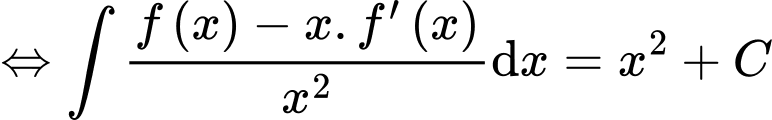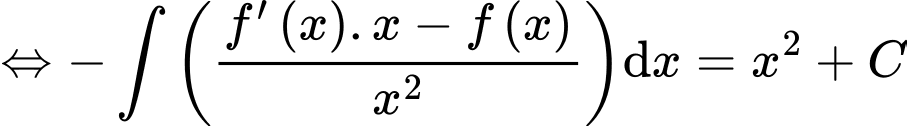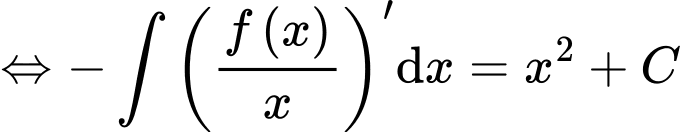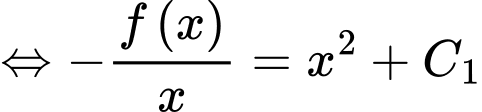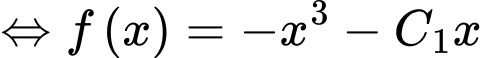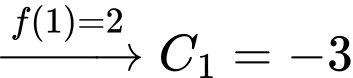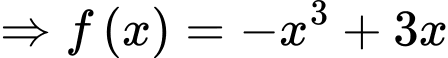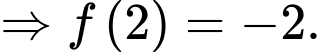Đáp án Bài tập tự luyện số 2
Câu 1 [147872]: Tìm họ nguyên hàm của hàm số 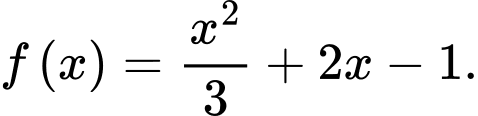
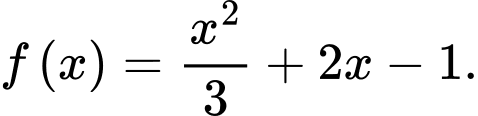
Ta có 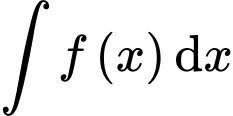
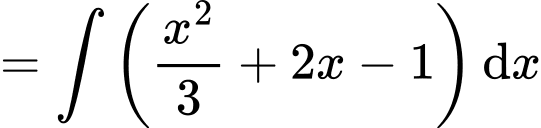
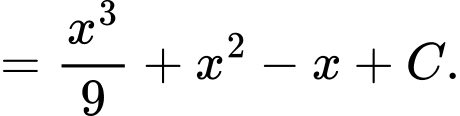
Chọn đáp án D. Đáp án: D
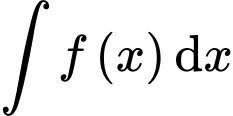
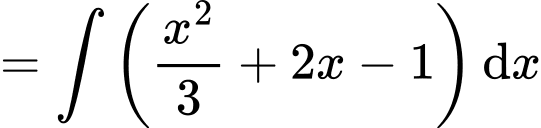
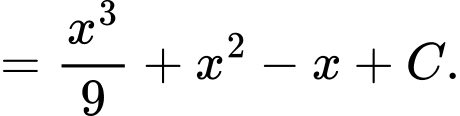
Chọn đáp án D. Đáp án: D
Câu 2 [389365]: Nếu 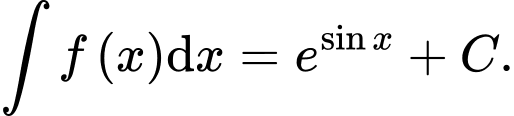 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng?
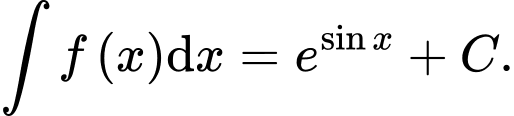 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng? A, 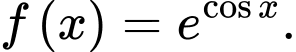
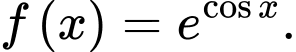
B, 

C, 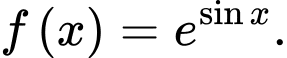
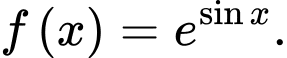
D, 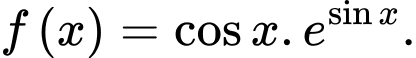
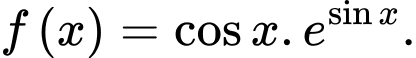
Ta có: 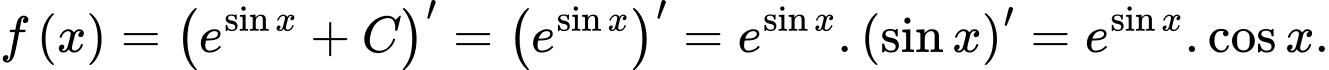 Chọn D. Đáp án: D
Chọn D. Đáp án: D
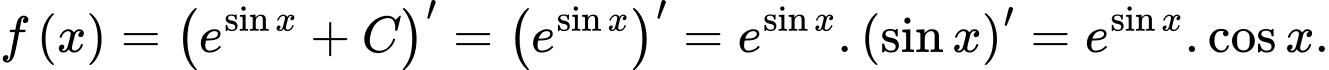 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 3 [383122]: [MĐ2] Biết 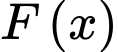 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 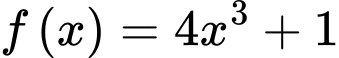 và
và  . Tính giá trị của
. Tính giá trị của 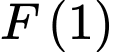 .
.
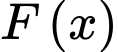 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 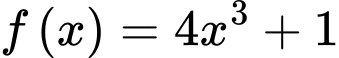 và
và  . Tính giá trị của
. Tính giá trị của 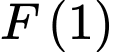 .
. A, 1.
B, 2.
C, 3.
D, 0.
Ta có 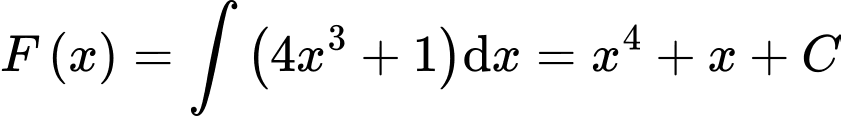 .
.
Mặt khác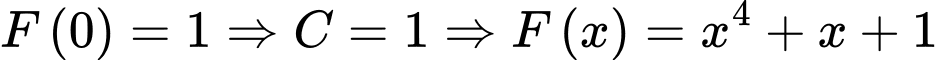 .
.
Do đó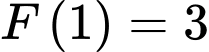 . Đáp án: C
. Đáp án: C
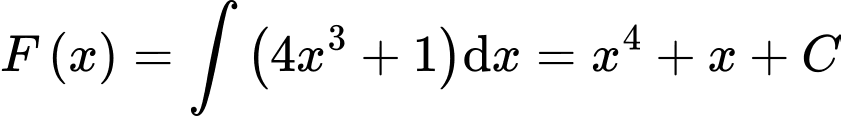 .
.
Mặt khác
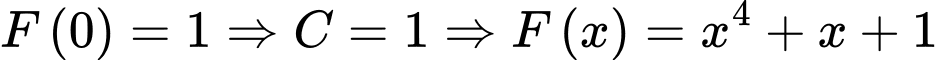 .
.
Do đó
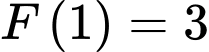 . Đáp án: C
. Đáp án: C
Câu 4 [148030]: Cho 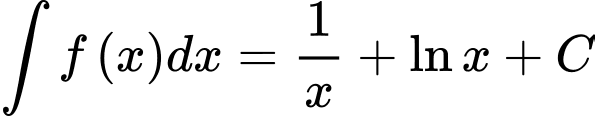 (với
(với  là hằng số tùy ý), trên miền
là hằng số tùy ý), trên miền 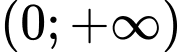 chọn đẳng thức đúng về hàm số
chọn đẳng thức đúng về hàm số 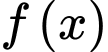 .
.
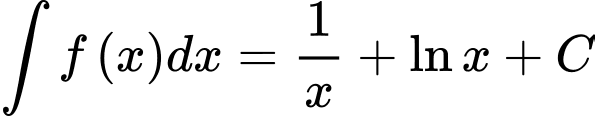 (với
(với  là hằng số tùy ý), trên miền
là hằng số tùy ý), trên miền 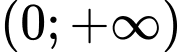 chọn đẳng thức đúng về hàm số
chọn đẳng thức đúng về hàm số 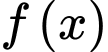 .
. A, 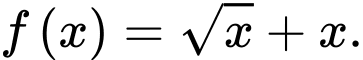
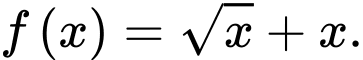
B, 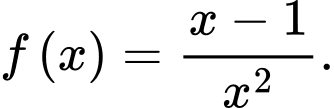
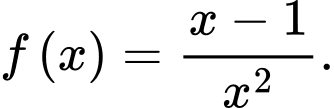
C, 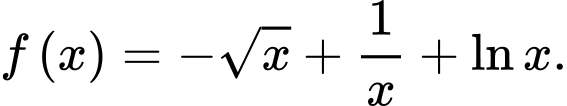
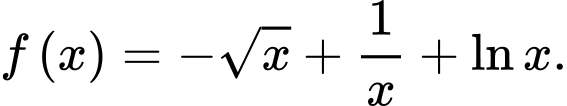
D, 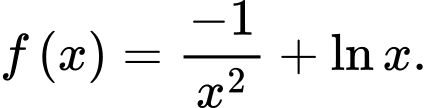
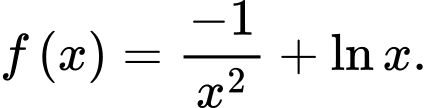
Ta có 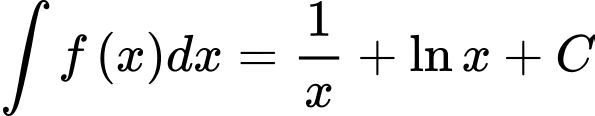
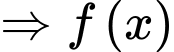
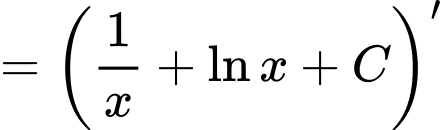
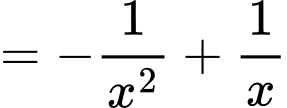
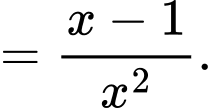
Chọn đáp án B. Đáp án: B
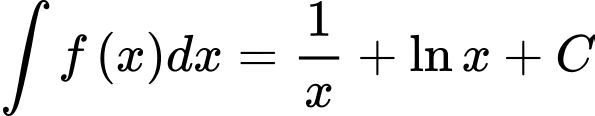
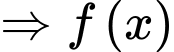
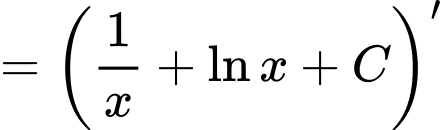
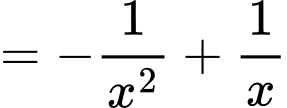
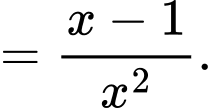
Chọn đáp án B. Đáp án: B
Câu 5 [389366]: Nguyên hàm của hàm số 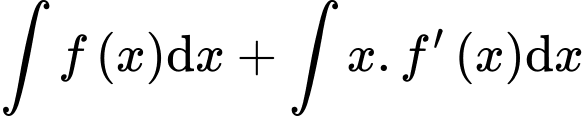 bằng
bằng
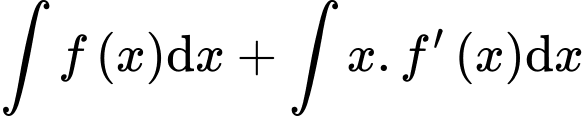 bằng
bằng A, 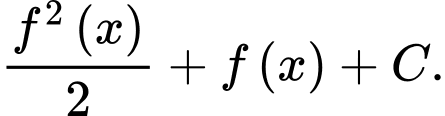
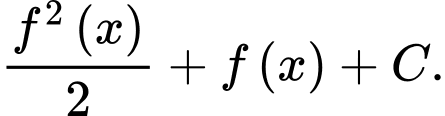
B, 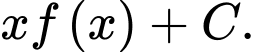
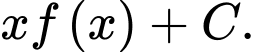
C, 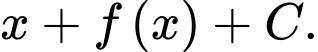
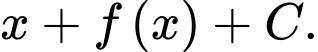
D, 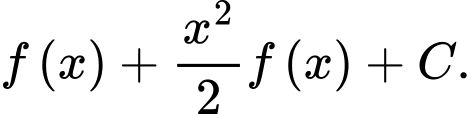
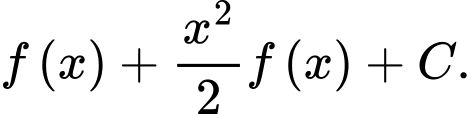
Ta có: 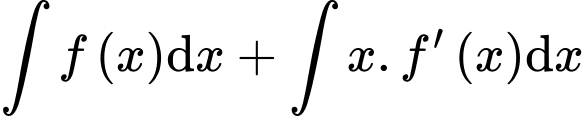
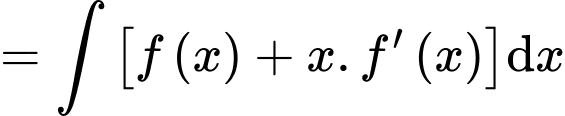
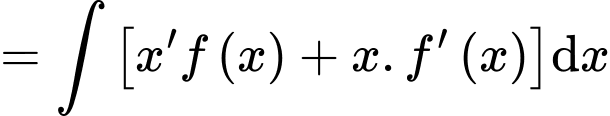
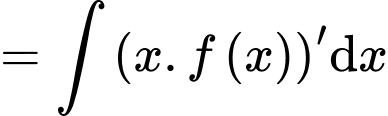

Chọn B. Đáp án: B
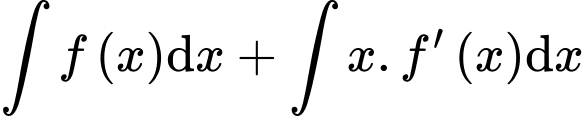
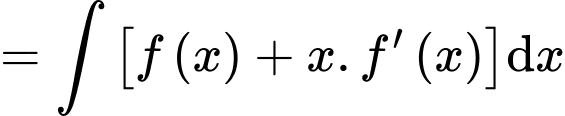
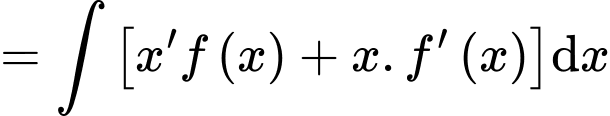
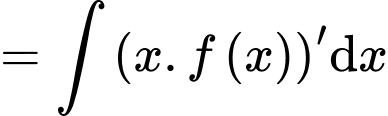

Chọn B. Đáp án: B
Câu 6 [389367]: Biết rằng 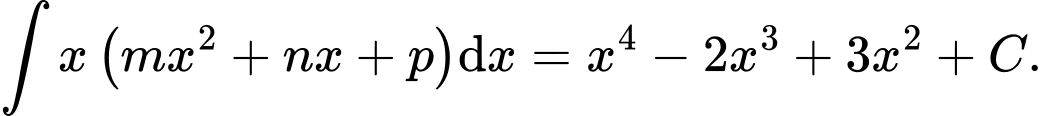 Tính giá trị của
Tính giá trị của 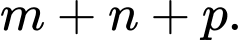
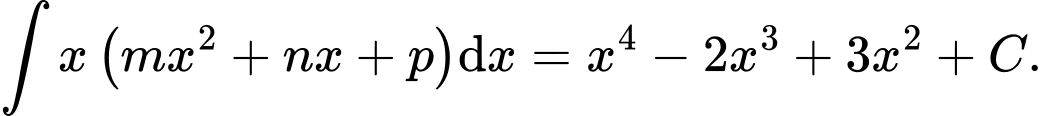 Tính giá trị của
Tính giá trị của 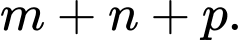
A, 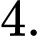
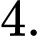
B, 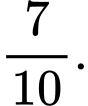
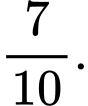
C, 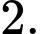
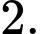
D, 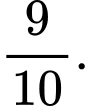
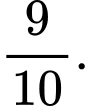
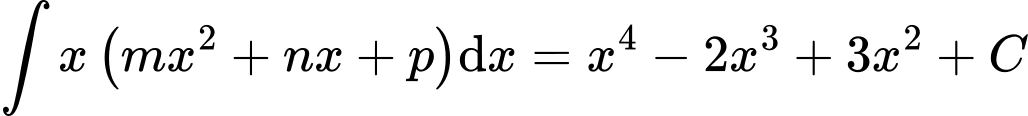
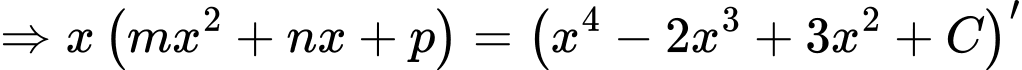
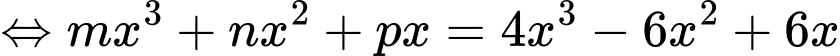
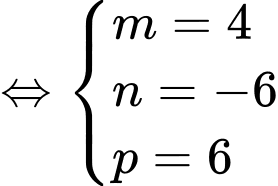
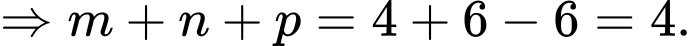 Đáp án: A
Đáp án: A
Câu 7 [148225]: Cho 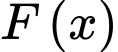 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 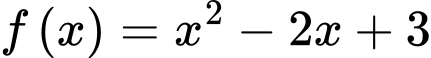 thỏa mãn
thỏa mãn  , giá trị của
, giá trị của 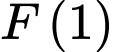 bằng
bằng
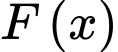 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 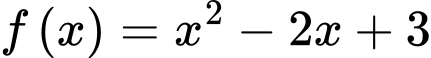 thỏa mãn
thỏa mãn  , giá trị của
, giá trị của 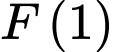 bằng
bằng A, 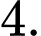
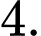
B, 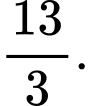
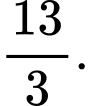
C, 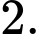
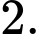
D, 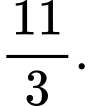
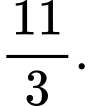
Ta có 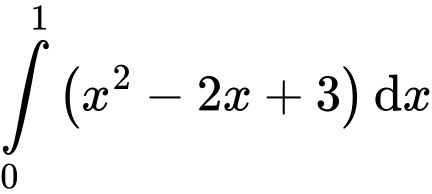
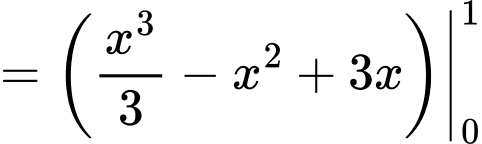
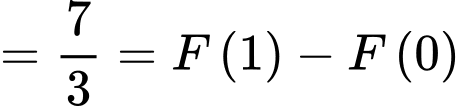
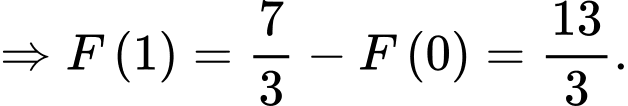
Chọn đáp án B. Đáp án: B
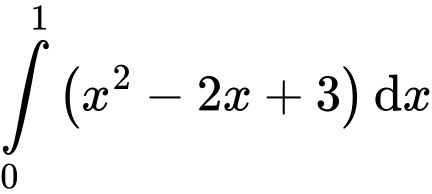
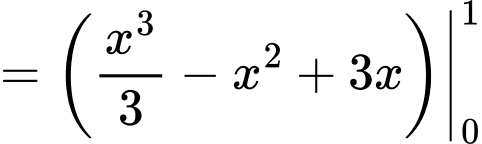
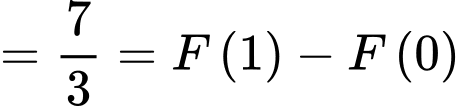
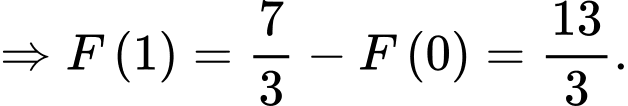
Chọn đáp án B. Đáp án: B
Câu 8 [389368]: Cho hàm số 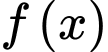 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 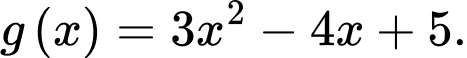 Tính
Tính 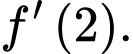
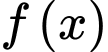 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 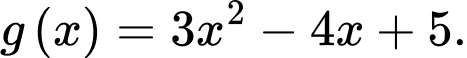 Tính
Tính 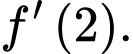
A, 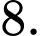
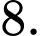
B, 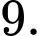
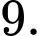
C, 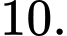
D, 
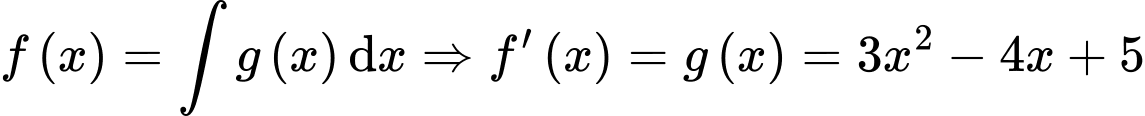
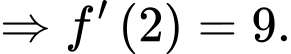
Câu 9 [389369]: Biết rằng 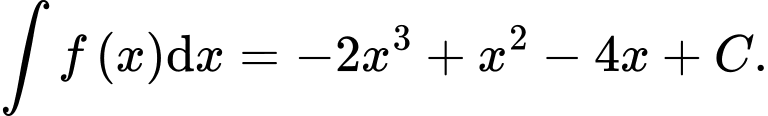 Tính giá trị của
Tính giá trị của 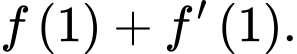
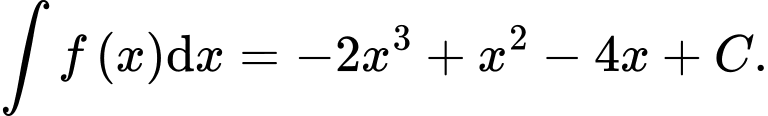 Tính giá trị của
Tính giá trị của 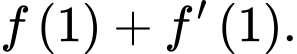
A, 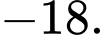
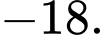
B, 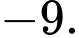
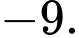
C, 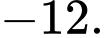
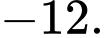
D, 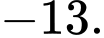
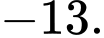
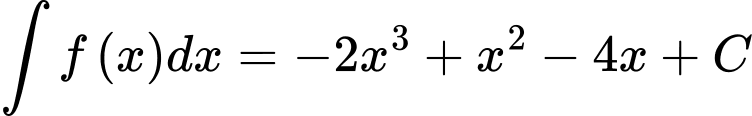
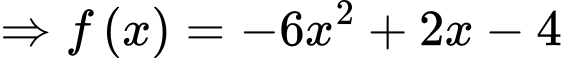
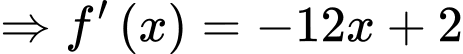
Khi đó:
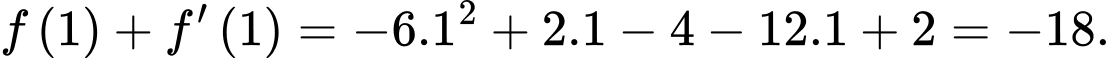 Chọn đáp án A. Đáp án: A
Chọn đáp án A. Đáp án: A
Câu 10 [148228]: Cho 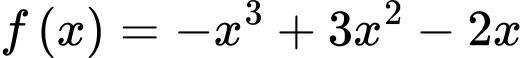 . Một nguyên hàm
. Một nguyên hàm 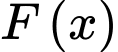 của
của 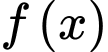 thỏa mãn
thỏa mãn 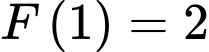 là
là
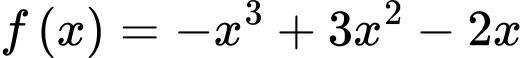 . Một nguyên hàm
. Một nguyên hàm 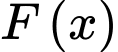 của
của 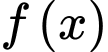 thỏa mãn
thỏa mãn 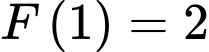 là
là A, 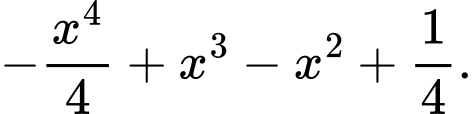
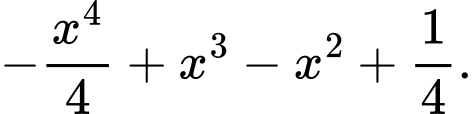
B, 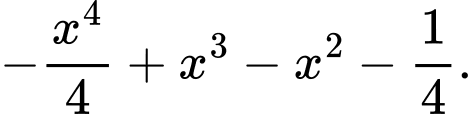
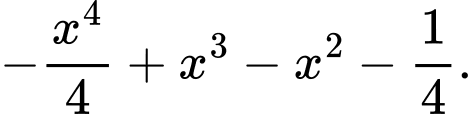
C, 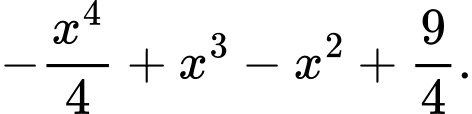
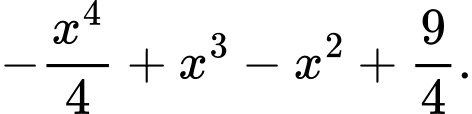
D, 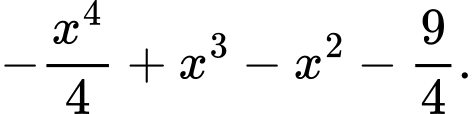
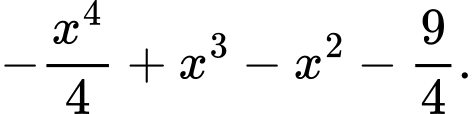
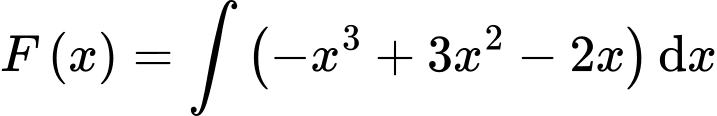
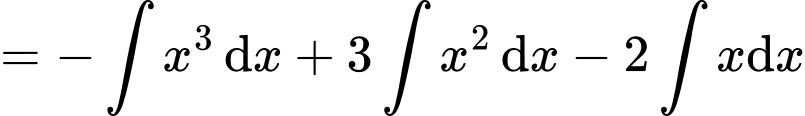
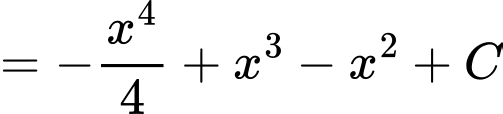
Mà
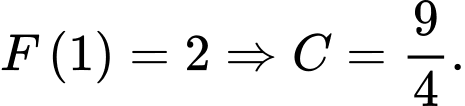
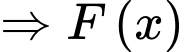
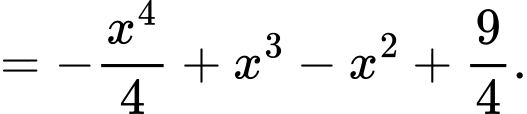
Chọn đáp án C. Đáp án: C
Câu 11 [389370]: Biết rằng 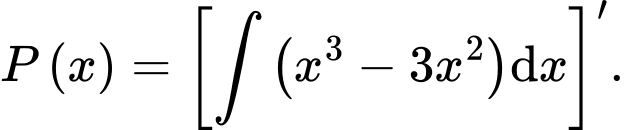 Tính giá trị của
Tính giá trị của 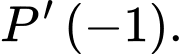
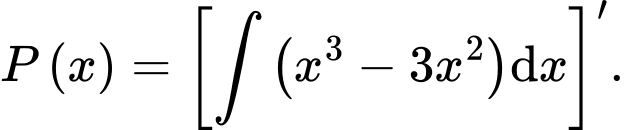 Tính giá trị của
Tính giá trị của 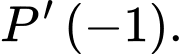
A, 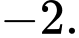
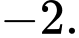
B, 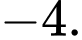
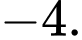
C, 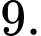
D, 
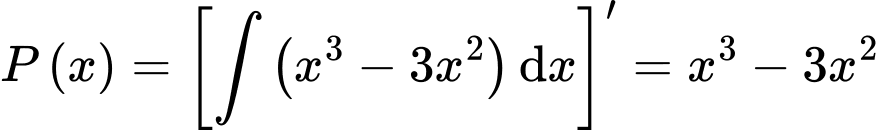
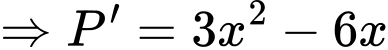
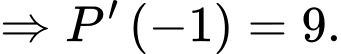 Đáp án: C
Đáp án: C
Câu 12 [389371]: Cho hàm số 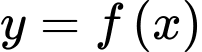 liên tục trên
liên tục trên  thoả mãn
thoả mãn 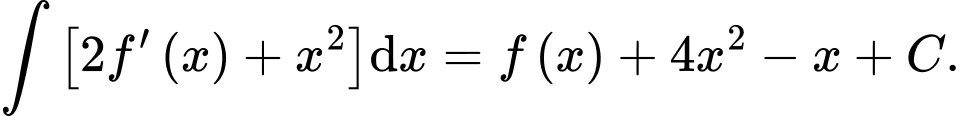 Hệ số góc của tiếp tuyến của đồ thị hàm số
Hệ số góc của tiếp tuyến của đồ thị hàm số 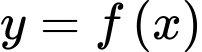 tại điểm
tại điểm 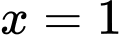 bằng
bằng
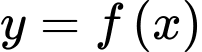 liên tục trên
liên tục trên 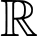 thoả mãn
thoả mãn 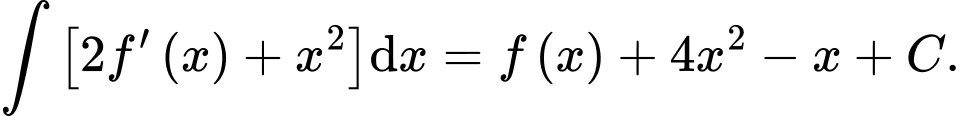 Hệ số góc của tiếp tuyến của đồ thị hàm số
Hệ số góc của tiếp tuyến của đồ thị hàm số 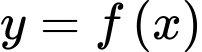 tại điểm
tại điểm 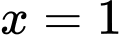 bằng
bằng A, 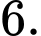
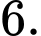
B, 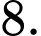
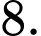
C, 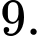
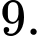
D, 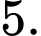
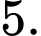
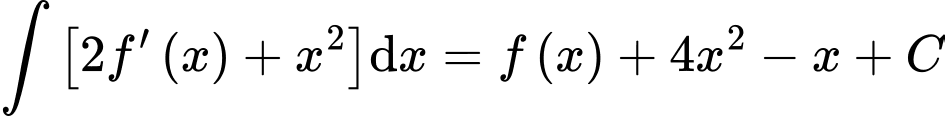
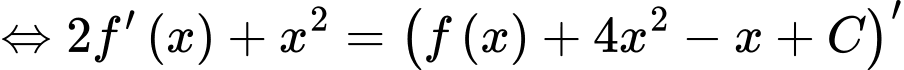
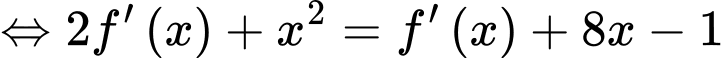
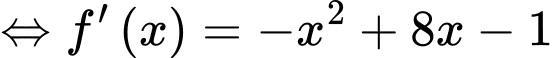
Vậy hệ số góc của tiếp tuyến tại điểm
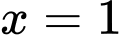 là
là 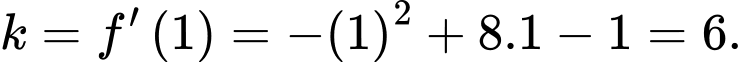
Chọn đápn án A. Đáp án: A
Câu 13 [389372]: Biết rằng 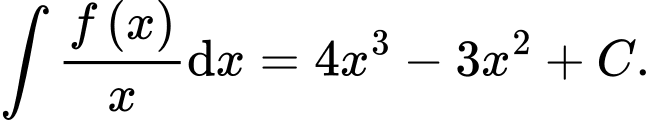 Giá trị của
Giá trị của 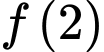 bằng:
bằng:
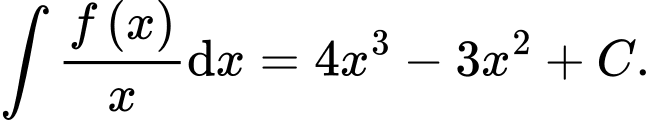 Giá trị của
Giá trị của 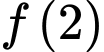 bằng:
bằng: A, 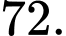
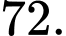
B, 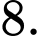
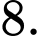
C, 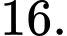
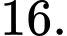
D, 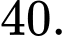
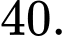
Ta có 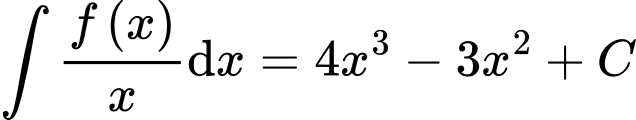
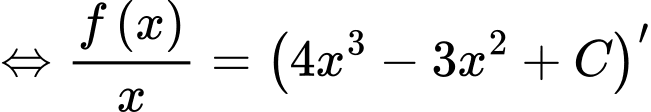
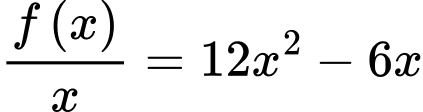
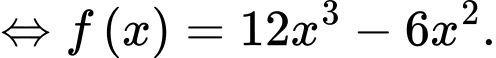
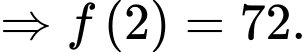
Chọn đáp án A. Đáp án: A
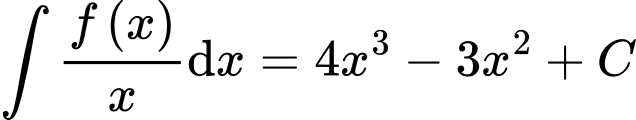
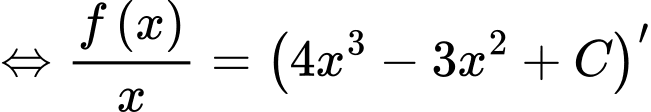
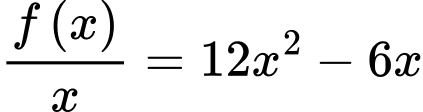
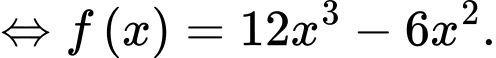
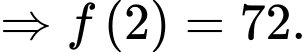
Chọn đáp án A. Đáp án: A
Câu 14 [148286]: Tìm nguyên hàm 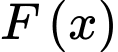 của hàm số
của hàm số 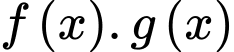 , biết
, biết 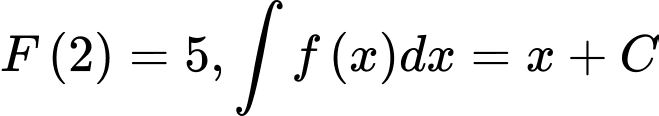 và
và 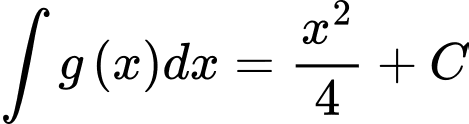 .
.
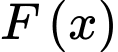 của hàm số
của hàm số 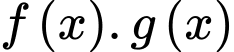 , biết
, biết 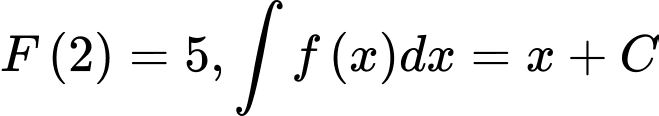 và
và 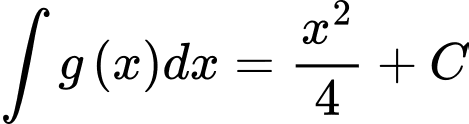 .
. A, 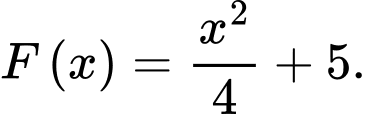
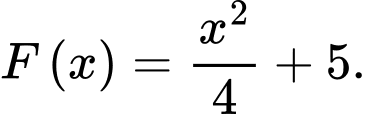
B, 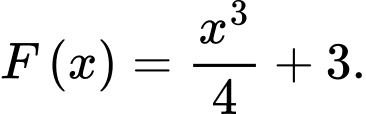
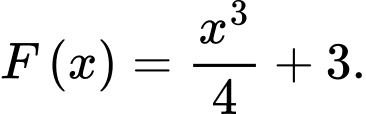
C, 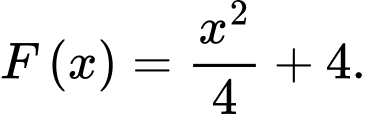
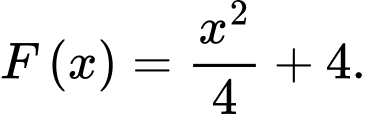
D, 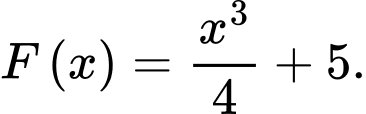
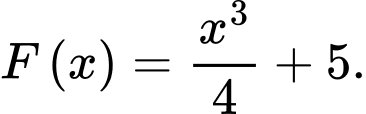
Ta có 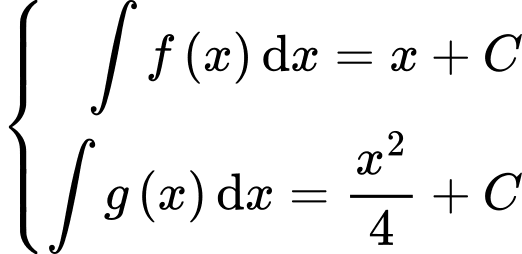
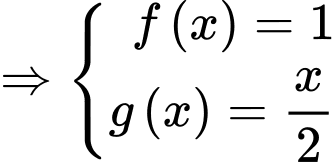
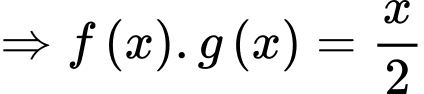
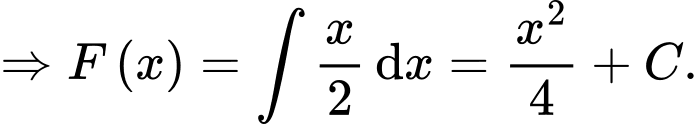
Mặt khác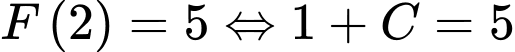
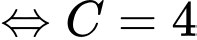
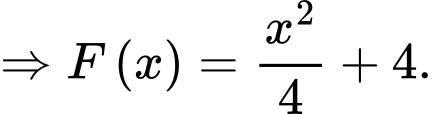
Chọn đáp án C. Đáp án: C
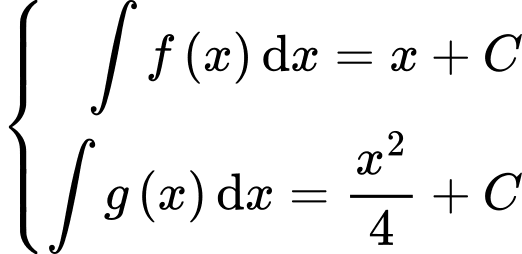
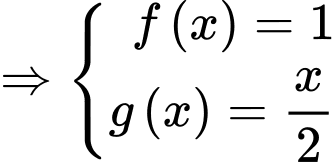
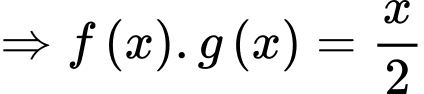
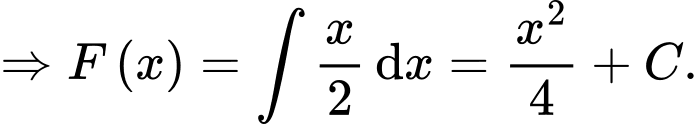
Mặt khác
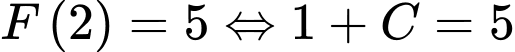
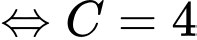
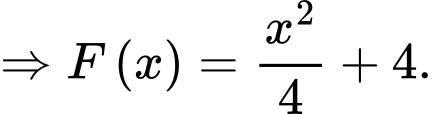
Chọn đáp án C. Đáp án: C
Câu 15 [386276]: Cho hàm số 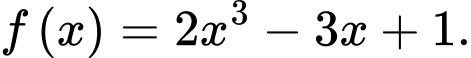 Gọi
Gọi 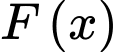 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 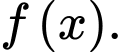 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
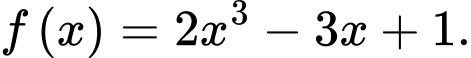 Gọi
Gọi 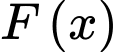 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 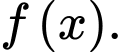 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) 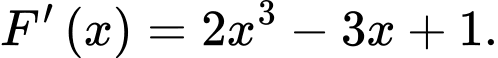
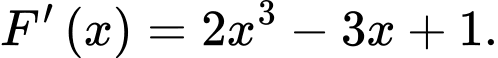
B, b) 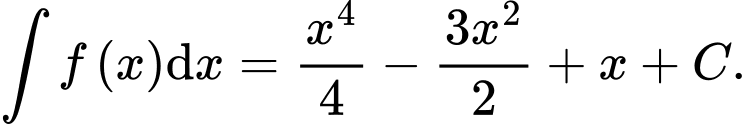
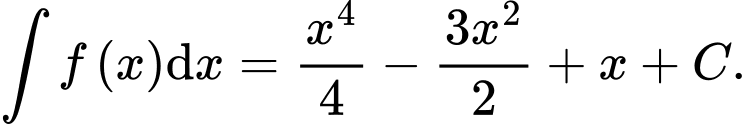
C, c) Nếu 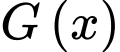 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 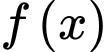 thì
thì 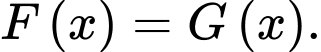
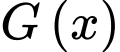 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 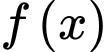 thì
thì 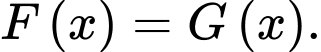
D, d) Nếu 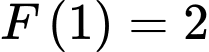 thì
thì 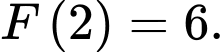
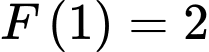 thì
thì 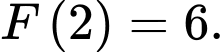
a) Đúng. 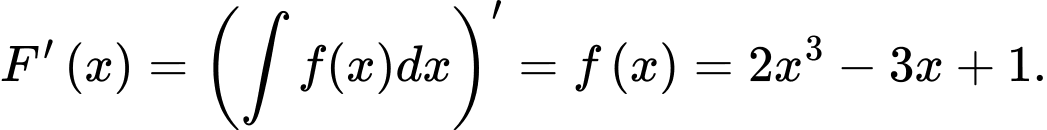
b) Sai.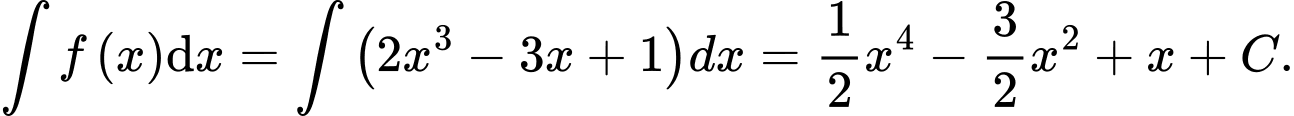
c) Sai. Một hàm số có nhiều nguyên hàm khác nhau.
d) Đúng.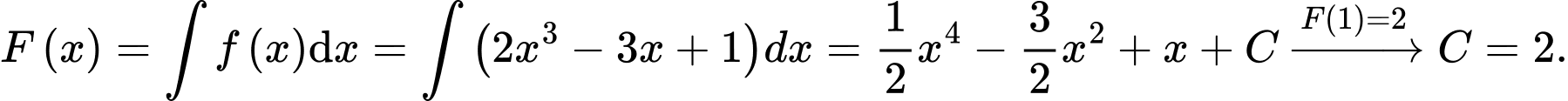
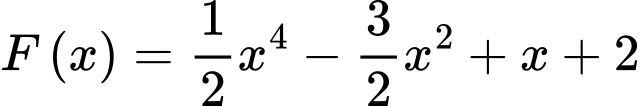
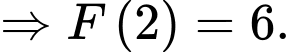
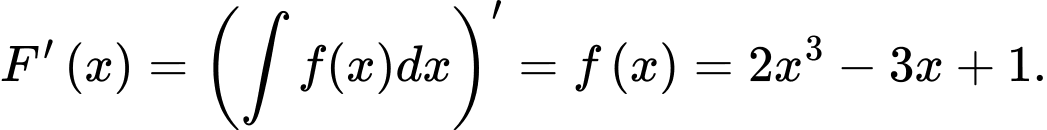
b) Sai.
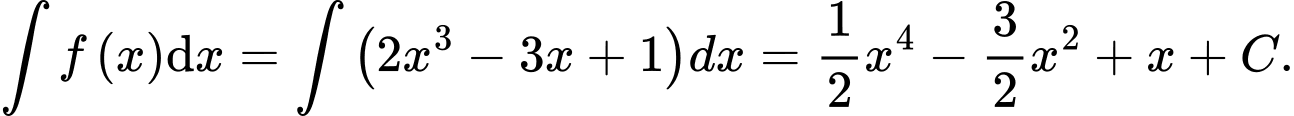
c) Sai. Một hàm số có nhiều nguyên hàm khác nhau.
d) Đúng.
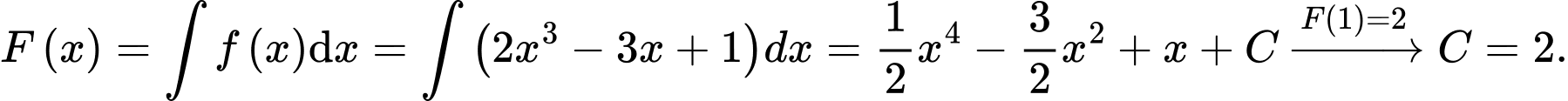
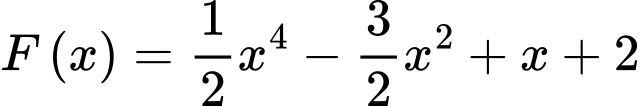
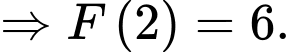
Câu 16 [161574]: Cho hàm số 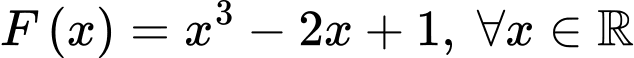 một nguyên hàm của hàm số
một nguyên hàm của hàm số 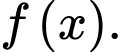 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
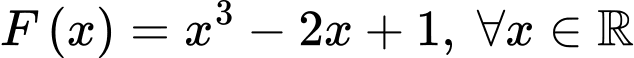 một nguyên hàm của hàm số
một nguyên hàm của hàm số 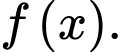 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai? A, a) 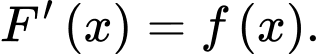
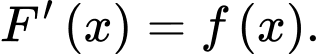
B, b) 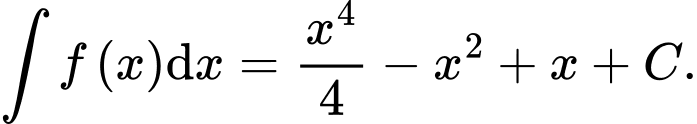
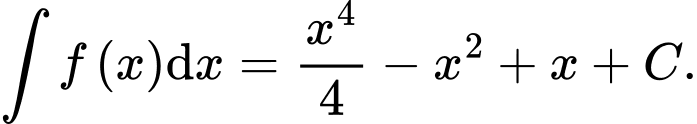
C, c) Nếu hàm số 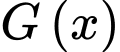 cũng là một nguyên hàm của hàm số
cũng là một nguyên hàm của hàm số 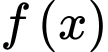 và
và 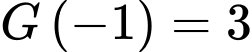 thì
thì 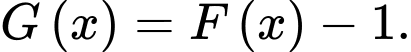
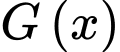 cũng là một nguyên hàm của hàm số
cũng là một nguyên hàm của hàm số 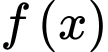 và
và 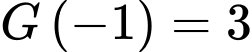 thì
thì 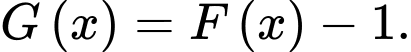
D, d) Nếu hàm số 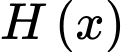 cũng là một nguyên hàm của hàm số
cũng là một nguyên hàm của hàm số 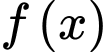 và
và 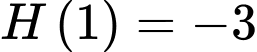 thì
thì
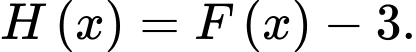
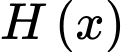 cũng là một nguyên hàm của hàm số
cũng là một nguyên hàm của hàm số 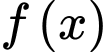 và
và 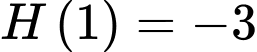 thì
thì 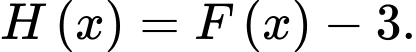
a) Đúng. 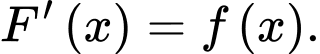
b) Sai.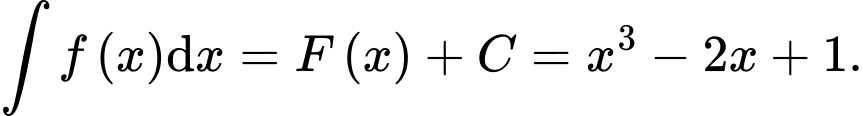
c) Sai.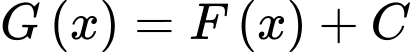 mà
mà 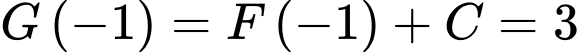
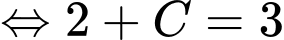
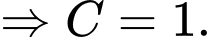
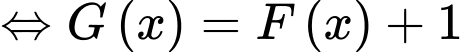
d) Đúng.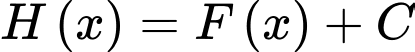
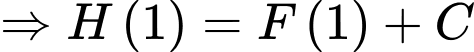

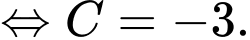
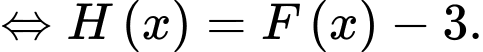
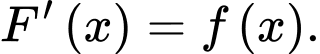
b) Sai.
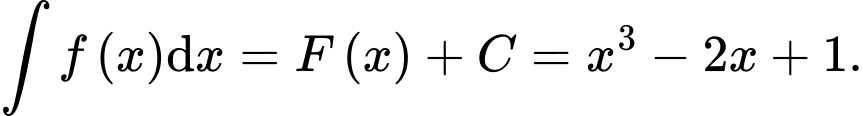
c) Sai.
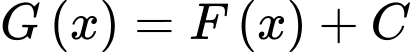 mà
mà 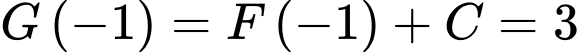
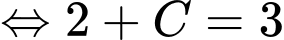
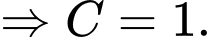
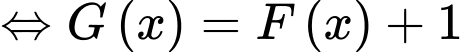
d) Đúng.
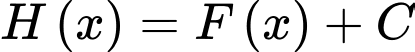
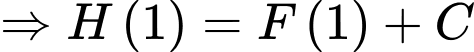

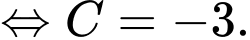
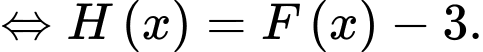
Câu 17 [161575]: Cho hàm số 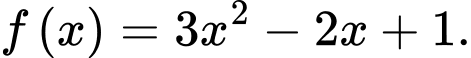 Gọi
Gọi 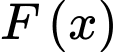 là họ nguyên hàm của hàm số
là họ nguyên hàm của hàm số 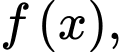
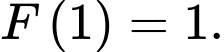 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
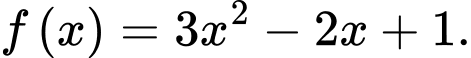 Gọi
Gọi 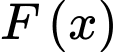 là họ nguyên hàm của hàm số
là họ nguyên hàm của hàm số 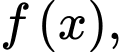
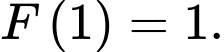 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai? A, a)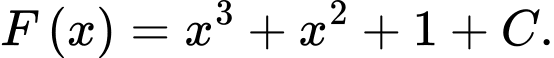
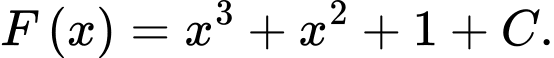
B, b) Giá trị 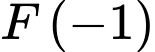 bằng
bằng 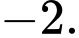
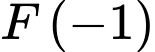 bằng
bằng 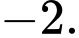
C, c) Họ nguyên hàm của hàm số 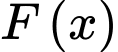 bằng
bằng 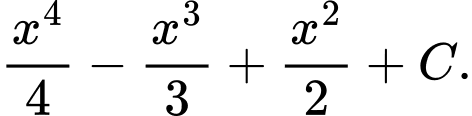
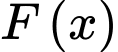 bằng
bằng 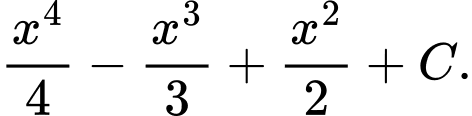
D, d) Họ nguyên hàm của hàm số 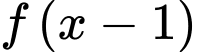 bằng
bằng 
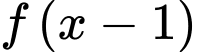 bằng
bằng 
a) Sai
Ta có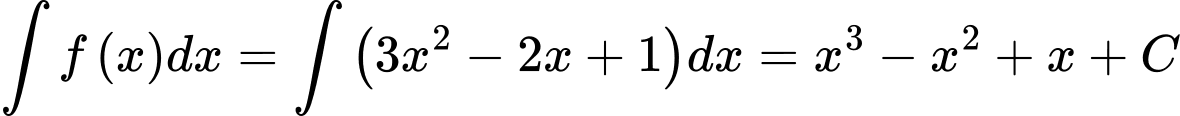
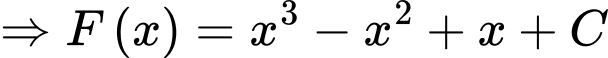
b) Sai
Ta có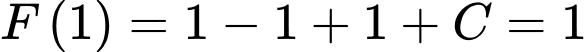
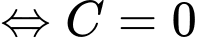
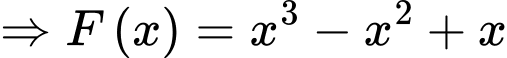
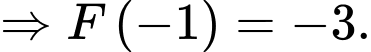
c) Đúng
Ta có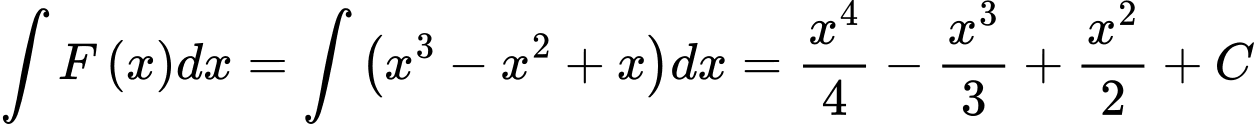
d) Đúng
Ta có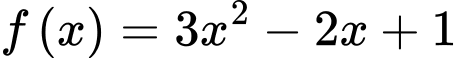
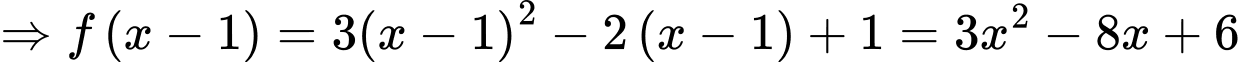
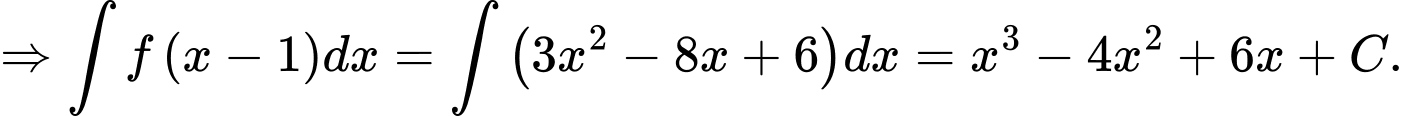
Ta có
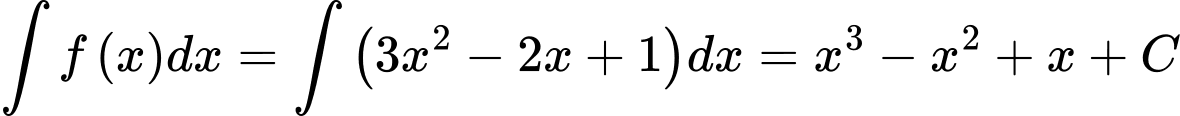
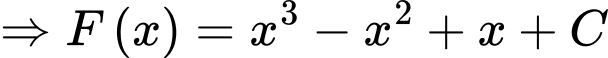
b) Sai
Ta có
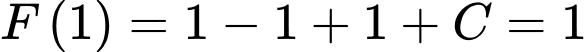
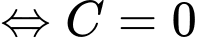
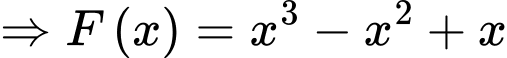
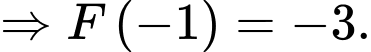
c) Đúng
Ta có
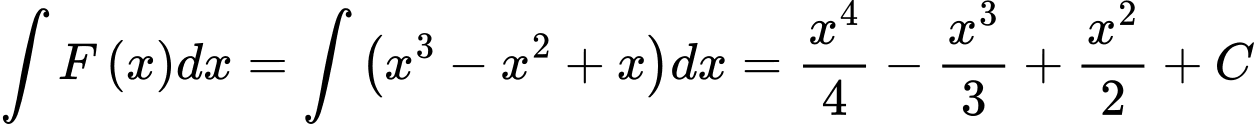
d) Đúng
Ta có
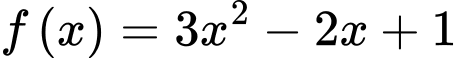
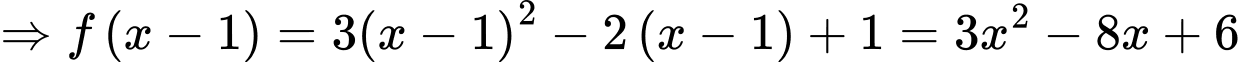
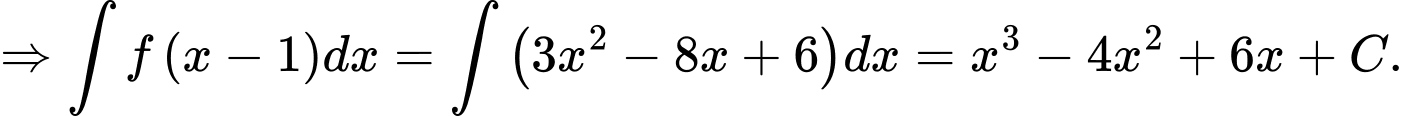
Câu 18 [389381]: Cho hàm số 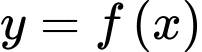 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 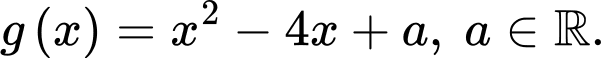 Biết rằng
Biết rằng 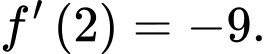 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
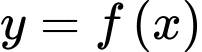 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 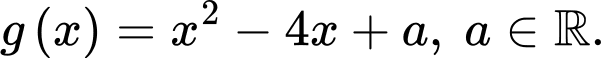 Biết rằng
Biết rằng 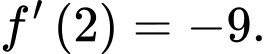 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) 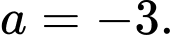
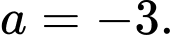
B, b) Tiếp tuyến của đồ thị hàm số 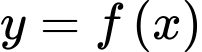 tại điểm có hoành độ
tại điểm có hoành độ 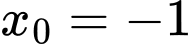 có hệ số góc bằng
có hệ số góc bằng 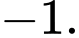
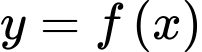 tại điểm có hoành độ
tại điểm có hoành độ 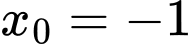 có hệ số góc bằng
có hệ số góc bằng 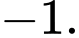
C, c) Hàm số 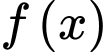 đồng biến trên khoảng
đồng biến trên khoảng 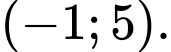
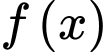 đồng biến trên khoảng
đồng biến trên khoảng 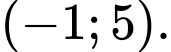
D, d) Nếu 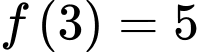 thì
thì 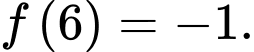
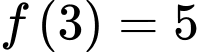 thì
thì 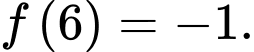
a) Sai. 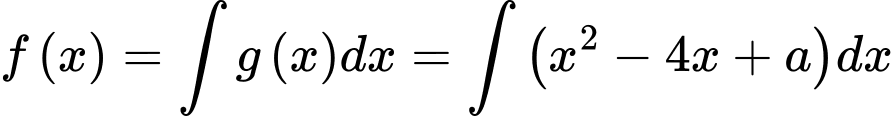
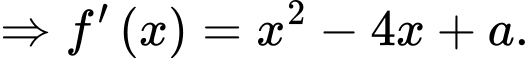
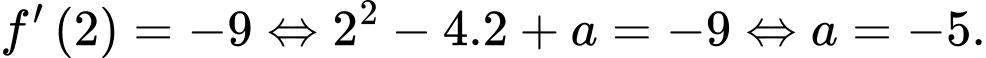
b) Sai. Tiếp tuyến của đồ thị hàm số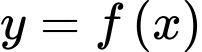 tại điểm có hoành độ
tại điểm có hoành độ 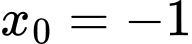 có hệ số góc bằng
có hệ số góc bằng 
c) Sai.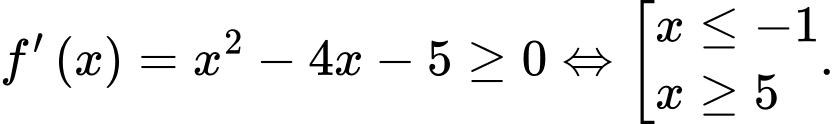
Hàm số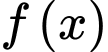 đồng biến trên khoảng
đồng biến trên khoảng 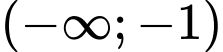 và
và 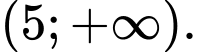
d) Đúng.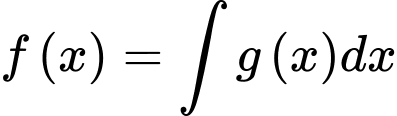
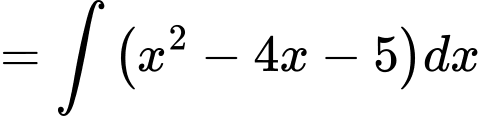
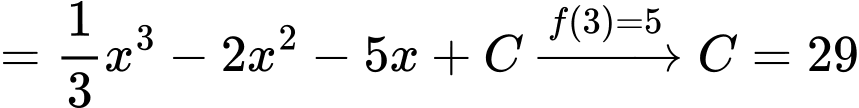
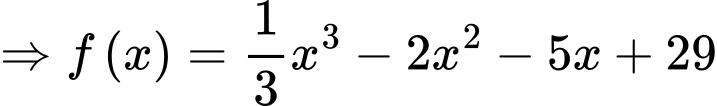

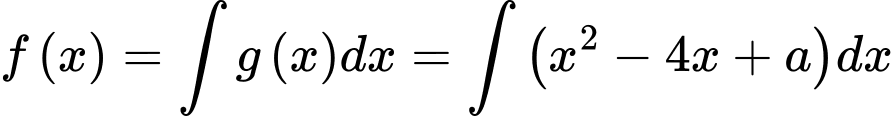
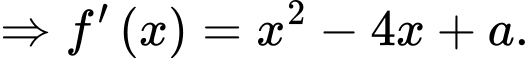
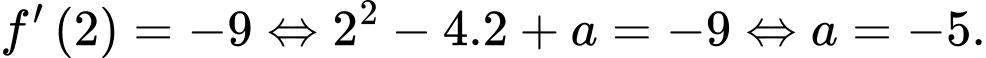
b) Sai. Tiếp tuyến của đồ thị hàm số
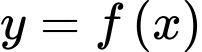 tại điểm có hoành độ
tại điểm có hoành độ 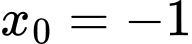 có hệ số góc bằng
có hệ số góc bằng 
c) Sai.
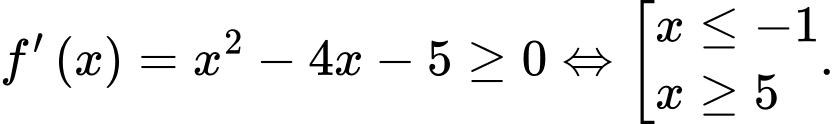
Hàm số
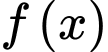 đồng biến trên khoảng
đồng biến trên khoảng 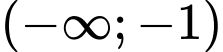 và
và 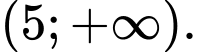
d) Đúng.
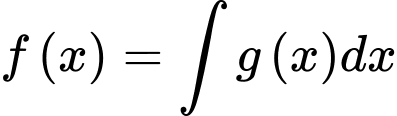
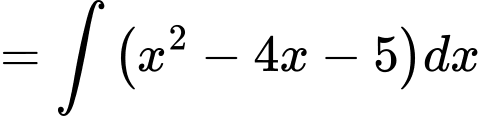
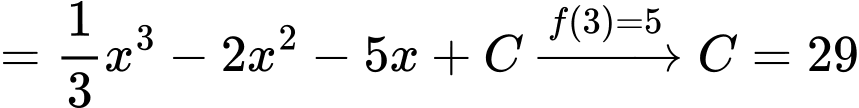
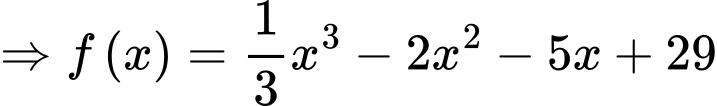

Câu 19 [386656]: Cho hàm số 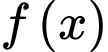 thoả mãn
thoả mãn 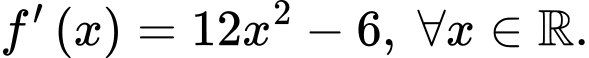 Gọi
Gọi  là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 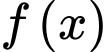 thoả mãn
thoả mãn 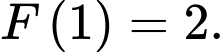 Biết
Biết 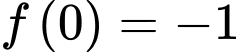 , xét tính đúng sai của các mệnh đề sau:
, xét tính đúng sai của các mệnh đề sau:
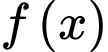 thoả mãn
thoả mãn 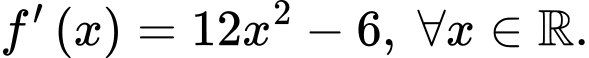 Gọi
Gọi  là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 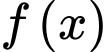 thoả mãn
thoả mãn 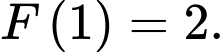 Biết
Biết 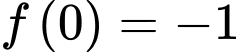 , xét tính đúng sai của các mệnh đề sau:
, xét tính đúng sai của các mệnh đề sau: A, a) 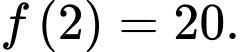
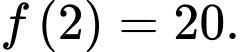
B, b) 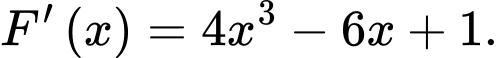
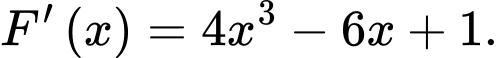
C, c) 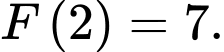
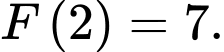
D, d) 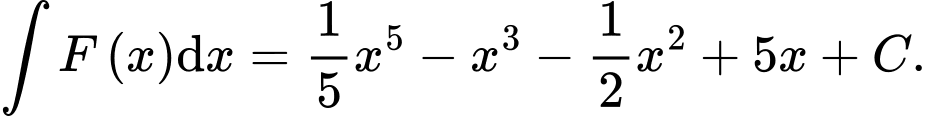
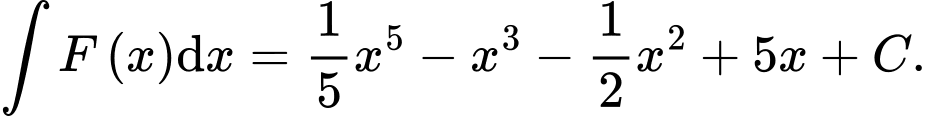
Ta có: 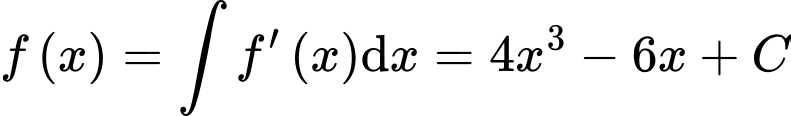
Lại có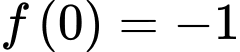
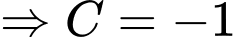
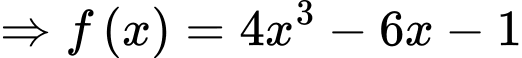
Suy ra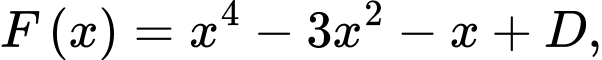 mà
mà 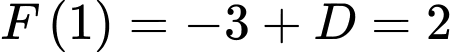

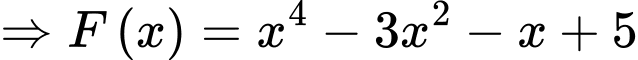
a) Sai.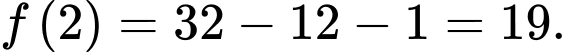
b) Sai.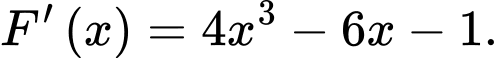
c) Đúng.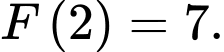
d) Đúng.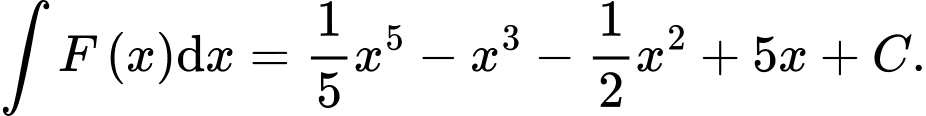
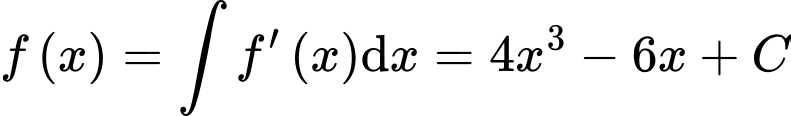
Lại có
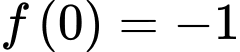
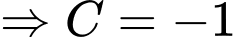
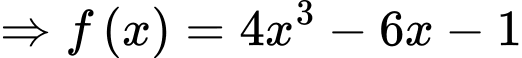
Suy ra
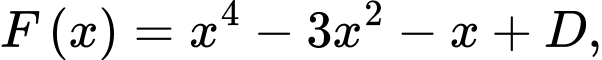 mà
mà 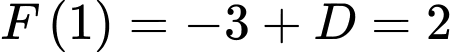

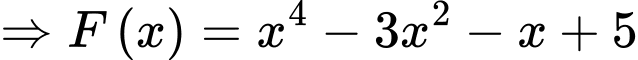
a) Sai.
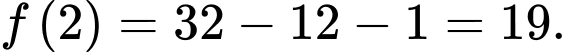
b) Sai.
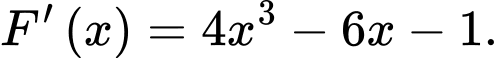
c) Đúng.
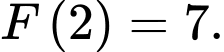
d) Đúng.
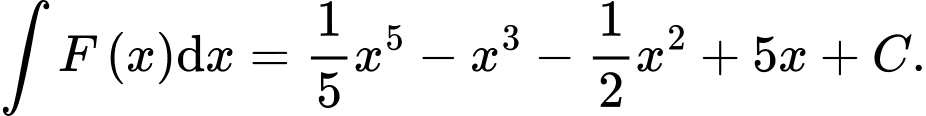
Câu 20 [161486]: Cho hàm số 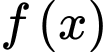 liên tục trên
liên tục trên 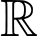 thoả mãn:
thoả mãn: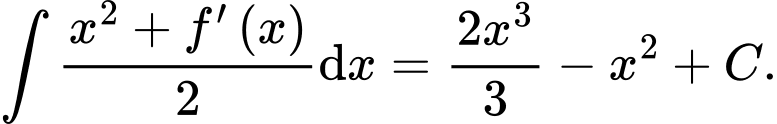 Biết rằng
Biết rằng 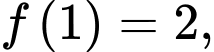 các mệnh đề sau đúng hay sai?
các mệnh đề sau đúng hay sai?
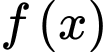 liên tục trên
liên tục trên 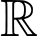 thoả mãn:
thoả mãn: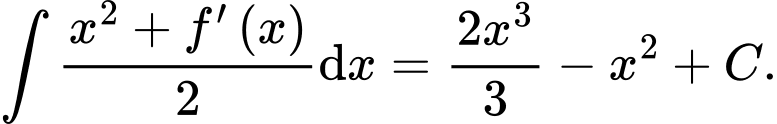 Biết rằng
Biết rằng 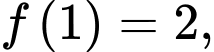 các mệnh đề sau đúng hay sai?
các mệnh đề sau đúng hay sai? A, a) 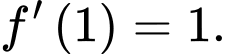
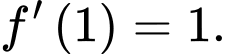
B, b) Hàm số 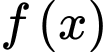 có hai điểm cực trị.
có hai điểm cực trị.
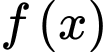 có hai điểm cực trị.
có hai điểm cực trị.C, c) Phương trình 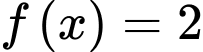 có ba nghiệm thực phân biệt.
có ba nghiệm thực phân biệt.
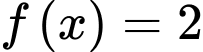 có ba nghiệm thực phân biệt.
có ba nghiệm thực phân biệt.D, d) 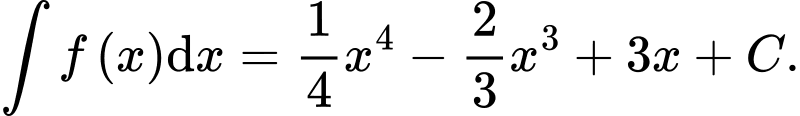
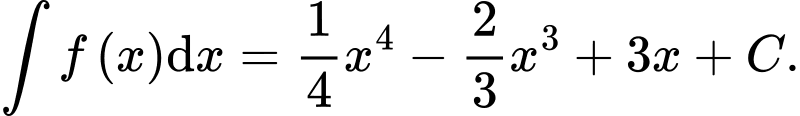
Ta có: 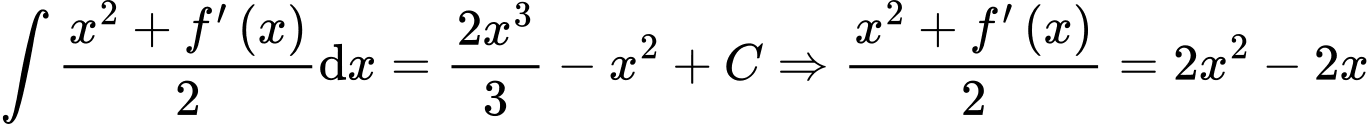
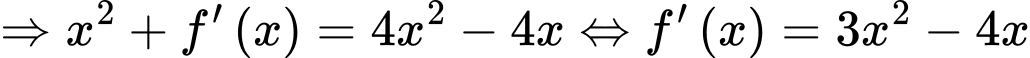
a) Sai.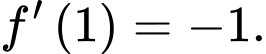
b) Đúng.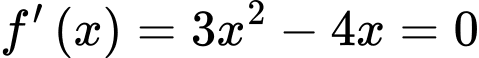 có hai nghiệm phân biệt nên hàm số
có hai nghiệm phân biệt nên hàm số 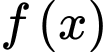 có hai điểm cực trị.
có hai điểm cực trị.
c) Đúng.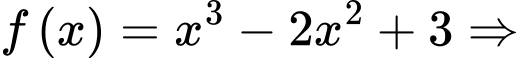 Phương trình
Phương trình 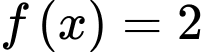 có ba nghiệm thực phân biệt.
có ba nghiệm thực phân biệt.
d) Đúng.
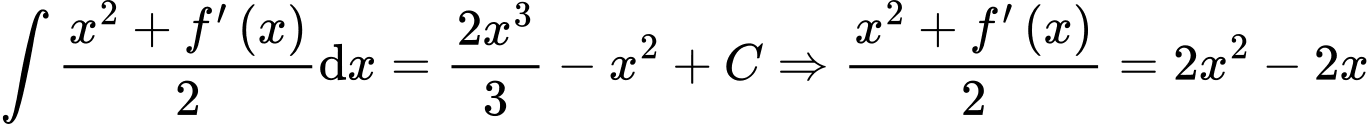
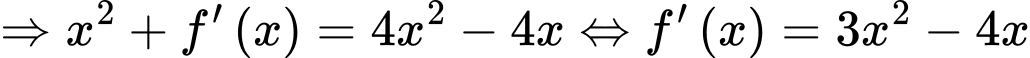
a) Sai.
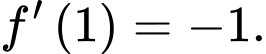
b) Đúng.
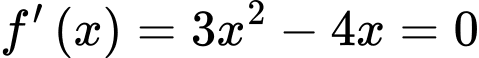 có hai nghiệm phân biệt nên hàm số
có hai nghiệm phân biệt nên hàm số 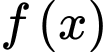 có hai điểm cực trị.
có hai điểm cực trị.
c) Đúng.
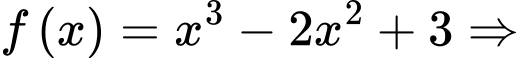 Phương trình
Phương trình 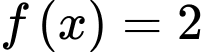 có ba nghiệm thực phân biệt.
có ba nghiệm thực phân biệt.
d) Đúng.
Câu 21 [389382]: Cho hàm số 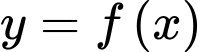 liên tục trên
liên tục trên 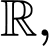 thoả mãn
thoả mãn 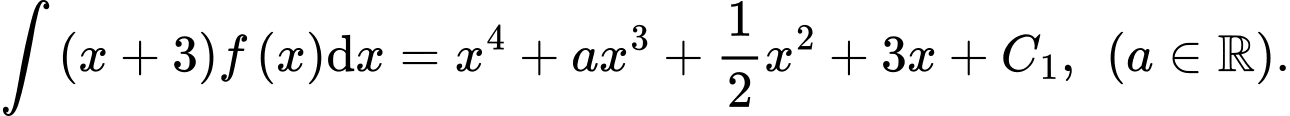 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
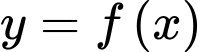 liên tục trên
liên tục trên 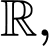 thoả mãn
thoả mãn 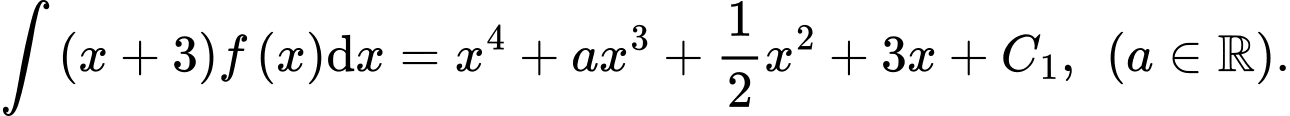 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) 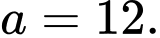
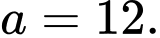
B, b) 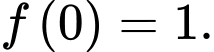
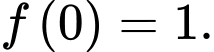
C, c) 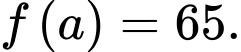
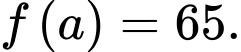
D, d) 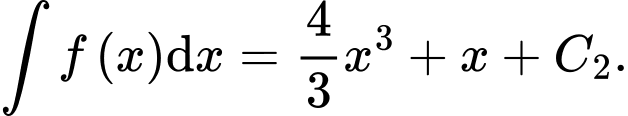
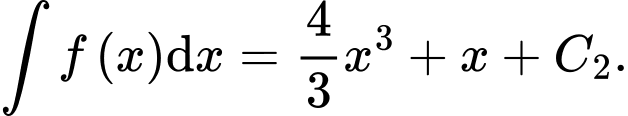
Lưu ý: Bài toán này thầy đính chính lại: Thêm dữ kiện "Hàm số liên tục trên R".
a) Sai.
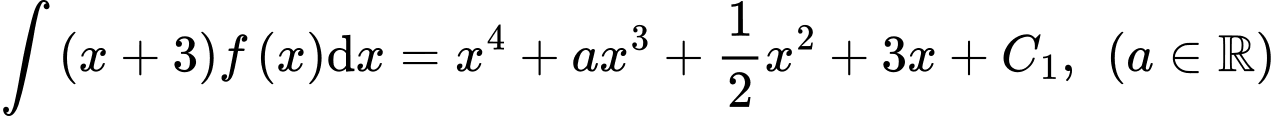
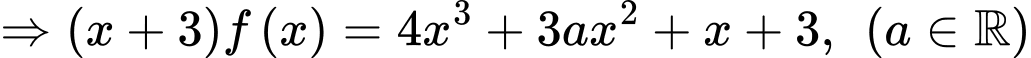
Vì hàm số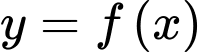 liên tục trên
liên tục trên 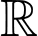 nên hàm số liên tục tại
nên hàm số liên tục tại 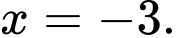 Thay
Thay 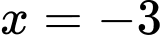 vào 2 vế của phương trình trên, ta được
vào 2 vế của phương trình trên, ta được
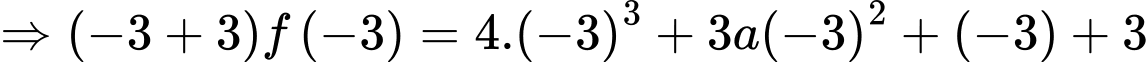
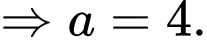
b) Đúng.
Ta có: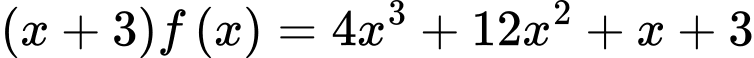
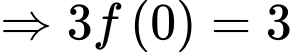

c) Đúng.
Vì nên ở í c) ta cần tính
nên ở í c) ta cần tính 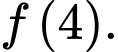
Ta có: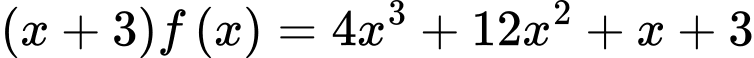
Thay vào phương trình trên, ta được
vào phương trình trên, ta được
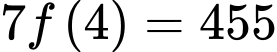
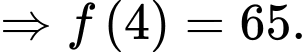
d) Đúng.
Ta có: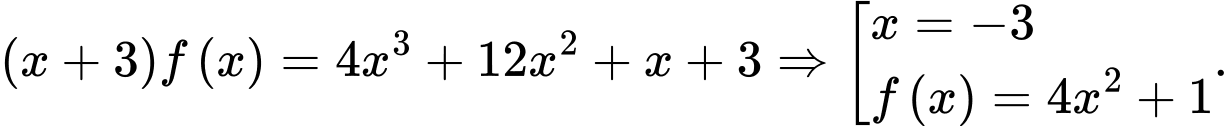
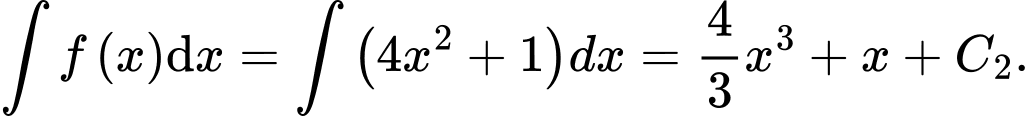
a) Sai.
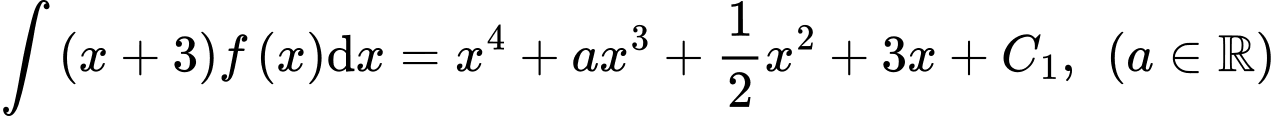
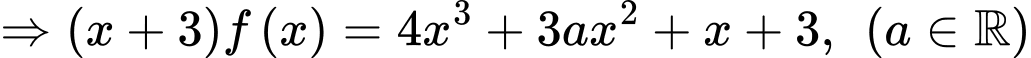
Vì hàm số
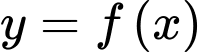 liên tục trên
liên tục trên 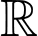 nên hàm số liên tục tại
nên hàm số liên tục tại 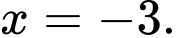 Thay
Thay 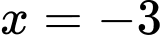 vào 2 vế của phương trình trên, ta được
vào 2 vế của phương trình trên, ta được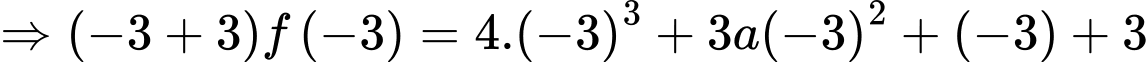
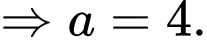
b) Đúng.
Ta có:
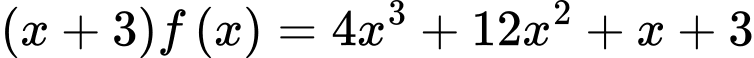
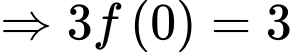

c) Đúng.
Vì
 nên ở í c) ta cần tính
nên ở í c) ta cần tính 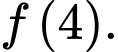
Ta có:
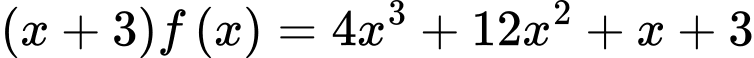
Thay
 vào phương trình trên, ta được
vào phương trình trên, ta được
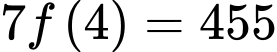
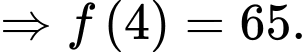
d) Đúng.
Ta có:
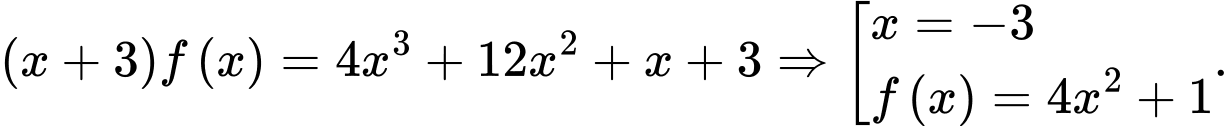
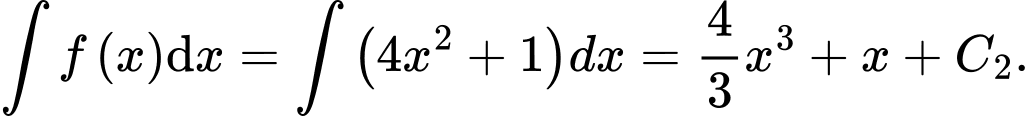
Câu 22 [161578]: Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi 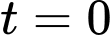 là thời điểm viên đạn được bắn lên), vận tốc của viên đạn là
là thời điểm viên đạn được bắn lên), vận tốc của viên đạn là  . Tính độ cao lớn nhất của viên đạn tính từ mặt đất (làm tròn kết quả đến hàng đơn vị của mét).
. Tính độ cao lớn nhất của viên đạn tính từ mặt đất (làm tròn kết quả đến hàng đơn vị của mét).
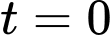 là thời điểm viên đạn được bắn lên), vận tốc của viên đạn là
là thời điểm viên đạn được bắn lên), vận tốc của viên đạn là  . Tính độ cao lớn nhất của viên đạn tính từ mặt đất (làm tròn kết quả đến hàng đơn vị của mét).
. Tính độ cao lớn nhất của viên đạn tính từ mặt đất (làm tròn kết quả đến hàng đơn vị của mét).
Điền đáp số: 
Độ cao của viên đạn tại thời điểm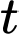 giây là
giây là 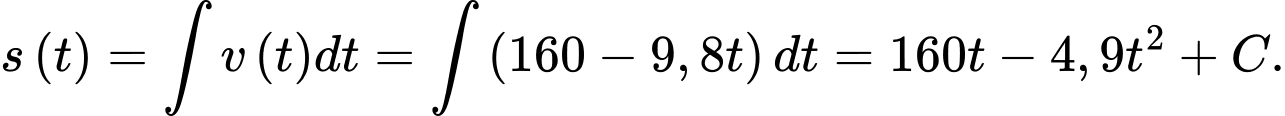
Tại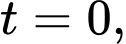 ta có
ta có 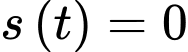 nên
nên 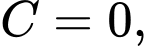 vậy có
vậy có 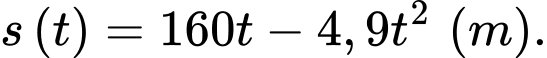
Độ cao lớn nhất của viên đạn đạt được khi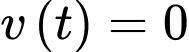
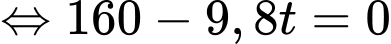
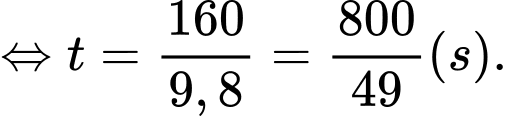
Khi đó ta có độ cao lớn nhất của viên đạn đạt được là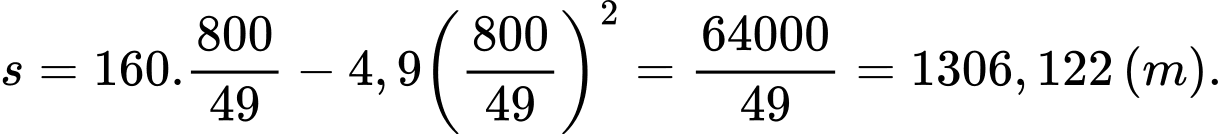
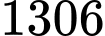
Độ cao của viên đạn tại thời điểm
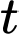 giây là
giây là 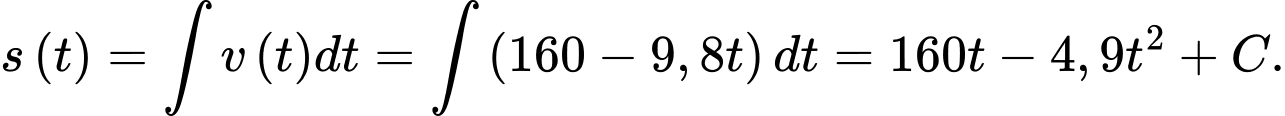
Tại
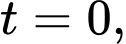 ta có
ta có 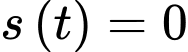 nên
nên 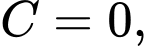 vậy có
vậy có 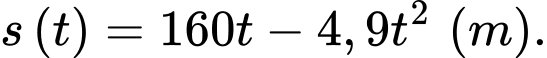
Độ cao lớn nhất của viên đạn đạt được khi
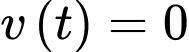
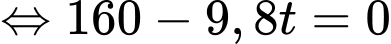
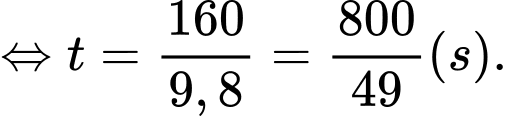
Khi đó ta có độ cao lớn nhất của viên đạn đạt được là
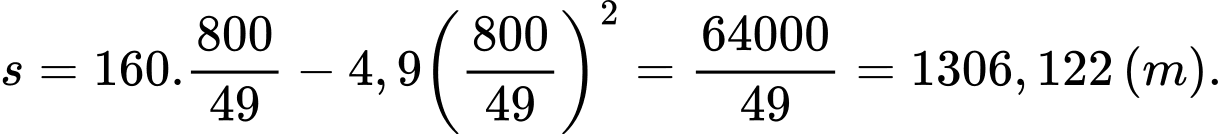
Câu 23 [389386]: Biết rằng 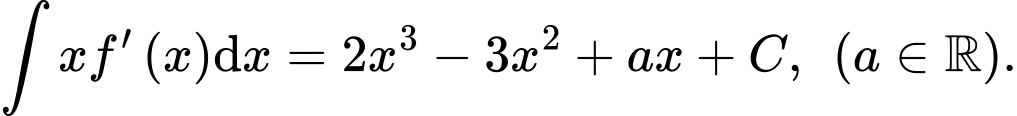 Biết hệ số góc của tiếp tuyến của đồ thị hàm số
Biết hệ số góc của tiếp tuyến của đồ thị hàm số 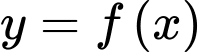 tại điểm có hoành độ
tại điểm có hoành độ 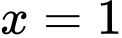 là
là 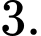 Tính giá trị của
Tính giá trị của 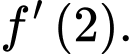 XIn lỗi các em, câu hỏi này đề bị lỗi
Thầy xin đính chính câu hỏi
XIn lỗi các em, câu hỏi này đề bị lỗi
Thầy xin đính chính câu hỏi
Cho hàm số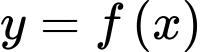 liên tục trên
liên tục trên 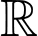 và thoả mãn
và thoả mãn 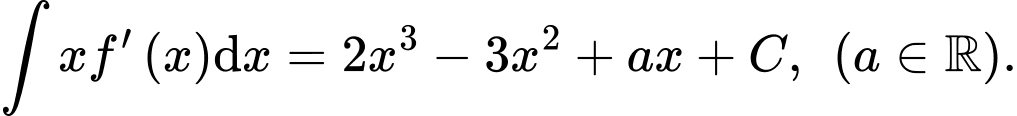
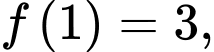 tính giá trị của
tính giá trị của 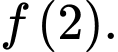
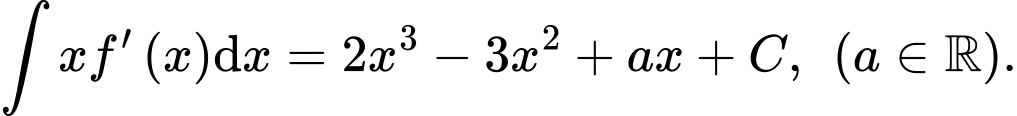 Biết hệ số góc của tiếp tuyến của đồ thị hàm số
Biết hệ số góc của tiếp tuyến của đồ thị hàm số 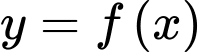 tại điểm có hoành độ
tại điểm có hoành độ 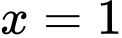 là
là 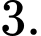 Tính giá trị của
Tính giá trị của 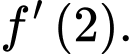 XIn lỗi các em, câu hỏi này đề bị lỗi
Thầy xin đính chính câu hỏi
XIn lỗi các em, câu hỏi này đề bị lỗi
Thầy xin đính chính câu hỏi
Cho hàm số
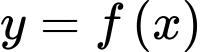 liên tục trên
liên tục trên 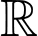 và thoả mãn
và thoả mãn 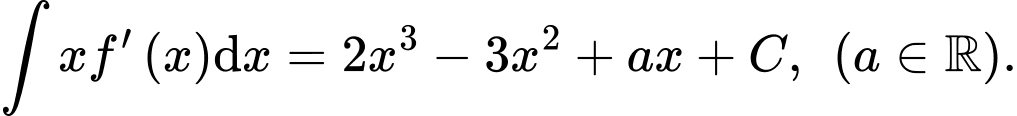
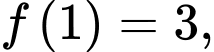 tính giá trị của
tính giá trị của 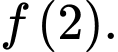
Ta có 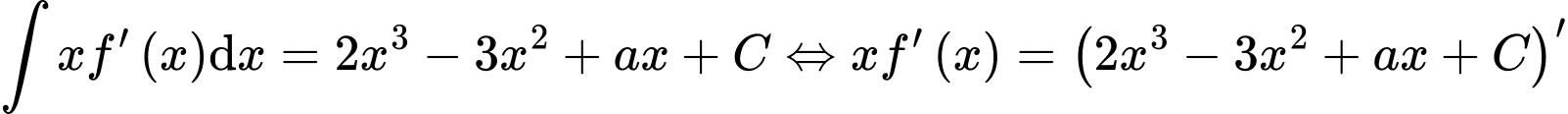
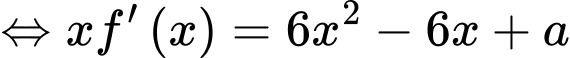 (1)
(1)
Hàm số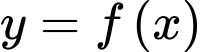 liên tục trên
liên tục trên 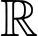 nên hàm số
nên hàm số 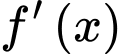 liên tục trên
liên tục trên 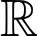
Thay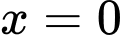 vào (1) ta được:
vào (1) ta được: 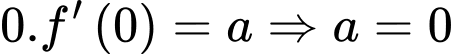
Khi đó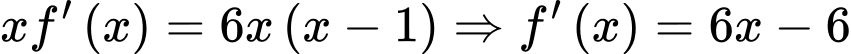
Suy ra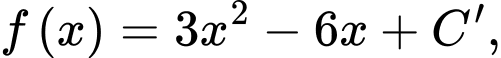 mặt khác
mặt khác 
Vậy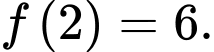
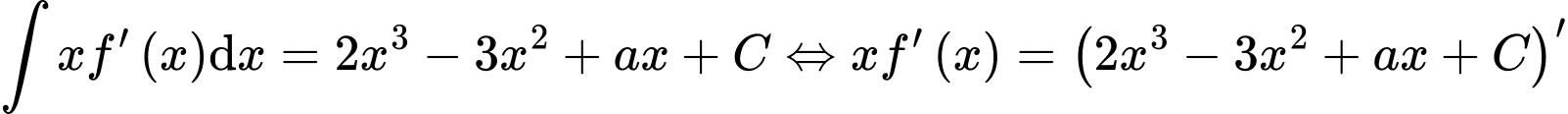
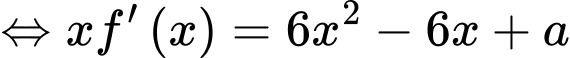 (1)
(1)
Hàm số
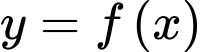 liên tục trên
liên tục trên 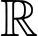 nên hàm số
nên hàm số 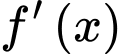 liên tục trên
liên tục trên 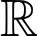
Thay
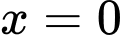 vào (1) ta được:
vào (1) ta được: 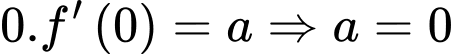
Khi đó
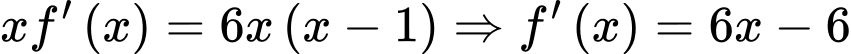
Suy ra
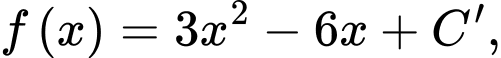 mặt khác
mặt khác 
Vậy
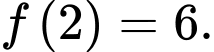
Câu 24 [389388]: Cho hàm số 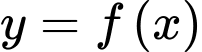 có đạo hàm cấp hai trên
có đạo hàm cấp hai trên 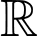 thoả mãn
thoả mãn 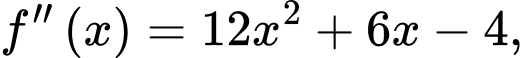
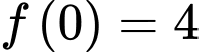 và
và 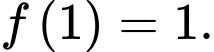 Tính
Tính 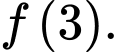
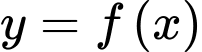 có đạo hàm cấp hai trên
có đạo hàm cấp hai trên 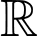 thoả mãn
thoả mãn 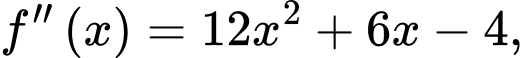
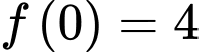 và
và 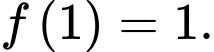 Tính
Tính 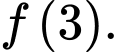
Ta có 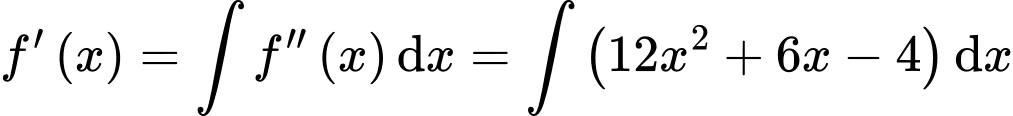
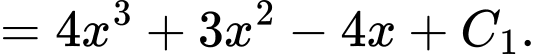
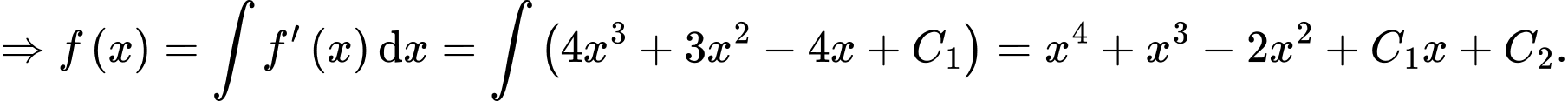
Theo giả thiết, ta có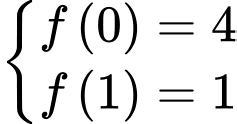
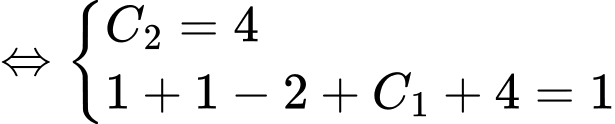
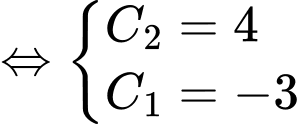
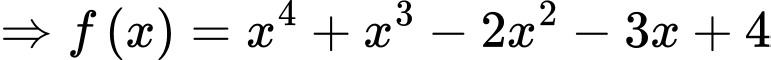
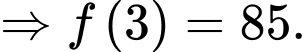
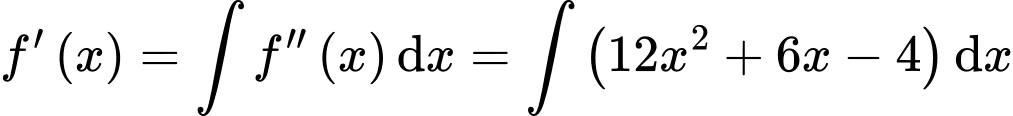
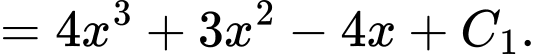
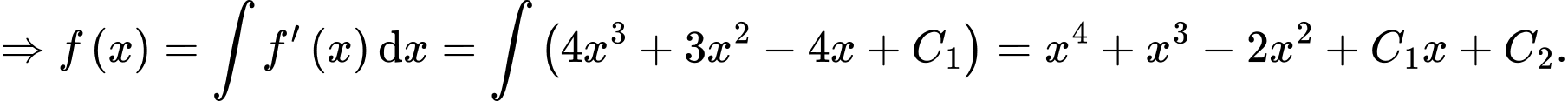
Theo giả thiết, ta có
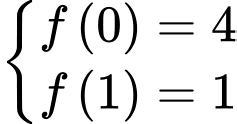
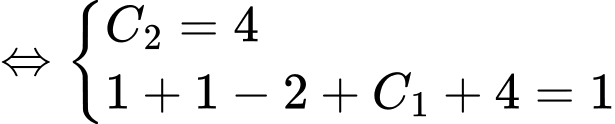
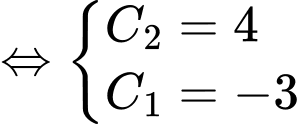
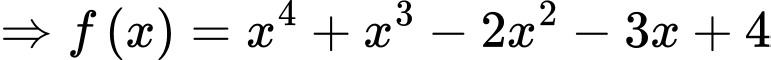
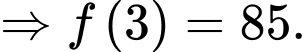
Câu 25 [212392]: Cho hàm số 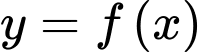 có đạo hàm là
có đạo hàm là 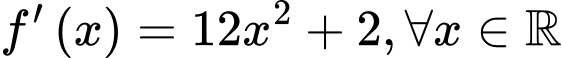 và
và 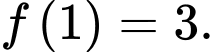 Biết
Biết 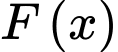 là nguyên hàm của
là nguyên hàm của 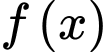 thỏa mãn
thỏa mãn 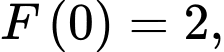 khi đó
khi đó 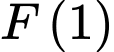 bằng
bằng
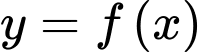 có đạo hàm là
có đạo hàm là 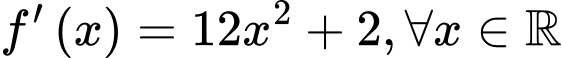 và
và 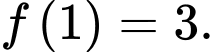 Biết
Biết 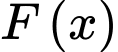 là nguyên hàm của
là nguyên hàm của 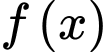 thỏa mãn
thỏa mãn 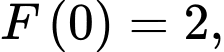 khi đó
khi đó 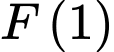 bằng
bằng A, 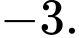
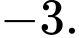
B, 1.
C, 2.
D, 7.
Chọn B
Ta có: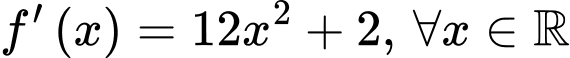
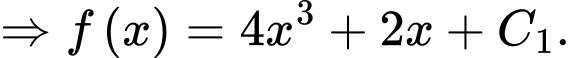
Mà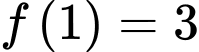
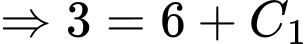
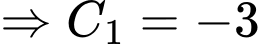
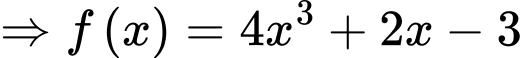

Lại có:
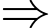
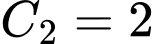
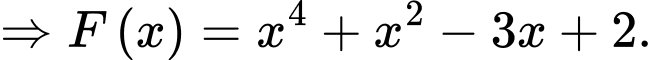
Khi đó: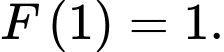
Cách khác: Ta có: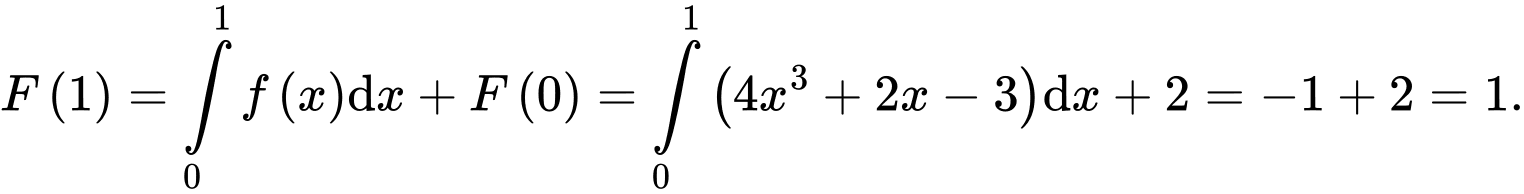 Đáp án: B
Đáp án: B
Ta có:
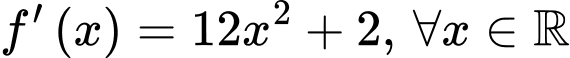
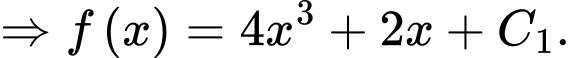
Mà
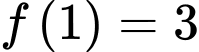
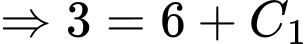
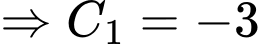
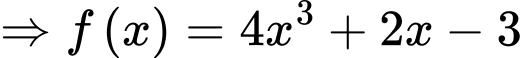

Lại có:

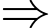
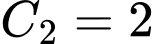
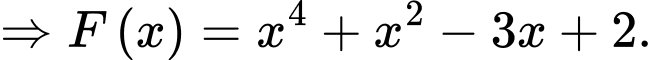
Khi đó:
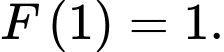
Cách khác: Ta có:
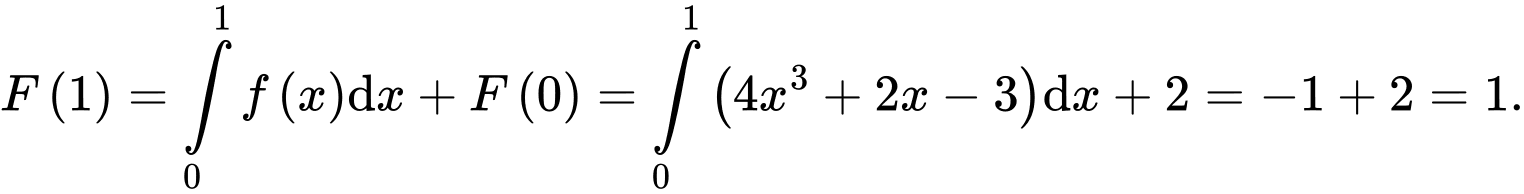 Đáp án: B
Đáp án: B
Câu 26 [389387]: Biết rằng 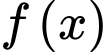 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 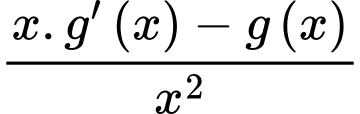 thoả mãn
thoả mãn 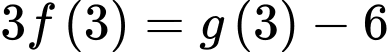 và
và 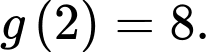 Tính giá trị của
Tính giá trị của 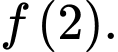
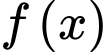 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 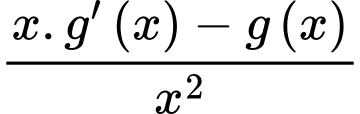 thoả mãn
thoả mãn 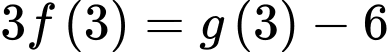 và
và 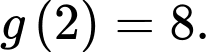 Tính giá trị của
Tính giá trị của 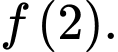
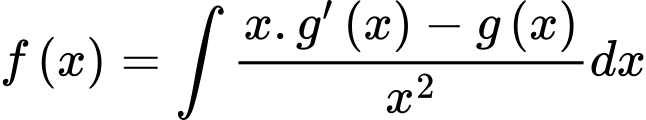
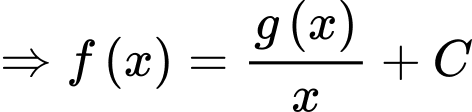
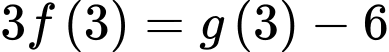
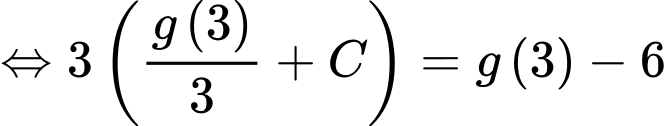
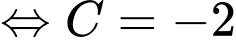
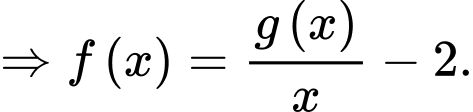
Khi đó,
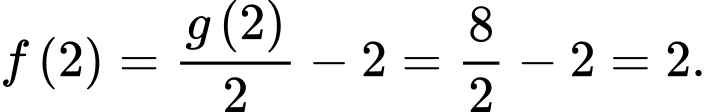
Câu 27 [389390]: Cho hàm số 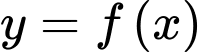 có đồ thị như hình vẽ bên. Tiếp tuyến của đồ thị hàm số tại điểm
có đồ thị như hình vẽ bên. Tiếp tuyến của đồ thị hàm số tại điểm 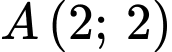 cắt trục hoành tại điểm có hoành độ
cắt trục hoành tại điểm có hoành độ 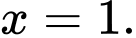 Biết rằng
Biết rằng 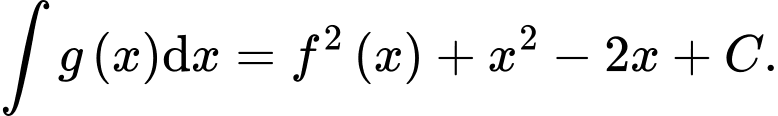 Tính giá trị của
Tính giá trị của 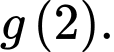
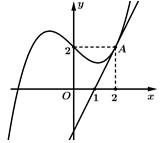
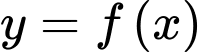 có đồ thị như hình vẽ bên. Tiếp tuyến của đồ thị hàm số tại điểm
có đồ thị như hình vẽ bên. Tiếp tuyến của đồ thị hàm số tại điểm 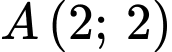 cắt trục hoành tại điểm có hoành độ
cắt trục hoành tại điểm có hoành độ 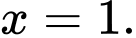 Biết rằng
Biết rằng 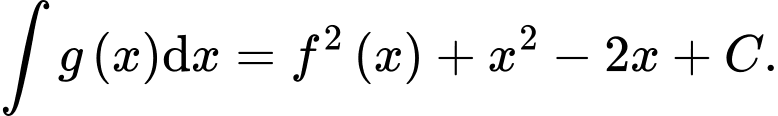 Tính giá trị của
Tính giá trị của 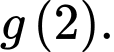

Phương trình tiếp tuyến của 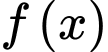 tại điểm
tại điểm 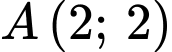 suy ra
suy ra 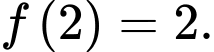
Giả sử phương trình tiếp tuyến của hàm số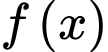 có dạng:
có dạng: 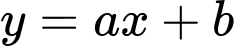 với
với 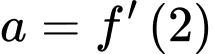
Ta có hệ phương trình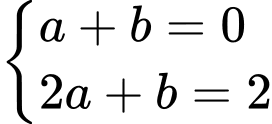
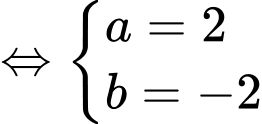
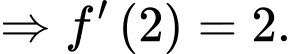
Ta có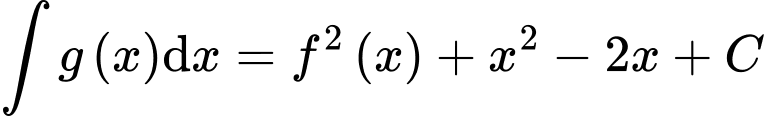
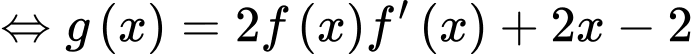
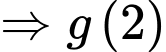
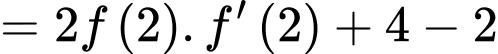
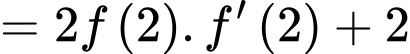

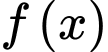 tại điểm
tại điểm 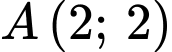 suy ra
suy ra 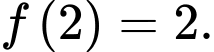
Giả sử phương trình tiếp tuyến của hàm số
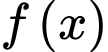 có dạng:
có dạng: 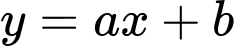 với
với 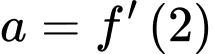
Ta có hệ phương trình
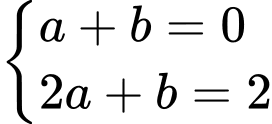
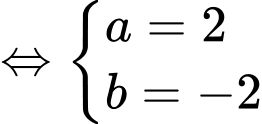
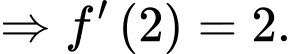
Ta có
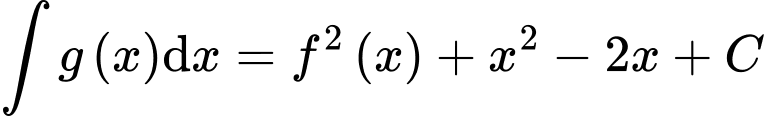
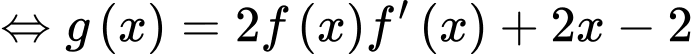
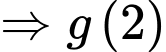
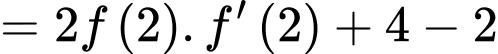
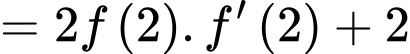

Câu 28 [389391]: Biết rằng 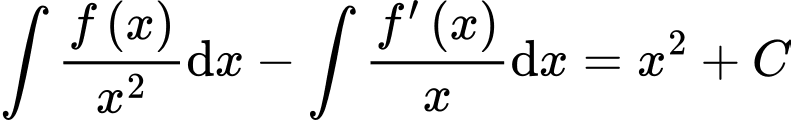 và
và 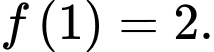 Tính giá trị của
Tính giá trị của 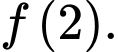
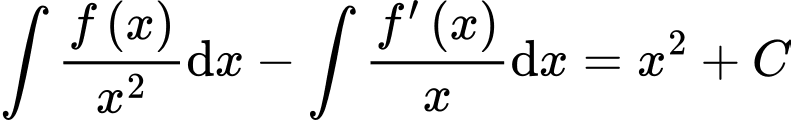 và
và 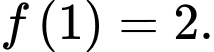 Tính giá trị của
Tính giá trị của