Đáp án Bài tập tự luyện
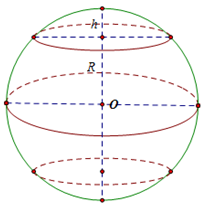
Câu 1 [151694]: Một khối cầu có bán kính là 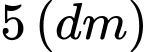 , người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng
, người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng 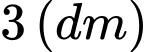 để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
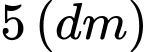 , người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng
, người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng 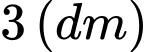 để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.
A, 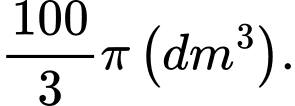
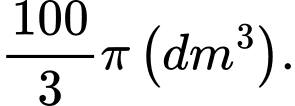
B, 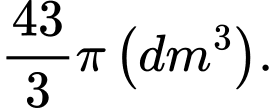
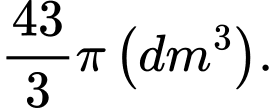
C, 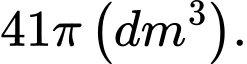
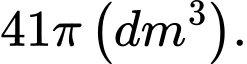
D, 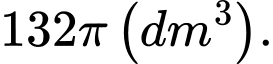
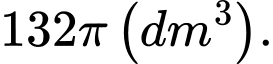
 Đáp án: D
Đáp án: D
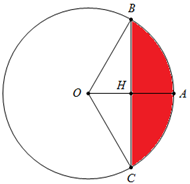
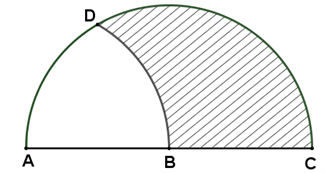
Câu 2 [151703]: Cho hình phẳng  giới hạn bởi cung tròn
giới hạn bởi cung tròn 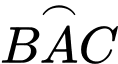 của đường tròn tâm
của đường tròn tâm  bán kính
bán kính  và dây cung
và dây cung 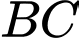 vuông góc với
vuông góc với 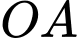 tại
tại 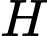 và
và 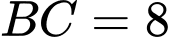 (hình vẽ). Tính thể tích
(hình vẽ). Tính thể tích  của vật thể tròn xoay tạo được khi quay hình phẳng
của vật thể tròn xoay tạo được khi quay hình phẳng  xung quanh
xung quanh 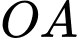 .
.
 giới hạn bởi cung tròn
giới hạn bởi cung tròn 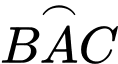 của đường tròn tâm
của đường tròn tâm  bán kính
bán kính  và dây cung
và dây cung 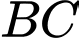 vuông góc với
vuông góc với 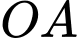 tại
tại  và
và 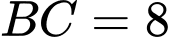 (hình vẽ). Tính thể tích
(hình vẽ). Tính thể tích  của vật thể tròn xoay tạo được khi quay hình phẳng
của vật thể tròn xoay tạo được khi quay hình phẳng  xung quanh
xung quanh 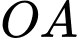 .
.
A, 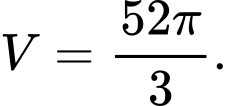
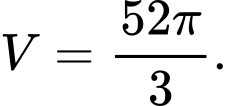
B, 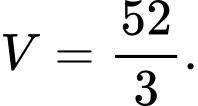
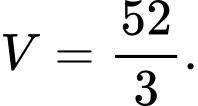
C, 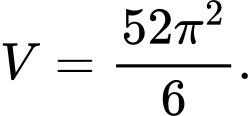
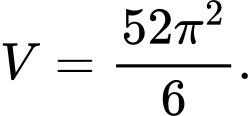
D, 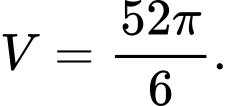
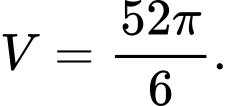
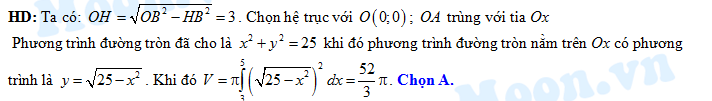 Đáp án: A
Đáp án: A
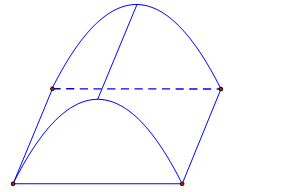
Câu 3 [151712]: Để chuẩn bị cho hội trại do Đoàn trường tổ chức, lớp 12A dự định dựng một cái lều trại có dạng hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang  mét, chiều dài
mét, chiều dài 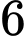 mét, đỉnh trại cách nền
mét, đỉnh trại cách nền 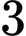 mét. Tính thể tích phần không gian bên trong lều trại.
mét. Tính thể tích phần không gian bên trong lều trại.
 mét, chiều dài
mét, chiều dài 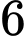 mét, đỉnh trại cách nền
mét, đỉnh trại cách nền 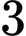 mét. Tính thể tích phần không gian bên trong lều trại.
mét. Tính thể tích phần không gian bên trong lều trại.
A, 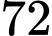 .
.
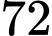 .
.B, 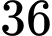 .
.
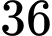 .
.C, 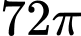 .
.
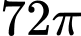 .
.D, 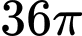 .
.
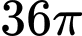 .
. Đáp án: B
Đáp án: B
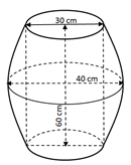
Câu 4 [15924]: Một thùng đựng Bia hơi (có dạng như hình vẽ) có đường kính đáy là 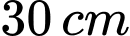 , đường kính lớn nhất của nhân thùng là
, đường kính lớn nhất của nhân thùng là 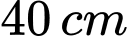 , chiều cao thùng là
, chiều cao thùng là 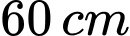 , cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng Bia hơi gần nhất với số nào sau đây? (với giả thiết độ dày thùng Bia không đáng kể)
, cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng Bia hơi gần nhất với số nào sau đây? (với giả thiết độ dày thùng Bia không đáng kể)
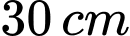 , đường kính lớn nhất của nhân thùng là
, đường kính lớn nhất của nhân thùng là 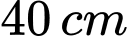 , chiều cao thùng là
, chiều cao thùng là 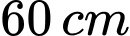 , cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng Bia hơi gần nhất với số nào sau đây? (với giả thiết độ dày thùng Bia không đáng kể)
, cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng Bia hơi gần nhất với số nào sau đây? (với giả thiết độ dày thùng Bia không đáng kể)
A, 70 (lít).
B, 62 (lít).
C, 60 (lít).
D, 64 (lít).
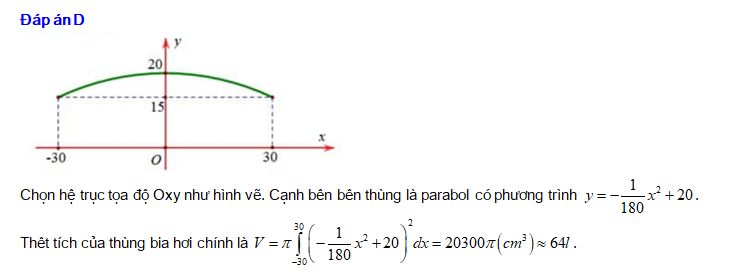 Đáp án: D
Đáp án: D
Câu 5 [151704]: Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây:
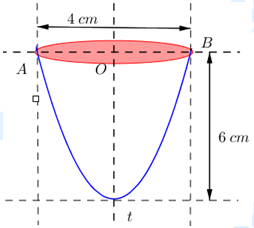
Người ta đo được đường kính của miệng ly là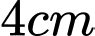 và chiều cao là
và chiều cao là 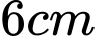 . Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một Parabol. Tính thể tích
. Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một Parabol. Tính thể tích 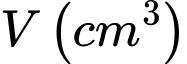 của vật đã cho.
của vật đã cho.

Người ta đo được đường kính của miệng ly là
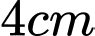 và chiều cao là
và chiều cao là 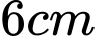 . Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một Parabol. Tính thể tích
. Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng qua trục đối xứng là một Parabol. Tính thể tích 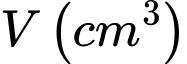 của vật đã cho.
của vật đã cho. A, 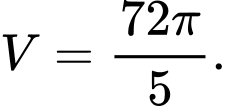
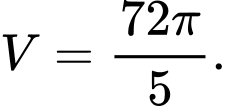
B, 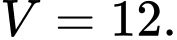
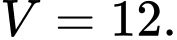
C, 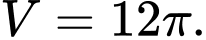
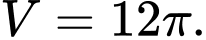
D, 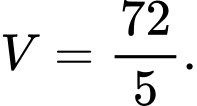
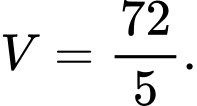
Thể tích của vật là thể tích khối tròn xoay khi quay hình  giới hạn bởi các đường
giới hạn bởi các đường 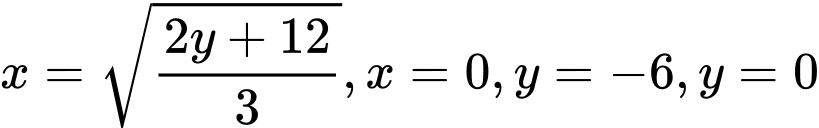 quanh trục tung.
quanh trục tung.
Khi đó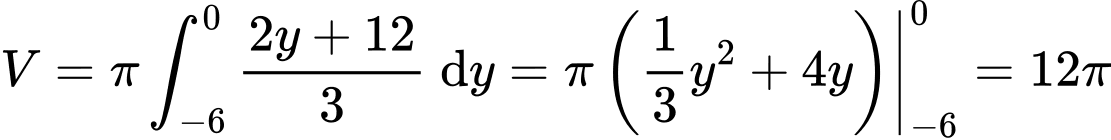
Chọn C. Đáp án: C
 giới hạn bởi các đường
giới hạn bởi các đường 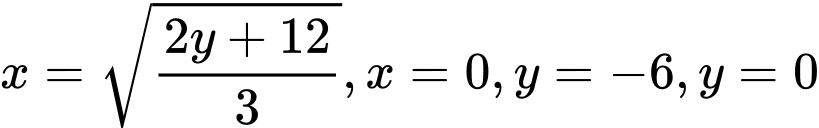 quanh trục tung.
quanh trục tung.
Khi đó
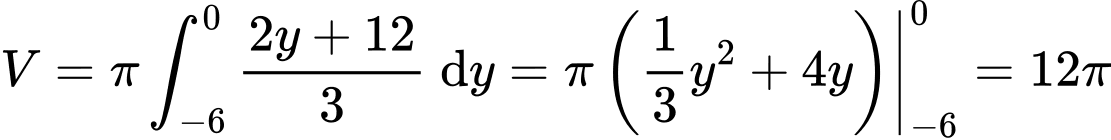
Chọn C. Đáp án: C
Câu 6 [151696]: Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 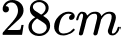 , trục nhỏ
, trục nhỏ 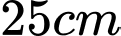 . Biết cứ
. Biết cứ  dưa hấu sẽ làm được cốc sinh tố giá
dưa hấu sẽ làm được cốc sinh tố giá 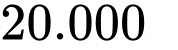 . Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
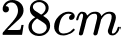 , trục nhỏ
, trục nhỏ 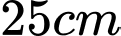 . Biết cứ
. Biết cứ  dưa hấu sẽ làm được cốc sinh tố giá
dưa hấu sẽ làm được cốc sinh tố giá 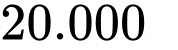 . Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể. A, 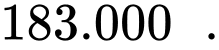
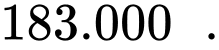
B, 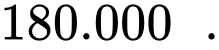
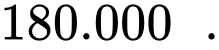
C, 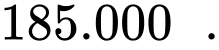
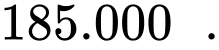
D, 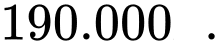
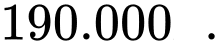
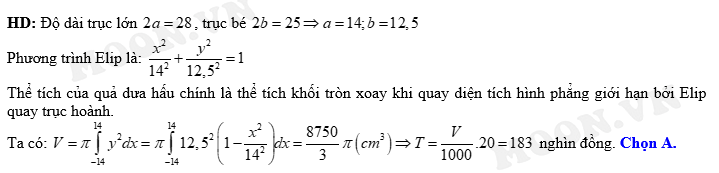 Đáp án: A
Đáp án: A
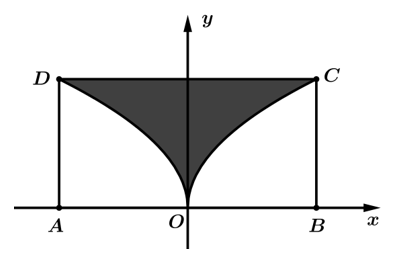
Câu 7 [408110]: Từ hình chữ nhật 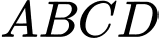 có chiều dài
có chiều dài 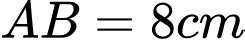 và chiều rộng
và chiều rộng 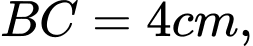 người ta cắt bỏ miền
người ta cắt bỏ miền  được giới hạn bởi cạnh
được giới hạn bởi cạnh 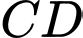 của hình chữ nhật và hai nửa đường thẳng parabol có chung đỉnh là trung điểm cạnh
của hình chữ nhật và hai nửa đường thẳng parabol có chung đỉnh là trung điểm cạnh  chúng lần lượt đi qua hai đầu mút
chúng lần lượt đi qua hai đầu mút 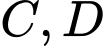 của hình chứ nhất đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục
của hình chứ nhất đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục  để tạo nên một đồ vật làm trang trí, thể thế của vật trang trí đó bằng bao nhiêu
để tạo nên một đồ vật làm trang trí, thể thế của vật trang trí đó bằng bao nhiêu 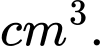 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.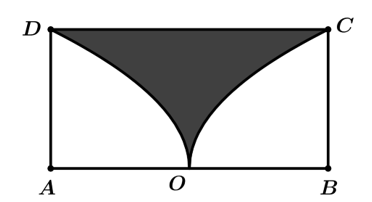
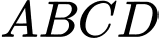 có chiều dài
có chiều dài 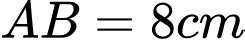 và chiều rộng
và chiều rộng 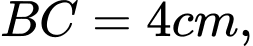 người ta cắt bỏ miền
người ta cắt bỏ miền  được giới hạn bởi cạnh
được giới hạn bởi cạnh 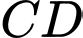 của hình chữ nhật và hai nửa đường thẳng parabol có chung đỉnh là trung điểm cạnh
của hình chữ nhật và hai nửa đường thẳng parabol có chung đỉnh là trung điểm cạnh  chúng lần lượt đi qua hai đầu mút
chúng lần lượt đi qua hai đầu mút 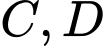 của hình chứ nhất đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục
của hình chứ nhất đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục  để tạo nên một đồ vật làm trang trí, thể thế của vật trang trí đó bằng bao nhiêu
để tạo nên một đồ vật làm trang trí, thể thế của vật trang trí đó bằng bao nhiêu  Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.
Chọn hệ trục toạ độ như hình vẽ.
Phương trình Parabol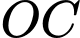 có dạng:
có dạng: 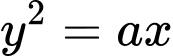
Mặt khác Parabol đi qua điểm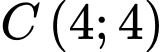
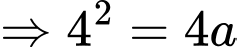
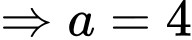
Khi đó phương trình đường cong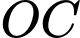 là
là 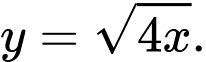
Thể tích của vật thể thu được là: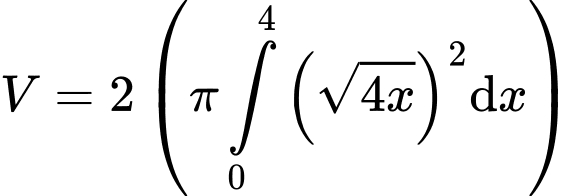
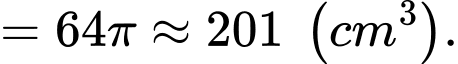

Phương trình Parabol
 có dạng:
có dạng: 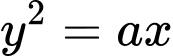
Mặt khác Parabol đi qua điểm
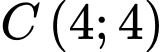
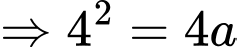
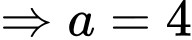
Khi đó phương trình đường cong
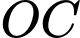 là
là 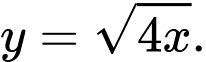
Thể tích của vật thể thu được là:
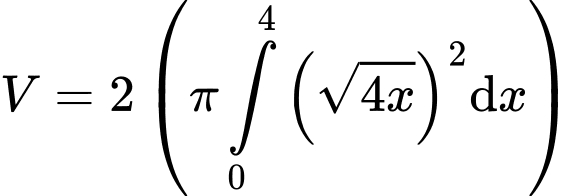
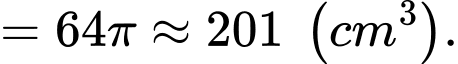
Câu 8 [408108]: Một vật trang trí có dạng khối tròn xoay được tạo thành khi quay miền  (Phần gạch sọc trong hình vẽ bên dưới) quanh trục
(Phần gạch sọc trong hình vẽ bên dưới) quanh trục 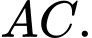 Biết rằng
Biết rằng 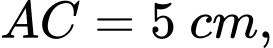
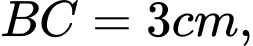 miền
miền  được giới hạn bởi đoạn thẳng
được giới hạn bởi đoạn thẳng  , cung tròn
, cung tròn 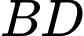 có tâm
có tâm 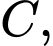 đường tròn elip
đường tròn elip 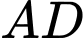 có trục
có trục 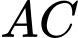 và
và 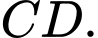 Thể tích của vật trang trí bằng bao nhiêu
Thể tích của vật trang trí bằng bao nhiêu 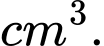 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.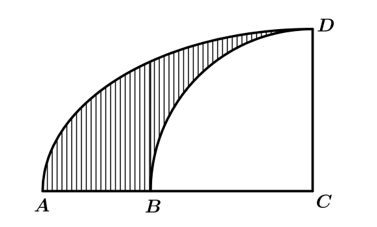
 (Phần gạch sọc trong hình vẽ bên dưới) quanh trục
(Phần gạch sọc trong hình vẽ bên dưới) quanh trục  Biết rằng
Biết rằng 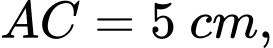
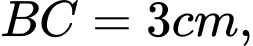 miền
miền  được giới hạn bởi đoạn thẳng
được giới hạn bởi đoạn thẳng  , cung tròn
, cung tròn 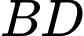 có tâm
có tâm 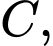 đường tròn elip
đường tròn elip 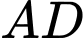 có trục
có trục 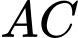 và
và 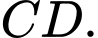 Thể tích của vật trang trí bằng bao nhiêu
Thể tích của vật trang trí bằng bao nhiêu 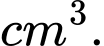 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.
Chọn hệ trục với  trùng với
trùng với  như hình vẽ.
như hình vẽ. 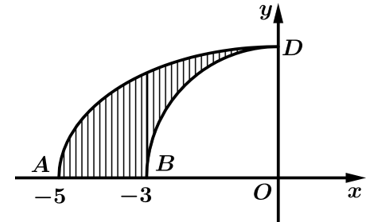
 trùng với
trùng với  như hình vẽ.
như hình vẽ. Phương trình nửa đường tròn là 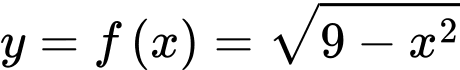
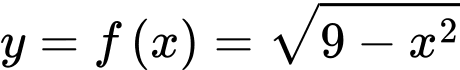
Phương trình Elip là: 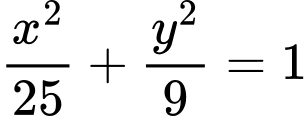 suy ra phương trình đường cong Elip phía trên là
suy ra phương trình đường cong Elip phía trên là 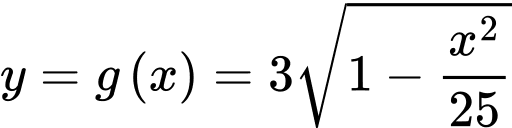
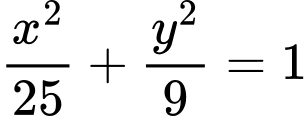 suy ra phương trình đường cong Elip phía trên là
suy ra phương trình đường cong Elip phía trên là 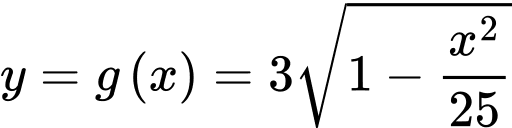
Thể tích khối tròn xoay cần tìm là 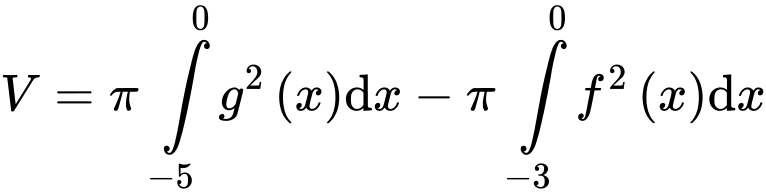
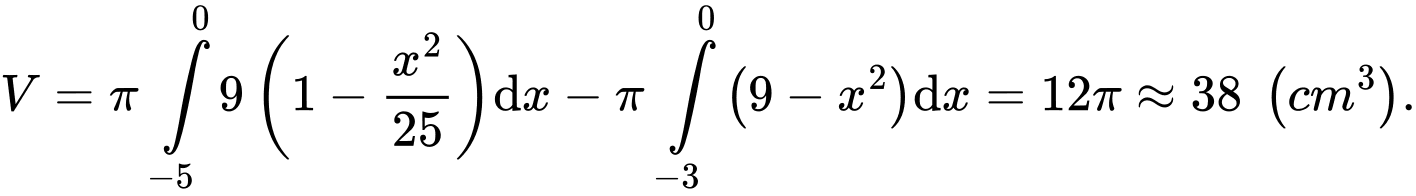
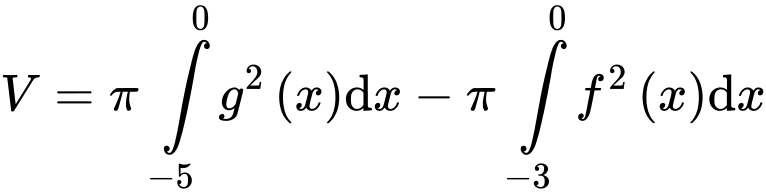
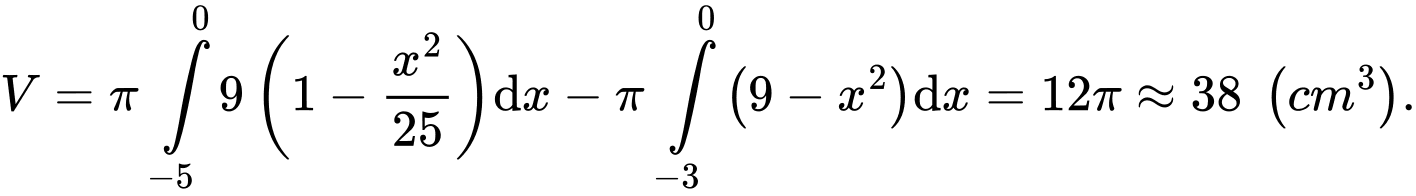

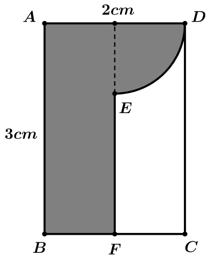
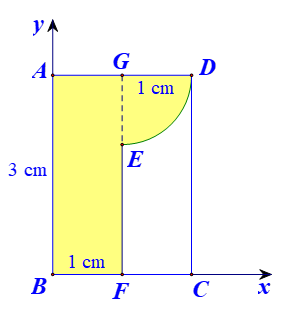
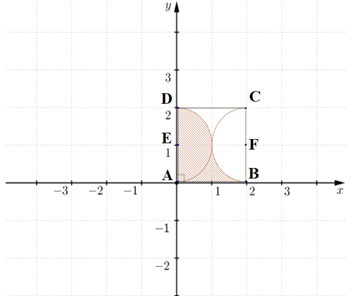
Câu 9 [398640]: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền  (phần gạch chéo trong hình vẽ) quanh trục
(phần gạch chéo trong hình vẽ) quanh trục 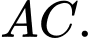 Biết rằng
Biết rằng 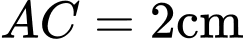 ,
, 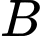 là trung điểm
là trung điểm 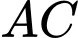 , miền
, miền  được giới hạn bởi đoạn thẳng
được giới hạn bởi đoạn thẳng 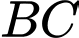 và các cung tròn bán kính
và các cung tròn bán kính 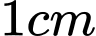 có tâm
có tâm  và
và  Thể tích vật trang trí đó bằng bao nhiêu cm3. Viết kết quả làm tròn đến hang phần chục.
Thể tích vật trang trí đó bằng bao nhiêu cm3. Viết kết quả làm tròn đến hang phần chục.
 (phần gạch chéo trong hình vẽ) quanh trục
(phần gạch chéo trong hình vẽ) quanh trục  Biết rằng
Biết rằng 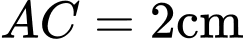 ,
, 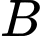 là trung điểm
là trung điểm 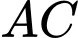 , miền
, miền  được giới hạn bởi đoạn thẳng
được giới hạn bởi đoạn thẳng 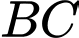 và các cung tròn bán kính
và các cung tròn bán kính 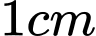 có tâm
có tâm 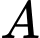 và
và 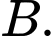 Thể tích vật trang trí đó bằng bao nhiêu cm3. Viết kết quả làm tròn đến hang phần chục.
Thể tích vật trang trí đó bằng bao nhiêu cm3. Viết kết quả làm tròn đến hang phần chục. 
A, 2,9 cm3.
B, 3,5 cm3.
C, 1,7 cm3.
D, 4,2 cm3.
Chọn A.
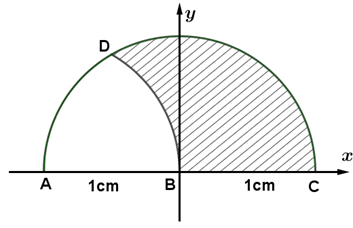
Chọn hệ trục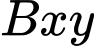 như hình vẽ
như hình vẽ
Khi đó mặt phẳng được giới hạn bởi hai cung tròn:
được giới hạn bởi hai cung tròn: 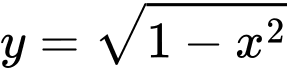 và
và 
Hoành độ giao điểm của hai cung tròn này là nghiệm của phương trình
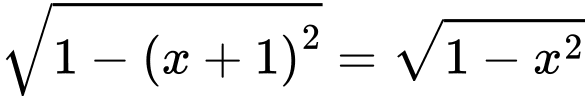
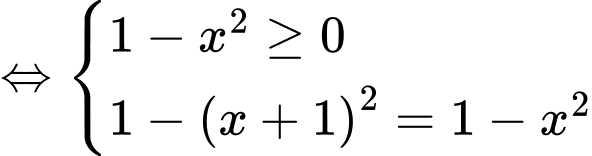
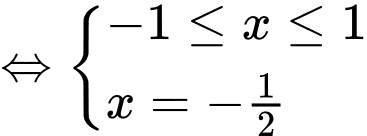
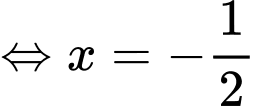
Khi đó miền phẳng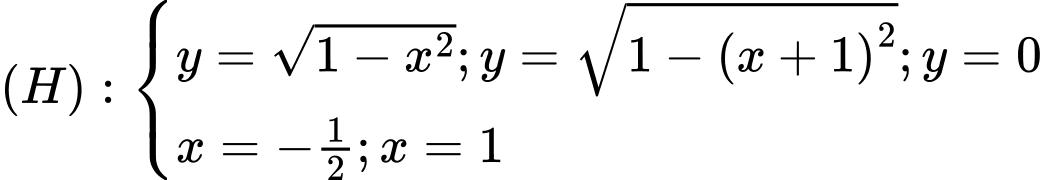
Vậy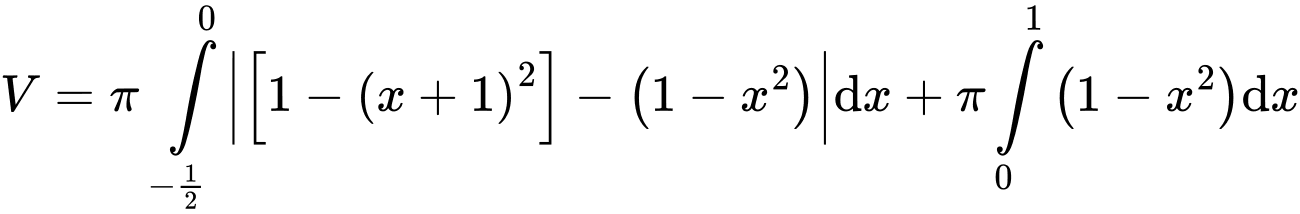
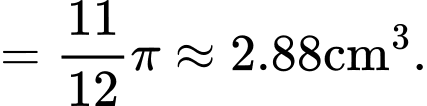 Đáp án: A
Đáp án: A

Chọn hệ trục
 như hình vẽ
như hình vẽ
Khi đó mặt phẳng
 được giới hạn bởi hai cung tròn:
được giới hạn bởi hai cung tròn: 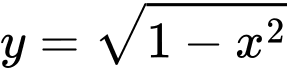 và
và 
Hoành độ giao điểm của hai cung tròn này là nghiệm của phương trình
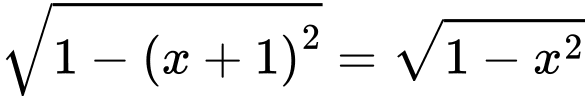
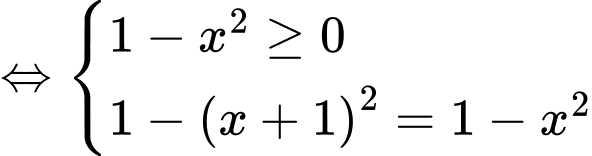
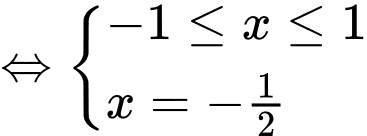
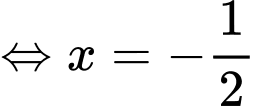
Khi đó miền phẳng
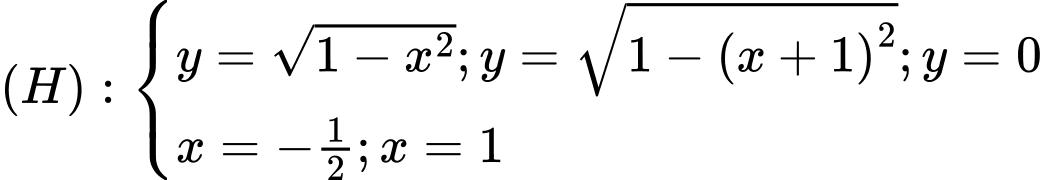
Vậy
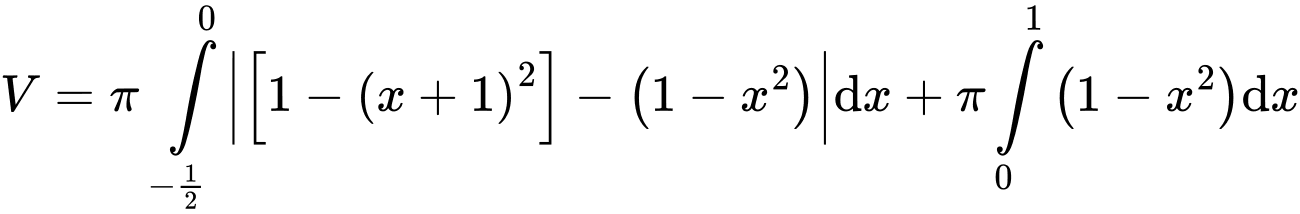
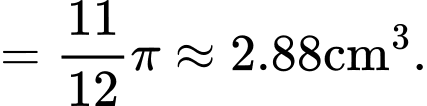 Đáp án: A
Đáp án: A
Câu 10 [408109]: Một vật trang trí có dạng khối tròn xoay tạo thành khi quay miền  được giới hạn bởi đường gấp khúc
được giới hạn bởi đường gấp khúc 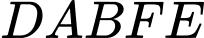 và cung tròn
và cung tròn 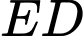 (phần tô đậm trong hình bên) xung quanh trục
(phần tô đậm trong hình bên) xung quanh trục  . Biết
. Biết  là hình chữ nhật cạnh
là hình chữ nhật cạnh 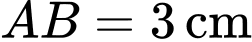 ,
, 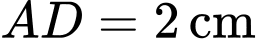 ;
;  là trung điểm của
là trung điểm của 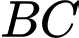 ; điểm
; điểm 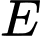 cách
cách 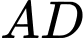 một đoạn bằng
một đoạn bằng 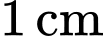 . Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười theo đơn vị
. Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười theo đơn vị 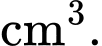
 được giới hạn bởi đường gấp khúc
được giới hạn bởi đường gấp khúc  và cung tròn
và cung tròn  (phần tô đậm trong hình bên) xung quanh trục
(phần tô đậm trong hình bên) xung quanh trục  . Biết
. Biết 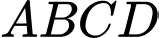 là hình chữ nhật cạnh
là hình chữ nhật cạnh 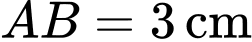 ,
, 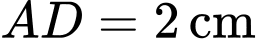 ;
; 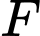 là trung điểm của
là trung điểm của 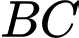 ; điểm
; điểm 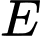 cách
cách 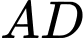 một đoạn bằng
một đoạn bằng 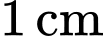 . Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười theo đơn vị
. Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười theo đơn vị 

+ Gắn hệ trục
 như hình vẽ.
như hình vẽ.Gọi
 là trung điểm
là trung điểm 
+ Gọi
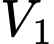 là thể tích khối trụ được sinh ra khi quay hình chữ nhật
là thể tích khối trụ được sinh ra khi quay hình chữ nhật 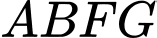 quanh trục
quanh trục  gọi
gọi 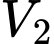 là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi cung tròn đi qua
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi cung tròn đi qua 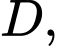
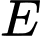 và cạnh
và cạnh 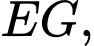
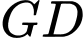 quanh
quanh 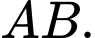
+ Ta có:
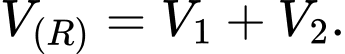
+
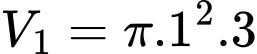
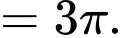
+ Phương trình đường tròn đi qua
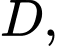
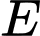 là
là 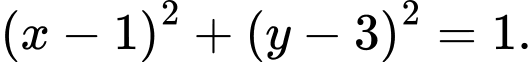
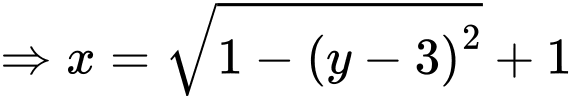
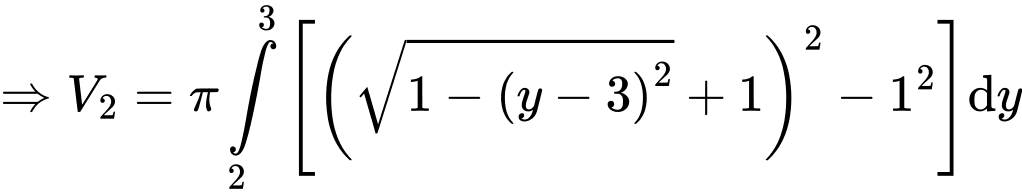
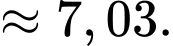
+ Vậy thể tích khối tròn xoay cần tìm bằng
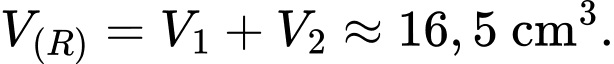
Câu 11 [408479]: Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có hình dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng 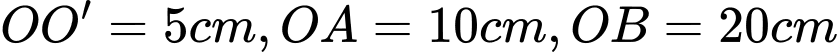 , đường cong
, đường cong  là một phần của parabol có đỉnh là điểm
là một phần của parabol có đỉnh là điểm 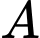 . Thể tích của chiếc mũ bằng bao nhiêu
. Thể tích của chiếc mũ bằng bao nhiêu 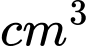 . Viết kết quả làm tròn đến hàng đơn vị
. Viết kết quả làm tròn đến hàng đơn vị
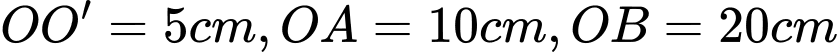 , đường cong
, đường cong  là một phần của parabol có đỉnh là điểm
là một phần của parabol có đỉnh là điểm 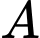 . Thể tích của chiếc mũ bằng bao nhiêu
. Thể tích của chiếc mũ bằng bao nhiêu 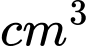 . Viết kết quả làm tròn đến hàng đơn vị
. Viết kết quả làm tròn đến hàng đơn vị 

Lưu ý: 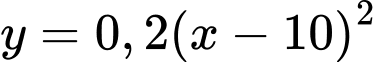
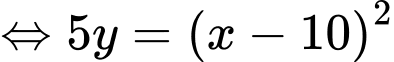
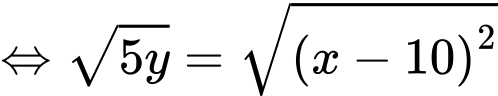
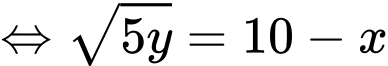 (Vì
(Vì  )
)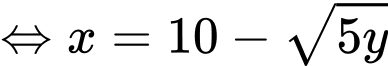
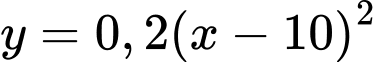
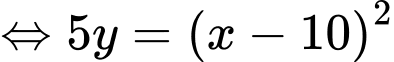
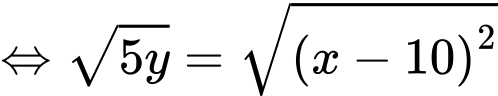
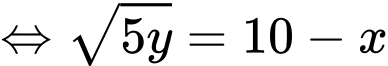 (Vì
(Vì  )
)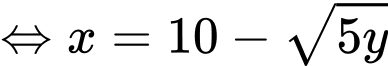
Câu 12 [395596]: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền  (phần gạch chéo trong hình vẽ bên) quanh trục
(phần gạch chéo trong hình vẽ bên) quanh trục 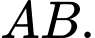 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh  ,
, 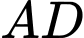 của hình vuông
của hình vuông 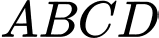 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 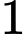 cm với tâm lần lượt là trung điểm của các cạnh
cm với tâm lần lượt là trung điểm của các cạnh 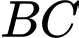 ,
, 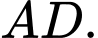
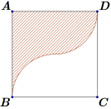
Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười
 (phần gạch chéo trong hình vẽ bên) quanh trục
(phần gạch chéo trong hình vẽ bên) quanh trục 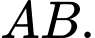 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh  ,
, 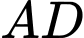 của hình vuông
của hình vuông 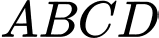 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng  cm với tâm lần lượt là trung điểm của các cạnh
cm với tâm lần lượt là trung điểm của các cạnh 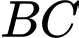 ,
, 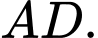

Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười
Điền đáp án: 10,5.
Chọn hệ trục tọa độ sao cho trục
sao cho trục  chứa cạnh
chứa cạnh  và
và 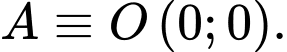
Khi đó và
và 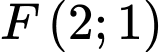 với
với 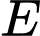 ,
, 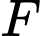 lần lượt là trung điểm của
lần lượt là trung điểm của 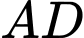 ,
, 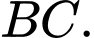
Khi đó đường tròn tâm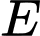 chứa cung tròn
chứa cung tròn 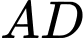 là
là 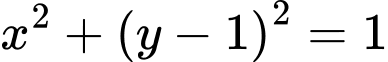 và đường tròn tâm
và đường tròn tâm  chứa cung tròn
chứa cung tròn  là
là 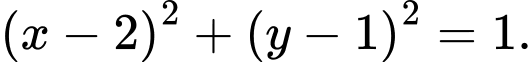
Suy ra phương trình cung trên của đường tròn tâm là
là 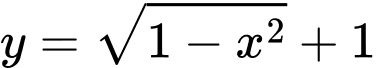 và phương trình cung dưới của của đường tròn tâm
và phương trình cung dưới của của đường tròn tâm  là
là 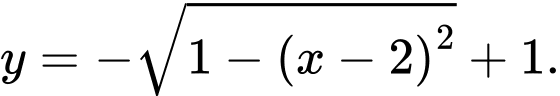
Khi đó, thể tích vật thể trang trí là
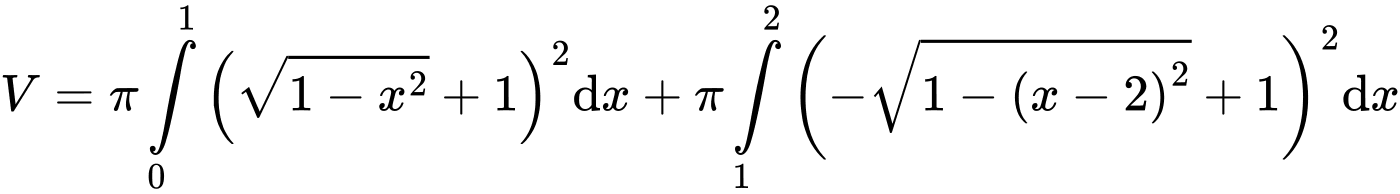
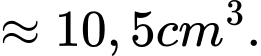

Chọn hệ trục tọa độ
 sao cho trục
sao cho trục  chứa cạnh
chứa cạnh  và
và 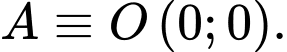
Khi đó
 và
và 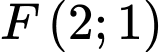 với
với 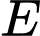 ,
, 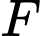 lần lượt là trung điểm của
lần lượt là trung điểm của 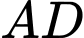 ,
, 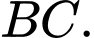
Khi đó đường tròn tâm
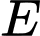 chứa cung tròn
chứa cung tròn 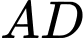 là
là 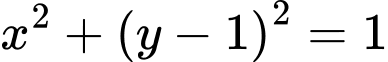 và đường tròn tâm
và đường tròn tâm  chứa cung tròn
chứa cung tròn  là
là 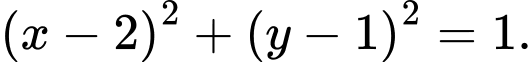
Suy ra phương trình cung trên của đường tròn tâm
 là
là 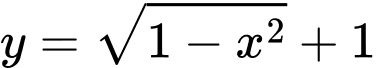 và phương trình cung dưới của của đường tròn tâm
và phương trình cung dưới của của đường tròn tâm  là
là 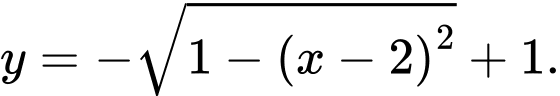
Khi đó, thể tích vật thể trang trí là
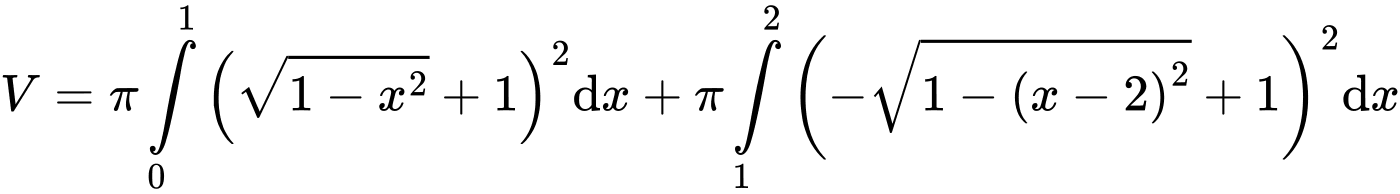
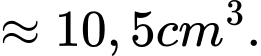
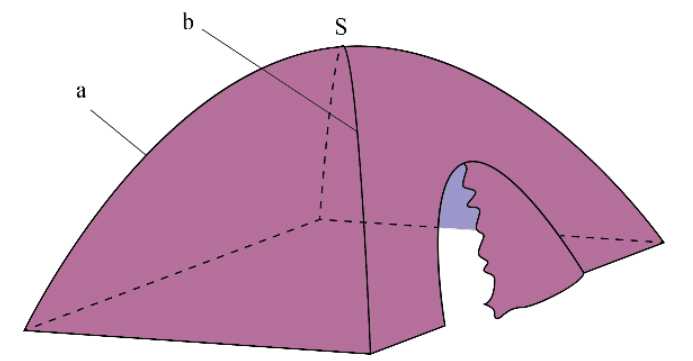
Câu 13 [204876]: Một chiếc lều vải du lịch dạng hình cong như hình vẽ. Khung chính bao gồm đáy là hình vuông cạnh 2 m và hai xương dây 𝑎, 𝑏 nằm trên các đường parabol đỉnh 𝑆. Biết chiều cao của lều là 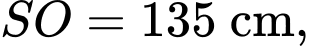 𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị
𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị 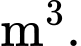 Viết kết quả dưới dạng số thập phân.
Viết kết quả dưới dạng số thập phân.
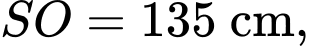 𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị
𝑂 là tâm của đáy. Tính thể tích chiếc lều theo đơn vị 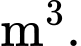 Viết kết quả dưới dạng số thập phân.
Viết kết quả dưới dạng số thập phân.
Điền đáp án: 2,7.
Gắn hệ trục như hình vẽ.
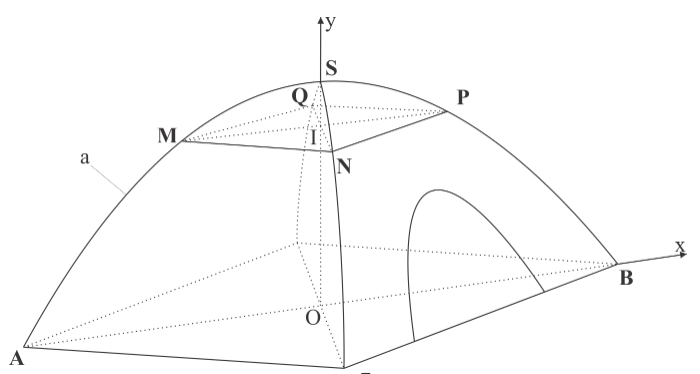
Ta tính được
Gọi phương trình của đường thẳng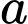 là
là 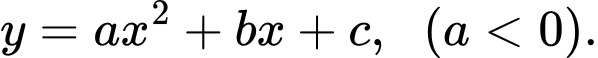
Ta có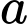 đi qua các điểm
đi qua các điểm
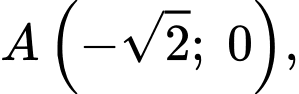
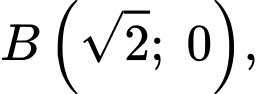
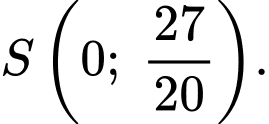
Suy ra ta có hệ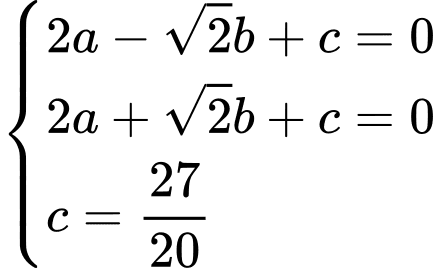
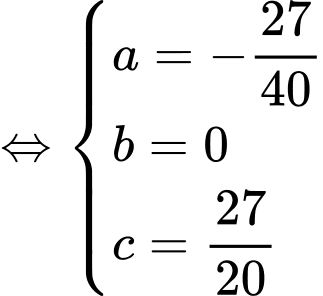
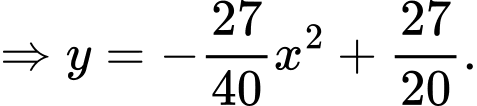
Gọi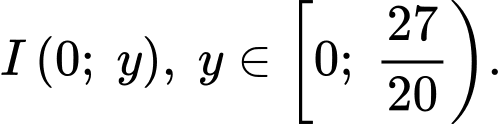
Mặt phẳng vuông góc tại
tại  cắt hình đa cho theo 1 thiết diện là hình vuông
cắt hình đa cho theo 1 thiết diện là hình vuông 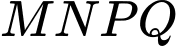 có diện tích
có diện tích 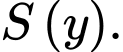
Theo giả thiết trên các điểm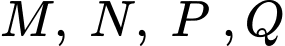 cùng có tung độ bằng
cùng có tung độ bằng 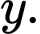 Mà hai điểm
Mà hai điểm  thuộc đường
thuộc đường 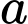 có phương trình
có phương trình 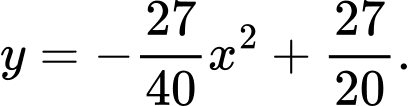
Suy ra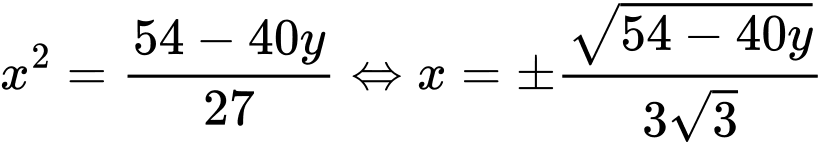
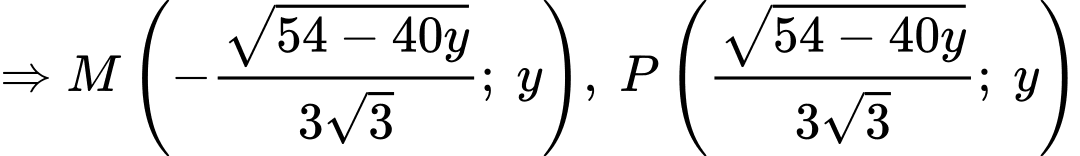
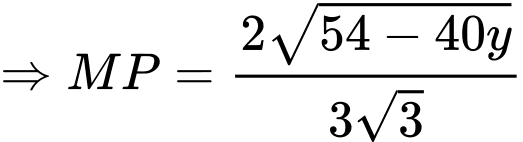
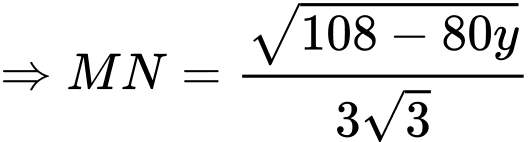
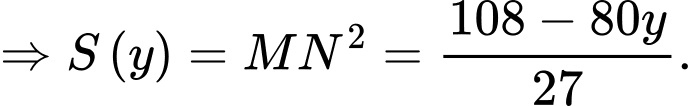
Suy ra thể tích chiếc lều là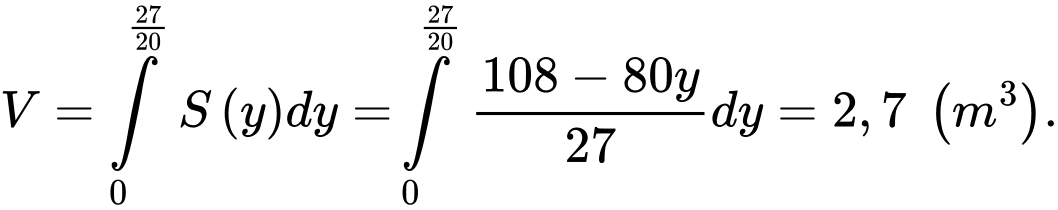
Gắn hệ trục như hình vẽ.

Ta tính được

Gọi phương trình của đường thẳng
 là
là 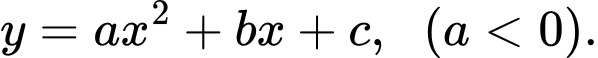
Ta có
 đi qua các điểm
đi qua các điểm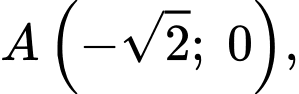
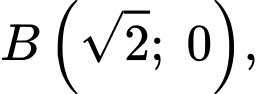
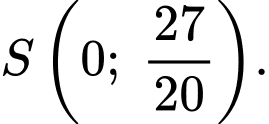
Suy ra ta có hệ
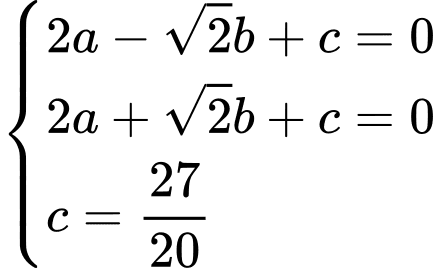
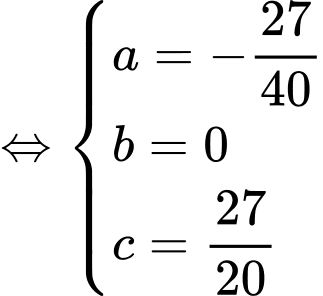
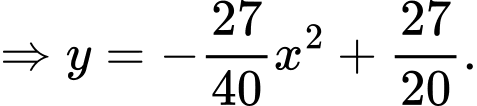
Gọi
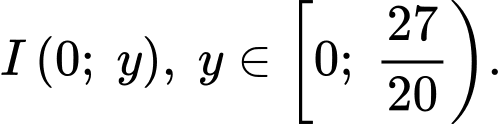
Mặt phẳng vuông góc
 tại
tại  cắt hình đa cho theo 1 thiết diện là hình vuông
cắt hình đa cho theo 1 thiết diện là hình vuông 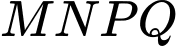 có diện tích
có diện tích 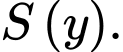
Theo giả thiết trên các điểm
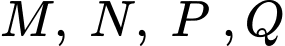 cùng có tung độ bằng
cùng có tung độ bằng 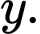 Mà hai điểm
Mà hai điểm  thuộc đường
thuộc đường 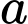 có phương trình
có phương trình 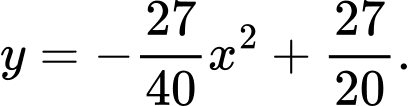
Suy ra
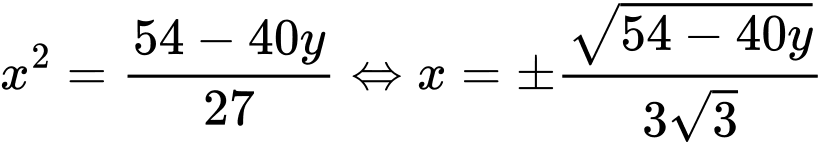
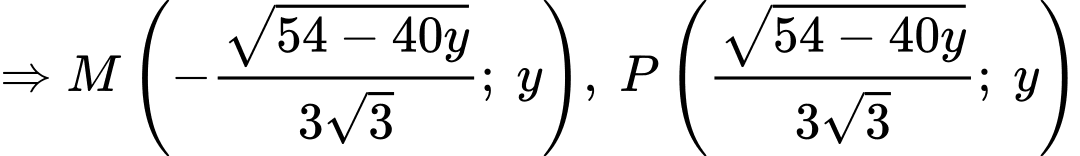
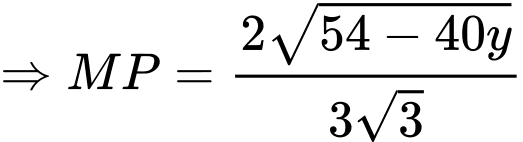
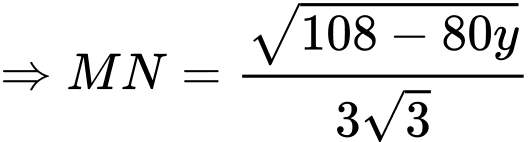
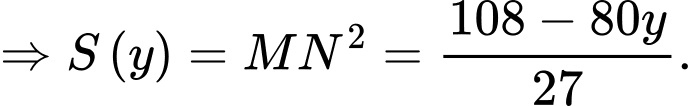
Suy ra thể tích chiếc lều là
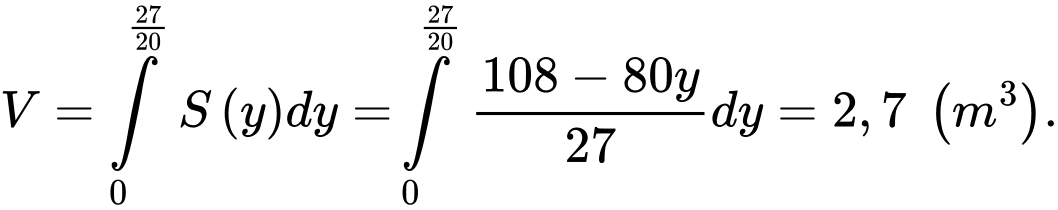
Câu 14 [151705]: Một chiếc đồng hồ cát như hình vẽ, gồm hai phần đối xứng nhau qua mặt nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt nằm ngang. Ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao 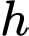 của mực cát bằng
của mực cát bằng 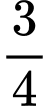 chiều cao của bên đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi
chiều cao của bên đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi 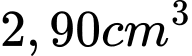 /
/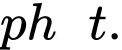 Khi chiều cao của cát còn
Khi chiều cao của cát còn 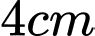 thì bề mặt trên cùng của cát tạo thành một đường tròn chu vi
thì bề mặt trên cùng của cát tạo thành một đường tròn chu vi 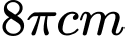 (xem hình). Biết sau 30 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu
(xem hình). Biết sau 30 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu 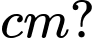 (Kết quả làm tròn đến hàng đơn vị).
(Kết quả làm tròn đến hàng đơn vị).
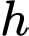 của mực cát bằng
của mực cát bằng 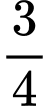 chiều cao của bên đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi
chiều cao của bên đó (xem hình). Cát chảy từ trên xuống dưới với lưu lượng không đổi 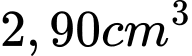 /
/ Khi chiều cao của cát còn
Khi chiều cao của cát còn 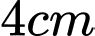 thì bề mặt trên cùng của cát tạo thành một đường tròn chu vi
thì bề mặt trên cùng của cát tạo thành một đường tròn chu vi 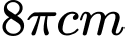 (xem hình). Biết sau 30 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu
(xem hình). Biết sau 30 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài là bao nhiêu 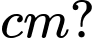 (Kết quả làm tròn đến hàng đơn vị).
(Kết quả làm tròn đến hàng đơn vị). A, 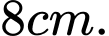
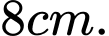
B, 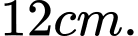
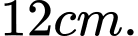
C, 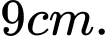
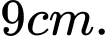
D, 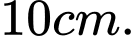
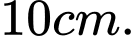
 Đáp án: D
Đáp án: D
Câu 15 [151706]: Bạn A có một cốc thủy tinh hình trụ, đường kính trong lòng đáy cốc là 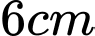 , chiều cao trong lòng cốc là
, chiều cao trong lòng cốc là 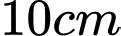 đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Thể tích lượng nước trong cốc là bao nhiêu cm^3.
đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Thể tích lượng nước trong cốc là bao nhiêu cm^3.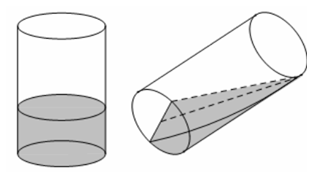
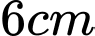 , chiều cao trong lòng cốc là
, chiều cao trong lòng cốc là 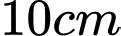 đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Thể tích lượng nước trong cốc là bao nhiêu cm^3.
đang đựng một lượng nước. Bạn A nghiêng cốc nước, vừa lúc khi nước chạm miệng cốc thì ở đáy mực nước trùng với đường kính đáy. Thể tích lượng nước trong cốc là bao nhiêu cm^3.
A, 

B, 

C, 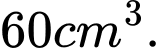
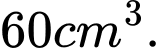
D, 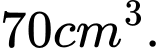
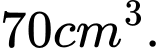
 Đáp án: C
Đáp án: C
Câu 16 [151709]: Từ một khúc gỗ hình trụ có đường kính 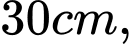 người ta cắt khúc gỗ theo một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc
người ta cắt khúc gỗ theo một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc 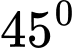 để lấy một hình nêm (xem hình minh họa dưới đây).
để lấy một hình nêm (xem hình minh họa dưới đây).
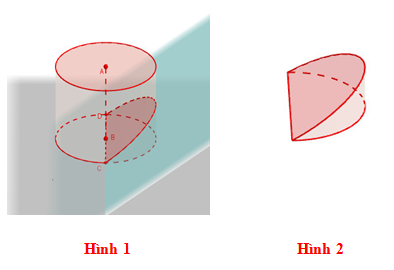
Kí hiệu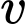 là thể tích của hình nêm (Hình 2). Tính
là thể tích của hình nêm (Hình 2). Tính 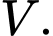
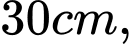 người ta cắt khúc gỗ theo một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc
người ta cắt khúc gỗ theo một mặt phẳng đi qua đường kính đáy và nghiêng với đáy một góc 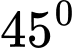 để lấy một hình nêm (xem hình minh họa dưới đây).
để lấy một hình nêm (xem hình minh họa dưới đây).
Kí hiệu
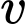 là thể tích của hình nêm (Hình 2). Tính
là thể tích của hình nêm (Hình 2). Tính 
A, 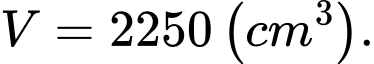
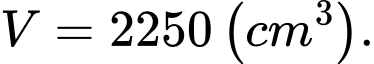
B, 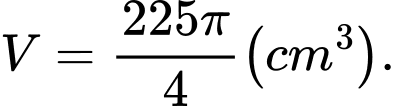
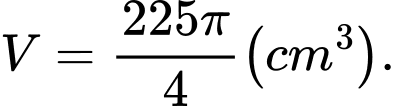
C, 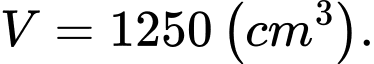
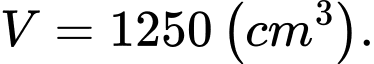
D, 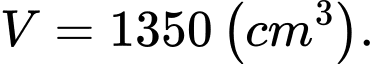
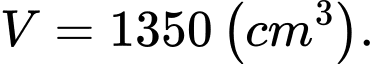
 Đáp án: A
Đáp án: A
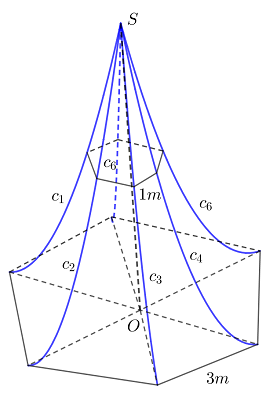
Câu 17 [151711]: Người ta dựng một cái lều vải  có dạng hình chóp lục giác đều như hình vẽ dưới. Đáy của
có dạng hình chóp lục giác đều như hình vẽ dưới. Đáy của  là một hình lục giác đều cạnh
là một hình lục giác đều cạnh 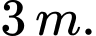 Chiều cao
Chiều cao  (
( vuông góc với mặt phẳng đáy). Các cạnh bên của
vuông góc với mặt phẳng đáy). Các cạnh bên của  là các sợi
là các sợi 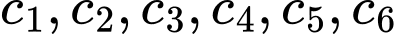 nằm trên các đường parabol có trục đối xứng song song với
nằm trên các đường parabol có trục đối xứng song song với  Giả sử giao tuyến (nếu có) của
Giả sử giao tuyến (nếu có) của  với mặt phẳng
với mặt phẳng 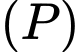 vuông góc với
vuông góc với 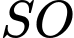 là một lục giác đều và khi
là một lục giác đều và khi 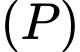 đi qua trung điểm
đi qua trung điểm 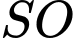 thì lục giác đều cạnh bằng
thì lục giác đều cạnh bằng 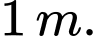 Tính thể tích phần không gian bên trong cái lều
Tính thể tích phần không gian bên trong cái lều  đó.
đó.
 có dạng hình chóp lục giác đều như hình vẽ dưới. Đáy của
có dạng hình chóp lục giác đều như hình vẽ dưới. Đáy của  là một hình lục giác đều cạnh
là một hình lục giác đều cạnh 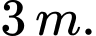 Chiều cao
Chiều cao  (
(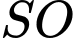 vuông góc với mặt phẳng đáy). Các cạnh bên của
vuông góc với mặt phẳng đáy). Các cạnh bên của  là các sợi
là các sợi 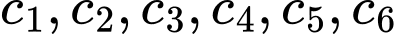 nằm trên các đường parabol có trục đối xứng song song với
nằm trên các đường parabol có trục đối xứng song song với  Giả sử giao tuyến (nếu có) của
Giả sử giao tuyến (nếu có) của  với mặt phẳng
với mặt phẳng 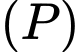 vuông góc với
vuông góc với 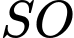 là một lục giác đều và khi
là một lục giác đều và khi 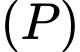 đi qua trung điểm
đi qua trung điểm 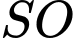 thì lục giác đều cạnh bằng
thì lục giác đều cạnh bằng 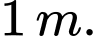 Tính thể tích phần không gian bên trong cái lều
Tính thể tích phần không gian bên trong cái lều  đó.
đó.
A, 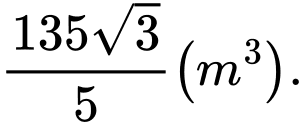
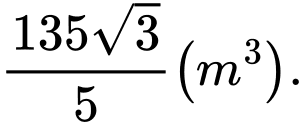
B, 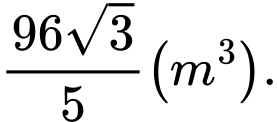
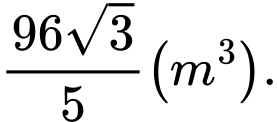
C, 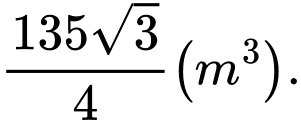
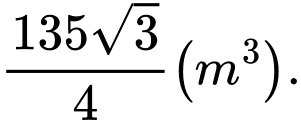
D, 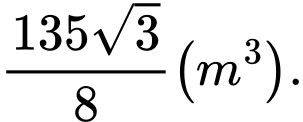
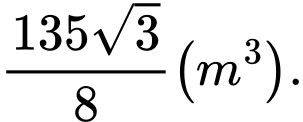
 Đáp án: D
Đáp án: D
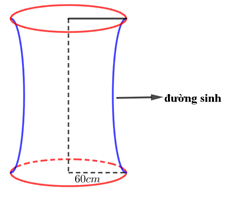
Câu 18 [151713]: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lơn bằng 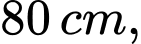 độ dài trục bé bằng
độ dài trục bé bằng 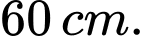 Tính thể tích
Tính thể tích  của trống (kết quả làm tròn đến hàng đơn vị).
của trống (kết quả làm tròn đến hàng đơn vị).
 độ dài trục bé bằng
độ dài trục bé bằng 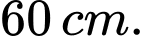 Tính thể tích
Tính thể tích  của trống (kết quả làm tròn đến hàng đơn vị).
của trống (kết quả làm tròn đến hàng đơn vị).
A, 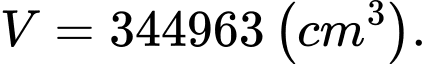
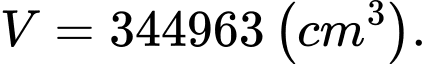
B, 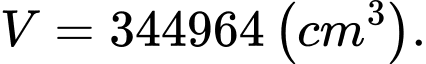
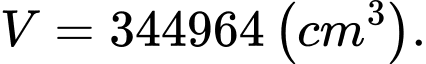
C, 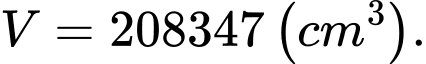
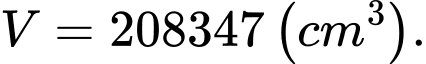
D, 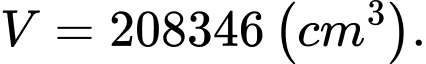
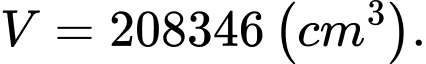
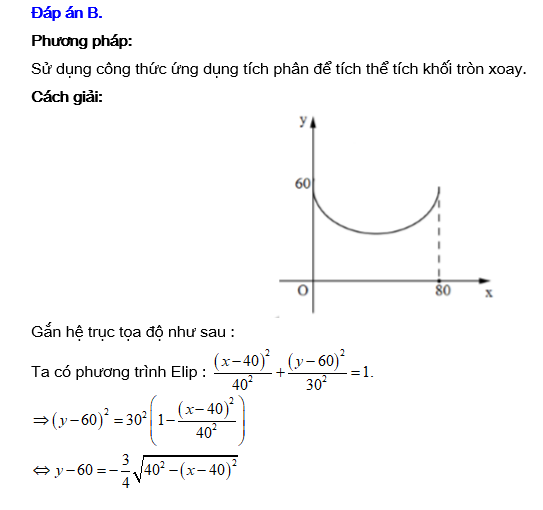
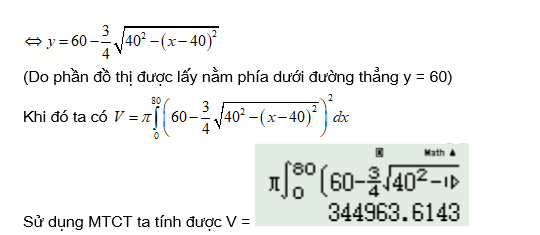 Đáp án: B
Đáp án: B
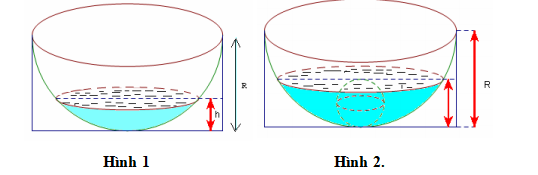
Câu 19 [140098]: Một chậu nước hình bán cầu bằng nhôm có bán kính 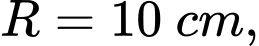 đặt trong một khung hình hộp chữ nhật (hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao
đặt trong một khung hình hộp chữ nhật (hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao 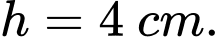 Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (hình 2). Bán kính của viên bi gần bằng
Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (hình 2). Bán kính của viên bi gần bằng
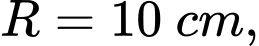 đặt trong một khung hình hộp chữ nhật (hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao
đặt trong một khung hình hộp chữ nhật (hình 1). Trong chậu có chứa sẵn một khối nước hình chỏm cầu có chiều cao 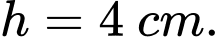 Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (hình 2). Bán kính của viên bi gần bằng
Người ta bỏ vào chậu một viên bi hình cầu bằng kim loại thì mặt nước dâng lên vừa phủ kín viên bi (hình 2). Bán kính của viên bi gần bằng
A, 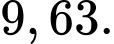
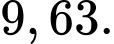
B, 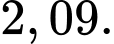
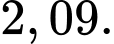
C, 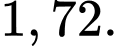
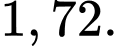
D, 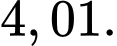
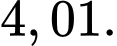
 Đáp án: B
Đáp án: B
Câu 20 [151716]: Gọi  là phần giao nhau của hai khối một phần tư hình trụ có bán kính bằng a (xem hình vẽ bên). Tính thể tích của
là phần giao nhau của hai khối một phần tư hình trụ có bán kính bằng a (xem hình vẽ bên). Tính thể tích của 
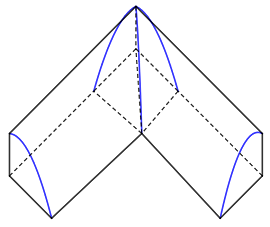
 là phần giao nhau của hai khối một phần tư hình trụ có bán kính bằng a (xem hình vẽ bên). Tính thể tích của
là phần giao nhau của hai khối một phần tư hình trụ có bán kính bằng a (xem hình vẽ bên). Tính thể tích của 

A, 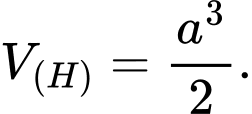
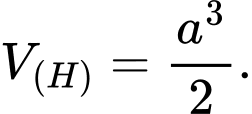
B, 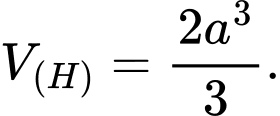
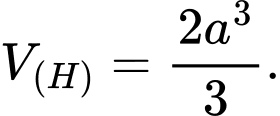
C, 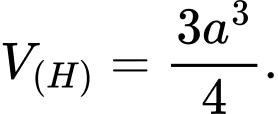
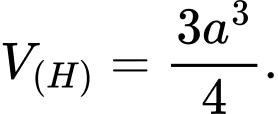
D, 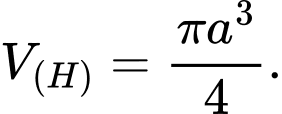
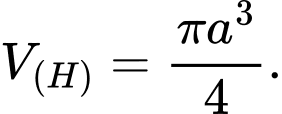
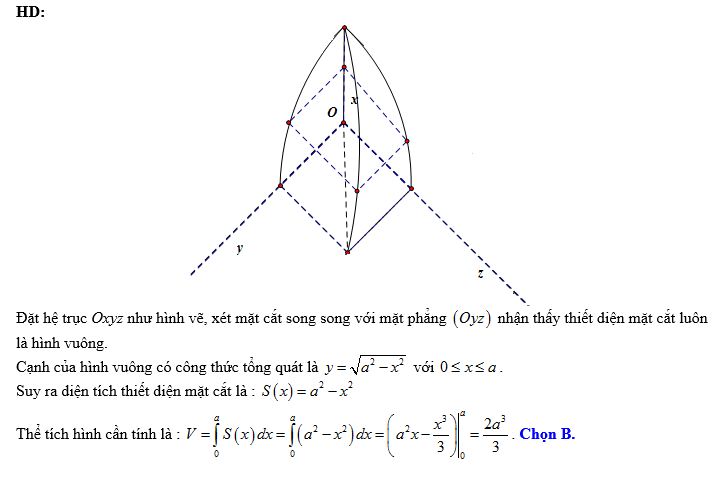 Đáp án: B
Đáp án: B
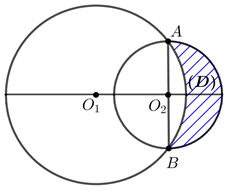
Câu 21 [151717]: Cho 2 đường tròn 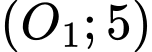 và
và 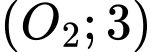 cắt nhau tại 2 điểm
cắt nhau tại 2 điểm 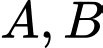 sao cho
sao cho  là 1 đường kính của đường tròn
là 1 đường kính của đường tròn 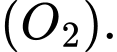 Gọi
Gọi 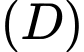 là hình thẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay
là hình thẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay 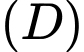 quanh trục
quanh trục 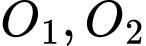 ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
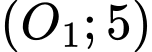 và
và 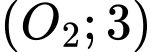 cắt nhau tại 2 điểm
cắt nhau tại 2 điểm 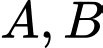 sao cho
sao cho  là 1 đường kính của đường tròn
là 1 đường kính của đường tròn 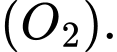 Gọi
Gọi 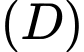 là hình thẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay
là hình thẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay 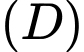 quanh trục
quanh trục 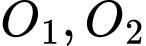 ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
A, 

B, 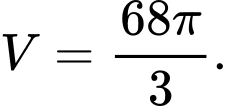
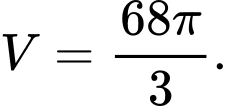
C, 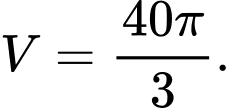
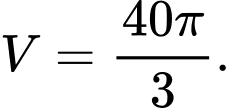
D, 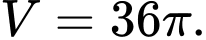
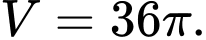
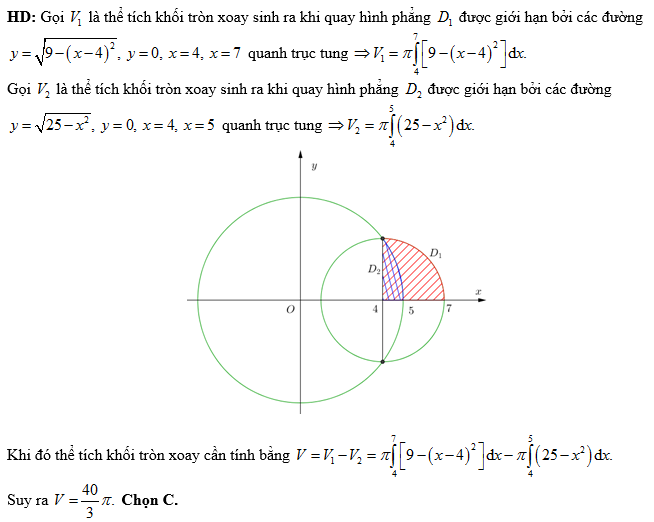 Đáp án: C
Đáp án: C
Câu 22 [151718]: Ta vẽ hai nửa đường tròn như hình vẽ dưới, trong đó đường kính của nửa đường tròn lớn gấp đôi đường kính của nửa đường tròn nhỏ. Biết rằng nửa hình tròn đường kính  có diện tích là
có diện tích là 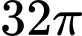 và
và 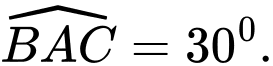 Tính thể tích của vật thể tròn xoay được tạo thành khi quay hình
Tính thể tích của vật thể tròn xoay được tạo thành khi quay hình  (phần tô đậm) xung quanh đường thẳng
(phần tô đậm) xung quanh đường thẳng 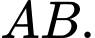
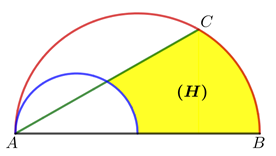
 có diện tích là
có diện tích là 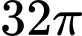 và
và 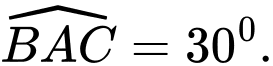 Tính thể tích của vật thể tròn xoay được tạo thành khi quay hình
Tính thể tích của vật thể tròn xoay được tạo thành khi quay hình  (phần tô đậm) xung quanh đường thẳng
(phần tô đậm) xung quanh đường thẳng 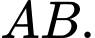

A, 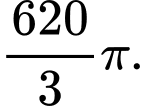
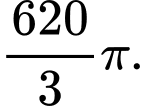
B, 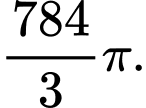
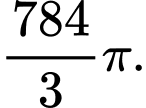
C, 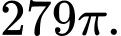
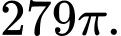
D, 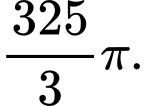
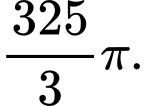
Đáp án: B
Câu 23 [151719]: Ông An có một cái bình đựng rượu, thân bình có hai phần: phần phía dưới là hình nón cụt, phần trên là hình cầu bị cắt bỏ 2 đầu chỏm (hình 1).
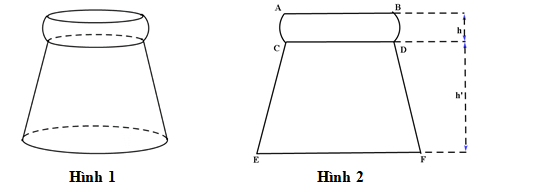
Thiết diện qua trục của bình như hình 2. Biết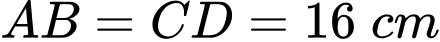 ,
,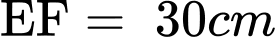 ,
, 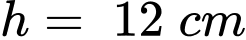 ,
, 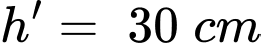 và giá mỗi lít rượu là
và giá mỗi lít rượu là  đồng. Hỏi số tiền ông An cần để đổ đầy bình rượu là bao nhiêu nghìn đồng (giả sử độ dày của vỏ bình rượu không đáng kể)?. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng?
đồng. Hỏi số tiền ông An cần để đổ đầy bình rượu là bao nhiêu nghìn đồng (giả sử độ dày của vỏ bình rượu không đáng kể)?. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng?

Thiết diện qua trục của bình như hình 2. Biết
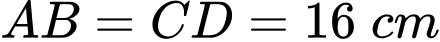 ,
,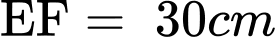 ,
, 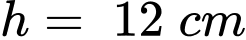 ,
, 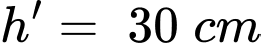 và giá mỗi lít rượu là
và giá mỗi lít rượu là  đồng. Hỏi số tiền ông An cần để đổ đầy bình rượu là bao nhiêu nghìn đồng (giả sử độ dày của vỏ bình rượu không đáng kể)?. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng?
đồng. Hỏi số tiền ông An cần để đổ đầy bình rượu là bao nhiêu nghìn đồng (giả sử độ dày của vỏ bình rượu không đáng kể)?. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng? A, 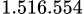 đồng.
đồng.
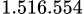 đồng.
đồng.B, 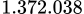 đồng.
đồng.
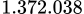 đồng.
đồng.C, 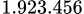 đồng.
đồng.
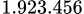 đồng.
đồng.D, 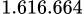 đồng.
đồng.
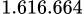 đồng.
đồng.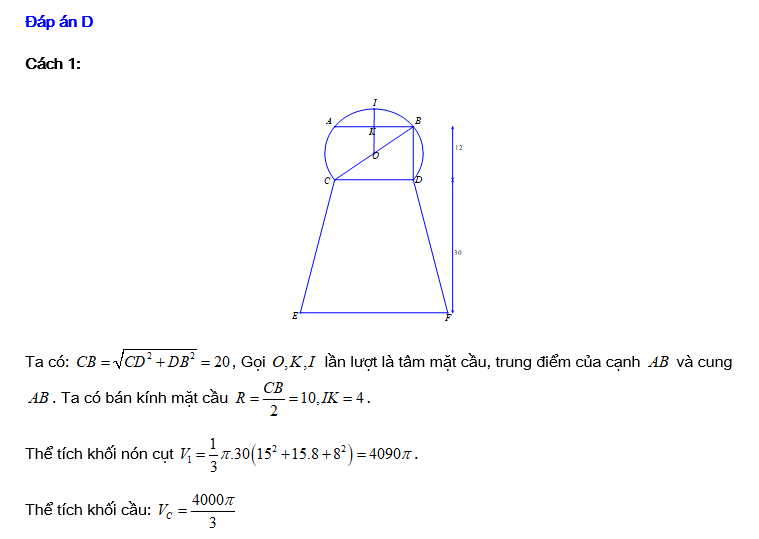
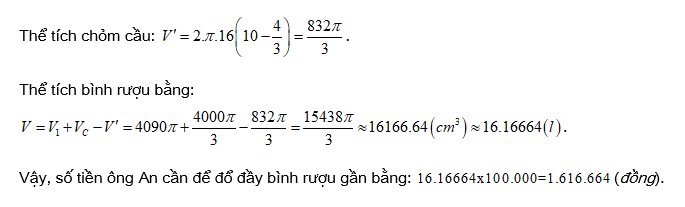 Đáp án: D
Đáp án: D
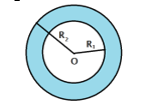
Câu 24 [408423]: Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiều bằng như hình vẽ với bán kính đường tròn nhỏ 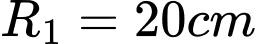 , bán kính đường tròn lớn
, bán kính đường tròn lớn 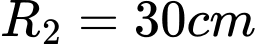 và mặt cắt bởi mặt phẳng đi qua trục vuông góc với mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày của vỏ săm. Thể tích không khí được chứa bên trong săm la bao nhiêu
và mặt cắt bởi mặt phẳng đi qua trục vuông góc với mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày của vỏ săm. Thể tích không khí được chứa bên trong săm la bao nhiêu 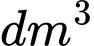 . Viết kết quả làm tròn đến hàng phần chục.
. Viết kết quả làm tròn đến hàng phần chục.
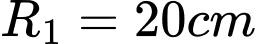 , bán kính đường tròn lớn
, bán kính đường tròn lớn 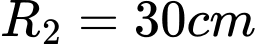 và mặt cắt bởi mặt phẳng đi qua trục vuông góc với mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày của vỏ săm. Thể tích không khí được chứa bên trong săm la bao nhiêu
và mặt cắt bởi mặt phẳng đi qua trục vuông góc với mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày của vỏ săm. Thể tích không khí được chứa bên trong săm la bao nhiêu 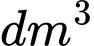 . Viết kết quả làm tròn đến hàng phần chục.
. Viết kết quả làm tròn đến hàng phần chục.
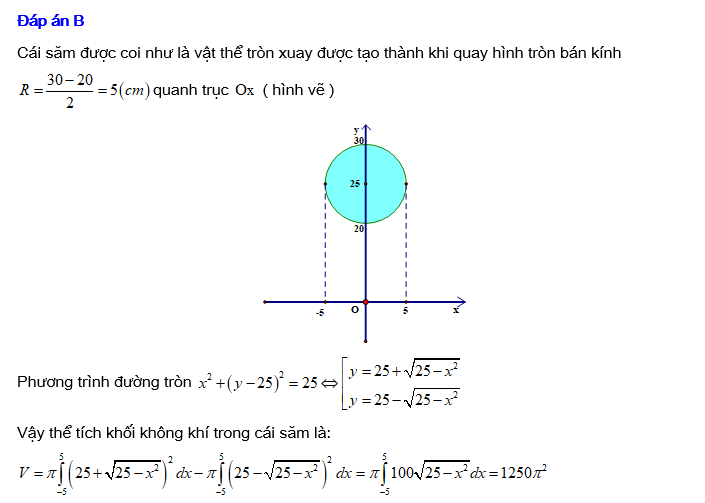
Thể tích săm là 12,3 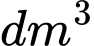
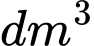
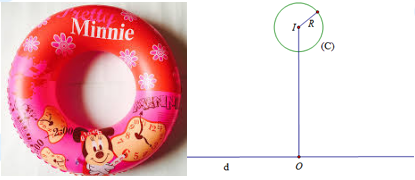
Câu 25 [408422]: Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt có được bằng cách quay đường tròn  quanh trục
quanh trục 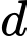 ). Biết rằng
). Biết rằng 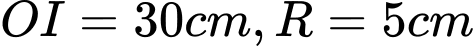 . Thể tích
. Thể tích  của chiếc phao la bao nhiêu lít. Viết kết quả làm tròn đến một chữ số thập phân
của chiếc phao la bao nhiêu lít. Viết kết quả làm tròn đến một chữ số thập phân
 quanh trục
quanh trục  ). Biết rằng
). Biết rằng 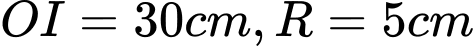 . Thể tích
. Thể tích  của chiếc phao la bao nhiêu lít. Viết kết quả làm tròn đến một chữ số thập phân
của chiếc phao la bao nhiêu lít. Viết kết quả làm tròn đến một chữ số thập phân

Thể tích phao là 14,8 lít