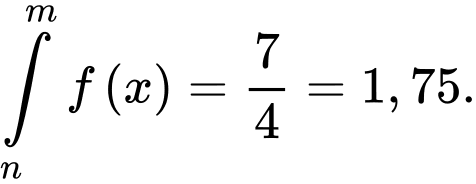Đáp án Bài tập tự luyện số 1
Câu 1 [45972]: Cho đường thẳng 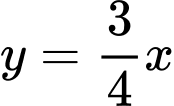 và parabol
và parabol 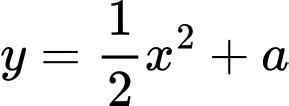 (
(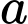 là tham số thực dương). Gọi
là tham số thực dương). Gọi 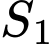 và
và 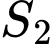 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi 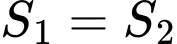 thì
thì 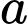 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
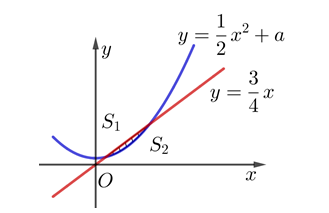
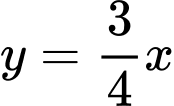 và parabol
và parabol 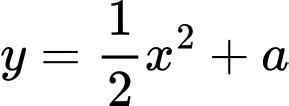 (
(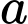 là tham số thực dương). Gọi
là tham số thực dương). Gọi 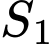 và
và 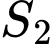 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi 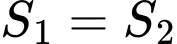 thì
thì 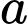 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
A, 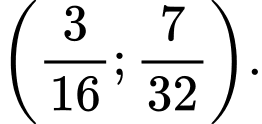
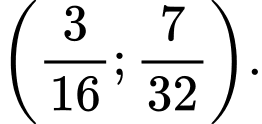
B, 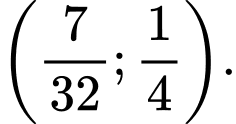
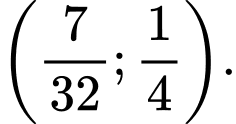
C, 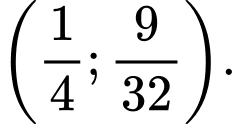
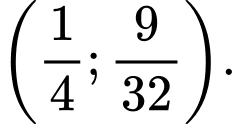
D, 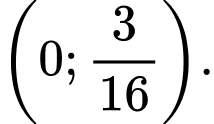
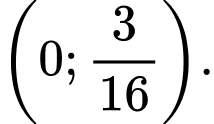
HD: Gọi 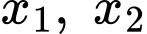 lần lượt là 2 nghiệm của phương trình hoành độ giao điểm
lần lượt là 2 nghiệm của phương trình hoành độ giao điểm 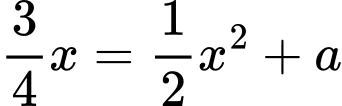 và giả sử
và giả sử 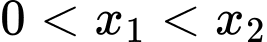 .
.
Do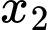 là nghiệm của phương trình
là nghiệm của phương trình 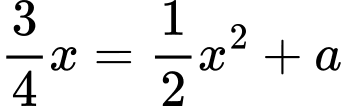 nên
nên 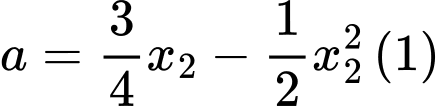
Bài ra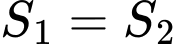 suy ra
suy ra 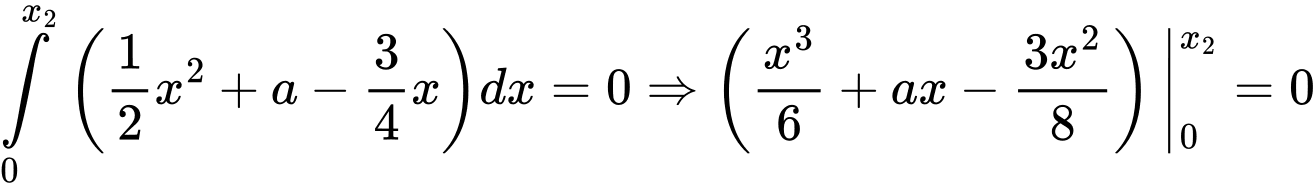
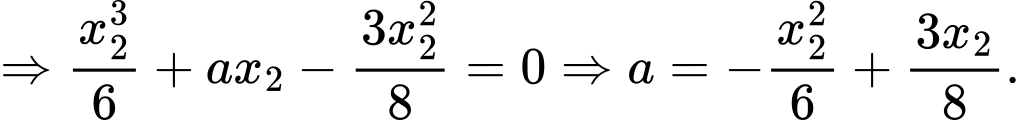
Kết hợp với (1) ta được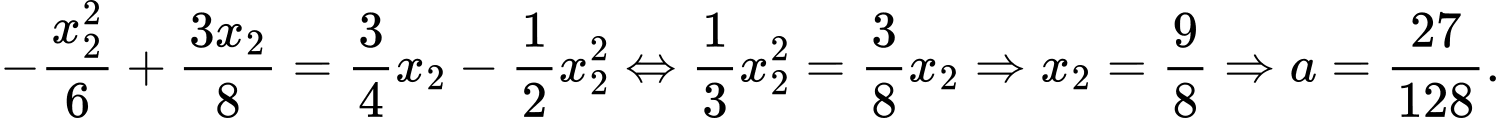
Chọn A. Đáp án: A
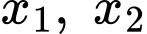 lần lượt là 2 nghiệm của phương trình hoành độ giao điểm
lần lượt là 2 nghiệm của phương trình hoành độ giao điểm 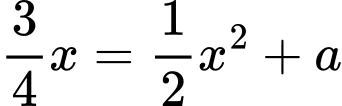 và giả sử
và giả sử 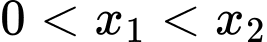 .
.Do
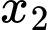 là nghiệm của phương trình
là nghiệm của phương trình 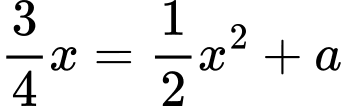 nên
nên 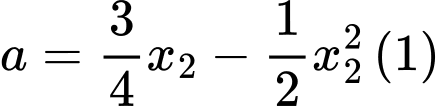
Bài ra
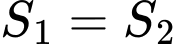 suy ra
suy ra 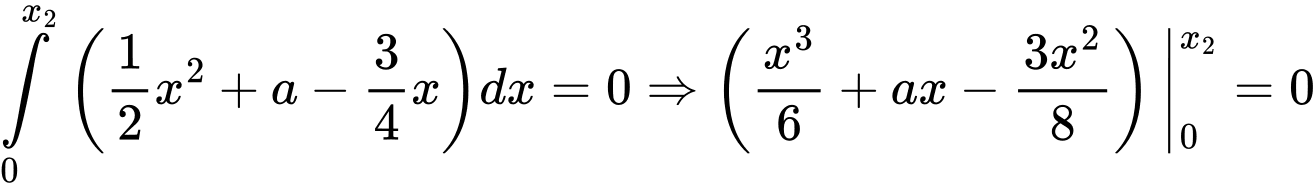
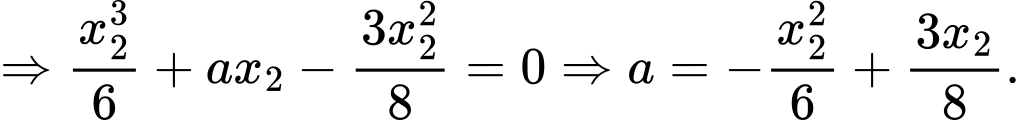
Kết hợp với (1) ta được
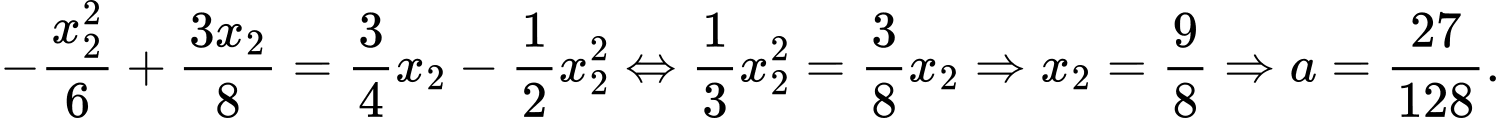
Chọn A. Đáp án: A
Câu 2 [46026]: Cho đường thẳng 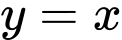 và parabol
và parabol 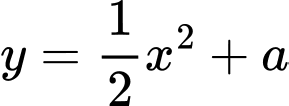 (a là tham số thực dương). Gọi
(a là tham số thực dương). Gọi 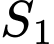 và
và 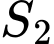 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi 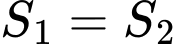 thì
thì 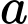 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
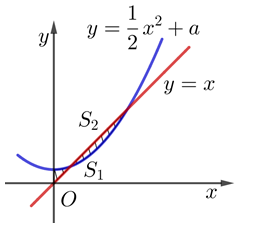
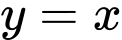 và parabol
và parabol 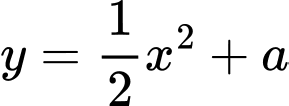 (a là tham số thực dương). Gọi
(a là tham số thực dương). Gọi 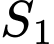 và
và 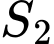 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi 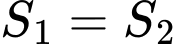 thì
thì 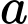 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
A, 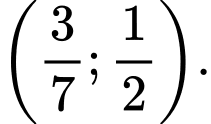
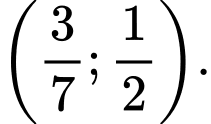
B, 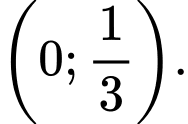
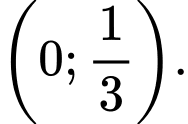
C, 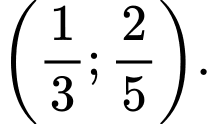
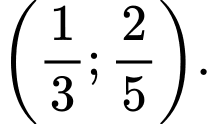
D, 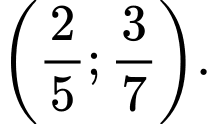
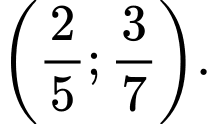
Gọi 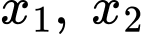 lần lượt là 2 nghiệm của phương trình hoành độ giao điểm
lần lượt là 2 nghiệm của phương trình hoành độ giao điểm 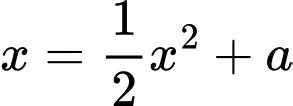 và giả sử
và giả sử 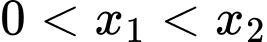 .
.
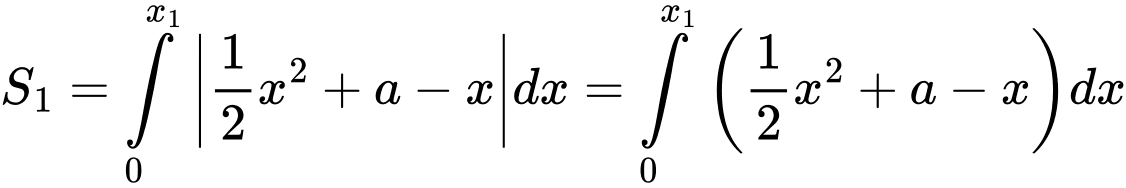 và
và 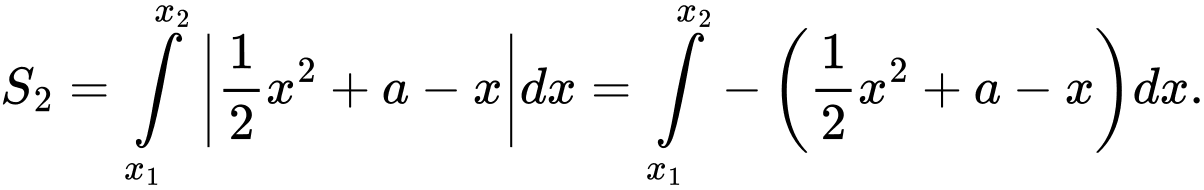
Bài ra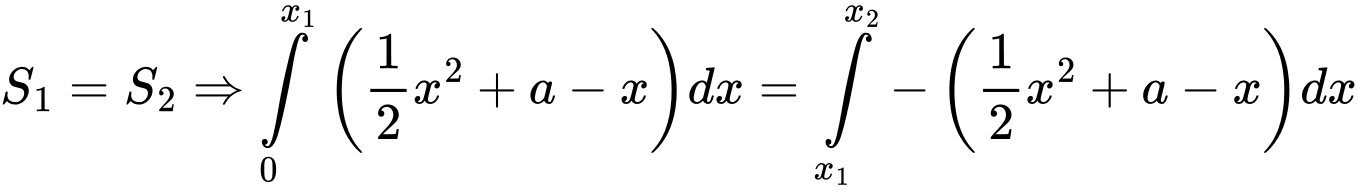
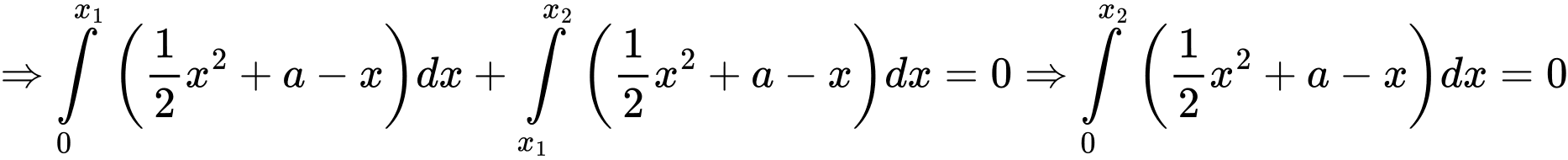
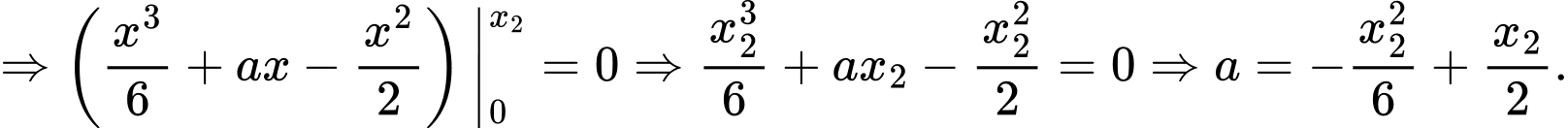
Do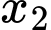 là nghiệm của phương trình
là nghiệm của phương trình 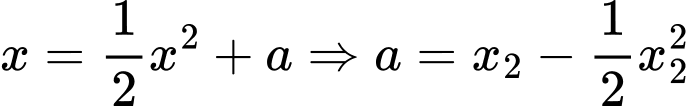
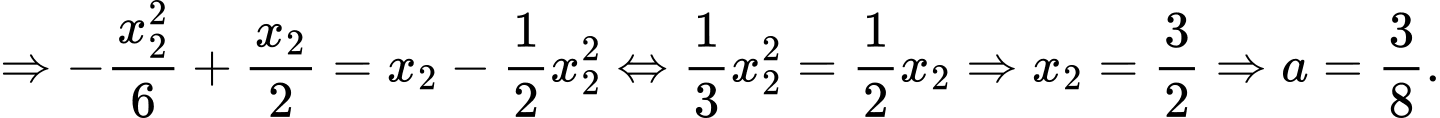 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
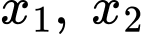 lần lượt là 2 nghiệm của phương trình hoành độ giao điểm
lần lượt là 2 nghiệm của phương trình hoành độ giao điểm 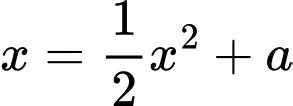 và giả sử
và giả sử 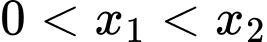 .
. 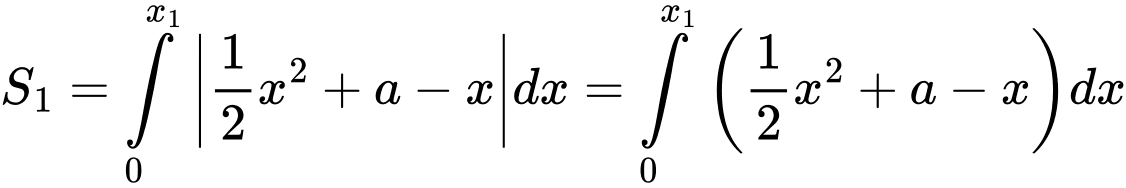 và
và 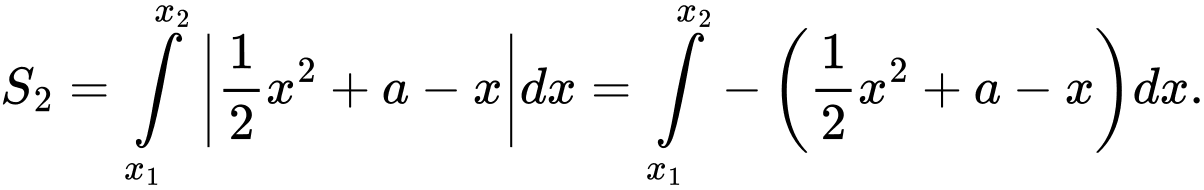
Bài ra
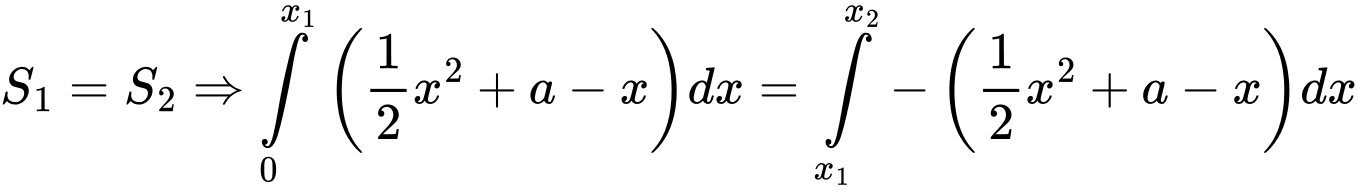
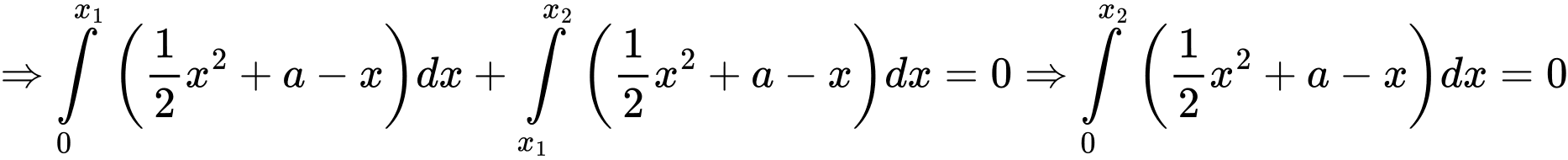
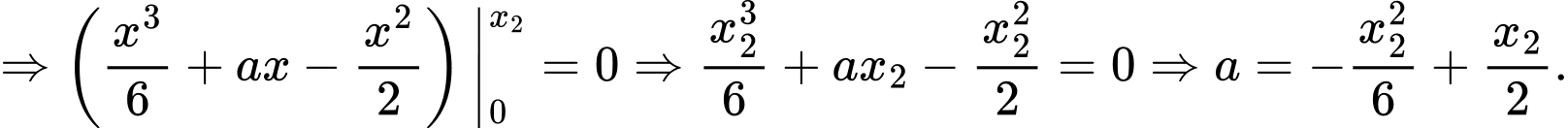
Do
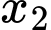 là nghiệm của phương trình
là nghiệm của phương trình 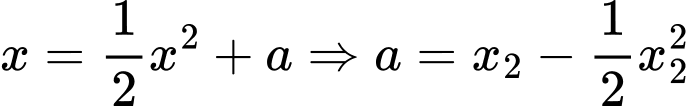
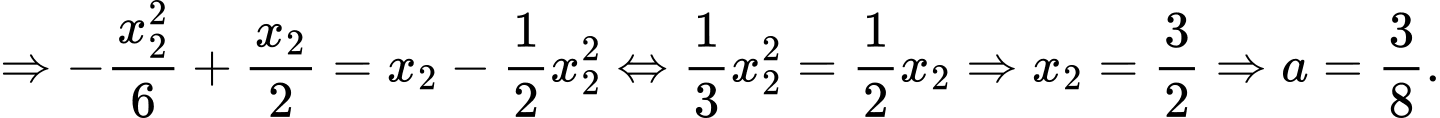 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
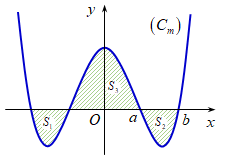
Câu 3 [311993]: Cho hàm số 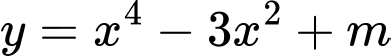 có đồ thị
có đồ thị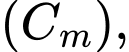 với
với 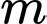 là tham số thực. Giả sử
là tham số thực. Giả sử 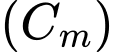 cắt trục
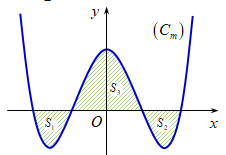
cắt trục 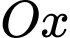 tại bốn điểm phân biệt như hình vẽ. Gọi
tại bốn điểm phân biệt như hình vẽ. Gọi 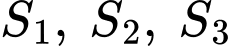 là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm giá trị thực của tham số
là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm giá trị thực của tham số 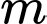 để
để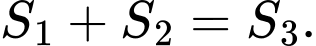
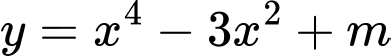 có đồ thị
có đồ thị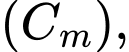 với
với 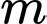 là tham số thực. Giả sử
là tham số thực. Giả sử 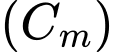 cắt trục
cắt trục 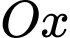 tại bốn điểm phân biệt như hình vẽ. Gọi
tại bốn điểm phân biệt như hình vẽ. Gọi 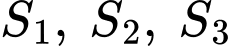 là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm giá trị thực của tham số
là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm giá trị thực của tham số 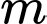 để
để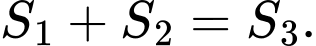

A, 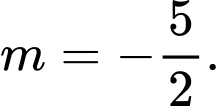
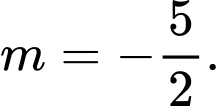
B, 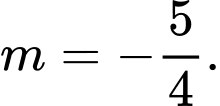
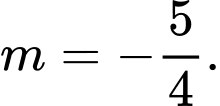
C, 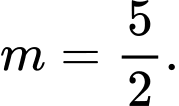
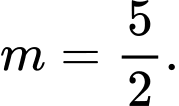
D, 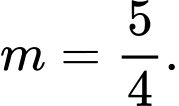
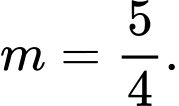
HD: Ta có 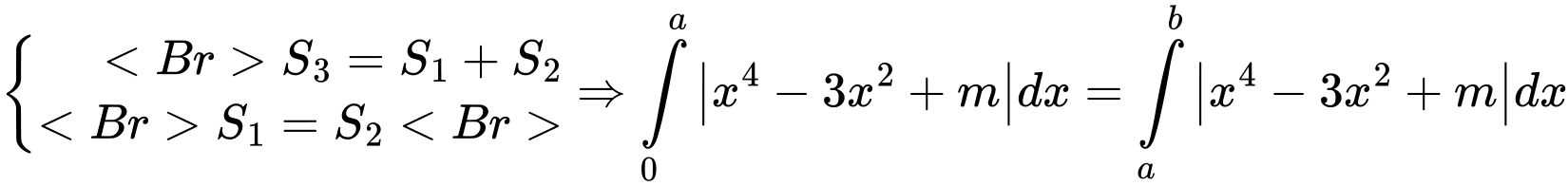
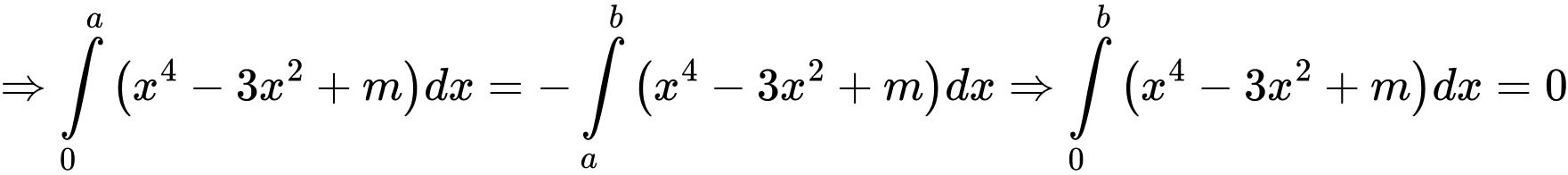
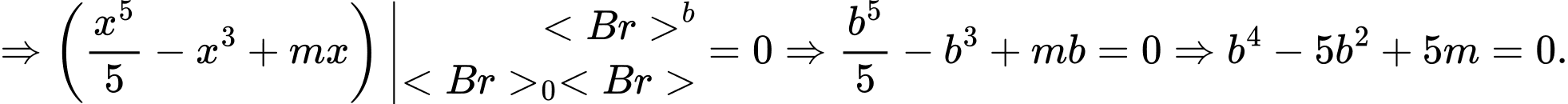
Mà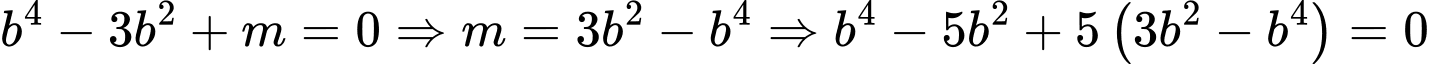
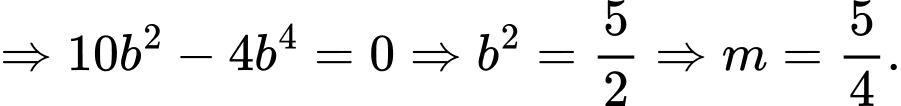
Chọn D.
Đáp án: D
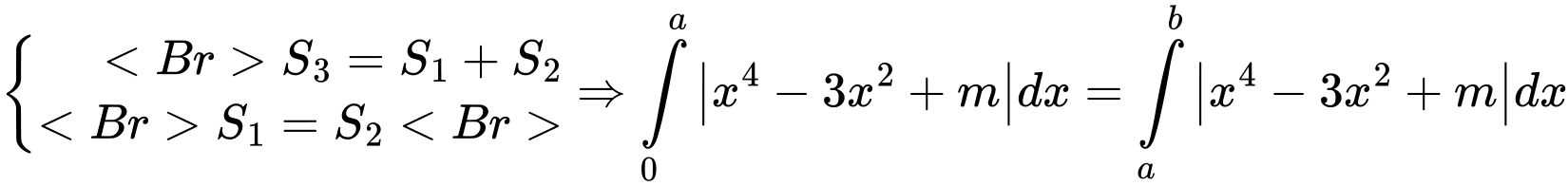

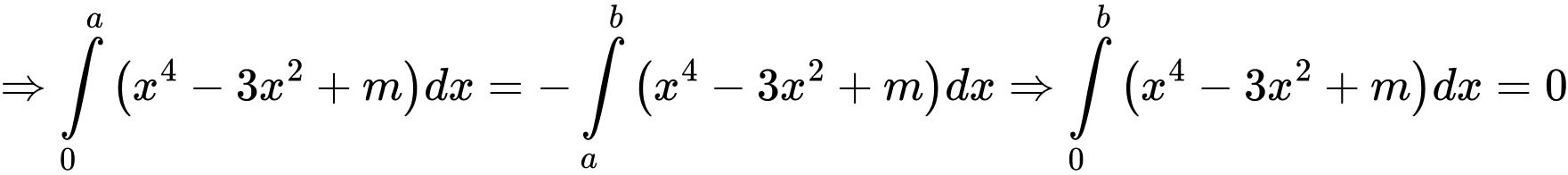
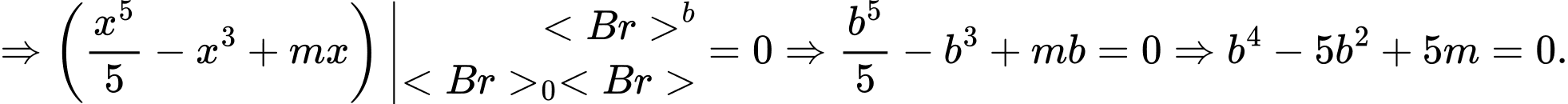
Mà
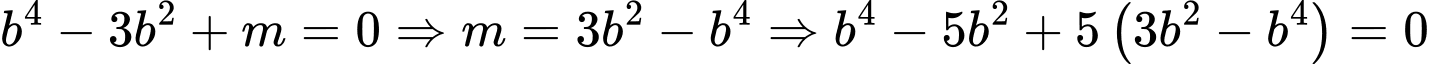
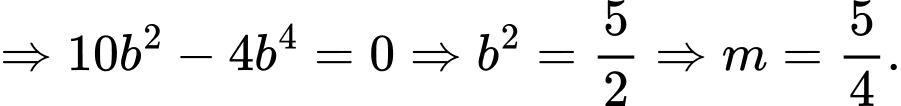
Chọn D.
Đáp án: D
Câu 4 [132954]: Cho hai hàm số 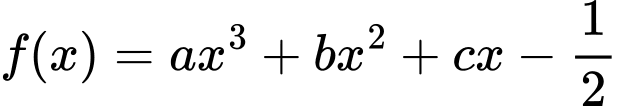 và
và 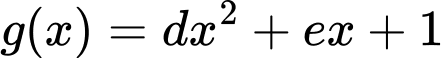 ,
, 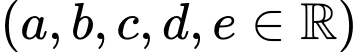 . Biết rằng đồ thị của hàm số
. Biết rằng đồ thị của hàm số 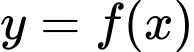 và
và 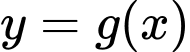 cắt nhau tại ba điểm có hoàng độ lần lượt là
cắt nhau tại ba điểm có hoàng độ lần lượt là 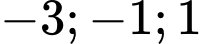 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
![668556[de].png](https://asset.moon.vn/img/ai/Teachers/rongden_167/2019/THPTQG2018/668556[de].png)
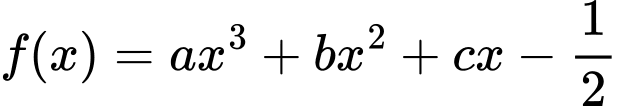 và
và 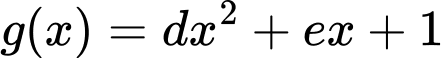 ,
, 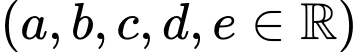 . Biết rằng đồ thị của hàm số
. Biết rằng đồ thị của hàm số 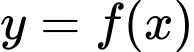 và
và 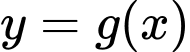 cắt nhau tại ba điểm có hoàng độ lần lượt là
cắt nhau tại ba điểm có hoàng độ lần lượt là 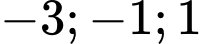 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
![668556[de].png](https://asset.moon.vn/img/ai/Teachers/rongden_167/2019/THPTQG2018/668556[de].png)
A, 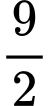 .
.
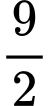 .
.B, 8.
C, 4.
D, 5.
Phương trình hoành độ giao điểm của hai hàm số đã cho là
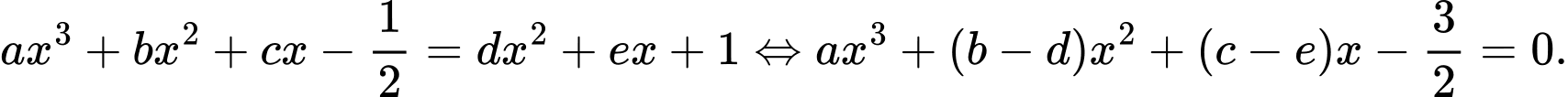
Phương trình có các nghiệm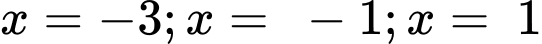
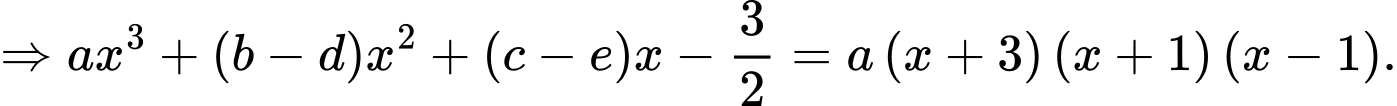
Cho hệ số tự do của hai vế bằng nhau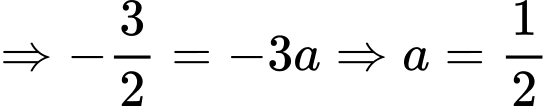
Diện tích hình phẳng cần tính là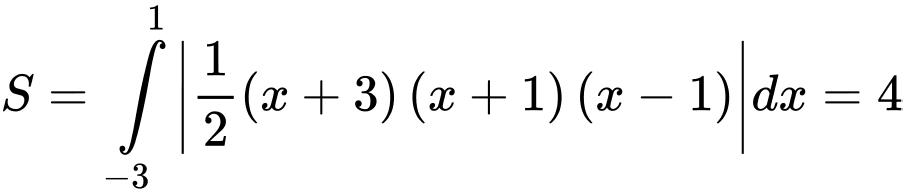 (bấm máy tính). Chọn C.
Đáp án: C
(bấm máy tính). Chọn C.
Đáp án: C
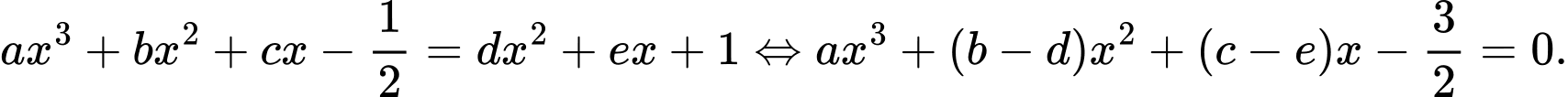
Phương trình có các nghiệm
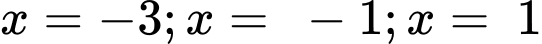
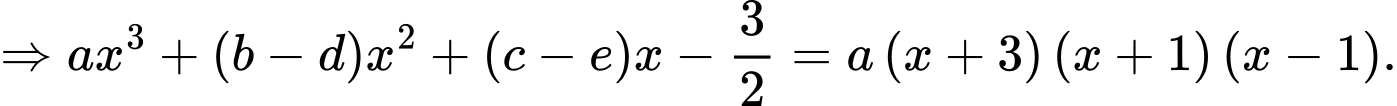
Cho hệ số tự do của hai vế bằng nhau
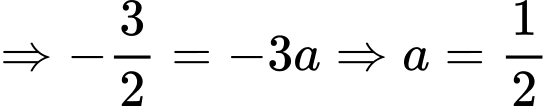
Diện tích hình phẳng cần tính là
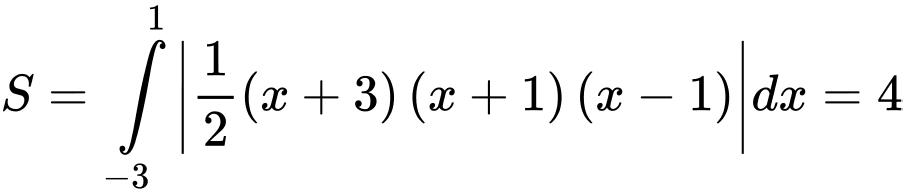 (bấm máy tính). Chọn C.
Đáp án: C
(bấm máy tính). Chọn C.
Đáp án: C
Câu 5 [135960]: Cho hai hàm số 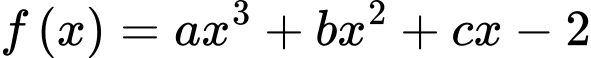 và
và 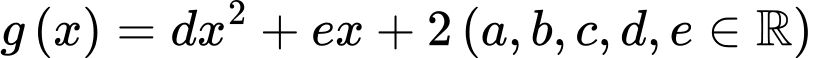 . Biết rằng đồ thị của hàm số
. Biết rằng đồ thị của hàm số 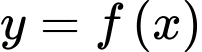 và
và 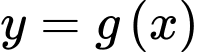 cắt nhau tại ba điểm có hoành độ lần lượt là
cắt nhau tại ba điểm có hoành độ lần lượt là 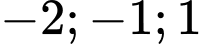 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
![668901[de].png](https://asset.moon.vn/img/ai/Teachers/rongden_167/2019/THPTQG2018/668901[de].png)
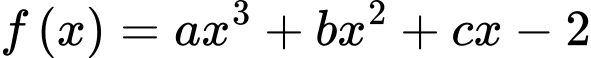 và
và 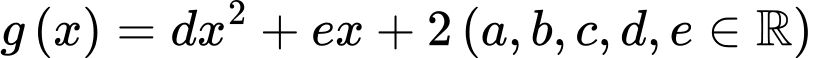 . Biết rằng đồ thị của hàm số
. Biết rằng đồ thị của hàm số 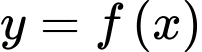 và
và 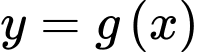 cắt nhau tại ba điểm có hoành độ lần lượt là
cắt nhau tại ba điểm có hoành độ lần lượt là 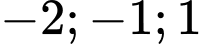 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
![668901[de].png](https://asset.moon.vn/img/ai/Teachers/rongden_167/2019/THPTQG2018/668901[de].png)
A, 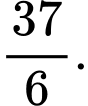
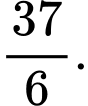
B, 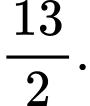
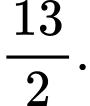
C, 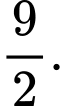
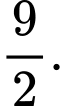
D, 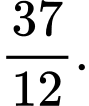
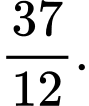
HD: Phương trình hoành độ giao điểm của hai hàm số đã cho là

Phương trình có các nghiệm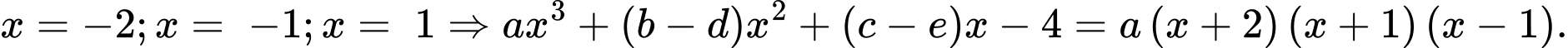
Cho hệ số tự do của hai vế bằng nhau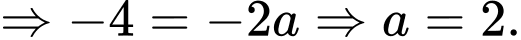
Diện tích hình phẳng cần tính là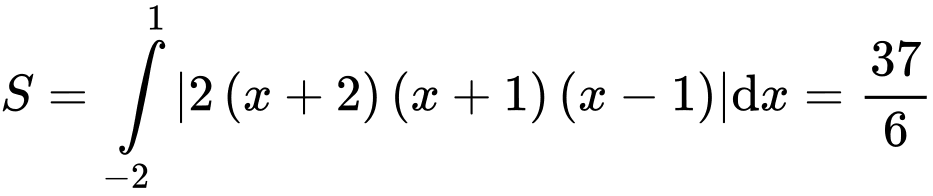 (bấm máy tính). Chọn A.
Đáp án: A
(bấm máy tính). Chọn A.
Đáp án: A

Phương trình có các nghiệm
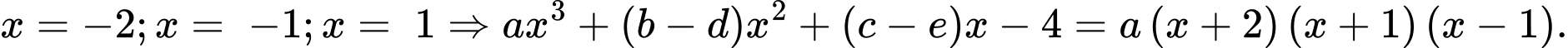
Cho hệ số tự do của hai vế bằng nhau
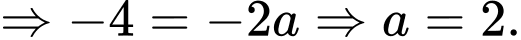
Diện tích hình phẳng cần tính là
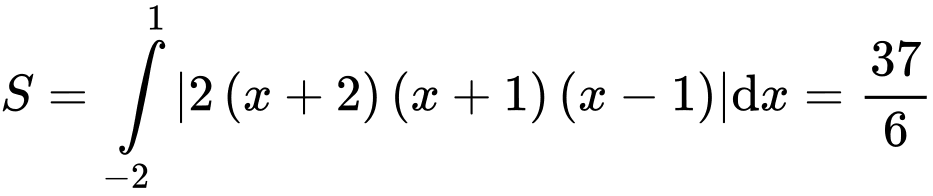 (bấm máy tính). Chọn A.
Đáp án: A
(bấm máy tính). Chọn A.
Đáp án: A
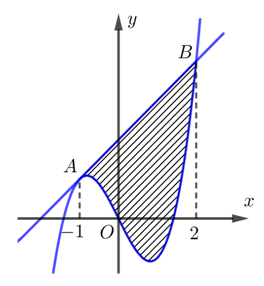
Câu 6 [9679]: Cho hàm số 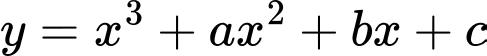 có đồ thị
có đồ thị  . Biết rằng tiếp tuyến
. Biết rằng tiếp tuyến 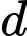 của
của  tại điểm
tại điểm 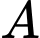 có hoành độ bằng
có hoành độ bằng 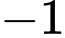 cắt
cắt  tại
tại 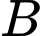 có hoành độ bằng
có hoành độ bằng 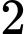 (xem hình vẽ). Diện tích hình phẳng giới hạn bởi
(xem hình vẽ). Diện tích hình phẳng giới hạn bởi 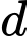 và
và  (phần gạch chéo trong hình vẽ) bằng
(phần gạch chéo trong hình vẽ) bằng
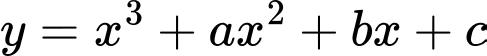 có đồ thị
có đồ thị  . Biết rằng tiếp tuyến
. Biết rằng tiếp tuyến 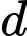 của
của  tại điểm
tại điểm 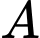 có hoành độ bằng
có hoành độ bằng 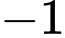 cắt
cắt  tại
tại 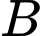 có hoành độ bằng
có hoành độ bằng 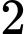 (xem hình vẽ). Diện tích hình phẳng giới hạn bởi
(xem hình vẽ). Diện tích hình phẳng giới hạn bởi 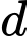 và
và  (phần gạch chéo trong hình vẽ) bằng
(phần gạch chéo trong hình vẽ) bằng
A, 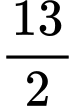 .
.
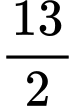 .
.B, 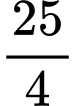 .
.
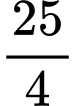 .
.C, 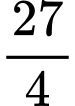 .
.
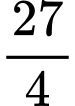 .
.D, 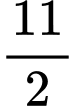 .
.
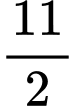 .
.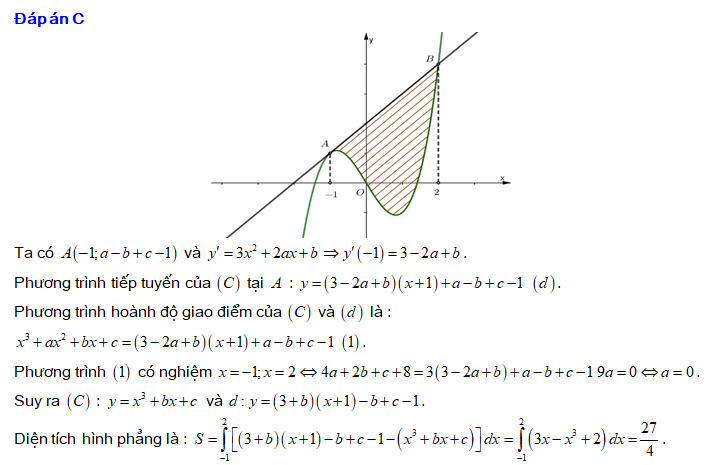 Đáp án: C
Đáp án: C
Câu 7 [789821]: Cho 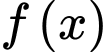 là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm
là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm 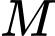 có hoành độ bằng
có hoành độ bằng 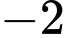 cắt đồ thị tại điểm thứ hai là
cắt đồ thị tại điểm thứ hai là 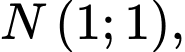 cắt
cắt 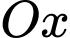 tại điểm có hoành độ bằng 4. Biết diện tích phần gạch chéo là
tại điểm có hoành độ bằng 4. Biết diện tích phần gạch chéo là 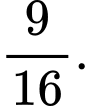 Tính tích phân
Tính tích phân 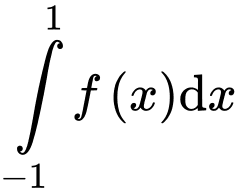
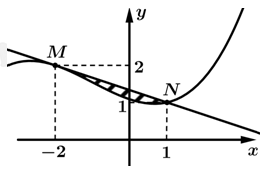
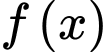 là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm
là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm 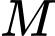 có hoành độ bằng
có hoành độ bằng 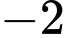 cắt đồ thị tại điểm thứ hai là
cắt đồ thị tại điểm thứ hai là 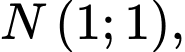 cắt
cắt 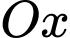 tại điểm có hoành độ bằng 4. Biết diện tích phần gạch chéo là
tại điểm có hoành độ bằng 4. Biết diện tích phần gạch chéo là 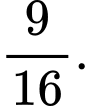 Tính tích phân
Tính tích phân 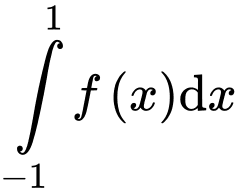

A, 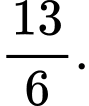
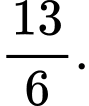
B, 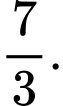
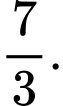
C, 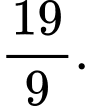
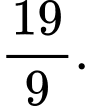
D, 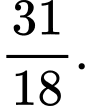
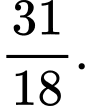
HD: Phương trình đường thẳng tiếp tuyến là 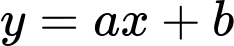
Lại có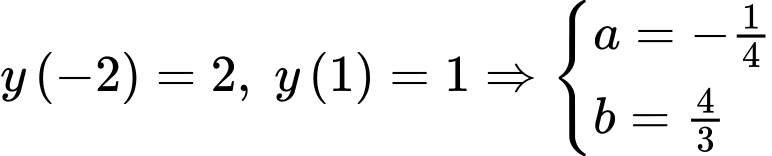
Ta có: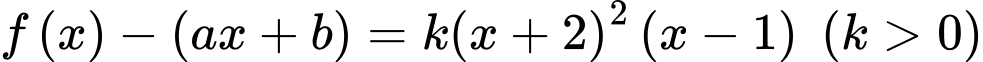
Lại có: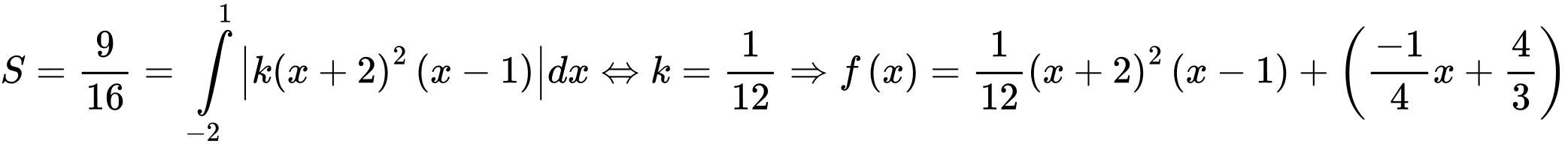
Vậy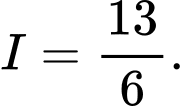 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
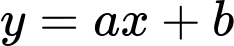
Lại có
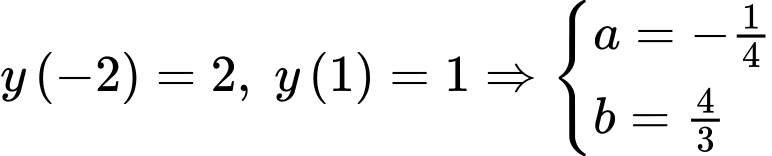
Ta có:
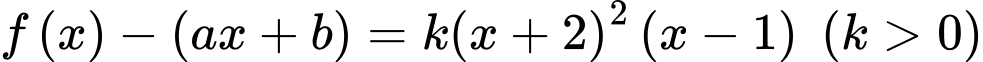
Lại có:
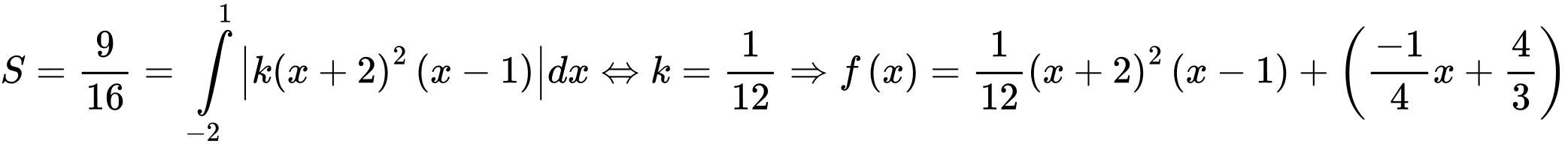
Vậy
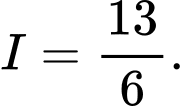 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
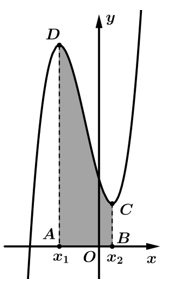
Câu 8 [408532]: Cho hàm số đa thức bậc ba 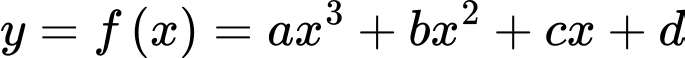 đạt cực trị tại
đạt cực trị tại 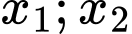 và
và 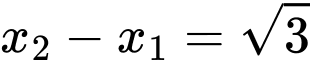 , có đồ thị như hình vẽ. Biết
, có đồ thị như hình vẽ. Biết 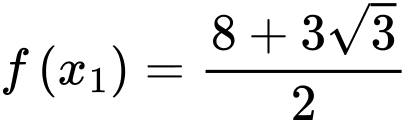 và diện tích hình thang cong
và diện tích hình thang cong 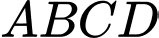 ở hình vẽ (phần tô đậm) là
ở hình vẽ (phần tô đậm) là 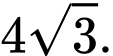 Tính
Tính 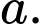
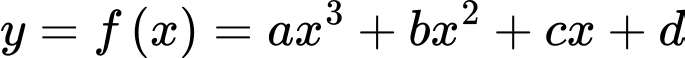 đạt cực trị tại
đạt cực trị tại 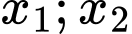 và
và 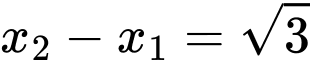 , có đồ thị như hình vẽ. Biết
, có đồ thị như hình vẽ. Biết 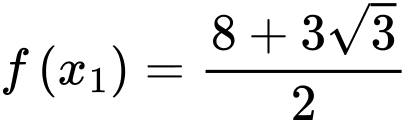 và diện tích hình thang cong
và diện tích hình thang cong 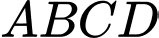 ở hình vẽ (phần tô đậm) là
ở hình vẽ (phần tô đậm) là 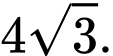 Tính
Tính 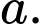

Không mất tính tổng quát ta tịnh tiến đồ thị hàm số sang phải (hình vẽ)
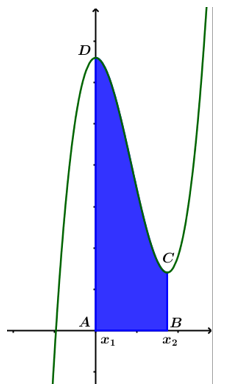
Sao cho: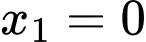 (gốc toạ độ) theo giả thiết:
(gốc toạ độ) theo giả thiết: 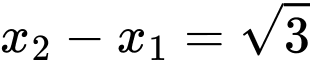
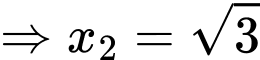
Mà hàm số đa thức bậc ba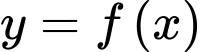 đạt cực trị tại
đạt cực trị tại 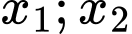 nên
nên
Do đó ta giả sử: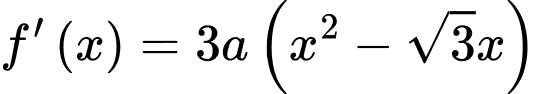
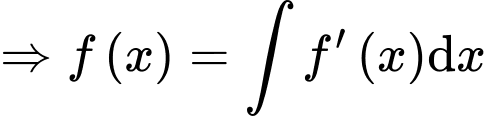
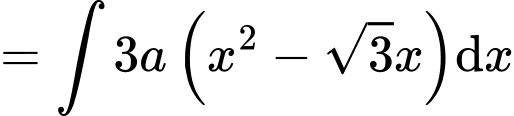
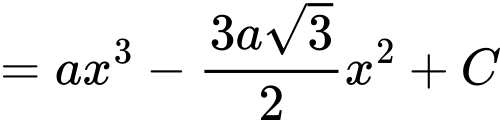
Mà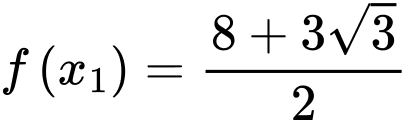
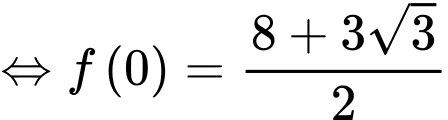
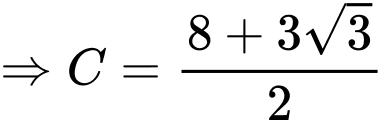
Suy ra: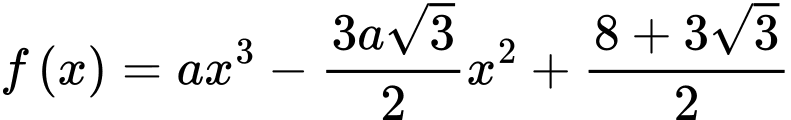
Lại có: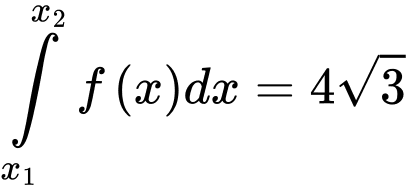
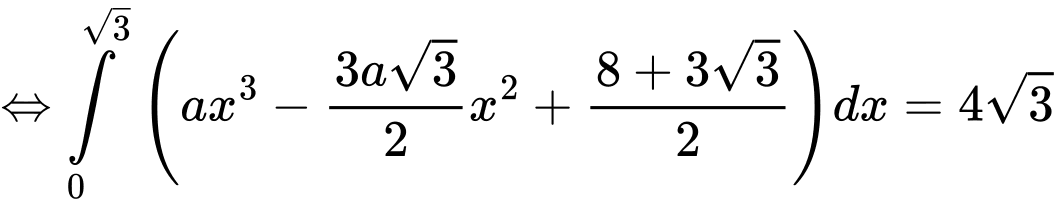
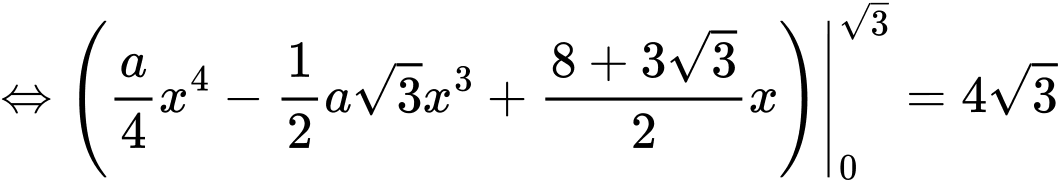
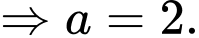

Sao cho:
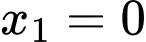 (gốc toạ độ) theo giả thiết:
(gốc toạ độ) theo giả thiết: 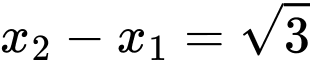
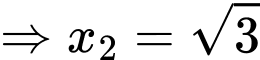
Mà hàm số đa thức bậc ba
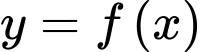 đạt cực trị tại
đạt cực trị tại 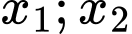 nên
nên
Do đó ta giả sử:
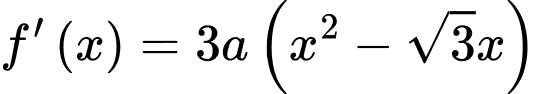
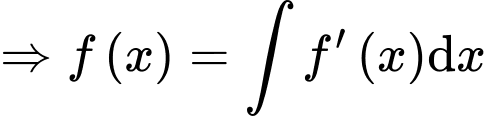
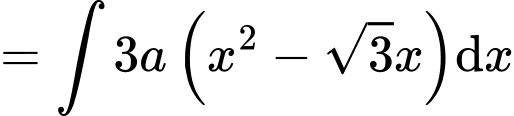
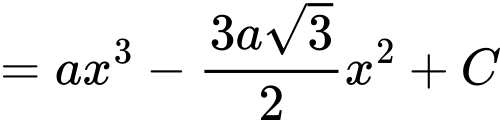
Mà
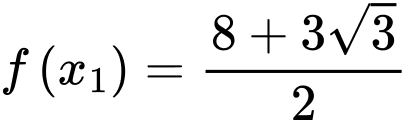
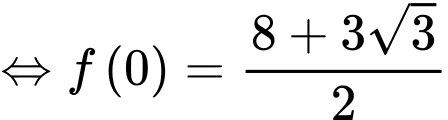
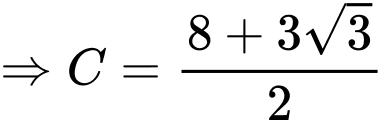
Suy ra:
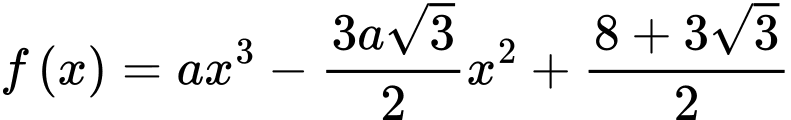
Lại có:
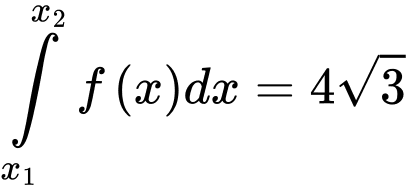
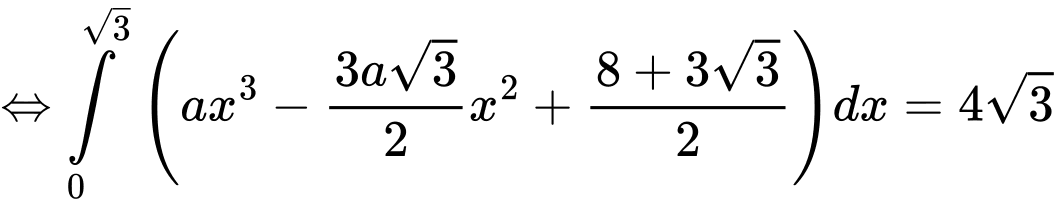
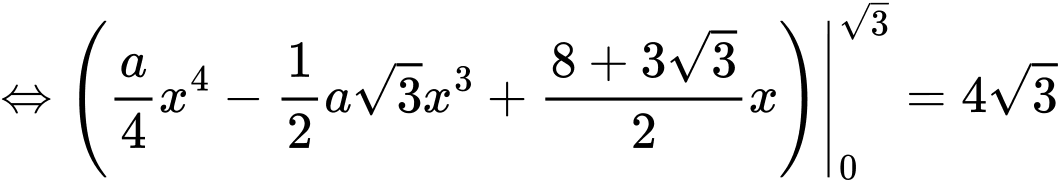
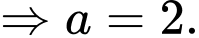
Câu 9 [222289]: Cho hàm số 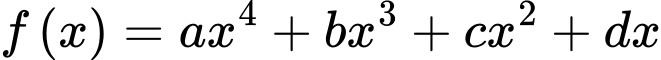 có ba điểm cực trị là
có ba điểm cực trị là 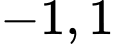 và 3. Gọi
và 3. Gọi 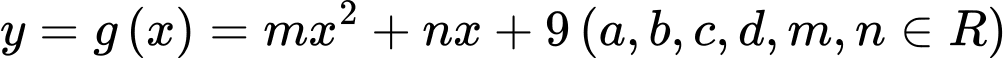 là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số
là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số 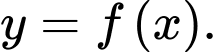 Tính diện tích hình phẳng giới hạn bởi hai đường cong
Tính diện tích hình phẳng giới hạn bởi hai đường cong 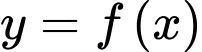 và
và 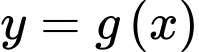
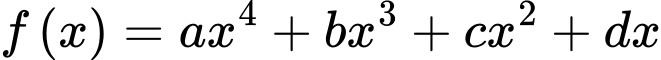 có ba điểm cực trị là
có ba điểm cực trị là 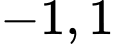 và 3. Gọi
và 3. Gọi 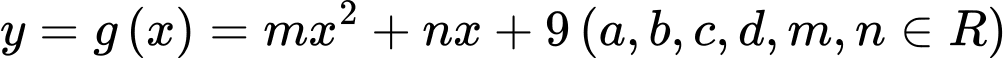 là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số
là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số 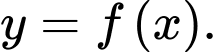 Tính diện tích hình phẳng giới hạn bởi hai đường cong
Tính diện tích hình phẳng giới hạn bởi hai đường cong 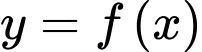 và
và 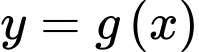
A, 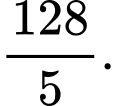
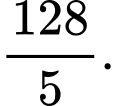
B, 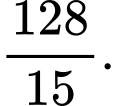
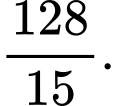
C, 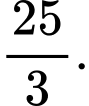
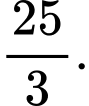
D, 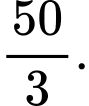
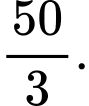
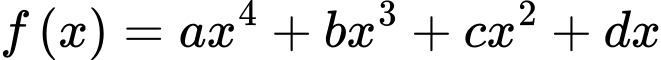
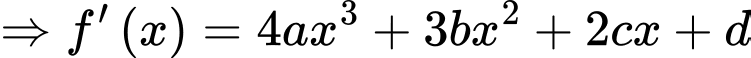
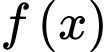 có ba điểm cực trị là
có ba điểm cực trị là 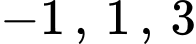

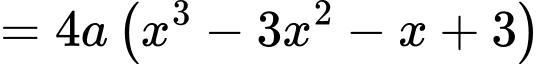
Do
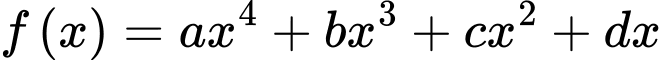 nên phương trình không có hệ số tự do.
nên phương trình không có hệ số tự do.
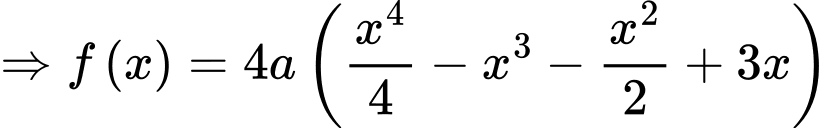
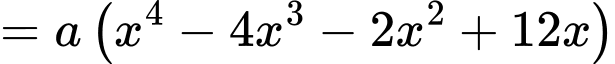
Lại có: Đồ thị hàm số
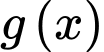 đi qua ba điểm cực trị của đồ thị
đi qua ba điểm cực trị của đồ thị 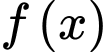 nên ta có:
nên ta có:
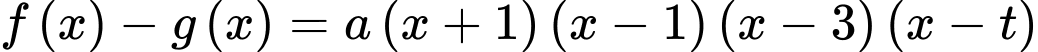

Cân bằng hệ số của
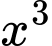 ta có:
ta có:
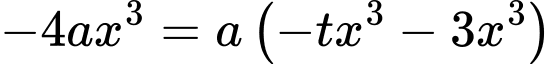
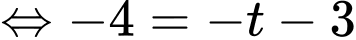
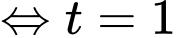
Cân bằng hệ số tự do hai vế, ta có:
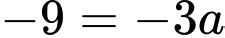
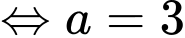
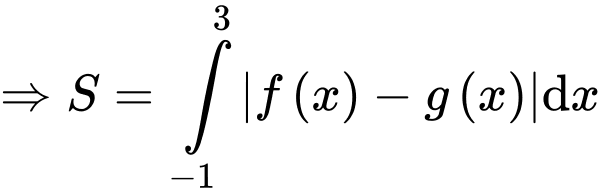
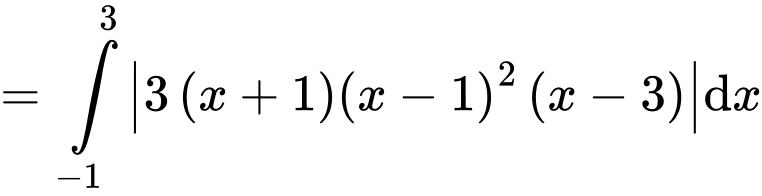
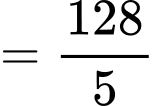
Đáp án: A Đáp án: A
Câu 10 [971913]: Cho hàm số 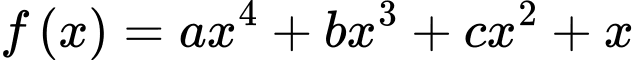 và
và 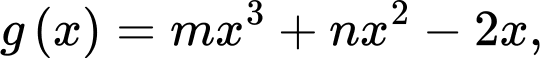 với
với 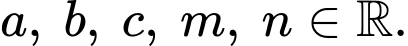 Biết hàm số
Biết hàm số 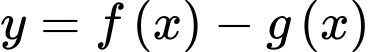 có 3 điểm cực trị là
có 3 điểm cực trị là 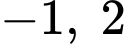 và
và 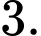 Diện tích hình phẳng giới hạn bởi các đường
Diện tích hình phẳng giới hạn bởi các đường 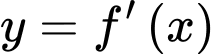 và
và 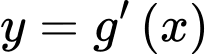 bằng
bằng
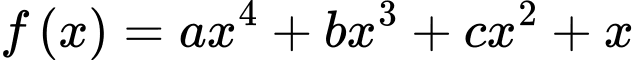 và
và 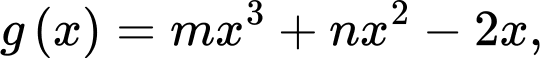 với
với 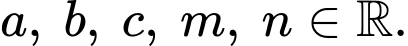 Biết hàm số
Biết hàm số 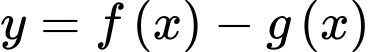 có 3 điểm cực trị là
có 3 điểm cực trị là 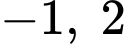 và
và 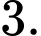 Diện tích hình phẳng giới hạn bởi các đường
Diện tích hình phẳng giới hạn bởi các đường 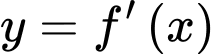 và
và 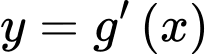 bằng
bằng A, 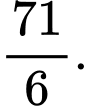
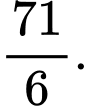
B, 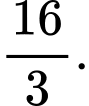
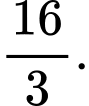
C, 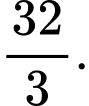
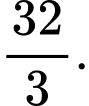
D, 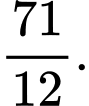
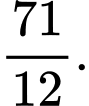
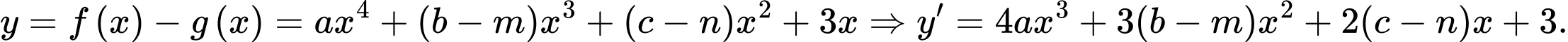
Hàm số 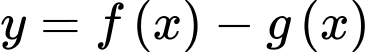 có 3 điểm cực trị là
có 3 điểm cực trị là 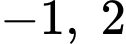 và 3 nên
và 3 nên 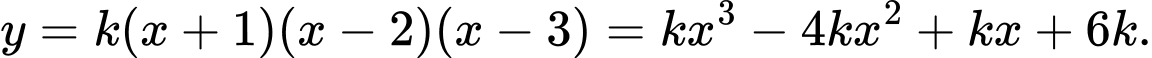
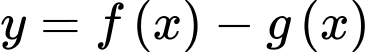 có 3 điểm cực trị là
có 3 điểm cực trị là 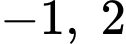 và 3 nên
và 3 nên 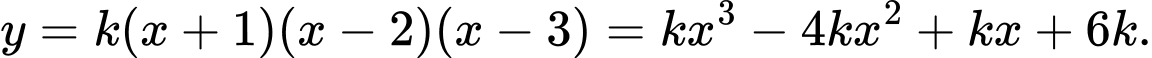
Đồng nhất hệ số ta có: 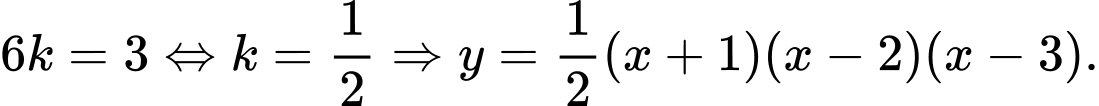
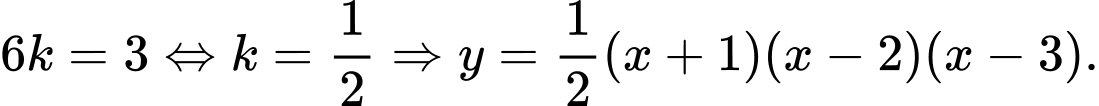
Diện tích hình phẳng giới hạn bởi các đường 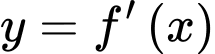 và
và 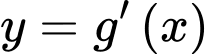 bằng
bằng
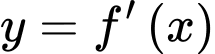 và
và 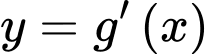 bằng
bằng 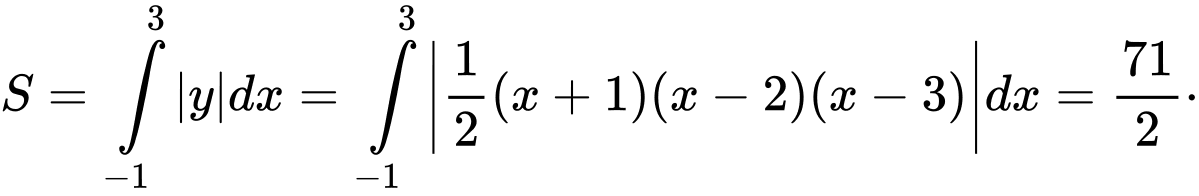
Chọn đáp án D.
Câu 11 [212396]: Cho hàm số 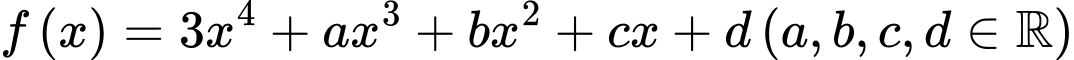 có ba điểm cực trị là
có ba điểm cực trị là 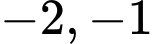 và 1. Gọi
và 1. Gọi 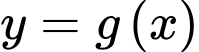 là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số
là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số 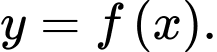 Diện tích hình phẳng giới hạn bởi hai đường
Diện tích hình phẳng giới hạn bởi hai đường 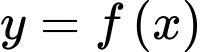 và
và 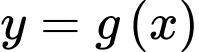 bằng
bằng
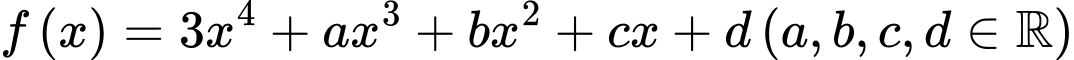 có ba điểm cực trị là
có ba điểm cực trị là 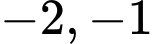 và 1. Gọi
và 1. Gọi 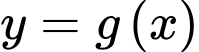 là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số
là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số 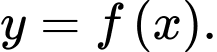 Diện tích hình phẳng giới hạn bởi hai đường
Diện tích hình phẳng giới hạn bởi hai đường 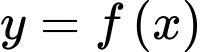 và
và 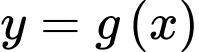 bằng
bằng A, 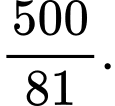
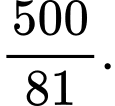
B, 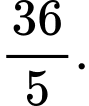
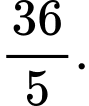
C, 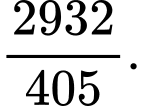
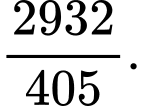
D, 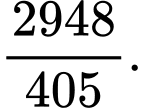
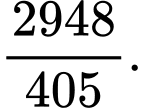
Chọn D
Do 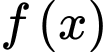 có ba điểm cực trị là
có ba điểm cực trị là 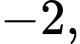
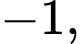
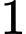 nên:
nên:
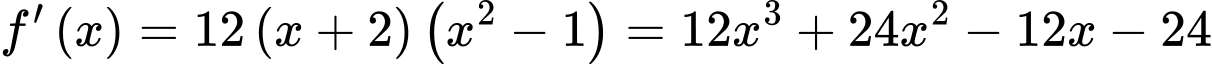
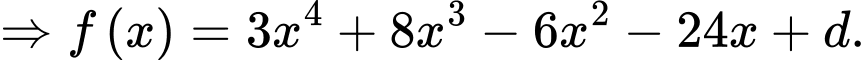
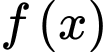 có ba điểm cực trị là
có ba điểm cực trị là 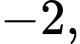
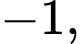
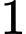 nên:
nên:
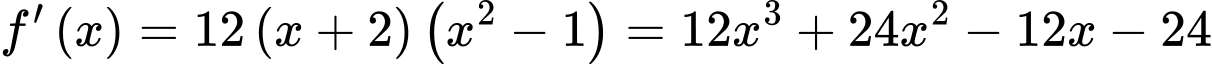
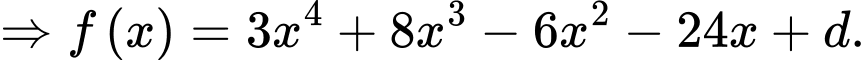
Thực hiện phép chia 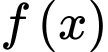 cho
cho 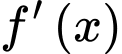 ta được:
ta được:
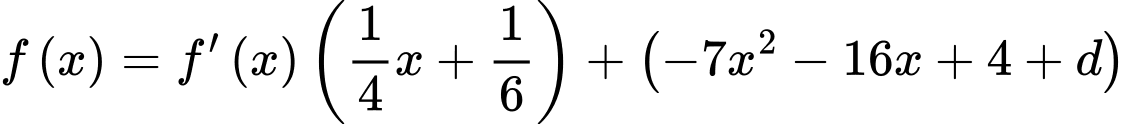
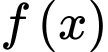 cho
cho 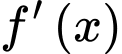 ta được:
ta được:
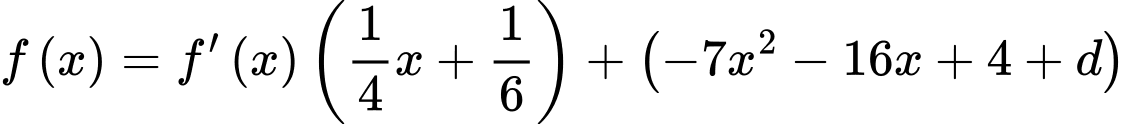
Mà 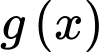 là parabol qua các điểm cực trị của
là parabol qua các điểm cực trị của 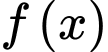 nên
nên 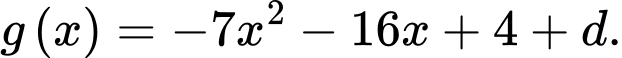
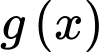 là parabol qua các điểm cực trị của
là parabol qua các điểm cực trị của 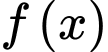 nên
nên 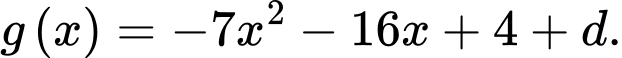
Xét phương trình hoành độ giao điểm: 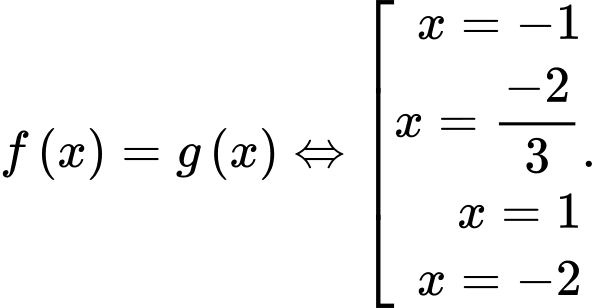
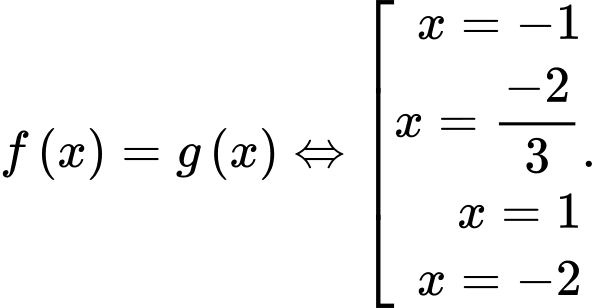
Khi đó diện tích hình phẳng giới hạn bởi 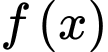 và
và 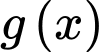 là:
là:
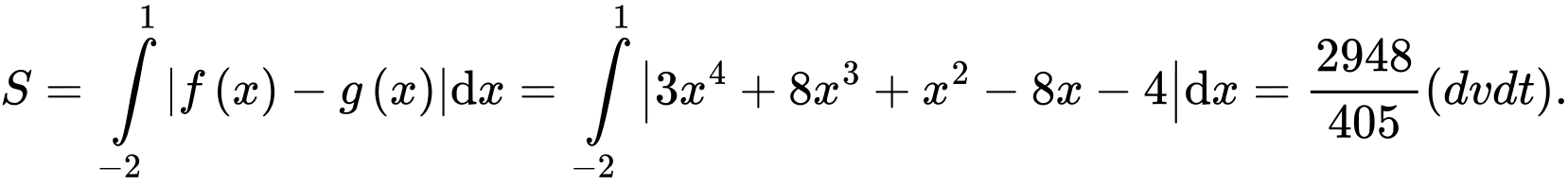
Đáp án: D 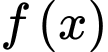 và
và 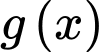 là:
là:
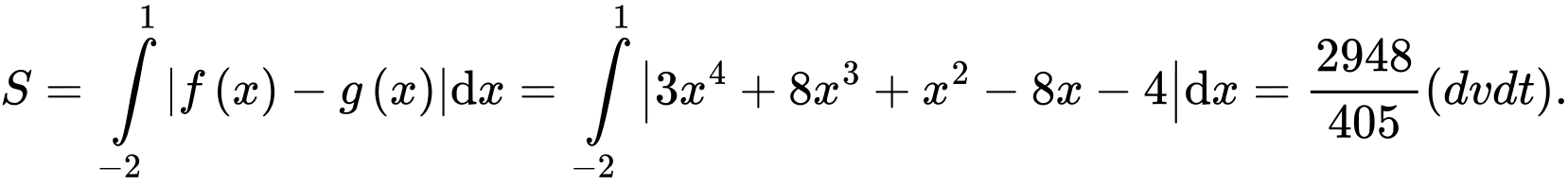
Câu 12 [151385]: Cho hàm số 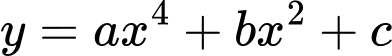 có đồ thị
có đồ thị  biết rằng
biết rằng  đi qua điểm
đi qua điểm 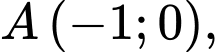 tiếp tuyến
tiếp tuyến 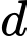 tại
tại 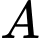 của
của  cắt
cắt  tại hai điểm có hoành độ lần lượt là
tại hai điểm có hoành độ lần lượt là  và
và 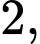 diện tích hình phẳng giới hạn bởi
diện tích hình phẳng giới hạn bởi 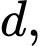 đồ thị
đồ thị  và hai đường thẳng
và hai đường thẳng 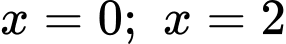 có diện tích bằng
có diện tích bằng 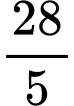 (phần gạch chéo trong hình vẽ).
(phần gạch chéo trong hình vẽ).
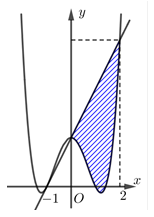
Diện tích hình phẳng giới hạn bởi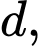 đồ thị
đồ thị  và hai đường thẳng
và hai đường thẳng 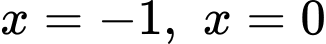 có diện tích bằng
có diện tích bằng
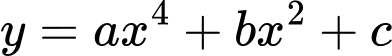 có đồ thị
có đồ thị  biết rằng
biết rằng  đi qua điểm
đi qua điểm 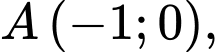 tiếp tuyến
tiếp tuyến 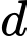 tại
tại 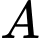 của
của  cắt
cắt  tại hai điểm có hoành độ lần lượt là
tại hai điểm có hoành độ lần lượt là  và
và 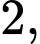 diện tích hình phẳng giới hạn bởi
diện tích hình phẳng giới hạn bởi 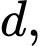 đồ thị
đồ thị  và hai đường thẳng
và hai đường thẳng 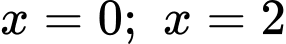 có diện tích bằng
có diện tích bằng 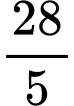 (phần gạch chéo trong hình vẽ).
(phần gạch chéo trong hình vẽ).
Diện tích hình phẳng giới hạn bởi
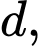 đồ thị
đồ thị  và hai đường thẳng
và hai đường thẳng 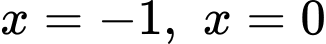 có diện tích bằng
có diện tích bằng A, 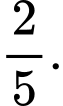
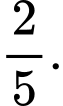
B, 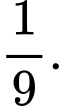
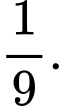
C, 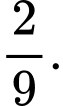
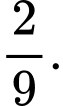
D, 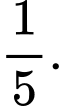
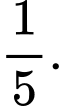
 Đáp án: D
Đáp án: D
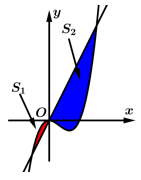
Câu 13 [971726]: [Đề Sở Phú Thọ-2021]: Cho đường cong 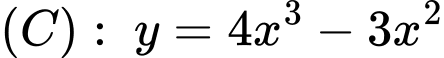 và đường thẳng
và đường thẳng 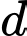 đi qua gốc tọa độ
đi qua gốc tọa độ  tạo thành hai miền phẳng có diện tích
tạo thành hai miền phẳng có diện tích 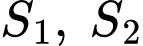 như hình vẽ. Khi
như hình vẽ. Khi 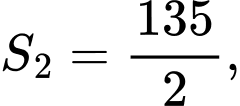 tính
tính 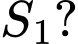
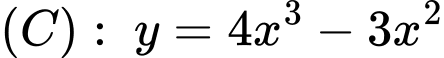 và đường thẳng
và đường thẳng 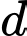 đi qua gốc tọa độ
đi qua gốc tọa độ  tạo thành hai miền phẳng có diện tích
tạo thành hai miền phẳng có diện tích 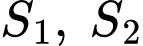 như hình vẽ. Khi
như hình vẽ. Khi 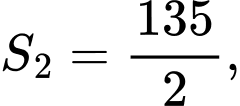 tính
tính 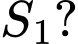

A, 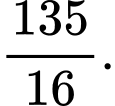
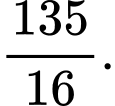
B, 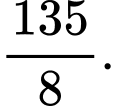
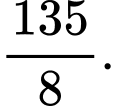
C, 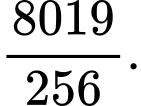
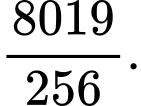
D, 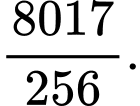
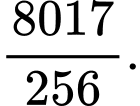
HD: Phương trình 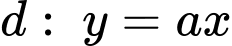 , ta giả sử 2 đồ thị cắt nhau tại các điểm
, ta giả sử 2 đồ thị cắt nhau tại các điểm 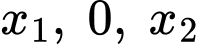 Khi đó
Khi đó 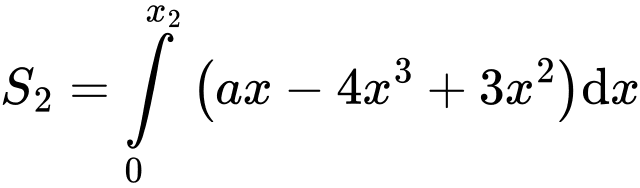 và
và 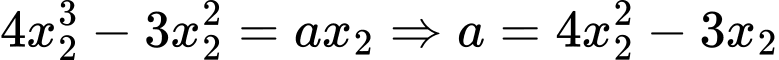 Thế vào ta được
Thế vào ta được 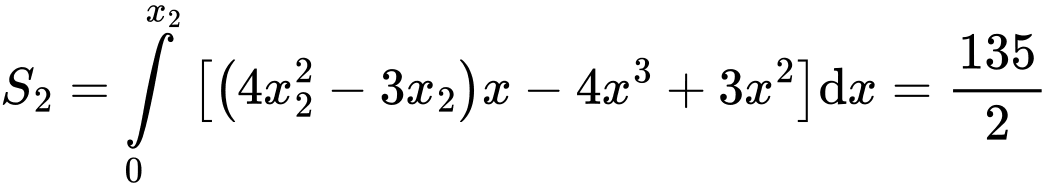 (chỗ này có slove được ko các em nhỉ???)
Suy ra
(chỗ này có slove được ko các em nhỉ???)
Suy ra 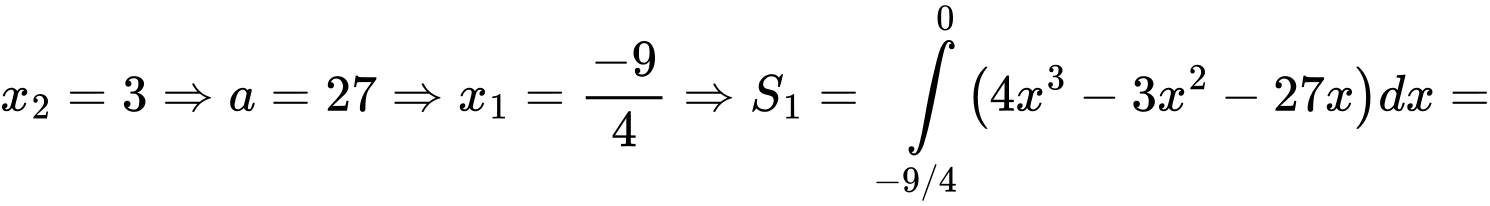
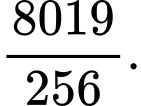 Chọn C. Đáp án: C
Chọn C. Đáp án: C
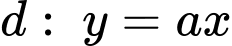 , ta giả sử 2 đồ thị cắt nhau tại các điểm
, ta giả sử 2 đồ thị cắt nhau tại các điểm 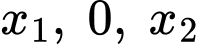 Khi đó
Khi đó 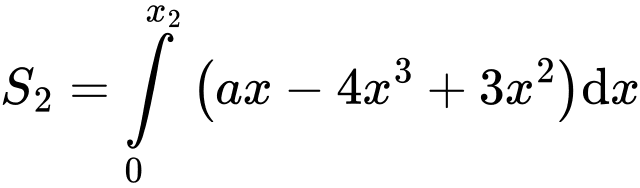 và
và 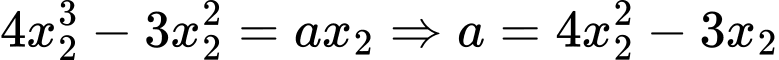 Thế vào ta được
Thế vào ta được 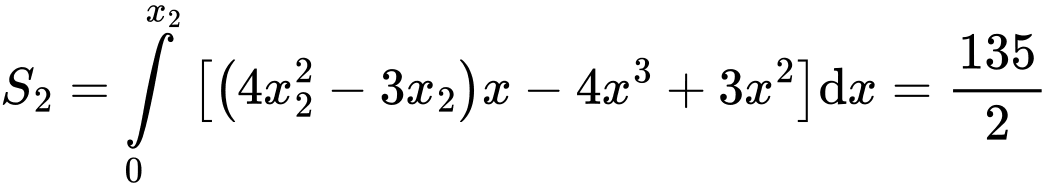 (chỗ này có slove được ko các em nhỉ???)
Suy ra
(chỗ này có slove được ko các em nhỉ???)
Suy ra 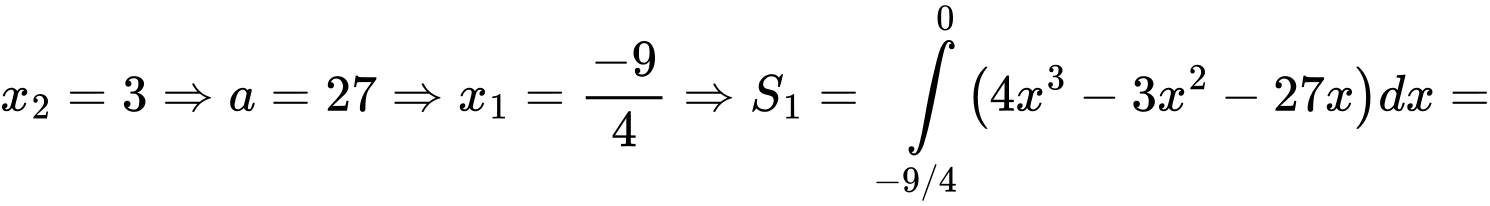
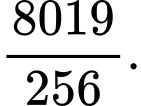 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 14 [205520]: Cho đường cong 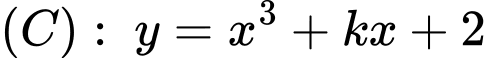 và Parabol
và Parabol 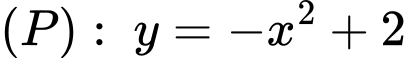 tạo thành hai miền phẳng có diện tích
tạo thành hai miền phẳng có diện tích 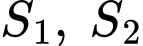 như hình vẽ bên. Biết
như hình vẽ bên. Biết 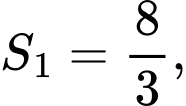 giá trị của
giá trị của 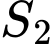 bằng
bằng =kphan2de1/44,cau44.png)
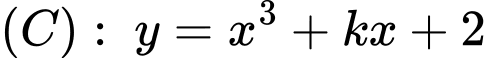 và Parabol
và Parabol 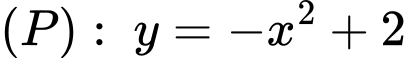 tạo thành hai miền phẳng có diện tích
tạo thành hai miền phẳng có diện tích 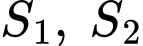 như hình vẽ bên. Biết
như hình vẽ bên. Biết 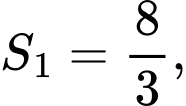 giá trị của
giá trị của 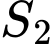 bằng
bằng =kphan2de1/44,cau44.png)
A, 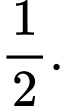
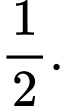
B, 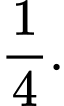
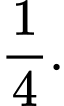
C, 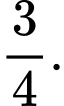
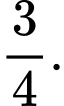
D, 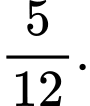
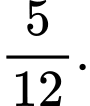
Phương trình hoành độ giao điểm: 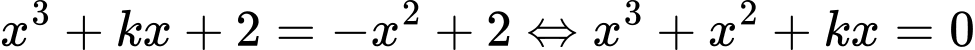
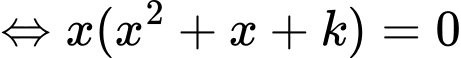
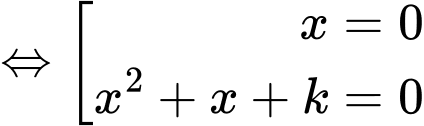
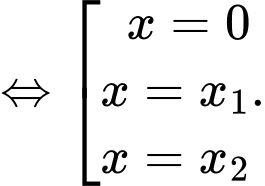
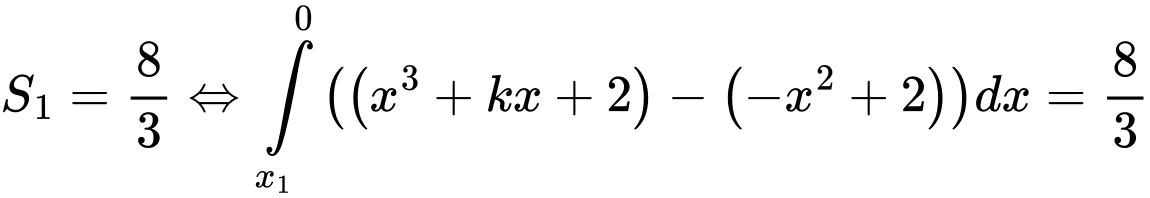
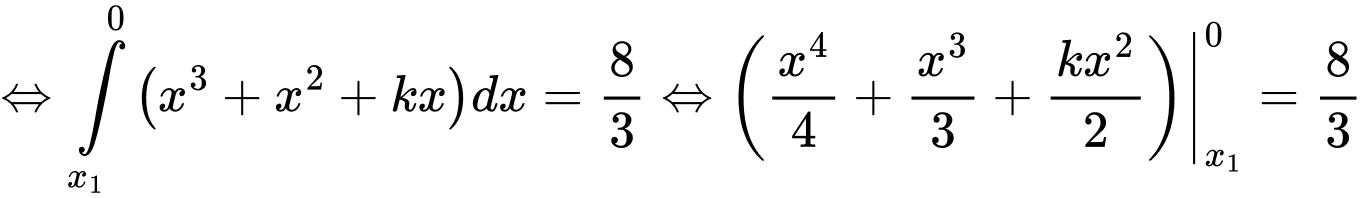
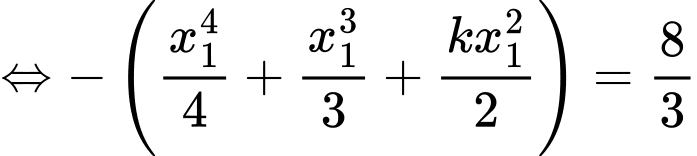
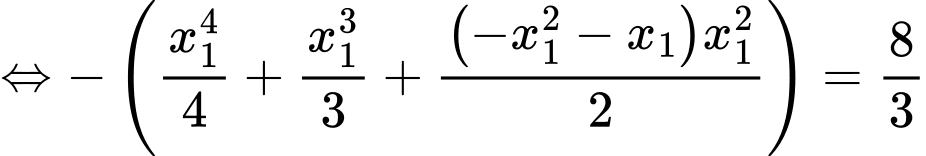
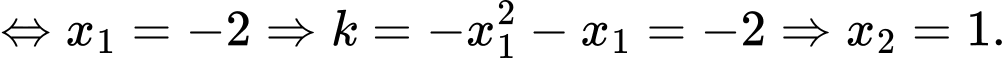
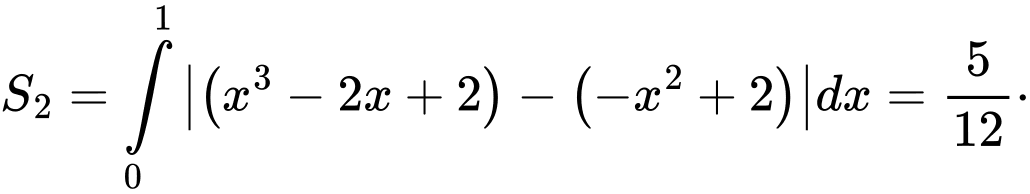
Chọn đáp án D. Đáp án: D
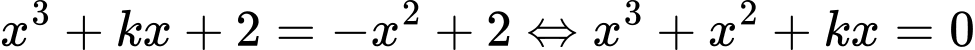
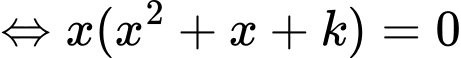
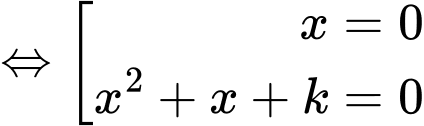
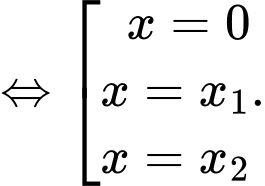
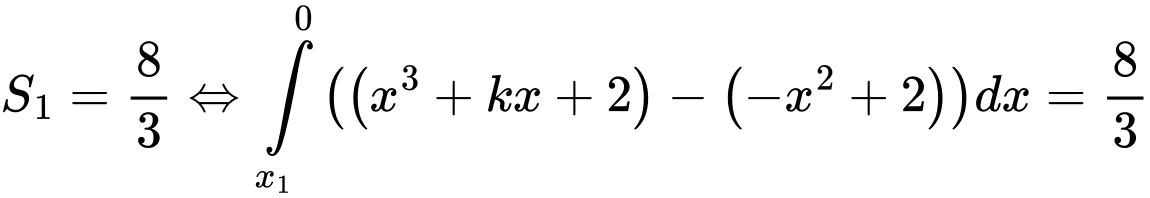
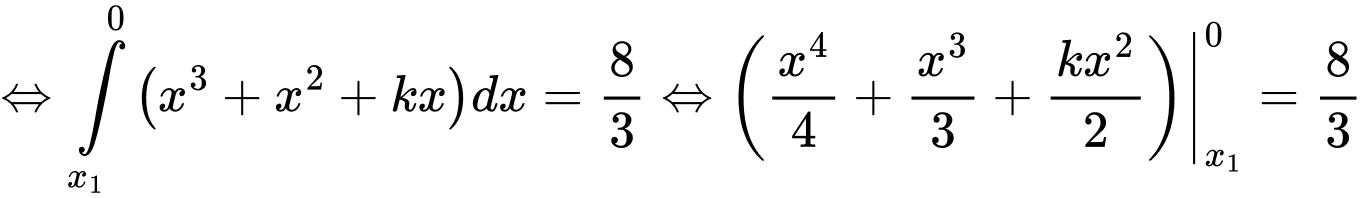
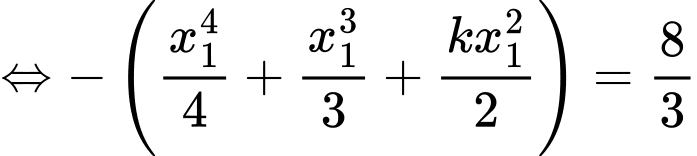
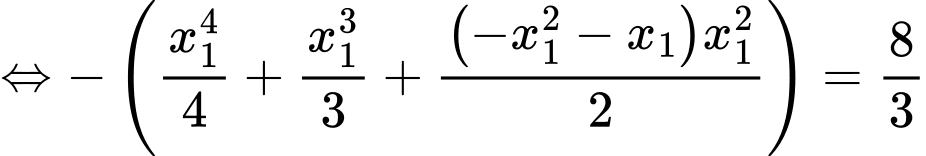
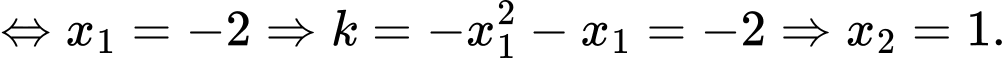
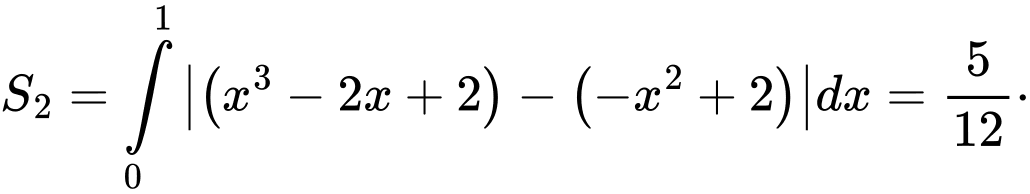
Chọn đáp án D.
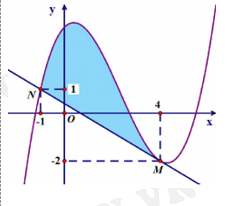
Câu 15 [903749]: Cho 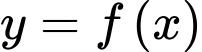 là một hàm số bậc 3 có đồ thị
là một hàm số bậc 3 có đồ thị  như hình vẽ. Tiếp tuyến
như hình vẽ. Tiếp tuyến  của
của  tại điểm
tại điểm 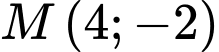 cắt đồ thị hàm số tại điểm thứ hai là
cắt đồ thị hàm số tại điểm thứ hai là 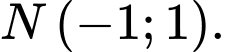 Biết diện tích hình phẳng giới hạn bởi
Biết diện tích hình phẳng giới hạn bởi  và tiếp tuyến
và tiếp tuyến  (phần tô đậm) bằng
(phần tô đậm) bằng 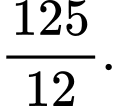 Tính
Tính 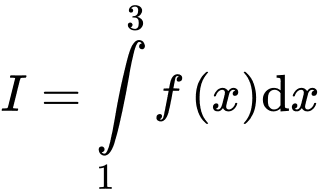
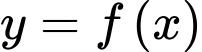 là một hàm số bậc 3 có đồ thị
là một hàm số bậc 3 có đồ thị  như hình vẽ. Tiếp tuyến
như hình vẽ. Tiếp tuyến  của
của  tại điểm
tại điểm 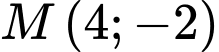 cắt đồ thị hàm số tại điểm thứ hai là
cắt đồ thị hàm số tại điểm thứ hai là 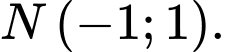 Biết diện tích hình phẳng giới hạn bởi
Biết diện tích hình phẳng giới hạn bởi  và tiếp tuyến
và tiếp tuyến  (phần tô đậm) bằng
(phần tô đậm) bằng 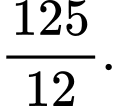 Tính
Tính 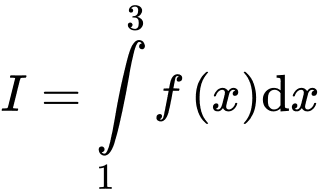

A, 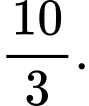
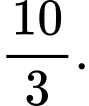
B, 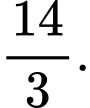
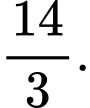
C, 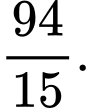
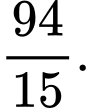
D, 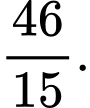
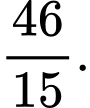
Đặt 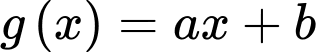
Theo đồ thị ta thấy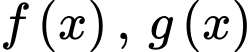 cắt nhau tại các điểm có tung độ lần lượt là
cắt nhau tại các điểm có tung độ lần lượt là 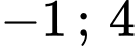 nên ta có:
nên ta có:
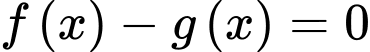
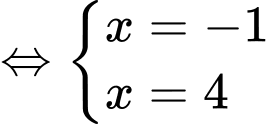
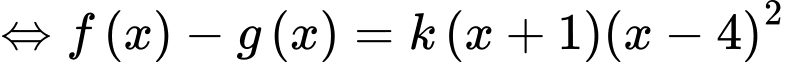
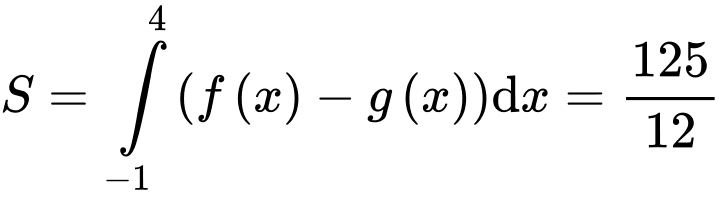
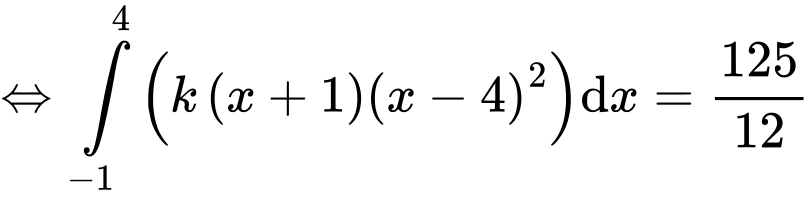
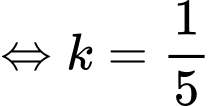
Có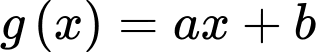 đi qua 2 điểm
đi qua 2 điểm 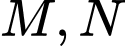 ta có hệ phương trình:
ta có hệ phương trình:
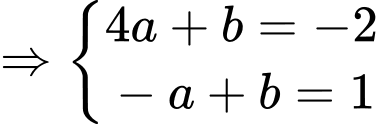
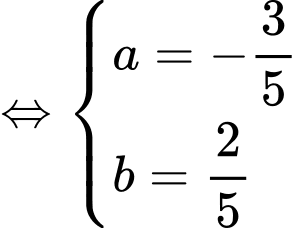
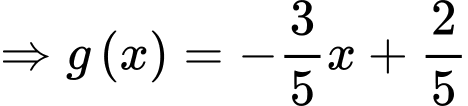
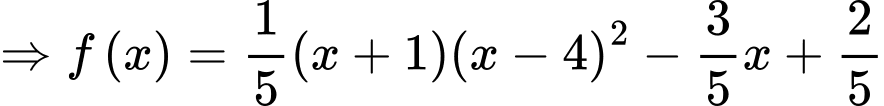
Vậy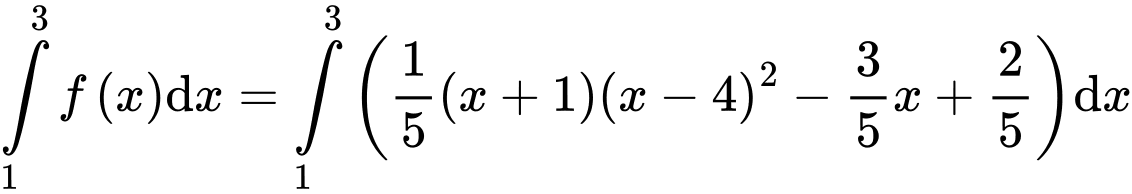
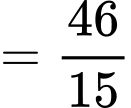
Đáp án: D Đáp án: D
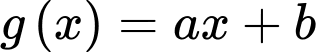
Theo đồ thị ta thấy
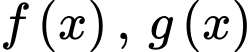 cắt nhau tại các điểm có tung độ lần lượt là
cắt nhau tại các điểm có tung độ lần lượt là 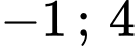 nên ta có:
nên ta có: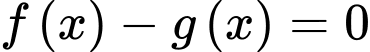
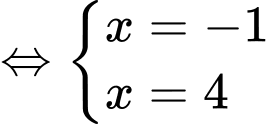
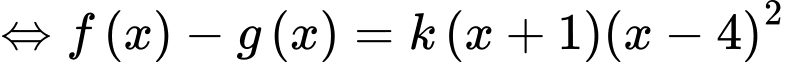
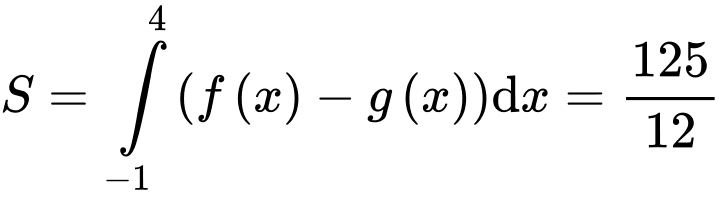
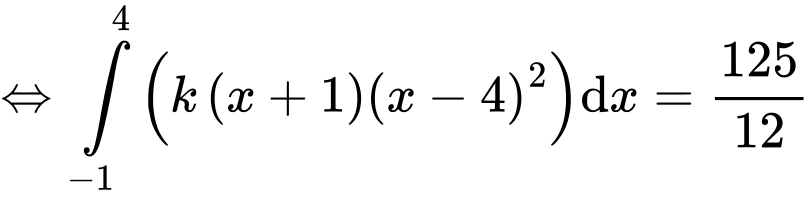
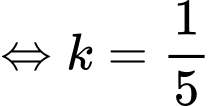
Có
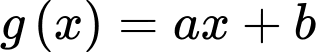 đi qua 2 điểm
đi qua 2 điểm 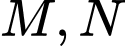 ta có hệ phương trình:
ta có hệ phương trình: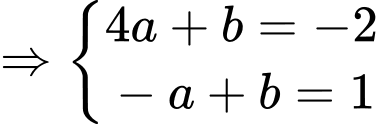
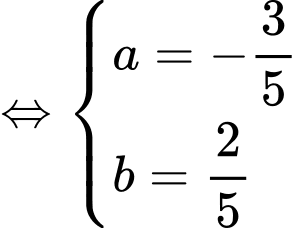
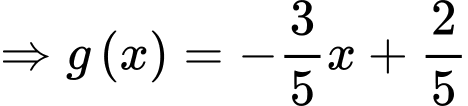
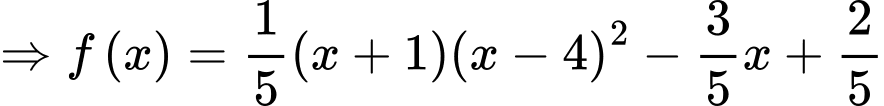
Vậy
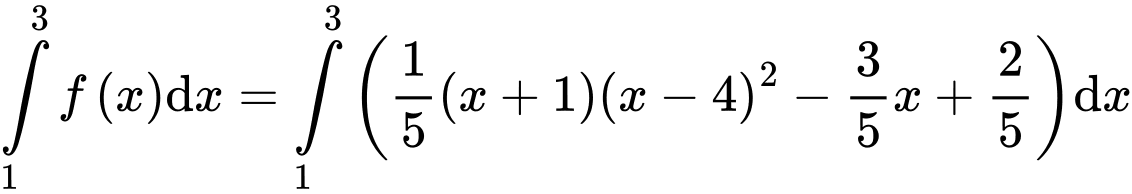
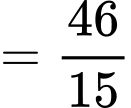
Đáp án: D Đáp án: D
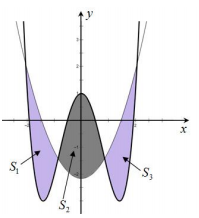
Câu 16 [971729]: [Trích đề thị xã Quảng Trị 2021]: Cho hàm số bậc bốn 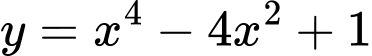 và Parabol
và Parabol 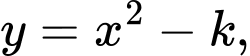 với
với 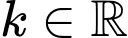 có đồ thị như hình vẽ bên. Gọi
có đồ thị như hình vẽ bên. Gọi 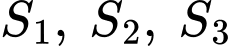 lần lượt là diện tích của phần hình phẳng được tô đậm tương ứng trong hình vẽ. Khi
lần lượt là diện tích của phần hình phẳng được tô đậm tương ứng trong hình vẽ. Khi 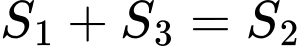 thi
thi 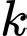 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
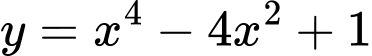 và Parabol
và Parabol 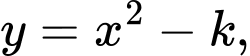 với
với 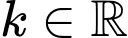 có đồ thị như hình vẽ bên. Gọi
có đồ thị như hình vẽ bên. Gọi 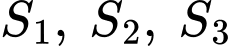 lần lượt là diện tích của phần hình phẳng được tô đậm tương ứng trong hình vẽ. Khi
lần lượt là diện tích của phần hình phẳng được tô đậm tương ứng trong hình vẽ. Khi 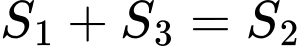 thi
thi 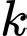 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? 
A, 

B, 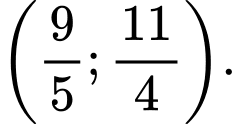
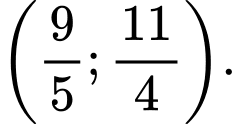
C, 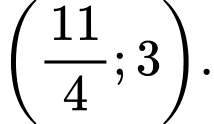
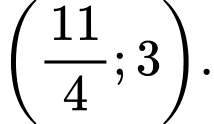
D, 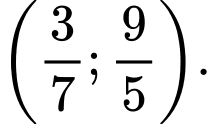
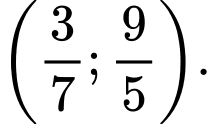
Đồ thị hàm số 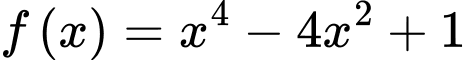 cắt
cắt 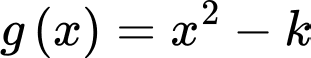 tại 4 điểm phân biệt, giả sử 2 điểm ngoài cùng là
tại 4 điểm phân biệt, giả sử 2 điểm ngoài cùng là 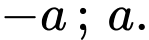
Ta có: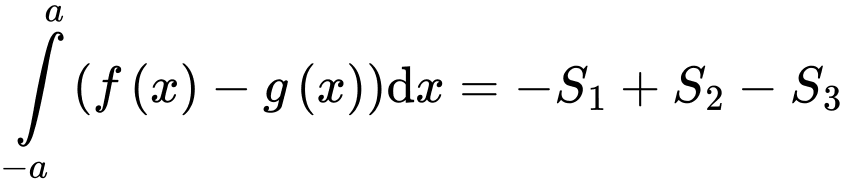
Mà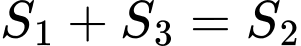
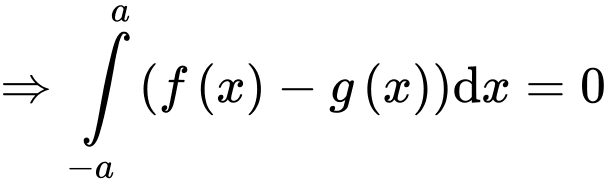
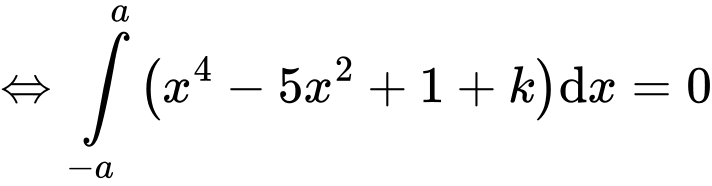
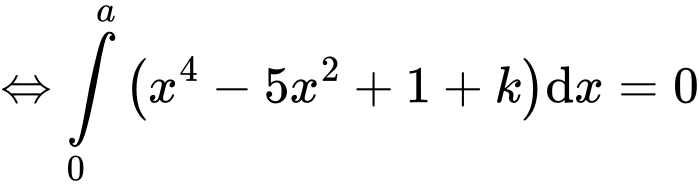
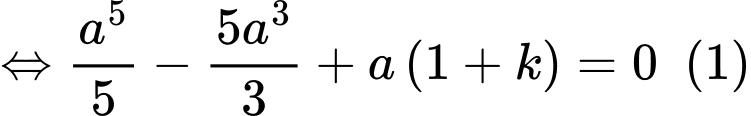
Áp dụng tính chất tích phân có:
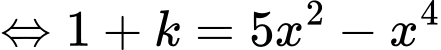
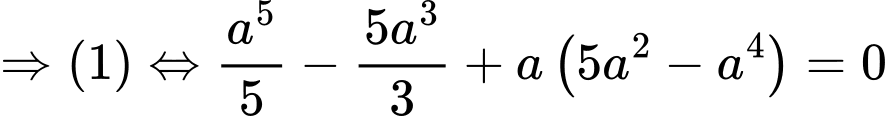
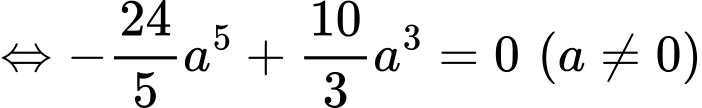
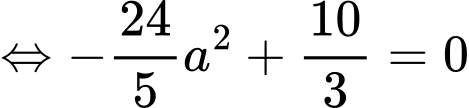
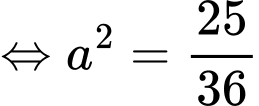
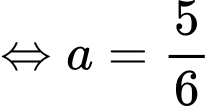
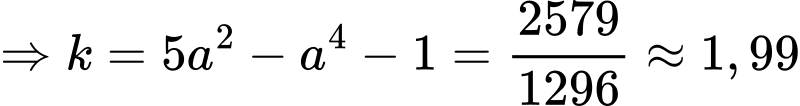
Đáp án: B. Đáp án: B
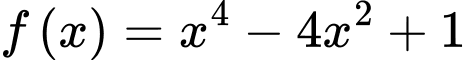 cắt
cắt 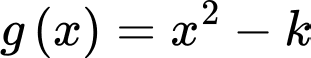 tại 4 điểm phân biệt, giả sử 2 điểm ngoài cùng là
tại 4 điểm phân biệt, giả sử 2 điểm ngoài cùng là 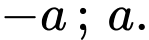
Ta có:
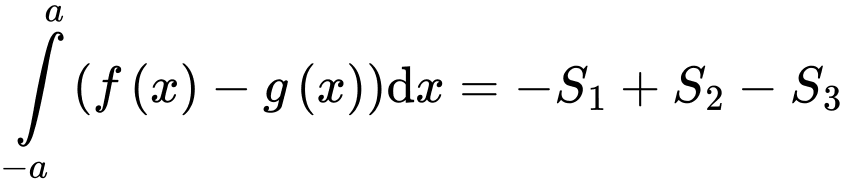
Mà
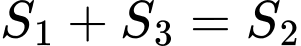
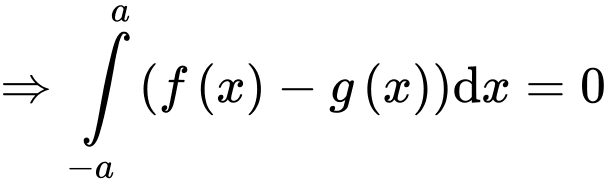
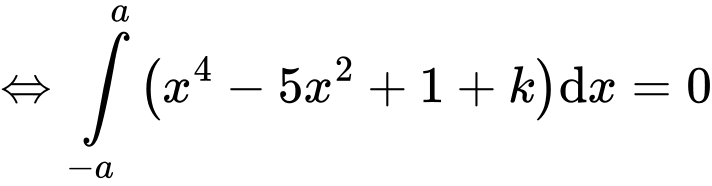
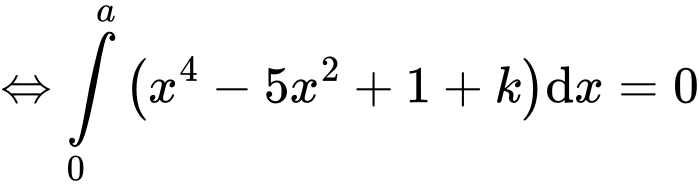
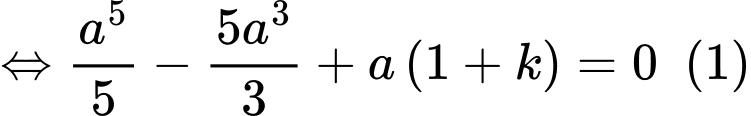
Áp dụng tính chất tích phân có:

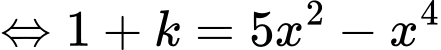
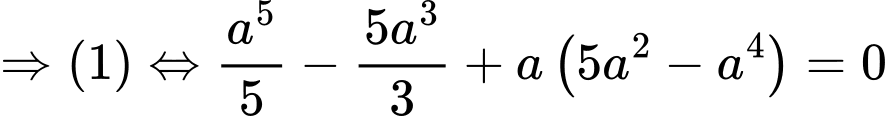
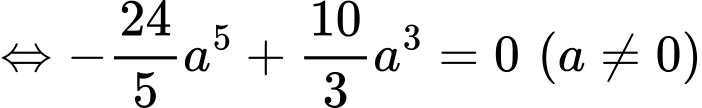
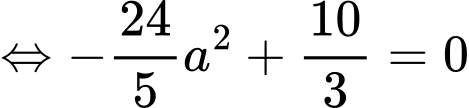
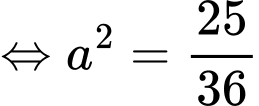
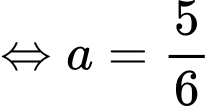
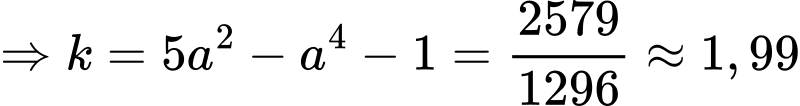
Đáp án: B. Đáp án: B
Câu 17 [159448]: Biết đồ thị hàm số 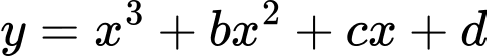 có đúng hai điểm chung
có đúng hai điểm chung 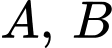 với trục hoành, đồng thời hình phẳng giới hạn bởi đồ thị hàm số
với trục hoành, đồng thời hình phẳng giới hạn bởi đồ thị hàm số 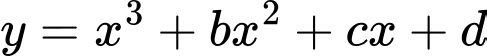 và trục hoành có diện tích bằng
và trục hoành có diện tích bằng 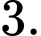 Tính
Tính 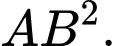
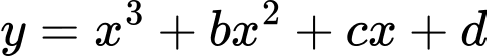 có đúng hai điểm chung
có đúng hai điểm chung 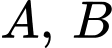 với trục hoành, đồng thời hình phẳng giới hạn bởi đồ thị hàm số
với trục hoành, đồng thời hình phẳng giới hạn bởi đồ thị hàm số 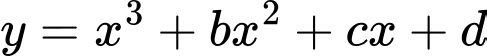 và trục hoành có diện tích bằng
và trục hoành có diện tích bằng 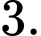 Tính
Tính 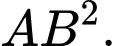
Giả sử đồ thị hàm số 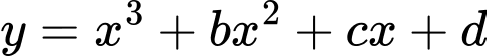 cắt trục hoành tại điểm
cắt trục hoành tại điểm 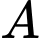 và tiếp xúc với trục hoành tại điểm
và tiếp xúc với trục hoành tại điểm 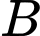 trong đó hoành độ hai điểm
trong đó hoành độ hai điểm 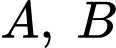 lần lượt là
lần lượt là 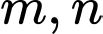 như hình vẽ
như hình vẽ
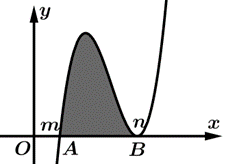
Khi đó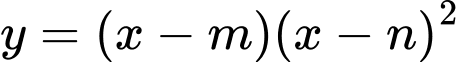 và
và
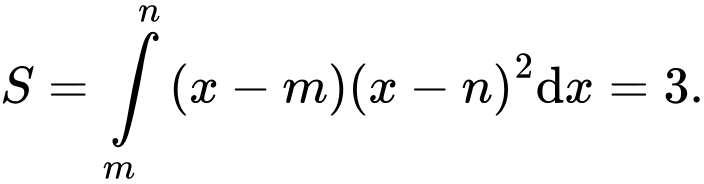
Để đơn giản bài toán ta có thể chọn hệ trục toạ độ mới với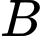 là gốc toạ độ
là gốc toạ độ
Ta chọn: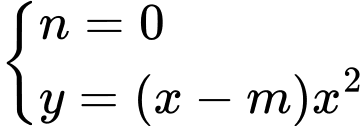 và
và 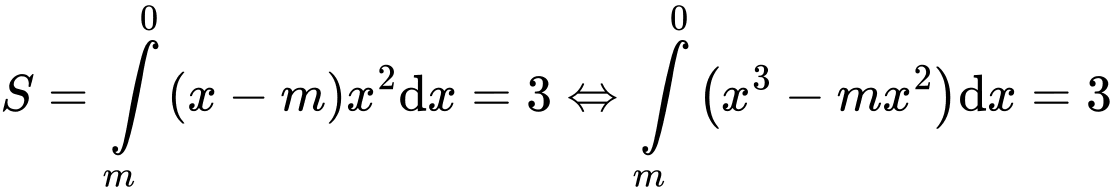

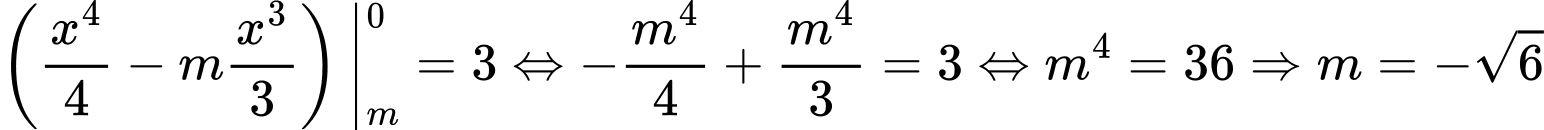 (do
(do  )
) Vậy 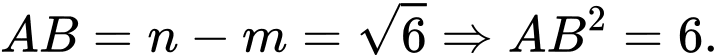
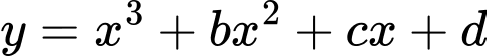 cắt trục hoành tại điểm
cắt trục hoành tại điểm 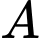 và tiếp xúc với trục hoành tại điểm
và tiếp xúc với trục hoành tại điểm 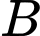 trong đó hoành độ hai điểm
trong đó hoành độ hai điểm 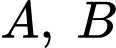 lần lượt là
lần lượt là 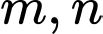 như hình vẽ
như hình vẽ

Khi đó
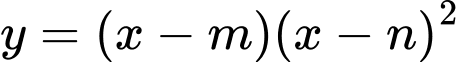 và
và 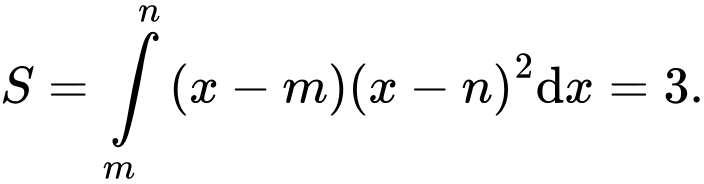
Để đơn giản bài toán ta có thể chọn hệ trục toạ độ mới với
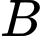 là gốc toạ độ
là gốc toạ độ
Ta chọn:
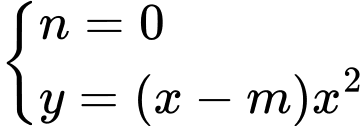 và
và 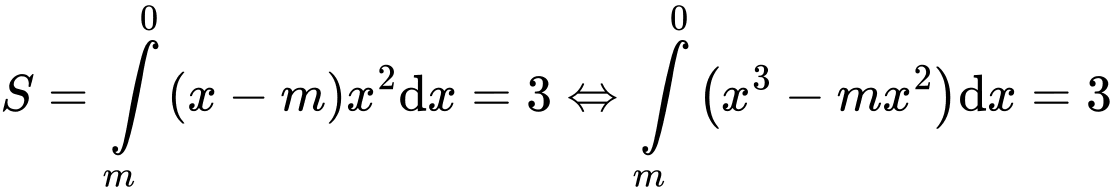

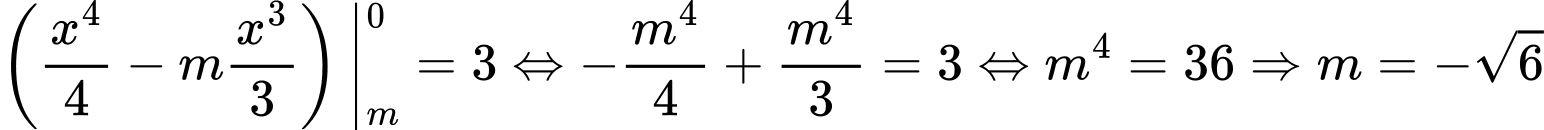 (do
(do  )
) 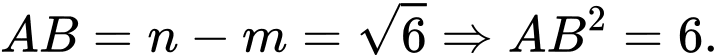
Câu 18 [159439]: Cho hàm số 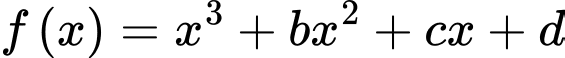 có đồ thị
có đồ thị  và
và 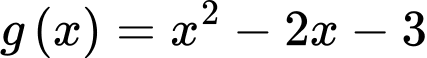 có đồ thị là
có đồ thị là 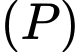 . Biết đồ thị
. Biết đồ thị  tiếp xúc với
tiếp xúc với 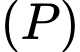 tại điểm
tại điểm 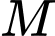 và cắt
và cắt 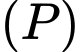 tại điểm
tại điểm 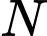 , với
, với 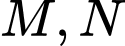 có hoành độ lần lượt là
có hoành độ lần lượt là 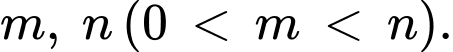 Biết
Biết 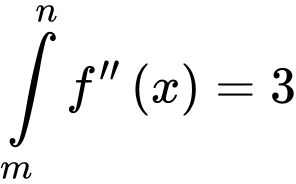 và độ dài
và độ dài 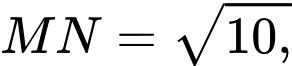 khi đó
khi đó 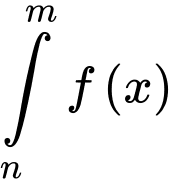 bằng bao nhiêu?
bằng bao nhiêu?
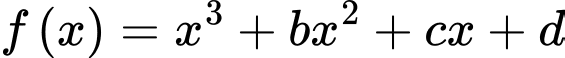 có đồ thị
có đồ thị  và
và 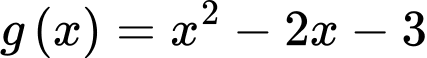 có đồ thị là
có đồ thị là 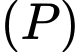 . Biết đồ thị
. Biết đồ thị  tiếp xúc với
tiếp xúc với 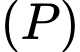 tại điểm
tại điểm 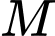 và cắt
và cắt 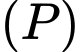 tại điểm
tại điểm 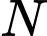 , với
, với 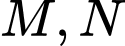 có hoành độ lần lượt là
có hoành độ lần lượt là 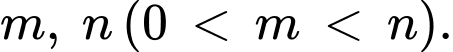 Biết
Biết 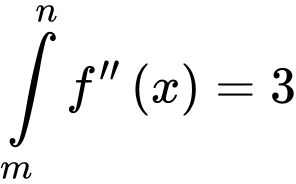 và độ dài
và độ dài 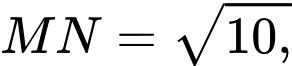 khi đó
khi đó 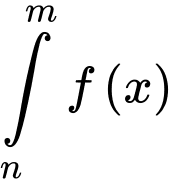 bằng bao nhiêu?
bằng bao nhiêu?
Phương trình hoành độ giao điểm:
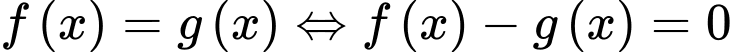

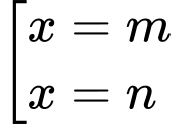 .
.
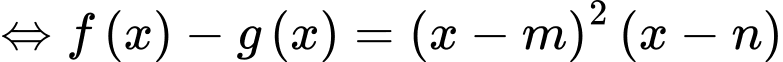 .
.
Đạo hàm 2 vế ta được:
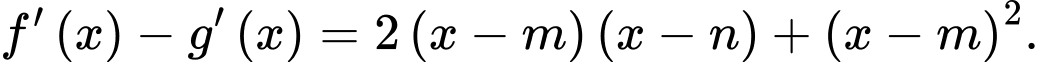
Mà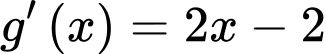
Khi đó ta có
Với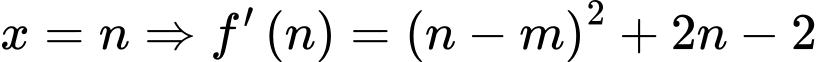
Với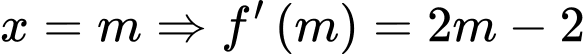
Mặt khác
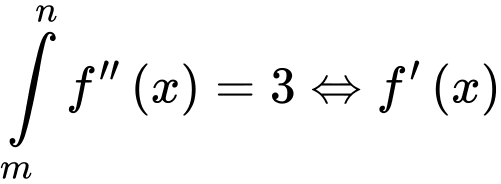
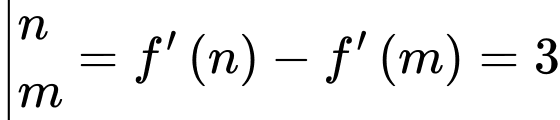
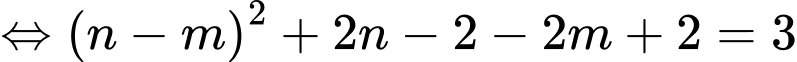
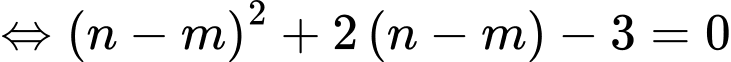

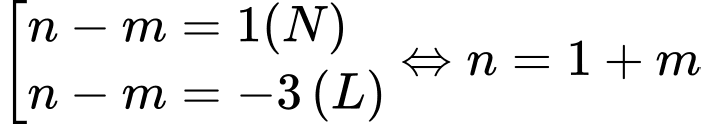
Nên tọa độ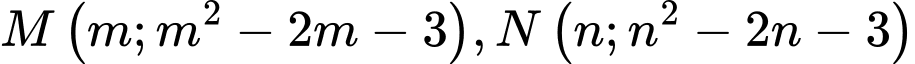 Với
Với 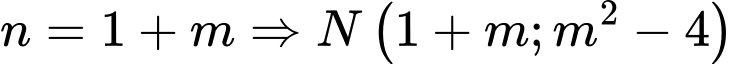 .
.
Mà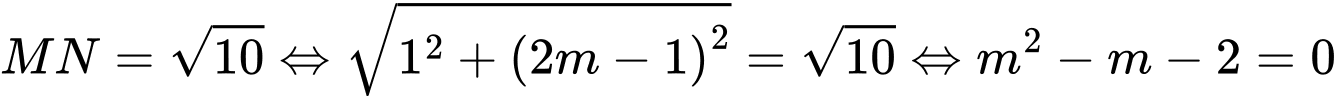

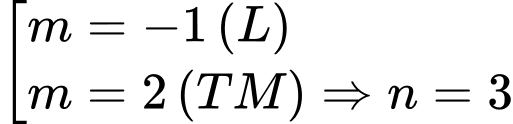 .
.
Ta có:
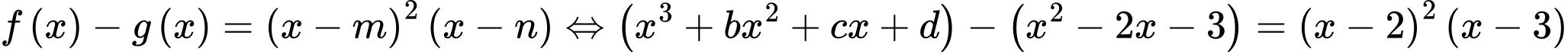
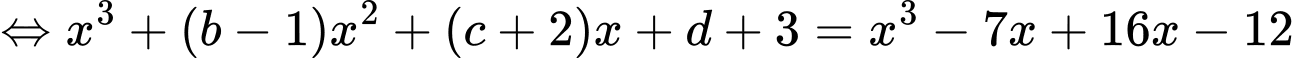
Đồng nhất thức ta có: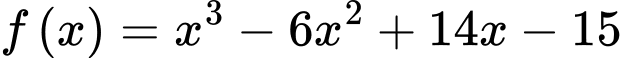
Vậy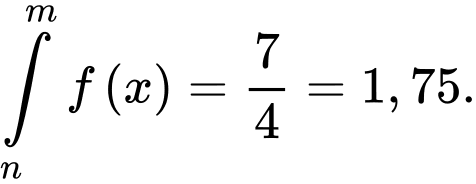
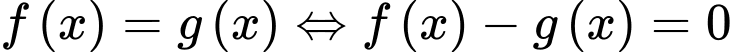

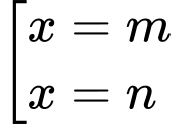 .
.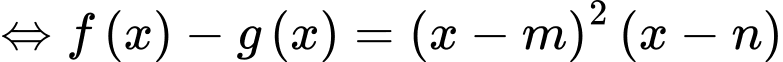 .
.Đạo hàm 2 vế ta được:
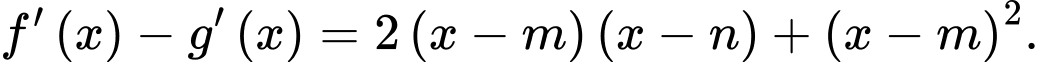
Mà
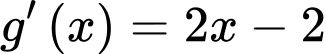
Khi đó ta có
Với
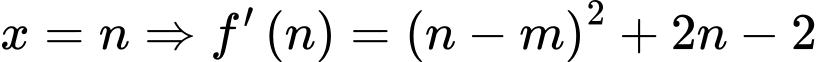
Với
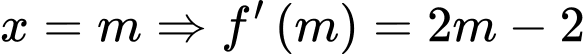
Mặt khác
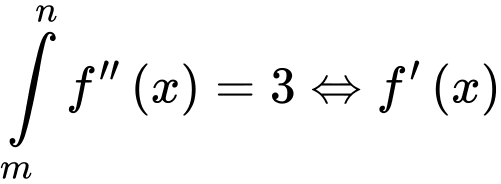
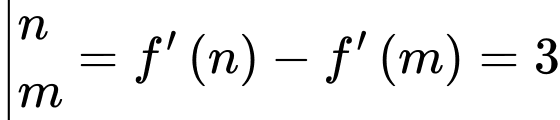
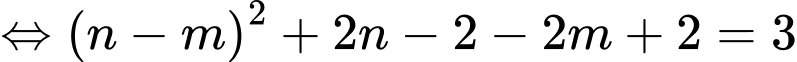
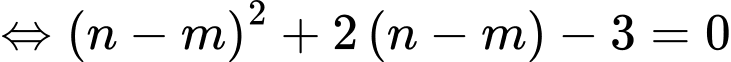

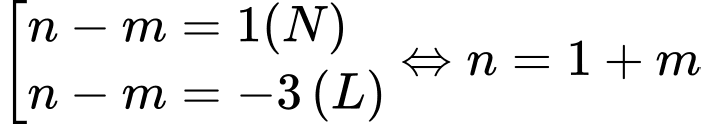
Nên tọa độ
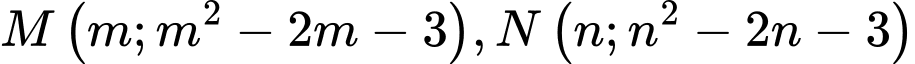 Với
Với 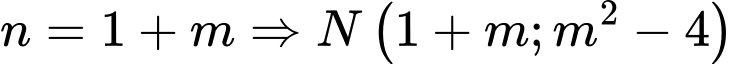 .
.Mà
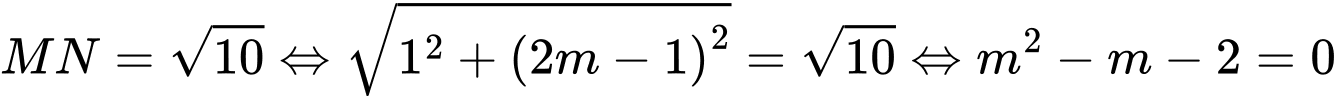

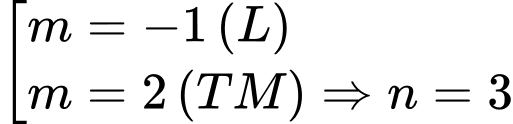 .
.Ta có:
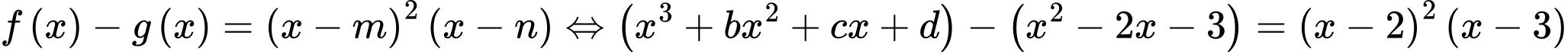
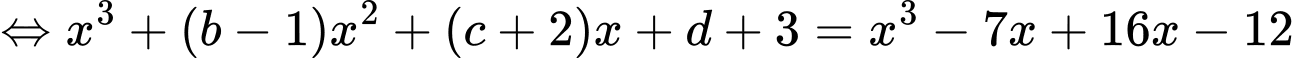
Đồng nhất thức ta có:
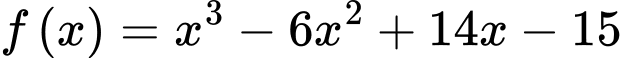
Vậy