Đáp án Bài tập tự luyện số 2
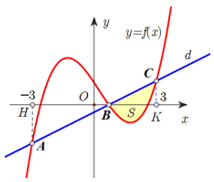
Câu 1 [903987]: Cho đồ thị hàm số bậc ba 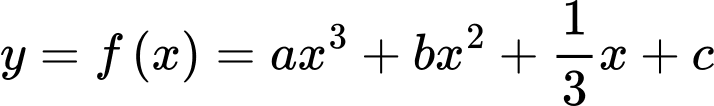 và đường thẳng
và đường thẳng 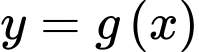 có đồ thị như hình vẽ sau:
có đồ thị như hình vẽ sau: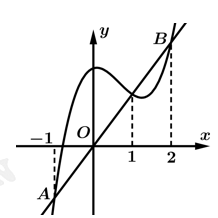
Biết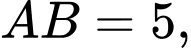 diện tích hình phẳng giới hạn bởi đồ thị hàm số
diện tích hình phẳng giới hạn bởi đồ thị hàm số 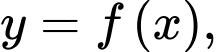 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 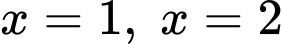 bằng
bằng
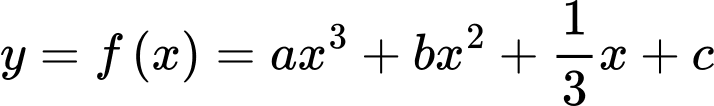 và đường thẳng
và đường thẳng 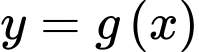 có đồ thị như hình vẽ sau:
có đồ thị như hình vẽ sau:
Biết
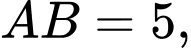 diện tích hình phẳng giới hạn bởi đồ thị hàm số
diện tích hình phẳng giới hạn bởi đồ thị hàm số 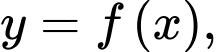 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 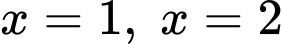 bằng
bằng A, 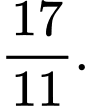
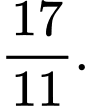
B, 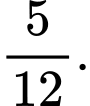
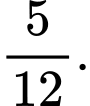
C, 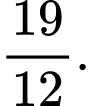
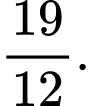
D, 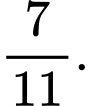
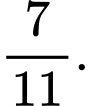
Dựa vào đồ thị hàm số, ta thấy phương trình 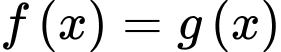 có 3 nghiệm phân biệt
có 3 nghiệm phân biệt 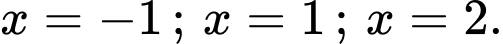
Suy ra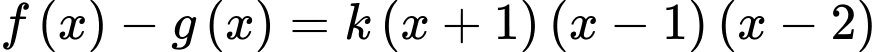
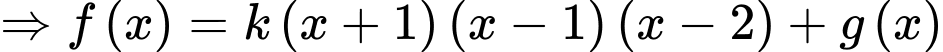
Dựa vào hình vẽ, ta thấy hàm số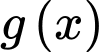 là 1 đường thẳng đi qua gốc toạ độ
là 1 đường thẳng đi qua gốc toạ độ 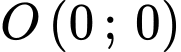
Nên suy ra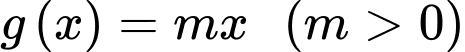 (do đồ thị hàm số đi lên)
(do đồ thị hàm số đi lên)
Vì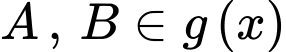
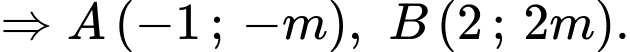
Theo giả thiết, ta có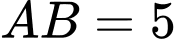
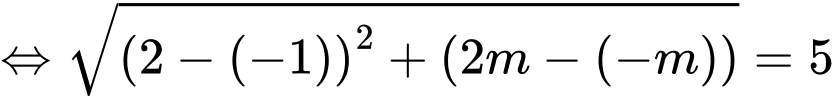
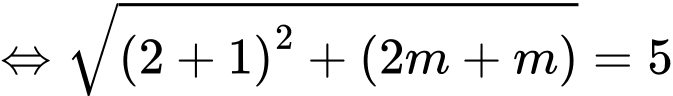
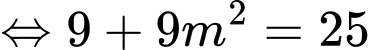
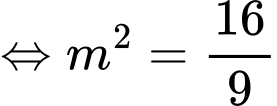
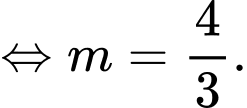
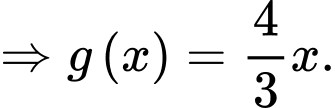
Ta có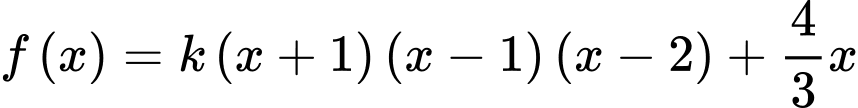
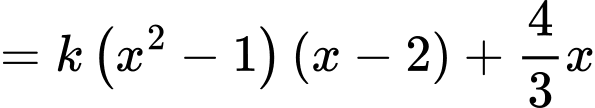
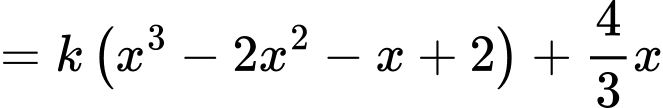
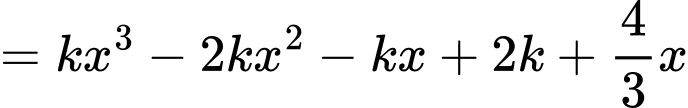
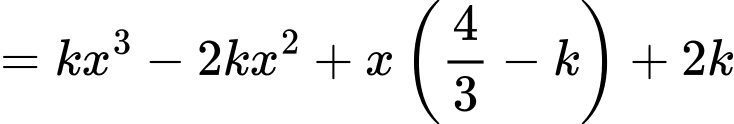
Dựa vào hệ số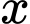 của
của 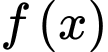 ở đề bài, suy ra
ở đề bài, suy ra 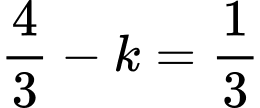
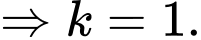
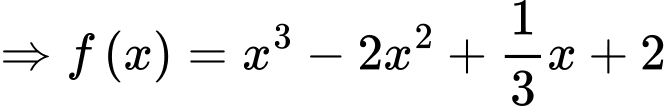
Suy ra diện tích hình phẳng giới hạn bởi đồ thị hàm số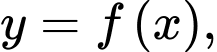 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 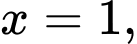
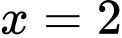 là
là 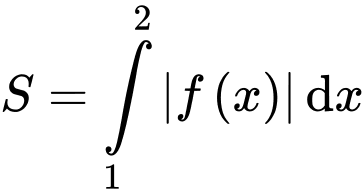
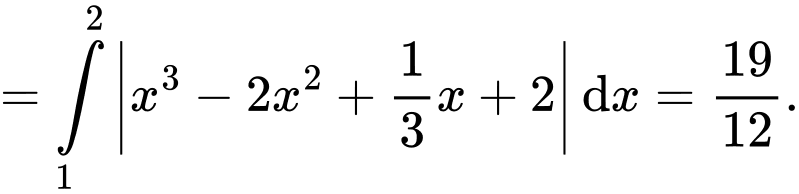
Chọn C. Đáp án: C
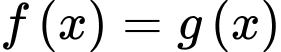 có 3 nghiệm phân biệt
có 3 nghiệm phân biệt 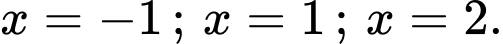
Suy ra
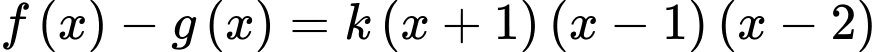
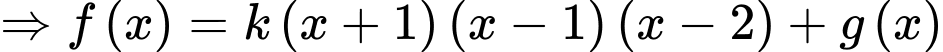
Dựa vào hình vẽ, ta thấy hàm số
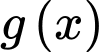 là 1 đường thẳng đi qua gốc toạ độ
là 1 đường thẳng đi qua gốc toạ độ 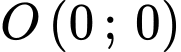
Nên suy ra
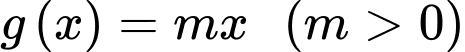 (do đồ thị hàm số đi lên)
(do đồ thị hàm số đi lên)
Vì
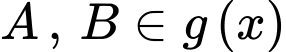
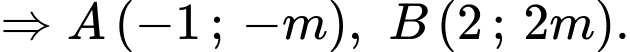
Theo giả thiết, ta có
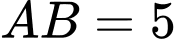
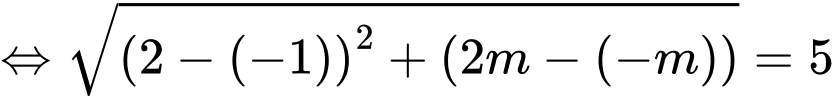
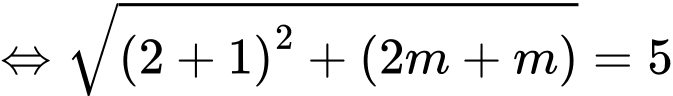
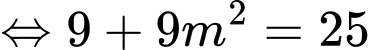
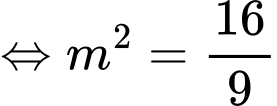
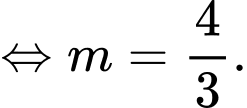
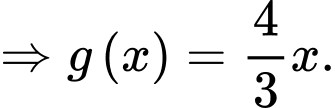
Ta có
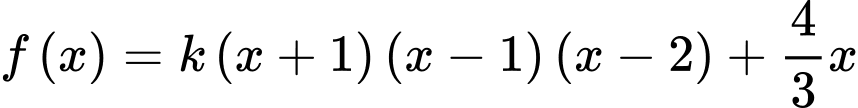
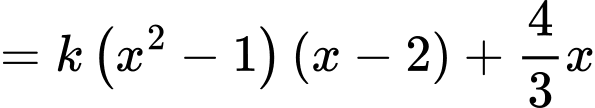
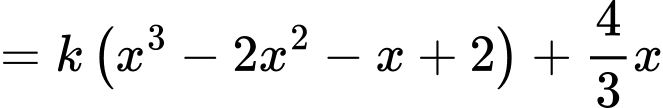
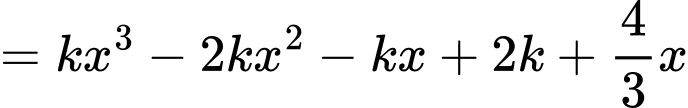
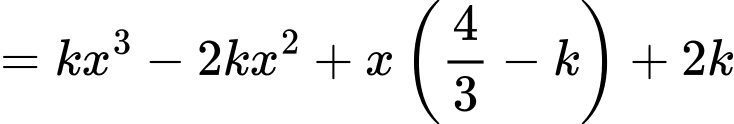
Dựa vào hệ số
 của
của 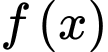 ở đề bài, suy ra
ở đề bài, suy ra 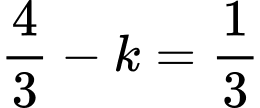
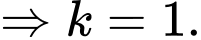
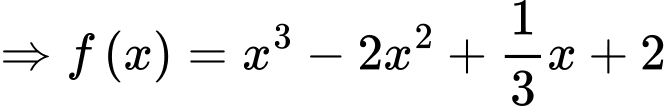
Suy ra diện tích hình phẳng giới hạn bởi đồ thị hàm số
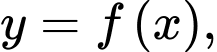 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 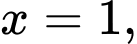
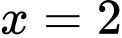 là
là 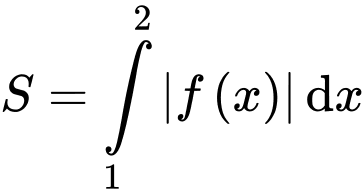
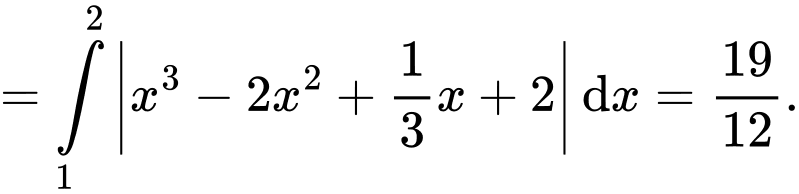
Chọn C. Đáp án: C
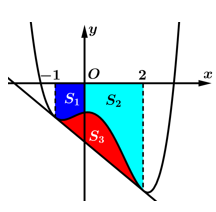
Câu 2 [903302]: Cho hàm số 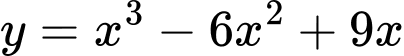 và
và 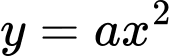 có đồ thị như hình vẽ. Gọi
có đồ thị như hình vẽ. Gọi 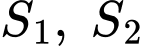 lần lượt là diện tích hình phẳng được tô đậm trong hình vẽ bên. Biết rằng
lần lượt là diện tích hình phẳng được tô đậm trong hình vẽ bên. Biết rằng 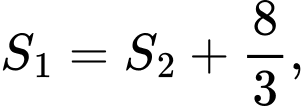 khi đó giá trị
khi đó giá trị 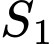 gần giá trị nào nhất trong các giá trị sau:
gần giá trị nào nhất trong các giá trị sau:
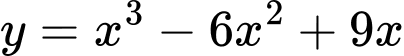 và
và 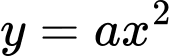 có đồ thị như hình vẽ. Gọi
có đồ thị như hình vẽ. Gọi 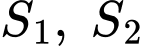 lần lượt là diện tích hình phẳng được tô đậm trong hình vẽ bên. Biết rằng
lần lượt là diện tích hình phẳng được tô đậm trong hình vẽ bên. Biết rằng 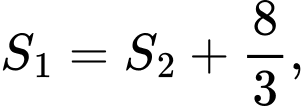 khi đó giá trị
khi đó giá trị 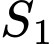 gần giá trị nào nhất trong các giá trị sau:
gần giá trị nào nhất trong các giá trị sau: 
A, 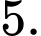
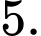
B, 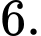
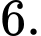
C, 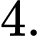
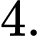
D, 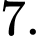
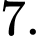
Đặt 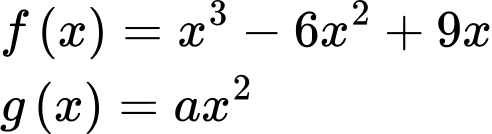
Ta có Phương trình hoành độ giao điểm:
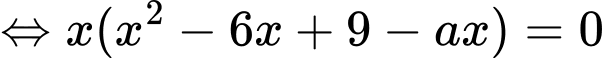
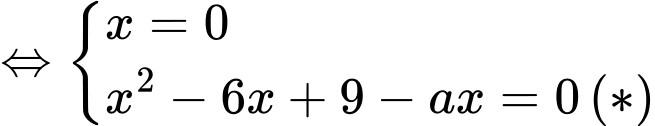
Giả sử có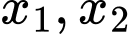 là 2 nghiệm dương của phương trình (*)
là 2 nghiệm dương của phương trình (*)
Ta có: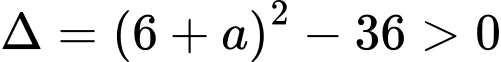
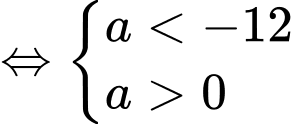
Theo Vi-ét, ta có: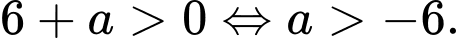
Vậy
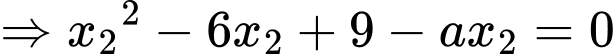
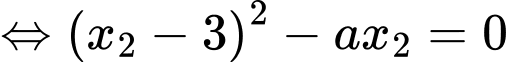
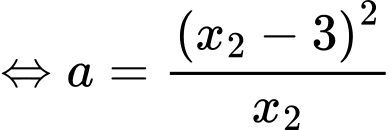
Lại có: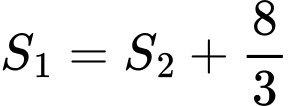
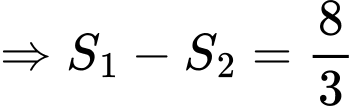
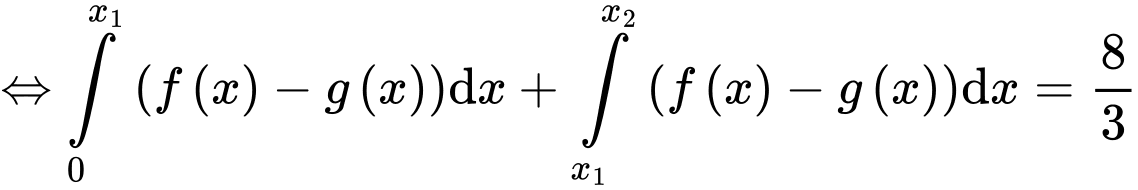
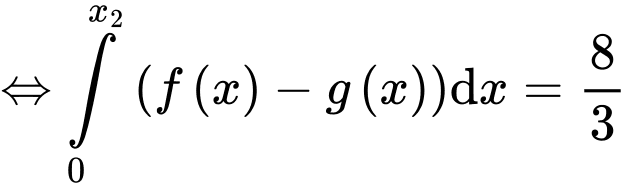
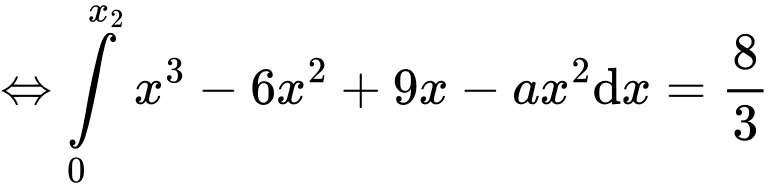
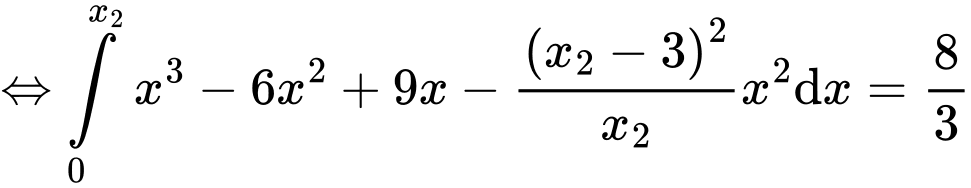
Giải phương trình ta được: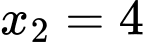
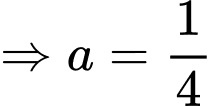
Theo Vi-ét có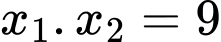
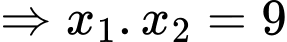
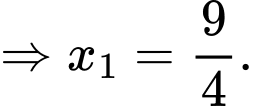
Từ đó, ta tính được: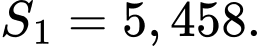
Suy ra chọn A. Đáp án: A
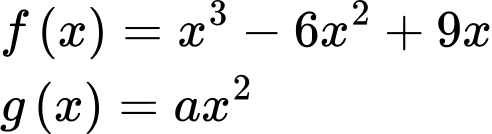
Ta có Phương trình hoành độ giao điểm:

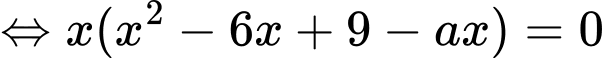
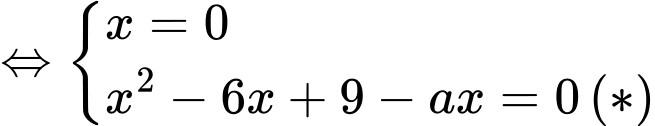
Giả sử có
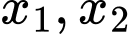 là 2 nghiệm dương của phương trình (*)
là 2 nghiệm dương của phương trình (*)
Ta có:
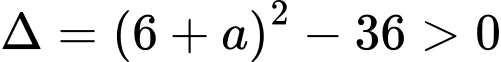
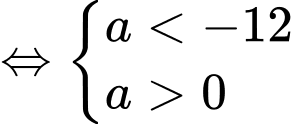
Theo Vi-ét, ta có:
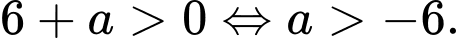
Vậy

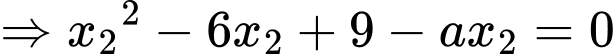
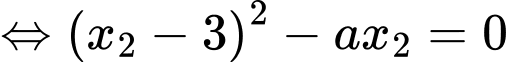
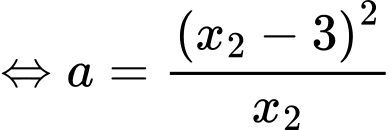
Lại có:
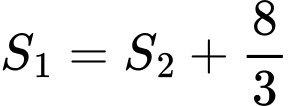
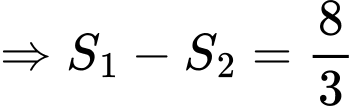
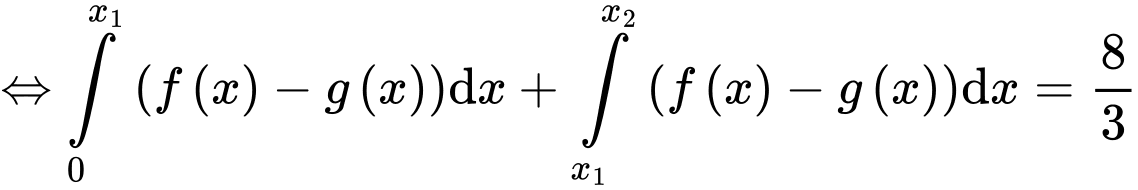
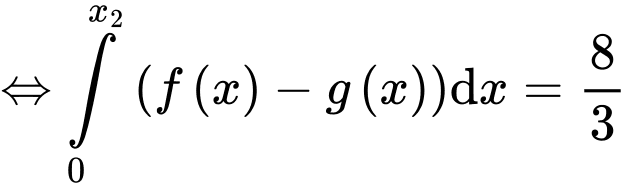
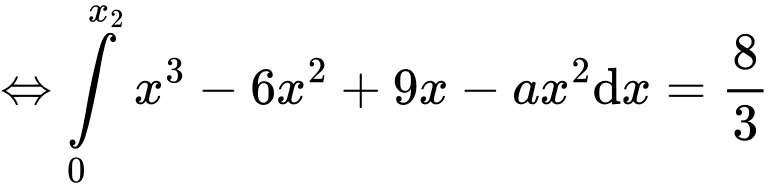
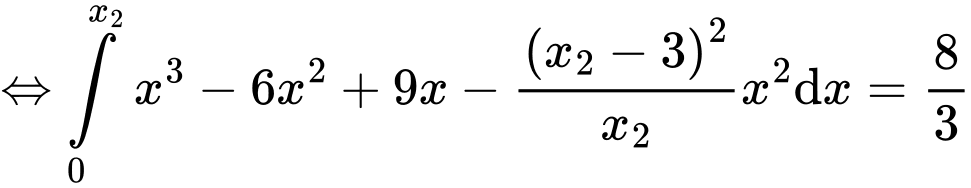
Giải phương trình ta được:
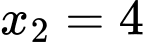
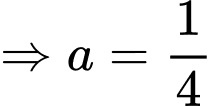
Theo Vi-ét có
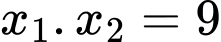
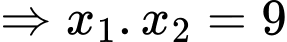
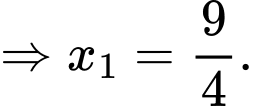
Từ đó, ta tính được:
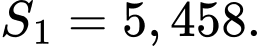
Suy ra chọn A. Đáp án: A
Câu 3 [229562]: Cho hàm số bậc ba 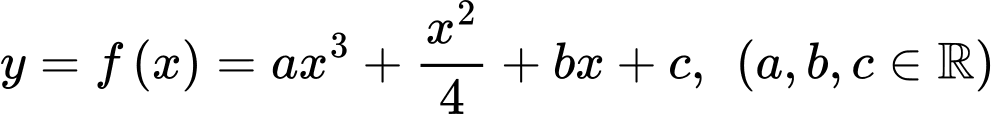 và parabol
và parabol 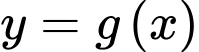 cắt nhau tại 3 điểm
cắt nhau tại 3 điểm 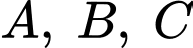 có hoành độ là
có hoành độ là 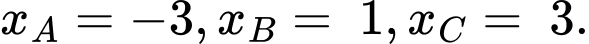 Biết rằng
Biết rằng 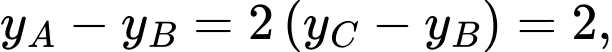 tính diện tích hình phẳng giới hạn bởi hai đồ thị
tính diện tích hình phẳng giới hạn bởi hai đồ thị 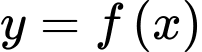 và
và 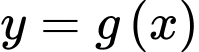
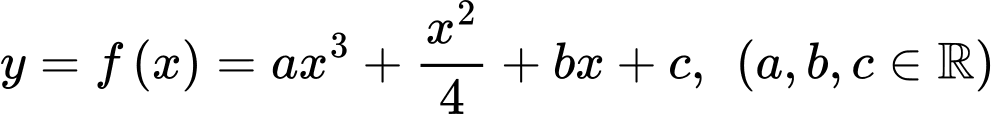 và parabol
và parabol 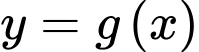 cắt nhau tại 3 điểm
cắt nhau tại 3 điểm 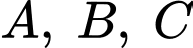 có hoành độ là
có hoành độ là 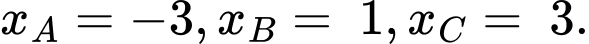 Biết rằng
Biết rằng 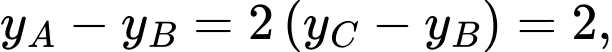 tính diện tích hình phẳng giới hạn bởi hai đồ thị
tính diện tích hình phẳng giới hạn bởi hai đồ thị 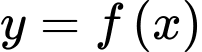 và
và 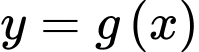
A, 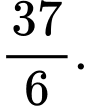
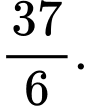
B, 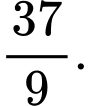
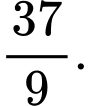
C, 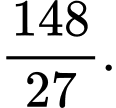
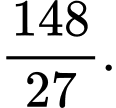
D, 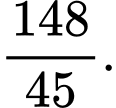
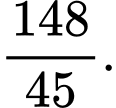
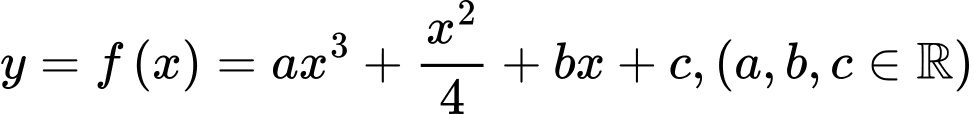
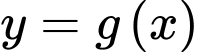
Hai hàm số cắt nhau tại 3 điểm
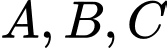 với
với 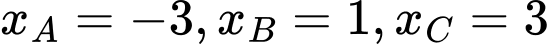
Từ gt ta có:
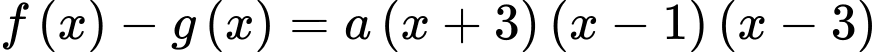
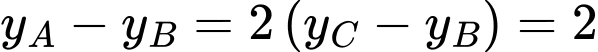
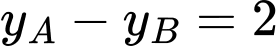
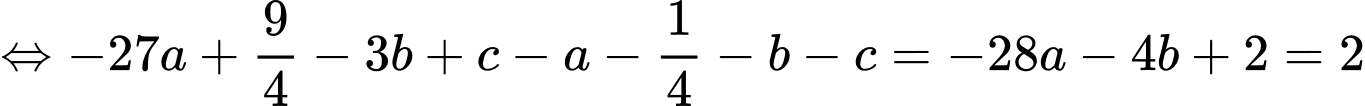
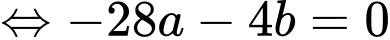
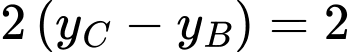
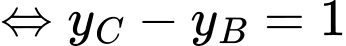
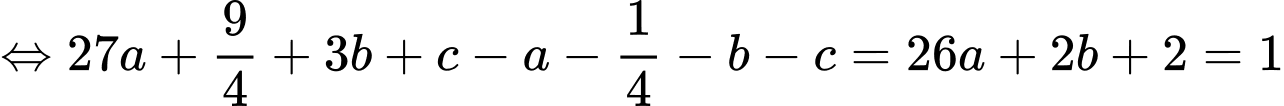
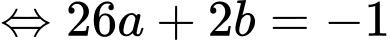
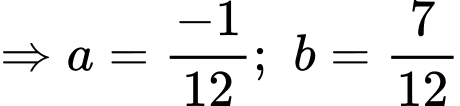
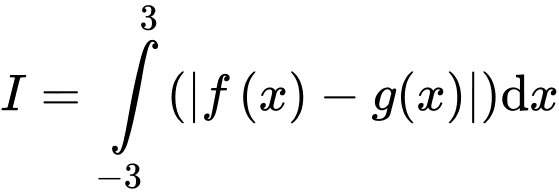
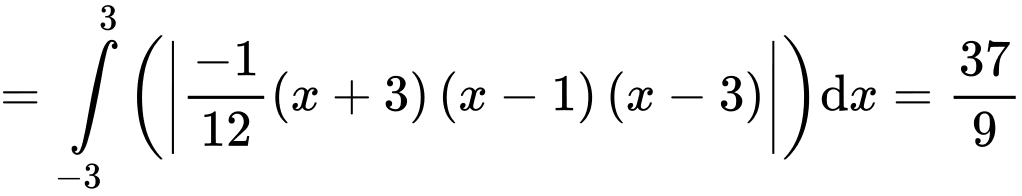
Đáp án B. Đáp án: B
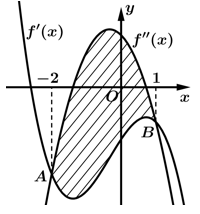
Câu 4 [383276]: Xét 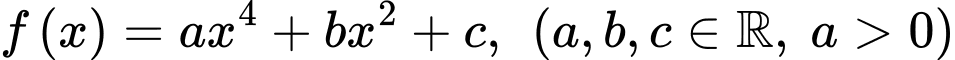 sao cho đồ thị hàm số
sao cho đồ thị hàm số 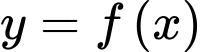 có ba điểm cực trị là
có ba điểm cực trị là 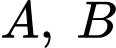 và
và 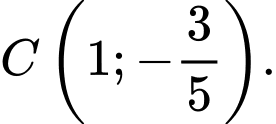 Gọi
Gọi 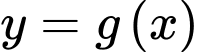 là hàm số bậc hai có đồ thị đi qua ba điểm
là hàm số bậc hai có đồ thị đi qua ba điểm 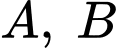 và
và  Khi hình phẳng giới hạn bởi đồ thị của hai hàm số
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số 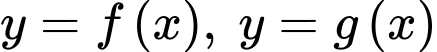 và hai đường thẳng
và hai đường thẳng 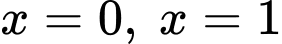 có diện tích bằng
có diện tích bằng 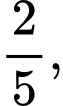 tích phân
tích phân 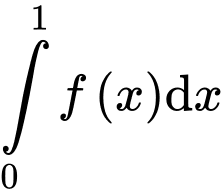 bằng
bằng
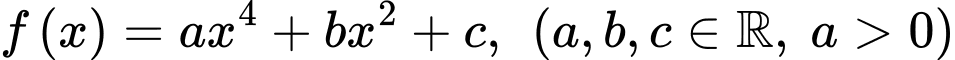 sao cho đồ thị hàm số
sao cho đồ thị hàm số 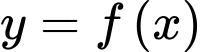 có ba điểm cực trị là
có ba điểm cực trị là 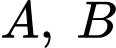 và
và 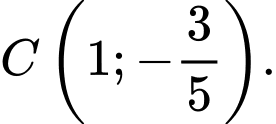 Gọi
Gọi 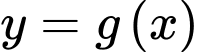 là hàm số bậc hai có đồ thị đi qua ba điểm
là hàm số bậc hai có đồ thị đi qua ba điểm 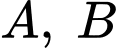 và
và  Khi hình phẳng giới hạn bởi đồ thị của hai hàm số
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số 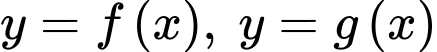 và hai đường thẳng
và hai đường thẳng 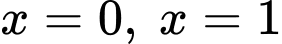 có diện tích bằng
có diện tích bằng 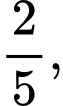 tích phân
tích phân 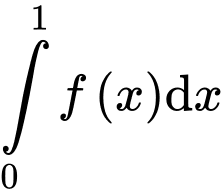 bằng
bằng A, 
B, 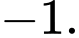
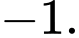
C, 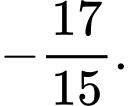
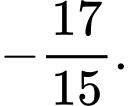
D, 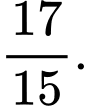
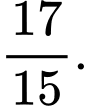
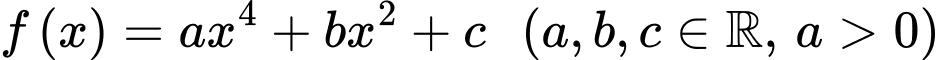
 có 3 cực trị tại 3 điểm
có 3 cực trị tại 3 điểm 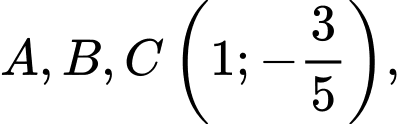
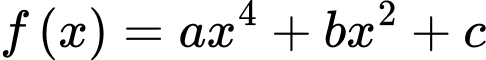 là phương trình trùng phương nên ta có:
là phương trình trùng phương nên ta có: 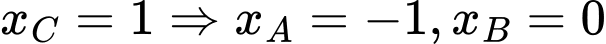
Theo gt ta có:
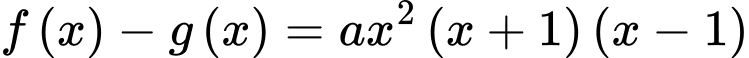
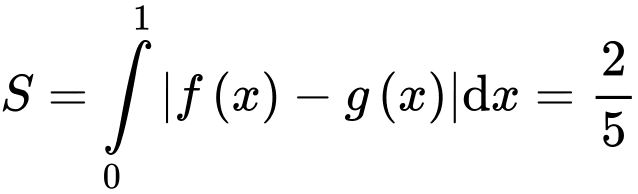
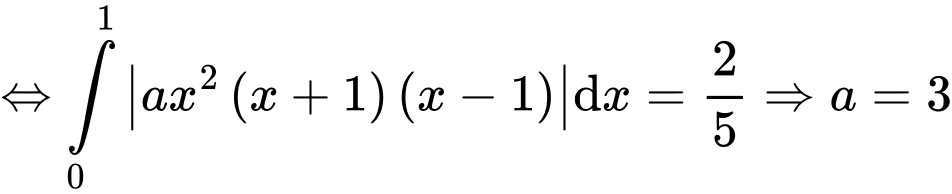
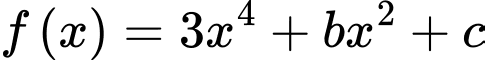
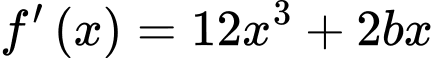
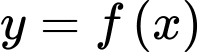 có 3 cực trị tại 3 điểm
có 3 cực trị tại 3 điểm 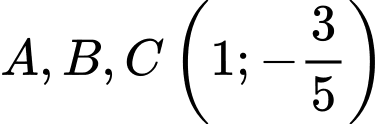
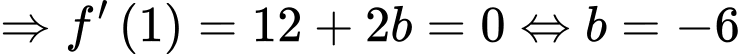
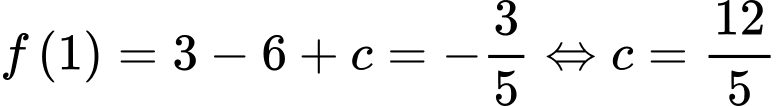
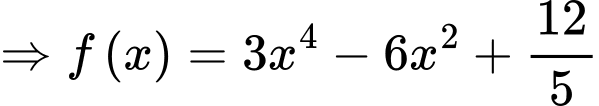
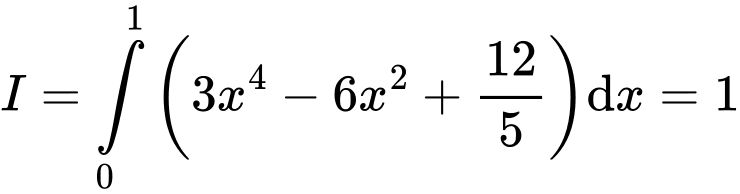
Câu 5 [228044]: Cho hàm số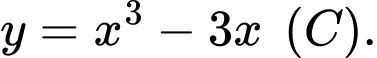 Tiếp tuyến của đồ thị
Tiếp tuyến của đồ thị tại điểm
tại điểm  có hoành độ âm cắt
có hoành độ âm cắt tại điểm thứ hai là
tại điểm thứ hai là 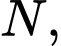 tiếp tuyến tại
tiếp tuyến tại 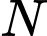 của
của  cắt
cắt  tại điểm thứ hai là
tại điểm thứ hai là 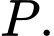 Biết diện tích hình phẳng giới hạn bởi đường thẳng
Biết diện tích hình phẳng giới hạn bởi đường thẳng 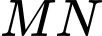 và đồ thị
và đồ thị  bằng
bằng Tính diện tích hình phẳng giới hạn bởi đường thẳng
Tính diện tích hình phẳng giới hạn bởi đường thẳng 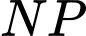 và đồ thị
và đồ thị 
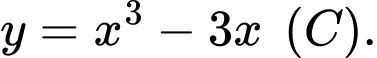 Tiếp tuyến của đồ thị
Tiếp tuyến của đồ thị tại điểm
tại điểm 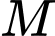 có hoành độ âm cắt
có hoành độ âm cắt tại điểm thứ hai là
tại điểm thứ hai là 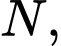 tiếp tuyến tại
tiếp tuyến tại 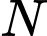 của
của  cắt
cắt  tại điểm thứ hai là
tại điểm thứ hai là 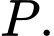 Biết diện tích hình phẳng giới hạn bởi đường thẳng
Biết diện tích hình phẳng giới hạn bởi đường thẳng 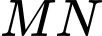 và đồ thị
và đồ thị  bằng
bằng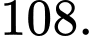 Tính diện tích hình phẳng giới hạn bởi đường thẳng
Tính diện tích hình phẳng giới hạn bởi đường thẳng 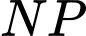 và đồ thị
và đồ thị 
A, 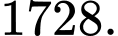
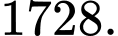
B, 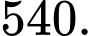
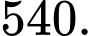
C, 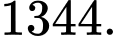
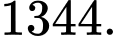
D, 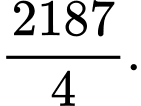
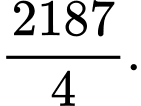
 Đáp án: A
Đáp án: A
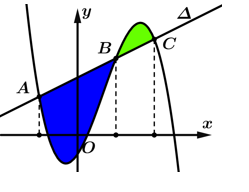
Câu 6 [230720]: Cho hàm số 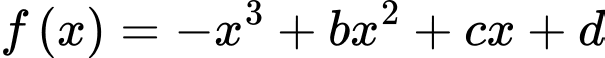
 có đồ thị
có đồ thị  Gọi
Gọi 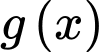 là hàm số bậc nhất có đồ thị là đường thẳng
là hàm số bậc nhất có đồ thị là đường thẳng  cắt đồ thị
cắt đồ thị  tại ba điểm
tại ba điểm 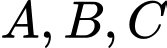 sao cho
sao cho 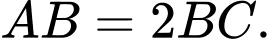 Gọi
Gọi 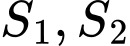 lần lượt là diện tích các hình phẳng được tô đậm trong hình vẽ. Biết
lần lượt là diện tích các hình phẳng được tô đậm trong hình vẽ. Biết 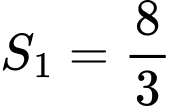 , tính
, tính 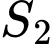 .
.
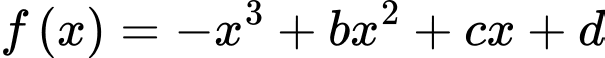
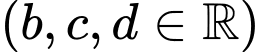 có đồ thị
có đồ thị  Gọi
Gọi 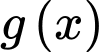 là hàm số bậc nhất có đồ thị là đường thẳng
là hàm số bậc nhất có đồ thị là đường thẳng  cắt đồ thị
cắt đồ thị  tại ba điểm
tại ba điểm 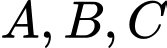 sao cho
sao cho 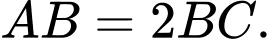 Gọi
Gọi 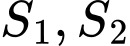 lần lượt là diện tích các hình phẳng được tô đậm trong hình vẽ. Biết
lần lượt là diện tích các hình phẳng được tô đậm trong hình vẽ. Biết 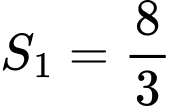 , tính
, tính 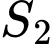 .
.
A, 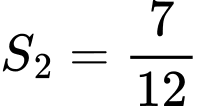 .
.
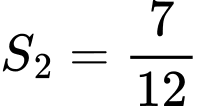 .
.B, 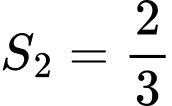 .
.
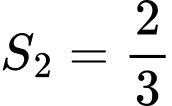 .
.C, 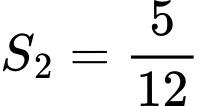 .
.
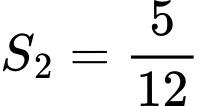 .
.D, 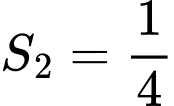 .
.
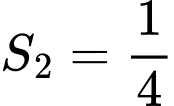 .
.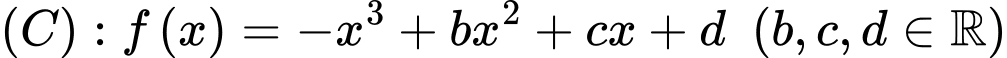
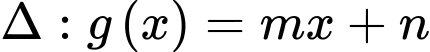
 tại 3 điểm
tại 3 điểm 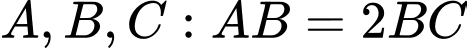
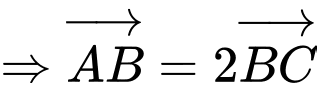
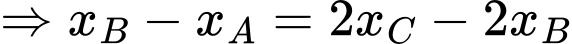
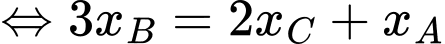
Giả sử ta đặt
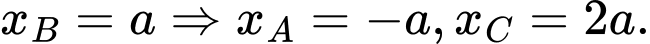
Theo bài ta có:
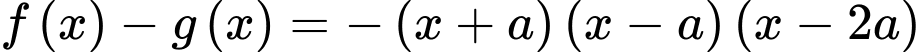
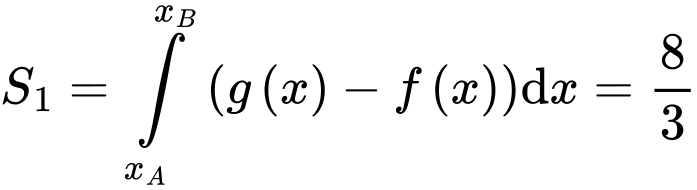
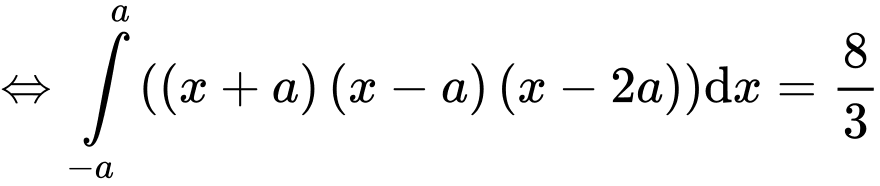
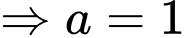
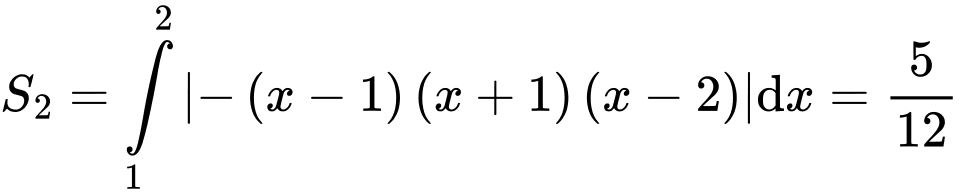
Đáp án C. Đáp án: C
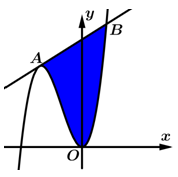
Câu 7 [906089]: Cho hàm số 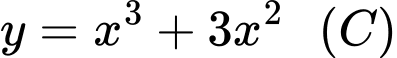 . Tiếp tuyến
. Tiếp tuyến 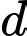 của đồ thị hàm số
của đồ thị hàm số  cắt
cắt  tại 2 điểm
tại 2 điểm 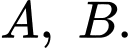 Biết diện tích hình phẳng giới hạn bởi
Biết diện tích hình phẳng giới hạn bởi 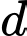 và
và  bằng
bằng 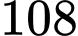 (tham khảo hình vẽ). Tính độ dài đoạn thẳng
(tham khảo hình vẽ). Tính độ dài đoạn thẳng 
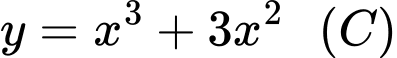 . Tiếp tuyến
. Tiếp tuyến 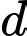 của đồ thị hàm số
của đồ thị hàm số  cắt
cắt  tại 2 điểm
tại 2 điểm 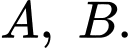 Biết diện tích hình phẳng giới hạn bởi
Biết diện tích hình phẳng giới hạn bởi 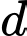 và
và  bằng
bằng 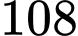 (tham khảo hình vẽ). Tính độ dài đoạn thẳng
(tham khảo hình vẽ). Tính độ dài đoạn thẳng 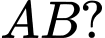

A, 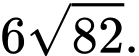
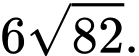
B, 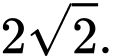
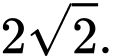
C, 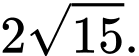
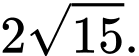
D, 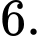
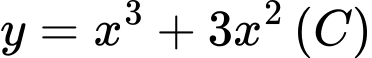
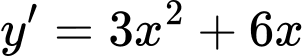
Ta có Phương trình tiếp tuyến d tại A là
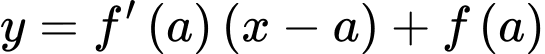
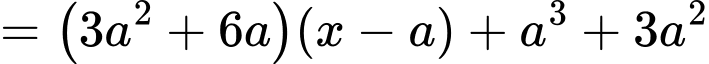
Tiếp tuyến d cắt hàm số
 tại 2 điểm A và B, ta có PT hoành độ giao điểm:
tại 2 điểm A và B, ta có PT hoành độ giao điểm:
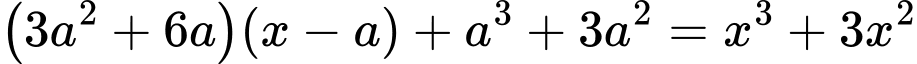
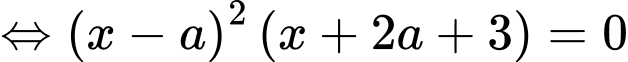
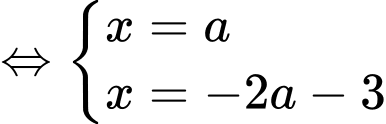
Ta có:
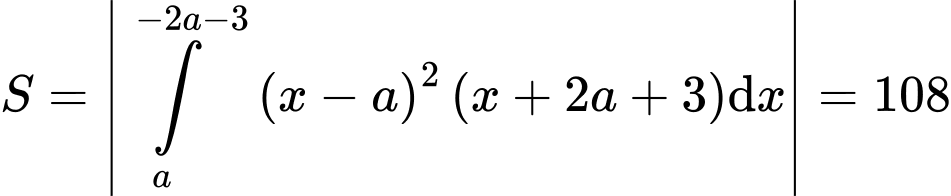
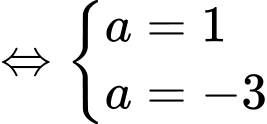
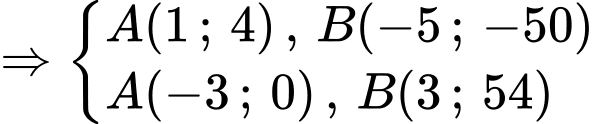
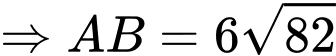
Suy ra, chọn đáp án A. Đáp án: A
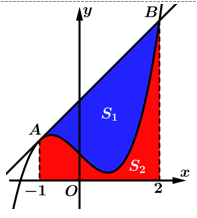
Câu 8 [905967]: Cho hàm số 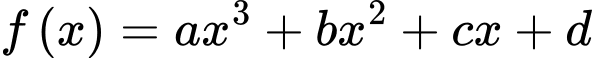 có đồ thị
có đồ thị  Biết rằng tiếp tuyến
Biết rằng tiếp tuyến 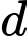 của
của  tại điểm
tại điểm 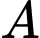 có hoành độ
có hoành độ 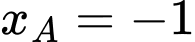 cắt
cắt  tại
tại 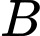 có hoành độ
có hoành độ 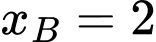 (xem hình vẽ). Trong hình vẽ bên có
(xem hình vẽ). Trong hình vẽ bên có 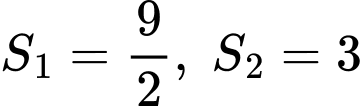 và
và 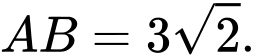 Tích phân
Tích phân 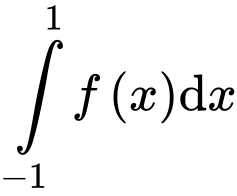 bằng
bằng
 có đồ thị
có đồ thị  Biết rằng tiếp tuyến
Biết rằng tiếp tuyến 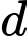 của
của  tại điểm
tại điểm 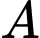 có hoành độ
có hoành độ 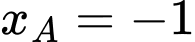 cắt
cắt  tại
tại 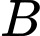 có hoành độ
có hoành độ 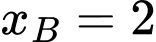 (xem hình vẽ). Trong hình vẽ bên có
(xem hình vẽ). Trong hình vẽ bên có 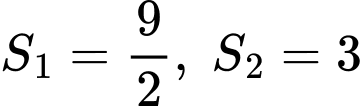 và
và 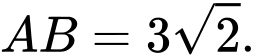 Tích phân
Tích phân 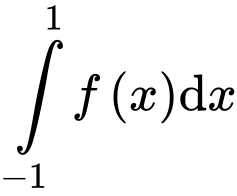 bằng
bằng 
A, 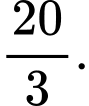
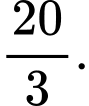
B, 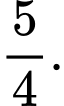
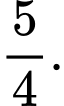
C, 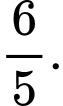
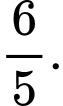
D, 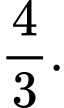
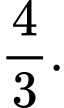
Giả sử 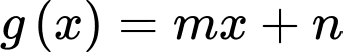 là phương trình tiếp tuyến
là phương trình tiếp tuyến 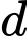 của
của 
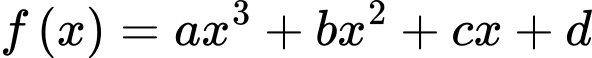
Ta có: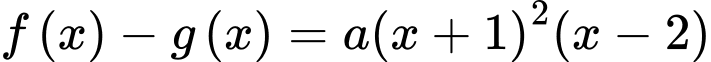
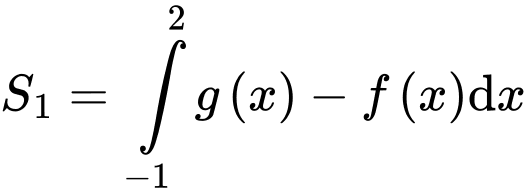
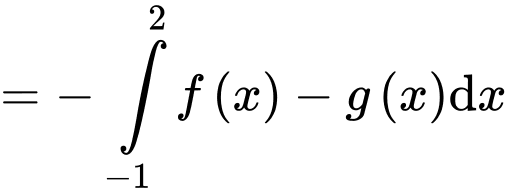
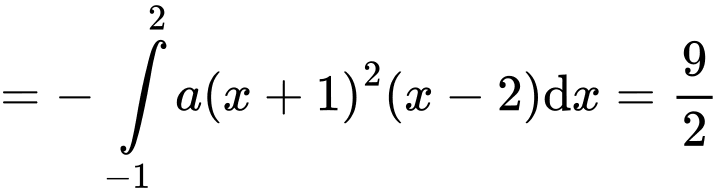
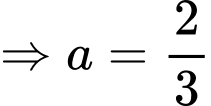
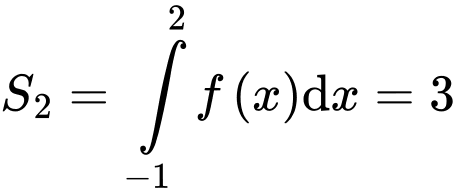
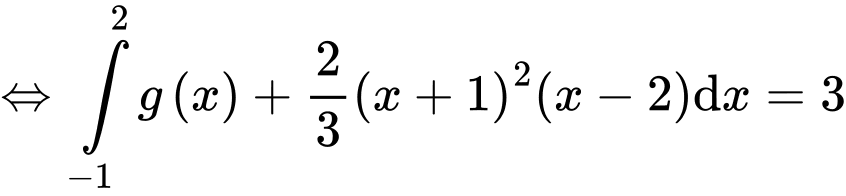
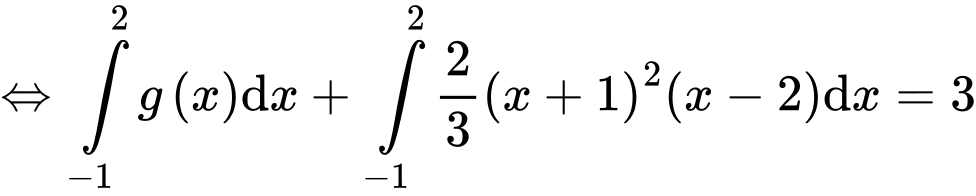
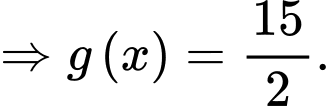
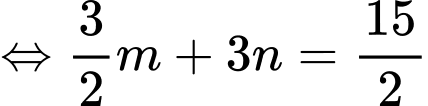
Có: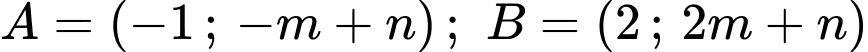

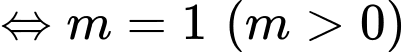
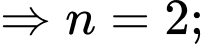
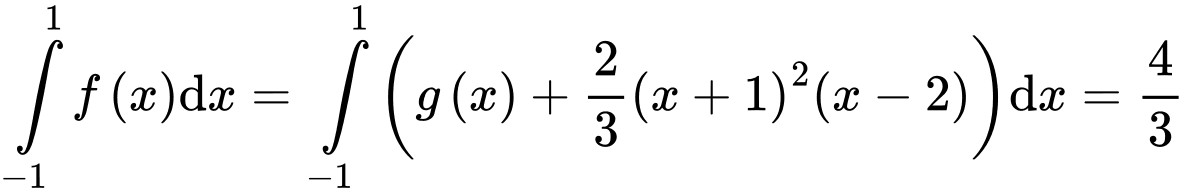
Suy ra, chọn D. Đáp án: D
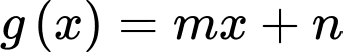 là phương trình tiếp tuyến
là phương trình tiếp tuyến 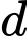 của
của 
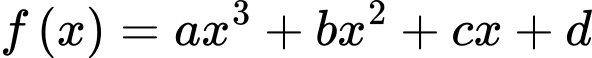
Ta có:
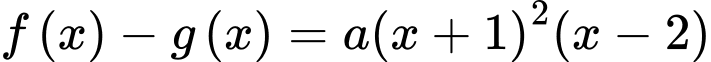
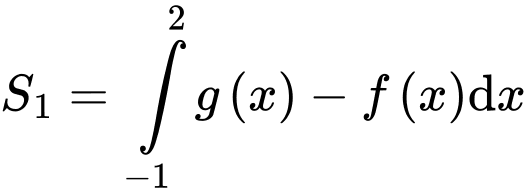
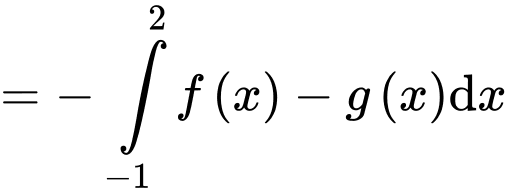
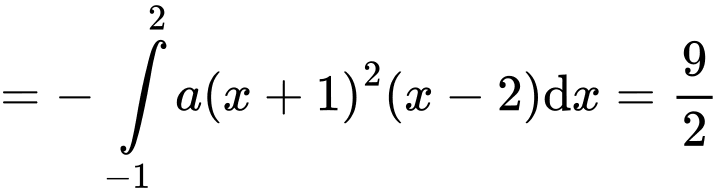
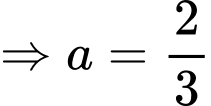
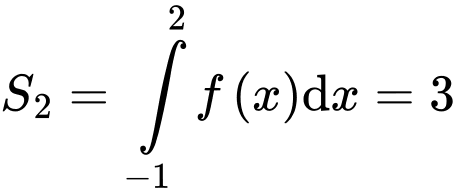
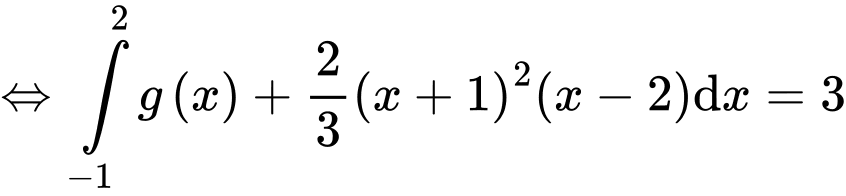
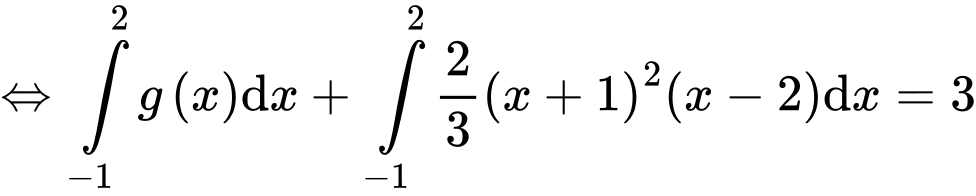
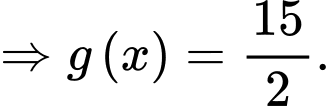
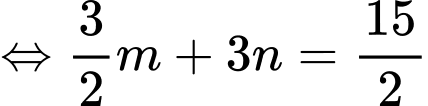
Có:
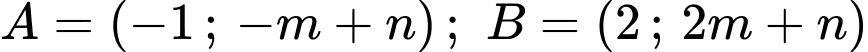

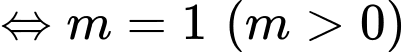
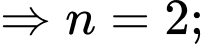
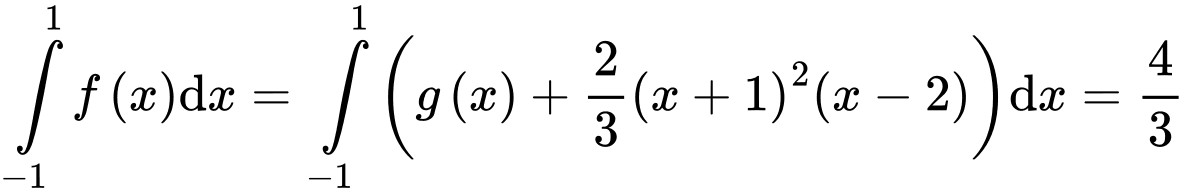
Suy ra, chọn D. Đáp án: D
Câu 9 [904754]: Cho hàm số 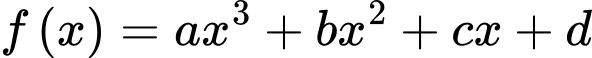 và đường thẳng
và đường thẳng 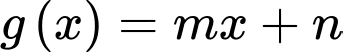 (a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ
(a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ  Gọi
Gọi 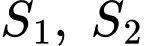 là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng
là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng 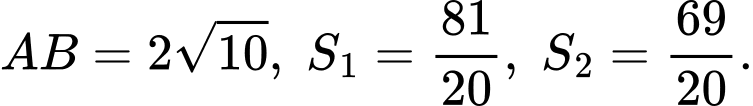 Tích phân
Tích phân 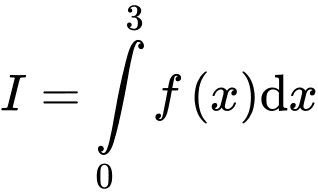 gần giá trị nguyên nào nhất?
gần giá trị nguyên nào nhất?
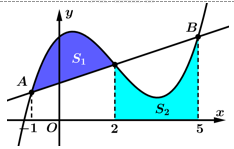
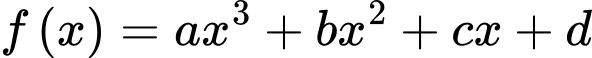 và đường thẳng
và đường thẳng 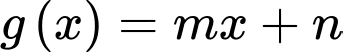 (a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ
(a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ  Gọi
Gọi 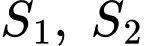 là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng
là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng 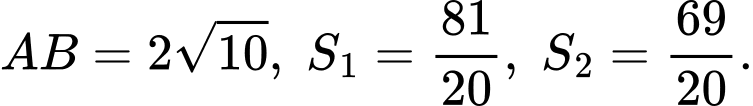 Tích phân
Tích phân 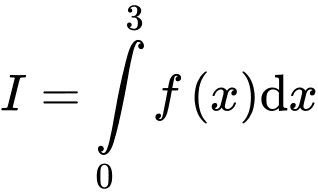 gần giá trị nguyên nào nhất?
gần giá trị nguyên nào nhất?
A, 8.
B, 9.
C, 6.
D, 7.
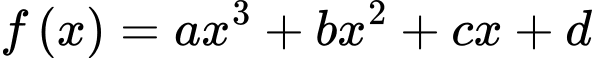
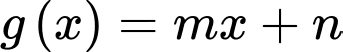
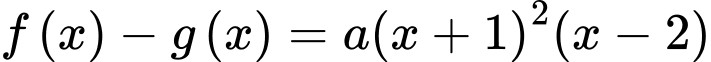
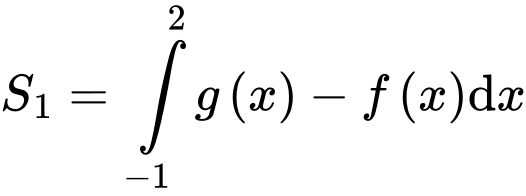
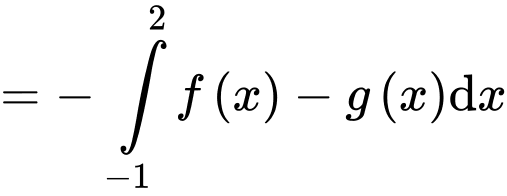
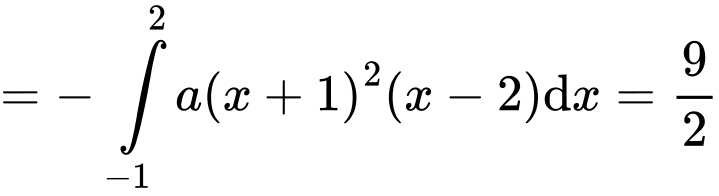
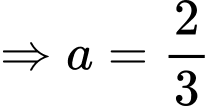
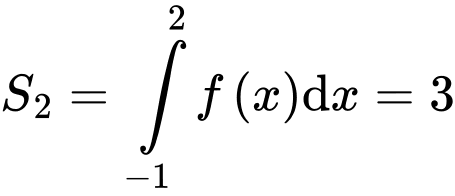
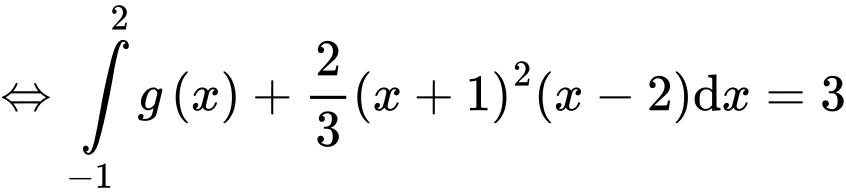
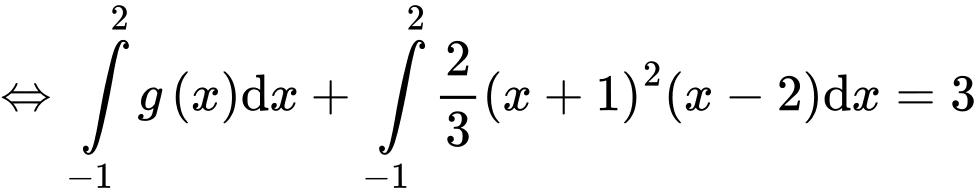
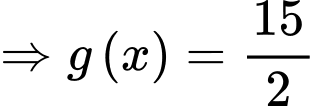
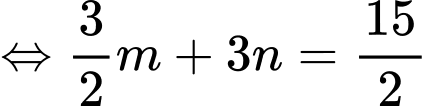
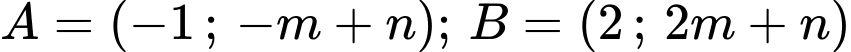


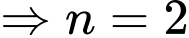
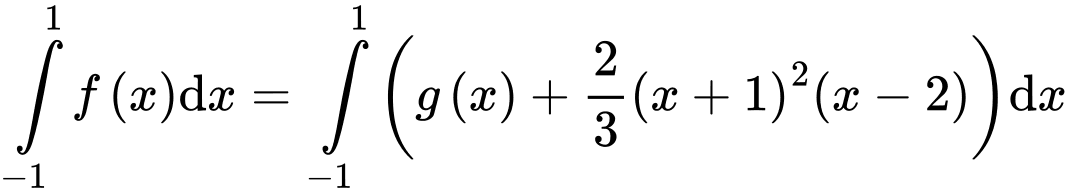
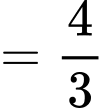
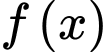 cắt
cắt 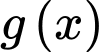 tại 3 điểm có hoành độ
tại 3 điểm có hoành độ 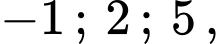 suy ra:
suy ra:
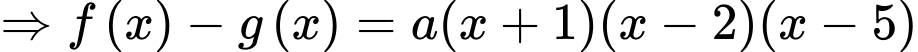
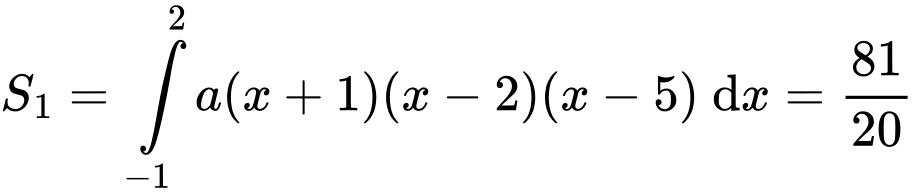
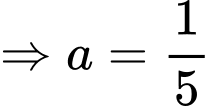
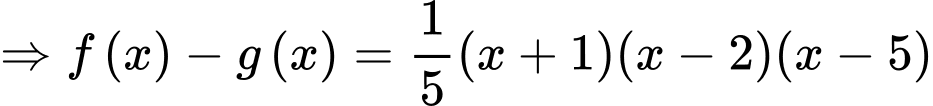
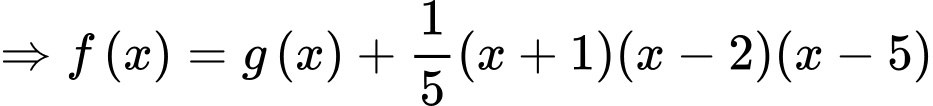
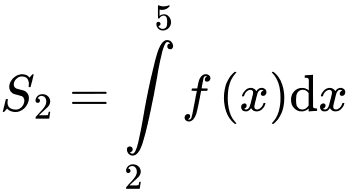
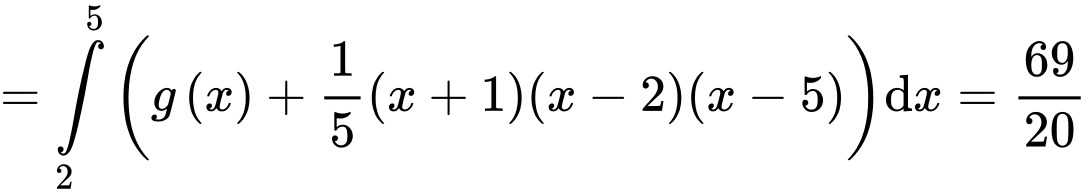
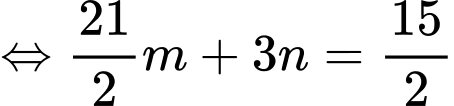
Có
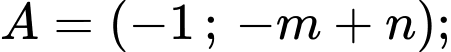
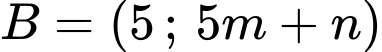
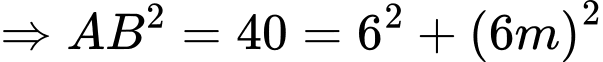
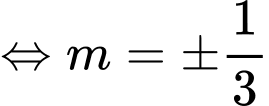
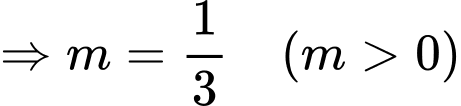
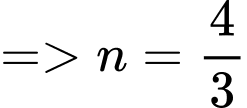
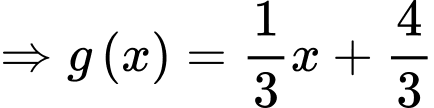
Vậy
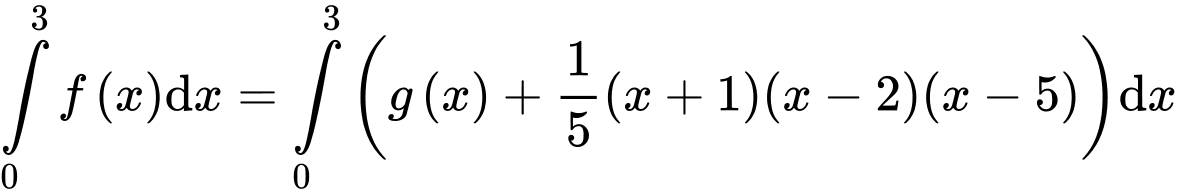
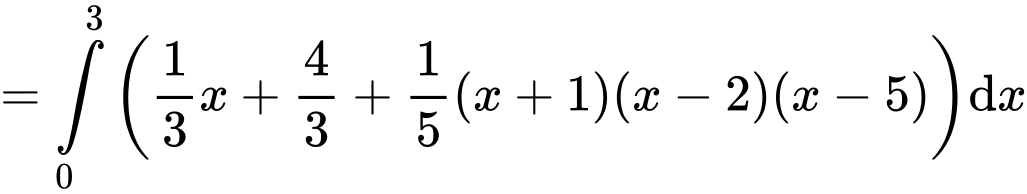
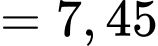
Suy ra, chọn D. Đáp án: D
Câu 10 [227489]: Cho hàm số 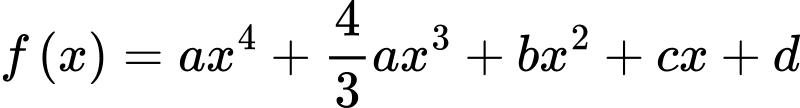 với
với  là các số thực. Đồ thị của hai hàm số
là các số thực. Đồ thị của hai hàm số 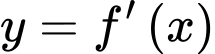 và
và 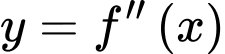 cắt nhau tại các điểm trong đó có hai điểm là
cắt nhau tại các điểm trong đó có hai điểm là 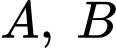 (như hình vẽ). Biết diện tích miền gạch chéo bằng
(như hình vẽ). Biết diện tích miền gạch chéo bằng 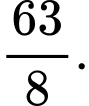 Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 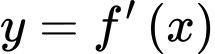 và
và 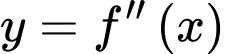 .
.
 với
với  là các số thực. Đồ thị của hai hàm số
là các số thực. Đồ thị của hai hàm số 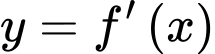 và
và 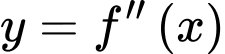 cắt nhau tại các điểm trong đó có hai điểm là
cắt nhau tại các điểm trong đó có hai điểm là 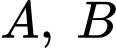 (như hình vẽ). Biết diện tích miền gạch chéo bằng
(như hình vẽ). Biết diện tích miền gạch chéo bằng 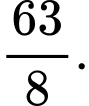 Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 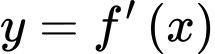 và
và 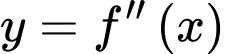 .
.
A, 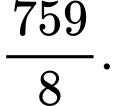
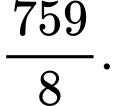
B, 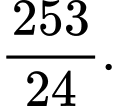
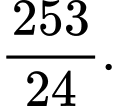
C, 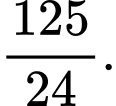
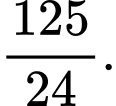
D, 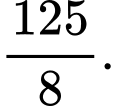
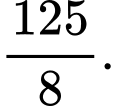
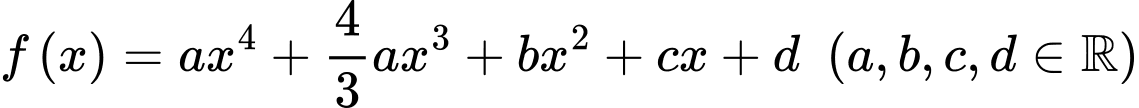
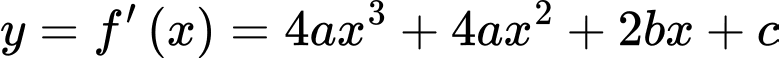
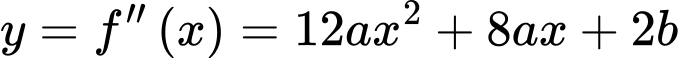
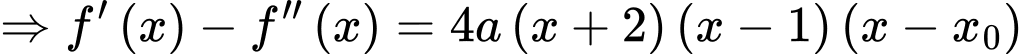
Cân bằng hệ số của
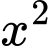 ta có:
ta có: 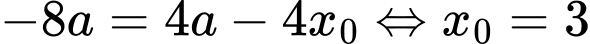
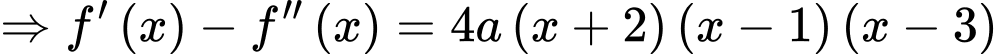
Theo bài ta có:
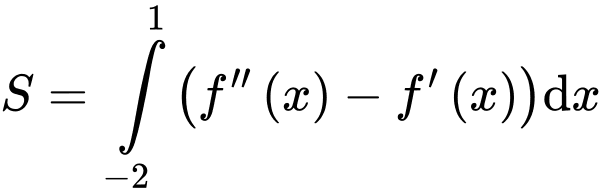
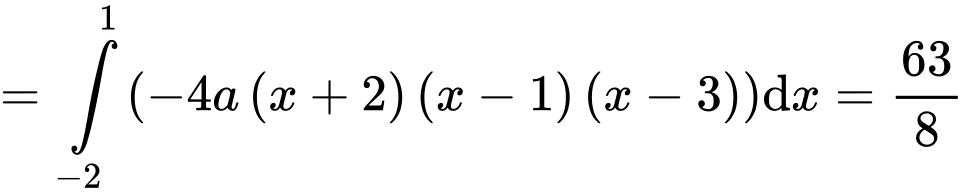
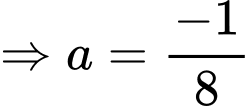
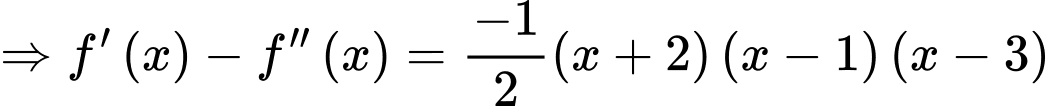
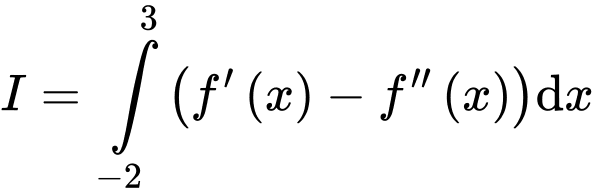
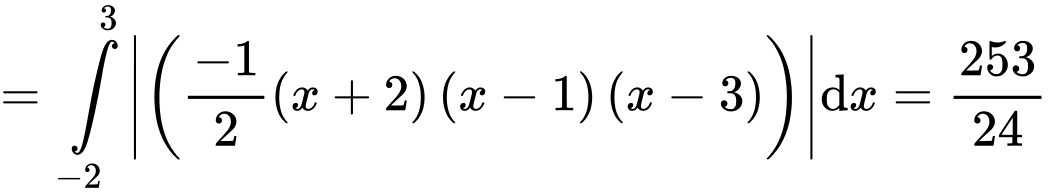
Đáp án B Đáp án: B
Câu 11 [908488]: Cho hàm số 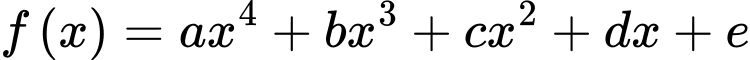 và đường thẳng
và đường thẳng 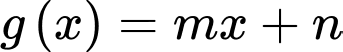 tiếp xúc nhau tại 2 điểm có hoành độ
tiếp xúc nhau tại 2 điểm có hoành độ 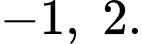 Trong hình vẽ bên có
Trong hình vẽ bên có 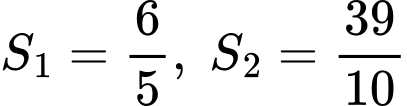 và
và 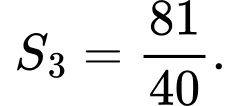 Tính tích phân
Tính tích phân 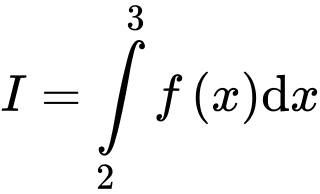
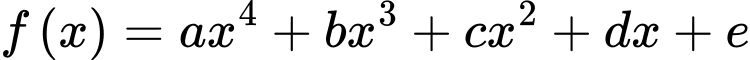 và đường thẳng
và đường thẳng 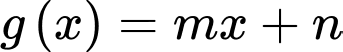 tiếp xúc nhau tại 2 điểm có hoành độ
tiếp xúc nhau tại 2 điểm có hoành độ 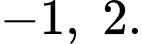 Trong hình vẽ bên có
Trong hình vẽ bên có 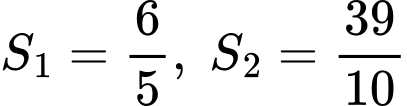 và
và 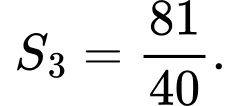 Tính tích phân
Tính tích phân 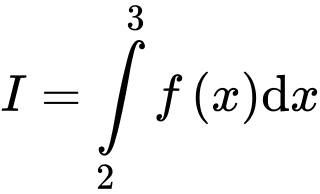

A, .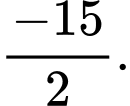
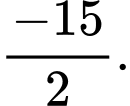
B, 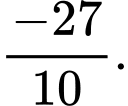
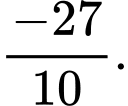
C, 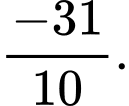
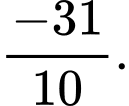
D, 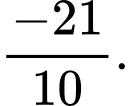
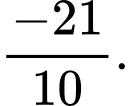
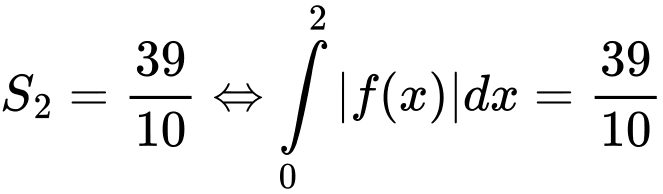
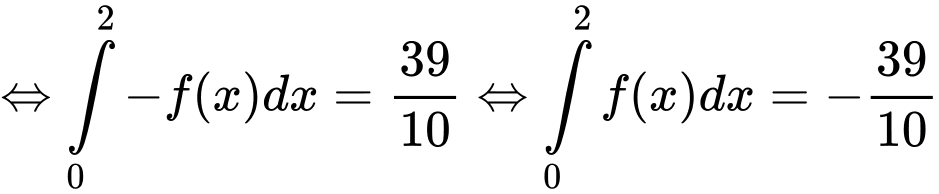
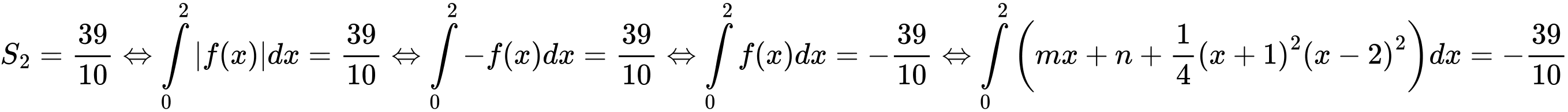
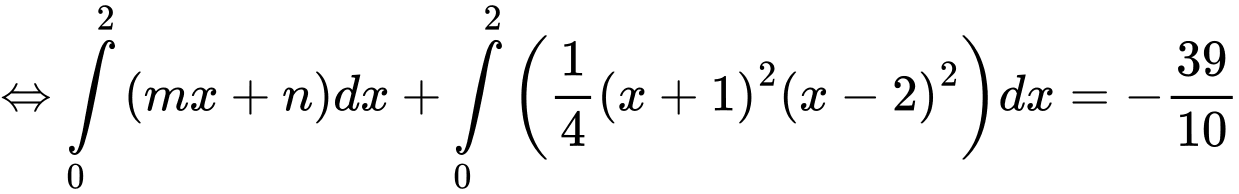
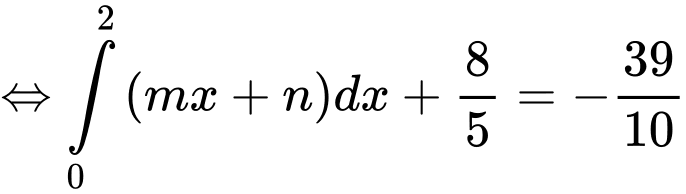
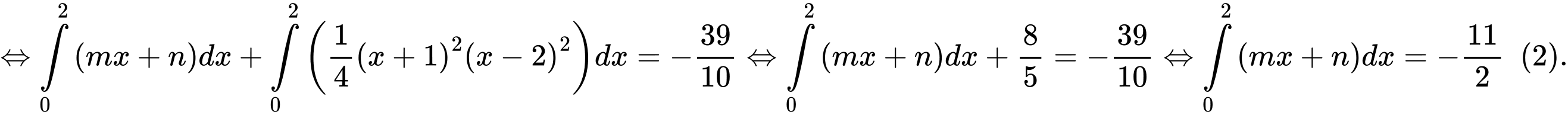
Từ (1) và (2) ta có:
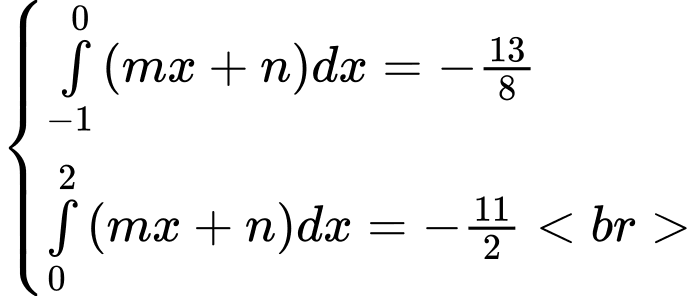
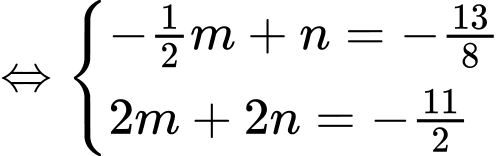
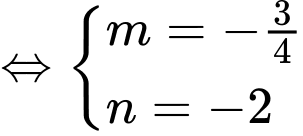
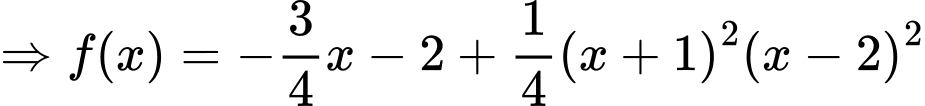
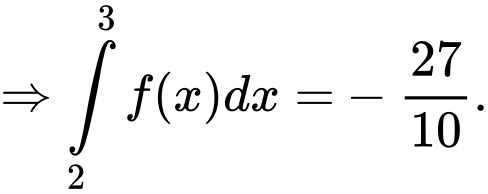
Chọn đáp án B. Đáp án: B
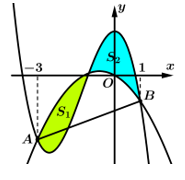
Câu 12 [907817]: Cho hàm số 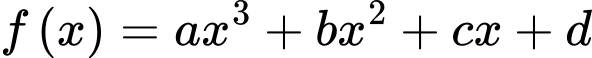 và
và 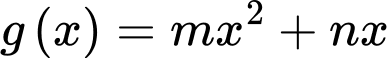 cắt nhau tại 3 điểm có hoành độ
cắt nhau tại 3 điểm có hoành độ  như hình vẽ bên. Biết rằng
như hình vẽ bên. Biết rằng 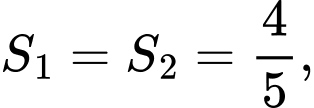
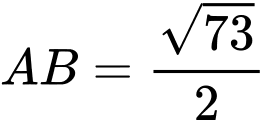 và
và 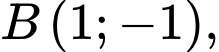 tính tích phân
tính tích phân 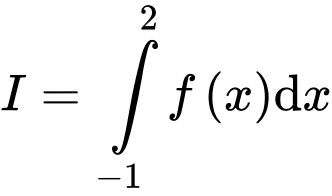
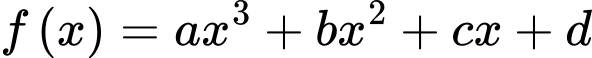 và
và 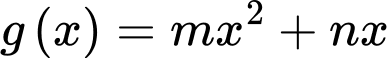 cắt nhau tại 3 điểm có hoành độ
cắt nhau tại 3 điểm có hoành độ  như hình vẽ bên. Biết rằng
như hình vẽ bên. Biết rằng 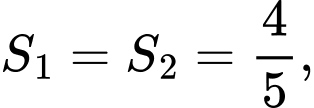
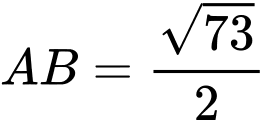 và
và 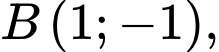 tính tích phân
tính tích phân 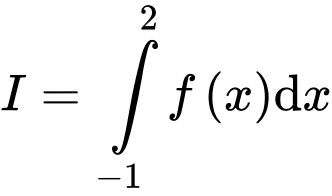

A, 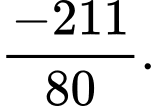
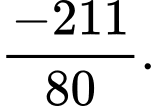
B, 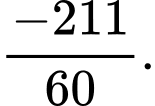
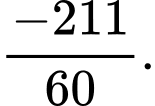
C, 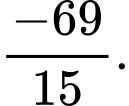
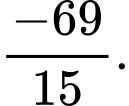
D, 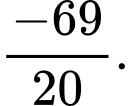
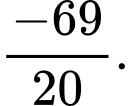
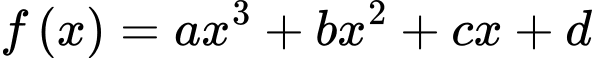
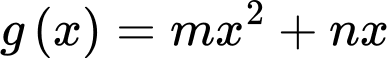
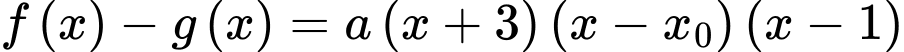
Theo bài ta có:
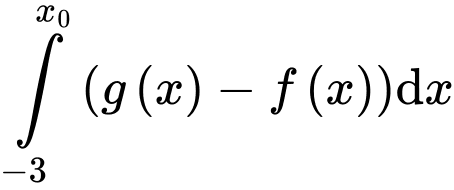
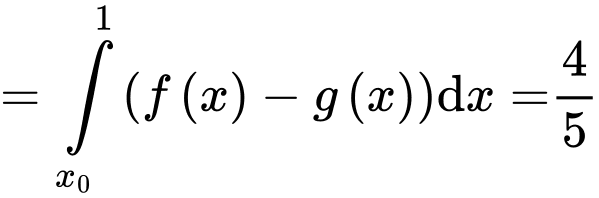
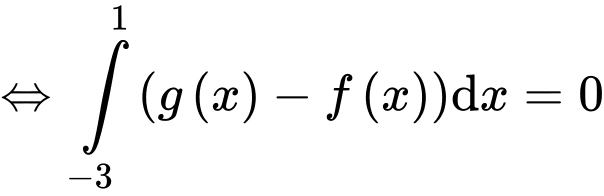
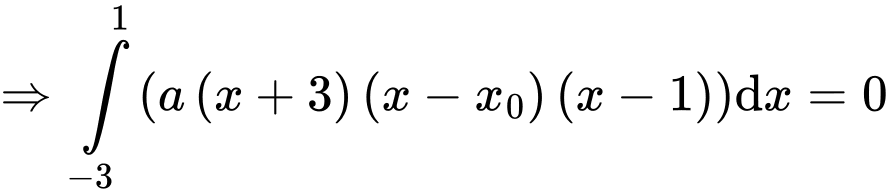
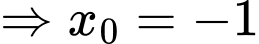
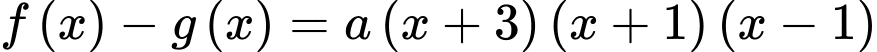
Lại có:
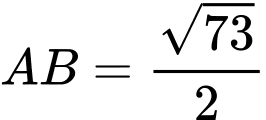
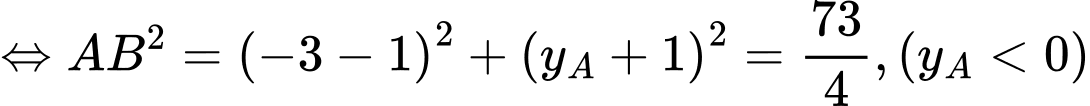
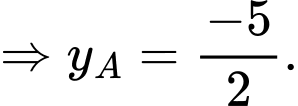
Có
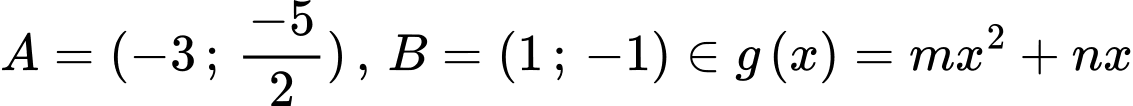
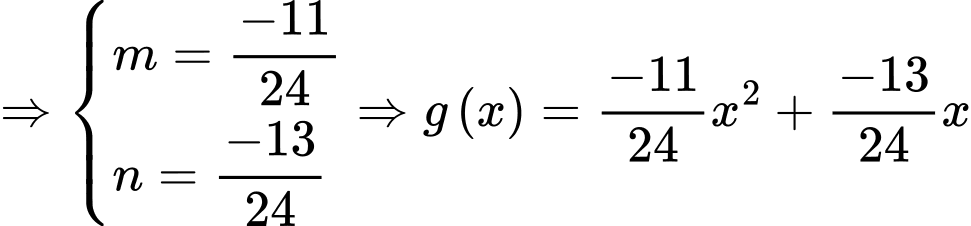
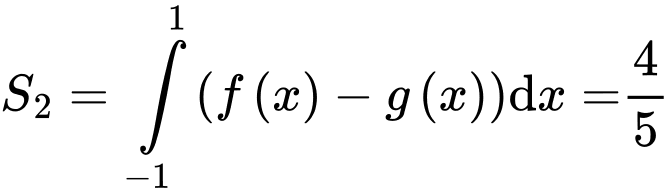
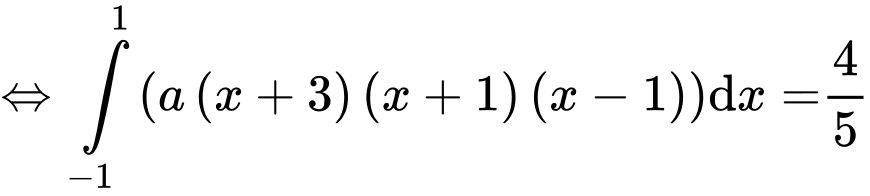
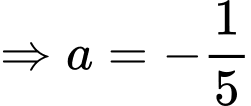
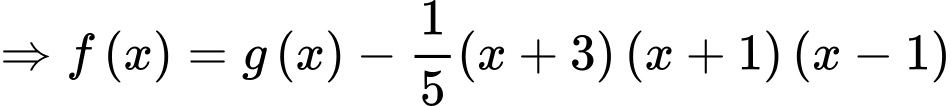
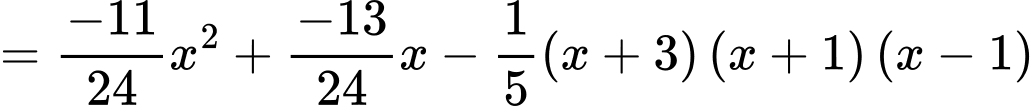
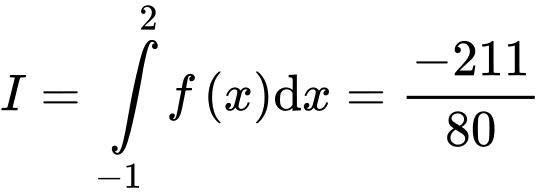
Từ đó, suy ra chọn đáp án A. Đáp án: A
Câu 13 [906158]: Cho hàm số đa thức bậc bốn 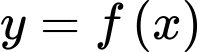 và đường thẳng
và đường thẳng 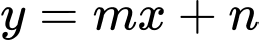 tiếp xúc nhau tại điểm
tiếp xúc nhau tại điểm  và cắt nhau tại điểm
và cắt nhau tại điểm 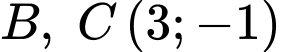 trong đó
trong đó 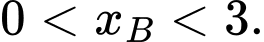 Biết rằng
Biết rằng 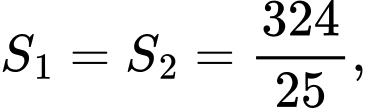 tích phân
tích phân 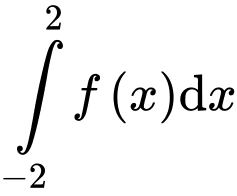 gần giá trị nguyên nào nhất
gần giá trị nguyên nào nhất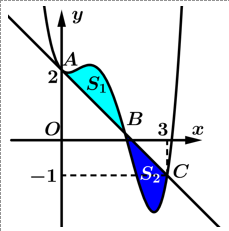
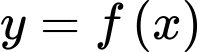 và đường thẳng
và đường thẳng 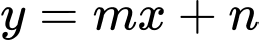 tiếp xúc nhau tại điểm
tiếp xúc nhau tại điểm  và cắt nhau tại điểm
và cắt nhau tại điểm 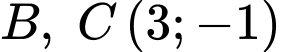 trong đó
trong đó 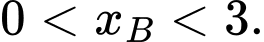 Biết rằng
Biết rằng 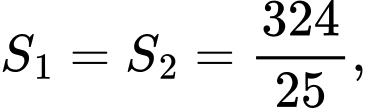 tích phân
tích phân 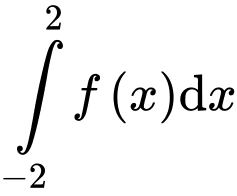 gần giá trị nguyên nào nhất
gần giá trị nguyên nào nhất
A, 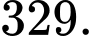
B, 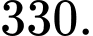
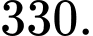
C, 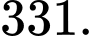
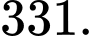
D, 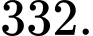
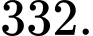
Hàm số đa thức bậc bốn 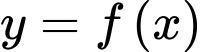 và đường thẳng
và đường thẳng 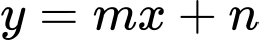 tiếp xúc nhau tại điểm
tiếp xúc nhau tại điểm  và cắt nhau tại điểm
và cắt nhau tại điểm 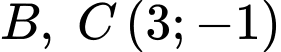 nên
nên 
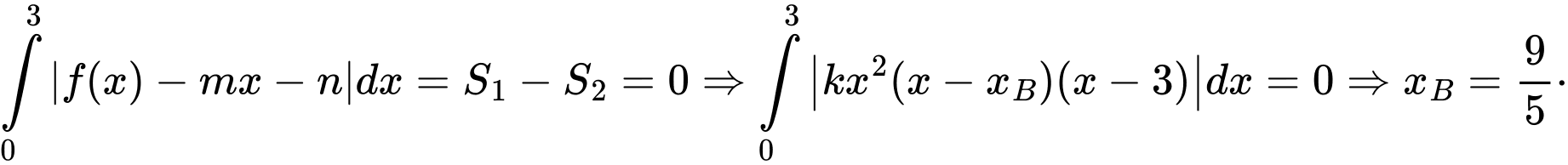
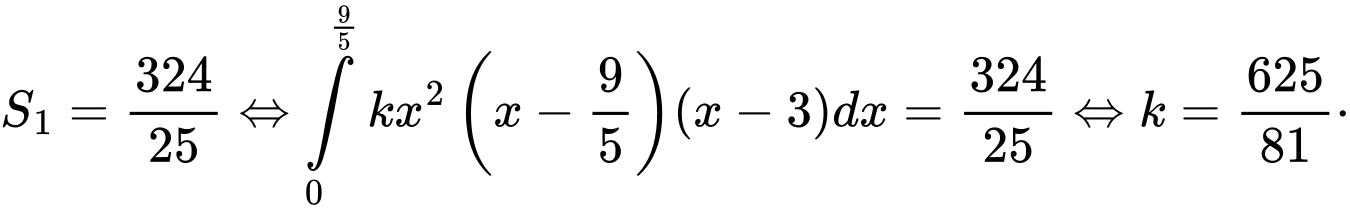
Phương trình đường thẳng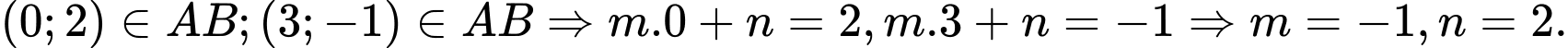
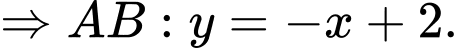
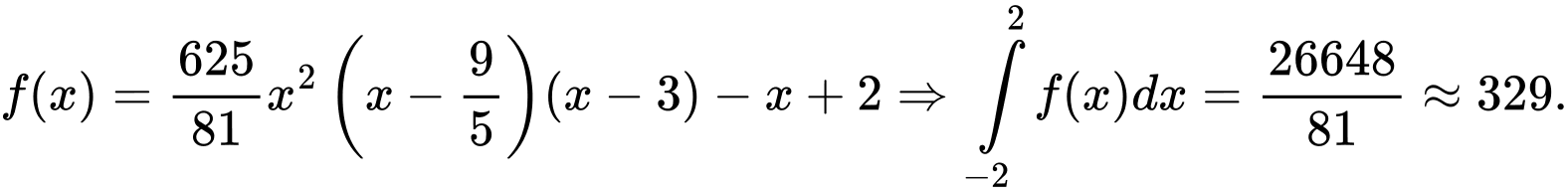
Chọn đáp án A. Đáp án: A
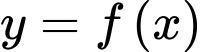 và đường thẳng
và đường thẳng 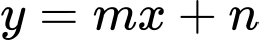 tiếp xúc nhau tại điểm
tiếp xúc nhau tại điểm  và cắt nhau tại điểm
và cắt nhau tại điểm 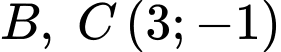 nên
nên 
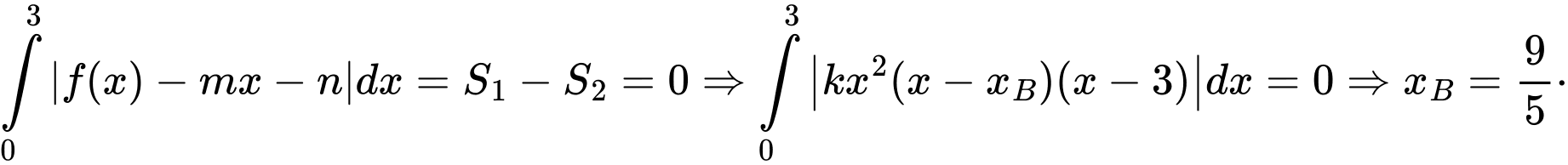
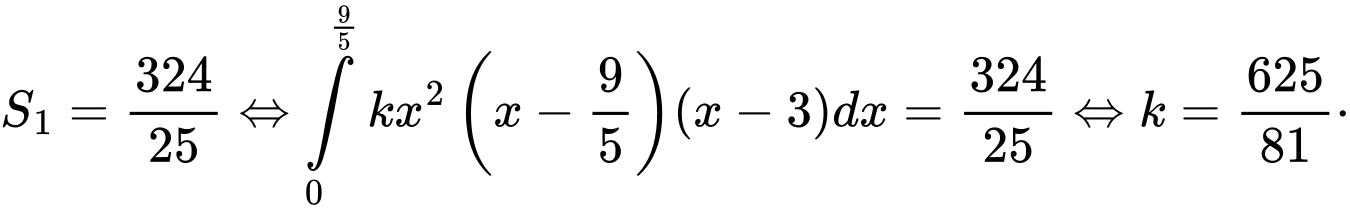
Phương trình đường thẳng
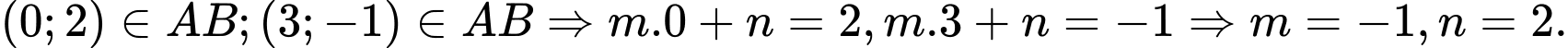
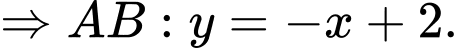
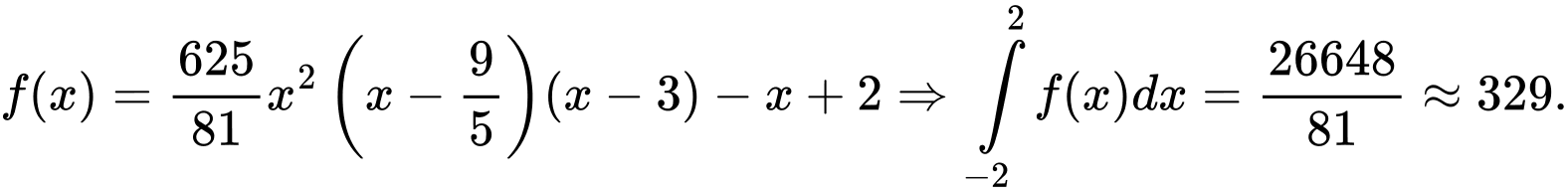
Chọn đáp án A. Đáp án: A
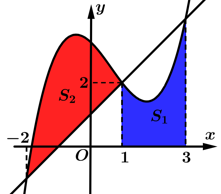
Câu 14 [904641]: Cho hàm số 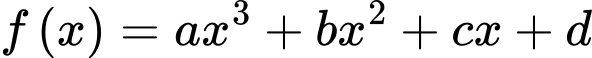 và đường thẳng
và đường thẳng 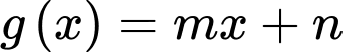 (a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ
(a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ  trong đó có điểm
trong đó có điểm 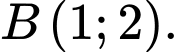 Gọi
Gọi 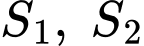 là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng
là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng 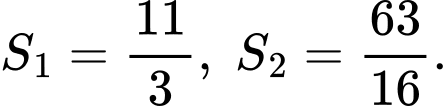 Tích phân
Tích phân 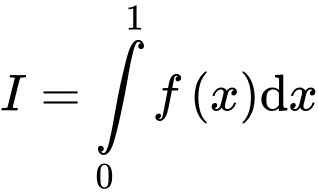 gần giá trị nào nhất trong các giá trị sau
gần giá trị nào nhất trong các giá trị sau
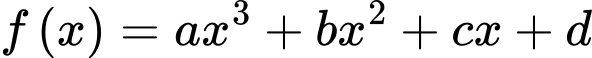 và đường thẳng
và đường thẳng 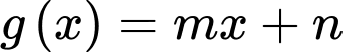 (a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ
(a,b,c,d,m,n là số thực) cắt nhau tại 3 điểm có hoành độ  trong đó có điểm
trong đó có điểm 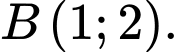 Gọi
Gọi 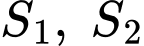 là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng
là diện tích hình phẳng được tô đậm như hình vẽ (tham khảo hình vẽ). Biết rằng 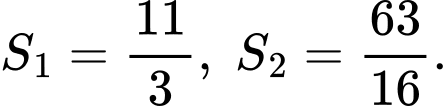 Tích phân
Tích phân 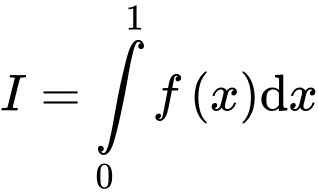 gần giá trị nào nhất trong các giá trị sau
gần giá trị nào nhất trong các giá trị sau
A, 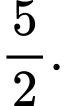
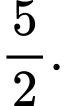
B, 
C, 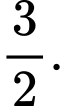
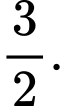
D, 
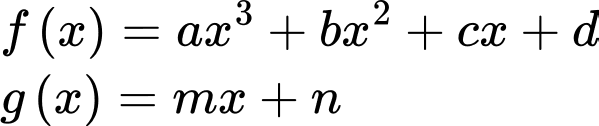
 cắt
cắt 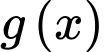 tại 3 điểm có hoành độ -2,1,3, suy ra:
tại 3 điểm có hoành độ -2,1,3, suy ra: 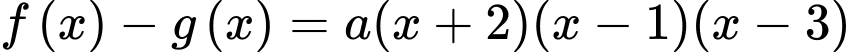
Ta có:
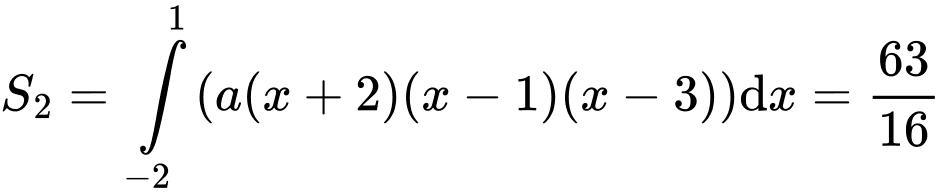
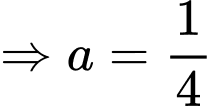
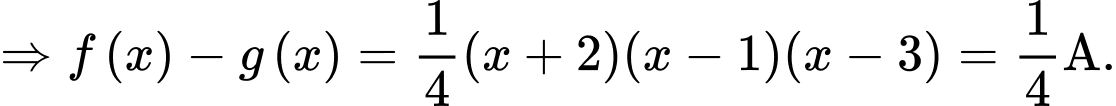
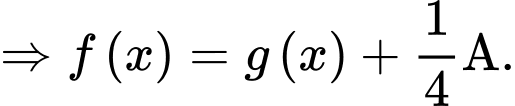
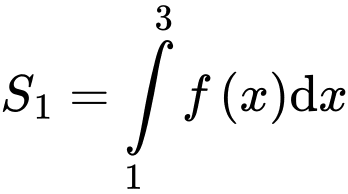
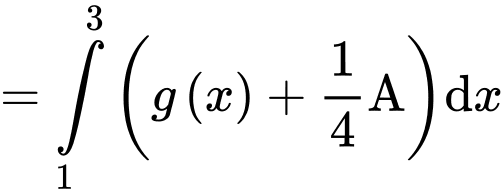
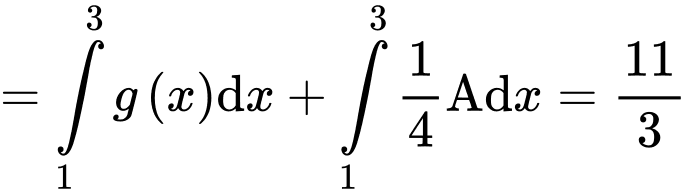
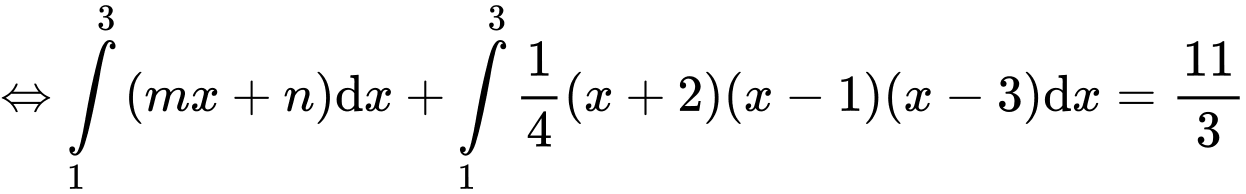
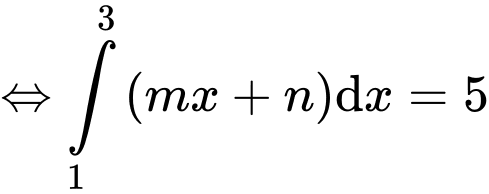

Lại có:
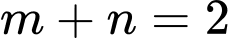
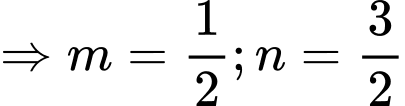
Vậy
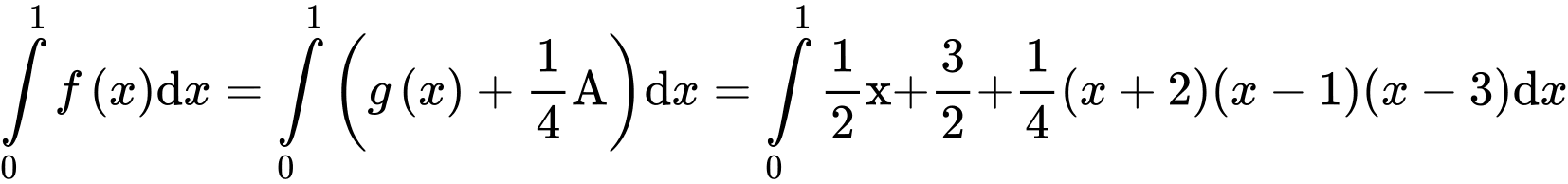
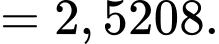
Suy ra chọn A. Đáp án: A
Câu 15 [906687]: Cho đồ thị hàm số 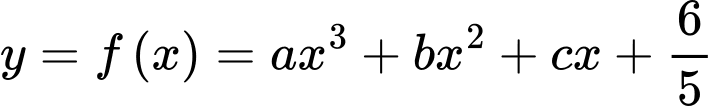 cắt đường thẳng
cắt đường thẳng 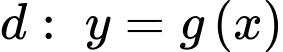 tại ba điểm
tại ba điểm 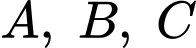 với
với 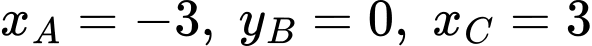 như hình vẽ. Gọi
như hình vẽ. Gọi  lần lượt là hình chiếu của
lần lượt là hình chiếu của 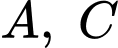 trên trục
trên trục 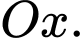 Biết rằng
Biết rằng 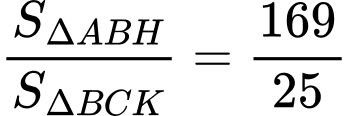 và diện tích phần tô đậm bằng
và diện tích phần tô đậm bằng 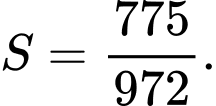 Giá trị của
Giá trị của 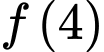 bằng
bằng
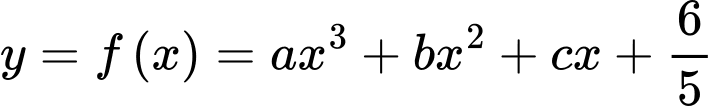 cắt đường thẳng
cắt đường thẳng 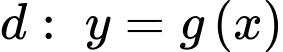 tại ba điểm
tại ba điểm  với
với 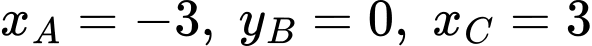 như hình vẽ. Gọi
như hình vẽ. Gọi  lần lượt là hình chiếu của
lần lượt là hình chiếu của 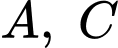 trên trục
trên trục 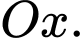 Biết rằng
Biết rằng 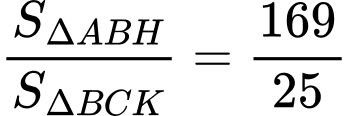 và diện tích phần tô đậm bằng
và diện tích phần tô đậm bằng 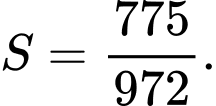 Giá trị của
Giá trị của 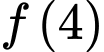 bằng
bằng 
A, 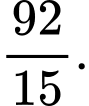
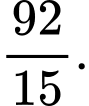
B, 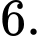
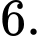
C, 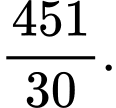
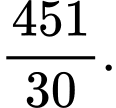
D, 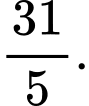
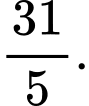
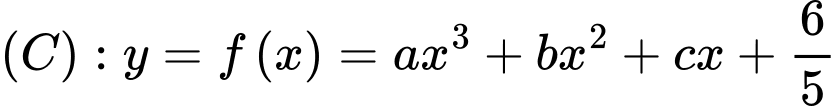
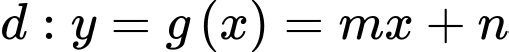
Theo gt,
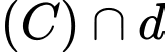 tại 3 điểm
tại 3 điểm 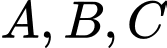 với
với 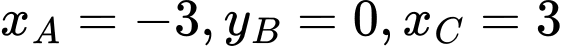
Có
 là hình chiếu của
là hình chiếu của  trên trục
trên trục 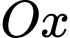
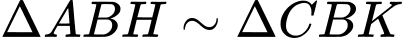
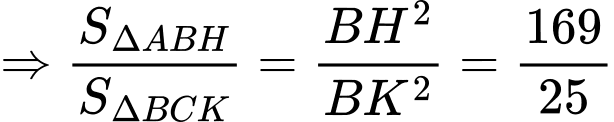
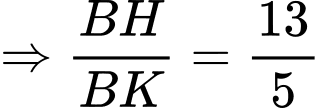
Lại có:

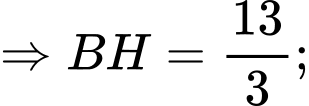
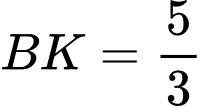
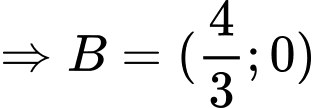
Có:
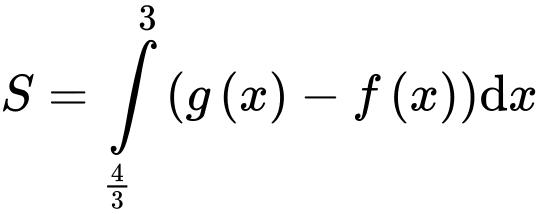
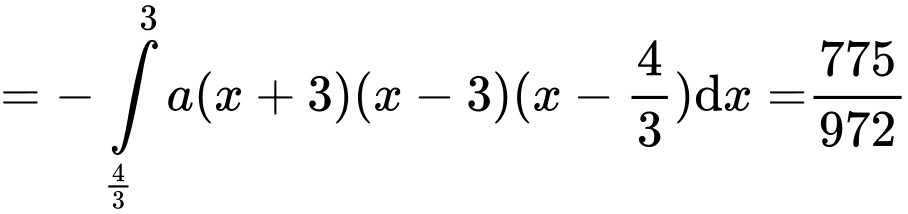
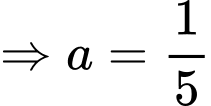
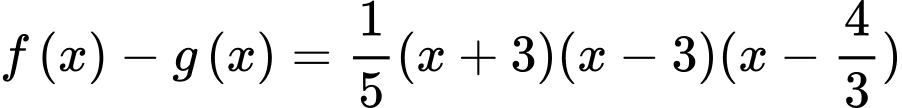 ta xét hệ số tự do
ta xét hệ số tự do
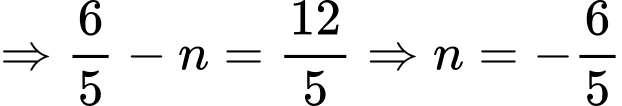
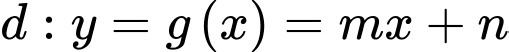 đi qua điểm
đi qua điểm 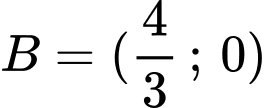
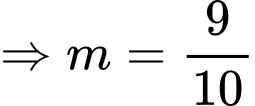
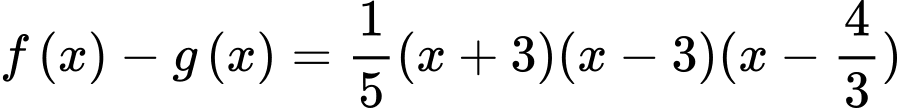
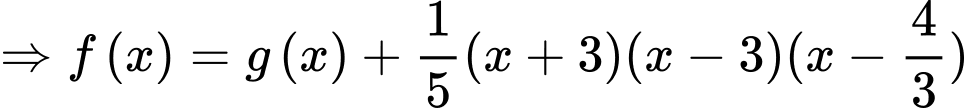
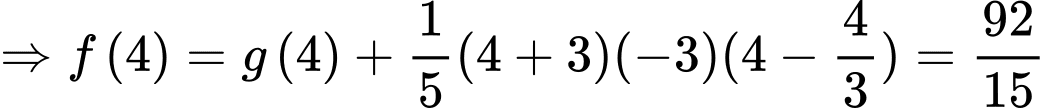
Suy ra, chọn đáp án A. Đáp án: A
Câu 16 [907228]: Cho Parabol 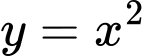 và đường thẳng
và đường thẳng 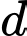 thay đổi luôn đi qua điểm
thay đổi luôn đi qua điểm  và cắt parabol
và cắt parabol 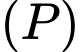 tại 2 điểm phân biệt
tại 2 điểm phân biệt 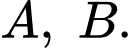 Gọi
Gọi 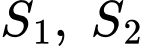 là diện tích hình phẳng trong hình vẽ bên, biết rằng
là diện tích hình phẳng trong hình vẽ bên, biết rằng 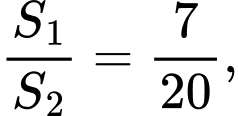 khi đó độ dài đoạn thẳng
khi đó độ dài đoạn thẳng  gần giá trị nào nhất sau đây
gần giá trị nào nhất sau đây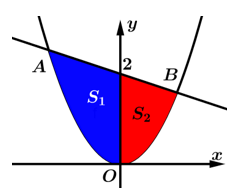
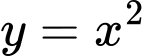 và đường thẳng
và đường thẳng 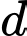 thay đổi luôn đi qua điểm
thay đổi luôn đi qua điểm  và cắt parabol
và cắt parabol 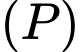 tại 2 điểm phân biệt
tại 2 điểm phân biệt 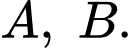 Gọi
Gọi 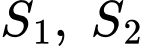 là diện tích hình phẳng trong hình vẽ bên, biết rằng
là diện tích hình phẳng trong hình vẽ bên, biết rằng 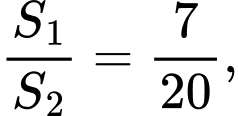 khi đó độ dài đoạn thẳng
khi đó độ dài đoạn thẳng  gần giá trị nào nhất sau đây
gần giá trị nào nhất sau đây
A, 3.
B, 4.
C, 5.
D, 6.
Phương trình đường thẳng AB là: 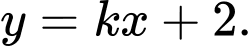
Phương trình hoành độ giao điểm: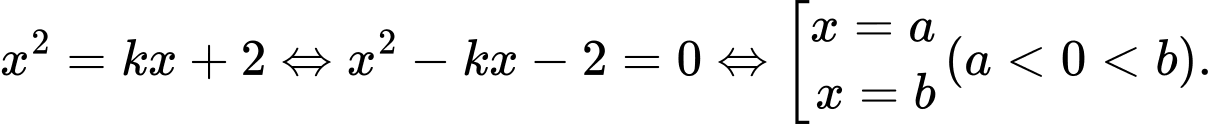
Khi đó: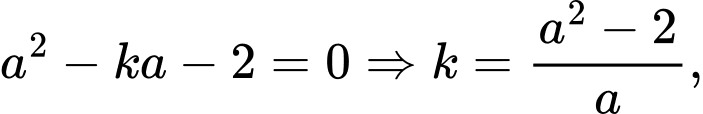
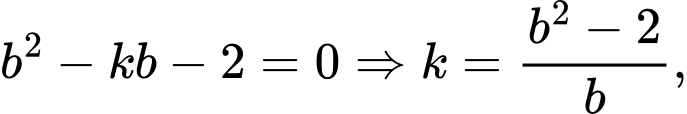
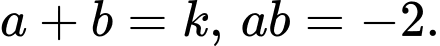
Ta có: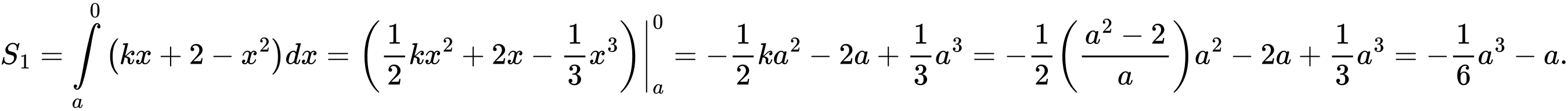
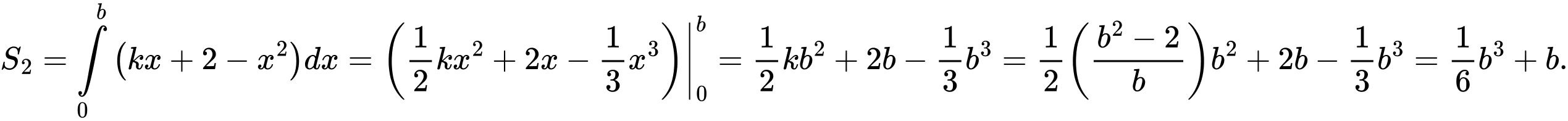
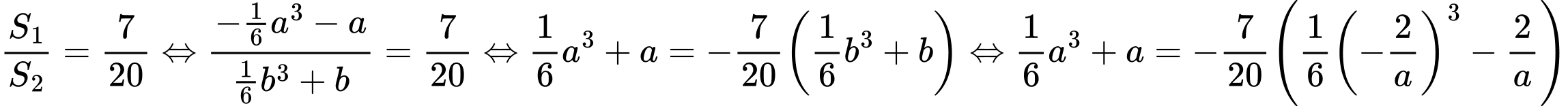
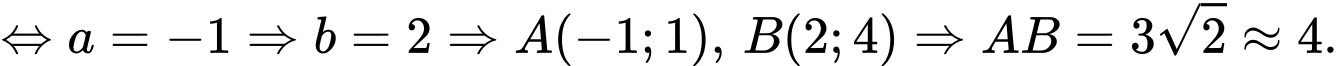 Đáp án: B
Đáp án: B
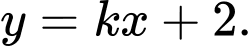
Phương trình hoành độ giao điểm:
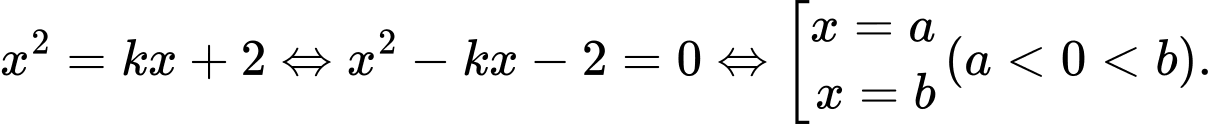
Khi đó:
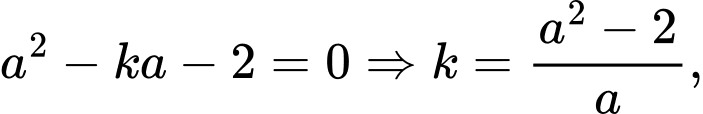
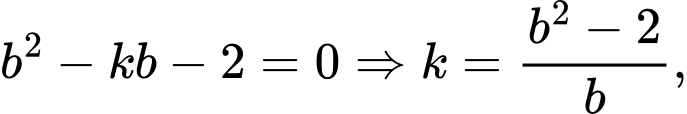
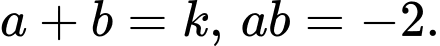
Ta có:
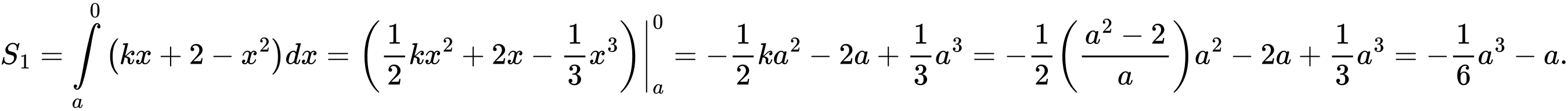
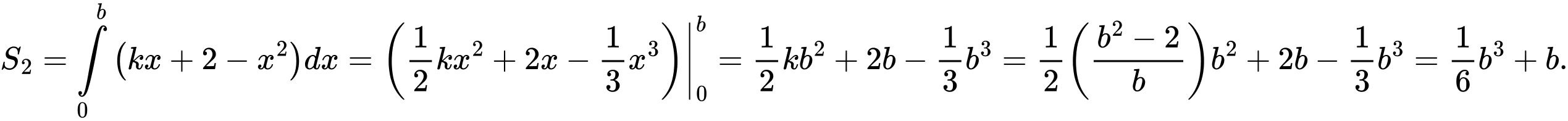
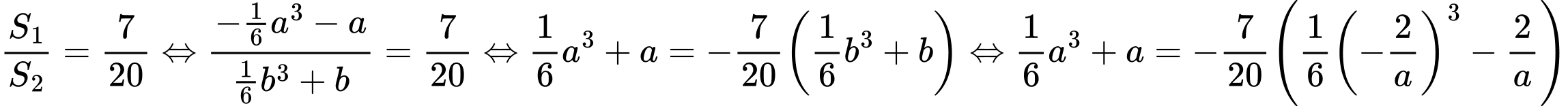
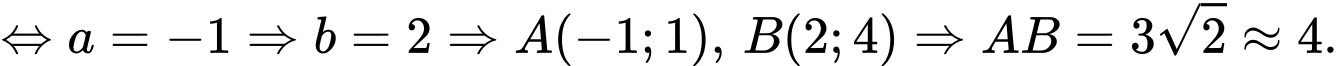 Đáp án: B
Đáp án: B