Đáp án Bài tập tự luyện
Câu 1 [899530]: Trong không gian 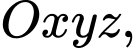 cho mặt phẳng
cho mặt phẳng 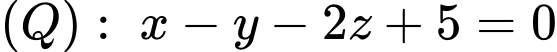 và điểm
và điểm 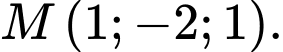 Khoảng cách từ điểm
Khoảng cách từ điểm 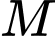 đến mặt phẳng
đến mặt phẳng  bằng
bằng
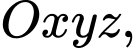 cho mặt phẳng
cho mặt phẳng 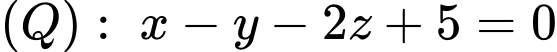 và điểm
và điểm 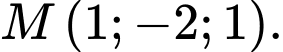 Khoảng cách từ điểm
Khoảng cách từ điểm 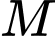 đến mặt phẳng
đến mặt phẳng  bằng
bằng A, 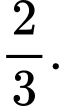
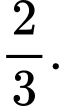
B, 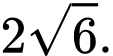
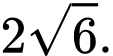
C, 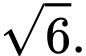
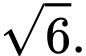
D, 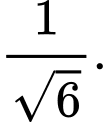
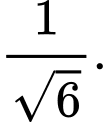
Áp dụng công thức ta có: 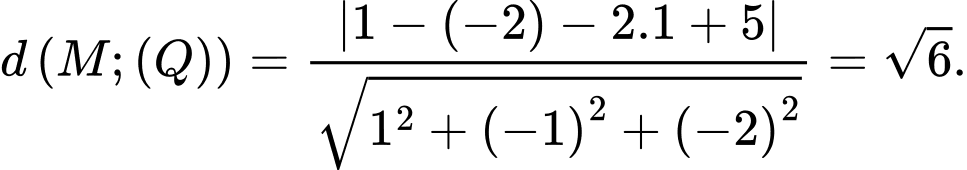 Chọn C. Đáp án: C
Chọn C. Đáp án: C
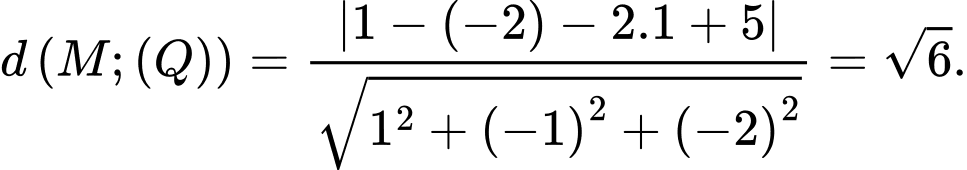 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 2 [57293]: Trong không gian 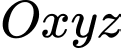 , khoảng cách từ điểm
, khoảng cách từ điểm 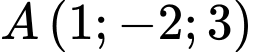 đến
đến 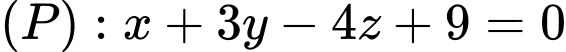 là
là
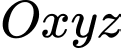 , khoảng cách từ điểm
, khoảng cách từ điểm 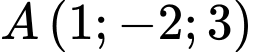 đến
đến 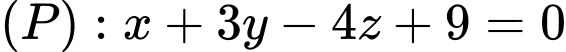 là
là A, 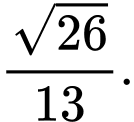
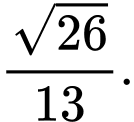
B, 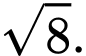
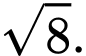
C, 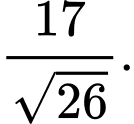
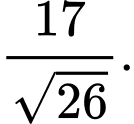
D, 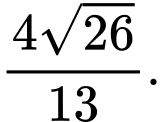
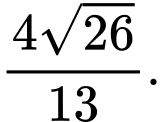
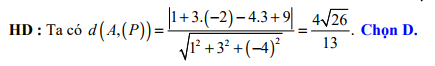 Đáp án: D
Đáp án: D
Câu 3 [57309]: Trong không gian 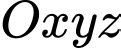 cho mặt phẳng
cho mặt phẳng 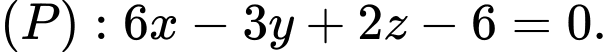 Tính khoảng cách
Tính khoảng cách 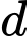 từ điểm
từ điểm 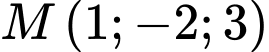 đến mặt phẳng
đến mặt phẳng 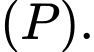
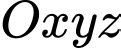 cho mặt phẳng
cho mặt phẳng 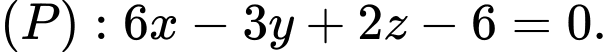 Tính khoảng cách
Tính khoảng cách 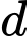 từ điểm
từ điểm 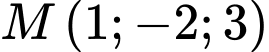 đến mặt phẳng
đến mặt phẳng 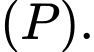
A, 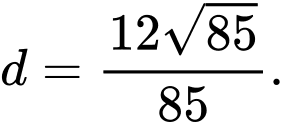
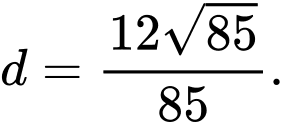
B, 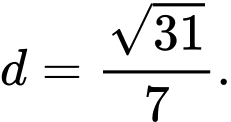
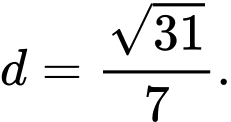
C, 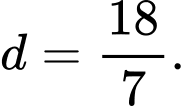
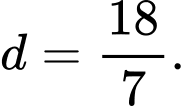
D, 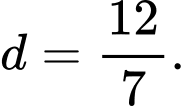
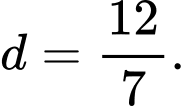
HD: Khoảng cách từ điểm 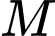 đến mặt phẳng
đến mặt phẳng 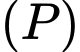 là
là 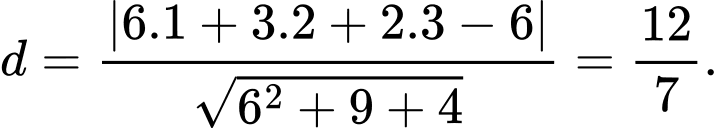 Chọn D. Đáp án: D
Chọn D. Đáp án: D
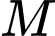 đến mặt phẳng
đến mặt phẳng 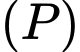 là
là 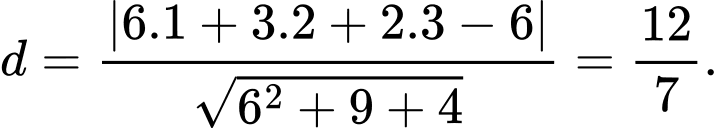 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 4 [360649]: Khoảng cách từ điểm 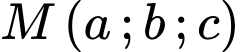 đến mặt phẳng
đến mặt phẳng 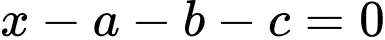 là:
là:
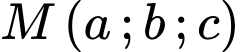 đến mặt phẳng
đến mặt phẳng 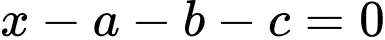 là:
là: A, 

B, 

C, 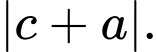
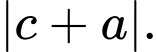
D, 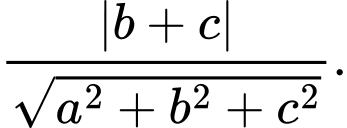
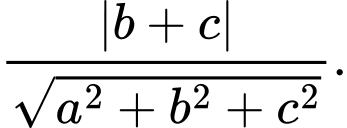
Khoảng cách từ 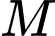 đến mặt phẳng
đến mặt phẳng 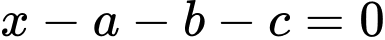 bằng
bằng
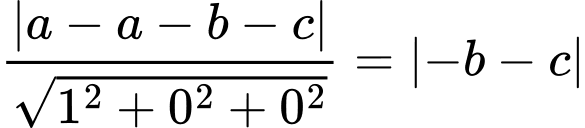
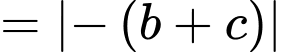
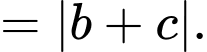 Chọn B. Đáp án: B
Chọn B. Đáp án: B
 đến mặt phẳng
đến mặt phẳng 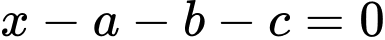 bằng
bằng 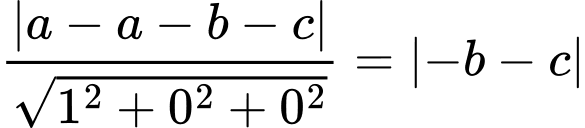
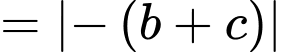
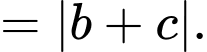 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 5 [322584]: Trong không gian 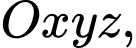 khoảng cách giữa hai mặt phẳng
khoảng cách giữa hai mặt phẳng  và
và 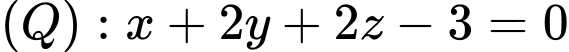 bằng
bằng
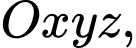 khoảng cách giữa hai mặt phẳng
khoảng cách giữa hai mặt phẳng  và
và 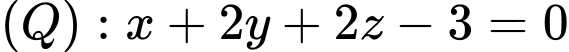 bằng
bằng A, 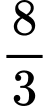
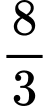
B, 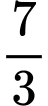
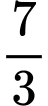
C, 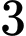
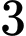
D, 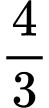
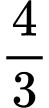
Chọn đáp án B.
Ta có: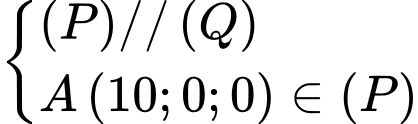
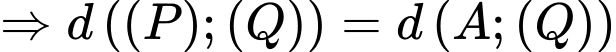
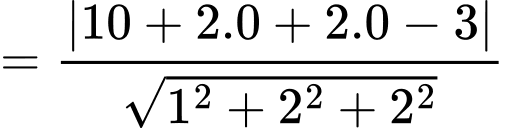
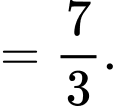 Đáp án: B
Đáp án: B
Ta có:
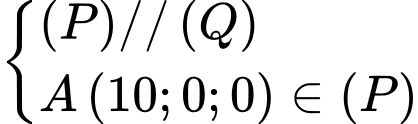
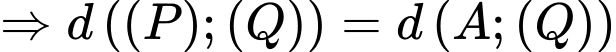
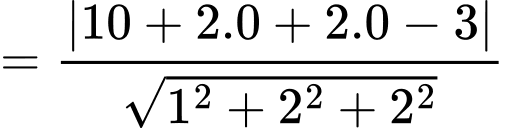
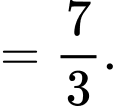 Đáp án: B
Đáp án: B
Câu 6 [899536]: Trong không gian 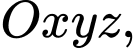 cho hai mặt phẳng song song
cho hai mặt phẳng song song 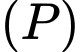 và
và  lần lượt có phương trình
lần lượt có phương trình 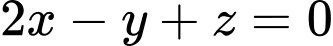 và
và 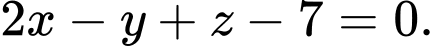 Khoảng cách giữa hai mặt phẳng
Khoảng cách giữa hai mặt phẳng 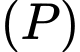 và
và  bằng
bằng
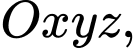 cho hai mặt phẳng song song
cho hai mặt phẳng song song 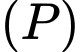 và
và  lần lượt có phương trình
lần lượt có phương trình 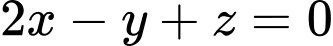 và
và 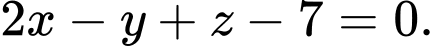 Khoảng cách giữa hai mặt phẳng
Khoảng cách giữa hai mặt phẳng 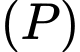 và
và  bằng
bằng A, 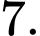
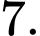
B, 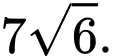
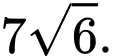
C, 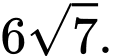
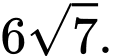
D, 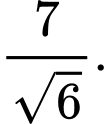
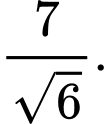
Xét 2 mặt phẳng 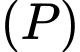 và
và  ta có:
ta có: 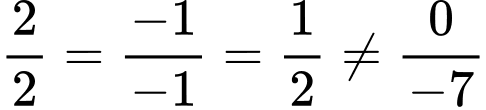 nên
nên 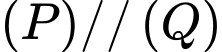 .
.
Do đó: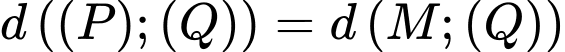 với
với 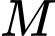 là điểm bất kì thuộc
là điểm bất kì thuộc 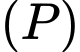 .
.
Chọn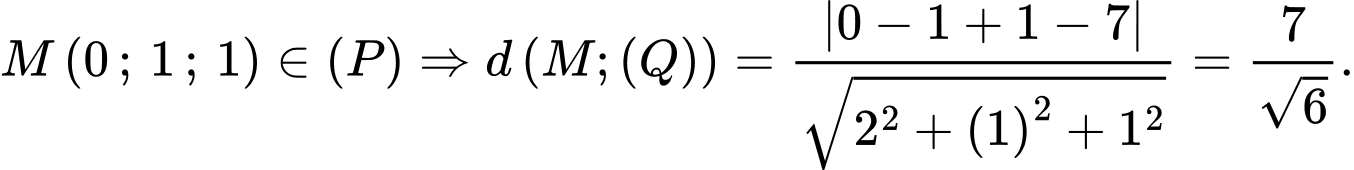 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
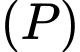 và
và  ta có:
ta có: 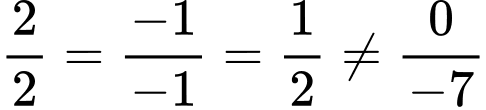 nên
nên 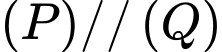 .
. Do đó:
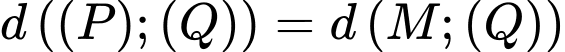 với
với 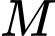 là điểm bất kì thuộc
là điểm bất kì thuộc 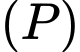 .
. Chọn
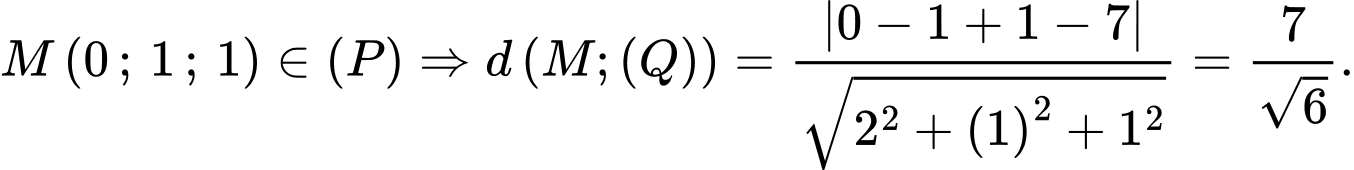 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 7 [57310]: Trong không gian tọa độ 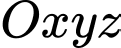 , cho
, cho 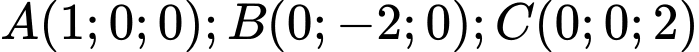 . Tính khoảng cách từ điểm
. Tính khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng 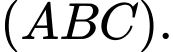
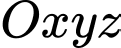 , cho
, cho 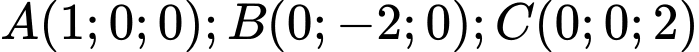 . Tính khoảng cách từ điểm
. Tính khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng 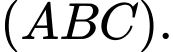
A, 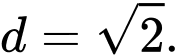
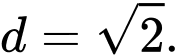
B, 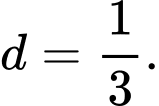
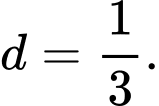
C, 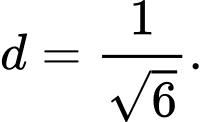
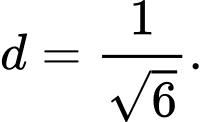
D, 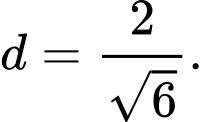
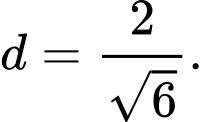
 Đáp án: D
Đáp án: D
Câu 8 [899531]: Trong không gian tọa độ 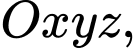 cho các điểm
cho các điểm  Khoảng cách từ gốc tọa độ
Khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 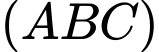 bằng
bằng
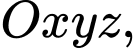 cho các điểm
cho các điểm  Khoảng cách từ gốc tọa độ
Khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 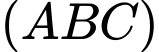 bằng
bằng A, 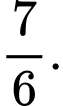
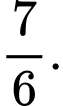
B, 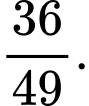
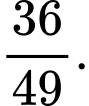
C, 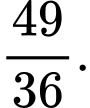
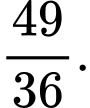
D, 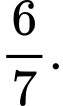
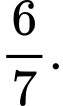
Phương trình mặt phẳng 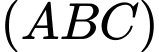 theo đoạn chắn là
theo đoạn chắn là
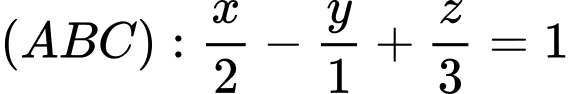 hay
hay 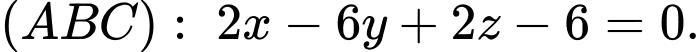
Khoảng cách từ gốc tọa độ đến mặt phẳng
đến mặt phẳng 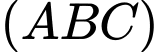 là
là 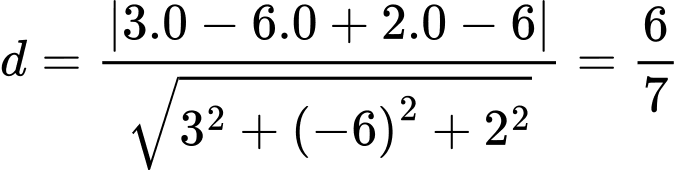 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
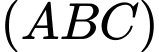 theo đoạn chắn là
theo đoạn chắn là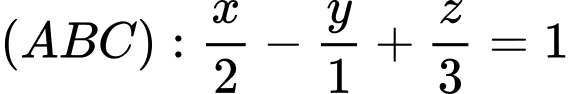 hay
hay 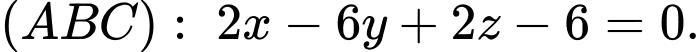
Khoảng cách từ gốc tọa độ
 đến mặt phẳng
đến mặt phẳng 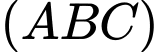 là
là 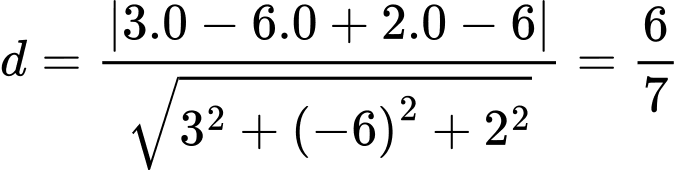 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
Câu 9 [398642]: Trong không gian 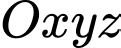 , cho các điểm
, cho các điểm 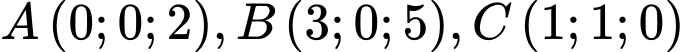 và
và 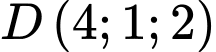 . Khoảng cách từ
. Khoảng cách từ 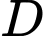 đến mặt phẳng
đến mặt phẳng 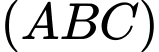 bằng
bằng
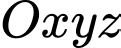 , cho các điểm
, cho các điểm 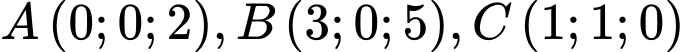 và
và 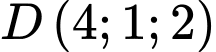 . Khoảng cách từ
. Khoảng cách từ 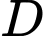 đến mặt phẳng
đến mặt phẳng 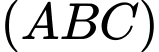 bằng
bằng A,  .
.
 .
. B, 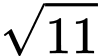 .
.
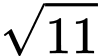 .
.C, 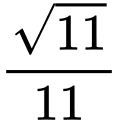 .
.
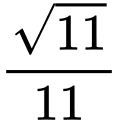 .
.D, 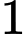 .
.
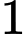 .
.
Ta có 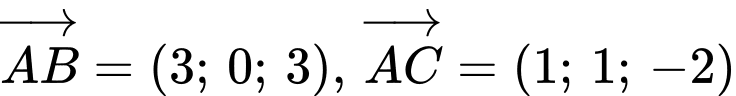 Mặt phẳng
Mặt phẳng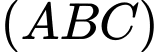 có vectơ pháp tuyến
có vectơ pháp tuyến 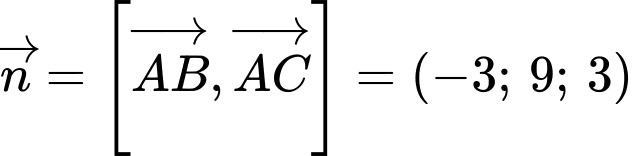 Phương trình mặt phẳng
Phương trình mặt phẳng 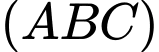 là :
là : 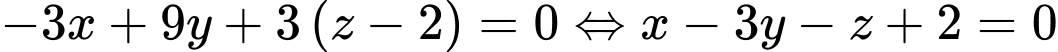 Khoảng cách từ
Khoảng cách từ 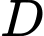 đến mặt phẳng
đến mặt phẳng 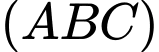 là
là
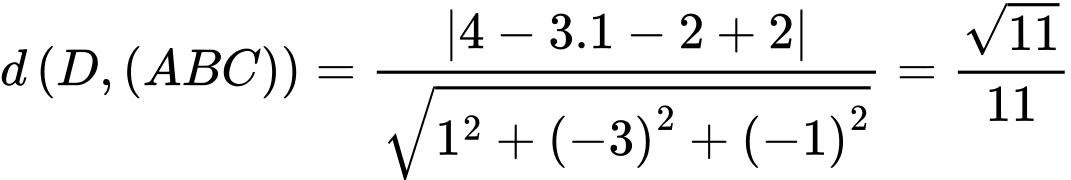 . Đáp án: C
. Đáp án: C
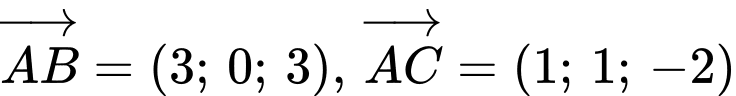 Mặt phẳng
Mặt phẳng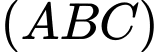 có vectơ pháp tuyến
có vectơ pháp tuyến 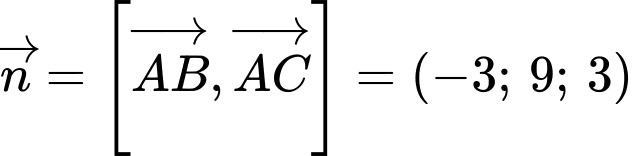 Phương trình mặt phẳng
Phương trình mặt phẳng 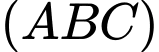 là :
là : 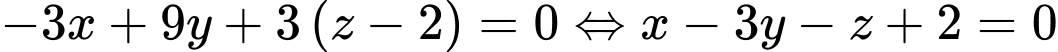 Khoảng cách từ
Khoảng cách từ 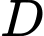 đến mặt phẳng
đến mặt phẳng 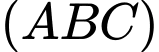 là
là
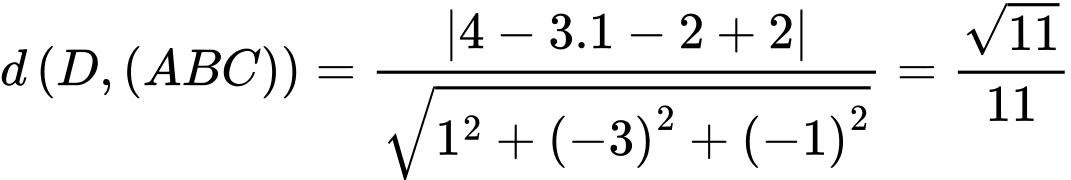 . Đáp án: C
. Đáp án: C
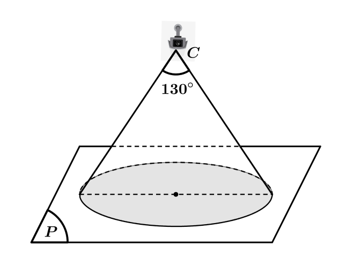
Câu 10 [408111]: Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz, camera được đặt tại điểm 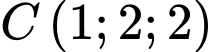 và chiếu thẳng về phía mặt phẳng
và chiếu thẳng về phía mặt phẳng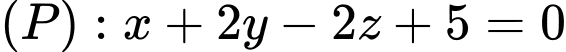 . Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
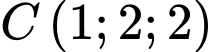 và chiếu thẳng về phía mặt phẳng
và chiếu thẳng về phía mặt phẳng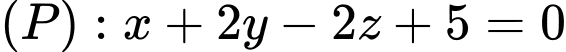 . Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
A, 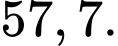
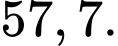
B, 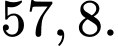
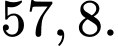
C, 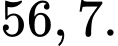
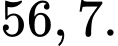
D, 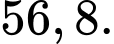
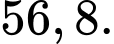
Chọn B.
Khoảng cách từ điểm C tới mặt phẳng (P) là
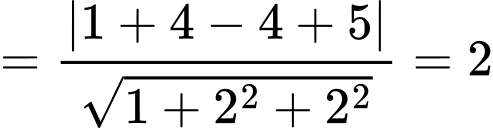
Khoảng cách từ điểm C tới mặt phẳng (P) là

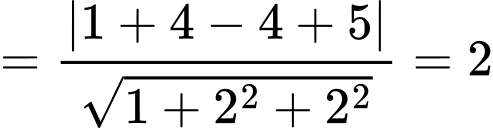
Vùng quan sát là diện tích hình tròn tâm H bán kính HA và vùng quan sát có diện tích
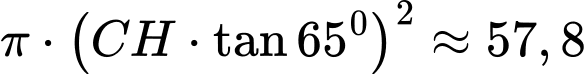 .
.
Đáp án: B 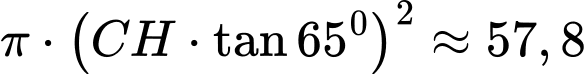 .
.
Câu 11 [392345]: Trong không gian với hệ toạ độ 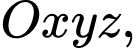 cho hình chóp
cho hình chóp  có đáy là hình chữ nhật và các điểm
có đáy là hình chữ nhật và các điểm 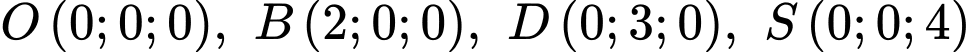 . Các mệnh đề sau đúng hay sai.
. Các mệnh đề sau đúng hay sai.
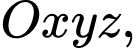 cho hình chóp
cho hình chóp  có đáy là hình chữ nhật và các điểm
có đáy là hình chữ nhật và các điểm 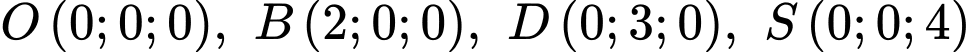 . Các mệnh đề sau đúng hay sai.
. Các mệnh đề sau đúng hay sai. A, a) Toạ độ điểm  là
là 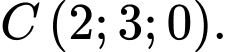
 là
là 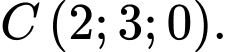
B, b) Phương trình đường thẳng 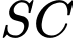 là
là 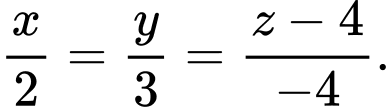
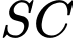 là
là 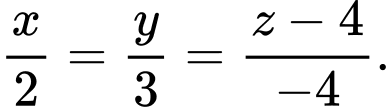
C, c) Phương trình mặt phẳng 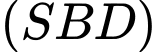 là
là 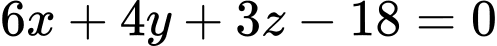
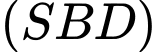 là
là 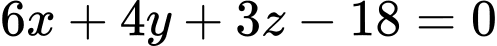
D, d) Khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng 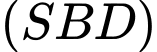 là
là 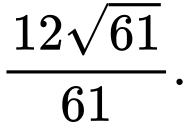
 đến mặt phẳng
đến mặt phẳng 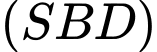 là
là 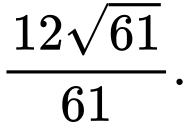
a) Đúng b) Đúng c) Sai d) Đúng
a)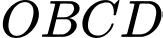 là hình bình hành
là hình bình hành 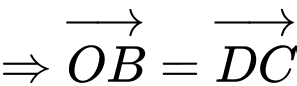
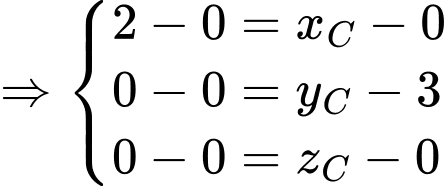
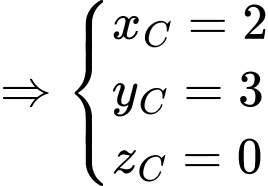
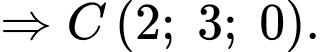
b) Phương trình đường thẳng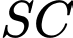 là
là 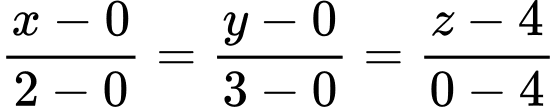 hay
hay 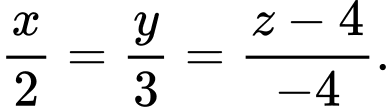
c) Phương trình mặt phẳng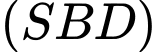 là
là 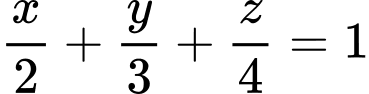 hay
hay 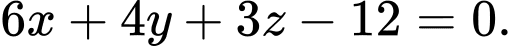
d) Khoảng cách từ điểm đến mặt phẳng
đến mặt phẳng 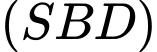 là
là
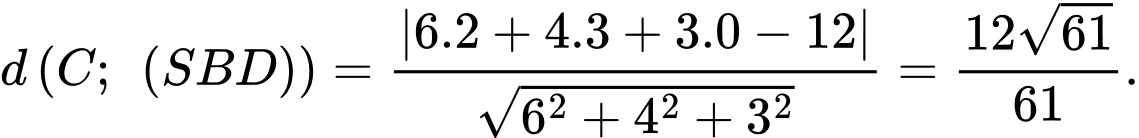
a)
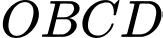 là hình bình hành
là hình bình hành 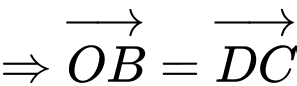
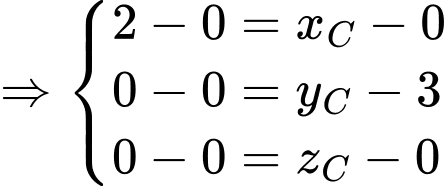
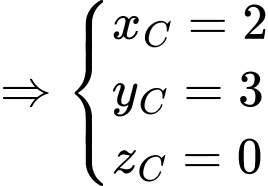
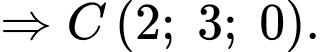
b) Phương trình đường thẳng
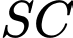 là
là 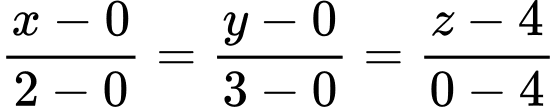 hay
hay 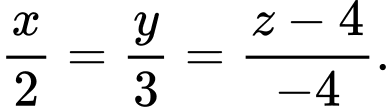
c) Phương trình mặt phẳng
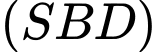 là
là 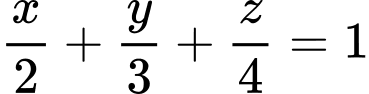 hay
hay 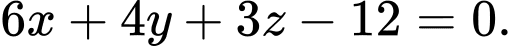
d) Khoảng cách từ điểm
 đến mặt phẳng
đến mặt phẳng 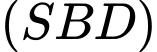 là
là 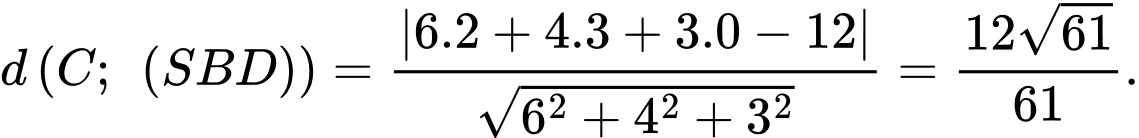
Câu 12 [405662]: Cho hình chóp 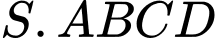 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 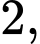 điểm
điểm  là trung điểm của cạnh
là trung điểm của cạnh 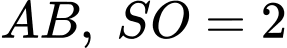 và
và 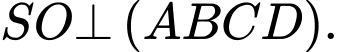 Bằng cách gắn hệ trục toạ độ
Bằng cách gắn hệ trục toạ độ 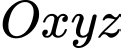 như hình vẽ. Xác định tính đúng sai của các mệnh đề sau:
như hình vẽ. Xác định tính đúng sai của các mệnh đề sau: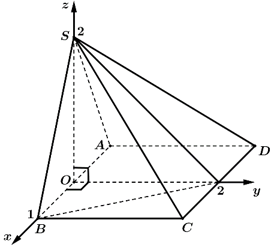
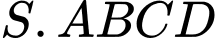 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 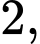 điểm
điểm  là trung điểm của cạnh
là trung điểm của cạnh 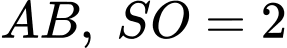 và
và 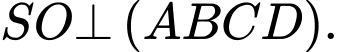 Bằng cách gắn hệ trục toạ độ
Bằng cách gắn hệ trục toạ độ 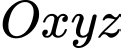 như hình vẽ. Xác định tính đúng sai của các mệnh đề sau:
như hình vẽ. Xác định tính đúng sai của các mệnh đề sau:
a) Đúng b) Sai c) Đúng d) Sai
a, Dựa vào hình vẽ dễ thấy toạ độ điểm là
là 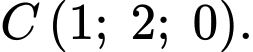
b, Ta có: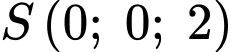 ;
; 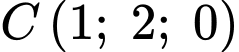 ;
; 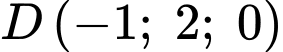
Suy ra toạ độ trọng tâm của tam giác
của tam giác 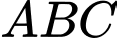 là
là
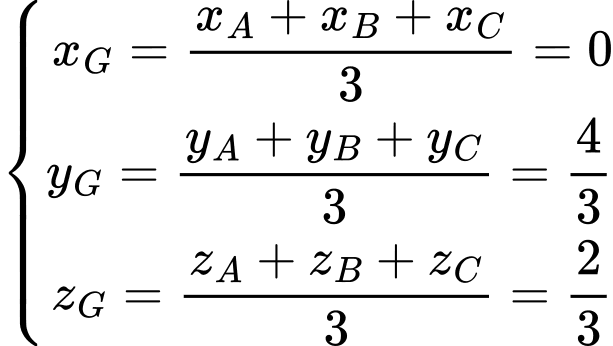
Vậy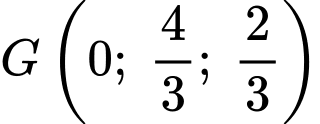
c, Ta có: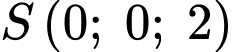 ;
; 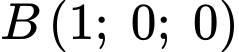 ;
; 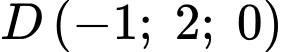
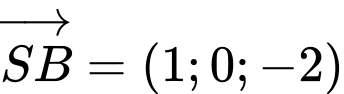 ;
; 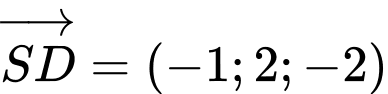
Suy ra vectơ pháp tuyến của mặt phẳng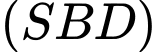 có toạ độ là
có toạ độ là 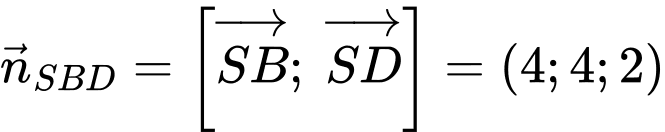
Hay mặt phẳng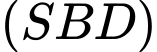 có vectơ pháp tuyến là
có vectơ pháp tuyến là 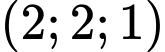
Vậy phương trình mặt phẳng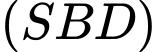 đi qua điểm
đi qua điểm 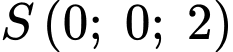 và có vectơ pháp tuyến
và có vectơ pháp tuyến 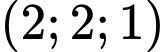 là
là 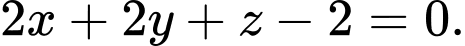
d, Khoảng cách từ đến mặt phẳng
đến mặt phẳng 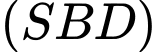 là
là 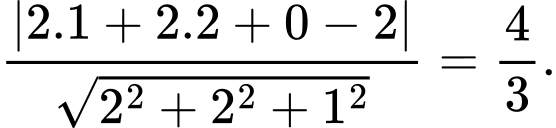
a, Dựa vào hình vẽ dễ thấy toạ độ điểm
 là
là 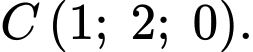
b, Ta có:
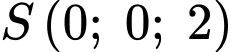 ;
; 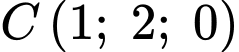 ;
; 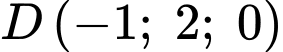
Suy ra toạ độ trọng tâm
 của tam giác
của tam giác 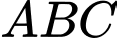 là
là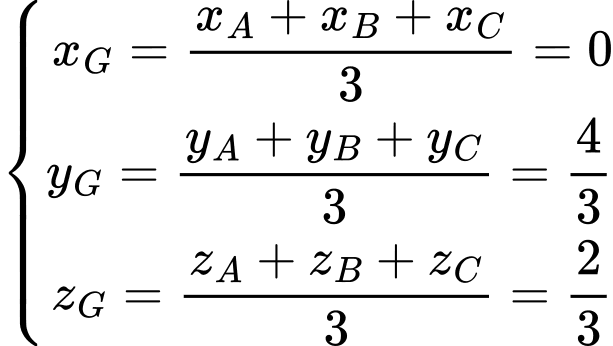
Vậy
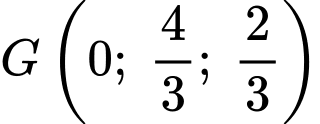
c, Ta có:
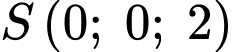 ;
; 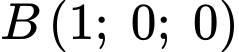 ;
; 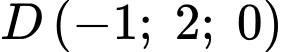
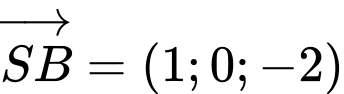 ;
; 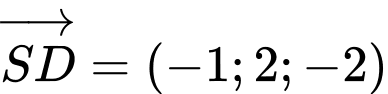
Suy ra vectơ pháp tuyến của mặt phẳng
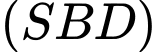 có toạ độ là
có toạ độ là 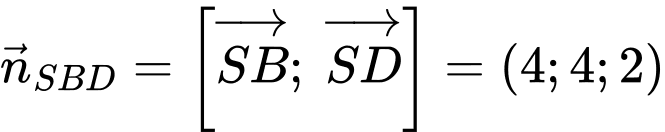
Hay mặt phẳng
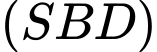 có vectơ pháp tuyến là
có vectơ pháp tuyến là 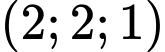
Vậy phương trình mặt phẳng
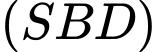 đi qua điểm
đi qua điểm 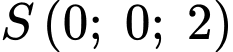 và có vectơ pháp tuyến
và có vectơ pháp tuyến 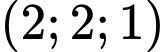 là
là 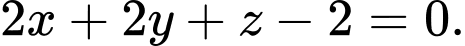
d, Khoảng cách từ
 đến mặt phẳng
đến mặt phẳng 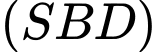 là
là 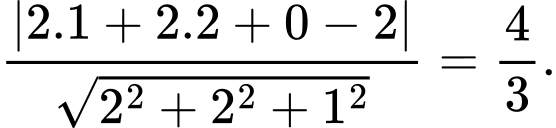
Câu 13 [405663]: Cho hình chóp đều 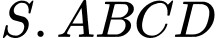 có đáy
có đáy 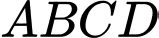 là hình vuông cạnh bằng
là hình vuông cạnh bằng 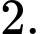 Gọi
Gọi  là tâm của đáy và
là tâm của đáy và 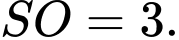 Điểm
Điểm  là trọng tâm tam giác
là trọng tâm tam giác 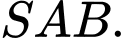 Bằng cách gắn hệ trục toạ độ
Bằng cách gắn hệ trục toạ độ 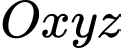 như hình vẽ. Xác định tính đúng sai của các mệnh đề sau:
như hình vẽ. Xác định tính đúng sai của các mệnh đề sau: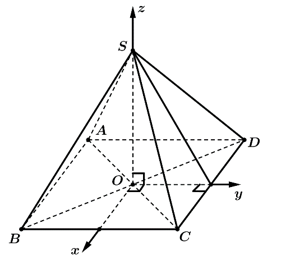
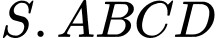 có đáy
có đáy 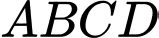 là hình vuông cạnh bằng
là hình vuông cạnh bằng 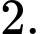 Gọi
Gọi  là tâm của đáy và
là tâm của đáy và 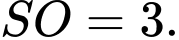 Điểm
Điểm  là trọng tâm tam giác
là trọng tâm tam giác 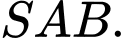 Bằng cách gắn hệ trục toạ độ
Bằng cách gắn hệ trục toạ độ 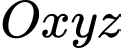 như hình vẽ. Xác định tính đúng sai của các mệnh đề sau:
như hình vẽ. Xác định tính đúng sai của các mệnh đề sau:
A, a) Toạ độ điểm  là
là 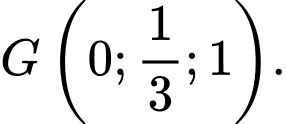
 là
là 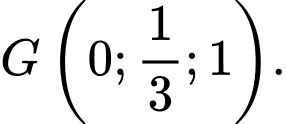
B, b) Phương trình đường thẳng 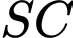 là:
là: 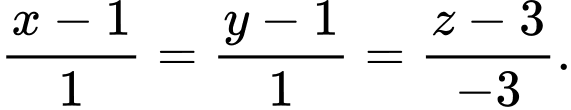
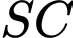 là:
là: 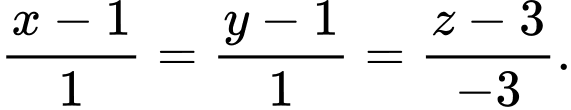
C, c) Phương trình mặt phẳng  là
là 
 là
là 
D, d) Khoảng cách từ điểm 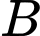 đến mặt phẳng
đến mặt phẳng  là
là 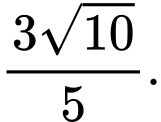
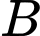 đến mặt phẳng
đến mặt phẳng  là
là 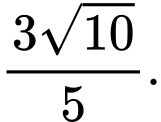
a) Sai b) Sai c) Đúng d) Đúng
a, Dựa vào hình vẽ dễ thấy 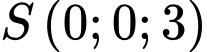 ;
; 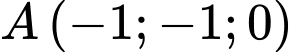 ;
; 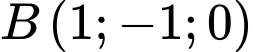
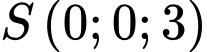 ;
; 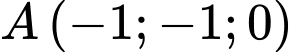 ;
; 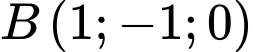
Vì  là trọng tâm tam giác
là trọng tâm tam giác 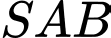 nên toạ độ điểm
nên toạ độ điểm  là
là
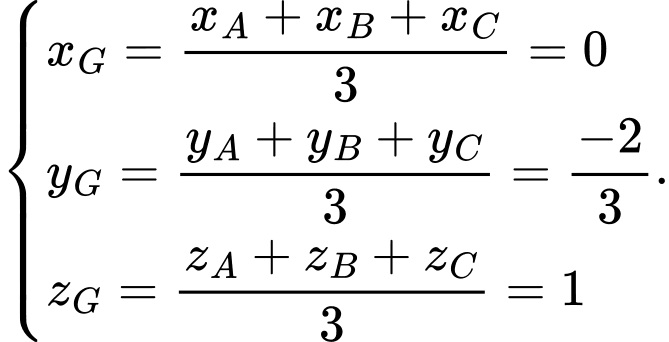 Vậy
Vậy 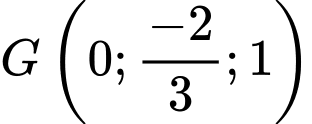
 là trọng tâm tam giác
là trọng tâm tam giác 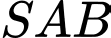 nên toạ độ điểm
nên toạ độ điểm  là
là
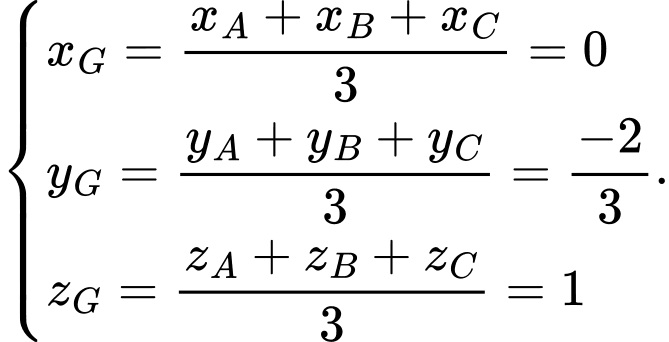 Vậy
Vậy 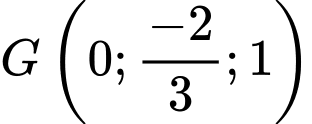
b, Ta có: 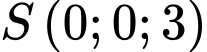 ;
; 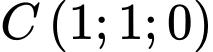 .
.
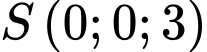 ;
; 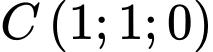 .
. Suy ra 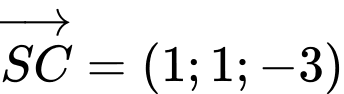
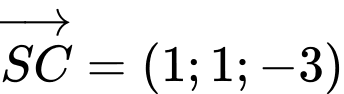
Phương trình đường thẳng 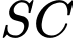 có vecto chỉ phương
có vecto chỉ phương 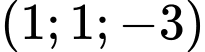 và đi qua điểm
và đi qua điểm 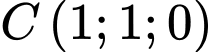 là
là
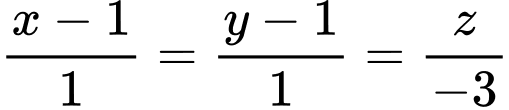
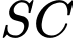 có vecto chỉ phương
có vecto chỉ phương 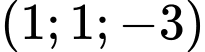 và đi qua điểm
và đi qua điểm 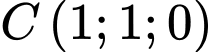 là
là
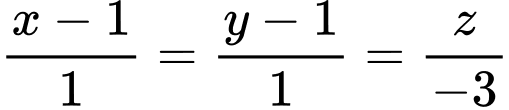
c, Ta có: 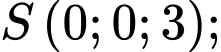
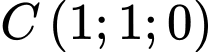 ;
; 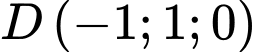
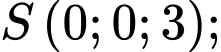
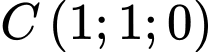 ;
; 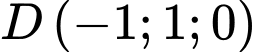
Suy ra 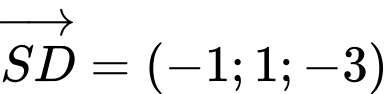 ;
; 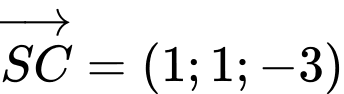
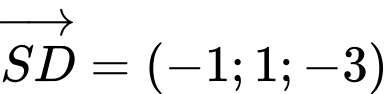 ;
; 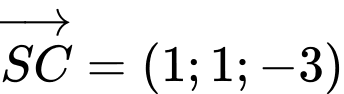
Vectơ pháp tuyến của mặt phẳng  có toạ độ là
có toạ độ là 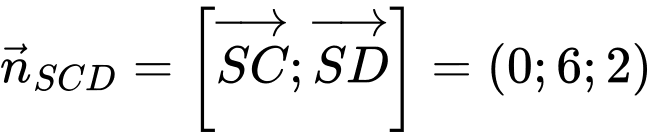
 có toạ độ là
có toạ độ là 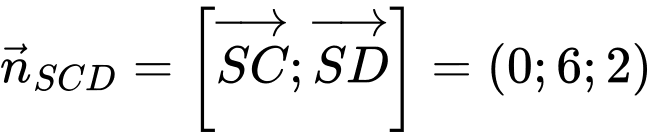
Hay mặt phẳng  có vectơ pháp tuyến là
có vectơ pháp tuyến là 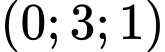
 có vectơ pháp tuyến là
có vectơ pháp tuyến là 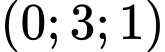
Vậy mặt phẳng  đi qua
đi qua 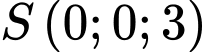 và có vecto pháp tuyến
và có vecto pháp tuyến 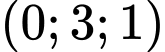 có phương trình là
có phương trình là

 đi qua
đi qua 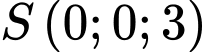 và có vecto pháp tuyến
và có vecto pháp tuyến 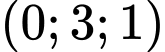 có phương trình là
có phương trình là

d) Khoảng cách từ điểm 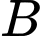 đến mặt phẳng
đến mặt phẳng  là
là 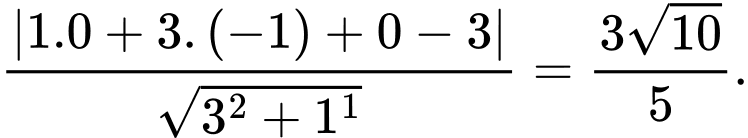
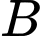 đến mặt phẳng
đến mặt phẳng  là
là 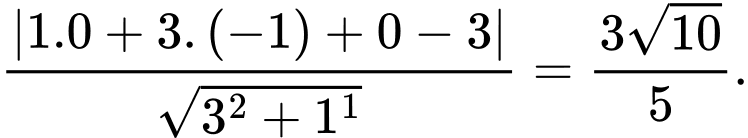
Câu 14 [405664]: Trong không gian với hệ toạ độ 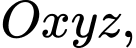 cho hình hộp chữ nhật
cho hình hộp chữ nhật  có các điểm
có các điểm 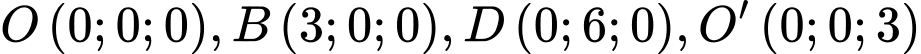 (Hình vẽ).Gọi
(Hình vẽ).Gọi  là trọng tâm tam giác
là trọng tâm tam giác 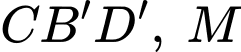 là trung điểm của
là trung điểm của 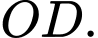 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.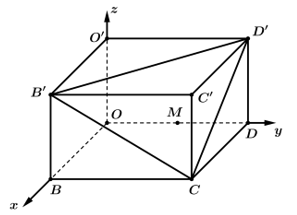
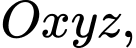 cho hình hộp chữ nhật
cho hình hộp chữ nhật  có các điểm
có các điểm 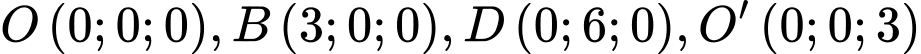 (Hình vẽ).Gọi
(Hình vẽ).Gọi  là trọng tâm tam giác
là trọng tâm tam giác 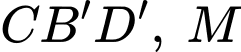 là trung điểm của
là trung điểm của 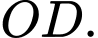 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
A, a) Toạ độ điểm  là
là 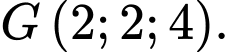
 là
là 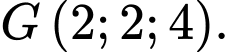
B, b) Diện tích tam giác 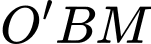 bằng
bằng 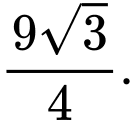
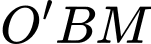 bằng
bằng 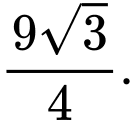
C, c) Phương trình mặt phẳng 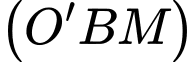 là
là 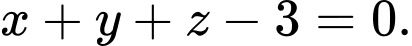
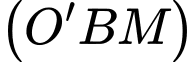 là
là 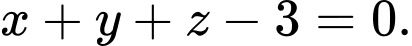
D, d) Thể tích khối chóp 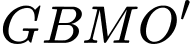 bằng
bằng 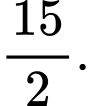
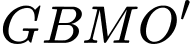 bằng
bằng 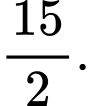
a) Sai b) Sai c) Đúng d) Đúng
a) Ta có: 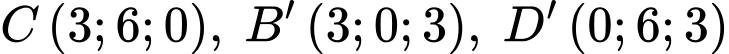 suy ra
suy ra 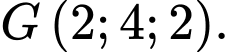 Sai
Sai
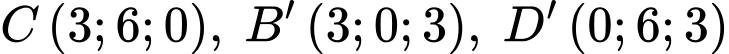 suy ra
suy ra 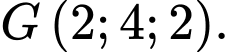 Sai
Sai b) Tam giác 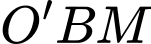 là tam giác đều có cạnh bằng
là tam giác đều có cạnh bằng 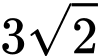 nên có diện tích là
nên có diện tích là 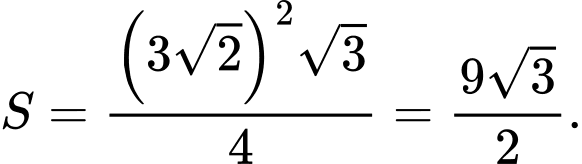 Sai.
Sai.
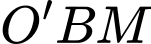 là tam giác đều có cạnh bằng
là tam giác đều có cạnh bằng 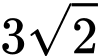 nên có diện tích là
nên có diện tích là 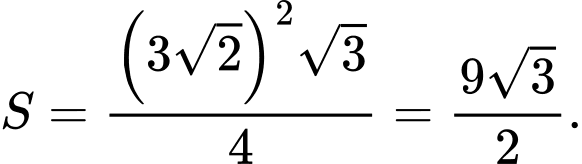 Sai.
Sai. c) Phương trình mặt phẳng 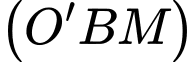 là
là 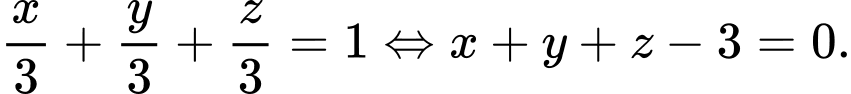 Đúng.
Đúng.
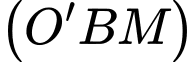 là
là 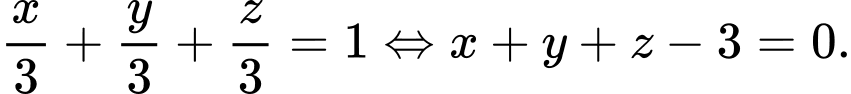 Đúng.
Đúng. d) 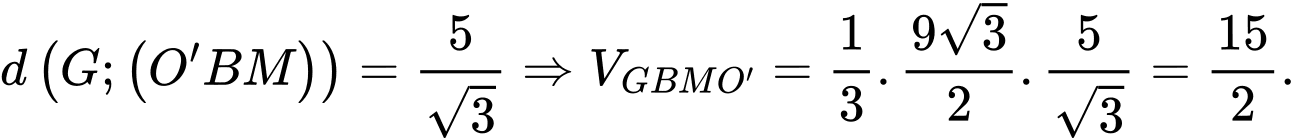 Đúng.
Đúng.
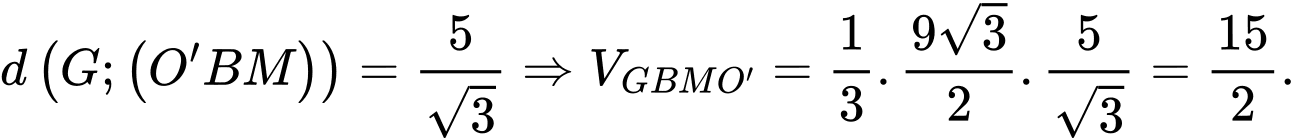 Đúng.
Đúng.
Câu 15 [392346]: Trong không gian toạ độ 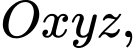 cho hai mặt phẳng
cho hai mặt phẳng 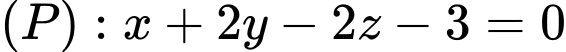 và
và 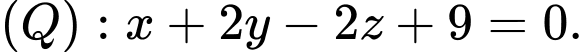 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
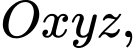 cho hai mặt phẳng
cho hai mặt phẳng 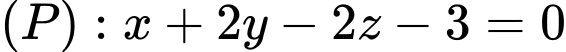 và
và 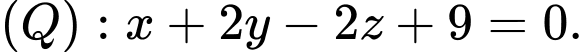 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai. A, a) Mặt phẳng 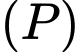 đi qua điểm
đi qua điểm 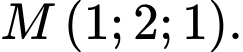
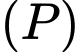 đi qua điểm
đi qua điểm 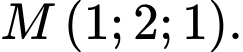
B, b) Khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 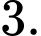
 đến mặt phẳng
đến mặt phẳng  bằng
bằng 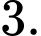
C, c) Khoảng cách giữa hai mặt phẳng 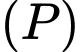 và
và  bằng
bằng 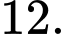
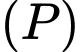 và
và  bằng
bằng 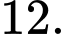
D, d) Mặt phẳng  song song và cách đều hai mặt phẳng
song song và cách đều hai mặt phẳng 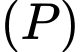 và
và  có phương trình là
có phương trình là 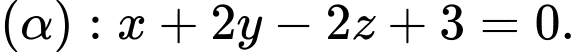
 song song và cách đều hai mặt phẳng
song song và cách đều hai mặt phẳng 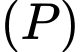 và
và  có phương trình là
có phương trình là 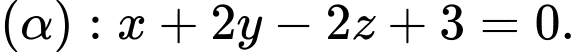
a) Đúng b) Đúng c) Sai d) Đúng
a) Mặt phẳng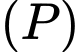 đi qua điểm
đi qua điểm 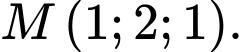
b) Khoảng cách từ gốc toạ độ đến mặt phẳng
đến mặt phẳng  bằng
bằng 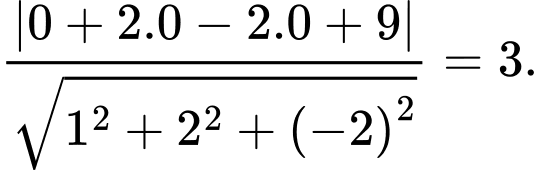
c) Khoảng cách giữa hai mặt phẳng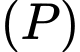 và
và  bằng
bằng 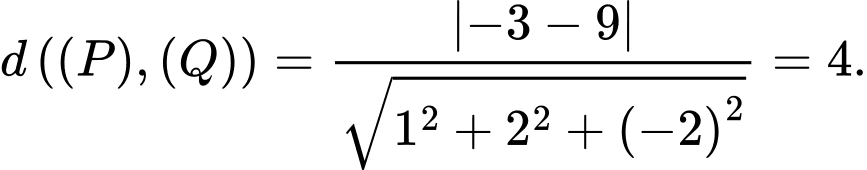
d) Gọi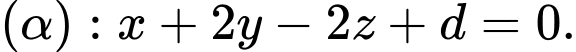
Lấy điểm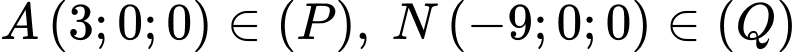
Khoảng cách giữa hai mặt phẳng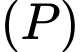 và
và  bằng
bằng
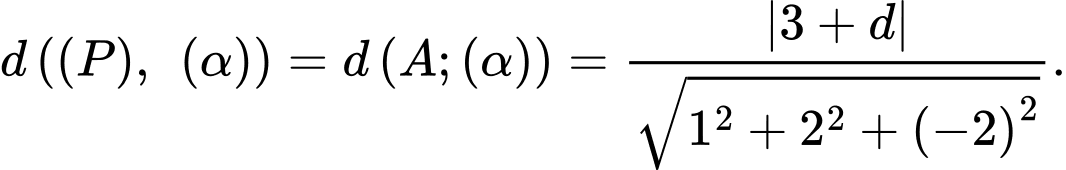
Khoảng cách giữa hai mặt phẳng và
và  bằng
bằng
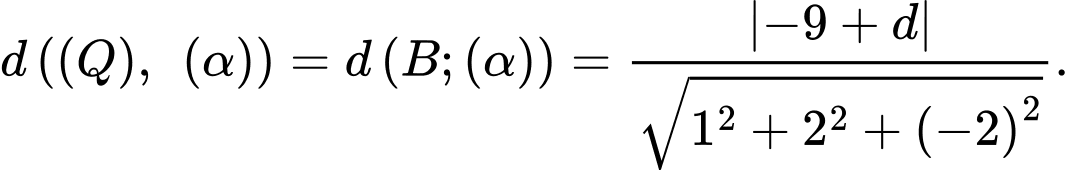
Khi đó: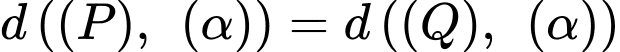
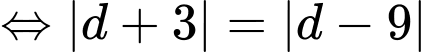
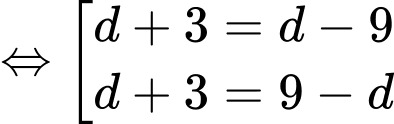
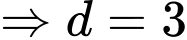 nên
nên 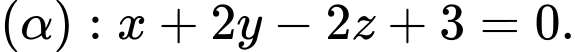
a) Mặt phẳng
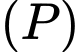 đi qua điểm
đi qua điểm 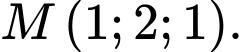
b) Khoảng cách từ gốc toạ độ
 đến mặt phẳng
đến mặt phẳng  bằng
bằng 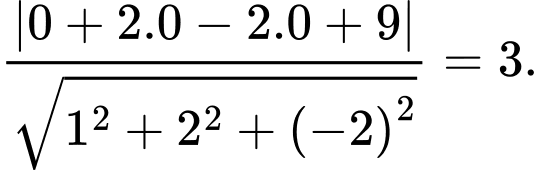
c) Khoảng cách giữa hai mặt phẳng
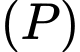 và
và  bằng
bằng 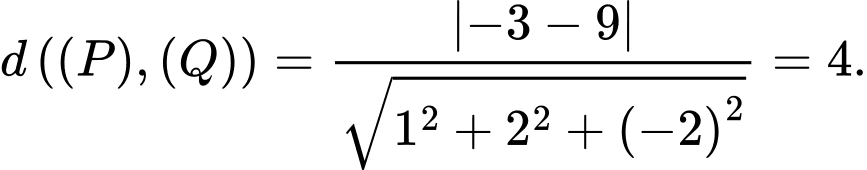
d) Gọi
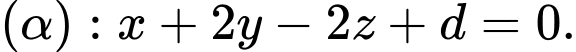
Lấy điểm
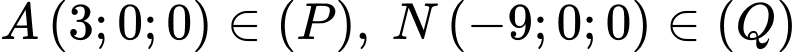
Khoảng cách giữa hai mặt phẳng
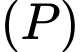 và
và  bằng
bằng 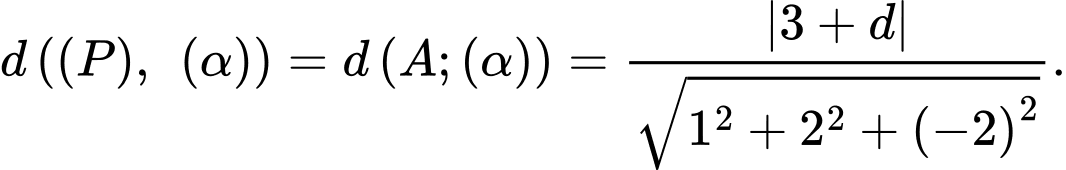
Khoảng cách giữa hai mặt phẳng
 và
và  bằng
bằng 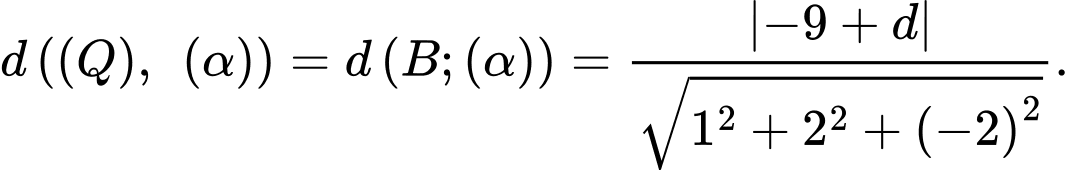
Khi đó:
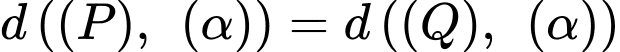
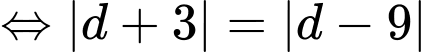
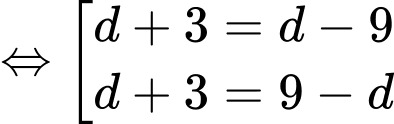
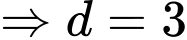 nên
nên 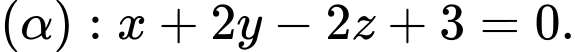
Câu 16 [392347]: Trong không gian toạ độ 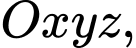 cho ba điểm
cho ba điểm 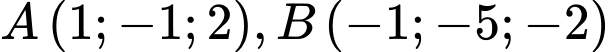 và
và 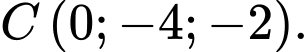 Gọi
Gọi 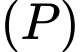 là mặt phẳng trung trực của đoạn thẳng
là mặt phẳng trung trực của đoạn thẳng 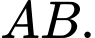 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
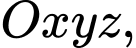 cho ba điểm
cho ba điểm 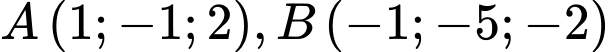 và
và 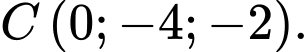 Gọi
Gọi 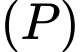 là mặt phẳng trung trực của đoạn thẳng
là mặt phẳng trung trực của đoạn thẳng 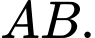 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai. A, a) 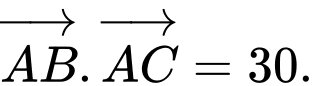
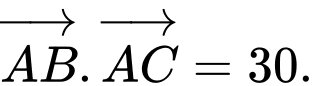
B, b) Phương trình đường thẳng  là:
là: 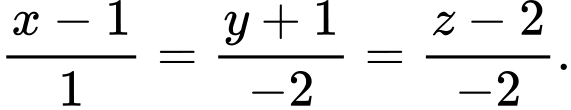
 là:
là: 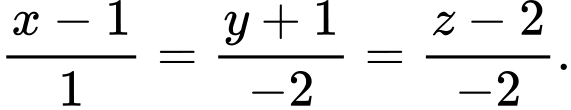
C, c) Khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng 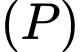 bằng
bằng 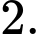
 đến mặt phẳng
đến mặt phẳng 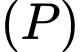 bằng
bằng 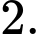
D, d) Khoảng cách từ điểm 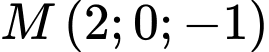 đến mặt phẳng
đến mặt phẳng 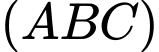 bằng
bằng 
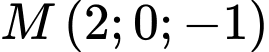 đến mặt phẳng
đến mặt phẳng 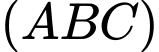 bằng
bằng 
a) Đúng b) Sai c) Đúng d) Đúng
a)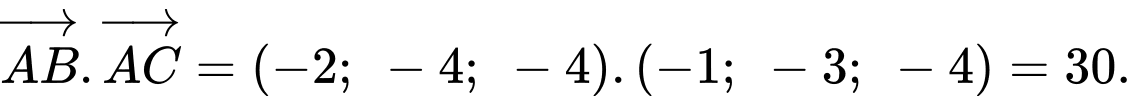
b) Phương trình đường thẳng là
là 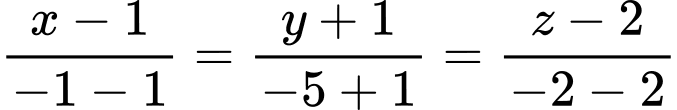
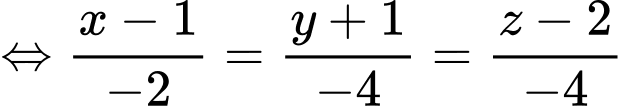 hay
hay 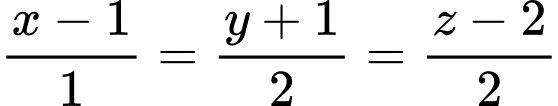
c) Gọi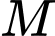 là trung điểm của
là trung điểm của 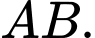 Khi đó:
Khi đó: 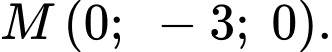
Ta có: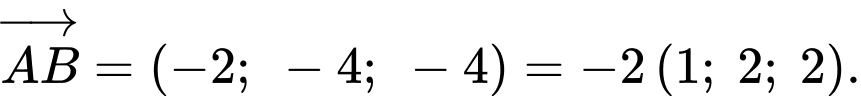
Gọi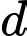 là đường trung trực của
là đường trung trực của  thì
thì 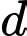 đi qua
đi qua 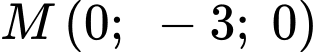 và nhận
và nhận 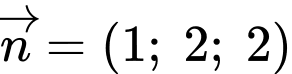 làm VTPT.
làm VTPT.
Phương trình đường thẳng trung trực của là
là 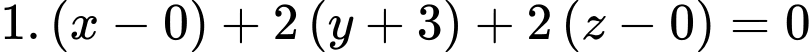 hay
hay 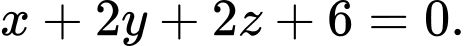
Khoảng cách từ điểm đến mặt phẳng
đến mặt phẳng 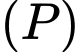 bằng
bằng 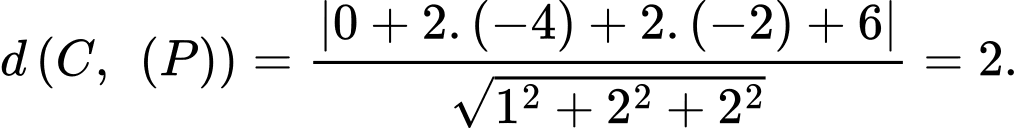
d)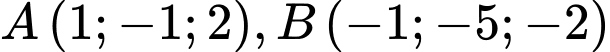 và
và 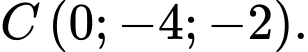
Ta có: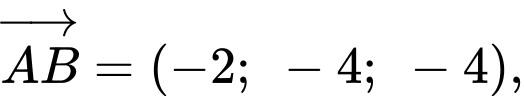
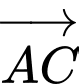
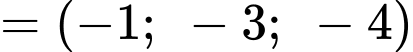
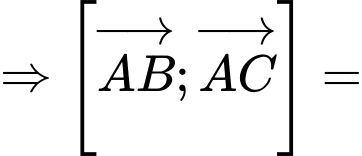
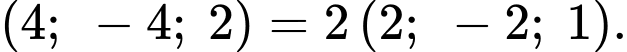
Phương trình mặt phẳng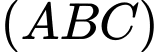 là
là 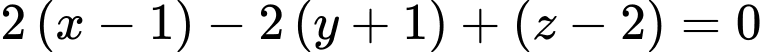

Khoảng cách từ điểm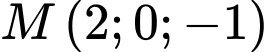 đến mặt phẳng
đến mặt phẳng 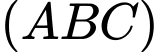 bằng
bằng 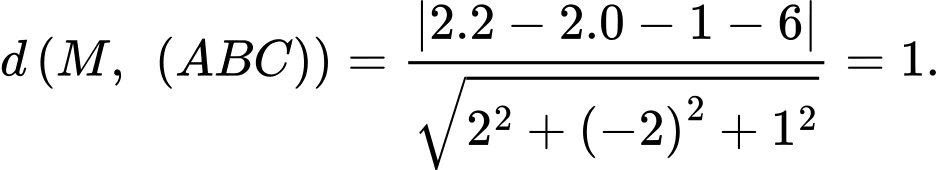
a)
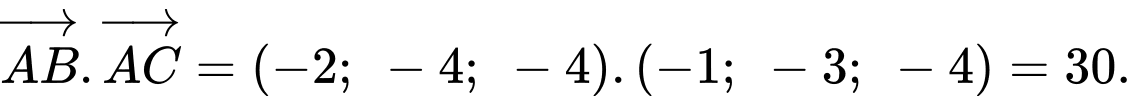
b) Phương trình đường thẳng
 là
là 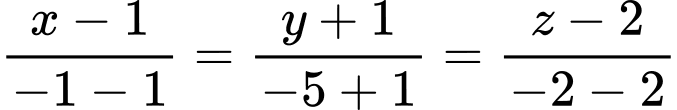
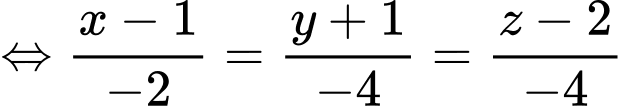 hay
hay 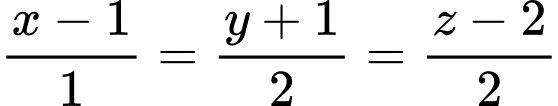
c) Gọi
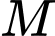 là trung điểm của
là trung điểm của 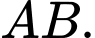 Khi đó:
Khi đó: 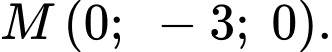
Ta có:
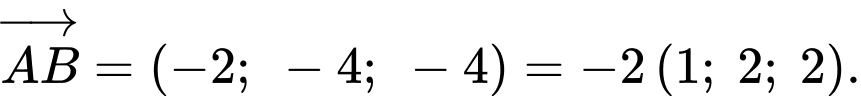
Gọi
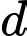 là đường trung trực của
là đường trung trực của  thì
thì 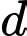 đi qua
đi qua 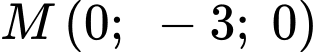 và nhận
và nhận 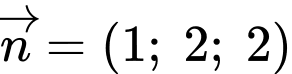 làm VTPT.
làm VTPT. Phương trình đường thẳng trung trực của
 là
là 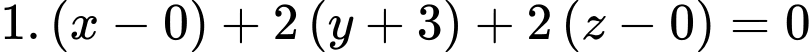 hay
hay 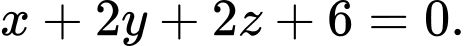
Khoảng cách từ điểm
 đến mặt phẳng
đến mặt phẳng 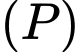 bằng
bằng 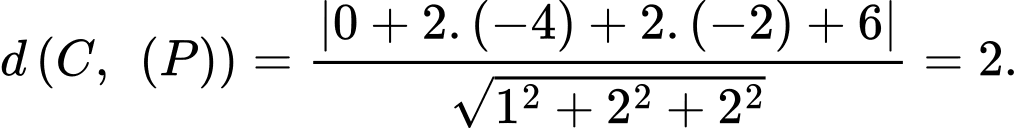
d)
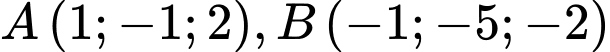 và
và 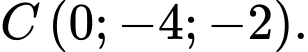
Ta có:
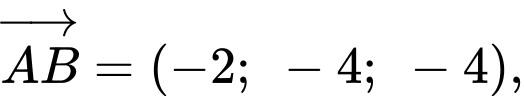
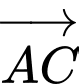
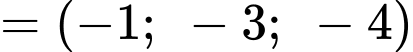
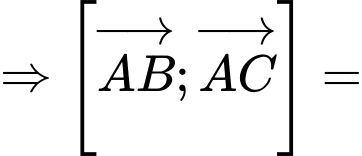
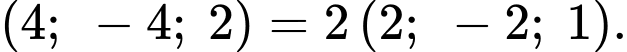
Phương trình mặt phẳng
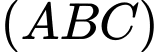 là
là 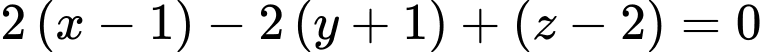

Khoảng cách từ điểm
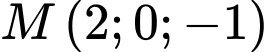 đến mặt phẳng
đến mặt phẳng 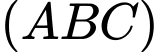 bằng
bằng 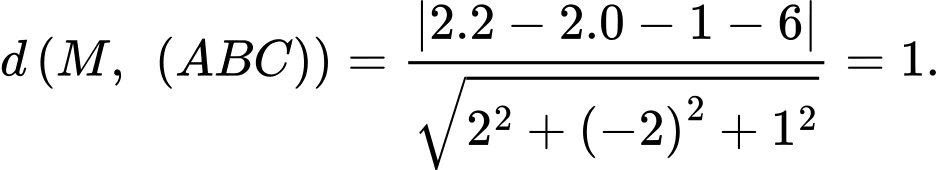
Câu 17 [392348]: Trong không gian tọa độ 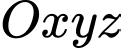 , cho
, cho 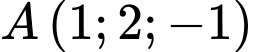 và hai mặt phẳng
và hai mặt phẳng 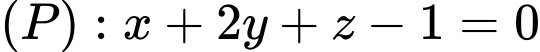 và
và 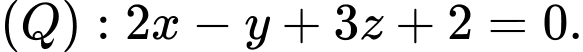 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
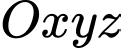 , cho
, cho 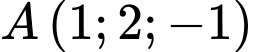 và hai mặt phẳng
và hai mặt phẳng 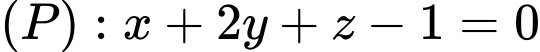 và
và 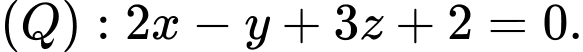 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai. A, a) Một vectơ pháp tuyến của mặt phẳng 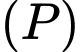 là
là 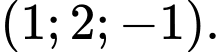
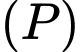 là
là 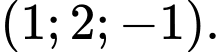
B, b) Khoảng cách từ điểm 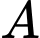 đến mặt phẳng
đến mặt phẳng 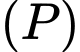 bằng
bằng 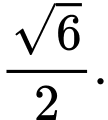
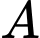 đến mặt phẳng
đến mặt phẳng 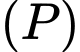 bằng
bằng 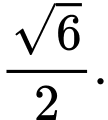
C, c) Đường thẳng giao tuyến của hai mặt phẳng 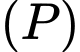 và
và  có một vectơ chỉ phương là
có một vectơ chỉ phương là 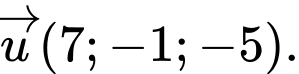
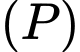 và
và  có một vectơ chỉ phương là
có một vectơ chỉ phương là 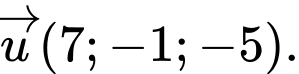
D, d) Gọi  là mặt phẳng qua
là mặt phẳng qua 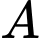 đồng thời vuông góc với hai mặt phẳng
đồng thời vuông góc với hai mặt phẳng 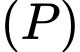 và
và  thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 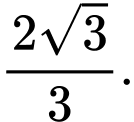
 là mặt phẳng qua
là mặt phẳng qua 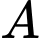 đồng thời vuông góc với hai mặt phẳng
đồng thời vuông góc với hai mặt phẳng 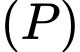 và
và  thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 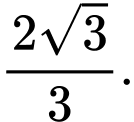
a) Sai b) Đúng c) Đúng d) Đúng
a) Một vectơ pháp tuyến của mặt phẳng 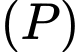 là
là 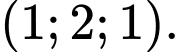
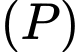 là
là 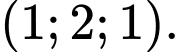
b) Khoảng cách từ điểm 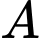 đến mặt phẳng
đến mặt phẳng 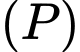 bằng
bằng 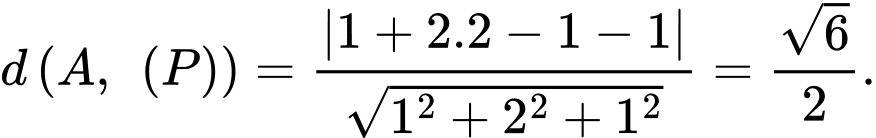
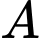 đến mặt phẳng
đến mặt phẳng  bằng
bằng 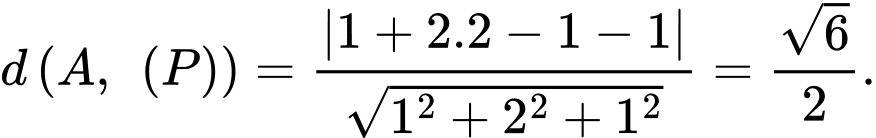
c) Đường thẳng giao tuyến của hai mặt phẳng  và
và  có một vectơ chỉ phương là
có một vectơ chỉ phương là 
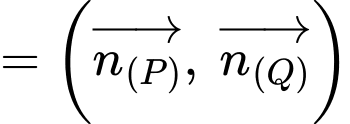
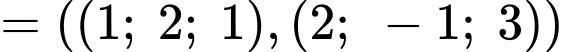
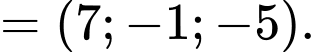
 và
và  có một vectơ chỉ phương là
có một vectơ chỉ phương là 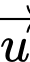
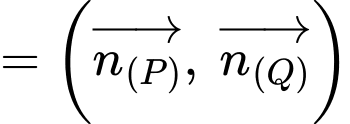
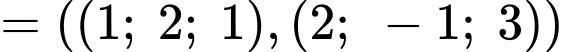
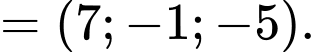
d) Gọi  là mặt phẳng qua
là mặt phẳng qua 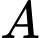 và vuông góc với hai mặt phẳng
và vuông góc với hai mặt phẳng 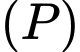 và
và  thì phương trình mặt phẳng
thì phương trình mặt phẳng  là
là 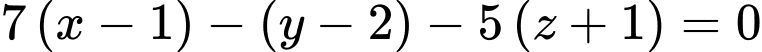 hay
hay 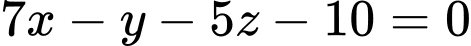
 là mặt phẳng qua
là mặt phẳng qua 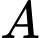 và vuông góc với hai mặt phẳng
và vuông góc với hai mặt phẳng 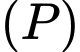 và
và  thì phương trình mặt phẳng
thì phương trình mặt phẳng  là
là 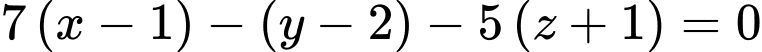 hay
hay 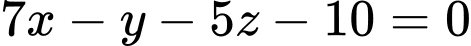
Khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 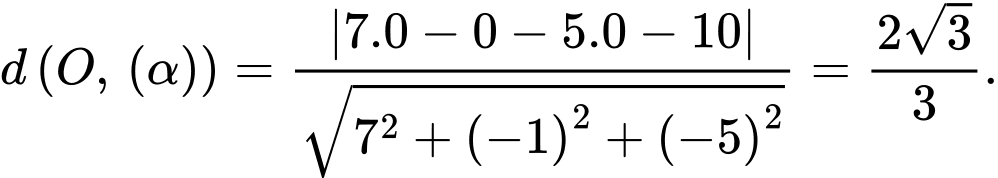
 đến mặt phẳng
đến mặt phẳng  bằng
bằng 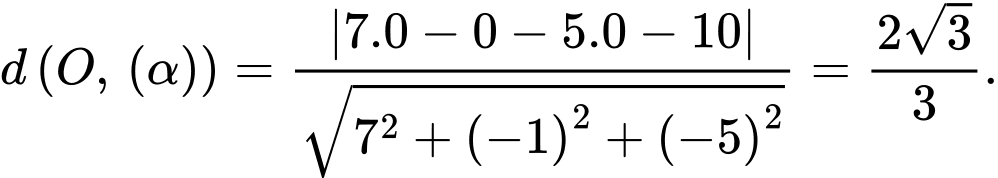
Câu 18 [392349]: Trong không gian toạ độ 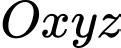 , cho 2 điểm
, cho 2 điểm 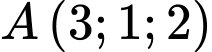 và
và 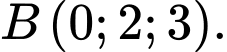 Gọi
Gọi 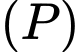 là mặt phẳng qua hai điểm
là mặt phẳng qua hai điểm 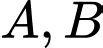 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 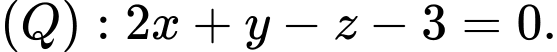 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
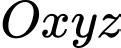 , cho 2 điểm
, cho 2 điểm 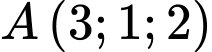 và
và 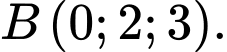 Gọi
Gọi 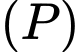 là mặt phẳng qua hai điểm
là mặt phẳng qua hai điểm 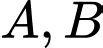 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 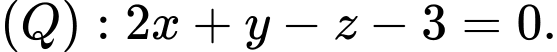 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai. A, a) Độ dài đoạn thẳng  bằng
bằng 
 bằng
bằng 
B, b) Phương trình đường thẳng  là
là 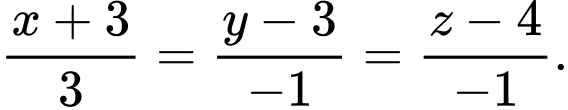
 là
là 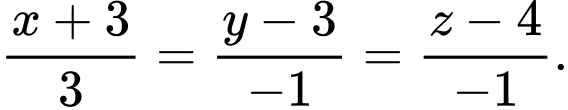
C, c) Khoảng cách từ điểm 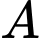 đến mặt phẳng
đến mặt phẳng  bằng
bằng 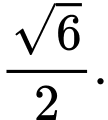
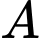 đến mặt phẳng
đến mặt phẳng  bằng
bằng 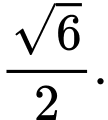
D, d) Khoảng cách từ điểm 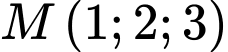 đến mặt phẳng
đến mặt phẳng 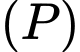 bằng
bằng 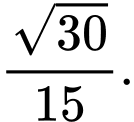
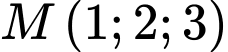 đến mặt phẳng
đến mặt phẳng 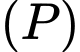 bằng
bằng 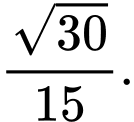
a) Đúng b) Đúng c) Sai d) Đúng 
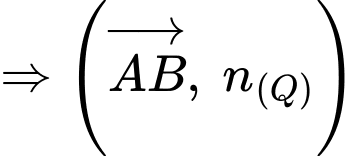
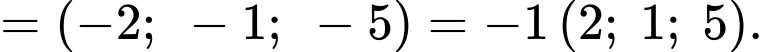
a) Độ dài đoạn thẳng  bằng
bằng 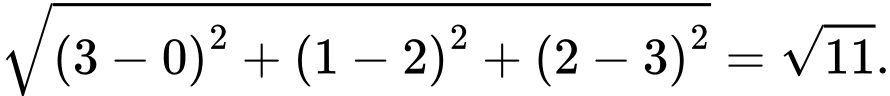
 bằng
bằng 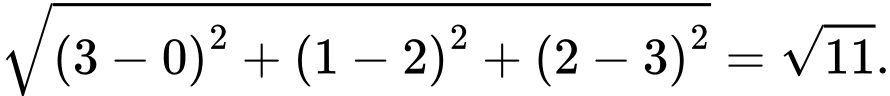
b) Phương trình đường thẳng  là
là 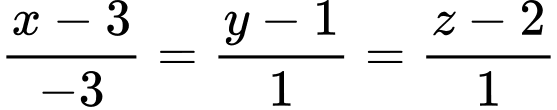
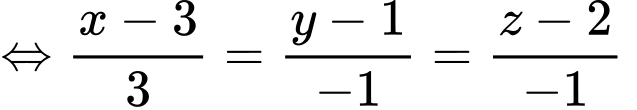 \
\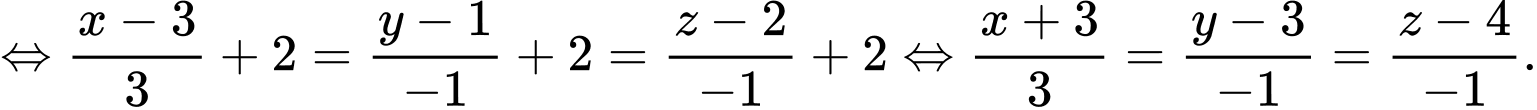
 là
là 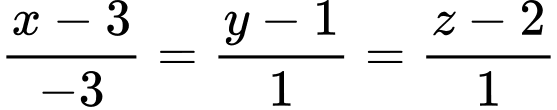
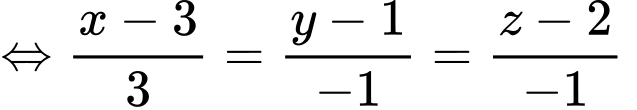 \
\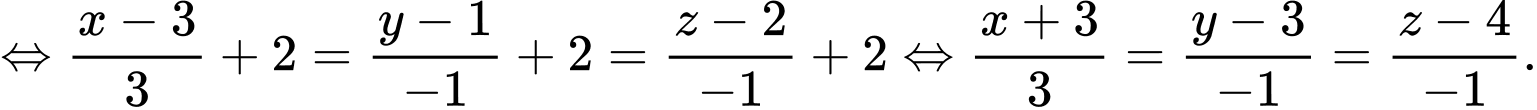
c) Khoảng cách từ điểm 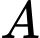 đến mặt phẳng
đến mặt phẳng  bằng
bằng 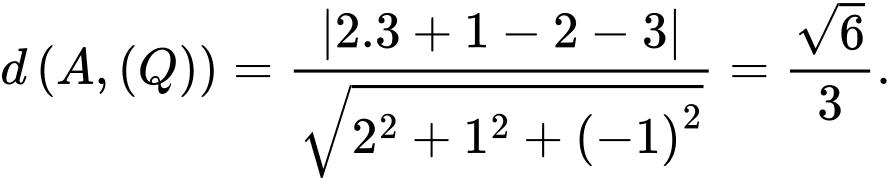
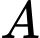 đến mặt phẳng
đến mặt phẳng  bằng
bằng 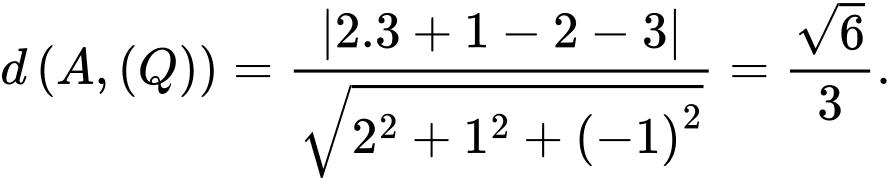
d) Ta có:
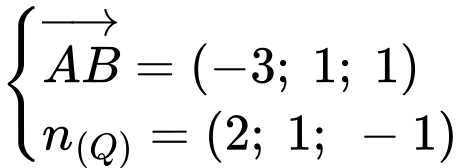
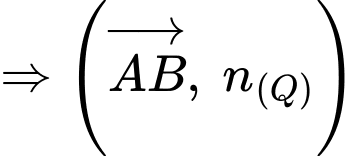
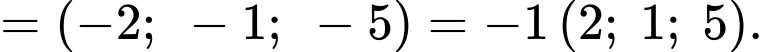
Mặt phẳng 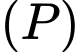 qua hai điểm
qua hai điểm  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng  là
là
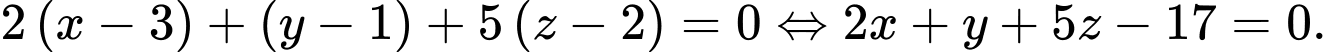
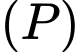 qua hai điểm
qua hai điểm  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng  là
là
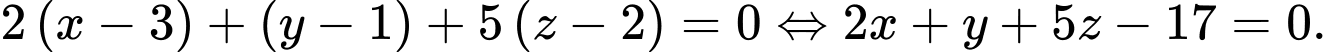
Khoảng cách từ điểm 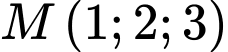 đến mặt phẳng
đến mặt phẳng 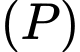 bằng
bằng 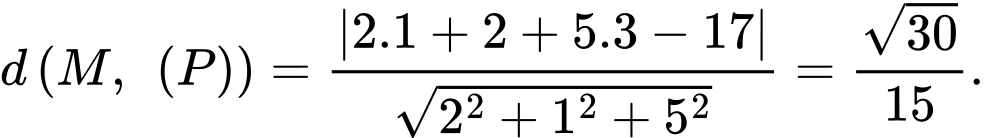
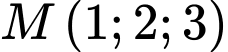 đến mặt phẳng
đến mặt phẳng 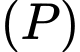 bằng
bằng 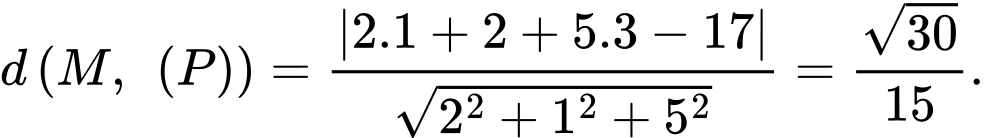
Câu 19 [163887]: Cho hình lập phương  có
có 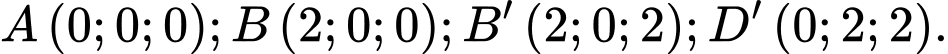 Gọi
Gọi 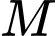 lần lượt là trung điểm của
lần lượt là trung điểm của 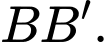 Xét tính đúng sai của các phát biểu sau:
Xét tính đúng sai của các phát biểu sau:
 có
có 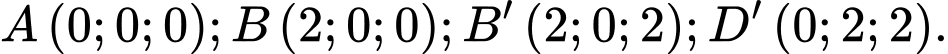 Gọi
Gọi 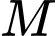 lần lượt là trung điểm của
lần lượt là trung điểm của 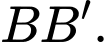 Xét tính đúng sai của các phát biểu sau:
Xét tính đúng sai của các phát biểu sau: A,
a) Phương trình mặt phẳng 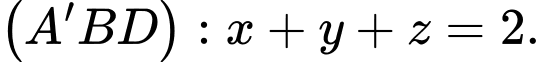
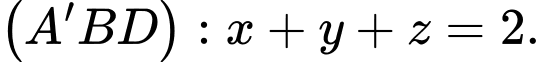
B,
b) 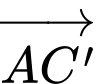 là một vecto pháp tuyến của mặt phẳng
là một vecto pháp tuyến của mặt phẳng 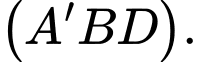
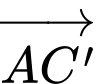 là một vecto pháp tuyến của mặt phẳng
là một vecto pháp tuyến của mặt phẳng 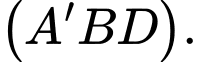
C,
c) Khoảng cách 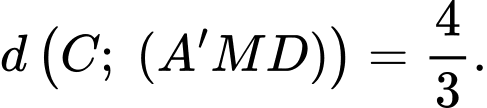
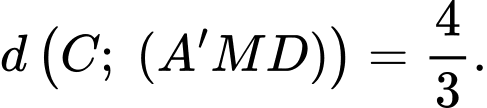
D,
d) Điểm 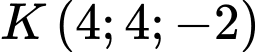 thuộc mặt phẳng
thuộc mặt phẳng 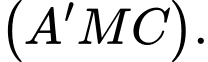
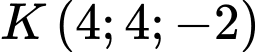 thuộc mặt phẳng
thuộc mặt phẳng 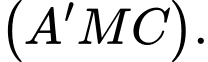
Gắn hệ trục tọa độ như hình vẽ: 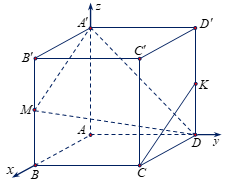
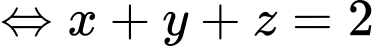

Ta có: 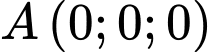 ,
, 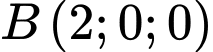 ,
, 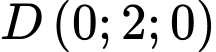 ,
, 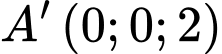 ,
, 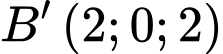 ,
,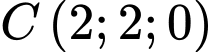 ,
, 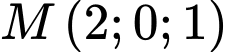 ,
, 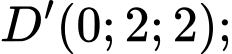 ,
, 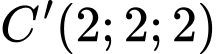
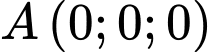 ,
, 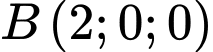 ,
, 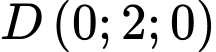 ,
, 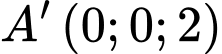 ,
, 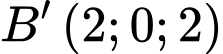 ,
,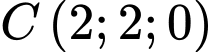 ,
, 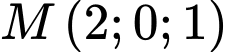 ,
, 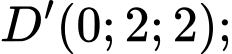 ,
, 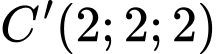
a) Đúng
Ta có phương trình mặt phẳng 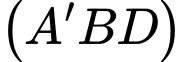 là phương trình mặt chắn, nên
là phương trình mặt chắn, nên 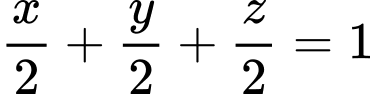
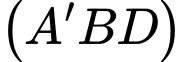 là phương trình mặt chắn, nên
là phương trình mặt chắn, nên 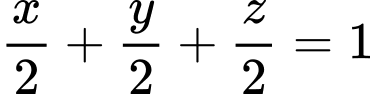
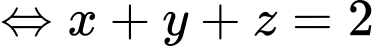
b) Đúng
Ta có 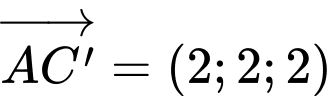 - là một vecto pháp tuyến của mặt phẳng
- là một vecto pháp tuyến của mặt phẳng 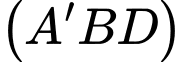 .
.
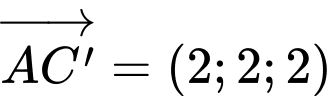 - là một vecto pháp tuyến của mặt phẳng
- là một vecto pháp tuyến của mặt phẳng 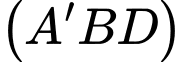 .
. c) Sai
Phương trình 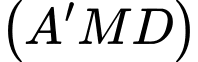 là
là 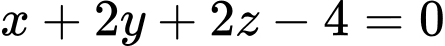 .
.
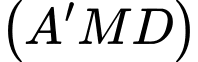 là
là 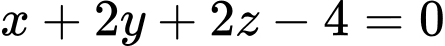 .
. Do đó: 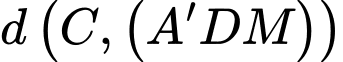
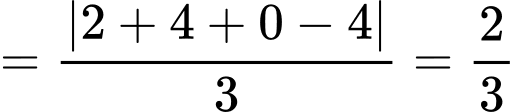 .
.
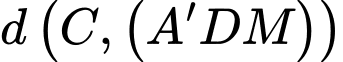
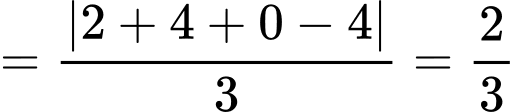 .
. d) Đúng.
Ta có : 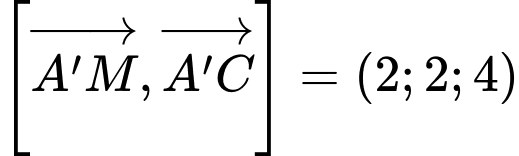 , nên phương trình mặt phẳng
, nên phương trình mặt phẳng 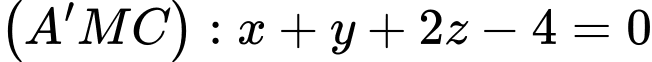 .
.
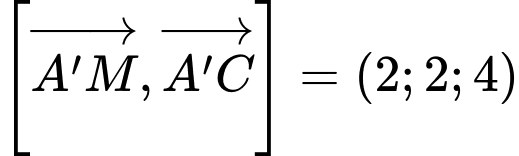 , nên phương trình mặt phẳng
, nên phương trình mặt phẳng 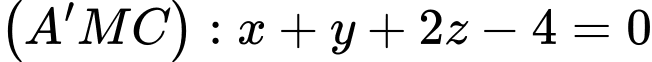 .
. Lại có 
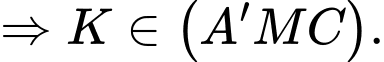

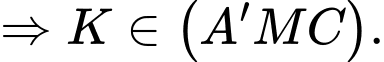
Câu 20 [57311]: Trong không gian với hệ trục tọa độ 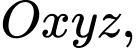 cho mặt phẳng
cho mặt phẳng 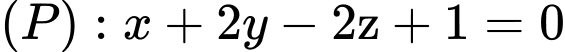 và điểm
và điểm 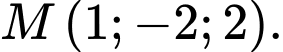 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 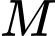 đến mặt phẳng
đến mặt phẳng 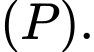
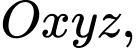 cho mặt phẳng
cho mặt phẳng 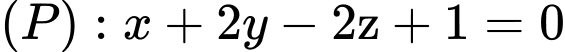 và điểm
và điểm 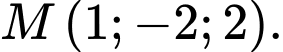 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 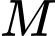 đến mặt phẳng
đến mặt phẳng 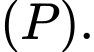
A, 

B, 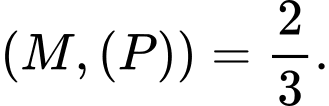
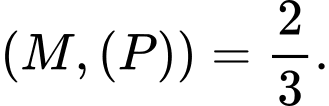
C, 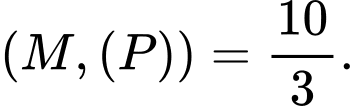
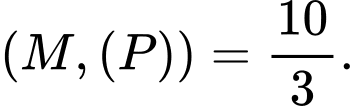
D, 

HD: Ta có: 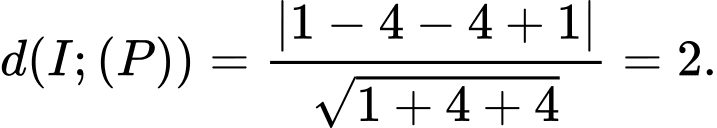 Chọn A. Đáp án: A
Chọn A. Đáp án: A
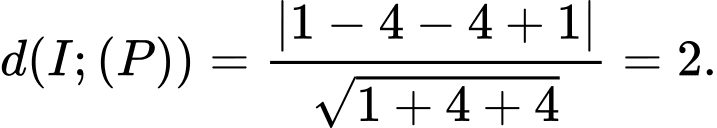 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 21 [57147]: Khoảng cách giữa hai mặt phẳng 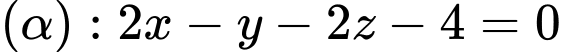 và
và 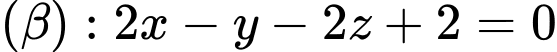 là
là
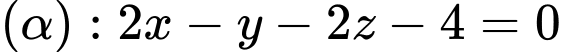 và
và 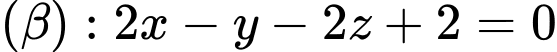 là
là A, 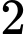 .
.
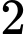 .
.B, 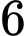 .
.
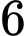 .
.C, 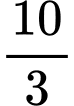 .
.
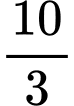 .
.D, 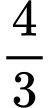 .
.
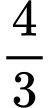 .
.
Đáp án A.
Ta có: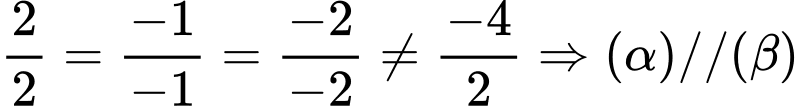 .
.
Chọn: .
.
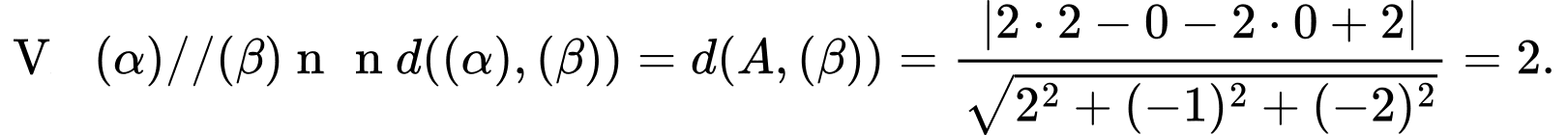 Đáp án: A
Đáp án: A
Ta có:
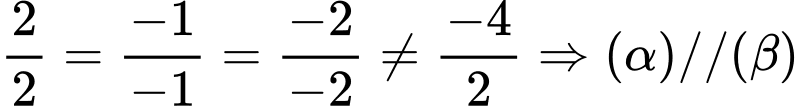 .
.
Chọn:
 .
.
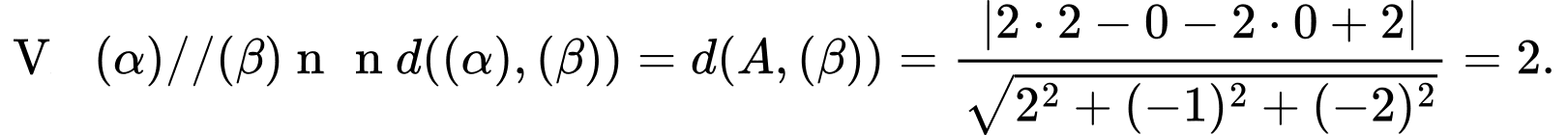 Đáp án: A
Đáp án: A
Câu 22 [405665]: Trong không gian toạ độ 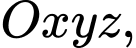 gọi
gọi 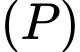 là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng 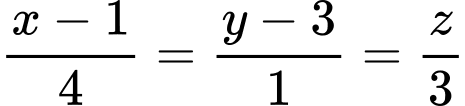 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 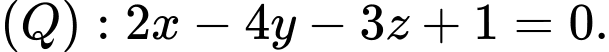 Khoảng cách từ điểm
Khoảng cách từ điểm 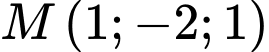 đến mặt phẳng
đến mặt phẳng 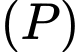 bằng
bằng
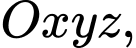 gọi
gọi 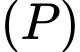 là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng 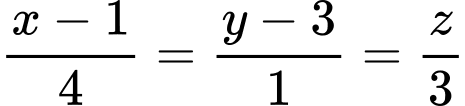 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 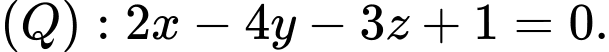 Khoảng cách từ điểm
Khoảng cách từ điểm 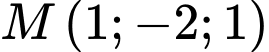 đến mặt phẳng
đến mặt phẳng 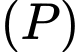 bằng
bằng
Đường thẳng 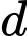 đi qua điểm
đi qua điểm 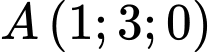 và có vectơ chỉ phương
và có vectơ chỉ phương 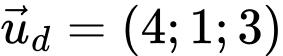
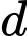 đi qua điểm
đi qua điểm 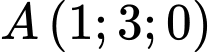 và có vectơ chỉ phương
và có vectơ chỉ phương 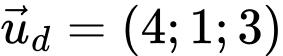
Mặt phẳng  có vectơ pháp tuyến
có vectơ pháp tuyến 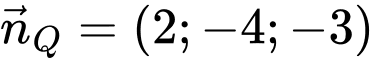
 có vectơ pháp tuyến
có vectơ pháp tuyến 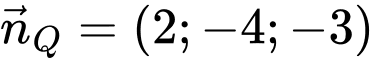
Mặt phẳng 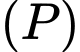 chứa đường thẳng
chứa đường thẳng 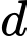 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng  có vectơ pháp tuyến là
có vectơ pháp tuyến là 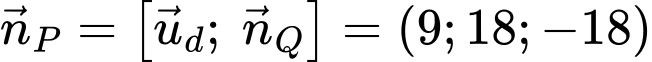
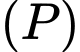 chứa đường thẳng
chứa đường thẳng 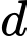 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng  có vectơ pháp tuyến là
có vectơ pháp tuyến là 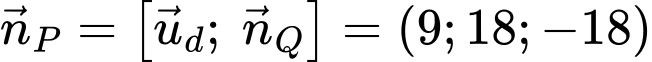
Hay mặt phẳng 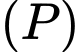 có vectơ pháp tuyến là
có vectơ pháp tuyến là 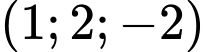
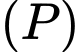 có vectơ pháp tuyến là
có vectơ pháp tuyến là 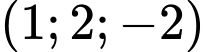
Mặt phẳng 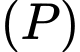 đi qua
đi qua 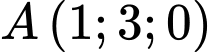 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 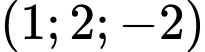 có phương trình là
có phương trình là
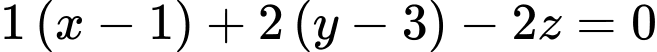
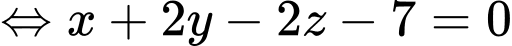
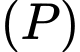 đi qua
đi qua 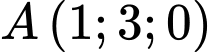 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 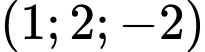 có phương trình là
có phương trình là
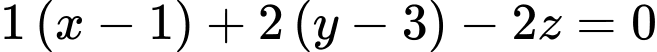
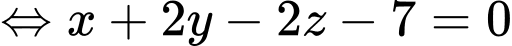
Vậy khoảng cách từ điểm 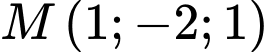 đến mặt phẳng
đến mặt phẳng 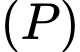 là
là 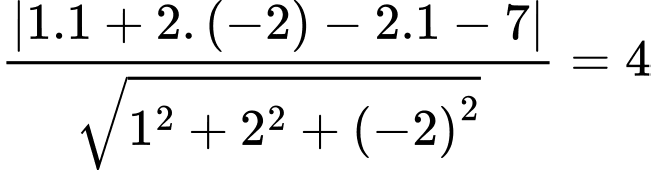 .
.
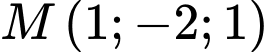 đến mặt phẳng
đến mặt phẳng 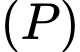 là
là 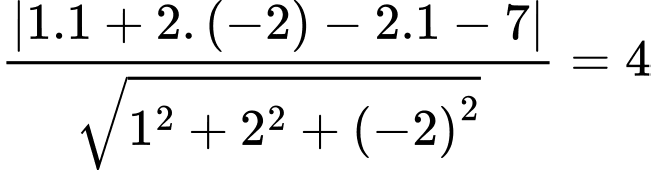 .
.
Câu 23 [405666]: Trong không gian toạ độ 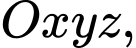 gọi
gọi 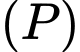 là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng 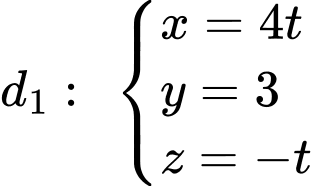 và song song với đường thẳng
và song song với đường thẳng 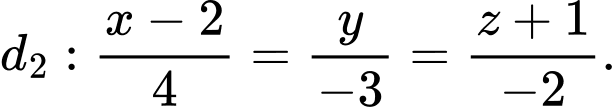 Khoảng cách từ điểm
Khoảng cách từ điểm 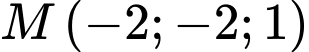 đến mặt phẳng
đến mặt phẳng 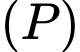 bằng:
bằng:
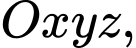 gọi
gọi 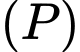 là mặt phẳng chứa đường thẳng
là mặt phẳng chứa đường thẳng 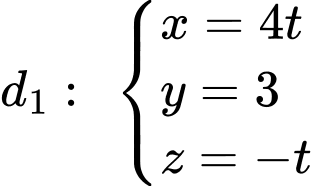 và song song với đường thẳng
và song song với đường thẳng 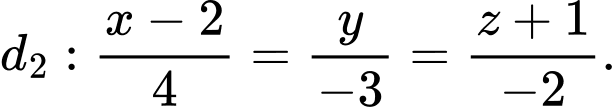 Khoảng cách từ điểm
Khoảng cách từ điểm 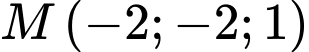 đến mặt phẳng
đến mặt phẳng 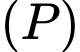 bằng:
bằng:
Đường thẳng 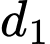 đi qua điểm
đi qua điểm 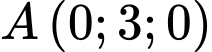 và có vecto chỉ phương
và có vecto chỉ phương 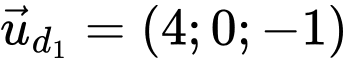
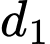 đi qua điểm
đi qua điểm 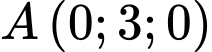 và có vecto chỉ phương
và có vecto chỉ phương 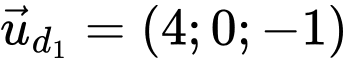
Đường thẳng 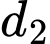 có vecto chỉ phương
có vecto chỉ phương 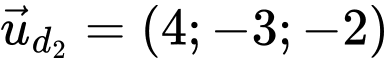
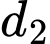 có vecto chỉ phương
có vecto chỉ phương 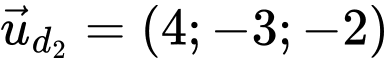
Mặt phẳng 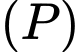 chứa đường thẳng
chứa đường thẳng 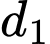 và song song với đường thẳng
và song song với đường thẳng 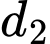 có 1 vecto pháp tuyến là
có 1 vecto pháp tuyến là 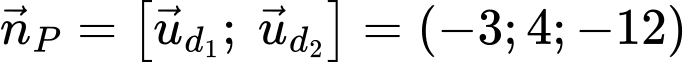
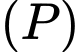 chứa đường thẳng
chứa đường thẳng 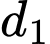 và song song với đường thẳng
và song song với đường thẳng 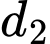 có 1 vecto pháp tuyến là
có 1 vecto pháp tuyến là 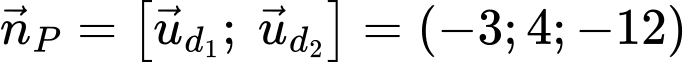
Mặt phẳng 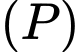 đi qua
đi qua 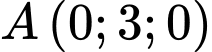 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 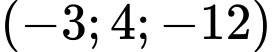 có phương trình là
có phương trình là

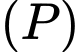 đi qua
đi qua 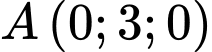 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 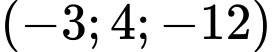 có phương trình là
có phương trình là

Vậy khoảng cách từ điểm 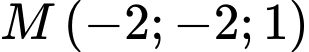 đến mặt phẳng
đến mặt phẳng 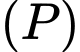 là
là 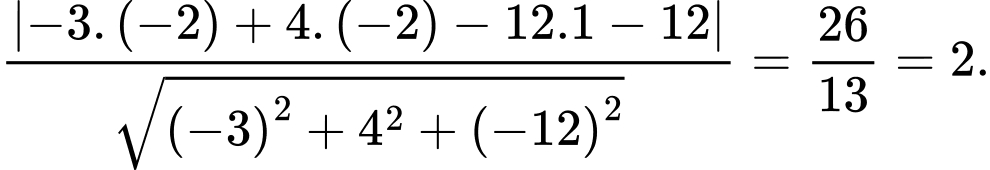
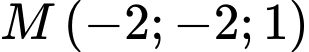 đến mặt phẳng
đến mặt phẳng 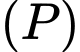 là
là