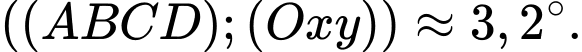Đáp án Bài tập tự luyện số 2
Câu 1 [57136]: Trong không gian 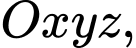 cho hai mặt phẳng
cho hai mặt phẳng 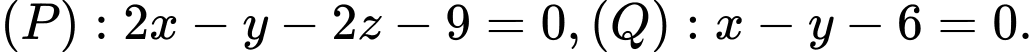 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 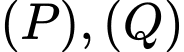 bằng
bằng
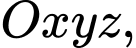 cho hai mặt phẳng
cho hai mặt phẳng 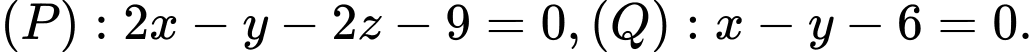 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 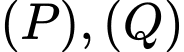 bằng
bằng A, 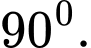
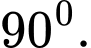
B, 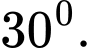
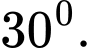
C, 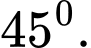
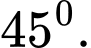
D, 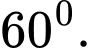
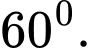
Đáp án C.
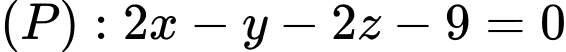 có 1 VTPT là
có 1 VTPT là 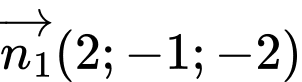
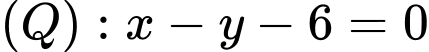 có 1 VTPT là
có 1 VTPT là 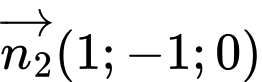
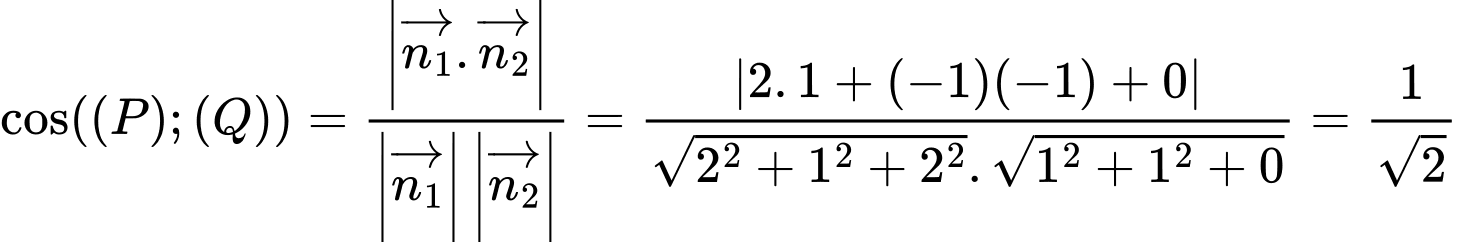
 Đáp án: C
Đáp án: C
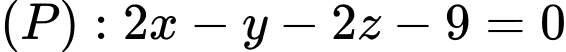 có 1 VTPT là
có 1 VTPT là 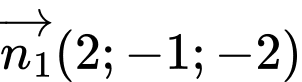
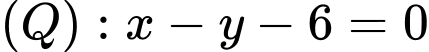 có 1 VTPT là
có 1 VTPT là 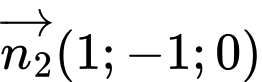
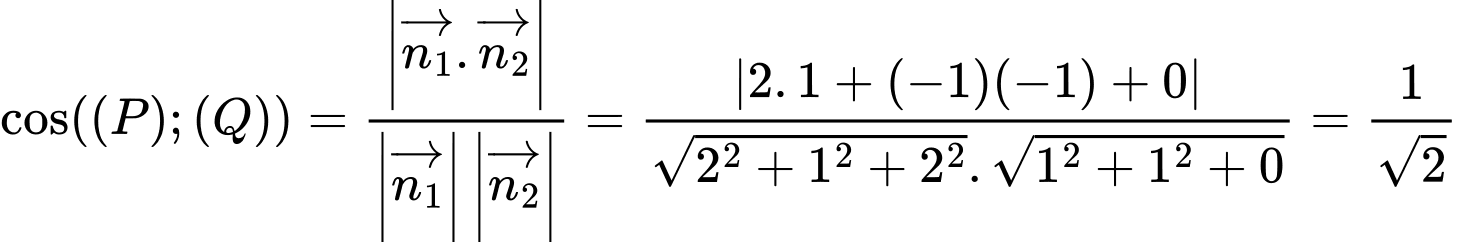
 Đáp án: C
Đáp án: C
Câu 2 [57132]: Trong không gian với hệ tọa độ  góc hợp bởi mặt phẳng
góc hợp bởi mặt phẳng 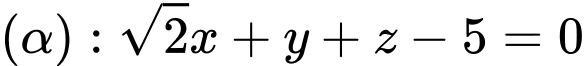 và mặt phẳng
và mặt phẳng 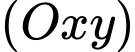 là
là
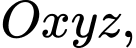 góc hợp bởi mặt phẳng
góc hợp bởi mặt phẳng 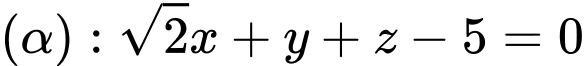 và mặt phẳng
và mặt phẳng 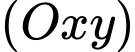 là
là A, 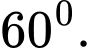
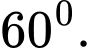
B, 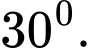
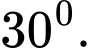
C, 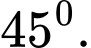
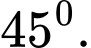
D, 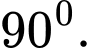
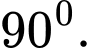
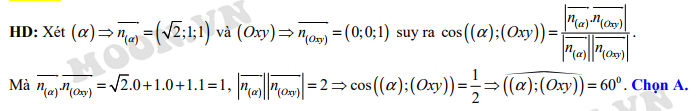 Đáp án: A
Đáp án: A
Câu 3 [57271]: Trong không gian 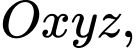 cho đường thẳng
cho đường thẳng 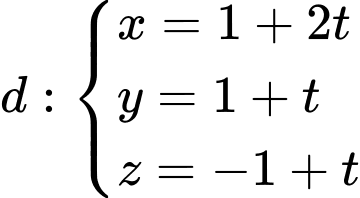 và mặt phẳng
và mặt phẳng 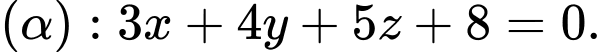 Góc giữa
Góc giữa  và
và  là
là
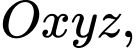 cho đường thẳng
cho đường thẳng 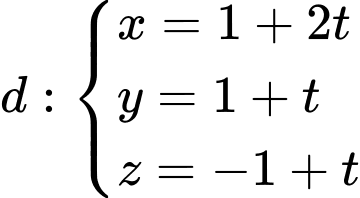 và mặt phẳng
và mặt phẳng 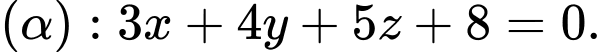 Góc giữa
Góc giữa  và
và  là
là A, 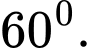
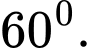
B, 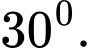
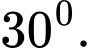
C, 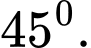
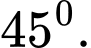
D, 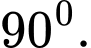
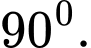
Xét 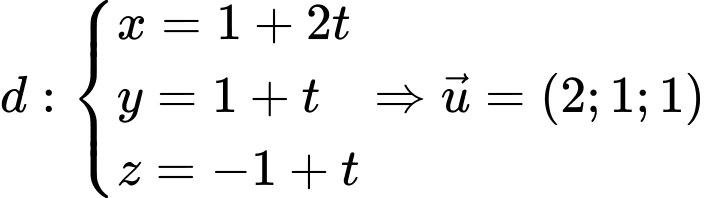 và
và 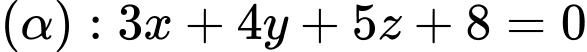
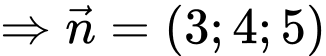
Áp dụng công thức tính góc giữa đường thẳng và mặt phẳng, ta có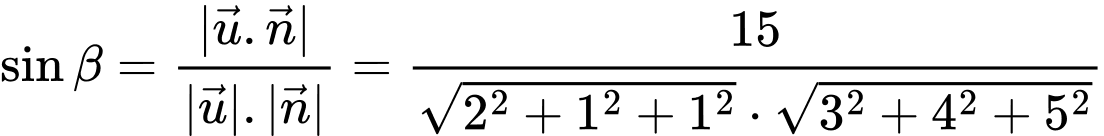
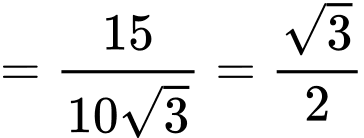
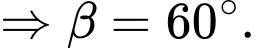
Chọn đáp án A. Đáp án: A
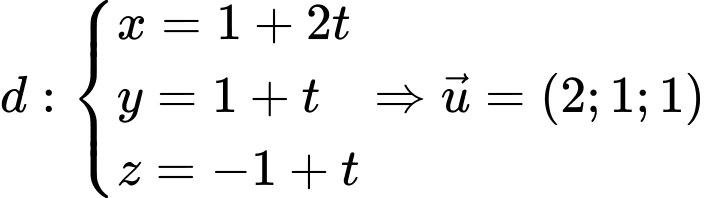 và
và 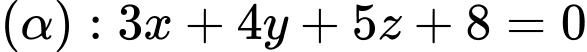
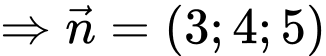
Áp dụng công thức tính góc giữa đường thẳng và mặt phẳng, ta có
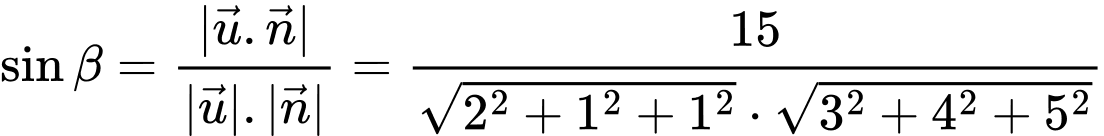
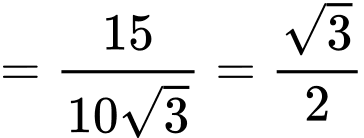
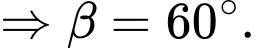
Chọn đáp án A. Đáp án: A
Câu 4 [57273]: Trong không gian với hệ tọa độ 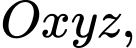 cho mặt phẳng
cho mặt phẳng 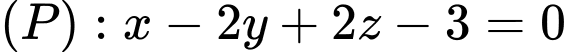 và đường thẳng
và đường thẳng 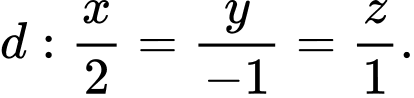 Tính sin của góc giữa đường thẳng
Tính sin của góc giữa đường thẳng 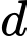 và mặt phẳng
và mặt phẳng 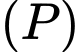

 cho mặt phẳng
cho mặt phẳng 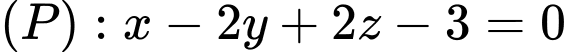 và đường thẳng
và đường thẳng 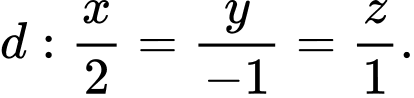 Tính sin của góc giữa đường thẳng
Tính sin của góc giữa đường thẳng 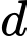 và mặt phẳng
và mặt phẳng 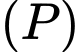

A, 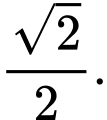
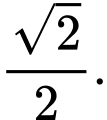
B, 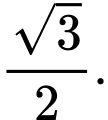
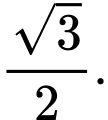
C, 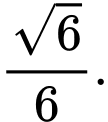
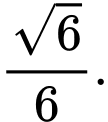
D, 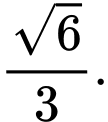
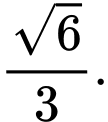
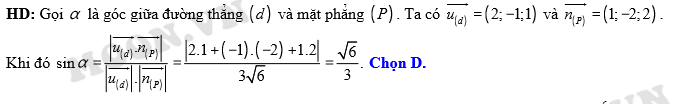 Đáp án: D
Đáp án: D
Câu 5 [879527]: Trong không gian tọa độ 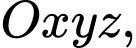 cho hai mặt phẳng
cho hai mặt phẳng 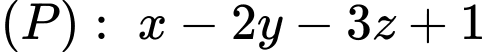 và
và 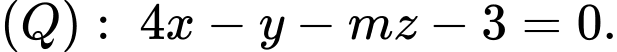 Tìm giá trị của tham số
Tìm giá trị của tham số 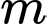 để góc giữa hai mặt phẳng
để góc giữa hai mặt phẳng 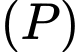 và
và  bằng
bằng 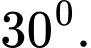
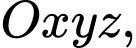 cho hai mặt phẳng
cho hai mặt phẳng 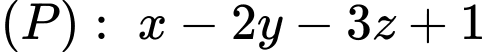 và
và 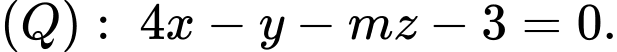 Tìm giá trị của tham số
Tìm giá trị của tham số 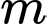 để góc giữa hai mặt phẳng
để góc giữa hai mặt phẳng 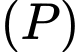 và
và  bằng
bằng 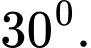
A, 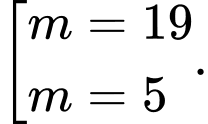
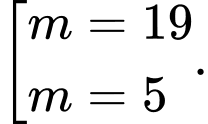
B, 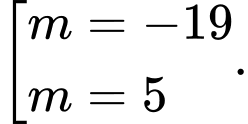
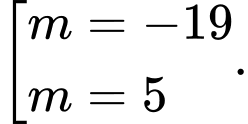
C, 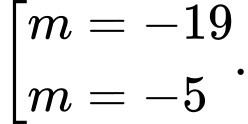
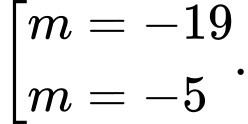
D, 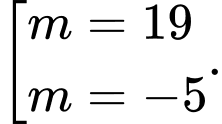
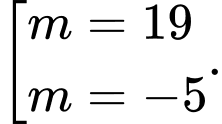
Các vectơ pháp tuyến của mặt phẳng 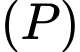 và
và  lần lượt là
lần lượt là 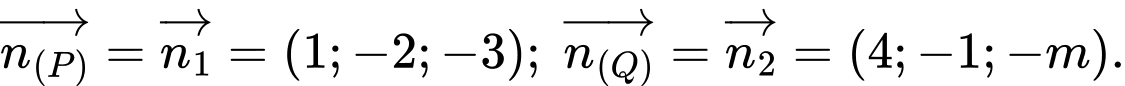
Khi đó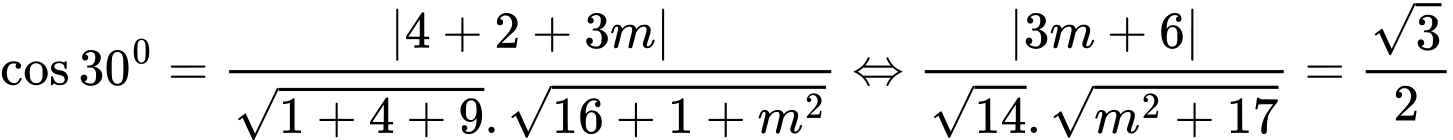
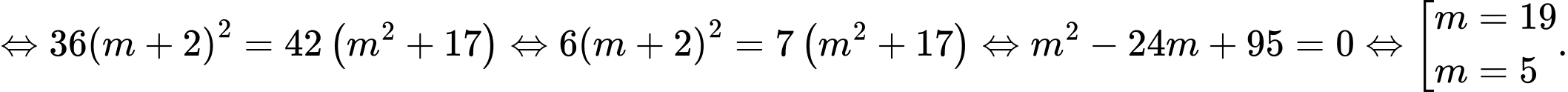 Chọn A. Đáp án: A
Chọn A. Đáp án: A
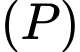 và
và  lần lượt là
lần lượt là 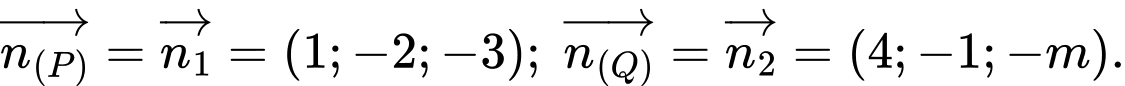
Khi đó
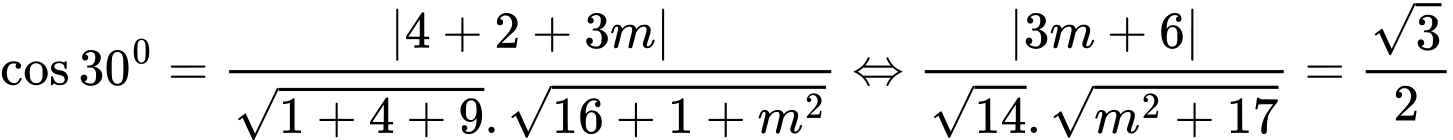
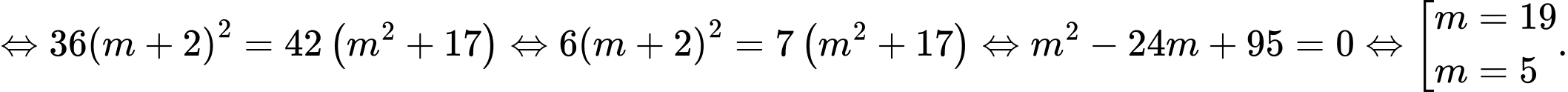 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 6 [405671]: Trong không gian tọa độ  cho hai mặt phẳng
cho hai mặt phẳng 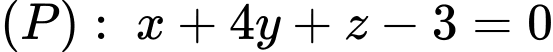 và
và 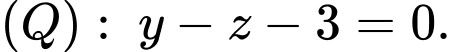 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
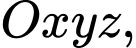 cho hai mặt phẳng
cho hai mặt phẳng 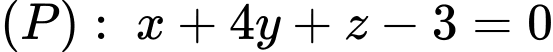 và
và 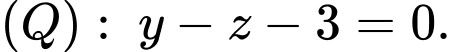 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Một vectơ pháp tuyến của mặt phẳng  là
là 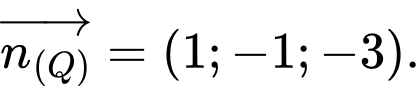
 là
là 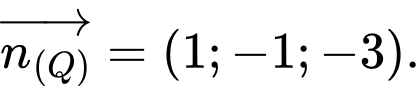
B, b) Khoảng cách từ điểm 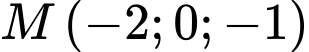 đến mặt phẳng
đến mặt phẳng 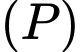 bằng
bằng 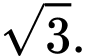
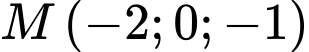 đến mặt phẳng
đến mặt phẳng 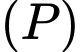 bằng
bằng 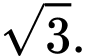
C, c) Góc giữa hai mặt phẳng 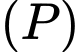 và
và  bằng
bằng 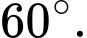
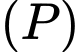 và
và  bằng
bằng 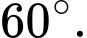
D, d) Gọi  là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 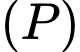 và
và  thì
thì  có một vectơ chỉ phương là
có một vectơ chỉ phương là 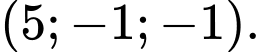
 là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 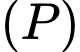 và
và  thì
thì  có một vectơ chỉ phương là
có một vectơ chỉ phương là 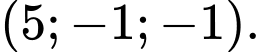
a) Sai.
Một vectơ pháp tuyến của mặt phẳng là
là 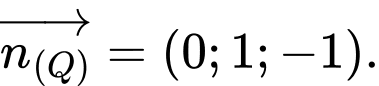
b) Sai.
Khoảng cách từ điểm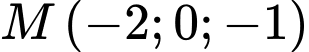 đến mặt phẳng
đến mặt phẳng 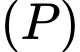 là
là 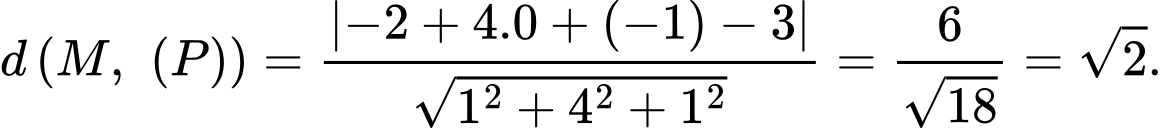
c) Đúng.
Các vectơ pháp tuyến của mặt phẳng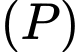 và
và  lần lượt là
lần lượt là 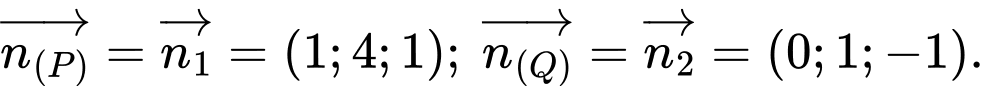
Khi đó: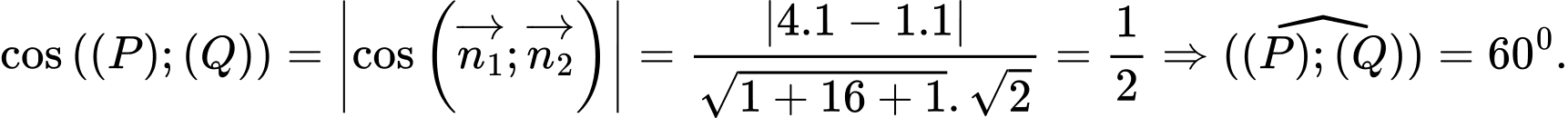
d) Đúng.
Vectơ pháp tuyến của mặt phẳng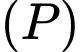 và
và  lần lượt là
lần lượt là 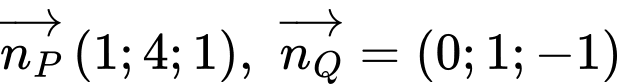
Suy ra một vectơ chỉ phương của là
là 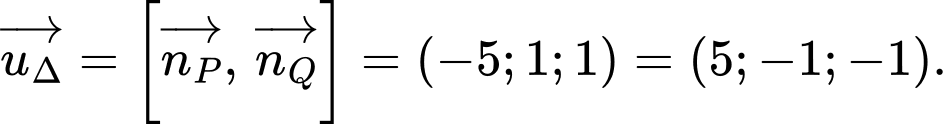
Một vectơ pháp tuyến của mặt phẳng
 là
là 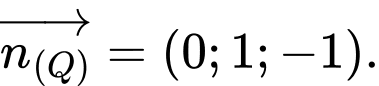
b) Sai.
Khoảng cách từ điểm
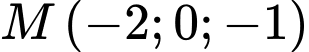 đến mặt phẳng
đến mặt phẳng 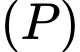 là
là 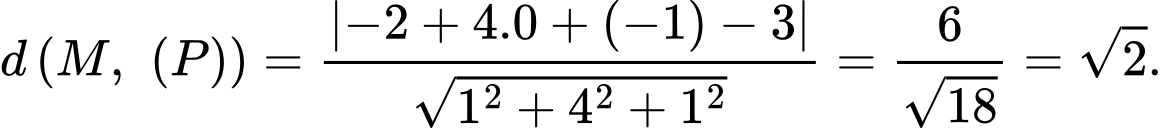
c) Đúng.
Các vectơ pháp tuyến của mặt phẳng
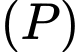 và
và  lần lượt là
lần lượt là 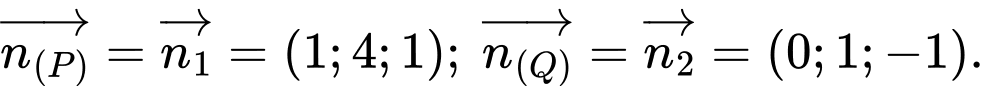
Khi đó:
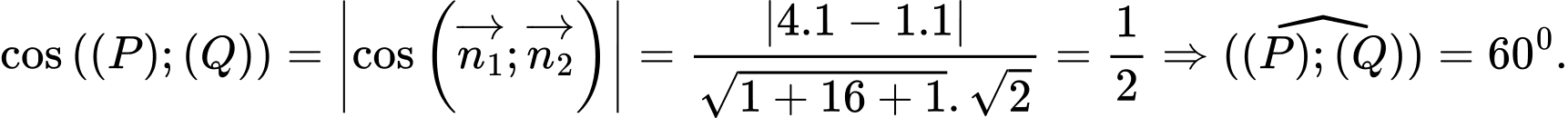
d) Đúng.
Vectơ pháp tuyến của mặt phẳng
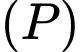 và
và  lần lượt là
lần lượt là 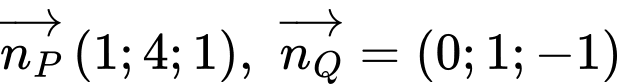
Suy ra một vectơ chỉ phương của
 là
là 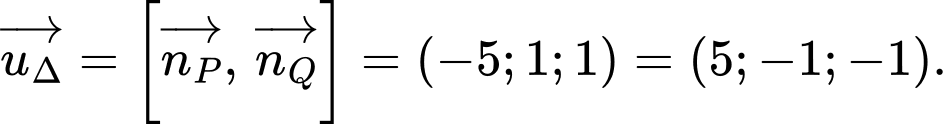
Câu 7 [405675]: Trong không gian  cho hai đường thẳng
cho hai đường thẳng 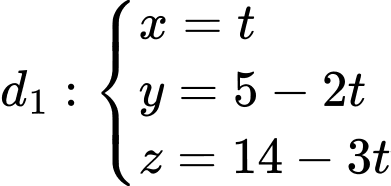 và
và 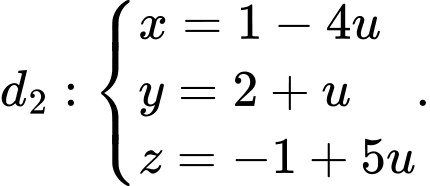 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
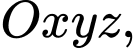 cho hai đường thẳng
cho hai đường thẳng 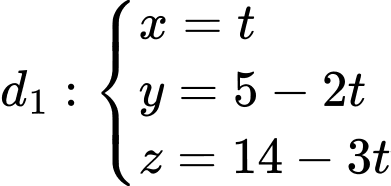 và
và 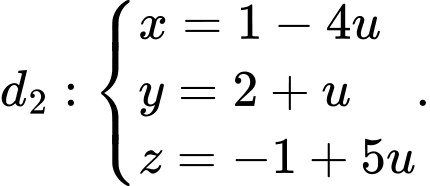 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Một vectơ chỉ phương của đường thẳng 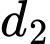 là
là 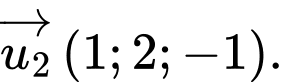
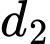 là
là 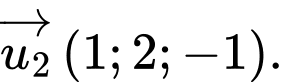
B, b) Góc giữa 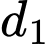 và
và 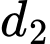 bằng
bằng 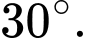
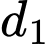 và
và 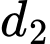 bằng
bằng 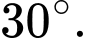
C, c) 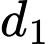 và
và 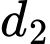 là hai đường thẳng chéo nhau.
là hai đường thẳng chéo nhau.
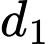 và
và 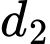 là hai đường thẳng chéo nhau.
là hai đường thẳng chéo nhau.D, d) Gọi  là mặt phẳng chứa
là mặt phẳng chứa 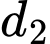 và song song với
và song song với 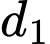 thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ 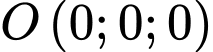 đến mặt phẳng
đến mặt phẳng  bằng
bằng 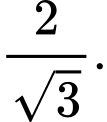
 là mặt phẳng chứa
là mặt phẳng chứa 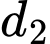 và song song với
và song song với 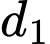 thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ 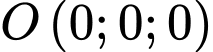 đến mặt phẳng
đến mặt phẳng  bằng
bằng 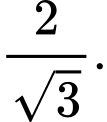
a) Sai.
Một vectơ chỉ phương của đường thẳng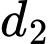 là
là 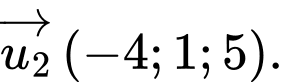
b) Đúng.
Vectơ chỉ phương của đường thẳng là
là 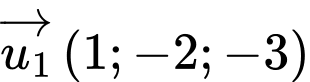
Vectơ chỉ phương của đường thẳng là
là 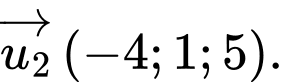
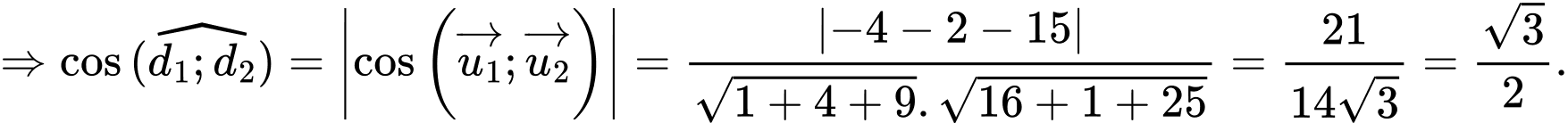
Suy ra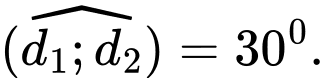
c) Đúng.
Nhắc lại: Hai đường thẳng chéo nhau là hai đường thẳng không song song và cũng không cắt nhau.
Cách 1: (ta chứng minh hai đường thẳng không cắt nhau và cũng không song song với nhau)
+) Xét hệ phương trình
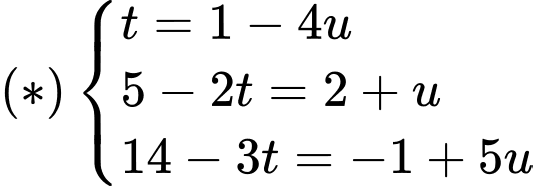
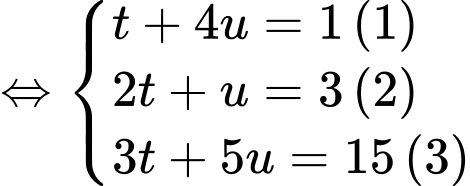
Từ phương trình và
và  ta tìm được
ta tìm được 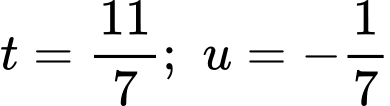
Thay vào ta được
ta được 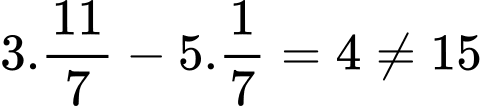
Suy ra hệ vô nghiệm
vô nghiệm
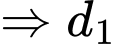 không cắt
không cắt 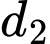
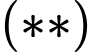
+) Ta có vectơ chỉ phương của hai đường thẳng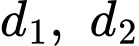 lần lượt là
lần lượt là 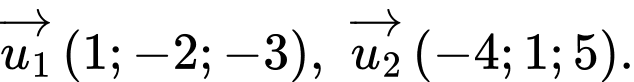
Ta thấy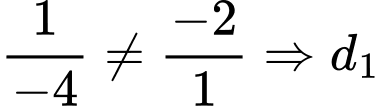 không song song với
không song song với 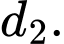

Từ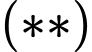 và
và  suy ra
suy ra 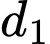 và
và 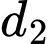 chéo nhau.
chéo nhau.
Cách 2: (ta so sánh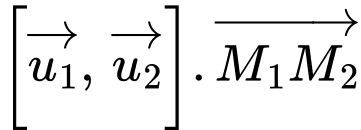 với
với  nếu
nếu 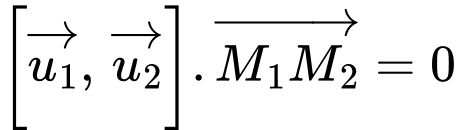 thì hai đường thẳng đồng phẳng tức không chéo nhau; nếu
thì hai đường thẳng đồng phẳng tức không chéo nhau; nếu 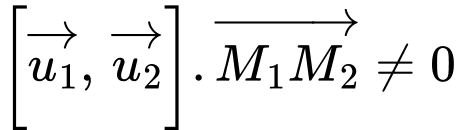 thì hai đường thẳng không đồng phẳng tức hai đường thẳng chéo nhau)
thì hai đường thẳng không đồng phẳng tức hai đường thẳng chéo nhau)
Ta có vectơ chỉ phương của hai đường thẳng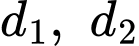 lần lượt là
lần lượt là
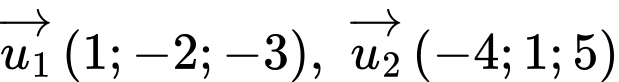
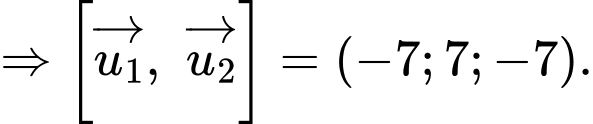 Chọn
Chọn 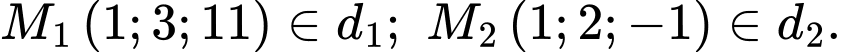
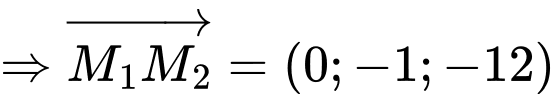
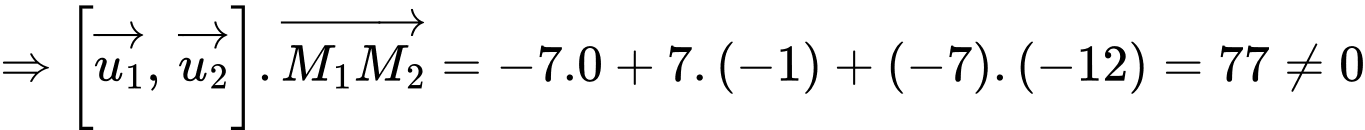
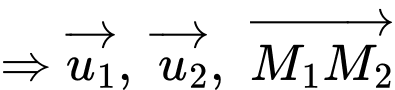 không đồng phẳng
không đồng phẳng 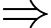
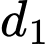 và
và 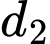 chéo nhau.
chéo nhau.
d) Đúng.
Mặt phẳng có hai vectơ chỉ phương là
có hai vectơ chỉ phương là 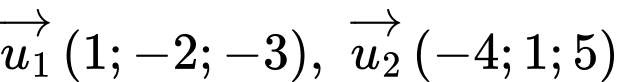
Suy ra một vectơ pháp tuyến của là
là 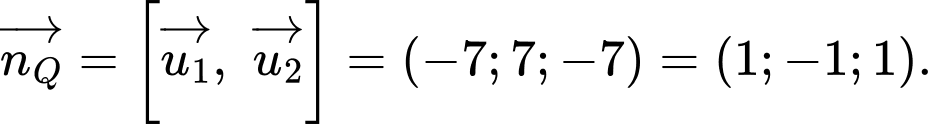
Mặt phẳng đi qua
đi qua 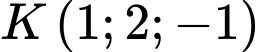 và có vectơ pháp tuyến
và có vectơ pháp tuyến 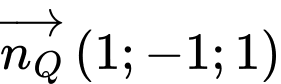 có phương trình tổng quát là
có phương trình tổng quát là 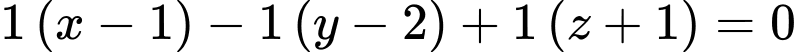
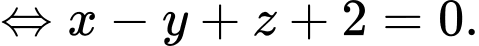
Suy ra khoảng cách từ gốc toạ độ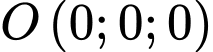 đến mặt phẳng
đến mặt phẳng  là
là 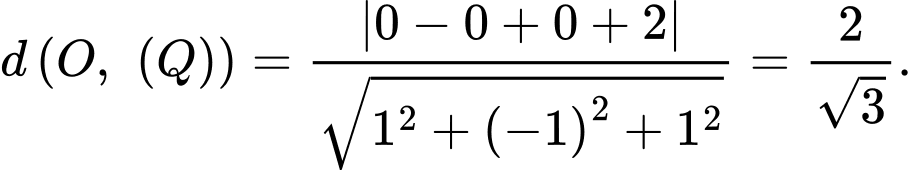
Một vectơ chỉ phương của đường thẳng
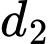 là
là 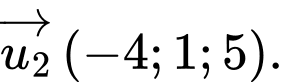
b) Đúng.
Vectơ chỉ phương của đường thẳng
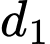 là
là 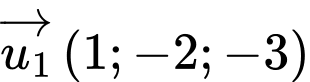
Vectơ chỉ phương của đường thẳng
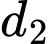 là
là 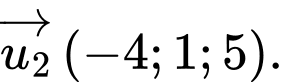
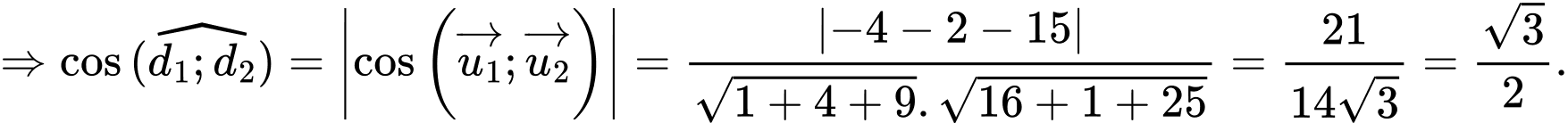
Suy ra
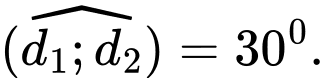
c) Đúng.
Nhắc lại: Hai đường thẳng chéo nhau là hai đường thẳng không song song và cũng không cắt nhau.
Cách 1: (ta chứng minh hai đường thẳng không cắt nhau và cũng không song song với nhau)
+) Xét hệ phương trình
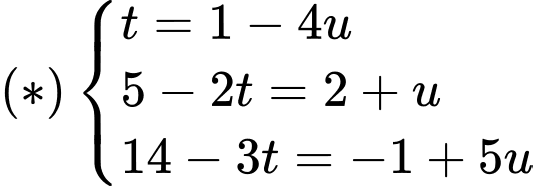
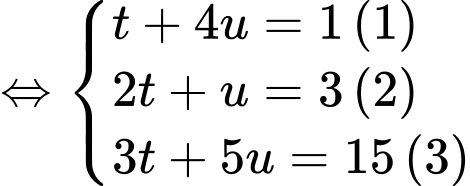
Từ phương trình
 và
và  ta tìm được
ta tìm được 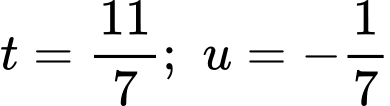
Thay vào
 ta được
ta được 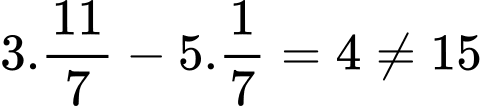
Suy ra hệ
 vô nghiệm
vô nghiệm
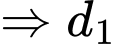 không cắt
không cắt 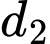
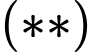
+) Ta có vectơ chỉ phương của hai đường thẳng
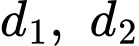 lần lượt là
lần lượt là 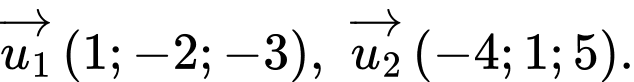
Ta thấy
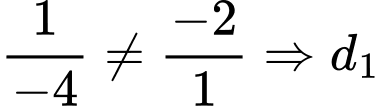 không song song với
không song song với 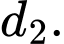

Từ
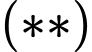 và
và  suy ra
suy ra 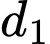 và
và 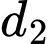 chéo nhau.
chéo nhau.
Cách 2: (ta so sánh
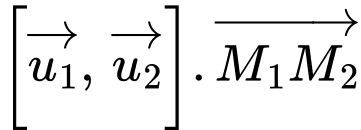 với
với  nếu
nếu 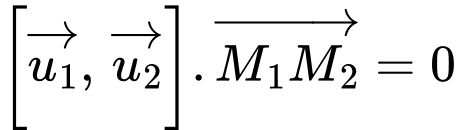 thì hai đường thẳng đồng phẳng tức không chéo nhau; nếu
thì hai đường thẳng đồng phẳng tức không chéo nhau; nếu 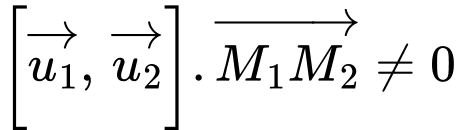 thì hai đường thẳng không đồng phẳng tức hai đường thẳng chéo nhau)
thì hai đường thẳng không đồng phẳng tức hai đường thẳng chéo nhau)
Ta có vectơ chỉ phương của hai đường thẳng
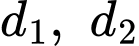 lần lượt là
lần lượt là
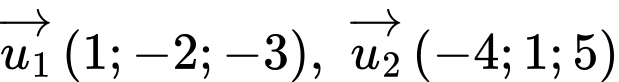
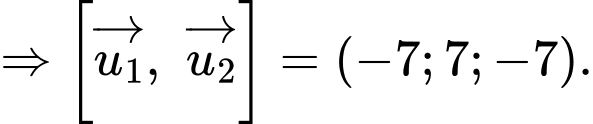 Chọn
Chọn 
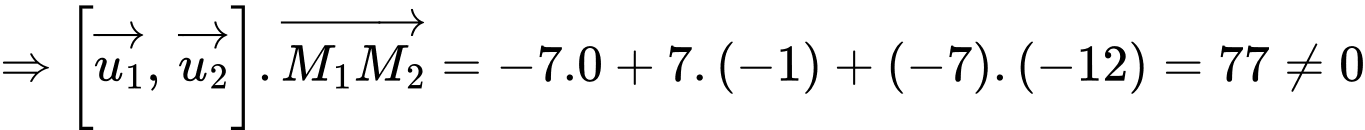
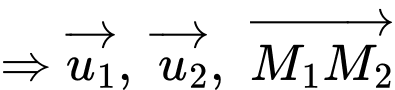 không đồng phẳng
không đồng phẳng 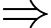
 và
và 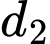 chéo nhau.
chéo nhau.
d) Đúng.
Mặt phẳng
 có hai vectơ chỉ phương là
có hai vectơ chỉ phương là 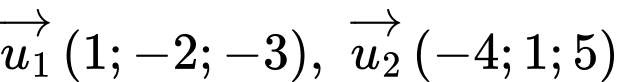
Suy ra một vectơ pháp tuyến của
 là
là 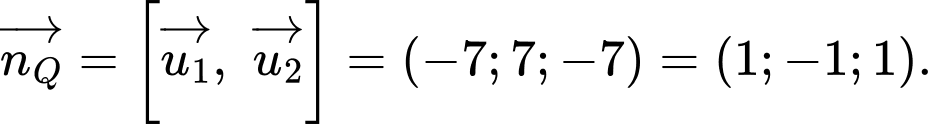
Mặt phẳng
 đi qua
đi qua 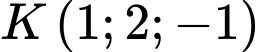 và có vectơ pháp tuyến
và có vectơ pháp tuyến 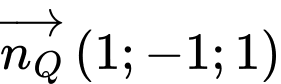 có phương trình tổng quát là
có phương trình tổng quát là 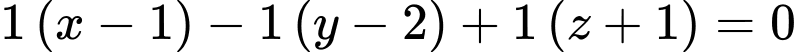
Suy ra khoảng cách từ gốc toạ độ
 đến mặt phẳng
đến mặt phẳng  là
là 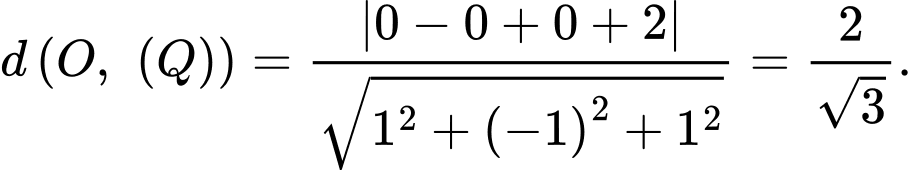
Câu 8 [405676]: Trong không gian với hệ tọa độ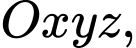 cho mặt phẳng
cho mặt phẳng 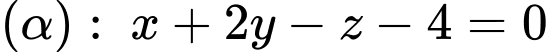 và đường thẳng
và đường thẳng 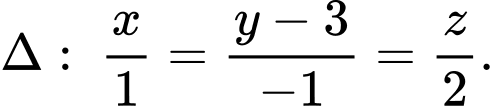 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
 cho mặt phẳng
cho mặt phẳng 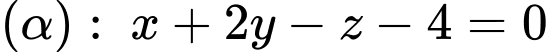 và đường thẳng
và đường thẳng 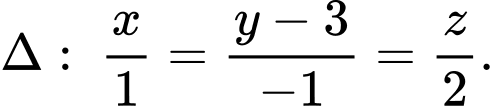 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Một vectơ chỉ phương của đường thẳng  là
là 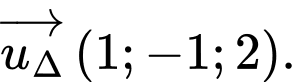
 là
là 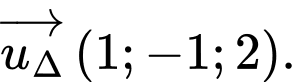
B, b) Khoảng cách từ điểm 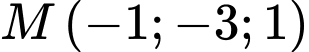 đến mặt phẳng
đến mặt phẳng  bằng
bằng 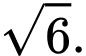
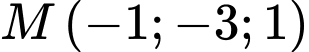 đến mặt phẳng
đến mặt phẳng  bằng
bằng 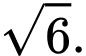
C, c) Góc giữa đường thẳng  và mặt phẳng
và mặt phẳng  bằng
bằng 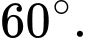
 và mặt phẳng
và mặt phẳng  bằng
bằng 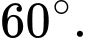
D, d) Gọi 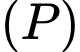 là mặt phẳng chứa
là mặt phẳng chứa  và vuông góc với
và vuông góc với  thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 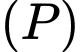 bằng
bằng 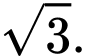
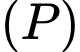 là mặt phẳng chứa
là mặt phẳng chứa  và vuông góc với
và vuông góc với  thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 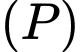 bằng
bằng 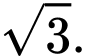
a) Đúng.
b) Sai.
Khoảng cách từ điểm 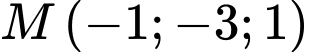 đến mặt phẳng
đến mặt phẳng  là
là 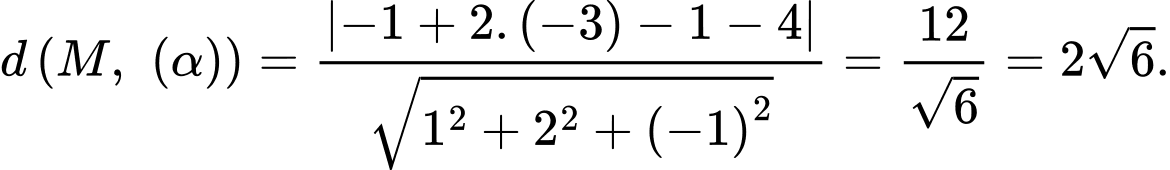
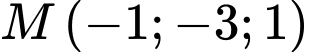 đến mặt phẳng
đến mặt phẳng  là
là 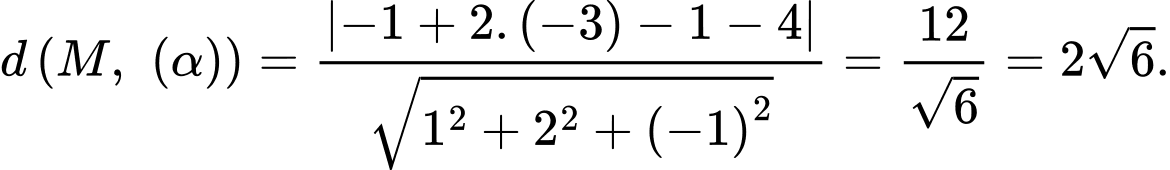
c) Sai.
Đường thẳng  có vectơ chỉ phương là
có vectơ chỉ phương là 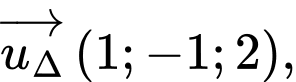 mặt phẳng
mặt phẳng  có vectơ pháp tuyến là
có vectơ pháp tuyến là 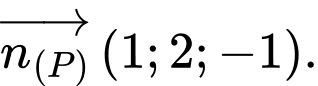
 có vectơ chỉ phương là
có vectơ chỉ phương là 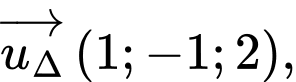 mặt phẳng
mặt phẳng 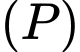 có vectơ pháp tuyến là
có vectơ pháp tuyến là 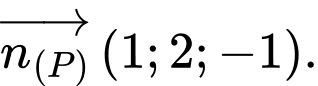
Gọi 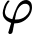 là góc giữa d và
là góc giữa d và 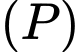 thì:
thì:
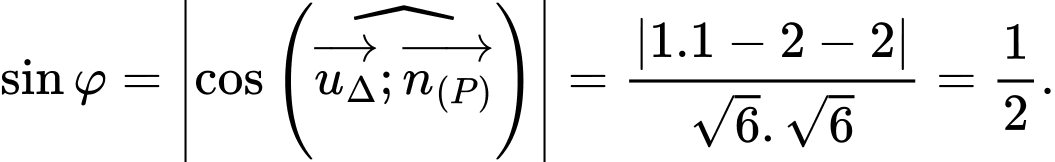
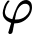 là góc giữa d và
là góc giữa d và 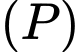 thì:
thì:
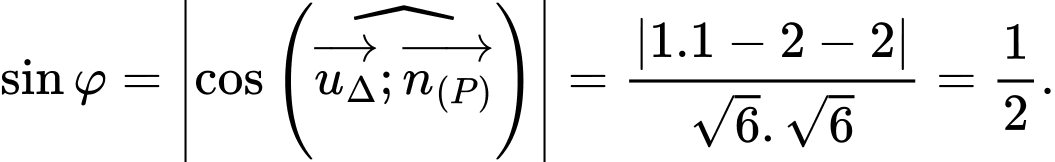
Suy ra 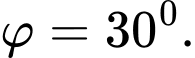
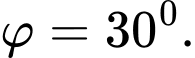
d) Đúng.
Vì 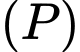 chứa
chứa  và vuông góc với
và vuông góc với  nên sẽ có hai vectơ chỉ phương là
nên sẽ có hai vectơ chỉ phương là 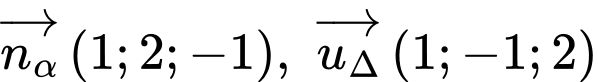
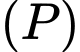 chứa
chứa  và vuông góc với
và vuông góc với  nên sẽ có hai vectơ chỉ phương là
nên sẽ có hai vectơ chỉ phương là 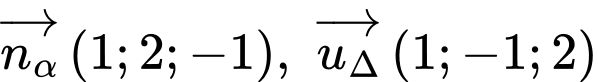
Suy ra một vectơ pháp tuyến của mặt phẳng 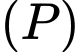 là
là 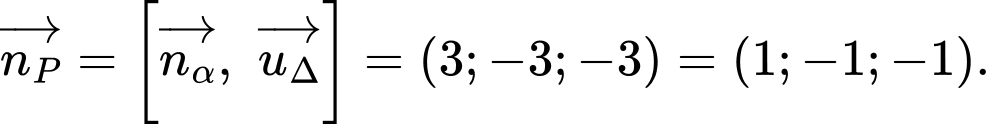
 là
là 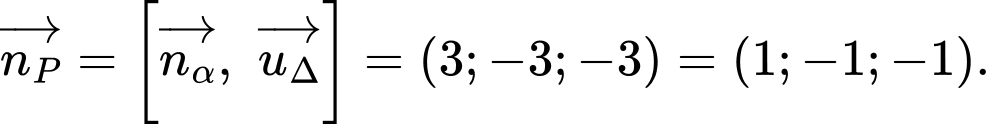
Mặt phẳng  đi qua
đi qua 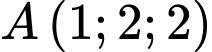 và có vectơ pháp tuyến
và có vectơ pháp tuyến 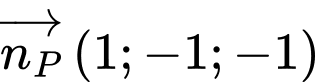 có phương trình tổng quát là
có phương trình tổng quát là 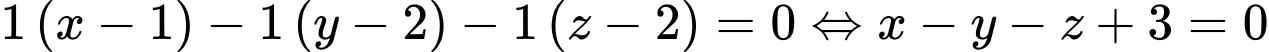
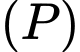 đi qua
đi qua 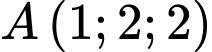 và có vectơ pháp tuyến
và có vectơ pháp tuyến 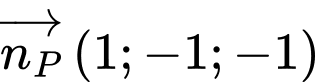 có phương trình tổng quát là
có phương trình tổng quát là 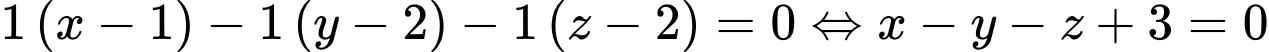
Suy ra khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 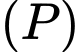 là
là 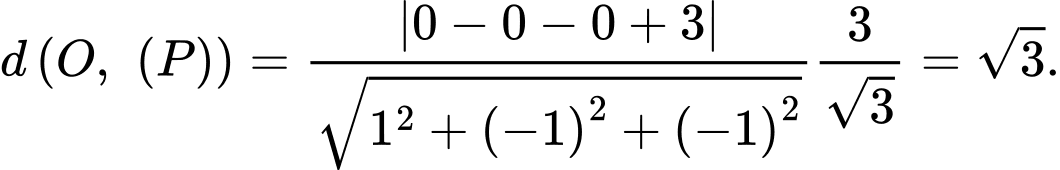
 đến mặt phẳng
đến mặt phẳng 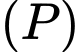 là
là 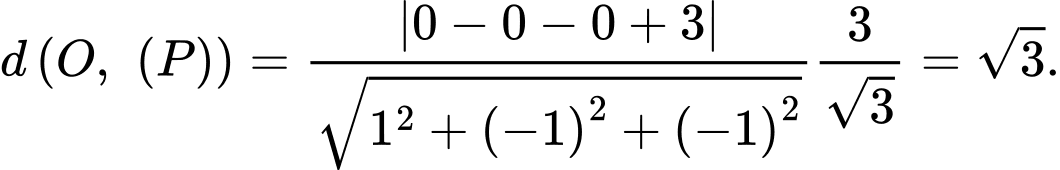
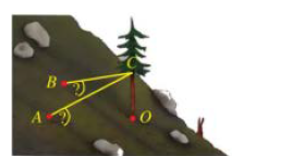
Câu 9 [163892]: Trên một sườn núi (có độ nghiêng đều), người ta trồng một cây thông và muốn giữ nó không bị nghiêng bằng hai sợi dây neo như hình. Giả thiết cây thông mọc thẳng đứng và trong một hệ toạ độ phù hợp, các điểm  (gốc cây thông) và
(gốc cây thông) và  (nơi buộc dây neo) có toạ độ tương ứng là
(nơi buộc dây neo) có toạ độ tương ứng là 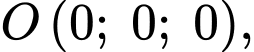
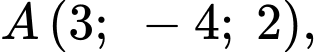
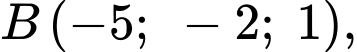 đơn vị trên mỗi trục toạ độ là mét. Biết rằng hai dây neo đều được buộc vào cây thông tại điểm
đơn vị trên mỗi trục toạ độ là mét. Biết rằng hai dây neo đều được buộc vào cây thông tại điểm 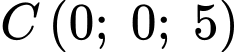 và được kéo căng tạo thành các đoạn thẳng. Các mệnh đề sau đúng hay sai.
và được kéo căng tạo thành các đoạn thẳng. Các mệnh đề sau đúng hay sai.
 (gốc cây thông) và
(gốc cây thông) và  (nơi buộc dây neo) có toạ độ tương ứng là
(nơi buộc dây neo) có toạ độ tương ứng là 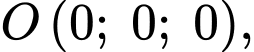
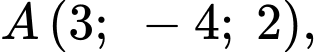
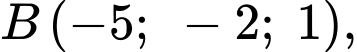 đơn vị trên mỗi trục toạ độ là mét. Biết rằng hai dây neo đều được buộc vào cây thông tại điểm
đơn vị trên mỗi trục toạ độ là mét. Biết rằng hai dây neo đều được buộc vào cây thông tại điểm 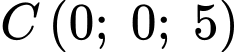 và được kéo căng tạo thành các đoạn thẳng. Các mệnh đề sau đúng hay sai.
và được kéo căng tạo thành các đoạn thẳng. Các mệnh đề sau đúng hay sai.
A, a) 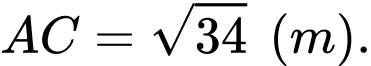
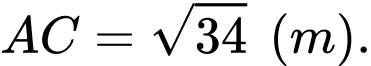
B, b) Một vectơ pháp tuyến của mặt phẳng 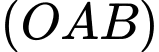 là
là 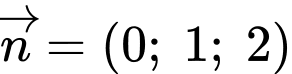
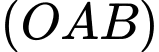 là
là 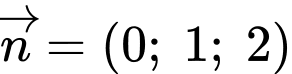
C, c) Góc giữa  so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là
so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là 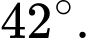
 so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là
so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là 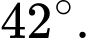
D, d) Góc giữa 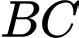 so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là
so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là 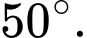
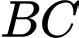 so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là
so với mặt phẳng sườn núi (làm tròn đến hàng đơn vị của độ) là 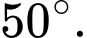
Thầy Tuấn-Xin lỗi các em về lỗi đề (sách 3000 bài tập nên không thể tránh khỏi trong lần đầu xuất bản) - Các em sửa lại đề theo đề Web nhé!. Cảm ơn các em nhiều! (bài này thêm toạ độ A)
a) Đúng.
Do điểm 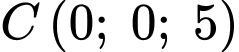 nên
nên 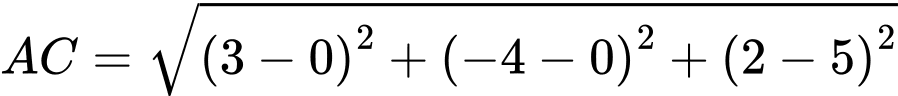

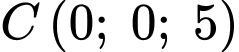 nên
nên 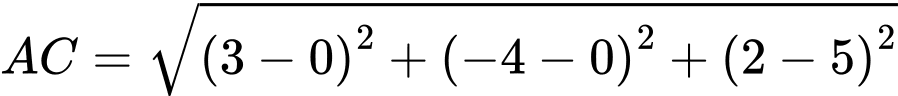

b) Đúng.
Ta có: 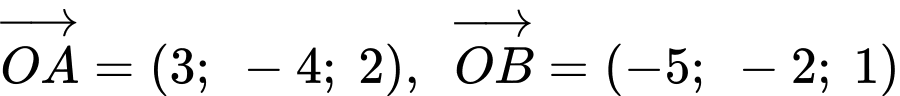 nên
nên 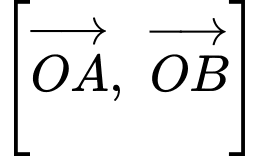
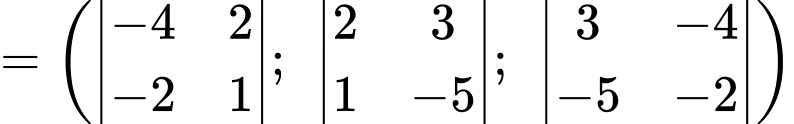
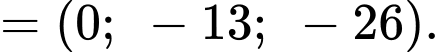
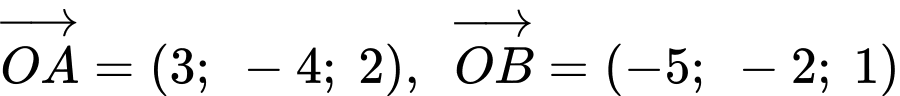 nên
nên 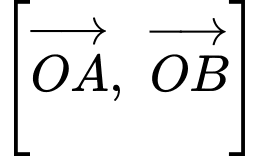
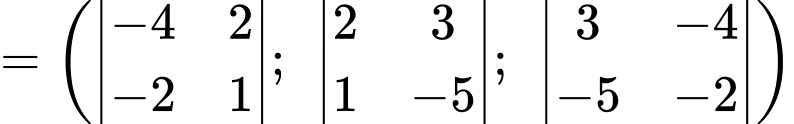
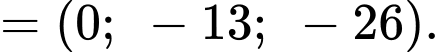
Vì thế, vectơ 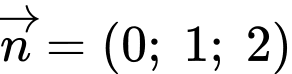 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 
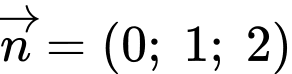 là một vectơ pháp tuyến của mặt phẳng
là một vectơ pháp tuyến của mặt phẳng 
Mặt khác, do 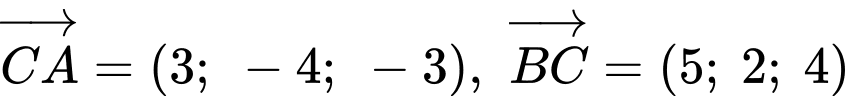 nên ta có:
nên ta có:
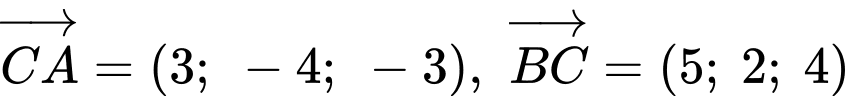 nên ta có:
nên ta có: c) Sai.
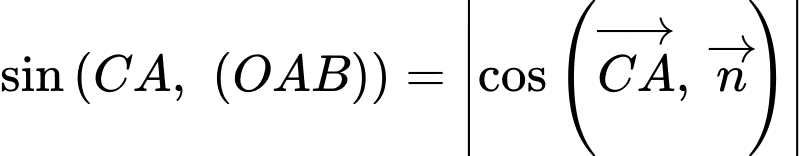
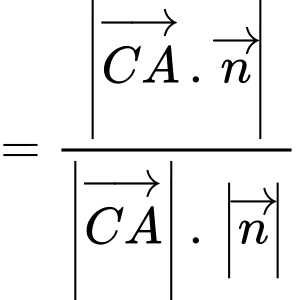
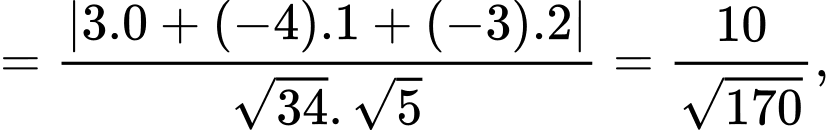
suy ra
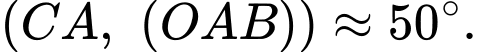
Vậy góc tạo bởi dây neo  và mặt phẳng sườn núi là khoảng
và mặt phẳng sườn núi là khoảng 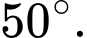
 và mặt phẳng sườn núi là khoảng
và mặt phẳng sườn núi là khoảng 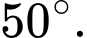
d) Sai.
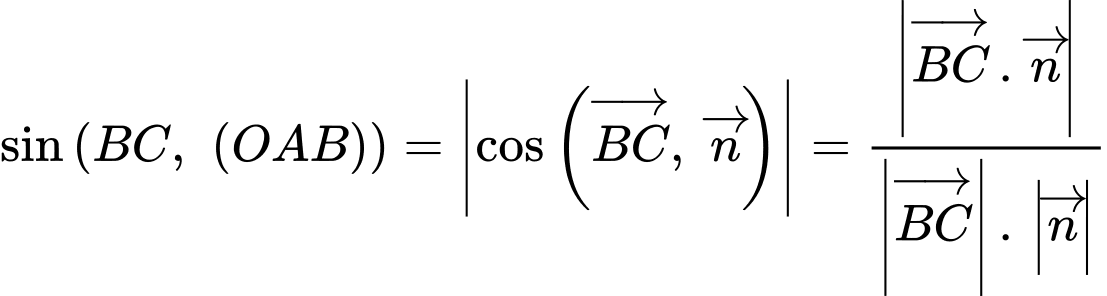
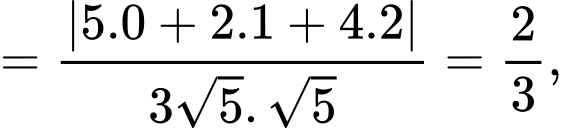
suy ra
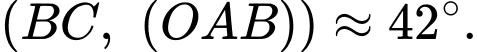
Vậy góc tạo bởi dây neo 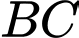 và mặt phẳng sườn núi là khoảng
và mặt phẳng sườn núi là khoảng 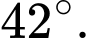
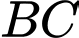 và mặt phẳng sườn núi là khoảng
và mặt phẳng sườn núi là khoảng 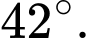
Câu 10 [202965]: Trong không gian với hệ toạ độ 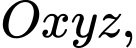 một cabin cáp treo xuất phát từ điểm
một cabin cáp treo xuất phát từ điểm 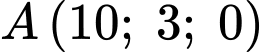 và chuyển động đều theo cáp có vectơ chỉ phương là
và chuyển động đều theo cáp có vectơ chỉ phương là 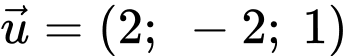 với tốc độ là
với tốc độ là 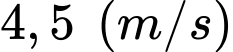 (đơn vị trên mỗi trục toạ độ là mét). Các mệnh đề sau đúng hay sai
(đơn vị trên mỗi trục toạ độ là mét). Các mệnh đề sau đúng hay sai
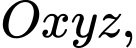 một cabin cáp treo xuất phát từ điểm
một cabin cáp treo xuất phát từ điểm 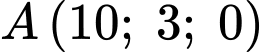 và chuyển động đều theo cáp có vectơ chỉ phương là
và chuyển động đều theo cáp có vectơ chỉ phương là 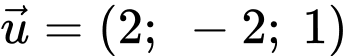 với tốc độ là
với tốc độ là 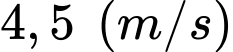 (đơn vị trên mỗi trục toạ độ là mét). Các mệnh đề sau đúng hay sai
(đơn vị trên mỗi trục toạ độ là mét). Các mệnh đề sau đúng hay sai
A, a) Phương trình đường cáp là 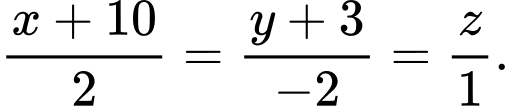
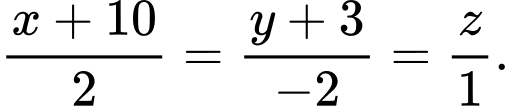
B, b) Giả sử sau 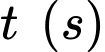 kể từ xuất phát
kể từ xuất phát 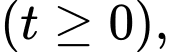 cabin đến điểm
cabin đến điểm 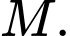 Toạ độ của điểm
Toạ độ của điểm 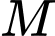 theo
theo 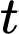 là
là 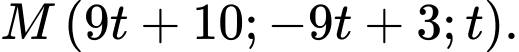
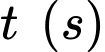 kể từ xuất phát
kể từ xuất phát 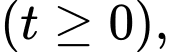 cabin đến điểm
cabin đến điểm  Toạ độ của điểm
Toạ độ của điểm 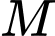 theo
theo 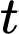 là
là 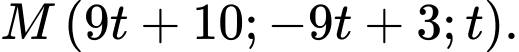
C, c) Cabin dừng ở điểm 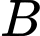 có hoành độ
có hoành độ 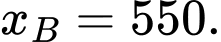 Độ dài quãng đường
Độ dài quãng đường  (làm tròn kết quả đến hàng đơn vị của mét) bằng
(làm tròn kết quả đến hàng đơn vị của mét) bằng 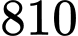 mét.
mét.
 có hoành độ
có hoành độ 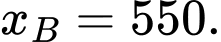 Độ dài quãng đường
Độ dài quãng đường  (làm tròn kết quả đến hàng đơn vị của mét) bằng
(làm tròn kết quả đến hàng đơn vị của mét) bằng 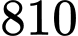 mét.
mét.D, d) Đường cáp  tạo với mặt phẳng
tạo với mặt phẳng 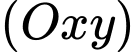 góc (làm tròn kết quả đến hàng đơn vị của độ) là
góc (làm tròn kết quả đến hàng đơn vị của độ) là 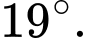
 tạo với mặt phẳng
tạo với mặt phẳng 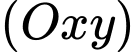 góc (làm tròn kết quả đến hàng đơn vị của độ) là
góc (làm tròn kết quả đến hàng đơn vị của độ) là 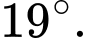
a. Sai. 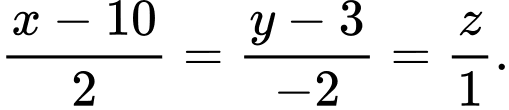
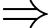
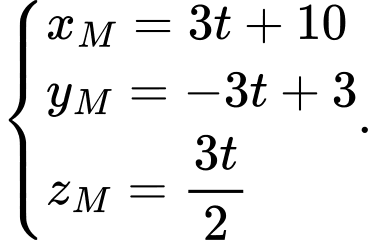
Phương trình chính tắc của đường cáp là:
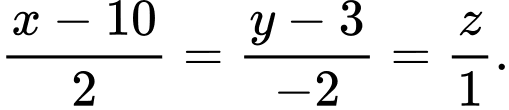
b. Sai.
Do tốc độ chuyển động của cabin là 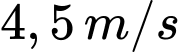 nên độ dài
nên độ dài  bằng
bằng 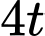 (m).
(m).
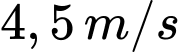 nên độ dài
nên độ dài  bằng
bằng 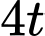 (m).
(m). Vì vậy 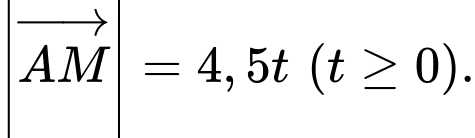
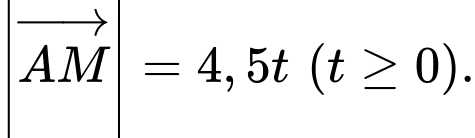
Do hai vectơ 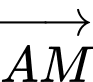 và
và 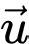 là cùng phương và cùng hướng nên
là cùng phương và cùng hướng nên 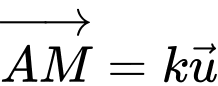 với
với 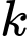 là số thực dương nào đó.
là số thực dương nào đó.
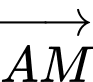 và
và 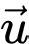 là cùng phương và cùng hướng nên
là cùng phương và cùng hướng nên 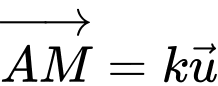 với
với 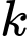 là số thực dương nào đó.
là số thực dương nào đó. Suy ra 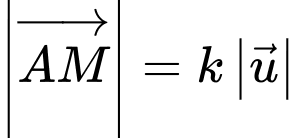
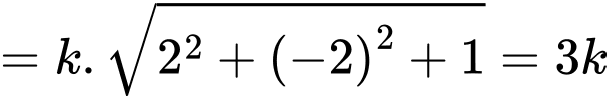
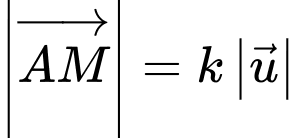
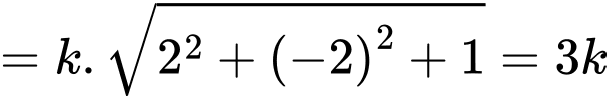
Do đó 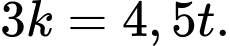 Suy ra
Suy ra 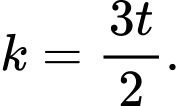 Vì thế, ta có:
Vì thế, ta có: 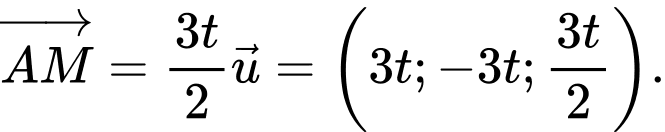
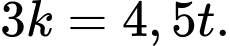 Suy ra
Suy ra 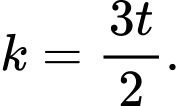 Vì thế, ta có:
Vì thế, ta có: 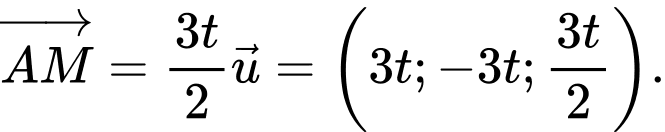
Gọi toạ độ của điểm 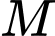 là
là 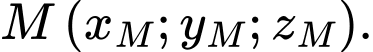
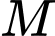 là
là 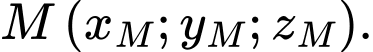
Do 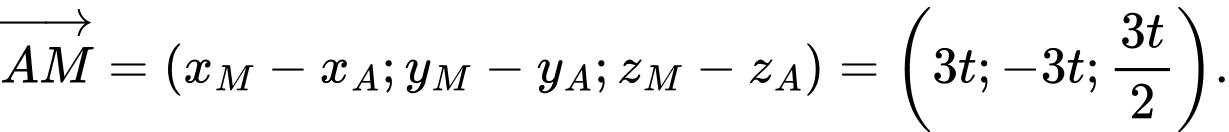
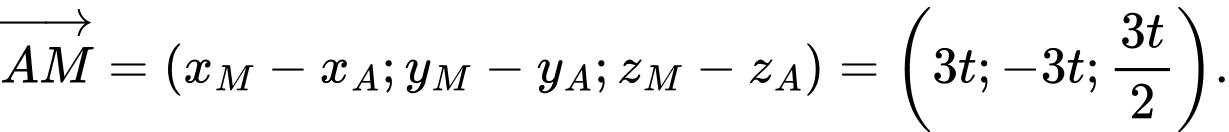
Nên 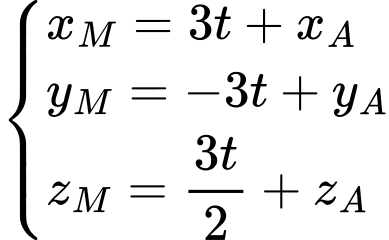
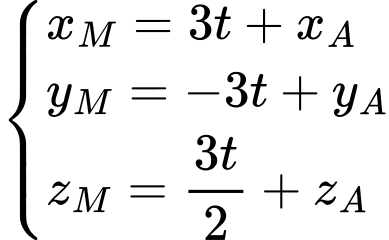
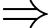
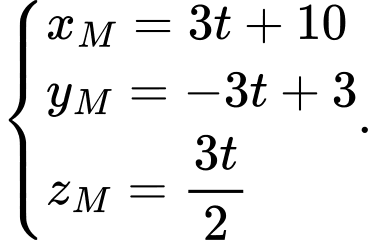
Vậy điểm 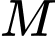 có toạ độ là
có toạ độ là 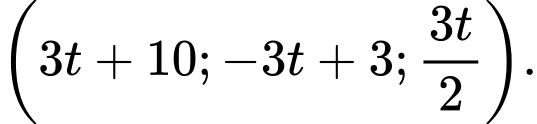
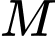 có toạ độ là
có toạ độ là 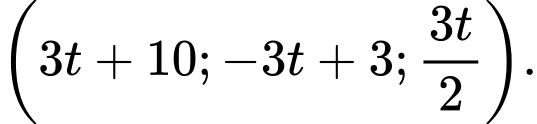
c. Đúng.
Do 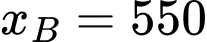 nên
nên 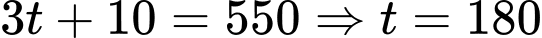
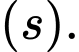
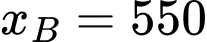 nên
nên 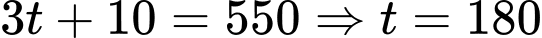
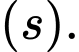
Do đó, ta có điểm 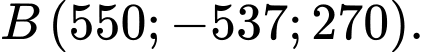
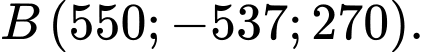
Vậy 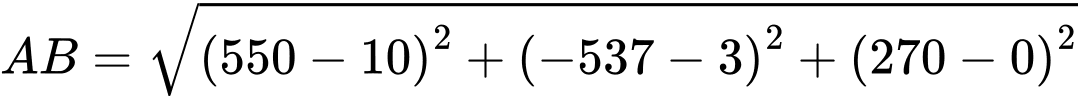

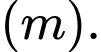
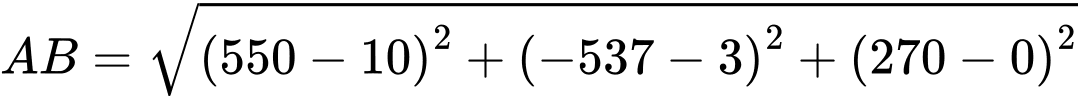

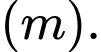
d. Đúng.
Đường thẳng  có vectơ chỉ phương
có vectơ chỉ phương 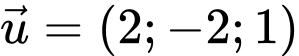 và mặt phẳng
và mặt phẳng  có vectơ pháp tuyến
có vectơ pháp tuyến 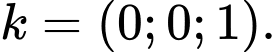
 có vectơ chỉ phương
có vectơ chỉ phương 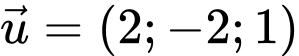 và mặt phẳng
và mặt phẳng 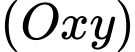 có vectơ pháp tuyến
có vectơ pháp tuyến 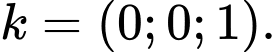
Do đó, ta có:
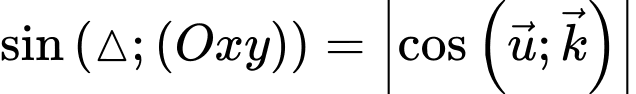
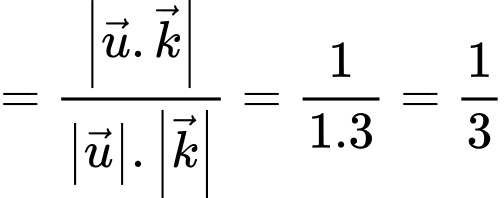
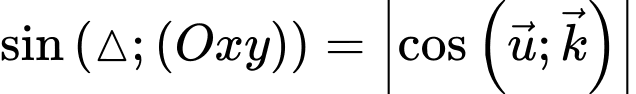
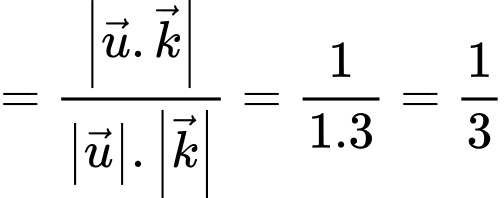
Vậy 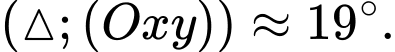
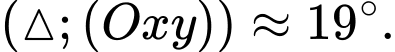
Câu 11 [57133]: Trong không gian với hệ trục tọa độ  cho điểm
cho điểm 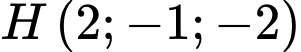 là hình chiếu vuông góc của gốc tọa độ
là hình chiếu vuông góc của gốc tọa độ  xuống mặt phẳng
xuống mặt phẳng 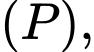 số đo góc giữa mặt phẳng
số đo góc giữa mặt phẳng 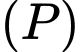 và mặt phẳng
và mặt phẳng  có phương trình
có phương trình 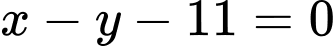 bằng bao nhiêu độ
bằng bao nhiêu độ
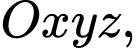 cho điểm
cho điểm 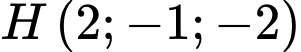 là hình chiếu vuông góc của gốc tọa độ
là hình chiếu vuông góc của gốc tọa độ  xuống mặt phẳng
xuống mặt phẳng  số đo góc giữa mặt phẳng
số đo góc giữa mặt phẳng  và mặt phẳng
và mặt phẳng  có phương trình
có phương trình 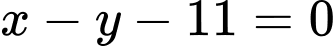 bằng bao nhiêu độ
bằng bao nhiêu độ A, 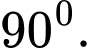
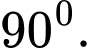
B, 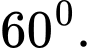
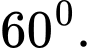
C, 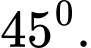
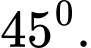
D, 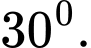
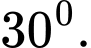
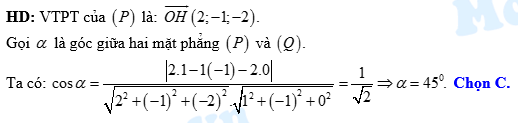 Đáp án: C
Đáp án: C
Câu 12 [57257]: Trong không gian với hệ tọa độ 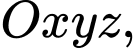 cho bốn điểm
cho bốn điểm 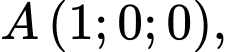
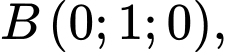
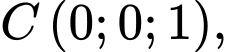 và
và 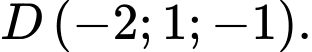 Góc giữa hai cạnh
Góc giữa hai cạnh  và
và 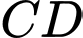 có số đo là bao nhiêu độ
có số đo là bao nhiêu độ
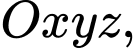 cho bốn điểm
cho bốn điểm 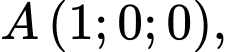
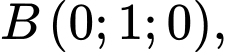
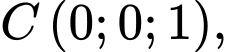 và
và 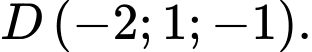 Góc giữa hai cạnh
Góc giữa hai cạnh  và
và 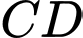 có số đo là bao nhiêu độ
có số đo là bao nhiêu độ A, 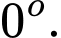
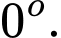
B, 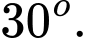
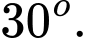
C, 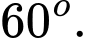
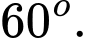
D, 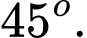
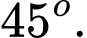
 Đáp án: D
Đáp án: D
Câu 13 [867060]: Trong không gian với hệ tọa độ 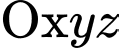 cho đường thẳng
cho đường thẳng 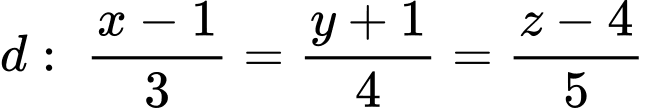 và mặt phẳng
và mặt phẳng 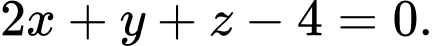 Góc hợp giữa đường thẳng
Góc hợp giữa đường thẳng 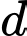 và mặt phẳng
và mặt phẳng 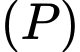 là bao nhiêu độ?
là bao nhiêu độ?
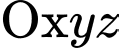 cho đường thẳng
cho đường thẳng 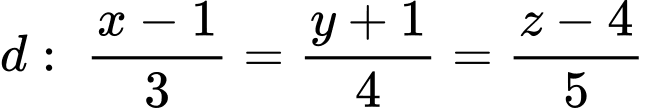 và mặt phẳng
và mặt phẳng 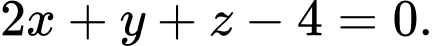 Góc hợp giữa đường thẳng
Góc hợp giữa đường thẳng 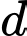 và mặt phẳng
và mặt phẳng 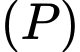 là bao nhiêu độ?
là bao nhiêu độ? A, 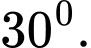
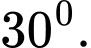
B, 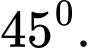
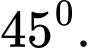
C, 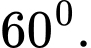
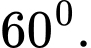
D, 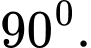
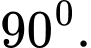
Đường thẳng 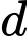 có vectơ chỉ phương là
có vectơ chỉ phương là 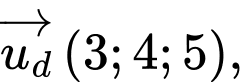 mặt phẳng
mặt phẳng 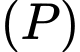 có vectơ pháp tuyến là
có vectơ pháp tuyến là 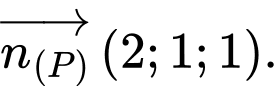 Gọi
Gọi 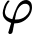 là góc giữa d và
là góc giữa d và 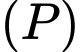 thì:
thì:
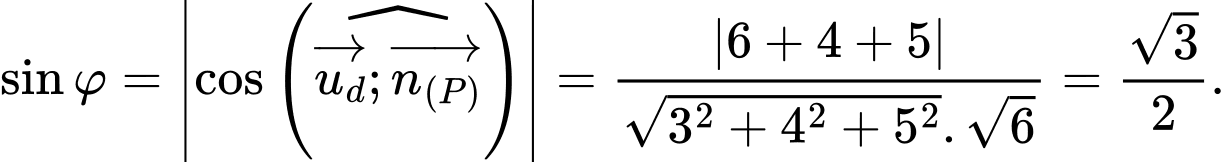 Suy ra
Suy ra 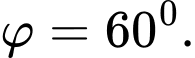 Chọn C.
Chọn C.
Đáp án: C
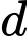 có vectơ chỉ phương là
có vectơ chỉ phương là 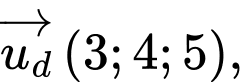 mặt phẳng
mặt phẳng  có vectơ pháp tuyến là
có vectơ pháp tuyến là 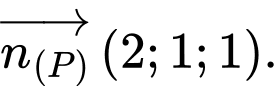 Gọi
Gọi 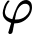 là góc giữa d và
là góc giữa d và 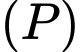 thì:
thì: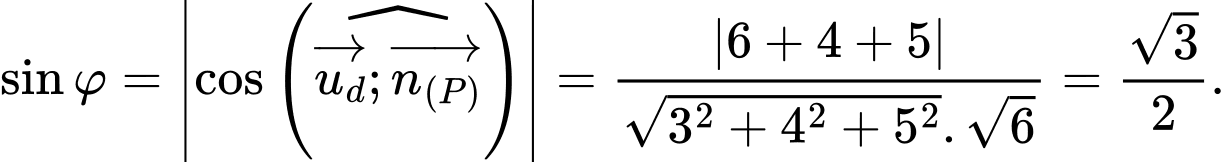 Suy ra
Suy ra 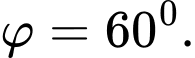 Chọn C.
Chọn C.
Đáp án: C
Câu 14 [57276]: Trong không gian với hệ tọa độ 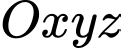 cho mặt phẳng
cho mặt phẳng 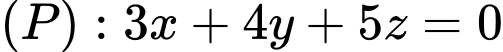 và đường thẳng
và đường thẳng 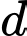 là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 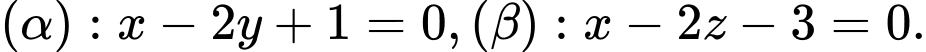 Gọi
Gọi 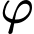 là góc giữa đường thẳng
là góc giữa đường thẳng 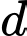 và mặt phẳng
và mặt phẳng 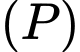
 Số đo góc
Số đo góc 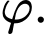 bằng bao nhiêu độ?
bằng bao nhiêu độ?
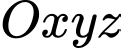 cho mặt phẳng
cho mặt phẳng 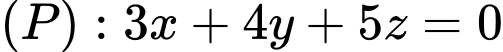 và đường thẳng
và đường thẳng  là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 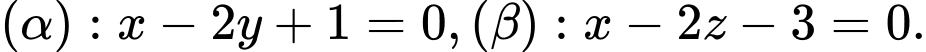 Gọi
Gọi 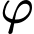 là góc giữa đường thẳng
là góc giữa đường thẳng 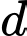 và mặt phẳng
và mặt phẳng 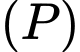
 Số đo góc
Số đo góc 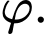 bằng bao nhiêu độ?
bằng bao nhiêu độ? A, 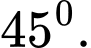
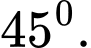
B, 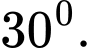
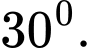
C, 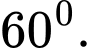
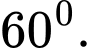
D, 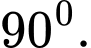
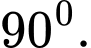
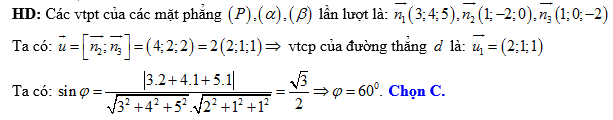 Đáp án: C
Đáp án: C
Câu 15 [899529]: Cho đường thẳng 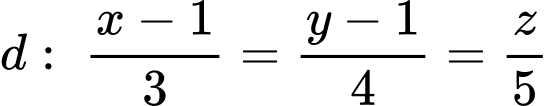 và mặt phẳng
và mặt phẳng 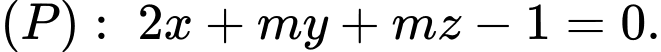 Gọi
Gọi 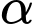 là góc giữa đường thẳng
là góc giữa đường thẳng 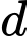 và mặt phẳng
và mặt phẳng 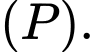 Gọi
Gọi 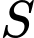 là tập hợp các giá trị của
là tập hợp các giá trị của 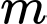 sao cho
sao cho 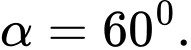 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 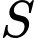 bằng bao nhiêu?
bằng bao nhiêu?
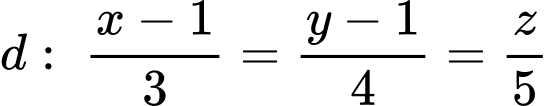 và mặt phẳng
và mặt phẳng 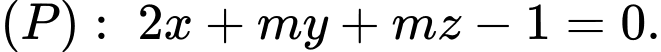 Gọi
Gọi 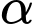 là góc giữa đường thẳng
là góc giữa đường thẳng 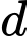 và mặt phẳng
và mặt phẳng 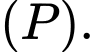 Gọi
Gọi 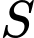 là tập hợp các giá trị của
là tập hợp các giá trị của 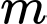 sao cho
sao cho 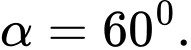 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 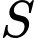 bằng bao nhiêu?
bằng bao nhiêu? A, 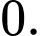
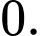
B, 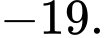
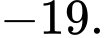
C, 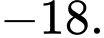
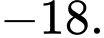
D, 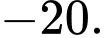
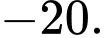
Ta có 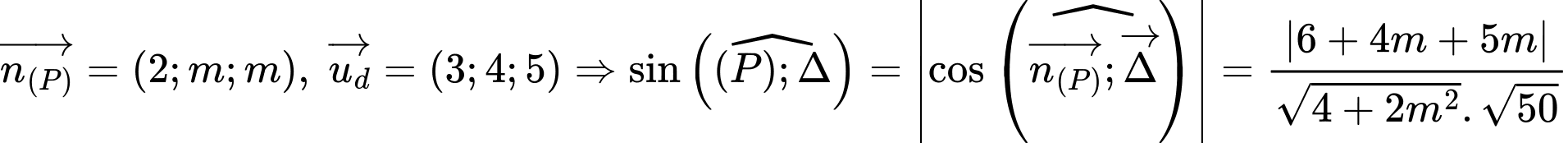
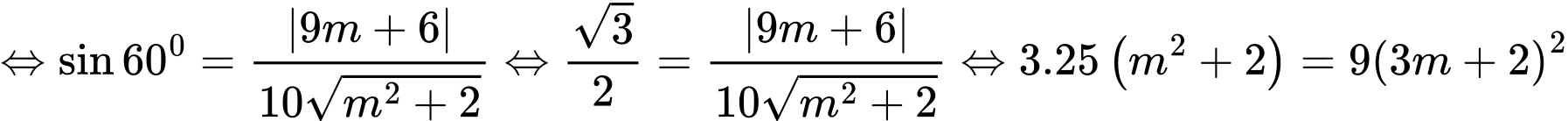
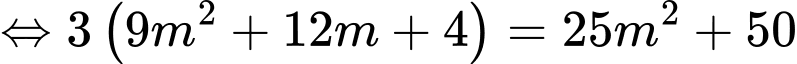
 Đáp án: C
Đáp án: C
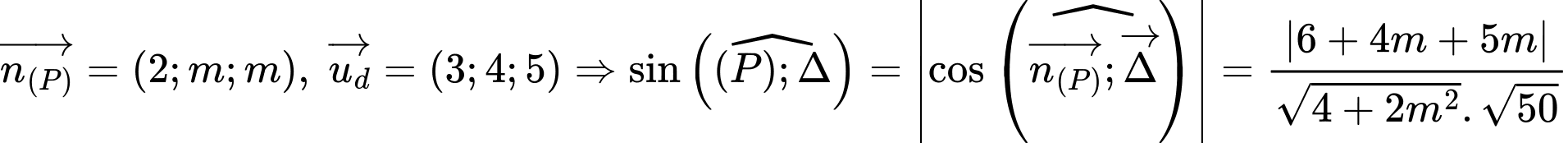
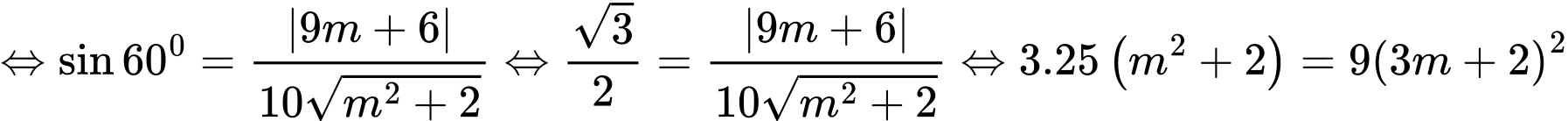
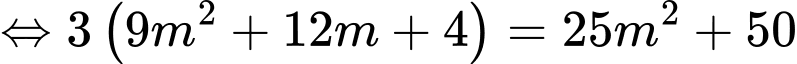
 Đáp án: C
Đáp án: C
Câu 16 [161474]: Cho hình chóp 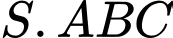 có
có 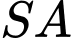 vuông góc với mặt phẳng
vuông góc với mặt phẳng 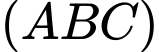 ,
, 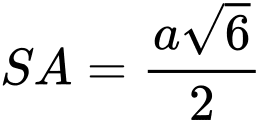 , tam giác
, tam giác 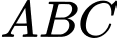 vuông tại
vuông tại 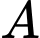 và
và 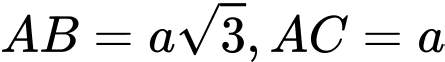 (minh hoạ như hình bên).
(minh hoạ như hình bên).
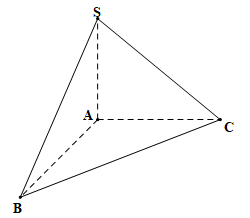
Góc giữa mặt phẳng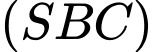 và mặt phẳng
và mặt phẳng 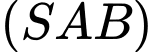 bằng
bằng
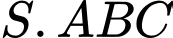 có
có 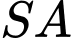 vuông góc với mặt phẳng
vuông góc với mặt phẳng 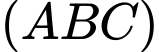 ,
, 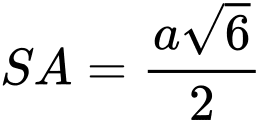 , tam giác
, tam giác 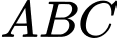 vuông tại
vuông tại 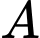 và
và 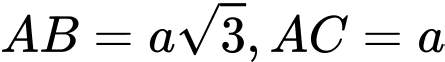 (minh hoạ như hình bên).
(minh hoạ như hình bên). 
Góc giữa mặt phẳng
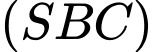 và mặt phẳng
và mặt phẳng 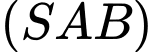 bằng
bằng
Chọn C
Cách 1:
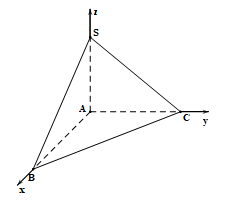
Gắn hệ trục toạ độ như hình vẽ, ta có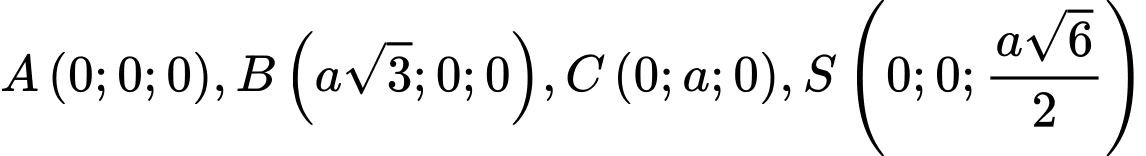 .
.
Mặt phẳng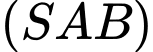 vuông góc với AC ≡ Oy nên nhận
vuông góc với AC ≡ Oy nên nhận 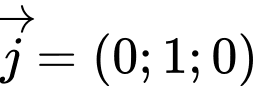 là vectơ pháp tuyến.
là vectơ pháp tuyến.
Ta có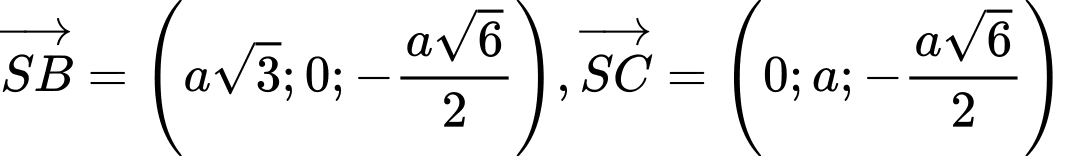
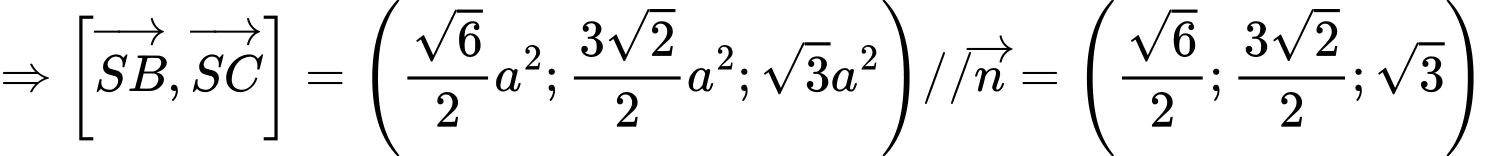
Mặt phẳng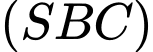 nhận vectơ
nhận vectơ 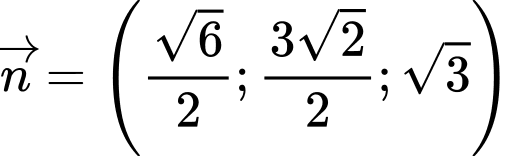 là vectơ pháp tuyến.
là vectơ pháp tuyến.
Gọi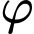 là góc giữa mặt phẳng
là góc giữa mặt phẳng 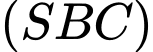 và mặt phẳng
và mặt phẳng 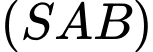 .
.
Ta có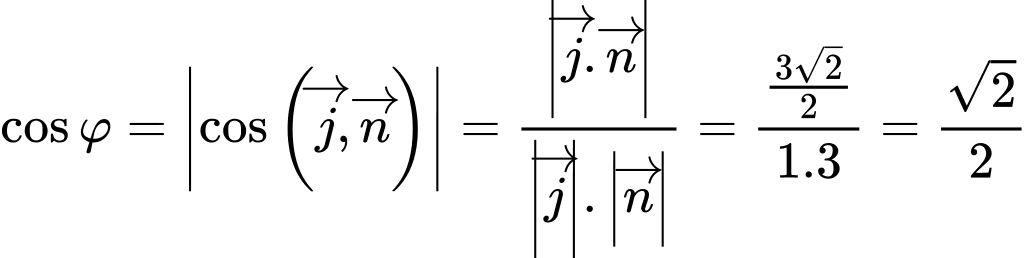
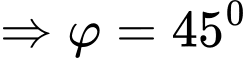 .
.
Vậy góc giữa mặt phẳng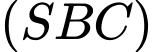 và mặt phẳng
và mặt phẳng 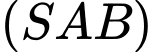 bằng
bằng 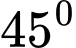 .
.
Cách 1:

Gắn hệ trục toạ độ như hình vẽ, ta có
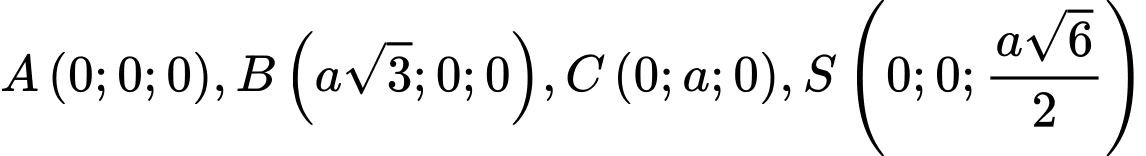 .
.Mặt phẳng
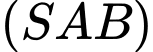 vuông góc với AC ≡ Oy nên nhận
vuông góc với AC ≡ Oy nên nhận 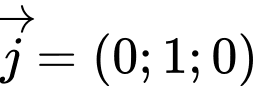 là vectơ pháp tuyến.
là vectơ pháp tuyến.Ta có
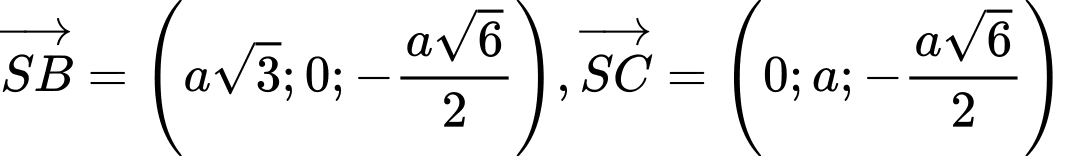
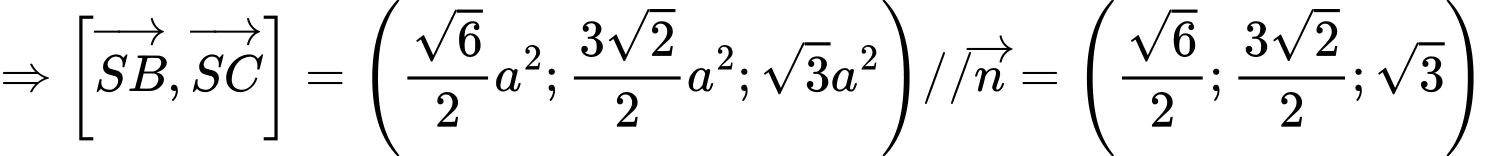
Mặt phẳng
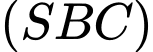 nhận vectơ
nhận vectơ 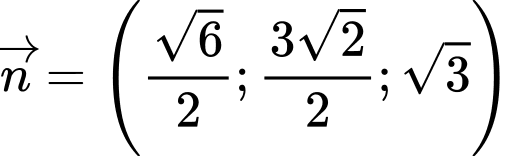 là vectơ pháp tuyến.
là vectơ pháp tuyến.Gọi
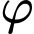 là góc giữa mặt phẳng
là góc giữa mặt phẳng 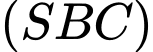 và mặt phẳng
và mặt phẳng 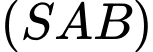 .
.Ta có
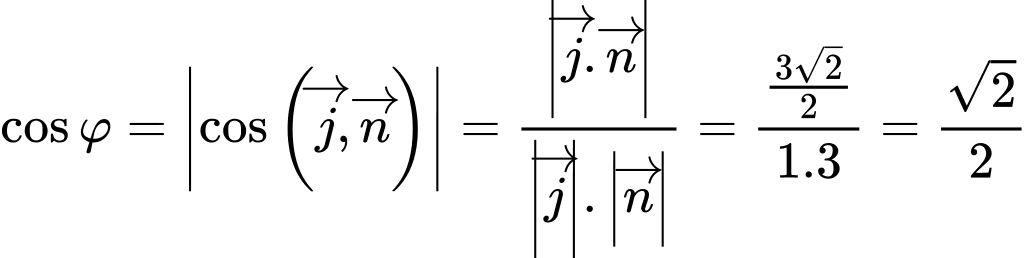
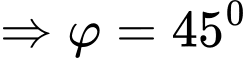 .
.Vậy góc giữa mặt phẳng
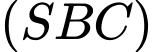 và mặt phẳng
và mặt phẳng 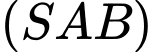 bằng
bằng 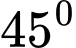 .
.
Câu 17 [202979]: Trong không gian với hệ toạ độ 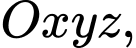 cho hình chóp
cho hình chóp 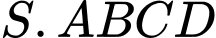 có
có 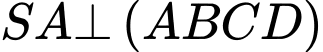 và đáy
và đáy 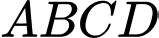 là hình vuông,
là hình vuông, 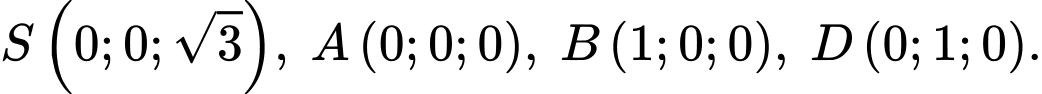 Gọi
Gọi 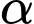 là góc giữa hai mặt phẳng
là góc giữa hai mặt phẳng 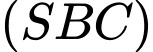 và
và 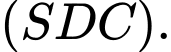 Giá trị
Giá trị 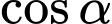 bằng bao nhiêu. Viết kết quả dưới dạng số thập phân.
bằng bao nhiêu. Viết kết quả dưới dạng số thập phân.
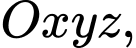 cho hình chóp
cho hình chóp 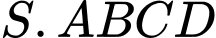 có
có 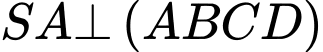 và đáy
và đáy 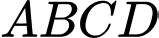 là hình vuông,
là hình vuông, 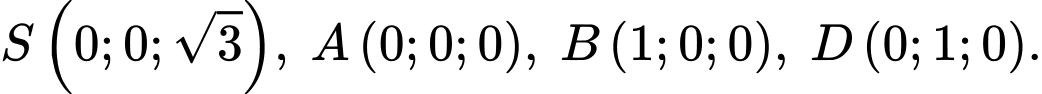 Gọi
Gọi 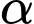 là góc giữa hai mặt phẳng
là góc giữa hai mặt phẳng 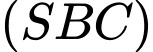 và
và 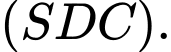 Giá trị
Giá trị 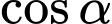 bằng bao nhiêu. Viết kết quả dưới dạng số thập phân.
bằng bao nhiêu. Viết kết quả dưới dạng số thập phân. 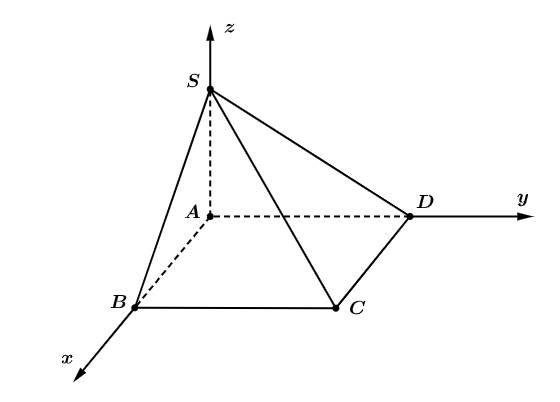
Ghép trục toạ độ như hình, với
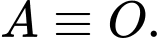
Suy ra toạ độ điểm
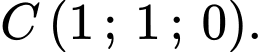
+) Mặt phẳng
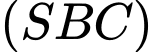 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 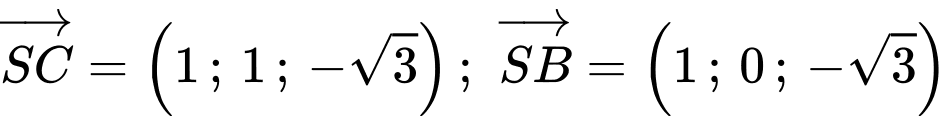
Suy ra vectơ pháp tuyến của mp
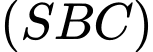 là
là 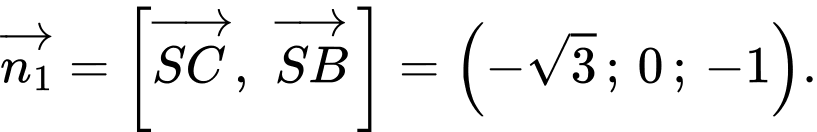
+) Mặt phẳng
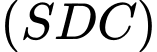 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 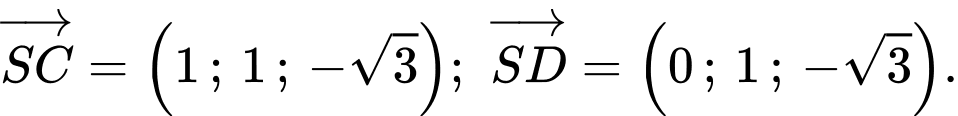
Suy ra vectơ pháp tuyến của mp
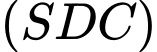 là
là 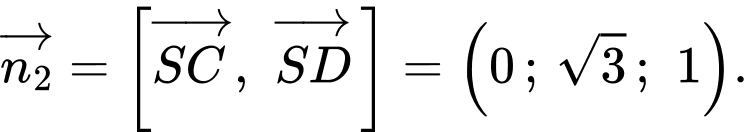
Suy ra
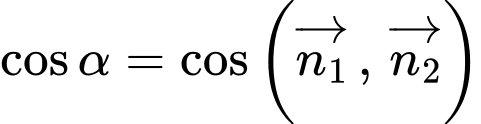
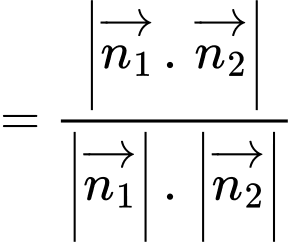
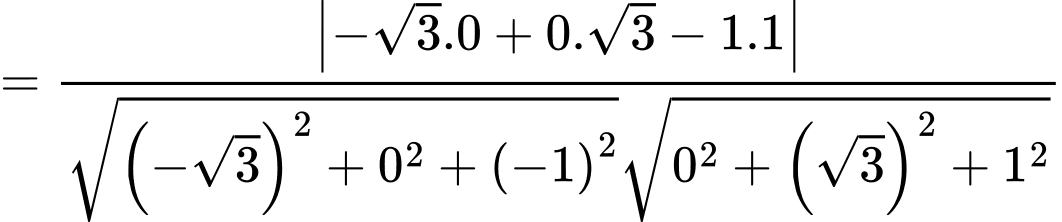
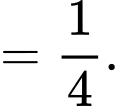
Câu 18 [202980]: Giải bài toán sau bằng phương pháp toạ độ. Cho hình chóp 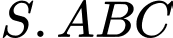 có đáy
có đáy 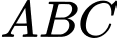 là tam giác vuông cân,
là tam giác vuông cân, 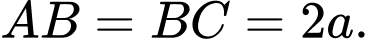 Tam giác
Tam giác 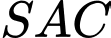 cân tại
cân tại 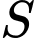 và nằm trong mặt phẳng vuông góc với
và nằm trong mặt phẳng vuông góc với  Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 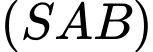 và
và 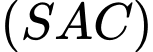 bằng bao nhiêu độ?.
bằng bao nhiêu độ?.
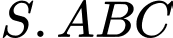 có đáy
có đáy 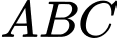 là tam giác vuông cân,
là tam giác vuông cân, 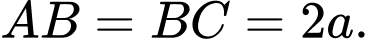 Tam giác
Tam giác 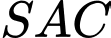 cân tại
cân tại 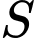 và nằm trong mặt phẳng vuông góc với
và nằm trong mặt phẳng vuông góc với  Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 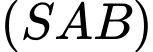 và
và 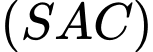 bằng bao nhiêu độ?.
bằng bao nhiêu độ?.
Gọi 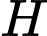 là trung điểm của
là trung điểm của 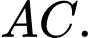 Ta có
Ta có
+) (vì
(vì 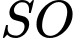 là đường trung tuyến của tam giác cân
là đường trung tuyến của tam giác cân 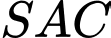 )
)
+) (vì
(vì 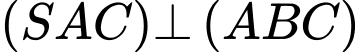 mà
mà 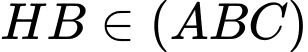 ).
).
Nên ta chọn hệ trục toạ độ như hình vẽ và xét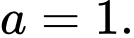
 là gốc toạ độ.
là gốc toạ độ.
+) Xét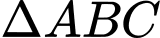 vuông cân tại
vuông cân tại 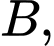 ta có
ta có
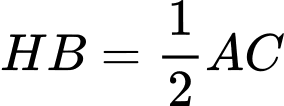
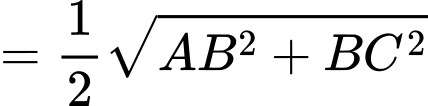
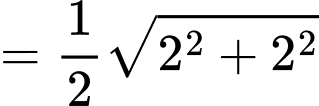
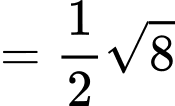

Suy ra toạ độ điểm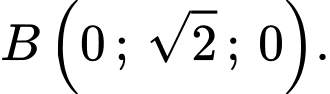
+) Xét tam giác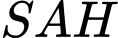 vuông tại
vuông tại 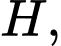 ta có
ta có
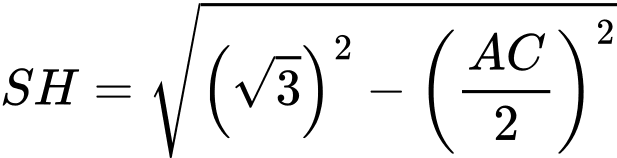
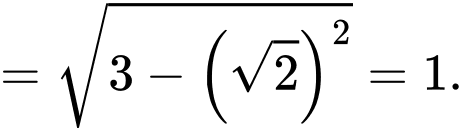
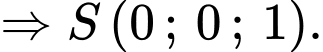
+) Giả sử toạ độ điểm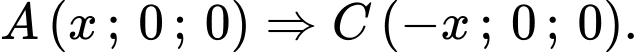
(vì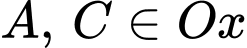 và
và 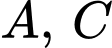 đối xứng nhau qua gốc toạ độ
đối xứng nhau qua gốc toạ độ 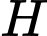 )
)
Ta có
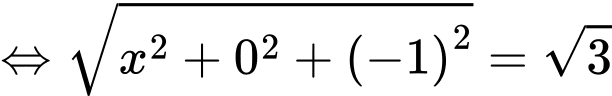

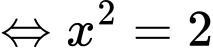
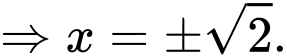
Chọn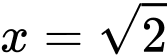
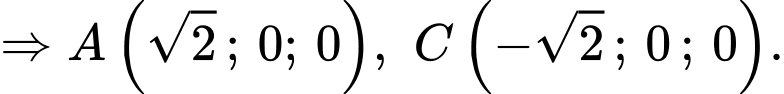
+) Mặt phẳng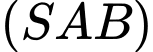 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 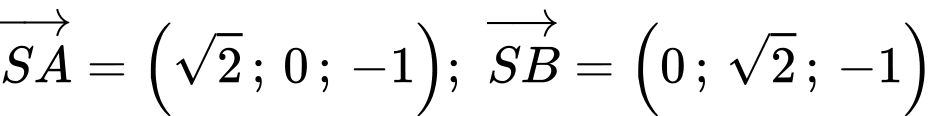
Suy ra vectơ pháp tuyến của mp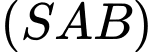 là
là 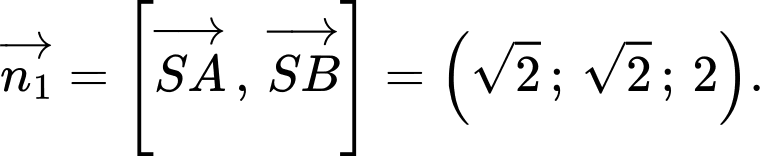
+) Mặt phẳng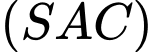 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 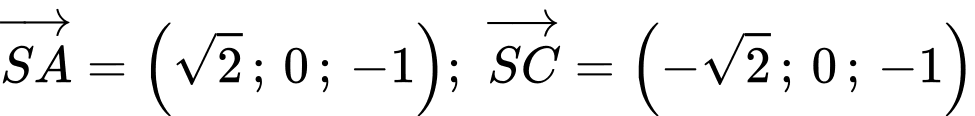
Suy ra vectơ pháp tuyến của mp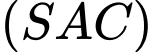 là
là 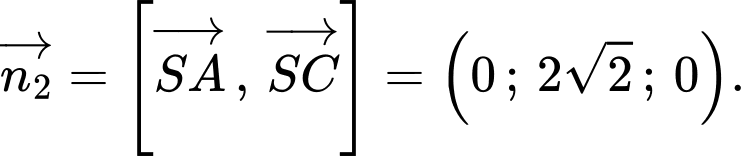
Suy ra góc giữa hai mặt phẳng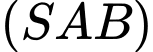 và
và 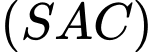 là
là
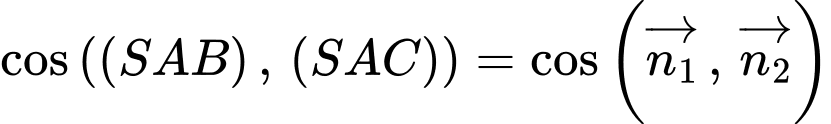
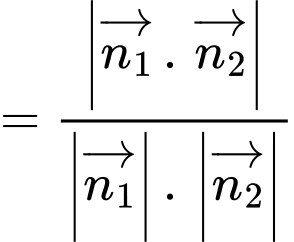
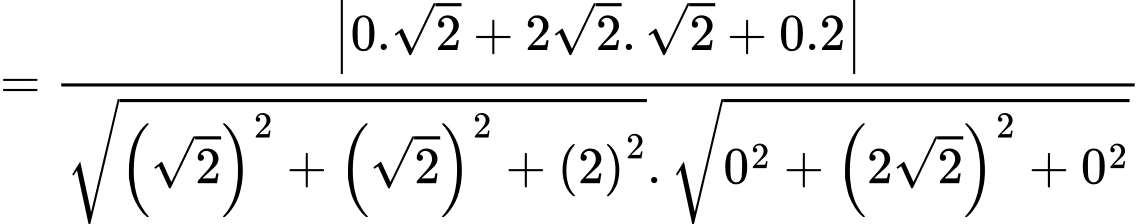
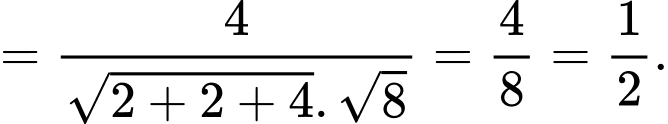
Suy ra góc giữa hai mp bằng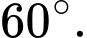
 là trung điểm của
là trung điểm của 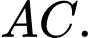 Ta có
Ta có
+)
 (vì
(vì 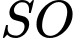 là đường trung tuyến của tam giác cân
là đường trung tuyến của tam giác cân 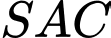 )
)
+)
 (vì
(vì 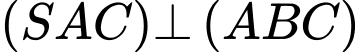 mà
mà 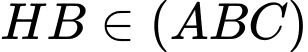 ).
).
Nên ta chọn hệ trục toạ độ như hình vẽ và xét
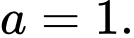
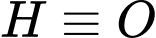 là gốc toạ độ.
là gốc toạ độ.
+) Xét
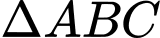 vuông cân tại
vuông cân tại 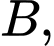 ta có
ta có
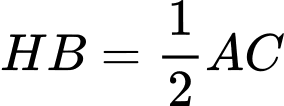
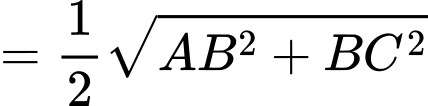
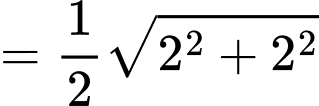
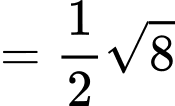

Suy ra toạ độ điểm
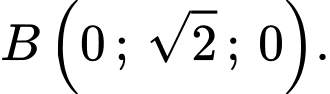
+) Xét tam giác
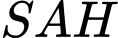 vuông tại
vuông tại 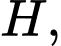 ta có
ta có
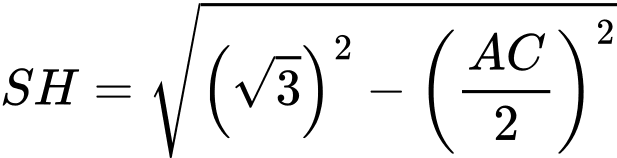
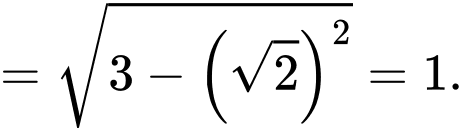
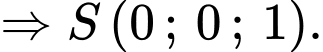
+) Giả sử toạ độ điểm
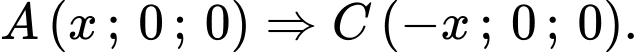
(vì
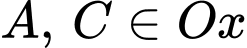 và
và 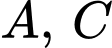 đối xứng nhau qua gốc toạ độ
đối xứng nhau qua gốc toạ độ 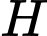 )
)
Ta có

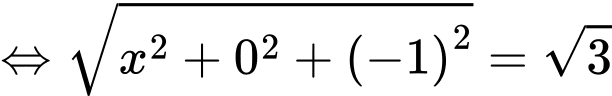

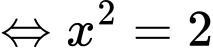
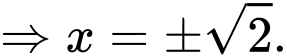
Chọn
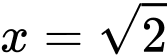
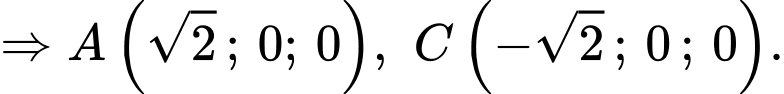
+) Mặt phẳng
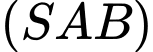 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 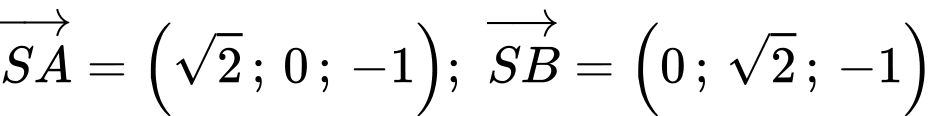
Suy ra vectơ pháp tuyến của mp
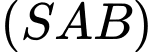 là
là 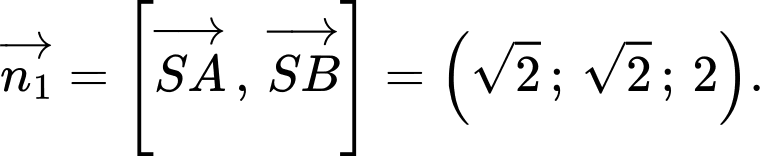
+) Mặt phẳng
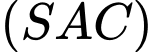 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 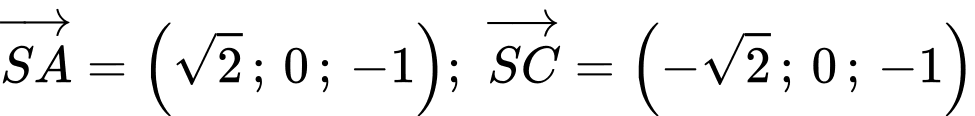
Suy ra vectơ pháp tuyến của mp
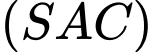 là
là 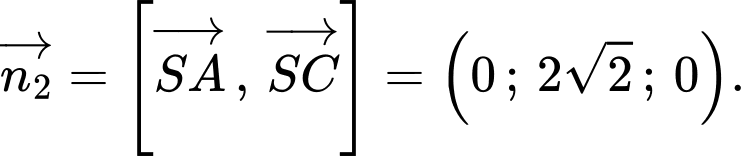
Suy ra góc giữa hai mặt phẳng
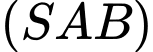 và
và 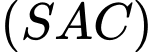 là
là
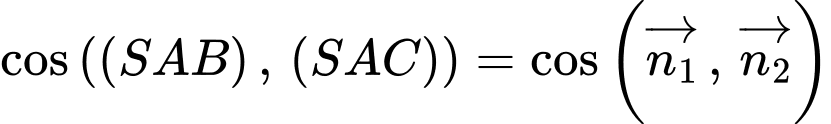
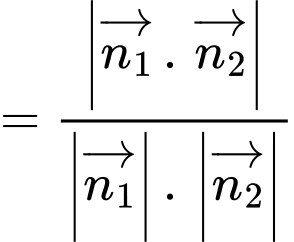
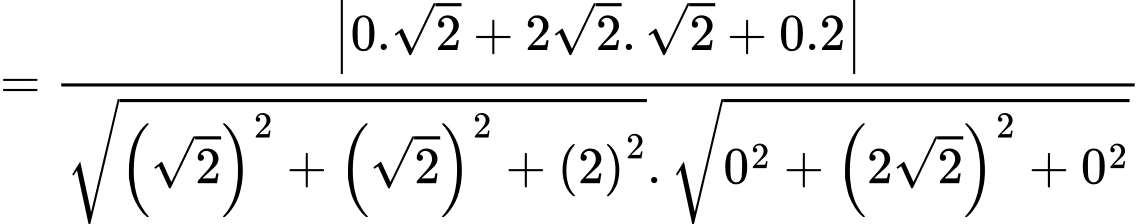
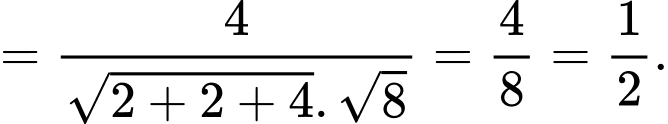
Suy ra góc giữa hai mp bằng
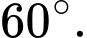
Câu 19 [202971]: Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau  người ta thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài
người ta thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 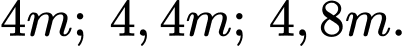 Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Viết kết quả làm tròn đến hàng phần chục.
Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Viết kết quả làm tròn đến hàng phần chục.
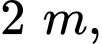 người ta thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài
người ta thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 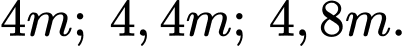 Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Viết kết quả làm tròn đến hàng phần chục.
Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Viết kết quả làm tròn đến hàng phần chục. 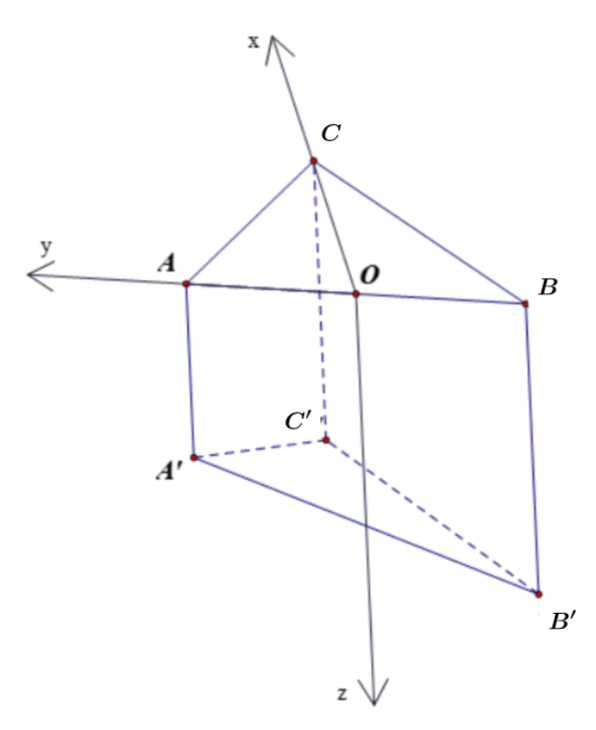
Gọi
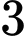 điểm cách nhau
điểm cách nhau 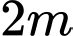 trên mặt nước là
trên mặt nước là 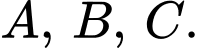
Vị trí thả rọi xuống đáy bể lần lượt là
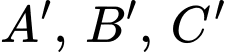 sao cho
sao cho 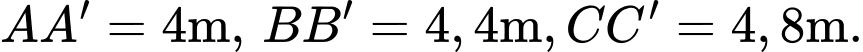
Chọn gốc toạ độ
 tại trung điểm
tại trung điểm 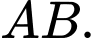
Khi đó,
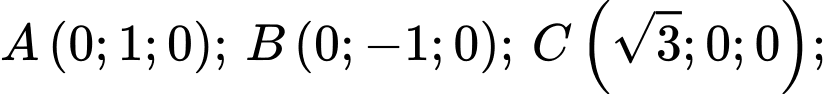
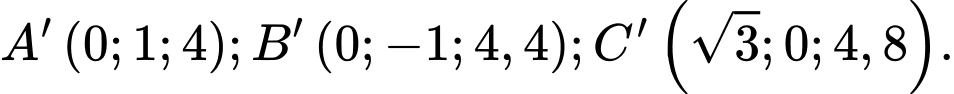
Ta có:
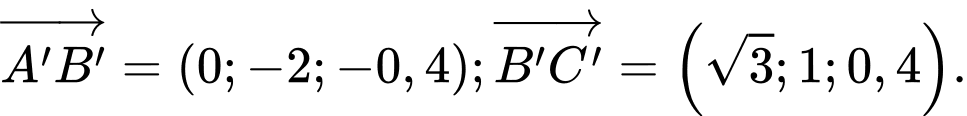
Mặt phẳng
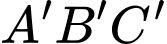 nhận
nhận 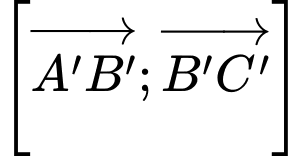 làm một vectơ pháp tuyến.
làm một vectơ pháp tuyến. Ta có:
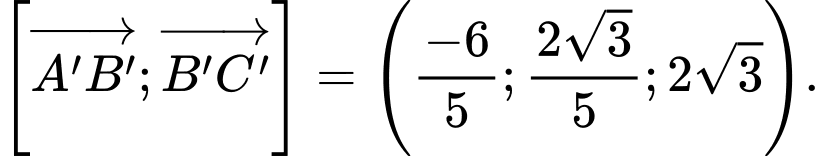
Mặt phẳng đáy bể là mp
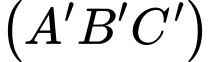 nên có vectơ pháp tuyến là
nên có vectơ pháp tuyến là 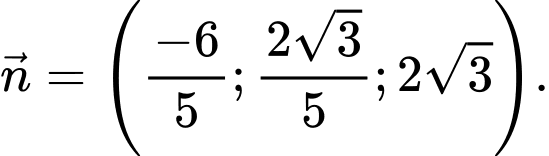
Mặt phẳng ngang (mặt nước) là mp
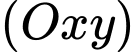 có vectơ pháp tuyến là
có vectơ pháp tuyến là 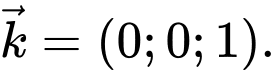
Nên góc giữa hai mặt phẳng đáy bể và mặt phẳng ngang là:
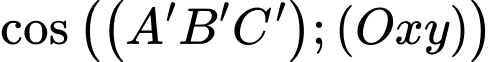
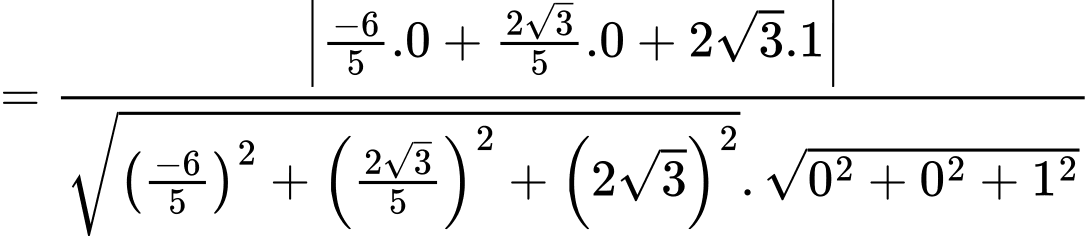
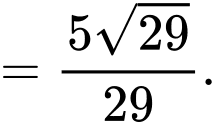
Suy ra
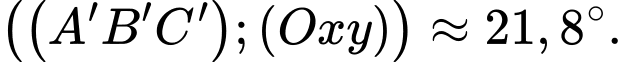
Vậy đáy bể nghiêng so với mặt phẳng nằm ngang một góc khoảng
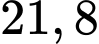 độ.
độ.Cách khác:
Xét
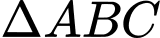 đều cạnh
đều cạnh 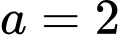
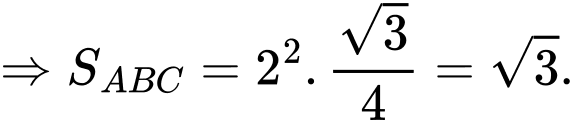
Ta có:
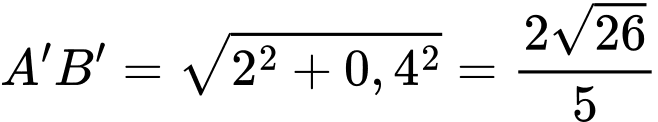
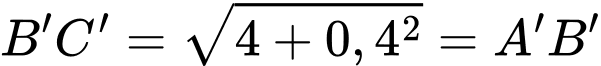
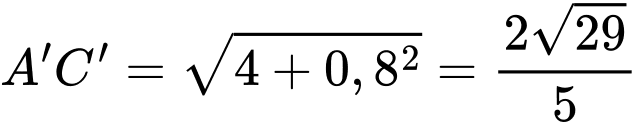
Xét
 có đường cao từ đỉnh
có đường cao từ đỉnh 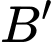 là
là 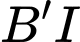
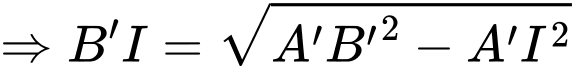
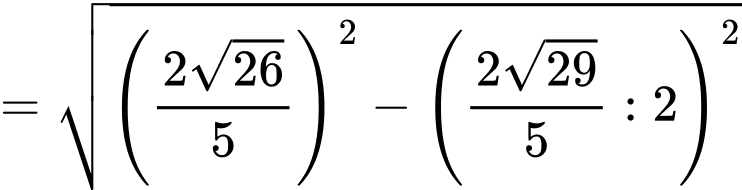
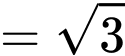
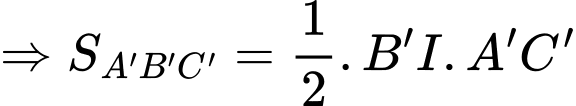
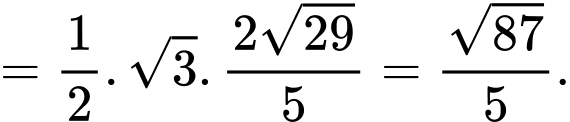
Ta có:
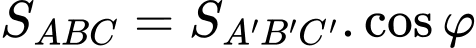
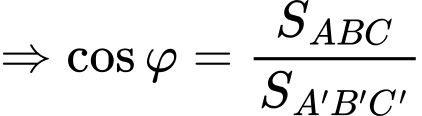
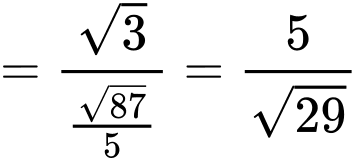
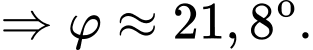
Câu 20 [202972]: Trong một bể hình lập phương cạnh 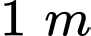 có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành
có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành 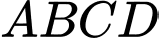 và khoảng cách từ các điểm
và khoảng cách từ các điểm 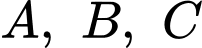 đến đáy bể tương ứng là
đến đáy bể tương ứng là 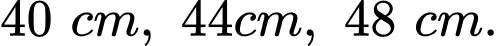
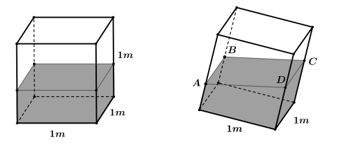
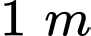 có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành
có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành 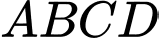 và khoảng cách từ các điểm
và khoảng cách từ các điểm 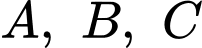 đến đáy bể tương ứng là
đến đáy bể tương ứng là 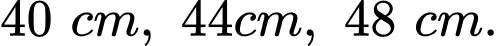

Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ? Viết kết quả làm tròn đến hàng phần chục.
Chọn hệ trục toạ độ  như hình vẽ.
như hình vẽ.
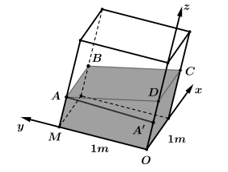
Khi đó,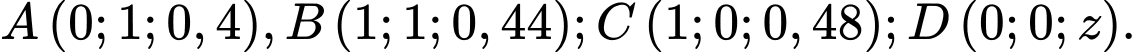
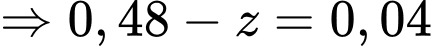
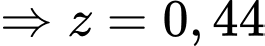
 như hình vẽ.
như hình vẽ. 
Khi đó,
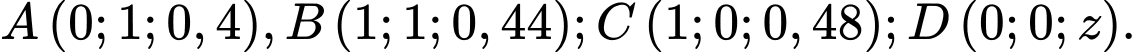
Suy ra 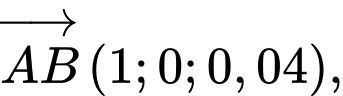
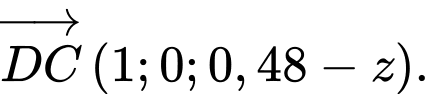
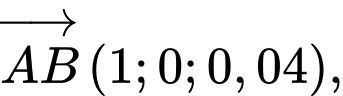
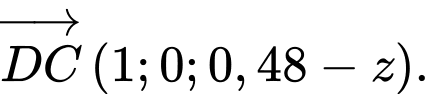
Vì 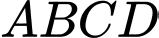 là hình bình hành nên
là hình bình hành nên 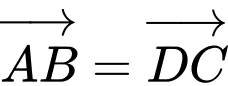
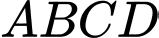 là hình bình hành nên
là hình bình hành nên 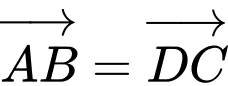
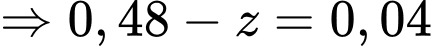
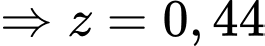
Do đó, 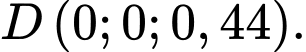
Đáy bể nằm trong mặt phẳng có phương trình là
Ta có: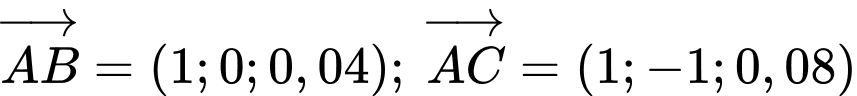
Suy ra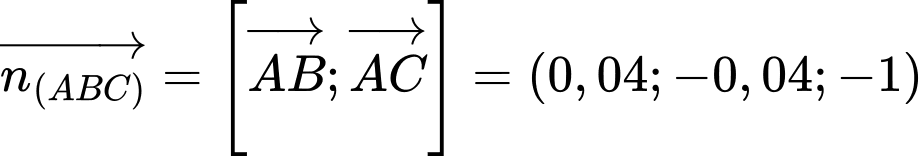
Do đó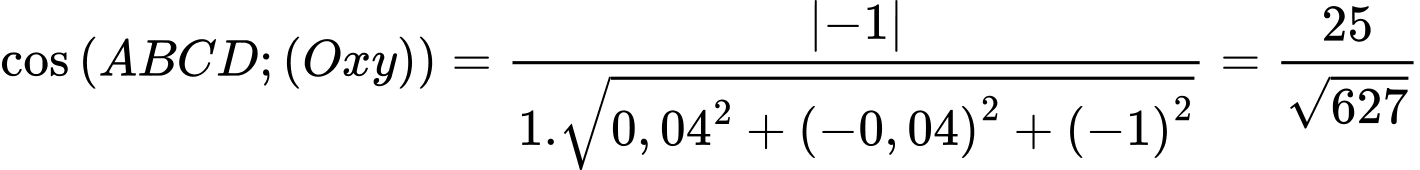
Suy ra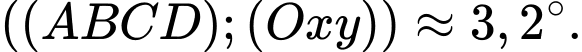
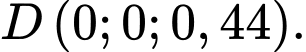
Đáy bể nằm trong mặt phẳng có phương trình là

Ta có:
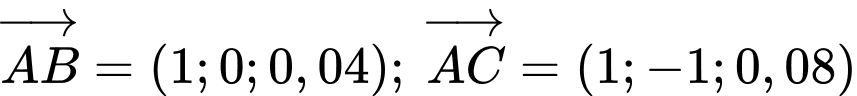
Suy ra
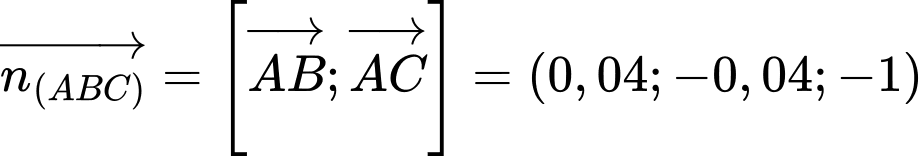
Do đó
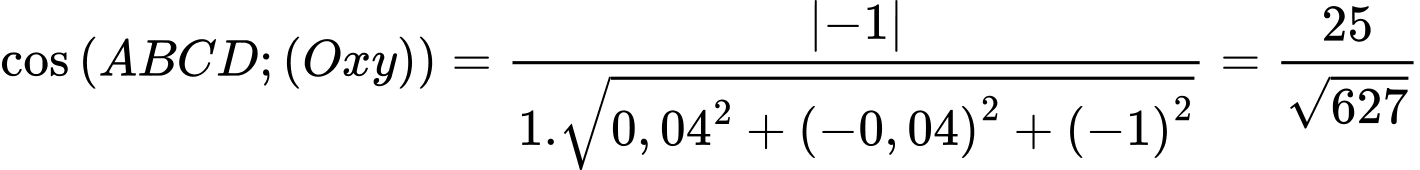
Suy ra