Đáp án Bài tập tự luyện
Câu 1 [58380]: Trong không gian với hệ tọa độ 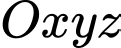 cho đường thẳng
cho đường thẳng 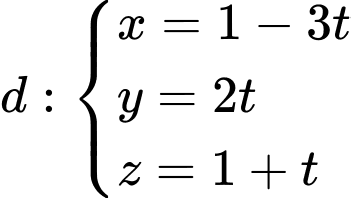
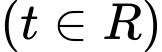 và mặt phẳng
và mặt phẳng  Tìm tọa độ giao điểm của
Tìm tọa độ giao điểm của 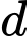 và
và 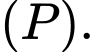
 cho đường thẳng
cho đường thẳng 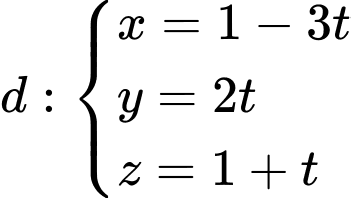
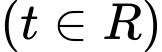 và mặt phẳng
và mặt phẳng  Tìm tọa độ giao điểm của
Tìm tọa độ giao điểm của 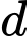 và
và 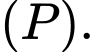
A, 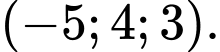
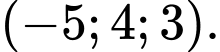
B, 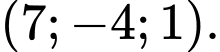
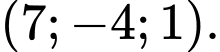
C, 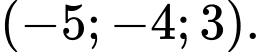
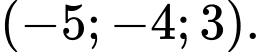
D, 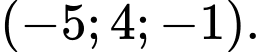
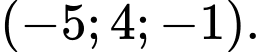
Gọi  là giao điểm của đường thẳng
là giao điểm của đường thẳng 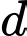 và mặt phẳng
và mặt phẳng 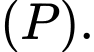
Vì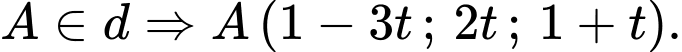
Mà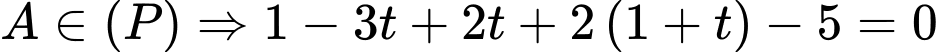
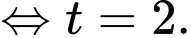
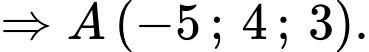 Chọn A. Đáp án: A
Chọn A. Đáp án: A
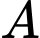 là giao điểm của đường thẳng
là giao điểm của đường thẳng 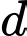 và mặt phẳng
và mặt phẳng 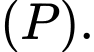
Vì
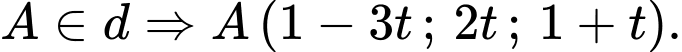
Mà
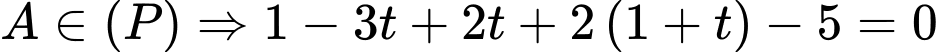
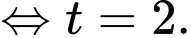
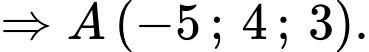 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 2 [55848]: Trong không gian với hệ tọa độ 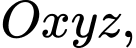 tọa độ giao điểm của
tọa độ giao điểm của 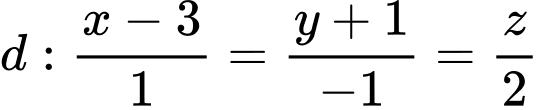 và mặt phẳng
và mặt phẳng 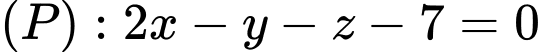 là
là
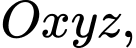 tọa độ giao điểm của
tọa độ giao điểm của 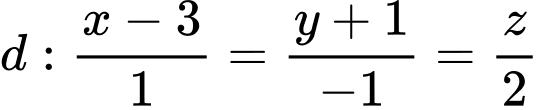 và mặt phẳng
và mặt phẳng 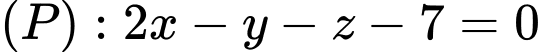 là
là A, 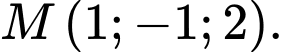
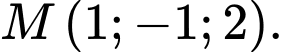
B, 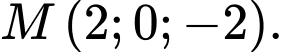
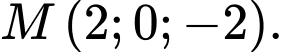
C, 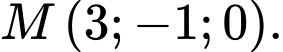
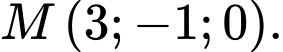
D, 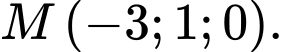
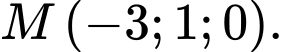
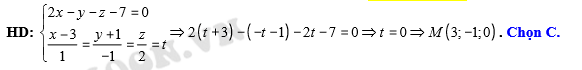 Đáp án: C
Đáp án: C
Câu 3 [58373]: Gọi 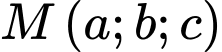 là giao điểm của đường thẳng
là giao điểm của đường thẳng 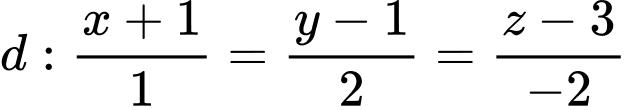 và mặt phẳng
và mặt phẳng 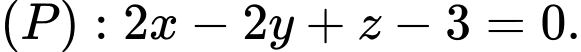 Khi đó tổng
Khi đó tổng 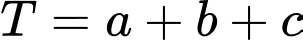 bằng
bằng
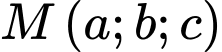 là giao điểm của đường thẳng
là giao điểm của đường thẳng 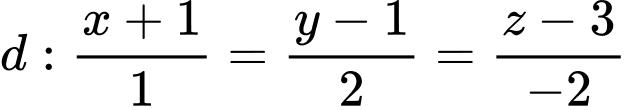 và mặt phẳng
và mặt phẳng 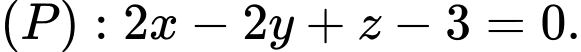 Khi đó tổng
Khi đó tổng 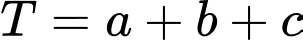 bằng
bằng A, 5.
B, 4.
C, 6.
D, 2.
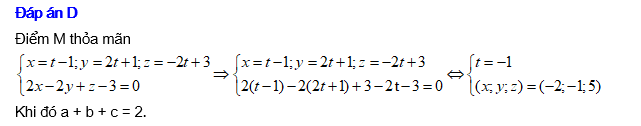 Đáp án: D
Đáp án: D
Câu 4 [58374]: Trong không gian 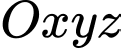 , cho hai điểm
, cho hai điểm 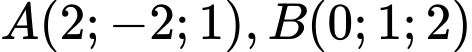 . Tọa độ điểm
. Tọa độ điểm 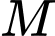 thuộc mặt phẳng
thuộc mặt phẳng 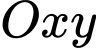 sao cho ba điểm
sao cho ba điểm 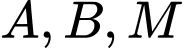 thẳng hàng là
thẳng hàng là
 , cho hai điểm
, cho hai điểm 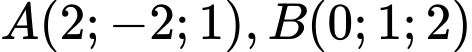 . Tọa độ điểm
. Tọa độ điểm 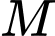 thuộc mặt phẳng
thuộc mặt phẳng 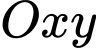 sao cho ba điểm
sao cho ba điểm 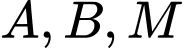 thẳng hàng là
thẳng hàng là A, 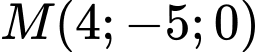 .
.
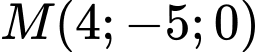 .
.B, 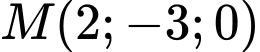 .
.
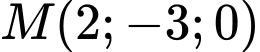 .
.C, 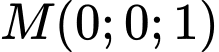 .
.
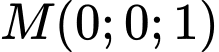 .
.D, 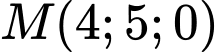 .
.
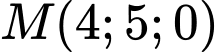 .
. Đáp án: A
Đáp án: A
Câu 5 [55827]: Trong không gian với hệ tọa độ 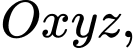 cho đường thẳng
cho đường thẳng 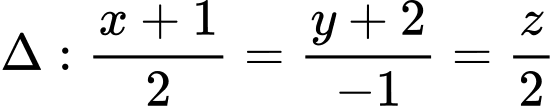 . Tìm tọa độ điểm
. Tìm tọa độ điểm 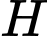 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 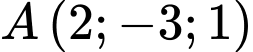 lên
lên 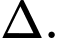
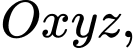 cho đường thẳng
cho đường thẳng 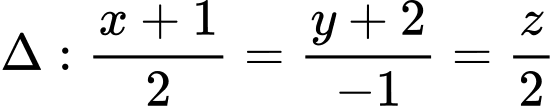 . Tìm tọa độ điểm
. Tìm tọa độ điểm 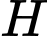 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 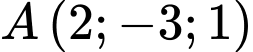 lên
lên 
A, 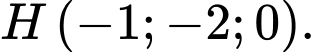
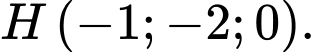
B, 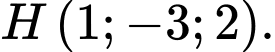
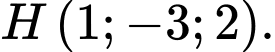
C, 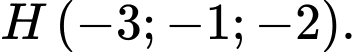
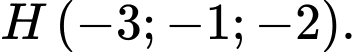
D, 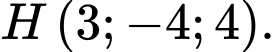
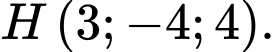
 Đáp án: B
Đáp án: B
Câu 6 [58217]: Cho điểm  và đường thẳng
và đường thẳng  Hình chiếu
Hình chiếu 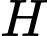 của
của 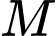 trên đường thẳng
trên đường thẳng 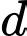 có tọa độ là
có tọa độ là
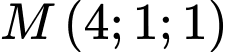 và đường thẳng
và đường thẳng 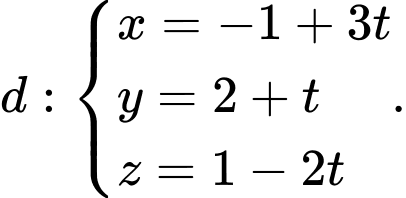 Hình chiếu
Hình chiếu 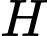 của
của 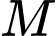 trên đường thẳng
trên đường thẳng 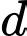 có tọa độ là
có tọa độ là A, 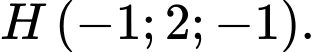
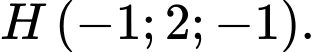
B, 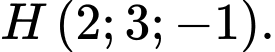
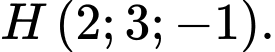
C, 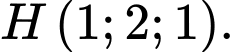
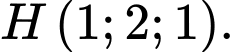
D, 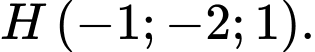
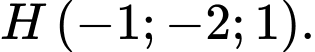
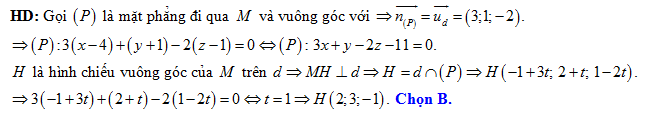 Đáp án: B
Đáp án: B
Câu 7 [55821]: Trong không gian tọa độ  cho đường thẳng
cho đường thẳng 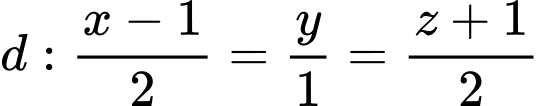 điểm
điểm 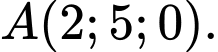 Tọa độ hình chiếu vuông góc của
Tọa độ hình chiếu vuông góc của 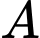 trên
trên 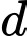 là
là
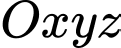 cho đường thẳng
cho đường thẳng 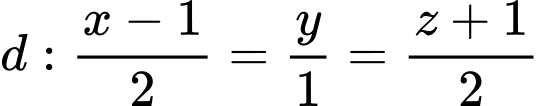 điểm
điểm 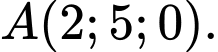 Tọa độ hình chiếu vuông góc của
Tọa độ hình chiếu vuông góc của 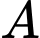 trên
trên 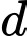 là
là A, 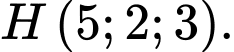
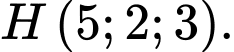
B, 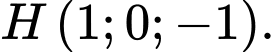
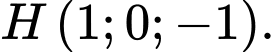
C, 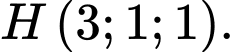
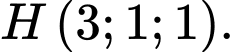
D, 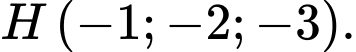
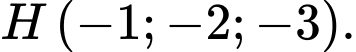
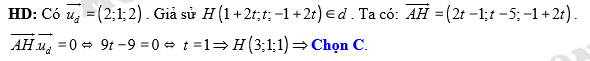 Đáp án: C
Đáp án: C
Câu 8 [55828]: Trong không gian với hệ tọa độ 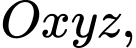 cho tam giác
cho tam giác 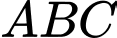 biết
biết 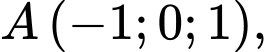
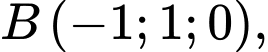
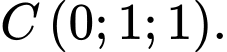 Đường cao
Đường cao 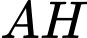 của tam giác
của tam giác 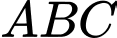 có vectơ chỉ phương là vectơ nào trong các vectơ sau?
có vectơ chỉ phương là vectơ nào trong các vectơ sau?
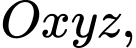 cho tam giác
cho tam giác  biết
biết 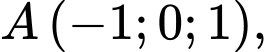
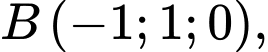
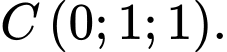 Đường cao
Đường cao 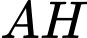 của tam giác
của tam giác 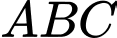 có vectơ chỉ phương là vectơ nào trong các vectơ sau?
có vectơ chỉ phương là vectơ nào trong các vectơ sau? A, 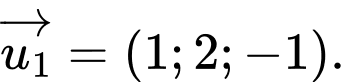
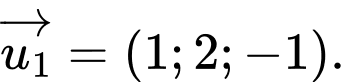
B, 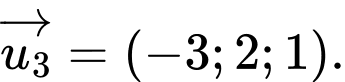
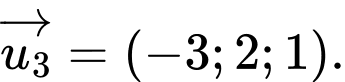
C, 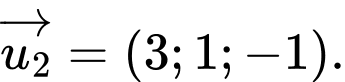
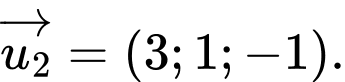
D, 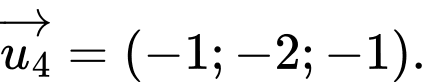
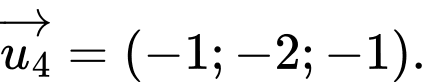
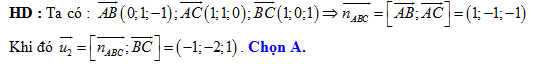 Đáp án: A
Đáp án: A
Câu 9 [58415]: Trong không gian với hệ trục tọa độ  , cho điểm
, cho điểm 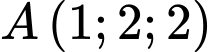 và đường thẳng
và đường thẳng 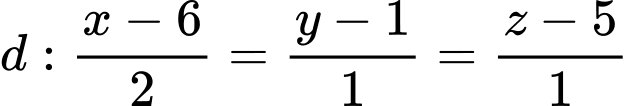 . Tìm tọa độ điểm
. Tìm tọa độ điểm  đối xứng với
đối xứng với 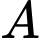 qua
qua 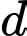 .
.
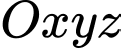 , cho điểm
, cho điểm 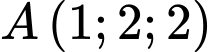 và đường thẳng
và đường thẳng 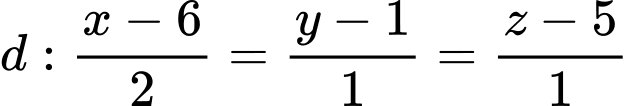 . Tìm tọa độ điểm
. Tìm tọa độ điểm 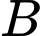 đối xứng với
đối xứng với 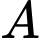 qua
qua 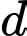 .
. A, 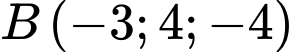 .
.
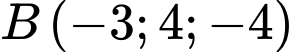 .
.B, 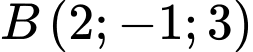 .
.
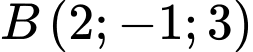 .
.C, 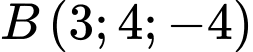 .
.
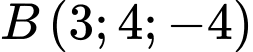 .
.D, 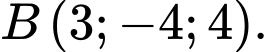
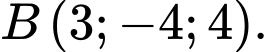
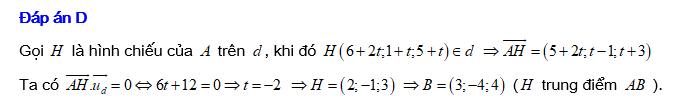 Đáp án: D
Đáp án: D
Câu 10 [58417]: Trong không gian 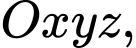 cho đường thẳng
cho đường thẳng 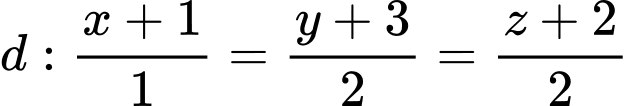 và điểm
và điểm 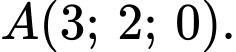 Tìm tọa độ điểm đối xứng của điểm
Tìm tọa độ điểm đối xứng của điểm 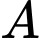 qua đường thẳng
qua đường thẳng 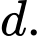
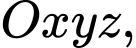 cho đường thẳng
cho đường thẳng 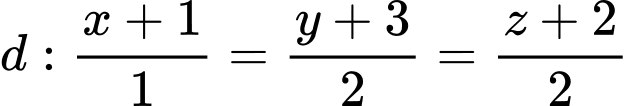 và điểm
và điểm 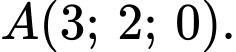 Tìm tọa độ điểm đối xứng của điểm
Tìm tọa độ điểm đối xứng của điểm 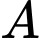 qua đường thẳng
qua đường thẳng 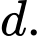
A, 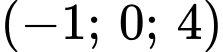 .
.
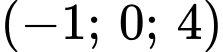 .
.B, 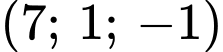 .
.
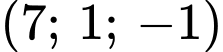 .
.C, 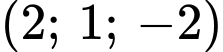 .
.
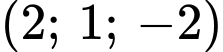 .
.D, 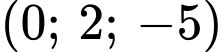 .
.
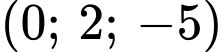 .
.
Gọi 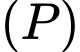 là mặt phẳng đi qua
là mặt phẳng đi qua 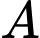 và vuông góc với đường thẳng
và vuông góc với đường thẳng 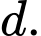
Phương trình của mặt phẳng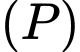 là
là 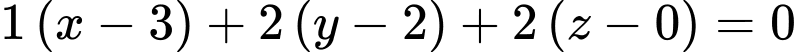
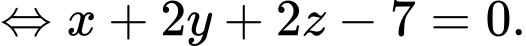
Gọi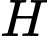 là hình chiếu của
là hình chiếu của 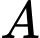 lên đường thẳng
lên đường thẳng 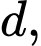 khi đó
khi đó 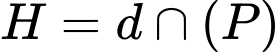
Suy ra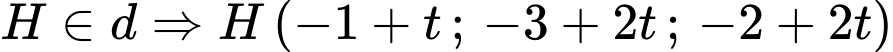
Mặt khác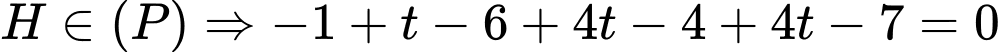
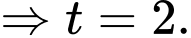
Vậy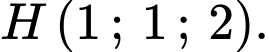
Gọi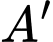 là điểm đối xứng với
là điểm đối xứng với 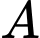 qua đường thẳng
qua đường thẳng 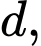 khi đó
khi đó 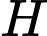 là trung điểm của
là trung điểm của 
Suy ra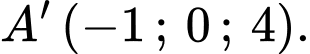
Chọn A. Đáp án: A
 là mặt phẳng đi qua
là mặt phẳng đi qua  và vuông góc với đường thẳng
và vuông góc với đường thẳng 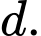
Phương trình của mặt phẳng
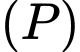 là
là 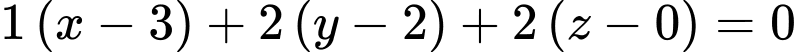
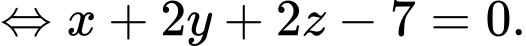
Gọi
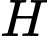 là hình chiếu của
là hình chiếu của 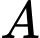 lên đường thẳng
lên đường thẳng 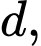 khi đó
khi đó 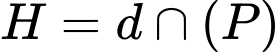
Suy ra
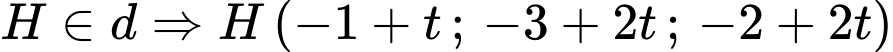
Mặt khác
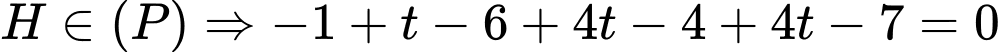
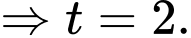
Vậy
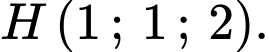
Gọi
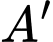 là điểm đối xứng với
là điểm đối xứng với 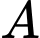 qua đường thẳng
qua đường thẳng 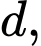 khi đó
khi đó 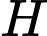 là trung điểm của
là trung điểm của 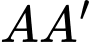
Suy ra
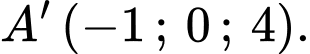
Chọn A. Đáp án: A
Câu 11 [55829]: Trong không gian với với hệ tọa độ 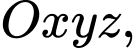 cho
cho 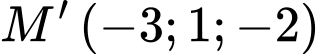 là hình chiếu của
là hình chiếu của 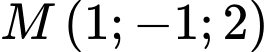 lên mặt phẳng
lên mặt phẳng  Phương trình mặt phẳng
Phương trình mặt phẳng  là
là
 cho
cho 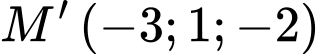 là hình chiếu của
là hình chiếu của 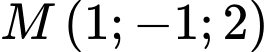 lên mặt phẳng
lên mặt phẳng 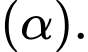 Phương trình mặt phẳng
Phương trình mặt phẳng  là
là A, 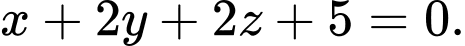
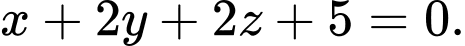
B, 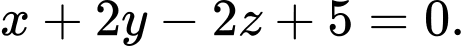
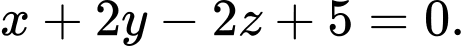
C, 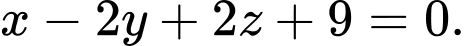
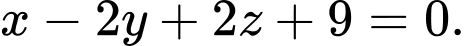
D, 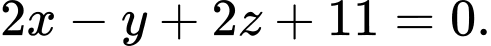
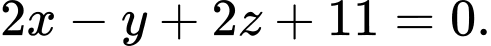
HD: Ta có  qua
qua 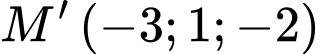 và nhận
và nhận 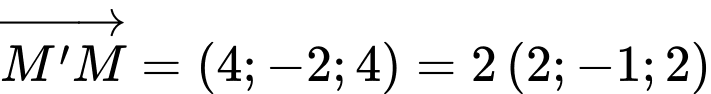 là 1 VTPT
là 1 VTPT
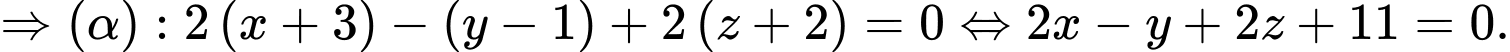 Chọn D Đáp án: D
Chọn D Đáp án: D
 qua
qua 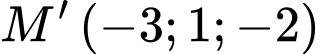 và nhận
và nhận 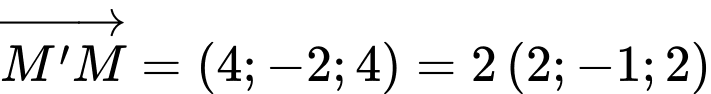 là 1 VTPT
là 1 VTPT
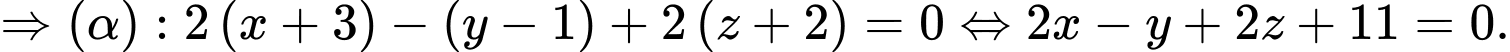 Chọn D Đáp án: D
Chọn D Đáp án: D
Câu 12 [58386]: Trong không gian với hệ trục tọa độ 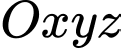 , hình chiếu vuông góc của điểm
, hình chiếu vuông góc của điểm 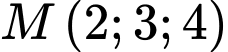 trên mặt phẳng
trên mặt phẳng 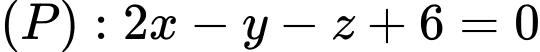 là điểm nào dưới đây?
là điểm nào dưới đây?
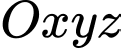 , hình chiếu vuông góc của điểm
, hình chiếu vuông góc của điểm 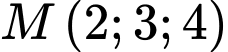 trên mặt phẳng
trên mặt phẳng 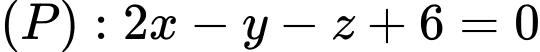 là điểm nào dưới đây?
là điểm nào dưới đây? A, 
B, 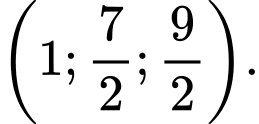
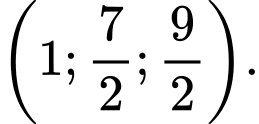
C, 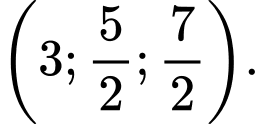
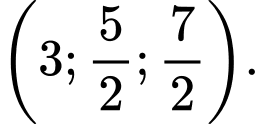
D, 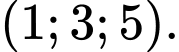
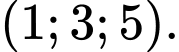
 Đáp án: B
Đáp án: B
Câu 13 [405677]: Trong không gian 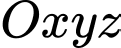 , cho đường thẳng
, cho đường thẳng 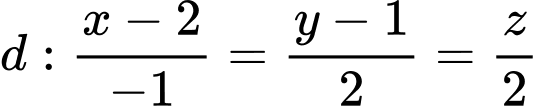 và
mặt phẳng
và
mặt phẳng 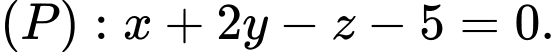 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
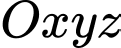 , cho đường thẳng
, cho đường thẳng 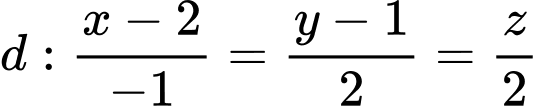 và
mặt phẳng
và
mặt phẳng 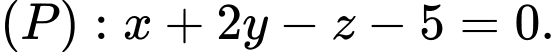 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Đường thẳng 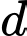 đi qua điểm
đi qua điểm 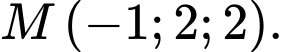
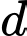 đi qua điểm
đi qua điểm 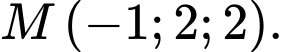
B, b) Khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 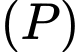 bằng
bằng 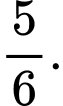
 đến mặt phẳng
đến mặt phẳng 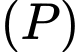 bằng
bằng 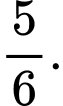
C, c) Tọa độ giao điểm của 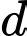 và
và 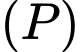 là
là 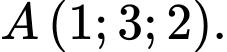
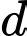 và
và 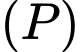 là
là 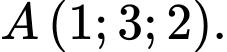
D, d) Gọi 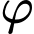 là góc giữa đường thẳng
là góc giữa đường thẳng 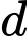 và mặt phẳng
và mặt phẳng 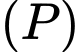 thì
thì 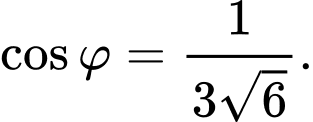
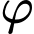 là góc giữa đường thẳng
là góc giữa đường thẳng 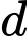 và mặt phẳng
và mặt phẳng 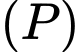 thì
thì 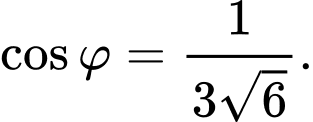
a) Sai. 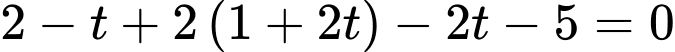
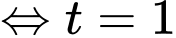 Với
Với 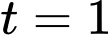
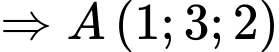 là tọa độ giao điểm của đường thẳng và mặt phẳng.
là tọa độ giao điểm của đường thẳng và mặt phẳng.
b) Sai.
Khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 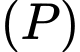 là
là 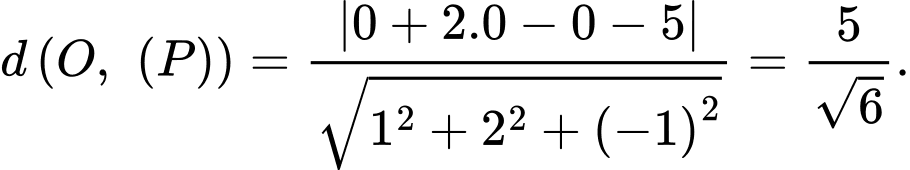
 đến mặt phẳng
đến mặt phẳng 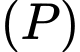 là
là 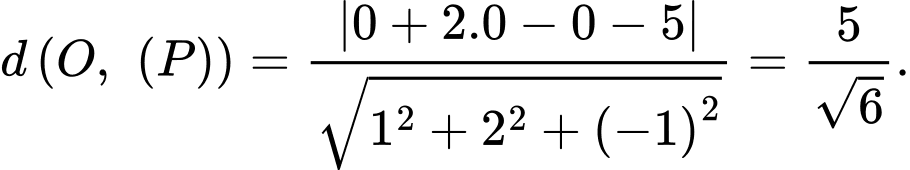
c) Đúng.
Phương trình tham số của đường thẳng 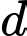 là
là 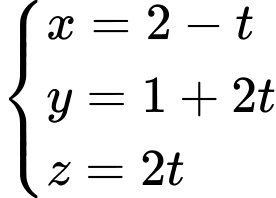
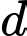 là
là 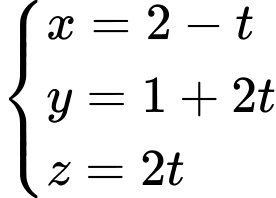
Gọi 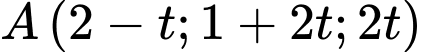 thuộc đường thẳng
thuộc đường thẳng  thay tọa độ điểm
thay tọa độ điểm 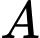 vào mặt phẳng
vào mặt phẳng 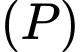 ta được:
ta được:
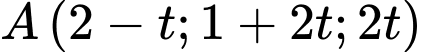 thuộc đường thẳng
thuộc đường thẳng 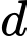 thay tọa độ điểm
thay tọa độ điểm 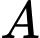 vào mặt phẳng
vào mặt phẳng 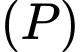 ta được:
ta được: 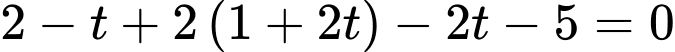
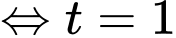 Với
Với 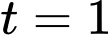
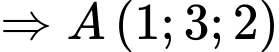 là tọa độ giao điểm của đường thẳng và mặt phẳng.
là tọa độ giao điểm của đường thẳng và mặt phẳng. d) Sai.
Vectơ chỉ phương của đường thẳng 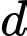 là
là 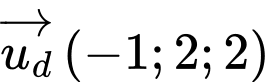 và vectơ pháp tuyến của mặt phẳng
và vectơ pháp tuyến của mặt phẳng 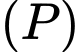 là
là 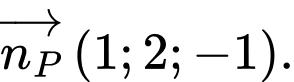
 là
là 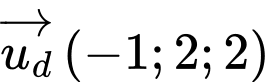 và vectơ pháp tuyến của mặt phẳng
và vectơ pháp tuyến của mặt phẳng 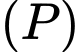 là
là 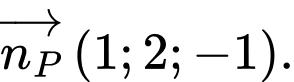
Suy ra 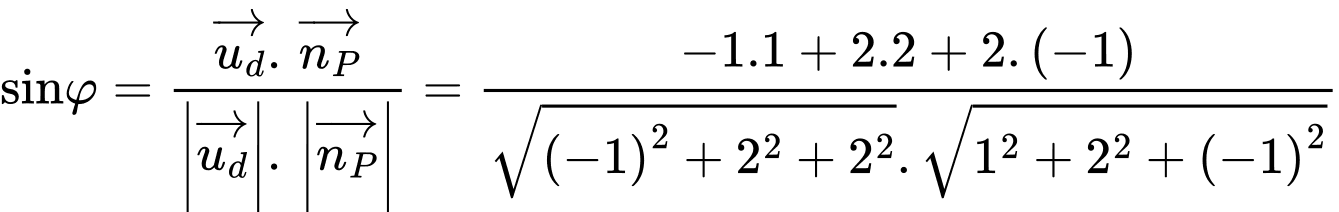
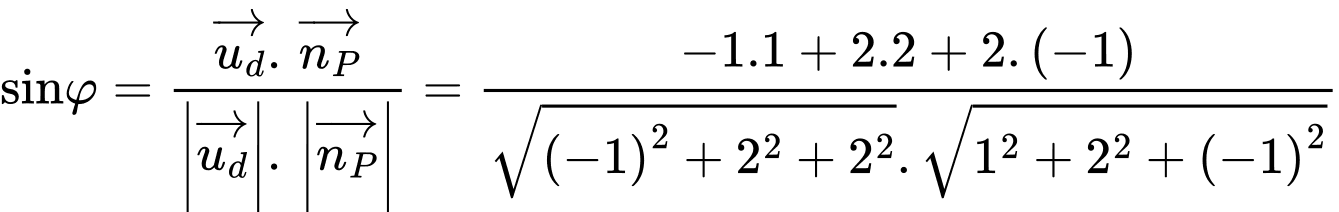
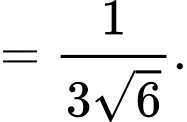
Câu 14 [405678]: Trong không gian với hệ tọa độ 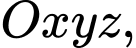 cho điểm
cho điểm 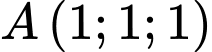 và đường thẳng
và đường thẳng 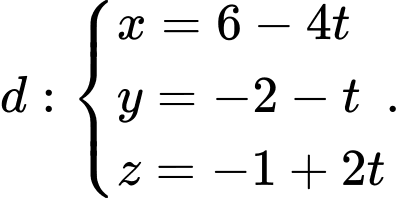 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
 cho điểm
cho điểm 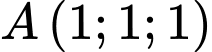 và đường thẳng
và đường thẳng 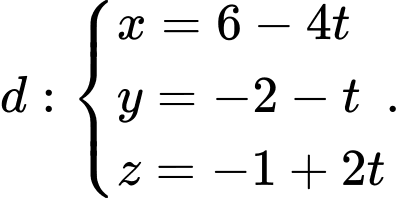 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Một vectơ chỉ phương của đường thẳng 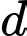 là
là 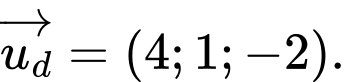
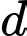 là
là 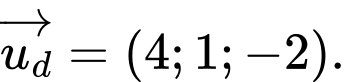
B, b) Đường thẳng 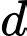 đi qua điểm
đi qua điểm 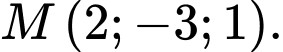
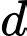 đi qua điểm
đi qua điểm 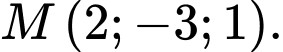
C, c) Gọi  là mặt phẳng qua điểm
là mặt phẳng qua điểm 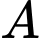 và chứa đường thẳng
và chứa đường thẳng 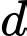 thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 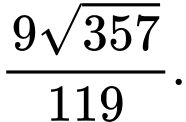
 là mặt phẳng qua điểm
là mặt phẳng qua điểm 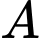 và chứa đường thẳng
và chứa đường thẳng 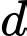 thì khoảng cách từ gốc toạ độ
thì khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng 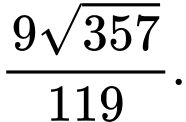
D, d) Gọi 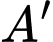 là hình chiếu vuông góc của
là hình chiếu vuông góc của 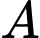 trên
trên 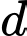 thì hoành độ của điểm
thì hoành độ của điểm 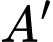 bằng
bằng 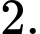
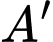 là hình chiếu vuông góc của
là hình chiếu vuông góc của 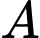 trên
trên 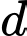 thì hoành độ của điểm
thì hoành độ của điểm 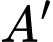 bằng
bằng 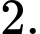
a) Đúng.
b) Đúng.
c) Đúng.
Đường thẳng 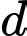 đi qua điểm
đi qua điểm 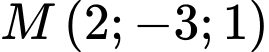 và có vectơ chỉ phương
và có vectơ chỉ phương 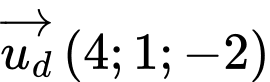
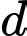 đi qua điểm
đi qua điểm 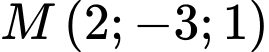 và có vectơ chỉ phương
và có vectơ chỉ phương 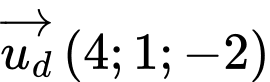
Suy ra 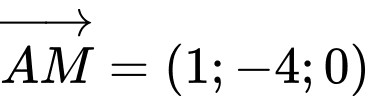
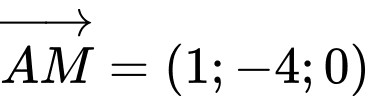
Mặt phẳng  đi qua điểm
đi qua điểm 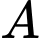 và chứa đường thẳng
và chứa đường thẳng 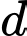 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là
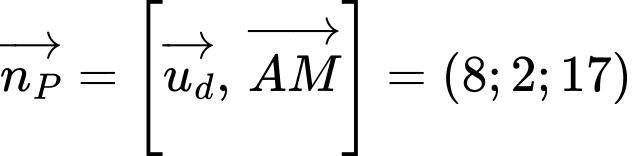
 đi qua điểm
đi qua điểm  và chứa đường thẳng
và chứa đường thẳng 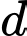 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là
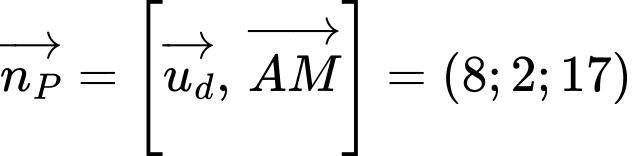
Suy ra phương trình mặt phẳng  là
là 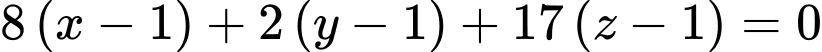
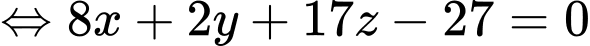
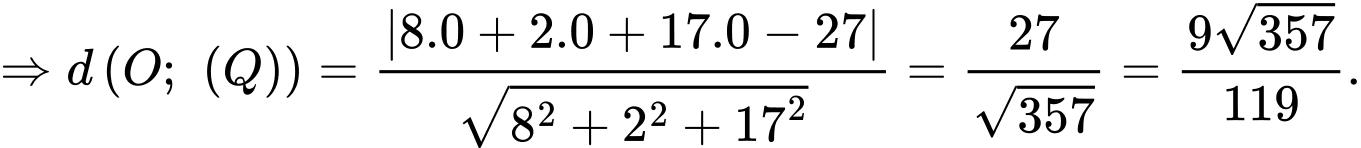
 là
là 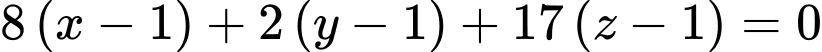
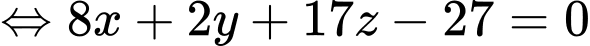
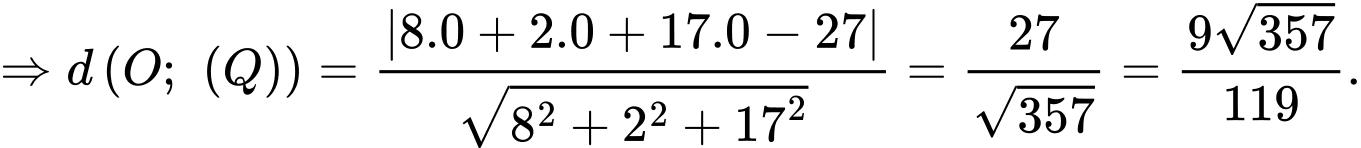
d) Đúng.
Gọi 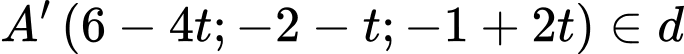
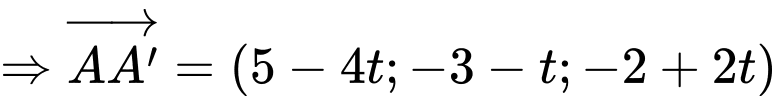 Vì
Vì 
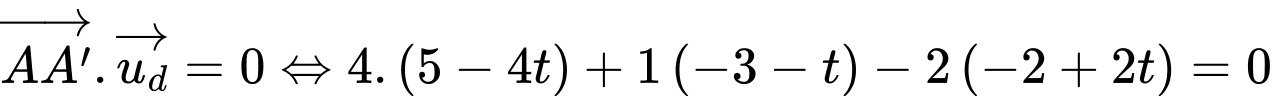
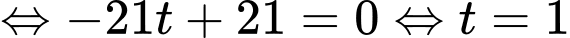
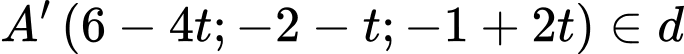
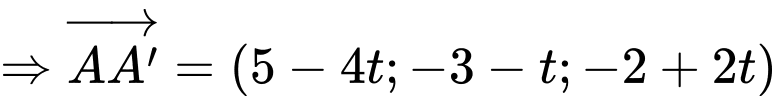 Vì
Vì 
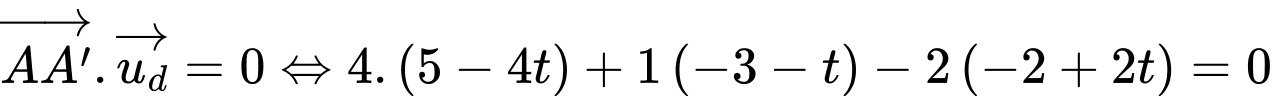
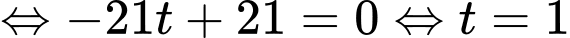
Suy ra hoành độ của điểm 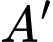 là
là 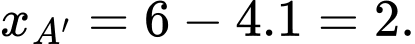
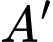 là
là 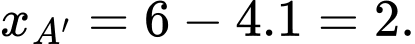
Câu 15 [405679]: Trong không gian tọa độ 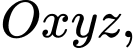 cho mặt phẳng
cho mặt phẳng 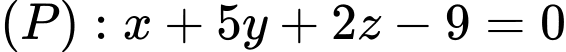 và điểm
và điểm 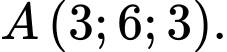 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
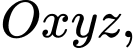 cho mặt phẳng
cho mặt phẳng 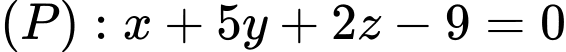 và điểm
và điểm 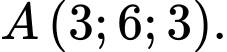 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Một vectơ pháp tuyến của mặt phẳng 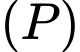 là
là 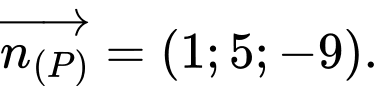
 là
là 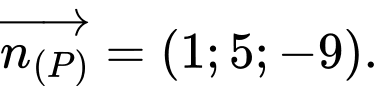
B, b) Khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng  bằng
bằng 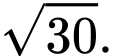
 đến mặt phẳng
đến mặt phẳng 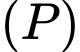 bằng
bằng 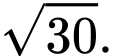
C, c) Đường thẳng qua 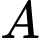 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 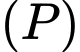 có phương trình tham số là
có phương trình tham số là 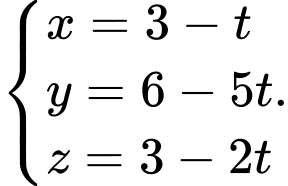
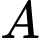 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng  có phương trình tham số là
có phương trình tham số là 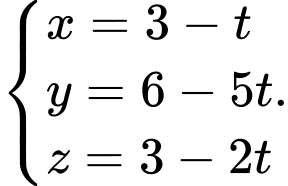
D, d) Gọi 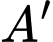 là hình chiếu vuông góc của
là hình chiếu vuông góc của 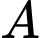 trên
trên 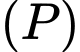 thì tung độ của điểm
thì tung độ của điểm 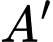 bằng
bằng 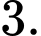
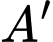 là hình chiếu vuông góc của
là hình chiếu vuông góc của 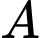 trên
trên 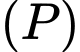 thì tung độ của điểm
thì tung độ của điểm 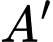 bằng
bằng 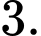
a) Sai.
Một vectơ pháp tuyến của mặt phẳng  là
là 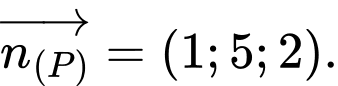
 là
là 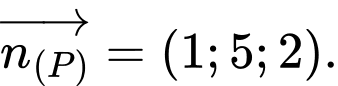
b) Đúng.
Khoảng cách từ điểm 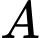 đến mặt phẳng
đến mặt phẳng 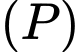 là
là 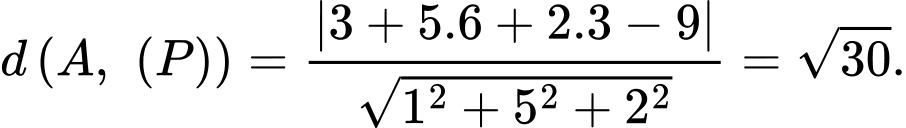
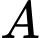 đến mặt phẳng
đến mặt phẳng 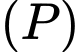 là
là 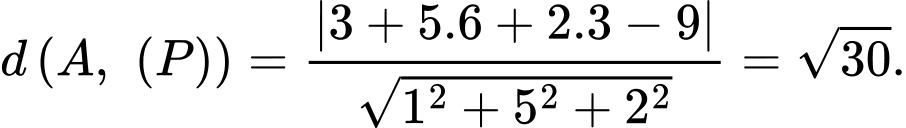
c) Đúng.
Gọi  là đường thẳng qua
là đường thẳng qua  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 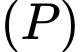
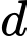 là đường thẳng qua
là đường thẳng qua 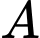 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 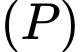
Vì 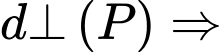
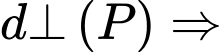
Một vectơ chỉ phương của đường thẳng 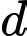 là
là 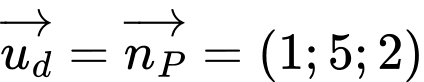
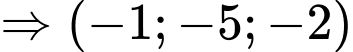 cũng là một vectơ chỉ phương của đường thẳng
cũng là một vectơ chỉ phương của đường thẳng 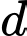
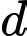 là
là 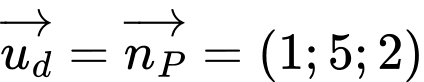
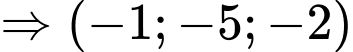 cũng là một vectơ chỉ phương của đường thẳng
cũng là một vectơ chỉ phương của đường thẳng 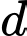
Phương trình đường thẳng 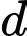 là
là 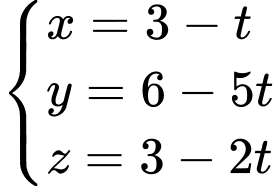
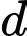 là
là 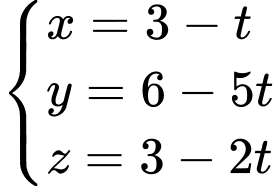
d) Sai.
Từ bước c) ta có phương trình đường thẳng 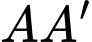 là
là 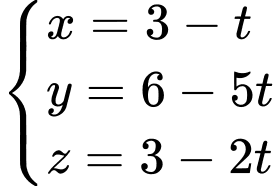
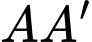 là
là 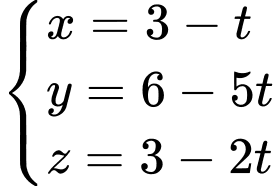
Gọi 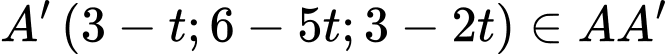
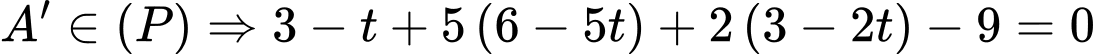
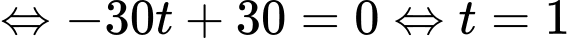
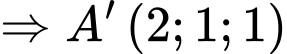
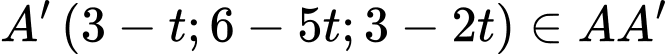
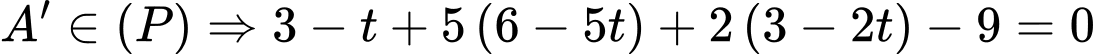
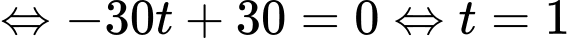
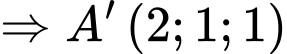
Vậy tung độ của 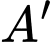 bằng
bằng 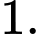
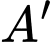 bằng
bằng 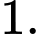
Câu 16 [405680]: Trong không gian với hệ tọa độ 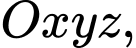 cho điểm
cho điểm 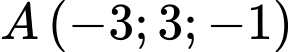 và mặt phẳng
và mặt phẳng 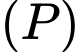 có phương trình
có phương trình 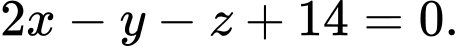 Gọi
Gọi 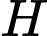 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 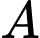 trên mặt phẳng
trên mặt phẳng 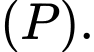 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 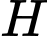 đến mặt phẳng
đến mặt phẳng 
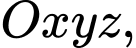 cho điểm
cho điểm 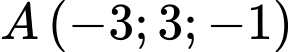 và mặt phẳng
và mặt phẳng 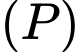 có phương trình
có phương trình 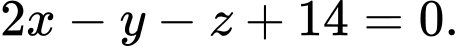 Gọi
Gọi 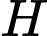 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 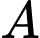 trên mặt phẳng
trên mặt phẳng 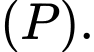 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 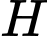 đến mặt phẳng
đến mặt phẳng 
Vì 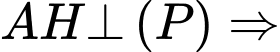
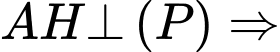
Một vectơ chỉ phương của đường thẳng  là
là 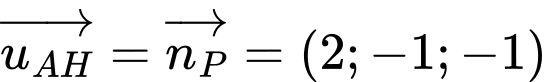
 là
là 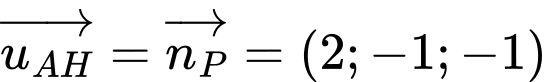
Phương trình đường thẳng 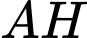 là
là 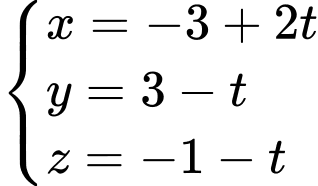
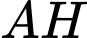 là
là 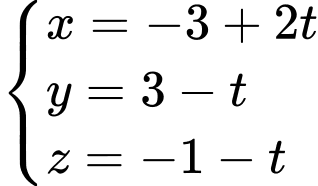
Gọi 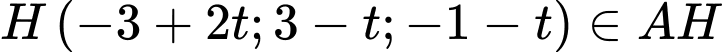
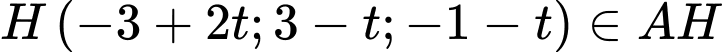
Ta có 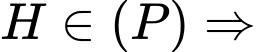
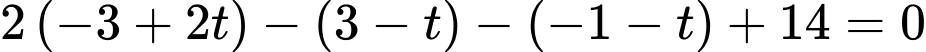
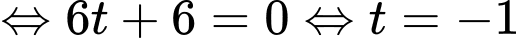

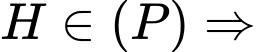
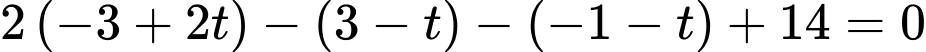
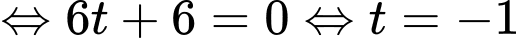

Mặt phẳng 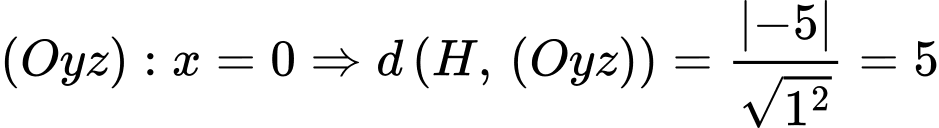
Câu 17 [405681]: Trong không gian với hệ tọa độ 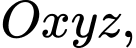 tọa độ hình chiếu vuông góc của điểm
tọa độ hình chiếu vuông góc của điểm 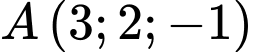 trên mặt phẳng
trên mặt phẳng 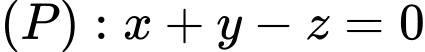 là
là 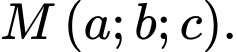 Tính
Tính 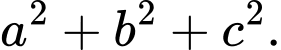
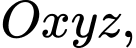 tọa độ hình chiếu vuông góc của điểm
tọa độ hình chiếu vuông góc của điểm 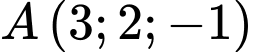 trên mặt phẳng
trên mặt phẳng 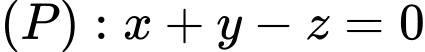 là
là 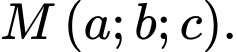 Tính
Tính 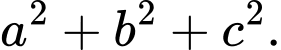
Ta có 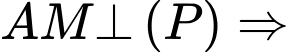
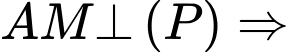
Một vectơ chỉ phương của đường thẳng  là
là 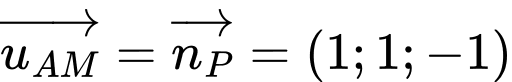
 là
là 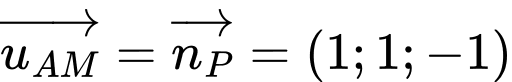
Suy ra phương trình tham số của đường thẳng  là
là 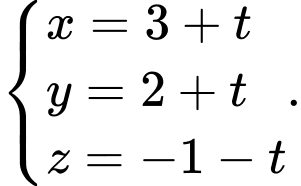
 là
là 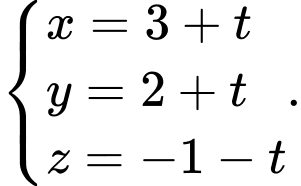
Gọi 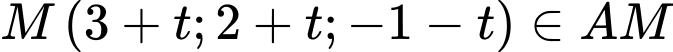
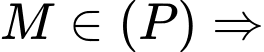
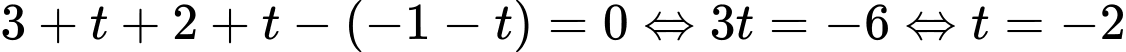
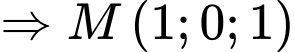
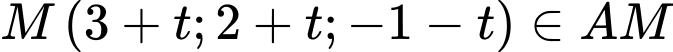
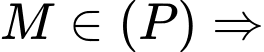
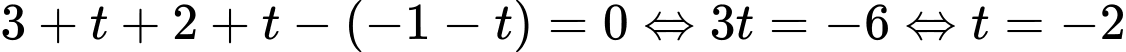
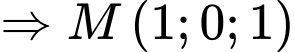
Vậy 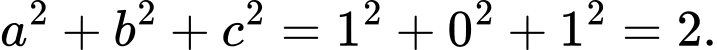
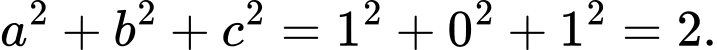
Câu 18 [405682]: Trong không gian với hệ tọa độ 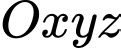 , cho
, cho 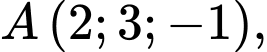
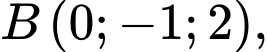
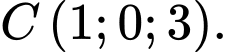 Tọa độ chân đường cao hạ từ đỉnh
Tọa độ chân đường cao hạ từ đỉnh 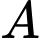 của tam giác
của tam giác 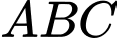 có tọa độ là
có tọa độ là 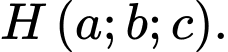 Tính
Tính 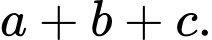
 , cho
, cho 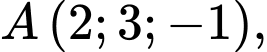
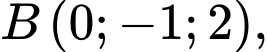
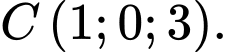 Tọa độ chân đường cao hạ từ đỉnh
Tọa độ chân đường cao hạ từ đỉnh 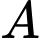 của tam giác
của tam giác 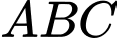 có tọa độ là
có tọa độ là 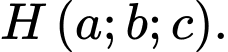 Tính
Tính 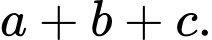
Ta có : 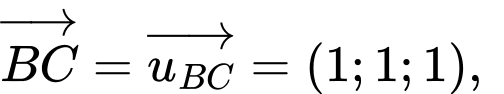 gọi
gọi 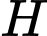 là chân đường cao hạ từ
là chân đường cao hạ từ 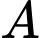 xuống
xuống 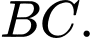
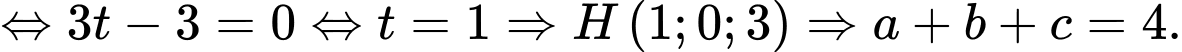
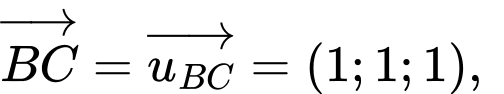 gọi
gọi  là chân đường cao hạ từ
là chân đường cao hạ từ  xuống
xuống 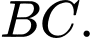
Phương trình đường thẳng BC là 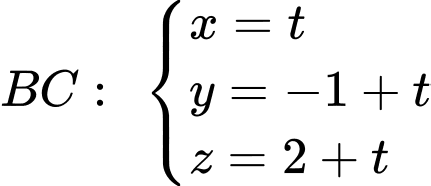 .
.
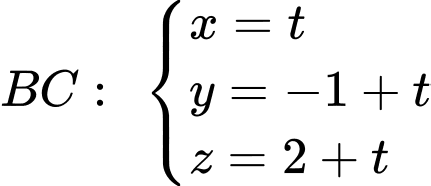 .
. Gọi 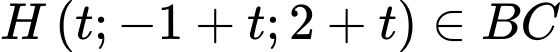 ta có:
ta có: 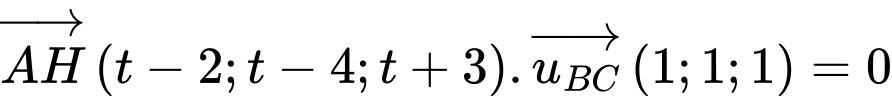
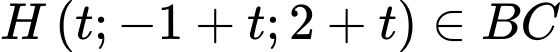 ta có:
ta có: 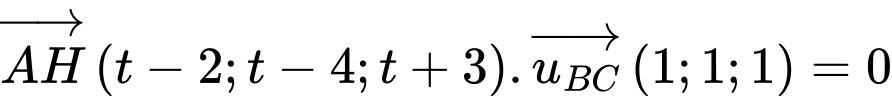
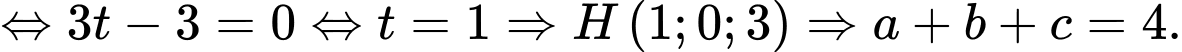
Câu 19 [405683]: Trong không gian với hê tọa độ 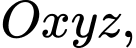 cho điểm
cho điểm 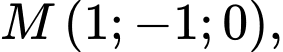 mặt phẳng
mặt phẳng 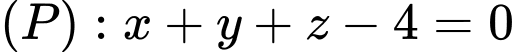 và đường thẳng
và đường thẳng 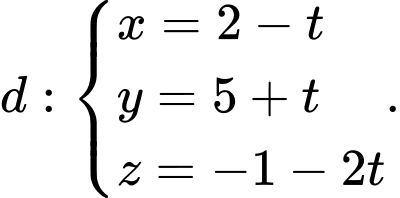 Điểm
Điểm 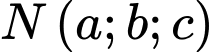 thuộc
thuộc 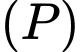 sao cho đường thẳng
sao cho đường thẳng 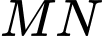 song song với
song song với 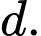 Tính
Tính 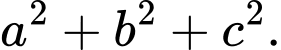
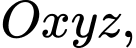 cho điểm
cho điểm 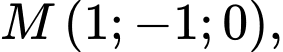 mặt phẳng
mặt phẳng 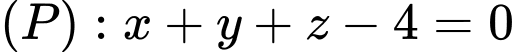 và đường thẳng
và đường thẳng 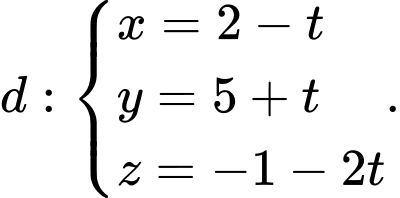 Điểm
Điểm 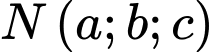 thuộc
thuộc 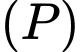 sao cho đường thẳng
sao cho đường thẳng 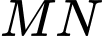 song song với
song song với 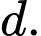 Tính
Tính 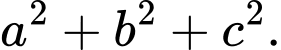
Ta có 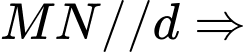
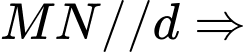
Một vectơ chỉ phương của 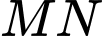 là
là 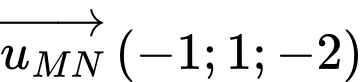
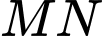 là
là 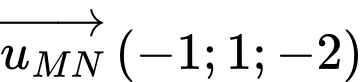
Suy ra phương trình đường thẳng 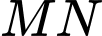 là
là 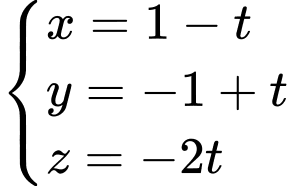
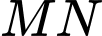 là
là 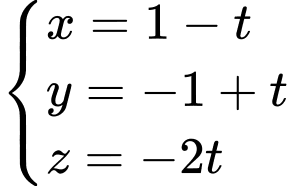
Gọi 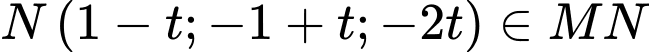
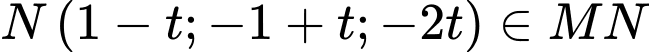
Vì 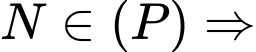
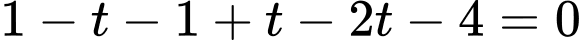
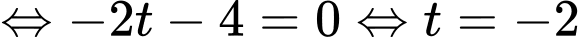
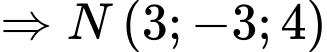
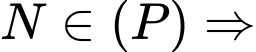
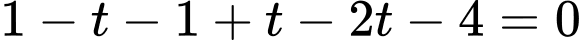
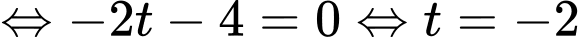
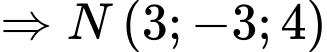
Vậy 

Câu 20 [405684]: Trong không gian với hê tọa độ 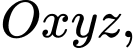 gọi
gọi 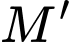 là điểm đối xứng của điểm
là điểm đối xứng của điểm 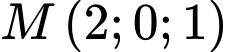 qua đường thẳng
qua đường thẳng 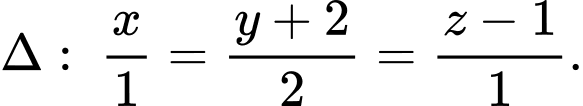 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 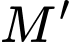 đến mặt phẳng
đến mặt phẳng 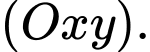
 gọi
gọi 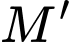 là điểm đối xứng của điểm
là điểm đối xứng của điểm 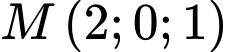 qua đường thẳng
qua đường thẳng 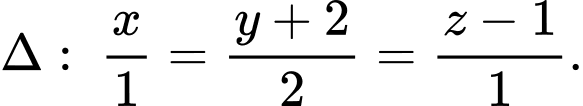 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 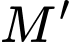 đến mặt phẳng
đến mặt phẳng 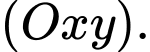
Vì 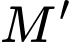 là điểm đối xứng của
là điểm đối xứng của 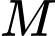 qua đường thẳng
qua đường thẳng  nên ta có
nên ta có 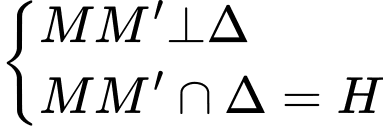
 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 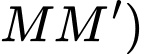
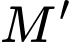 là điểm đối xứng của
là điểm đối xứng của 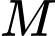 qua đường thẳng
qua đường thẳng  nên ta có
nên ta có 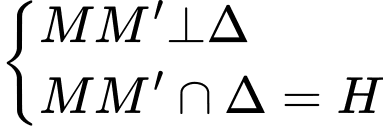
 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 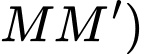
Gọi 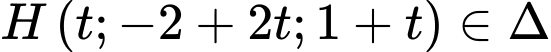
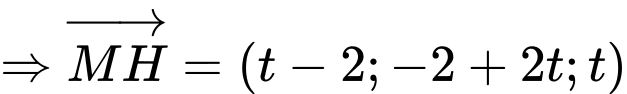
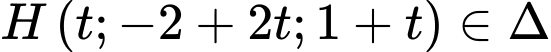
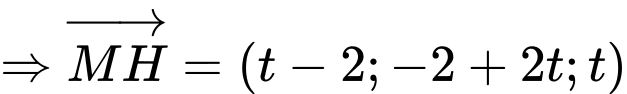
Vì 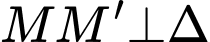 nên
nên 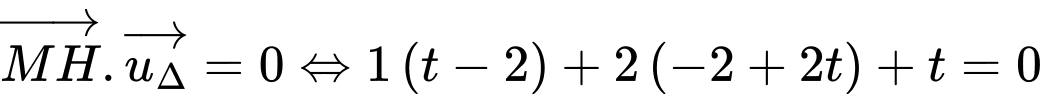
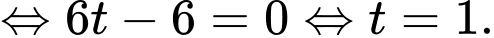
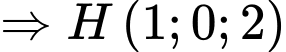
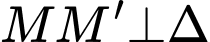 nên
nên 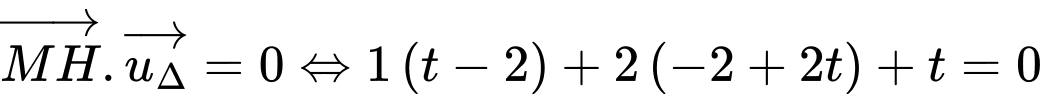
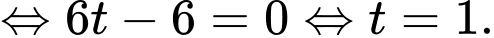
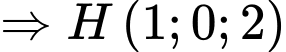
Giả sử 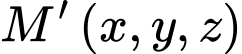 Ta có
Ta có 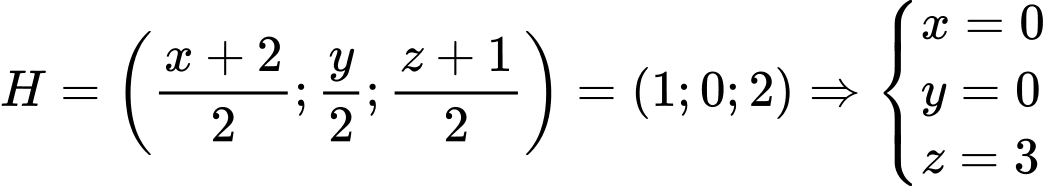

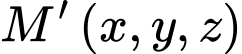 Ta có
Ta có 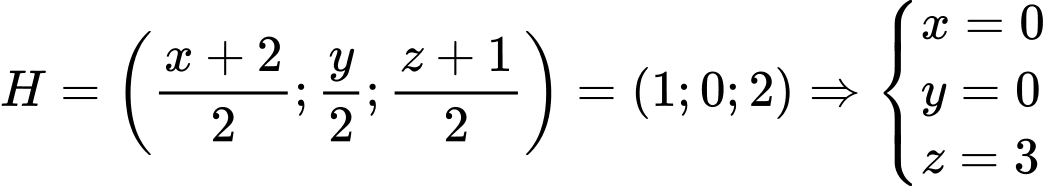

Ta có 
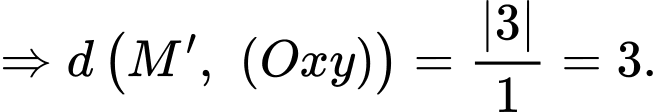
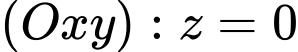
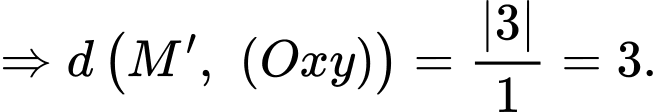
Câu 21 [405685]: Trong không gian với hê tọa độ 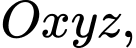 điểm đối xứng với điểm
điểm đối xứng với điểm 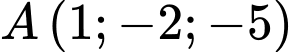 qua đường thẳng
qua đường thẳng 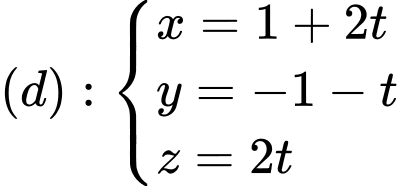 là điểm
là điểm 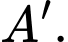 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 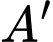 đến mặt phẳng
đến mặt phẳng 
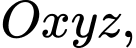 điểm đối xứng với điểm
điểm đối xứng với điểm 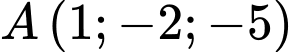 qua đường thẳng
qua đường thẳng 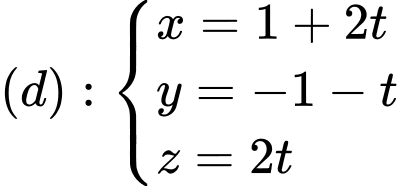 là điểm
là điểm 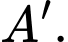 Tính khoảng cách từ điểm
Tính khoảng cách từ điểm 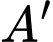 đến mặt phẳng
đến mặt phẳng 
Gọi 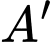 là điểm đối xứng của qua
là điểm đối xứng của qua 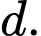
Gọi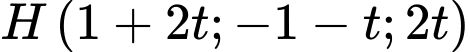 ta có:
ta có:
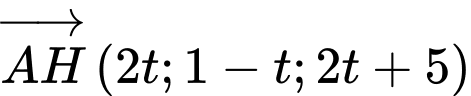
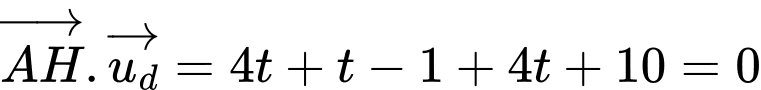
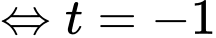
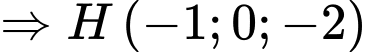
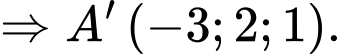
Khi đó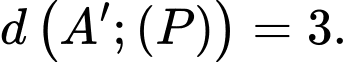
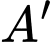 là điểm đối xứng của qua
là điểm đối xứng của qua 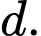
Gọi
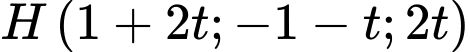 ta có:
ta có:
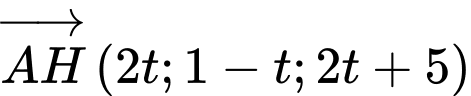
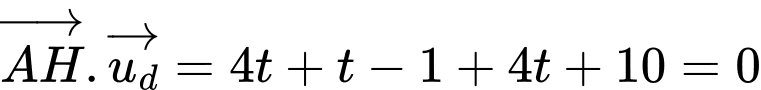
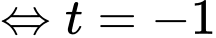
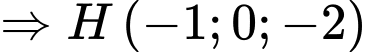
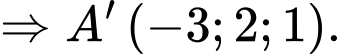
Khi đó
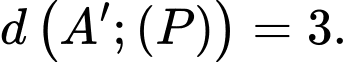
Câu 22 [405686]: Trong không gian tọa độ  , cho tứ diện
, cho tứ diện  có
có 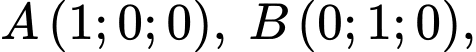
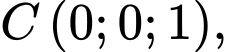
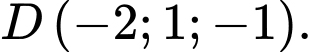 Tọa độ chân đường cao hạ từ đỉnh
Tọa độ chân đường cao hạ từ đỉnh  của tứ diện là
của tứ diện là 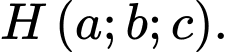 Tính
Tính 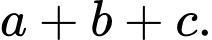
 , cho tứ diện
, cho tứ diện 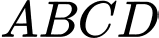 có
có 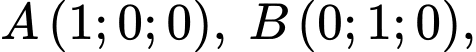
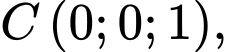
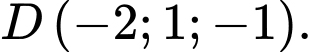 Tọa độ chân đường cao hạ từ đỉnh
Tọa độ chân đường cao hạ từ đỉnh 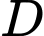 của tứ diện là
của tứ diện là 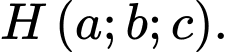 Tính
Tính 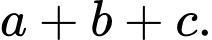
Phương trình mặt phẳng 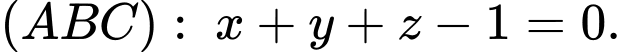
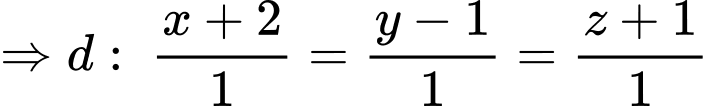
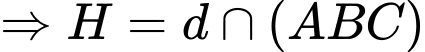 .
.
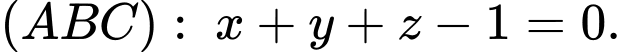
Phương trình đường thằng qua D và vuông góc với 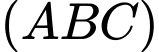 có vectơ chỉ phương là
có vectơ chỉ phương là 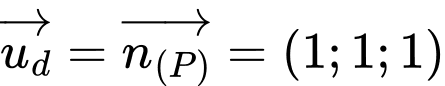
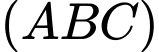 có vectơ chỉ phương là
có vectơ chỉ phương là 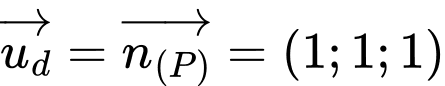
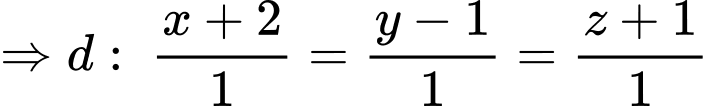
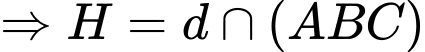 .
. Gọi 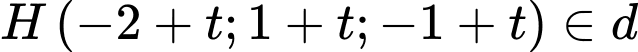
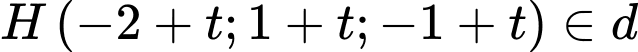
Do 
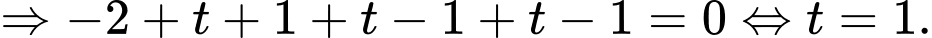
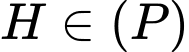
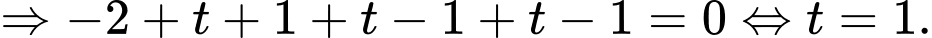
Vậy 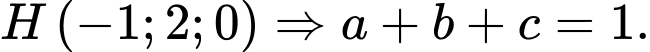
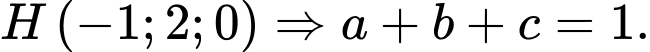
Câu 23 [405687]: Cho hai điểm 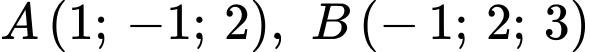 và đường thẳng
và đường thẳng 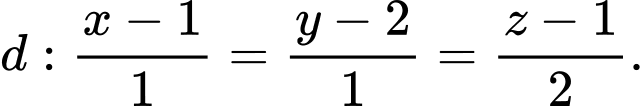 Tìm điểm
Tìm điểm 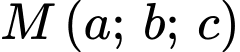 thuộc
thuộc 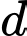 sao cho
sao cho 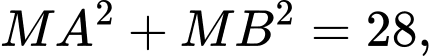 biết
biết  Tính giá trị
Tính giá trị 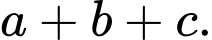
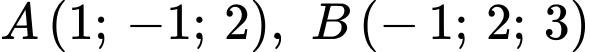 và đường thẳng
và đường thẳng 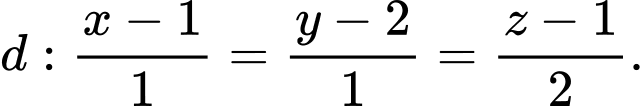 Tìm điểm
Tìm điểm 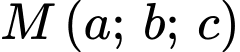 thuộc
thuộc 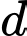 sao cho
sao cho 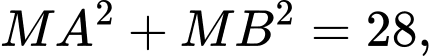 biết
biết  Tính giá trị
Tính giá trị 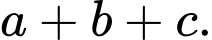
Gọi 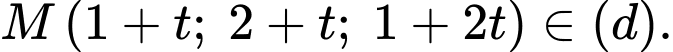
Khi đó:
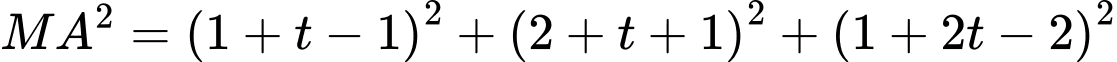
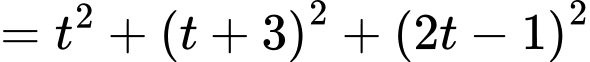
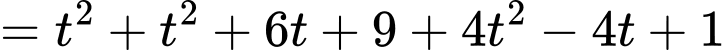
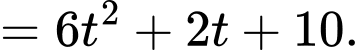
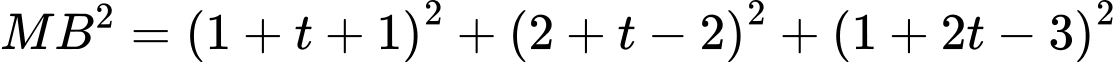
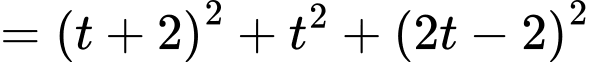
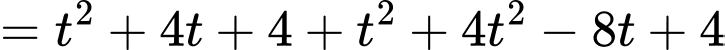
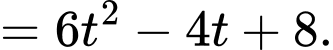
Do đó: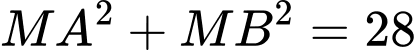
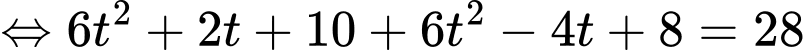
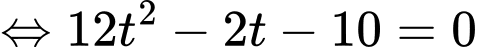
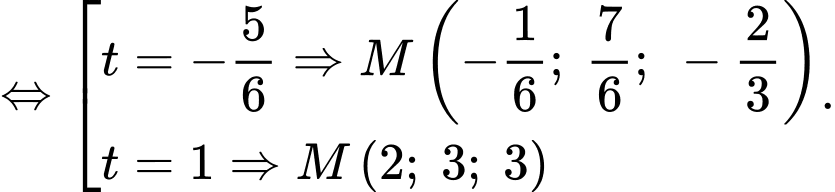
Do
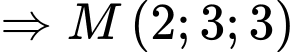
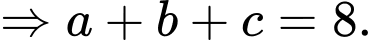
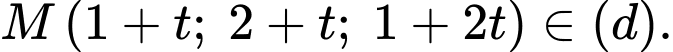
Khi đó:
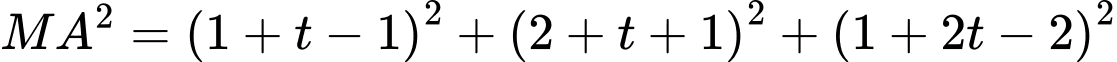
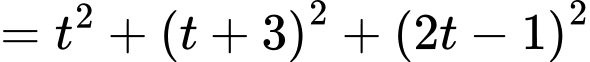
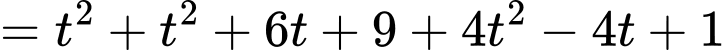
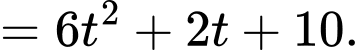
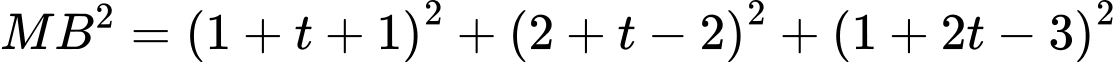
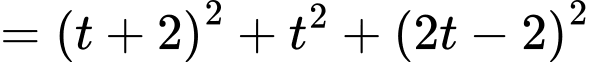
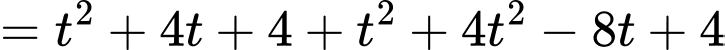
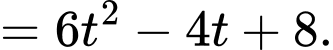
Do đó:
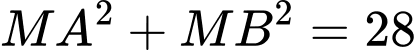
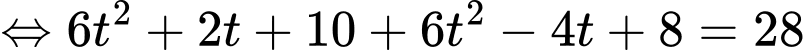
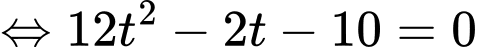
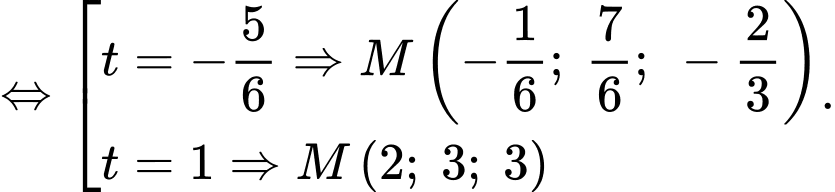
Do

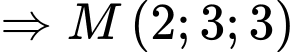
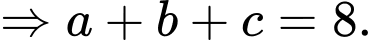
Câu 24 [405688]: Trong không gian với hệ trục tọa độ  cho đường thẳng
cho đường thẳng 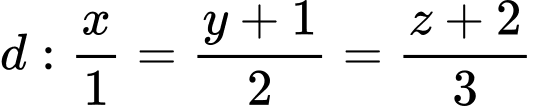 và mặt phẳng có phương trình
và mặt phẳng có phương trình 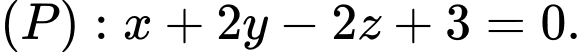 Gọi
Gọi 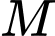 là điểm có hoành độ âm thuộc
là điểm có hoành độ âm thuộc 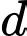 sao cho khoảng cách từ
sao cho khoảng cách từ 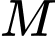 đến mặt phẳng
đến mặt phẳng 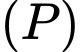 bằng 2. Tung độ của điểm
bằng 2. Tung độ của điểm 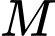 bằng bao nhiêu ?
bằng bao nhiêu ?
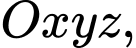 cho đường thẳng
cho đường thẳng 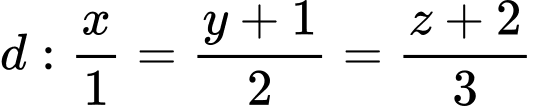 và mặt phẳng có phương trình
và mặt phẳng có phương trình 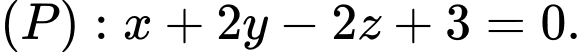 Gọi
Gọi 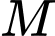 là điểm có hoành độ âm thuộc
là điểm có hoành độ âm thuộc 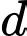 sao cho khoảng cách từ
sao cho khoảng cách từ 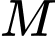 đến mặt phẳng
đến mặt phẳng 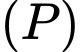 bằng 2. Tung độ của điểm
bằng 2. Tung độ của điểm 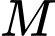 bằng bao nhiêu ?
bằng bao nhiêu ?
Gọi 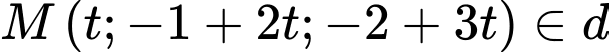
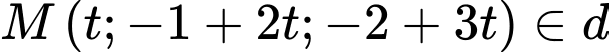
Vì 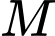 có hoành độ âm nên
có hoành độ âm nên 
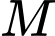 có hoành độ âm nên
có hoành độ âm nên 
Ta có 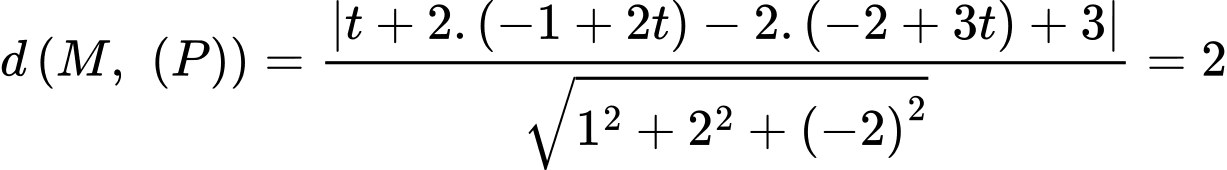
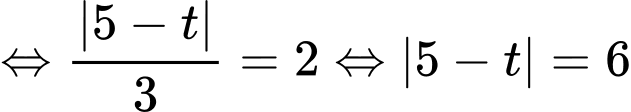
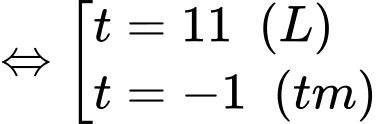
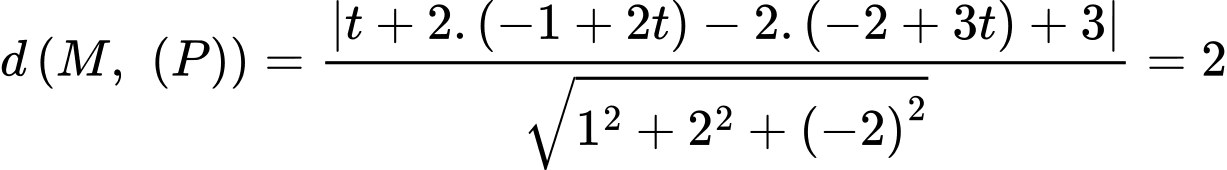
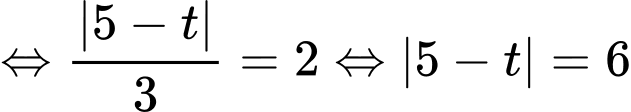
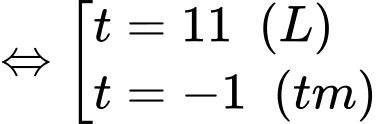
Vậy tung độ của điểm 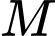 là
là 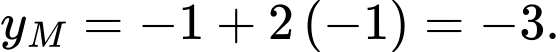
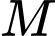 là
là 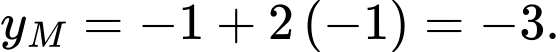
Câu 25 [80373]: Trong không gian 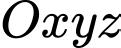 , cho mặt phẳng
, cho mặt phẳng 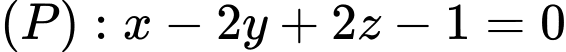 và đường thẳng
và đường thẳng 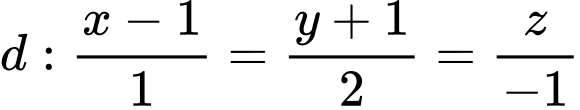 . Biết điểm
. Biết điểm 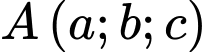 ,
, 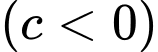 là điểm nằm trên đường thẳng
là điểm nằm trên đường thẳng 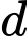 và cách
và cách 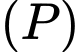 một khoảng bằng
một khoảng bằng 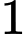 . Tính tổng
. Tính tổng 
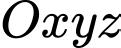 , cho mặt phẳng
, cho mặt phẳng 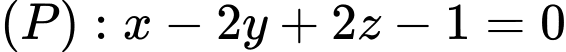 và đường thẳng
và đường thẳng 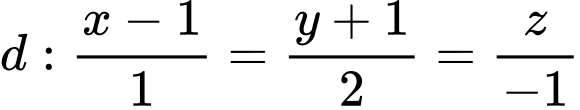 . Biết điểm
. Biết điểm 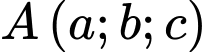 ,
, 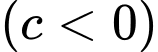 là điểm nằm trên đường thẳng
là điểm nằm trên đường thẳng 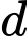 và cách
và cách 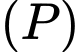 một khoảng bằng
một khoảng bằng 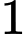 . Tính tổng
. Tính tổng 
A, 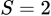 .
.
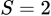 .
.B, 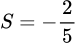 .
.
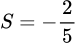 .
.C, 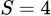 .
.
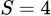 .
.D, 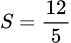 .
.
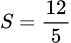 .
. Đáp án: A
Đáp án: A
Câu 26 [58249]: Trong không gian 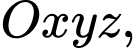 cho mặt phẳng
cho mặt phẳng 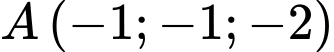 và mặt phẳng
và mặt phẳng 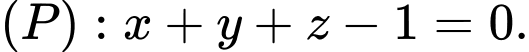 Gọi
Gọi 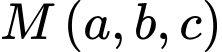 là điểm thuộc
là điểm thuộc 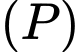 sao cho độ dài
sao cho độ dài  ngắn nhất. Tính
ngắn nhất. Tính 
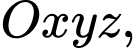 cho mặt phẳng
cho mặt phẳng 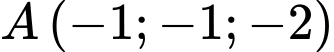 và mặt phẳng
và mặt phẳng 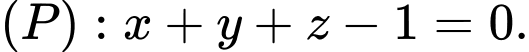 Gọi
Gọi 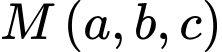 là điểm thuộc
là điểm thuộc 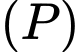 sao cho độ dài
sao cho độ dài  ngắn nhất. Tính
ngắn nhất. Tính 
A, 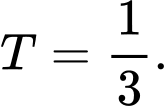
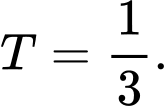
B, 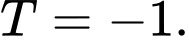
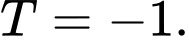
C, 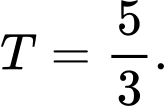
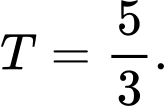
D, 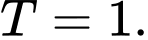
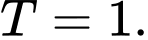
Chọn đáp án D.
Độ dài là ngắn nhất khi và chỉ khi
là ngắn nhất khi và chỉ khi 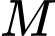 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 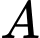 xuống mặt phẳng
xuống mặt phẳng  Vì
Vì 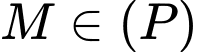 nên ta có
nên ta có 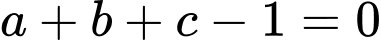
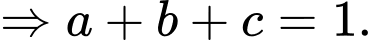
Vậy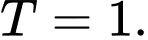 Đáp án: D
Đáp án: D
Độ dài
 là ngắn nhất khi và chỉ khi
là ngắn nhất khi và chỉ khi 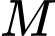 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 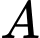 xuống mặt phẳng
xuống mặt phẳng 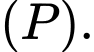 Vì
Vì 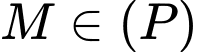 nên ta có
nên ta có 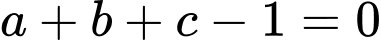
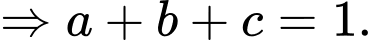
Vậy
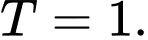 Đáp án: D
Đáp án: D
Câu 27 [55825]: Trong không gian với hệ tọa độ 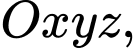 cho điểm
cho điểm 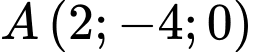 và đường thẳng
và đường thẳng 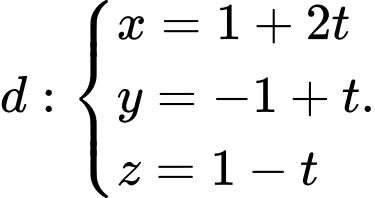 Gọi
Gọi 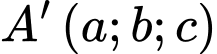 là điểm đối xứng với
là điểm đối xứng với 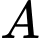 qua
qua 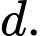 Khi đó, tổng
Khi đó, tổng 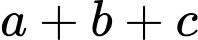 là
là
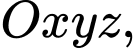 cho điểm
cho điểm 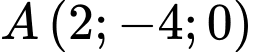 và đường thẳng
và đường thẳng 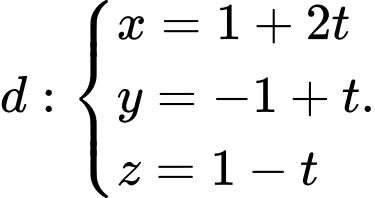 Gọi
Gọi 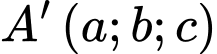 là điểm đối xứng với
là điểm đối xứng với 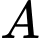 qua
qua 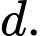 Khi đó, tổng
Khi đó, tổng 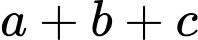 là
là A, 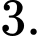
B, 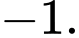
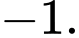
C, 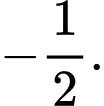
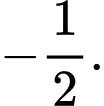
D, 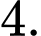
 Đáp án: D
Đáp án: D
Câu 28 [408486]: Trong không gian 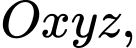 cho hai điểm
cho hai điểm  và mặt phẳng
và mặt phẳng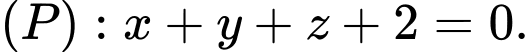 Gọi
Gọi 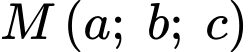 với
với 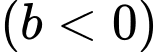 thuộc mặt phẳng
thuộc mặt phẳng 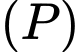 sao cho
sao cho 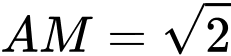 và mặt phẳng
và mặt phẳng 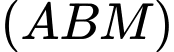 vuông góc với mặt phẳng
vuông góc với mặt phẳng 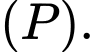 Tính
Tính 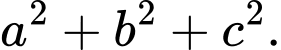
Đáp số:………………
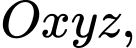 cho hai điểm
cho hai điểm  và mặt phẳng
và mặt phẳng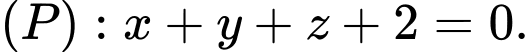 Gọi
Gọi 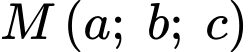 với
với 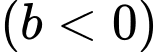 thuộc mặt phẳng
thuộc mặt phẳng 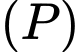 sao cho
sao cho 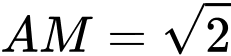 và mặt phẳng
và mặt phẳng 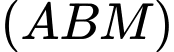 vuông góc với mặt phẳng
vuông góc với mặt phẳng 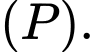 Tính
Tính 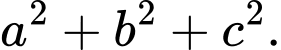
Đáp số:………………
Ta có: 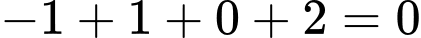 nên
nên 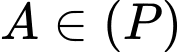 với
với 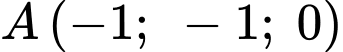 và
và 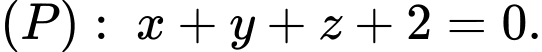
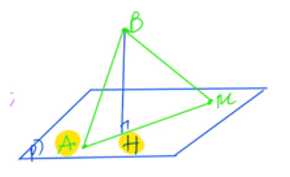
Gọi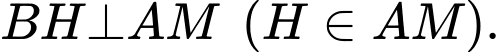
Mà,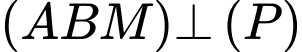
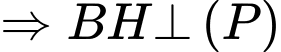
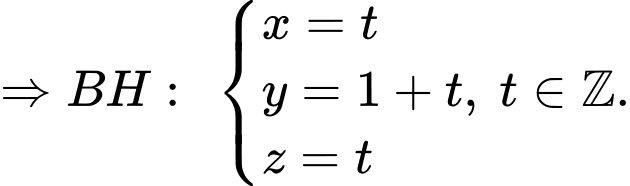
Ta có: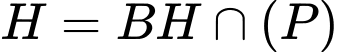
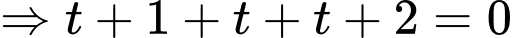
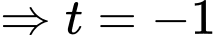
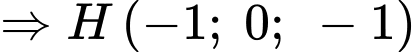
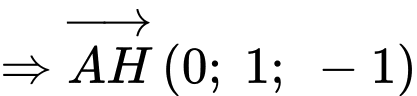
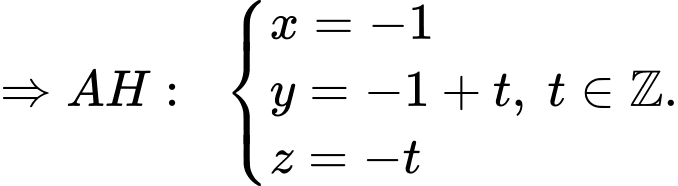

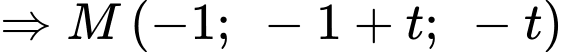
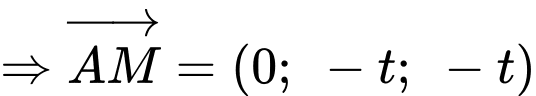
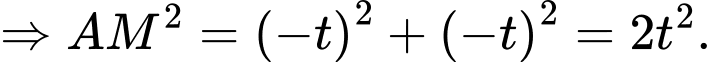
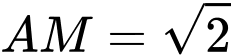
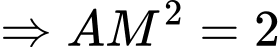
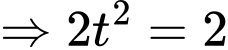
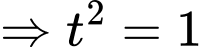
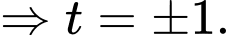
Với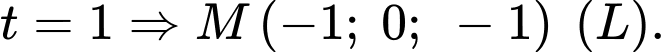
Với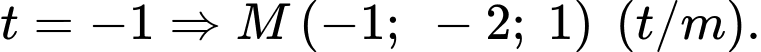
Vậy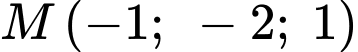 và
và 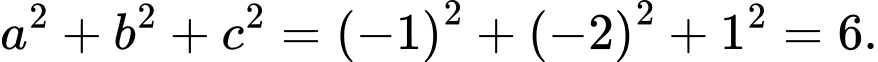
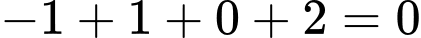 nên
nên 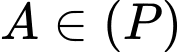 với
với 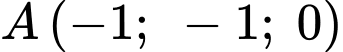 và
và 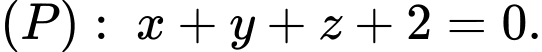

Gọi
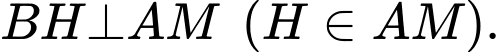
Mà,
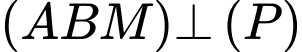
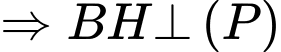
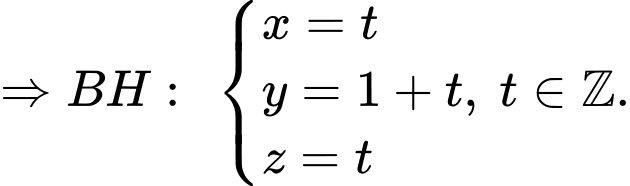
Ta có:
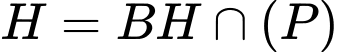
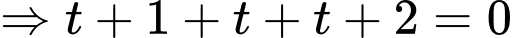
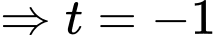
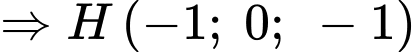
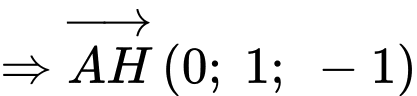
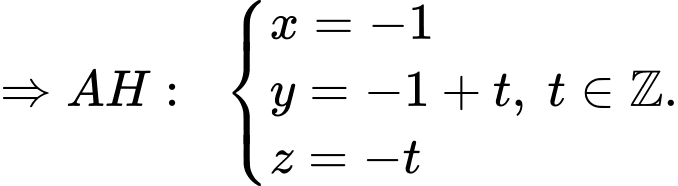

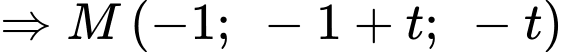
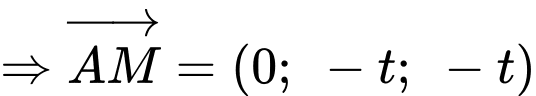
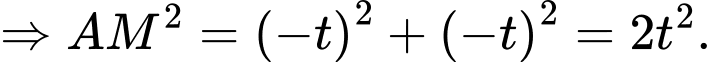
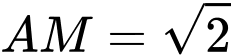
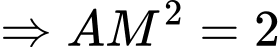
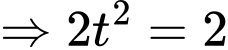
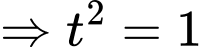
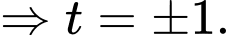
Với
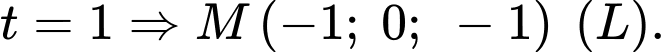
Với
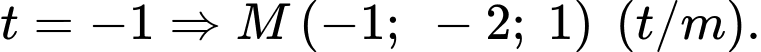
Vậy
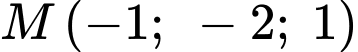 và
và