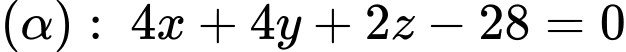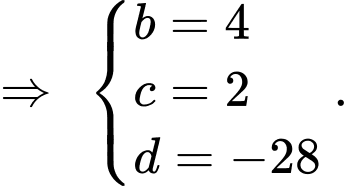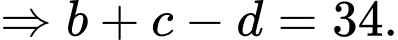Đáp án Bài tập tự luyện
Câu 1 [53372]: Trong không gian với hệ trục tọa độ 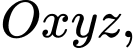 mặt phẳng đi qua các điểm
mặt phẳng đi qua các điểm 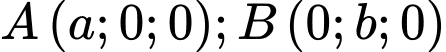 và
và 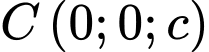 với
với 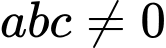 có phương trình là
có phương trình là
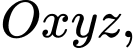 mặt phẳng đi qua các điểm
mặt phẳng đi qua các điểm 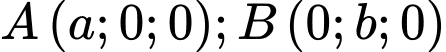 và
và 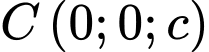 với
với 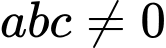 có phương trình là
có phương trình là A, 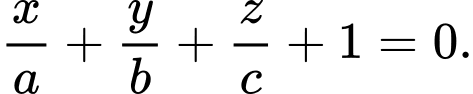
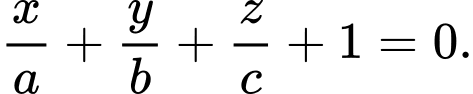
B, 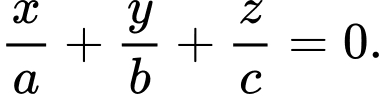
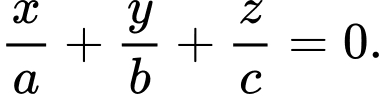
C, 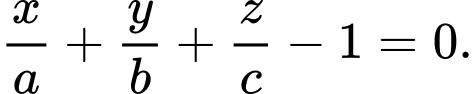
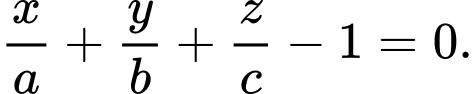
D, 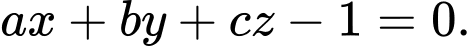
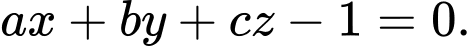
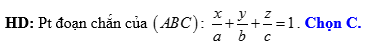 Đáp án: C
Đáp án: C
Câu 2 [899291]: Trong không gian với hệ trục tọa độ 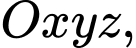 cho ba điểm
cho ba điểm 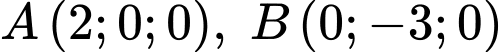 và
và 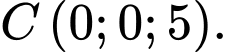 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 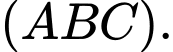
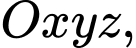 cho ba điểm
cho ba điểm 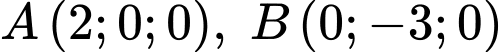 và
và 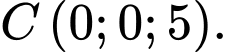 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 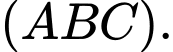
A, 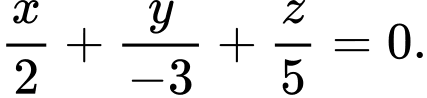
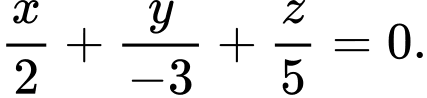
B, 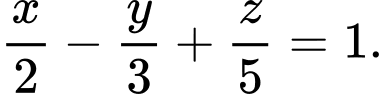
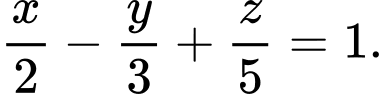
C, 

D, 

Chọn B.
Phương trình đoạn chắn của mặt phẳng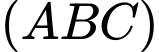 là:
là: 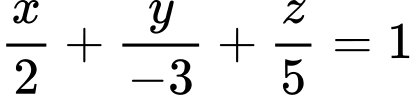 hay
hay 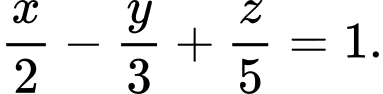 Đáp án: B
Đáp án: B
Phương trình đoạn chắn của mặt phẳng
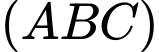 là:
là: 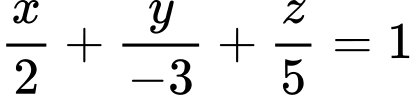 hay
hay 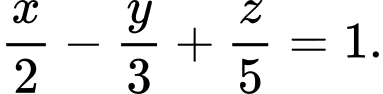 Đáp án: B
Đáp án: B
Câu 3 [53364]: Trong không gian với hệ tọa độ 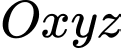 , cho 3 điểm
, cho 3 điểm 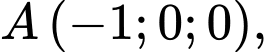
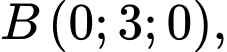
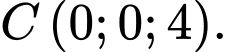 Phương trình nào dưới đây là phương trình của
Phương trình nào dưới đây là phương trình của 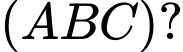
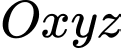 , cho 3 điểm
, cho 3 điểm 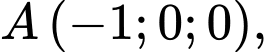
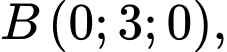
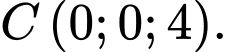 Phương trình nào dưới đây là phương trình của
Phương trình nào dưới đây là phương trình của 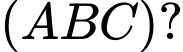
A, 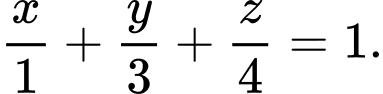
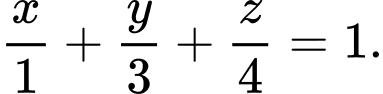
B, 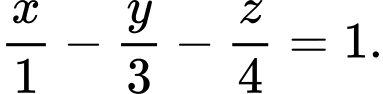
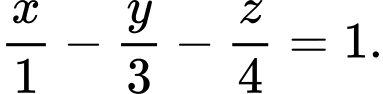
C, 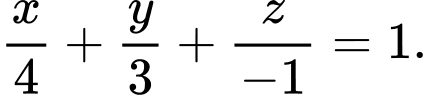
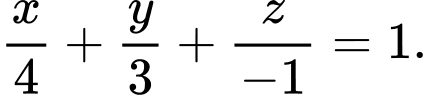
D, 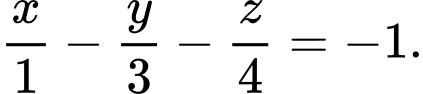
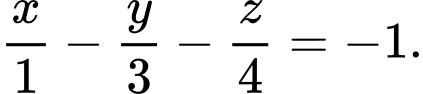
Ta có 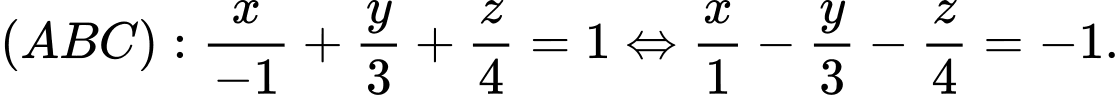 Chọn D Đáp án: D
Chọn D Đáp án: D
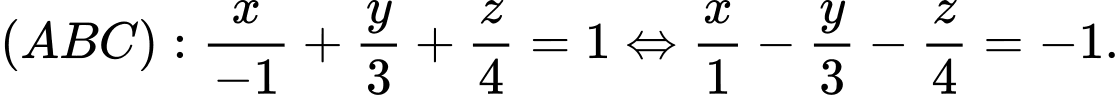 Chọn D Đáp án: D
Chọn D Đáp án: D
Câu 4 [185135]: Trong không gian với hệ tọa độ 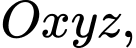 mặt phẳng
mặt phẳng 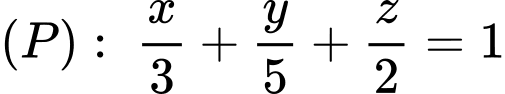 cắt trục
cắt trục 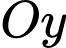 tại điểm có tọa độ là
tại điểm có tọa độ là
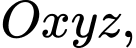 mặt phẳng
mặt phẳng 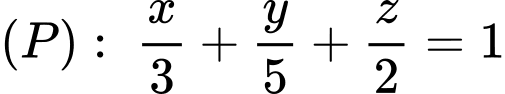 cắt trục
cắt trục 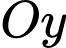 tại điểm có tọa độ là
tại điểm có tọa độ là A, 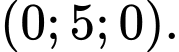
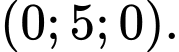
B, 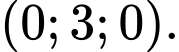
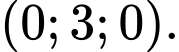
C, 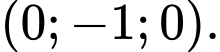
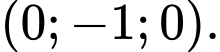
D, 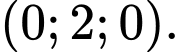
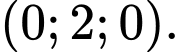
Điểm thuộc trục 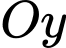 có hoành độ và cao độ bằng 0
có hoành độ và cao độ bằng 0
Cho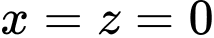 ta được
ta được 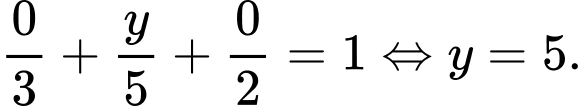
Vậy giao điểm của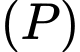 với
với 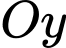 là điểm
là điểm 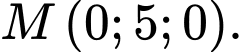 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
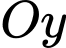 có hoành độ và cao độ bằng 0
có hoành độ và cao độ bằng 0
Cho
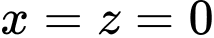 ta được
ta được 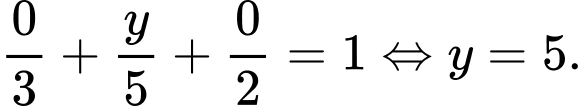
Vậy giao điểm của
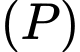 với
với 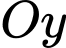 là điểm
là điểm 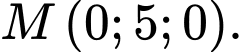 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 5 [53386]: Trong không gian với hệ tọa độ 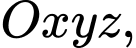 cho ba điểm
cho ba điểm 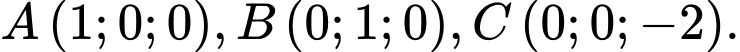 Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng 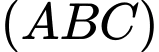 ?
?
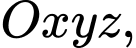 cho ba điểm
cho ba điểm 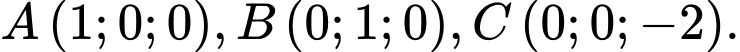 Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng
Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng 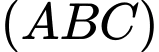 ?
? A, 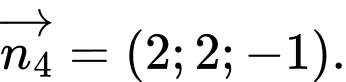
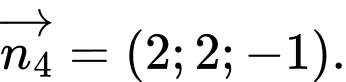
B, 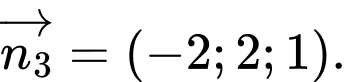
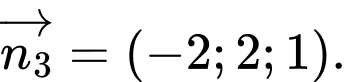
C, 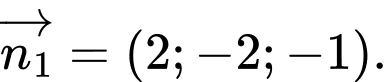
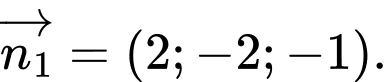
D, 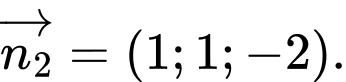
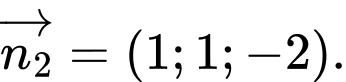
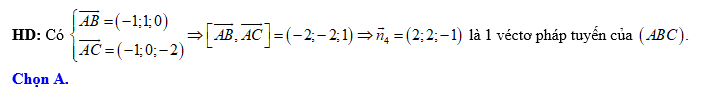 Đáp án: A
Đáp án: A
Câu 6 [810101]: Trong không gian 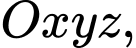 cho mặt phẳng
cho mặt phẳng 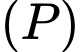 có phương trình là
có phương trình là 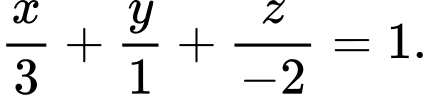 Véc tơ nào sau đây là một véc tơ pháp tuyến của
Véc tơ nào sau đây là một véc tơ pháp tuyến của 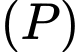 ?
?
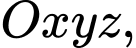 cho mặt phẳng
cho mặt phẳng 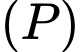 có phương trình là
có phương trình là 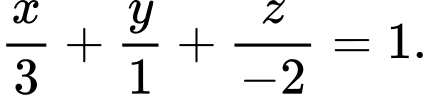 Véc tơ nào sau đây là một véc tơ pháp tuyến của
Véc tơ nào sau đây là một véc tơ pháp tuyến của 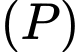 ?
? A, 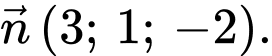
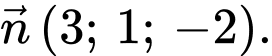
B, 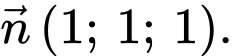
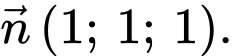
C, 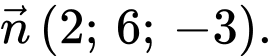
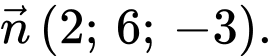
D, 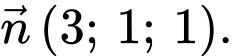
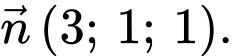
Chọn đáp án C.
Mặt phẳng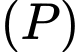 có phương trình là
có phương trình là 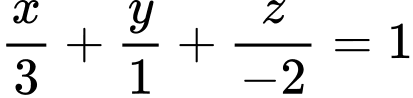
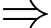 VTPT
VTPT 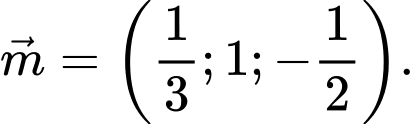
Vậy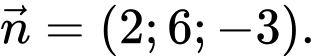 Đáp án: C
Đáp án: C
Mặt phẳng
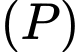 có phương trình là
có phương trình là 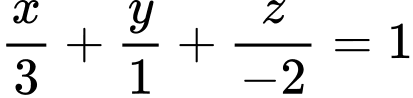
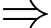 VTPT
VTPT 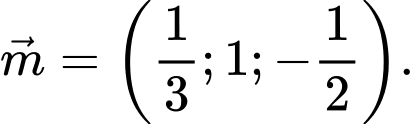
Vậy
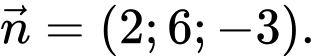 Đáp án: C
Đáp án: C
Câu 7 [899292]: Trong không gian tọa độ 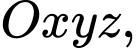 cho ba điểm
cho ba điểm 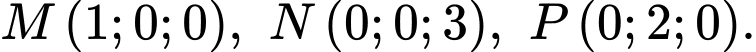 Lập phương trình mặt phẳng
Lập phương trình mặt phẳng 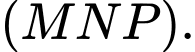
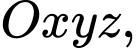 cho ba điểm
cho ba điểm 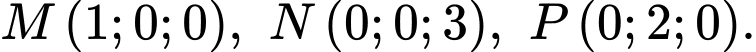 Lập phương trình mặt phẳng
Lập phương trình mặt phẳng 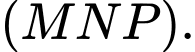
A, 

B, 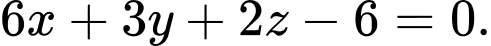
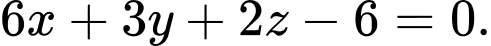
C, 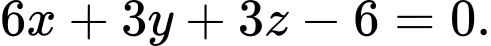
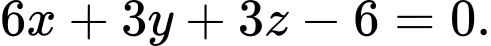
D, 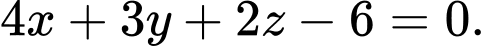
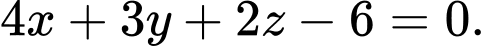
Chọn B.
Phương trình mặt phẳng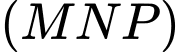 theo đoạn chắn là
theo đoạn chắn là 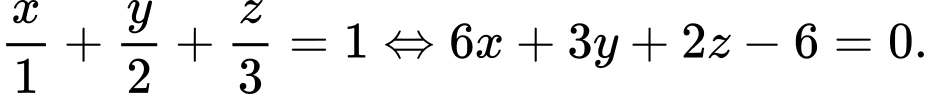 Đáp án: B
Đáp án: B
Phương trình mặt phẳng
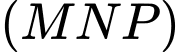 theo đoạn chắn là
theo đoạn chắn là 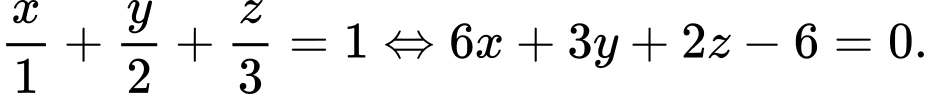 Đáp án: B
Đáp án: B
Câu 8 [53374]: Trong không gian với hệ trục tọa độ 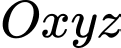 , cho
, cho 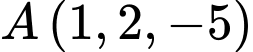 . Gọi
. Gọi 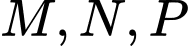 là hình chiếu của
là hình chiếu của 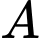 lên các trục
lên các trục 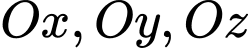 . Phương trình mặt phẳng
. Phương trình mặt phẳng 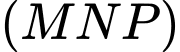 là
là
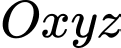 , cho
, cho 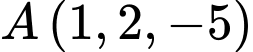 . Gọi
. Gọi 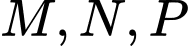 là hình chiếu của
là hình chiếu của 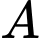 lên các trục
lên các trục 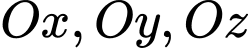 . Phương trình mặt phẳng
. Phương trình mặt phẳng 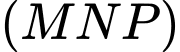 là
là A, 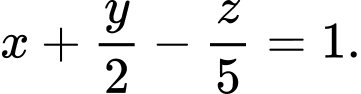
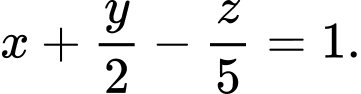
B, 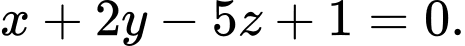
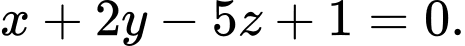
C, 

D, 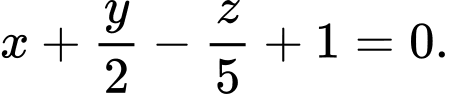
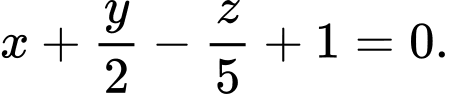
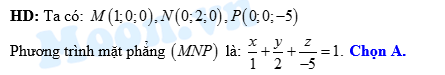 Đáp án: A
Đáp án: A
Câu 9 [53383]: Trong không gian với hệ trục tọa độ 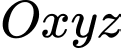 , cho điểm
, cho điểm 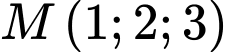 . Gọi
. Gọi 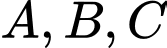 lần lượt là hình chiếu vuông góc của điểm
lần lượt là hình chiếu vuông góc của điểm 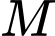 trên các trục
trên các trục 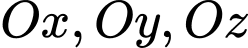 . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng 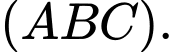
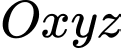 , cho điểm
, cho điểm 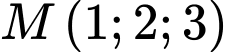 . Gọi
. Gọi 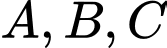 lần lượt là hình chiếu vuông góc của điểm
lần lượt là hình chiếu vuông góc của điểm 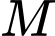 trên các trục
trên các trục 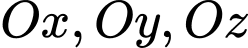 . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng 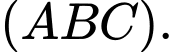
A, 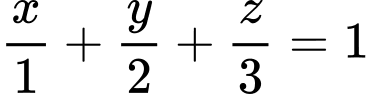 .
.
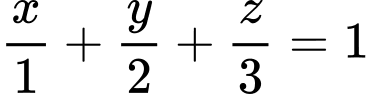 .
.B, 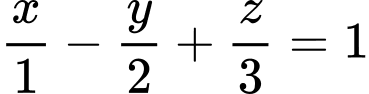 .
.
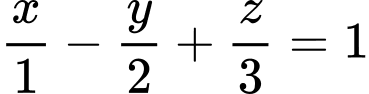 .
.C, 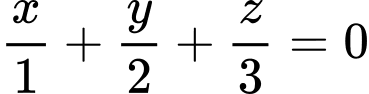 .
.
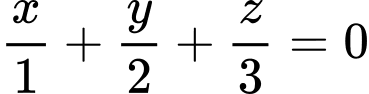 .
.D, 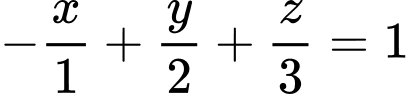 .
.
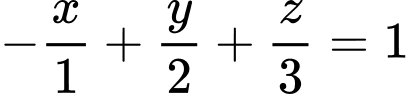 .
. Đáp án: A
Đáp án: A
Câu 10 [899293]: Trong không gian với hệ trục tọa độ 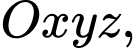 cho
cho 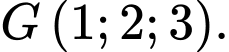 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 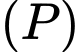 đi qua điểm
đi qua điểm  và cắt các trục tọa độ tại ba điểm phân biệt
và cắt các trục tọa độ tại ba điểm phân biệt 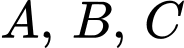 sao cho
sao cho  là trọng tâm tam giác
là trọng tâm tam giác 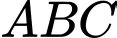 .
.
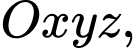 cho
cho 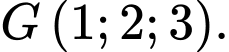 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 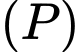 đi qua điểm
đi qua điểm  và cắt các trục tọa độ tại ba điểm phân biệt
và cắt các trục tọa độ tại ba điểm phân biệt 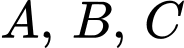 sao cho
sao cho  là trọng tâm tam giác
là trọng tâm tam giác 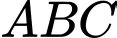 .
. A, 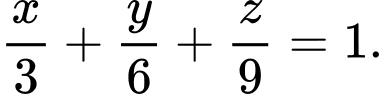
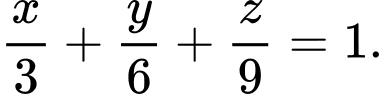
B, 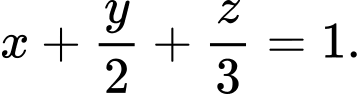
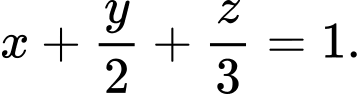
C, 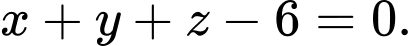
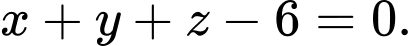
D, 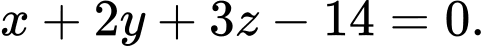
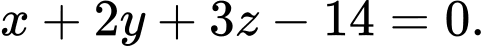
Gọi tọa độ các điểm 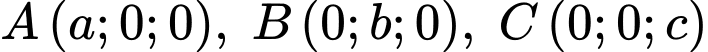 .
.
Phương trình đoạn chắn của mặt phẳng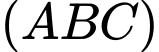 là:
là: 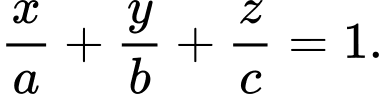
Do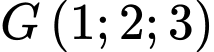 là trọng tâm tam giác ABC nên ta có:
là trọng tâm tam giác ABC nên ta có: 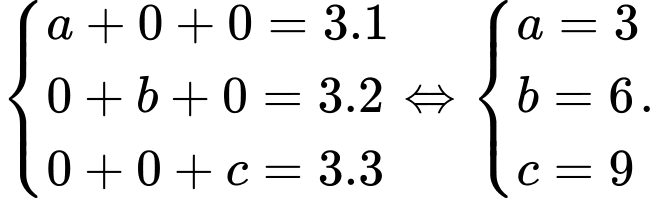
Do đó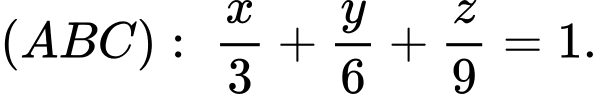 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
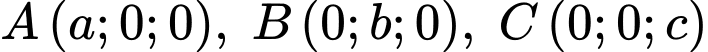 .
. Phương trình đoạn chắn của mặt phẳng
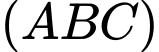 là:
là: 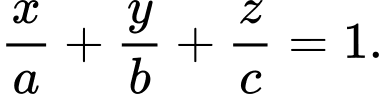
Do
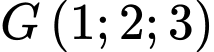 là trọng tâm tam giác ABC nên ta có:
là trọng tâm tam giác ABC nên ta có: 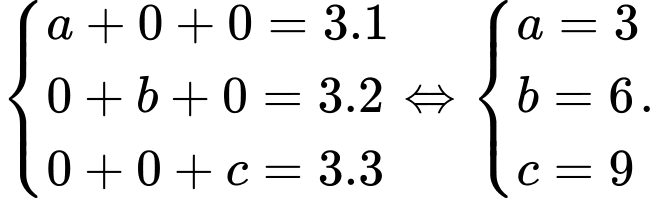
Do đó
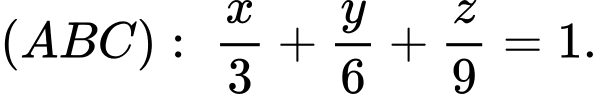 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 11 [53378]: Trong không gian 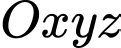 , cho điểm
, cho điểm 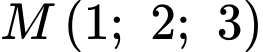 . Phương trình mặt phẳng
. Phương trình mặt phẳng 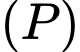 đi qua
đi qua 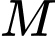 cắt các trục
cắt các trục 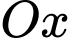 ,
, 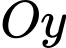 ,
,  lần lượt tại
lần lượt tại 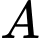 ,
, 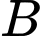 ,
,  sao cho
sao cho 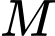 là trọng tâm tam giác
là trọng tâm tam giác 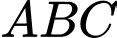 là
là
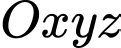 , cho điểm
, cho điểm 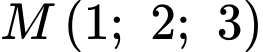 . Phương trình mặt phẳng
. Phương trình mặt phẳng 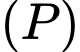 đi qua
đi qua 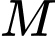 cắt các trục
cắt các trục 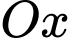 ,
, 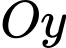 ,
,  lần lượt tại
lần lượt tại 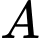 ,
, 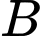 ,
,  sao cho
sao cho 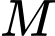 là trọng tâm tam giác
là trọng tâm tam giác 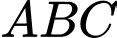 là
là A, 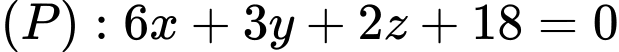 .
.
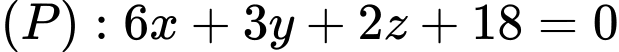 .
.B, 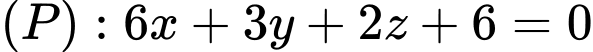 .
.
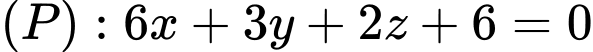 .
.C, 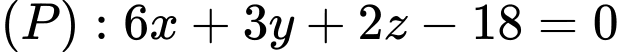 .
.
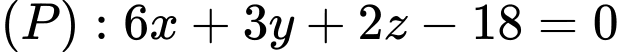 .
.D, 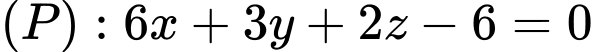 .
.
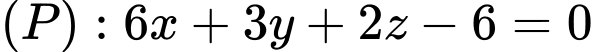 .
.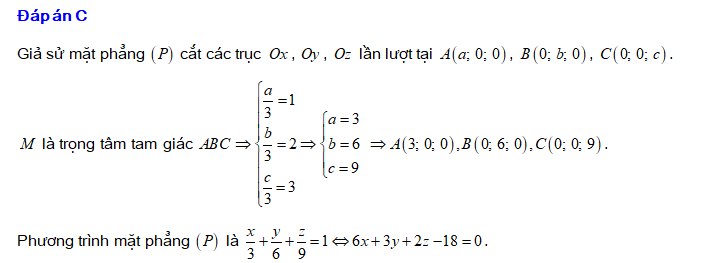 Đáp án: C
Đáp án: C
Câu 12 [899294]: Trong không gian với hệ tọa độ 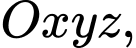 cho điểm
cho điểm 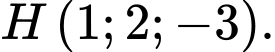 Tìm phương trình mặt phẳng
Tìm phương trình mặt phẳng  cắt các trục tọa độ
cắt các trục tọa độ 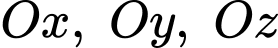 lần lượt tại 3 điểm
lần lượt tại 3 điểm 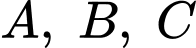 sao cho
sao cho 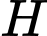 là trực tâm tam giác
là trực tâm tam giác 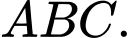
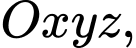 cho điểm
cho điểm 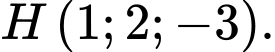 Tìm phương trình mặt phẳng
Tìm phương trình mặt phẳng  cắt các trục tọa độ
cắt các trục tọa độ 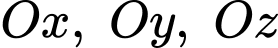 lần lượt tại 3 điểm
lần lượt tại 3 điểm 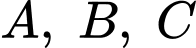 sao cho
sao cho 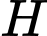 là trực tâm tam giác
là trực tâm tam giác 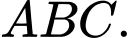
A, 

B, 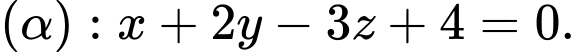
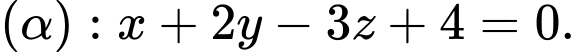
C, 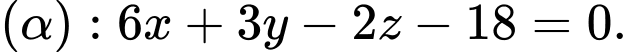
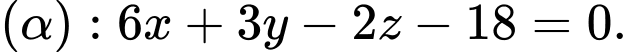
D, 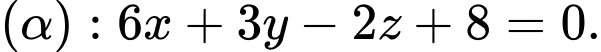
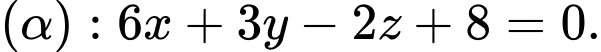
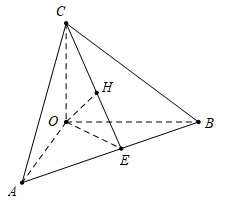
Với ví dụ này ta nên chứng minh tính chất
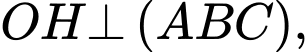 khi đó mặt phẳng
khi đó mặt phẳng  đi qua điểm
đi qua điểm 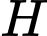 và nhận
và nhận 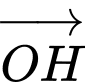 là một vectơ pháp tuyến. Do
là một vectơ pháp tuyến. Do 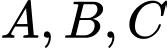 lần lượt thuộc các trục
lần lượt thuộc các trục 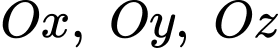 nên ta có:
nên ta có: 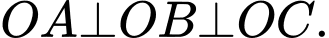
Khi đó
 nên
nên 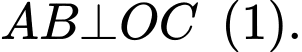
Do
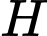 là trực tâm tam giác
là trực tâm tam giác 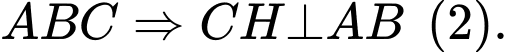
Từ
 và
và 
Tương tự ta có:
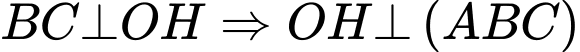
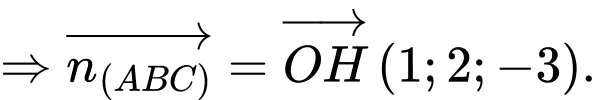
Phương trình mặt phẳng
 qua
qua 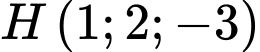 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 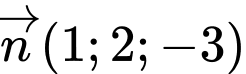 là
là 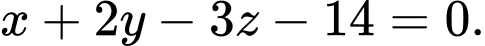 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 13 [53361]: Trong không gian 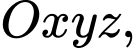 phương trình mặt phẳng qua ba điểm
phương trình mặt phẳng qua ba điểm 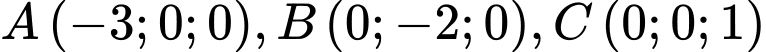 được viết dưới dạng
được viết dưới dạng 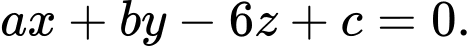 Giá trị của
Giá trị của 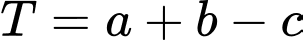 là
là
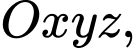 phương trình mặt phẳng qua ba điểm
phương trình mặt phẳng qua ba điểm 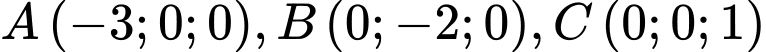 được viết dưới dạng
được viết dưới dạng 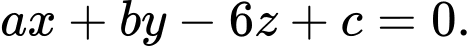 Giá trị của
Giá trị của 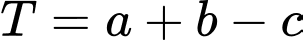 là
là
Phương trình mặt phẳng (ABCP) : 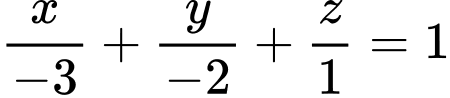
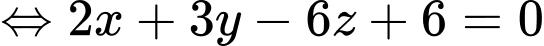
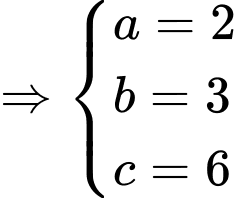
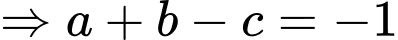 . Đáp án: D
. Đáp án: D
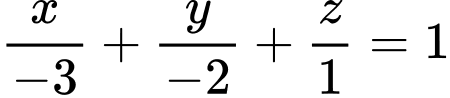
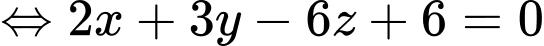
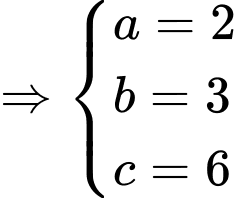
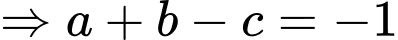 . Đáp án: D
. Đáp án: D
Câu 14 [163888]: Trong không gian với hệ trục toạ độ 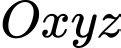 (đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí
(đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí 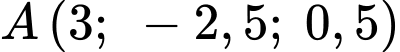 và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí 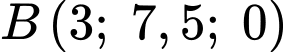 trên đường băng. Có một lớp mây được mô phỏng bởi một mặt phẳng
trên đường băng. Có một lớp mây được mô phỏng bởi một mặt phẳng  đi qua ba điểm
đi qua ba điểm 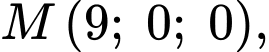
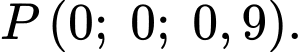 Độ cao của máy bay khi xuyên qua đám mây để hạ cánh là bao nhiêu km?
Độ cao của máy bay khi xuyên qua đám mây để hạ cánh là bao nhiêu km?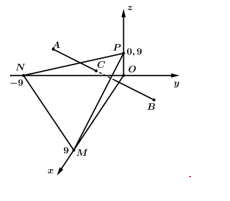
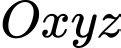 (đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí
(đơn vị trên mỗi trục toạ độ là kilômét), một máy bay đang ở vị trí 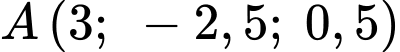 và sẽ hạ cánh ở vị trí
và sẽ hạ cánh ở vị trí 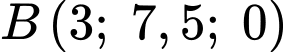 trên đường băng. Có một lớp mây được mô phỏng bởi một mặt phẳng
trên đường băng. Có một lớp mây được mô phỏng bởi một mặt phẳng  đi qua ba điểm
đi qua ba điểm 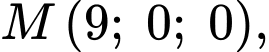
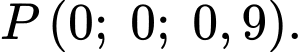 Độ cao của máy bay khi xuyên qua đám mây để hạ cánh là bao nhiêu km?
Độ cao của máy bay khi xuyên qua đám mây để hạ cánh là bao nhiêu km?
Giả sử điểm 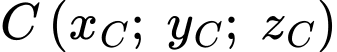 là vị trí mà máy bay xuyên qua đám mây để hạ cánh, suy ra
là vị trí mà máy bay xuyên qua đám mây để hạ cánh, suy ra 
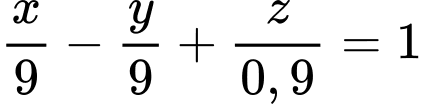
 .
. 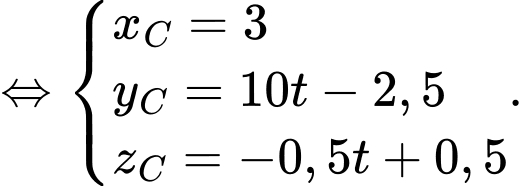
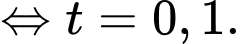 Suy ra
Suy ra 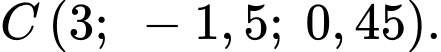
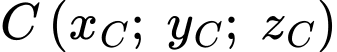 là vị trí mà máy bay xuyên qua đám mây để hạ cánh, suy ra
là vị trí mà máy bay xuyên qua đám mây để hạ cánh, suy ra 
Áp dụng phương trình mặt phẳng theo đoạn chắn, ta thấy mặt phẳng  có phương trình là:
có phương trình là:
 có phương trình là:
có phương trình là: 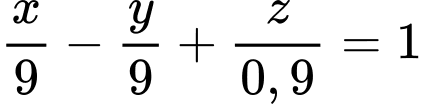
 .
. Suy ra 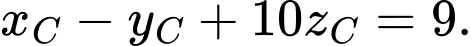
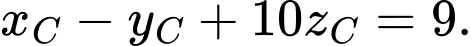
Mặt khác, vì 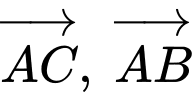 là hai vectơ cùng hướng nên tồn tại số thực
là hai vectơ cùng hướng nên tồn tại số thực  sao cho
sao cho 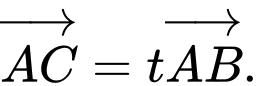
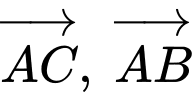 là hai vectơ cùng hướng nên tồn tại số thực
là hai vectơ cùng hướng nên tồn tại số thực  sao cho
sao cho 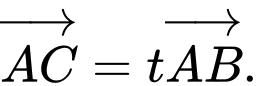
Do 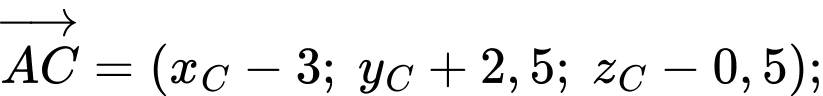
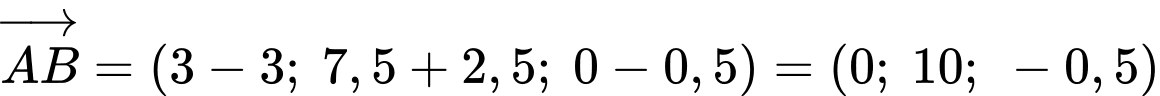
nên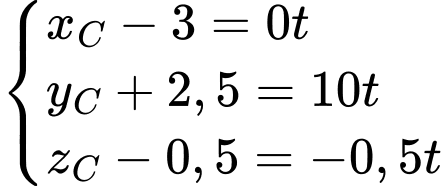
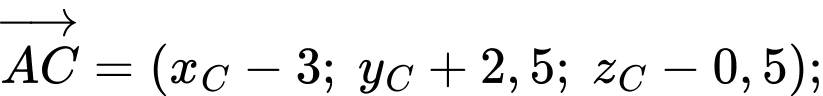
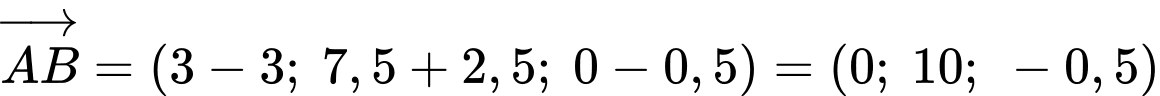
nên
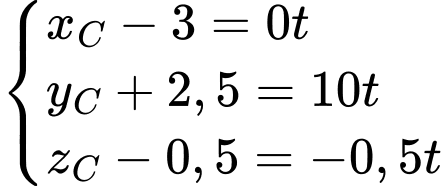
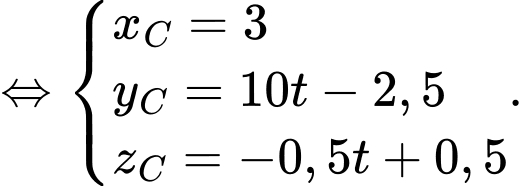
Vì 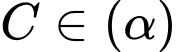 nên
nên 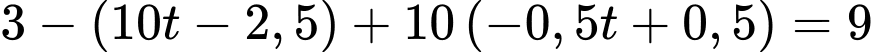
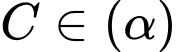 nên
nên 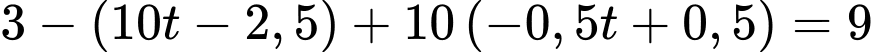
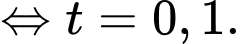 Suy ra
Suy ra 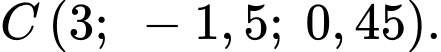
Vậy tại vị trí 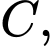 độ cao máy bay là
độ cao máy bay là 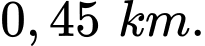
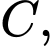 độ cao máy bay là
độ cao máy bay là 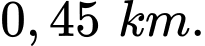
Câu 15 [398966]: Trong không gian tọa độ phương trình mặt phẳng chứa điểm 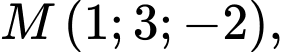 cắt các tia
cắt các tia 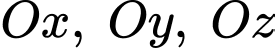 lần lượt tại
lần lượt tại 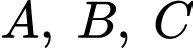 sao cho
sao cho 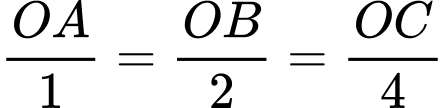 là
là 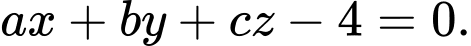 Tính
Tính 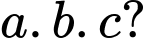
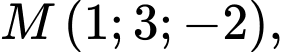 cắt các tia
cắt các tia 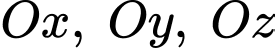 lần lượt tại
lần lượt tại 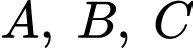 sao cho
sao cho 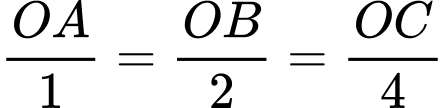 là
là 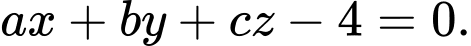 Tính
Tính 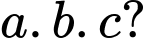
Phương trình mặt chắn cắt tia 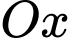 tại
tại 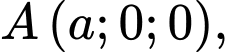 cắt tia
cắt tia 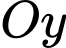 tại
tại 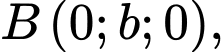 cắt tia
cắt tia  tại
tại 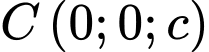 có dạng là
có dạng là 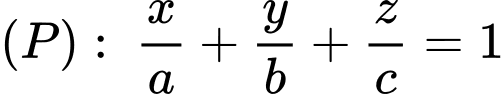

Theo bài ra ta có: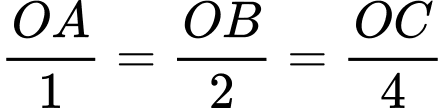
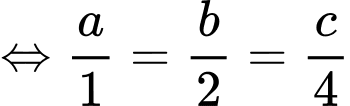
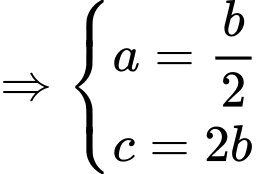
Vì
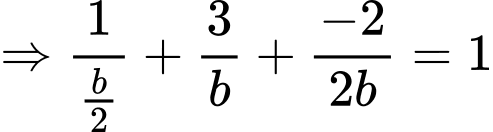
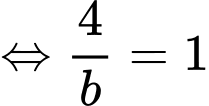
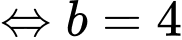
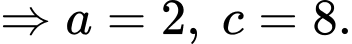
Vậy phường trình mặt phẳng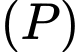 là
là 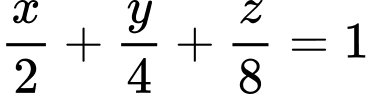 hay
hay 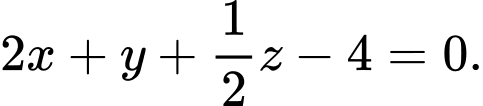
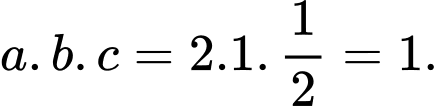
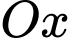 tại
tại 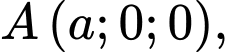 cắt tia
cắt tia 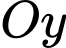 tại
tại 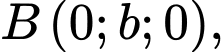 cắt tia
cắt tia  tại
tại 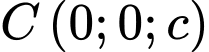 có dạng là
có dạng là 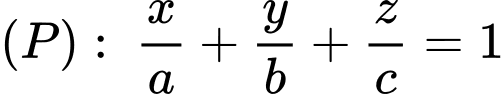

Theo bài ra ta có:
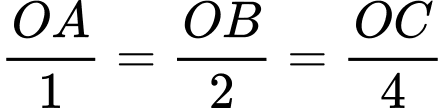
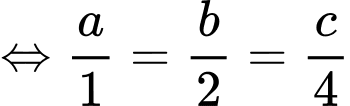
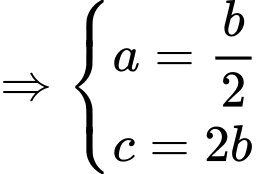
Vì

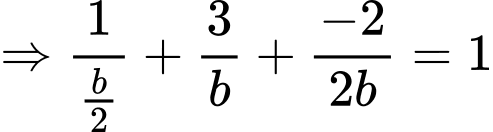
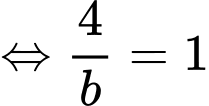
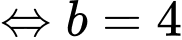
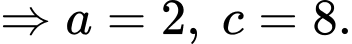
Vậy phường trình mặt phẳng
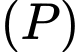 là
là 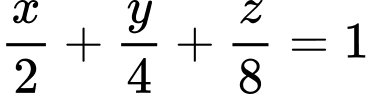 hay
hay 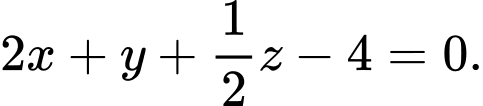
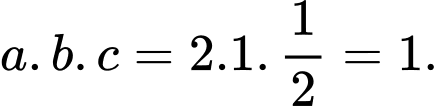
Câu 16 [398967]: Trong không gian với hệ tọa độ 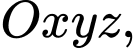 gọi
gọi 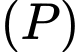 là mặt phẳng đi qua
là mặt phẳng đi qua 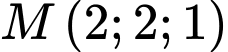 và cắt các tia
và cắt các tia 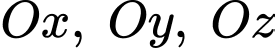 lần lượt tại
lần lượt tại 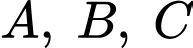 sao cho
sao cho 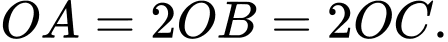
Phương trình mặt phẳng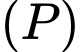 là
là 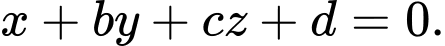 Tính
Tính 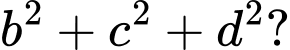
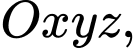 gọi
gọi 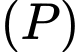 là mặt phẳng đi qua
là mặt phẳng đi qua 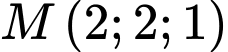 và cắt các tia
và cắt các tia 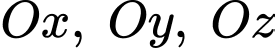 lần lượt tại
lần lượt tại 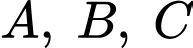 sao cho
sao cho 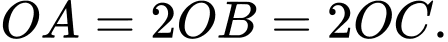
Phương trình mặt phẳng
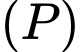 là
là 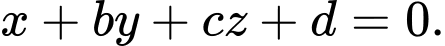 Tính
Tính 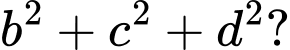
Điền đáp án: 72.
Gọi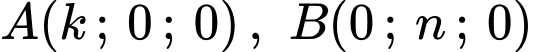 và
và 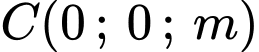 với
với 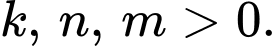
Phương trình mặt phẳng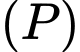 là
là 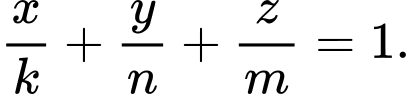
Mà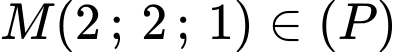 suy ra
suy ra 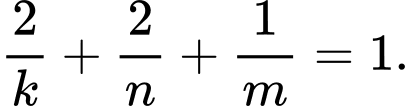
Mà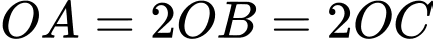
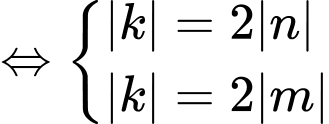
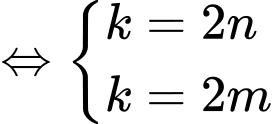
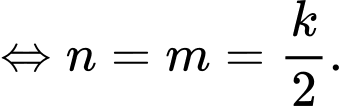
Khi đó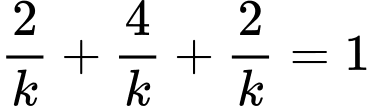
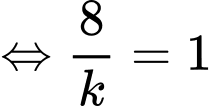
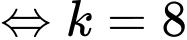
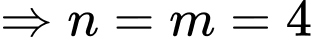
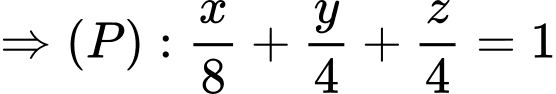
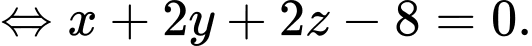
Vậy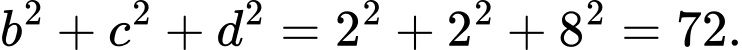
Gọi
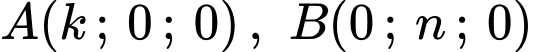 và
và 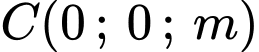 với
với 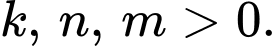
Phương trình mặt phẳng
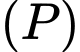 là
là 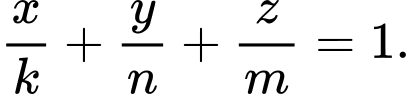
Mà
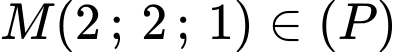 suy ra
suy ra 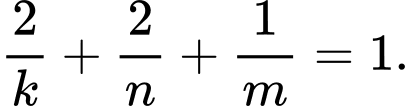
Mà
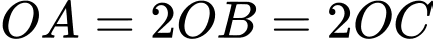
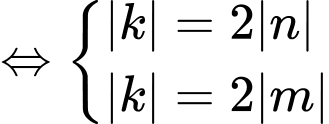
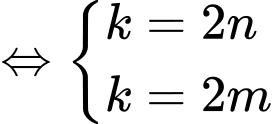
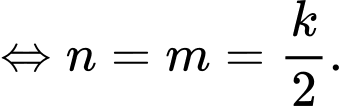
Khi đó
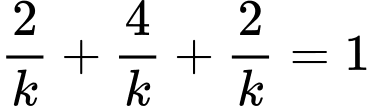
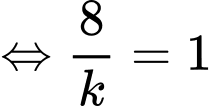
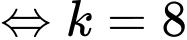
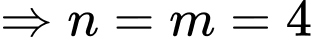
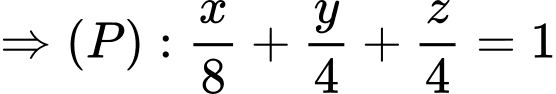
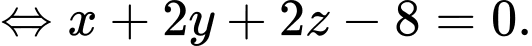
Vậy
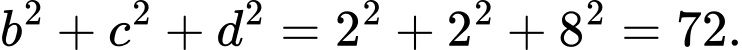
Câu 17 [398968]: Trong không gian với hệ tọa độ 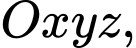 mặt phẳng
mặt phẳng  chắn các trục
chắn các trục 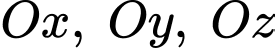 lần lượt tại
lần lượt tại 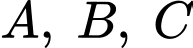 sao cho
sao cho 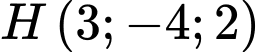 là trực tâm của tam giác
là trực tâm của tam giác 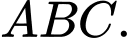
Phương trình mặt phẳng có dạng
có dạng 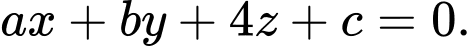 Tính
Tính 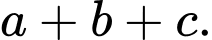
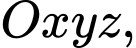 mặt phẳng
mặt phẳng  chắn các trục
chắn các trục 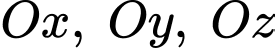 lần lượt tại
lần lượt tại 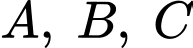 sao cho
sao cho 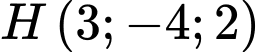 là trực tâm của tam giác
là trực tâm của tam giác 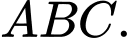
Phương trình mặt phẳng
 có dạng
có dạng 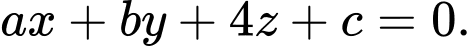 Tính
Tính 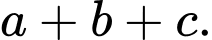
Điền đáp án: 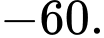

Gọi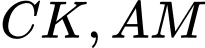 là hai đường cao của tam giác
là hai đường cao của tam giác 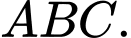
Suy ra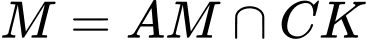
Ta có: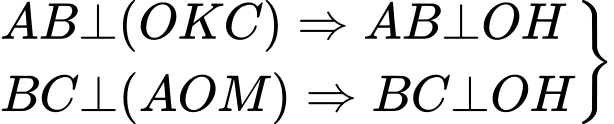
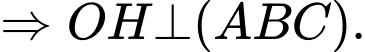
Mặt phẳng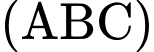 đi qua điểm H và nhận
đi qua điểm H và nhận  làm một VTPT.
làm một VTPT.
Nên mặt phẳng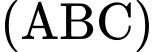 có phương trình:
có phương trình: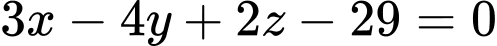
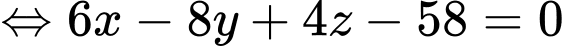
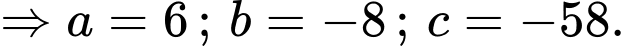


Gọi
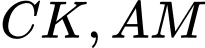 là hai đường cao của tam giác
là hai đường cao của tam giác 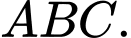
Suy ra
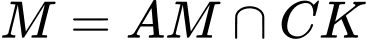
Ta có:
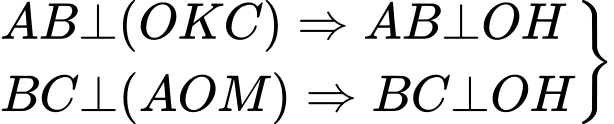
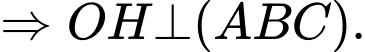
Mặt phẳng
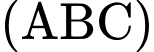 đi qua điểm H và nhận
đi qua điểm H và nhận  làm một VTPT.
làm một VTPT.Nên mặt phẳng
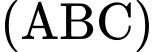 có phương trình:
có phương trình: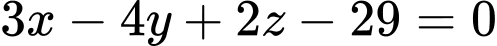
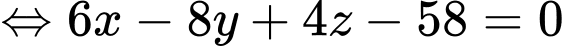
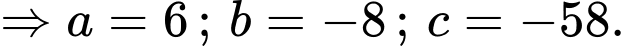

Câu 18 [398970]: Trong không gian với hệ tọa độ 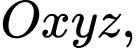 mặt phẳng
mặt phẳng  đi qua điểm
đi qua điểm  và chắn trên tia
và chắn trên tia  một đoạn dài gấp đôi các đoạn chắn trên các tia
một đoạn dài gấp đôi các đoạn chắn trên các tia 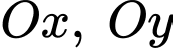 có phương trình là
có phương trình là 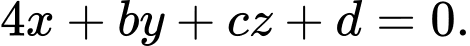 Tính
Tính 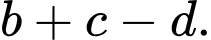
Đáp án:……………………………….
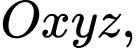 mặt phẳng
mặt phẳng  đi qua điểm
đi qua điểm  và chắn trên tia
và chắn trên tia  một đoạn dài gấp đôi các đoạn chắn trên các tia
một đoạn dài gấp đôi các đoạn chắn trên các tia 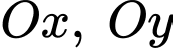 có phương trình là
có phương trình là 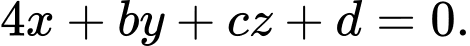 Tính
Tính 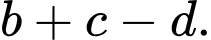
Đáp án:……………………………….
HD: Giả sử mặt phẳng  cắt các tia
cắt các tia 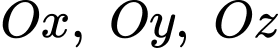 lần lượt tại các điểm
lần lượt tại các điểm 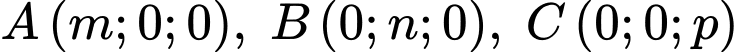 thì phương trình mặt phẳng
thì phương trình mặt phẳng  là:
là: 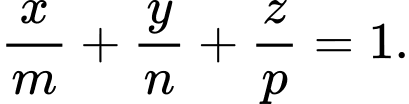
Chú ý rằng cắt các tia
cắt các tia 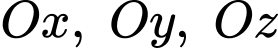 nên ta có điều kiện
nên ta có điều kiện 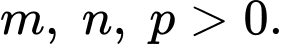
Theo bài ra ta có: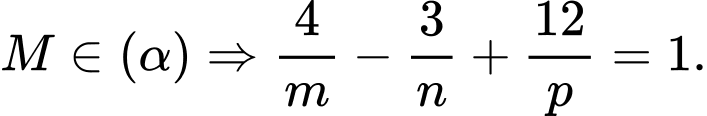
Mặt khác theo giả thiết ta suy ra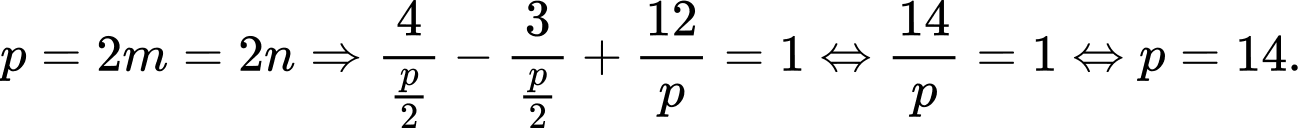
Do đó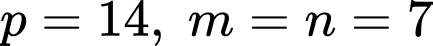
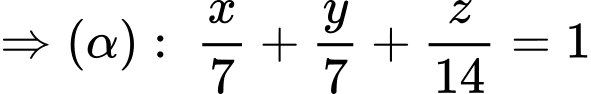
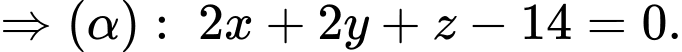
Hay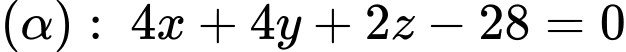
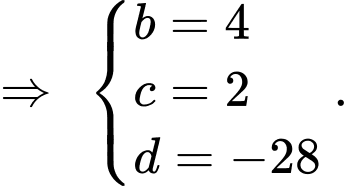
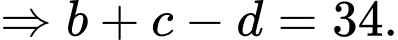
 cắt các tia
cắt các tia 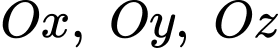 lần lượt tại các điểm
lần lượt tại các điểm 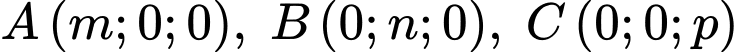 thì phương trình mặt phẳng
thì phương trình mặt phẳng  là:
là: 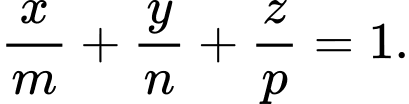
Chú ý rằng
 cắt các tia
cắt các tia 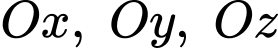 nên ta có điều kiện
nên ta có điều kiện 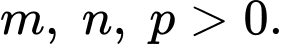
Theo bài ra ta có:
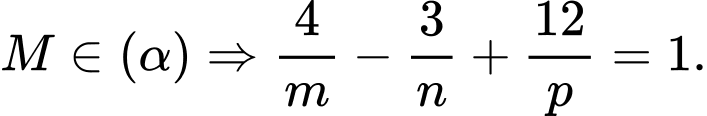
Mặt khác theo giả thiết ta suy ra
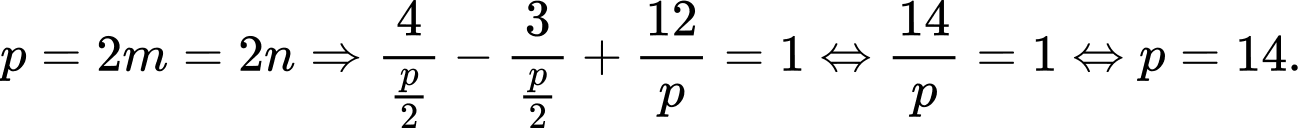
Do đó
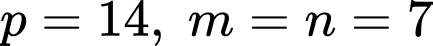
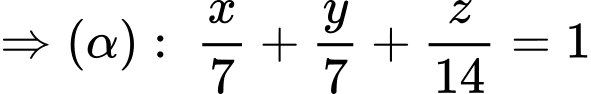
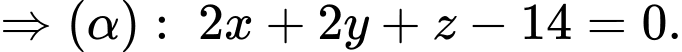
Hay