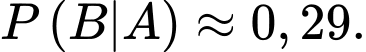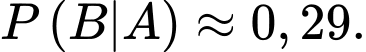Đáp án Bài tập tự luyện đề 2
Câu 1 [378752]: Trong số 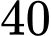 học sinh lớp 12A, có
học sinh lớp 12A, có 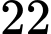 em đăng kí thi ngành Kinh tế,
em đăng kí thi ngành Kinh tế, 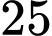 em đăng kí thi ngành Luật,
em đăng kí thi ngành Luật, 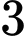 em không đăng kí thi cả hai ngành này. Chọn ngẫu nhiên một học sinh, biết rằng em đó đăng kí thi ngành luật. Xác suất để em đó đăng kí thi ngành Kinh tế là
em không đăng kí thi cả hai ngành này. Chọn ngẫu nhiên một học sinh, biết rằng em đó đăng kí thi ngành luật. Xác suất để em đó đăng kí thi ngành Kinh tế là
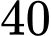 học sinh lớp 12A, có
học sinh lớp 12A, có 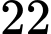 em đăng kí thi ngành Kinh tế,
em đăng kí thi ngành Kinh tế, 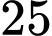 em đăng kí thi ngành Luật,
em đăng kí thi ngành Luật, 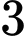 em không đăng kí thi cả hai ngành này. Chọn ngẫu nhiên một học sinh, biết rằng em đó đăng kí thi ngành luật. Xác suất để em đó đăng kí thi ngành Kinh tế là
em không đăng kí thi cả hai ngành này. Chọn ngẫu nhiên một học sinh, biết rằng em đó đăng kí thi ngành luật. Xác suất để em đó đăng kí thi ngành Kinh tế là A, 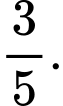
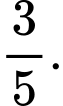
B, 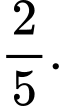
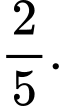
C, 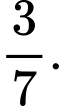
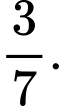
D, 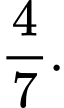
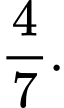
Số em học sinh đăng kí cả luật và kinh tế là: 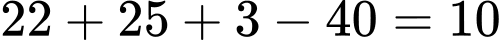
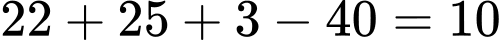
Gọi A là biến cố: em đó đăng kí ngành kinh tế
B là biến cố: Em đó đăng kí ngành luật
Ta có: 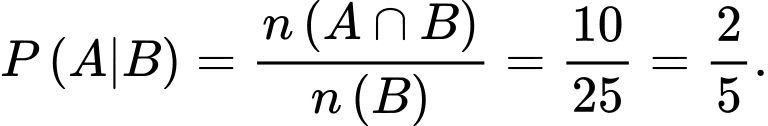 Chọn B.
Chọn B.
Đáp án: B 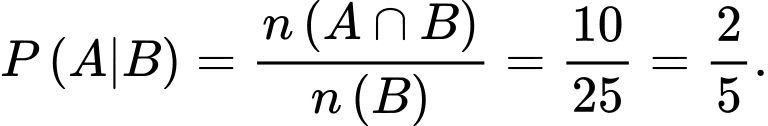 Chọn B.
Chọn B.
Câu 2 [360668]: Một doanh nghiệp trước khi xuất khẩu áo sơ mi phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 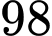 % sản phẩm làm ra qua được lần kiểm tra thứ nhất và
% sản phẩm làm ra qua được lần kiểm tra thứ nhất và 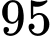 % sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.
% sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.
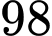 % sản phẩm làm ra qua được lần kiểm tra thứ nhất và
% sản phẩm làm ra qua được lần kiểm tra thứ nhất và 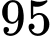 % sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.
% sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu. A, 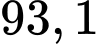
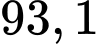
B, 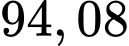
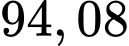
C, 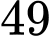
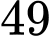
D, 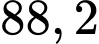
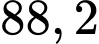
Gọi A là biến cố: “chiếc áo sơ mi trong lô hàng S được chọn qua được lần kiểm tra thứ nhất”, B là biến cố: “chiếc áo sơ mi trong lô hàng S được chọn qua được lần kiểm tra thứ hai”, C là biến cố: “chiếc áo sơ mi được chọn đủ tiêu chuẩn xuất khẩu”.
Theo bài ra ta có: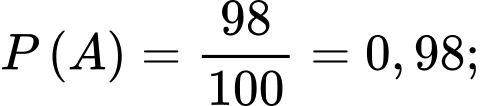
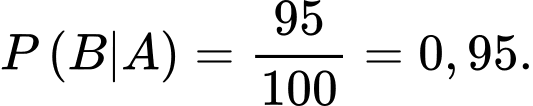
Một chiếc áo đủ tiêu chuẩn xuất khẩu khi cả hai lần kiểm tra chất lượng sản phẩm đều đạt. Xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là:
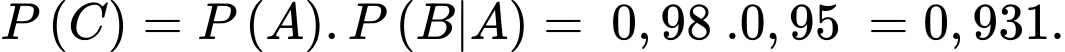
Chọn đáp án A. Đáp án: A
Theo bài ra ta có:
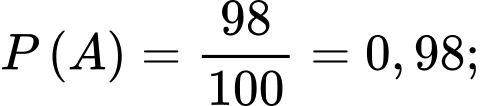
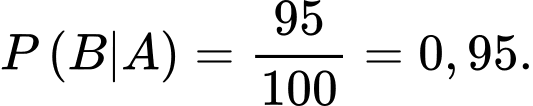
Một chiếc áo đủ tiêu chuẩn xuất khẩu khi cả hai lần kiểm tra chất lượng sản phẩm đều đạt. Xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là:
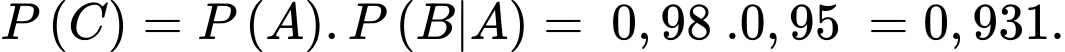
Chọn đáp án A. Đáp án: A
Câu 3 [378730]: Bạn An có một túi gồm một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 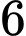 chiếc kẹo
sô cô la đen, còn lại
chiếc kẹo
sô cô la đen, còn lại 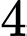 chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên
chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên 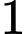 chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp
chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp 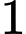 chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được
chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được 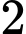 chiếc kẹo sô cô la đen là
chiếc kẹo sô cô la đen là
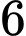 chiếc kẹo
sô cô la đen, còn lại
chiếc kẹo
sô cô la đen, còn lại 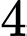 chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên
chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên 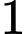 chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp
chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp 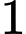 chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được
chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được 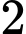 chiếc kẹo sô cô la đen là
chiếc kẹo sô cô la đen là A, 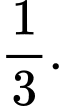
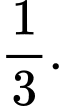
B, 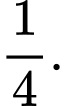
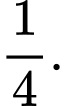
C, 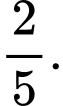
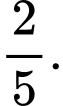
D, 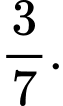
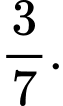
Gọi 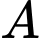 là biến cố chiếc kéo thứ nhất là sô cô la đen,
là biến cố chiếc kéo thứ nhất là sô cô la đen, 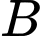 là biến cố chiếc kéo thứ nhất là sô cô la đen. Khi đó xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là
là biến cố chiếc kéo thứ nhất là sô cô la đen. Khi đó xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là 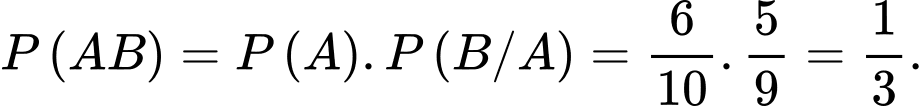 Đáp án: A
Đáp án: A
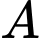 là biến cố chiếc kéo thứ nhất là sô cô la đen,
là biến cố chiếc kéo thứ nhất là sô cô la đen, 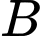 là biến cố chiếc kéo thứ nhất là sô cô la đen. Khi đó xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là
là biến cố chiếc kéo thứ nhất là sô cô la đen. Khi đó xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là 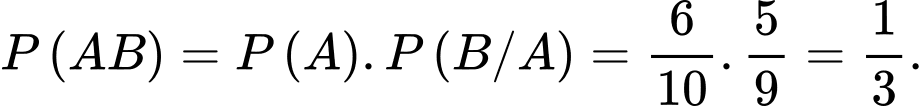
Chọn A.
Câu 4 [135794]: [Trích SGK Cánh Diều]: Có hai linh kiện điện tử, xác suất để mỗi linh kiện hỏng trong một thời điểm bất kì lần lượt là: 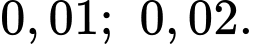 Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.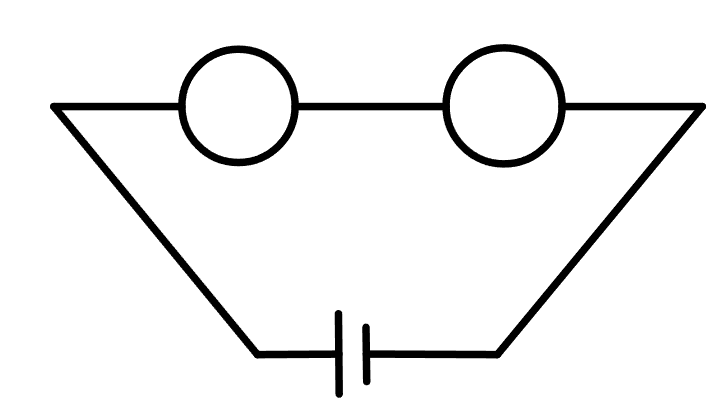
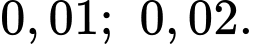 Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
A, 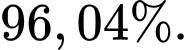
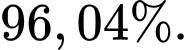
B, 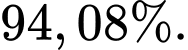
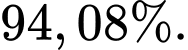
C, 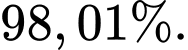
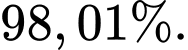
D, 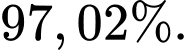
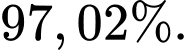
Xác suất để trong mạch điện có dòng điện chạy qua là 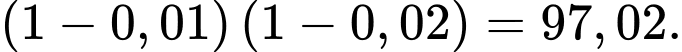 Chọn D. Đáp án: D
Chọn D. Đáp án: D
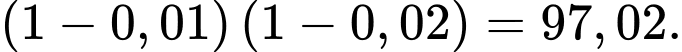 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 5 [135795]: [Trích SGK Cánh Diều]: Có hai linh kiện điện tử, xác suất để mỗi linh kiện hỏng trong một thời điểm bất kì lần lượt là: 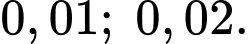 Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.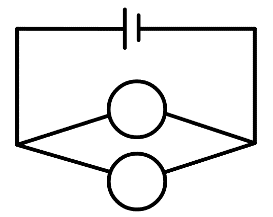
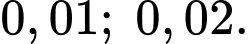 Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
Hai linh kiện đó được lắp vào một mạch điện theo sơ đồ ở hình vẽ. Hãy tính xác suất để trong mạch điện có dòng điện chạy qua.
A, 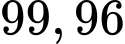
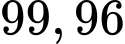
B, 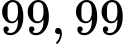
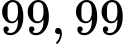
C, 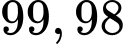
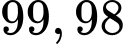
D, 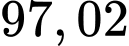
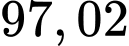
Xác suất để trong mạch điện có dòng điện chạy qua là 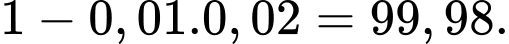 Chọn C. Đáp án: C
Chọn C. Đáp án: C
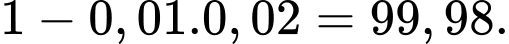 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 6 [135800]: Trong một trò chơi rút thăm trúng thưởng, có 10 lá thăm trong đó có 3 lá thăm có thưởng và 7 lá thăm không có thưởng. Người chơi rút ngẫu nhiên lần lượt hai lá thăm theo phương thức không hoàn lại. Biết rằng trong lần rút đầu tiên, người chơi rút được lá thăm không có thưởng. Bốn bạn học sinh đã giải thích về xác xuất người chơi rút được lá thăm có thưởng trong lần rút thăm thứ hai như sau:
• Bạn Mai: “Vì có 3 lá thăm có thưởng trong 10 lá thăm nên xác suất người chơi rút được lá thăm có thưởng trong lần rút thứ hai là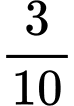 ”
”
• Bạn Ngọc: “Vì lần đầu tiên người chơi rút được lá thăm không có thưởng nên số lá thăm còn lại là 9 trong đó có 3 lá thăm có thưởng nên xác suất người chơi rút được lá thăm có thưởng trong lần rút thứ hai là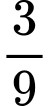 ”
”
• Bạn Phong: “Vì người chơi rút hai lá thăm trong đó có một lá thăm đầu không có thưởng và một lá thăm thứ hai có thưởng nên xác suất để rút được lá thăm thứ hai có thưởng là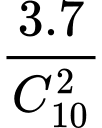 ”
”
• Bạn Quang: “Vì xác suất để rút được lá thăm không có thưởng là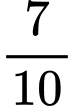 và xác suất rút được lá thăm có thưởng là
và xác suất rút được lá thăm có thưởng là 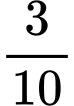 nên xác suất để lần thứ hai rút được lá thăm có thưởng khi biết lần đầu rút được lá thăm không có thưởng là
nên xác suất để lần thứ hai rút được lá thăm có thưởng khi biết lần đầu rút được lá thăm không có thưởng là 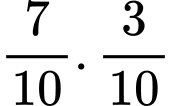 ”.
”.
• Bạn Mai: “Vì có 3 lá thăm có thưởng trong 10 lá thăm nên xác suất người chơi rút được lá thăm có thưởng trong lần rút thứ hai là
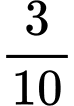 ”
” • Bạn Ngọc: “Vì lần đầu tiên người chơi rút được lá thăm không có thưởng nên số lá thăm còn lại là 9 trong đó có 3 lá thăm có thưởng nên xác suất người chơi rút được lá thăm có thưởng trong lần rút thứ hai là
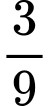 ”
” • Bạn Phong: “Vì người chơi rút hai lá thăm trong đó có một lá thăm đầu không có thưởng và một lá thăm thứ hai có thưởng nên xác suất để rút được lá thăm thứ hai có thưởng là
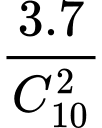 ”
” • Bạn Quang: “Vì xác suất để rút được lá thăm không có thưởng là
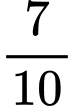 và xác suất rút được lá thăm có thưởng là
và xác suất rút được lá thăm có thưởng là 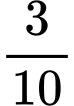 nên xác suất để lần thứ hai rút được lá thăm có thưởng khi biết lần đầu rút được lá thăm không có thưởng là
nên xác suất để lần thứ hai rút được lá thăm có thưởng khi biết lần đầu rút được lá thăm không có thưởng là 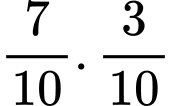 ”.
”. Trong bốn bạn trên, bạn nào giải thích đúng?
A, Bạn Mai.
B, Bạn Ngọc.
C, Bạn Phong.
D, Bạn Quang.
Vì lần đầu tiên người chơi rút được lá thăm không có thưởng nên số lá thăm còn lại là 9 trong đó có 3 lá thăm có thưởng nên xác suất người chơi rút được lá thăm có thưởng trong lần rút thứ hai là 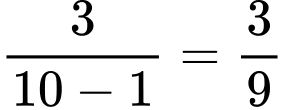 ” Đáp án: B
” Đáp án: B
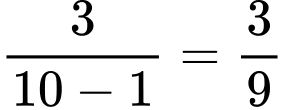 ” Đáp án: B
” Đáp án: B
Câu 7 [145405]: Trong 1 khu phố, tỷ lệ người mắc bệnh tim là 6%; mắc bệnh phổi là 8% và mắc cả hai bệnh là 5%. Chọn ngẫu nhiên 1 người trong khu phố đó. Tính xác suất để người đó không mắc cả 2 bệnh tim và bệnh phổi.
A, 92%.
B, 95%.
C, 93%.
D, 91%.
Gọi A là biến cố: Người đó mắc bệnh tim
B là biến cố: Người đó mắc bệnh phổi
Ta có: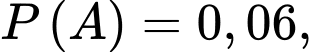
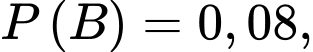
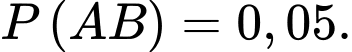
Suy ra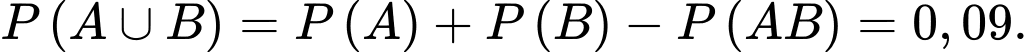
Do đó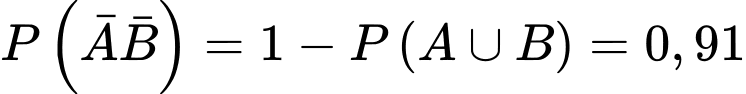
Chọn D. Đáp án: D
B là biến cố: Người đó mắc bệnh phổi
Ta có:
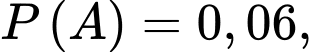
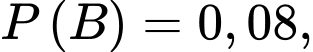
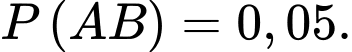
Suy ra
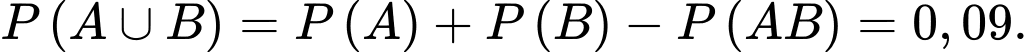
Do đó
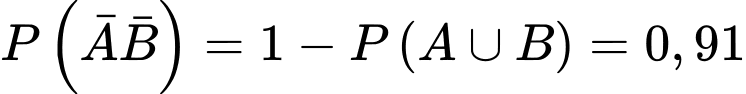
Chọn D. Đáp án: D
Câu 8 [134769]: Cho 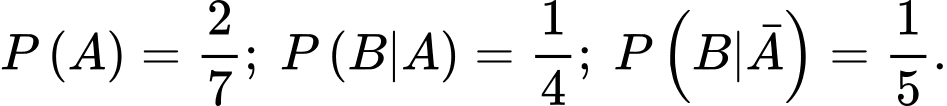 Giá trị
Giá trị 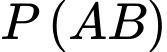 là
là
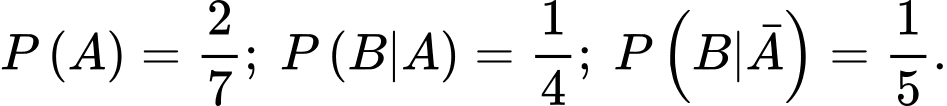 Giá trị
Giá trị 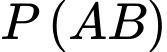 là
là A, 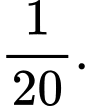
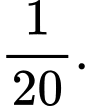
B, 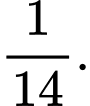
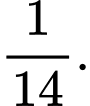
C, 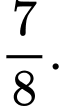
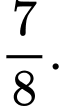
D, 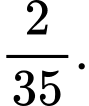
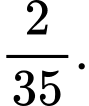
Ta có: 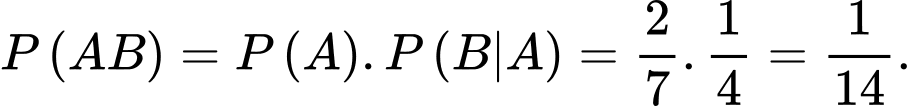 Chọn B. Đáp án: B
Chọn B. Đáp án: B
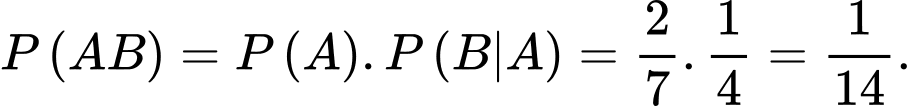 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 9 [134800]: Cho hai biến cố 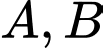 có có
có có 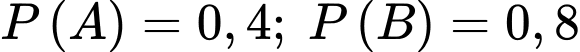 và
và 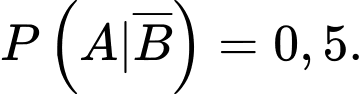 Tính
Tính 
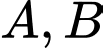 có có
có có 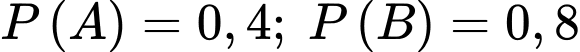 và
và 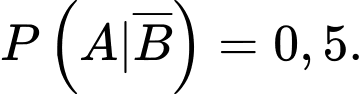 Tính
Tính 
A, 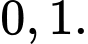
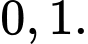
B, 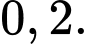
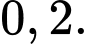
C, 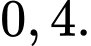
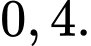
D, 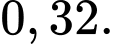
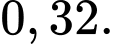
Ta có: 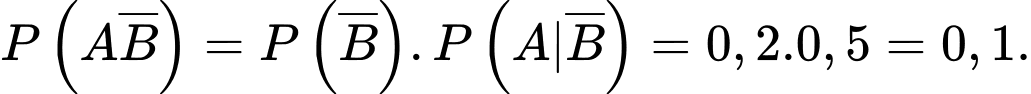 Chọn A. Đáp án: A
Chọn A. Đáp án: A
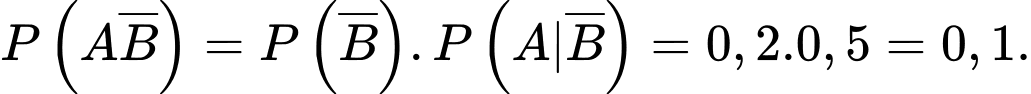 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 10 [134803]: Cho 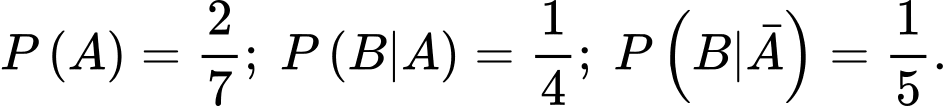 Giá trị
Giá trị  là
là
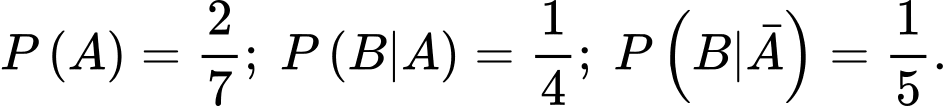 Giá trị
Giá trị  là
là A, 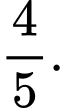
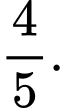
B, 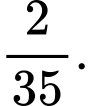
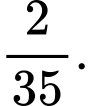
C, 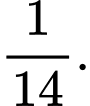
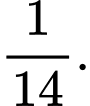
D, 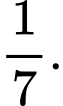
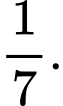
Chọn đáp án D.
Ta có: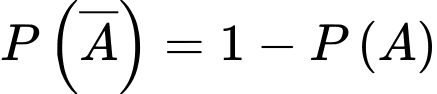
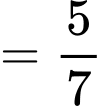
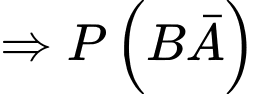
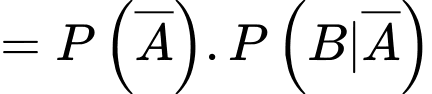
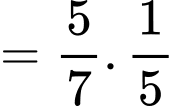
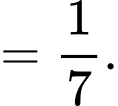 Đáp án: D
Đáp án: D
Ta có:
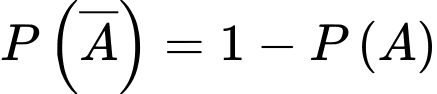
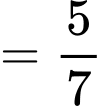
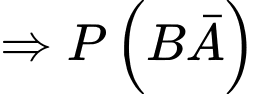
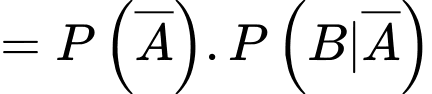
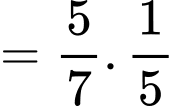
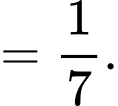 Đáp án: D
Đáp án: D
Câu 11 [134807]: Cho hai biến cố 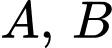 sao cho
sao cho 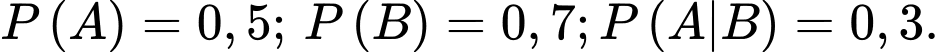 Tính
Tính 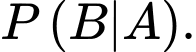
 sao cho
sao cho 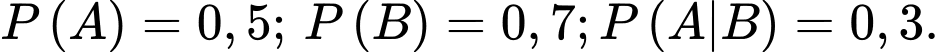 Tính
Tính 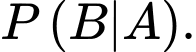
A, 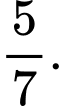
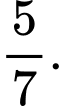
B, 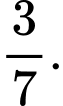
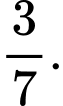
C, 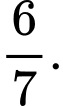
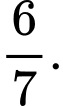
D, 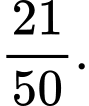
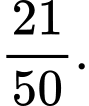
Chọn đáp án D.
Ta có: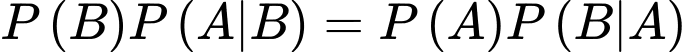
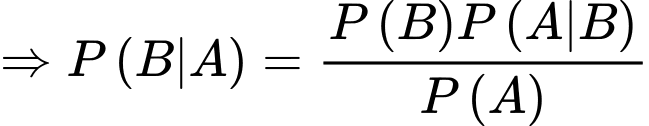
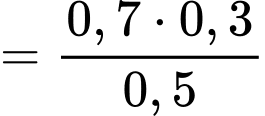
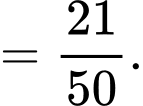 Đáp án: D
Đáp án: D
Ta có:
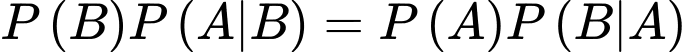
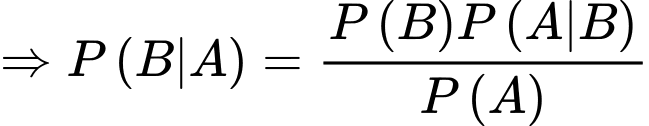
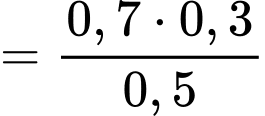
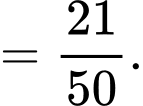 Đáp án: D
Đáp án: D
Câu 12 [145267]: Cho hai biến cố 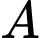 và
và 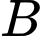 có
có 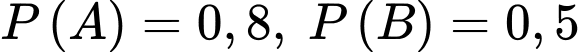 và
và 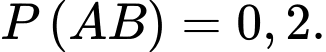 Xác suất của biến cố
Xác suất của biến cố 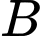 không xảy ra với điều kiện biến cố
không xảy ra với điều kiện biến cố 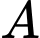 xảy ra là
xảy ra là
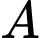 và
và 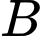 có
có 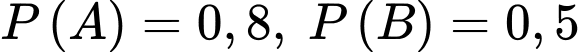 và
và 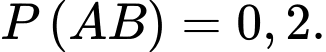 Xác suất của biến cố
Xác suất của biến cố 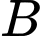 không xảy ra với điều kiện biến cố
không xảy ra với điều kiện biến cố 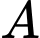 xảy ra là
xảy ra là A, 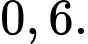
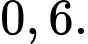
B, 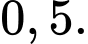
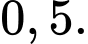
C, 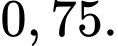
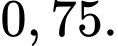
D, 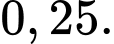
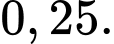
Ta có: 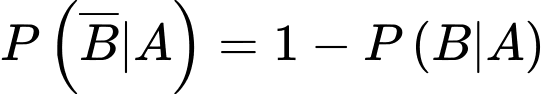
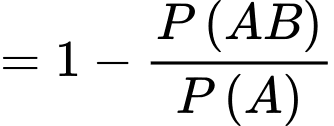
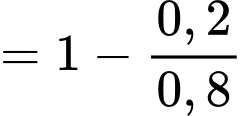
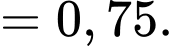
Chọn C. Đáp án: C
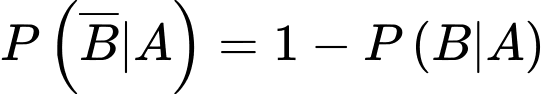
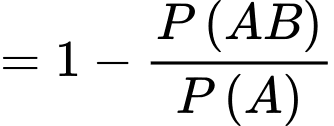
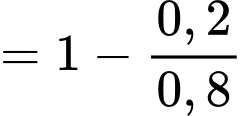
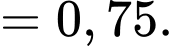
Chọn C. Đáp án: C
Câu 13 [145266]: [Trích SGK Chân Trời Sáng Tạo]: Một nhà máy thực hiện khảo sát toàn bộ công nhân về sự hài lòng của họ về điều kiện làm việc tại phân xưởng. Kết quả khảo sát như sau:
Gặp ngẫu nhiên một công nhân của nhà máy. Gọi A là biến cố “Công nhân đó làm việc tại phân xưởng I” và B là biến cố “Công nhân đó hài lòng với điều kiện làm việc tại phân xưởng”. Gặp ngẫu nhiên một công nhân của nhà máy. Gọi A là biến cố “Công nhân đó làm việc tại phân xưởng I” và B là biến cố “Công nhân đó hài lòng với điều kiện làm việc tại phân xưởng”. Xác suất của biến cố B với điều kiện A không xảy ra là

A, 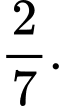
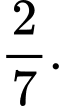
B, 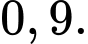
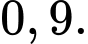
C, 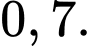
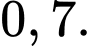
D, 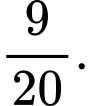
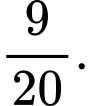
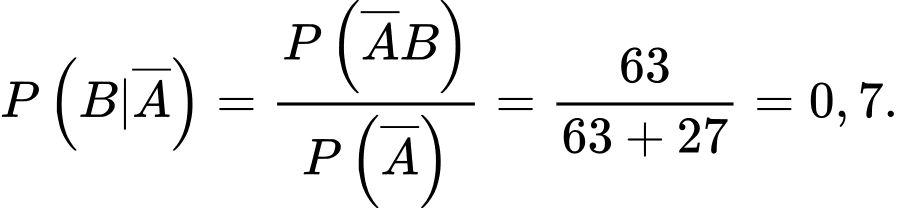 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 14 [134811]: Cho hai biến cố 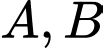 có
có 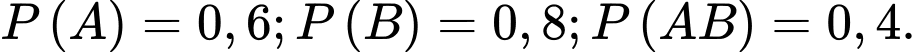 Tính xác suất của biến cố
Tính xác suất của biến cố 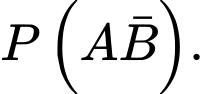
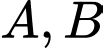 có
có 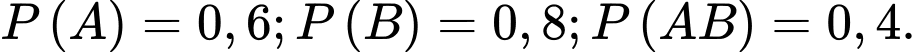 Tính xác suất của biến cố
Tính xác suất của biến cố 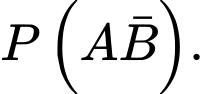
A, 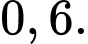
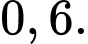
B, 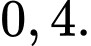
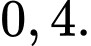
C, 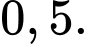
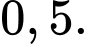
D, 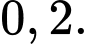
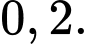
Vì  và
và  là hai biến cố xung khắc và
là hai biến cố xung khắc và  nên theo tính chất của xác suất, ta có:
nên theo tính chất của xác suất, ta có: 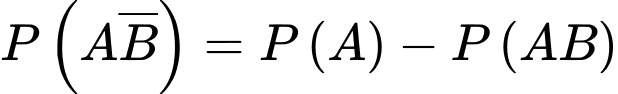
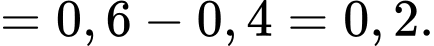
Chọn D. Đáp án: D
 và
và  là hai biến cố xung khắc và
là hai biến cố xung khắc và  nên theo tính chất của xác suất, ta có:
nên theo tính chất của xác suất, ta có: 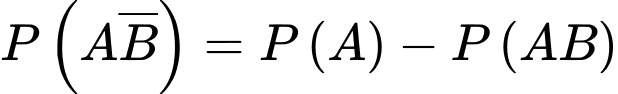
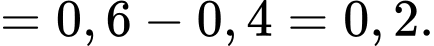
Chọn D. Đáp án: D
Câu 15 [134813]: Cho hai biến cố A và B có 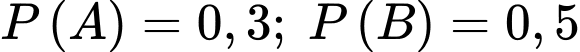 và
và  Tính
Tính 
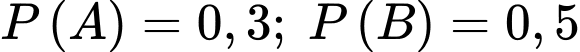 và
và  Tính
Tính 
A, 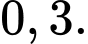
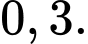
B, 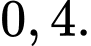
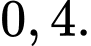
C, 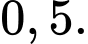
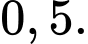
D, 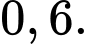
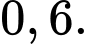
Chọn đáp án A.
Ta có: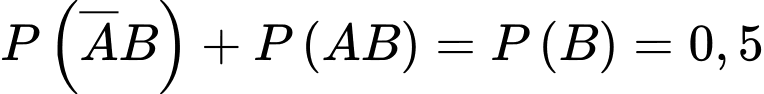
Mặt khác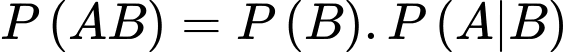
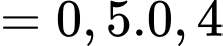
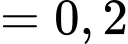
Suy ra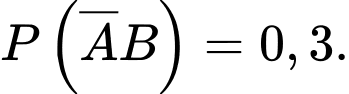 Đáp án: A
Đáp án: A
Ta có:
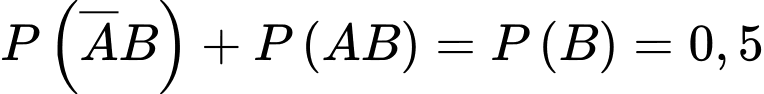
Mặt khác
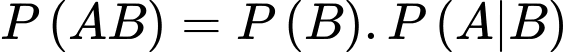
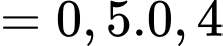
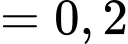
Suy ra
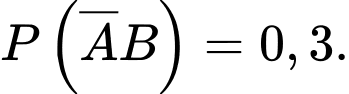 Đáp án: A
Đáp án: A
Câu 16 [134808]: Cho hai biến cố 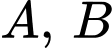 sao cho
sao cho 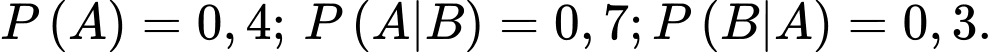 Tính
Tính 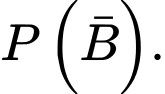
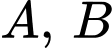 sao cho
sao cho 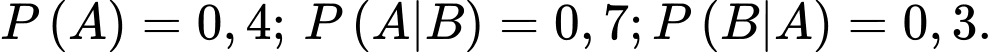 Tính
Tính 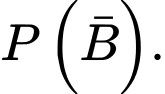
A, 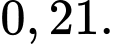
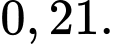
B, 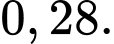
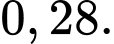
C, 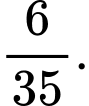
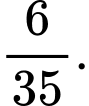
D, 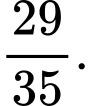
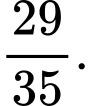
Ta có: 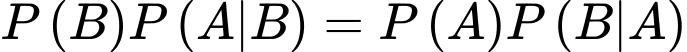
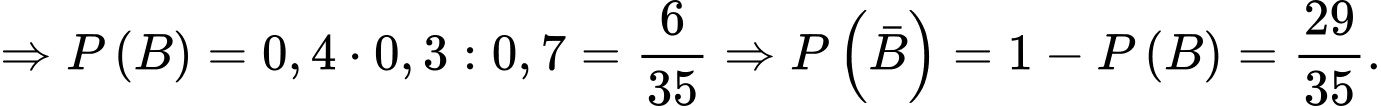
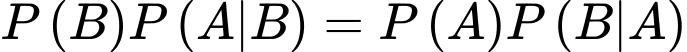
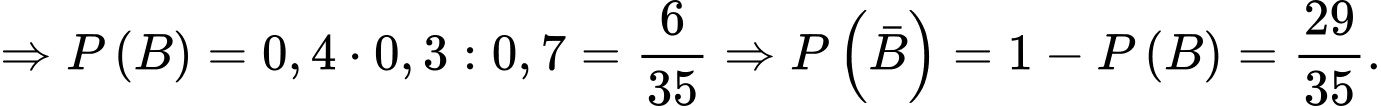
Chọn D.
Đáp án: D
Câu 17 [145261]: [Trích SGK Cùng Khám Phá]: Cho 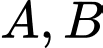 là các biến cố thoả mãn
là các biến cố thoả mãn 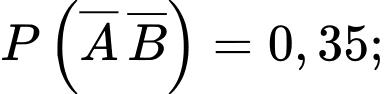
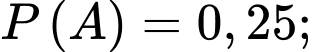
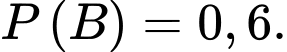 Giá trị của
Giá trị của  bằng
bằng
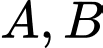 là các biến cố thoả mãn
là các biến cố thoả mãn 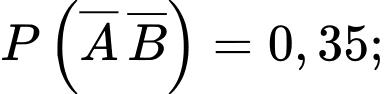
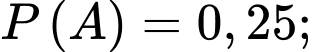
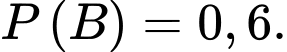 Giá trị của
Giá trị của  bằng
bằng A, 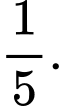
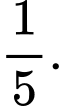
B, 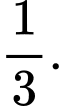
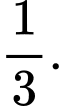
C, 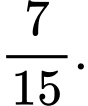
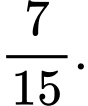
D, 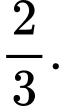
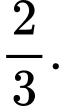
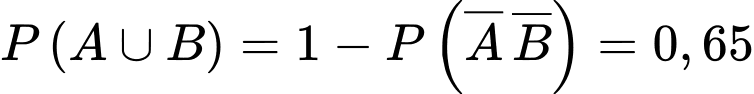
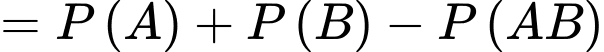
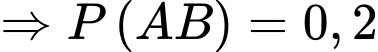
Do đó
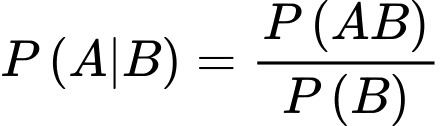
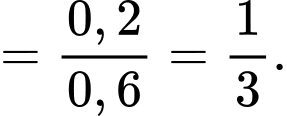
Chọn B. Đáp án: B
Câu 18 [135751]: Trong một bình có 5 quả cầu trắng và 3 quả cầu đen. Lấy ngẫu nhiên lần lượt 2 quả cầu theo phương thức không hoàn lại. Tính xác suất để lần thứ hai lấy được cầu trắng với điều kiện lần thứ nhất đã lấy được cầu đen
A, 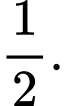
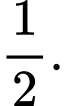
B, 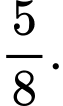
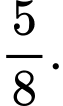
C, 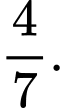
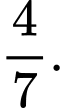
D, 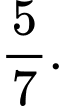
Gọi 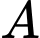 là biến cố lần thứ hai rút được cầu trắng.
là biến cố lần thứ hai rút được cầu trắng. 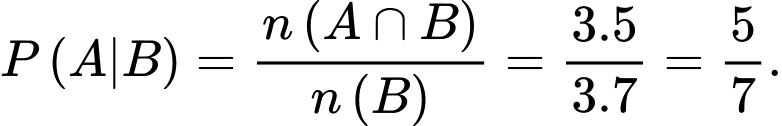 Đáp án: D
Đáp án: D
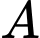 là biến cố lần thứ hai rút được cầu trắng.
là biến cố lần thứ hai rút được cầu trắng. B là biến cố lần thứ nhất rút được quả cầu đen (lần 2 rút được quả cầu gì cũng được)
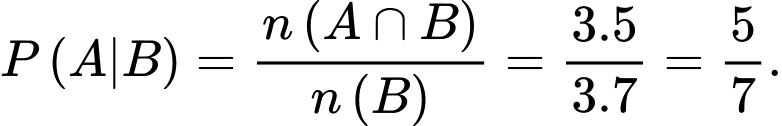
Chọn D.
Câu 19 [376889]: Trong 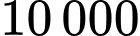 áo sơ mi xuất khẩu của một doanh nghiệp dệt may có
áo sơ mi xuất khẩu của một doanh nghiệp dệt may có 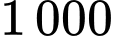 áo sơ mi trắng. Các áo sơ mi trắng đó gồm ba cỡ: 40, 41, 42, trong đó có 200 áo cỡ 40. Chọn ra ngẫu nhiên một chiếc áo trong
áo sơ mi trắng. Các áo sơ mi trắng đó gồm ba cỡ: 40, 41, 42, trong đó có 200 áo cỡ 40. Chọn ra ngẫu nhiên một chiếc áo trong 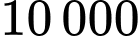 áo sơ mi xuất khẩu. Giả sử chiếc áo sơ mi được chọn ra là áo sơ mi trắng. Tính xác suất để chiếc áo sơ mi đó cỡ 40.
áo sơ mi xuất khẩu. Giả sử chiếc áo sơ mi được chọn ra là áo sơ mi trắng. Tính xác suất để chiếc áo sơ mi đó cỡ 40.
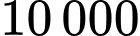 áo sơ mi xuất khẩu của một doanh nghiệp dệt may có
áo sơ mi xuất khẩu của một doanh nghiệp dệt may có 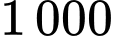 áo sơ mi trắng. Các áo sơ mi trắng đó gồm ba cỡ: 40, 41, 42, trong đó có 200 áo cỡ 40. Chọn ra ngẫu nhiên một chiếc áo trong
áo sơ mi trắng. Các áo sơ mi trắng đó gồm ba cỡ: 40, 41, 42, trong đó có 200 áo cỡ 40. Chọn ra ngẫu nhiên một chiếc áo trong 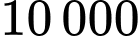 áo sơ mi xuất khẩu. Giả sử chiếc áo sơ mi được chọn ra là áo sơ mi trắng. Tính xác suất để chiếc áo sơ mi đó cỡ 40.
áo sơ mi xuất khẩu. Giả sử chiếc áo sơ mi được chọn ra là áo sơ mi trắng. Tính xác suất để chiếc áo sơ mi đó cỡ 40. A, 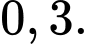
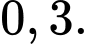
B, 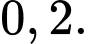
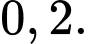
C, 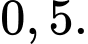
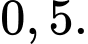
D, 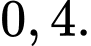
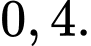
Gọi 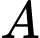 là biến cố chiếc sơ mi đó cỡ 40.
là biến cố chiếc sơ mi đó cỡ 40.
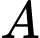 là biến cố chiếc sơ mi đó cỡ 40.
là biến cố chiếc sơ mi đó cỡ 40. Gọi 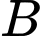 là biến cố chiếc sơ mi được chọn ra là áo sơ mi trắng
là biến cố chiếc sơ mi được chọn ra là áo sơ mi trắng
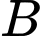 là biến cố chiếc sơ mi được chọn ra là áo sơ mi trắng
là biến cố chiếc sơ mi được chọn ra là áo sơ mi trắng Ta phải tính 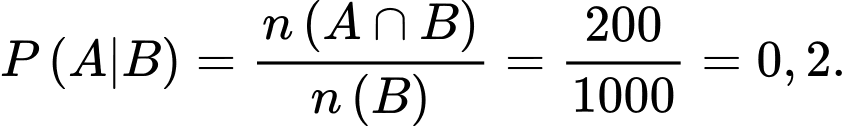
Đáp án: B 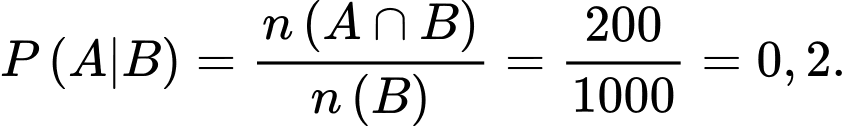
Chọn B.
Câu 20 [135752]: Một hộp có 8 viên bi màu đỏ và 5 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Có 5 viên bi trong hộp được đánh số, trong đó có 3 viên bi màu đỏ và 2 viên bi màu vàng. Lấy ngẫu nhiên một viên bi trong hộp. Tính xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số.
A, 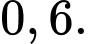
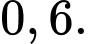
B, 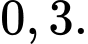
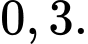
C, 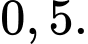
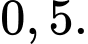
D, 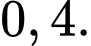
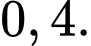
Gọi 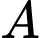 là biến cố viên bi lấy ra có màu đỏ.
là biến cố viên bi lấy ra có màu đỏ.
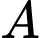 là biến cố viên bi lấy ra có màu đỏ.
là biến cố viên bi lấy ra có màu đỏ. Gọi 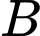 là biến cố viên bi đó được đánh số.
là biến cố viên bi đó được đánh số.
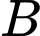 là biến cố viên bi đó được đánh số.
là biến cố viên bi đó được đánh số. Ta phải tính 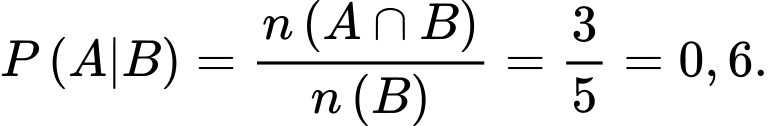
Đáp án: A 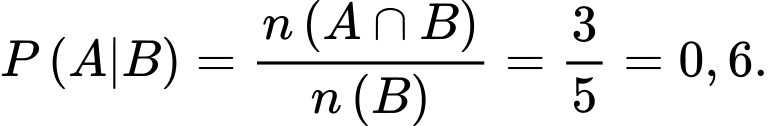
Chọn A.
Câu 21 [360660]: Một hộp có 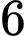 quả bóng màu xanh,
quả bóng màu xanh, 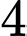 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
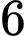 quả bóng màu xanh,
quả bóng màu xanh, 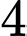 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh. A, 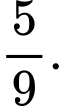
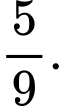
B, 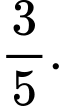
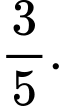
C, 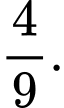
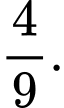
D, 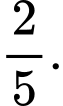
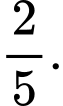
Gọi 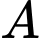 là biến cố lần thứ hai lấy được quả bóng màu đỏ.
là biến cố lần thứ hai lấy được quả bóng màu đỏ.
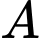 là biến cố lần thứ hai lấy được quả bóng màu đỏ.
là biến cố lần thứ hai lấy được quả bóng màu đỏ. Gọi 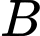 là biến cố lần thứ nhất lấy được quả bóng màu xanh.
là biến cố lần thứ nhất lấy được quả bóng màu xanh.
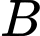 là biến cố lần thứ nhất lấy được quả bóng màu xanh.
là biến cố lần thứ nhất lấy được quả bóng màu xanh. Ta phải tính 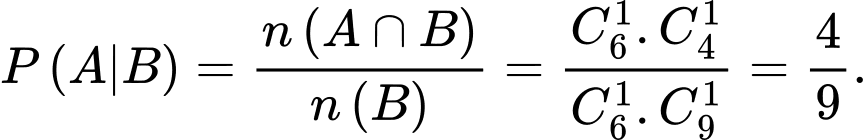
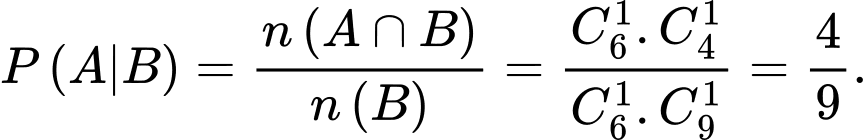
Chọn C.
Đáp án: C
Câu 22 [135807]: Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T, xác suất để một ngày có gió là 0,6; nếu ngày có gió thì xác suất có mưa là 0,4; nếu ngày không có gió thì xác suất
có mưa là 0,2. Gọi G là biến cố "Ngày có gió" và M là biến cố "Ngày có mưa". Các mệnh đề sau đúng hay sai.
A, a) Xác suất để một ngày không có gió là 0,4.
B, b) Nếu ngày không có gió thì xác suất không có mưa là 0,8.
C, c) Trong một ngày, xác suất để trời vừa có gió và vừa có mưa là 0,36
D, d) Trong một ngày, xác suất để trời không có gió nhưng có mưa là 0,12.
a) Đúng. Xác suất bằng 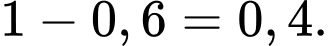
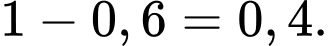
b) Đúng. Xác suất bằng 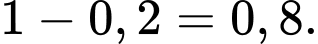
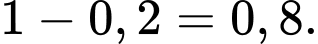
c) Sai. Xác suất bằng 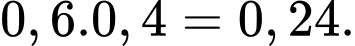
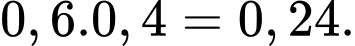
d) Sai. Xác suất bằng 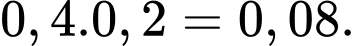
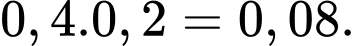
Câu 23 [135815]: Cho sơ đồ hình cây như hình vẽ. Các mệnh đề sau đúng hay sai.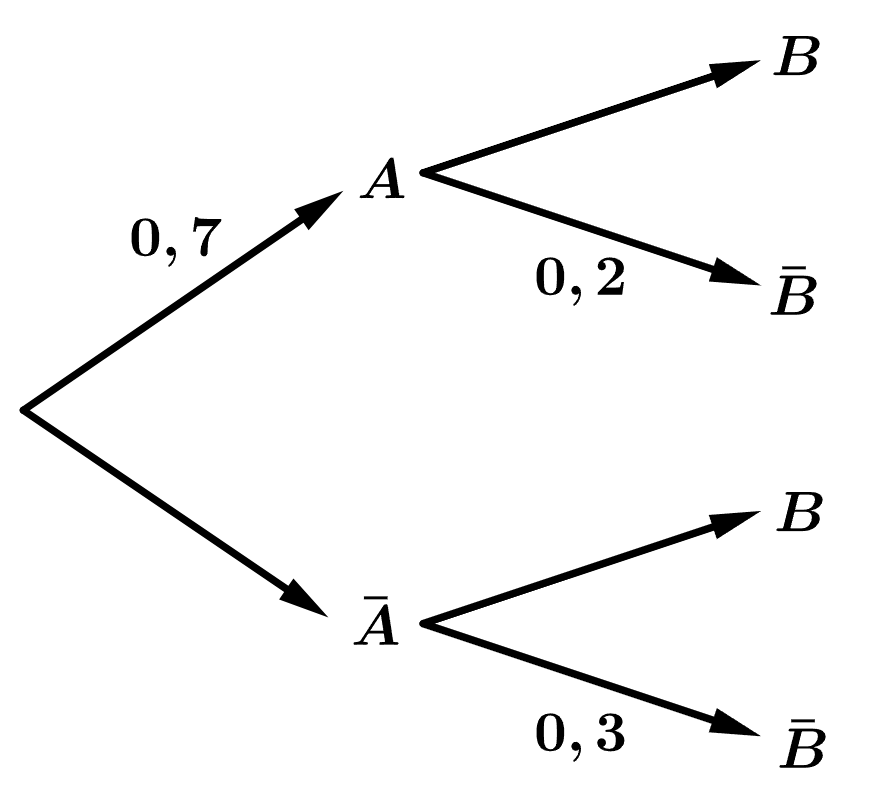

A, a) 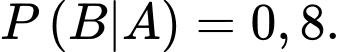
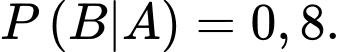
B, b) Xác suất của biến cố 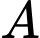 và
và 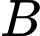 đều xảy ra là
đều xảy ra là 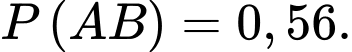
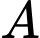 và
và 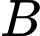 đều xảy ra là
đều xảy ra là 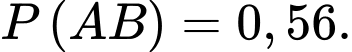
C, c) Xác suất của biến cố 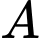 và
và  đều không xảy ra là
đều không xảy ra là 
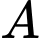 và
và  đều không xảy ra là
đều không xảy ra là 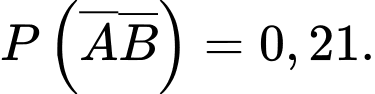
D, d) Xác suất của biến cố 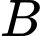 là
là 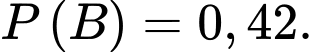
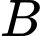 là
là 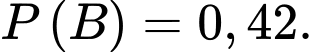
a) Đúng. 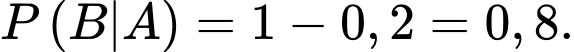
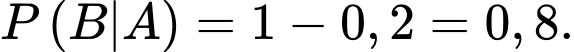
b) Đúng. Xác suất của biến cố 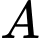 và
và  đều xảy ra là
đều xảy ra là 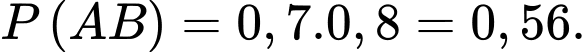
 và
và  đều xảy ra là
đều xảy ra là 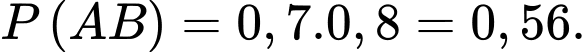
c) Sai. Xác suất của biến cố 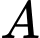 và
và 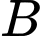 đều không xảy ra là
đều không xảy ra là 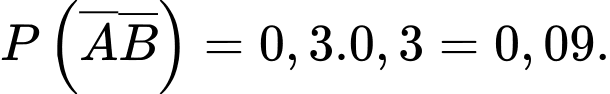
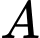 và
và 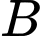 đều không xảy ra là
đều không xảy ra là 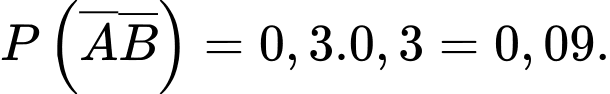
d) Sai. Xác suất của biến cố  là
là 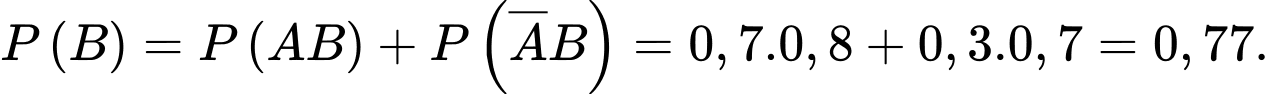
 là
là 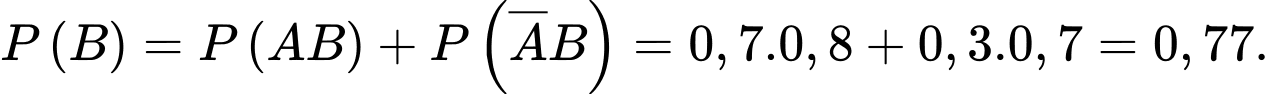
Câu 24 [145265]: Cho sơ đồ hình cây 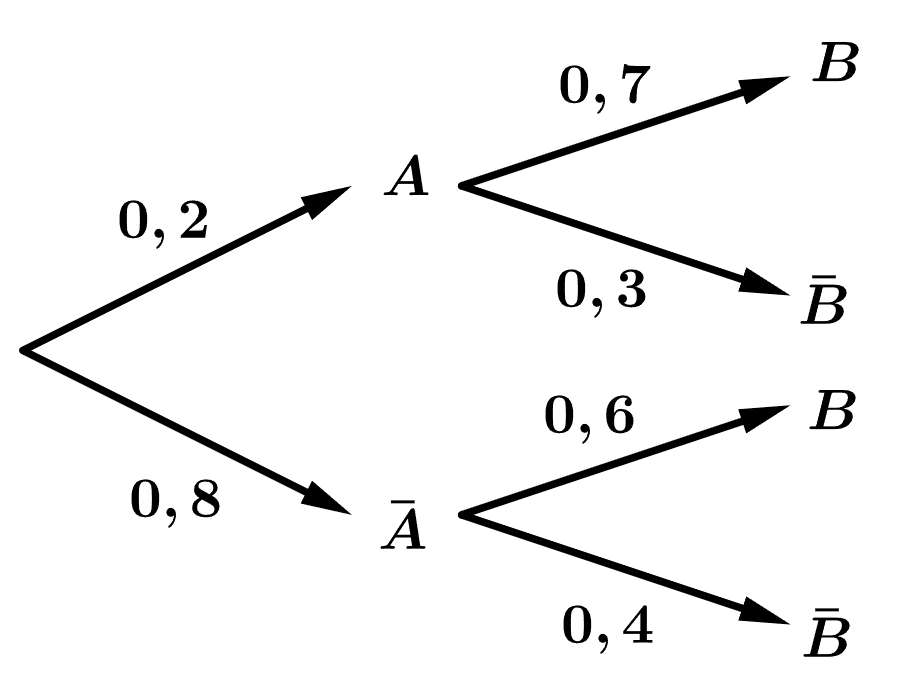

Các mệnh đề sau đúng hay sai?
a) Đúng. Ta có: 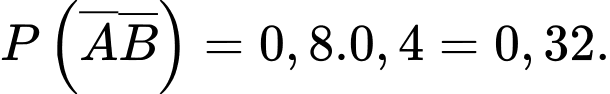
b) Sai. Xác suất của biến cố B là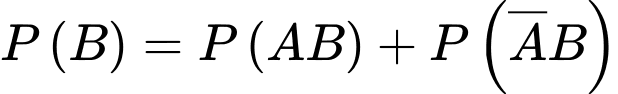
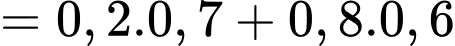
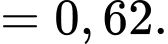
c) Sai. Xác suất điều kiện P(A | B) là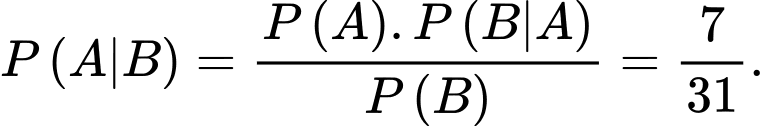
d) Sai.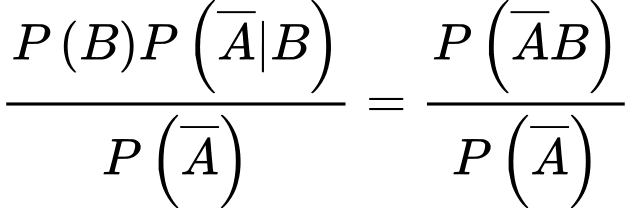
b) Sai. Xác suất của biến cố B là
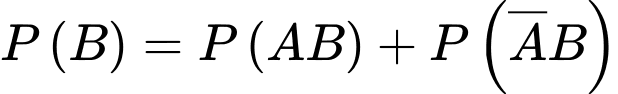
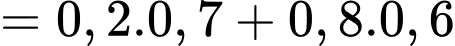
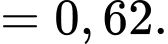
c) Sai. Xác suất điều kiện P(A | B) là
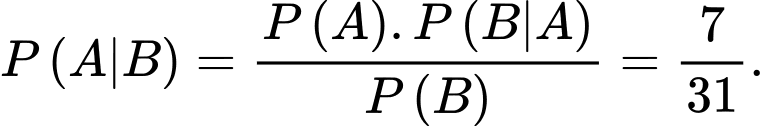
d) Sai.
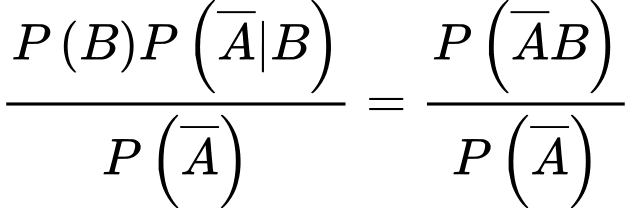
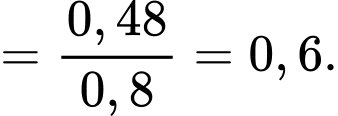
Câu 25 [135860]: Một xí nghiệp có 3 ô tô hoạt động độc lập. Xác suất để trong một ngày các ô tô bị hỏng tương ứng là 0,1; 0,2; 0,15. Tìm xác suất để trong một ngày có đúng một ô tô bị hỏng. Viết kết quả làm tròn đến hàng phần trăm.
Xác suất để trong một ngày có đúng một ô tô bị hỏng là: (nghĩa là chỉ có 1 xe bị hỏng, còn 2 xe còn lại không bị hỏng)
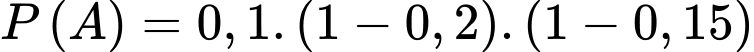
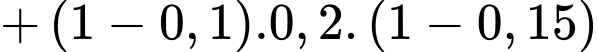
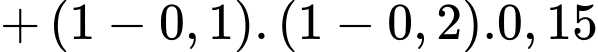
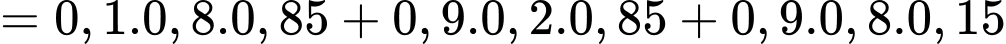
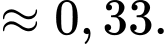
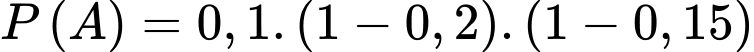
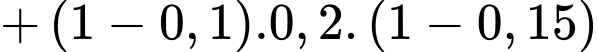
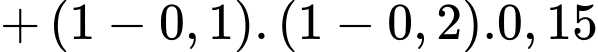
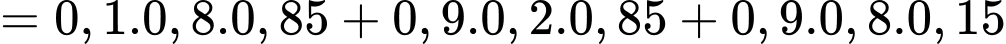
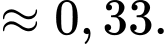
Câu 26 [143805]: Trong thời gian có dịch ở một vung cứ 100 người mắc dịch thì có 10 người phải cấp cứu. Xác suất gặp một người mắc dịch và phải đi cấp cứu ở vùng đó là 0,06. Tìm tỷ lệ mắc bệnh dịch của vùng đó.
Đặt A – gặp người mắc dịch, B – gặp người bị cấp cứu và ta
phải tìm P(A).
phải tìm P(A).
Từ đầu bài ta có: P(B|A) = 10/100 = 0,1; P(AB) =0,06.
Mặt khác P(B|A) = P(AB)/P(A), từ đo suy ra 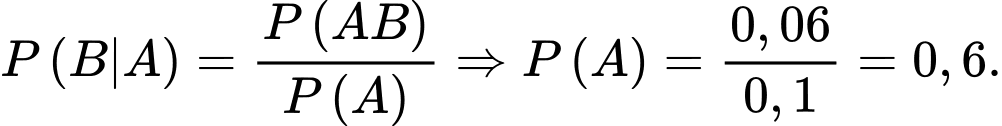
Câu 27 [145403]: Một lớp có 3 tổ sinh viên: tổ I có 12 người, tổ II có 10 người và tổ III có 15 người. Chọn ngẫu nhiên ra một nhóm sinh viên gồm 4 người. Biết trong nhóm có đúng một sinh viên tổ I, tính xác suất để trong nhóm đó có đúng một sinh viên tổ III. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố: “Trong nhóm có đúng 1 sinh viên tổ 1”
B là biến cố: Trong nhóm có đúng 1 sinh viên tổ 3”
Ta có: 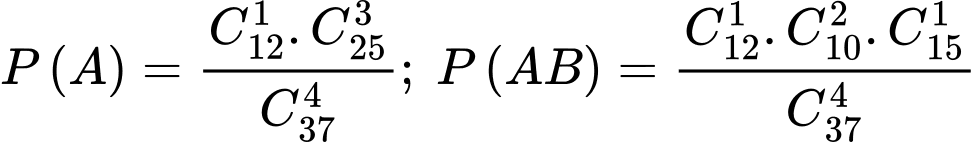
Suy ra