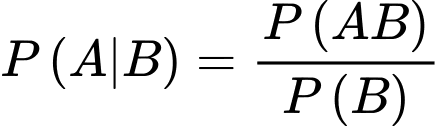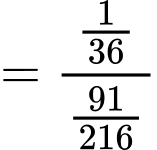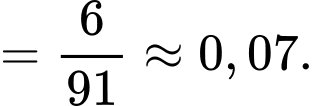Đáp án Bài tập tự luyện đề 3
Câu 1 [134814]: Cho hai biến cố 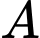 và
và 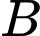 có
có 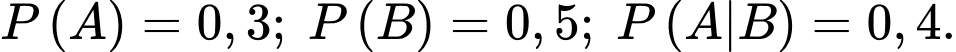 Tính
Tính 
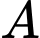 và
và 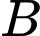 có
có 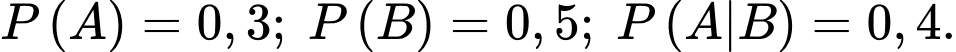 Tính
Tính 
A, 0,2.
B, 0,4.
C, 0,6.
D, 0,8.
Ta có: 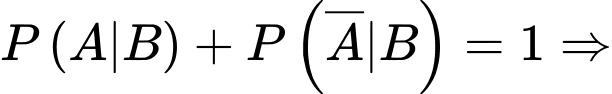
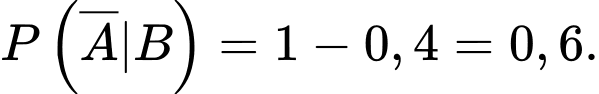 Đáp án: C
Đáp án: C
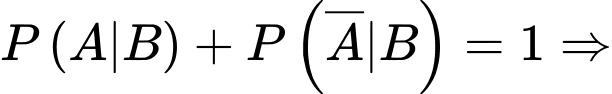
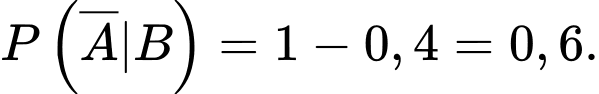 Đáp án: C
Đáp án: C
Câu 2 [134819]: Cho hai biến cố 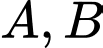 có
có 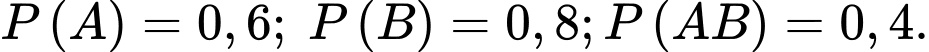 Tính xác suất của biến cố
Tính xác suất của biến cố 
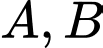 có
có 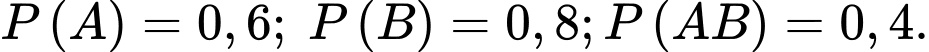 Tính xác suất của biến cố
Tính xác suất của biến cố 
A, 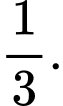
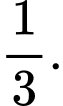
B, 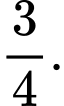
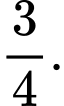
C, 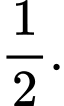
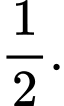
D, 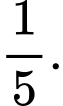
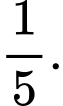
Ta có: 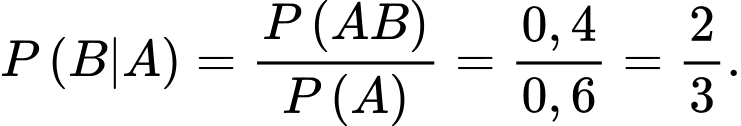
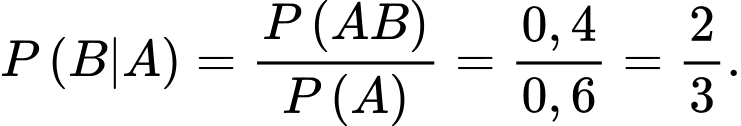
Mặt khác: 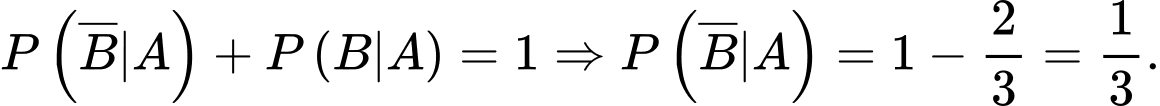
Đáp án: A 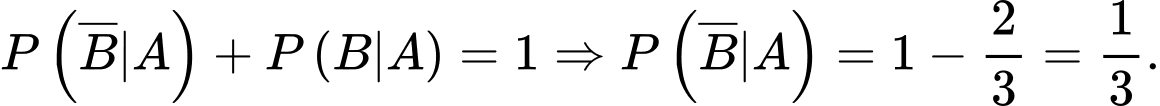
Chọn A.
Câu 3 [134823]: Cho hai biến cố 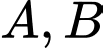 có có
có có 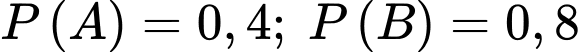 và
và 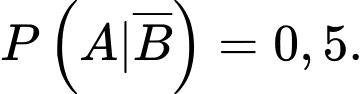 Tính
Tính 
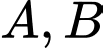 có có
có có 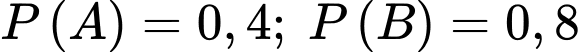 và
và 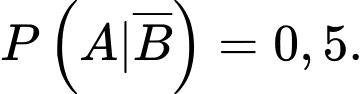 Tính
Tính 
A, 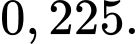
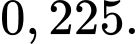
B, 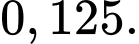
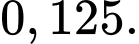
C, 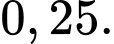
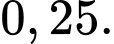
D, 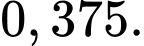
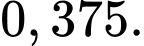
Ta có: 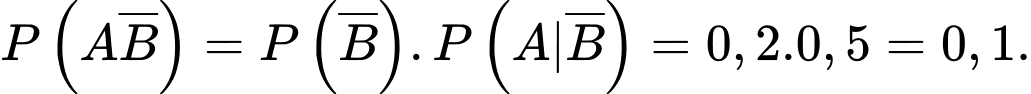
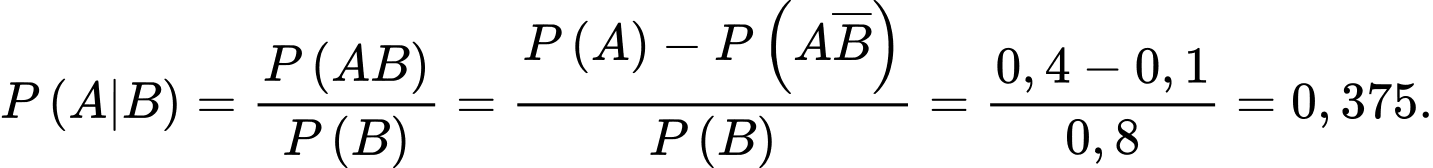
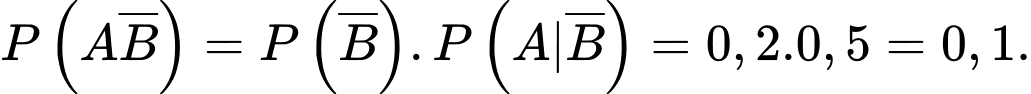
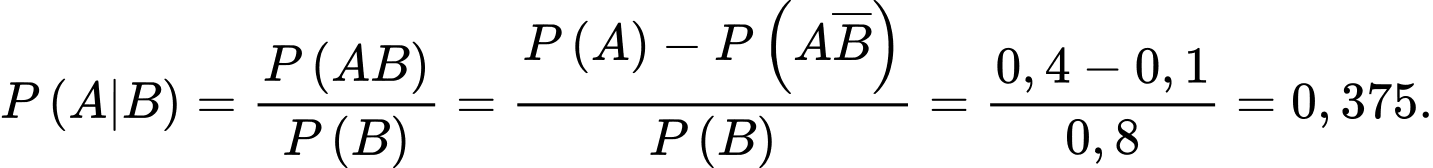
Chọn D.
Đáp án: D
Câu 4 [134824]: Một cửa hàng sách ước lượng rằng trong tổng số các khách hàng đến cửa hàng có 30% khách cần hỏi nhân viên bán hàng, 20% khách mua sách và 15% khách thực hiện cả
hai điều trên. Gặp ngẫu nhiên một khách trong nhà sách. Tính xác suất để người này không mua sách, biết rằng người này đã hỏi nhân viên bán hàng.
A, 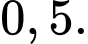
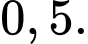
B, 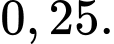
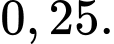
C, 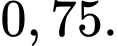
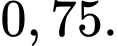
D, 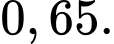
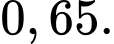
Gọi A là biến cố “khách hàng hỏi nhân viên bán hàng”
B là biến cố “khách hàng mua sách”
Khi đó 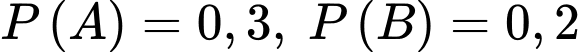 và
và 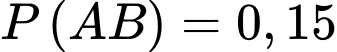 ta cần tính
ta cần tính 
Đáp án: A 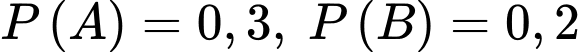 và
và 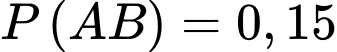 ta cần tính
ta cần tính 
Mặt khác 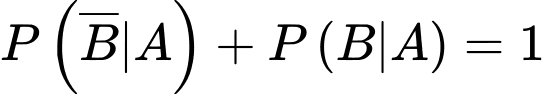 mà
mà 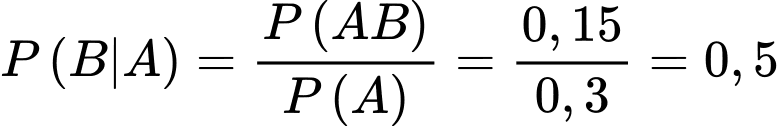
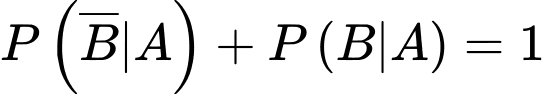 mà
mà 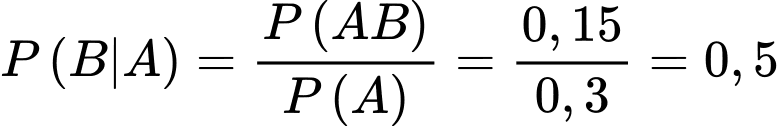
Suy ra 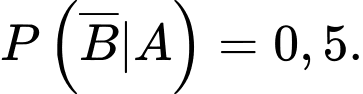
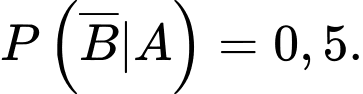
Chọn A.
Câu 5 [134825]: [Trích SGK Cùng Khám Phá]: Trong cuộc khảo sát 300 gia đình ở một khu vực, người ta nhận thấy có 90% gia đình có ti vi và 60% gia đình có máy tính bàn. Mỗi gia đình đều có ít nhất một trong hai thiết bị này. Chọn ngẫu nhiên một gia đình. Tính xác suất gia đình đó có máy tính bàn trong nhóm các gia đình có ti vi.
A, 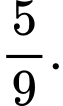
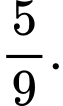
B, 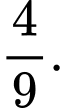
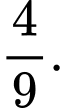
C, 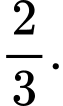
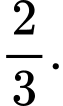
D, 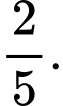
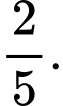
Gọi A là biến cố: “ gia đình có ti vi” và B là biến cố “ gia đình có máy tính bàn”
Ta có: 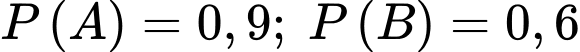 và
và 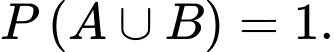
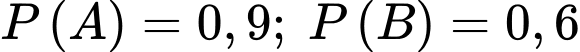 và
và 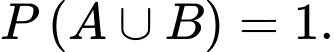
Lại có: 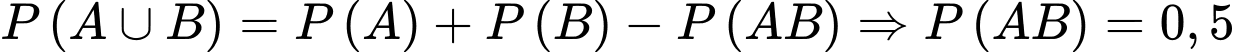
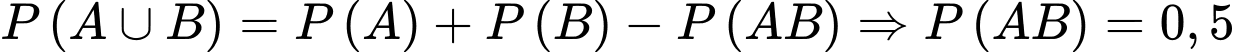
Ta cần tính 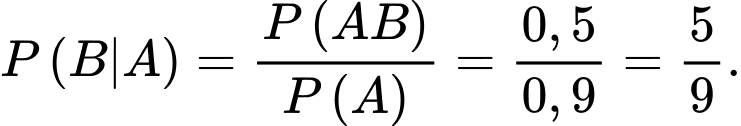
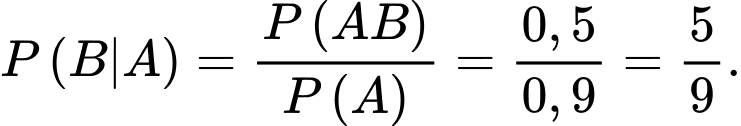
Chọn A.
Câu 6 [360661]: Trong hộp đựng  chiếc thẻ cùng loại có
chiếc thẻ cùng loại có 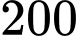 chiếc thẻ màu vàng. Trên mỗi chiếc thẻ màu vàng có ghi một trong năm số:
chiếc thẻ màu vàng. Trên mỗi chiếc thẻ màu vàng có ghi một trong năm số: 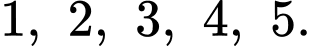 Có
Có 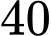 chiếc thẻ màu vàng ghi số
chiếc thẻ màu vàng ghi số 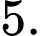 Chọn ra ngẫu nhiên một chiếc thẻ trong hộp đựng thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác suất để chiếc thẻ đó ghi số
Chọn ra ngẫu nhiên một chiếc thẻ trong hộp đựng thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác suất để chiếc thẻ đó ghi số 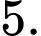
 chiếc thẻ cùng loại có
chiếc thẻ cùng loại có 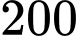 chiếc thẻ màu vàng. Trên mỗi chiếc thẻ màu vàng có ghi một trong năm số:
chiếc thẻ màu vàng. Trên mỗi chiếc thẻ màu vàng có ghi một trong năm số: 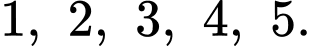 Có
Có 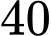 chiếc thẻ màu vàng ghi số
chiếc thẻ màu vàng ghi số 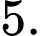 Chọn ra ngẫu nhiên một chiếc thẻ trong hộp đựng thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác suất để chiếc thẻ đó ghi số
Chọn ra ngẫu nhiên một chiếc thẻ trong hộp đựng thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác suất để chiếc thẻ đó ghi số 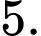
A, 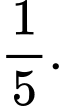
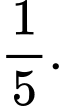
B, 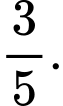
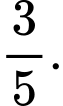
C, 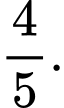
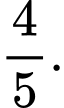
D, 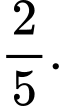
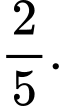
Gọi 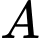 là biến cố chiếc thẻ được chọn ghi số 5.
là biến cố chiếc thẻ được chọn ghi số 5.
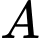 là biến cố chiếc thẻ được chọn ghi số 5.
là biến cố chiếc thẻ được chọn ghi số 5. Gọi 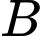 là biến cố chiếc thẻ được chọn có màu vàng.
là biến cố chiếc thẻ được chọn có màu vàng.
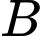 là biến cố chiếc thẻ được chọn có màu vàng.
là biến cố chiếc thẻ được chọn có màu vàng. Ta phải tính 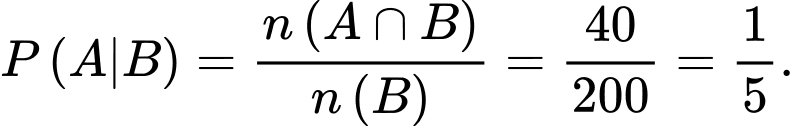
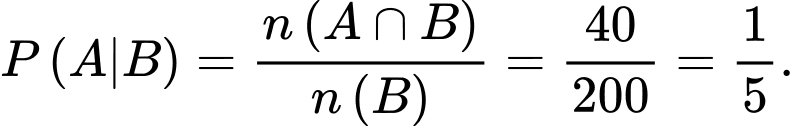
Chọn A.
Đáp án: A
Câu 7 [135780]: Một túi có  hộp sữa chua dâu và
hộp sữa chua dâu và  hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có
hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có  hộp sữa chua trong túi là sữa chua không đường, trong đó có
hộp sữa chua trong túi là sữa chua không đường, trong đó có 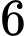 hộp sữa chua dâu và
hộp sữa chua dâu và 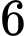 hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
 hộp sữa chua dâu và
hộp sữa chua dâu và  hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có
hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có  hộp sữa chua trong túi là sữa chua không đường, trong đó có
hộp sữa chua trong túi là sữa chua không đường, trong đó có 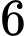 hộp sữa chua dâu và
hộp sữa chua dâu và 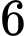 hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường. A, 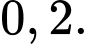
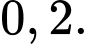
B, 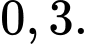
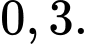
C, 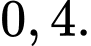
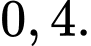
D, 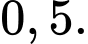
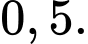
Gọi 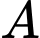 là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu.
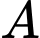 là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu. Gọi 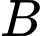 là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường.
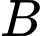 là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường. Ta phải tính 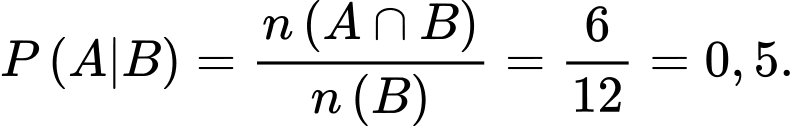
Đáp án: D 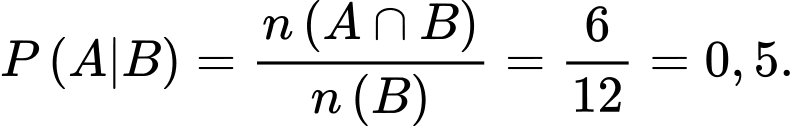
Chọn D.
Câu 8 [135801]: Một thủ quỹ có một chùm chìa khóa gồm 9 chiếc chìa giống hệt nhau trong đó chỉ có 2 chìa có thể mở được tủ sắt. Anh ta thử ngẫu nhiên từng chìa (chìa không trúng được bỏ ra trong lần thử kế tiếp). Tìm xác suất để anh ta mở được tủ vào đúng lần thứ ba.
A, 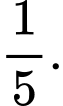
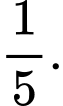
B, 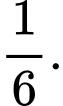
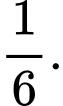
C, 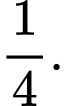
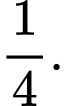
D, 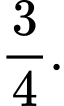
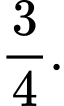
Chọn đáp án B.
Số cách sử dụng chìa khoá đến lần thứ ba là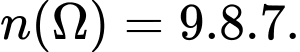
Số cách mở được cửa ở lần thứ ba là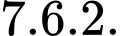
Xác suất cần tính bằng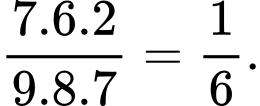 Đáp án: B
Đáp án: B
Số cách sử dụng chìa khoá đến lần thứ ba là
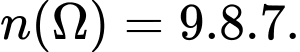
Số cách mở được cửa ở lần thứ ba là
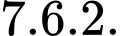
Xác suất cần tính bằng
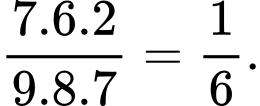 Đáp án: B
Đáp án: B
Câu 9 [135684]: Một cuộc khảo sát 1000 người về hoạt động thể dục thấy có 80% số người thích đi bộ và 60% thích đạp xe vào buổi sáng và tất cả mọi người đều tham gia ít nhất một
trong hai hoạt động trên. Chọn ngẫu nhiên một người hoạt động thể dục. Nếu gặp
được người thích đi xe đạp thì xác suất mà người đó không thích đi bộ là bao nhiêu?
A, 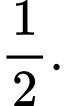
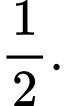
B, 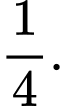
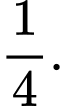
C, 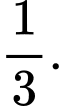
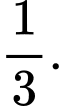
D, 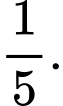
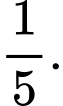
Gọi A là biến cố: “ người đó thích đi bộ” và B là biến cố “ người đó thích đi xe đạp”
Ta có: 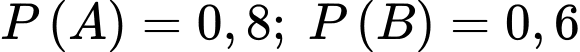 và
và 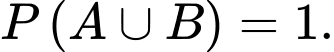
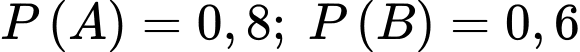 và
và 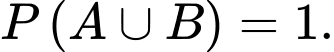
Lại có: 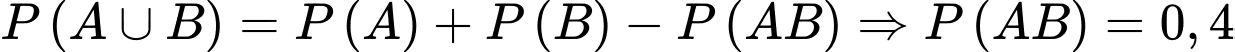
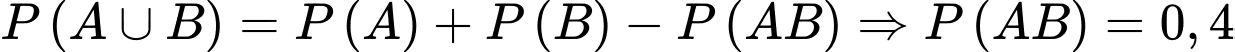
Ta cần tính 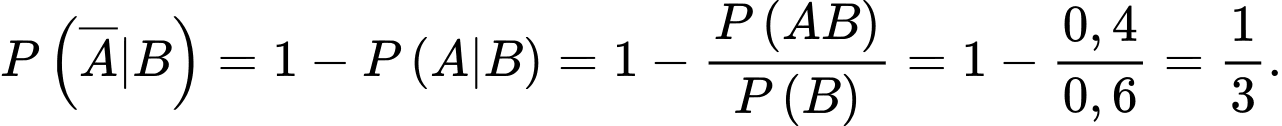
Đáp án: C 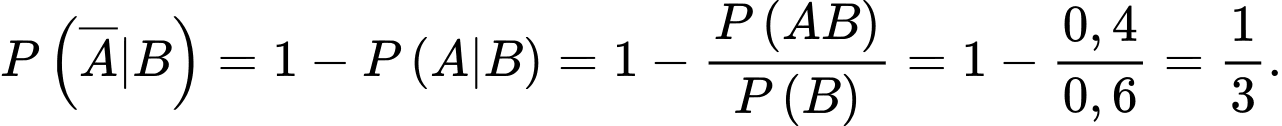
Chọn C.
Câu 10 [360667]: Cho hai xúc xắc cân đối và đồng chất. Gieo lần lượt từng xúc xắc trong hai xúc xắc đó. Tính xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 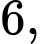 biết rằng xúc xắc thứ nhất xuất hiện mặt
biết rằng xúc xắc thứ nhất xuất hiện mặt 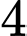 chấm.
chấm.
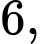 biết rằng xúc xắc thứ nhất xuất hiện mặt
biết rằng xúc xắc thứ nhất xuất hiện mặt 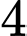 chấm.
chấm. A, 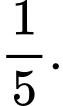
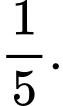
B, 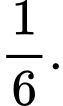
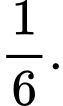
C, 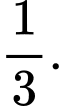
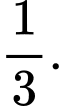
D, 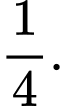
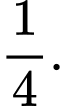
Gọi 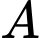 là biến cố tổng số chấm xuất hiện trên hai xúc xắc bằng 6.
là biến cố tổng số chấm xuất hiện trên hai xúc xắc bằng 6.
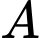 là biến cố tổng số chấm xuất hiện trên hai xúc xắc bằng 6.
là biến cố tổng số chấm xuất hiện trên hai xúc xắc bằng 6. Gọi 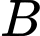 là biến cố xúc xắc thứ nhất xuất hiện mặt 4 chấm.
là biến cố xúc xắc thứ nhất xuất hiện mặt 4 chấm.
 là biến cố xúc xắc thứ nhất xuất hiện mặt 4 chấm.
là biến cố xúc xắc thứ nhất xuất hiện mặt 4 chấm. Khi đó, 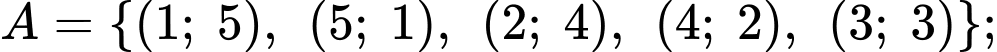
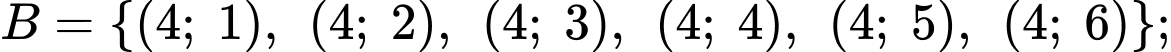
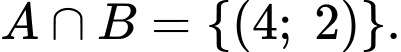
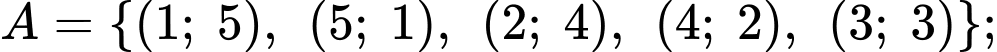
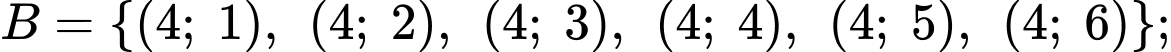
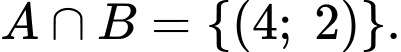
Ta phải tính 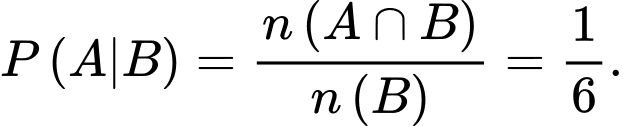
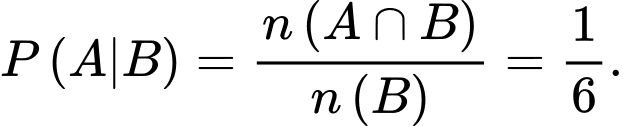
Chọn B.
Đáp án: B
Câu 11 [378714]: Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn  nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt
nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt 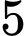 chấm.
chấm.
 nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt
nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt 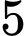 chấm.
chấm. A, 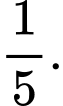
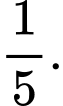
B, 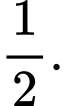
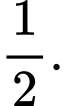
C, 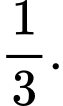
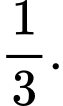
D, 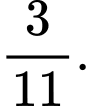
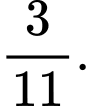
"Câu hỏi này thầy đính chính là phương án D nhé các em"
Gọi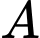 là biến cố tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn
là biến cố tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 
Gọi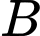 là biến cố có ít nhất một con xúc xắc xuất hiện mặt
là biến cố có ít nhất một con xúc xắc xuất hiện mặt 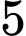 chấm.
chấm.
Khi đó,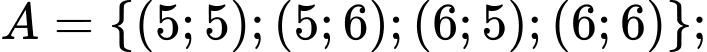
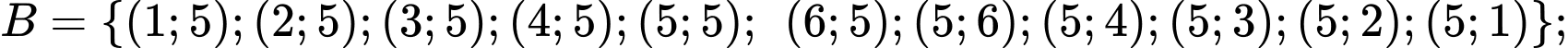
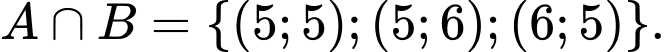
Ta phải tính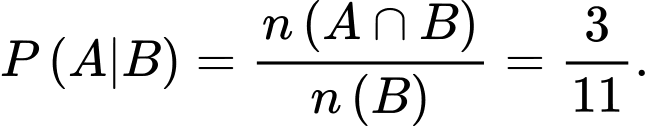 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Gọi
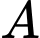 là biến cố tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn
là biến cố tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 
Gọi
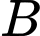 là biến cố có ít nhất một con xúc xắc xuất hiện mặt
là biến cố có ít nhất một con xúc xắc xuất hiện mặt 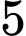 chấm.
chấm. Khi đó,
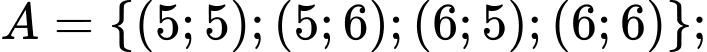
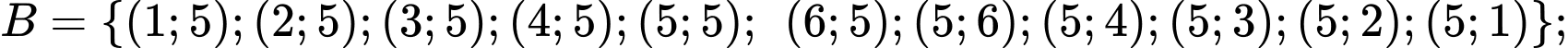
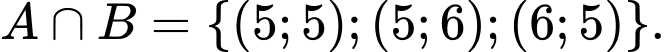
Ta phải tính
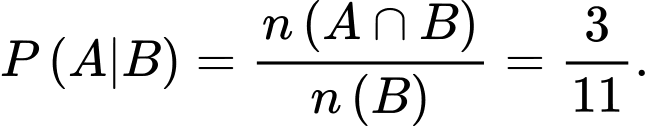 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 12 [135701]: Cho hai biến cố 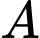 và
và 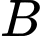 với
với 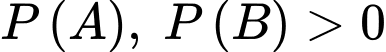 và
và 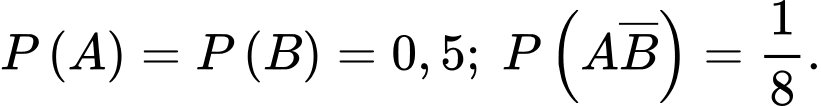 Tính
Tính 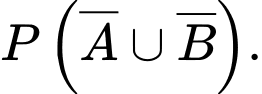
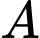 và
và 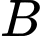 với
với 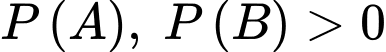 và
và 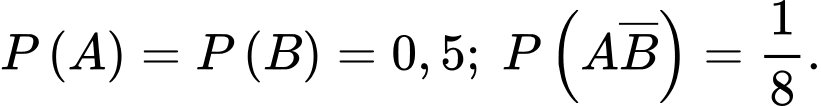 Tính
Tính 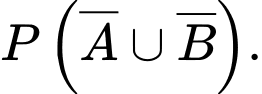
A, 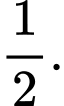
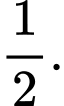
B, 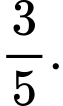
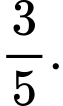
C, 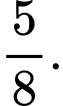
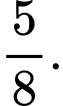
D, 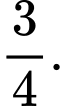
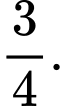
Ta có: 

Lại có: 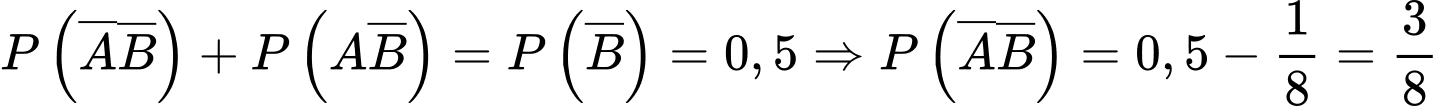 nên
nên 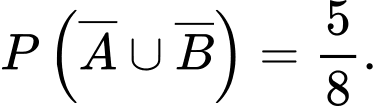
Đáp án: C 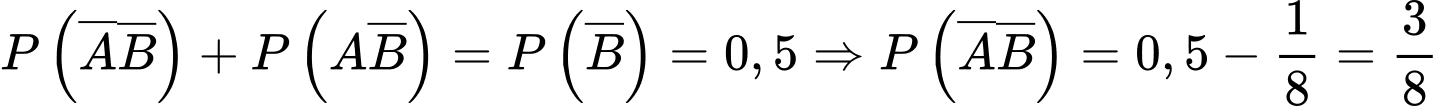 nên
nên 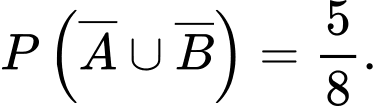
Câu 13 [135703]: Cho hai biến cố 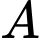 và
và 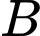 với
với 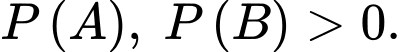 Biết
Biết 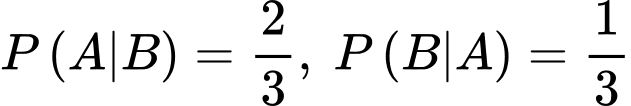 và
và 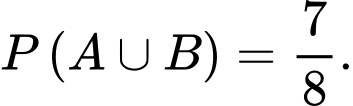 Tính
Tính 
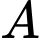 và
và 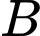 với
với 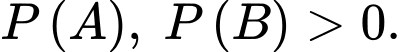 Biết
Biết 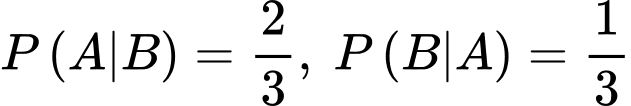 và
và 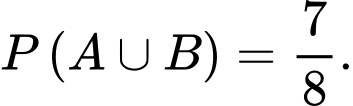 Tính
Tính 
A, 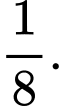
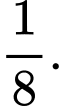
B, 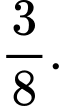
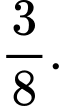
C, 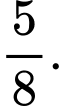
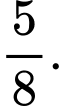
D, 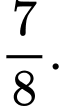
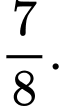
Từ 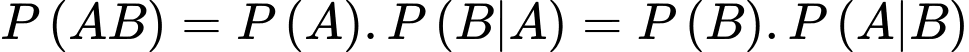
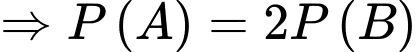
Vậy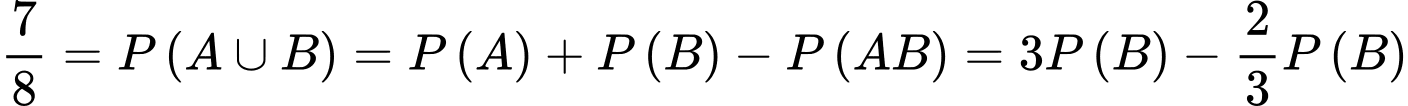 hay
hay 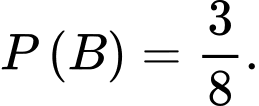
Chọn B. Đáp án: B
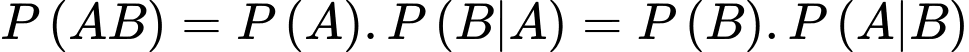
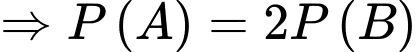
Vậy
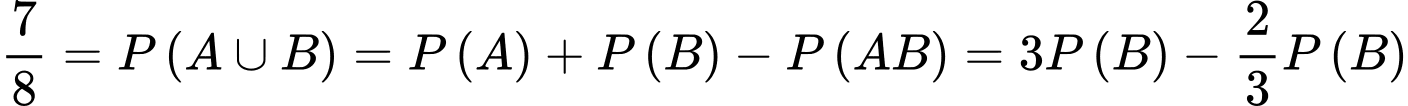 hay
hay 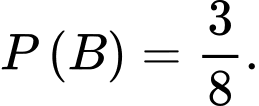
Chọn B. Đáp án: B
Câu 14 [135792]: Một gia đình có 2 đứa trẻ. Biết rằng có ít nhất 1 đứa trẻ là con gái và xác suất sinh con trai và con gái ở mỗi lần sinh là bằng nhau. Xác suất cả 2 đứa trẻ đều là con gái bằng
A, 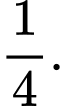
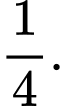
B, 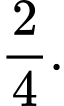
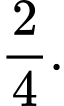
C, 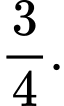
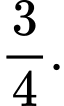
D, 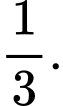
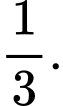
Do gia đình có 2 đứa trẻ nên sẽ có thể xảy ra 4 khả năng: (trai, trai), (gái, gái), (gái, trai), (trai, gái).
Gọi 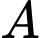 là biến cố “Cả hai đứa trẻ đều là con gái” và
là biến cố “Cả hai đứa trẻ đều là con gái” và 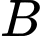 là biến cố “Có ít nhất một đứa trẻ là con gái” thì có
là biến cố “Có ít nhất một đứa trẻ là con gái” thì có 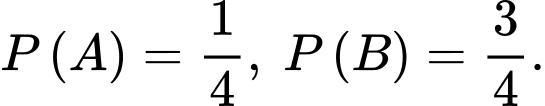
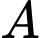 là biến cố “Cả hai đứa trẻ đều là con gái” và
là biến cố “Cả hai đứa trẻ đều là con gái” và 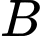 là biến cố “Có ít nhất một đứa trẻ là con gái” thì có
là biến cố “Có ít nhất một đứa trẻ là con gái” thì có 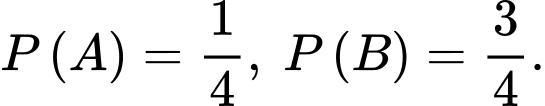
Lại có: 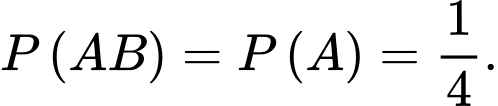
Đáp án: D 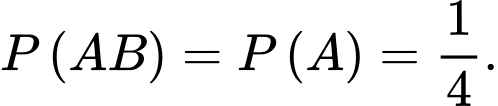
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là 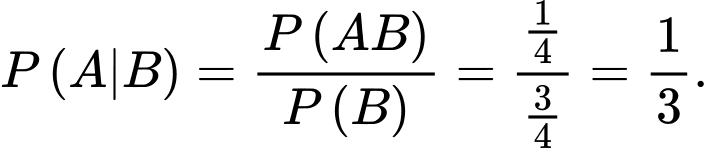
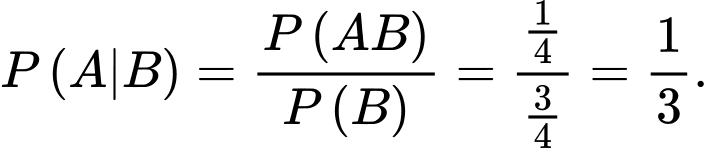
Chọn D.
Câu 15 [135818]: Một xạ thủ bán vào bia số 1 và bia số 2. Xác suất để xạ thủ đó bắn trúng bia số 1 là 0,8 và bắn trúng bia số 2 là 0,9. Xác suất để xạ thủ đó bắn trúng cả hai bia là 0,75. Xét hai biến cố: A: “Xạ thủ đó bắn trúng bia số 1”; B: “Xạ thủ đó bắn trúng bia số 2”. Các mệnh đề sau đúng hay sai.
Xét hai biến cố sau: A: “Xạ thủ đó bắn trúng bia số 1”; B: “Xạ thủ đó bắn trúng bia số 2”. 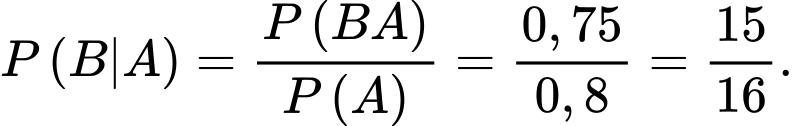
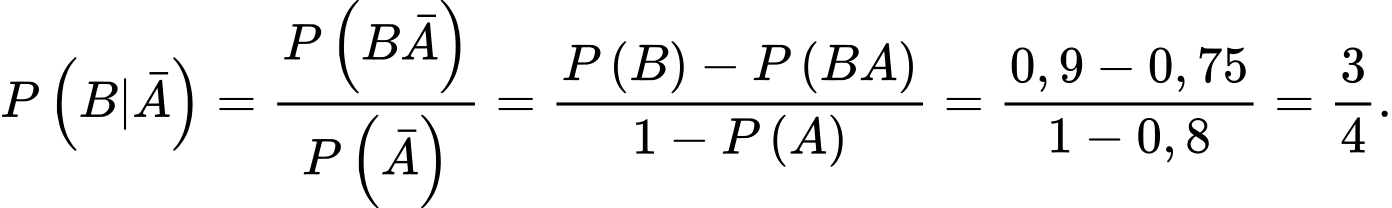
Ta có 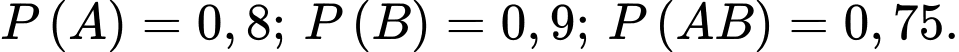
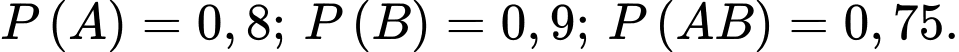
a) Đúng. 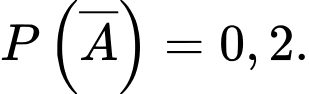
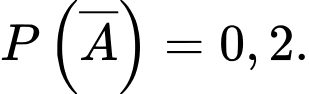
b) Sai. Ta có: 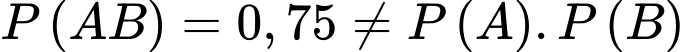 nên hai biến cố A và B không độc lập.
nên hai biến cố A và B không độc lập.
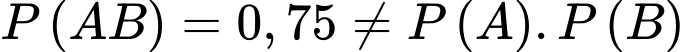 nên hai biến cố A và B không độc lập.
nên hai biến cố A và B không độc lập. c) Đúng. Nếu xạ thủ đó bắn trúng bia số 1, xác suất để xạ thủ đó bắn trúng bia số 2 là
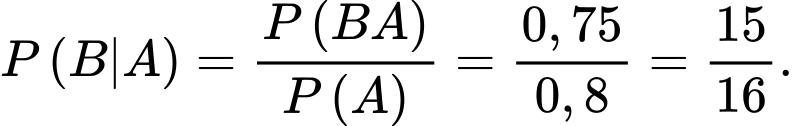
d) Sai. Biết xạ thủ đó bắn không trúng bia số 1, xác suất để xạ thủ đó bắn trúng bia số 2 là
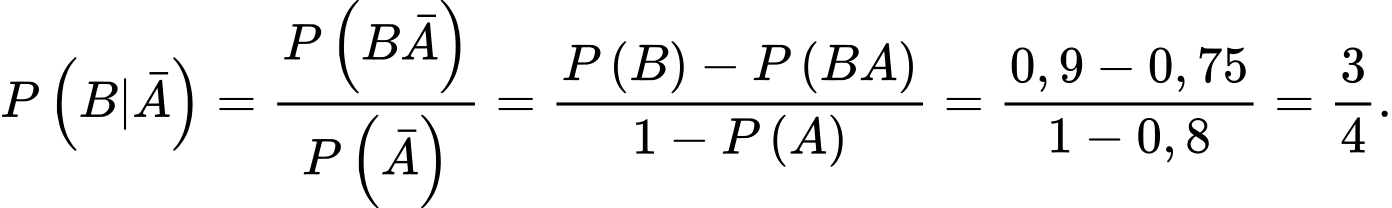
Câu 16 [135850]: Tại một vùng, tỷ lệ người dân nghiện hút thuốc lá là 20%, tỷ lệ người dân nghiện uống rượu là 14%, tỷ lệ người dân vừa nghiện hút thuốc vừa nghiện uống rượu là 9%. Các mệnh đề sau đúng hay sai.
A, a) Tỷ lệ người dân nghiện hút thuốc nhưng không nghiện uống rượu là 0,11.
B, b) Tỷ lệ người dân không nghiện hút thuốc và không nghiện uống rượu là 0,75.
C, c) Chọn ngẫu nhiên một người dân ở vùng này. Nếu biết rằng người đó nghiện hút thuốc thì xác suất người đó cũng nghiện uống rượu là 0,45.
D, d) Chọn ngẫu nhiên một người dân ở vùng này. Nếu biết người đó nghiện uống rượu thì xác suất người đó không nghiện hút thuốc là 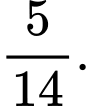
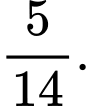
Xét hai biến cố sau: A: “người đó nghiện hút thuốc”; B: “Người đó nghiện uống rượu”.
Ta có 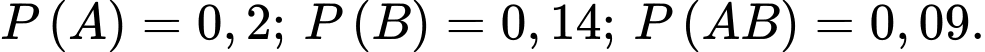
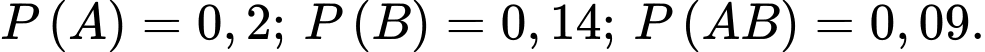
a) Đúng. 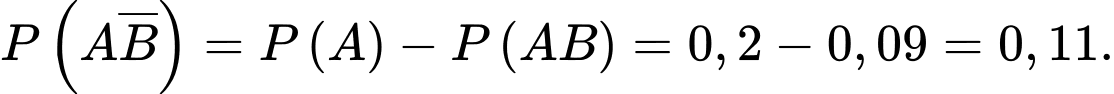
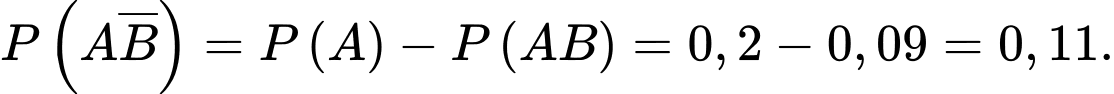
b) Đúng. Ta có: 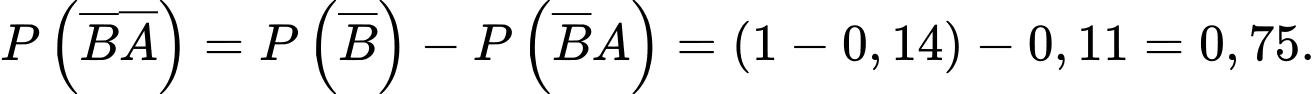
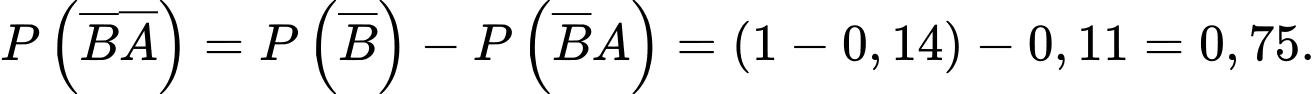
c) Đúng. 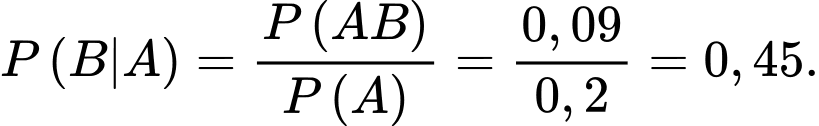
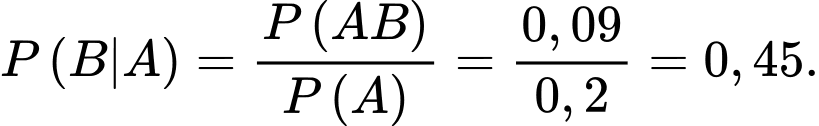
d) Đúng. 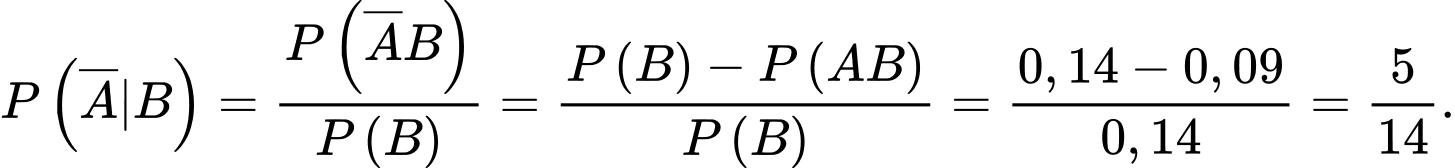
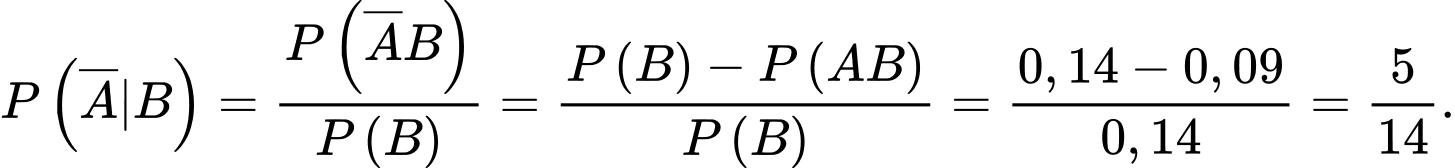
Câu 17 [135855]: Một cuộc thi có 2 vòng. Vòng 1 lấy 90% thí sinh. Vòng 2 lấy 80% thí sinh của vòng 1. Các mệnh đề sau đúng hay sai.
A, a) Xác suất thí sinh đó đỗ cuộc thi là 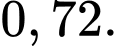
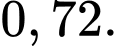
B, b) Xác suất bị loại của thí sinh ở vòng 2 là 0,08.
C, c) Xác suất thí sinh bị loại ở vòng 2 biết rằng thí sinh đó bị loại là 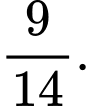
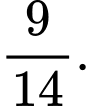
D, d) Xác suất để thí sinh đỗ cuộc thi biết rằng thí sinh đó vượt qua vòng 1 là 0,8.
Thứ tự đáp án: Đúng, Sai, Đúng, Đúng.
Xét các biến cố sau:
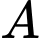 là biến cố “Thí sinh đó đỗ cuộc thi”
là biến cố “Thí sinh đó đỗ cuộc thi”
 là biến cố “Thí sinh đó không đỗ cuộc thi”
là biến cố “Thí sinh đó không đỗ cuộc thi”
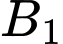 là biến cố “Thí sinh đó qua vòng 1”
là biến cố “Thí sinh đó qua vòng 1”
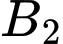 là biến cố “Thí sinh đó qua vòng 2”
là biến cố “Thí sinh đó qua vòng 2”
Từ giả thiết:
Vòng 1 lấy 90% thí sinh tức có 90% thí sinh qua vòng 1 nên xác suất thí sinh đó qua vòng 1 là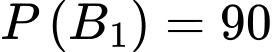 Theo tính chất xác suất, ta suy ra
Theo tính chất xác suất, ta suy ra 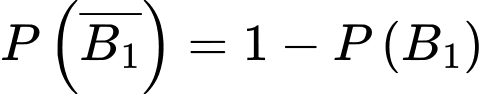
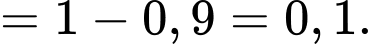
Tương tự, vì vòng 2 lấy 80% thí sinh của vòng 1 tức có 80% vượt qua vòng 2 nên ta có xác suất thí sinh đó qua vòng 2 là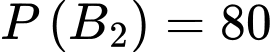 Và theo tính chất xác suất, ta suy ra
Và theo tính chất xác suất, ta suy ra 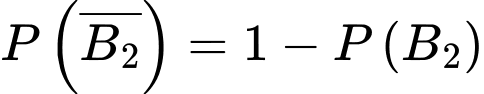
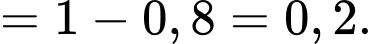
a) Thí sinh đó đỗ cuộc thi khi và chỉ khi thí sinh đó qua vòng 1 và qua vòng 2 nên xác suất thí sinh đó đỗ cuộc thi là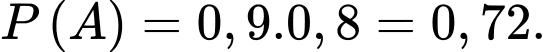
 Mệnh đề đúng.
Mệnh đề đúng.
b) Xác suất bị loại của thí sinh ở vòng 2 là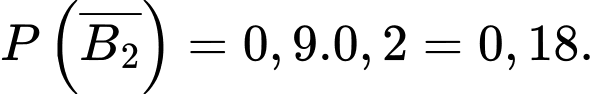
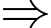 Mệnh đề sai.
Mệnh đề sai.
c) YCBT Tính
Tính 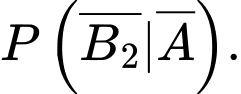
Ta có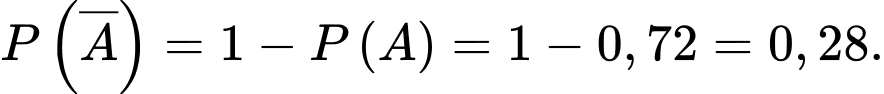 (tính chất xác suất)
(tính chất xác suất)
Theo công thức xác suất có điều kiện, ta có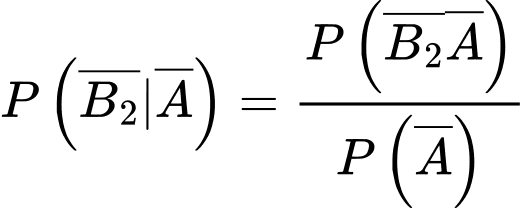
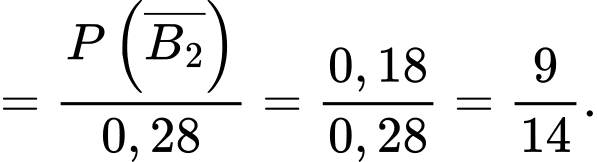
(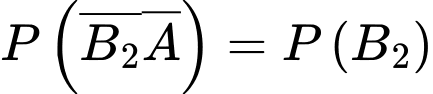 vì
vì 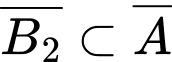 nên
nên 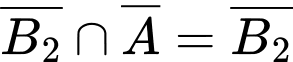 )
)
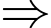 Mệnh đề đúng.
Mệnh đề đúng.
d) YCBT Tính
Tính 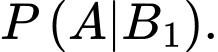
Theo công thức Bayes, ta có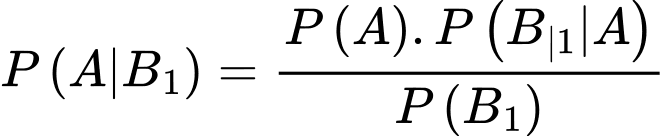
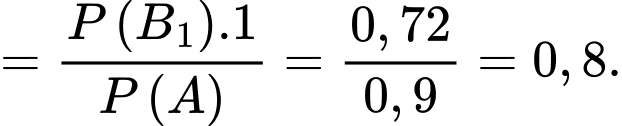
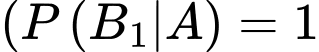 vì
vì 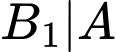 là biến cố qua vòng 1 khi biết thí sinh đó đỗ, thì đây là biến cố chắc chắn xảy ra, do đó có xác suất bằng 1)
là biến cố qua vòng 1 khi biết thí sinh đó đỗ, thì đây là biến cố chắc chắn xảy ra, do đó có xác suất bằng 1)
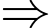 Mệnh đề đúng.
Mệnh đề đúng.
Xét các biến cố sau:
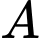 là biến cố “Thí sinh đó đỗ cuộc thi”
là biến cố “Thí sinh đó đỗ cuộc thi”
 là biến cố “Thí sinh đó không đỗ cuộc thi”
là biến cố “Thí sinh đó không đỗ cuộc thi”
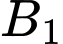 là biến cố “Thí sinh đó qua vòng 1”
là biến cố “Thí sinh đó qua vòng 1”
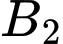 là biến cố “Thí sinh đó qua vòng 2”
là biến cố “Thí sinh đó qua vòng 2”
Từ giả thiết:
Vòng 1 lấy 90% thí sinh tức có 90% thí sinh qua vòng 1 nên xác suất thí sinh đó qua vòng 1 là
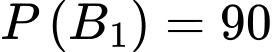 Theo tính chất xác suất, ta suy ra
Theo tính chất xác suất, ta suy ra 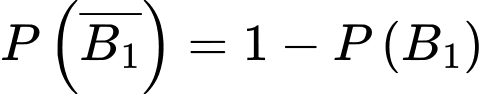
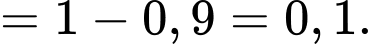
Tương tự, vì vòng 2 lấy 80% thí sinh của vòng 1 tức có 80% vượt qua vòng 2 nên ta có xác suất thí sinh đó qua vòng 2 là
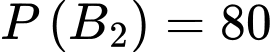 Và theo tính chất xác suất, ta suy ra
Và theo tính chất xác suất, ta suy ra 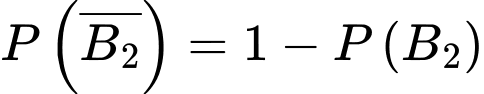
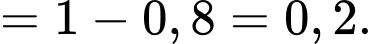
a) Thí sinh đó đỗ cuộc thi khi và chỉ khi thí sinh đó qua vòng 1 và qua vòng 2 nên xác suất thí sinh đó đỗ cuộc thi là
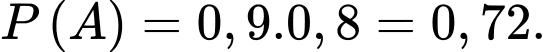
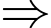 Mệnh đề đúng.
Mệnh đề đúng.
b) Xác suất bị loại của thí sinh ở vòng 2 là
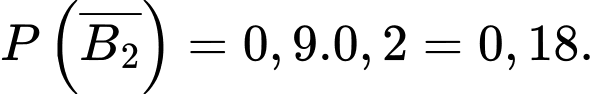
 Mệnh đề sai.
Mệnh đề sai.
c) YCBT
 Tính
Tính 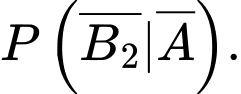
Ta có
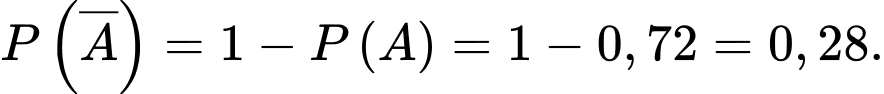 (tính chất xác suất)
(tính chất xác suất)
Theo công thức xác suất có điều kiện, ta có
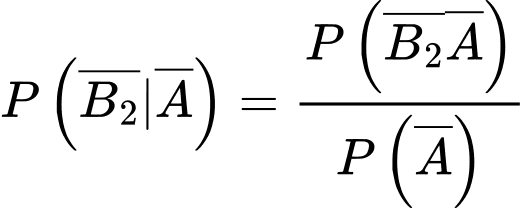
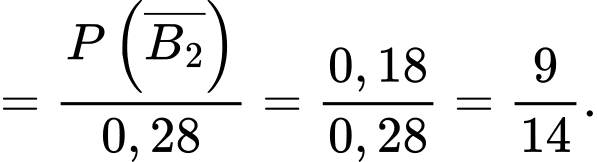
(
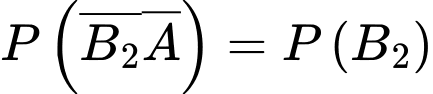 vì
vì 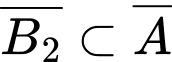 nên
nên 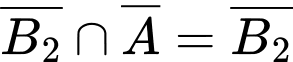 )
)
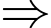 Mệnh đề đúng.
Mệnh đề đúng.
d) YCBT
 Tính
Tính 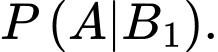
Theo công thức Bayes, ta có
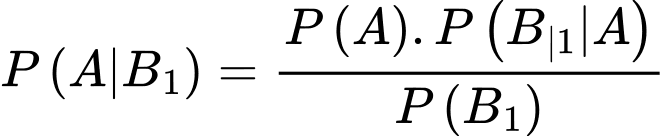
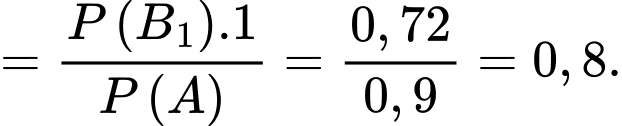
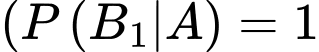 vì
vì 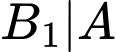 là biến cố qua vòng 1 khi biết thí sinh đó đỗ, thì đây là biến cố chắc chắn xảy ra, do đó có xác suất bằng 1)
là biến cố qua vòng 1 khi biết thí sinh đó đỗ, thì đây là biến cố chắc chắn xảy ra, do đó có xác suất bằng 1)
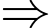 Mệnh đề đúng.
Mệnh đề đúng.
Câu 18 [143804]: Một công ty cần tuyển 2 nhân viên, có 6 người nộp đơn trong đó có 2 nam và 4 nữ. Biết rằng khả năng được tuyển của mỗi người là như nhau. Xét tính đúng sai của các mệnh đề sau:
A, a) Xác suất để cả hai người được chọn là nữ là 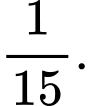
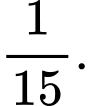
B, b) Xác suất để ít nhất một nữ được chọn là 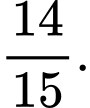
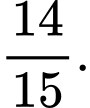
C, c) Xác suất để cả hai nữ được chọn nếu biết rằng có ít nhất một nữ đã
được chọn là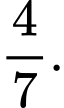
được chọn là
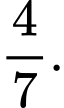
D, d) Giả sử Hoa là một trong 4 nữ. Xác suất để Hoa được chọn nếu biết rằng có ít nhất một nữ được chọn là 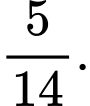
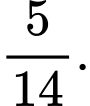
a) Sai. Xác suất cả hai người được chọn đều là nữ là 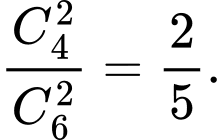
b) Đúng. Xác suất cả hai người được chọn đều là nam là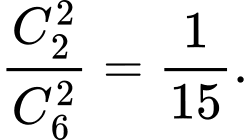
Do vậy xác suất để ít nhất một nữ được chọn là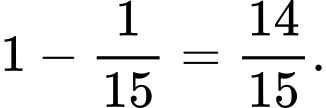
c) Sai. Gọi A là biến cố: “Cả hai nữ được chọn” và B là biến cố: Ít nhất một nữ được chọn”
Ta có: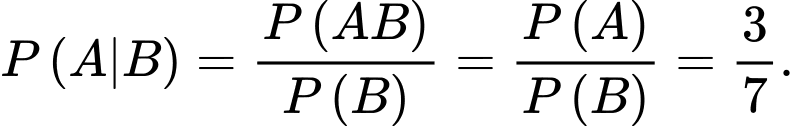
d) Đúng. Gọi C là biến cố: “Hoa được chọn” thì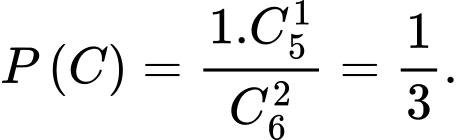
Ta có: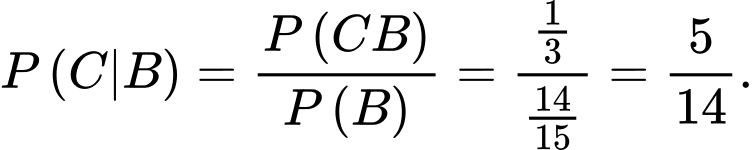
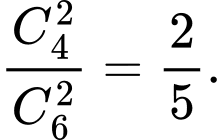
b) Đúng. Xác suất cả hai người được chọn đều là nam là
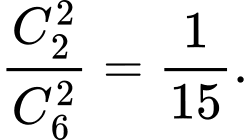
Do vậy xác suất để ít nhất một nữ được chọn là
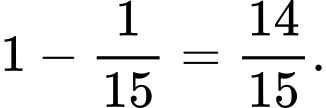
c) Sai. Gọi A là biến cố: “Cả hai nữ được chọn” và B là biến cố: Ít nhất một nữ được chọn”
Ta có:
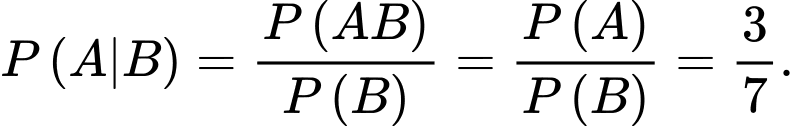
d) Đúng. Gọi C là biến cố: “Hoa được chọn” thì
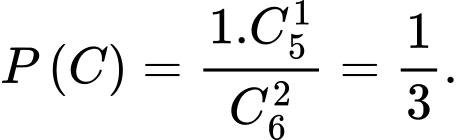
Ta có:
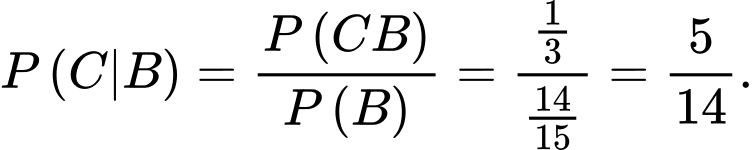
Câu 19 [145406]: Ba xạ thủ A, B, C độc lập với nhau cùng bắn súng vào bia. Xác suất bắn trúng bia của 3 người A, B và C tương ứng là 0,7, 0,6 và 0,9. Xét tính đúng sai của các mệnh đề sau:
A, a) Xác suất để có duy nhất một xạ thủ bắn trúng bia là 0,154.
B, b) Xác suất để có đúng hai xạ thủ bắn trúng bia là 0,456.
C, c) Xác suất để có ít nhất một xạ thủ bắn trúng bia là 0,988.
D, d) Xác suất để xạ thủ A bắn trúng bia biết rằng có hai xạ thủ bắn trúng bia là 0,648.
Gọi 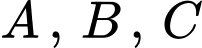 là biến cố xạ thủ
là biến cố xạ thủ 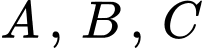 bắn trúng bia.
bắn trúng bia.
Ta có: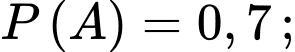
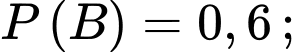
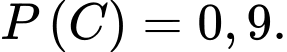
Các biến cố độc lập.
a) Đúng. Vì: Xác suất duy nhất một xạ thủ bắn trúng:
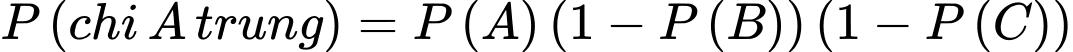
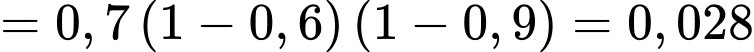
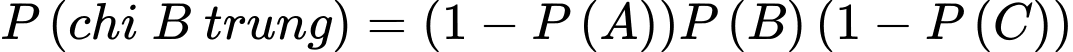
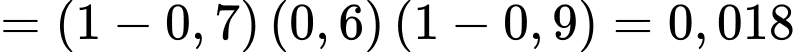
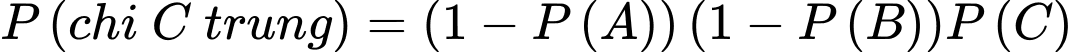
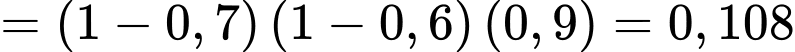
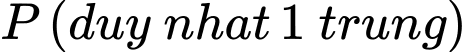
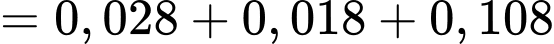
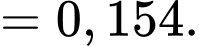
b) Đúng. Vì: Xác suất đúng hai xạ thủ bắn trúng:
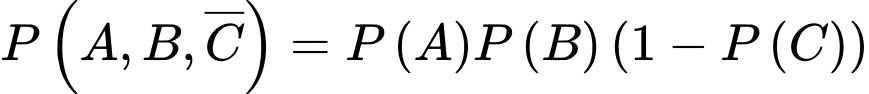
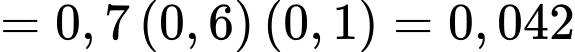

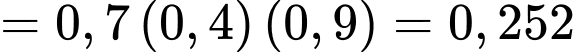
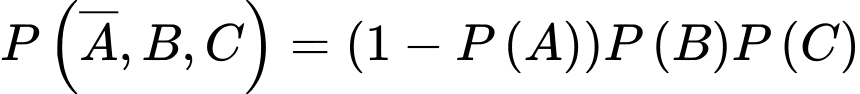
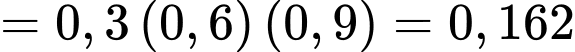
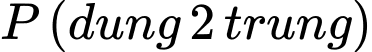
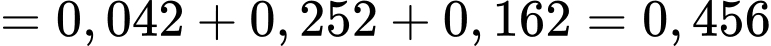
c) Đúng. Vì: Xác suất ít nhất một xạ thủ bắn trúng:
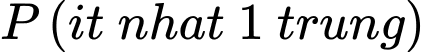
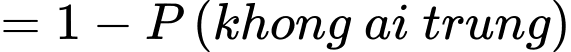
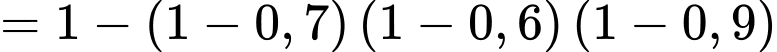
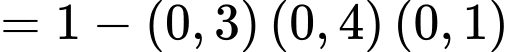
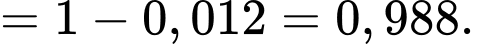
d) Sai. Vì: Xác suất xạ thủ A trúng biết có 2 xạ thủ trúng:
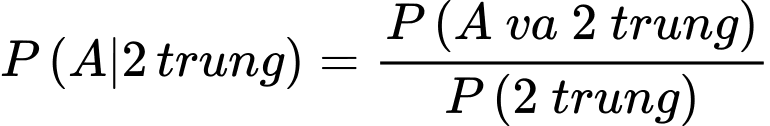
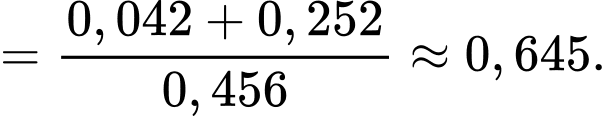
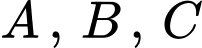 là biến cố xạ thủ
là biến cố xạ thủ 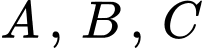 bắn trúng bia.
bắn trúng bia.
Ta có:
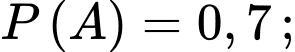
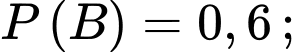
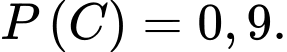
Các biến cố độc lập.
a) Đúng. Vì: Xác suất duy nhất một xạ thủ bắn trúng:
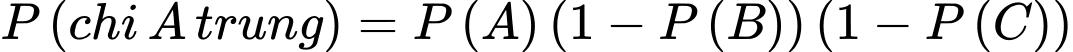
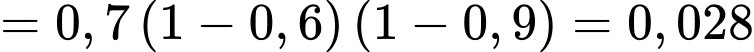
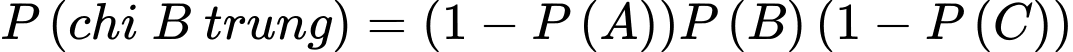
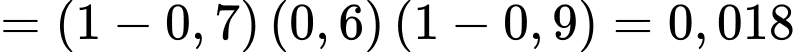
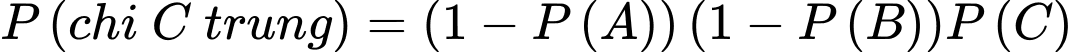
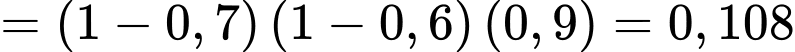
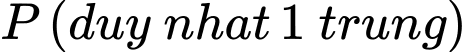
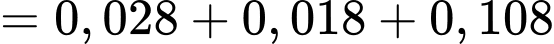
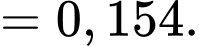
b) Đúng. Vì: Xác suất đúng hai xạ thủ bắn trúng:
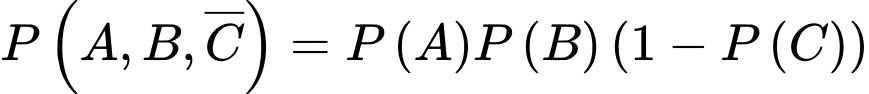
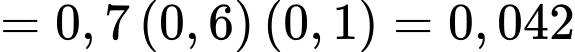

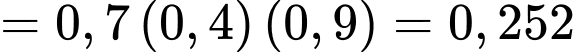
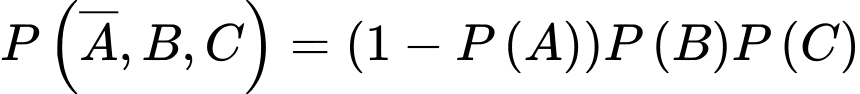
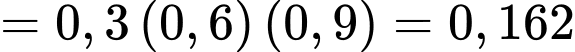
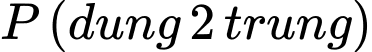
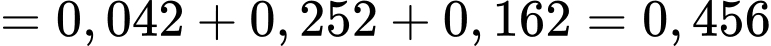
c) Đúng. Vì: Xác suất ít nhất một xạ thủ bắn trúng:
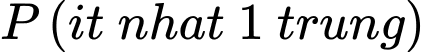
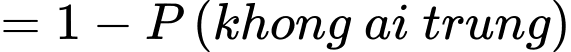
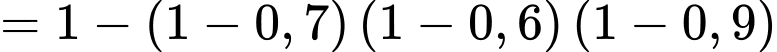
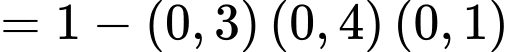
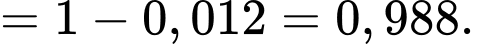
d) Sai. Vì: Xác suất xạ thủ A trúng biết có 2 xạ thủ trúng:
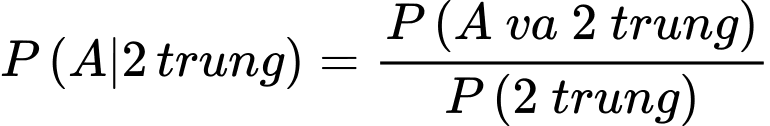
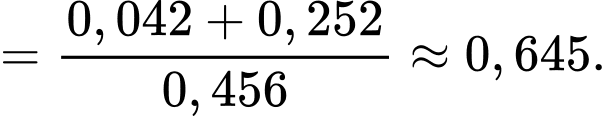
Câu 20 [146098]: Đội tuyển cầu lông của Trường THPT-X có 3 vận động viên, mỗi vận động viên thi đấu một trận. Xác suất thắng trận của các vận viên A, B, C lần lượt là: 0,9; 0,7; 0,8. Xét tính đúng sai của các mệnh đề sau:
A, a) Xác suất để đội tuyển thẳng cả ba trận bằng 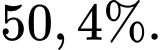
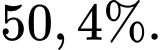
B, b) Xác suất để đội tuyển thắng ít nhất một trận là 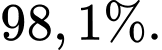
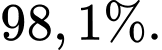
C, c) Xác suất để đội tuyển thắng hai trận là 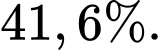
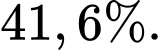
D, d) Biết rằng đội tuyển thắng 2 trận. Xác suất để C thua xấp xỉ 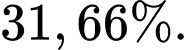
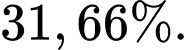
a) Đúng. Xác suất để đội tuyển thẳng cả ba trân bằng 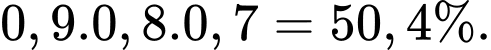
b) Sai. Xác suất để đội tuyển thắng ít nhất một trận là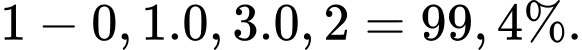
c) Sai. Xác suất để đội tuyển thắng hai trận là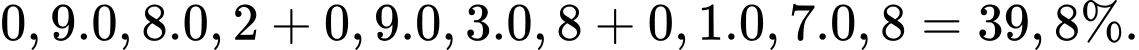
d) Đúng.
Gọi A là biến cố: Đội tuyển thắng hai trận
B là biến cố: C thua
Ta có: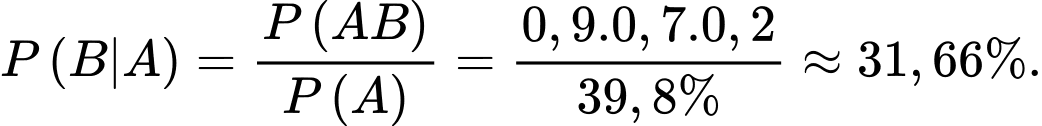
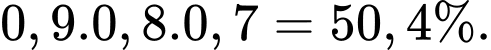
b) Sai. Xác suất để đội tuyển thắng ít nhất một trận là
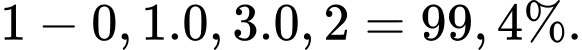
c) Sai. Xác suất để đội tuyển thắng hai trận là
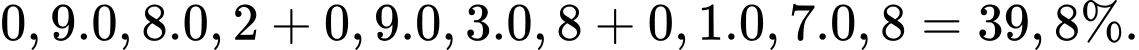
d) Đúng.
Gọi A là biến cố: Đội tuyển thắng hai trận
B là biến cố: C thua
Ta có:
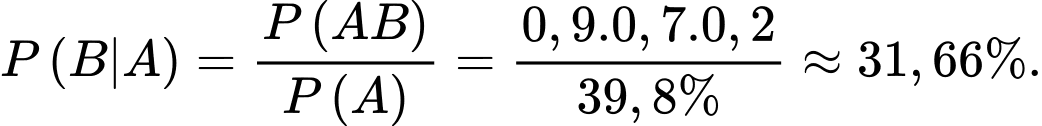
Câu 21 [146101]: Trong 1 lô hàng 10 sản phẩm có 2 sản phẩm xấu, chọn không hoàn lại để phát hiện ra 2 sản phẩm xấu, khi nào chọn được sản phẩm xấu thứ 2 thì dừng lại. Xét tính đúng sai của các mệnh đề sau:
A, a) Xác suất dừng lại ở lần chọn thứ hai là 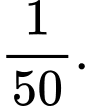
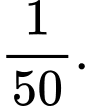
B, b) Xác suất dừng lại ở lần chọn thứ 3 là 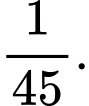
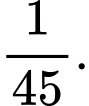
C, c) Biết rằng đã chọn được sản phẩm xấu ở lần chọn thứ nhất, xác suất dừng lại ở lần chọn thứ 4 là 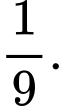
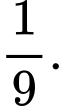
D, d) Nếu việc kiểm tra dừng lại ở lần chọn thứ 3, xác suất lần chọn đầu được sản phẩm xấu là 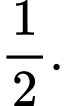
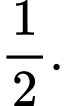
a) Sai. Xác suất dừng lại ở lần chọn thứ hai là 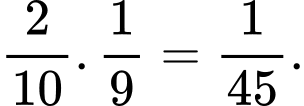
b) Sai. Xác suất dừng lại ở lần chọn thứ 3 là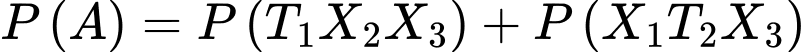
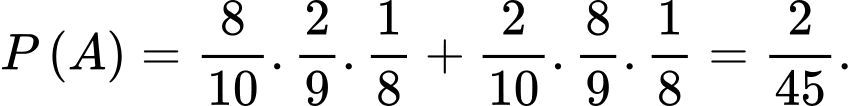
c) Đúng. Biết rằng đã chọn được sản phẩm xấu ở lần chọn thứ nhất, xác suất dừng lại ở lần chọn thứ 4 là
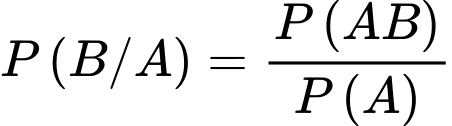
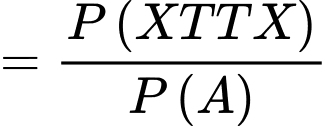
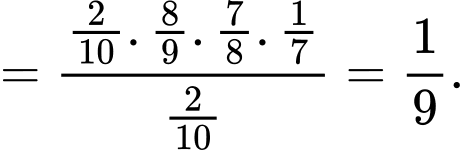
d) Đúng. Gọi B là biến cố: Lần đầu chọn được sản phẩm xấu
Ta có: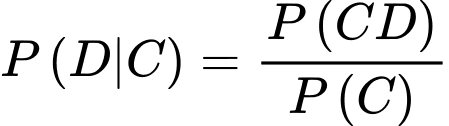
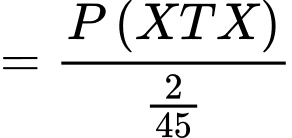
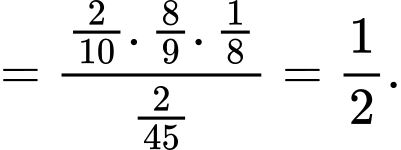
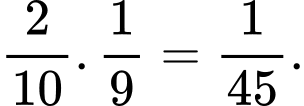
b) Sai. Xác suất dừng lại ở lần chọn thứ 3 là
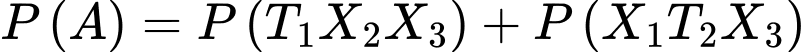
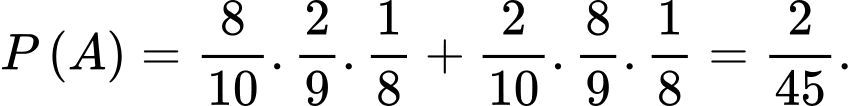
c) Đúng. Biết rằng đã chọn được sản phẩm xấu ở lần chọn thứ nhất, xác suất dừng lại ở lần chọn thứ 4 là
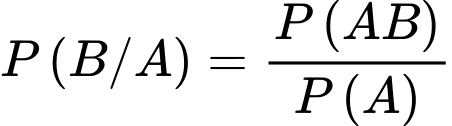
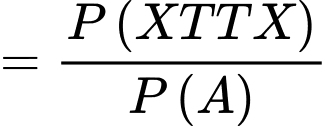
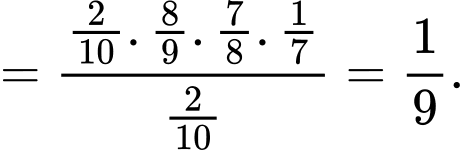
d) Đúng. Gọi B là biến cố: Lần đầu chọn được sản phẩm xấu
Ta có:
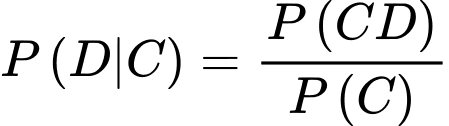
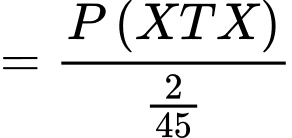
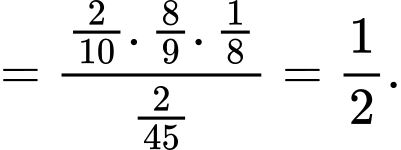
Câu 22 [135692]: Theo thống kê ở các gia đình có hai con thì xác suất để con thứ nhất và con thứ hai đều là trai là 0,27 và hai con đều là gái là 0,23, còn xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau. Chọn ngẫu nhiên một gia đình thì gặp gia đình có con thứ nhất là gái, tìm xác suất để con thứ hai là trai. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố "con thứ nhất là con gái” và B là biến cố "con thứ hai là con trai thì theo đề bài ta có: 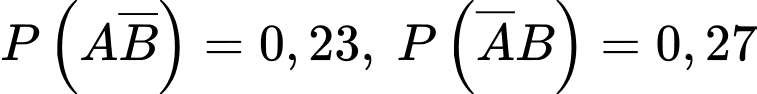
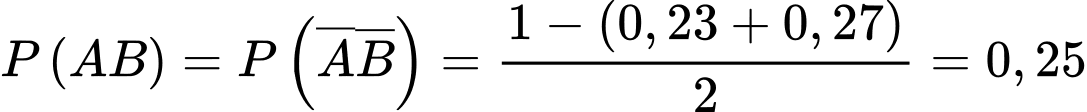
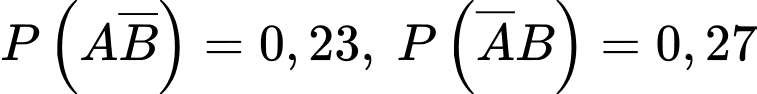
Vì xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau nên
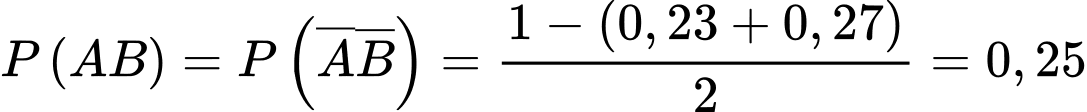
Ta cần tính: 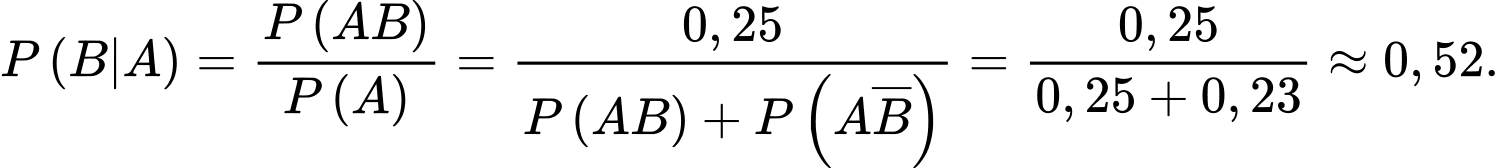
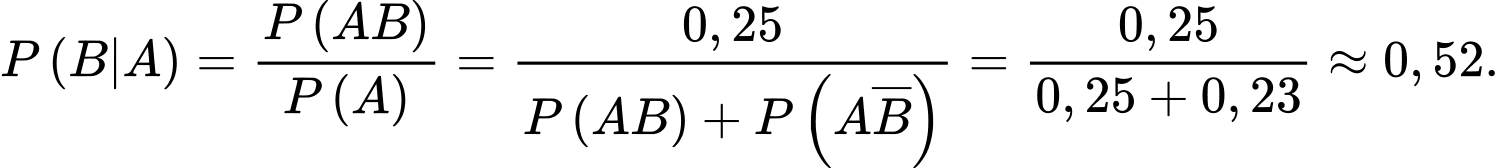
Câu 23 [146672]: Một lô hàng có 6 sản phẩm tốt, 4 sản phẩm xấu. Lấy ngẫu nhiên không hoàn lại từng sản phẩm cho đến khi lấy được 2 sản phẩm tốt thì ngừng, Biết đã ngừng lại ở lần lấy sản phẩm thứ 4. Tính xác suất để lần lấy thứ nhất lấy được sản phẩm tốt. Viết kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,33.
Gọi A là biến cố: lần thứ nhất lấy được sản phẩm tốt
B là biến cố: Ngưng lại ở lần thứ 4
Ta có: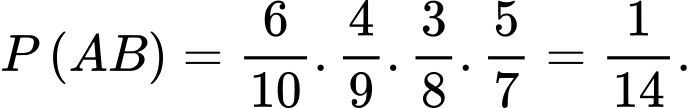
Mặt khác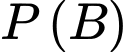
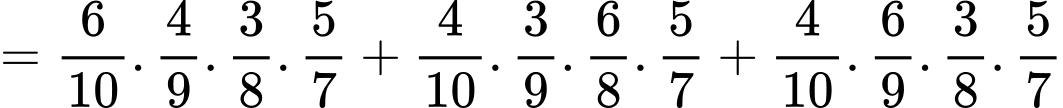
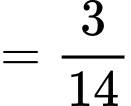
Do đó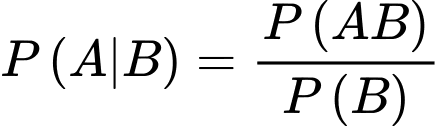
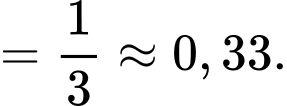
Gọi A là biến cố: lần thứ nhất lấy được sản phẩm tốt
B là biến cố: Ngưng lại ở lần thứ 4
Ta có:
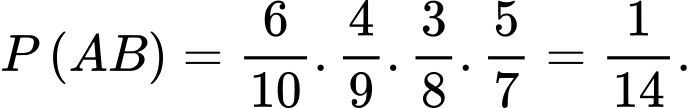
Mặt khác
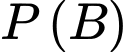
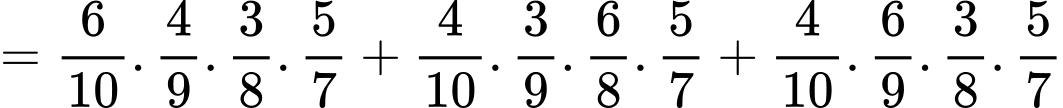
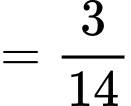
Do đó
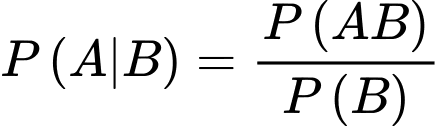
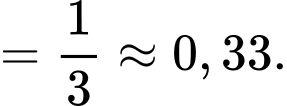
Câu 24 [135871]: Một gia đình có 3 đứa trẻ. Biết rằng có ít nhất 2 đứa trẻ là con trai và xác suất sinh con trai và con gái là như nhau ở mỗi lần sinh. Xác suất để gia đình có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái bằng bao nhiêu?
Do gia đình có 3 đứa trẻ nên sẽ có thể xảy ra 8 khả năng: (trai, trai, trai), (gái, gái, gái), (gái, trai, trai), (trai, gái, trai), (trai, trai, gái), (trai, gái, gái), (gái, trai, gái), (gái, gái, trai).
Gọi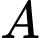 là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và
là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và 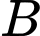 là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có
là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có 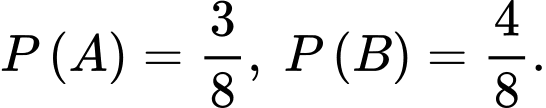
Do nếu xảy ra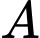 thì đương nhiên sẽ xảy ra
thì đương nhiên sẽ xảy ra 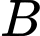 nên ta có:
nên ta có: 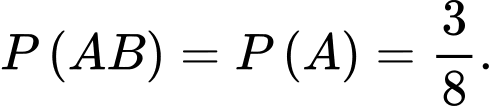
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là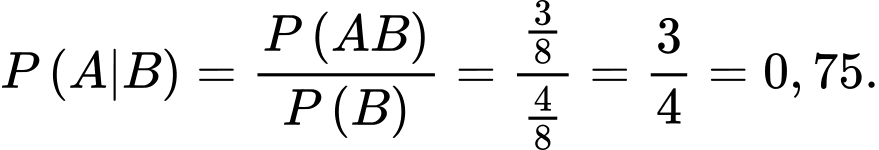
Gọi
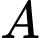 là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và
là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và 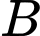 là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có
là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có 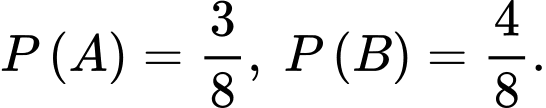
Do nếu xảy ra
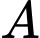 thì đương nhiên sẽ xảy ra
thì đương nhiên sẽ xảy ra 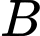 nên ta có:
nên ta có: 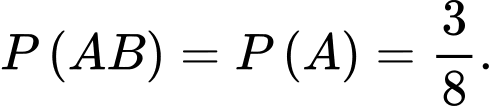
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là
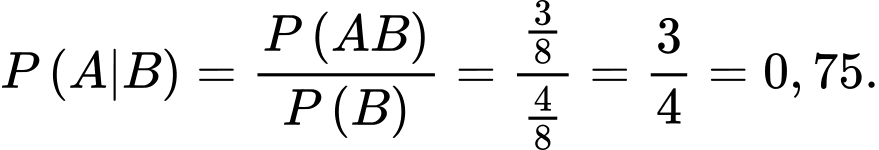
Câu 25 [135872]: Gieo đồng thời ba con xúc xắc cân đối đồng chất. Tính xác suất để tổng số chấm xuất hiện trên ba con bằng 8 biết rằng ít nhất có một con xuất hiện mặt 5 chấm. Viết kết quả làm tròn đến hàng phần trăm.
Không gian mẫu gồm các phần tử 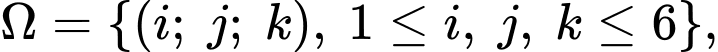 trong đó bộ số
trong đó bộ số 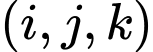 kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt
kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt 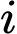 chấm, con xúc xắc thứ hai xuất hiện mặt
chấm, con xúc xắc thứ hai xuất hiện mặt 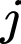 chấm và con xúc xắc thứ ba xuất hiện mặt
chấm và con xúc xắc thứ ba xuất hiện mặt 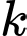 chấm”.
chấm”.
Gọi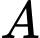 là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,
là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,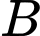 là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
Ta có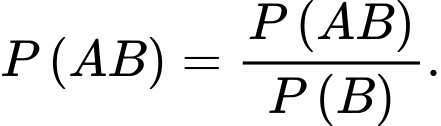
Vì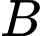 là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên
là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên 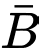 là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó
là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó 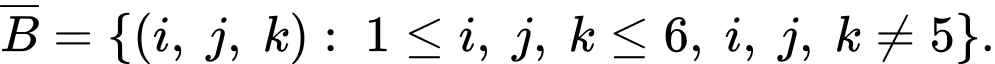
Suy ra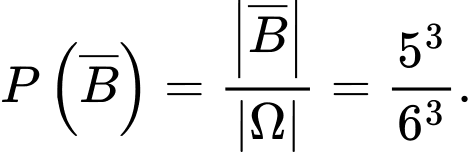
Do đó,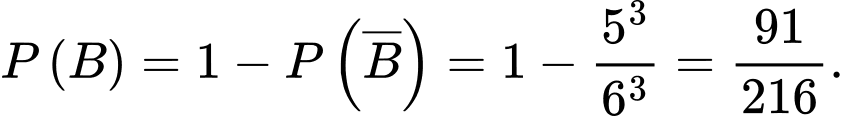
Ta thấy là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó:
là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó: 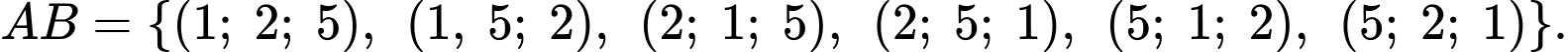
Suy ra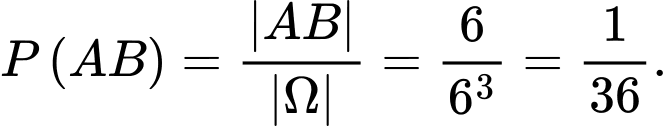
Vậy xác suất cần tìm là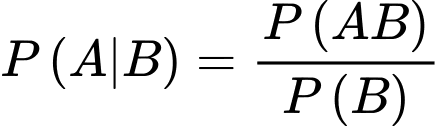
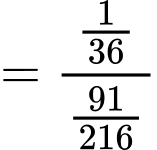
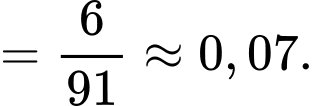
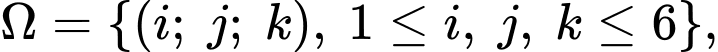 trong đó bộ số
trong đó bộ số 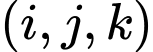 kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt
kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt 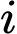 chấm, con xúc xắc thứ hai xuất hiện mặt
chấm, con xúc xắc thứ hai xuất hiện mặt 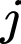 chấm và con xúc xắc thứ ba xuất hiện mặt
chấm và con xúc xắc thứ ba xuất hiện mặt 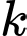 chấm”.
chấm”.
Gọi
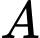 là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,
là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”,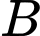 là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”.
Ta có
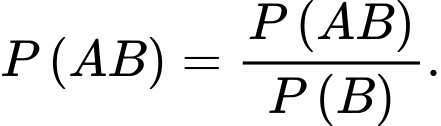
Vì
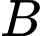 là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên
là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên 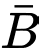 là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó
là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó 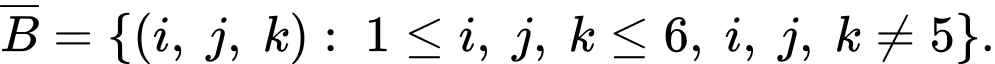
Suy ra
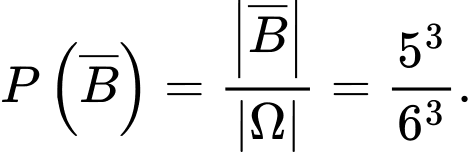
Do đó,
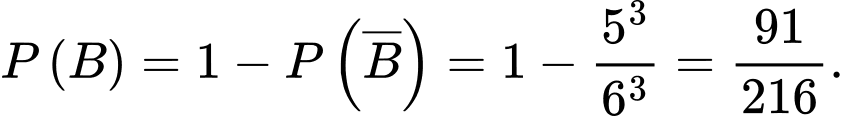
Ta thấy
 là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó:
là biến cố: “ Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó: 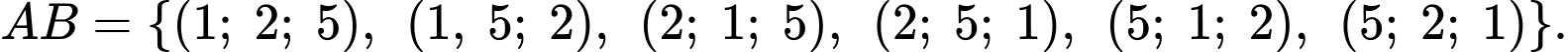
Suy ra
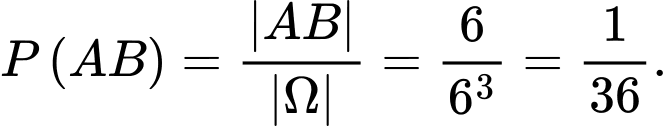
Vậy xác suất cần tìm là