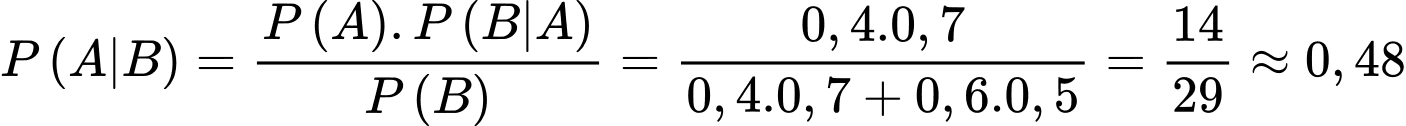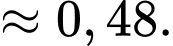Đáp án Bài tập tự luyện đề 2
Câu 1 [143817]: Cho hai biến cố ngẫu nhiên 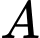 và
và 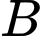 có
có 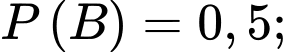
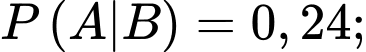
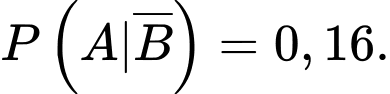 Khi đó,
Khi đó,  bằng
bằng
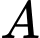 và
và 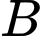 có
có 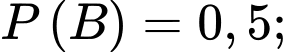
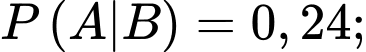
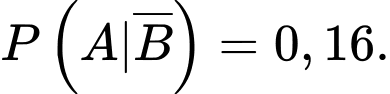 Khi đó,
Khi đó,  bằng
bằng A, 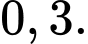
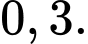
B, 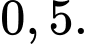
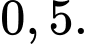
C, 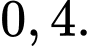
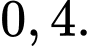
D, 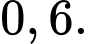
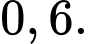
Áp dụng công thức Bayes ta có:
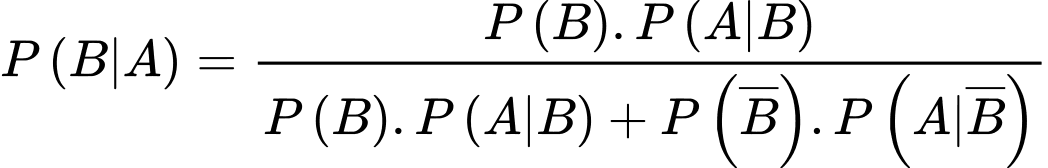
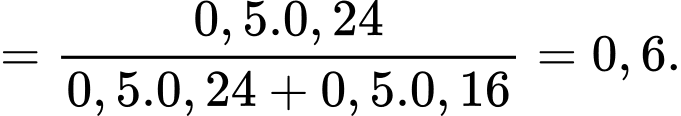
Chọn D. Đáp án: D
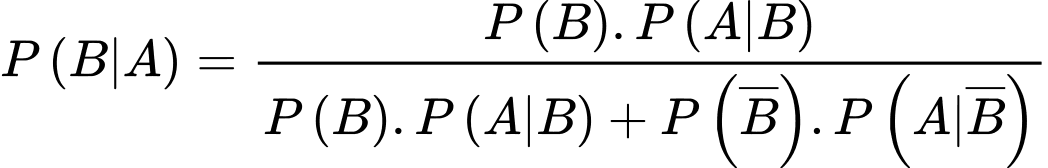
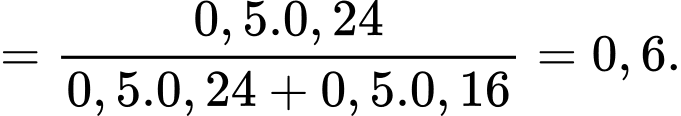
Chọn D. Đáp án: D
Câu 2 [143818]: Một xét nghiệm Covid - 19 cho kết quả dương tính với 90% các trường hợp thực sự nhiễm virus và cho kết quả âm tính với 80% các trường hợp thực sự không nhiễm virus. Biết rằng tỉ lệ người nhiễm Covid - 19 trong một cộng đồng nào đó là 1%. Một người trong cộng đồng đó có kết quả xét nghiệm dương tính. Xác suất để người đó thực sự bị nhiễm virus là
A, 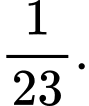
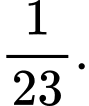
B, 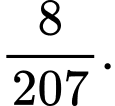
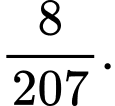
C, 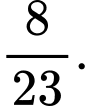
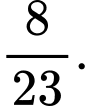
D, 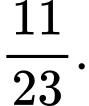
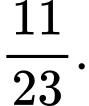
Gọi A là biến cố người đó bị nhiễm virus 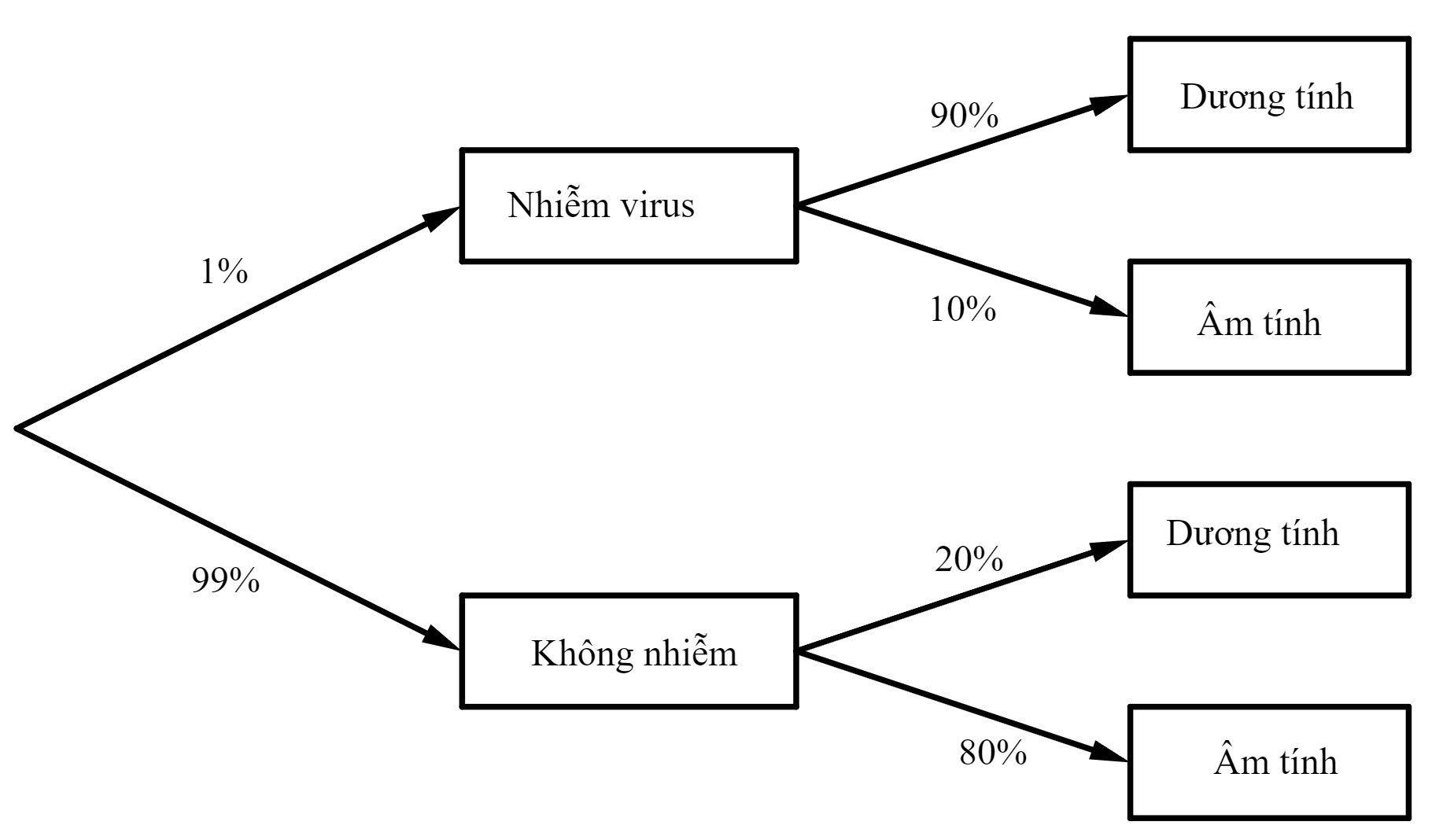
B là biến cố “Người được chọn ra có xét nghiệm dương tính”.
Xác suất để người đó có kết quả dương tính là: 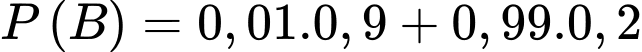
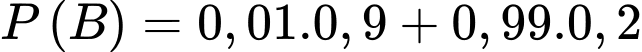

Xác suất để người đó thực sự bị nhiễm virus là 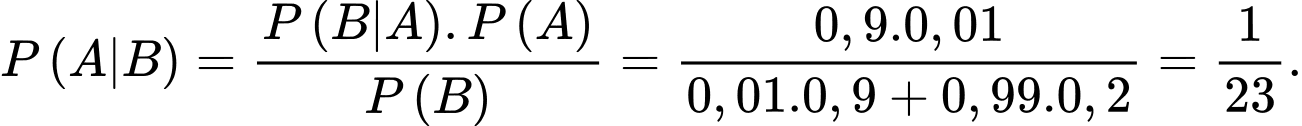
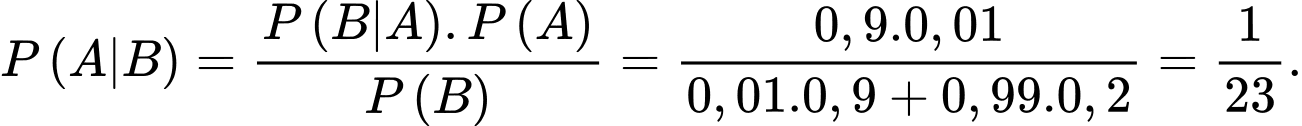
Chọn A.
Đáp án: A
Câu 3 [145260]: [Trích SGK Cùng Khám Phá]: Kết quả khảo sát tại một xã cho thấy có 20% cư dân hút thuốc lá. Tỉ lệ cư dân thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp trong số những người hút thuốc lá và không hút thuốc lá lần lượt là 70% và 15%. Nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp thì xác suất người đó có hút thuốc lá là khoảng bao nhiêu phần trăm?
A, 46%.
B, 58%.
C, 26%.
D, 54%.
Giả sử ta gặp một cư dân của xã, gọi 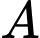 là biến cố "Người đó có hút thuốc lá" và
là biến cố "Người đó có hút thuốc lá" và 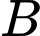 là biến cố "Người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp".
là biến cố "Người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp".
Ta có: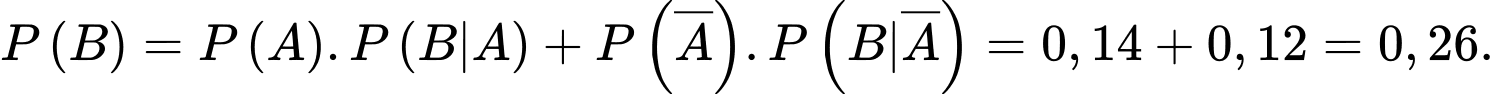
Theo công thức Bayes, ta có: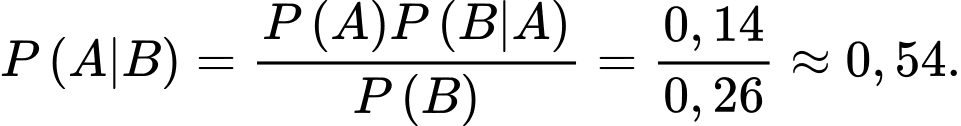
Vậy nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp thì xác suất người đó có hút thuốc lá là khoảng 54%. Chọn D. Đáp án: D
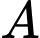 là biến cố "Người đó có hút thuốc lá" và
là biến cố "Người đó có hút thuốc lá" và 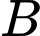 là biến cố "Người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp".
là biến cố "Người đó thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp".Ta có:
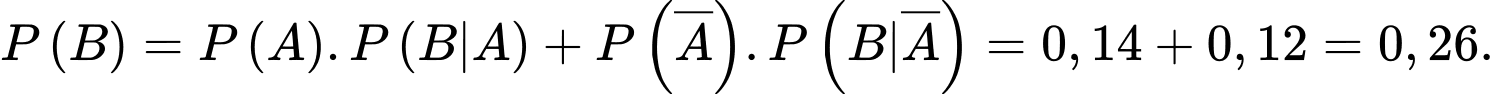
Theo công thức Bayes, ta có:
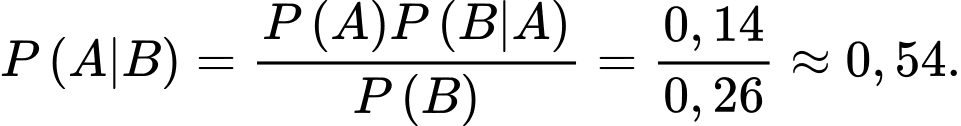
Vậy nếu ta gặp một cư dân của xã thường xuyên gặp các vấn đề sức khoẻ về đường hô hấp thì xác suất người đó có hút thuốc lá là khoảng 54%. Chọn D. Đáp án: D
Câu 4 [143819]: Tỷ lệ sản phẩm tốt của máy thứ nhất là 99%, của máy thứ hai là 98%. Một lô
sản phẩm gồm 40% sản phẩm của máy thứ nhất và 60% sản phẩm của máy thứ hai.
Người ta lấy ngẫu nhiên ra một sản phẩm để kiểm tra thấy là sản phẩm tốt. Tìm xác suất
để sản phẩm đó do máy thứ nhất sản xuất.
A, 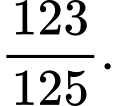
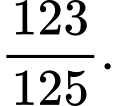
B, 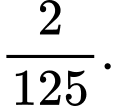
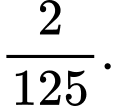
C, 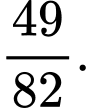
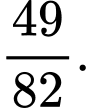
D, 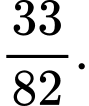
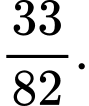
Gọi A là biến cố “Sản phẩm kiểm tra là sản phẩm tốt” 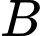 là biến cố “Sản phẩm do máy thứ nhất sản xuất”.
là biến cố “Sản phẩm do máy thứ nhất sản xuất”.  là biến cố “Sản phẩm do máy thứ hai sản xuất”.
là biến cố “Sản phẩm do máy thứ hai sản xuất”. 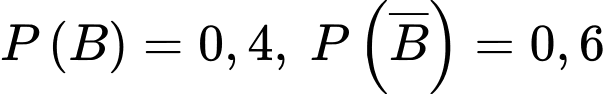
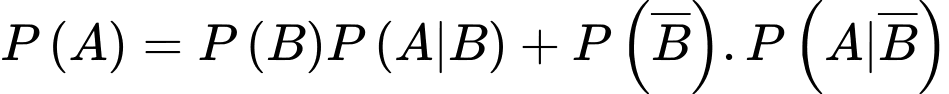
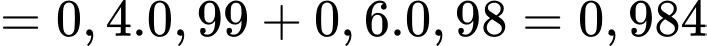
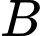 là biến cố “Sản phẩm do máy thứ nhất sản xuất”.
là biến cố “Sản phẩm do máy thứ nhất sản xuất”.  là biến cố “Sản phẩm do máy thứ hai sản xuất”.
là biến cố “Sản phẩm do máy thứ hai sản xuất”. 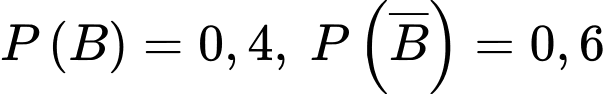
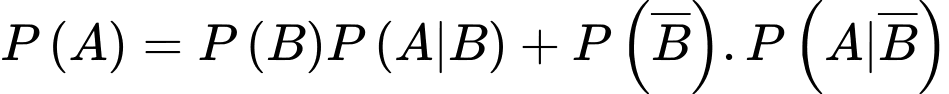
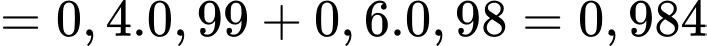
Suy ra 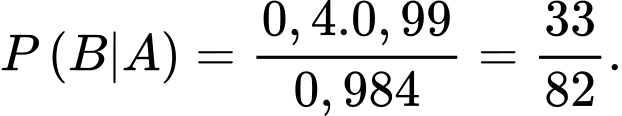
Đáp án: D 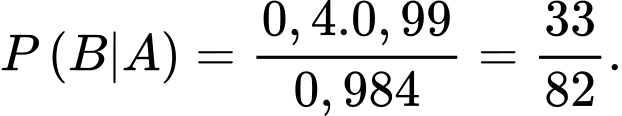
Chọn D.
Câu 5 [143820]: Tỷ lệ người nghiện thuốc là ở một vùng là 30%. Biết rằng tỷ lệ người bị viêm họng trong số những người nghiện thuốc là 60%, còn tỷ lệ người bị viêm họng trong số những người không nghiện là 40%. Lấy ngẫu nhiên một người thấy người ấy không bị viêm họng. Tính xác suất người đó nghiện thuốc lá
A, 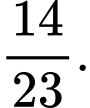
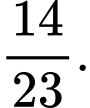
B, 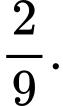
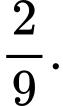
C, 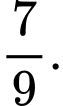
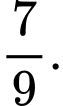
D, 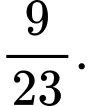
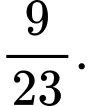
Gọi  là biến cố “Người ấy không bị viêm họng”
là biến cố “Người ấy không bị viêm họng”
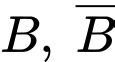 lần lượt là biến cố : “Người ấy nghiện thuốc lá” và “ Người ấy không nghiện thuốc lá”
lần lượt là biến cố : “Người ấy nghiện thuốc lá” và “ Người ấy không nghiện thuốc lá” 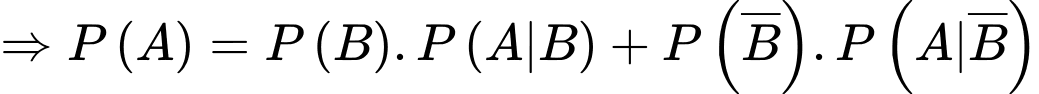
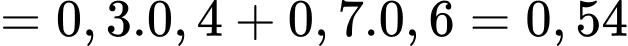
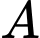 là biến cố “Người ấy không bị viêm họng”
là biến cố “Người ấy không bị viêm họng”
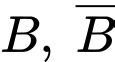 lần lượt là biến cố : “Người ấy nghiện thuốc lá” và “ Người ấy không nghiện thuốc lá”
lần lượt là biến cố : “Người ấy nghiện thuốc lá” và “ Người ấy không nghiện thuốc lá” Ta có: 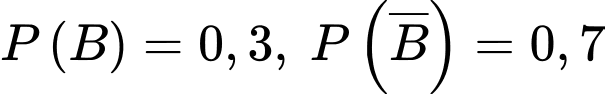
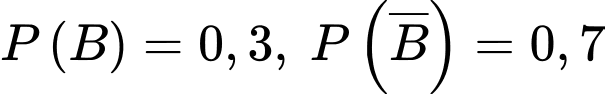
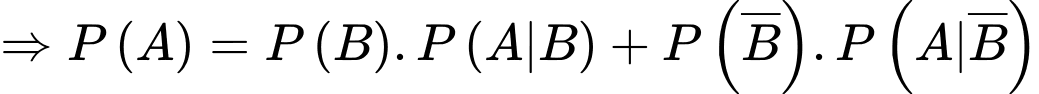
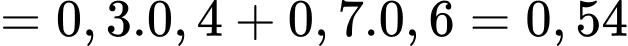
Do đó 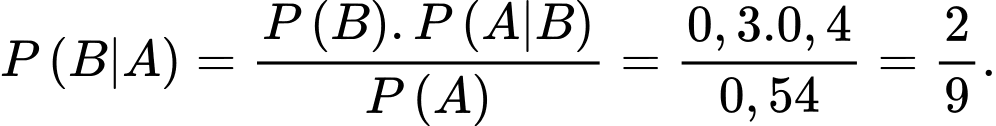 Chọn B.
Chọn B.
Đáp án: B 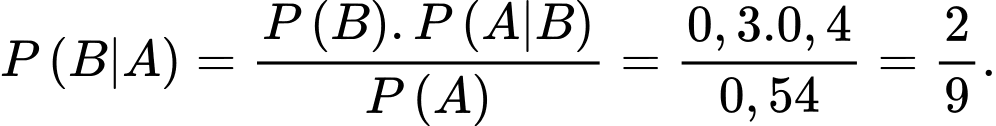 Chọn B.
Chọn B.
Câu 6 [145262]: [Trích SGK Cùng Khám Phá]: Một bệnh viện đang xét nghiệm cho một số bệnh nhân để xác định liệu họ có nhiễm virus X hay không. Xác suất để một bệnh nhân bị nhiễm virus X là 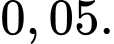 Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là
Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là 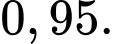 Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là
Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là 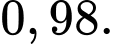 Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là
Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là
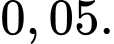 Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là
Khi xét nghiệm, nếu một bệnh nhân bị nhiễm thì xác suất để kết quả xét nghiệm dương tính là 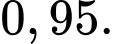 Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là
Nếu một bệnh nhân không bị nhiễm thì xác suất để kết quả xét nghiệm âm tính là 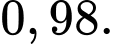 Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là
Một bệnh nhân được chọn ngẫu nhiên và có kết quả xét nghiệm dương tính. Xác suất để bệnh nhân đó thực sự bị nhiễm virus X là A, 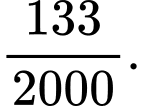
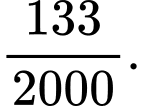
B, 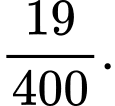
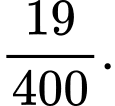
C, 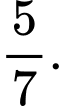
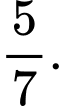
D, 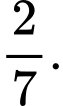
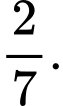
HD: 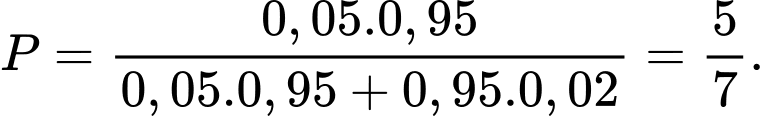 Chọn C. Đáp án: C
Chọn C. Đáp án: C
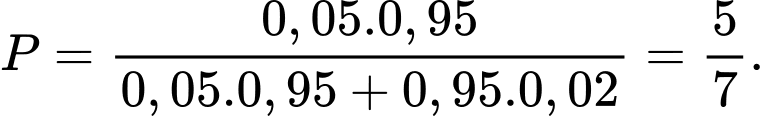 Chọn C. Đáp án: C
Chọn C. Đáp án: C
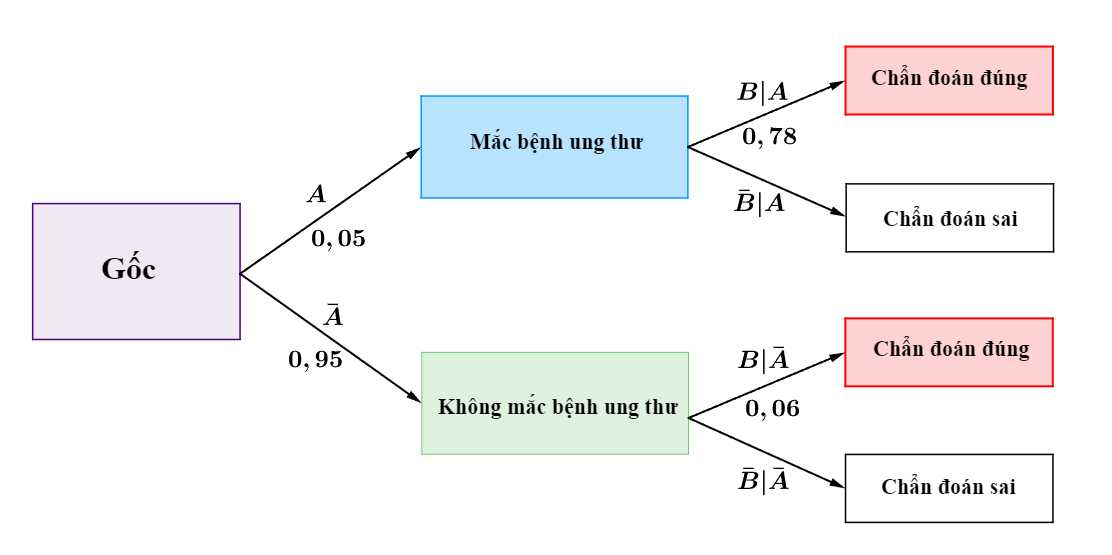
Câu 7 [145263]: Trích SGK Cùng Khám Phá]: Ở một địa phương X, xác suất để một người lớn trên 40 tuổi mắc bệnh ung thư là 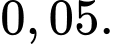 Xác suất bác sĩ chẩn đoán đúng một người mắc bệnh ung thư là
Xác suất bác sĩ chẩn đoán đúng một người mắc bệnh ung thư là 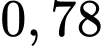 và chẩn đoán sai (không bị ung thư nhưng được chẩn đoán mắc bệnh) là
và chẩn đoán sai (không bị ung thư nhưng được chẩn đoán mắc bệnh) là 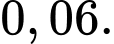 Xác suất để một người thật sự mắc bệnh ung thư khi nhận được kết quả chẩn đoán bị ung thư bằng
Xác suất để một người thật sự mắc bệnh ung thư khi nhận được kết quả chẩn đoán bị ung thư bằng
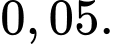 Xác suất bác sĩ chẩn đoán đúng một người mắc bệnh ung thư là
Xác suất bác sĩ chẩn đoán đúng một người mắc bệnh ung thư là 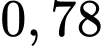 và chẩn đoán sai (không bị ung thư nhưng được chẩn đoán mắc bệnh) là
và chẩn đoán sai (không bị ung thư nhưng được chẩn đoán mắc bệnh) là 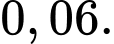 Xác suất để một người thật sự mắc bệnh ung thư khi nhận được kết quả chẩn đoán bị ung thư bằng
Xác suất để một người thật sự mắc bệnh ung thư khi nhận được kết quả chẩn đoán bị ung thư bằng A, 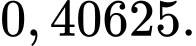
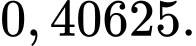
B, 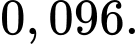
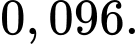
C, 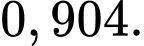
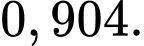
D, 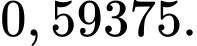
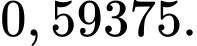
Chọn đáp án A.
Gọi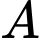 là biến cố “Người đó mắc bệnh ung thư”. Khi đó,
là biến cố “Người đó mắc bệnh ung thư”. Khi đó,  là biến cố “Người đó không mắc bệnh ung thư”.
là biến cố “Người đó không mắc bệnh ung thư”.
Gọi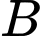 là biến cố “Chẩn đoán đúng” và
là biến cố “Chẩn đoán đúng” và 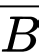 là biến cố “Chẩn đoán sai”.
là biến cố “Chẩn đoán sai”.
Yêu cầu bài toán: Tính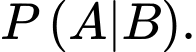 Theo công thức xác suất có điều kiện,
Theo công thức xác suất có điều kiện, 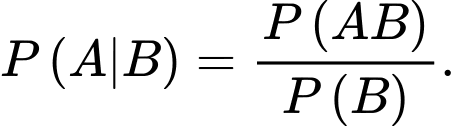
Từ dữ kiện bài cho, ta có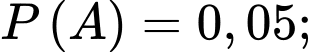
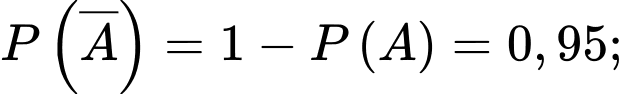
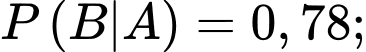
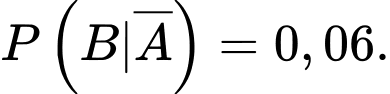
Ta có sơ đồ cây như sau:
Áp dụng công thức xác suất toàn phần, ta có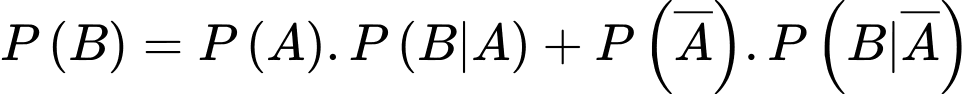
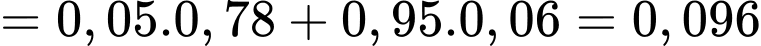
Áp dụng công thức xác suất có điều kiện, ta có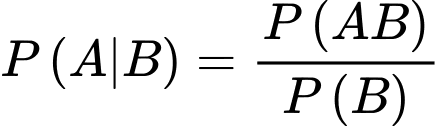
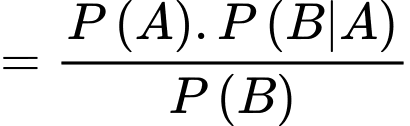
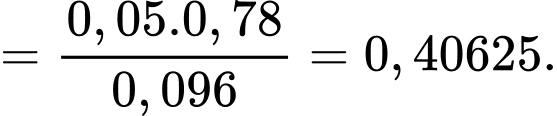 Đáp án: A
Đáp án: A
Gọi
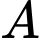 là biến cố “Người đó mắc bệnh ung thư”. Khi đó,
là biến cố “Người đó mắc bệnh ung thư”. Khi đó,  là biến cố “Người đó không mắc bệnh ung thư”.
là biến cố “Người đó không mắc bệnh ung thư”.
Gọi
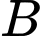 là biến cố “Chẩn đoán đúng” và
là biến cố “Chẩn đoán đúng” và 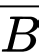 là biến cố “Chẩn đoán sai”.
là biến cố “Chẩn đoán sai”.
Yêu cầu bài toán: Tính
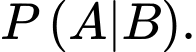 Theo công thức xác suất có điều kiện,
Theo công thức xác suất có điều kiện, 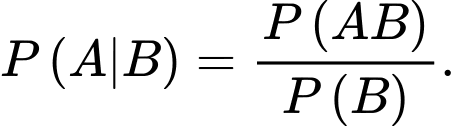
Từ dữ kiện bài cho, ta có
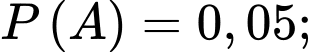
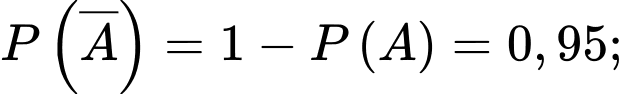
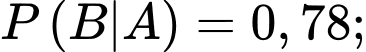
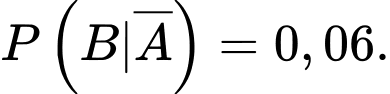
Ta có sơ đồ cây như sau:

Áp dụng công thức xác suất toàn phần, ta có
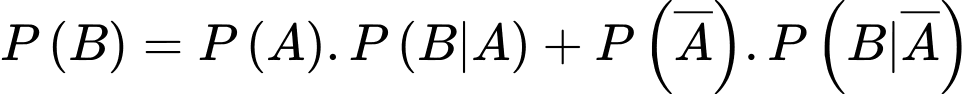
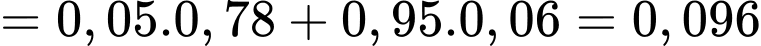
Áp dụng công thức xác suất có điều kiện, ta có
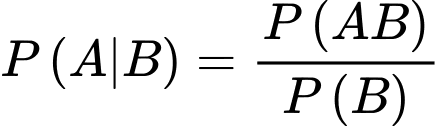
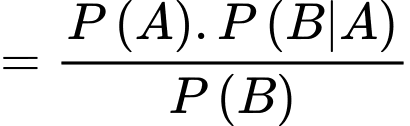
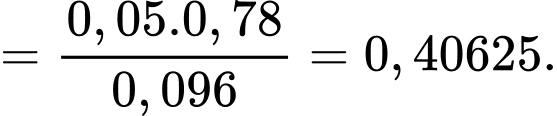 Đáp án: A
Đáp án: A
Câu 8 [143821]: Có hai đội thi đấu môn Bắn súng. Đội I có 6 vận động viên, đội II có 8 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên trong hai đội. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.
A, 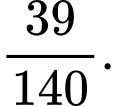
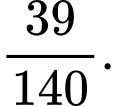
B, 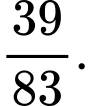
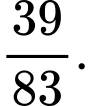
C, 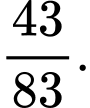
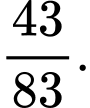
D, 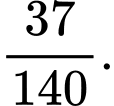
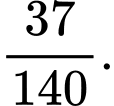
Gọi A là biến cố: “ Vận động viên được chọn thuộc đội I”; 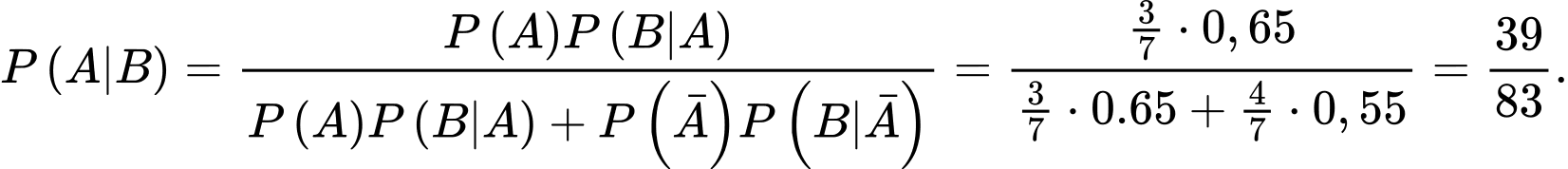
B là biến cố: “Vận động viên được huy chương vàng”.
Ta có 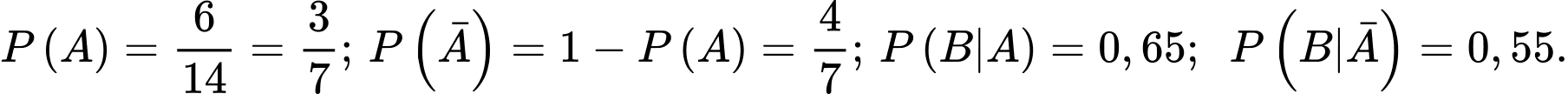
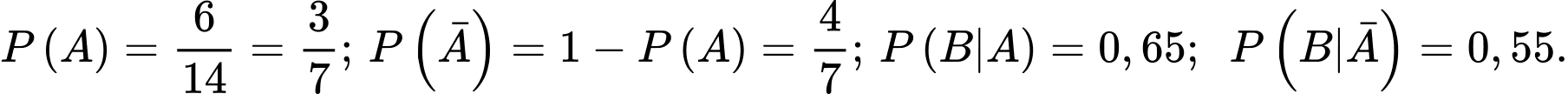
Xác suất để vận động viên được chọn thuộc đội I khi anh ấy đạt huy chương vàng được tính theo công thức Bayes:
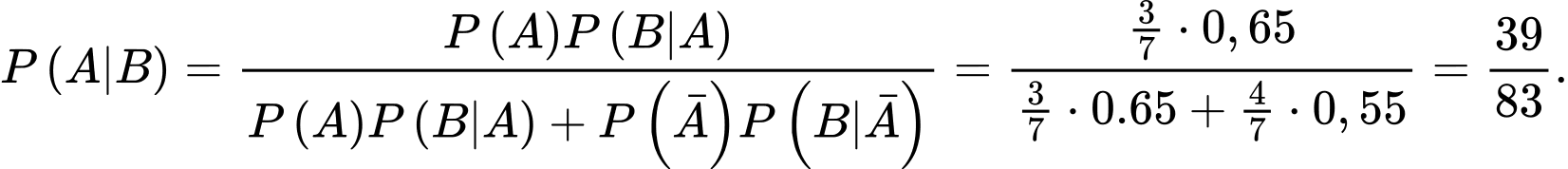
Chọn B.
Đáp án: B
Câu 9 [145269]: [Trích SGK Chân Trời Sáng Tạo]: Trong một trường học, tỉ lệ học sinh nữ là 52%. Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là 18% và 15%. Gặp ngẫu nhiên 1 học sinh của trường. Biết rằng học sinh có tham gia câu lạc bộ nghệ thuật. Tính xác suất học sinh đó là nam.
A, 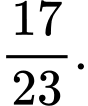
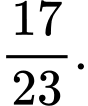
B, 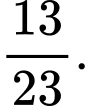
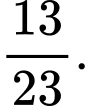
C, 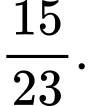
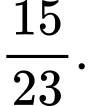
D, 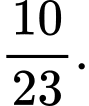
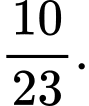
Gọi A là biến cố "Học sinh được chọn là học sinh nữ" và B là biến cố "Học sinh được chọn tham gia câu lạc bộ nghệ thuật".
Ta có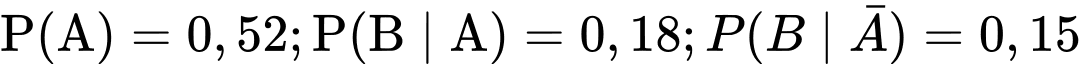 .
.
Suy ra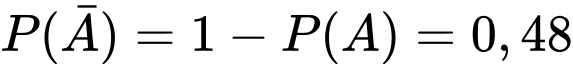 .
.

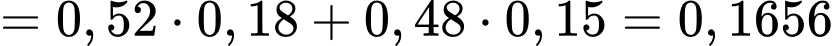
Cần tính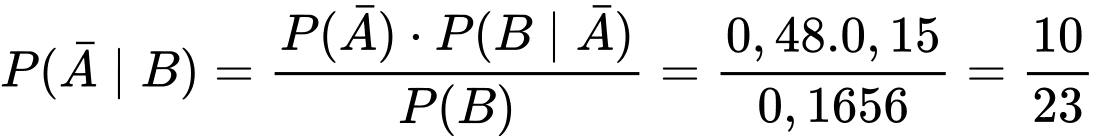 .
.
Chọn D. Đáp án: D
Ta có
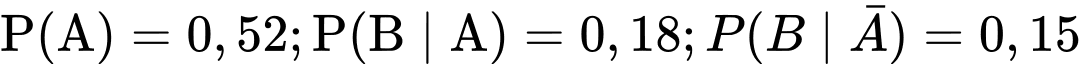 .
.
Suy ra
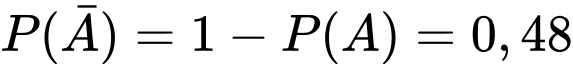 .
.

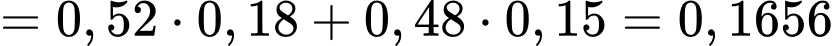
Cần tính
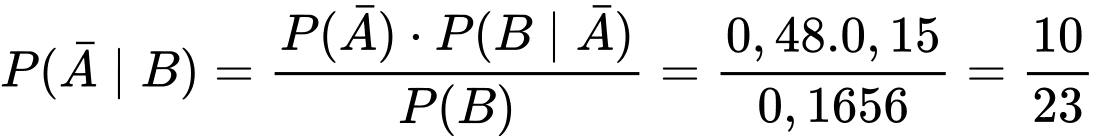 .
.
Chọn D. Đáp án: D
Câu 10 [143822]: Túi I chứa 4 quả bóng trắng và 6 quả bóng đen, túi II khác chứa 4 quả bóng trắng và 3 quả bóng đen. Lấy ngẫu nhiên một quả bóng từ một trong các túi và thấy nó có màu đen. Xác suất để nó được rút ra từ Túi I bằng
A, 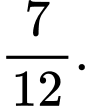
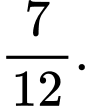
B, 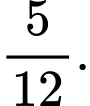
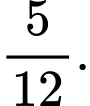
C, 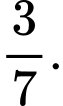
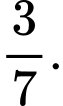
D, 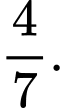
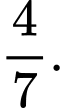
Gọi 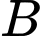 là biến cố chọn được túi I,
là biến cố chọn được túi I, 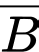 là biến cố chọn được túi II và
là biến cố chọn được túi II và 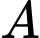 là biến cố lấy được bi đen.
là biến cố lấy được bi đen. 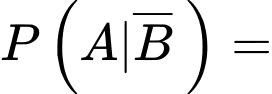 P(rút một quả bóng đen từ Túi II)
P(rút một quả bóng đen từ Túi II) 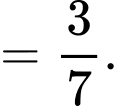
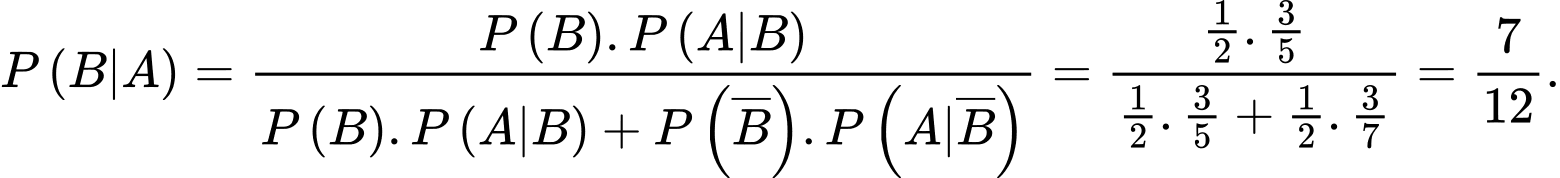 Đáp án: A
Đáp án: A
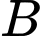 là biến cố chọn được túi I,
là biến cố chọn được túi I, 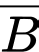 là biến cố chọn được túi II và
là biến cố chọn được túi II và 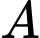 là biến cố lấy được bi đen.
là biến cố lấy được bi đen. Sau đó, 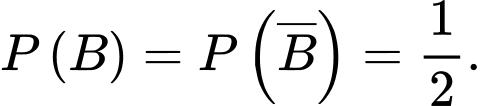
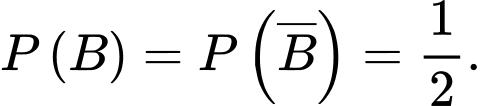
Ngoài ra, 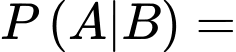 P(rút một quả bóng đen từ Túi I)
P(rút một quả bóng đen từ Túi I) 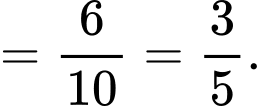
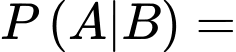 P(rút một quả bóng đen từ Túi I)
P(rút một quả bóng đen từ Túi I) 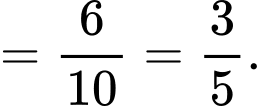
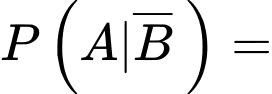 P(rút một quả bóng đen từ Túi II)
P(rút một quả bóng đen từ Túi II) 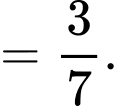
Bằng cách sử dụng định lý Bayes, xác suất lấy được một quả bóng đen từ túi I ra khỏi hai túi là:
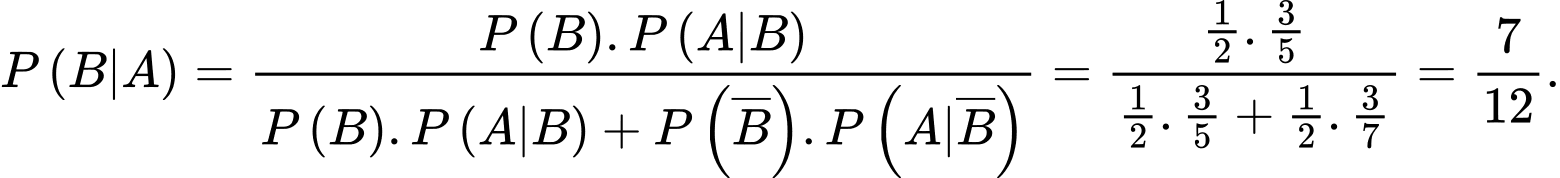
Chọn A.
Câu 11 [144409]: Một người đàn ông được biết là cứ mỗi ba lần thì người đó sẽ nói sự thật 2 lần. Anh ta tung một con súc sắc và báo cáo rằng con số thu được là bốn. Xác suất để số thu được thực sự là số bốn bằng
A, 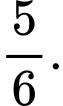
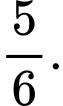
B, 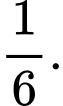
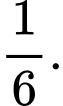
C, 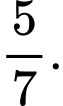
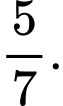
D, 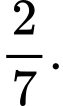
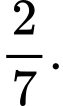
Gọi 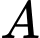 là biến cố người đàn ông báo cáo rằng đã đạt được số bốn.
là biến cố người đàn ông báo cáo rằng đã đạt được số bốn.  Xác suất bốn không xảy ra
Xác suất bốn không xảy ra 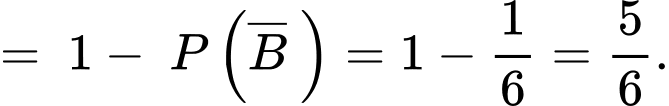
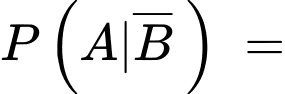 Xác suất người đàn ông báo cáo là bốn và nó không phải là bốn
Xác suất người đàn ông báo cáo là bốn và nó không phải là bốn 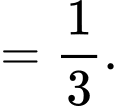
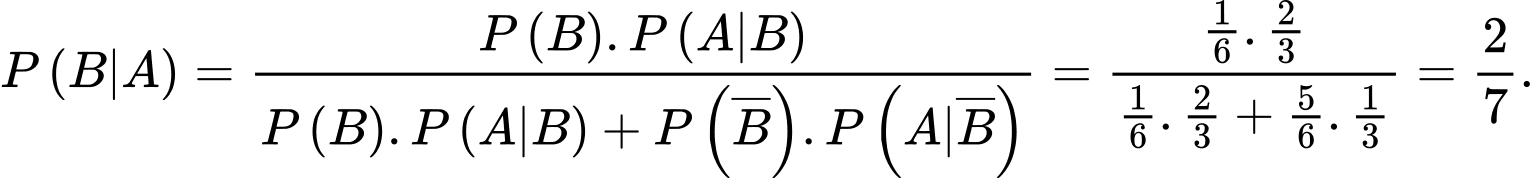 Đáp án: D
Đáp án: D
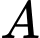 là biến cố người đàn ông báo cáo rằng đã đạt được số bốn.
là biến cố người đàn ông báo cáo rằng đã đạt được số bốn. Gọi 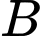 là biến cố thu được bốn và
là biến cố thu được bốn và 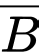 là biến cố bù của nó.
là biến cố bù của nó.
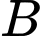 là biến cố thu được bốn và
là biến cố thu được bốn và 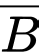 là biến cố bù của nó.
là biến cố bù của nó. Khi đó, 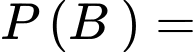 Xác suất xảy ra bốn
Xác suất xảy ra bốn 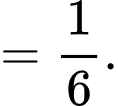
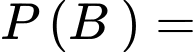 Xác suất xảy ra bốn
Xác suất xảy ra bốn 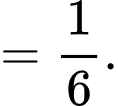
 Xác suất bốn không xảy ra
Xác suất bốn không xảy ra 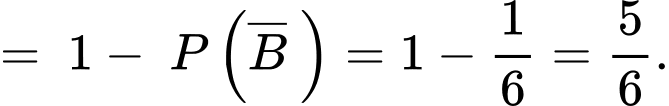
Ngoài ra, 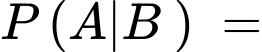 Xác suất người đàn ông báo cáo là bốn và thực tế là bốn
Xác suất người đàn ông báo cáo là bốn và thực tế là bốn 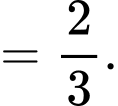
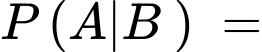 Xác suất người đàn ông báo cáo là bốn và thực tế là bốn
Xác suất người đàn ông báo cáo là bốn và thực tế là bốn 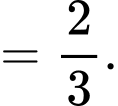
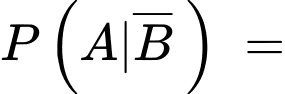 Xác suất người đàn ông báo cáo là bốn và nó không phải là bốn
Xác suất người đàn ông báo cáo là bốn và nó không phải là bốn 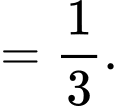
Bằng cách sử dụng định lý Bayes, xác suất mà số thu được thực tế là số 4 bằng
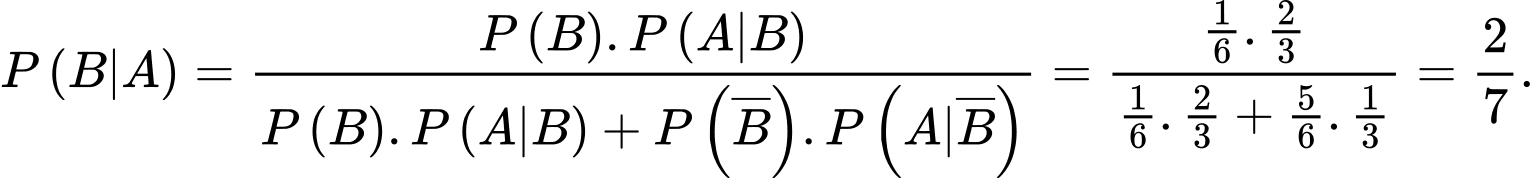
Chọn D.
Câu 12 [144766]: Một nhà máy có hai xưởng sản xuất: xưởng I chiếm 65% tổng sản phẩm, xưởng II chiếm 35%. Biết rằng tỉ lệ sản phẩm đạt chất lượng tốt của xưởng I là 90% và xưởng II là 85%. Xét 1 sản phẩm không đạt chất lượng. Tính xác suất đó là sản phẩm do xưởng II sản xuất.
A, 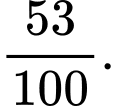
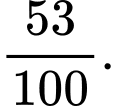
B, 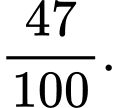
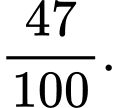
C, 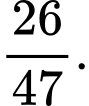
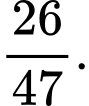
D, 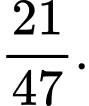
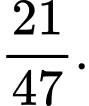
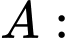 ” sản phẩm lấy ra không đạt chất lượng”,
” sản phẩm lấy ra không đạt chất lượng”, 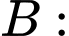 ”sản phẩm do xưởng I sản xuất”,
”sản phẩm do xưởng I sản xuất”, 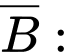 ”sản phẩm do xưởng II sản xuất”.
”sản phẩm do xưởng II sản xuất”. Khi đó, 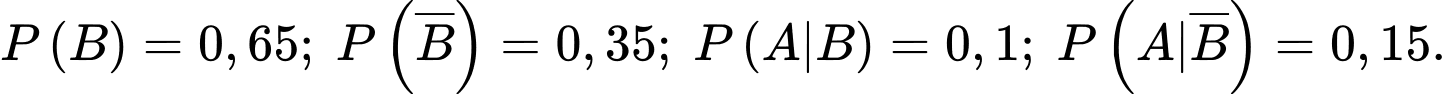
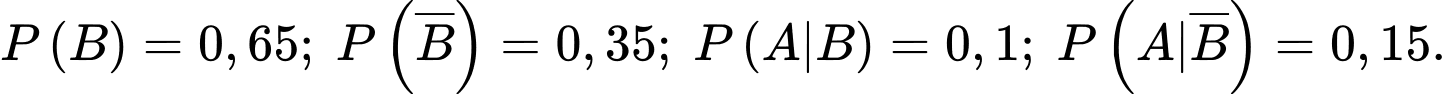
Xác suất đó là sản phẩm do xưởng II sản xuất nếu nó không đạt chất lượng là
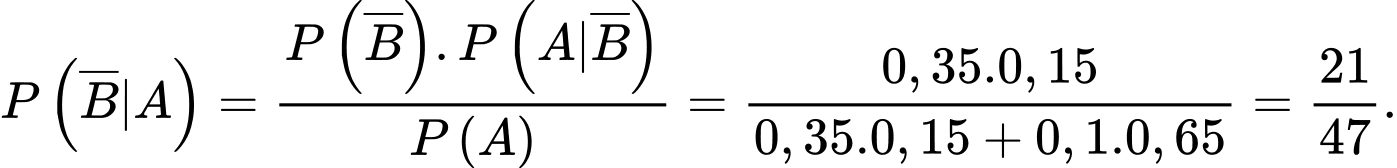
Chọn D.
Câu 13 [144829]: Một nhà máy sản xuất bóng đèn có tỷ lệ bóng đèn đạt tiêu chuẩn là 80%. Trước khi xuất ra thị trường, mỗi bóng đèn đều được qua kiểm tra chất lượng. Vì sự kiểm tra không thể tuyệt đối hoàn hảo nên một bóng đèn tốt có xác suất 0,9 được công nhận là tốt và một bóng đèn hỏng có xác suất 0,95 bị loại bỏ. Tỷ lệ bóng đèn đạt tiêu chuẩn sau khi qua khâu kiểm tra chất lượng là bao nhiêu phần trăm. Làm tròn kết quả đến hàng phần chục.
A, 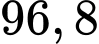
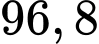
B, 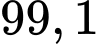
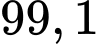
C, 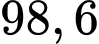
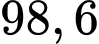
D, 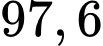
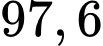
Ta có sơ đồ hình cây sau
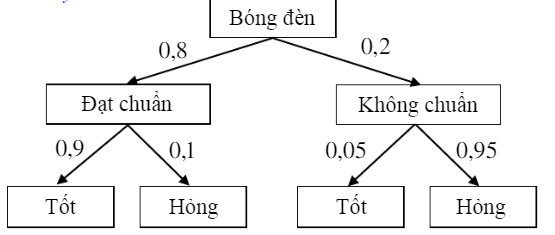
Đáp án: C

A là biến cố “Bóng đèn được công nhận là tốt”
B là biến cố “Bóng đèn đạt chuẩn”
Khi đó 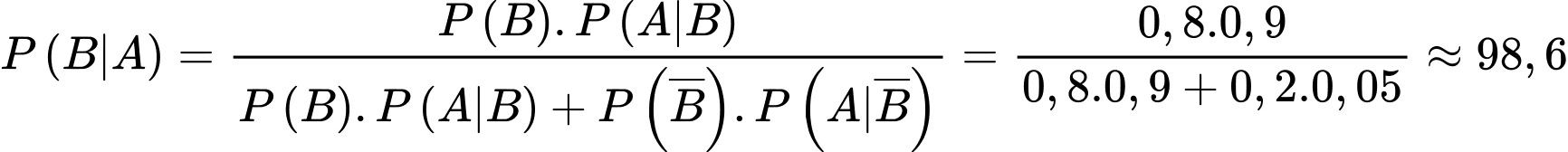
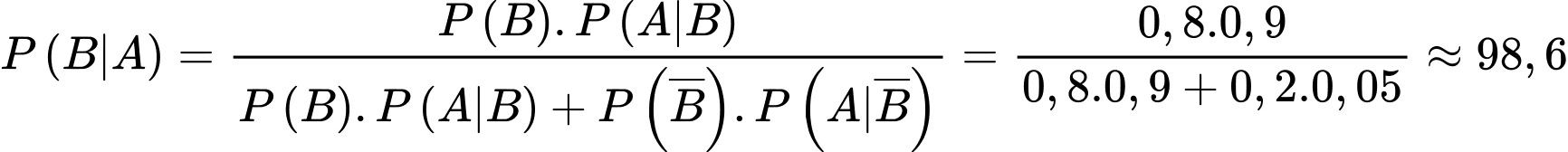
Chọn C.
Câu 14 [144831]: Một nhà máy có hai máy I và II. Máy I sản xuất 40% số lượng sản phẩm và Máy II sản xuất 60% số lượng sản phẩm. Có 4% mặt hàng do Máy I sản xuất bị lỗi và 5% sản phẩm do Máy II sản xuất bị lỗi. Một vật phẩm được rút ngẫu nhiên. Xét tính đúng sai của các mệnh đề sau:
A, a) Nếu vật phẩm được sản xuất bởi máy I thì xác suất sản phẩm đó bị lỗi là 0,04.
B, b) Xác suất để vật lấy ra được tạo bởi máy II và không bị lỗi là 0,384.
C, c) Xác suất để vật lấy ra không bị lỗi là 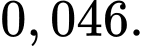
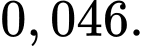
D, d) Nếu vật được rút ra bị lỗi, xác suất để vật đó được tạo ra bởi Máy II bằng 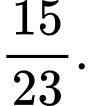
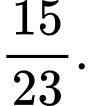
Gọi 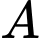 là sự kiện các vật phẩm được sản xuất bởi Máy-I,
là sự kiện các vật phẩm được sản xuất bởi Máy-I,
 là sự kiện các vật phẩm được sản xuất bởi Máy-II.
là sự kiện các vật phẩm được sản xuất bởi Máy-II. 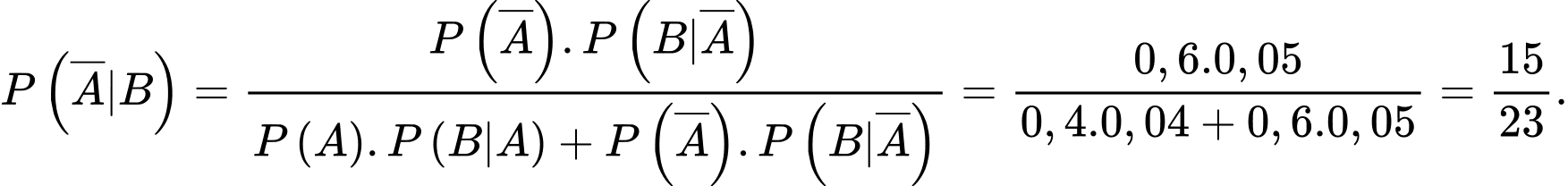
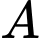 là sự kiện các vật phẩm được sản xuất bởi Máy-I,
là sự kiện các vật phẩm được sản xuất bởi Máy-I,
 là sự kiện các vật phẩm được sản xuất bởi Máy-II.
là sự kiện các vật phẩm được sản xuất bởi Máy-II. Gọi 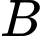 là biến cố rút được một sản phẩm bị lỗi.
là biến cố rút được một sản phẩm bị lỗi.
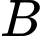 là biến cố rút được một sản phẩm bị lỗi.
là biến cố rút được một sản phẩm bị lỗi. Khi đó: 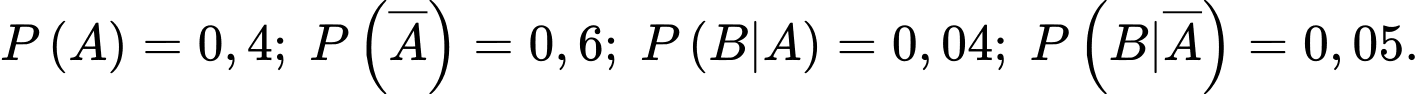
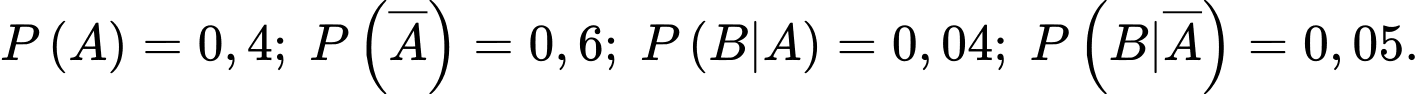
a) Đúng.
b) Sai. 

c) Sai. Theo công thức xác suất toàn phần.
Xác xuất để vật lấy ra bị lỗi là 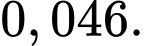
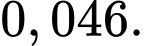
Xác suất vật lấy ra không bị lỗi là 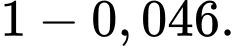
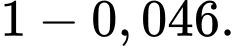
d) Đúng. Theo định lý Bayes, ta có:
Nếu vật được rút ra bị lỗi, xác suất để vật đó được tạo ra bởi Máy I là:
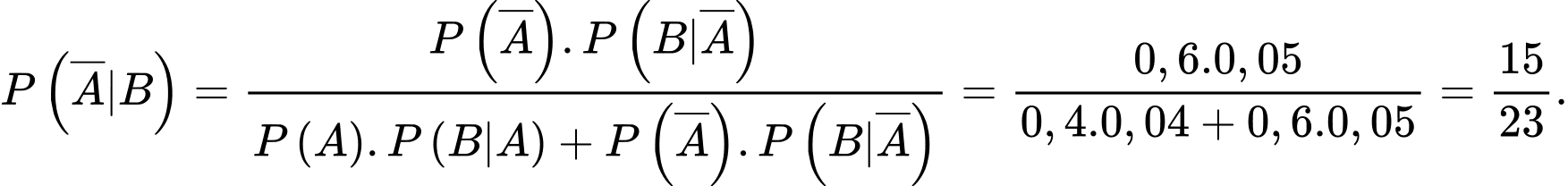
Câu 15 [145264]: [Trích SGK Kết Nối Tri Thức]: Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 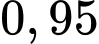 và một thư đúng (không phải là thư rác) bị chặn với xác suất
và một thư đúng (không phải là thư rác) bị chặn với xác suất 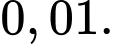 Thống kê cho thấy tỉ lệ thư rác là
Thống kê cho thấy tỉ lệ thư rác là 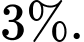 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai.
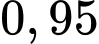 và một thư đúng (không phải là thư rác) bị chặn với xác suất
và một thư đúng (không phải là thư rác) bị chặn với xác suất 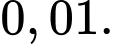 Thống kê cho thấy tỉ lệ thư rác là
Thống kê cho thấy tỉ lệ thư rác là 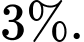 Các mệnh đề sau đúng hay sai.
Các mệnh đề sau đúng hay sai. A, a) Xác suất để thư đó bị chặn là 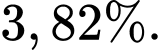
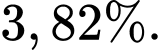
B, b) Chọn ngẫu nhiên một thư bị chặn. Xác suất để đó là thư rác xấp xỉ 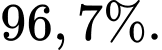
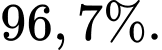
C, c) Chọn ngẫu nhiên một thư không bị chặn. Xác suất để đó là thư đúng xấp xỉ 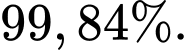
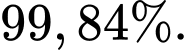
D, d) Trong số các thư không bị chặn, có xấp xỉ 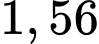 là thư rác.
là thư rác.
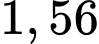 là thư rác.
là thư rác.
a) Đúng. Xác suất để thư đó bị chặn là 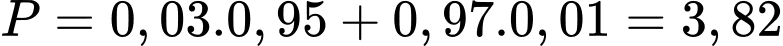
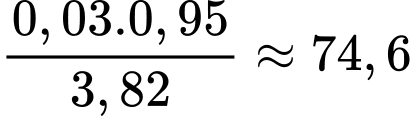
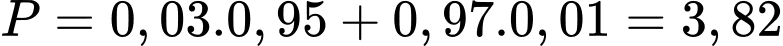
b) Sai. Chọn ngẫu nhiên một thư bị chặn. Xác suất để đó là thư rác là
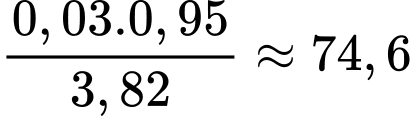
c) Đúng. Chọn ngẫu nhiên một thư không bị chặn. Xác suất để đó là thư đúng là 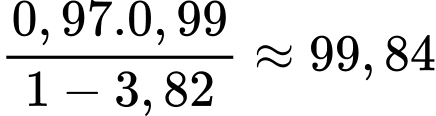
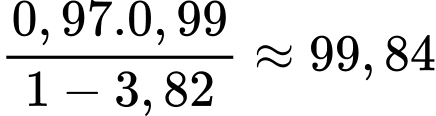
d) Sai. Chọn 1 thư không bị chặn, xác suất nó là thư rác là: 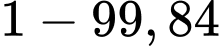
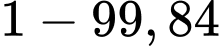
Câu 16 [144879]: Có 6 khẩu súng cũ và 4 khẩu súng mới, trong đó xác suất trúng khi bắn bằng súng
cũ là 0,8, còn súng mới là 0,95. Một người lấy ngẫu nhiên một khẩu súng và bắn một mục tiêu. Các mệnh đề sau đúng hay sai.
A, a) Xác suất để người đó bắn khẩu súng cũ là 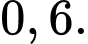
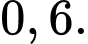
B, b) Xác suất để người đó bắn khẩu súng mới và trúng mục tiêu là 0,57
C, c) Xác suất để người đó bắn trúng mục tiêu là 0,86.
D, d) Giả sử người đó bắn trúng mục tiêu thì xác suất người đó dùng súng mới là cao hơn.
Gọi 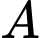 là biến cố người đó bắn súng mới thì
là biến cố người đó bắn súng mới thì 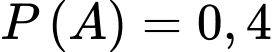
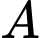 là biến cố người đó bắn súng mới thì
là biến cố người đó bắn súng mới thì 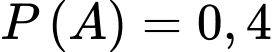
Khi đó xác suất người đã bắn súng cũ là 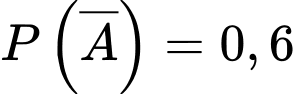
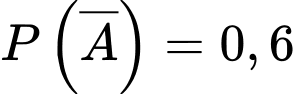
Gọi 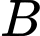 là biến cố người đó bắn trúng thì ta có:
là biến cố người đó bắn trúng thì ta có: 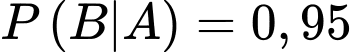 và
và 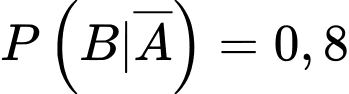
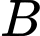 là biến cố người đó bắn trúng thì ta có:
là biến cố người đó bắn trúng thì ta có: 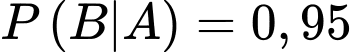 và
và 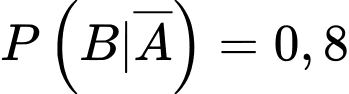
a) Đúng.
b) Sai. Xác suất để người đó bắn khẩu súng mới và trúng mục tiêu là 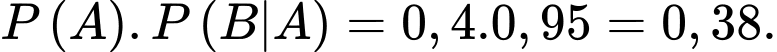
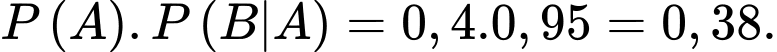
c) Đúng. Xác suất để người đó bắn trúng mục tiêu là 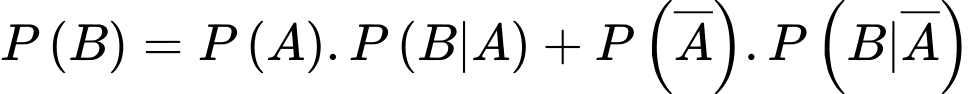
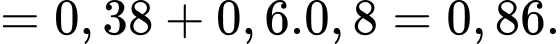
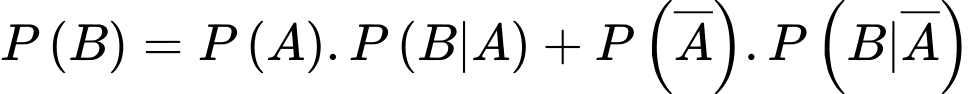
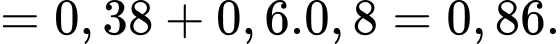
d) Sai. Ta có: 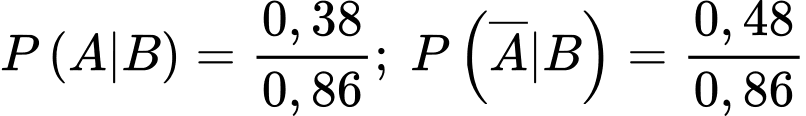 nên
nên 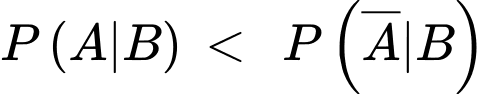 nên xác suất người đó dùng súng cũ là cao hơn.
nên xác suất người đó dùng súng cũ là cao hơn.
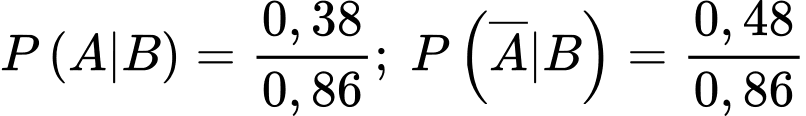 nên
nên 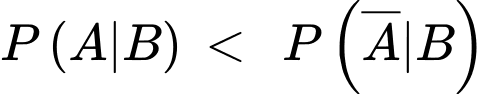 nên xác suất người đó dùng súng cũ là cao hơn.
nên xác suất người đó dùng súng cũ là cao hơn.
Câu 17 [144885]: Trong một trạm cấp cứu bỏng : 80% bệnh nhân bỏng do nóng, 20% bỏng do hóa chất. Loại bỏng do nóng có 30% bi biến chứng, loại bỏng do hóa chất có 50% bị biến chứng. Các mệnh đề sau đúng hay sai.
A, Loại bỏng do nóng có 70% không bị biến chứng.
B, Chọn ngẫu nhiên một bệnh án. Xác suất để gặp bệnh án của bệnh nhân bị bỏng nóng và không bị biến chứng là 0,4.
C, Chọn ngẫu nhiên một bệnh án. Xác suất để gặp một bệnh án của bệnh nhân bị biến chứng là 0,34.
D, Rút ngẫu nhiên được một bệnh án của một bệnh nhân bị biến chứng. Xác suất để bệnh án đó là của bệnh nhân bị biến chứng do hoá chất gây ra là 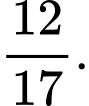
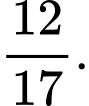
a) Đúng.
b) Sai.  là biến cố “Bệnh nhân bị bỏng nóng”.
là biến cố “Bệnh nhân bị bỏng nóng”. 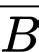 là biến cố “Bệnh nhân bị bỏng hoá chất”.
là biến cố “Bệnh nhân bị bỏng hoá chất”.
Chọn ngẫu nhiên một bệnh án. Xác suất để gặp bệnh án của bệnh nhân bị bỏnổng nóng và không bị biến chứng là 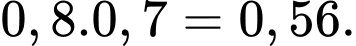
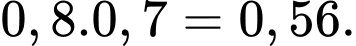
Gọi A là biến cố: “ Bệnh nhân có bệnh án của bệnh nhân bị biến chứng”
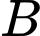 là biến cố “Bệnh nhân bị bỏng nóng”.
là biến cố “Bệnh nhân bị bỏng nóng”. 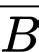 là biến cố “Bệnh nhân bị bỏng hoá chất”.
là biến cố “Bệnh nhân bị bỏng hoá chất”. Ta có: 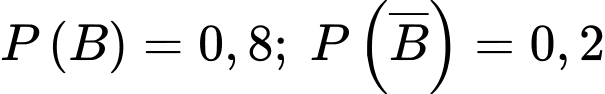 và
và 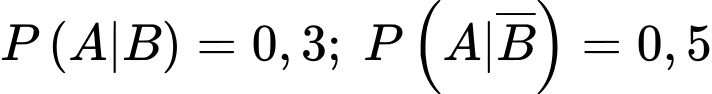
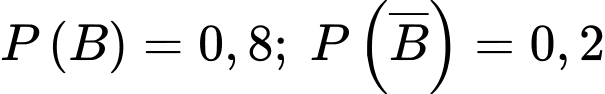 và
và 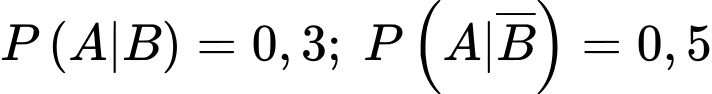
c) Đúng: 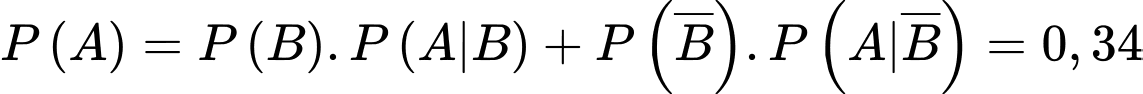
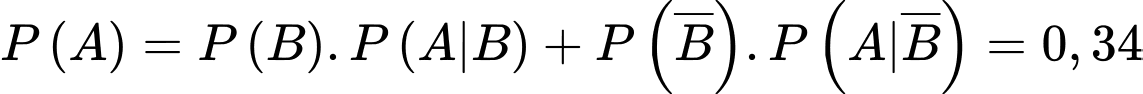
d) Sai. 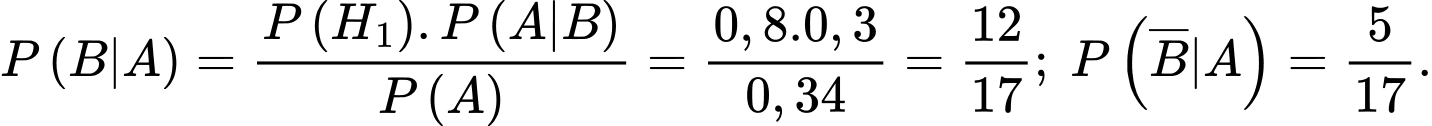
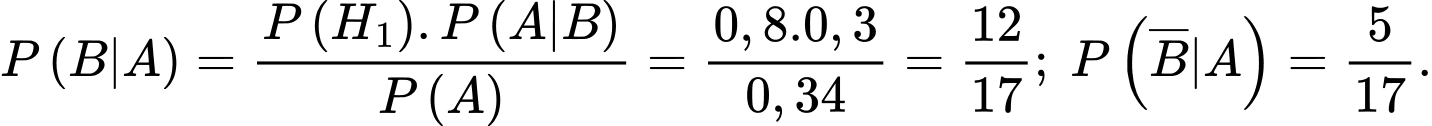
Câu 18 [144894]: Một công ty xây dựng có 2 kỹ sư điều hành. Kỹ sư-1 thực hiện 60% công việc của công ty. Kỹ sư-2 thực hiện 40% công việc của công ty. Kinh nghiệm trước đây cho thấy xác suất xảy ra sai sót khi kỹ sư 1 thực hiện công việc là 0,03, trong khi xác suất xảy ra sai sót trong công việc của kỹ sư 2 là 0,04. Các mệnh đề sau đúng hay sai.
A, a) Xác suất để một công việc do kĩ sư 1 thực hiện và không xảy ra lỗi là 0,388.
B, b) Xác suất để xảy ra một lỗi trong công việc là 0,034.
C, c) Giả sử xảy ra một lỗi trong công việc, xác suất để lỗi đó do kỹ sư 1 thực hiện là 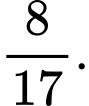
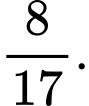
D, d) Giả sử xảy ra một lỗi trong công việc, thì xác suất xảy ra lỗi của kỹ sư 1 lớn hơn khả năng xảy ra lỗi của kỹ sư 2.
Gọi 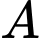 là sự kiện thực hiện công việc của kỹ sư-1,
là sự kiện thực hiện công việc của kỹ sư-1,  là sự kiện thực hiện công việc của kỹ sư-2. Gọi
là sự kiện thực hiện công việc của kỹ sư-2. Gọi 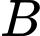 là biến cố xảy ra lỗi trong công việc.
là biến cố xảy ra lỗi trong công việc. 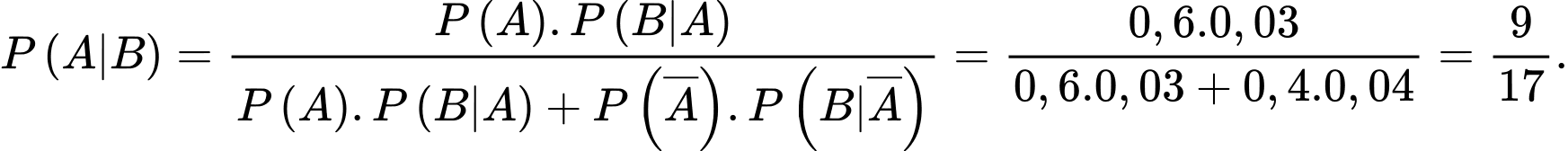
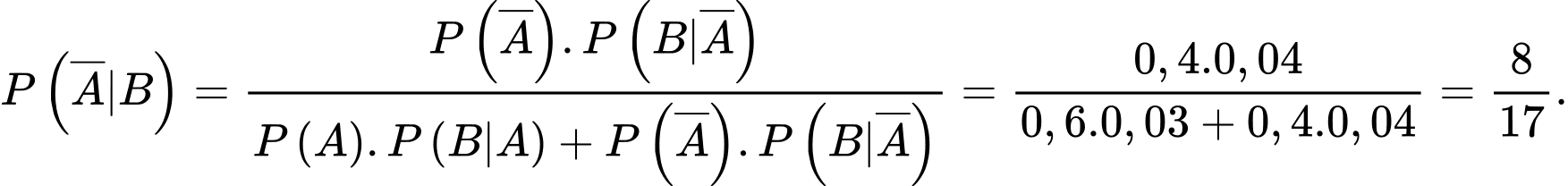
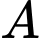 là sự kiện thực hiện công việc của kỹ sư-1,
là sự kiện thực hiện công việc của kỹ sư-1,  là sự kiện thực hiện công việc của kỹ sư-2. Gọi
là sự kiện thực hiện công việc của kỹ sư-2. Gọi  là biến cố xảy ra lỗi trong công việc.
là biến cố xảy ra lỗi trong công việc. Khi đó: 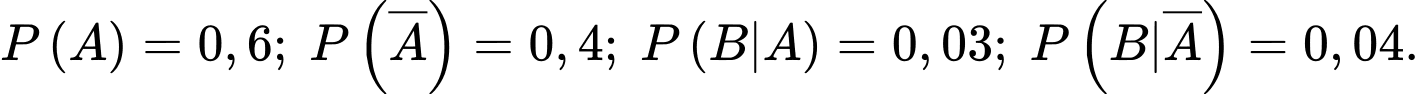
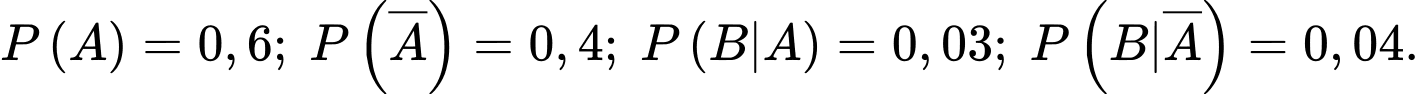
Vì  là các biến cố toàn diện và loại trừ lẫn nhau, theo định lý Bayes, ta có:
là các biến cố toàn diện và loại trừ lẫn nhau, theo định lý Bayes, ta có:
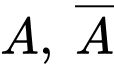 là các biến cố toàn diện và loại trừ lẫn nhau, theo định lý Bayes, ta có:
là các biến cố toàn diện và loại trừ lẫn nhau, theo định lý Bayes, ta có: a) Sai. Xác suất để một công việc do kĩ sư 1 thực hiện và không xảy ra lỗi là 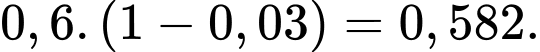
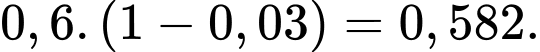
b) Đúng. Xác suất để xảy ra một lỗi trong công việc là 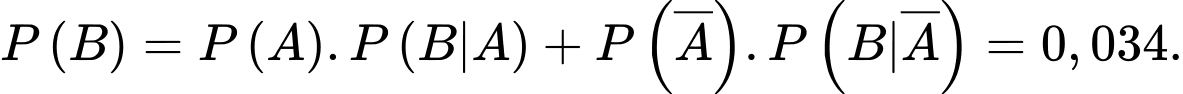
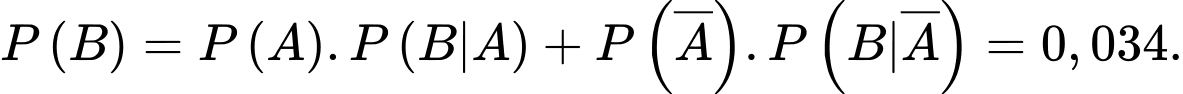
c) Sai. Xác suất để lỗi đó được kỹ sư-1 thực hiện là:
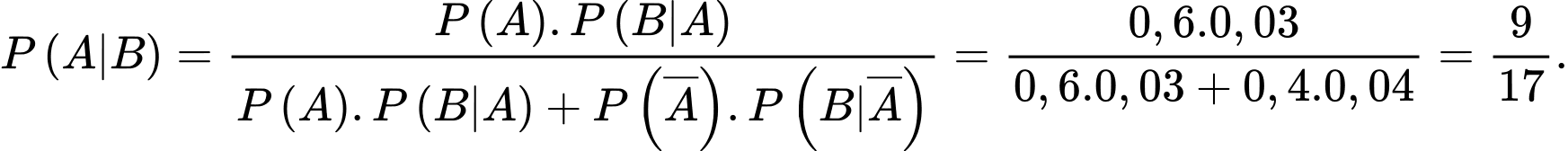
d) Đúng. Xác suất để lỗi đó được kỹ sư-2 thực hiện là:
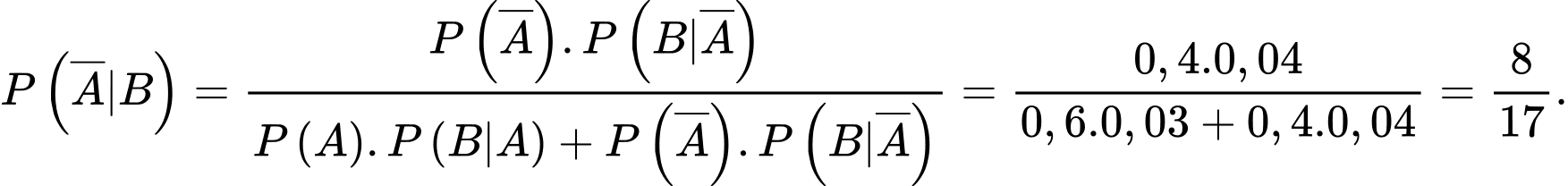
Vậy khả năng xảy ra lỗi của kỹ sư-1 lớn hơn khả năng xảy ra lỗi của kỹ sư-2. Vì vậy, người ta có thể đoán rằng lỗi nghiêm trọng có thể do kỹ sư-1 thực hiện.
Câu 19 [145230]: Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của các dự án lần lượt là 0,4 và 0,5. Khả năng thắng thầu của 2 dự án là 0,3. Gọi A, B lần lượt là biến cố thắng thầu dự án 1 và dự án 2. Các mệnh đề sau đúng hay sai.
A, a) A và B là hai biến cố độc lập.
B, b) Xác suất để công ty thắng thầu đúng một dự án là 0,3.
C, c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là 0,75.
D, d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là 0,5.
Tóm tắt đề bài: P(A)=0,4 , P(B)=0,5 , P(AB)=0,3
a) Sai. Do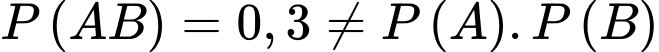 nên A và B là hai biến cố không độc lập.
nên A và B là hai biến cố không độc lập.
b) Đúng. Xác suất để công ty thắng thầu đúng một dự án là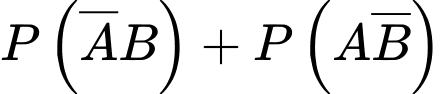
Lại có: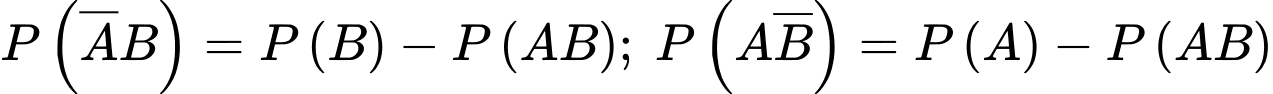
Suy ra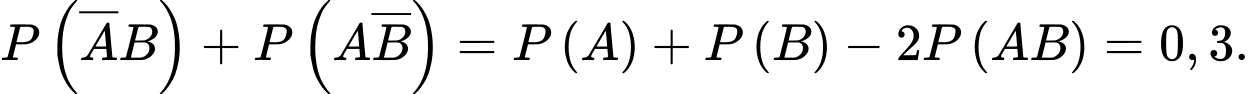
c) Đúng. Gọi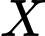 là biến cố thắng dự 2 biết thắng dự án 1
là biến cố thắng dự 2 biết thắng dự án 1
Khi đó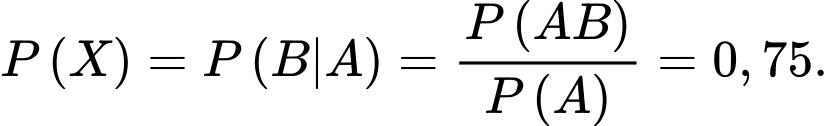
d) Sai.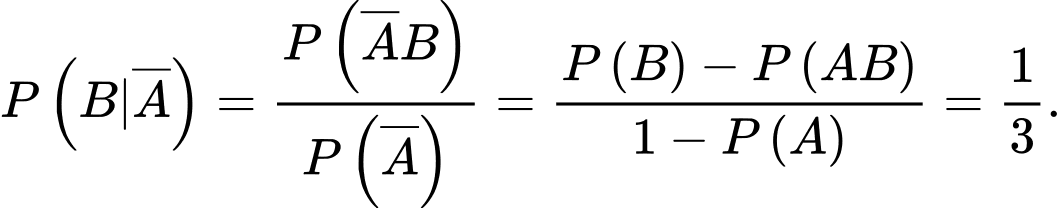
a) Sai. Do
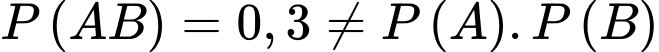 nên A và B là hai biến cố không độc lập.
nên A và B là hai biến cố không độc lập.
b) Đúng. Xác suất để công ty thắng thầu đúng một dự án là
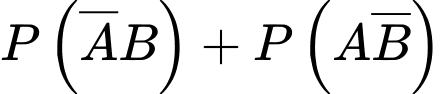
Lại có:
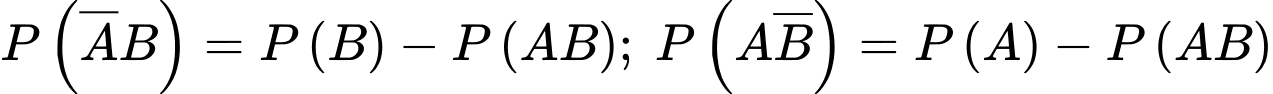
Suy ra
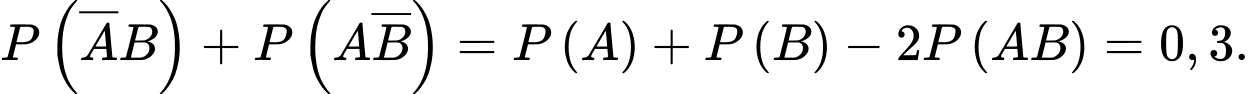
c) Đúng. Gọi
 là biến cố thắng dự 2 biết thắng dự án 1
là biến cố thắng dự 2 biết thắng dự án 1
Khi đó
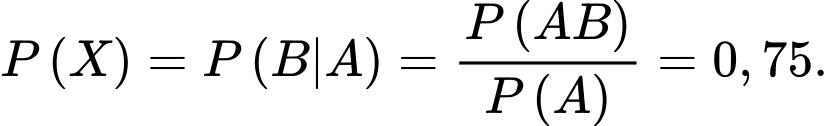
d) Sai.
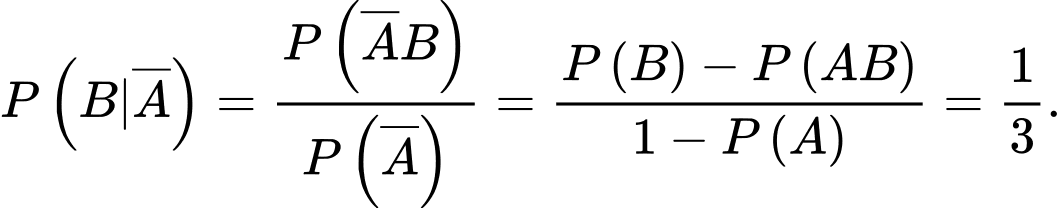
Câu 20 [145231]: Một học sinh làm 2 bài tập kế tiếp. Xác suất làm đúng bài thứ nhất là 0,7. Nếu làm đúng bài thứ nhất thì khả năng làm đúng bài thứ 2 là 0,8, nhưng nếu làm sai bài thứ 1 thì khả năng làm đúng bài thứ 2 là 0,2. Các mệnh đề sau đúng hay sai.
A, a) Xác suất làm sai bài thứ nhất là 0,3.
B, b) Xác suất làm đúng ít nhất 1 bài là 0,76.
C, c) Xác suất làm đúng bài 1 biết rằng làm đúng bài 2 là 0,8.
D, d) Xác suất làm đúng cả 2 bài, biết rằng làm đúng ít nhất một bài là 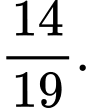
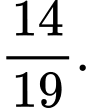
Gọi A là biến cố làm đúng bài 1. Gọi B là biến cố làm đúng bài 2
Ta có: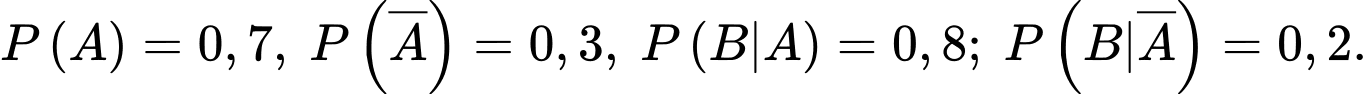
a) Đúng.
b) Đúng. Xác suất làm sai cả hai bài là:
Suy ra xác suất làm đúng ít nhất một bài là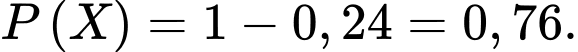
c) Sai.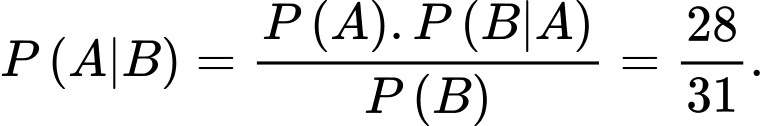
d) Đúng. Xác suất làm đúng cả hai bài là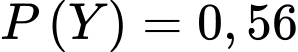
Xác suất làm đúng cả 2 bài, biết rằng làm đúng ít nhất một bài là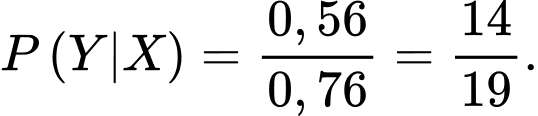
Ta có:
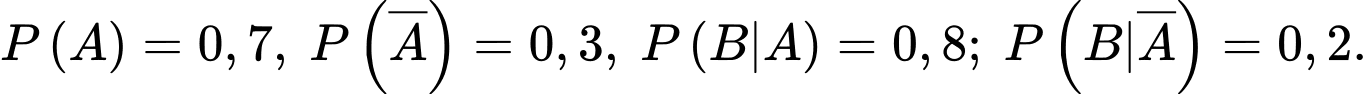
a) Đúng.
b) Đúng. Xác suất làm sai cả hai bài là:

Suy ra xác suất làm đúng ít nhất một bài là
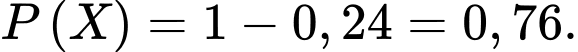
c) Sai.
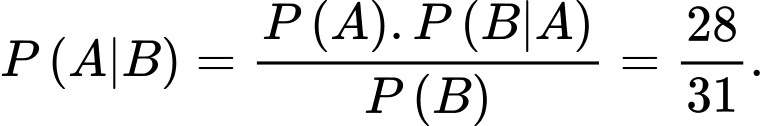
d) Đúng. Xác suất làm đúng cả hai bài là
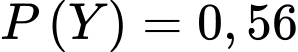
Xác suất làm đúng cả 2 bài, biết rằng làm đúng ít nhất một bài là
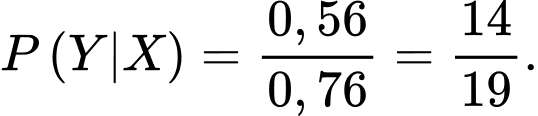
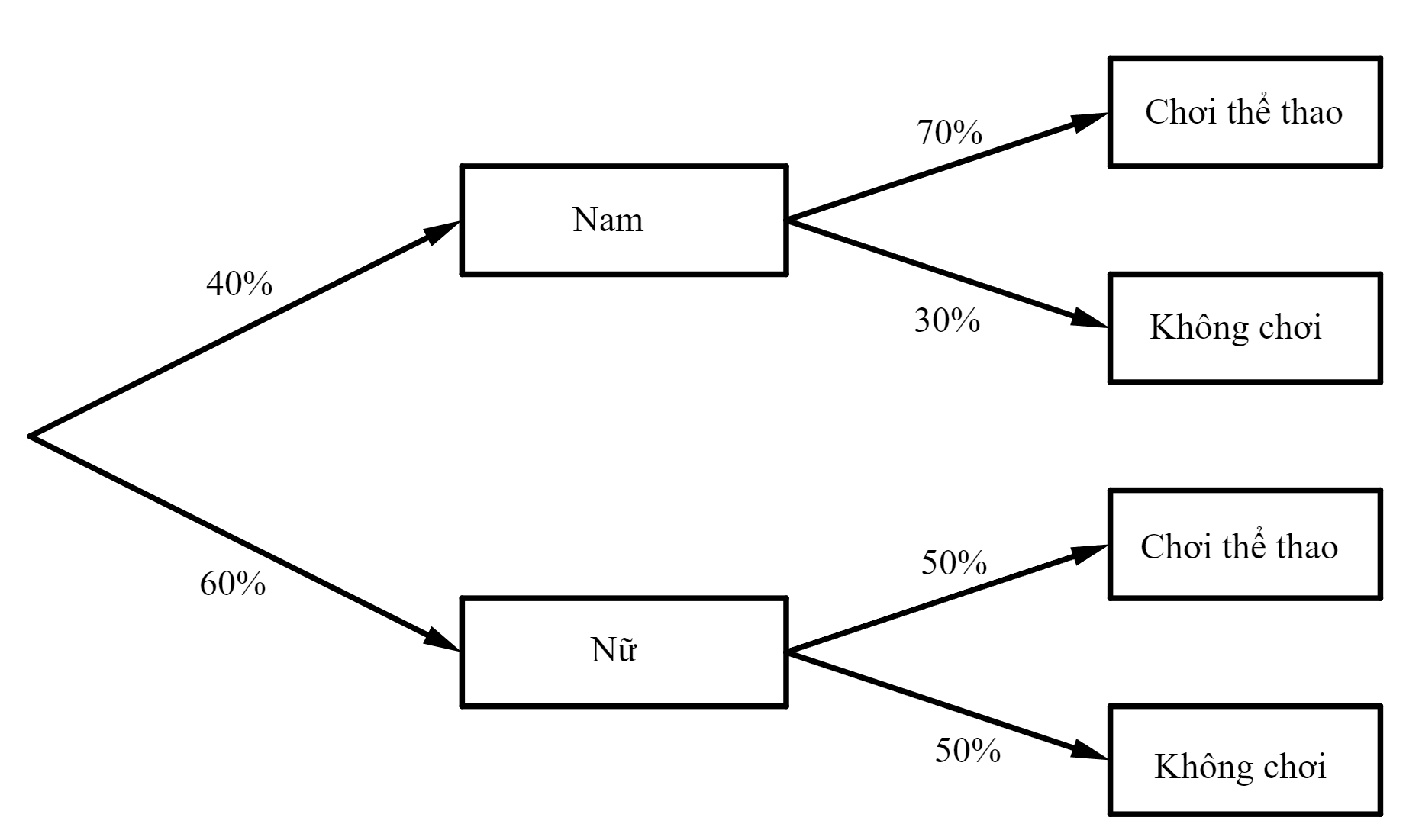
Câu 21 [145233]: Trong một cuộc khảo sát về việc có chơi thể thao hay không có 40% nam và 60% nữ tham gia. Kết quả cho thấy có 30% nam và 50% nữ không chơi thể thao. Chọn ngẫu nhiên một người trong số người được khảo sát. Biết người đó chơi thể thao. Tính xác suất để người được chọn là nam. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố “Người được chọn là nam”; 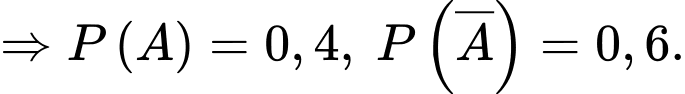 Từ đề bài ta có
Từ đề bài ta có 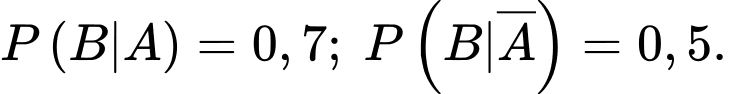

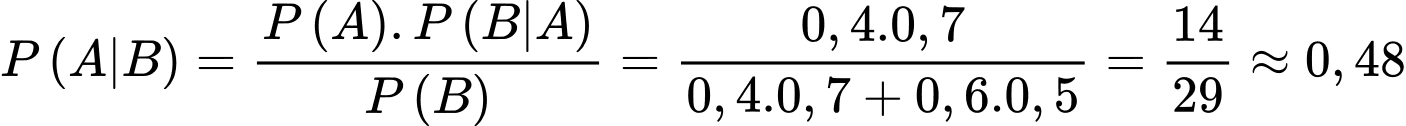 Vậy xác suất để người được chọn là nam khi biết người đó chơi thể thao là
Vậy xác suất để người được chọn là nam khi biết người đó chơi thể thao là 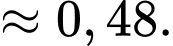
B là biến cố “Người được chọn chơi thể thao”.
Khi đó  là biến cố “Người được chọn là nữ”
là biến cố “Người được chọn là nữ”
 là biến cố “Người được chọn là nữ”
là biến cố “Người được chọn là nữ” 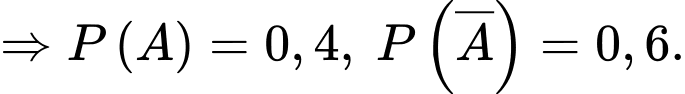 Từ đề bài ta có
Từ đề bài ta có 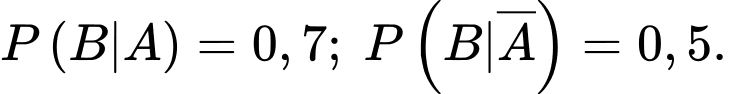


Áp dụng công thức Bayes ta có: