Đáp án Bài tập tự luyện đề 3
Câu 1 [145232]: Ô cửa bí mật (Let's Make a Deal) là một trò chơi trên truyền hình nổi tiếng ở Mỹ. Nội dung trò chơi như sau:
• Người chơi được mời lên sân khấu và đứng trước ba cánh cửa đóng kín. Sau một cánh cửa có chiếc ô tô, sau mỗi cánh cửa còn lại là một con lừa. Người chơi được yêu cầu chọn ngẫu nhiên một cánh cửa, nhưng không được mở ra.
• Tiếp đó người quản trò tuyên bố sẽ mở ngẫu nhiên một trong hai cánh cửa người chơi không chọn mà sau cửa đó là con lừa. Người quản trò hỏi người chơi muốn giữ nguyên sự lựa chọn ban đầu của mình hay muốn chuyển sang cửa chưa mở còn lại.
Giả sử người chơi chọn cửa số 1. Kí hiệu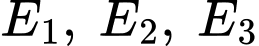
tương ứng là các biến cố: “Sau ô cửa số 1 có ô tô"; "Sau ô cửa số 2 có ô tô"; "Sau ô cửa số 3 có ô tô" và 
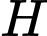là biến cố: "Người quản trò mở một ô cửa có chứa con lừa”. Các mệnh đề sau đúng hay sai.
• Người chơi được mời lên sân khấu và đứng trước ba cánh cửa đóng kín. Sau một cánh cửa có chiếc ô tô, sau mỗi cánh cửa còn lại là một con lừa. Người chơi được yêu cầu chọn ngẫu nhiên một cánh cửa, nhưng không được mở ra.
• Tiếp đó người quản trò tuyên bố sẽ mở ngẫu nhiên một trong hai cánh cửa người chơi không chọn mà sau cửa đó là con lừa. Người quản trò hỏi người chơi muốn giữ nguyên sự lựa chọn ban đầu của mình hay muốn chuyển sang cửa chưa mở còn lại.
Giả sử người chơi chọn cửa số 1. Kí hiệu
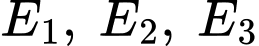tương ứng là các biến cố: “Sau ô cửa số 1 có ô tô"; "Sau ô cửa số 2 có ô tô"; "Sau ô cửa số 3 có ô tô" và 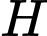là biến cố: "Người quản trò mở một ô cửa có chứa con lừa”. Các mệnh đề sau đúng hay sai.A, a)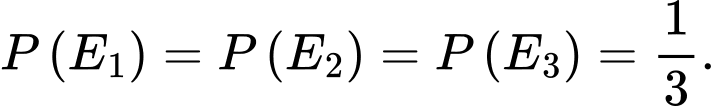 
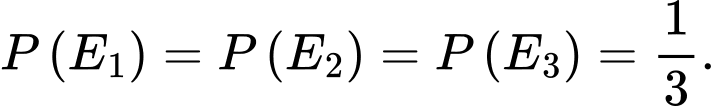
B, b)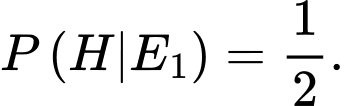 
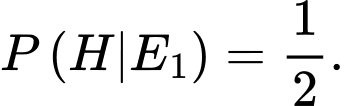
C, c)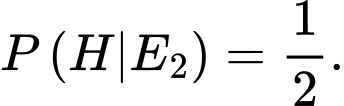 
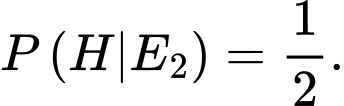
D, d) Sau khi người quản trò mở cánh cửa số 3 và thấy con lừa, lúc này người chơi nên chuyển sang ô cửa số 2 để xác suất chiến thắng sẽ cao hơn.
a) Đúng.
b) Sai.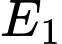
xảy ra và người chơi đã chọn cổng 1
Cổng 2 và 3 đều là lừa.
Vậy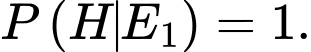
c) Đúng.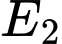
xảy ra, người chơi đã chọn cổng 1
Sẽ có một cổng ra xe (cổng 2) và một cổng ra lừa (cổng 3).
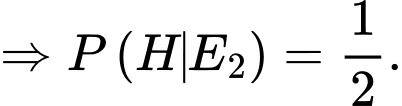
d) Sai.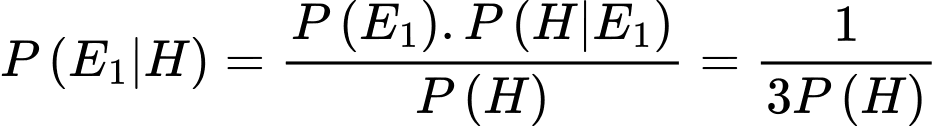
và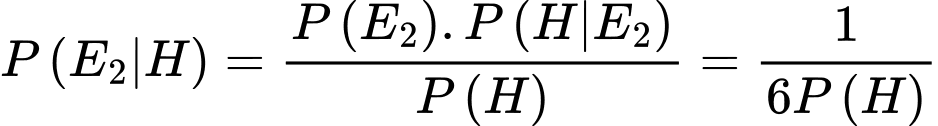 
Khi đó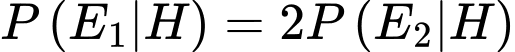
nên nếu người chơi chuyển sang ô cửa số 2 thì xác suất chiến thắng sẽ giảm gấp đôi.
b) Sai.
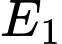xảy ra và người chơi đã chọn cổng 1 Cổng 2 và 3 đều là lừa.Vậy
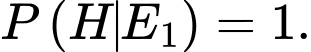
c) Đúng.
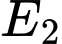xảy ra, người chơi đã chọn cổng 1 Sẽ có một cổng ra xe (cổng 2) và một cổng ra lừa (cổng 3). 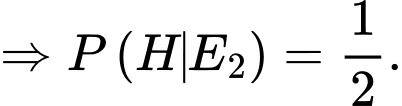d) Sai.
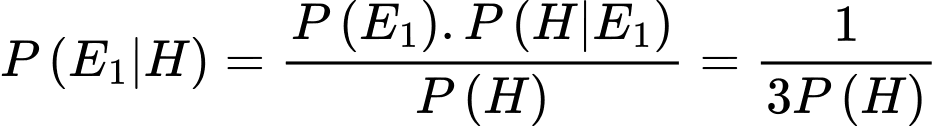và 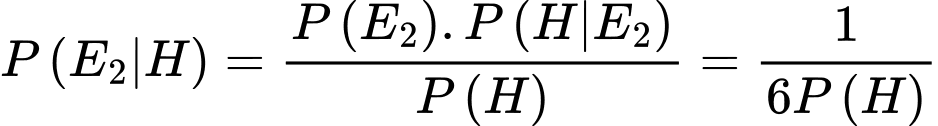Khi đó
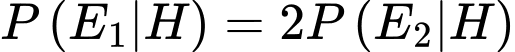nên nếu người chơi chuyển sang ô cửa số 2 thì xác suất chiến thắng sẽ giảm gấp đôi.
Câu 2 [145234]: Dây chuyền lắp ráp nhận được các chi tiết do hai máy sản xuất. Trung bình máy thứ nhất cung cấp 60% chi tiết, máy thứ hai cung cấp 40% chi tiết. Có 90% chi tiết do máy thứ nhất sản xuất là đạt tiêu chuẩn, còn 85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền một sản phẩm, thấy nó đạt tiêu chuẩn. Xác suất để sản phẩm đó do máy thứ nhất sản xuất bằng bao nhiêu? Kết quả làm tròn đến hàng phần trăm.
Gọi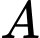 
là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”, 
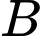là biến cố: “Chi tiết do máy thứ nhất sản xuất” và 
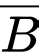là biến cố: “Chi tiết do máy thứ hai sản xuất”. Ta cần tính xác suất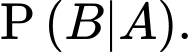 
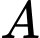là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”, 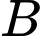là biến cố: “Chi tiết do máy thứ nhất sản xuất” và 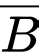là biến cố: “Chi tiết do máy thứ hai sản xuất”. Ta cần tính xác suất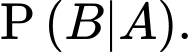 Khi đó,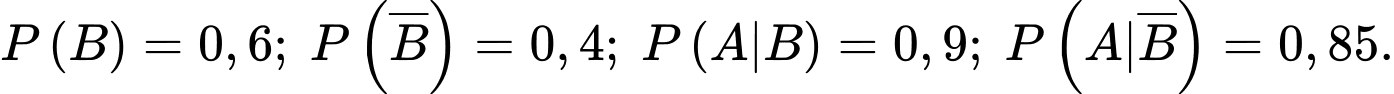 
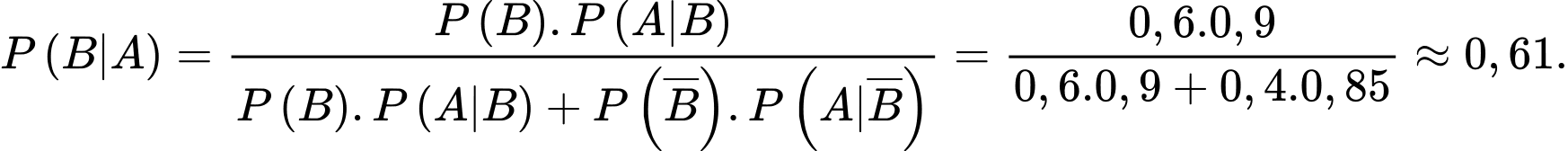
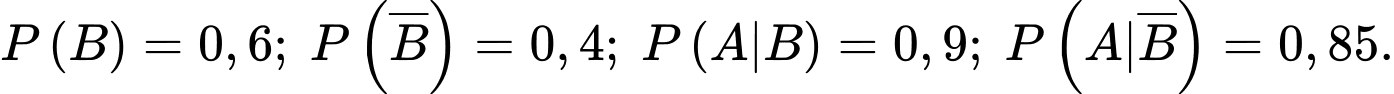
Xác suất để sản phẩm đó do máy thứ nhất sản xuất bằng
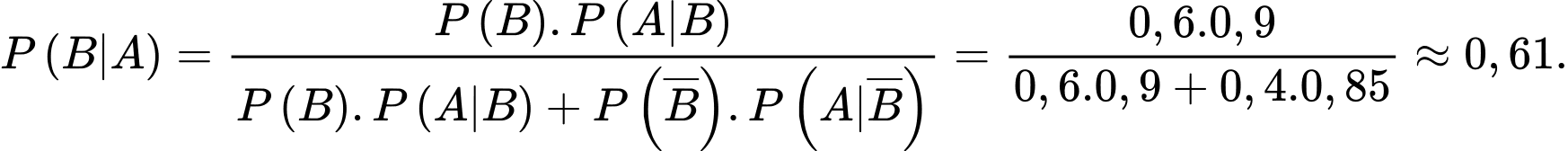
Câu 3 [145235]: Một công nhân đi làm ở thành phố khi trở về nhà có 2 cách: hoặc đi theo đường ngầm hoặc đi qua cầu. Biết rằng ông ta đi lối đường ngầm trong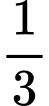 
các trường hợp, còn lại đi lối cầu. Nếu đi lối đường ngầm 75% trường hợp ông ta về đến nhà trước 6 giờ tối; còn nếu đi lối cầu chỉ có 70% trường hợp (nhưng đi lối cầu thích hơn). Tìm xác suất để công nhân đó đã đi lối cầu biết rằng ông ta về đến nhà sau 6 giờ tối. Viết kết quả làm tròn đến hàng phần trăm.
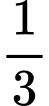các trường hợp, còn lại đi lối cầu. Nếu đi lối đường ngầm 75% trường hợp ông ta về đến nhà trước 6 giờ tối; còn nếu đi lối cầu chỉ có 70% trường hợp (nhưng đi lối cầu thích hơn). Tìm xác suất để công nhân đó đã đi lối cầu biết rằng ông ta về đến nhà sau 6 giờ tối. Viết kết quả làm tròn đến hàng phần trăm.
Gọi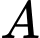 
là biến cố “Ông ta về đến nha sau 6 giờ tối”
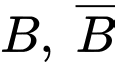lần lượt là biến cố : “Ông ta đi đường ngầm” và “ Ông ta đi lối cầu”
Ta có: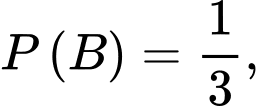
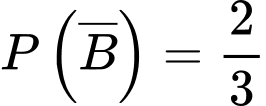
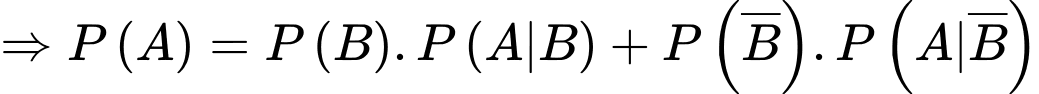
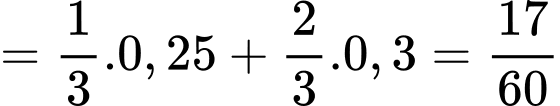
Do đó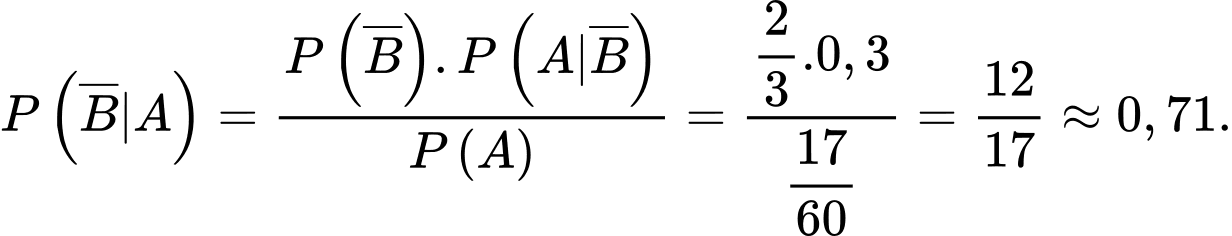
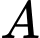là biến cố “Ông ta về đến nha sau 6 giờ tối” 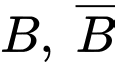lần lượt là biến cố : “Ông ta đi đường ngầm” và “ Ông ta đi lối cầu”Ta có:
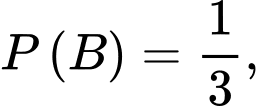
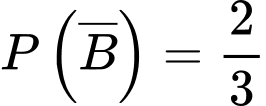
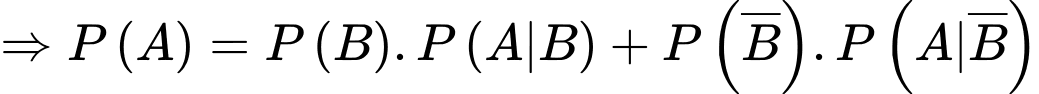
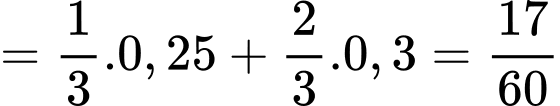
Do đó
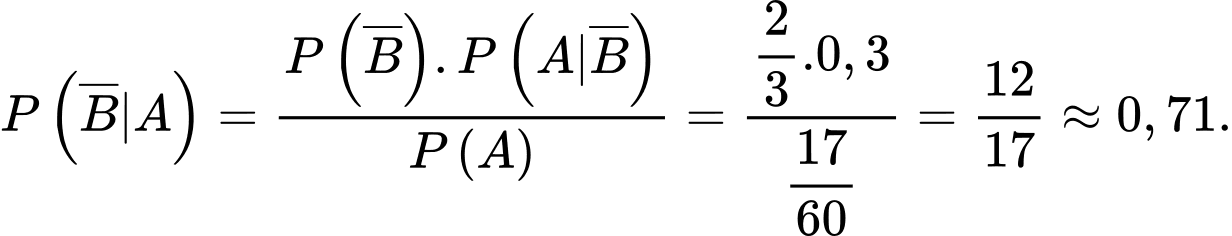
Câu 4 [378720]: Trong một kho rượu có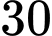 
là rượu loại I. Chọn ngẫu nhiên một chai rượu đưa cho ông Tùng, một người sành rượu, để nếm thử. Biết rằng, một chai rượu loại I có xác suất 
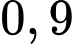để ông Tùng xác nhận là loại I; một chai rượu không phải loại I có xác suất 
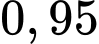để ông Tùng xác nhận đây không phải là loại I. Sau khi nếm, ông Tùng xác nhận đây là rượu loại I. Tính xác suất để chai rượu đúng là rượu loại I. Viết kết quả làm tròn đến hàng phần trăm.
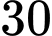là rượu loại I. Chọn ngẫu nhiên một chai rượu đưa cho ông Tùng, một người sành rượu, để nếm thử. Biết rằng, một chai rượu loại I có xác suất 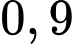để ông Tùng xác nhận là loại I; một chai rượu không phải loại I có xác suất 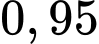để ông Tùng xác nhận đây không phải là loại I. Sau khi nếm, ông Tùng xác nhận đây là rượu loại I. Tính xác suất để chai rượu đúng là rượu loại I. Viết kết quả làm tròn đến hàng phần trăm.
A là biến cố: ông Tùng nhận đây là rượu loại I
B là biến cố: chai rượu đúng là loại I
Ta có: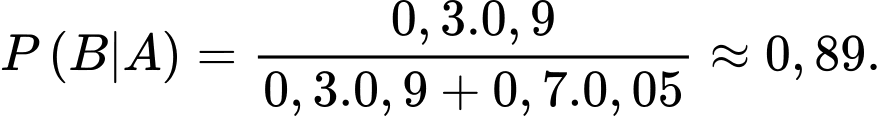 
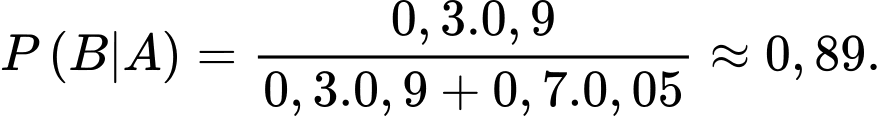
Câu 5 [145236]: Tỉ lệ người đến khám tại một bệnh viện mắc bệnh A là 60%, trong số những người mắc bệnh A có 50% mắc cả bệnh B, còn trong số những người không mắc bệnh A có 70% mắc bệnh B. Nếu người được khám không mắc bệnh B tìm xác suất để người đó không mắc bệnh A. Viết kết quả làm tròn đến hàng phần trăm.
a) Gọi A là biến cố “ người đi khám mắc bệnh B”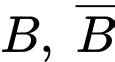 
lần lượt là biến cố người khám mặc bệnh A và không mắc bệnh A
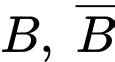lần lượt là biến cố người khám mặc bệnh A và không mắc bệnh A Ta có: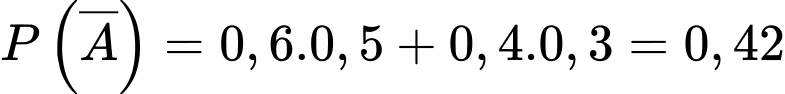 
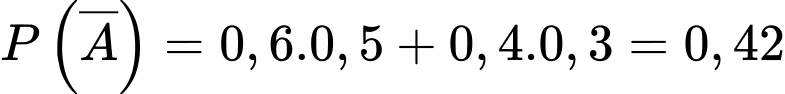
Suy ra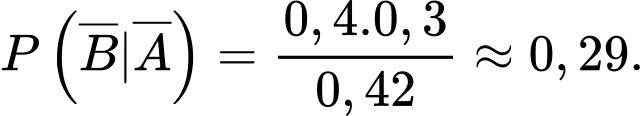 
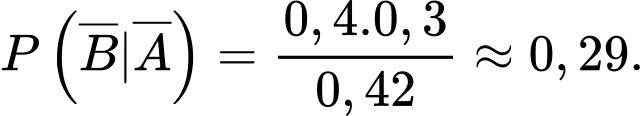
Câu 6 [145237]: Giả sử có mội loại bệnh mà tỉ lệ người mắc bệnh là 0,01%. Giả sử có một loại xét nghiệm, nếu một người bị bệnh thì xác suất xét nghiệm ra dương tính là 90%, nếu một người không bị bệnh thì xác suất ra dương tính là 5%. Khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm)?
Xét hai biến cố: B: “Người được chọn ra mắc bệnh”;
A: “Người được chọn ra có xét nghiệm dương tính”.
Ta có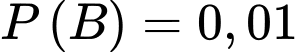
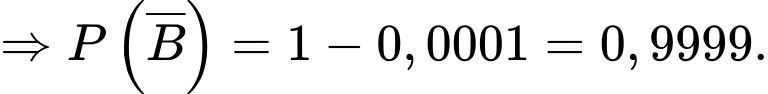
Trong số những người không mắc bệnh nhưng có 5% số người có xét nghiệm dương tính nên
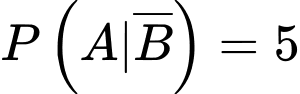
Vì ai mắc bệnh có xác suất xét nghiệm dương tính nên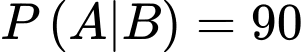
Khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó là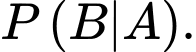
Áp dụng công thức Bayes, ta có
%
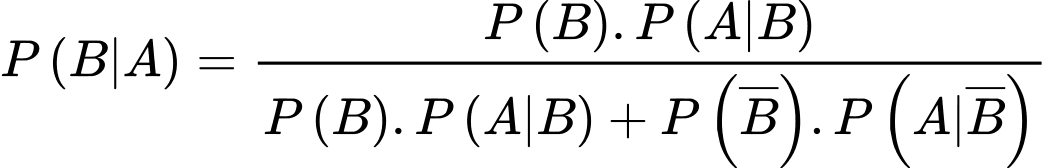
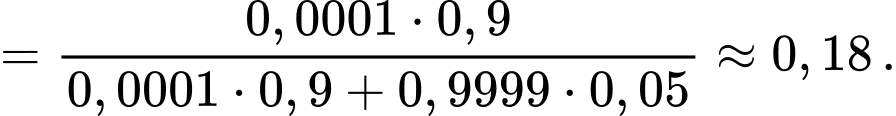A: “Người được chọn ra có xét nghiệm dương tính”.
Ta có
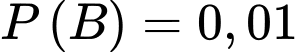
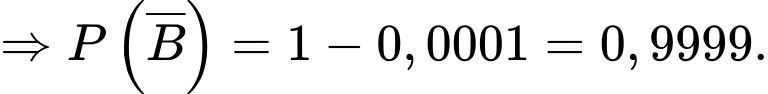
Trong số những người không mắc bệnh nhưng có 5% số người có xét nghiệm dương tính nên
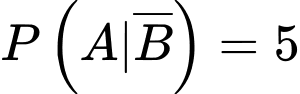
Vì ai mắc bệnh có xác suất xét nghiệm dương tính nên
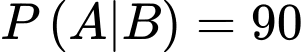
Khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó là
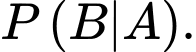
Áp dụng công thức Bayes, ta có
%
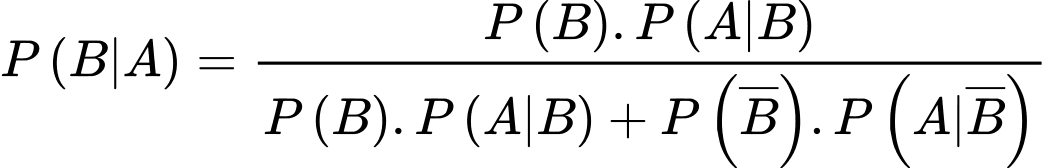
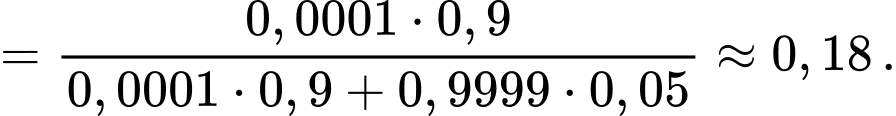Câu 7 [145268]: [SGK Chân Trời Sáng Tạo]: Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có 99% các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật. Viết kết quả làm tròn đến hàng phần trăm.
A là biến cố: hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay
B là biến cố: Vật thể đó là mục tiêu thật
Ta có: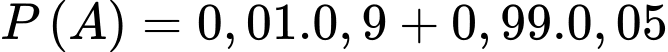 
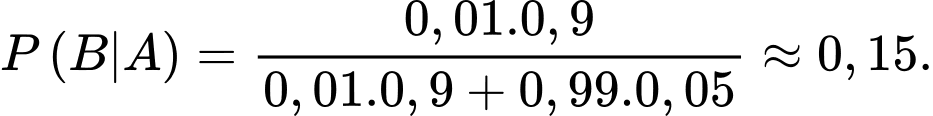
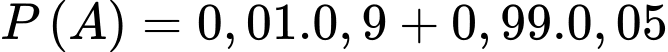và 
và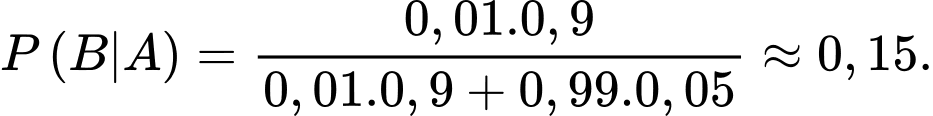
Câu 8 [378768]: Trong một tuần, Sơn chọn ngẫu nhiên ba ngày chạy bộ buổi sáng. Nếu chạy bộ thị xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là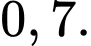 
Nếu không chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 
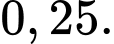Chọn ngẫu nhiên một ngày trong tuần của Sơn. Tính xác suất để hôm đó Sơn chạy bộ nếu biết rằng bữa sáng hôm đó Sơn có ăn thêm một quả trứng. Viết kết quả làm tròn đến hàng phần trăm.
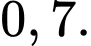Nếu không chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 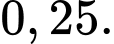Chọn ngẫu nhiên một ngày trong tuần của Sơn. Tính xác suất để hôm đó Sơn chạy bộ nếu biết rằng bữa sáng hôm đó Sơn có ăn thêm một quả trứng. Viết kết quả làm tròn đến hàng phần trăm.
Gọi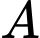 
là biến cố: “Sơn chạy bộ buổi sáng”;
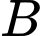là biến cố: “Sơn ăn thêm một quả trứng trong bữa sáng”.
Khi đó, xác suất để hôm đó Sơn chạy bộ nếu biết rằng bữa sáng hôm đó Sơn có ăn thêm một quả trứng chính là xác suất có điều kiện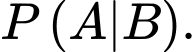
Vì trong một tuần, Sơn chọn ngẫu nhiên ba ngày chạy bộ buổi sáng nên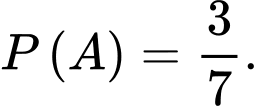
Suy ra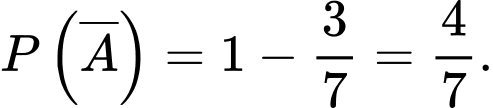
Nếu chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 0,7, do đó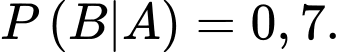
Nếu không chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 0,25, do đó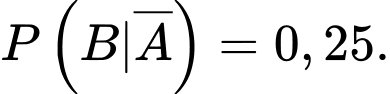
Áp dụng công thức Bayes, ta có: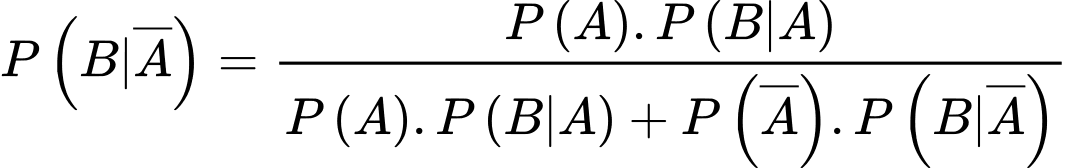
.
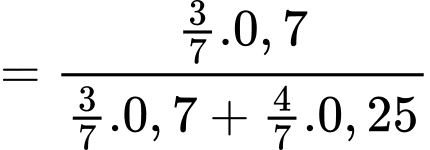
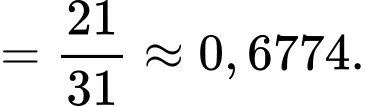Vậy xác suất để hôm đó Sơn chạy bộ nếu biết rằng bữa sáng hôm đó Sơn có ăn thêm một quả trứng xấp xỉ bằng 0,6774.
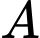là biến cố: “Sơn chạy bộ buổi sáng”; 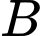là biến cố: “Sơn ăn thêm một quả trứng trong bữa sáng”. Khi đó, xác suất để hôm đó Sơn chạy bộ nếu biết rằng bữa sáng hôm đó Sơn có ăn thêm một quả trứng chính là xác suất có điều kiện
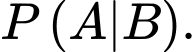
Vì trong một tuần, Sơn chọn ngẫu nhiên ba ngày chạy bộ buổi sáng nên
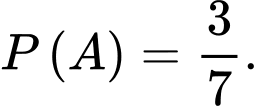
Suy ra
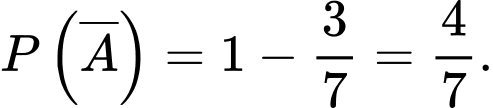
Nếu chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 0,7, do đó
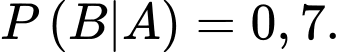
Nếu không chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 0,25, do đó
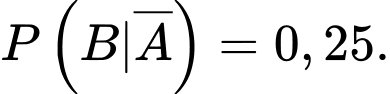
Áp dụng công thức Bayes, ta có:
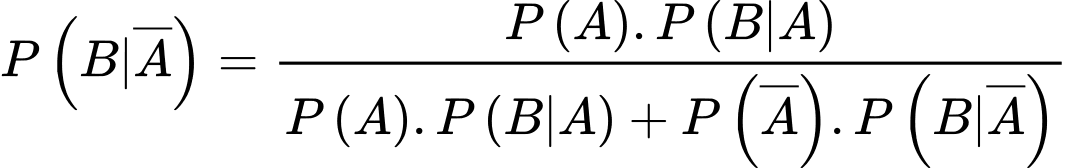
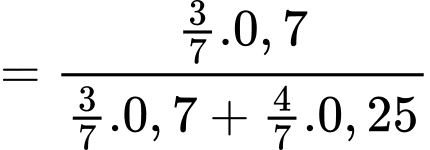
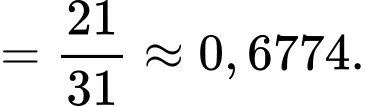. Vậy xác suất để hôm đó Sơn chạy bộ nếu biết rằng bữa sáng hôm đó Sơn có ăn thêm một quả trứng xấp xỉ bằng 0,6774.
Câu 9 [145270]: [Trích SGK Chân Trời Sáng Tạo]: Ở một khu rừng nọ có 7 chú lùn, trong đó có 4 chú luôn nói thật, 3 chú còn lại nói thật với xác suất 0,5. Bạn Tuyết gặp ngẫu nhiên một chú lùn. Biết rằng chú lùn mà bạn Tuyết gặp tự nhận mình là người luôn nói thật. Tính xác suất để chú lùn đó luôn nói thật. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố “Chú lùn đó luôn nói thật” và B là biến cố “Chú lùn đó tự nhận mình luôn nói thật”.
Ta có: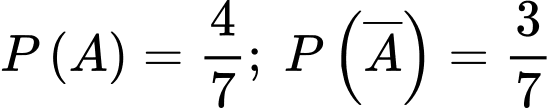
Khi đó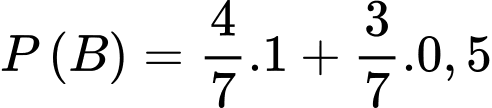
suy ra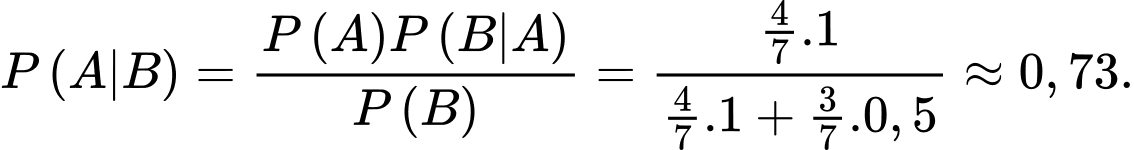 
Ta có:
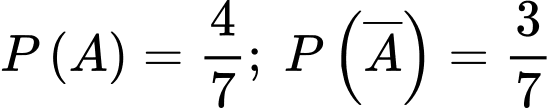
Khi đó
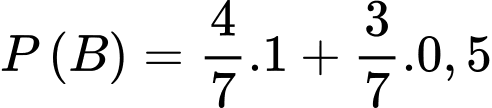suy ra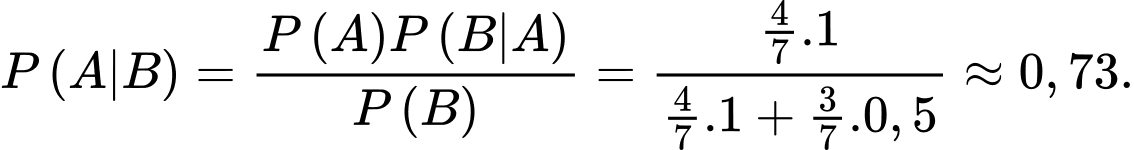
Câu 10 [145238]: Một trạm chỉ phát hai loại tín hiệu A và B với xác suất tương ứng là 0,84 và 0,16. Do có nhiễu trên đường truyền nên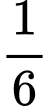 
tín hiệu A bị méo và được thu như là tín hiệu B, còn 
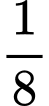tín hiệu B bị méo thành tín hiệu A. Giả sử thu được tín hiệu A, xác suất để thu được đúng tín hiệu lúc phát là bao nhiêu. Viết kết quả làm tròn đến hàng phần trăm.
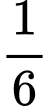tín hiệu A bị méo và được thu như là tín hiệu B, còn 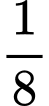tín hiệu B bị méo thành tín hiệu A. Giả sử thu được tín hiệu A, xác suất để thu được đúng tín hiệu lúc phát là bao nhiêu. Viết kết quả làm tròn đến hàng phần trăm.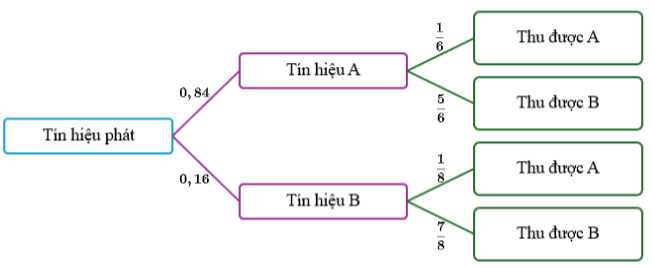 
Gọi
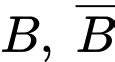lần lượt là biến cố "phát ra tín hiệu A, B". Khi đó 
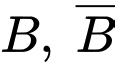tạo thành hệ đầy đủ. Ta có: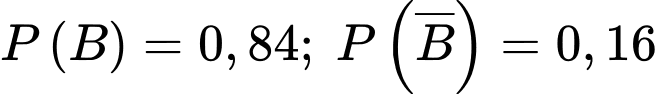 
Gọi
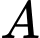là biến cố thu được tín hiệu A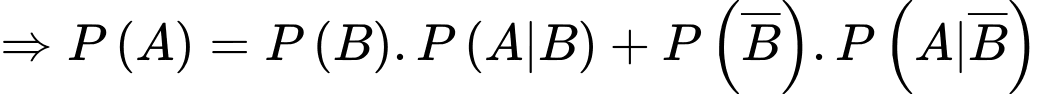
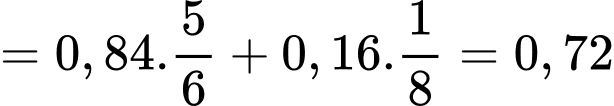
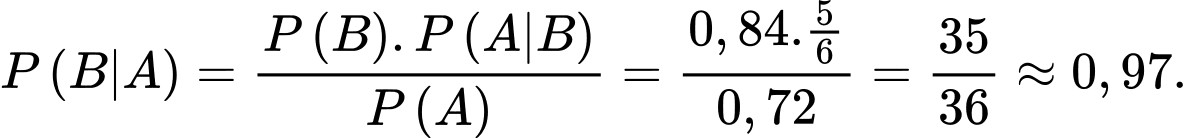
Câu 11 [373332]: Người ta điều tra thấy ở một địa phương nọ có 2% tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ởđịa phương đó, người ta nhận thấy có 10% là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần? Viết kết quả làm tròn đến hàng phần chục.
Gọi A là biến cố:Người đó sử dụng điện thoại khi lái xe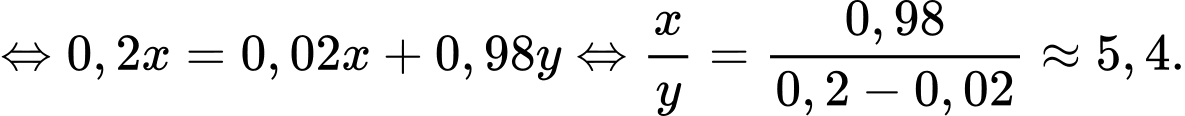 
B là biến cố: Người đó gây tai nạn
Ta có: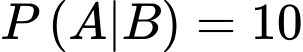 
ta cần tính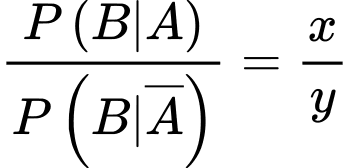 
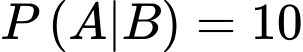ta cần tính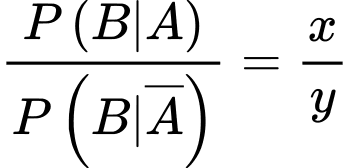 Lại có: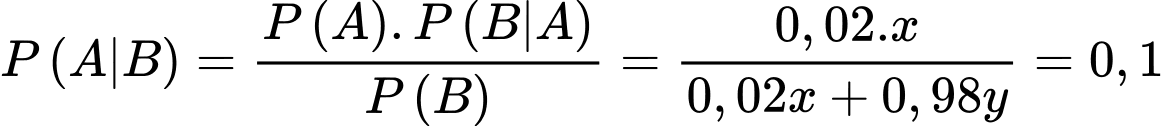 
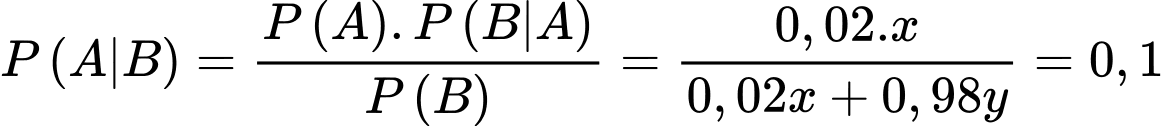
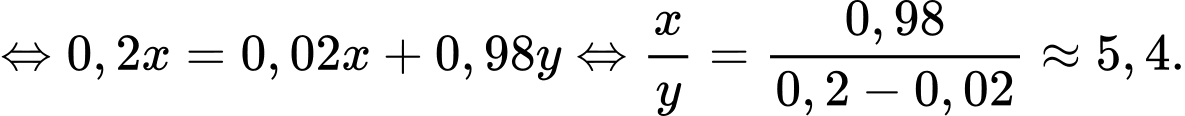
Câu 12 [378736]: Một loại vaccine được tiêm ở địa phương X. Người có bệnh nền thì với xác suất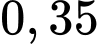 
có phản ứng phụ sau tiêm; người không có bệnh nền thì chỉ có phản ứng phụ sau tiêm với xác suất 
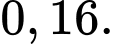Chọn ngẫu nhiên một người được tiêm vaccine và người này có phản ứng phụ. Tinh xác suất để người này có bệnh nền, biết rằng tỉ lệ người có bệnh nền ở địa phương X là 18%. Viết kết quả làm tròn đến hàng phần trăm.
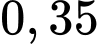có phản ứng phụ sau tiêm; người không có bệnh nền thì chỉ có phản ứng phụ sau tiêm với xác suất 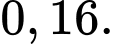Chọn ngẫu nhiên một người được tiêm vaccine và người này có phản ứng phụ. Tinh xác suất để người này có bệnh nền, biết rằng tỉ lệ người có bệnh nền ở địa phương X là 18%. Viết kết quả làm tròn đến hàng phần trăm. 
Câu 13 [145239]: [Trích SGK Cánh Diều]: Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác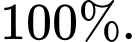 
Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 
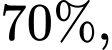còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 
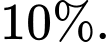Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 
con trên 
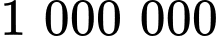con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Spring, 2005). Khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là 
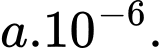Tìm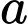 
viết kết quả làm tròn đến hàng đơn vị.
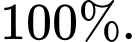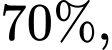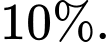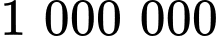Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là con trên con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Spring, 2005). Khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là 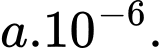Tìm 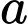viết kết quả làm tròn đến hàng đơn vị.
Điền đáp án: 91
Xét hai biến cố:
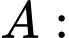“Con bò được chọn không bị mắc bệnh bò điên”.
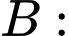“Con bò được chọn ra có phản ứng dương tính”.
Vì tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con nên tỉ lệ bò mắc bệnh bò điên ở Hà Lan là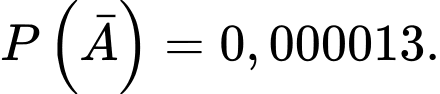
Suy ra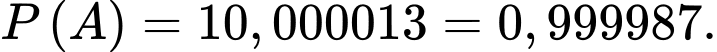
Trong số những con bò không bị mắc bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm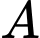
là 10%, suy ra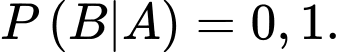 
Khi con bò mắc bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm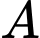
là 70% nên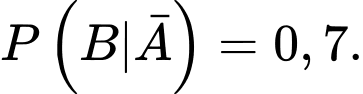 
Ta thấy xác suất mắc bệnh bò điên của một con bò ở Hà Lan xét nghiệm có phản ứng dương tính với xét nghiệm A chính là
Áp dụng công thức Bayes, ta có:
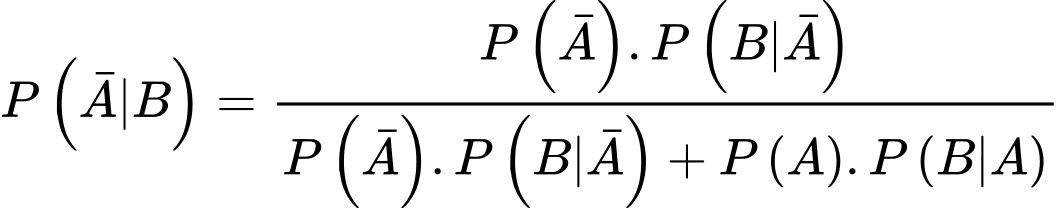
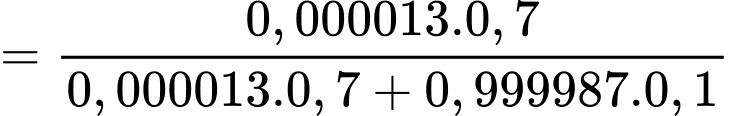
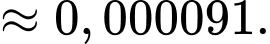
Vậy khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm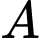
thì xác suất để nó bị mắc bệnh bò điên là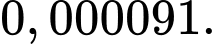 
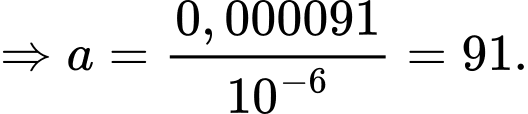
Xét hai biến cố:
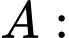“Con bò được chọn không bị mắc bệnh bò điên”.
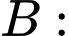“Con bò được chọn ra có phản ứng dương tính”.
Vì tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con nên tỉ lệ bò mắc bệnh bò điên ở Hà Lan là
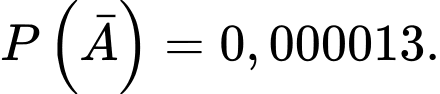
Suy ra
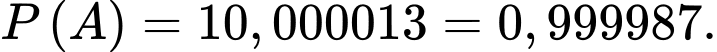
Trong số những con bò không bị mắc bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm
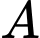là 10%, suy ra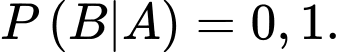
Khi con bò mắc bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm
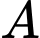là 70% nên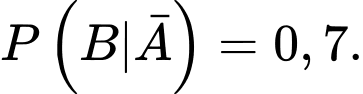
Ta thấy xác suất mắc bệnh bò điên của một con bò ở Hà Lan xét nghiệm có phản ứng dương tính với xét nghiệm A chính là
Áp dụng công thức Bayes, ta có:
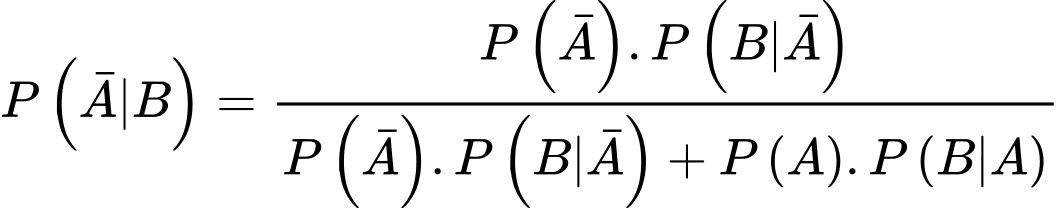
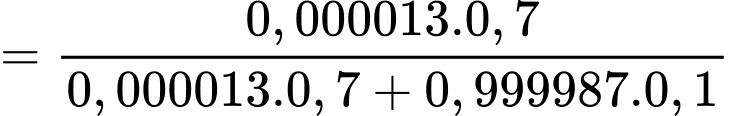
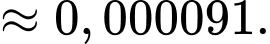
Vậy khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm
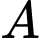thì xác suất để nó bị mắc bệnh bò điên là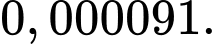
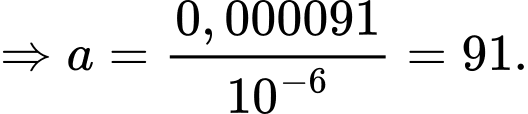
Câu 14 [145271]: [Trích SGK Chân Trời Sáng Tạo]: Có hai cái hộp giống nhau, hộp thứ nhất chứa 5 quả bóng bàn màu trắng và 3 quả bóng bàn màu vàng, hộp thứ hai chứa 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Minh lấy ra ngẫu nhiên 1 quả bóng từ hộp thứ nhất. Nếu quả bóng đó là bóng vàng thì Minh lấy ra ngẫu nhiên đồng thời 2 quả bóng từ hộp thứ hai, còn nếu quả bóng đó màu trắng thì Minh lấy ra ngẫu nhiên đồng thời 3 quả bóng từ hộp thứ hai. Biết rằng các quả bóng lấy ra từ hộp thứ hai đều có màu trắng. Tính xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng. Viết kết quả làm tròn đến hàng phần trăm.
A là biến cố: Minh lấy được quả bóng vàng lần thứ nhất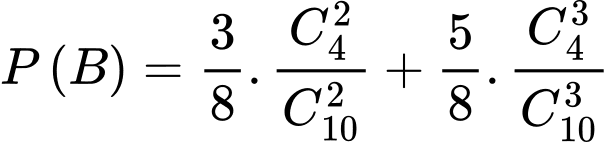 
suy ra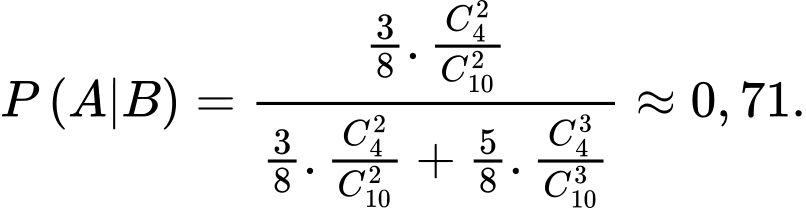 
B là biến cố: Các quả bóng lấy ra từ hộp thứ hai đều có màu trắng.
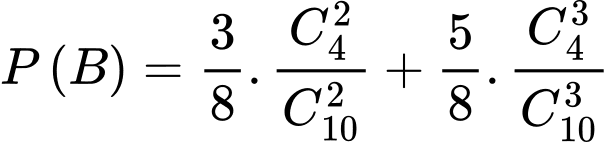suy ra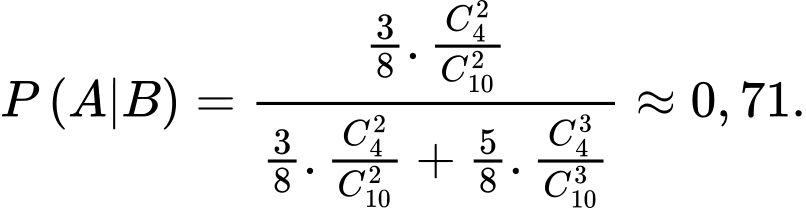
Câu 15 [145272]: [Trích SGK Chân Trời Sáng Tạo]: Hộp thứ nhất có 1 viên bi xanh và 5 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 5 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 2 viên bi từ hộp thứ hai. Biết rằng 2 viên bi lấy ra từ hộp thứ hai đều là bi đỏ. Tính xác suất để 2 viên bi lấy ra từ hộp thứ nhất cũng đều là bi đỏ. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố: 2 viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ
B là biến cố: “2 viên bi lấy ra từ hộp thứ hai là bi đỏ”
Ta có: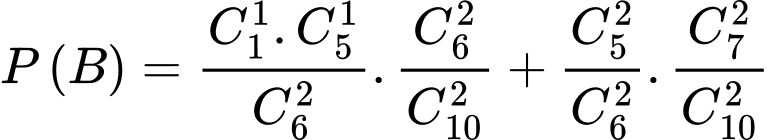
Xác suất cần tìm là: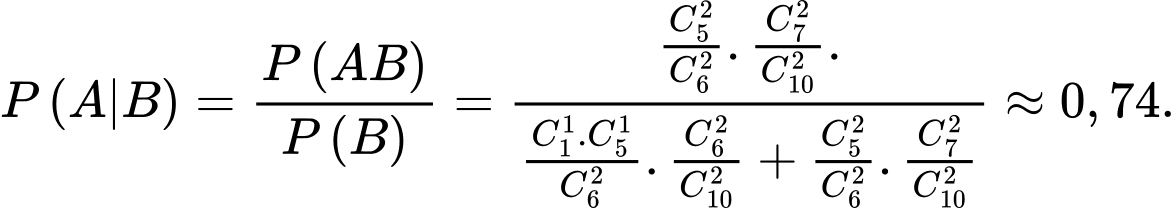
B là biến cố: “2 viên bi lấy ra từ hộp thứ hai là bi đỏ”
Ta có:
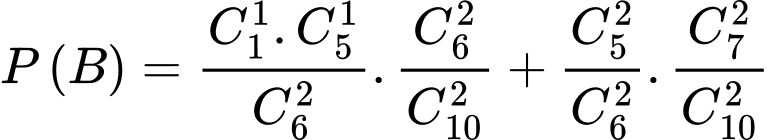
Xác suất cần tìm là:
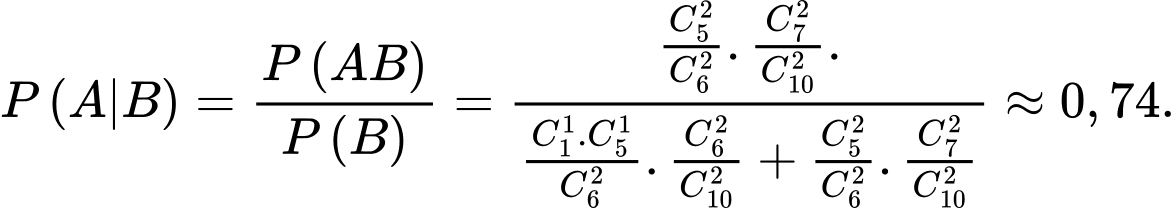
Câu 16 [145402]: [Trích SGK Chân Trời Sáng Tạo]: Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai. Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ, tính xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố: Viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ
B là biến cố: “2 Viên bi lấy ra từ hộp thứ 2 là bi đỏ.
Ta có: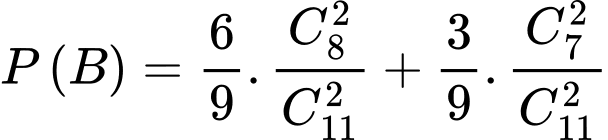
Suy ra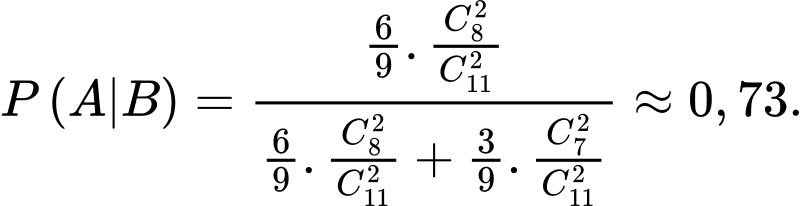
Ta có:
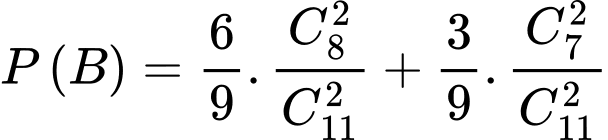
Suy ra
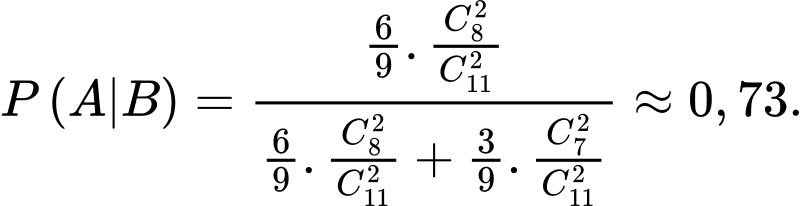
Câu 17 [145404]: Có 2 hộp áo; hộp một có 10 áo trong đó có 1 phế phẩm; hộp hai có 8 áo trong đó có 2 phế phẩm. Lấy ngẫu nhiên 1 áo từ hộp một bỏ sang hộp hai; sau đó từ hộp này chọn ngẫu nhiên ra 2 áo. Xác suất để cả 2 áo này đều là phế phẩm là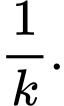 
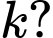
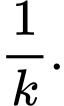Tìm 
Tìm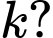
Gọi A là biến cố: Hai áo được lấy sau cùng là phế phẩm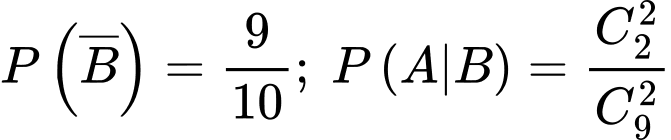 
B là biến cố: Lấy được phế phẩm từ hộp 1 sang hộp 2
Ta có: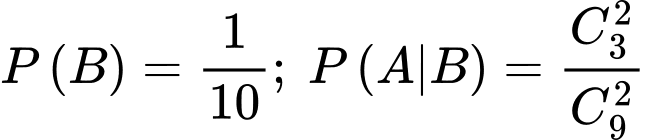 
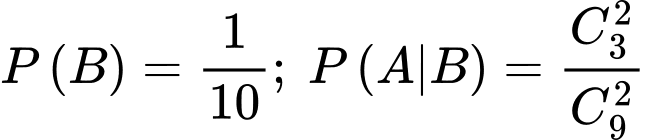
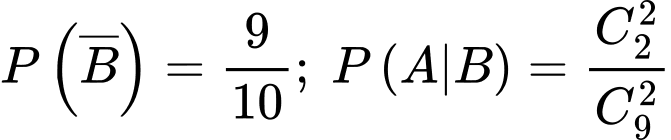
Suy ra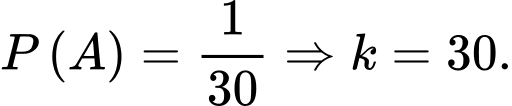 
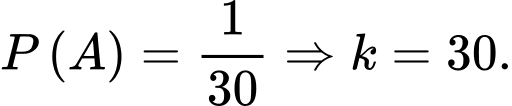
Câu 18 [378767]: Có hai chuồng gà. Chuồng I có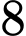 
con gà trống và 
con gà mái. Chuồng II có 
con gà trống và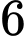 
con gà mái. An bắt ngẫu nhiên một con gà từ chuồng II đem thả vào chuồng I. Sau đó, Bình bắt ngẫu nhiên một con gà từ chuồng I.
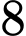con gà trống và con gà mái. Chuồng II có con gà trống và 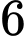con gà mái. An bắt ngẫu nhiên một con gà từ chuồng II đem thả vào chuồng I. Sau đó, Bình bắt ngẫu nhiên một con gà từ chuồng I.Giả sử Bình bắt được con gà mái. Tính xác suất để Bình bắt được con gà mái của chuồng I.Viết kết quả làm tròn đến hàng phần trăm.
Khi đó,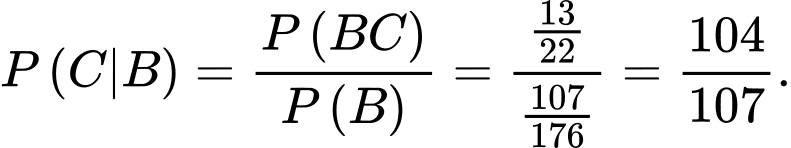 
Vậy nếu Bình bắt được con gà mái thì xác suất để Bình bắt được con gà mái của chuồng I là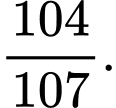 
Câu 19 [145240]: Có hai chuồng thỏ. Chuồng thứ nhất có 5 con thỏ đen và 10 con thỏ trắng. Chuồng thứ hai có 3 thỏ trắng và 7 thỏ đen. Từ chuồng thứ hai ta bắt ngẫu nhiên một con thỏ cho vào chuồng thứ nhất và sau đó lại bắt ngẫu nhiên một con thỏ ở chuồng thứ nhất ra thì được một chú thỏ trắng. Tính xác suất để con thỏ trắng này là của chuồng thứ nhất. Viết kết quả làm tròn đến hàng phần trăm.
Gọi biến cố A: “Lấy lần 1 ra được thỏ trắng”;
B: “Lấy lần 2 ra được thỏ trắng”;
Ta có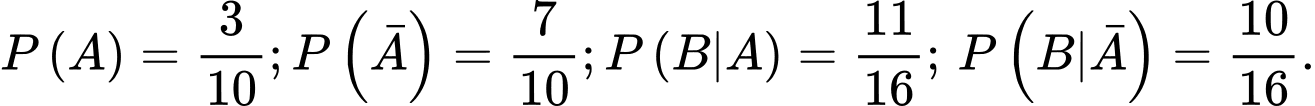 
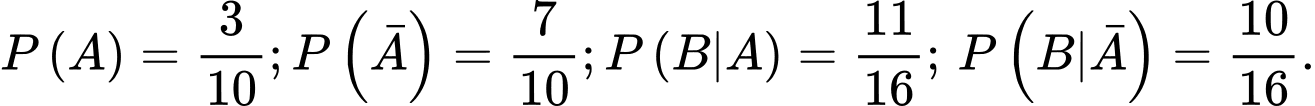
Lại có: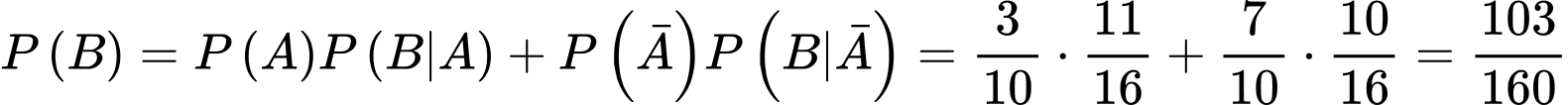 
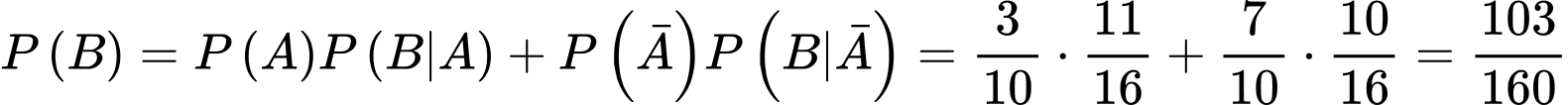
Gọi 
là biến cố: Thỏ trắng bắt lần hai là thỏ thuộc chuồng thứ nhất
là biến cố: Thỏ trắng bắt lần hai là thỏ thuộc chuồng thứ nhất Khi đó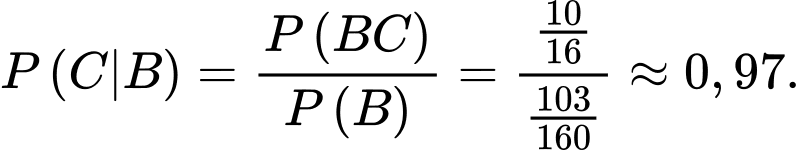 
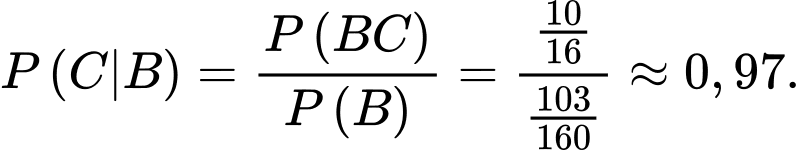
Câu 20 [145241]: Tại một phòng khám chuyên khoa tỷ lệ người đến khám có bệnh là 83%. Theo thống kê biết rằng nếu chẩn đoán có bệnh thì đúng tới 90%, còn nếu chẩn đoán không bệnh thì chỉ đúng 80%. Xác suất chẩn đoán đúng là bao nhiêu?
Gọi A là biến cố: “Người đến khám có bệnh” và B là biến cố: “Phòng khám chẩn đoán có bệnh”
Ta có:
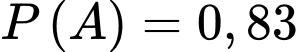. Xác suất chuẩn đoán đúng khi có bệnh là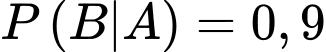 
Xác suất chuẩn đoán đúng khi không có bệnh là:
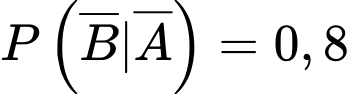
Suy ra: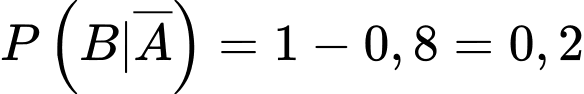
Xác suất không có bệnh là: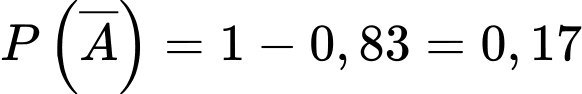
Áp dụng công thức có điều kiện ta tính xác suất chuẩn đoán có bệnh:
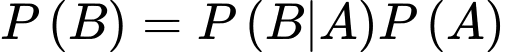
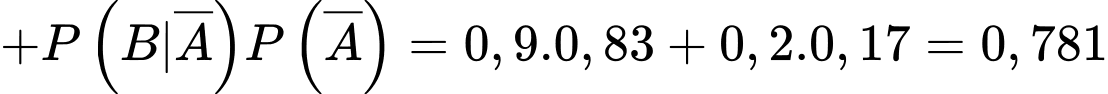
Xác suất chuẩn đoán đúng bao gồm cả trường hợp chuẩn đoán đúng có bệnh và chuẩn đoán đúng không bệnh là
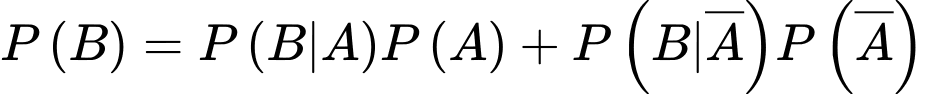
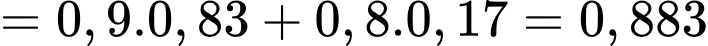
Đáp án: 0,883.
Ta có:
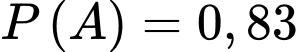. Xác suất chuẩn đoán đúng khi có bệnh là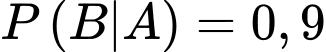 Xác suất chuẩn đoán đúng khi không có bệnh là:
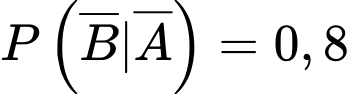
Suy ra:
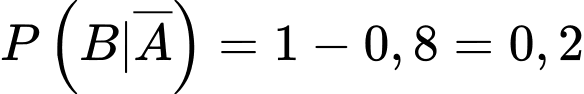
Xác suất không có bệnh là:
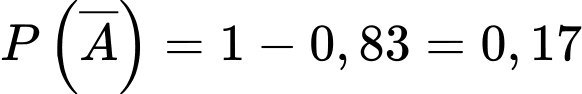
Áp dụng công thức có điều kiện ta tính xác suất chuẩn đoán có bệnh:
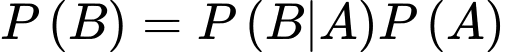
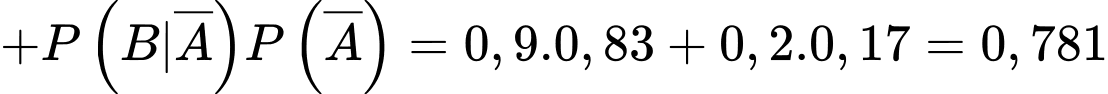
Xác suất chuẩn đoán đúng bao gồm cả trường hợp chuẩn đoán đúng có bệnh và chuẩn đoán đúng không bệnh là
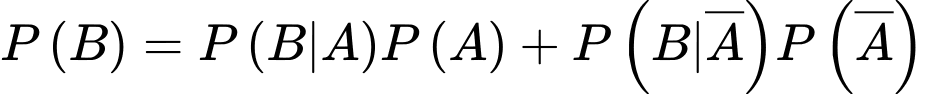
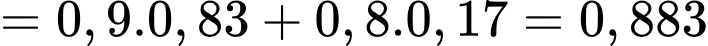
Đáp án: 0,883.