Đáp án Bài tập tự luyện
Câu 1 [139849]: Tìm nguyên hàm 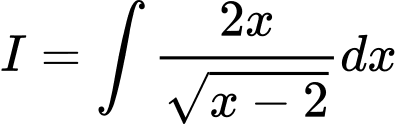 .
.
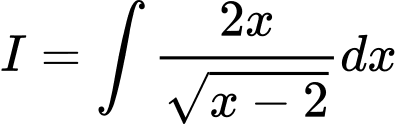 .
. A, 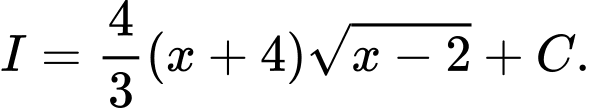
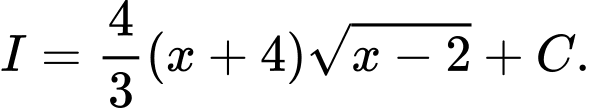
B, 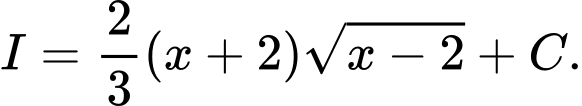
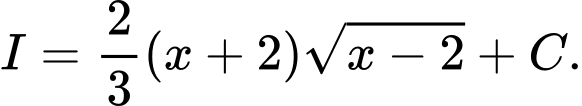
C, 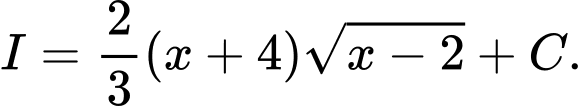
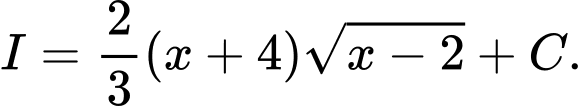
D, 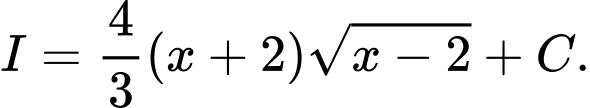
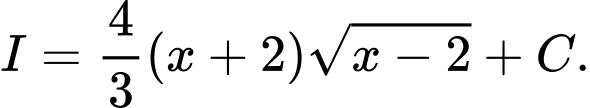
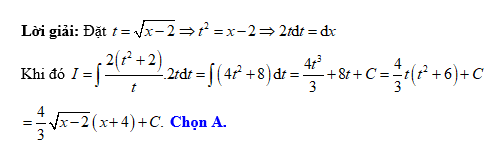 Đáp án: A
Đáp án: A
Câu 2 [139850]: Tìm nguyên hàm 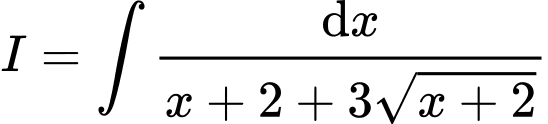 .
.
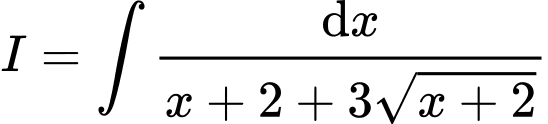 .
. A, 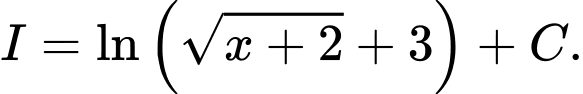
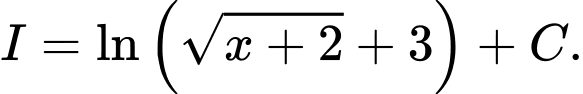
B, 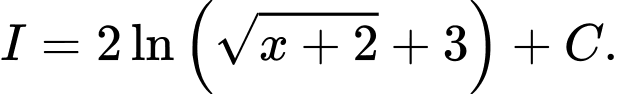
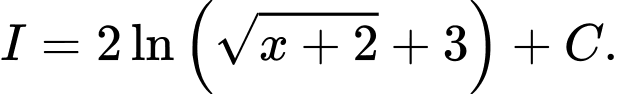
C, 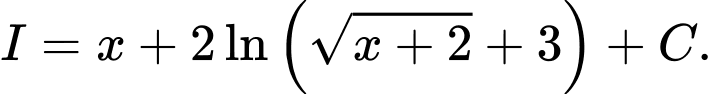
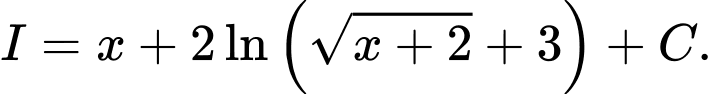
D, 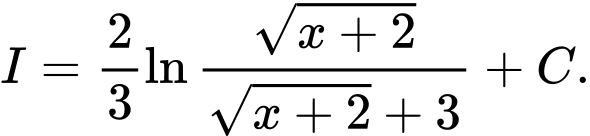
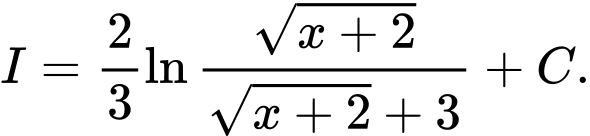
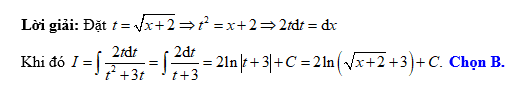 Đáp án: B
Đáp án: B
Câu 3 [139851]: Tìm nguyên hàm 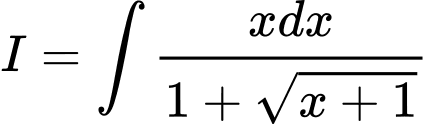 .
.
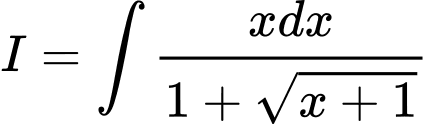 .
. A, 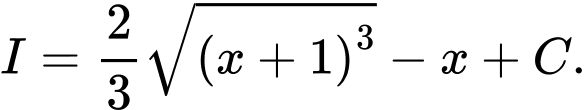
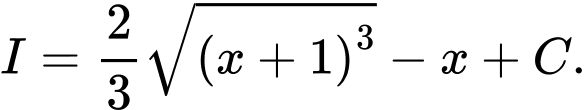
B, 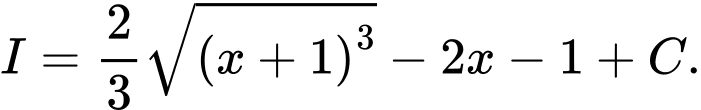
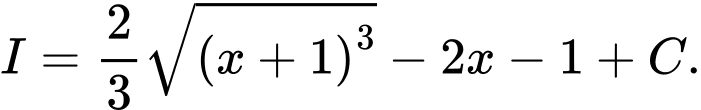
C, 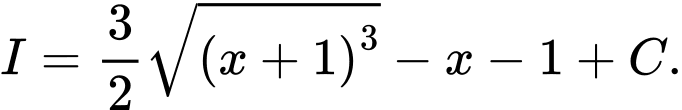
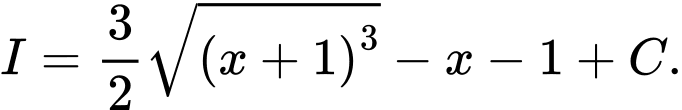
D, 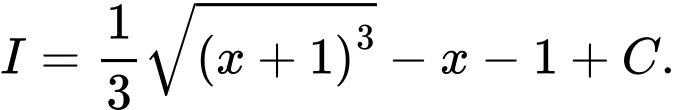
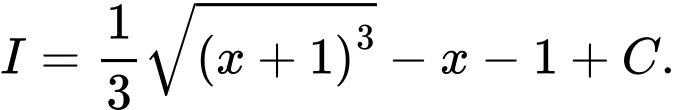
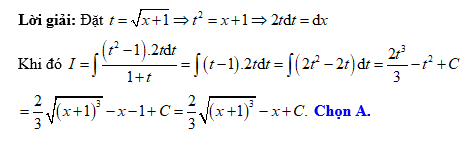 Đáp án: A
Đáp án: A
Câu 4 [148916]: Xét nguyên hàm 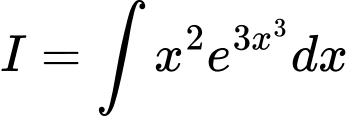 . Đặt
. Đặt 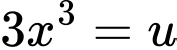 thu được . Tính giá trị tổng .
thu được . Tính giá trị tổng .
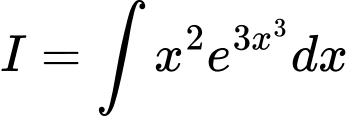 . Đặt
. Đặt 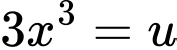 thu được . Tính giá trị tổng .
thu được . Tính giá trị tổng . 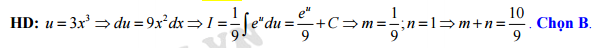 Đáp án: B
Đáp án: B
Câu 5 [148821]: Tìm nguyên hàm 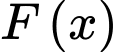 của hàm số
của hàm số 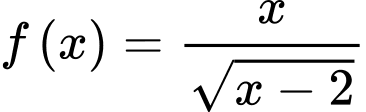 thỏa mãn
thỏa mãn 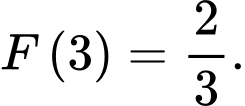
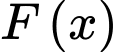 của hàm số
của hàm số 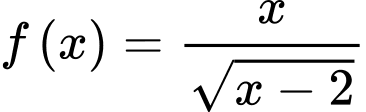 thỏa mãn
thỏa mãn 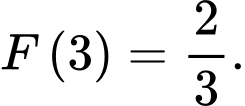
A, 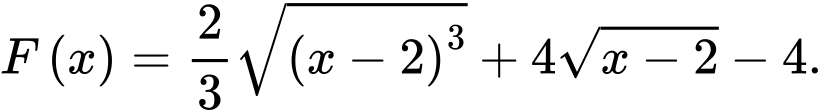
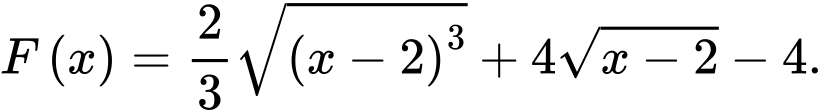
B, 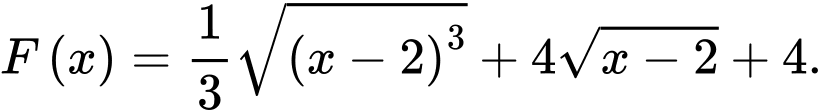
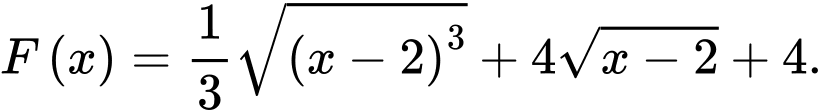
C, 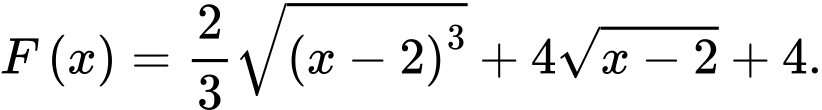
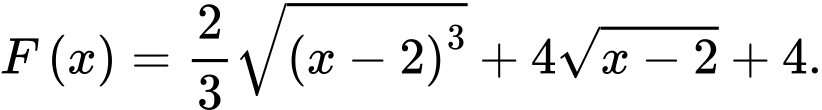
D, 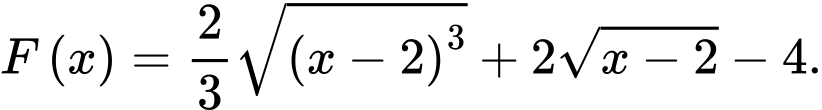
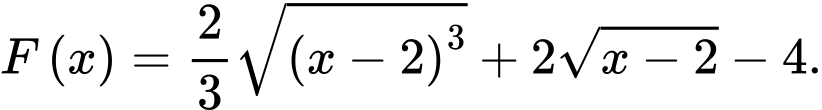
HD: Ta có 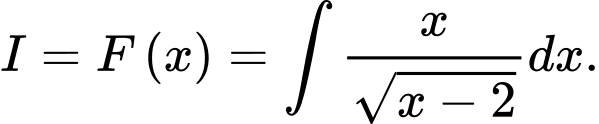
Đặt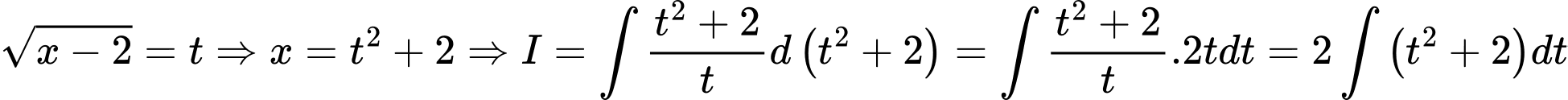
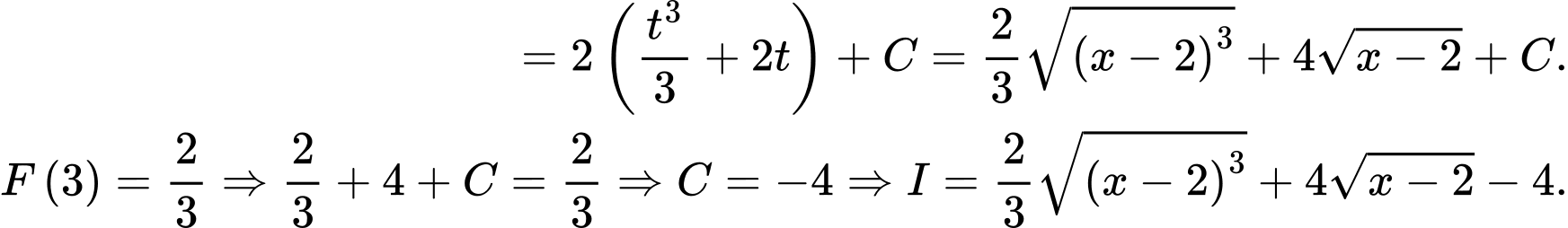
Chọn A. Đáp án: A
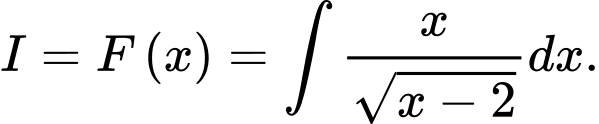
Đặt
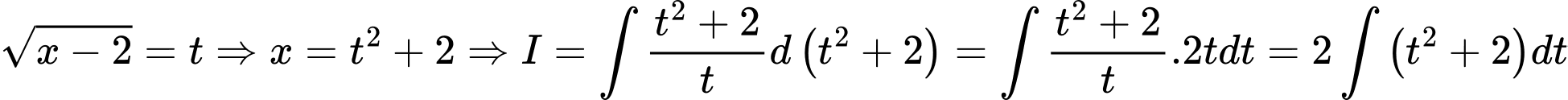
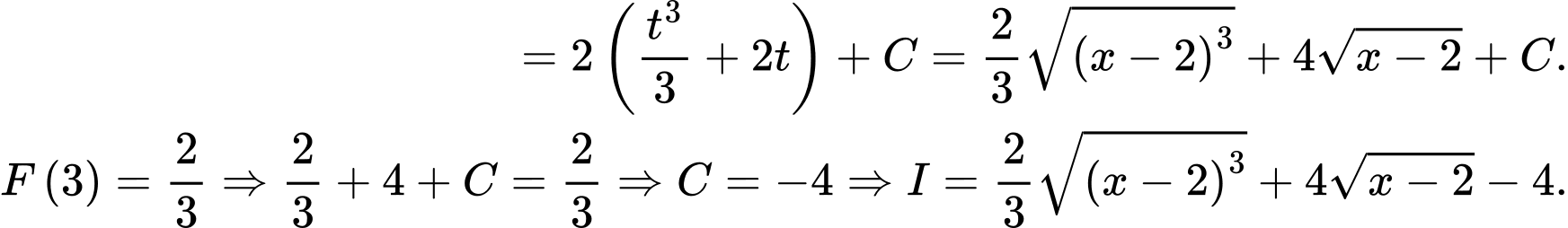
Chọn A. Đáp án: A
Câu 6 [148876]: Nguyên hàm của hàm số 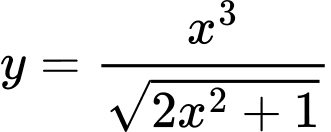 bằng
bằng
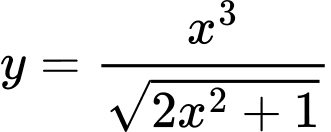 bằng
bằng A, 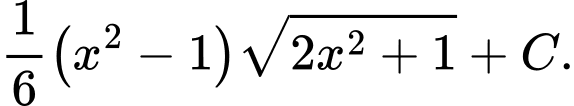
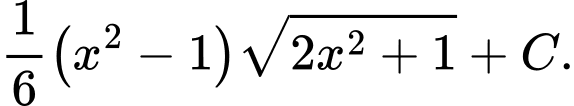
B, 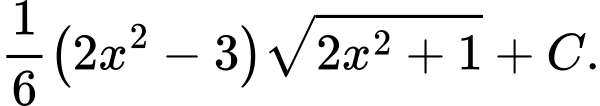
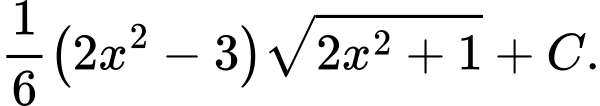
C, 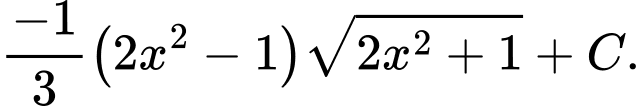
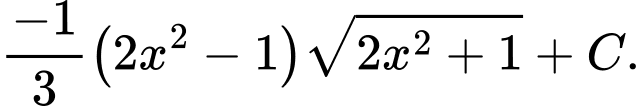
D, 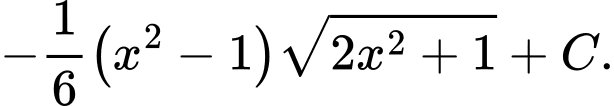
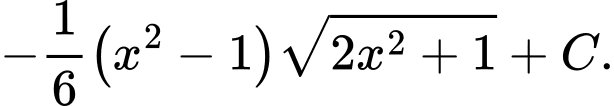
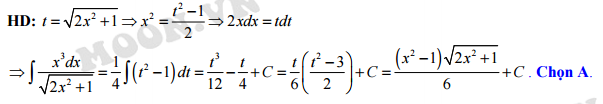 Đáp án: A
Đáp án: A
Câu 7 [145495]: Cho 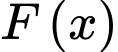 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 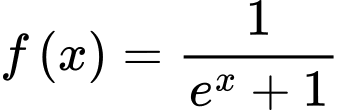 thỏa mãn
thỏa mãn 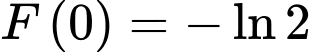 . Tìm tập nghiệm
. Tìm tập nghiệm 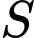 của phương trình
của phương trình 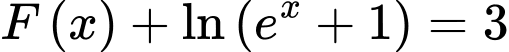 .
.
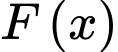 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 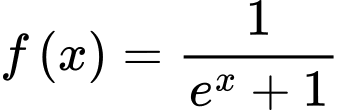 thỏa mãn
thỏa mãn 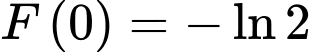 . Tìm tập nghiệm
. Tìm tập nghiệm 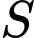 của phương trình
của phương trình 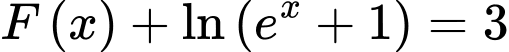 .
. A, 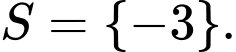
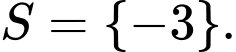
B, 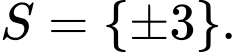
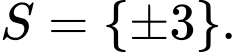
C, 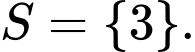
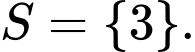
D, 

Ta có: 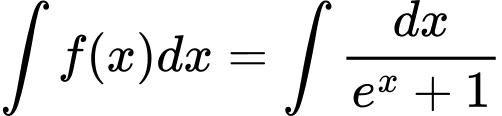
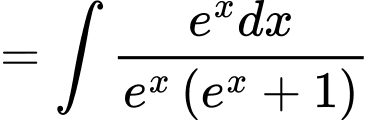
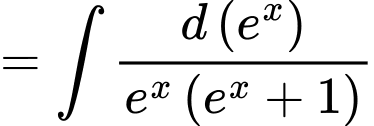
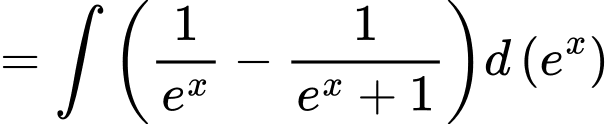
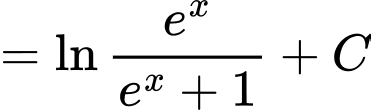 (Do
(Do  ).
).
Khi đó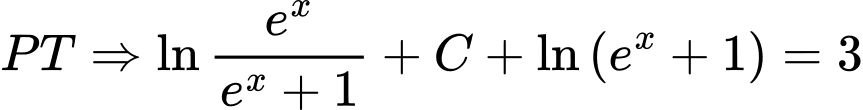
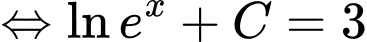
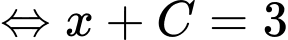 Mặt khác
Mặt khác
Chọn đáp án Đáp án: C
Đáp án: C
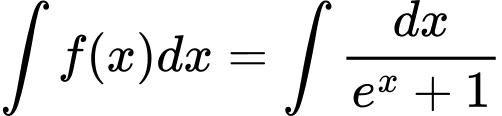
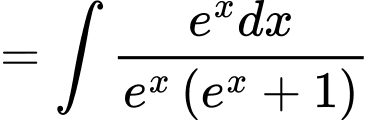
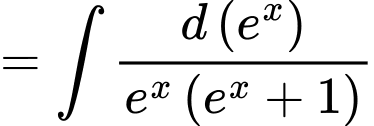
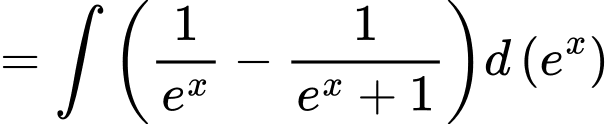
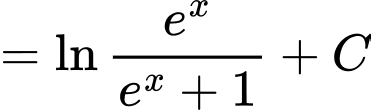 (Do
(Do  ).
).
Khi đó
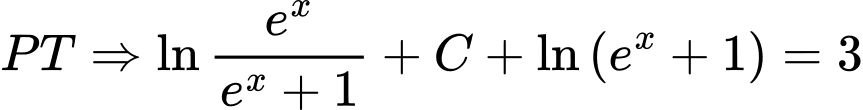
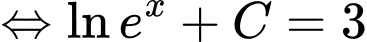
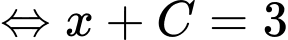 Mặt khác
Mặt khác Chọn đáp án
 Đáp án: C
Đáp án: C
Câu 8 [120788]: Tìm nguyên hàm 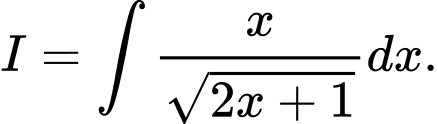
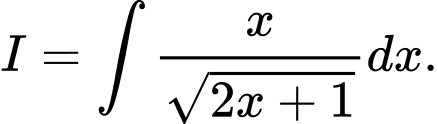
A, 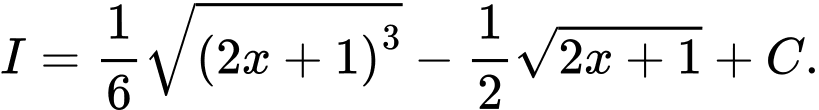
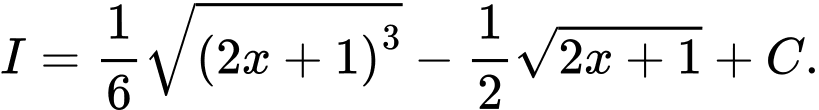
B, 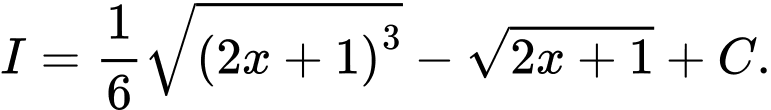
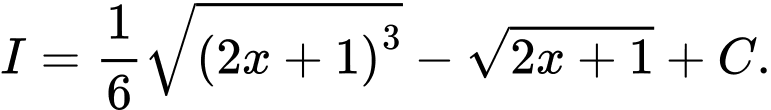
C, 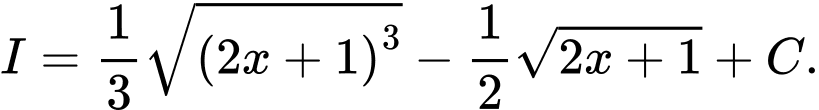
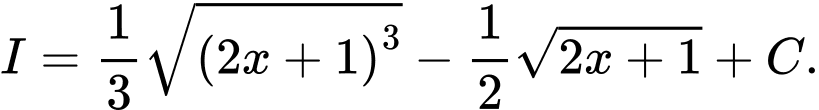
D, 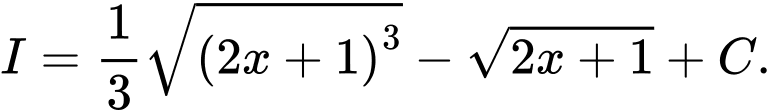
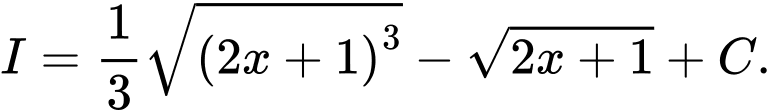
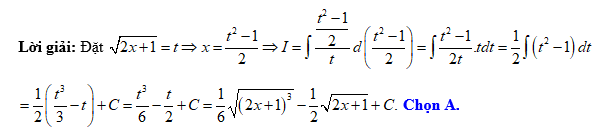 Đáp án: A
Đáp án: A
Câu 9 [148868]: Tìm nguyên hàm 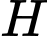 của hàm số
của hàm số 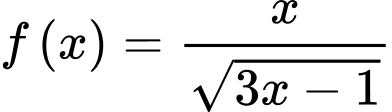 .
.
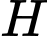 của hàm số
của hàm số 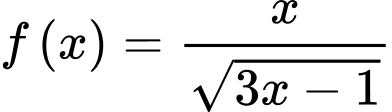 .
. A, 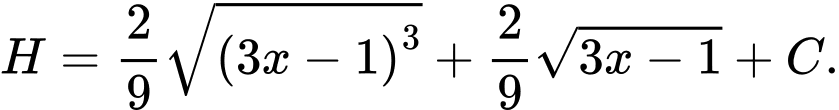
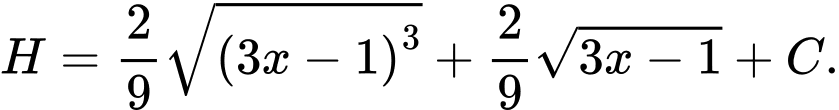
B, 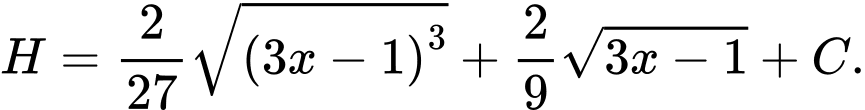
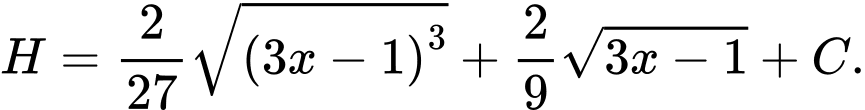
C, 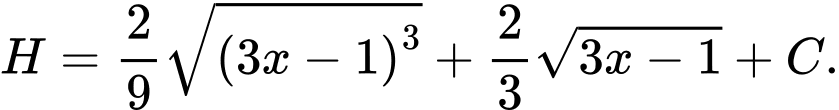
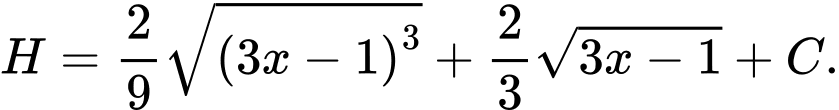
D, 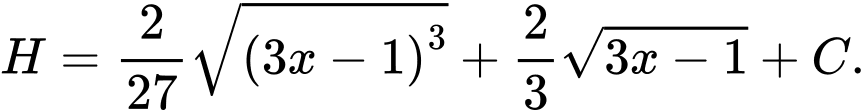
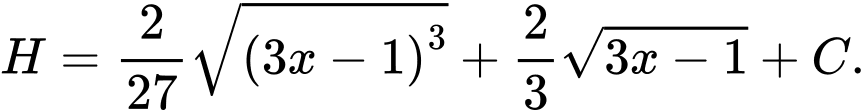
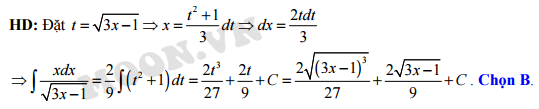 Đáp án: B
Đáp án: B
Câu 10 [148869]: Tìm nguyên hàm 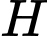 của hàm số
của hàm số 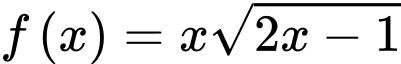 .
.
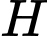 của hàm số
của hàm số 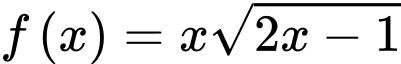 .
. A, 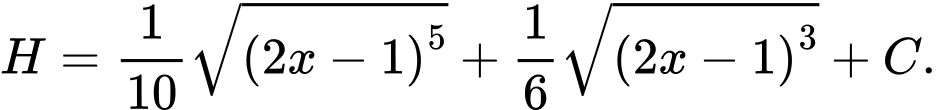
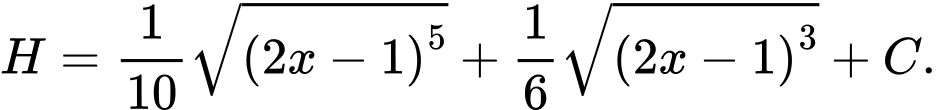
B, 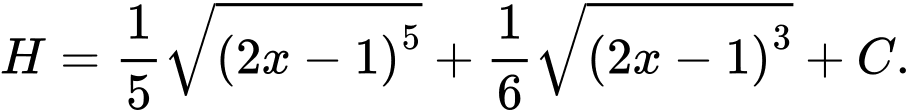
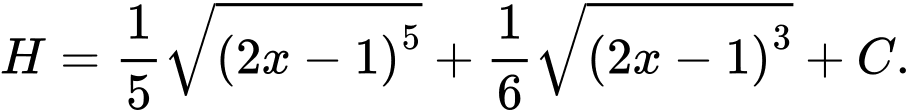
C, 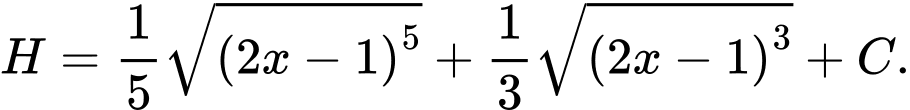
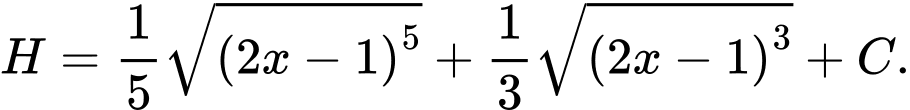
D, 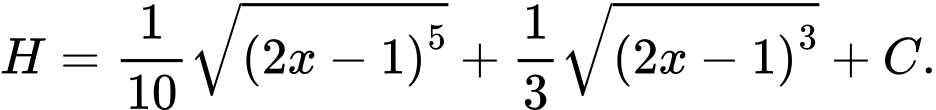
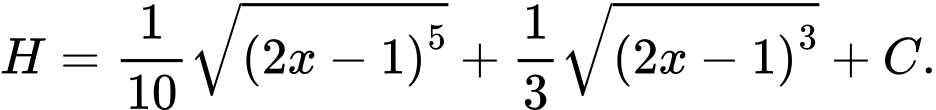
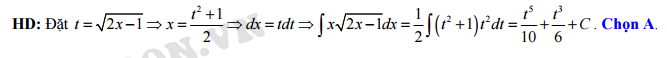 Đáp án: A
Đáp án: A
Câu 11 [148904]: Tìm nguyên hàm 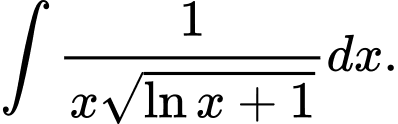
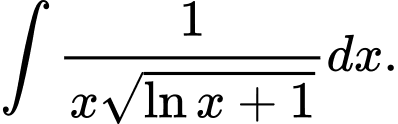
A, 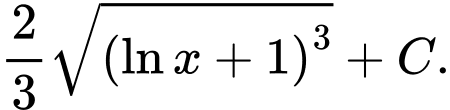
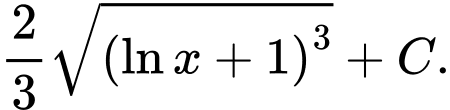
B, 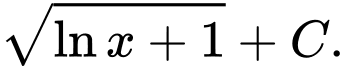
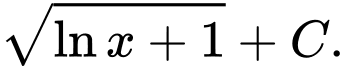
C, 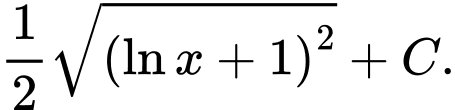
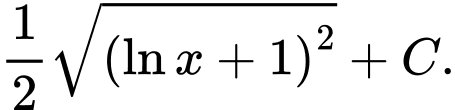
D, 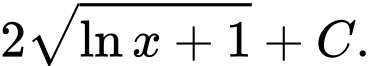
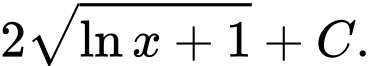
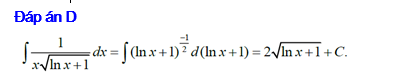 Đáp án: D
Đáp án: D
Câu 12 [148900]: Tìm nguyên hàm của hàm số 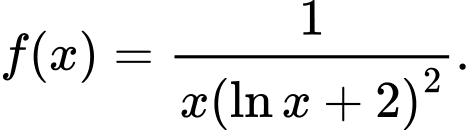
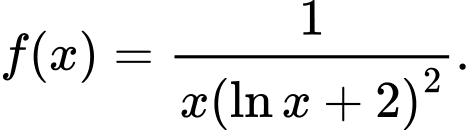
A, 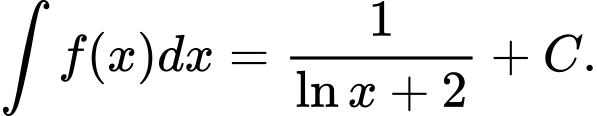
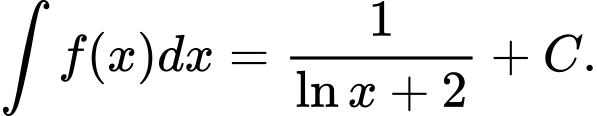
B, 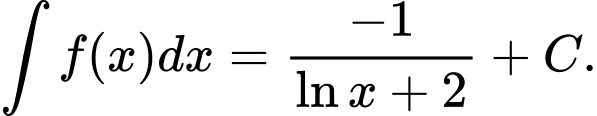
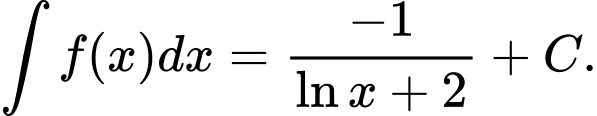
C, 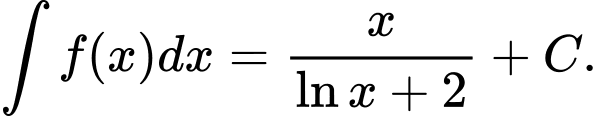
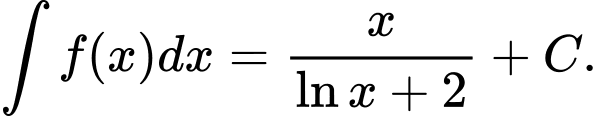
D, 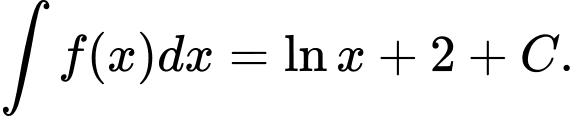
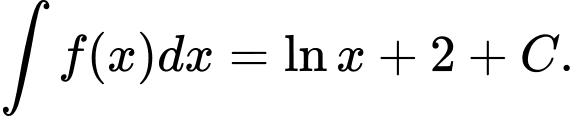
 Đáp án: B
Đáp án: B
Câu 13 [148907]: Tính 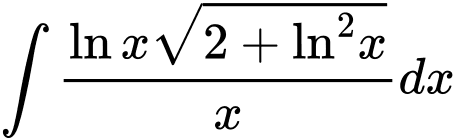 .
.
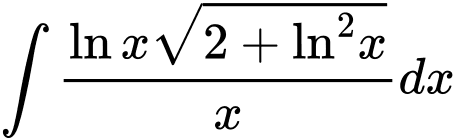 .
. A, 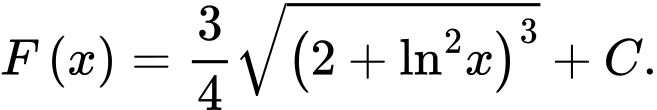
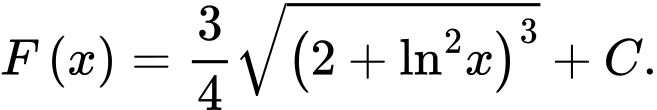
B, 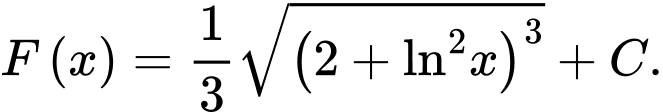
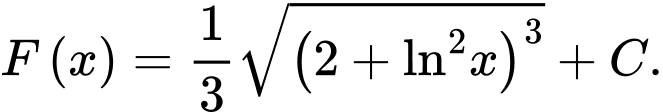
C, 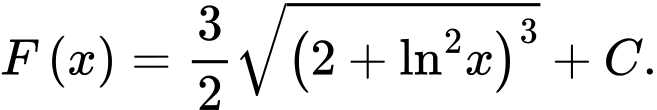
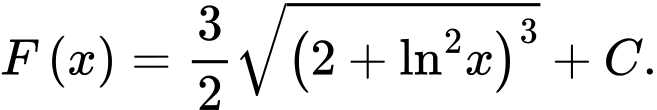
D, 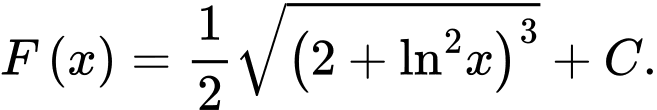
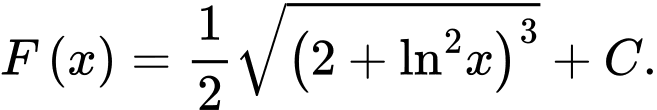
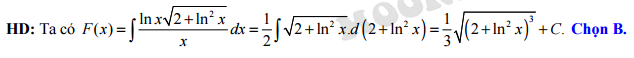 Đáp án: B
Đáp án: B
Câu 14 [148908]: 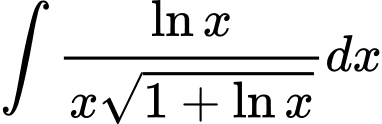 bằng
bằng
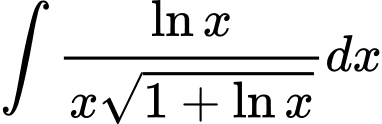 bằng
bằng A, 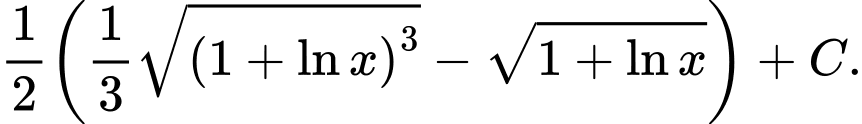
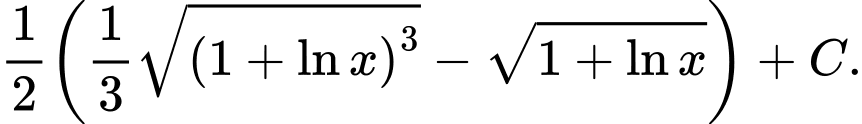
B, 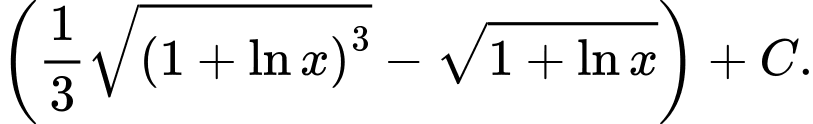
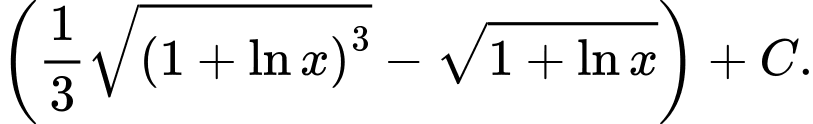
C, 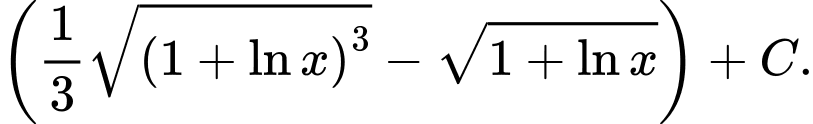
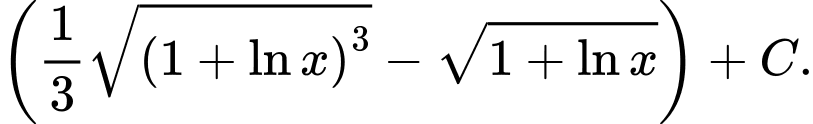
D, 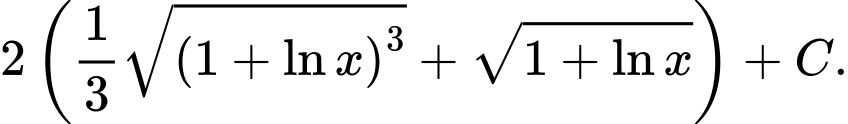
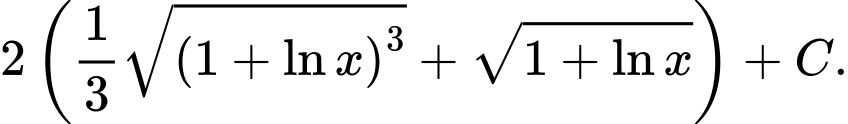
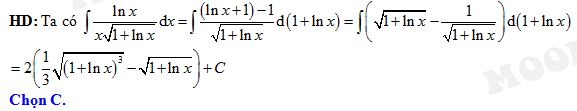 Đáp án: C
Đáp án: C
Câu 15 [120797]: Tìm nguyên hàm 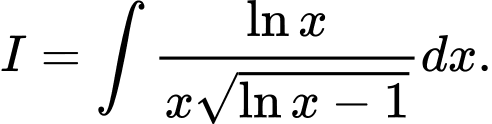
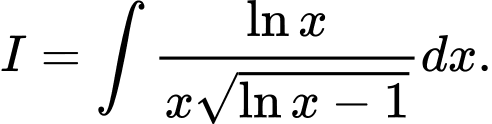
A, 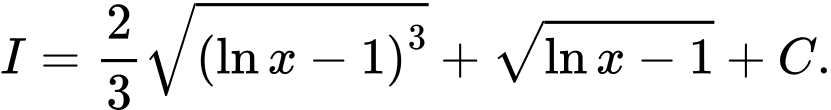
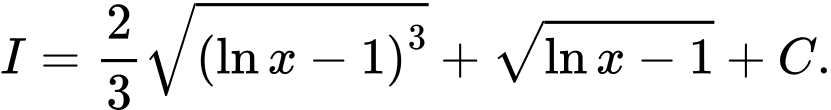
B, 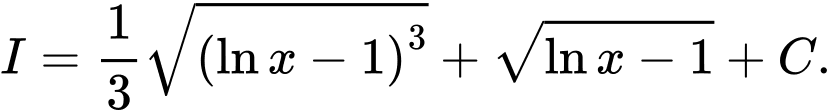
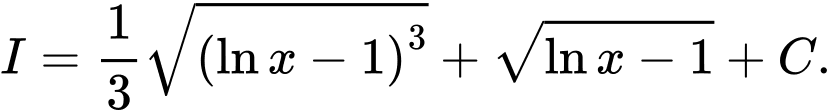
C, 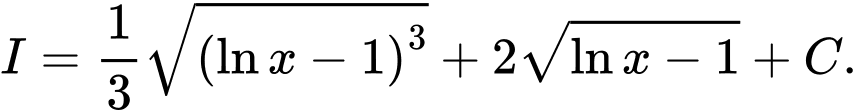
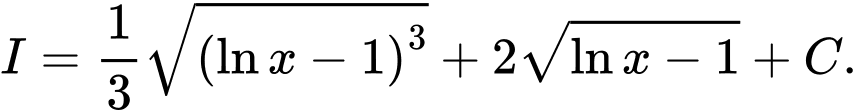
D, 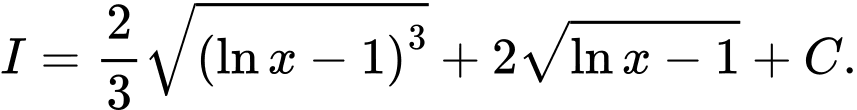
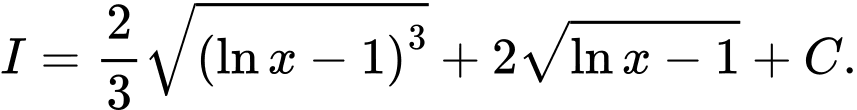
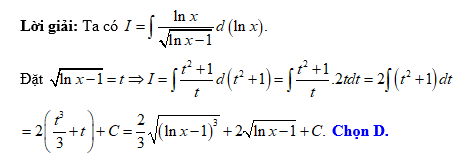 Đáp án: D
Đáp án: D
Câu 16 [148819]: Cho 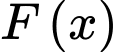 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 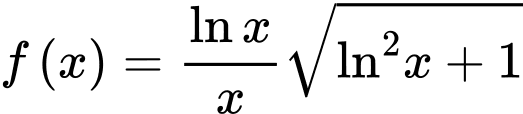 thỏa mãn
thỏa mãn 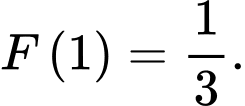 Tính
Tính 
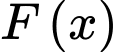 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 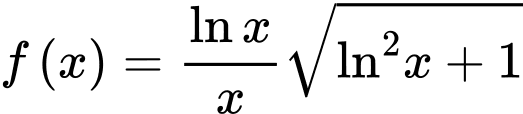 thỏa mãn
thỏa mãn 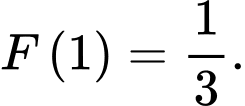 Tính
Tính 
A, 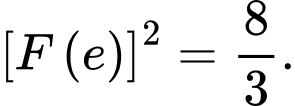
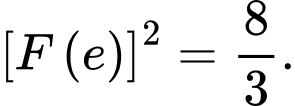
B, 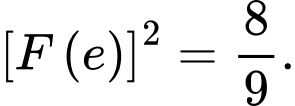
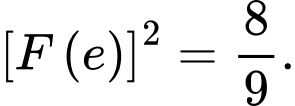
C, 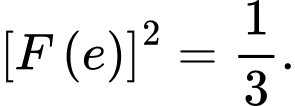
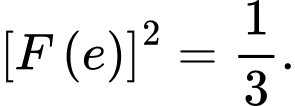
D, 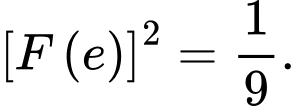
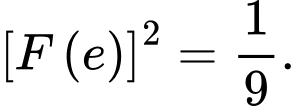
HD: Ta có 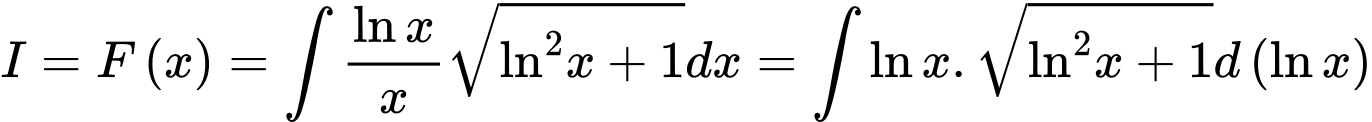
Đặt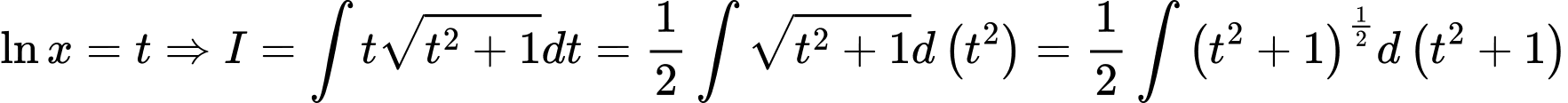
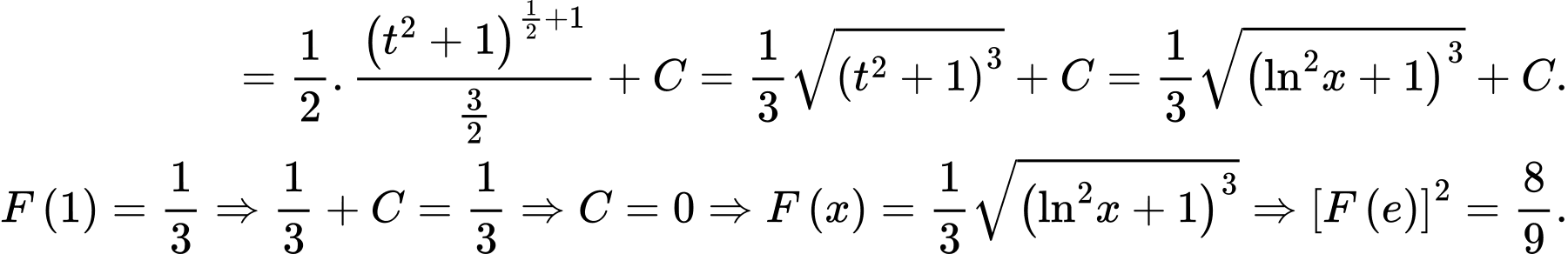
Chọn B. Đáp án: B
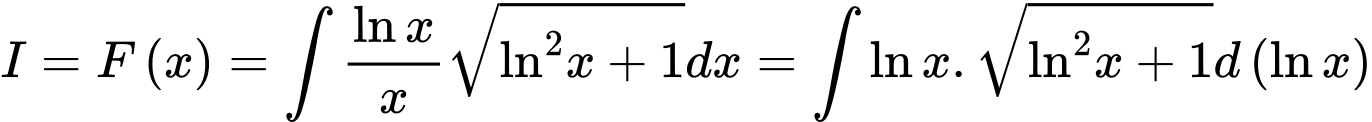
Đặt
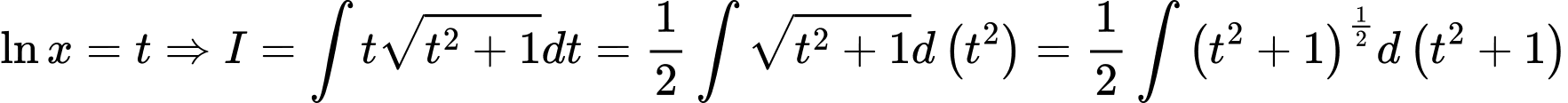
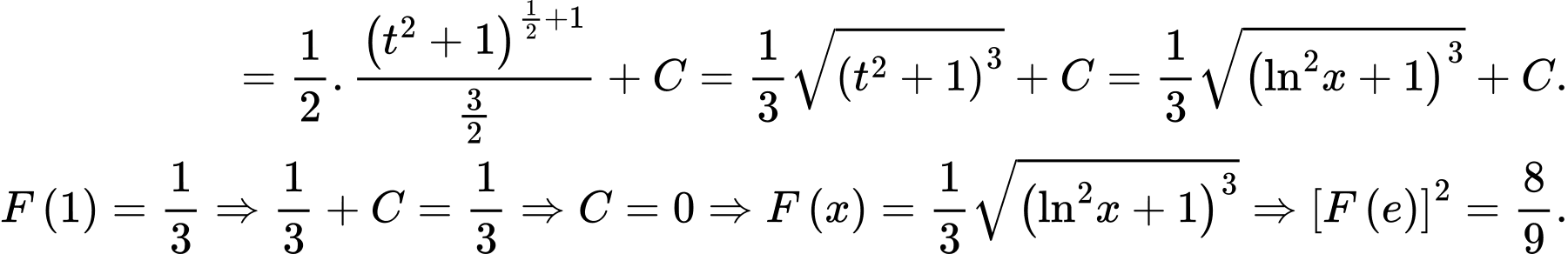
Chọn B. Đáp án: B
Câu 17 [516406]: Cho hàm số 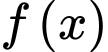 có
có 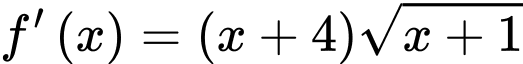 với mọi
với mọi  và
và 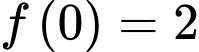 . Tích phân
. Tích phân 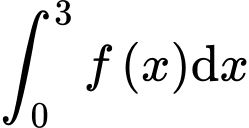 bằng
bằng
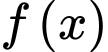 có
có 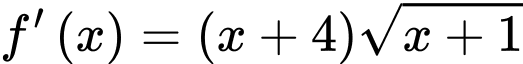 với mọi
với mọi  và
và 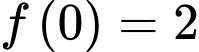 . Tích phân
. Tích phân 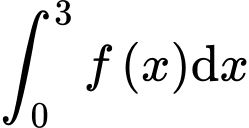 bằng
bằng A, 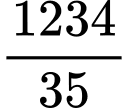 .
.
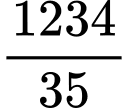 .
.B, 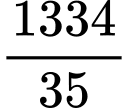 .
.
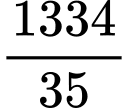 .
.C, 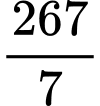 .
.
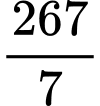 .
.D, 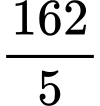 .
.
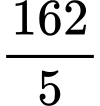 .
.
Chọn B
Xét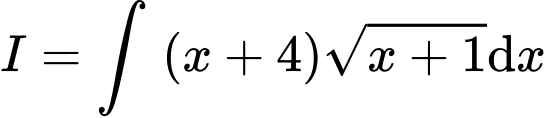 , đặt
, đặt 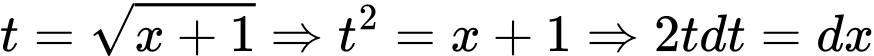 . Khi đó:
. Khi đó:
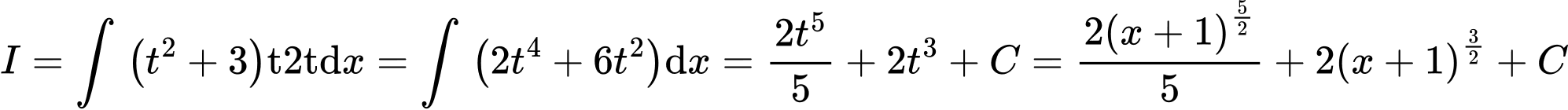 .
.
Suy ra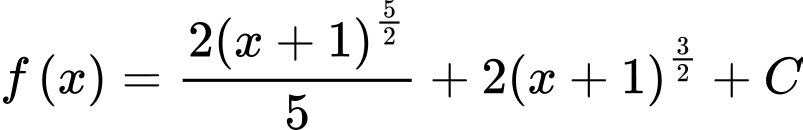 . Thay
. Thay 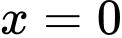 :
: 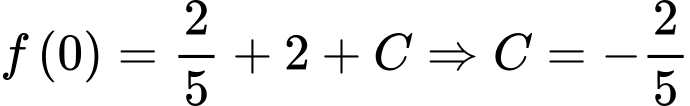 . Do đó
. Do đó 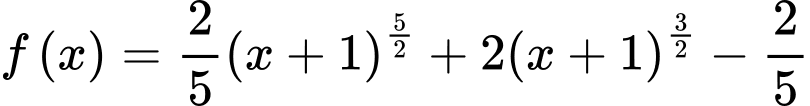 .
.
Khi đó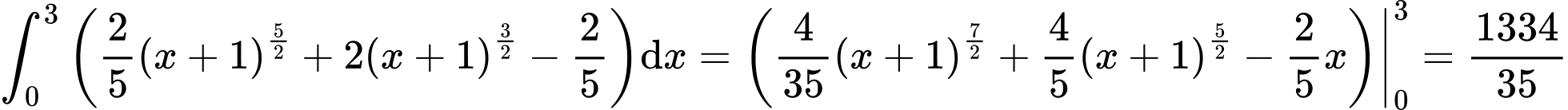 . Đáp án: B
. Đáp án: B
Xét
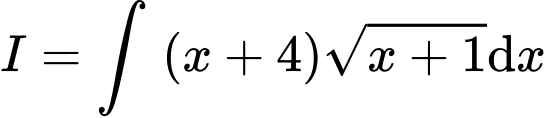 , đặt
, đặt 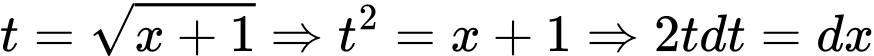 . Khi đó:
. Khi đó: 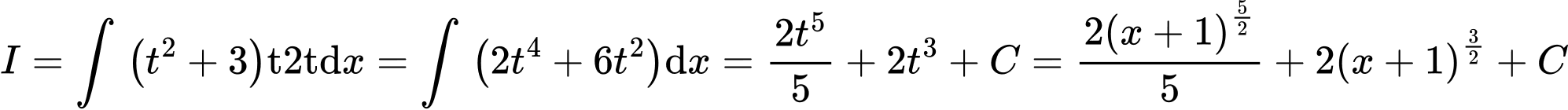 .
. Suy ra
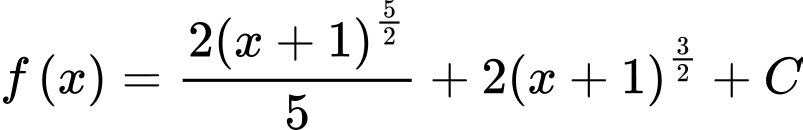 . Thay
. Thay 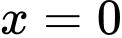 :
: 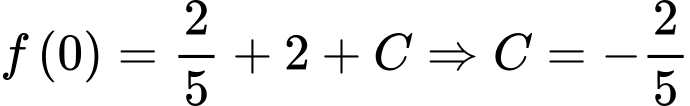 . Do đó
. Do đó 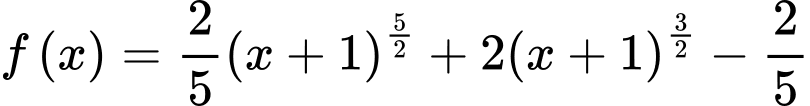 .
. Khi đó
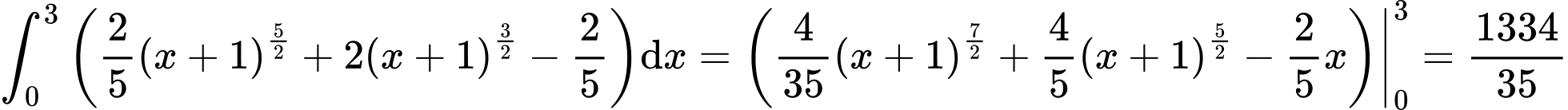 . Đáp án: B
. Đáp án: B
Câu 18 [516400]: Cho hàm số 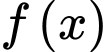 thỏa mãn
thỏa mãn 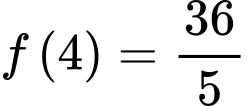 và
và 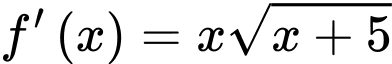 ,
, 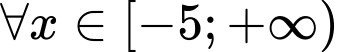 . Khi đó
. Khi đó 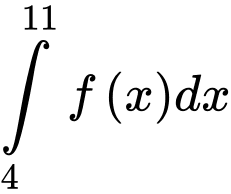 bằng
bằng
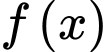 thỏa mãn
thỏa mãn 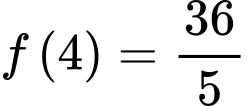 và
và 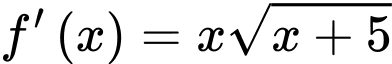 ,
, 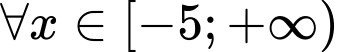 . Khi đó
. Khi đó 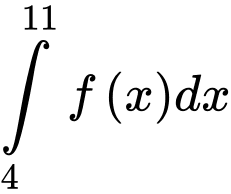 bằng
bằng A, 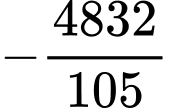 .
.
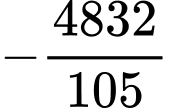 .
.B, 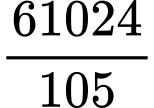 .
.
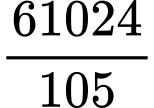 .
.C, 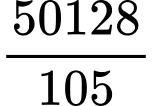 .
.
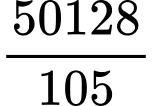 .
.D, 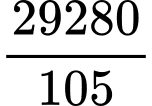 .
.
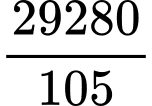 .
.
Chọn B
Ta có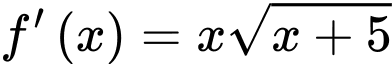 nên
nên 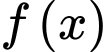 là một nguyên hàm của
là một nguyên hàm của 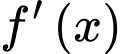 .
.
Có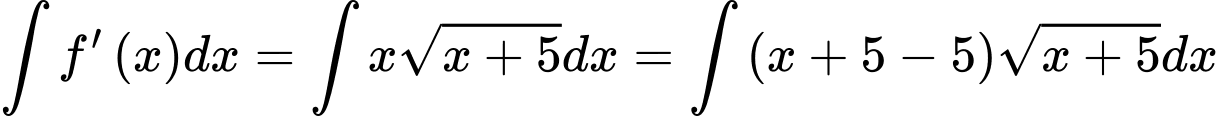
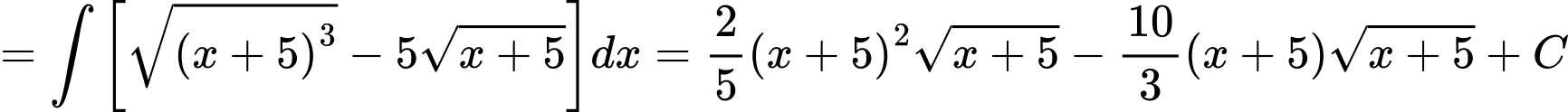 .
.
Do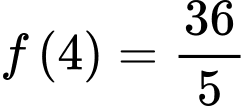 nên
nên 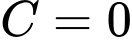 , hay
, hay 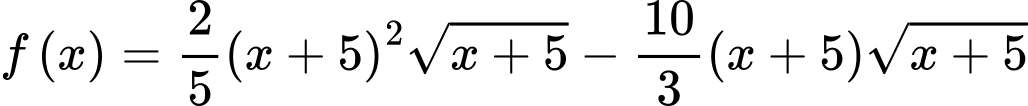 .
.
Suy ra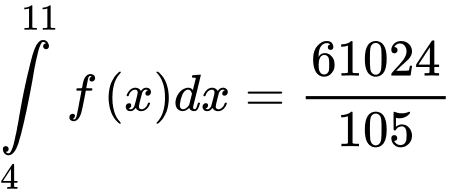 . Đáp án: B
. Đáp án: B
Ta có
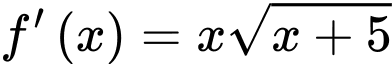 nên
nên 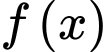 là một nguyên hàm của
là một nguyên hàm của 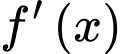 .
. Có
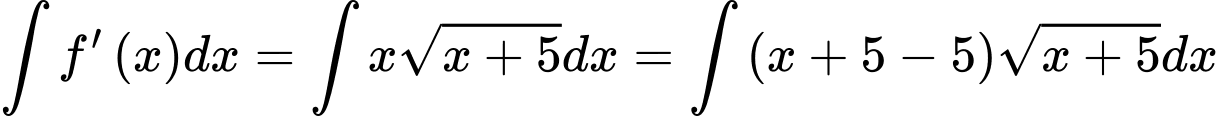
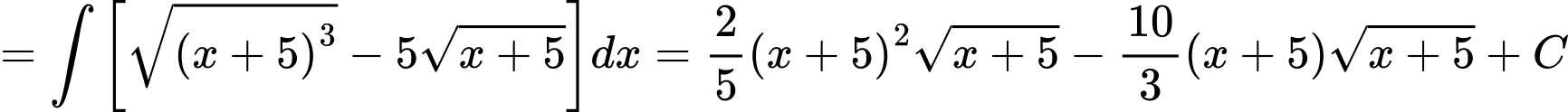 .
. Do
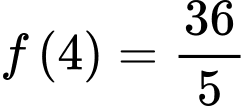 nên
nên 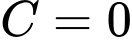 , hay
, hay 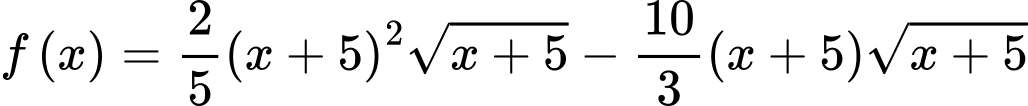 .
. Suy ra
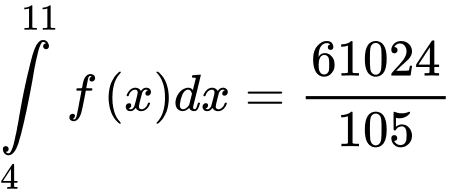 . Đáp án: B
. Đáp án: B
Câu 19 [516298]: Cho hàm số 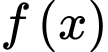 có
có 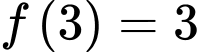 và
và 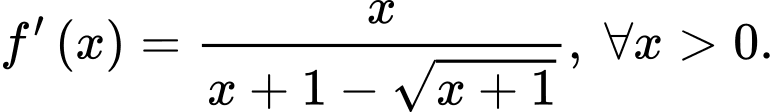 Khi đó
Khi đó 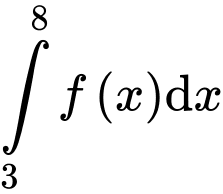 bằng
bằng
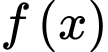 có
có 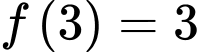 và
và 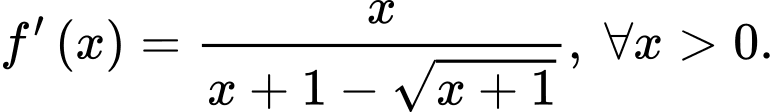 Khi đó
Khi đó 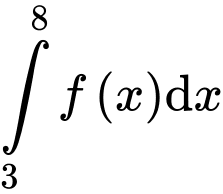 bằng
bằng A, 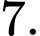
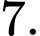
B, 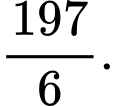
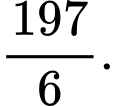
C, 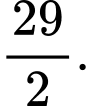
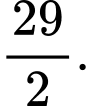
D, 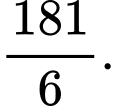
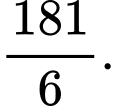
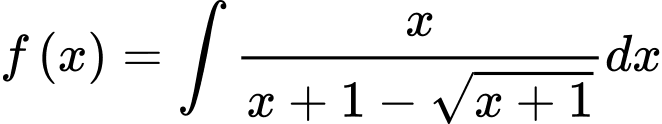 .
. Đặt
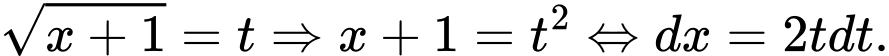
Thay:
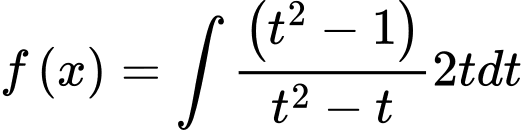
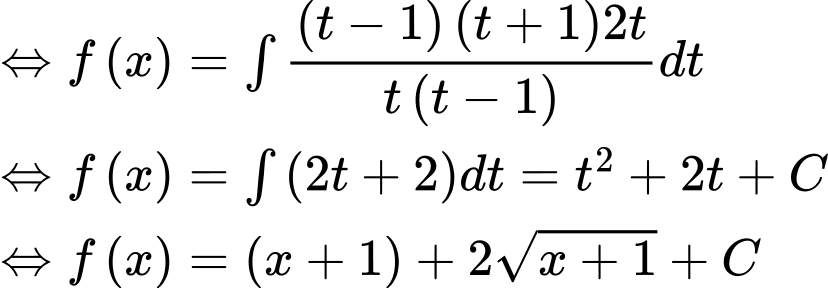
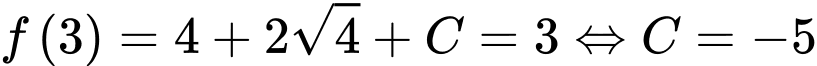 .
.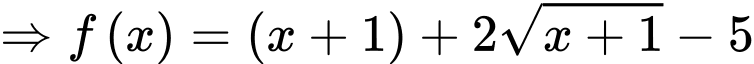 .
. Vậy
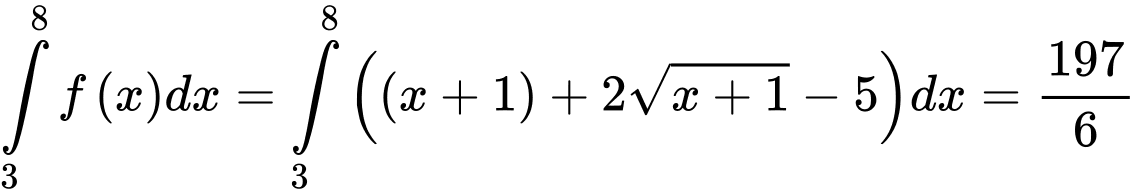 . Đáp án: B
. Đáp án: B
Câu 20 [516299]: Cho hàm số 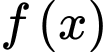 có
có 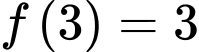 và
và 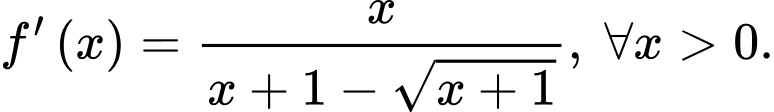 Khi đó
Khi đó 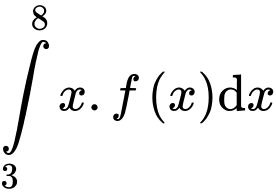 bằng
bằng
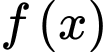 có
có 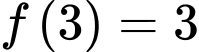 và
và 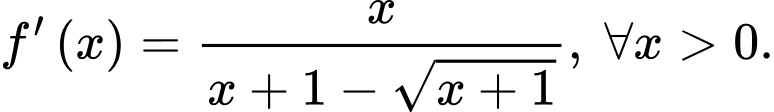 Khi đó
Khi đó 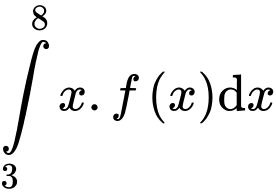 bằng
bằng A, 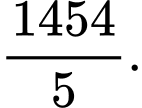
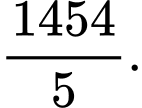
B, 
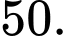
C, 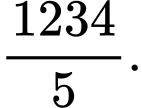
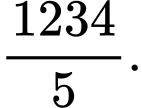
D, 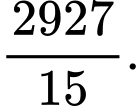
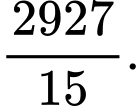
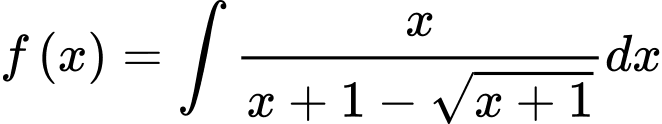 .
. Đặt
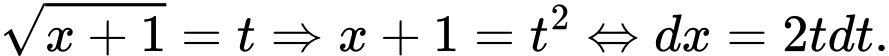
Thay:
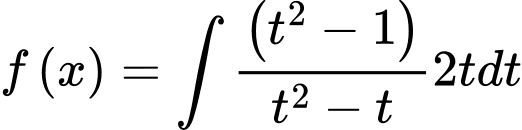
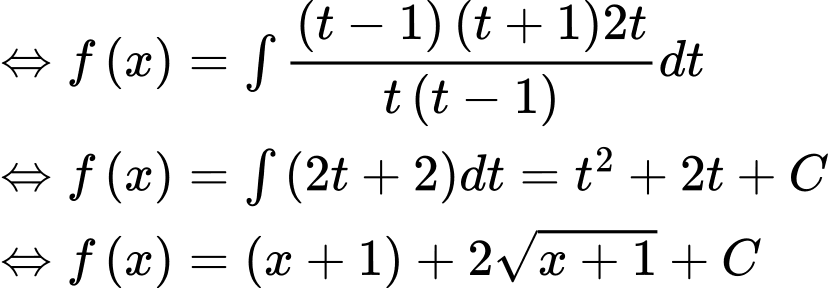
Ta có:
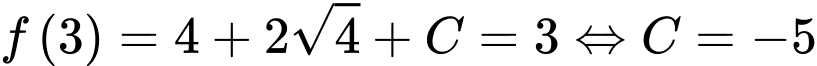 .
.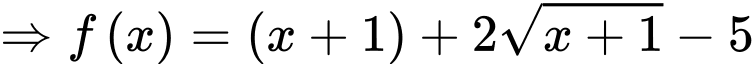 .
. Vậy
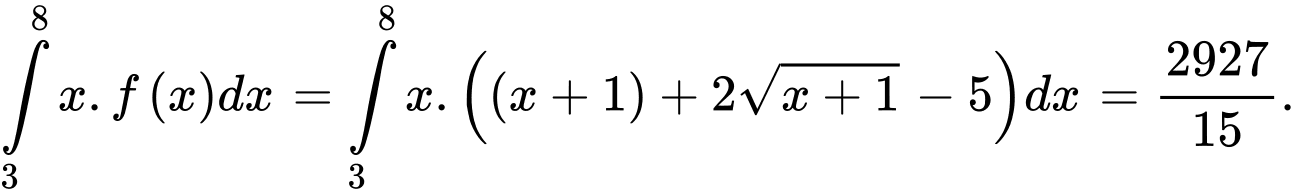 . Đáp án: D
. Đáp án: D