Đáp án Bài tập tự luyện số 2
Câu 1 [340654]: Cho 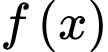 là hàm dương và có đạo hàm liên tục trên
là hàm dương và có đạo hàm liên tục trên 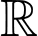 thỏa mãn
thỏa mãn 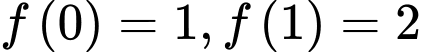 . Biết tích phân
. Biết tích phân 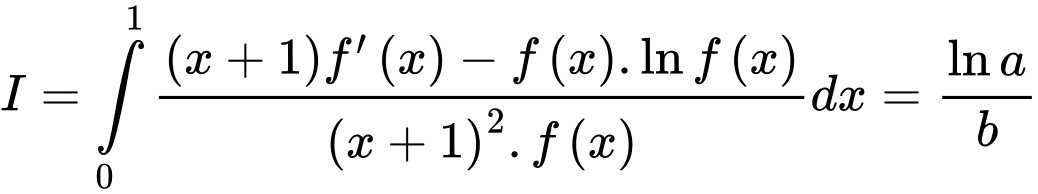 trong đó
trong đó 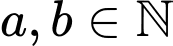 ;
; 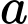 và
và 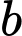 là hai số nguyên tố. Tính
là hai số nguyên tố. Tính 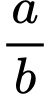 .
.
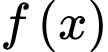 là hàm dương và có đạo hàm liên tục trên
là hàm dương và có đạo hàm liên tục trên 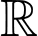 thỏa mãn
thỏa mãn 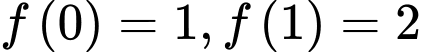 . Biết tích phân
. Biết tích phân 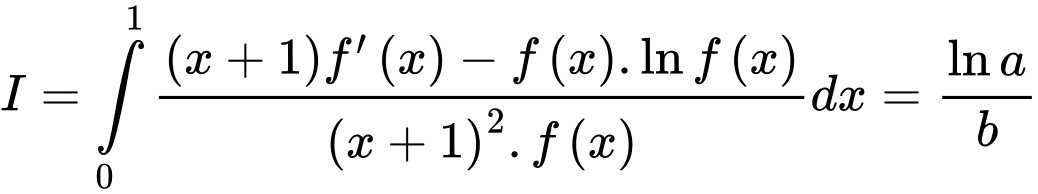 trong đó
trong đó 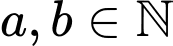 ;
; 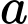 và
và 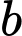 là hai số nguyên tố. Tính
là hai số nguyên tố. Tính 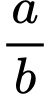 .
. A, 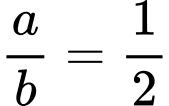 .
.
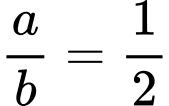 .
.B, 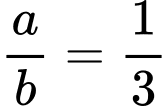 .
.
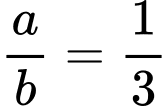 .
.C, 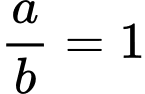 .
.
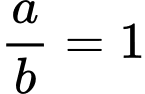 .
.D, 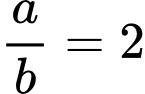 .
.
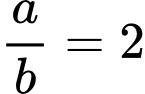 .
.
Chọn C
Ta có: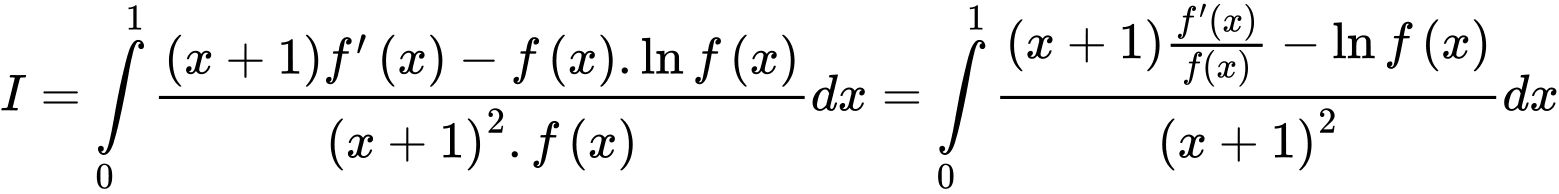 .
.
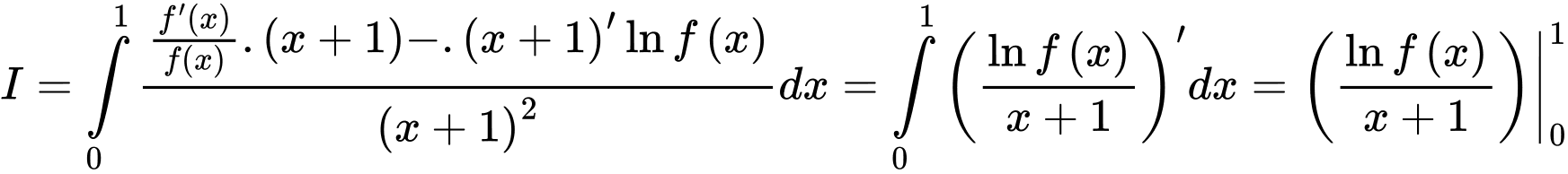 .
.
Hay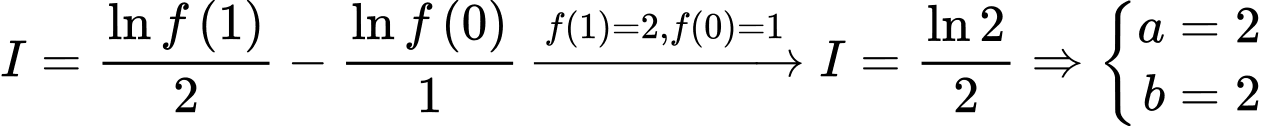 . Do đó
. Do đó 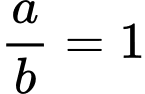 . Đáp án: C
. Đáp án: C
Ta có:
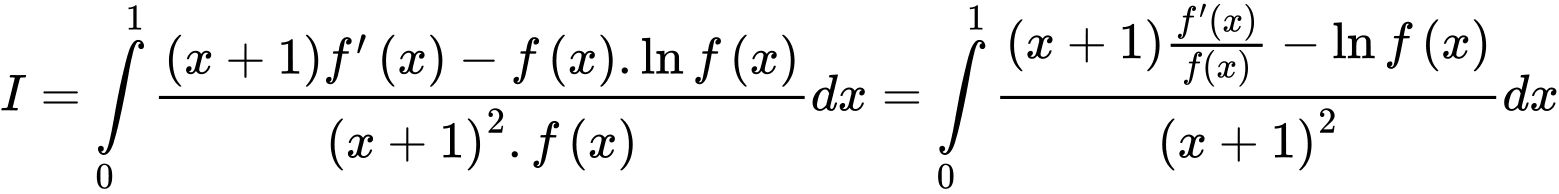 .
.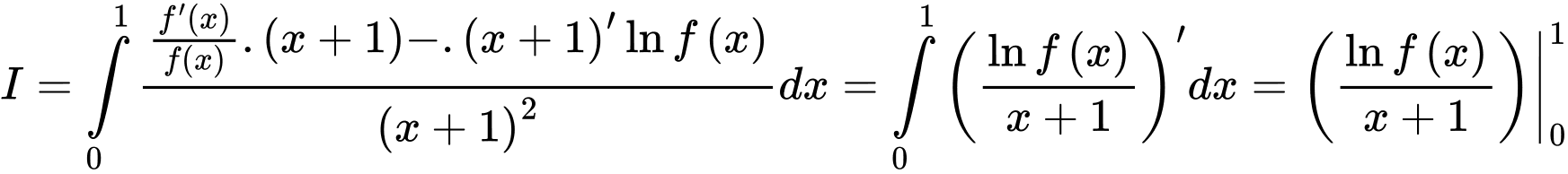 .
.Hay
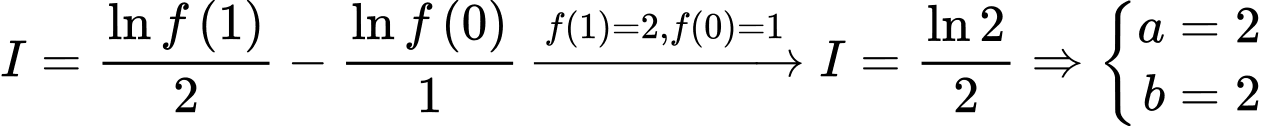 . Do đó
. Do đó 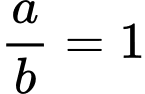 . Đáp án: C
. Đáp án: C
Câu 2 [516241]: Cho hàm số 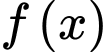 có đạo hàm liên tục trên
có đạo hàm liên tục trên 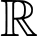 và thỏa mãn
và thỏa mãn 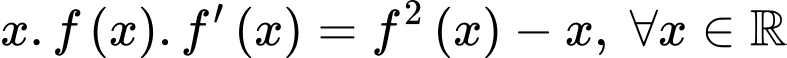 và có
và có 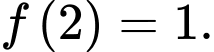 Tính tích phân
Tính tích phân 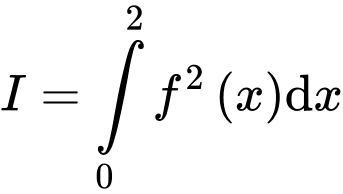
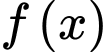 có đạo hàm liên tục trên
có đạo hàm liên tục trên 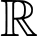 và thỏa mãn
và thỏa mãn 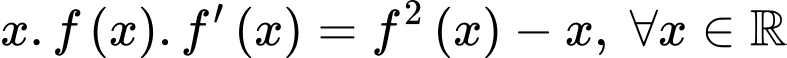 và có
và có 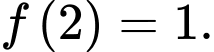 Tính tích phân
Tính tích phân 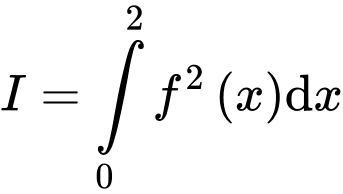
A, 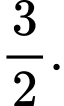
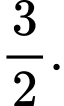
B, 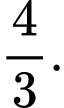
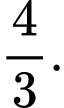
C, 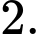
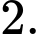
D, 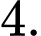
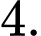
 Đáp án: C
Đáp án: C
Câu 3 [151772]: Cho hàm số 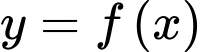 liên tục trên
liên tục trên 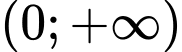 và thỏa
và thỏa 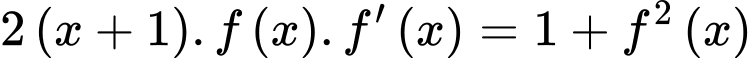 ,
,  ;
; 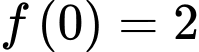 . Khi đó giá trị
. Khi đó giá trị 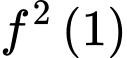 bằng
bằng
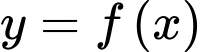 liên tục trên
liên tục trên 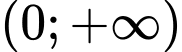 và thỏa
và thỏa 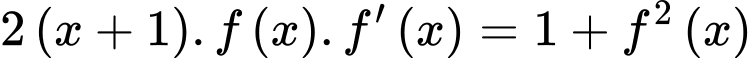 ,
,  ;
; 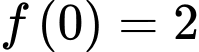 . Khi đó giá trị
. Khi đó giá trị 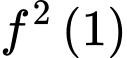 bằng
bằng A, 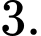
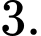
B, 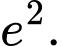
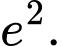
C, 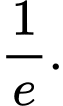
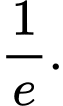
D, 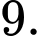
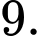
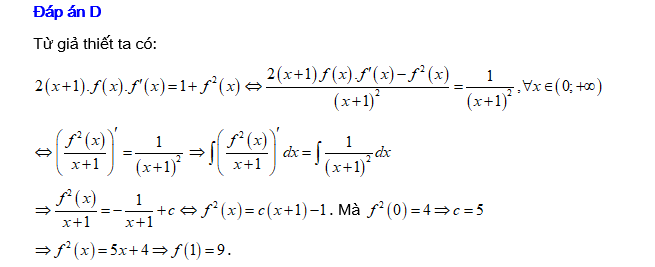 Đáp án: D
Đáp án: D
Câu 4 [516242]: Cho hàm số 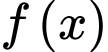 nhận giá trị dương và có đạo hàm liên tục trên đoạn
nhận giá trị dương và có đạo hàm liên tục trên đoạn 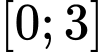 biết
biết 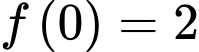 và
và 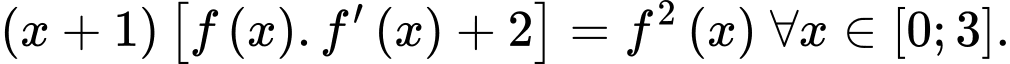 Khi đó
Khi đó 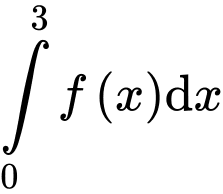 bằng
bằng
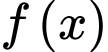 nhận giá trị dương và có đạo hàm liên tục trên đoạn
nhận giá trị dương và có đạo hàm liên tục trên đoạn 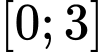 biết
biết 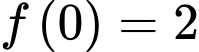 và
và 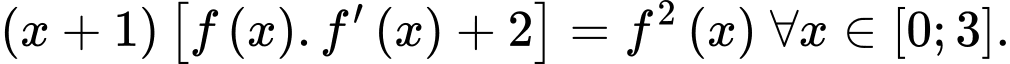 Khi đó
Khi đó 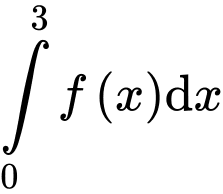 bằng
bằng A, 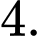
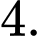
B, 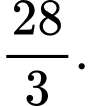
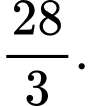
C, 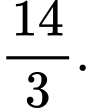
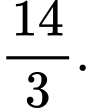
D, 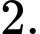
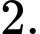
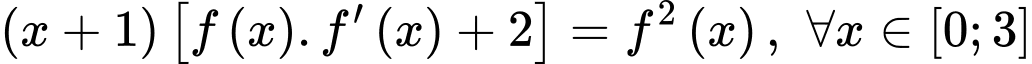
Đặt
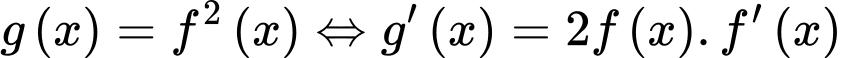
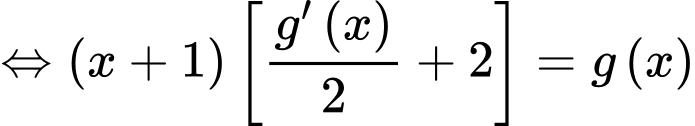
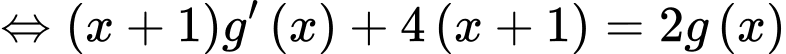
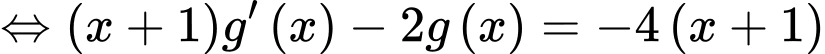
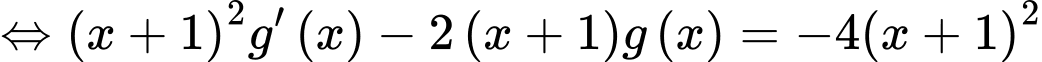
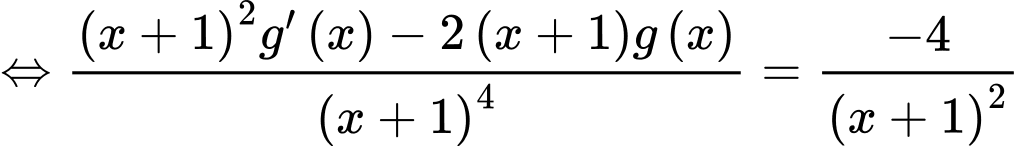
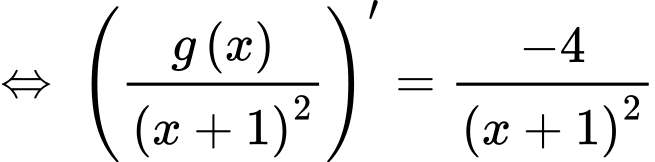
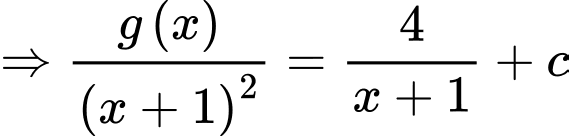
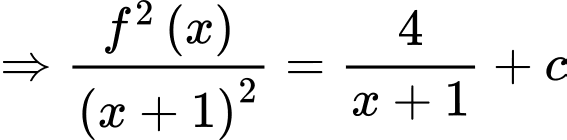
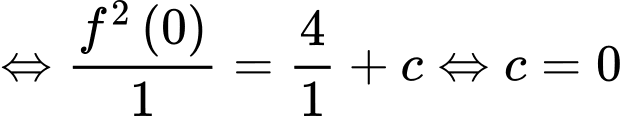 với
với 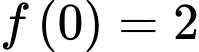
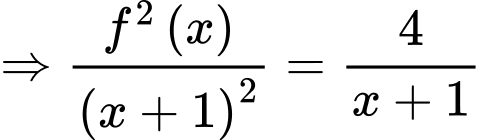
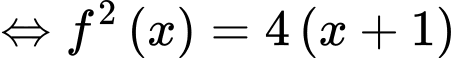
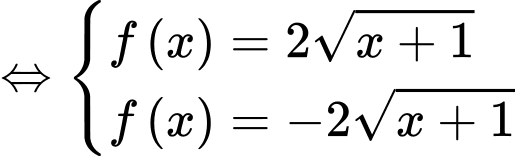
Suy ra
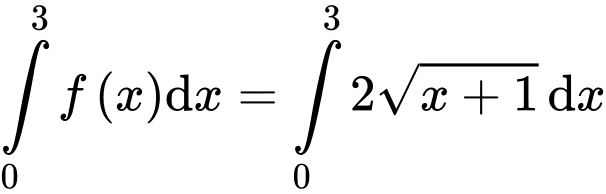
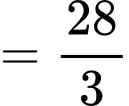
Đáp án B Đáp án: B
Câu 5 [516243]: Cho hàm số 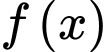 có đạo hàm liên tục trên
có đạo hàm liên tục trên 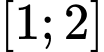 và thỏa mãn
và thỏa mãn 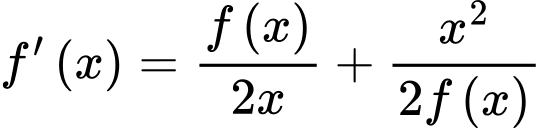 với mọi
với mọi 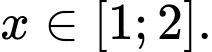 Biết
Biết 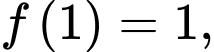 tính tích phân
tính tích phân 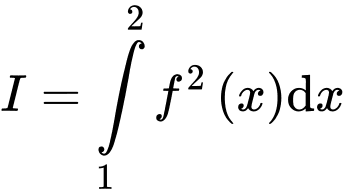
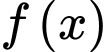 có đạo hàm liên tục trên
có đạo hàm liên tục trên 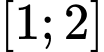 và thỏa mãn
và thỏa mãn 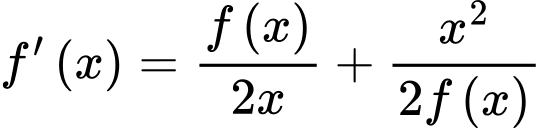 với mọi
với mọi 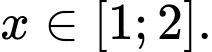 Biết
Biết 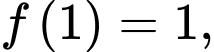 tính tích phân
tính tích phân 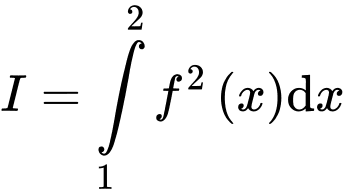
A, 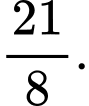
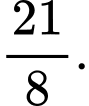
B, 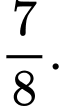
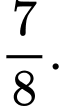
C, 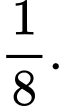
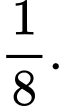
D, 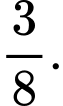
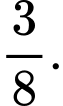
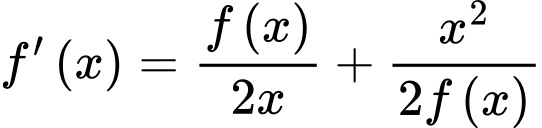
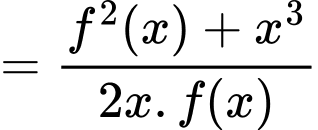
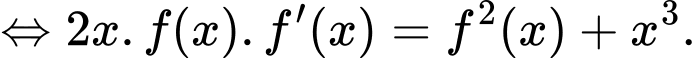
Đặt 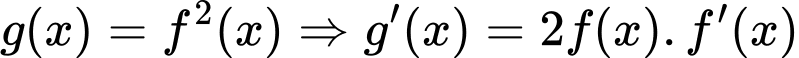
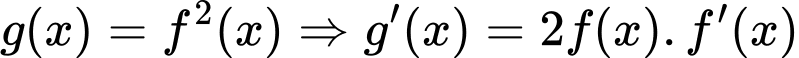
Phương trình đã cho trở thành:
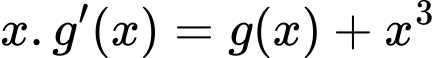
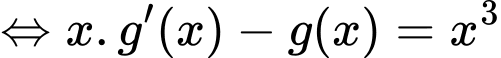
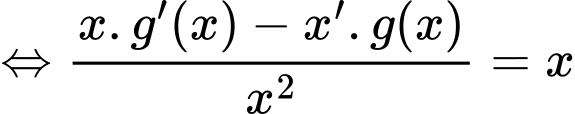
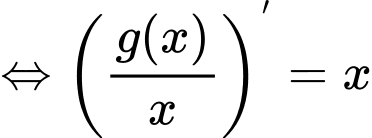
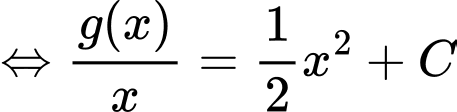
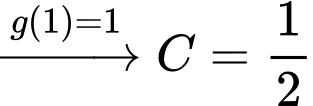
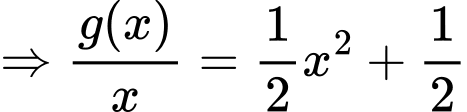
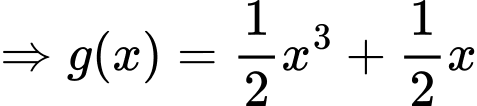
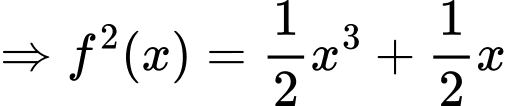
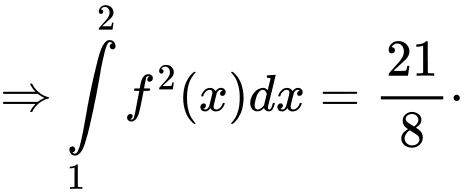
Chọn đáp án A.
Câu 6 [516245]: Cho hàm số 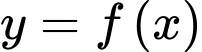 liên tục trên
liên tục trên 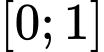 thỏa mãn
thỏa mãn 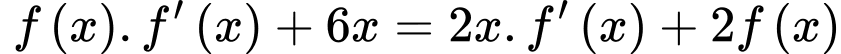 và
và 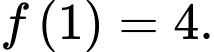 Tính giá trị của
Tính giá trị của 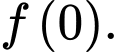
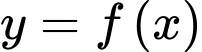 liên tục trên
liên tục trên 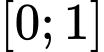 thỏa mãn
thỏa mãn 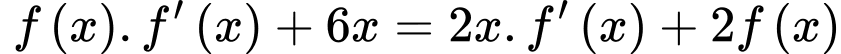 và
và 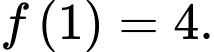 Tính giá trị của
Tính giá trị của 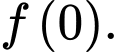
A, 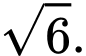
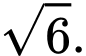
B, 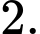
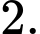
C, 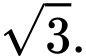
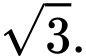
D, 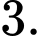
Cho 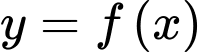 liên tục trên
liên tục trên 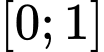
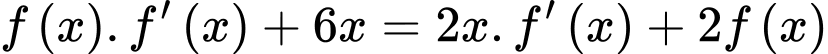
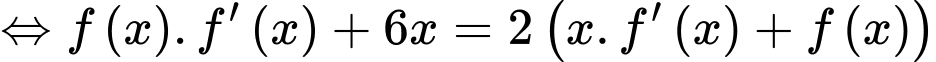
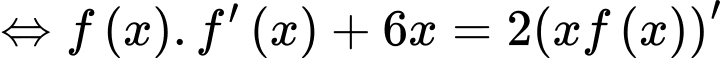
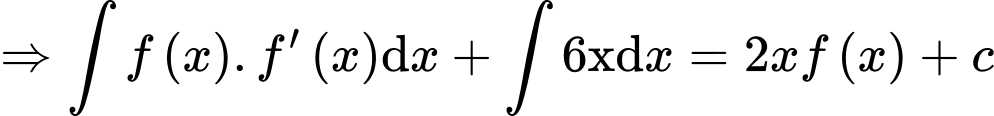
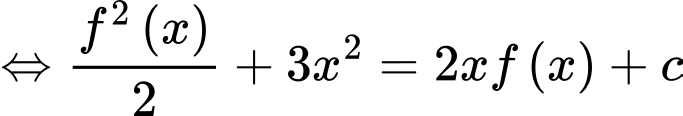
Ta có: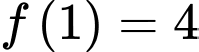
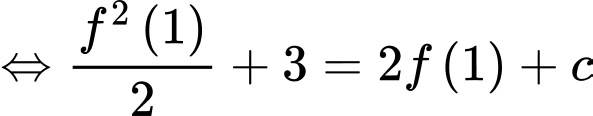
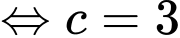
Tại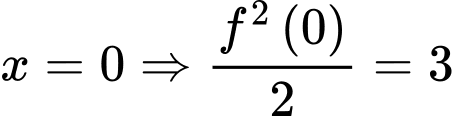
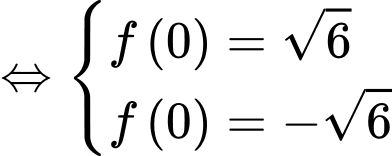
Đáp án A Đáp án: A
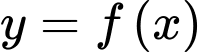 liên tục trên
liên tục trên 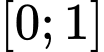
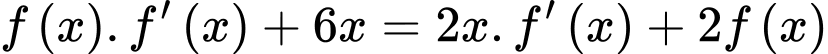
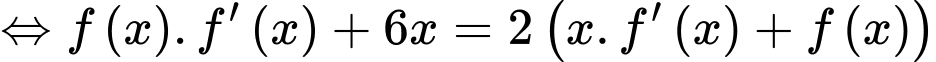
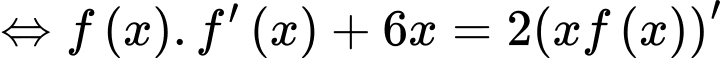
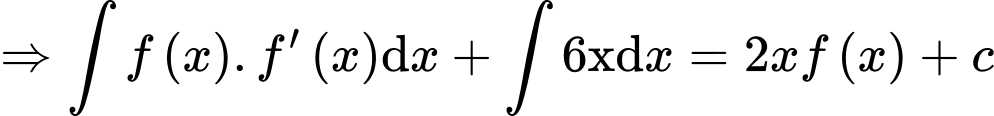
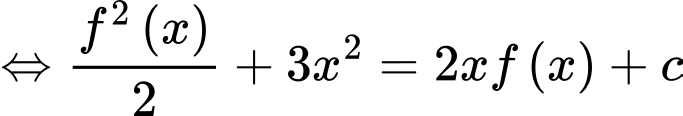
Ta có:
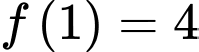
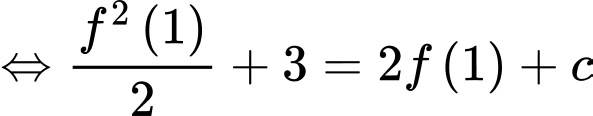
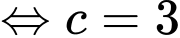
Tại
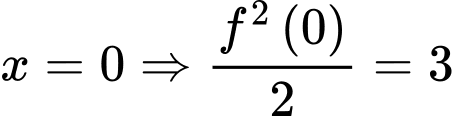
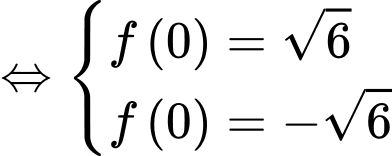
Đáp án A Đáp án: A
Câu 7 [516405]: Cho hàm số 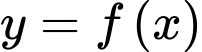 xác định và dương trên khoảng
xác định và dương trên khoảng 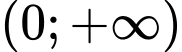 , thỏa mãn
, thỏa mãn 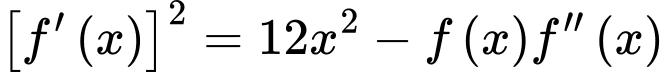 với mọi
với mọi 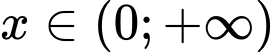 và
và 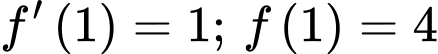 . Giá trị của
. Giá trị của 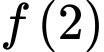 bằng
bằng
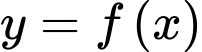 xác định và dương trên khoảng
xác định và dương trên khoảng 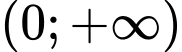 , thỏa mãn
, thỏa mãn 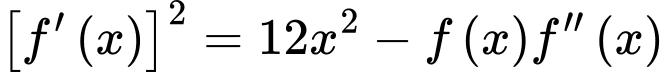 với mọi
với mọi 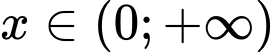 và
và 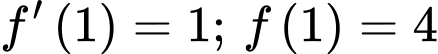 . Giá trị của
. Giá trị của 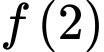 bằng
bằng A, 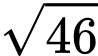 .
.
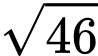 .
.B, 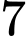 .
.
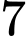 .
.C, 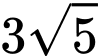 .
.
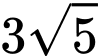 .
.D, 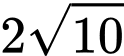 .
.
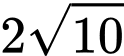 .
.
Chọn A
Ta có:
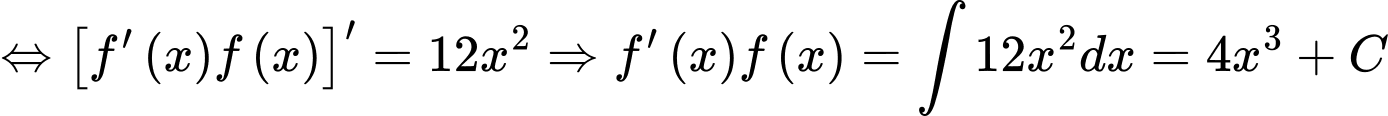 .
.
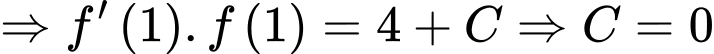
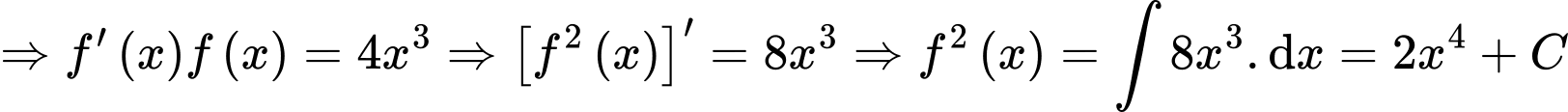 .
.
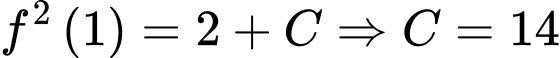
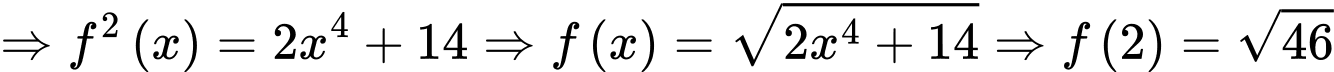 . Đáp án: A
. Đáp án: A
Ta có:

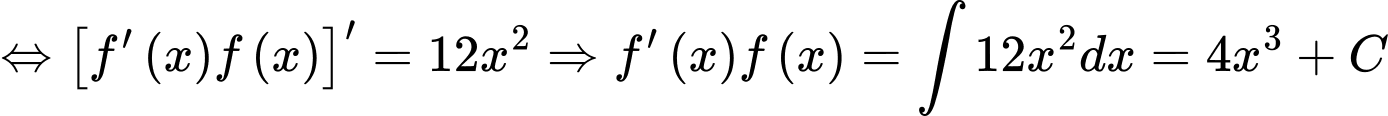 .
. 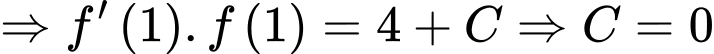
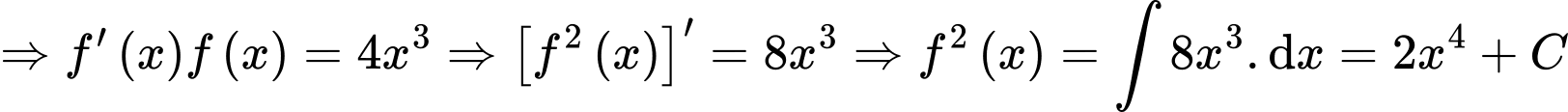 .
. 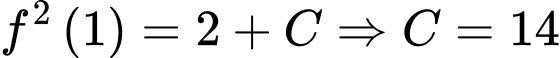
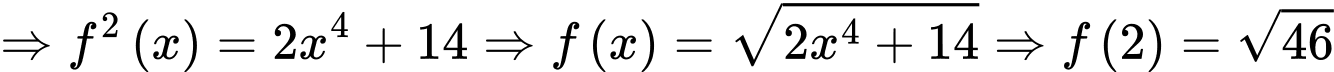 . Đáp án: A
. Đáp án: A
Câu 8 [151761]: Cho hàm số 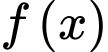 thỏa mãn
thỏa mãn 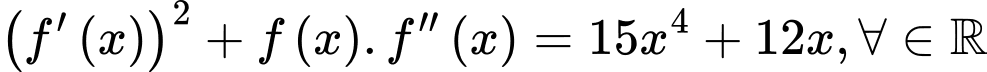 và
và 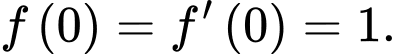 Giá trị của
Giá trị của 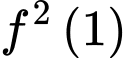 bằng
bằng
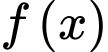 thỏa mãn
thỏa mãn 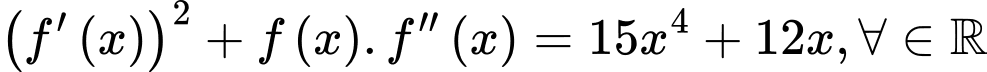 và
và 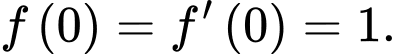 Giá trị của
Giá trị của 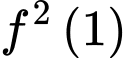 bằng
bằng A, 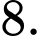
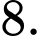
B, 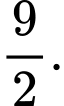
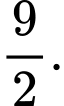
C, 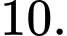
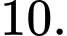
D, 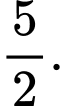
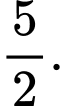
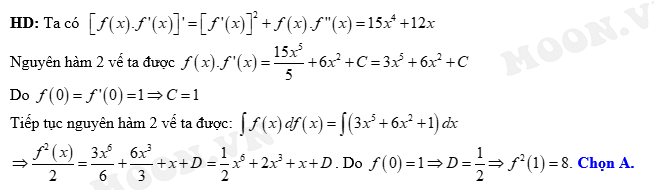 Đáp án: A
Đáp án: A
Câu 9 [801947]: Cho hàm số 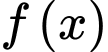 liên tục và có đạo hàm xác định trên
liên tục và có đạo hàm xác định trên 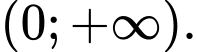 Biết rằng
Biết rằng 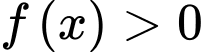 với mọi
với mọi 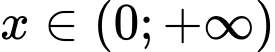 thỏa mãn
thỏa mãn 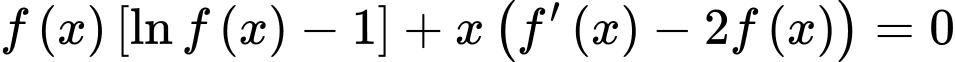 và lnf(2)-lnf(1)=1 Giá trị tích phân
và lnf(2)-lnf(1)=1 Giá trị tích phân 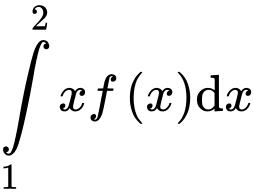 nằm trong khoảng nào dưới đây?
nằm trong khoảng nào dưới đây?
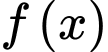 liên tục và có đạo hàm xác định trên
liên tục và có đạo hàm xác định trên 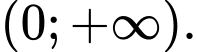 Biết rằng
Biết rằng 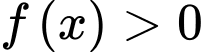 với mọi
với mọi 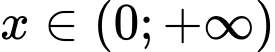 thỏa mãn
thỏa mãn 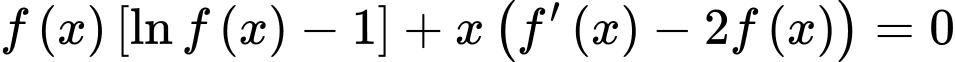 và lnf(2)-lnf(1)=1 Giá trị tích phân
và lnf(2)-lnf(1)=1 Giá trị tích phân 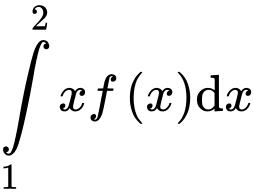 nằm trong khoảng nào dưới đây?
nằm trong khoảng nào dưới đây? A, 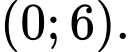
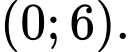
B, 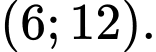
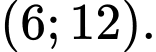
C, 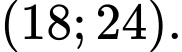
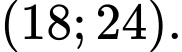
D, 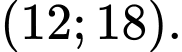
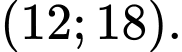
HD: Chọn C
Từ giả thiết suy ra: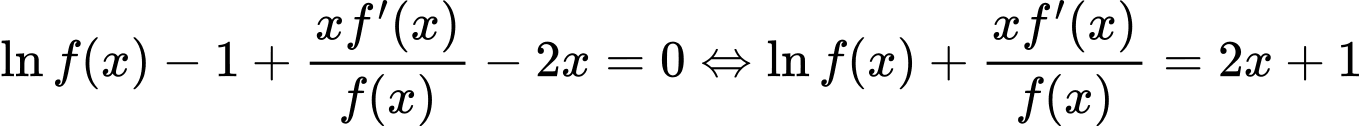
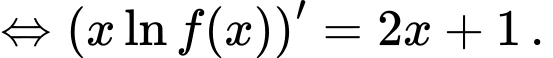
Nguyên hàm 2 vế, ta được: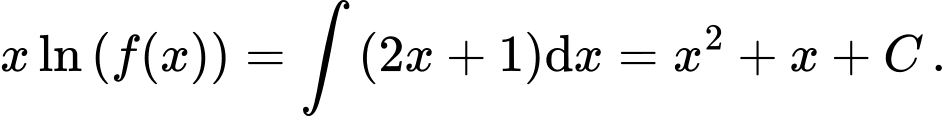
Thay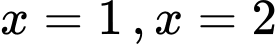 vào 2 vế, ta được:
vào 2 vế, ta được:
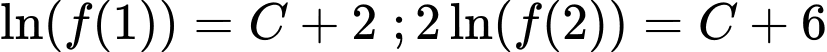
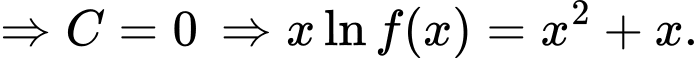
Vì ta có:
ta có: 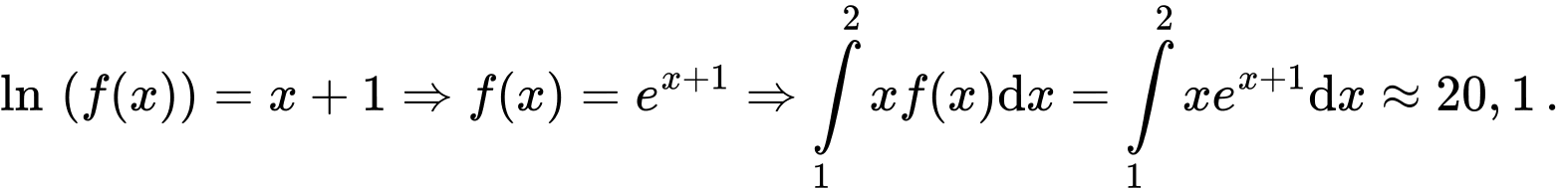 Đáp án: C
Đáp án: C
Từ giả thiết suy ra:
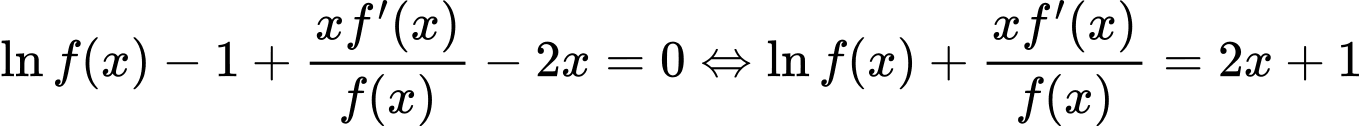
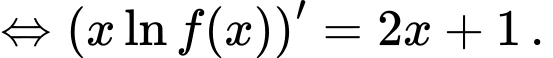
Nguyên hàm 2 vế, ta được:
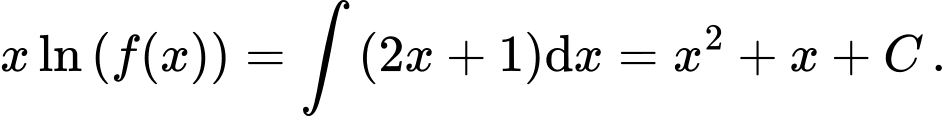
Thay
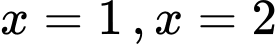 vào 2 vế, ta được:
vào 2 vế, ta được: 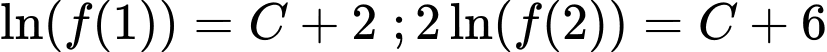
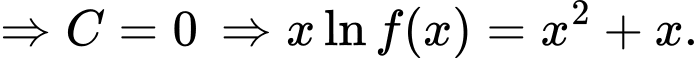
Vì
 ta có:
ta có: 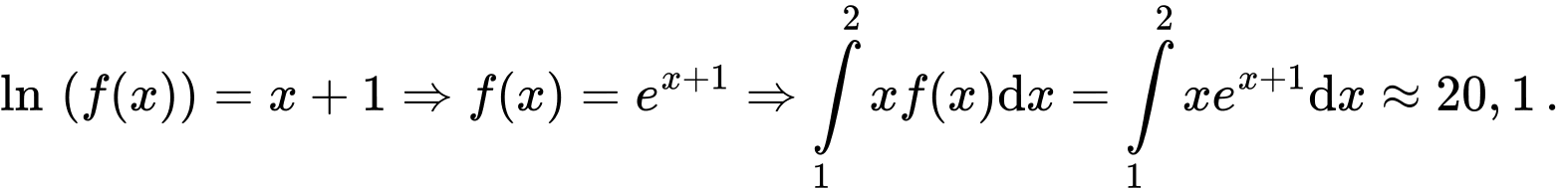 Đáp án: C
Đáp án: C
Câu 10 [184702]: [Câu 48 – Mã 103]: Cho hàm số 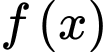 nhận giá trị dương trên khoảng
nhận giá trị dương trên khoảng 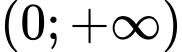 , có đạo hàm trên khoảng đó và thỏa mãn
, có đạo hàm trên khoảng đó và thỏa mãn 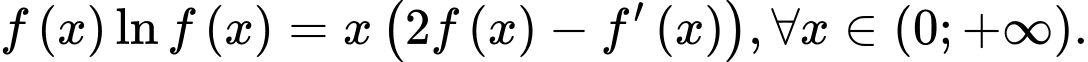 Biết
Biết 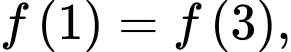 giá trị
giá trị 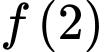 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
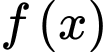 nhận giá trị dương trên khoảng
nhận giá trị dương trên khoảng 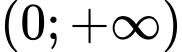 , có đạo hàm trên khoảng đó và thỏa mãn
, có đạo hàm trên khoảng đó và thỏa mãn 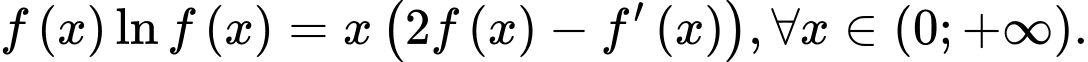 Biết
Biết 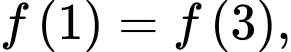 giá trị
giá trị 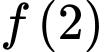 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? A, 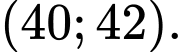
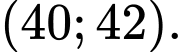
B, 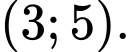
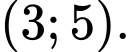
C, 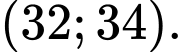
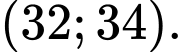
D, 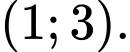
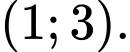
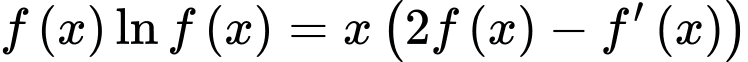
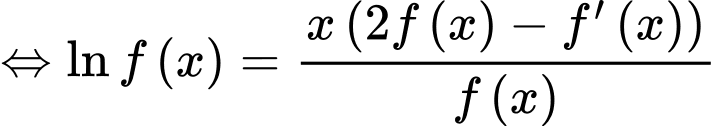
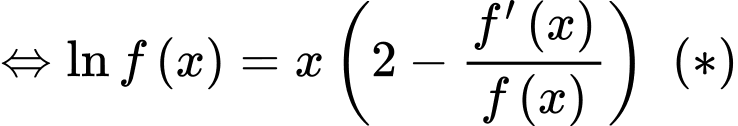
Đặt
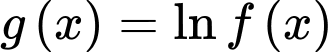
PT
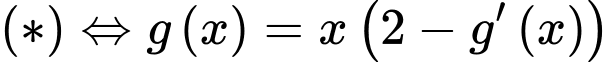
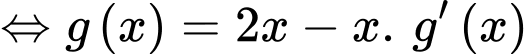
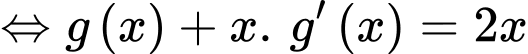
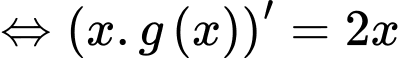
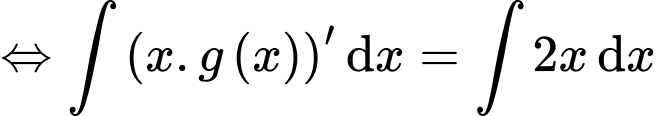
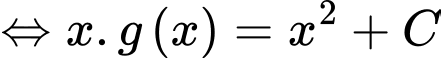
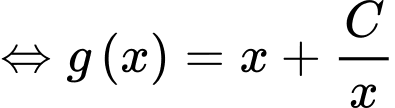
Ta có
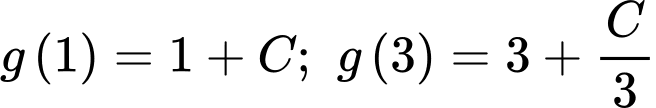
Vì
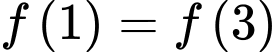
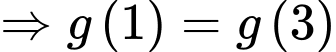
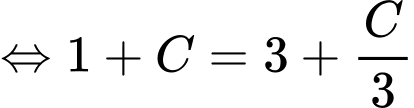


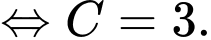
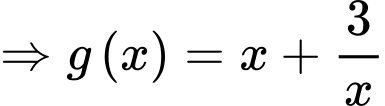
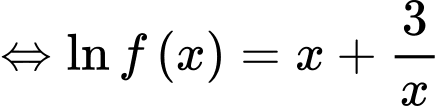
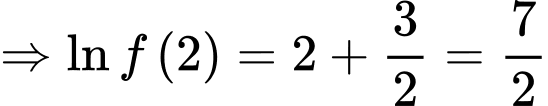
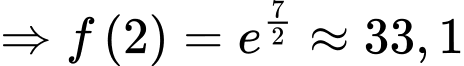
Chọn C. Đáp án: C
Câu 11 [184823]: [Câu 42 – Mã 104]: Cho hàm số 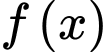 nhận giá trị dương trên khoảng
nhận giá trị dương trên khoảng 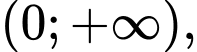 có đạo hàm trên khoảng đó và thỏa mãn
có đạo hàm trên khoảng đó và thỏa mãn 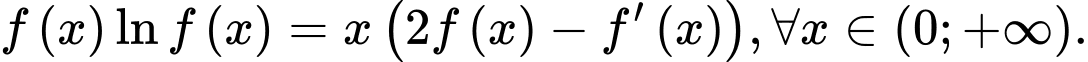 Biết
Biết 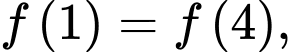 giá trị
giá trị 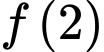 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây?
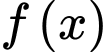 nhận giá trị dương trên khoảng
nhận giá trị dương trên khoảng 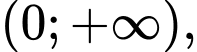 có đạo hàm trên khoảng đó và thỏa mãn
có đạo hàm trên khoảng đó và thỏa mãn 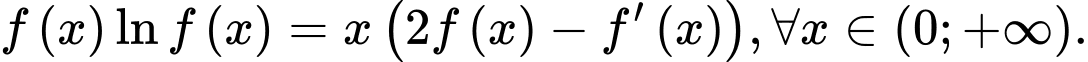 Biết
Biết 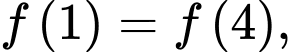 giá trị
giá trị 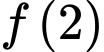 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? A, 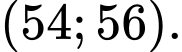
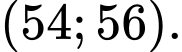
B, 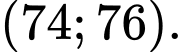
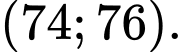
C, 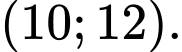
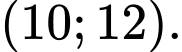
D, 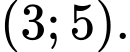
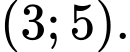
Ta có 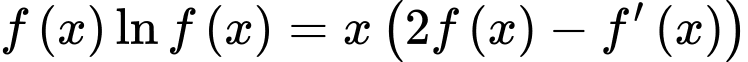
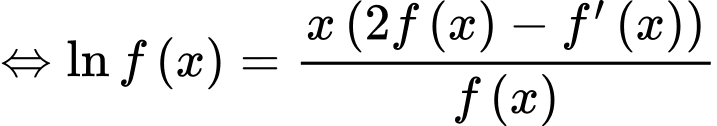
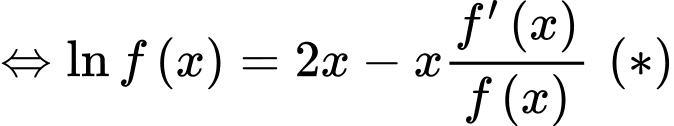
Đặt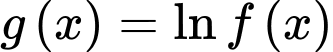
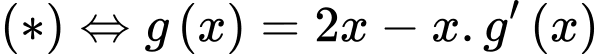
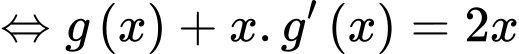
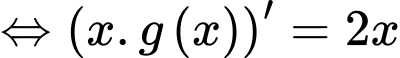
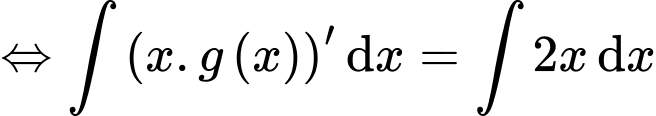
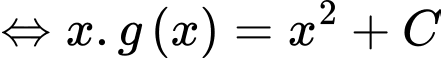
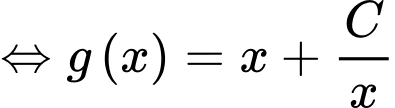
Ta có: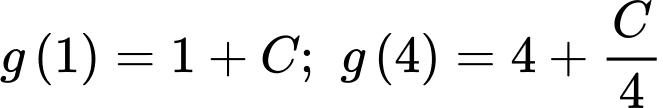
Vì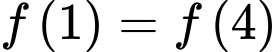
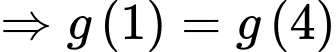
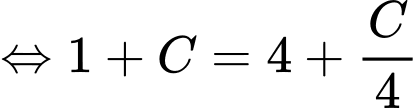
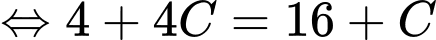
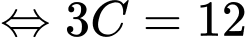
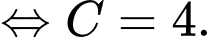
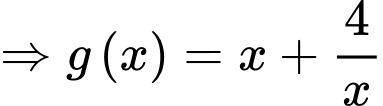
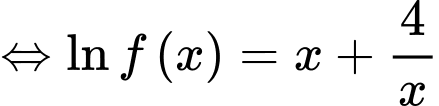
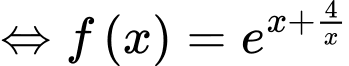
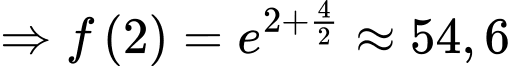
Chọn A. Đáp án: A
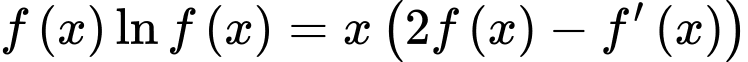
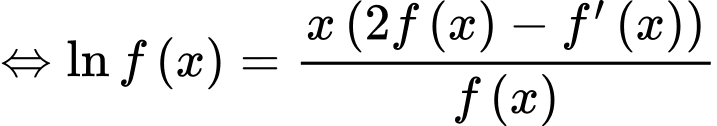
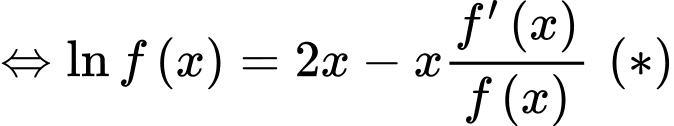
Đặt
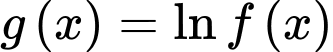
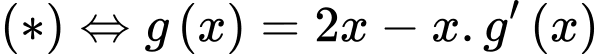
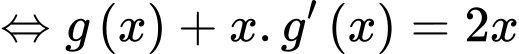
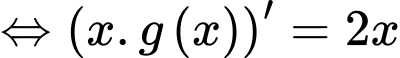
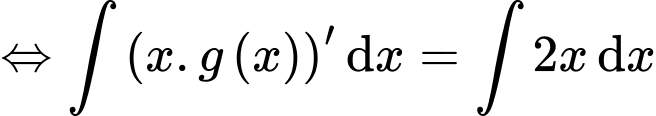
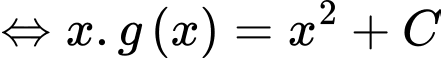
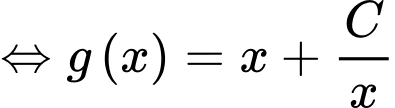
Ta có:
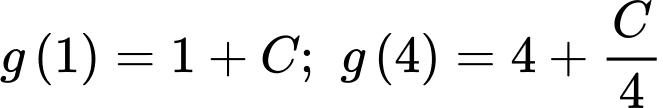
Vì
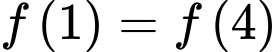
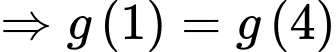
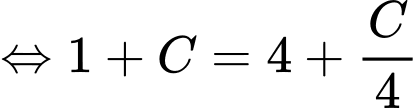
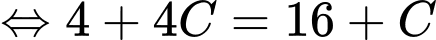
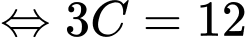
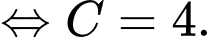
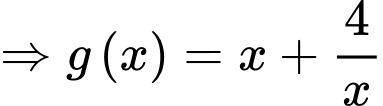
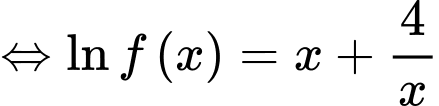
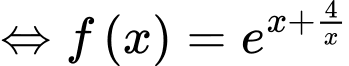
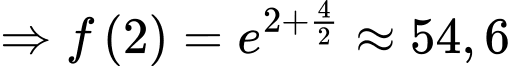
Chọn A. Đáp án: A
Câu 12 [904830]: Cho hàm số 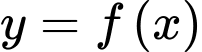 có đạo hàm và nhận giá trị dương với
có đạo hàm và nhận giá trị dương với  . Biết
. Biết 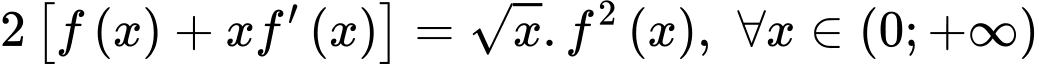 và
và 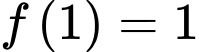 . Giá trị
. Giá trị 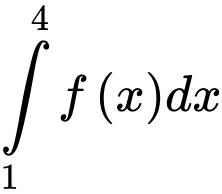 bằng
bằng
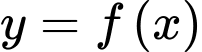 có đạo hàm và nhận giá trị dương với
có đạo hàm và nhận giá trị dương với  . Biết
. Biết 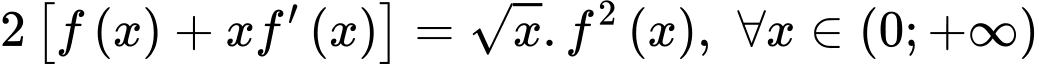 và
và 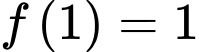 . Giá trị
. Giá trị 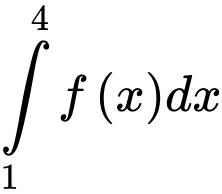 bằng
bằng A, 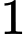 .
.
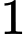 .
.B, 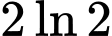 .
.
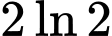 .
.C, 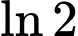 .
.
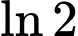 .
.D, 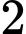 .
.
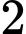 .
.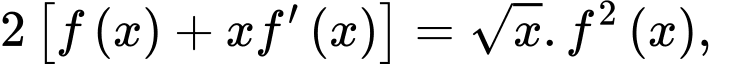

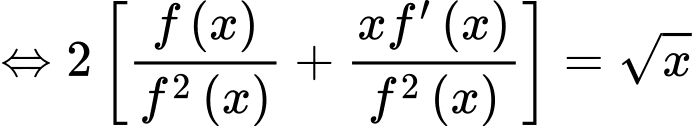
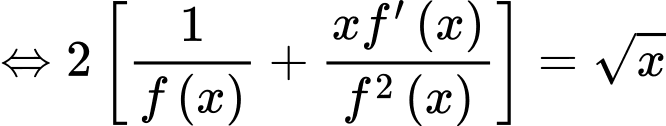
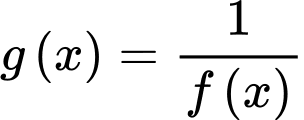
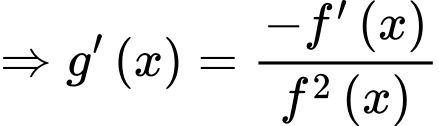
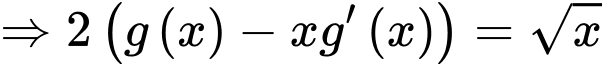
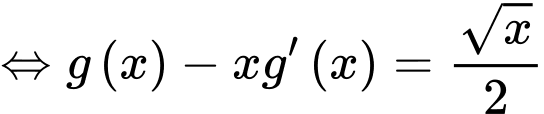
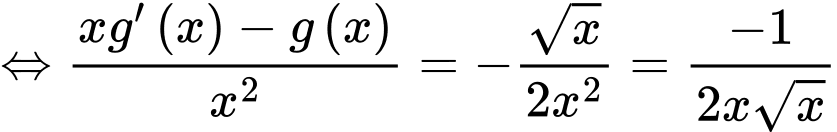
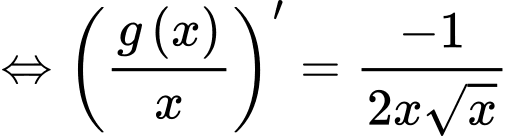
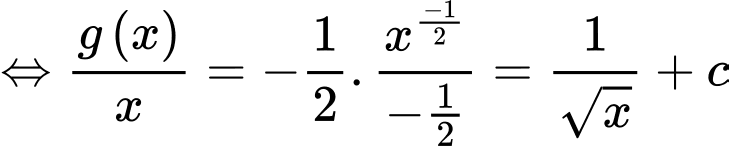
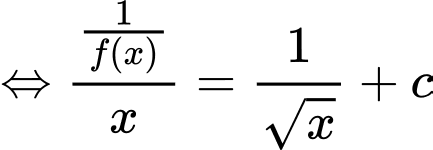
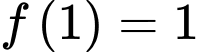
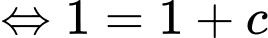
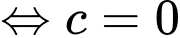
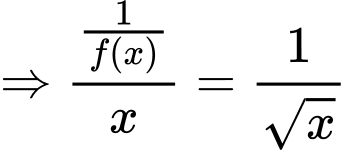
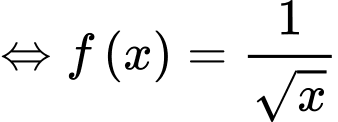
Ta có:
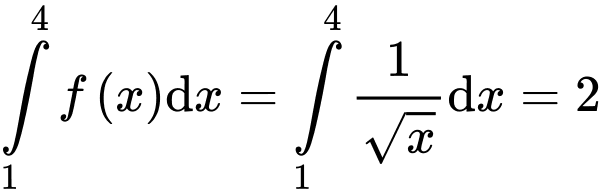
Đáp án D Đáp án: D
Câu 13 [903991]: Cho hàm số 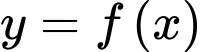 luôn nhận giá trị dương và có đạo hàm cấp hai trên khoảng
luôn nhận giá trị dương và có đạo hàm cấp hai trên khoảng 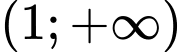 đồng thời thỏa mãn điều kiện
đồng thời thỏa mãn điều kiện 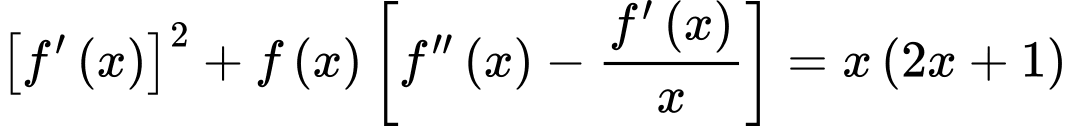 và
và 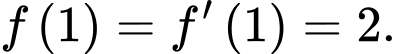 Tính giá trị của
Tính giá trị của 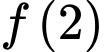
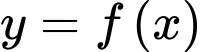 luôn nhận giá trị dương và có đạo hàm cấp hai trên khoảng
luôn nhận giá trị dương và có đạo hàm cấp hai trên khoảng 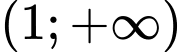 đồng thời thỏa mãn điều kiện
đồng thời thỏa mãn điều kiện 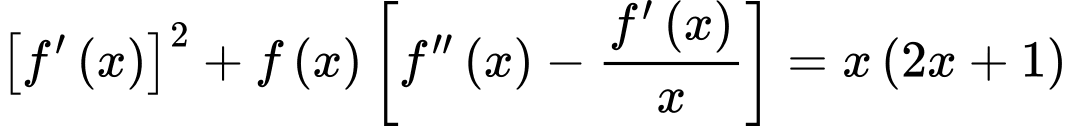 và
và 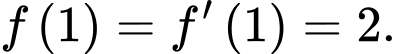 Tính giá trị của
Tính giá trị của 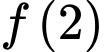
A, 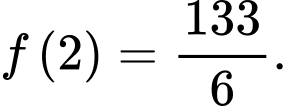
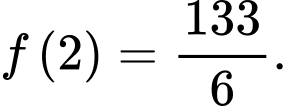
B, 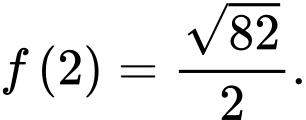
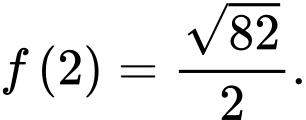
C, 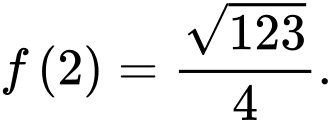
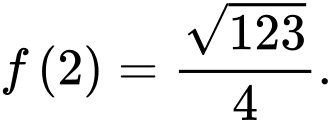
D, 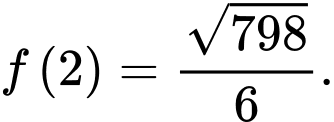
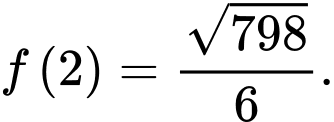
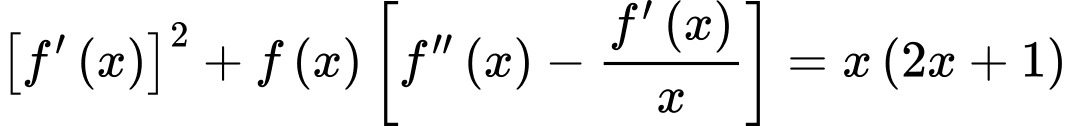
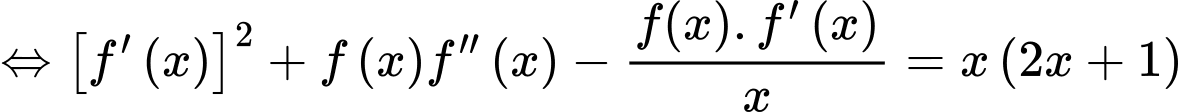
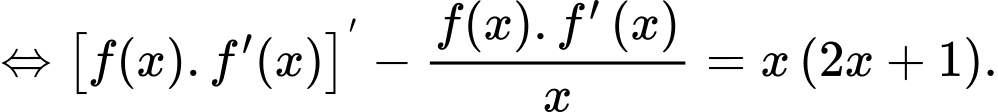
Đặt 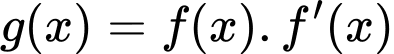 khi đó phương trình trở thành:
khi đó phương trình trở thành:
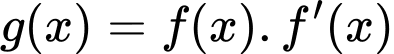 khi đó phương trình trở thành:
khi đó phương trình trở thành: 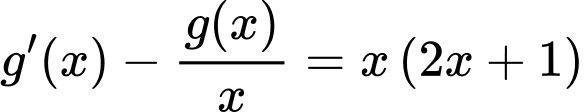
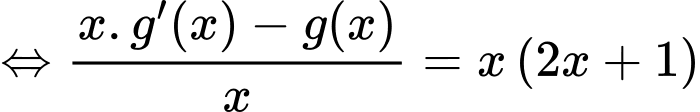
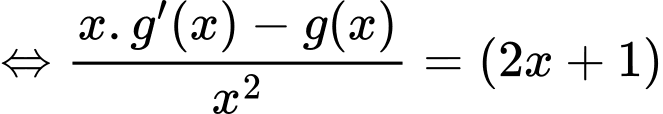
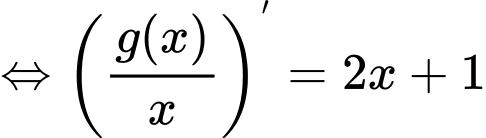
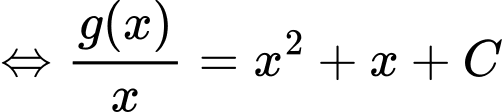
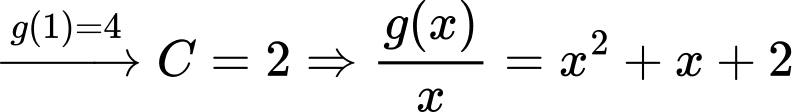
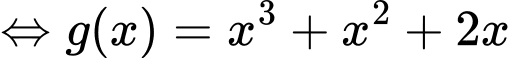
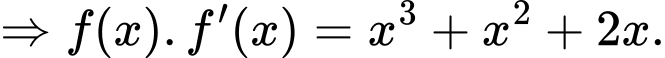
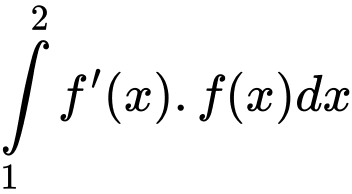
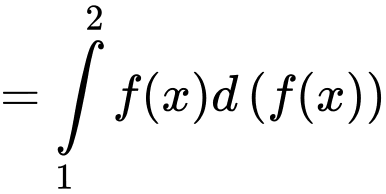
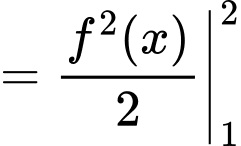
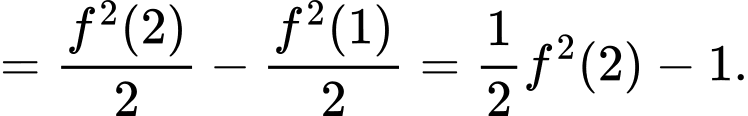
Mặt khác: 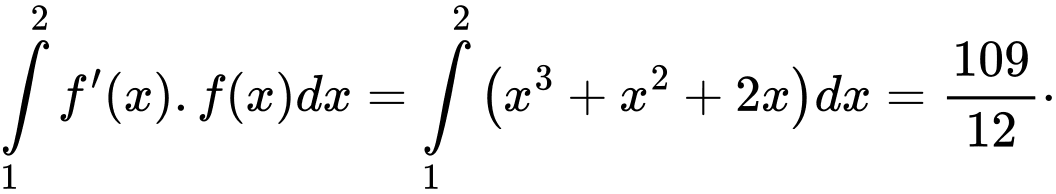
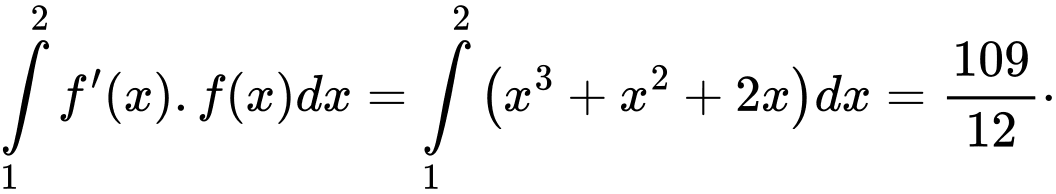
Do đó: 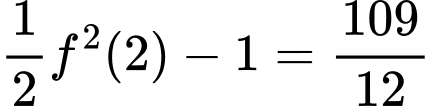
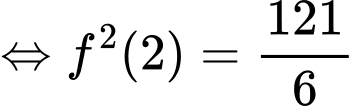
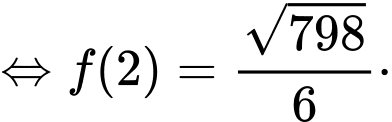
Đáp án: D 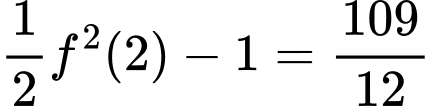
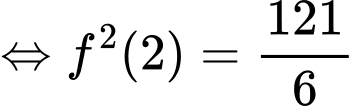
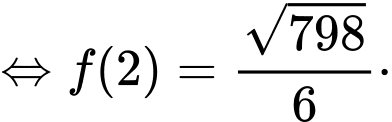
Chọn đáp án D.
Câu 14 [903989]: Cho hàm số 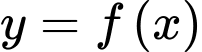 có đạo hàm liên tục và nhận giá trị dương trên khoảng
có đạo hàm liên tục và nhận giá trị dương trên khoảng 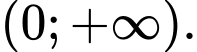 Biết
Biết 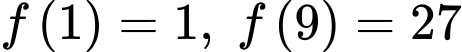 và
và 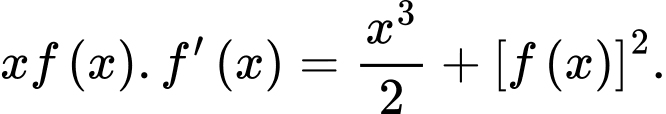 Giá trị của tích phân
Giá trị của tích phân 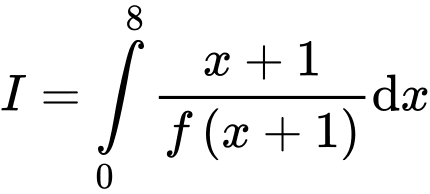 bằng
bằng
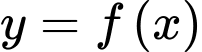 có đạo hàm liên tục và nhận giá trị dương trên khoảng
có đạo hàm liên tục và nhận giá trị dương trên khoảng 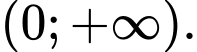 Biết
Biết 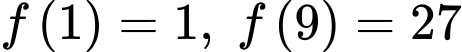 và
và 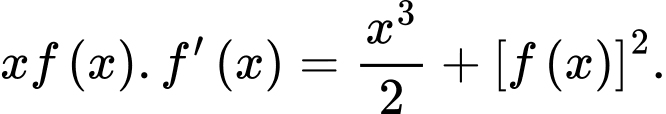 Giá trị của tích phân
Giá trị của tích phân 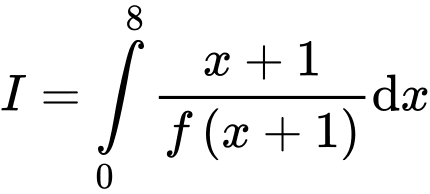 bằng
bằng A, 
B, 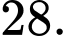
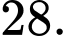
C, 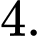
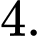
D, 
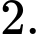
Đặt 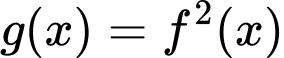 khi đó phương trình trở thành:
khi đó phương trình trở thành: 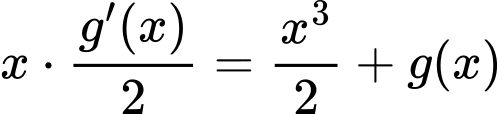
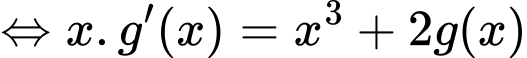
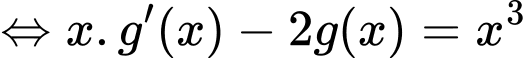
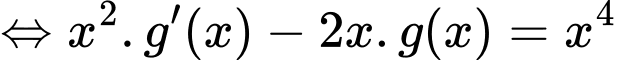
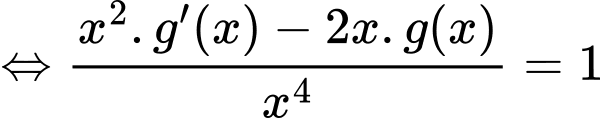
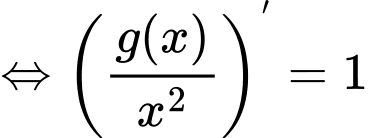
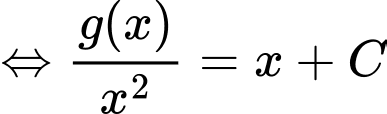
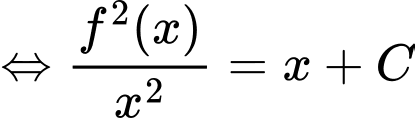
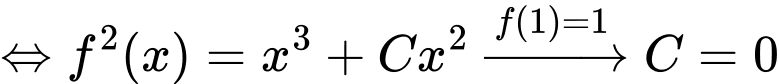

 khi đó phương trình trở thành:
khi đó phương trình trở thành: 
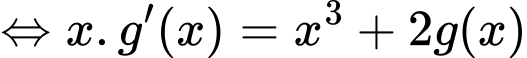
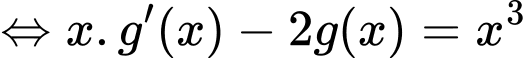
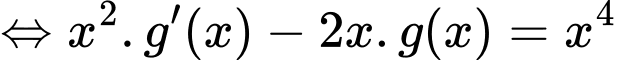
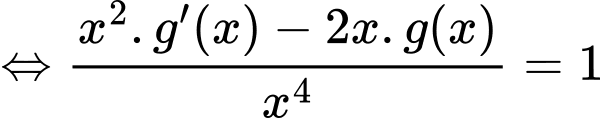
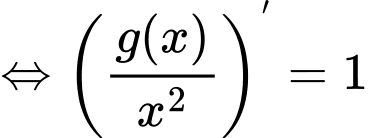
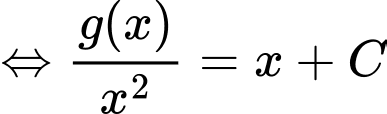
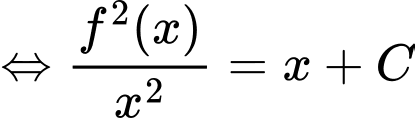
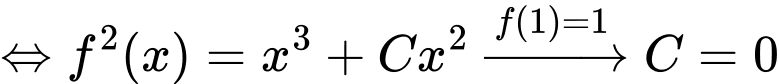

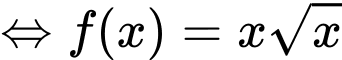
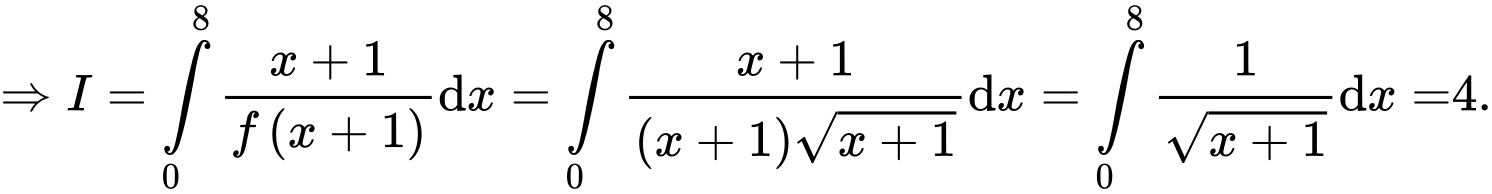
Chọn đáp án C.
Đáp án: C
Câu 15 [789750]: (THPT NGHĨA HƯNG NĐ - GK2-2018-2019) Cho hàm số 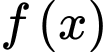 thỏa mãn
thỏa mãn 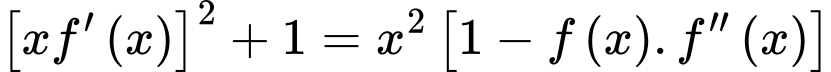 với mọi
với mọi 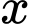 dương. Biết
dương. Biết 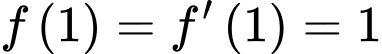 . Giá trị
. Giá trị 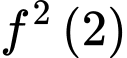 bằng
bằng
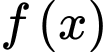 thỏa mãn
thỏa mãn 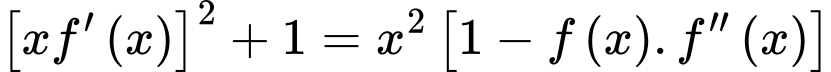 với mọi
với mọi 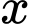 dương. Biết
dương. Biết 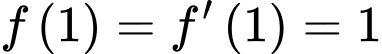 . Giá trị
. Giá trị 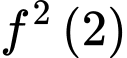 bằng
bằng A, 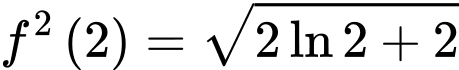 .
.
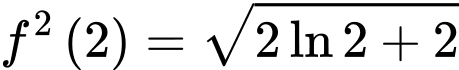 .
.B, 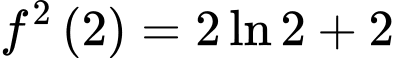 .
.
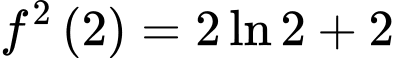 .
.C, 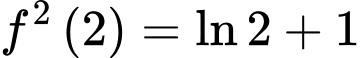 .
.
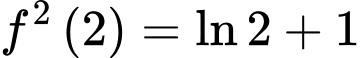 .
.D, 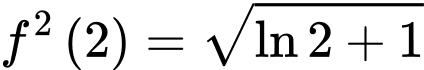 .
.
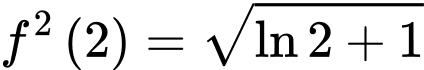 .
.
Ta có: 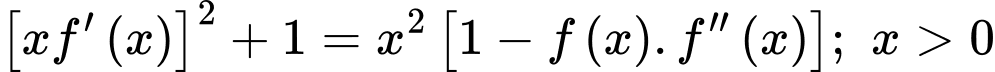
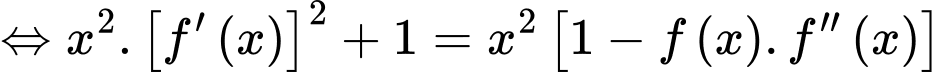
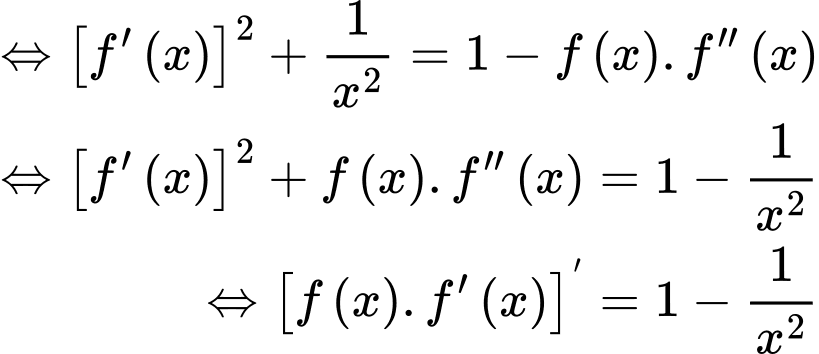
Do đó: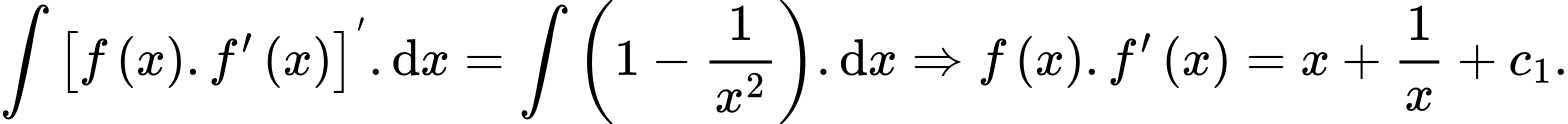
Vì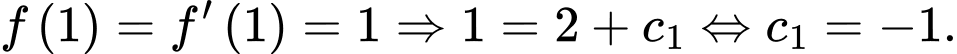
Nên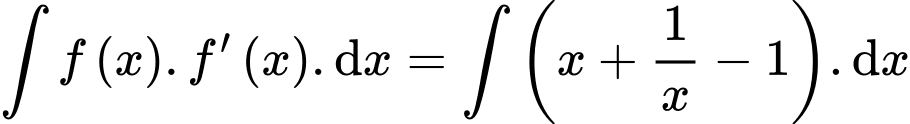
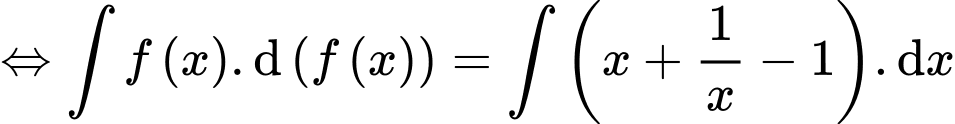
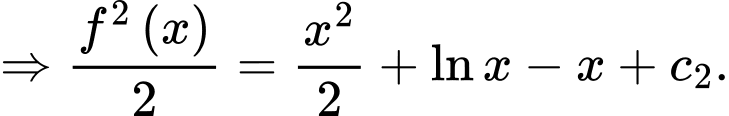 Vì
Vì 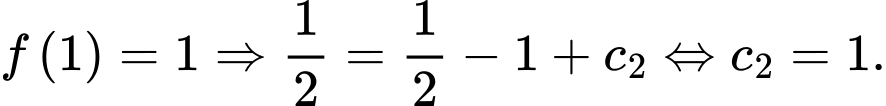
Vậy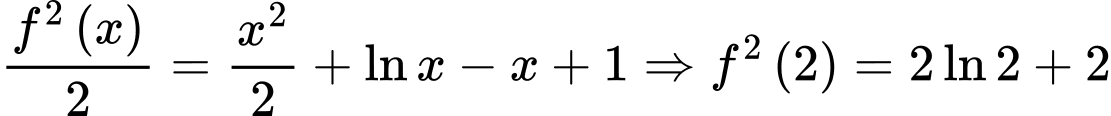 . Đáp án: B
. Đáp án: B
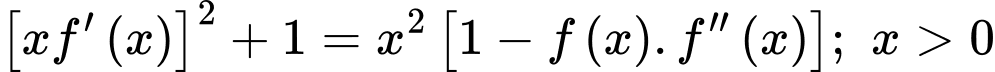
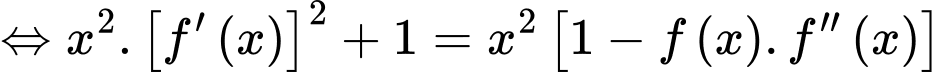
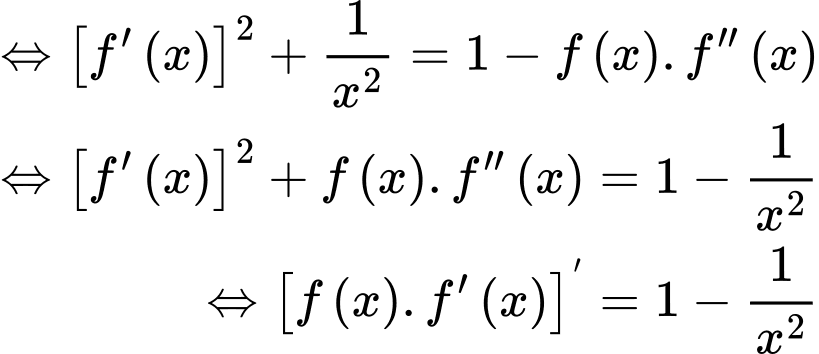
Do đó:
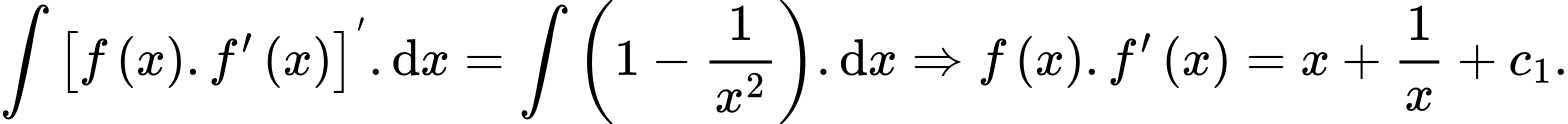
Vì
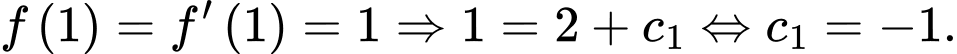
Nên
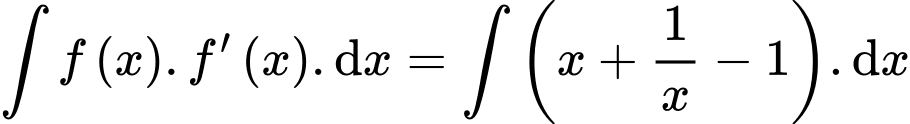
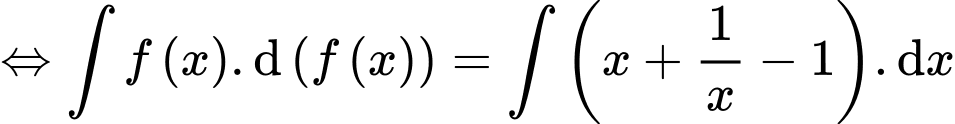
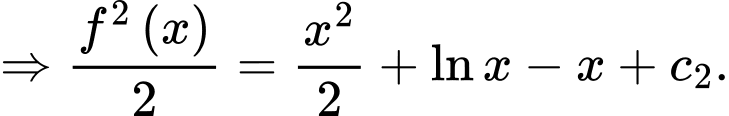 Vì
Vì 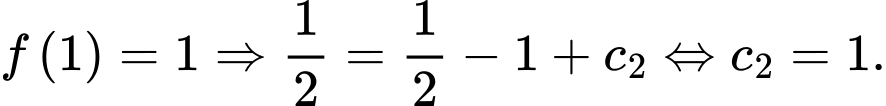
Vậy
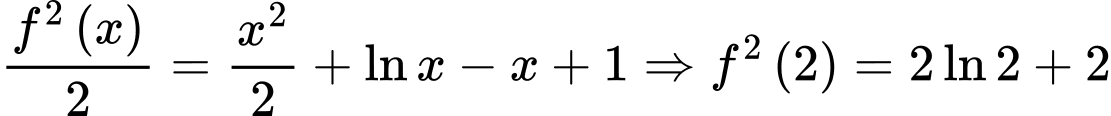 . Đáp án: B
. Đáp án: B
Câu 16 [512821]: Cho hàm số 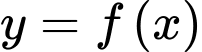 liên tục trên khoảng
liên tục trên khoảng 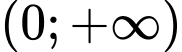 . Biết
. Biết 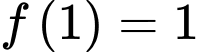 và
và 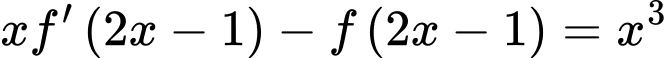 ,
,  . Giá trị
. Giá trị 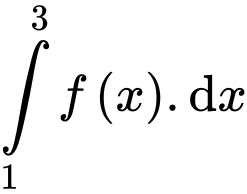 bằng
bằng
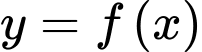 liên tục trên khoảng
liên tục trên khoảng 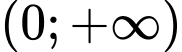 . Biết
. Biết 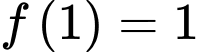 và
và 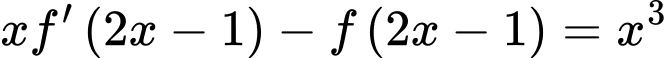 ,
,  . Giá trị
. Giá trị 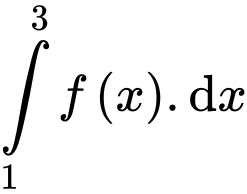 bằng
bằng A, 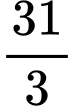 .
.
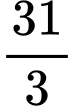 .
.B, 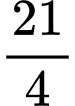 .
.
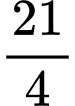 .
.C,  .
.
 .
.D, 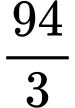 .
.
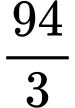 .
.
Chọn A
Với , ta có
, ta có 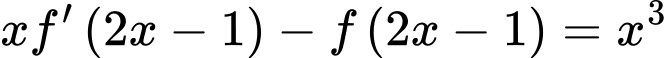
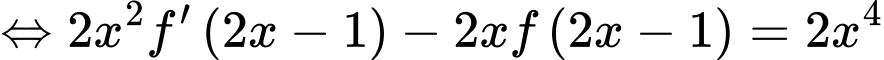
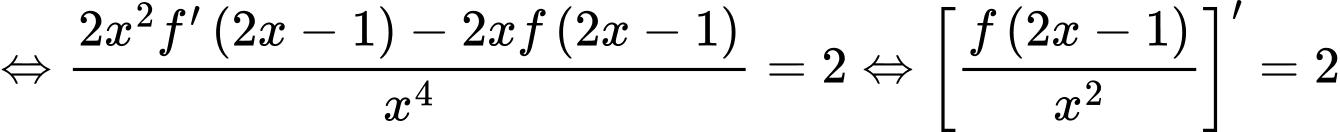 .
.
Suy ra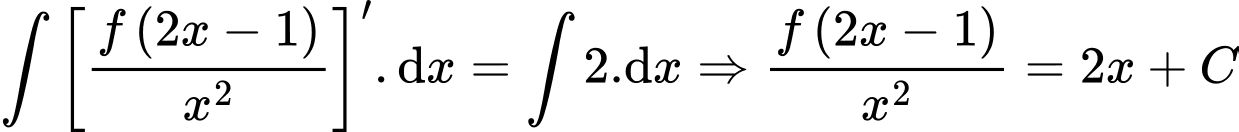 .
.
Mà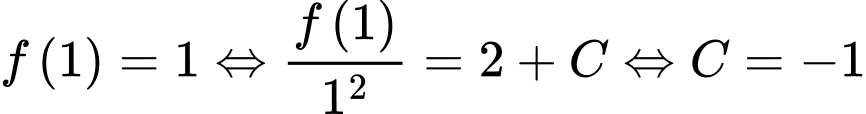 . Suy ra
. Suy ra 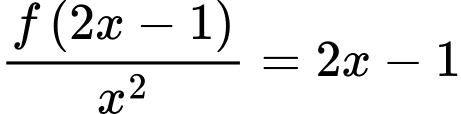
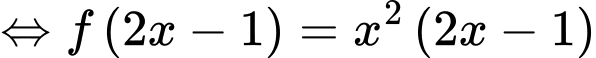 .
.
Do đó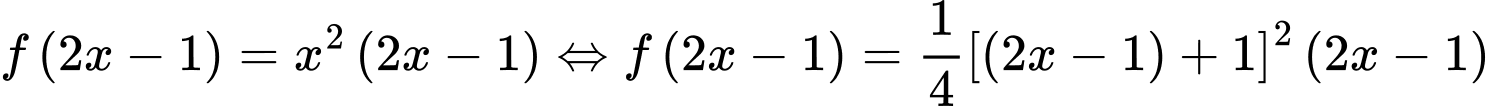 .
.
Suy ra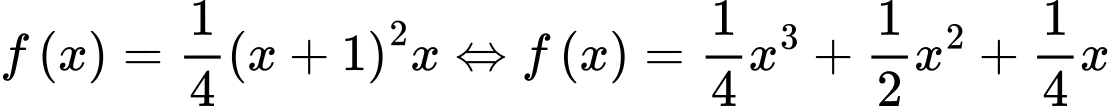 .
.
Vậy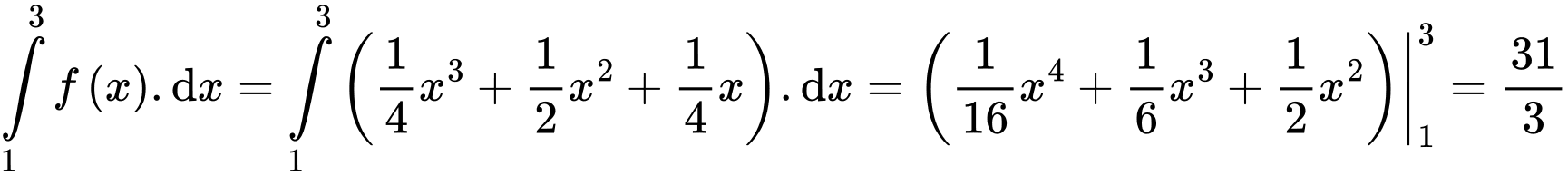 . Đáp án: A
. Đáp án: A
Với
 , ta có
, ta có 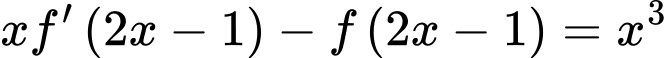
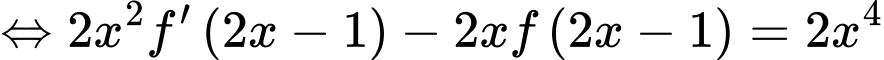
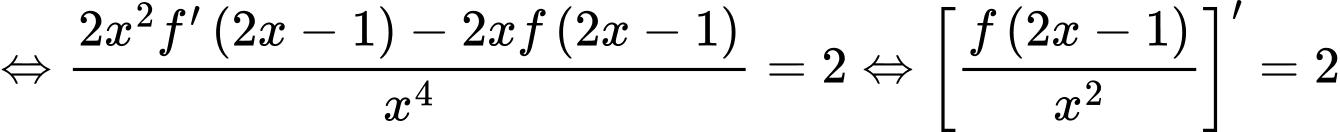 .
.Suy ra
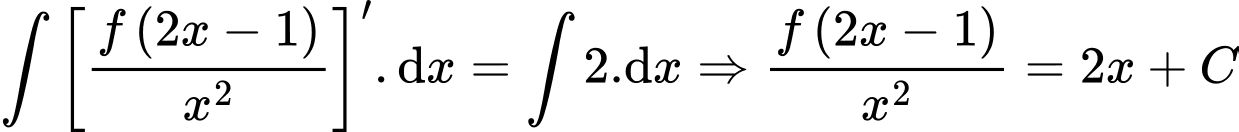 .
.Mà
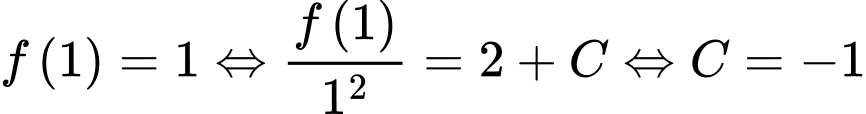 . Suy ra
. Suy ra 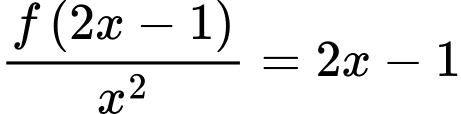
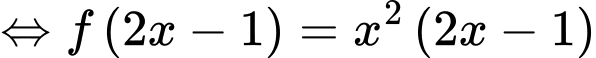 .
.Do đó
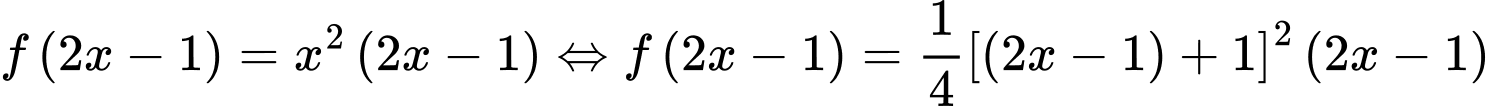 .
.Suy ra
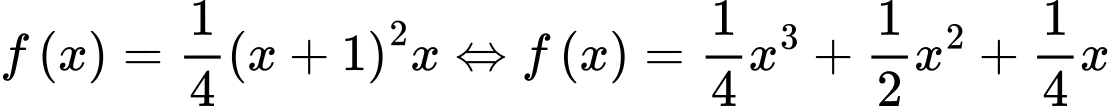 .
.Vậy
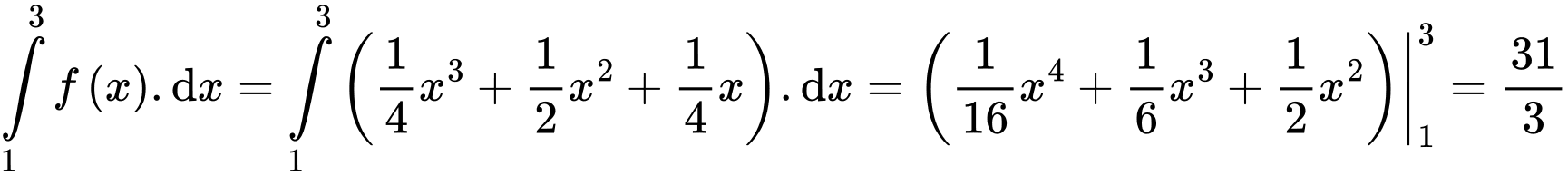 . Đáp án: A
. Đáp án: A
Câu 17 [789742]: (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hàm số 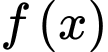 liên tục trên khoảng
liên tục trên khoảng 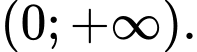 Biết
Biết 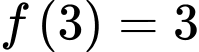 và
và 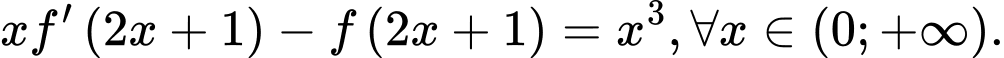 Giá trị của
Giá trị của 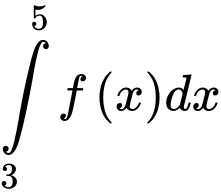 bằng
bằng
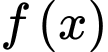 liên tục trên khoảng
liên tục trên khoảng 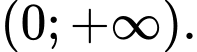 Biết
Biết 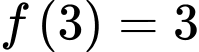 và
và 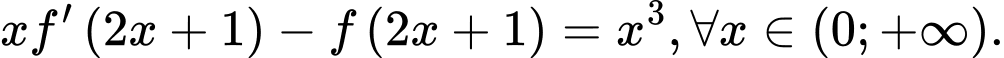 Giá trị của
Giá trị của 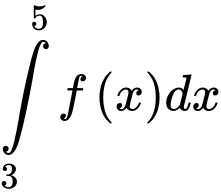 bằng
bằng A,  .
.
 .
.B, 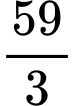 .
.
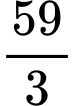 .
.C, 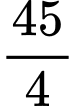 .
.
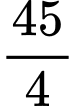 .
.D, 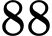 .
.
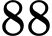 .
.
Chọn B
Ta có:
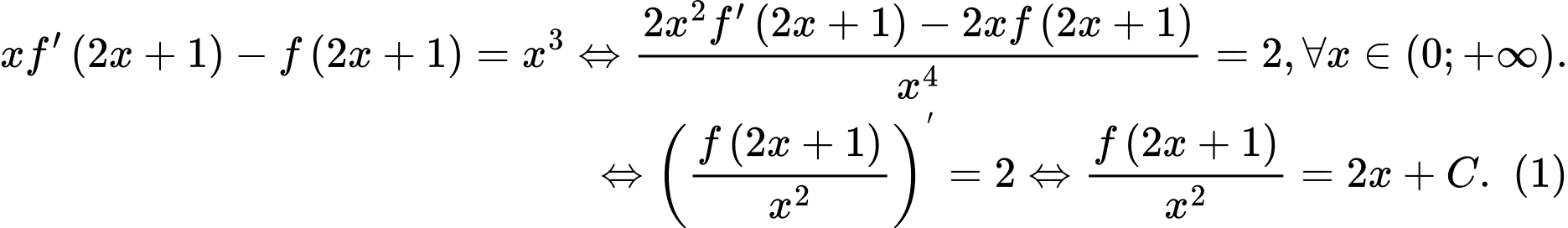 Cho
Cho 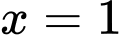 từ
từ 
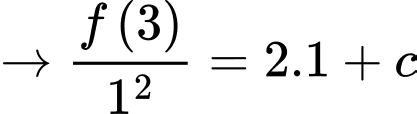 \Rightarrow \int\limits_1^2 {f\left( {2x + 1} \right)} dx = \int\limits_1^2 {\left( {2{x^3} + {x^2}} \right)} dx = \left. {\left( {2\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3}} \right)} \right|_1^2 = \frac{{59}}{6}. \Rightarrow \int\limits_3^5 {f\left( x \right)} dx = 2\int\limits_1^2 {f\left( {2x + 1} \right)} dx = \frac{{59}}{3}. Đáp án: B
\Rightarrow \int\limits_1^2 {f\left( {2x + 1} \right)} dx = \int\limits_1^2 {\left( {2{x^3} + {x^2}} \right)} dx = \left. {\left( {2\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3}} \right)} \right|_1^2 = \frac{{59}}{6}. \Rightarrow \int\limits_3^5 {f\left( x \right)} dx = 2\int\limits_1^2 {f\left( {2x + 1} \right)} dx = \frac{{59}}{3}. Đáp án: B
Ta có:
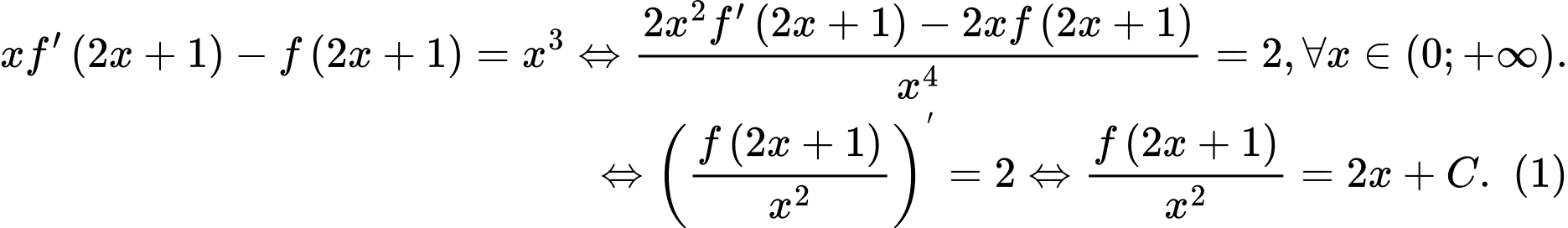 Cho
Cho 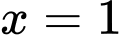 từ
từ 
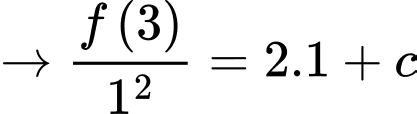 \Rightarrow \int\limits_1^2 {f\left( {2x + 1} \right)} dx = \int\limits_1^2 {\left( {2{x^3} + {x^2}} \right)} dx = \left. {\left( {2\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3}} \right)} \right|_1^2 = \frac{{59}}{6}. \Rightarrow \int\limits_3^5 {f\left( x \right)} dx = 2\int\limits_1^2 {f\left( {2x + 1} \right)} dx = \frac{{59}}{3}. Đáp án: B
\Rightarrow \int\limits_1^2 {f\left( {2x + 1} \right)} dx = \int\limits_1^2 {\left( {2{x^3} + {x^2}} \right)} dx = \left. {\left( {2\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3}} \right)} \right|_1^2 = \frac{{59}}{6}. \Rightarrow \int\limits_3^5 {f\left( x \right)} dx = 2\int\limits_1^2 {f\left( {2x + 1} \right)} dx = \frac{{59}}{3}. Đáp án: B
Câu 18 [151766]: Cho hàm số 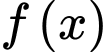 có đạo hàm liên tục trên
có đạo hàm liên tục trên 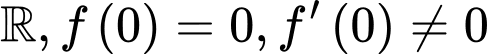 và thỏa mãn hệ thức
và thỏa mãn hệ thức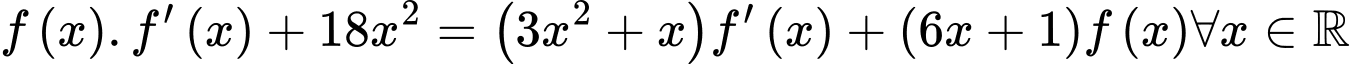 . Biết
. Biết 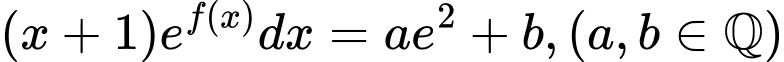 .Giá trị của
.Giá trị của 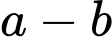 bằng
bằng
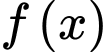 có đạo hàm liên tục trên
có đạo hàm liên tục trên 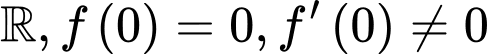 và thỏa mãn hệ thức
và thỏa mãn hệ thức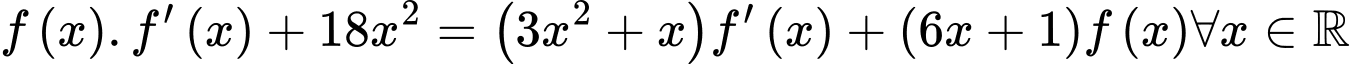 . Biết
. Biết 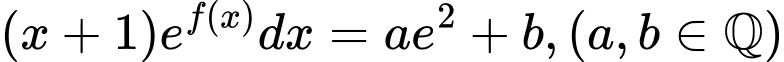 .Giá trị của
.Giá trị của 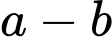 bằng
bằng A, 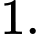
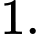
B, 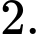
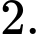
C, 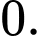
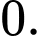
D, 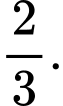
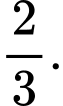
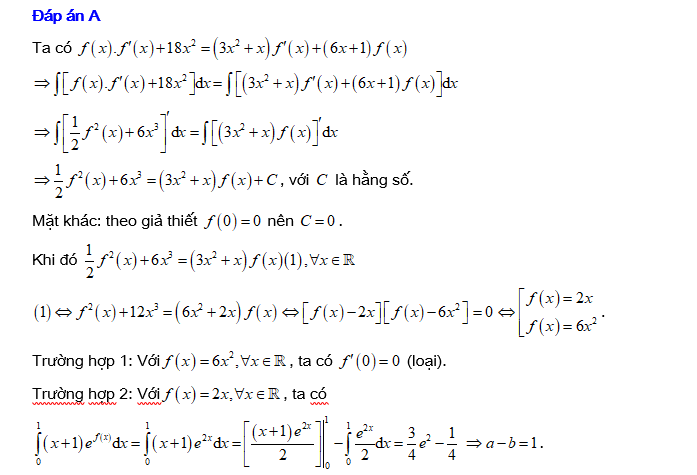 Đáp án: A
Đáp án: A
Câu 19 [789340]: Cho hàm số 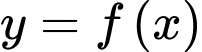 có đạo hàm trên khoảng
có đạo hàm trên khoảng 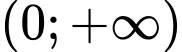 thỏa mãn
thỏa mãn 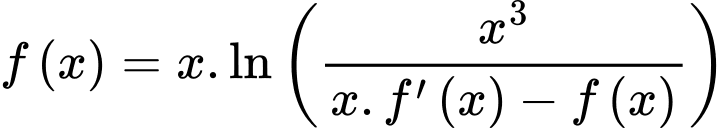 và
và 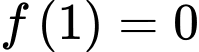 . Tính tích phân
. Tính tích phân 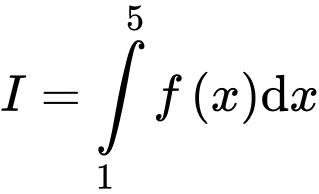 .
.
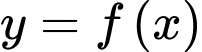 có đạo hàm trên khoảng
có đạo hàm trên khoảng 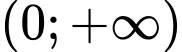 thỏa mãn
thỏa mãn 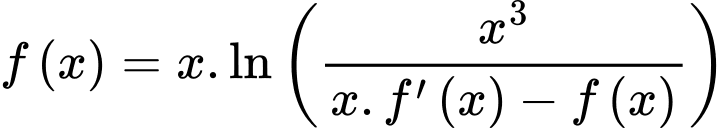 và
và 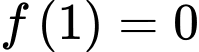 . Tính tích phân
. Tính tích phân 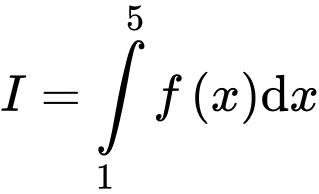 .
. A, 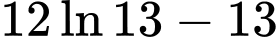 .
.
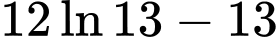 .
.B, 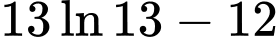 .
.
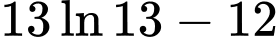 .
.C, 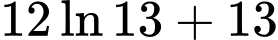 .
.
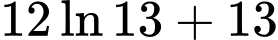 .
.D, 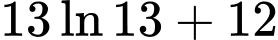 .
.
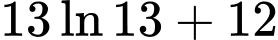 .
.
Chọn B
Từ giả thiết và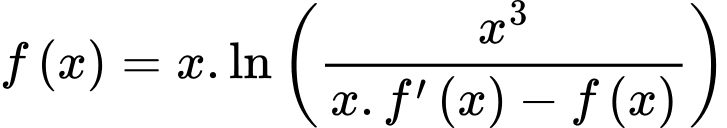
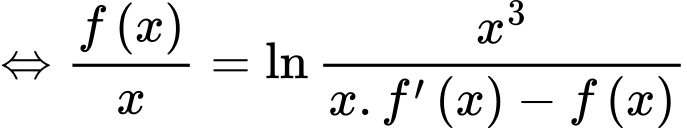
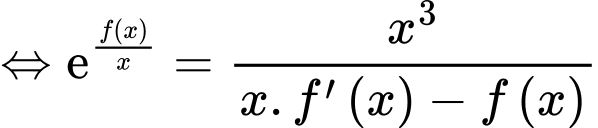
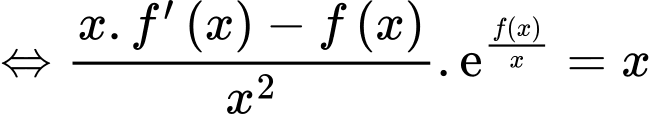
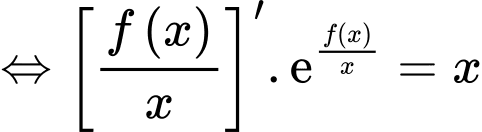 (1)
(1)
Lấy nguyên hàm hai vế của (1) suy ra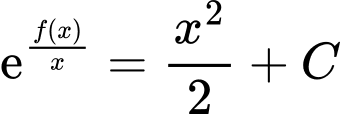 .
.
Do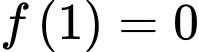
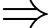
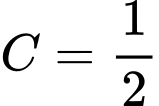 , nên
, nên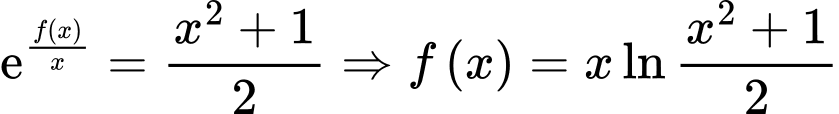 với
với 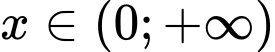 .
.
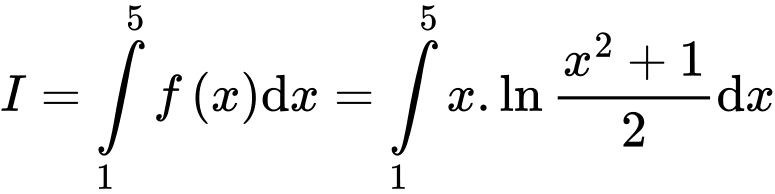 (2).
(2).
Đặt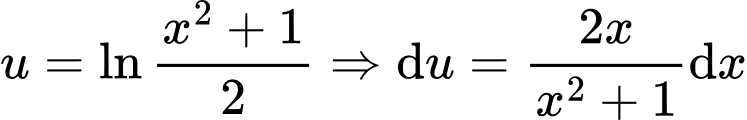 ;
; 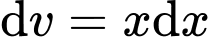 , chọn
, chọn 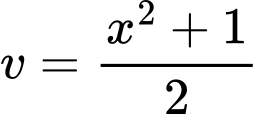 .
.
Theo công thức tích phân từng phần, ta được:
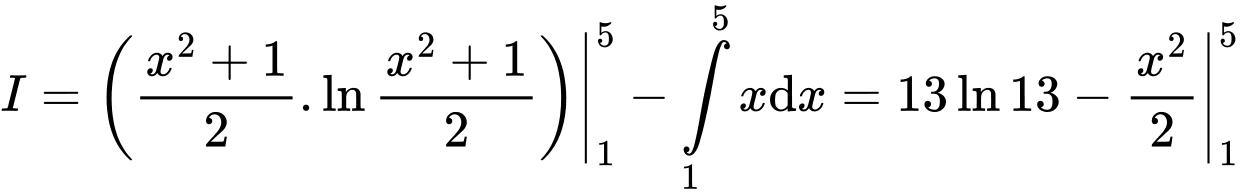
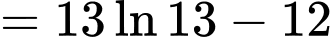 . Đáp án: B
. Đáp án: B
Từ giả thiết và
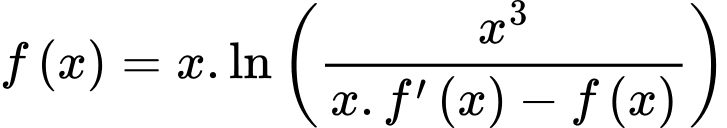
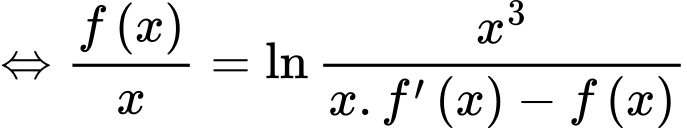
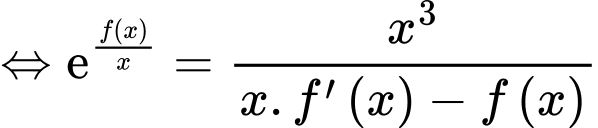
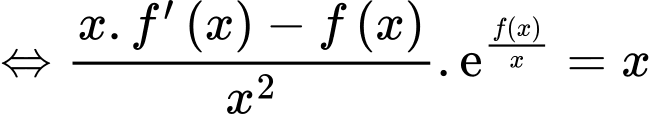
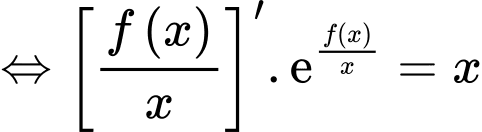 (1)
(1) Lấy nguyên hàm hai vế của (1) suy ra
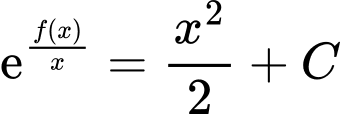 .
.Do
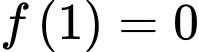
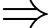
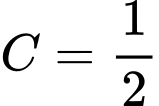 , nên
, nên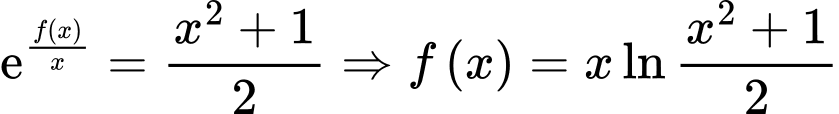 với
với 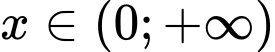 .
.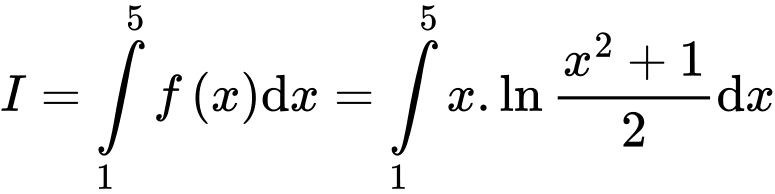 (2).
(2). Đặt
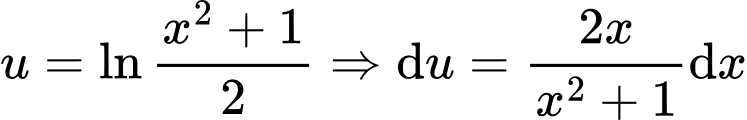 ;
; 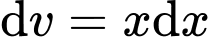 , chọn
, chọn 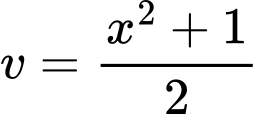 .
.Theo công thức tích phân từng phần, ta được:
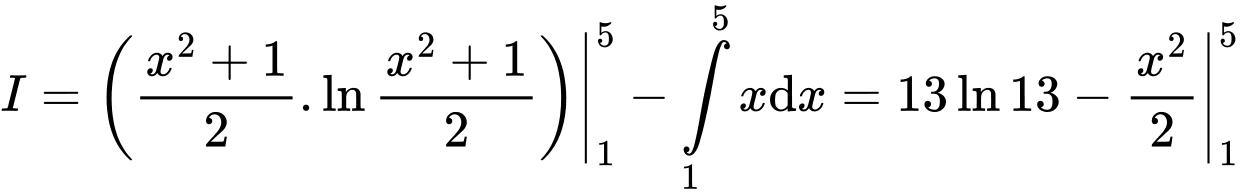
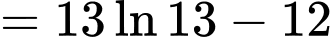 . Đáp án: B
. Đáp án: B