Đáp án Bài tập tự luyện
Câu 1 [133148]: Cho 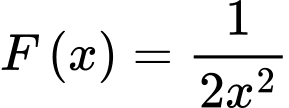 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 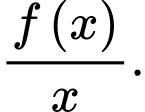 Tìm nguyên hàm của hàm số
Tìm nguyên hàm của hàm số 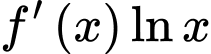
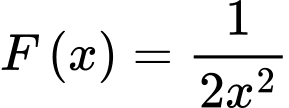 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 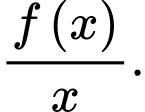 Tìm nguyên hàm của hàm số
Tìm nguyên hàm của hàm số 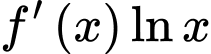
A, 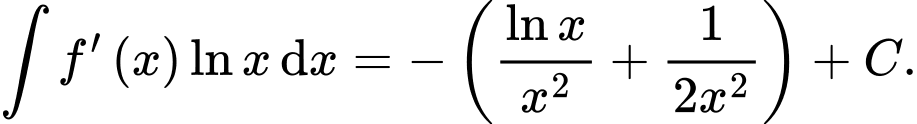
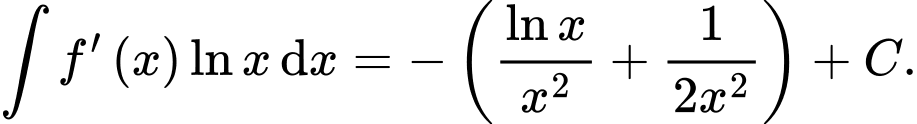
B, 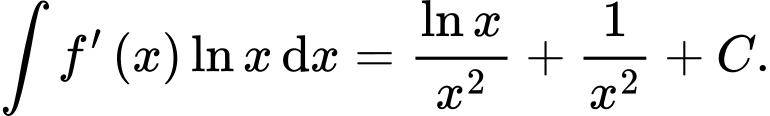
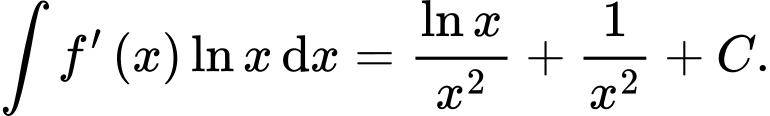
C, 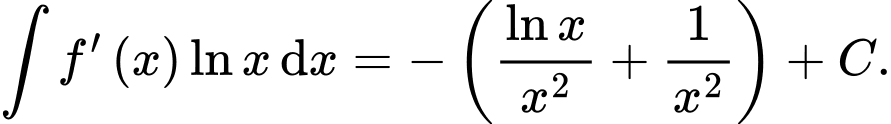
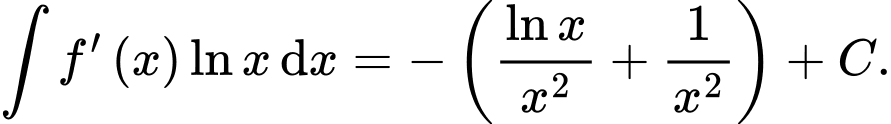
D, 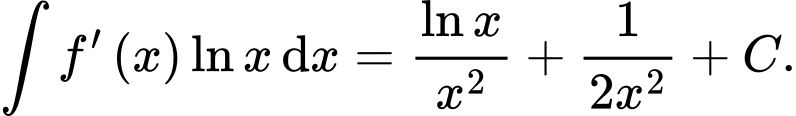
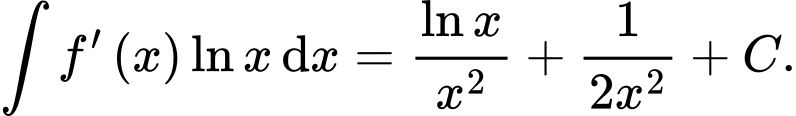
Cách 1: Do 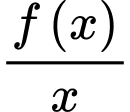 là nguyên hàm của hàm số
là nguyên hàm của hàm số 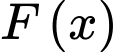 nên
nên 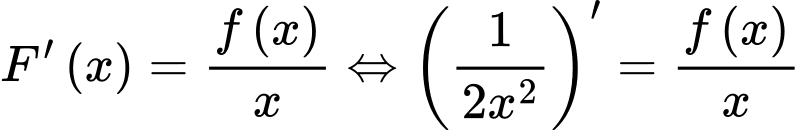
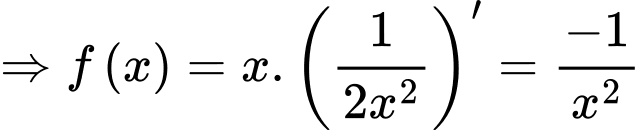 và
và 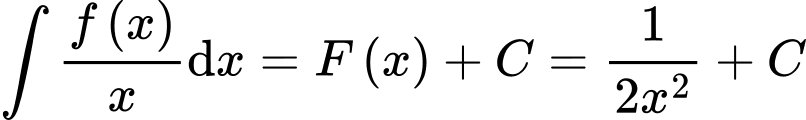
Xét nguyên hàm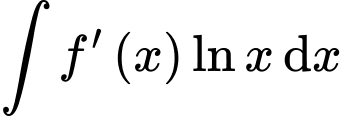 ta đặt
ta đặt 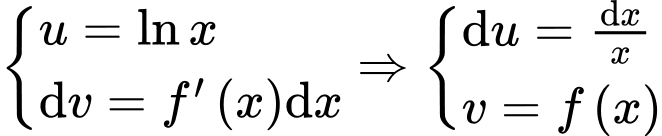
Do đó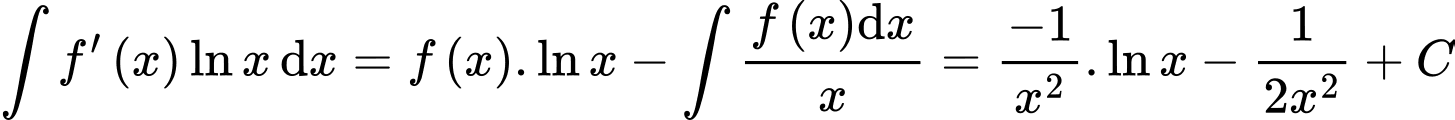
Cách 2: Ta có: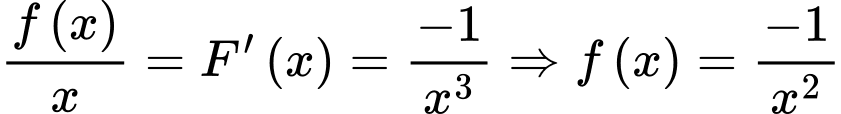 suy ra
suy ra 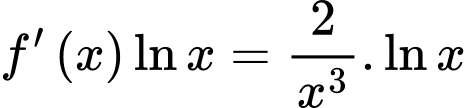 .
.
Đặt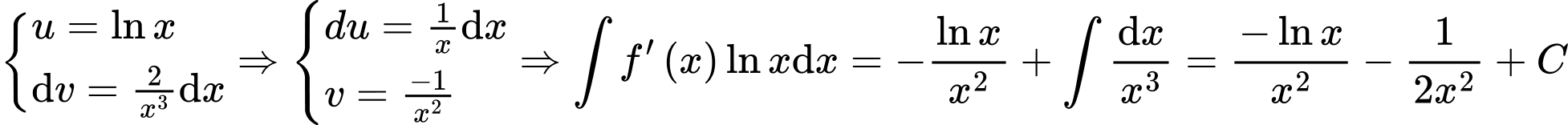 . Chọn A.
Đáp án: A
. Chọn A.
Đáp án: A
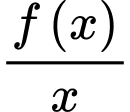 là nguyên hàm của hàm số
là nguyên hàm của hàm số 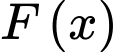 nên
nên 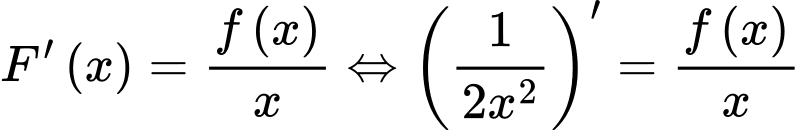
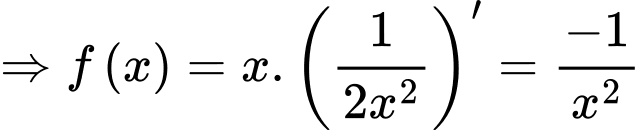 và
và 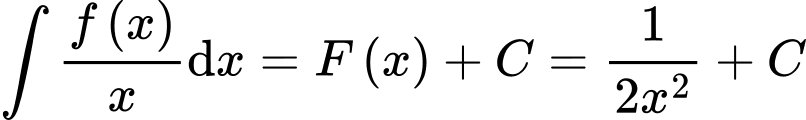
Xét nguyên hàm
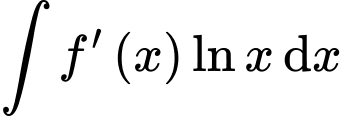 ta đặt
ta đặt 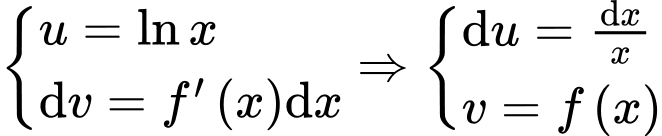
Do đó
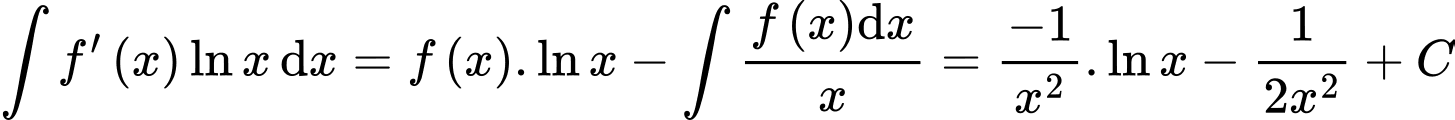
Cách 2: Ta có:
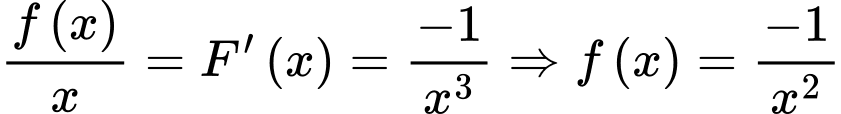 suy ra
suy ra 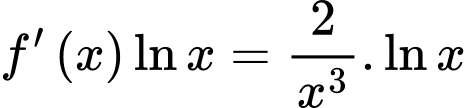 .
.
Đặt
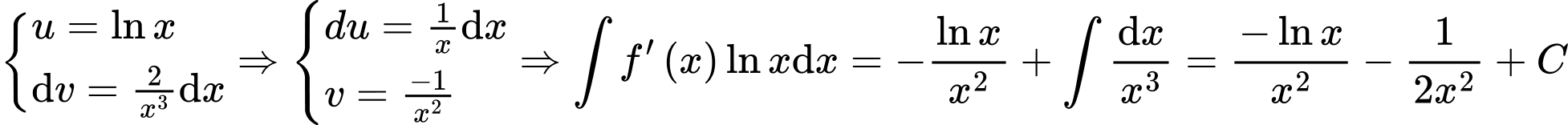 . Chọn A.
Đáp án: A
. Chọn A.
Đáp án: A
Câu 2 [139650]: Cho 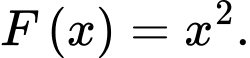 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 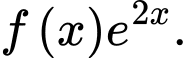 Tìm nguyên hàm của hàm số
Tìm nguyên hàm của hàm số 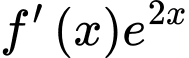
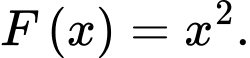 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 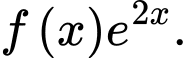 Tìm nguyên hàm của hàm số
Tìm nguyên hàm của hàm số 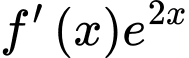
A, 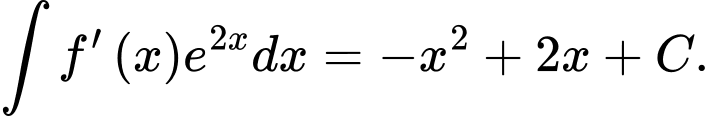
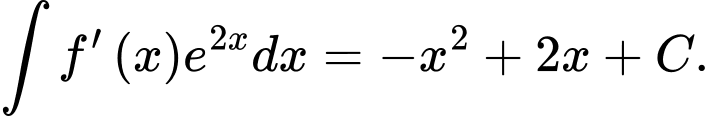
B, 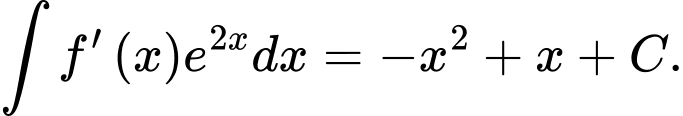
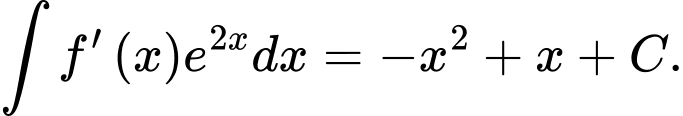
C, 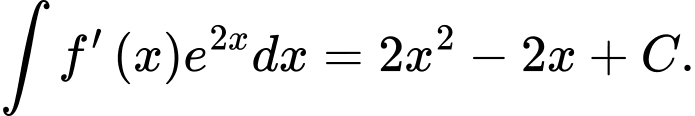
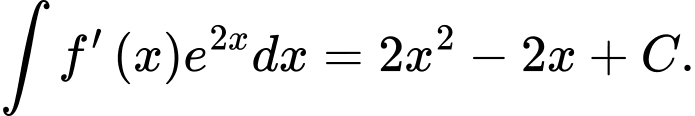
D, 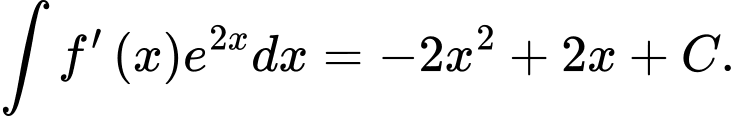
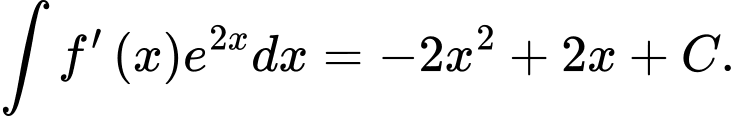
Ta có 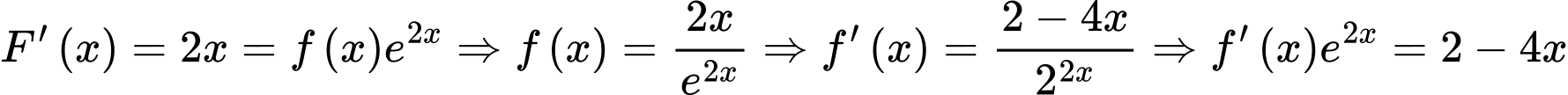
Suy ra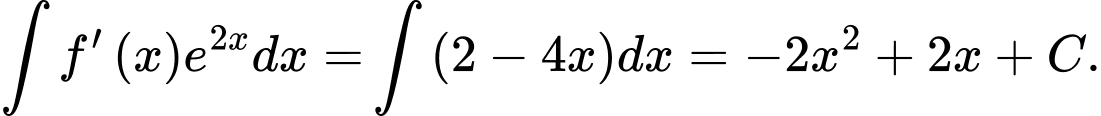 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
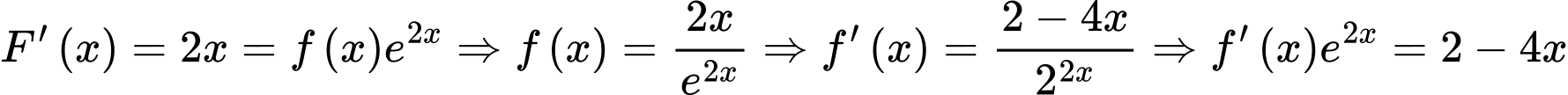
Suy ra
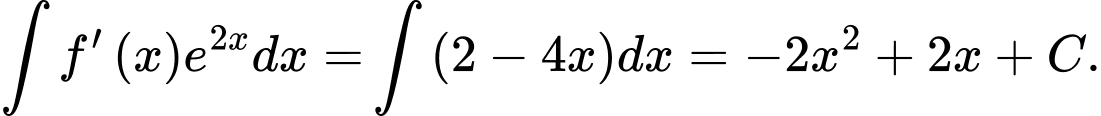 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 3 [677930]: Cho hàm số 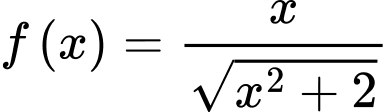 . Họ tất cả các nguyên hàm của hàm số
. Họ tất cả các nguyên hàm của hàm số 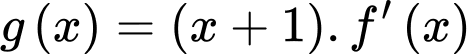 là
là
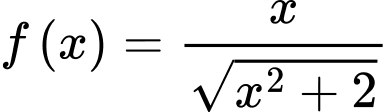 . Họ tất cả các nguyên hàm của hàm số
. Họ tất cả các nguyên hàm của hàm số 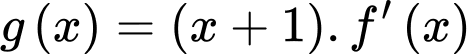 là
là A, 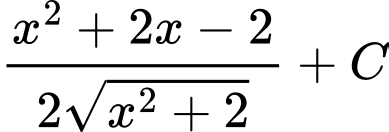 .
.
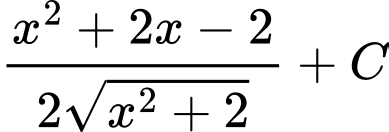 .
.B, 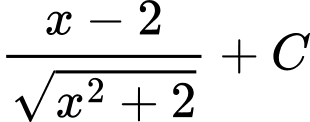 .
.
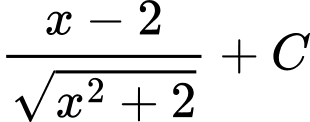 .
.C, 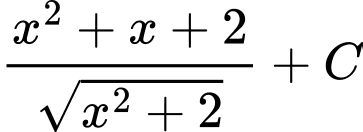 .
.
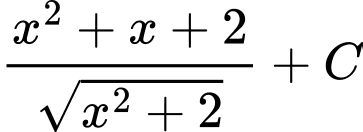 .
.D, 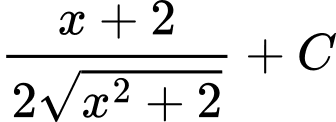 .
.
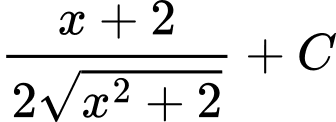 .
.
Chọn B.
Tính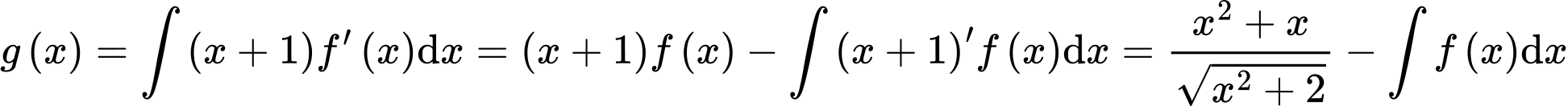
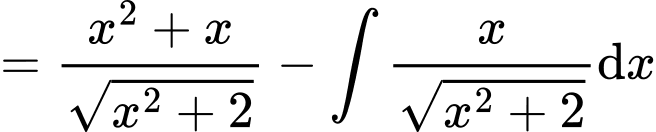
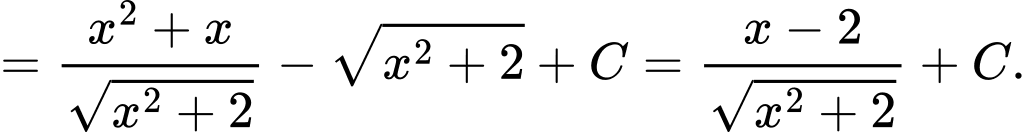 Đáp án: B
Đáp án: B
Tính
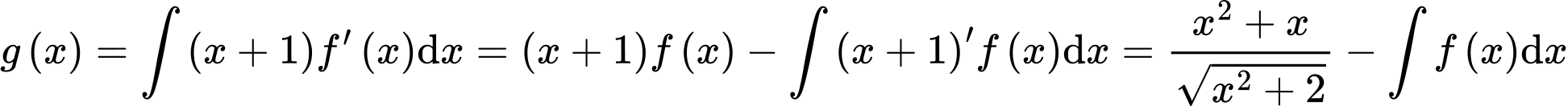
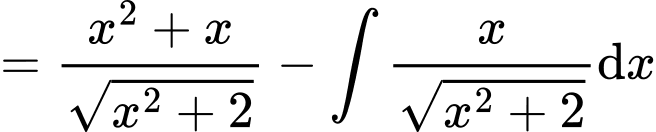
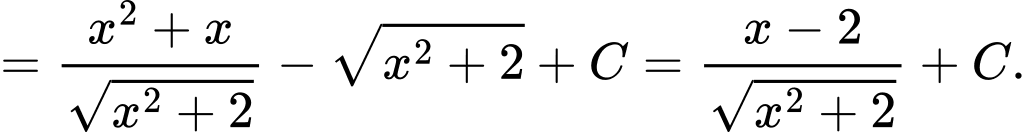 Đáp án: B
Đáp án: B
Câu 4 [516234]: Cho hàm số 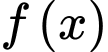 liên tục trên
liên tục trên 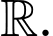 Biết
Biết 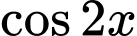 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 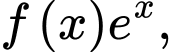 họ tất cả các nguyên hàm của hàm số
họ tất cả các nguyên hàm của hàm số  là
là
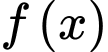 liên tục trên
liên tục trên 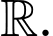 Biết
Biết 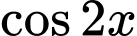 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 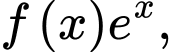 họ tất cả các nguyên hàm của hàm số
họ tất cả các nguyên hàm của hàm số  là
là A, 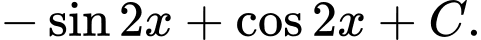
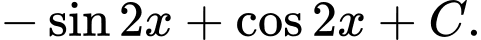
B, 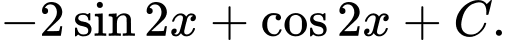
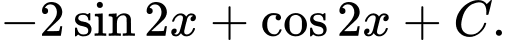
C, 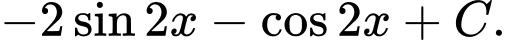
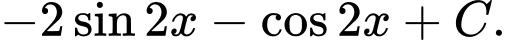
D, 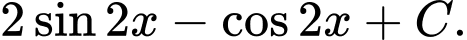
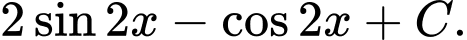
Ta có: 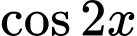 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 
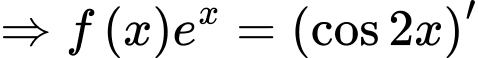
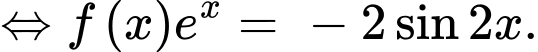
Lại có: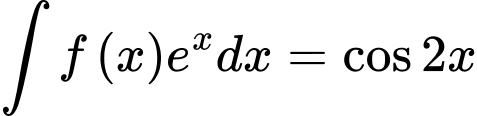
Đặt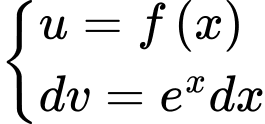

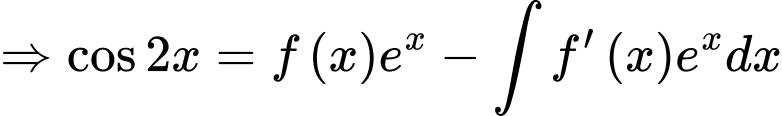
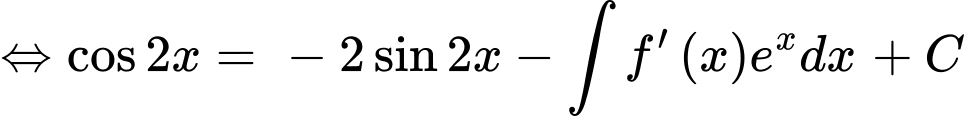
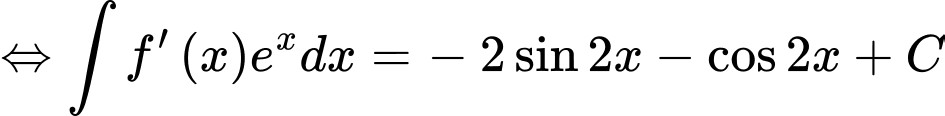 Đáp án: C
Đáp án: C
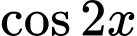 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 
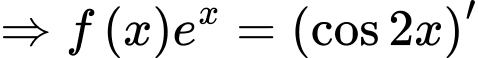
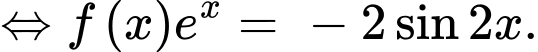
Lại có:
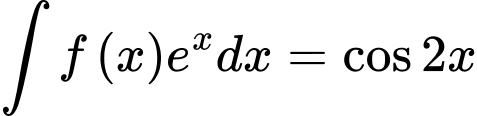
Đặt
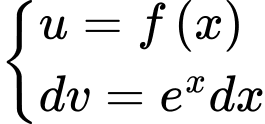

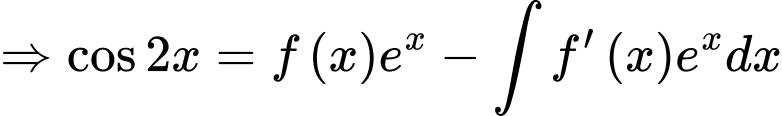
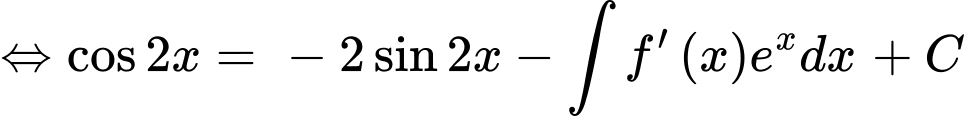
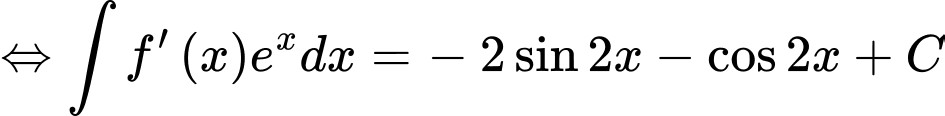 Đáp án: C
Đáp án: C
Câu 5 [516235]: Cho 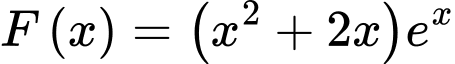 là một nguyên hàm của
là một nguyên hàm của 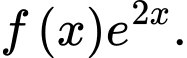 Tìm họ nguyên hàm của hàm số
Tìm họ nguyên hàm của hàm số 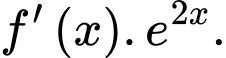
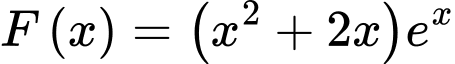 là một nguyên hàm của
là một nguyên hàm của 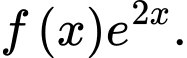 Tìm họ nguyên hàm của hàm số
Tìm họ nguyên hàm của hàm số 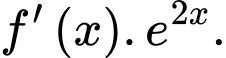
A, 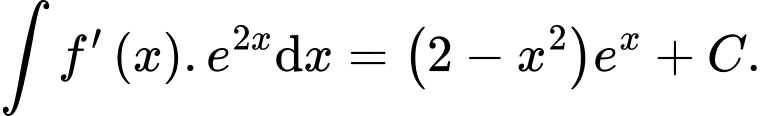
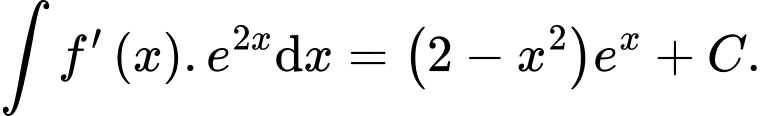
B, 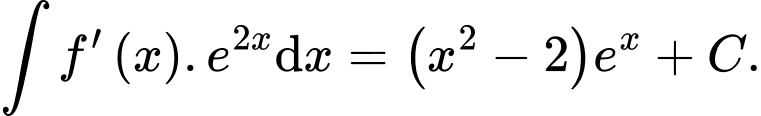
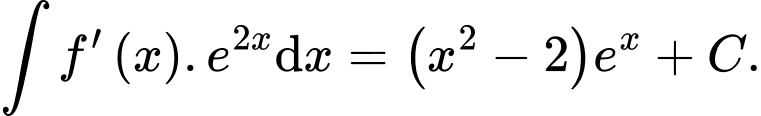
C, 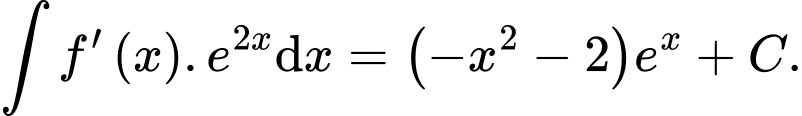
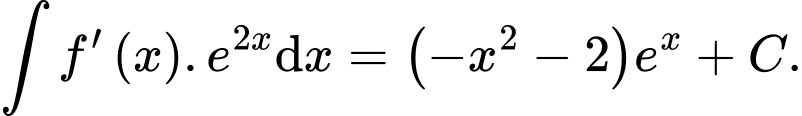
D, 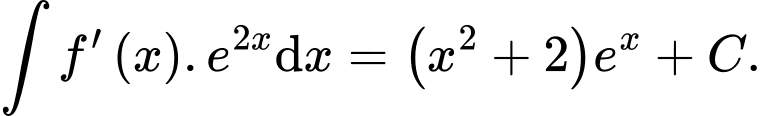
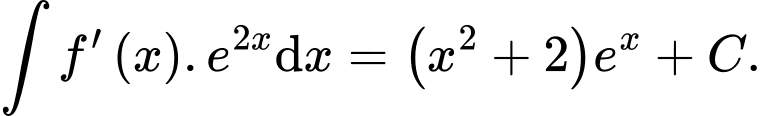

Câu 6 [148251]: Cho hàm số 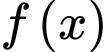 thỏa mãn
thỏa mãn 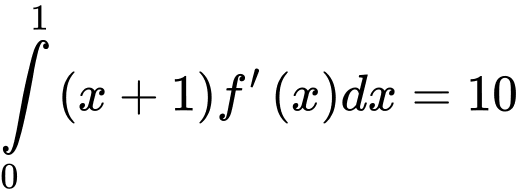 và
và 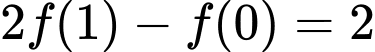 . Tính
. Tính 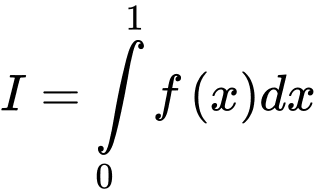 .
.
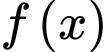 thỏa mãn
thỏa mãn 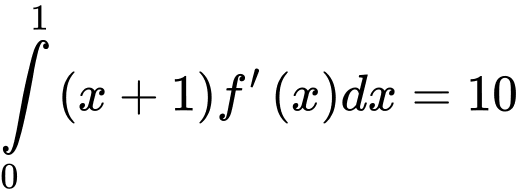 và
và 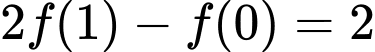 . Tính
. Tính 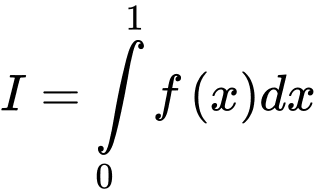 .
. A, 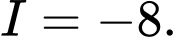
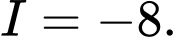
B, 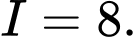
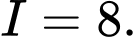
C, 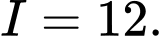
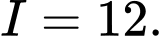
D, 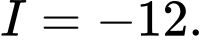
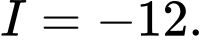
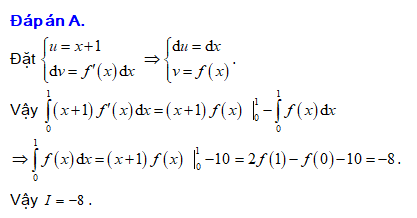 Đáp án: A
Đáp án: A
Câu 7 [149494]: Cho hàm số 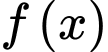 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 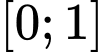 thỏa mãn
thỏa mãn 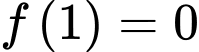 ,
, 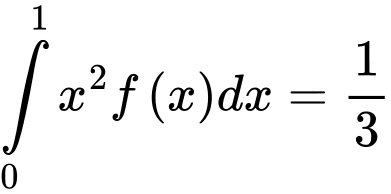 Tính
Tính 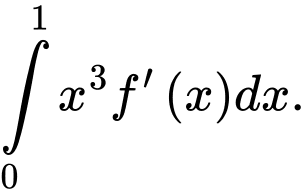
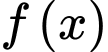 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 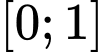 thỏa mãn
thỏa mãn 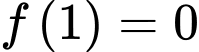 ,
, 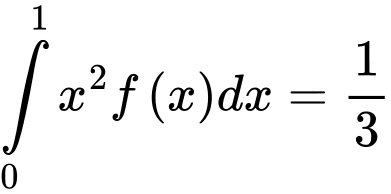 Tính
Tính 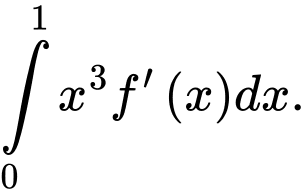
A, 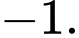
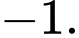
B, 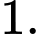
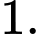
C, 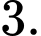
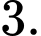
D, 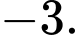
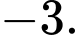
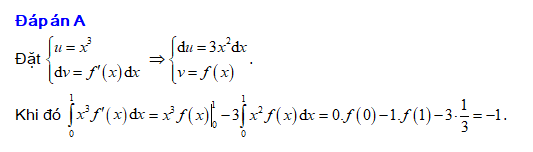 Đáp án: A
Đáp án: A
Câu 8 [149481]: Cho hàm số 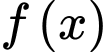 có đạo hàm liên tục trên
có đạo hàm liên tục trên 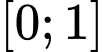 và thỏa mãn:
và thỏa mãn: 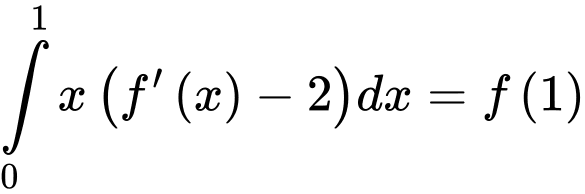 . Tính giá trị của
. Tính giá trị của 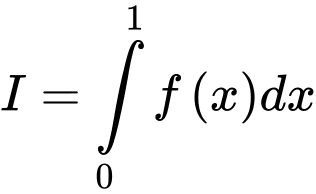 .
.
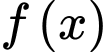 có đạo hàm liên tục trên
có đạo hàm liên tục trên 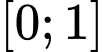 và thỏa mãn:
và thỏa mãn: 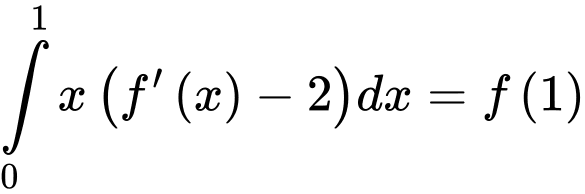 . Tính giá trị của
. Tính giá trị của 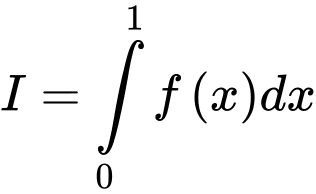 .
. A, 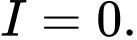
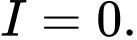
B, 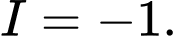
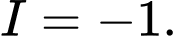
C, 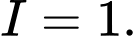
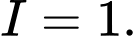
D, 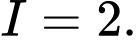
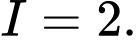
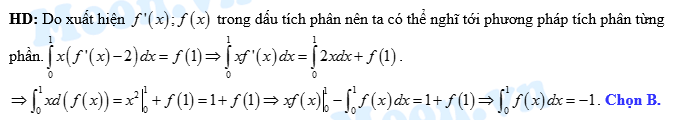 Đáp án: B
Đáp án: B
Câu 9 [140550]: Cho 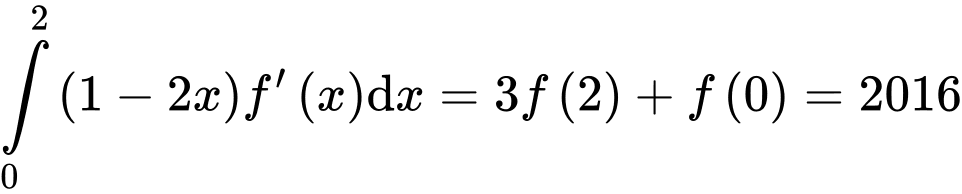 . Tích phân
. Tích phân 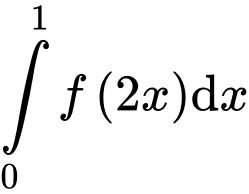 bằng
bằng
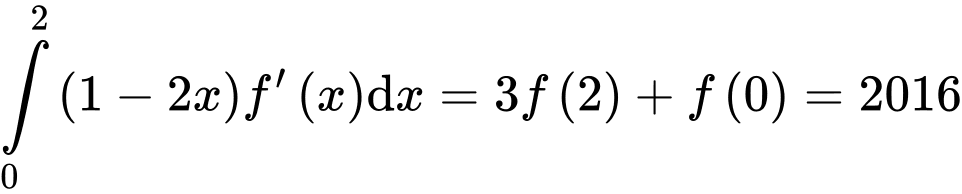 . Tích phân
. Tích phân 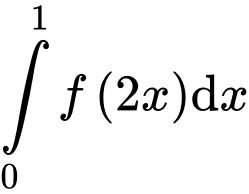 bằng
bằng A, 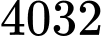 .
.
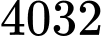 .
.B, 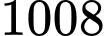 .
.
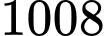 .
.C,  .
.
 .
.D,  .
.
 .
.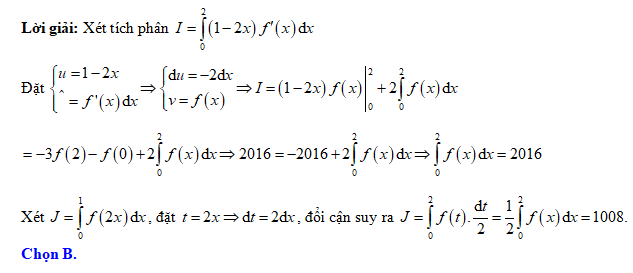 Đáp án: B
Đáp án: B
Câu 10 [45975]: Cho hàm số 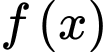 có đạo hàm liên tục trên
có đạo hàm liên tục trên 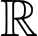 . Biết
. Biết 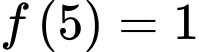 và
và 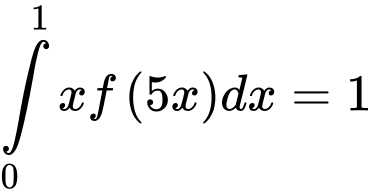 , khi đó
, khi đó 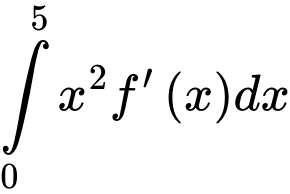 bằng
bằng
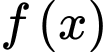 có đạo hàm liên tục trên
có đạo hàm liên tục trên 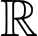 . Biết
. Biết 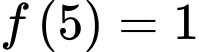 và
và 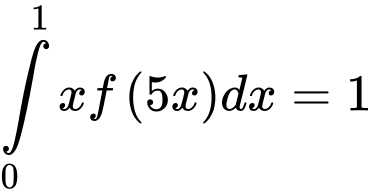 , khi đó
, khi đó 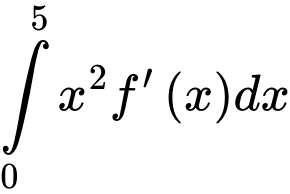 bằng
bằng A, 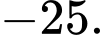
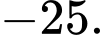
B, 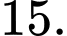
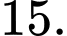
C, 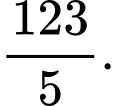
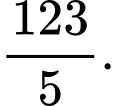
D, 
HD: Ta có 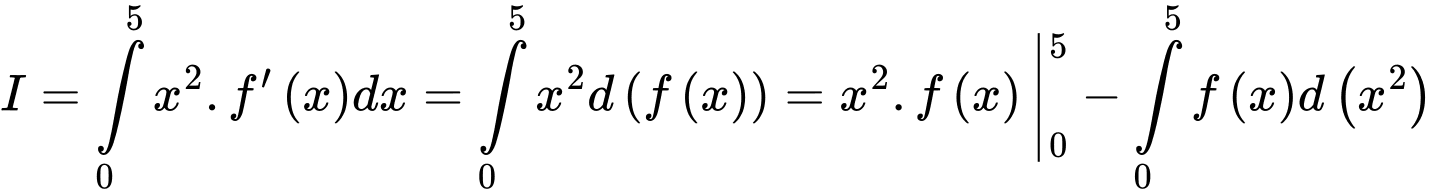
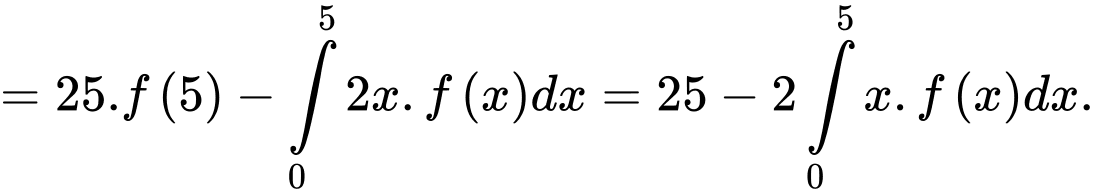
Xét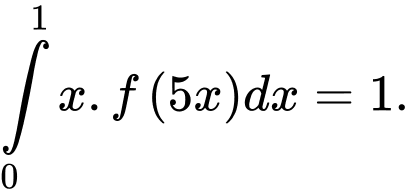 Đặt
Đặt 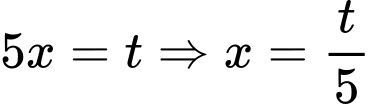
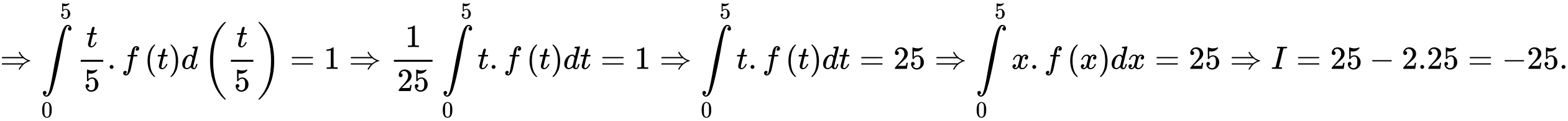
Chọn A. Đáp án: A
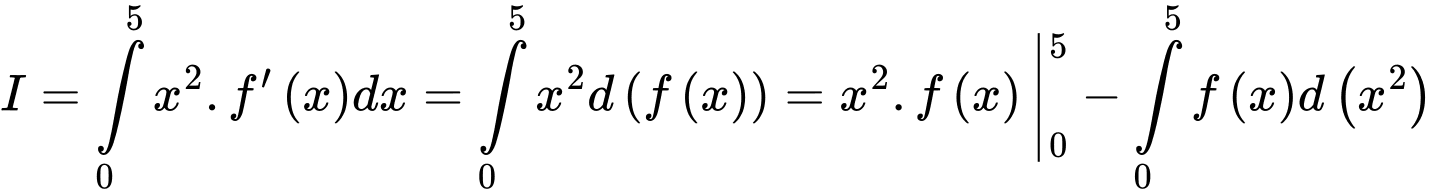
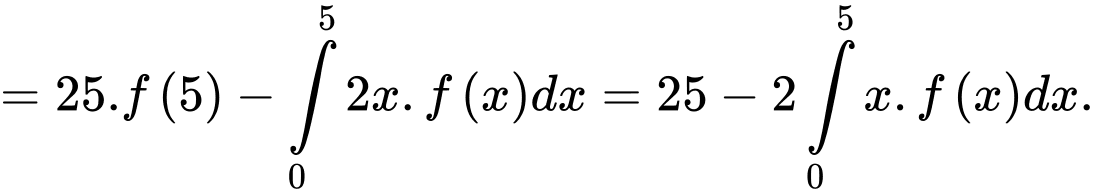
Xét
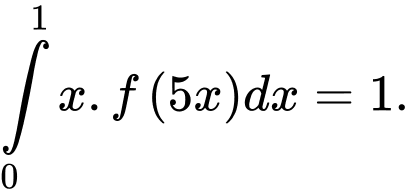 Đặt
Đặt 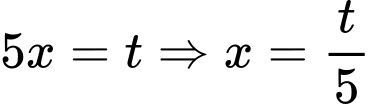
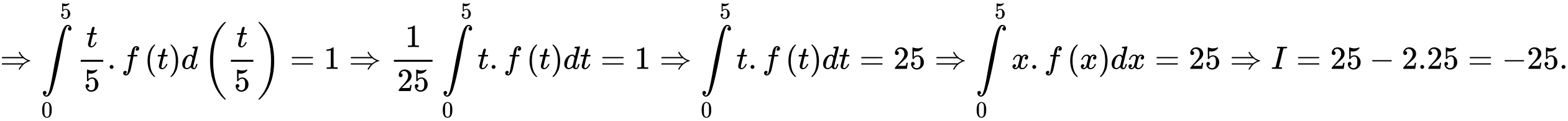
Chọn A. Đáp án: A
Câu 11 [46022]: Cho hàm số 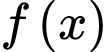 có đạo hàm liên tục trên
có đạo hàm liên tục trên 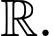 Biết
Biết 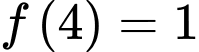 và
và 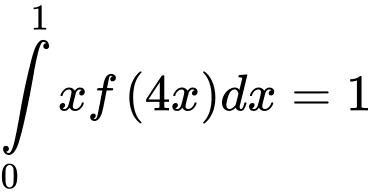 , khi đó
, khi đó 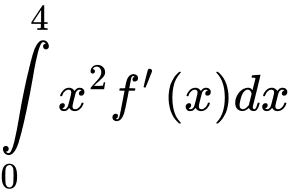 bằng
bằng
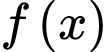 có đạo hàm liên tục trên
có đạo hàm liên tục trên 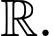 Biết
Biết 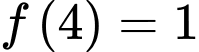 và
và 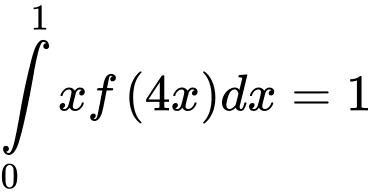 , khi đó
, khi đó 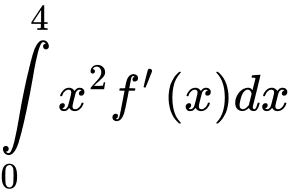 bằng
bằng A, 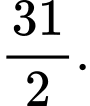
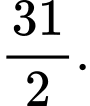
B, 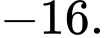
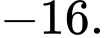
C, 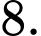
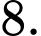
D, 
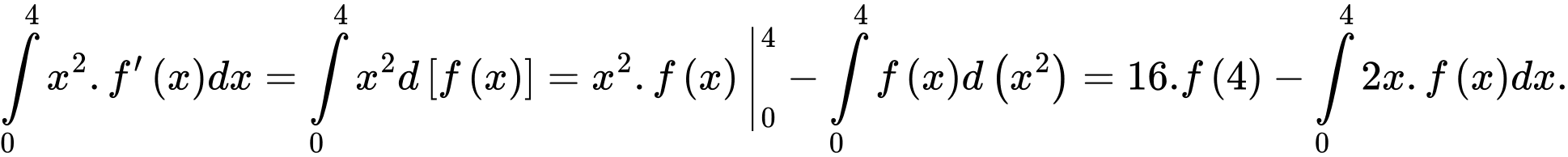
Xét
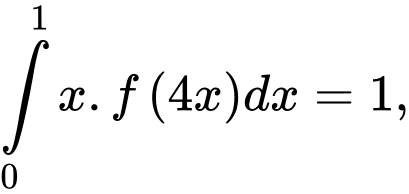 đặt
đặt 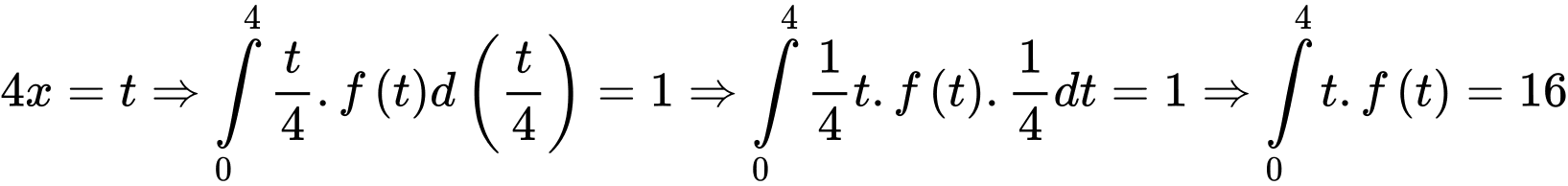
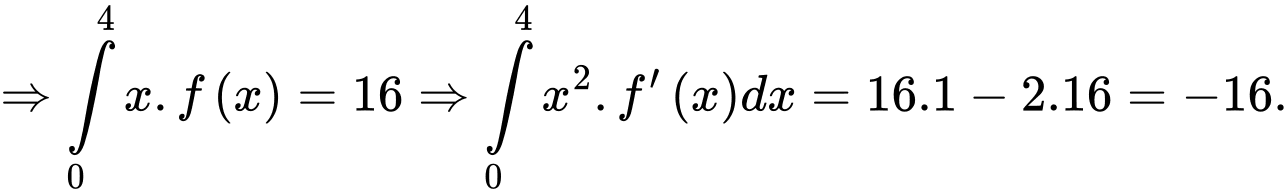 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 12 [789418]: Cho hàm số 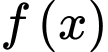 liên tục và có đạo hàm cấp hai trên
liên tục và có đạo hàm cấp hai trên 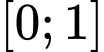 thỏa
thỏa 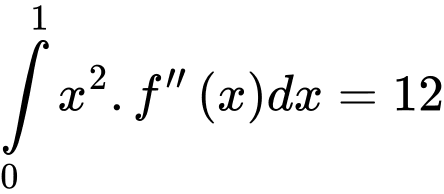 và
và 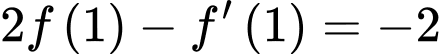 . Tính
. Tính 
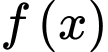 liên tục và có đạo hàm cấp hai trên
liên tục và có đạo hàm cấp hai trên 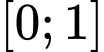 thỏa
thỏa 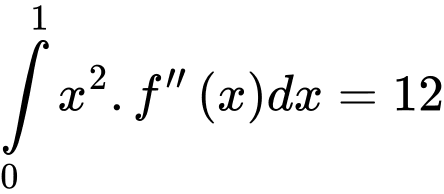 và
và 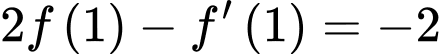 . Tính
. Tính 
A,  .
.
 .
.B, 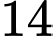 .
.
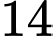 .
.C, 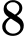 .
.
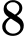 .
.D, 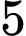 .
.
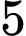 .
.
Chọn D
Đặt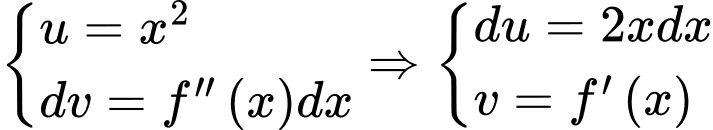 . Khi đó
. Khi đó 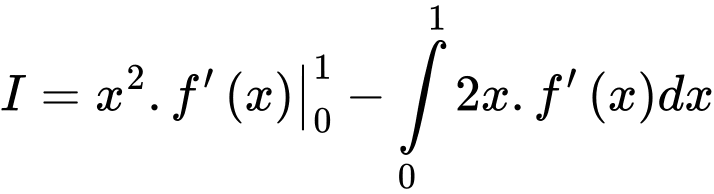 .
.
Đặt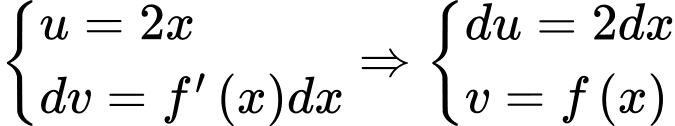 . Suy ra
. Suy ra 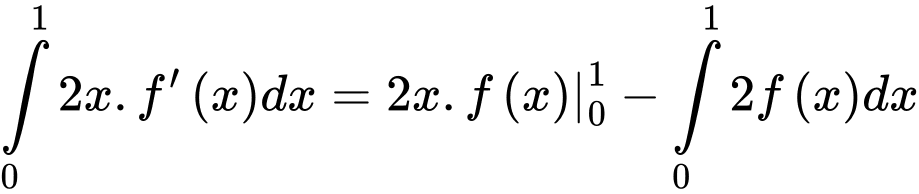
Do đó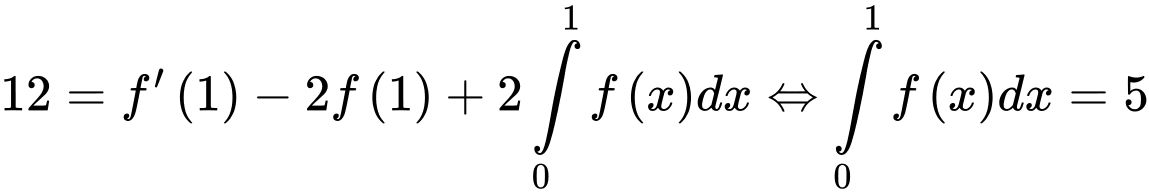 Đáp án: D
Đáp án: D
Đặt
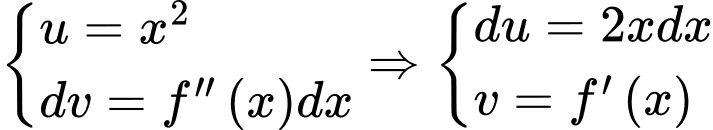 . Khi đó
. Khi đó 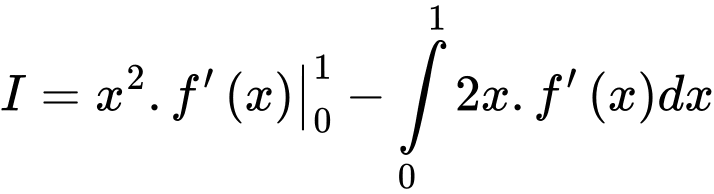 .
.Đặt
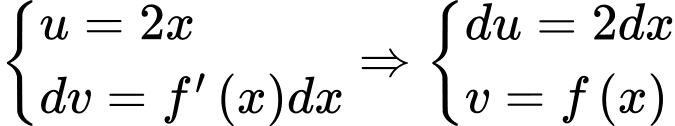 . Suy ra
. Suy ra 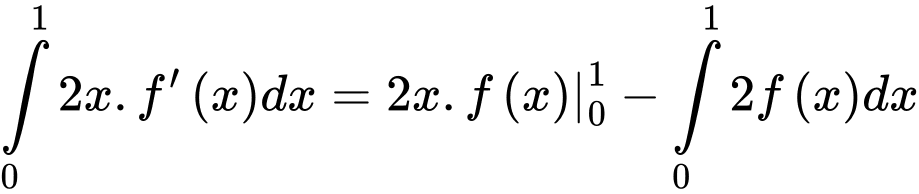
Do đó
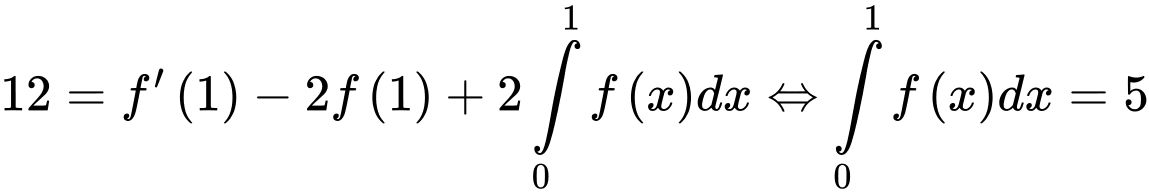 Đáp án: D
Đáp án: D
Câu 13 [516403]: Cho hàm số 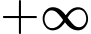 liên tục trên
liên tục trên 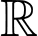 và
và 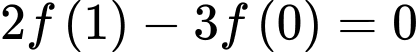 ,
, 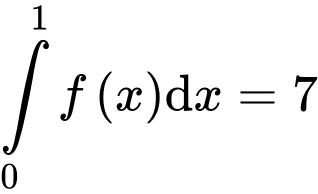 . Tính
. Tính 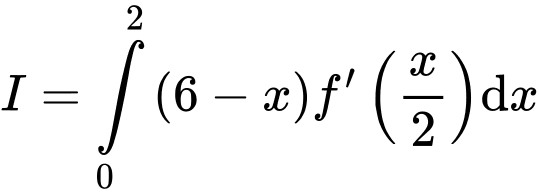
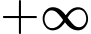 liên tục trên
liên tục trên 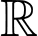 và
và 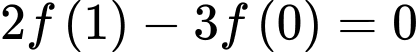 ,
, 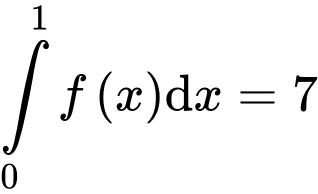 . Tính
. Tính 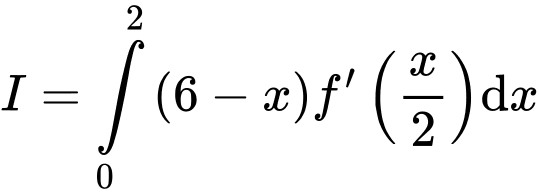
A, 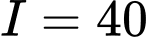 .
.
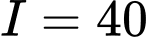 .
.B, 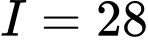 .
.
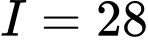 .
.C, 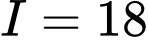 .
.
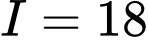 .
.D, 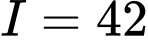 .
.
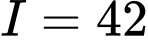 .
.
Chọn B
Xét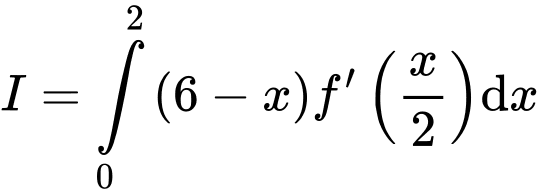
Đặt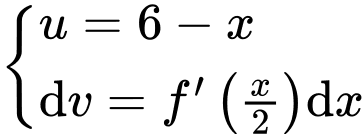
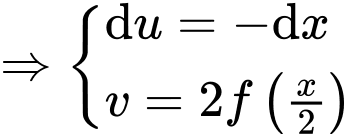 .
.
Khi đó: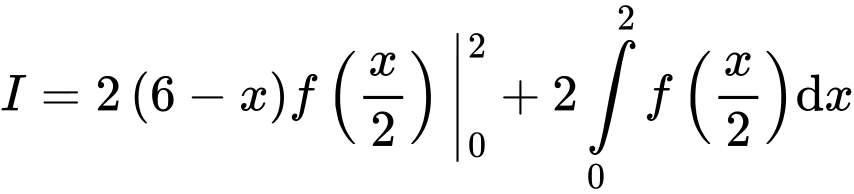
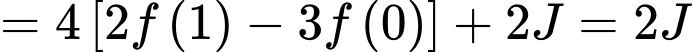 .
.
Xét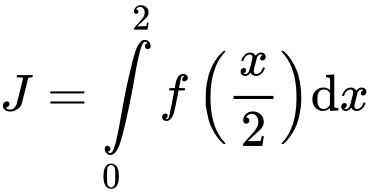
+ Đặt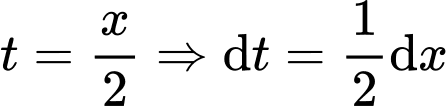 .
.
+ Đổi cận :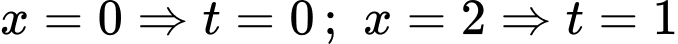 .
.
Lúc này: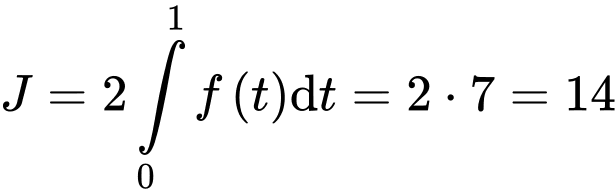 .
.
Vậy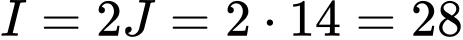 . Đáp án: B
. Đáp án: B
Xét
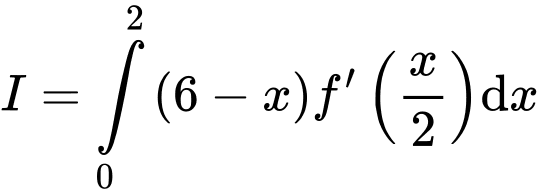
Đặt
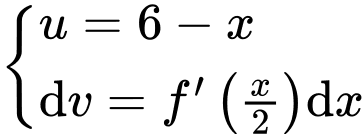
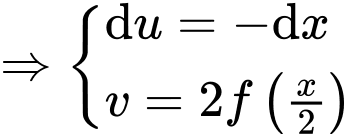 .
. Khi đó:
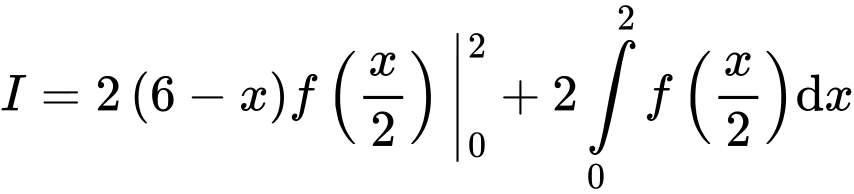
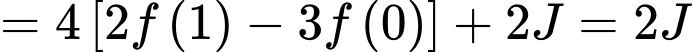 .
. Xét
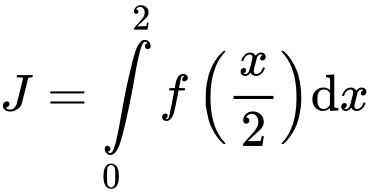
+ Đặt
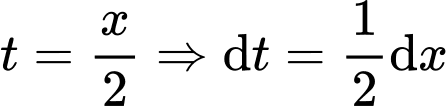 .
. + Đổi cận :
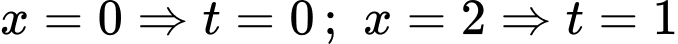 .
. Lúc này:
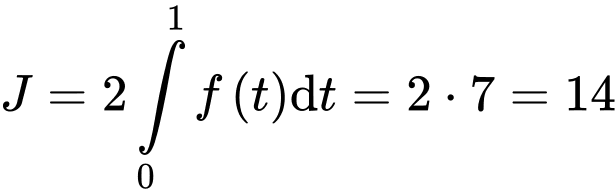 .
. Vậy
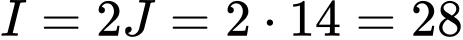 . Đáp án: B
. Đáp án: B
Câu 14 [147261]: Cho hàm số 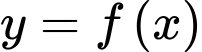 liên tục trên
liên tục trên 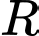 thỏa mãn
thỏa mãn 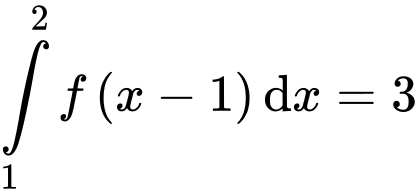 và
và 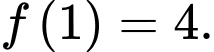 Khi đó tích phân
Khi đó tích phân 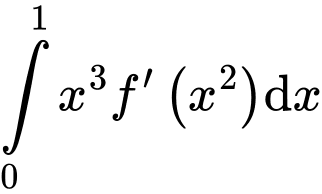 bằng
bằng
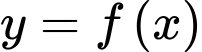 liên tục trên
liên tục trên 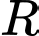 thỏa mãn
thỏa mãn 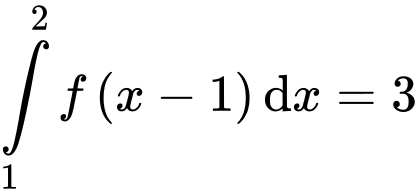 và
và 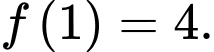 Khi đó tích phân
Khi đó tích phân 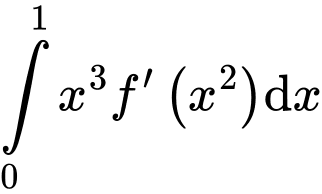 bằng
bằng A, 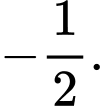
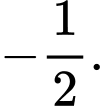
B, 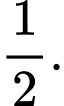
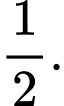
C, 

D, 1.
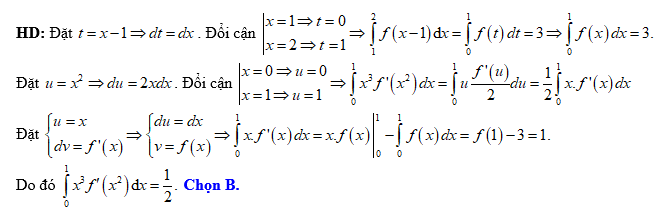 Đáp án: B
Đáp án: B
Câu 15 [140551]: Cho hàm số 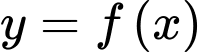 thỏa mãn điều kiện
thỏa mãn điều kiện 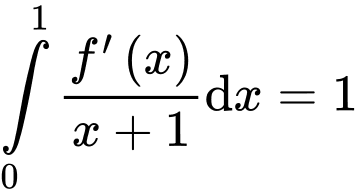 và
và 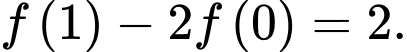 Tính tích phân
Tính tích phân 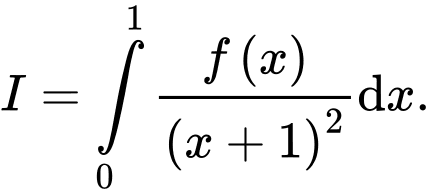
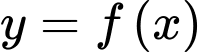 thỏa mãn điều kiện
thỏa mãn điều kiện 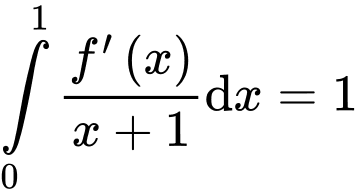 và
và 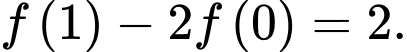 Tính tích phân
Tính tích phân 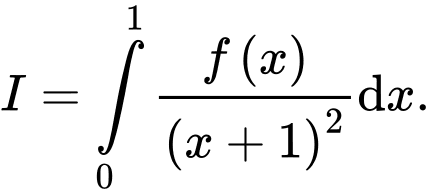
A, 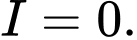
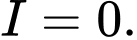
B, 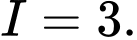
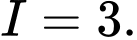
C, 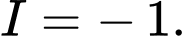
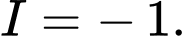
D, 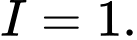
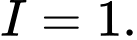
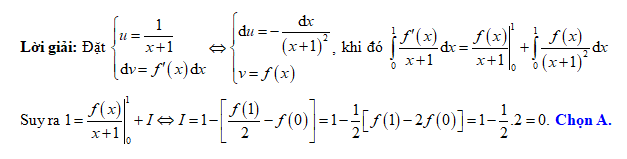 Đáp án: A
Đáp án: A
Câu 16 [146743]: Cho hàm số 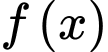 có
có 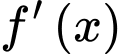 và
và 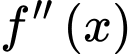 liên tục trên đoạn
liên tục trên đoạn 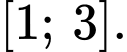 Biết
Biết 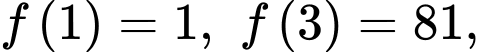
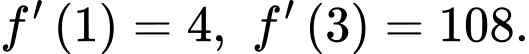 Giá trị của
Giá trị của 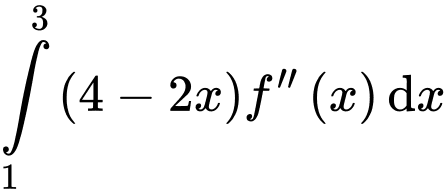 bằng
bằng
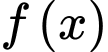 có
có 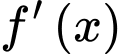 và
và 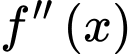 liên tục trên đoạn
liên tục trên đoạn 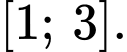 Biết
Biết 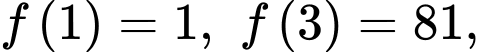
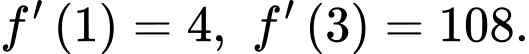 Giá trị của
Giá trị của 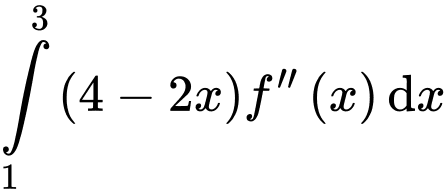 bằng
bằng A, 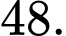
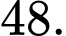
B, 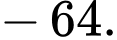
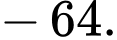
C, 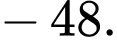
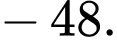
D, 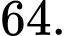
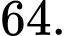
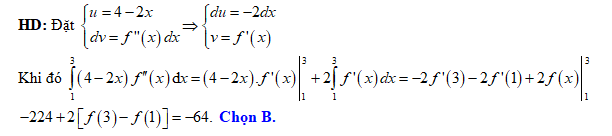 Đáp án: B
Đáp án: B
Câu 17 [149496]: Cho hàm số 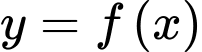 liên tục và có đạo hàm trên
liên tục và có đạo hàm trên 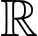 thỏa mãn
thỏa mãn 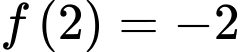 ;
; 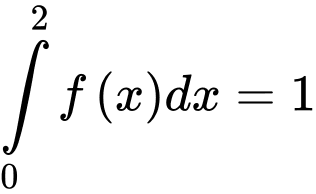 . Tính tích phân
. Tính tích phân 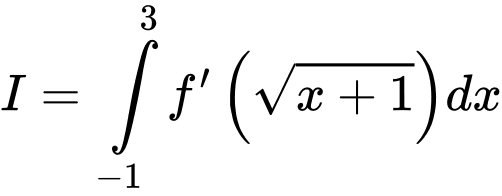 .
.
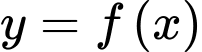 liên tục và có đạo hàm trên
liên tục và có đạo hàm trên 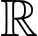 thỏa mãn
thỏa mãn 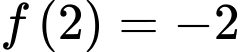 ;
; 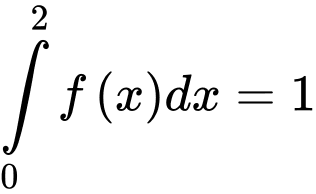 . Tính tích phân
. Tính tích phân 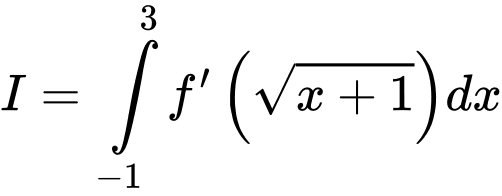 .
. A, 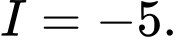
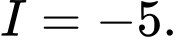
B, 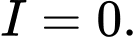
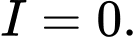
C, 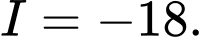
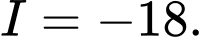
D, 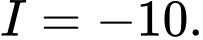
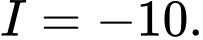
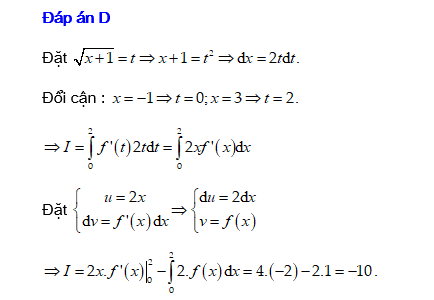 Đáp án: D
Đáp án: D
Câu 18 [516294]: Nếu 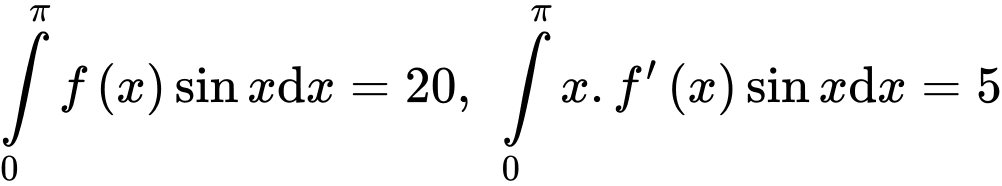 thì
thì 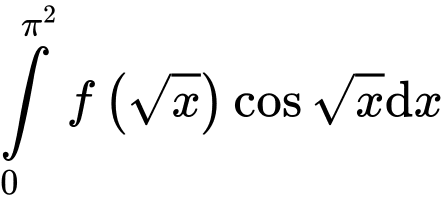 bằng
bằng
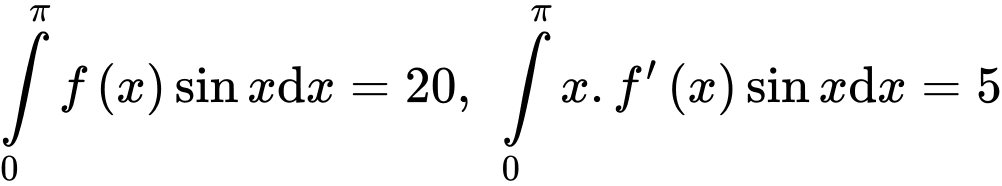 thì
thì 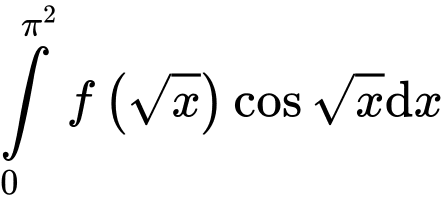 bằng
bằng A, 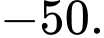
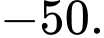
B, 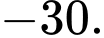
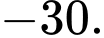
C, 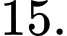
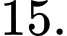
D, 
Đặt 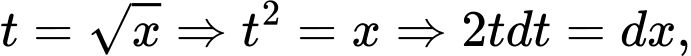 Khi đó:
Khi đó:
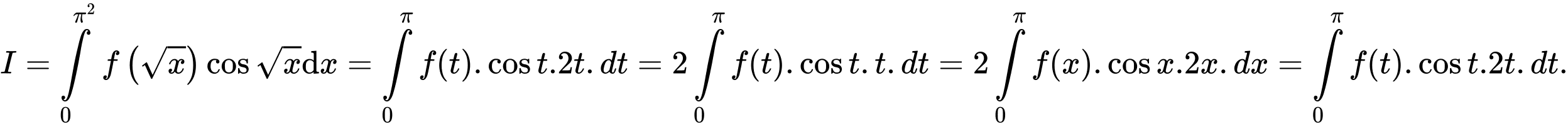
Đặt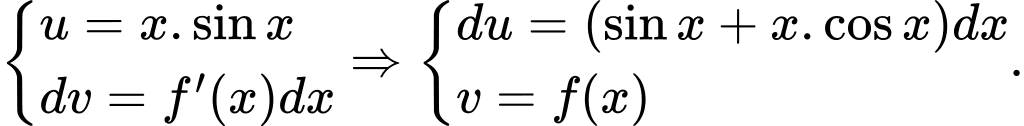
Khi đó: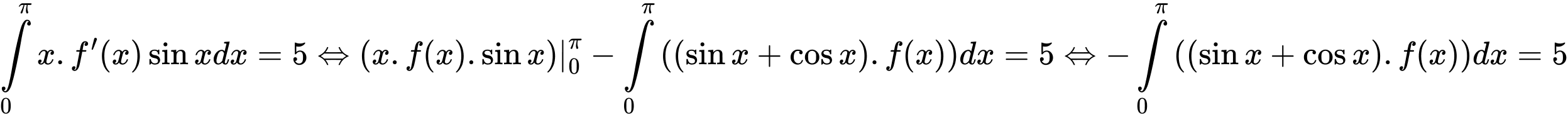
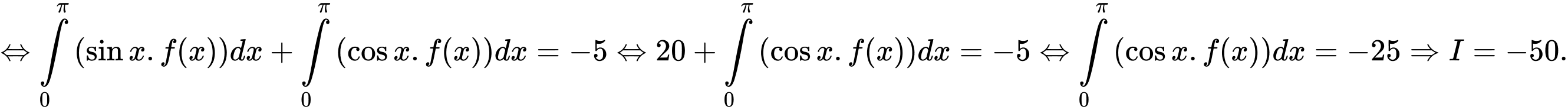
Chọn đáp án A. Đáp án: A
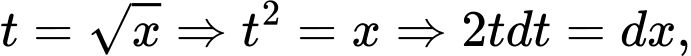 Khi đó:
Khi đó: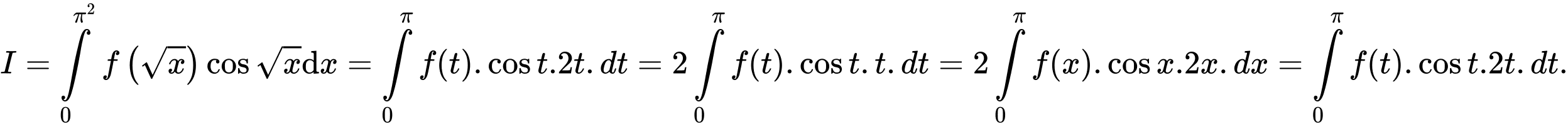
Đặt
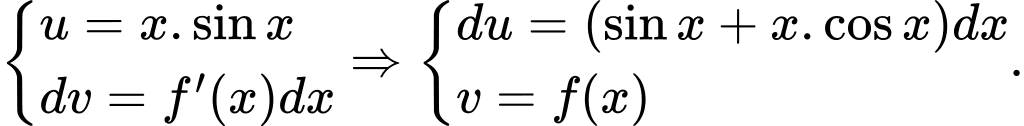
Khi đó:
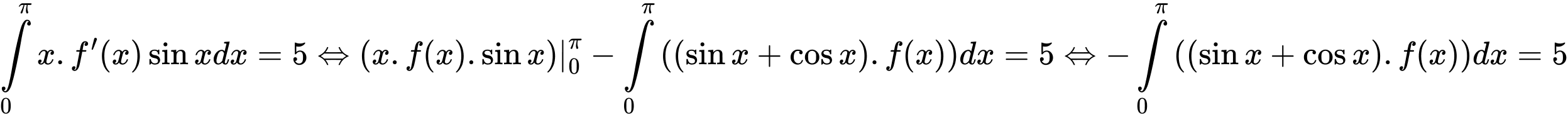
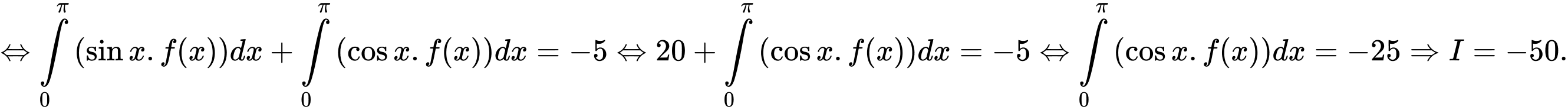
Chọn đáp án A. Đáp án: A
Câu 19 [516297]: Cho hàm số 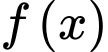 có đạo hàm trên
có đạo hàm trên 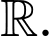 Biết
Biết 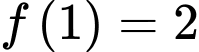 và
và 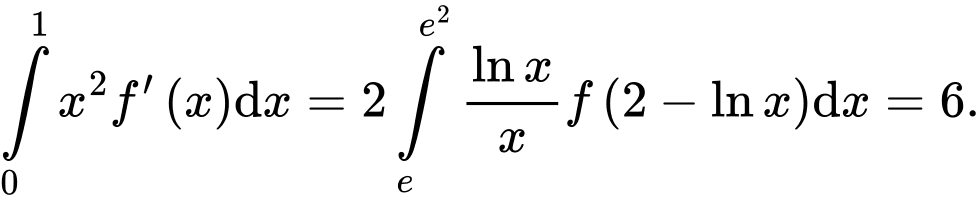 Giá trị của
Giá trị của 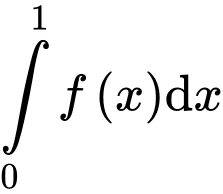 bằng
bằng
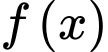 có đạo hàm trên
có đạo hàm trên 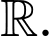 Biết
Biết 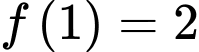 và
và 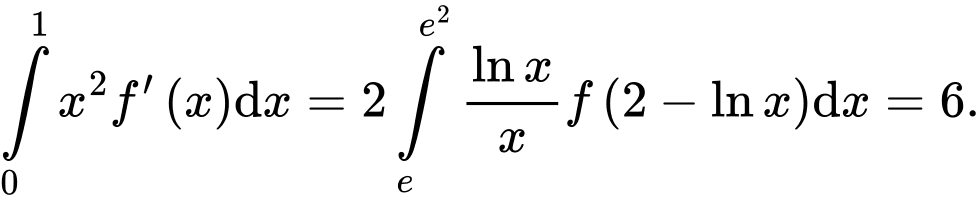 Giá trị của
Giá trị của 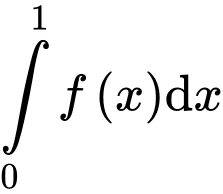 bằng
bằng A, 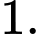
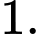
B, 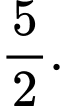
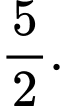
C, 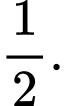
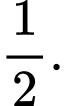
D, 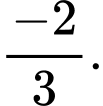
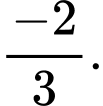
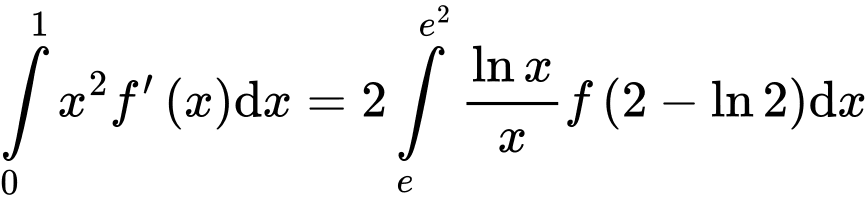
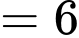
Đặt
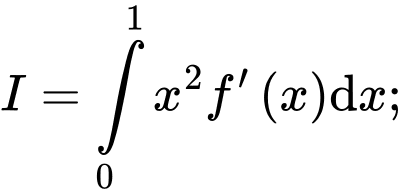
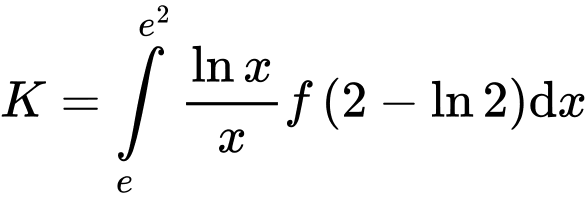
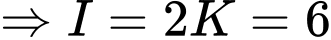
Tính
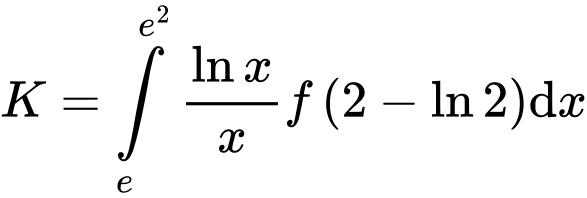
Đặt
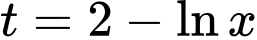
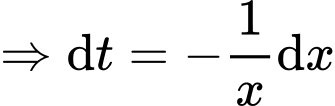 đổi cận
đổi cận 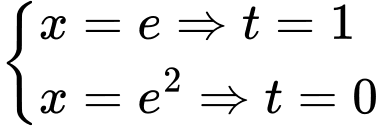
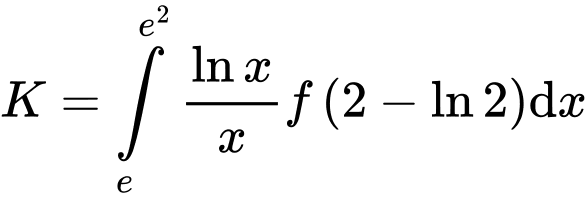
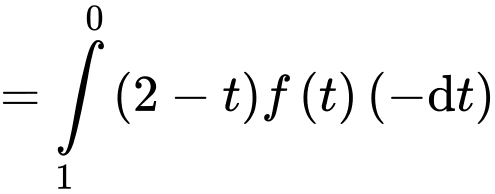
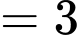
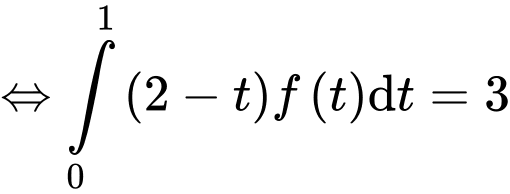
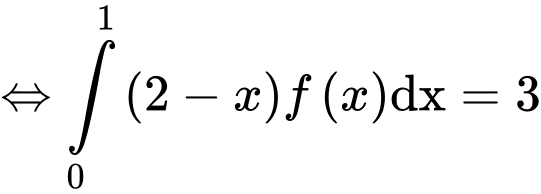
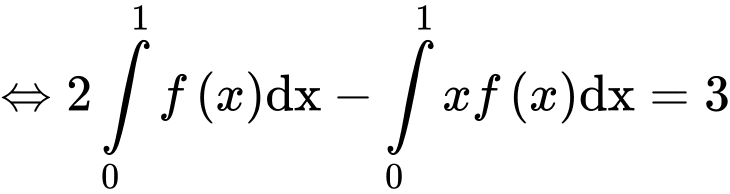 (1)
(1)
Tính
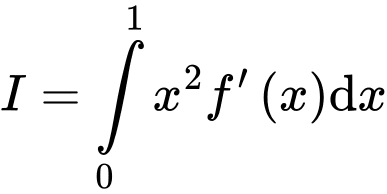
Đặt
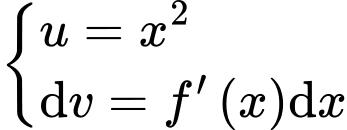
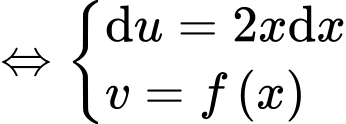
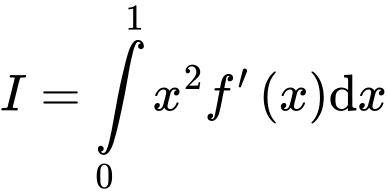
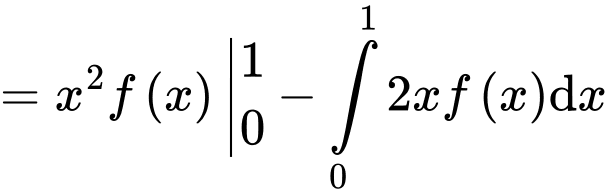
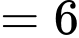
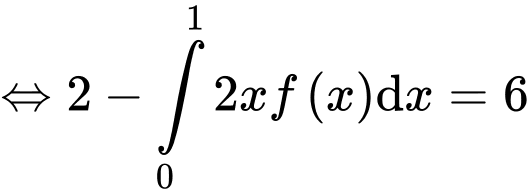
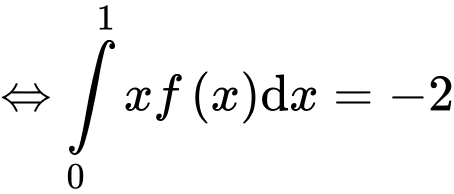 (2)
(2)
Từ (1) và (2) ta suy ra:
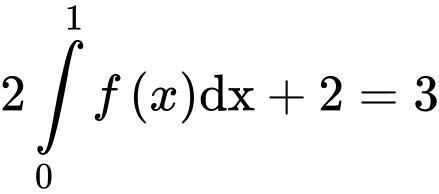
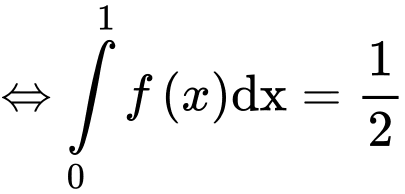
Đáp án C Đáp án: C
Câu 20 [907820]: Cho hàm số 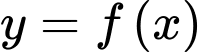 có đạo hàm trên . Biết
có đạo hàm trên . Biết 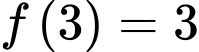 và
và 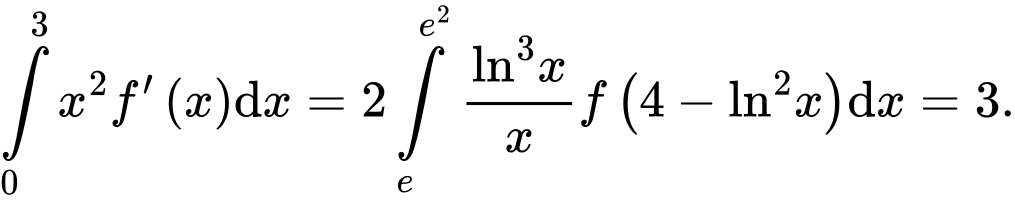 Giá trị của
Giá trị của 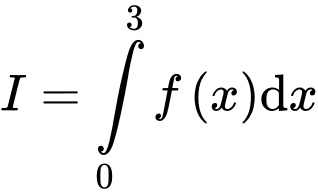 bằng
bằng
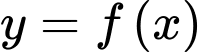 có đạo hàm trên . Biết
có đạo hàm trên . Biết 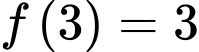 và
và 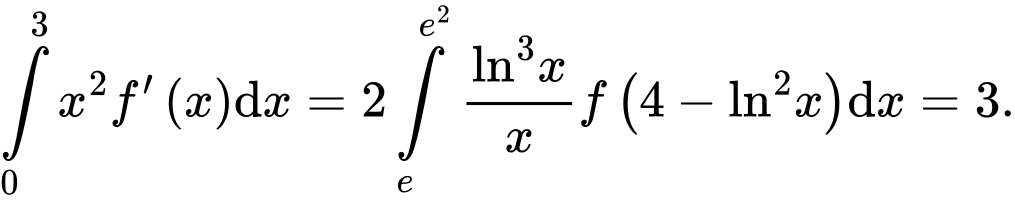 Giá trị của
Giá trị của 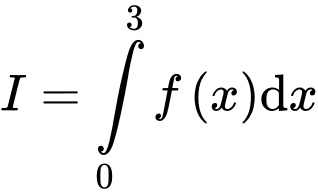 bằng
bằng A, 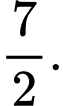
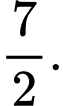
B, 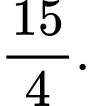
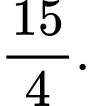
C, 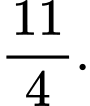
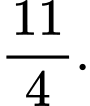
D, 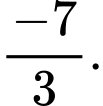
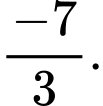
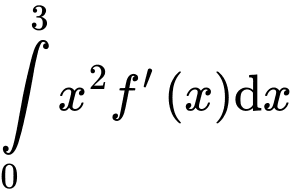
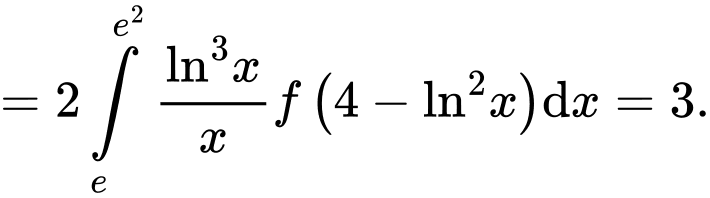
Xét
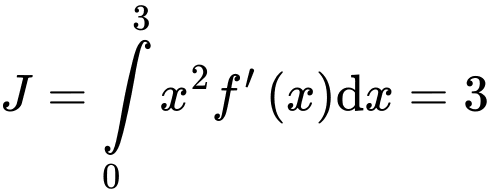
Đặt
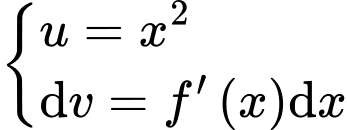
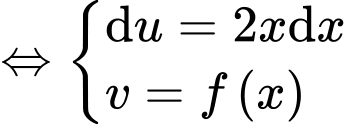
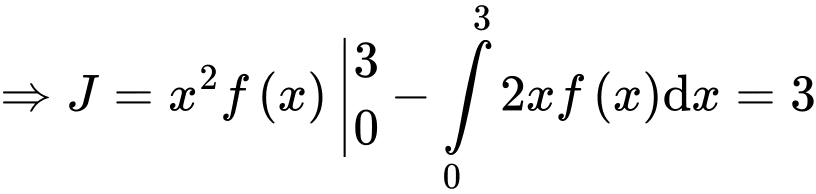
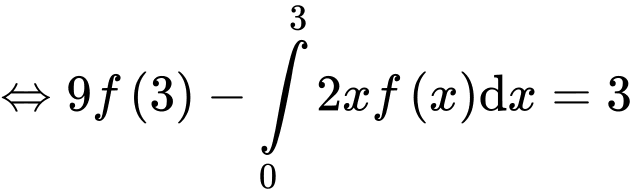
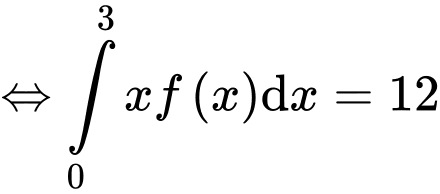
Xét
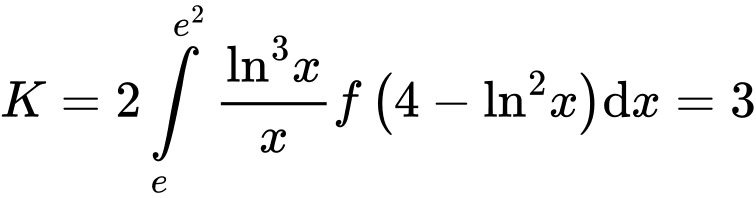
Đặt
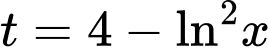
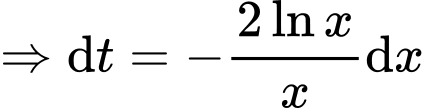
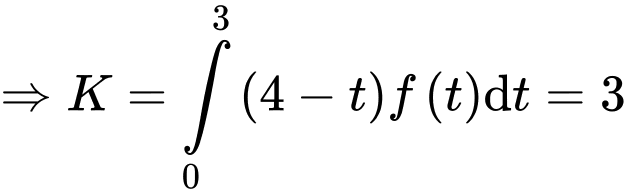
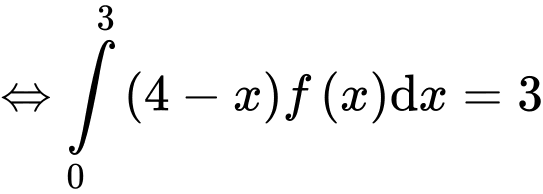
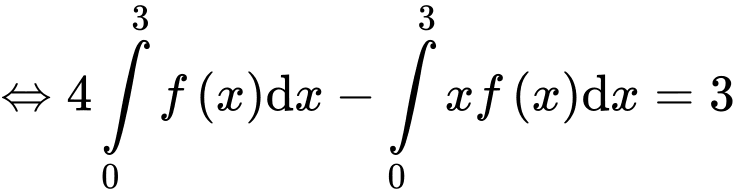
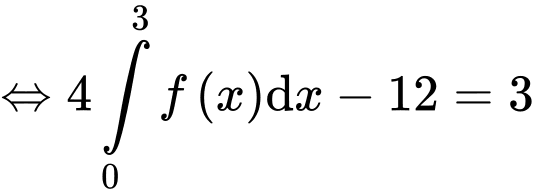
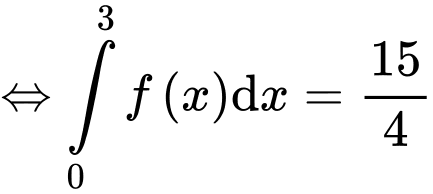
Đáp án B Đáp án: B
Câu 21 [507477]: Cho hàm số 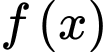 xác định và liên tục trên
xác định và liên tục trên 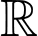 . Gọi
. Gọi 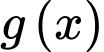 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 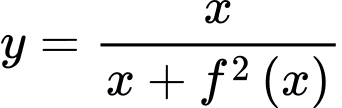 . Biết
. Biết 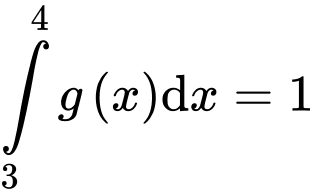 và
và 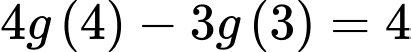 . Tích phân
. Tích phân 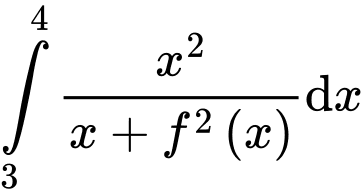 bằng
bằng
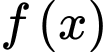 xác định và liên tục trên
xác định và liên tục trên 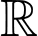 . Gọi
. Gọi 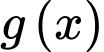 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 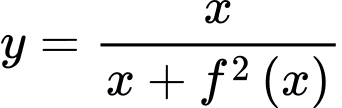 . Biết
. Biết 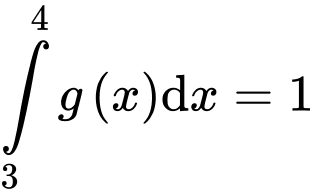 và
và 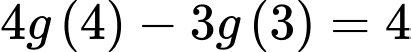 . Tích phân
. Tích phân 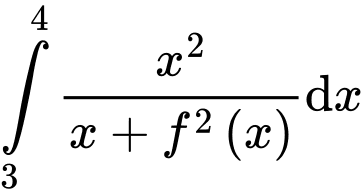 bằng
bằng A, 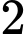 .
.
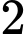 .
.B, 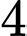 .
.
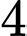 .
.C, 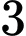 .
.
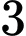 .
.D, 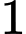 .
.
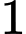 .
.
Chọn C
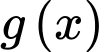 là một nguyên hàm của
là một nguyên hàm của 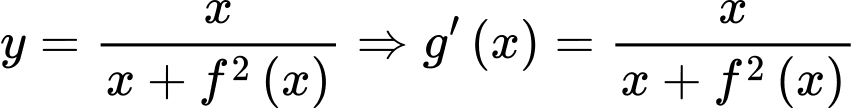 .
.
Đặt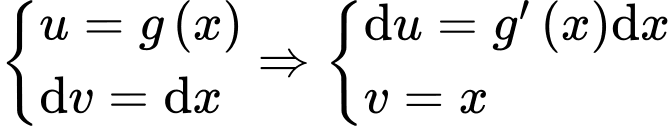
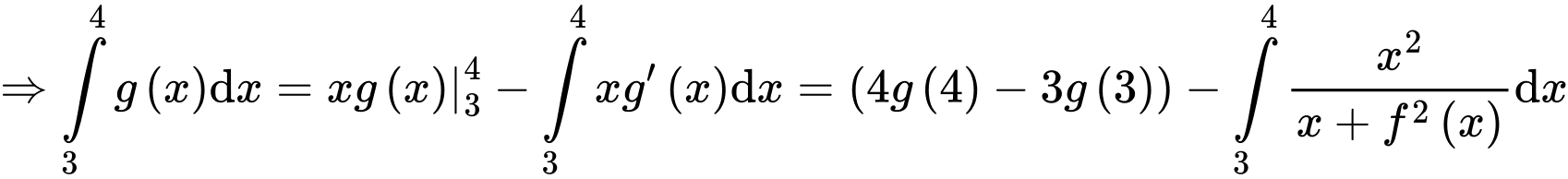
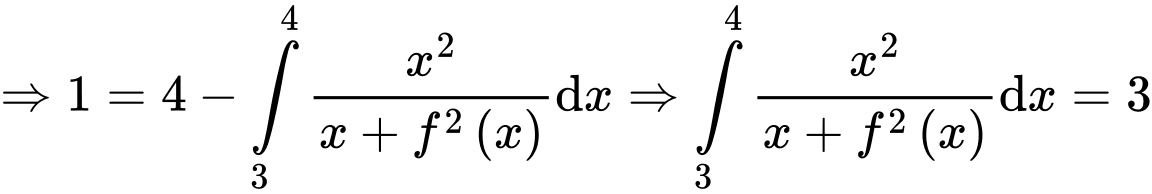 . Đáp án: C
. Đáp án: C
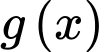 là một nguyên hàm của
là một nguyên hàm của 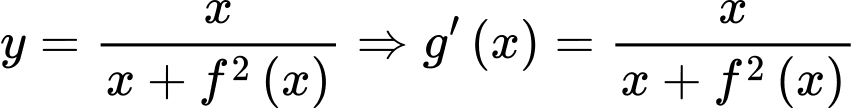 .
.Đặt
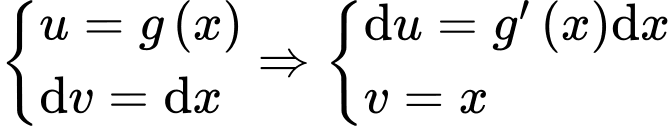
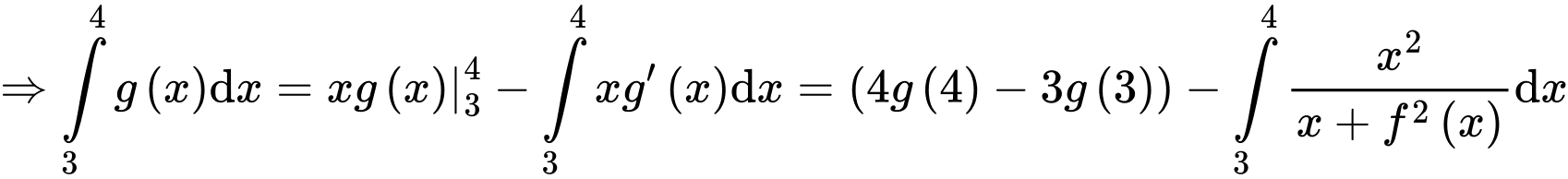
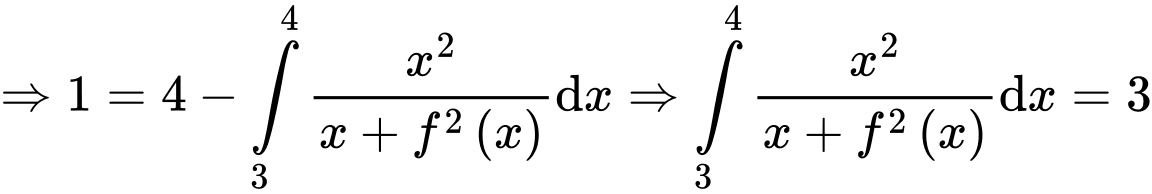 . Đáp án: C
. Đáp án: C
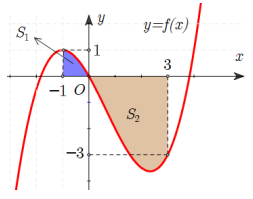
Câu 22 [906685]: Cho đồ thị hàm số 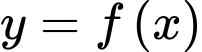 có đạo hàm liên tục trên và có đồ thị như hình vẽ bên. Diện tích hình phẳng giới hạn
có đạo hàm liên tục trên và có đồ thị như hình vẽ bên. Diện tích hình phẳng giới hạn
bởi đồ thị hàm số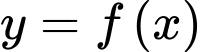 và trục hoành lần lượt là
và trục hoành lần lượt là 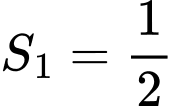 và
và 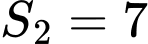 (như hình vẽ). Giá trị của
(như hình vẽ). Giá trị của 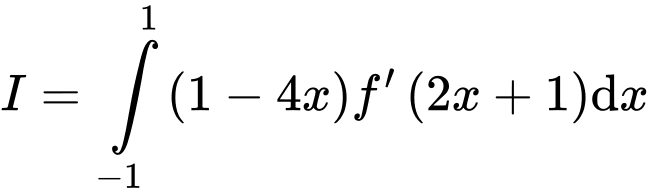 bằng
bằng
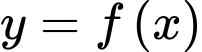 có đạo hàm liên tục trên và có đồ thị như hình vẽ bên. Diện tích hình phẳng giới hạn
có đạo hàm liên tục trên và có đồ thị như hình vẽ bên. Diện tích hình phẳng giới hạnbởi đồ thị hàm số
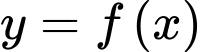 và trục hoành lần lượt là
và trục hoành lần lượt là 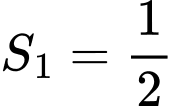 và
và 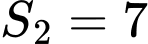 (như hình vẽ). Giá trị của
(như hình vẽ). Giá trị của 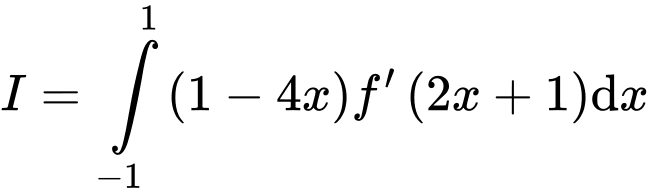 bằng
bằng 
A, 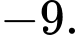
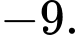
B, 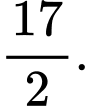
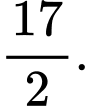
C, 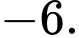
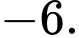
D, 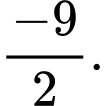
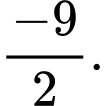
Đặt 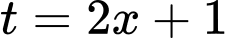
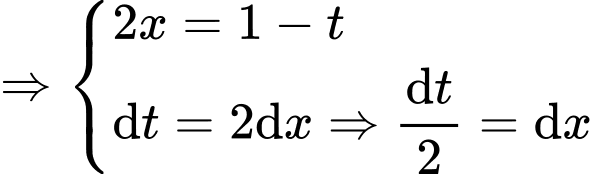
Đổi cận:
Với
Với
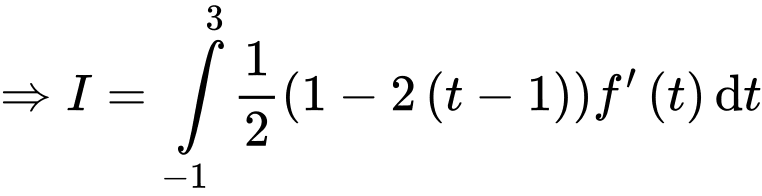
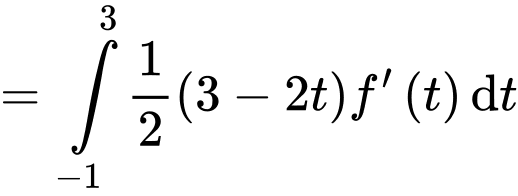
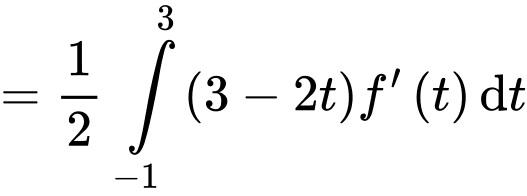
Sử dụng tích phân từng phần, ta đặt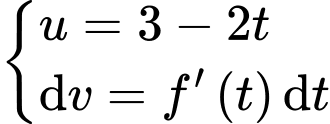
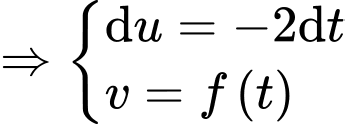
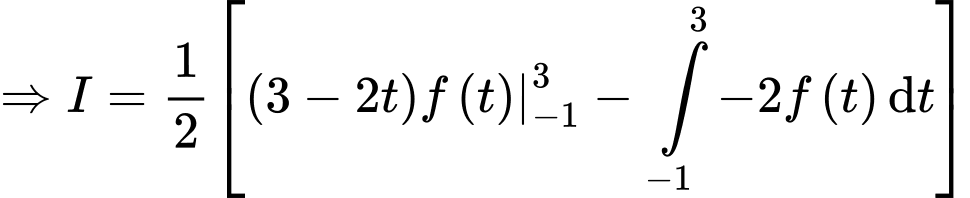
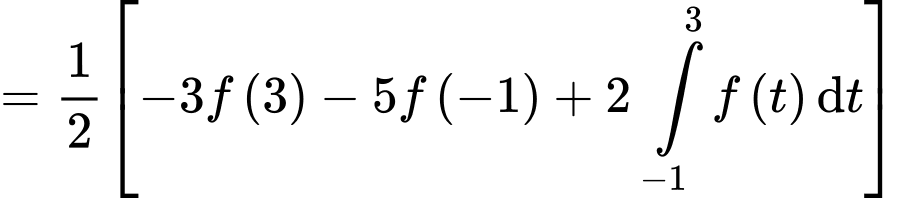 (quan sát đồ thị hàm số
(quan sát đồ thị hàm số 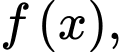 ta thấy
ta thấy 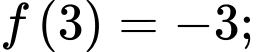
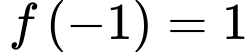 )
)
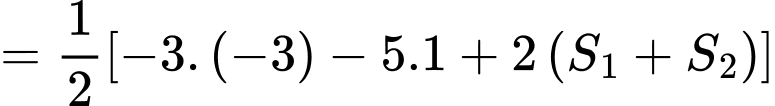
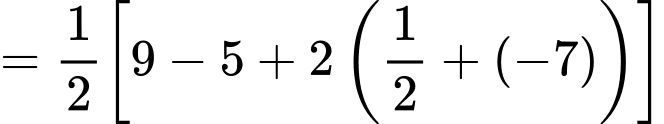
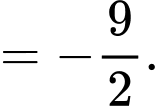
Chọn D. Đáp án: D
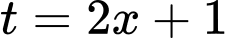
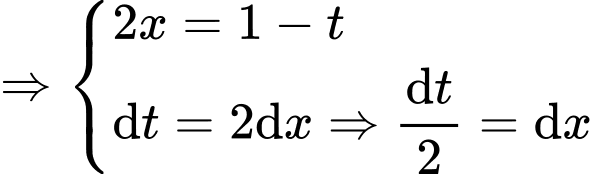
Đổi cận:
Với

Với

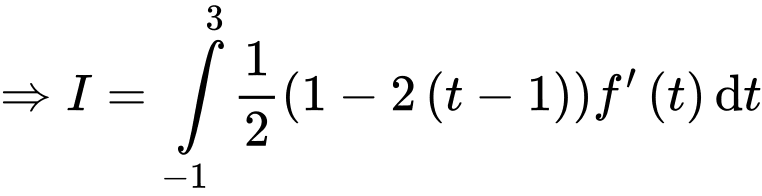
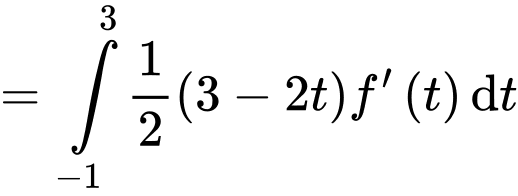
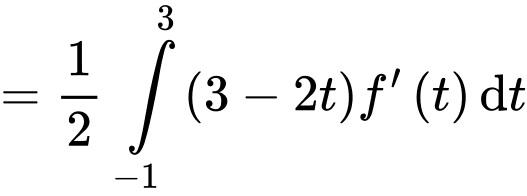
Sử dụng tích phân từng phần, ta đặt
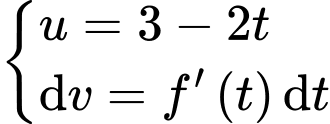
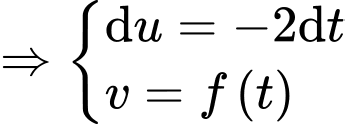
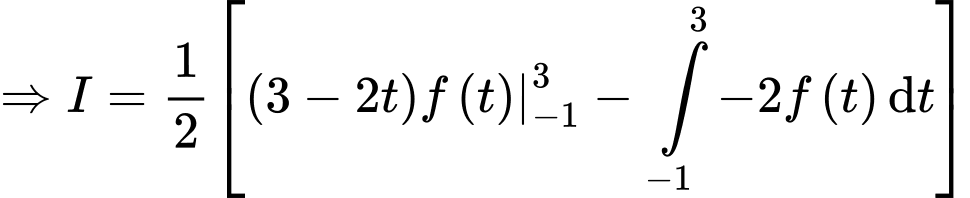
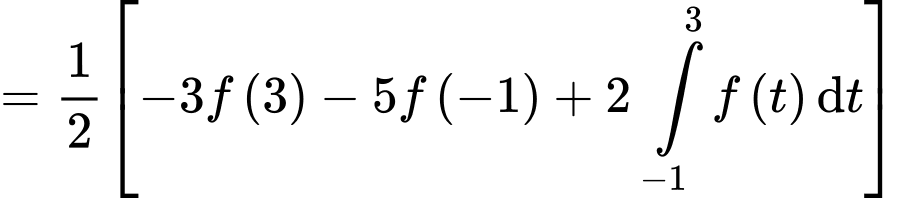 (quan sát đồ thị hàm số
(quan sát đồ thị hàm số 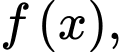 ta thấy
ta thấy 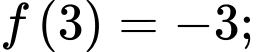
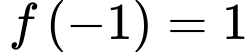 )
)
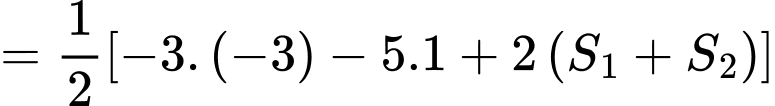
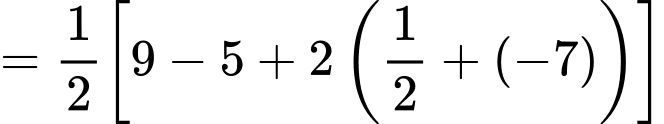
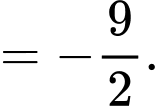
Chọn D. Đáp án: D
Câu 23 [905466]: Cho hàm số 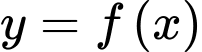 có đạo hàm liên tục trên và có đồ thị như hình vẽ. Ký hiệu
có đạo hàm liên tục trên và có đồ thị như hình vẽ. Ký hiệu 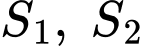 lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số
lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số 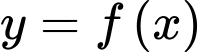 và trục hoành ( hình vẽ). Biết rằng
và trục hoành ( hình vẽ). Biết rằng 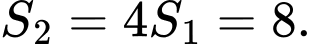 Giá trị của tích phân
Giá trị của tích phân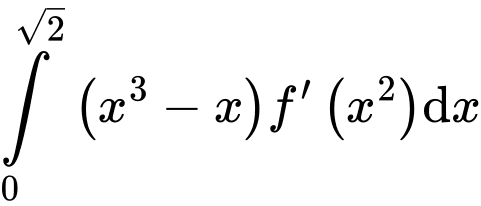 bằng
bằng 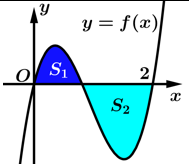
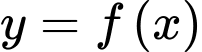 có đạo hàm liên tục trên và có đồ thị như hình vẽ. Ký hiệu
có đạo hàm liên tục trên và có đồ thị như hình vẽ. Ký hiệu 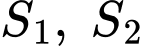 lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số
lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số 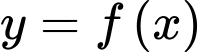 và trục hoành ( hình vẽ). Biết rằng
và trục hoành ( hình vẽ). Biết rằng 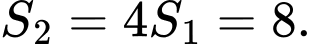 Giá trị của tích phân
Giá trị của tích phân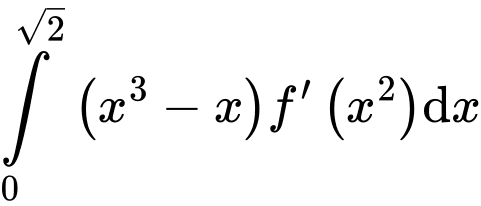 bằng
bằng 
A, 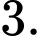
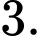
B, 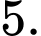
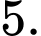
C, 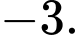
D, 
Ta có 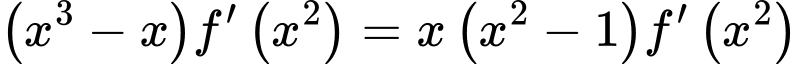
Đặt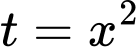

Đổi cận:
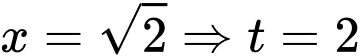
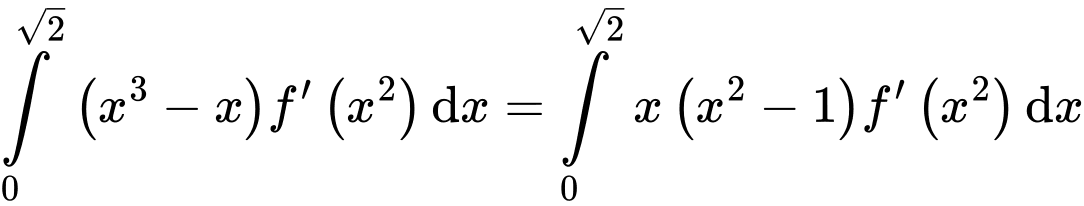
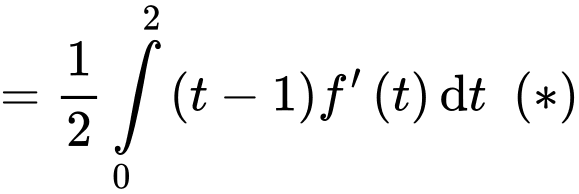
Đặt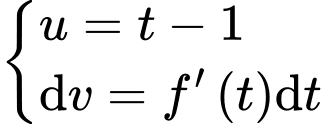
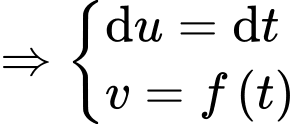
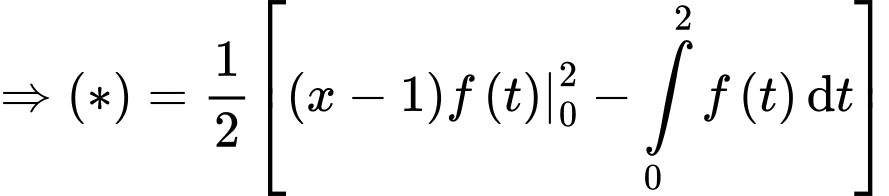
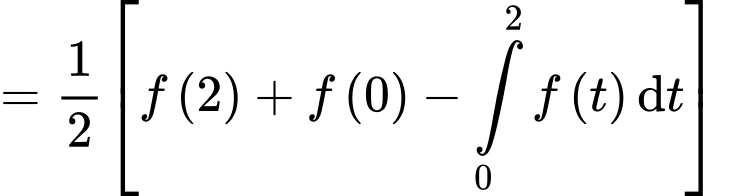 (Quan sát đồ thị hàm số
(Quan sát đồ thị hàm số 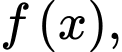 ta thấy
ta thấy 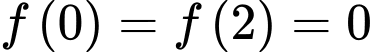 )
)
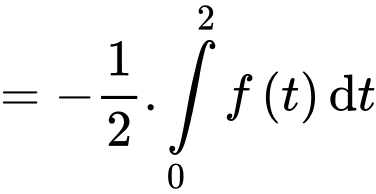
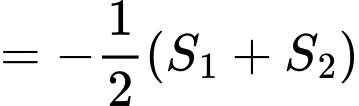
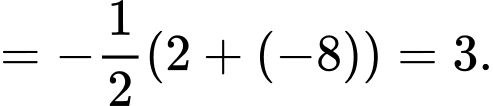
Chọn A. Đáp án: A
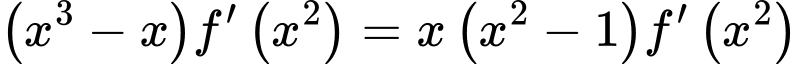
Đặt
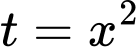

Đổi cận:

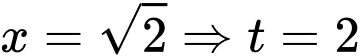
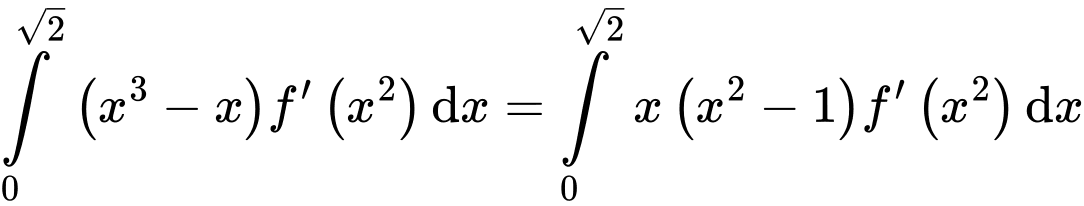
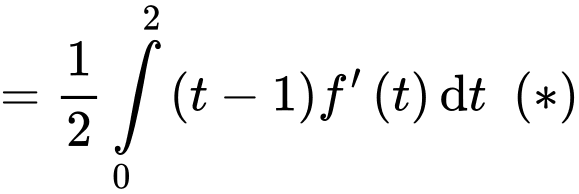
Đặt
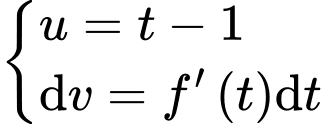
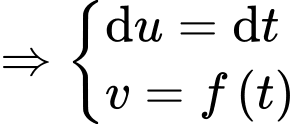
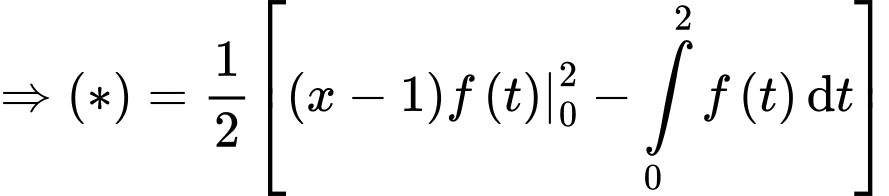
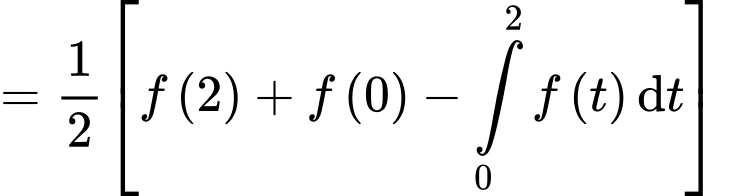 (Quan sát đồ thị hàm số
(Quan sát đồ thị hàm số 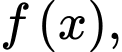 ta thấy
ta thấy 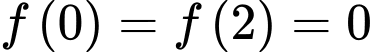 )
)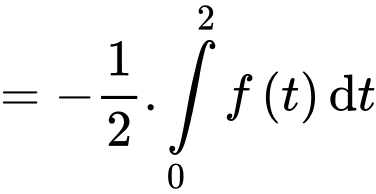
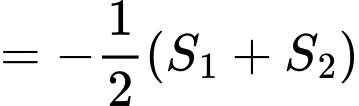
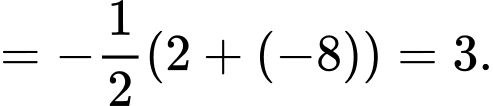
Chọn A. Đáp án: A
Câu 24 [184695]: Cho hàm số bậc hai 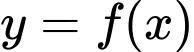 có đồ thị
có đồ thị 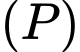 và đường thẳng
và đường thẳng 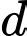 cắt
cắt 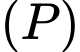 tại hai điểm như trong hình bên. Biết rằng hình phẳng giới hạn bởi
tại hai điểm như trong hình bên. Biết rằng hình phẳng giới hạn bởi 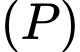 và
và 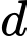 có diện tích
có diện tích 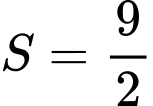 . Tích phân
. Tích phân 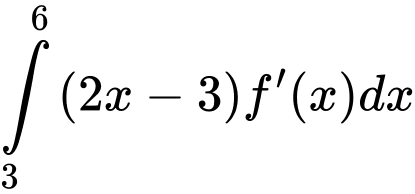 bằng
bằng
a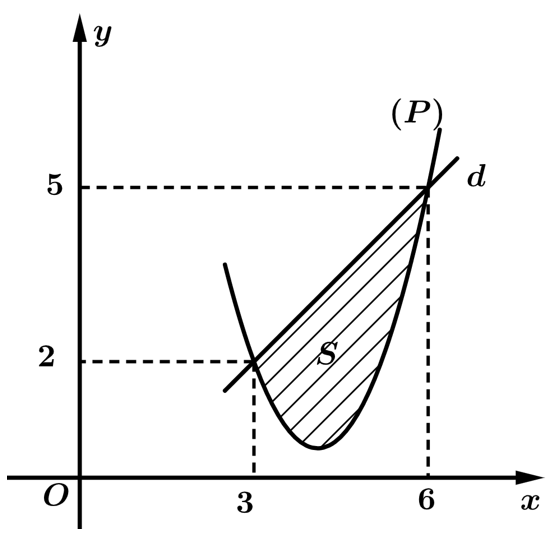
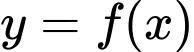 có đồ thị
có đồ thị 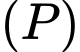 và đường thẳng
và đường thẳng 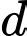 cắt
cắt 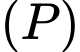 tại hai điểm như trong hình bên. Biết rằng hình phẳng giới hạn bởi
tại hai điểm như trong hình bên. Biết rằng hình phẳng giới hạn bởi 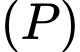 và
và 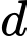 có diện tích
có diện tích 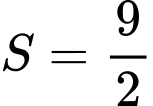 . Tích phân
. Tích phân 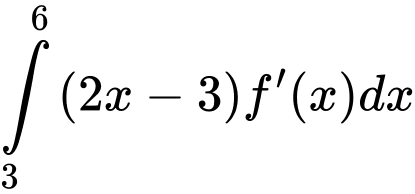 bằng
bằnga

A, 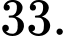
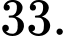
B, 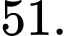
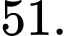
C, 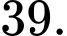
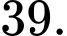
D, 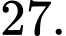
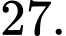
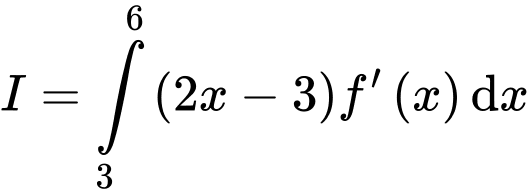
Đặt
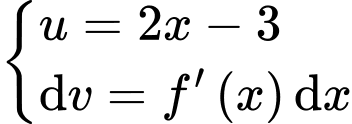
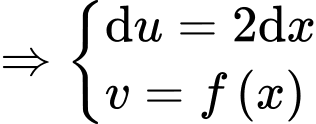
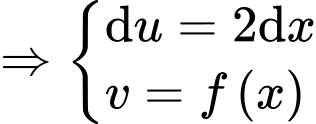
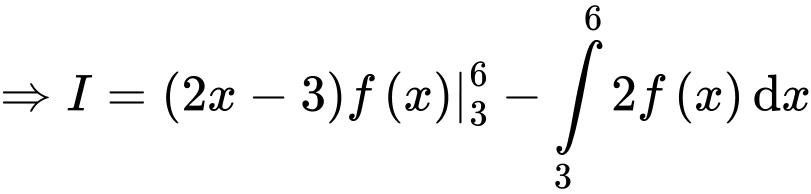
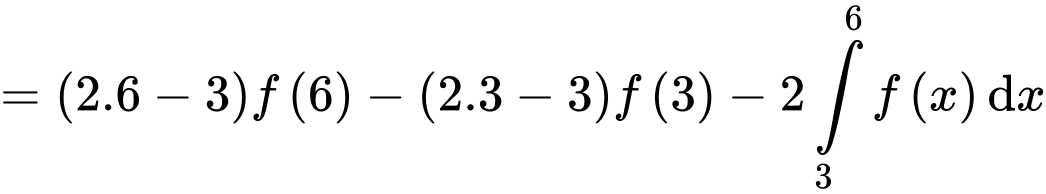
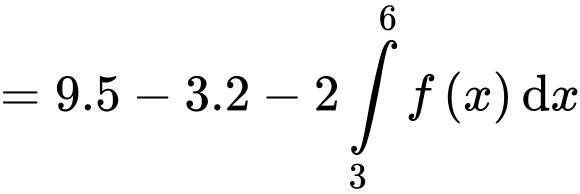
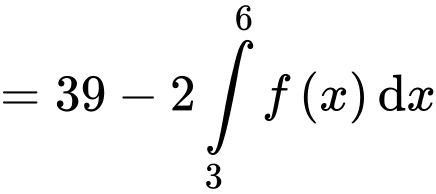
Giả sử đường thẳng
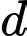 có phương trình
có phương trình 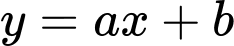
Ta kí hiệu như hình vẽ.
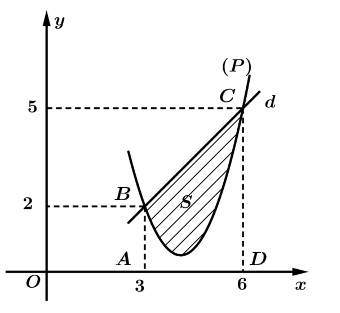
Dựa vào đồ thị hàm số ta có
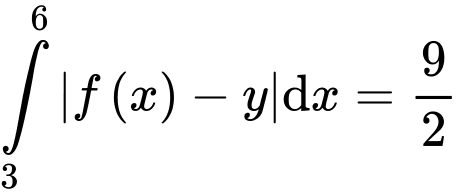
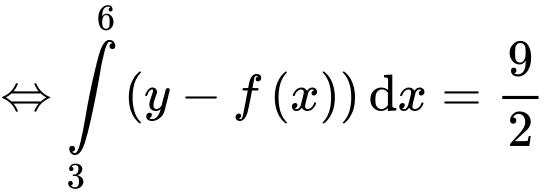
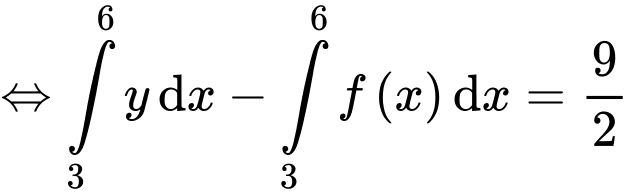
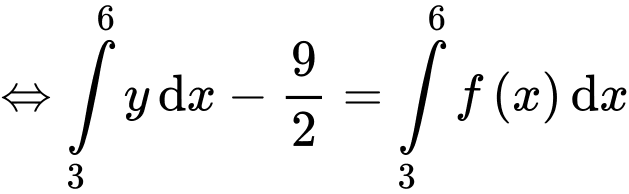
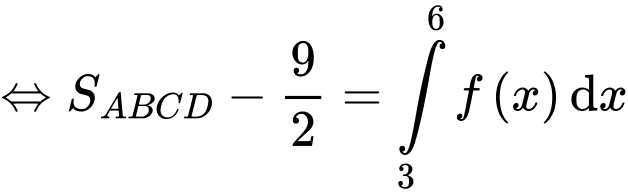
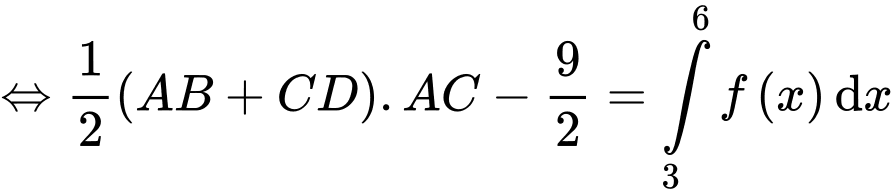
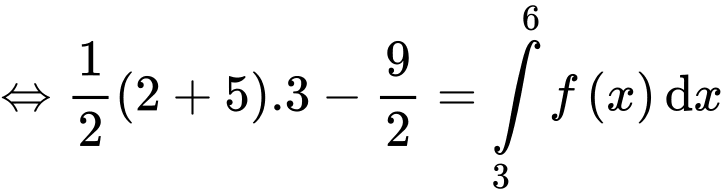
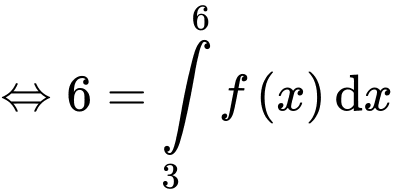
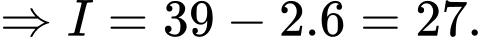
Chọn D. Đáp án: D
Câu 25 [907647]: Cho hàm số 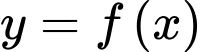 có đạo hàm trên . Biết
có đạo hàm trên . Biết 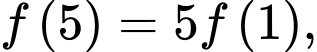 và
và 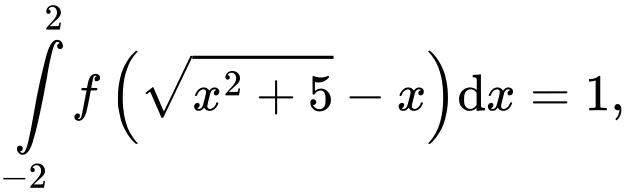
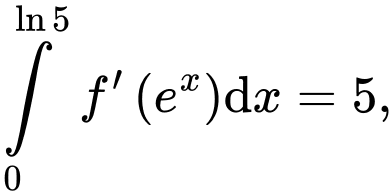 tính tích phân
tính tích phân 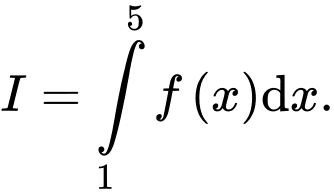
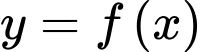 có đạo hàm trên . Biết
có đạo hàm trên . Biết 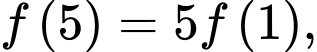 và
và 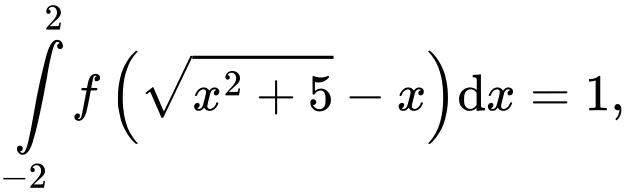
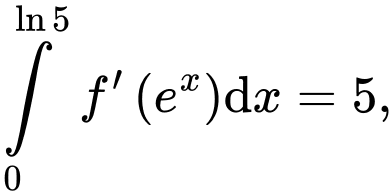 tính tích phân
tính tích phân 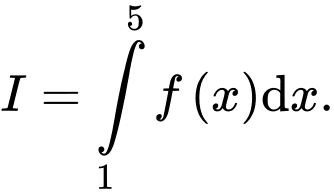
A, 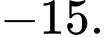
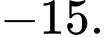
B, 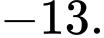
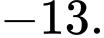
C, 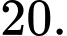
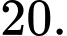
D, 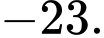
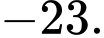
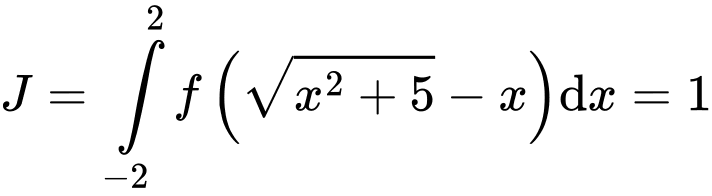
Đặt
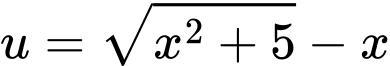
Ta có
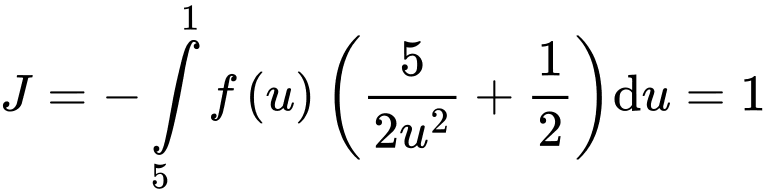
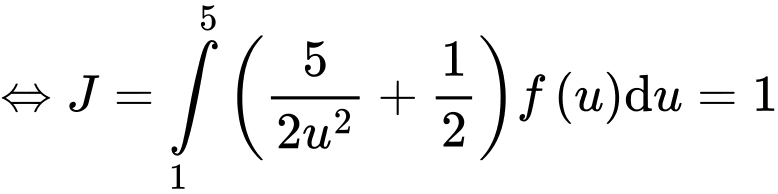
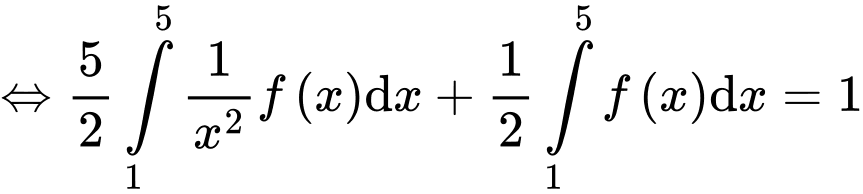
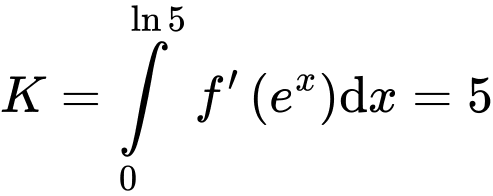
Đặt
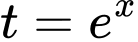
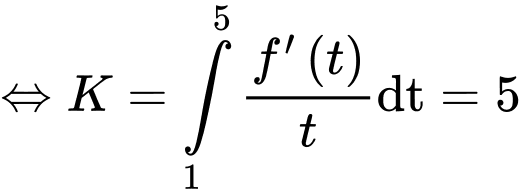
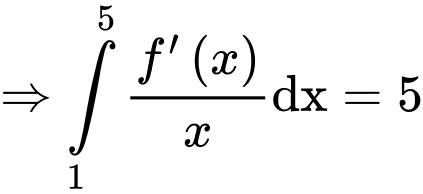
Đặt
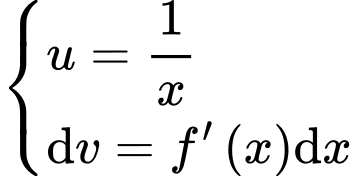
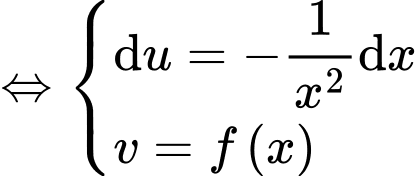
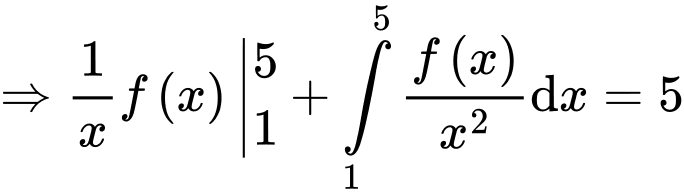
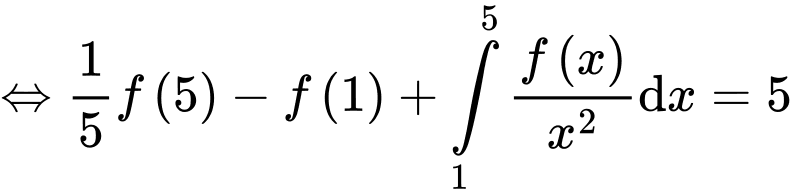
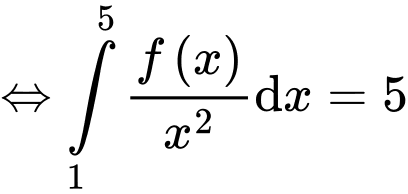
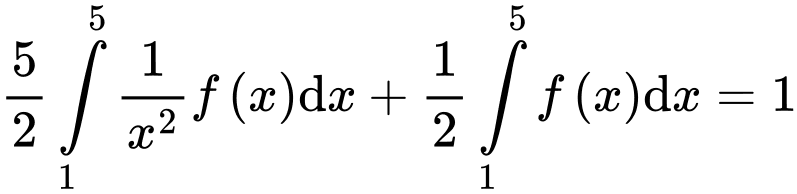
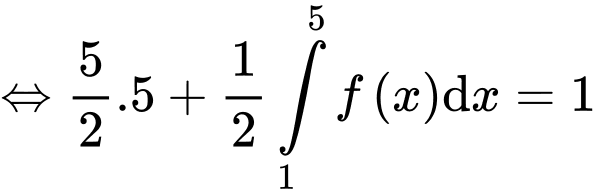
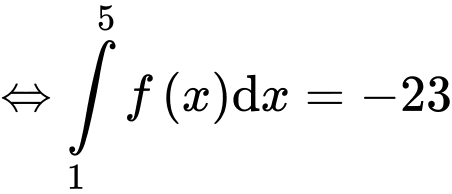
Đáp án D Đáp án: D