Đáp án Bài tập tự luyện số 1
Câu 1 [140077]: Cho hàm số 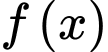 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 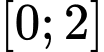 thỏa mãn
thỏa mãn 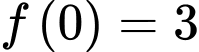 và
và 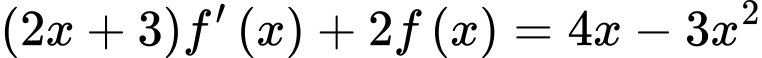 . Tính
. Tính 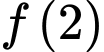 bằng
bằng
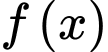 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 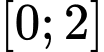 thỏa mãn
thỏa mãn 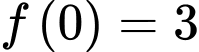 và
và 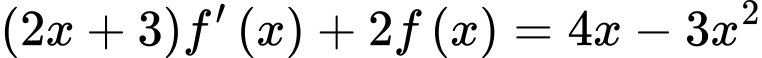 . Tính
. Tính 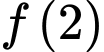 bằng
bằng A, 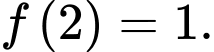
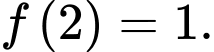
B, 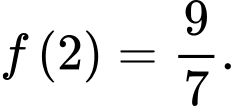
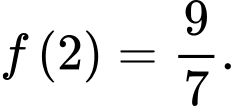
C, 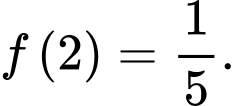
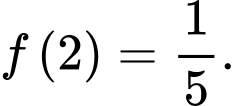
D, 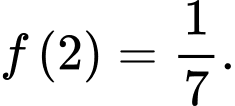
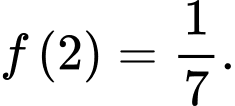
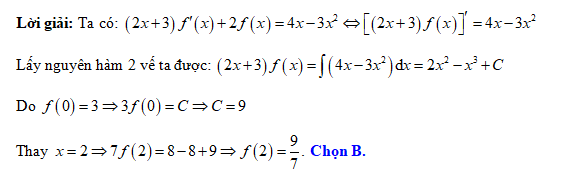 Đáp án: B
Đáp án: B
Câu 2 [140080]: Cho hàm số 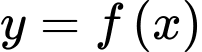 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 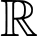 . Biết rằng
. Biết rằng 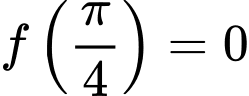 và
và 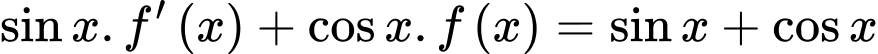 . Tính giá trị của
. Tính giá trị của 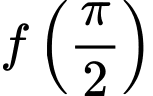 .
.
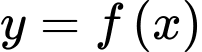 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 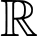 . Biết rằng
. Biết rằng 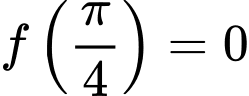 và
và 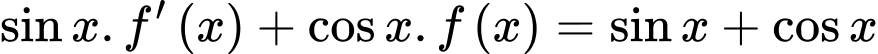 . Tính giá trị của
. Tính giá trị của 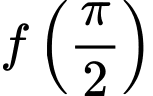 .
. A, 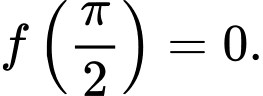
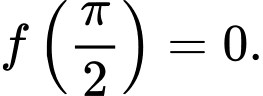
B, 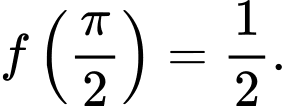
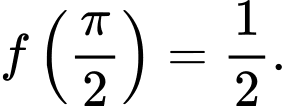
C, 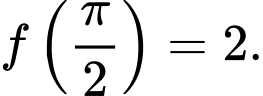
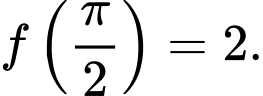
D, 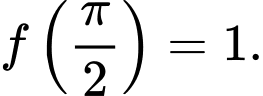
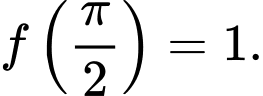
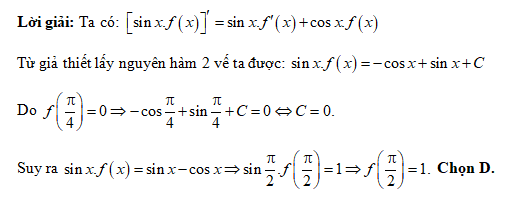 Đáp án: D
Đáp án: D
Câu 3 [136463]: Cho hàm số 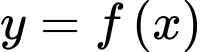 có đạo hàm liên tục trên
có đạo hàm liên tục trên 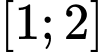 thỏa mãn
thỏa mãn 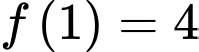 và
và 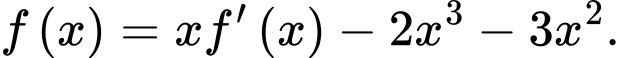 Tính giá trị
Tính giá trị 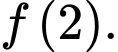
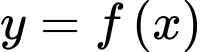 có đạo hàm liên tục trên
có đạo hàm liên tục trên 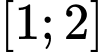 thỏa mãn
thỏa mãn 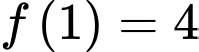 và
và 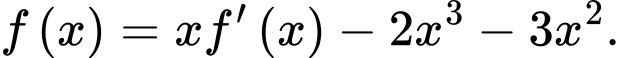 Tính giá trị
Tính giá trị 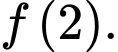
A, 5.
B, 20.
C, 10.
D, 15.
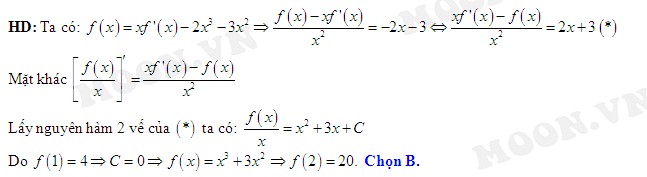 Đáp án: B
Đáp án: B
Câu 4 [140079]: Cho hàm số 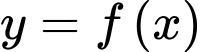 có đạo hàm liên tục trên
có đạo hàm liên tục trên 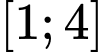 thỏa mãn
thỏa mãn 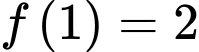 và
và 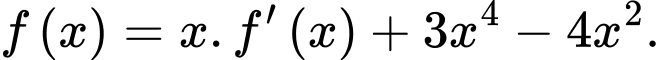 Tính giá trị
Tính giá trị 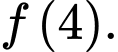
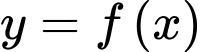 có đạo hàm liên tục trên
có đạo hàm liên tục trên 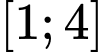 thỏa mãn
thỏa mãn 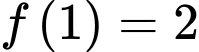 và
và 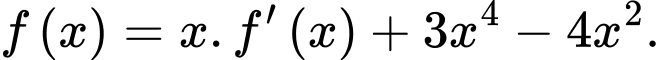 Tính giá trị
Tính giá trị 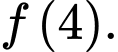
A, 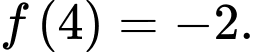
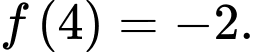
B, 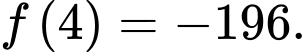
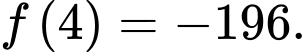
C, 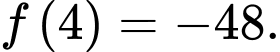
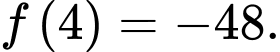
D, 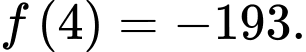
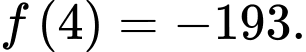
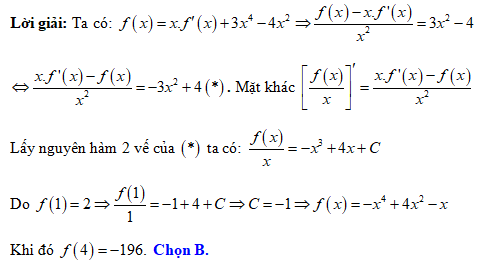 Đáp án: B
Đáp án: B
Câu 5 [136470]: (Cẩm Bình – Hà Tĩnh) Cho hàm số 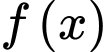 có đạo hàm liên tục trên
có đạo hàm liên tục trên 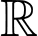 thỏa mãn
thỏa mãn 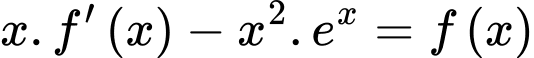 và
và 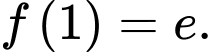 Tính tích phân
Tính tích phân 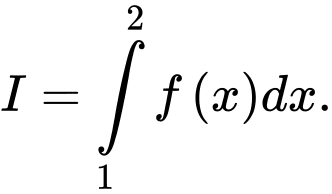
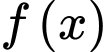 có đạo hàm liên tục trên
có đạo hàm liên tục trên 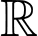 thỏa mãn
thỏa mãn 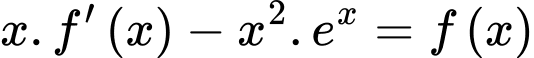 và
và 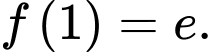 Tính tích phân
Tính tích phân 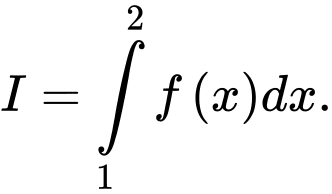
A, 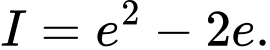
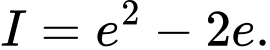
B, 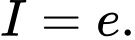
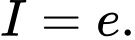
C, 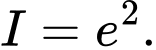
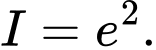
D, 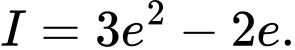
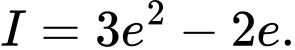
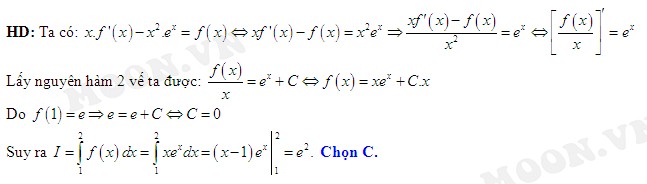 Đáp án: C
Đáp án: C
Câu 6 [11854]: Cho hàm số 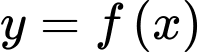 có đạo hàm cấp 2 trên
có đạo hàm cấp 2 trên 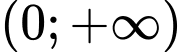 thỏa mãn
thỏa mãn 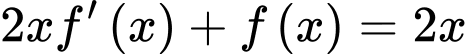 ,
,  và
và 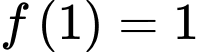 . Giá trị của biểu thức
. Giá trị của biểu thức 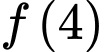 là
là
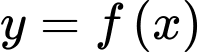 có đạo hàm cấp 2 trên
có đạo hàm cấp 2 trên 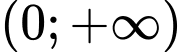 thỏa mãn
thỏa mãn 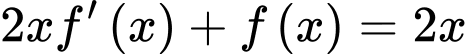 ,
,  và
và 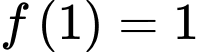 . Giá trị của biểu thức
. Giá trị của biểu thức 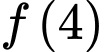 là
là A, 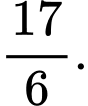
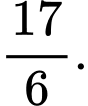
B, 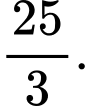
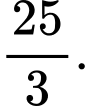
C, 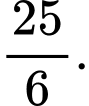
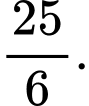
D, 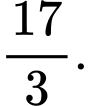
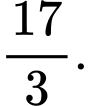
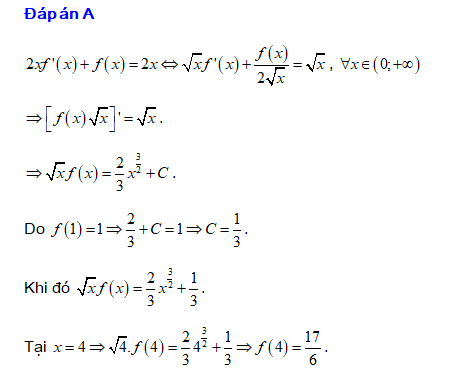 Đáp án: A
Đáp án: A
Câu 7 [398645]: Cho hàm số 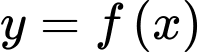 liên tục trên khoảng
liên tục trên khoảng 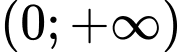 thỏa mãn
thỏa mãn 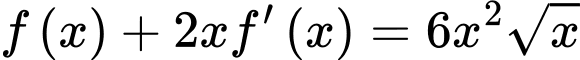 ,
,  và
và 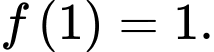 Giá trị của
Giá trị của 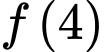 bằng
bằng
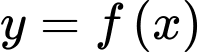 liên tục trên khoảng
liên tục trên khoảng 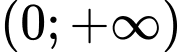 thỏa mãn
thỏa mãn 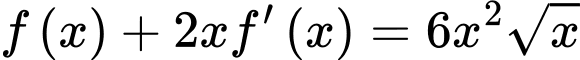 ,
,  và
và 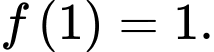 Giá trị của
Giá trị của 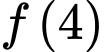 bằng
bằng A, 69.
B, 16.
C, 96.
D, 32.
Chọn D
Theo giả thiết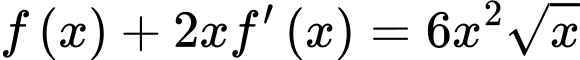 ,
, 

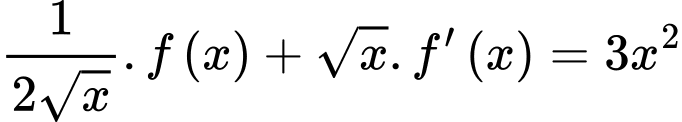

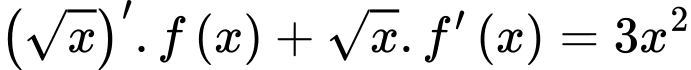

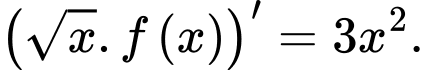 Lấy nguyên hàm cả hai vế ta được
Lấy nguyên hàm cả hai vế ta được 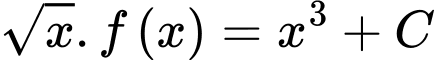
Vì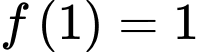 nên
nên  Do đó
Do đó  Vậy
Vậy 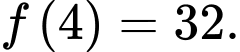 Đáp án: D
Đáp án: D
Theo giả thiết
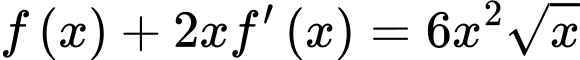 ,
, 

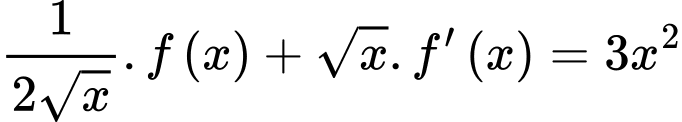

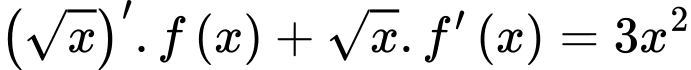

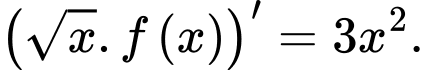 Lấy nguyên hàm cả hai vế ta được
Lấy nguyên hàm cả hai vế ta được 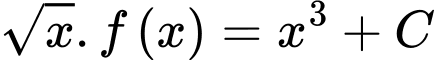
Vì
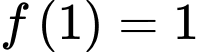 nên
nên  Do đó
Do đó  Vậy
Vậy 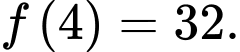 Đáp án: D
Đáp án: D
Câu 8 [398638]: Cho hàm số 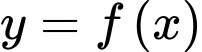 có đạo hàm trên
có đạo hàm trên 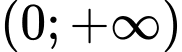 và thỏa mãn
và thỏa mãn 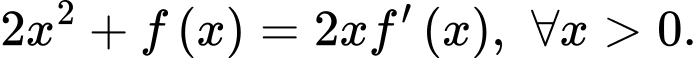 Biết
Biết 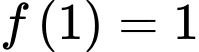 , giá trị của
, giá trị của 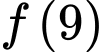 bằng
bằng
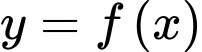 có đạo hàm trên
có đạo hàm trên 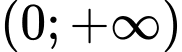 và thỏa mãn
và thỏa mãn 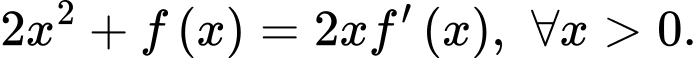 Biết
Biết 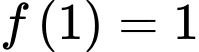 , giá trị của
, giá trị của 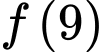 bằng
bằng A, 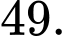
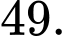
B, 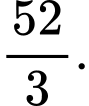
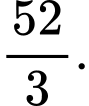
C, 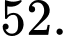
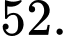
D, 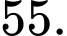
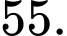
Chọn D
Với , ta có:
, ta có:
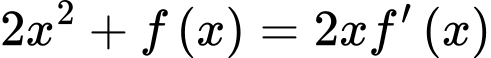
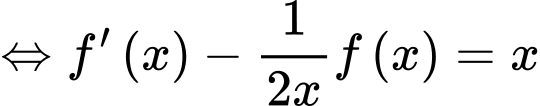
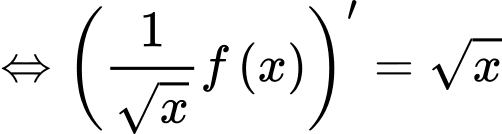
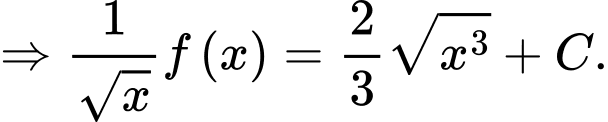
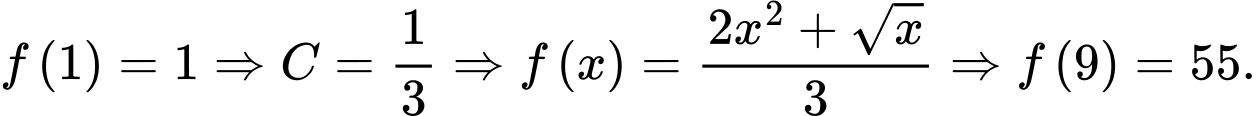 Đáp án: D
Đáp án: D
Với
 , ta có:
, ta có: 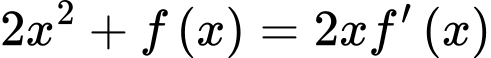
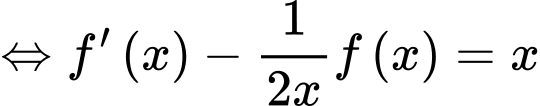
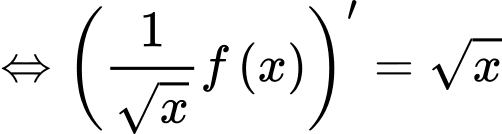
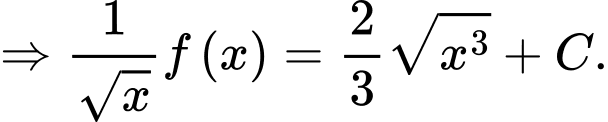
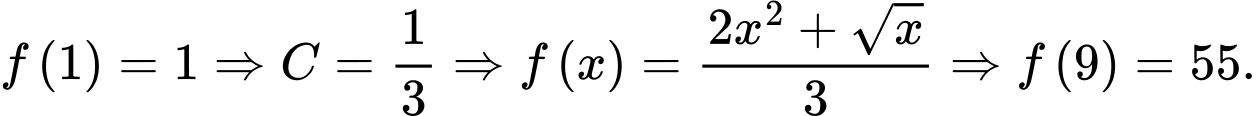 Đáp án: D
Đáp án: D
Câu 9 [150055]: [Trích đề MH ĐGNL Hà Nội]: Cho hàm số 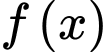 xác định và có đạo hàm trên khoảng
xác định và có đạo hàm trên khoảng 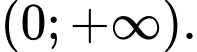 Biết rằng
Biết rằng 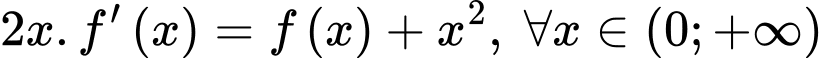 và
và 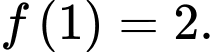 Tính
Tính 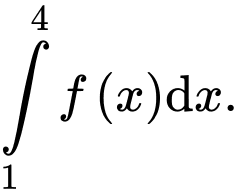
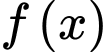 xác định và có đạo hàm trên khoảng
xác định và có đạo hàm trên khoảng 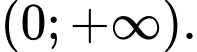 Biết rằng
Biết rằng 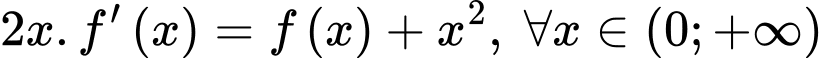 và
và 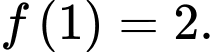 Tính
Tính 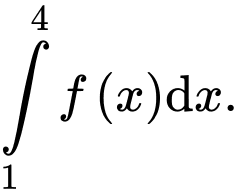
A, 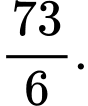
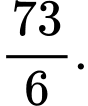
B, 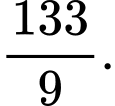
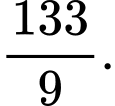
C, 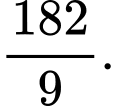
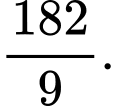
D, 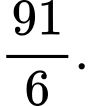
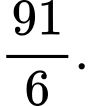
Ta có: 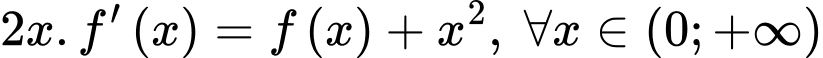
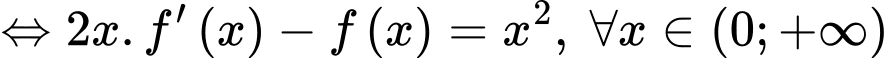
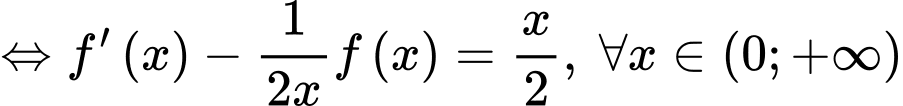
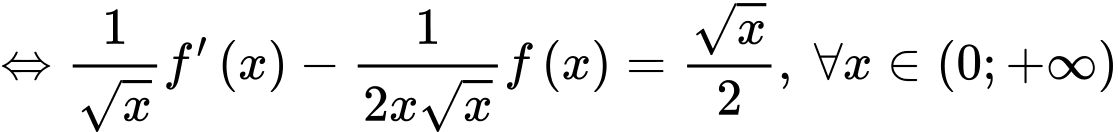
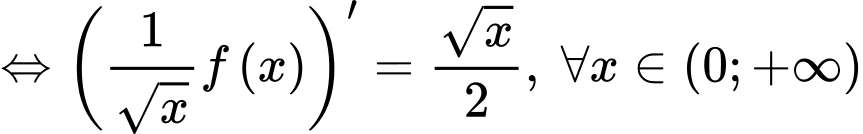
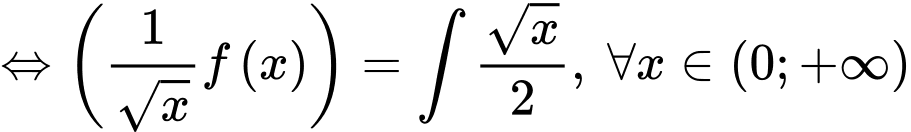
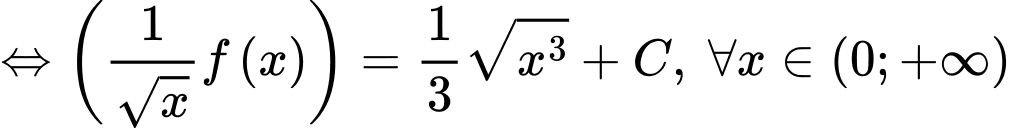
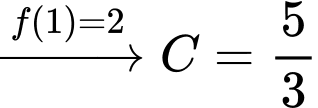
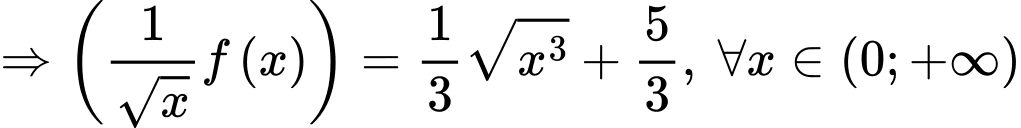
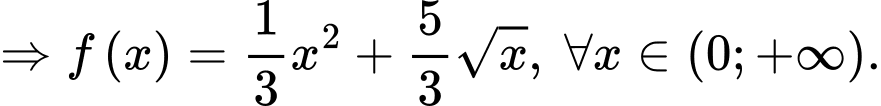
Vậy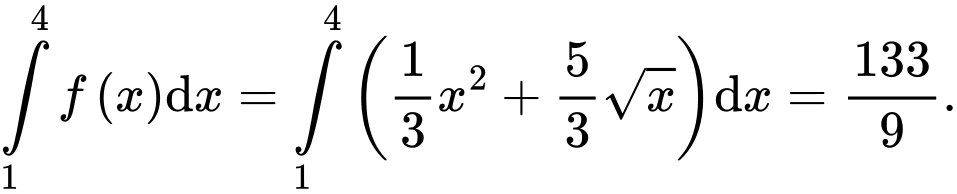 Đáp án: B
Đáp án: B
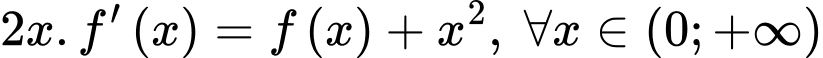
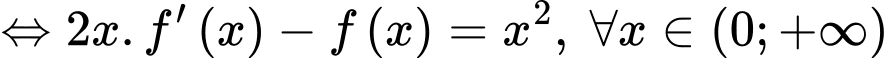
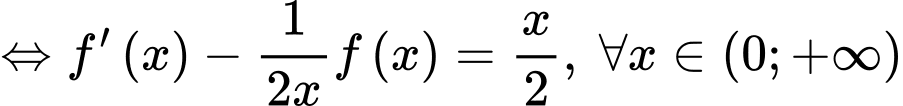
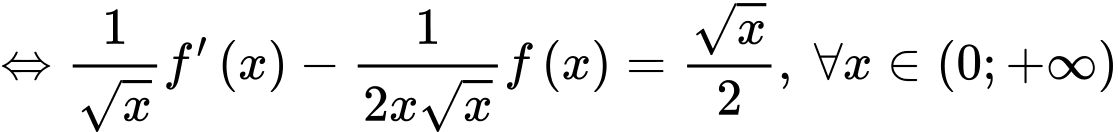
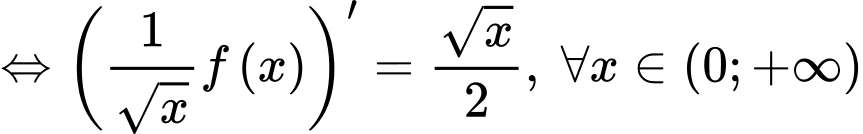
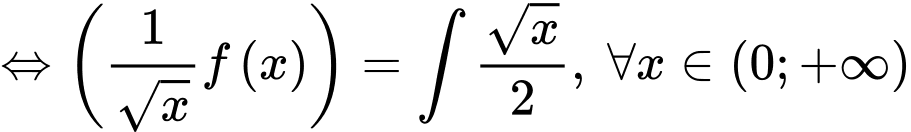
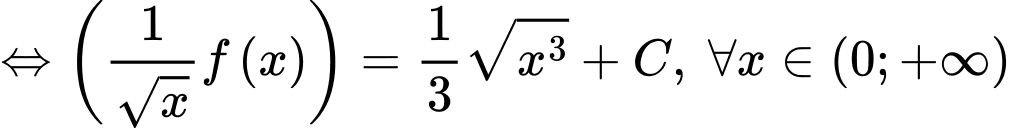
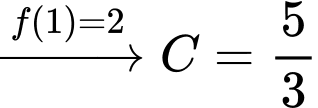
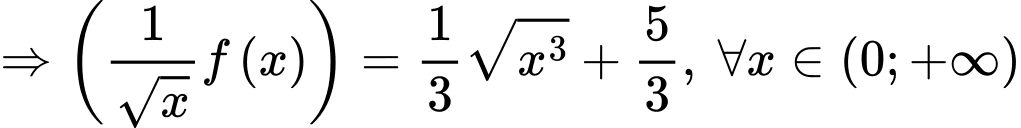
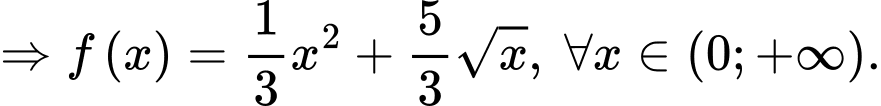
Vậy
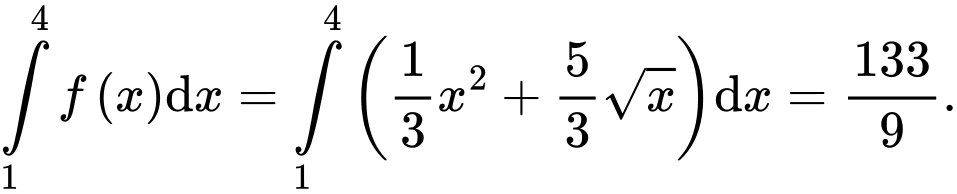 Đáp án: B
Đáp án: B
Câu 10 [136468]: (Quỳnh Lưu 1 Nghệ An – Lần 1) Cho hàm số 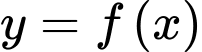 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 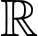 thỏa mãn
thỏa mãn 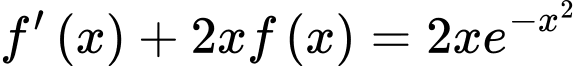 và
và 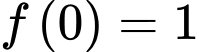 . Tính
. Tính 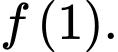
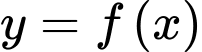 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 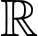 thỏa mãn
thỏa mãn 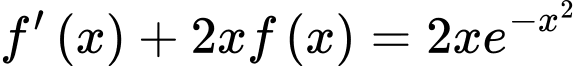 và
và 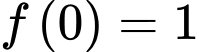 . Tính
. Tính 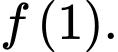
A, 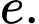
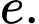
B, 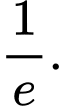
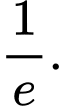
C, 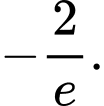
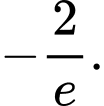
D, 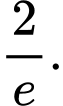
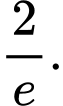
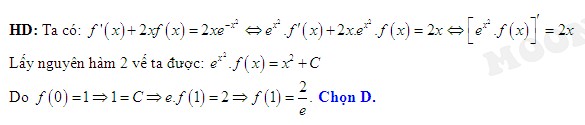 Đáp án: D
Đáp án: D
Câu 11 [151767]: Cho hàm số 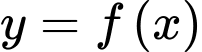 liên tục trên khoảng
liên tục trên khoảng 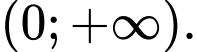 Biết
Biết 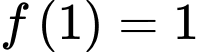 và
và 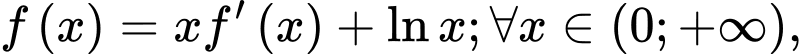 giá trị
giá trị 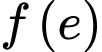 bằng
bằng
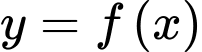 liên tục trên khoảng
liên tục trên khoảng 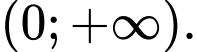 Biết
Biết 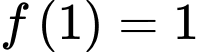 và
và 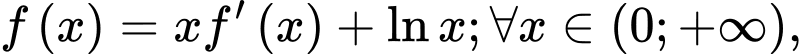 giá trị
giá trị 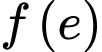 bằng
bằng A, 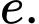
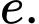
B, 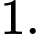
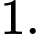
C, 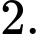
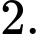
D, 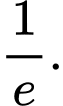
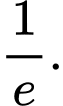
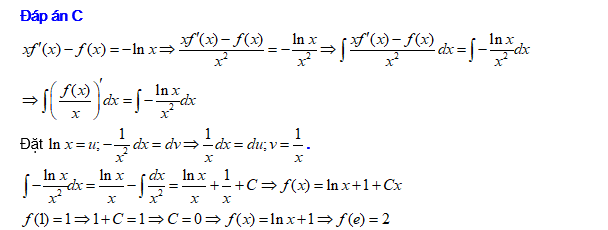 Đáp án: C
Đáp án: C
Câu 12 [516239]: Cho hàm số 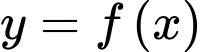 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 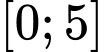 và thỏa mãn
và thỏa mãn 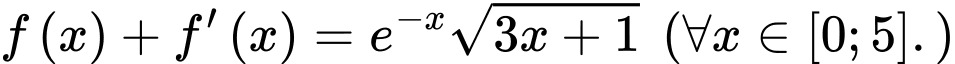 Biết
Biết 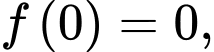 tính
tính 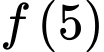
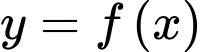 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 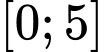 và thỏa mãn
và thỏa mãn 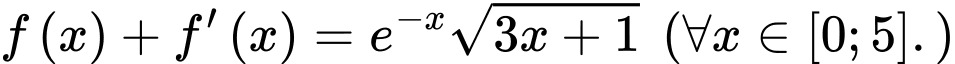 Biết
Biết 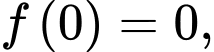 tính
tính 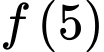
A, 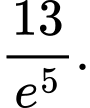
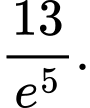
B, 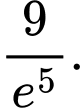
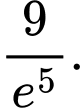
C, 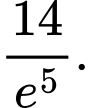
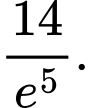
D, 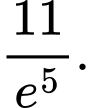
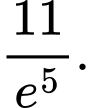
Ta có:
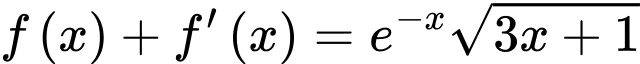
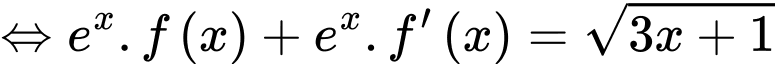
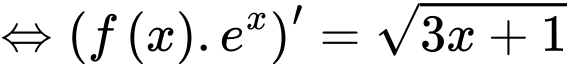
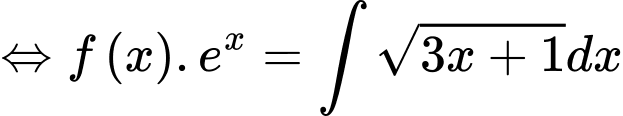
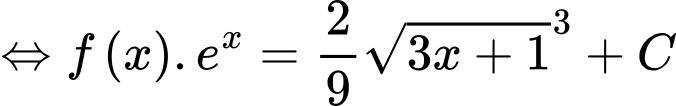
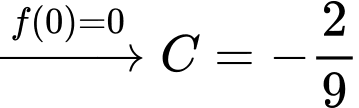
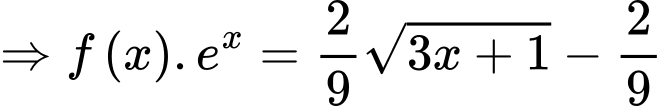
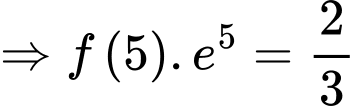
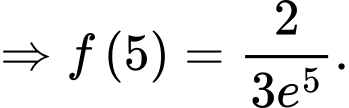 Đáp án: C
Đáp án: C
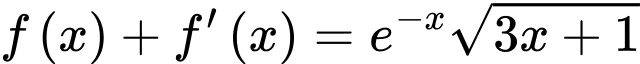
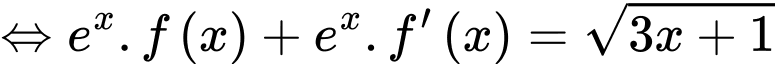
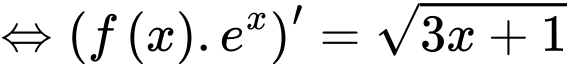
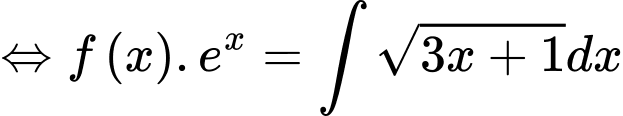
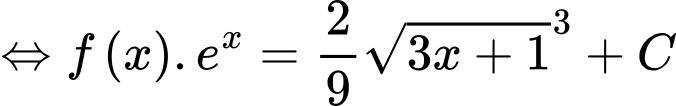
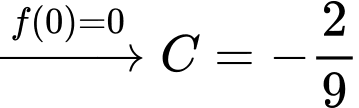
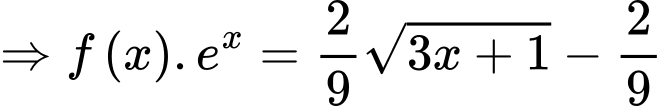
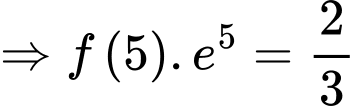
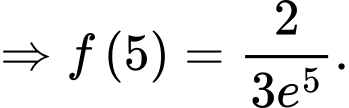 Đáp án: C
Đáp án: C
Câu 13 [151774]: Cho hàm số 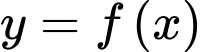 liên tục trên
liên tục trên 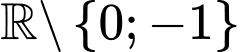 biết rằng hàm số thỏa mãn điều kiện
biết rằng hàm số thỏa mãn điều kiện 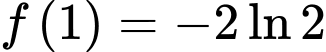
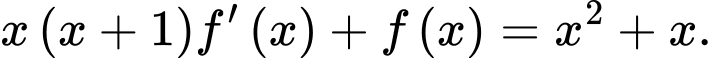 Giá trị
Giá trị 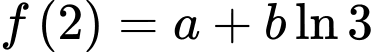
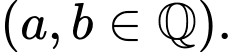 Tính giá trị
Tính giá trị 
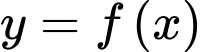 liên tục trên
liên tục trên 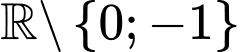 biết rằng hàm số thỏa mãn điều kiện
biết rằng hàm số thỏa mãn điều kiện 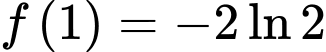
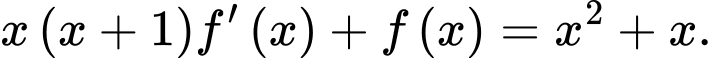 Giá trị
Giá trị 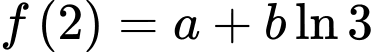
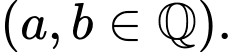 Tính giá trị
Tính giá trị 
A, 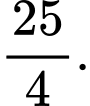
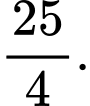
B, 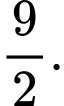
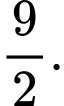
C, 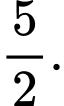
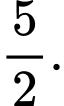
D, 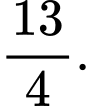
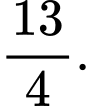
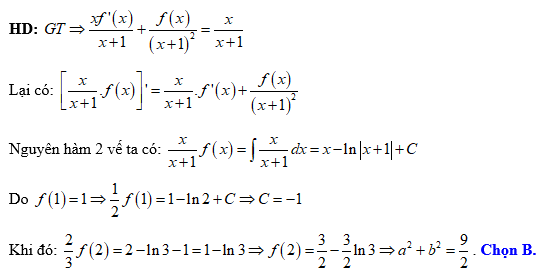 Đáp án: B
Đáp án: B
Câu 14 [399925]: Cho hàm số 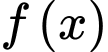 nhận giá trị dương trên khoảng
nhận giá trị dương trên khoảng 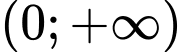 và có đạo hàm trên khoảng đó. Biết
và có đạo hàm trên khoảng đó. Biết 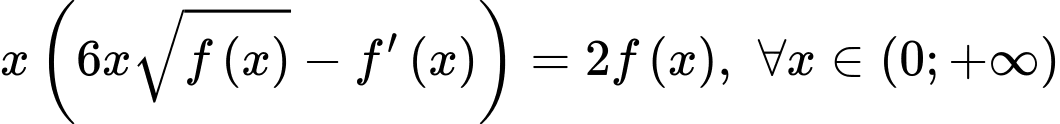 và
và 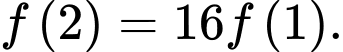 Tính
Tính 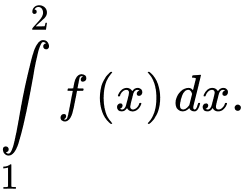
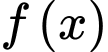 nhận giá trị dương trên khoảng
nhận giá trị dương trên khoảng 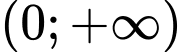 và có đạo hàm trên khoảng đó. Biết
và có đạo hàm trên khoảng đó. Biết 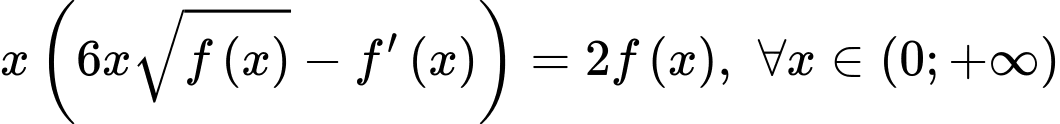 và
và 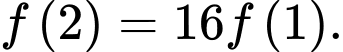 Tính
Tính 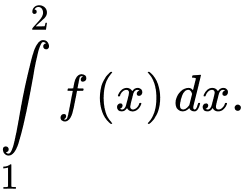
A, 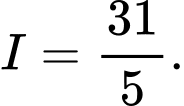
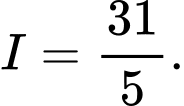
B, 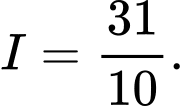
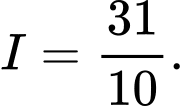
C, 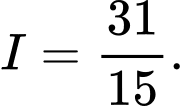
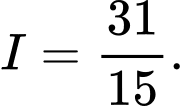
D, 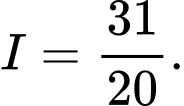
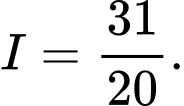
Chọn A
Ta có: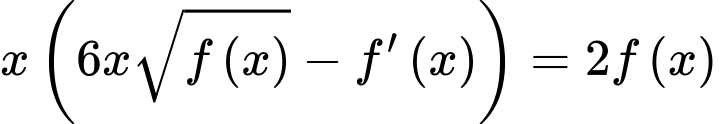
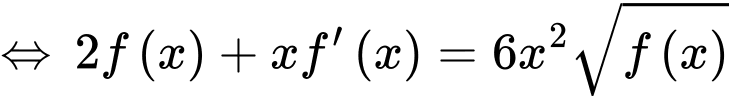
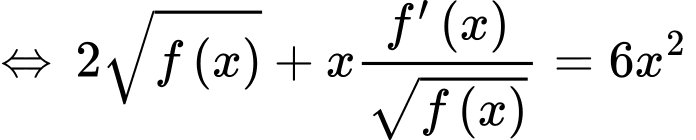
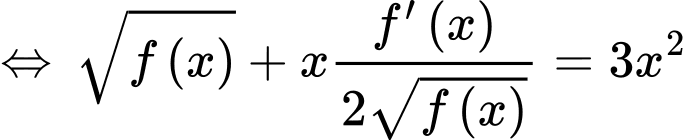
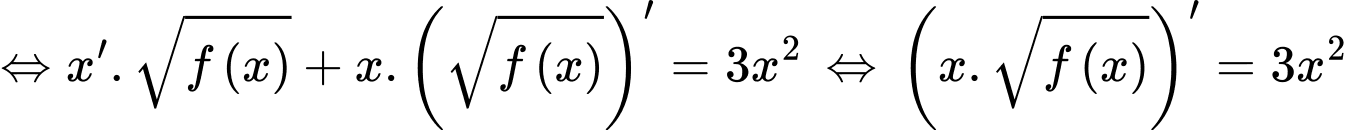
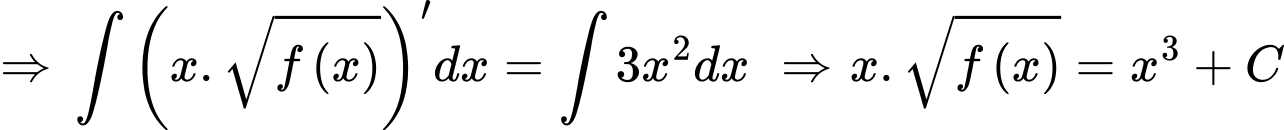
Chọn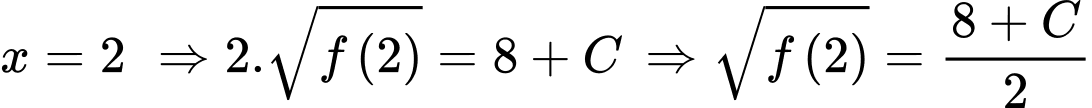
Chọn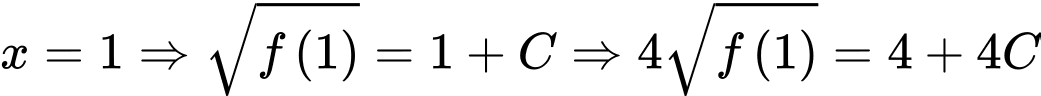
Mà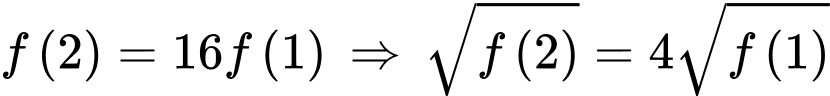
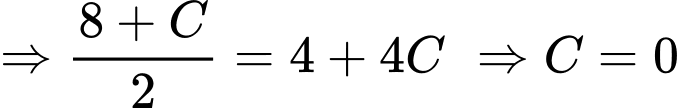
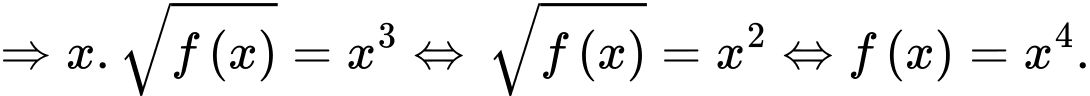
Vậy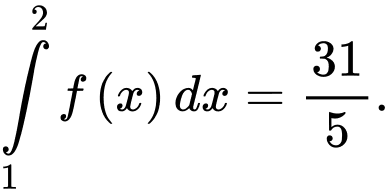 Đáp án: A
Đáp án: A
Ta có:
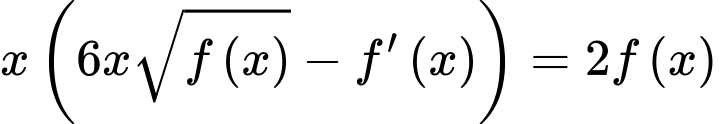
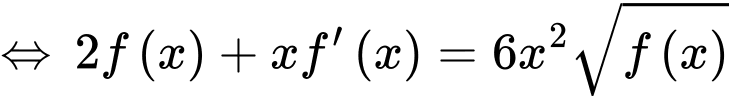
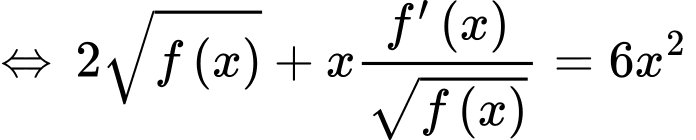
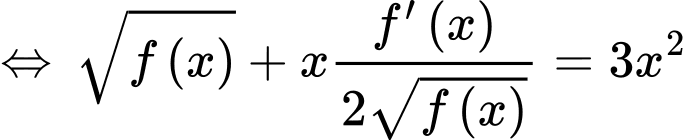
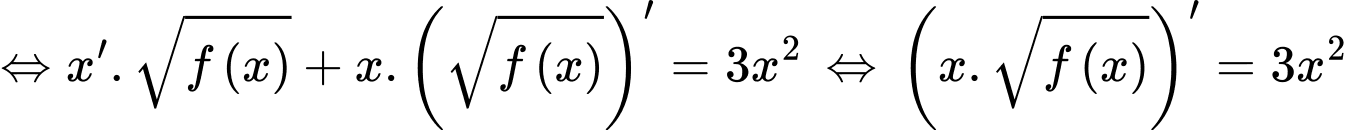
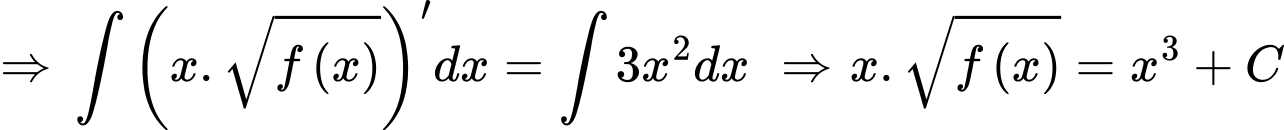
Chọn
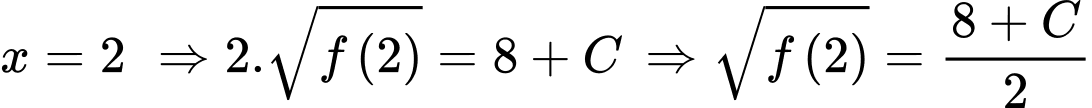
Chọn
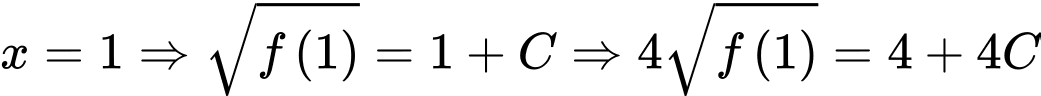
Mà
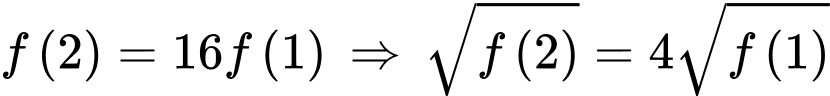
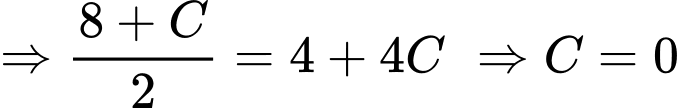
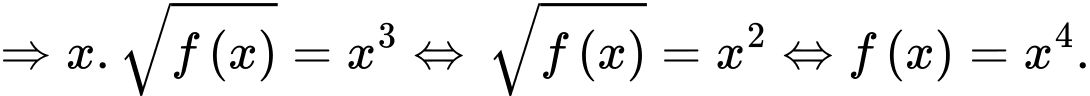
Vậy
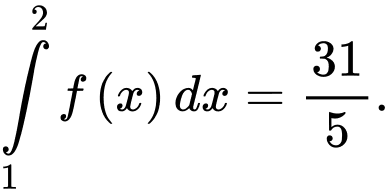 Đáp án: A
Đáp án: A
Câu 15 [803778]: Giả sử 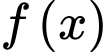 là hàm có đạo hàm liên tục trên khoảng
là hàm có đạo hàm liên tục trên khoảng 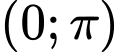 và
và 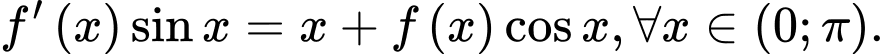 Biết
Biết 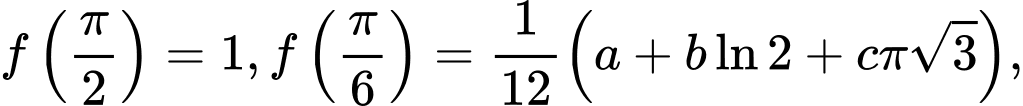 với
với 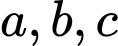 là các số nguyên. Giá trị
là các số nguyên. Giá trị 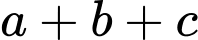 bằng
bằng
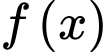 là hàm có đạo hàm liên tục trên khoảng
là hàm có đạo hàm liên tục trên khoảng 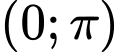 và
và 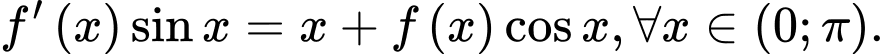 Biết
Biết 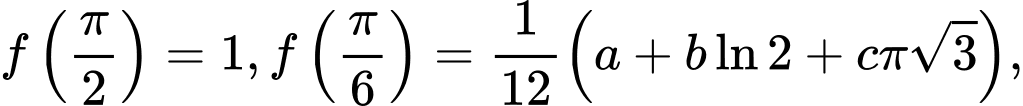 với
với 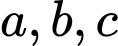 là các số nguyên. Giá trị
là các số nguyên. Giá trị 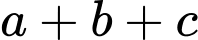 bằng
bằng A, 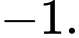
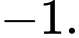
B, 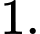
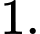
C, 

D, 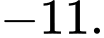
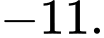
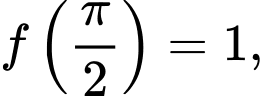
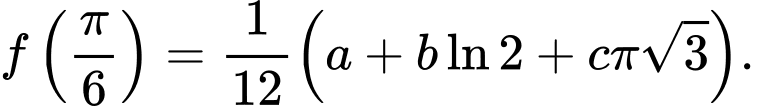
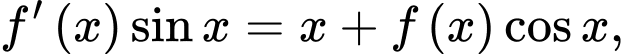
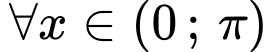
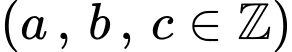
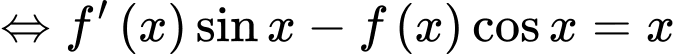
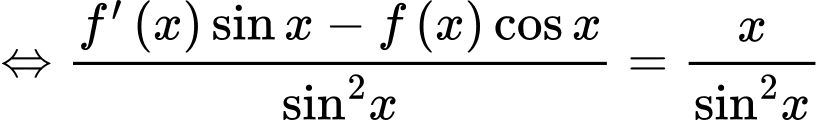
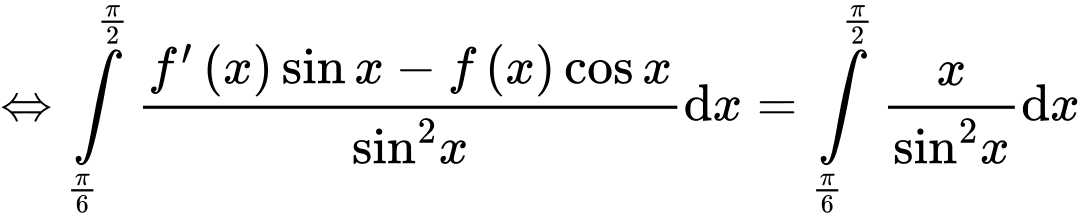
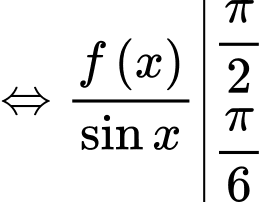
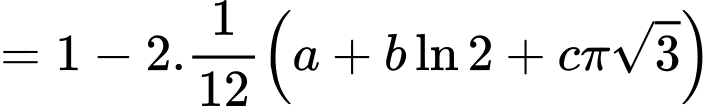
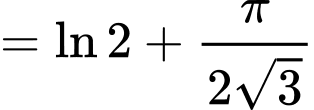
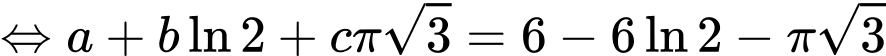
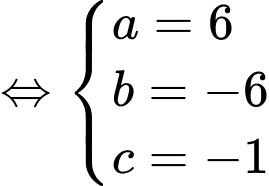

Đáp án A. Đáp án: A
Câu 16 [789740]: (Chuyên Chu Văn An - 2020) Cho hàm số 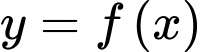 liên tục, có đạo hàm trên
liên tục, có đạo hàm trên 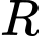 thỏa mãn điều kiện
thỏa mãn điều kiện 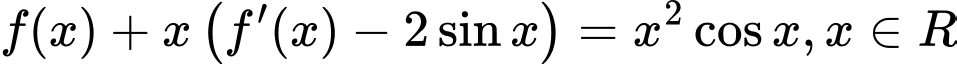 và
và 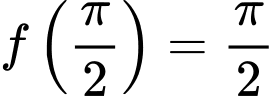 .Tính
.Tính 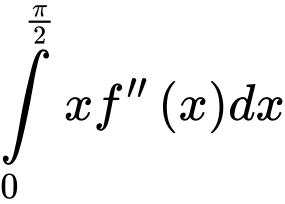
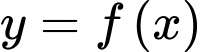 liên tục, có đạo hàm trên
liên tục, có đạo hàm trên 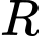 thỏa mãn điều kiện
thỏa mãn điều kiện 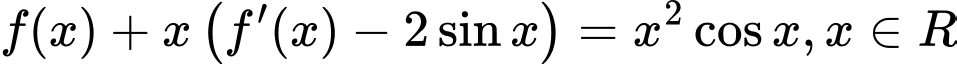 và
và 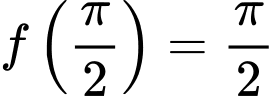 .Tính
.Tính 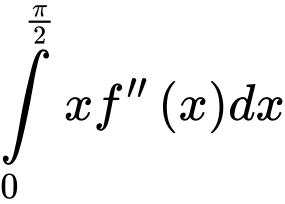
A,  .
.
 .
.B, 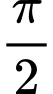 .
.
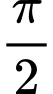 .
.C, 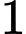 .
.
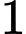 .
.D, 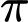 .
.
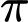 .
.
Chọn A
Từ giả thiết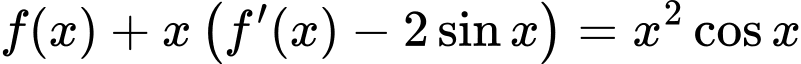
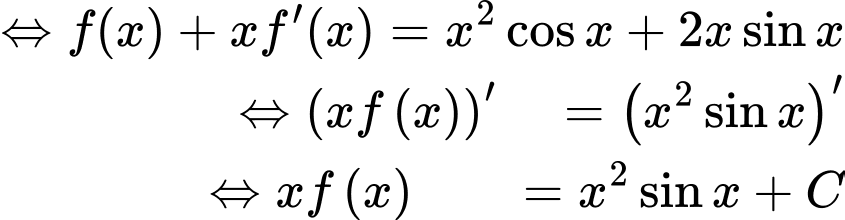
Mặt khác: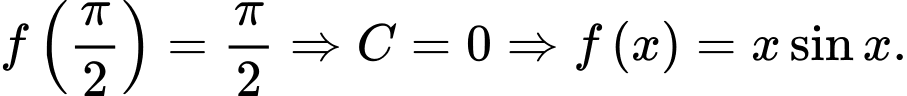
Ta có: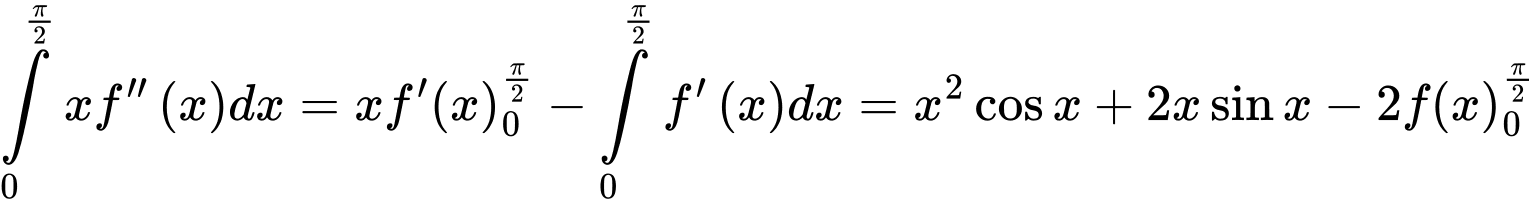
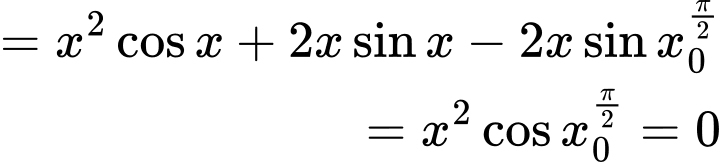
Đáp án: A
Từ giả thiết
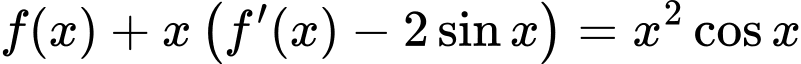
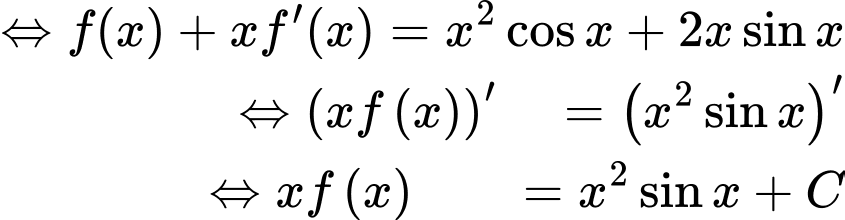
Mặt khác:
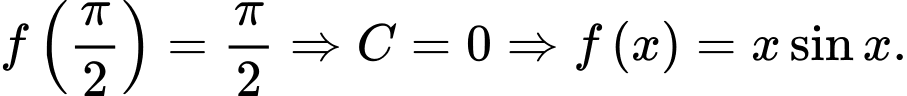
Ta có:
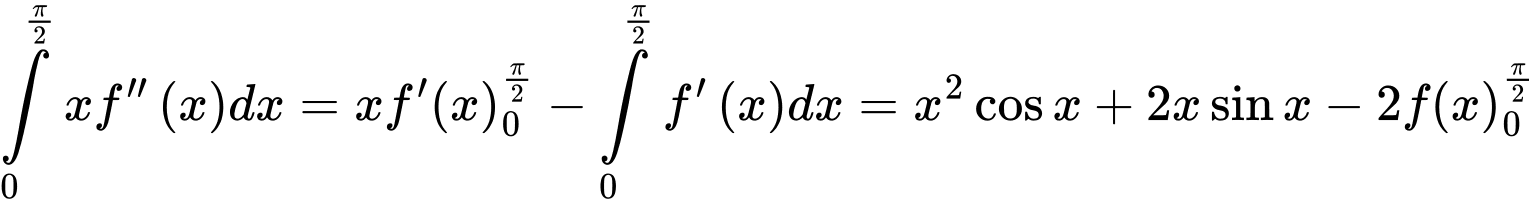
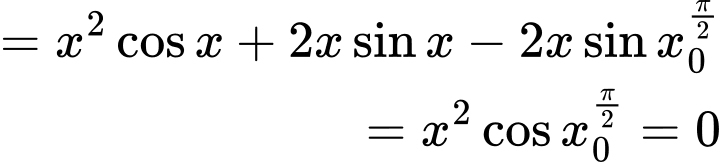
Đáp án: A
Câu 17 [789748]: Cho hàm số 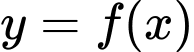 liên tục trên đoạn
liên tục trên đoạn 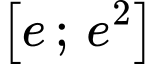 . Biết
. Biết 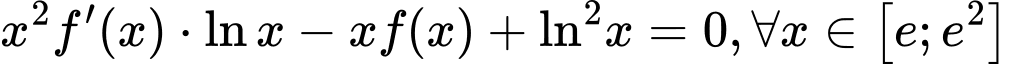 và
và 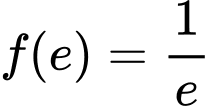 . Tính tích phân
. Tính tích phân 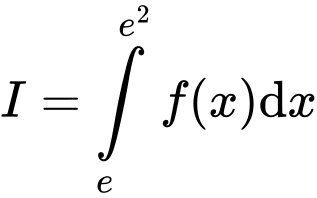 .
.
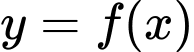 liên tục trên đoạn
liên tục trên đoạn 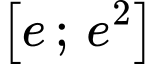 . Biết
. Biết 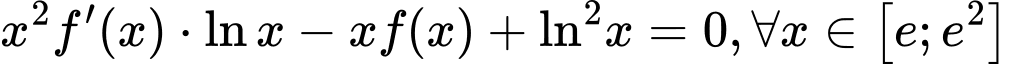 và
và 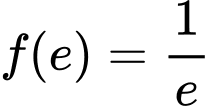 . Tính tích phân
. Tính tích phân 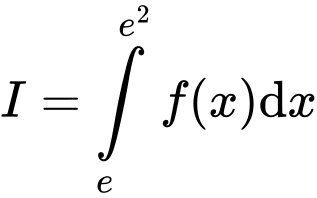 .
. A,  .
.
 .
.B, 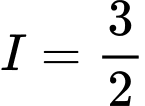 .
.
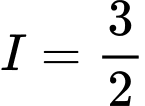 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn B
Ta có: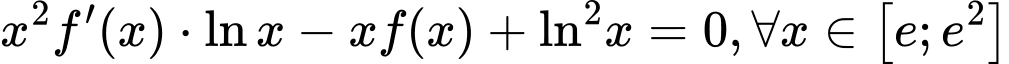
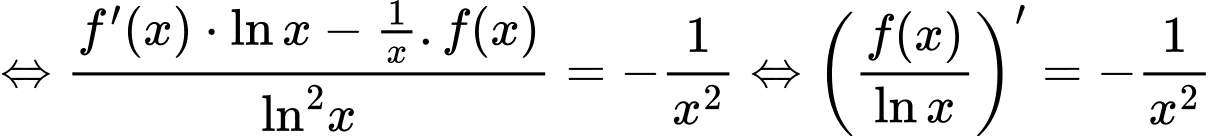
Lấy nguyên hàm hai vế ta được: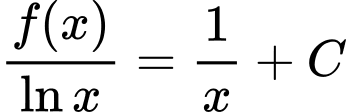 theo đề bài ta có
theo đề bài ta có 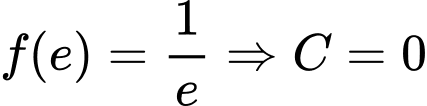
suy ra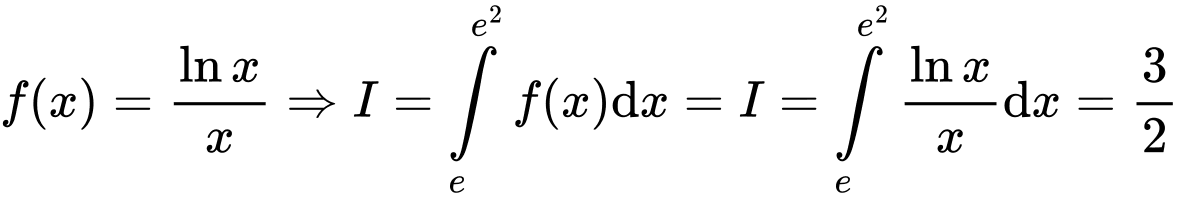 . Đáp án: B
. Đáp án: B
Ta có:
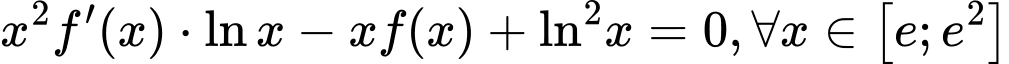
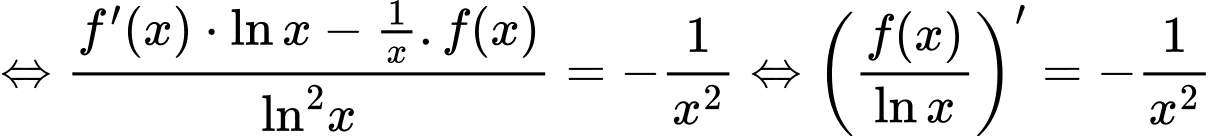
Lấy nguyên hàm hai vế ta được:
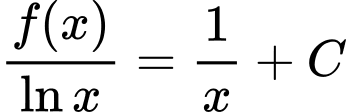 theo đề bài ta có
theo đề bài ta có 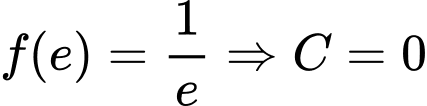
suy ra
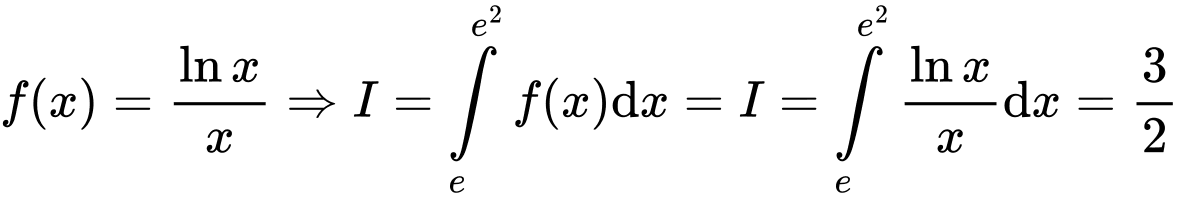 . Đáp án: B
. Đáp án: B
Câu 18 [516395]: Cho hàm số 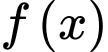 có
có 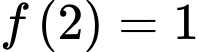 và
và 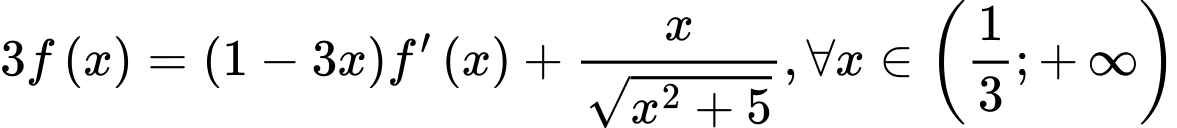 . Khi đó
. Khi đó 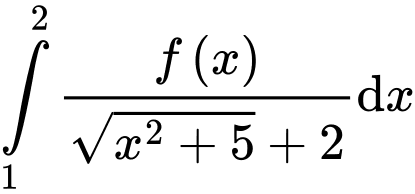 bằng
bằng
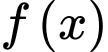 có
có 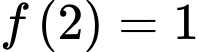 và
và 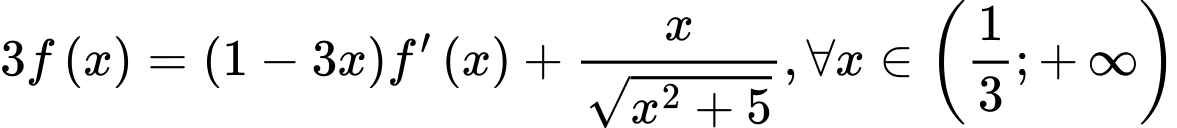 . Khi đó
. Khi đó 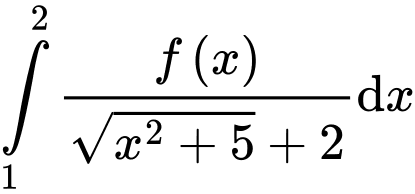 bằng
bằng A, 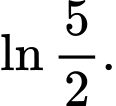
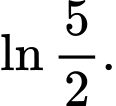
B, 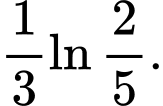
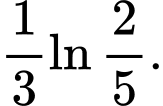
C, 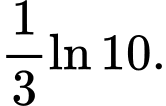
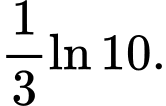
D, 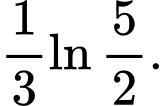
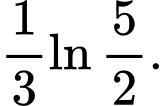
Chọn D
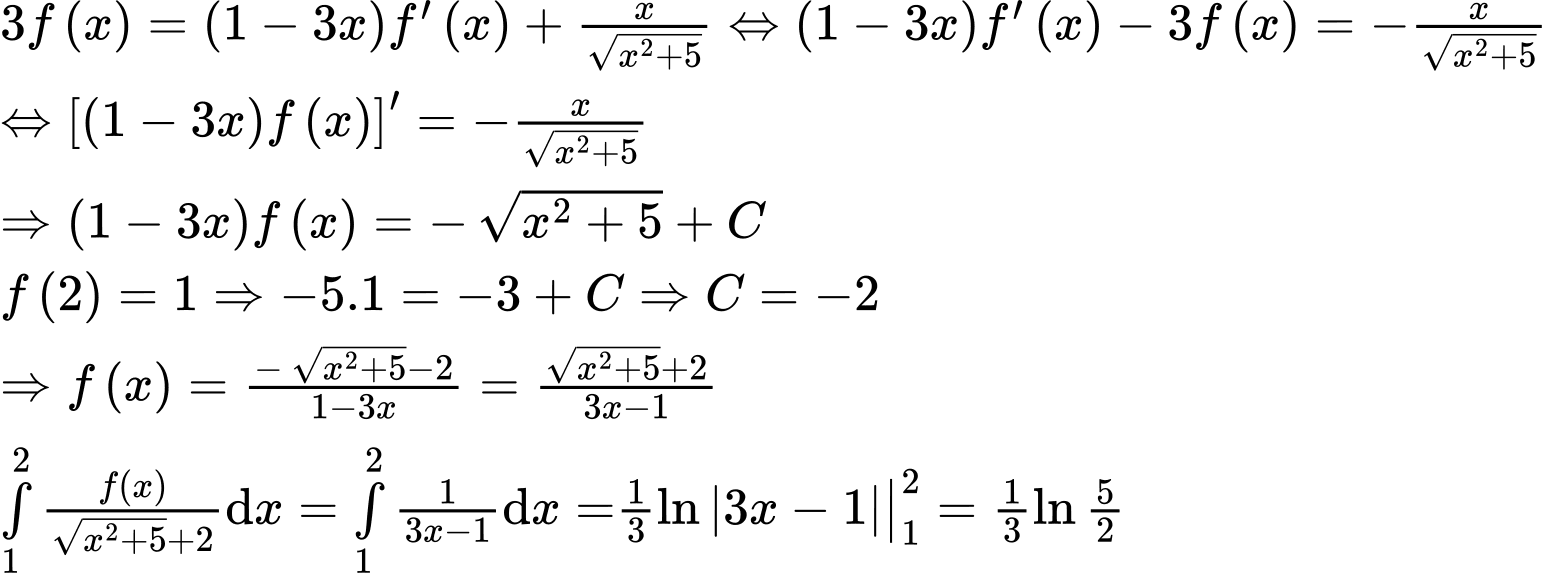 Đáp án: D
Đáp án: D
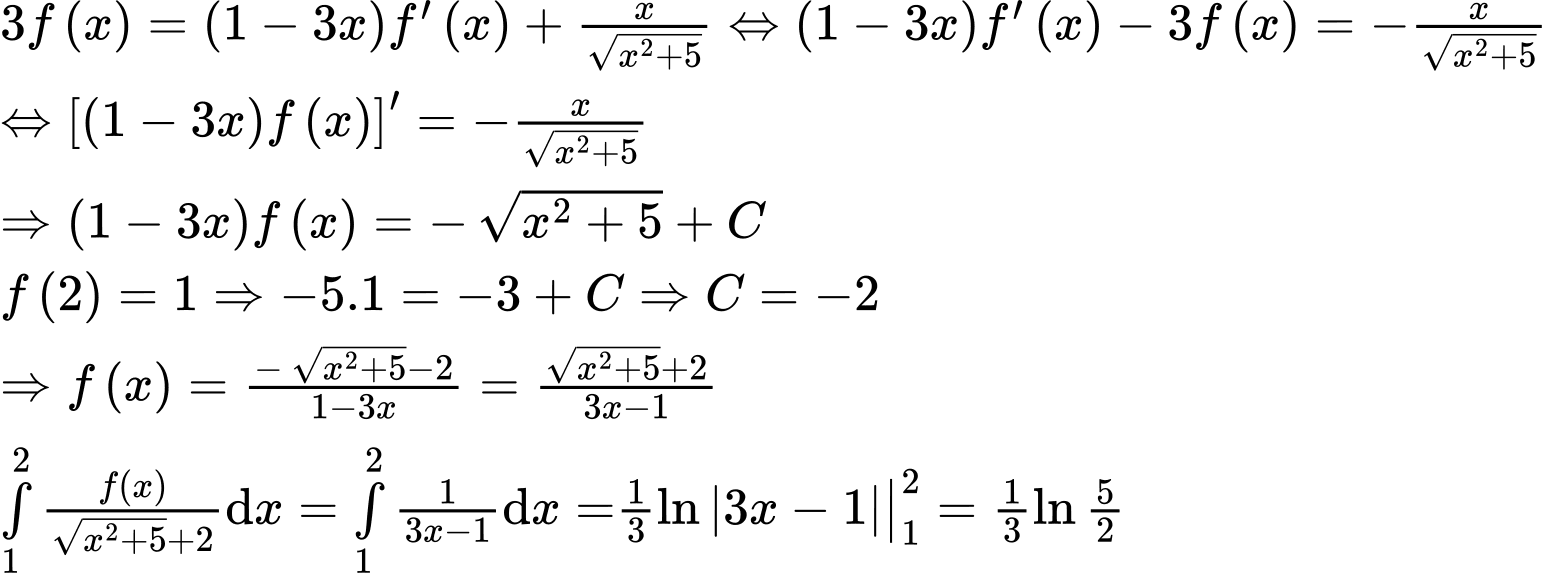 Đáp án: D
Đáp án: D
Câu 19 [771749]: [MĐ3] Cho hàm số 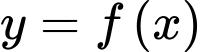 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 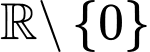 và thỏa mãn
và thỏa mãn 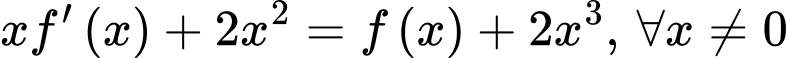 ,
, 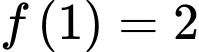 . Diện tích hình phẳng giới hạn bởi các đường
. Diện tích hình phẳng giới hạn bởi các đường 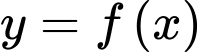 và
và 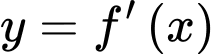
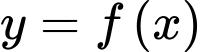 có đạo hàm và liên tục trên
có đạo hàm và liên tục trên 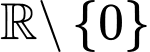 và thỏa mãn
và thỏa mãn 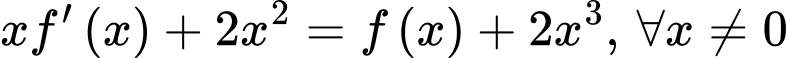 ,
, 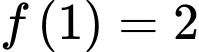 . Diện tích hình phẳng giới hạn bởi các đường
. Diện tích hình phẳng giới hạn bởi các đường 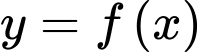 và
và 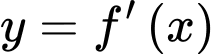
A, 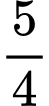 .
.
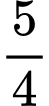 .
.B, 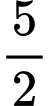 .
.
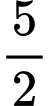 .
.C, 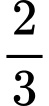 .
.
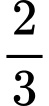 .
.D, 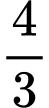 .
.
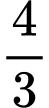 .
.
Chọn D
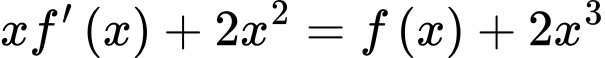
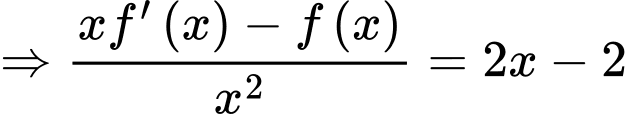
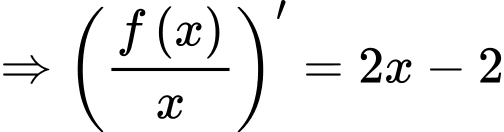
Lấy nguyên hàm 2 vế, ta có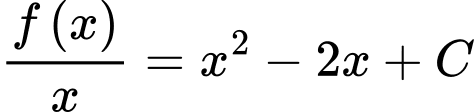
Với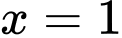 suy ra
suy ra 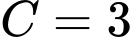 hay
hay 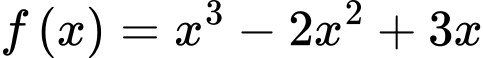 và
và 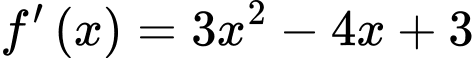 .
.
Xét phương trình hoành độ giao điểm :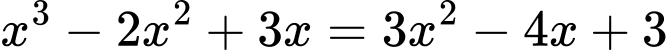

Giao điểm đồ thị hàm số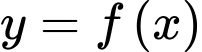 và
và 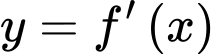 là
là 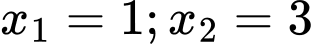 .
.
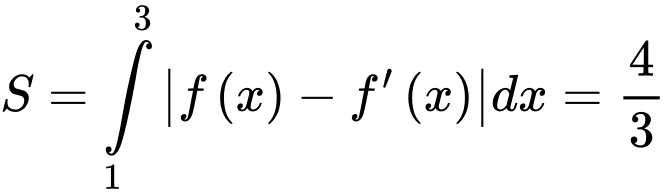 . Đáp án: D
. Đáp án: D
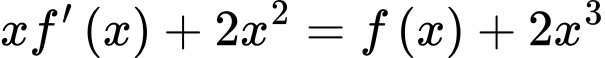
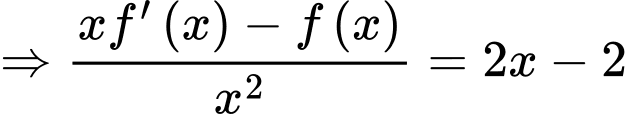
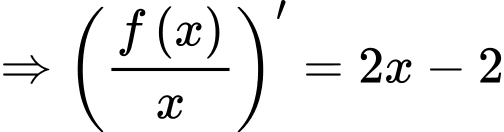
Lấy nguyên hàm 2 vế, ta có
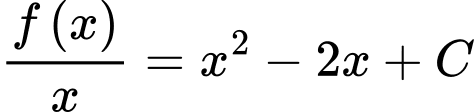
Với
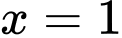 suy ra
suy ra 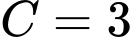 hay
hay 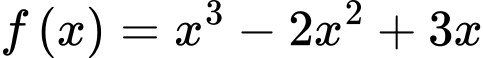 và
và 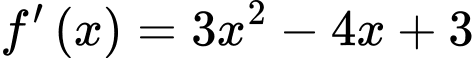 .
.
Xét phương trình hoành độ giao điểm :
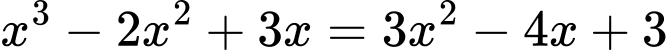

Giao điểm đồ thị hàm số
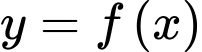 và
và 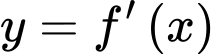 là
là 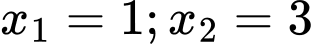 .
.
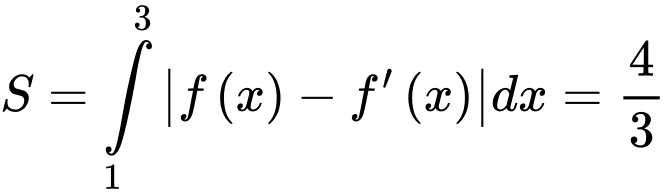 . Đáp án: D
. Đáp án: D
Câu 20 [736644]: [MĐ4] Cho hàm số 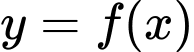 thỏa mãn
thỏa mãn 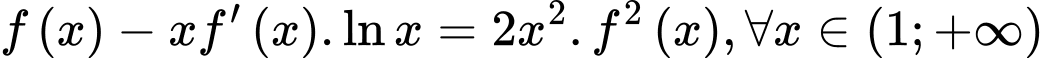 . Biết
. Biết 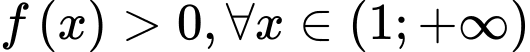 và
và 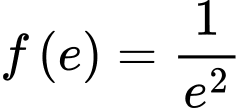 . Tính diện tích S của hình phẳng được giới hạn bởi các đường
. Tính diện tích S của hình phẳng được giới hạn bởi các đường 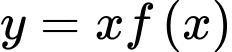 ,
, 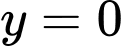 ,
, 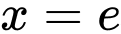 và
và 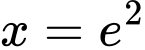 .
.
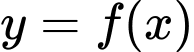 thỏa mãn
thỏa mãn 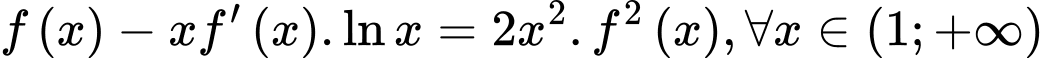 . Biết
. Biết 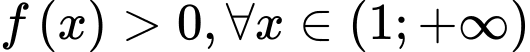 và
và 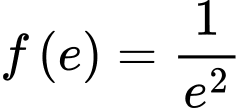 . Tính diện tích S của hình phẳng được giới hạn bởi các đường
. Tính diện tích S của hình phẳng được giới hạn bởi các đường 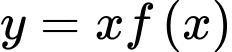 ,
, 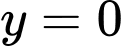 ,
, 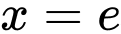 và
và 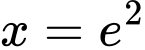 .
. A, 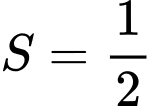 .
.
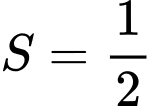 .
.B, 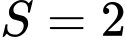 .
.
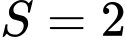 .
.C, 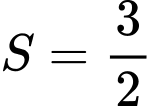 .
.
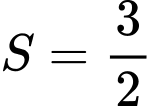 .
.D, 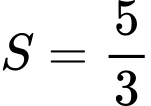 .
.
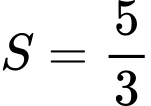 .
.
Ta có: 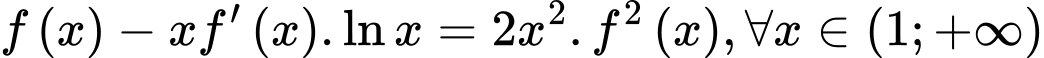
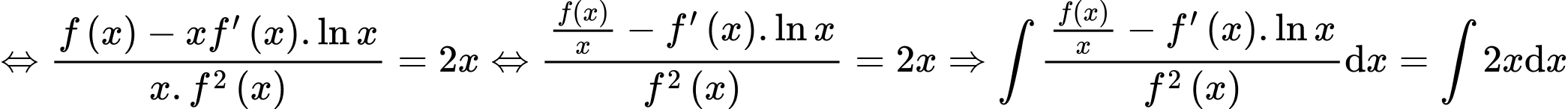
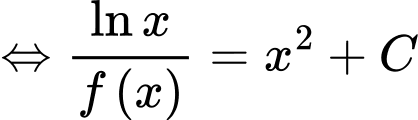 (1)
(1)
Thay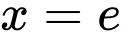 vào (1)
vào (1) 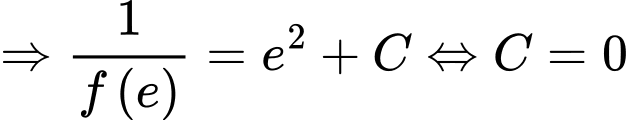 vì
vì 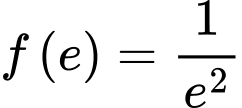
Khi đó,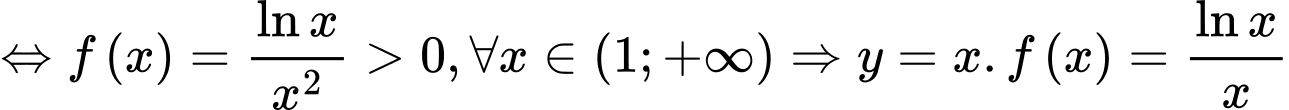
Như vậy, diện tích S của hình phẳng được giới hạn bởi các đường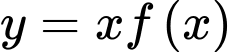 ,
, 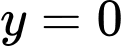 ,
, 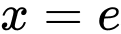 và
và 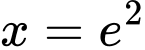 là
là 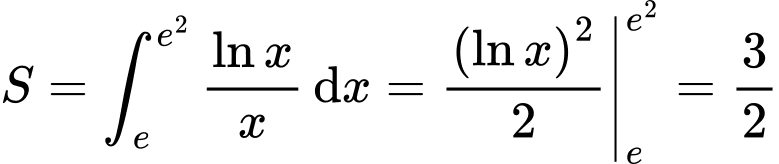 . Đáp án: C
. Đáp án: C
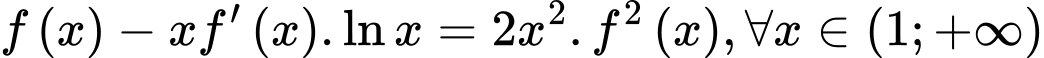
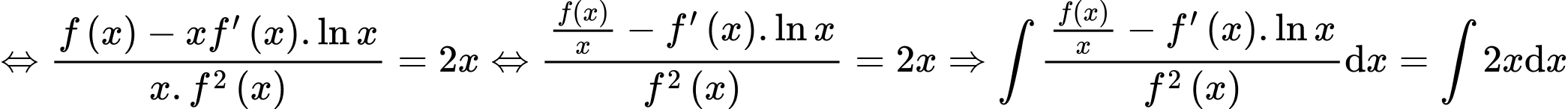
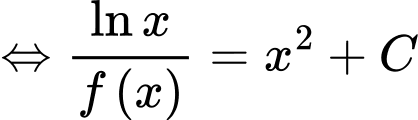 (1)
(1)
Thay
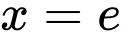 vào (1)
vào (1) 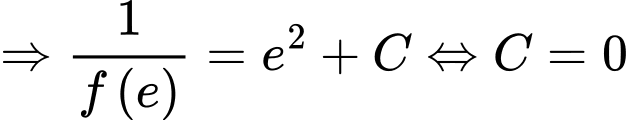 vì
vì 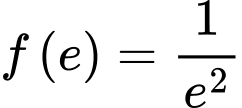
Khi đó,
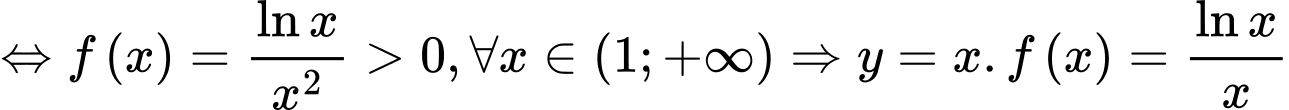
Như vậy, diện tích S của hình phẳng được giới hạn bởi các đường
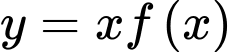 ,
, 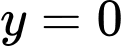 ,
, 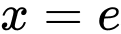 và
và 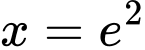 là
là 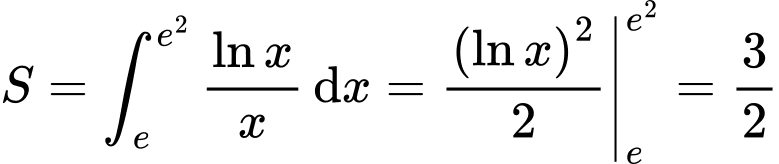 . Đáp án: C
. Đáp án: C
Câu 21 [735252]: [MĐ3] Cho hàm số 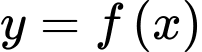 có đạo hàm liên tục trên
có đạo hàm liên tục trên 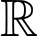 và thỏa mãn
và thỏa mãn 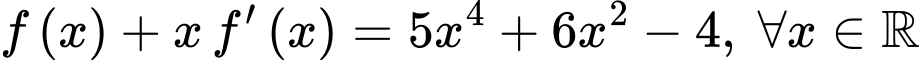 . Diện tích hình phẳng giới hạn bởi các đường
. Diện tích hình phẳng giới hạn bởi các đường 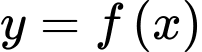 và
và 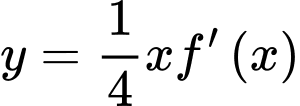 bằng
bằng
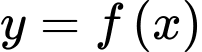 có đạo hàm liên tục trên
có đạo hàm liên tục trên 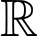 và thỏa mãn
và thỏa mãn 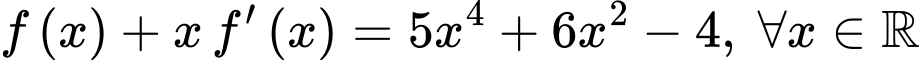 . Diện tích hình phẳng giới hạn bởi các đường
. Diện tích hình phẳng giới hạn bởi các đường 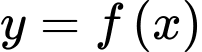 và
và 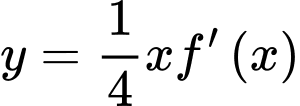 bằng
bằng A, 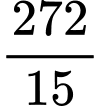 .
.
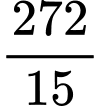 .
.B, 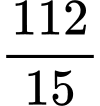 .
.
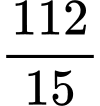 .
.C, 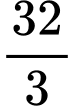 .
.
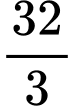 .
.D, 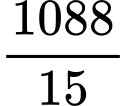 .
.
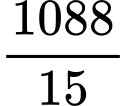 .
.
Ta có 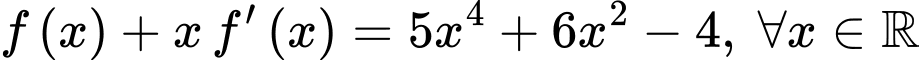 .
.
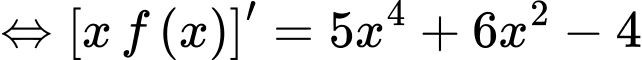
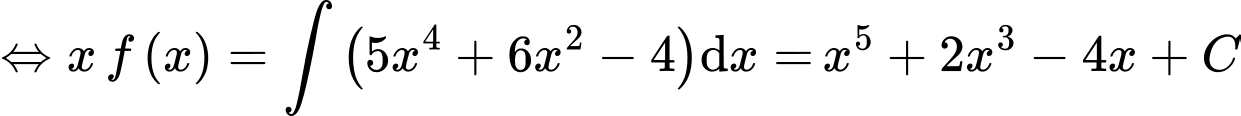 .
.
Với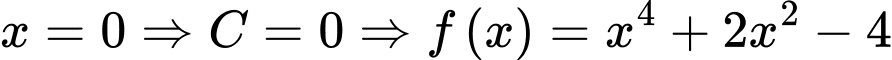
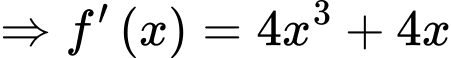
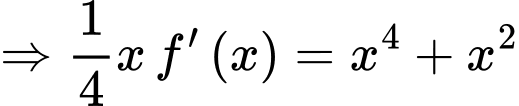 .
.
Xét phương trình hoành độ giao điểm: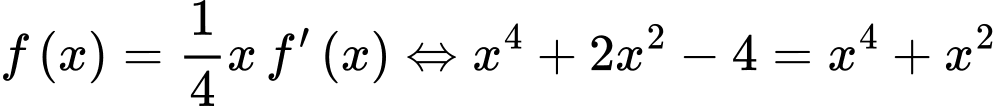
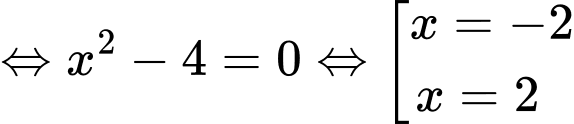 .
.
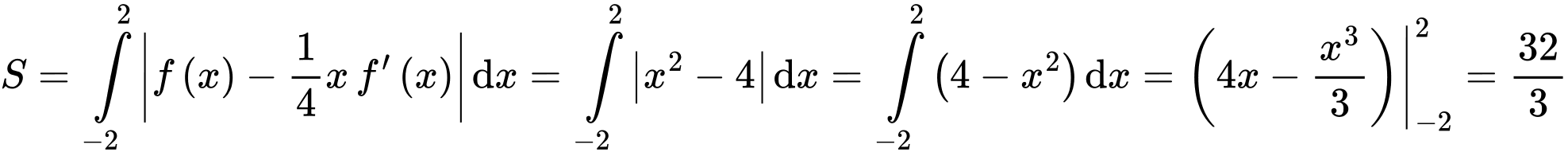 . Đáp án: C
. Đáp án: C
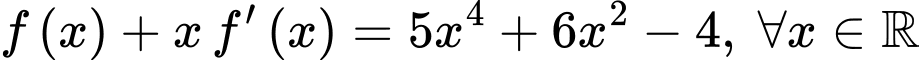 .
.
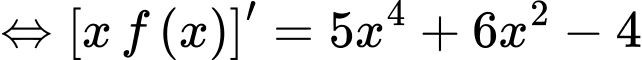
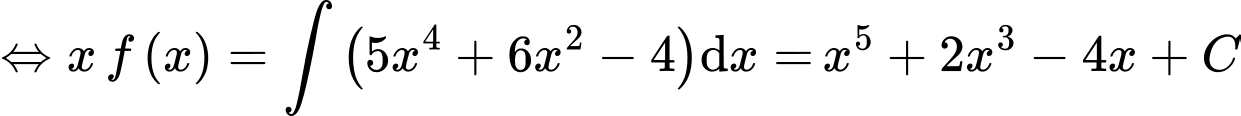 .
.
Với
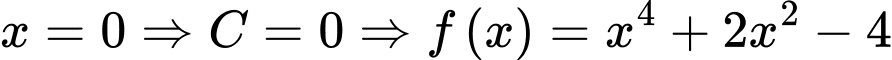
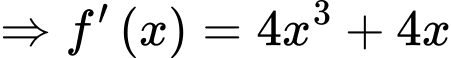
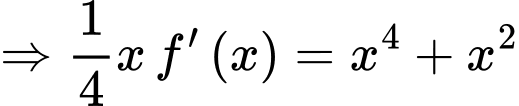 .
.
Xét phương trình hoành độ giao điểm:
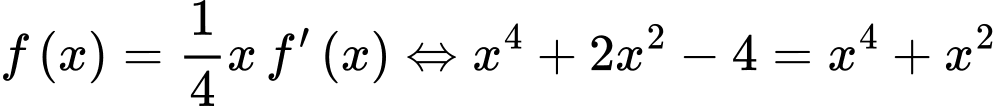
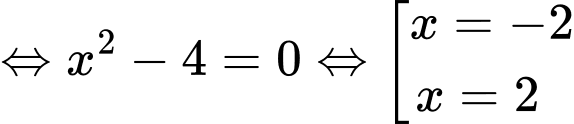 .
.
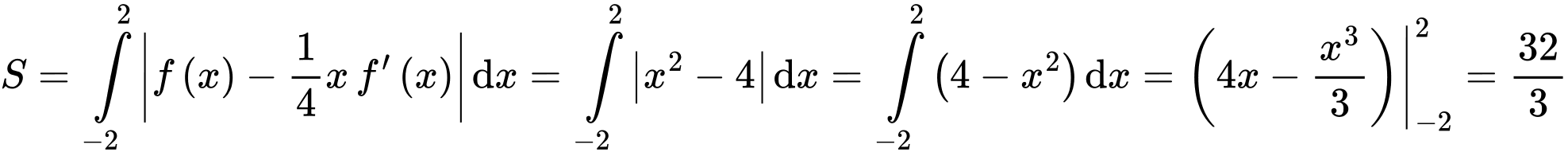 . Đáp án: C
. Đáp án: C
Câu 22 [398643]: Cho hàm số 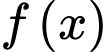 thoả mãn
thoả mãn 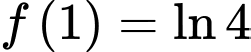 và
và 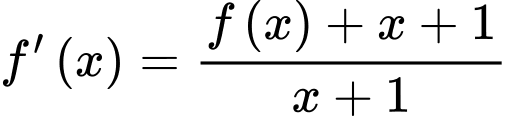 với mọi
với mọi  Giá trị của
Giá trị của 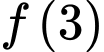 bằng
bằng
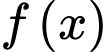 thoả mãn
thoả mãn 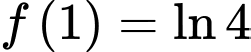 và
và 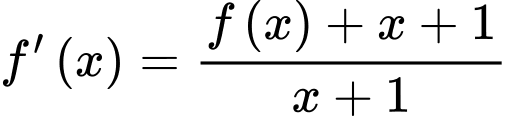 với mọi
với mọi  Giá trị của
Giá trị của 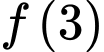 bằng
bằng A, 

B, 

C, 

D, 

Ta có: 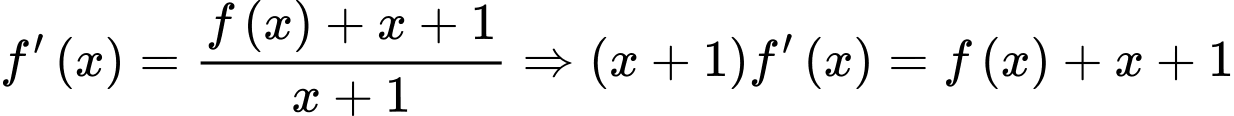
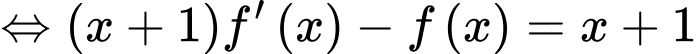
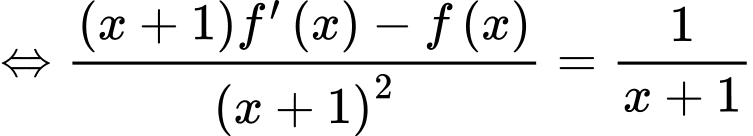
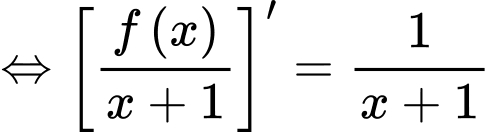 Lấy nguyên hàm 2 vế ta được:
Lấy nguyên hàm 2 vế ta được: 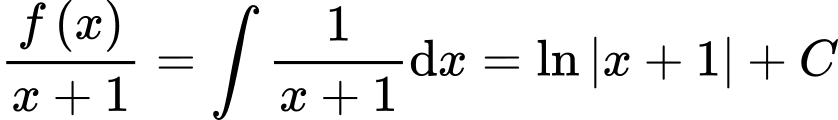 Thay
Thay 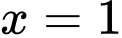 vào ta có:
vào ta có: 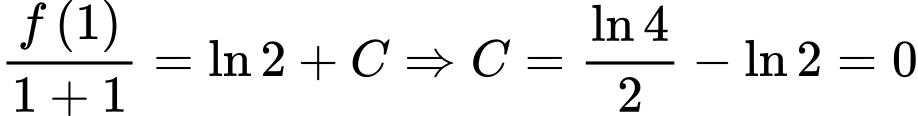 Do đó:
Do đó: 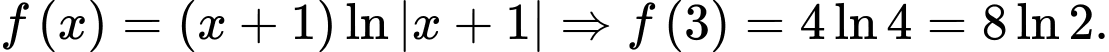 Đáp án: A
Đáp án: A
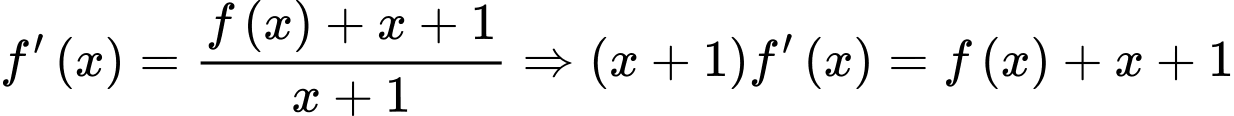
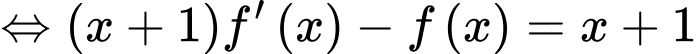
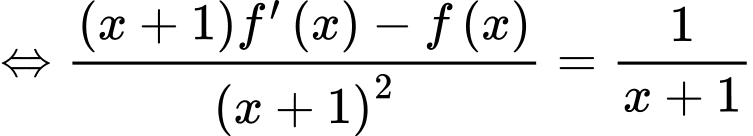
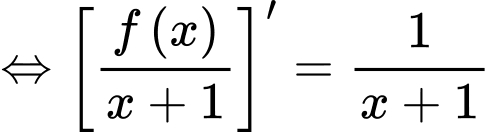 Lấy nguyên hàm 2 vế ta được:
Lấy nguyên hàm 2 vế ta được: 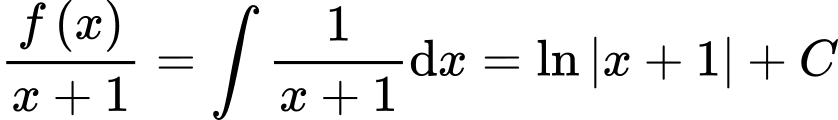 Thay
Thay 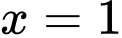 vào ta có:
vào ta có: 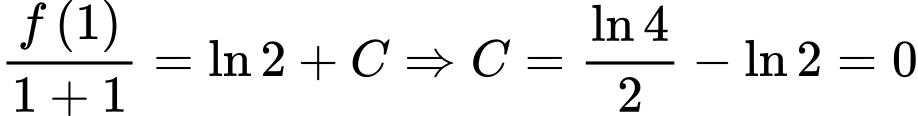 Do đó:
Do đó: 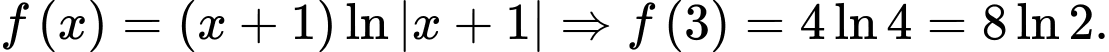 Đáp án: A
Đáp án: A
Câu 23 [408533]: Cho hàm số 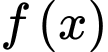 nhận giá trị dương, có đạo hàm liên tục trên khoảng
nhận giá trị dương, có đạo hàm liên tục trên khoảng 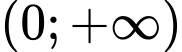 thỏa mãn
thỏa mãn 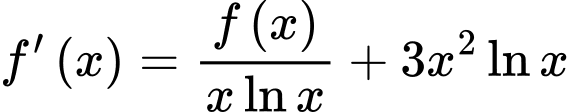 và
và 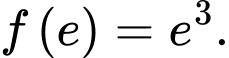 Tích phân
Tích phân 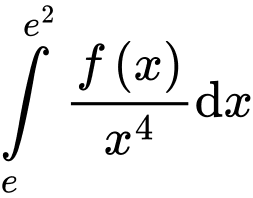 bằng bao nhiêu?
bằng bao nhiêu?
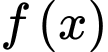 nhận giá trị dương, có đạo hàm liên tục trên khoảng
nhận giá trị dương, có đạo hàm liên tục trên khoảng 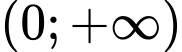 thỏa mãn
thỏa mãn 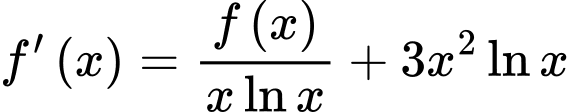 và
và 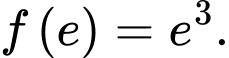 Tích phân
Tích phân 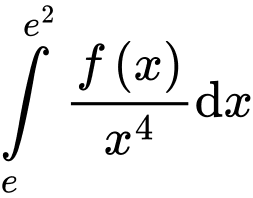 bằng bao nhiêu?
bằng bao nhiêu?
Ta có: 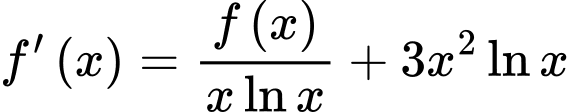 . Nhân hai vế với
. Nhân hai vế với 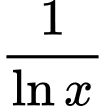 ,ta được
,ta được
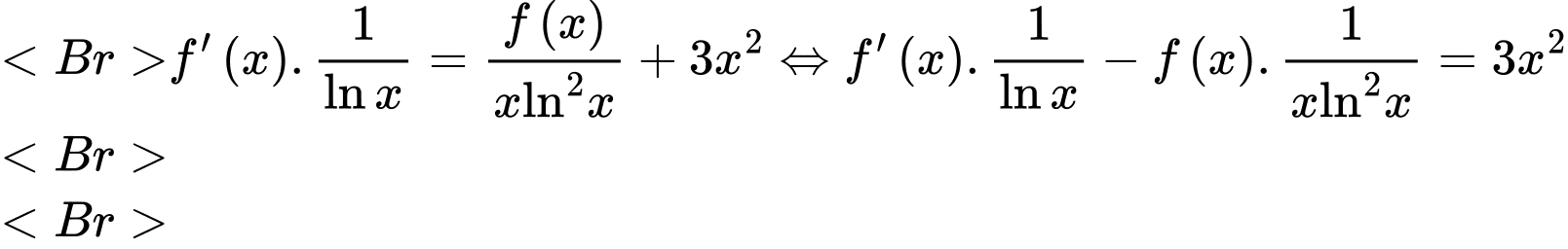
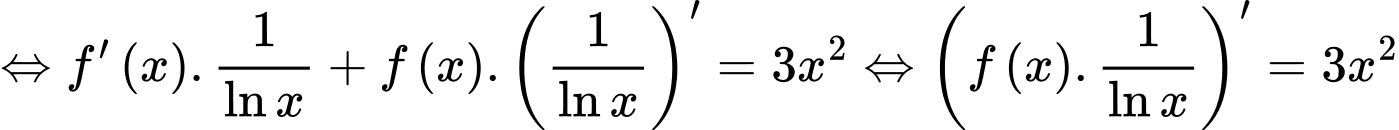 .
.
Nguyên hàm hai vế, ta được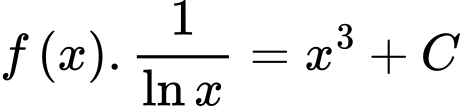 .
.
Vì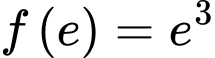 nên
nên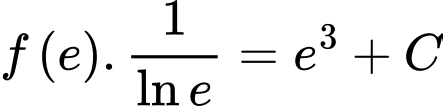
 .
.
Vậy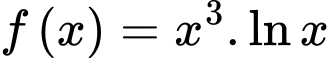
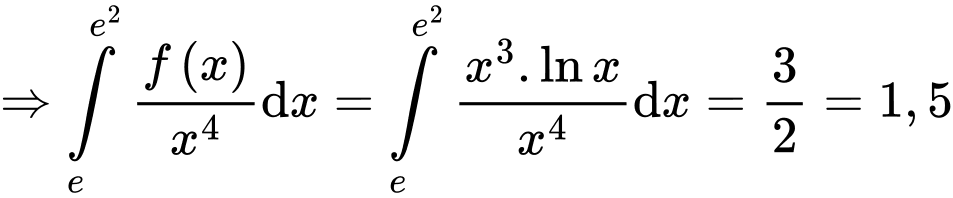 .
.
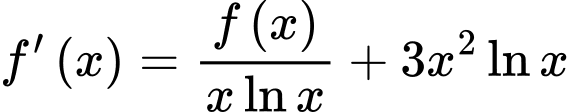 . Nhân hai vế với
. Nhân hai vế với 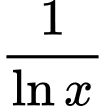 ,ta được
,ta được
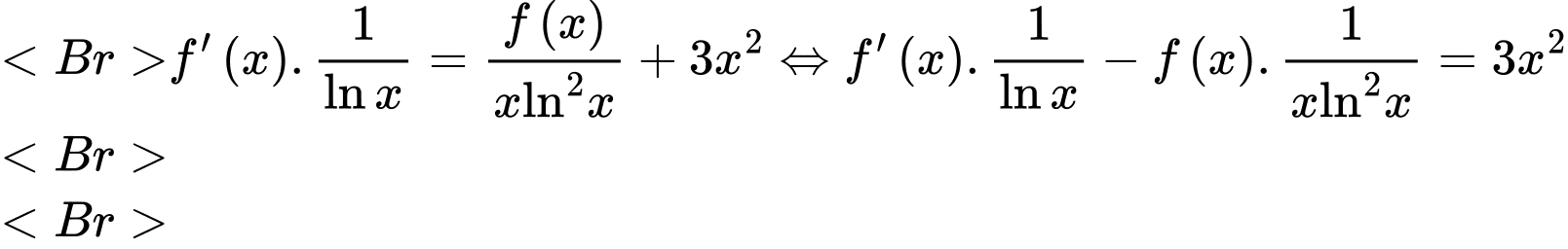
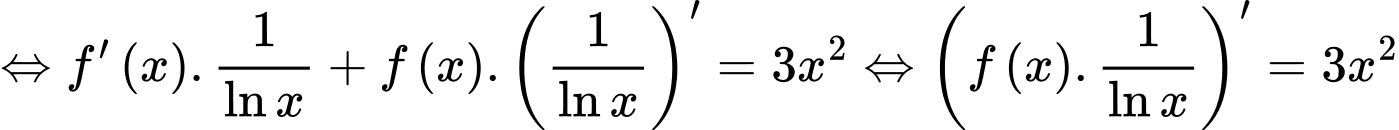 .
.
Nguyên hàm hai vế, ta được
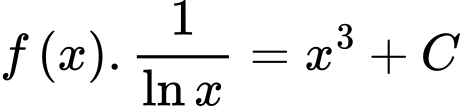 .
.
Vì
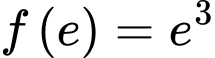 nên
nên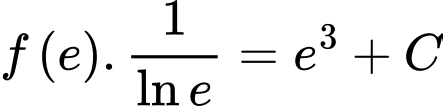
 .
.
Vậy
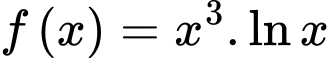
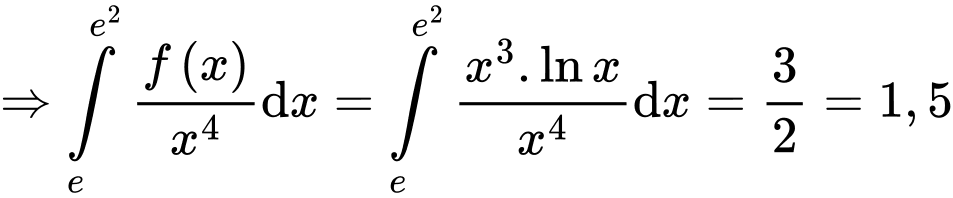 .
.
Câu 24 [789339]: Cho hàm số 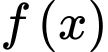 nhận giá trị dương thỏa mãn
nhận giá trị dương thỏa mãn 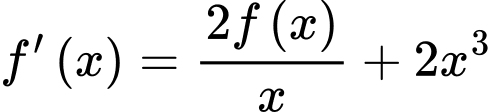 ,
, 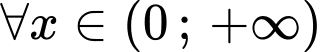 và
và 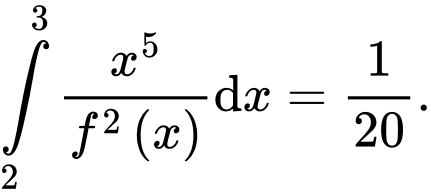 Giá trị của biểu thức
Giá trị của biểu thức  bằng bao nhiêu?
bằng bao nhiêu?
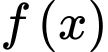 nhận giá trị dương thỏa mãn
nhận giá trị dương thỏa mãn 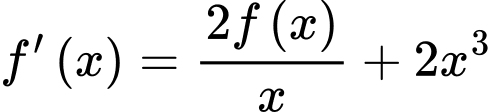 ,
, 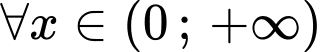 và
và 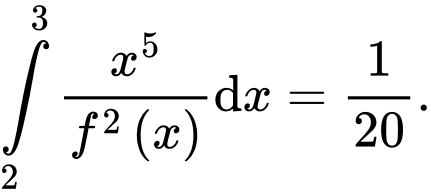 Giá trị của biểu thức
Giá trị của biểu thức  bằng bao nhiêu?
bằng bao nhiêu? A, 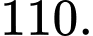
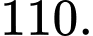
B, 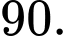
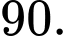
C, 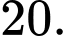
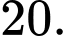
D, 
Chọn A
Với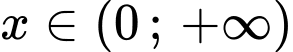 :
:
Ta có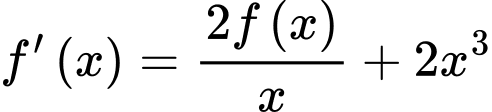
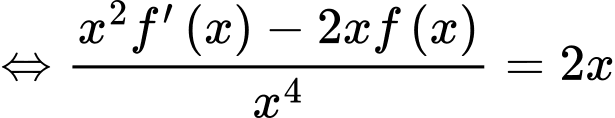
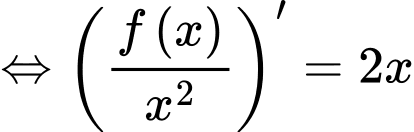
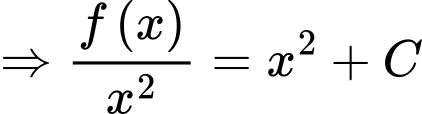
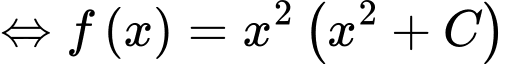 .
.
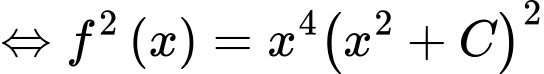 .
.
Khi đó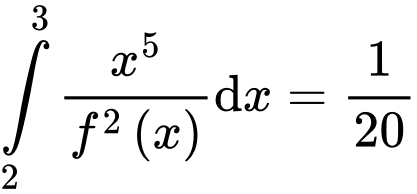
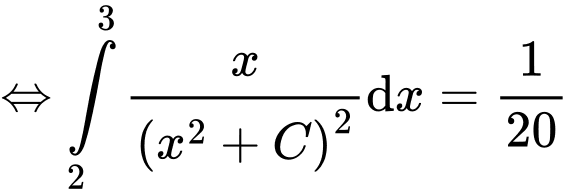
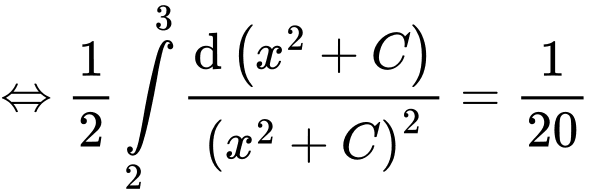
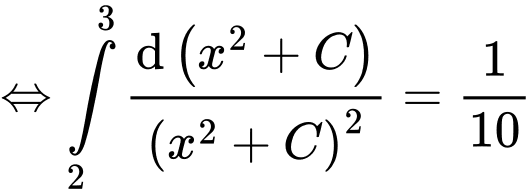
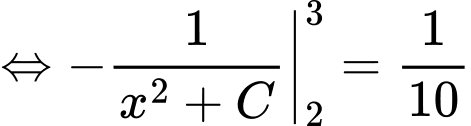
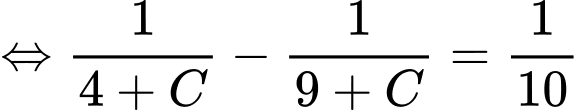
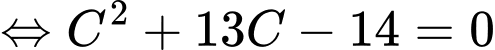
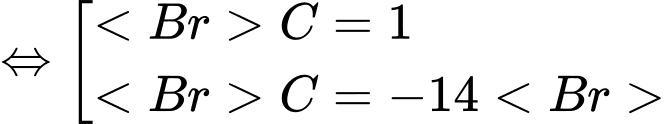 .
.
+ Với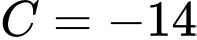
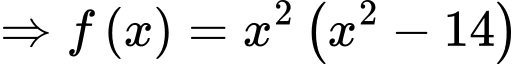 .
.
Chọn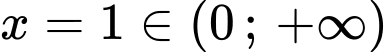 ta được
ta được 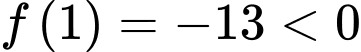 (vô lý vì
(vô lý vì 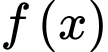 là hàm số dương).
là hàm số dương).
+ Với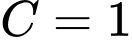
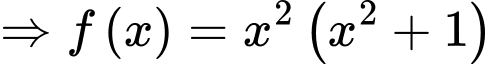 là hàm số dương.
là hàm số dương.
Khi đó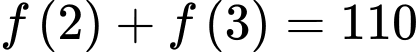 . Đáp án: A
. Đáp án: A
Với
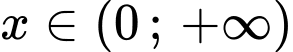 :
:Ta có
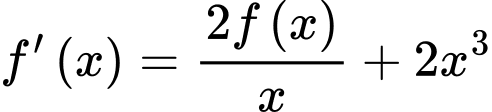
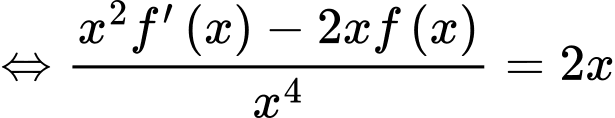
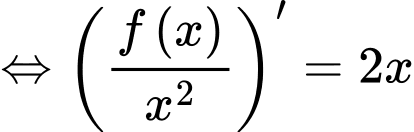
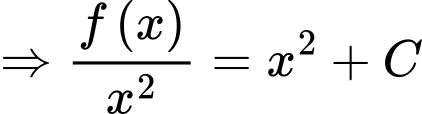
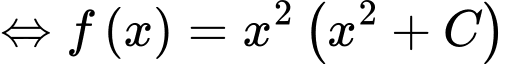 .
.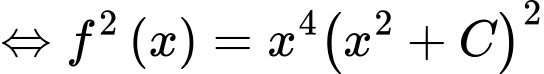 .
.Khi đó
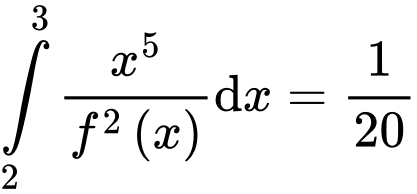
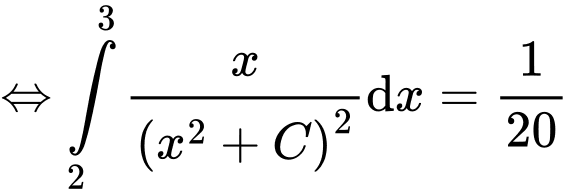
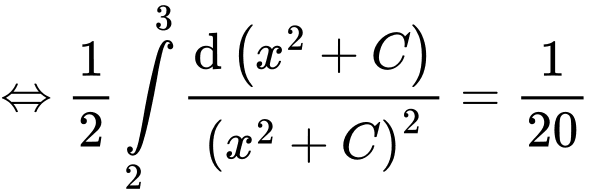
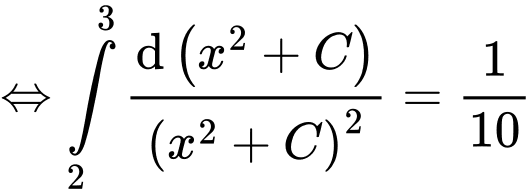
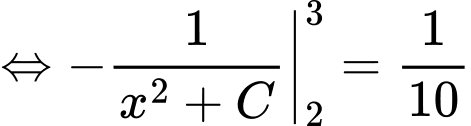
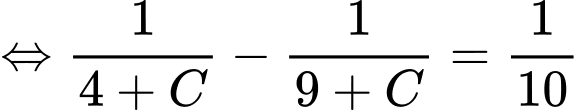
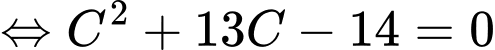
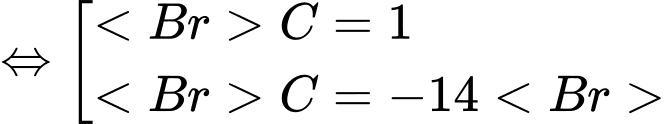 .
.+ Với
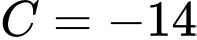
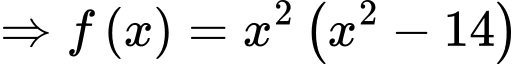 .
.Chọn
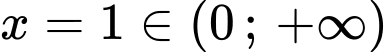 ta được
ta được 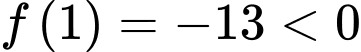 (vô lý vì
(vô lý vì 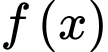 là hàm số dương).
là hàm số dương). + Với
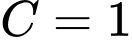
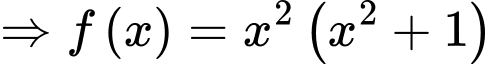 là hàm số dương.
là hàm số dương. Khi đó
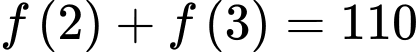 . Đáp án: A
. Đáp án: A