Đáp án Bài tập tự luyện số 2
Câu 1 [58242]: Trong không gian với hệ tọa độ 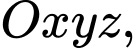 cho tứ diện
cho tứ diện 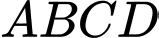 có
có 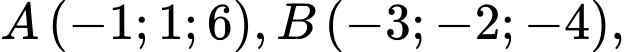
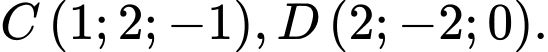 Điểm
Điểm 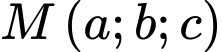 thuộc đường thẳng
thuộc đường thẳng 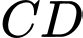 sao cho tam giác
sao cho tam giác 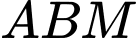 có chu vi nhỏ nhất. Tính
có chu vi nhỏ nhất. Tính 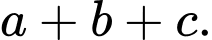
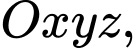 cho tứ diện
cho tứ diện 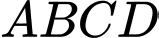 có
có 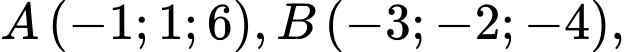
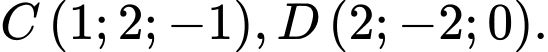 Điểm
Điểm 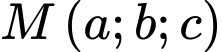 thuộc đường thẳng
thuộc đường thẳng 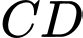 sao cho tam giác
sao cho tam giác 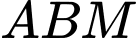 có chu vi nhỏ nhất. Tính
có chu vi nhỏ nhất. Tính 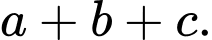
A, 1.
B, 2.
C, 3.
D, 0.
 Đáp án: A
Đáp án: A
Câu 2 [58259]: Trong không gian với hệ tọa độ 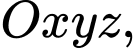 cho các điểm
cho các điểm 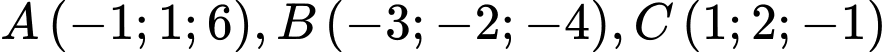 và
và  Gọi
Gọi 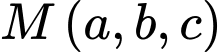 làm điểm thuộc đường thẳng
làm điểm thuộc đường thẳng 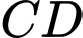 sao cho tam giác
sao cho tam giác 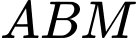 có chu vi nhỏ nhất. Tính
có chu vi nhỏ nhất. Tính 
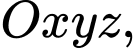 cho các điểm
cho các điểm 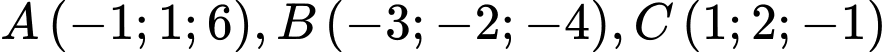 và
và  Gọi
Gọi 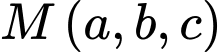 làm điểm thuộc đường thẳng
làm điểm thuộc đường thẳng 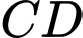 sao cho tam giác
sao cho tam giác 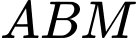 có chu vi nhỏ nhất. Tính
có chu vi nhỏ nhất. Tính 
A, 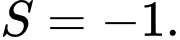
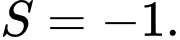
B, 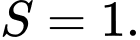
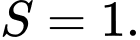
C, 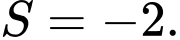
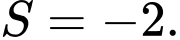
D, 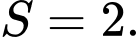
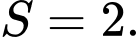
 Đáp án: B
Đáp án: B
Câu 3 [58349]: Trong không gian tọa độ 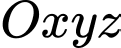 cho các điểm
cho các điểm 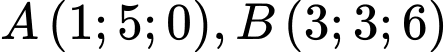 và đường thẳng
và đường thẳng 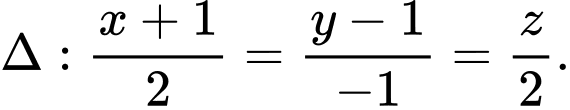 Gọi
Gọi 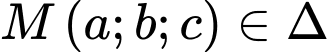 sao cho chu vi tam giác
sao cho chu vi tam giác 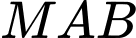 đạt giá trị nhỏ nhất. Tính tổng
đạt giá trị nhỏ nhất. Tính tổng 
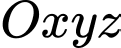 cho các điểm
cho các điểm 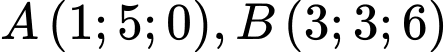 và đường thẳng
và đường thẳng 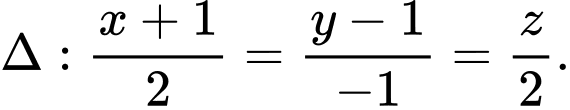 Gọi
Gọi 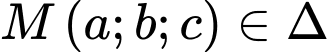 sao cho chu vi tam giác
sao cho chu vi tam giác 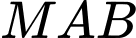 đạt giá trị nhỏ nhất. Tính tổng
đạt giá trị nhỏ nhất. Tính tổng 
A, 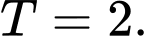
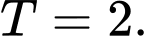
B, 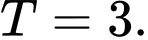
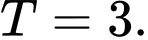
C, 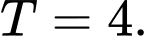
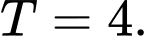
D, 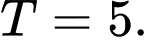
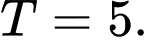
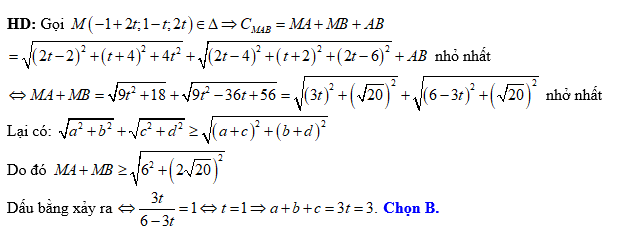 Đáp án: B
Đáp án: B
Câu 4 [57836]: Trong không gian  cho hai điểm
cho hai điểm 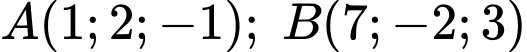 và đường thẳng
và đường thẳng  có phương trình:
có phương trình: 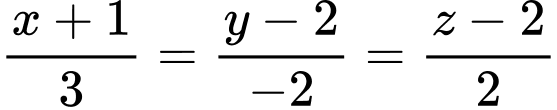 . Điểm
. Điểm 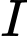 thuộc
thuộc  sao cho
sao cho  nhỏ nhất. Hoành độ của điểm
nhỏ nhất. Hoành độ của điểm 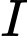 là
là
 cho hai điểm
cho hai điểm 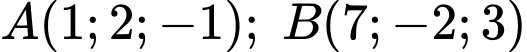 và đường thẳng
và đường thẳng  có phương trình:
có phương trình: 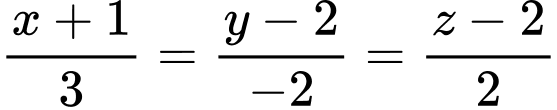 . Điểm
. Điểm 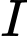 thuộc
thuộc  sao cho
sao cho  nhỏ nhất. Hoành độ của điểm
nhỏ nhất. Hoành độ của điểm  là
là A, 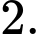
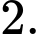
B, 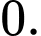
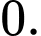
C, 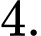
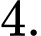
D, 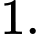
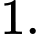
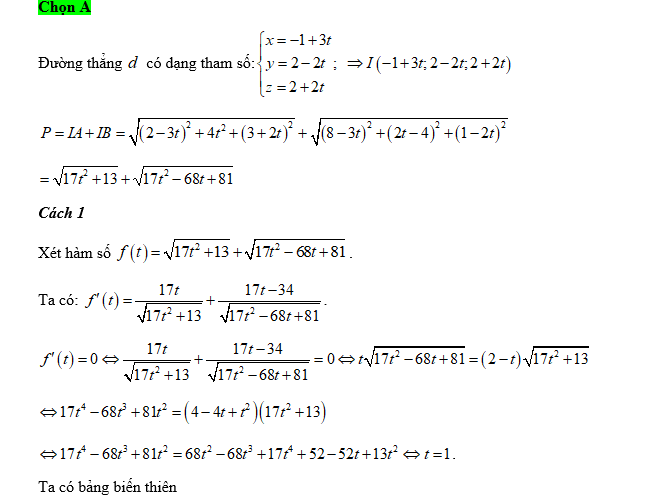
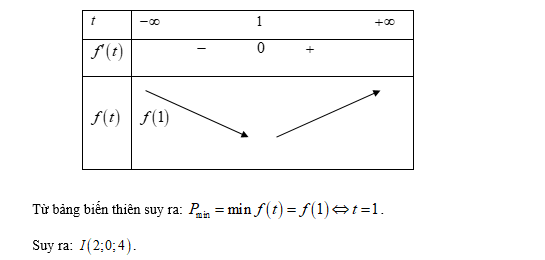 Đáp án: A
Đáp án: A
Câu 5 [58247]: Trong không gian với hệ tọa độ 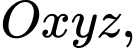 cho các điểm
cho các điểm 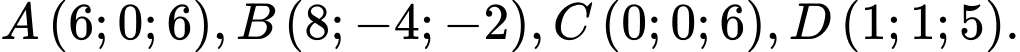 Gọi
Gọi 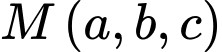 thuộc đường thẳng
thuộc đường thẳng  sao cho diện tích tam giác
sao cho diện tích tam giác  nhỏ nhất . Tính tam giác của biểu thức
nhỏ nhất . Tính tam giác của biểu thức 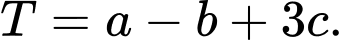
 cho các điểm
cho các điểm 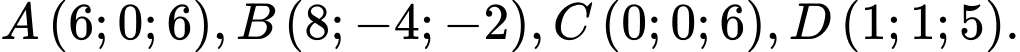 Gọi
Gọi 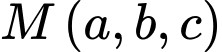 thuộc đường thẳng
thuộc đường thẳng 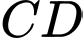 sao cho diện tích tam giác
sao cho diện tích tam giác 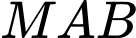 nhỏ nhất . Tính tam giác của biểu thức
nhỏ nhất . Tính tam giác của biểu thức 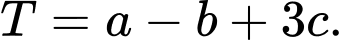
A, 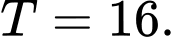
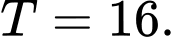
B, 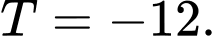
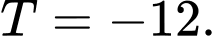
C, 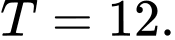
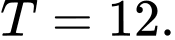
D, 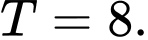
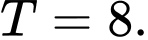
 Đáp án: C
Đáp án: C
Câu 6 [58255]: Trong không gian với hệ tọa độ 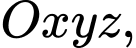 cho hai điểm
cho hai điểm 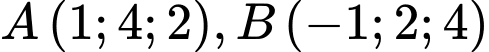 và đường thẳng
và đường thẳng 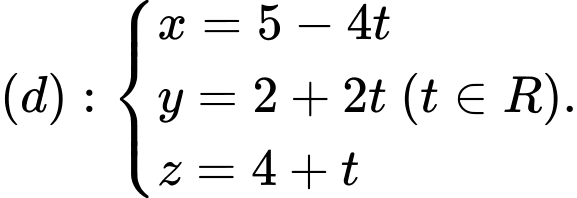 Cho
Cho 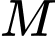 là một điểm thuộc đường thẳng
là một điểm thuộc đường thẳng 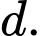 Tìm giá nhỏ nhất của diện tích tam giác
Tìm giá nhỏ nhất của diện tích tam giác 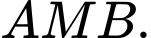
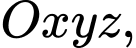 cho hai điểm
cho hai điểm 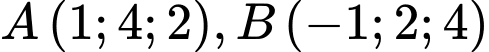 và đường thẳng
và đường thẳng 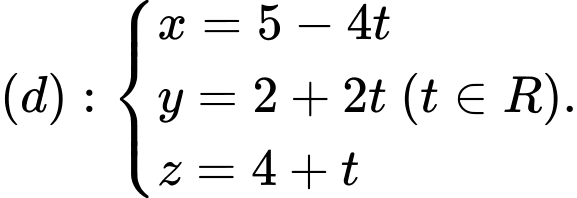 Cho
Cho  là một điểm thuộc đường thẳng
là một điểm thuộc đường thẳng  Tìm giá nhỏ nhất của diện tích tam giác
Tìm giá nhỏ nhất của diện tích tam giác 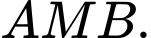
A, 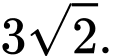
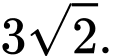
B, 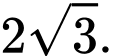
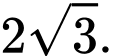
C, 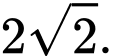
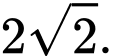
D, 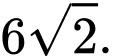
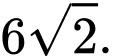
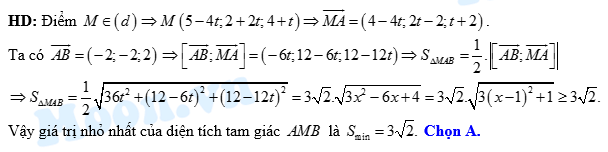 Đáp án: A
Đáp án: A
Câu 7 [55873]: Trong không gian với hệ tọa độ 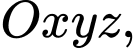 cho các điểm
cho các điểm 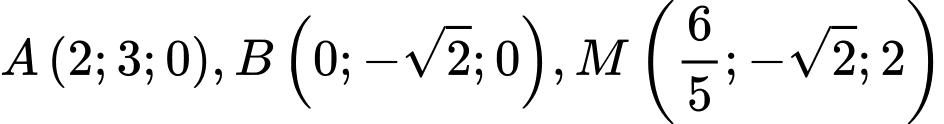 và các đường thẳng
và các đường thẳng 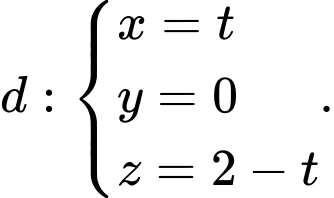 Điểm
Điểm  thuộc
thuộc  sao cho chu vi tam giác
sao cho chu vi tam giác  nhỏ nhất thì độ dài
nhỏ nhất thì độ dài  bằng
bằng
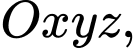 cho các điểm
cho các điểm 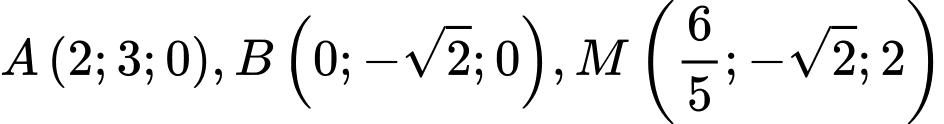 và các đường thẳng
và các đường thẳng 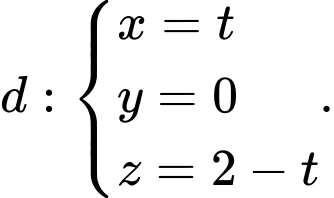 Điểm
Điểm  thuộc
thuộc 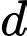 sao cho chu vi tam giác
sao cho chu vi tam giác 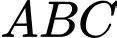 nhỏ nhất thì độ dài
nhỏ nhất thì độ dài 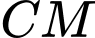 bằng
bằng A, 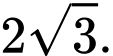
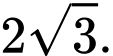
B, 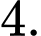
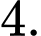
C, 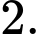
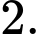
D, 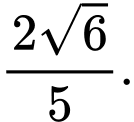
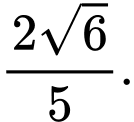
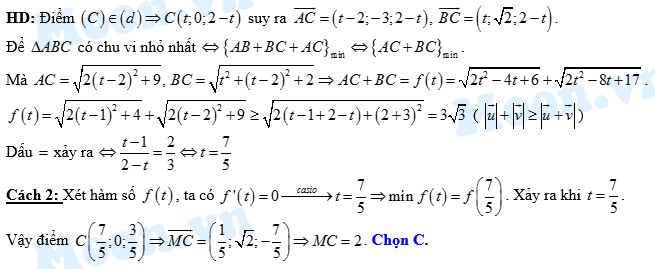 Đáp án: C
Đáp án: C
Câu 8 [82101]: Trong không gian với hệ tọa độ 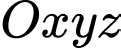 , cho điểm
, cho điểm 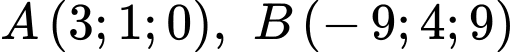 và đường thẳng
và đường thẳng 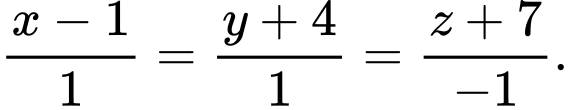 Gọi
Gọi  là điểm thuộc mặt phẳng
là điểm thuộc mặt phẳng  sao cho
sao cho  đạt giá trị lớn nhất. Tính
đạt giá trị lớn nhất. Tính 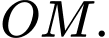
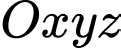 , cho điểm
, cho điểm 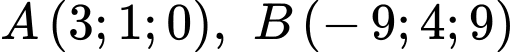 và đường thẳng
và đường thẳng 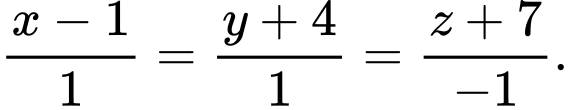 Gọi
Gọi 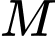 là điểm thuộc mặt phẳng
là điểm thuộc mặt phẳng 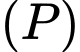 sao cho
sao cho  đạt giá trị lớn nhất. Tính
đạt giá trị lớn nhất. Tính 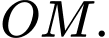
A, 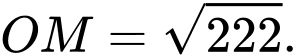
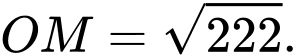
B, 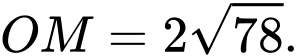
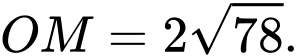
C, 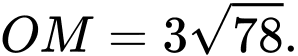
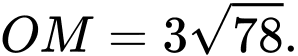
D, 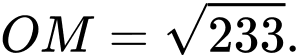
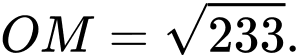
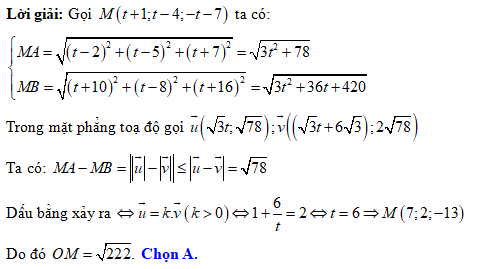 Đáp án: A
Đáp án: A
Câu 9 [82102]: Trong không gian toạ độ 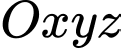 cho 2 điểm
cho 2 điểm 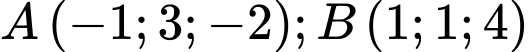 và đường thẳng
và đường thẳng 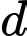 có phương trình
có phương trình 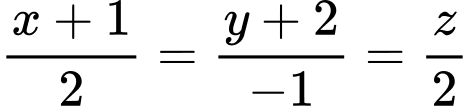 . Gọi
. Gọi 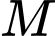 là điểm thuộc
là điểm thuộc 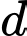 sao cho chu vi tam giác
sao cho chu vi tam giác 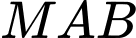 nhỏ nhất. Khi đó độ dài
nhỏ nhất. Khi đó độ dài 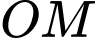 là.
là.
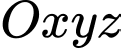 cho 2 điểm
cho 2 điểm 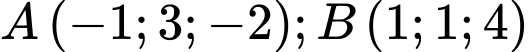 và đường thẳng
và đường thẳng 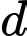 có phương trình
có phương trình 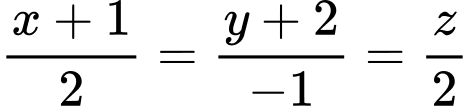 . Gọi
. Gọi 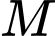 là điểm thuộc
là điểm thuộc 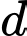 sao cho chu vi tam giác
sao cho chu vi tam giác 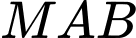 nhỏ nhất. Khi đó độ dài
nhỏ nhất. Khi đó độ dài 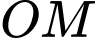 là.
là. A, 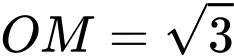 .
.
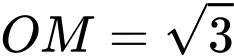 .
.B, 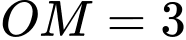 .
.
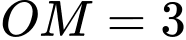 .
.C, 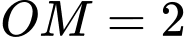 .
.
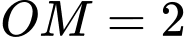 .
.D, 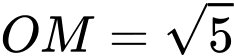 .
.
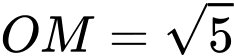 .
.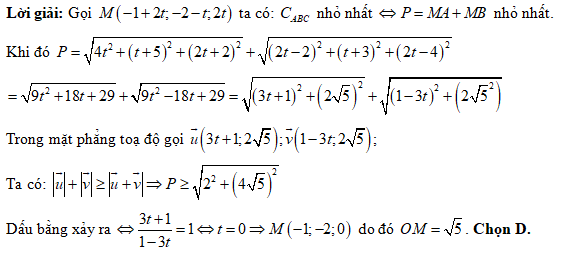 Đáp án: D
Đáp án: D
Câu 10 [59157]: Trong không gian với hệ trục tọa độ  , cho hai đường thẳng
, cho hai đường thẳng 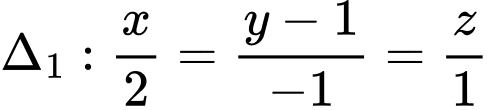 và
và 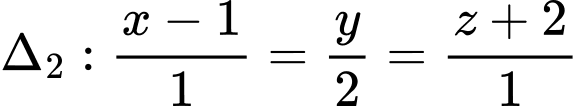 . Một mặt phẳng
. Một mặt phẳng 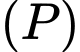 vuông góc với
vuông góc với 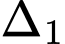 , cắt trục
, cắt trục  tại
tại 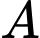 và cắt
và cắt 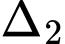 tại
tại 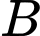 . Tìm độ dài nhỏ nhất của đoạn
. Tìm độ dài nhỏ nhất của đoạn  .
.
 , cho hai đường thẳng
, cho hai đường thẳng 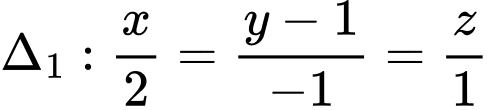 và
và 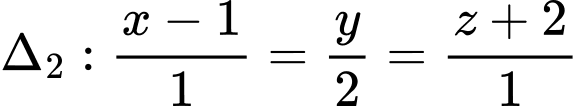 . Một mặt phẳng
. Một mặt phẳng 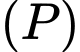 vuông góc với
vuông góc với 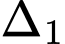 , cắt trục
, cắt trục  tại
tại 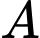 và cắt
và cắt 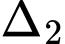 tại
tại 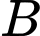 . Tìm độ dài nhỏ nhất của đoạn
. Tìm độ dài nhỏ nhất của đoạn  .
. A, 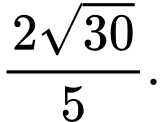
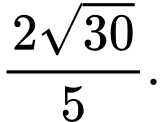
B, 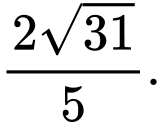
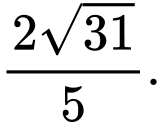
C, 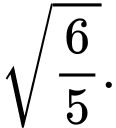
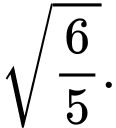
D, 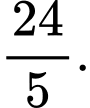
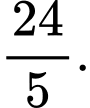
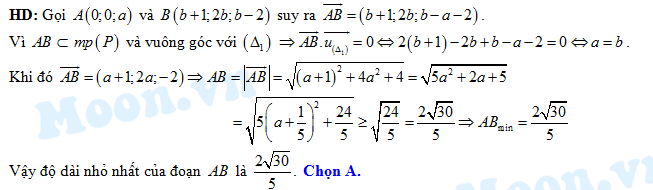 Đáp án: A
Đáp án: A
Câu 11 [57823]: Trong không gian 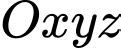 , cho hai điểm
, cho hai điểm 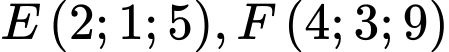 . Gọi
. Gọi  là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 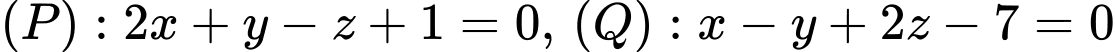 . Điểm
. Điểm 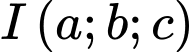 thuộc
thuộc  sao cho biểu thức
sao cho biểu thức 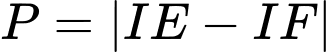 lớn nhất. Tính
lớn nhất. Tính 
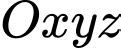 , cho hai điểm
, cho hai điểm 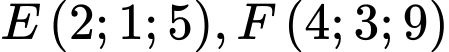 . Gọi
. Gọi  là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 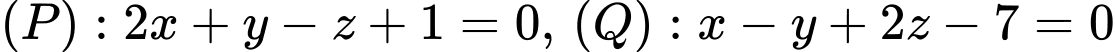 . Điểm
. Điểm 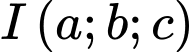 thuộc
thuộc  sao cho biểu thức
sao cho biểu thức 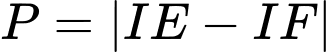 lớn nhất. Tính
lớn nhất. Tính 
A, 4.
B, 1.
C, 3.
D, 2.
 Đáp án: A
Đáp án: A
Câu 12 [81197]: Trong không gian với hệ tọa độ 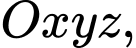 cho 2 điểm
cho 2 điểm 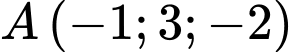 và
và 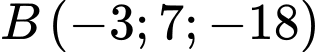 và mặt phẳng
và mặt phẳng 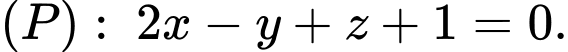 Điểm
Điểm 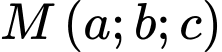 thuộc
thuộc 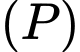 sao cho
sao cho  nhỏ nhất. Tính giá trị của biểu thức
nhỏ nhất. Tính giá trị của biểu thức 
 cho 2 điểm
cho 2 điểm 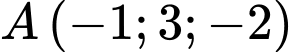 và
và 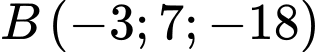 và mặt phẳng
và mặt phẳng 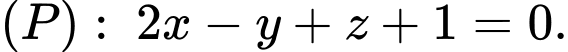 Điểm
Điểm 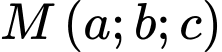 thuộc
thuộc 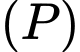 sao cho
sao cho  nhỏ nhất. Tính giá trị của biểu thức
nhỏ nhất. Tính giá trị của biểu thức 
A, 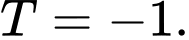
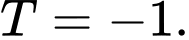
B, 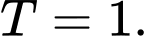
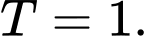
C, 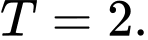
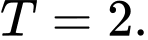
D, 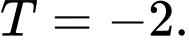
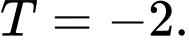
 Đáp án: B
Đáp án: B
Câu 13 [81198]: Trong không gian với hệ tọa độ 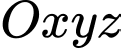 , cho mặt phẳng
, cho mặt phẳng 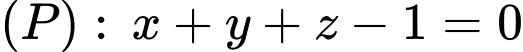 và hai điểm
và hai điểm 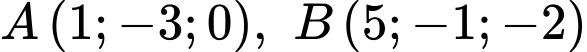 . Điểm
. Điểm 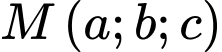 nằm trên
nằm trên 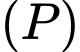 và
và  lớn nhất. Giá trị tích
lớn nhất. Giá trị tích 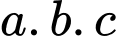 bằng
bằng
 , cho mặt phẳng
, cho mặt phẳng 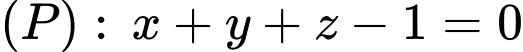 và hai điểm
và hai điểm 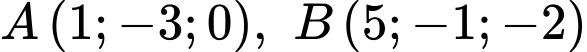 . Điểm
. Điểm 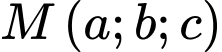 nằm trên
nằm trên 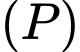 và
và  lớn nhất. Giá trị tích
lớn nhất. Giá trị tích 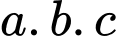 bằng
bằng A, 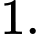
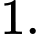
B, 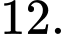
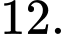
C, 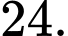
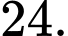
D, 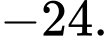
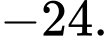
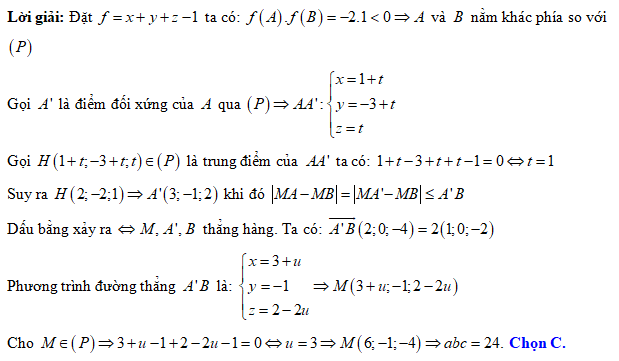 Đáp án: C
Đáp án: C
Câu 14 [81199]: Trong không gian toạ độ 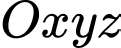 cho mặt phẳng
cho mặt phẳng 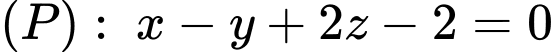 và 2 điểm
và 2 điểm 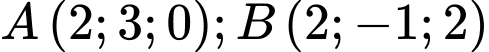 . Điểm
. Điểm 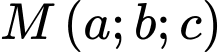 thuộc mặt phẳng
thuộc mặt phẳng 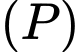 sao cho
sao cho  lớn nhất. Tính giá trị của biểu thức
lớn nhất. Tính giá trị của biểu thức 
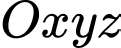 cho mặt phẳng
cho mặt phẳng 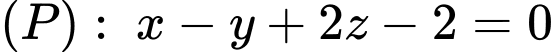 và 2 điểm
và 2 điểm 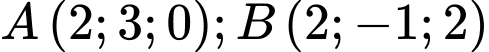 . Điểm
. Điểm 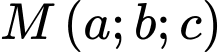 thuộc mặt phẳng
thuộc mặt phẳng  sao cho
sao cho  lớn nhất. Tính giá trị của biểu thức
lớn nhất. Tính giá trị của biểu thức 
A, 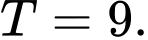
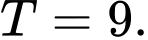
B, 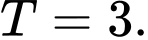
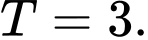
C, 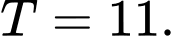
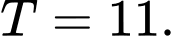
D, 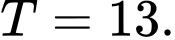
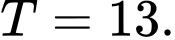
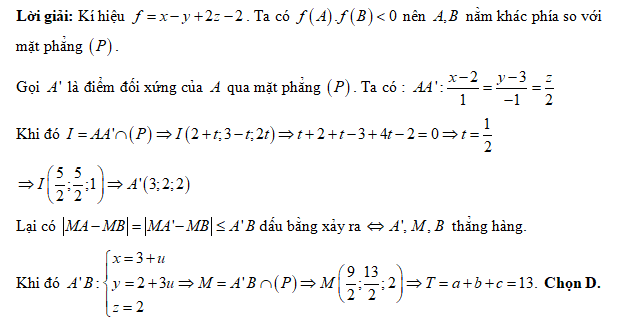 Đáp án: D
Đáp án: D
Câu 15 [81200]: Trong không gian toạ độ 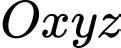 cho mặt phẳng
cho mặt phẳng 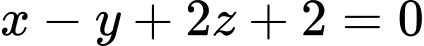 và 2 điểm
và 2 điểm 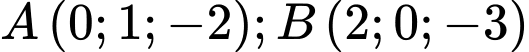 . Gọi
. Gọi 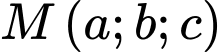 là điểm thuộc mặt phẳng
là điểm thuộc mặt phẳng 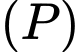 sao cho
sao cho  nhỏ nhất. Tính giá trị của biểu thức
nhỏ nhất. Tính giá trị của biểu thức 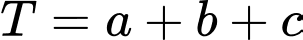 .
.
 cho mặt phẳng
cho mặt phẳng 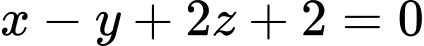 và 2 điểm
và 2 điểm 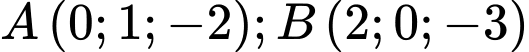 . Gọi
. Gọi 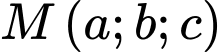 là điểm thuộc mặt phẳng
là điểm thuộc mặt phẳng 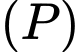 sao cho
sao cho  nhỏ nhất. Tính giá trị của biểu thức
nhỏ nhất. Tính giá trị của biểu thức 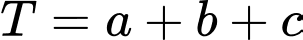 .
. A, 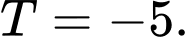
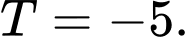
B, 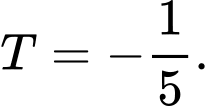
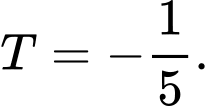
C, 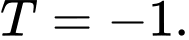
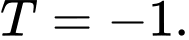
D, 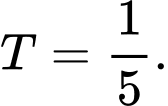
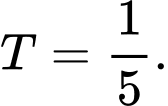
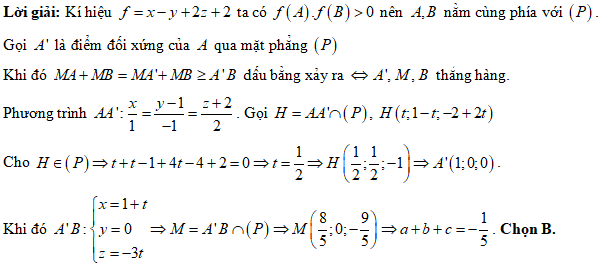 Đáp án: B
Đáp án: B
Câu 16 [57824]: Trong không gian với hệ trục tọa độ 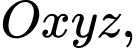 cho hai điểm
cho hai điểm 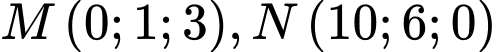 và mặt phẳng
và mặt phẳng 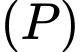 có phương trình
có phương trình 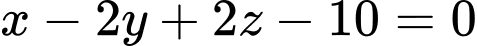 . Điểm
. Điểm 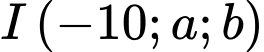 thuộc mặt phẳng
thuộc mặt phẳng 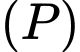 sao cho
sao cho 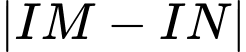 lớn nhất. Khi đó tổng
lớn nhất. Khi đó tổng 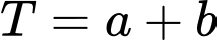 bằng
bằng
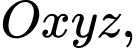 cho hai điểm
cho hai điểm 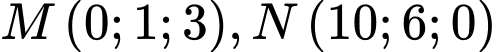 và mặt phẳng
và mặt phẳng 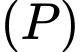 có phương trình
có phương trình 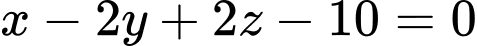 . Điểm
. Điểm 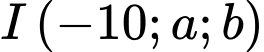 thuộc mặt phẳng
thuộc mặt phẳng 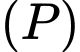 sao cho
sao cho 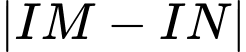 lớn nhất. Khi đó tổng
lớn nhất. Khi đó tổng 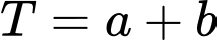 bằng
bằng A, 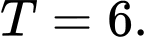
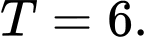
B, 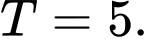
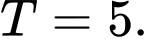
C, 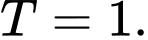
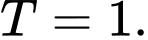
D, 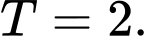
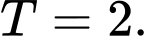
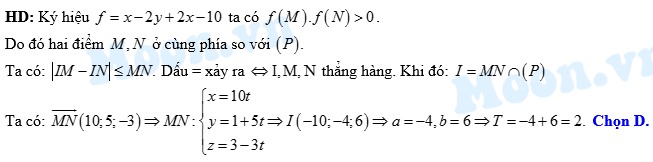 Đáp án: D
Đáp án: D
Câu 17 [58239]: Trong không gian 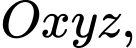 cho hai điểm
cho hai điểm 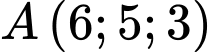 và
và 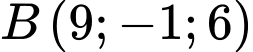 . Trên mặt phẳng
. Trên mặt phẳng 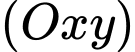 , lấy điểm
, lấy điểm 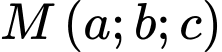 sao cho
sao cho  bé nhất. Tính
bé nhất. Tính  .
.
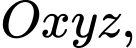 cho hai điểm
cho hai điểm 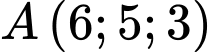 và
và 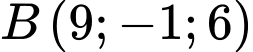 . Trên mặt phẳng
. Trên mặt phẳng 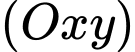 , lấy điểm
, lấy điểm 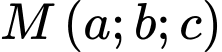 sao cho
sao cho  bé nhất. Tính
bé nhất. Tính  .
. A, 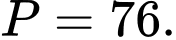
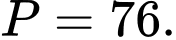
B, 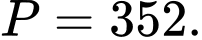
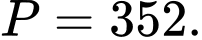
C, 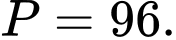
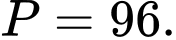
D, 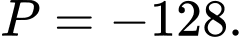
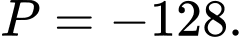
Phương trình mặt phẳng 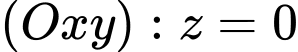
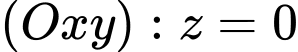
Do 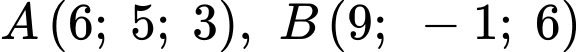 nằm cùng phía so với mặt phẳng
nằm cùng phía so với mặt phẳng 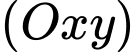
Đáp án: A 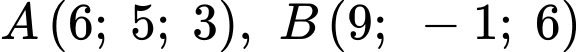 nằm cùng phía so với mặt phẳng
nằm cùng phía so với mặt phẳng 
Gọi 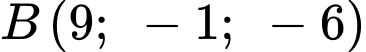 là điểm đối xứng của
là điểm đối xứng của  qua mặt phẳng
qua mặt phẳng 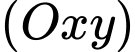
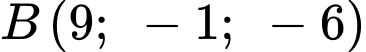 là điểm đối xứng của
là điểm đối xứng của 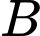 qua mặt phẳng
qua mặt phẳng 
Ta có 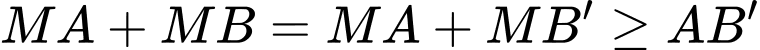 Dấu “=” xảy ra khi và chỉ khi
Dấu “=” xảy ra khi và chỉ khi 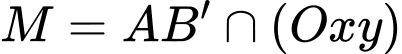
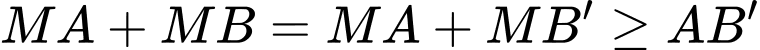 Dấu “=” xảy ra khi và chỉ khi
Dấu “=” xảy ra khi và chỉ khi 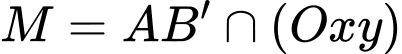
Phương trình đường thẳng  là
là 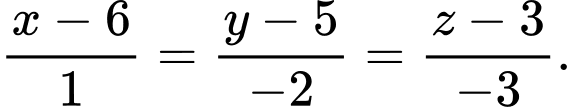
 là
là 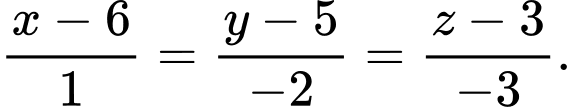
Suy ra 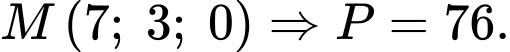
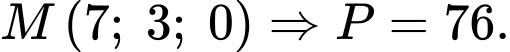
Chọn đáp án A.
Câu 18 [58240]: Trong không gian với hệ tọa độ 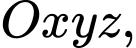 cho 3 điểm
cho 3 điểm 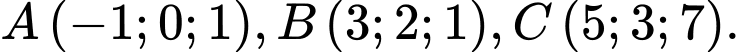 Gọi
Gọi 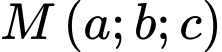 là điểm thỏa mãn
là điểm thỏa mãn  và
và  đạt giá trị nhỏ nhất. Tìm
đạt giá trị nhỏ nhất. Tìm 
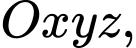 cho 3 điểm
cho 3 điểm 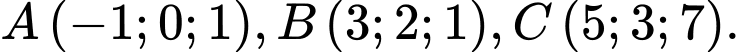 Gọi
Gọi 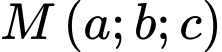 là điểm thỏa mãn
là điểm thỏa mãn  và
và  đạt giá trị nhỏ nhất. Tìm
đạt giá trị nhỏ nhất. Tìm 
A, 

B, 

C, 

D, 

Ta có 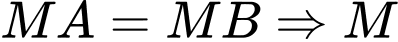 thuộc mặt phẳng trung trực của đoạn thẳng
thuộc mặt phẳng trung trực của đoạn thẳng 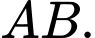
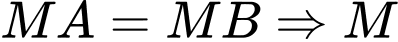 thuộc mặt phẳng trung trực của đoạn thẳng
thuộc mặt phẳng trung trực của đoạn thẳng 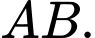
Gọi 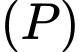 là mặt phẳng trung trực của
là mặt phẳng trung trực của 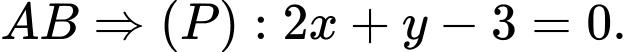
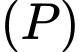 là mặt phẳng trung trực của
là mặt phẳng trung trực của 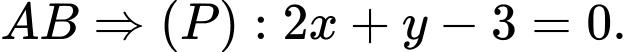
Lại có 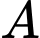 và
và  nằm hai phía của mặt phẳng
nằm hai phía của mặt phẳng 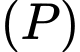
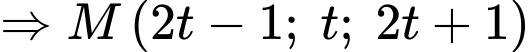
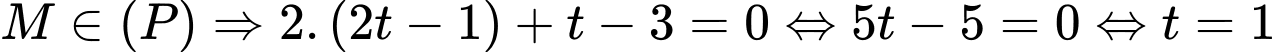
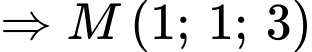
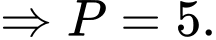
Đáp án: D 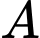 và
và  nằm hai phía của mặt phẳng
nằm hai phía của mặt phẳng 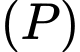
Do đó 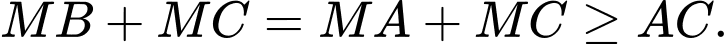
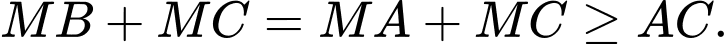
Dấu “=” xảy ra khi và chỉ khi 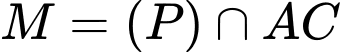
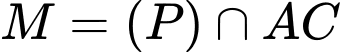
Phương trình đường thẳng 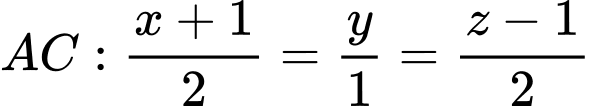
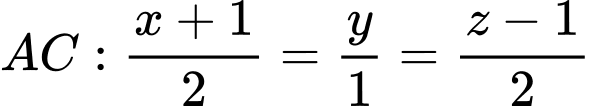
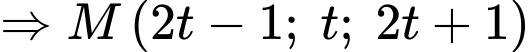
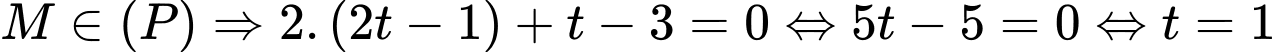
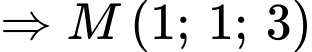
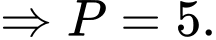
Chọn đáp án D.
Câu 19 [57835]: Trong không gian  , cho ba điểm
, cho ba điểm 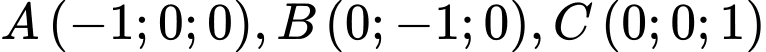 và mặt phẳng
và mặt phẳng 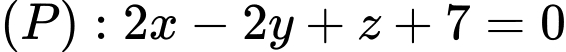 . Xét
. Xét  , giá trị nhỏ nhất của
, giá trị nhỏ nhất của 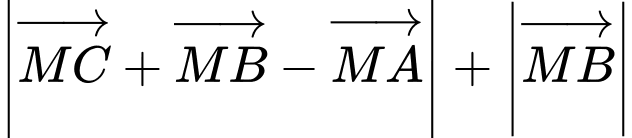 bằng
bằng
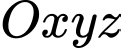 , cho ba điểm
, cho ba điểm 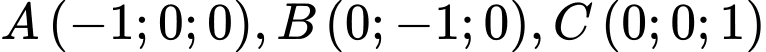 và mặt phẳng
và mặt phẳng 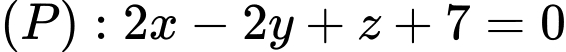 . Xét
. Xét 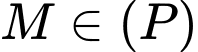 , giá trị nhỏ nhất của
, giá trị nhỏ nhất của 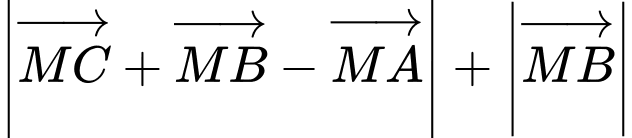 bằng
bằng A, 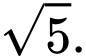
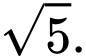
B, 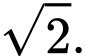
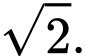
C, 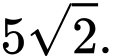
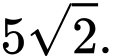
D, 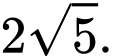
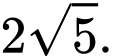
 Đáp án: C
Đáp án: C
Câu 20 [81201]: Trong không gian với hệ tọa độ 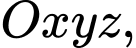 cho
cho 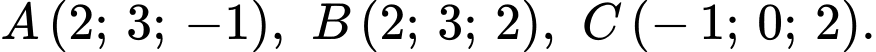 Tìm tọa độ điểm
Tìm tọa độ điểm 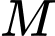 thuộc mặt phẳng
thuộc mặt phẳng 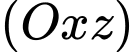 để
để 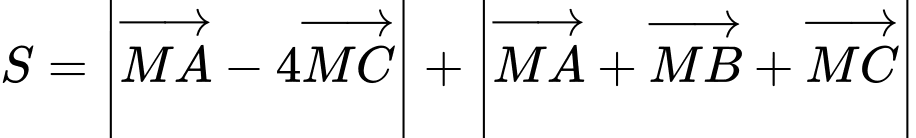 nhỏ nhất.
nhỏ nhất.
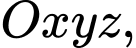 cho
cho 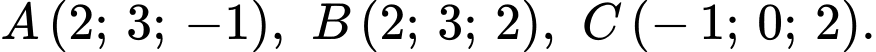 Tìm tọa độ điểm
Tìm tọa độ điểm 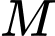 thuộc mặt phẳng
thuộc mặt phẳng 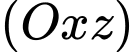 để
để 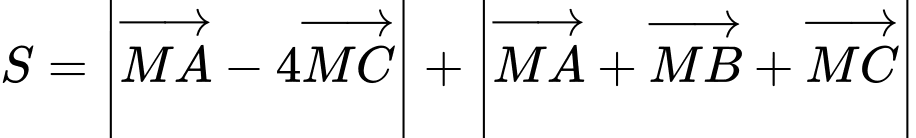 nhỏ nhất.
nhỏ nhất. A, 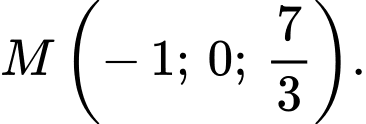
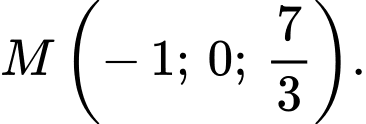
B, 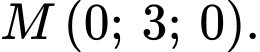
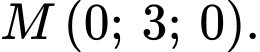
C, 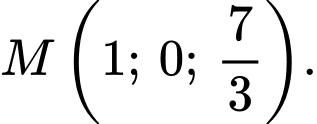
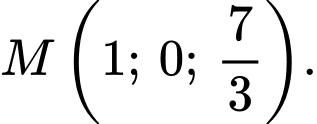
D, 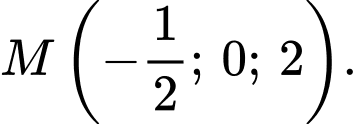
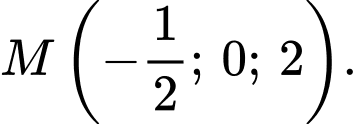
 Đáp án: A
Đáp án: A