Đáp án Bài tập tự luyện
Câu 1 [57771]: Trong không gian với hệ tọa độ 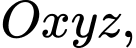 cho đường thẳng
cho đường thẳng 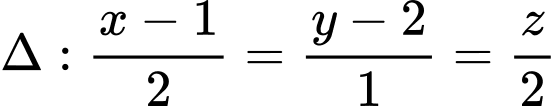 và mặt phẳng
và mặt phẳng 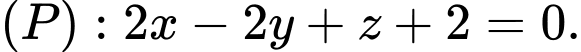 Mặt phẳng
Mặt phẳng  chứa
chứa  và tạo với
và tạo với 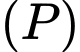 một góc nhỏ nhất có phương trình dạng
một góc nhỏ nhất có phương trình dạng 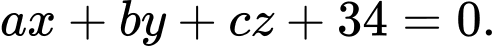 Tính tích
Tính tích 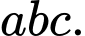
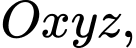 cho đường thẳng
cho đường thẳng 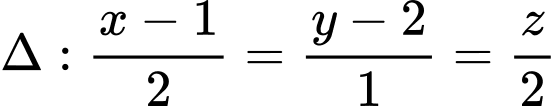 và mặt phẳng
và mặt phẳng 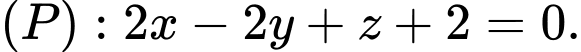 Mặt phẳng
Mặt phẳng  chứa
chứa  và tạo với
và tạo với 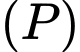 một góc nhỏ nhất có phương trình dạng
một góc nhỏ nhất có phương trình dạng 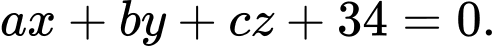 Tính tích
Tính tích 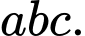
A, 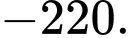
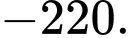
B, 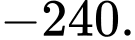
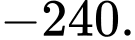
C, 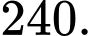
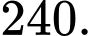
D, 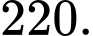
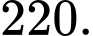
Ta có 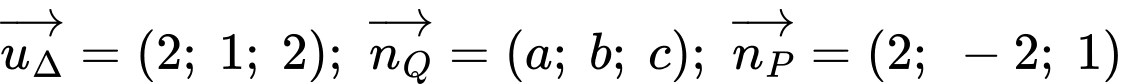
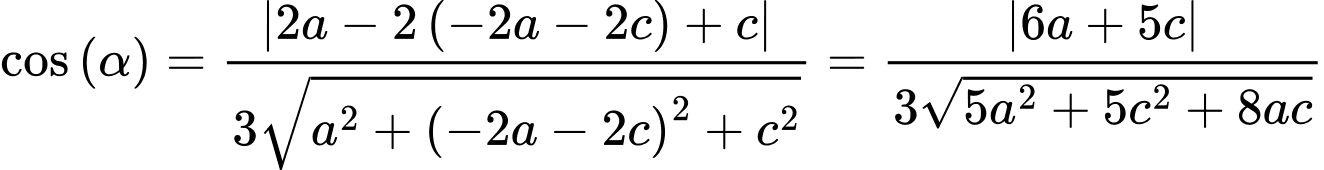
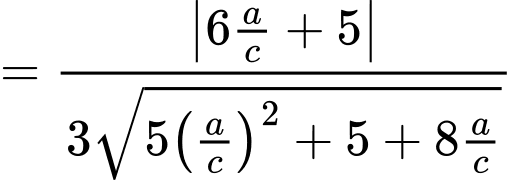 (chia cả tử và mẫu cho c)
(chia cả tử và mẫu cho c) 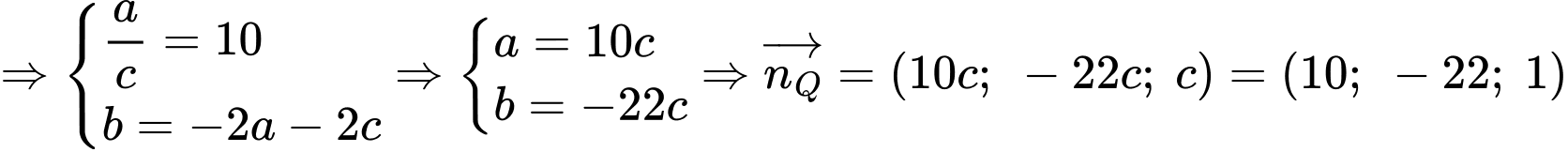
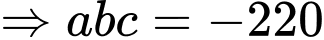
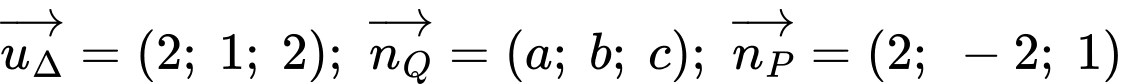
Vì 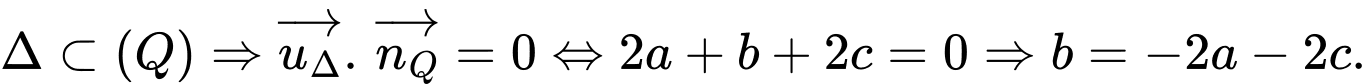
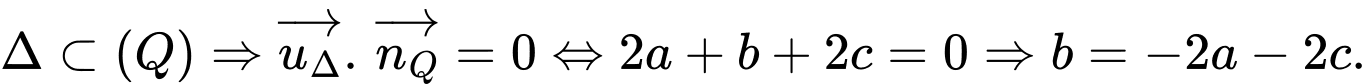
Gọi 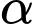 là góc giữa hai mặt phẳng
là góc giữa hai mặt phẳng 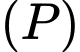 và
và 
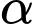 là góc giữa hai mặt phẳng
là góc giữa hai mặt phẳng 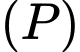 và
và 
Ta có 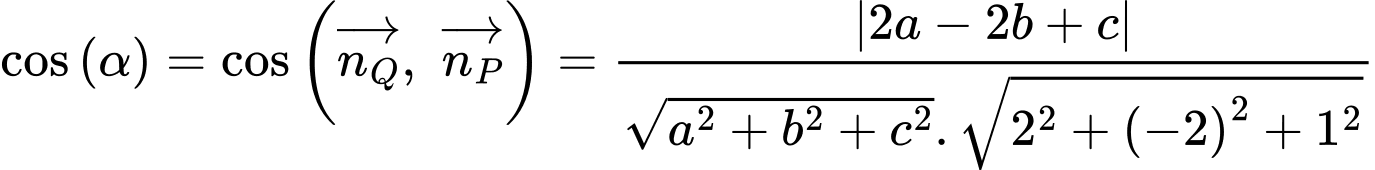
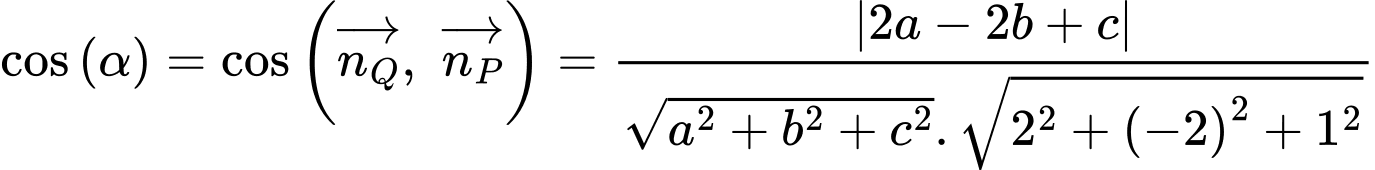
Thay 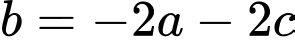 vào biểu thức trên ta được
vào biểu thức trên ta được
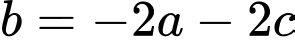 vào biểu thức trên ta được
vào biểu thức trên ta được 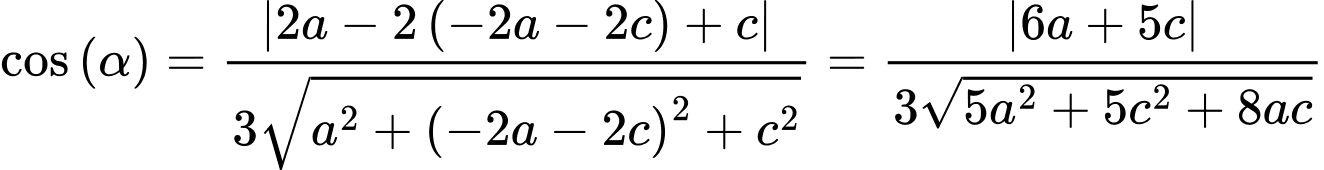
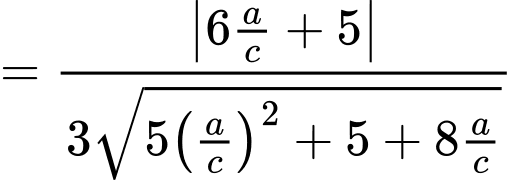 (chia cả tử và mẫu cho c)
(chia cả tử và mẫu cho c) Ta có 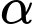 là nhỏ nhất
là nhỏ nhất 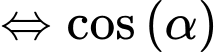 là lớn nhất
là lớn nhất
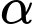 là nhỏ nhất
là nhỏ nhất 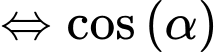 là lớn nhất
là lớn nhất Đặt 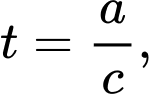 xét hàm số
xét hàm số 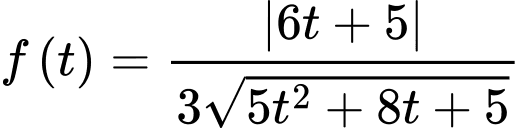
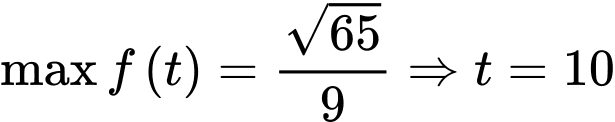
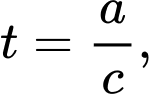 xét hàm số
xét hàm số 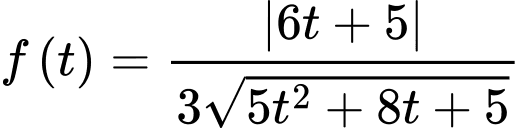
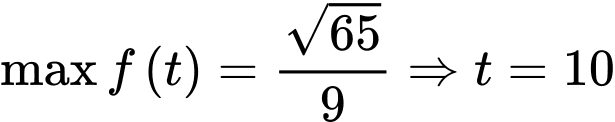
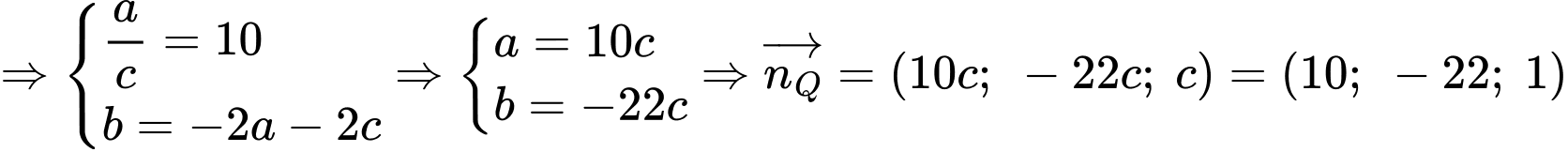
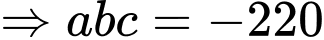
Chọn đáp án A.
Đáp án: A
Câu 2 [953306]: Trong không gian tọa độ 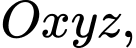 cho các đường thẳng
cho các đường thẳng 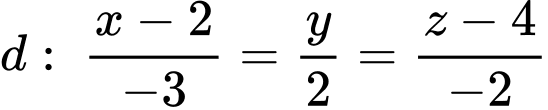 và
và 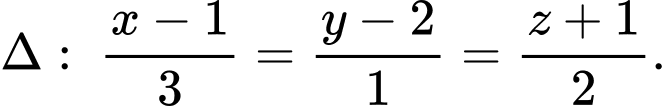 Biết rằng trong tất cả các mặt phẳng chứa
Biết rằng trong tất cả các mặt phẳng chứa  thì mặt phẳng
thì mặt phẳng 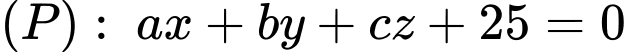 tạo với
tạo với 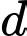 góc lớn nhất. Tính
góc lớn nhất. Tính 
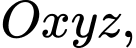 cho các đường thẳng
cho các đường thẳng 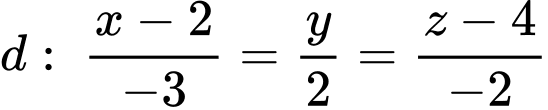 và
và 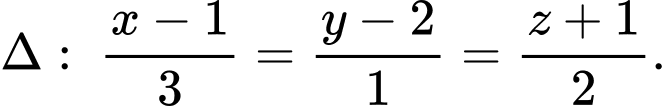 Biết rằng trong tất cả các mặt phẳng chứa
Biết rằng trong tất cả các mặt phẳng chứa  thì mặt phẳng
thì mặt phẳng 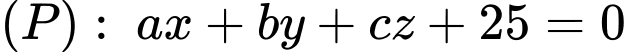 tạo với
tạo với 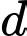 góc lớn nhất. Tính
góc lớn nhất. Tính 
A, 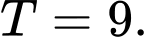
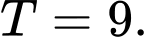
B, 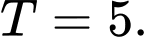
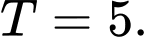
C, 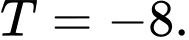
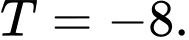
D, 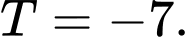
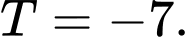
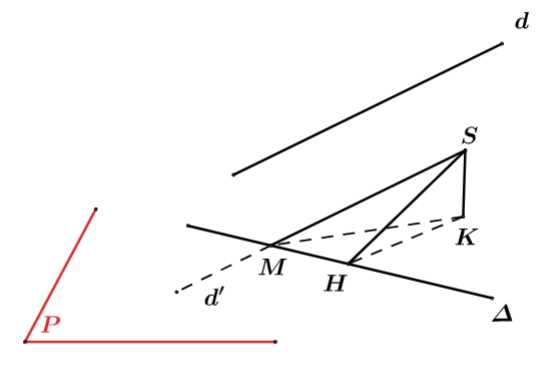
Gọi
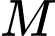 là điểm bất kì thuộc
là điểm bất kì thuộc 
Gọi
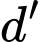 là đường thẳng qua
là đường thẳng qua 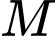 và song song với
và song song với 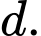 Khi đó ta có
Khi đó ta có 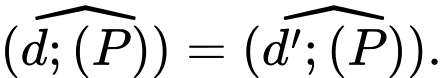
Lấy
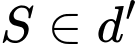 bất kì, kẻ
bất kì, kẻ 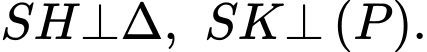
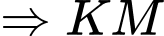 là hình chiếu vuông góc của
là hình chiếu vuông góc của 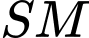 lên
lên 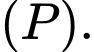

Xét tam giác vuông
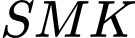 ta có
ta có 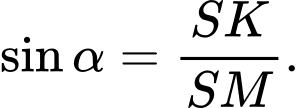
Để
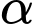 lớn nhất thì
lớn nhất thì 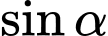 lớn nhất
lớn nhất 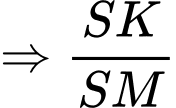 lớn nhất.
lớn nhất.
Ta có:
 (do
(do 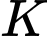 là hình chiếu
là hình chiếu 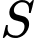 trên
trên 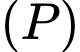 )
)
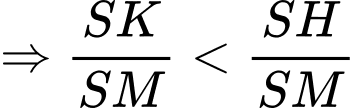 với
với 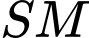 cố định.
cố định.
Ta có:
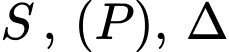 cố định
cố định 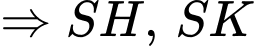 không đổi.
không đổi.
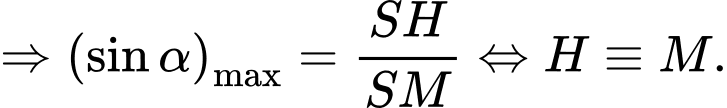
Khi đó
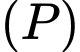 chứa
chứa  và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 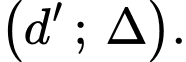
Lấy
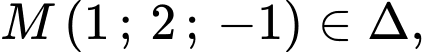 phương trình đường thẳng
phương trình đường thẳng 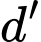 là
là 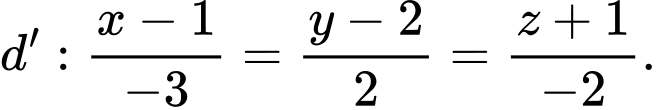
Gọi
 là mặt phẳng chứa
là mặt phẳng chứa 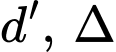
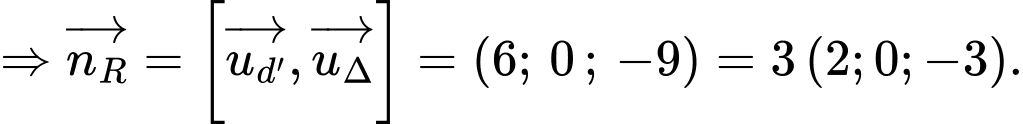
Ta có:
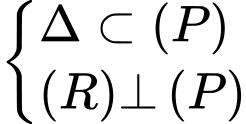
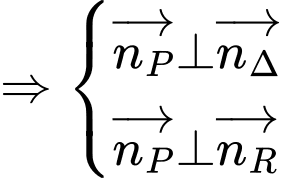
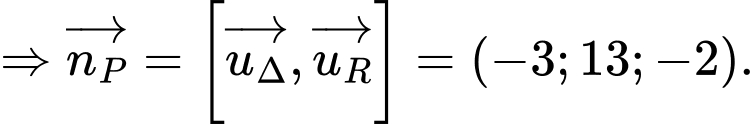
Suy ra, phương trình mặt phẳng
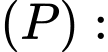


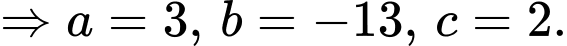
Vậy
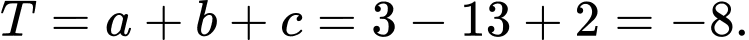
Đáp án: C. Đáp án: C
Câu 3 [57772]: Trong không gian với hệ tọa độ 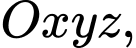 cho hai đường thẳng
cho hai đường thẳng 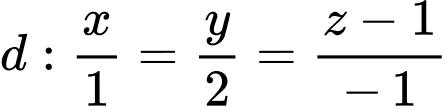 và
và 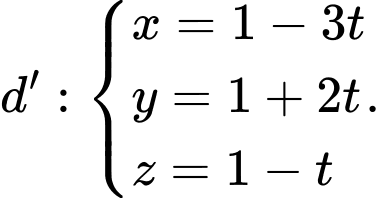 Mặt phẳng
Mặt phẳng 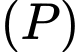 chứa
chứa 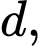 tạo với đường thẳng
tạo với đường thẳng 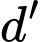 một góc lớn nhất đi qua điểm nào dưới đây?
một góc lớn nhất đi qua điểm nào dưới đây?
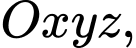 cho hai đường thẳng
cho hai đường thẳng 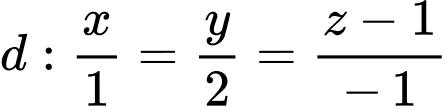 và
và 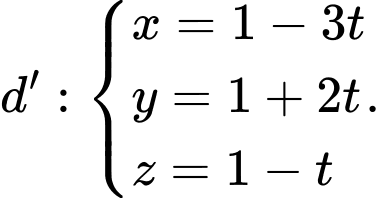 Mặt phẳng
Mặt phẳng 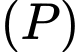 chứa
chứa 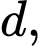 tạo với đường thẳng
tạo với đường thẳng 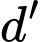 một góc lớn nhất đi qua điểm nào dưới đây?
một góc lớn nhất đi qua điểm nào dưới đây? A, 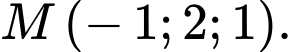
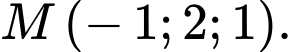
B, 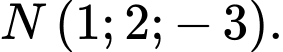
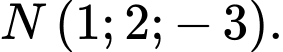
C, 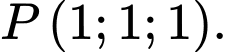
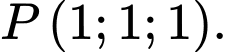
D, 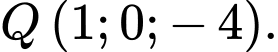
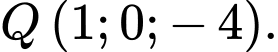
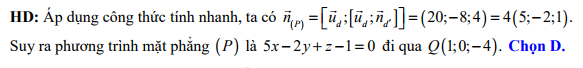 Đáp án: D
Đáp án: D
Câu 4 [57775]: Trong không gian với hệ tọa độ 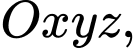 cho hai điểm
cho hai điểm 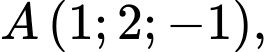
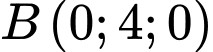 và mặt phẳng
và mặt phẳng 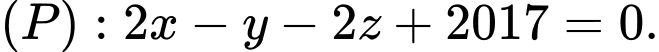 Gọi
Gọi  là mặt phẳng đi qua
là mặt phẳng đi qua 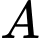 và
và 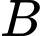 và tạo với
và tạo với 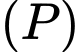 góc nhỏ nhất bằng
góc nhỏ nhất bằng 
 Tính
Tính 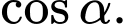
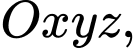 cho hai điểm
cho hai điểm 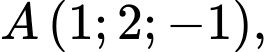
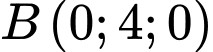 và mặt phẳng
và mặt phẳng 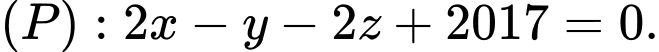 Gọi
Gọi  là mặt phẳng đi qua
là mặt phẳng đi qua 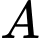 và
và 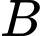 và tạo với
và tạo với 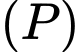 góc nhỏ nhất bằng
góc nhỏ nhất bằng 
 Tính
Tính 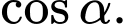
A, 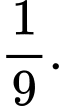
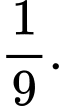
B, 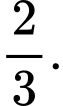
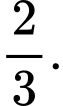
C, 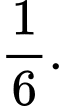
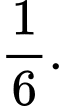
D, 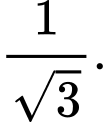
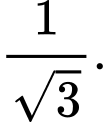
 Đáp án: D
Đáp án: D
Câu 5 [57783]: Trong không gian với hệ tọa độ 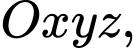 cho đường thẳng
cho đường thẳng 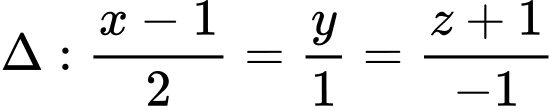 và mặt phẳng có phương trình
và mặt phẳng có phương trình 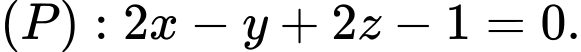 Gọi
Gọi  là mặt phẳng chứa
là mặt phẳng chứa  tạo với
tạo với 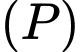 một góc nhỏ nhất
một góc nhỏ nhất Biết rằng mặt phẳng
Biết rằng mặt phẳng  có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 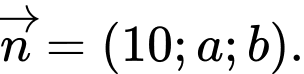 Hệ thức nào sau đây là đúng?
Hệ thức nào sau đây là đúng?
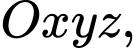 cho đường thẳng
cho đường thẳng 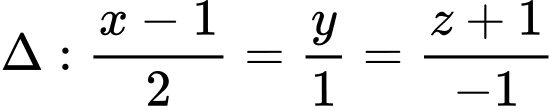 và mặt phẳng có phương trình
và mặt phẳng có phương trình 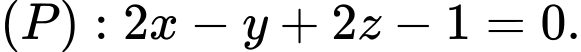 Gọi
Gọi  là mặt phẳng chứa
là mặt phẳng chứa  tạo với
tạo với 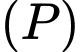 một góc nhỏ nhất
một góc nhỏ nhất Biết rằng mặt phẳng
Biết rằng mặt phẳng  có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 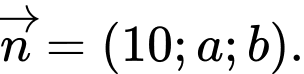 Hệ thức nào sau đây là đúng?
Hệ thức nào sau đây là đúng? A, 

B, 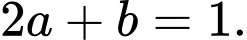
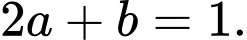
C, 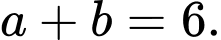
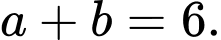
D, 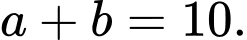
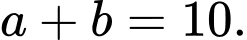
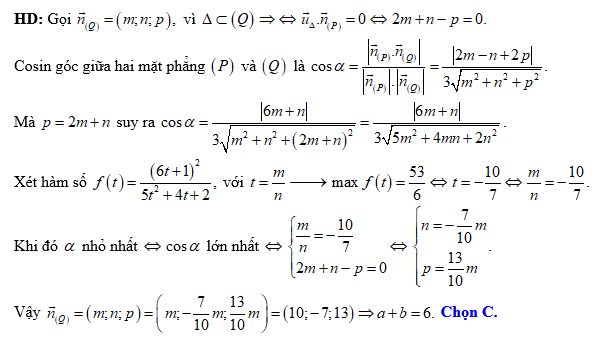 Đáp án: C
Đáp án: C
Câu 6 [57785]: Gọi 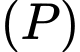 là mặt phẳng chứa trục
là mặt phẳng chứa trục 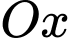
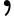 và tạo với đường thẳng
và tạo với đường thẳng 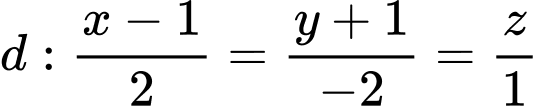 một góc lớn nhất
một góc lớn nhất  Hỏi
Hỏi 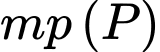 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây?
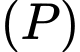 là mặt phẳng chứa trục
là mặt phẳng chứa trục 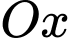
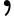 và tạo với đường thẳng
và tạo với đường thẳng 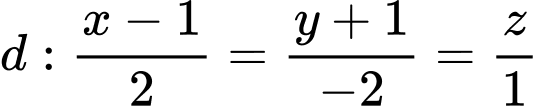 một góc lớn nhất
một góc lớn nhất  Hỏi
Hỏi 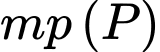 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây? A, 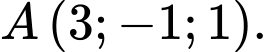
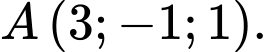
B, 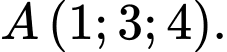
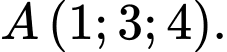
C, 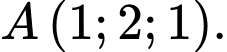
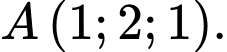
D, 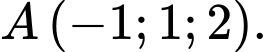
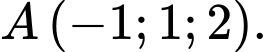
 Đáp án: D
Đáp án: D
Câu 7 [80571]: Trong không gian 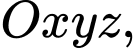 cho hai điểm
cho hai điểm 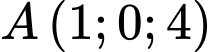 và
và 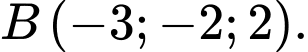 Gọi
Gọi 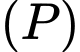 là phương trình mặt phẳng đi qua 2 điểm
là phương trình mặt phẳng đi qua 2 điểm 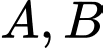 sao cho
sao cho 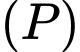 tạo với mặt phẳng
tạo với mặt phẳng 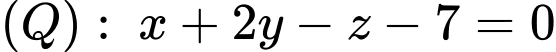 một góc nhỏ nhất. Mặt phẳng
một góc nhỏ nhất. Mặt phẳng 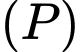 đi qua điểm nào trong các điểm sau?
đi qua điểm nào trong các điểm sau?
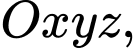 cho hai điểm
cho hai điểm 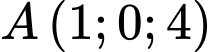 và
và 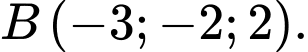 Gọi
Gọi 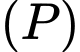 là phương trình mặt phẳng đi qua 2 điểm
là phương trình mặt phẳng đi qua 2 điểm 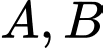 sao cho
sao cho 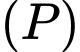 tạo với mặt phẳng
tạo với mặt phẳng 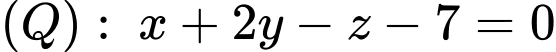 một góc nhỏ nhất. Mặt phẳng
một góc nhỏ nhất. Mặt phẳng 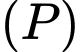 đi qua điểm nào trong các điểm sau?
đi qua điểm nào trong các điểm sau? A, 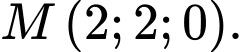
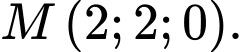
B, 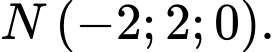
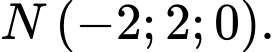
C, 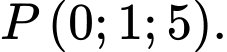
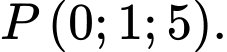
D, 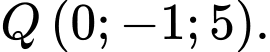
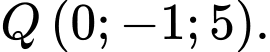
 Đáp án: C
Đáp án: C
Câu 8 [80572]: Trong không gian 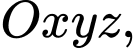 cho đường thẳng
cho đường thẳng 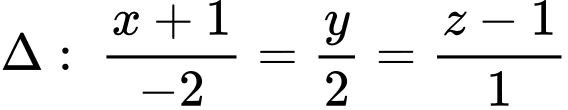 và đường thẳng
và đường thẳng 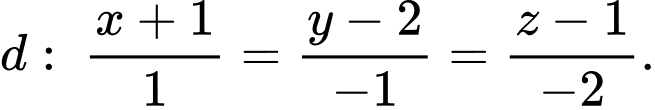 Gọi
Gọi 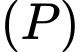 là mặt phẳng chứa
là mặt phẳng chứa 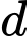 và tạo với
và tạo với  một góc lớn nhất. Tính khoảng cách từ gốc tọa độ
một góc lớn nhất. Tính khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 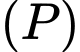 khi đó
khi đó
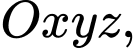 cho đường thẳng
cho đường thẳng 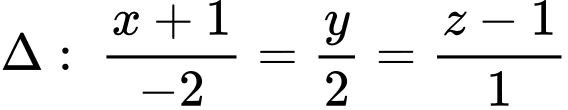 và đường thẳng
và đường thẳng 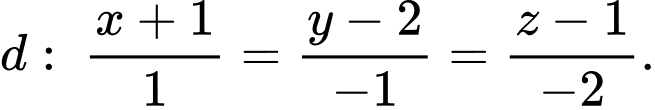 Gọi
Gọi 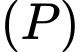 là mặt phẳng chứa
là mặt phẳng chứa 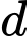 và tạo với
và tạo với  một góc lớn nhất. Tính khoảng cách từ gốc tọa độ
một góc lớn nhất. Tính khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 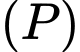 khi đó
khi đó A, 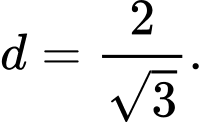
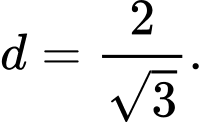
B, 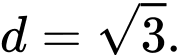
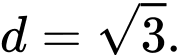
C, 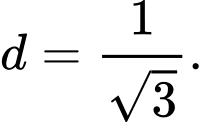
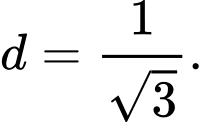
D, 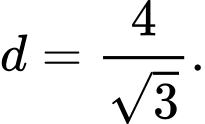
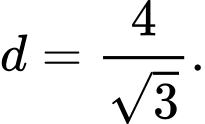
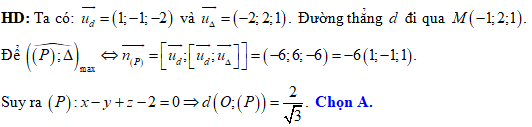 Đáp án: A
Đáp án: A
Câu 9 [80574]: Trong không gian 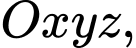 cho hai đường thẳng
cho hai đường thẳng 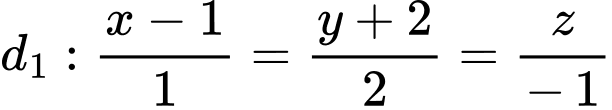 và
và 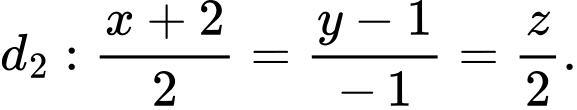 Phương trình mặt phẳng
Phương trình mặt phẳng 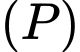 chứa
chứa 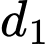 sao cho góc giữa mặt phẳng
sao cho góc giữa mặt phẳng 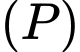 và đường thẳng
và đường thẳng 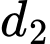 là lớn nhất là
là lớn nhất là 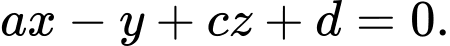 Giá trị của
Giá trị của  bằng
bằng
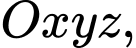 cho hai đường thẳng
cho hai đường thẳng 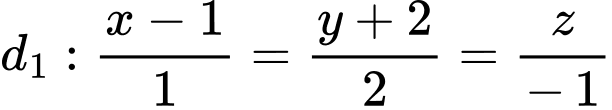 và
và 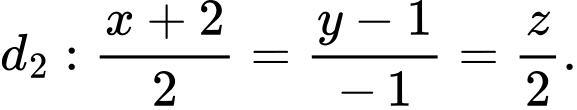 Phương trình mặt phẳng
Phương trình mặt phẳng 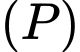 chứa
chứa 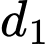 sao cho góc giữa mặt phẳng
sao cho góc giữa mặt phẳng 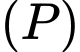 và đường thẳng
và đường thẳng 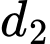 là lớn nhất là
là lớn nhất là 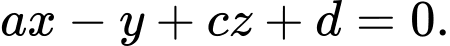 Giá trị của
Giá trị của  bằng
bằng A, 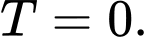
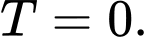
B, 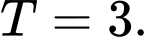
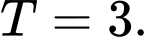
C, 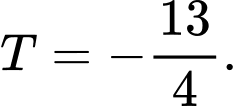
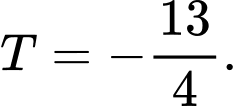
D, 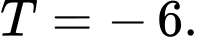
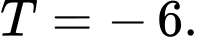
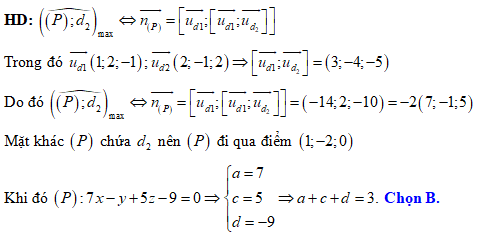 Đáp án: B
Đáp án: B
Câu 10 [80577]: Trong không gian với hệ trục tọa độ 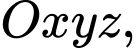 cho mặt phẳng
cho mặt phẳng 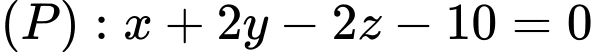 và hai điểm
và hai điểm 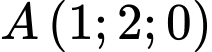 ,
, 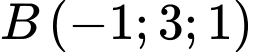 . Gọi
. Gọi  là một mặt phẳng đi qua
là một mặt phẳng đi qua 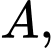
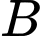 đồng thời tạo với
đồng thời tạo với 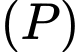 một góc nhỏ nhất. Biết rằng phương trình tổng quát của mặt phẳng
một góc nhỏ nhất. Biết rằng phương trình tổng quát của mặt phẳng  là:
là: 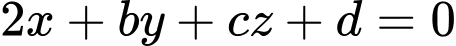 , với
, với 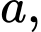
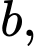
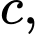
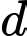 là những số thực. Khi đó giá trị của tổng
là những số thực. Khi đó giá trị của tổng  bằng
bằng
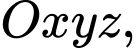 cho mặt phẳng
cho mặt phẳng 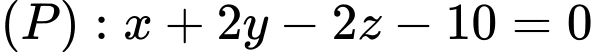 và hai điểm
và hai điểm 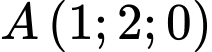 ,
, 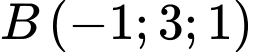 . Gọi
. Gọi  là một mặt phẳng đi qua
là một mặt phẳng đi qua 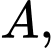
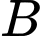 đồng thời tạo với
đồng thời tạo với 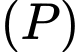 một góc nhỏ nhất. Biết rằng phương trình tổng quát của mặt phẳng
một góc nhỏ nhất. Biết rằng phương trình tổng quát của mặt phẳng  là:
là: 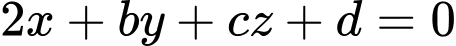 , với
, với 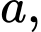
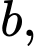
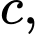
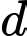 là những số thực. Khi đó giá trị của tổng
là những số thực. Khi đó giá trị của tổng  bằng
bằng A, 
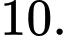
B, 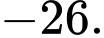
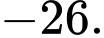
C, 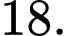
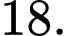
D, 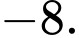
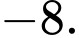
 Đáp án: B
Đáp án: B
Câu 11 [80582]: Trong không gian 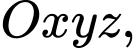 cho hai điểm
cho hai điểm 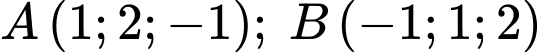 . Gọi
. Gọi  là phương trình mặt phẳng đi qua 2 điểm
là phương trình mặt phẳng đi qua 2 điểm 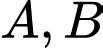 sao cho
sao cho  tạo với mặt phẳng
tạo với mặt phẳng 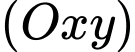 một góc nhỏ nhất. Khoảng cách từ gốc tọa độ
một góc nhỏ nhất. Khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng
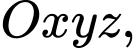 cho hai điểm
cho hai điểm 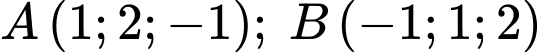 . Gọi
. Gọi  là phương trình mặt phẳng đi qua 2 điểm
là phương trình mặt phẳng đi qua 2 điểm 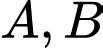 sao cho
sao cho  tạo với mặt phẳng
tạo với mặt phẳng 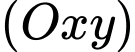 một góc nhỏ nhất. Khoảng cách từ gốc tọa độ
một góc nhỏ nhất. Khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng  bằng
bằng A, 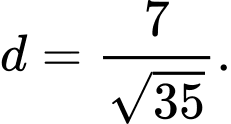
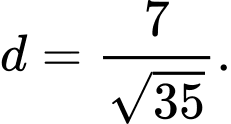
B, 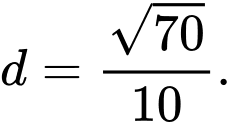
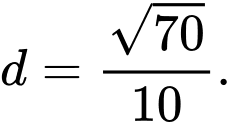
C, 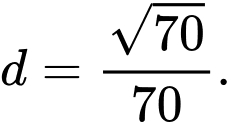
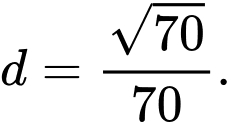
D, 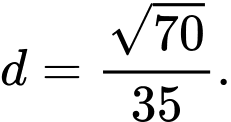
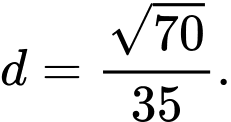
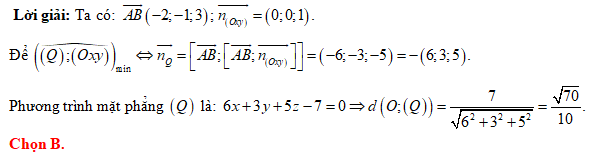 Đáp án: B
Đáp án: B
Câu 12 [100318]: Trong không gian tọa độ 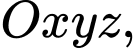 cho đường thẳng
cho đường thẳng 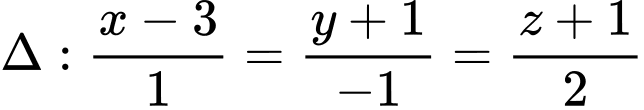 và mặt phẳng
và mặt phẳng 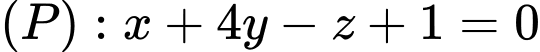 . Gọi
. Gọi  là mặt phẳng chứa
là mặt phẳng chứa  sao cho góc giữa
sao cho góc giữa 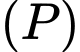 và
và  nhỏ nhất. Biết mặt phẳng
nhỏ nhất. Biết mặt phẳng  có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 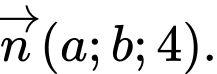 Tính giá trị của biểu thức
Tính giá trị của biểu thức 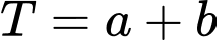
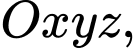 cho đường thẳng
cho đường thẳng 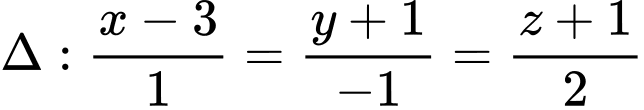 và mặt phẳng
và mặt phẳng 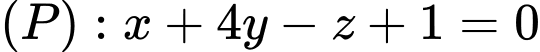 . Gọi
. Gọi  là mặt phẳng chứa
là mặt phẳng chứa  sao cho góc giữa
sao cho góc giữa 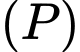 và
và  nhỏ nhất. Biết mặt phẳng
nhỏ nhất. Biết mặt phẳng  có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 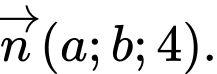 Tính giá trị của biểu thức
Tính giá trị của biểu thức 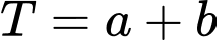
A, 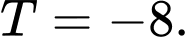
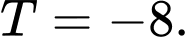
B, 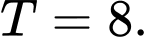
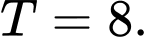
C, 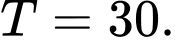
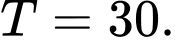
D, 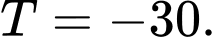
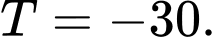
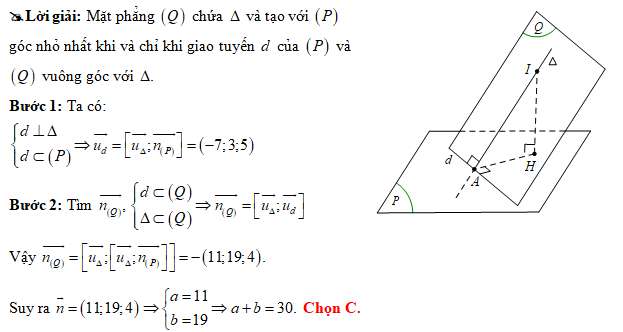 Đáp án: C
Đáp án: C
Câu 13 [100321]: Trong không gian 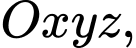 cho đường thẳng
cho đường thẳng 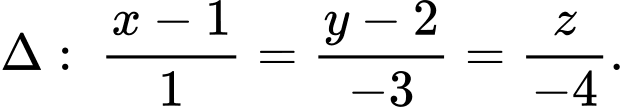 Gọi
Gọi 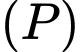 là mặt phẳng đi qua 2 điểm
là mặt phẳng đi qua 2 điểm 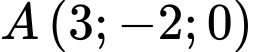 và
và 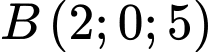 tạo với
tạo với  một góc lớn nhất. Tính khoảng cách từ gốc tọa độ
một góc lớn nhất. Tính khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 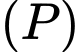 khi đó
khi đó
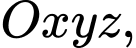 cho đường thẳng
cho đường thẳng 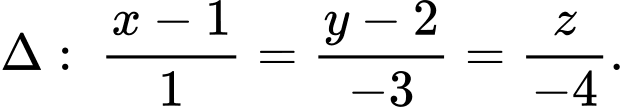 Gọi
Gọi 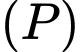 là mặt phẳng đi qua 2 điểm
là mặt phẳng đi qua 2 điểm 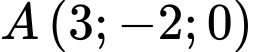 và
và 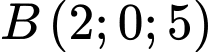 tạo với
tạo với  một góc lớn nhất. Tính khoảng cách từ gốc tọa độ
một góc lớn nhất. Tính khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 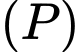 khi đó
khi đó A, 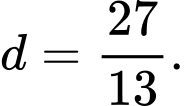
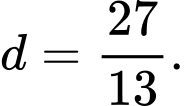
B, 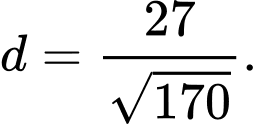
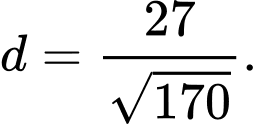
C, 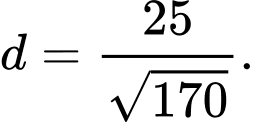
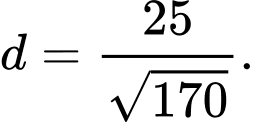
D, 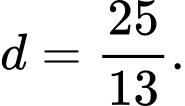
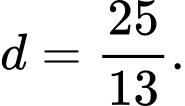
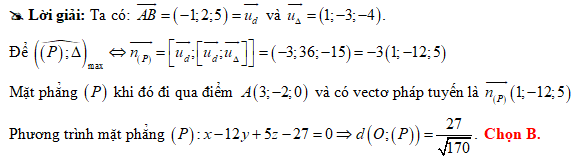 Đáp án: B
Đáp án: B
Câu 14 [57784]: Trong không gian 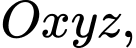 cho đường thẳng
cho đường thẳng 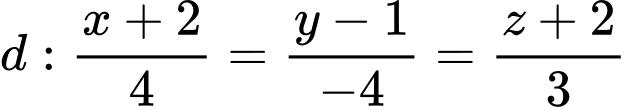 và mặt phẳng
và mặt phẳng 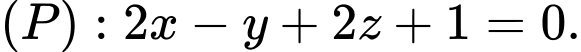 Đường thẳng
Đường thẳng  đi qua
đi qua 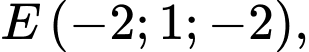 song song với
song song với 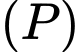 đồng thời tạo với
đồng thời tạo với 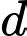 góc bé nhất
góc bé nhất  Biết rằng
Biết rằng  có một vectơ chỉ phương
có một vectơ chỉ phương 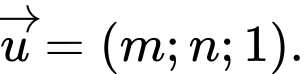 Tính
Tính 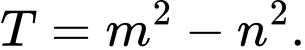
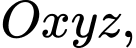 cho đường thẳng
cho đường thẳng 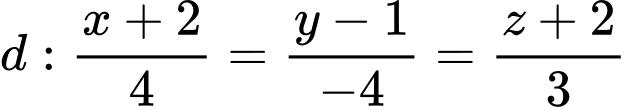 và mặt phẳng
và mặt phẳng 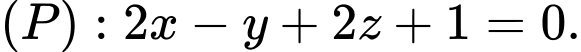 Đường thẳng
Đường thẳng  đi qua
đi qua 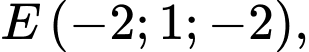 song song với
song song với 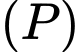 đồng thời tạo với
đồng thời tạo với 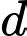 góc bé nhất
góc bé nhất  Biết rằng
Biết rằng  có một vectơ chỉ phương
có một vectơ chỉ phương 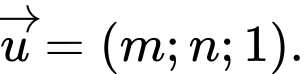 Tính
Tính 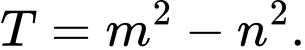
A, 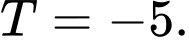
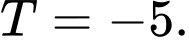
B, 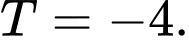
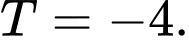
C, 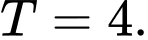
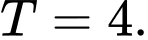
D, 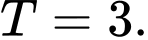
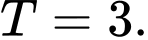
 Đáp án: B
Đáp án: B
Câu 15 [57774]: Trong không gian với hệ trục tọa độ 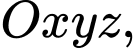 gọi
gọi 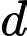 là đường thẳng đi qua
là đường thẳng đi qua 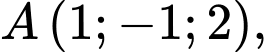 song song với mp
song song với mp 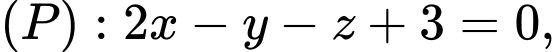 đồng thời tạo với đường thẳng
đồng thời tạo với đường thẳng 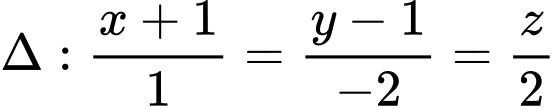 một góc lớn nhất. Phương trình của đường thẳng
một góc lớn nhất. Phương trình của đường thẳng 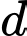 là
là
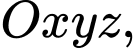 gọi
gọi 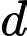 là đường thẳng đi qua
là đường thẳng đi qua 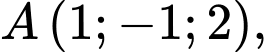 song song với mp
song song với mp 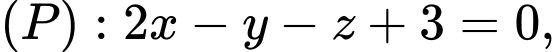 đồng thời tạo với đường thẳng
đồng thời tạo với đường thẳng 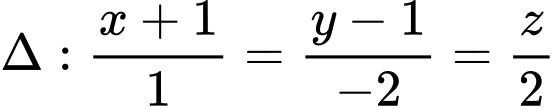 một góc lớn nhất. Phương trình của đường thẳng
một góc lớn nhất. Phương trình của đường thẳng 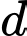 là
là A, 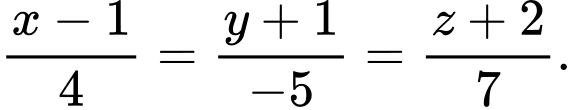
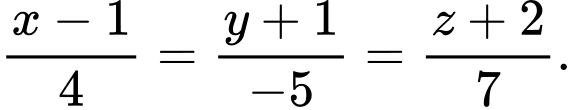
B, 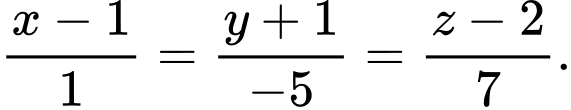
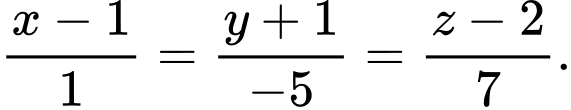
C, 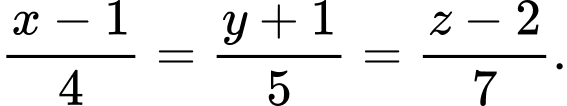
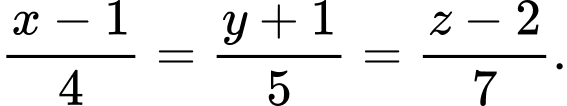
D, 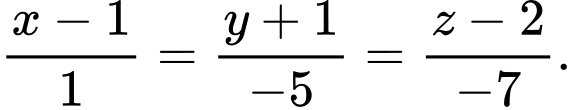
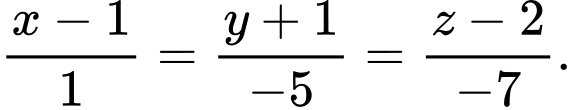
 Đáp án: B
Đáp án: B
Câu 16 [57780]: Trong không gian 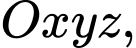 cho hai đường thẳng
cho hai đường thẳng 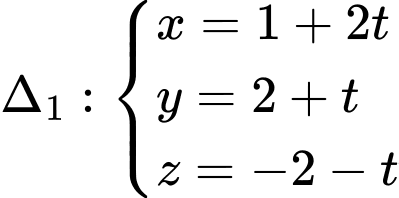 và
và 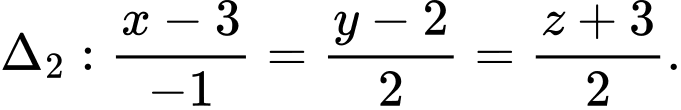 Gọi
Gọi 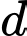 là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 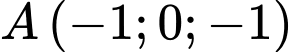 cắt đường thẳng
cắt đường thẳng 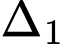 và tạo với đường thẳng
và tạo với đường thẳng 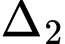 một góc lớn nhất. Phương trình đường thẳng
một góc lớn nhất. Phương trình đường thẳng 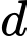 là
là
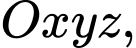 cho hai đường thẳng
cho hai đường thẳng 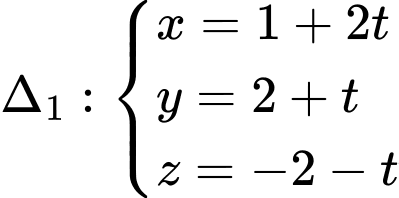 và
và 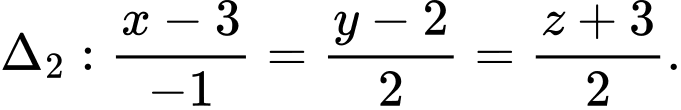 Gọi
Gọi 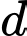 là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 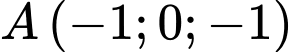 cắt đường thẳng
cắt đường thẳng 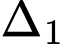 và tạo với đường thẳng
và tạo với đường thẳng  một góc lớn nhất. Phương trình đường thẳng
một góc lớn nhất. Phương trình đường thẳng 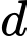 là
là A, 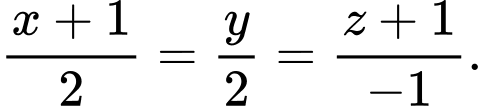
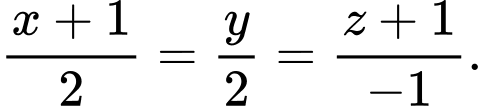
B, 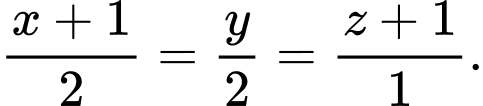
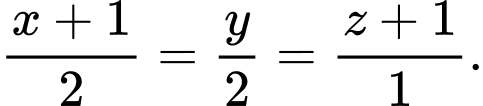
C, 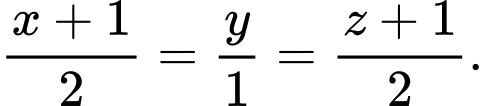
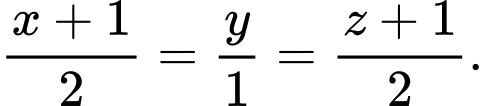
D, 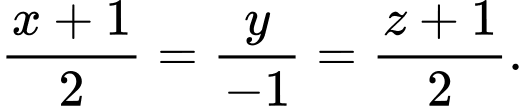
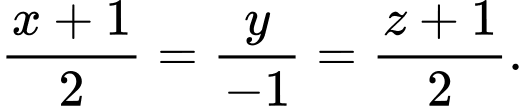
HD: Gọi 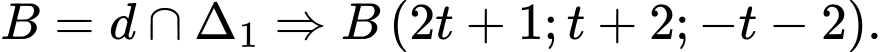
Ta có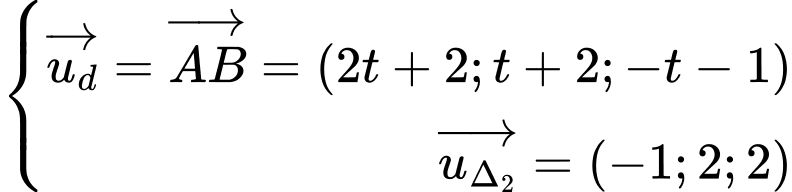
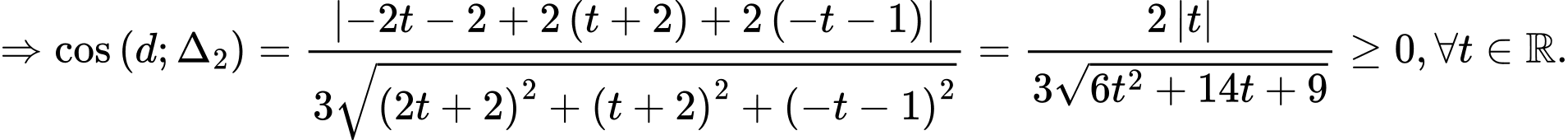
Góc giữa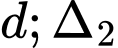 lớn nhất
lớn nhất 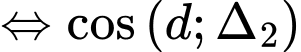 nhỏ nhất
nhỏ nhất 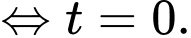
Khi đó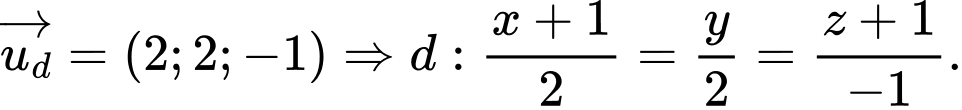 Chọn A Đáp án: A
Chọn A Đáp án: A
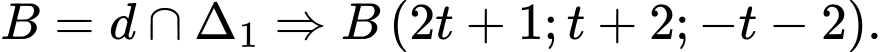
Ta có
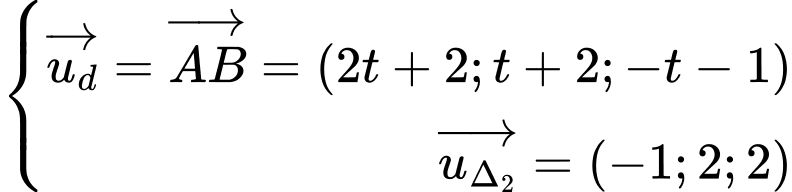
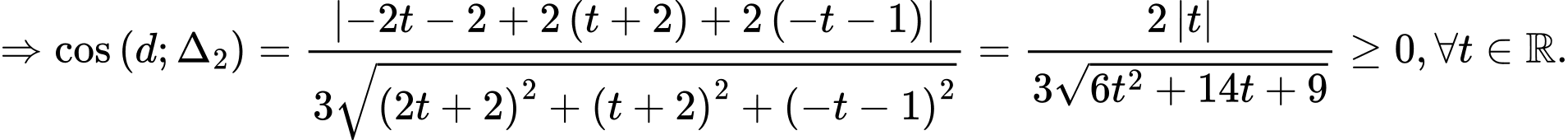
Góc giữa
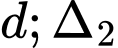 lớn nhất
lớn nhất 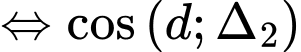 nhỏ nhất
nhỏ nhất 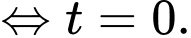
Khi đó
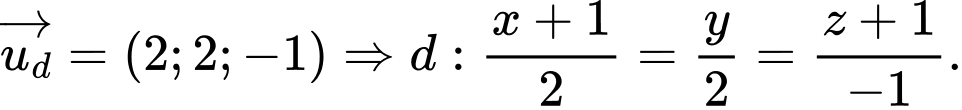 Chọn A Đáp án: A
Chọn A Đáp án: A
Câu 17 [57782]: Đường thẳng  đi qua điểm
đi qua điểm 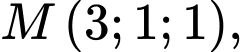 nằm trong mặt phẳng
nằm trong mặt phẳng 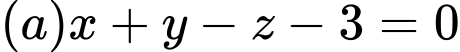 và tạo với đường thẳng
và tạo với đường thẳng 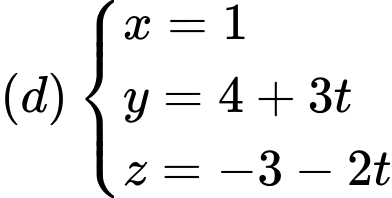 một góc nhỏ nhất thì phương trình của
một góc nhỏ nhất thì phương trình của  là
là
 đi qua điểm
đi qua điểm 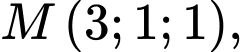 nằm trong mặt phẳng
nằm trong mặt phẳng 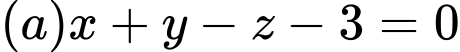 và tạo với đường thẳng
và tạo với đường thẳng 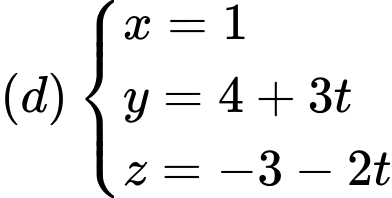 một góc nhỏ nhất thì phương trình của
một góc nhỏ nhất thì phương trình của  là
là A, 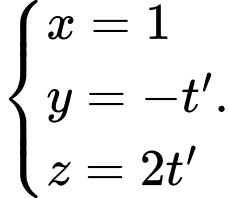
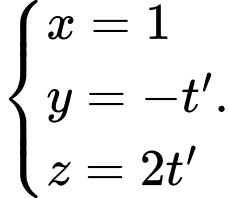
B, 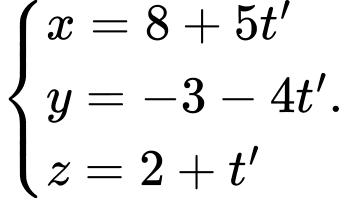
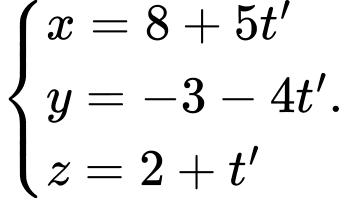
C, 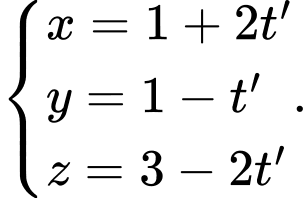
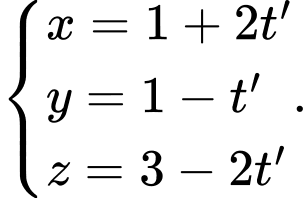
D, 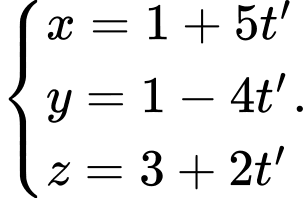
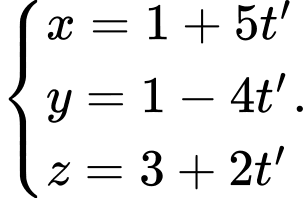
 Đáp án: B
Đáp án: B
Câu 18 [80583]: Trong không gian 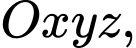 cho hai đường thẳng
cho hai đường thẳng 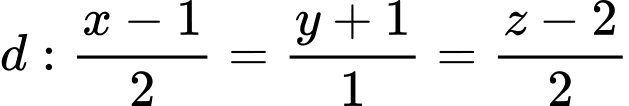 và
và 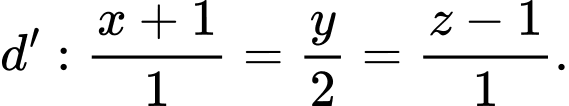 Phương trình mặt phẳng chứa đường thẳng
Phương trình mặt phẳng chứa đường thẳng 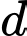 và tạo với đường thẳng
và tạo với đường thẳng 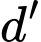 một góc lớn nhất là
một góc lớn nhất là
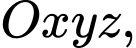 cho hai đường thẳng
cho hai đường thẳng 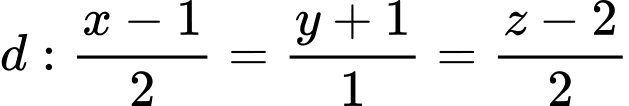 và
và 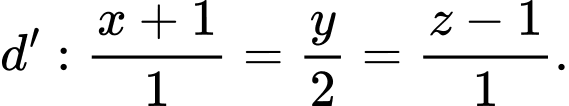 Phương trình mặt phẳng chứa đường thẳng
Phương trình mặt phẳng chứa đường thẳng 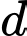 và tạo với đường thẳng
và tạo với đường thẳng 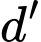 một góc lớn nhất là
một góc lớn nhất là A, 

B, 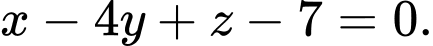
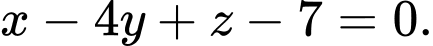
C, 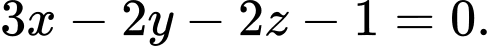
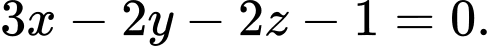
D, 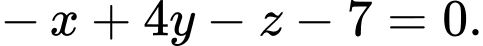
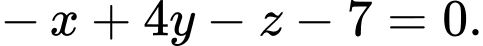
 Đáp án: B
Đáp án: B
Câu 19 [80584]: Trong không gian 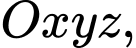 cho hai đường thẳng
cho hai đường thẳng 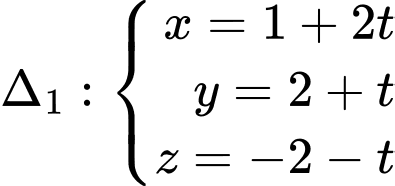 và
và 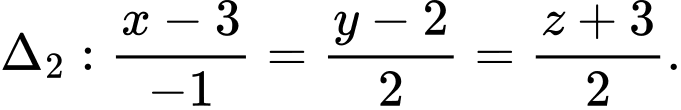 Gọi
Gọi 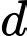 là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 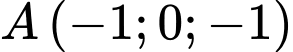 cắt đường thẳng
cắt đường thẳng 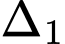 và tạo với đường thẳng
và tạo với đường thẳng 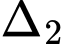 một góc lớn nhất. Phương trình đường thẳng
một góc lớn nhất. Phương trình đường thẳng 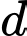 là
là
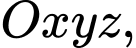 cho hai đường thẳng
cho hai đường thẳng 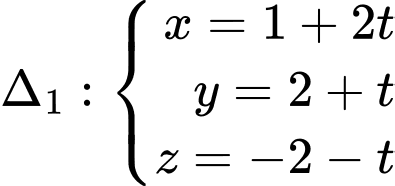 và
và 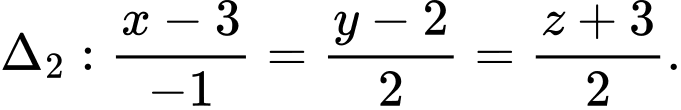 Gọi
Gọi 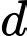 là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 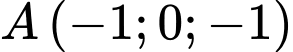 cắt đường thẳng
cắt đường thẳng 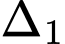 và tạo với đường thẳng
và tạo với đường thẳng  một góc lớn nhất. Phương trình đường thẳng
một góc lớn nhất. Phương trình đường thẳng  là
là A, 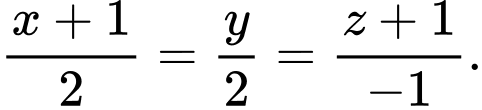
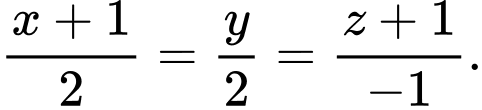
B, 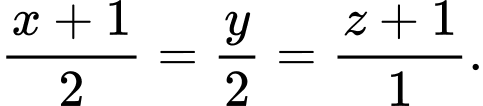
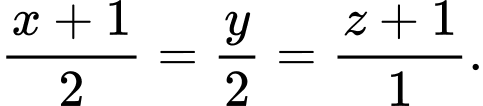
C, 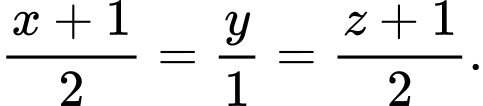
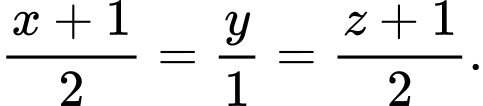
D, 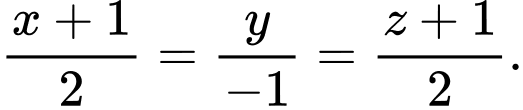
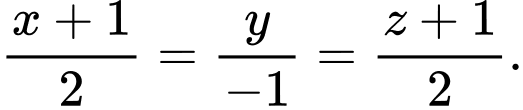
Ta có VTCP của 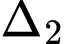 là
là 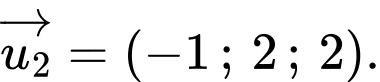
Gọi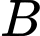 là giao điểm của
là giao điểm của 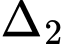 và
và 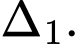
Suy ra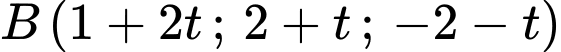
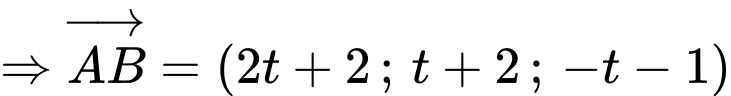
Gọi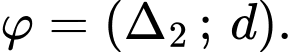
Khi đó
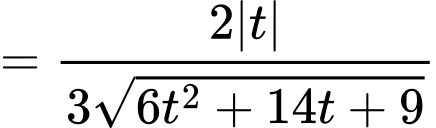
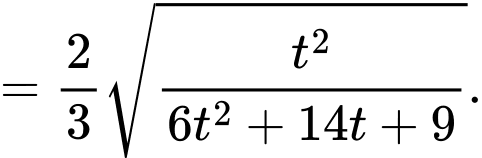
Đặt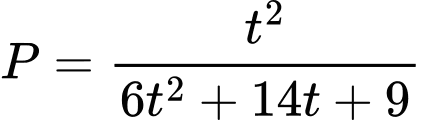
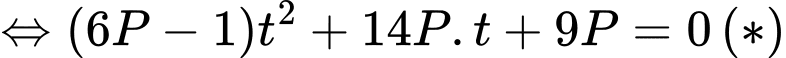
TH1 :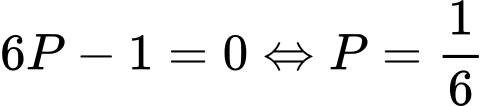 khi
khi 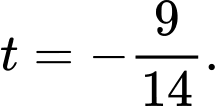
TH2 :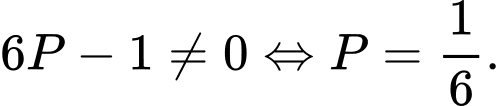
Phương trình có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi 
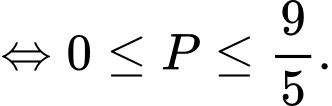
Nhận xét góc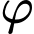 càng lớn thì
càng lớn thì 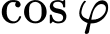 càng nhỏ.
càng nhỏ.
Từ đó suy ra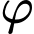 lớn nhất khi và chỉ khỉ
lớn nhất khi và chỉ khỉ 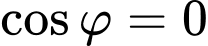 nên
nên 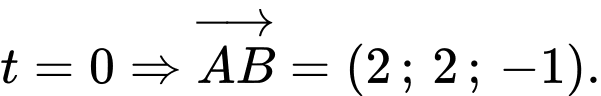
Phương trình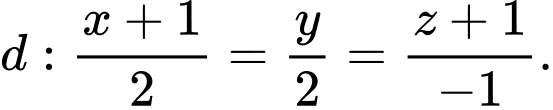
Chọn đáp án D. Đáp án: D
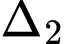 là
là 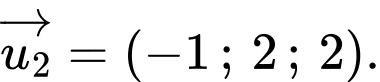
Gọi
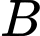 là giao điểm của
là giao điểm của 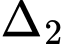 và
và 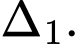
Suy ra
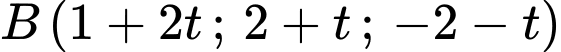
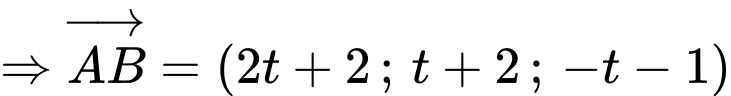
Gọi
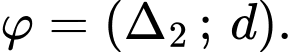
Khi đó

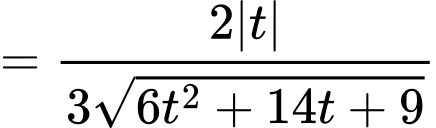
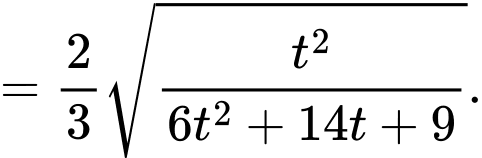
Đặt
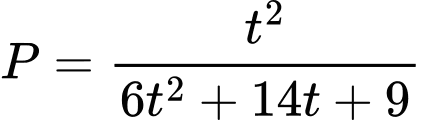
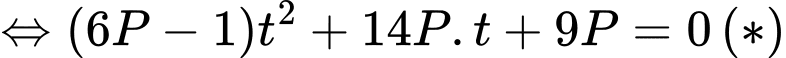
TH1 :
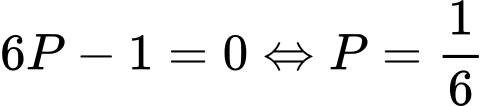 khi
khi 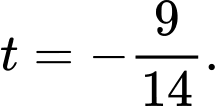
TH2 :
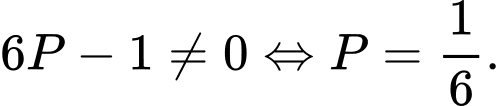
Phương trình
 có nghiệm khi và chỉ khi
có nghiệm khi và chỉ khi 
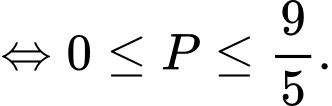
Nhận xét góc
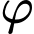 càng lớn thì
càng lớn thì 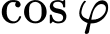 càng nhỏ.
càng nhỏ. Từ đó suy ra
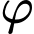 lớn nhất khi và chỉ khỉ
lớn nhất khi và chỉ khỉ 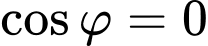 nên
nên 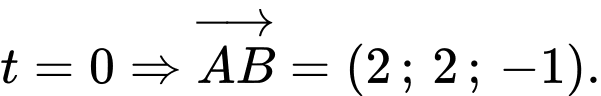
Phương trình
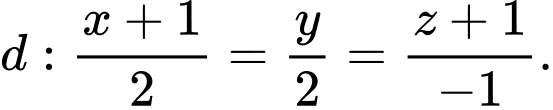
Chọn đáp án D. Đáp án: D
Câu 20 [100323]: Trong không gian với hệ tọa độ 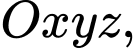 cho điểm
cho điểm 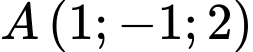 và đường
và đường 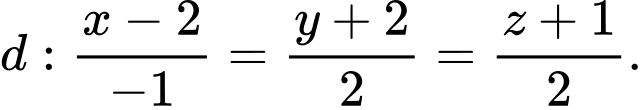 Đường thẳng đi qua A nằm trong mặt phẳng
Đường thẳng đi qua A nằm trong mặt phẳng 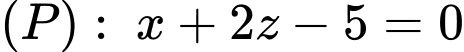 sao cho góc giữa và
sao cho góc giữa và 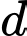 nhỏ nhất có một vectơ chỉ phương là
nhỏ nhất có một vectơ chỉ phương là 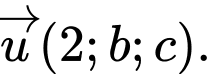 Tính giá trị của biểu thức
Tính giá trị của biểu thức 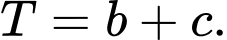
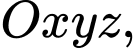 cho điểm
cho điểm 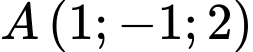 và đường
và đường 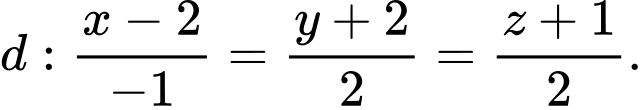 Đường thẳng đi qua A nằm trong mặt phẳng
Đường thẳng đi qua A nằm trong mặt phẳng 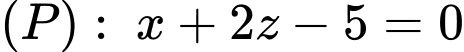 sao cho góc giữa và
sao cho góc giữa và 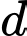 nhỏ nhất có một vectơ chỉ phương là
nhỏ nhất có một vectơ chỉ phương là 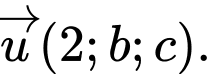 Tính giá trị của biểu thức
Tính giá trị của biểu thức 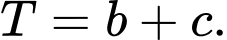
A, 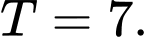
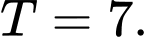
B, 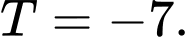
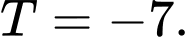
C, 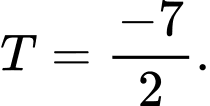
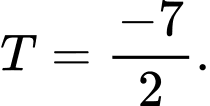
D, 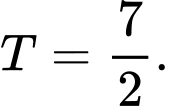
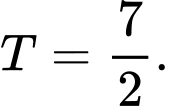
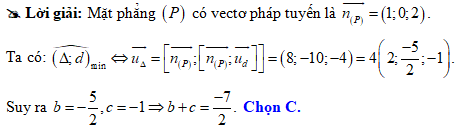 Đáp án: C
Đáp án: C
Câu 21 [100324]: Trong không gian với hệ tọa độ  Đường thẳng
Đường thẳng 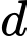 đi qua
đi qua 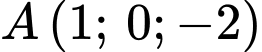 và cắt
và cắt 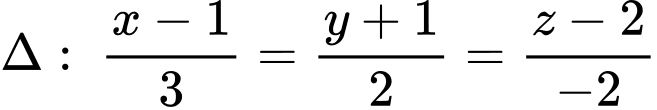 sao cho góc giữa đường thẳng d và mặt phẳng
sao cho góc giữa đường thẳng d và mặt phẳng 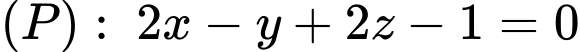 lớn nhất có một vectơ chỉ phương là
lớn nhất có một vectơ chỉ phương là 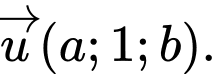 Giá trị của biểu thức
Giá trị của biểu thức 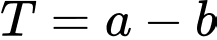 là
là
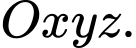 Đường thẳng
Đường thẳng 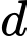 đi qua
đi qua 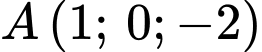 và cắt
và cắt 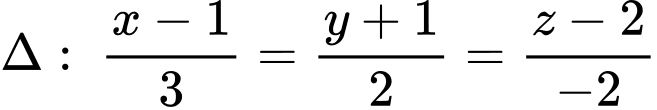 sao cho góc giữa đường thẳng d và mặt phẳng
sao cho góc giữa đường thẳng d và mặt phẳng 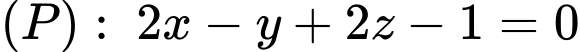 lớn nhất có một vectơ chỉ phương là
lớn nhất có một vectơ chỉ phương là 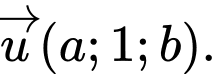 Giá trị của biểu thức
Giá trị của biểu thức 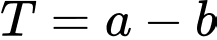 là
là A, 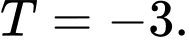
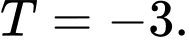
B, 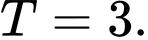
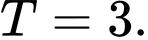
C, 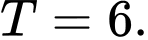
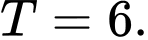
D, 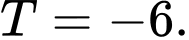
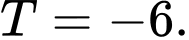
 Đáp án: C
Đáp án: C
Câu 22 [100325]: Trong không gian với hệ tọa độ 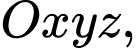 đường thẳng
đường thẳng  đi qua
đi qua 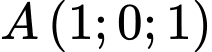 , nằm trong mặt phẳng
, nằm trong mặt phẳng 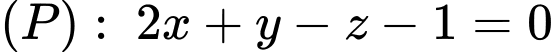 và tạo với đường thẳng
và tạo với đường thẳng 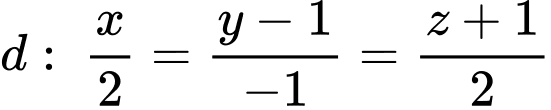 một góc nhỏ nhất. Biết
một góc nhỏ nhất. Biết 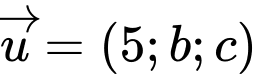 là một vectơ chỉ phương của đường thẳng
là một vectơ chỉ phương của đường thẳng 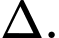 Tìm
Tìm 
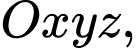 đường thẳng
đường thẳng  đi qua
đi qua 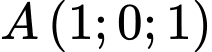 , nằm trong mặt phẳng
, nằm trong mặt phẳng 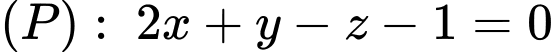 và tạo với đường thẳng
và tạo với đường thẳng 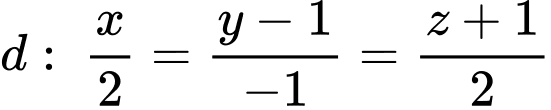 một góc nhỏ nhất. Biết
một góc nhỏ nhất. Biết 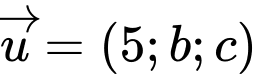 là một vectơ chỉ phương của đường thẳng
là một vectơ chỉ phương của đường thẳng 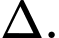 Tìm
Tìm 
A, 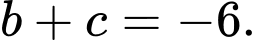
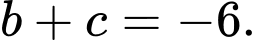
B, 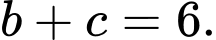
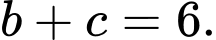
C, 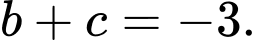
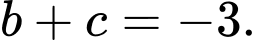
D, 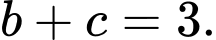
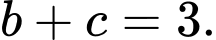
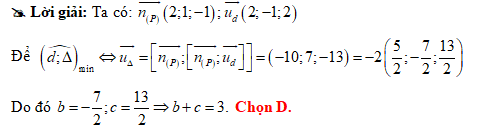 Đáp án: D
Đáp án: D
Câu 23 [100327]: Trong không gian với hệ tọa độ 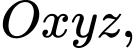 gọi
gọi 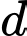 là đường thẳng song song với
là đường thẳng song song với 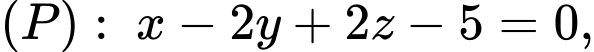 đồng thời tạo với mặt phẳng
đồng thời tạo với mặt phẳng 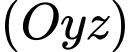 một góc lớn nhất là
một góc lớn nhất là 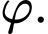 Tính
Tính 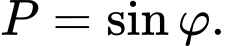
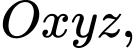 gọi
gọi 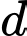 là đường thẳng song song với
là đường thẳng song song với 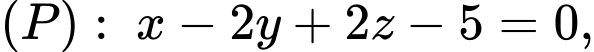 đồng thời tạo với mặt phẳng
đồng thời tạo với mặt phẳng 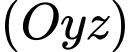 một góc lớn nhất là
một góc lớn nhất là 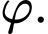 Tính
Tính 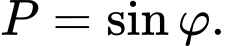
A, 

B, 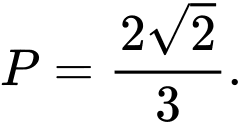
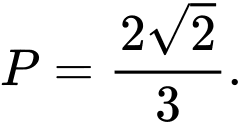
C, 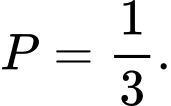
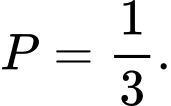
D, 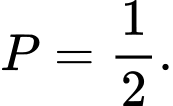
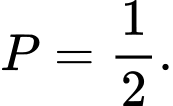
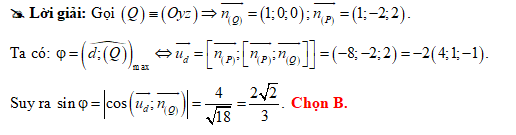 Đáp án: B
Đáp án: B
Câu 24 [100328]: Trong không gian với hệ tọa độ 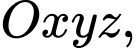 cho mặt phẳng
cho mặt phẳng 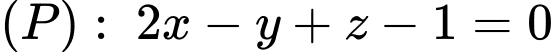 điểm
điểm 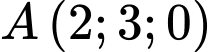 thuộc mặt phẳng
thuộc mặt phẳng 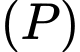 và đường thẳng
và đường thẳng 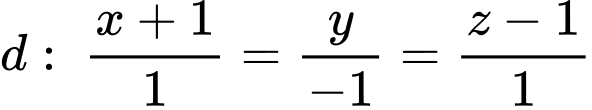 . Đường thẳng
. Đường thẳng 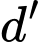 qua
qua 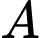 nằm trong
nằm trong 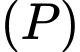 sao cho góc giữa hai đường thẳng
sao cho góc giữa hai đường thẳng 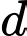 và
và 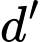 nhỏ nhất đi qua điểm nào trong các điểm sau
nhỏ nhất đi qua điểm nào trong các điểm sau
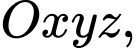 cho mặt phẳng
cho mặt phẳng 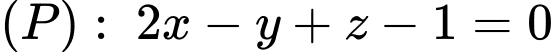 điểm
điểm 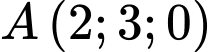 thuộc mặt phẳng
thuộc mặt phẳng 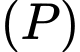 và đường thẳng
và đường thẳng 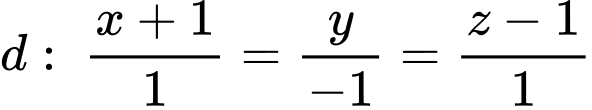 . Đường thẳng
. Đường thẳng 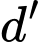 qua
qua 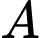 nằm trong
nằm trong 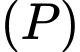 sao cho góc giữa hai đường thẳng
sao cho góc giữa hai đường thẳng 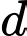 và
và 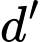 nhỏ nhất đi qua điểm nào trong các điểm sau
nhỏ nhất đi qua điểm nào trong các điểm sau A, 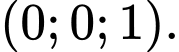
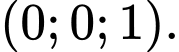
B, 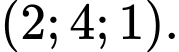
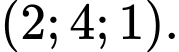
C, 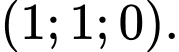
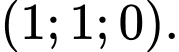
D, 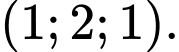
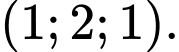
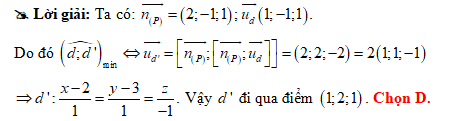 Đáp án: D
Đáp án: D
Câu 25 [100329]: Cho mặt phẳng 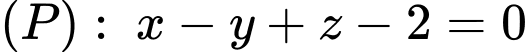 điểm
điểm 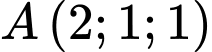 thuộc mặt phẳng
thuộc mặt phẳng 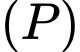 và đường thẳng
và đường thẳng 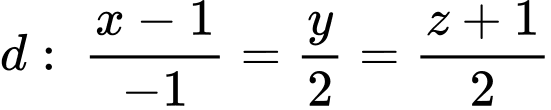 . Đường thẳng
. Đường thẳng 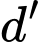 qua
qua 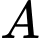 nằm trong
nằm trong 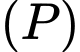 sao cho góc giữa hai đường thẳng
sao cho góc giữa hai đường thẳng 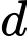 và
và 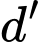 nhỏ nhất cắt mặt phẳng
nhỏ nhất cắt mặt phẳng 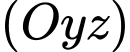 tại điểm
tại điểm 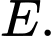 Tính
Tính 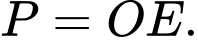
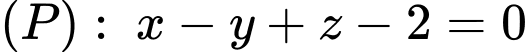 điểm
điểm 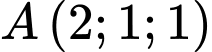 thuộc mặt phẳng
thuộc mặt phẳng 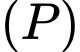 và đường thẳng
và đường thẳng 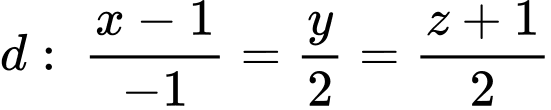 . Đường thẳng
. Đường thẳng 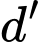 qua
qua 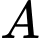 nằm trong
nằm trong 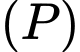 sao cho góc giữa hai đường thẳng
sao cho góc giữa hai đường thẳng 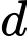 và
và 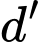 nhỏ nhất cắt mặt phẳng
nhỏ nhất cắt mặt phẳng 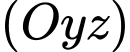 tại điểm
tại điểm 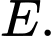 Tính
Tính 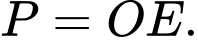
A, 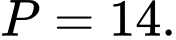
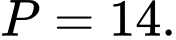
B, 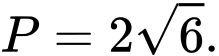
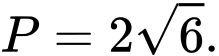
C, 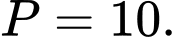
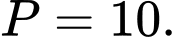
D, 

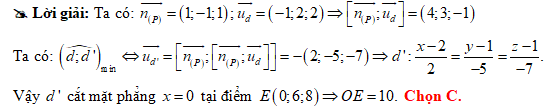 Đáp án: C
Đáp án: C