Đáp án Bài tập tự luyện số 1
Câu 1 [81694]: [Đề thi THPT QG năm 2018] Trong không gian 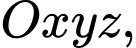 cho mặt cầu
cho mặt cầu 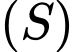 có tâm
có tâm 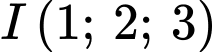 và đi qua điểm
và đi qua điểm 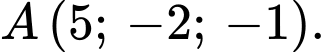 Xét các điểm
Xét các điểm 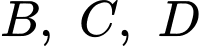 thuộc
thuộc 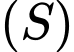 sao cho
sao cho 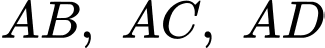 đôi một vuông góc với nhau. Thể tích của khối tứ diện
đôi một vuông góc với nhau. Thể tích của khối tứ diện 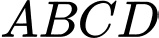 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng
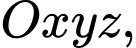 cho mặt cầu
cho mặt cầu 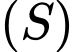 có tâm
có tâm 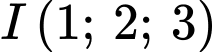 và đi qua điểm
và đi qua điểm 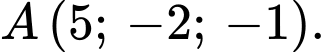 Xét các điểm
Xét các điểm 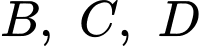 thuộc
thuộc 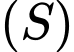 sao cho
sao cho 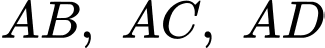 đôi một vuông góc với nhau. Thể tích của khối tứ diện
đôi một vuông góc với nhau. Thể tích của khối tứ diện 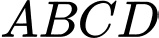 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng A, 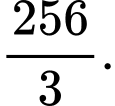
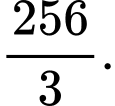
B, 256.
C, 128.
D, 

 Đáp án: A
Đáp án: A
Câu 2 [398655]: Trong không gian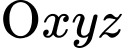 , cho ba điểm
, cho ba điểm 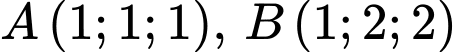 và
và 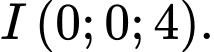 Mặt cầu
Mặt cầu 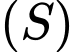 đi qua hai điểm
đi qua hai điểm 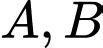 và tiếp xúc mặt phẳng
và tiếp xúc mặt phẳng 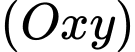 tại điểm
tại điểm  Giá trị lớn nhất của
Giá trị lớn nhất của 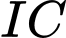 bằng
bằng
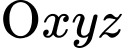 , cho ba điểm
, cho ba điểm 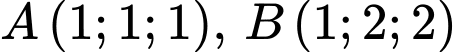 và
và 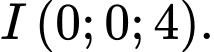 Mặt cầu
Mặt cầu 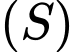 đi qua hai điểm
đi qua hai điểm 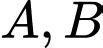 và tiếp xúc mặt phẳng
và tiếp xúc mặt phẳng 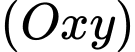 tại điểm
tại điểm  Giá trị lớn nhất của
Giá trị lớn nhất của 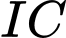 bằng
bằng A, 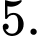
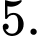
B, 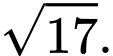
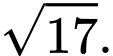
C, 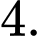
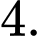
D, 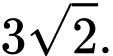
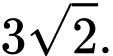
Ta có 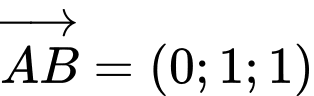 , nên phương trình đường thẳng
, nên phương trình đường thẳng  là:
là: 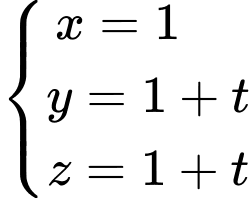 .
.
Gọi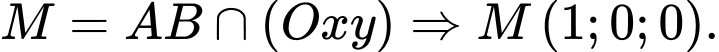
Khi đó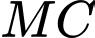 là một tiếp tuyến với mặt cầu
là một tiếp tuyến với mặt cầu 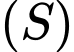 ta có:
ta có: 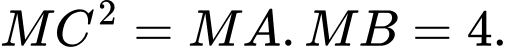
Do nên
nên 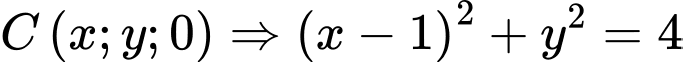
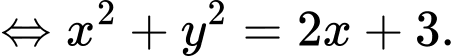
Mặt khác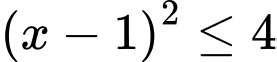
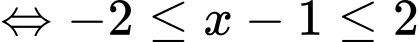

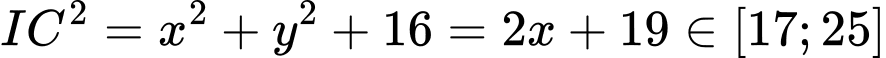
 Đáp án: A
Đáp án: A
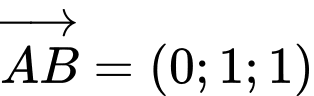 , nên phương trình đường thẳng
, nên phương trình đường thẳng  là:
là: 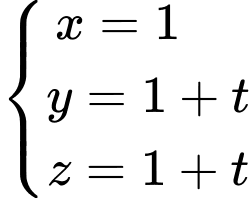 .
.
Gọi
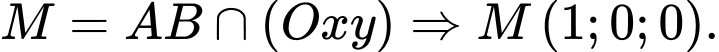
Khi đó
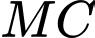 là một tiếp tuyến với mặt cầu
là một tiếp tuyến với mặt cầu 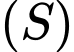 ta có:
ta có: 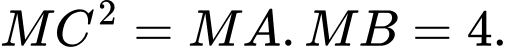
Do
 nên
nên 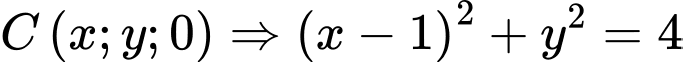
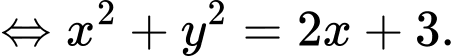
Mặt khác
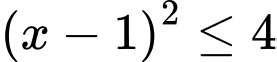
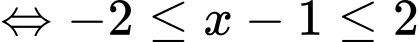

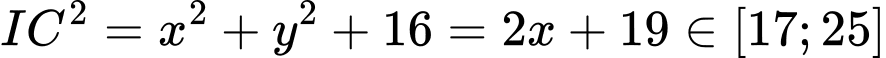
 Đáp án: A
Đáp án: A
Câu 3 [618084]: Trong không gian 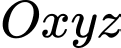 , cho đường thẳng
, cho đường thẳng 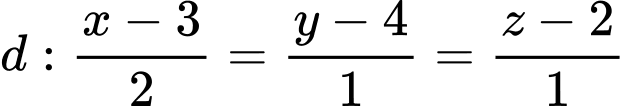 và 2 điểm
và 2 điểm 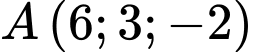 ,
, 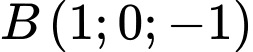 . Gọi
. Gọi  là đường thẳng đi qua
là đường thẳng đi qua 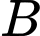 , vuông góc với
, vuông góc với 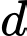 và thỏa mãn khoảng cách từ
và thỏa mãn khoảng cách từ 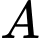 đến
đến  là nhỏ nhất. Một vectơ chỉ phương của
là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ
có tọa độ
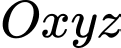 , cho đường thẳng
, cho đường thẳng 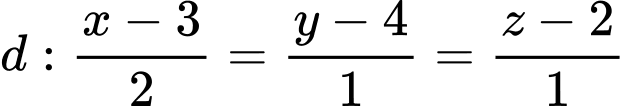 và 2 điểm
và 2 điểm 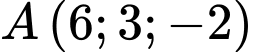 ,
, 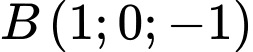 . Gọi
. Gọi  là đường thẳng đi qua
là đường thẳng đi qua 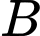 , vuông góc với
, vuông góc với 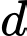 và thỏa mãn khoảng cách từ
và thỏa mãn khoảng cách từ 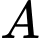 đến
đến  là nhỏ nhất. Một vectơ chỉ phương của
là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ
có tọa độ A, 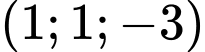 .
.
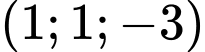 .
.B, 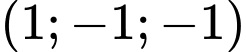 .
.
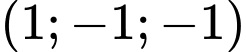 .
.C, 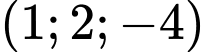 .
.
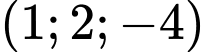 .
.D, 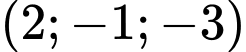 .
.
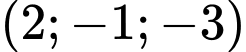 .
. Đáp án: A
Đáp án: A
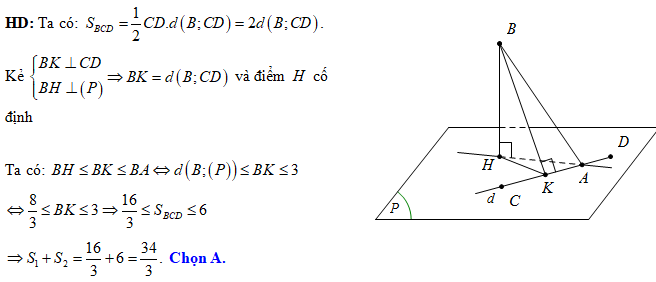
Câu 4 [81996]: Trong không gian với hệ trục tọa độ 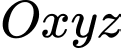 , cho hai điểm
, cho hai điểm 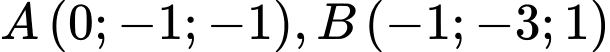 . Giả sử
. Giả sử 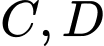 là hai điểm di động trên mặt phẳng
là hai điểm di động trên mặt phẳng 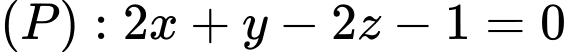 sao cho
sao cho 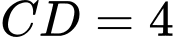 và
và  thẳng hàng. Gọi
thẳng hàng. Gọi 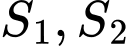 lần lượt là diện tích lớn nhất và nhỏ nhất của tam giác
lần lượt là diện tích lớn nhất và nhỏ nhất của tam giác  . Khi đó tổng
. Khi đó tổng  có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
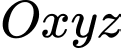 , cho hai điểm
, cho hai điểm 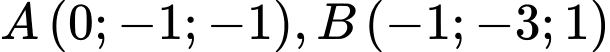 . Giả sử
. Giả sử 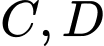 là hai điểm di động trên mặt phẳng
là hai điểm di động trên mặt phẳng 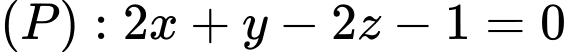 sao cho
sao cho 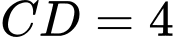 và
và  thẳng hàng. Gọi
thẳng hàng. Gọi 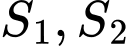 lần lượt là diện tích lớn nhất và nhỏ nhất của tam giác
lần lượt là diện tích lớn nhất và nhỏ nhất của tam giác  . Khi đó tổng
. Khi đó tổng  có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu? A, 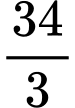 .
.
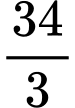 .
.B, 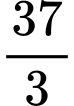 .
.
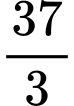 .
.C, 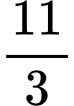 .
.
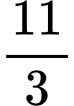 .
.D, 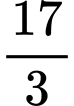 .
.
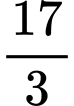 .
. Đáp án: A
Đáp án: A
Câu 5 [58275]: Trong không gian với hệ tọa độ 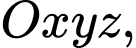 cho điểm
cho điểm 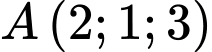 và mặt phẳng
và mặt phẳng 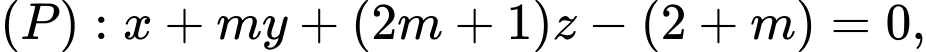 với
với 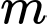 là tham số. Gọi điểm
là tham số. Gọi điểm 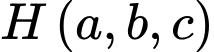 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 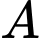 trên
trên 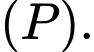 Tính
Tính  khi khoảng cách từ điểm
khi khoảng cách từ điểm 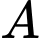 đến
đến 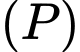 lớn nhất
lớn nhất
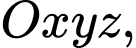 cho điểm
cho điểm 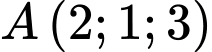 và mặt phẳng
và mặt phẳng 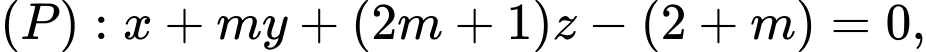 với
với 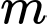 là tham số. Gọi điểm
là tham số. Gọi điểm 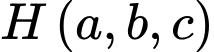 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 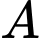 trên
trên 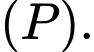 Tính
Tính  khi khoảng cách từ điểm
khi khoảng cách từ điểm 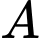 đến
đến 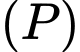 lớn nhất
lớn nhất A, 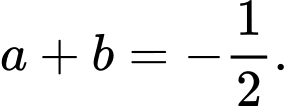
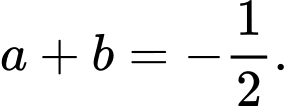
B, 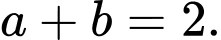
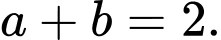
C, 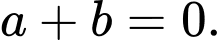
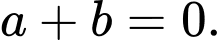
D, 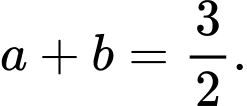
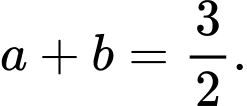
 Đáp án: D
Đáp án: D
Câu 6 [59138]: Trong không gian với hệ tọa độ 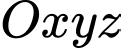 , cho mặt phẳng
, cho mặt phẳng 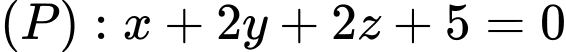 và mặt cầu có phương trình
và mặt cầu có phương trình 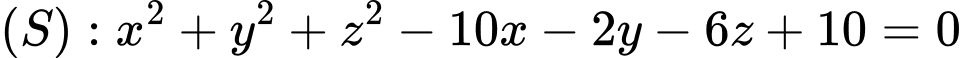 . Từ một điểm
. Từ một điểm 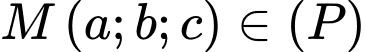 kẻ đường thẳng
kẻ đường thẳng  tiếp xúc với mặt cầu
tiếp xúc với mặt cầu 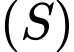 tại điểm
tại điểm 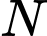 . Khi
. Khi 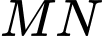 nhỏ nhất, tổng
nhỏ nhất, tổng 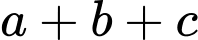 bằng
bằng
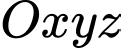 , cho mặt phẳng
, cho mặt phẳng 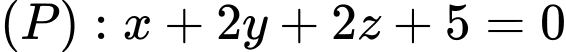 và mặt cầu có phương trình
và mặt cầu có phương trình 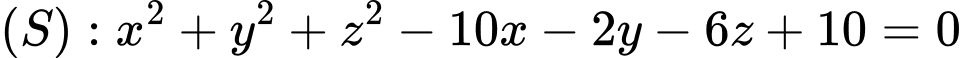 . Từ một điểm
. Từ một điểm 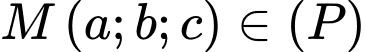 kẻ đường thẳng
kẻ đường thẳng  tiếp xúc với mặt cầu
tiếp xúc với mặt cầu 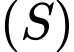 tại điểm
tại điểm 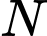 . Khi
. Khi 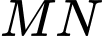 nhỏ nhất, tổng
nhỏ nhất, tổng 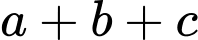 bằng
bằng A, 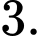
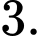
B, 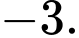
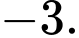
C, 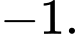
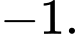
D, 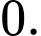
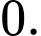
 Đáp án: C
Đáp án: C
Câu 7 [59102]: Trong không gian 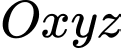 , cho ba đường thẳng
, cho ba đường thẳng  và
và 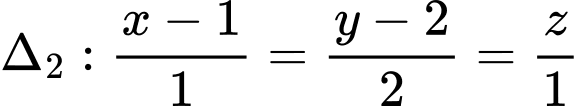 . Đường thẳng
. Đường thẳng  vuông góc với
vuông góc với 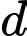 đồng thời cắt
đồng thời cắt 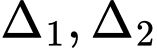 tương ứng tại
tương ứng tại  sao cho độ dài
sao cho độ dài 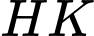 nhỏ nhất. Biết rằng
nhỏ nhất. Biết rằng  có một vectơ chỉ phương là
có một vectơ chỉ phương là 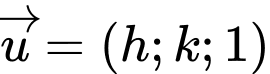 . Giá trị của
. Giá trị của 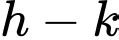 bằng
bằng
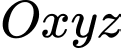 , cho ba đường thẳng
, cho ba đường thẳng  và
và 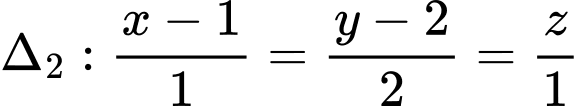 . Đường thẳng
. Đường thẳng  vuông góc với
vuông góc với 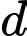 đồng thời cắt
đồng thời cắt 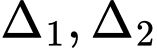 tương ứng tại
tương ứng tại  sao cho độ dài
sao cho độ dài 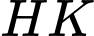 nhỏ nhất. Biết rằng
nhỏ nhất. Biết rằng  có một vectơ chỉ phương là
có một vectơ chỉ phương là 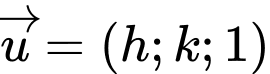 . Giá trị của
. Giá trị của 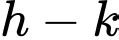 bằng
bằng A, 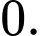
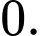
B, 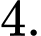
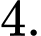
C, 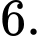
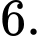
D, 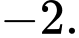
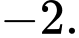
 Đáp án: A
Đáp án: A
Câu 8 [904820]: Trong không gian 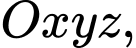 cho hình chóp
cho hình chóp 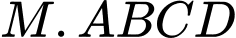 có đỉnh
có đỉnh 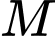 thay đổi luôn nằm trên mặt cầu
thay đổi luôn nằm trên mặt cầu 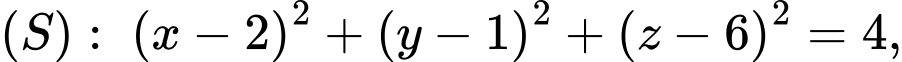 đáy
đáy 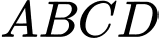 là hình vuông có tâm
là hình vuông có tâm 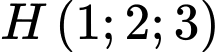 và điểm
và điểm 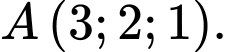 Khi đó thể tích lớn nhất của khối chóp
Khi đó thể tích lớn nhất của khối chóp 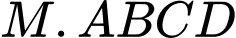 bằng
bằng
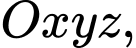 cho hình chóp
cho hình chóp 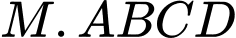 có đỉnh
có đỉnh 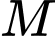 thay đổi luôn nằm trên mặt cầu
thay đổi luôn nằm trên mặt cầu 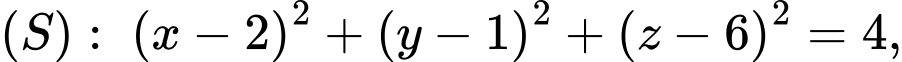 đáy
đáy 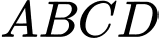 là hình vuông có tâm
là hình vuông có tâm 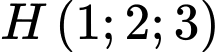 và điểm
và điểm 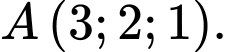 Khi đó thể tích lớn nhất của khối chóp
Khi đó thể tích lớn nhất của khối chóp 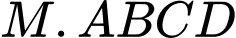 bằng
bằng A, 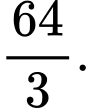
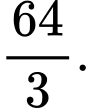
B, 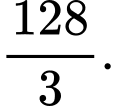
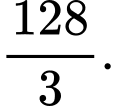
C, 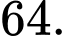
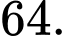
D, 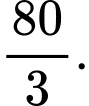
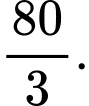
Hình chóp 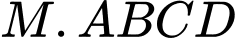 có đỉnh
có đỉnh 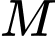 thay đổi luôn năm trên mặt cầu
thay đổi luôn năm trên mặt cầu 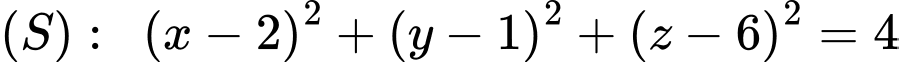
Đáy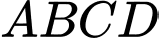 là hình vuông có tâm
là hình vuông có tâm 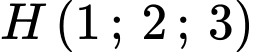 và điểm
và điểm 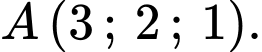
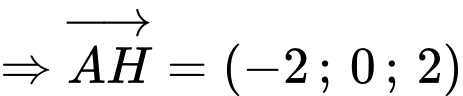
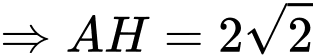
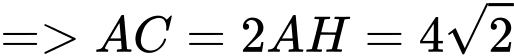
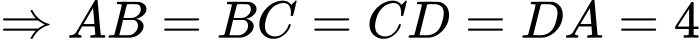
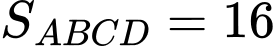
Có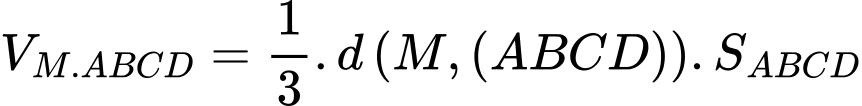
Suy ra, để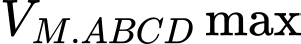 thì
thì 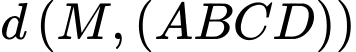 phải đạt giá trị lớn nhất. Suy ra
phải đạt giá trị lớn nhất. Suy ra 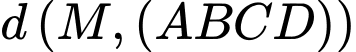 phải đi qua
phải đi qua 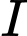 và có hình chiếu
và có hình chiếu 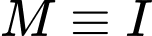 tại
tại 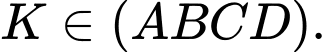
Giả sử, hình chiếu của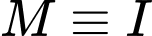 nằm trên
nằm trên 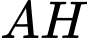 hay
hay 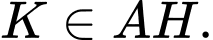
Ta có, Phương trình đường thẳng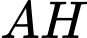 :
: 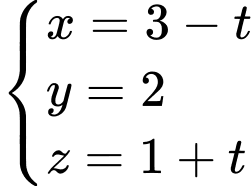
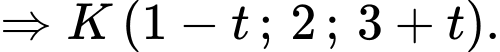
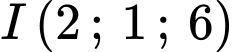
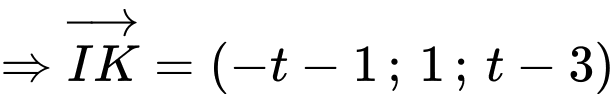
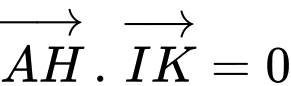
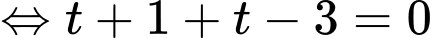
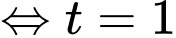
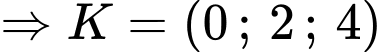
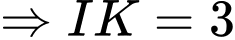
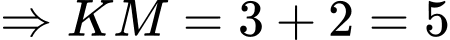
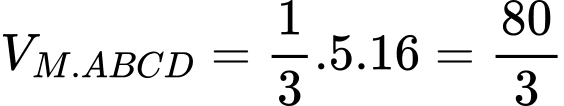
Đáp án D. Đáp án: D
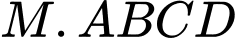 có đỉnh
có đỉnh 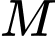 thay đổi luôn năm trên mặt cầu
thay đổi luôn năm trên mặt cầu 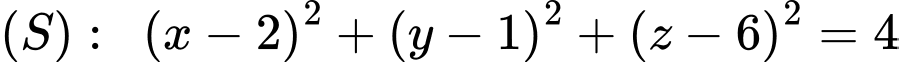
Đáy
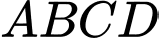 là hình vuông có tâm
là hình vuông có tâm 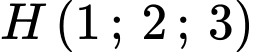 và điểm
và điểm 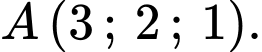
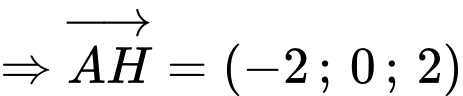
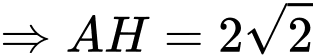
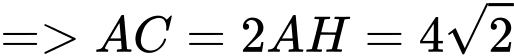
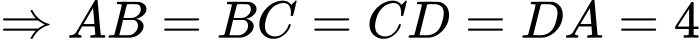
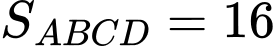
Có
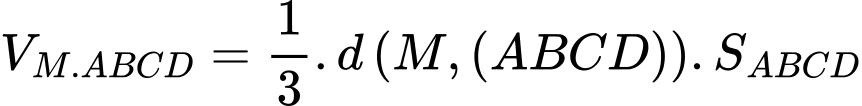
Suy ra, để
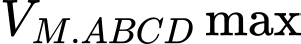 thì
thì 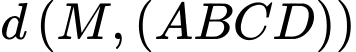 phải đạt giá trị lớn nhất. Suy ra
phải đạt giá trị lớn nhất. Suy ra 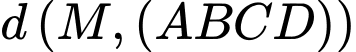 phải đi qua
phải đi qua 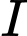 và có hình chiếu
và có hình chiếu 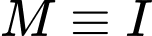 tại
tại 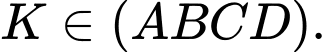
Giả sử, hình chiếu của
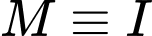 nằm trên
nằm trên 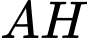 hay
hay 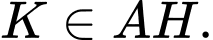
Ta có, Phương trình đường thẳng
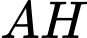 :
: 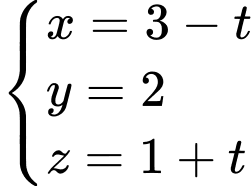
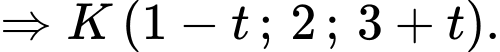
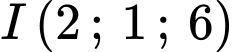
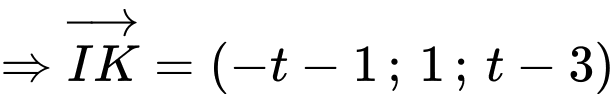
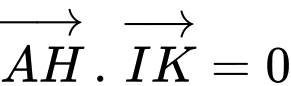
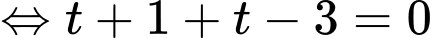
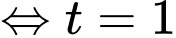
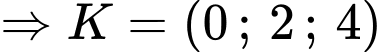
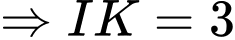
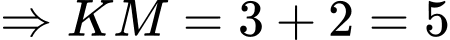
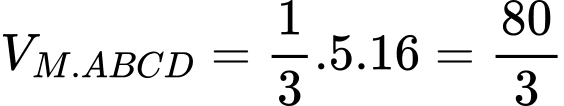
Đáp án D. Đáp án: D
Câu 9 [81693]: [Đề thi THPT QG năm 2019] Trong không gian 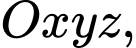 cho điểm
cho điểm 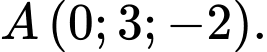 Xét đường thẳng
Xét đường thẳng 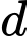 thay đổi song song với trục
thay đổi song song với trục  và cách trục
và cách trục  một khoảng bằng
một khoảng bằng 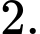 Khi khoảng cách từ
Khi khoảng cách từ 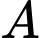 đến
đến 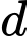 nhỏ nhất,
nhỏ nhất, 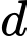 đi qua điểm nào dưới đây.
đi qua điểm nào dưới đây.
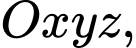 cho điểm
cho điểm 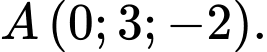 Xét đường thẳng
Xét đường thẳng 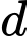 thay đổi song song với trục
thay đổi song song với trục  và cách trục
và cách trục  một khoảng bằng
một khoảng bằng 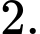 Khi khoảng cách từ
Khi khoảng cách từ 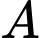 đến
đến 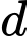 nhỏ nhất,
nhỏ nhất, 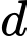 đi qua điểm nào dưới đây.
đi qua điểm nào dưới đây. A, 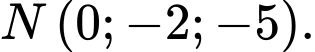
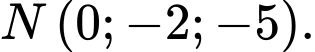
B, 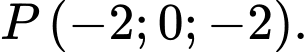
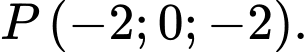
C, 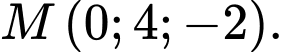
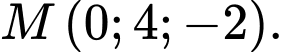
D, 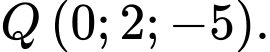
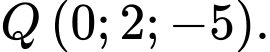
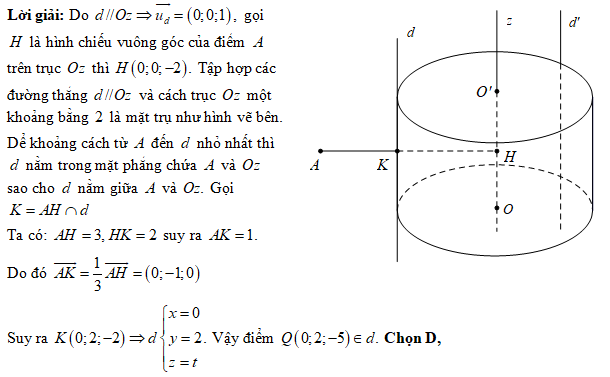 Đáp án: D
Đáp án: D
Câu 10 [58260]: Trong không gian với hệ tọa độ 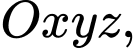 cho đường thẳng
cho đường thẳng 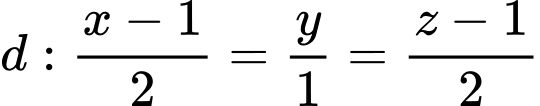 và điểm
và điểm 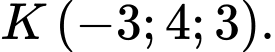 Viết phương trình đường thẳng
Viết phương trình đường thẳng 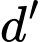 song song với
song song với 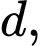 cách
cách 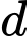 một khoảng bằng 3 và cách điểm
một khoảng bằng 3 và cách điểm 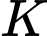 một khoảng nhỏ nhất.
một khoảng nhỏ nhất.
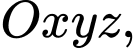 cho đường thẳng
cho đường thẳng 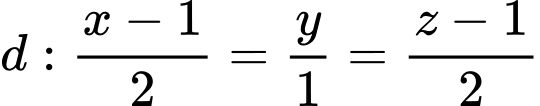 và điểm
và điểm 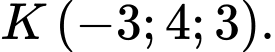 Viết phương trình đường thẳng
Viết phương trình đường thẳng 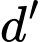 song song với
song song với 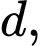 cách
cách 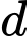 một khoảng bằng 3 và cách điểm
một khoảng bằng 3 và cách điểm 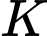 một khoảng nhỏ nhất.
một khoảng nhỏ nhất. A, 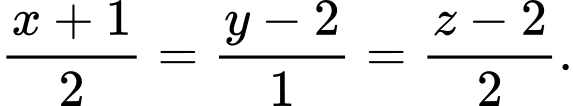
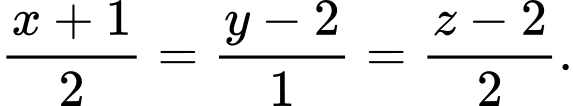
B, 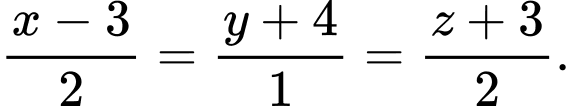
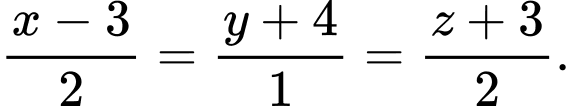
C, 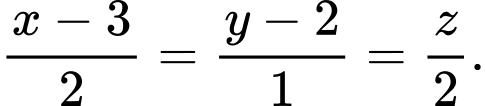
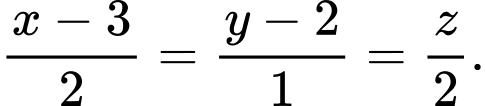
D, 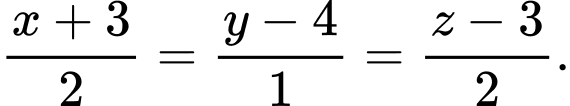
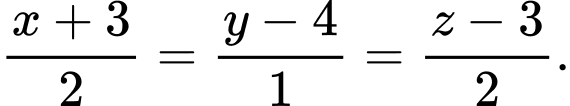
 Đáp án: A
Đáp án: A
Câu 11 [905970]: Trong không gian 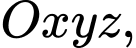 cho mặt cầu
cho mặt cầu 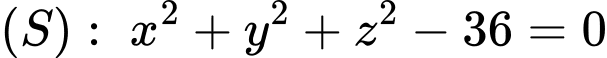 và mặt phẳng
và mặt phẳng 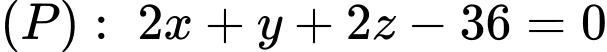 và điểm
và điểm 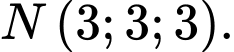 Từ một điểm
Từ một điểm 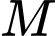 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 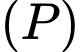 kẻ các tiếp tuyến phân biệt
kẻ các tiếp tuyến phân biệt 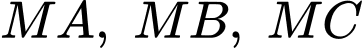 đến
đến 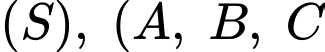 là các tiếp điểm). Khi khoảng cách từ
là các tiếp điểm). Khi khoảng cách từ 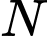 đến mặt phẳng
đến mặt phẳng 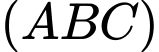 lớn nhất thì phương trình mặt phẳng
lớn nhất thì phương trình mặt phẳng 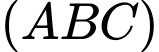 là
là 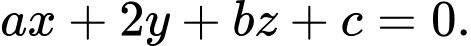 Giá trị của biểu thức
Giá trị của biểu thức 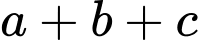 là
là
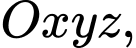 cho mặt cầu
cho mặt cầu 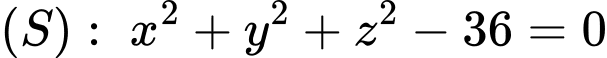 và mặt phẳng
và mặt phẳng 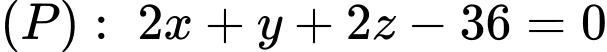 và điểm
và điểm 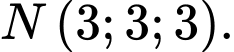 Từ một điểm
Từ một điểm 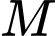 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 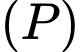 kẻ các tiếp tuyến phân biệt
kẻ các tiếp tuyến phân biệt 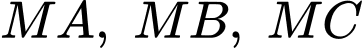 đến
đến 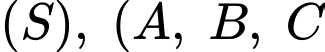 là các tiếp điểm). Khi khoảng cách từ
là các tiếp điểm). Khi khoảng cách từ 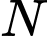 đến mặt phẳng
đến mặt phẳng 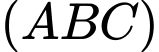 lớn nhất thì phương trình mặt phẳng
lớn nhất thì phương trình mặt phẳng 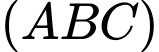 là
là 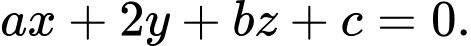 Giá trị của biểu thức
Giá trị của biểu thức 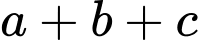 là
là A, 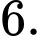
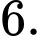
B, 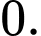
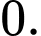
C, 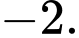
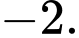
D, 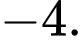
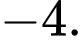
Trong không gian 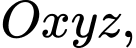 mặt cầu
mặt cầu 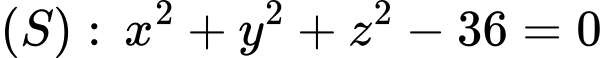
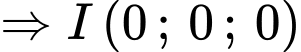
Mặt phẳng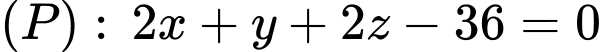 và điểm
và điểm 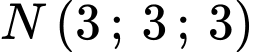
Giả sử: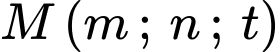 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 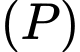

Các tiếp tuyến phân biệt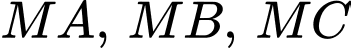 đến
đến 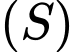
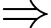
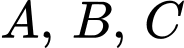 luôn nhìn
luôn nhìn 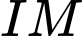 dưới một góc vuông.
dưới một góc vuông.
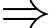 Luôn tồn tại mặt cầu ngoại tiếp
Luôn tồn tại mặt cầu ngoại tiếp  tâm là trung điểm
tâm là trung điểm 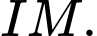
Gọi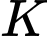 là trung điểm
là trung điểm 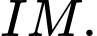
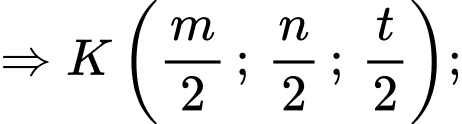
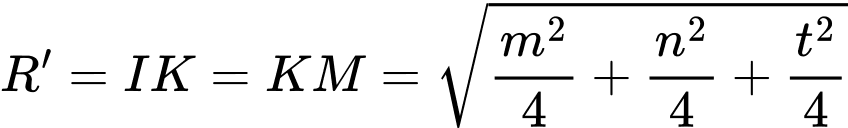
Phương trình mặt cầu: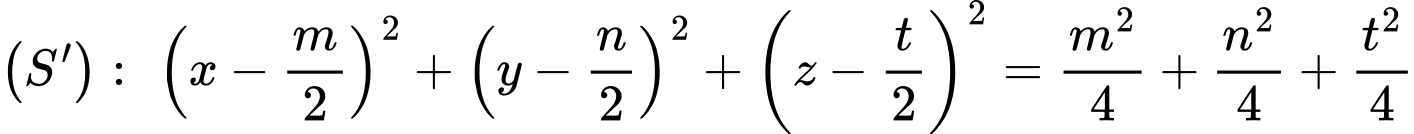
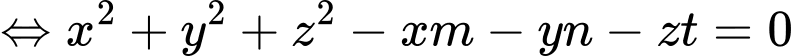
Dễ dàng thấy được mặt cầu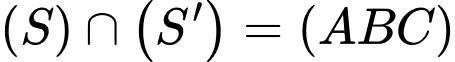
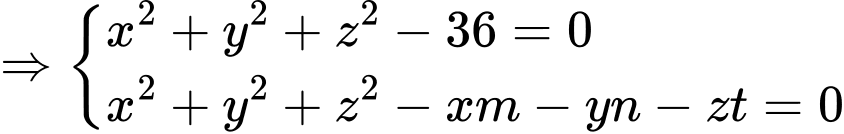
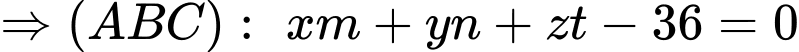
Ta có, mặt phẳng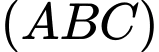 luôn đi qua điểm cố định
luôn đi qua điểm cố định 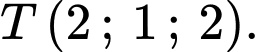
Gọi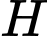 là hình chiếu của
là hình chiếu của 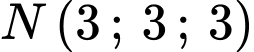 trên mặt phẳng
trên mặt phẳng 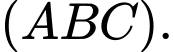
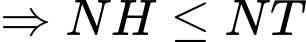
Vậy khoảng cách từ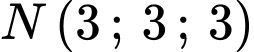 đến mặt phẳng
đến mặt phẳng 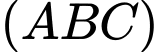 lớn nhất khi và chỉ khi
lớn nhất khi và chỉ khi
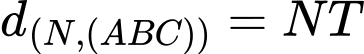
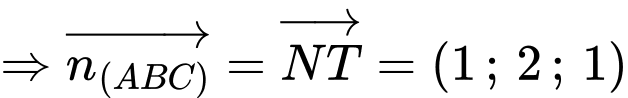
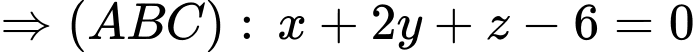
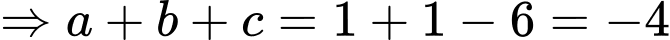
Đáp án: A Đáp án: D
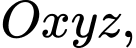 mặt cầu
mặt cầu 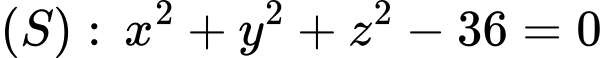
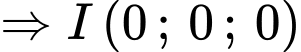
Mặt phẳng
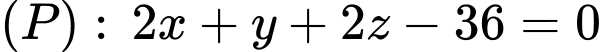 và điểm
và điểm 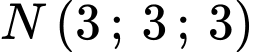
Giả sử:
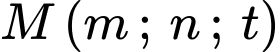 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 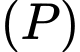

Các tiếp tuyến phân biệt
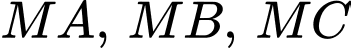 đến
đến 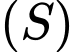
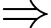
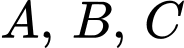 luôn nhìn
luôn nhìn 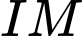 dưới một góc vuông.
dưới một góc vuông.
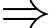 Luôn tồn tại mặt cầu ngoại tiếp
Luôn tồn tại mặt cầu ngoại tiếp  tâm là trung điểm
tâm là trung điểm 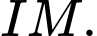
Gọi
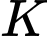 là trung điểm
là trung điểm 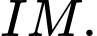
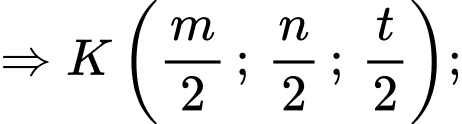
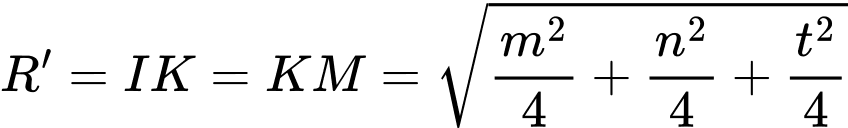
Phương trình mặt cầu:
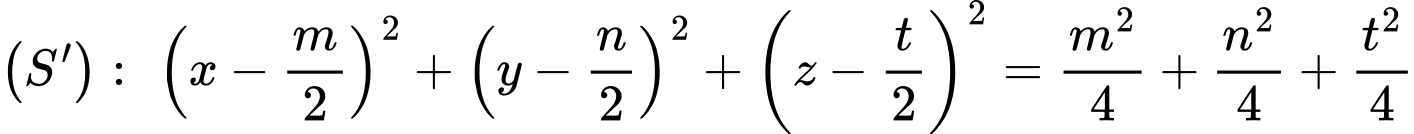
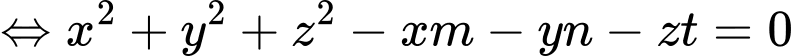
Dễ dàng thấy được mặt cầu
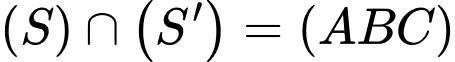
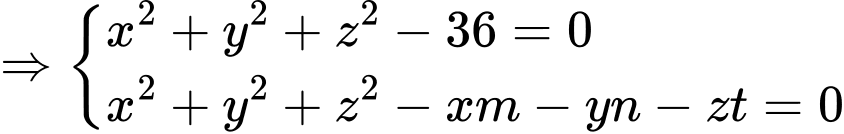
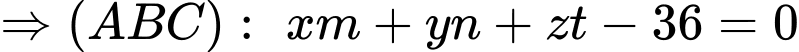
Ta có, mặt phẳng
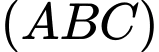 luôn đi qua điểm cố định
luôn đi qua điểm cố định 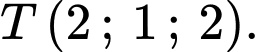
Gọi
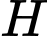 là hình chiếu của
là hình chiếu của 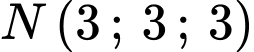 trên mặt phẳng
trên mặt phẳng 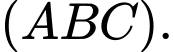
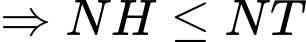
Vậy khoảng cách từ
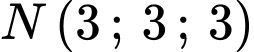 đến mặt phẳng
đến mặt phẳng 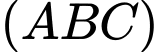 lớn nhất khi và chỉ khi
lớn nhất khi và chỉ khi
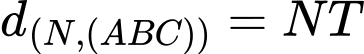
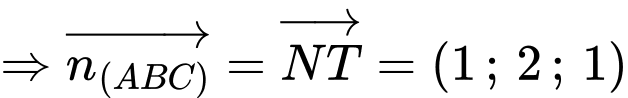
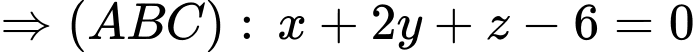
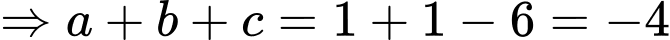
Đáp án: A Đáp án: D
Câu 12 [59108]: Trong không gian tọa độ 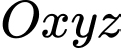 cho ba mặt phẳng
cho ba mặt phẳng 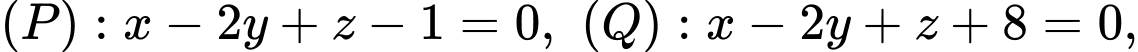
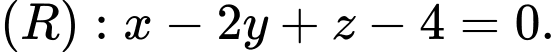 Một đường thẳng
Một đường thẳng 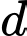 thay đổi cắt ba mặt phẳng
thay đổi cắt ba mặt phẳng  lần lượt tại
lần lượt tại 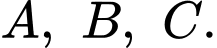 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 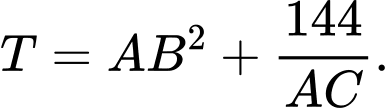
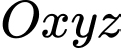 cho ba mặt phẳng
cho ba mặt phẳng 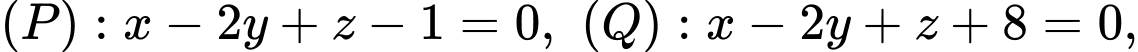
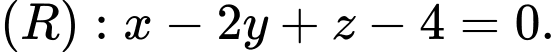 Một đường thẳng
Một đường thẳng 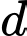 thay đổi cắt ba mặt phẳng
thay đổi cắt ba mặt phẳng  lần lượt tại
lần lượt tại 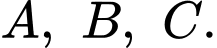 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 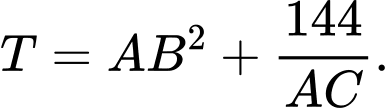
A, 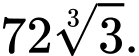
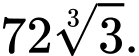
B, 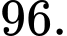
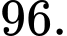
C, 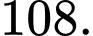
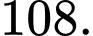
D, 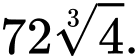
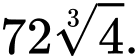
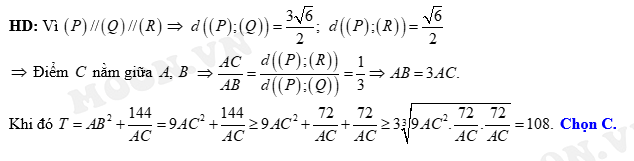 Đáp án: C
Đáp án: C
Câu 13 [216407]: Trong không gian tọa độ 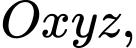 cho 3 điểm
cho 3 điểm 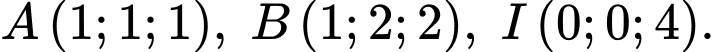 Mặt cầu
Mặt cầu 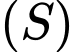 đi qua hai điểm
đi qua hai điểm 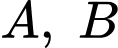 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 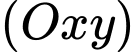 tại điểm
tại điểm  Giá trị lớn nhất của độ dài đoạn thẳng
Giá trị lớn nhất của độ dài đoạn thẳng 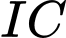 bằng
bằng
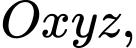 cho 3 điểm
cho 3 điểm 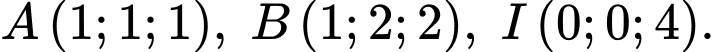 Mặt cầu
Mặt cầu 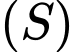 đi qua hai điểm
đi qua hai điểm 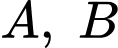 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 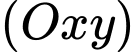 tại điểm
tại điểm  Giá trị lớn nhất của độ dài đoạn thẳng
Giá trị lớn nhất của độ dài đoạn thẳng 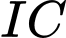 bằng
bằng A, 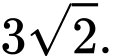
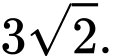
B, 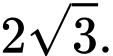
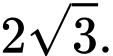
C, 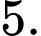
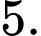
D, 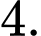
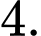
Gọi 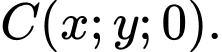
Phương trình đường thẳng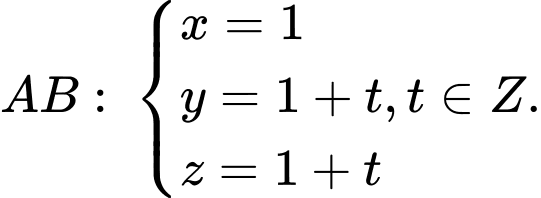
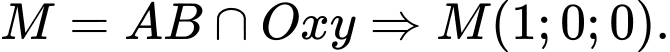
Ta có: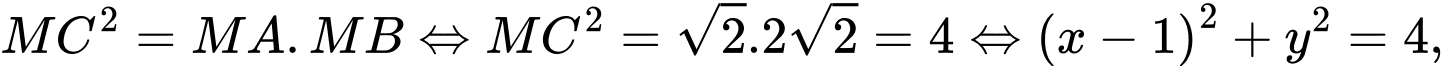 với
với 
Ta có: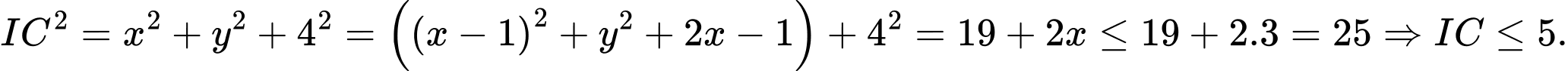
Dấu bằng xảy ra khi: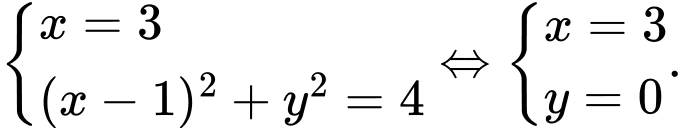
Vậy giá trị lớn nhất của độ dài đoạn thẳng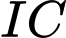 là
là 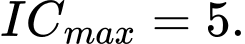
Chọn đáp án C. Đáp án: C
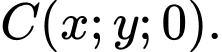
Phương trình đường thẳng
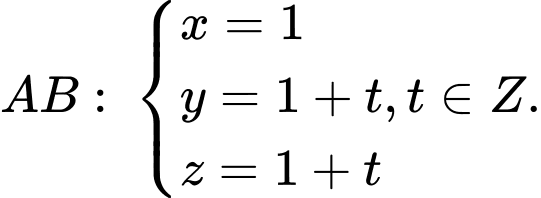
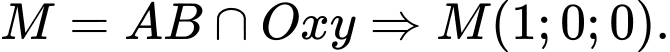
Ta có:
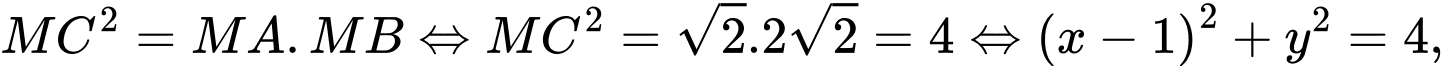 với
với 
Ta có:
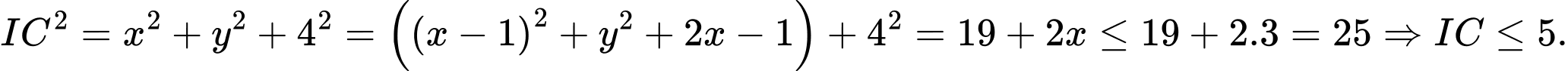
Dấu bằng xảy ra khi:
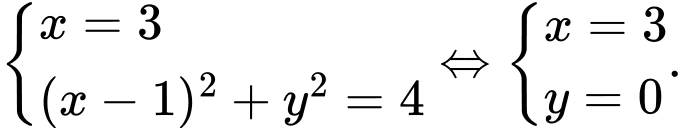
Vậy giá trị lớn nhất của độ dài đoạn thẳng
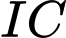 là
là 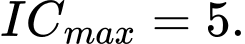
Chọn đáp án C. Đáp án: C
Câu 14 [224505]: Trong không gian 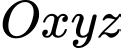 , cho mặt cầu
, cho mặt cầu 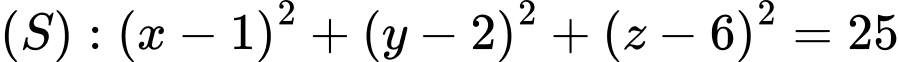 và ba điểm
và ba điểm 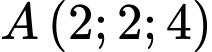 ,
, 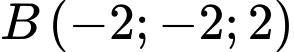 ,
, 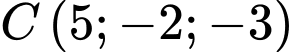 . Điểm
. Điểm 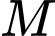 nằm trên
nằm trên 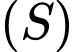 và cách đều hai điểm
và cách đều hai điểm 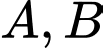 . Độ dài đoạn thẳng
. Độ dài đoạn thẳng 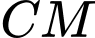 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng
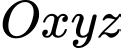 , cho mặt cầu
, cho mặt cầu 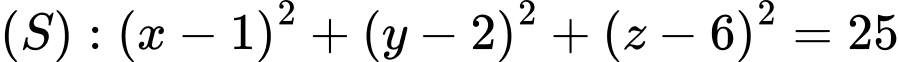 và ba điểm
và ba điểm 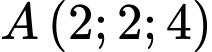 ,
, 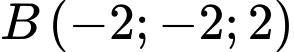 ,
, 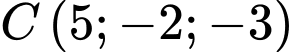 . Điểm
. Điểm 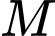 nằm trên
nằm trên 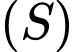 và cách đều hai điểm
và cách đều hai điểm 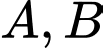 . Độ dài đoạn thẳng
. Độ dài đoạn thẳng 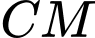 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng A, 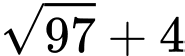 .
.
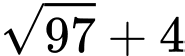 .
.B, 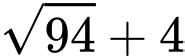 .
.
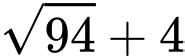 .
.C, 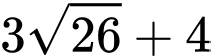 .
.
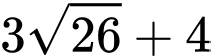 .
.D, 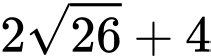 .
.
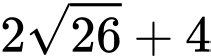 .
.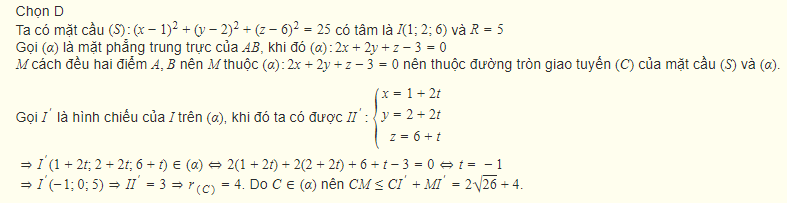 Đáp án: D
Đáp án: D
Câu 15 [59226]: Trong không gian với hệ tọa độ 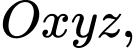 cho hai điểm
cho hai điểm 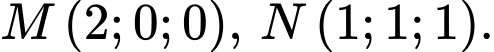 Mặt phẳng
Mặt phẳng 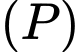 thay đổi nhưng luôn qua
thay đổi nhưng luôn qua 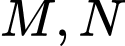 và cắt các tia
và cắt các tia 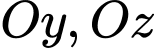 lần lượt tại
lần lượt tại 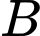 và
và  (với
(với 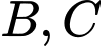 không trùng
không trùng  ). Tính giá trị nhỏ nhất
). Tính giá trị nhỏ nhất 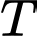 của biểu thức
của biểu thức 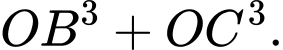
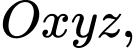 cho hai điểm
cho hai điểm 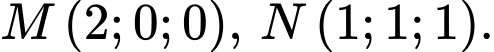 Mặt phẳng
Mặt phẳng 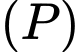 thay đổi nhưng luôn qua
thay đổi nhưng luôn qua 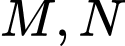 và cắt các tia
và cắt các tia 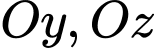 lần lượt tại
lần lượt tại 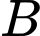 và
và  (với
(với 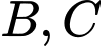 không trùng
không trùng  ). Tính giá trị nhỏ nhất
). Tính giá trị nhỏ nhất 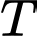 của biểu thức
của biểu thức 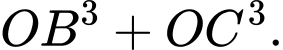
A, 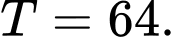
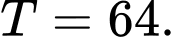
B, 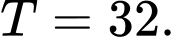
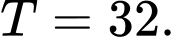
C, 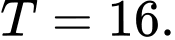
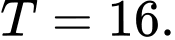
D, 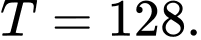
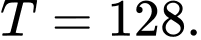
 Đáp án: D
Đáp án: D
Câu 16 [59164]: Trong không gian 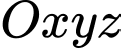 cho mặt cầu
cho mặt cầu 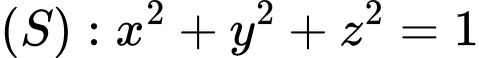 . Điểm
. Điểm 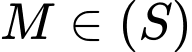 có tọa độ dương; mặt phẳng
có tọa độ dương; mặt phẳng 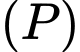 tiếp xúc với
tiếp xúc với 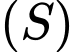 tại
tại 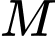 cắt các tia
cắt các tia 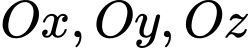 tại các điểm
tại các điểm 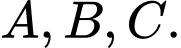 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 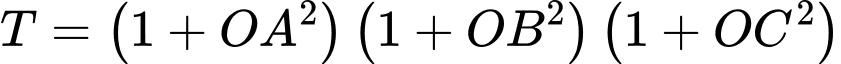 là
là
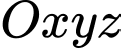 cho mặt cầu
cho mặt cầu 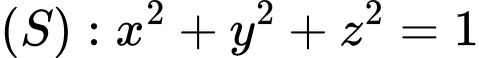 . Điểm
. Điểm 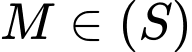 có tọa độ dương; mặt phẳng
có tọa độ dương; mặt phẳng 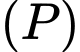 tiếp xúc với
tiếp xúc với 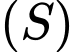 tại
tại 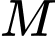 cắt các tia
cắt các tia 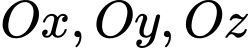 tại các điểm
tại các điểm 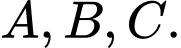 Giá trị nhỏ nhất của biểu thức
Giá trị nhỏ nhất của biểu thức 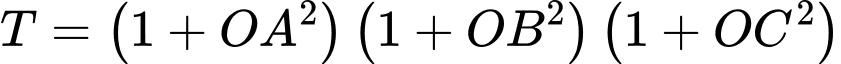 là
là A, 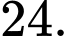
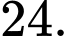
B, 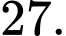
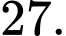
C, 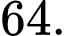
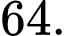
D, 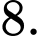
 Đáp án: C
Đáp án: C
Câu 17 [216027]: Trong không gian 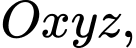 cho mặt cầu
cho mặt cầu 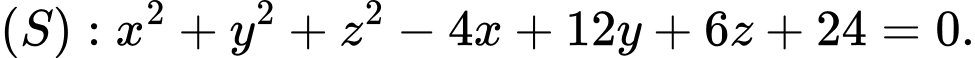 Hai điểm
Hai điểm 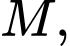
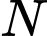 thuộc
thuộc 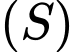 sao cho
sao cho 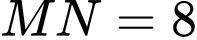 và
và 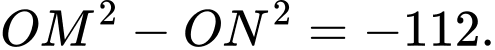 Khoảng cách từ
Khoảng cách từ  đến đường thẳng
đến đường thẳng 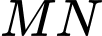 bằng
bằng
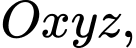 cho mặt cầu
cho mặt cầu 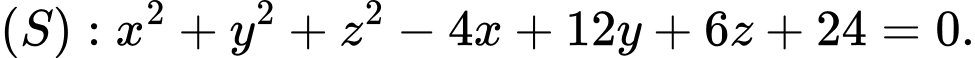 Hai điểm
Hai điểm 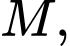
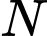 thuộc
thuộc 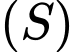 sao cho
sao cho 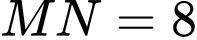 và
và 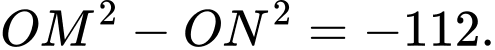 Khoảng cách từ
Khoảng cách từ  đến đường thẳng
đến đường thẳng 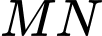 bằng
bằng A, 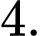
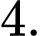
B, 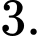
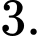
C, 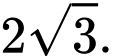
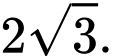
D, 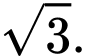
Chọn B
Phương trình mặt cầu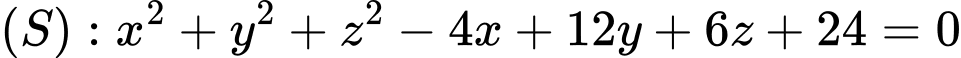 ;
;
Ta có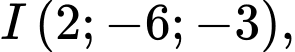
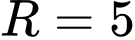 và
và 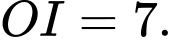
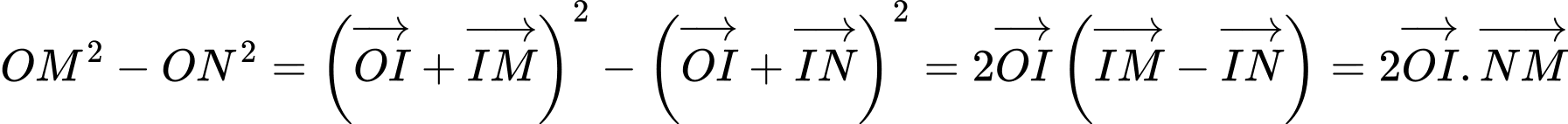
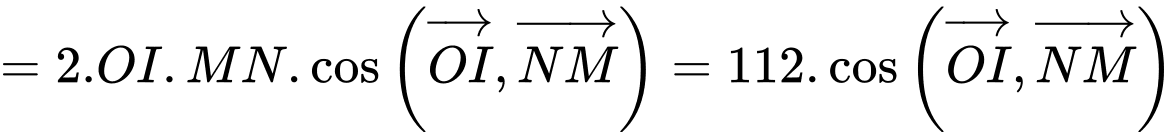
Khi đó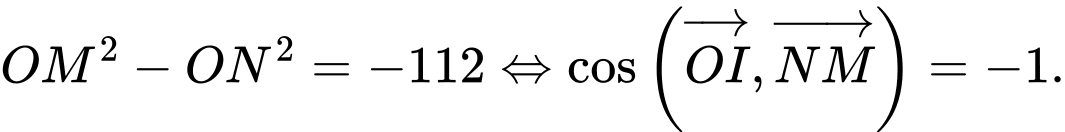
Suy ra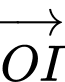 và
và  ngược hướng hay
ngược hướng hay 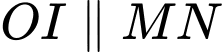 (vì
(vì 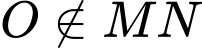 ).
).
Vậy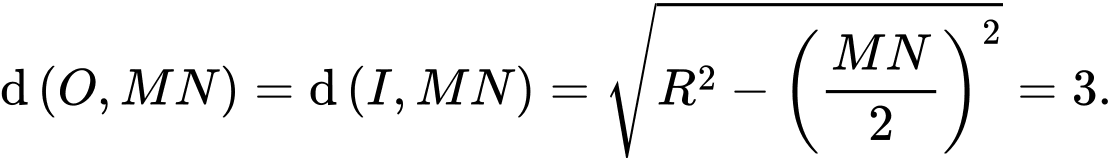 Đáp án: B
Đáp án: B
Phương trình mặt cầu
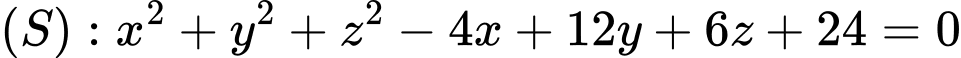 ;
;
Ta có
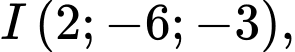
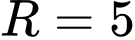 và
và 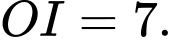
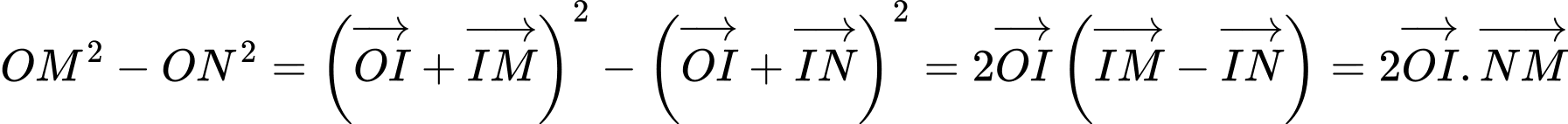
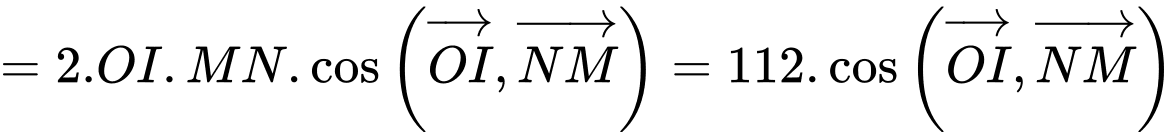
Khi đó
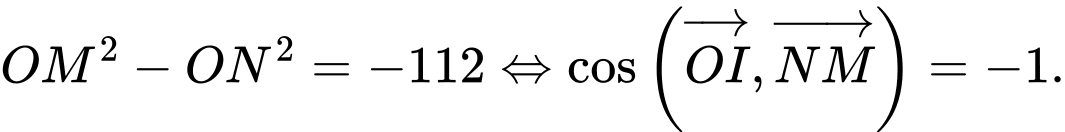
Suy ra
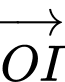 và
và  ngược hướng hay
ngược hướng hay 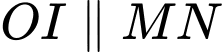 (vì
(vì 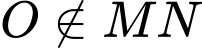 ).
).
Vậy
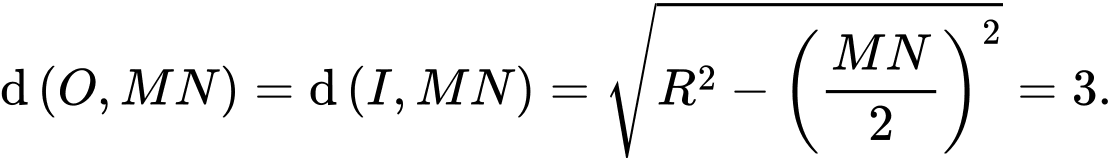 Đáp án: B
Đáp án: B
Câu 18 [908234]: Trong không gian với hệ trục 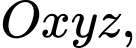 cho hai mặt phẳng
cho hai mặt phẳng 
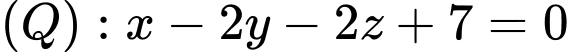 và mặt cầu
và mặt cầu 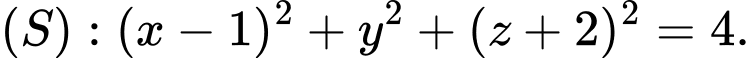 Gọi
Gọi 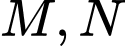 lần lượt là hai điểm nằm trên
lần lượt là hai điểm nằm trên 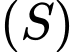 và
và  sao cho
sao cho 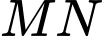 luôn vuông góc với
luôn vuông góc với 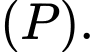 Giá trị nhỏ nhất và lớn nhất của
Giá trị nhỏ nhất và lớn nhất của 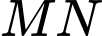 tương ứng là
tương ứng là 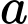 và
và 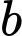 . Khi đó
. Khi đó  là
là
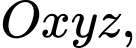 cho hai mặt phẳng
cho hai mặt phẳng 
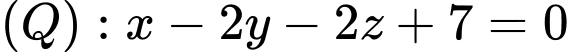 và mặt cầu
và mặt cầu 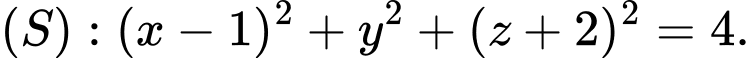 Gọi
Gọi 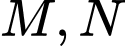 lần lượt là hai điểm nằm trên
lần lượt là hai điểm nằm trên 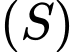 và
và  sao cho
sao cho 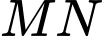 luôn vuông góc với
luôn vuông góc với 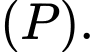 Giá trị nhỏ nhất và lớn nhất của
Giá trị nhỏ nhất và lớn nhất của 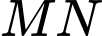 tương ứng là
tương ứng là 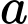 và
và 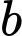 . Khi đó
. Khi đó  là
là A, 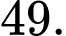
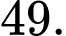
B, 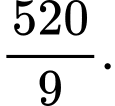
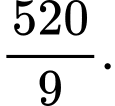
C, 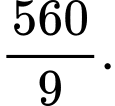
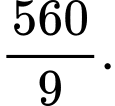
D, 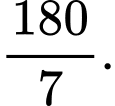
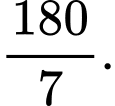
Trong không gian tọa độ
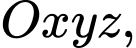 cho 2 mặt phẳng
cho 2 mặt phẳng 
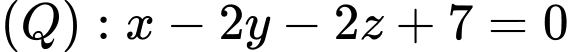 và mặt cầu
và mặt cầu 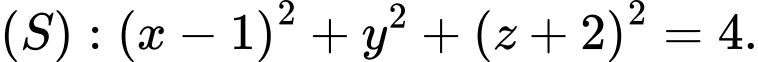
Có:
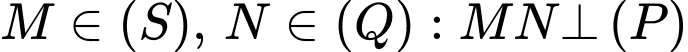
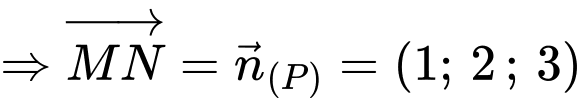
Có:
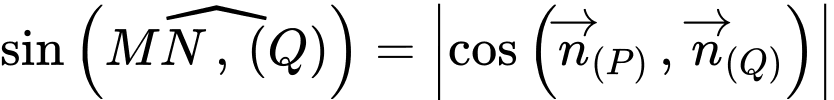
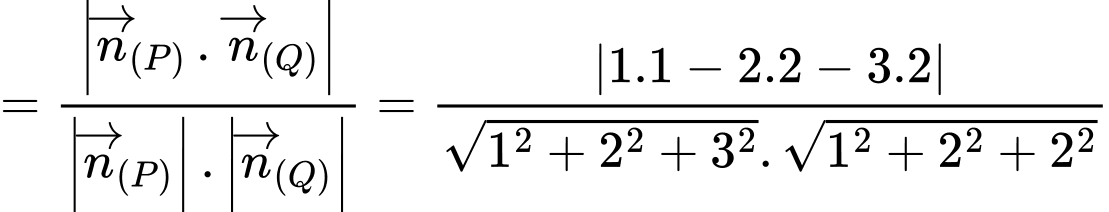
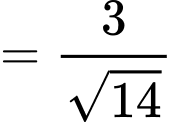
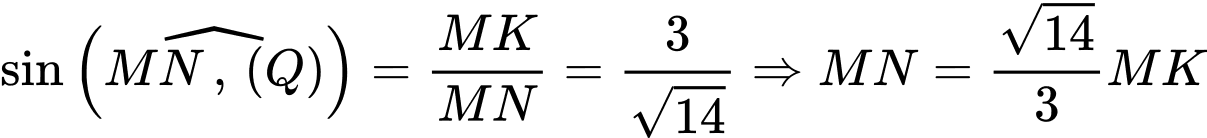
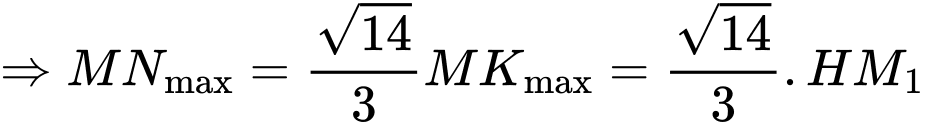
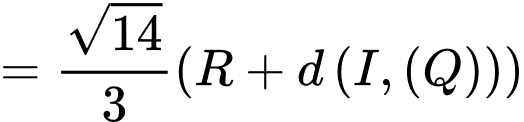
Có
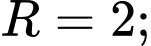
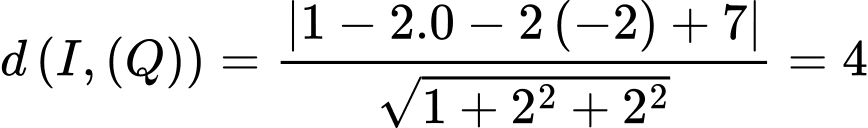
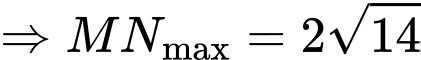
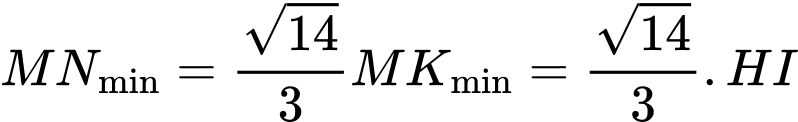
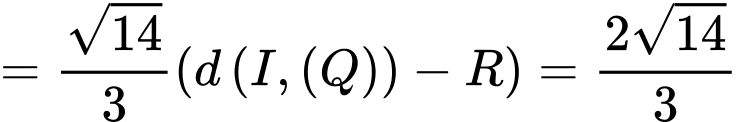
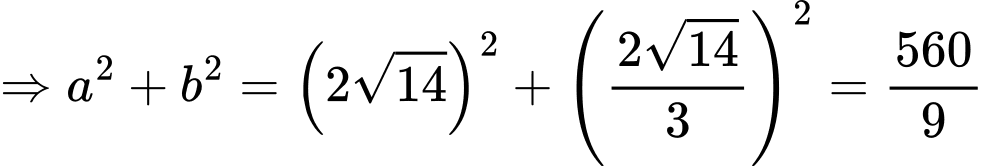
Đáp án C. Đáp án: C
Câu 19 [398637]: Trong không gian 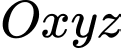 , cho mặt cầu
, cho mặt cầu 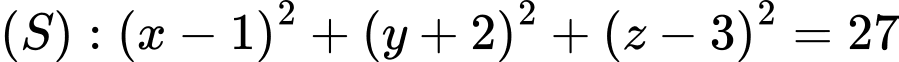 . Gọi
. Gọi  là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 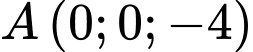 ,
, 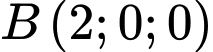 và cắt
và cắt 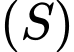 theo giao tuyến là đường tròn
theo giao tuyến là đường tròn  . Gọi
. Gọi 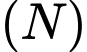 là khối nón có đỉnh là tâm của
là khối nón có đỉnh là tâm của 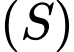 , đáy là hình tròn
, đáy là hình tròn  Khi
Khi 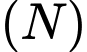 có thể tích lớn nhất, mặt phẳng
có thể tích lớn nhất, mặt phẳng  có phương trình dạng
có phương trình dạng 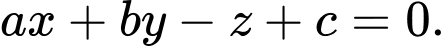 Giá trị của
Giá trị của 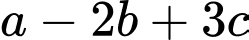 bằng
bằng
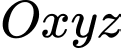 , cho mặt cầu
, cho mặt cầu 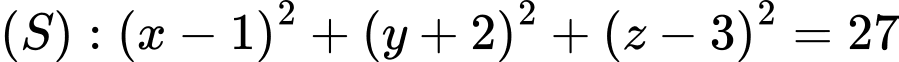 . Gọi
. Gọi  là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 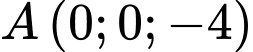 ,
, 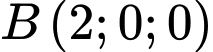 và cắt
và cắt 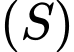 theo giao tuyến là đường tròn
theo giao tuyến là đường tròn  . Gọi
. Gọi 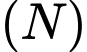 là khối nón có đỉnh là tâm của
là khối nón có đỉnh là tâm của 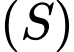 , đáy là hình tròn
, đáy là hình tròn  Khi
Khi 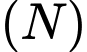 có thể tích lớn nhất, mặt phẳng
có thể tích lớn nhất, mặt phẳng  có phương trình dạng
có phương trình dạng 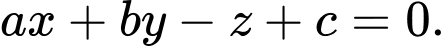 Giá trị của
Giá trị của 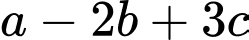 bằng
bằng A, 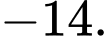
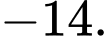
B, 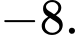
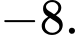
C, 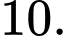
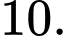
D, 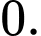
Chọn A
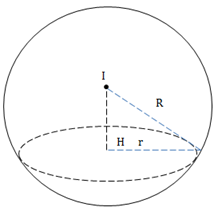
Mặt cầu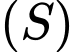 có tâm
có tâm  và bán kính
và bán kính 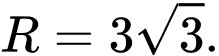
Gọi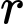 là bán kính đường tròn
là bán kính đường tròn  và
và 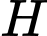 là hình chiếu của
là hình chiếu của 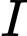 lên
lên 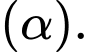
Đặt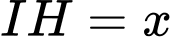 ta có
ta có 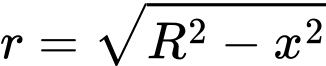
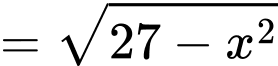
Vậy thể tích khối nón tạo được là
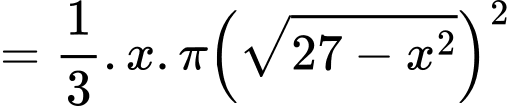
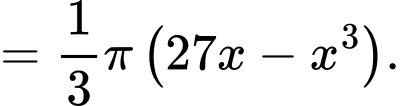
Gọi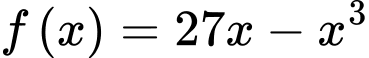 với
với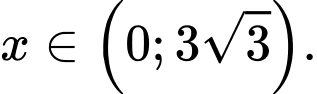 Thể tích nón lớn nhất khi
Thể tích nón lớn nhất khi 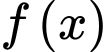 đạt giá trị lớn nhất
đạt giá trị lớn nhất
Ta có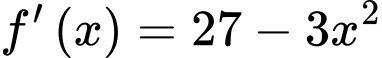
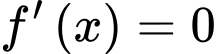
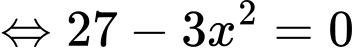
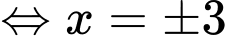
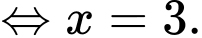
Bảng biến thiên :
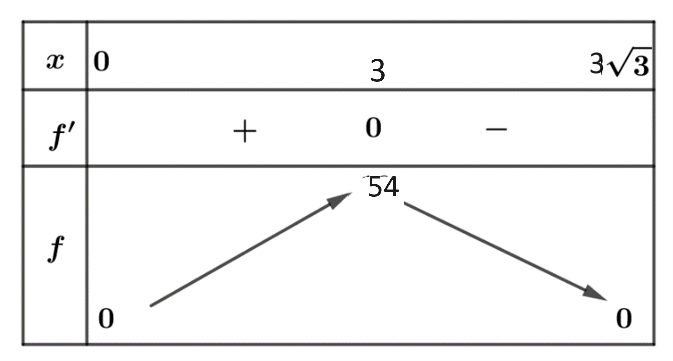
Vậy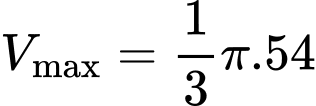
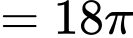 khi
khi 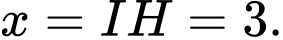
Mặt phẳng
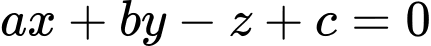 đi qua hai điểm
đi qua hai điểm 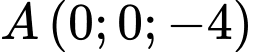
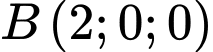 ,
,
nên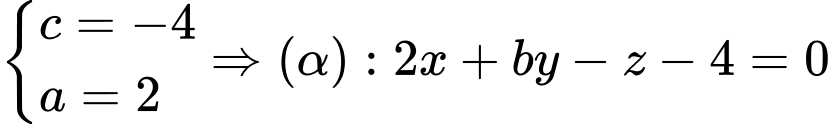
Và
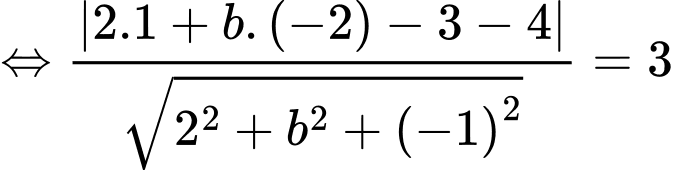

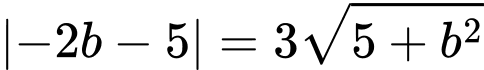
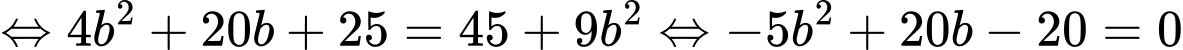
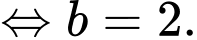
Vậy giá trị của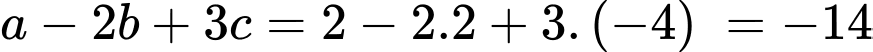 Đáp án: A
Đáp án: A

Mặt cầu
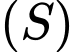 có tâm
có tâm  và bán kính
và bán kính 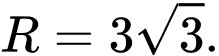
Gọi
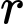 là bán kính đường tròn
là bán kính đường tròn  và
và 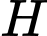 là hình chiếu của
là hình chiếu của 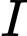 lên
lên 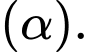
Đặt
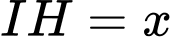 ta có
ta có 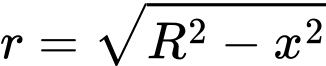
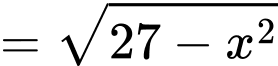
Vậy thể tích khối nón tạo được là

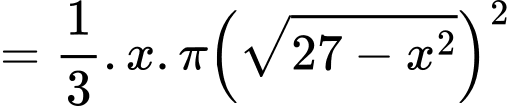
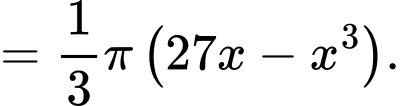
Gọi
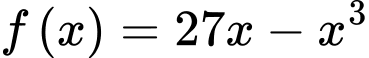 với
với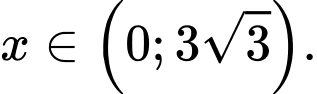 Thể tích nón lớn nhất khi
Thể tích nón lớn nhất khi 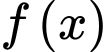 đạt giá trị lớn nhất
đạt giá trị lớn nhấtTa có
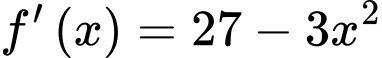
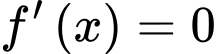
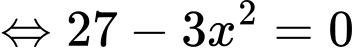
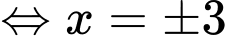
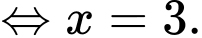
Bảng biến thiên :

Vậy
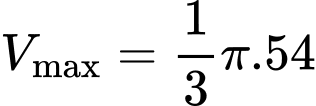
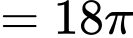 khi
khi 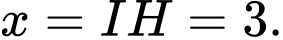
Mặt phẳng

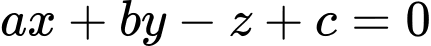 đi qua hai điểm
đi qua hai điểm 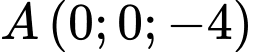
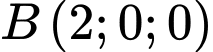 ,
,nên
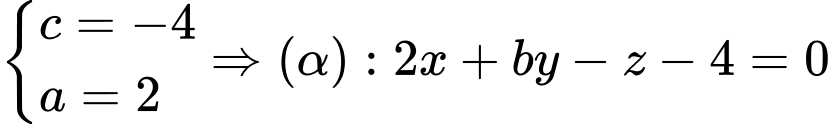
Và

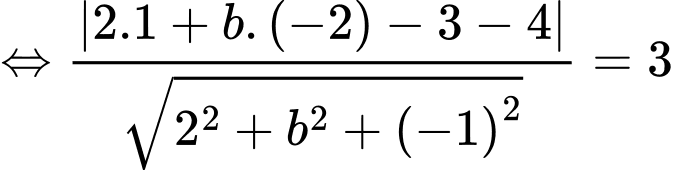

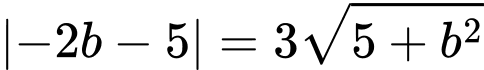
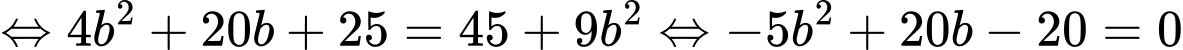
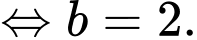
Vậy giá trị của
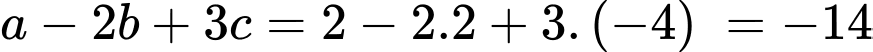 Đáp án: A
Đáp án: A
Câu 20 [903750]: Trong không gian 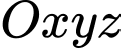 cho các điểm
cho các điểm 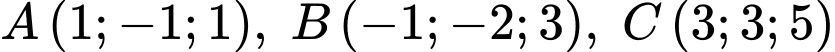 và mặt cầu
và mặt cầu 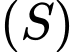 có tâm
có tâm 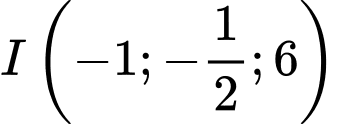 bán kính
bán kính  Gọi
Gọi 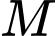 là điểm thuộc mặt cầu
là điểm thuộc mặt cầu 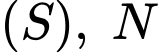 là điểm thỏa mãn
là điểm thỏa mãn 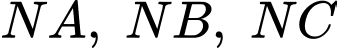 hợp với mặt phẳng
hợp với mặt phẳng 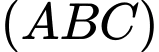 các góc bằng nhau. Tìm giá trị nhỏ nhất của
các góc bằng nhau. Tìm giá trị nhỏ nhất của 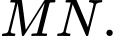
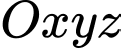 cho các điểm
cho các điểm 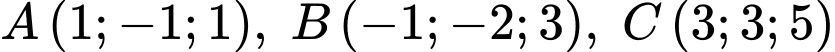 và mặt cầu
và mặt cầu 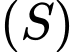 có tâm
có tâm 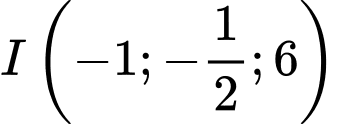 bán kính
bán kính  Gọi
Gọi 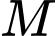 là điểm thuộc mặt cầu
là điểm thuộc mặt cầu 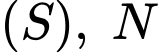 là điểm thỏa mãn
là điểm thỏa mãn 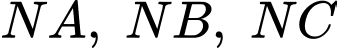 hợp với mặt phẳng
hợp với mặt phẳng 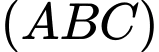 các góc bằng nhau. Tìm giá trị nhỏ nhất của
các góc bằng nhau. Tìm giá trị nhỏ nhất của 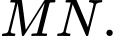
A, 4.
B, 3.
C, 2.
D, 1.
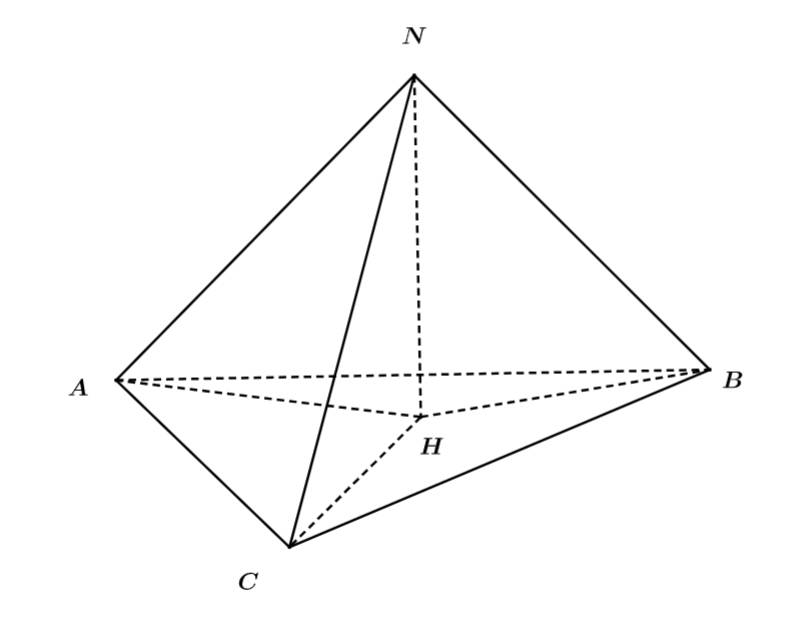
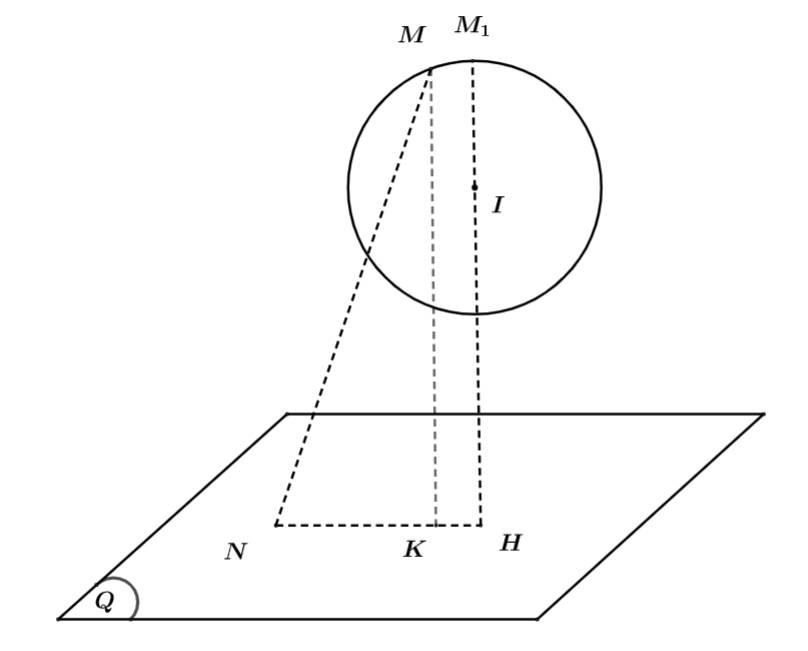
Theo giả thuyết: thỏa mãn
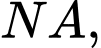

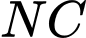 hợp với mặt phẳng
hợp với mặt phẳng 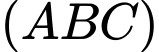 các góc bằng nhau.
các góc bằng nhau.=>Hình chiếu của N trên mặt phẳng
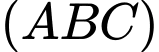 sẽ trùng với tâm đường tròn ngoại tiếp
sẽ trùng với tâm đường tròn ngoại tiếp 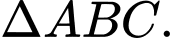
Xét
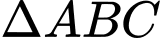 có:
có: 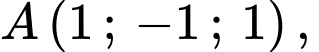
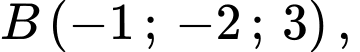
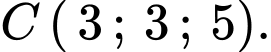
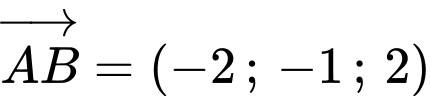
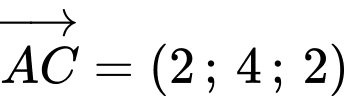
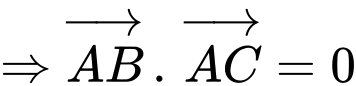
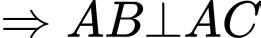
=>
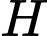 là trung điểm
là trung điểm 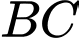
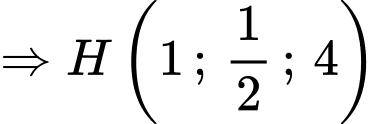
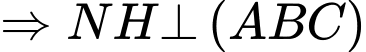
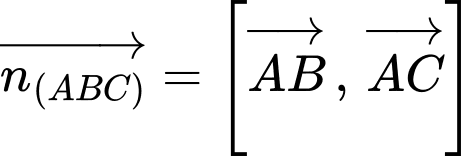
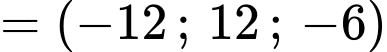
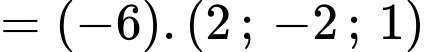
Ta có phương trình đường thẳng NH đi qua H và nhận vecto
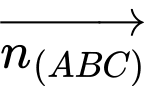 làm vecto chỉ phương:
làm vecto chỉ phương: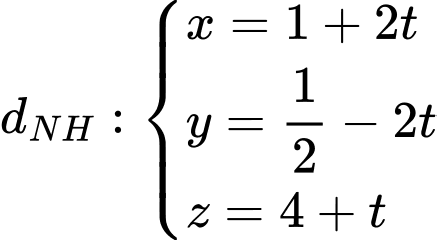
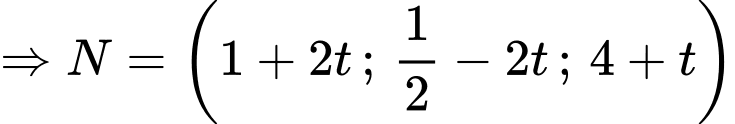
Ta có:
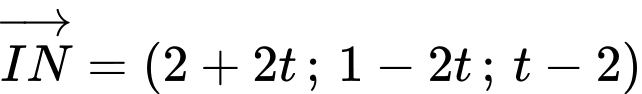
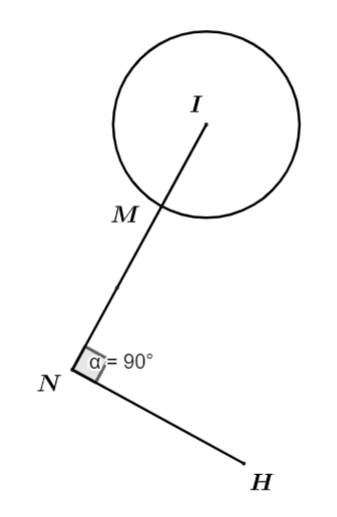
Để khoảng cách
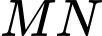 nhỏ nhất thì khoảng cách
nhỏ nhất thì khoảng cách 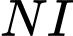 phải ngắn nhất
phải ngắn nhất 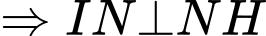
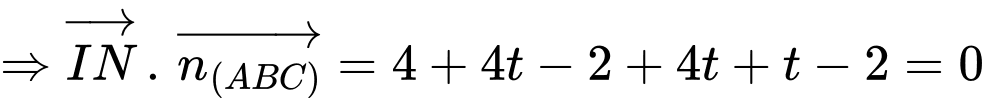
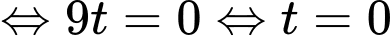
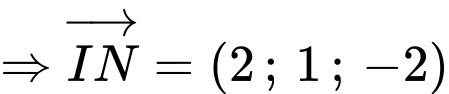
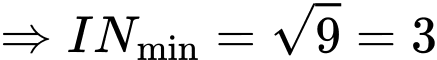
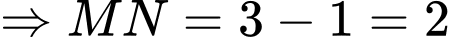
Đáp án C Đáp án: C