Đáp án Bài tập tự luyện số 2
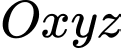 , cho hai điểm
, cho hai điểm 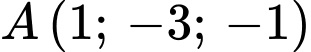 ,
, 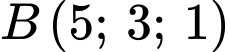 và mặt phẳng
và mặt phẳng 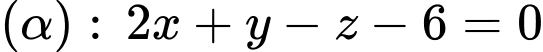 . Mặt cầu
. Mặt cầu 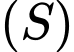 tâm
tâm 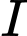 có bán kính
có bán kính 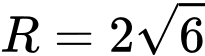 , đi qua điểm
, đi qua điểm 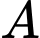 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng  tại điểm
tại điểm 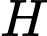 . Độ dài ngắn nhất của đoạn
. Độ dài ngắn nhất của đoạn 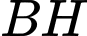 bằng
bằng 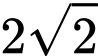 .
.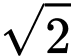 .
.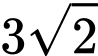 .
.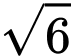 .
.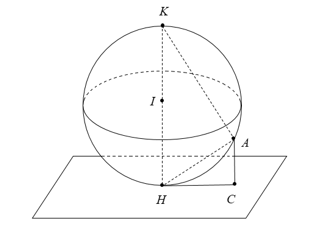
Gọi
 là hình chiếu vuông góc của
là hình chiếu vuông góc của 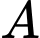 lên mặt phẳng
lên mặt phẳng  . Ta có:
. Ta có: 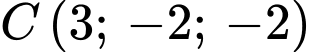 và
và 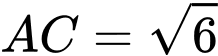 .
.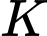 là điểm đối xứng với
là điểm đối xứng với 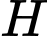 qua
qua 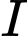 nên
nên 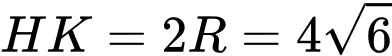 .
.Hai tam giác
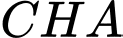 và
và 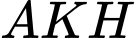 đồng dạng nên
đồng dạng nên 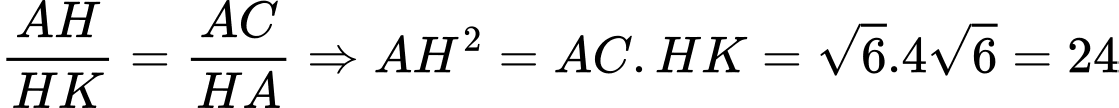 .
.Tam giác
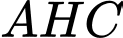 vuông tại
vuông tại  , ta có:
, ta có: 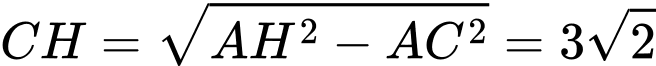 .
.Ta thấy
 là điểm cố định và
là điểm cố định và 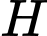 di động cùng thuộc mặt phẳng
di động cùng thuộc mặt phẳng  mà
mà 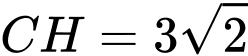 nên
nên 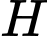 thuộc đường tròn
thuộc đường tròn  nằm trong mặt phẳng
nằm trong mặt phẳng  có tâm
có tâm  và bán kính
và bán kính 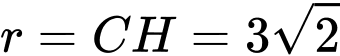 .
.Gọi
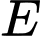 là hình chiếu vuông góc của
là hình chiếu vuông góc của 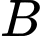 lên mặt phẳng
lên mặt phẳng  . Ta có:
. Ta có: 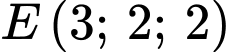 .
.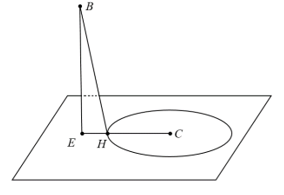
Tam giác
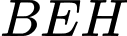 vuông tại
vuông tại 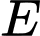 , ta có:
, ta có:  .
.Độ dài đoạn
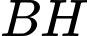 ngắn nhất khi
ngắn nhất khi 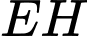 ngắn nhất.
ngắn nhất. Mà
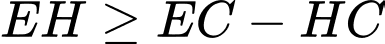 nên
nên 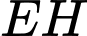 ngắn nhất khi
ngắn nhất khi  .
.Vậy độ dài ngắn nhất của đoạn
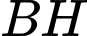 bằng
bằng 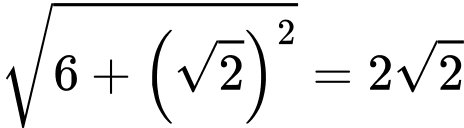 . Đáp án: A
. Đáp án: A 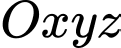 , cho các điểm
, cho các điểm 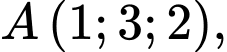
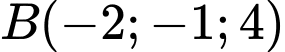 và hai điểm
và hai điểm 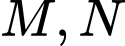 thay đổi trên mặt phẳng
thay đổi trên mặt phẳng 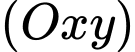 sao cho
sao cho 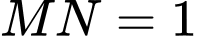 . Giá trị nhỏ nhất của
. Giá trị nhỏ nhất của  là
là 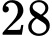 .
.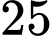 .
.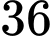 .
.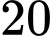 .
. Đáp án: A
Đáp án: A 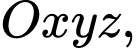 cho điểm
cho điểm 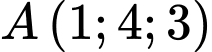 và mặt phẳng
và mặt phẳng 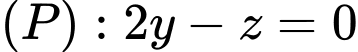 . Biết điểm
. Biết điểm 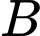 thuộc
thuộc 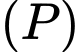 , điểm
, điểm  thuộc
thuộc 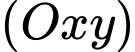 sao cho chu vi tam giác
sao cho chu vi tam giác 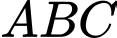 nhỏ nhất. Hỏi giá trị nhỏ nhất đó là
nhỏ nhất. Hỏi giá trị nhỏ nhất đó là 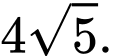
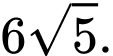
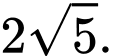
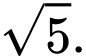
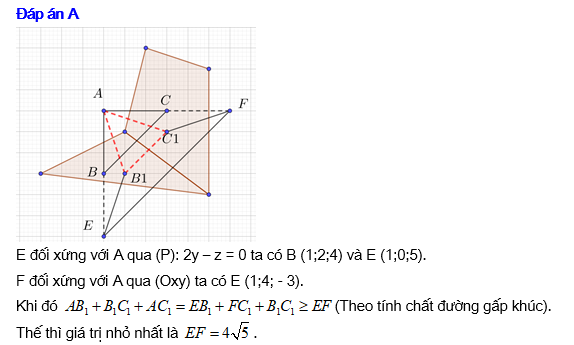 Đáp án: A
Đáp án: A 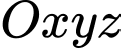 , cho điểm
, cho điểm 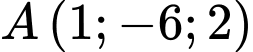 và mặt phẳng
và mặt phẳng 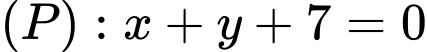 . Điểm
. Điểm 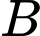 thay đổi thuộc
thay đổi thuộc  ; điểm
; điểm  thay đổi thuộc mặt phẳng
thay đổi thuộc mặt phẳng 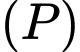 . Biết rằng tam giác
. Biết rằng tam giác 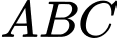 có chu vi nhỏ nhất. Tọa độ điểm
có chu vi nhỏ nhất. Tọa độ điểm 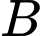 là
là 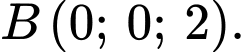
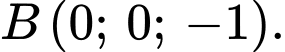
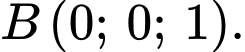
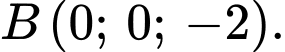
 Đáp án: A
Đáp án: A 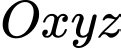 , cho ba điểm
, cho ba điểm 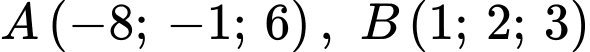 và
và 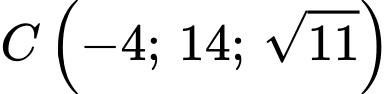 . Điểm
. Điểm 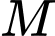 di động trên mặt cầu
di động trên mặt cầu 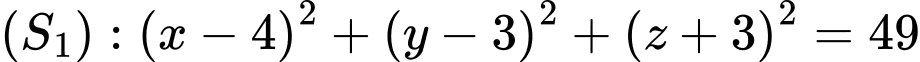 sao cho tam giác
sao cho tam giác 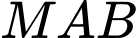 có
có 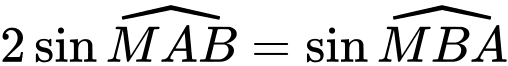 . Giá trị nhỏ nhất của đoạn thẳng
. Giá trị nhỏ nhất của đoạn thẳng 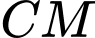 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? 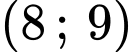 .
.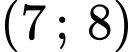 .
.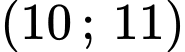 .
.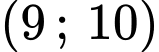 .
.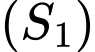 có tâm
có tâm 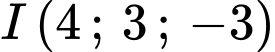 , bán kính
, bán kính 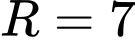 .
.
+
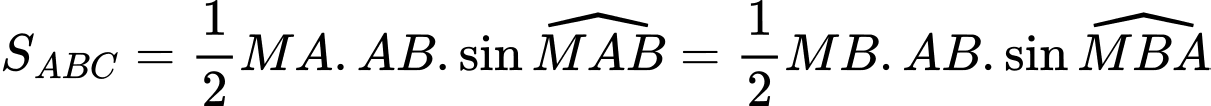 và
và 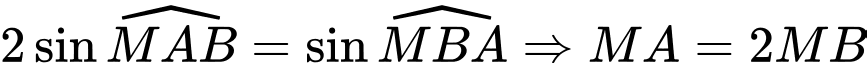 .
.
Gọi
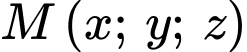 , từ
, từ 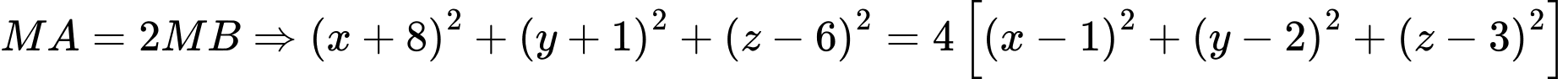
 điểm
điểm 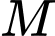 di động trên mặt cầu
di động trên mặt cầu 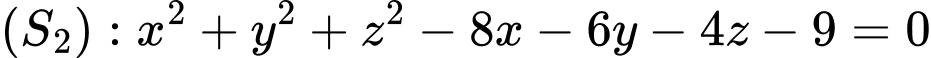 .
.
Từ đó suy ra điểm
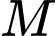 di động trên đường tròn
di động trên đường tròn 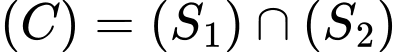 , nằm trên
, nằm trên 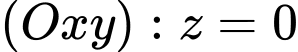 và có tâm
và có tâm 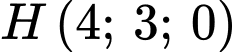 , bán kính
, bán kính 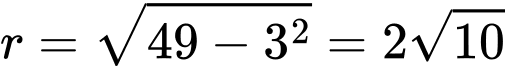 .
.
Gọi
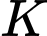 là hình chiếu vuông góc của
là hình chiếu vuông góc của 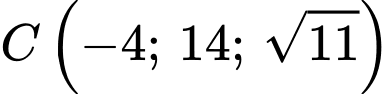 lên
lên 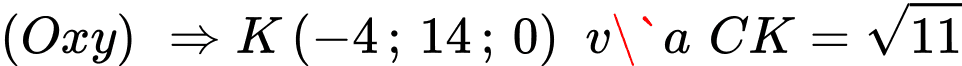 .
.
Ta có:
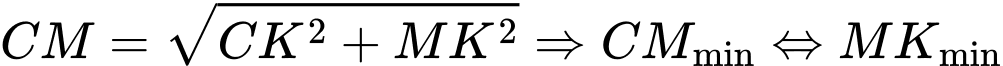 và
và 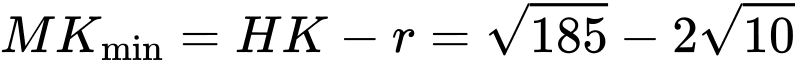 .
.
Vậy
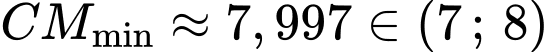 . Đáp án: B
. Đáp án: B 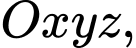 gọi
gọi 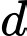 là đường thẳng đi qua
là đường thẳng đi qua 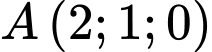 , song song với mặt phẳng
, song song với mặt phẳng 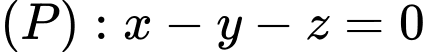 và có tổng khoảng cách từ các điểm
và có tổng khoảng cách từ các điểm 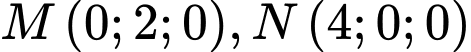 tới đường thẳng
tới đường thẳng 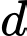 có giá trị nhỏ nhất. Vectơ chỉ phương
có giá trị nhỏ nhất. Vectơ chỉ phương 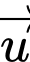 của
của 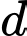 có tọa độ là
có tọa độ là 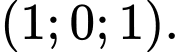
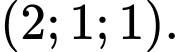
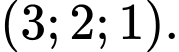
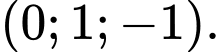
 Đáp án: A
Đáp án: A 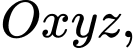 cho điểm
cho điểm 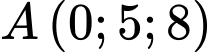 và hai mặt cầu
và hai mặt cầu 
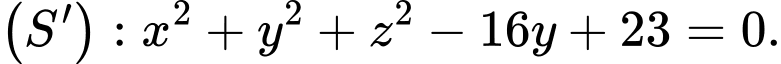 Gọi
Gọi 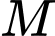 là điểm thuộc cả hai mặt cầu
là điểm thuộc cả hai mặt cầu 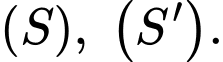 Khoảng cách
Khoảng cách  nhỏ nhất bằng
nhỏ nhất bằng 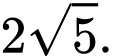
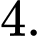
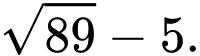
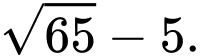
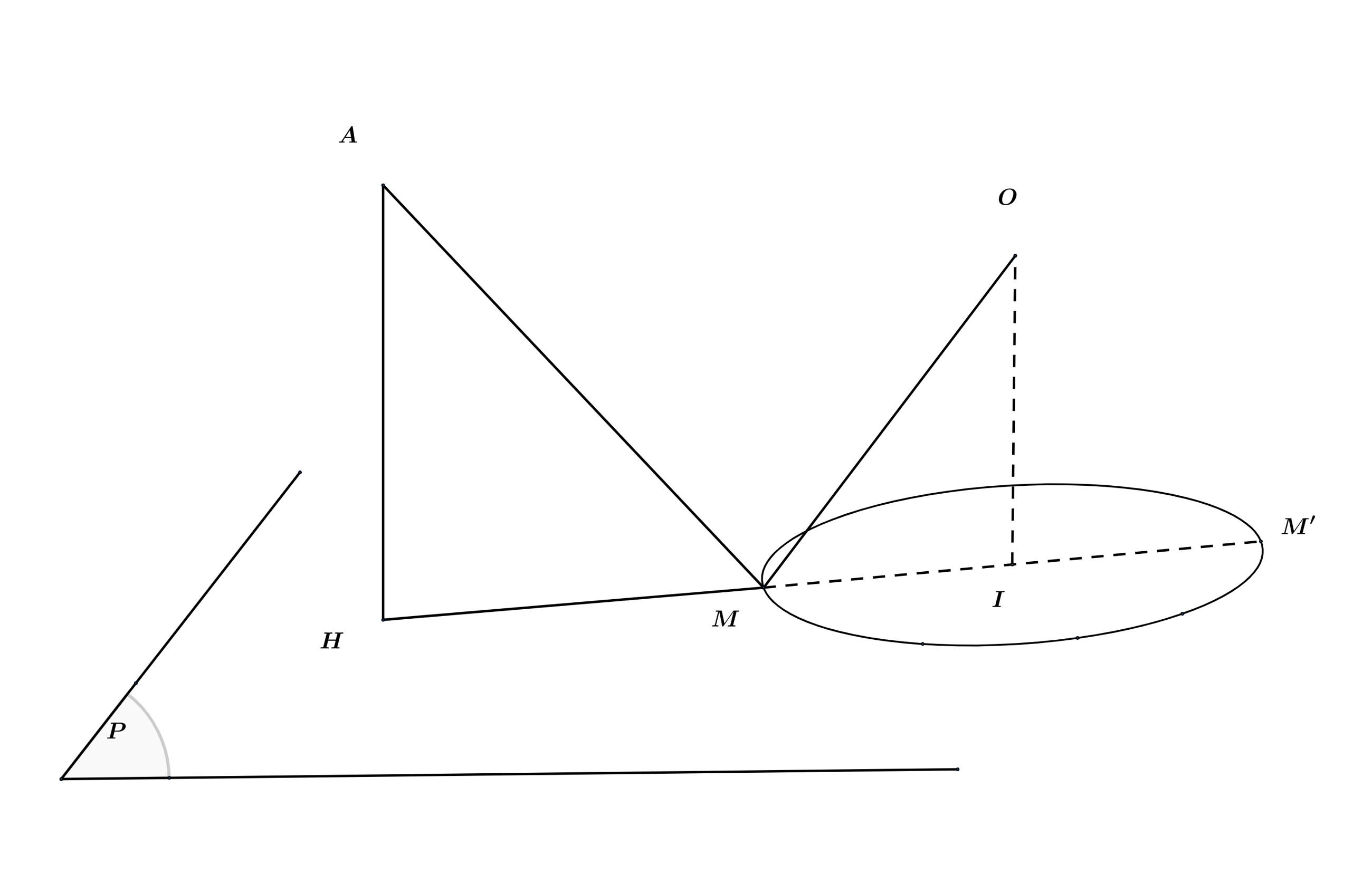
Hai mặt cầu 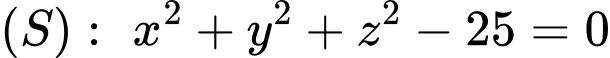 và
và 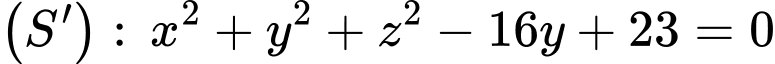 cắt nhau tại mặt phẳng
cắt nhau tại mặt phẳng 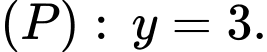
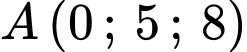 :
: 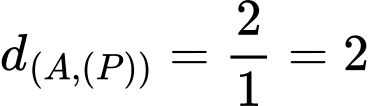
 Hình chiếu của
Hình chiếu của 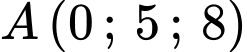 lên mặt phẳng
lên mặt phẳng 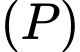 là:
là: 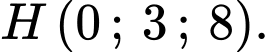
Ta có: Tâm mặt phẳng hình tròn 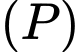 được cắt bởi hai mặt cầu là
được cắt bởi hai mặt cầu là 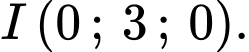
Xét 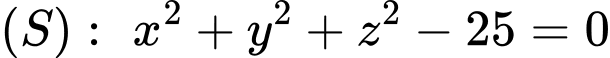 có: Tâm
có: Tâm 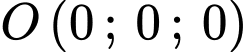 và bán kính
và bán kính 
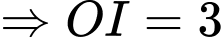 và
và 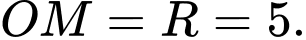
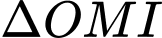 vuông tại
vuông tại 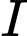
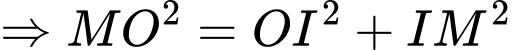
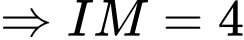
Có: 
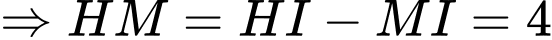
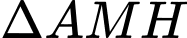 vuông tại
vuông tại 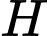
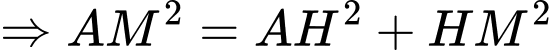
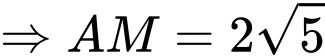
Đáp án: A
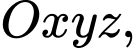 cho đường thẳng
cho đường thẳng 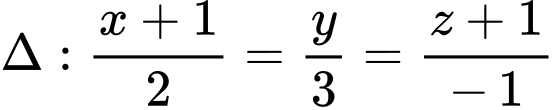 và hai điểm
và hai điểm 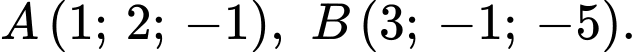 Gọi
Gọi 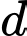 là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 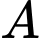 và cắt đường thẳng
và cắt đường thẳng  sao cho khoảng cách từ
sao cho khoảng cách từ 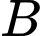 đến đường thẳng
đến đường thẳng 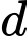 lớn nhất,
lớn nhất, 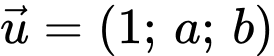 là vectơ chỉ phương của đường thẳng
là vectơ chỉ phương của đường thẳng 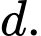 Giá trị của
Giá trị của 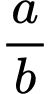 bằng
bằng 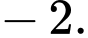
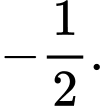
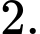
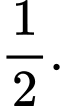
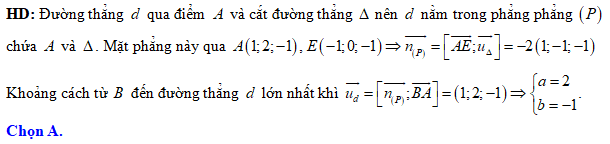 Đáp án: A
Đáp án: A 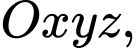 cho hai điểm
cho hai điểm 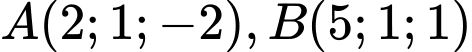 và mặt cầu
và mặt cầu  Xét đường thẳng
Xét đường thẳng 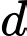 đi qua
đi qua 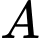 và tiếp xúc với
và tiếp xúc với 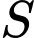 sao cho khoảng cách từ
sao cho khoảng cách từ 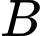 đến
đến 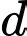 nhỏ nhất. Phương trình của đường thẳng
nhỏ nhất. Phương trình của đường thẳng 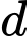 là
là 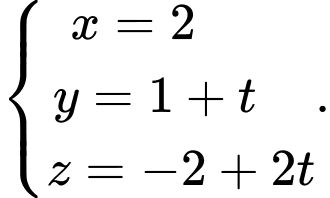
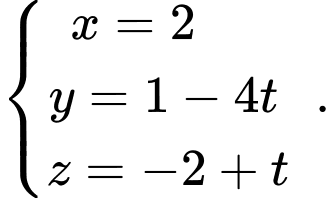
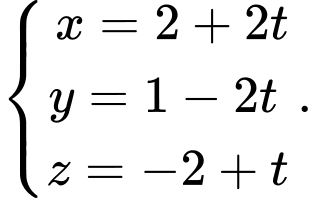
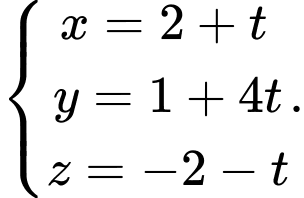
 Đáp án: C
Đáp án: C 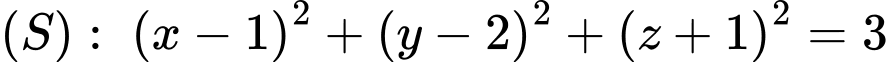 và đường thẳng
và đường thẳng 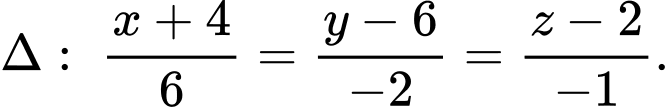 Từ điểm
Từ điểm 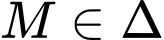 kẻ các tiếp tuyến đến mặt cầu
kẻ các tiếp tuyến đến mặt cầu 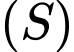 và gọi
và gọi  là tập hợp các tiếp điểm. Biết khi diện tích hình phẳng giới hạn bởi
là tập hợp các tiếp điểm. Biết khi diện tích hình phẳng giới hạn bởi  đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì  thuộc mặt phẳng
thuộc mặt phẳng 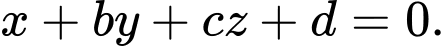 Tìm
Tìm 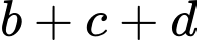
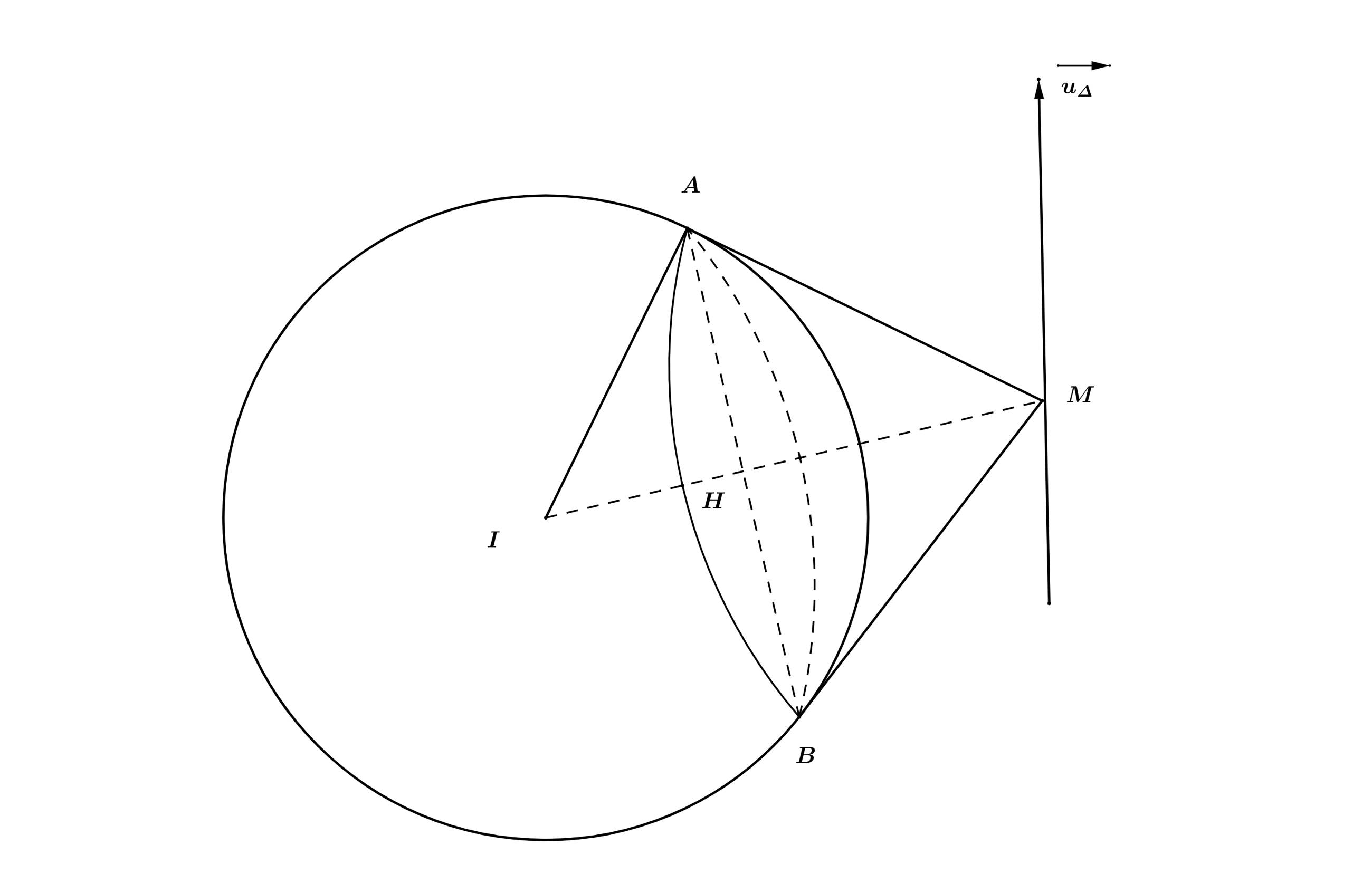
Mặt cầu
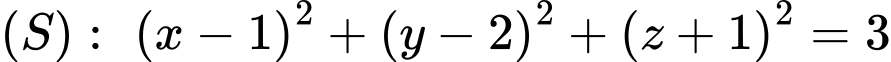 có tâm
có tâm 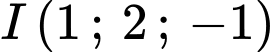 và bán kính
và bán kính 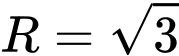
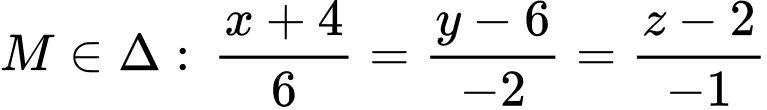
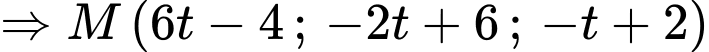
Từ
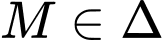 ta kẻ các đường tiếp tuyến đến mặt cầu
ta kẻ các đường tiếp tuyến đến mặt cầu 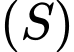 tạo thành hình tròn
tạo thành hình tròn  tập hợp các điểm.
tập hợp các điểm.Diện tích giới hạn bởi
 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi 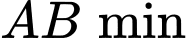 hay
hay 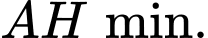
Xét
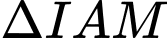 vuông tại
vuông tại 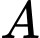 :
: 
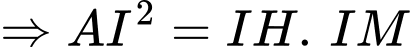
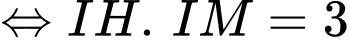
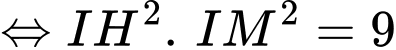
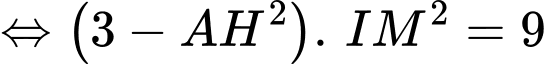
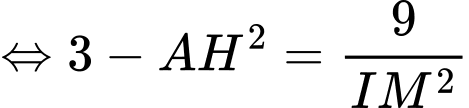
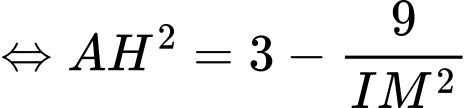
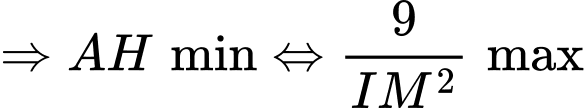
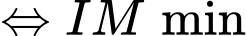
Ta có:
 khi và chỉ khi
khi và chỉ khi 
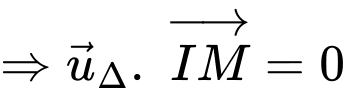
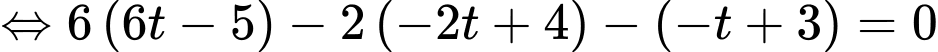
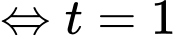
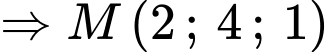
Có
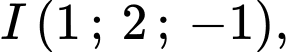
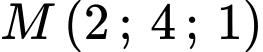
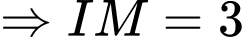
Lại có:
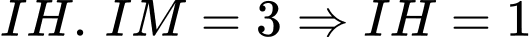
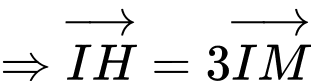
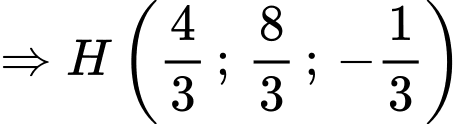
Ta có phương trình mặt phẳng chứa
 đi qua
đi qua 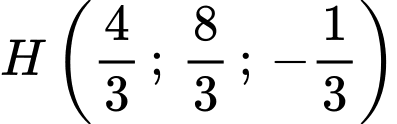 và có vecto pháp tuyến là
và có vecto pháp tuyến là 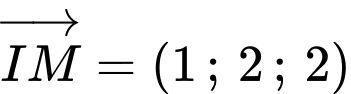 :
: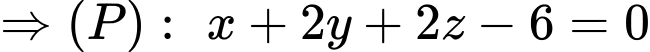
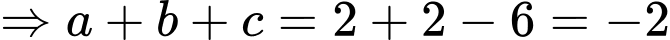
Đáp án: B Đáp án: B
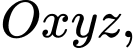 cho mặt phẳng
cho mặt phẳng  các điểm
các điểm 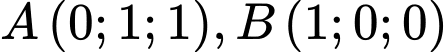 (
(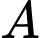 và
và 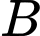 nằm trên mặt phẳng
nằm trên mặt phẳng 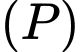 ) và mặt cầu
) và mặt cầu 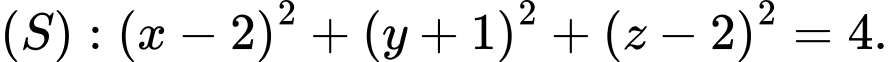
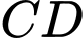 là một đường kính thay đổi của
là một đường kính thay đổi của 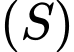 sao cho
sao cho 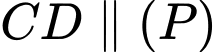 và bốn điểm
và bốn điểm 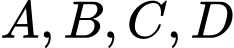 tạo thành một tứ diện. Giá trị lớn nhất của thể tích tứ diện
tạo thành một tứ diện. Giá trị lớn nhất của thể tích tứ diện 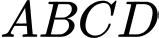 bằng
bằng 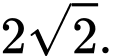
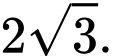
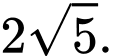
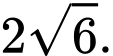
 Đáp án: A
Đáp án: A 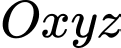 , cho mặt cầu
, cho mặt cầu 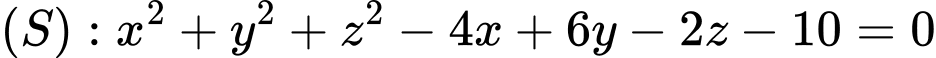 và điểm
và điểm 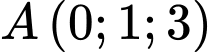 . Bốn điểm
. Bốn điểm 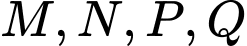 thay đổi trên mặt cầu sao cho tứ giác
thay đổi trên mặt cầu sao cho tứ giác 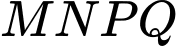 là hình vuông. Khi khối chóp
là hình vuông. Khi khối chóp 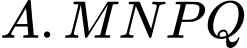 có thể tích lớn nhất thì mặt phẳng chứa bốn điểm
có thể tích lớn nhất thì mặt phẳng chứa bốn điểm 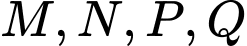 có phương trình là
có phương trình là 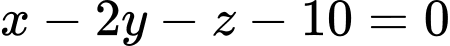 .
.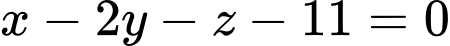 .
.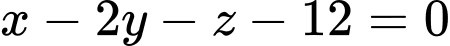 .
.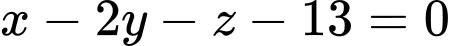 .
.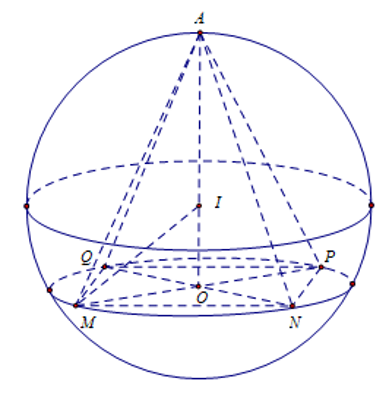
Nhận thấy điểm
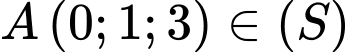 nên đây chính là bài toán tìm thể tích lớn nhất của khối chóp tứ giác đều nội tiếp mặt cầu
nên đây chính là bài toán tìm thể tích lớn nhất của khối chóp tứ giác đều nội tiếp mặt cầu 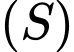 . Gọi
. Gọi  là tâm của hình vuông
là tâm của hình vuông 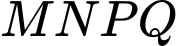 .
. 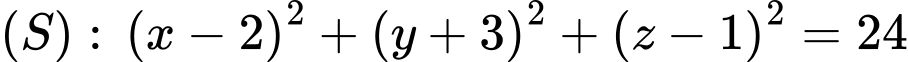
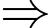 tâm mặt cầu
tâm mặt cầu  , bán kính
, bán kính 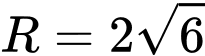
Đặt
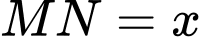 , với
, với 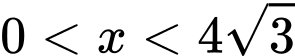 .
. 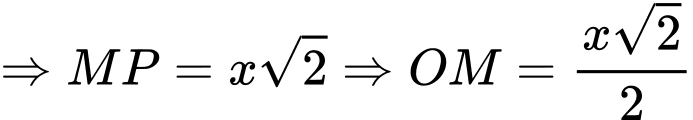 ;
; 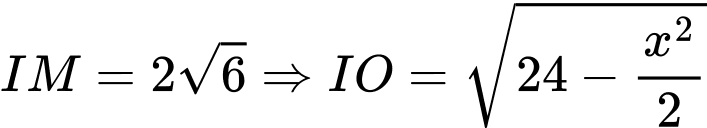
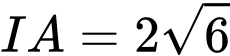
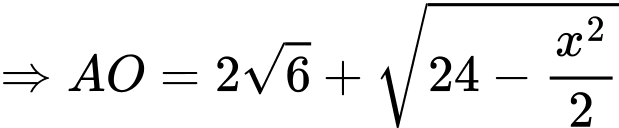
Thể tích khối chóp
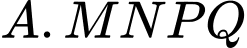 bằng
bằng 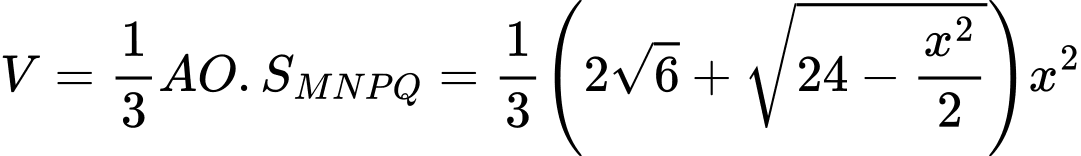
Đặt
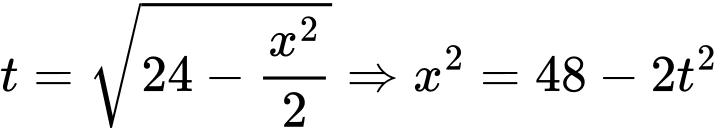 , với
, với 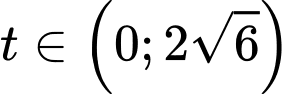
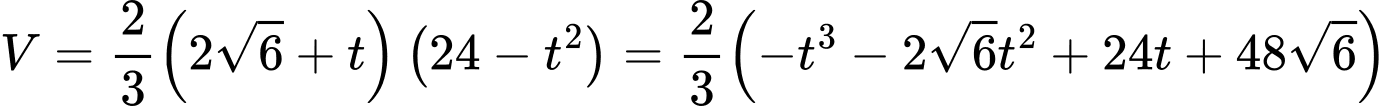
Xét hàm số
 , với
, với 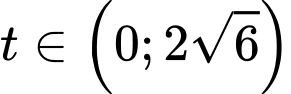

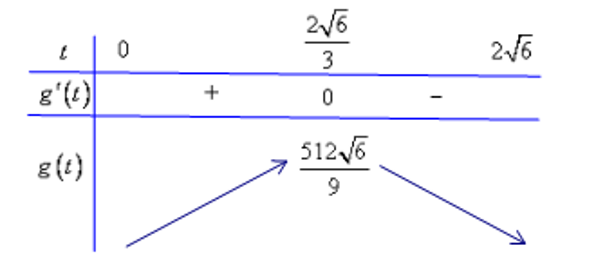
Từ bảng biến thiên suy ra
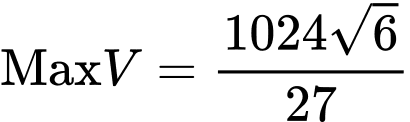 khi
khi 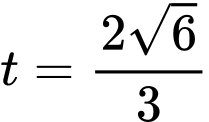
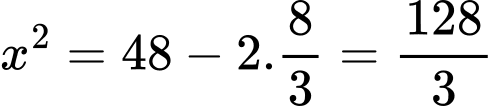
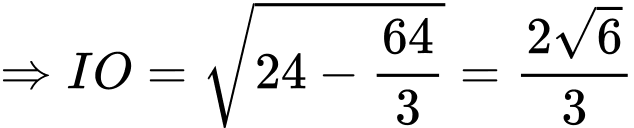
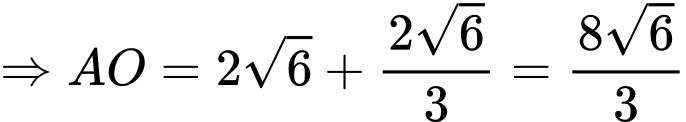
Vì mặt phẳng
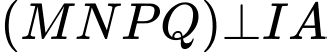 nên mặt phẳng
nên mặt phẳng 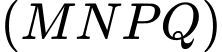 nhận véc tơ
nhận véc tơ 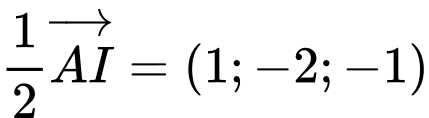 làm véctơ pháp tuyến nên phương trình có dạng:
làm véctơ pháp tuyến nên phương trình có dạng: 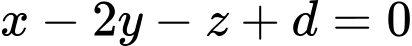
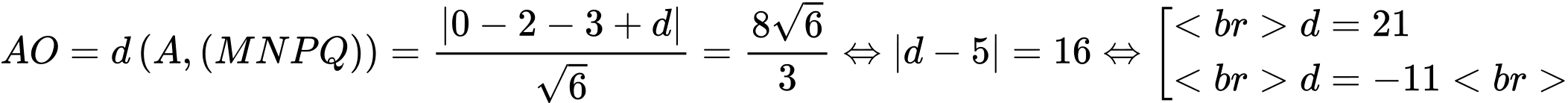
 hoặc
hoặc 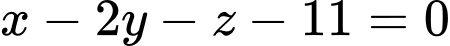 .
. Vì
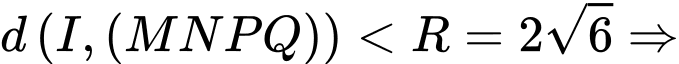
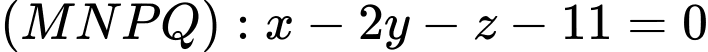
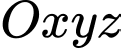 cho mặt cầu
cho mặt cầu 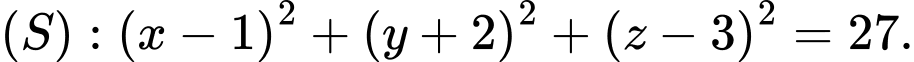 Gọi
Gọi  là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 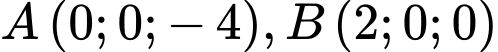 và cắt
và cắt 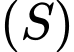 theo giao tuyến là đường tròn
theo giao tuyến là đường tròn  sao cho khối nón có đỉnh là tâm của
sao cho khối nón có đỉnh là tâm của 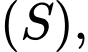 đáy là
đáy là  có thể tích lớn nhất. Biết mặt phẳng
có thể tích lớn nhất. Biết mặt phẳng  có phương trình dạng
có phương trình dạng 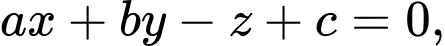 khi đó
khi đó 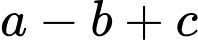 bằng
bằng 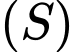 có tâm
có tâm 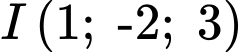 và bán kính
và bán kính 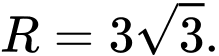
Điểm
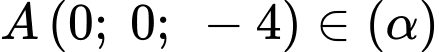
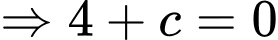
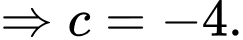
Điểm
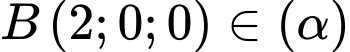

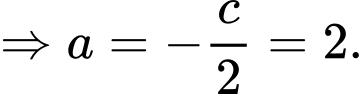
Mặt phẳng
 có dạng
có dạng 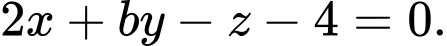
Gọi
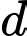 là khoảng cách từ tâm
là khoảng cách từ tâm 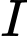 đến mặt phẳng
đến mặt phẳng  và
và 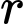 là bán kính của đường tròn
là bán kính của đường tròn 
Khi đó khối nón có đỉnh
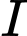 và đáy là đường tròn
và đáy là đường tròn  có thể tích là:
có thể tích là: 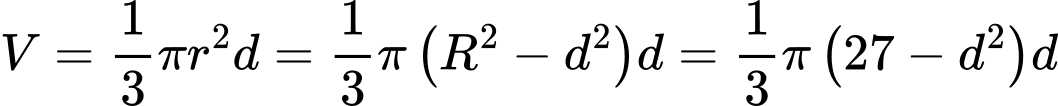
Đặt
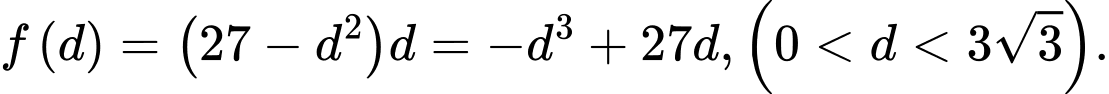
Suy ra
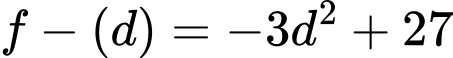 và
và 
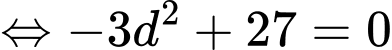
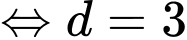 (vì
(vì 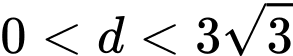 ).
). Bảng biến thiên:

Dựa vào bảng biến thiên, ta thấy
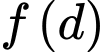 đạt giá trị lớn nhất khi
đạt giá trị lớn nhất khi  hay thể tích khối nón đạt giá trị lớn nhất khi
hay thể tích khối nón đạt giá trị lớn nhất khi 
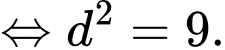
Mà
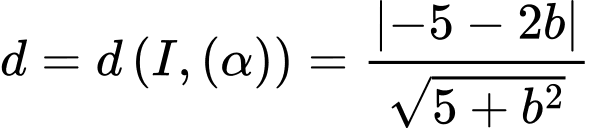 nên
nên 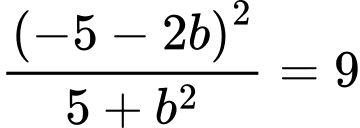
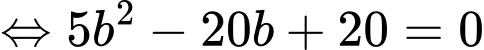
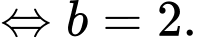
Vậy
 Đáp án: A
Đáp án: A 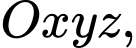 cho hai điểm
cho hai điểm 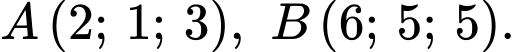 Gọi
Gọi  là mặt cầu có đường kính
là mặt cầu có đường kính 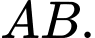 Mặt phẳng
Mặt phẳng 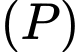 vuông góc với đoạn
vuông góc với đoạn  tại
tại 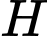 sao cho khối nón đỉnh
sao cho khối nón đỉnh 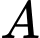 và đáy là hình tròn tâm
và đáy là hình tròn tâm 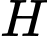 (giao của mặt cầu
(giao của mặt cầu 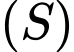 và mặt phẳng
và mặt phẳng 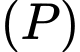 ) có thể tích lớn nhất, biết rằng
) có thể tích lớn nhất, biết rằng 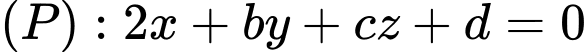 với
với 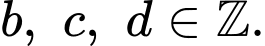 Tính
Tính 
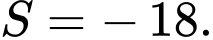
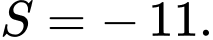
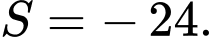
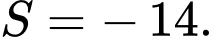
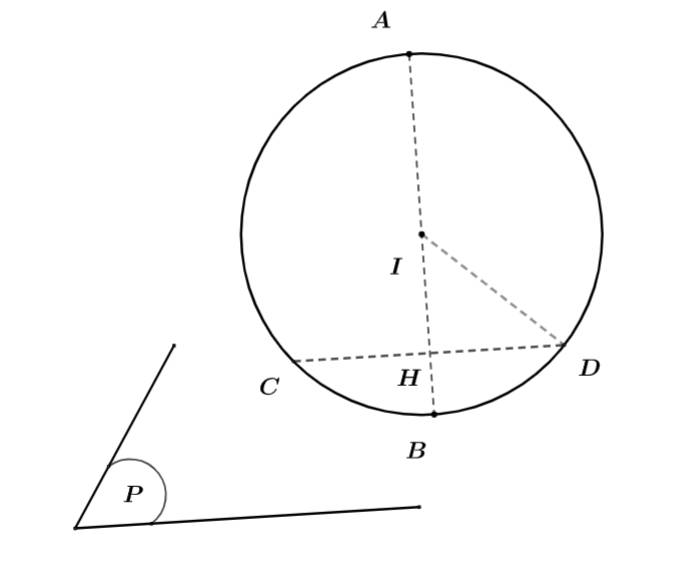
Trên hệ trục tọa độ
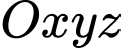 cho
cho 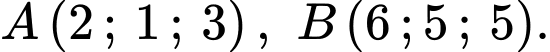
Mặt cầu
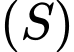 có đường kính
có đường kính 
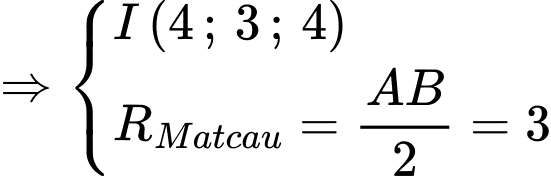
Mặt phẳng
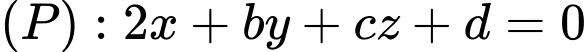 vuông góc với
vuông góc với  tại
tại 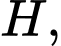
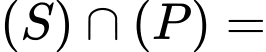 hình tròn tâm
hình tròn tâm 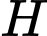
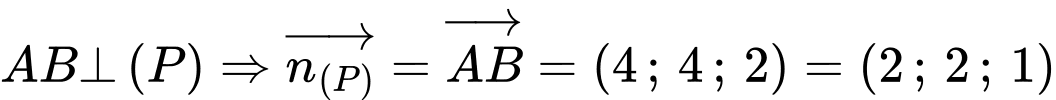
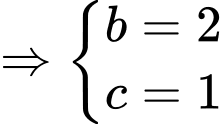
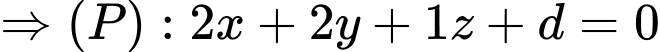
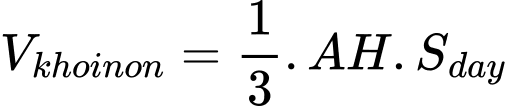
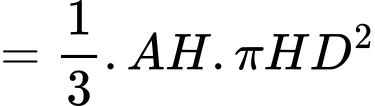
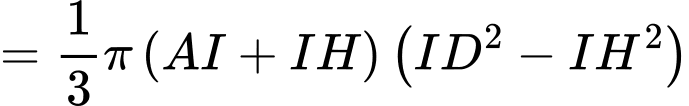
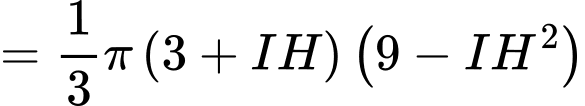
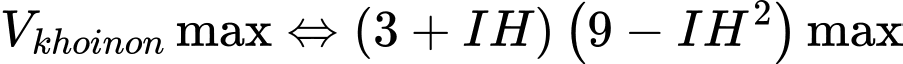
Đặt
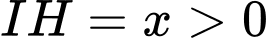
Ta có:
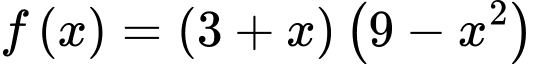
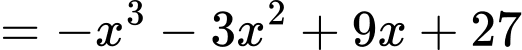
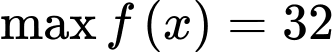
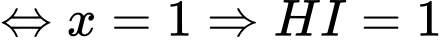
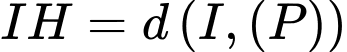
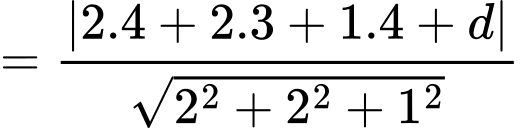
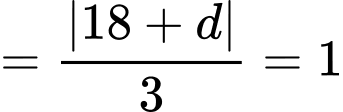
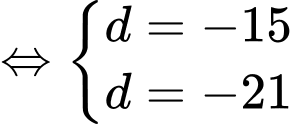
Vì
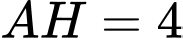

Vậy
Đáp án A Đáp án: A
 cho đường thẳng
cho đường thẳng 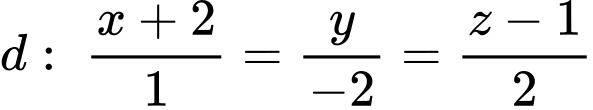 và mặt cầu
và mặt cầu 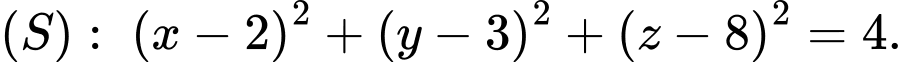 Hai điểm
Hai điểm 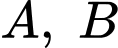 thay đổi trên
thay đổi trên 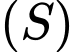 sao cho tiếp diện của
sao cho tiếp diện của 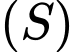 tại
tại 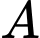 và
và 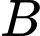 vuông góc với nhau. Đường thẳng qua
vuông góc với nhau. Đường thẳng qua 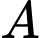 song song với
song song với 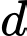 cắt mặt phẳng
cắt mặt phẳng 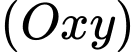 tại
tại 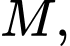 đường thẳng qua
đường thẳng qua 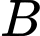 song song với
song song với 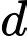 cắt mặt phẳng
cắt mặt phẳng 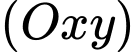 tại
tại 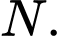 Tìm giá trị lớn nhất của tổng
Tìm giá trị lớn nhất của tổng 
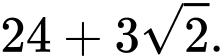
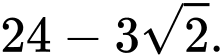
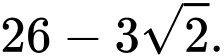
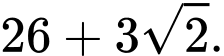
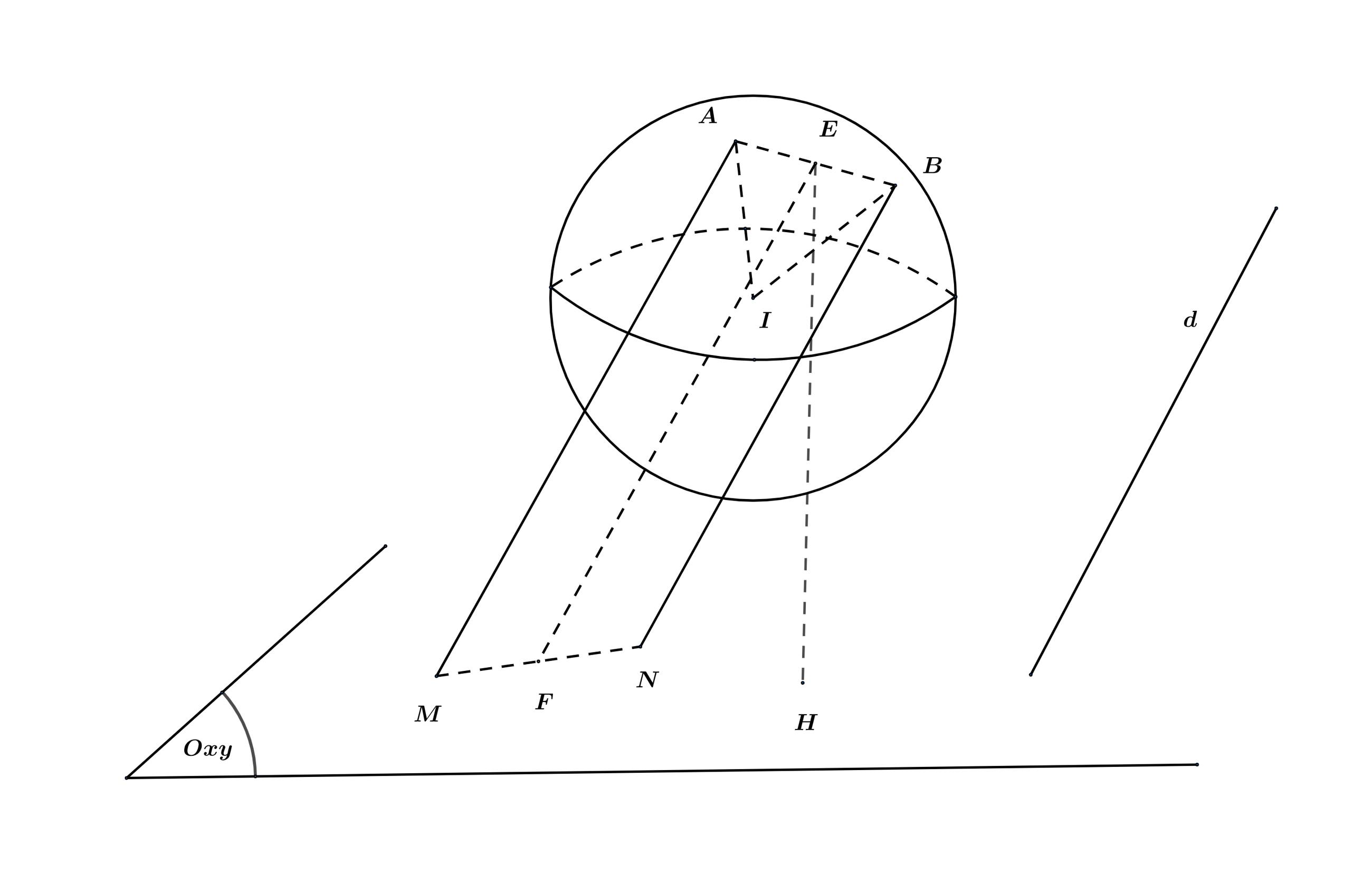
Theo giả thiết, ta có:
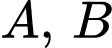 là hai điểm thay đổi trên
là hai điểm thay đổi trên 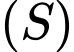
Gọi
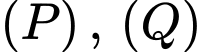 lần lượt là tiếp diện của mặt cầu
lần lượt là tiếp diện của mặt cầu 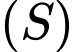 tại hai điểm
tại hai điểm 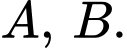
 lần lượt là vecto pháp tuyến của
lần lượt là vecto pháp tuyến của 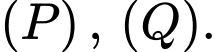
Hai thiết diện vuông góc với nhau

Theo giả thiết, lại có:
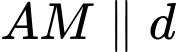 và
và 

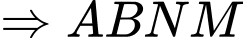 là hình thang. Gọi
là hình thang. Gọi 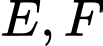 lần lượt là trung điểm của
lần lượt là trung điểm của 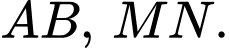
Áp dụng tính chất đường trung bình của hình thang, ta có:
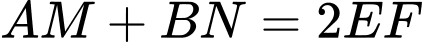

Xét
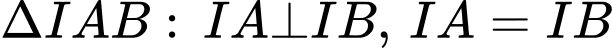
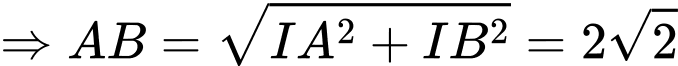
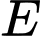 là trung điểm
là trung điểm 
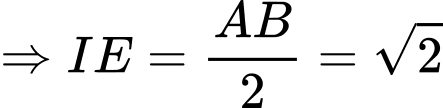
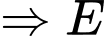 luôn nằm trên mặt cầu
luôn nằm trên mặt cầu 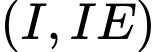
Có:
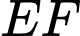 là đường trung bình của hình thang
là đường trung bình của hình thang 
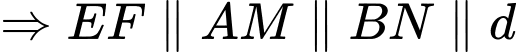
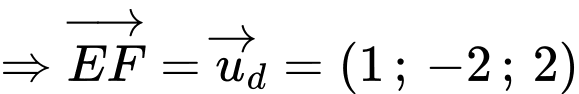
Gọi
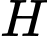 là hình chiếu của
là hình chiếu của 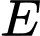 trên
trên 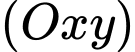
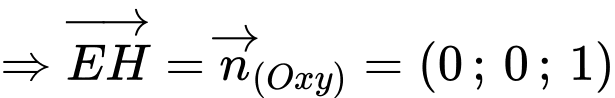
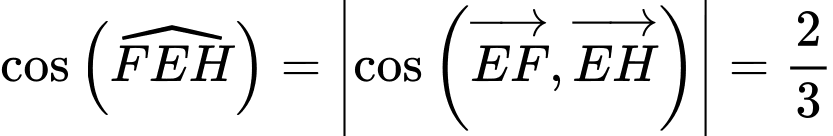
Có:
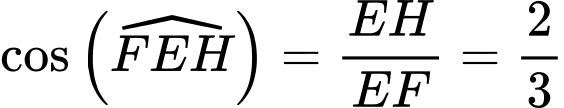
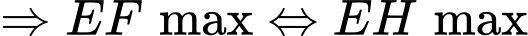

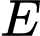 nằm trên đỉnh mặt cầu
nằm trên đỉnh mặt cầu 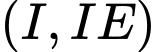
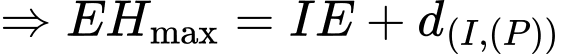
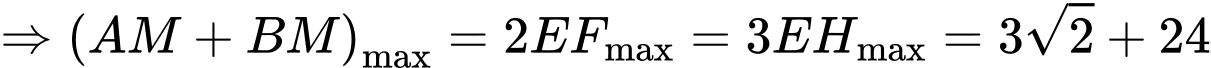
Đáp án: A. Đáp án: A
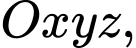 cho mặt cầu
cho mặt cầu 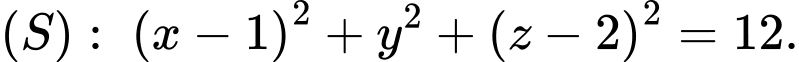 Biết rẳng từ một điểm
Biết rẳng từ một điểm 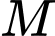 thuộc mặt phẳng
thuộc mặt phẳng 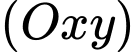 ta luôn kẻ được ba tiếp tuyến
ta luôn kẻ được ba tiếp tuyến 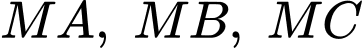 đôi một vuông góc với nhau đến mặt cầu
đôi một vuông góc với nhau đến mặt cầu 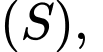 (trong đó
(trong đó 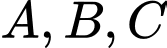 là các tiếp điểm). Tính giá trị lớn nhất của
là các tiếp điểm). Tính giá trị lớn nhất của 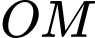
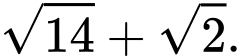
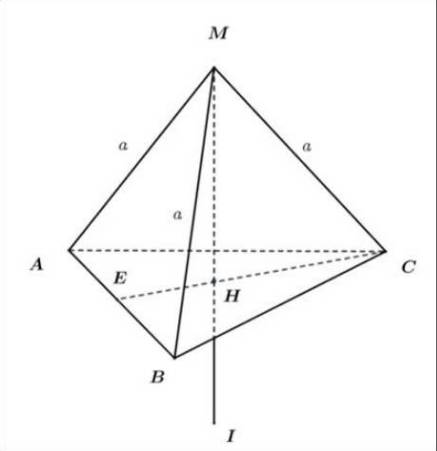
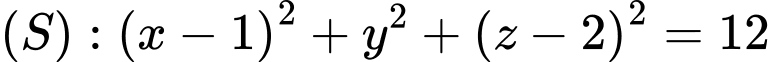
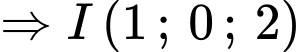
Từ
 ta luôn kẻ được ba tiếp tuyến
ta luôn kẻ được ba tiếp tuyến 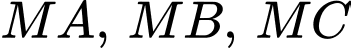 đôi một vuông góc với nhau.
đôi một vuông góc với nhau.Có
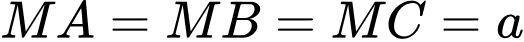
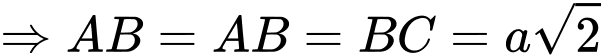
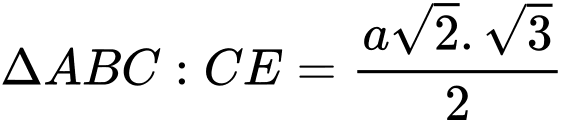
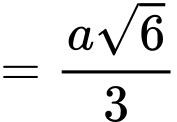
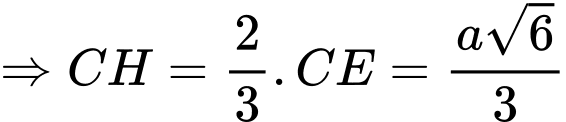
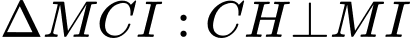
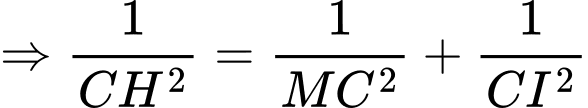
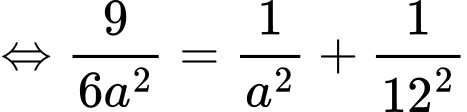
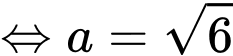
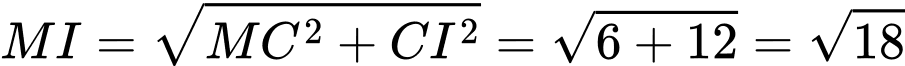
+ Hình chiếu
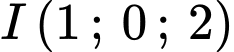 lên
lên 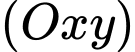 :
: 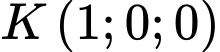
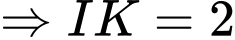
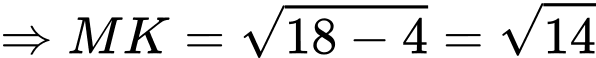

Đáp án B. Đáp án: B
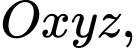 cho ba điểm
cho ba điểm 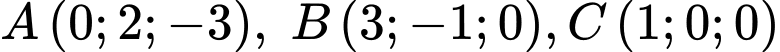 và mặt phẳng
và mặt phẳng 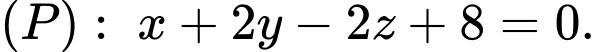 Điểm
Điểm 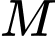 nằm trên mặt phẳng
nằm trên mặt phẳng 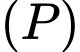 sao cho
sao cho 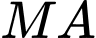 và
và 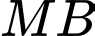 đều tạo với mặt phẳng
đều tạo với mặt phẳng 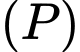 các góc bằng nhau. Tính khoảng cách lớn nhất của đoạn
các góc bằng nhau. Tính khoảng cách lớn nhất của đoạn 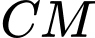
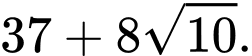
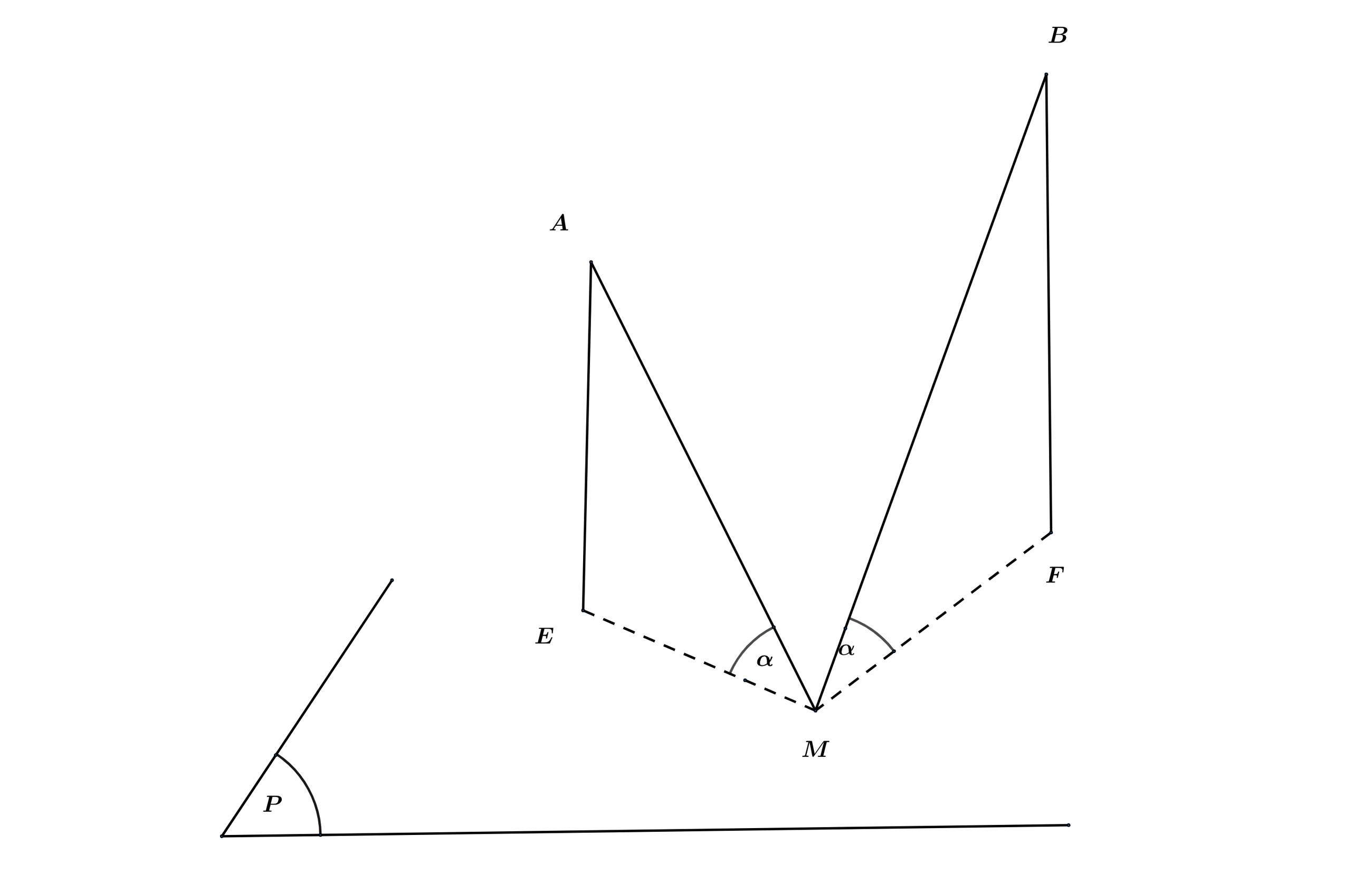
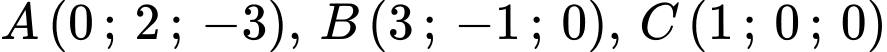
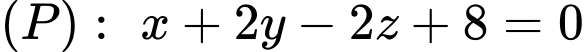
Ta có:
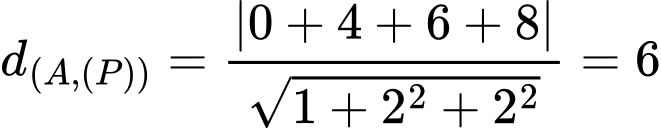
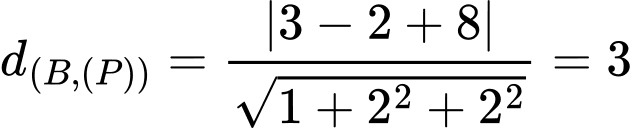
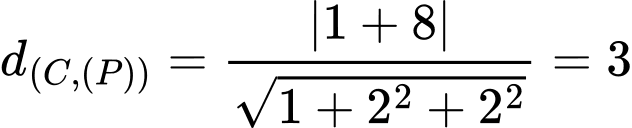
Theo giả thiết, ta có: 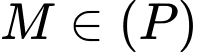 sao cho
sao cho 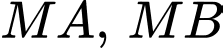 tạo với mặt phẳng
tạo với mặt phẳng 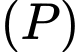 góc bẳng nhau.
góc bẳng nhau.
Gọi hình chiếu của 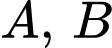 trên mặt phẳng
trên mặt phẳng 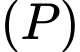 lần lượt là
lần lượt là 

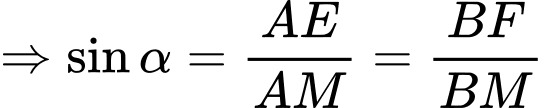
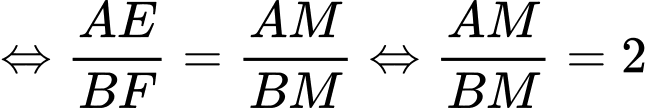
 luôn nằm trên mặt cầu có tâm
luôn nằm trên mặt cầu có tâm 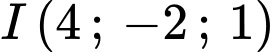 và bán kính
và bán kính 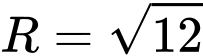
Lại có: 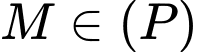
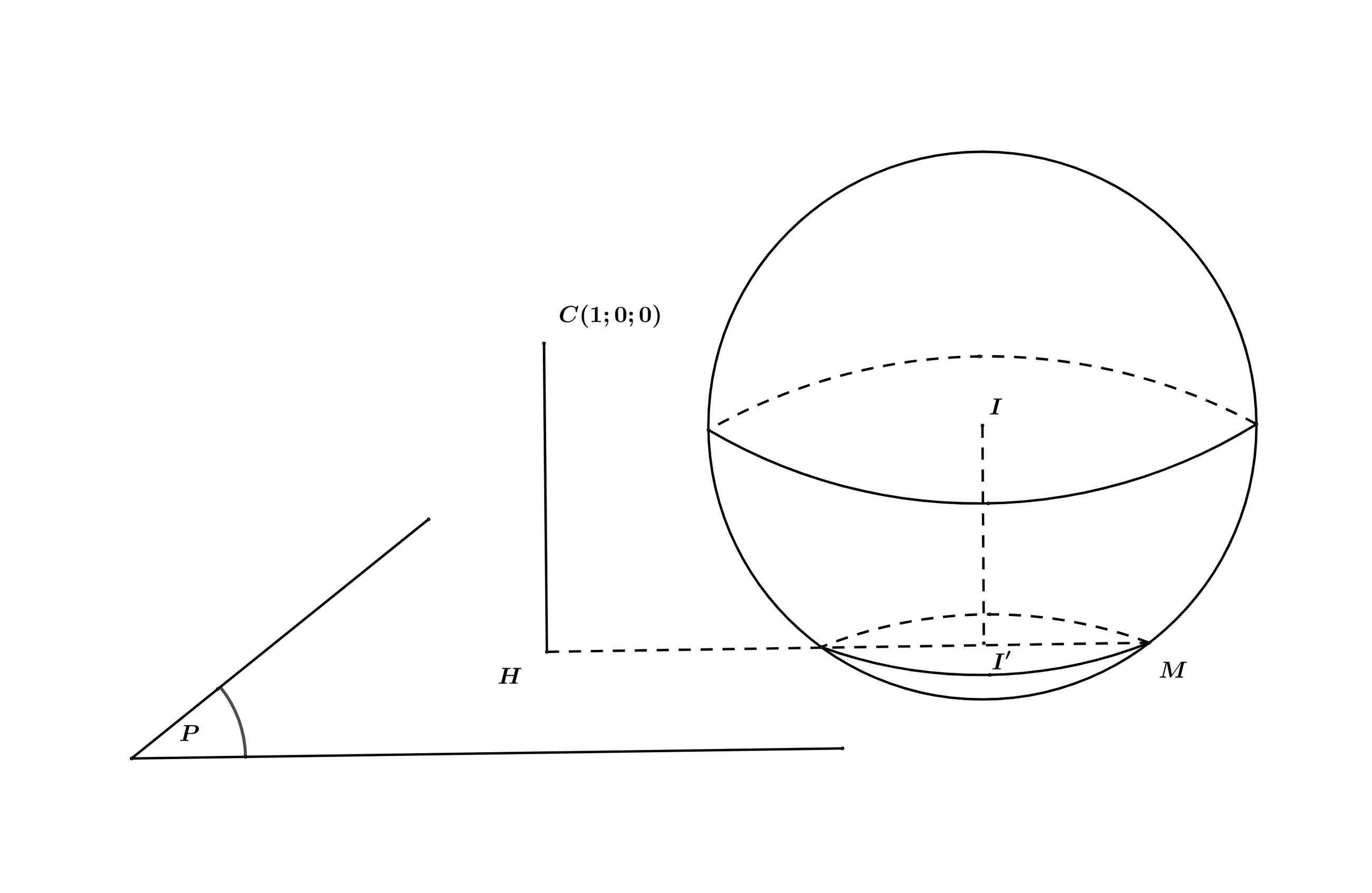
Khoảng cách từ  đến
đến 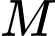 đạt giá trị lớn nhất khi và khi hình chiếu của
đạt giá trị lớn nhất khi và khi hình chiếu của  trên mặt phẳng
trên mặt phẳng 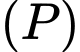 là xa nhất, hay
là xa nhất, hay 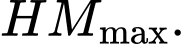
Có: 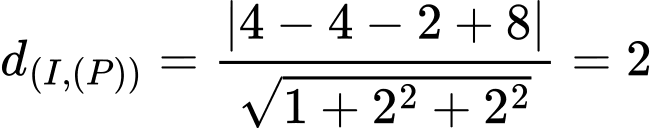
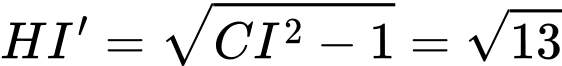
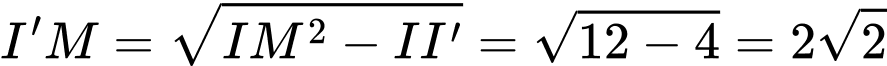
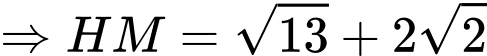
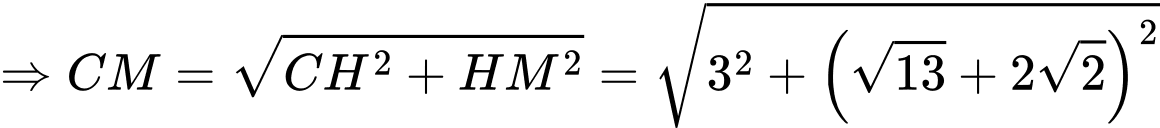
Đáp án: 7,099019.
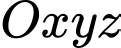 , cho hai điểm
, cho hai điểm 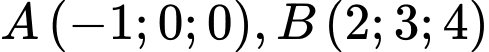 . Gọi
. Gọi 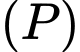 là mặt phẳng chứa đường tròn giao tuyến cảu hai mặt cầu
là mặt phẳng chứa đường tròn giao tuyến cảu hai mặt cầu 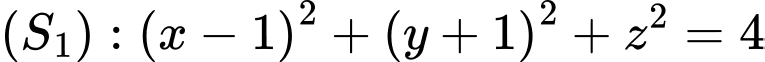 và
và 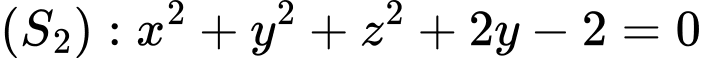 . Xét hai điểm
. Xét hai điểm 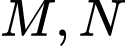 bất kì thuộc
bất kì thuộc 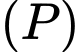 sao cho
sao cho 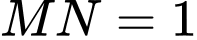 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức  bằng
bằng 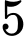 .
.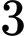 .
.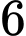 .
.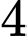 .
.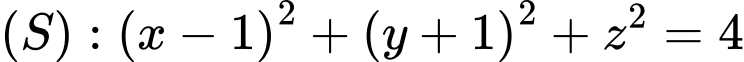 có tâm
có tâm 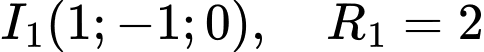
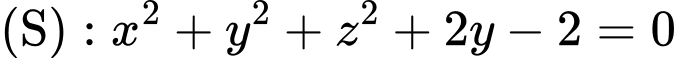 có tâm
có tâm 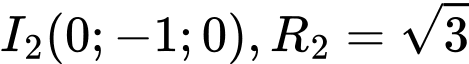
Ta có 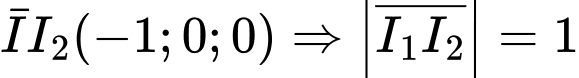
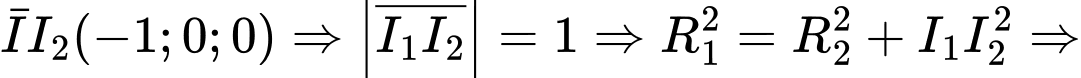 tâm đường tròn thiết diện chính là
tâm đường tròn thiết diện chính là 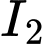
Phương trình 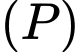 qua
qua 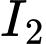 và nhận
và nhận 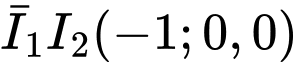 làm VTPT là:
làm VTPT là: 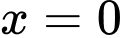
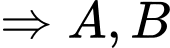 khác phía so với
khác phía so với 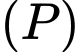
Xét tiết diện thả̉ng chứa 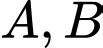 và hai hình chiếu
và hai hình chiếu 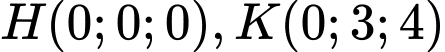 của
của 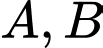 lên
lên 
Ta có 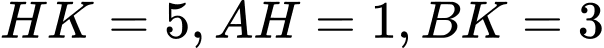
Ta tìm  nhỏ nhất
nhỏ nhất
Gọi 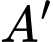 là ảnh cùa
là ảnh cùa 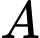 qua phép tịnh tiến theo
qua phép tịnh tiến theo 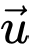 (cùng hướng với
(cùng hướng với 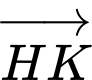 và có độ dài bằng 1 )
và có độ dài bằng 1 )
Ta có 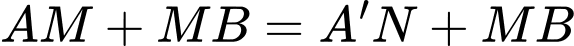 nhȯ nhất khi
nhȯ nhất khi 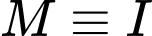 , khi đó
, khi đó 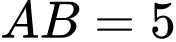 .
.
Chọn đáp án A.
 Đáp án: A
Đáp án: A
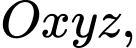 cho
cho 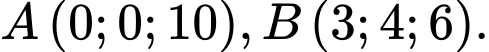 Xét các điểm
Xét các điểm 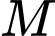 thay đổi sao cho tam giác
thay đổi sao cho tam giác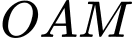 không có góc tù và có diện tích bằng
không có góc tù và có diện tích bằng 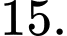 Giá trị nhỏ nhất của độ dài đoạn thẳng
Giá trị nhỏ nhất của độ dài đoạn thẳng 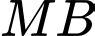 thuộc khoảng nào dưới đây?
thuộc khoảng nào dưới đây? 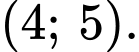
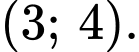
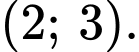
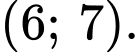
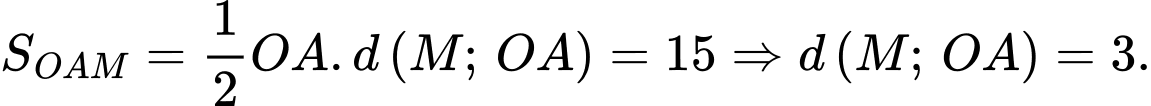
Suy ra:
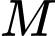 di động trên mặt trụ, bán kính bằng
di động trên mặt trụ, bán kính bằng 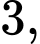 trục là
trục là 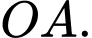
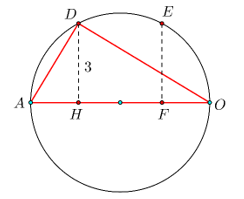
Xét điểm
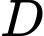 như hình vẽ,
như hình vẽ, 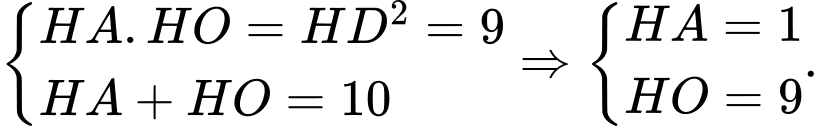
Vì
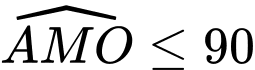 nên giới hạn của
nên giới hạn của 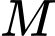 là hai mặt trụ với trục
là hai mặt trụ với trục 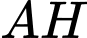 và
và 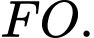
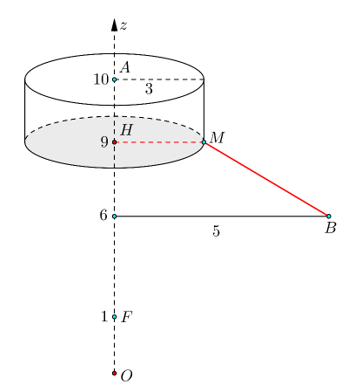
Vì hình chiếu của
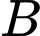 cách
cách 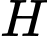 gần hơn nên
gần hơn nên 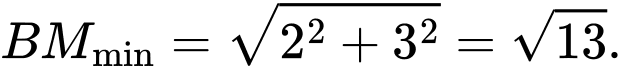 Đáp án: B
Đáp án: B 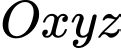 cho mặt phẳng
cho mặt phẳng 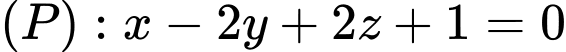 và điểm
và điểm 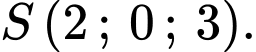 Đường thẳng
Đường thẳng  có phương trình tham số
có phương trình tham số 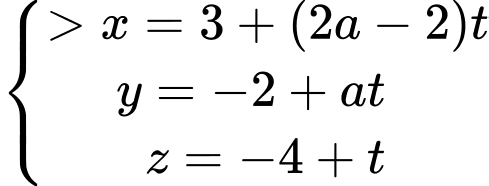 , trong đó
, trong đó 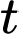 là tham số và
là tham số và 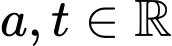 . Gọi
. Gọi  là mặt phẳng chứa
là mặt phẳng chứa 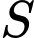 và
và  , đường thẳng vuông góc với
, đường thẳng vuông góc với  tại S cắt
tại S cắt 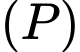 tại
tại 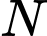 . Khoảng cách
. Khoảng cách 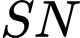 ngắn nhất bằng
ngắn nhất bằng 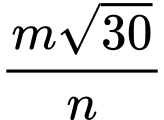 ,
,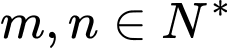 và
và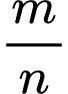 tối giản. Tính giá trị biểu thức
tối giản. Tính giá trị biểu thức 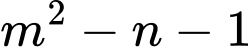 .
.  .
.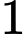 .
.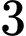 .
.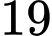 .
.