Đáp án Bài tập tự luyện số 3
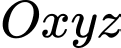 , cho điểm
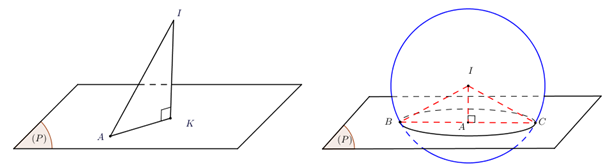
, cho điểm 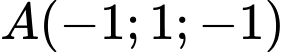 và mặt cầu
và mặt cầu  tâm
tâm 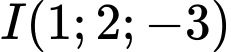 , bán kính
, bán kính 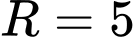 . Mặt phẳng
. Mặt phẳng 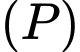 đi qua
đi qua 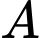 và cắt
và cắt 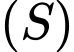 theo giao tuyến là đường tròn
theo giao tuyến là đường tròn  . Gọi
. Gọi 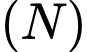 là khối nón có đỉnh
là khối nón có đỉnh 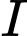 và nhận
và nhận  làm đường tròn đáy. Tính bán kính của
làm đường tròn đáy. Tính bán kính của  khi thể tích khối nón
khi thể tích khối nón 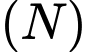 đạt giá trị lớn nhất
đạt giá trị lớn nhất 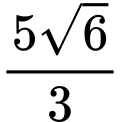 .
.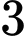 .
.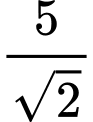 .
.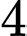 .
.
Ta có:
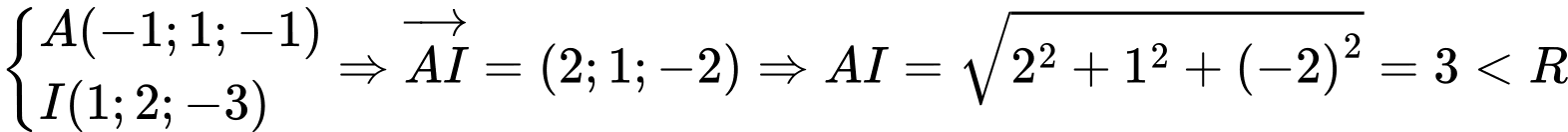
Suy ra điểm
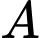 nằm bên trong mặt cầu
nằm bên trong mặt cầu Gọi
 là hình chiếu của
là hình chiếu của  lên mặt phẳng
lên mặt phẳng 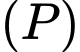 và
và 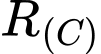 là bán kính đường tròn giao tuyến
là bán kính đường tròn giao tuyến 
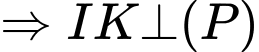 và
và 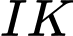 cũng chính là đường cao của khối nón
cũng chính là đường cao của khối nón 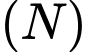 . Mà
. Mà 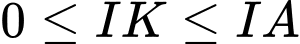 với
với 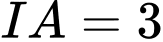 nên
nên Ta đặt
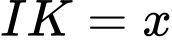

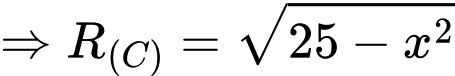
Suy ra
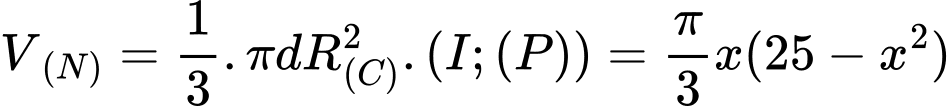
Xét hàm
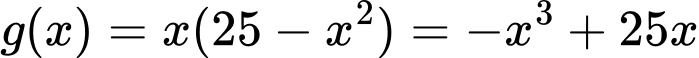
 có
có 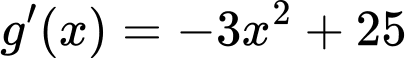
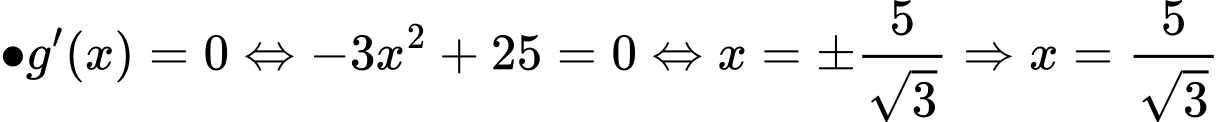
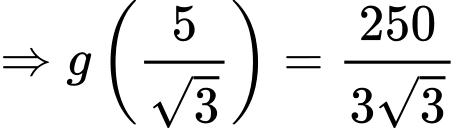
Bảng biến thiên hàm
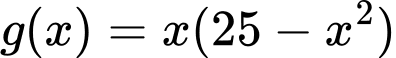 như sau:
như sau: 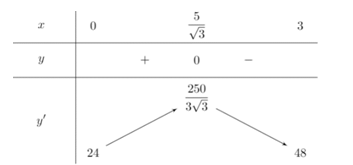
Dựa vào BBT ta kết luận được
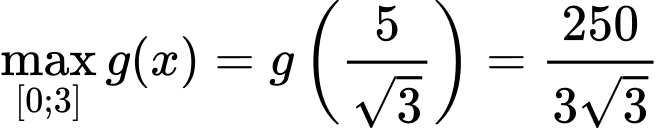
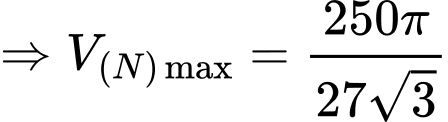 khi
khi 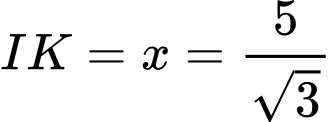
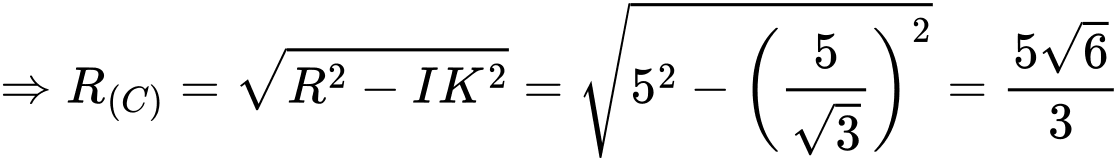 Đáp án: A
Đáp án: A 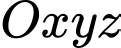 , cho hai điểm
, cho hai điểm 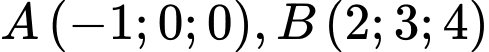 . Gọi
. Gọi 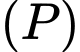 là mặt phẳng chứa đường tròn giao tuyến cảu hai mặt cầu
là mặt phẳng chứa đường tròn giao tuyến cảu hai mặt cầu 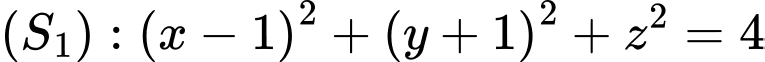 và
và 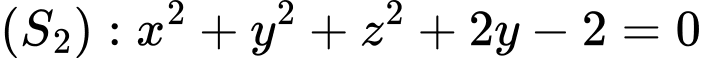 . Xét hai điểm
. Xét hai điểm 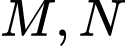 bất kì thuộc
bất kì thuộc 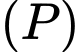 sao cho
sao cho 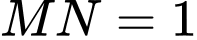 . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức  bằng
bằng 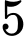 .
.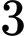 .
.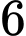 .
.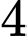 .
.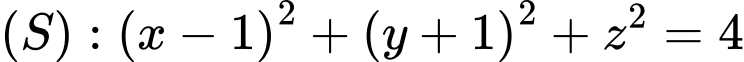 có tâm
có tâm 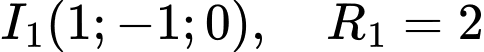
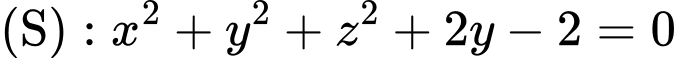 có tâm
có tâm 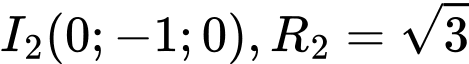
Ta có 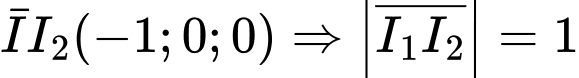
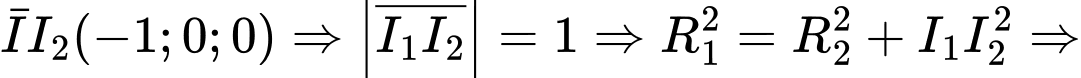 tâm đường tròn thiết diện chính là
tâm đường tròn thiết diện chính là 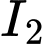
Phương trình 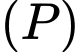 qua
qua 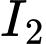 và nhận
và nhận 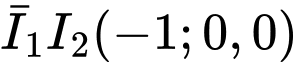 làm VTPT là:
làm VTPT là: 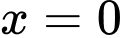
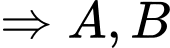 khác phía so với
khác phía so với 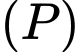
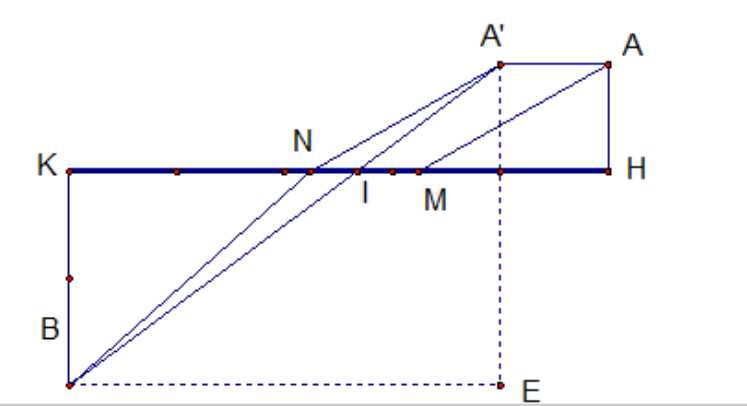
Xét tiết diện thả̉ng chứa 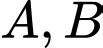 và hai hình chiếu
và hai hình chiếu 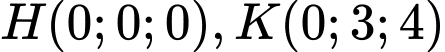 của
của 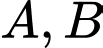 lên
lên 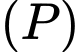
Ta có 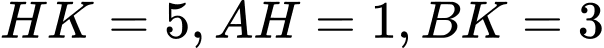
Ta tìm  nhỏ nhất
nhỏ nhất
Gọi 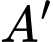 là ảnh cùa
là ảnh cùa 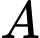 qua phép tịnh tiến theo
qua phép tịnh tiến theo 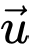 (cùng hướng với
(cùng hướng với 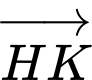 và có độ dài bằng 1 )
và có độ dài bằng 1 )
Ta có 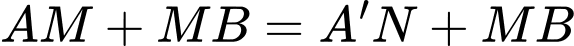 nhȯ nhất khi
nhȯ nhất khi 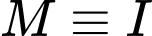 , khi đó
, khi đó 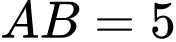 .
.
Chọn đáp án A.
 Đáp án: A
Đáp án: A
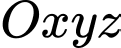 , cho hình nón
, cho hình nón  có đỉnh
có đỉnh 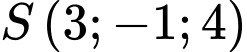 và đường tròn đáy có tâm
và đường tròn đáy có tâm 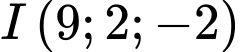 , bán kính
, bán kính  không đổi. Hình trụ
không đổi. Hình trụ  có một đường tròn đáy tâm
có một đường tròn đáy tâm 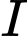 , đường tròn đáy còn lại có tâm
, đường tròn đáy còn lại có tâm 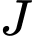 và đường tròn này nằm trên mặt xung quanh của hình nón
và đường tròn này nằm trên mặt xung quanh của hình nón 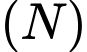 . Khi
. Khi 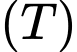 có thể tích lớn nhất thì mặt phẳng chứa đường tròn tâm
có thể tích lớn nhất thì mặt phẳng chứa đường tròn tâm 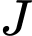 có phương trình
có phương trình 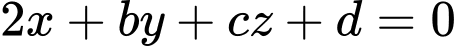 . Tính
. Tính 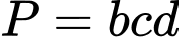
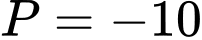 .
.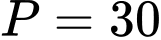 .
.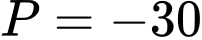 .
.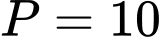 .
.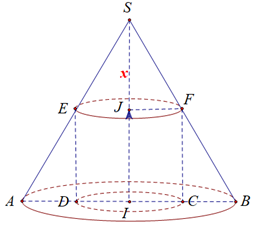
Xét mặt phẳng
 qua trục của hình nón, cắt hình nón
qua trục của hình nón, cắt hình nón 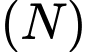 và hình trụ
và hình trụ 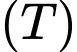 theo tam giác
theo tam giác 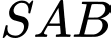 và hình chữ nhật
và hình chữ nhật 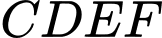 (như hình). Đặt
(như hình). Đặt 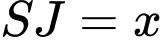 (
(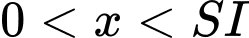 ) .
) . Khi đó hình trụ
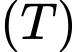 có chiều cao
có chiều cao 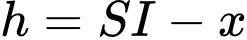 , bán kính
, bán kính 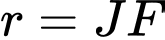 .
.Trong mp
 :
: 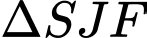 và
và 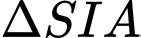 đồng dạng nên
đồng dạng nên 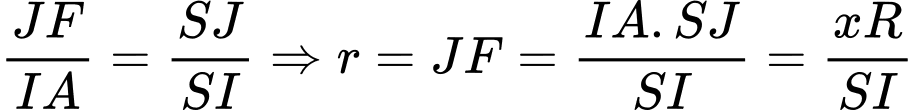 .
.Thể tích khối trụ
 là:
là: 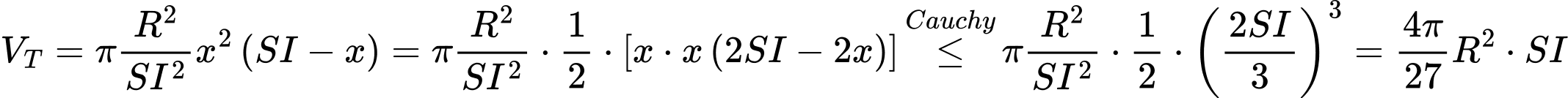
Dấu bằng xảy ra khi
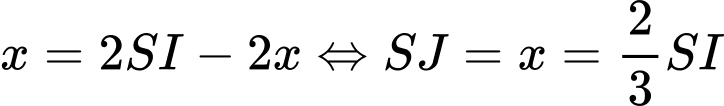 .
.Khi
 có thể tích lớn nhất thì
có thể tích lớn nhất thì 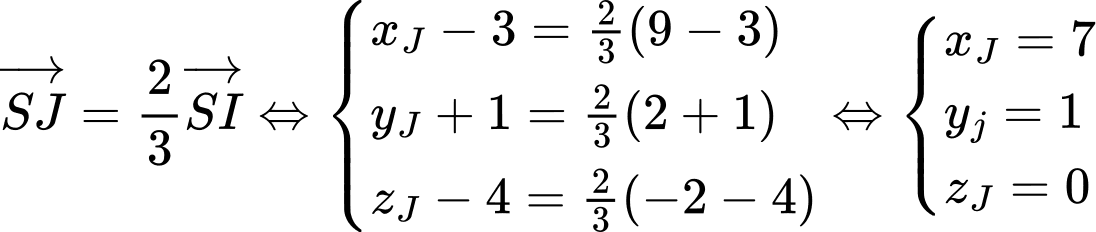
Khi đó mặt phẳng chứa đường tròn đáy tâm
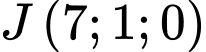 và nhận
và nhận 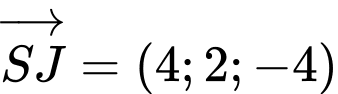 hay
hay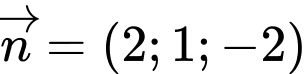 làm VTPT nên có phương trình
làm VTPT nên có phương trình 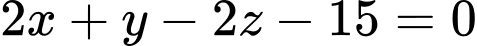 .
. Mà theo giả thiết mp đó có phương trình
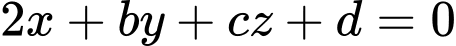 , do đó
, do đó 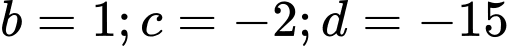 .
.Vậy
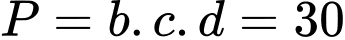 . Đáp án: B
. Đáp án: B 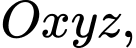 cho hai điểm
cho hai điểm 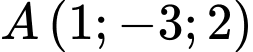 và
và 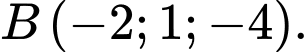 Xét hai điểm
Xét hai điểm 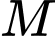 và
và 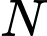 thay đổi thuộc mặt phẳng
thay đổi thuộc mặt phẳng 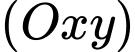 sao cho
sao cho 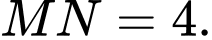 Giá trị lớn nhất của
Giá trị lớn nhất của 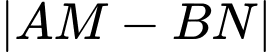 bằng
bằng 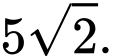
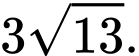


Chọn D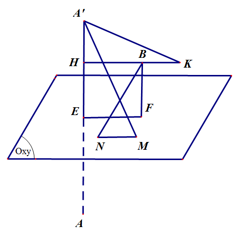
Dễ thấy  ,
, 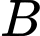 nằm hai phía của mặt phẳng
nằm hai phía của mặt phẳng 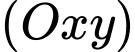 .
.
Gọi 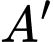 đối xứng với
đối xứng với 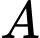 qua mặt phẳng
qua mặt phẳng 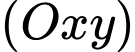 suy ra
suy ra 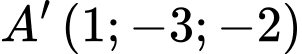 ,
, 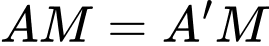 .
.
Gọi 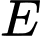 và
và 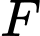 lần lượt là hình chiếu của
lần lượt là hình chiếu của 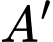 và
và 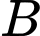 lên mặt phẳng
lên mặt phẳng 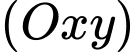 , ta có
, ta có 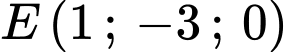 ,
, 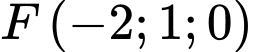 . Do đó
. Do đó 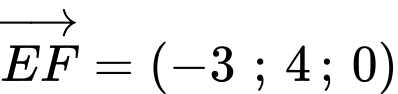
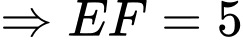 .
.
Dựng 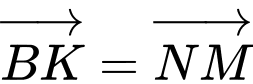 suy ra
suy ra 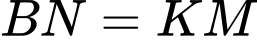 . Vậy
. Vậy 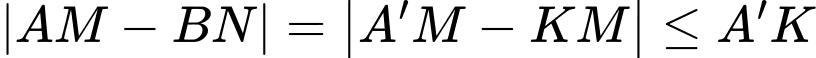 .
.
Ta đi tìm giá trị lớn nhất của  .
.
Do 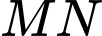 nằm trên mặt phẳng
nằm trên mặt phẳng 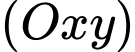 ,
, 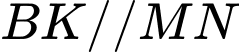 nên
nên  .
.
Suy ra 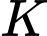 nằm trên mặt phẳng chứa
nằm trên mặt phẳng chứa 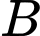 , song song với
, song song với  .
.
Mà 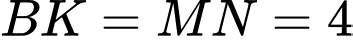 nên quỹ tích
nên quỹ tích 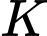 là đường tròn
là đường tròn 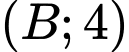 .
.
Kẻ 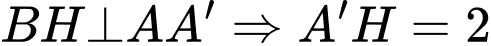 .
.
Có 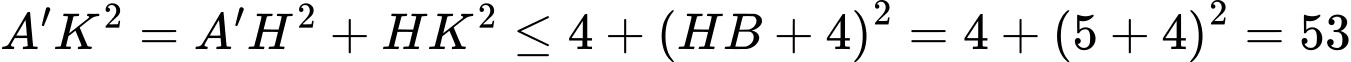 .
.
Dấu "=" xảy ra khi 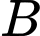 nằm giữa
nằm giữa  .
.
Vậy GTLN của 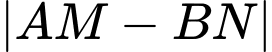 là
là  .
.
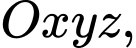 cho hai điểm
cho hai điểm 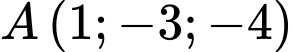 và
và 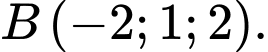 Xét hai điểm
Xét hai điểm  và
và  thay đổi thuộc mặt phẳng
thay đổi thuộc mặt phẳng 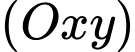 sao cho
sao cho 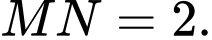 Giá trị lớn nhất của
Giá trị lớn nhất của 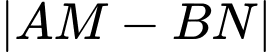 bằng
bằng 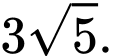

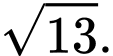
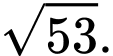

Dễ thấy
 ,
,  nằm hai phía của mặt phẳng
nằm hai phía của mặt phẳng 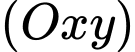 .
. Gọi
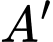 đối xứng với
đối xứng với 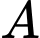 qua mặt phẳng
qua mặt phẳng 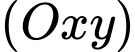 suy ra
suy ra 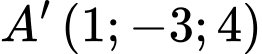 ,
, 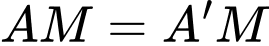 .
.Gọi
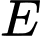 và
và 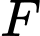 lần lượt là hình chiếu của
lần lượt là hình chiếu của 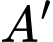 và
và 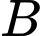 lên mặt phẳng
lên mặt phẳng 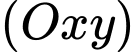 , ta có
, ta có
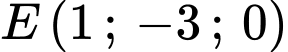 ,
, 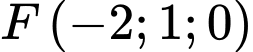 . Do đó
. Do đó 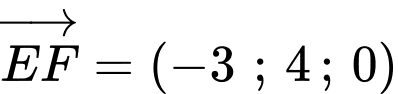
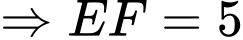 .
.Dựng
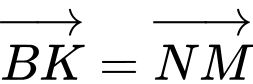 suy ra
suy ra 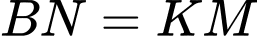 . Vậy
. Vậy 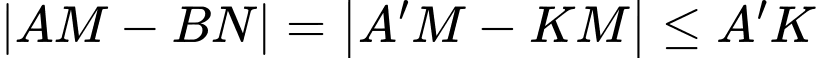 .
.Ta đi tìm giá trị lớn nhất của
 .
.Do
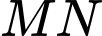 nằm trên mặt phẳng
nằm trên mặt phẳng 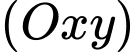 ,
, 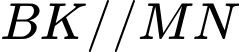 nên
nên  .
. Suy ra
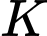 nằm trên mặt phẳng chứa
nằm trên mặt phẳng chứa 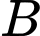 , song song với
, song song với  .
. Mà
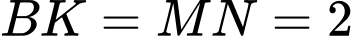 nên quỹ tích
nên quỹ tích 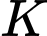 là đường tròn
là đường tròn 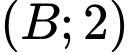 .
.Kẻ
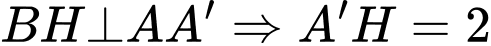 .
.Có
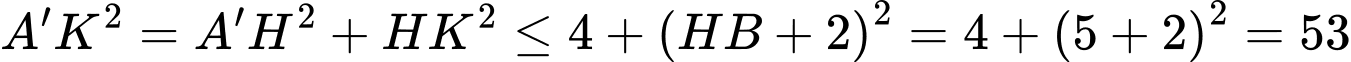 .
. Dấu "=" xảy ra khi
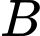 nằm giữa
nằm giữa  .
.Vậy GTLN của
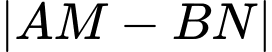 là
là 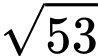 . Đáp án: D
. Đáp án: D 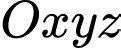 cho hai điểm
cho hai điểm 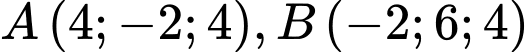 và đường thẳng
và đường thẳng 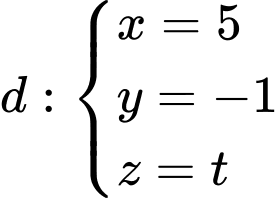 . Gọi
. Gọi 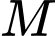 là điểm di động thuộc mặt phẳng
là điểm di động thuộc mặt phẳng 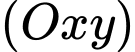 sao cho
sao cho 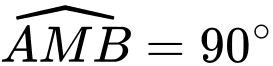 và
và 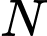 là điểm di động thuộc
là điểm di động thuộc 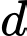 . Tìm giá trị nhỏ nhất của
. Tìm giá trị nhỏ nhất của 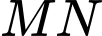 ?
? 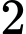
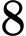
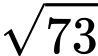
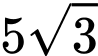
Ta có:
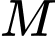 là điểm di động thuộc mặt phẳng
là điểm di động thuộc mặt phẳng 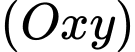 nên suy ra
nên suy ra 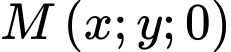
Mà
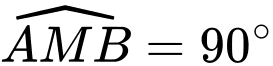 nện suy ra
nện suy ra 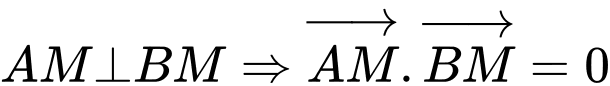
Ta lại có:
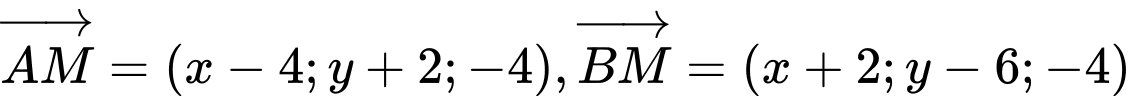 như vậy phương trình trên tương đương với:
như vậy phương trình trên tương đương với: 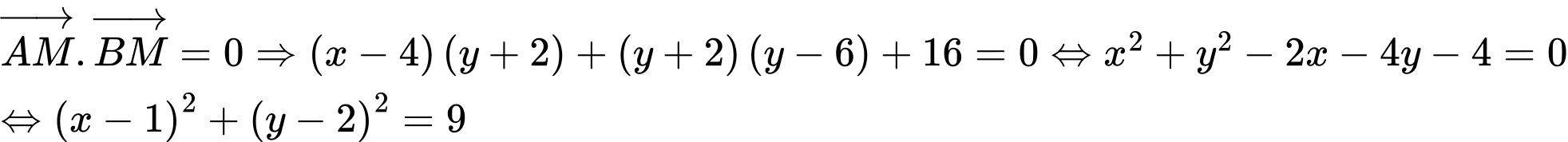
Suy ra tập hợp các điểm thuộc mặt phẳng
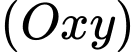 là một đường tròn
là một đường tròn  có tâm
có tâm 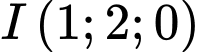 vá bán kính
vá bán kính 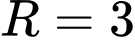 với đường tròn
với đường tròn  là giao tuyến giữa mặt cầu đường kính
là giao tuyến giữa mặt cầu đường kính  và mặt phẳng
và mặt phẳng 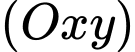
Gọi
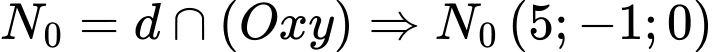 mà ta có
mà ta có 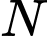 là điểm di động thuộc
là điểm di động thuộc 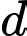 nên suy ra ta có:
nên suy ra ta có: 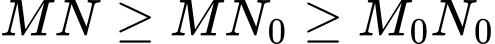 với
với 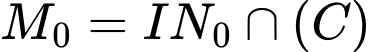
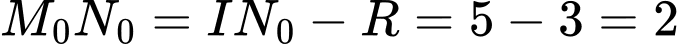 nên suy ra giá trị nhỏ nhất của
nên suy ra giá trị nhỏ nhất của 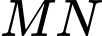 bằng 2 với dấu bằng xảy ra khi
bằng 2 với dấu bằng xảy ra khi
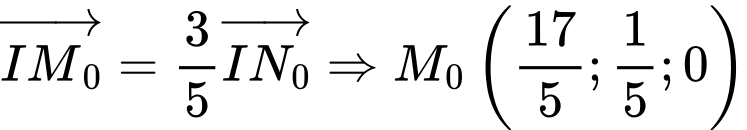 Đáp án: A
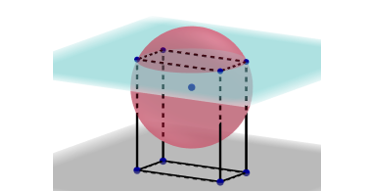
Đáp án: A  , cho mặt phẳng
, cho mặt phẳng  và mặt cầu
và mặt cầu 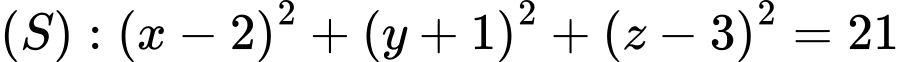 . Một khối hộp chữ nhật
. Một khối hộp chữ nhật  có bốn đỉnh nằm trên mặt phẳng
có bốn đỉnh nằm trên mặt phẳng 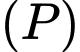 và bốn đỉnh còn lại nằm trên mặt cầu
và bốn đỉnh còn lại nằm trên mặt cầu 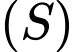 . Khi
. Khi  có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của
có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của  nằm trên mặt cầu
nằm trên mặt cầu 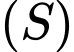 là
là 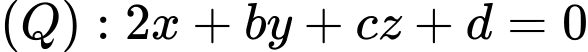 . Giá trị
. Giá trị 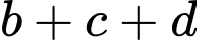 bằng
bằng 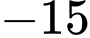 .
.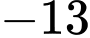 .
.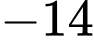 .
.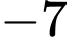 .
.
Ta có mặt cầu
 có tâm
có tâm  và bán kính
và bán kính 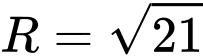 và
và  .
.Do
 là hình hộp chữ nhật nên
là hình hộp chữ nhật nên 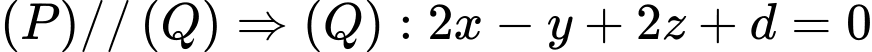 .
.Khi đó
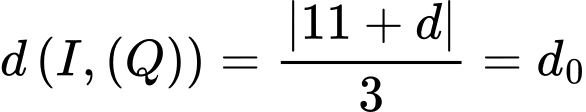 Ta có bán kính đường tròn ngoại tiếp bốn điểm của khối hộp nằm trên mặt cầu là
Ta có bán kính đường tròn ngoại tiếp bốn điểm của khối hộp nằm trên mặt cầu là 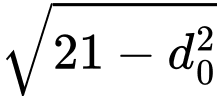
Gọi
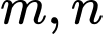 là hai cạnh của hình chữ nhật, khi đó diện tích hình chữ nhật là
là hai cạnh của hình chữ nhật, khi đó diện tích hình chữ nhật là 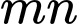
Áp dụng bất đẳng thức
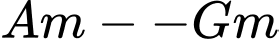 :
: 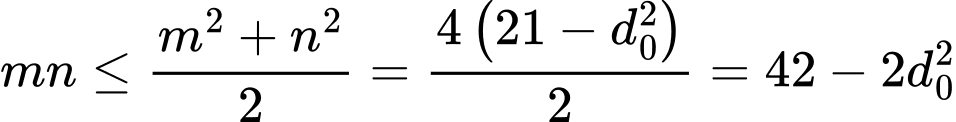
Ta có thể tích của khối hộp
 là
là 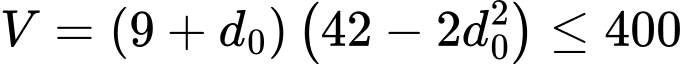
Đẳng thức xảy ra khi
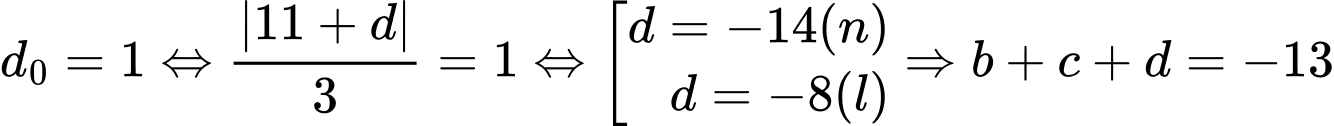 . Đáp án: B
. Đáp án: B  cho điểm
cho điểm 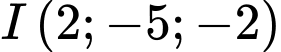 và mặt cầu
và mặt cầu 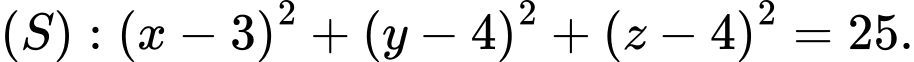 Gọi
Gọi  là giao tuyến của
là giao tuyến của 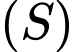 và mặt phẳng
và mặt phẳng 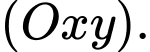 Lấy hai điểm M, N trên
Lấy hai điểm M, N trên  sao cho
sao cho 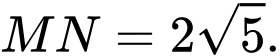 Khi tứ diện OAMN có thể tích lớn nhất thì đường thẳng MN đi qua điểm nào dưới đây?
Khi tứ diện OAMN có thể tích lớn nhất thì đường thẳng MN đi qua điểm nào dưới đây? 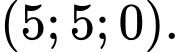
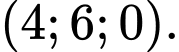
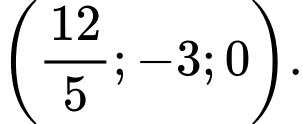
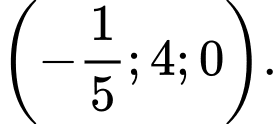
 Đáp án: A
Đáp án: A 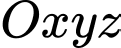 , cho hai điểm
, cho hai điểm 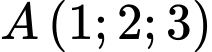 ,
, 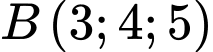 và mặt phẳng
và mặt phẳng  . Gọi
. Gọi  là một đường thẳng thay đổi nằm trong mặt phẳng
là một đường thẳng thay đổi nằm trong mặt phẳng  Gọi
Gọi 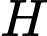 ,
, 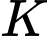 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 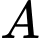 ,
, 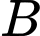 trên
trên  . Biết rằng khi
. Biết rằng khi  thì trung điểm của
thì trung điểm của 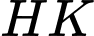 luôn thuộc một đường thẳng
luôn thuộc một đường thẳng 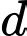 cố định, phương trình của đường thẳng
cố định, phương trình của đường thẳng 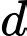 là
là 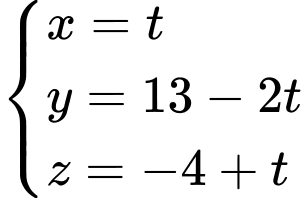 .
.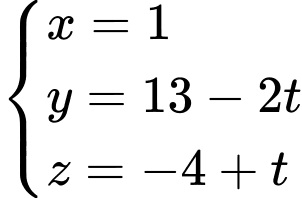 .
.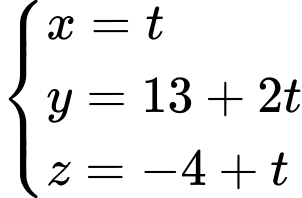 .
.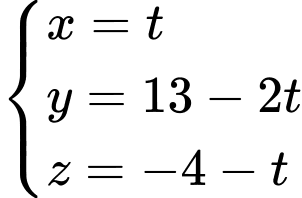 .
. Đáp án: A
Đáp án: A  cho mặt cầu
cho mặt cầu 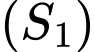 có tâm
có tâm 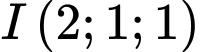 bán kính bằng 4 và mặt cầu
bán kính bằng 4 và mặt cầu 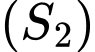 có tâm
có tâm 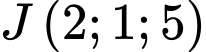 bán kính bằng 2.
bán kính bằng 2. 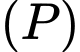 là mặt phẳng thay đổi tiếp xúc với hai mặt cầu
là mặt phẳng thay đổi tiếp xúc với hai mặt cầu 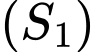 ,
, 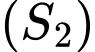 . Đặt
. Đặt 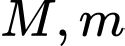 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm  đến
đến 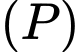 . Giá trị
. Giá trị  bằng
bằng 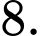
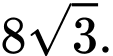

 Đáp án: C
Đáp án: C 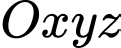 , cho mặt cầu
, cho mặt cầu 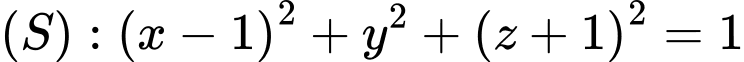 và các điểm
và các điểm 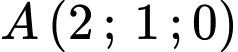 ,
, 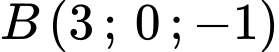 . Gọi
. Gọi 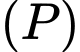 và
và  lần lượt là hai mặt phẳng chứa tất cả các tiếp điểm của các tiếp tuyến kẻ từ
lần lượt là hai mặt phẳng chứa tất cả các tiếp điểm của các tiếp tuyến kẻ từ 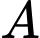 đến
đến 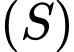 và từ
và từ 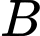 đến
đến 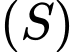 . Tìm tọa độ điểm
. Tìm tọa độ điểm 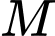 nằm trên giao tuyến của hai mặt phẳng
nằm trên giao tuyến của hai mặt phẳng 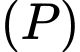 và
và  sao cho diện tích tam giác
sao cho diện tích tam giác 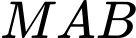 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. 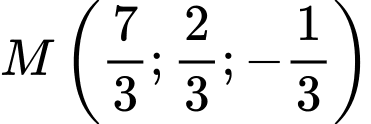 .
.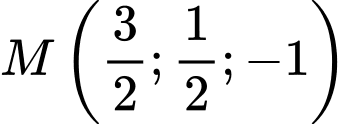 .
.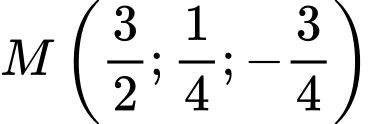 .
.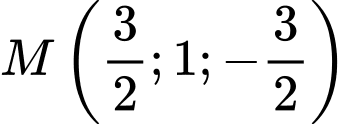 .
.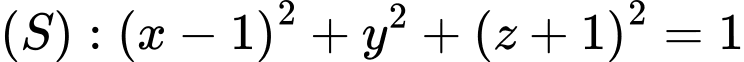
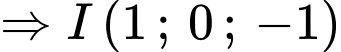
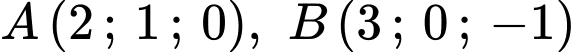
-
 lần lượt là hai mặt phẳng chứa tất cả các tiếp điểm của các tiếp tuyến kẻ từ
lần lượt là hai mặt phẳng chứa tất cả các tiếp điểm của các tiếp tuyến kẻ từ 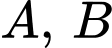 đến
đến 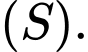
-Giả sử điểm
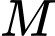 là tiếp điểm của tiếp tuyến kẻ từ
là tiếp điểm của tiếp tuyến kẻ từ 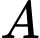
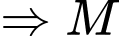 luôn nhìn
luôn nhìn 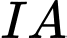 dưới một góc vuông
dưới một góc vuông
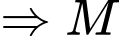 luôn nằm trên mặt cầu có đường kính là
luôn nằm trên mặt cầu có đường kính là 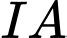 : có tâm là
: có tâm là 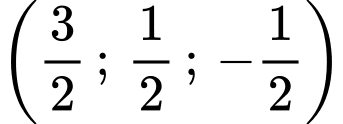
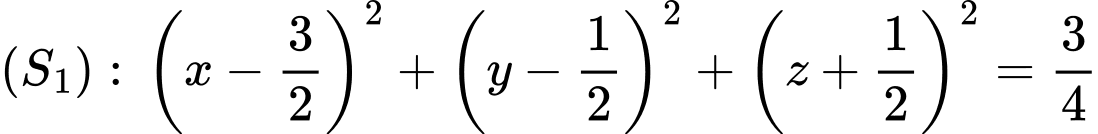
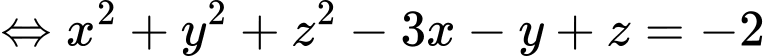
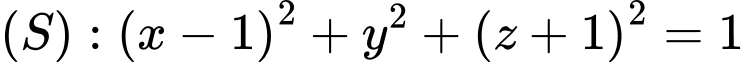
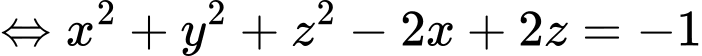
Hiệu 2 phương trình mặt cầu ta được phương trình mặt phẳng giao giữa hai mặt cầu:
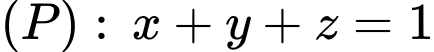
Tương tự, ta tìm được phương trình mặt phẳng
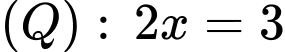
Lại có:
 nằm trên giao tuyến của hai mặt phẳng
nằm trên giao tuyến của hai mặt phẳng 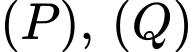 nên ta tìm được phương trình đường thẳng giao tuyến của hai mặt phẳng là:
nên ta tìm được phương trình đường thẳng giao tuyến của hai mặt phẳng là:
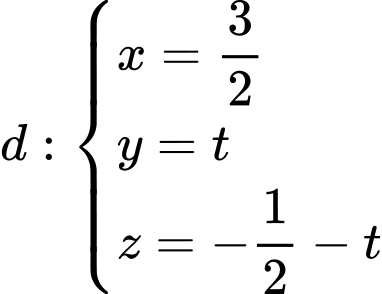
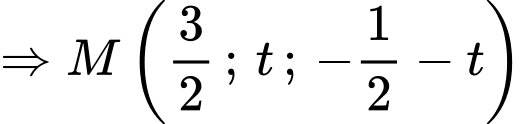
Gọi
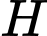 là hình chiếu của
là hình chiếu của 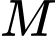 trên
trên 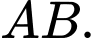
Để
 đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì 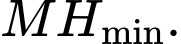 Suy ra,
Suy ra, 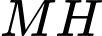 phải là đường vuông góc chung của
phải là đường vuông góc chung của 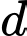 và
và 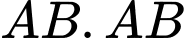 :
: 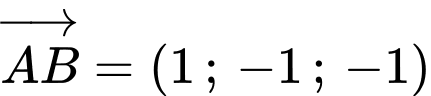
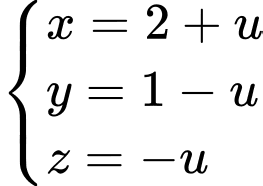
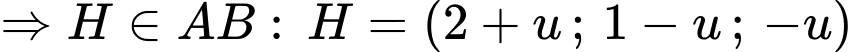
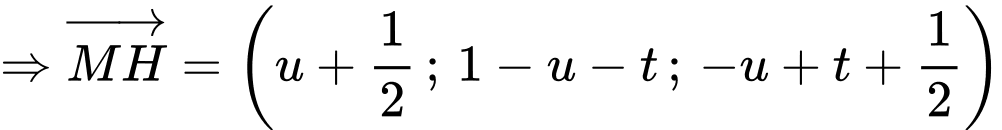
Có:
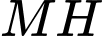 là đường vuông góc chung của
là đường vuông góc chung của 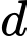 và
và 
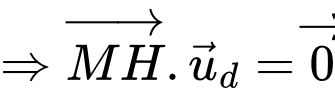
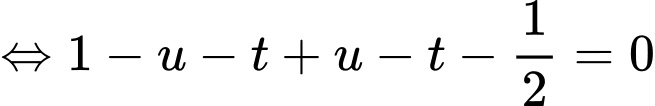
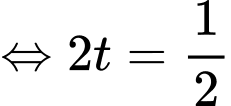
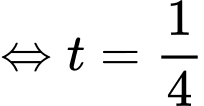
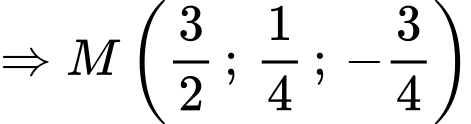
Đáp án: C. Đáp án: C
 , cho mặt cầu
, cho mặt cầu 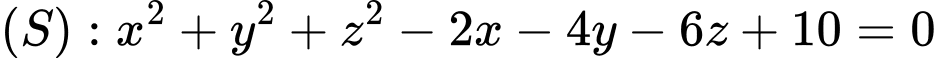 . Xét đường thẳng
. Xét đường thẳng 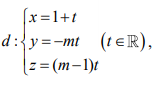 , với
, với  là tham số. Giả sử hai mặt phẳng
là tham số. Giả sử hai mặt phẳng  và
và  chứa đường thẳng
chứa đường thẳng 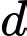 và lần lượt tiếp xúc với mặt cầu
và lần lượt tiếp xúc với mặt cầu 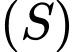 tại
tại 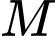 và
và 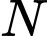 . Khi đoạn thẳng
. Khi đoạn thẳng 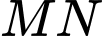 ngắn nhất thì mặt phẳng
ngắn nhất thì mặt phẳng  qua tâm của mặt cầu
qua tâm của mặt cầu 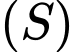 và vuông góc với đường thẳng
và vuông góc với đường thẳng 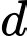 có dạng
có dạng 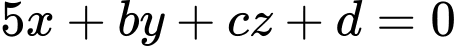 . Hãy tính
. Hãy tính  .
. 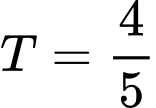 .
.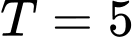 .
.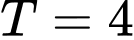 .
.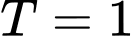 .
.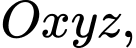 cho mặt cầu
cho mặt cầu 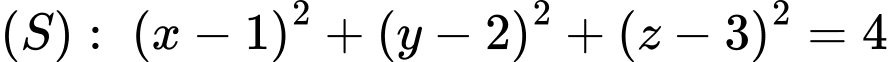 và đường thẳng
và đường thẳng 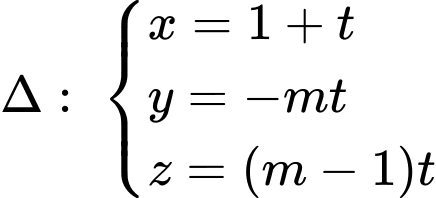 với
với 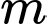 là tham số. Hai mặt phẳng
là tham số. Hai mặt phẳng 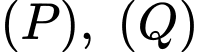 cùng chứa
cùng chứa  và tiếp xúc với mặt cầu
và tiếp xúc với mặt cầu 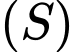 lần lượt tại
lần lượt tại  Khi độ dài
Khi độ dài 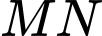 ngắn nhất thì
ngắn nhất thì 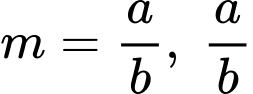 là phân số tối giản. Tính
là phân số tối giản. Tính 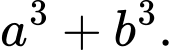
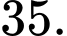
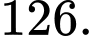
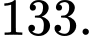
Gọi
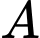 là hình chiếu của
là hình chiếu của 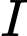 lên
lên  . Các tam giác
. Các tam giác 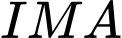 và
và 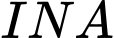 vuông tại
vuông tại 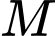 và
và 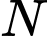
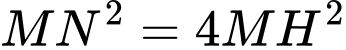 . Ta có:
. Ta có:
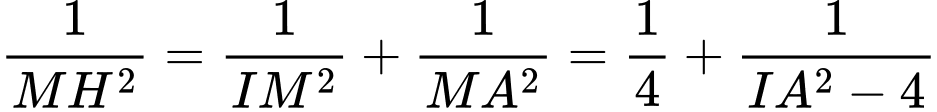
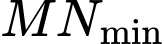
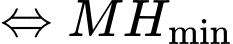
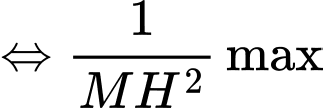
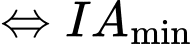
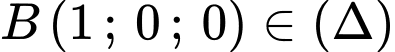 và
và 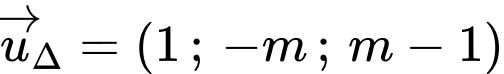
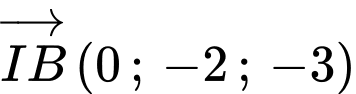
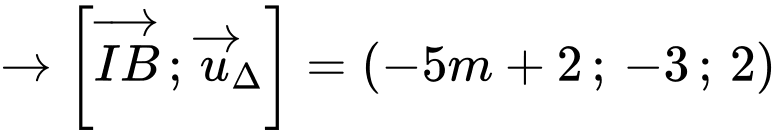
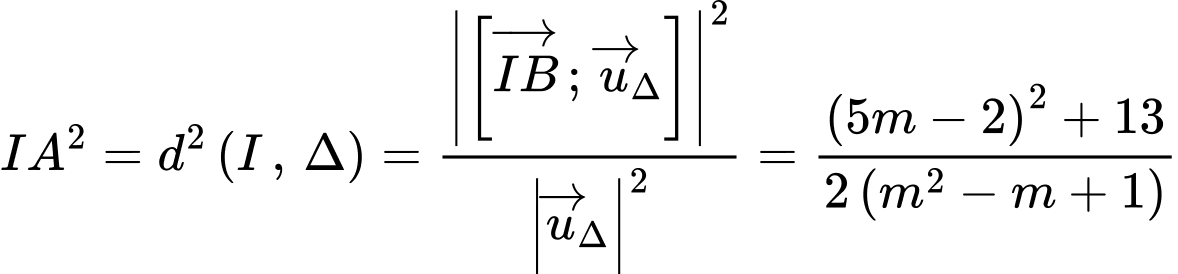
Đặt
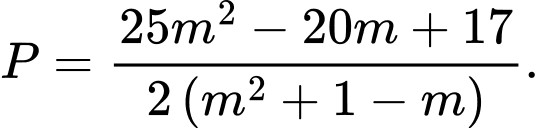 Ta có:
Ta có:
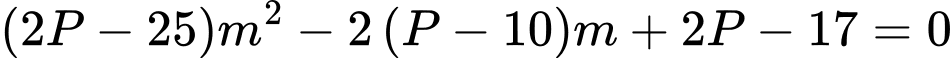 phương trình ẩn
phương trình ẩn 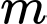 có nghiệm
có nghiệm
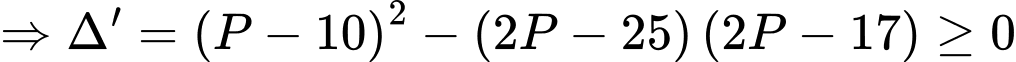
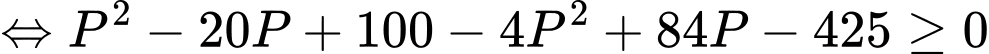
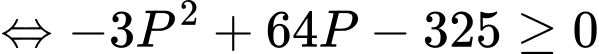
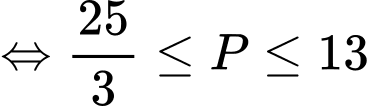
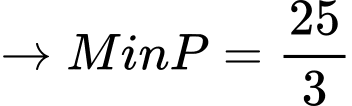
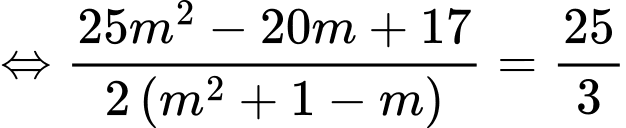
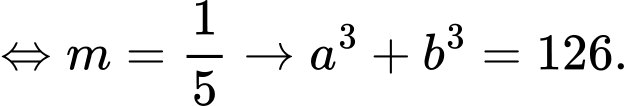 Đáp án: B
Đáp án: B 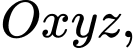 gọi
gọi 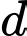 là đường thẳng đi qua
là đường thẳng đi qua 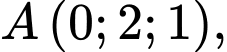 song song với mặt phẳng
song song với mặt phẳng 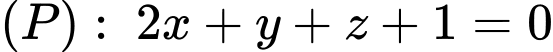 sao cho khoảng cách giữa
sao cho khoảng cách giữa 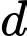 và
và 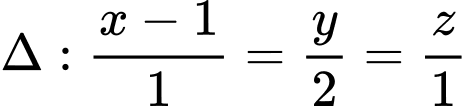 lớn nhất. Đường thẳng
lớn nhất. Đường thẳng 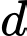 đi qua điểm nào trong các điểm sau:
đi qua điểm nào trong các điểm sau: 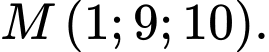
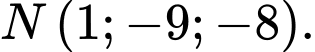
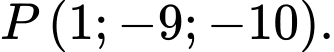
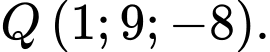
 Đáp án: D
Đáp án: D  phương trình đường thẳng
phương trình đường thẳng 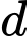 đi qua
đi qua 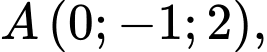 cắt đường thẳng
cắt đường thẳng 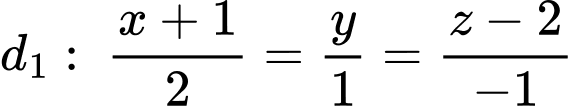 , sao cho khoảng cách giữa
, sao cho khoảng cách giữa 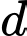 và
và 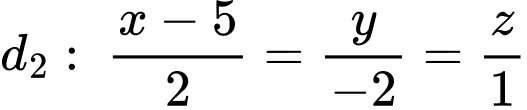 lớn nhất có một vectơ chỉ phương là
lớn nhất có một vectơ chỉ phương là 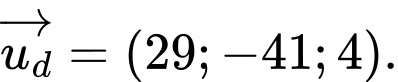
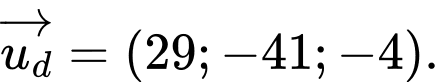
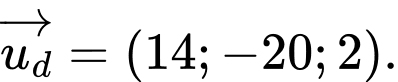
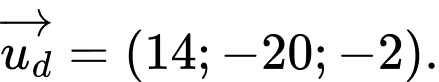
 Đáp án: A
Đáp án: A  , cho hai đường thẳng
, cho hai đường thẳng 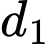 :
: 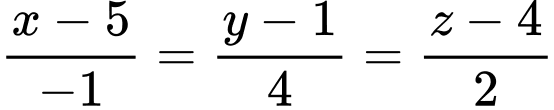 ;
; 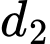 :
: 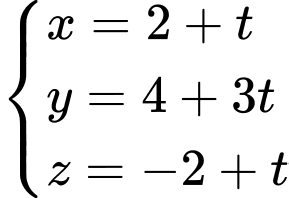 và điểm
và điểm 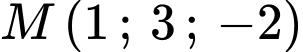 . Gọi
. Gọi  là đường thẳng đi qua điểm
là đường thẳng đi qua điểm 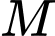 và cắt
và cắt 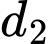 tại điểm
tại điểm 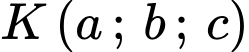 . Tính giá trị của biểu thức
. Tính giá trị của biểu thức 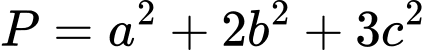 khi khoảng cách giữa hai đường thẳng
khi khoảng cách giữa hai đường thẳng 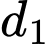 và
và  là lớn nhất:
là lớn nhất: 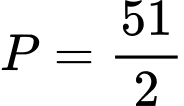 .
.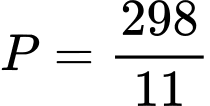 .
.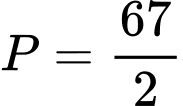 .
.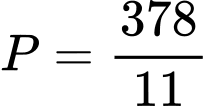 .
.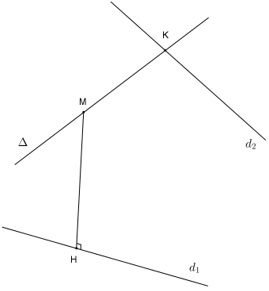
Gọi
 là mặt phẳng đi qua
là mặt phẳng đi qua 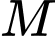 và vuông góc với
và vuông góc với 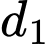 .
. Phương trình mặt phẳng
Phương trình mặt phẳng  là:
là:  hay
hay 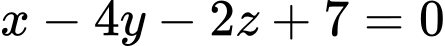
Gọi
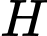 là hình chiếu của
là hình chiếu của 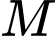 lên
lên 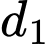

 Tọa độ điểm
Tọa độ điểm  thỏa mãn hệ:
thỏa mãn hệ: 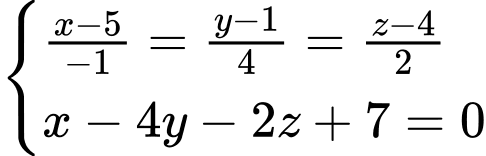

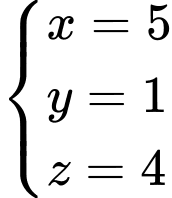
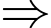
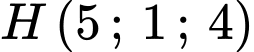 .
.Ta có:
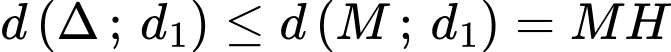 .
.Dấu bằng xảy ra

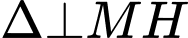 hay
hay  .
.Do
 nên tọa độ điểm
nên tọa độ điểm 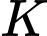 có dạng
có dạng  .
.Ta có:
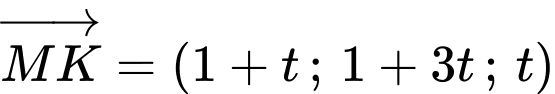 ;
; 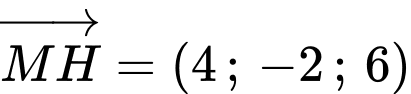 .
.Do
 nên
nên 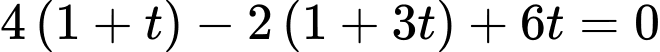

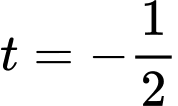
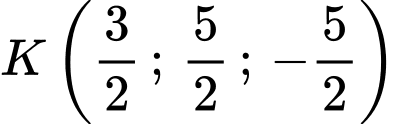 .
.
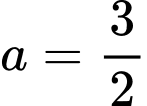 ;
; 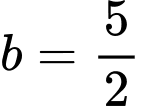 ;
; 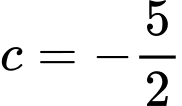
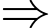
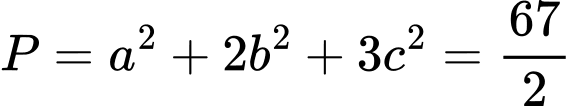 . Đáp án: C
. Đáp án: C  cho mặt cầu
cho mặt cầu  Có tất cả bao nhiêu điểm
Có tất cả bao nhiêu điểm 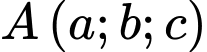 (
(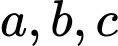 là các số nguyên) thuộc mặt phẳng
là các số nguyên) thuộc mặt phẳng 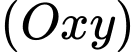 sao cho có ít nhất hai tiếp tuyến của
sao cho có ít nhất hai tiếp tuyến của 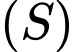 đi qua
đi qua 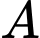 và hai tiếp tuyến đó vuông góc với nhau?
và hai tiếp tuyến đó vuông góc với nhau? 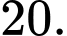
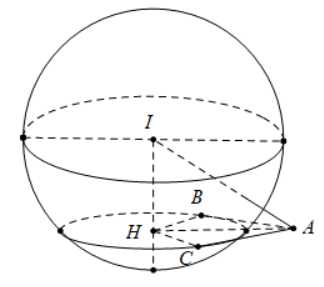
Gọi
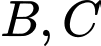 là các tiếp điếm và mặt phắng
là các tiếp điếm và mặt phắng 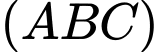 cắt mặt cầu đã cho (tâm
cắt mặt cầu đã cho (tâm 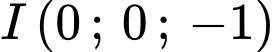 bán kính
bán kính 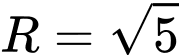 ) theo giao tuyến là đường tròn tâm
) theo giao tuyến là đường tròn tâm 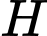 bán kính
bán kính 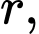 đặt
đặt 
Ta có:
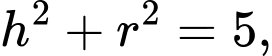 do
do 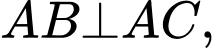

 suy ra
suy ra 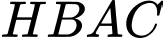 là hình vuông nên
là hình vuông nên 
Lại có:
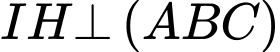
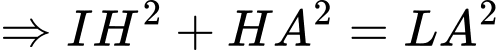
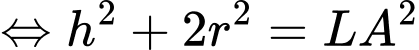
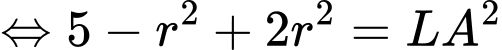
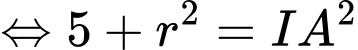
Mặt khác
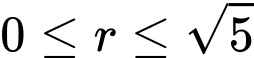
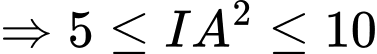
Điểm
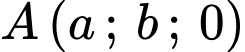 nên
nên 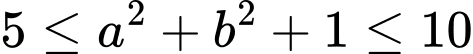
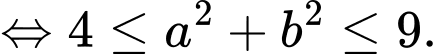
Do
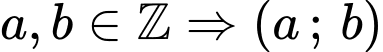 là các cặp
là các cặp 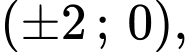
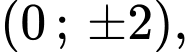
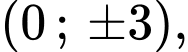
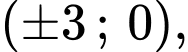
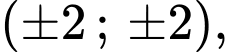
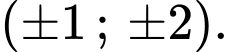
Vậy có 20 cặp
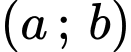 nên có 20 điểm
nên có 20 điểm 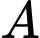 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán. Chọn đáp án A. Đáp án: A
 xét mặt cầu
xét mặt cầu 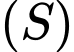 có tâm
có tâm 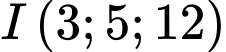 và bán kính
và bán kính 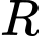 thay đổi. Có bao nhiêu giá trị nguyên của
thay đổi. Có bao nhiêu giá trị nguyên của 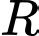 sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của
sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của 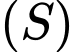 trong mặt phẳng
trong mặt phẳng 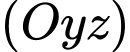 mà hai tiếp tuyến đó cùng đi qua
mà hai tiếp tuyến đó cùng đi qua  và góc giữa chúng không nhỏ hơn
và góc giữa chúng không nhỏ hơn 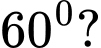
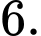
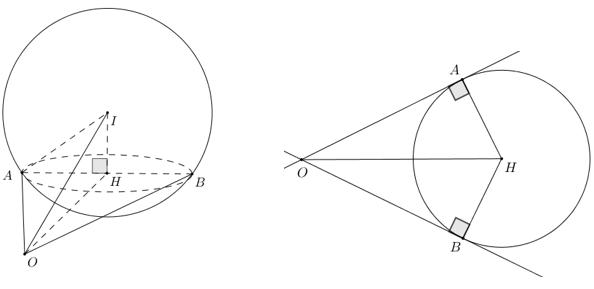
Giả sử 2 tiếp tuyến
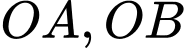 , theo giả thiết suy ra
, theo giả thiết suy ra 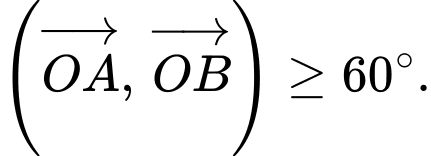 Suy ra
Suy ra 
Gọi
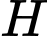 là hình chiếu của
là hình chiếu của 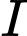 trên
trên 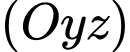 , suy ra
, suy ra 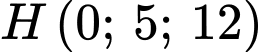 , suy ra
, suy ra 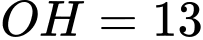
Xét tam giác
 có:
có: 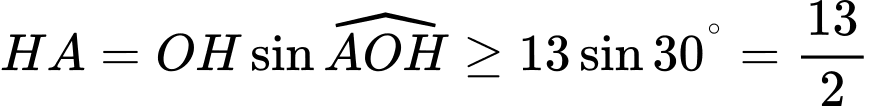
Ta có
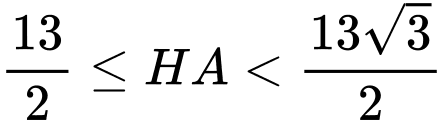

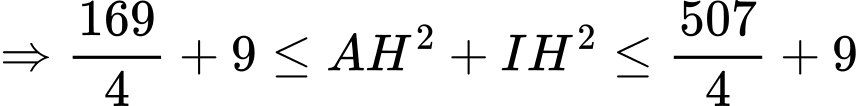
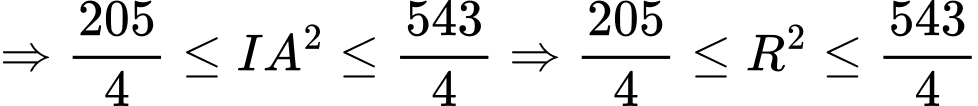 hay
hay 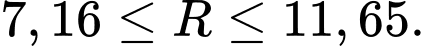
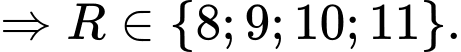
Vậy có tất cả 4 giá trị của
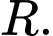
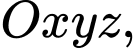 xét mặt cầu
xét mặt cầu 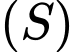 có tâm
có tâm 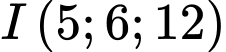 và bán kính
và bán kính 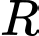 thay đổi. Có bao nhiêu giá trị nguyên của
thay đổi. Có bao nhiêu giá trị nguyên của 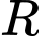 sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của
sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của 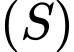 trong mặt phẳng
trong mặt phẳng 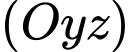 mà hai tiếp tuyến đó cùng đi qua
mà hai tiếp tuyến đó cùng đi qua  và góc giữa chúng không nhỏ hơn
và góc giữa chúng không nhỏ hơn 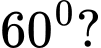
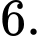

Giả sử 2 tiếp tuyến 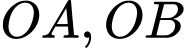 , theo giả thiết suy ra
, theo giả thiết suy ra 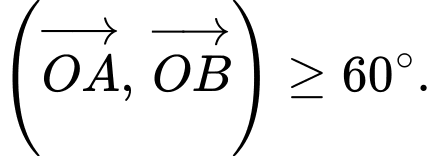 Suy ra
Suy ra 
Gọi 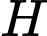 là hình chiếu của
là hình chiếu của 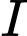 trên
trên 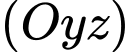 , suy ra
, suy ra 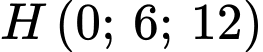 , suy ra
, suy ra 
Xét tam giác 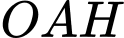 có:
có: 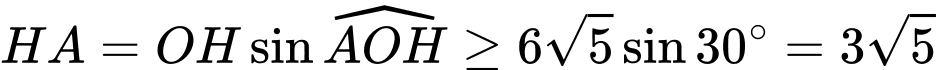
Ta có 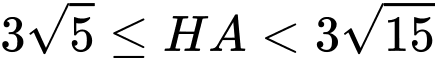
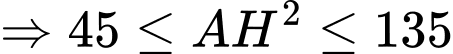
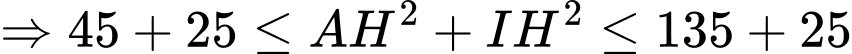
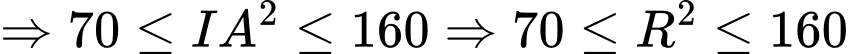 hay
hay 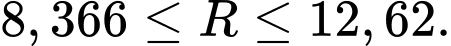
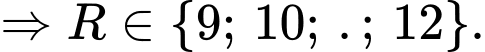
Vậy có tất cả 4 giá trị của 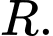
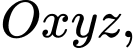 cho mặt cầu
cho mặt cầu 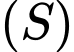 tâm
tâm 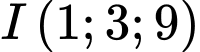 bán kính bằng 3. Gọi
bán kính bằng 3. Gọi 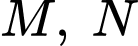 là hai điểm lần lượt thuộc hai trục
là hai điểm lần lượt thuộc hai trục 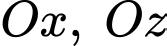 sao cho đường thẳng
sao cho đường thẳng 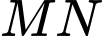 tiếp xúc với
tiếp xúc với 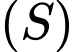 , đồng thời mặt cầu ngoại tiếp tứ diện
, đồng thời mặt cầu ngoại tiếp tứ diện 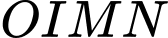 có bán kính bằng
có bán kính bằng 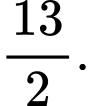 Gọi
Gọi 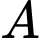 là tiếp điểm của
là tiếp điểm của 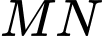 và
và 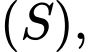 giá trị
giá trị  bằng
bằng 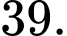
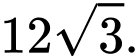
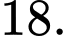
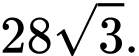
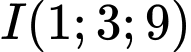 và
và 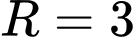 . Suy ra
. Suy ra 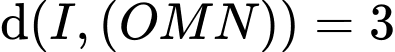
Vậy mặt cầu
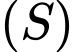 tiếp xúc
tiếp xúc 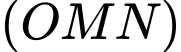 tại
tại 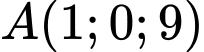
Gọi tọa độ
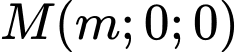 và
và 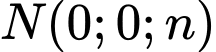
Ta có
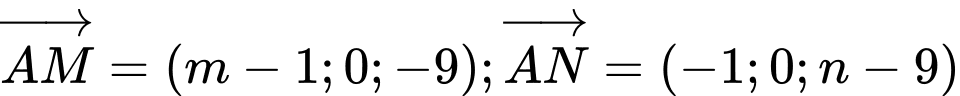
Do
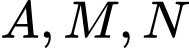 thẳng hàng nên
thẳng hàng nên 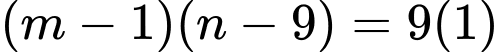
Do
 và
và  là trung điểm
là trung điểm 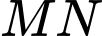 thì
thì 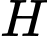 là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 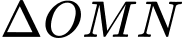
Suy ra
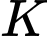 là tâm mặt cầu ngoại tiếp
là tâm mặt cầu ngoại tiếp 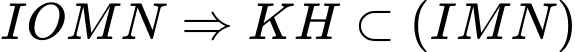
Bán kính đường tròn ngoại tiếp
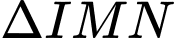 bằng
bằng 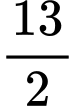 (đường tròn lớn)
(đường tròn lớn)
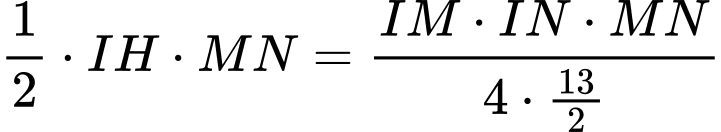
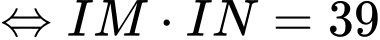
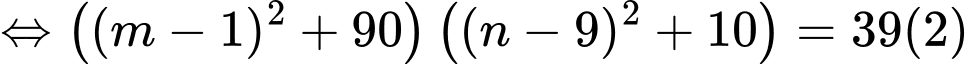
Từ
 và
và  suy ra
suy ra 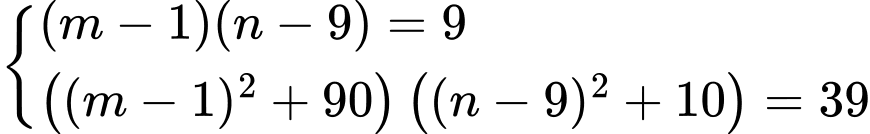
Đặt
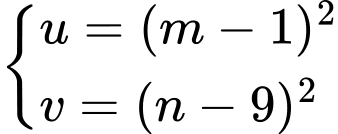 ta có hệ phương trình:
ta có hệ phương trình:
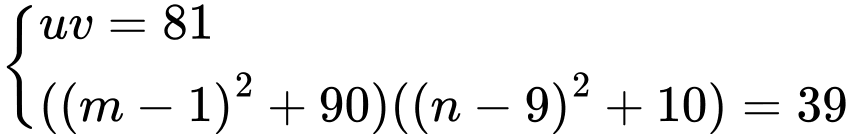
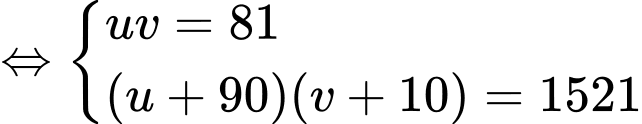
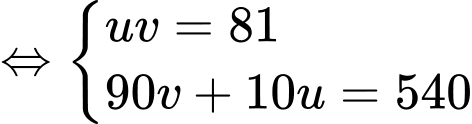
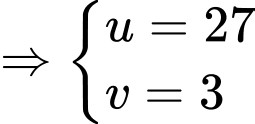
Vậy

Chọn B. Đáp án: B
Cho đường tròn
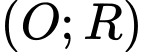 . Lấy điểm
. Lấy điểm 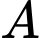 nằm ngoài đường tròn sao cho
nằm ngoài đường tròn sao cho 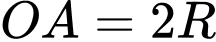 , vẽ các tiếp tuyến
, vẽ các tiếp tuyến 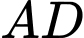 ,
, 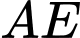 đến
đến  (
(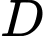 ,
, 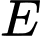 là tiếp điểm). Lấy
là tiếp điểm). Lấy  trên cung lớn
trên cung lớn 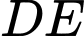 , vẽ
, vẽ  (
(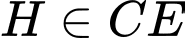 );
); 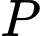 là trung điểm của
là trung điểm của 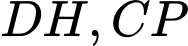 cắt đường tròn
cắt đường tròn  tại
tại  ,
, 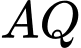 cắt
cắt  tại
tại 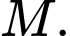
a) Chứng minh
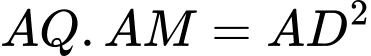 và tính
và tính 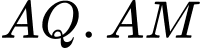 theo
theo 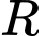 .
.
b) Gọi
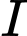 là giao điểm của
là giao điểm của 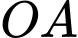 và
và 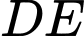 . Chứng minh tứ giác
. Chứng minh tứ giác 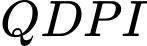 nội tiếp đường tròn.
nội tiếp đường tròn.
c) Chứng minh
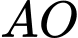 là tiếp tuyến của đường tròn ngoại tiếp
là tiếp tuyến của đường tròn ngoại tiếp 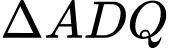 .
. 
a) Xét
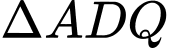 và
và  có:
có: 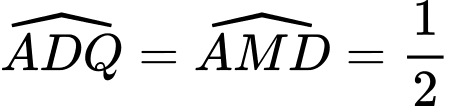 sđ;
sđ; 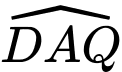 chung
chung
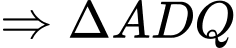 đồng dạng
đồng dạng  (g.g)
(g.g) 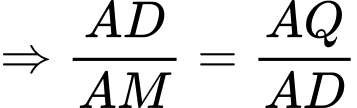
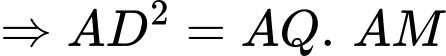
Xét
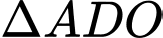 vuông tại
vuông tại  :
: 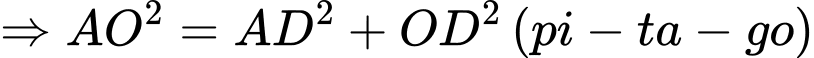
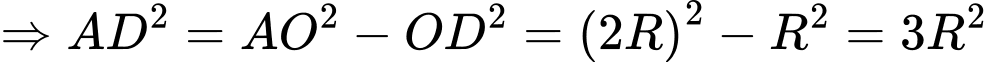
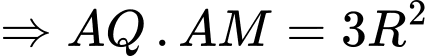 .
.
b) Ta có:
 và
và  (tính chất hai tiếp tuyến cắt nhau)
(tính chất hai tiếp tuyến cắt nhau)
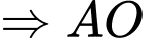 là đường trung trực của
là đường trung trực của 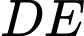
 tại
tại 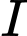 và
và 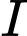 là trung điểm của
là trung điểm của 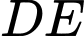 .
.
Xét
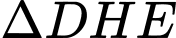 có:
có: 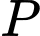 là trung điểm của
là trung điểm của 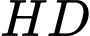 ,
, 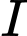 là trung điểm của
là trung điểm của 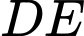
Suy ra
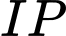 là đường trung bình của
là đường trung bình của 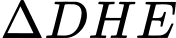

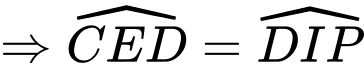 (hai góc đồng vị) mà
(hai góc đồng vị) mà 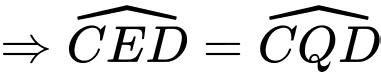 (cùng chắn )
(cùng chắn )
Suy ra

Xét tứ giác
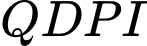 có
có  suy ra tứ giác
suy ra tứ giác 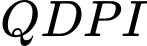 nội tiếp (tứ giác có hai đỉnh liên tiếp cùng nhìn một cạnh dưới góc bằng nhau).
nội tiếp (tứ giác có hai đỉnh liên tiếp cùng nhìn một cạnh dưới góc bằng nhau).
c) Xét
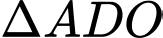 vuông tại
vuông tại 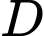 có
có  là đường cao suy ra
là đường cao suy ra 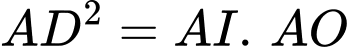 mà
mà 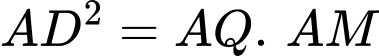 suy ra
suy ra 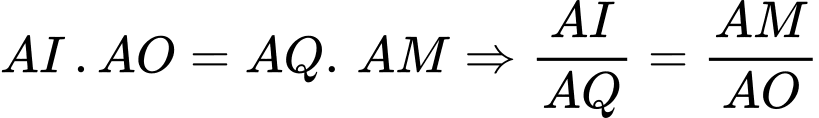
Xét
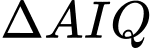 và
và 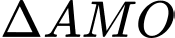 có:
có:  chung,
chung, 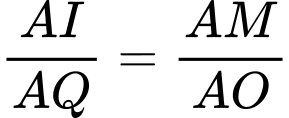 nên
nên 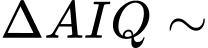
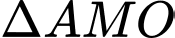 (c.g.c)
(c.g.c) 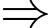
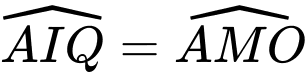
Ta lại có tứ giác
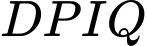 là tứ giác nội tiếp nên
là tứ giác nội tiếp nên 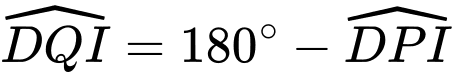
Mặt khác
 nên
nên 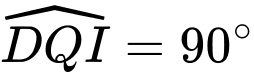 do đó
do đó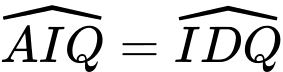 ( cùng phụ
( cùng phụ 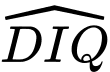 )
)
Và
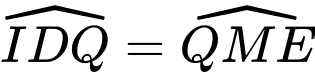 ( cùng chắn cung ) do vậy
( cùng chắn cung ) do vậy 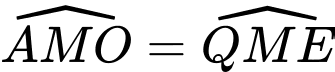
Từ đó 2 tia
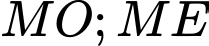 trùng nhau hay là 3 điểm
trùng nhau hay là 3 điểm 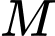 ,
,  ,
, 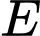 thẳng hàng.
thẳng hàng.
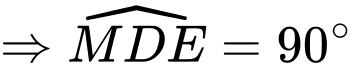 (góc nội tiếp chắn nửa đường tròn) suy ra
(góc nội tiếp chắn nửa đường tròn) suy ra  (cùng vuông với
(cùng vuông với 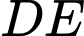 )
)
 (hai góc so le trong) mà
(hai góc so le trong) mà 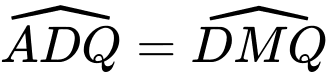 suy ra
suy ra 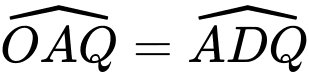 suy ra
suy ra 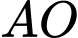 là tiếp tuyến của đường tròn ngoại tiếp
là tiếp tuyến của đường tròn ngoại tiếp 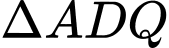
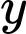 sao cho ứng với mỗi
sao cho ứng với mỗi 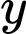 tồn tại đúng
tồn tại đúng 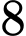 số thực
số thực 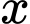 thoả mãn
thoả mãn 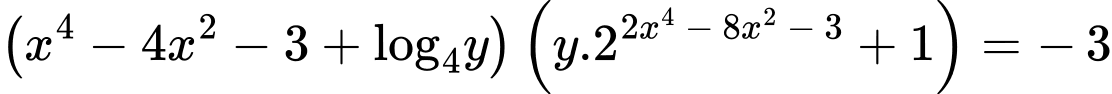 ?
? 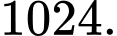
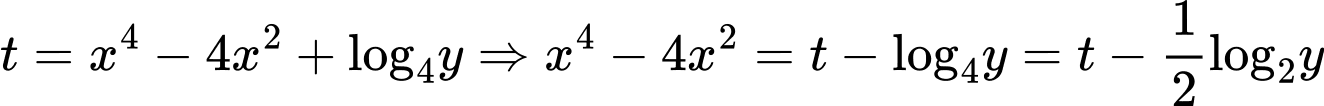
Phương trình được viết lại thành:
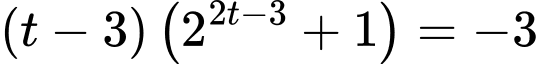
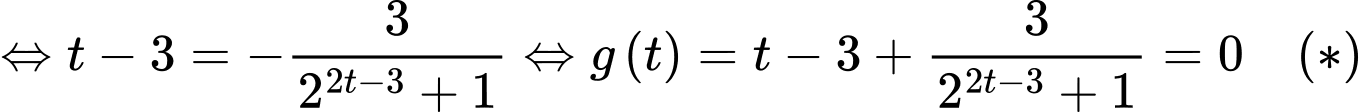 Ta có
Ta có 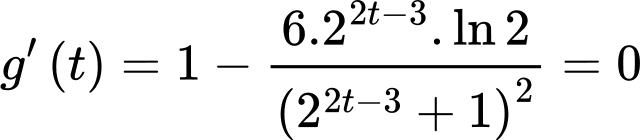 có đúng 2 nghiệm nên
có đúng 2 nghiệm nên  có tối đa 3 nghiệm.
có tối đa 3 nghiệm. Nhận thấy:
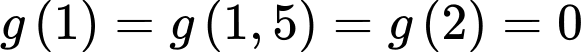 nên
nên 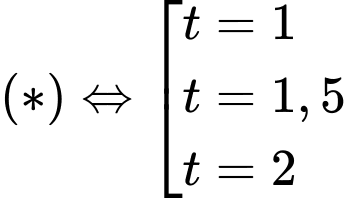
Suy ra
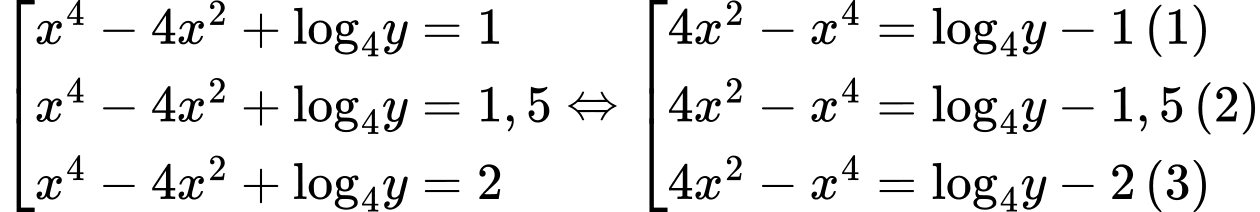
Ta có bảng biến thiên hàm số
 như sau:
như sau: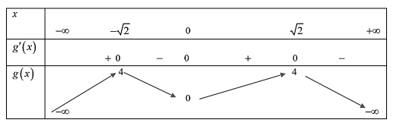
Để phương trình có đúng 8 nghiệm thực phân biệt thì ta xét các trường hợp sau: Trường hợp 1: Các phương trình
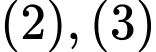 mỗi phương trình có 4 nghiệm.
mỗi phương trình có 4 nghiệm.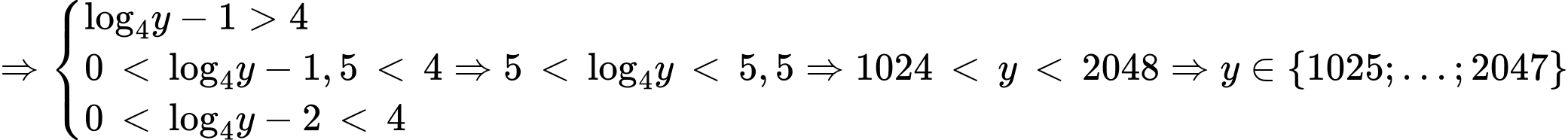
Trường hợp 2: Phương trình
 có
có 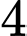 nghiệm và phương trình
nghiệm và phương trình 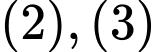 mỗi phương trình có 2 nghiệm.
mỗi phương trình có 2 nghiệm.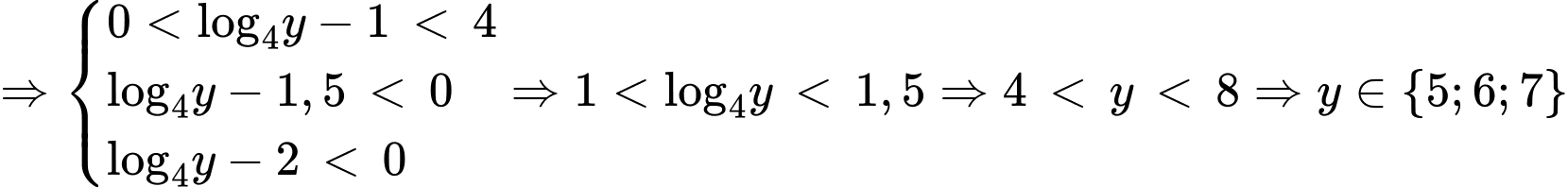 .
. Vậy có tất cả 1026 giá trị nguyên dương của
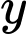 thoả mãn.
thoả mãn. Chọn đáp án D Đáp án: D
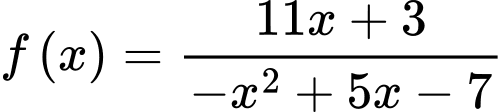 nhận giá trị dương khi và chỉ khi
nhận giá trị dương khi và chỉ khi 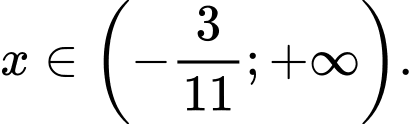
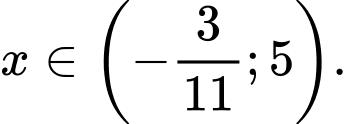
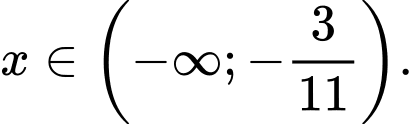
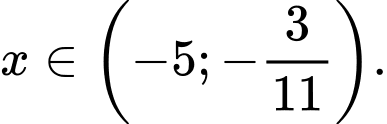
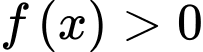
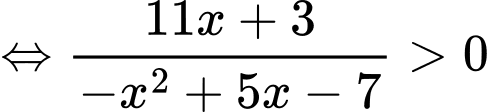
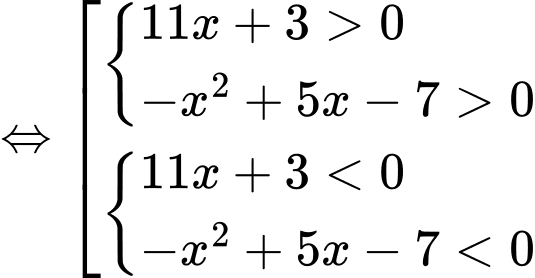
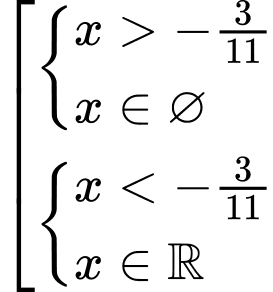
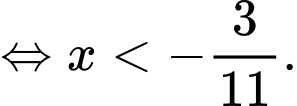 Chọn C. Đáp án: C
Chọn C. Đáp án: C