Đáp án Bài tập tự luyện số 1
Câu 1 [153550]: [Đề Mẫu ĐGNL TPHCM]: Gọi 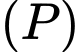 là mặt phẳng chứa điểm
là mặt phẳng chứa điểm 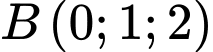 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm 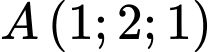 đến
đến 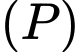 là lớn nhất. Phương trình của
là lớn nhất. Phương trình của 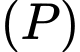 là
là
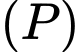 là mặt phẳng chứa điểm
là mặt phẳng chứa điểm 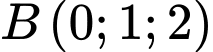 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm 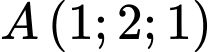 đến
đến 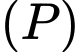 là lớn nhất. Phương trình của
là lớn nhất. Phương trình của 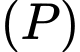 là
là A, 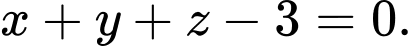
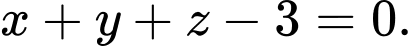
B, 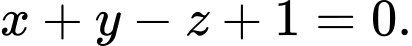
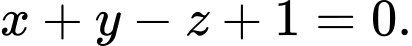
C, 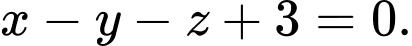
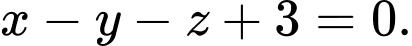
D, 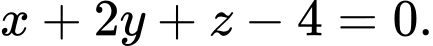
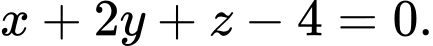
Ta có:  dấu bằng xảy ra khi và chỉ khi
dấu bằng xảy ra khi và chỉ khi 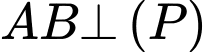
 dấu bằng xảy ra khi và chỉ khi
dấu bằng xảy ra khi và chỉ khi 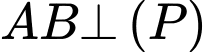
Khi đó 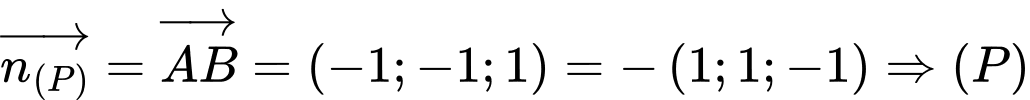
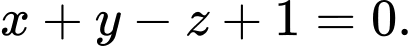
Đáp án: B 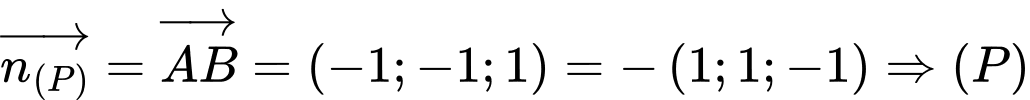
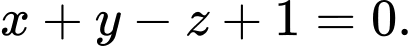
Chọn B.
Câu 2 [57936]: Trong không gian với hệ tọa độ 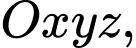 cho điểm
cho điểm 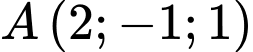 . Phương trình mặt phẳng
. Phương trình mặt phẳng 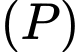 đi qua điểm
đi qua điểm 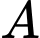 và cách gốc tọa độ
và cách gốc tọa độ  một khoảng cách lớn nhất là
một khoảng cách lớn nhất là
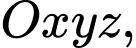 cho điểm
cho điểm 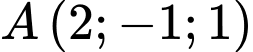 . Phương trình mặt phẳng
. Phương trình mặt phẳng 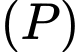 đi qua điểm
đi qua điểm 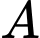 và cách gốc tọa độ
và cách gốc tọa độ  một khoảng cách lớn nhất là
một khoảng cách lớn nhất là A, 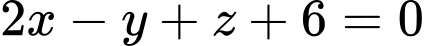 .
.
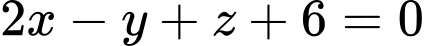 .
.B, 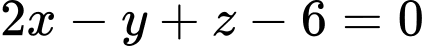 .
.
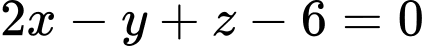 .
.C, 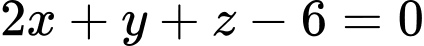 .
.
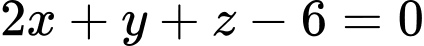 .
.D, 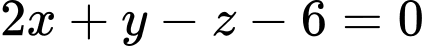 .
.
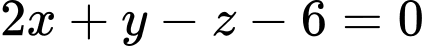 .
.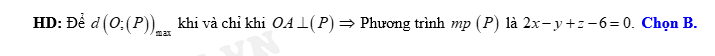
Đáp án: B
Câu 3 [234246]: [Đề thi TH THPT 2022]: Trong không gian 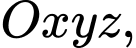 cho điểm
cho điểm 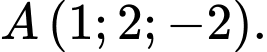 Gọi
Gọi 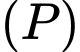 là mặt phẳng chứa trục
là mặt phẳng chứa trục 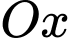 sao cho khoảng cách từ
sao cho khoảng cách từ 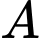 đến
đến 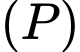 lớn nhất. Phương trình của
lớn nhất. Phương trình của 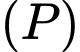 là
là
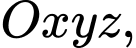 cho điểm
cho điểm 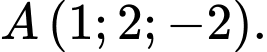 Gọi
Gọi 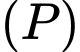 là mặt phẳng chứa trục
là mặt phẳng chứa trục 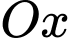 sao cho khoảng cách từ
sao cho khoảng cách từ 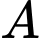 đến
đến 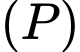 lớn nhất. Phương trình của
lớn nhất. Phương trình của 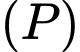 là
là A, 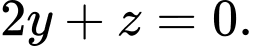
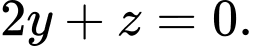
B, 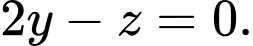
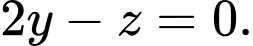
C, 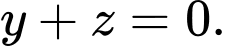
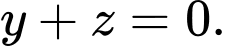
D, 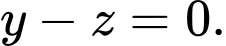
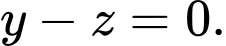
HD: Gọi 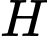 là hình chiếu của
là hình chiếu của 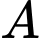 trên trục
trên trục 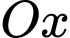 thì
thì 
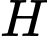 là hình chiếu của
là hình chiếu của 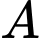 trên trục
trên trục 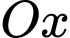 thì
thì 
Khi đó 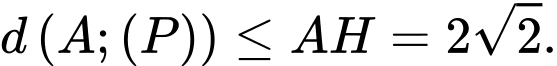
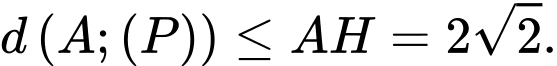
Dấu bằng xảy ra khi 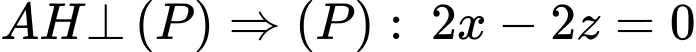 hay
hay 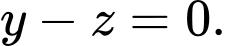
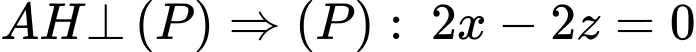 hay
hay 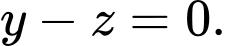
Chọn D.
Đáp án: D
Câu 4 [57962]: Gọi 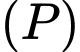 là mặt phẳng đi qua điểm
là mặt phẳng đi qua điểm 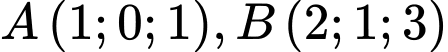 và cách gốc tọa độ
và cách gốc tọa độ  một khoảng lớn nhất .
một khoảng lớn nhất . 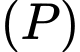 đi qua điểm nào sau đây?
đi qua điểm nào sau đây?
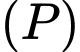 là mặt phẳng đi qua điểm
là mặt phẳng đi qua điểm 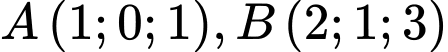 và cách gốc tọa độ
và cách gốc tọa độ  một khoảng lớn nhất .
một khoảng lớn nhất . 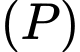 đi qua điểm nào sau đây?
đi qua điểm nào sau đây? A, 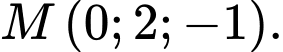
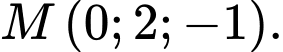
B, 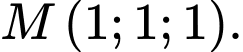
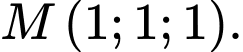
C, 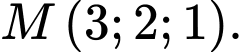
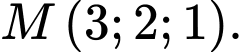
D, 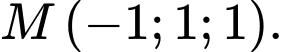
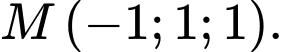
 Đáp án: C
Đáp án: C
Câu 5 [399915]: Trong không gian 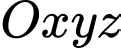 , gọi
, gọi 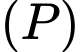 là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 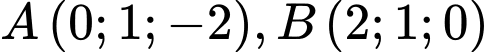 sao cho khoảng cách từ gốc tọa độ
sao cho khoảng cách từ gốc tọa độ  đến
đến 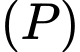 lớn nhất. Phương trình của mặt phẳng
lớn nhất. Phương trình của mặt phẳng 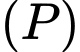 là
là
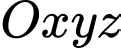 , gọi
, gọi 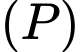 là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 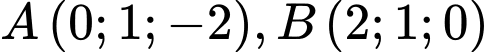 sao cho khoảng cách từ gốc tọa độ
sao cho khoảng cách từ gốc tọa độ  đến
đến 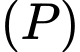 lớn nhất. Phương trình của mặt phẳng
lớn nhất. Phương trình của mặt phẳng 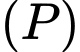 là
là A, 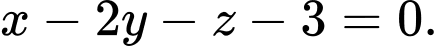
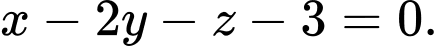
B, 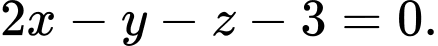
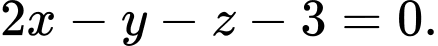
C, 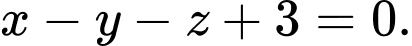
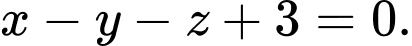
D, 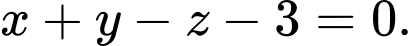
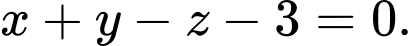
Chọn D
Có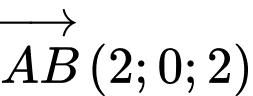 , đường thẳng
, đường thẳng  đi qua điểm
đi qua điểm 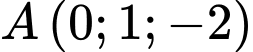 có véc tơ chỉ phương
có véc tơ chỉ phương 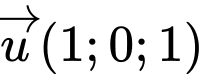 có phương trình tham số là
có phương trình tham số là 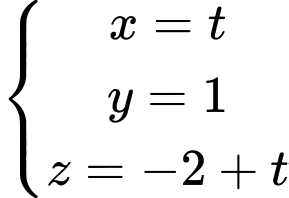
Gọi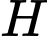 là hình chiếu của
là hình chiếu của  lên đường thẳng
lên đường thẳng  ta có
ta có 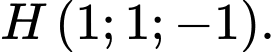
Gọi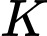 là hình chiếu của
là hình chiếu của  lên
lên 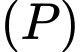 , ta luôn có
, ta luôn có 
Vậy nên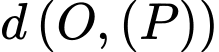 lớn nhất bằng
lớn nhất bằng 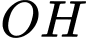 khi
khi 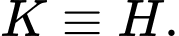
Khi đó mặt phẳng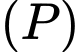 nhận véc tơ
nhận véc tơ 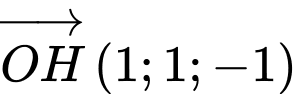 làm véc tơ pháp tuyến và đi qua điểm
làm véc tơ pháp tuyến và đi qua điểm 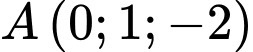 nên có phương trình
nên có phương trình 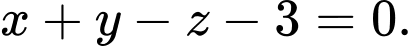 Đáp án: D
Đáp án: D
Có
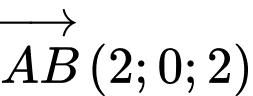 , đường thẳng
, đường thẳng  đi qua điểm
đi qua điểm 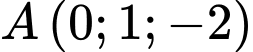 có véc tơ chỉ phương
có véc tơ chỉ phương 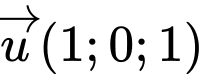 có phương trình tham số là
có phương trình tham số là 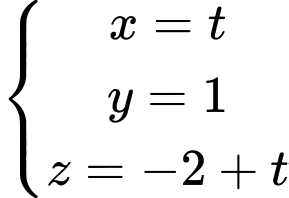
Gọi
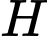 là hình chiếu của
là hình chiếu của  lên đường thẳng
lên đường thẳng  ta có
ta có 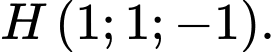
Gọi
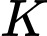 là hình chiếu của
là hình chiếu của  lên
lên 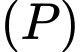 , ta luôn có
, ta luôn có 
Vậy nên
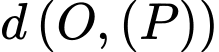 lớn nhất bằng
lớn nhất bằng 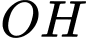 khi
khi 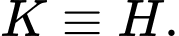
Khi đó mặt phẳng
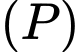 nhận véc tơ
nhận véc tơ 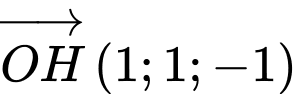 làm véc tơ pháp tuyến và đi qua điểm
làm véc tơ pháp tuyến và đi qua điểm 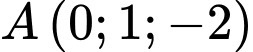 nên có phương trình
nên có phương trình 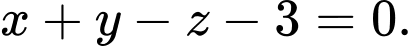 Đáp án: D
Đáp án: D
Câu 6 [57963]: Trong không gian với hệ tọa độ 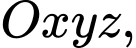 cho điểm
cho điểm 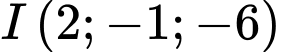 và đường thẳng
và đường thẳng 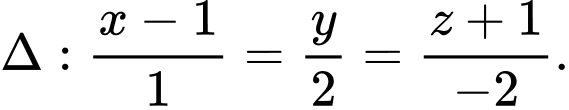 Gọi
Gọi 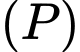 là mặt phẳng thay đổi luôn chứa đường thẳng
là mặt phẳng thay đổi luôn chứa đường thẳng 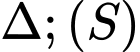 là mặt cầu có tâm
là mặt cầu có tâm 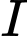 và tiếp xúc
và tiếp xúc 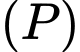 sao cho mặt cầu
sao cho mặt cầu 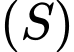 có bán kính lớn nhất. Tính
có bán kính lớn nhất. Tính 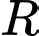 của mặt cầu
của mặt cầu 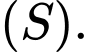
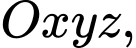 cho điểm
cho điểm 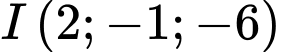 và đường thẳng
và đường thẳng 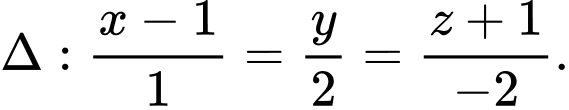 Gọi
Gọi 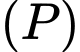 là mặt phẳng thay đổi luôn chứa đường thẳng
là mặt phẳng thay đổi luôn chứa đường thẳng 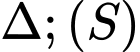 là mặt cầu có tâm
là mặt cầu có tâm 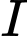 và tiếp xúc
và tiếp xúc 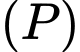 sao cho mặt cầu
sao cho mặt cầu 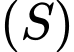 có bán kính lớn nhất. Tính
có bán kính lớn nhất. Tính 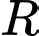 của mặt cầu
của mặt cầu 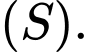
A, 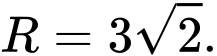
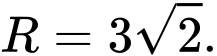
B, 

C, 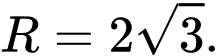
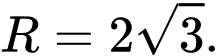
D, 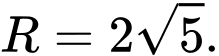
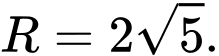
 Đáp án: A
Đáp án: A
Câu 7 [82649]: Trong không gian tọa độ 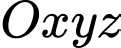 , cho các điểm
, cho các điểm 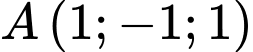 và đường thẳng
và đường thẳng 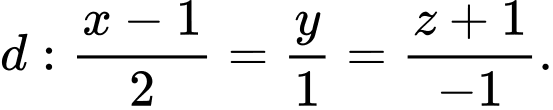 Gọi
Gọi 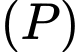 là mặt phẳng chứa d sao cho khoảng cách từ
là mặt phẳng chứa d sao cho khoảng cách từ 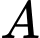 đến
đến 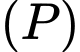 đạt giá trị lớn nhất. Biết
đạt giá trị lớn nhất. Biết 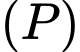 có dạng
có dạng 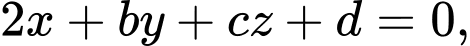 tính
tính 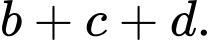
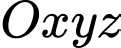 , cho các điểm
, cho các điểm 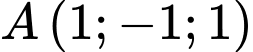 và đường thẳng
và đường thẳng 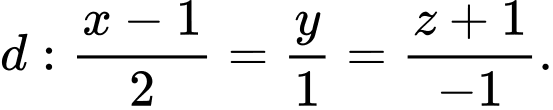 Gọi
Gọi 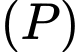 là mặt phẳng chứa d sao cho khoảng cách từ
là mặt phẳng chứa d sao cho khoảng cách từ 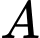 đến
đến 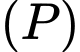 đạt giá trị lớn nhất. Biết
đạt giá trị lớn nhất. Biết 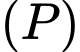 có dạng
có dạng 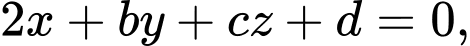 tính
tính 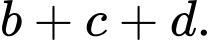
A, 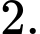
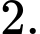
B, 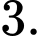
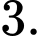
C, 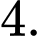
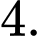
D, 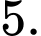
 Đáp án: B
Đáp án: B
Câu 8 [82650]: Trong không gian với hệ tọa độ 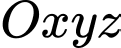 cho cho điểm
cho cho điểm 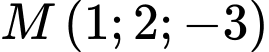 và đường thẳng
và đường thẳng 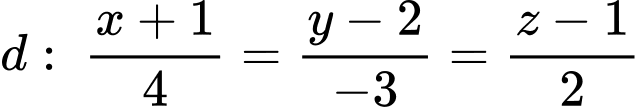 . Mặt phẳng
. Mặt phẳng 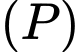 chứa đường thẳng
chứa đường thẳng 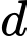 đồng thời cách điểm
đồng thời cách điểm 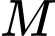 một khoảng lớn nhất có phương trình dạng
một khoảng lớn nhất có phương trình dạng 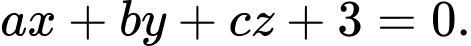 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
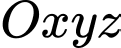 cho cho điểm
cho cho điểm 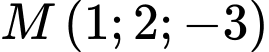 và đường thẳng
và đường thẳng 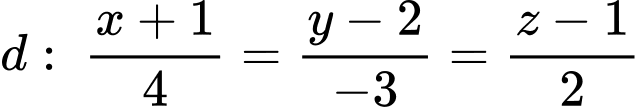 . Mặt phẳng
. Mặt phẳng 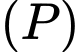 chứa đường thẳng
chứa đường thẳng 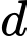 đồng thời cách điểm
đồng thời cách điểm 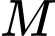 một khoảng lớn nhất có phương trình dạng
một khoảng lớn nhất có phương trình dạng 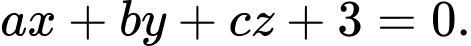 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
A, 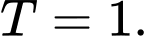
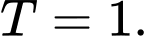
B, 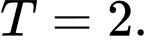
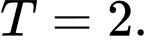
C, 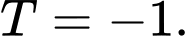
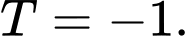
D, 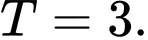
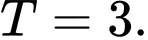
 Đáp án: C
Đáp án: C
Câu 9 [82651]: Trong không gian với hệ tọa độ 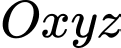 cho điểm
cho điểm 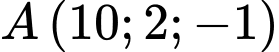 và đường thẳng
và đường thẳng 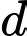 có phương trình
có phương trình 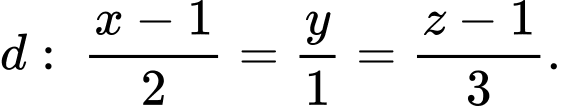 Mặt phẳng
Mặt phẳng 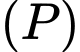 đi qua
đi qua 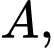 song song với
song song với 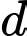 và khoảng cách từ
và khoảng cách từ 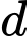 đến
đến 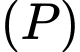 là lớn nhất có một vectơ pháp tuyến là
là lớn nhất có một vectơ pháp tuyến là 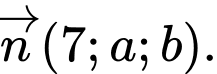 Tính giá trị của biểu thức
Tính giá trị của biểu thức 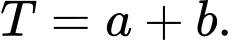
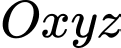 cho điểm
cho điểm 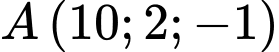 và đường thẳng
và đường thẳng 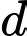 có phương trình
có phương trình 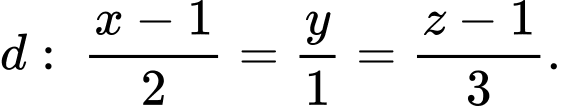 Mặt phẳng
Mặt phẳng 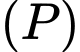 đi qua
đi qua 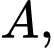 song song với
song song với 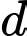 và khoảng cách từ
và khoảng cách từ 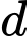 đến
đến 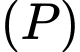 là lớn nhất có một vectơ pháp tuyến là
là lớn nhất có một vectơ pháp tuyến là 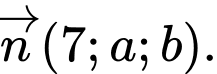 Tính giá trị của biểu thức
Tính giá trị của biểu thức 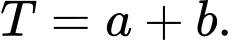
A, 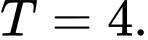
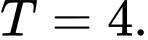
B, 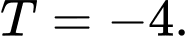
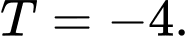
C, 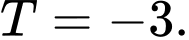
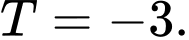
D, 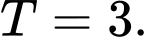
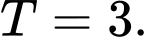
 Đáp án: B
Đáp án: B
Câu 10 [57935]: Trong không gian 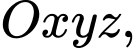 phương trình mặt phẳng
phương trình mặt phẳng 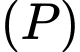 đi qua hai điểm
đi qua hai điểm 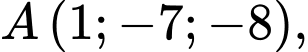
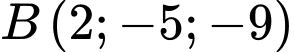 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm 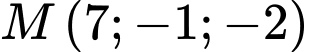 đến
đến 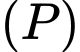 lớn nhất có một vectơ pháp tuyến là
lớn nhất có một vectơ pháp tuyến là 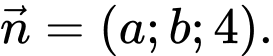 Giá trị của tổng
Giá trị của tổng  là
là
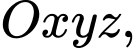 phương trình mặt phẳng
phương trình mặt phẳng 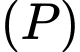 đi qua hai điểm
đi qua hai điểm 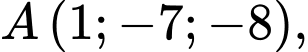
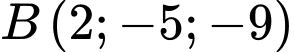 sao cho khoảng cách từ điểm
sao cho khoảng cách từ điểm 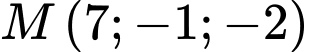 đến
đến 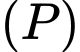 lớn nhất có một vectơ pháp tuyến là
lớn nhất có một vectơ pháp tuyến là 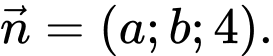 Giá trị của tổng
Giá trị của tổng  là
là A, 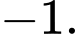
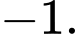
B, 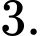
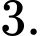
C, 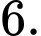
D, 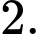
Ta có 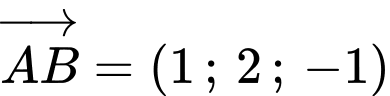
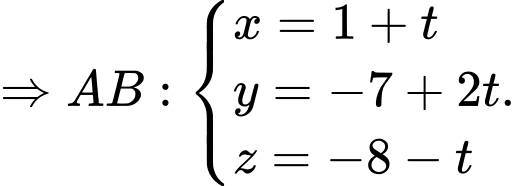
Gọi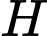 là hình chiếu của
là hình chiếu của 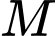 lên đường thẳng
lên đường thẳng 
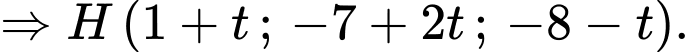
Suy ra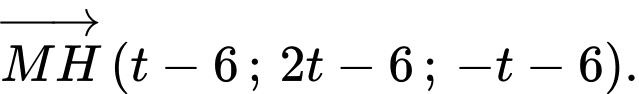
Vì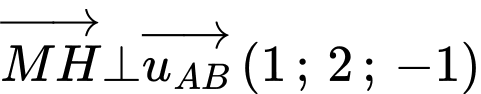
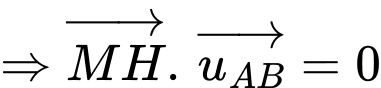
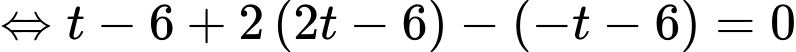

Khoảng cách từ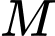 đến
đến 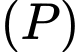 lớn nhất, suy ra
lớn nhất, suy ra 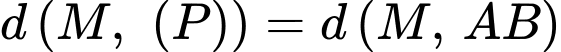
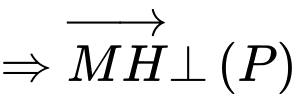
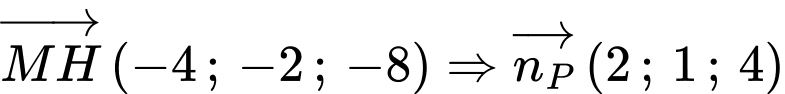
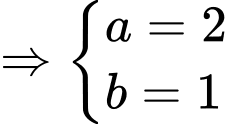
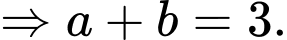
Chọn B. Đáp án: B
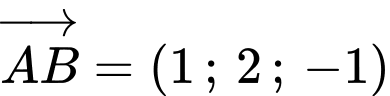
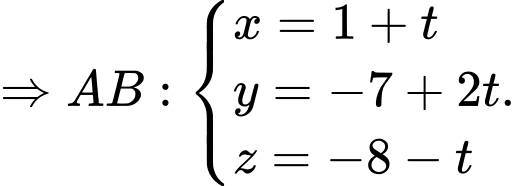
Gọi
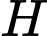 là hình chiếu của
là hình chiếu của 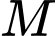 lên đường thẳng
lên đường thẳng 
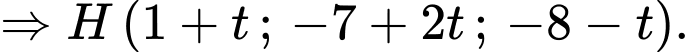
Suy ra
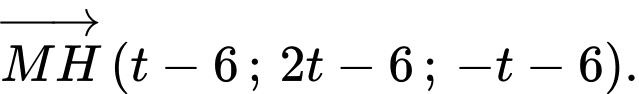
Vì
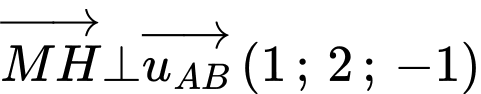
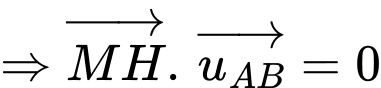
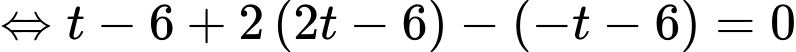

Khoảng cách từ
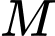 đến
đến 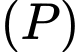 lớn nhất, suy ra
lớn nhất, suy ra 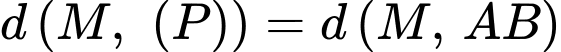
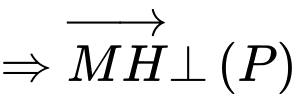
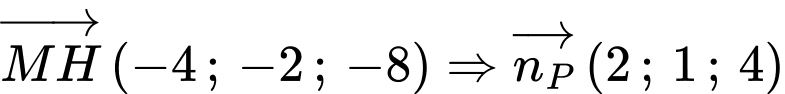
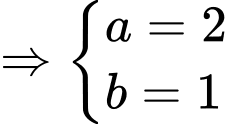
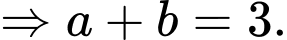
Chọn B. Đáp án: B
Câu 11 [82652]: Trong không gian tọa độ Oxyz cho đường thẳng 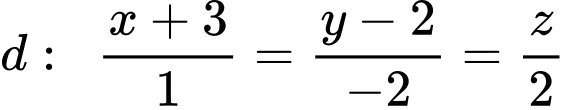 . Gọi
. Gọi  là đường thẳng qua
là đường thẳng qua 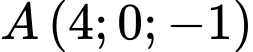 song song với
song song với 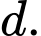 Mặt phẳng
Mặt phẳng 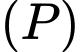 chứa
chứa  và khoảng cách giữa
và khoảng cách giữa 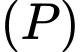 và đường thẳng
và đường thẳng 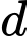 lớn nhất có phương trình dạng
lớn nhất có phương trình dạng 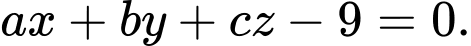 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
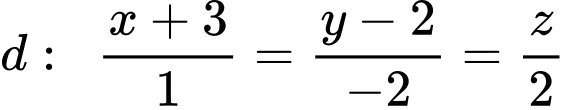 . Gọi
. Gọi  là đường thẳng qua
là đường thẳng qua 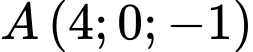 song song với
song song với 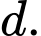 Mặt phẳng
Mặt phẳng 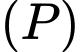 chứa
chứa  và khoảng cách giữa
và khoảng cách giữa 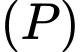 và đường thẳng
và đường thẳng 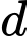 lớn nhất có phương trình dạng
lớn nhất có phương trình dạng 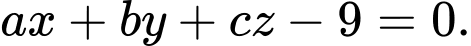 Tính giá trị của biểu thức
Tính giá trị của biểu thức 
A, 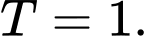
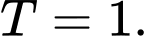
B, 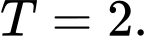
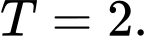
C, 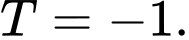
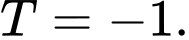
D, 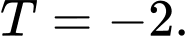
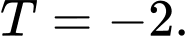
Phương trình đường thẳng 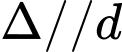 là
là 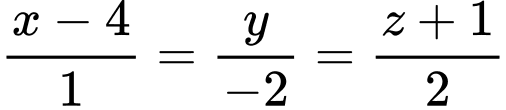
Đường thẳng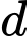 đi qua điểm
đi qua điểm 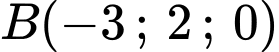 ta có:
ta có: 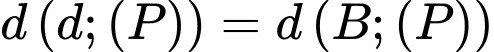 lớn nhất khi và chỉ khi
lớn nhất khi và chỉ khi
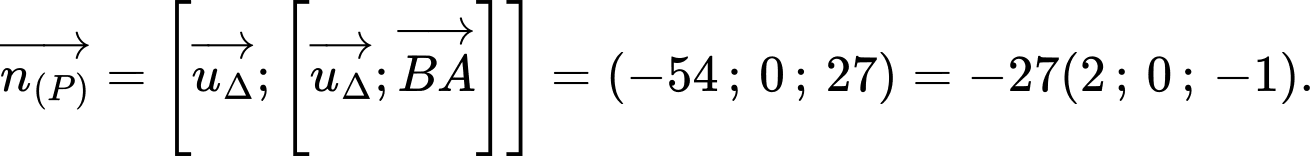
Phương trình mặt phẳng qua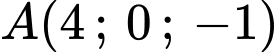 và có vectơ pháp tuyến
và có vectơ pháp tuyến 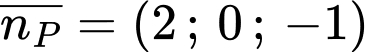 là:
là:
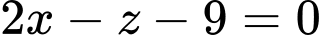
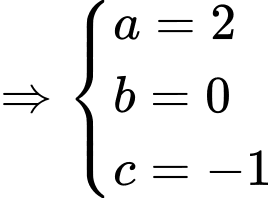
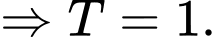
Chọn đáp án A Đáp án: A
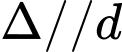 là
là 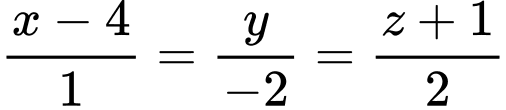
Đường thẳng
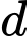 đi qua điểm
đi qua điểm 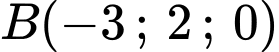 ta có:
ta có: 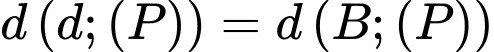 lớn nhất khi và chỉ khi
lớn nhất khi và chỉ khi
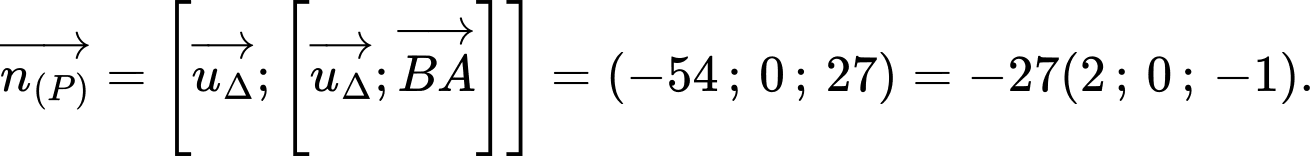
Phương trình mặt phẳng qua
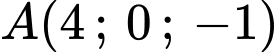 và có vectơ pháp tuyến
và có vectơ pháp tuyến 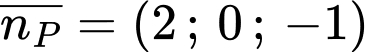 là:
là:
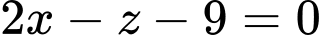
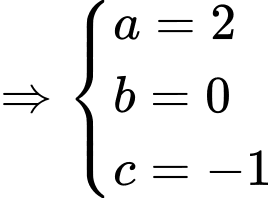
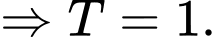
Chọn đáp án A Đáp án: A
Câu 12 [82654]: [Đề thi THPT QG năm 2017] Trong không gian với hệ tọa độ 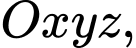 cho hai điểm
cho hai điểm 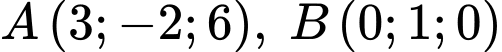 và mặt cầu
và mặt cầu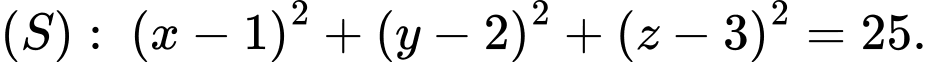 Mặt phẳng
Mặt phẳng 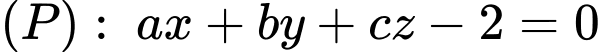 đi qua
đi qua 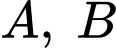 và cắt
và cắt 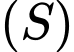 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính 
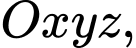 cho hai điểm
cho hai điểm 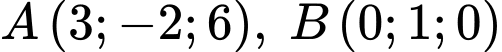 và mặt cầu
và mặt cầu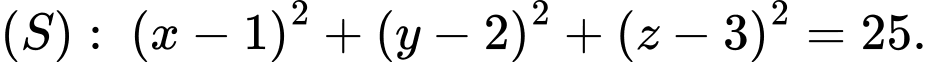 Mặt phẳng
Mặt phẳng 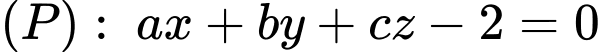 đi qua
đi qua 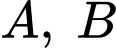 và cắt
và cắt 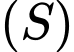 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính 
A, 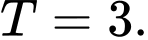
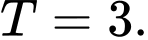
B, 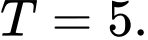
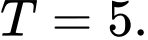
C, 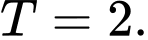
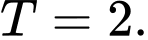
D, 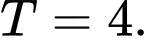
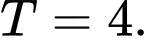
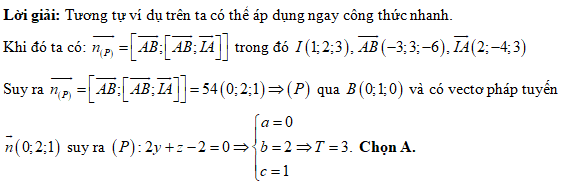 Đáp án: A
Đáp án: A
Câu 13 [82655]: Trong không gian với hệ tọa độ 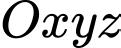 cho cho điểm
cho cho điểm 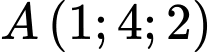 và đường thẳng
và đường thẳng 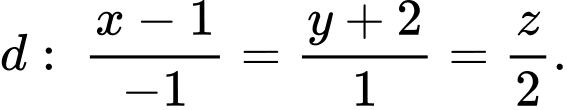 Mặt phẳng
Mặt phẳng 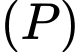 chứa đường thẳng
chứa đường thẳng 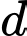 đồng thời cách điểm
đồng thời cách điểm 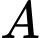 một khoảng lớn nhất có một vectơ pháp tuyến là
một khoảng lớn nhất có một vectơ pháp tuyến là 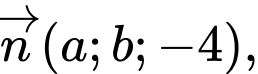 tính
tính 
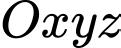 cho cho điểm
cho cho điểm 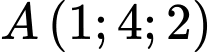 và đường thẳng
và đường thẳng 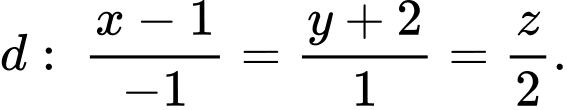 Mặt phẳng
Mặt phẳng 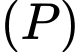 chứa đường thẳng
chứa đường thẳng 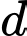 đồng thời cách điểm
đồng thời cách điểm 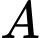 một khoảng lớn nhất có một vectơ pháp tuyến là
một khoảng lớn nhất có một vectơ pháp tuyến là 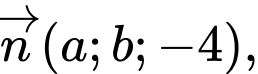 tính
tính 
A, 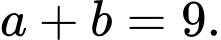
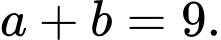
B, 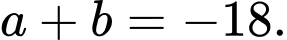
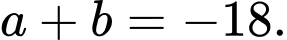
C, 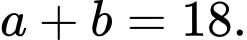
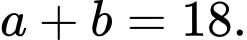
D, 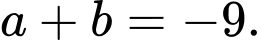
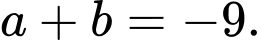
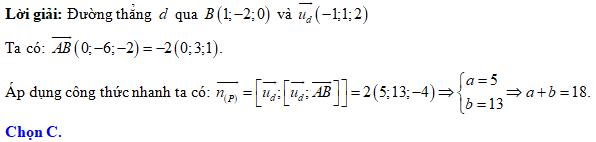 Đáp án: C
Đáp án: C
Câu 14 [82656]: Trong không gian 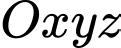 , cho điểm
, cho điểm 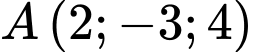 , đường thẳng
, đường thẳng 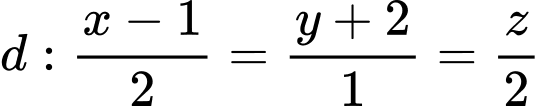 và mặt cầu
và mặt cầu 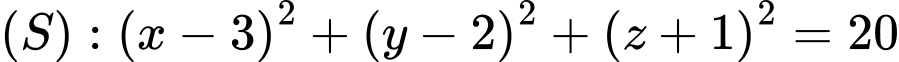 . Mặt phẳng
. Mặt phẳng 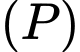 chứa đường thẳng
chứa đường thẳng 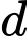 thỏa mãn khoảng cách từ điểm
thỏa mãn khoảng cách từ điểm 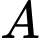 đến
đến 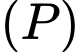 lớn nhất. Mặt cầu
lớn nhất. Mặt cầu 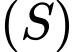 cắt
cắt 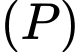 theo đường tròn có bán kính bằng
theo đường tròn có bán kính bằng
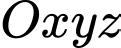 , cho điểm
, cho điểm 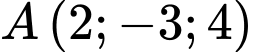 , đường thẳng
, đường thẳng 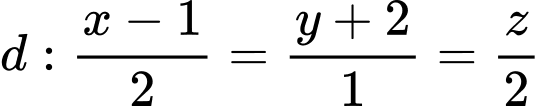 và mặt cầu
và mặt cầu 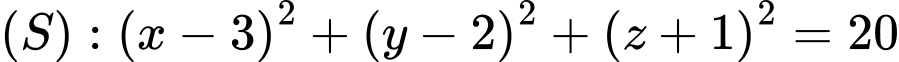 . Mặt phẳng
. Mặt phẳng 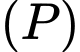 chứa đường thẳng
chứa đường thẳng 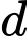 thỏa mãn khoảng cách từ điểm
thỏa mãn khoảng cách từ điểm 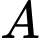 đến
đến 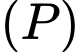 lớn nhất. Mặt cầu
lớn nhất. Mặt cầu 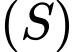 cắt
cắt 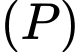 theo đường tròn có bán kính bằng
theo đường tròn có bán kính bằng A, 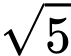 .
.
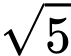 .
.B, 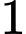 .
.
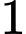 .
.C, 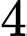 .
.
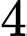 .
.D, 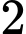 .
.
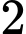 .
. Đáp án: D
Đáp án: D
Câu 15 [57951]: Trong không gian với hệ tọa độ 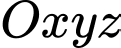 , cho điểm
, cho điểm 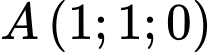 và đường thẳng
và đường thẳng 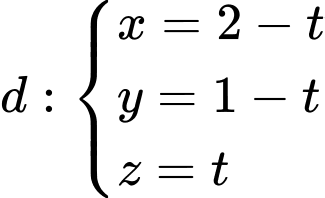 . Mặt phẳng
. Mặt phẳng 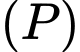 qua
qua 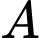 , song song với
, song song với 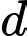 đồng thời khoảng cách từ gốc tọa
đồng thời khoảng cách từ gốc tọa  đến
đến 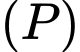 lớn nhất. Biết
lớn nhất. Biết 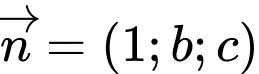 là 1 vectơ pháp tuyến của
là 1 vectơ pháp tuyến của 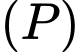 . Tính
. Tính 
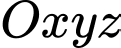 , cho điểm
, cho điểm 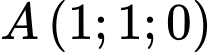 và đường thẳng
và đường thẳng 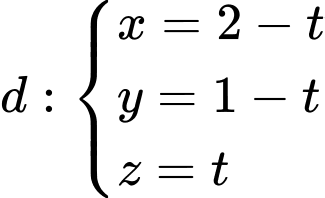 . Mặt phẳng
. Mặt phẳng 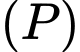 qua
qua 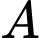 , song song với
, song song với 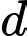 đồng thời khoảng cách từ gốc tọa
đồng thời khoảng cách từ gốc tọa  đến
đến 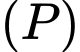 lớn nhất. Biết
lớn nhất. Biết 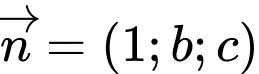 là 1 vectơ pháp tuyến của
là 1 vectơ pháp tuyến của 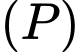 . Tính
. Tính 
A, 0.
B, 3.
C, 1.
D, 2.
Chọn đáp án B.
Gọi phương trình mặt phẳng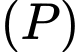 có dạng
có dạng 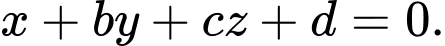
Ta có: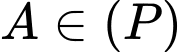
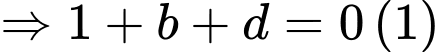 và
và 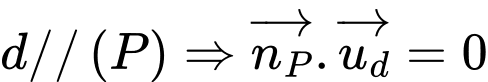
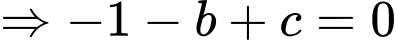
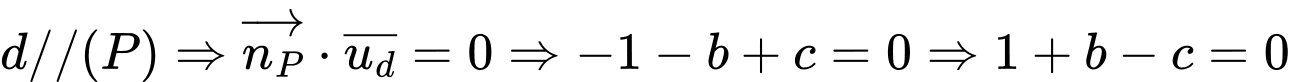
Từ (1), (2)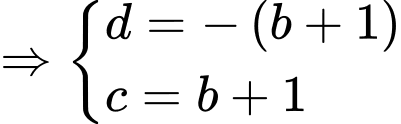
Do đó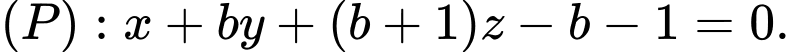
Xét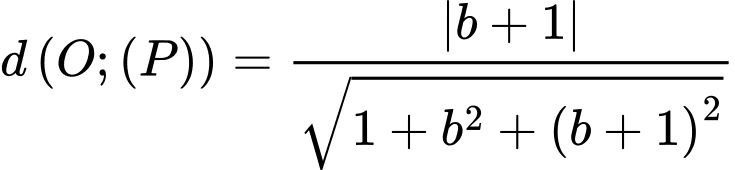
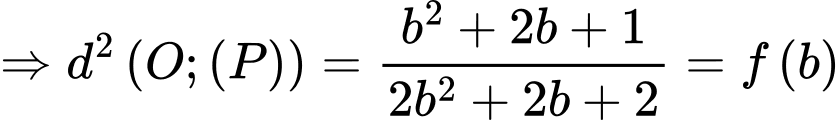
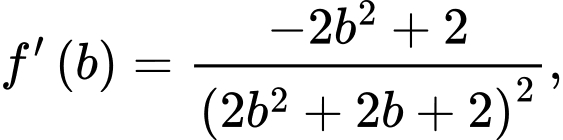
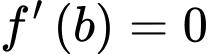
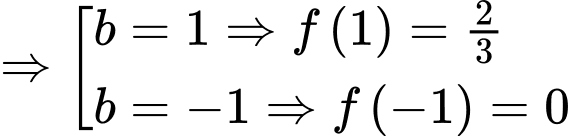
Đồng thời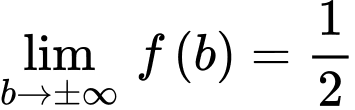
Lập bảng biến thiên, ta được
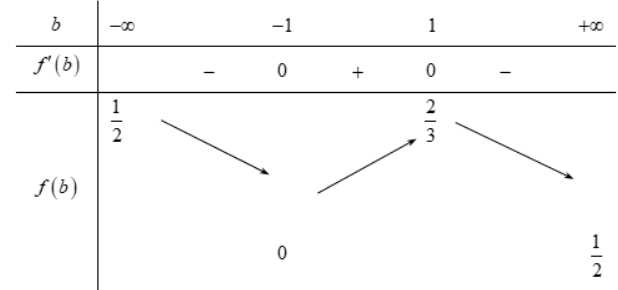
Dựa vào bảng biến thiên ta thấy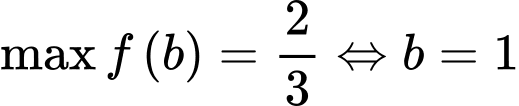
Do đó
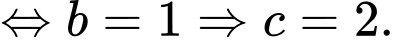
Vậy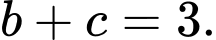 Đáp án: B
Đáp án: B
Gọi phương trình mặt phẳng
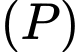 có dạng
có dạng 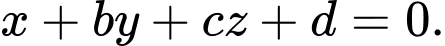
Ta có:
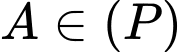
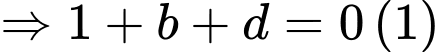 và
và 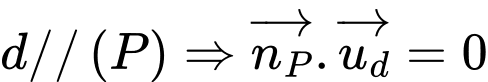
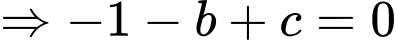
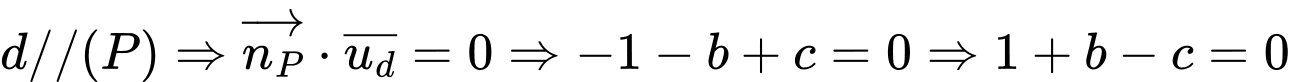
Từ (1), (2)
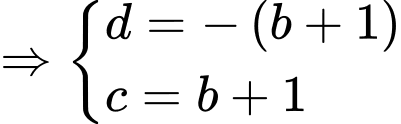
Do đó
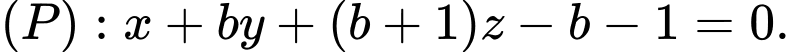
Xét
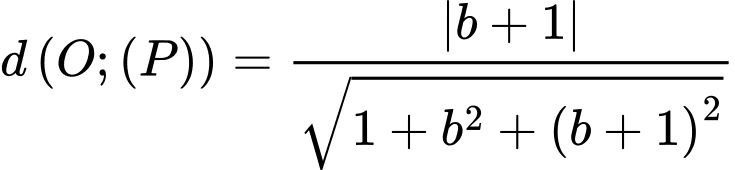
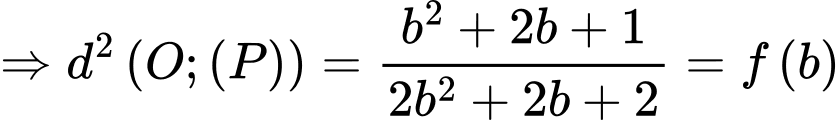
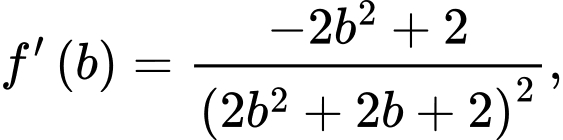
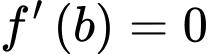
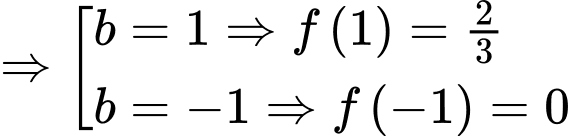
Đồng thời
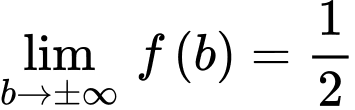
Lập bảng biến thiên, ta được

Dựa vào bảng biến thiên ta thấy
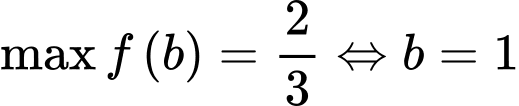
Do đó

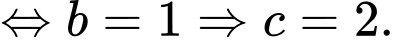
Vậy
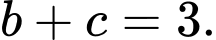 Đáp án: B
Đáp án: B
Câu 16 [57959]: Trong không gian với hệ trục tọa độ 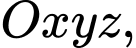 cho điểm
cho điểm 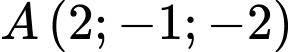 và đường thẳng
và đường thẳng 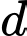 có phương trình
có phương trình 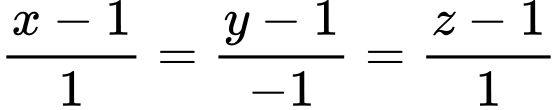 . Gọi
. Gọi 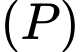 là mặt phẳng đi qua điểm
là mặt phẳng đi qua điểm 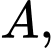 song song với đường thẳng
song song với đường thẳng 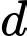 và khoảng cách từ đường thẳng
và khoảng cách từ đường thẳng 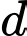 tới mặt phẳng
tới mặt phẳng 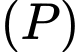 là lớn nhất. Khi đó mặt phẳng
là lớn nhất. Khi đó mặt phẳng 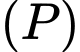 vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây?
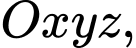 cho điểm
cho điểm 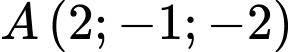 và đường thẳng
và đường thẳng 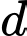 có phương trình
có phương trình 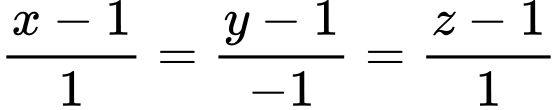 . Gọi
. Gọi 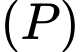 là mặt phẳng đi qua điểm
là mặt phẳng đi qua điểm 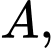 song song với đường thẳng
song song với đường thẳng 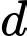 và khoảng cách từ đường thẳng
và khoảng cách từ đường thẳng 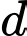 tới mặt phẳng
tới mặt phẳng 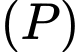 là lớn nhất. Khi đó mặt phẳng
là lớn nhất. Khi đó mặt phẳng 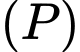 vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây? A, 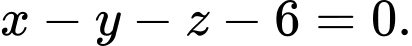
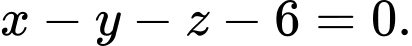
B, 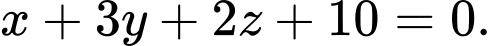
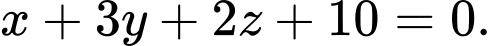
C, 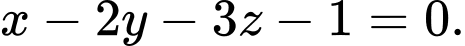
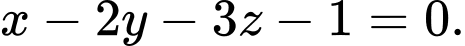
D, 

 Đáp án: D
Đáp án: D
Câu 17 [57938]: Trong không gian với hệ tọa độ 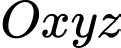 , cho mặt cầu
, cho mặt cầu 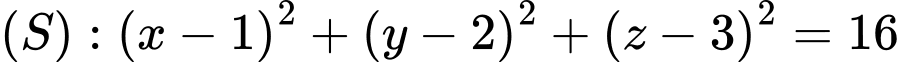 và các điểm
và các điểm 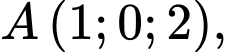
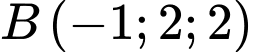 . Gọi
. Gọi 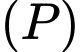 là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 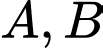 sao cho thiết diện của mặt phẳng
sao cho thiết diện của mặt phẳng 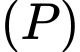 và mặt cầu
và mặt cầu 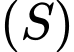 có diện tích nhỏ nhất. Khi đó phương trình (P) có dạng
có diện tích nhỏ nhất. Khi đó phương trình (P) có dạng 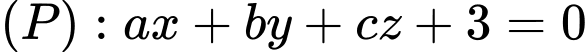 . Tính giá trị của
. Tính giá trị của 
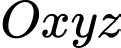 , cho mặt cầu
, cho mặt cầu 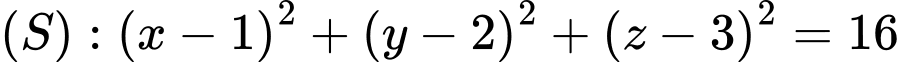 và các điểm
và các điểm 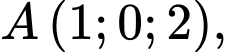
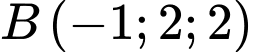 . Gọi
. Gọi 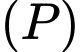 là mặt phẳng đi qua hai điểm
là mặt phẳng đi qua hai điểm 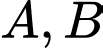 sao cho thiết diện của mặt phẳng
sao cho thiết diện của mặt phẳng 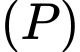 và mặt cầu
và mặt cầu 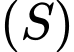 có diện tích nhỏ nhất. Khi đó phương trình (P) có dạng
có diện tích nhỏ nhất. Khi đó phương trình (P) có dạng 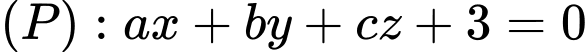 . Tính giá trị của
. Tính giá trị của 
A, 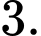
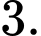
B, 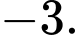
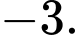
C, 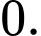
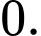
D, 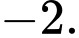
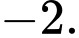
 Đáp án: B
Đáp án: B
Câu 18 [57947]: Trong không gian 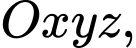 cho mặt cầu
cho mặt cầu 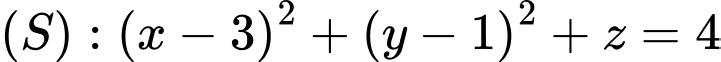 và đường thẳng
và đường thẳng 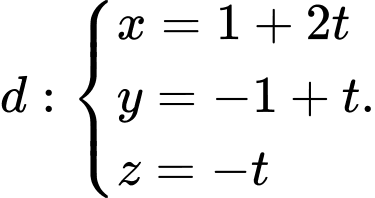 Gọi
Gọi 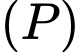 là mặt phẳng chứa
là mặt phẳng chứa 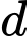 và cắt
và cắt 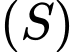 theo một đường tròn có bán kính nhỏ nhất, phương trình của
theo một đường tròn có bán kính nhỏ nhất, phương trình của 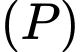 là
là
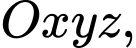 cho mặt cầu
cho mặt cầu 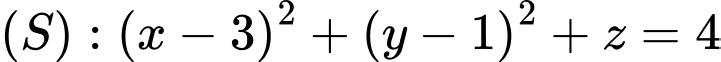 và đường thẳng
và đường thẳng 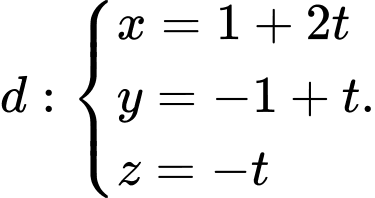 Gọi
Gọi 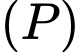 là mặt phẳng chứa
là mặt phẳng chứa 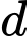 và cắt
và cắt 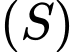 theo một đường tròn có bán kính nhỏ nhất, phương trình của
theo một đường tròn có bán kính nhỏ nhất, phương trình của 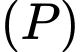 là
là A, 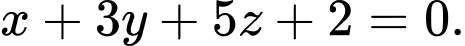
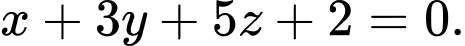
B, 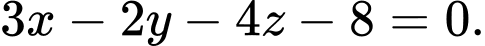
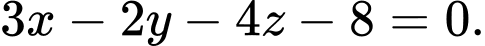
C, 

D, 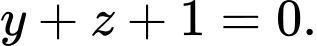
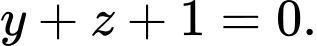
 Đáp án: D
Đáp án: D
Câu 19 [57950]: Trong không gian với hệ tọa độ 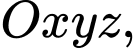 cho mặt cầu
cho mặt cầu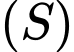 có phương trình
có phương trình 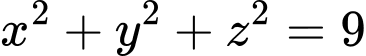 và điểm
và điểm 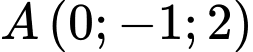 . Gọi
. Gọi 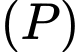 là mặt phẳng qua
là mặt phẳng qua 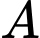 và cắt mặt cầu
và cắt mặt cầu 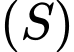 theo một đường tròn có chu vi nhỏ nhất. Phương trình của
theo một đường tròn có chu vi nhỏ nhất. Phương trình của 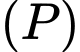 là
là
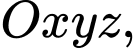 cho mặt cầu
cho mặt cầu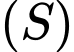 có phương trình
có phương trình 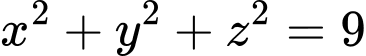 và điểm
và điểm 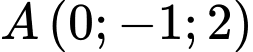 . Gọi
. Gọi 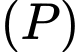 là mặt phẳng qua
là mặt phẳng qua 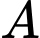 và cắt mặt cầu
và cắt mặt cầu 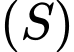 theo một đường tròn có chu vi nhỏ nhất. Phương trình của
theo một đường tròn có chu vi nhỏ nhất. Phương trình của 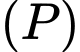 là
là A, 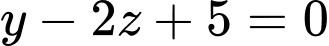 .
.
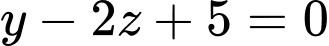 .
.B, 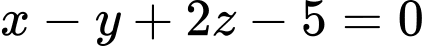 .
.
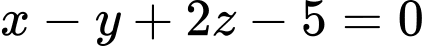 .
.C, 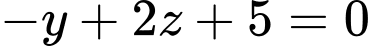 .
.
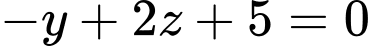 .
.D, 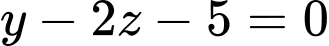 .
.
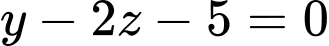 .
. Đáp án: A
Đáp án: A
Câu 20 [57953]: Trong không gian với hệ tọa độ 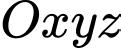 , cho mặt cầu
, cho mặt cầu 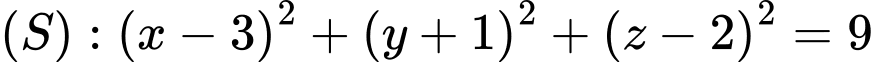 và điểm
và điểm 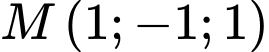 . Mặt phẳng
. Mặt phẳng 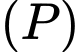 đi qua
đi qua 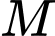 và cắt
và cắt 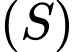 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Biết phương trình mặt phẳng
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Biết phương trình mặt phẳng 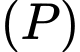 có dạng
có dạng 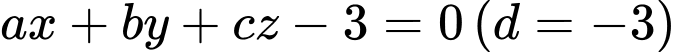 . Tính
. Tính 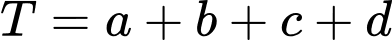 .
.
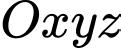 , cho mặt cầu
, cho mặt cầu 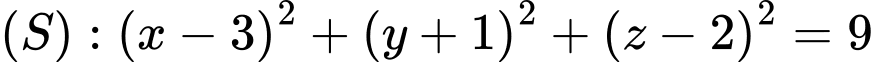 và điểm
và điểm 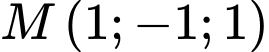 . Mặt phẳng
. Mặt phẳng 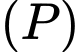 đi qua
đi qua 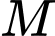 và cắt
và cắt 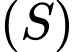 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Biết phương trình mặt phẳng
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Biết phương trình mặt phẳng 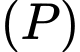 có dạng
có dạng 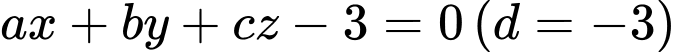 . Tính
. Tính 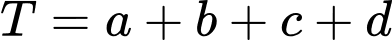 .
. A, 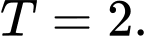
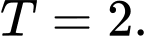
B, 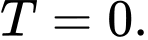
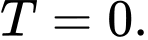
C, 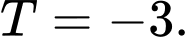
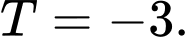
D, 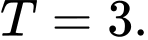
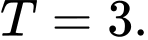
 Đáp án: B
Đáp án: B
Câu 21 [57954]: Cho mặt cầu 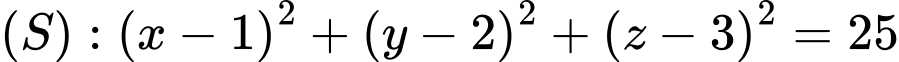 và hai điểm
và hai điểm 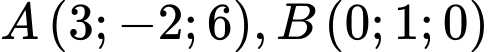 . Giả sử
. Giả sử 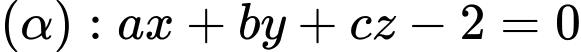 đi qua
đi qua 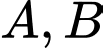 và cắt
và cắt 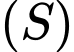 theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính 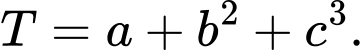
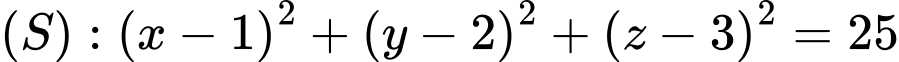 và hai điểm
và hai điểm 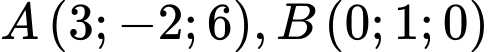 . Giả sử
. Giả sử 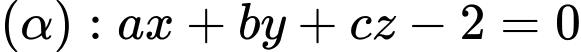 đi qua
đi qua 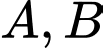 và cắt
và cắt 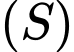 theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính 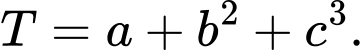
A, 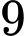 .
.
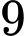 .
.B,  .
.
 .
.C, 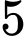 .
.
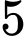 .
.D, 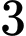 .
.
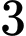 .
. Đáp án: C
Đáp án: C
Câu 22 [57957]: Trong không gian với hệ trục tọa độ 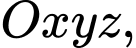 cho điểm
cho điểm 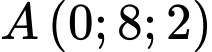 và mặt cầu
và mặt cầu 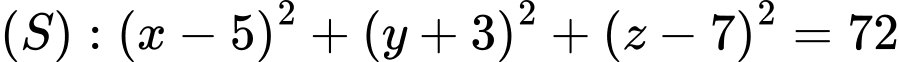 và điểm
và điểm 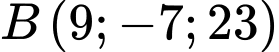 . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng 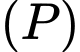 đi qua
đi qua 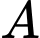 và tiếp xúc với
và tiếp xúc với 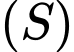 sao cho khoảng cách từ
sao cho khoảng cách từ 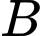 đến
đến 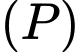 là lớn nhất. Giả sử
là lớn nhất. Giả sử 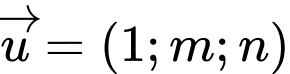 là một vectơ pháp tuyến của
là một vectơ pháp tuyến của 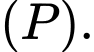 Khi đó
Khi đó 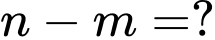
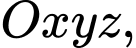 cho điểm
cho điểm 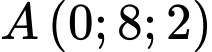 và mặt cầu
và mặt cầu 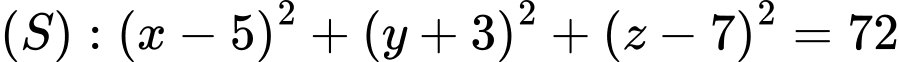 và điểm
và điểm 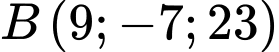 . Viết phương trình mặt phẳng
. Viết phương trình mặt phẳng 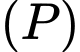 đi qua
đi qua 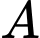 và tiếp xúc với
và tiếp xúc với 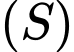 sao cho khoảng cách từ
sao cho khoảng cách từ 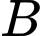 đến
đến 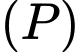 là lớn nhất. Giả sử
là lớn nhất. Giả sử 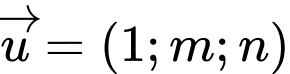 là một vectơ pháp tuyến của
là một vectơ pháp tuyến của 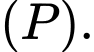 Khi đó
Khi đó 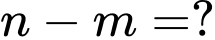
A, 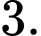
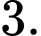
B, 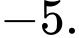
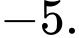
C, 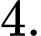
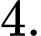
D, 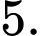
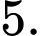

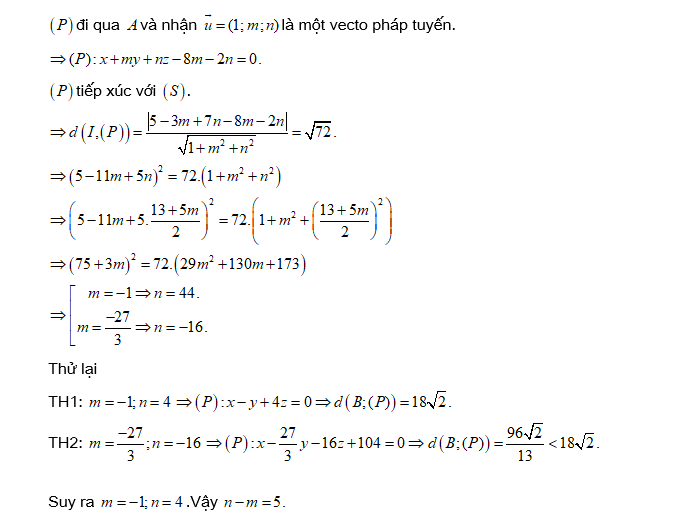 Đáp án: D
Đáp án: D
Câu 23 [53369]: Trong không gian với hệ tọa độ 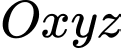 , gọi
, gọi 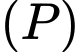 là mặt phẳng đi qua
là mặt phẳng đi qua 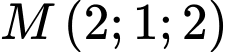 và cắt các tia
và cắt các tia 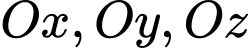 lần lượt tại
lần lượt tại 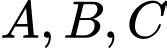 sao cho thể tích của khối tứ diện
sao cho thể tích của khối tứ diện 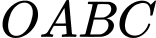 là nhỏ nhất. Phương trình mặt phẳng
là nhỏ nhất. Phương trình mặt phẳng 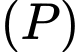 là
là
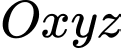 , gọi
, gọi 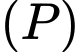 là mặt phẳng đi qua
là mặt phẳng đi qua 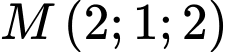 và cắt các tia
và cắt các tia 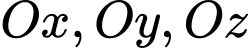 lần lượt tại
lần lượt tại 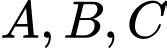 sao cho thể tích của khối tứ diện
sao cho thể tích của khối tứ diện 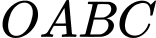 là nhỏ nhất. Phương trình mặt phẳng
là nhỏ nhất. Phương trình mặt phẳng 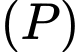 là
là A, 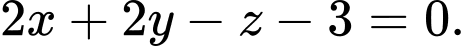
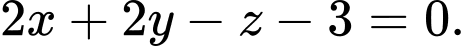
B, 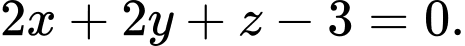
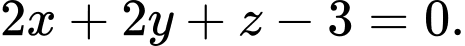
C, 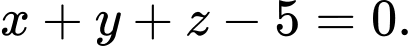
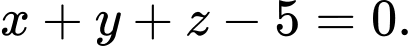
D, 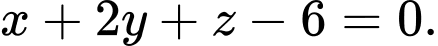
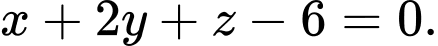
 Đáp án: D
Đáp án: D
Câu 24 [53397]: Trong không gian với hệ tọa độ 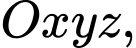 cho điểm
cho điểm 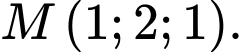 Mặt phẳng
Mặt phẳng  thay đổi đi qua
thay đổi đi qua 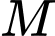 lần lượt cắt các tia
lần lượt cắt các tia 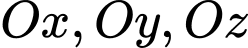 tại
tại 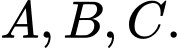 Giá trị nhỏ nhất của thể tích khối tứ diện
Giá trị nhỏ nhất của thể tích khối tứ diện 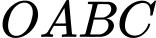 là
là
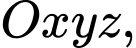 cho điểm
cho điểm 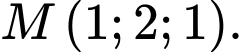 Mặt phẳng
Mặt phẳng  thay đổi đi qua
thay đổi đi qua 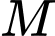 lần lượt cắt các tia
lần lượt cắt các tia 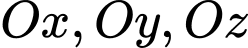 tại
tại 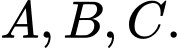 Giá trị nhỏ nhất của thể tích khối tứ diện
Giá trị nhỏ nhất của thể tích khối tứ diện 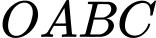 là
là A, 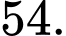
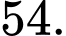
B, 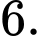
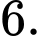
C, 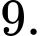
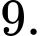
D, 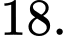
Chọn đáp án C.
Giả sử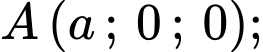
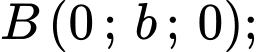
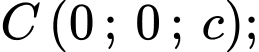
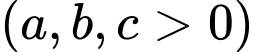
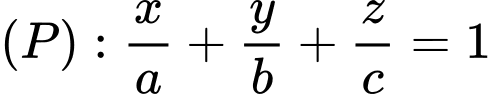 đi qua
đi qua 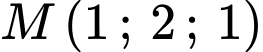
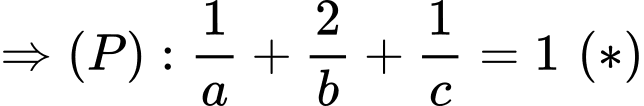
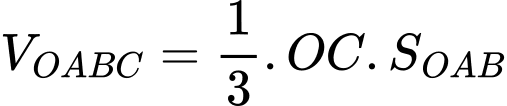
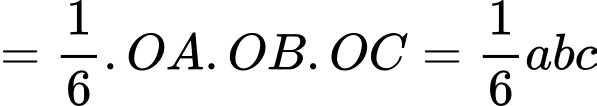
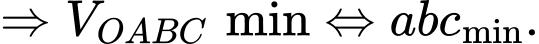
Theo bất đẳng thức Co-si ta có:
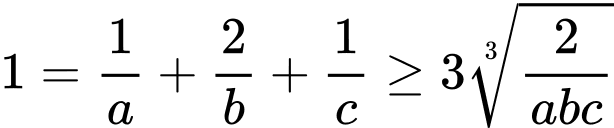
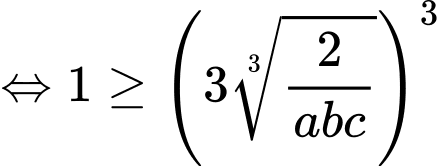
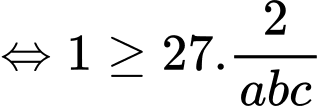
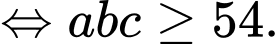
Dấu “=” xảy ra khi và chỉ khi: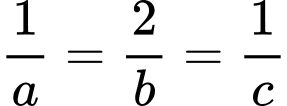
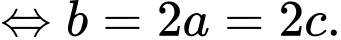
Vậy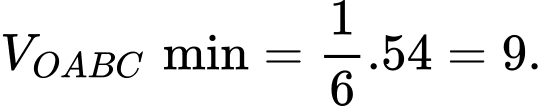 Đáp án: C
Đáp án: C
Giả sử
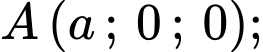
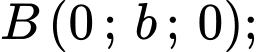
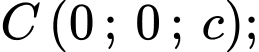
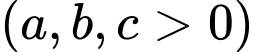
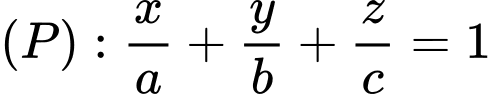 đi qua
đi qua 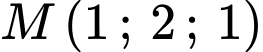
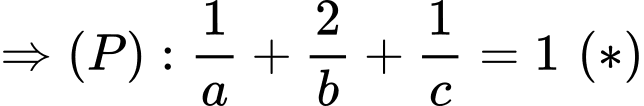
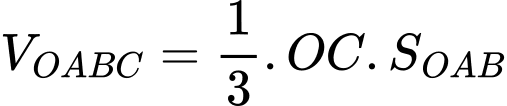
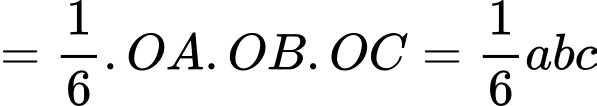
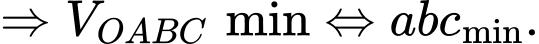
Theo bất đẳng thức Co-si ta có:
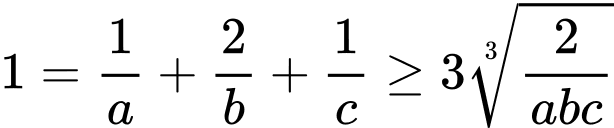
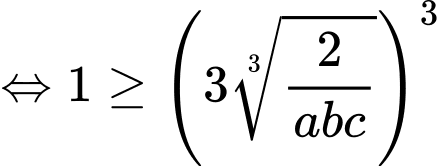
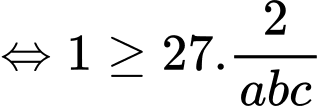
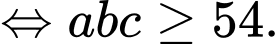
Dấu “=” xảy ra khi và chỉ khi:
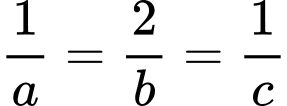
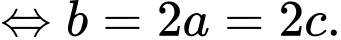
Vậy
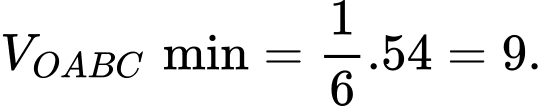 Đáp án: C
Đáp án: C
Câu 25 [53375]: Trong không gian với hệ tọa độ 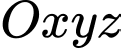 , mặt phẳng
, mặt phẳng 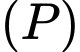 đi qua điểm
đi qua điểm 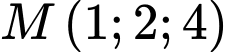 và cắt các trục tọa độ
và cắt các trục tọa độ 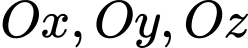 lần lượt tại
lần lượt tại 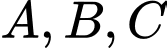 thỏa mãn
thỏa mãn 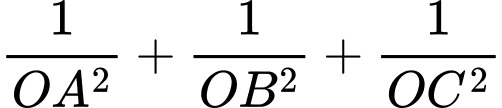 nhỏ nhất. Mặt phẳng
nhỏ nhất. Mặt phẳng 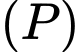 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây?
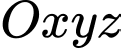 , mặt phẳng
, mặt phẳng 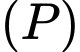 đi qua điểm
đi qua điểm 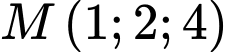 và cắt các trục tọa độ
và cắt các trục tọa độ 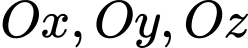 lần lượt tại
lần lượt tại 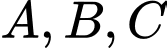 thỏa mãn
thỏa mãn 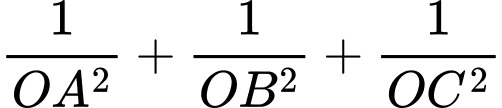 nhỏ nhất. Mặt phẳng
nhỏ nhất. Mặt phẳng 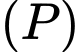 đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây? A, 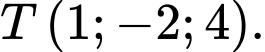
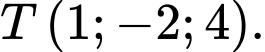
B, 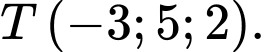
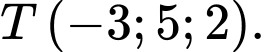
C, 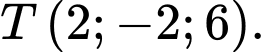
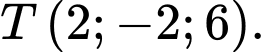
D, 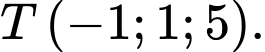
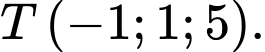
 Đáp án: D
Đáp án: D
Câu 26 [899298]: Trong không gian với hệ trục tọa độ 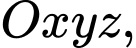 cho
cho 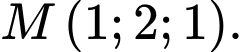 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 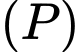 qua
qua 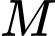 lần lượt cắt các trục
lần lượt cắt các trục 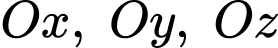 lần lượt tại
lần lượt tại 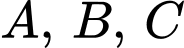 sao cho
sao cho 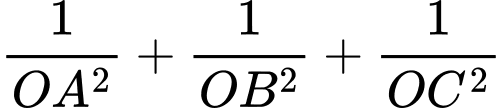 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
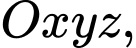 cho
cho 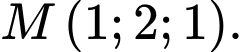 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 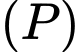 qua
qua 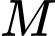 lần lượt cắt các trục
lần lượt cắt các trục 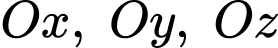 lần lượt tại
lần lượt tại 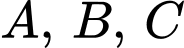 sao cho
sao cho 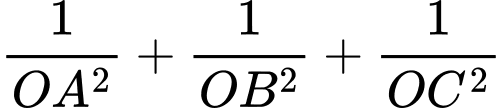 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất. A, 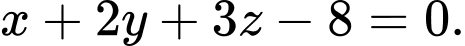
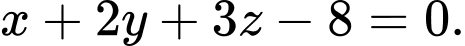
B, 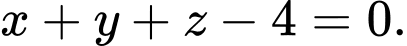
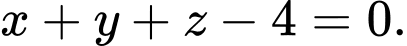
C, 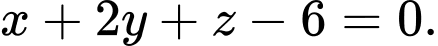
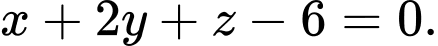
D, 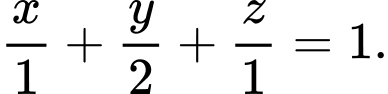
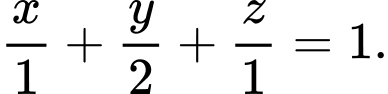
Gọi tọa độ các điểm 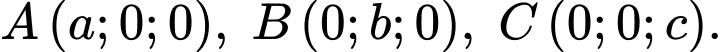
Phương trình đoạn chắn của mặt phẳng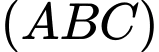 là:
là: 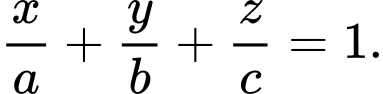
Điểm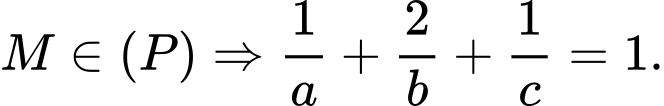 Xét
Xét 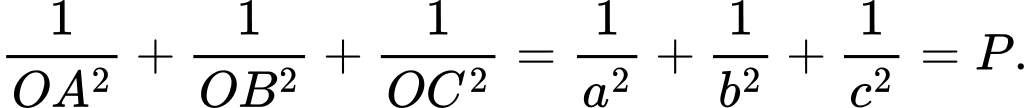
Lại có: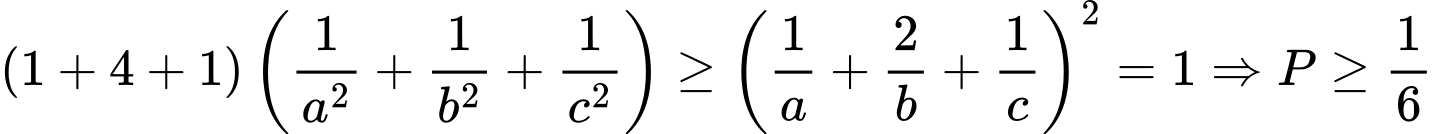 (Theo BĐT Bunhiacopxki).
(Theo BĐT Bunhiacopxki).
Dấu bằng xảy ra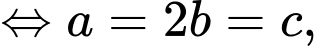 kết hợp
kết hợp 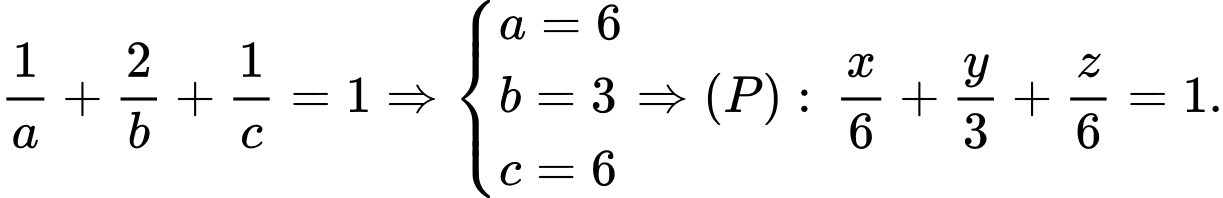
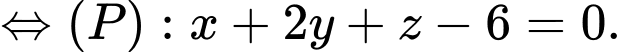 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
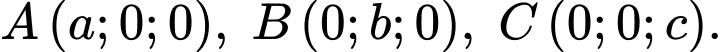
Phương trình đoạn chắn của mặt phẳng
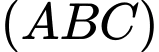 là:
là: 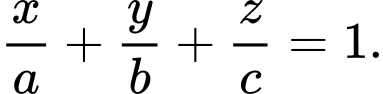
Điểm
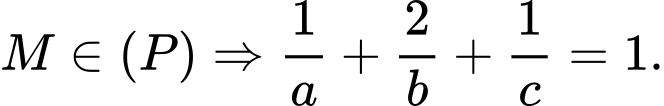 Xét
Xét 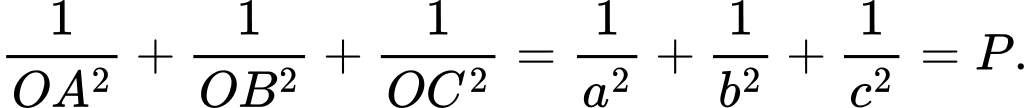
Lại có:
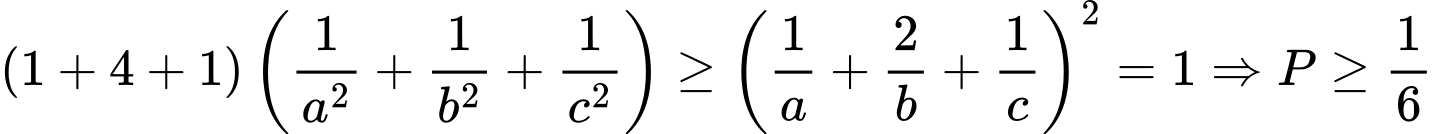 (Theo BĐT Bunhiacopxki).
(Theo BĐT Bunhiacopxki). Dấu bằng xảy ra
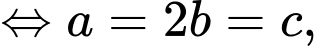 kết hợp
kết hợp 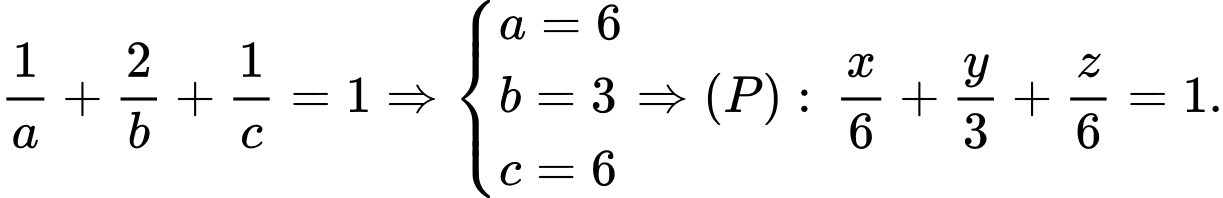
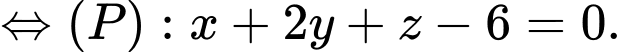 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 27 [82000]: Trong không gian với hệ tọa độ 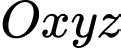 gọi
gọi 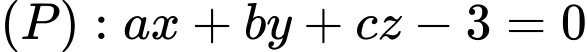 (với
(với 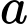 ,
, 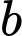 ,
,  là các số nguyên không đồng thời bằng 0) là phương trình mặt phẳng đi qua hai điểm
là các số nguyên không đồng thời bằng 0) là phương trình mặt phẳng đi qua hai điểm 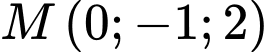 ,
, 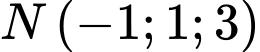 và không đi qua điểm
và không đi qua điểm 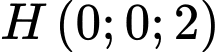 . Biết rằng khoảng cách từ
. Biết rằng khoảng cách từ 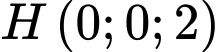 đến mặt phẳng
đến mặt phẳng 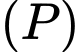 đạt giá trị lớn nhất. Tổng
đạt giá trị lớn nhất. Tổng 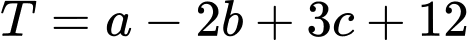 bằng
bằng
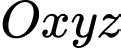 gọi
gọi 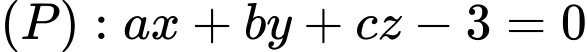 (với
(với 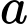 ,
, 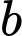 ,
,  là các số nguyên không đồng thời bằng 0) là phương trình mặt phẳng đi qua hai điểm
là các số nguyên không đồng thời bằng 0) là phương trình mặt phẳng đi qua hai điểm 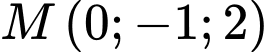 ,
, 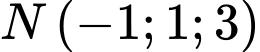 và không đi qua điểm
và không đi qua điểm 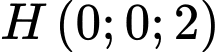 . Biết rằng khoảng cách từ
. Biết rằng khoảng cách từ 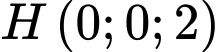 đến mặt phẳng
đến mặt phẳng 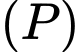 đạt giá trị lớn nhất. Tổng
đạt giá trị lớn nhất. Tổng 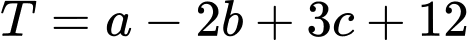 bằng
bằng A, 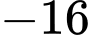 .
.
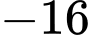 .
.B, 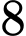 .
.
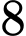 .
.C,  .
.
 .
.D, 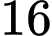 .
.
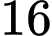 .
.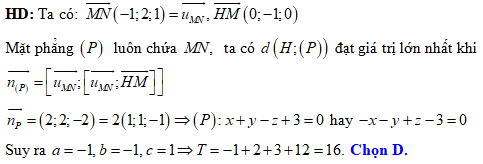 Đáp án: D
Đáp án: D
Câu 28 [809361]: Trong không gian toạ độ 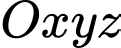 , cho bốn điểm
, cho bốn điểm 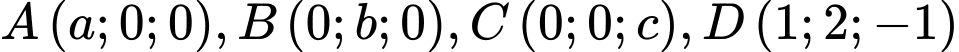 , với
, với 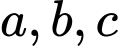 là các số thực khác
là các số thực khác  . Biết rằng bốn điểm
. Biết rằng bốn điểm 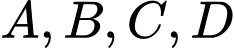 đồng phẳng khi khoảng cách từ gốc toạ độ
đồng phẳng khi khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 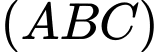 là lớn nhất, giá trị
là lớn nhất, giá trị 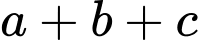 bằng
bằng
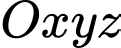 , cho bốn điểm
, cho bốn điểm 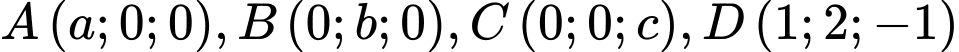 , với
, với 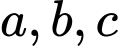 là các số thực khác
là các số thực khác  . Biết rằng bốn điểm
. Biết rằng bốn điểm 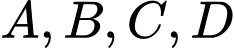 đồng phẳng khi khoảng cách từ gốc toạ độ
đồng phẳng khi khoảng cách từ gốc toạ độ  đến mặt phẳng
đến mặt phẳng 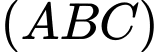 là lớn nhất, giá trị
là lớn nhất, giá trị 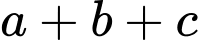 bằng
bằng A, 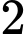 .
.
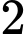 .
.B, 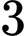 .
.
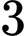 .
.C,  .
.
 .
.D, 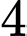 .
.
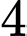 .
.
Chọn B
Ta có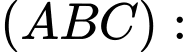
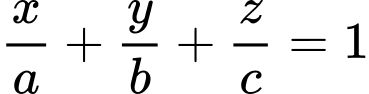 và
và 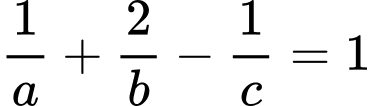 .
.
Gọi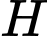 là hình chiếu của
là hình chiếu của  lên
lên 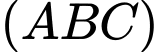 suy ra
suy ra 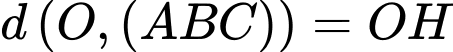 nên
nên 
Vậy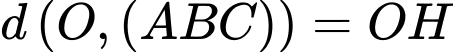 lớn nhất bằng
lớn nhất bằng 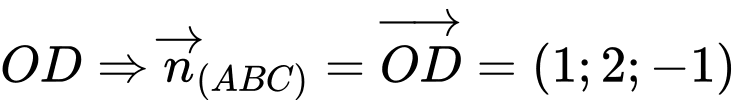 .
.
Khi đó mặt phẳng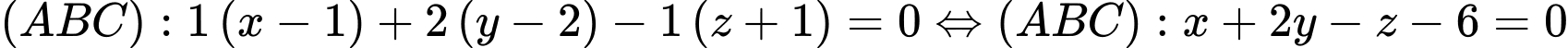 .
.
Ta có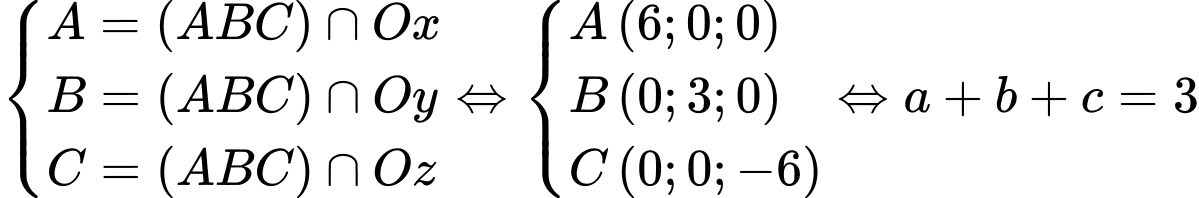 . Đáp án: B
. Đáp án: B
Ta có
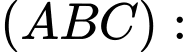
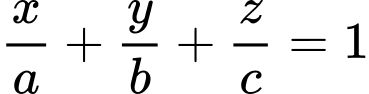 và
và 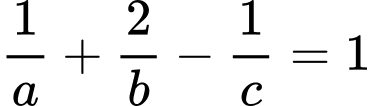 .
.Gọi
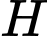 là hình chiếu của
là hình chiếu của  lên
lên 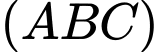 suy ra
suy ra 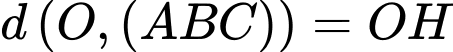 nên
nên 
Vậy
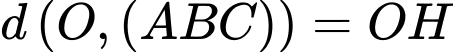 lớn nhất bằng
lớn nhất bằng 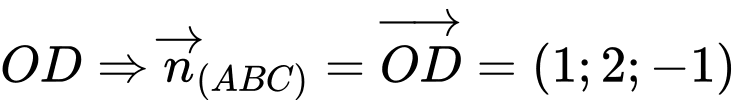 .
.Khi đó mặt phẳng
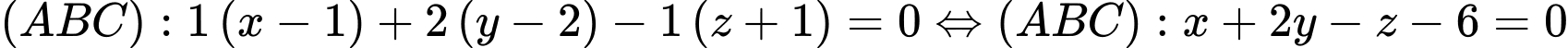 .
.Ta có
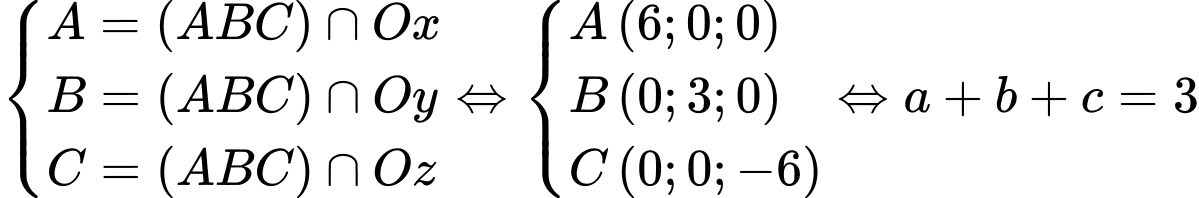 . Đáp án: B
. Đáp án: B