Đáp án Bài tập tự luyện số 2
Câu 1 [58252]: Trong không gian 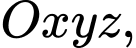 cho đểm
cho đểm 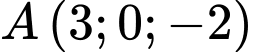 và mặt cầu
và mặt cầu 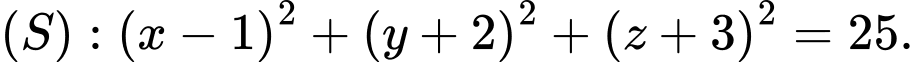 Một đường thẳng
Một đường thẳng 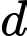 đi qua
đi qua 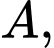 cắt mặt cầu tại hai điểm
cắt mặt cầu tại hai điểm  Độ dài ngắn nhất của
Độ dài ngắn nhất của 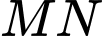 là
là
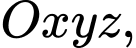 cho đểm
cho đểm 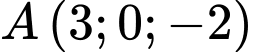 và mặt cầu
và mặt cầu 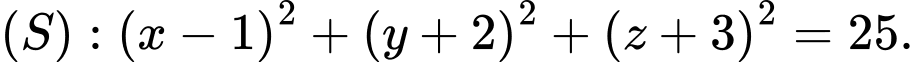 Một đường thẳng
Một đường thẳng 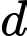 đi qua
đi qua 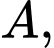 cắt mặt cầu tại hai điểm
cắt mặt cầu tại hai điểm  Độ dài ngắn nhất của
Độ dài ngắn nhất của 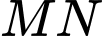 là
là A, 6.
B, 10.
C, 4.
D, 8.
 Đáp án: D
Đáp án: D
Câu 2 [80459]: Trong không gian tọa độ 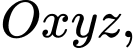 cho các điểm
cho các điểm 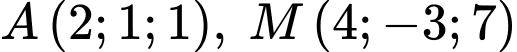 và mặt phẳng
và mặt phẳng 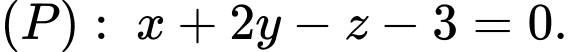 Đường thẳng d nằm trong
Đường thẳng d nằm trong 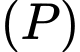 đi qua A và cách
đi qua A và cách 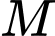 một khoảng lớn nhất có một vectơ chỉ phương là
một khoảng lớn nhất có một vectơ chỉ phương là 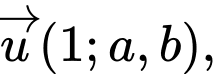 tính giá trị của biểu thức
tính giá trị của biểu thức 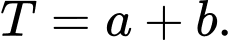
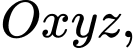 cho các điểm
cho các điểm 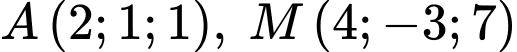 và mặt phẳng
và mặt phẳng 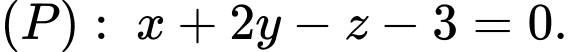 Đường thẳng d nằm trong
Đường thẳng d nằm trong 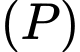 đi qua A và cách
đi qua A và cách 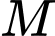 một khoảng lớn nhất có một vectơ chỉ phương là
một khoảng lớn nhất có một vectơ chỉ phương là 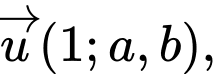 tính giá trị của biểu thức
tính giá trị của biểu thức 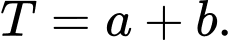
A, 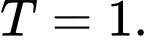
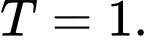
B, 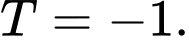
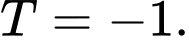
C, 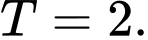
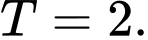
D, 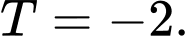
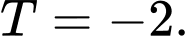
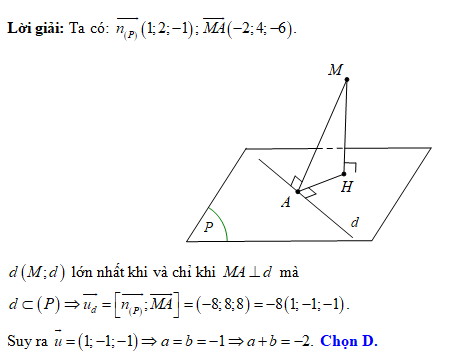 Đáp án: D
Đáp án: D
Câu 3 [80460]: Cho các điểm 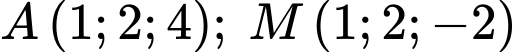 và
và 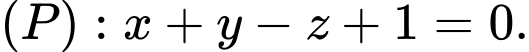 Lập phương trình đường
Lập phương trình đường 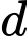 nằm trong
nằm trong 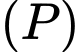 đi qua A và cách
đi qua A và cách 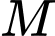 một khoảng nhỏ nhất.
một khoảng nhỏ nhất.
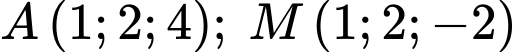 và
và 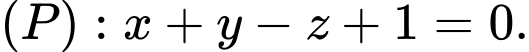 Lập phương trình đường
Lập phương trình đường 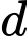 nằm trong
nằm trong 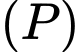 đi qua A và cách
đi qua A và cách 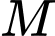 một khoảng nhỏ nhất.
một khoảng nhỏ nhất. A, 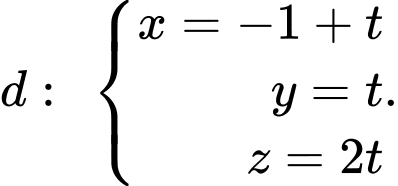
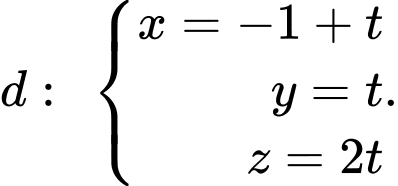
B, 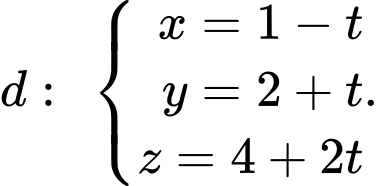
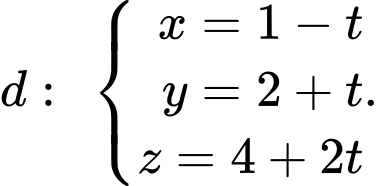
C, 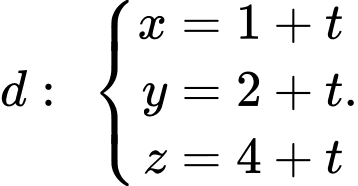
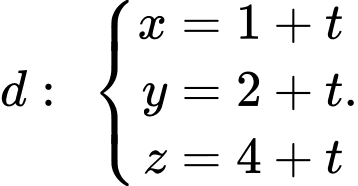
D, 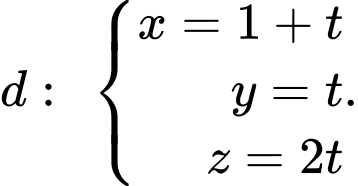
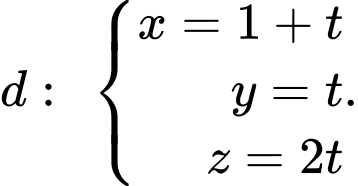

 Đáp án: A
Đáp án: A
Câu 4 [80461]: [Đề thi Chuyên ĐH Vinh năm 2019] Trong không gian 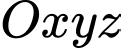 , cho đường thẳng
, cho đường thẳng 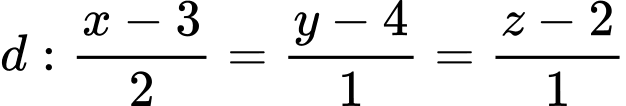 và 2 điểm
và 2 điểm 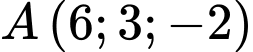 ,
, 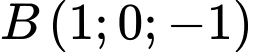 . Gọi
. Gọi  là đường thẳng đi qua
là đường thẳng đi qua 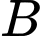 , vuông góc với
, vuông góc với 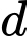 và thỏa mãn khoảng cách từ
và thỏa mãn khoảng cách từ 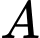 đến
đến  là nhỏ nhất. Một vectơ chỉ phương của
là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ là
có tọa độ là
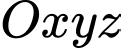 , cho đường thẳng
, cho đường thẳng 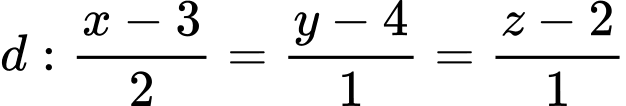 và 2 điểm
và 2 điểm 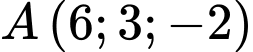 ,
, 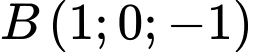 . Gọi
. Gọi  là đường thẳng đi qua
là đường thẳng đi qua 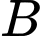 , vuông góc với
, vuông góc với 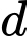 và thỏa mãn khoảng cách từ
và thỏa mãn khoảng cách từ 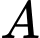 đến
đến  là nhỏ nhất. Một vectơ chỉ phương của
là nhỏ nhất. Một vectơ chỉ phương của  có tọa độ là
có tọa độ là A, 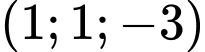 .
.
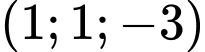 .
.B, 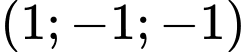 .
.
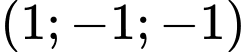 .
.C, 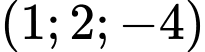 .
.
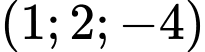 .
.D, 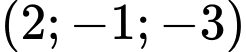 .
.
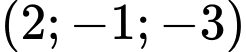 .
.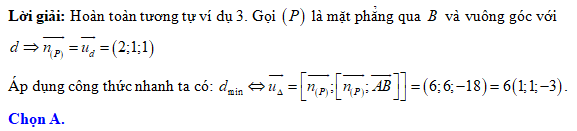 Đáp án: A
Đáp án: A
Câu 5 [80462]: Trong không gian với hệ tọa độ 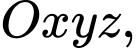 cho đường thẳng
cho đường thẳng 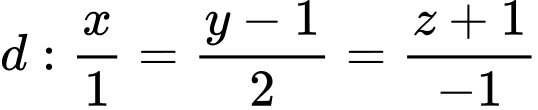 và 2 điểm
và 2 điểm 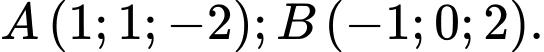 Viết phương trình đường thẳng
Viết phương trình đường thẳng  đi qua
đi qua 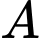 , vuông góc với
, vuông góc với 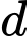 sao cho khoảng cách từ
sao cho khoảng cách từ 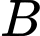 đến
đến  là nhỏ nhất.
là nhỏ nhất.
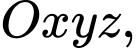 cho đường thẳng
cho đường thẳng 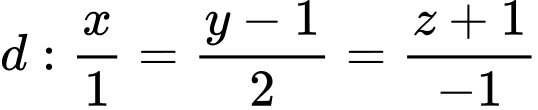 và 2 điểm
và 2 điểm 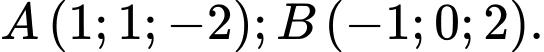 Viết phương trình đường thẳng
Viết phương trình đường thẳng  đi qua
đi qua 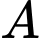 , vuông góc với
, vuông góc với 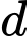 sao cho khoảng cách từ
sao cho khoảng cách từ 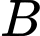 đến
đến  là nhỏ nhất.
là nhỏ nhất. A, 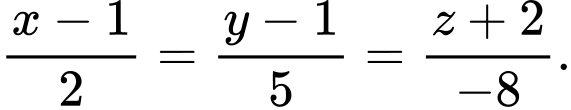
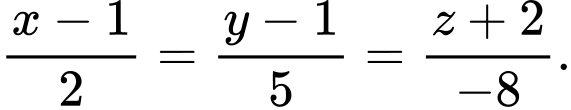
B, 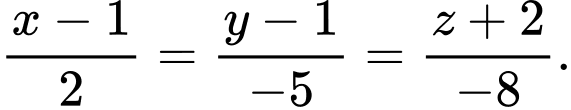
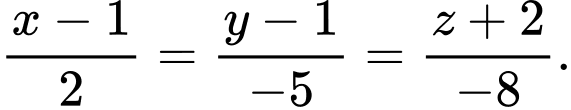
C, 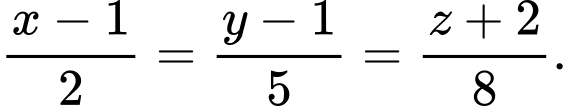
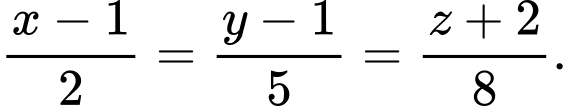
D, 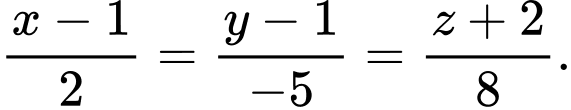
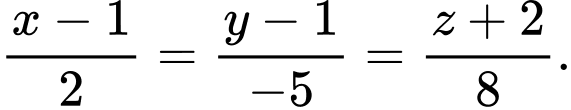
 Đáp án: B
Đáp án: B
Câu 6 [80463]: Trong không gian với hệ tọa độ 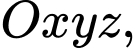 cho 2 điểm
cho 2 điểm 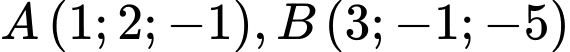 và đường thẳng
và đường thẳng 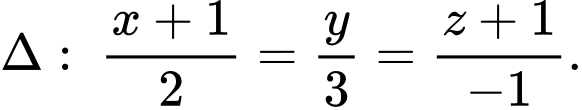 Gọi
Gọi 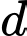 là đường thẳng đi qua
là đường thẳng đi qua 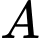 và cắt đường thẳng
và cắt đường thẳng  sao cho khoảng cách từ
sao cho khoảng cách từ 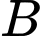 đến
đến 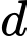 là lớn nhất, đường thẳng
là lớn nhất, đường thẳng 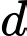 có một vectơ chỉ phương là
có một vectơ chỉ phương là 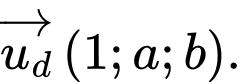 Giả trị của biểu thức
Giả trị của biểu thức 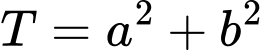 là
là
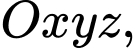 cho 2 điểm
cho 2 điểm 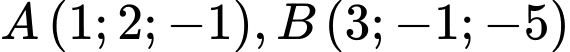 và đường thẳng
và đường thẳng 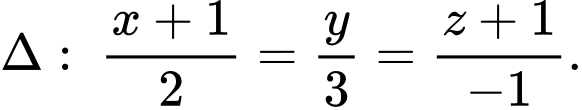 Gọi
Gọi 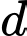 là đường thẳng đi qua
là đường thẳng đi qua 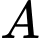 và cắt đường thẳng
và cắt đường thẳng  sao cho khoảng cách từ
sao cho khoảng cách từ 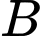 đến
đến 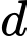 là lớn nhất, đường thẳng
là lớn nhất, đường thẳng 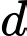 có một vectơ chỉ phương là
có một vectơ chỉ phương là 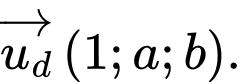 Giả trị của biểu thức
Giả trị của biểu thức 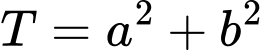 là
là A, 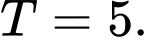
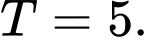
B, 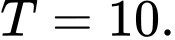
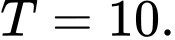
C, 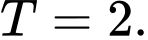
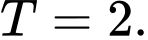
D, 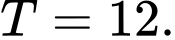
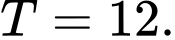
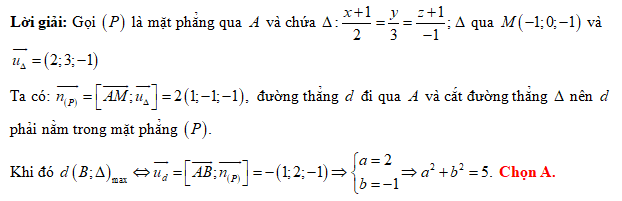 Đáp án: A
Đáp án: A
Câu 7 [57945]: Trong không gian 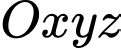 , cho hai điểm
, cho hai điểm 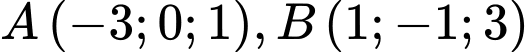 và mặt phẳng
và mặt phẳng 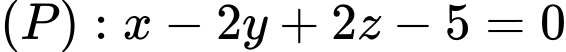 . Đường thẳng
. Đường thẳng 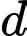 đi qua
đi qua 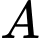 , song song với mặt phẳng
, song song với mặt phẳng 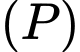 sao cho khoảng cách từ
sao cho khoảng cách từ 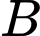 đến đường thẳng
đến đường thẳng 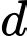 nhỏ nhất. Đường thẳng
nhỏ nhất. Đường thẳng 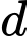 có một VTCP là
có một VTCP là 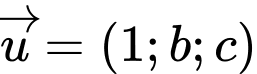 khi đó
khi đó 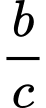 bằng
bằng
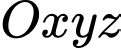 , cho hai điểm
, cho hai điểm 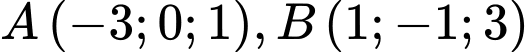 và mặt phẳng
và mặt phẳng 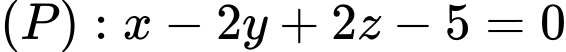 . Đường thẳng
. Đường thẳng 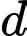 đi qua
đi qua 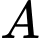 , song song với mặt phẳng
, song song với mặt phẳng 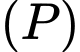 sao cho khoảng cách từ
sao cho khoảng cách từ 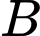 đến đường thẳng
đến đường thẳng 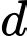 nhỏ nhất. Đường thẳng
nhỏ nhất. Đường thẳng 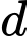 có một VTCP là
có một VTCP là 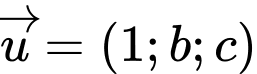 khi đó
khi đó 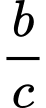 bằng
bằng A, 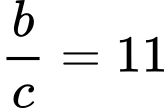 .
.
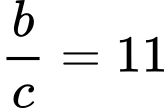 .
.B, 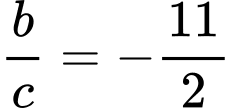 .
.
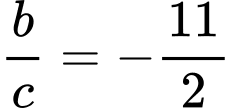 .
.C, 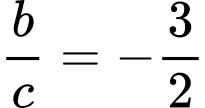 .
.
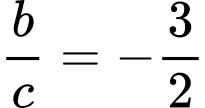 .
.D, 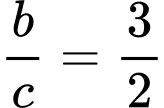 .
.
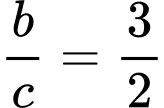 .
. Đáp án: B
Đáp án: B
Câu 8 [58283]: Trong không gian với hệ tọa độ 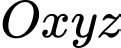 , cho hai điểm
, cho hai điểm 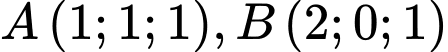 và mặt phẳng
và mặt phẳng  Viết phương trình chính tắc của đường thẳng
Viết phương trình chính tắc của đường thẳng 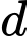 đi qua
đi qua 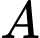 , song song với mặt phẳng
, song song với mặt phẳng 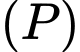 sao cho khoảng cách từ
sao cho khoảng cách từ 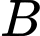 đến
đến 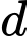 lớn nhất.
lớn nhất.
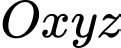 , cho hai điểm
, cho hai điểm 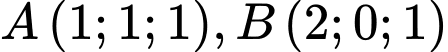 và mặt phẳng
và mặt phẳng  Viết phương trình chính tắc của đường thẳng
Viết phương trình chính tắc của đường thẳng 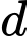 đi qua
đi qua 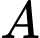 , song song với mặt phẳng
, song song với mặt phẳng 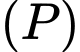 sao cho khoảng cách từ
sao cho khoảng cách từ 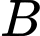 đến
đến 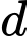 lớn nhất.
lớn nhất. A, 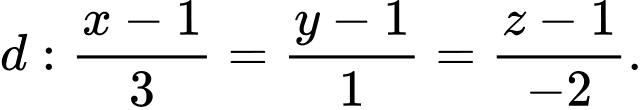
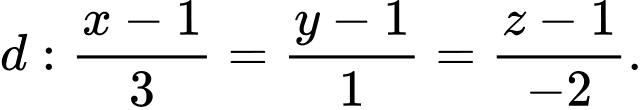
B, 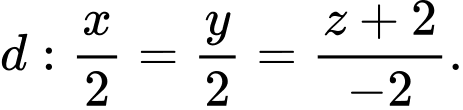
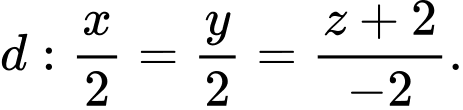
C, 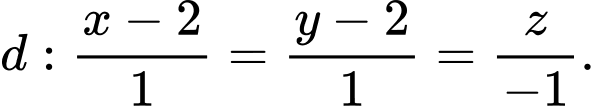
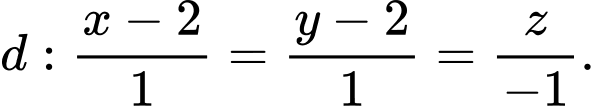
D, 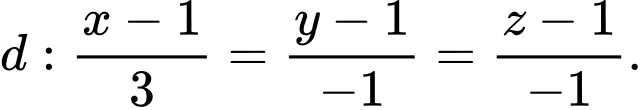
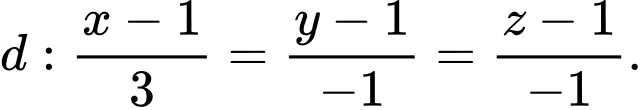
 Đáp án: C
Đáp án: C
Câu 9 [58295]: Trong không gian với hệ tọa độ 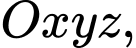 cho hai điểm
cho hai điểm 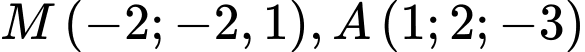 và đường thẳng
và đường thẳng 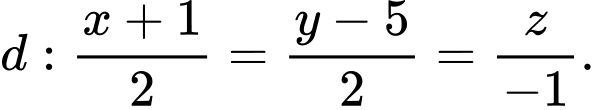 Tìm vectơ chỉ phương
Tìm vectơ chỉ phương 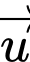 của đường thẳng
của đường thẳng  đi qua
đi qua 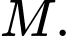 Vuông góc với đường thẳng
Vuông góc với đường thẳng 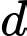 đồng thời cách điểm
đồng thời cách điểm 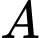 một khoảng bé nhất.
một khoảng bé nhất.
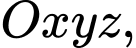 cho hai điểm
cho hai điểm 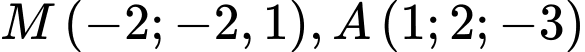 và đường thẳng
và đường thẳng 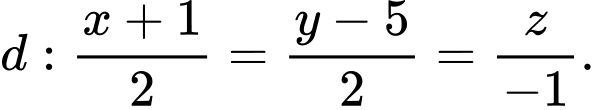 Tìm vectơ chỉ phương
Tìm vectơ chỉ phương 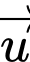 của đường thẳng
của đường thẳng  đi qua
đi qua 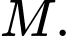 Vuông góc với đường thẳng
Vuông góc với đường thẳng 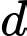 đồng thời cách điểm
đồng thời cách điểm 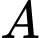 một khoảng bé nhất.
một khoảng bé nhất. A, 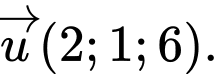
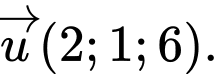
B, 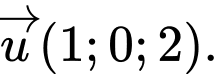
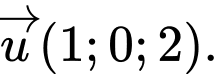
C, 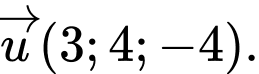
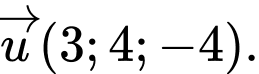
D, 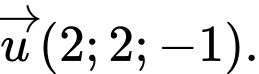
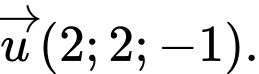
 Đáp án: B
Đáp án: B
Câu 10 [58286]: Trong không gian với hệ tọa độ 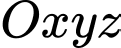 . Cho hai điểm
. Cho hai điểm 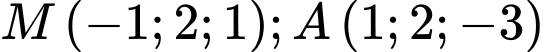 và đường thẳng
và đường thẳng 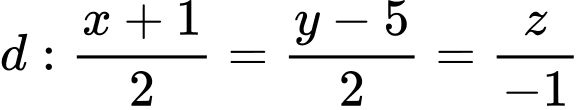 vectơ
chỉ phương
vectơ
chỉ phương 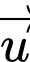 của đường thẳng
của đường thẳng  đi qua
đi qua 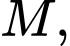 vuông góc với đường thẳng
vuông góc với đường thẳng 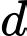 đồng thời cách điểm
đồng thời cách điểm 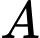 một khoảng lớn nhất.
một khoảng lớn nhất.
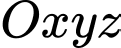 . Cho hai điểm
. Cho hai điểm 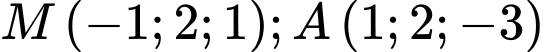 và đường thẳng
và đường thẳng 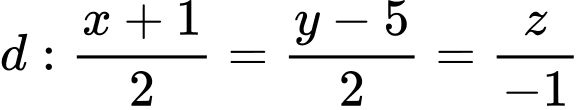 vectơ
chỉ phương
vectơ
chỉ phương 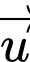 của đường thẳng
của đường thẳng  đi qua
đi qua 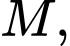 vuông góc với đường thẳng
vuông góc với đường thẳng 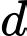 đồng thời cách điểm
đồng thời cách điểm 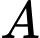 một khoảng lớn nhất.
một khoảng lớn nhất. A, 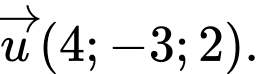
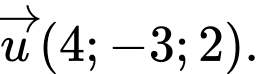
B, 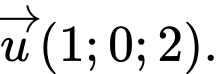
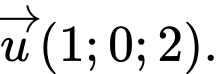
C, 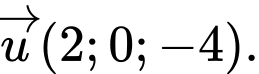
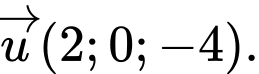
D, 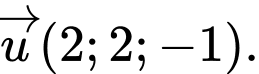
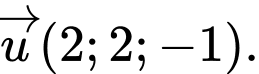
 Đáp án: A
Đáp án: A
Câu 11 [58294]: Trong không gian với hệ tọa độ 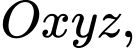 cho mặt phẳng
cho mặt phẳng 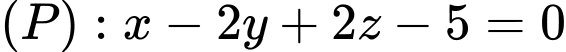 và hai điểm
và hai điểm 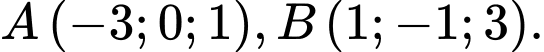 Trong tất cả các đường thẳng đi qua
Trong tất cả các đường thẳng đi qua 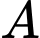 và song song với mặt phẳng
và song song với mặt phẳng 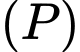 , gọi
, gọi  là đường thẳng sao cho khoảng cách từ
là đường thẳng sao cho khoảng cách từ 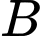 đến
đến  là lớn nhất. Hãy viết phương trình đường thẳng
là lớn nhất. Hãy viết phương trình đường thẳng 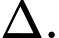
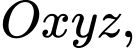 cho mặt phẳng
cho mặt phẳng 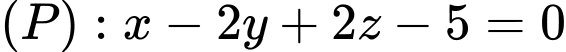 và hai điểm
và hai điểm 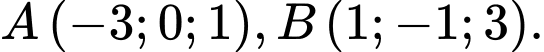 Trong tất cả các đường thẳng đi qua
Trong tất cả các đường thẳng đi qua 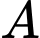 và song song với mặt phẳng
và song song với mặt phẳng 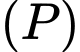 , gọi
, gọi  là đường thẳng sao cho khoảng cách từ
là đường thẳng sao cho khoảng cách từ 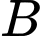 đến
đến  là lớn nhất. Hãy viết phương trình đường thẳng
là lớn nhất. Hãy viết phương trình đường thẳng 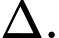
A, 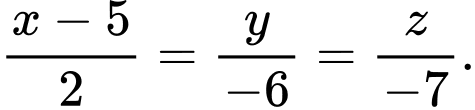
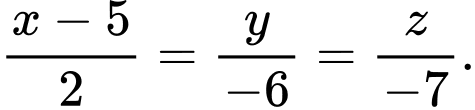
B, 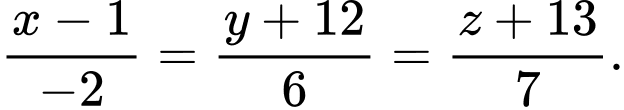
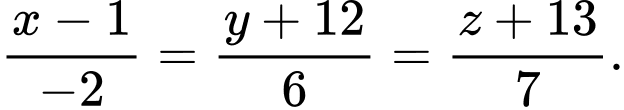
C, 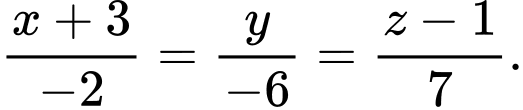
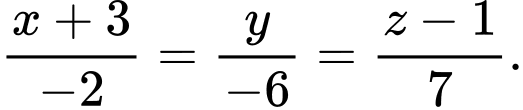
D, 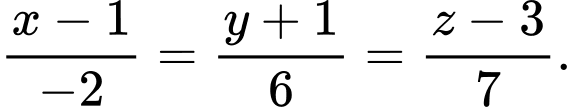
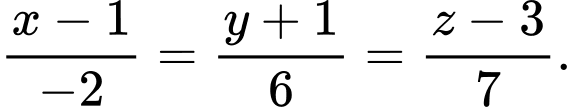
 Đáp án: B
Đáp án: B
Câu 12 [58288]: Trong không gian với hệ tọa độ 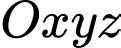 , cho điểm
, cho điểm 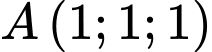 , và mặt phẳng
, và mặt phẳng  , gọi
, gọi 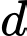 là đường thẳng đi qua
là đường thẳng đi qua 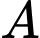 song song với
song song với 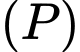 và cách
và cách 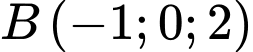 một khoảng ngắn nhất. Hỏi
một khoảng ngắn nhất. Hỏi 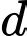 nhận vectơ nào dưới đây là vectơ chỉ phương?
nhận vectơ nào dưới đây là vectơ chỉ phương?
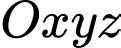 , cho điểm
, cho điểm 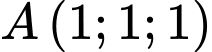 , và mặt phẳng
, và mặt phẳng  , gọi
, gọi 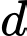 là đường thẳng đi qua
là đường thẳng đi qua 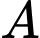 song song với
song song với 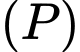 và cách
và cách 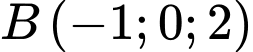 một khoảng ngắn nhất. Hỏi
một khoảng ngắn nhất. Hỏi 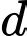 nhận vectơ nào dưới đây là vectơ chỉ phương?
nhận vectơ nào dưới đây là vectơ chỉ phương? A, 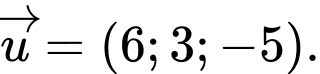
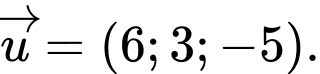
B, 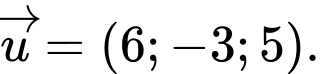
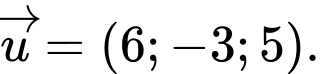
C, 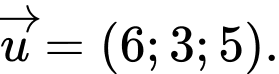
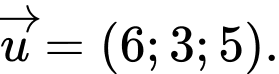
D, 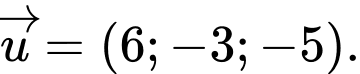
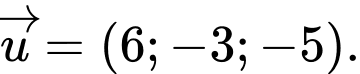
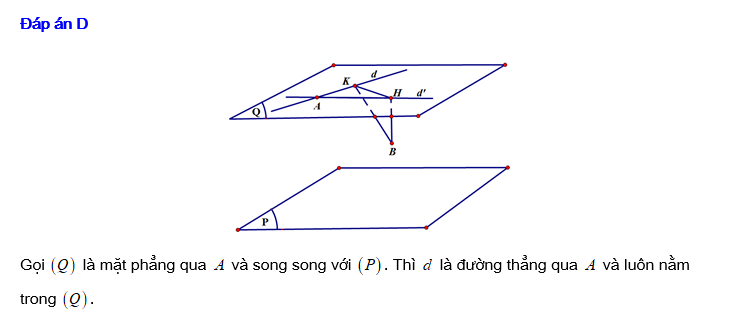
 Đáp án: D
Đáp án: D
Câu 13 [58289]: Viết phương trình đường thẳng 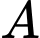 đi qua
đi qua 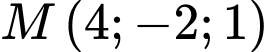 , song song với mặt phẳng
, song song với mặt phẳng 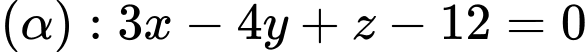 và cách
và cách 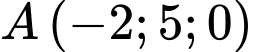 một khoảng lớn nhất.
một khoảng lớn nhất.
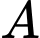 đi qua
đi qua 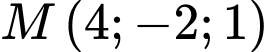 , song song với mặt phẳng
, song song với mặt phẳng 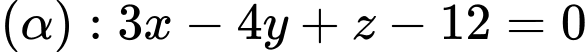 và cách
và cách 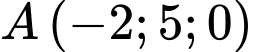 một khoảng lớn nhất.
một khoảng lớn nhất. A, 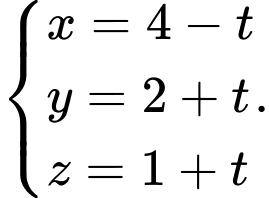
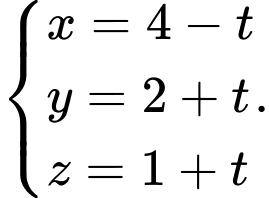
B, 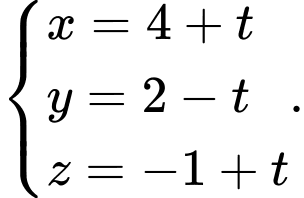
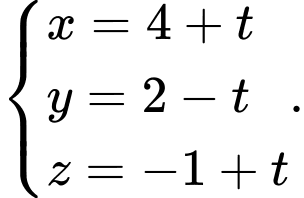
C, 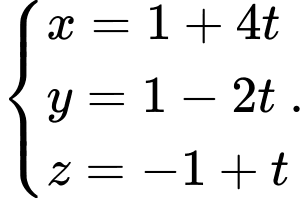
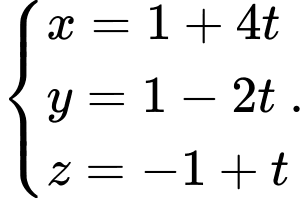
D, 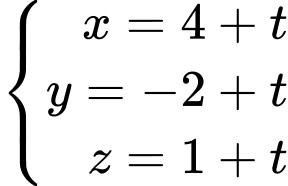 .
.
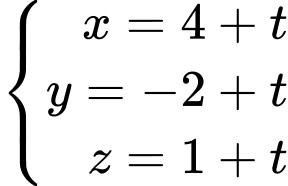 .
. Đáp án: D
Đáp án: D
Câu 14 [58293]: Gọi 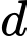 là đường thẳng đi qua gốc tọa độ
là đường thẳng đi qua gốc tọa độ  và vuông góc với đường thẳng
và vuông góc với đường thẳng 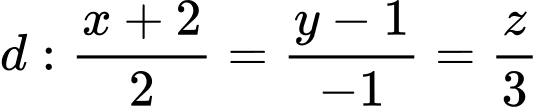 và cách điểm
và cách điểm 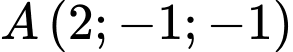 một khoảng lớn nhất. Hỏi
một khoảng lớn nhất. Hỏi 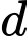 đi qua điểm nào sau đây?
đi qua điểm nào sau đây?
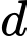 là đường thẳng đi qua gốc tọa độ
là đường thẳng đi qua gốc tọa độ  và vuông góc với đường thẳng
và vuông góc với đường thẳng 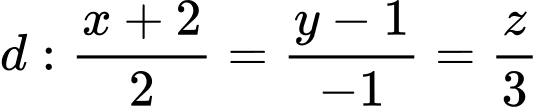 và cách điểm
và cách điểm 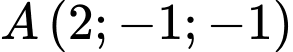 một khoảng lớn nhất. Hỏi
một khoảng lớn nhất. Hỏi 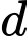 đi qua điểm nào sau đây?
đi qua điểm nào sau đây? A, 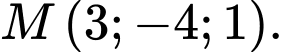
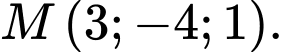
B, 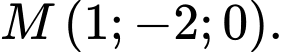
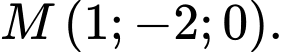
C, 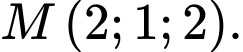
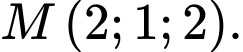
D, 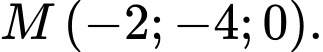
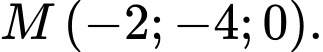
 Đáp án: D
Đáp án: D
Câu 15 [80464]: [Đề thi THPT QG năm 2017] Trong không gian 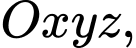 cho mặt cầu
cho mặt cầu 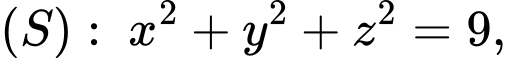 điểm
điểm 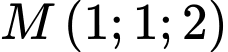 và mặt phẳng
và mặt phẳng 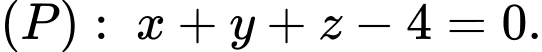 Gọi
Gọi  là đường thẳng qua
là đường thẳng qua 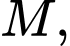 thuộc mặt phẳng
thuộc mặt phẳng 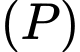 và cắt
và cắt 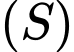 tại hai điểm
tại hai điểm 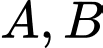 sao cho
sao cho  nhỏ nhất. Biết
nhỏ nhất. Biết  có một vectơ chỉ phương là
có một vectơ chỉ phương là 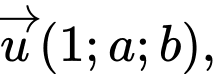 tính
tính 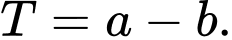
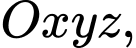 cho mặt cầu
cho mặt cầu 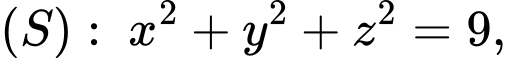 điểm
điểm 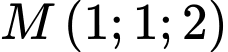 và mặt phẳng
và mặt phẳng 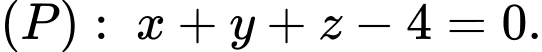 Gọi
Gọi  là đường thẳng qua
là đường thẳng qua 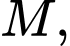 thuộc mặt phẳng
thuộc mặt phẳng 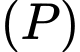 và cắt
và cắt 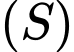 tại hai điểm
tại hai điểm 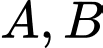 sao cho
sao cho  nhỏ nhất. Biết
nhỏ nhất. Biết  có một vectơ chỉ phương là
có một vectơ chỉ phương là 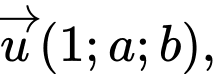 tính
tính 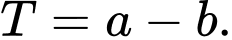
A, 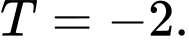
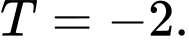
B, 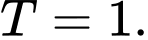
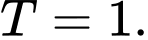
C, 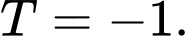
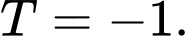
D, 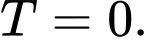
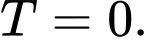
 Đáp án: C
Đáp án: C
Câu 16 [80465]: [Đề thi tham khảo năm 2019] Trong không gian 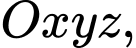 cho điểm
cho điểm 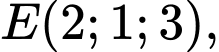 mặt phẳng
mặt phẳng 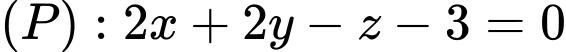 và mặt cầu
và mặt cầu 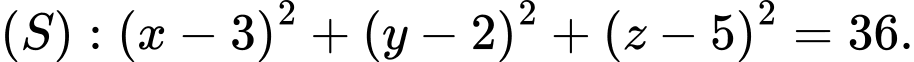 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 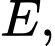 nằm trong
nằm trong 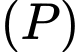 và cắt
và cắt 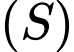 tại hai điểm có khoảng cách nhỏ nhất. Phương trình của
tại hai điểm có khoảng cách nhỏ nhất. Phương trình của  là
là
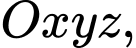 cho điểm
cho điểm 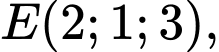 mặt phẳng
mặt phẳng 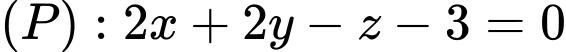 và mặt cầu
và mặt cầu 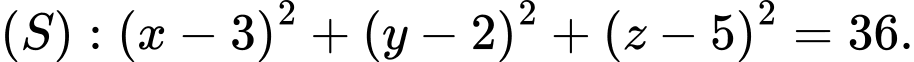 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 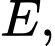 nằm trong
nằm trong 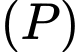 và cắt
và cắt 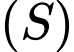 tại hai điểm có khoảng cách nhỏ nhất. Phương trình của
tại hai điểm có khoảng cách nhỏ nhất. Phương trình của  là
là A, 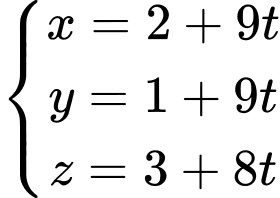
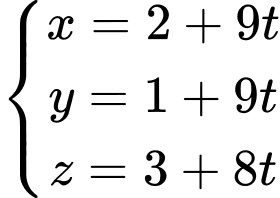
B, 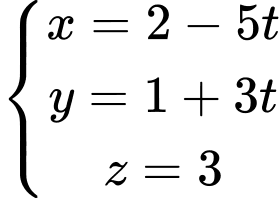
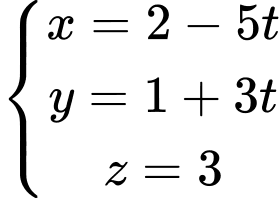
C, 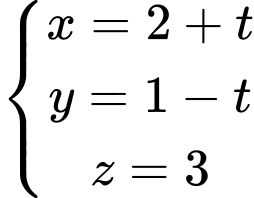
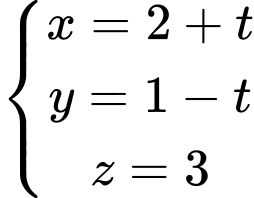
D, 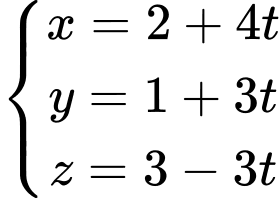
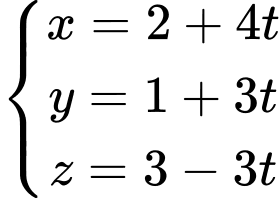
 Đáp án: C
Đáp án: C
Câu 17 [80466]: Trong không gian tọa độ 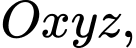 cho đường thẳng
cho đường thẳng 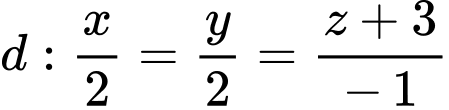 và mặt cầu
và mặt cầu 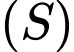 có phương trình
có phương trình 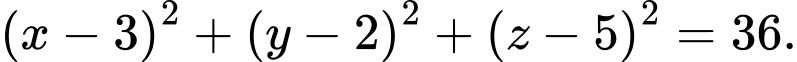 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 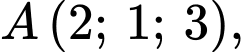 vuông góc với đường thẳng
vuông góc với đường thẳng 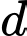 và cắt
và cắt 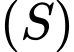 tại hai điểm có khoảng cách lớn nhất. Khi đó đường thẳng
tại hai điểm có khoảng cách lớn nhất. Khi đó đường thẳng  có một véc tơ chỉ phương là
có một véc tơ chỉ phương là 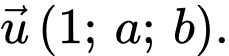 Tính
Tính 
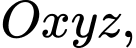 cho đường thẳng
cho đường thẳng 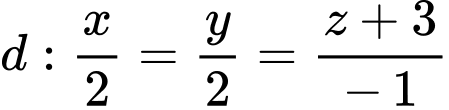 và mặt cầu
và mặt cầu 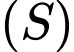 có phương trình
có phương trình 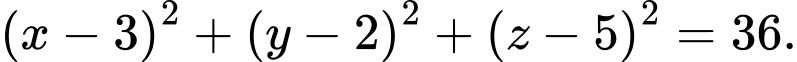 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 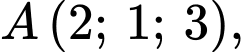 vuông góc với đường thẳng
vuông góc với đường thẳng 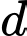 và cắt
và cắt 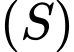 tại hai điểm có khoảng cách lớn nhất. Khi đó đường thẳng
tại hai điểm có khoảng cách lớn nhất. Khi đó đường thẳng  có một véc tơ chỉ phương là
có một véc tơ chỉ phương là 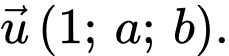 Tính
Tính 
A, 4.
B, 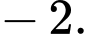
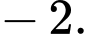
C, 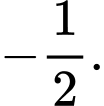
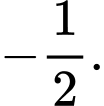
D, 5.
 Đáp án: D
Đáp án: D
Câu 18 [58284]: Trong không gian với hệ tọa độ 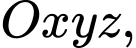 cho điểm
cho điểm 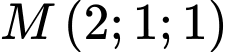 và mặt phẳng
và mặt phẳng 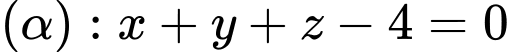 và mặt cầu
và mặt cầu 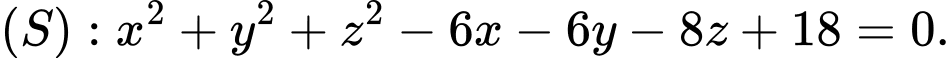 Phương trình đường thẳng
Phương trình đường thẳng  đi qua
đi qua 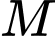 và nằm trong
và nằm trong 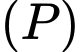 cắt mặt cầu
cắt mặt cầu 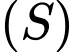 theo một đoạn thẳng có độ dài nhỏ nhất là
theo một đoạn thẳng có độ dài nhỏ nhất là
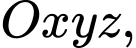 cho điểm
cho điểm 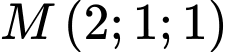 và mặt phẳng
và mặt phẳng 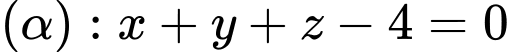 và mặt cầu
và mặt cầu 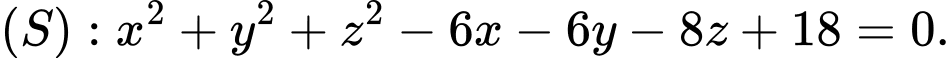 Phương trình đường thẳng
Phương trình đường thẳng  đi qua
đi qua 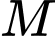 và nằm trong
và nằm trong 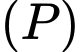 cắt mặt cầu
cắt mặt cầu 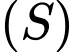 theo một đoạn thẳng có độ dài nhỏ nhất là
theo một đoạn thẳng có độ dài nhỏ nhất là A, 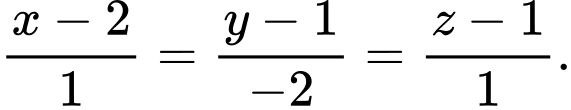
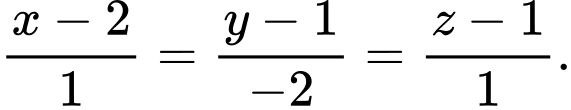
B, 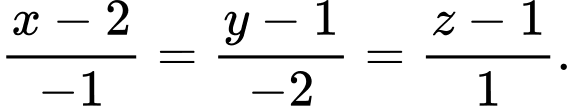
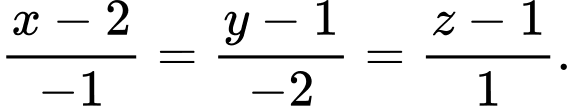
C, 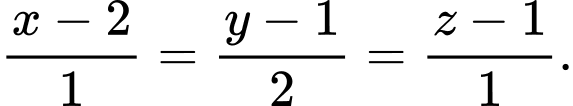
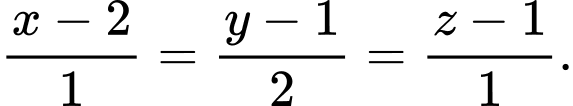
D, 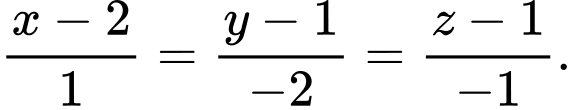
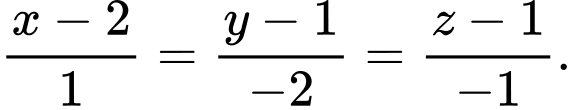
 Đáp án: A
Đáp án: A
Câu 19 [58291]: Trong không gian với hệ tọa độ 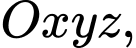 cho mặt phẳng
cho mặt phẳng 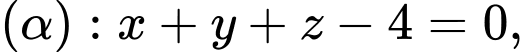 mặt cầu
mặt cầu 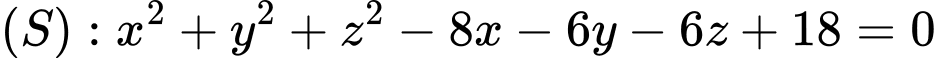 và điểm
và điểm 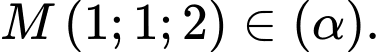 Đường thẳng
Đường thẳng 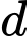 đi qua
đi qua 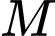 nằm trong mặt phẳng
nằm trong mặt phẳng  và cắt mặt cầu
và cắt mặt cầu 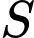 tại hai điểm phân biệt
tại hai điểm phân biệt 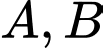 sao cho dây cung
sao cho dây cung  có độ dài nhỏ nhất. Đường thẳng
có độ dài nhỏ nhất. Đường thẳng 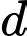 có một vectơ chỉ phương là
có một vectơ chỉ phương là
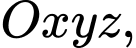 cho mặt phẳng
cho mặt phẳng 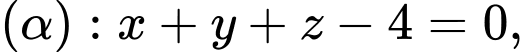 mặt cầu
mặt cầu 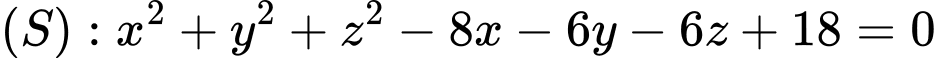 và điểm
và điểm 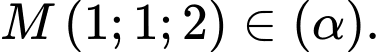 Đường thẳng
Đường thẳng 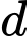 đi qua
đi qua 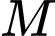 nằm trong mặt phẳng
nằm trong mặt phẳng  và cắt mặt cầu
và cắt mặt cầu 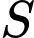 tại hai điểm phân biệt
tại hai điểm phân biệt 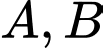 sao cho dây cung
sao cho dây cung  có độ dài nhỏ nhất. Đường thẳng
có độ dài nhỏ nhất. Đường thẳng 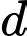 có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 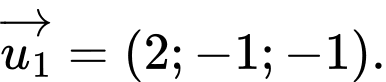
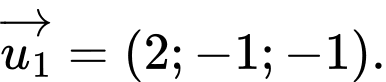
B, 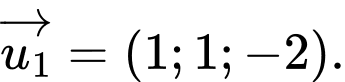
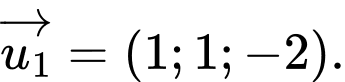
C, 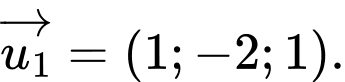
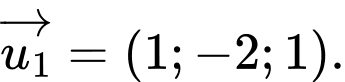
D, 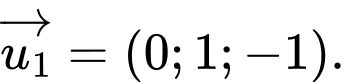
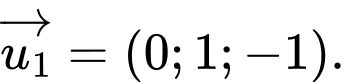
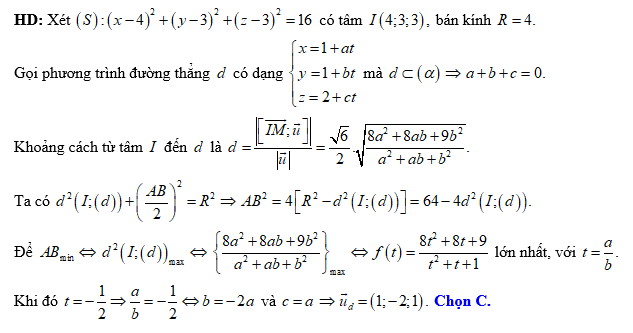 Đáp án: C
Đáp án: C
Câu 20 [58290]: Trong không gian với hệ tọa độ 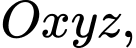 cho mặt phẳng
cho mặt phẳng 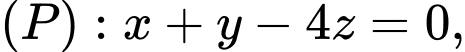 đường thẳng
đường thẳng 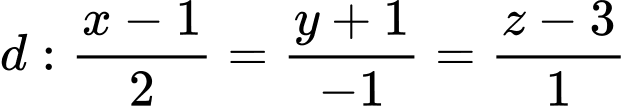 và điểm
và điểm 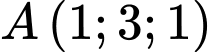 thuộc mặt phẳng
thuộc mặt phẳng 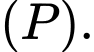 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 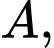 nằm trong mặt phẳng
nằm trong mặt phẳng 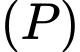 và cách
và cách 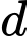 một khoảng lớn nhất. Gọi
một khoảng lớn nhất. Gọi 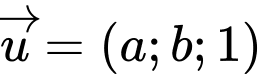 là một vectơ chỉ phương của đường thẳng
là một vectơ chỉ phương của đường thẳng 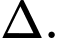 Tính
Tính 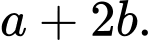
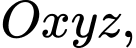 cho mặt phẳng
cho mặt phẳng 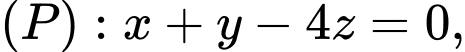 đường thẳng
đường thẳng 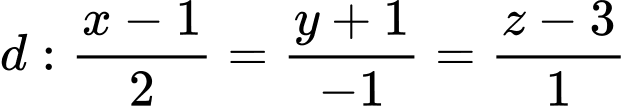 và điểm
và điểm 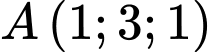 thuộc mặt phẳng
thuộc mặt phẳng 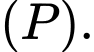 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 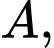 nằm trong mặt phẳng
nằm trong mặt phẳng 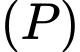 và cách
và cách 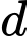 một khoảng lớn nhất. Gọi
một khoảng lớn nhất. Gọi 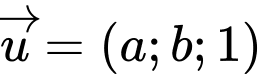 là một vectơ chỉ phương của đường thẳng
là một vectơ chỉ phương của đường thẳng 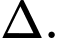 Tính
Tính 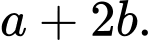
A, 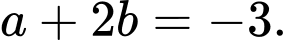
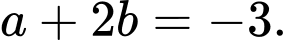
B, 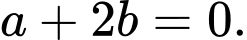
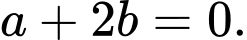
C, 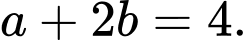
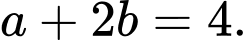
D, 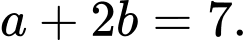
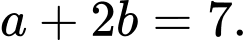
 Đáp án: A
Đáp án: A