DẠNG 1: Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn
Câu 1 [581895]: Giá trị nhỏ nhất của hàm số 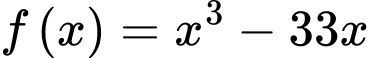 trên đoạn
trên đoạn 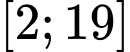 bằng
bằng
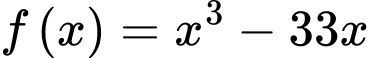 trên đoạn
trên đoạn 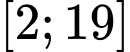 bằng
bằng A, 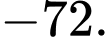
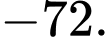
B, 

C, 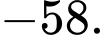
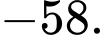
D, 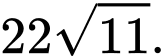
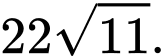
Chọn B
Ta có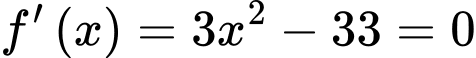
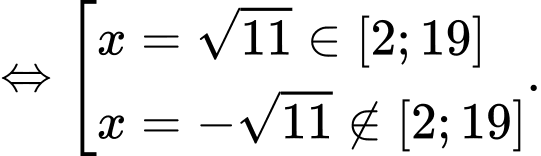
Khi đó ta có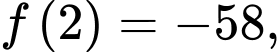
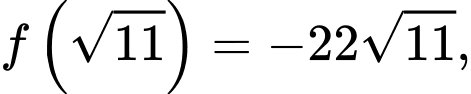
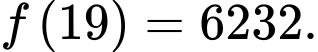
Vậy Đáp án: B
Đáp án: B
Ta có
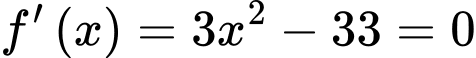
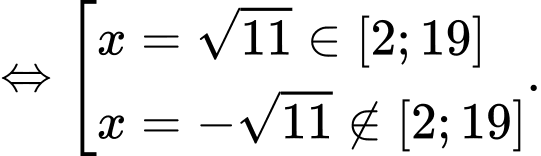
Khi đó ta có
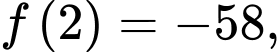
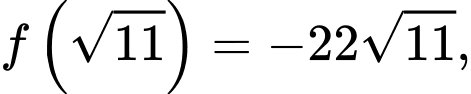
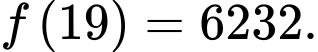
Vậy
 Đáp án: B
Đáp án: B
Câu 2 [581896]: Giá trị nhỏ nhất của hàm số 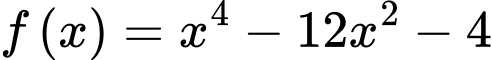 trên đoạn
trên đoạn 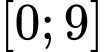 bằng
bằng
Trả lời: ………………
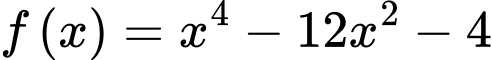 trên đoạn
trên đoạn 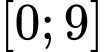 bằng
bằng
Trả lời: ………………
Ta có: 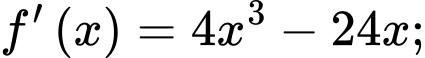
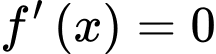
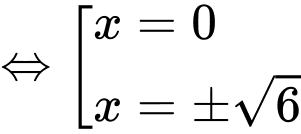
Tính được: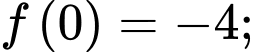
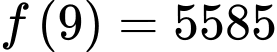 và
và 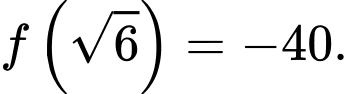
Suy ra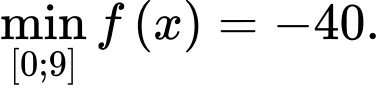
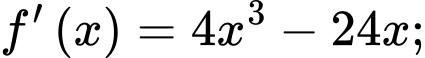
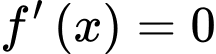
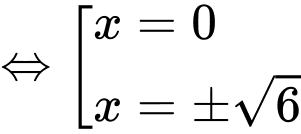
Tính được:
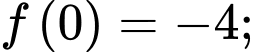
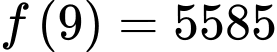 và
và 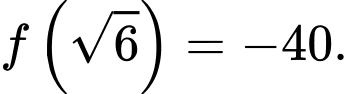
Suy ra
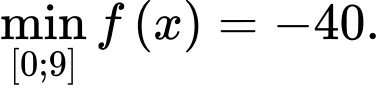
DẠNG 2: Tìm m để GTLN – GTNN của hàm số thỏa mãn điều kiện cho trước
Câu 3 [581897]: Cho hàm số 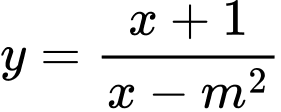 (
(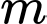 là tham số thực) thỏa mãn
là tham số thực) thỏa mãn 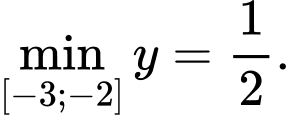 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
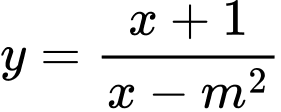 (
(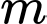 là tham số thực) thỏa mãn
là tham số thực) thỏa mãn 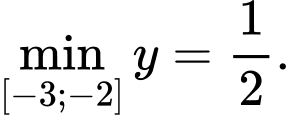 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng? A, 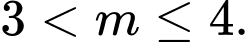
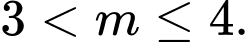
B, 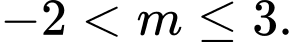
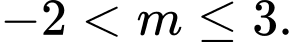
C, 

D, 

Chọn B
+TXĐ: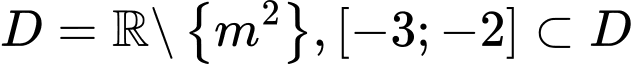
+ Ta có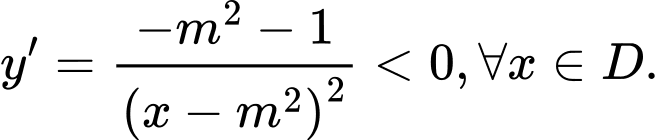
Nên hàm số nghịch biến trên từng khoảng xác định.
Nên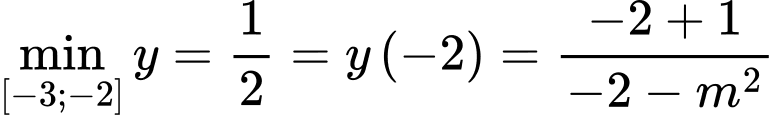
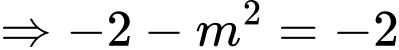
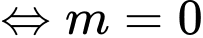
 Đáp án: B
Đáp án: B
+TXĐ:
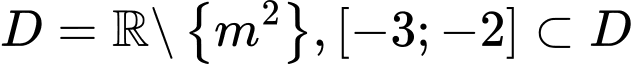
+ Ta có
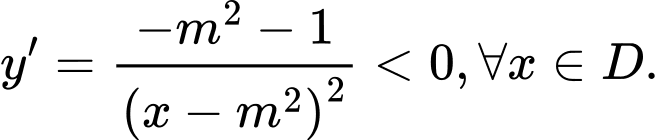
Nên hàm số nghịch biến trên từng khoảng xác định.
Nên
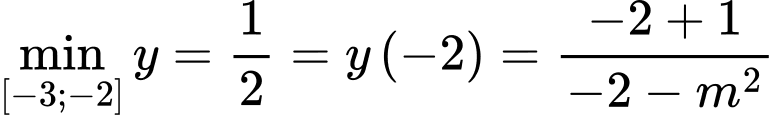
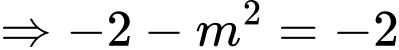
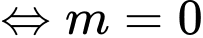
 Đáp án: B
Đáp án: B
Câu 4 [581898]: Tìm các giá trị của tham số 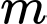 để giá trị nhỏ nhất của hàm số
để giá trị nhỏ nhất của hàm số 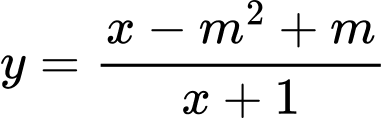 trên đoạn
trên đoạn 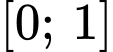 bằng
bằng 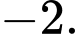
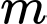 để giá trị nhỏ nhất của hàm số
để giá trị nhỏ nhất của hàm số 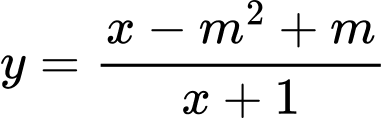 trên đoạn
trên đoạn 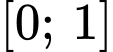 bằng
bằng 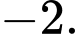
A, 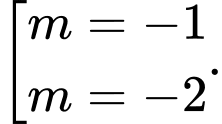
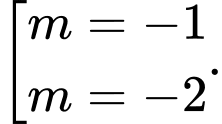
B, 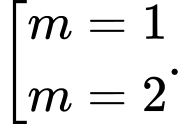
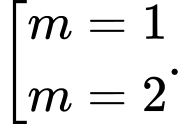
C, 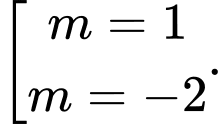
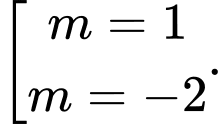
D, 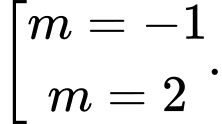
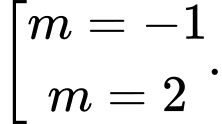
Chọn D
Tập xác định: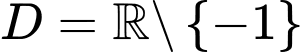
Hàm số đã cho liên tục trên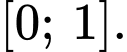
Ta có: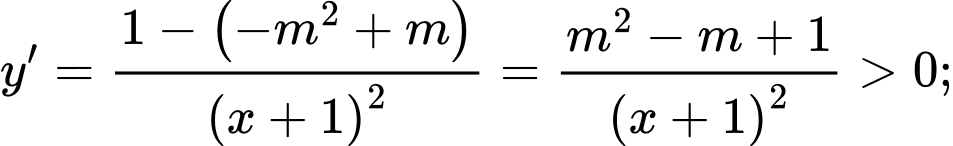
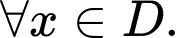
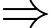 Hàm số đồng biến trên đoạn
Hàm số đồng biến trên đoạn 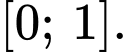
Trên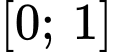 hàm số đạt giá trị nhỏ nhất tại
hàm số đạt giá trị nhỏ nhất tại 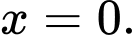
Ta có: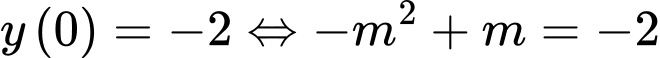
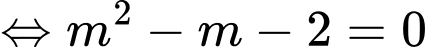
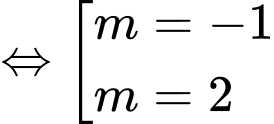 Đáp án: D
Đáp án: D
Tập xác định:
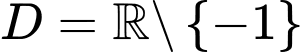
Hàm số đã cho liên tục trên
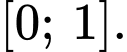
Ta có:
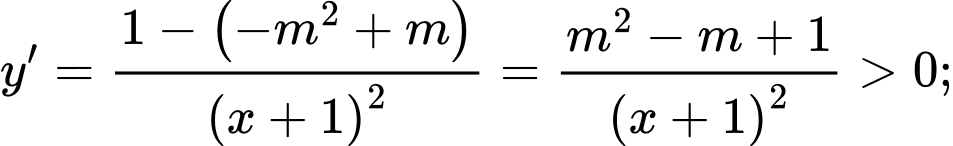
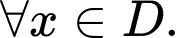
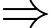 Hàm số đồng biến trên đoạn
Hàm số đồng biến trên đoạn 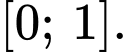
Trên
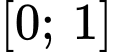 hàm số đạt giá trị nhỏ nhất tại
hàm số đạt giá trị nhỏ nhất tại 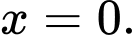
Ta có:
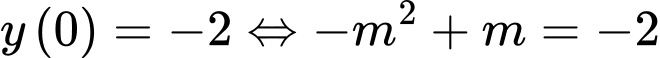
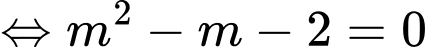
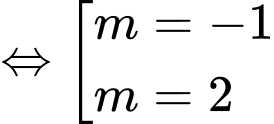 Đáp án: D
Đáp án: D DẠNG 3: Tìm m để GTLN – GTNN của hàm số chứa dấu giá trị tuyệt đối thỏa mãn điều kiện cho trước
Câu 5 [581899]: Tìm 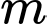 để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số 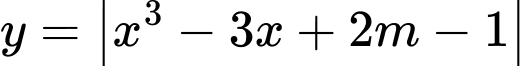 trên đoạn
trên đoạn 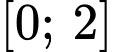 là nhỏ nhất. Giá trị của
là nhỏ nhất. Giá trị của 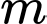 thuộc khoảng nào?
thuộc khoảng nào?
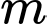 để giá trị lớn nhất của hàm số
để giá trị lớn nhất của hàm số 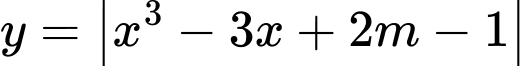 trên đoạn
trên đoạn 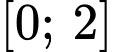 là nhỏ nhất. Giá trị của
là nhỏ nhất. Giá trị của 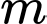 thuộc khoảng nào?
thuộc khoảng nào? A, 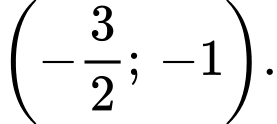
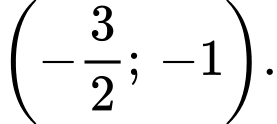
B, 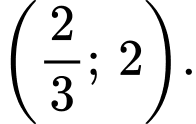
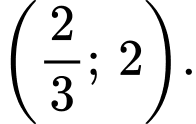
C, 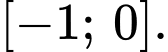
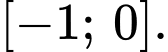
D, 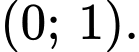
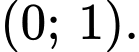
Chọn D
Xét hàm số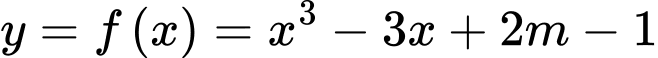 trên đoạn
trên đoạn 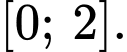
Ta có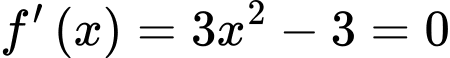
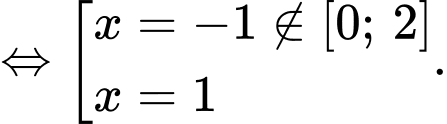
Ta có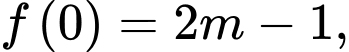
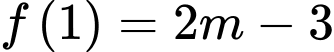 và
và 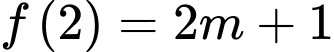
Suy ra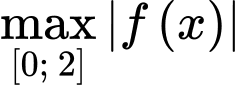
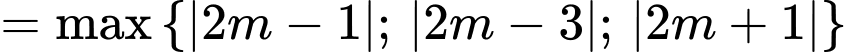
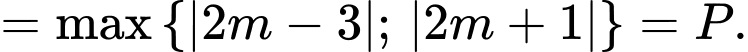
Trường hợp 1: Xét
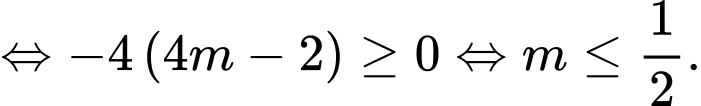
Khi đó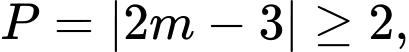
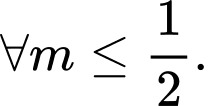 Suy ra
Suy ra 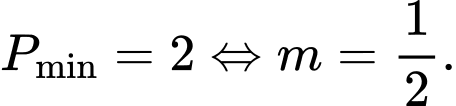
Trường hợp 2: Xét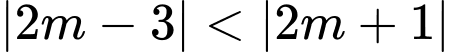
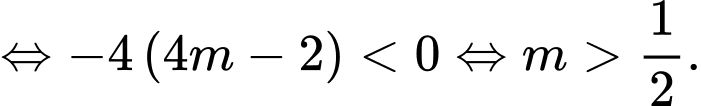
Khi đó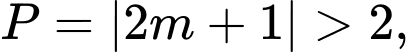
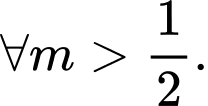 Suy ra
Suy ra  không tồn tại.
không tồn tại.
Vậy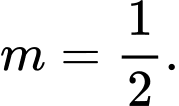 Đáp án: D
Đáp án: D
Xét hàm số
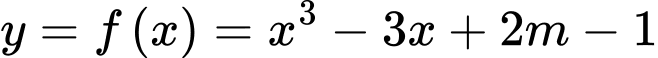 trên đoạn
trên đoạn 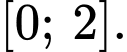
Ta có
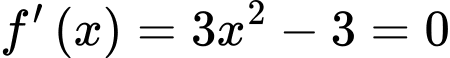
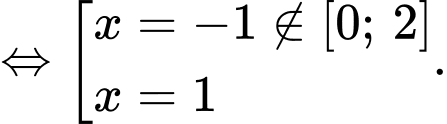
Ta có
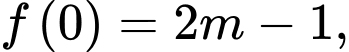
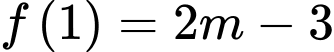 và
và 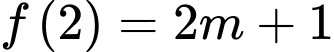
Suy ra
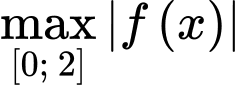
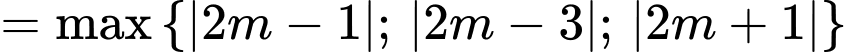
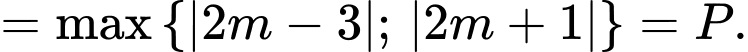
Trường hợp 1: Xét

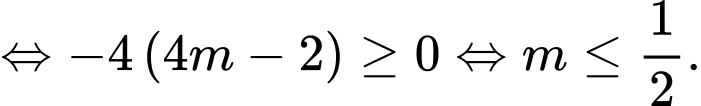
Khi đó
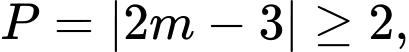
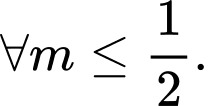 Suy ra
Suy ra 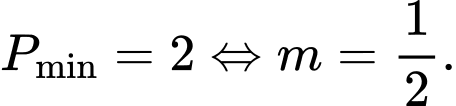
Trường hợp 2: Xét
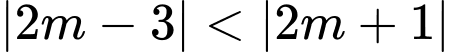
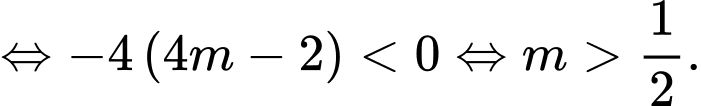
Khi đó
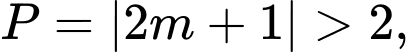
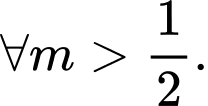 Suy ra
Suy ra  không tồn tại.
không tồn tại.Vậy
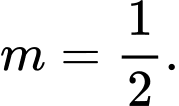 Đáp án: D
Đáp án: D
Câu 6 [581900]: Gọi 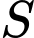 là tập hợp tất cả các giá trị của tham số thực
là tập hợp tất cả các giá trị của tham số thực 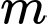 sao cho giá trị lớn nhất của hàm số
sao cho giá trị lớn nhất của hàm số 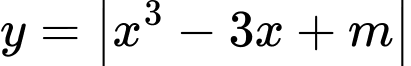 trên đoạn
trên đoạn 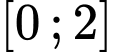 bằng
bằng 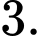 Số phần tử của S là
Số phần tử của S là
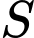 là tập hợp tất cả các giá trị của tham số thực
là tập hợp tất cả các giá trị của tham số thực 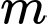 sao cho giá trị lớn nhất của hàm số
sao cho giá trị lớn nhất của hàm số 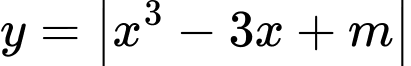 trên đoạn
trên đoạn 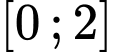 bằng
bằng 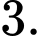 Số phần tử của S là
Số phần tử của S là A, 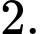
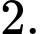
B, 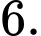
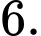
C, 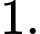
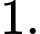
D, 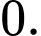
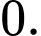
Chọn A
Xét hàm số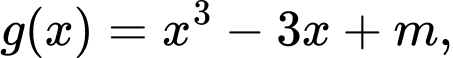 ta có
ta có 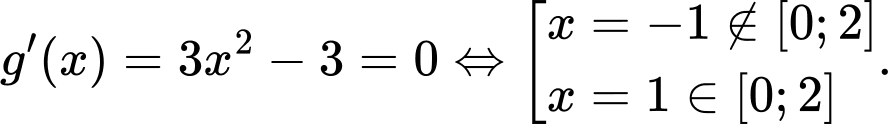
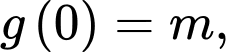
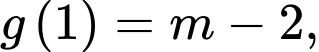
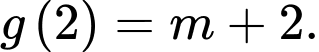
Vậy giá trị lớn nhất của hàm số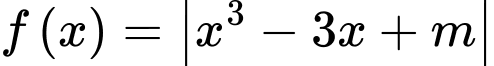 bằng max của
bằng max của 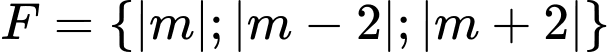
TH1: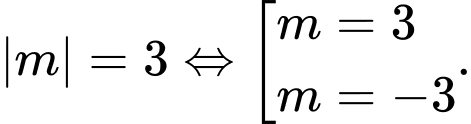
Với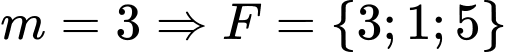 loại vì max bằng 5.
loại vì max bằng 5.
Với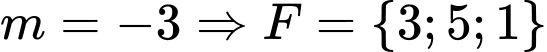 loại vì max bằng 5.
loại vì max bằng 5.
TH2: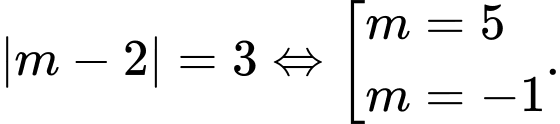
Với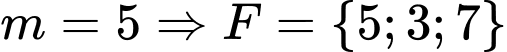 loại vì max bằng 7.
loại vì max bằng 7.
Với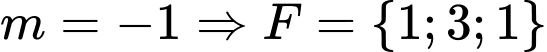 có max bẳng 3. Chọn
có max bẳng 3. Chọn 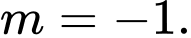
TH3: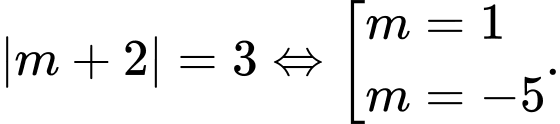
Với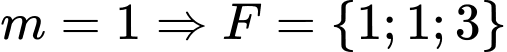 có max bằng 3. Chọn
có max bằng 3. Chọn 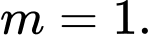
Với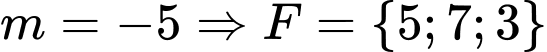 loại vì max bẳng 7.
loại vì max bẳng 7.
Vậy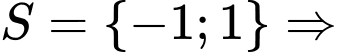 có 2 giá trị
có 2 giá trị 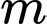 thoả mãn yêu cầu đề bài.
Đáp án: A
thoả mãn yêu cầu đề bài.
Đáp án: A
Xét hàm số
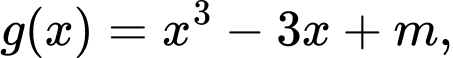 ta có
ta có 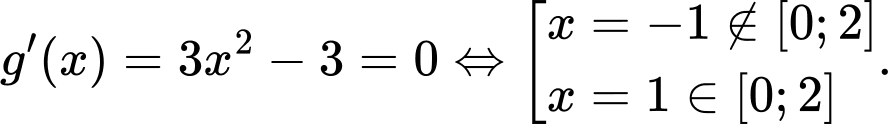
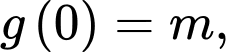
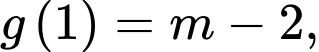
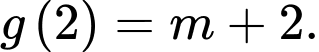
Vậy giá trị lớn nhất của hàm số
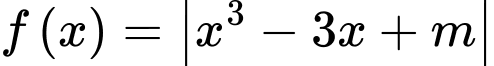 bằng max của
bằng max của 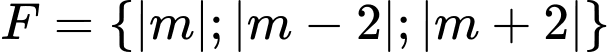
TH1:
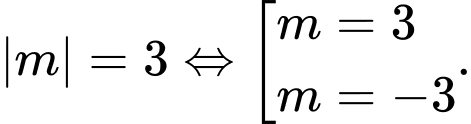
Với
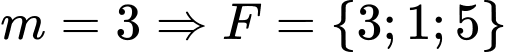 loại vì max bằng 5.
loại vì max bằng 5.
Với
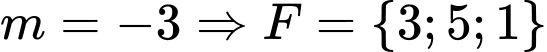 loại vì max bằng 5.
loại vì max bằng 5.
TH2:
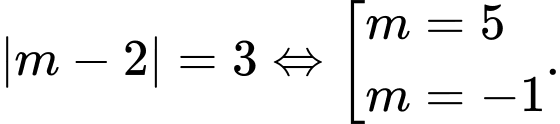
Với
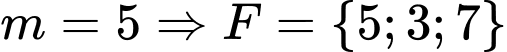 loại vì max bằng 7.
loại vì max bằng 7.
Với
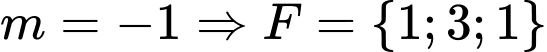 có max bẳng 3. Chọn
có max bẳng 3. Chọn 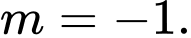
TH3:
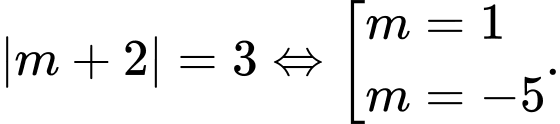
Với
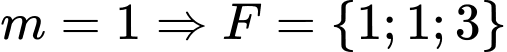 có max bằng 3. Chọn
có max bằng 3. Chọn 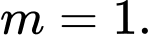
Với
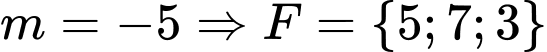 loại vì max bẳng 7.
loại vì max bẳng 7.
Vậy
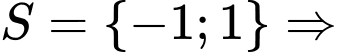 có 2 giá trị
có 2 giá trị 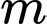 thoả mãn yêu cầu đề bài.
Đáp án: A
thoả mãn yêu cầu đề bài.
Đáp án: A DẠNG 4: Dùng phương pháp hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Câu 7 [581901]: Cho 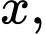
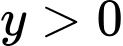 thỏa mãn
thỏa mãn 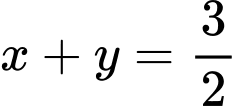 và biểu thức
và biểu thức 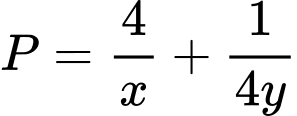 đạt giá trị nhỏ nhất. Tính
đạt giá trị nhỏ nhất. Tính 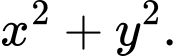
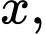
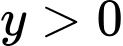 thỏa mãn
thỏa mãn 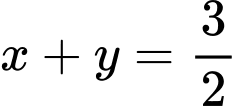 và biểu thức
và biểu thức 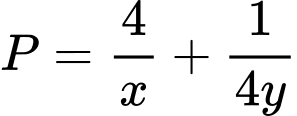 đạt giá trị nhỏ nhất. Tính
đạt giá trị nhỏ nhất. Tính 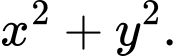
A, 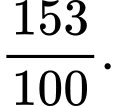
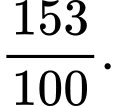
B, 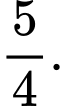
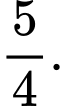
C, 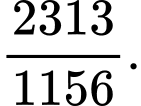
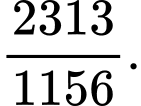
D, 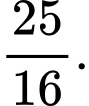
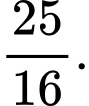
Chọn A
Từ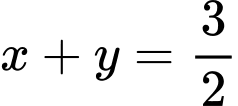 suy ra
suy ra 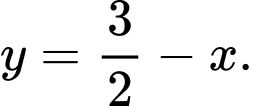 Ta có:
Ta có: 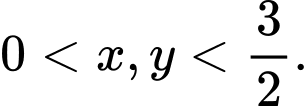
Xét hàm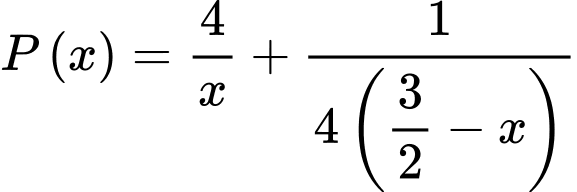
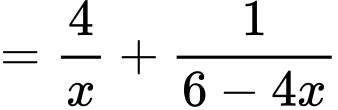 trên khoảng
trên khoảng 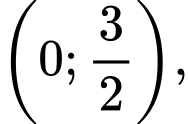 ta có:
ta có:
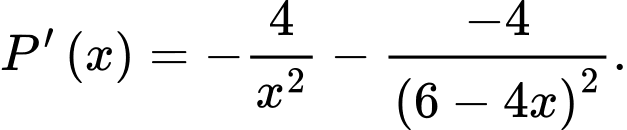
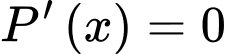
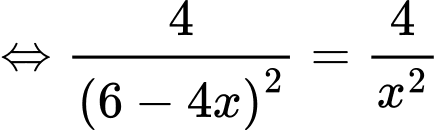
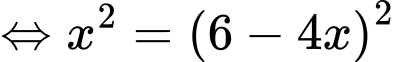
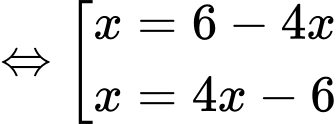
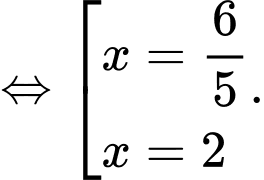
Bảng biến thiên của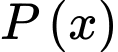 trên
trên 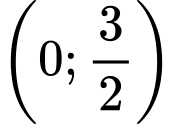 :
:
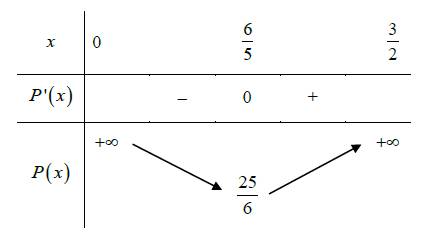
Dựa vào bảng biến thiên ta thấy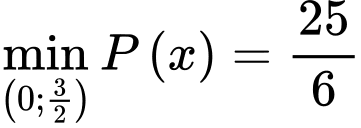 khi
khi 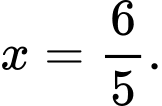
Với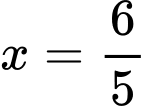 thì
thì 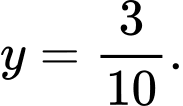
Như vậy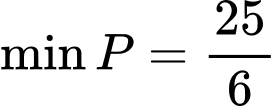 khi
khi 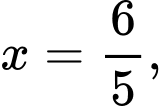
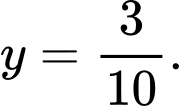
Khi đó,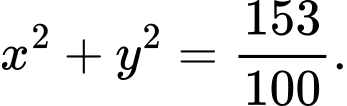 Đáp án: A
Đáp án: A
Từ
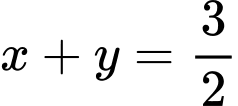 suy ra
suy ra 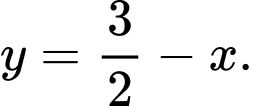 Ta có:
Ta có: 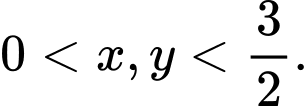
Xét hàm
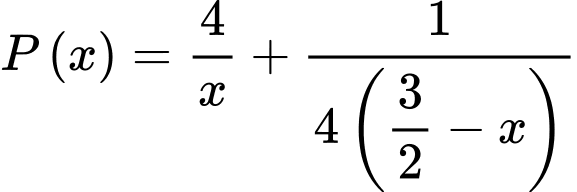
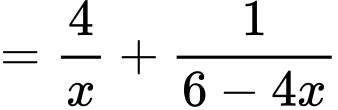 trên khoảng
trên khoảng 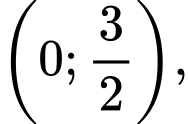 ta có:
ta có: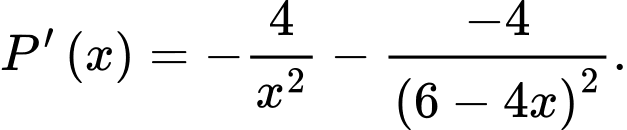
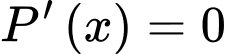
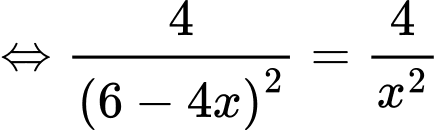
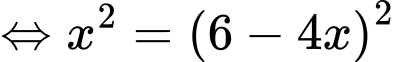
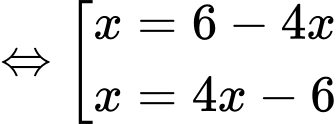
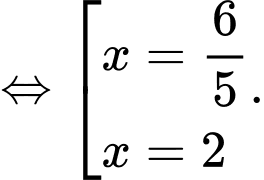
Bảng biến thiên của
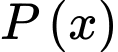 trên
trên 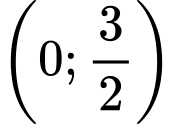 :
:
Dựa vào bảng biến thiên ta thấy
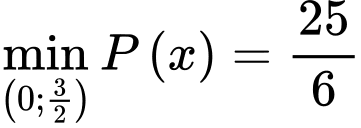 khi
khi 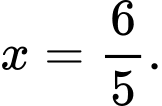
Với
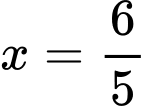 thì
thì 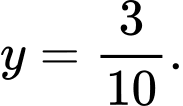
Như vậy
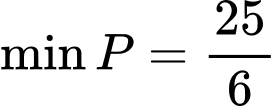 khi
khi 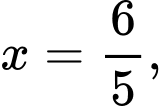
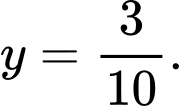
Khi đó,
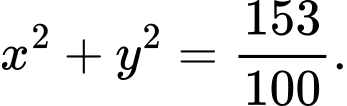 Đáp án: A
Đáp án: A