1. Khái niệm tính đơn điệu của hàm số
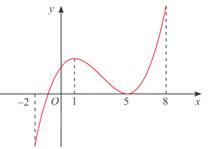
Câu 1 [581809]: Tìm các khoảng đơn điệu của hàm số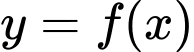 
có đồ thị cho ở Hình.
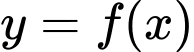có đồ thị cho ở Hình.
Hàm số đồng biến trên các khoảng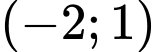 
và 
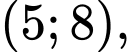nghịch biến trên khoảng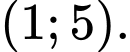 
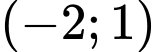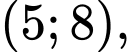và nghịch biến trên khoảng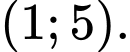
Câu 2 [581810]: Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số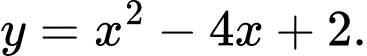 
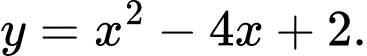
Tập xác định của hàm số là 
Ta có: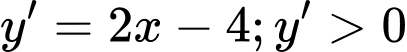
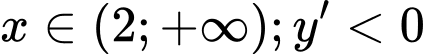với 
với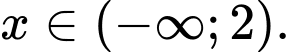 
Do đó, hàm số đồng biến trên khoảng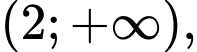
nghịch biến trên khoảng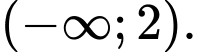 
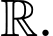
Ta có:
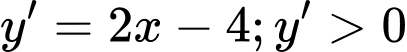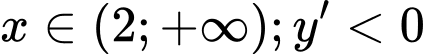với với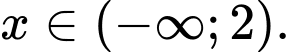
Do đó, hàm số đồng biến trên khoảng
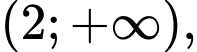nghịch biến trên khoảng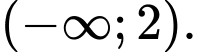
2. Sử dụng bảng biến thiên xét tính đơn điệu của hàm số
Câu 3 [581811]: Tìm các khoảng đơn điệu của hàm số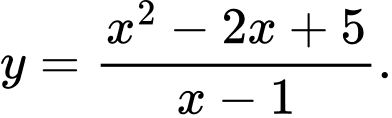 
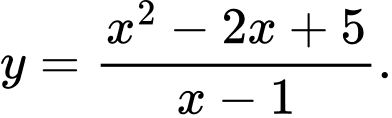
Tập xác định của hàm số là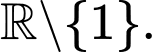 
Ta có: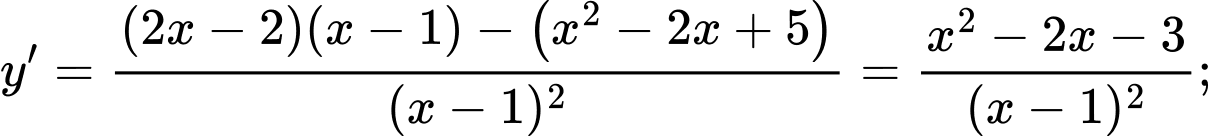
hoặc 
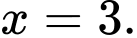
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng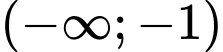
và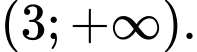 
Hàm số nghịch biến trên các khoảng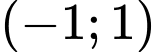
và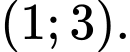 
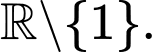
Ta có:
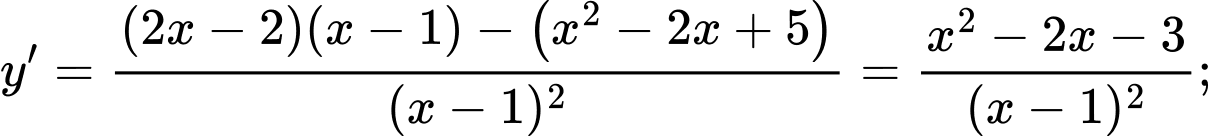
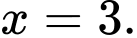
hoặc Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng
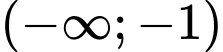và 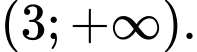Hàm số nghịch biến trên các khoảng
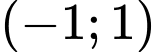và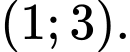
Câu 4 [581812]: Xét chiều biến thiên của hàm số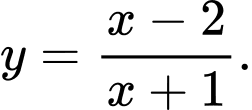 
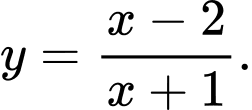
Tập xác định của hàm số là 
Ta có: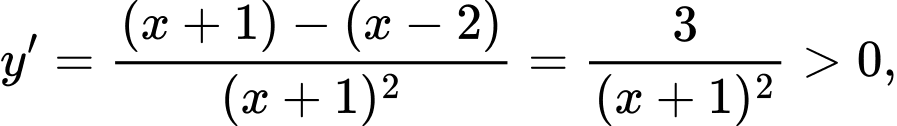
với mọi 
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
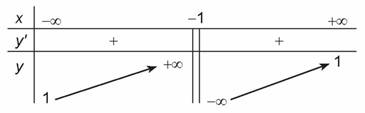
Hàm số đồng biến trên các khoảng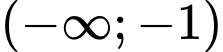
và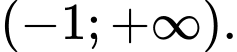 
Ta có:
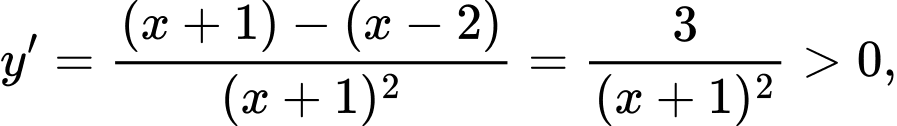với mọi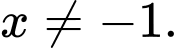 Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng
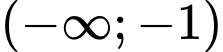và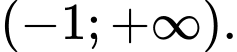
Câu 5 [581813]: Tìm các khoảng đơn điệu của hàm số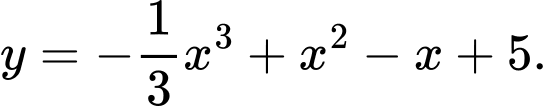 
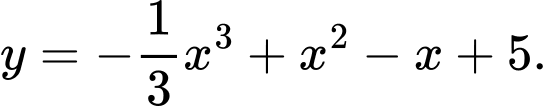
- Hàm số đã cho có tập xác định là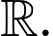 
- Ta có: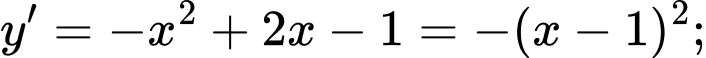
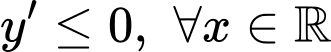và 
Bảng biến thiên của hàm số như sau:
Vậy hàm số nghịch biến trên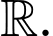
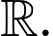
- Ta có:
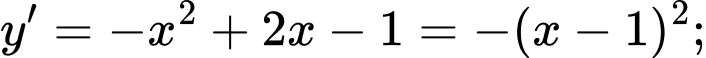
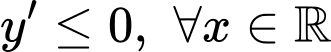và Bảng biến thiên của hàm số như sau:
Vậy hàm số nghịch biến trên