DẠNG 1: TỐC ĐỘ THAY ĐỔI CỦA MỘT ĐẠI LƯỢNG
Câu 1 [581993]: Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hinh hoá bằng hàm số 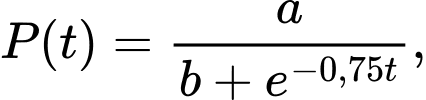 trong đó thời gian
trong đó thời gian 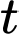 được tính bằng giờ. Tại thời điểm ban đầu
được tính bằng giờ. Tại thời điểm ban đầu 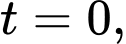 quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của
quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của 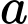 và
và 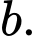 Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?
Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?
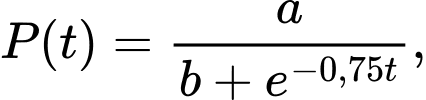 trong đó thời gian
trong đó thời gian 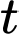 được tính bằng giờ. Tại thời điểm ban đầu
được tính bằng giờ. Tại thời điểm ban đầu 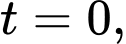 quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của
quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của 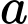 và
và 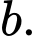 Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?
Theo mô hình này, điều gì xảy ra với quần thể nấm men về lâu dài?
Ta có: 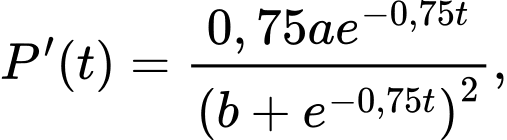

Theo đề bài, ta có: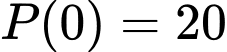 và
và 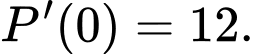 Do đó, ta có hệ phương trình:
Do đó, ta có hệ phương trình:
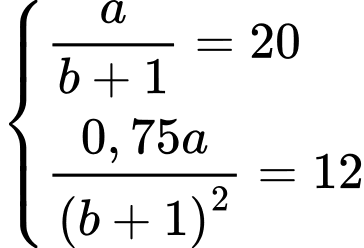
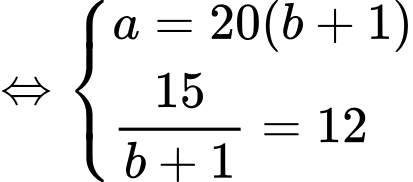
Giải hệ phương trình này, ta được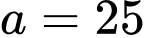 và
và 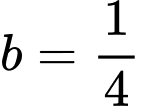 .
.
Khi đó,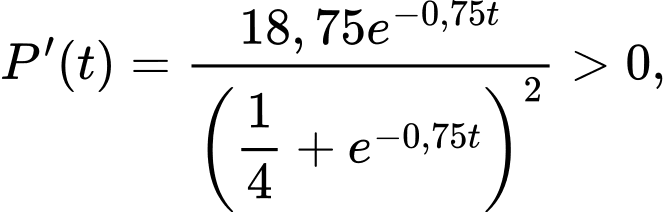
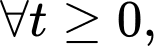 tức là số lượng quần thể nấm men luôn tăng.
tức là số lượng quần thể nấm men luôn tăng.
Tuy nhiên, do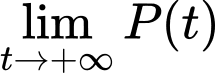
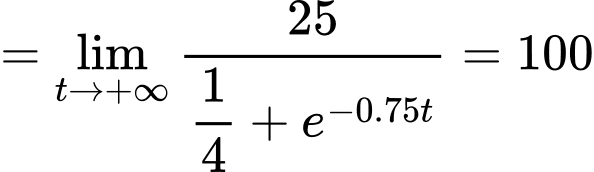 nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
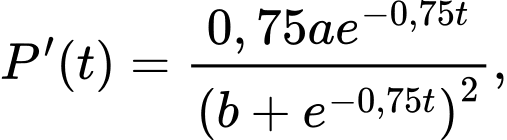

Theo đề bài, ta có:
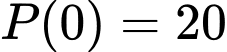 và
và 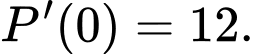 Do đó, ta có hệ phương trình:
Do đó, ta có hệ phương trình: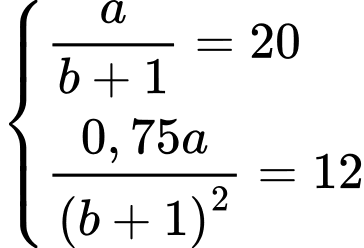
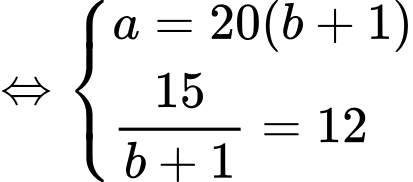
Giải hệ phương trình này, ta được
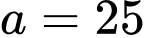 và
và 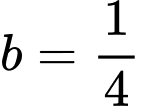 .
.Khi đó,
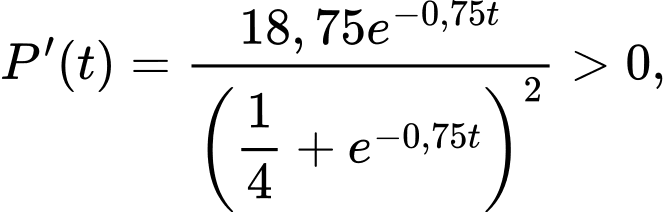
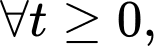 tức là số lượng quần thể nấm men luôn tăng.
tức là số lượng quần thể nấm men luôn tăng. Tuy nhiên, do
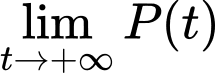
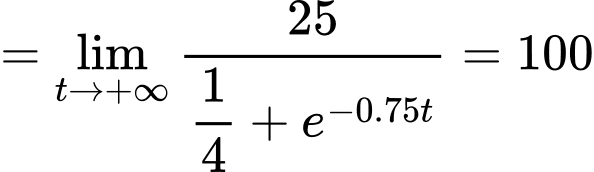 nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
nên số lượng quần thể nấm men tăng nhưng không vượt quá 100 tế bào.
Câu 2 [581994]: Giả sử chi phí 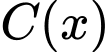 (nghìn đồng) để sản xuất
(nghìn đồng) để sản xuất 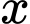 đơn vị của một loại hàng hoá nào đó được cho bởi hàm số
đơn vị của một loại hàng hoá nào đó được cho bởi hàm số 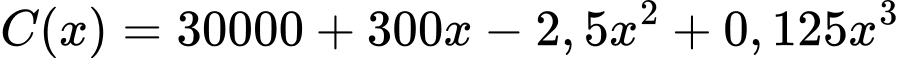 .
.
a) Tìm hàm chi phí biên.
b) Tìm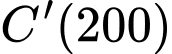 và giải thích ý nghĩa.
và giải thích ý nghĩa.
c) So sánh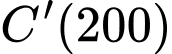 với chi phí sản xuất đơn vị hàng hoá thứ 201.
với chi phí sản xuất đơn vị hàng hoá thứ 201.
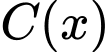 (nghìn đồng) để sản xuất
(nghìn đồng) để sản xuất 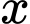 đơn vị của một loại hàng hoá nào đó được cho bởi hàm số
đơn vị của một loại hàng hoá nào đó được cho bởi hàm số 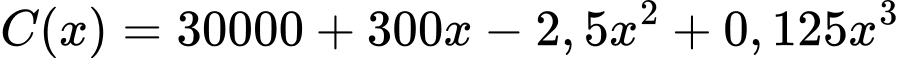 .
.a) Tìm hàm chi phí biên.
b) Tìm
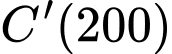 và giải thích ý nghĩa.
và giải thích ý nghĩa. c) So sánh
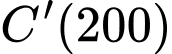 với chi phí sản xuất đơn vị hàng hoá thứ 201.
với chi phí sản xuất đơn vị hàng hoá thứ 201.
a) Hàm chi phí biên là 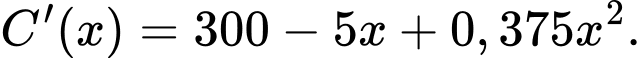
b) Ta có: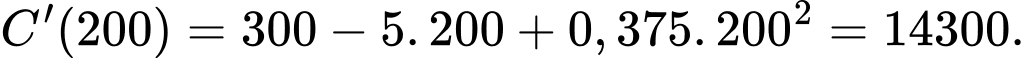
Chi phí biên tại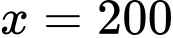 là 14300 nghìn đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hoá tiếp theo
là 14300 nghìn đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hoá tiếp theo
(đơn vị hàng hoá thứ 201) là khoảng 14300 nghìn đồng.
c) Chi phí sản xuất đơn vị hàng hoá thứ 201 là
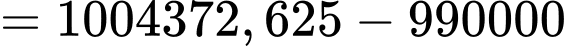
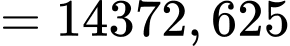 (nghìn đồng)
(nghìn đồng)
Giá trị này xấp xỉ với chi phí biên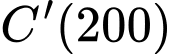 đã tính ở câu b.
đã tính ở câu b.
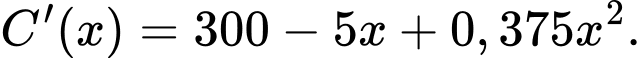
b) Ta có:
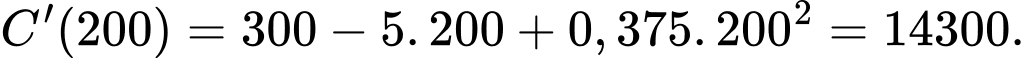
Chi phí biên tại
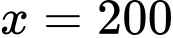 là 14300 nghìn đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hoá tiếp theo
là 14300 nghìn đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hoá tiếp theo(đơn vị hàng hoá thứ 201) là khoảng 14300 nghìn đồng.
c) Chi phí sản xuất đơn vị hàng hoá thứ 201 là

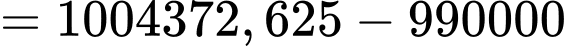
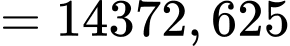 (nghìn đồng)
(nghìn đồng) Giá trị này xấp xỉ với chi phí biên
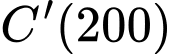 đã tính ở câu b.
đã tính ở câu b.
Câu 3 [581995]: Để loại bỏ 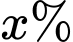 chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là
chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là 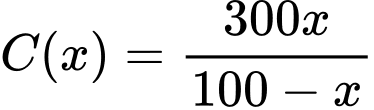 (triệu đồng),
(triệu đồng),  Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Khảo sát sự biến thiên và vẽ đồ thị của hàm số  Tự đó, hãy cho biết:
Tự đó, hãy cho biết:
a) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi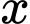 tăng?
tăng?
b) Có thể loại bỏ được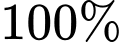 chất gây ô nhiễm không khí không? Vì sao?
chất gây ô nhiễm không khí không? Vì sao?
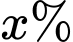 chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là
chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là 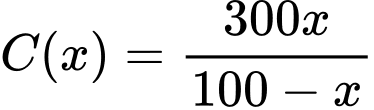 (triệu đồng),
(triệu đồng),  Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Khảo sát sự biến thiên và vẽ đồ thị của hàm số  Tự đó, hãy cho biết:
Tự đó, hãy cho biết: a) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi
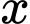 tăng?
tăng? b) Có thể loại bỏ được
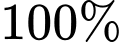 chất gây ô nhiễm không khí không? Vì sao?
chất gây ô nhiễm không khí không? Vì sao?
Xét hàm số 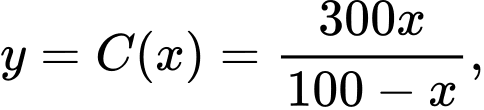

Ta có:
-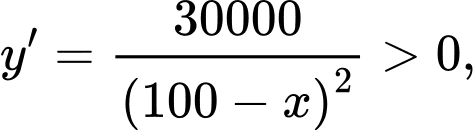 với mọi
với mọi 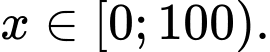
Do đó hàm số luôn đồng biến trên nửa khoảng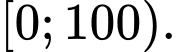
-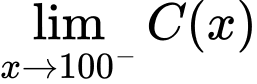
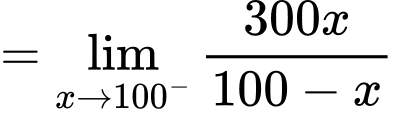
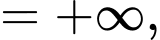 nên đồ thị hàm số có tiệm cận đứng là
nên đồ thị hàm số có tiệm cận đứng là 
Bảng biến thiên:
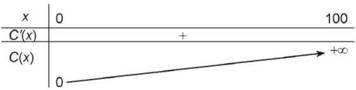
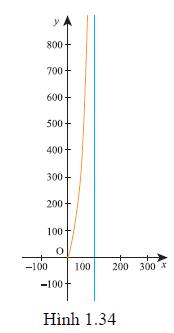
Đồ thị hàm số như Hình 1.34.
a) Chi phí cần bỏ ra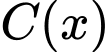 sẽ luôn tăng khi
sẽ luôn tăng khi 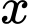 tăng.
tăng.
b) Vì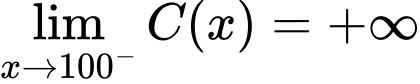 (hàm số
(hàm số 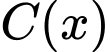 không xác định khi
không xác định khi 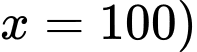 nên nhà máy không thể loại bỏ
nên nhà máy không thể loại bỏ 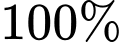 chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa)
chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa)
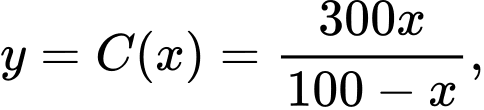

Ta có:
-
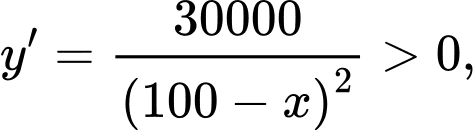 với mọi
với mọi 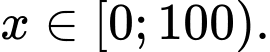
Do đó hàm số luôn đồng biến trên nửa khoảng
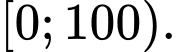
-
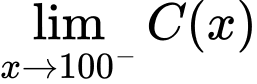
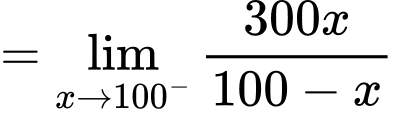
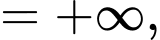 nên đồ thị hàm số có tiệm cận đứng là
nên đồ thị hàm số có tiệm cận đứng là 
Bảng biến thiên:

Đồ thị hàm số như Hình 1.34.

a) Chi phí cần bỏ ra
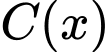 sẽ luôn tăng khi
sẽ luôn tăng khi 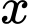 tăng.
tăng. b) Vì
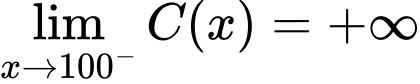 (hàm số
(hàm số 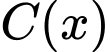 không xác định khi
không xác định khi 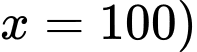 nên nhà máy không thể loại bỏ
nên nhà máy không thể loại bỏ 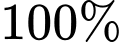 chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa)
chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa) DẠNG 2: BÀI TOÁN TỐI ƯU HÓA
Nhóm 1: Bài toán về quãng đường
Câu 4 [581996]: Một công ty muốn làm một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển 6km. Giá để xây đường ống trên bờ là 30.000USD mỗi km, và 50.000USD mỗi km để xây dưới nước. B’ là điểm trên bờ biển sao cho BB’ vuông góc với bờ biển. Khoảng cách từ A đến B’ là 11km. Vị trí C trên đoạn AB’ sao cho khi nối ống theo ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng:
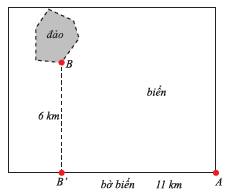

A, 6.5km.
B, 6km.
C, 0km.
D, 9km.
Đặt 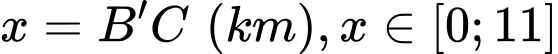
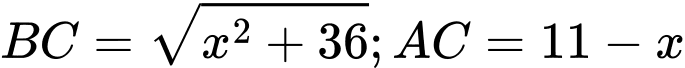
Chi phí xây dựng đường ống là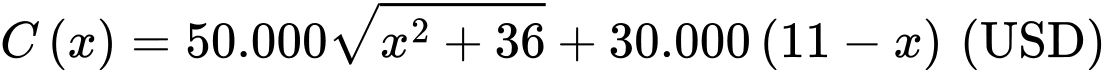
Hàm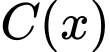 , xác định, liên tục trên [0;11] và
, xác định, liên tục trên [0;11] và 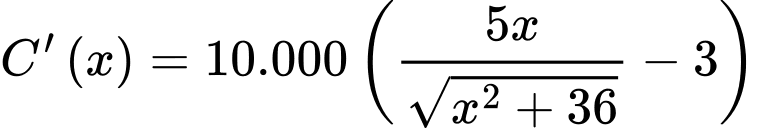
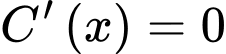
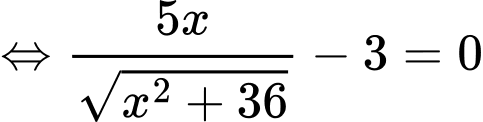
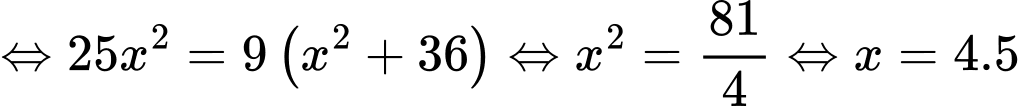
Khoảng cách từ đến
đến 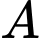 là
là 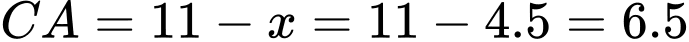
Chọn A. Đáp án: A
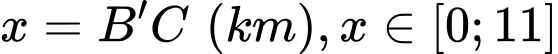
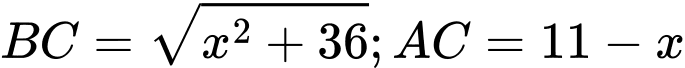
Chi phí xây dựng đường ống là
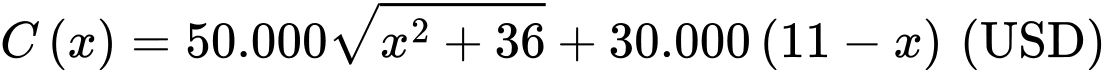
Hàm
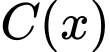 , xác định, liên tục trên [0;11] và
, xác định, liên tục trên [0;11] và 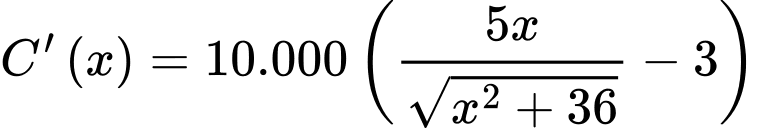
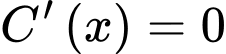
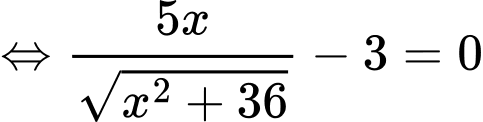
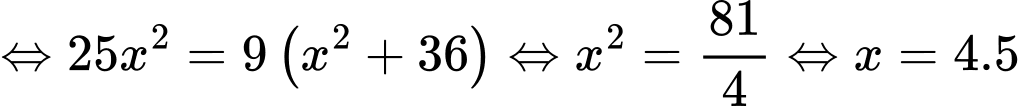
Khoảng cách từ
 đến
đến 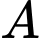 là
là 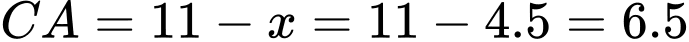
Chọn A. Đáp án: A
Nhóm 2: Bài toán diện tích hình phẳng
Câu 5 [581997]: Cho hình chữ nhật có diện tích bằng  Hỏi mỗi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất?
Hỏi mỗi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất?
 Hỏi mỗi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất?
Hỏi mỗi kích thước của nó bằng bao nhiêu để chu vi của nó nhỏ nhất? A, 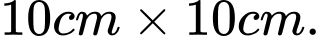
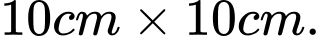
B, 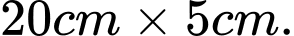
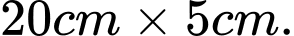
C, 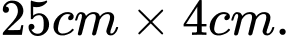
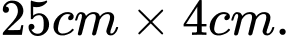
D, Đáp án khác.
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là:  và
và 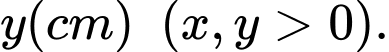
Chu vi hình chữ nhật là: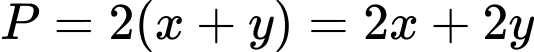
Theo đề bài thì: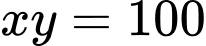 hay
hay 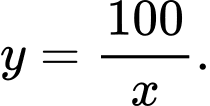 Do đó:
Do đó: 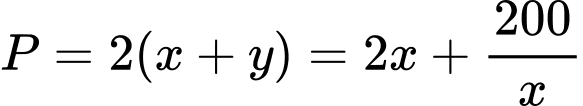 với
với 
Đạo hàm: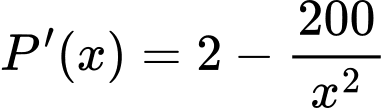
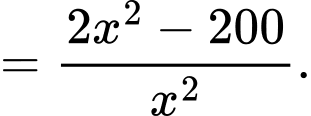 Cho
Cho 
Lập bảng biến thiên ta được: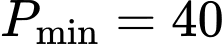 khi
khi 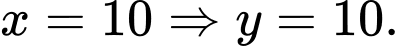
Kết luận: Kích thước của hình chữ nhật là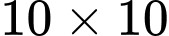 (là hình vuông).
(là hình vuông).
Lưu ý: Có thể đánh giá bằng BĐT Cô-si: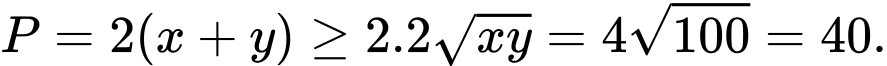 Đáp án: A
Đáp án: A
 và
và 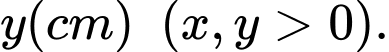
Chu vi hình chữ nhật là:
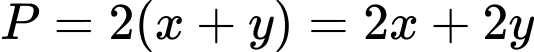
Theo đề bài thì:
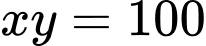 hay
hay 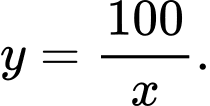 Do đó:
Do đó: 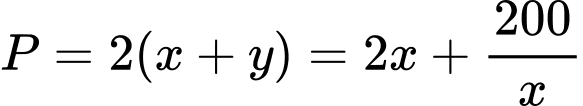 với
với 
Đạo hàm:
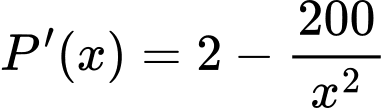
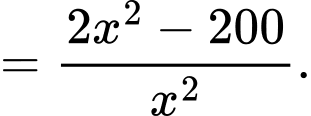 Cho
Cho 
Lập bảng biến thiên ta được:
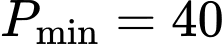 khi
khi 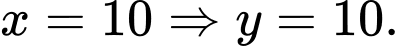
Kết luận: Kích thước của hình chữ nhật là
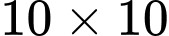 (là hình vuông).
(là hình vuông). Lưu ý: Có thể đánh giá bằng BĐT Cô-si:
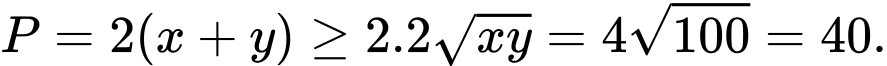 Đáp án: A
Đáp án: A Nhóm 3: Bài toán liên hệ diện tích, thể tích
Câu 6 [581998]: Người ta phải cưa một thân cây hình trụ có đường kính 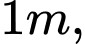 chiều dài
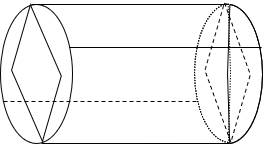
chiều dài 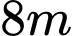 để được một cây xà hình khối chữ nhật như hình vẽ. Hỏi thể tích cực đại của khối gỗ sau khi cưa xong là bao nhiêu?
để được một cây xà hình khối chữ nhật như hình vẽ. Hỏi thể tích cực đại của khối gỗ sau khi cưa xong là bao nhiêu?
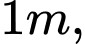 chiều dài
chiều dài 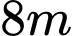 để được một cây xà hình khối chữ nhật như hình vẽ. Hỏi thể tích cực đại của khối gỗ sau khi cưa xong là bao nhiêu?
để được một cây xà hình khối chữ nhật như hình vẽ. Hỏi thể tích cực đại của khối gỗ sau khi cưa xong là bao nhiêu?
Gọi 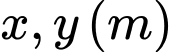 là các cạnh của tiết diện. Theo Định lí Pitago ta có:
là các cạnh của tiết diện. Theo Định lí Pitago ta có: 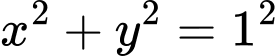 (đường kính của thân cây là
(đường kính của thân cây là 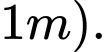 Thể tích của cây xà sẽ cực đại khi diện tích của tiết diện là cực đại, nghĩa là khi
Thể tích của cây xà sẽ cực đại khi diện tích của tiết diện là cực đại, nghĩa là khi 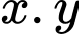 cực đại. Ta có:
cực đại. Ta có:
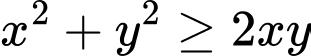
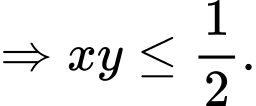 Dấu xảy ra khi
Dấu xảy ra khi 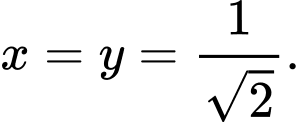
Thể tích khối gỗ sau khi cưa xong: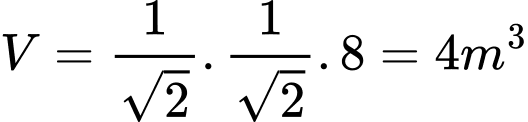 (tiết diện là hình vuông).
(tiết diện là hình vuông).
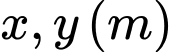 là các cạnh của tiết diện. Theo Định lí Pitago ta có:
là các cạnh của tiết diện. Theo Định lí Pitago ta có: 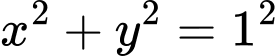 (đường kính của thân cây là
(đường kính của thân cây là 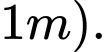 Thể tích của cây xà sẽ cực đại khi diện tích của tiết diện là cực đại, nghĩa là khi
Thể tích của cây xà sẽ cực đại khi diện tích của tiết diện là cực đại, nghĩa là khi 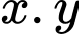 cực đại. Ta có:
cực đại. Ta có: 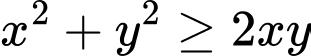
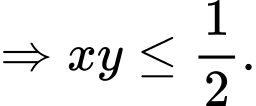 Dấu xảy ra khi
Dấu xảy ra khi 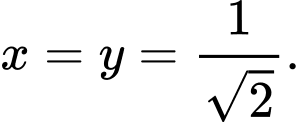
Thể tích khối gỗ sau khi cưa xong:
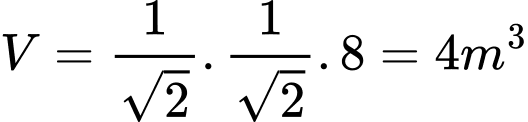 (tiết diện là hình vuông).
(tiết diện là hình vuông). Nhóm 4: Bài toán kinh tế
Câu 7 [581999]: Một nhà phân tích thị trường làm việc cho một công ty sản xuất thiết bị gia dụng nhận thấy rằng nếu công ty sản xuất và bán 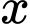 chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là
chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là 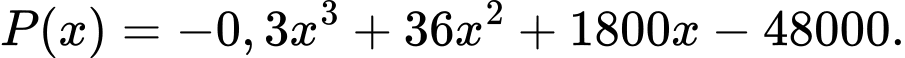 Khảo sát sự biến thiên và vẽ đồ thị hàm số
Khảo sát sự biến thiên và vẽ đồ thị hàm số 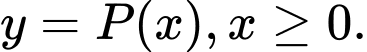 Sử dụng đồ thị đã vẽ để trả lời các câu hỏi sau:
Sử dụng đồ thị đã vẽ để trả lời các câu hỏi sau:
a) Khi chỉ sản xuất một vài máy xay sinh tố, công ty sẽ bị lỗ (vì lúc này lợi nhuận âm). Hỏi hằng tháng công ty phải sản xuất ít nhất bao nhiêu chiếc máy xay sinh tố để hoà vốn?
b) Lợi nhuận lớn nhất mà công ty có thể đạt được là bao nhiêu? Công ty có nên sản xuất 200 chiếc máy xay sinh tố hằng tháng hay không?
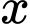 chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là
chiếc máy xay sinh tố hằng tháng thì lợi nhuận thu được (nghìn đồng) là 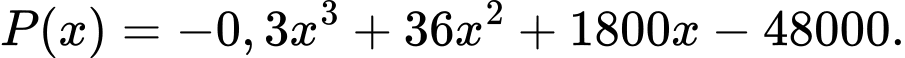 Khảo sát sự biến thiên và vẽ đồ thị hàm số
Khảo sát sự biến thiên và vẽ đồ thị hàm số 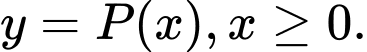 Sử dụng đồ thị đã vẽ để trả lời các câu hỏi sau:
Sử dụng đồ thị đã vẽ để trả lời các câu hỏi sau: a) Khi chỉ sản xuất một vài máy xay sinh tố, công ty sẽ bị lỗ (vì lúc này lợi nhuận âm). Hỏi hằng tháng công ty phải sản xuất ít nhất bao nhiêu chiếc máy xay sinh tố để hoà vốn?
b) Lợi nhuận lớn nhất mà công ty có thể đạt được là bao nhiêu? Công ty có nên sản xuất 200 chiếc máy xay sinh tố hằng tháng hay không?
Xét hàm số 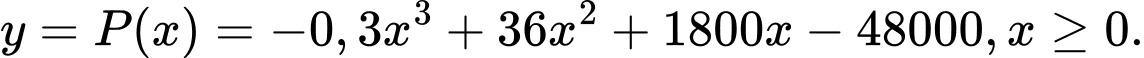
Ta có:
-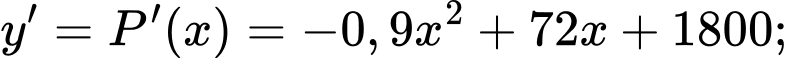
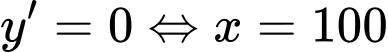 (vì
(vì 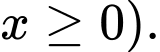
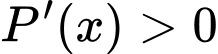 với mọi
với mọi 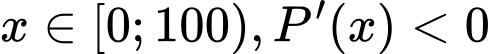 với mọi
với mọi 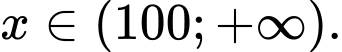
Do đó hàm số đồng biến trên nửa khoảng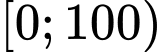 và nghịch biến trên khoảng
và nghịch biến trên khoảng 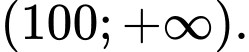
Tại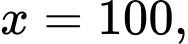 hàm số đạt cực đại và
hàm số đạt cực đại và 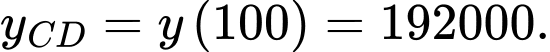
-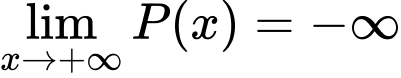 .
.
Bảng biến thiên:
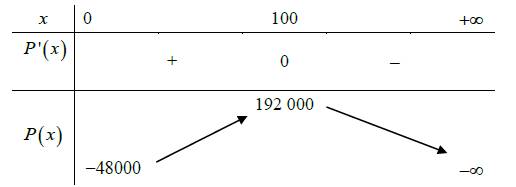
Đồ thị hàm số như Hình 1.36 (ở đây ta lấy một đơn vị trên trục hoành bằng 1000 đơn vị trên trục tung).
Từ đồ thị đã vẽ suy ra:
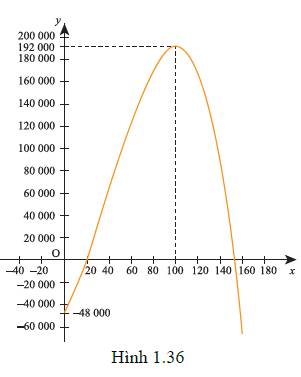
a) Đồ thị xuất phát từ điểm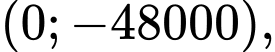 ở phia dưới trục hoành (tức là công ty đang bị lõm), và giao với trục hoành tại điểm đầu tiên có hoành độ
ở phia dưới trục hoành (tức là công ty đang bị lõm), và giao với trục hoành tại điểm đầu tiên có hoành độ 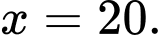 Do đó, hằng tháng công ty cần sản xuất ít nhất 20 chiếc máy xay sinh tố để hoà vốn.
Do đó, hằng tháng công ty cần sản xuất ít nhất 20 chiếc máy xay sinh tố để hoà vốn.
b) Từ đồ thị ta thấy khi sản xuất hơn 100 chiếc máy xay sinh tố mỗi tháng thì càng sản xuất nhiều lợi nhuận càng giảm. Do đó, công ty không nên sản xuất 200 chiếc máy xay sinh tố hằng tháng.
Lợi nhuận lớn nhất mà công ty có thể thu được là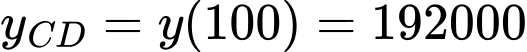 (nghìn đồng), tức là 192 triệu đồng, đạt được khi sản xuất đúng 100 chiếc máy xay sinh tố mỗi tháng.
(nghìn đồng), tức là 192 triệu đồng, đạt được khi sản xuất đúng 100 chiếc máy xay sinh tố mỗi tháng.
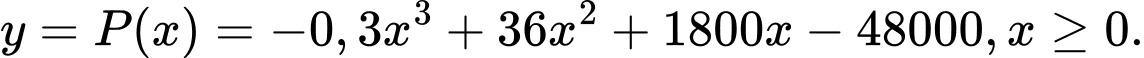
Ta có:
-
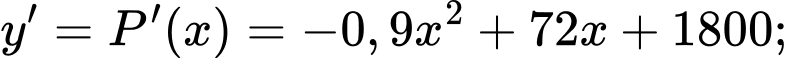
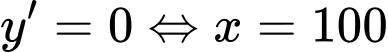 (vì
(vì 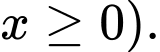
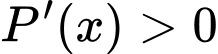 với mọi
với mọi 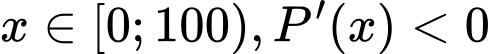 với mọi
với mọi 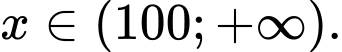
Do đó hàm số đồng biến trên nửa khoảng
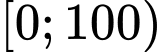 và nghịch biến trên khoảng
và nghịch biến trên khoảng 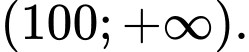
Tại
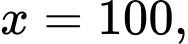 hàm số đạt cực đại và
hàm số đạt cực đại và 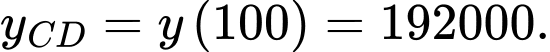
-
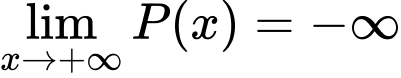 .
.Bảng biến thiên:

Đồ thị hàm số như Hình 1.36 (ở đây ta lấy một đơn vị trên trục hoành bằng 1000 đơn vị trên trục tung).
Từ đồ thị đã vẽ suy ra:

a) Đồ thị xuất phát từ điểm
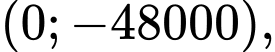 ở phia dưới trục hoành (tức là công ty đang bị lõm), và giao với trục hoành tại điểm đầu tiên có hoành độ
ở phia dưới trục hoành (tức là công ty đang bị lõm), và giao với trục hoành tại điểm đầu tiên có hoành độ 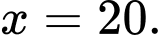 Do đó, hằng tháng công ty cần sản xuất ít nhất 20 chiếc máy xay sinh tố để hoà vốn.
Do đó, hằng tháng công ty cần sản xuất ít nhất 20 chiếc máy xay sinh tố để hoà vốn. b) Từ đồ thị ta thấy khi sản xuất hơn 100 chiếc máy xay sinh tố mỗi tháng thì càng sản xuất nhiều lợi nhuận càng giảm. Do đó, công ty không nên sản xuất 200 chiếc máy xay sinh tố hằng tháng.
Lợi nhuận lớn nhất mà công ty có thể thu được là
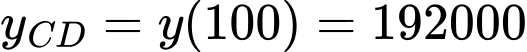 (nghìn đồng), tức là 192 triệu đồng, đạt được khi sản xuất đúng 100 chiếc máy xay sinh tố mỗi tháng.
(nghìn đồng), tức là 192 triệu đồng, đạt được khi sản xuất đúng 100 chiếc máy xay sinh tố mỗi tháng.