Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582002]: Công suất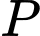 
(đơn vị 
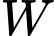) của một mạch điện được cung cấp bởi một nguồn pin 
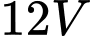được cho bởi công thức 
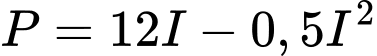với 
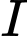(đơn vị 
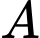) là cường độ dòng điện. Tìm công suất tối đa của mạch điện.
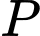(đơn vị 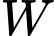) của một mạch điện được cung cấp bởi một nguồn pin 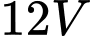được cho bởi công thức 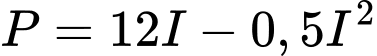với 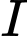(đơn vị 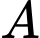) là cường độ dòng điện. Tìm công suất tối đa của mạch điện. A, 
B, 
C,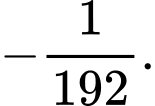 
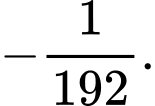
D,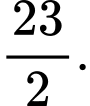 
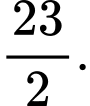
Chọn A
Xét hàm số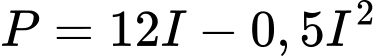
với 
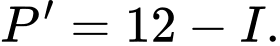
Bảng biến thiên:
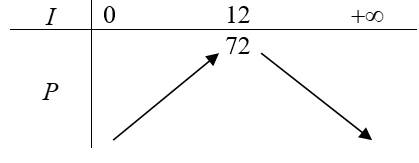
Công suất tối đa của mạch điện là
đạt được khi cường độ dòng điện là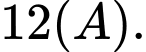 
Đáp án: A
Xét hàm số
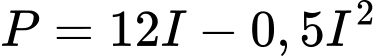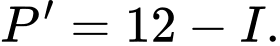
với Bảng biến thiên:
Công suất tối đa của mạch điện là
đạt được khi cường độ dòng điện là 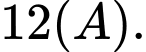Đáp án: A
Câu 2 [582003]: Khi nuôi cá thí nghiệm trong hồ, một nhà khoa học đã nhận thấy rằng: nếu trên mỗi đơn vị diện tích của mặt hồ có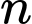 
con cá thì trung bình mỗi con cá sau một vụ cân nặng là 
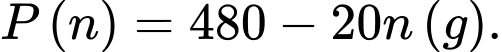Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
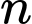con cá thì trung bình mỗi con cá sau một vụ cân nặng là 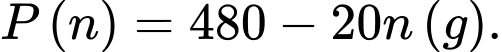Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất? A, 14.
B, 13.
C, 12.
D, 11.
Chọn C
Gọi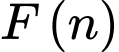
là hàm cân nặng của 
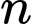con cá sau vụ thu hoạch trên một đơn vị diện tích
Ta có: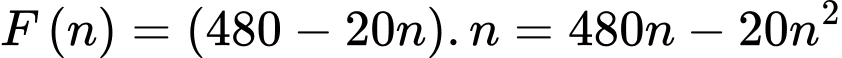
Để sau một vụ thu hoạch được nhiều cá nhất thì cân nặng của n con cá trên một đơn vị diện tích của mặt hồ là lớn nhất.
Bài toán trở thành tìm
sao cho F(n) đạt GTLN.
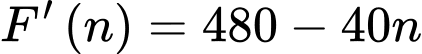
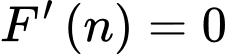
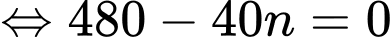
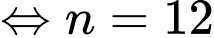
Học sinh tự lập bảng biến thiên.
Vậy phải thả 12 con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất. Đáp án: C
Gọi
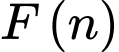là hàm cân nặng của 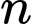con cá sau vụ thu hoạch trên một đơn vị diện tíchTa có:
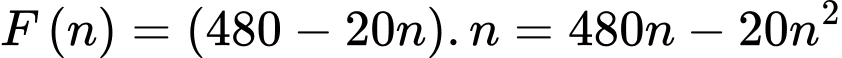
Để sau một vụ thu hoạch được nhiều cá nhất thì cân nặng của n con cá trên một đơn vị diện tích của mặt hồ là lớn nhất.
Bài toán trở thành tìm
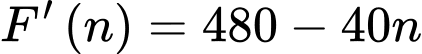
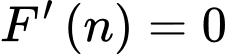
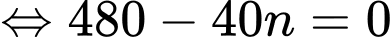
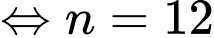
sao cho F(n) đạt GTLN. Học sinh tự lập bảng biến thiên.
Vậy phải thả 12 con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất. Đáp án: C
Câu 3 [582004]: Để giảm nhiệt độ trong phòng từ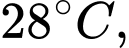 
một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi 
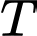(đơn vị 
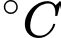) là nhiệt độ phòng ở phút thứ 
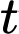được cho bởi công thức 
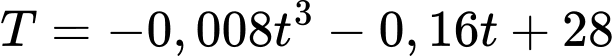với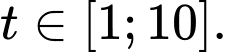 
Tìm nhiệt độ thấp nhất trong phòng đạt được trong thời gian 10 phút kể từ khi hệ thống làm mát bắt đầu hoạt động.
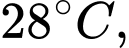một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi 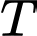(đơn vị 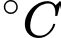) là nhiệt độ phòng ở phút thứ 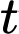được cho bởi công thức 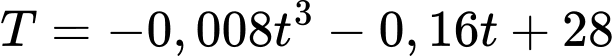với 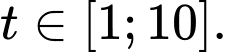Tìm nhiệt độ thấp nhất trong phòng đạt được trong thời gian 10 phút kể từ khi hệ thống làm mát bắt đầu hoạt động. A,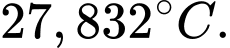 
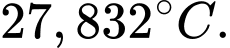
B,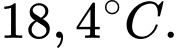 
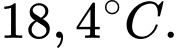
C,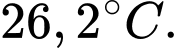 
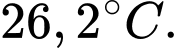
D,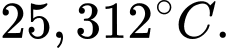 
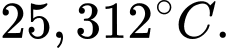
Chọn B
Xét hàm số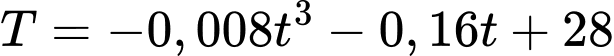
với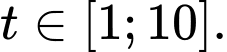 
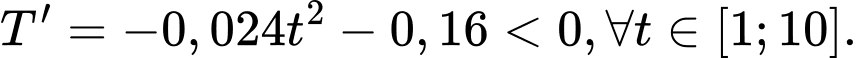
Suy ra hàm số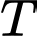
nghịch biến trên đoạn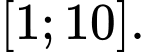 
Nhiệt độ thấp nhất trong phòng đạt được là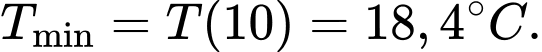
Đáp án: B
Xét hàm số
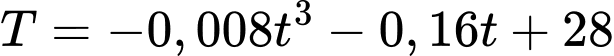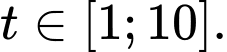
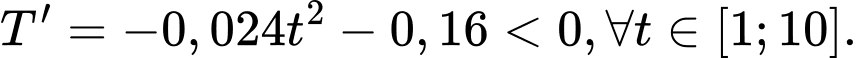
với Suy ra hàm số
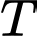nghịch biến trên đoạn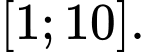 Nhiệt độ thấp nhất trong phòng đạt được là
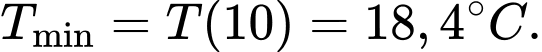Đáp án: B
Câu 4 [582005]: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000 đồng mỗi tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ 100.000 đồng mỗi tháng thì có thêm 2 căn hộ bị bỏ trống. Muốn có thu nhập cao nhất, công ty đó phải cho thuê với giá mỗi căn hộ là bao nhiêu?
A, 2.250.000.
B, 2.350.000.
C, 2.450.000.
D, 2.550.000.
Chọn A
Gọi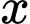
là giá thuê thực tế của mỗi căn hộ, (
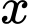: đồng; 
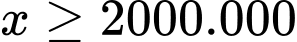đồng)
Ta có thể lập luận như sau:
Tăng giá 100.000 đồng thì có 2 căn hộ bị bỏ trống.
Tăng giá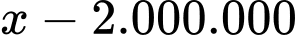
đồng thì có bao nhiêu căn hộ bị bỏ trống.
Theo quy tắc tam xuất ta có số căn hộ bị bỏ trống là:
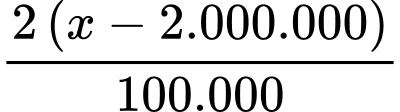
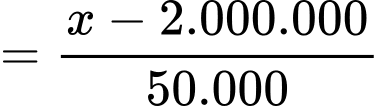
Do đó khi cho thuê với giá x đồng thì số căn hộ cho thuê là:
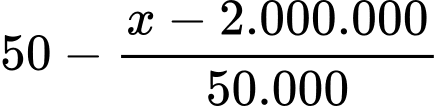
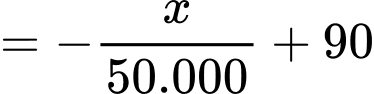
Gọi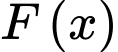
là hàm lợi nhuận thu được khi cho thuê các căn hộ, (F(x): đồng).
Ta có: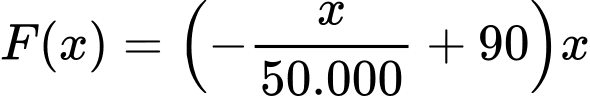
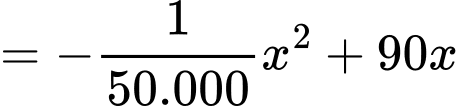( bằng số căn hộ cho thuê nhân với giá cho thuê mỗi căn hộ).
Bài toán trở thành tìm GTLN của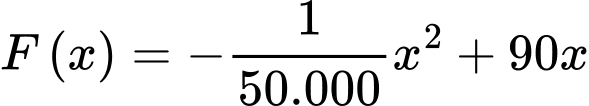
, ĐK: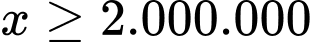 
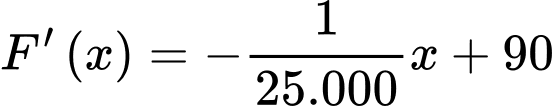
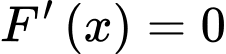
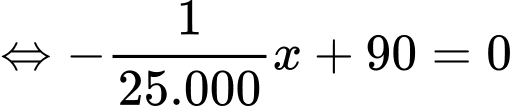
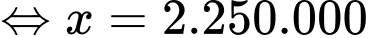
Bảng biến thiên:
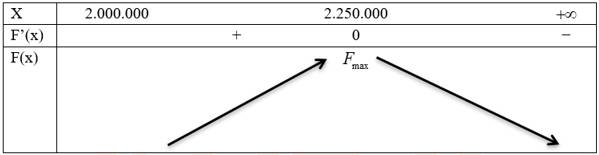
Suy ra F(x) đạt giá trị lớn nhất khi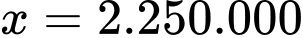
Vậy công ty phải cho thuê với giá 2.250.000 đồng mỗi căn hộ thì được lãi lớn nhất.
Nhận xét:
Sau khi tìm được hàm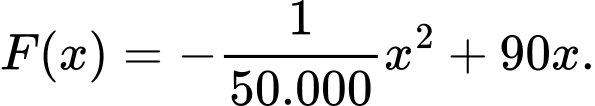
Ta không cần phải đi khảo sát và vẽ bảng biến thiên như trên. Đề đã cho bốn đáp án x, ta dùng phím CALC của MTCT để thay lần lượt các giá trị vào, cái nào làm cho F(x) lớn nhất chính là giá trị cần tìm. Đáp án: A
Gọi
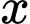là giá thuê thực tế của mỗi căn hộ, (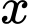: đồng; 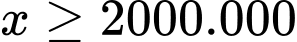đồng) Ta có thể lập luận như sau:
Tăng giá 100.000 đồng thì có 2 căn hộ bị bỏ trống.
Tăng giá
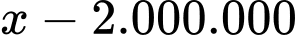đồng thì có bao nhiêu căn hộ bị bỏ trống. Theo quy tắc tam xuất ta có số căn hộ bị bỏ trống là:
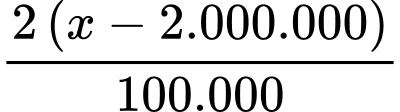
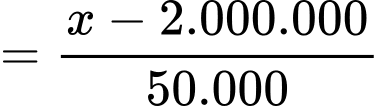
Do đó khi cho thuê với giá x đồng thì số căn hộ cho thuê là:
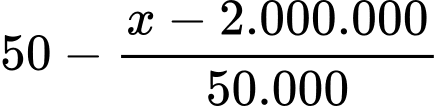
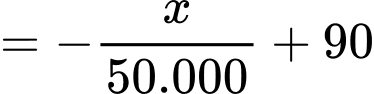
Gọi
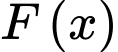là hàm lợi nhuận thu được khi cho thuê các căn hộ, (F(x): đồng). Ta có:
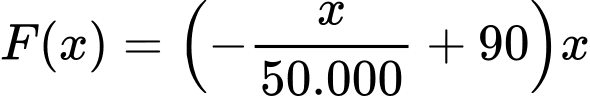
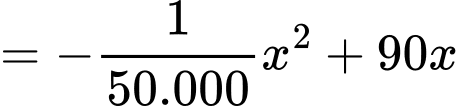( bằng số căn hộ cho thuê nhân với giá cho thuê mỗi căn hộ). Bài toán trở thành tìm GTLN của
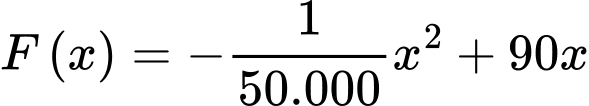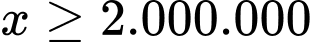
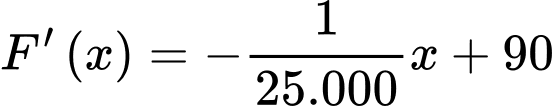
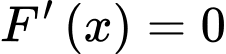
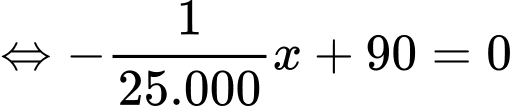
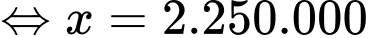
, ĐK: Bảng biến thiên:
Suy ra F(x) đạt giá trị lớn nhất khi
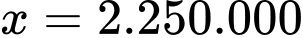
Vậy công ty phải cho thuê với giá 2.250.000 đồng mỗi căn hộ thì được lãi lớn nhất.
Nhận xét:
Sau khi tìm được hàm
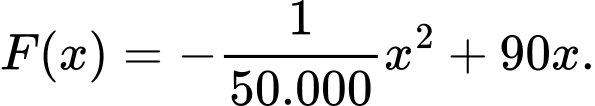Ta không cần phải đi khảo sát và vẽ bảng biến thiên như trên. Đề đã cho bốn đáp án x, ta dùng phím CALC của MTCT để thay lần lượt các giá trị vào, cái nào làm cho F(x) lớn nhất chính là giá trị cần tìm. Đáp án: A
Câu 5 [582006]: Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm là 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.
A, 44.000đ.
B, 43.000đ.
C, 42.000đ.
D, 41.000đ.
Chọn C
Gọi x là giá bán thực tế của mỗi quả bưởi Đoan Hùng, (x: đồng;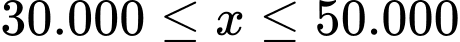
đồng).
Ta có thể lập luận như sau:
Giá 50.000 đồng thì bán được 40 quả bưởi
Giảm giá 5.000 đồng thì bán được thêm 50 quả.
Giảm giá 50.000 – x thì bán được thêm bao nhiêu quả?
Theo quy tắc tam xuất số quả bán thêm được là:
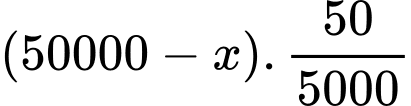
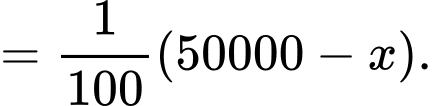
Do đó Số quả bưởi bán được tương ứng với giá bán x:
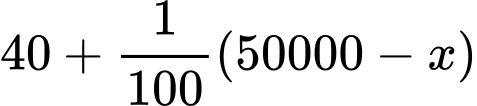
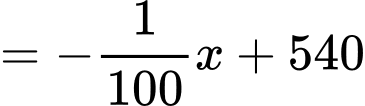
Gọi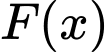
là hàm lợi nhuận thu được (
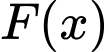: đồng).
Ta có: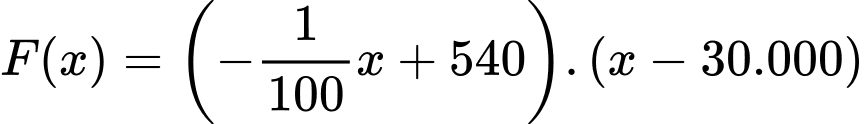
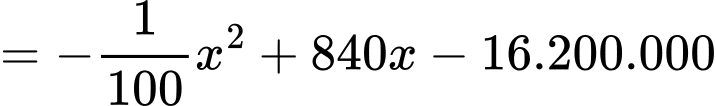
Bài toán trở thành tìm GTLN của
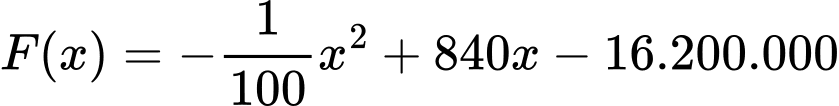, Đk: 
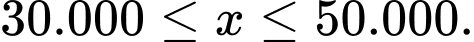
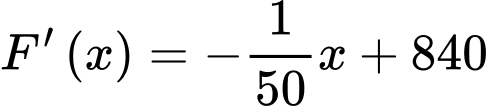
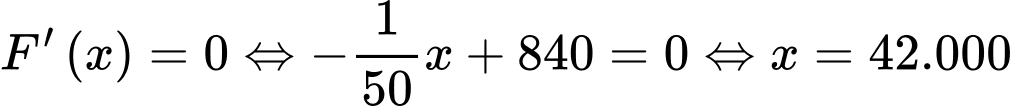
Vì hàm F(x) liên tục trên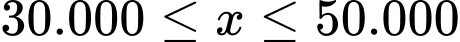
nên ta có:
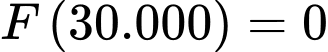
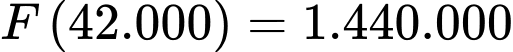
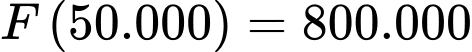
Vậy vớ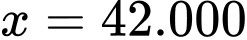i
thì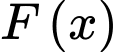 
đạt GTLN.
Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi quả bưởi Đoan Hùng là 42.000 đồng. Đáp án: C
Gọi x là giá bán thực tế của mỗi quả bưởi Đoan Hùng, (x: đồng;
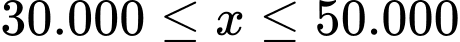đồng). Ta có thể lập luận như sau:
Giá 50.000 đồng thì bán được 40 quả bưởi
Giảm giá 5.000 đồng thì bán được thêm 50 quả.
Giảm giá 50.000 – x thì bán được thêm bao nhiêu quả?
Theo quy tắc tam xuất số quả bán thêm được là:
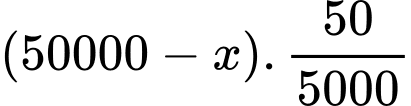
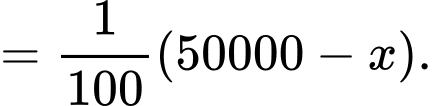
Do đó Số quả bưởi bán được tương ứng với giá bán x:
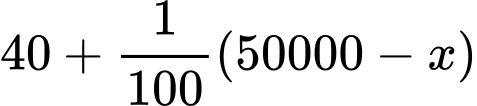
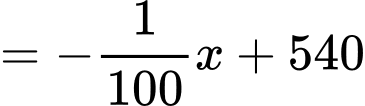
Gọi
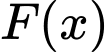là hàm lợi nhuận thu được (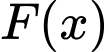: đồng). Ta có:
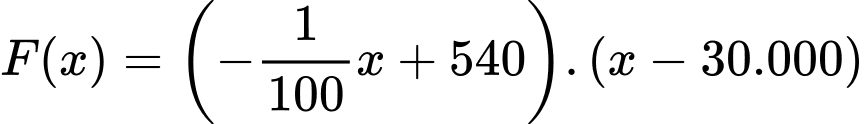
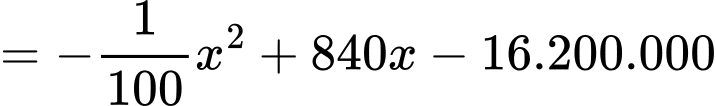
Bài toán trở thành tìm GTLN của
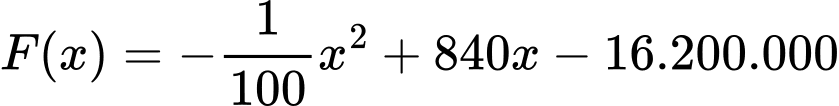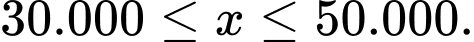
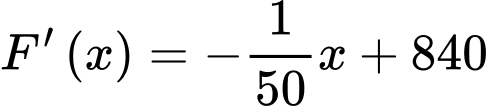
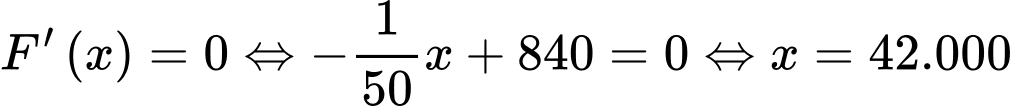
, Đk: Vì hàm F(x) liên tục trên
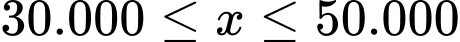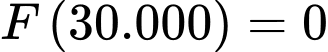
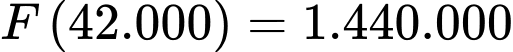
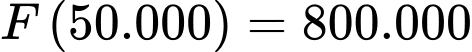
nên ta có: Vậy với
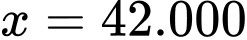thì 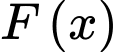đạt GTLN. Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi quả bưởi Đoan Hùng là 42.000 đồng. Đáp án: C
Câu 6 [582007]: Độ giảm huyết áp của một bệnh nhân được đo bởi công thức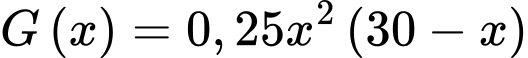 
trong đó 
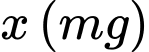và 
là lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng bao nhiêu:
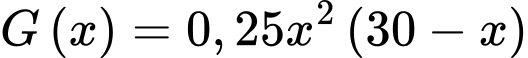trong đó 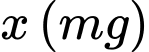và là lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng bao nhiêu: A, 15mg.
B, 30mg.
C, 40mg.
D, 20mg.
Chọn D
Ta có: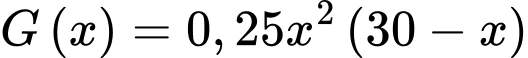
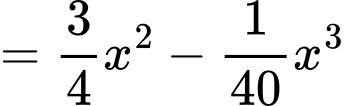
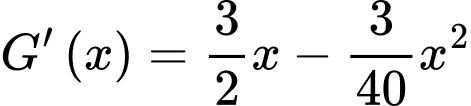
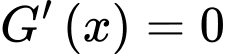
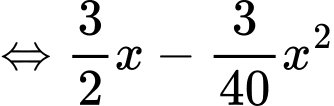
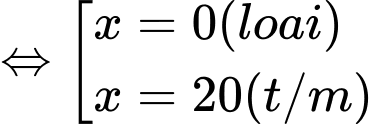
Bảng biến thiên:
Dựa vào bảng biến thiên thì bênh nhân cần tiêm một lượng thuốc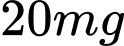
Đáp án: D
Ta có:
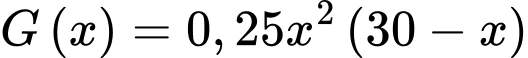
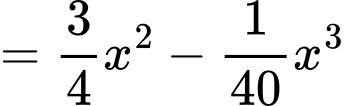
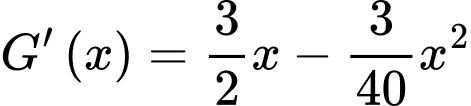
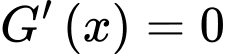
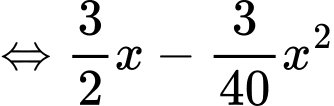
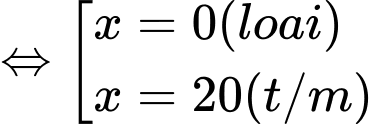
Bảng biến thiên:
Dựa vào bảng biến thiên thì bênh nhân cần tiêm một lượng thuốc
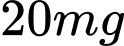Đáp án: D
Câu 7 [582008]: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ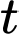 
là 
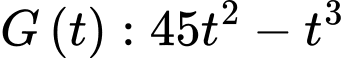, (kết quả khảo sát được trong 10 tháng vừa qua). Nếu xem 
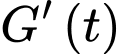là tốc độ truyền bệnh (người / ngày) tại thời điểm 
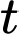thì tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ:
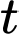là 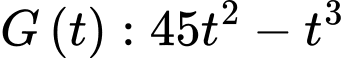, (kết quả khảo sát được trong 10 tháng vừa qua). Nếu xem 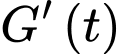là tốc độ truyền bệnh (người / ngày) tại thời điểm 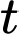thì tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ: A, 25.
B, 30.
C, 20.
D, 15.
Chọn D
Ta có:
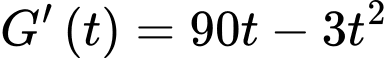
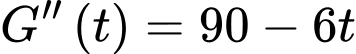
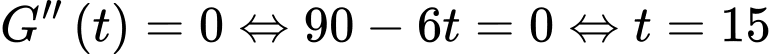
Bảng biến thiên:
Vậy tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ 15. Đáp án: D
Ta có:
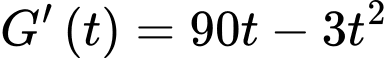
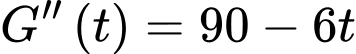
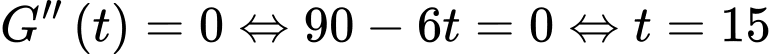
Bảng biến thiên:
Vậy tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ 15. Đáp án: D
Câu 8 [582009]: Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu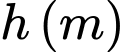 
của mực nước trong kênh tính theo thời gian 
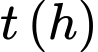trong ngày cho bởi công thức 
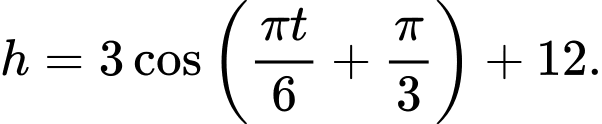Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
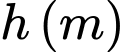của mực nước trong kênh tính theo thời gian 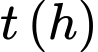trong ngày cho bởi công thức 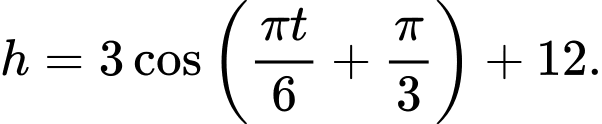Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất? A,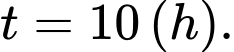 
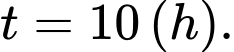
B,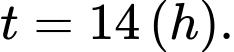 
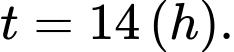
C,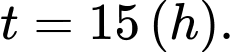 
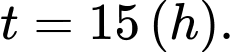
D,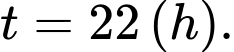 
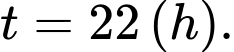
Chọn A
Ta có:
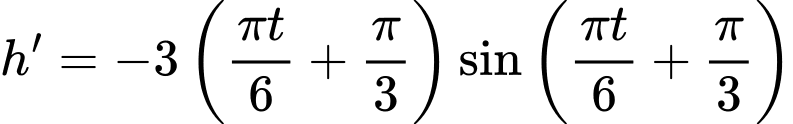
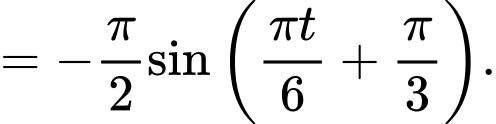
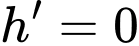
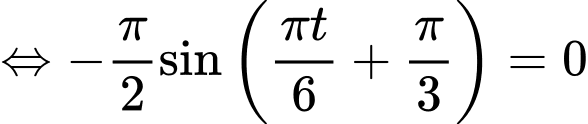
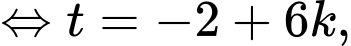
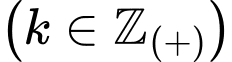
ở đây ta chỉ cần xét một số giá trị
Bảng biến thiên:
Ta suy ra được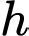
đạt GTLN khi 
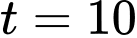(h)
Lưu ý: Ngoài cách trên ta có thể làm như sau
Vì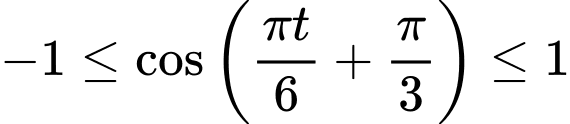
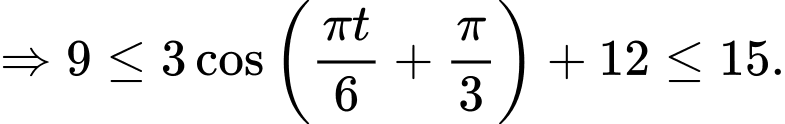
Vậy để h lớn nhất thì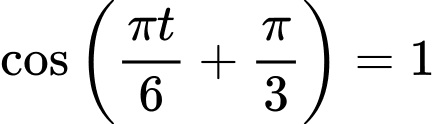
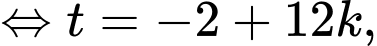
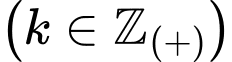
Vậy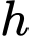
đạt GTLN khi 
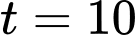(h) Đáp án: A
Ta có:
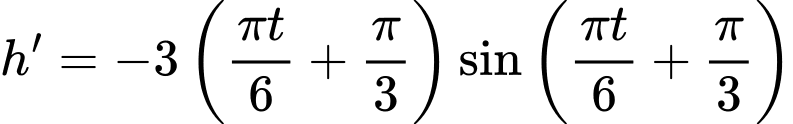
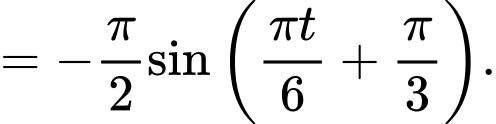
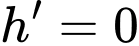
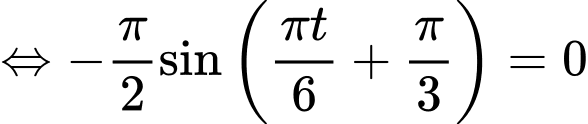
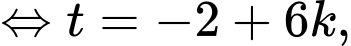
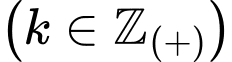
ở đây ta chỉ cần xét một số giá trị
Bảng biến thiên:
Ta suy ra được
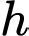đạt GTLN khi 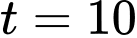(h) Lưu ý: Ngoài cách trên ta có thể làm như sau
Vì
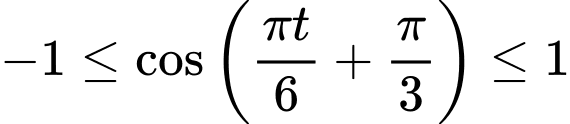
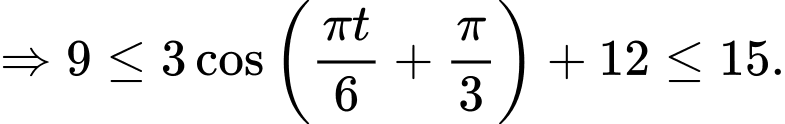
Vậy để h lớn nhất thì
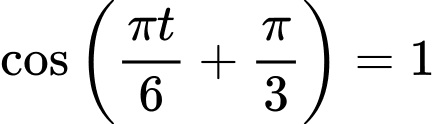
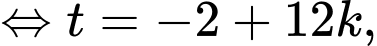
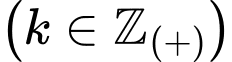
Vậy
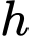đạt GTLN khi 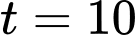(h) Đáp án: A
Câu 9 [582010]: Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính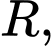 
nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp?
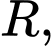nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp? A,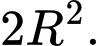 
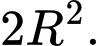
B,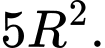 
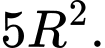
C,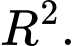 
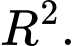
D,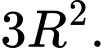 
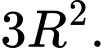
Chọn C
Gọi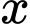
là độ dài cạnh của hình chữ nhật không nằm dọc theo đường kính của hình tròn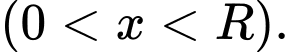 
Độ dài cạnh còn lại của hình chữ nhật là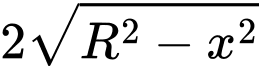
Ta có diện tích của hình chữ nhật là: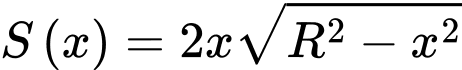
Bài toán trở thành tìm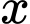
để S(x) đạt GTLN.
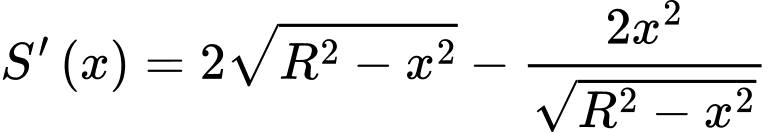
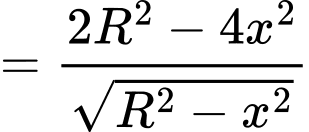
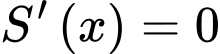
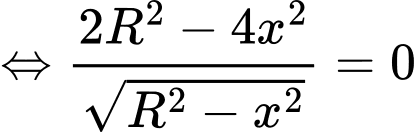
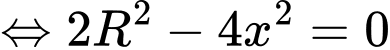
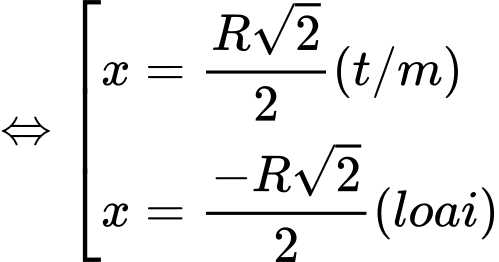
BBT:
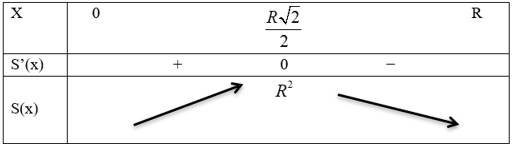
Vậy diện tích lớn nhất của hình chữ nhật là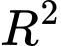
Đáp án: C
Gọi
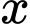là độ dài cạnh của hình chữ nhật không nằm dọc theo đường kính của hình tròn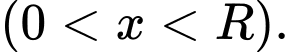 Độ dài cạnh còn lại của hình chữ nhật là
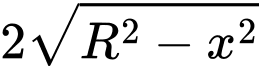
Ta có diện tích của hình chữ nhật là:
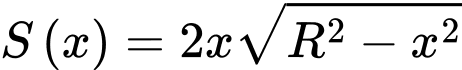
Bài toán trở thành tìm
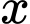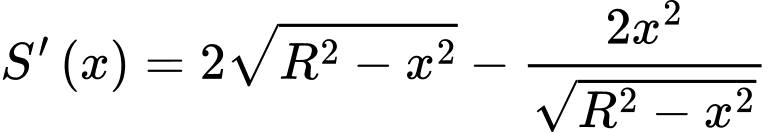
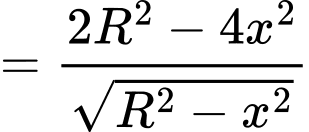
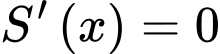
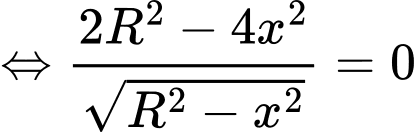
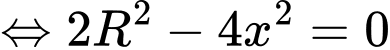
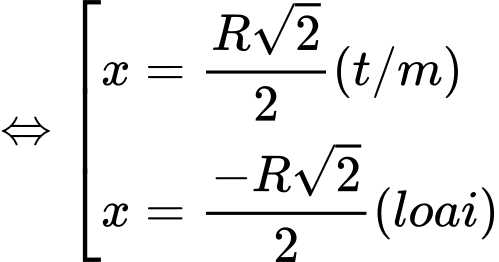
để S(x) đạt GTLN. BBT:
Vậy diện tích lớn nhất của hình chữ nhật là
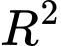Đáp án: C
Câu 10 [582011]: Một xe khách đi từ Việt Trì về Hà Nội chở tối đa được là 60 hành khách một chuyến. Nếu một chuyến chở được m hành khách thì giá tiền cho mỗi hành khách được tính là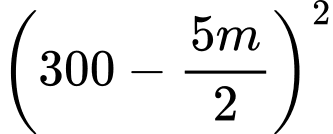 
đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận mỗi chuyến xe là lớn nhất?
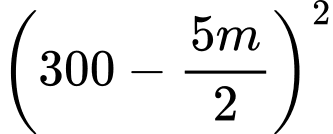đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận mỗi chuyến xe là lớn nhất? A, 30.
B, 40.
C, 50.
D, 60.
Chọn B
Gọi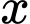
là số hành khách trên mỗi chuyến xe để số tiền thu được là lớn nhất,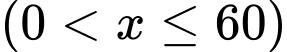 
Gọi F(x) là hàm lợi nhuận thu được (F(x): đồng)
Số tiền thu được:
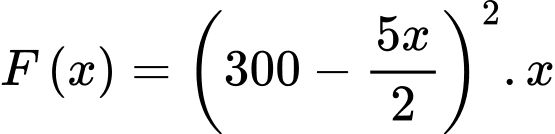
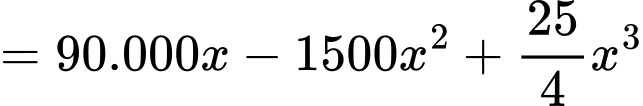
Bài toán trở thành tìm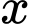
để F(x) đạt giá trị lớn nhất.
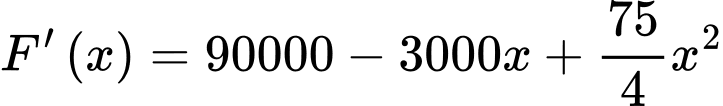
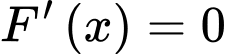
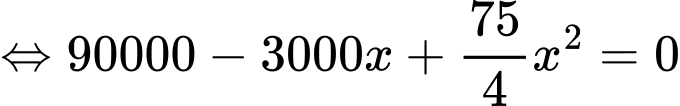
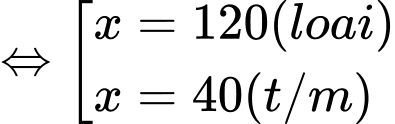
Bảng biến thiên
Vậy để thu được số tiền lớn nhất thì trên mỗi chuyến xe khách đó phải chở 40 người. Đáp án: B
Gọi
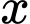là số hành khách trên mỗi chuyến xe để số tiền thu được là lớn nhất,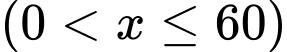 Gọi F(x) là hàm lợi nhuận thu được (F(x): đồng)
Số tiền thu được:
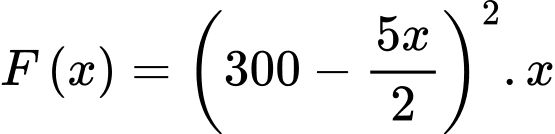
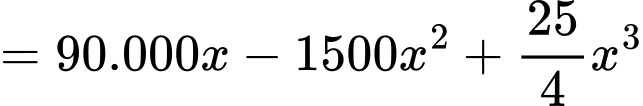
Bài toán trở thành tìm
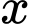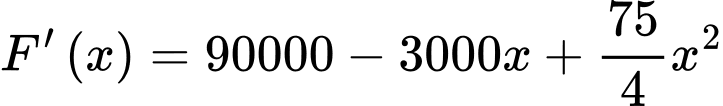
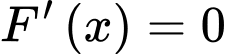
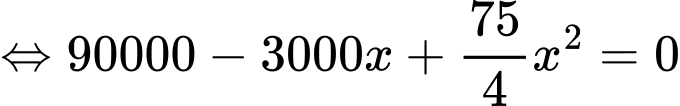
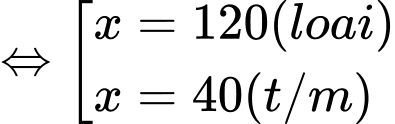
để F(x) đạt giá trị lớn nhất. Bảng biến thiên
Vậy để thu được số tiền lớn nhất thì trên mỗi chuyến xe khách đó phải chở 40 người. Đáp án: B
Câu 11 [582012]: Gia đình ông Thanh nuôi tôm với diện tích ao nuôi là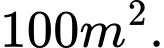 
Vụ tôm vừa qua ông nuôi với mật độ là 
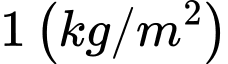tôm giống và sản lượng tôm khi thu hoạch được khoảng 2 tấn tôm. Với kinh nghiệm nuôi tôm nhiều năm, ông cho biết cứ thả giảm đi 
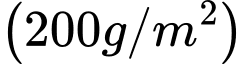tôm giống thì sản lượng tôm thu hoạch được 2,2 tấn tôm. Vậy vụ tới ông phải thả bao nhiêu kg tôm giống để đạt sản lượng tôm cho thu hoạch là lớn nhất? (Giả sử không có dịch bệnh, hao hụt khi nuôi tôm giống).
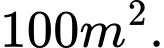Vụ tôm vừa qua ông nuôi với mật độ là 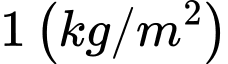tôm giống và sản lượng tôm khi thu hoạch được khoảng 2 tấn tôm. Với kinh nghiệm nuôi tôm nhiều năm, ông cho biết cứ thả giảm đi 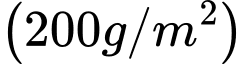tôm giống thì sản lượng tôm thu hoạch được 2,2 tấn tôm. Vậy vụ tới ông phải thả bao nhiêu kg tôm giống để đạt sản lượng tôm cho thu hoạch là lớn nhất? (Giả sử không có dịch bệnh, hao hụt khi nuôi tôm giống). A,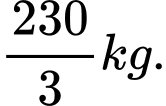 
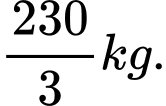
B, 
C, 
D,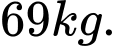 
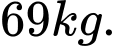
Chọn A
Số Kg tôm giống mà ông Thanh thả vụ vừa qua: 100.1= 100(kg).
Gọi x (0Khối lượng trung bình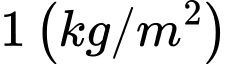 
tôm giống thu hoạch được: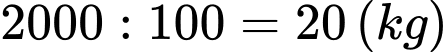 
Khi giảm 0,2 kg tôm giống thì thì sản lượng tôm thu hoạch tăng thêm là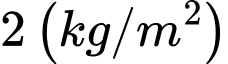
Gọi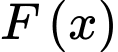
là hàm sản lượng tôm thu được vụ tới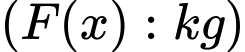 
Vậy sản lượng tôm thu hoạch được trong vụ tới có pt tổng quát là:
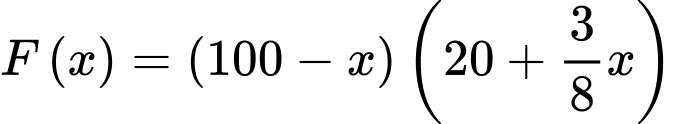
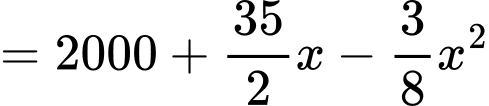
Bài toán trở thành tìm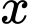
để F(x) lớn nhất.
Ta có:
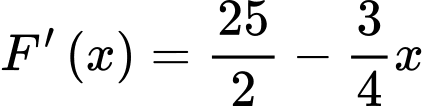
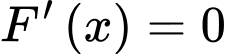
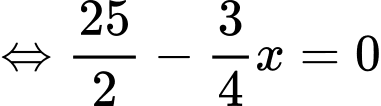
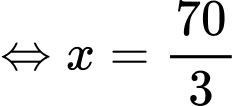
Bảng biến thiên
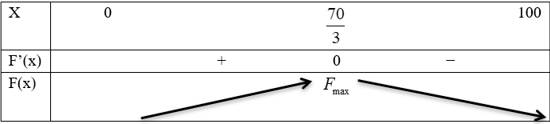
Vậy vụ tới ông Thanh phải thả số kg tôm giống là:
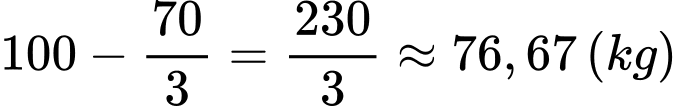
Nhận xét:
Làm sao ta có thể tìm được hàm F(x) và tìm được hệ số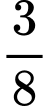
Ta có thể hiểu đơn giản như sau: nếu ta không giảm số lượng tôm giống thì sản lượng tôm thu hoạch được là: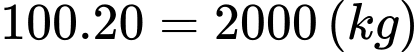
tôm.
Nếu ta giảm số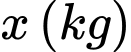
tôm giống thì số tôm giống cần thả là 
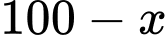và số kg tôm thu hoạch được là: 
Theo giả thiết tôm giống giảm 0,2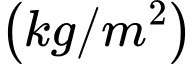
thì 
giảm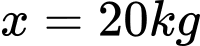 
, sản lượng thu được là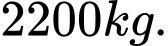 
Ta có: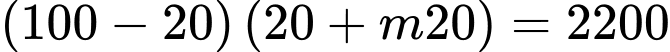
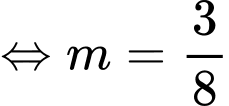
Đáp án: A
Số Kg tôm giống mà ông Thanh thả vụ vừa qua: 100.1= 100(kg).
Gọi x (0
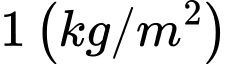tôm giống thu hoạch được: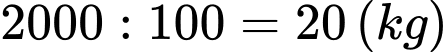 Khi giảm 0,2 kg tôm giống thì thì sản lượng tôm thu hoạch tăng thêm là
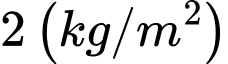
Gọi
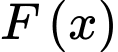là hàm sản lượng tôm thu được vụ tới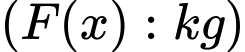 Vậy sản lượng tôm thu hoạch được trong vụ tới có pt tổng quát là:
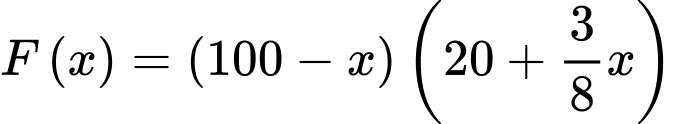
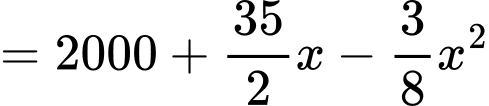
Bài toán trở thành tìm
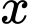để F(x) lớn nhất. Ta có:
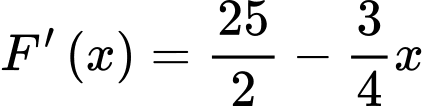
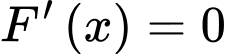
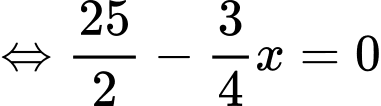
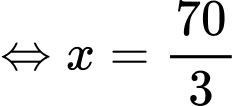
Bảng biến thiên
Vậy vụ tới ông Thanh phải thả số kg tôm giống là:
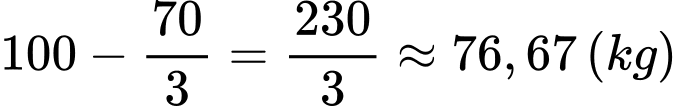
Nhận xét:
Làm sao ta có thể tìm được hàm F(x) và tìm được hệ số
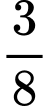
Ta có thể hiểu đơn giản như sau: nếu ta không giảm số lượng tôm giống thì sản lượng tôm thu hoạch được là:
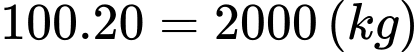tôm. Nếu ta giảm số
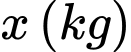tôm giống thì số tôm giống cần thả là 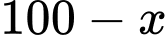và số kg tôm thu hoạch được là: Theo giả thiết tôm giống giảm 0,2
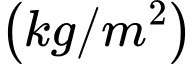thì giảm 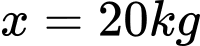, sản lượng thu được là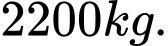 Ta có:
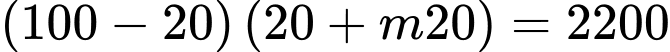
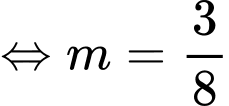
Câu 12 [582013]: Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất.
A, 480 ngàn.
B, 50 ngàn.
C, 450 ngàn.
D, 80 ngàn.
Chọn C
Gọi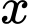
(ngàn đồng) là giá phòng khách sạn cần đặt ra, 
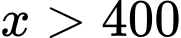(đơn vị: ngàn đồng).
Giá chênh lệch sau khi tăng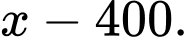
Số phòng cho thuê giảm nếu giá là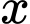
: 
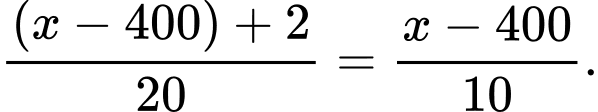
Số phòng cho thuê với gi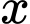á
là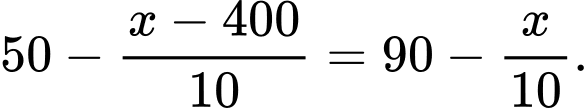 
Tổng doanh thu trong ngày là: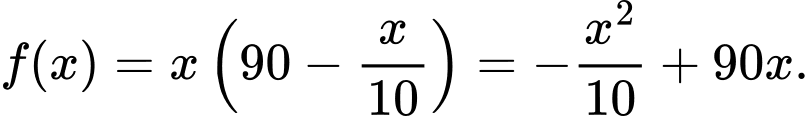
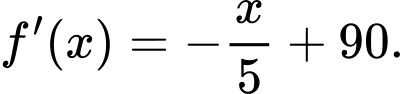
Bảng biến thiên:
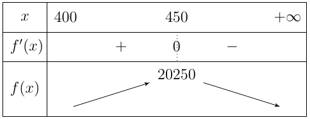
Dựa vào bảng biến thiên ta thấy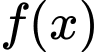
đạt giá trị lớn nhất khi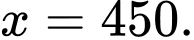 
Vậy nếu cho thuê với giá 450 ngàn đồng thì sẽ có doanh thu cao nhất trong ngày là 2.025.000 đồng. Đáp án: C
Gọi
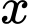(ngàn đồng) là giá phòng khách sạn cần đặt ra, 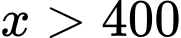(đơn vị: ngàn đồng). Giá chênh lệch sau khi tăng
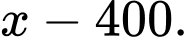
Số phòng cho thuê giảm nếu giá là
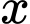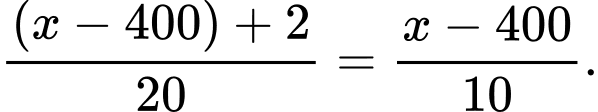
: Số phòng cho thuê với giá
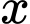là 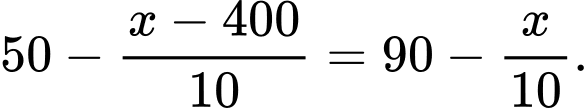Tổng doanh thu trong ngày là:
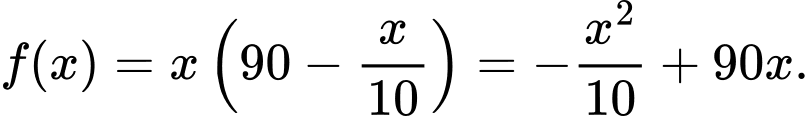
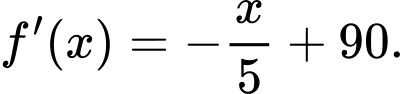
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy
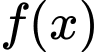đạt giá trị lớn nhất khi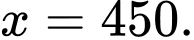 Vậy nếu cho thuê với giá 450 ngàn đồng thì sẽ có doanh thu cao nhất trong ngày là 2.025.000 đồng. Đáp án: C
Câu 13 [582014]: Một màn ảnh hình chữ nhật cao 1,4 mét và đặt ở độ cao 1,8 mét so với tầm mắt (tính từ đầu mép dưới của màn hình BC). Xác định vị trí nhìn từ phía O, sao cho nhìn rõ màn hình BC nhất? Biết rằng góc 
là góc nhọn.
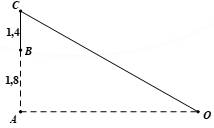
là góc nhọn. A,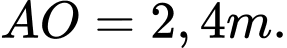 
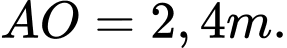
B,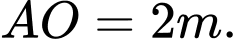 
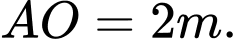
C,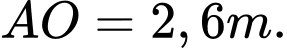 
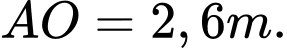
D,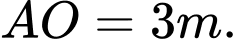 
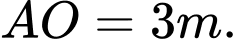
Chọn A
Đặt độ dài cạnh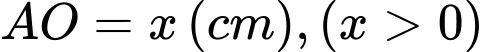
Suy ra:
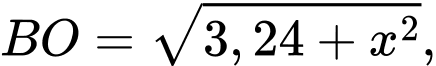
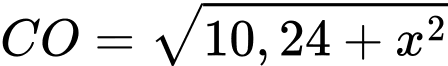
Ta sử dụng định lí cosin trong tam giác OBC ta có:
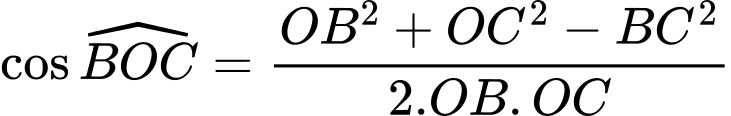
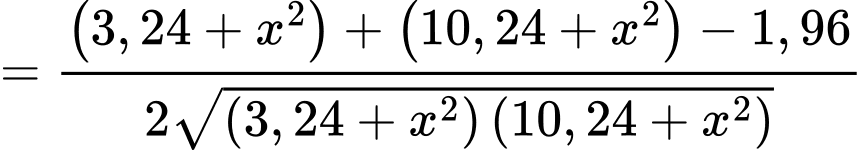
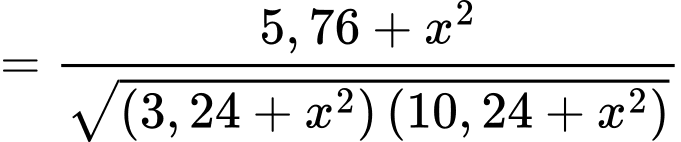
Vì góc
là góc nhọn nên bài toán trở thành bài toán tìm 
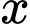để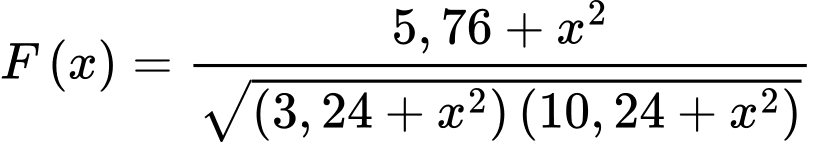 
đạt GTNN.
Đặt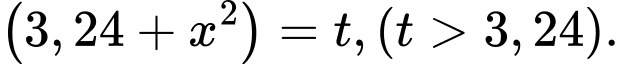
Suy ra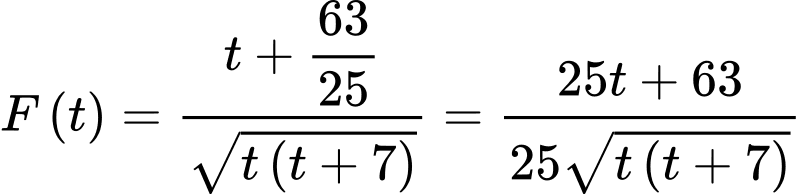
Ta tìm t để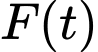
nhận giá trị nhỏ nhất.
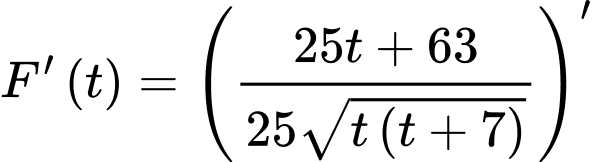
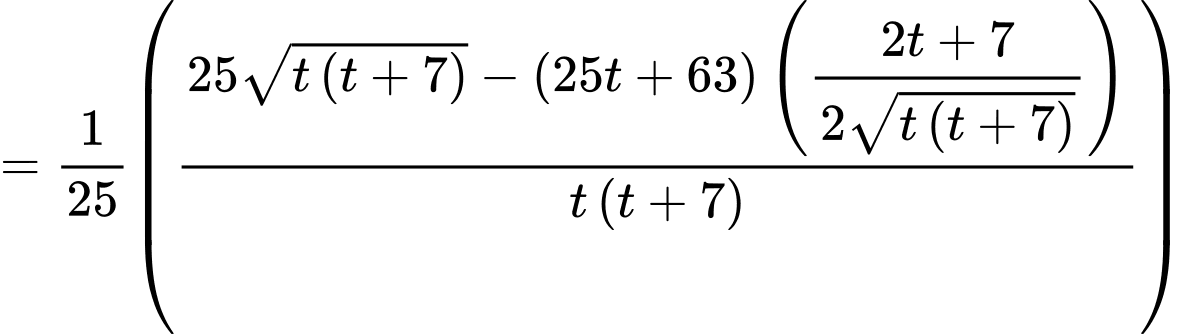
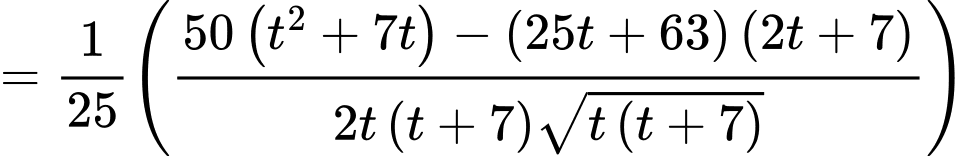
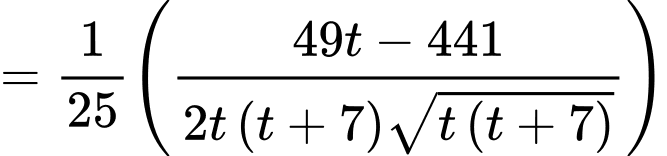
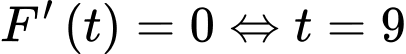
BBT
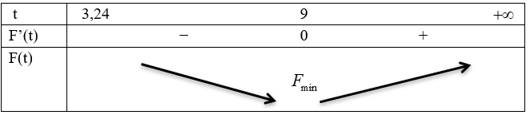
Thay vào đặt ta có: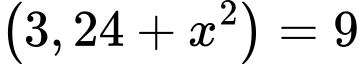
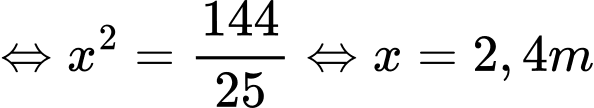
Vậy để nhìn rõ nhất thì AO =2,4 m. Đáp án: A
Đặt độ dài cạnh
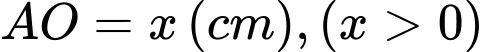
Suy ra:
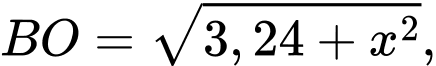
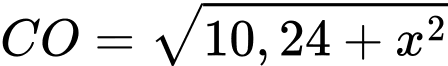
Ta sử dụng định lí cosin trong tam giác OBC ta có:
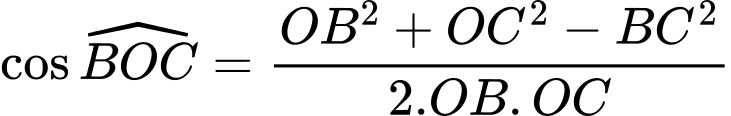
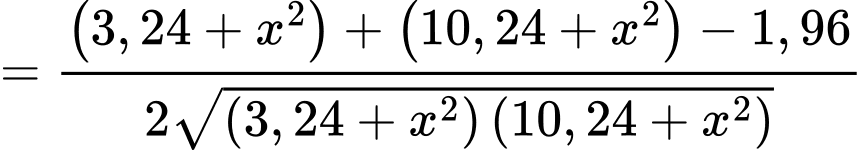
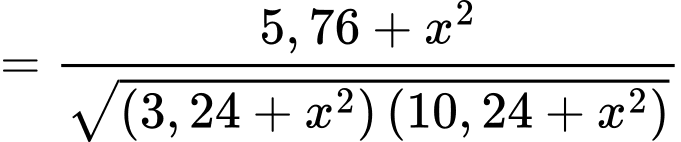
Vì góc
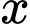là góc nhọn nên bài toán trở thành bài toán tìm để 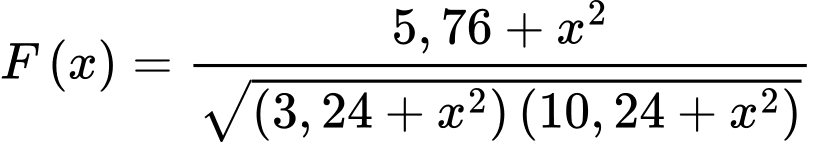đạt GTNN. Đặt
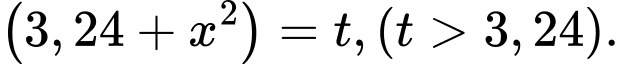
Suy ra
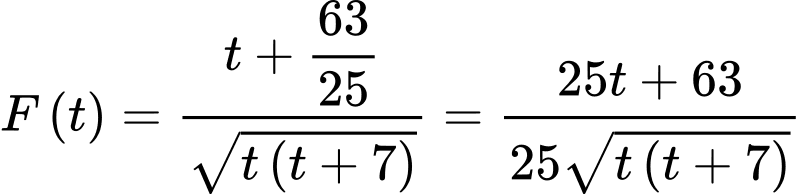
Ta tìm t để
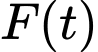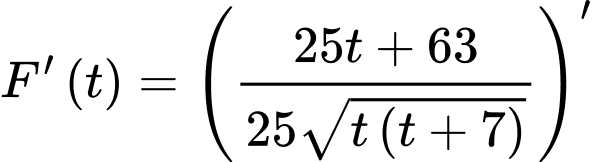
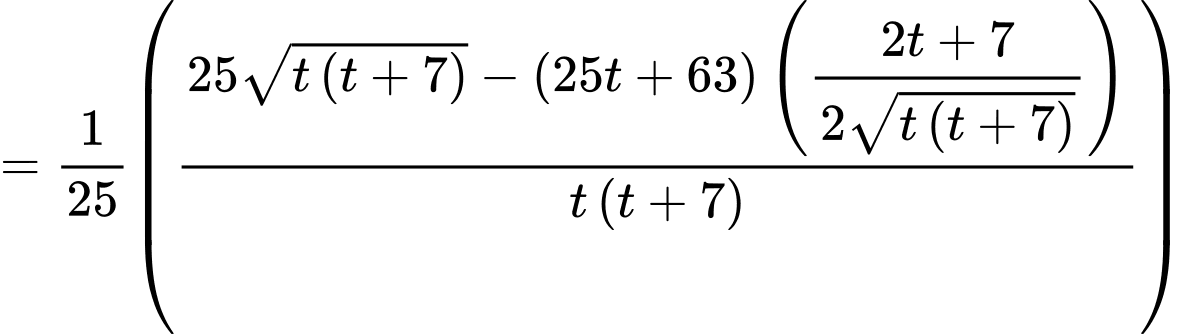
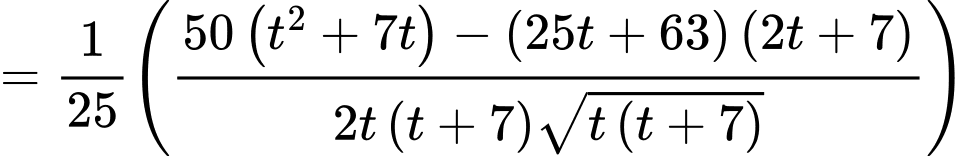
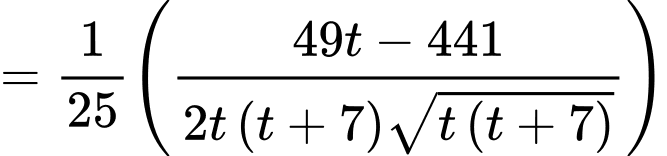
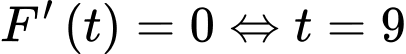
nhận giá trị nhỏ nhất. BBT
Thay vào đặt ta có:
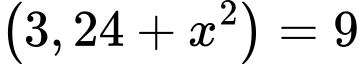
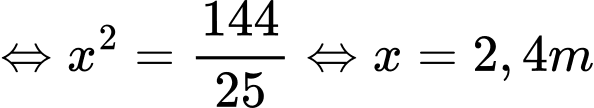
Vậy để nhìn rõ nhất thì AO =2,4 m. Đáp án: A
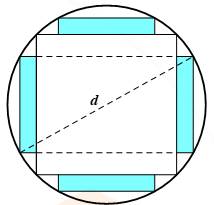
Câu 14 [582015]: Một khúc gỗ tròn hình trụ cần xẻ thành một chiếc xà có tiết diện ngang là hình vuông và 4 miếng phụ như hình vẽ. Hãy xác định kích thước của các miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. Biết đường kính khúc gỗ là d.
A, Rộng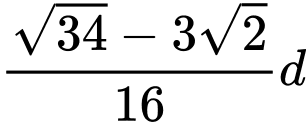 
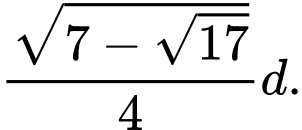
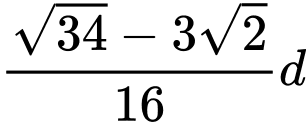, dài 
, dài 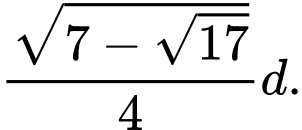B, Rộng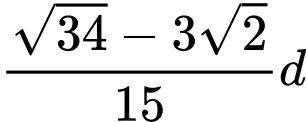 
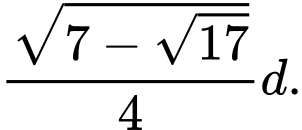
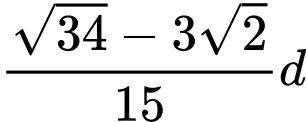, dài 
, dài 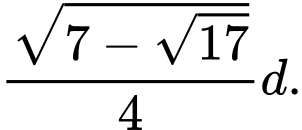C, Rộng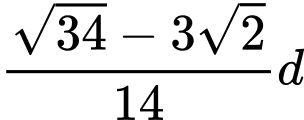 
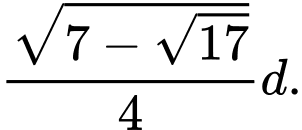
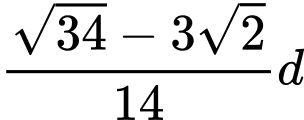, dài 
, dài 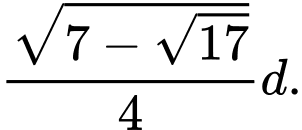D, Rộng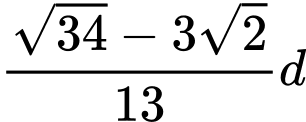 
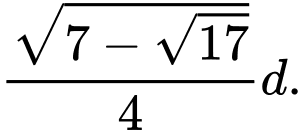
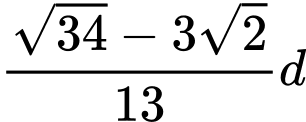, dài 
, dài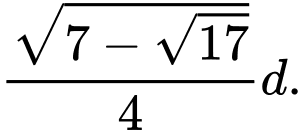
Chọn A
Gọi chiều dài và chiều rộng của miếng phụ lần lượt là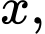
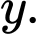Đường kính của khúc gỗ là 
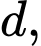khi đó tiết diện ngang của thanh xà có độ dài cạnh là 
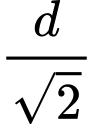và 
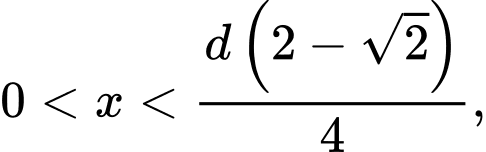
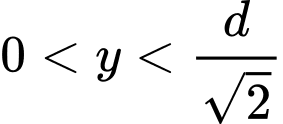
Theo đề bài ta được hình chữ nhật
như hình vẽ, theo định lý Pitago ta có:
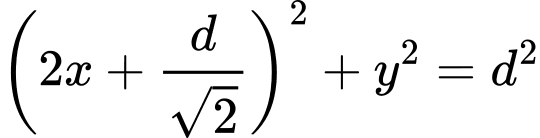
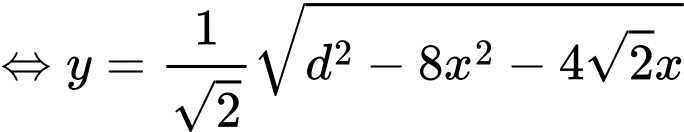
Do đó, miếng phụ có diện tích là:
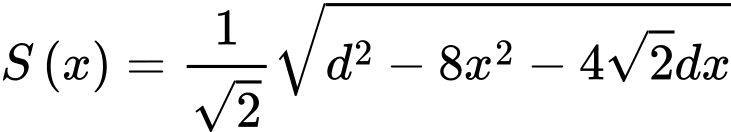với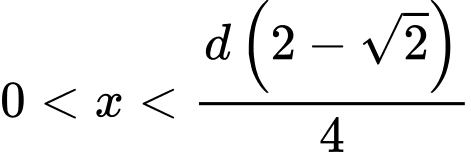 
Bài toán trở thành tìm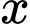
để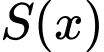 
đạt GTLN.
Ta có:
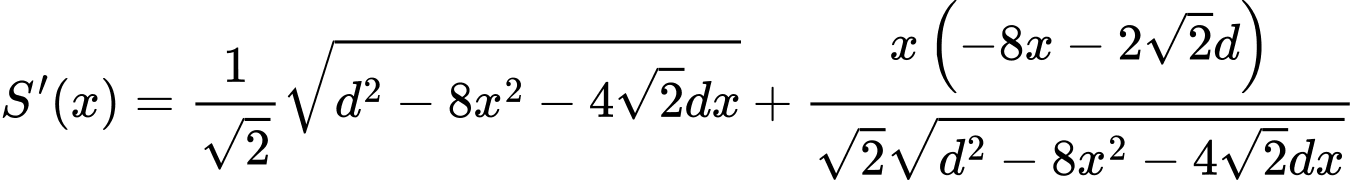
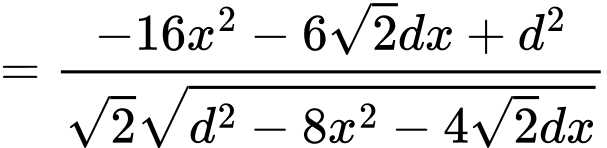
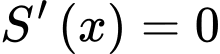
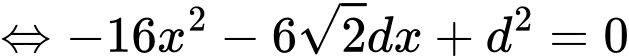
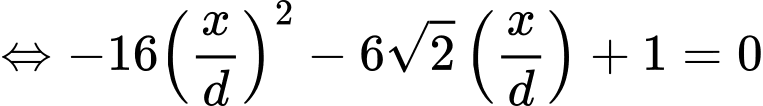
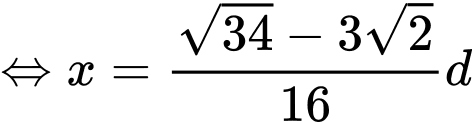
BBT
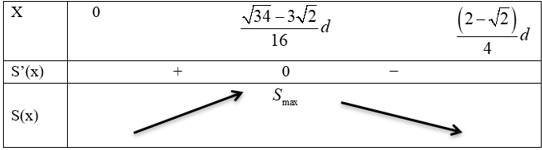
Vậy miếng phụ có kích thước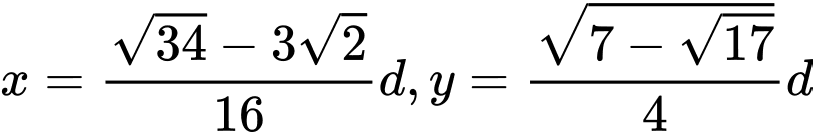
Đáp án: A
Gọi chiều dài và chiều rộng của miếng phụ lần lượt là
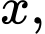
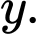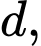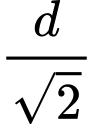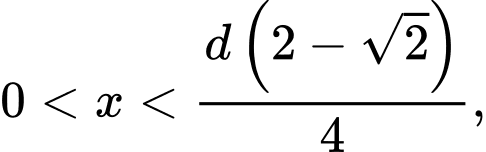
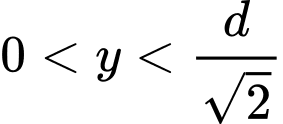
Đường kính của khúc gỗ là khi đó tiết diện ngang của thanh xà có độ dài cạnh là và Theo đề bài ta được hình chữ nhật
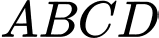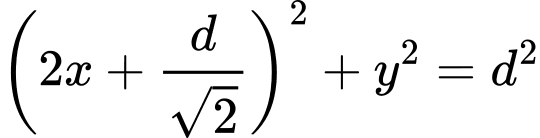
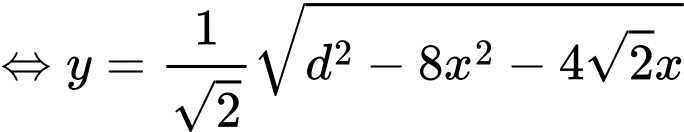
như hình vẽ, theo định lý Pitago ta có: Do đó, miếng phụ có diện tích là:
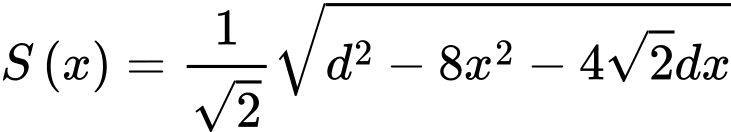với 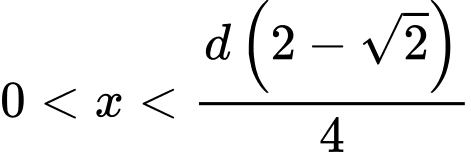Bài toán trở thành tìm
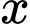để 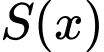đạt GTLN. Ta có:
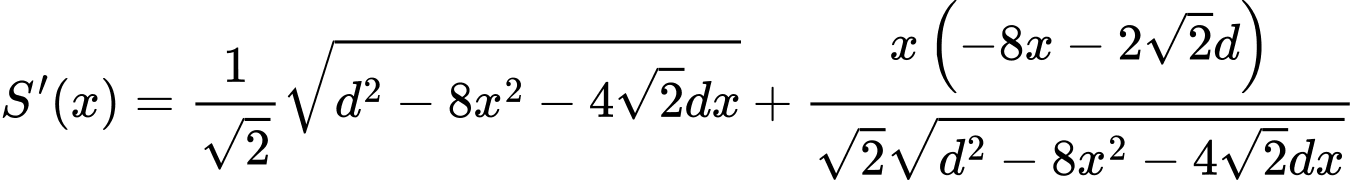
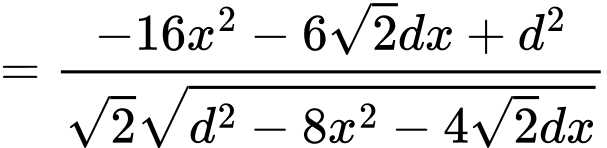
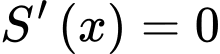
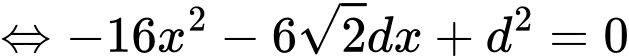
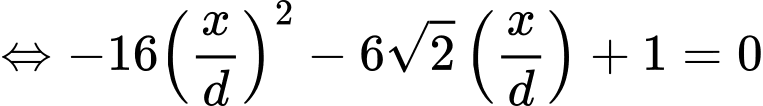
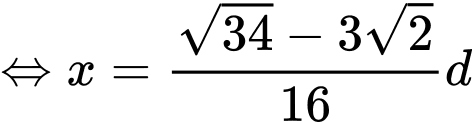
BBT
Vậy miếng phụ có kích thước
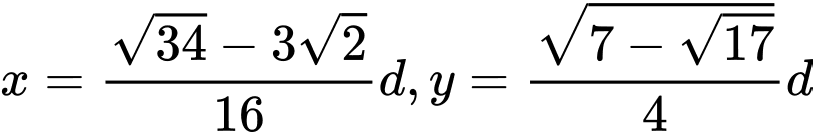Đáp án: A
Câu 15 [582016]: Nhà Long muốn xây một hồ chứa nước có dạng một khối hộp chữ nhật có nắp đậy có thể tích bằng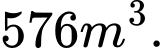 
Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá tiền thuê nhân công để xây hồ tính theo 
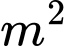là 
đồng/m2. Hãy xác định kích thước của hồ chứa nước sao cho chi phí thuê nhân công là ít nhất và chi phí đó là bao nhiêu?
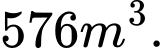Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá tiền thuê nhân công để xây hồ tính theo 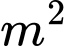là đồng/m2. Hãy xác định kích thước của hồ chứa nước sao cho chi phí thuê nhân công là ít nhất và chi phí đó là bao nhiêu? A, Rộng 6m, dài 12m, cao 8m. Tiền: 216 triệu.
B, Rộng 6m, dài 12m, cao 8m. Tiền: 215 triệu.
C, Rộng 6m, dài 12m, cao 8m. Tiền: 214 triệu.
D, Rộng 6m, dài 12m, cao 8m. Tiền: 213 triệu.
Chọn A
Gọi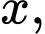
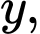
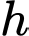lần lượt là chiều dài, chiều rộng, chiều cao của hồ chứa nước,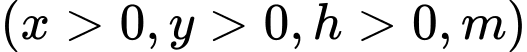 
Ta có: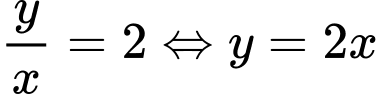
Thể tích hồ chứa nước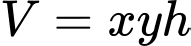
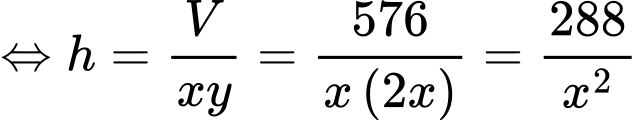
Diện tích cần xây dựng hồ chứa nước:
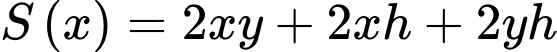
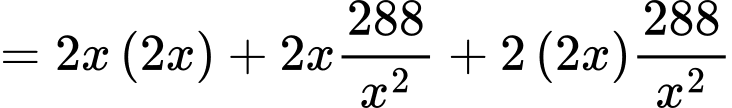
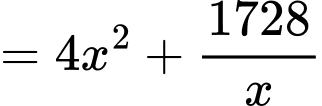
Để chi phí nhân công là ít nhất thì diện tích cần xây dựng là nhỏ nhất, mà vẫn đạt thể tích như mong muốn.
Bài toán trở thành tìm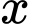
để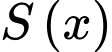 
nhỏ nhất.
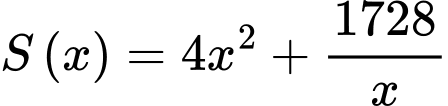
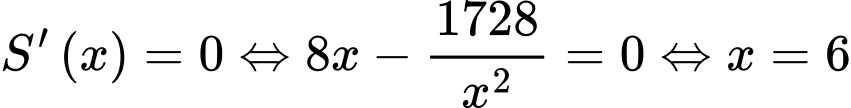
BBT
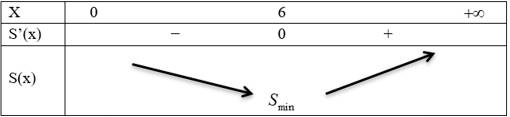
Vậy kích thước của hồ là: rộng 6m, dài 12m, cao 8m. Diện tích cần xây: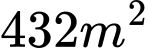
Chi phí ít nhất là: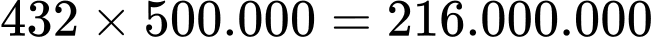
Đáp án: A
Gọi
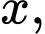
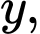
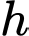lần lượt là chiều dài, chiều rộng, chiều cao của hồ chứa nước,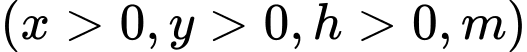 Ta có:
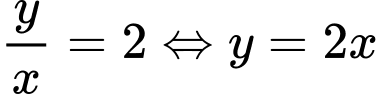
Thể tích hồ chứa nước
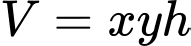
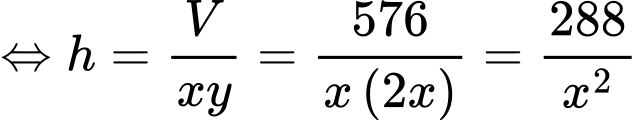
Diện tích cần xây dựng hồ chứa nước:
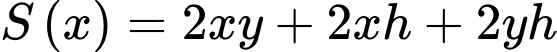
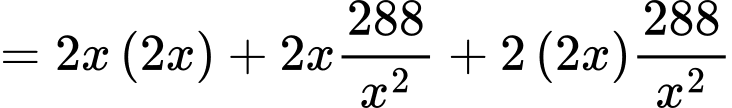
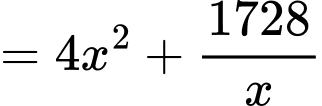
Để chi phí nhân công là ít nhất thì diện tích cần xây dựng là nhỏ nhất, mà vẫn đạt thể tích như mong muốn.
Bài toán trở thành tìm
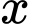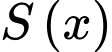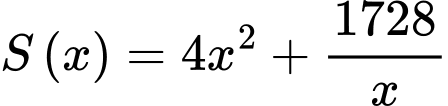
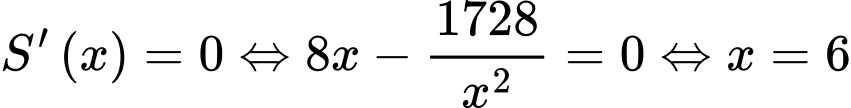
để nhỏ nhất. BBT
Vậy kích thước của hồ là: rộng 6m, dài 12m, cao 8m. Diện tích cần xây:
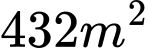
Chi phí ít nhất là:
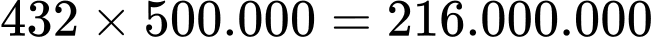Đáp án: A Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 16 [582017]: Thể tích nước của một bề bơi sau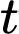 
phút bơm tính theo công thức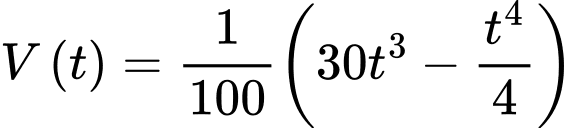 
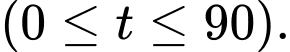Tốc độ bơm nước tại thời điểm 
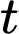được tính bởi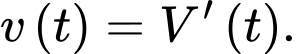 
a) Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
b) Tốc độ bơm luôn giảm.
c) Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
d) Cả a), b), c) đều sai.
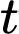phút bơm tính theo công thức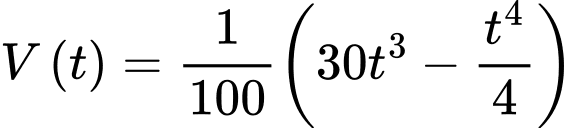 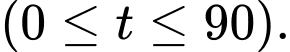Tốc độ bơm nước tại thời điểm 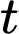được tính bởi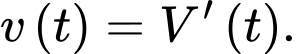 a) Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
b) Tốc độ bơm luôn giảm.
c) Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
d) Cả a), b), c) đều sai.
Xét hàm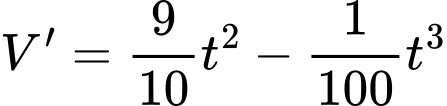 
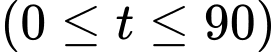
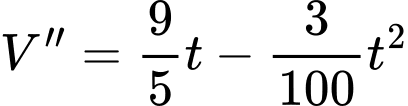
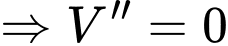khi 
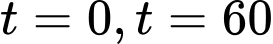
Dựa vào bảng biến thiên, Ta có hàm số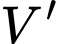
đồng biến trên 
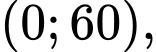nghịch biến trên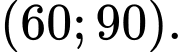 
Vậy chỉ có khẳng định a) đúng.
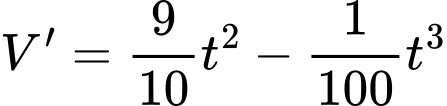
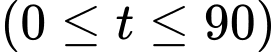
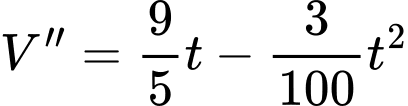
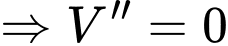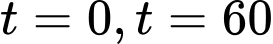
khi Dựa vào bảng biến thiên, Ta có hàm số
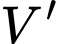đồng biến trên 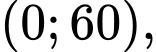nghịch biến trên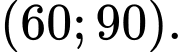 Vậy chỉ có khẳng định a) đúng.
Câu 17 [582018]: Một vật chuyển động theo quy luật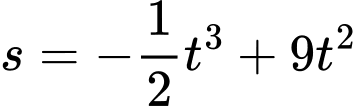 
với 
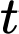(giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và 
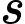(mét) là quãng đường vật đi được trong khoảng thời gian đó.
a) Vật chuyển động được 400 m trong 10 giây đầu tiên.
b) Vật chuyển động được 300 m trong 10 giây đầu tiên.
c) Trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng 400 m/s.
d) Trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng 54 m/s.
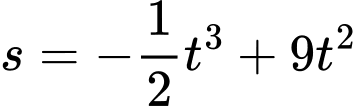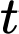với (giây) là khoảng thời gian tính từ lúc bắt đầu chuyển động và 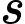(mét) là quãng đường vật đi được trong khoảng thời gian đó.a) Vật chuyển động được 400 m trong 10 giây đầu tiên.
b) Vật chuyển động được 300 m trong 10 giây đầu tiên.
c) Trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng 400 m/s.
d) Trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng 54 m/s.
Quãng đường vật chuyển động được trong 10 giây đầu: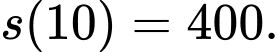 
Do đó a) đúng, b) sai.
Vận tốc tại thời điểm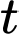
là 
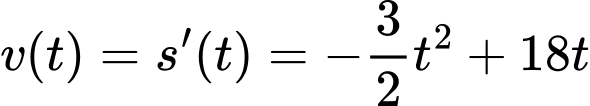với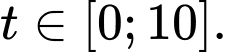 
Ta có :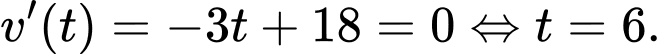
Suy ra: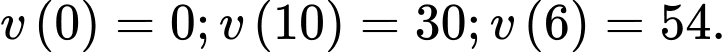
Vậy vận tốc lớn nhất của vật đạt được bằng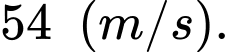
Do đó d) đúng, c) sai.
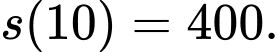Do đó a) đúng, b) sai. Vận tốc tại thời điểm
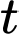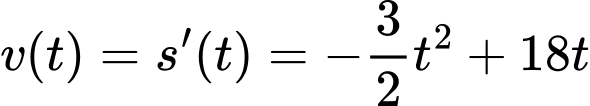là với 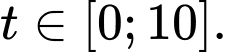Ta có :
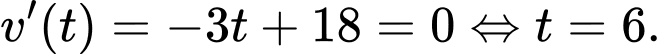
Suy ra:
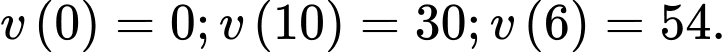
Vậy vận tốc lớn nhất của vật đạt được bằng
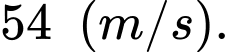
Do đó d) đúng, c) sai.
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582019]: Ông Thanh nuôi cá chim ở một cái ao có diện tích là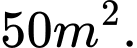 
Vụ trước ông nuôi với mật độ là 
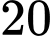con/m2 và thu được 1,5 tấn cá. Theo kinh nghiệm nuôi cá của mình thì cứ thả giảm đi 8 con/m2 thì mỗi con cá khi thu hoạch tăng lên 0,5kg. Vậy vụ tới ông phải thả bao nhiêu con cá giống để được tổng năng suất khi thu hoạch là cao nhất? Giả sử không có hao hụt khi nuôi.
TRẢ LỜI: ……………………….
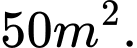Vụ trước ông nuôi với mật độ là 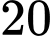con/m2 và thu được 1,5 tấn cá. Theo kinh nghiệm nuôi cá của mình thì cứ thả giảm đi 8 con/m2 thì mỗi con cá khi thu hoạch tăng lên 0,5kg. Vậy vụ tới ông phải thả bao nhiêu con cá giống để được tổng năng suất khi thu hoạch là cao nhất? Giả sử không có hao hụt khi nuôi.TRẢ LỜI: ……………………….
Trả lời: 1100
Vụ đầu, ông Thanh thả với mật độ 
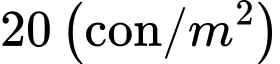ở cái ao có diện tích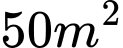 
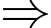Tổng số cá là: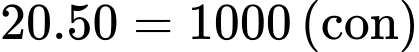 
- Vì thu hoạch được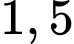
tấn 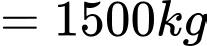cá 
cá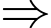 
Khối lượng mỗi con cá sau thu hoạch là: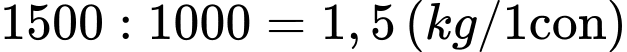 
Gọi số cá thả giảm đi là 
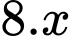(con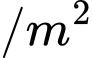
), thì mỗi con cá khi thu hoạch tăng lên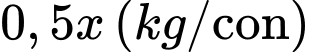 
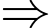Khối lượng mỗi con cá sau thu hoạch là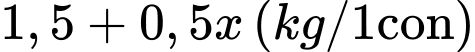 
- Trên toàn bộ ao, số cá thả giảm đi là: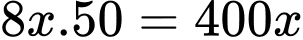
(con)
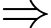Vụ sau, ông Thanh thả số cá là: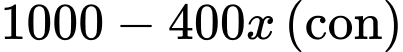 
Do đó, tổng khối lượng cá vụ sau là:
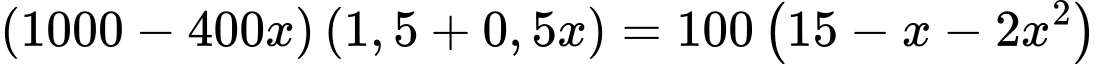
Đặt 
- Đạo hàm: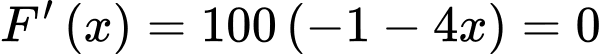
- Xét phương trình
BBT
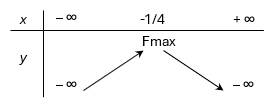
Vậy ông thanh phải thả số cá giống trong vụ này là: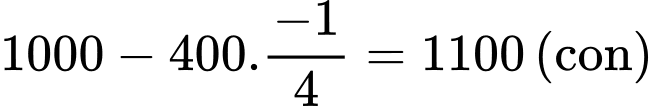
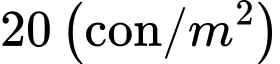Vụ đầu, ông Thanh thả với mật độ ở cái ao có diện tích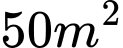 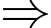Tổng số cá là: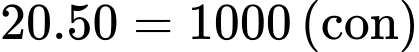 - Vì thu hoạch được
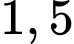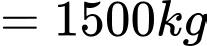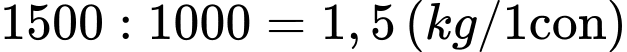
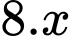tấn cá cá Khối lượng mỗi con cá sau thu hoạch là: Gọi số cá thả giảm đi là (con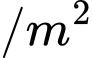), thì mỗi con cá khi thu hoạch tăng lên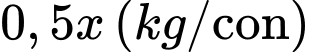 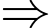Khối lượng mỗi con cá sau thu hoạch là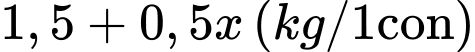 - Trên toàn bộ ao, số cá thả giảm đi là:
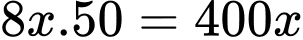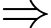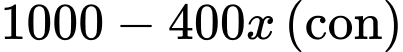
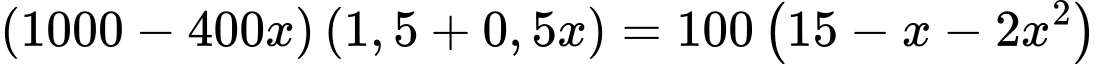
(con) Vụ sau, ông Thanh thả số cá là: Do đó, tổng khối lượng cá vụ sau là: Đặt - Đạo hàm:
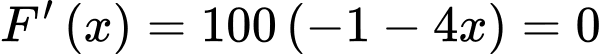
- Xét phương trình
BBT
Vậy ông thanh phải thả số cá giống trong vụ này là:
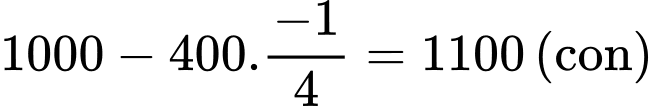
Câu 19 [582020]: Người ta cần làm một hộp theo dạng một khối lăng trụ đều không nắp với thể tích lớn nhất từ một miếng tôn hình vuông có cạnh là 1 mét. Thể tích của hộp cần làm.
TRẢ LỜI: ……………………….
TRẢ LỜI: ……………………….
Trả lời: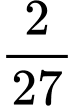 
Giả sử mỗi góc cắt đi một hình vuông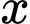
dm.
Khi đó chiều cao của hình hộp là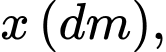
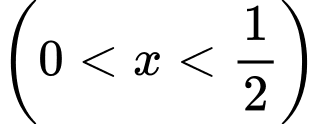
Và cạnh đáy của hộp là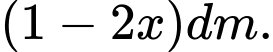
Vậy thể tích của hộp là: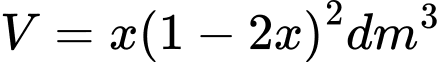
Ta có:
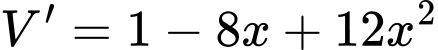
Phương trình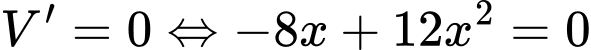
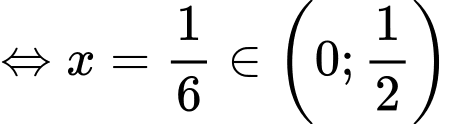
BBT
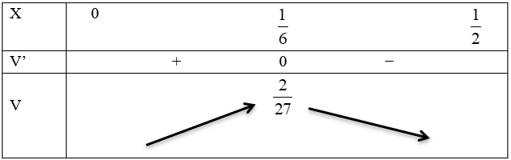
Vậy thể tích cần tìm là: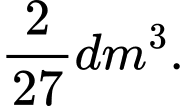
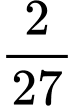
Giả sử mỗi góc cắt đi một hình vuông
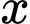dm. Khi đó chiều cao của hình hộp là
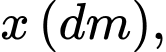
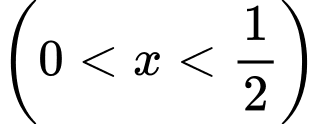
Và cạnh đáy của hộp là
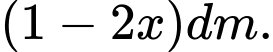
Vậy thể tích của hộp là:
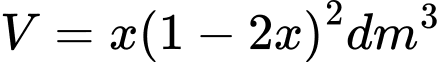
Ta có:
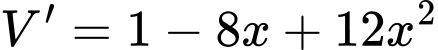
Phương trình
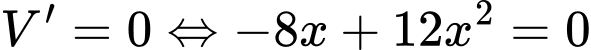
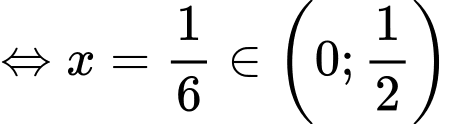
BBT
Vậy thể tích cần tìm là:
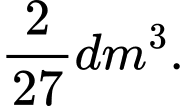
Câu 20 [582021]: Công ty HSA&TSA Việt Nam muốn làm đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển 6km. Giá thành để xây đường ống trên bờ là 50.000USD mỗi km, và 130.000USD mỗi km để xây dưới nước. B’ là điểm trên bờ sao cho BB’ vuông góc với bờ biển. Khoảng cách từ A đến B’ là 9km. Vị trí C trên đoạn AB’ sao cho khi nối ống theo hướng ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng:
TRẢ LỜI: ……………………….
TRẢ LỜI: ……………………….
Trả lời: 13/2
Ta đặt: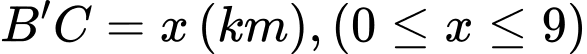
Ta có:
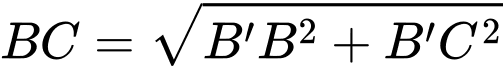
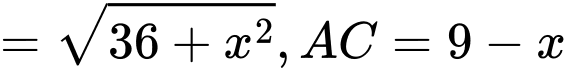
Gọi F(x) là hàm chi phí xây dựng đường ống nước từ ACB
Ta có: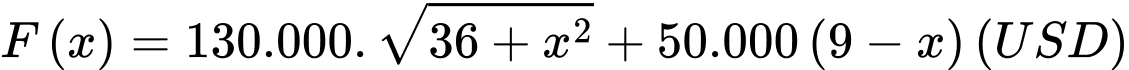
Bài toán trở thành tìm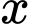
sao cho 
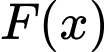đạt GTNN.
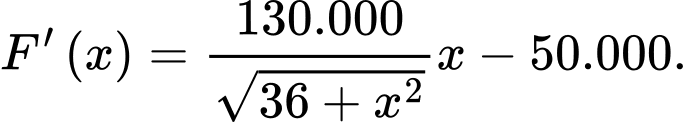
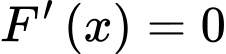
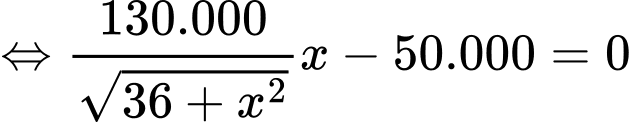
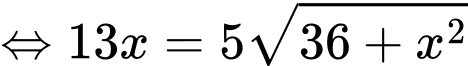
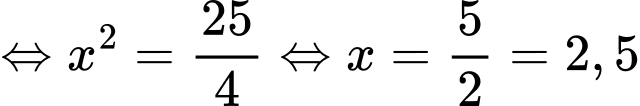
Vì F(x) là hàm liên tục trên đoạn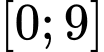
nên ta có:
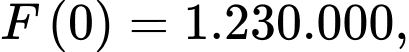
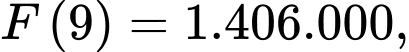
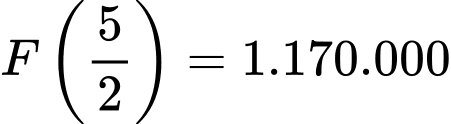
Vậy chi phí nhỏ nhất khi C cách A khoảng bằng 9km-2,5km=6,5km.
Ta đặt:
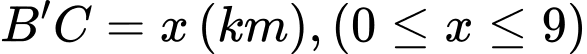
Ta có:
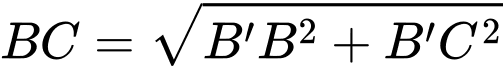
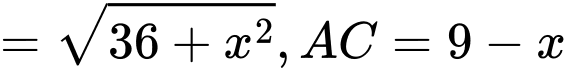
Gọi F(x) là hàm chi phí xây dựng đường ống nước từ ACB
Ta có:
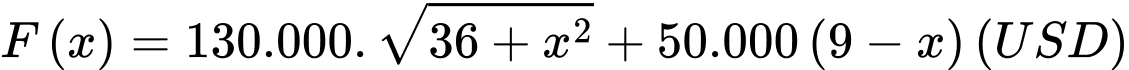
Bài toán trở thành tìm
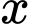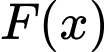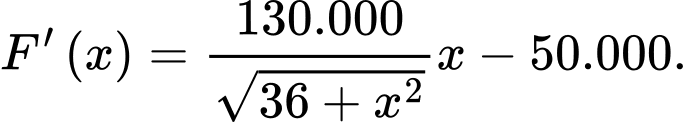
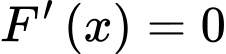
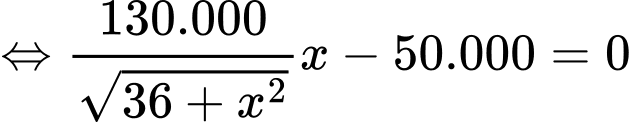
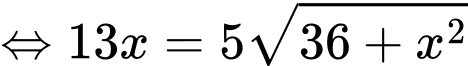
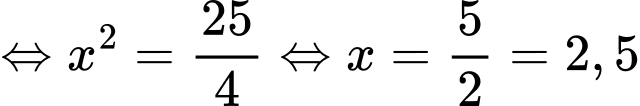
sao cho đạt GTNN. Vì F(x) là hàm liên tục trên đoạn
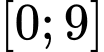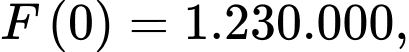
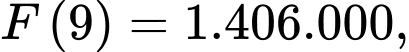
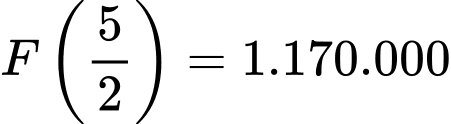
nên ta có: Vậy chi phí nhỏ nhất khi C cách A khoảng bằng 9km-2,5km=6,5km.
Dạng câu hỏi: Câu hỏi kéo thả.
Câu 21 [582022]: Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục tọa độ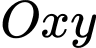
được mô phỏng như hình vẽ
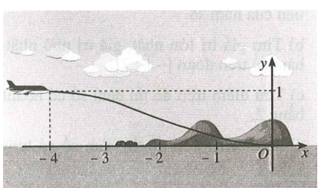
Biết đường bay của nó có dạng đồ thị hàm số bậc ba. Vị trí bắt đầu hạ cánh có tọa độ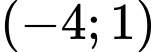
là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm số
Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất ______ dặm? (biết đơn vị trên hệ trục tọa độ là dặm)
Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang là ______ dặm
Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục tọa độ
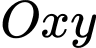được mô phỏng như hình vẽBiết đường bay của nó có dạng đồ thị hàm số bậc ba. Vị trí bắt đầu hạ cánh có tọa độ
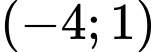là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm sốKhi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất ______ dặm? (biết đơn vị trên hệ trục tọa độ là dặm)
Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang là ______ dặm
Đáp án
Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất __0,84375____ dặm? (biết đơn vị trên hệ trục tọa độ là dặm)
Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang là __2____ dặm
Giải thích
Gọi hàm số thỏa mãn :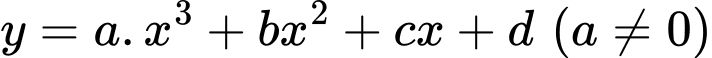
là hàm số biểu diễn đường bay của máy bay
Dựa vào tọa độ cực đại, cực tiểu của đồ thị hàm số dễ dàng tìm được hàm số thỏa mãn là: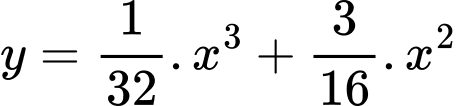
Theo hình vẽ, khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm tương ứng với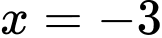
Khi đó thay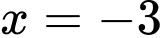
ta được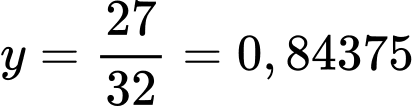 
Vậy khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất __0,84375____ dặm
Cũng như vậy, khi máy bay ở độ cao 0,5 dặm tương ứng với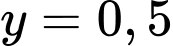
, khi đó ta giải được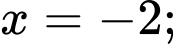 
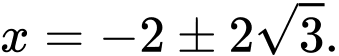Do 
nên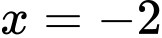 
là giá trị thỏa mãn
Vậy khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang là ___2___ dặm
Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất __0,84375____ dặm? (biết đơn vị trên hệ trục tọa độ là dặm)
Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang là __2____ dặm
Giải thích
Gọi hàm số thỏa mãn :
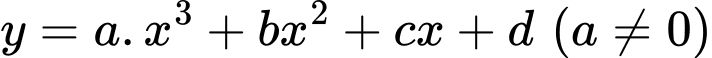là hàm số biểu diễn đường bay của máy bayDựa vào tọa độ cực đại, cực tiểu của đồ thị hàm số dễ dàng tìm được hàm số thỏa mãn là:
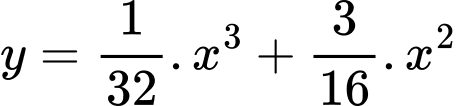
Theo hình vẽ, khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm tương ứng với
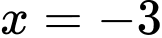
Khi đó thay
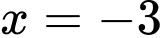ta được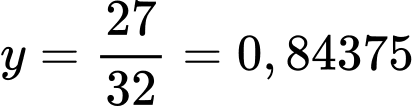 Vậy khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất __0,84375____ dặm
Cũng như vậy, khi máy bay ở độ cao 0,5 dặm tương ứng với
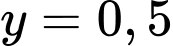, khi đó ta giải được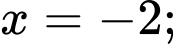 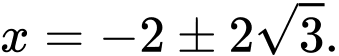Do nên 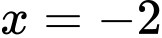là giá trị thỏa mãnVậy khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang là ___2___ dặm