DẠNG 1: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ CHO TRƯỚC
Câu 1 [580391]: Hàm số 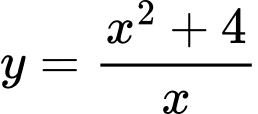 nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào?
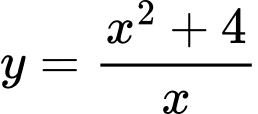 nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào?
- Hàm số đã cho có tập xác định là 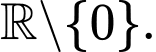
- Ta có: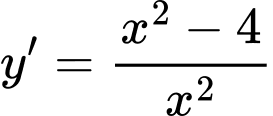 với
với 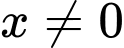 ;
;
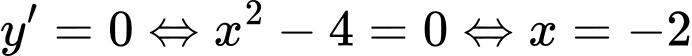 hoặc
hoặc 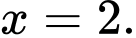
Bảng biến thiên của hàm số như sau:
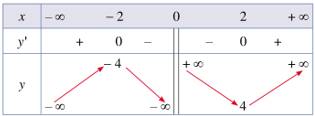
Vậy hàm số đồng biến trên mỗi khoảng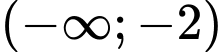 và
và 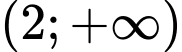 ; nghịch biến trên mỗi khoảng
; nghịch biến trên mỗi khoảng 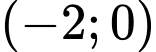 và
và 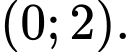
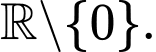
- Ta có:
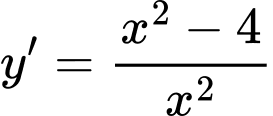 với
với 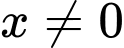 ;
;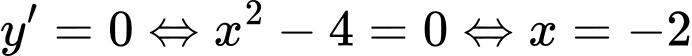 hoặc
hoặc 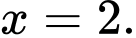
Bảng biến thiên của hàm số như sau:

Vậy hàm số đồng biến trên mỗi khoảng
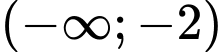 và
và 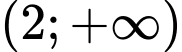 ; nghịch biến trên mỗi khoảng
; nghịch biến trên mỗi khoảng 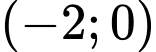 và
và 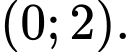
Câu 2 [580392]: Cho hàm số 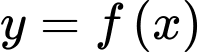 liên tục trên
liên tục trên 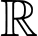 và có đạo hàm
và có đạo hàm 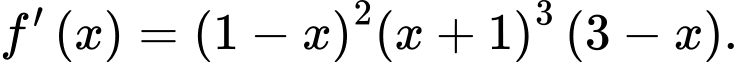 Hàm số
Hàm số 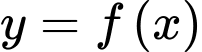 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
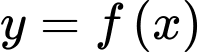 liên tục trên
liên tục trên 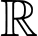 và có đạo hàm
và có đạo hàm 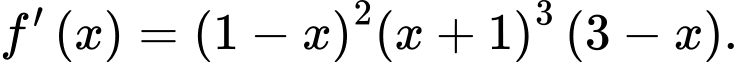 Hàm số
Hàm số 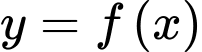 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 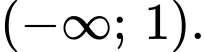
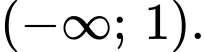
B, 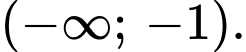
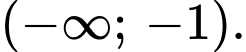
C, 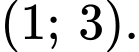
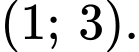
D, 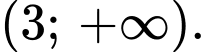
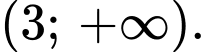
Chọn C
Ta có: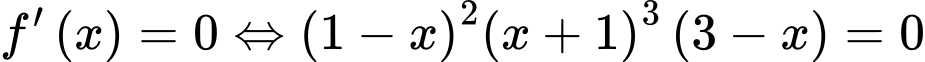
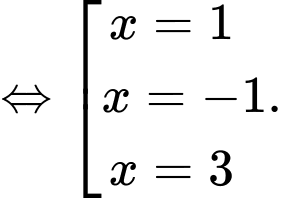
Bảng xét dấu:

Hàm số đồng biến trên các khoảng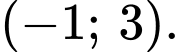 Đáp án: C
Đáp án: C
Ta có:
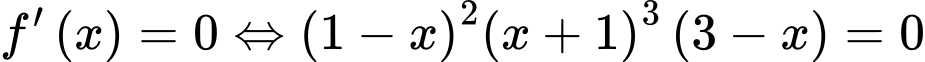
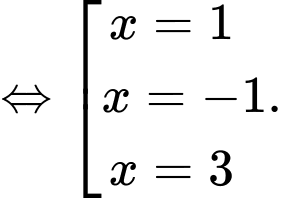
Bảng xét dấu:

Hàm số đồng biến trên các khoảng
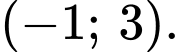 Đáp án: C
Đáp án: C DẠNG 2: TÌM m ĐỂ HÀM SỐ ĐƠN ĐIỆU TRÊN MỘT KHOẢNG
Câu 3 [580393]: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số 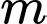 để hàm số hàm số
để hàm số hàm số 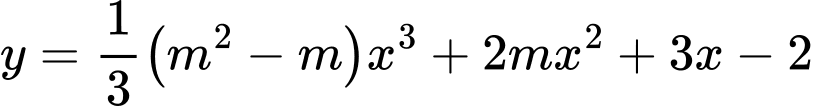 đồng biến trên khoảng
đồng biến trên khoảng 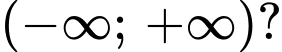
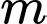 để hàm số hàm số
để hàm số hàm số 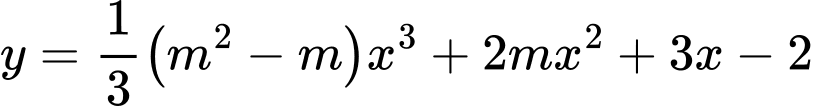 đồng biến trên khoảng
đồng biến trên khoảng 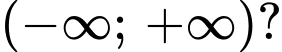
Đáp án: 4
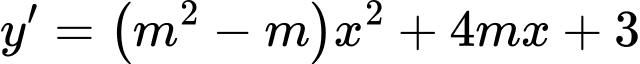
Hàm số đã cho đồng biến trên khoảng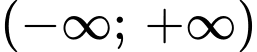
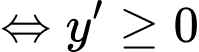 với
với 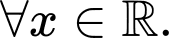
+ Với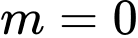 ta có
ta có 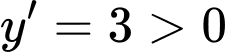 với
với 
Hàm số đồng biến trên khoảng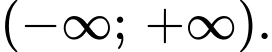
+ Với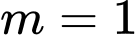 ta có
ta có 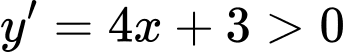
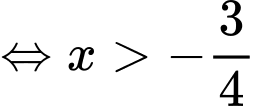
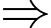
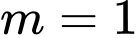 không thảo mãn.
không thảo mãn.
+ Với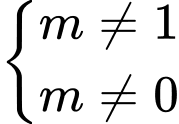 ta có
ta có 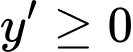 với
với 
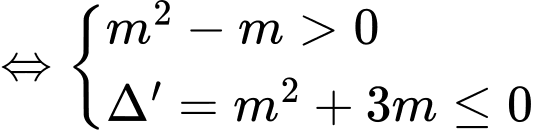
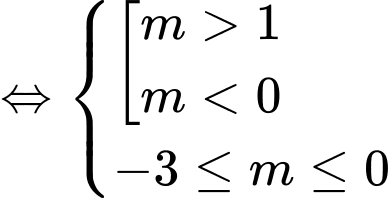

Tổng hợp các trường hợp ta được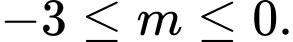

Vậy có 4 giá trị nguyên của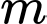 thỏa mãn bài ra.
thỏa mãn bài ra.
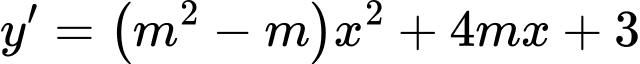
Hàm số đã cho đồng biến trên khoảng
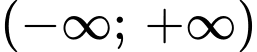
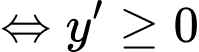 với
với 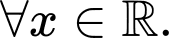
+ Với
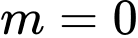 ta có
ta có 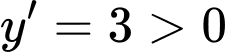 với
với 
Hàm số đồng biến trên khoảng
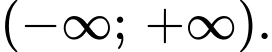
+ Với
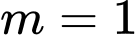 ta có
ta có 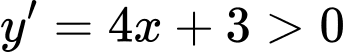
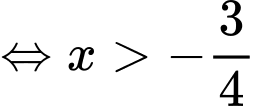
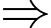
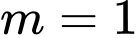 không thảo mãn.
không thảo mãn. + Với
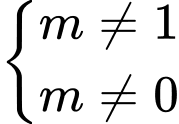 ta có
ta có 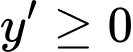 với
với 
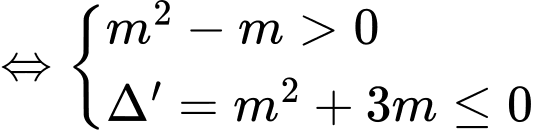
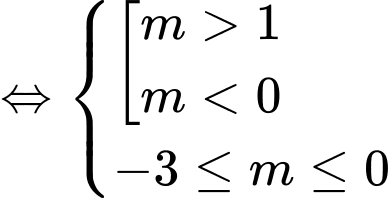

Tổng hợp các trường hợp ta được
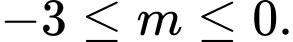

Vậy có 4 giá trị nguyên của
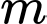 thỏa mãn bài ra.
thỏa mãn bài ra.
Câu 4 [580394]: Tìm 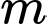 để hàm số
để hàm số 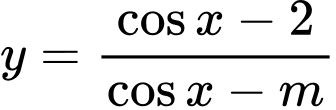 đồng biến trên khoảng
đồng biến trên khoảng 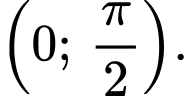
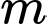 để hàm số
để hàm số 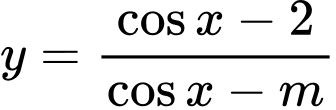 đồng biến trên khoảng
đồng biến trên khoảng 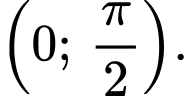
A, 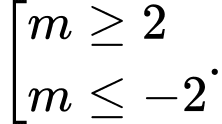
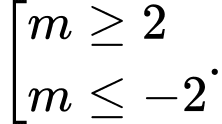
B, 

C, 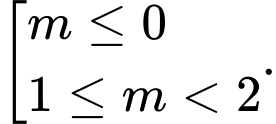
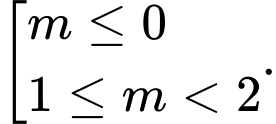
D, 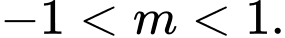
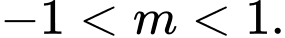
Chọn B
Đặt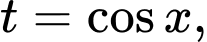 ta phát biểu lại bài toán như sau:
ta phát biểu lại bài toán như sau:
Tìm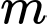 để hàm số
để hàm số 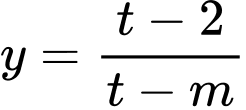 nghịch biến trên
nghịch biến trên 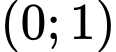
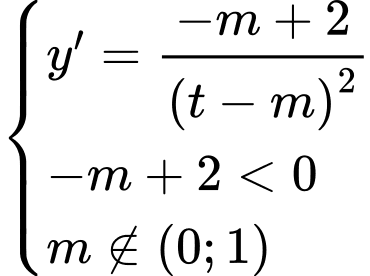
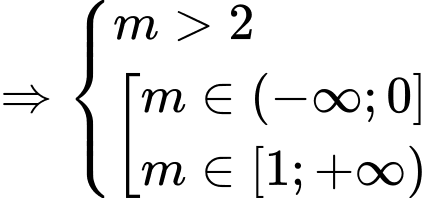
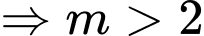 Đáp án: B
Đáp án: B
Đặt
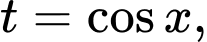 ta phát biểu lại bài toán như sau:
ta phát biểu lại bài toán như sau: Tìm
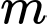 để hàm số
để hàm số 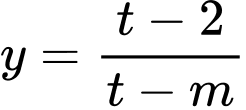 nghịch biến trên
nghịch biến trên 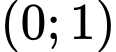
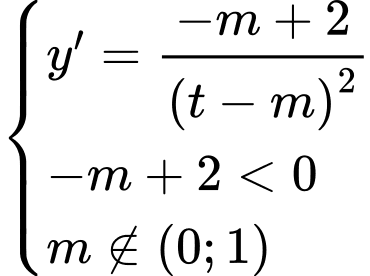
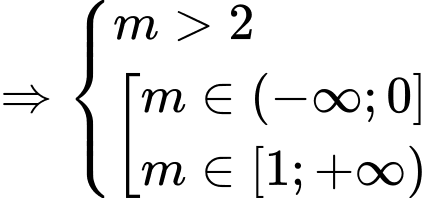
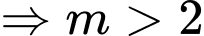 Đáp án: B
Đáp án: B
Câu 5 [580395]: Có bao nhiêu giá trị nguyên của tham số 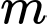 để hàm số
để hàm số 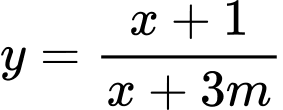 nghịch biến trên khoảng
nghịch biến trên khoảng 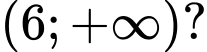
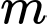 để hàm số
để hàm số 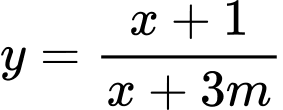 nghịch biến trên khoảng
nghịch biến trên khoảng 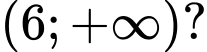
Đáp án: 3
Tập xác định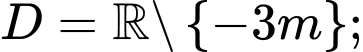
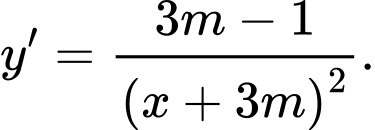
Hàm số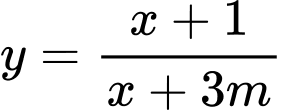 nghịch biến trên khoảng
nghịch biến trên khoảng 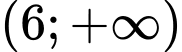 khi và chỉ khi:
khi và chỉ khi:
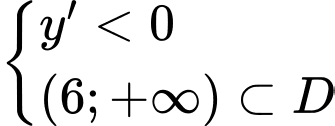
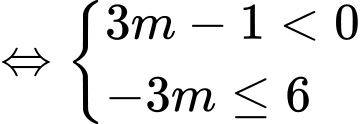
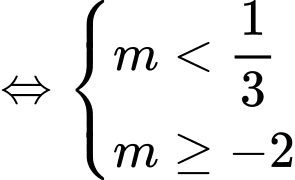
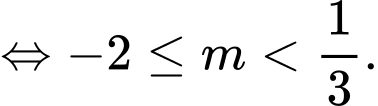
Vì

Tập xác định
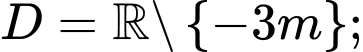
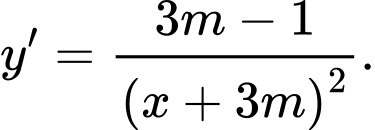
Hàm số
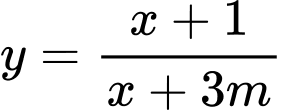 nghịch biến trên khoảng
nghịch biến trên khoảng 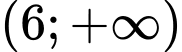 khi và chỉ khi:
khi và chỉ khi: 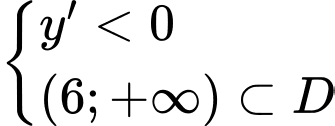
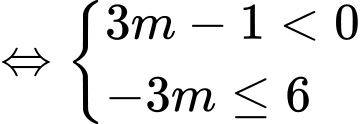
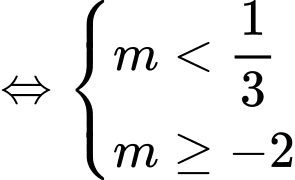
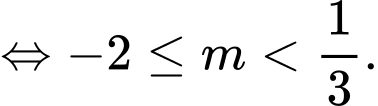
Vì


DẠNG 3: TÌM KHOẢNG ĐƠN ĐIỆU CỦA HÀM SỐ G(X) KHI BIẾT ĐỒ THỊ, BẢNG BIẾN THIÊN CỦA HÀM SỐ F’(X)
Câu 6 [580396]: Cho hàm số 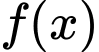 , bảng xét dấu của
, bảng xét dấu của 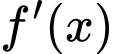 như sau:
như sau:
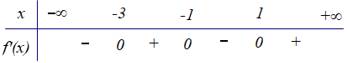
Hàm số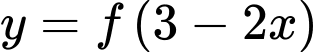 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
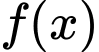 , bảng xét dấu của
, bảng xét dấu của 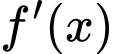 như sau:
như sau: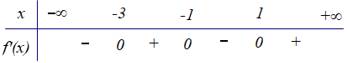
Hàm số
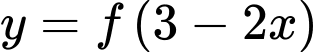 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 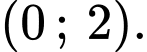
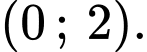
B, 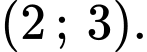
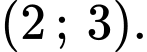
C, 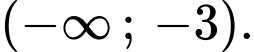
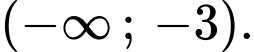
D, 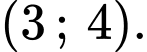
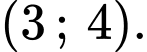
Chọn D
Ta có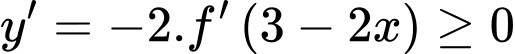
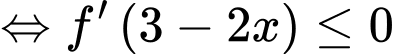
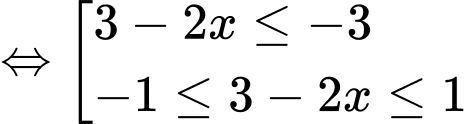
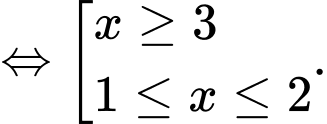 Đáp án: D
Đáp án: D
Ta có
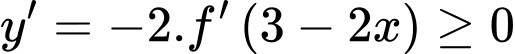
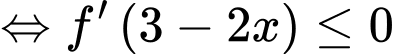
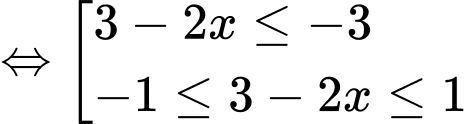
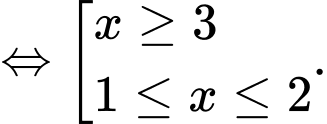 Đáp án: D
Đáp án: D
Câu 7 [580397]: Cho hàm số 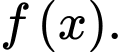 Hàm số
Hàm số 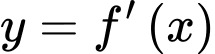 có đồ thị như hình bên. Hàm số
có đồ thị như hình bên. Hàm số 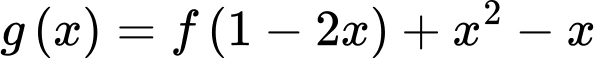 nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào?
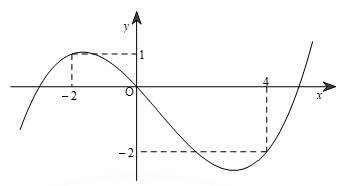
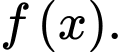 Hàm số
Hàm số 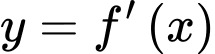 có đồ thị như hình bên. Hàm số
có đồ thị như hình bên. Hàm số 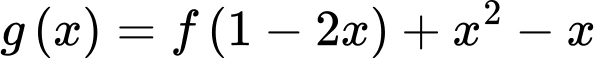 nghịch biến trên khoảng nào?
nghịch biến trên khoảng nào?
Ta có : 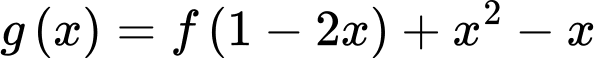
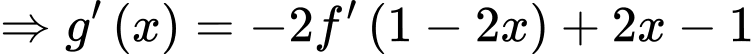
Đặt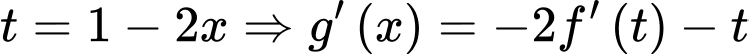
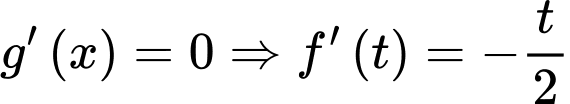
Vẽ đường thẳng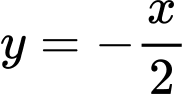 và đồ thị hàm số
và đồ thị hàm số 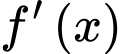 trên cùng một hệ trục
trên cùng một hệ trục
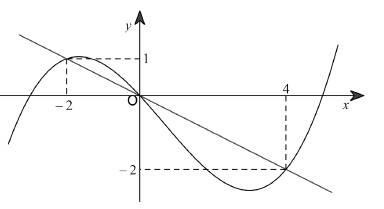
Hàm số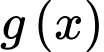 nghịch biến
nghịch biến 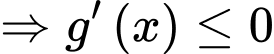
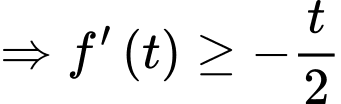
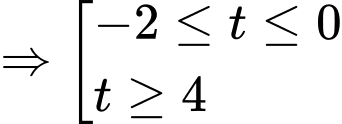
Như vậy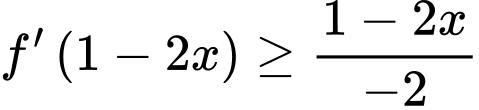
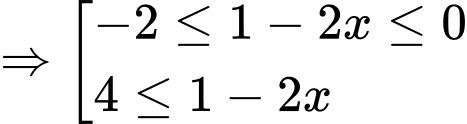
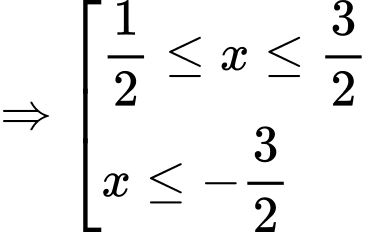
Vậy hàm số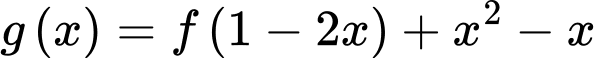 nghịch biến trên các khoảng
nghịch biến trên các khoảng 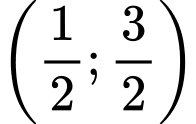 và
và 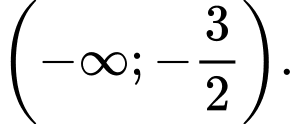
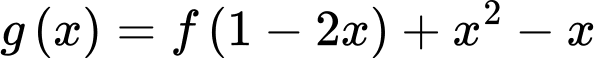
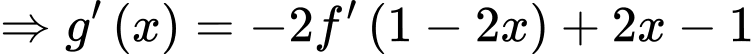
Đặt
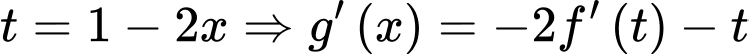
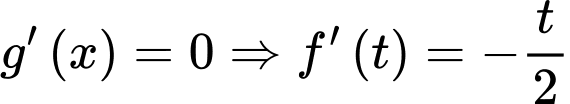
Vẽ đường thẳng
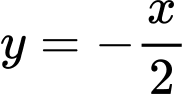 và đồ thị hàm số
và đồ thị hàm số 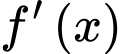 trên cùng một hệ trục
trên cùng một hệ trục
Hàm số
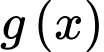 nghịch biến
nghịch biến 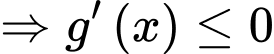
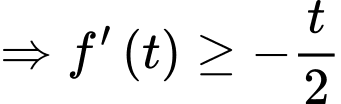
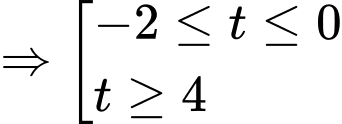
Như vậy
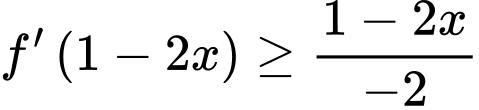
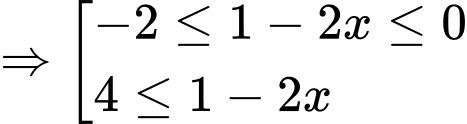
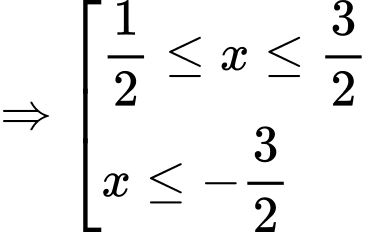
Vậy hàm số
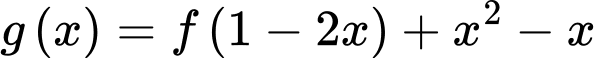 nghịch biến trên các khoảng
nghịch biến trên các khoảng 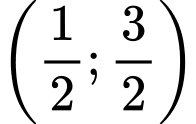 và
và 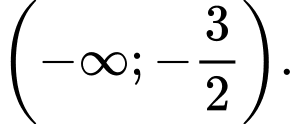
Câu 8 [580398]: Cho hàm số 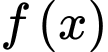 có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau:
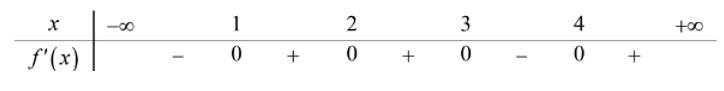
Hàm số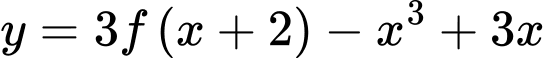 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
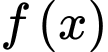 có bảng xét dấu của đạo hàm như sau:
có bảng xét dấu của đạo hàm như sau: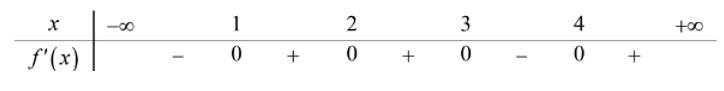
Hàm số
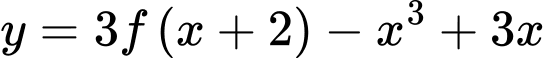 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 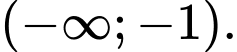
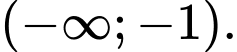
B, 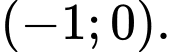
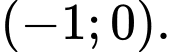
C, 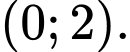
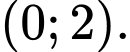
D, 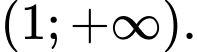
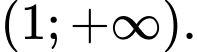
Chọn B
Ta có: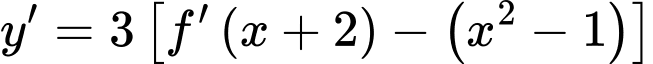
Với
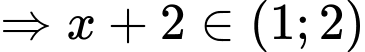
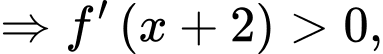 lại có
lại có 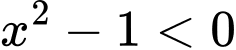
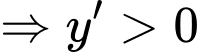
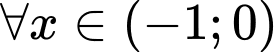
Vậy hàm số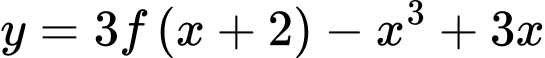 đồng biến trên khoảng
đồng biến trên khoảng 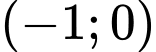 Đáp án: B
Đáp án: B
Ta có:
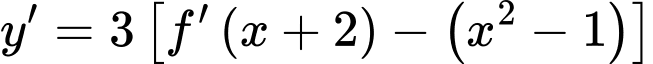
Với

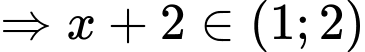
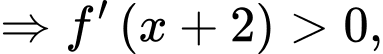 lại có
lại có 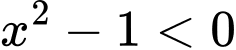
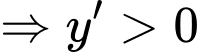
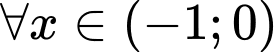
Vậy hàm số
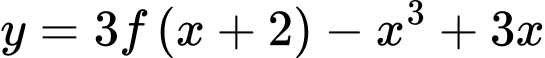 đồng biến trên khoảng
đồng biến trên khoảng 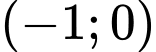 Đáp án: B
Đáp án: B DẠNG 4: BÀI TOÁN HÀM ẨN, HÀM HỢP LIÊN QUAN ĐẾN THAM SỐ VÀ MỘT SỐ BÀI TOÁN KHÁC
Câu 9 [580399]: Cho hàm số 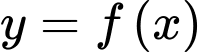 có đạo hàm liên tục trên
có đạo hàm liên tục trên 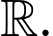 Biết hàm số
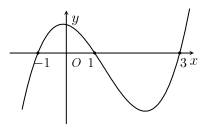
Biết hàm số 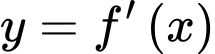 có đồ thị như hình vẽ. Gọi
có đồ thị như hình vẽ. Gọi 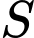 là tập hợp các giá trị nguyên
là tập hợp các giá trị nguyên  để hàm số
để hàm số 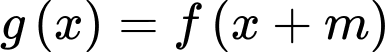 nghịch biến trên khoảng
nghịch biến trên khoảng 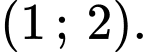 Hỏi
Hỏi 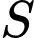 có bao nhiêu phần tử?
có bao nhiêu phần tử?
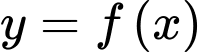 có đạo hàm liên tục trên
có đạo hàm liên tục trên 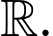 Biết hàm số
Biết hàm số 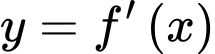 có đồ thị như hình vẽ. Gọi
có đồ thị như hình vẽ. Gọi 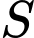 là tập hợp các giá trị nguyên
là tập hợp các giá trị nguyên  để hàm số
để hàm số 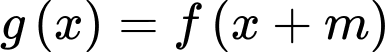 nghịch biến trên khoảng
nghịch biến trên khoảng 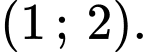 Hỏi
Hỏi 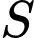 có bao nhiêu phần tử?
có bao nhiêu phần tử?
A, 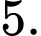
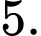
B, 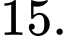
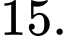
C, 

D, 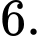
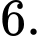
Chọn A
Ta có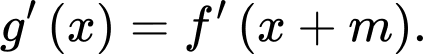
Vì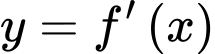 liên tục trên
liên tục trên 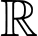 nên
nên 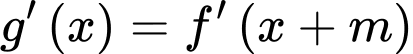 cũng liên tục trên
cũng liên tục trên 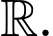
Căn cứ vào đồ thị hàm số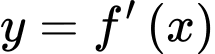 ta thấy
ta thấy
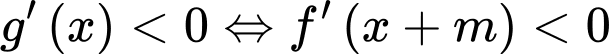
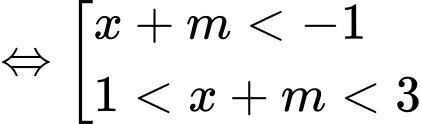
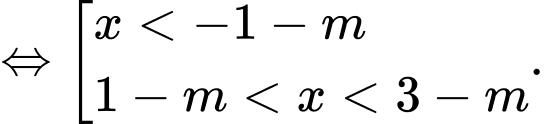
Hàm số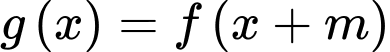 nghịch biến trên khoảng
nghịch biến trên khoảng 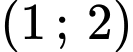
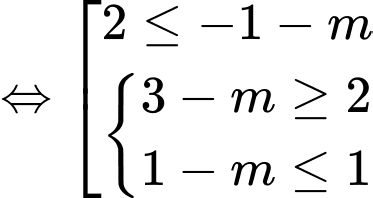
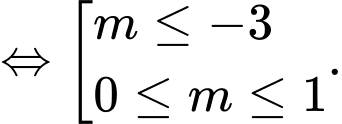
Mà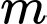 là số nguyên thuộc đoạn
là số nguyên thuộc đoạn 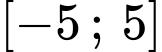 nên ta có
nên ta có 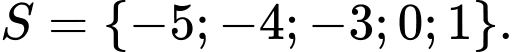
Vậy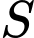 có 5 phần tử. Đáp án: A
có 5 phần tử. Đáp án: A
Ta có
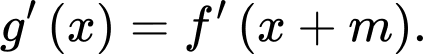
Vì
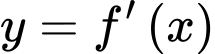 liên tục trên
liên tục trên 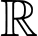 nên
nên 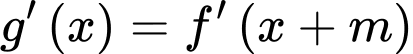 cũng liên tục trên
cũng liên tục trên 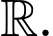
Căn cứ vào đồ thị hàm số
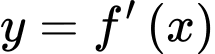 ta thấy
ta thấy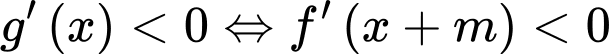
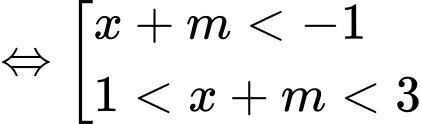
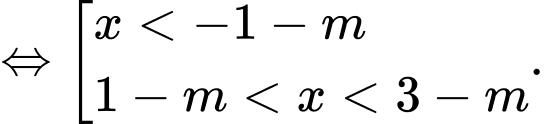
Hàm số
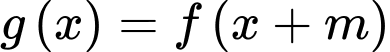 nghịch biến trên khoảng
nghịch biến trên khoảng 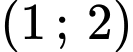
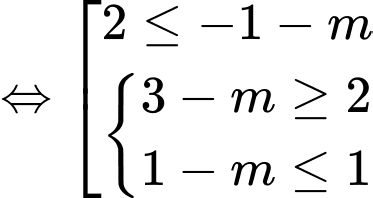
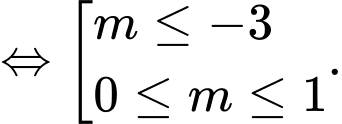
Mà
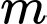 là số nguyên thuộc đoạn
là số nguyên thuộc đoạn 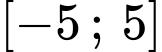 nên ta có
nên ta có 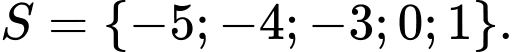
Vậy
 có 5 phần tử. Đáp án: A
có 5 phần tử. Đáp án: A