Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [580400]: Hàm số nào dưới đây đồng biến trên tập 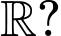
A, 
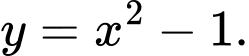
B, 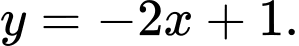
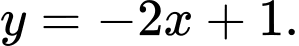
C, 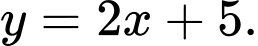
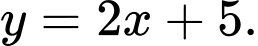
D, 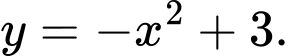
Đáp án: C
Câu 2 [580401]: Cho hàm số 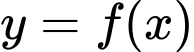 có bảng biến thiên như hình sau
có bảng biến thiên như hình sau
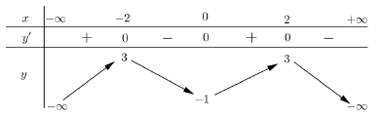
Hàm số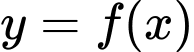 nghịch biến trên khoảng nào dưới đây ?
nghịch biến trên khoảng nào dưới đây ?
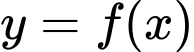 có bảng biến thiên như hình sau
có bảng biến thiên như hình sau
Hàm số
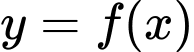 nghịch biến trên khoảng nào dưới đây ?
nghịch biến trên khoảng nào dưới đây ? A, 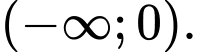
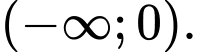
B, 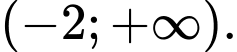
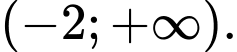
C, 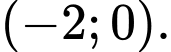
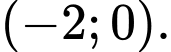
D, 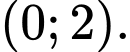
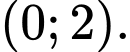
Đáp án: C
Câu 3 [580402]: Cho hàm số 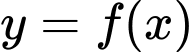 có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
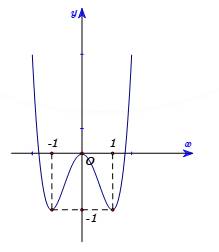
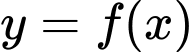 có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A, Hàm số đồng biến trên khoảng 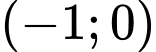 và
và 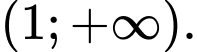
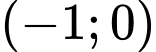 và
và 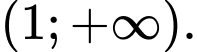
B, Hàm số nghịch biến trên khoảng 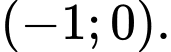
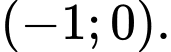
C, Hàm số đồng biến trên khoảng  và
và 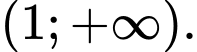
 và
và 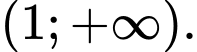
D, Hàm số nghịch biến trên khoảng 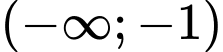 và
và 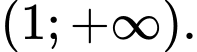
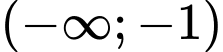 và
và 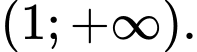
Đáp án: A
Câu 4 [580403]: Cho hàm số 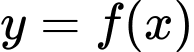 có bảng xét dấu của đạo hàm
có bảng xét dấu của đạo hàm

Hàm số đồng biến trên khoảng nào dưới đây?
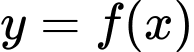 có bảng xét dấu của đạo hàm
có bảng xét dấu của đạo hàm
Hàm số đồng biến trên khoảng nào dưới đây?
A, 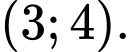
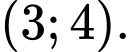
B, 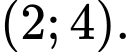
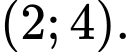
C, 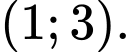
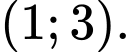
D, 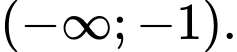
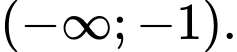
Đáp án: C
Câu 5 [580404]: Cho hàm số 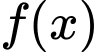 có đạo hàm
có đạo hàm 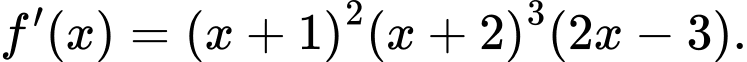 Hàm số
Hàm số 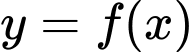 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
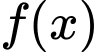 có đạo hàm
có đạo hàm 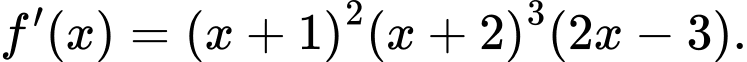 Hàm số
Hàm số 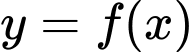 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 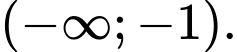
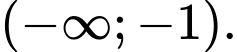
B, 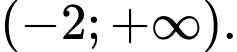
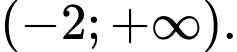
C, 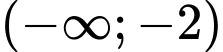 và
và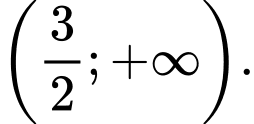
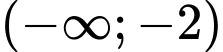 và
và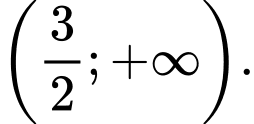
D, 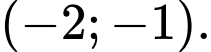
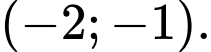
Đáp án: C
Câu 6 [580405]: Đường cong của hình vẽ bên là đồ thị của hàm số 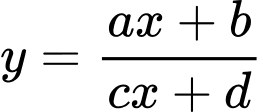 với
với 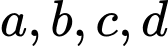 là các số thực.
là các số thực.
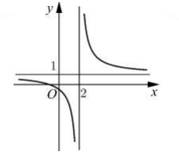
Mệnh đề nào sau đây là đúng?
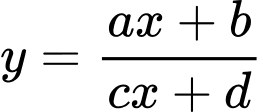 với
với 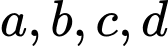 là các số thực.
là các số thực. 
Mệnh đề nào sau đây là đúng?
A, 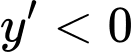 với
với 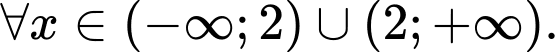
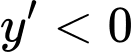 với
với 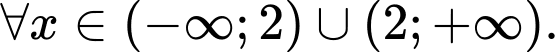
B, 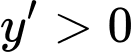 với
với 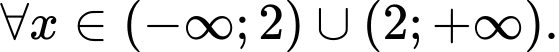
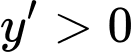 với
với 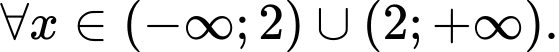
C, 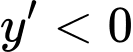 với
với 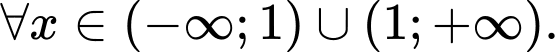
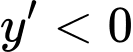 với
với 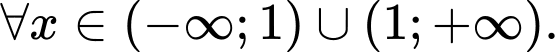
D, 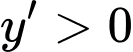 với
với 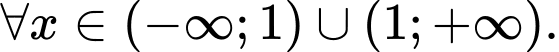
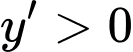 với
với 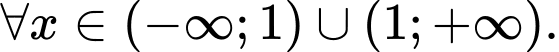
Đáp án: A
Câu 7 [580406]: Hàm số 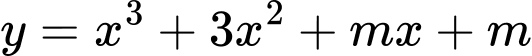 đồng biến trên tập xác định khi giá trị của
đồng biến trên tập xác định khi giá trị của 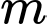 là:
là:
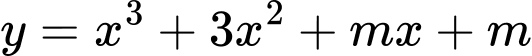 đồng biến trên tập xác định khi giá trị của
đồng biến trên tập xác định khi giá trị của 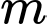 là:
là: A, 

B, 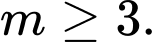
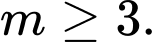
C, 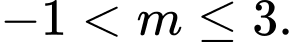
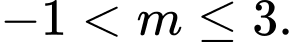
D, 

Chọn B
Tập xác định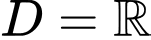
Tính đạo hàm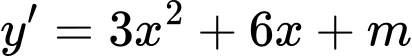
Để hàm số đồng biến trên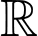
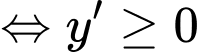
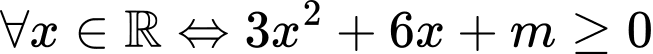 với mọi
với mọi  (*)
(*)
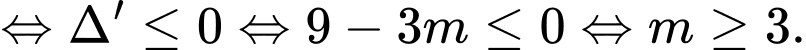 Đáp án: B
Đáp án: B
Tập xác định
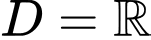
Tính đạo hàm
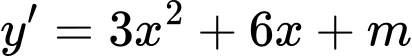
Để hàm số đồng biến trên
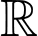
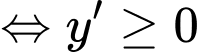
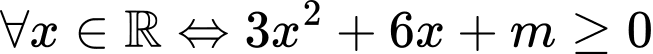 với mọi
với mọi 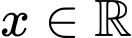 (*)
(*) 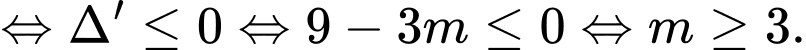 Đáp án: B
Đáp án: B
Câu 8 [580407]: Giá trị của 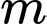 để hàm số
để hàm số 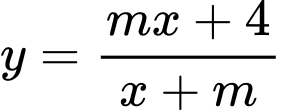 nghịch biến trên mỗi khoảng xác định là:
nghịch biến trên mỗi khoảng xác định là:
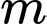 để hàm số
để hàm số 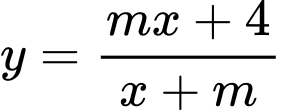 nghịch biến trên mỗi khoảng xác định là:
nghịch biến trên mỗi khoảng xác định là: A, 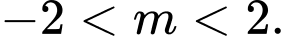
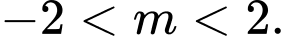
B, 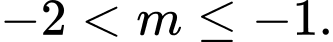
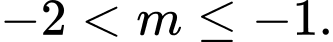
C, 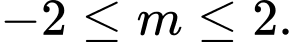
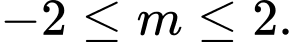
D, 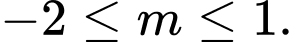
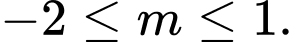
Chọn A
Tập xác định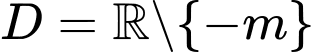
Tính đạo hàm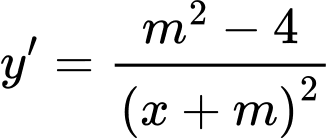
Để hàm số nghịch biến trên mỗi khoảng xác định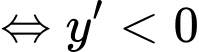

 Đáp án: A
Đáp án: A
Tập xác định
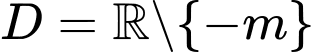
Tính đạo hàm
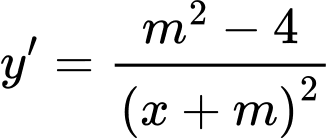
Để hàm số nghịch biến trên mỗi khoảng xác định
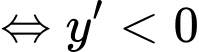

 Đáp án: A
Đáp án: A
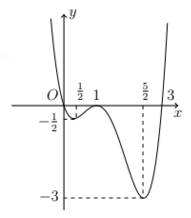
Câu 9 [580408]: Cho hàm số 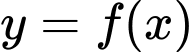 có đạo hàm
có đạo hàm 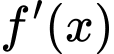 trên khoảng
trên khoảng 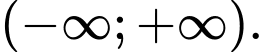 Đồ thị của hàm số
Đồ thị của hàm số 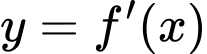 như hình vẽ. Hàm số
như hình vẽ. Hàm số 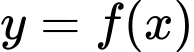 nghịch biến trên khoảng nào trong các khoảng sau?
nghịch biến trên khoảng nào trong các khoảng sau?
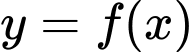 có đạo hàm
có đạo hàm 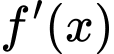 trên khoảng
trên khoảng 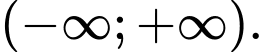 Đồ thị của hàm số
Đồ thị của hàm số 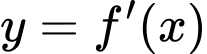 như hình vẽ. Hàm số
như hình vẽ. Hàm số 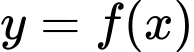 nghịch biến trên khoảng nào trong các khoảng sau?
nghịch biến trên khoảng nào trong các khoảng sau?
A, 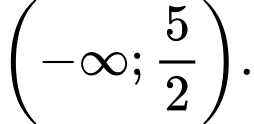
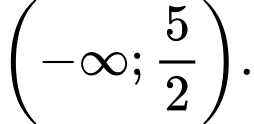
B, 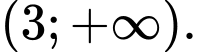
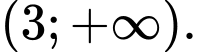
C, 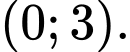
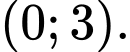
D, 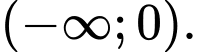
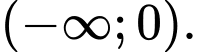
Chọn C
Dựa vào đồ thị thấy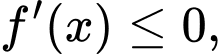
 nên hàm số
nên hàm số 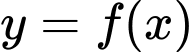 nghịch biến trên khoảng
nghịch biến trên khoảng 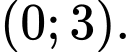 Đáp án: C
Đáp án: C
Dựa vào đồ thị thấy
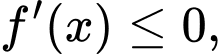
 nên hàm số
nên hàm số 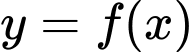 nghịch biến trên khoảng
nghịch biến trên khoảng 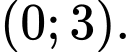 Đáp án: C
Đáp án: C
Câu 10 [580409]: Cho hàm số 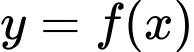 có đạo hàm
có đạo hàm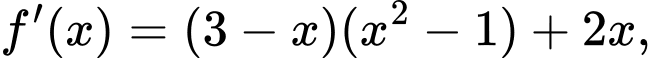 Hỏi hàm số
Hỏi hàm số 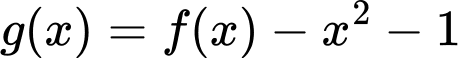 đồng biến trên khoảng nào trong các khoảng dưới đây ?
đồng biến trên khoảng nào trong các khoảng dưới đây ?
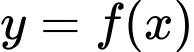 có đạo hàm
có đạo hàm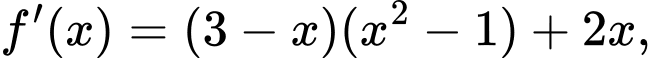 Hỏi hàm số
Hỏi hàm số 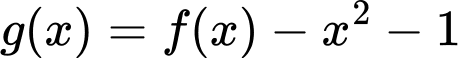 đồng biến trên khoảng nào trong các khoảng dưới đây ?
đồng biến trên khoảng nào trong các khoảng dưới đây ? A, 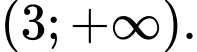
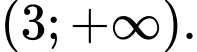
B, 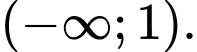
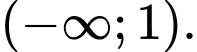
C, 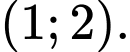
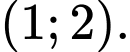
D, 

Chọn C
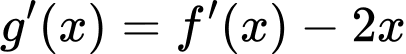
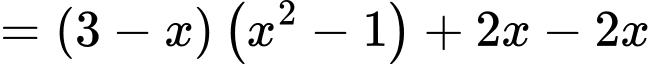
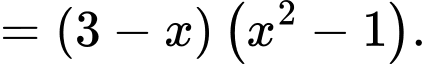
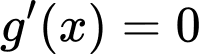
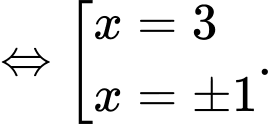
Bảng xét dấu :
:

Từ bảng xét dấu trên ta thấy hàm số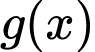 đồng biến trên khoảng
đồng biến trên khoảng 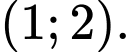 Đáp án: C
Đáp án: C
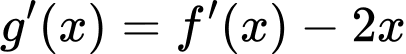
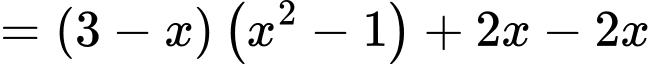
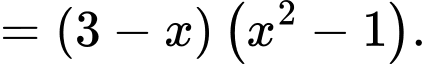
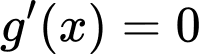
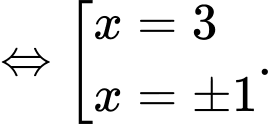
Bảng xét dấu
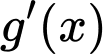 :
: 
Từ bảng xét dấu trên ta thấy hàm số
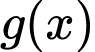 đồng biến trên khoảng
đồng biến trên khoảng 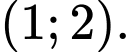 Đáp án: C
Đáp án: C
Câu 11 [580410]: Tìm tất cả giá trị của tham số 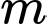 để hàm số
để hàm số 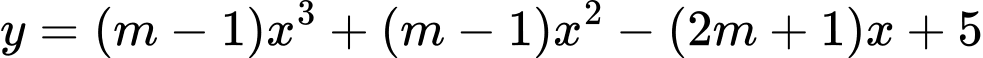 nghịch biến trên tập xác định.
nghịch biến trên tập xác định.
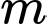 để hàm số
để hàm số 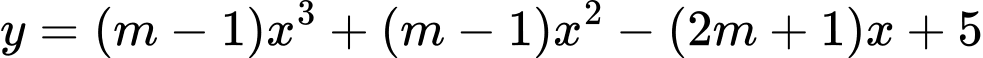 nghịch biến trên tập xác định.
nghịch biến trên tập xác định. A, 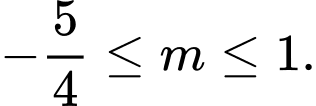
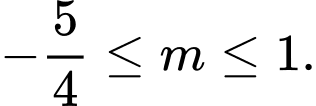
B, 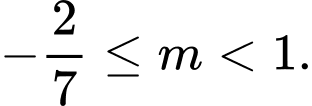
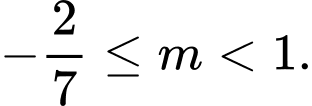
C, 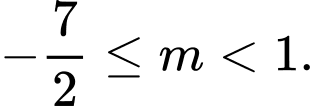
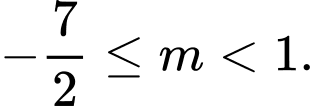
D, 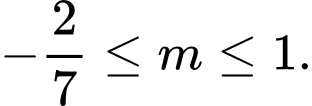
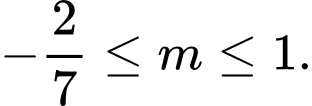
Chọn D
Tập xác định: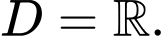
Ta có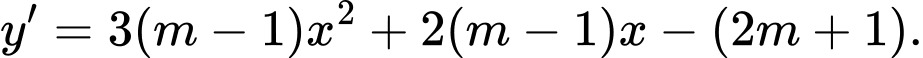
Xét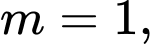 ta có
ta có 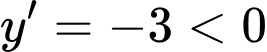
 nên nghịch biến trên tập xác định.
nên nghịch biến trên tập xác định.
Xét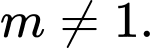 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi 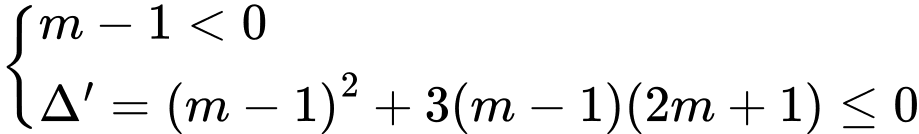
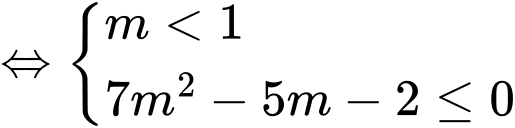
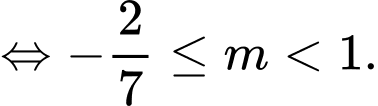
Vậy với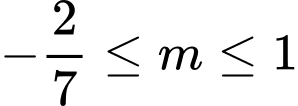 thì hàm số
thì hàm số 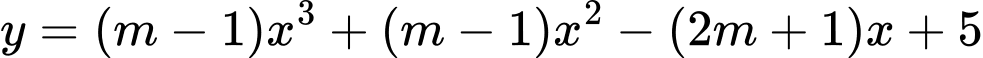 nghịch biến trên tập xác định. Đáp án: D
nghịch biến trên tập xác định. Đáp án: D
Tập xác định:
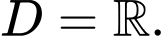
Ta có
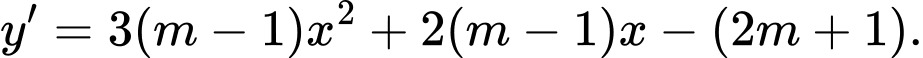
Xét
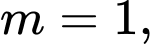 ta có
ta có 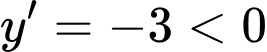
 nên nghịch biến trên tập xác định.
nên nghịch biến trên tập xác định. Xét
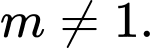 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi
Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi 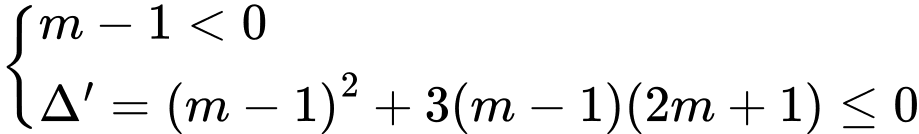
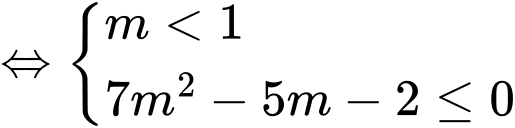
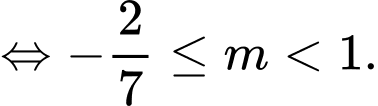
Vậy với
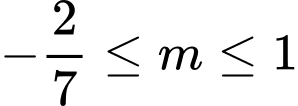 thì hàm số
thì hàm số 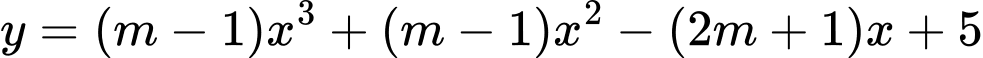 nghịch biến trên tập xác định. Đáp án: D
nghịch biến trên tập xác định. Đáp án: D
Câu 12 [580411]: Tìm các giá trị của tham số 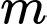 để hàm số
để hàm số 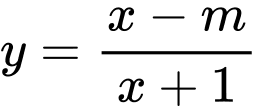 đồng biến trên các khoảng xác định của nó.
đồng biến trên các khoảng xác định của nó.
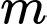 để hàm số
để hàm số 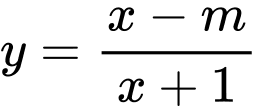 đồng biến trên các khoảng xác định của nó.
đồng biến trên các khoảng xác định của nó. A, 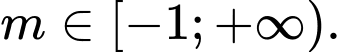
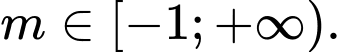
B, 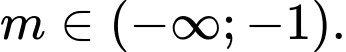
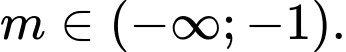
C, 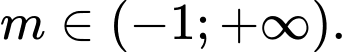
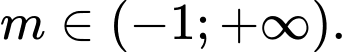
D, 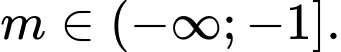
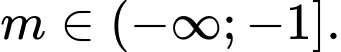
Chon C
Tập xác định: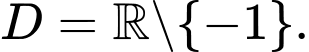
Ta có: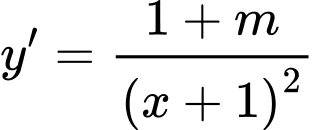
Hàm số đồng biến trên các khoảng xác định của nó khi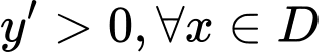
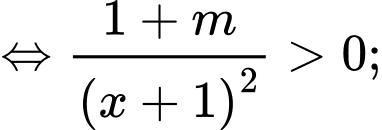

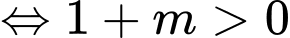
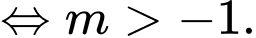 Đáp án: C
Đáp án: C
Tập xác định:
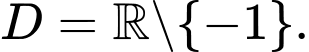
Ta có:
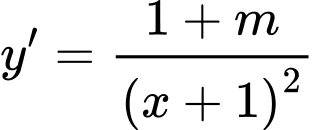
Hàm số đồng biến trên các khoảng xác định của nó khi
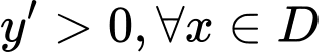
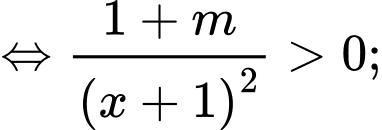

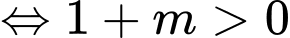
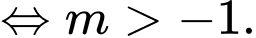 Đáp án: C
Đáp án: C
Câu 13 [580412]: Tập hợp các giá trị thực của 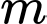 để hàm số
để hàm số 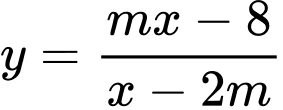 (1) đồng biến trên khoảng
(1) đồng biến trên khoảng 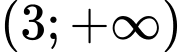 là
là
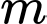 để hàm số
để hàm số 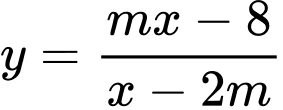 (1) đồng biến trên khoảng
(1) đồng biến trên khoảng 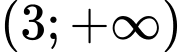 là
là A, 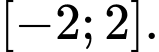
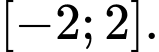
B, 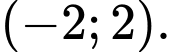
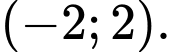
C, 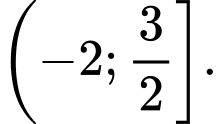
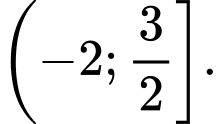
D, 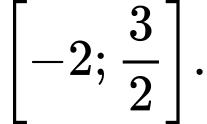
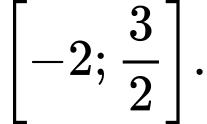
Chọn C
TXĐ: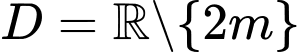
Ta có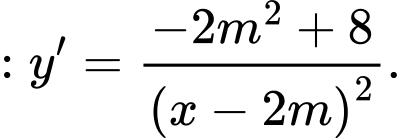 Để hàm số (1) đồng biến trên
Để hàm số (1) đồng biến trên 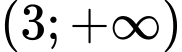 thì :
thì :
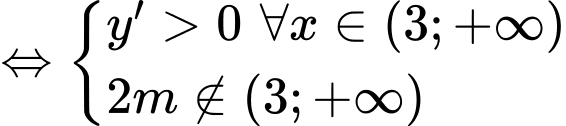
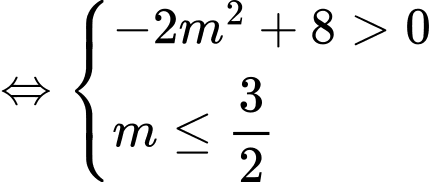
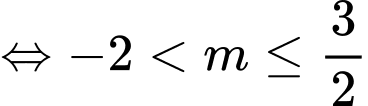 Đáp án: C
Đáp án: C
TXĐ:
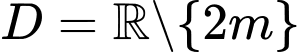
Ta có
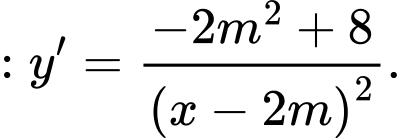 Để hàm số (1) đồng biến trên
Để hàm số (1) đồng biến trên 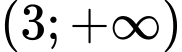 thì :
thì : 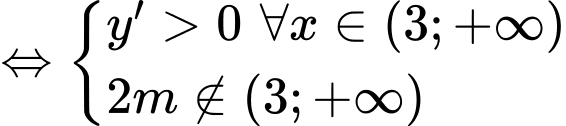
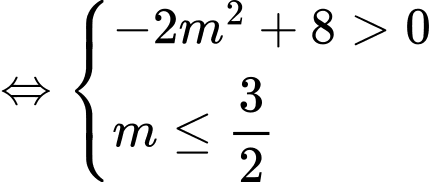
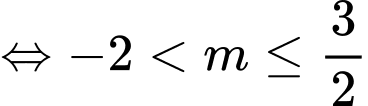 Đáp án: C
Đáp án: C
Câu 14 [580413]: Cho hàm số 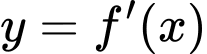 có đồ thị như hình vẽ
có đồ thị như hình vẽ
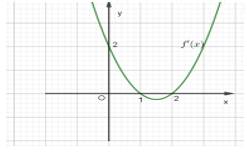
Hàm số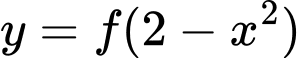 đồng biến trên khoảng nào dưới đây
đồng biến trên khoảng nào dưới đây
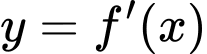 có đồ thị như hình vẽ
có đồ thị như hình vẽ
Hàm số
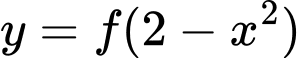 đồng biến trên khoảng nào dưới đây
đồng biến trên khoảng nào dưới đây A, 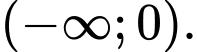
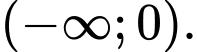
B, 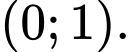
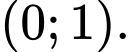
C, 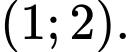
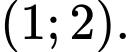
D, 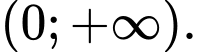
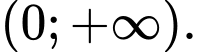
Chọn B
Hàm số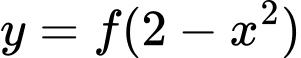 có
có 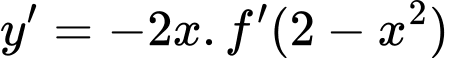
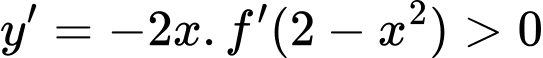
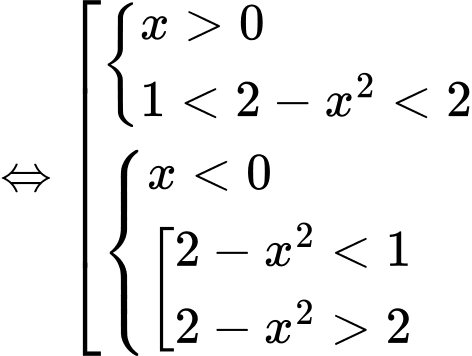
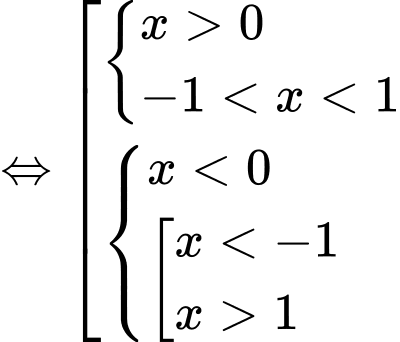
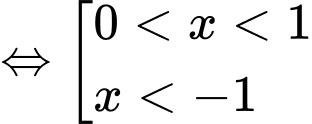
Do đó hàm số đồng biến trên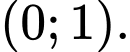 Đáp án: B
Đáp án: B
Hàm số
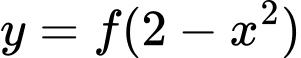 có
có 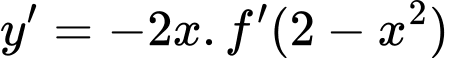
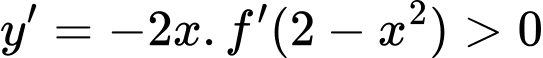
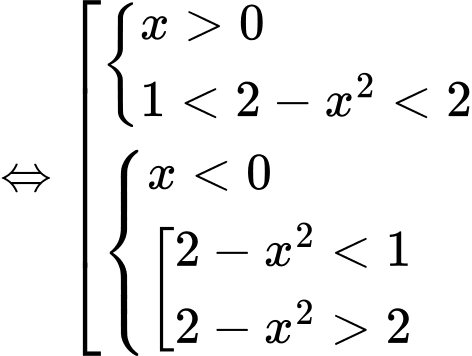
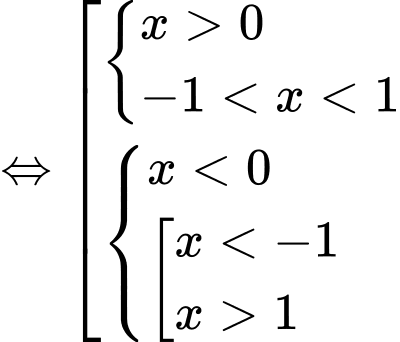
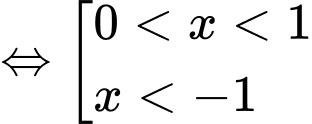
Do đó hàm số đồng biến trên
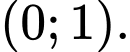 Đáp án: B
Đáp án: B
Câu 15 [580414]: Tìm tất cả các giá trị của tham số 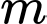 để hàm số
để hàm số 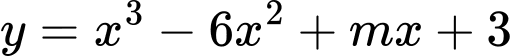 đồng biến trên khoảng
đồng biến trên khoảng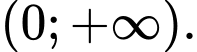
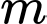 để hàm số
để hàm số 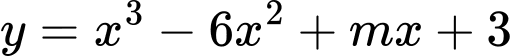 đồng biến trên khoảng
đồng biến trên khoảng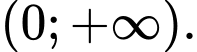
A, 

B, 

C, 

D, 

Chọn D
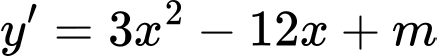
Hàm số đã cho đồng biến trên khoảng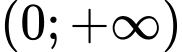 khi và chi khi
khi và chi khi  với mọi
với mọi 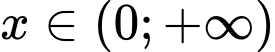
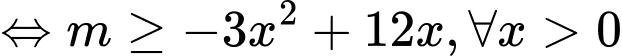
Xét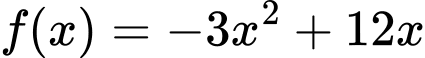 với
với 
Ta có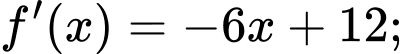
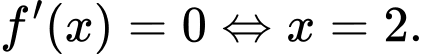
Bảng biến thiên:
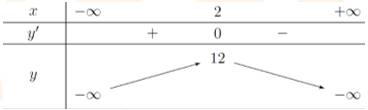
Dựa vào bảng biến thiên, ta được giá trị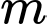 thỏa mãn yêu cầu bài toán là
thỏa mãn yêu cầu bài toán là  Đáp án: D
Đáp án: D
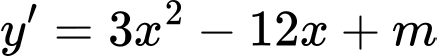
Hàm số đã cho đồng biến trên khoảng
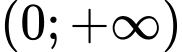 khi và chi khi
khi và chi khi  với mọi
với mọi 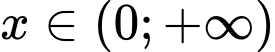
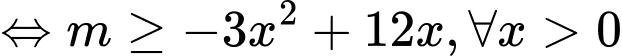
Xét
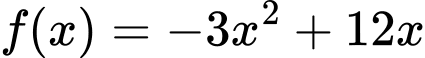 với
với 
Ta có
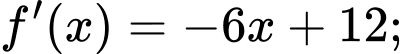
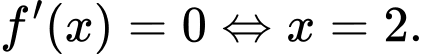
Bảng biến thiên:

Dựa vào bảng biến thiên, ta được giá trị
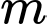 thỏa mãn yêu cầu bài toán là
thỏa mãn yêu cầu bài toán là  Đáp án: D
Đáp án: D Dạng câu hỏi: Câu trắc nghiệm đúng sai.
Câu 16 [580415]: Cho hàm số 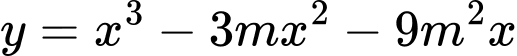 (tham số
(tham số 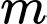 ). Khi đó:
). Khi đó:
a) Khi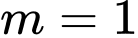 thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 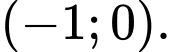
b) Nếu thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 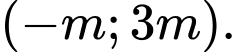
c) Nếu thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 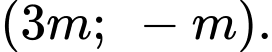
d) Biết hàm số nghịch biến trên khoảng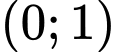 khi
khi  hoặc
hoặc 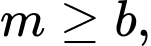 khi đó
khi đó 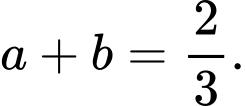
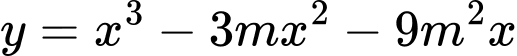 (tham số
(tham số 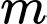 ). Khi đó:
). Khi đó:a) Khi
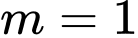 thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 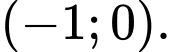
b) Nếu
 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 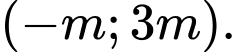
c) Nếu
 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 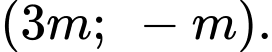
d) Biết hàm số nghịch biến trên khoảng
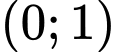 khi
khi  hoặc
hoặc 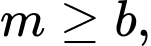 khi đó
khi đó 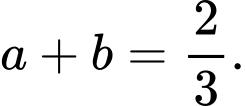
a) Sai
b) Đúng
c) Đúng
d) Sai
Tập xác định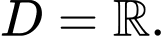
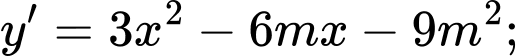
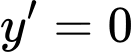

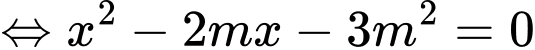
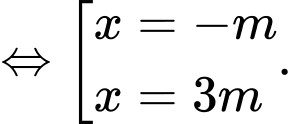
• Nếu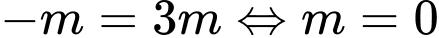 thì
thì 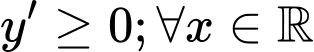 nên hàm số không có khoảng nghịch biến.
nên hàm số không có khoảng nghịch biến.
• Nếu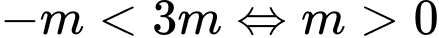 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 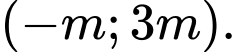
Do đó hàm số nghịch biến trên khoảng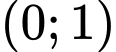
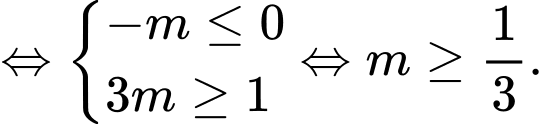
Kết hợp với điều kiện ta được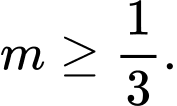
• Nếu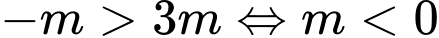 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 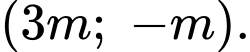
Do đó hàm số nghịch biến trên khoảng
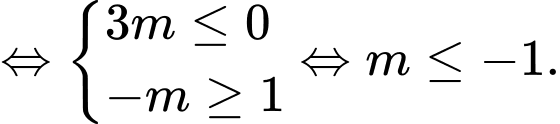
Kết hợp với điều kiện ta được
Vậy hàm số nghịch biến trên khoảng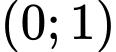 khi
khi  hoặc
hoặc 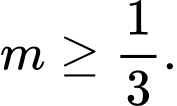
b) Đúng
c) Đúng
d) Sai
Tập xác định
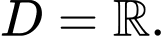
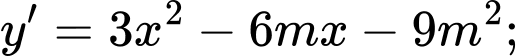
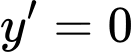

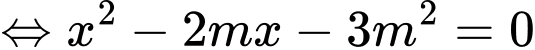
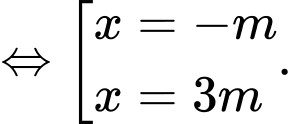
• Nếu
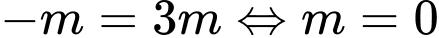 thì
thì 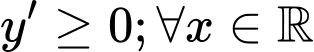 nên hàm số không có khoảng nghịch biến.
nên hàm số không có khoảng nghịch biến. • Nếu
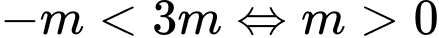 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 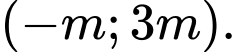
Do đó hàm số nghịch biến trên khoảng
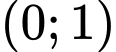
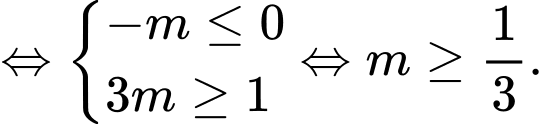
Kết hợp với điều kiện ta được
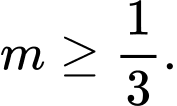
• Nếu
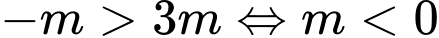 thì hàm số nghịch biến trên khoảng
thì hàm số nghịch biến trên khoảng 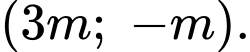
Do đó hàm số nghịch biến trên khoảng
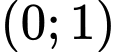
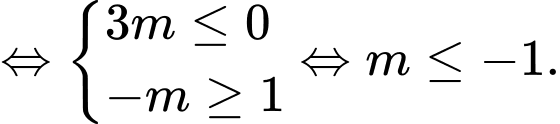
Kết hợp với điều kiện ta được

Vậy hàm số nghịch biến trên khoảng
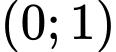 khi
khi  hoặc
hoặc 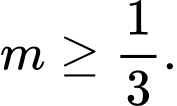
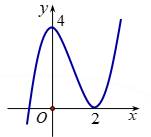
Câu 17 [580416]: Cho hàm số 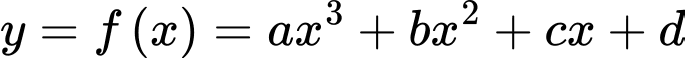 có đồ thị như hình bên. Đặt
có đồ thị như hình bên. Đặt 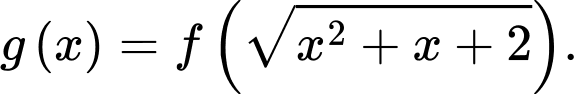
Khi đó:
a)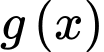 nghịch biến trên khoảng
nghịch biến trên khoảng 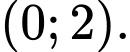
b)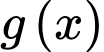 đồng biến trên khoảng
đồng biến trên khoảng 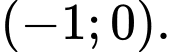
c)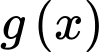 nghịch biến trên khoảng
nghịch biến trên khoảng 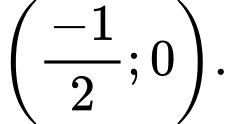
d) đồng biến trên khoảng
đồng biến trên khoảng 
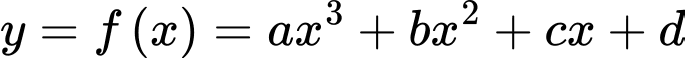 có đồ thị như hình bên. Đặt
có đồ thị như hình bên. Đặt 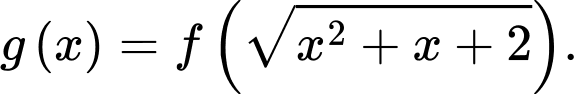

Khi đó:
a)
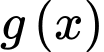 nghịch biến trên khoảng
nghịch biến trên khoảng 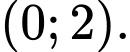
b)
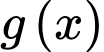 đồng biến trên khoảng
đồng biến trên khoảng 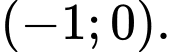
c)
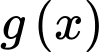 nghịch biến trên khoảng
nghịch biến trên khoảng 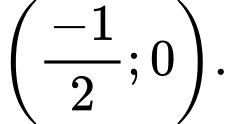
d)
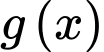 đồng biến trên khoảng
đồng biến trên khoảng 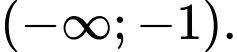
a) Sai
b) Sai
c) Đúng
d) Sai
Hàm số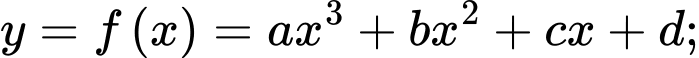
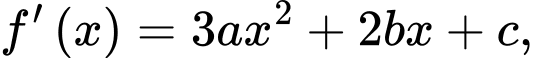 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Do đó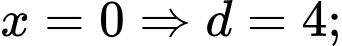
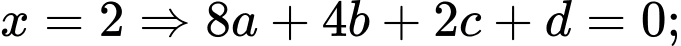
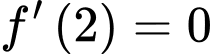
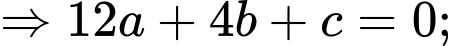
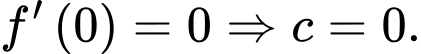
Tìm được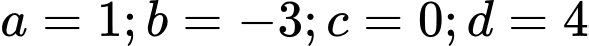 và hàm số
và hàm số 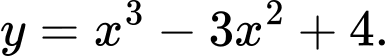
Ta có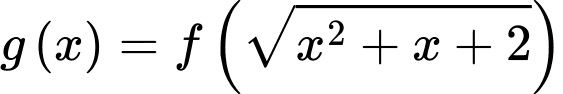
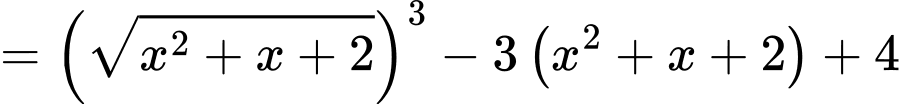
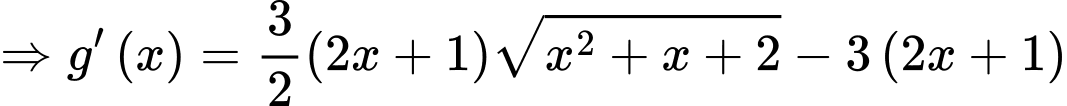
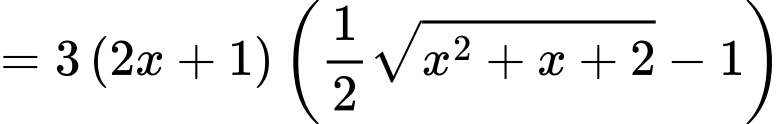 ;
;
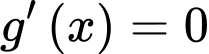
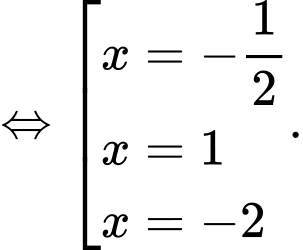
Bảng xét dấu của hàm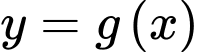 :
:
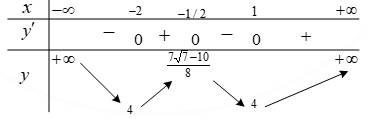
Vậy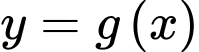 nghịch biến trên khoảng
nghịch biến trên khoảng 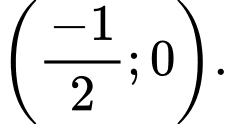
b) Sai
c) Đúng
d) Sai
Hàm số
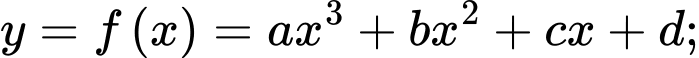
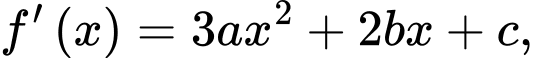 có đồ thị như hình vẽ.
có đồ thị như hình vẽ. Do đó
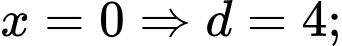
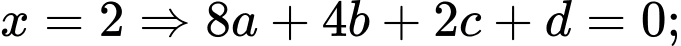
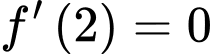
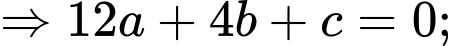
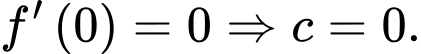
Tìm được
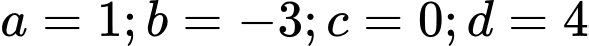 và hàm số
và hàm số 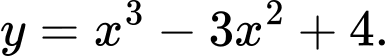
Ta có
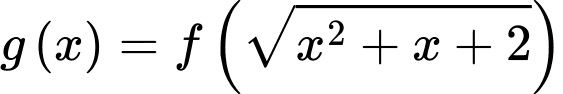
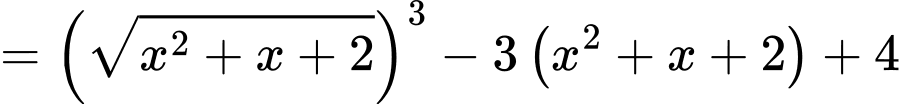
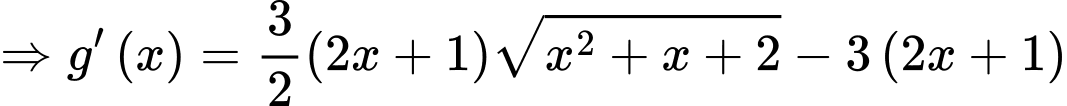
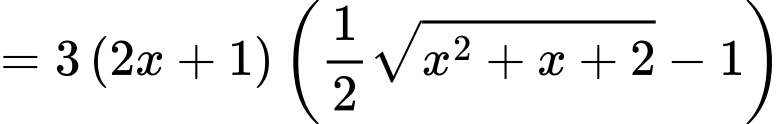 ;
; 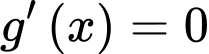
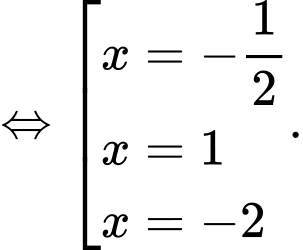
Bảng xét dấu của hàm
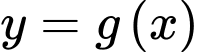 :
:
Vậy
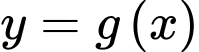 nghịch biến trên khoảng
nghịch biến trên khoảng 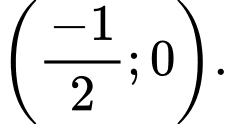
Dạng câu hỏi: Câu trả lời ngắn.
Câu 18 [580417]: Có bao nhiêu giá trị nguyên dương của tham số 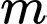 để hàm số
để hàm số 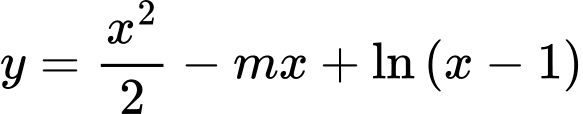 đồng biến trên khoảng
đồng biến trên khoảng 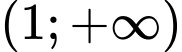 ?
?
Trả lời: __________
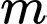 để hàm số
để hàm số 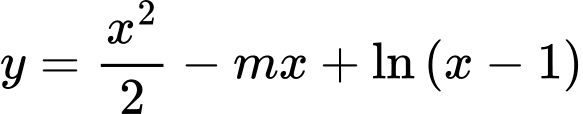 đồng biến trên khoảng
đồng biến trên khoảng 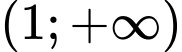 ?
?Trả lời: __________
Ta có 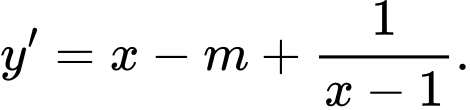
Để hàm số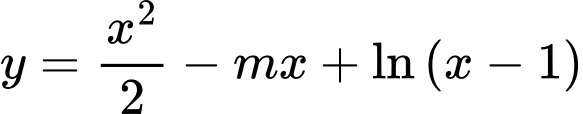 đồng biến trên khoảng
đồng biến trên khoảng 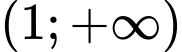 thì
thì 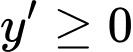 với
với 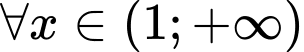
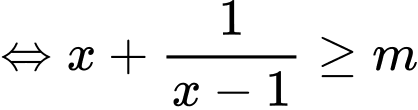 với
với 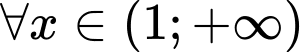
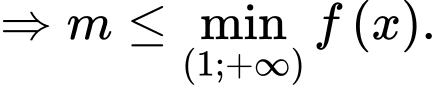
Xét hàm số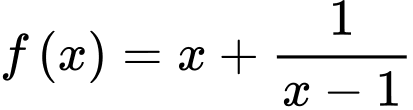 trên khoảng
trên khoảng 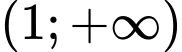 ta có
ta có
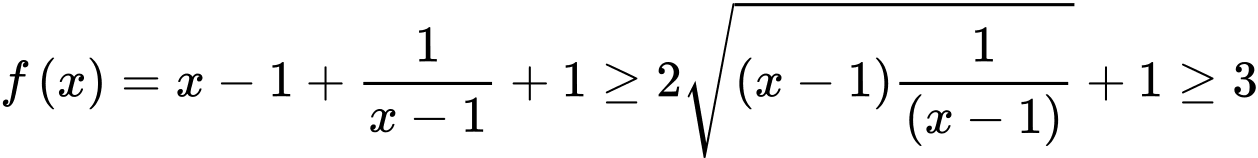
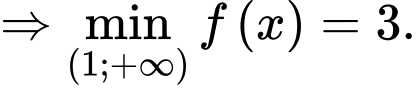
Do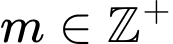 nên
nên 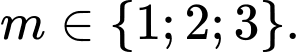
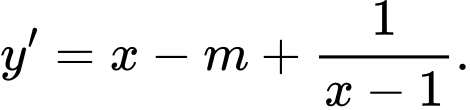
Để hàm số
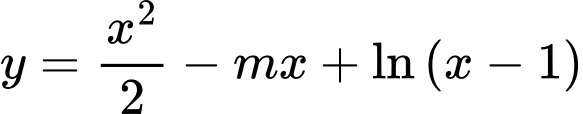 đồng biến trên khoảng
đồng biến trên khoảng 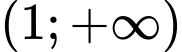 thì
thì 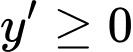 với
với 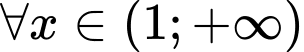
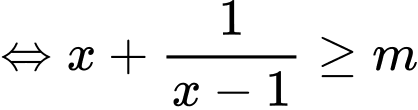 với
với 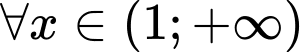
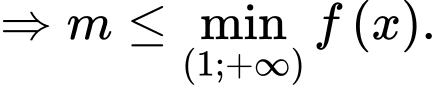
Xét hàm số
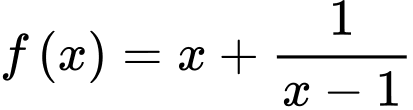 trên khoảng
trên khoảng 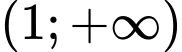 ta có
ta có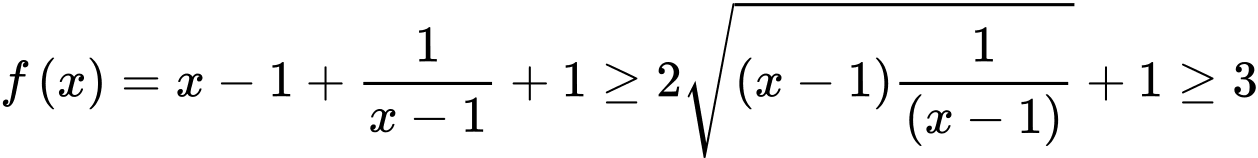
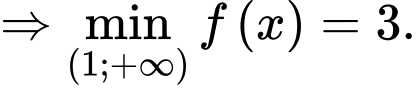
Do
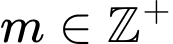 nên
nên 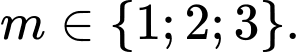
Câu 19 [580418]: Cho hàm số 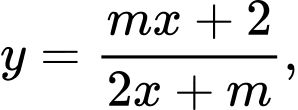
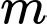 là tham số thực. Gọi
là tham số thực. Gọi 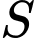 là tập hợp tất cả các giá trị nguyên của tham số
là tập hợp tất cả các giá trị nguyên của tham số 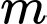 để hàm số nghịch biến trên khoảng
để hàm số nghịch biến trên khoảng 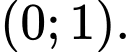 Tìm số phần tử của
Tìm số phần tử của 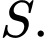
Trả lời: __________
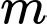 là tham số thực. Gọi
là tham số thực. Gọi 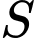 là tập hợp tất cả các giá trị nguyên của tham số
là tập hợp tất cả các giá trị nguyên của tham số 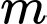 để hàm số nghịch biến trên khoảng
để hàm số nghịch biến trên khoảng 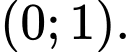 Tìm số phần tử của
Tìm số phần tử của 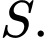
Trả lời: __________
Tập xác định 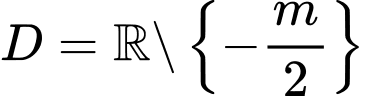
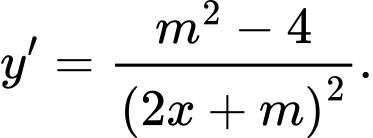
Yêu cầu bài toán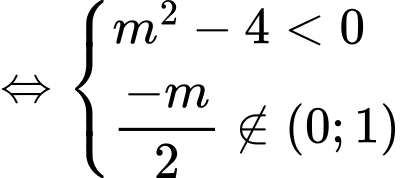
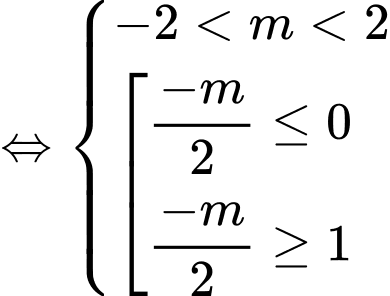
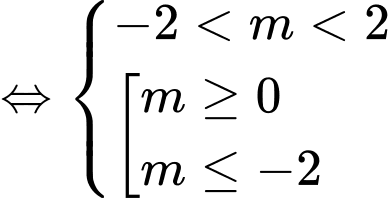
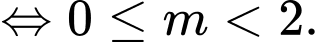
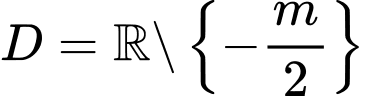
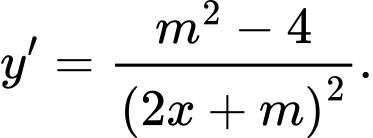
Yêu cầu bài toán
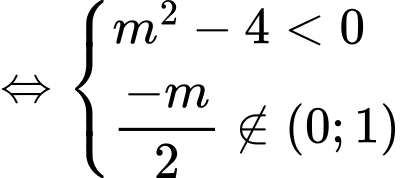
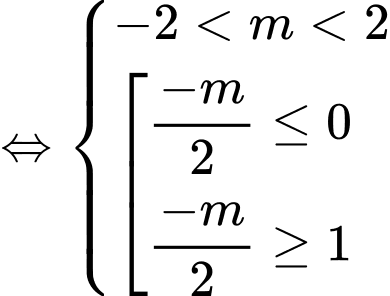
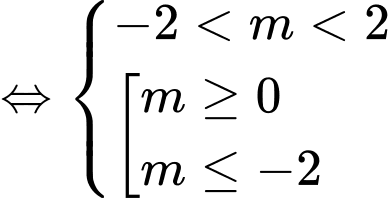
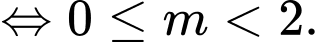
Câu 20 [580419]: Gọi 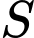 là tập hợp các giá trị nguyên dương của
là tập hợp các giá trị nguyên dương của 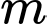 để hàm số
để hàm số 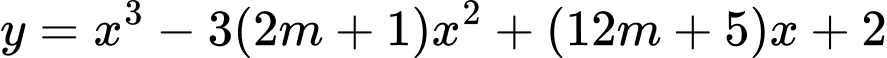 đồng biến trên khoảng
đồng biến trên khoảng 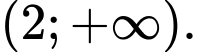 Số phần tử của
Số phần tử của 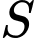 bằng
bằng
Trả lời: __________
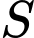 là tập hợp các giá trị nguyên dương của
là tập hợp các giá trị nguyên dương của 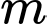 để hàm số
để hàm số 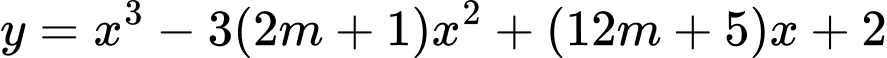 đồng biến trên khoảng
đồng biến trên khoảng 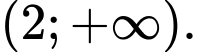 Số phần tử của
Số phần tử của  bằng
bằngTrả lời: __________
Tập xác định 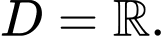
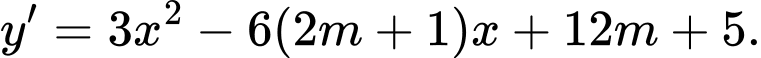
Hàm số đồng biến trong khoảng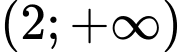 khi
khi 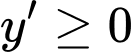 ,
, 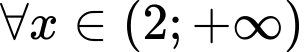
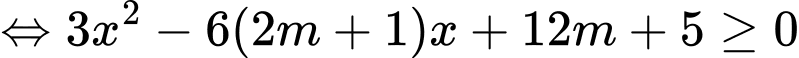 ,
, 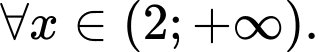
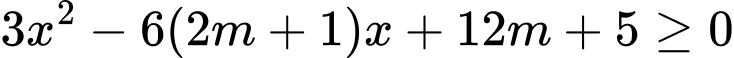
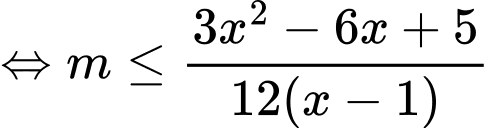
Xét hàm số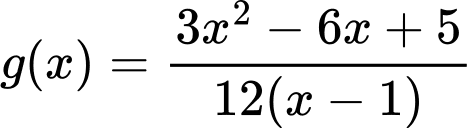 với
với 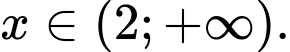
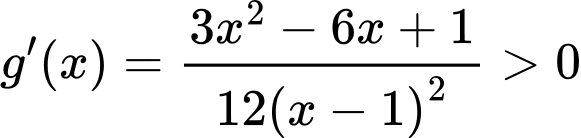 với
với 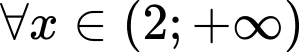
 hàm số
hàm số 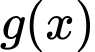 đồng biến trên khoảng
đồng biến trên khoảng 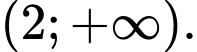
Do đó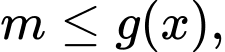
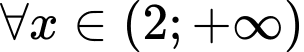
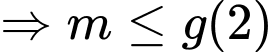
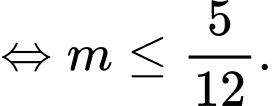
Vậy không có giá trị nguyên dương nào của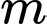 thỏa mãn bài toán.
thỏa mãn bài toán.
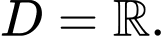
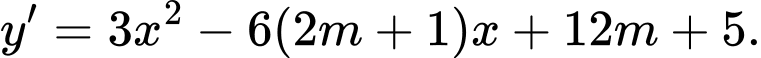
Hàm số đồng biến trong khoảng
 khi
khi 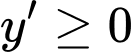 ,
, 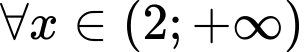
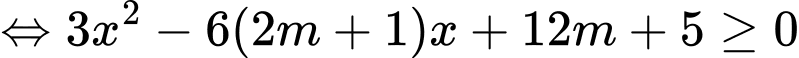 ,
, 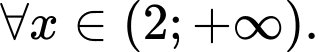
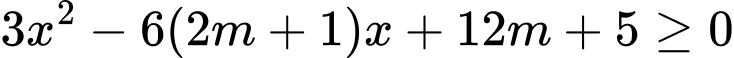
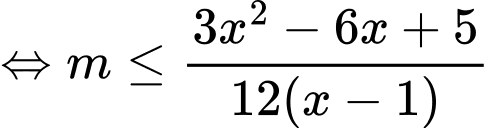
Xét hàm số
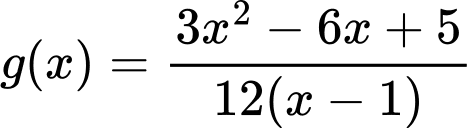 với
với 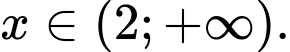
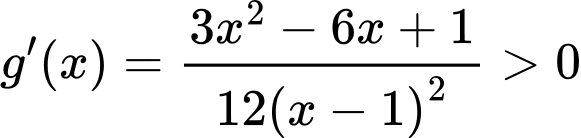 với
với 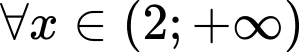
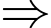 hàm số
hàm số 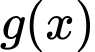 đồng biến trên khoảng
đồng biến trên khoảng 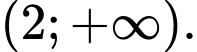
Do đó
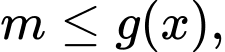
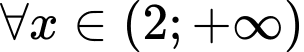
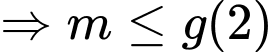
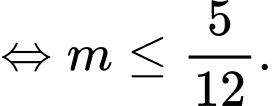
Vậy không có giá trị nguyên dương nào của
 thỏa mãn bài toán.
thỏa mãn bài toán. Dạng câu hỏi: Câu hỏi kéo thả.
Câu 21 [581087]: Cho hàm số 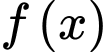 xác định trên
xác định trên 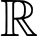 và có đồ thị hàm số
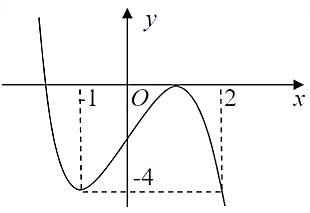
và có đồ thị hàm số 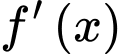 là đường cong như hình bên dưới.
là đường cong như hình bên dưới.
Kéo ô thích hợp thả vào vị trí tương ứng để hoàn thành các câu sau:

Đặt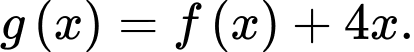 Khi đó hàm số
Khi đó hàm số 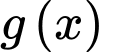 đồng biến trên khoảng __________và nghịch biến trên khoảng__________
đồng biến trên khoảng __________và nghịch biến trên khoảng__________
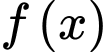 xác định trên
xác định trên 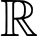 và có đồ thị hàm số
và có đồ thị hàm số 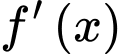 là đường cong như hình bên dưới.
là đường cong như hình bên dưới.
Kéo ô thích hợp thả vào vị trí tương ứng để hoàn thành các câu sau:

Đặt
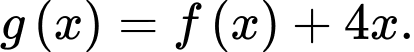 Khi đó hàm số
Khi đó hàm số 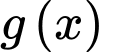 đồng biến trên khoảng __________và nghịch biến trên khoảng__________
đồng biến trên khoảng __________và nghịch biến trên khoảng__________
Đáp án
Đặt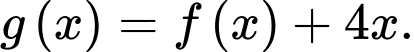 Khi đó hàm số
Khi đó hàm số 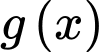 đồng biến trên khoảng
đồng biến trên khoảng  và nghịch biến trên khoảng
và nghịch biến trên khoảng 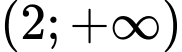
Phương pháp giải
a) Tính số nghiệm của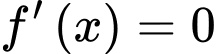
b) Xét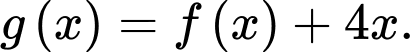
Lời giải
Dễ thấy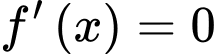 có đúng 1 nghiệm bội lẻ duy nhất a < −1 nên hàm số
có đúng 1 nghiệm bội lẻ duy nhất a < −1 nên hàm số 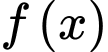 có đúng 1 cực trị.
có đúng 1 cực trị.
Xét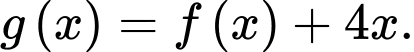
Ta có: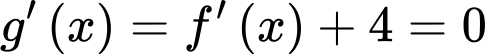
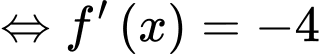
Lập bảng xét dấu của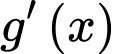

Vậy hàm số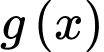 đồng biến trên khoảng (−∞;2) và nghịch biến trên khoảng (2;+∞).
đồng biến trên khoảng (−∞;2) và nghịch biến trên khoảng (2;+∞).
Đặt
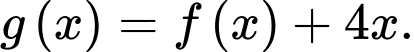 Khi đó hàm số
Khi đó hàm số 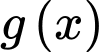 đồng biến trên khoảng
đồng biến trên khoảng  và nghịch biến trên khoảng
và nghịch biến trên khoảng 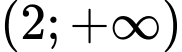
Phương pháp giải
a) Tính số nghiệm của
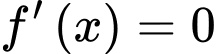
b) Xét
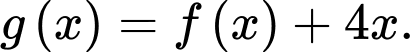
Lời giải
Dễ thấy
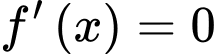 có đúng 1 nghiệm bội lẻ duy nhất a < −1 nên hàm số
có đúng 1 nghiệm bội lẻ duy nhất a < −1 nên hàm số 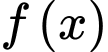 có đúng 1 cực trị.
có đúng 1 cực trị. Xét
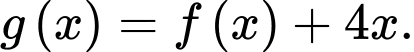
Ta có:
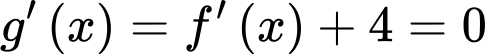
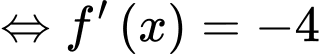
Lập bảng xét dấu của
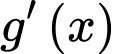

Vậy hàm số
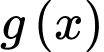 đồng biến trên khoảng (−∞;2) và nghịch biến trên khoảng (2;+∞).
đồng biến trên khoảng (−∞;2) và nghịch biến trên khoảng (2;+∞).