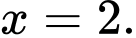Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [581830]: Cho hàm số 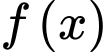 có đạo hàm là
có đạo hàm là 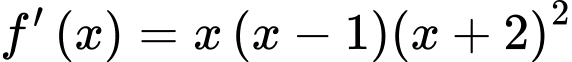
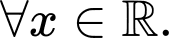 Số điểm cực trị của hàm số là?
Số điểm cực trị của hàm số là?
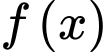 có đạo hàm là
có đạo hàm là 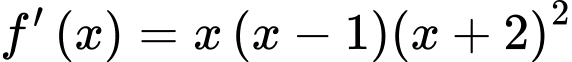
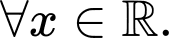 Số điểm cực trị của hàm số là?
Số điểm cực trị của hàm số là? A, 
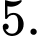
B, 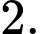
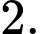
C, 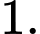
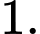
D, 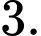
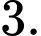
Chọn B
Ta có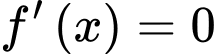
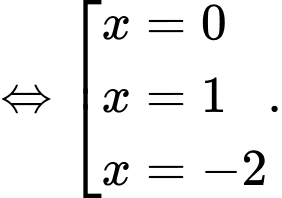
Do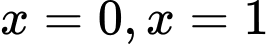 là nghiệm đơn, còn các nghiệm và
là nghiệm đơn, còn các nghiệm và 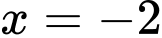 là nghiệm bội chẵn nên
là nghiệm bội chẵn nên 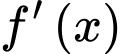 chỉ đổi khi đi qua
chỉ đổi khi đi qua  Đáp án: B
Đáp án: B
Ta có
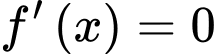
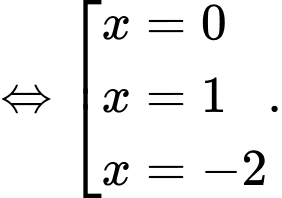
Do
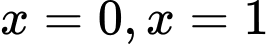 là nghiệm đơn, còn các nghiệm và
là nghiệm đơn, còn các nghiệm và 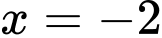 là nghiệm bội chẵn nên
là nghiệm bội chẵn nên 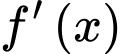 chỉ đổi khi đi qua
chỉ đổi khi đi qua  Đáp án: B
Đáp án: B
Câu 2 [581831]: Tìm giá trị thực của tham số 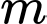 để hàm số
để hàm số 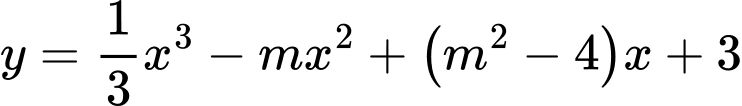 đạt cực đại tại
đạt cực đại tại 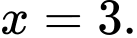
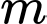 để hàm số
để hàm số 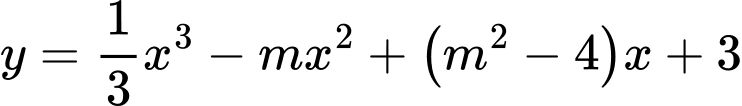 đạt cực đại tại
đạt cực đại tại 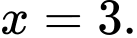
A, 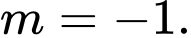
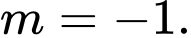
B, 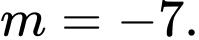
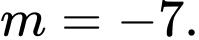
C, 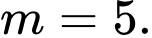
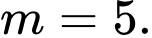
D, 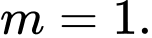
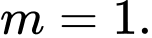
Chọn C
Ta có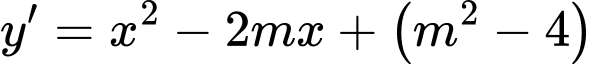 ;
; 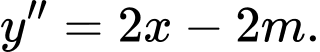
Hàm số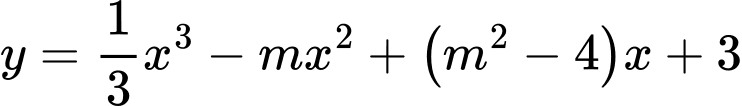 đạt cực đại tại
đạt cực đại tại 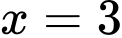 khi và chỉ khi:
khi và chỉ khi: 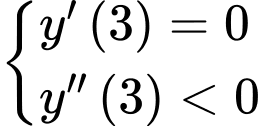
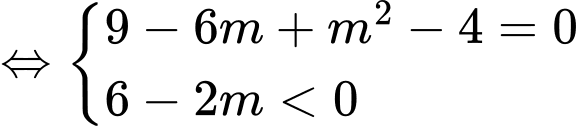
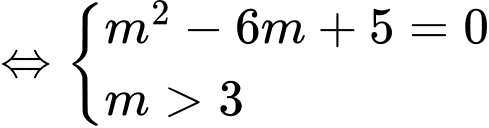
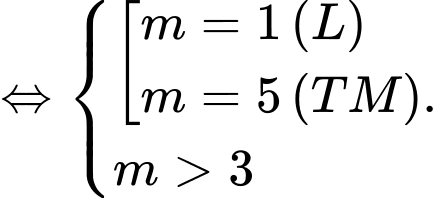
Vậy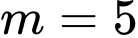 là giá trị cần tìm.
Đáp án: C
là giá trị cần tìm.
Đáp án: C
Ta có
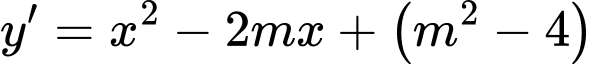 ;
; 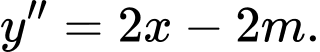
Hàm số
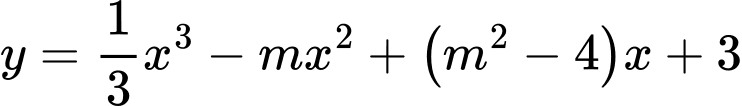 đạt cực đại tại
đạt cực đại tại 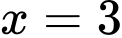 khi và chỉ khi:
khi và chỉ khi: 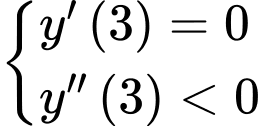
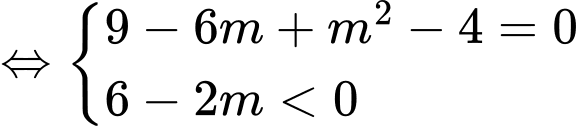
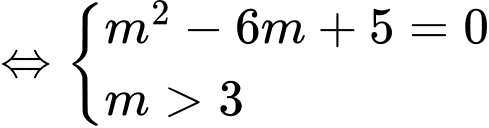
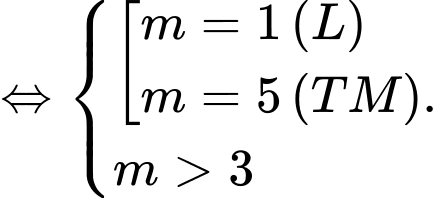
Vậy
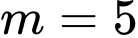 là giá trị cần tìm.
Đáp án: C
là giá trị cần tìm.
Đáp án: C
Câu 3 [581832]: Cho hàm số 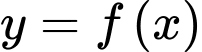 xác định trên tập số thực
xác định trên tập số thực 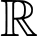 và có đạo hàm
và có đạo hàm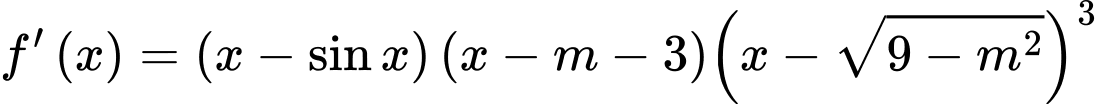
 (
(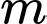 là tham số). Có bao nhiêu giá trị nguyên của
là tham số). Có bao nhiêu giá trị nguyên của 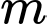 để hàm số
để hàm số 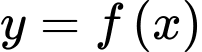 đạt cực tiểu tại
đạt cực tiểu tại 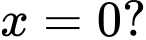
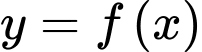 xác định trên tập số thực
xác định trên tập số thực 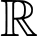 và có đạo hàm
và có đạo hàm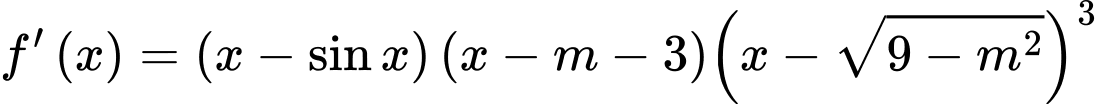
 (
(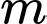 là tham số). Có bao nhiêu giá trị nguyên của
là tham số). Có bao nhiêu giá trị nguyên của 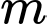 để hàm số
để hàm số 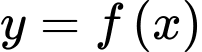 đạt cực tiểu tại
đạt cực tiểu tại 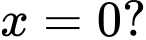
A, 6.
B, 7.
C, 5.
D, 4.
Chọn A
Điều kiện
TH1: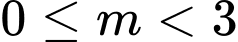 ta có BTT
ta có BTT
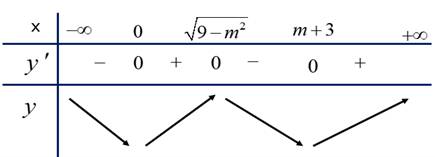
TH2: ta có BTT
ta có BTT
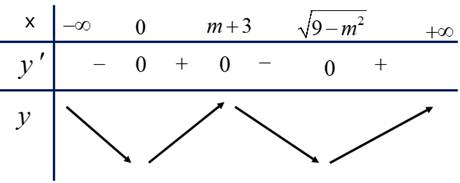
TH3: ta có BTT
ta có BTT
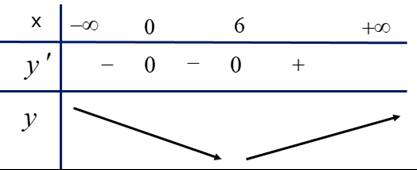
Từ đó suy ra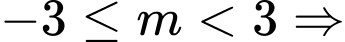 có 6 giá trị nguyên của
có 6 giá trị nguyên của 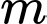 thỏa mãn. Đáp án: A
thỏa mãn. Đáp án: A
Điều kiện

TH1:
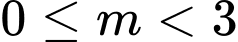 ta có BTT
ta có BTT
TH2:
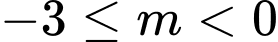 ta có BTT
ta có BTT
TH3:
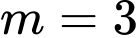 ta có BTT
ta có BTT
Từ đó suy ra
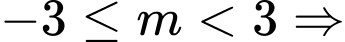 có 6 giá trị nguyên của
có 6 giá trị nguyên của 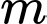 thỏa mãn. Đáp án: A
thỏa mãn. Đáp án: A
Câu 4 [581833]: Tìm tất cả các giá trị của tham số 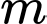 để hàm số
để hàm số 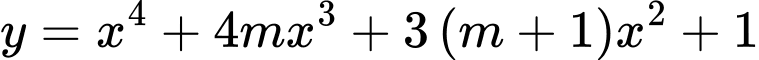 có cực tiểu mà không có cực đại.
có cực tiểu mà không có cực đại.
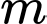 để hàm số
để hàm số 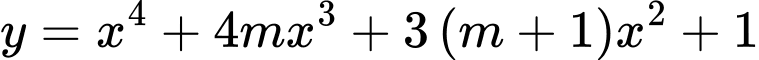 có cực tiểu mà không có cực đại.
có cực tiểu mà không có cực đại. A, 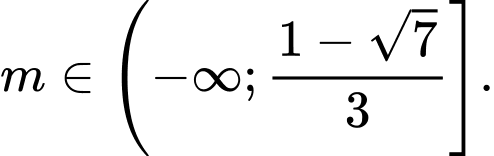
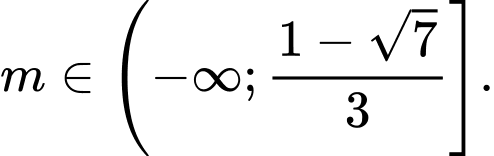
B, 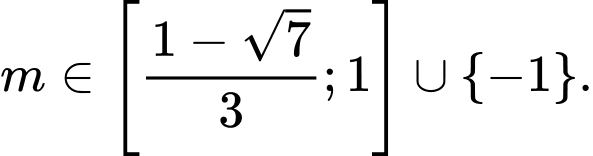
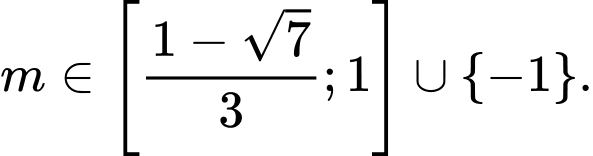
C, 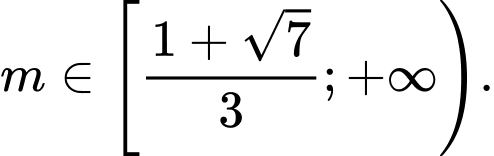
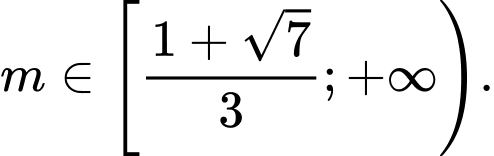
D, 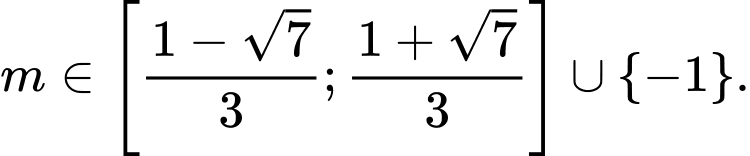
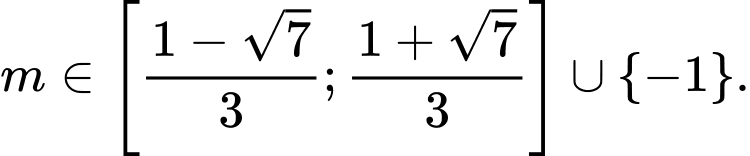
Chọn D
Ta có: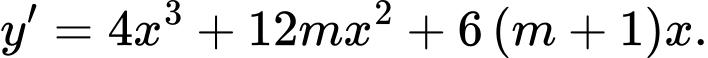
+ TH1: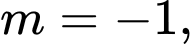 ta có:
ta có: 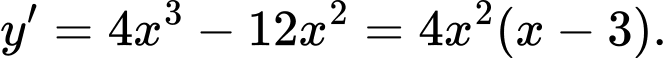
Bảng xét dấu

Hàm số có 1 cực tiểu duy nhất.
Ta có: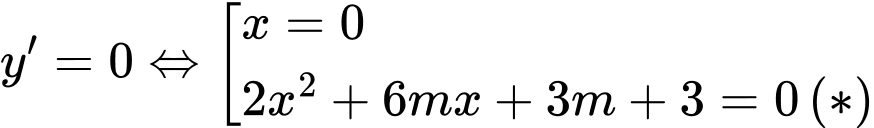
+ TH2: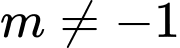
Để hàm số đã cho chỉ có một cực tiểu thì phương trình không có hai nghiệm phân biệt
không có hai nghiệm phân biệt
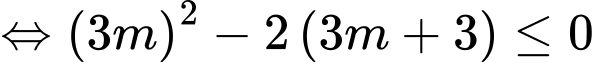
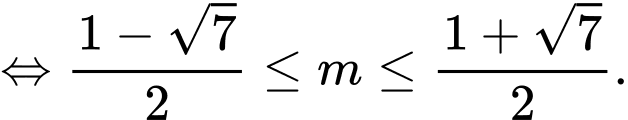
Vậy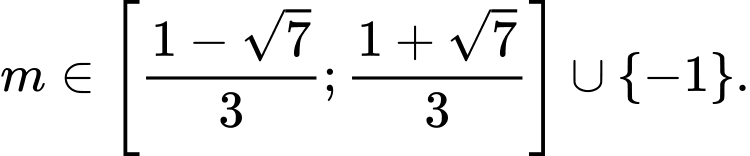 Đáp án: D
Đáp án: D
Ta có:
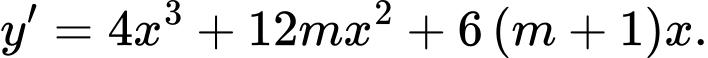
+ TH1:
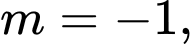 ta có:
ta có: 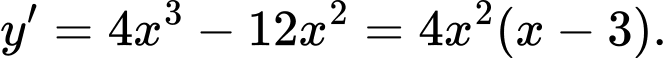
Bảng xét dấu

Hàm số có 1 cực tiểu duy nhất.
Ta có:
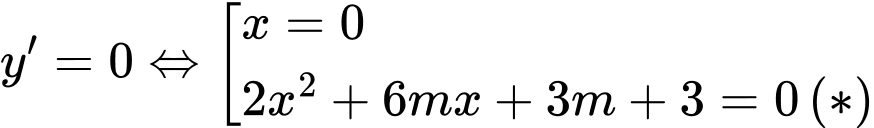
+ TH2:
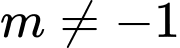
Để hàm số đã cho chỉ có một cực tiểu thì phương trình
 không có hai nghiệm phân biệt
không có hai nghiệm phân biệt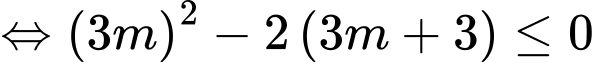
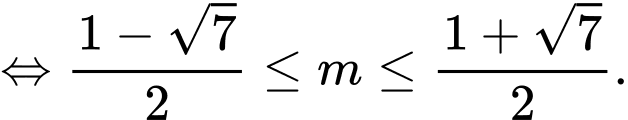
Vậy
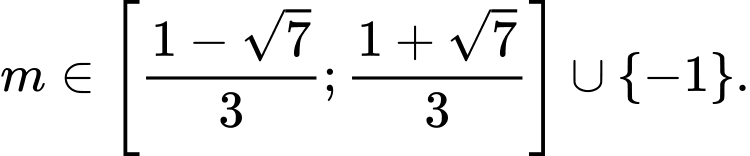 Đáp án: D
Đáp án: D
Câu 5 [581834]: Đồ thị hàm số 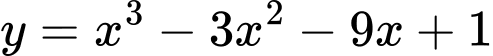 có hai cực trị
có hai cực trị 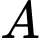 và
và 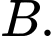 Điểm nào dưới đây thuộc đường thẳng
Điểm nào dưới đây thuộc đường thẳng 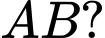
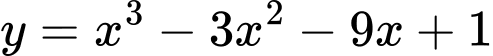 có hai cực trị
có hai cực trị 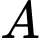 và
và 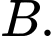 Điểm nào dưới đây thuộc đường thẳng
Điểm nào dưới đây thuộc đường thẳng 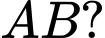
A, 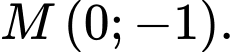
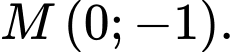
B, 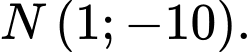
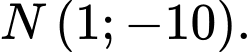
C, 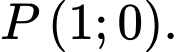
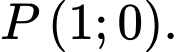
D, 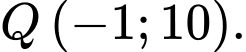
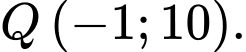
Chọn B
Ta có: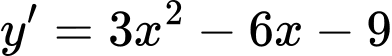 thực hiện phép chia
thực hiện phép chia 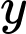 cho
cho 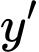 ta được số dư là
ta được số dư là 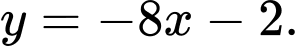 Như thế điểm
Như thế điểm 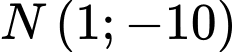 thuộc đường thẳng
thuộc đường thẳng 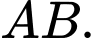 Đáp án: B
Đáp án: B
Ta có:
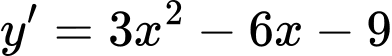 thực hiện phép chia
thực hiện phép chia 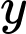 cho
cho 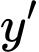 ta được số dư là
ta được số dư là 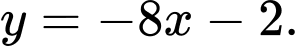 Như thế điểm
Như thế điểm 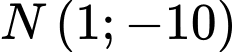 thuộc đường thẳng
thuộc đường thẳng 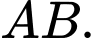 Đáp án: B
Đáp án: B
Câu 6 [581835]: Biết 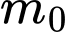 là giá trị của tham số
là giá trị của tham số 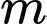 để hàm số
để hàm số 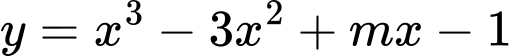 có hai điểm cực trị
có hai điểm cực trị 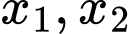 sao cho
sao cho 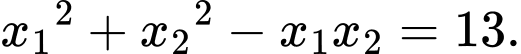 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
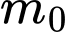 là giá trị của tham số
là giá trị của tham số 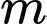 để hàm số
để hàm số 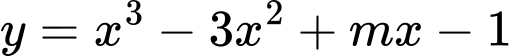 có hai điểm cực trị
có hai điểm cực trị 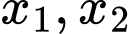 sao cho
sao cho 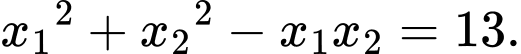 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng? A, 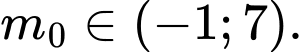
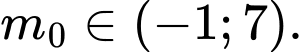
B, 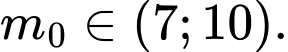
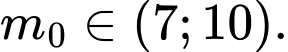
C, 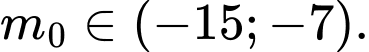
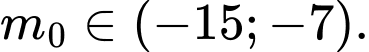
D, 

TXĐ: 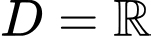
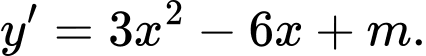
Xét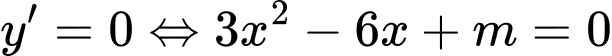 ;
; 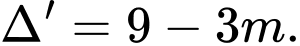
Hàm số có hai điểm cực trị
Hai điểm cực trị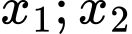 là nghiệm của
là nghiệm của 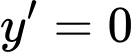 nên:
nên: 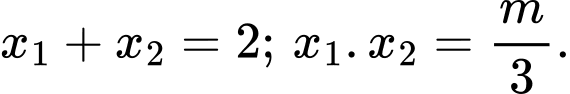
Để

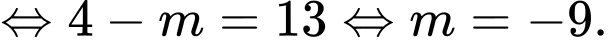
Vậy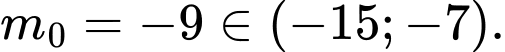 Đáp án: C
Đáp án: C
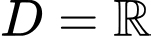
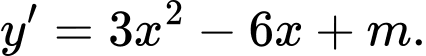
Xét
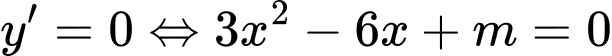 ;
; 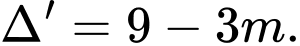
Hàm số có hai điểm cực trị

Hai điểm cực trị
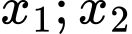 là nghiệm của
là nghiệm của 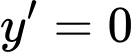 nên:
nên: 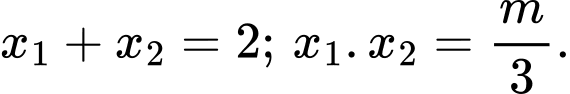
Để


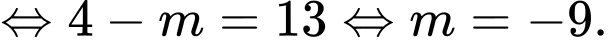
Vậy
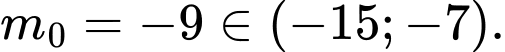 Đáp án: C
Đáp án: C
Câu 7 [581836]: Cho hàm số  có bảng biến thiên như hình bên.
có bảng biến thiên như hình bên.
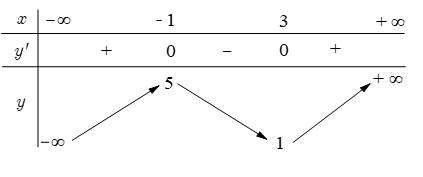
Giá trị cực tiểu của hàm số bằng
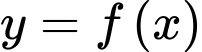 có bảng biến thiên như hình bên.
có bảng biến thiên như hình bên. 
Giá trị cực tiểu của hàm số bằng
A, 1.
B, 3.
C, 5.
D, 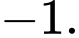
Đáp án: A
Câu 8 [581837]: Cho hàm số 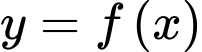 xác định và liên tục trên
xác định và liên tục trên 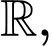 có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Hàm số có điểm cực tiểu là
có điểm cực tiểu là
 xác định và liên tục trên
xác định và liên tục trên  có đồ thị như hình vẽ.
có đồ thị như hình vẽ.
Hàm số
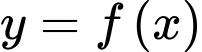 có điểm cực tiểu là
có điểm cực tiểu là A, 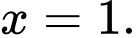
B, 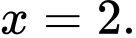
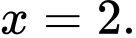
C, 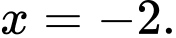
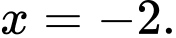
D, 

Đáp án: A
Câu 9 [581838]: Tìm giá trị thực của tham số 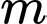 đề hàm số
đề hàm số 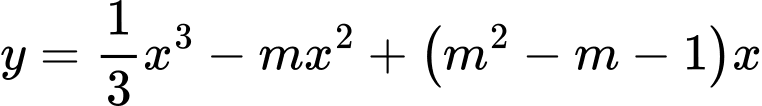 đạt cực đại tại
đạt cực đại tại 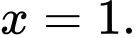
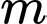 đề hàm số
đề hàm số 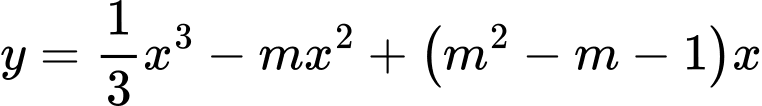 đạt cực đại tại
đạt cực đại tại 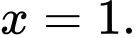
A, 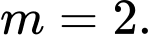
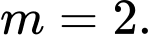
B, 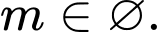
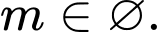
C, 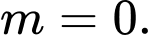
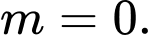
D, 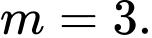
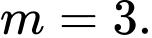
Chọn D
Tập xác định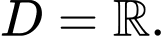
Ta có: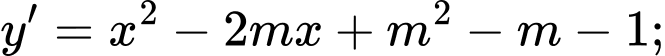
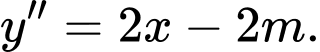
Hàm số đạt cực đại tại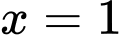 suy ra
suy ra 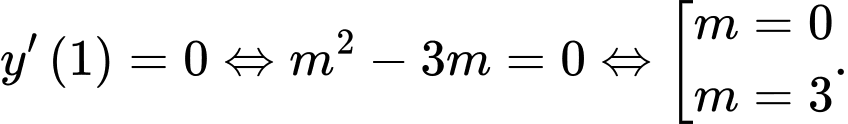
Với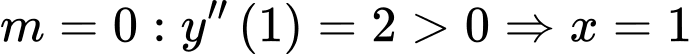 là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm số
Với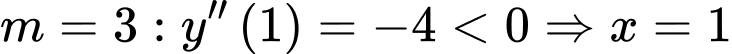 là điểm cực đại của hàm số.
là điểm cực đại của hàm số.
Vậy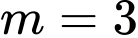 là giá trị cần tìm. Đáp án: D
là giá trị cần tìm. Đáp án: D
Tập xác định
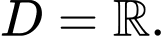
Ta có:
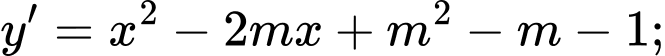
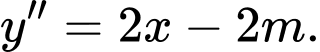
Hàm số đạt cực đại tại
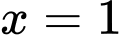 suy ra
suy ra 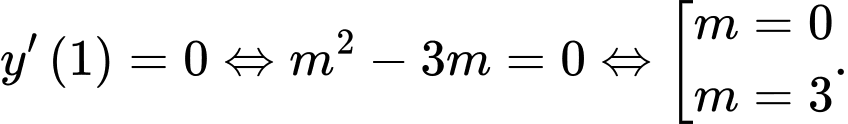
Với
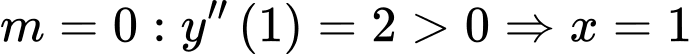 là điểm cực tiểu của hàm số
là điểm cực tiểu của hàm sốVới
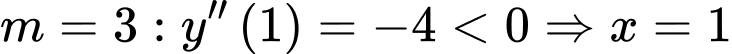 là điểm cực đại của hàm số.
là điểm cực đại của hàm số.Vậy
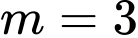 là giá trị cần tìm. Đáp án: D
là giá trị cần tìm. Đáp án: D
Câu 10 [581839]: Tìm tất cả các giá trị thực của tham số 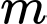 để hàm số
để hàm số 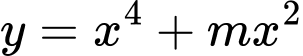 đạt cực tiều tại
đạt cực tiều tại 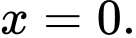
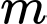 để hàm số
để hàm số 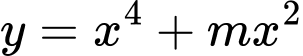 đạt cực tiều tại
đạt cực tiều tại 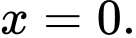
A, 

B, 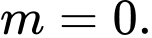
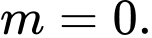
C, 

D, 

Chọn C
Ta có: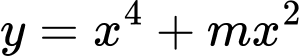
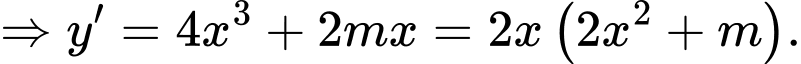
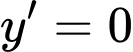
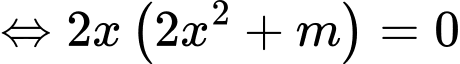
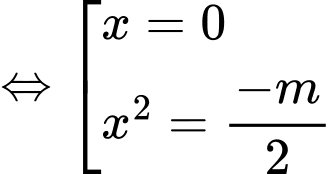
• Nếu ta có bảng biến thiên:
ta có bảng biến thiên:
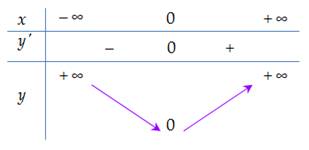
Suy ra hàm số đạt cực tiểu tại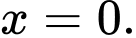
• Nếu ta có bảng biến thiên:
ta có bảng biến thiên:
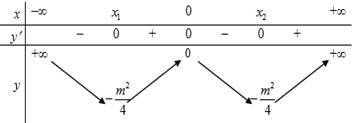
Suy ra hàm số đạt cực đại tại Vậy hàm số đạt cực tiểu tại
Vậy hàm số đạt cực tiểu tại 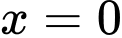 khi
khi  Đáp án: C
Đáp án: C
Ta có:
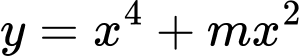
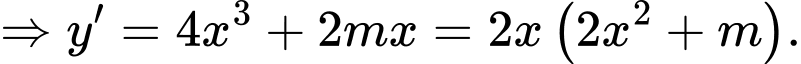
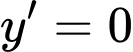
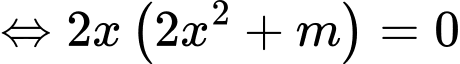
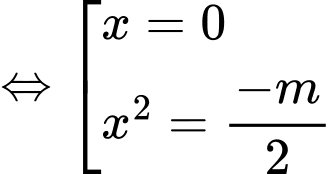
• Nếu
 ta có bảng biến thiên:
ta có bảng biến thiên:
Suy ra hàm số đạt cực tiểu tại
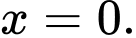
• Nếu
 ta có bảng biến thiên:
ta có bảng biến thiên:
Suy ra hàm số đạt cực đại tại
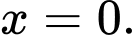 Vậy hàm số đạt cực tiểu tại
Vậy hàm số đạt cực tiểu tại 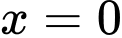 khi
khi  Đáp án: C
Đáp án: C
Câu 11 [581840]: Tìm tất cả các giá trị thực của tham số 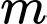 để hàm số
để hàm số 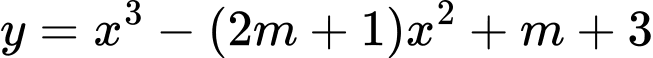 có điểm cực trị?
có điểm cực trị?
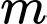 để hàm số
để hàm số 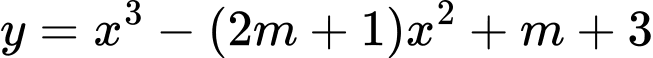 có điểm cực trị?
có điểm cực trị? A, 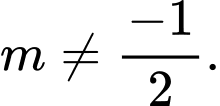
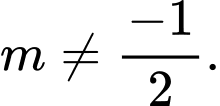
B, 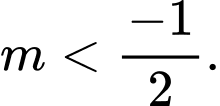
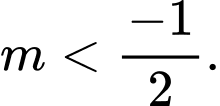
C, 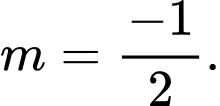
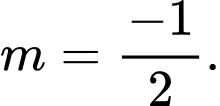
D, 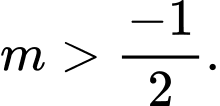
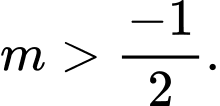
Chọn A
Tập xác định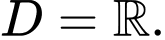
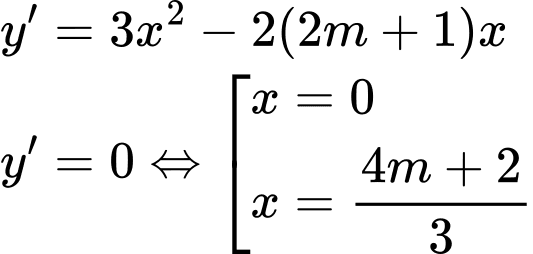
- Ta có: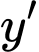 là hàm bậc hai, có nghiệm
là hàm bậc hai, có nghiệm 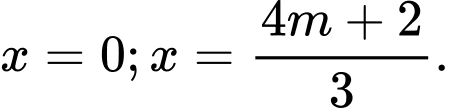
Hàm số có điềm cực trị khi và chỉ khi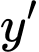 dổi dấu suy ra hàm số có diểm cực trị khi và chỉ khi
dổi dấu suy ra hàm số có diểm cực trị khi và chỉ khi
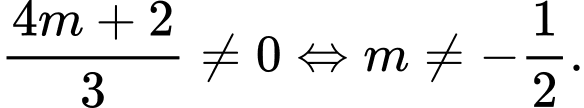
Sai lầm dễ mắc phải:
Sử dụng sai điều kiện:
+) Hàm số đạt cực trị khi và chì khi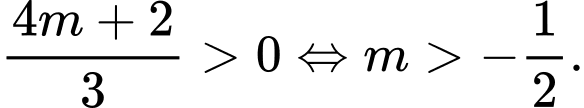 Chọn phương án D.
Chọn phương án D.
+) Hàm số đạt cực trị khi và chỉ khi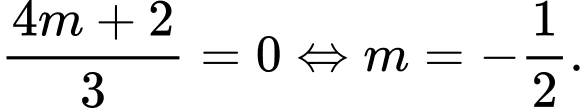 Chọn phương án C.
Chọn phương án C.
+) Hàm số đạt cực trị khi và chỉ khi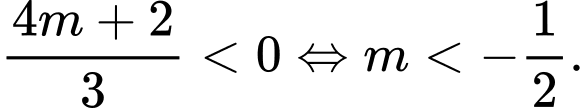 Chọn phương án B. Đáp án: A
Chọn phương án B. Đáp án: A
Tập xác định
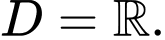
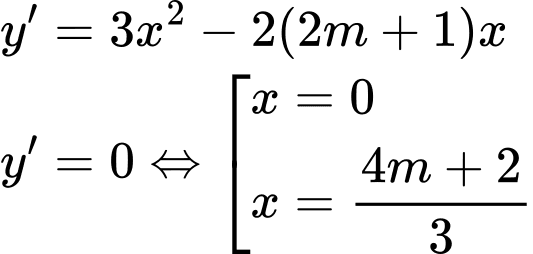
- Ta có:
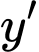 là hàm bậc hai, có nghiệm
là hàm bậc hai, có nghiệm 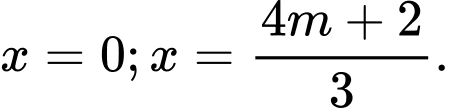
Hàm số có điềm cực trị khi và chỉ khi
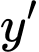 dổi dấu suy ra hàm số có diểm cực trị khi và chỉ khi
dổi dấu suy ra hàm số có diểm cực trị khi và chỉ khi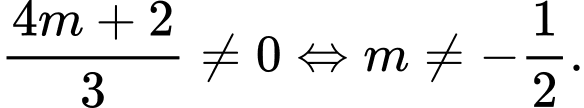
Sai lầm dễ mắc phải:
Sử dụng sai điều kiện:
+) Hàm số đạt cực trị khi và chì khi
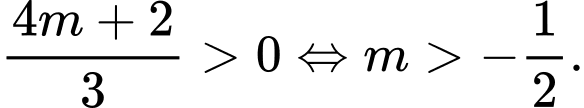 Chọn phương án D.
Chọn phương án D.+) Hàm số đạt cực trị khi và chỉ khi
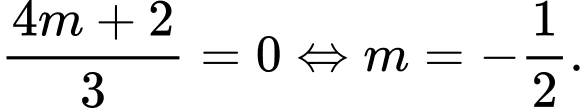 Chọn phương án C.
Chọn phương án C.+) Hàm số đạt cực trị khi và chỉ khi
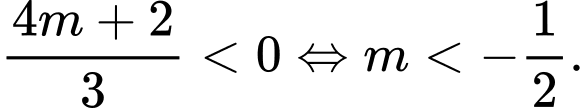 Chọn phương án B. Đáp án: A
Chọn phương án B. Đáp án: A
Câu 12 [581841]: Cho hàm số 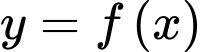 có đạo hàm liên tục trên
có đạo hàm liên tục trên 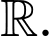 Đồ thị hàm số
Đồ thị hàm số 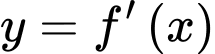 như hình vẽ sau:
như hình vẽ sau:
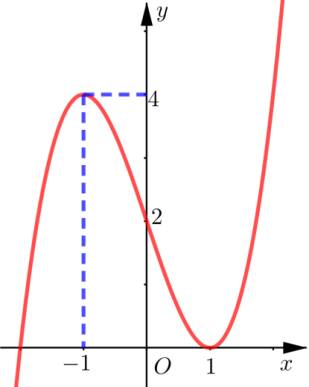
Số điểm cực trị của hàm số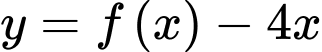 là
là
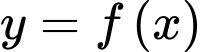 có đạo hàm liên tục trên
có đạo hàm liên tục trên 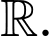 Đồ thị hàm số
Đồ thị hàm số 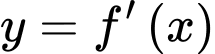 như hình vẽ sau:
như hình vẽ sau:
Số điểm cực trị của hàm số
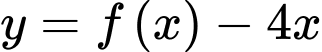 là
là A, 2.
B, 3.
C, 4.
D, 1.
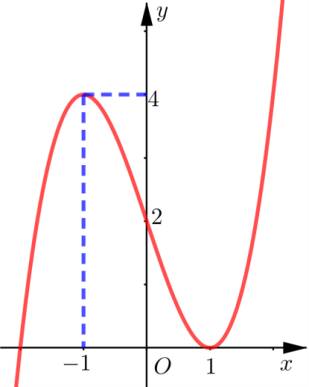
Đặt :
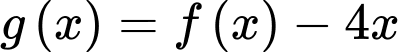
Ta có:
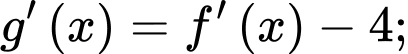
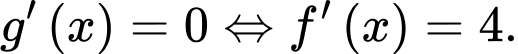
Dựa vào đồ thị, suy ra phương trình
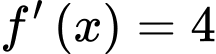 có 2 nghiệm
có 2 nghiệm 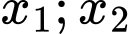 trong đó
trong đó 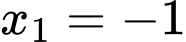 là nghiệm kép và
là nghiệm kép và  là nghiệm đơn.
là nghiệm đơn.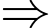 phương trình
phương trình 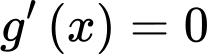 có 2 nghiệm
có 2 nghiệm 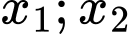 nhưng
nhưng 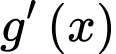 đổi dấu duy nhất 1 lần khi qua nghiệm
đổi dấu duy nhất 1 lần khi qua nghiệm 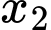 này. Vậy hàm số
này. Vậy hàm số 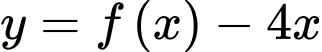 có một điểm cực trị.
có một điểm cực trị.Sai lầm dễ mắc phải:
Ta có:
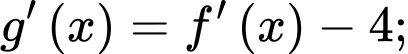

Dựa vào đồ thị, suy ra phương trình
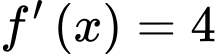 có 2 nghiệm phân biệt
có 2 nghiệm phân biệt 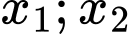 do đó
do đó 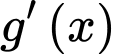 có 2 nghiệm phân biệt suy ra hàm số
có 2 nghiệm phân biệt suy ra hàm số 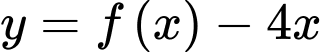 có hai điểm cực trị. Chọn A. Đáp án: D
có hai điểm cực trị. Chọn A. Đáp án: D
Câu 13 [581842]: Tìm 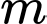 để đồ thị hàm số
để đồ thị hàm số 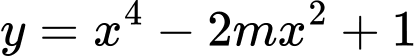 có ba điểm cực trị
có ba điểm cực trị 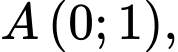
 thỏa mãn
thỏa mãn 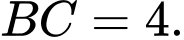
 để đồ thị hàm số
để đồ thị hàm số 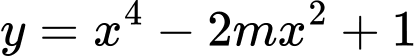 có ba điểm cực trị
có ba điểm cực trị 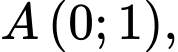
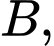
 thỏa mãn
thỏa mãn 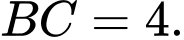
A, 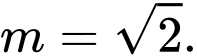
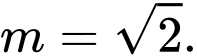
B, 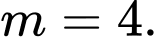
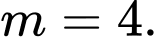
C, 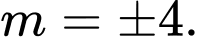
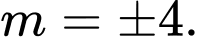
D, 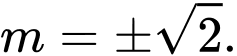
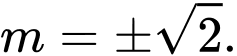
Chọn B
Tập xác định: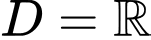 .
.
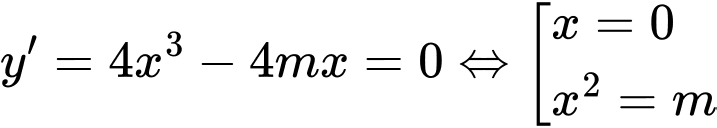
Hàm số đã cho có ba điểm cực trị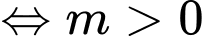 .
.
Tọa độ điểm cực trị của đồ thị hàm số:
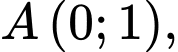
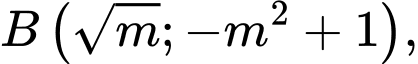
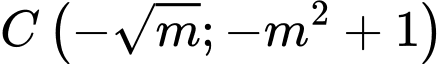
Theo giả thiết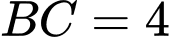
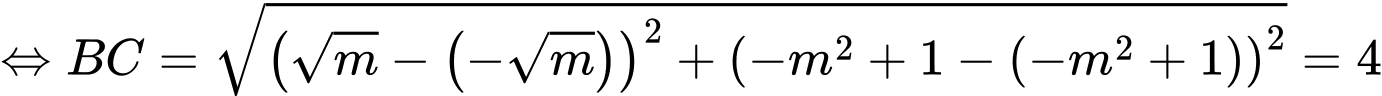
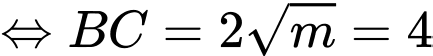
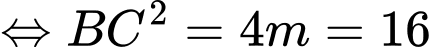
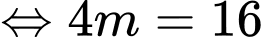
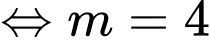 ( thỏa mãn). Đáp án: B
( thỏa mãn). Đáp án: B
Tập xác định:
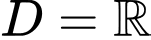 .
.
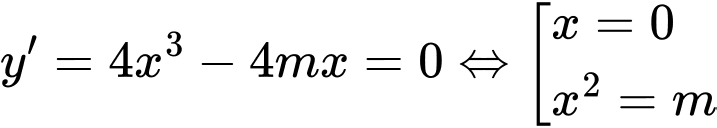
Hàm số đã cho có ba điểm cực trị
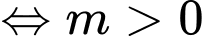 .
.
Tọa độ điểm cực trị của đồ thị hàm số:
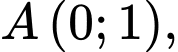
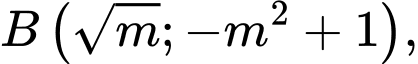
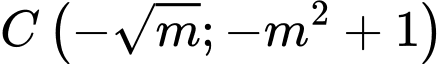
Theo giả thiết
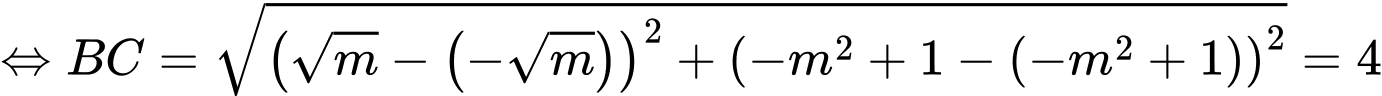
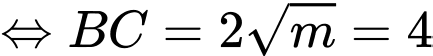
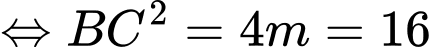
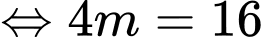
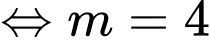 ( thỏa mãn). Đáp án: B
( thỏa mãn). Đáp án: B
Câu 14 [581843]: Tìm tất cả các giá trị thực của tham số 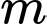 sao cho đồ thị của hàm số
sao cho đồ thị của hàm số 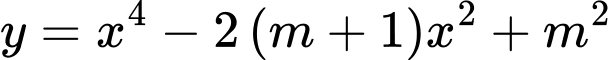 có ba điểm cực trị tạo thành một tam giác vuông cân.
có ba điểm cực trị tạo thành một tam giác vuông cân.
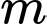 sao cho đồ thị của hàm số
sao cho đồ thị của hàm số 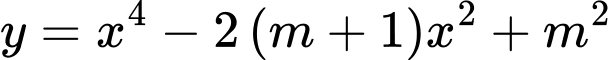 có ba điểm cực trị tạo thành một tam giác vuông cân.
có ba điểm cực trị tạo thành một tam giác vuông cân. A, 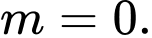
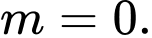
B, 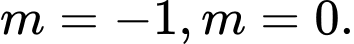
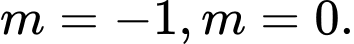
C, 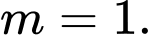
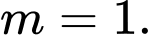
D, 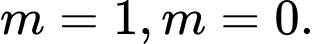
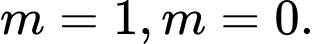
Chọn A
Cách 1: Phương pháp tự luận
Ta có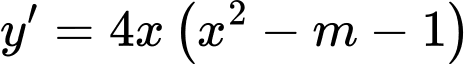
Xét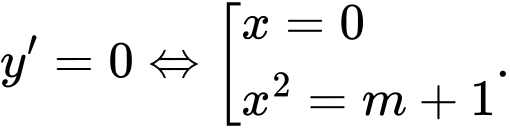
Để đồ thị số có ba điểm cực trị thì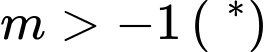
Tọa độ ba điểm cực trị là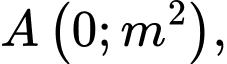
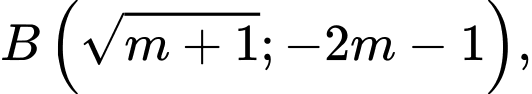
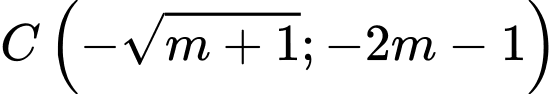
Gọi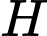 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 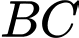 thì
thì 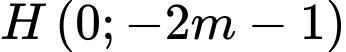
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi
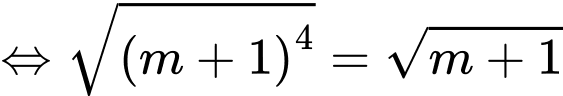
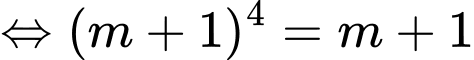
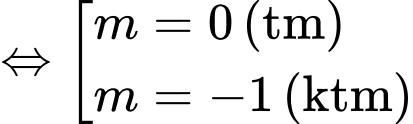 .
.
Chú ý: điều kiện ba điểm cực trị lập thành tam giác vuông cân có thể sử dụng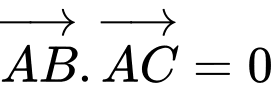 hoặc
hoặc 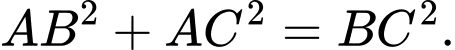
Cách 2: Phương pháp trắc nghiệm
Điều kiện để đồ thị hàm trùng phương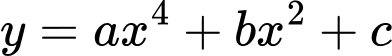 có ba điểm cực trị là
có ba điểm cực trị là 
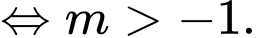
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi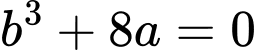
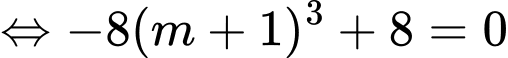
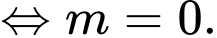 Đáp án: A
Đáp án: A
Cách 1: Phương pháp tự luận
Ta có
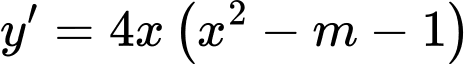
Xét
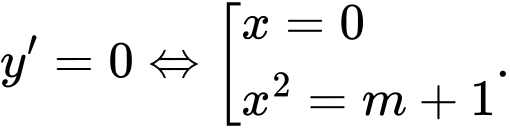
Để đồ thị số có ba điểm cực trị thì
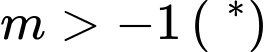
Tọa độ ba điểm cực trị là
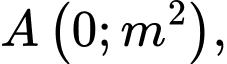
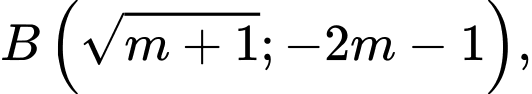
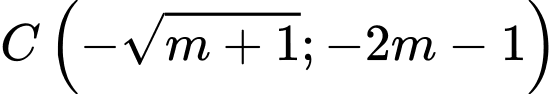
Gọi
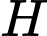 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 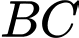 thì
thì 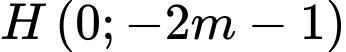
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi

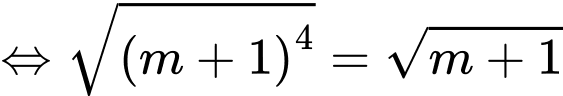
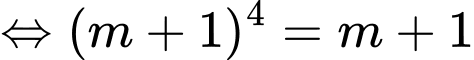
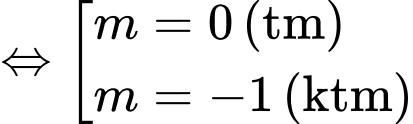 .
.Chú ý: điều kiện ba điểm cực trị lập thành tam giác vuông cân có thể sử dụng
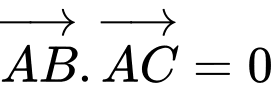 hoặc
hoặc 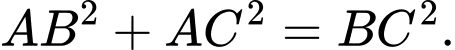
Cách 2: Phương pháp trắc nghiệm
Điều kiện để đồ thị hàm trùng phương
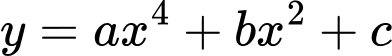 có ba điểm cực trị là
có ba điểm cực trị là 
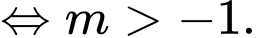
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi
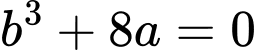
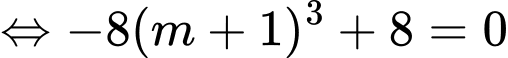
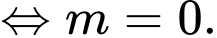 Đáp án: A
Đáp án: A
Câu 15 [581844]: Cho hàm số 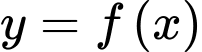 có đúng ba điểm cực trị là
có đúng ba điểm cực trị là 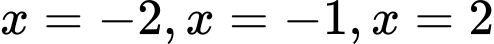 và có đạo hàm liên tục trên
và có đạo hàm liên tục trên 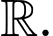 Khi đó hàm số
Khi đó hàm số 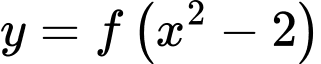 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
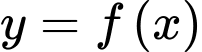 có đúng ba điểm cực trị là
có đúng ba điểm cực trị là 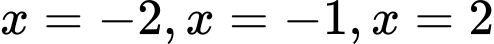 và có đạo hàm liên tục trên
và có đạo hàm liên tục trên 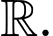 Khi đó hàm số
Khi đó hàm số 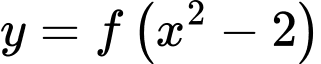 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 5.
B, 8.
C, 6.
D, 4.
Chọn A
Vì hàm số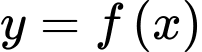 có đúng ba điểm cực trị là
có đúng ba điểm cực trị là 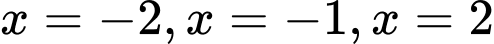 và có đạo hàm liên tục trên
và có đạo hàm liên tục trên 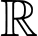 nên
nên 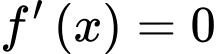 có ba nghiệm là
có ba nghiệm là 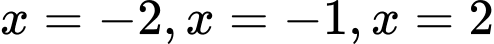 (ba nghiệm bội lẻ).
(ba nghiệm bội lẻ).
Xét hàm số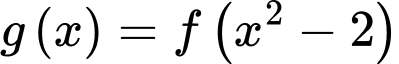 có
có 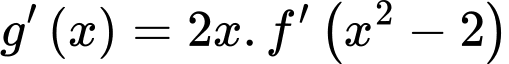 ;
;
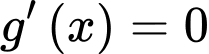
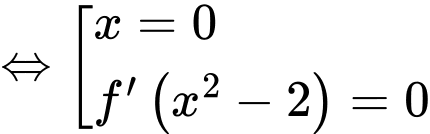
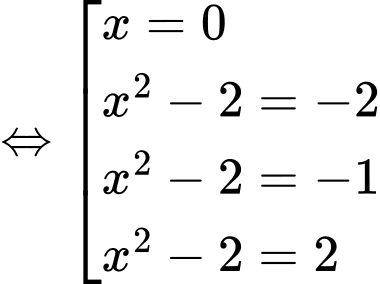
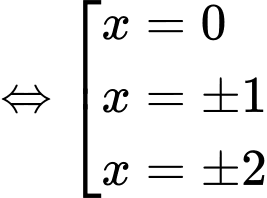
Do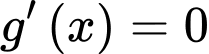 có các nghiệm bội lẻ
có các nghiệm bội lẻ 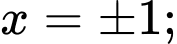
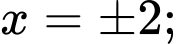
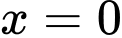 suy ra
suy ra 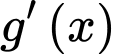 đổi dấu năm lần nên hàm số
đổi dấu năm lần nên hàm số 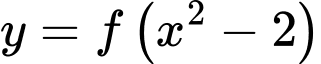 có năm điểm cực trị.
có năm điểm cực trị.
Sai lầm dễ mắc phải:
Tính sai đạo hàm hàm hợp :
Xét hàm số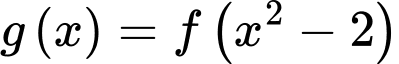 có
có
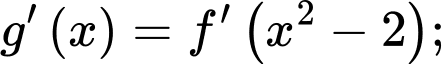
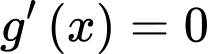
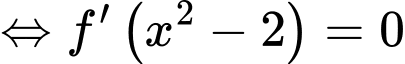
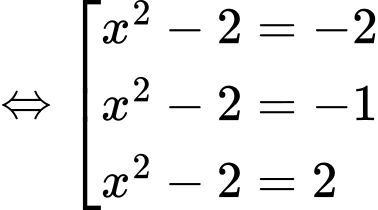
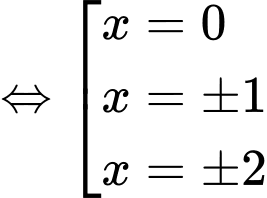
Do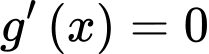 có các nghiệm bội lẻ
có các nghiệm bội lẻ 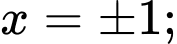
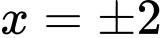 và
và 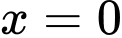 là nghiệm bội chẵn
là nghiệm bội chẵn 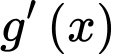 đổi dấu bốn lần nên hàm số
đổi dấu bốn lần nên hàm số 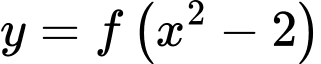 có bốn điểm cực trị. Chọn D. Đáp án: A
có bốn điểm cực trị. Chọn D. Đáp án: A
Vì hàm số
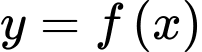 có đúng ba điểm cực trị là
có đúng ba điểm cực trị là 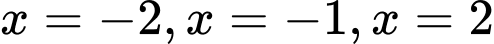 và có đạo hàm liên tục trên
và có đạo hàm liên tục trên  nên
nên 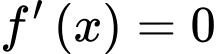 có ba nghiệm là
có ba nghiệm là 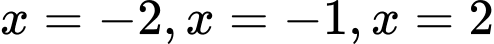 (ba nghiệm bội lẻ).
(ba nghiệm bội lẻ).Xét hàm số
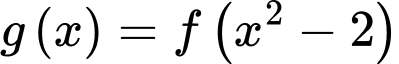 có
có 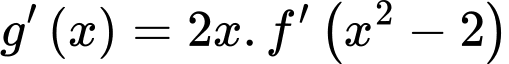 ;
;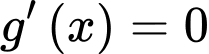
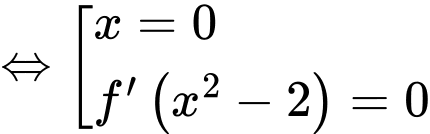
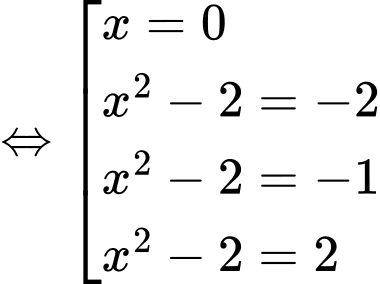
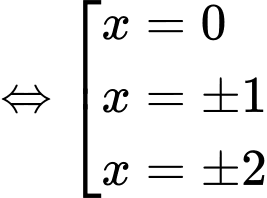
Do
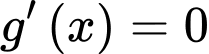 có các nghiệm bội lẻ
có các nghiệm bội lẻ 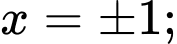
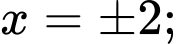
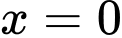 suy ra
suy ra 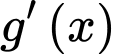 đổi dấu năm lần nên hàm số
đổi dấu năm lần nên hàm số 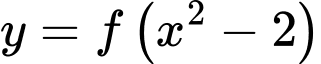 có năm điểm cực trị.
có năm điểm cực trị.Sai lầm dễ mắc phải:
Tính sai đạo hàm hàm hợp :
Xét hàm số
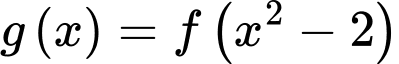 có
có 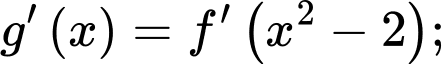
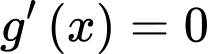
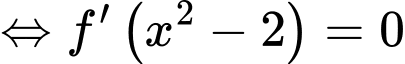
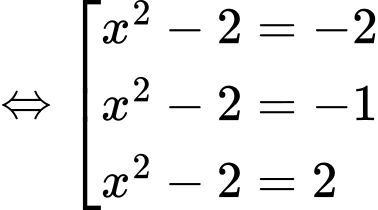
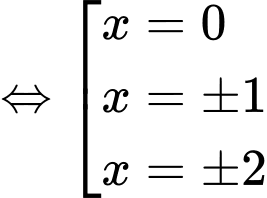
Do
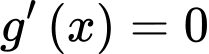 có các nghiệm bội lẻ
có các nghiệm bội lẻ 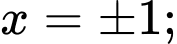
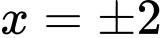 và
và 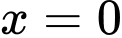 là nghiệm bội chẵn
là nghiệm bội chẵn 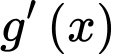 đổi dấu bốn lần nên hàm số
đổi dấu bốn lần nên hàm số 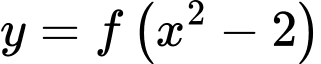 có bốn điểm cực trị. Chọn D. Đáp án: A
có bốn điểm cực trị. Chọn D. Đáp án: A Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai)
Câu 16 [581845]: Cho hàm số 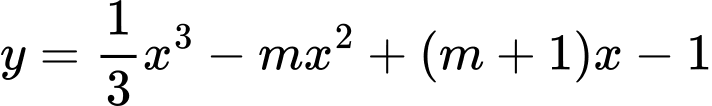 (
(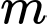 là tham số). Khi đó:
là tham số). Khi đó:
a) Với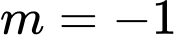 thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 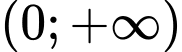
b) Với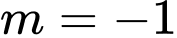 thì đồ thị hàm số có một điểm cực tiểu là
thì đồ thị hàm số có một điểm cực tiểu là 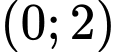
c) Ta có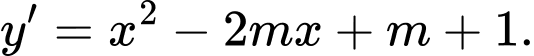
d) Để hàm số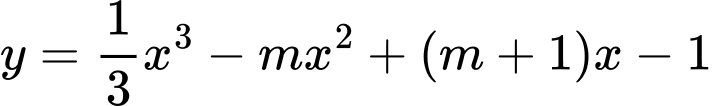 đạt cực đại tại
đạt cực đại tại 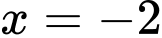 thì
thì 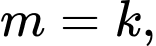 khi đó phương trình
khi đó phương trình 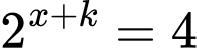 có nghiệm là
có nghiệm là 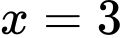
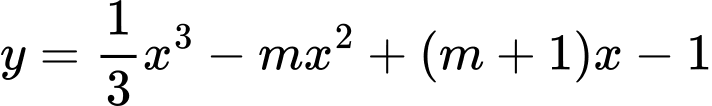 (
(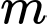 là tham số). Khi đó:
là tham số). Khi đó:a) Với
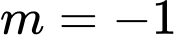 thì hàm số đồng biến trên khoảng
thì hàm số đồng biến trên khoảng 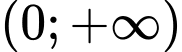
b) Với
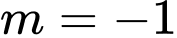 thì đồ thị hàm số có một điểm cực tiểu là
thì đồ thị hàm số có một điểm cực tiểu là 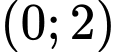
c) Ta có
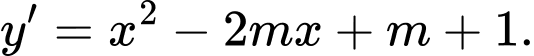
d) Để hàm số
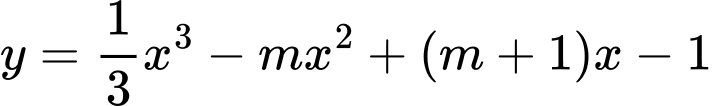 đạt cực đại tại
đạt cực đại tại 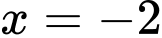 thì
thì 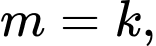 khi đó phương trình
khi đó phương trình 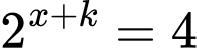 có nghiệm là
có nghiệm là 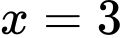
a) Đ
b) S
c) Đ
d) Đ
Ta có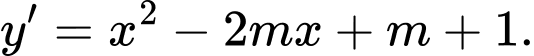
Giả sử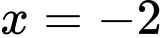 là điểm cực đại của hàm số đã cho, khi đó
là điểm cực đại của hàm số đã cho, khi đó 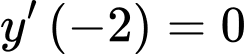
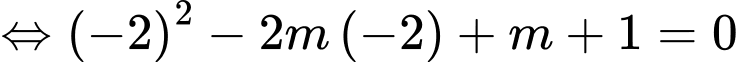

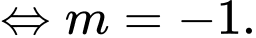
Với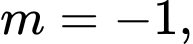 ta có
ta có 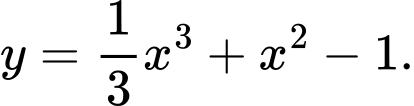
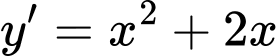 ;
;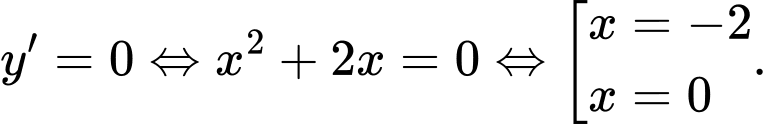
Ta có bảng biến thiên:
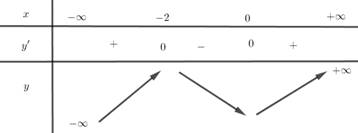
Dựa vào bảng biến thiên, ta kết luận là giá trị cần tìm.
là giá trị cần tìm.
d) Khi đó
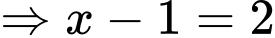
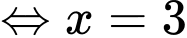
b) S
c) Đ
d) Đ
Ta có
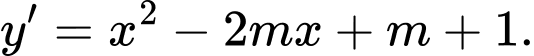
Giả sử
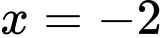 là điểm cực đại của hàm số đã cho, khi đó
là điểm cực đại của hàm số đã cho, khi đó 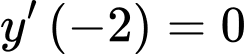
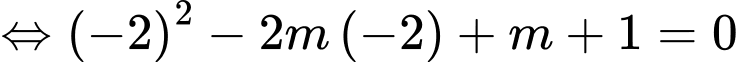

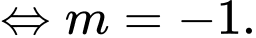
Với
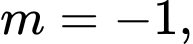 ta có
ta có 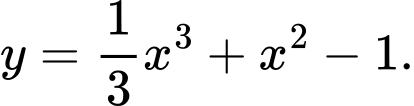
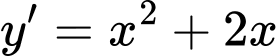 ;
;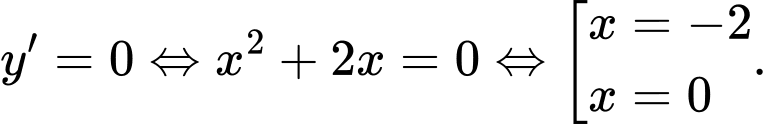
Ta có bảng biến thiên:

Dựa vào bảng biến thiên, ta kết luận
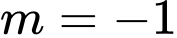 là giá trị cần tìm.
là giá trị cần tìm.d) Khi đó
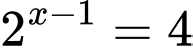
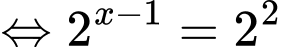
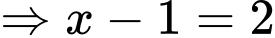
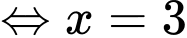
Câu 17 [581846]: Cho hàm số 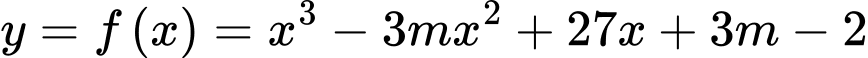 (
(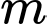 là tham số). Khi đó:
là tham số). Khi đó:
a) Khi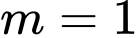 thì
thì 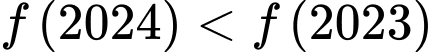
b) Khi thì hàm số có 2 điểm cực trị
thì hàm số có 2 điểm cực trị
c) Khi thì hàm số có 2 điểm cực trị
thì hàm số có 2 điểm cực trị
d) Gọi S là tập các giá trị dương của tham số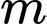 sao cho hàm số
sao cho hàm số 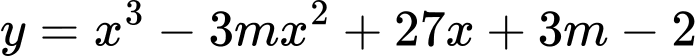 đạt cực trị tại
đạt cực trị tại 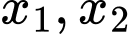 thỏa mãn
thỏa mãn 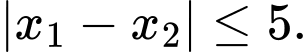 Biết
Biết  Khi đó
Khi đó 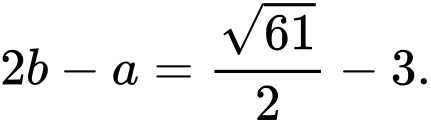
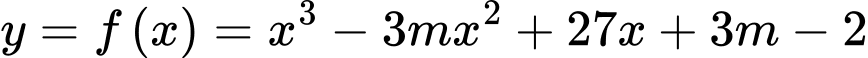 (
(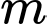 là tham số). Khi đó:
là tham số). Khi đó:a) Khi
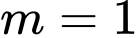 thì
thì 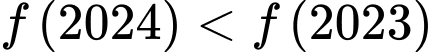
b) Khi
 thì hàm số có 2 điểm cực trị
thì hàm số có 2 điểm cực trịc) Khi
 thì hàm số có 2 điểm cực trị
thì hàm số có 2 điểm cực trịd) Gọi S là tập các giá trị dương của tham số
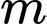 sao cho hàm số
sao cho hàm số 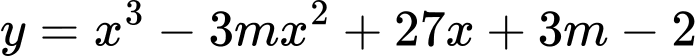 đạt cực trị tại
đạt cực trị tại 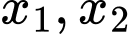 thỏa mãn
thỏa mãn 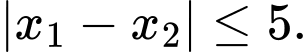 Biết
Biết  Khi đó
Khi đó 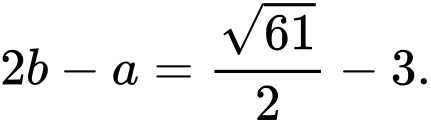
a) S
b) Đ
c) Đ
d) S
+) Ta có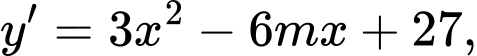
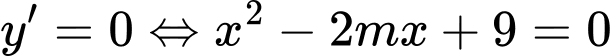

a) Khi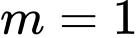 thì nên hàm số đồng biến trên khoảng
thì nên hàm số đồng biến trên khoảng 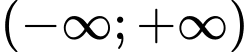 suy ra
suy ra 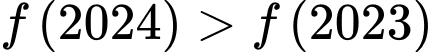
+) Theo giả thiết hàm số đạt cực trị tại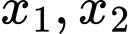
 phương trình
phương trình  có 2 nghiệm phân biệt
có 2 nghiệm phân biệt
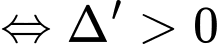

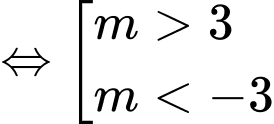 (*)
(*)
+) Với điều kiện (*) thì phương trình có
có 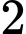 nghiệm
nghiệm 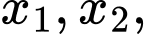 theo Vi-ét ta có:
theo Vi-ét ta có: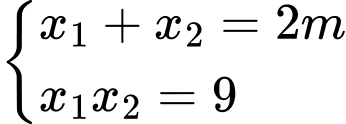
+) Ta lại có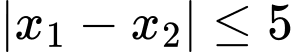
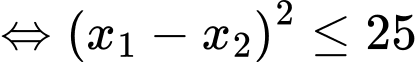
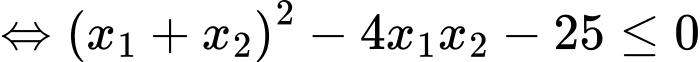

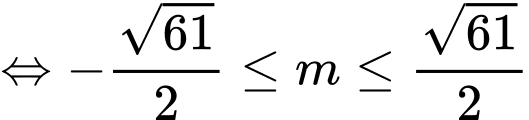 (**)
(**)
+) Kết hợp (*), (**) và điều kiện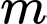 dương ta được:
dương ta được: 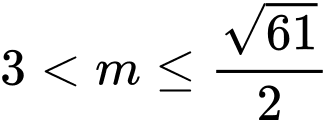
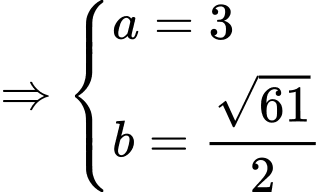
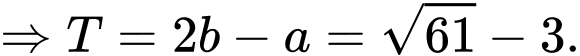
b) Đ
c) Đ
d) S
+) Ta có
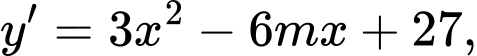
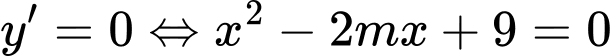

a) Khi
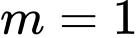 thì nên hàm số đồng biến trên khoảng
thì nên hàm số đồng biến trên khoảng 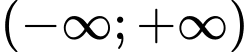 suy ra
suy ra 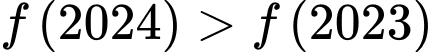
+) Theo giả thiết hàm số đạt cực trị tại
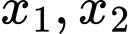
 phương trình
phương trình  có 2 nghiệm phân biệt
có 2 nghiệm phân biệt 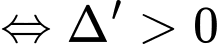

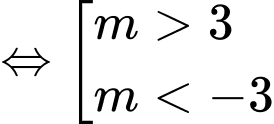 (*)
(*)+) Với điều kiện (*) thì phương trình
 có
có 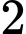 nghiệm
nghiệm 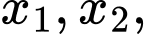 theo Vi-ét ta có:
theo Vi-ét ta có: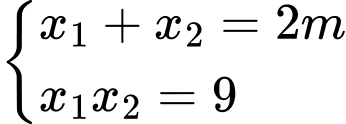
+) Ta lại có
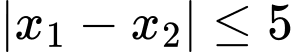
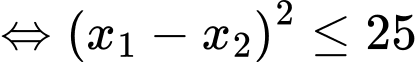
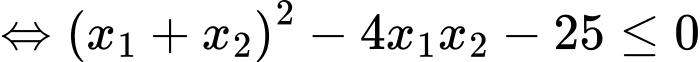

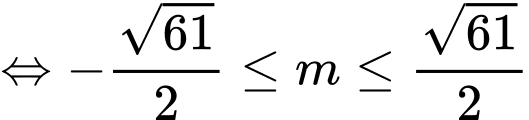 (**)
(**)+) Kết hợp (*), (**) và điều kiện
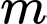 dương ta được:
dương ta được: 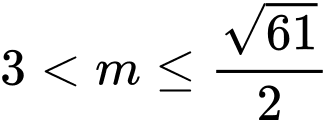
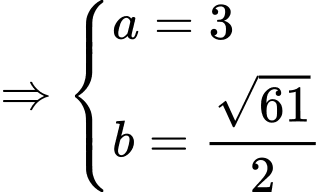
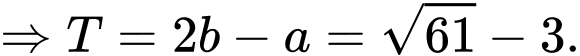
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [581847]: Cho hàm số 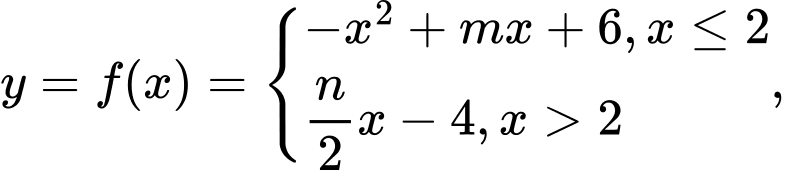
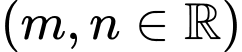 liên tục trên
liên tục trên 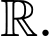 Hỏi có tất cá bao nhiêu giá trị nguyên của tham số
Hỏi có tất cá bao nhiêu giá trị nguyên của tham số 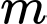 để hàm số
để hàm số 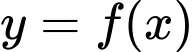 có đúng hai điểm cực trị?
có đúng hai điểm cực trị?
Trả lời: …..…….….
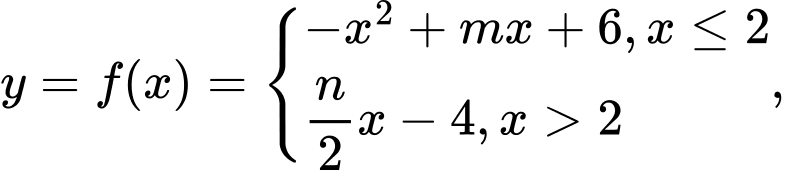
 liên tục trên
liên tục trên  Hỏi có tất cá bao nhiêu giá trị nguyên của tham số
Hỏi có tất cá bao nhiêu giá trị nguyên của tham số 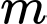 để hàm số
để hàm số 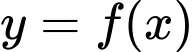 có đúng hai điểm cực trị?
có đúng hai điểm cực trị?Trả lời: …..…….….
Trả lời: …..6…….
Hàm số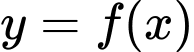 liên tục trên khi
liên tục trên khi 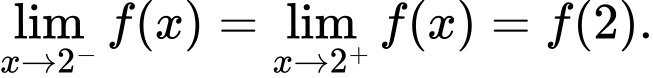
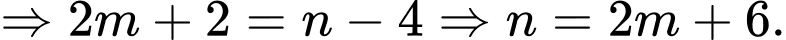
Ta có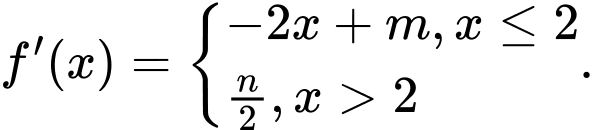
Rõ ràng, trên khoảng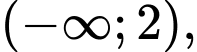 phương trình
phương trình 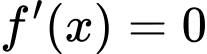 chỉ có tối đa 1 nghiệm (bội lẻ) và trên khoảng
chỉ có tối đa 1 nghiệm (bội lẻ) và trên khoảng 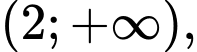 phương trình
phương trình 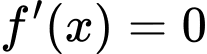 vô nghiệm.
vô nghiệm.
 hàm số
hàm số 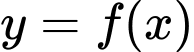 có đúng hai điểm cực trị khi và chỉ khi:
có đúng hai điểm cực trị khi và chỉ khi:
Phương trình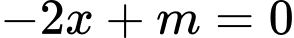 có một nghiệm
có một nghiệm  và đạo hàm của hàm số đổi dấu khi đi qua điểm
và đạo hàm của hàm số đổi dấu khi đi qua điểm 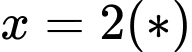
Phương trình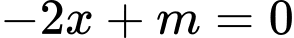 có nghiệm
có nghiệm 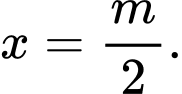
Mà
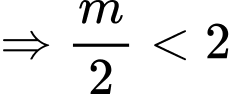
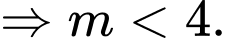
Khi đó bảng xét dấu của trên
trên  là:
là:
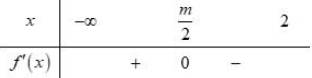
Như vậy, để thỏa mãn điều kiện suy ra
suy ra 
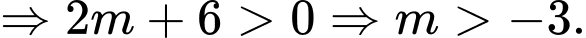
Kết hợp điều kiện, suy ra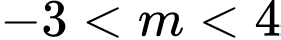
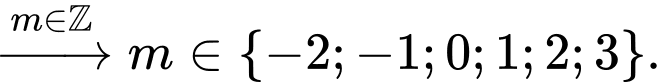
Như vậy có 6 giá trị nguyên của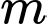 thỏa mãn bài toán.
thỏa mãn bài toán.
Hàm số
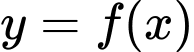 liên tục trên khi
liên tục trên khi 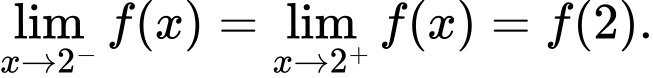
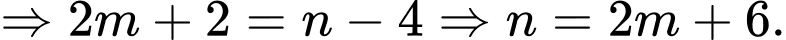
Ta có
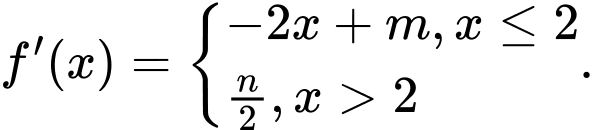
Rõ ràng, trên khoảng
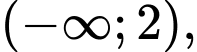 phương trình
phương trình 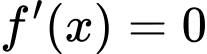 chỉ có tối đa 1 nghiệm (bội lẻ) và trên khoảng
chỉ có tối đa 1 nghiệm (bội lẻ) và trên khoảng 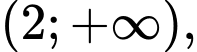 phương trình
phương trình 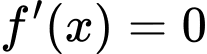 vô nghiệm.
vô nghiệm. hàm số
hàm số 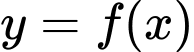 có đúng hai điểm cực trị khi và chỉ khi:
có đúng hai điểm cực trị khi và chỉ khi:Phương trình
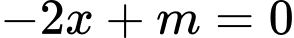 có một nghiệm
có một nghiệm  và đạo hàm của hàm số đổi dấu khi đi qua điểm
và đạo hàm của hàm số đổi dấu khi đi qua điểm 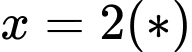
Phương trình
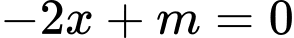 có nghiệm
có nghiệm 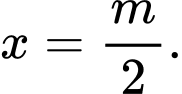
Mà

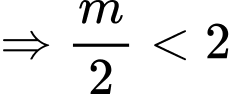
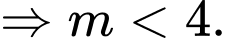
Khi đó bảng xét dấu của
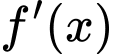 trên
trên  là:
là: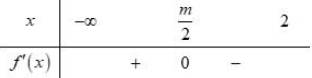
Như vậy, để thỏa mãn điều kiện
 suy ra
suy ra 
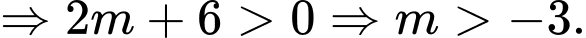
Kết hợp điều kiện, suy ra
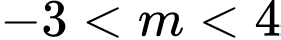
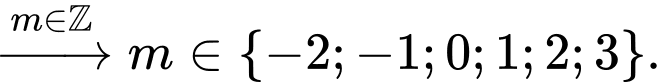
Như vậy có 6 giá trị nguyên của
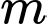 thỏa mãn bài toán.
thỏa mãn bài toán.
Câu 19 [581848]: Có bao nhiêu giá trị nguyên của tham số 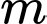 để đồ thị hàm số
để đồ thị hàm số 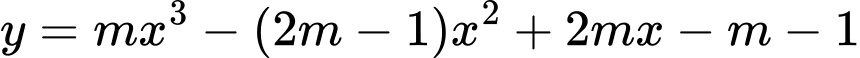 có hai điểm cực trị nằm về hai phía của trục hoành?
có hai điểm cực trị nằm về hai phía của trục hoành?
Trả lời: …………….
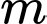 để đồ thị hàm số
để đồ thị hàm số 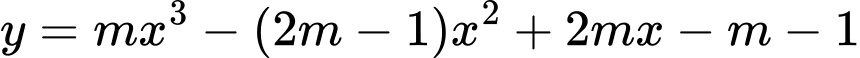 có hai điểm cực trị nằm về hai phía của trục hoành?
có hai điểm cực trị nằm về hai phía của trục hoành?Trả lời: …………….
Trả lời: …1…….
Đồ thị hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành khi và chỉ khi phương trình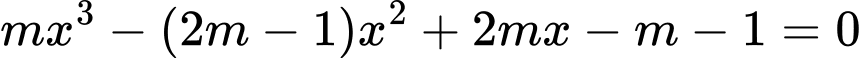 (1) có 3 nghiệm phân biệt.
(1) có 3 nghiệm phân biệt.
Ta có (1)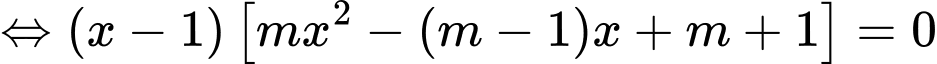
Phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi phương trình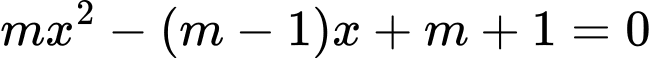 có 2 nghiệm phân biệt khác 1
có 2 nghiệm phân biệt khác 1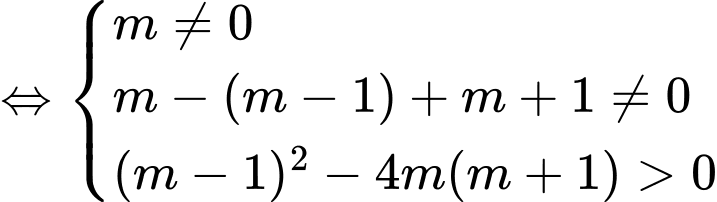
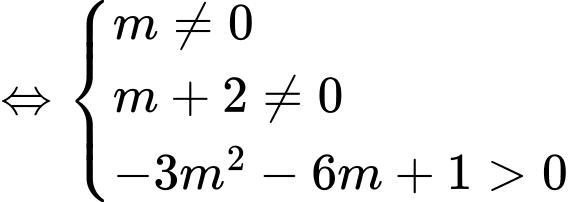
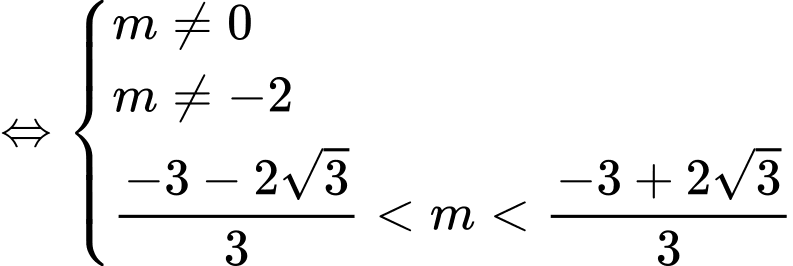
Do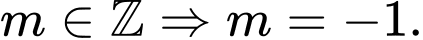
Đồ thị hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành khi và chỉ khi phương trình
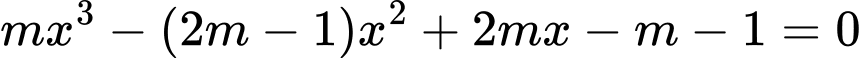 (1) có 3 nghiệm phân biệt.
(1) có 3 nghiệm phân biệt.Ta có (1)
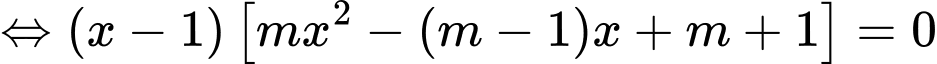
Phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi phương trình
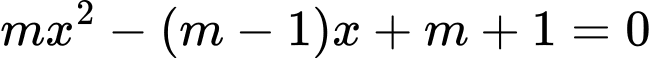 có 2 nghiệm phân biệt khác 1
có 2 nghiệm phân biệt khác 1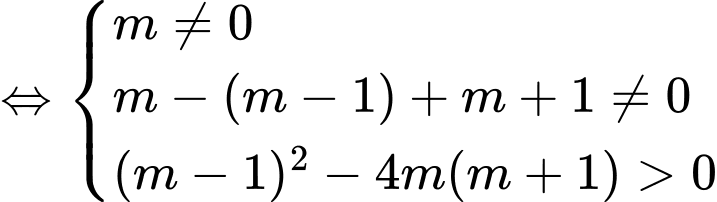
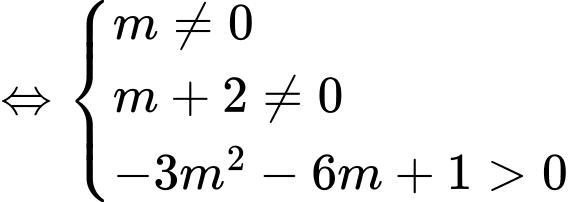
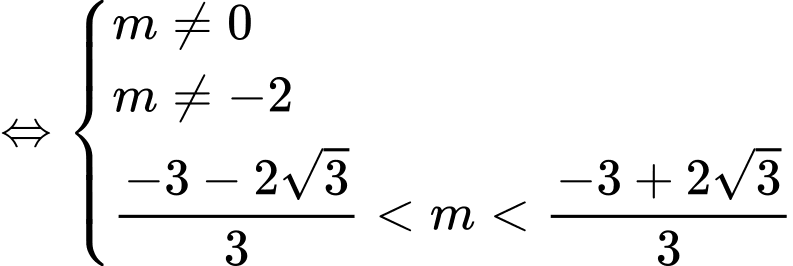
Do
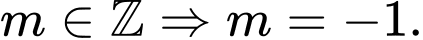
Câu 20 [581849]: Cho hàm số 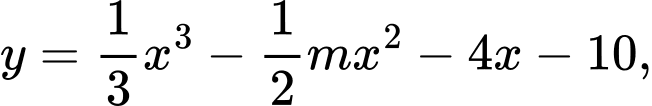 với
với 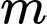 là tham số; gọi
là tham số; gọi 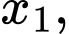
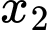 là các điểm cực trị của hàm số đã cho. Tính giá trị lớn nhất của biểu thức
là các điểm cực trị của hàm số đã cho. Tính giá trị lớn nhất của biểu thức 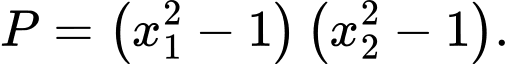
Trả lời: …………….
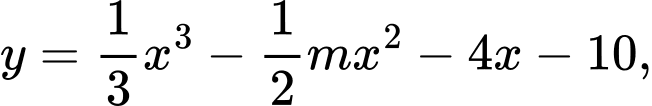 với
với 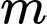 là tham số; gọi
là tham số; gọi 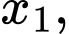
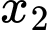 là các điểm cực trị của hàm số đã cho. Tính giá trị lớn nhất của biểu thức
là các điểm cực trị của hàm số đã cho. Tính giá trị lớn nhất của biểu thức 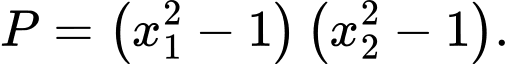
Trả lời: …………….
Trả lời: ……9…….
Tập xác định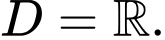
Đạo hàm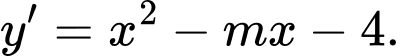
Khi đó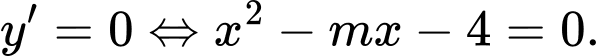
Ta có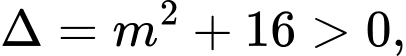
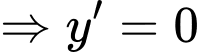 luôn có hai nghiệm phân biệt hay hàm số luôn có hai điểm cực trị
luôn có hai nghiệm phân biệt hay hàm số luôn có hai điểm cực trị 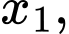
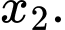
Do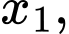
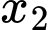 là hai nghiệm phân biệt của
là hai nghiệm phân biệt của 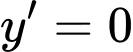 nên theo định lý Viet ta có
nên theo định lý Viet ta có 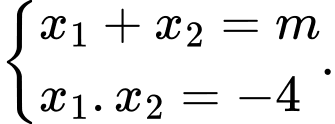
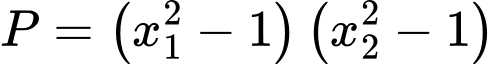
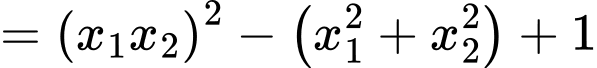
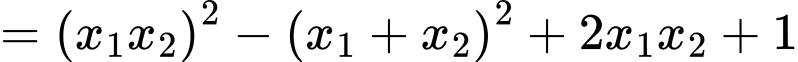
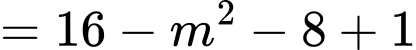
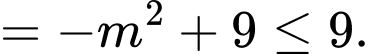
Do đó giá trị lớn nhất của biểu thức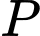 bằng
bằng 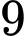
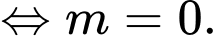
Tập xác định
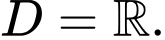
Đạo hàm
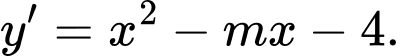
Khi đó
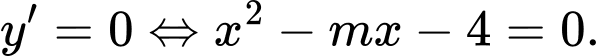
Ta có
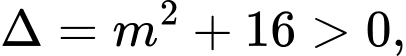
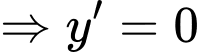 luôn có hai nghiệm phân biệt hay hàm số luôn có hai điểm cực trị
luôn có hai nghiệm phân biệt hay hàm số luôn có hai điểm cực trị 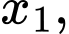
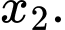
Do
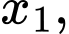
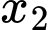 là hai nghiệm phân biệt của
là hai nghiệm phân biệt của 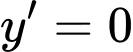 nên theo định lý Viet ta có
nên theo định lý Viet ta có 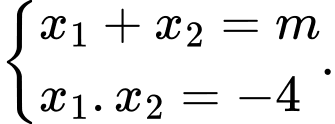
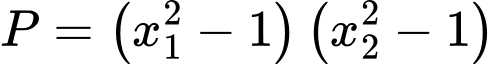
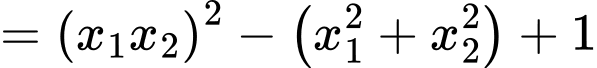
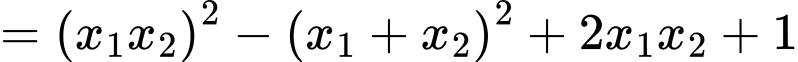
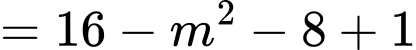
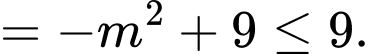
Do đó giá trị lớn nhất của biểu thức
 bằng
bằng 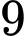
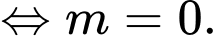
Dạng câu hỏi: Câu hỏi kéo thả
Câu 21 [581850]: Cho hàm số 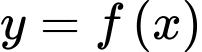 liên tục trên
liên tục trên 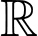 và đồ thị hàm số
và đồ thị hàm số 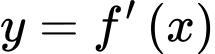 cho bởi hình vẽ bên. Đặt
cho bởi hình vẽ bên. Đặt 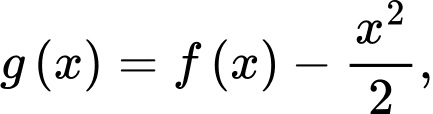

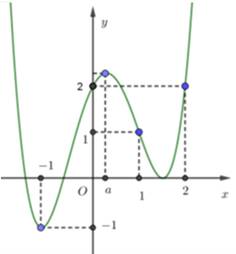
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Hàm số đạt cực đại tại
đạt cực đại tại  bằng _______.
bằng _______.
Hàm số đạt cực tiểu tại
đạt cực tiểu tại 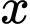 bằng _______.
bằng _______.
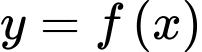 liên tục trên
liên tục trên 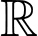 và đồ thị hàm số
và đồ thị hàm số 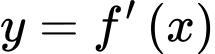 cho bởi hình vẽ bên. Đặt
cho bởi hình vẽ bên. Đặt 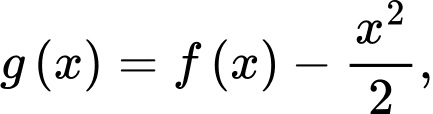


Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Hàm số
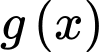 đạt cực đại tại
đạt cực đại tại 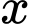 bằng _______.
bằng _______.Hàm số
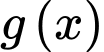 đạt cực tiểu tại
đạt cực tiểu tại  bằng _______.
bằng _______.
Đáp án
Hàm số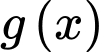 đạt cực đại tại
đạt cực đại tại  bằng 1.
bằng 1.
Hàm số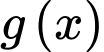 đạt cực tiểu tại
đạt cực tiểu tại 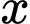 bằng 2.
bằng 2.
Giải thích
Ta có: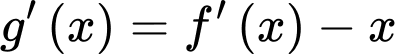
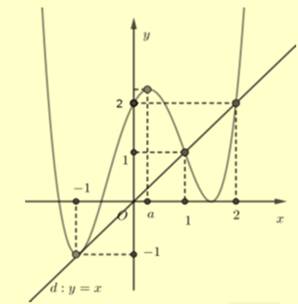
Từ đồ thị hàm số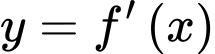 và đồ thị hàm số
và đồ thị hàm số 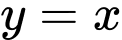 ta thấy:
ta thấy:
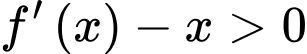 với
với 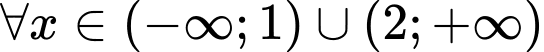 và
và 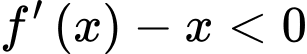 với
với 
Ta có bảng biến thiên của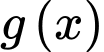
Vậy hàm số đạt cực đại tại
đạt cực đại tại  và đạt cực tiểu tại
và đạt cực tiểu tại 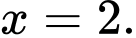
Hàm số
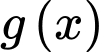 đạt cực đại tại
đạt cực đại tại 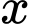 bằng 1.
bằng 1.Hàm số
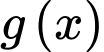 đạt cực tiểu tại
đạt cực tiểu tại 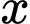 bằng 2.
bằng 2.Giải thích
Ta có:
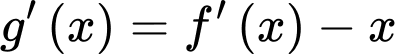

Từ đồ thị hàm số
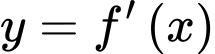 và đồ thị hàm số
và đồ thị hàm số 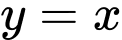 ta thấy:
ta thấy: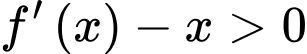 với
với 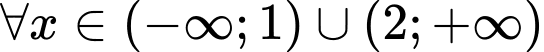 và
và 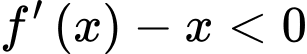 với
với 
Ta có bảng biến thiên của
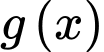

Vậy hàm số
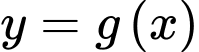 đạt cực đại tại
đạt cực đại tại 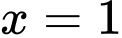 và đạt cực tiểu tại
và đạt cực tiểu tại