DẠNG 1: NGUYÊN HÀM CƠ BẢN
Câu 1 [580230]: Tìm nguyên hàm 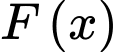 của hàm số
của hàm số 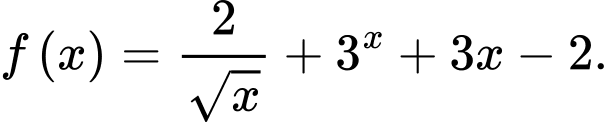
Trả lời: ………………..
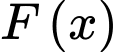 của hàm số
của hàm số 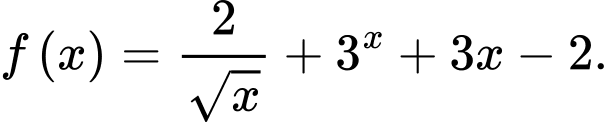
Trả lời: ………………..
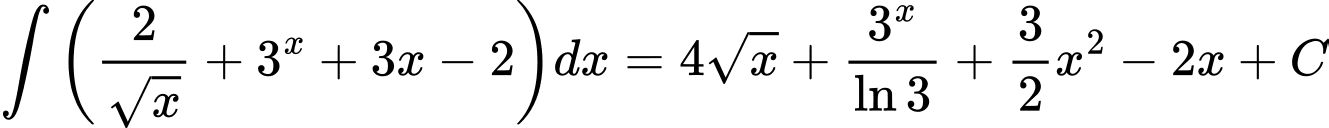
Câu 2 [580231]: Cho hàm số 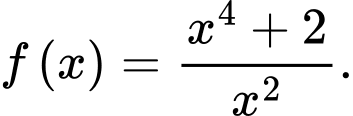 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
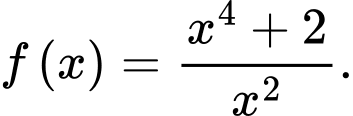 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng? A, 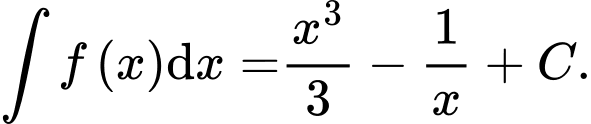
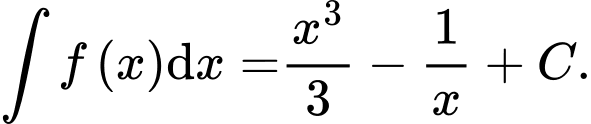
B, 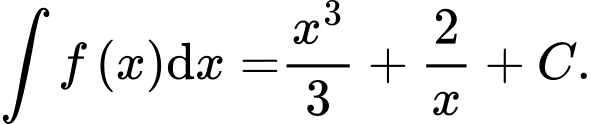
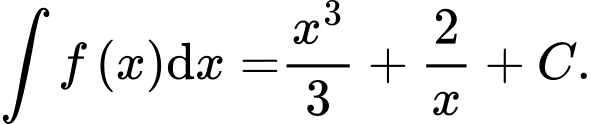
C, 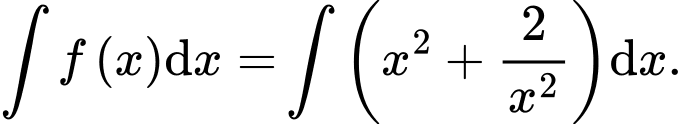
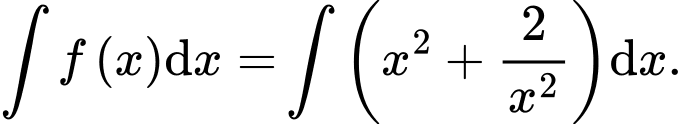
D, 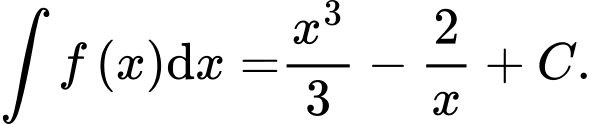
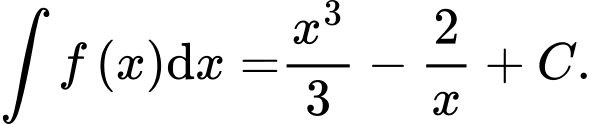
Ta có: 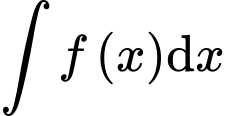
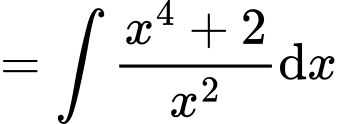
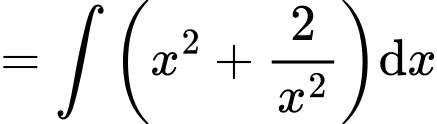
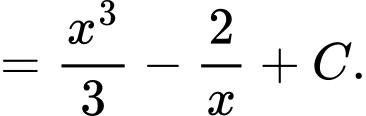
Chọn D Đáp án: D
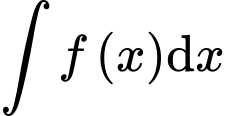
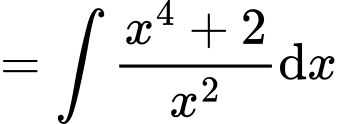
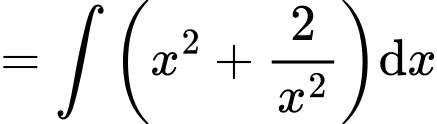
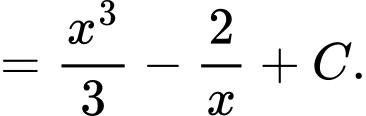
Chọn D Đáp án: D
DẠNG 2: NGUYÊN HÀM LƯỢNG GIÁC
Câu 3 [580232]: Tìm nguyên hàm 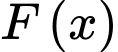 của hàm số
của hàm số 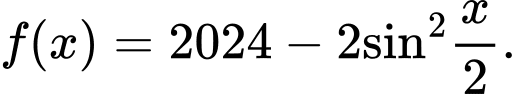
Trả lời: ………………..
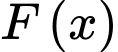 của hàm số
của hàm số 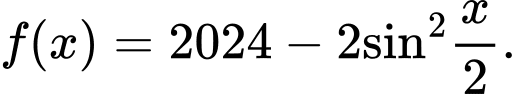
Trả lời: ………………..
Đáp án: 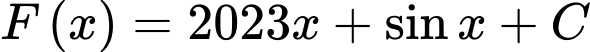
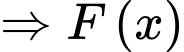
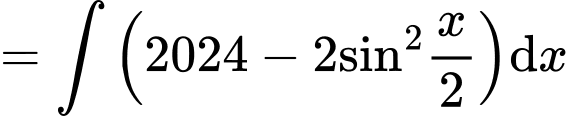
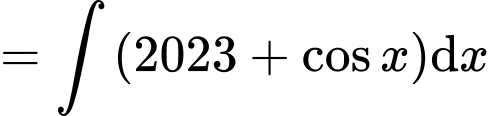

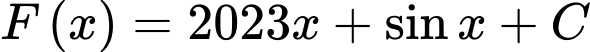
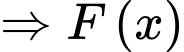
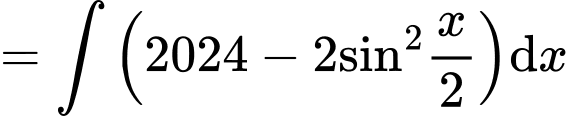
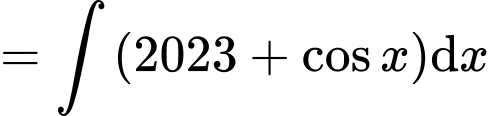

Câu 4 [580233]: Họ nguyên hàm của hàm số 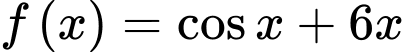 là
là
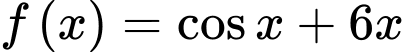 là
là A, 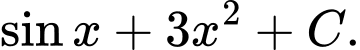
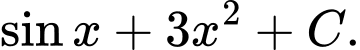
B, 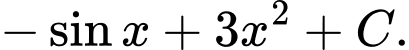
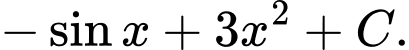
C, 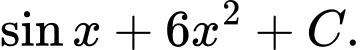
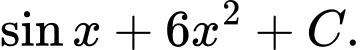
D, 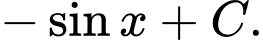
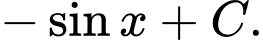
Chọn A.
Ta có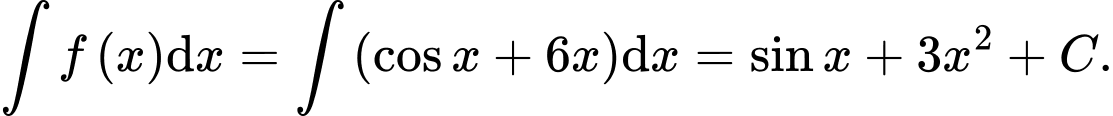 Đáp án: A
Đáp án: A
Ta có
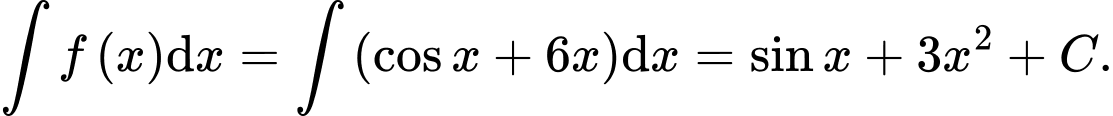 Đáp án: A
Đáp án: A DẠNG 3: NGUYÊN HÀM HÀM MŨ
Câu 5 [580234]: Nguyên hàm của hàm số 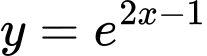 là
là
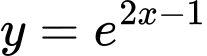 là
là A, 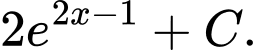
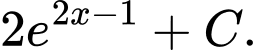
B, 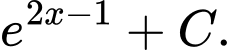
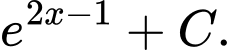
C, 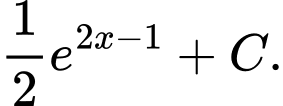
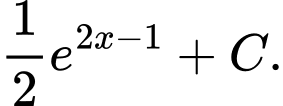
D, 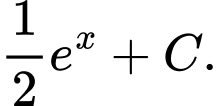
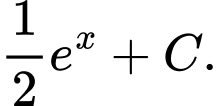
Chọn C.
Cách 1: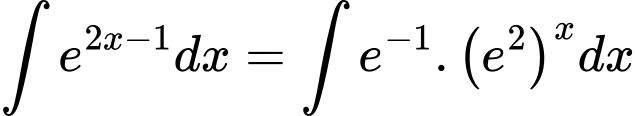
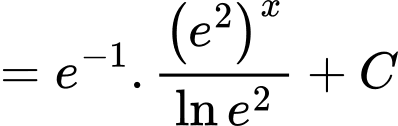
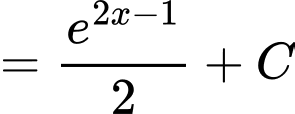
Cách 2: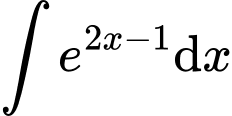
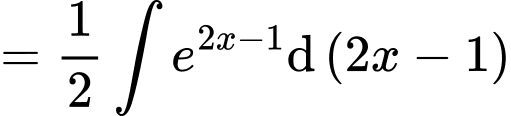
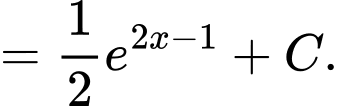 Đáp án: C
Đáp án: C
Cách 1:
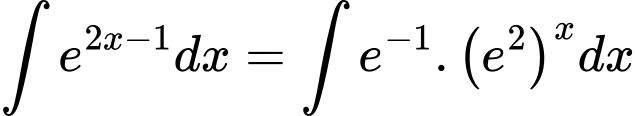
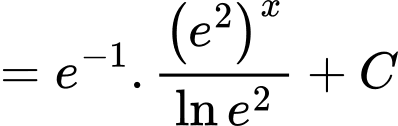
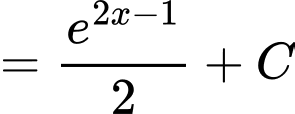
Cách 2:
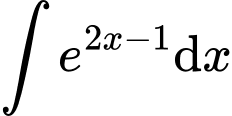
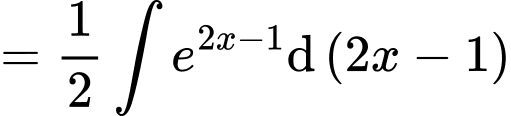
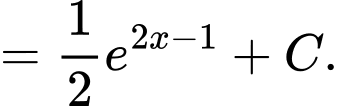 Đáp án: C
Đáp án: C
Câu 6 [580235]: Tìm 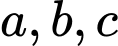 để
để 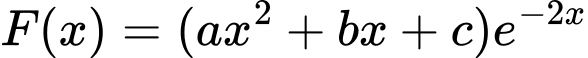 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 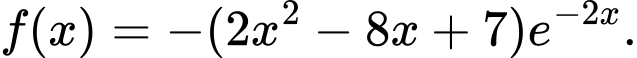
Trả lời: ………………..
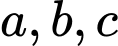 để
để 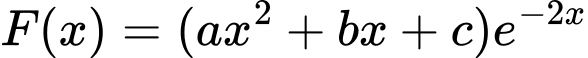 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 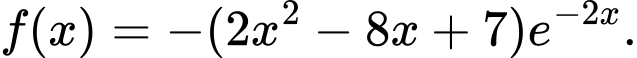
Trả lời: ………………..
Đáp án 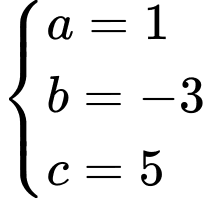
Vì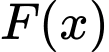 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 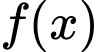 nên
nên 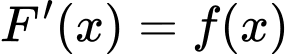
Ta có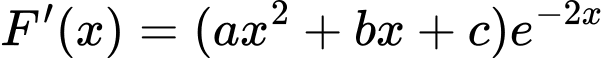
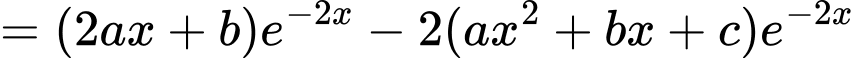
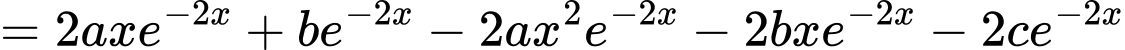
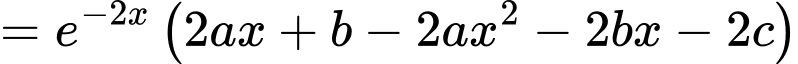
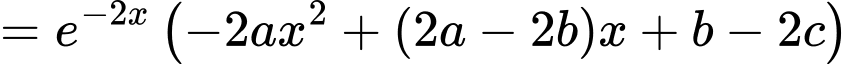
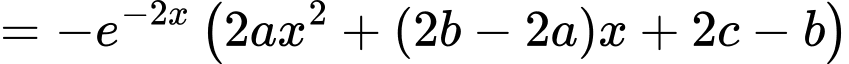
Do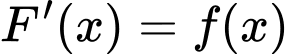 nên
nên 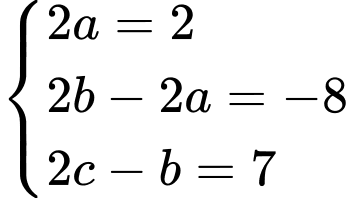
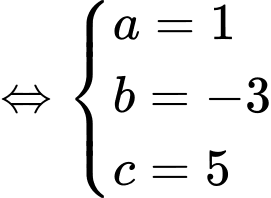
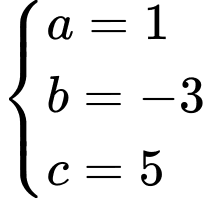
Vì
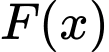 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 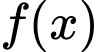 nên
nên 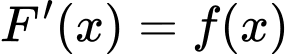
Ta có
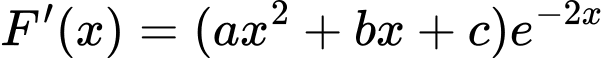
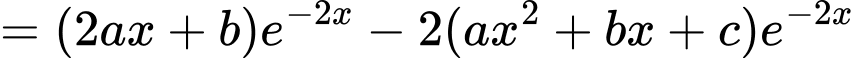
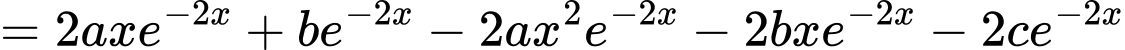
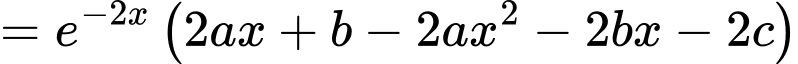
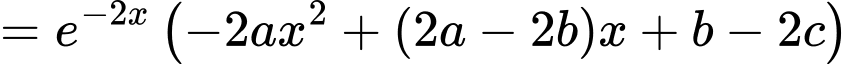
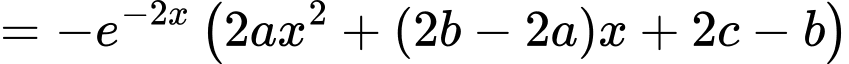
Do
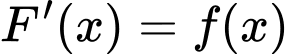 nên
nên 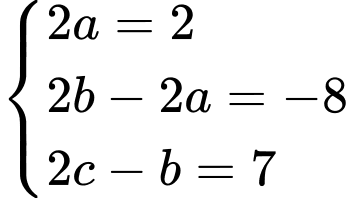
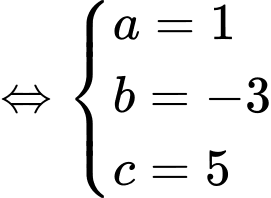
DẠNG 4: NGUYÊN HÀM CÓ ĐIỀU KIỆN
Câu 7 [580236]: Cho hàm số 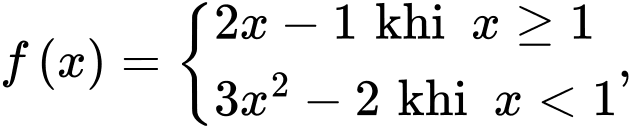 giả sử
giả sử 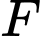 là nguyên hàm của
là nguyên hàm của 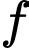 trên
trên 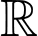 thỏa mãn
thỏa mãn 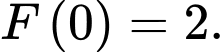 Giá trị của
Giá trị của  bằng
bằng
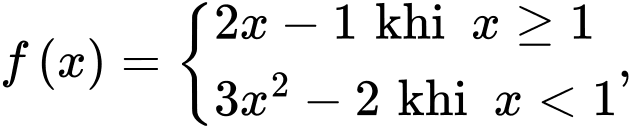 giả sử
giả sử 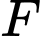 là nguyên hàm của
là nguyên hàm của 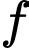 trên
trên 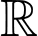 thỏa mãn
thỏa mãn 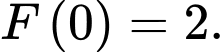 Giá trị của
Giá trị của  bằng
bằng A, 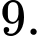
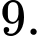
B, 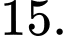
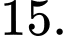
C, 

D, 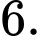
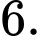
Chọn A.
Ta có:
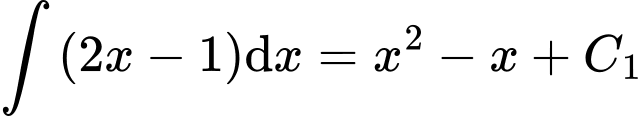 ;
;
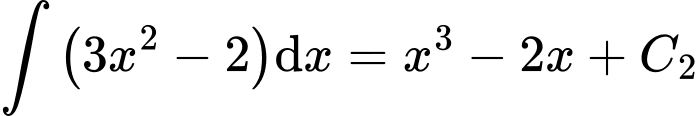
Suy ra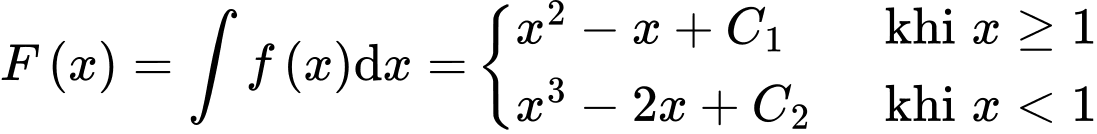
Mà ta có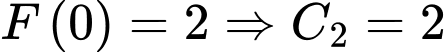
Mặt khác hàm số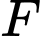 là nguyên hàm của
là nguyên hàm của 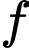 trên nên
trên nên 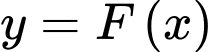 liên tục tại
liên tục tại 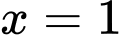
Suy ra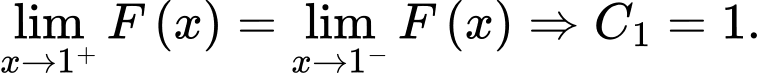
Khi đó ta có: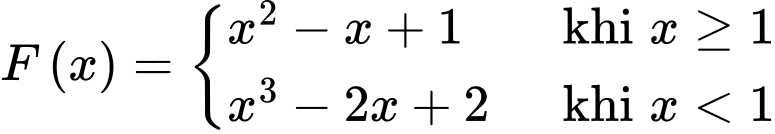 suy ra
suy ra 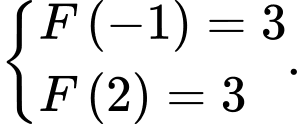
Vậy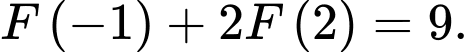 Đáp án: A
Đáp án: A
Ta có:
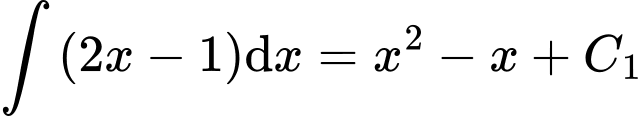 ;
; 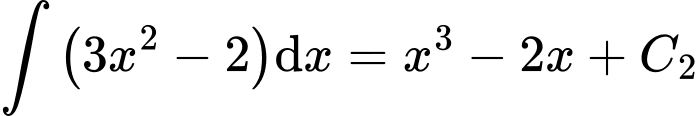
Suy ra
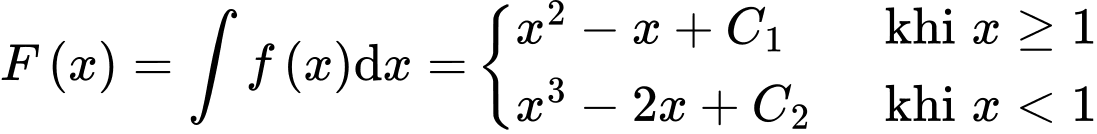
Mà ta có
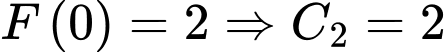
Mặt khác hàm số
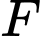 là nguyên hàm của
là nguyên hàm của 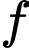 trên nên
trên nên 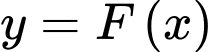 liên tục tại
liên tục tại 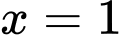
Suy ra
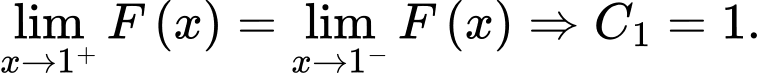
Khi đó ta có:
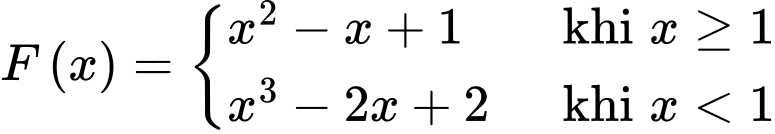 suy ra
suy ra 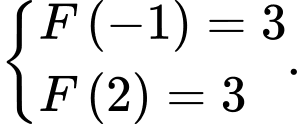
Vậy
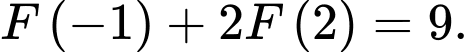 Đáp án: A
Đáp án: A DẠNG 5: NGUYÊN HÀM HÀM ẨN
Câu 8 [580237]: Cho hàm số 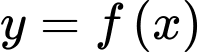 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 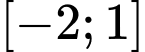 thỏa mãn
thỏa mãn 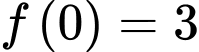 và
và 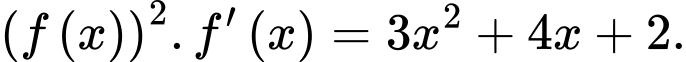 Giá trị
Giá trị 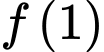 là
là
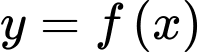 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 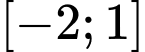 thỏa mãn
thỏa mãn 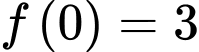 và
và 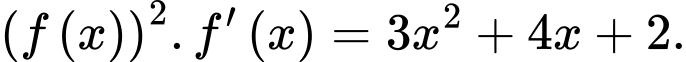 Giá trị
Giá trị 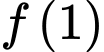 là
là
Ta có: 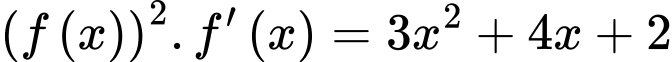 (*)
(*)
Lấy nguyên hàm 2 vế của phương trình trên ta được
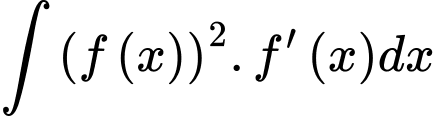
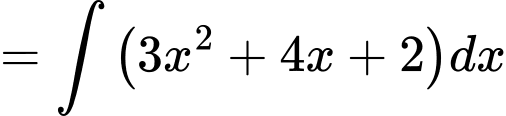
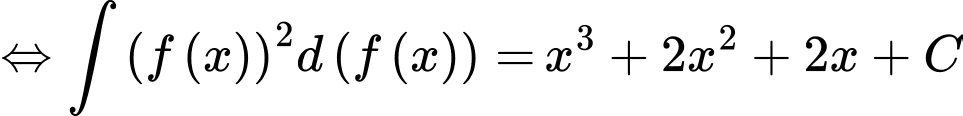
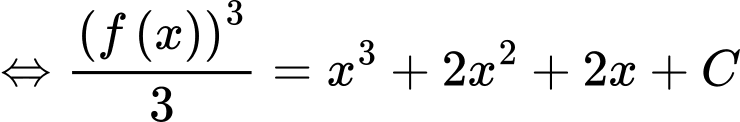
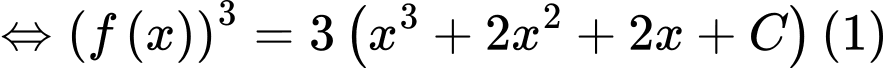
Theo đề bài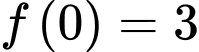 nên từ (1) ta có
nên từ (1) ta có 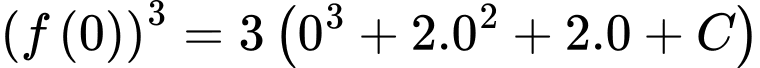
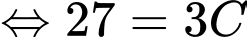
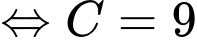
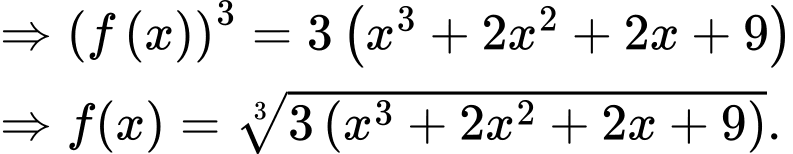
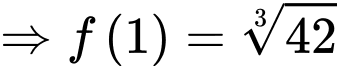
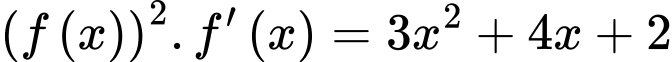 (*)
(*)Lấy nguyên hàm 2 vế của phương trình trên ta được
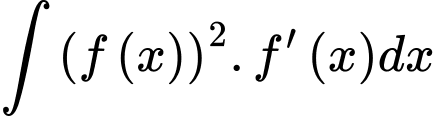
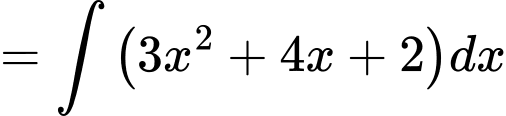
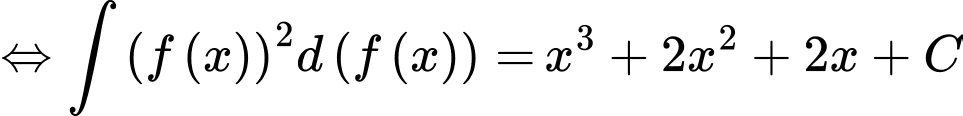
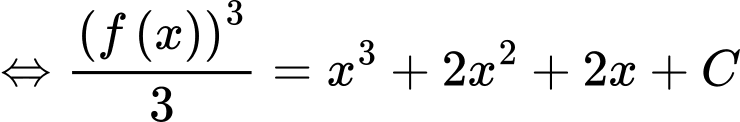
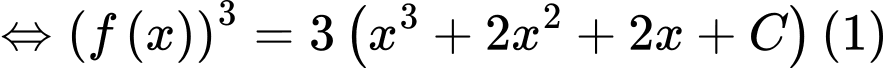
Theo đề bài
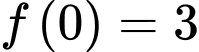 nên từ (1) ta có
nên từ (1) ta có 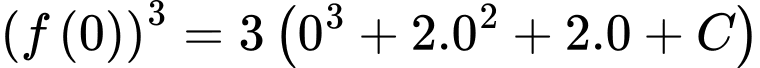
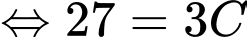
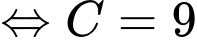
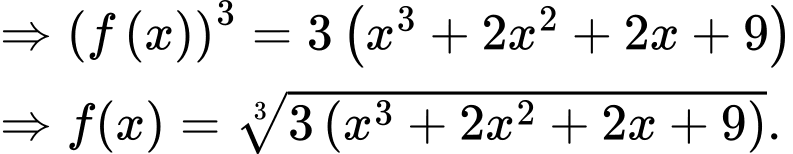
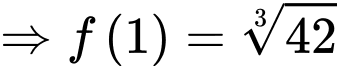
Câu 9 [580238]: Cho 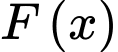 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 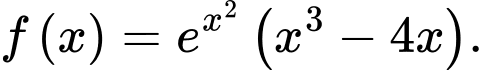 Hàm số
Hàm số 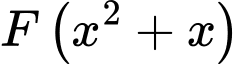 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
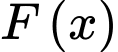 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 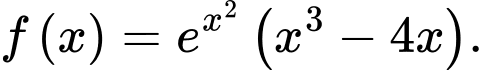 Hàm số
Hàm số 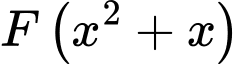 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 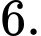
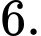
B, 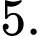
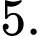
C, 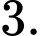
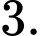
D, 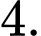
Chọn B.
Ta có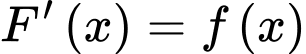
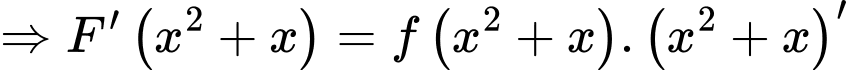
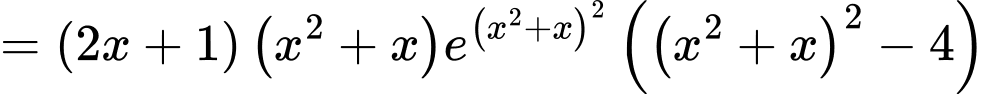
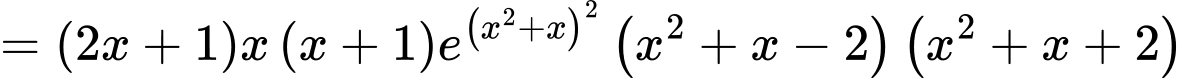
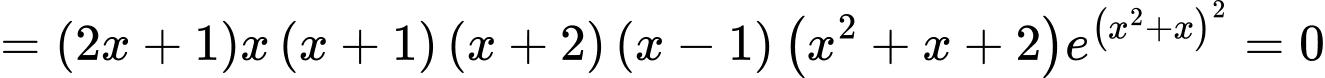
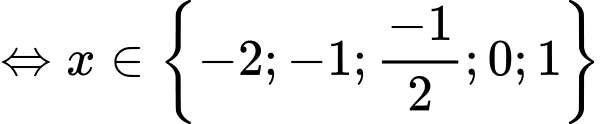
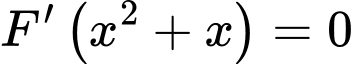 có 5 nghiệm đơn nên
có 5 nghiệm đơn nên 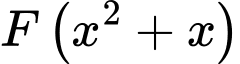 có 5 điểm cực trị. Đáp án: B
có 5 điểm cực trị. Đáp án: B
Ta có
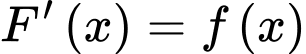
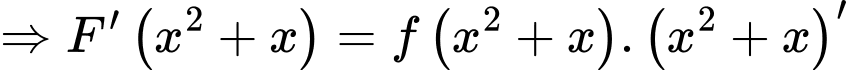
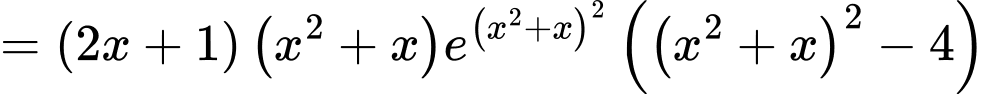
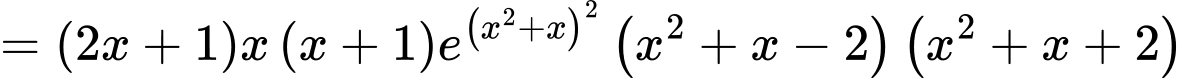
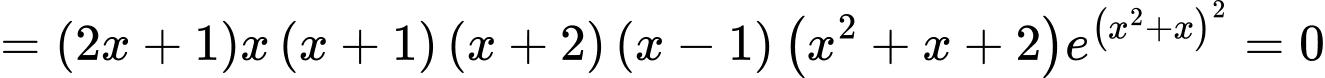
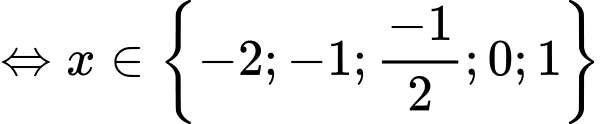
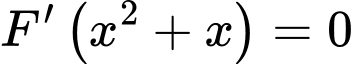 có 5 nghiệm đơn nên
có 5 nghiệm đơn nên 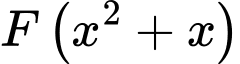 có 5 điểm cực trị. Đáp án: B
có 5 điểm cực trị. Đáp án: B