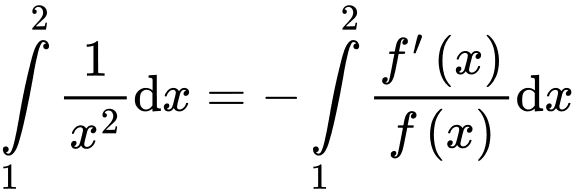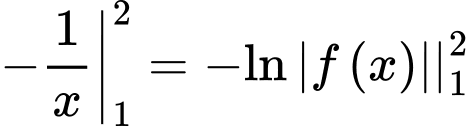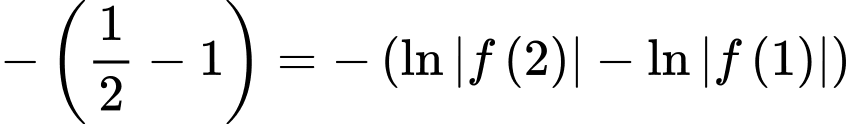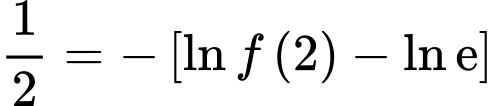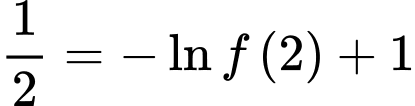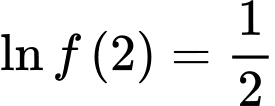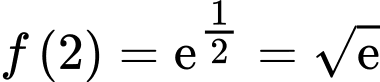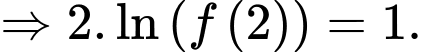Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [580265]: Biết 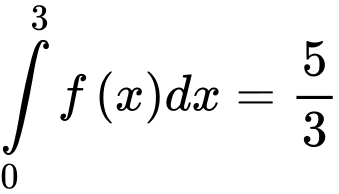 và
và 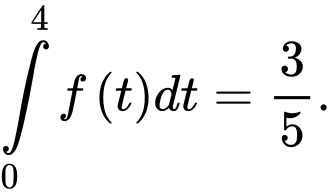 Tính
Tính 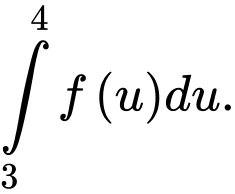
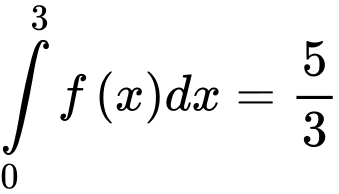 và
và 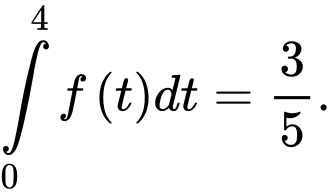 Tính
Tính 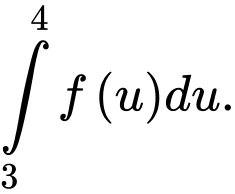
A, 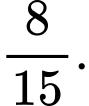
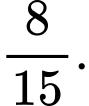
B, 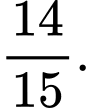
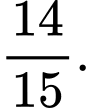
C, 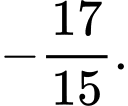
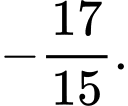
D, 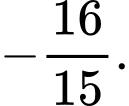
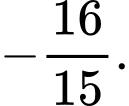
Chọn D
Ta có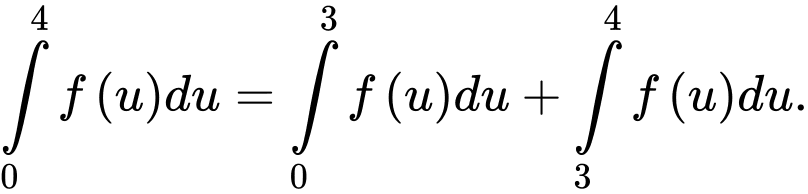
Mà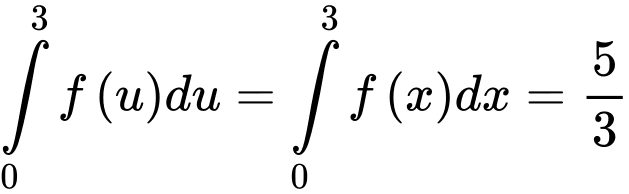 và
và 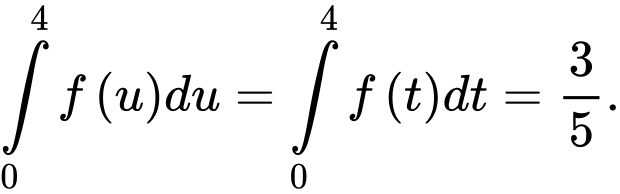
Nên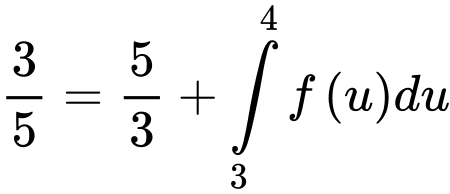
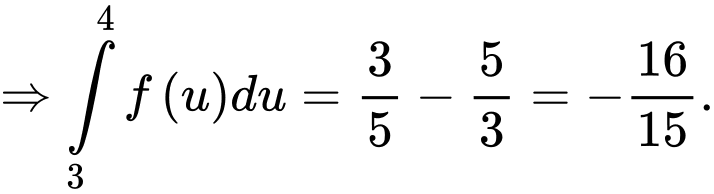 Đáp án: D
Đáp án: D
Ta có
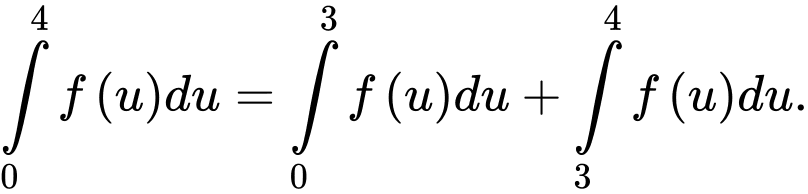
Mà
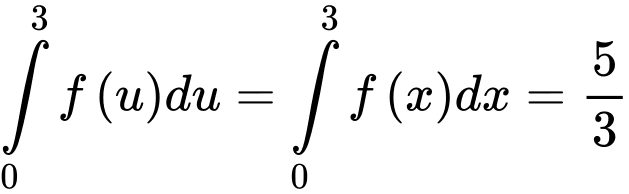 và
và 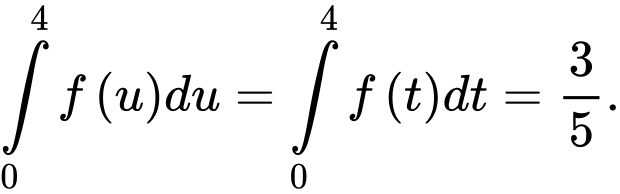
Nên
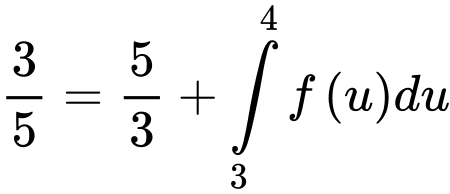
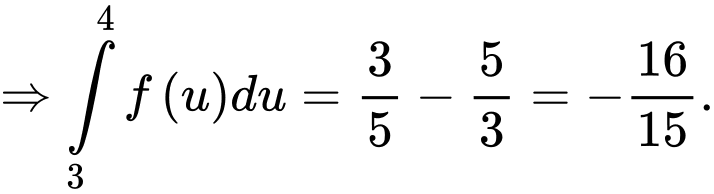 Đáp án: D
Đáp án: D
Câu 2 [580266]: Cho 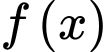 là hàm số liên tục trên
là hàm số liên tục trên 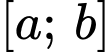 và
và 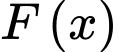 là nguyên hàm của
là nguyên hàm của 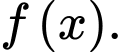 Khẳng định nào sau đây là đúng.
Khẳng định nào sau đây là đúng.
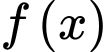 là hàm số liên tục trên
là hàm số liên tục trên 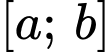 và
và 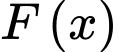 là nguyên hàm của
là nguyên hàm của 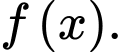 Khẳng định nào sau đây là đúng.
Khẳng định nào sau đây là đúng. A, 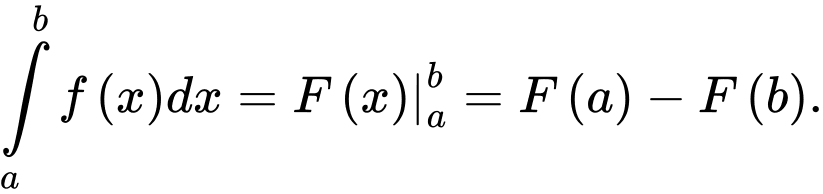
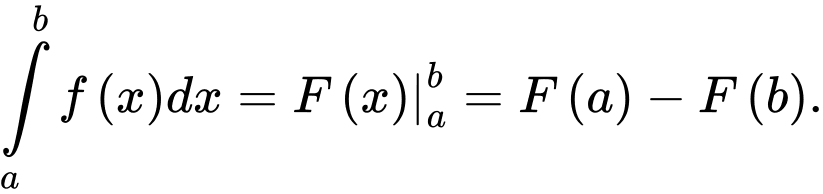
B, 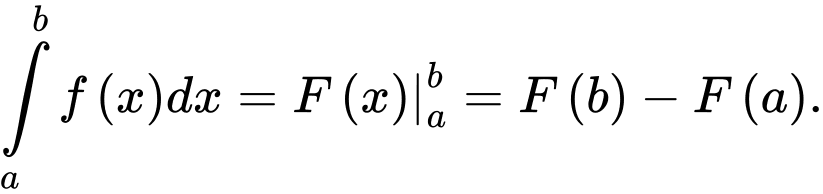
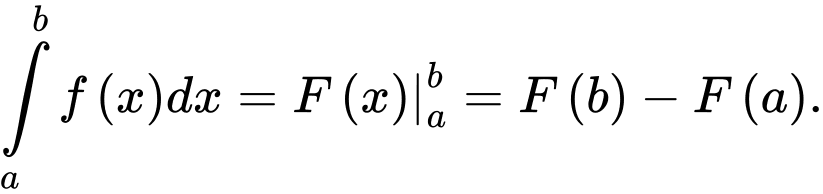
C, 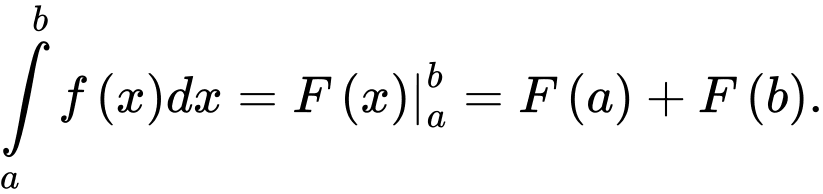
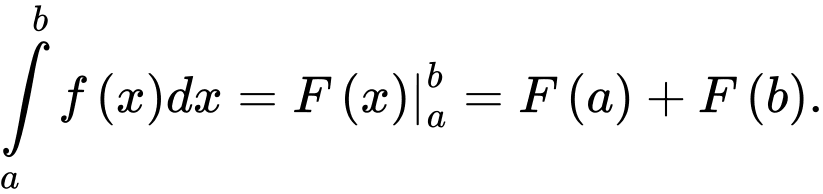
D, 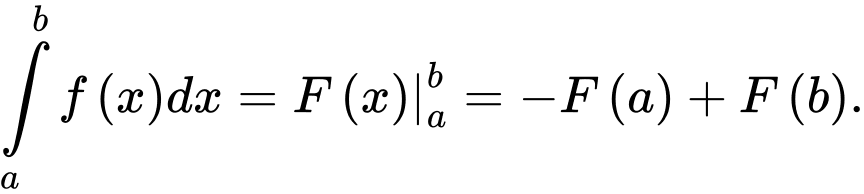
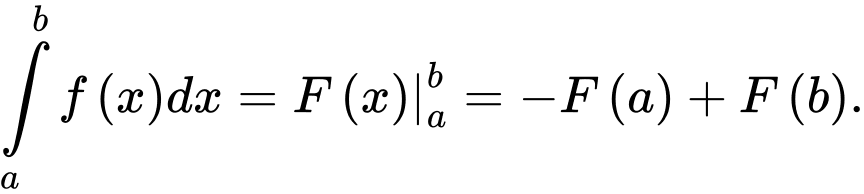
Chọn B
Áp dụng định nghĩa ta có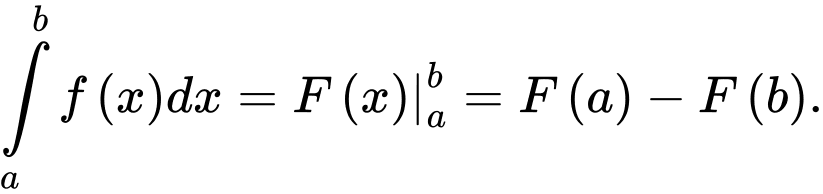 Đáp án: B
Đáp án: B
Áp dụng định nghĩa ta có
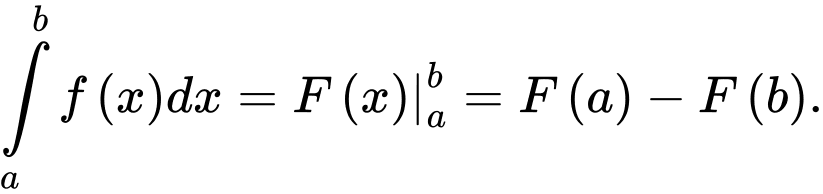 Đáp án: B
Đáp án: B
Câu 3 [580267]: Giả sử 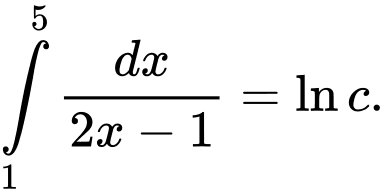 Giá trị của
Giá trị của  là
là
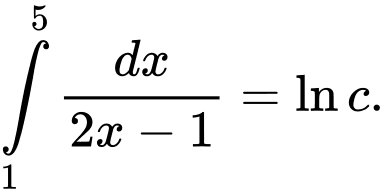 Giá trị của
Giá trị của  là
là A, 9.
B, 3.
C, 81.
D, 8.
Chọn B
Ta có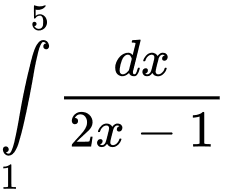
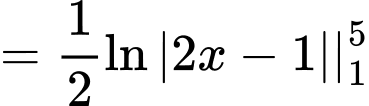
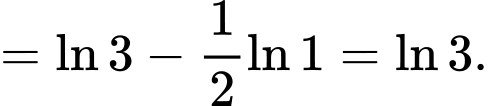
Do đó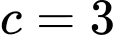 thỏa mãn yêu cầu bài toán. Đáp án: B
thỏa mãn yêu cầu bài toán. Đáp án: B
Ta có
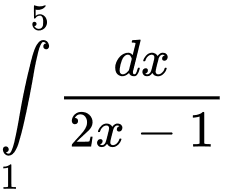
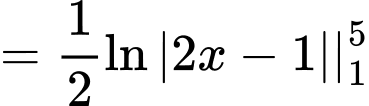
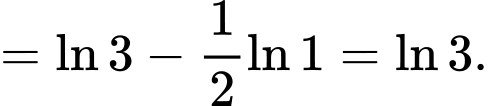
Do đó
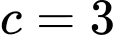 thỏa mãn yêu cầu bài toán. Đáp án: B
thỏa mãn yêu cầu bài toán. Đáp án: B
Câu 4 [580268]: Cho tích phân 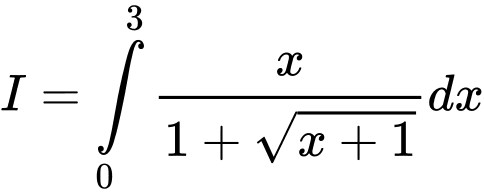 nếu đặt
nếu đặt 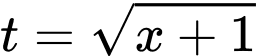 thì
thì 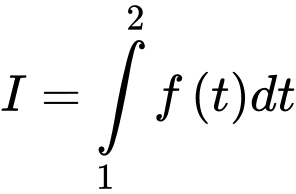 trong đó:
trong đó:
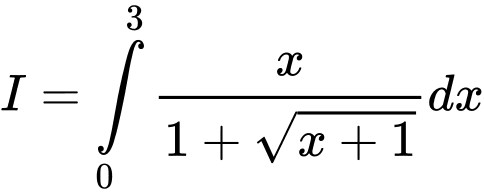 nếu đặt
nếu đặt 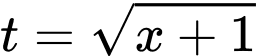 thì
thì 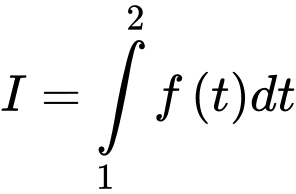 trong đó:
trong đó: A, 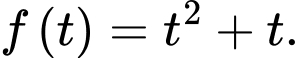
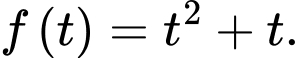
B, 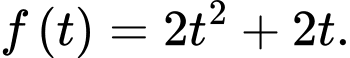
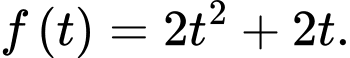
C, 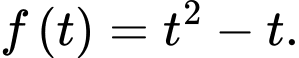
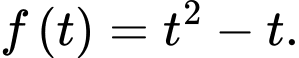
D, 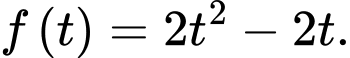
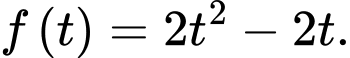
Chọn D
Đặt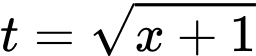
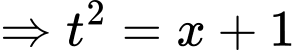
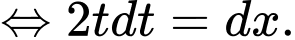
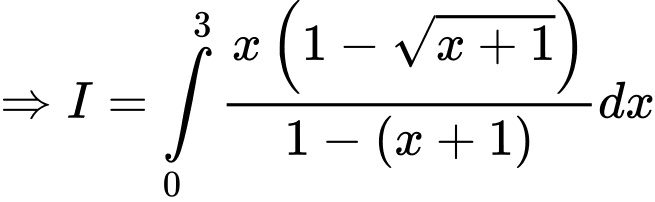
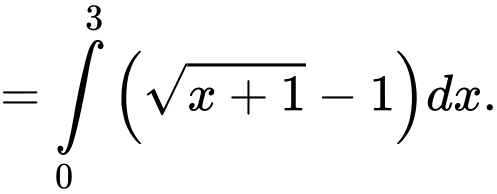
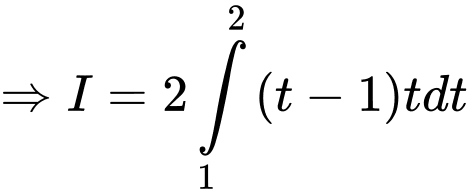
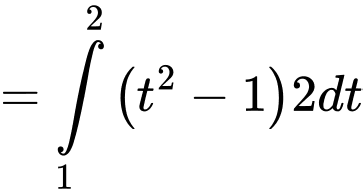
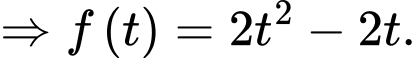 Đáp án: D
Đáp án: D
Đặt
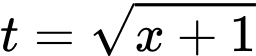
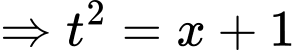
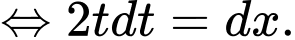
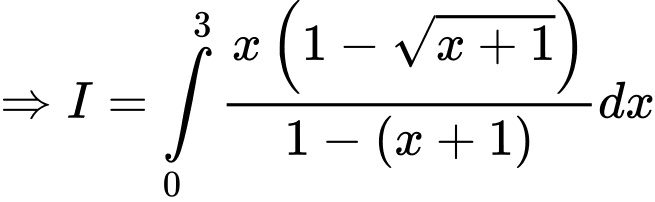
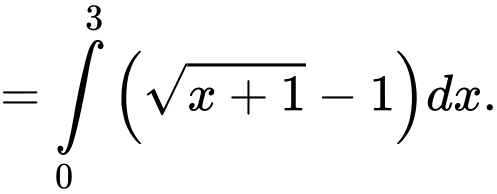
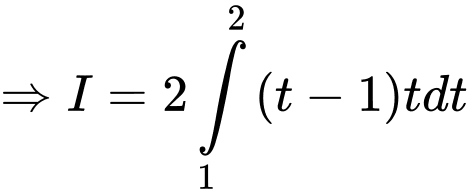
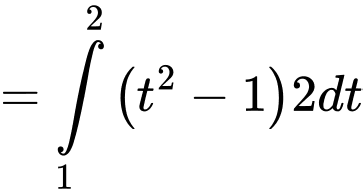
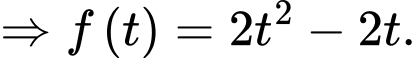 Đáp án: D
Đáp án: D
Câu 5 [580269]: Cho 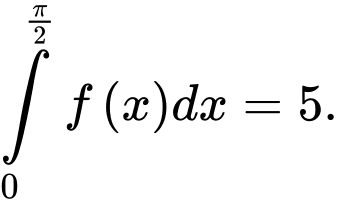 Tính
Tính 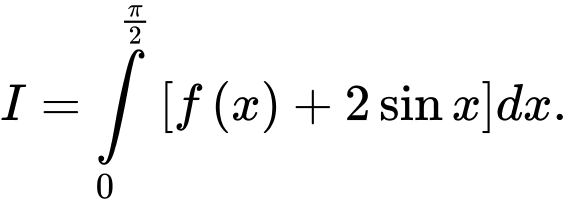
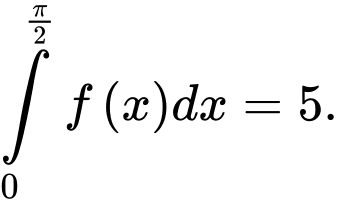 Tính
Tính 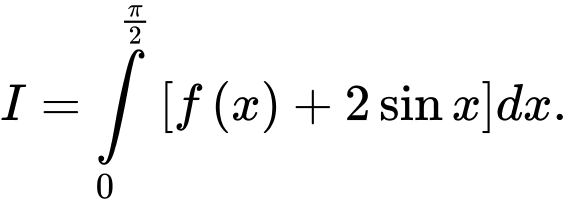
A, 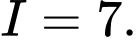
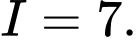
B, 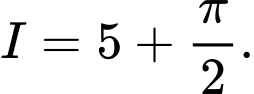
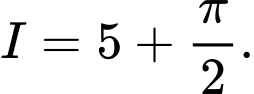
C, 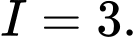
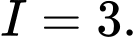
D, 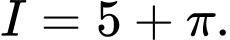
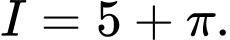
Chọn A
Ta có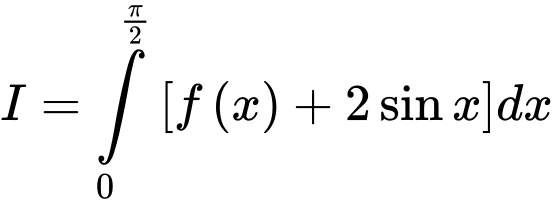
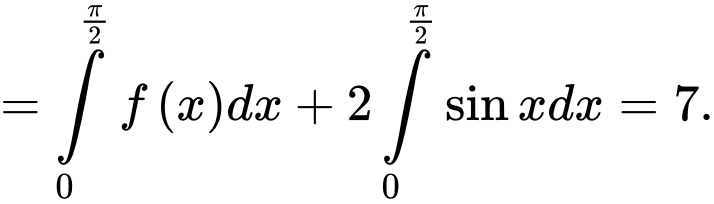 Đáp án: A
Đáp án: A
Ta có
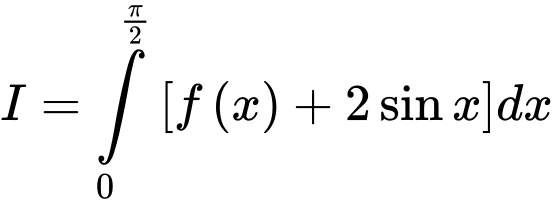
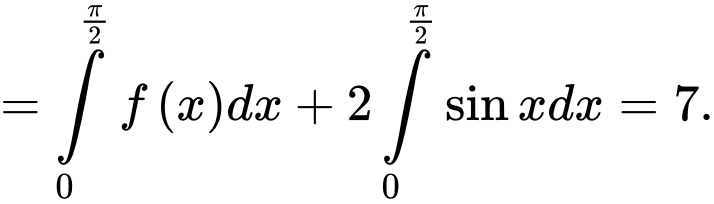 Đáp án: A
Đáp án: A
Câu 6 [580270]: Tính tích phân 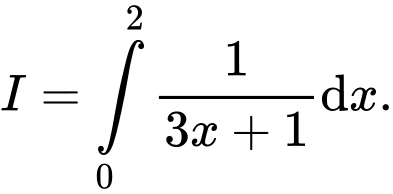
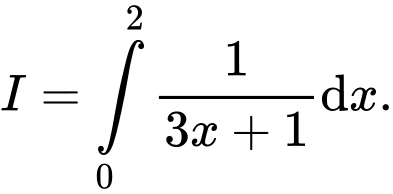
A, 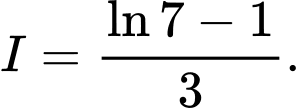
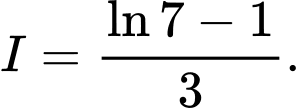
B, 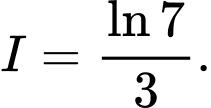
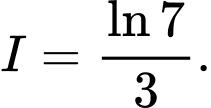
C, 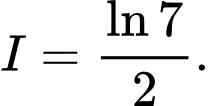
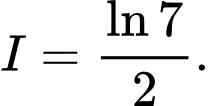
D, 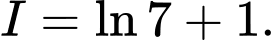
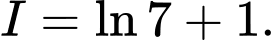
Chọn B
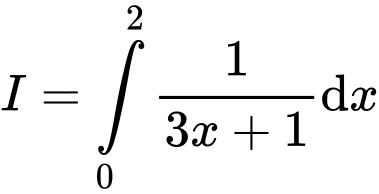
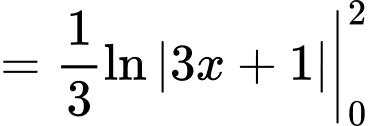
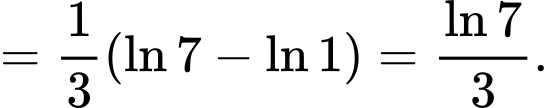 Đáp án: B
Đáp án: B
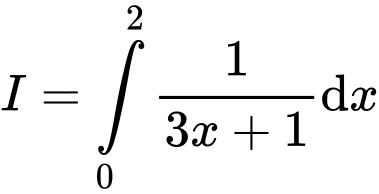
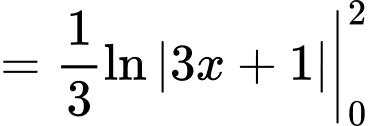
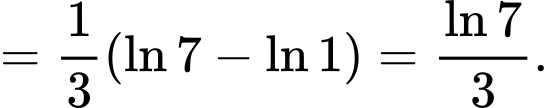 Đáp án: B
Đáp án: B
Câu 7 [580271]: Giá trị của tích phân 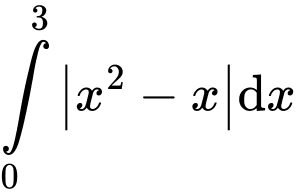 là
là 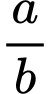 (với
(với 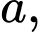
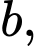 là các số tự nhiên và
là các số tự nhiên và 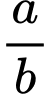 là phân số tối giản). Tổng
là phân số tối giản). Tổng  bằng
bằng
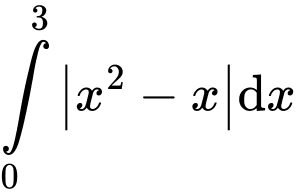 là
là 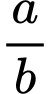 (với
(với 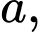
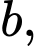 là các số tự nhiên và
là các số tự nhiên và 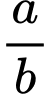 là phân số tối giản). Tổng
là phân số tối giản). Tổng  bằng
bằng A, 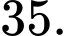
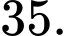
B, 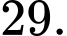
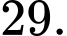
C, 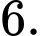
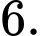
D, 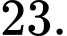
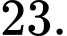
Chọn A
Ta có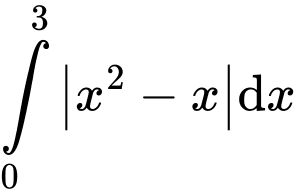
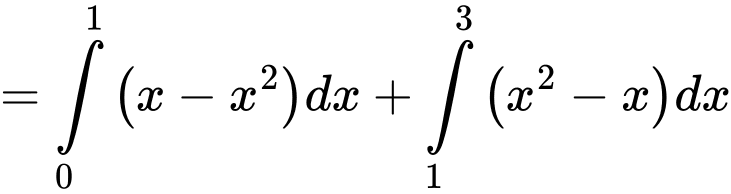
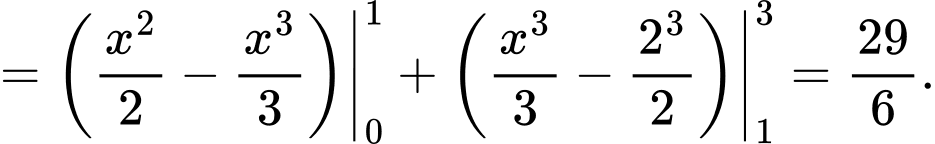
Vậy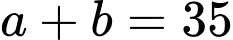 Đáp án: A
Đáp án: A
Ta có
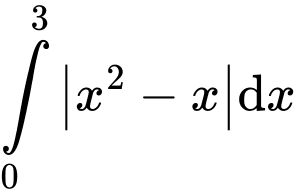
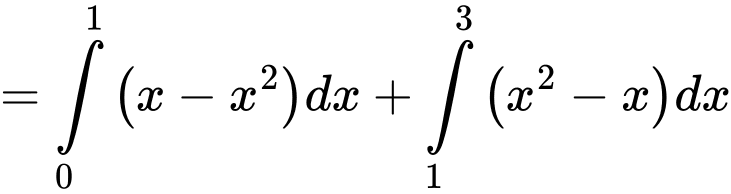
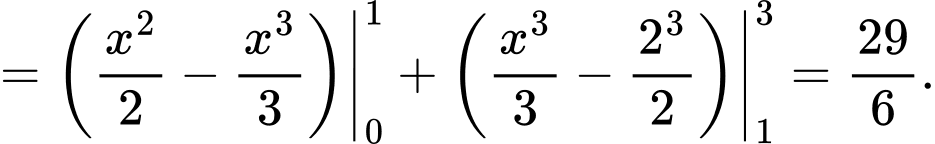
Vậy
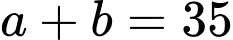 Đáp án: A
Đáp án: A
Câu 8 [580272]: Cho 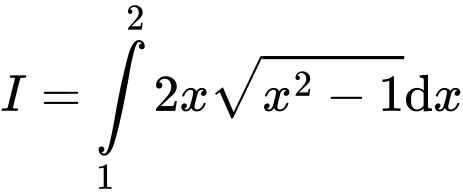 và
và 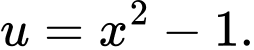 Chọn khẳng định sai trong các khẳng định sau:
Chọn khẳng định sai trong các khẳng định sau:
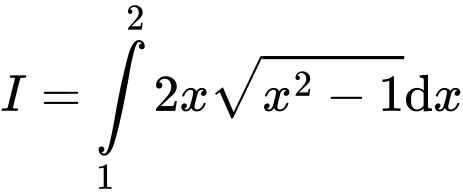 và
và 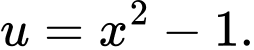 Chọn khẳng định sai trong các khẳng định sau:
Chọn khẳng định sai trong các khẳng định sau: A, 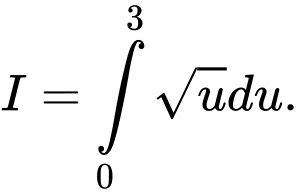
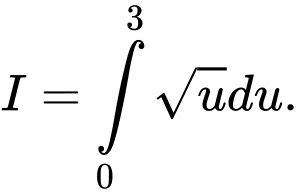
B, 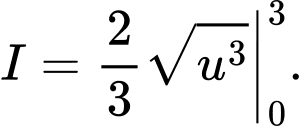
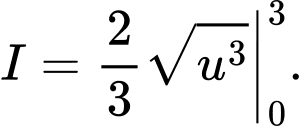
C, 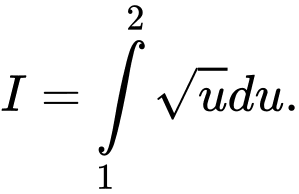
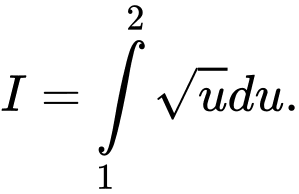
D, 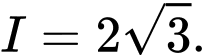
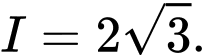
Chọn C
Đặt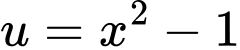
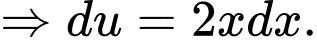
Đổi cận: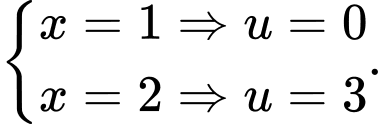
Suy ra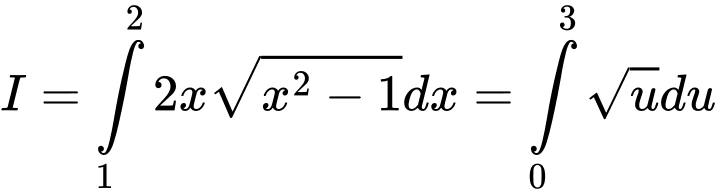
Do đó C sai. Đáp án: C
Đặt
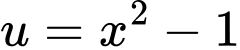
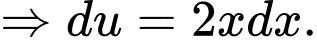
Đổi cận:
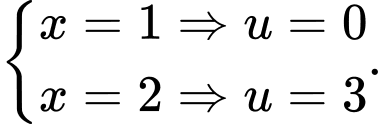
Suy ra
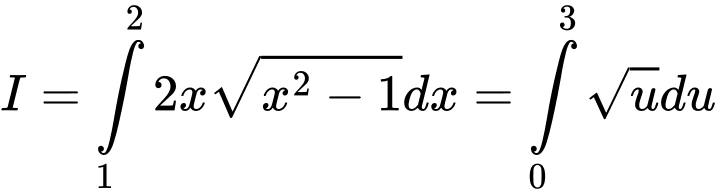
Do đó C sai. Đáp án: C
Câu 9 [580273]: Biết rằng tích phân 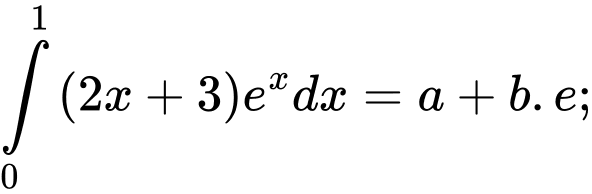
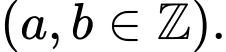 Tính giá trị biểu thức
Tính giá trị biểu thức 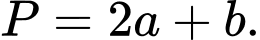
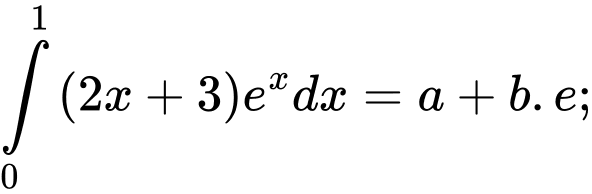
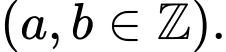 Tính giá trị biểu thức
Tính giá trị biểu thức 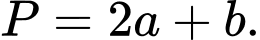
A, 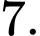
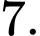
B, 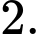
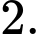
C, 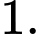
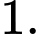
D, 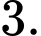
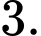
Chọn C
Đặt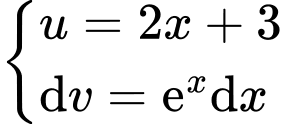
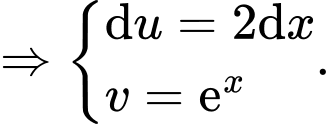
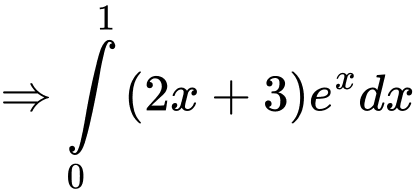
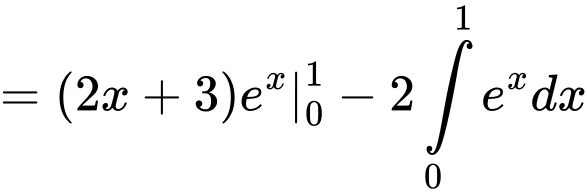
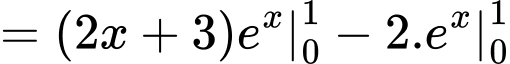
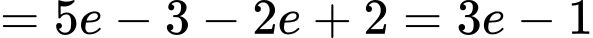

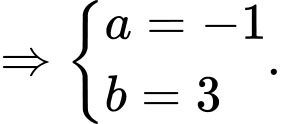
Vậy tích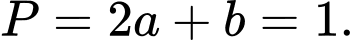 Đáp án: C
Đáp án: C
Đặt
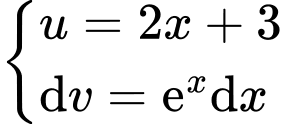
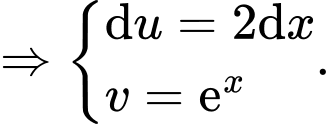
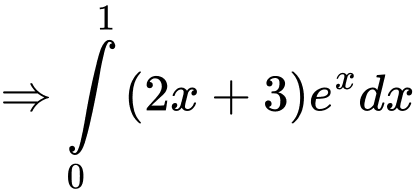
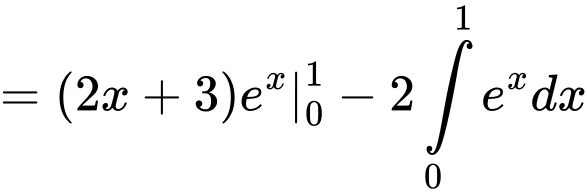
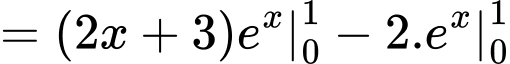
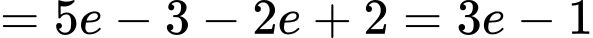

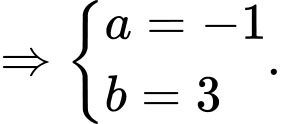
Vậy tích
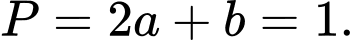 Đáp án: C
Đáp án: C
Câu 10 [580274]: Cho 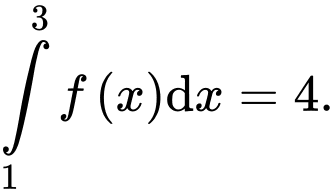 Khi đó
Khi đó 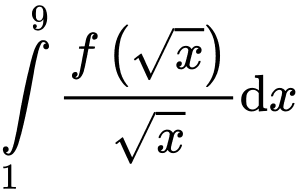 bằng
bằng
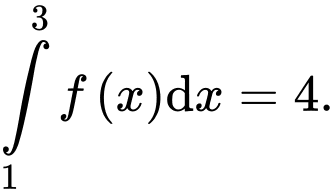 Khi đó
Khi đó 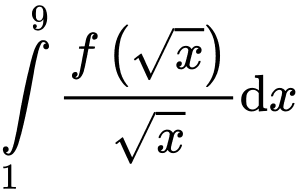 bằng
bằng A, 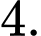
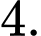
B, 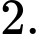
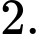
C, 
D, 
Chọn D
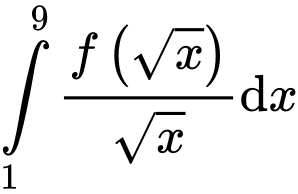
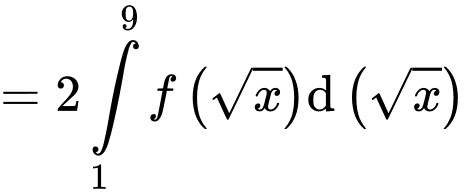
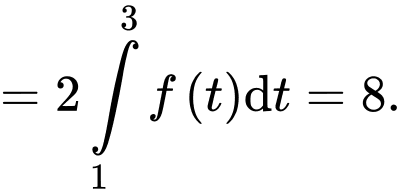 Đáp án: D
Đáp án: D
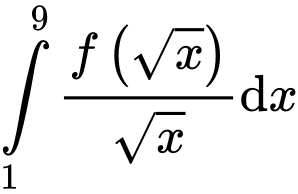
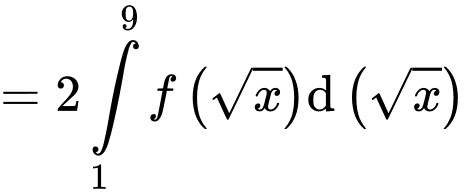
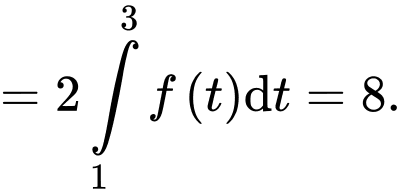 Đáp án: D
Đáp án: D
Câu 11 [580275]: Cho 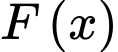 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 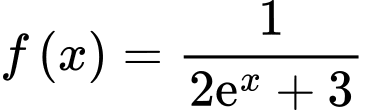 thỏa mãn
thỏa mãn 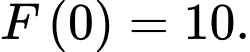 Tìm
Tìm 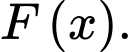
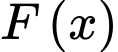 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 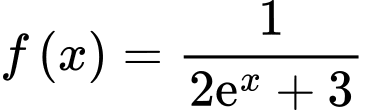 thỏa mãn
thỏa mãn 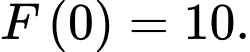 Tìm
Tìm 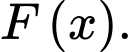
A, 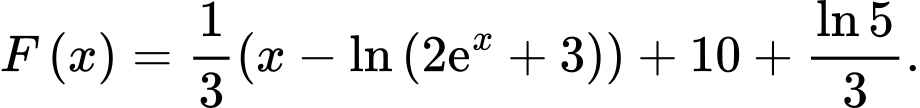
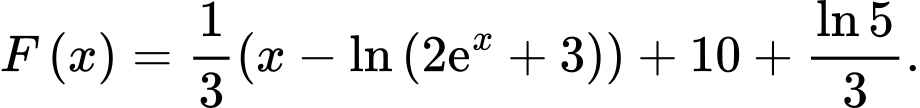
B, 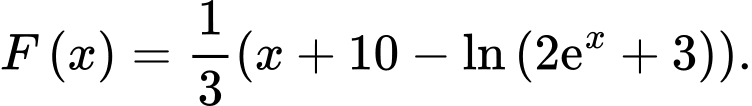
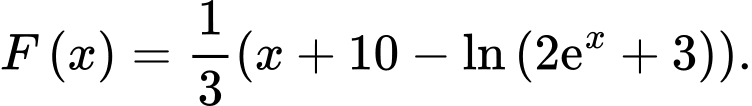
C, 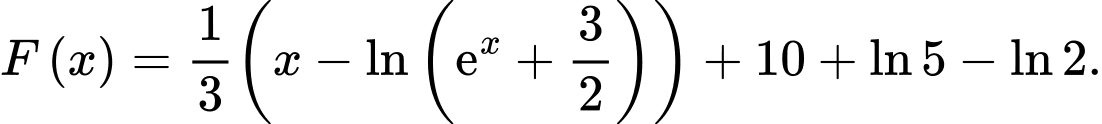
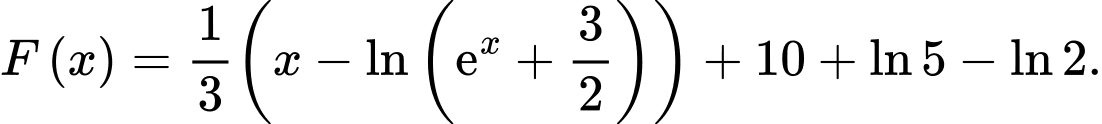
D, 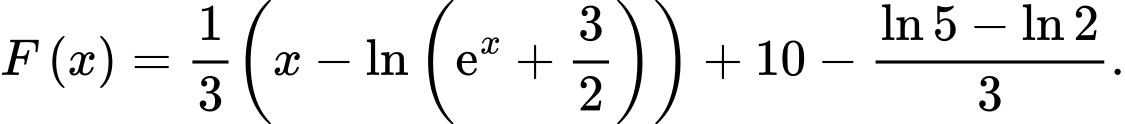
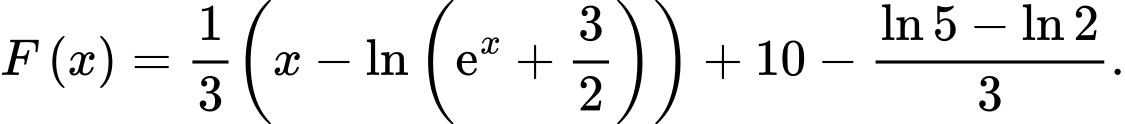
Chọn A
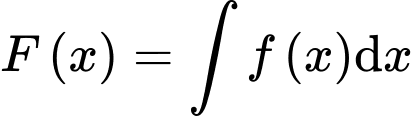
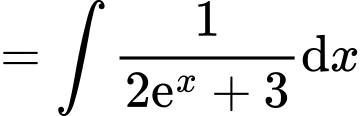
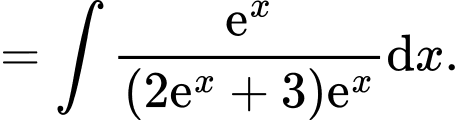
Đặt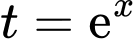
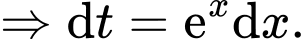 Suy ra
Suy ra
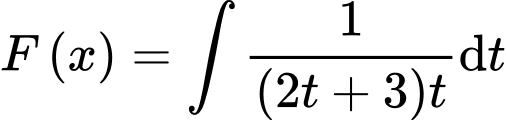
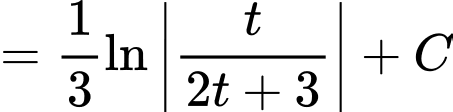
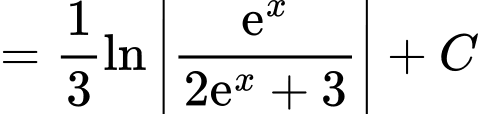
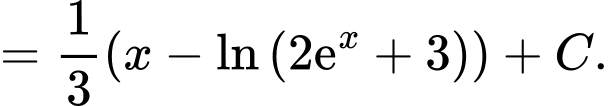
Vì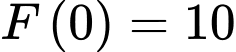 nên
nên 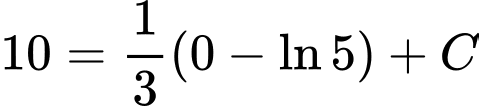
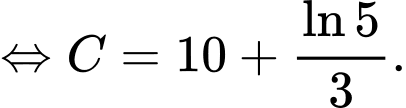
Vậy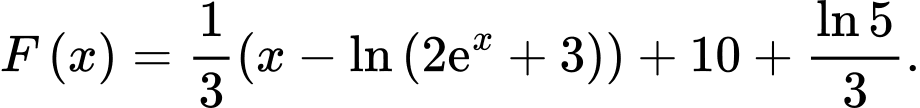 Đáp án: A
Đáp án: A
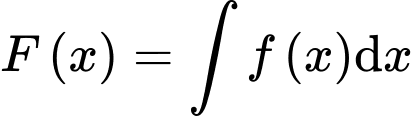
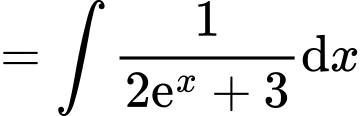
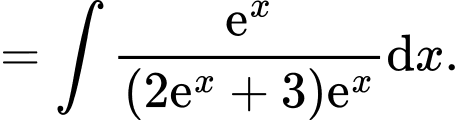
Đặt
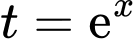
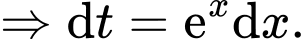 Suy ra
Suy ra
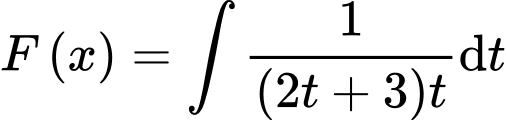
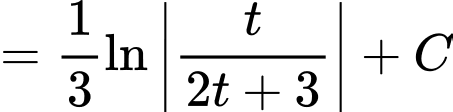
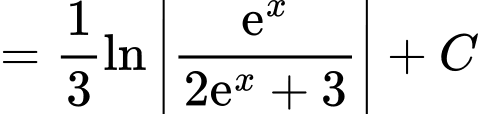
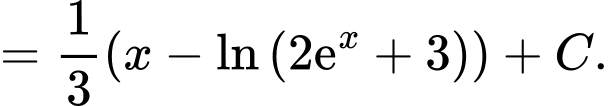
Vì
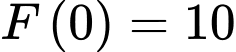 nên
nên 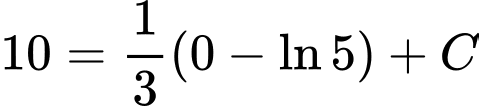
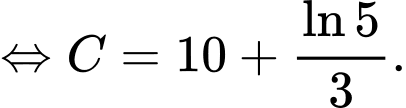
Vậy
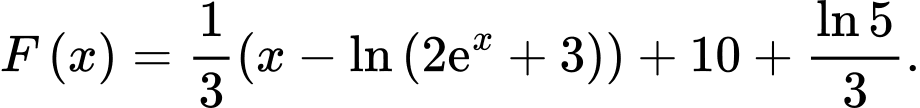 Đáp án: A
Đáp án: A
Câu 12 [580276]: Cho tích phân 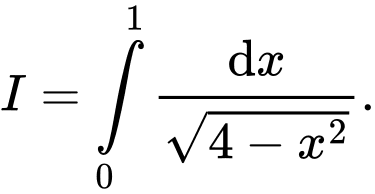 Nếu đổi biến số
Nếu đổi biến số 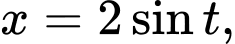
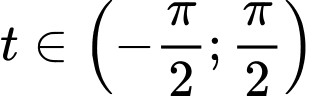 thì:
thì:
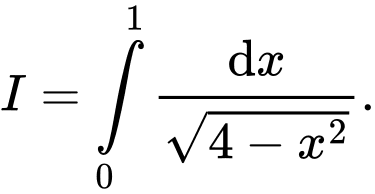 Nếu đổi biến số
Nếu đổi biến số 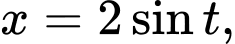
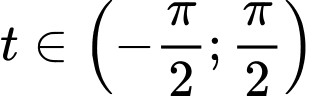 thì:
thì: A, 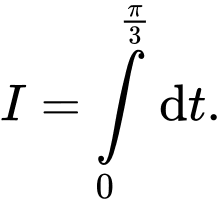
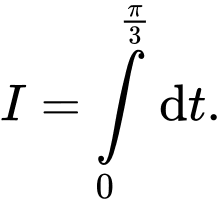
B, 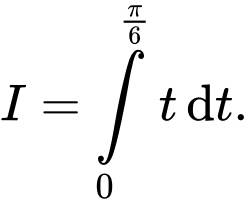
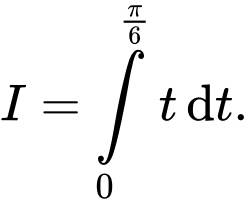
C, 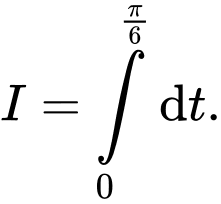
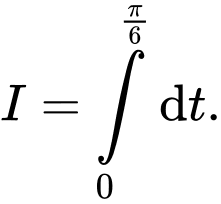
D, 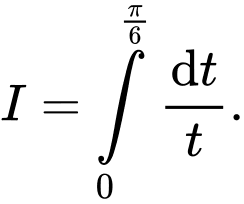
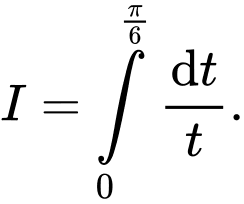
Chọn C
Đặt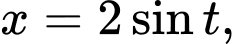
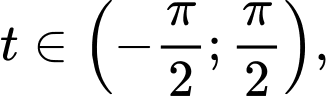
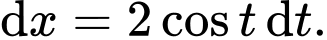
Đổi cận: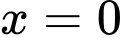
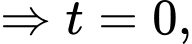
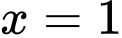
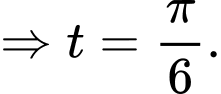
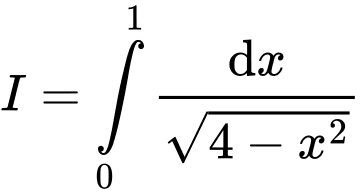
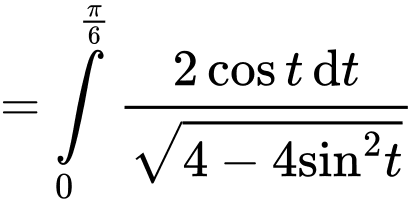
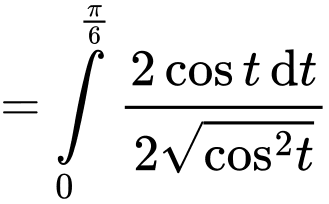
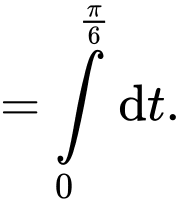 Đáp án: C
Đáp án: C
Đặt
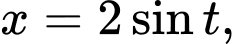
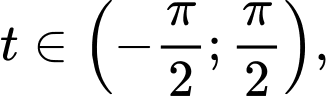
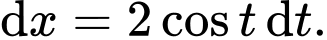
Đổi cận:
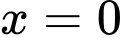
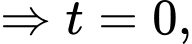
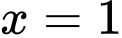
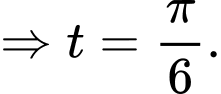
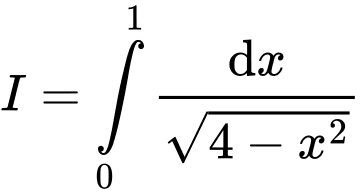
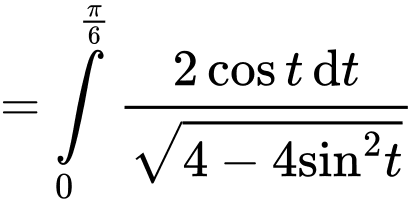
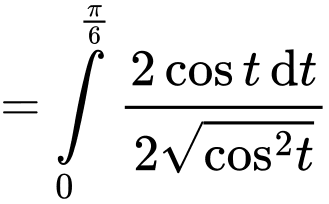
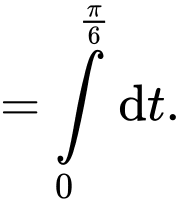 Đáp án: C
Đáp án: C
Câu 13 [580277]: Biết rằng 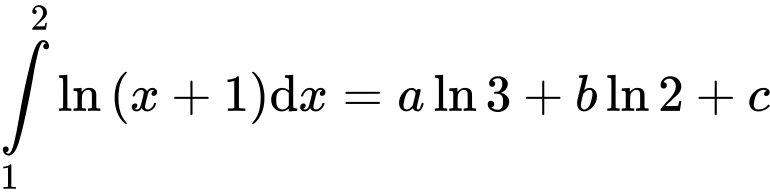 với
với 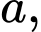
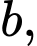
 là các số nguyên. Tính
là các số nguyên. Tính 
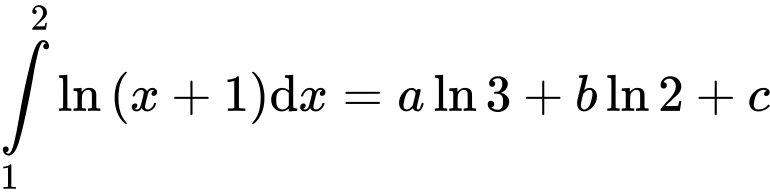 với
với 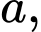
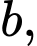
 là các số nguyên. Tính
là các số nguyên. Tính 
A, 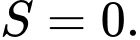
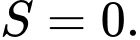
B, 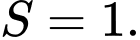
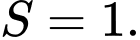
C, 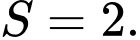
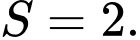
D, 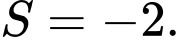
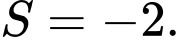
Đặt 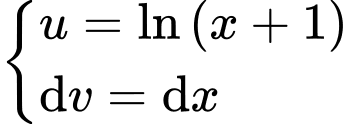
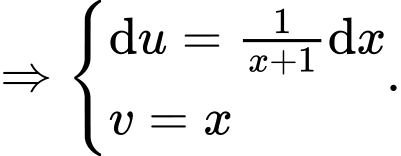
Khi đó, ta có: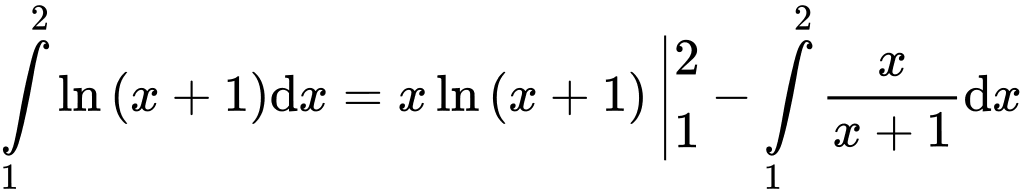
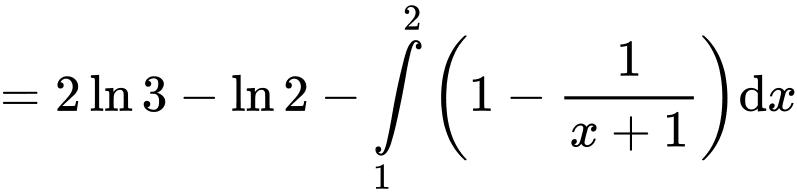
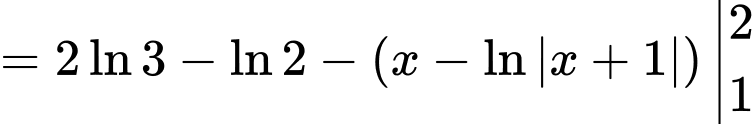
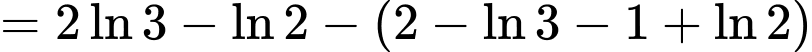
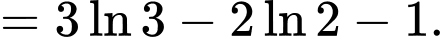
Suy ra
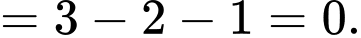 Đáp án: A
Đáp án: A
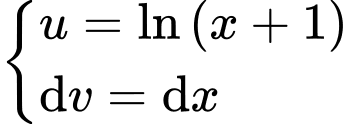
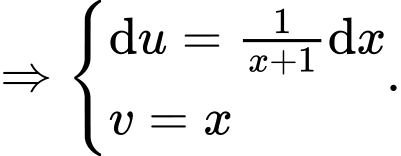
Khi đó, ta có:
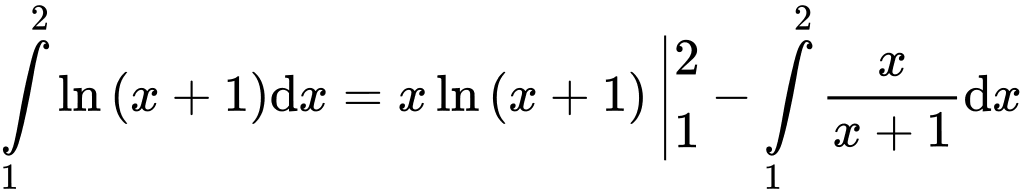
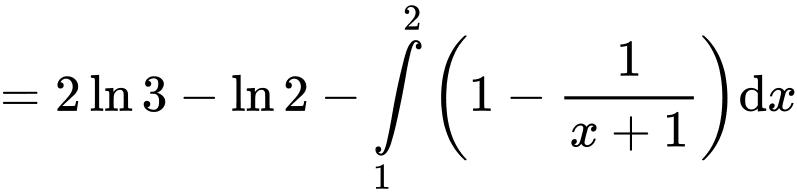
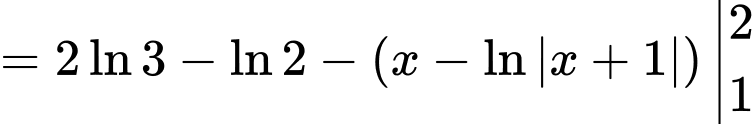
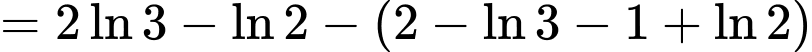
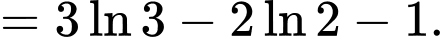
Suy ra

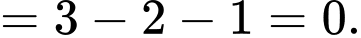 Đáp án: A
Đáp án: A
Câu 14 [580278]: Biết rằng tích phân 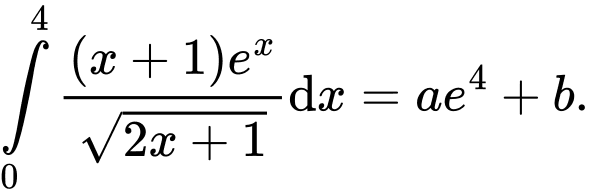 Tính
Tính 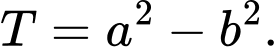
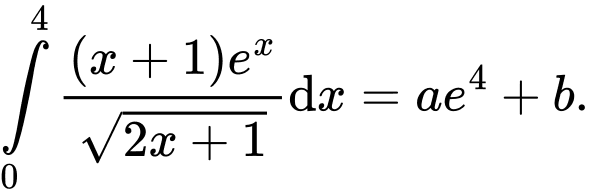 Tính
Tính 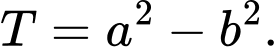
A, 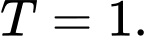
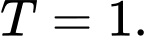
B, 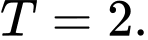
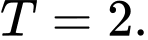
C, 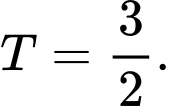
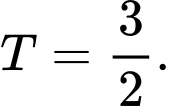
D, 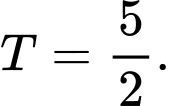
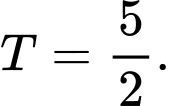
Ta có 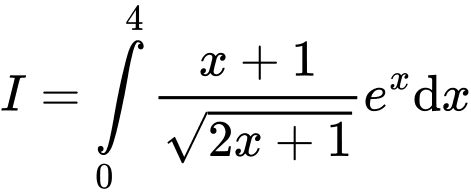
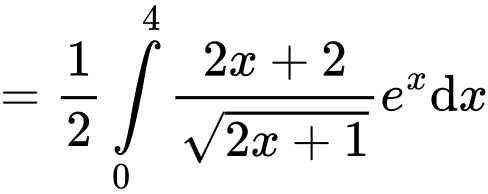
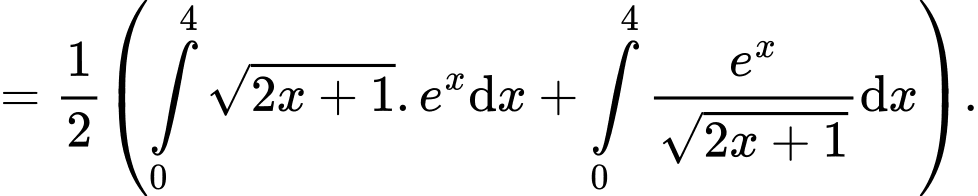
Xét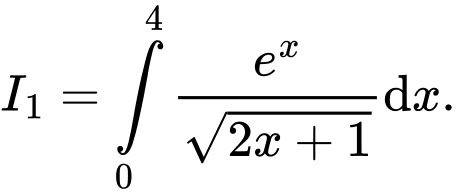
Đặt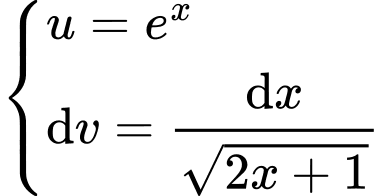
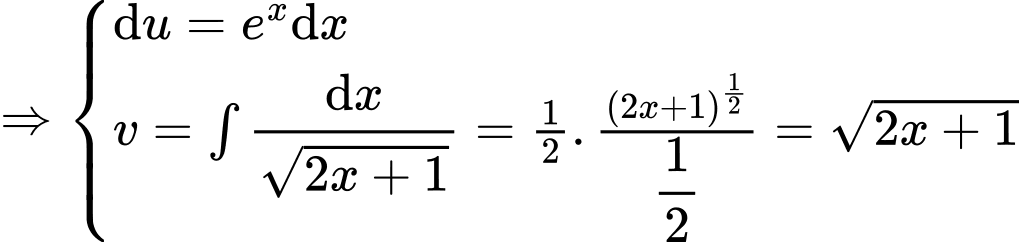
Do đó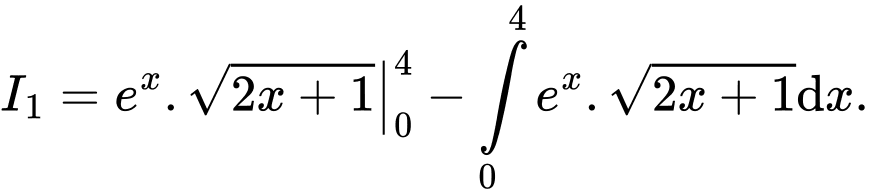
Suy ra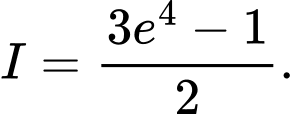 Khi đó
Khi đó 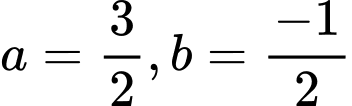
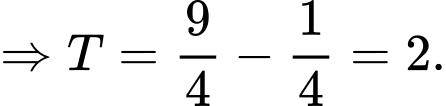 Đáp án: B
Đáp án: B
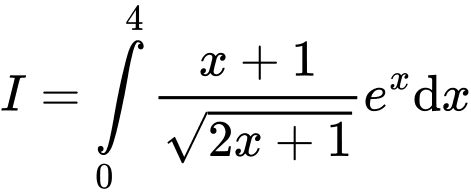
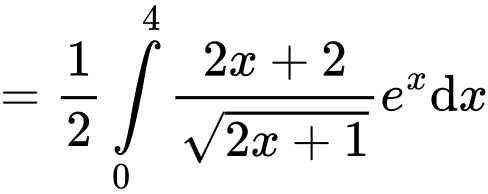
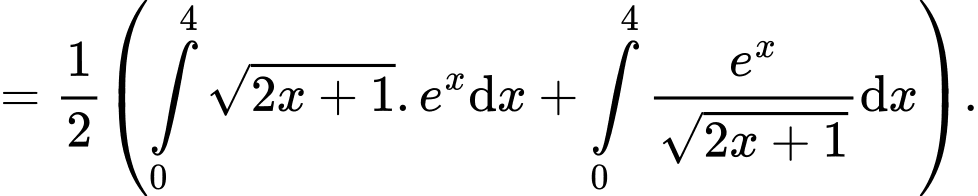
Xét
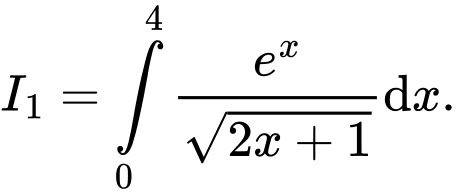
Đặt
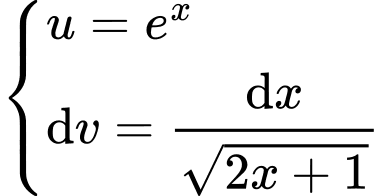
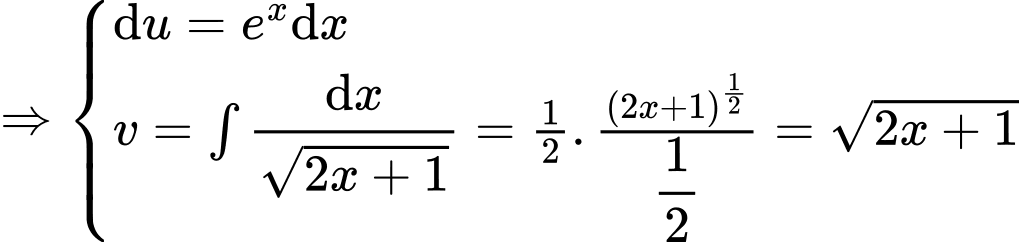
Do đó
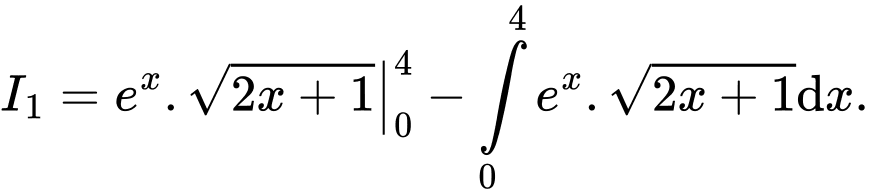
Suy ra
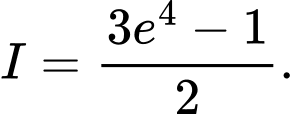 Khi đó
Khi đó 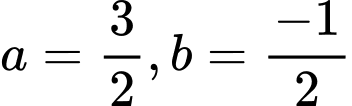
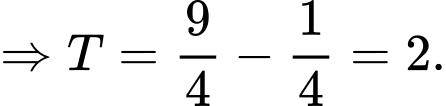 Đáp án: B
Đáp án: B
Câu 15 [580279]: Cho hàm số 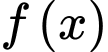 liên tục và nhận giá trị dương trên
liên tục và nhận giá trị dương trên 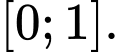 Biết
Biết 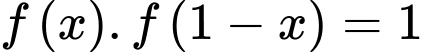 với
với  Tính giá trị
Tính giá trị 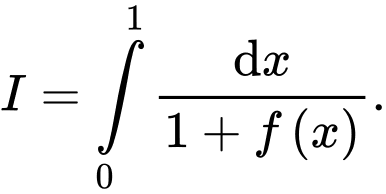
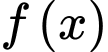 liên tục và nhận giá trị dương trên
liên tục và nhận giá trị dương trên 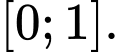 Biết
Biết 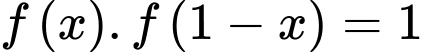 với
với  Tính giá trị
Tính giá trị 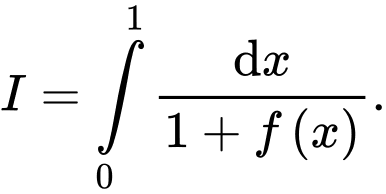
A, 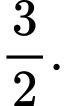
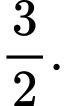
B, 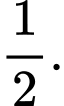
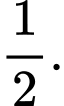
C, 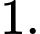
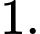
D, 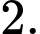
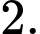
Ta có: 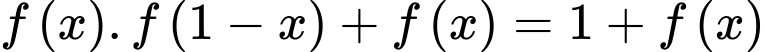
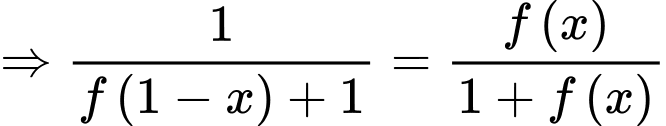
Xét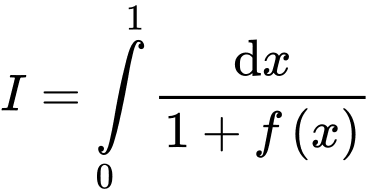
Đặt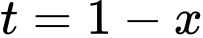
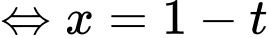
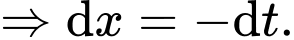
Đổi cận: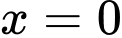
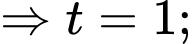
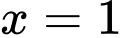
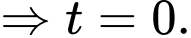
Khi đó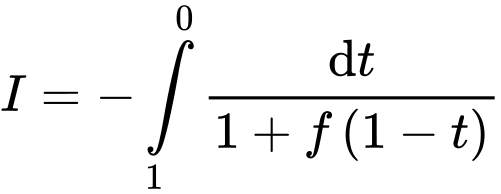
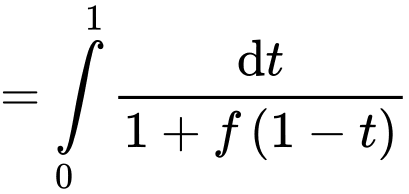
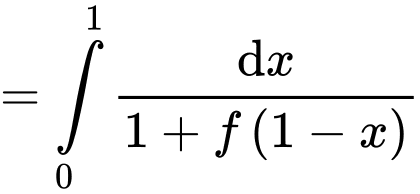
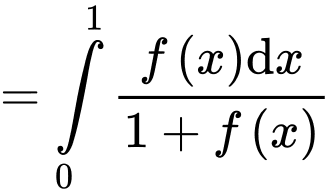
Mặt khác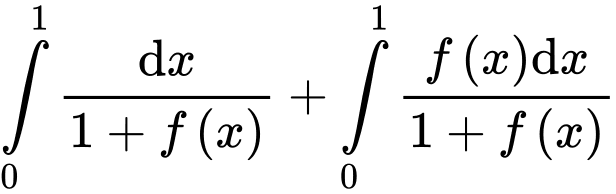
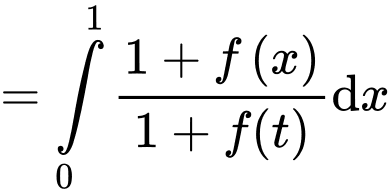
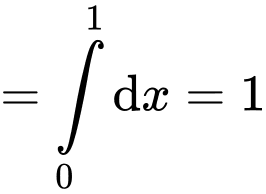 hay
hay 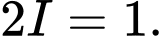
Vậy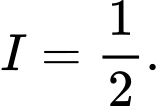 Đáp án: B
Đáp án: B
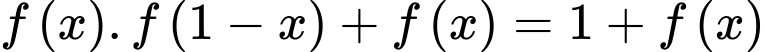
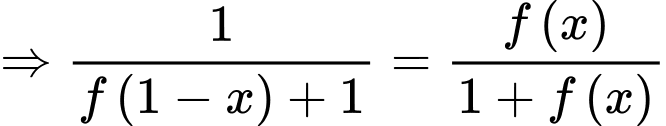
Xét
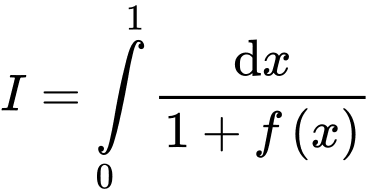
Đặt
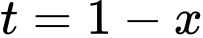
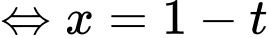
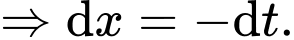
Đổi cận:
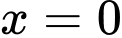
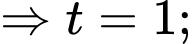
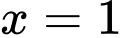
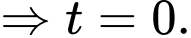
Khi đó
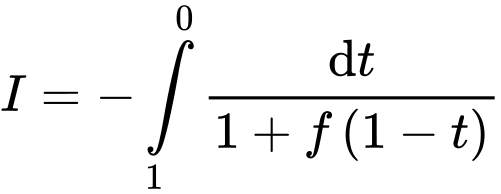
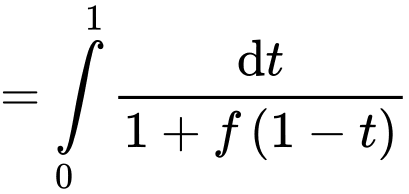
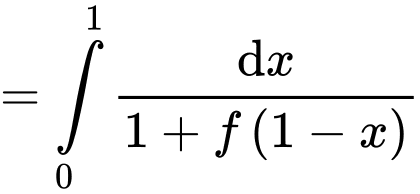
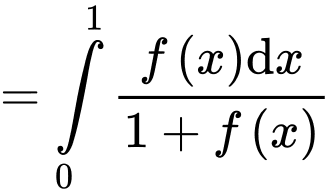
Mặt khác
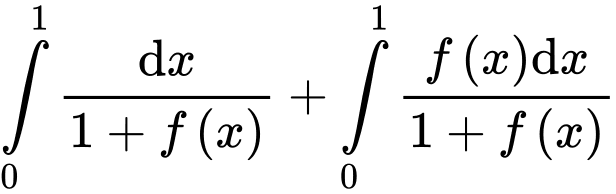
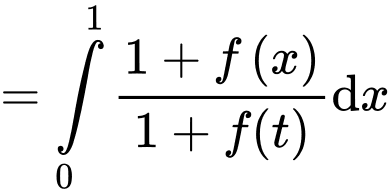
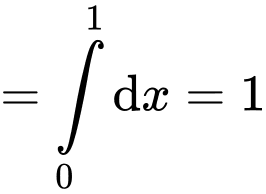 hay
hay 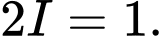
Vậy
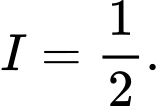 Đáp án: B
Đáp án: B Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 16 [580280]: Cho hai hàm số 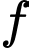 và
và 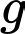 liên tục trên đoạn
liên tục trên đoạn 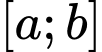 sao cho
sao cho 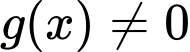 với mọi
với mọi 
Xét các khẳng định sau:
a)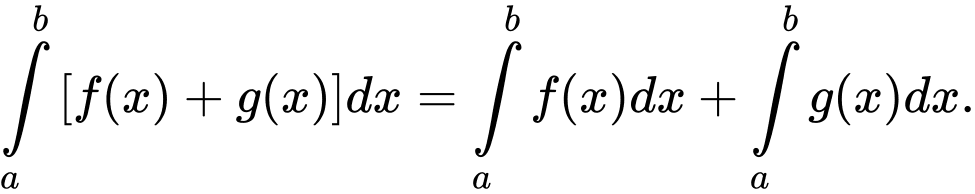
b)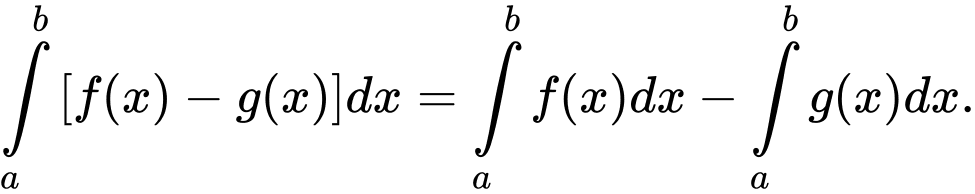
c)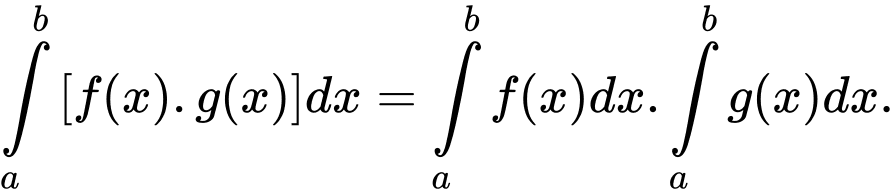
d)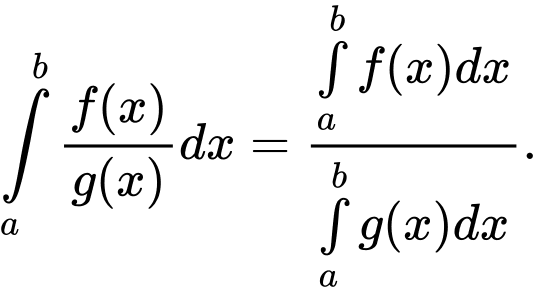
Xác định tính đúng sai trong các khẳng định trên.
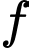 và
và 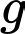 liên tục trên đoạn
liên tục trên đoạn 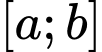 sao cho
sao cho 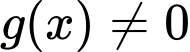 với mọi
với mọi 
Xét các khẳng định sau:
a)
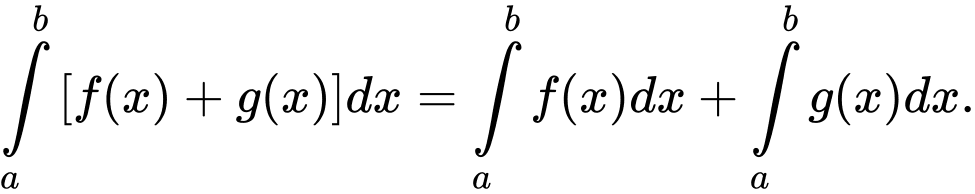
b)
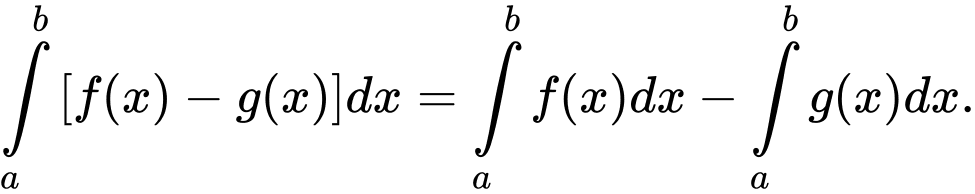
c)
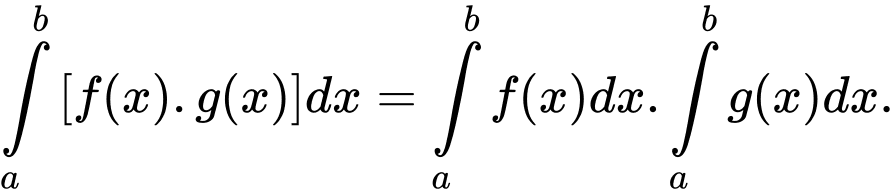
d)
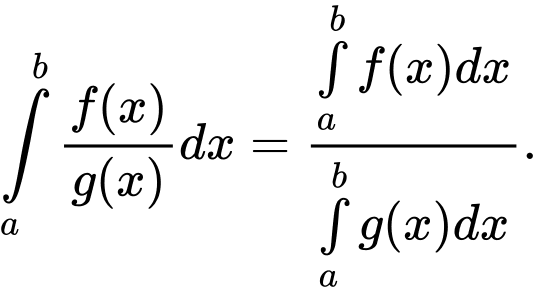
Xác định tính đúng sai trong các khẳng định trên.
a) Đ
b) Đ
c) S
d) S
Theo Sách giáo khoa Nâng cao lớp 12 (trang 151) có nêu: Tính chất của tích phân gồm có:
1.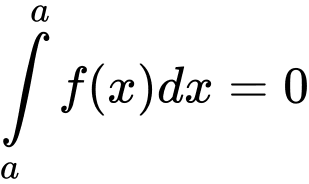
2.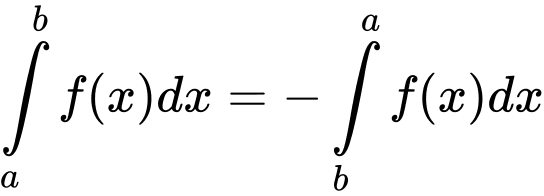
3.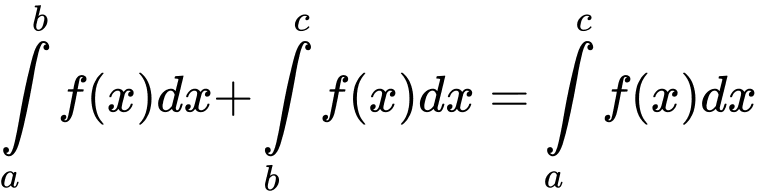 (
(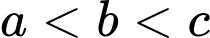 )
)
4.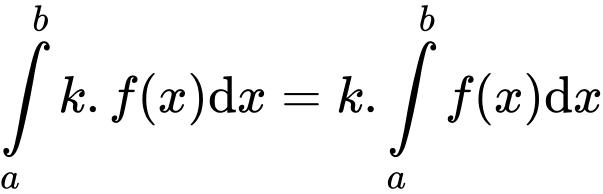

5.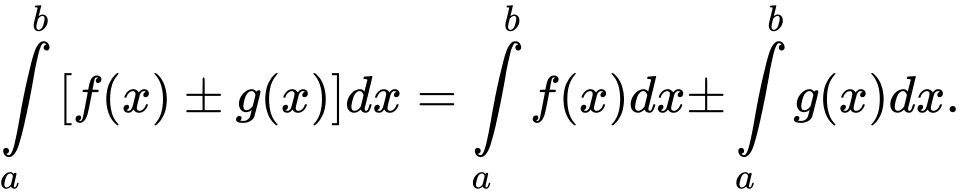
Do đó, các công thức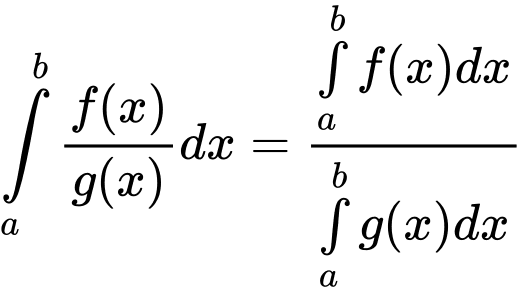 và
và 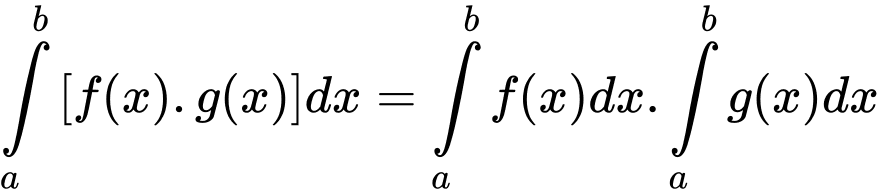 là sai.
là sai.
b) Đ
c) S
d) S
Theo Sách giáo khoa Nâng cao lớp 12 (trang 151) có nêu: Tính chất của tích phân gồm có:
1.
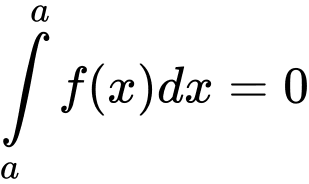
2.
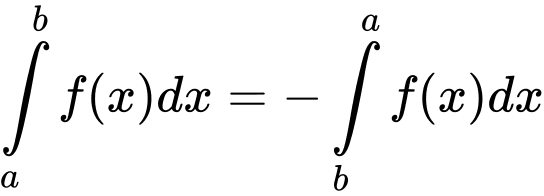
3.
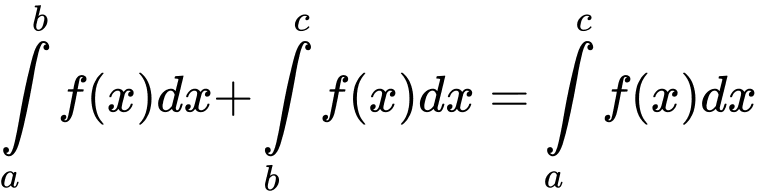 (
(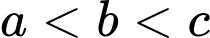 )
)
4.
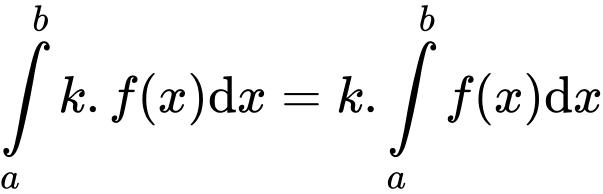

5.
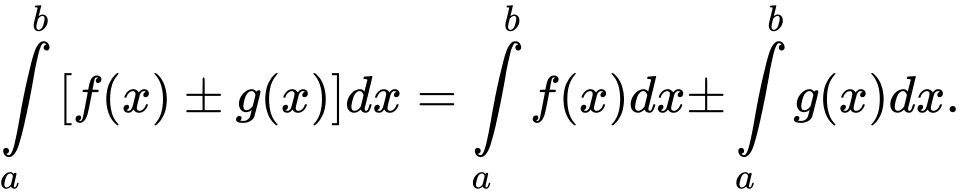
Do đó, các công thức
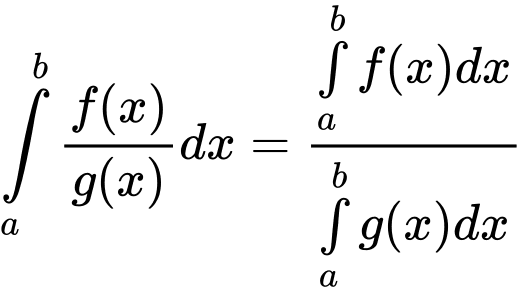 và
và 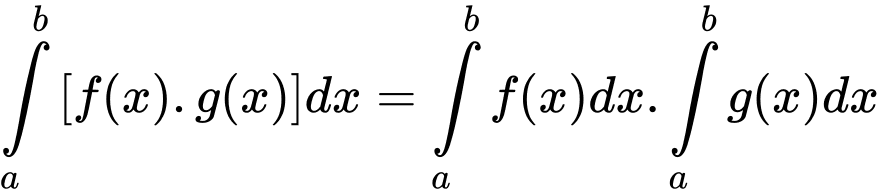 là sai.
là sai.
Câu 17 [580281]: Cho hàm số 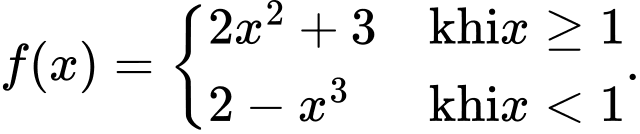 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
a)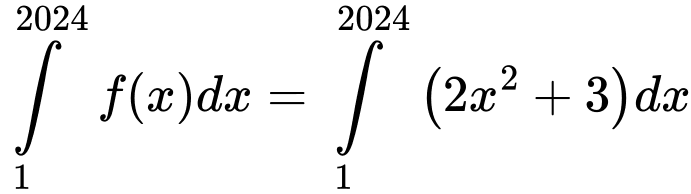
b)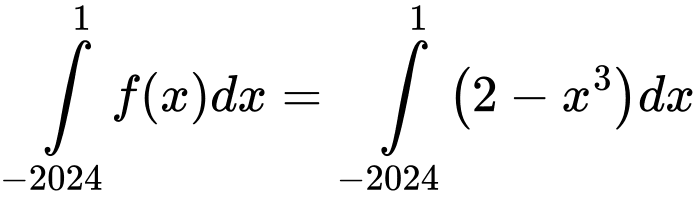
c)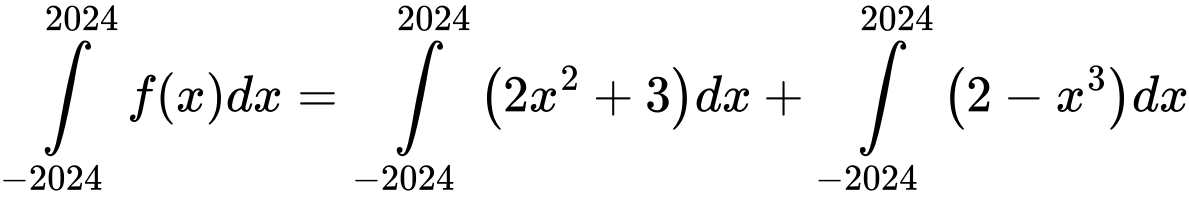
d)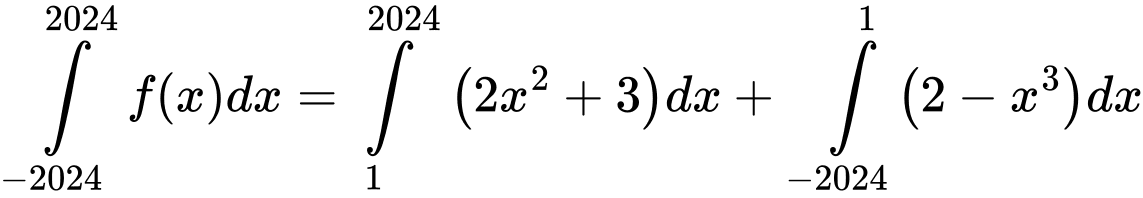
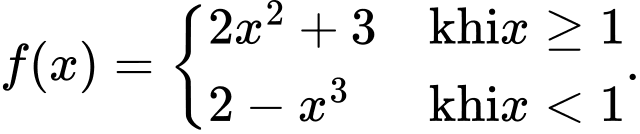 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
a)
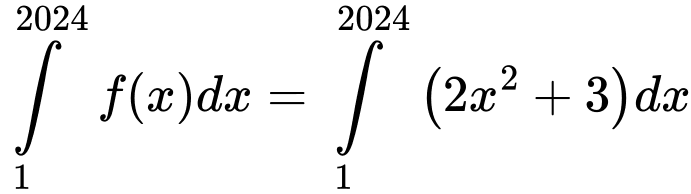
b)
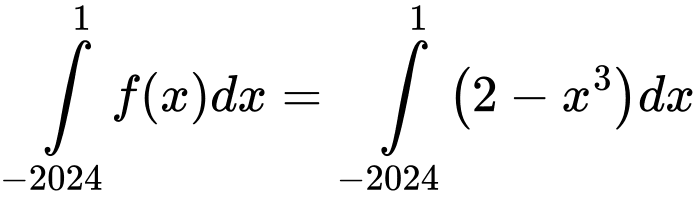
c)
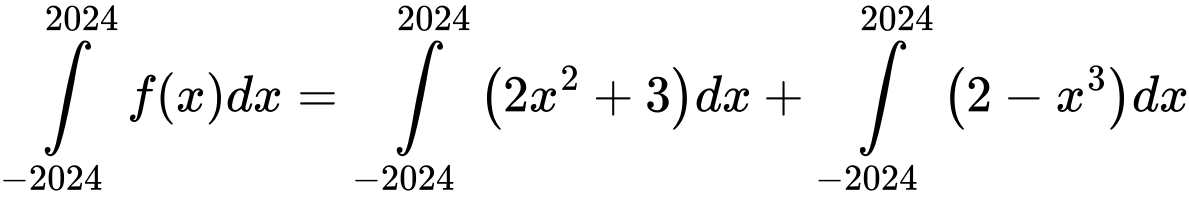
d)
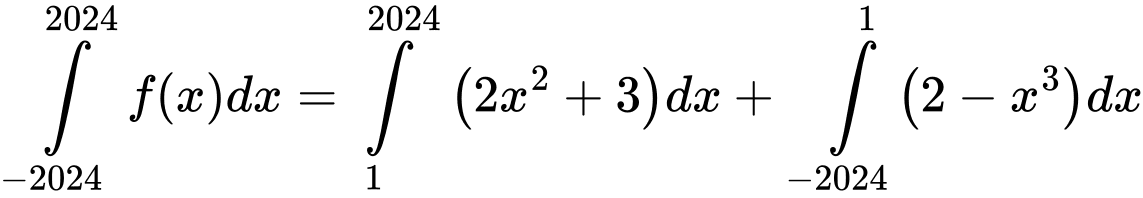
a) Đ
b) Đ
c) S
d) Đ
Do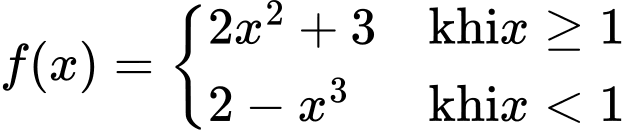 nên
nên
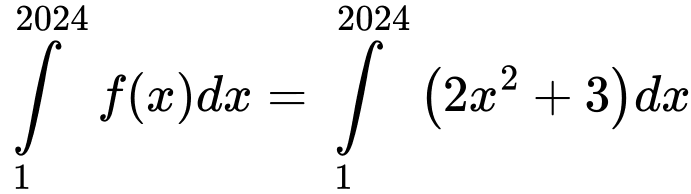
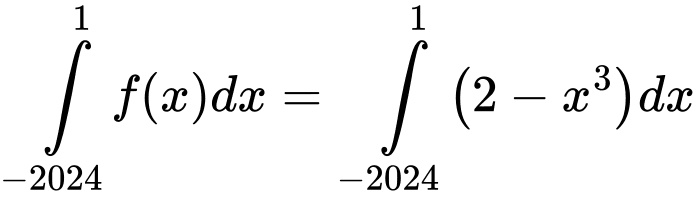
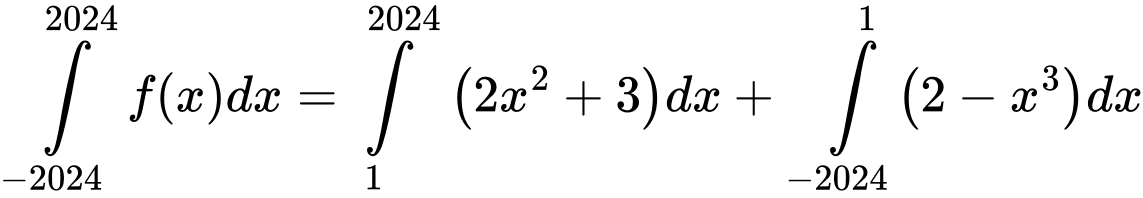
b) Đ
c) S
d) Đ
Do
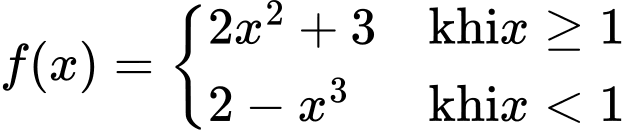 nên
nên
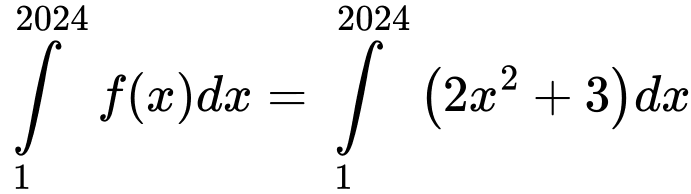
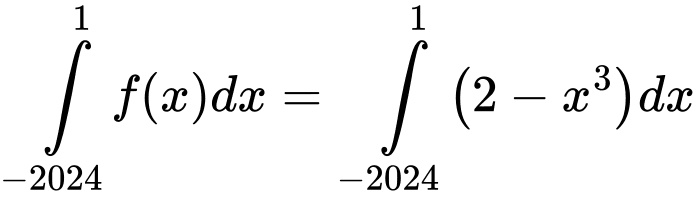
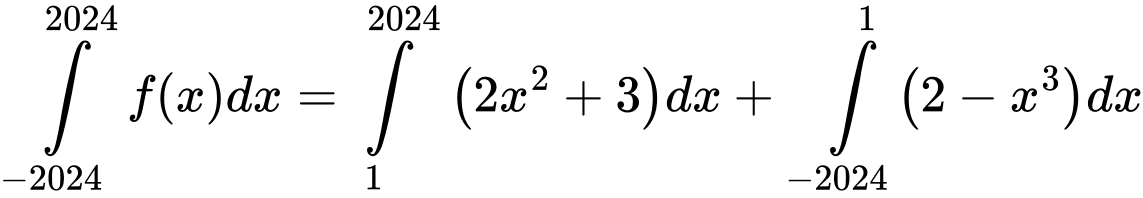
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [580282]: Cho hàm số 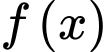 xác định, liên tục trên
xác định, liên tục trên 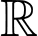 và thoả mãn
và thoả mãn 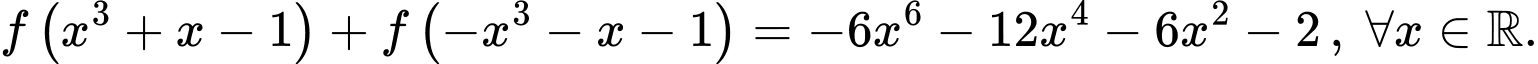 Tính tích phân
Tính tích phân 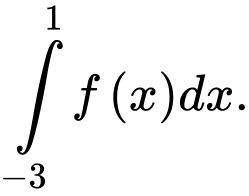
TRẢ LỜI:……………
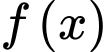 xác định, liên tục trên
xác định, liên tục trên 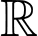 và thoả mãn
và thoả mãn 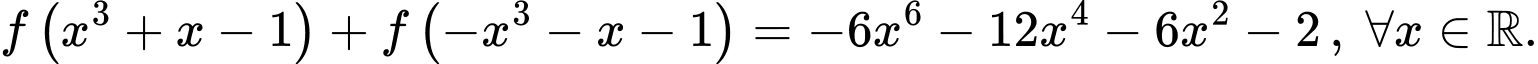 Tính tích phân
Tính tích phân 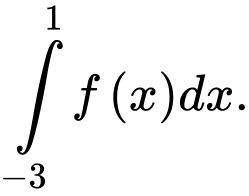
TRẢ LỜI:……………
Đặt 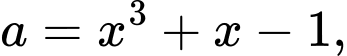 khi đó ta có
khi đó ta có 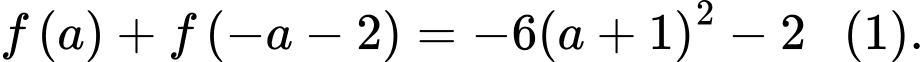 Hàm số
Hàm số 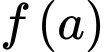 liên tục và xác định trên
liên tục và xác định trên 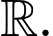
Lúc đó ycbt trở thành tính giá trị của tích phân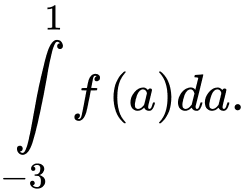
Lấy tích phân hai vế của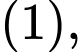 ta được
ta được 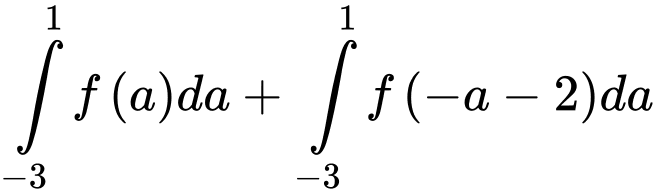
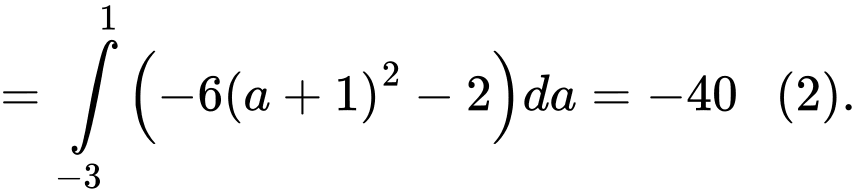
Từ tích phân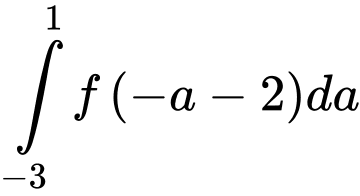 ta đặt
ta đặt 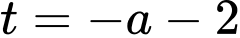

Khi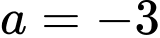
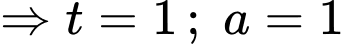

Tích phân trên chuyển thành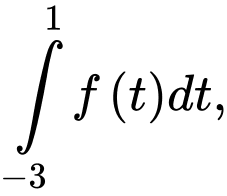 kết hợp với
kết hợp với  ta suy ra:
ta suy ra: 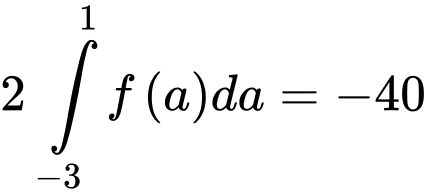
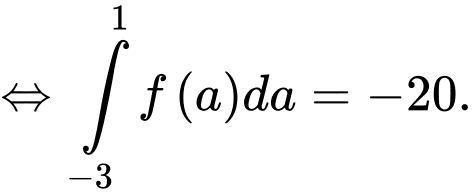
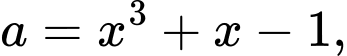 khi đó ta có
khi đó ta có 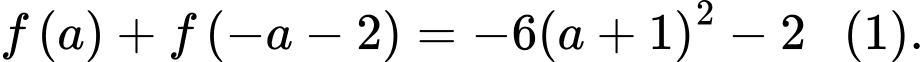 Hàm số
Hàm số 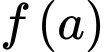 liên tục và xác định trên
liên tục và xác định trên 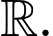
Lúc đó ycbt trở thành tính giá trị của tích phân
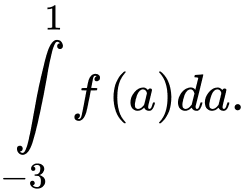
Lấy tích phân hai vế của
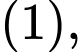 ta được
ta được 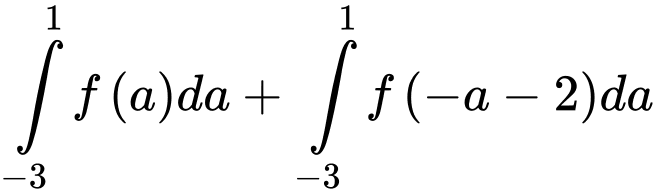
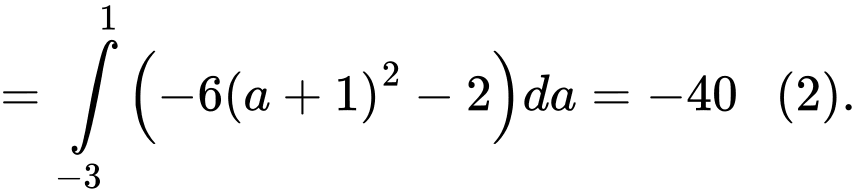
Từ tích phân
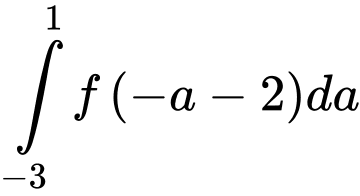 ta đặt
ta đặt 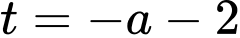

Khi
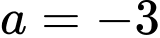
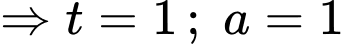

Tích phân trên chuyển thành
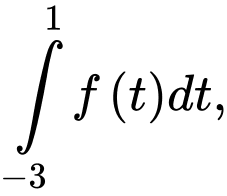 kết hợp với
kết hợp với  ta suy ra:
ta suy ra: 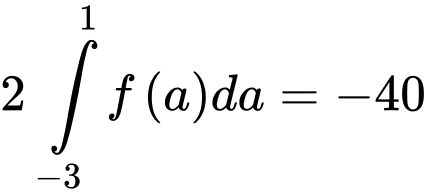
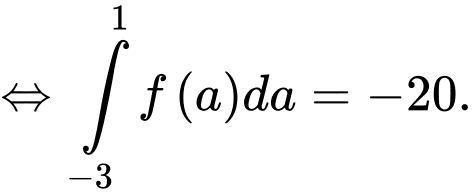
Câu 19 [580283]: Cho hàm số 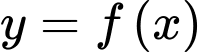 liên tục và có đạo hàm trên
liên tục và có đạo hàm trên 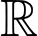 thỏa mãn
thỏa mãn 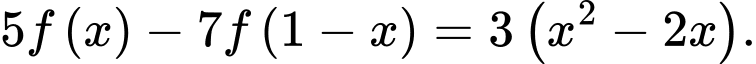 Biết rằng tích phân
Biết rằng tích phân 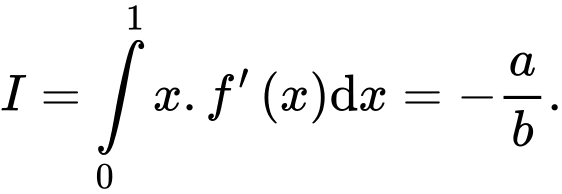 Tính
Tính 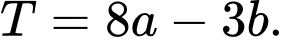
TRẢ LỜI:……………
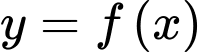 liên tục và có đạo hàm trên
liên tục và có đạo hàm trên  thỏa mãn
thỏa mãn 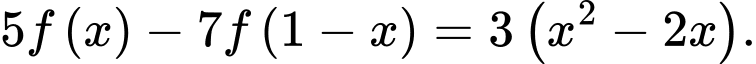 Biết rằng tích phân
Biết rằng tích phân 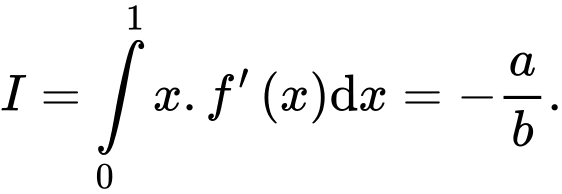 Tính
Tính 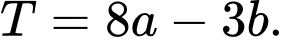
TRẢ LỜI:……………
Ta có: 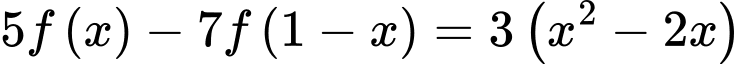
Lần lượt chọn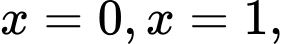 ta có hệ sau:
ta có hệ sau:
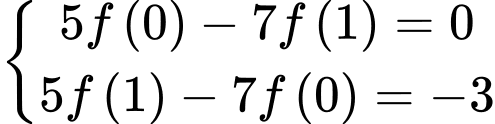
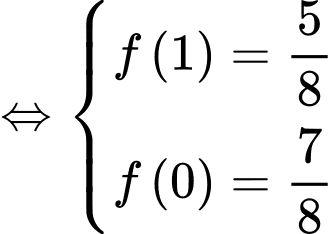
Tính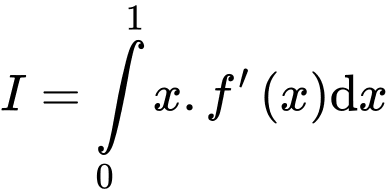
Đặt: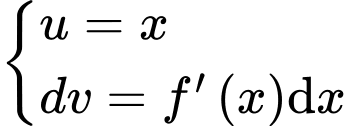
Chọn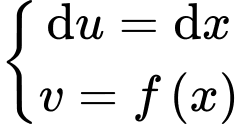
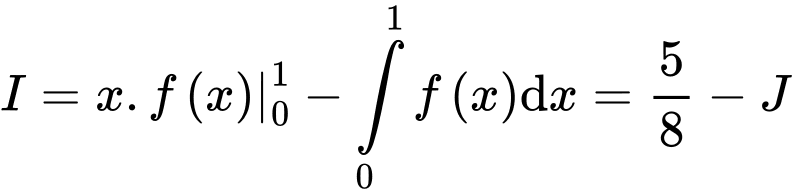
Đặt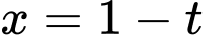
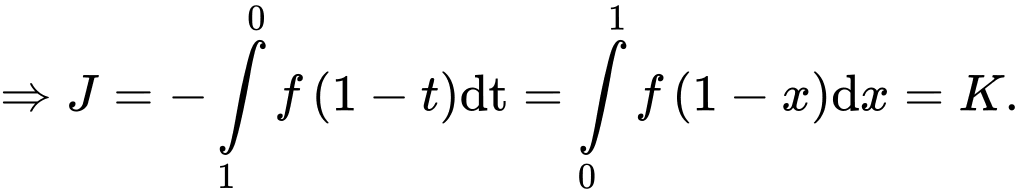
Suy ra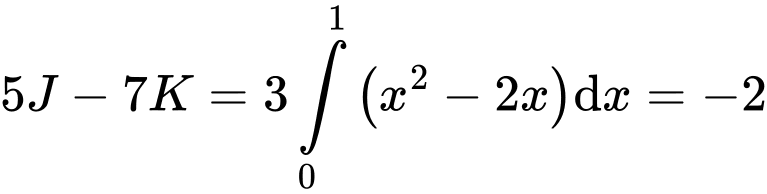
Ta có: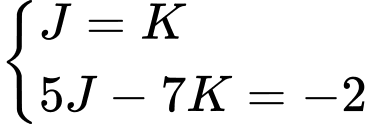
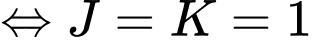
Vậy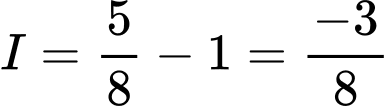
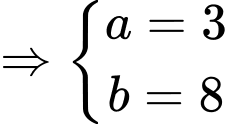
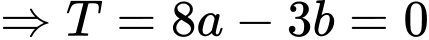
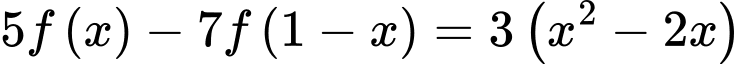
Lần lượt chọn
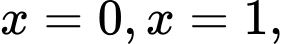 ta có hệ sau:
ta có hệ sau: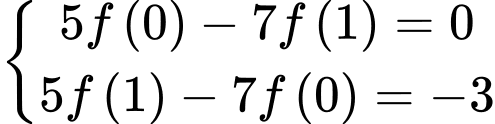
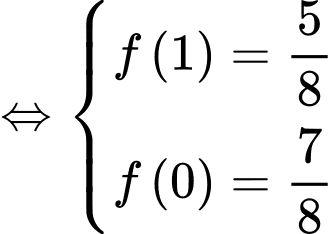
Tính
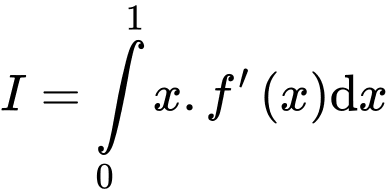
Đặt:
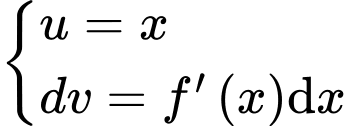
Chọn
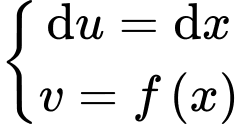
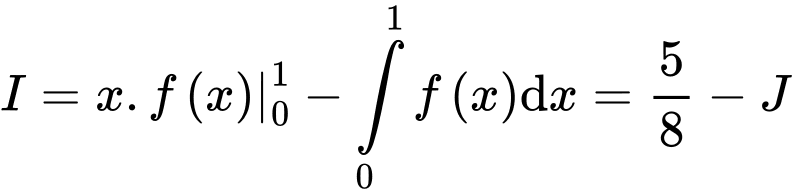
Đặt
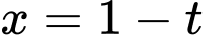
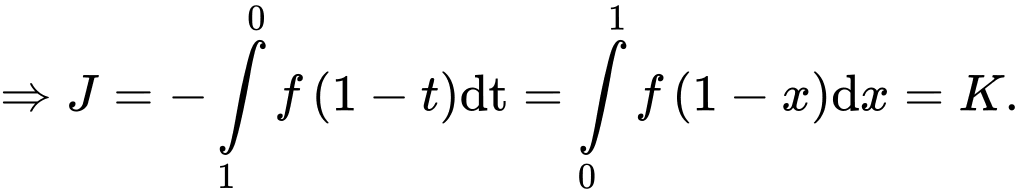
Suy ra
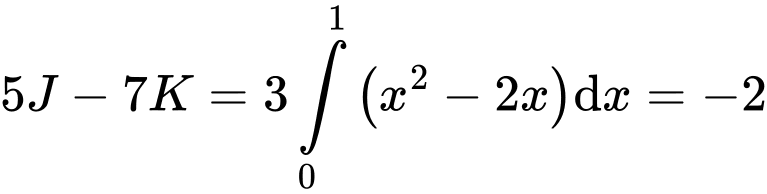
Ta có:
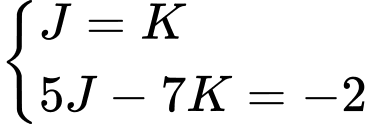
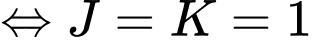
Vậy
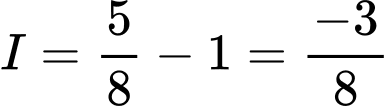
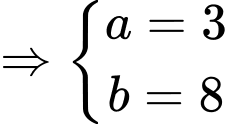
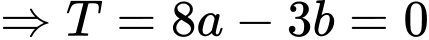
Câu 20 [580284]: Cho hàm số 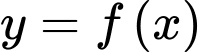 có đạo hàm liên tục trên khoảng
có đạo hàm liên tục trên khoảng  thỏa mãn
thỏa mãn 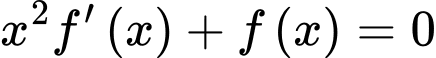 và
và 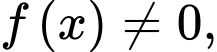
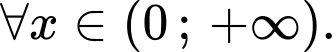 Tính
Tính 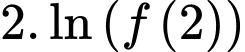 biết
biết 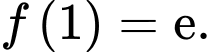
TRẢ LỜI:……………
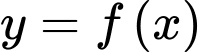 có đạo hàm liên tục trên khoảng
có đạo hàm liên tục trên khoảng  thỏa mãn
thỏa mãn 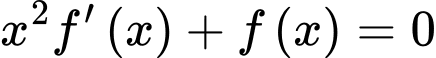 và
và 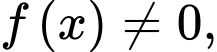
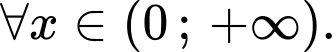 Tính
Tính 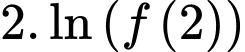 biết
biết 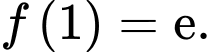
TRẢ LỜI:……………
Ta có 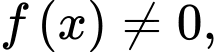
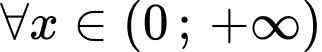
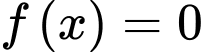 không có nghiệm trên khoảng
không có nghiệm trên khoảng 
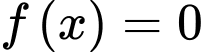 không có nghiệm trên khoảng
không có nghiệm trên khoảng 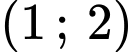
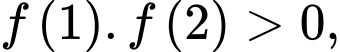
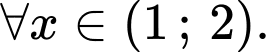
Mà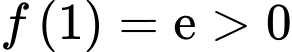 nên
nên 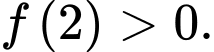
Do đó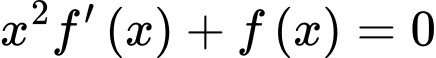

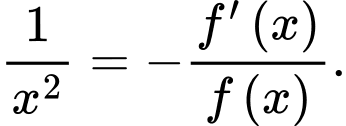
Suy ra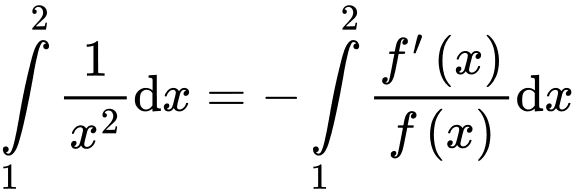

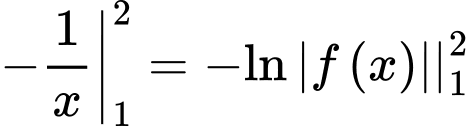

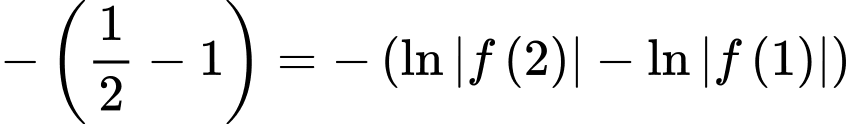

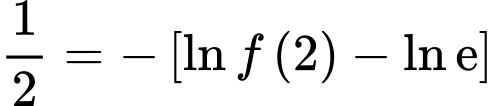

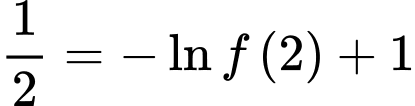

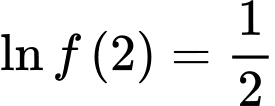

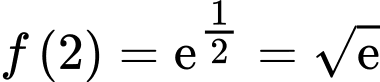
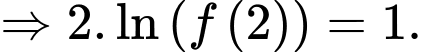
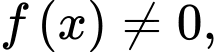
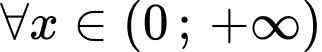
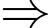
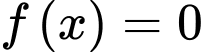 không có nghiệm trên khoảng
không có nghiệm trên khoảng 
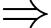
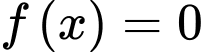 không có nghiệm trên khoảng
không có nghiệm trên khoảng 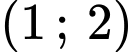
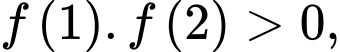
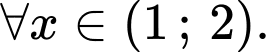
Mà
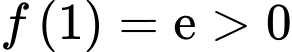 nên
nên 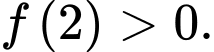
Do đó
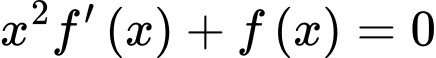

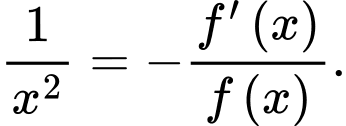
Suy ra