1. Dạng toán: Xác định vectơ chỉ phương của đường phẳng, xác định điểm thuộc và không thuộc đường phẳng
1.1. Phương pháp tư duy
1.2. Ví dụ áp dụng.
1.2. Ví dụ áp dụng.
Câu 1 [581661]: Trong không gian 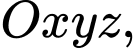 cho đường thẳng
cho đường thẳng 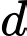 :
: 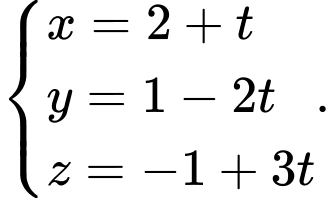 Vectơ nào dưới đây là một vectơ chỉ phương của
Vectơ nào dưới đây là một vectơ chỉ phương của 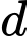 ?
?
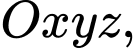 cho đường thẳng
cho đường thẳng 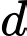 :
: 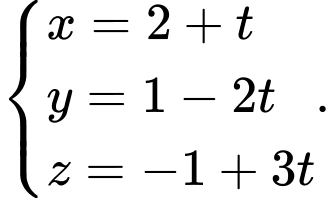 Vectơ nào dưới đây là một vectơ chỉ phương của
Vectơ nào dưới đây là một vectơ chỉ phương của 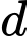 ?
? A, 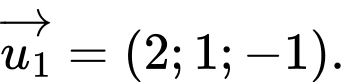
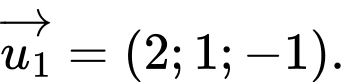
B, 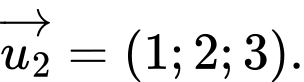
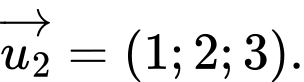
C, 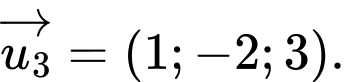
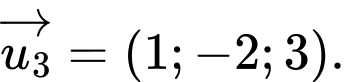
D, 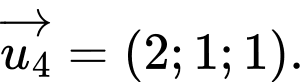
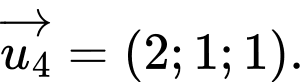
Chọn C.
Từ phương trình đường thẳng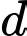 ta thấy vectơ
ta thấy vectơ 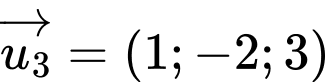 là một vectơ chỉ phương của
là một vectơ chỉ phương của 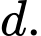 Đáp án: C
Đáp án: C
Từ phương trình đường thẳng
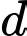 ta thấy vectơ
ta thấy vectơ 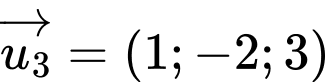 là một vectơ chỉ phương của
là một vectơ chỉ phương của 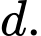 Đáp án: C
Đáp án: C
Câu 2 [581662]: Trong không gian 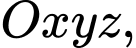 đường thẳng
đường thẳng 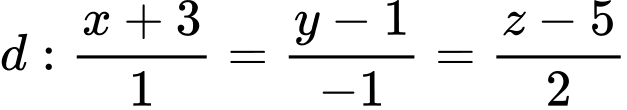 có một vectơ chỉ phương là
có một vectơ chỉ phương là
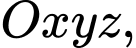 đường thẳng
đường thẳng 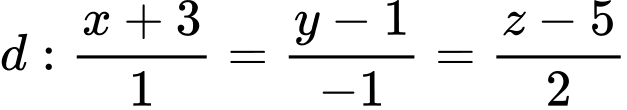 có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 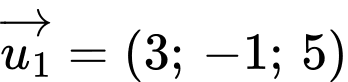
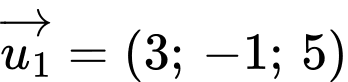
B, 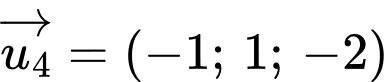
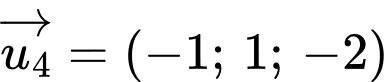
C, 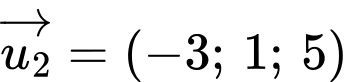
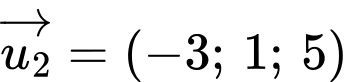
D, 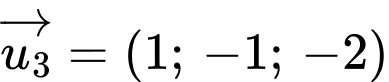
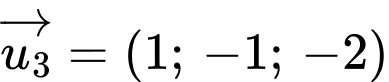
Chọn B
Đường thẳng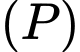 có một vectơ chỉ phương là
có một vectơ chỉ phương là 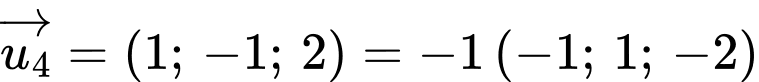
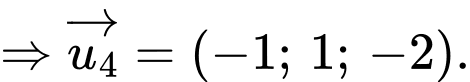 Đáp án: B
Đáp án: B
Đường thẳng
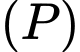 có một vectơ chỉ phương là
có một vectơ chỉ phương là 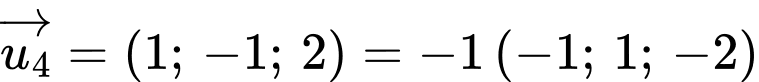
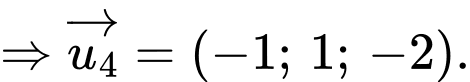 Đáp án: B
Đáp án: B
Câu 3 [581663]: Trong không gian với hệ toạ độ 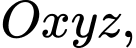 cho hai điểm
cho hai điểm 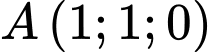 và
và 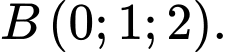 Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng 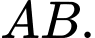
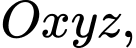 cho hai điểm
cho hai điểm 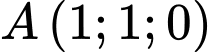 và
và 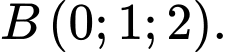 Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng
Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng 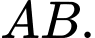
A, 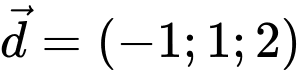
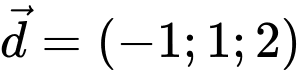
B, 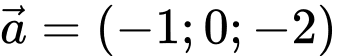
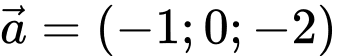
C, 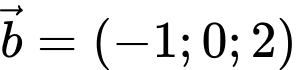
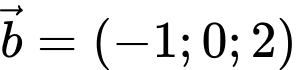
D, 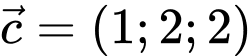
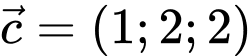
Chọn C
Ta có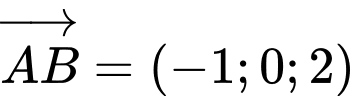 suy ra đường thẳng
suy ra đường thẳng  có VTCP là
có VTCP là 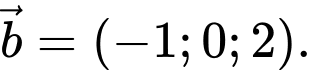 Đáp án: C
Đáp án: C
Ta có
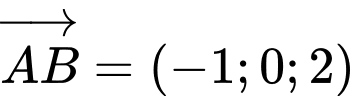 suy ra đường thẳng
suy ra đường thẳng  có VTCP là
có VTCP là 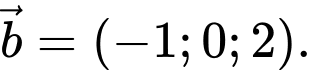 Đáp án: C
Đáp án: C 2. Dạng toán: Xét vị trí tương đối của hai đường thẳng
2.1. Phương pháp tư duy
2.2. Ví dụ áp dụng
2.2. Ví dụ áp dụng
Câu 4 [581664]: Trong không gian với hệ tọa độ 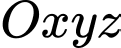 cho hai đường thẳng
cho hai đường thẳng 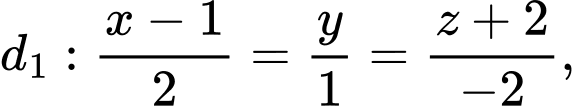
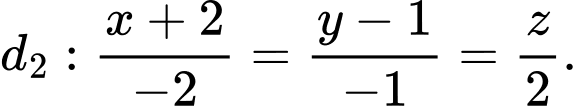 Xét vị trí tương đối của hai đường thẳng đã cho.
Xét vị trí tương đối của hai đường thẳng đã cho.
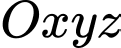 cho hai đường thẳng
cho hai đường thẳng 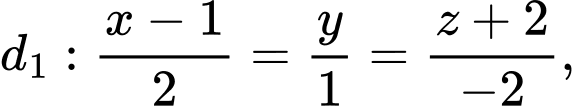
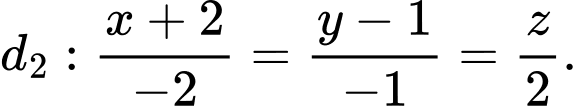 Xét vị trí tương đối của hai đường thẳng đã cho.
Xét vị trí tương đối của hai đường thẳng đã cho. A, Chéo nhau.
B, Trùng nhau.
C, Song song.
D, Cắt nhau.
Chọn C
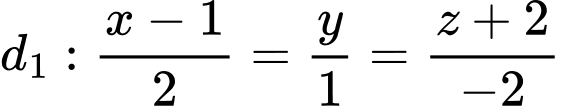
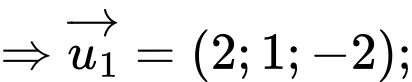
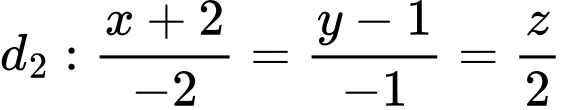

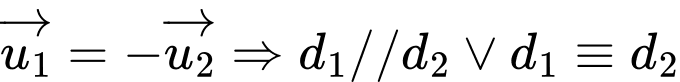
Điểm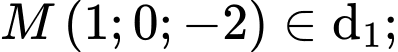
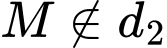 nên
nên Đáp án: C
Đáp án: C
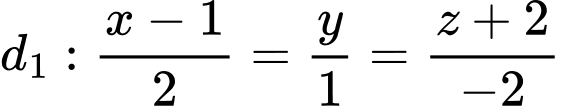
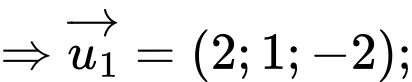
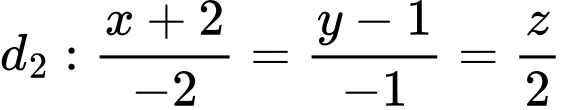

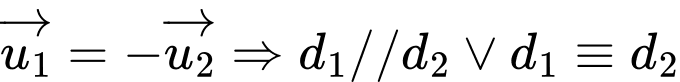
Điểm
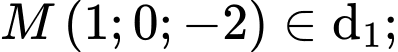
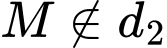 nên
nên Đáp án: C
Đáp án: C
Câu 5 [581665]: Trong không gian 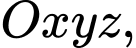 cho hai đường thẳng
cho hai đường thẳng 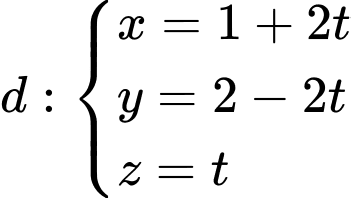 và
và 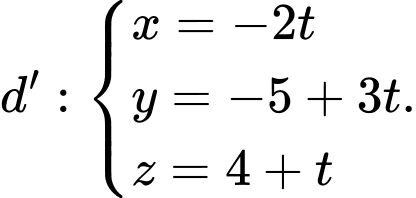 Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các mệnh đề sau, mệnh đề nào đúng?
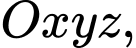 cho hai đường thẳng
cho hai đường thẳng 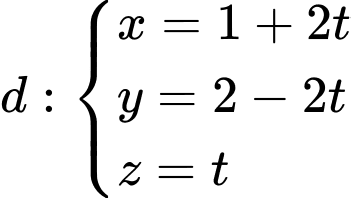 và
và 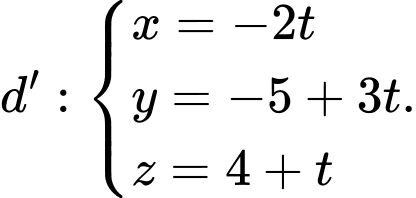 Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các mệnh đề sau, mệnh đề nào đúng? A, song song.
B, trùng nhau.
C, chéo nhau.
D, cắt nhau.
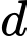 có VTCP
có VTCP 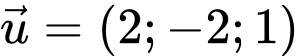 và đi qua
và đi qua 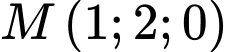
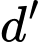 có VTCP
có VTCP 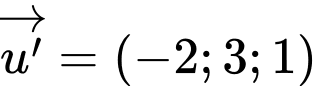 và đi qua
và đi qua 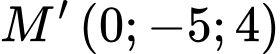
Từ đó ta có
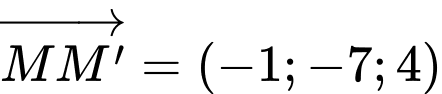 và
và 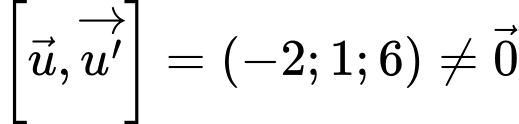
Lại có
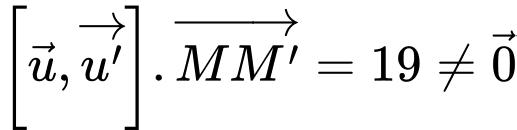
Suy ra
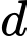 chéo nhau với
chéo nhau với 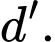 Đáp án: C
Đáp án: C
Câu 6 [581666]: Trong không gian 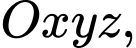 cho hai đường thẳng
cho hai đường thẳng 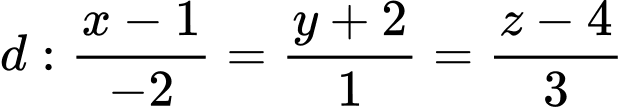 và
và 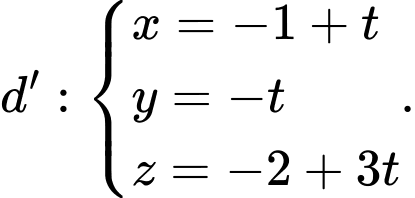 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
a) Tọa độ giao điểm I của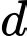 và
và 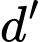 là
là 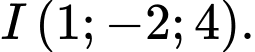
b) Tọa độ giao điểm I của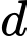 và
và 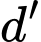 là
là 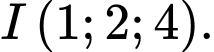
c) Đường thẳng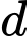 cắt đường thẳng
cắt đường thẳng 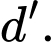
d) Đường thẳng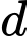 chéo đường thẳng
chéo đường thẳng 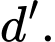
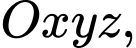 cho hai đường thẳng
cho hai đường thẳng 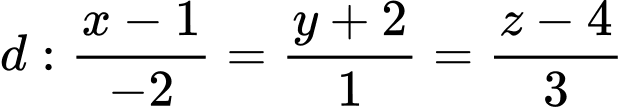 và
và 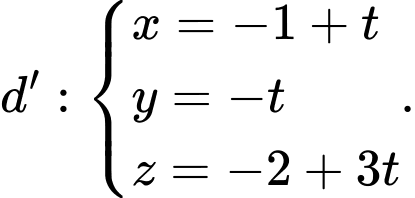 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?a) Tọa độ giao điểm I của
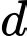 và
và 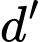 là
là 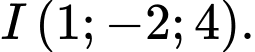
b) Tọa độ giao điểm I của
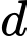 và
và 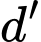 là
là 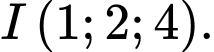
c) Đường thẳng
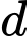 cắt đường thẳng
cắt đường thẳng 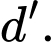
d) Đường thẳng
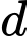 chéo đường thẳng
chéo đường thẳng 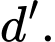
a) Đ
b) S
c) Đ
d) S
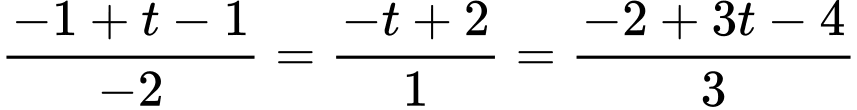
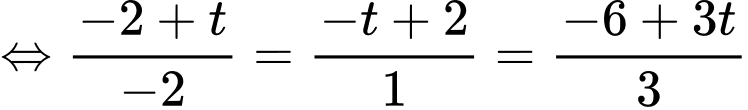
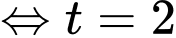
b) S
c) Đ
d) S
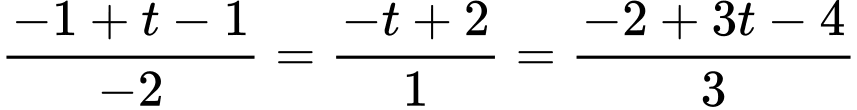
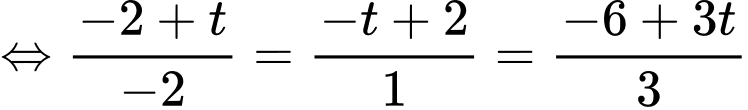
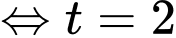
3. Dạng toán: Tính góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng
3.1. Phương pháp tư duy
3.2. Ví dụ áp dụng.
3.2. Ví dụ áp dụng.
Câu 7 [581667]: Gọi 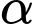 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 
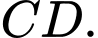 Khẳng định nào sau đây là khẳng định đúng:
Khẳng định nào sau đây là khẳng định đúng:
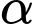 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 
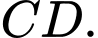 Khẳng định nào sau đây là khẳng định đúng:
Khẳng định nào sau đây là khẳng định đúng: A, 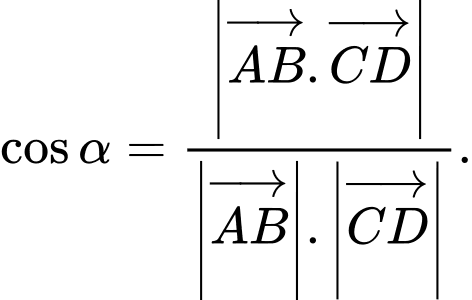
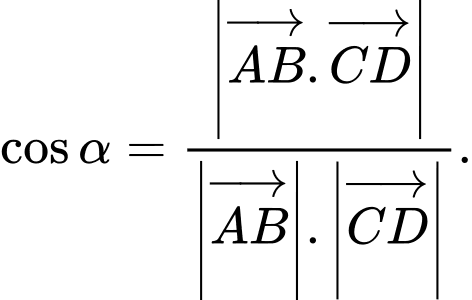
B, 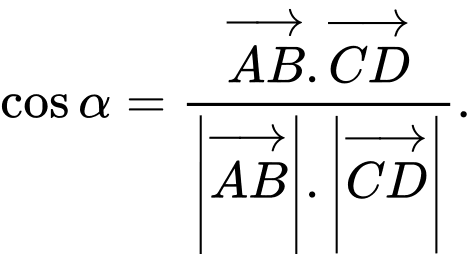
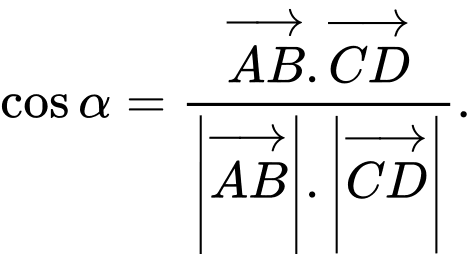
C, 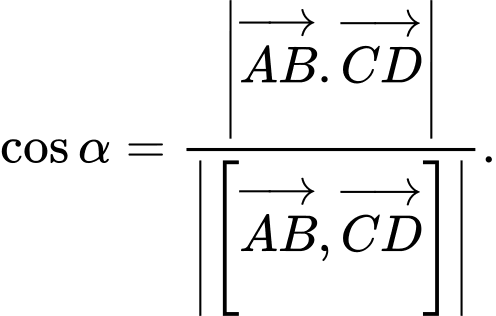
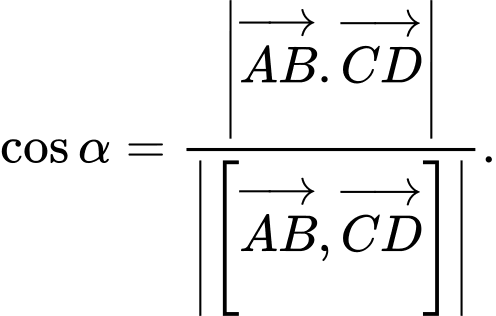
D, 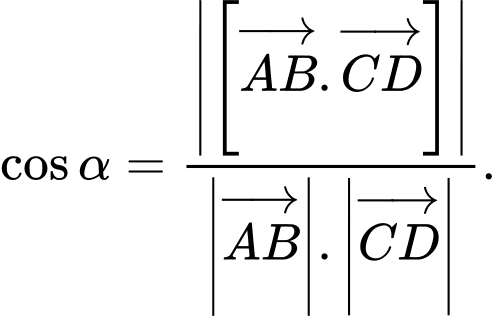
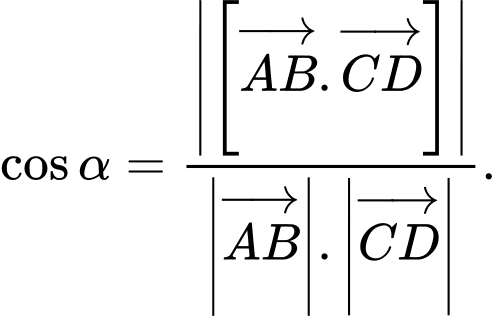
Áp dụng công thức ở lý thuyết. Đáp án: A
Câu 8 [581668]: Cho hai đường thẳng 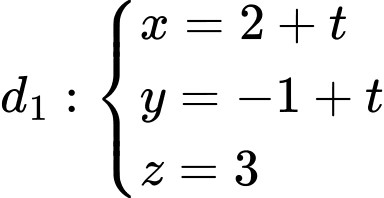 và
và 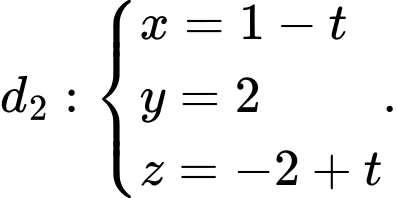 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng 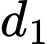 và
và 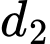 là:
là:
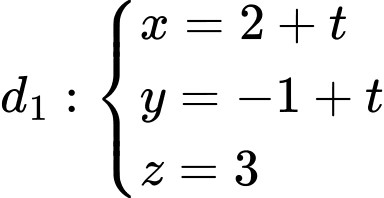 và
và 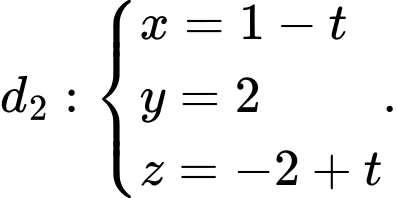 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng 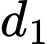 và
và 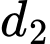 là:
là: A, 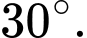
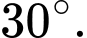
B, 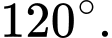
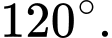
C, 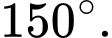
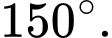
D, 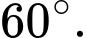
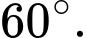
Gọi 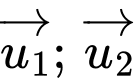 lần lượt là vectơ chỉ phương của đường thẳng
lần lượt là vectơ chỉ phương của đường thẳng 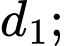
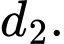
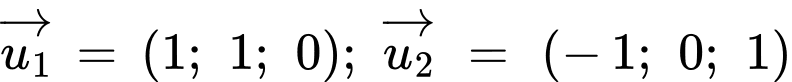
Áp dụng công thức ta có
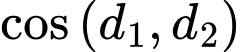
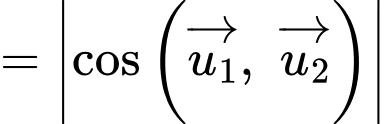
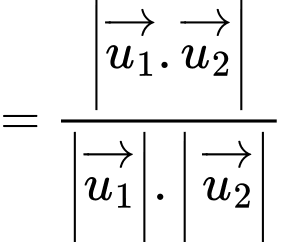
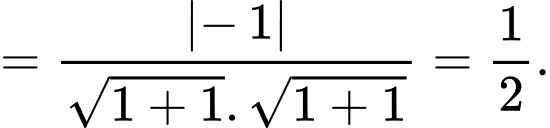
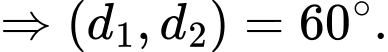 Đáp án: D
Đáp án: D
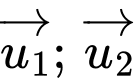 lần lượt là vectơ chỉ phương của đường thẳng
lần lượt là vectơ chỉ phương của đường thẳng 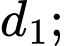
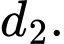
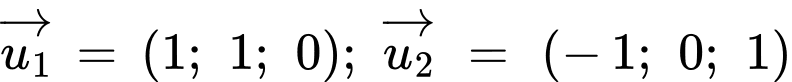
Áp dụng công thức ta có
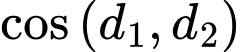
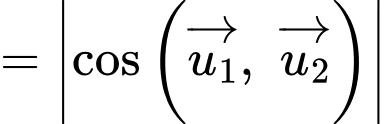
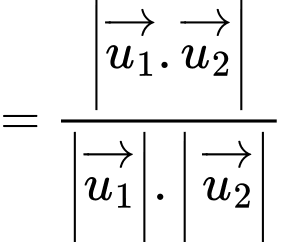
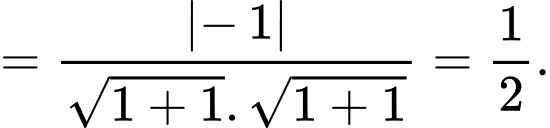
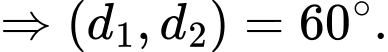 Đáp án: D
Đáp án: D
Câu 9 [581669]: Cho mặt phẳng 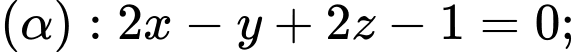
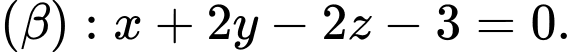 Cosin góc giữa mặt phẳng
Cosin góc giữa mặt phẳng  và mặt phẳng
và mặt phẳng  bằng:
bằng:
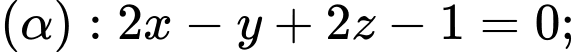
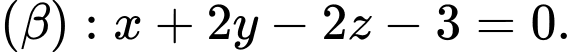 Cosin góc giữa mặt phẳng
Cosin góc giữa mặt phẳng  và mặt phẳng
và mặt phẳng  bằng:
bằng: A, 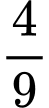
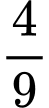
B, 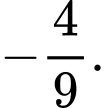
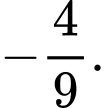
C, 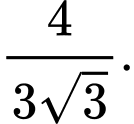
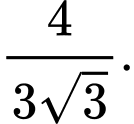
D, 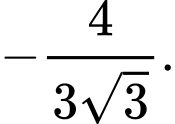
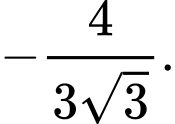
Gọi 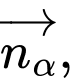
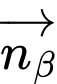 lần lượt là vectơ pháp tuyến của mặt phẳng
lần lượt là vectơ pháp tuyến của mặt phẳng  và
và 
Ta có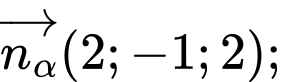
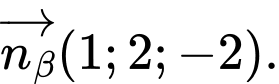
Áp dụng công thức:
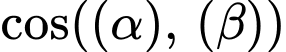
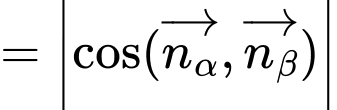
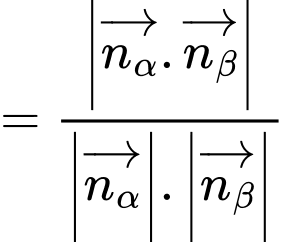
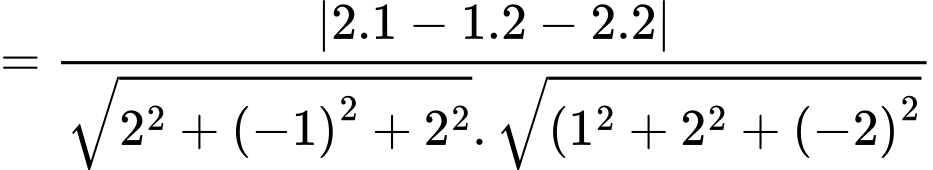
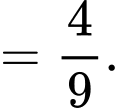 Đáp án: A
Đáp án: A
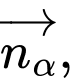
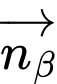 lần lượt là vectơ pháp tuyến của mặt phẳng
lần lượt là vectơ pháp tuyến của mặt phẳng  và
và 
Ta có
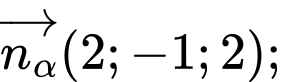
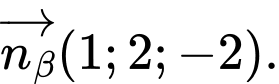
Áp dụng công thức:
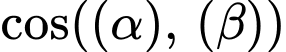
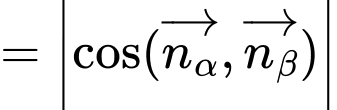
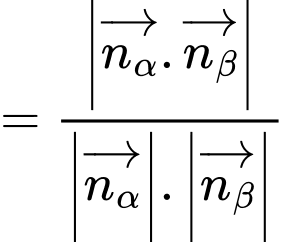
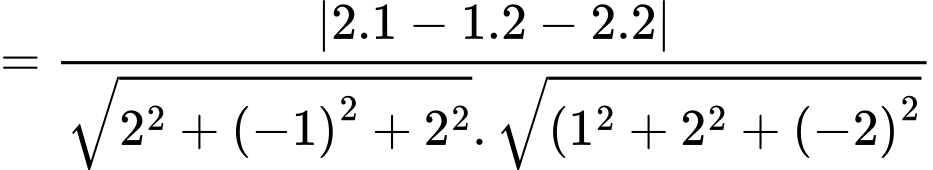
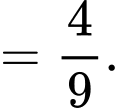 Đáp án: A
Đáp án: A 4. Dạng toán: Lập phương trình đường thẳng dạng cơ bản
4.1. Phương pháp tư duy
4.2. Ví dụ áp dụng.
4.2. Ví dụ áp dụng.
Câu 10 [581670]: Trong không gian 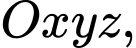 cho đường thẳng
cho đường thẳng 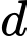 đi qua điểm
đi qua điểm 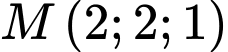 và có một vectơ chỉ phương
và có một vectơ chỉ phương 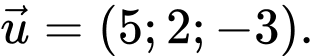 Phương trình của
Phương trình của 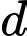 là:
là:
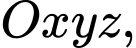 cho đường thẳng
cho đường thẳng 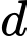 đi qua điểm
đi qua điểm 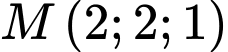 và có một vectơ chỉ phương
và có một vectơ chỉ phương 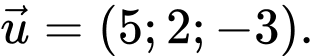 Phương trình của
Phương trình của 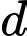 là:
là: A, 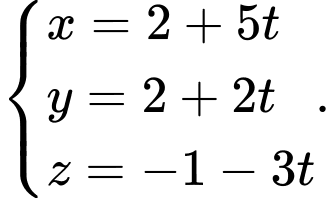
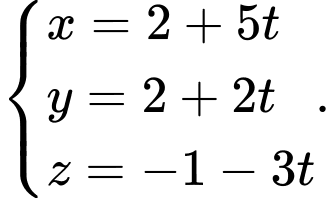
B, 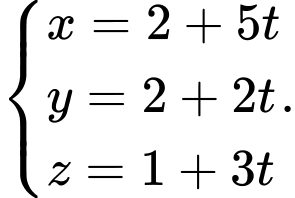
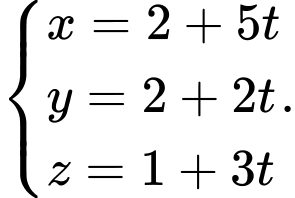
C, 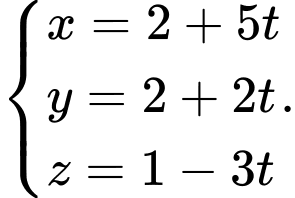
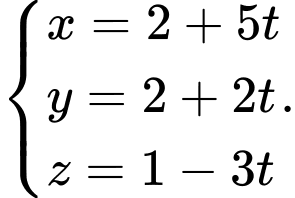
D, 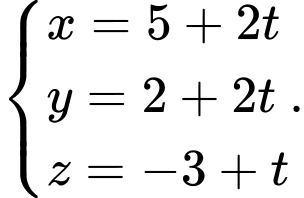
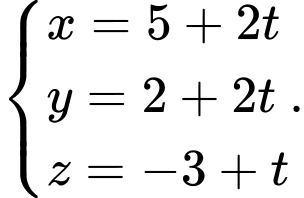
Đường thẳng 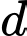 đi qua điểm
đi qua điểm 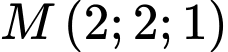 và có một vectơ chỉ phương
và có một vectơ chỉ phương 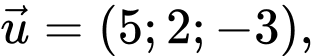 phương trình của
phương trình của 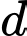 là
là 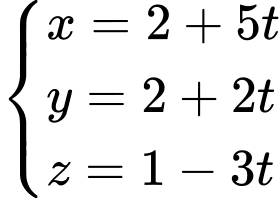 Đáp án: C
Đáp án: C
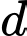 đi qua điểm
đi qua điểm 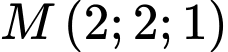 và có một vectơ chỉ phương
và có một vectơ chỉ phương 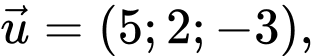 phương trình của
phương trình của 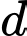 là
là 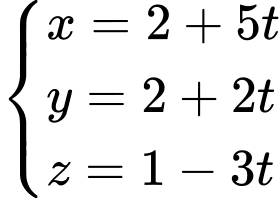 Đáp án: C
Đáp án: C
Câu 11 [581671]: Trong không gian tọa độ 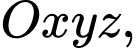 phương trình nào dưới đây là phương trình chính tắc của đường thẳng
phương trình nào dưới đây là phương trình chính tắc của đường thẳng 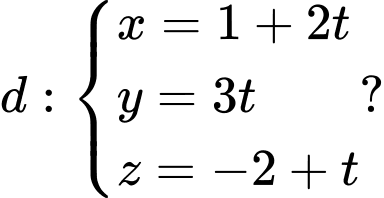
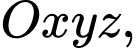 phương trình nào dưới đây là phương trình chính tắc của đường thẳng
phương trình nào dưới đây là phương trình chính tắc của đường thẳng 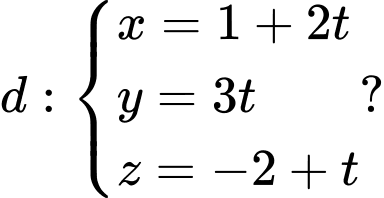
A, 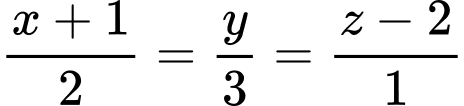
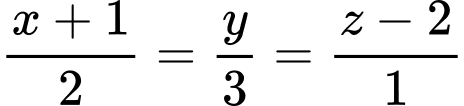
B, 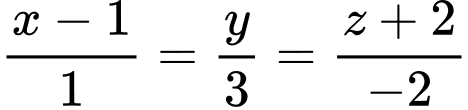
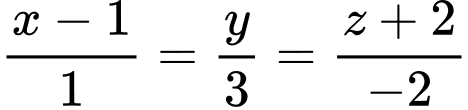
C, 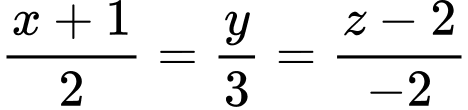
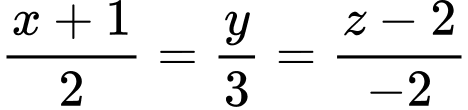
D, 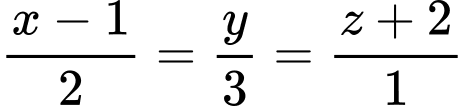
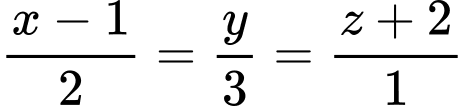
Do đường thẳng 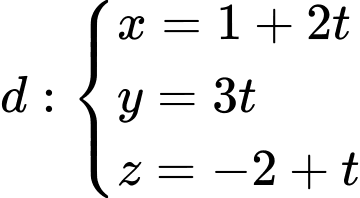 đi qua điểm
đi qua điểm 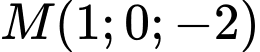 và có vectơ chỉ phương
và có vectơ chỉ phương 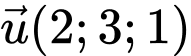 nên có phương trình chính tắc là
nên có phương trình chính tắc là 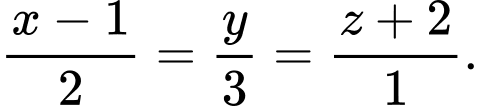 Đáp án: D
Đáp án: D
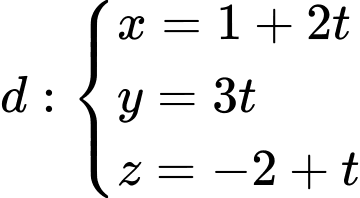 đi qua điểm
đi qua điểm 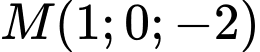 và có vectơ chỉ phương
và có vectơ chỉ phương 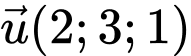 nên có phương trình chính tắc là
nên có phương trình chính tắc là 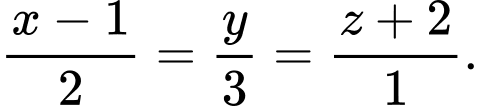 Đáp án: D
Đáp án: D
Câu 12 [581672]: Đường thẳng  là giao tuyến của 2 mặt phẳng:
là giao tuyến của 2 mặt phẳng:  và
và 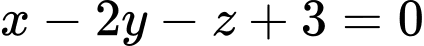 thì có phương trình là
thì có phương trình là
 là giao tuyến của 2 mặt phẳng:
là giao tuyến của 2 mặt phẳng:  và
và 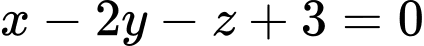 thì có phương trình là
thì có phương trình là A, 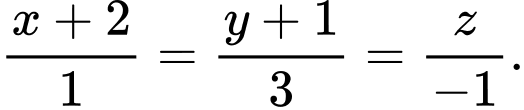
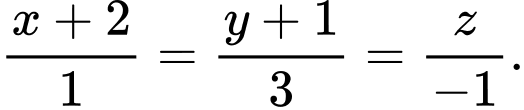
B, 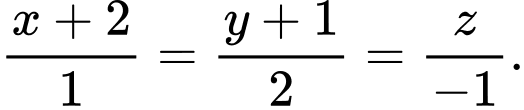
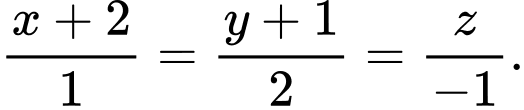
C, 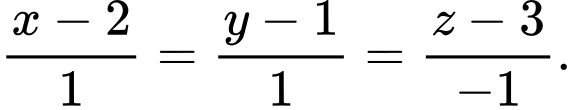
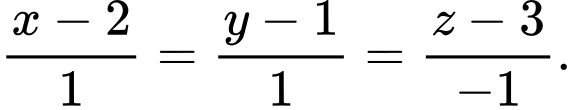
D, 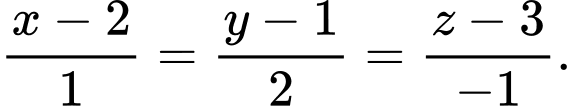
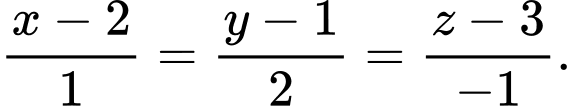
Vì  là giao tuyến của mặt phẳng
là giao tuyến của mặt phẳng 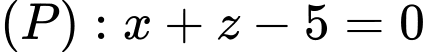 và
và 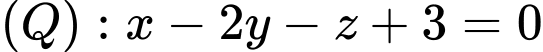 nên:
nên:
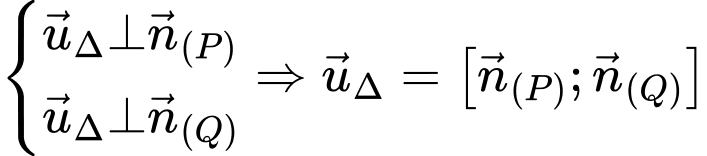
Mà: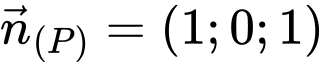 ;
; 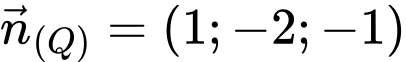
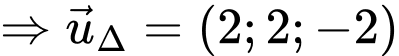
Chọn vecto chỉ phương của đường thẳng là:
là: 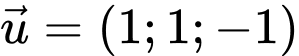
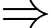 loại A,B,D.
loại A,B,D.
Chọn C.
Chú ý cách tìm phương trình đường thẳng :
:
Gọi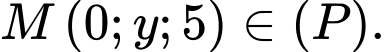 Để
Để 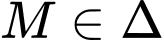 thì
thì 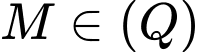
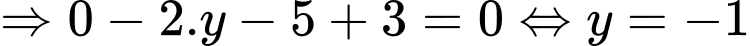
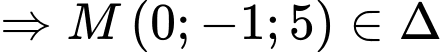
Phương trình đường thẳng đi qua
đi qua 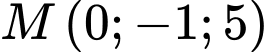 có VTCP
có VTCP 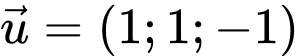 là:
là:
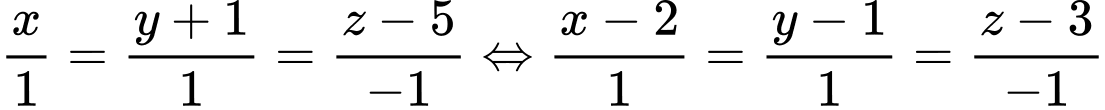 Đáp án: C
Đáp án: C
 là giao tuyến của mặt phẳng
là giao tuyến của mặt phẳng 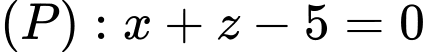 và
và 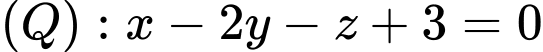 nên:
nên:
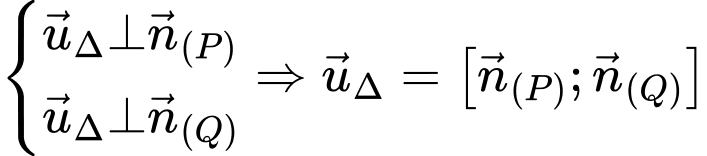
Mà:
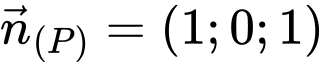 ;
; 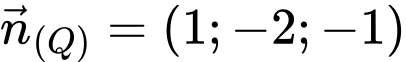
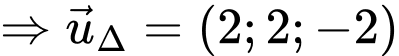
Chọn vecto chỉ phương của đường thẳng
 là:
là: 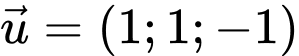
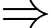 loại A,B,D.
loại A,B,D.
Chọn C.
Chú ý cách tìm phương trình đường thẳng
 :
:
Gọi
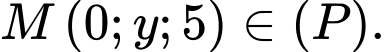 Để
Để 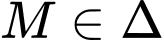 thì
thì 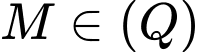
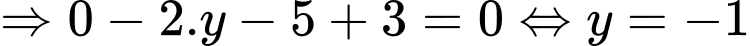
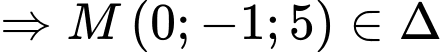
Phương trình đường thẳng
 đi qua
đi qua 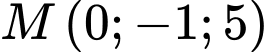 có VTCP
có VTCP 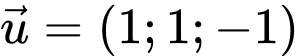 là:
là:
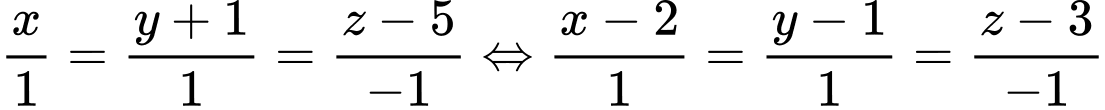 Đáp án: C
Đáp án: C 5. Dạng toán: Lập phương trình đường thẳng liên quan đến song song và vuông góc
5.1. Phương pháp tư duy
5.2. Ví dụ áp dụng.
5.2. Ví dụ áp dụng.
Câu 13 [581673]: Trong không gian 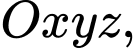 cho điểm
cho điểm 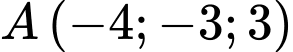 và mặt phẳng
và mặt phẳng 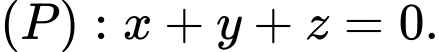 Đường thẳng đi qua
Đường thẳng đi qua 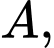 cắt trục
cắt trục  và song song với
và song song với 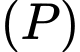 có phương trình là
có phương trình là
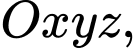 cho điểm
cho điểm 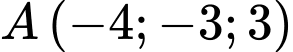 và mặt phẳng
và mặt phẳng 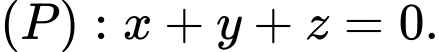 Đường thẳng đi qua
Đường thẳng đi qua 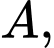 cắt trục
cắt trục  và song song với
và song song với 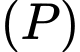 có phương trình là
có phương trình là A, 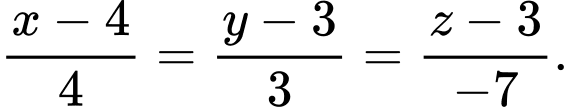
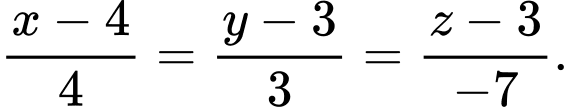
B, 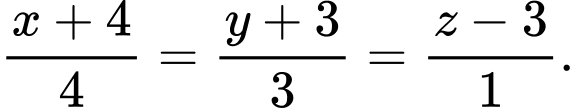
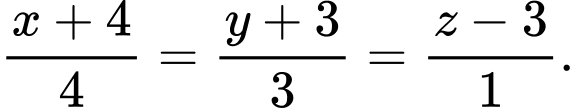
C, 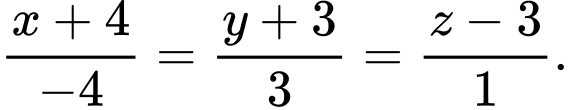
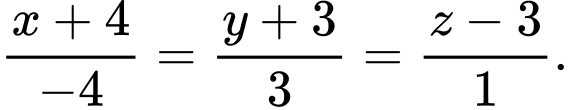
D, 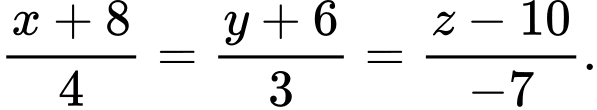
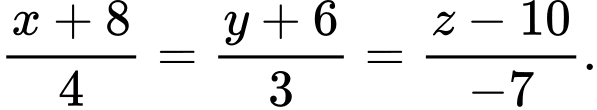
Gọi  là đường thẳng cần lập.
là đường thẳng cần lập.
Mặt phẳng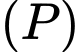 có một VTPT
có một VTPT 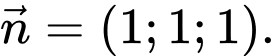
Theo đề, ta có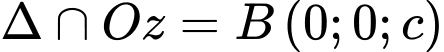
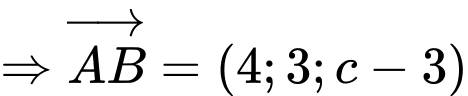 là một VTCP của
là một VTCP của 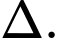
Khi đó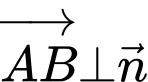
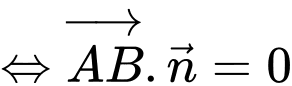
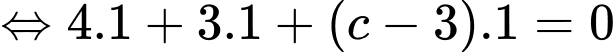
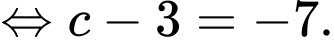
Suy ra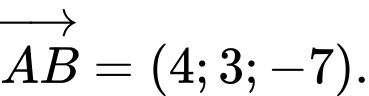
Vậy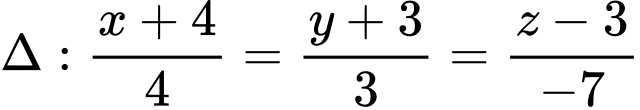 hay
hay 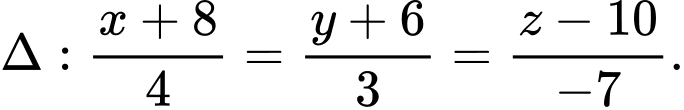 Đáp án: D
Đáp án: D
 là đường thẳng cần lập.
là đường thẳng cần lập.
Mặt phẳng
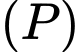 có một VTPT
có một VTPT 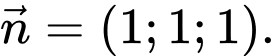
Theo đề, ta có
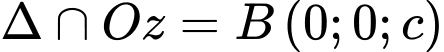
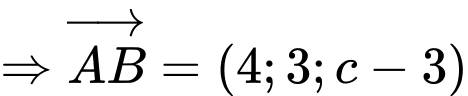 là một VTCP của
là một VTCP của 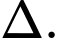
Khi đó
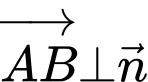
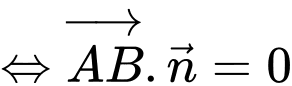
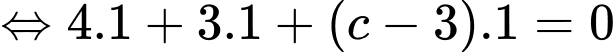
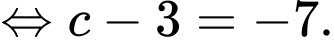
Suy ra
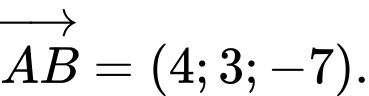
Vậy
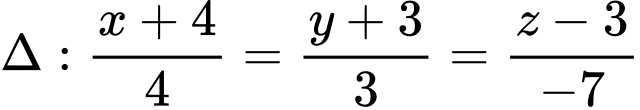 hay
hay 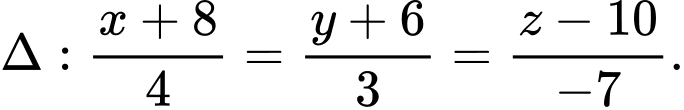 Đáp án: D
Đáp án: D
Câu 14 [581674]: Trong không gian 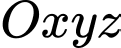 cho
cho 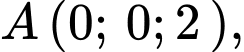
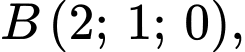
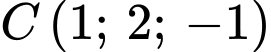 và
và 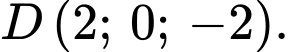 Đường thẳng đi qua
Đường thẳng đi qua 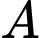 và vuông góc với
và vuông góc với 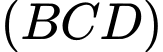 có phương trình là
có phương trình là
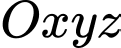 cho
cho 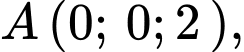
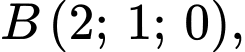
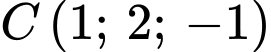 và
và 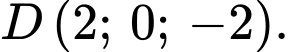 Đường thẳng đi qua
Đường thẳng đi qua 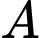 và vuông góc với
và vuông góc với 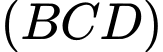 có phương trình là
có phương trình là A, 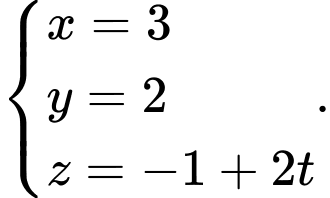
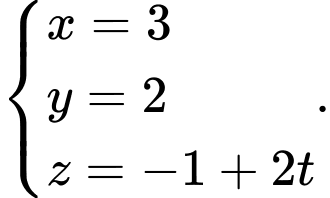
B, 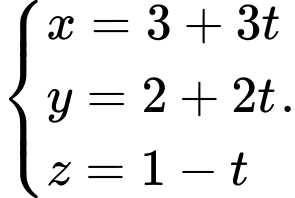
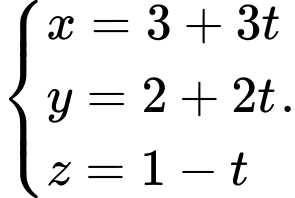
C, 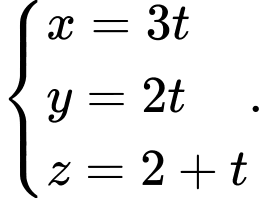
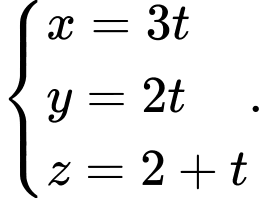
D, 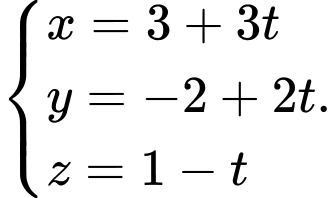
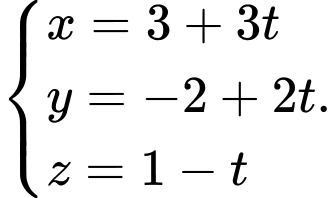
Gọi 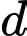 là đường thẳng đi qua
là đường thẳng đi qua 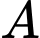 và vuông góc với
và vuông góc với 
Ta có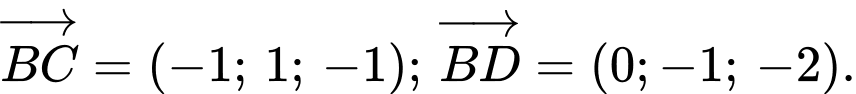
Mặt phẳng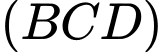 có vectơ pháp tuyến là
có vectơ pháp tuyến là 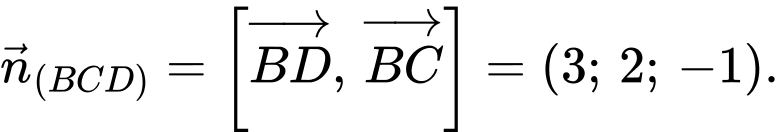
Gọi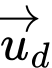 là vectơ chỉ phương của đường thẳng
là vectơ chỉ phương của đường thẳng 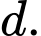
Vì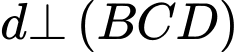 nên
nên 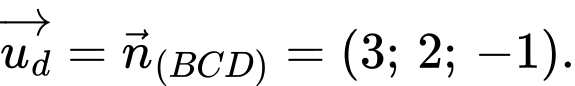
Đáp A và C có VTCP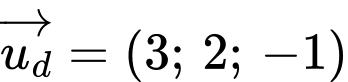 nên loại B và D.
nên loại B và D.
Ta thấy điểm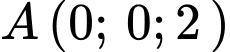 thuộc đáp án C nên loại A. Đáp án: B
thuộc đáp án C nên loại A. Đáp án: B
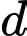 là đường thẳng đi qua
là đường thẳng đi qua 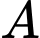 và vuông góc với
và vuông góc với 
Ta có
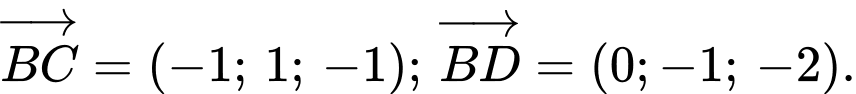
Mặt phẳng
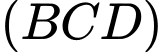 có vectơ pháp tuyến là
có vectơ pháp tuyến là 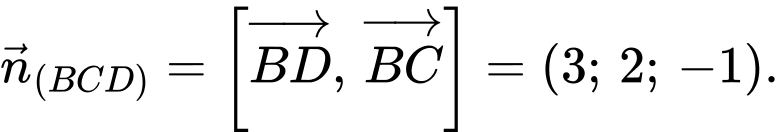
Gọi
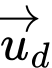 là vectơ chỉ phương của đường thẳng
là vectơ chỉ phương của đường thẳng 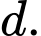
Vì
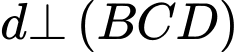 nên
nên 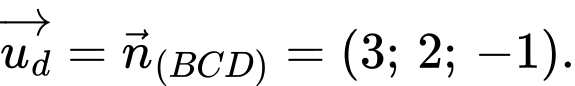
Đáp A và C có VTCP
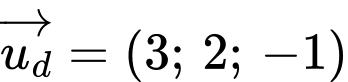 nên loại B và D.
nên loại B và D.Ta thấy điểm
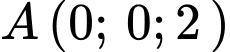 thuộc đáp án C nên loại A. Đáp án: B
thuộc đáp án C nên loại A. Đáp án: B
Câu 15 [581675]: Trong không gian với hệ toạ độ 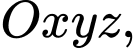 cho điểm
cho điểm 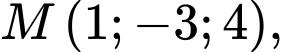 đường thẳng
đường thẳng 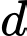 có phương trình:
có phương trình: 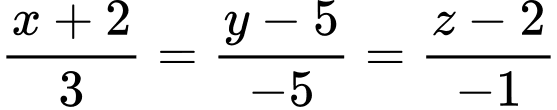 và mặt phẳng
và mặt phẳng 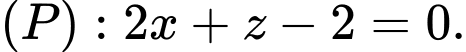 Viết phương trình đường thẳng
Viết phương trình đường thẳng  qua
qua 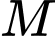 vuông góc với
vuông góc với 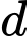 và song song với
và song song với 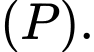
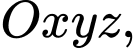 cho điểm
cho điểm 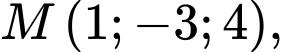 đường thẳng
đường thẳng 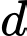 có phương trình:
có phương trình: 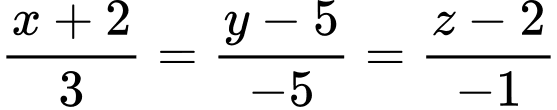 và mặt phẳng
và mặt phẳng 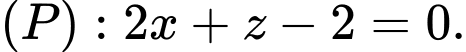 Viết phương trình đường thẳng
Viết phương trình đường thẳng  qua
qua 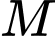 vuông góc với
vuông góc với 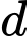 và song song với
và song song với 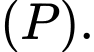
A, 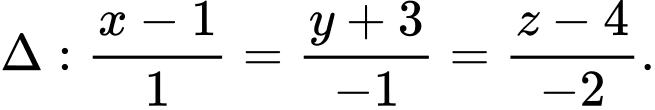
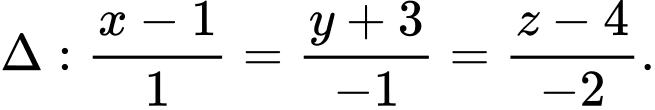
B, 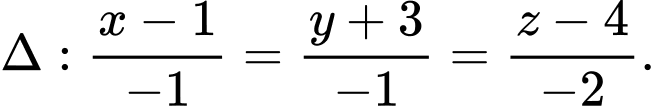
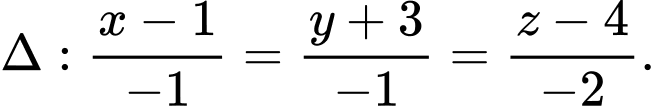
C, 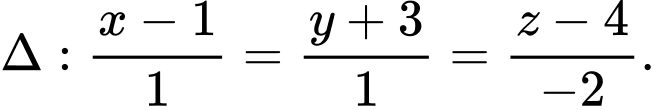
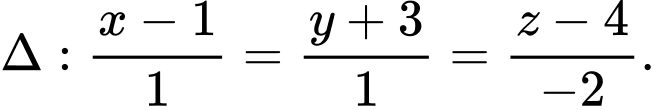
D, 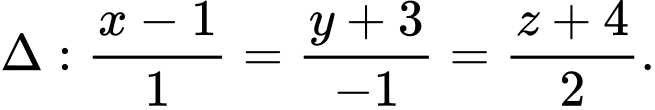
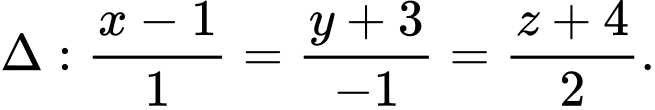
Ta có 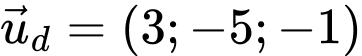 là vectơ chỉ phương của
là vectơ chỉ phương của 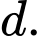
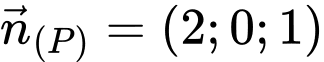 là vectơ pháp tuyến của
là vectơ pháp tuyến của 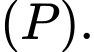
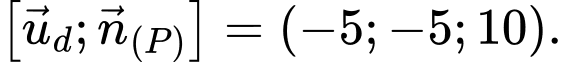
Do vuông góc với
vuông góc với 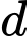 và song song với
và song song với 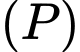 nên
nên 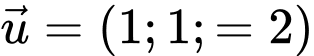 là vectơ chỉ phương của
là vectơ chỉ phương của 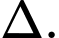
Khi đó, phương trình của là
là 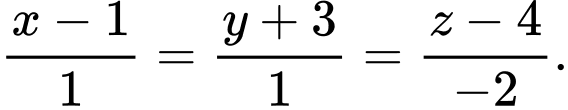 Đáp án: C
Đáp án: C
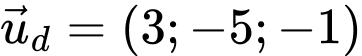 là vectơ chỉ phương của
là vectơ chỉ phương của 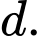
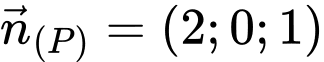 là vectơ pháp tuyến của
là vectơ pháp tuyến của 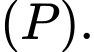
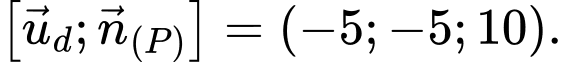
Do
 vuông góc với
vuông góc với 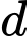 và song song với
và song song với 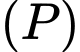 nên
nên 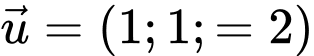 là vectơ chỉ phương của
là vectơ chỉ phương của 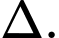
Khi đó, phương trình của
 là
là 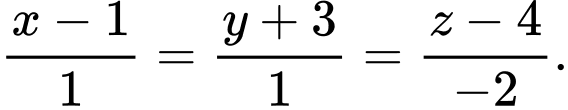 Đáp án: C
Đáp án: C 6. Dạng toán: Phương trình đường thẳng liên quan đến điểm đối xứng và hình chiếu
6.1. Phương pháp tư duy
6.2. Ví dụ áp dụng.
6.2. Ví dụ áp dụng.
Câu 16 [581676]: Trong không gian 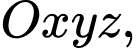 khoảng cách từ điểm
khoảng cách từ điểm 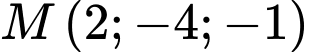 tới đường thẳng
tới đường thẳng 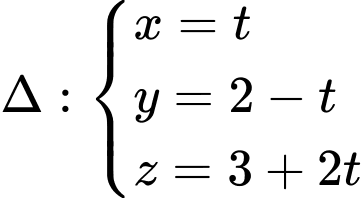 bằng
bằng
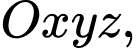 khoảng cách từ điểm
khoảng cách từ điểm 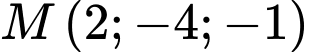 tới đường thẳng
tới đường thẳng 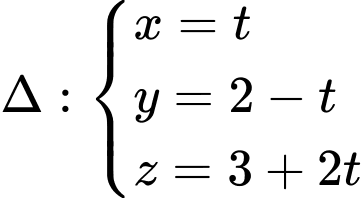 bằng
bằng A, 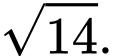
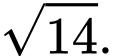
B, 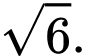
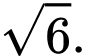
C, 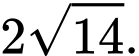
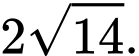
D, 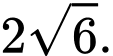
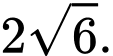
Đường thẳng  đi qua
đi qua 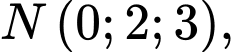 có vectơ chỉ phương
có vectơ chỉ phương 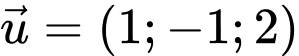
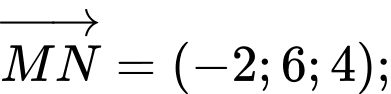
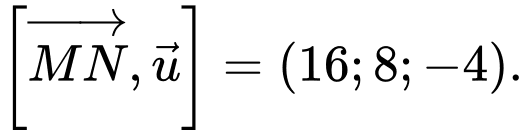
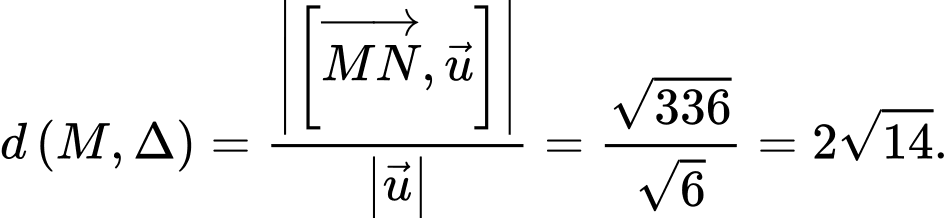 Đáp án: C
Đáp án: C
 đi qua
đi qua 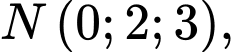 có vectơ chỉ phương
có vectơ chỉ phương 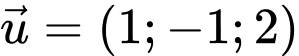
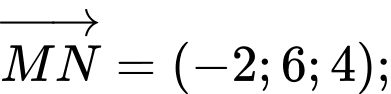
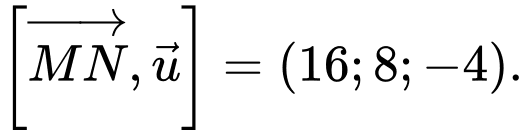
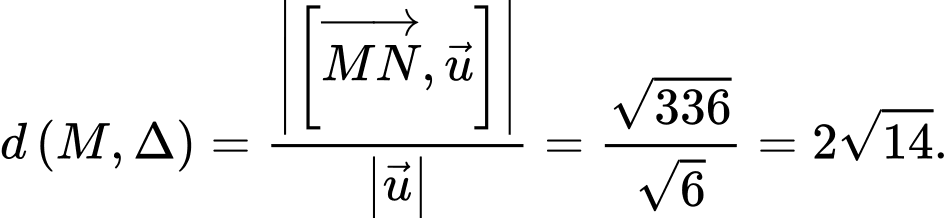 Đáp án: C
Đáp án: C
Câu 17 [581677]: Trong không gian 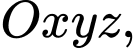 tọa độ hình chiếu vuông góc của
tọa độ hình chiếu vuông góc của 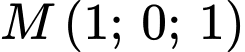 lên đường thẳng
lên đường thẳng 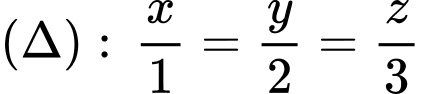 là
là
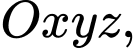 tọa độ hình chiếu vuông góc của
tọa độ hình chiếu vuông góc của 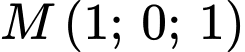 lên đường thẳng
lên đường thẳng 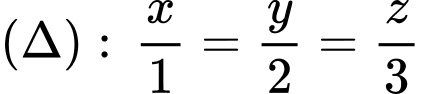 là
là A, 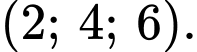
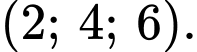
B, 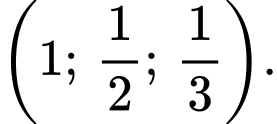
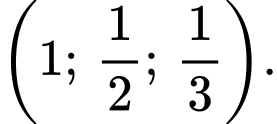
C, 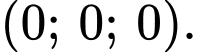
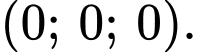
D, 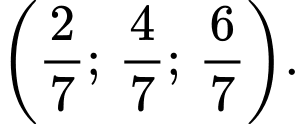
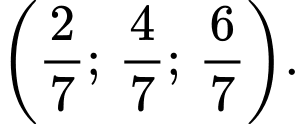
Đường thẳng  có vtcp
có vtcp 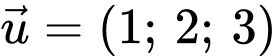 và có phương trình tham số là:
và có phương trình tham số là: 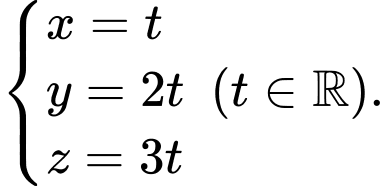
Gọi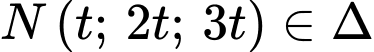 là hình chiếu vuông góc của
là hình chiếu vuông góc của 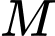 lên
lên 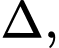 khi đó:
khi đó:
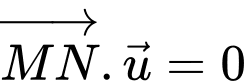
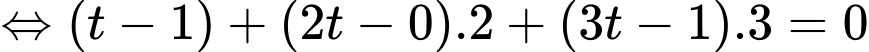
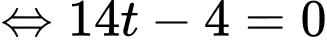
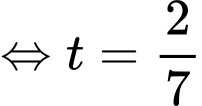
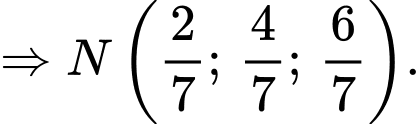 Đáp án: D
Đáp án: D
 có vtcp
có vtcp 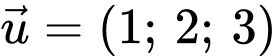 và có phương trình tham số là:
và có phương trình tham số là: 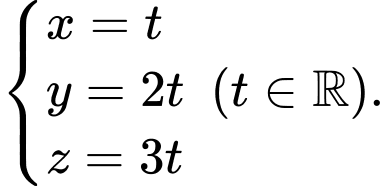
Gọi
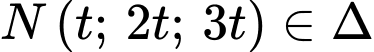 là hình chiếu vuông góc của
là hình chiếu vuông góc của 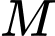 lên
lên 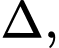 khi đó:
khi đó:
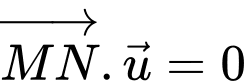
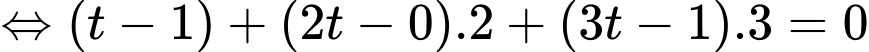
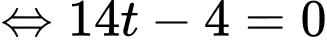
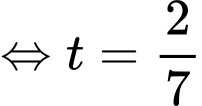
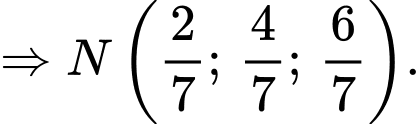 Đáp án: D
Đáp án: D
Câu 18 [581678]: Trong không gian 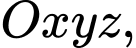 tọa độ hình chiếu vuông góc của điểm
tọa độ hình chiếu vuông góc của điểm 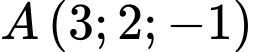 lên mặt phẳng
lên mặt phẳng 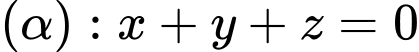 là:
là:
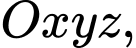 tọa độ hình chiếu vuông góc của điểm
tọa độ hình chiếu vuông góc của điểm 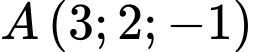 lên mặt phẳng
lên mặt phẳng 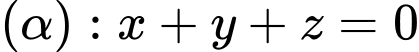 là:
là: A, 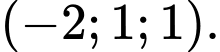
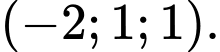
B, 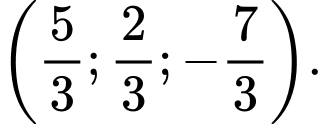
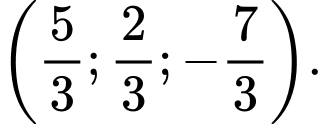
C, 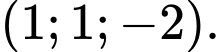
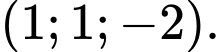
D, 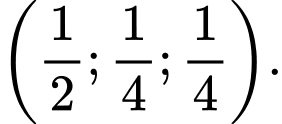
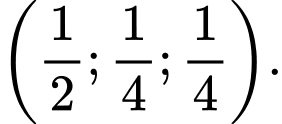
Gọi 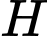 là hình chiếu của
là hình chiếu của 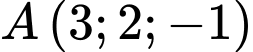 lên mặt phẳng
lên mặt phẳng 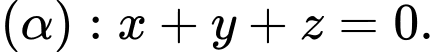 Khi đó:
Khi đó: 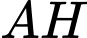 nhận
nhận 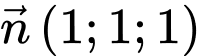 là vectơ chỉ phương suy ra phương trình
là vectơ chỉ phương suy ra phương trình 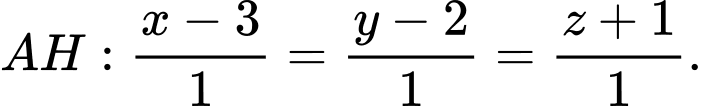
Do
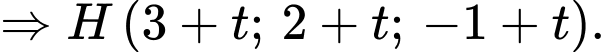
Do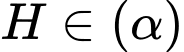

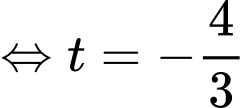
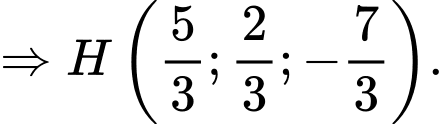 Đáp án: B
Đáp án: B
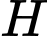 là hình chiếu của
là hình chiếu của 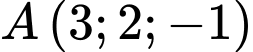 lên mặt phẳng
lên mặt phẳng 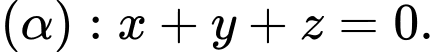 Khi đó:
Khi đó: 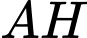 nhận
nhận 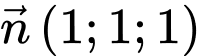 là vectơ chỉ phương suy ra phương trình
là vectơ chỉ phương suy ra phương trình 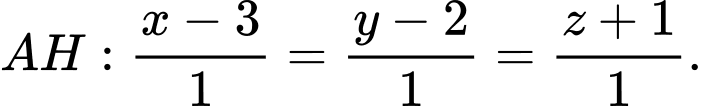
Do

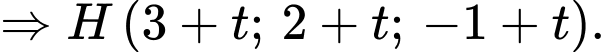
Do
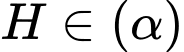

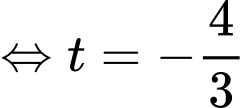
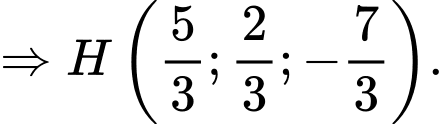 Đáp án: B
Đáp án: B 7. Dạng toán: Lập phương trình mặt phẳng liên quan đến đường thẳng
7.1. Phương pháp tư duy
7.2. Ví dụ áp dụng.
7.2. Ví dụ áp dụng.
Câu 19 [581679]: Trong không gian 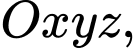 cho đường thẳng
cho đường thẳng 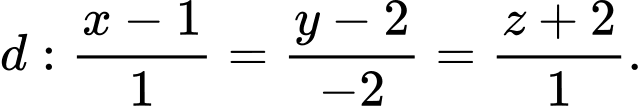 Mặt phẳng nào sau đây vuông góc với đường thẳng
Mặt phẳng nào sau đây vuông góc với đường thẳng 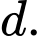
 cho đường thẳng
cho đường thẳng 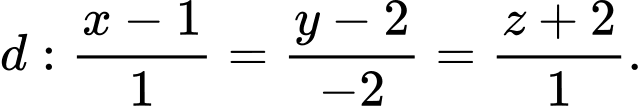 Mặt phẳng nào sau đây vuông góc với đường thẳng
Mặt phẳng nào sau đây vuông góc với đường thẳng 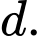
A, 

B, 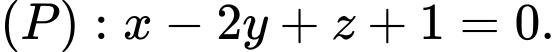
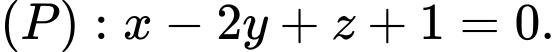
C, 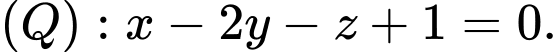
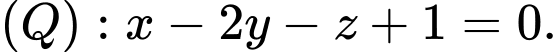
D, 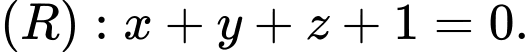
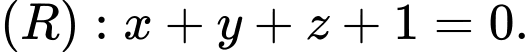
Đường thẳng vuông góc với mặt phẳng nếu vectơ chỉ phương của đường thẳng cùng phương với vectơ pháp tuyến của mặt phẳng.
Đường thẳng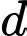 có một vectơ chỉ phương là
có một vectơ chỉ phương là 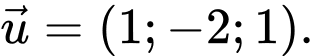
Mặt phẳng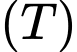 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 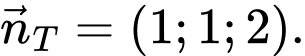 Do
Do 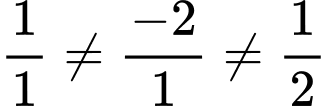 nên
nên 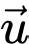 không cùng phương với
không cùng phương với 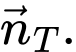 Do đó
Do đó 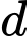 không vuông góc với
không vuông góc với 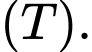
Mặt phẳng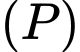 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 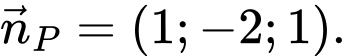 Do
Do 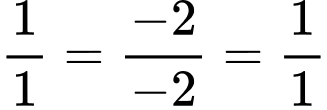 nên
nên 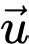 cùng phương với
cùng phương với 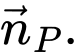 Do đó
Do đó 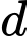 vuông góc với
vuông góc với 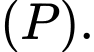
Mặt phẳng có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 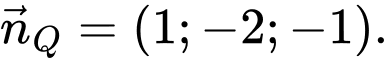 Do
Do 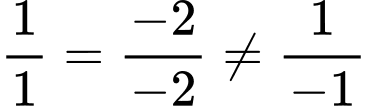 nên
nên 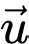 không cùng phương với
không cùng phương với 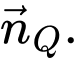 Do đó
Do đó 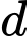 không vuông góc với
không vuông góc với 
Mặt phẳng có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 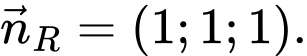 Do
Do 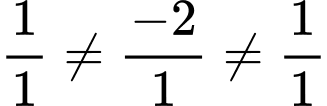 nên
nên 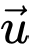 không cùng phương với
không cùng phương với 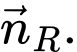 Do đó
Do đó 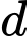 không vuông góc với
không vuông góc với 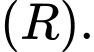 Đáp án: B
Đáp án: B
Đường thẳng
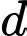 có một vectơ chỉ phương là
có một vectơ chỉ phương là 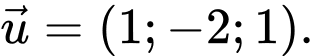
Mặt phẳng
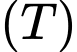 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 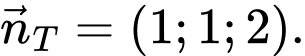 Do
Do 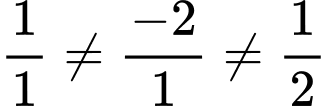 nên
nên 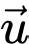 không cùng phương với
không cùng phương với 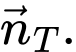 Do đó
Do đó 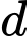 không vuông góc với
không vuông góc với 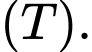
Mặt phẳng
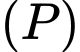 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 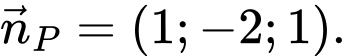 Do
Do 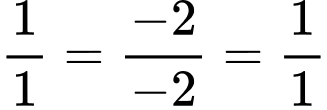 nên
nên 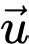 cùng phương với
cùng phương với 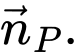 Do đó
Do đó 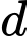 vuông góc với
vuông góc với 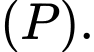
Mặt phẳng
 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 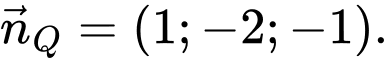 Do
Do 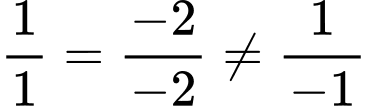 nên
nên 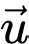 không cùng phương với
không cùng phương với 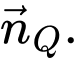 Do đó
Do đó 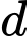 không vuông góc với
không vuông góc với 
Mặt phẳng
 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 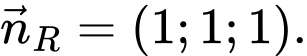 Do
Do 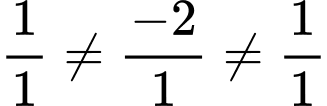 nên
nên 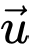 không cùng phương với
không cùng phương với 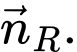 Do đó
Do đó 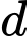 không vuông góc với
không vuông góc với  Đáp án: B
Đáp án: B
Câu 20 [581680]: Trong không gian 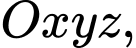 mặt phẳng chứa hai đường thẳng cắt nhau
mặt phẳng chứa hai đường thẳng cắt nhau 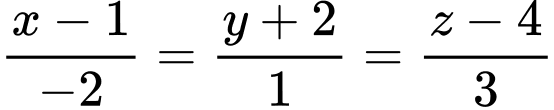 và
và 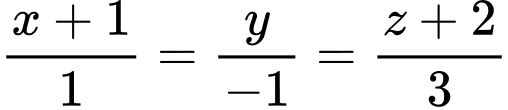 có phương trình là
có phương trình là
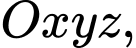 mặt phẳng chứa hai đường thẳng cắt nhau
mặt phẳng chứa hai đường thẳng cắt nhau 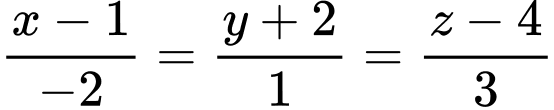 và
và 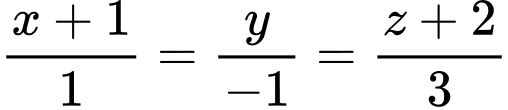 có phương trình là
có phương trình là
A, 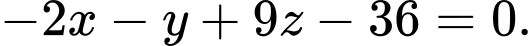
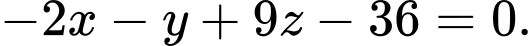
B, 

C, 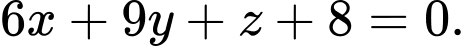
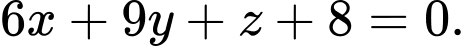
D, 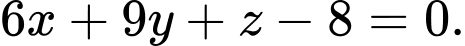
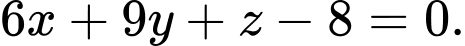
Đường thẳng 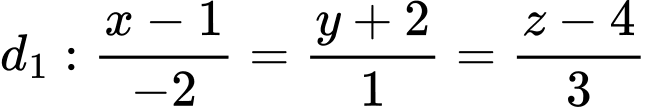 đi qua điểm
đi qua điểm 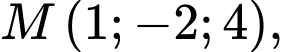 có một VTCP là
có một VTCP là 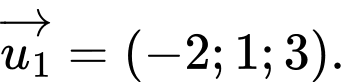
Đường thẳng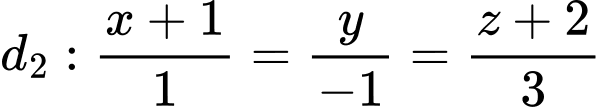 có một VTCP là
có một VTCP là 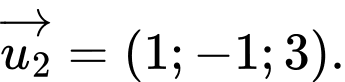
Mặt phẳng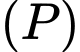 chứa hai đường thẳng cắt nhau
chứa hai đường thẳng cắt nhau 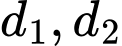
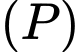 qua điểm
qua điểm 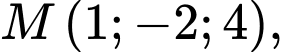 có một VTPT là
có một VTPT là 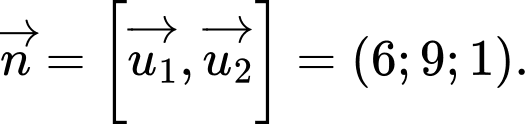
Phương trình mặt phẳng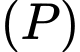 là :
là :
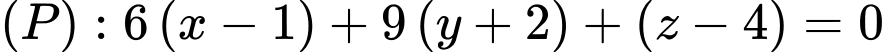
 Đáp án: C
Đáp án: C
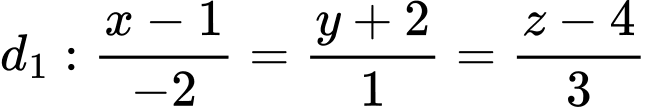 đi qua điểm
đi qua điểm 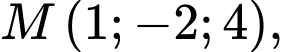 có một VTCP là
có một VTCP là 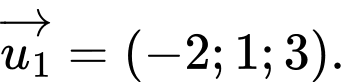
Đường thẳng
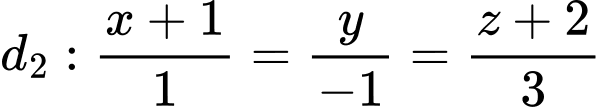 có một VTCP là
có một VTCP là 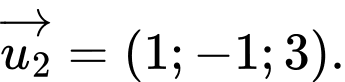
Mặt phẳng
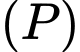 chứa hai đường thẳng cắt nhau
chứa hai đường thẳng cắt nhau 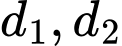
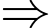
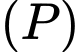 qua điểm
qua điểm 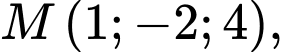 có một VTPT là
có một VTPT là 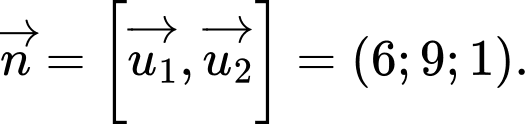
Phương trình mặt phẳng
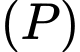 là :
là :
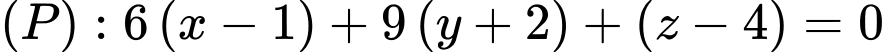
 Đáp án: C
Đáp án: C
Câu 21 [581681]: Trong không gian tọa độ 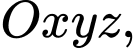 cho điểm
cho điểm 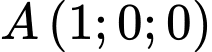 và đường thẳng
và đường thẳng 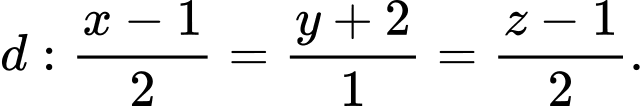 Viết phương trình mặt phẳng chứa điểm
Viết phương trình mặt phẳng chứa điểm 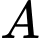 và đường thẳng
và đường thẳng 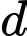 ?
?
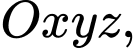 cho điểm
cho điểm 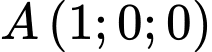 và đường thẳng
và đường thẳng 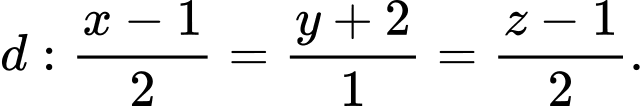 Viết phương trình mặt phẳng chứa điểm
Viết phương trình mặt phẳng chứa điểm 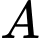 và đường thẳng
và đường thẳng 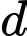 ?
? A, 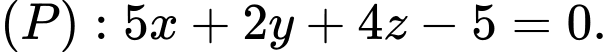
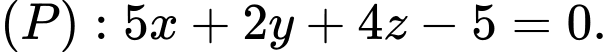
B, 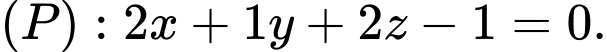
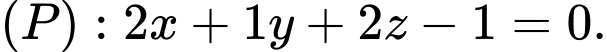
C, 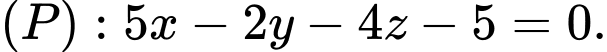
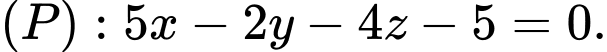
D, 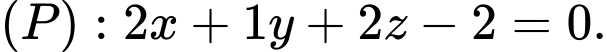
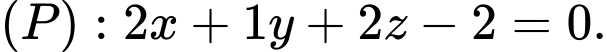
VTCP của 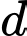 là
là 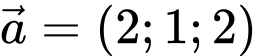 và
và 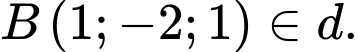
Khi đó: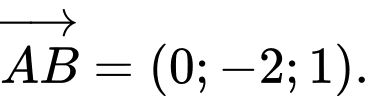
Do đó vectơ pháp tuyến của mặt phẳng là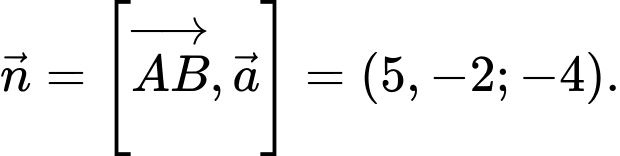
Từ đó suy ra phương trình mặt phẳng cần tìm là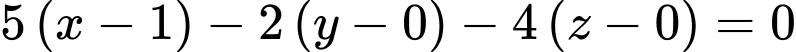 hay
hay 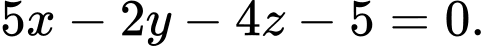 Đáp án: C
Đáp án: C
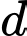 là
là 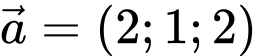 và
và 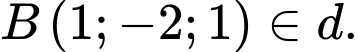
Khi đó:
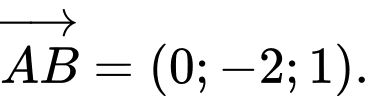
Do đó vectơ pháp tuyến của mặt phẳng là
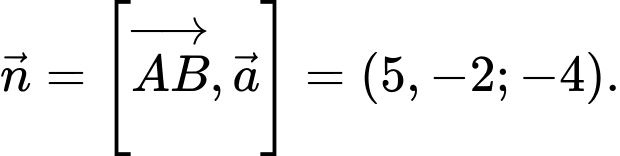
Từ đó suy ra phương trình mặt phẳng cần tìm là
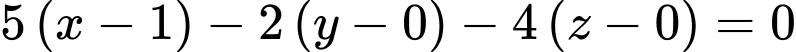 hay
hay 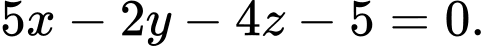 Đáp án: C
Đáp án: C 8. Dạng toán: Đường thẳng liên quan đến góc và khoảng cách
8.1. Phương pháp tư duy
8.2. Ví dụ áp dụng.
8.2. Ví dụ áp dụng.
Câu 22 [581682]: Trong không gian 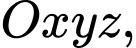 cho điểm
cho điểm 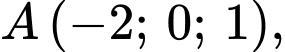 đường thẳng
đường thẳng 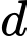 qua điểm
qua điểm 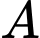 và tạo với trục góc
và tạo với trục góc 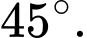 Phương trình đường thẳng
Phương trình đường thẳng 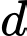 là
là
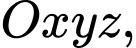 cho điểm
cho điểm 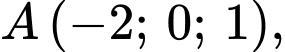 đường thẳng
đường thẳng 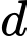 qua điểm
qua điểm 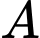 và tạo với trục góc
và tạo với trục góc 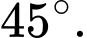 Phương trình đường thẳng
Phương trình đường thẳng 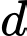 là
là A, 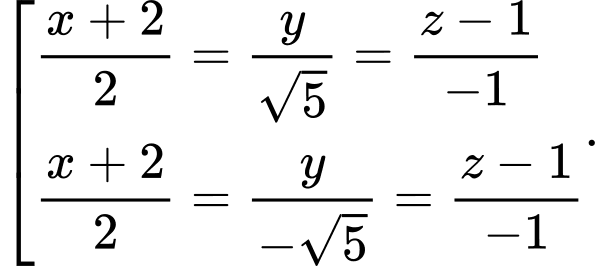
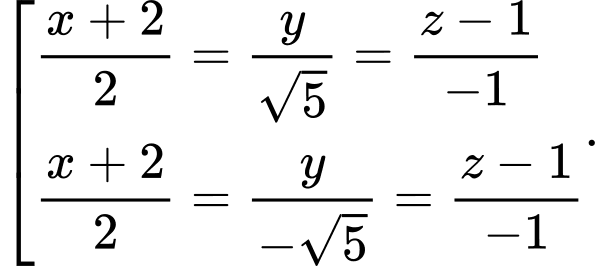
B, 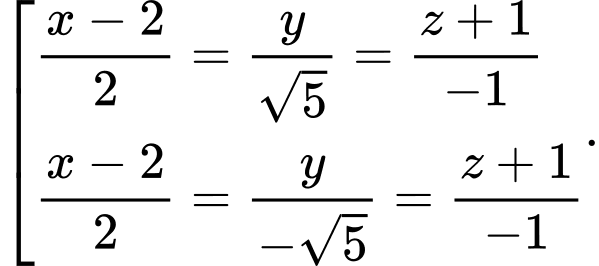
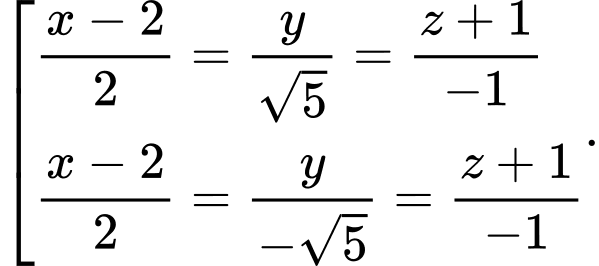
C, 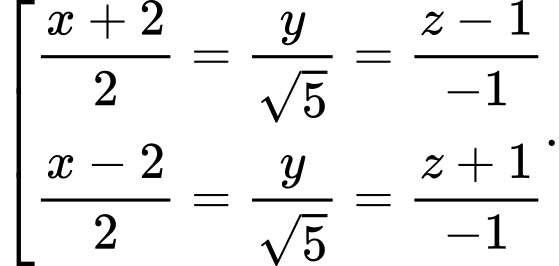
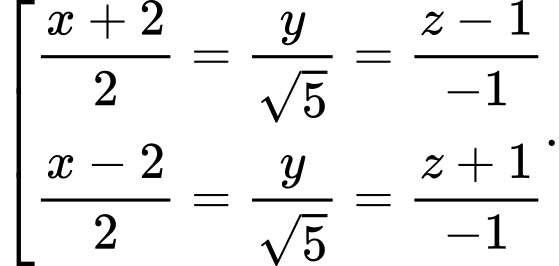
D, 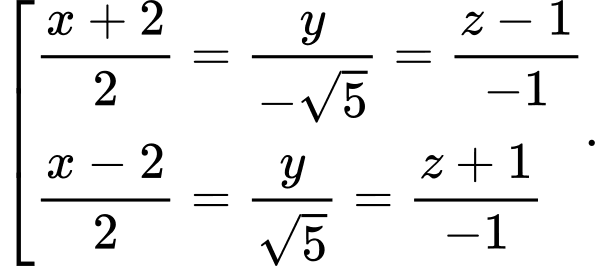
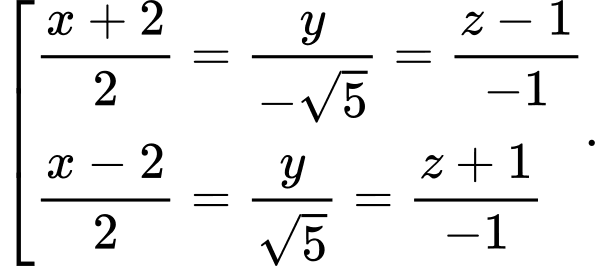
Cách 1: Điểm 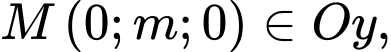
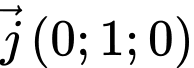 là vectơ chỉ phương của trục
là vectơ chỉ phương của trục 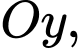
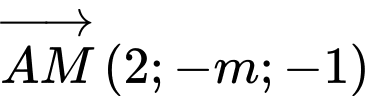
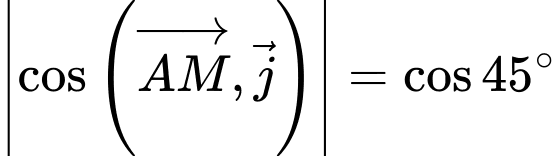
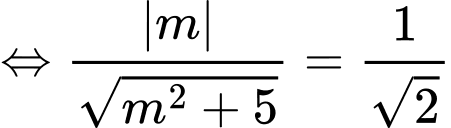
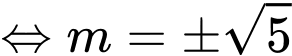 nên có 2 đường thẳng:
nên có 2 đường thẳng:
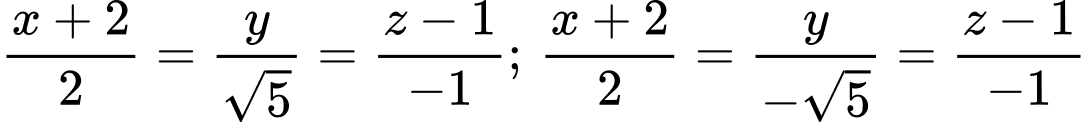
Cách 2: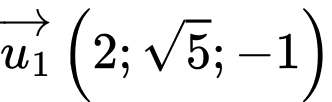
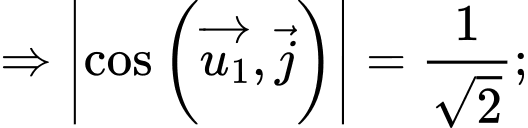
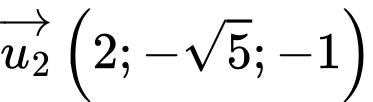
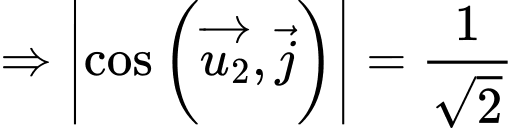
Đường thẳng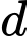 đi qua điểm
đi qua điểm 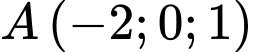 nên chọn đáp án A. Đáp án: A
nên chọn đáp án A. Đáp án: A
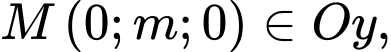
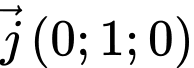 là vectơ chỉ phương của trục
là vectơ chỉ phương của trục 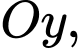
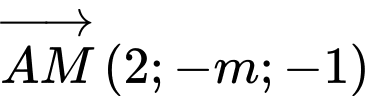
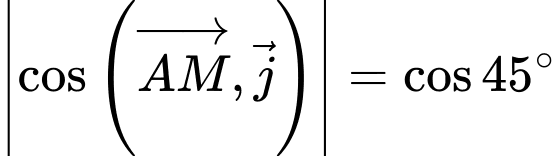
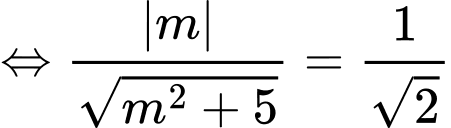
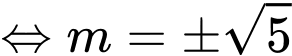 nên có 2 đường thẳng:
nên có 2 đường thẳng: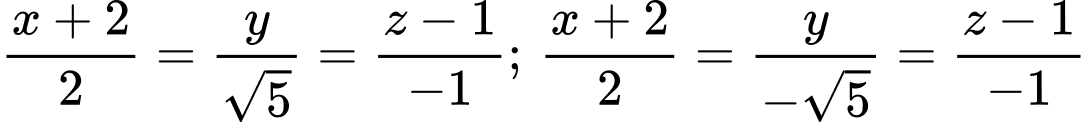
Cách 2:
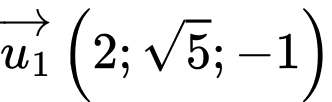
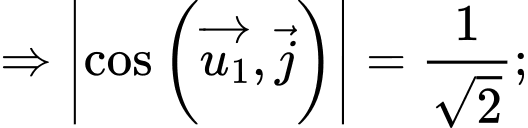
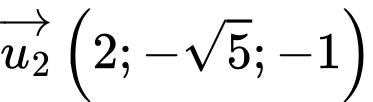
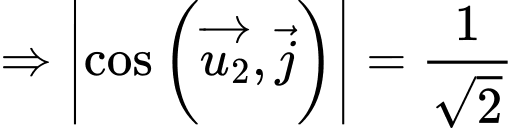
Đường thẳng
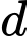 đi qua điểm
đi qua điểm 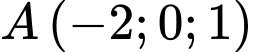 nên chọn đáp án A. Đáp án: A
nên chọn đáp án A. Đáp án: A
Câu 23 [581683]: Trong không gian với hệ tọa độ 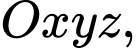 cho đường thẳng
cho đường thẳng 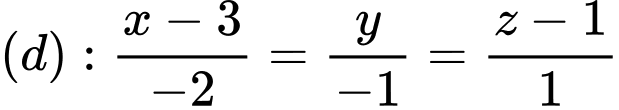 và điểm
và điểm 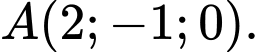 Khoảng cách từ điểm
Khoảng cách từ điểm 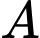 đến đường thẳng
đến đường thẳng  bằng
bằng
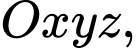 cho đường thẳng
cho đường thẳng 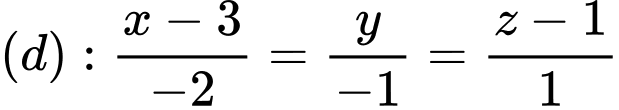 và điểm
và điểm 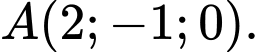 Khoảng cách từ điểm
Khoảng cách từ điểm 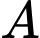 đến đường thẳng
đến đường thẳng  bằng
bằng A, 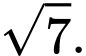
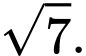
B, 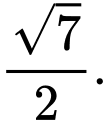
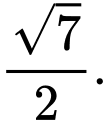
C, 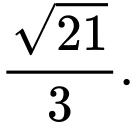
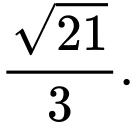
D, 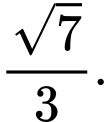
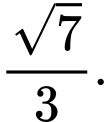
Gọi 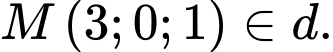
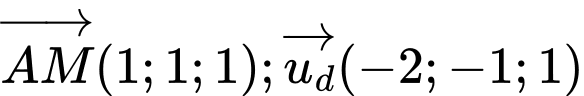
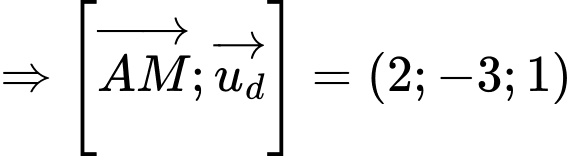
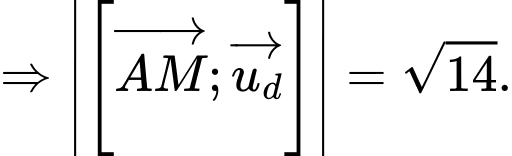
Vậy khoảng cách từ điểm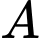 đến đường thẳng
đến đường thẳng  bằng
bằng 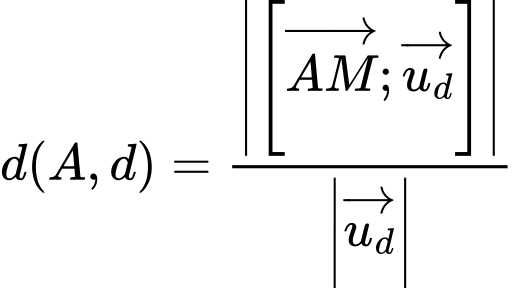
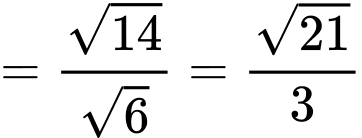 Đáp án: C
Đáp án: C
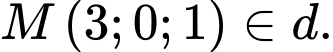
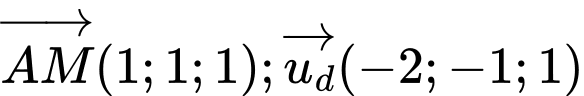
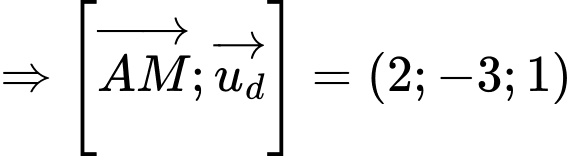
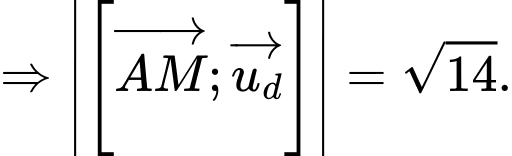
Vậy khoảng cách từ điểm
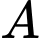 đến đường thẳng
đến đường thẳng  bằng
bằng 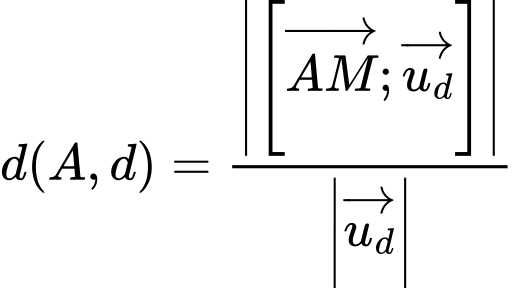
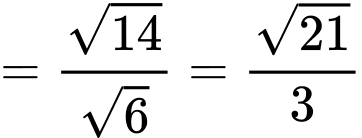 Đáp án: C
Đáp án: C
Câu 24 [581684]: Trong không gian với hệ tọa độ 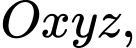 cho mặt phẳng
cho mặt phẳng 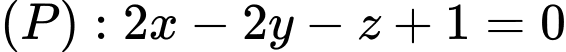 và đường thẳng
và đường thẳng 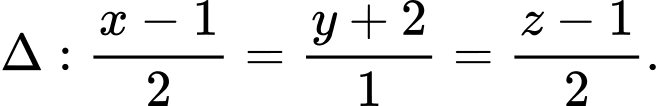 Tính khoảng cách
Tính khoảng cách 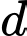 giữa
giữa  và
và 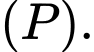
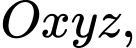 cho mặt phẳng
cho mặt phẳng 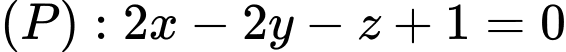 và đường thẳng
và đường thẳng 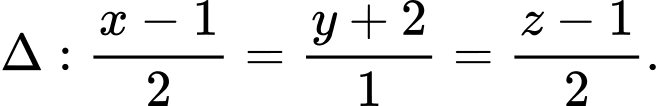 Tính khoảng cách
Tính khoảng cách 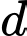 giữa
giữa  và
và 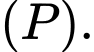
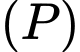 có vectơ pháp tuyến
có vectơ pháp tuyến 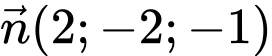 và đường thẳng
và đường thẳng  có vectơ chỉ phương
có vectơ chỉ phương 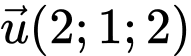 thỏa mãn
thỏa mãn 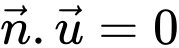 nên
nên  hoặc
hoặc 
Do đó: lấy
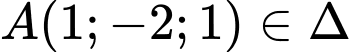 ta có:
ta có: 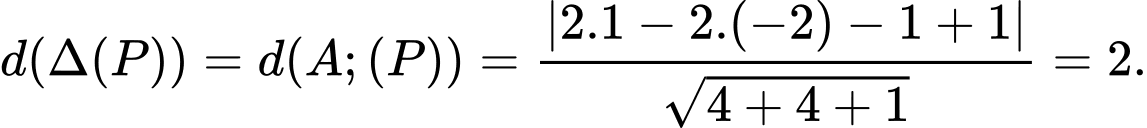
Đáp án: 2. Đáp án: A
9. Dạng toán: Vị trí tương đối của đường thẳng với mặt phẳng
9.1. Phương pháp tư duy
9.2. Ví dụ áp dụng.
9.2. Ví dụ áp dụng.
Câu 25 [581685]: Trong không gian với hệ tọa độ 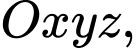 cho đường thẳng
cho đường thẳng 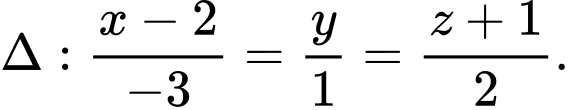 Gọi
Gọi 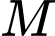 là giao điểm của
là giao điểm của  với mặt phẳng
với mặt phẳng 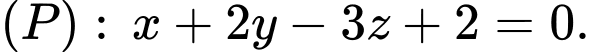 Tọa độ điểm
Tọa độ điểm 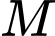 là
là
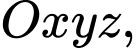 cho đường thẳng
cho đường thẳng 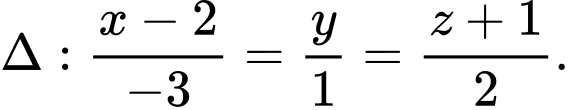 Gọi
Gọi 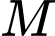 là giao điểm của
là giao điểm của  với mặt phẳng
với mặt phẳng 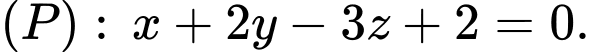 Tọa độ điểm
Tọa độ điểm 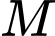 là
là A, 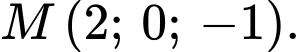
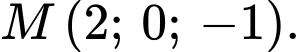
B, 

C, 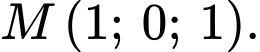
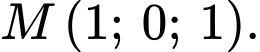
D, 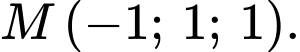
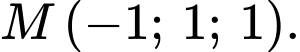
Tọa độ của điểm 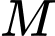 là nghiệm của hệ:
là nghiệm của hệ: 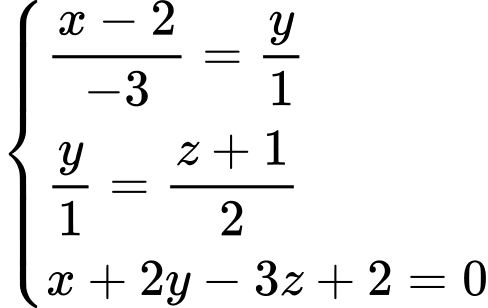
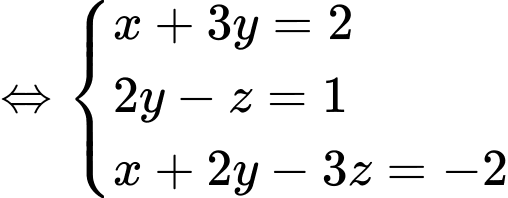
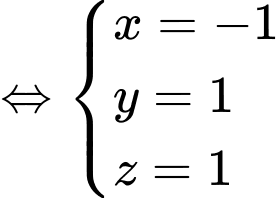 Đáp án: D
Đáp án: D
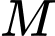 là nghiệm của hệ:
là nghiệm của hệ: 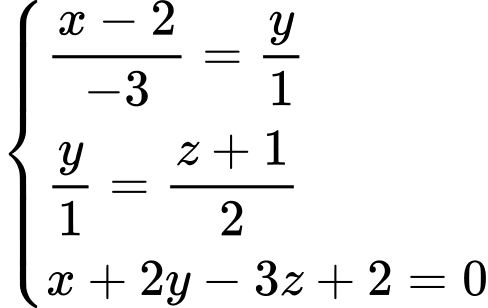
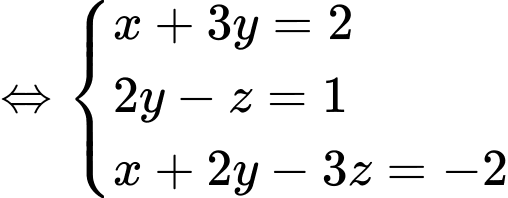
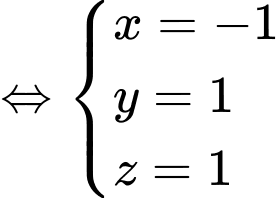 Đáp án: D
Đáp án: D
Câu 26 [581686]: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 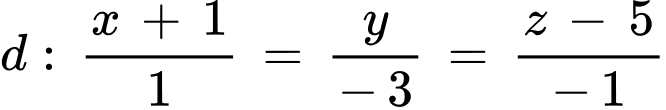 và mặt phẳng
và mặt phẳng 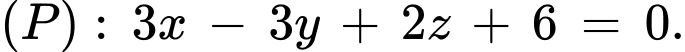 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
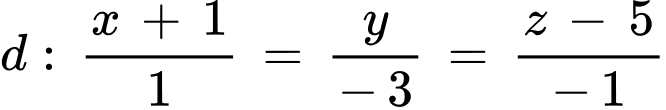 và mặt phẳng
và mặt phẳng 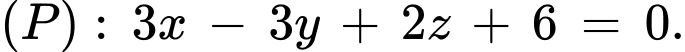 Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng? A, 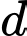 cắt và không vuông góc với
cắt và không vuông góc với 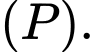
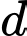 cắt và không vuông góc với
cắt và không vuông góc với 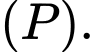
B, 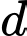 vuông góc với
vuông góc với 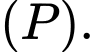
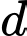 vuông góc với
vuông góc với 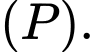
C, 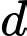 song song với
song song với 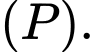
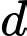 song song với
song song với 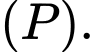
D, 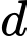 nằm trong
nằm trong 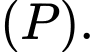
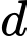 nằm trong
nằm trong 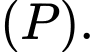
Đường thẳng 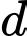 có vtcp
có vtcp 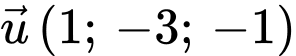
Mặt phẳng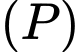 có vtpt
có vtpt 
Ta có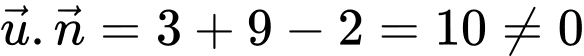 nên loại trường hợp
nên loại trường hợp 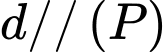 và
và 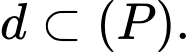
Lại có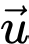 và
và 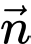 không cùng phương nên loại trường hợp
không cùng phương nên loại trường hợp 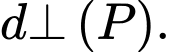
Vậy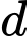 cắt và không vuông góc với
cắt và không vuông góc với 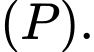 Đáp án: A
Đáp án: A
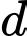 có vtcp
có vtcp 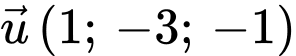
Mặt phẳng
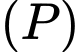 có vtpt
có vtpt 
Ta có
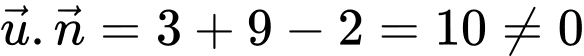 nên loại trường hợp
nên loại trường hợp 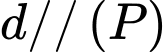 và
và 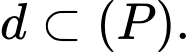
Lại có
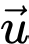 và
và 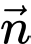 không cùng phương nên loại trường hợp
không cùng phương nên loại trường hợp 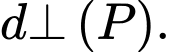
Vậy
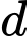 cắt và không vuông góc với
cắt và không vuông góc với 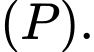 Đáp án: A
Đáp án: A
Câu 27 [581687]: Trong không gian 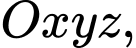 cho mặt phẳng
cho mặt phẳng 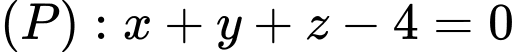 và đường thẳng
và đường thẳng 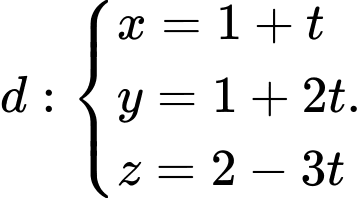 Số giao điểm của đường thẳng
Số giao điểm của đường thẳng 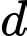 và mặt phẳng
và mặt phẳng 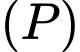 là:
là:
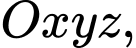 cho mặt phẳng
cho mặt phẳng 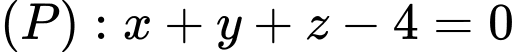 và đường thẳng
và đường thẳng 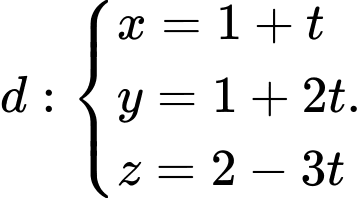 Số giao điểm của đường thẳng
Số giao điểm của đường thẳng 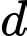 và mặt phẳng
và mặt phẳng 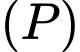 là:
là: A, Vô số.
B, 1.
C, Không có.
D, 2.
 có VTPT
có VTPT 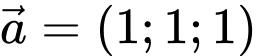
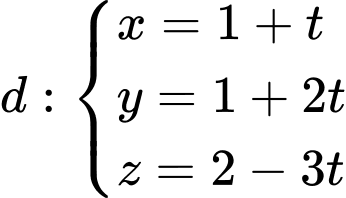 có VTCP
có VTCP 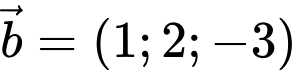
Ta có
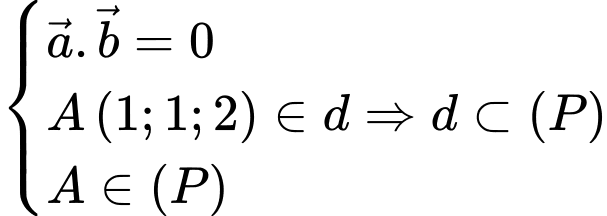 Đáp án: A
Đáp án: A