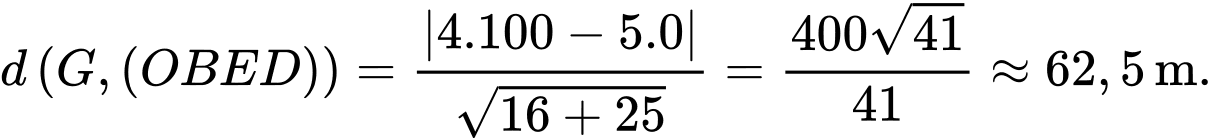1. Dạng toán: Xác định vectơ pháp tuyến của mặt phẳng, điểm thuộc và không thuộc mặt phẳng
1.1. Phương pháp tư duy
1.2. Ví dụ áp dụng.
1.2. Ví dụ áp dụng.
Câu 1 [581709]: Trong không gian 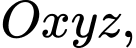 tọa độ một vectơ
tọa độ một vectơ 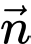 vuông góc với cả hai vectơ
vuông góc với cả hai vectơ 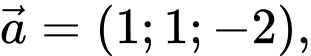
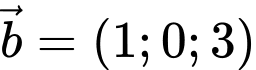 là
là
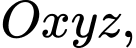 tọa độ một vectơ
tọa độ một vectơ 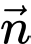 vuông góc với cả hai vectơ
vuông góc với cả hai vectơ 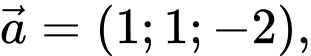
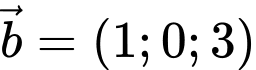 là
là A, 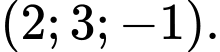
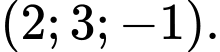
B, 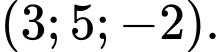
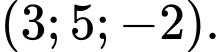
C, 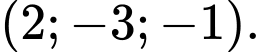
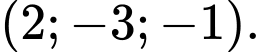
D, 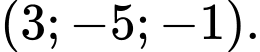
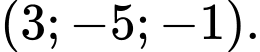
Ta có 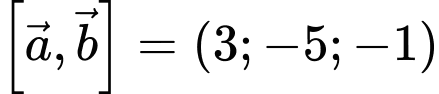 Đáp án: D
Đáp án: D
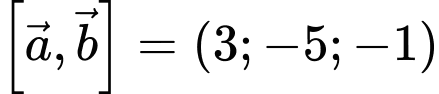 Đáp án: D
Đáp án: D
Câu 2 [581710]: Trong không gian  cho mặt phẳng
cho mặt phẳng 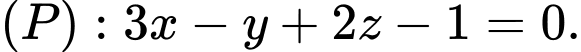 Vectơ nào dưới đây không phải là một vectơ pháp tuyến của
Vectơ nào dưới đây không phải là một vectơ pháp tuyến của 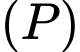 ?
?
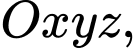 cho mặt phẳng
cho mặt phẳng 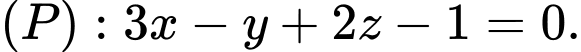 Vectơ nào dưới đây không phải là một vectơ pháp tuyến của
Vectơ nào dưới đây không phải là một vectơ pháp tuyến của 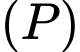 ?
? A, 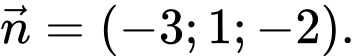
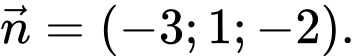
B, 
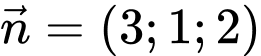
C, 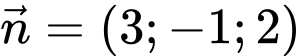
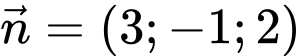
D, 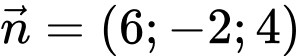
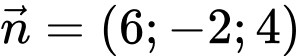
Vectơ pháp tuyến của  là:
là: 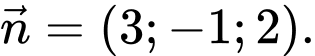
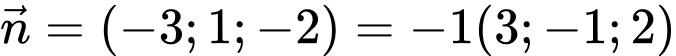 là một vectơ pháp tuyến của
là một vectơ pháp tuyến của 
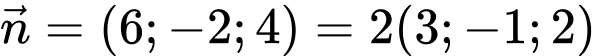 là một vectơ pháp tuyến của
là một vectơ pháp tuyến của  Đáp án: B
Đáp án: B
 là:
là: 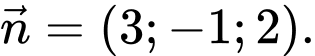
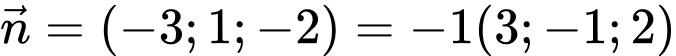 là một vectơ pháp tuyến của
là một vectơ pháp tuyến của 
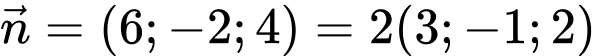 là một vectơ pháp tuyến của
là một vectơ pháp tuyến của  Đáp án: B
Đáp án: B
Câu 3 [581711]: Trong không gian 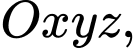 mặt phẳng
mặt phẳng 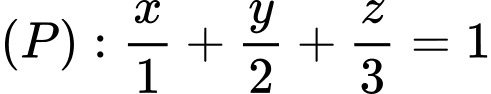 không đi qua điểm nào dưới đây?
không đi qua điểm nào dưới đây?
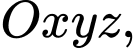 mặt phẳng
mặt phẳng 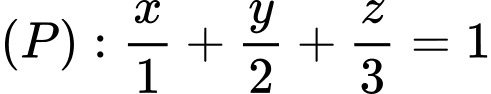 không đi qua điểm nào dưới đây?
không đi qua điểm nào dưới đây? A, 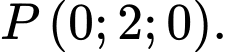
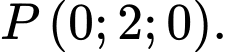
B, 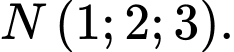
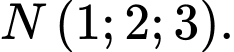
C, 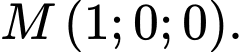
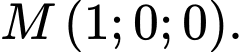
D, 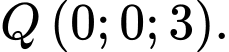
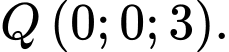
Thế tọa độ điểm 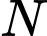 vào phương trình mặt phẳng
vào phương trình mặt phẳng 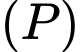 ta có:
ta có: 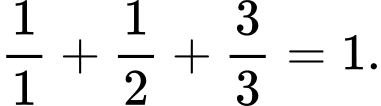
Vậy mặt phẳng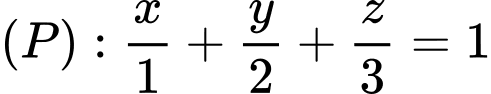 không đi qua điểm
không đi qua điểm 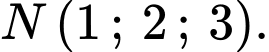 Đáp án: B
Đáp án: B
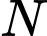 vào phương trình mặt phẳng
vào phương trình mặt phẳng 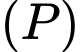 ta có:
ta có: 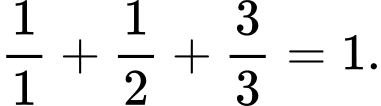
Vậy mặt phẳng
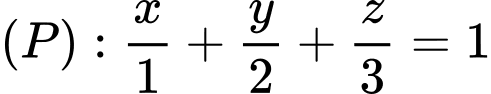 không đi qua điểm
không đi qua điểm 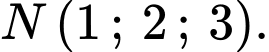 Đáp án: B
Đáp án: B 2. Dạng toán: Hai mặt phẳng song song, vuông góc. Khoảng cách một điểm đến mặt phẳng
2.1. Phương pháp tư duy
2.2. Ví dụ áp dụng
2.2. Ví dụ áp dụng
Câu 4 [581712]: Trong không gian với hệ tọa độ  cho mặt phẳng
cho mặt phẳng 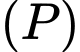 có phương trình:
có phương trình: 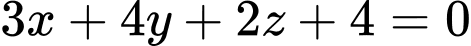 và điểm
và điểm 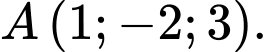 Tính khoảng cách
Tính khoảng cách 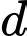 từ
từ 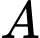 đến
đến 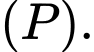
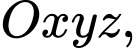 cho mặt phẳng
cho mặt phẳng 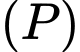 có phương trình:
có phương trình: 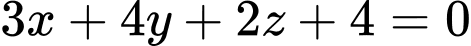 và điểm
và điểm 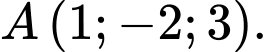 Tính khoảng cách
Tính khoảng cách 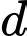 từ
từ 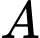 đến
đến 
A, 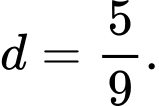
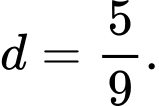
B, 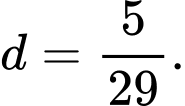
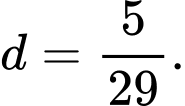
C, 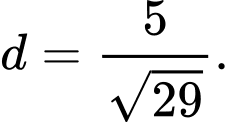
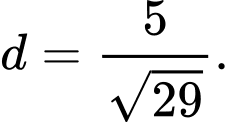
D, 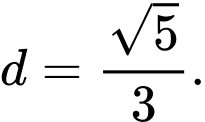
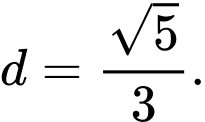
Khoảng cách 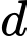 từ
từ  đến
đến  là
là 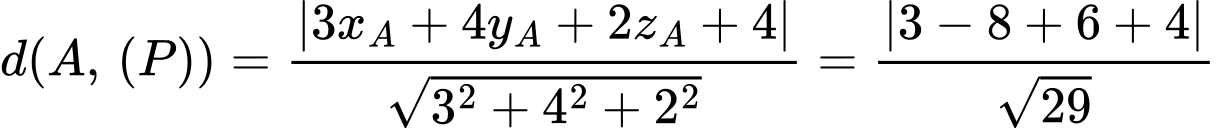
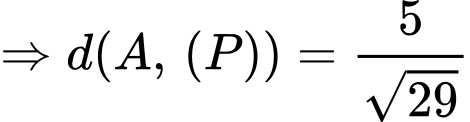 Đáp án: C
Đáp án: C
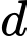 từ
từ 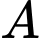 đến
đến 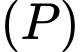 là
là 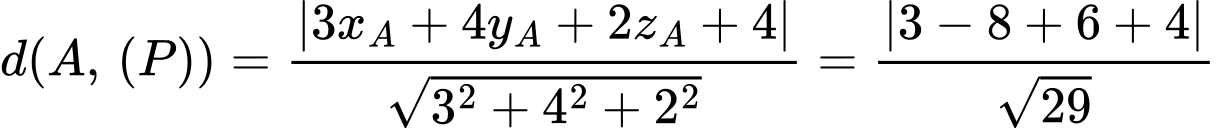
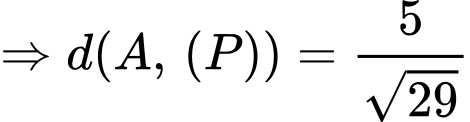 Đáp án: C
Đáp án: C
Câu 5 [581713]: Trong không gian 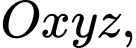 cho mặt phẳng
cho mặt phẳng 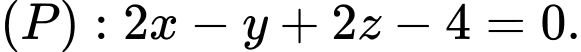 Gọi
Gọi 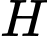 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 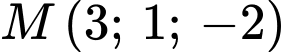 lên mặt phẳng
lên mặt phẳng 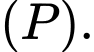 Độ dài đoạn thẳng
Độ dài đoạn thẳng 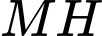 là
là
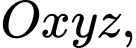 cho mặt phẳng
cho mặt phẳng 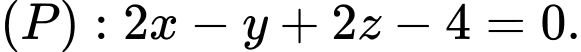 Gọi
Gọi 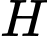 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 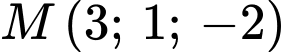 lên mặt phẳng
lên mặt phẳng 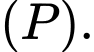 Độ dài đoạn thẳng
Độ dài đoạn thẳng 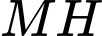 là
là A, 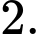
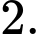
B, 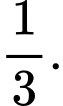
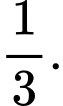
C, 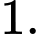
D, 
Khoảng cách từ điểm 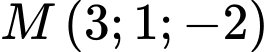 đến mặt phẳng
đến mặt phẳng 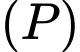 :
: 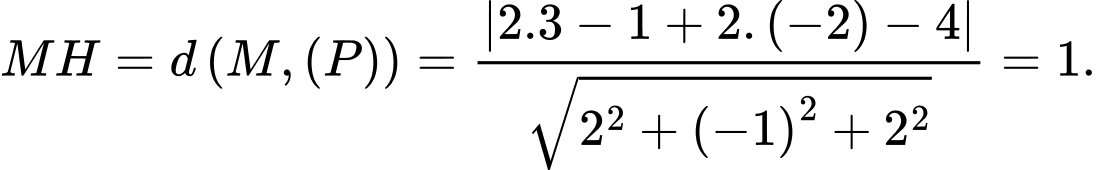 Đáp án: C
Đáp án: C
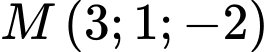 đến mặt phẳng
đến mặt phẳng 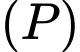 :
: 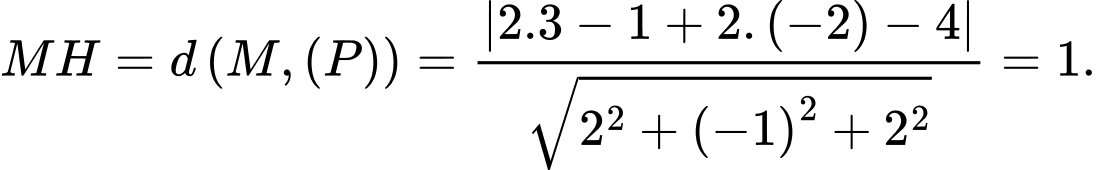 Đáp án: C
Đáp án: C
Câu 6 [581714]: Trong không gian 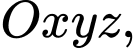 cho điểm
cho điểm 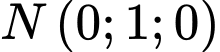 và hai mặt phẳng
và hai mặt phẳng 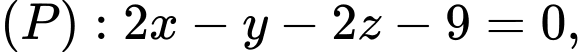
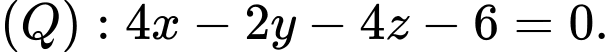 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
a) Hai mặt phẳng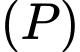 và
và  song song với nhau.
song song với nhau.
b) Khoảng cách điểm đến mặt phẳng bằng
bằng 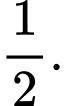
c) Khoảng cách giữa hai mặt phẳng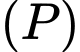 và
và  bằng
bằng 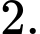
d) Khoảng cách giữa hai mặt phẳng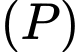 và
và  bằng
bằng 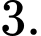
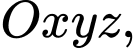 cho điểm
cho điểm 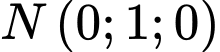 và hai mặt phẳng
và hai mặt phẳng 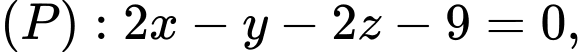
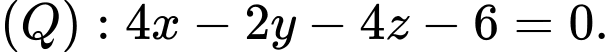 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
a) Hai mặt phẳng
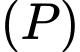 và
và  song song với nhau.
song song với nhau.
b) Khoảng cách điểm đến mặt phẳng
 bằng
bằng 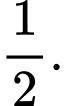
c) Khoảng cách giữa hai mặt phẳng
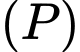 và
và  bằng
bằng 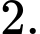
d) Khoảng cách giữa hai mặt phẳng
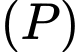 và
và  bằng
bằng 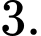
a) Đ
b) S
c) Đ
d) S
Hai mặt phẳng và
và  song song với nhau.
song song với nhau.
Trong mặt phẳng ta chọn điểm
ta chọn điểm 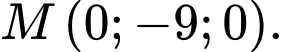 Tính khoảng cách từ
Tính khoảng cách từ 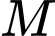 đến
đến  ta có:
ta có:
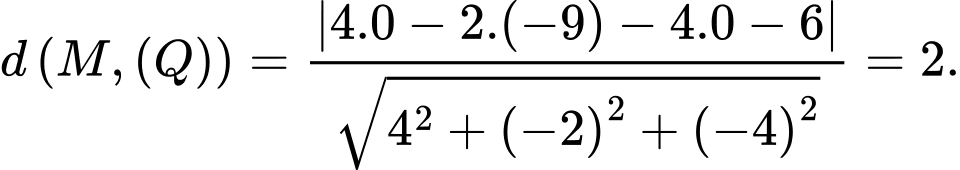
Vậy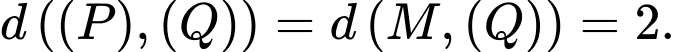
b) S
c) Đ
d) S
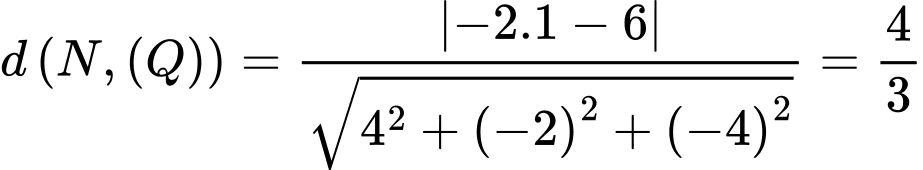
Hai mặt phẳng
 và
và  song song với nhau.
song song với nhau.
Trong mặt phẳng
 ta chọn điểm
ta chọn điểm 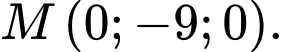 Tính khoảng cách từ
Tính khoảng cách từ 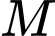 đến
đến  ta có:
ta có:
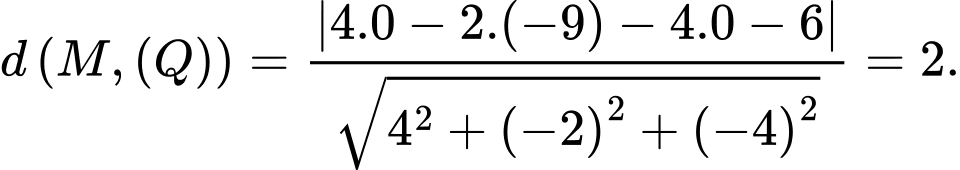
Vậy
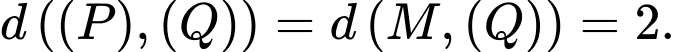
3. Dạng toán: Viết phương trình tổng quát mặt phẳng khi biết một điểm thuộc mặt phẳng và một vectơ pháp tuyến hoặc hai vectơ chỉ phương
3.1. Phương pháp tư duy
3.2. Ví dụ áp dụng.
3.2. Ví dụ áp dụng.
Câu 7 [581715]: Trong không gian với hệ tọa độ 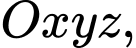 phương trình mặt phẳng qua
phương trình mặt phẳng qua 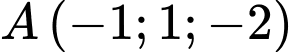 và có vectơ pháp tuyến
và có vectơ pháp tuyến 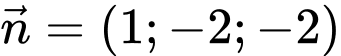 là
là
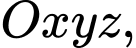 phương trình mặt phẳng qua
phương trình mặt phẳng qua 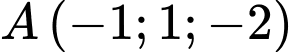 và có vectơ pháp tuyến
và có vectơ pháp tuyến 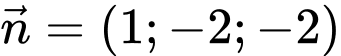 là
là A, 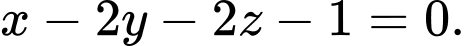
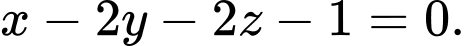
B, 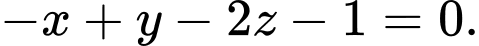
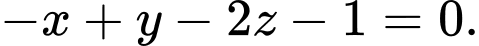
C, 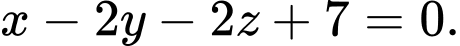
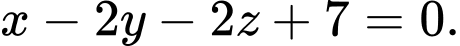
D, 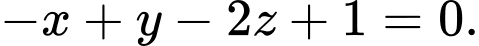
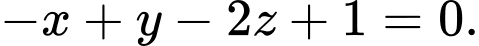
Mặt phẳng  đi qua
đi qua 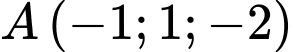 và có vectơ pháp tuyến
và có vectơ pháp tuyến 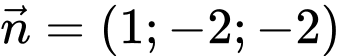 nên có phương trình
nên có phương trình
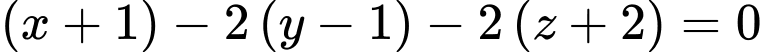
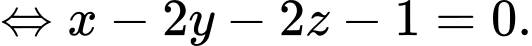
Vậy mặt phẳng cần tìm có phương trình: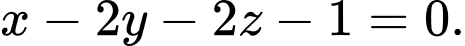 Đáp án: A
Đáp án: A
 đi qua
đi qua 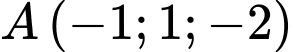 và có vectơ pháp tuyến
và có vectơ pháp tuyến 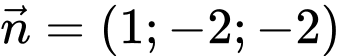 nên có phương trình
nên có phương trình
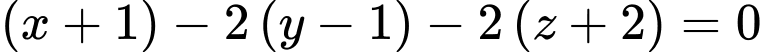
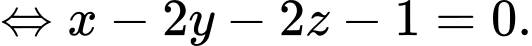
Vậy mặt phẳng cần tìm có phương trình:
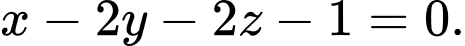 Đáp án: A
Đáp án: A
Câu 8 [581716]: Trong không gian với hệ toạ độ 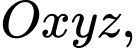 phương trình nào dưới đây là phương trình của mặt phẳng
phương trình nào dưới đây là phương trình của mặt phẳng 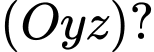
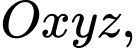 phương trình nào dưới đây là phương trình của mặt phẳng
phương trình nào dưới đây là phương trình của mặt phẳng 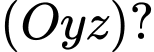
A, 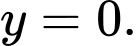
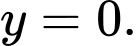
B, 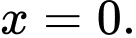
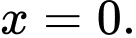
C, 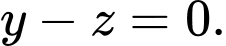
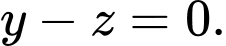
D, 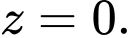
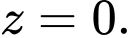
Mặt phẳng 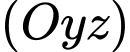 đi qua điểm
đi qua điểm 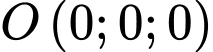 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 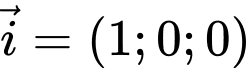 nên ta có phương trình mặt phẳng
nên ta có phương trình mặt phẳng  là :
là : 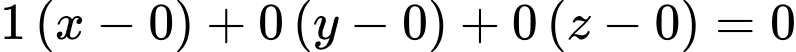
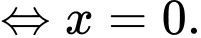 Đáp án: B
Đáp án: B
 đi qua điểm
đi qua điểm 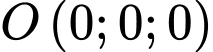 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 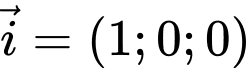 nên ta có phương trình mặt phẳng
nên ta có phương trình mặt phẳng 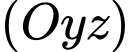 là :
là : 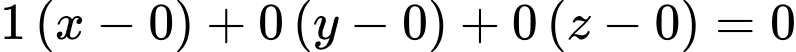
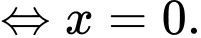 Đáp án: B
Đáp án: B
Câu 9 [581717]: Trong không gian với hệ tọa độ 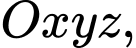 phương trình mặt phẳng
phương trình mặt phẳng 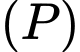 qua
qua 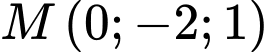 và có cặp vectơ chỉ phương
và có cặp vectơ chỉ phương 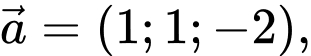
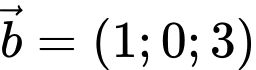 là
là
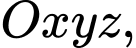 phương trình mặt phẳng
phương trình mặt phẳng 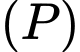 qua
qua 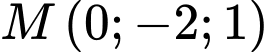 và có cặp vectơ chỉ phương
và có cặp vectơ chỉ phương 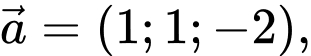
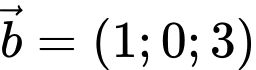 là
là A, 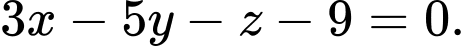
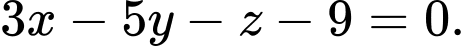
B, 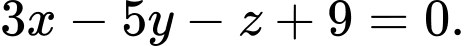
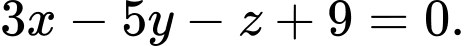
C, 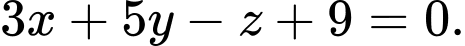
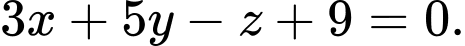
D, 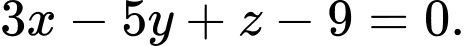
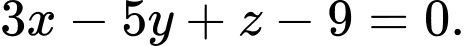
Ta có 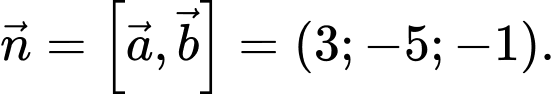
Mặt phẳng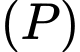 đi qua
đi qua 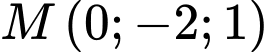 và có vectơ pháp tuyến
và có vectơ pháp tuyến 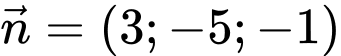 nên có phương trình
nên có phương trình
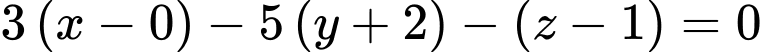

Vậy mặt phẳng cần tìm có phương trình: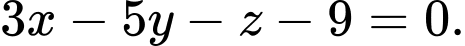 Đáp án: A
Đáp án: A
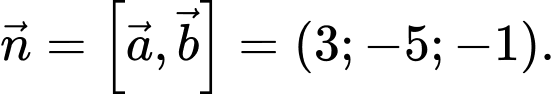
Mặt phẳng
 đi qua
đi qua 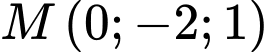 và có vectơ pháp tuyến
và có vectơ pháp tuyến 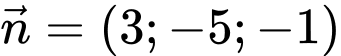 nên có phương trình
nên có phương trình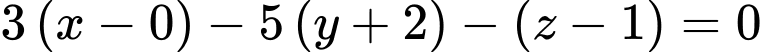

Vậy mặt phẳng cần tìm có phương trình:
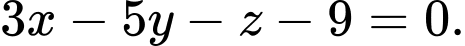 Đáp án: A
Đáp án: A 4. Dạng toán: Viết phương trình tổng quát mặt phẳng khi biết một vectơ pháp tuyến hoặc hai vectơ chỉ phương mà không biết điểm thuộc mặt phẳng
4.1. Phương pháp tư duy
4.2. Ví dụ áp dụng.
4.2. Ví dụ áp dụng.
Câu 10 [581718]: Trong không gian với hệ tọa độ 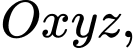 cho mặt phẳng
cho mặt phẳng 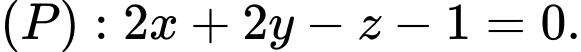 Mặt phẳng nào sau đây song song với
Mặt phẳng nào sau đây song song với 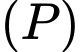 và cách
và cách 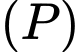 một khoảng bằng 3?
một khoảng bằng 3?
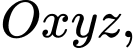 cho mặt phẳng
cho mặt phẳng 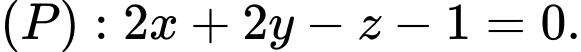 Mặt phẳng nào sau đây song song với
Mặt phẳng nào sau đây song song với 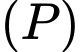 và cách
và cách 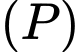 một khoảng bằng 3?
một khoảng bằng 3? A, 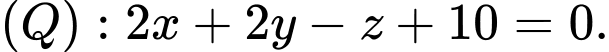
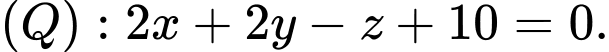
B, 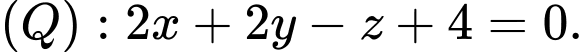
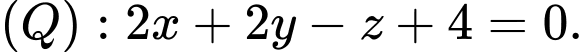
C, 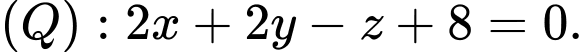
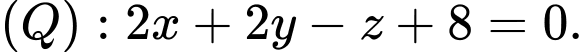
D, 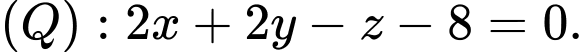
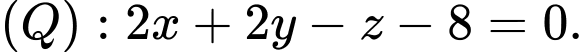
Mặt phẳng 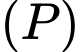 đi qua điểm
đi qua điểm 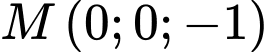 và có một vectơ pháp tuyến
và có một vectơ pháp tuyến 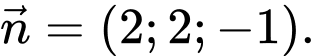
Mặt phẳng song song với
song song với 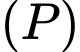 và cách
và cách 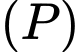 một khoảng bằng 3 nên có dạng
một khoảng bằng 3 nên có dạng 
Mặt khác ta có
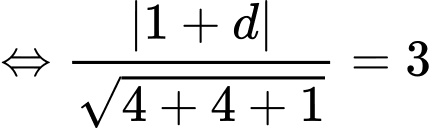
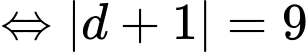
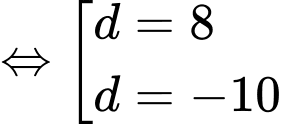 (thỏa mãn).
(thỏa mãn).
Do đó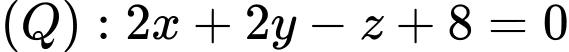 hoặc
hoặc 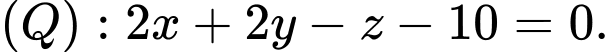 Đáp án: C
Đáp án: C
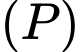 đi qua điểm
đi qua điểm 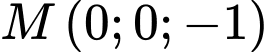 và có một vectơ pháp tuyến
và có một vectơ pháp tuyến 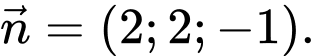
Mặt phẳng
 song song với
song song với  và cách
và cách  một khoảng bằng 3 nên có dạng
một khoảng bằng 3 nên có dạng 
Mặt khác ta có

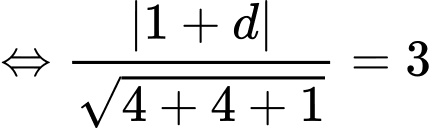
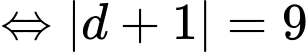
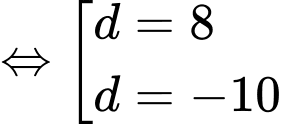 (thỏa mãn).
(thỏa mãn).
Do đó
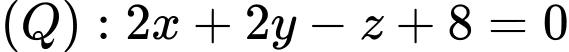 hoặc
hoặc 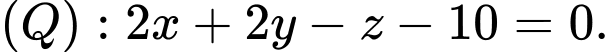 Đáp án: C
Đáp án: C
Câu 11 [581719]: Trong không gian  cho ba điểm
cho ba điểm 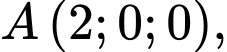
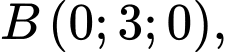
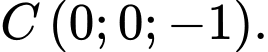 Phương trình của mặt phẳng
Phương trình của mặt phẳng  qua
qua 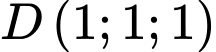 và song song với mặt phẳng
và song song với mặt phẳng 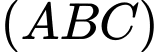 là
là
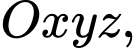 cho ba điểm
cho ba điểm 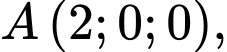
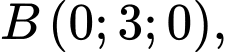
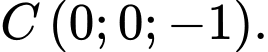 Phương trình của mặt phẳng
Phương trình của mặt phẳng 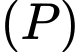 qua
qua 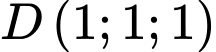 và song song với mặt phẳng
và song song với mặt phẳng 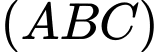 là
là A, 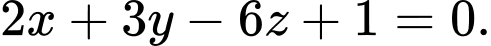
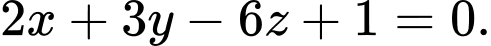
B, 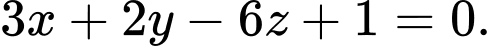
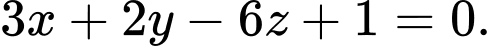
C, 

D, 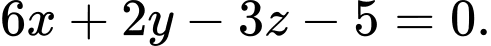
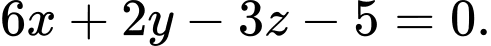
Phương trình đoạn chắn của mặt phẳng 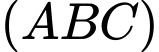 là:
là: 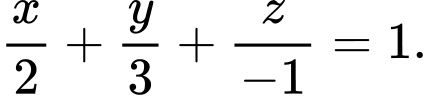
Mặt phẳng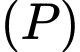 song song với mặt phẳng
song song với mặt phẳng 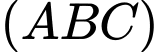 nên
nên
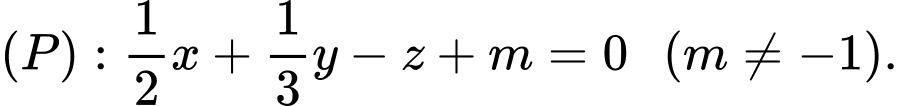
Do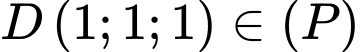 có:
có: 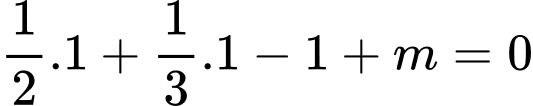
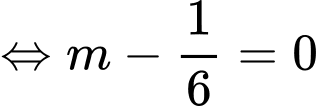
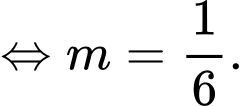
Vậy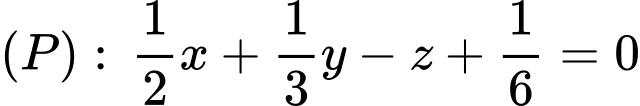
 Đáp án: B
Đáp án: B
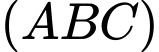 là:
là: 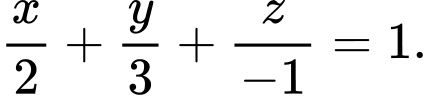
Mặt phẳng
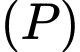 song song với mặt phẳng
song song với mặt phẳng 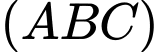 nên
nên
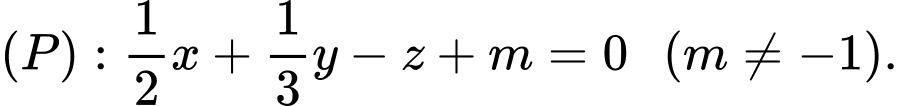
Do
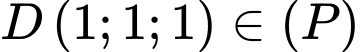 có:
có: 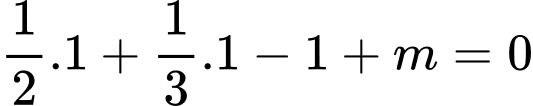
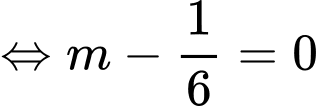
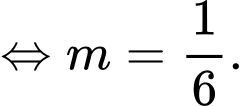
Vậy
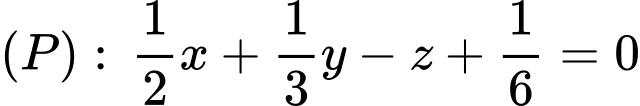
 Đáp án: B
Đáp án: B
Câu 12 [581720]: Trong không gian với hệ trục tọa độ  cho mặt phẳng
cho mặt phẳng 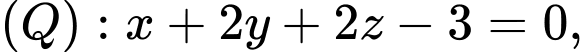 mặt phẳng
mặt phẳng 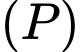 không qua
không qua  song song với mặt phẳng
song song với mặt phẳng  và
và  Phương trình mặt phẳng
Phương trình mặt phẳng 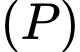 là
là
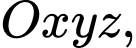 cho mặt phẳng
cho mặt phẳng 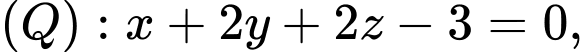 mặt phẳng
mặt phẳng 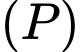 không qua
không qua  song song với mặt phẳng
song song với mặt phẳng  và
và  Phương trình mặt phẳng
Phương trình mặt phẳng 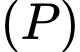 là
là A, 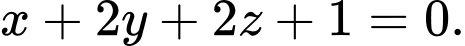
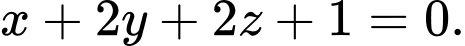
B, 

C, 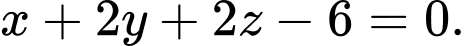
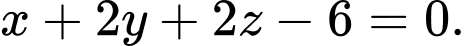
D, 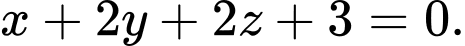
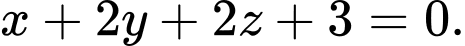
Vì mặt phẳng 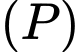 song song với mặt phẳng
song song với mặt phẳng 

Phương trình mặt phẳng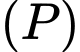 có dạng
có dạng 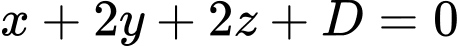
Gọi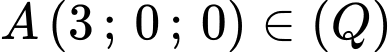
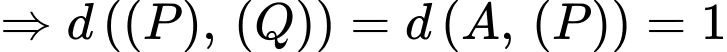
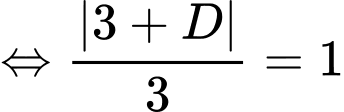
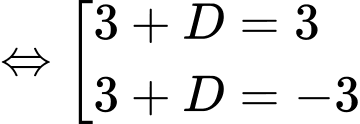
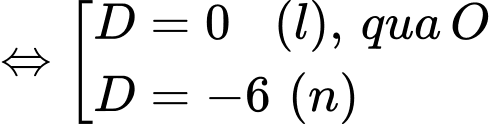 Đáp án: C
Đáp án: C
 song song với mặt phẳng
song song với mặt phẳng 

Phương trình mặt phẳng
 có dạng
có dạng 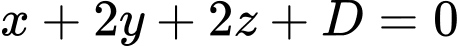
Gọi
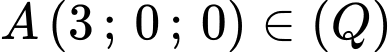
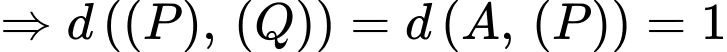
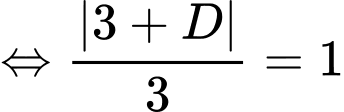
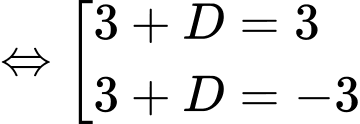
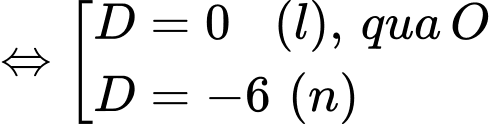 Đáp án: C
Đáp án: C 5. Dạng toán: Viết phương tình tổng quát mặt phẳng khi biết điểm thuộc mặt phẳng và không biết vectơ pháp tuyến hoặc không biết hai vectơ chỉ phương
5.1. Phương pháp tư duy
5.2. Ví dụ áp dụng.
5.2. Ví dụ áp dụng.
Câu 13 [581721]: Trong không gian 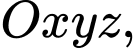 cho 3 điểm
cho 3 điểm 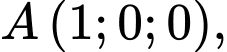
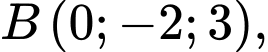
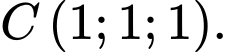 Gọi
Gọi 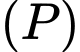 là mặt phẳng chứa
là mặt phẳng chứa 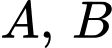 sao cho khoảng cách từ
sao cho khoảng cách từ  tới mặt phẳng
tới mặt phẳng 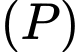 bằng
bằng 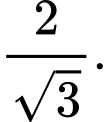 Phương trình mặt phẳng
Phương trình mặt phẳng 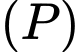 là
là
 cho 3 điểm
cho 3 điểm 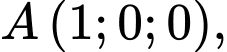
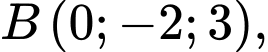
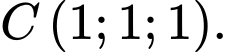 Gọi
Gọi 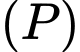 là mặt phẳng chứa
là mặt phẳng chứa 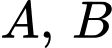 sao cho khoảng cách từ
sao cho khoảng cách từ  tới mặt phẳng
tới mặt phẳng 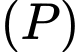 bằng
bằng 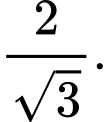 Phương trình mặt phẳng
Phương trình mặt phẳng 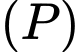 là
là A, 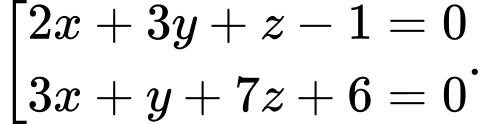
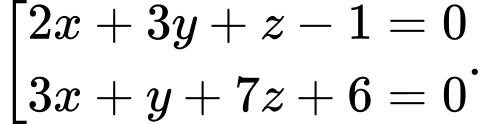
B, 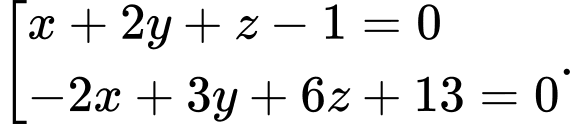
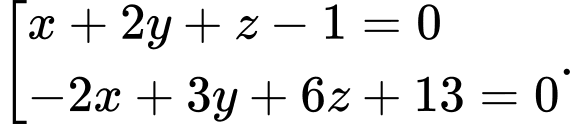
C, 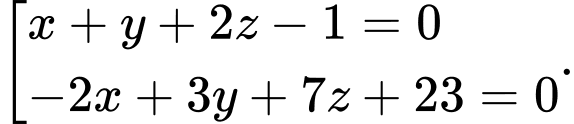
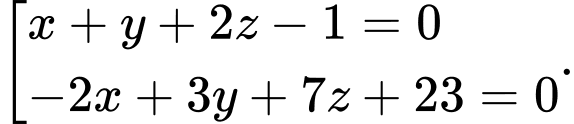
D, 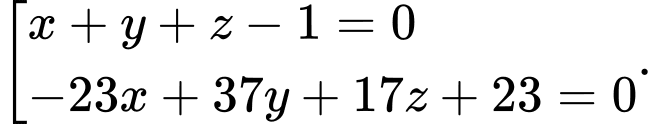
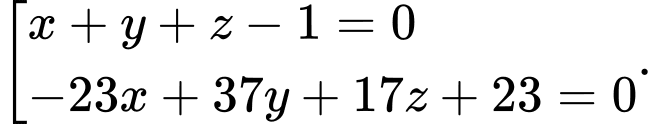
Gọi 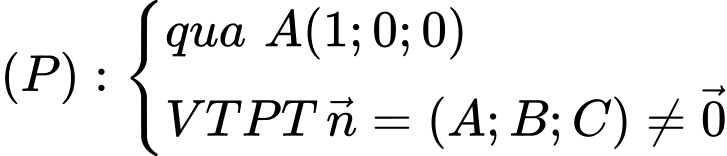
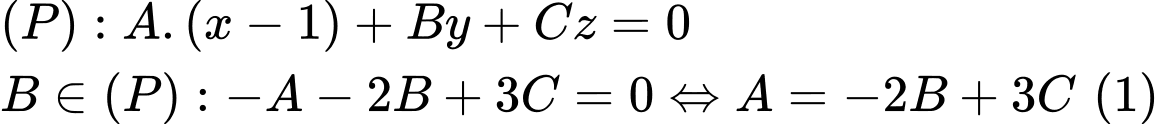
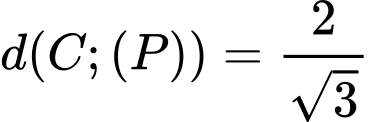
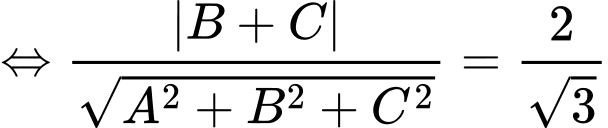
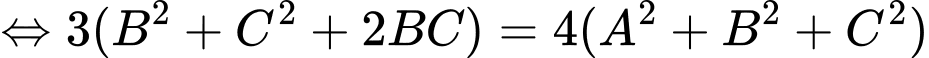
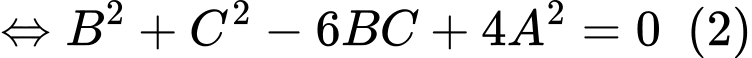
Thay vào
vào  ta có:
ta có: 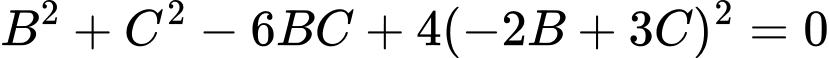
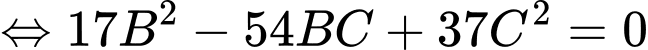
Cho
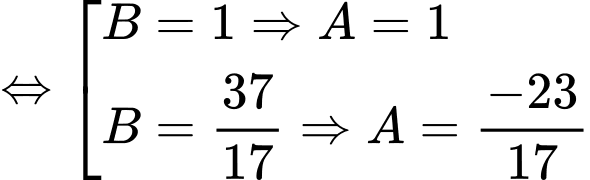
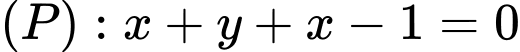
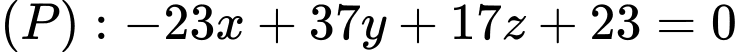 Đáp án: D
Đáp án: D
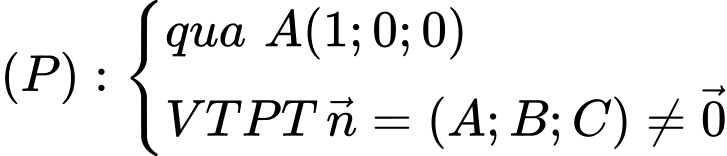
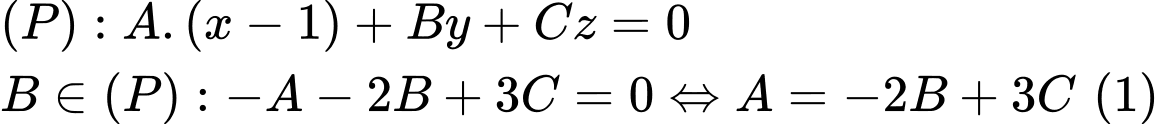
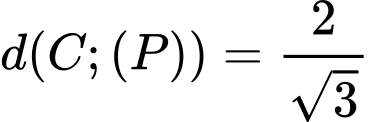
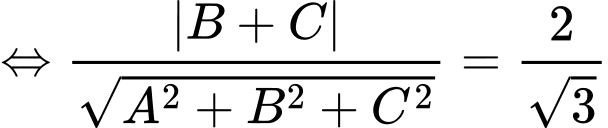
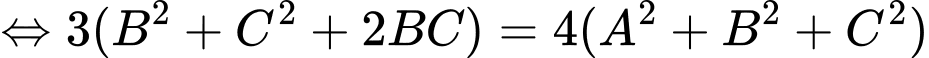
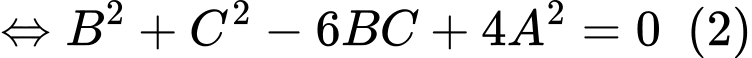
Thay
 vào
vào  ta có:
ta có: 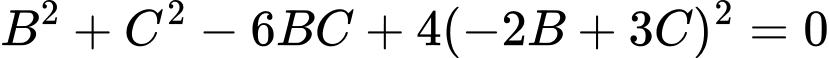
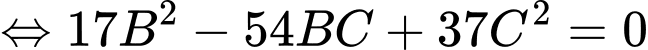
Cho

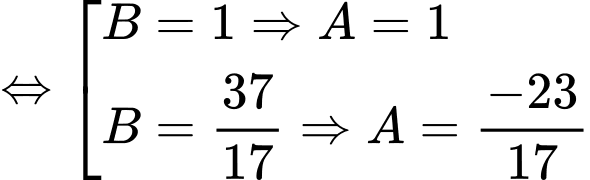
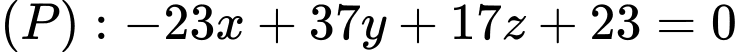 Đáp án: D
Đáp án: D
Câu 14 [581722]: Trong hệ trục tọa độ 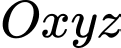 cho
cho 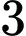 điểm
điểm 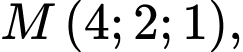
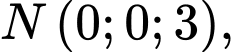
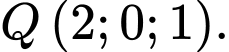 Viết phương trình mặt phẳng chứa
Viết phương trình mặt phẳng chứa 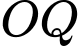 và cách đều
và cách đều 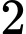 điểm
điểm 
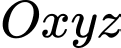 cho
cho 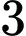 điểm
điểm 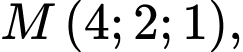
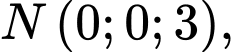
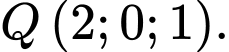 Viết phương trình mặt phẳng chứa
Viết phương trình mặt phẳng chứa 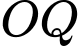 và cách đều
và cách đều 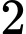 điểm
điểm 
A, 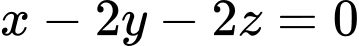 hoặc
hoặc 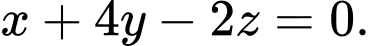
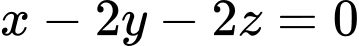 hoặc
hoặc 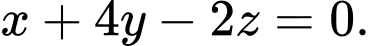
B,  hoặc
hoặc 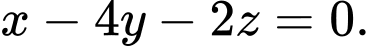
 hoặc
hoặc 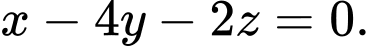
C, 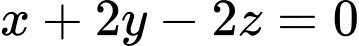 hoặc
hoặc 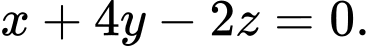
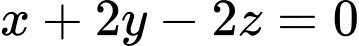 hoặc
hoặc 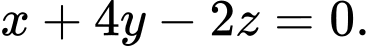
D, 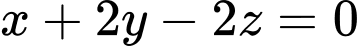 hoặc
hoặc 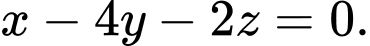
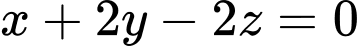 hoặc
hoặc 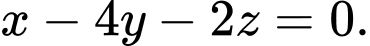
Gọi 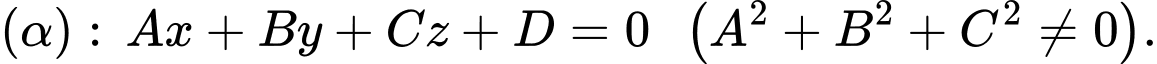
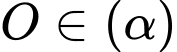 nên ta có:
nên ta có: 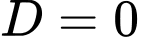

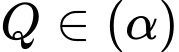 nên ta có:
nên ta có: 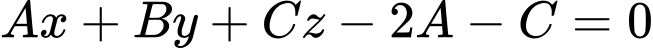

Từ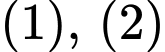
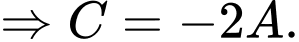
Theo đề bài: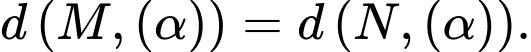
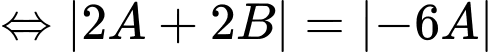
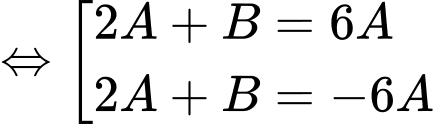
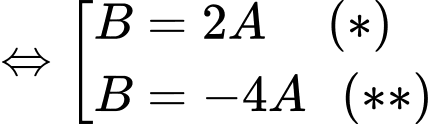
Từ Chọn
Chọn 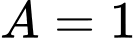
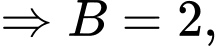
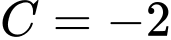
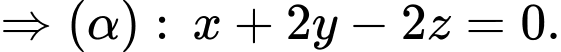
Từ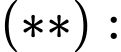 Chọn
Chọn 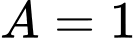
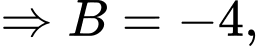
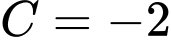
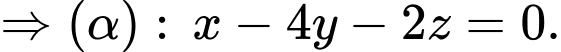 Đáp án: D
Đáp án: D
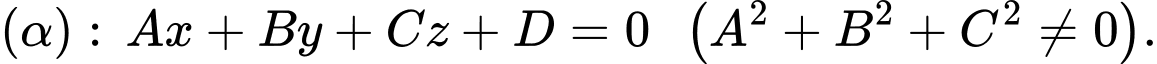
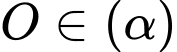 nên ta có:
nên ta có: 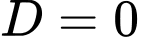

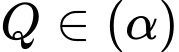 nên ta có:
nên ta có: 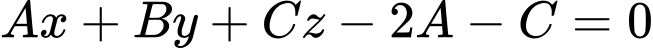

Từ
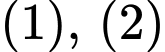
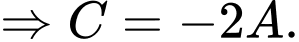
Theo đề bài:
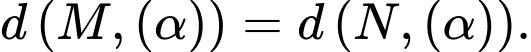
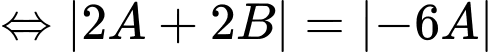
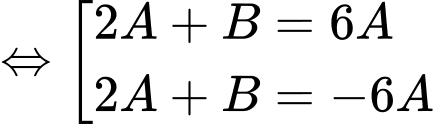
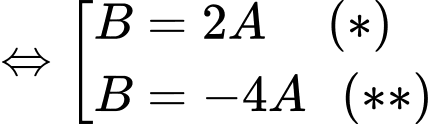
Từ
 Chọn
Chọn 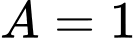
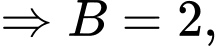
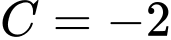
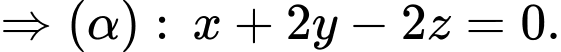
Từ
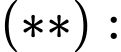 Chọn
Chọn 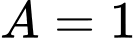
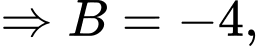
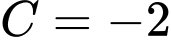
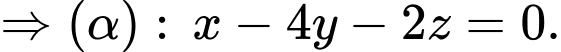 Đáp án: D
Đáp án: D
Câu 15 [581723]: Trong không gian với hệ trục tọa độ 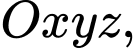 cho các điểm
cho các điểm 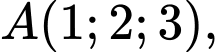
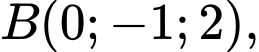
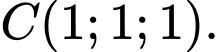 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 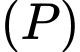 đi qua
đi qua 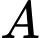 và gốc tọa độ
và gốc tọa độ  sao cho khoảng cách từ
sao cho khoảng cách từ 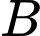 đến
đến 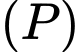 bằng khoảng cách từ
bằng khoảng cách từ  đến
đến 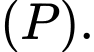
 cho các điểm
cho các điểm 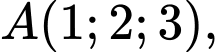
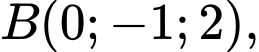
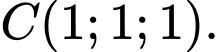 Viết phương trình mặt phẳng
Viết phương trình mặt phẳng 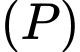 đi qua
đi qua 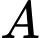 và gốc tọa độ
và gốc tọa độ  sao cho khoảng cách từ
sao cho khoảng cách từ 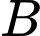 đến
đến 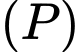 bằng khoảng cách từ
bằng khoảng cách từ  đến
đến 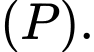
Đáp án: 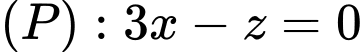 hoặc
hoặc 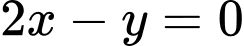
Vì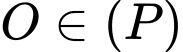 nên
nên 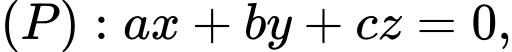 với
với 
Do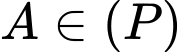
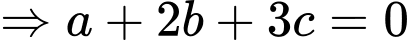 (1)
và
(1)
và 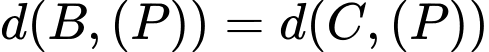
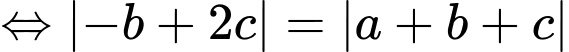 (2)
(2)
Từ (1) và (2)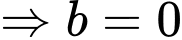 hoặc
hoặc 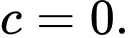
• Với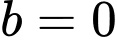 thì
thì 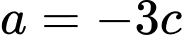
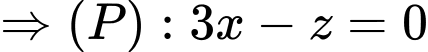
• Với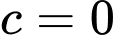 thì
thì 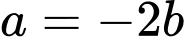
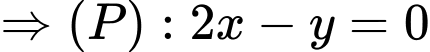
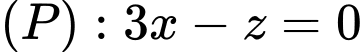 hoặc
hoặc 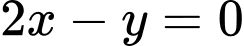
Vì
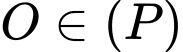 nên
nên 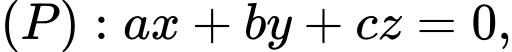 với
với 
Do
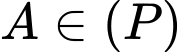
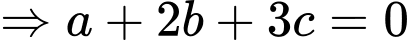 (1)
và
(1)
và 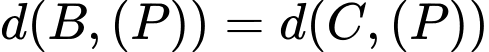
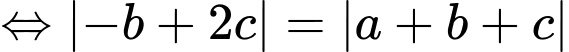 (2)
(2)
Từ (1) và (2)
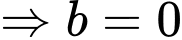 hoặc
hoặc 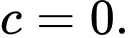
• Với
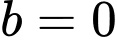 thì
thì 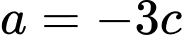
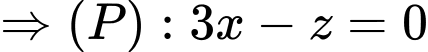
• Với
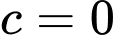 thì
thì 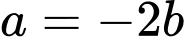
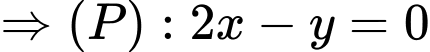
6. Dạng toán: Ứng dụng mặt phẳng trong không gian
6.1. Phương pháp tư duy
6.2. Ví dụ áp dụng.
6.2. Ví dụ áp dụng.
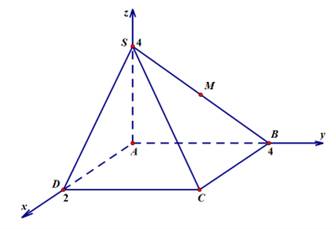
Câu 16 [581724]: Trong không gian với hệ tọa độ 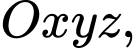 cho hình chóp
cho hình chóp 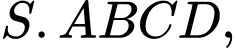 đáy
đáy 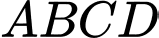 là hình chữ nhật. Biết
là hình chữ nhật. Biết 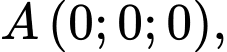
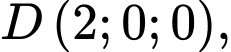
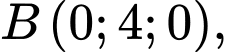
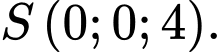 Gọi
Gọi 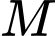 là trung điểm của
là trung điểm của 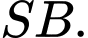 Tính khoảng cách từ
Tính khoảng cách từ 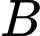 đến mặt phẳng
đến mặt phẳng 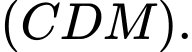
 cho hình chóp
cho hình chóp 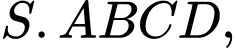 đáy
đáy  là hình chữ nhật. Biết
là hình chữ nhật. Biết 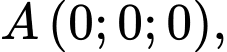
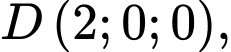
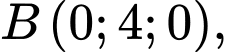
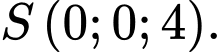 Gọi
Gọi 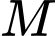 là trung điểm của
là trung điểm của 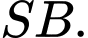 Tính khoảng cách từ
Tính khoảng cách từ 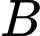 đến mặt phẳng
đến mặt phẳng 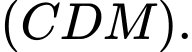
A, 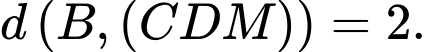
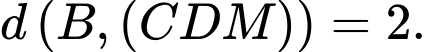
B, 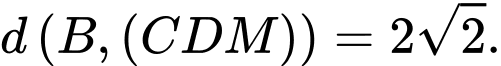
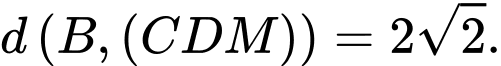
C, 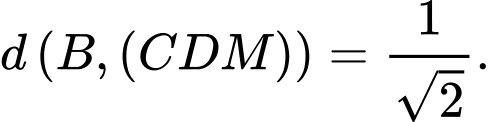
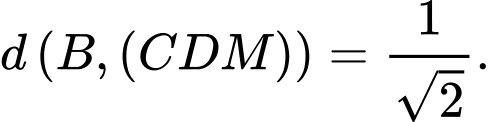
D, 

Tứ giác
 là hình chữ nhật nên
là hình chữ nhật nên 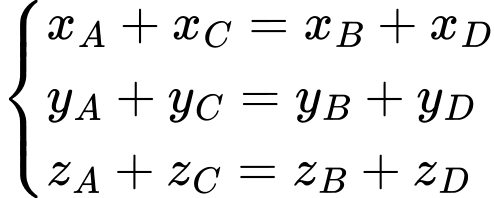
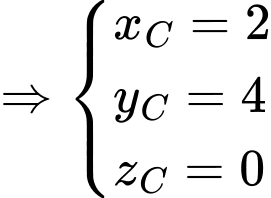
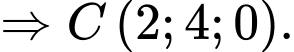
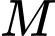 là trung điểm của
là trung điểm của 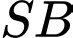

Viết phương trình mặt phẳng
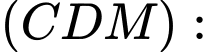
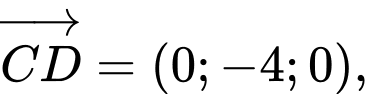
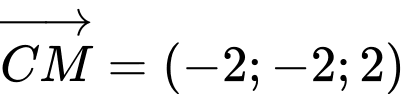
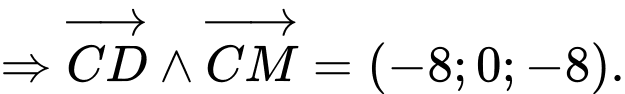
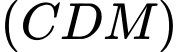 có một vectơ pháp tuyến
có một vectơ pháp tuyến 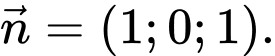
Suy ra
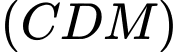 có phương trình:
có phương trình: 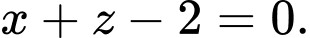
Vậy
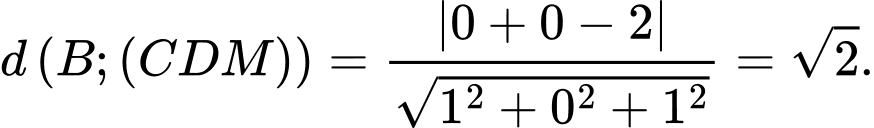 Đáp án: D
Đáp án: D
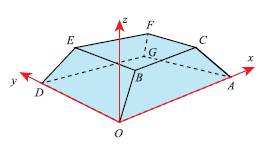
Câu 17 [581725]: Một sân vận động được xây dựng theo mô hình là hình chóp cụt  có hai đáy song song với nhau. Mặt sân
có hai đáy song song với nhau. Mặt sân  là hình chữ nhật và được gắn hệ trục
là hình chữ nhật và được gắn hệ trục 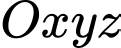 như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân
như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân  có chiều dài
có chiều dài 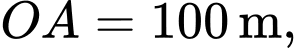 chiều rộng
chiều rộng 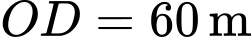 và tọa độ điểm
và tọa độ điểm 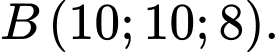
a) Lập phương trình mặt phẳng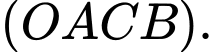
b) Tính khoảng cách từ điểm đến mặt phẳng
đến mặt phẳng 
 có hai đáy song song với nhau. Mặt sân
có hai đáy song song với nhau. Mặt sân 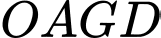 là hình chữ nhật và được gắn hệ trục
là hình chữ nhật và được gắn hệ trục  như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân
như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân  có chiều dài
có chiều dài 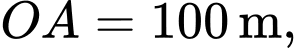 chiều rộng
chiều rộng 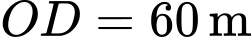 và tọa độ điểm
và tọa độ điểm 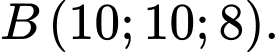

a) Lập phương trình mặt phẳng
b) Tính khoảng cách từ điểm
 đến mặt phẳng
đến mặt phẳng 

a) Lập phương trình mặt phẳng
Gắn hình chóp cụt
 vào hệ trục
vào hệ trục 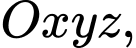 ta có:
ta có: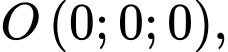
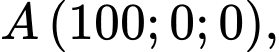
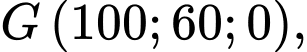
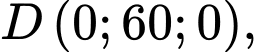
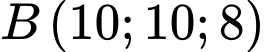
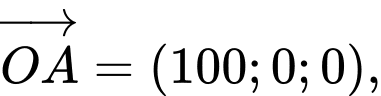
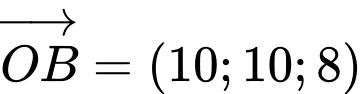
Vectơ pháp tuyến của mặt phẳng
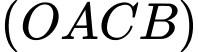 là
là 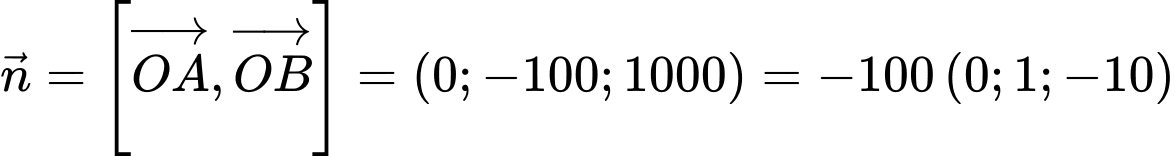
Phương trình mặt phẳng
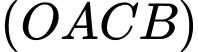 đi qua điểm
đi qua điểm 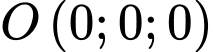 và có vectơ pháp tuyến
và có vectơ pháp tuyến 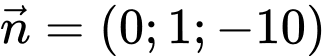 là:
là: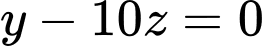
b) Tính khoảng cách từ điểm
 đến mặt phẳng
đến mặt phẳng 
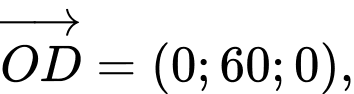
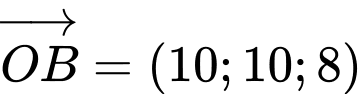
Vectơ pháp tuyến của mặt phẳng
 là
là 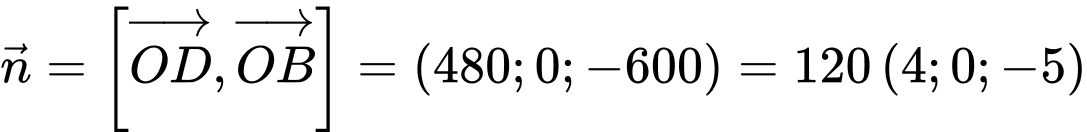
Phương trình mặt phẳng
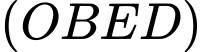 đi qua điểm
đi qua điểm 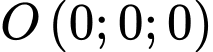 và có vectơ pháp tuyến
và có vectơ pháp tuyến 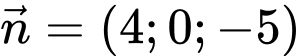 là:
là: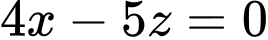
Khoảng cách từ điểm
 đến mặt phẳng
đến mặt phẳng  là:
là: