1. Dạng toán: Xác định các yếu tố cơ bản của mặt cầu
1.1. Phương pháp tư duy
1.2. Ví dụ áp dụng.
1.2. Ví dụ áp dụng.
Câu 1 [581747]: Trong không gian 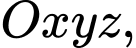 cho mặt cầu
cho mặt cầu 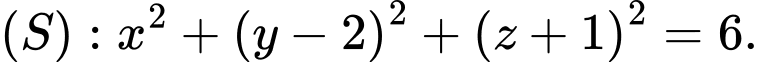 Đường kính của
Đường kính của 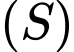 bằng
bằng
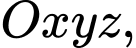 cho mặt cầu
cho mặt cầu 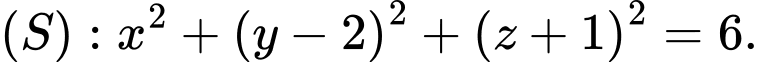 Đường kính của
Đường kính của 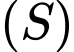 bằng
bằng A, 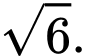
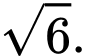
B, 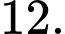
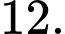
C, 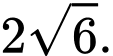
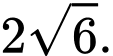
D, 
Chọn C.
Ta có bán kính của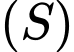 là
là 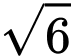 nên đường kính của
nên đường kính của 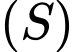 bằng
bằng 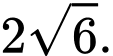 Đáp án: C
Đáp án: C
Ta có bán kính của
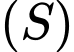 là
là 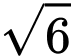 nên đường kính của
nên đường kính của 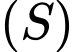 bằng
bằng 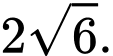 Đáp án: C
Đáp án: C
Câu 2 [581748]: Trong không gian 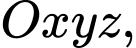 cho mặt cầu
cho mặt cầu 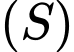 có tâm
có tâm 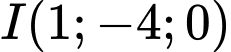 và bán kính bằng 3. Phương trình
của
và bán kính bằng 3. Phương trình
của 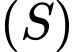 là
là
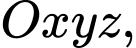 cho mặt cầu
cho mặt cầu 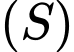 có tâm
có tâm 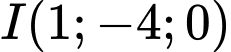 và bán kính bằng 3. Phương trình
của
và bán kính bằng 3. Phương trình
của 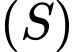 là
là A, 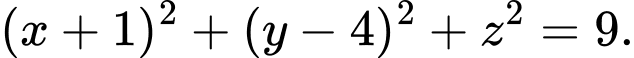
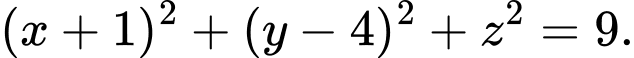
B, 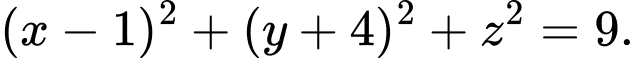
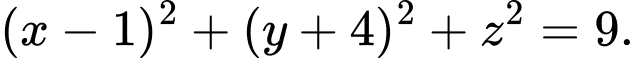
C, 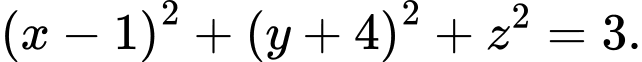
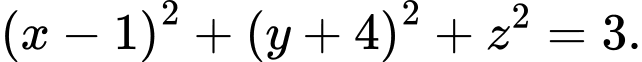
D, 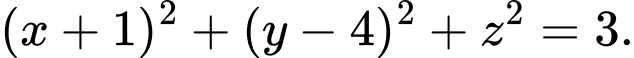
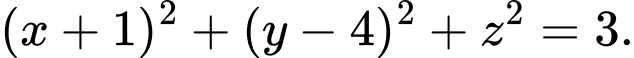
Chọn C.
Phương trình mặt cầu tâm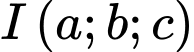 và bán kính bằng
và bán kính bằng 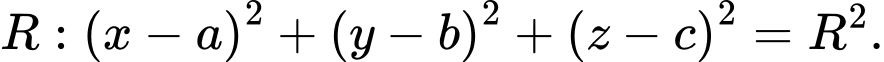
Mặt cầu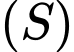 có tâm
có tâm 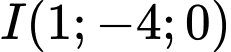 có bán kính 3 có phương trình là
có bán kính 3 có phương trình là 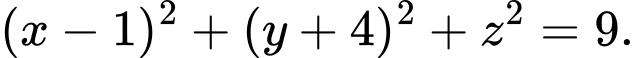 Đáp án: C
Đáp án: C
Phương trình mặt cầu tâm
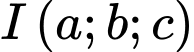 và bán kính bằng
và bán kính bằng 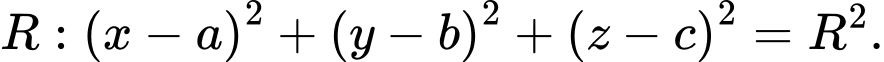
Mặt cầu
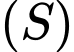 có tâm
có tâm 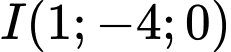 có bán kính 3 có phương trình là
có bán kính 3 có phương trình là 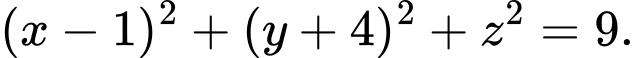 Đáp án: C
Đáp án: C
Câu 3 [581749]: Trong không gian với hệ tọa độ 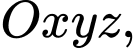 trong các mặt cầu dưới đây, mặt cầu nào có bán kính
trong các mặt cầu dưới đây, mặt cầu nào có bán kính 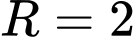
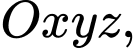 trong các mặt cầu dưới đây, mặt cầu nào có bán kính
trong các mặt cầu dưới đây, mặt cầu nào có bán kính 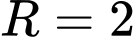
A, 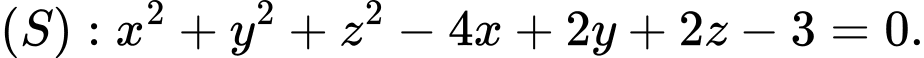
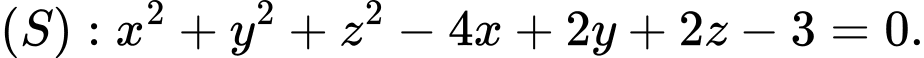
B, 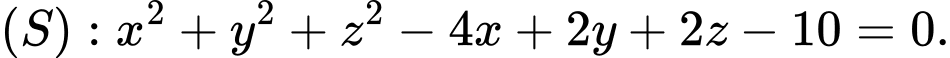
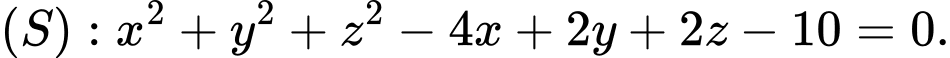
C, 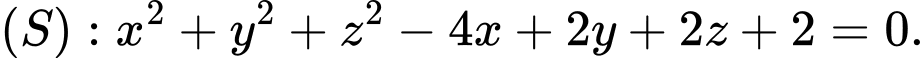
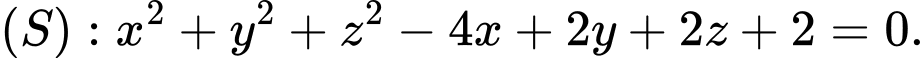
D, 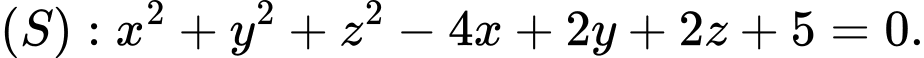
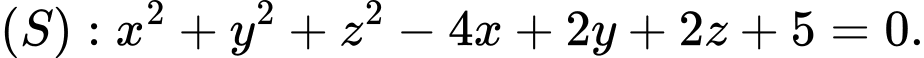
Chọn C
Ta có mặt cầu có bán kính là
có bán kính là 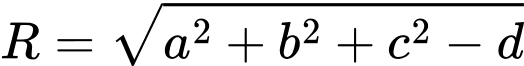
Trong đáp án C ta có: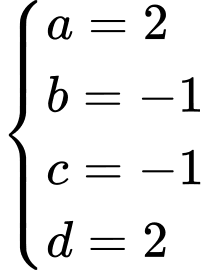
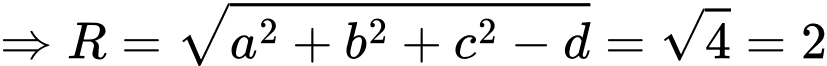 Đáp án: C
Đáp án: C
Ta có mặt cầu
 có bán kính là
có bán kính là 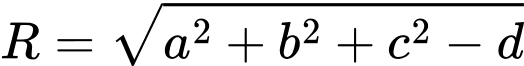
Trong đáp án C ta có:
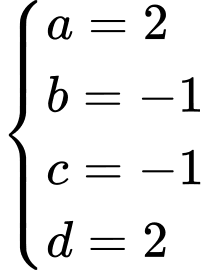
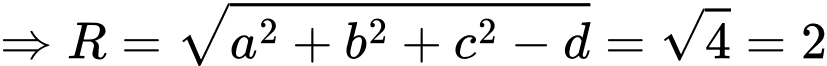 Đáp án: C
Đáp án: C 2. Dạng toán: Lập phương trình mặt cầu dạng cơ bản
2.1. Phương pháp tư duy
2.2. Ví dụ áp dụng
2.2. Ví dụ áp dụng
Câu 4 [581750]: Trong không gian 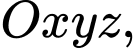 cho mặt cầu
cho mặt cầu 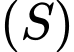 có tâm
có tâm 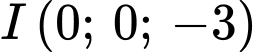 và đi qua điểm
và đi qua điểm 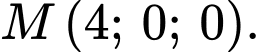 Phương trình của
Phương trình của 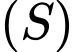 là
là
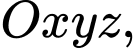 cho mặt cầu
cho mặt cầu 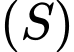 có tâm
có tâm 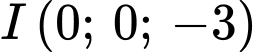 và đi qua điểm
và đi qua điểm 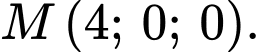 Phương trình của
Phương trình của 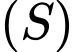 là
là A, 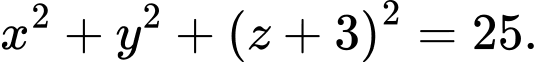
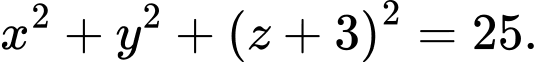
B, 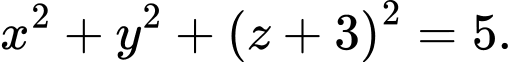
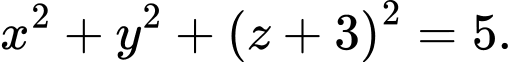
C, 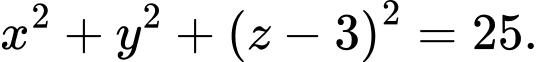
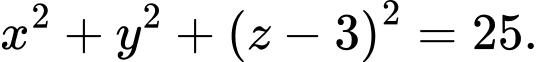
D, 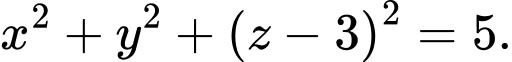
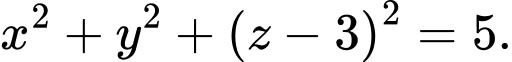
Chọn A
Phương trình mặt cầu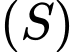 có tâm
có tâm 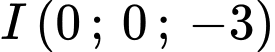 và bán kính
và bán kính 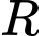 là:
là: 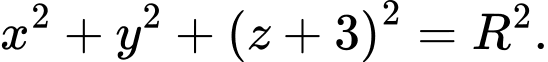
Ta có: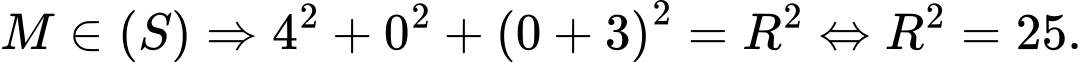
Vậy phương trình cần tìm là: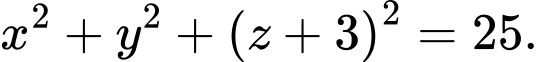 Đáp án: A
Đáp án: A
Phương trình mặt cầu
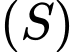 có tâm
có tâm 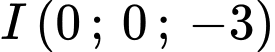 và bán kính
và bán kính 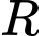 là:
là: 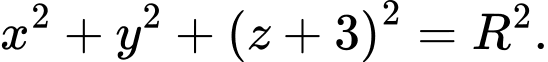
Ta có:
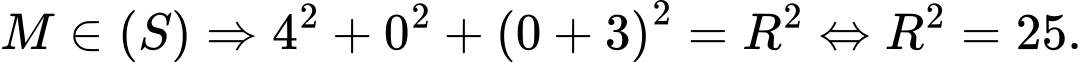
Vậy phương trình cần tìm là:
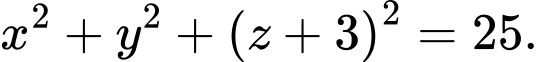 Đáp án: A
Đáp án: A
Câu 5 [581751]: Phương trình nào sau đây là phương trình mặt cầu 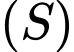 tâm
tâm 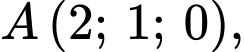 đi qua điểm
đi qua điểm 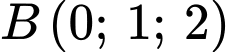 ?
?
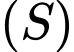 tâm
tâm 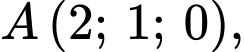 đi qua điểm
đi qua điểm 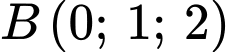 ?
? A, 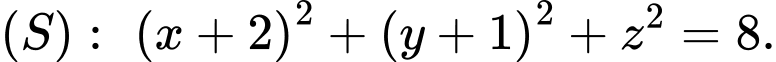
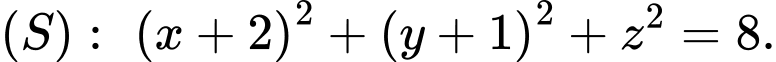
B, 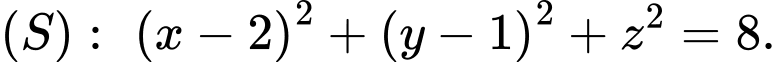
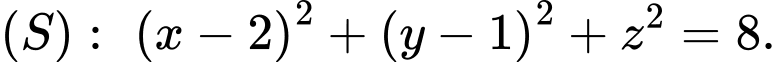
C, 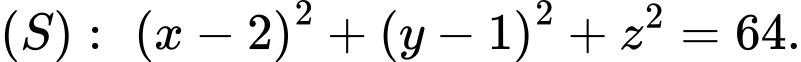
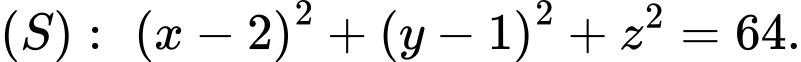
D, 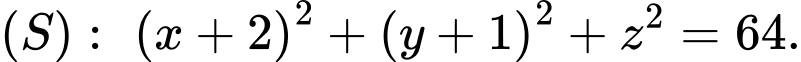
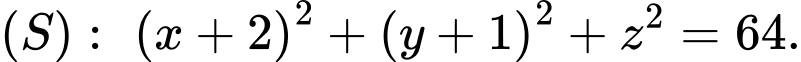
Chọn B
Vì mặt cầu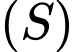 có tâm
có tâm 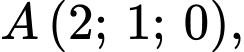 đi qua điểm
đi qua điểm 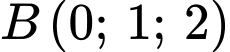 nên mặt cầu
nên mặt cầu 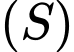 có tâm
có tâm 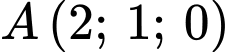 và nhận độ dài đoạn thẳng
và nhận độ dài đoạn thẳng  là bán kính.
là bán kính.
Ta có: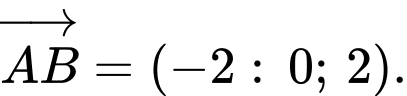
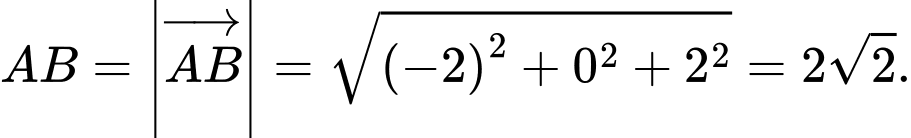 Suy ra:
Suy ra: 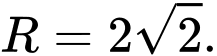
Vậy: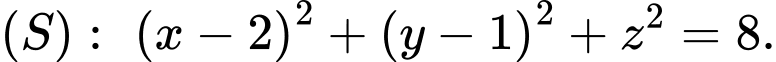 Đáp án: B
Đáp án: B
Vì mặt cầu
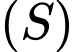 có tâm
có tâm 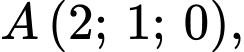 đi qua điểm
đi qua điểm 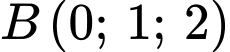 nên mặt cầu
nên mặt cầu 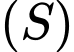 có tâm
có tâm 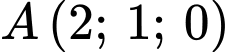 và nhận độ dài đoạn thẳng
và nhận độ dài đoạn thẳng  là bán kính.
là bán kính.
Ta có:
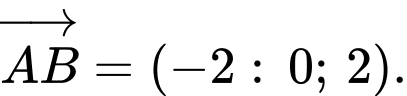
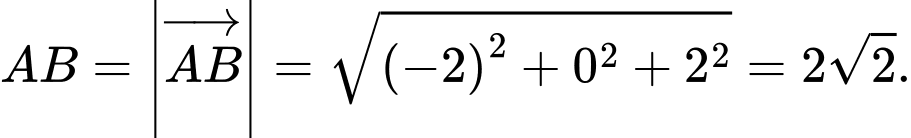 Suy ra:
Suy ra: 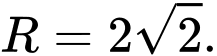
Vậy:
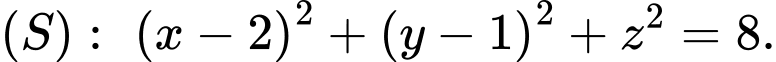 Đáp án: B
Đáp án: B
Câu 6 [581752]: Trong không gian với hệ trục tọa độ 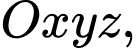 cho hai điểm
cho hai điểm 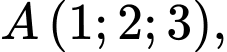
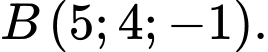 Phương trình mặt cầu đường kính
Phương trình mặt cầu đường kính  là
là
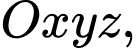 cho hai điểm
cho hai điểm 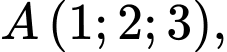
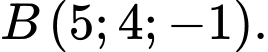 Phương trình mặt cầu đường kính
Phương trình mặt cầu đường kính  là
là A, 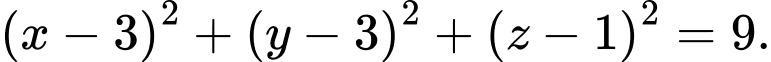
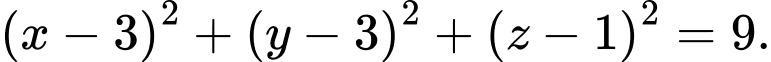
B, 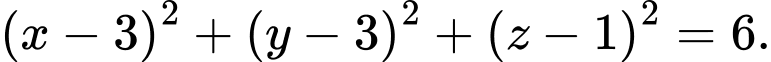
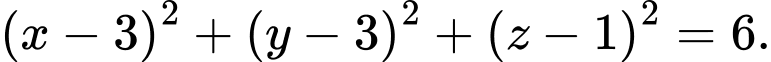
C, 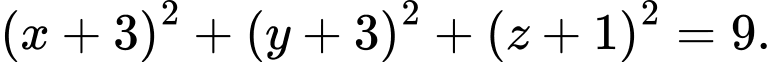
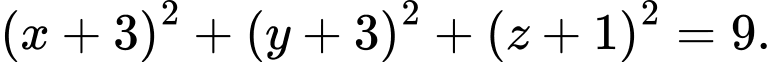
D, 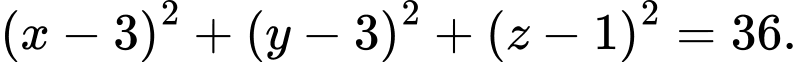
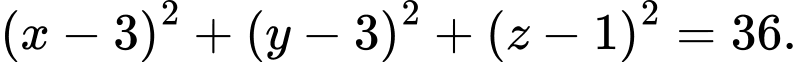
Chọn A
+ Gọi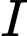 là trung điểm của
là trung điểm của 
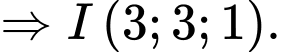
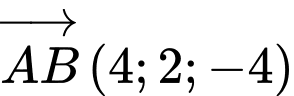
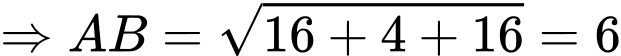
+ Mặt cầu đường kính có tâm
có tâm 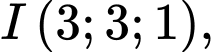 bán kính
bán kính 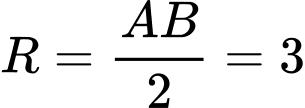 có phương trình là:
có phương trình là:
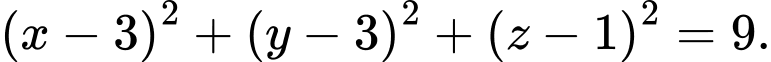 Đáp án: A
Đáp án: A
+ Gọi
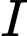 là trung điểm của
là trung điểm của 
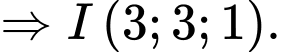
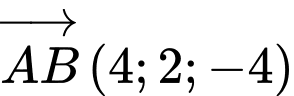
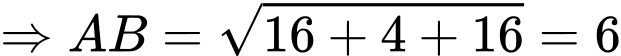
+ Mặt cầu đường kính
 có tâm
có tâm 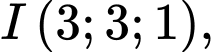 bán kính
bán kính 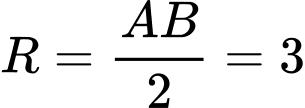 có phương trình là:
có phương trình là:
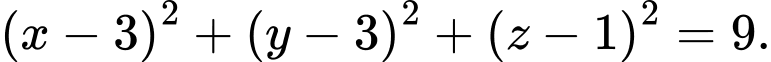 Đáp án: A
Đáp án: A 3. Dạng toán: Vị trí tương đối giữa mặt phẳng với mặt cầu
3.1. Phương pháp tư duy
3.2. Ví dụ áp dụng.
3.2. Ví dụ áp dụng.
Câu 7 [581753]: Trong không gian với hệ tọa độ 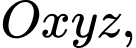 cho mặt cầu
cho mặt cầu 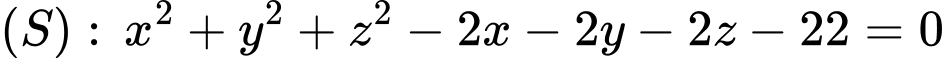 và mặt phẳng
và mặt phẳng 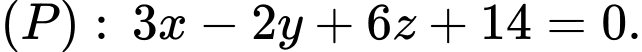 Khoảng cách từ tâm
Khoảng cách từ tâm 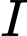 của mặt cầu
của mặt cầu 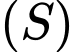 đến mặt phẳng
đến mặt phẳng 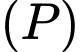 bằng
bằng
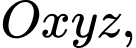 cho mặt cầu
cho mặt cầu 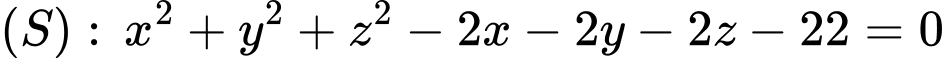 và mặt phẳng
và mặt phẳng 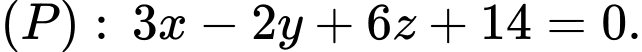 Khoảng cách từ tâm
Khoảng cách từ tâm 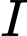 của mặt cầu
của mặt cầu 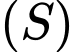 đến mặt phẳng
đến mặt phẳng 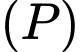 bằng
bằng A, 2.
B, 4.
C, 3.
D, 1.
Chọn C
Mặt cầu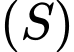 có tâm
có tâm 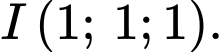 Vậy
Vậy 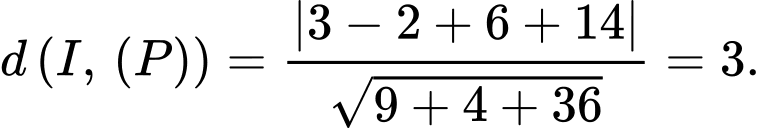
Mặt cầu
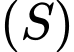 có tâm
có tâm 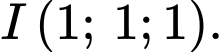 Vậy
Vậy 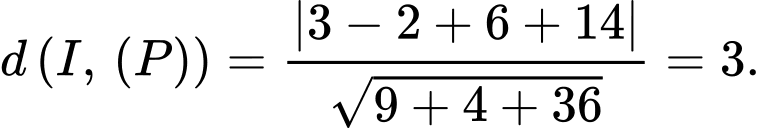
Câu 8 [581754]: Trong không gian với hệ tọa độ 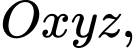 cho mặt cầu
cho mặt cầu 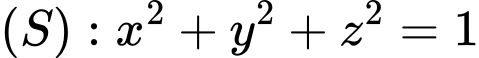 và mặt phẳng
và mặt phẳng 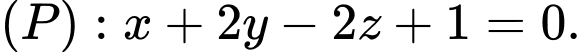 Tìm bán kính
Tìm bán kính 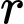 đường tròn giao tuyến của
đường tròn giao tuyến của 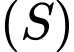 và
và 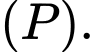
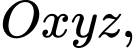 cho mặt cầu
cho mặt cầu 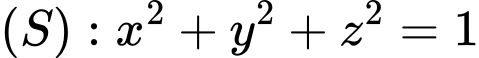 và mặt phẳng
và mặt phẳng 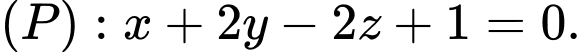 Tìm bán kính
Tìm bán kính 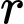 đường tròn giao tuyến của
đường tròn giao tuyến của 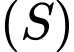 và
và 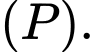
A, 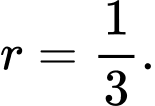
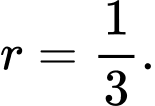
B, 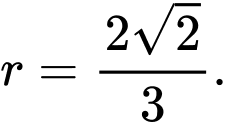
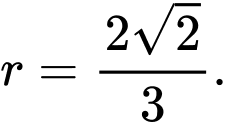
C, 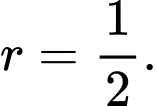
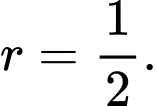
D, 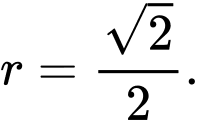
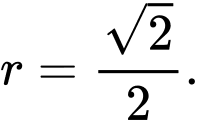
Chọn B
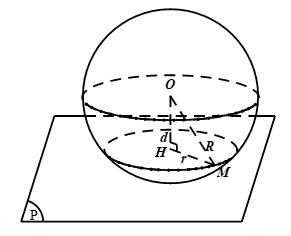
Mặt cầu có tâm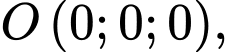 bán kính
bán kính 
Khoảng cách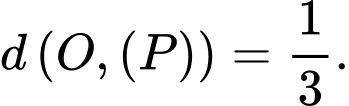
Bán kính đường tròn giao tuyến là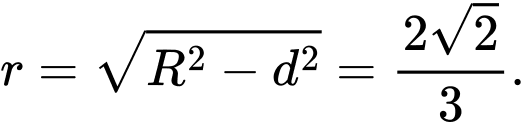 Đáp án: B
Đáp án: B

Mặt cầu có tâm
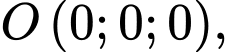 bán kính
bán kính 
Khoảng cách
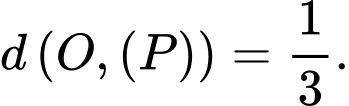
Bán kính đường tròn giao tuyến là
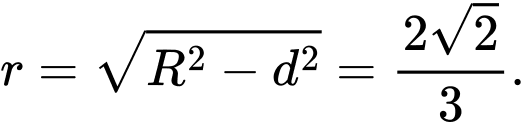 Đáp án: B
Đáp án: B
Câu 9 [581755]: Trong không gian 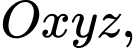 cho mặt cầu
cho mặt cầu 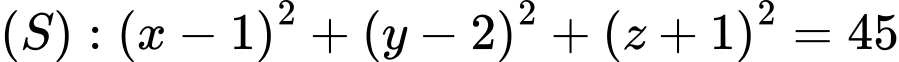 và mặt phẳng
và mặt phẳng 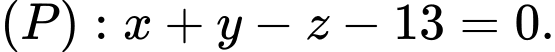 Mặt cầu
Mặt cầu 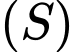 cắt mặt phẳng
cắt mặt phẳng 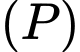 theo giao tuyến là đường tròn có tâm
theo giao tuyến là đường tròn có tâm 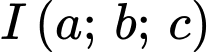 thì giá trị của
thì giá trị của 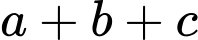 bằng
bằng
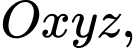 cho mặt cầu
cho mặt cầu 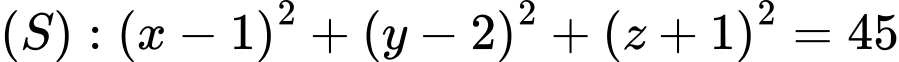 và mặt phẳng
và mặt phẳng 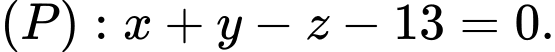 Mặt cầu
Mặt cầu 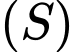 cắt mặt phẳng
cắt mặt phẳng 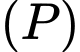 theo giao tuyến là đường tròn có tâm
theo giao tuyến là đường tròn có tâm 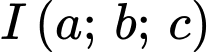 thì giá trị của
thì giá trị của 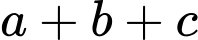 bằng
bằng A, 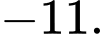
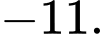
B, 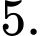
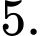
C, 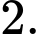
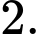
D, 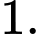
Chọn B
Mặt cầu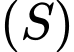 có tâm
có tâm 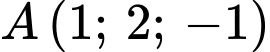 và bán kính
và bán kính 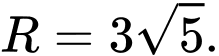
Mặt cầu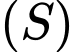 cắt mặt phẳng
cắt mặt phẳng 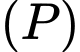 theo giao tuyến là đường tròn có tâm
theo giao tuyến là đường tròn có tâm 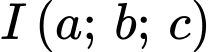
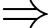
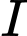 là hình chiếu của
là hình chiếu của 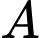 lên mp
lên mp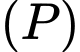
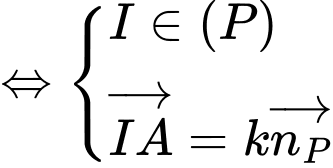
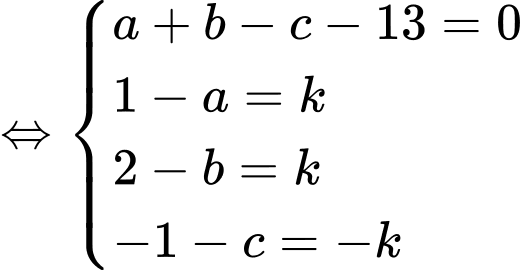
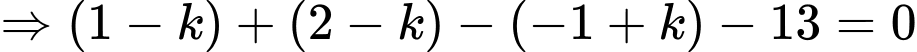
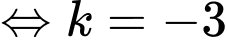
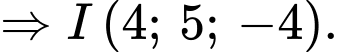
Vậy Đáp án: B
Đáp án: B
Mặt cầu
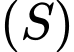 có tâm
có tâm 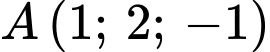 và bán kính
và bán kính 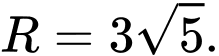
Mặt cầu
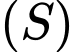 cắt mặt phẳng
cắt mặt phẳng 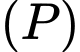 theo giao tuyến là đường tròn có tâm
theo giao tuyến là đường tròn có tâm 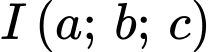
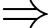
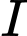 là hình chiếu của
là hình chiếu của 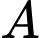 lên mp
lên mp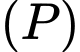
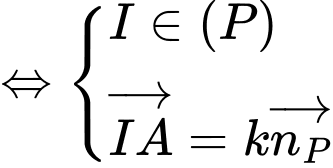
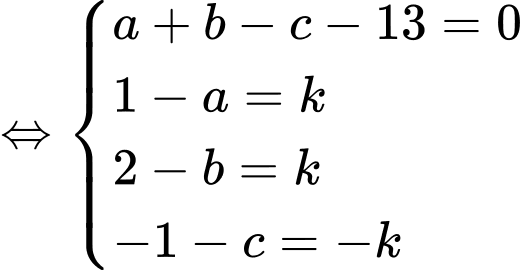
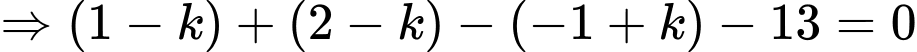
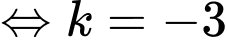
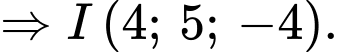
Vậy
 Đáp án: B
Đáp án: B 4. Dạng toán: Lập phương trình mặt cầu liên quan đến mặt phẳng
4.1. Phương pháp tư duy
4.2. Ví dụ áp dụng.
4.2. Ví dụ áp dụng.
Câu 10 [581756]: Trong không gian với hệ tọa độ 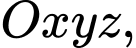 cho mặt cầu
cho mặt cầu 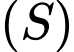 có tâm
có tâm 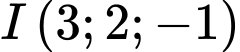 và đi qua điểm
và đi qua điểm 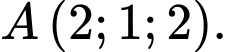 Mặt phẳng nào dưới đây tiếp xúc với
Mặt phẳng nào dưới đây tiếp xúc với 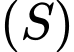 tại
tại 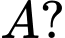
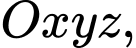 cho mặt cầu
cho mặt cầu 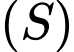 có tâm
có tâm 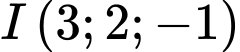 và đi qua điểm
và đi qua điểm 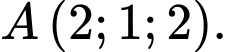 Mặt phẳng nào dưới đây tiếp xúc với
Mặt phẳng nào dưới đây tiếp xúc với 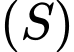 tại
tại 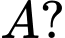
A, 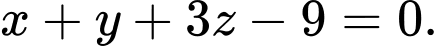
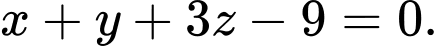
B, 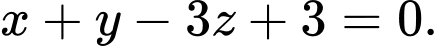
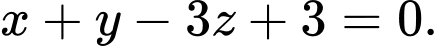
C, 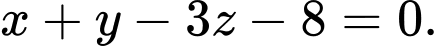
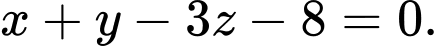
D, 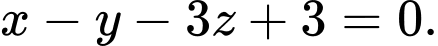
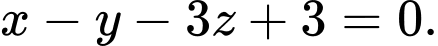
Chọn B
Gọi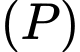 là mặt phẳng cần tìm. Khi đó,
là mặt phẳng cần tìm. Khi đó, 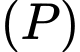 tiếp xúc với
tiếp xúc với 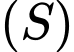 tại
tại 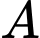 khi chỉ khi
khi chỉ khi 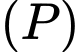 đi qua
đi qua 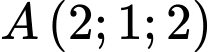 và nhận vectơ
và nhận vectơ 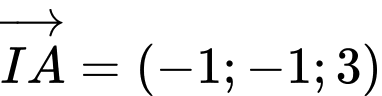 làm vectơ pháp tuyến. Phương trình mặt phẳng
làm vectơ pháp tuyến. Phương trình mặt phẳng 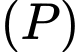 là
là 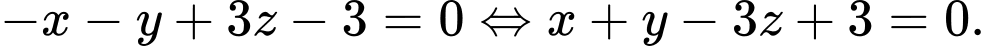 Đáp án: B
Đáp án: B
Gọi
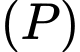 là mặt phẳng cần tìm. Khi đó,
là mặt phẳng cần tìm. Khi đó, 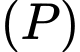 tiếp xúc với
tiếp xúc với 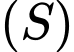 tại
tại 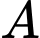 khi chỉ khi
khi chỉ khi 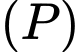 đi qua
đi qua 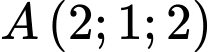 và nhận vectơ
và nhận vectơ 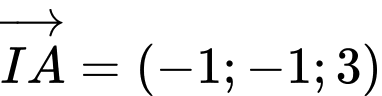 làm vectơ pháp tuyến. Phương trình mặt phẳng
làm vectơ pháp tuyến. Phương trình mặt phẳng 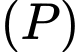 là
là 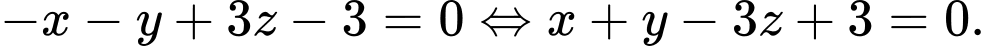 Đáp án: B
Đáp án: B
Câu 11 [581757]: Trong không gian với hệ tọa độ 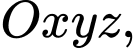 cho mặt phẳng
cho mặt phẳng 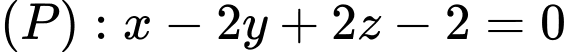 và điểm
và điểm 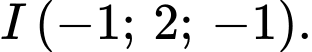 Viết phương trình mặt cầu
Viết phương trình mặt cầu 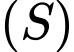 có tâm
có tâm 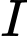 và cắt mặt phẳng
và cắt mặt phẳng 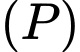 theo giao tuyến là đường tròn có bán kính bằng
theo giao tuyến là đường tròn có bán kính bằng 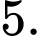
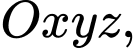 cho mặt phẳng
cho mặt phẳng 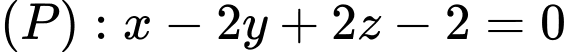 và điểm
và điểm 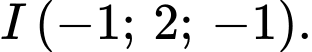 Viết phương trình mặt cầu
Viết phương trình mặt cầu 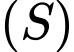 có tâm
có tâm 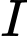 và cắt mặt phẳng
và cắt mặt phẳng 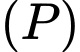 theo giao tuyến là đường tròn có bán kính bằng
theo giao tuyến là đường tròn có bán kính bằng 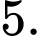
A, 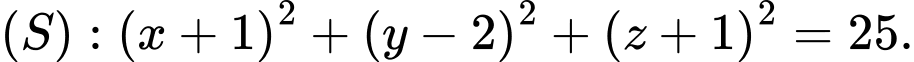
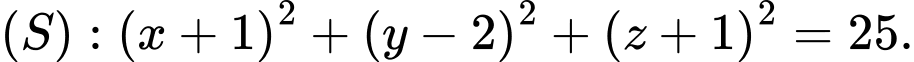
B, 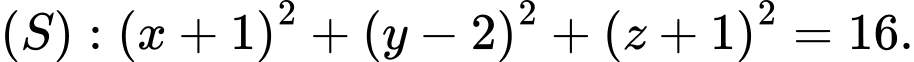
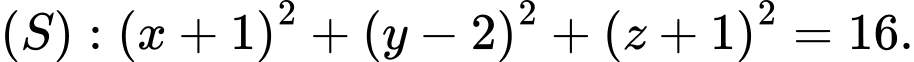
C, 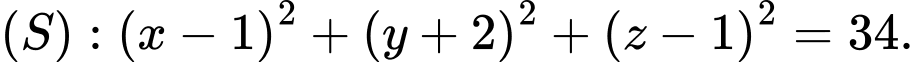
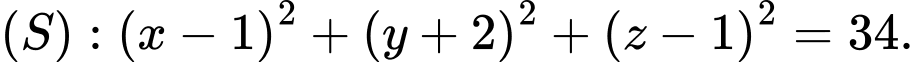
D, 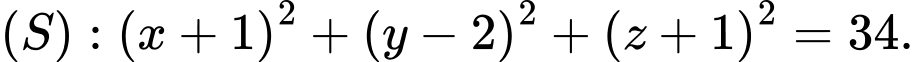
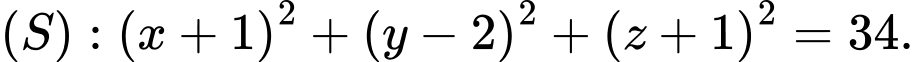
Chọn D
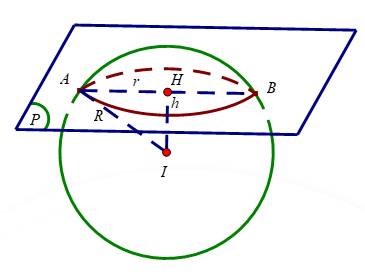
Gọi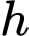 là khoảng cách từ tâm
là khoảng cách từ tâm 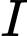 đến mặt phẳng
đến mặt phẳng  ta có:
ta có:
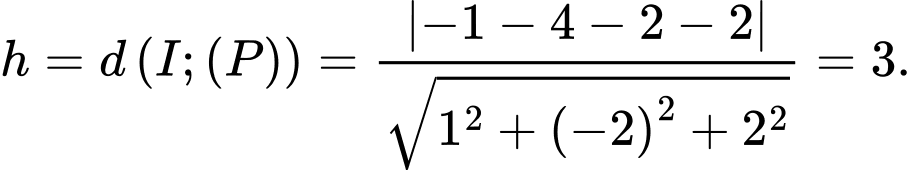
Bán kính mặt cầu là:
là: 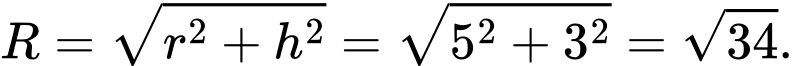
Phương trình mặt cầu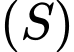 là:
là: 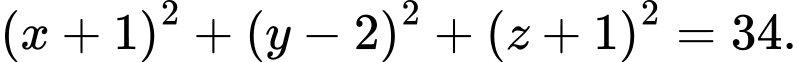 Đáp án: D
Đáp án: D

Gọi
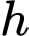 là khoảng cách từ tâm
là khoảng cách từ tâm 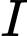 đến mặt phẳng
đến mặt phẳng 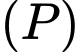 ta có:
ta có:
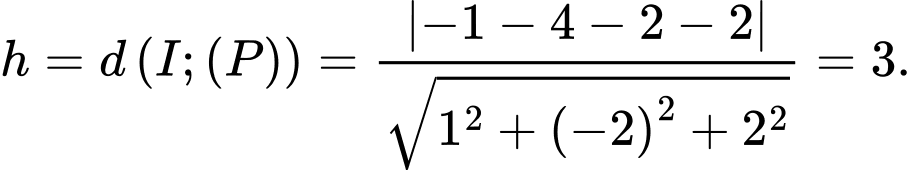
Bán kính mặt cầu
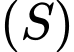 là:
là: 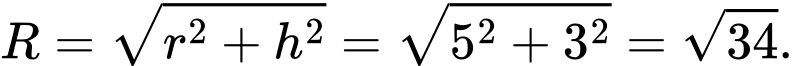
Phương trình mặt cầu
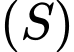 là:
là: 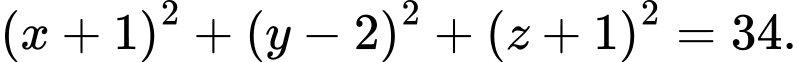 Đáp án: D
Đáp án: D
Câu 12 [581758]: Trong không gian với hệ trục tọa độ  phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm
phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm 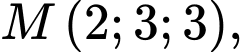
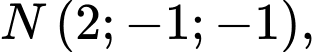
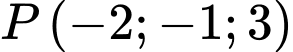 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 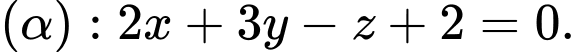
 phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm
phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm 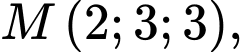
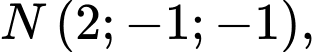
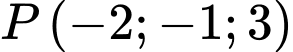 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 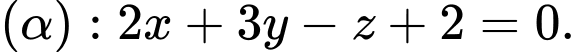
A, 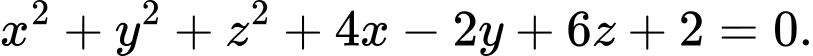
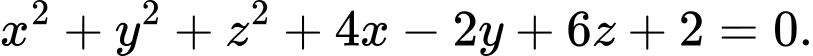
B, 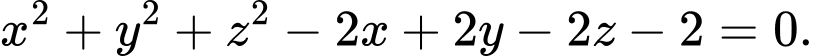
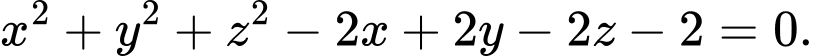
C, 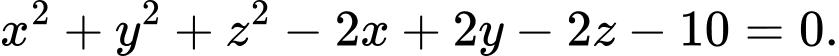
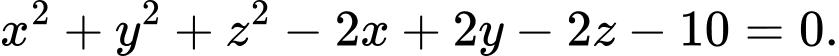
D, 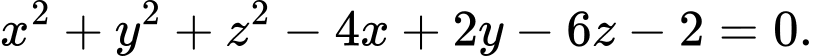
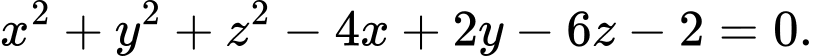
Chọn D.
Giả sử phương trình mặt cầu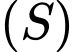 có dạng
có dạng 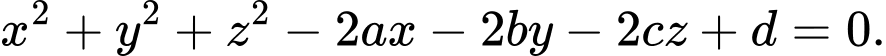
Điều kiện: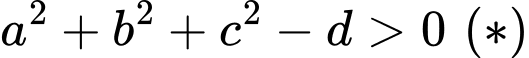
Vì mặt cầu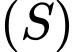 đi qua 3 điểm
đi qua 3 điểm 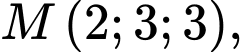
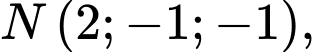
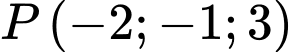 và có tâm
và có tâm 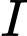 thuộc
thuộc 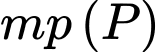 nên ta có hệ phương trình
nên ta có hệ phương trình 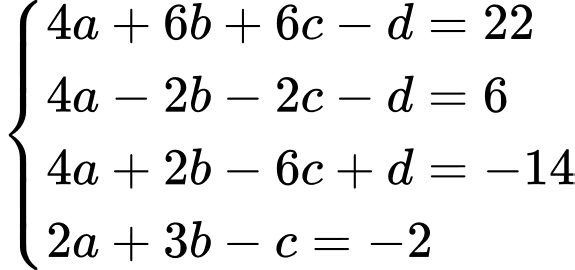
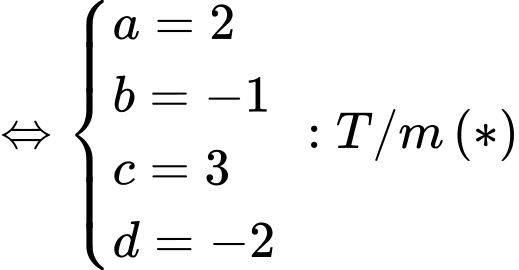
Vậy phương trình mặt cầu là: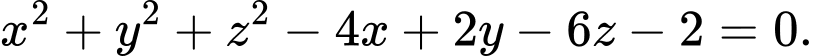 Đáp án: D
Đáp án: D
Giả sử phương trình mặt cầu
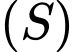 có dạng
có dạng 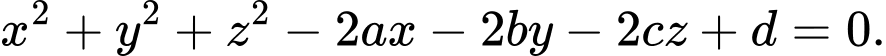
Điều kiện:
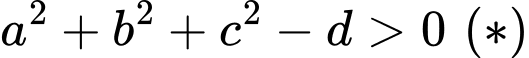
Vì mặt cầu
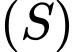 đi qua 3 điểm
đi qua 3 điểm 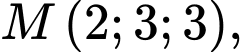
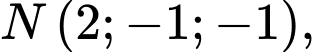
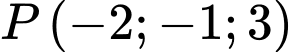 và có tâm
và có tâm 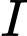 thuộc
thuộc 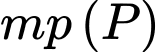 nên ta có hệ phương trình
nên ta có hệ phương trình 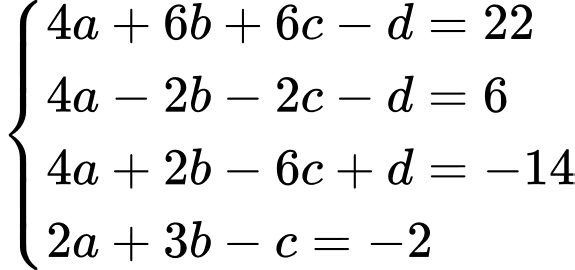
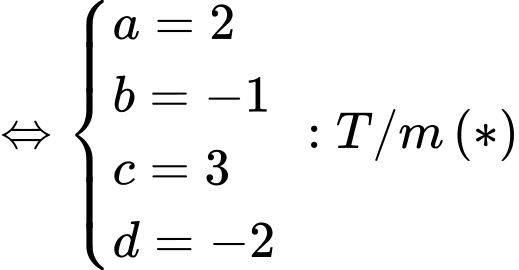
Vậy phương trình mặt cầu là:
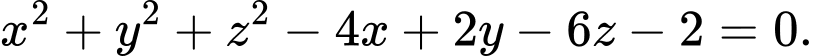 Đáp án: D
Đáp án: D 5. Dạng toán: Vị trí tương đối của đường thẳng với mặt cầu
5.1. Phương pháp tư duy
5.2. Ví dụ áp dụng.
5.2. Ví dụ áp dụng.
Câu 13 [581759]: Trong không gian 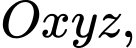 cho đường thẳng
cho đường thẳng 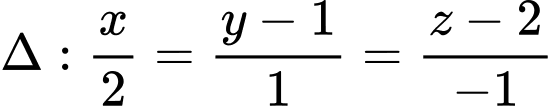 và và mặt cầu
và và mặt cầu 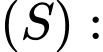
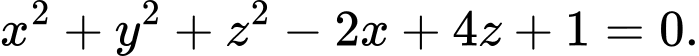 Số điểm chung của
Số điểm chung của  và
và 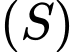 là:
là:
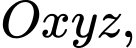 cho đường thẳng
cho đường thẳng 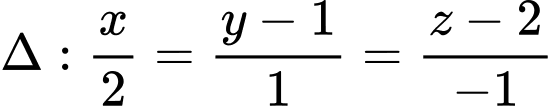 và và mặt cầu
và và mặt cầu 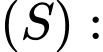
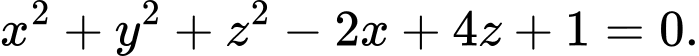 Số điểm chung của
Số điểm chung của  và
và 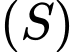 là:
là: A, 0.
B, 1.
C, 2.
D, 3.
Chọn A
Đường thẳng đi qua
đi qua 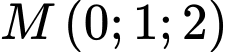 và có VTCP
và có VTCP 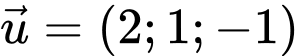
Mặt cầu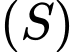 có tâm
có tâm 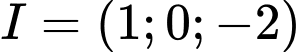 và bán kính
và bán kính 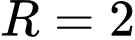
Ta có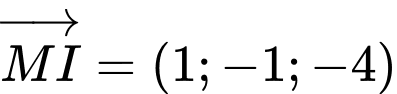 và
và 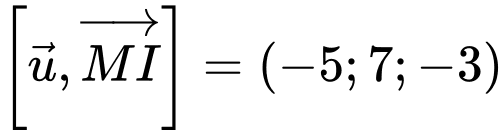
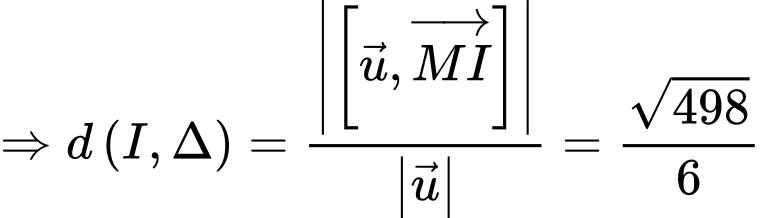
Vì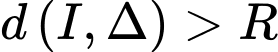 nên
nên  không cắt mặt cầu
không cắt mặt cầu 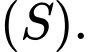 Đáp án: A
Đáp án: A
Đường thẳng
 đi qua
đi qua 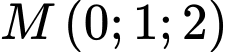 và có VTCP
và có VTCP 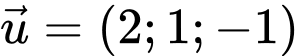
Mặt cầu
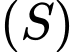 có tâm
có tâm 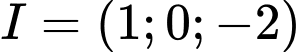 và bán kính
và bán kính 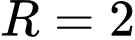
Ta có
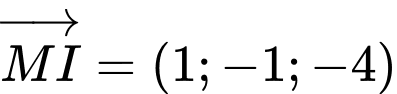 và
và 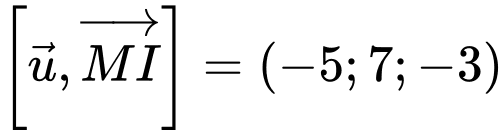
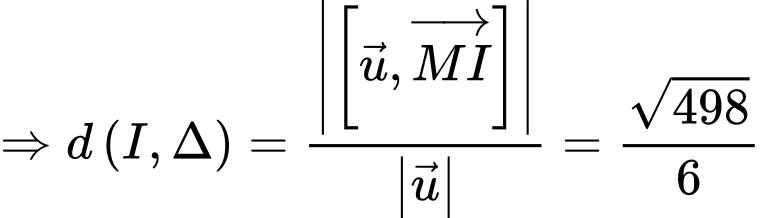
Vì
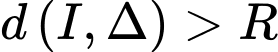 nên
nên  không cắt mặt cầu
không cắt mặt cầu 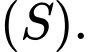 Đáp án: A
Đáp án: A
Câu 14 [581760]: Trong không gian 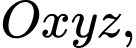 cho đường thẳng
cho đường thẳng 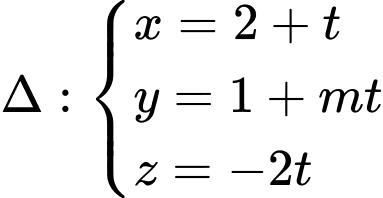 và mặt cầu
và mặt cầu 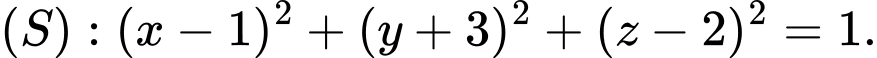 Giá trị của
Giá trị của 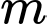 để đường thẳng
để đường thẳng  không cắt mặt cầu
không cắt mặt cầu 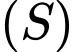 là:
là:
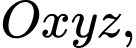 cho đường thẳng
cho đường thẳng 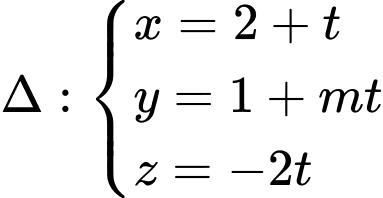 và mặt cầu
và mặt cầu 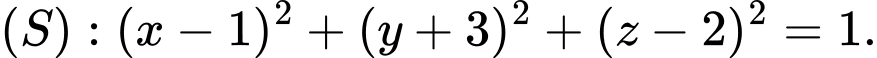 Giá trị của
Giá trị của 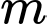 để đường thẳng
để đường thẳng  không cắt mặt cầu
không cắt mặt cầu 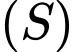 là:
là: A, 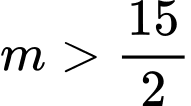 hoặc
hoặc 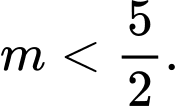
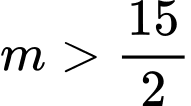 hoặc
hoặc 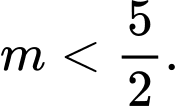
B, 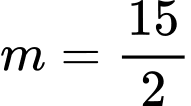 hoặc
hoặc 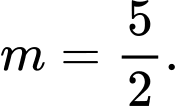
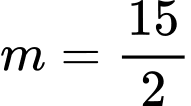 hoặc
hoặc 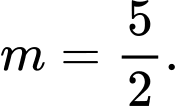
C, 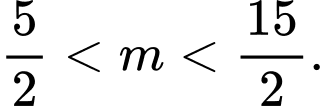
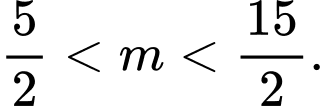
D, 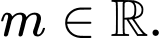
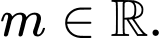
Chọn A
Từ phương trình đường thẳng và mặt cầu
và mặt cầu 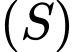 ta có
ta có
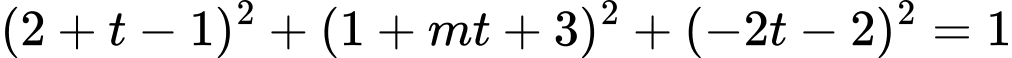
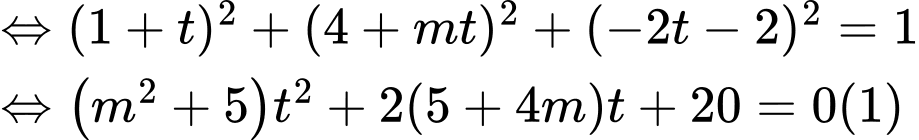
Để không cắt mặt cầu
không cắt mặt cầu 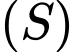 thì (1) vô nghiệm, hay (1) có
thì (1) vô nghiệm, hay (1) có 
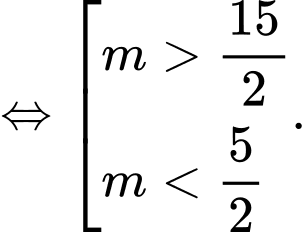 Đáp án: A
Đáp án: A
Từ phương trình đường thẳng
 và mặt cầu
và mặt cầu 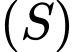 ta có
ta có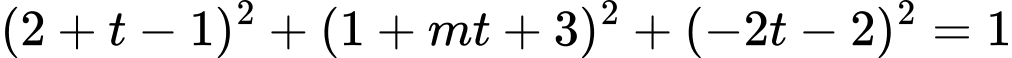
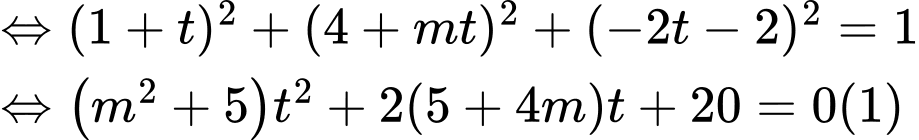
Để
 không cắt mặt cầu
không cắt mặt cầu 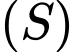 thì (1) vô nghiệm, hay (1) có
thì (1) vô nghiệm, hay (1) có 
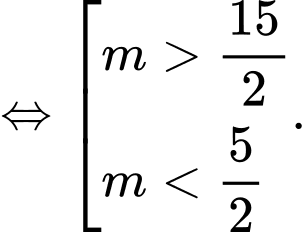 Đáp án: A
Đáp án: A
Câu 15 [581761]: Trong không gian với hệ tọa độ 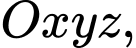 cho mặt phẳng
cho mặt phẳng 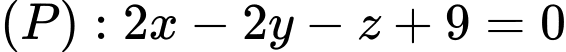 và mặt cầu
và mặt cầu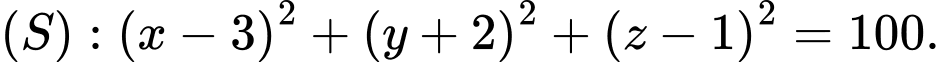 Mặt phẳng
Mặt phẳng 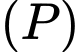 cắt mặt cầu
cắt mặt cầu 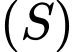 theo một đường tròn
theo một đường tròn  Tìm tọa độ tâm
Tìm tọa độ tâm 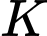 và bán kính
và bán kính 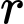 của đường tròn
của đường tròn  là
là
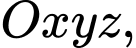 cho mặt phẳng
cho mặt phẳng 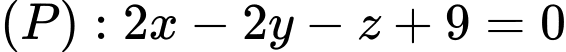 và mặt cầu
và mặt cầu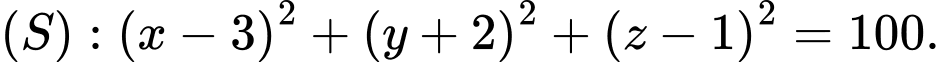 Mặt phẳng
Mặt phẳng 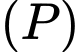 cắt mặt cầu
cắt mặt cầu 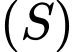 theo một đường tròn
theo một đường tròn  Tìm tọa độ tâm
Tìm tọa độ tâm 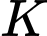 và bán kính
và bán kính 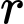 của đường tròn
của đường tròn  là
là A, 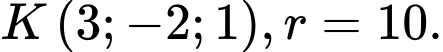
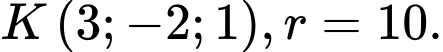
B, 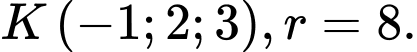
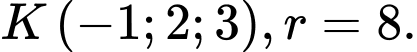
C, 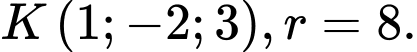
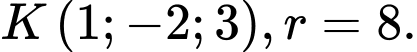
D, 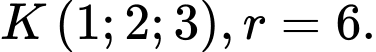
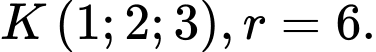
• Mặt cầu
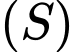 có tâm
có tâm 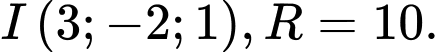
• Khoảng cách từ
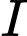 đến
đến 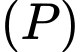 là
là 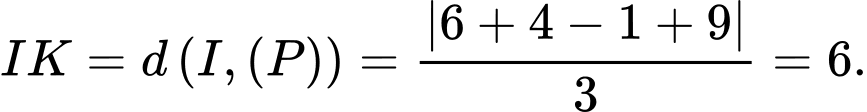
• Đường thẳng qua
 vuông góc với
vuông góc với 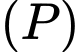 có phương trình tham số là
có phương trình tham số là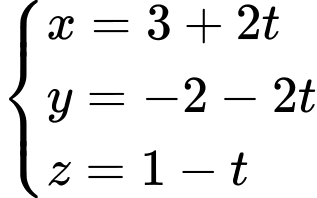 khi đó Tọa độ tâm
khi đó Tọa độ tâm 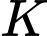 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình 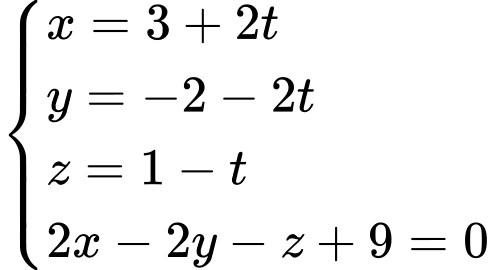

• Bán kính:
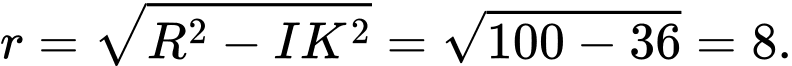 Đáp án: B
Đáp án: B 6. Dạng toán: Giá trị lớn nhất, giá trị nhỏ nhất liên quan đến mặt cầu
6.1. Phương pháp tư duy
6.2. Ví dụ áp dụng.
6.2. Ví dụ áp dụng.
Câu 16 [581762]: Trong không gian với hệ tọa độ 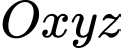 cho ba điểm
cho ba điểm 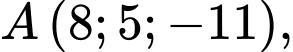
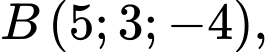
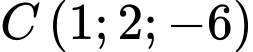 và mặt cầu
và mặt cầu 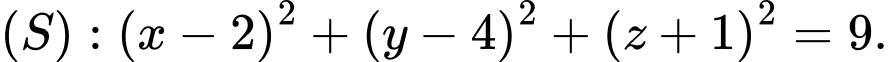 Gọi điểm
Gọi điểm 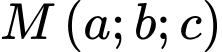 là điểm trên
là điểm trên 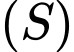 sao cho
sao cho 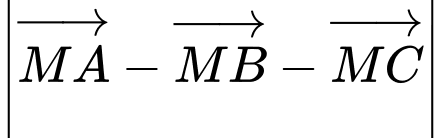 đạt giá trị nhỏ nhất. Hãy tìm
đạt giá trị nhỏ nhất. Hãy tìm 
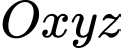 cho ba điểm
cho ba điểm 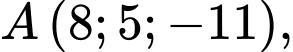
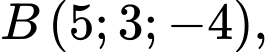
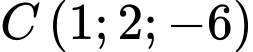 và mặt cầu
và mặt cầu 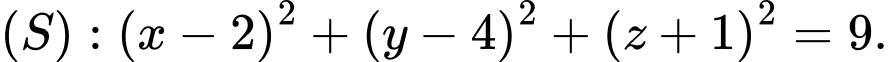 Gọi điểm
Gọi điểm 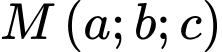 là điểm trên
là điểm trên 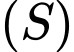 sao cho
sao cho 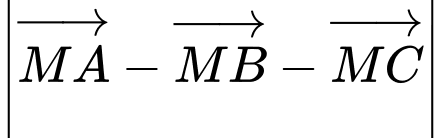 đạt giá trị nhỏ nhất. Hãy tìm
đạt giá trị nhỏ nhất. Hãy tìm 
A, 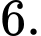
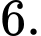
B, 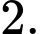
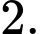
C, 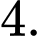
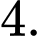
D, 9.
Chọn B
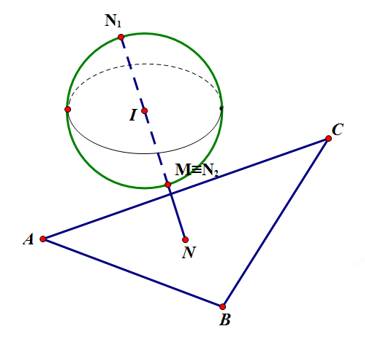
Gọi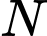 là điểm thỏa mãn
là điểm thỏa mãn 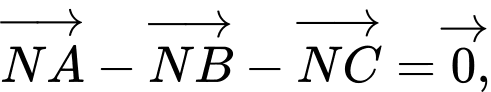 suy ra
suy ra 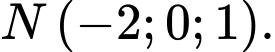
Khi đó: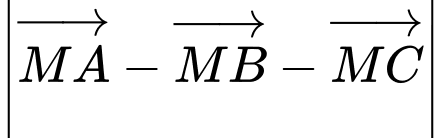
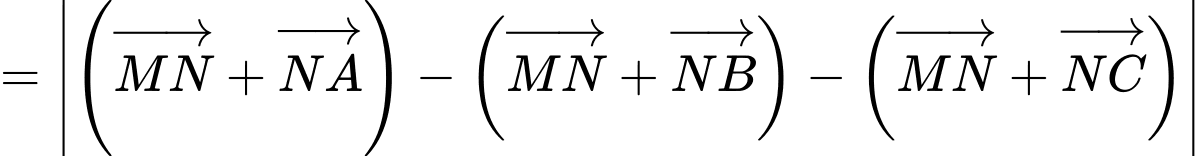
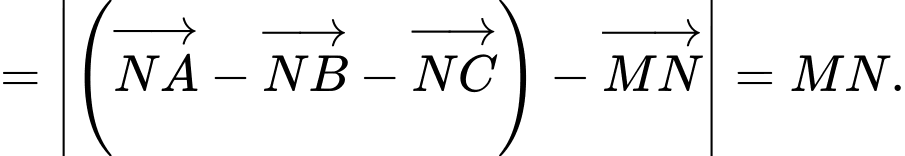
Suy ra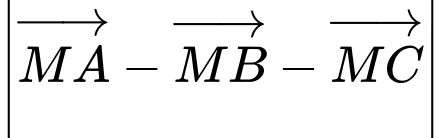 nhỏ nhất khi
nhỏ nhất khi 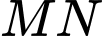 nhỏ nhất. Mặt cầu
nhỏ nhất. Mặt cầu 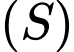 có tâm
có tâm 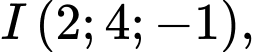 suy ra:
suy ra:
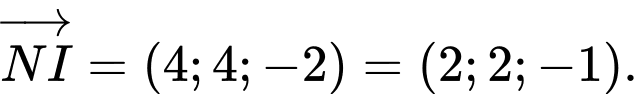 Phương trình
Phương trình 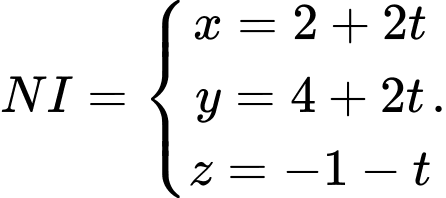 Thay phương trình
Thay phương trình 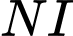 vào phương trình
vào phương trình 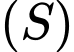 ta được:
ta được: 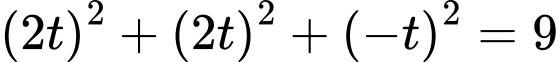
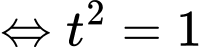
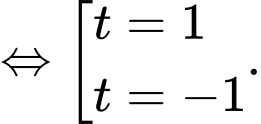
Suy ra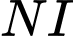 cắt
cắt 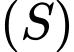 tại hai điểm phân biệt
tại hai điểm phân biệt 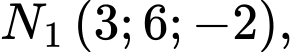
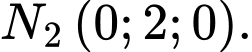
Vì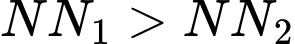 nên MN nhỏ nhất khi và chỉ khi
nên MN nhỏ nhất khi và chỉ khi 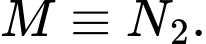 Vậy
Vậy 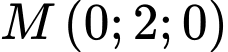 là điểm cần tìm.
là điểm cần tìm.
Suy ra: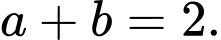 Đáp án: B
Đáp án: B

Gọi
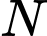 là điểm thỏa mãn
là điểm thỏa mãn 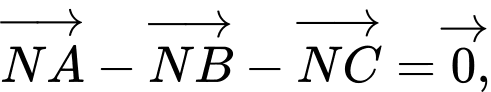 suy ra
suy ra 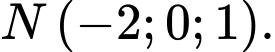
Khi đó:
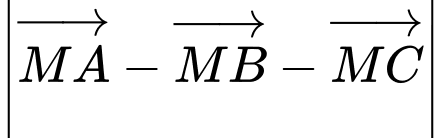
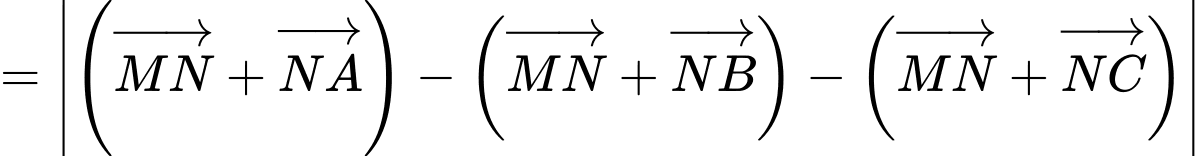
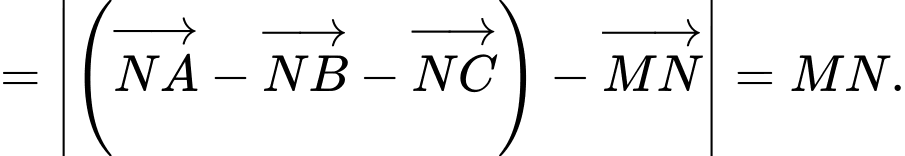
Suy ra
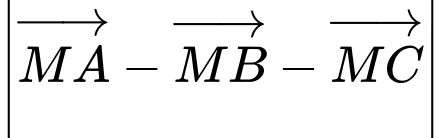 nhỏ nhất khi
nhỏ nhất khi 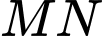 nhỏ nhất. Mặt cầu
nhỏ nhất. Mặt cầu 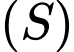 có tâm
có tâm 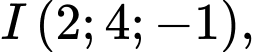 suy ra:
suy ra: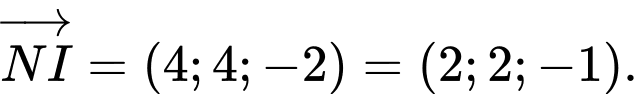 Phương trình
Phương trình 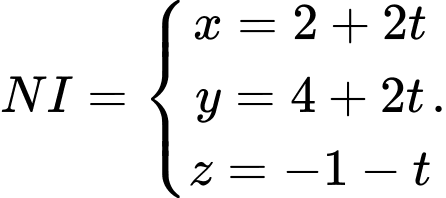 Thay phương trình
Thay phương trình 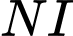 vào phương trình
vào phương trình 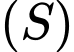 ta được:
ta được: 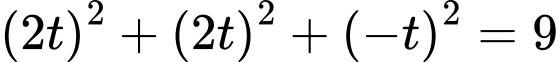
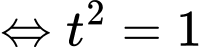
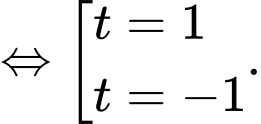
Suy ra
 cắt
cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 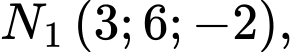
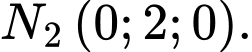
Vì
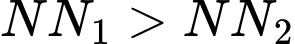 nên MN nhỏ nhất khi và chỉ khi
nên MN nhỏ nhất khi và chỉ khi 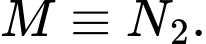 Vậy
Vậy 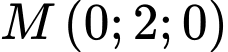 là điểm cần tìm.
là điểm cần tìm.Suy ra:
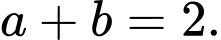 Đáp án: B
Đáp án: B
Câu 17 [581763]: Cho 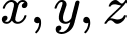 là ba số thực thỏa
là ba số thực thỏa 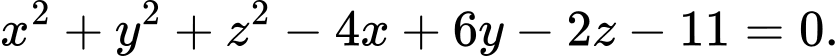 Tìm giá trị lớn nhất của
Tìm giá trị lớn nhất của 
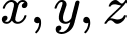 là ba số thực thỏa
là ba số thực thỏa 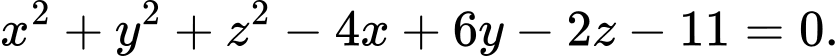 Tìm giá trị lớn nhất của
Tìm giá trị lớn nhất của 
A, 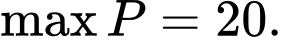
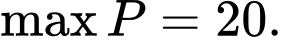
B, 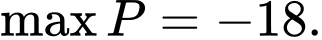
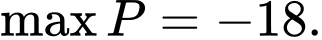
C, 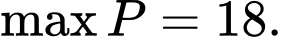
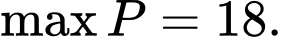
D, 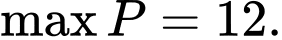
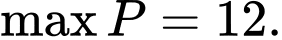
Chọn D
Ta có: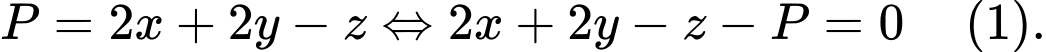
Lại có: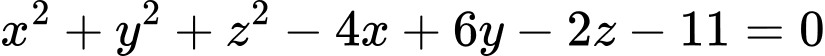
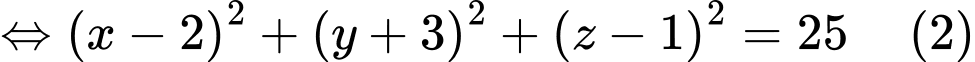
Xét trong hệ trục tọa độ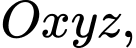 ta thấy
ta thấy  là phương trình của một mặt phẳng, gọi là
là phương trình của một mặt phẳng, gọi là 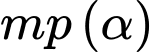 và
và  là phương trình của một mặt cầu
là phương trình của một mặt cầu 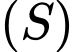 tâm
tâm 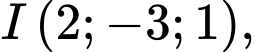 bán kính
bán kính 
Giá trị lớn nhất của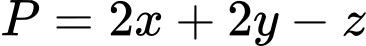 là giá trị lớn nhất của
là giá trị lớn nhất của 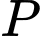 để
để  và
và 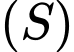 có điểm chung, điều này tương đương với
có điểm chung, điều này tương đương với 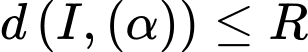
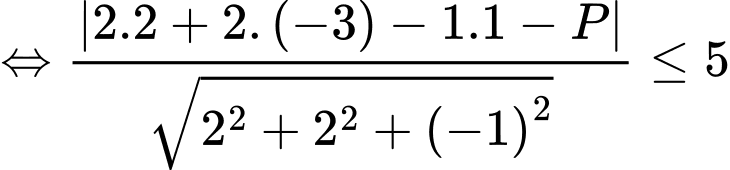
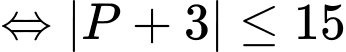

Vậy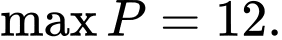 Đáp án: D
Đáp án: D
Ta có:
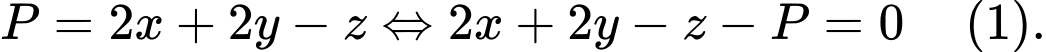
Lại có:
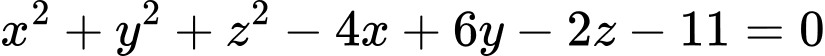
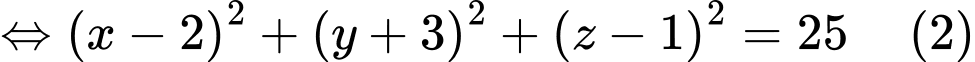
Xét trong hệ trục tọa độ
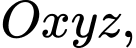 ta thấy
ta thấy  là phương trình của một mặt phẳng, gọi là
là phương trình của một mặt phẳng, gọi là 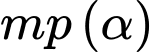 và
và  là phương trình của một mặt cầu
là phương trình của một mặt cầu 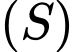 tâm
tâm 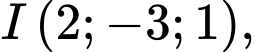 bán kính
bán kính 
Giá trị lớn nhất của
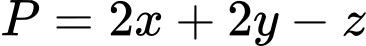 là giá trị lớn nhất của
là giá trị lớn nhất của 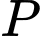 để
để  và
và 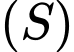 có điểm chung, điều này tương đương với
có điểm chung, điều này tương đương với 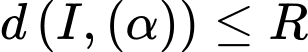
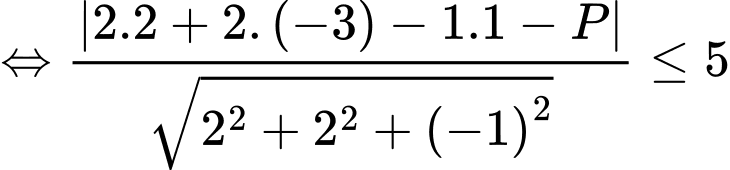
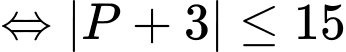

Vậy
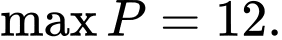 Đáp án: D
Đáp án: D
Câu 18 [581764]: Trong không gian với hệ tọa độ 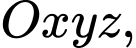 cho hai điểm
cho hai điểm 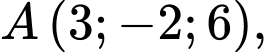
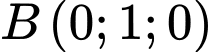 và mặt cầu
và mặt cầu 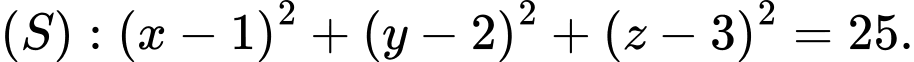 Mặt phẳng
Mặt phẳng 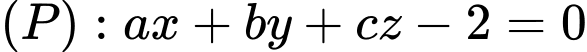 đi qua
đi qua 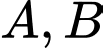 và cắt
và cắt 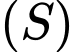 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính 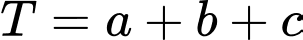
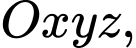 cho hai điểm
cho hai điểm 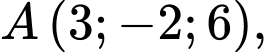
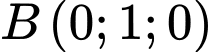 và mặt cầu
và mặt cầu 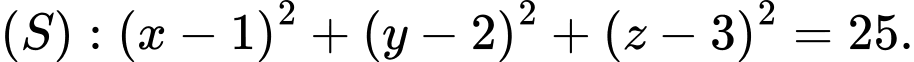 Mặt phẳng
Mặt phẳng 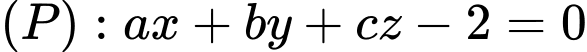 đi qua
đi qua 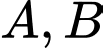 và cắt
và cắt 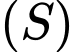 theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính 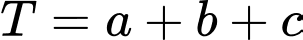
A, 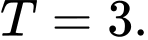
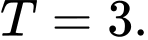
B, 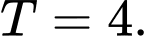
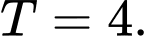
C, 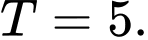
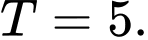
D, 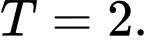
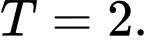
Chọn A
Cách 1:
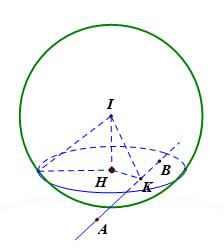
Mặt cầu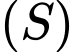 có tâm
có tâm 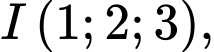 bán kính
bán kính 
Mặt phẳng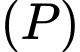 có vectơ pháp tuyến
có vectơ pháp tuyến 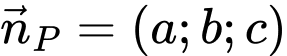
Theo giả thiết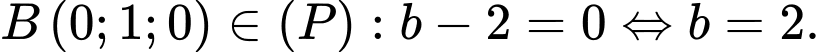
Ta có: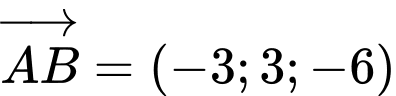 cùng phương với
cùng phương với 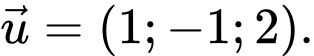
Phương trình đường thẳng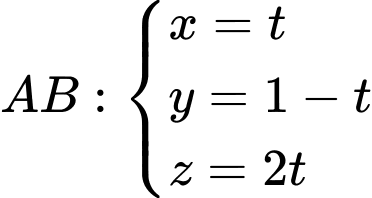
Gọi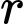 là bán kính đường tròn giao tuyến.
là bán kính đường tròn giao tuyến. 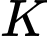 là hình chiếu vuông góc của
là hình chiếu vuông góc của 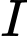 lên đường thẳng
lên đường thẳng 
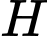 là hình chiếu vuông góc của
là hình chiếu vuông góc của 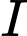 lên
lên 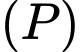
Ta có:
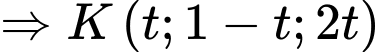
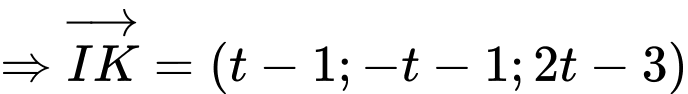

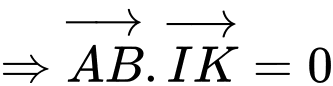
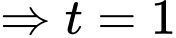
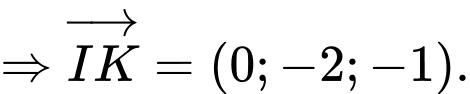
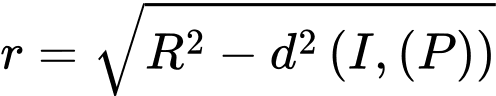
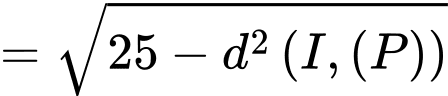
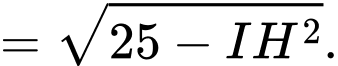
Ta có: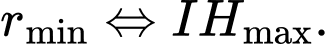
Mà

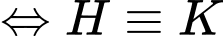
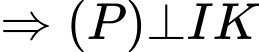
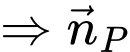 và
và 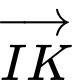 cùng phương.
cùng phương.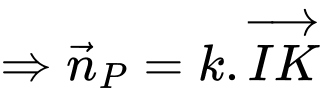
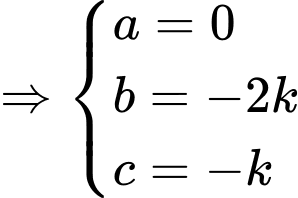
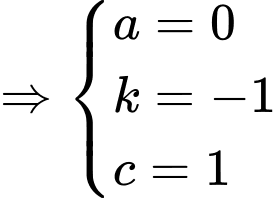
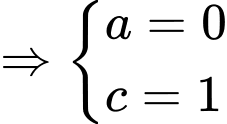
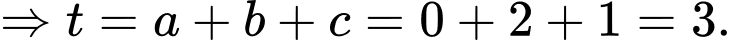
Cách 2:
Mặt cầu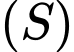 có tâm
có tâm 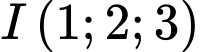 và bán kính
và bán kính 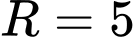
Ta có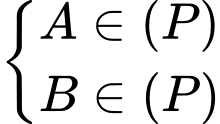
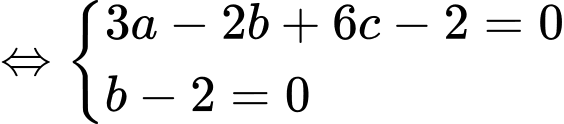
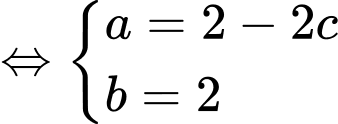
Bán kính của đường tròn giao tuyến là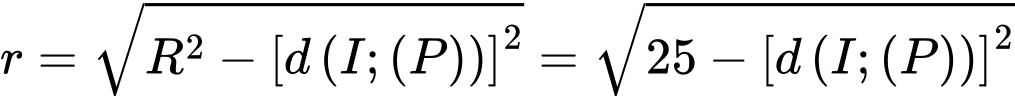
Bán kính của đường tròn giao tuyến nhỏ nhất khi và chỉ khi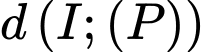 lớn nhất
lớn nhất
Ta có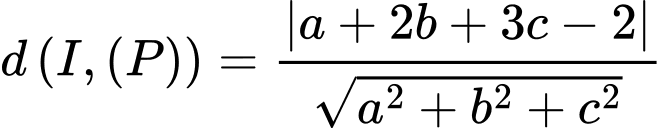
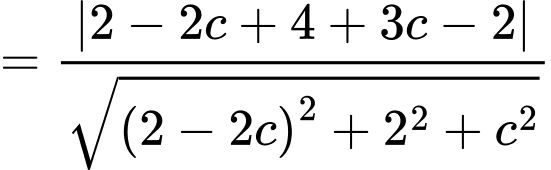
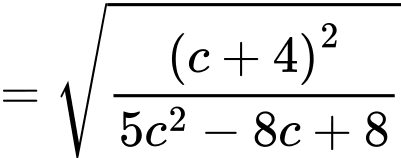
Xét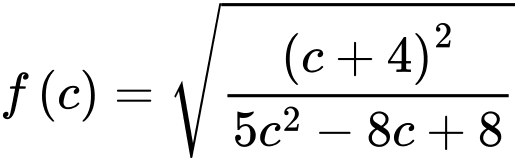
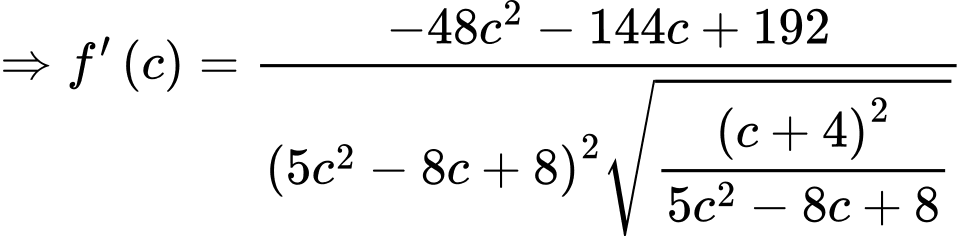
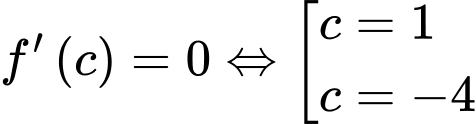
Bảng biến thiên
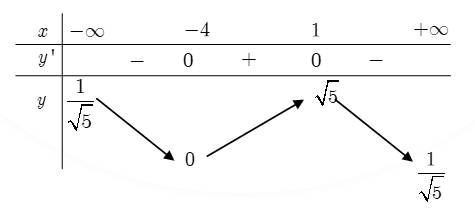
Vậy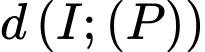 lớn nhất bằng
lớn nhất bằng 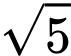 khi và chỉ khi
khi và chỉ khi 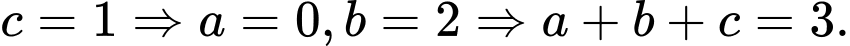 Đáp án: A
Đáp án: A
Cách 1:

Mặt cầu
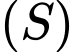 có tâm
có tâm 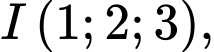 bán kính
bán kính 
Mặt phẳng
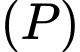 có vectơ pháp tuyến
có vectơ pháp tuyến 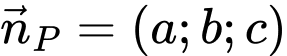
Theo giả thiết
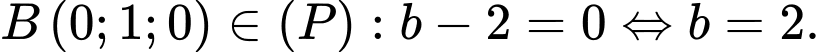
Ta có:
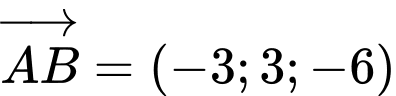 cùng phương với
cùng phương với 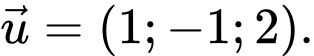
Phương trình đường thẳng
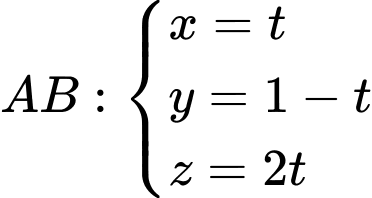
Gọi
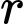 là bán kính đường tròn giao tuyến.
là bán kính đường tròn giao tuyến. 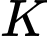 là hình chiếu vuông góc của
là hình chiếu vuông góc của 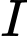 lên đường thẳng
lên đường thẳng 
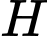 là hình chiếu vuông góc của
là hình chiếu vuông góc của 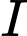 lên
lên 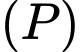
Ta có:

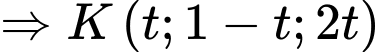
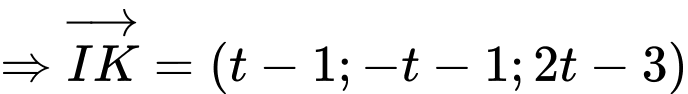

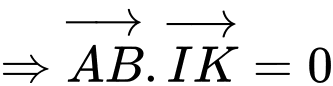
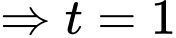
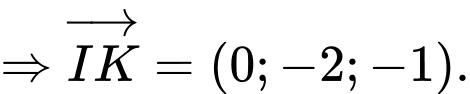
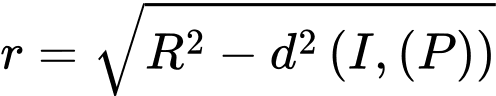
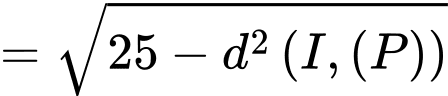
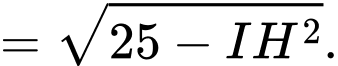
Ta có:
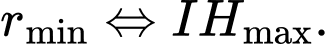
Mà


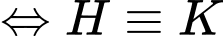
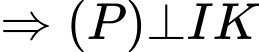
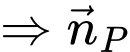 và
và 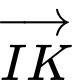 cùng phương.
cùng phương.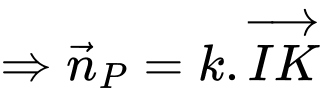
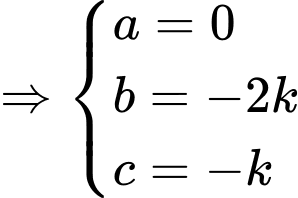
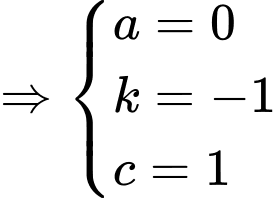
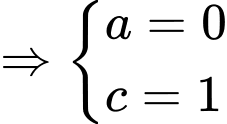
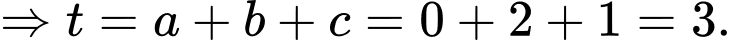
Cách 2:
Mặt cầu
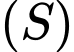 có tâm
có tâm 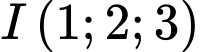 và bán kính
và bán kính 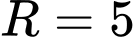
Ta có
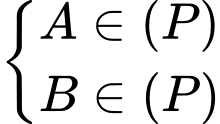
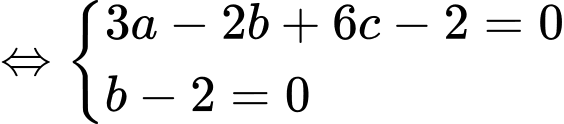
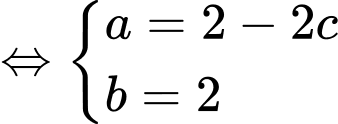
Bán kính của đường tròn giao tuyến là
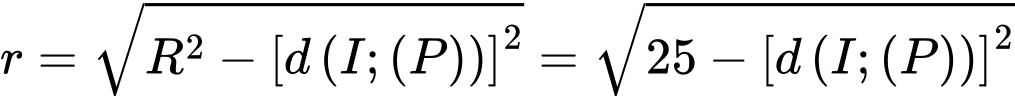
Bán kính của đường tròn giao tuyến nhỏ nhất khi và chỉ khi
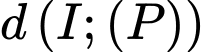 lớn nhất
lớn nhấtTa có
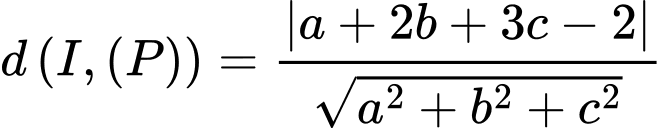
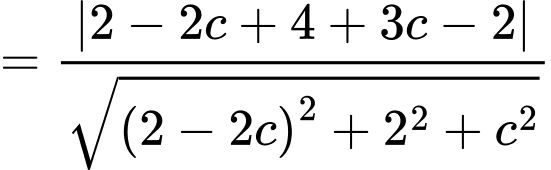
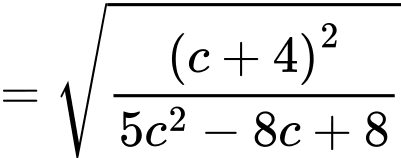
Xét
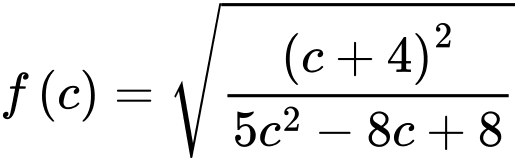
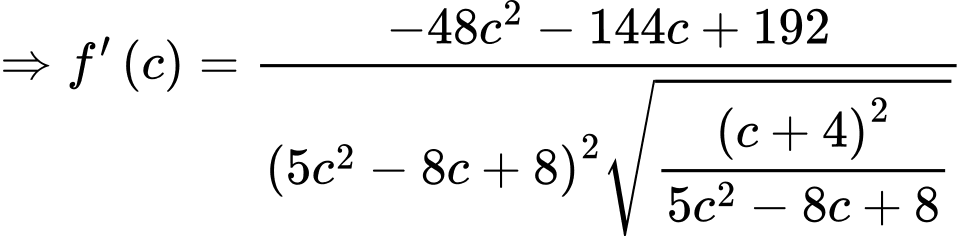
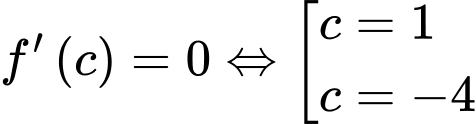
Bảng biến thiên

Vậy
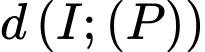 lớn nhất bằng
lớn nhất bằng 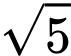 khi và chỉ khi
khi và chỉ khi 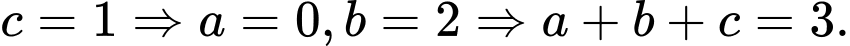 Đáp án: A
Đáp án: A