1. Dạng 1: Tính Giá Trị Biểu Thức Chứa Logarit
Câu 1 [582160]: Cho 2 số thực dương 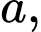
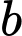 thỏa mãn
thỏa mãn 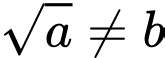 ,
, 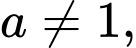
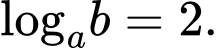 Tính
Tính 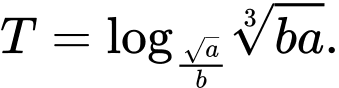
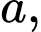
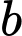 thỏa mãn
thỏa mãn 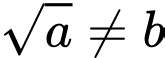 ,
, 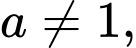
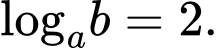 Tính
Tính 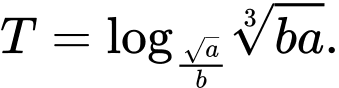
A, 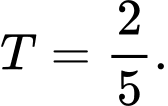
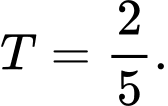
B, 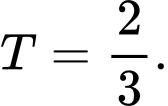
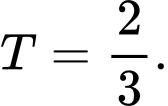
C, 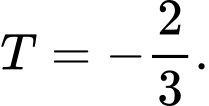
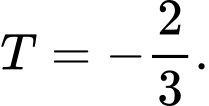
D, 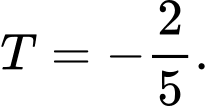
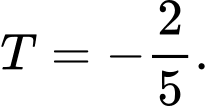
Ta có: 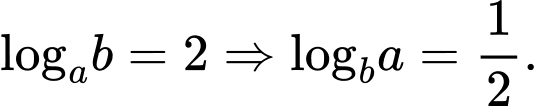
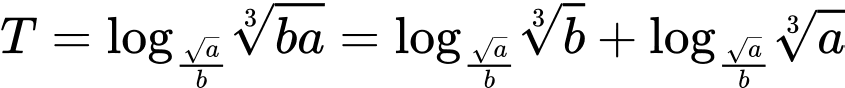
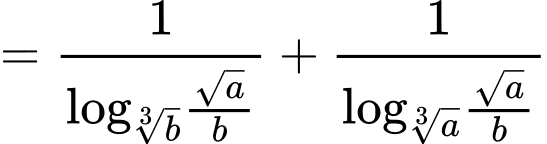
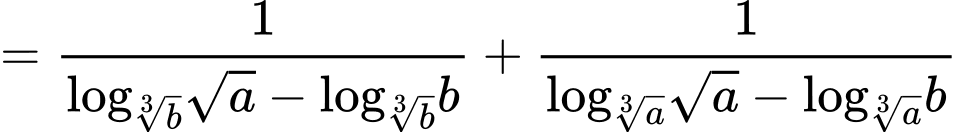 .
.
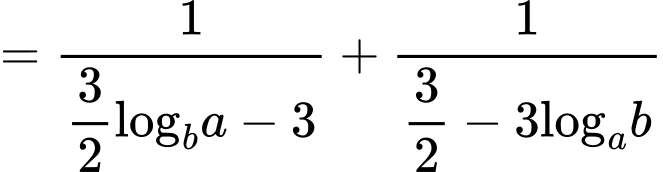 .
.
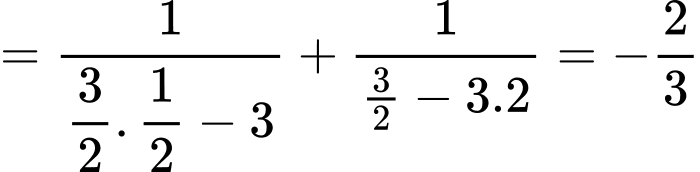 . Đáp án: C
. Đáp án: C
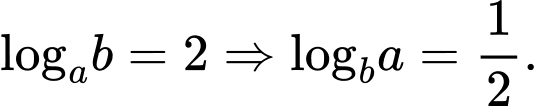
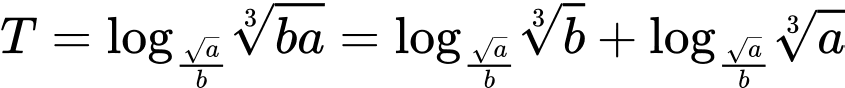
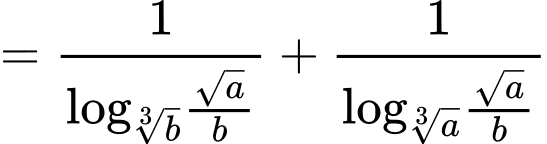
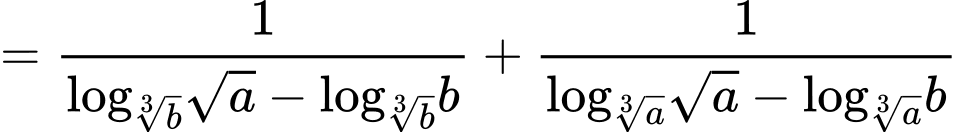 .
.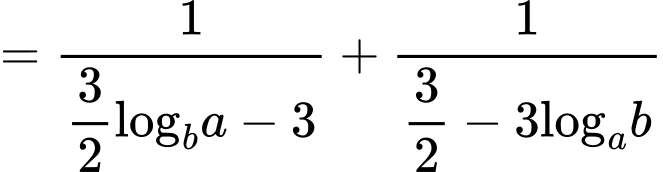 .
.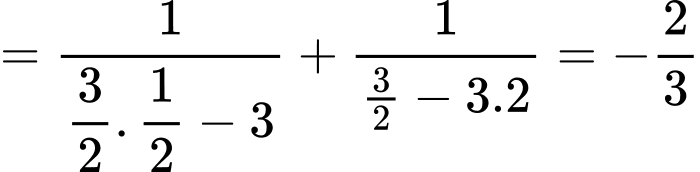 . Đáp án: C
. Đáp án: C 2. Dạng 2: Các Mệnh Đề Liên Quan Đến Logarit
Câu 2 [582161]: Với hai số thực bất kì 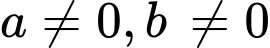 , khẳng định nào sau đây là khẳng định sai?
, khẳng định nào sau đây là khẳng định sai?
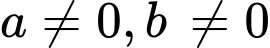 , khẳng định nào sau đây là khẳng định sai?
, khẳng định nào sau đây là khẳng định sai? A, 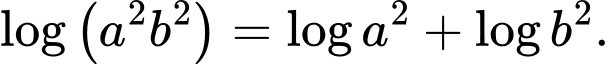
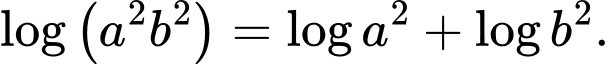
B, 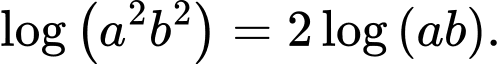
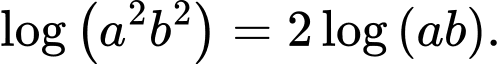
C, 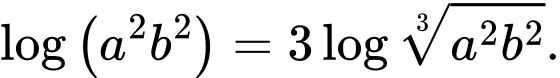
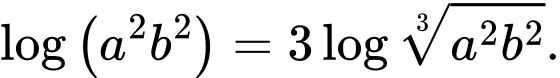
D, 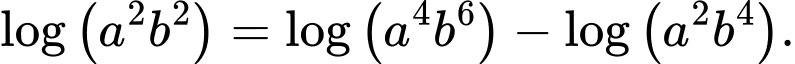
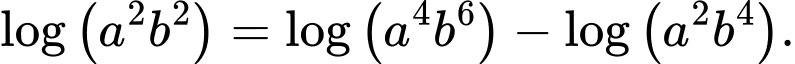
Với điều kiện 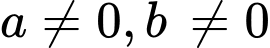 thì dấu
thì dấu 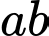 chưa đảm bảo lớn hơn 0 Đáp án: B
chưa đảm bảo lớn hơn 0 Đáp án: B
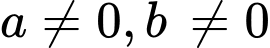 thì dấu
thì dấu 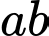 chưa đảm bảo lớn hơn 0 Đáp án: B
chưa đảm bảo lớn hơn 0 Đáp án: B
Câu 3 [582162]: Cho hai số thực dương 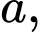
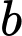 thỏa mãn
thỏa mãn 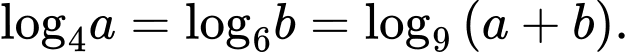 Tính
Tính 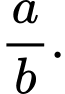
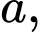
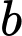 thỏa mãn
thỏa mãn 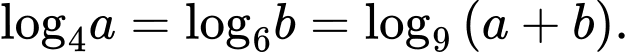 Tính
Tính 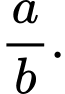
A, 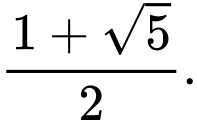
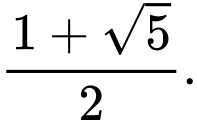
B, 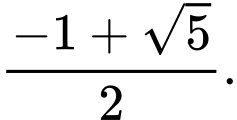
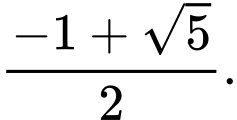
C, 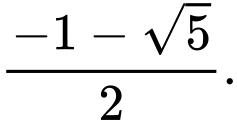
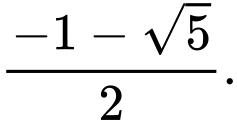
D, 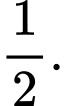
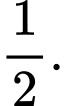
Đặt 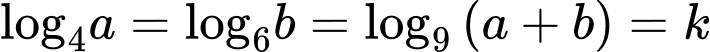
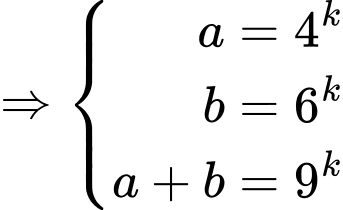
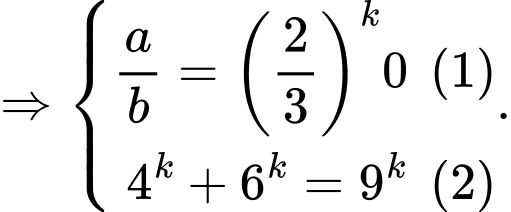
Có
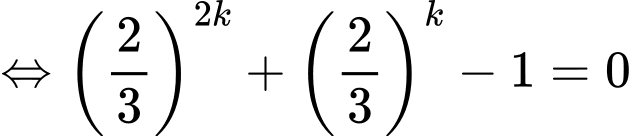

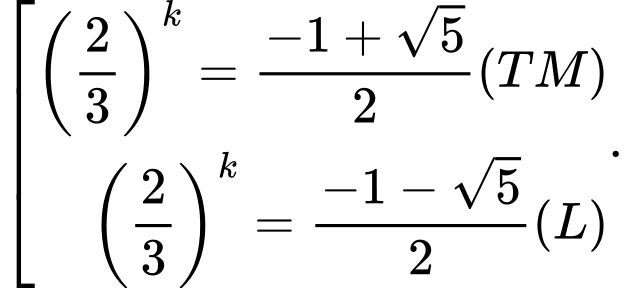
Do đó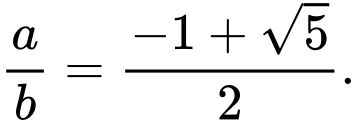 Đáp án: B
Đáp án: B
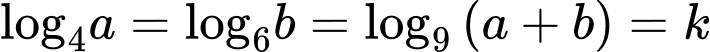
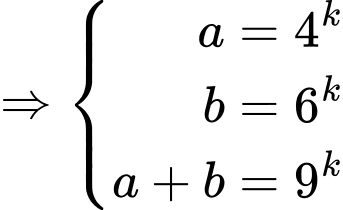
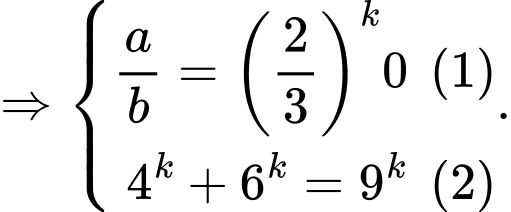
Có

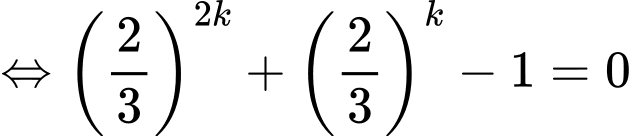

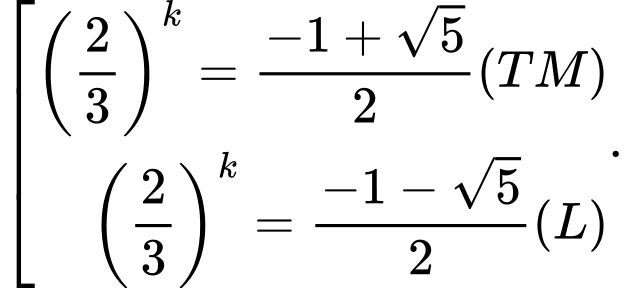
Do đó
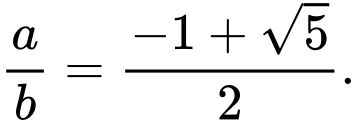 Đáp án: B
Đáp án: B 3. Dạng 3: Biểu Diễn Logarit Này Theo Logarit Khác
Câu 4 [582163]: Cho 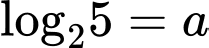 ;
; 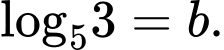 Tính
Tính 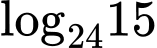 theo
theo 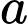 và
và 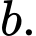
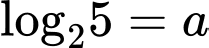 ;
; 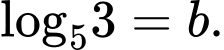 Tính
Tính 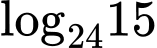 theo
theo 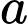 và
và 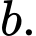
A, 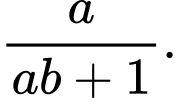
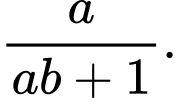
B, 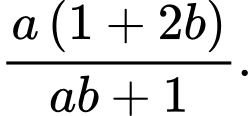
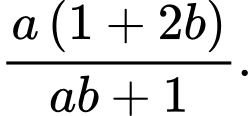
C, 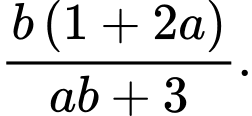
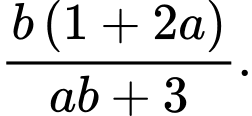
D, 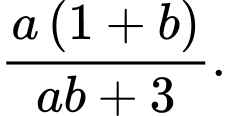
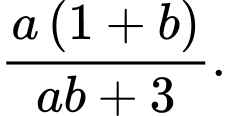
Ta có 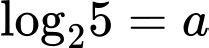
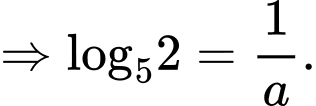
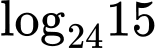
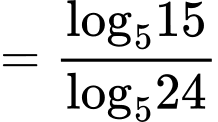
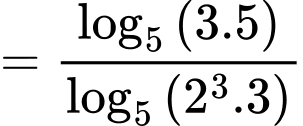
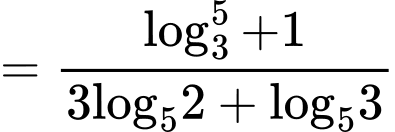
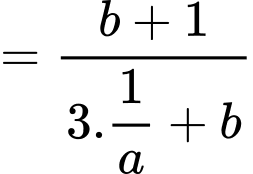
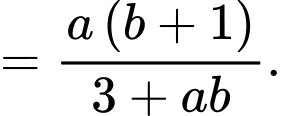 Đáp án: D
Đáp án: D
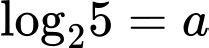
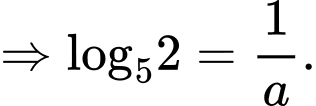
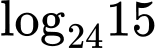
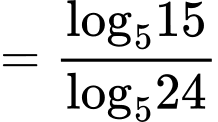
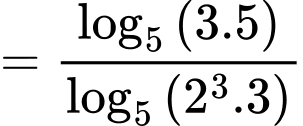
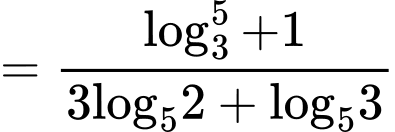
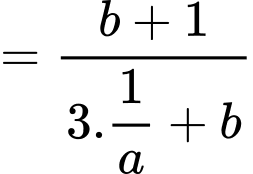
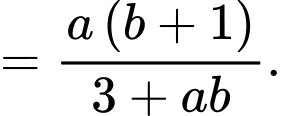 Đáp án: D
Đáp án: D
Câu 5 [582164]: Nếu 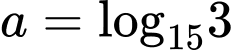 thì:
thì:
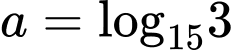 thì:
thì: A, 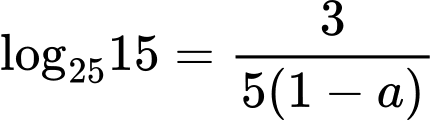 .
.
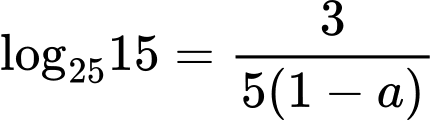 .
.B, 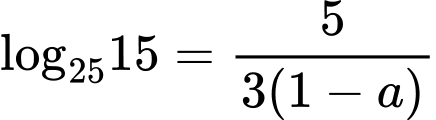 .
.
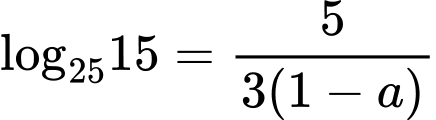 .
.C, 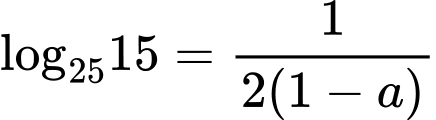 .
.
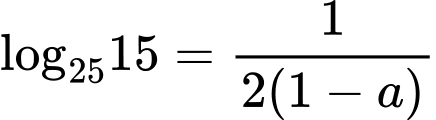 .
.D, 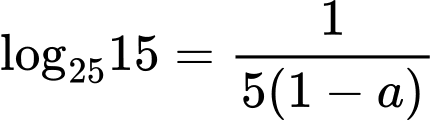 .
.
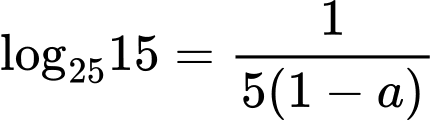 .
.
Có 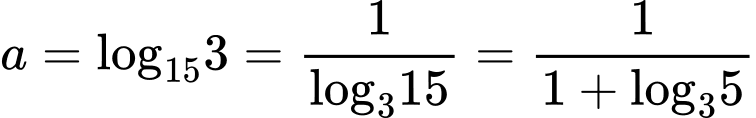
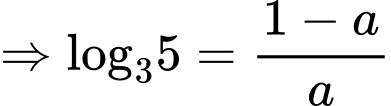
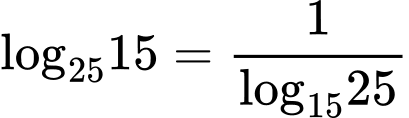
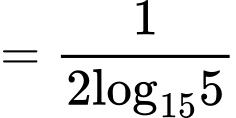
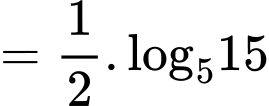
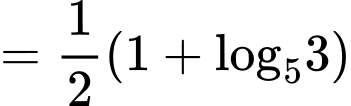
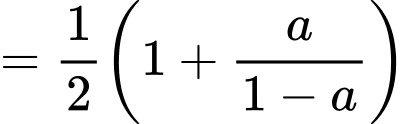
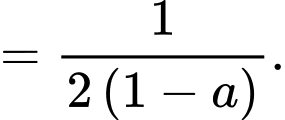 Đáp án: C
Đáp án: C
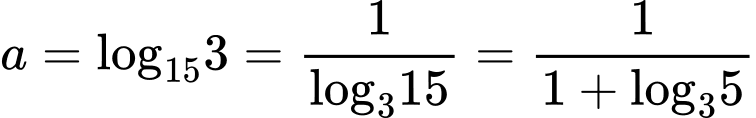
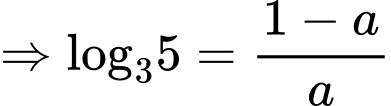
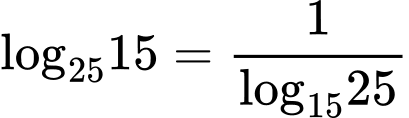
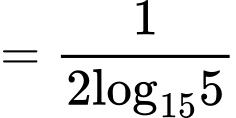
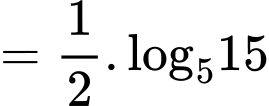
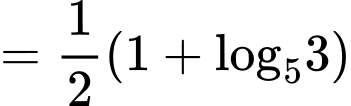
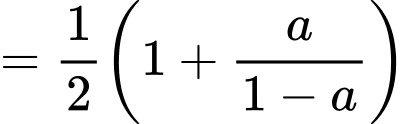
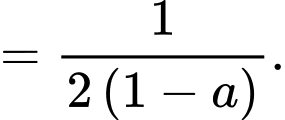 Đáp án: C
Đáp án: C 4. Dạng 4: Tìm Tập Xác Định Của Hàm Số
Câu 6 [582165]: Tìm tập xác định 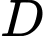 của hàm số
của hàm số 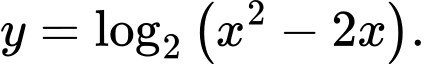
 của hàm số
của hàm số 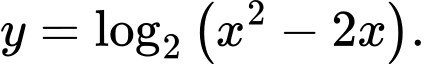
A, 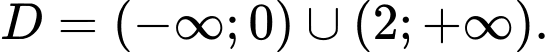
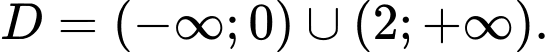
B, 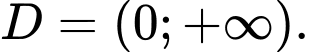
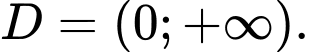
C, 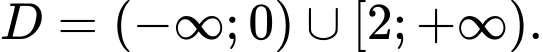
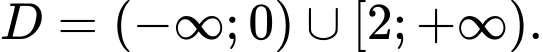
D, 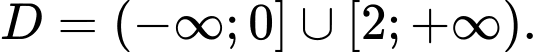
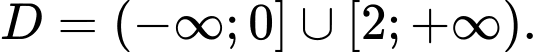
Biểu thức 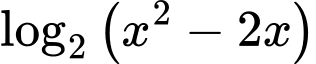 khi và chỉ khi
khi và chỉ khi 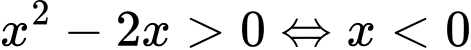 hoặc
hoặc 
Vậy tập xác định của hàm số là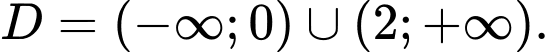 Đáp án: A
Đáp án: A
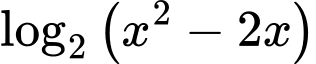 khi và chỉ khi
khi và chỉ khi 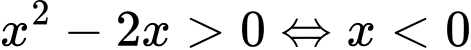 hoặc
hoặc 
Vậy tập xác định của hàm số là
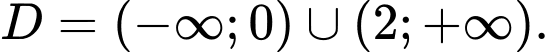 Đáp án: A
Đáp án: A
Câu 7 [582166]: Tìm tất cả các giá trị của m để hàm số 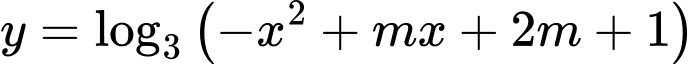 xác định với mọi
xác định với mọi 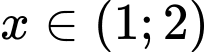
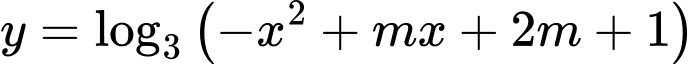 xác định với mọi
xác định với mọi 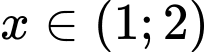
A, 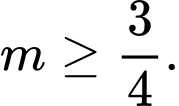
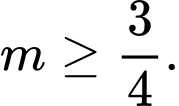
B, 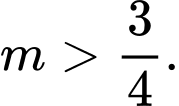
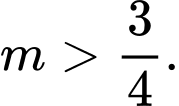
C, 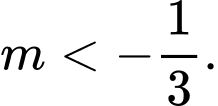
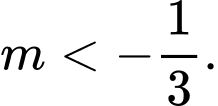
D, 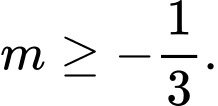
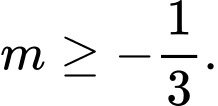
Hàm số xác định với mọi 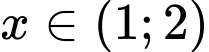 khi
khi 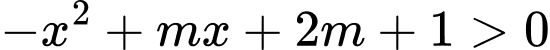 ,
, 
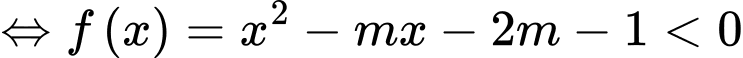 ,
, 
 có hai nghiệm thỏa
có hai nghiệm thỏa 
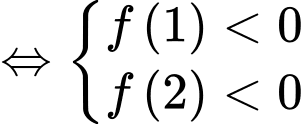
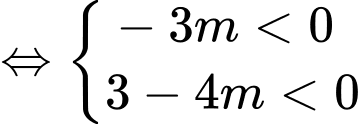
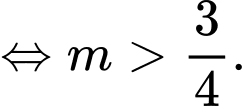 Đáp án: B
Đáp án: B
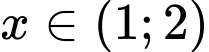 khi
khi 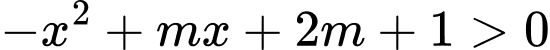 ,
, 
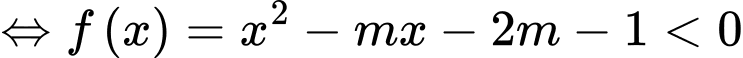 ,
, 
 có hai nghiệm thỏa
có hai nghiệm thỏa 
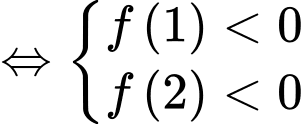
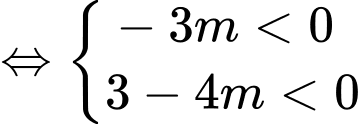
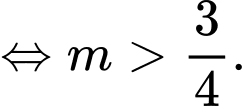 Đáp án: B
Đáp án: B 5. Dạng 5: Tính Đạo Hàm Các Cấp
Câu 8 [582167]: Đạo hàm của hàm số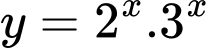 là:
là:
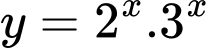 là:
là: A, 

B, 

C, 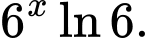
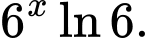
D, 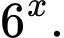
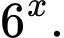
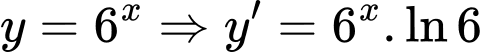 . Đáp án: C
. Đáp án: C
Câu 9 [582168]: Cho hàm số: 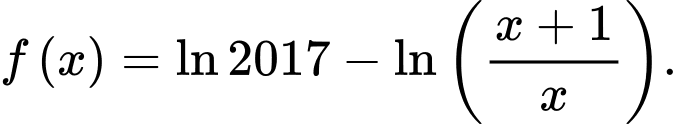 Tính tổng
Tính tổng 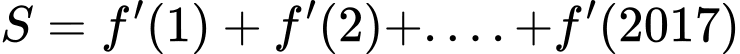 ?
?
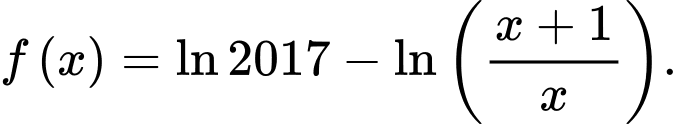 Tính tổng
Tính tổng 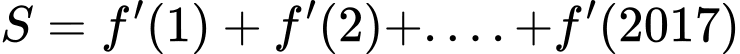 ?
? A, 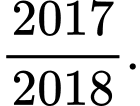
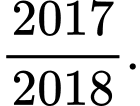
B, 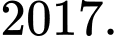
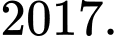
C, 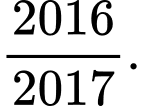
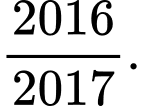
D, 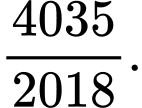
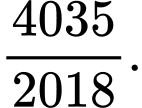
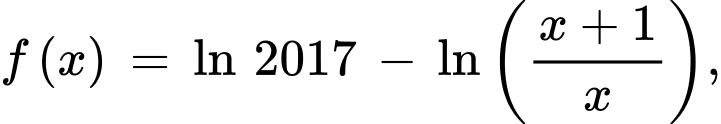
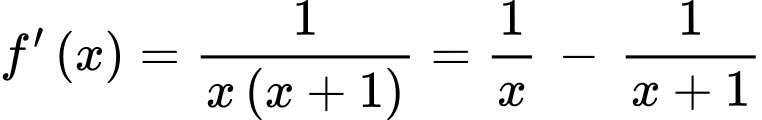
Ta có:
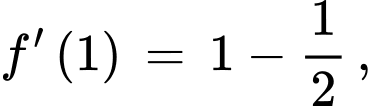
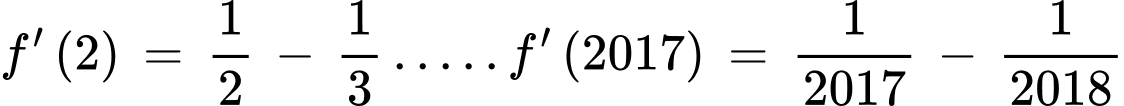
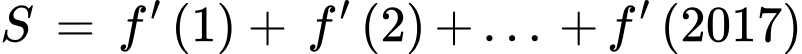
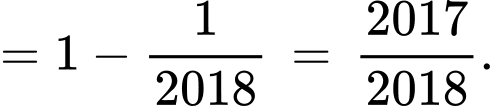 Đáp án: A
Đáp án: A 6. Dạng 6: Toán Max-Min Liên Quan Mũ Và Logarit
Câu 10 [582169]: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 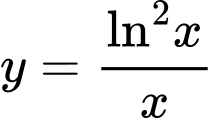 trên đoạn
trên đoạn 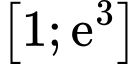 lần lượt là
lần lượt là
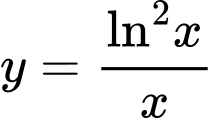 trên đoạn
trên đoạn 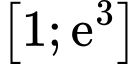 lần lượt là
lần lượt là A, 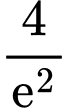 và
và 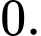
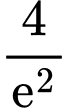 và
và 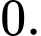
B, 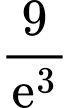 và
và 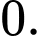
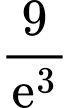 và
và 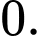
C, 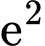 và
và 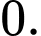
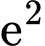 và
và 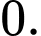
D, 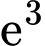 và
và 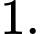
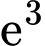 và
và 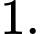
Ta có 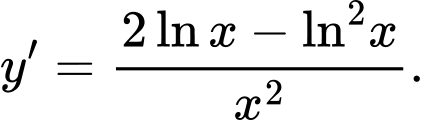 Khi đó
Khi đó 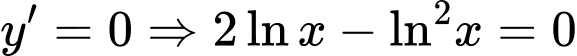
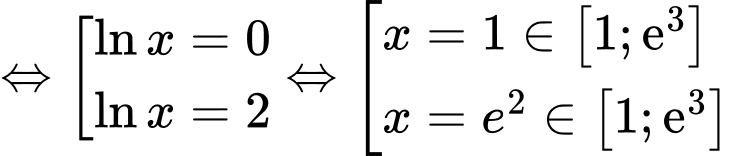
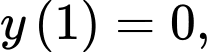
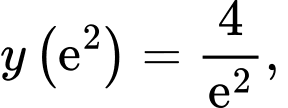
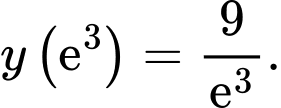
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là :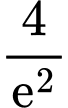 và
và 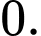 Đáp án: A
Đáp án: A
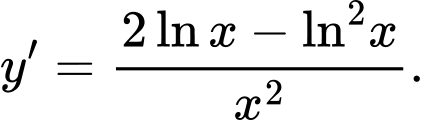 Khi đó
Khi đó 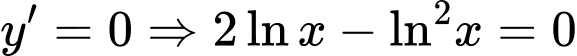
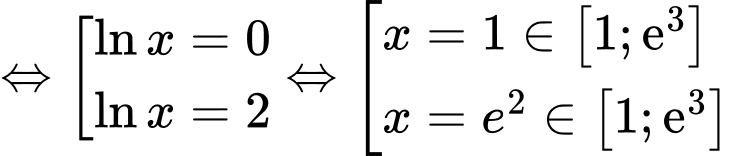
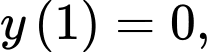
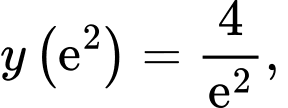
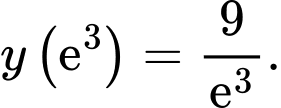
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là :
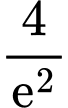 và
và  Đáp án: A
Đáp án: A
Câu 11 [582170]: Cho 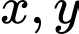 là số thực dương thỏa mãn
là số thực dương thỏa mãn 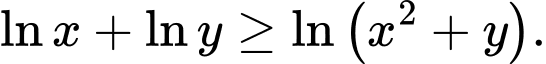 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 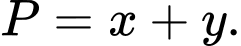
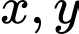 là số thực dương thỏa mãn
là số thực dương thỏa mãn 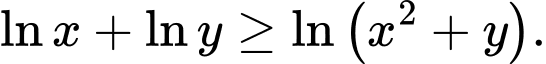 Tìm giá trị nhỏ nhất của
Tìm giá trị nhỏ nhất của 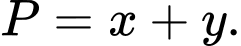
A, 

B, 

C, 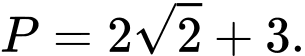
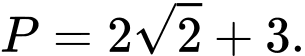
D, 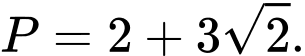
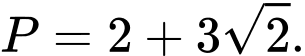
Từ 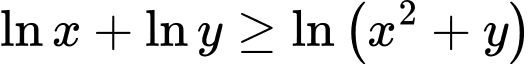
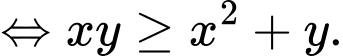 Ta xét:
Ta xét:
Nếu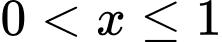 thì
thì 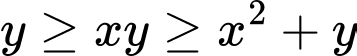
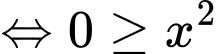 mâu thuẫn.
mâu thuẫn.
Nếu thì
thì 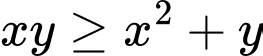
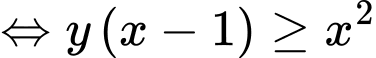
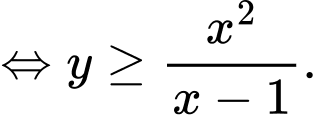
Vậy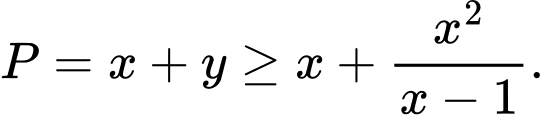
Ta có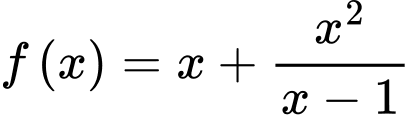 xét trên
xét trên 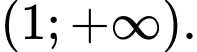 Có
Có 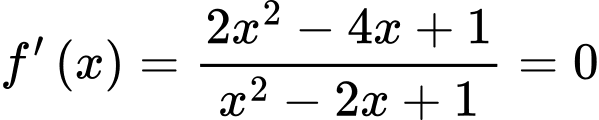
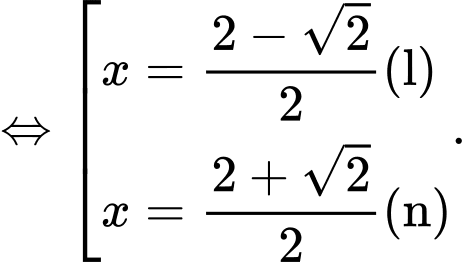
Vậy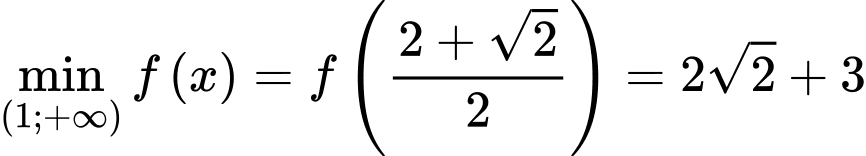 . Đáp án: C
. Đáp án: C
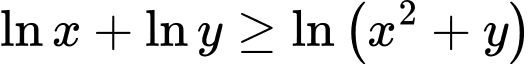
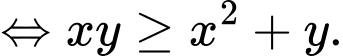 Ta xét:
Ta xét:Nếu
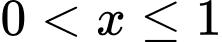 thì
thì 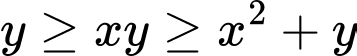
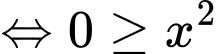 mâu thuẫn.
mâu thuẫn.Nếu
 thì
thì 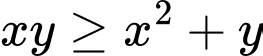
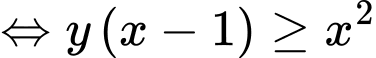
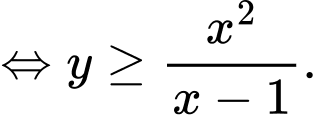
Vậy
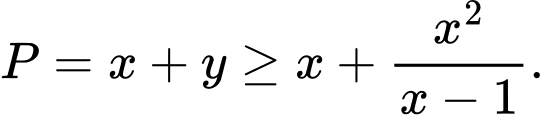
Ta có
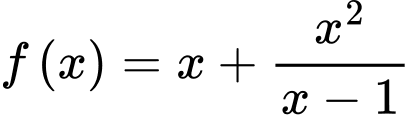 xét trên
xét trên 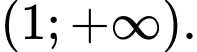 Có
Có 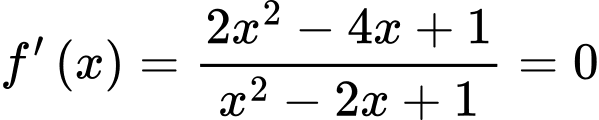
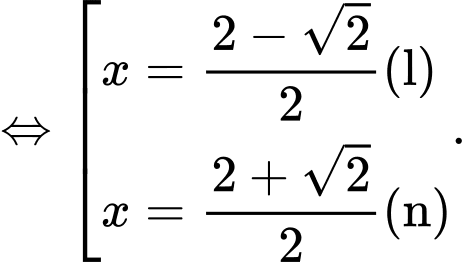
Vậy
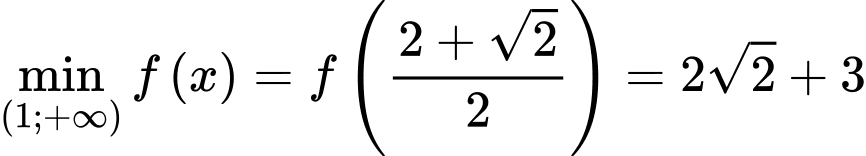 . Đáp án: C
. Đáp án: C
Câu 12 [582171]: Cho các số thực không âm 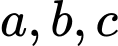 thỏa mãn
thỏa mãn  Gọi
Gọi 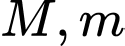 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 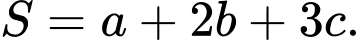 Giá trị của biểu thức
Giá trị của biểu thức 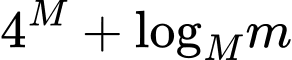 bằng
bằng
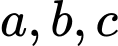 thỏa mãn
thỏa mãn  Gọi
Gọi 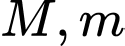 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 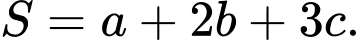 Giá trị của biểu thức
Giá trị của biểu thức 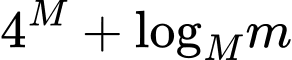 bằng
bằng A, 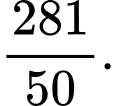
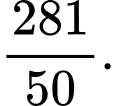
B, 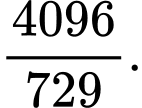
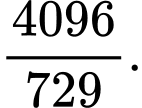
C, 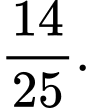
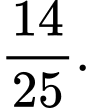
D, 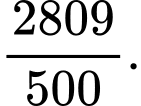
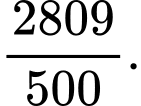
Đặt 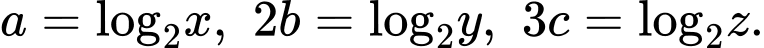
Ta có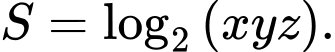
•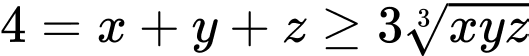
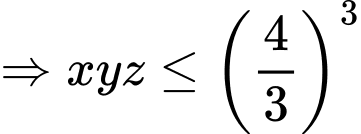

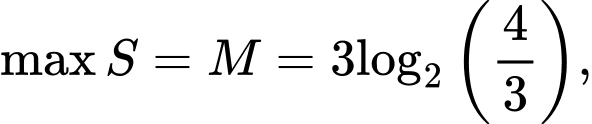 khi
khi 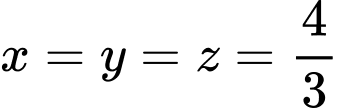
• Gọi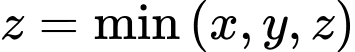
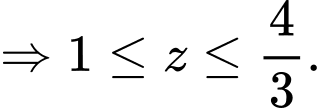
Do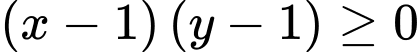
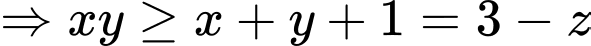
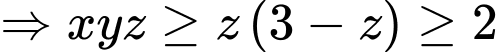 (vì
(vì 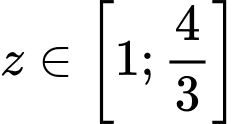
Suy ra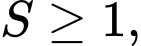 do đó
do đó 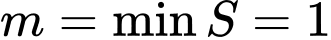 khi
khi 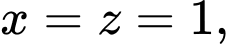
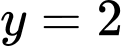
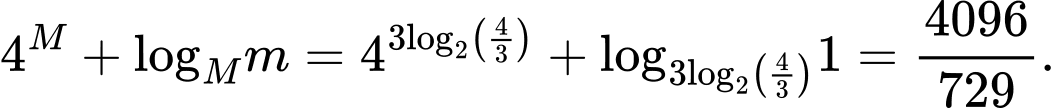 Đáp án: B
Đáp án: B
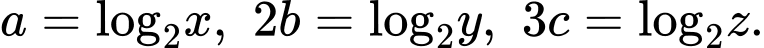
Ta có
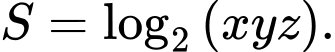
•
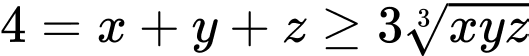
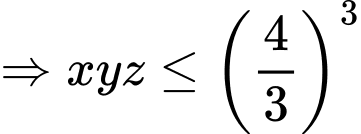

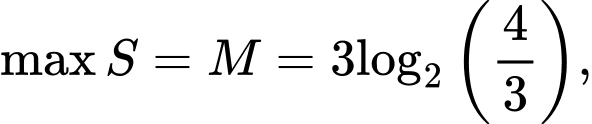 khi
khi 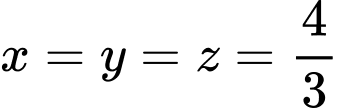
• Gọi
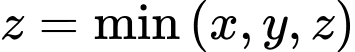
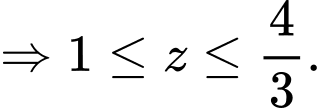
Do
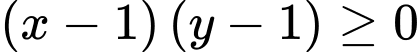
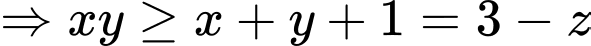
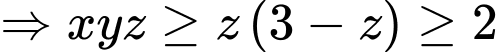 (vì
(vì 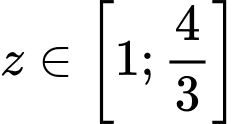
Suy ra
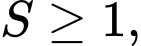 do đó
do đó 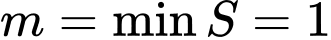 khi
khi 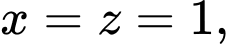
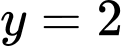
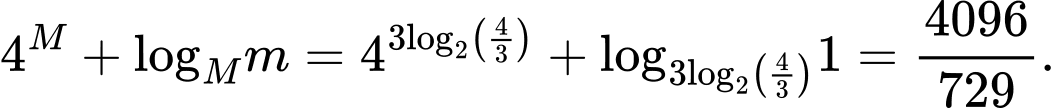 Đáp án: B
Đáp án: B 7. Dạng 7: Sự Biến Thiên Của Hàm Số Mũ – Logarit
Câu 13 [582172]: Hàm số nào sau đây đồng biến trên tập xác định của nó?
A, 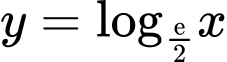 .
.
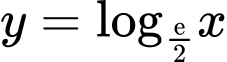 .
.B, 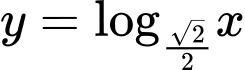 .
.
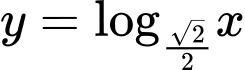 .
.C, 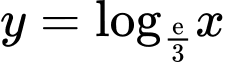 .
.
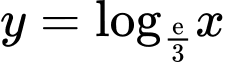 .
.D, 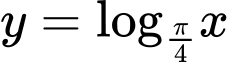 .
.
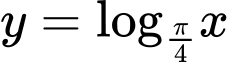 .
.
Ta thấy 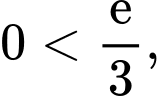
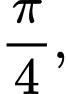
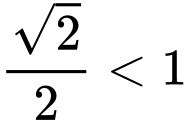 nên các hàm số ở B, C, D nghịch biến.
nên các hàm số ở B, C, D nghịch biến.
Vậy hàm số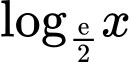 đồng biến trên tập xác định của nó, vì
đồng biến trên tập xác định của nó, vì 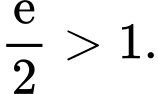 Đáp án: A
Đáp án: A
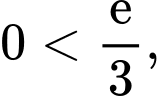
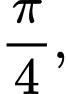
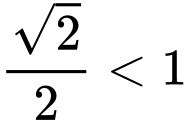 nên các hàm số ở B, C, D nghịch biến.
nên các hàm số ở B, C, D nghịch biến.Vậy hàm số
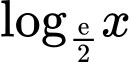 đồng biến trên tập xác định của nó, vì
đồng biến trên tập xác định của nó, vì 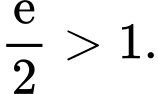 Đáp án: A
Đáp án: A
Câu 14 [582173]: Tìm tất cả các giá trị của tham số 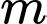 để hàm số
để hàm số 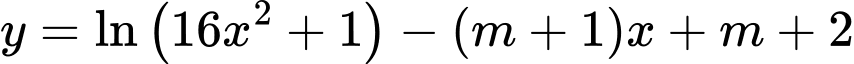 nghịch biến trên khoảng
nghịch biến trên khoảng 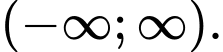
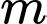 để hàm số
để hàm số 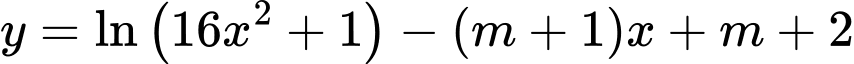 nghịch biến trên khoảng
nghịch biến trên khoảng 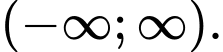
A, 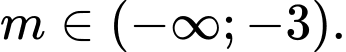
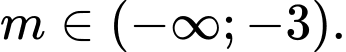
B, 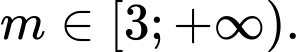
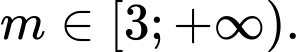
C, 

D, 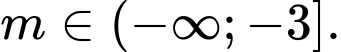
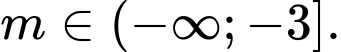
Ta có: 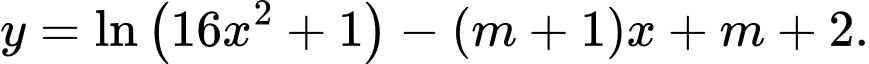
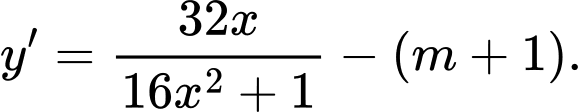
Hàm số nghịch biến trên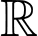 khi và chỉ khi
khi và chỉ khi 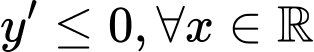
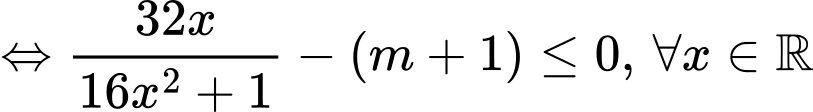 .
.
Cách 1: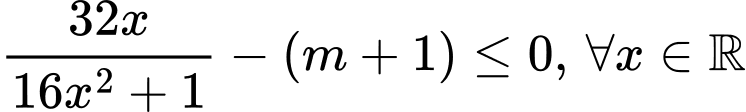
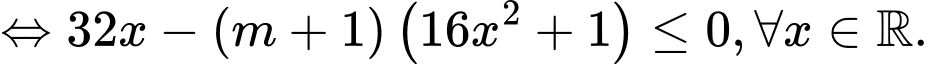
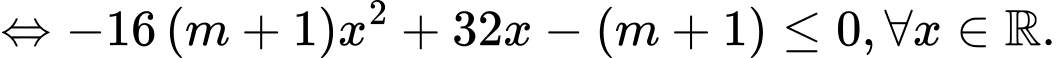
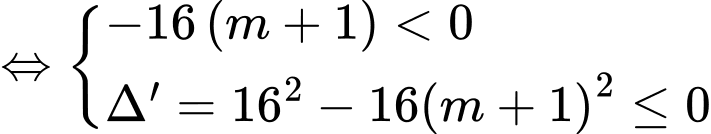
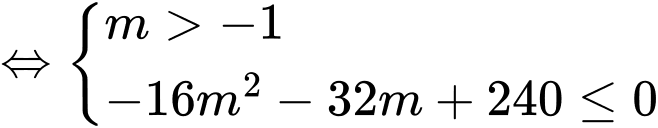
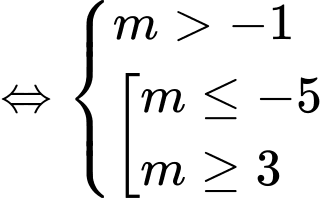
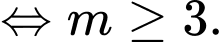
Cách 2: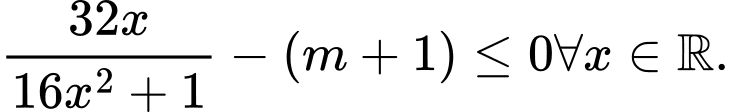
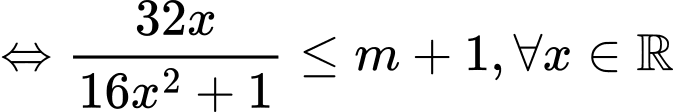
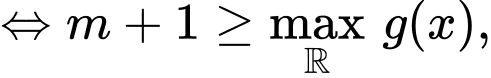 với
với 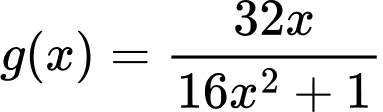 .
.
Ta có: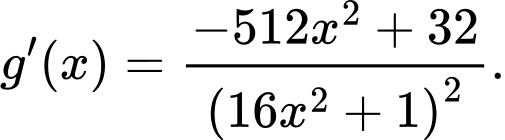
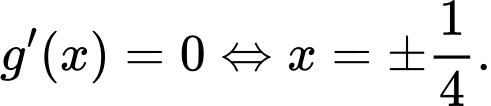
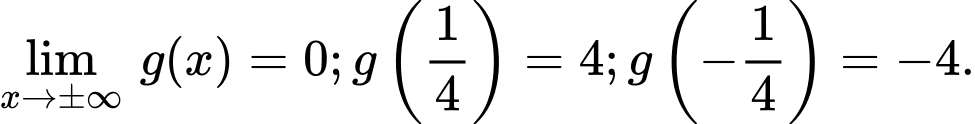
Bảng biến thiên:
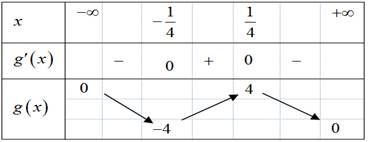
Dựa vào bảng biến thiên ta có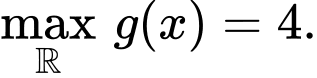
Do đó: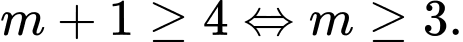 Đáp án: B
Đáp án: B
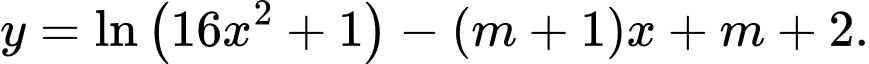
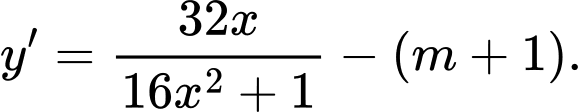
Hàm số nghịch biến trên
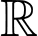 khi và chỉ khi
khi và chỉ khi 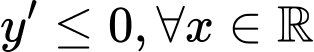
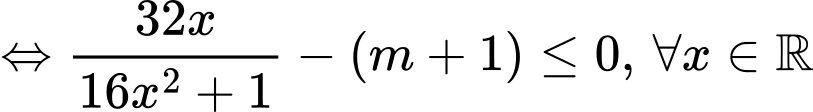 .
.Cách 1:
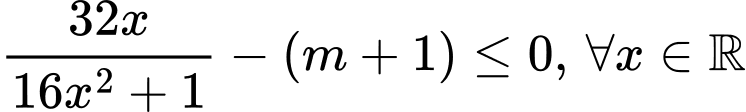
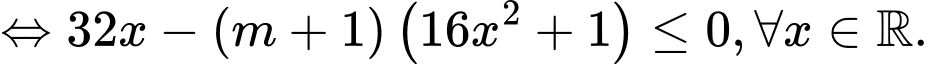
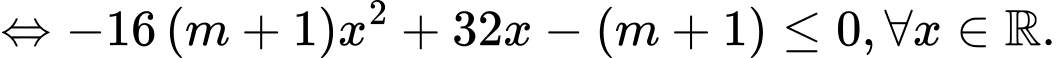
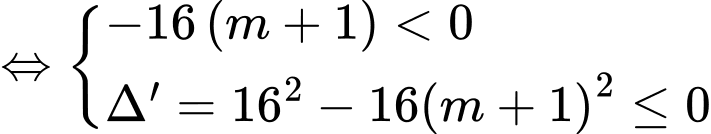
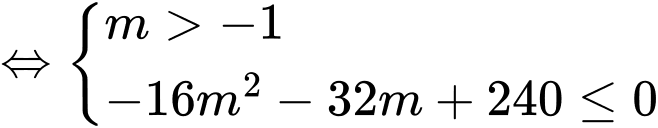
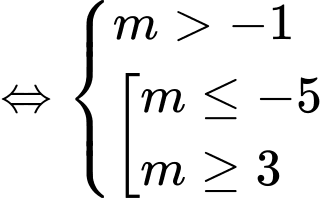
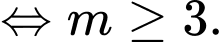
Cách 2:
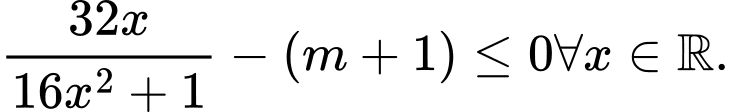
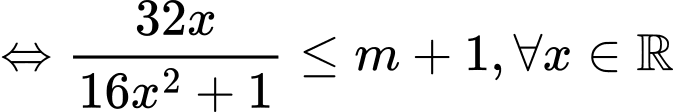
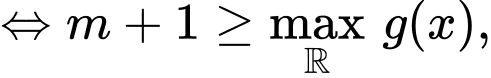 với
với 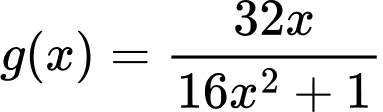 .
.Ta có:
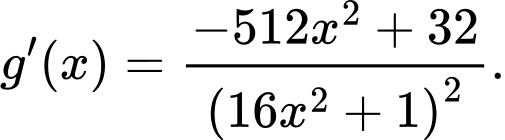
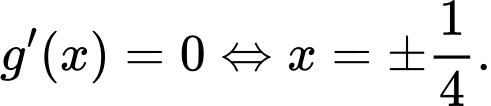
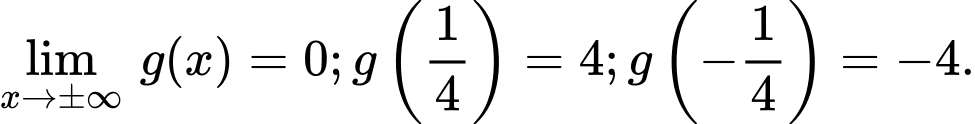
Bảng biến thiên:

Dựa vào bảng biến thiên ta có
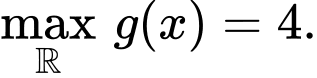
Do đó:
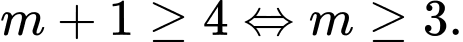 Đáp án: B
Đáp án: B 8. Dạng 8: Cực Trị Hàm Số Mũ – Logarit
Câu 15 [582174]: Hàm số 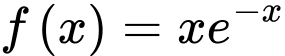 đạt cực đại tại điểm nào sau đây?
đạt cực đại tại điểm nào sau đây?
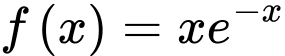 đạt cực đại tại điểm nào sau đây?
đạt cực đại tại điểm nào sau đây? A, 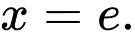
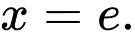
B, 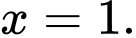
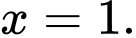
C, 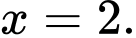
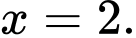
D, 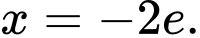
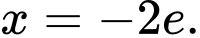
Tự luận: hàm số đai cực đại tại 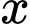 khi
khi 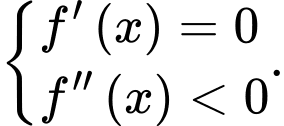
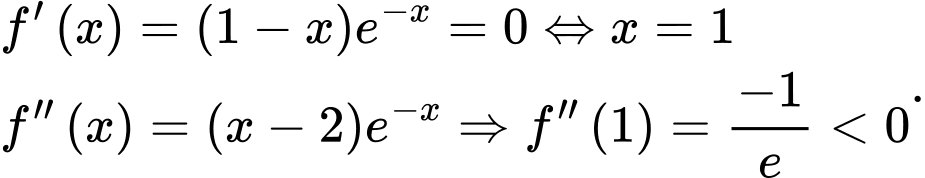
Trắc nghiệm: nhập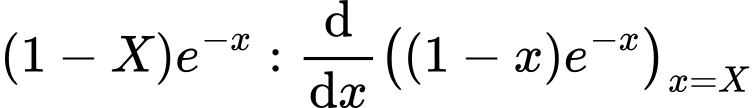
 CALC
CALC 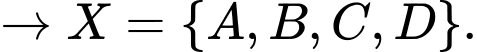 Đáp án: B
Đáp án: B
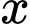 khi
khi 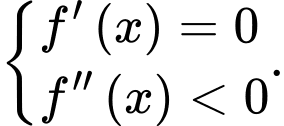
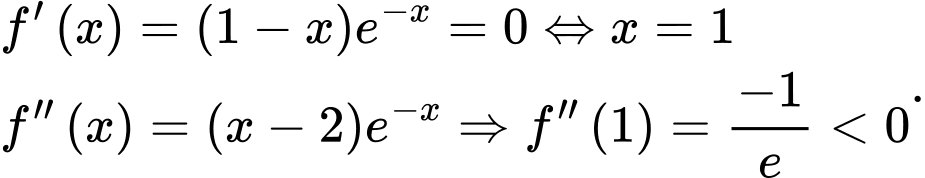
Trắc nghiệm: nhập
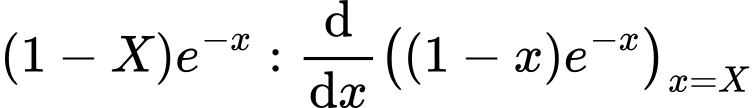
 CALC
CALC 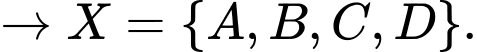 Đáp án: B
Đáp án: B
Câu 16 [582175]: Cho 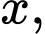
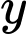 là các số thực thỏa mãn
là các số thực thỏa mãn 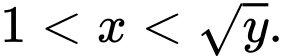 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 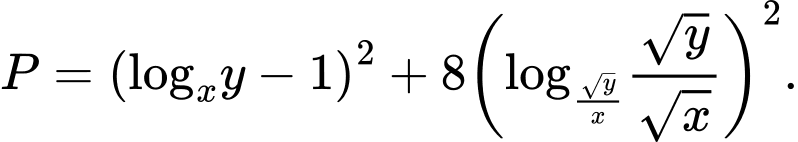
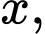
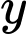 là các số thực thỏa mãn
là các số thực thỏa mãn 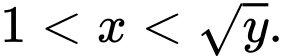 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức 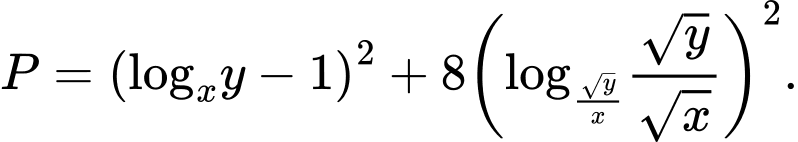
A, 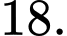
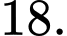
B, 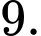
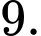
C, 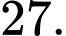
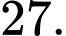
D, 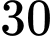
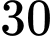
Ta có 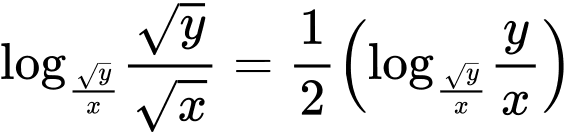
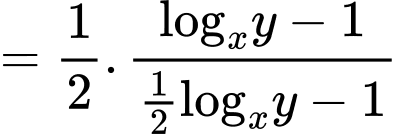
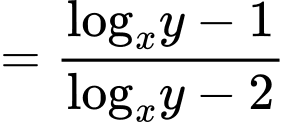
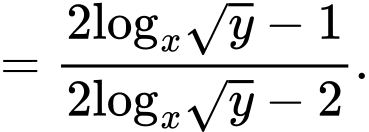
Suy ra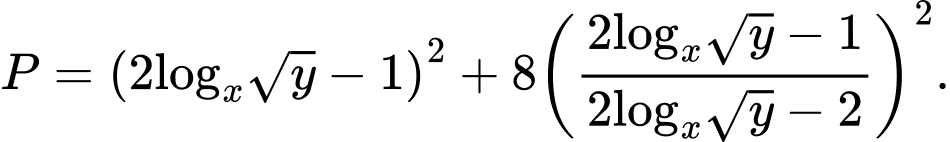
Đặt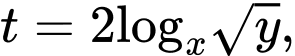 do
do 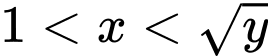
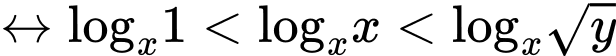
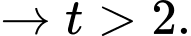
Ta có hàm số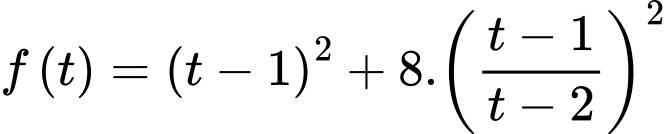 với
với 
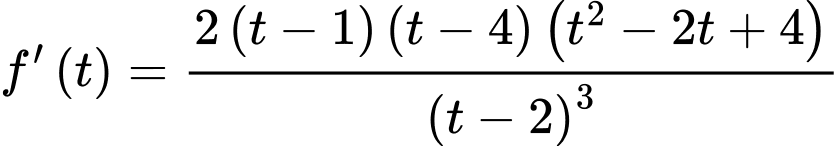 ;
; 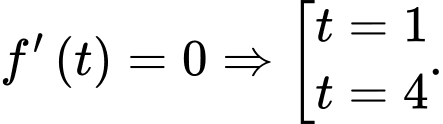
Lập bảng biến thiên trên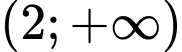 ta được
ta được
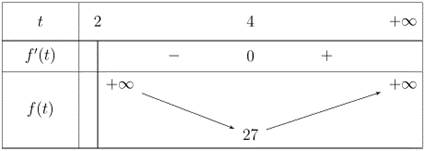
Vậy giá trị nhỏ nhất của biểu thức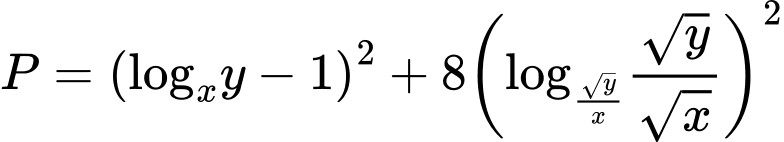 là
là 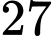 đạt được khi
đạt được khi

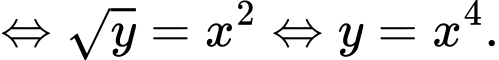
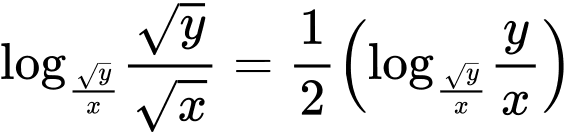
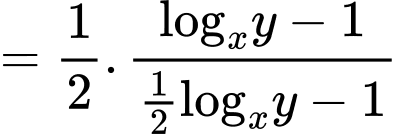
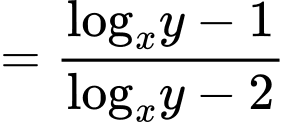
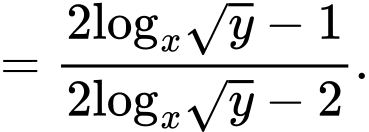
Suy ra
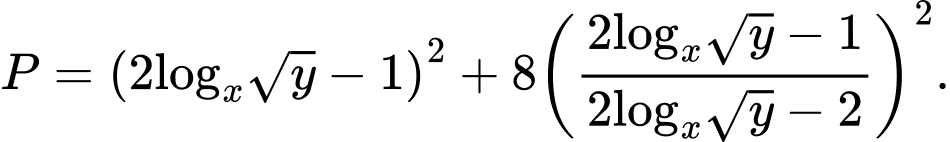
Đặt
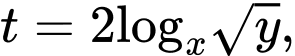 do
do 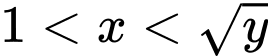
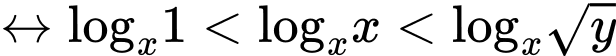
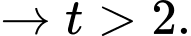
Ta có hàm số
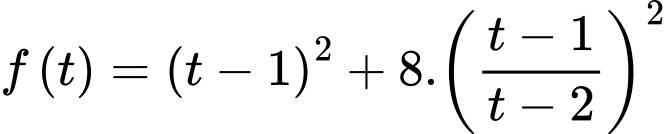 với
với 
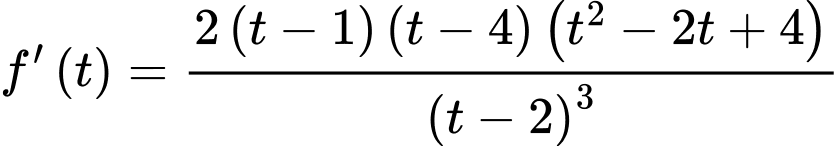 ;
; 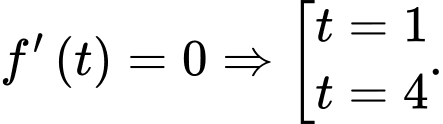
Lập bảng biến thiên trên
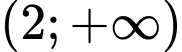 ta được
ta được
Vậy giá trị nhỏ nhất của biểu thức
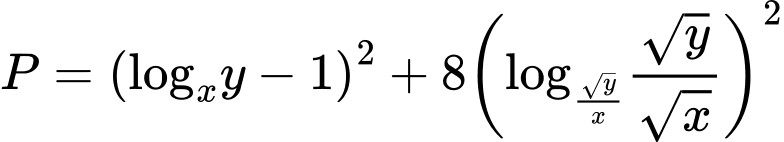 là
là 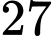 đạt được khi
đạt được khi 
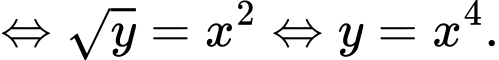
9. Dạng 9: Đồ Thị Hàm Số Mũ – Logarit
Câu 17 [582176]: Cho ba hàm số 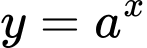 ,
, 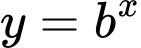 ,
, 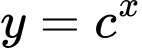 có đồ thị trên một mặt phẳng tọa độ
có đồ thị trên một mặt phẳng tọa độ 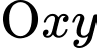 như hình vẽ dưới đây.
như hình vẽ dưới đây.
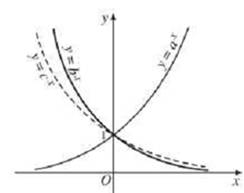
Mệnh đề nào sau đây là mệnh đề đúng?
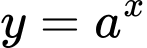 ,
, 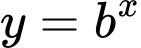 ,
, 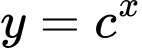 có đồ thị trên một mặt phẳng tọa độ
có đồ thị trên một mặt phẳng tọa độ 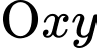 như hình vẽ dưới đây.
như hình vẽ dưới đây.
Mệnh đề nào sau đây là mệnh đề đúng?
A, 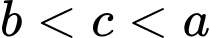 .
.
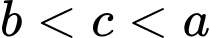 .
.B, 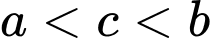 .
.
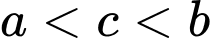 .
.C, 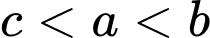 .
.
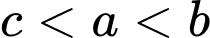 .
.D, 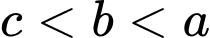 .
.
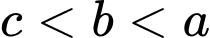 .
.
Dựa vào hình vẽ ba đồ thị ta thấy hàm số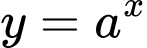 đồng biến trên
đồng biến trên 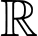 nên
nên 
Hàm số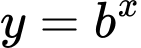 và
và 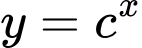 giảm trên
giảm trên  nên
nên  và
và  (loại B và C).
(loại B và C).
Nhìn vào đồ thị ta thấy với thì
thì  và với
và với  thì
thì  , do đó
, do đó 
Vậy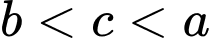 .
Đáp án: A
.
Đáp án: A
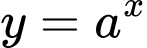 đồng biến trên
đồng biến trên  nên
nên 
Hàm số
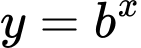 và
và 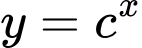 giảm trên
giảm trên 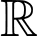 nên
nên  và
và  (loại B và C).
(loại B và C).
Nhìn vào đồ thị ta thấy với
 thì
thì  và với
và với  thì
thì  , do đó
, do đó 
Vậy
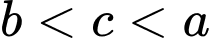 .
Đáp án: A
.
Đáp án: A 10. Dạng 10: Bài Toán Thực Tế
Câu 18 [582177]: Sự tăng trưởng của một loại vi khuẩn tuân theo công thức 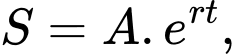 trong đó
trong đó 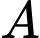 là số vi khuẩn ban đầu,
là số vi khuẩn ban đầu, 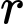 là tỷ lệ tăng trưởng,
là tỷ lệ tăng trưởng, 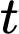 là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là
là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 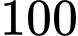 con và sau
con và sau 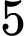 giờ có
giờ có  con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng
con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng 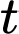 gần với kết quả nào sau đây nhất?
gần với kết quả nào sau đây nhất?
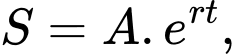 trong đó
trong đó 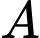 là số vi khuẩn ban đầu,
là số vi khuẩn ban đầu, 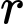 là tỷ lệ tăng trưởng,
là tỷ lệ tăng trưởng, 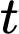 là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là
là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 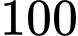 con và sau
con và sau 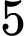 giờ có
giờ có  con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng
con. Để số lượng vi khuẩn ban đầu tăng gấp đôi thì thời gian tăng trưởng 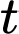 gần với kết quả nào sau đây nhất?
gần với kết quả nào sau đây nhất? A, 3 giờ 9 phút.
B, 3 giờ 2 phút.
C, 3 giờ 30 phút.
D, 3 giờ 18 phút.
Trước tiên, ta tìm tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này.
Từ giả thiết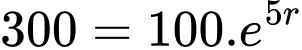
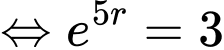
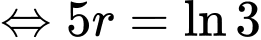
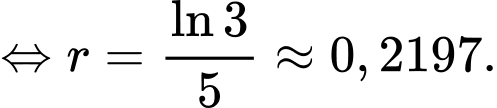
Từ công thức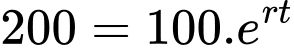
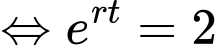
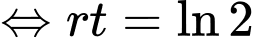
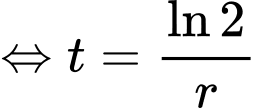
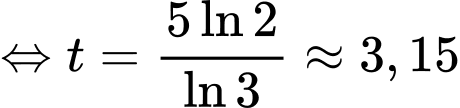 (giờ)
(giờ) 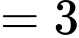 giờ 9 phút. Đáp án: A
giờ 9 phút. Đáp án: A
Từ giả thiết
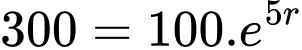
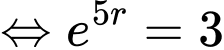
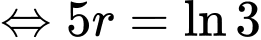
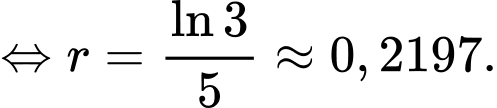
Từ công thức
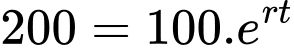
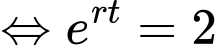
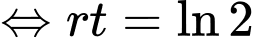
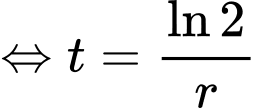
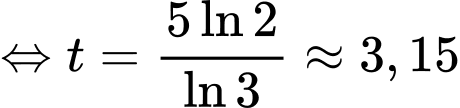 (giờ)
(giờ) 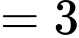 giờ 9 phút. Đáp án: A
giờ 9 phút. Đáp án: A