Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582178]: Tính giá trị của biểu thức 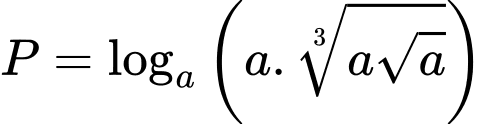 với
với 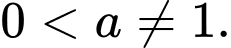
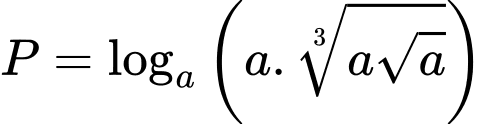 với
với 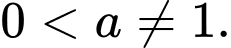
A, 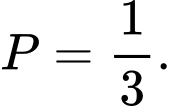
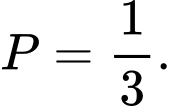
B, 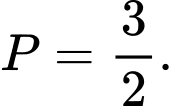
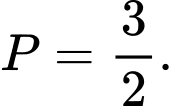
C, 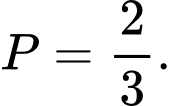
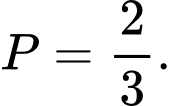
D, 

Ta có 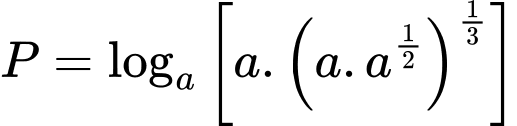

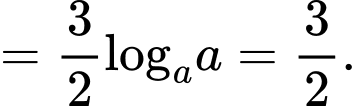
Chọn B.
Cách trắc nghiệm: Chọn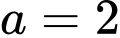 và bấm máy. Đáp án: B
và bấm máy. Đáp án: B
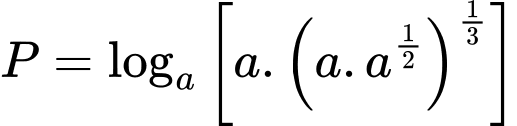

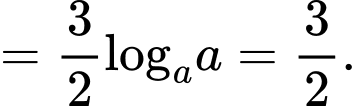
Chọn B.
Cách trắc nghiệm: Chọn
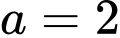 và bấm máy. Đáp án: B
và bấm máy. Đáp án: B
Câu 2 [582179]: Cho 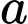 là số thực dương và khác
là số thực dương và khác 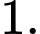 Tính giá trị biểu thức
Tính giá trị biểu thức 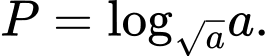
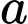 là số thực dương và khác
là số thực dương và khác 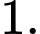 Tính giá trị biểu thức
Tính giá trị biểu thức 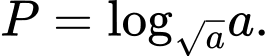
A, 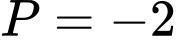 .
.
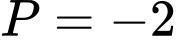 .
.B, 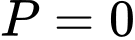 .
.
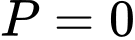 .
.C, 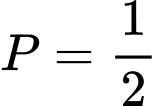 .
.
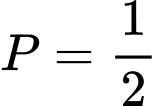 .
.D, 

Với 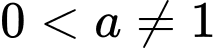 , ta có
, ta có 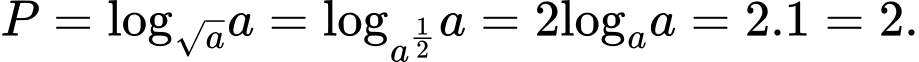 Đáp án: D
Đáp án: D
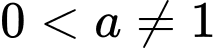 , ta có
, ta có 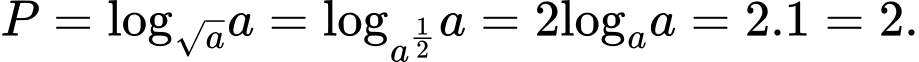 Đáp án: D
Đáp án: D
Câu 3 [582180]: Cho hàm số 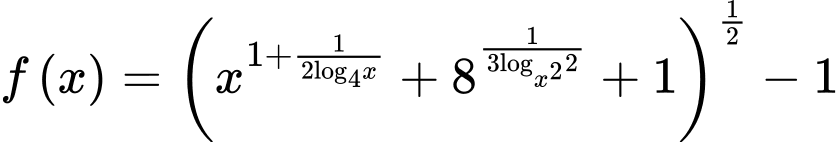 với
với 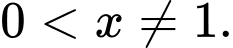 Tính giá trị biểu thức
Tính giá trị biểu thức 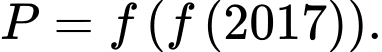
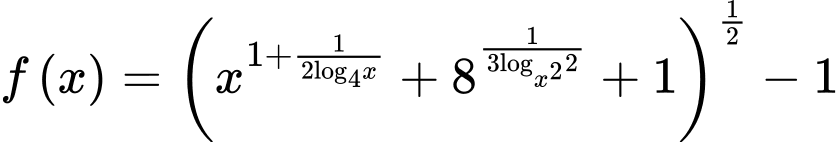 với
với 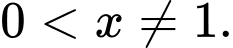 Tính giá trị biểu thức
Tính giá trị biểu thức 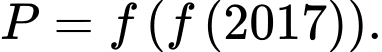
A, 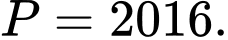
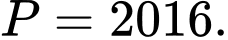
B, 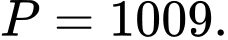
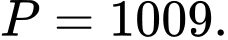
C, 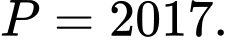
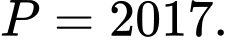
D, 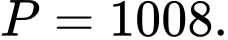
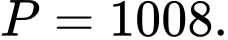
Ta có 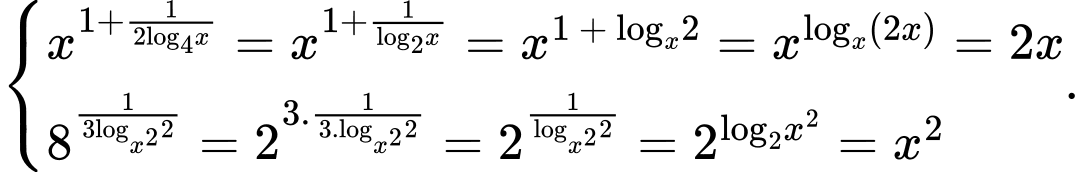
Khi đó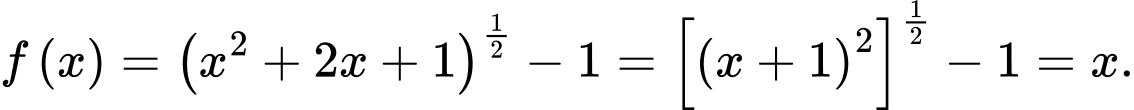
Suy ra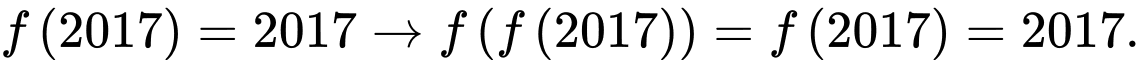 Đáp án: C
Đáp án: C
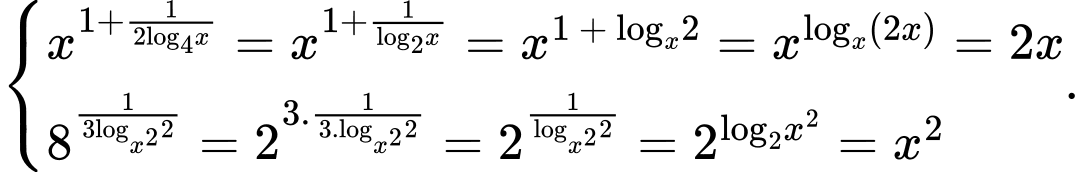
Khi đó
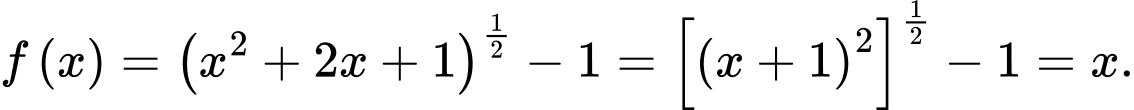
Suy ra
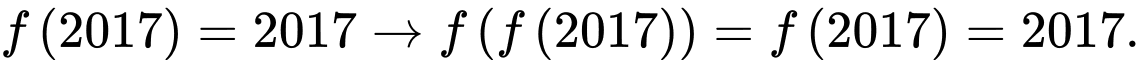 Đáp án: C
Đáp án: C
Câu 4 [582181]: Biết rằng hàm số 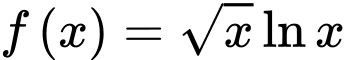 đạt giá trị lớn nhất trên đoạn
đạt giá trị lớn nhất trên đoạn 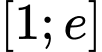 tại
tại 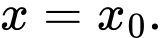 Mệnh đề nào sau đây là đúng?
Mệnh đề nào sau đây là đúng?
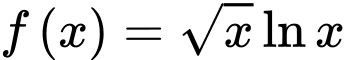 đạt giá trị lớn nhất trên đoạn
đạt giá trị lớn nhất trên đoạn 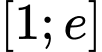 tại
tại 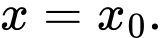 Mệnh đề nào sau đây là đúng?
Mệnh đề nào sau đây là đúng? A, 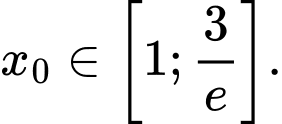
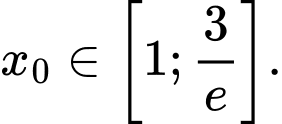
B, 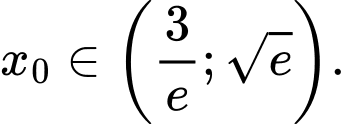
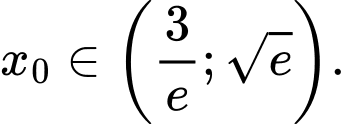
C, 

D, 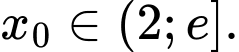
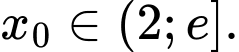
Hàm số xác định và liên tục trên đoạn 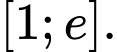
Đạo hàm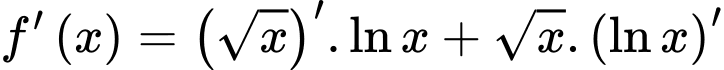
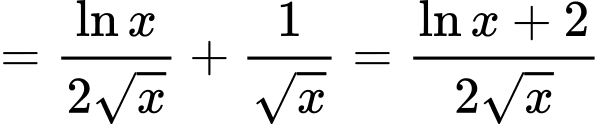
Suy ra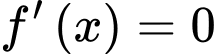
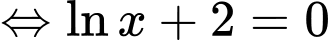
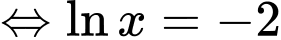
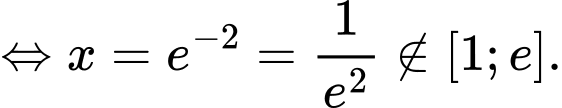
Ta có GTLN của hàm số bằng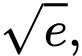 đạt tại
đạt tại 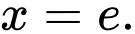
Chọn D.
Nhận xét. Ta có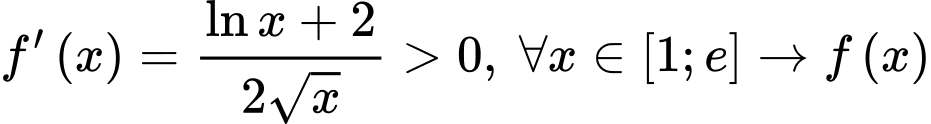 đồng biến trên
đồng biến trên 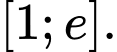 Đáp án: D
Đáp án: D
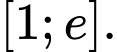
Đạo hàm
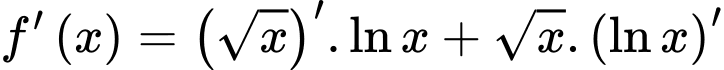
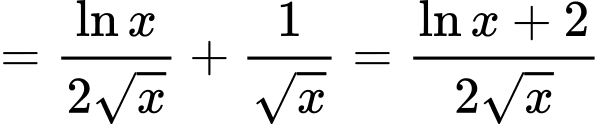
Suy ra
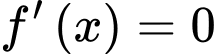
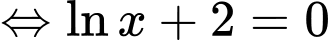
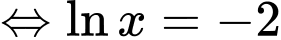
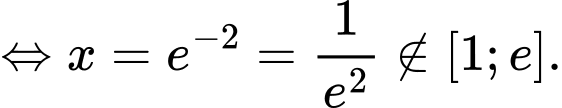
Ta có GTLN của hàm số bằng
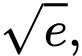 đạt tại
đạt tại 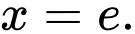
Chọn D.
Nhận xét. Ta có
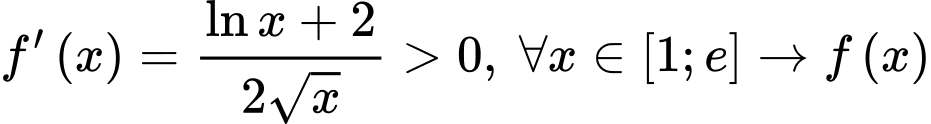 đồng biến trên
đồng biến trên 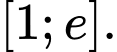 Đáp án: D
Đáp án: D
Câu 5 [582182]: Cho 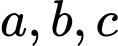 là các số thực dương khác
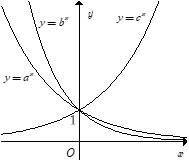
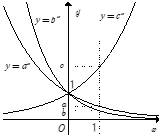
là các số thực dương khác  Hình vẽ bên là đồ thị của ba hàm số
Hình vẽ bên là đồ thị của ba hàm số 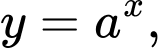
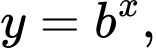
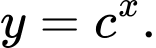 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
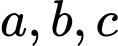 là các số thực dương khác
là các số thực dương khác 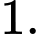 Hình vẽ bên là đồ thị của ba hàm số
Hình vẽ bên là đồ thị của ba hàm số 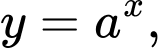
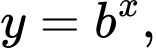
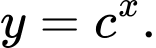 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
A, 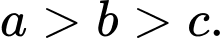
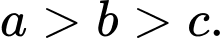
B, 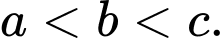
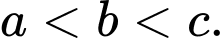
C, 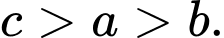
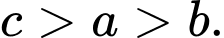
D, 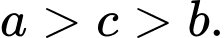
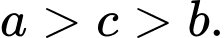
Ta thấy hàm 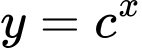 có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến
có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến 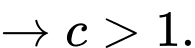
Còn hàm số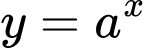 và
và 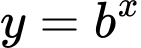 là những hàm nghịch biến
là những hàm nghịch biến 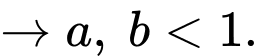 Từ đó loại được các đáp án A, D.
Từ đó loại được các đáp án A, D.
Từ đồ thị hàm số ta thấy tại cùng một giá trị thì đồ thị hàm số
thì đồ thị hàm số 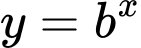 nằm trên đồ thị hàm số
nằm trên đồ thị hàm số 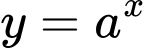 hay
hay 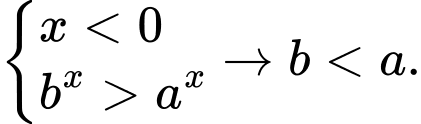 ví dụ
ví dụ 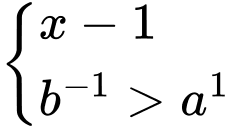
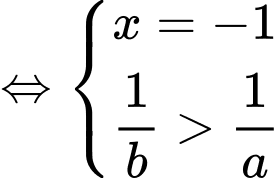
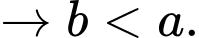
Vậy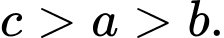
Chọn C.
Cách trắc nghiệm. Kẻ đường thẳng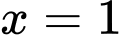 cắt đồ thị các hàm số
cắt đồ thị các hàm số 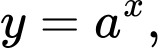
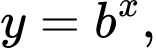
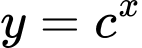 lần lượt tại các điểm có tung độ
lần lượt tại các điểm có tung độ 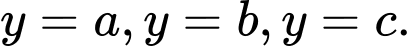 Dựa vào đồ thị ta thấy ngay
Dựa vào đồ thị ta thấy ngay 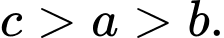
 Đáp án: C
Đáp án: C
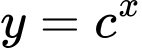 có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến
có đồ thị từ trái sang phải theo hướng đi lên nên là hàm đồng biến 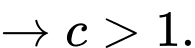
Còn hàm số
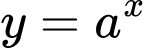 và
và 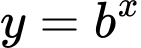 là những hàm nghịch biến
là những hàm nghịch biến 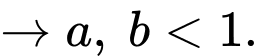 Từ đó loại được các đáp án A, D.
Từ đó loại được các đáp án A, D.Từ đồ thị hàm số ta thấy tại cùng một giá trị
 thì đồ thị hàm số
thì đồ thị hàm số 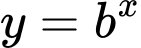 nằm trên đồ thị hàm số
nằm trên đồ thị hàm số 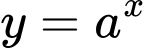 hay
hay 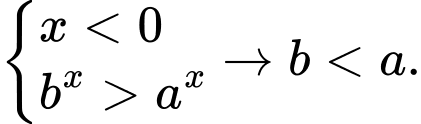 ví dụ
ví dụ 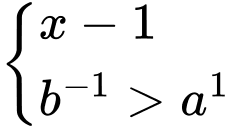
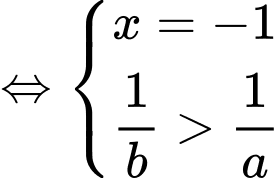
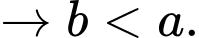
Vậy
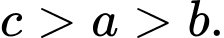
Chọn C.
Cách trắc nghiệm. Kẻ đường thẳng
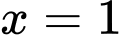 cắt đồ thị các hàm số
cắt đồ thị các hàm số 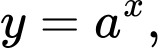
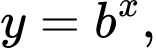
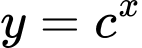 lần lượt tại các điểm có tung độ
lần lượt tại các điểm có tung độ 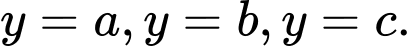 Dựa vào đồ thị ta thấy ngay
Dựa vào đồ thị ta thấy ngay 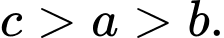
 Đáp án: C
Đáp án: C
Câu 6 [582183]: Cho 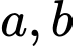 là các số thực dương khác
là các số thực dương khác 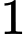 và thỏa mãn
và thỏa mãn 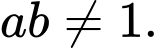 Rút gọn biểu thức
Rút gọn biểu thức 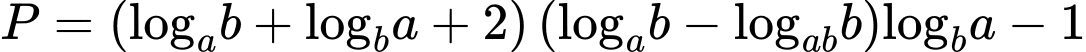 .
.
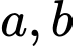 là các số thực dương khác
là các số thực dương khác 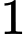 và thỏa mãn
và thỏa mãn 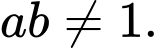 Rút gọn biểu thức
Rút gọn biểu thức 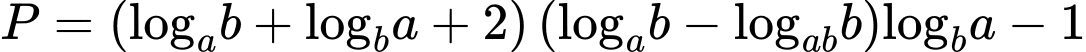 .
. A, 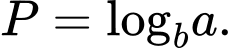
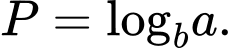
B, 

C, 

D, 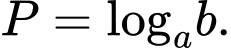
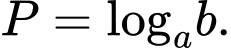
Từ giả thiết, ta có 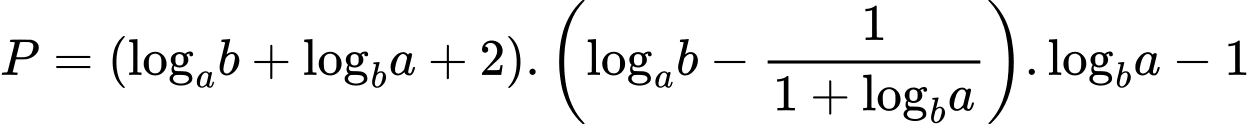
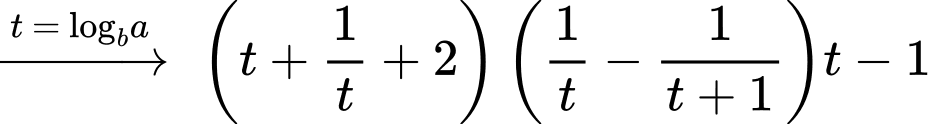
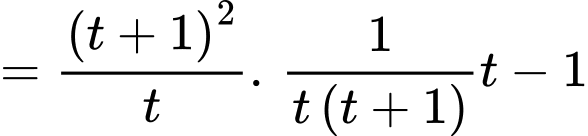
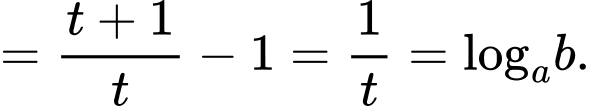
Chọn D. Đáp án: D
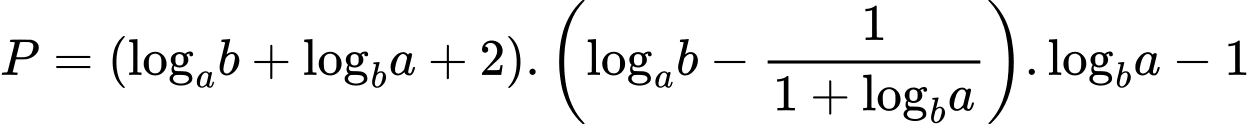
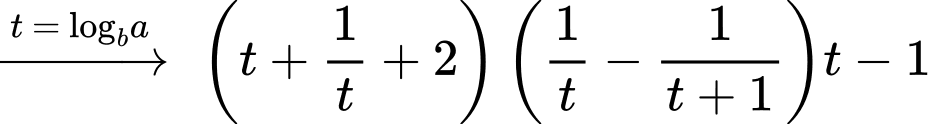
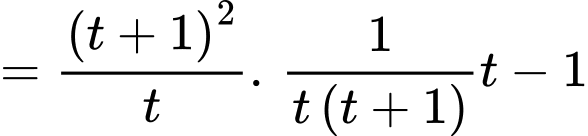
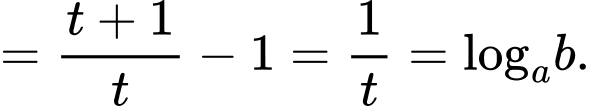
Chọn D. Đáp án: D
Câu 7 [582184]: Tìm tất cả các giá trị thực của tham số 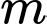 để hàm số
để hàm số 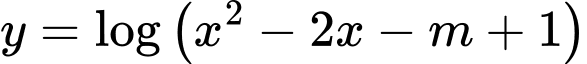 có tập xác định là
có tập xác định là
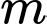 để hàm số
để hàm số 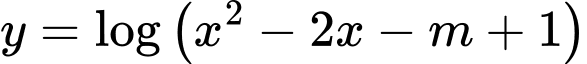 có tập xác định là
có tập xác định là A, 

B, 

C, 

D, 

Ycbt 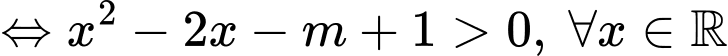
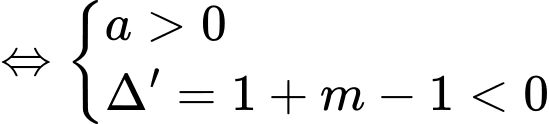
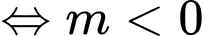
Chọn B. Đáp án: B
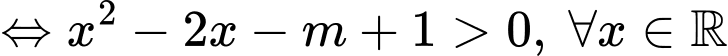
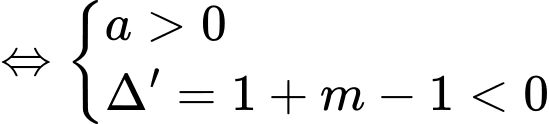
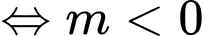
Chọn B. Đáp án: B
Câu 8 [582185]: Cho hàm số 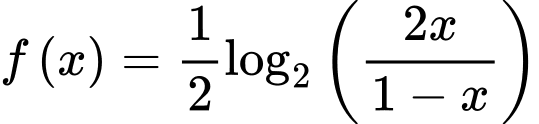 . Tính tổng
. Tính tổng 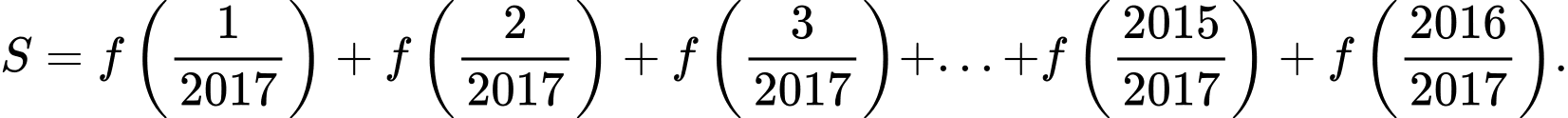
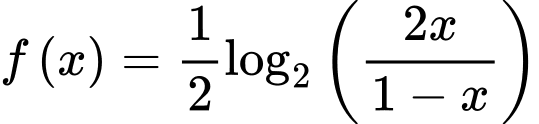 . Tính tổng
. Tính tổng 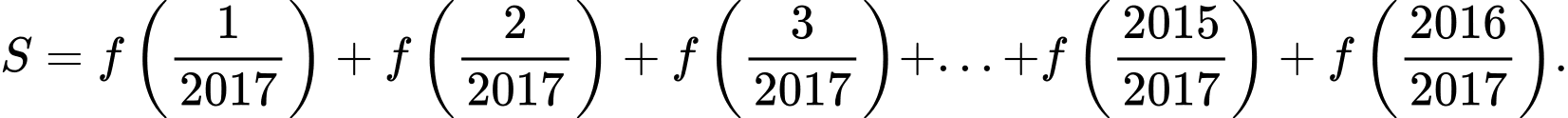
A, 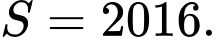
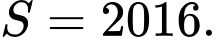
B, 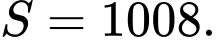
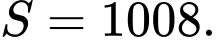
C, 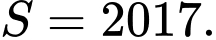
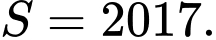
D, 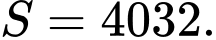
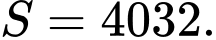
Xét 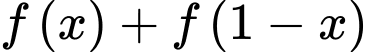
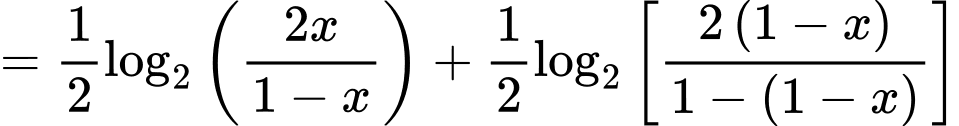
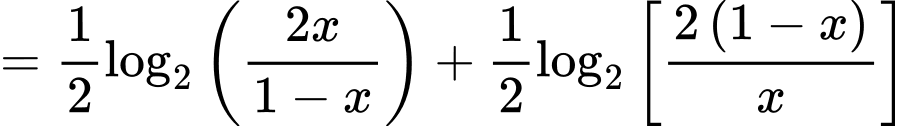
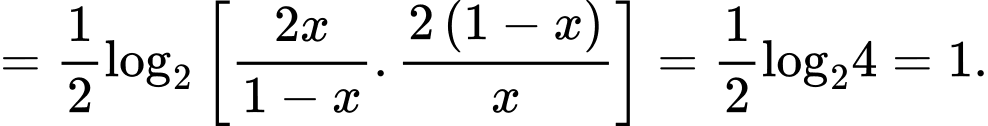
Áp dụng tính chất trên, ta được
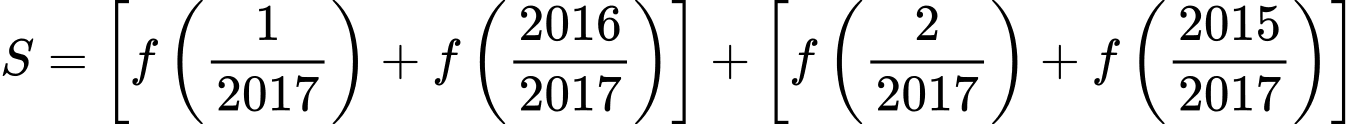
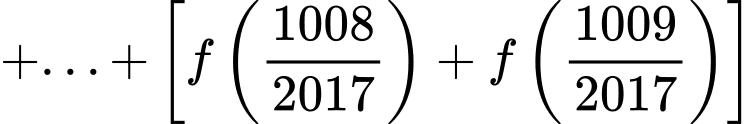
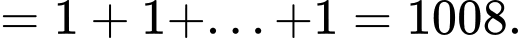 Đáp án: B
Đáp án: B
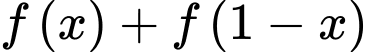
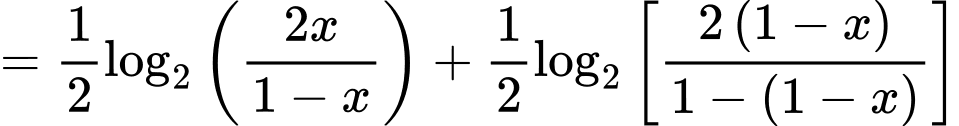
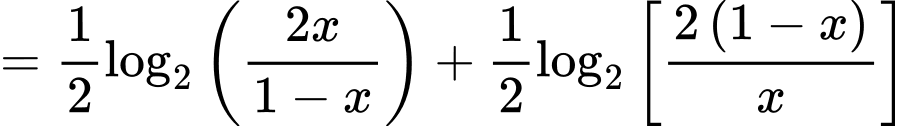
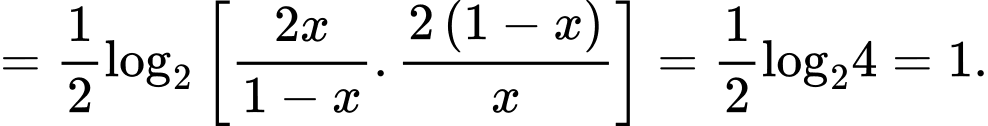
Áp dụng tính chất trên, ta được
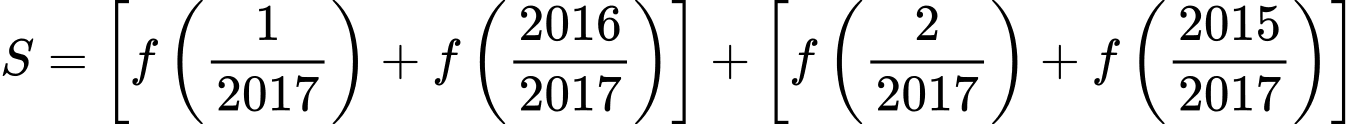
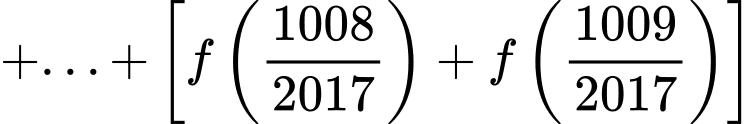
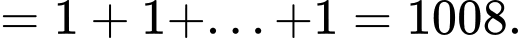 Đáp án: B
Đáp án: B
Câu 9 [582186]: Đặt 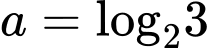 và
và 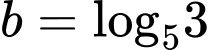 . Hãy biểu diễn
. Hãy biểu diễn 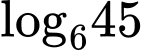 theo
theo 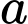 và
và 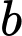 .
.
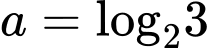 và
và 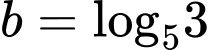 . Hãy biểu diễn
. Hãy biểu diễn 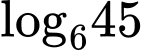 theo
theo 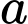 và
và 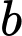 .
. A, 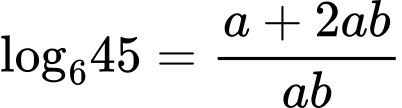 .
.
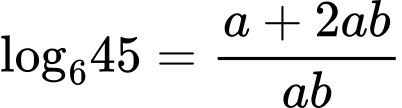 .
.B, 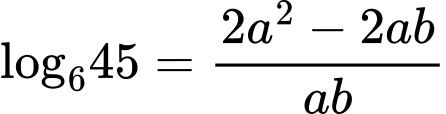 .
.
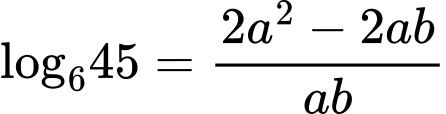 .
.C, 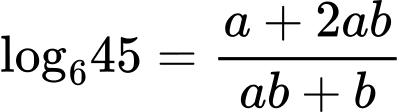 .
.
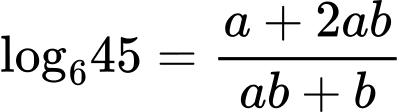 .
.D, 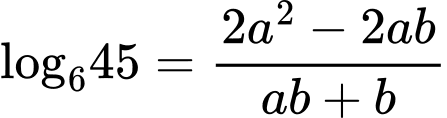 .
.
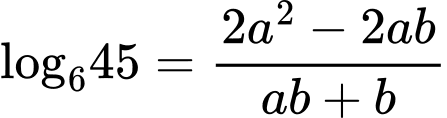 .
.
Ta có 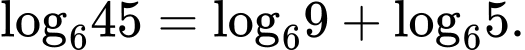
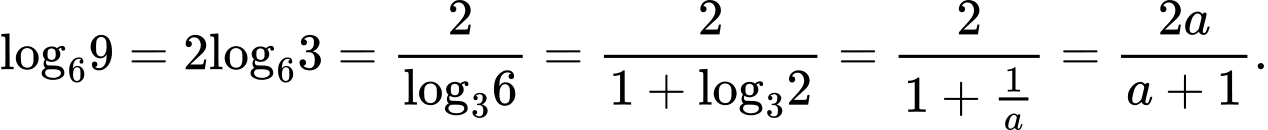
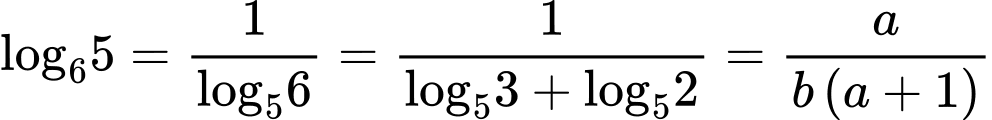 vì
vì 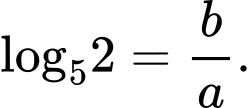
Vậy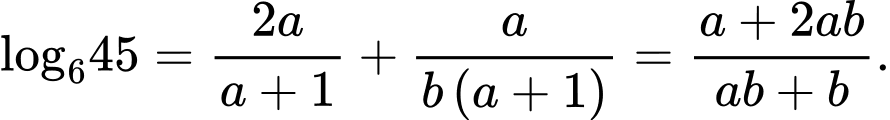 Đáp án: C
Đáp án: C
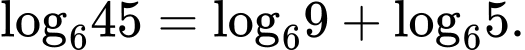
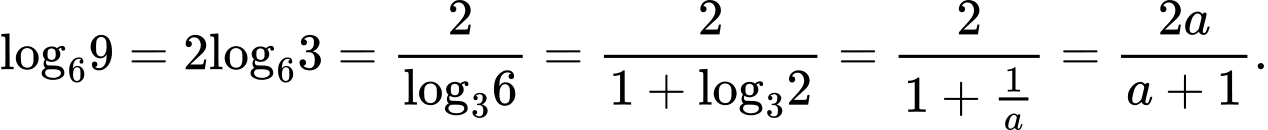
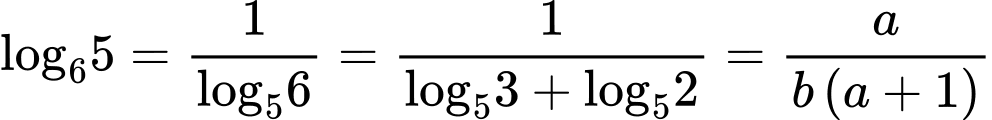 vì
vì 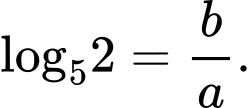
Vậy
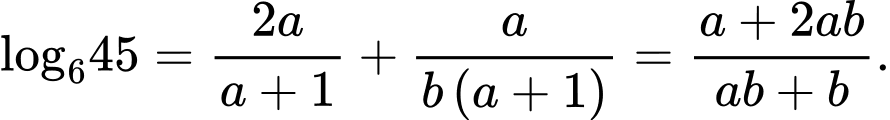 Đáp án: C
Đáp án: C
Câu 10 [582187]: Cho 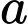 và
và 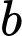 là các số thực dương khác
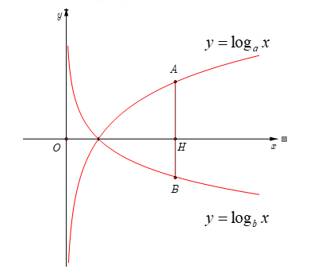
là các số thực dương khác 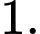 Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị
Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị  ,
, 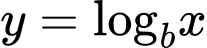 và trục hoành lần lượt tại
và trục hoành lần lượt tại 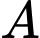 ,
,  và
và  ta đều có
ta đều có  (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
(hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
 và
và 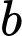 là các số thực dương khác
là các số thực dương khác 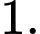 Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị
Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị  ,
, 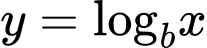 và trục hoành lần lượt tại
và trục hoành lần lượt tại  ,
, 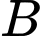 và
và 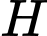 ta đều có
ta đều có  (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
(hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
A, 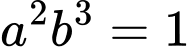 .
.
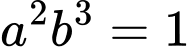 .
.B,  .
.
 .
.C, 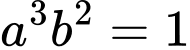 .
.
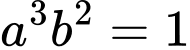 .
.D,  .
.
 .
.
Ta có 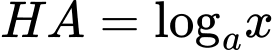 và
và 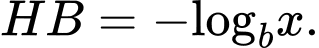
Do đó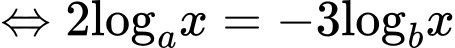
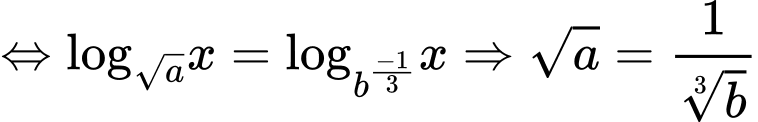
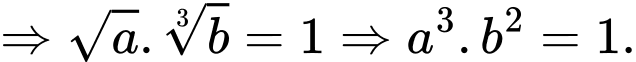 Đáp án: C
Đáp án: C
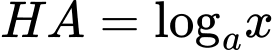 và
và 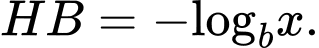
Do đó
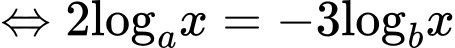
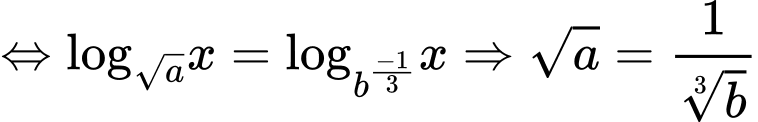
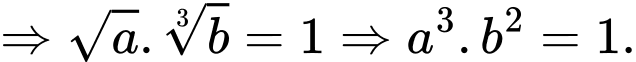 Đáp án: C
Đáp án: C
Câu 11 [582188]: Biết rằng năm 2001, dân số Việt Nam là 78685800 người và tỉ lệ tăng dân số năm đó là 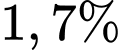 . Cho biết sự tăng dân số được ước tính theo công thức
. Cho biết sự tăng dân số được ước tính theo công thức 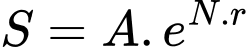 (trong đó
(trong đó 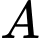 : là dân số của năm lấy làm mốc tính,
: là dân số của năm lấy làm mốc tính, 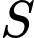 là dân số sau
là dân số sau 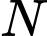 năm,
năm, 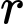 là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người?
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người?
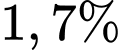 . Cho biết sự tăng dân số được ước tính theo công thức
. Cho biết sự tăng dân số được ước tính theo công thức 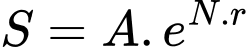 (trong đó
(trong đó 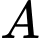 : là dân số của năm lấy làm mốc tính,
: là dân số của năm lấy làm mốc tính, 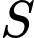 là dân số sau
là dân số sau 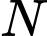 năm,
năm, 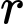 là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người?
là tỉ lệ tăng dân số hàng năm). Cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 120 triệu người? A, 2020.
B, 2022.
C, 2025.
D, 2026.
Ta có 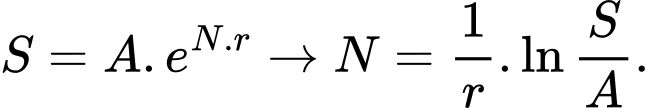
Để dân số nước ta ở mức 120 triệu người thì cần số năm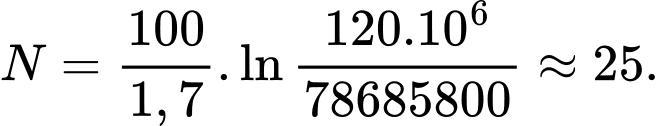
Lúc đấy là năm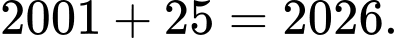
Chọn D. Đáp án: D
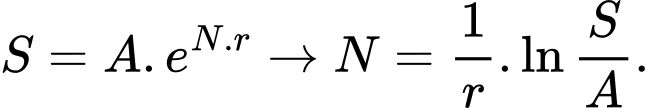
Để dân số nước ta ở mức 120 triệu người thì cần số năm
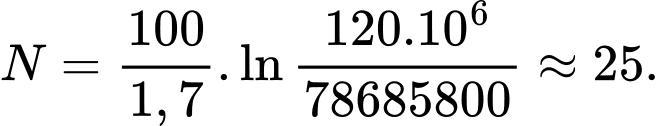
Lúc đấy là năm
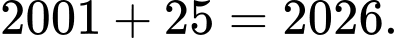
Chọn D. Đáp án: D
Câu 12 [582189]: Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ trái đất tăng thêm 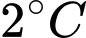 thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm
thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm 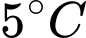 thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 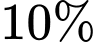 . Biết rằng nếu nhiệt độ trái đất tăng thêm
. Biết rằng nếu nhiệt độ trái đất tăng thêm 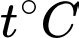 , tổng giá trị kinh tế toàn cầu giảm
, tổng giá trị kinh tế toàn cầu giảm 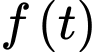 % thì
% thì 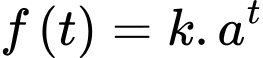 (trong đó
(trong đó 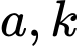 là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ
là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ  thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 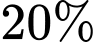 ?
?
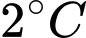 thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm
thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm 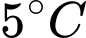 thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 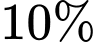 . Biết rằng nếu nhiệt độ trái đất tăng thêm
. Biết rằng nếu nhiệt độ trái đất tăng thêm 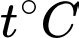 , tổng giá trị kinh tế toàn cầu giảm
, tổng giá trị kinh tế toàn cầu giảm 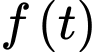 % thì
% thì 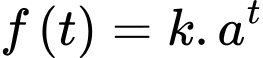 (trong đó
(trong đó 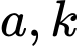 là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ
là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ  thì tổng giá trị kinh tế toàn cầu giảm
thì tổng giá trị kinh tế toàn cầu giảm 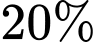 ?
? A, 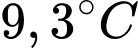 .
.
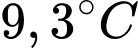 .
.B, 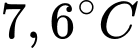 .
.
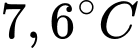 .
.C, 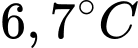 .
.
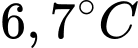 .
.D, 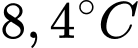 .
.
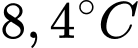 .
.
Theo đề bài, ta có 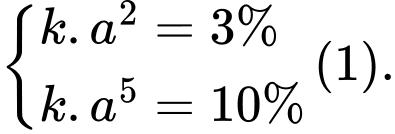 Cần tìm
Cần tìm 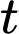 thỏa mãn
thỏa mãn 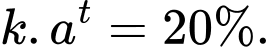
Từ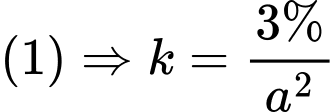 và
và 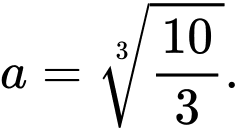
Khi đó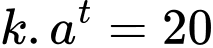 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
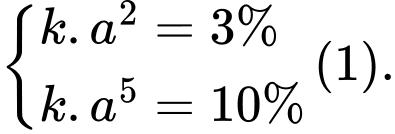 Cần tìm
Cần tìm 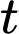 thỏa mãn
thỏa mãn 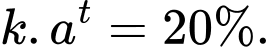
Từ
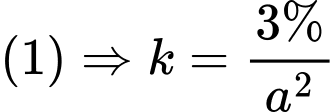 và
và 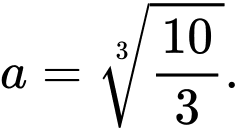
Khi đó
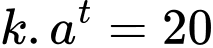 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 13 [582190]: Trong mặt phẳng với hệ tọa độ 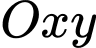 , cho hình vuông
, cho hình vuông 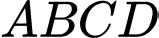 có diện tích bằng
có diện tích bằng 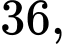 đường thẳng chứa cạnh
đường thẳng chứa cạnh  song song với trục
song song với trục  các đỉnh
các đỉnh 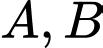 và
và  lần lượt nằm trên đồ thị của các hàm số
lần lượt nằm trên đồ thị của các hàm số 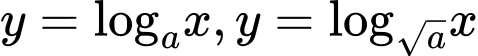 và
và 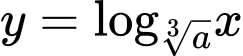 với
với 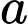 là số thực lớn hơn
là số thực lớn hơn 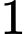 . Tìm
. Tìm 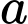 .
.
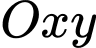 , cho hình vuông
, cho hình vuông 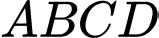 có diện tích bằng
có diện tích bằng 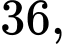 đường thẳng chứa cạnh
đường thẳng chứa cạnh  song song với trục
song song với trục  các đỉnh
các đỉnh 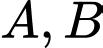 và
và  lần lượt nằm trên đồ thị của các hàm số
lần lượt nằm trên đồ thị của các hàm số 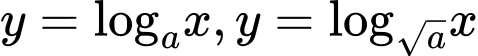 và
và 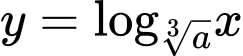 với
với 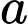 là số thực lớn hơn
là số thực lớn hơn 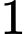 . Tìm
. Tìm 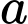 .
. A, 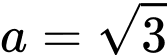 .
.
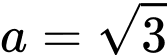 .
.B, 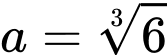 .
.
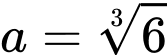 .
.C, 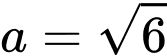 .
.
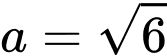 .
.D, 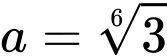 .
.
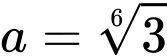 .
.
Do 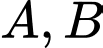 nằm trên đường thẳng
nằm trên đường thẳng 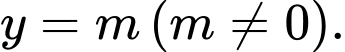
Lại có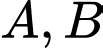 lần lượt nằm trên đồ thị của các hàm số
lần lượt nằm trên đồ thị của các hàm số 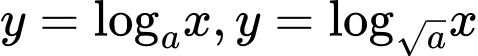 .
.
Từ đó suy ra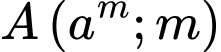 ,
, 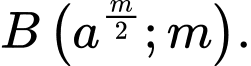
Vì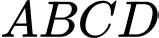 là hình vuông nên suy ra
là hình vuông nên suy ra 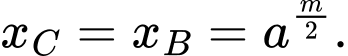
Lại có nằm trên đồ thị hàm số
nằm trên đồ thị hàm số 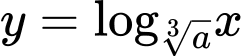 , suy ra
, suy ra 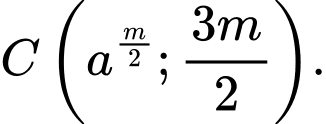
Theo đề bài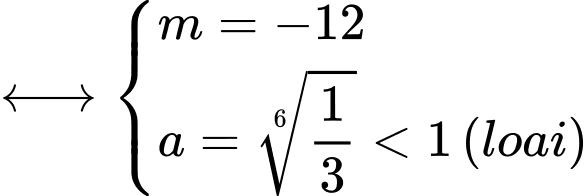
hoặc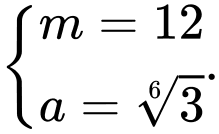 Đáp án: D
Đáp án: D
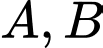 nằm trên đường thẳng
nằm trên đường thẳng 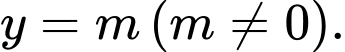
Lại có
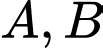 lần lượt nằm trên đồ thị của các hàm số
lần lượt nằm trên đồ thị của các hàm số 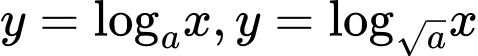 .
.Từ đó suy ra
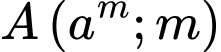 ,
, 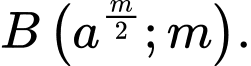
Vì
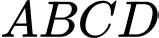 là hình vuông nên suy ra
là hình vuông nên suy ra 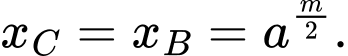
Lại có
 nằm trên đồ thị hàm số
nằm trên đồ thị hàm số 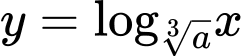 , suy ra
, suy ra 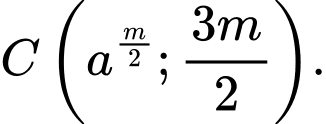
Theo đề bài
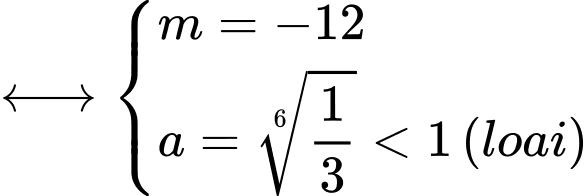
hoặc
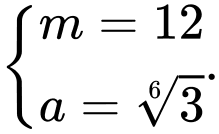 Đáp án: D
Đáp án: D
Câu 14 [582191]: Xét các số thực 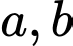 thỏa mãn
thỏa mãn  Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 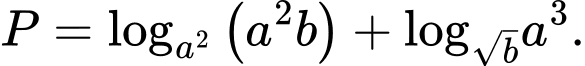
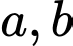 thỏa mãn
thỏa mãn  Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 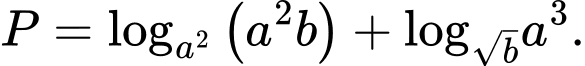
A, 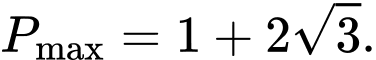
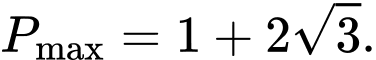
B, 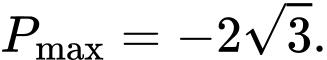
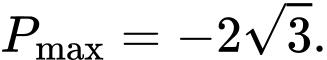
C, 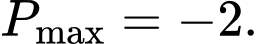
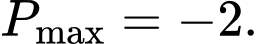
D, 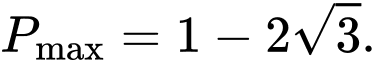
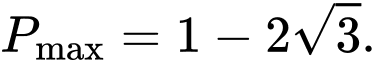
Ta có 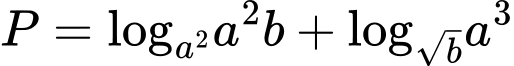
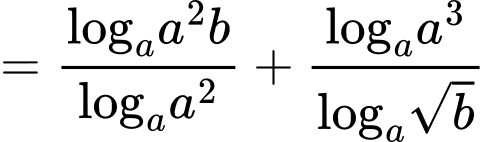
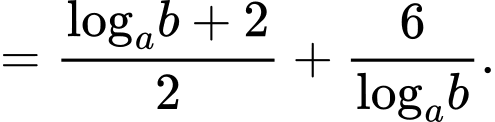
Đặt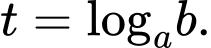 Do
Do
Khi đó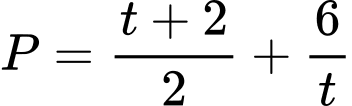
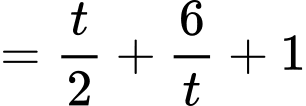
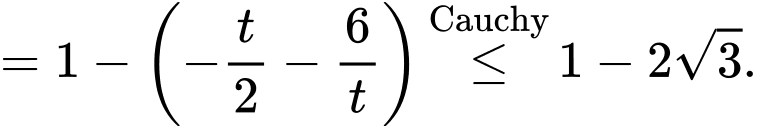
Chọn D.
Cách CASIO. Cho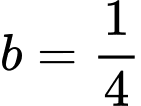 khi đó
khi đó 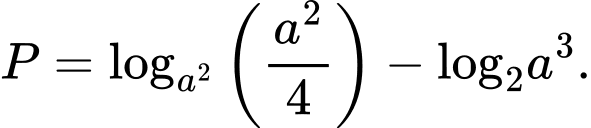
Dùng MODE 7 khảo sát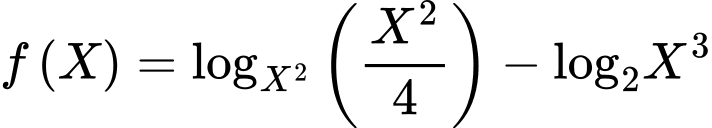 với
với 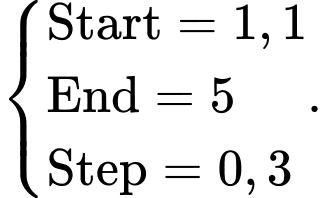
Quan sát bảng giá trị của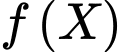 và so sánh với các đáp án ta chọn D. Đáp án: D
và so sánh với các đáp án ta chọn D. Đáp án: D
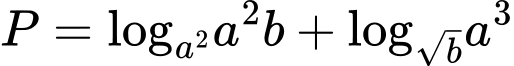
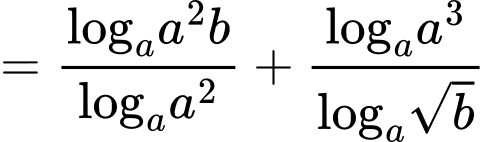
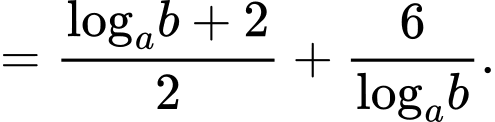
Đặt
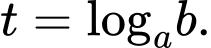 Do
Do Khi đó
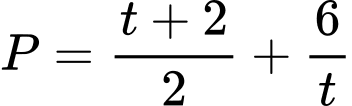
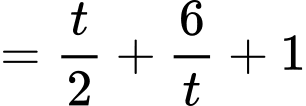
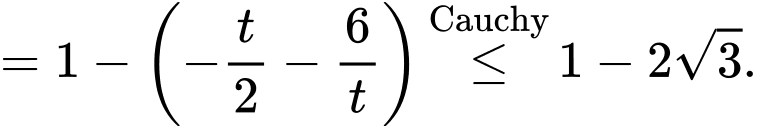
Chọn D.
Cách CASIO. Cho
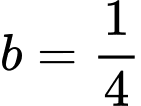 khi đó
khi đó 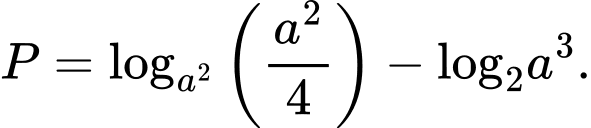
Dùng MODE 7 khảo sát
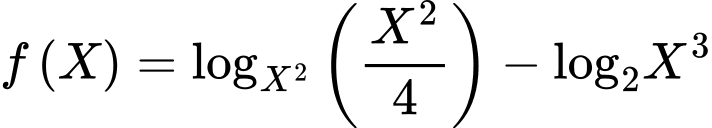 với
với 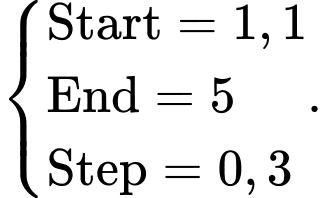
Quan sát bảng giá trị của
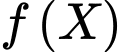 và so sánh với các đáp án ta chọn D. Đáp án: D
và so sánh với các đáp án ta chọn D. Đáp án: D
Câu 15 [582192]: Xét các số thực dương 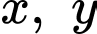 thỏa mãn
thỏa mãn 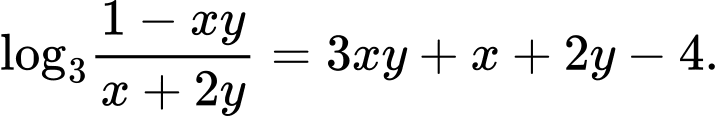 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 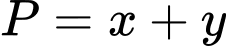 .
.
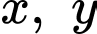 thỏa mãn
thỏa mãn 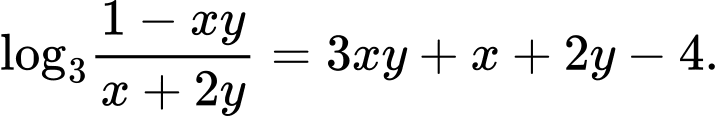 Tìm giá trị nhỏ nhất
Tìm giá trị nhỏ nhất  của biểu thức
của biểu thức 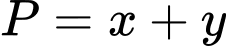 .
. A, 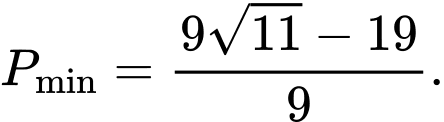
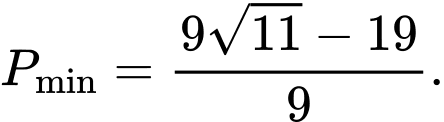
B, 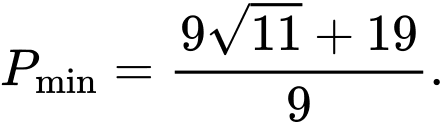
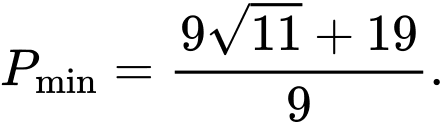
C, 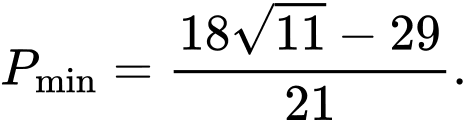
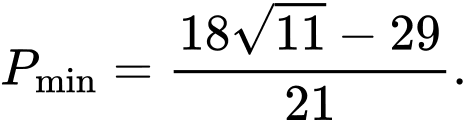
D, 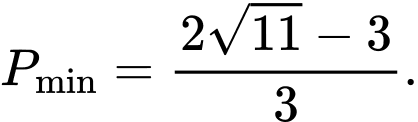
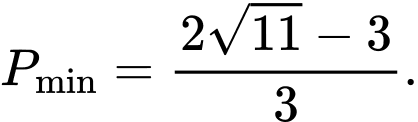
Điều kiện: 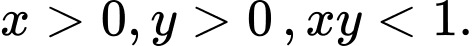
Ta có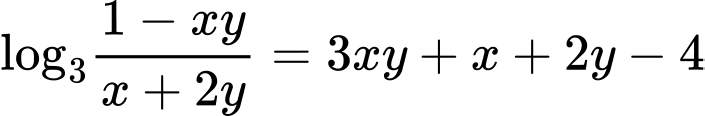
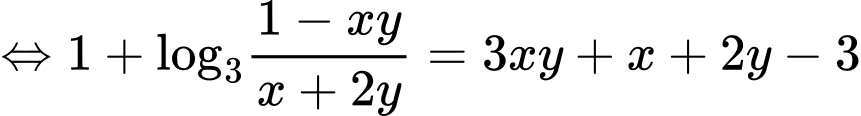
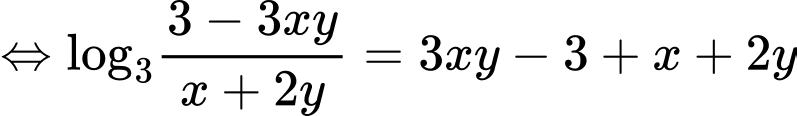
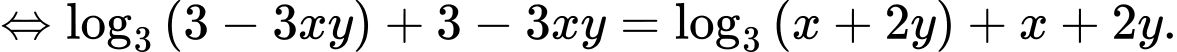

Xét hàm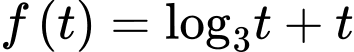 trên
trên 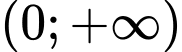 , ta có
, ta có 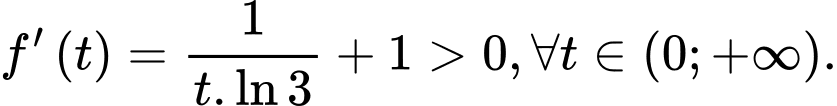
Từ đó suy ra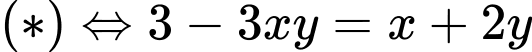
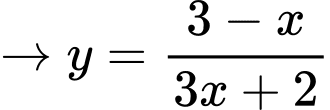
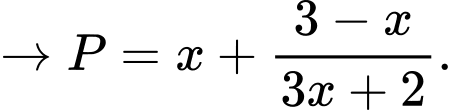
Xét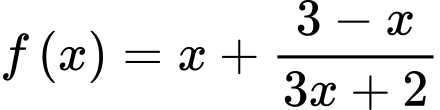 trên
trên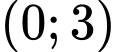 , ta được
, ta được 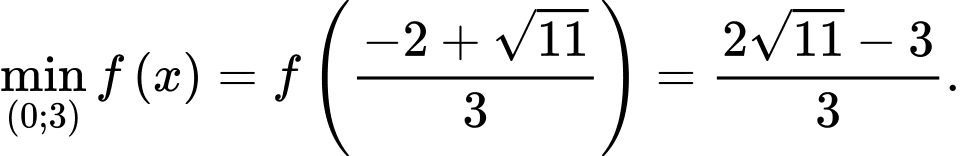
Chọn D.
Nhận xét. Do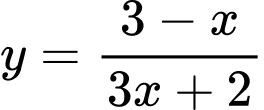 , mà
, mà 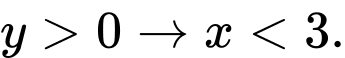 Kết hợp giả thiết ta có
Kết hợp giả thiết ta có  Đáp án: D
Đáp án: D
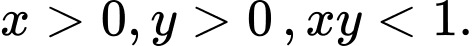
Ta có
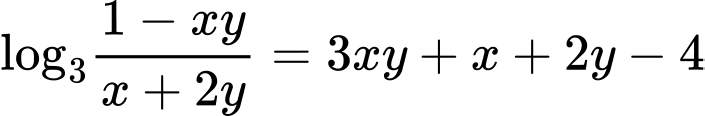
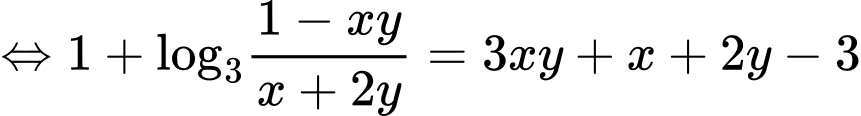
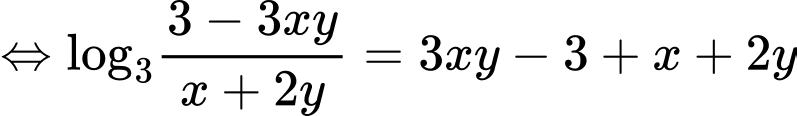
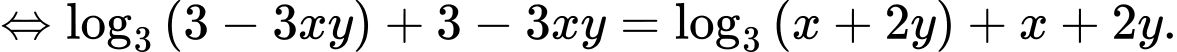

Xét hàm
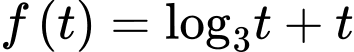 trên
trên 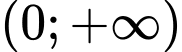 , ta có
, ta có 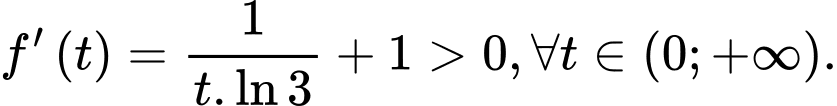
Từ đó suy ra
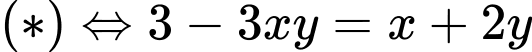
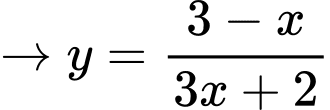
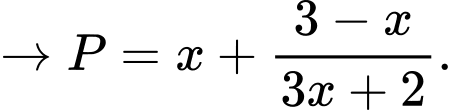
Xét
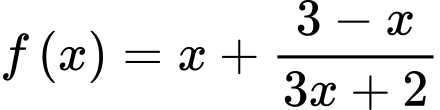 trên
trên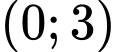 , ta được
, ta được 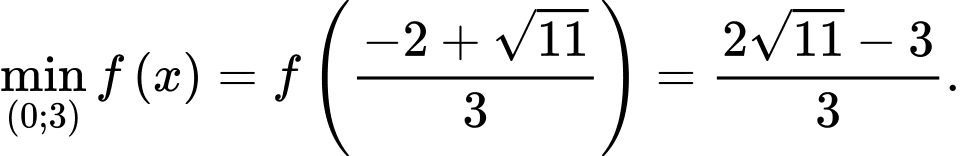
Chọn D.
Nhận xét. Do
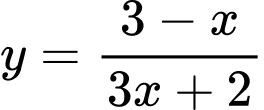 , mà
, mà 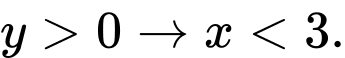 Kết hợp giả thiết ta có
Kết hợp giả thiết ta có  Đáp án: D
Đáp án: D Dạng câu hỏi: Câu trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 16, 17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 16 [582193]: Cho 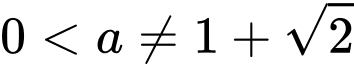 và các hàm
và các hàm 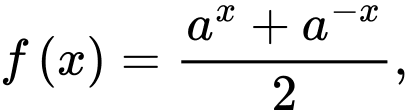
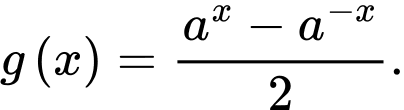 Xét tính đúng – sai của các khẳng định sau:
Xét tính đúng – sai của các khẳng định sau:
a)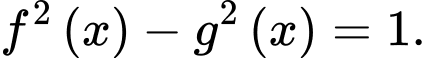
b)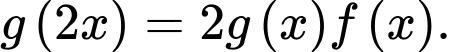
c)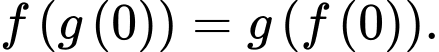
d)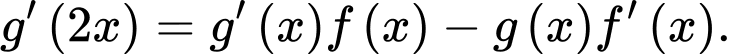
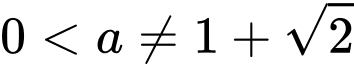 và các hàm
và các hàm 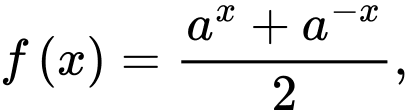
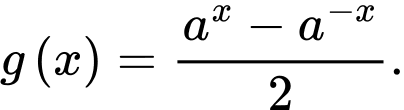 Xét tính đúng – sai của các khẳng định sau:
Xét tính đúng – sai của các khẳng định sau: a)
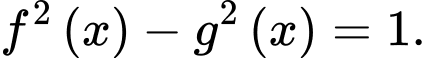
b)
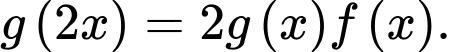
c)
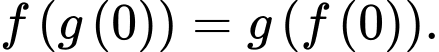
d)
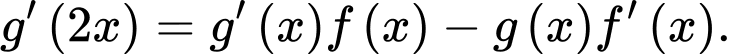
Ta có
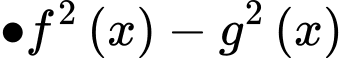
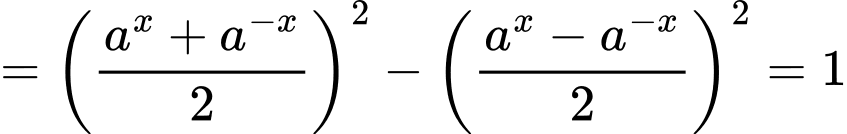
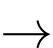 khẳng đinh a) đúng.
khẳng đinh a) đúng.
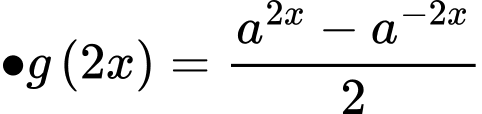
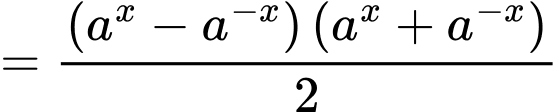
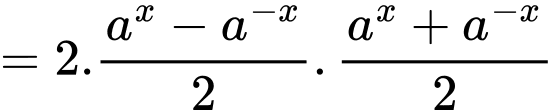
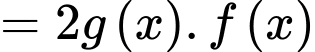
 khẳng đinh b) đúng.
khẳng đinh b) đúng.
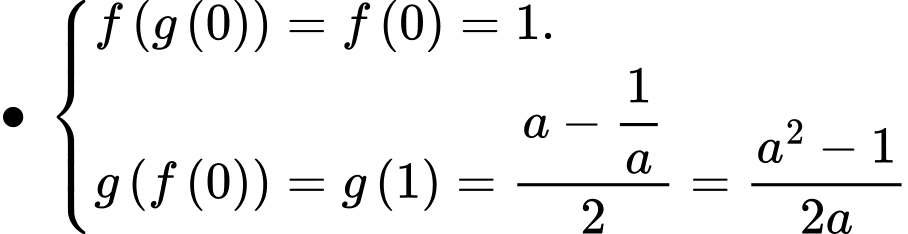
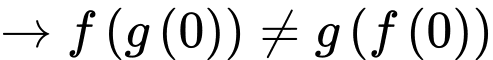
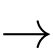 khẳng định c) sai.
khẳng định c) sai.
 Do
Do 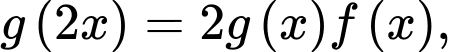 lấy đạo hàm hai vế (để ý là
lấy đạo hàm hai vế (để ý là 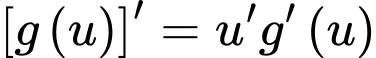 ), ta có:
), ta có: 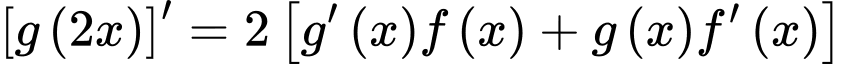
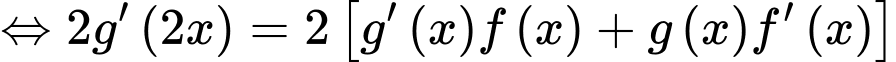
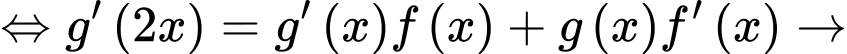 khẳng định d) sai.
khẳng định d) sai.
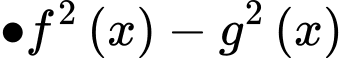
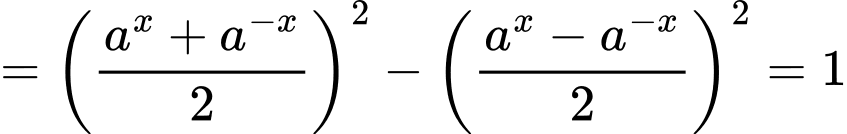
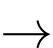 khẳng đinh a) đúng.
khẳng đinh a) đúng. 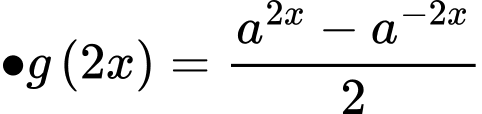
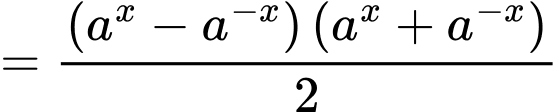
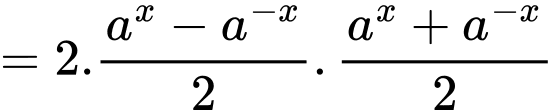
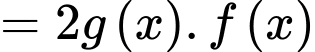
 khẳng đinh b) đúng.
khẳng đinh b) đúng.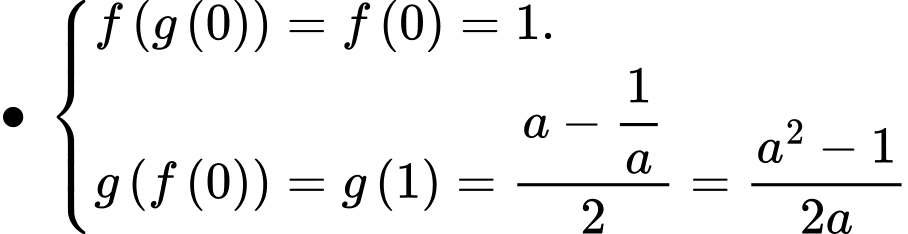
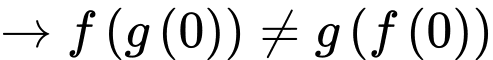
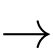 khẳng định c) sai.
khẳng định c) sai. Do
Do 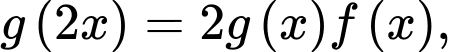 lấy đạo hàm hai vế (để ý là
lấy đạo hàm hai vế (để ý là 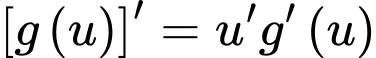 ), ta có:
), ta có: 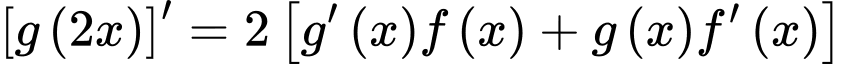
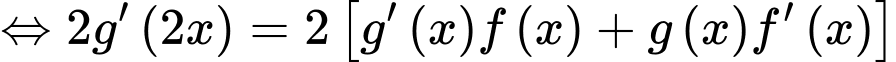
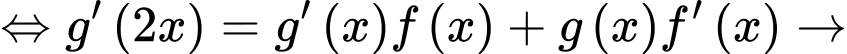 khẳng định d) sai.
khẳng định d) sai.
Câu 17 [582194]: Xét tính đúng – sai của các mệnh đề sau:
a) Hàm số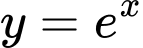 không chẵn cũng không lẻ
không chẵn cũng không lẻ
b) Hàm số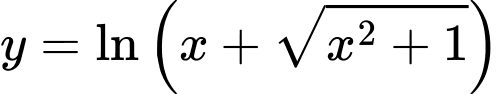 là hàm số lẻ.
là hàm số lẻ.
c) Hàm số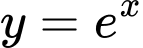 có tập giá trị là
có tập giá trị là 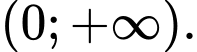
d) Hàm số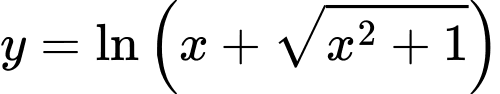 không chẵn cũng không lẻ.
không chẵn cũng không lẻ.
a) Hàm số
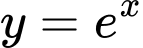 không chẵn cũng không lẻ
không chẵn cũng không lẻ b) Hàm số
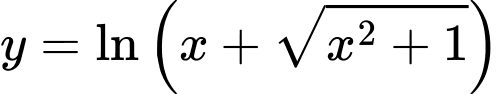 là hàm số lẻ.
là hàm số lẻ. c) Hàm số
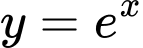 có tập giá trị là
có tập giá trị là 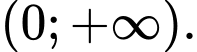
d) Hàm số
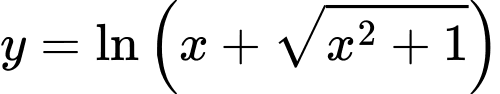 không chẵn cũng không lẻ.
không chẵn cũng không lẻ.
Ta có 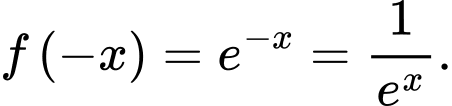 Do đó a) đúng.
Do đó a) đúng.
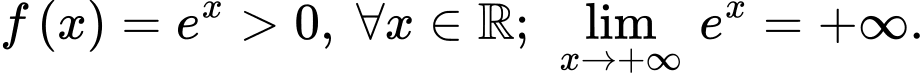 Do đó c) đúng.
Do đó c) đúng.
Xét hàm số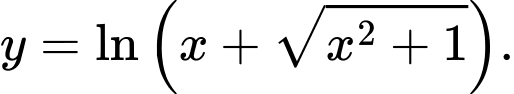
Ta có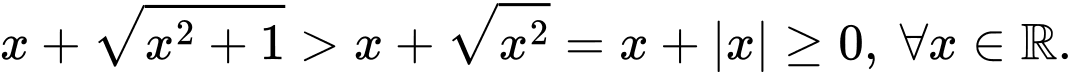
Do đó hàm số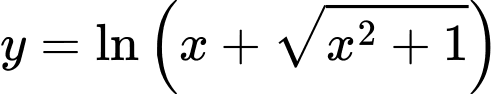 có TXĐ:
có TXĐ: 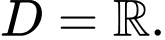 Rõ ràng
Rõ ràng 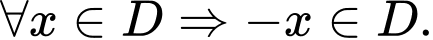
Ta có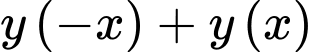
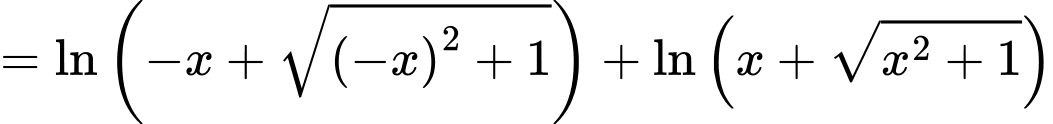
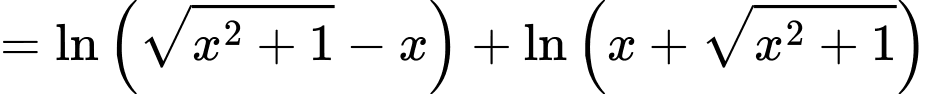

hay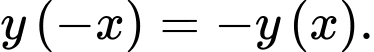
Suy ra hàm số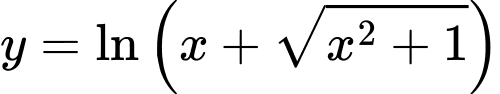 là hàm số lẻ. Do đó d) sai.
là hàm số lẻ. Do đó d) sai.
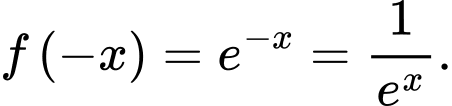 Do đó a) đúng.
Do đó a) đúng.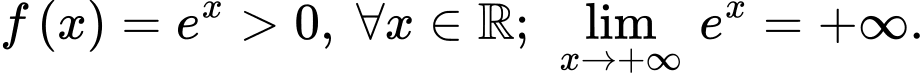 Do đó c) đúng.
Do đó c) đúng.Xét hàm số
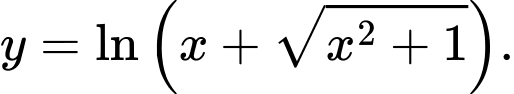
Ta có
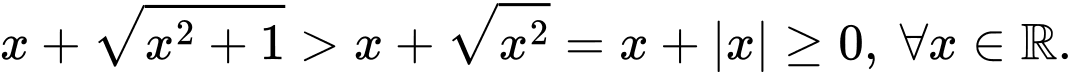
Do đó hàm số
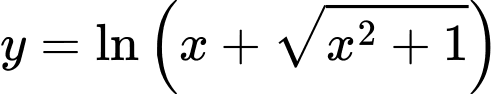 có TXĐ:
có TXĐ: 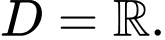 Rõ ràng
Rõ ràng 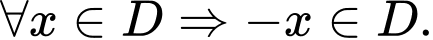
Ta có
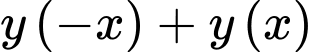
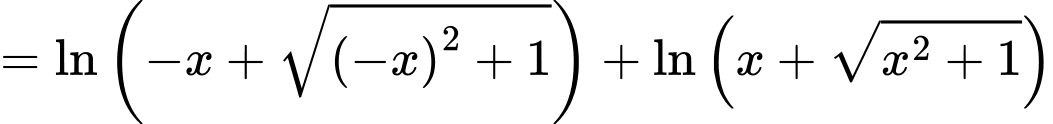
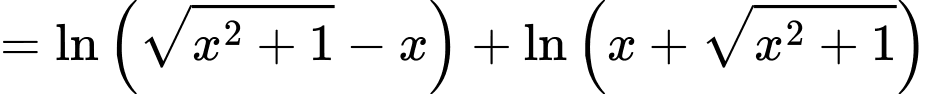

hay
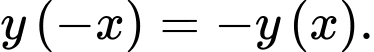
Suy ra hàm số
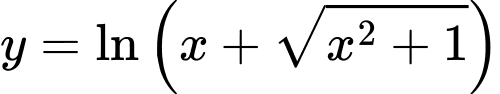 là hàm số lẻ. Do đó d) sai.
là hàm số lẻ. Do đó d) sai. Dạng câu hỏi: Trả lời ngắn
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582195]: Xét hàm số 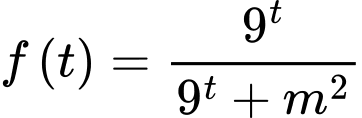 với
với 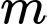 là tham số thực. Gọi
là tham số thực. Gọi 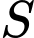 là tập hợp tất cả các giá trị của
là tập hợp tất cả các giá trị của 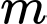 sao cho
sao cho 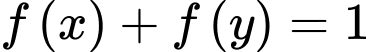 với mọi
với mọi 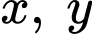 thỏa mãn
thỏa mãn 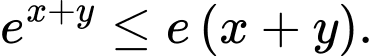 Tìm số phần tử của
Tìm số phần tử của 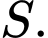
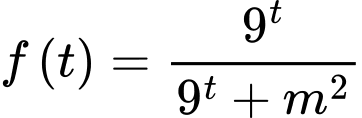 với
với 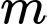 là tham số thực. Gọi
là tham số thực. Gọi 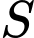 là tập hợp tất cả các giá trị của
là tập hợp tất cả các giá trị của 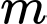 sao cho
sao cho 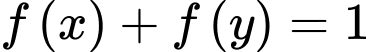 với mọi
với mọi 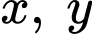 thỏa mãn
thỏa mãn 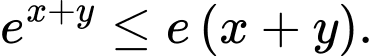 Tìm số phần tử của
Tìm số phần tử của 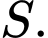
Xét hàm số 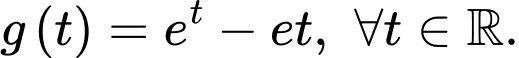 Ta có
Ta có 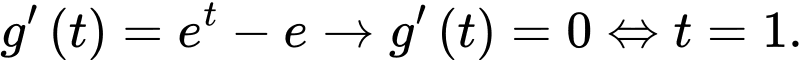
Lập bảng biến thiên ta thấy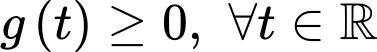 và đẳng thức xảy ra
và đẳng thức xảy ra 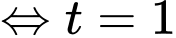 .
.
Ta có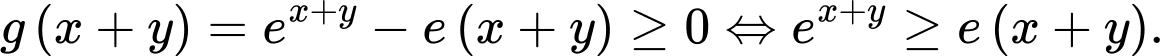
Kết hợp với giải thiết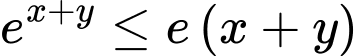 , suy ra
, suy ra 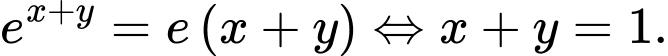
Chọn một bộ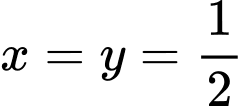 theo giả thiết, có
theo giả thiết, có 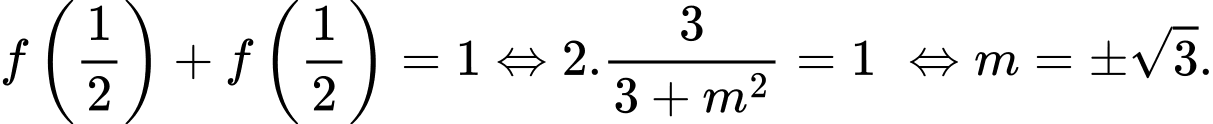
Vậy có hai giá trị m thỏa mãn yêu cầu.
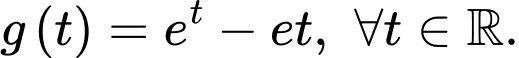 Ta có
Ta có 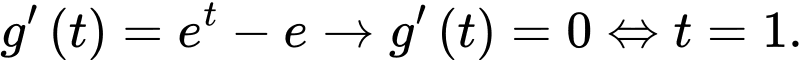
Lập bảng biến thiên ta thấy
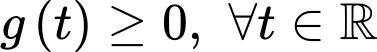 và đẳng thức xảy ra
và đẳng thức xảy ra 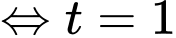 .
.Ta có
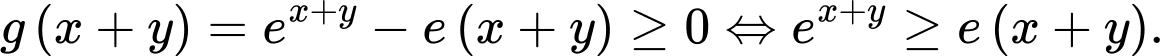
Kết hợp với giải thiết
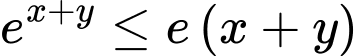 , suy ra
, suy ra 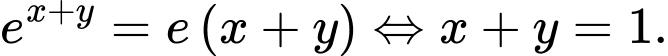
Chọn một bộ
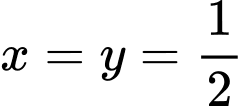 theo giả thiết, có
theo giả thiết, có 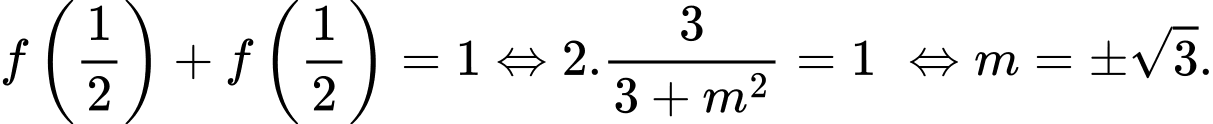
Vậy có hai giá trị m thỏa mãn yêu cầu.
Câu 19 [582196]: Xét các số nguyên dương 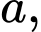
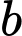 sao cho phương trình
sao cho phương trình 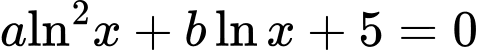 có hai nghiệm phân biệt
có hai nghiệm phân biệt 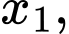
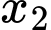 và phương trình
và phương trình 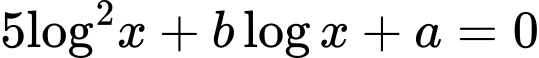 có hai nghiệm phân biệt
có hai nghiệm phân biệt 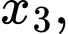
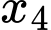 thỏa mãn
thỏa mãn  . Tính giá trị nhỏ nhất
. Tính giá trị nhỏ nhất  của
của 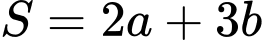
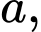
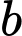 sao cho phương trình
sao cho phương trình 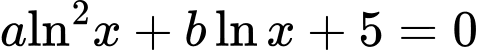 có hai nghiệm phân biệt
có hai nghiệm phân biệt 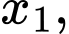
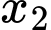 và phương trình
và phương trình 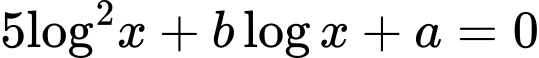 có hai nghiệm phân biệt
có hai nghiệm phân biệt 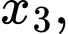
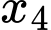 thỏa mãn
thỏa mãn  . Tính giá trị nhỏ nhất
. Tính giá trị nhỏ nhất  của
của 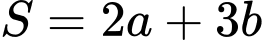
Điều kiện 
Phương trình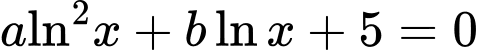 có hai nghiệm phân biệt
có hai nghiệm phân biệt 
Phương trình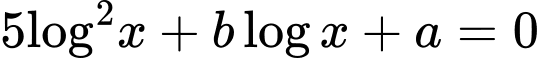 có hai nghiệm phân biệt
có hai nghiệm phân biệt 
Ta có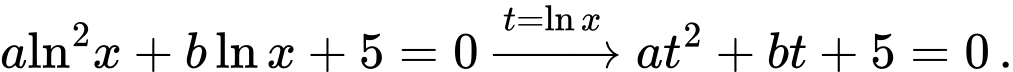

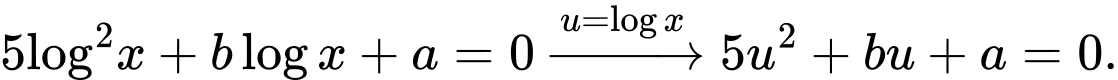

Với mỗi một nghiệm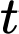 thì có một nghiệm
thì có một nghiệm 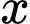 , một nghiệm
, một nghiệm 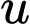 thì có một nghiệm
thì có một nghiệm 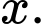
Ta có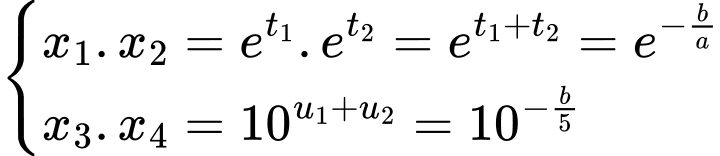 , kết hợp giả thiết
, kết hợp giả thiết 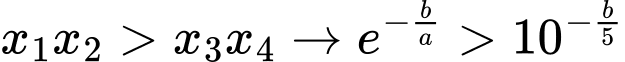
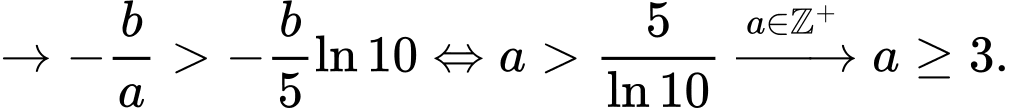
Suy ra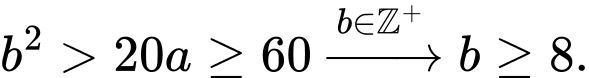
Vậy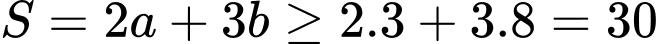 , suy ra
, suy ra 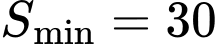 đạt được khi
đạt được khi 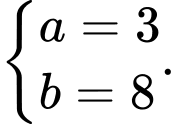

Phương trình
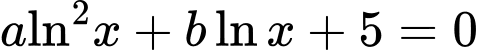 có hai nghiệm phân biệt
có hai nghiệm phân biệt 
Phương trình
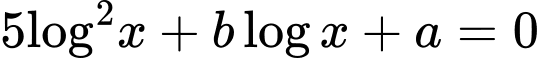 có hai nghiệm phân biệt
có hai nghiệm phân biệt 
Ta có
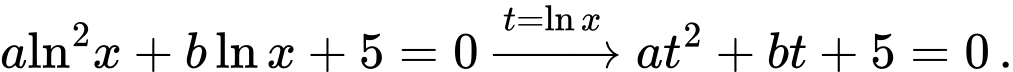

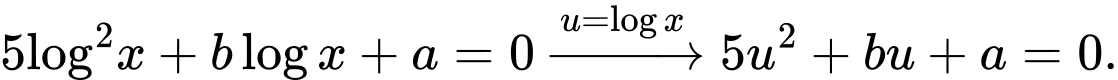

Với mỗi một nghiệm
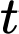 thì có một nghiệm
thì có một nghiệm 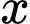 , một nghiệm
, một nghiệm 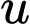 thì có một nghiệm
thì có một nghiệm 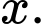
Ta có
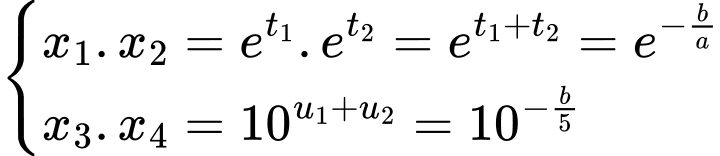 , kết hợp giả thiết
, kết hợp giả thiết 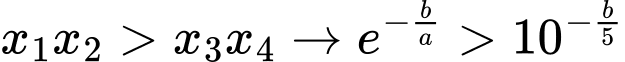
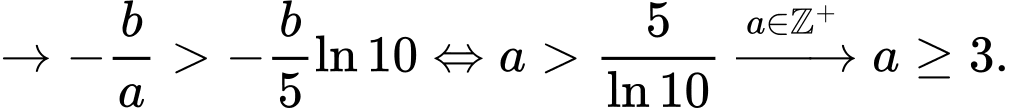
Suy ra
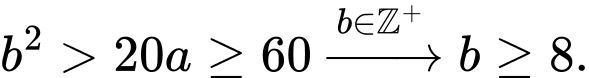
Vậy
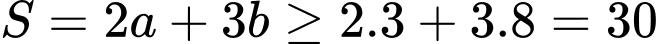 , suy ra
, suy ra 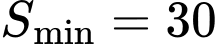 đạt được khi
đạt được khi 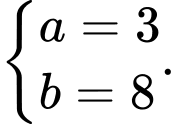
Câu 20 [582197]: Biết hai hàm số 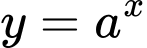 và
và 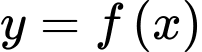 có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng
có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng 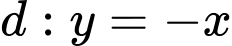 . Tính
. Tính 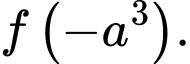
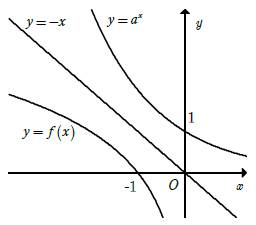
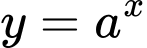 và
và 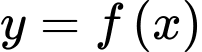 có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng
có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng 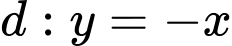 . Tính
. Tính 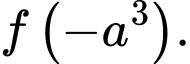

Giả sử 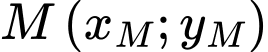 là điểm thuộc hàm số
là điểm thuộc hàm số 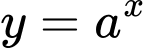 ;
; 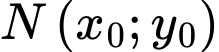 là điểm đối xứng của
là điểm đối xứng của 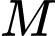 qua đường thẳng
qua đường thẳng 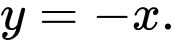
Gọi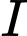 là trung điểm của .
là trung điểm của .
Vì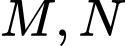 đối xứng nhau qua
đối xứng nhau qua
Ta có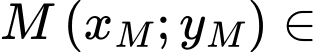 đồ thị
đồ thị 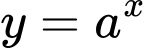 nên
nên 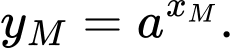
Do đó . Điều này chứng tỏ điểm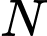 thuộc đồ thị hàm số
thuộc đồ thị hàm số 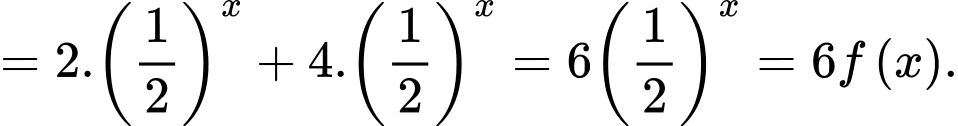
Khi đó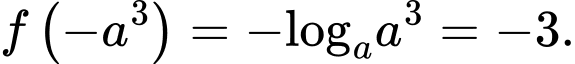
Cách 2. Lấy đối xứng đồ thị hàm số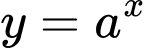 qua
qua 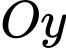 là được đồ thị hàm số
là được đồ thị hàm số 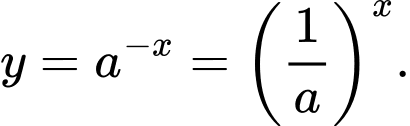
Lấy đối xứng đồ thị hàm số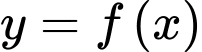 qua
qua 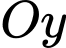 là được đồ thị hàm số
là được đồ thị hàm số 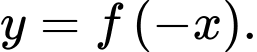
Theo giả thiết, ta có đồ thị hai hàm số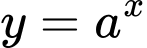 và
và 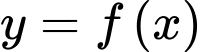 đối xứng nhau qua đường thẳng
đối xứng nhau qua đường thẳng 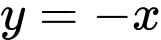 nên suy ra đồ thị của hai hàm số
nên suy ra đồ thị của hai hàm số 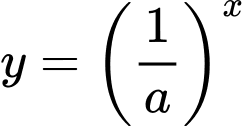 và
và 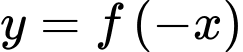 đối xứng nhau qua đường thẳng
đối xứng nhau qua đường thẳng 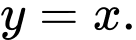

Theo lý thuyết (SGK) thì đồ thị của hai hàm số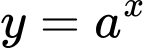 và
và  đối xứng nhau qua đường thẳng
đối xứng nhau qua đường thẳng 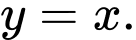

Từ và
và  , suy ra
, suy ra 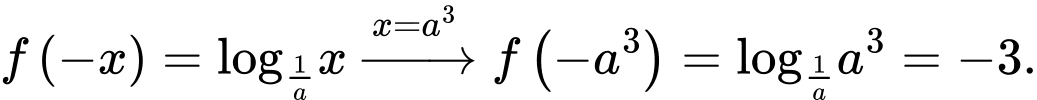
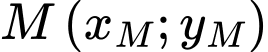 là điểm thuộc hàm số
là điểm thuộc hàm số 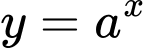 ;
; 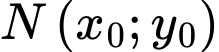 là điểm đối xứng của
là điểm đối xứng của 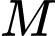 qua đường thẳng
qua đường thẳng 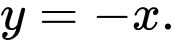
Gọi
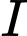 là trung điểm của .
là trung điểm của .Vì
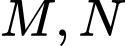 đối xứng nhau qua
đối xứng nhau qua Ta có
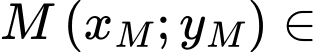 đồ thị
đồ thị 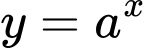 nên
nên 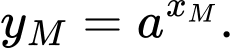
Do đó . Điều này chứng tỏ điểm
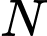 thuộc đồ thị hàm số
thuộc đồ thị hàm số 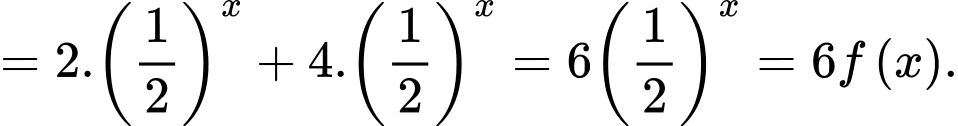
Khi đó
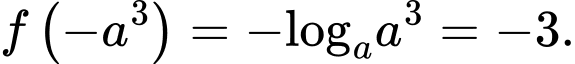
Cách 2. Lấy đối xứng đồ thị hàm số
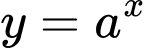 qua
qua 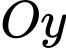 là được đồ thị hàm số
là được đồ thị hàm số 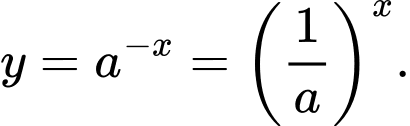
Lấy đối xứng đồ thị hàm số
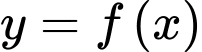 qua
qua 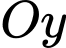 là được đồ thị hàm số
là được đồ thị hàm số 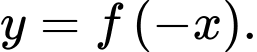
Theo giả thiết, ta có đồ thị hai hàm số
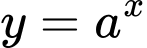 và
và 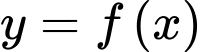 đối xứng nhau qua đường thẳng
đối xứng nhau qua đường thẳng 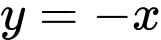 nên suy ra đồ thị của hai hàm số
nên suy ra đồ thị của hai hàm số 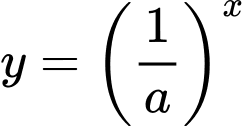 và
và 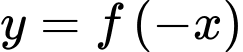 đối xứng nhau qua đường thẳng
đối xứng nhau qua đường thẳng 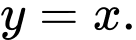

Theo lý thuyết (SGK) thì đồ thị của hai hàm số
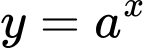 và
và  đối xứng nhau qua đường thẳng
đối xứng nhau qua đường thẳng 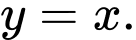

Từ
 và
và  , suy ra
, suy ra 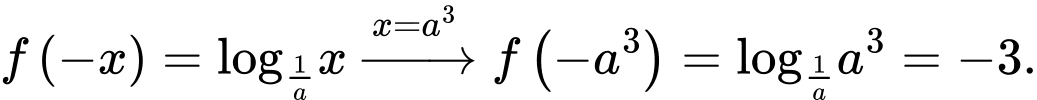
Dạng câu hỏi: Câu hỏi kéo thả
Câu 21 [582198]: Cho hàm số 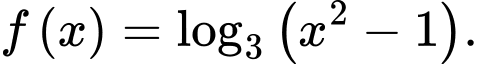
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Tại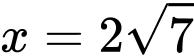 thì
thì 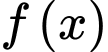 bằng _______.
bằng _______.
Số giá trị nguyên thuộc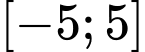 để hàm số có nghĩa là _______.
để hàm số có nghĩa là _______.
Phương trình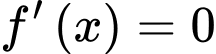 có nghiệm bằng _______.
có nghiệm bằng _______.
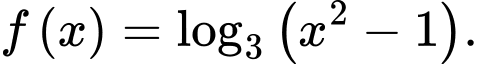
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Tại
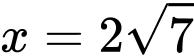 thì
thì 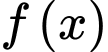 bằng _______.
bằng _______.Số giá trị nguyên thuộc
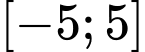 để hàm số có nghĩa là _______.
để hàm số có nghĩa là _______.Phương trình
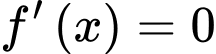 có nghiệm bằng _______.
có nghiệm bằng _______.
Tại 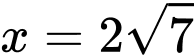 thì
thì 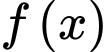 bằng 3 .
bằng 3 .
Số giá trị nguyên thuộc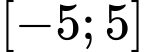 để hàm số có nghĩa là 8 .
để hàm số có nghĩa là 8 .
Phương trình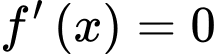 có nghiệm bằng 0 .
có nghiệm bằng 0 .
LỜI GIẢI
Vị trí thả 1: 3
Vị trí thả 2: 8
Vị trí thả 3: 0
Ta có:
Nhập ta được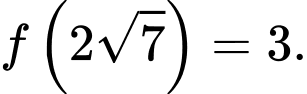
Điều kiện xác định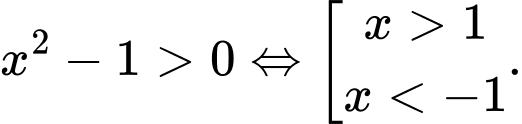 Vì
Vì 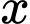 nguyên thuộc
nguyên thuộc 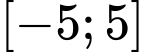 nên
nên
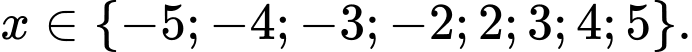
Vậy có 8 giá trị nguyên thỏa mãn.
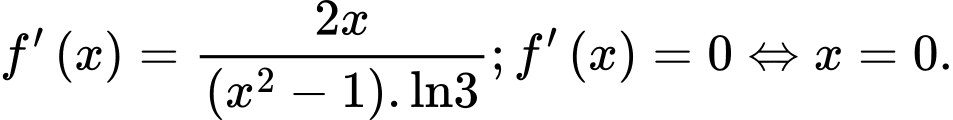
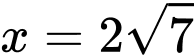 thì
thì 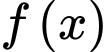 bằng 3 .
bằng 3 .Số giá trị nguyên thuộc
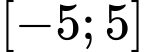 để hàm số có nghĩa là 8 .
để hàm số có nghĩa là 8 .Phương trình
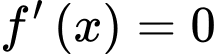 có nghiệm bằng 0 .
có nghiệm bằng 0 .LỜI GIẢI
Vị trí thả 1: 3
Vị trí thả 2: 8
Vị trí thả 3: 0
Ta có:
Nhập ta được
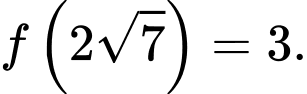
Điều kiện xác định
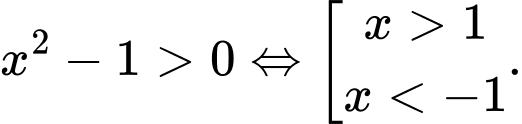 Vì
Vì 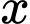 nguyên thuộc
nguyên thuộc 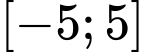 nên
nên 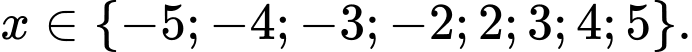
Vậy có 8 giá trị nguyên thỏa mãn.