I. Giải PT bằng phương pháp đưa về cùng cơ số hoặc lôgarit hóa – mũ hóa
Dạng 1: Giải phương trình mũ logarit bằng phương pháp đưa về cùng cơ số. Dùng các phép biến đổi về lũy thừa và logarit bằng phương pháp đưa về một trong các dạng sau:
Câu 1 [582199]: Phương trình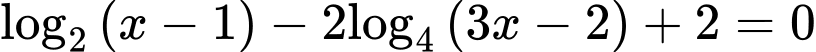 
có nghiệm nằm trong khoảng
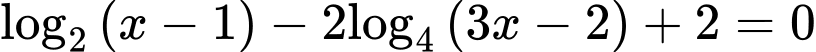có nghiệm nằm trong khoảng A,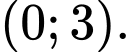 
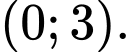
B,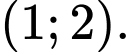 
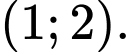
C,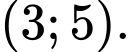 
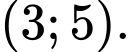
D,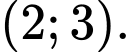 
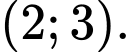
Điều kiện: 
Khi đó 
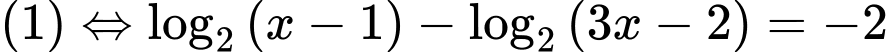
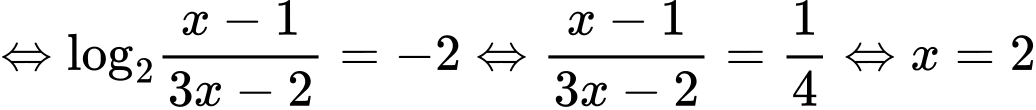
Vậy phương trình có nghiệm duy nhất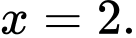
Đáp án: A
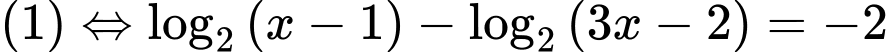
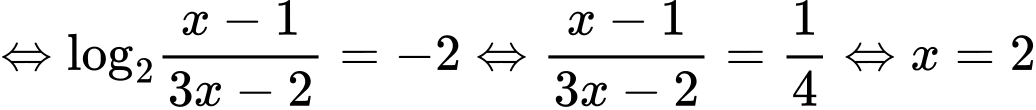
Khi đó Vậy phương trình có nghiệm duy nhất
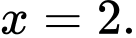Đáp án: A
Câu 2 [582200]: Tích hai nghiệm của phương trình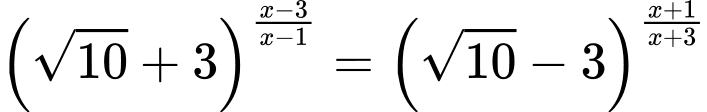 
nằm trong khoảng
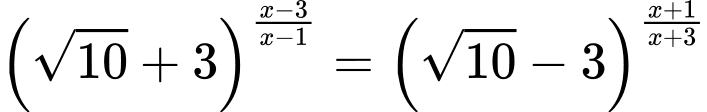nằm trong khoảng A,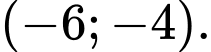 
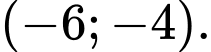
B,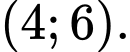 
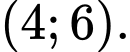
C,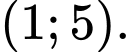 
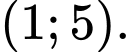
D,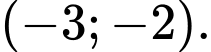 
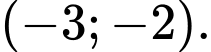
Điều kiện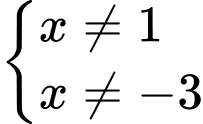 
Ta có phương trình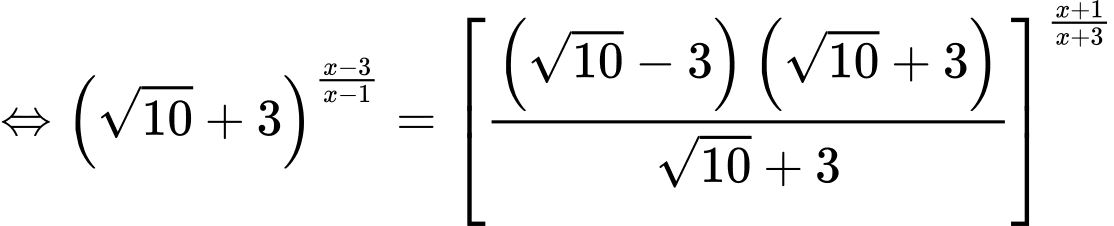
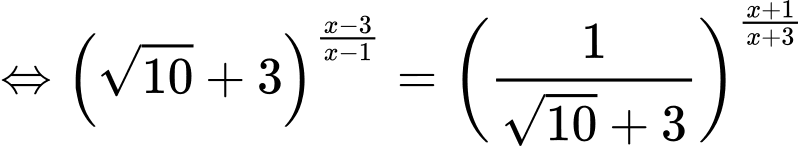
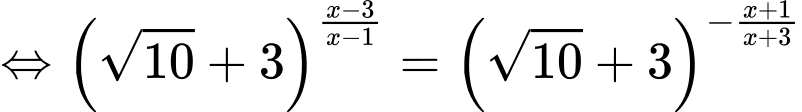
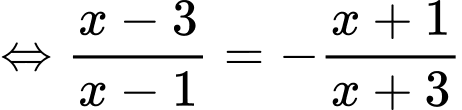
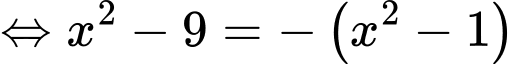
Vậy tích hai nghiệm của phương trình là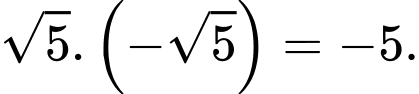
Đáp án: A
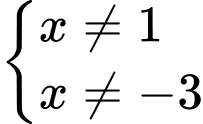
Ta có phương trình
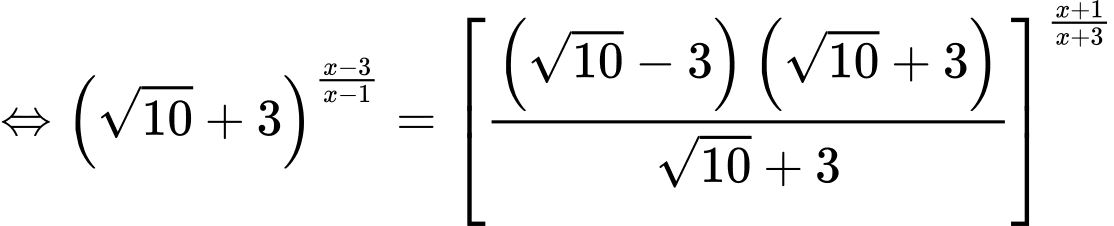
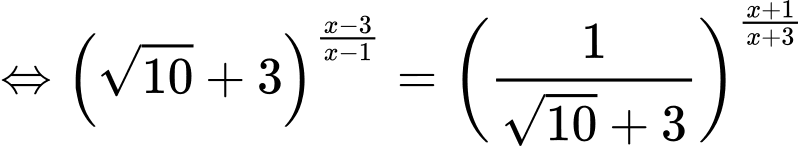
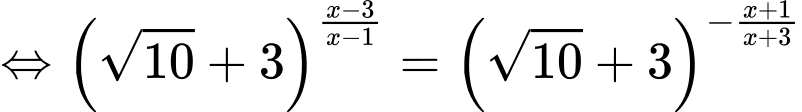
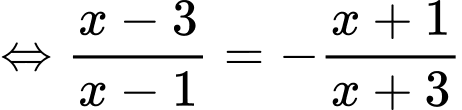
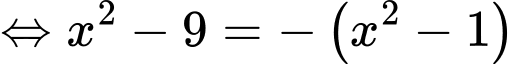
Vậy tích hai nghiệm của phương trình là
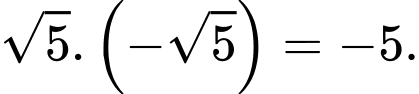Đáp án: A
Câu 3 [582201]: Tập nghiệm của bất phương trình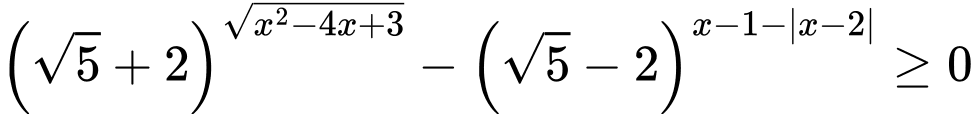 
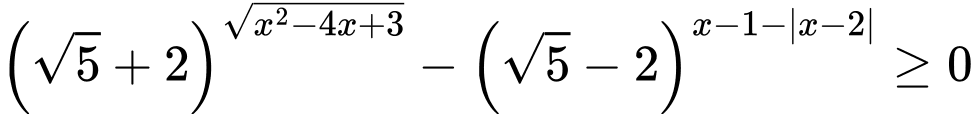là
là A,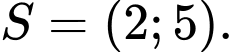 
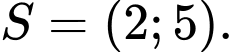
B,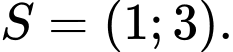 
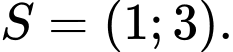
C, 
D,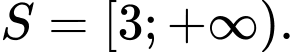 
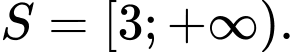
Điều kiện: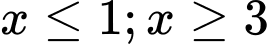 
.
Bất phương trình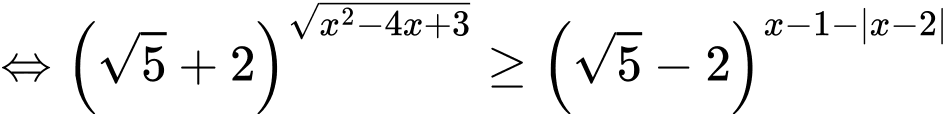
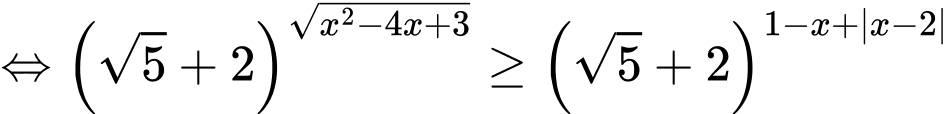
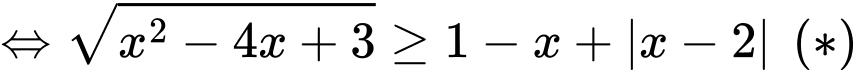
Với
thì 
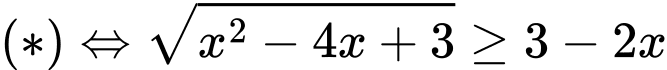: vô nghiệm.
Với
thì 
luôn đúng với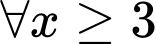 
.
Vậy bất phương trình có tập nghiệm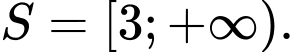
Đáp án: D
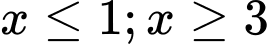.Bất phương trình
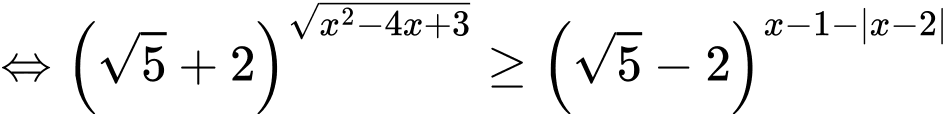
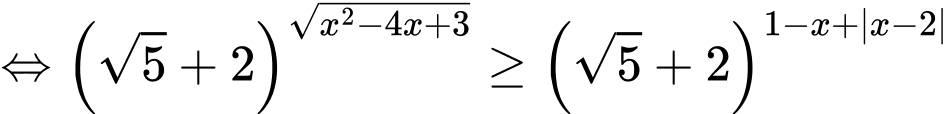
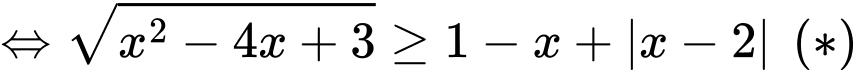
Với
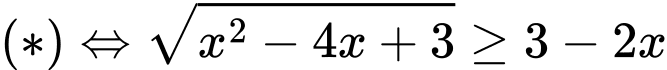thì : vô nghiệm. Với
thì luôn đúng với 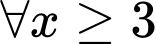.Vậy bất phương trình có tập nghiệm
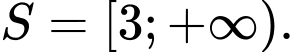Đáp án: D II. Phương pháp đặt ẩn phụ (dạng 1)
Loại 1: Phương trình dạng P(af(x))=0
Đặt t=af(x), (t>0). Phương trình trở thành P(t)=0
Đặt t=af(x), (t>0). Phương trình trở thành P(t)=0
Câu 4 [582202]: Phương trình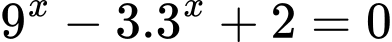 
có hai nghiệm là 
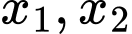với 
Giá trị của 
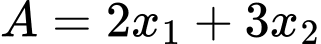là
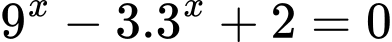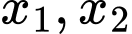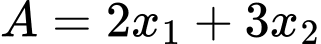có hai nghiệm là với Giá trị của là A, 0.
B,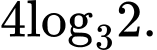 
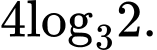
C,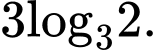 
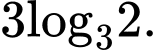
D, 2.
Nhận thấy ở đây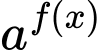 
chính là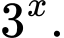 
Vậy nếu đặt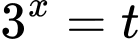
thì phương trình trở thành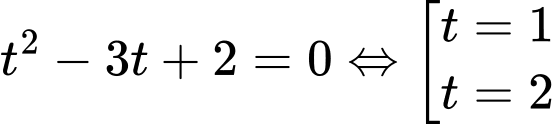 
Lúc này ta được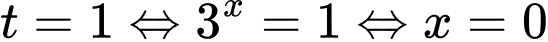
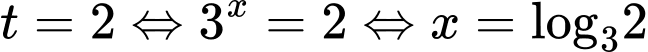
Vậy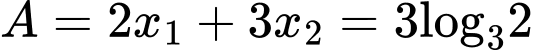
Đáp án: C
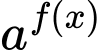chính là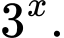 Vậy nếu đặt
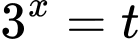thì phương trình trở thành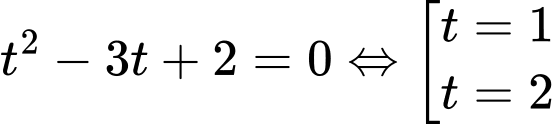 Lúc này ta được
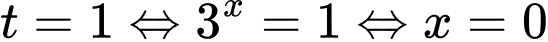
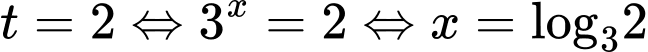
Vậy
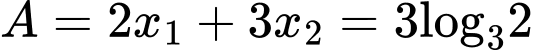Đáp án: C
Câu 5 [582203]: Tính tổng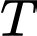 
tất cả các nghiệm của phương trình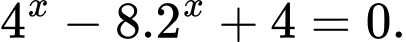 
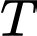tất cả các nghiệm của phương trình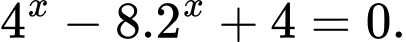 A,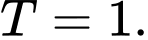 
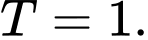
B,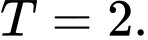 
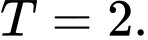
C,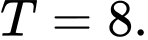 
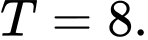
D,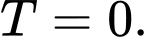 
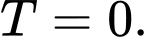
Cách 1: Ở đây nhiều độc giả sẽ bấm máy tính giải phương trình sau đó cộng hai nghiệm vào như sau:
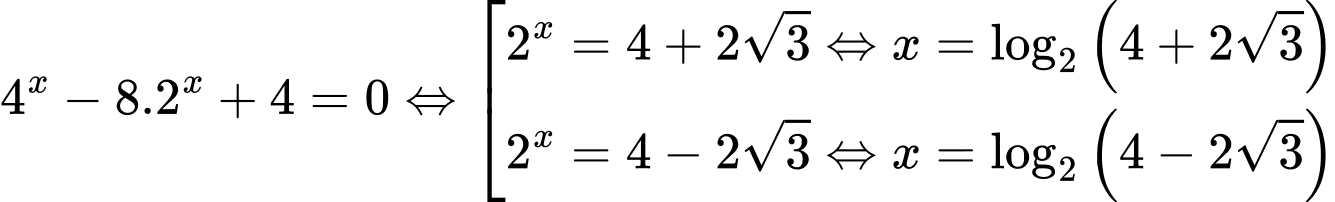
Sau đó ta có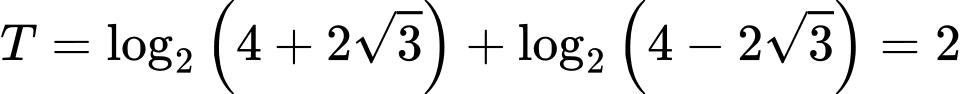
.
Nhận xét: Đây là cách giải khá dài, mà lại không nắm bắt được cách suy luận nhanh, thụ động vào máy tính với nghiệm lẻ.
Cách 2:
Ta thấy phương trình hỏi tổng các nghiệm của phương trình tức là
.
Mặt khác ta lại có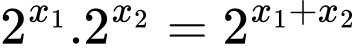
.
Mặt khác nếu coi phương trình đã cho là phương trình bậc hai đối với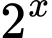
thì ta suy ra ngay 
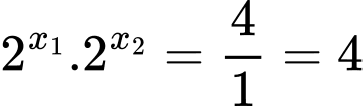(định lý Viet cho hai nghiệm của phương trình bậc hai).
Từ đây ta có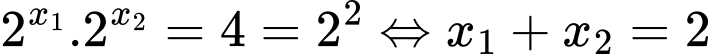
Đáp án: B
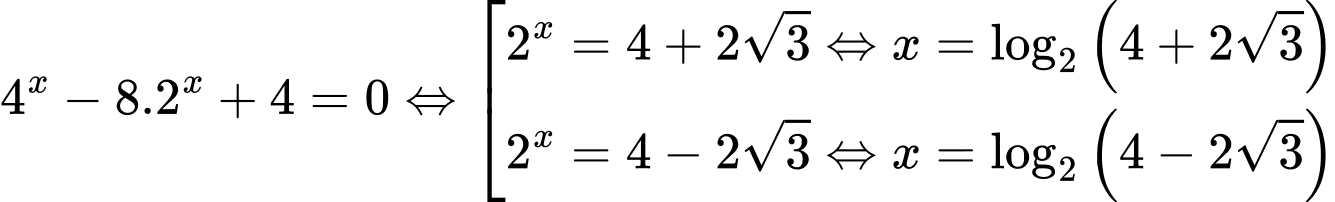
Sau đó ta có
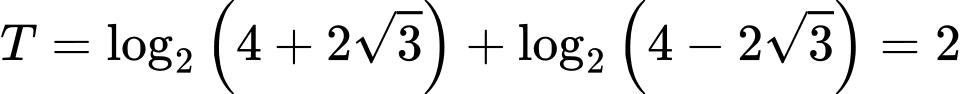.Nhận xét: Đây là cách giải khá dài, mà lại không nắm bắt được cách suy luận nhanh, thụ động vào máy tính với nghiệm lẻ.
Cách 2:
Ta thấy phương trình hỏi tổng các nghiệm của phương trình tức là
.Mặt khác ta lại có
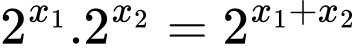.Mặt khác nếu coi phương trình đã cho là phương trình bậc hai đối với
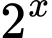thì ta suy ra ngay 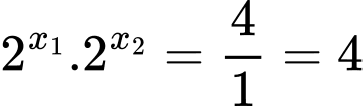(định lý Viet cho hai nghiệm của phương trình bậc hai).Từ đây ta có
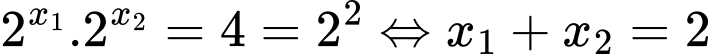Đáp án: B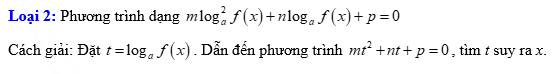 
Câu 6 [582204]: Cho phương trình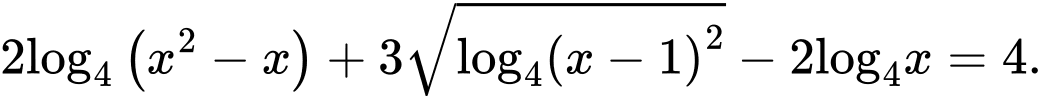 
Phương trình trên có một nghiệm 
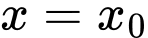nằm trong khoảng
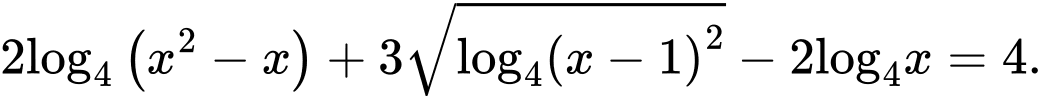Phương trình trên có một nghiệm 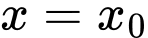nằm trong khoảng A,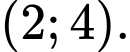 
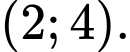
B,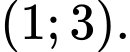 
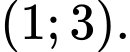
C,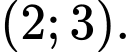 
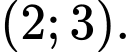
D,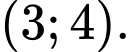 
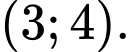
Cách 1:Điều kiện: 
Ta có phương trình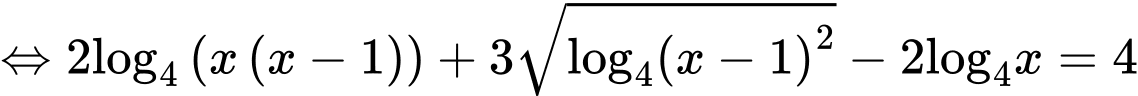
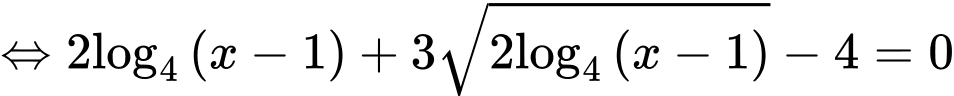
(ở đây ta biến đổi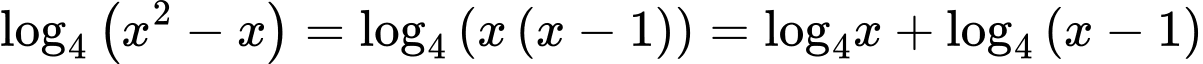
)
Vậy phương trình đã cho trở về dạng tổng quát, coi phương trình trên là phương trình bậc hai với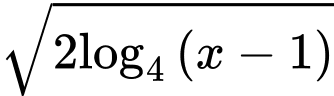
, lúc này bấm máy giải phương trình bậc hai ta được: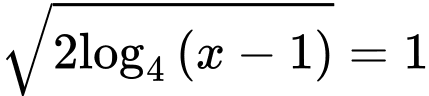 
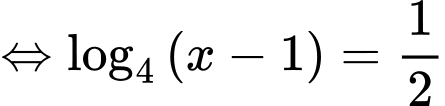
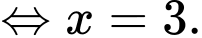Vậy ta chọn A.
Cách 2: Với các bài toán tìm xem nghiệm của phương trình này có nằm trong khoảng đã cho hay không, ta có thể nhanh chóng áp dụng định lý:
“Nếu hàm số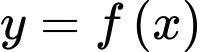
liên tục trên đoạn 
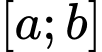và 
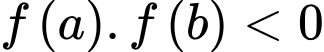thì tồn tại ít nhất một điểm 
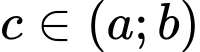sao cho 
.”
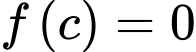Vậy như ở chủ đề 1, tôi đã giới thiệu về chức năng TABLE của máy tính cầm tay là lập ra các giá trị của hàm số trong một bảng. Ở đây ta sử dụng TABLE để xét xem hàm số có dổi dấu trong khoảng cho trước không.
Do đề bài cho khoảng hẹp, nên ở đây ta chỉ cần xét khoảng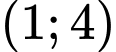
là có thể bao hàm được hết các phương án A, B, C, D.
Dùng máy tính nhập Lúc này nhập
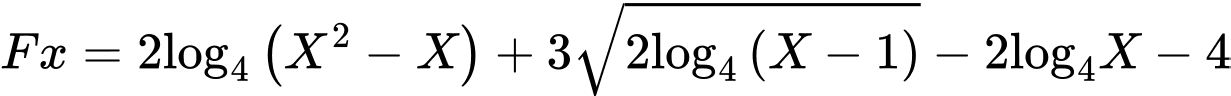
Lưu ý: Ở đây ta nhập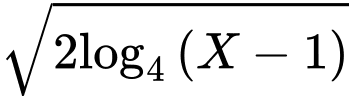
vào máy mà không nhập 
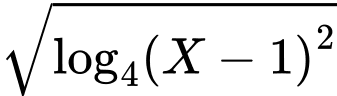bởi ở đây dấu mũ hai máy sẽ nhận là 
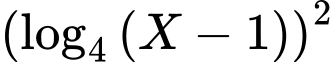chứ không phải nghĩa như ban đầu.
Chú ý: Nếu nhập vào máy tính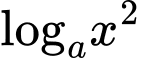
máy sẽ nhận dạng thành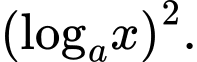 
Ấn 2 lần = bỏ qua Gx.
Lúc máy hiện START? ấn 1 =
END? 4 =
STEP? 0.5 =
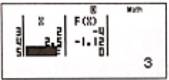
Máy hiện như hình bên. Lúc này ta thấy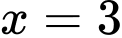
là nghiệm của phương trình.
Tuy nhiên với các bài toán khác ta có thể thấy hàm số đổi dấu khi đi qua 3 thì ta cũng có thể kết luận được phương án A. Đáp án: A
Ta có phương trình
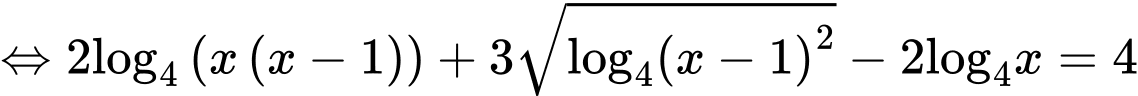
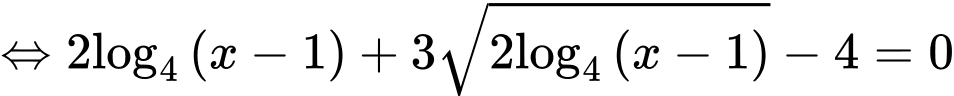
(ở đây ta biến đổi
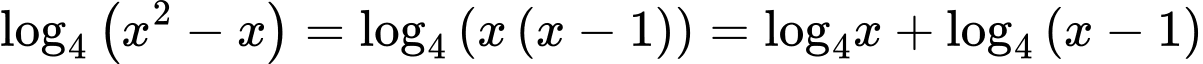)Vậy phương trình đã cho trở về dạng tổng quát, coi phương trình trên là phương trình bậc hai với
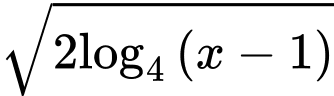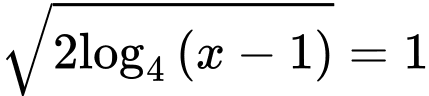
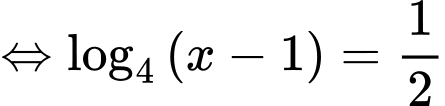
, lúc này bấm máy giải phương trình bậc hai ta được: 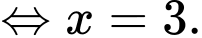Vậy ta chọn A.Cách 2: Với các bài toán tìm xem nghiệm của phương trình này có nằm trong khoảng đã cho hay không, ta có thể nhanh chóng áp dụng định lý:
“Nếu hàm số
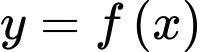liên tục trên đoạn 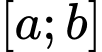và 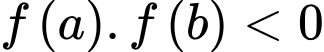thì tồn tại ít nhất một điểm 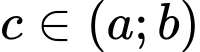sao cho 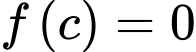.”Vậy như ở chủ đề 1, tôi đã giới thiệu về chức năng TABLE của máy tính cầm tay là lập ra các giá trị của hàm số trong một bảng. Ở đây ta sử dụng TABLE để xét xem hàm số có dổi dấu trong khoảng cho trước không.
Do đề bài cho khoảng hẹp, nên ở đây ta chỉ cần xét khoảng
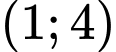là có thể bao hàm được hết các phương án A, B, C, D.Dùng máy tính nhập Lúc này nhập
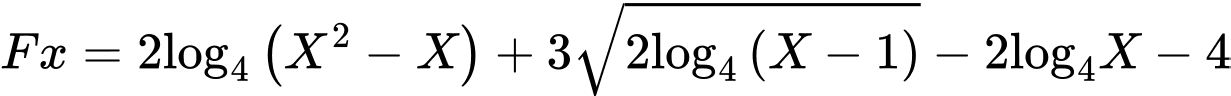
Lưu ý: Ở đây ta nhập
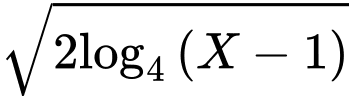vào máy mà không nhập 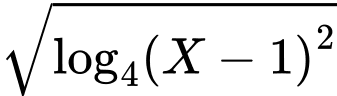bởi ở đây dấu mũ hai máy sẽ nhận là 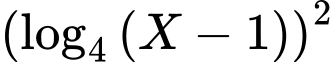chứ không phải nghĩa như ban đầu.Chú ý: Nếu nhập vào máy tính
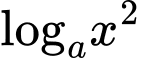máy sẽ nhận dạng thành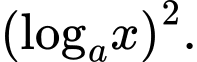 Ấn 2 lần = bỏ qua Gx.
Lúc máy hiện START? ấn 1 =
END? 4 =
STEP? 0.5 =
Máy hiện như hình bên. Lúc này ta thấy
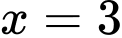là nghiệm của phương trình.Tuy nhiên với các bài toán khác ta có thể thấy hàm số đổi dấu khi đi qua 3 thì ta cũng có thể kết luận được phương án A. Đáp án: A
Câu 7 [582205]: Cho phương trình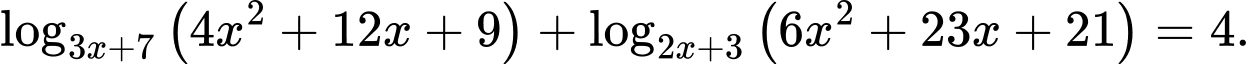 
Số nghiệm của phương trình trên là
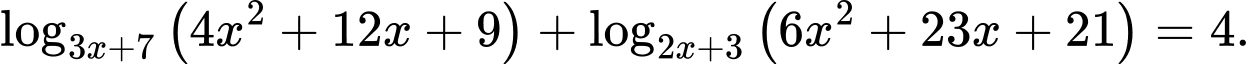Số nghiệm của phương trình trên là A, 2.
B, 1.
C, 0.
D, 3.
Điều kiện: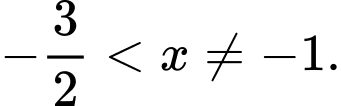 
="" phương="" trình="" đã="" cho="" tương="" đương="" với: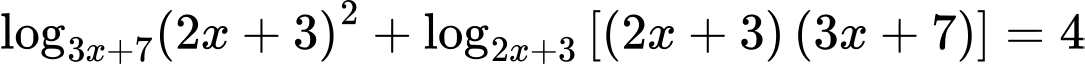
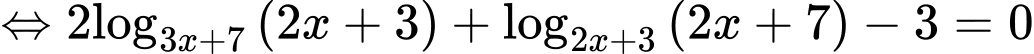(2)
Do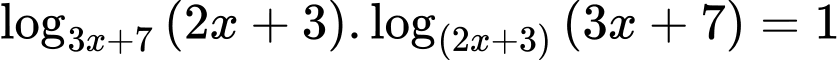
, nên nếu đặt
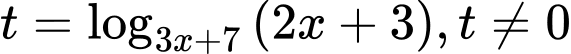thì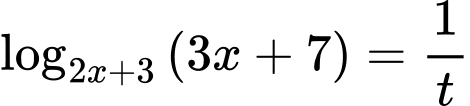 
.
Do đó phương trình (2) trở thành:
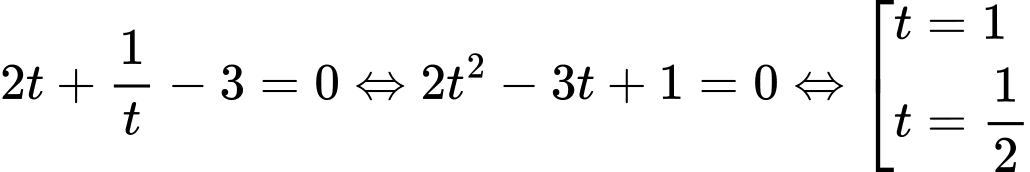
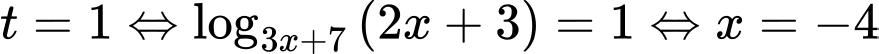
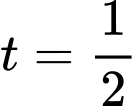
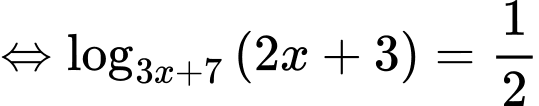
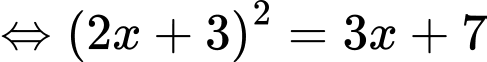
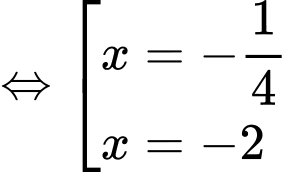
Đến đây nhiều độc giả có thể chọn A, hoặc D. Tuy nhiên so với điều kiện xác định thì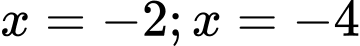
không thỏa mãn. Do vậy phương trình có nghiệm duy nhất 
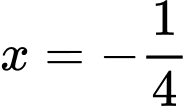. Đáp án: B
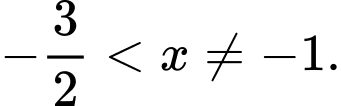="" phương="" trình="" đã="" cho="" tương="" đương="" với: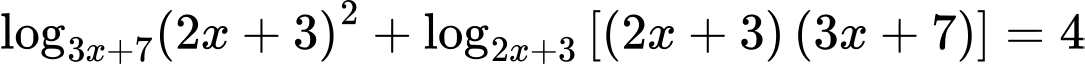 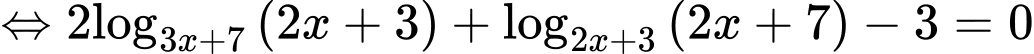(2)Do
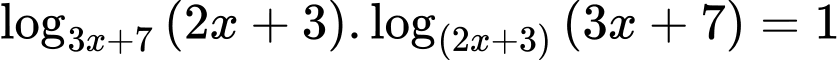, nên nếu đặt 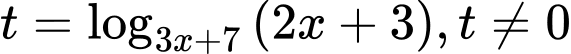thì 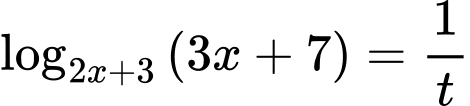.Do đó phương trình (2) trở thành:
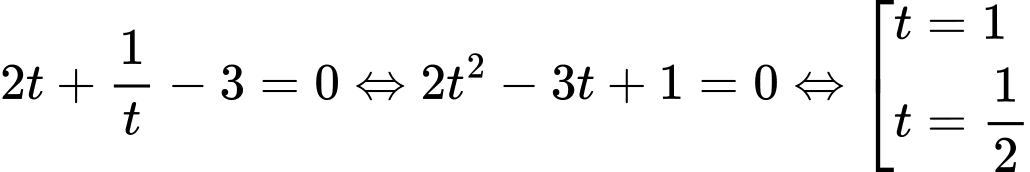
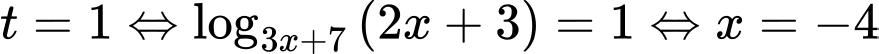
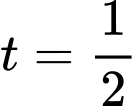
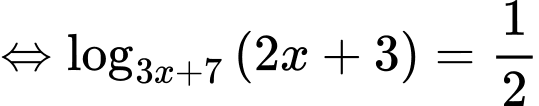
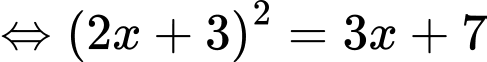
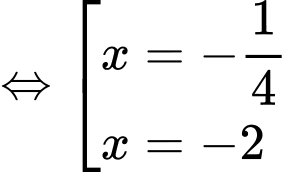
Đến đây nhiều độc giả có thể chọn A, hoặc D. Tuy nhiên so với điều kiện xác định thì
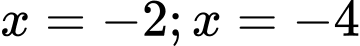không thỏa mãn. Do vậy phương trình có nghiệm duy nhất 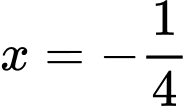. Đáp án: B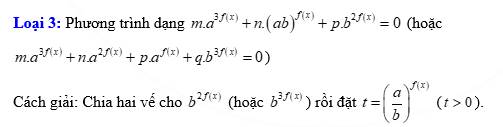 
Câu 8 [582206]: Tìm tích tất cả các nghiệm của phương trình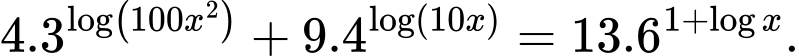 
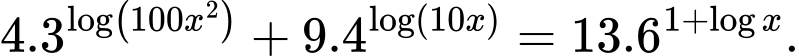
A, 100.
B, 10.
C, 1.
D,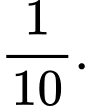 
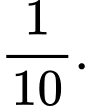
Điều kiện 
Ta có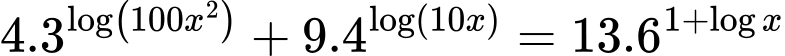
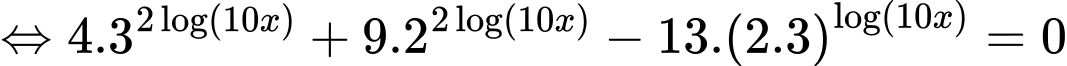
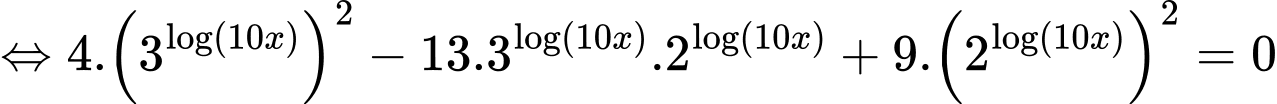
Với bài toán tự luận thông thường thì ta thường thực hiện đặt t, tuy nhiên ta có thể thấy đây là dạng phương trình đẳng cấp bậc hai, do vậy nếu ta nhập các hệ số và máy ta sẽ được kết quả là tỉ số giữa hai biến.
Vậy đến đây ta có thể sử dụng chọn giải phương trình bậc hai và lần lượt nhập các hệ số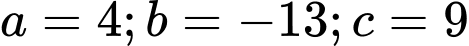
thì ta được hai nghiệm là: 
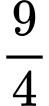và 1.
Tức là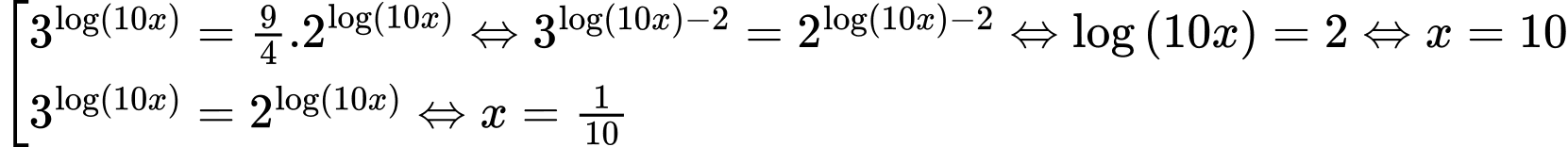
Vậy tích các nghiệm của phương trình là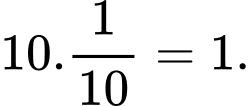
Chú ý: Khi đã hiểu bản chất của dạng toán, ta có thể bỏ qua các bước đặt và giải luôn phương trình bằng máy tính. Đáp án: C
Ta có
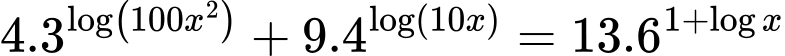
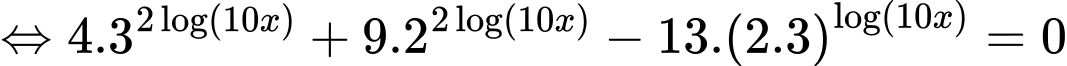
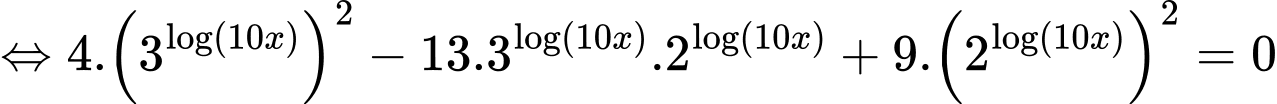
Với bài toán tự luận thông thường thì ta thường thực hiện đặt t, tuy nhiên ta có thể thấy đây là dạng phương trình đẳng cấp bậc hai, do vậy nếu ta nhập các hệ số và máy ta sẽ được kết quả là tỉ số giữa hai biến.
Vậy đến đây ta có thể sử dụng chọn giải phương trình bậc hai và lần lượt nhập các hệ số
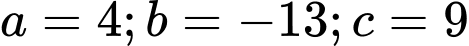thì ta được hai nghiệm là: 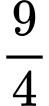và 1.Tức là
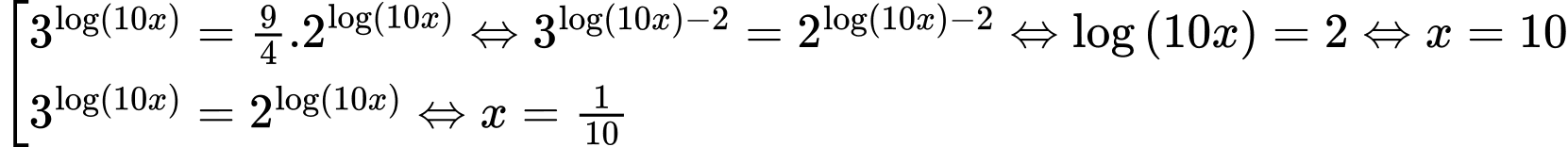
Vậy tích các nghiệm của phương trình là
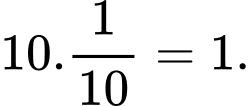
Chú ý: Khi đã hiểu bản chất của dạng toán, ta có thể bỏ qua các bước đặt và giải luôn phương trình bằng máy tính. Đáp án: C
Loại 4: Phương trình dạng m.af(x)+m.bf(x)+p=0, với ab=1
Cách giải: Giả sử a > 1, ta đặt t=af(x), t > 0, khi đó bf(x)=1/t.
Cách giải: Giả sử a > 1, ta đặt t=af(x), t > 0, khi đó bf(x)=1/t.
Câu 9 [582207]: Phương trình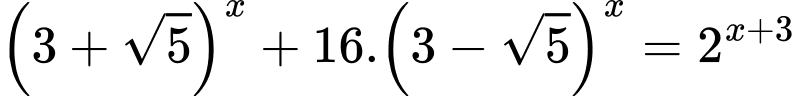 
có nghiệm
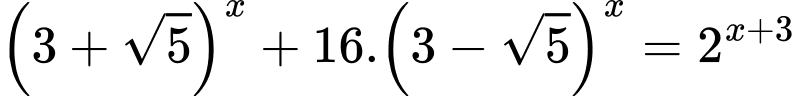có nghiệm A,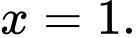 
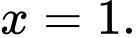
B,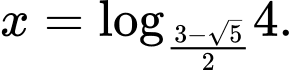 
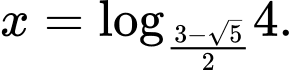
C,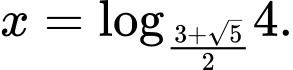 
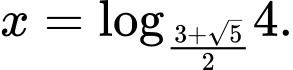
D, 0.
Phân tích: Do ở vế phải của phương trình chưa về dạng hằng số và
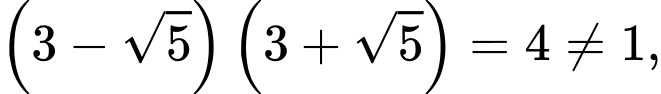nên ta phải biến đổi sao cho mất 
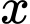ở vế phải đồng thời
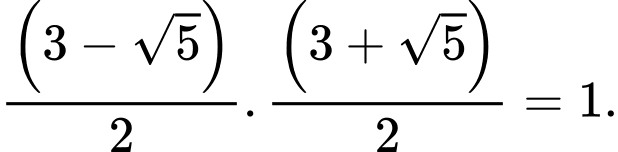Vậy ta sẽ chia cả hai vế của phương trình cho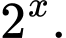 
Lời giải
Chia hai vế của phương trình cho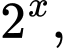
ta được
(*)
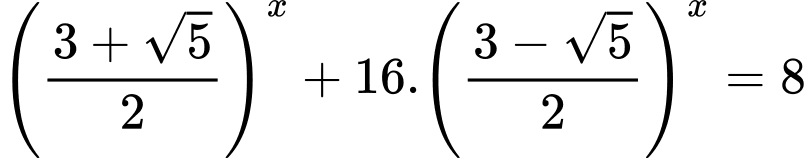Đặt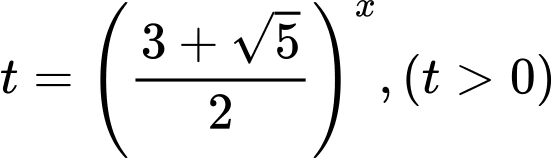
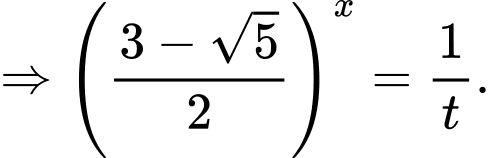
Khi đó phương trình (*) trở thành: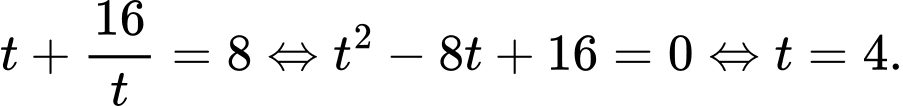
Vớ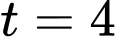i
thì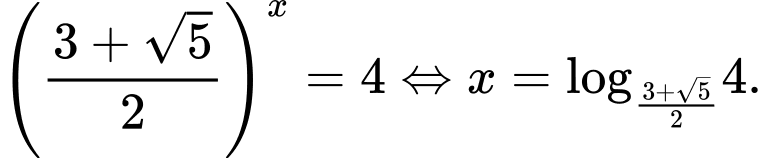 
Đáp án: C
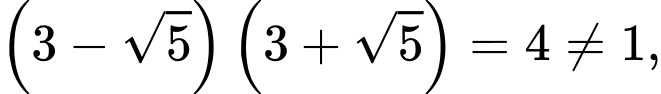nên ta phải biến đổi sao cho mất 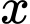ở vế phải đồng thời 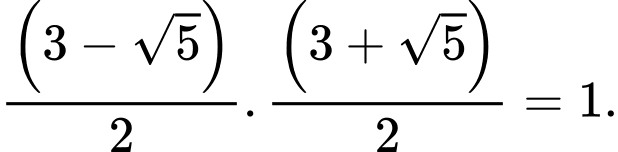Vậy ta sẽ chia cả hai vế của phương trình cho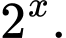 Lời giải
Chia hai vế của phương trình cho
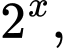ta được 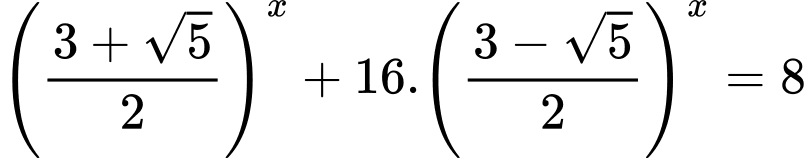(*)Đặt
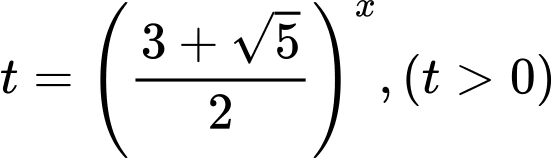
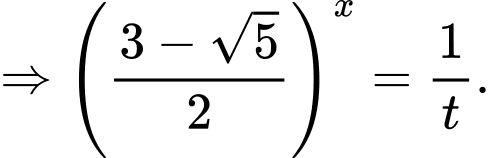
Khi đó phương trình (*) trở thành:
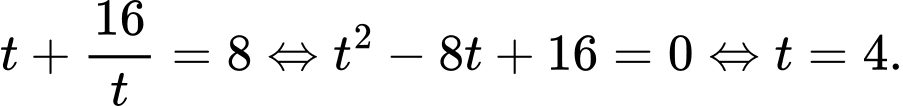
Với
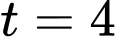thì 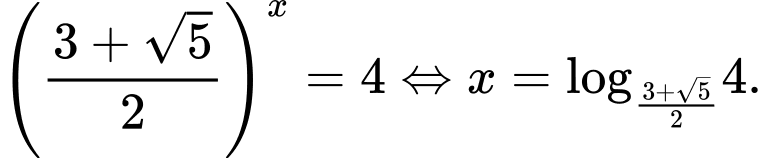Đáp án: C III. Phương pháp đặt ẩn phụ (dạng 2: đặt ẩn phụ không hoàn toàn)
Câu 10 [582208]: Nghiệm của phương trình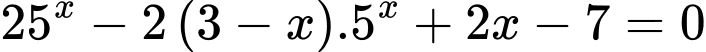 
nằm trong khoảng
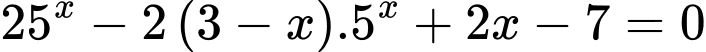nằm trong khoảng A,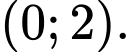 
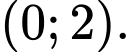
B,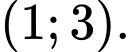 
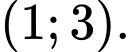
C,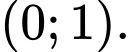 
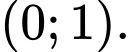
D,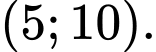 
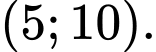
Cách 1: Đặt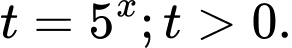 
Phương trình đã cho trở thành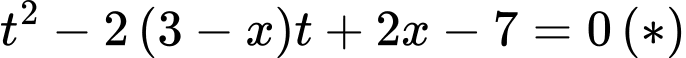
Ta có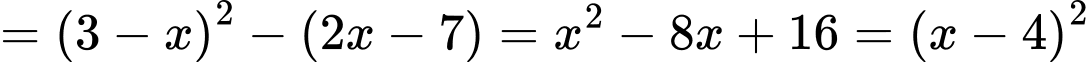
Do đó, phương trình (*) có hai nghiệm
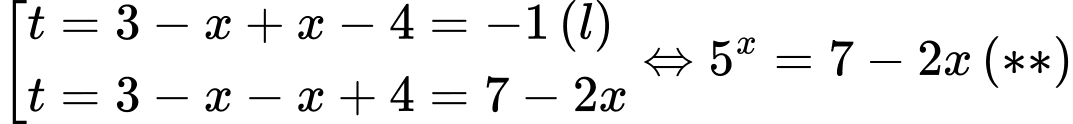
Vế trái của (**) là một hàm số đồng biến, vế phải là một hàm số nghịch biến. Nhận thấy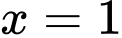
là nghiệm của phương trình, vậy phương trình có nghiệm là 
.
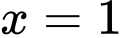Cách 2: Sử dụng máy tính cầm tay.
Do đề bài hỏi khoảng nghiệm của phương trình nên ta có thể dựa vào các khoảng để dò nghiệm phương trình bằng lệnh SHIFT SOLVE có sẵn trong máy tính.
Ta nhập phương trình và màn hình và sử dụng lệnh SHIFT SOLVE. Máy hỏi giá trị của x để thử thì ta sẽ chọn giá trị trong khoảng của từng phương án.
Ta bấm:
Máy sẽ hiện kết quả nghiệm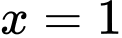
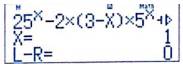
Đáp án: A
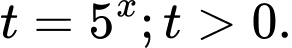
Phương trình đã cho trở thành
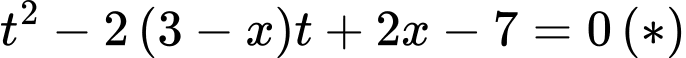
Ta có
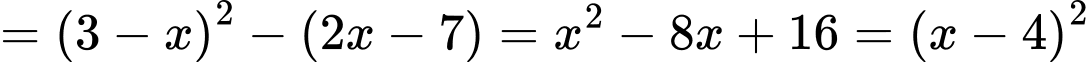
Do đó, phương trình (*) có hai nghiệm
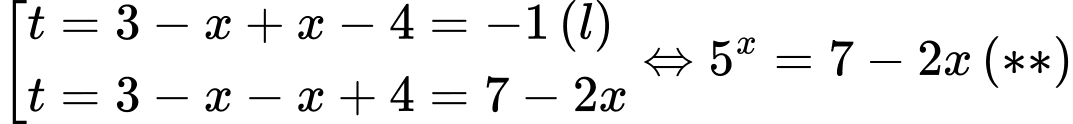
Vế trái của (**) là một hàm số đồng biến, vế phải là một hàm số nghịch biến. Nhận thấy
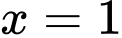là nghiệm của phương trình, vậy phương trình có nghiệm là 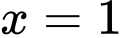.Cách 2: Sử dụng máy tính cầm tay.
Do đề bài hỏi khoảng nghiệm của phương trình nên ta có thể dựa vào các khoảng để dò nghiệm phương trình bằng lệnh SHIFT SOLVE có sẵn trong máy tính.
Ta nhập phương trình và màn hình và sử dụng lệnh SHIFT SOLVE. Máy hỏi giá trị của x để thử thì ta sẽ chọn giá trị trong khoảng của từng phương án.
Ta bấm:
Máy sẽ hiện kết quả nghiệm
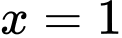
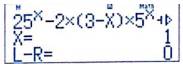
Đáp án: A
Câu 11 [582209]: Số nghiệm của phương trình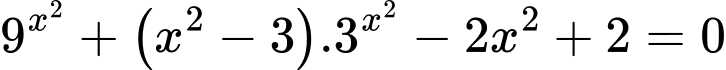 
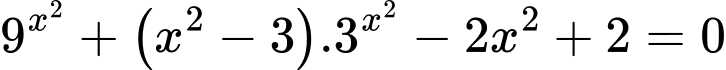là
là A, 0.
B, 1.
C, 2.
D, 3.
Đặt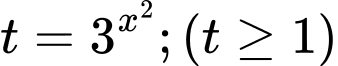 
.
Lúc đó phương trình tương đương với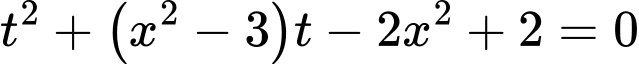
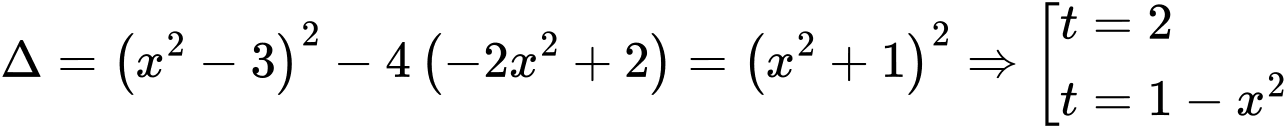
Khi đó: * Với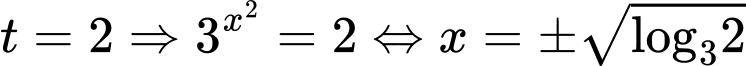
* Với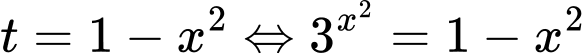
Ta có
.
Vậy phương trình đã cho có ba nghiệm phân biệt. Đáp án: D
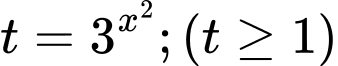.Lúc đó phương trình tương đương với
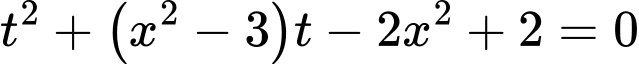
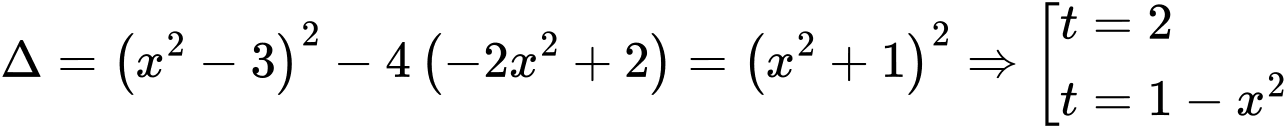
Khi đó: * Với
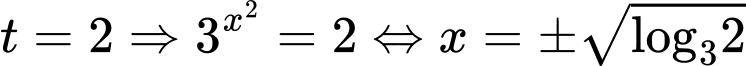
* Với
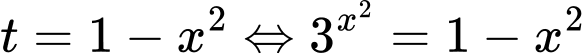
Ta có
.Vậy phương trình đã cho có ba nghiệm phân biệt. Đáp án: D
IV. Phương pháp logarit hóa, mũ hóa
Loại 1: Phương trình dạng af(x).bg(x)=c, với a,b,c > 0.
Cách giải: Ta lấy logarit hai vế cơ số a đưa về phương trình dạng
f(x)+g(x).logab=logac. (logarit hóa)
Loại 2: Với a > 0; a ≠ 1: logaf(x)=g(x) ⇒ f(x)=ag(x) (mũ hóa)
Cách giải: Ta lấy logarit hai vế cơ số a đưa về phương trình dạng
f(x)+g(x).logab=logac. (logarit hóa)
Loại 2: Với a > 0; a ≠ 1: logaf(x)=g(x) ⇒ f(x)=ag(x) (mũ hóa)
Câu 12 [582210]: Phương trình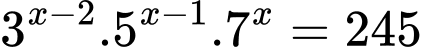 
có nghiệm là
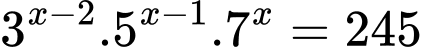có nghiệm là A,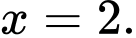 
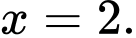
B,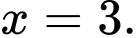 
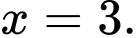
C,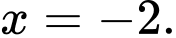 
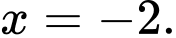
D,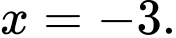 
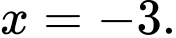
Do hai vế của phương trình đều dương nên lấy logarit cơ số 3 hai vế ta được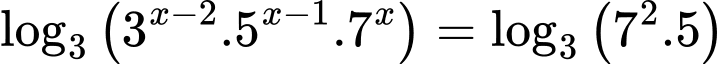 
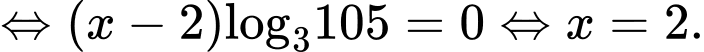Đáp án: A
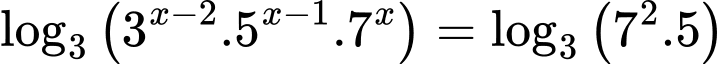
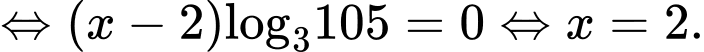Đáp án: A
Câu 13 [582211]: Tập nghiệm của bất phương trình 
là
là A,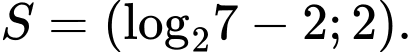 
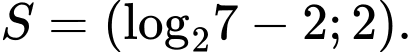
B,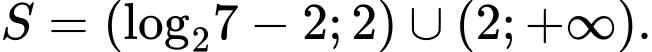 
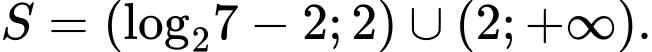
C,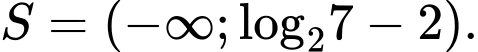 
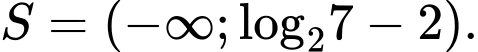
D,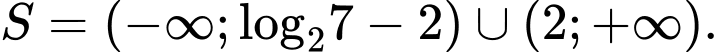 
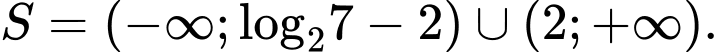
Tập xác định: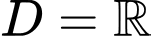 
Bất phương trình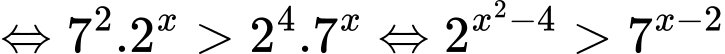
Lấy logarit cơ số 2 hai vế của bất phương trình ta được
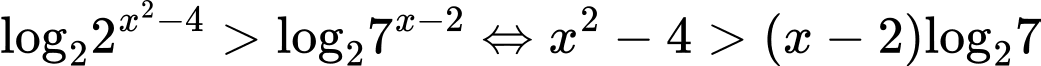
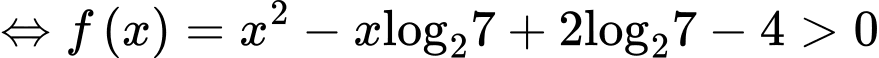
Ta có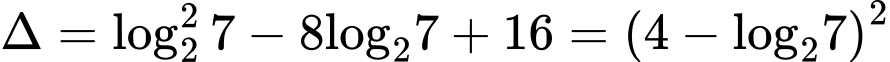
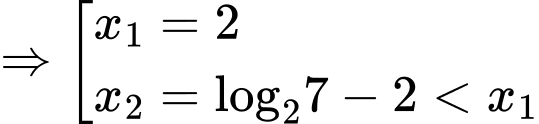
Vậy bất phương trình có nghiệm
hoặc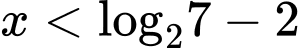 
. Đáp án: D
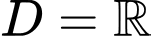
Bất phương trình
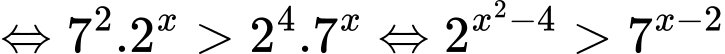
Lấy logarit cơ số 2 hai vế của bất phương trình ta được
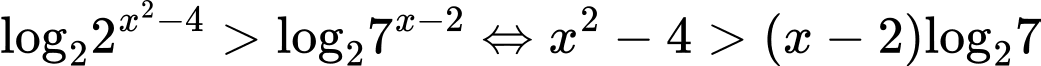
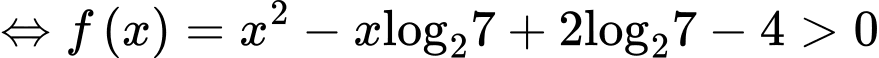
Ta có
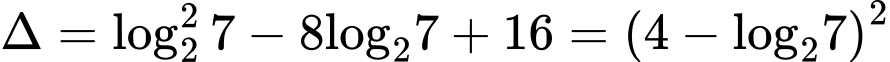
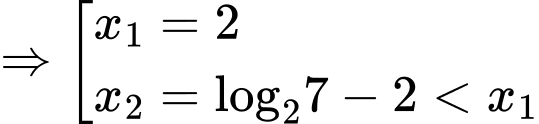
Vậy bất phương trình có nghiệm
hoặc 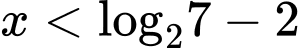. Đáp án: D V. Phương pháp sử dụng tính đơn điệu của hàm số
Phương trình đưa được về dạng f(u)=f(v).
Cách giải: Sử dụng tính chất: Cho hàm số y=f(x) đơn điệu trên tập D. Khi đó f(u)=f(v)⇒ u=v với mọi u,v ∈ D.
Cách giải: Sử dụng tính chất: Cho hàm số y=f(x) đơn điệu trên tập D. Khi đó f(u)=f(v)⇒ u=v với mọi u,v ∈ D.
Câu 14 [582212]: Phương trình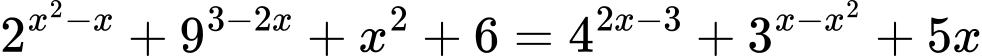 
có số nghiệm là
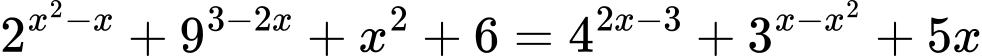có số nghiệm là A, 2.
B, 3.
C, 1.
D, 0.
Phương trình đã cho tương đương với
(*)
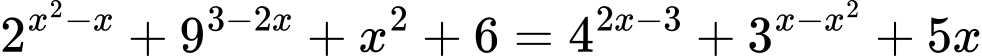
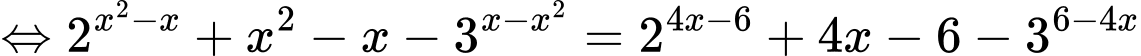Xét hàm số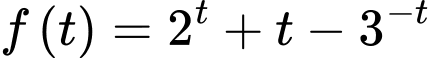
Có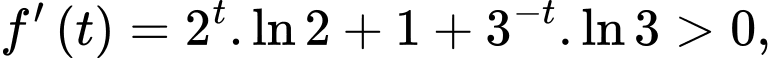
nên hàm số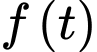 
đồng biến trên 
.
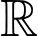Khi đó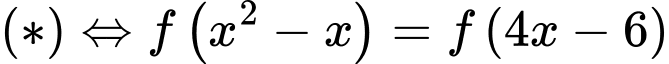
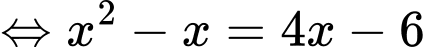
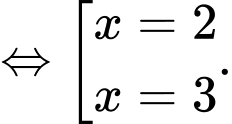Đáp án: A
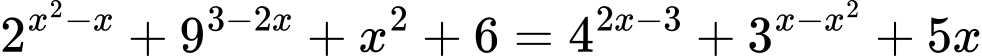
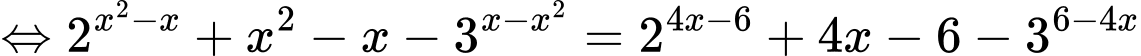(*)Xét hàm số
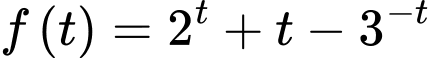
Có
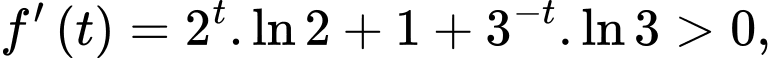
nên hàm số 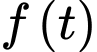đồng biến trên 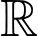.Khi đó
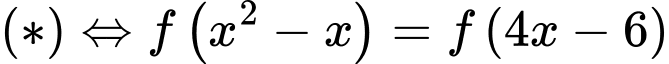
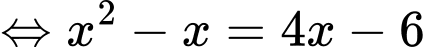
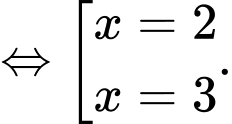Đáp án: A