Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
Câu 1 [582213]: Tìm tập 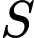 nghiệm của phương trình
nghiệm của phương trình 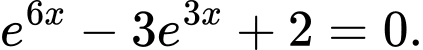
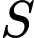 nghiệm của phương trình
nghiệm của phương trình 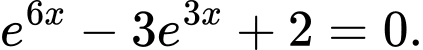
A, 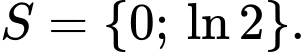
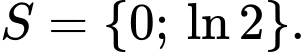
B, 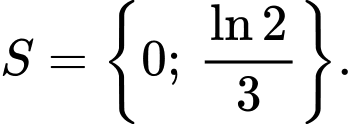
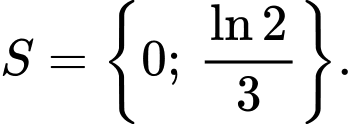
C, 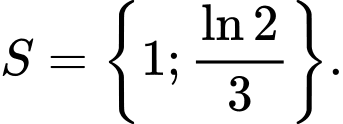
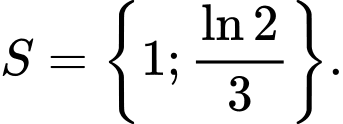
D, 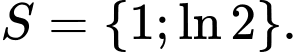
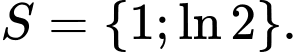
Đặt 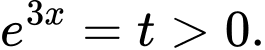 Phương trình trở thành
Phương trình trở thành 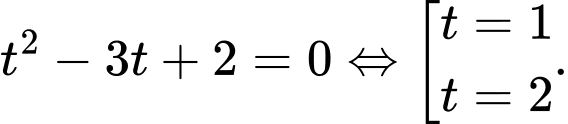
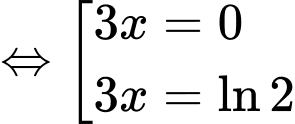
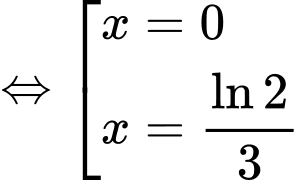 Đáp án: B
Đáp án: B
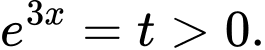 Phương trình trở thành
Phương trình trở thành 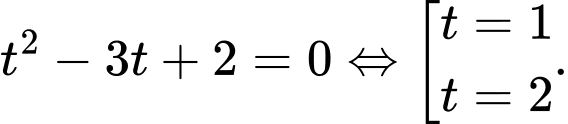
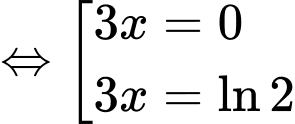
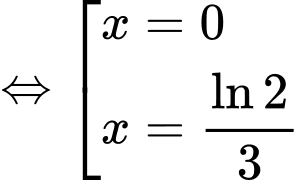 Đáp án: B
Đáp án: B
Câu 2 [582214]: Phương trình 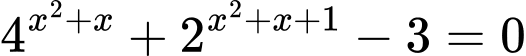 có bao nhiêu nghiệm không âm?
có bao nhiêu nghiệm không âm?
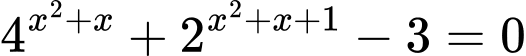 có bao nhiêu nghiệm không âm?
có bao nhiêu nghiệm không âm? A, 0.
B, 1.
C, 2.
D, 3.
Phương trình tương đương với 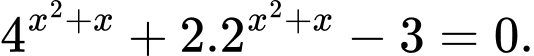
Đặt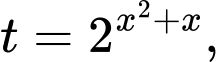
 Phương trình trở thành
Phương trình trở thành 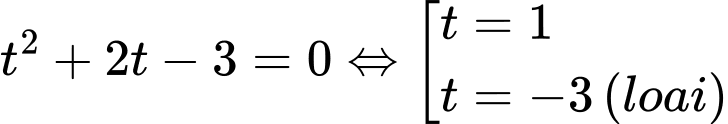 .
.
Với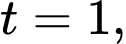 ta được
ta được 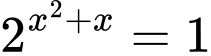

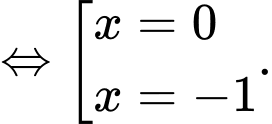
Vậy chỉ có duy nhất nghiệm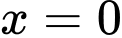 là nghiệm không âm. Đáp án: B
là nghiệm không âm. Đáp án: B
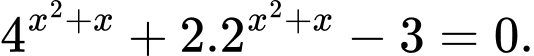
Đặt
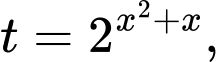
 Phương trình trở thành
Phương trình trở thành 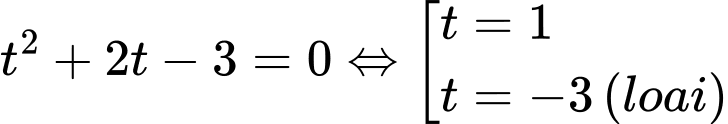 .
.Với
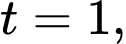 ta được
ta được 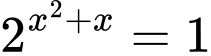

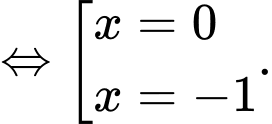
Vậy chỉ có duy nhất nghiệm
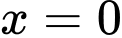 là nghiệm không âm. Đáp án: B
là nghiệm không âm. Đáp án: B
Câu 3 [582215]: Tính tổng 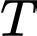 tất cả các nghiệm của phương trình
tất cả các nghiệm của phương trình 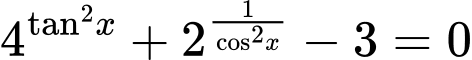 trên đoạn
trên đoạn 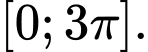
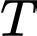 tất cả các nghiệm của phương trình
tất cả các nghiệm của phương trình 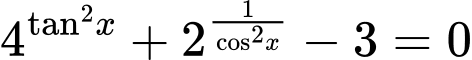 trên đoạn
trên đoạn 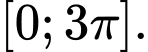
A, 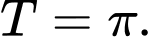
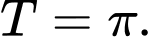
B, 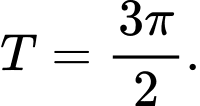
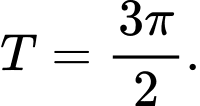
C, 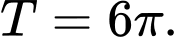
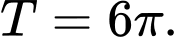
D, 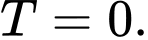
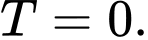
Điều kiện: 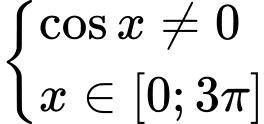
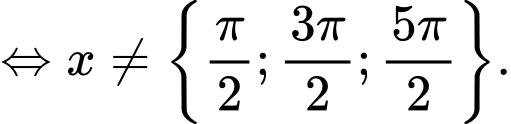
Ta có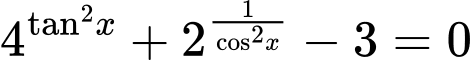
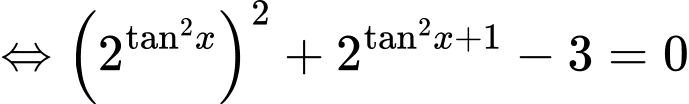
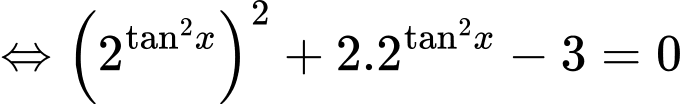
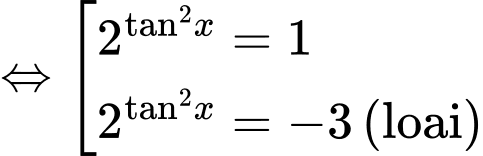
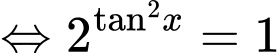

Vì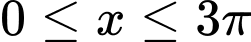
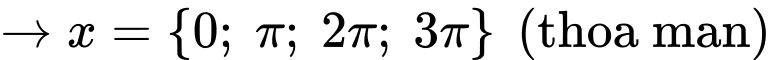
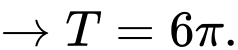 Đáp án: C
Đáp án: C
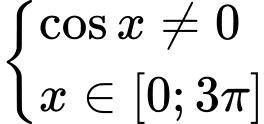
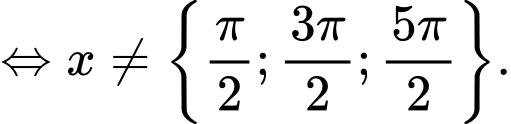
Ta có
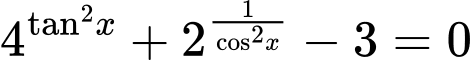
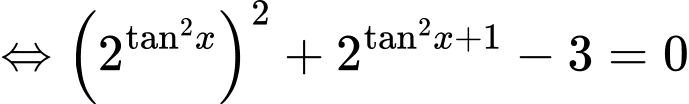
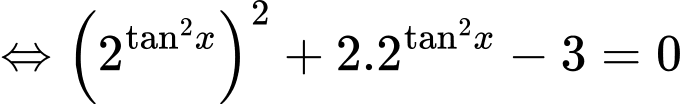
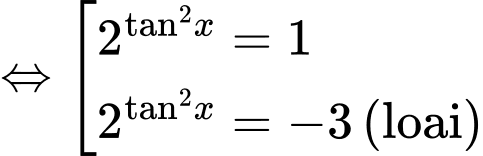
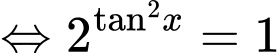

Vì
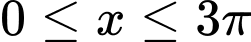
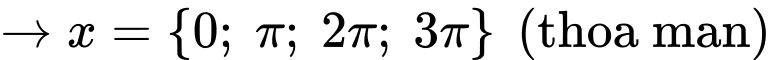
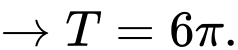 Đáp án: C
Đáp án: C
Câu 4 [582216]: Phương trình 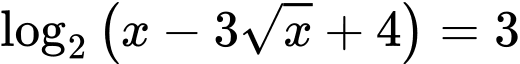 có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm?
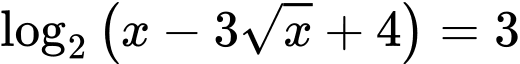 có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm? A, 4.
B, 1.
C, 2.
D, 0.
Phương trình 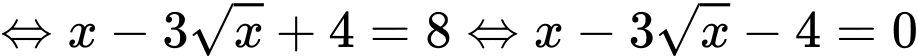
 Đáp án: B
Đáp án: B
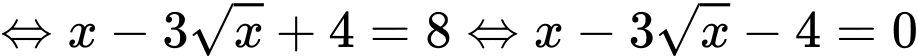
 Đáp án: B
Đáp án: B
Câu 5 [582217]: Tính 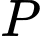 là tích tất cả các nghiệm của phương trình
là tích tất cả các nghiệm của phương trình 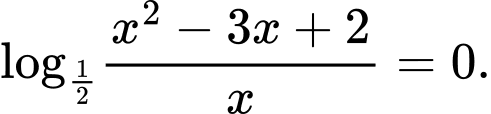
 là tích tất cả các nghiệm của phương trình
là tích tất cả các nghiệm của phương trình 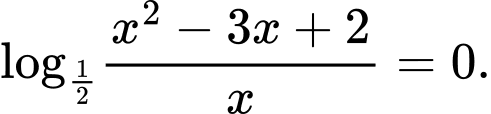
A, 

B, 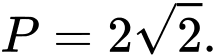
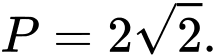
C, 

D, 

Phương trình 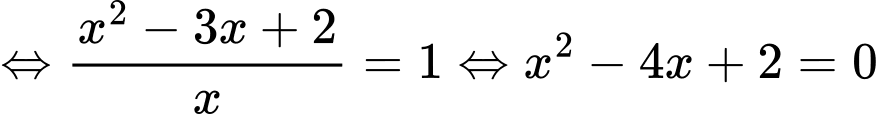
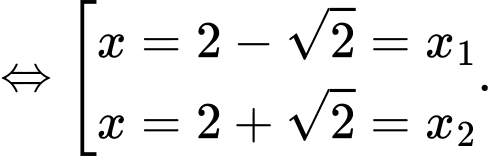
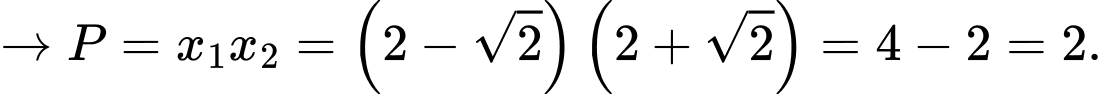
Chọn C.
Hoặc từ phương trình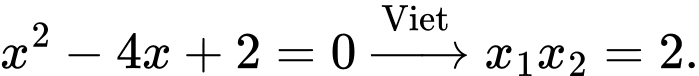 Đáp án: C
Đáp án: C
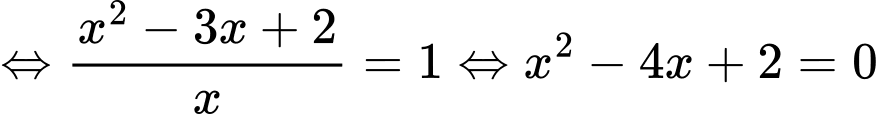
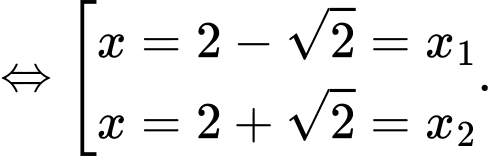
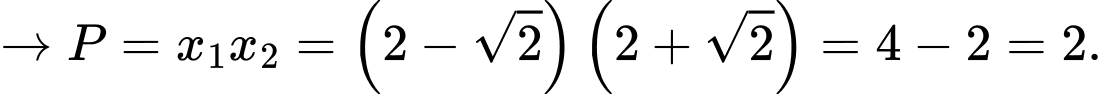
Chọn C.
Hoặc từ phương trình
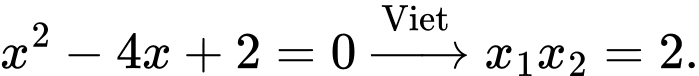 Đáp án: C
Đáp án: C
Câu 6 [582218]: Biết rằng phương trình 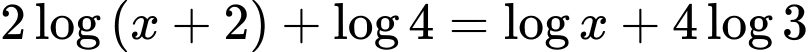 có hai nghiệm phân biệt
có hai nghiệm phân biệt 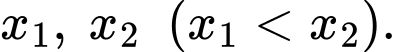 Tính
Tính 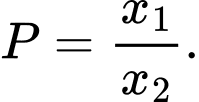
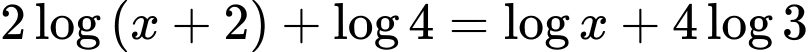 có hai nghiệm phân biệt
có hai nghiệm phân biệt 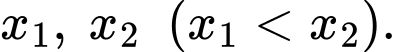 Tính
Tính 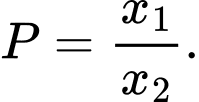
A, 

B, 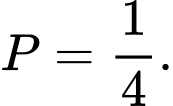
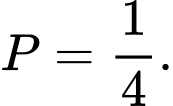
C, 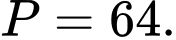
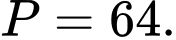
D, 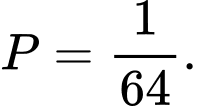
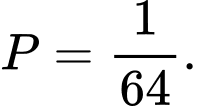
Điều kiện: 
Phương trình
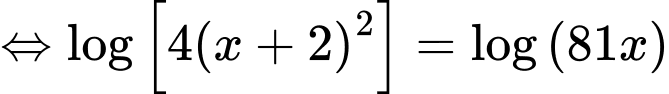

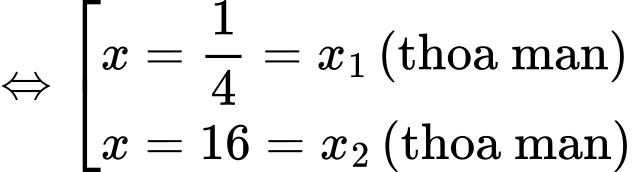
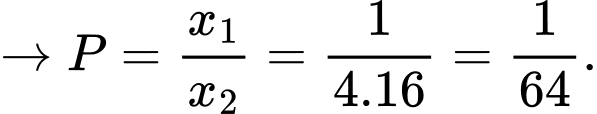 Đáp án: D
Đáp án: D

Phương trình

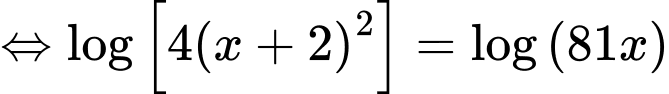

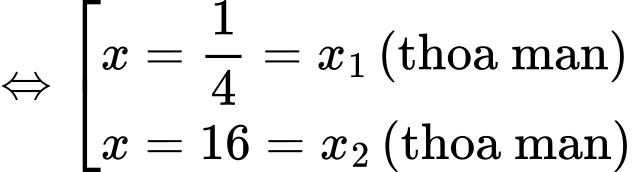
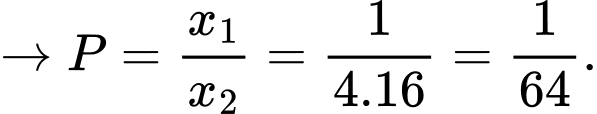 Đáp án: D
Đáp án: D
Câu 7 [582219]: Tìm giá trị thực của tham số 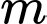 để phương trình
để phương trình 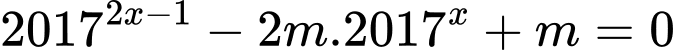 có hai nghiệm thực
có hai nghiệm thực 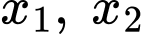 thỏa mãn
thỏa mãn 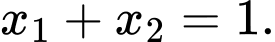
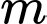 để phương trình
để phương trình 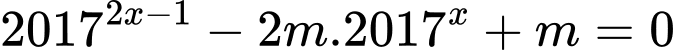 có hai nghiệm thực
có hai nghiệm thực 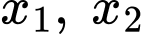 thỏa mãn
thỏa mãn 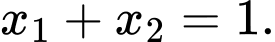
A, 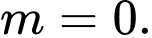
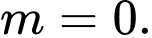
B, 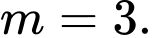
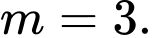
C, 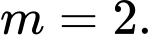
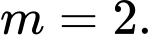
D, 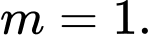
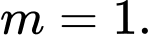
Phương trình 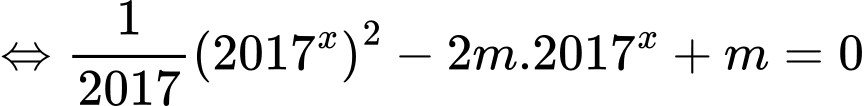
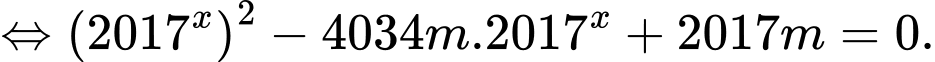
Giả sử phương trình có hai nghiệm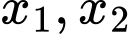 .
.
Theo Viet, ta có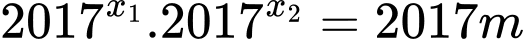
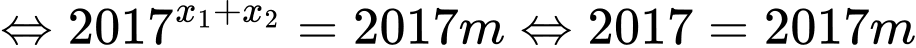
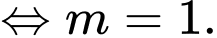
Thử lại với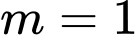 ta thấy thỏa mãn. Đáp án: D
ta thấy thỏa mãn. Đáp án: D
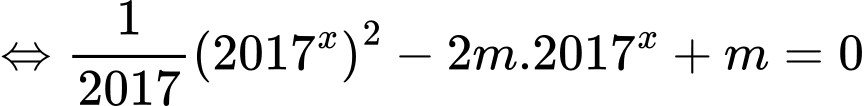
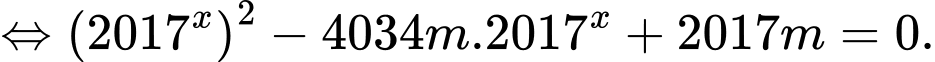
Giả sử phương trình có hai nghiệm
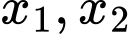 .
.Theo Viet, ta có
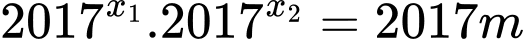
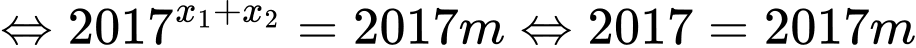
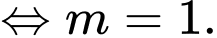
Thử lại với
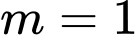 ta thấy thỏa mãn. Đáp án: D
ta thấy thỏa mãn. Đáp án: D
Câu 8 [582220]: Cho phương trình 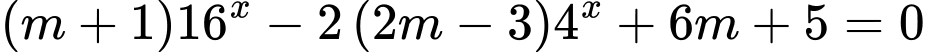 với
với 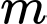 là tham số thực. Tập tất cả các giá trị của
là tham số thực. Tập tất cả các giá trị của 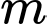 để phương trình có hai nghiệm trái dấu có dạng
để phương trình có hai nghiệm trái dấu có dạng 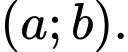 Tính
Tính 
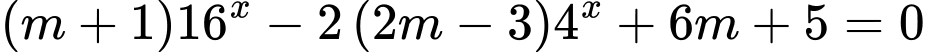 với
với 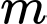 là tham số thực. Tập tất cả các giá trị của
là tham số thực. Tập tất cả các giá trị của 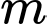 để phương trình có hai nghiệm trái dấu có dạng
để phương trình có hai nghiệm trái dấu có dạng 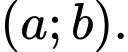 Tính
Tính 
A, 

B, 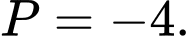
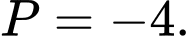
C, 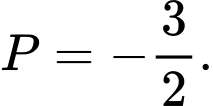
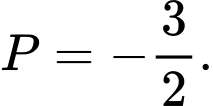
D, 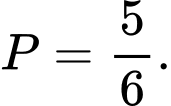
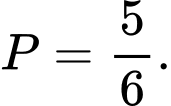
Đặt 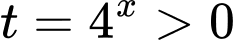 .
.
Phương trình trở thành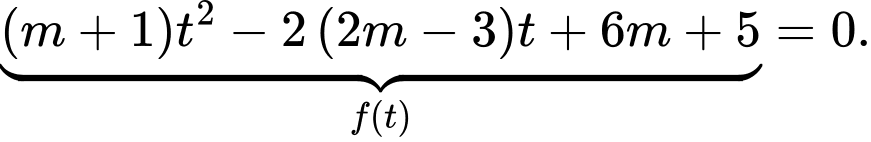

Phương trình đã cho có hai nghiệm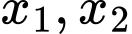 thỏa mãn
thỏa mãn 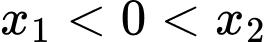
Ycbt phương trình
phương trình  có hai nghiệm
có hai nghiệm 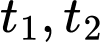 thỏa
thỏa 
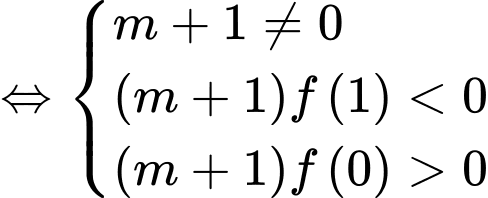
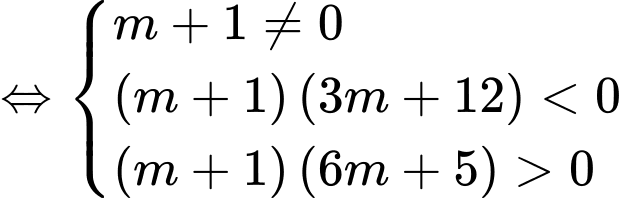
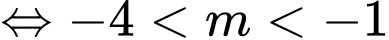 Đáp án: A
Đáp án: A
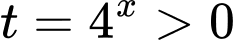 .
.Phương trình trở thành
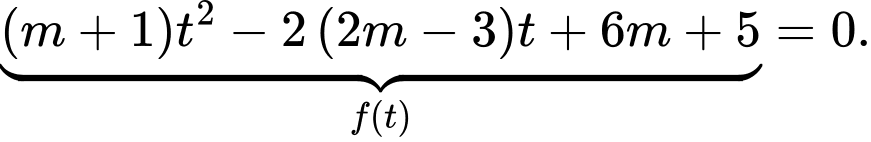

Phương trình đã cho có hai nghiệm
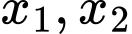 thỏa mãn
thỏa mãn 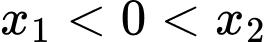
Ycbt
 phương trình
phương trình  có hai nghiệm
có hai nghiệm 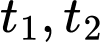 thỏa
thỏa 
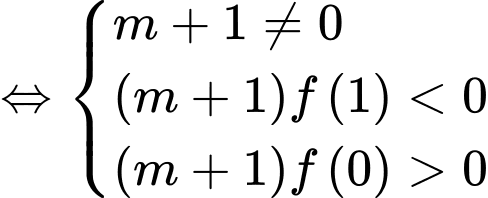
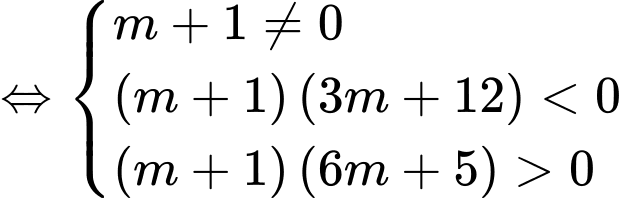
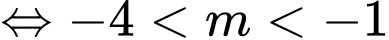 Đáp án: A
Đáp án: A
Câu 9 [582221]: Phương trình  có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm?
 có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm? A, 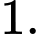
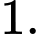
B, 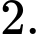
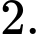
C, 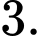
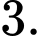
D, 
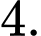
Đặt 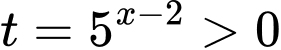 , phương trình trở thành
, phương trình trở thành 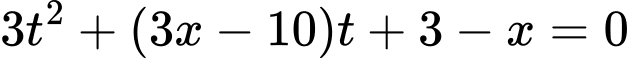 .
. 
Ta coi đây là phương trình bậc hai ẩn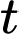 và có
và có 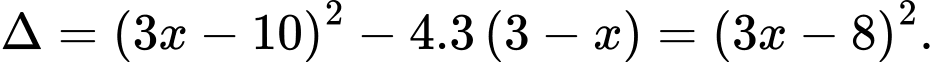
Suy ra phương trình có hai nghiệm:
có hai nghiệm: 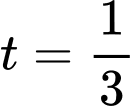 hoặc
hoặc 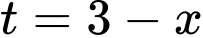 .
.
Với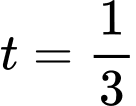
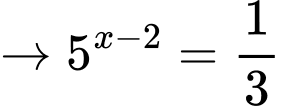
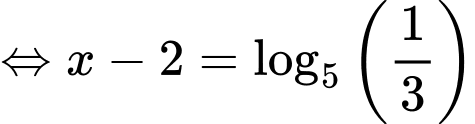
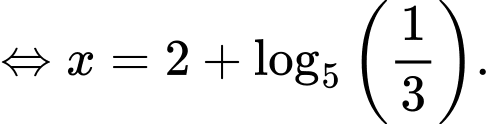
Với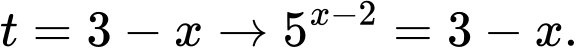
Dễ thấy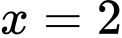 là nghiệm duy nhất (Vế trái là hàm đồng biến, vế phải là hàm nghịch biến).
là nghiệm duy nhất (Vế trái là hàm đồng biến, vế phải là hàm nghịch biến).
Vậy phương trình đã cho có hai nghiệm: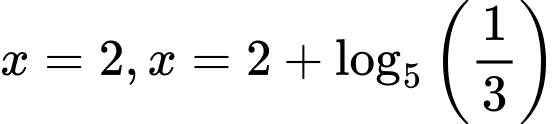 . Đáp án: B
. Đáp án: B
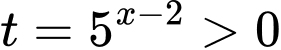 , phương trình trở thành
, phương trình trở thành 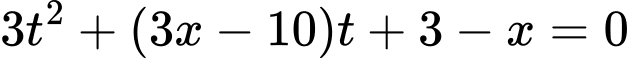 .
. 
Ta coi đây là phương trình bậc hai ẩn
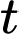 và có
và có 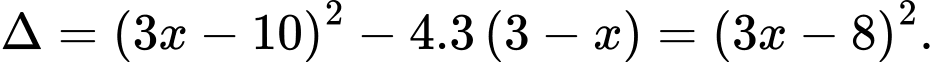
Suy ra phương trình
 có hai nghiệm:
có hai nghiệm: 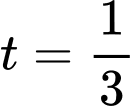 hoặc
hoặc 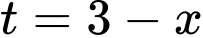 .
. Với
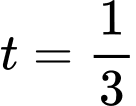
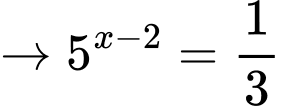
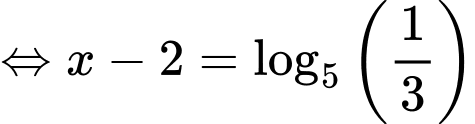
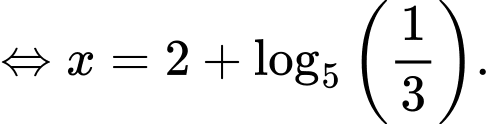
Với
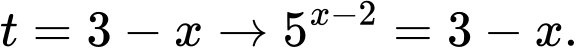
Dễ thấy
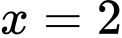 là nghiệm duy nhất (Vế trái là hàm đồng biến, vế phải là hàm nghịch biến).
là nghiệm duy nhất (Vế trái là hàm đồng biến, vế phải là hàm nghịch biến).Vậy phương trình đã cho có hai nghiệm:
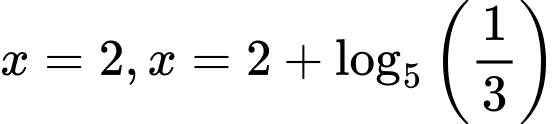 . Đáp án: B
. Đáp án: B
Câu 10 [582222]: Tính tổng 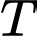 tất cả các nghiệm của phương trình
tất cả các nghiệm của phương trình 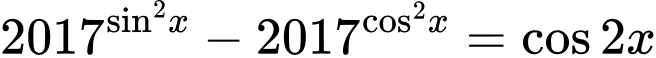 trên đoạn
trên đoạn 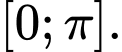
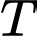 tất cả các nghiệm của phương trình
tất cả các nghiệm của phương trình 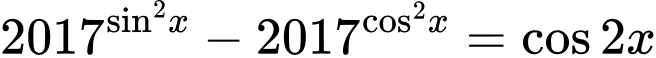 trên đoạn
trên đoạn 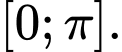
A, 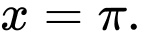
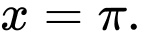
B, 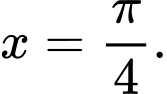
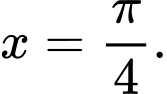
C, 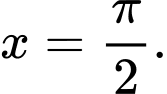
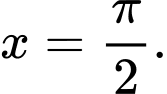
D, 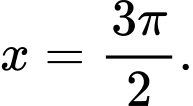
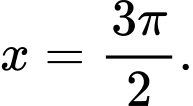
Phương trình 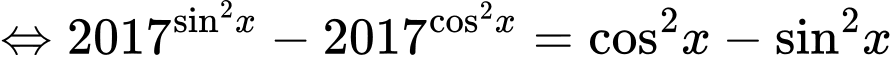
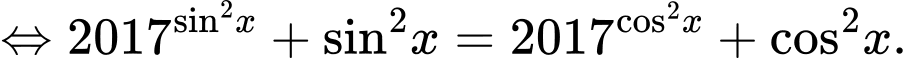

Xét hàm số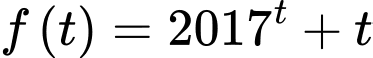 trên
trên 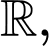 ta có
ta có 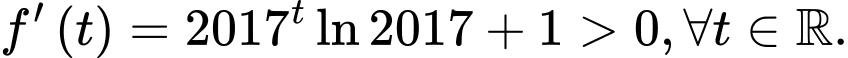
Suy ra hàm số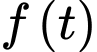 đồng biến trên
đồng biến trên 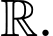
Nhận thấy có dạng
có dạng 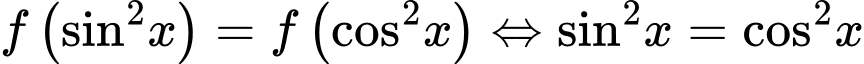
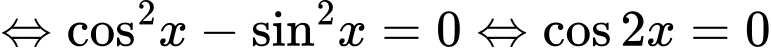
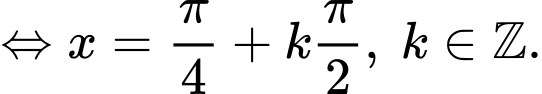
Vì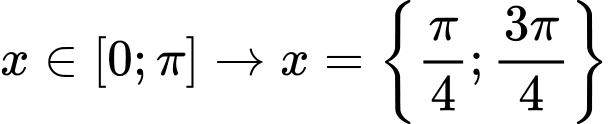
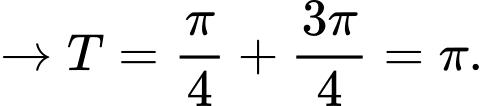 Đáp án: A
Đáp án: A
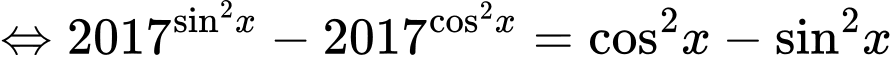
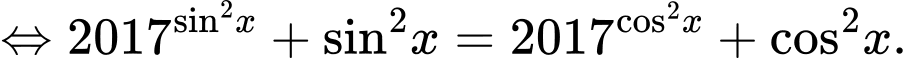

Xét hàm số
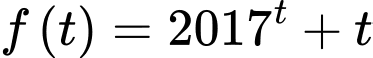 trên
trên 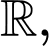 ta có
ta có 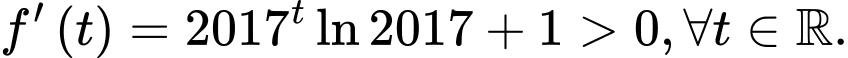
Suy ra hàm số
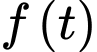 đồng biến trên
đồng biến trên 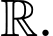
Nhận thấy
 có dạng
có dạng 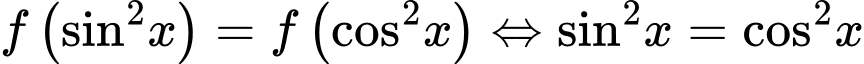
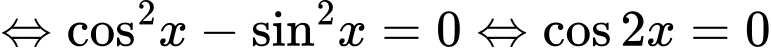
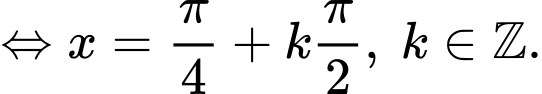
Vì
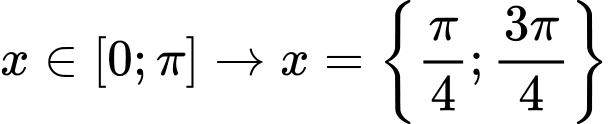
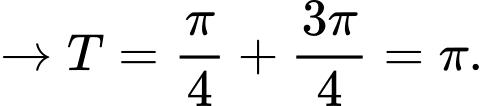 Đáp án: A
Đáp án: A
Câu 11 [582223]: Tìm tập nghiệm  của bất phương trình
của bất phương trình 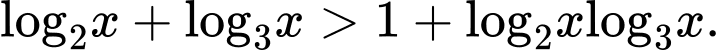
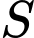 của bất phương trình
của bất phương trình 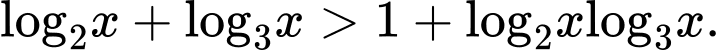
A, 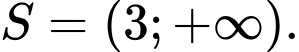
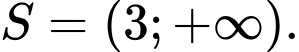
B, 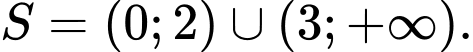
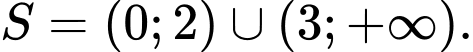
C, 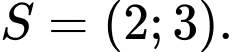
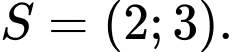
D, 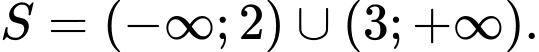
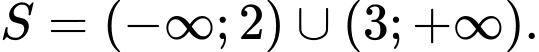
Điều kiện:  .
.
Bất phương trình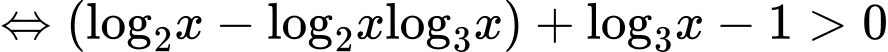
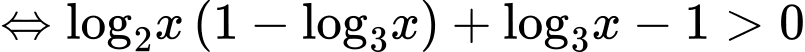
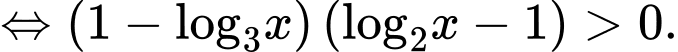

TH1: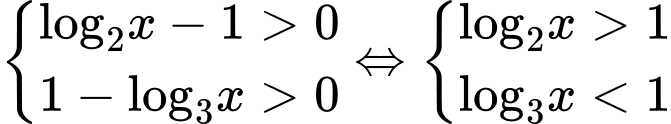
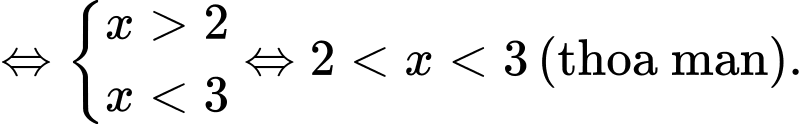
TH2: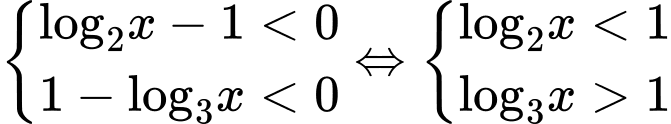 :
: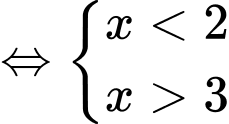 vô nghiệm.
vô nghiệm.
Vậy tập nghiệm của bất phương trình là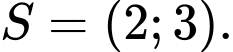
Chọn C. Đáp án: C
 .
.Bất phương trình
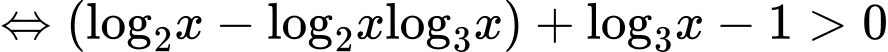
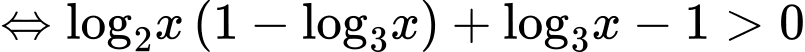
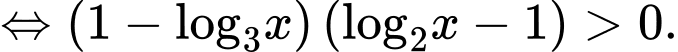

TH1:
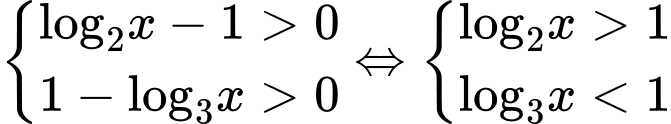
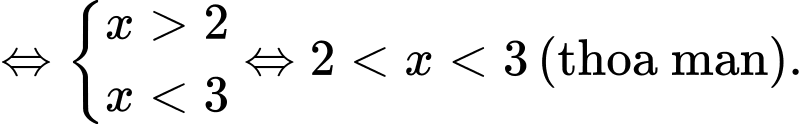
TH2:
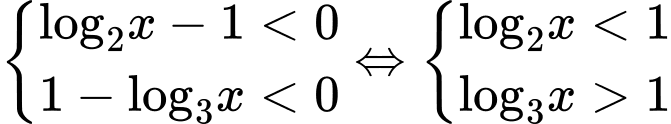 :
: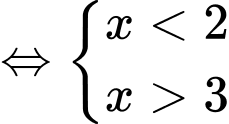 vô nghiệm.
vô nghiệm.Vậy tập nghiệm của bất phương trình là
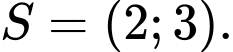
Chọn C. Đáp án: C
Câu 12 [582224]: Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình 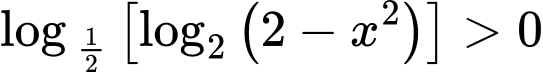 ?
?
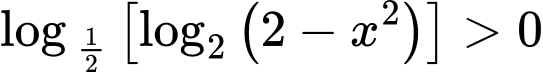 ?
? A, 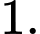
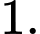
B, 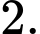
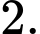
C, 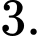
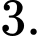
D, 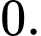
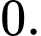
Điều kiện: 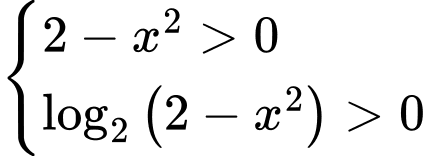
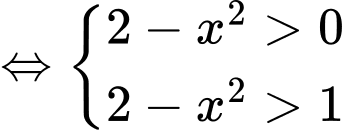

Bất phương trình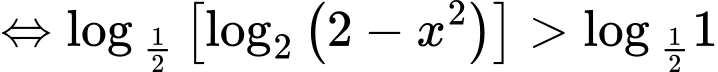
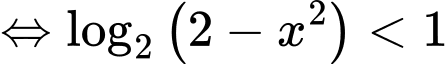
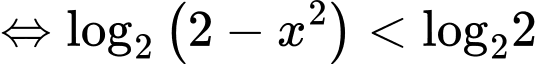
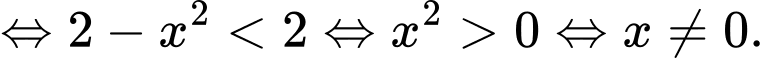
Đối chiếu điều kiện, bất phương trình có tập nghiệm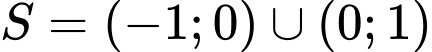 .
.
Suy ra không có số nguyên nào thuộc tập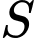 . Đáp án: D
. Đáp án: D
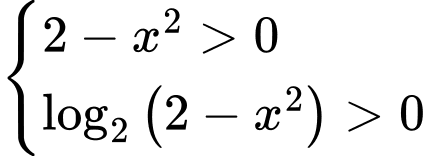
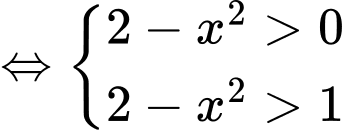

Bất phương trình
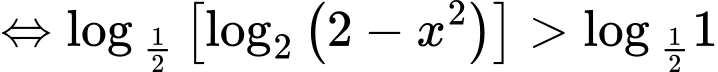
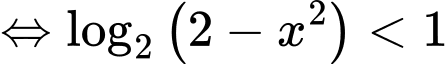
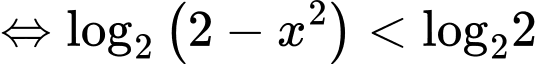
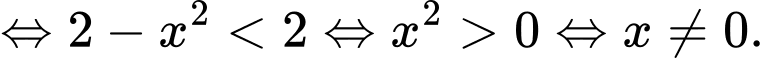
Đối chiếu điều kiện, bất phương trình có tập nghiệm
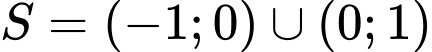 .
.Suy ra không có số nguyên nào thuộc tập
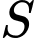 . Đáp án: D
. Đáp án: D
Câu 13 [582225]: Phương trình 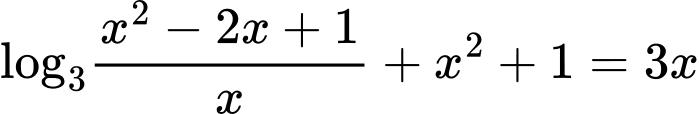 có tổng tất cả các nghiệm bằng:
có tổng tất cả các nghiệm bằng:
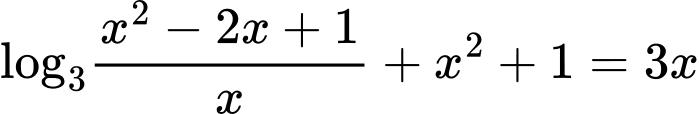 có tổng tất cả các nghiệm bằng:
có tổng tất cả các nghiệm bằng: A, 3.
B, 5.
C, 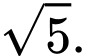
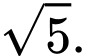
D, 2.
Điều kiện: 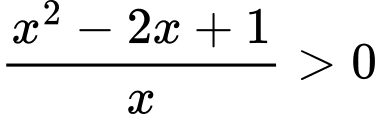
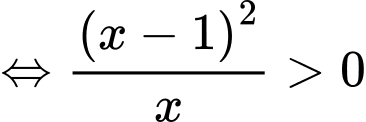
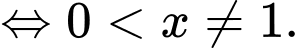
Phương trình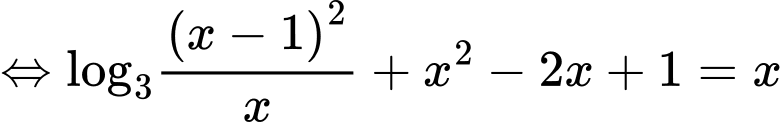
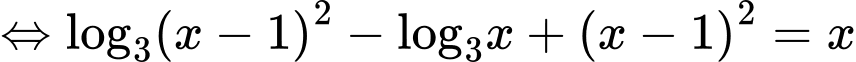
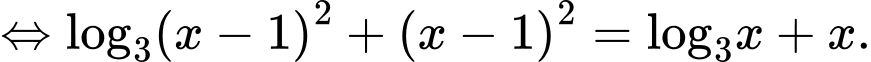

Xét hàm số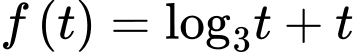 với
với  . Ta có
. Ta có 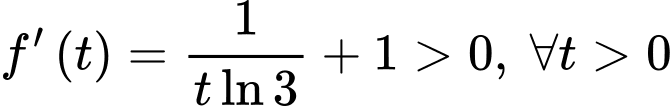 .
.
Suy ra hàm số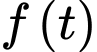 đồng biến trên
đồng biến trên 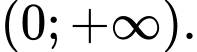
Nhận thấy có dạng
có dạng 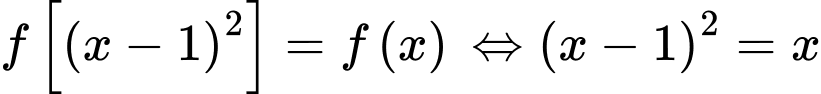
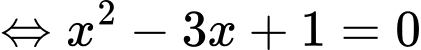
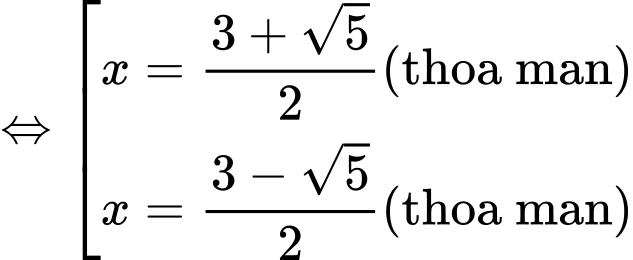 Đáp án: A
Đáp án: A
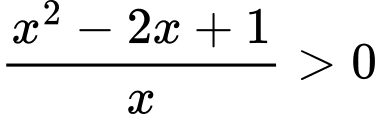
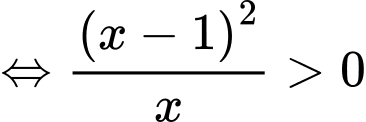
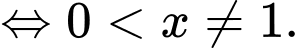
Phương trình
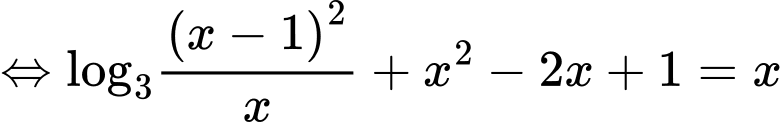
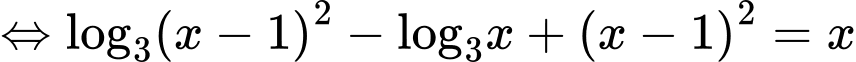
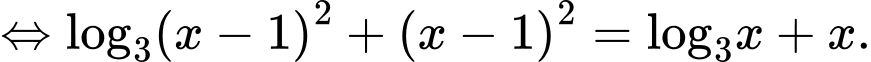

Xét hàm số
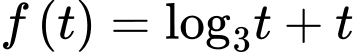 với
với  . Ta có
. Ta có 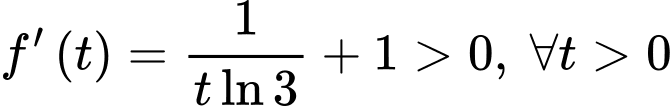 .
.Suy ra hàm số
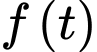 đồng biến trên
đồng biến trên 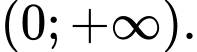
Nhận thấy
 có dạng
có dạng 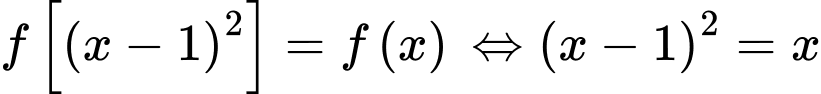
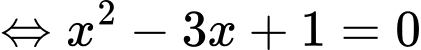
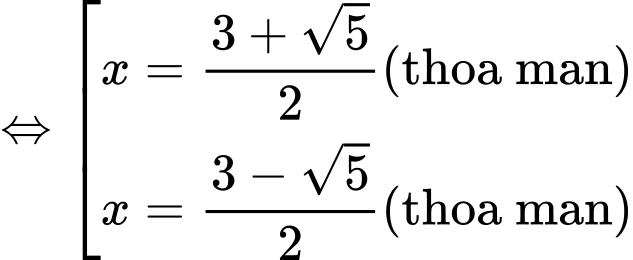 Đáp án: A
Đáp án: A
Câu 14 [582226]: Có bao nhiêu giá trị nguyên của 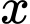 trong đoạn
trong đoạn 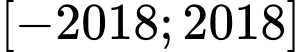 thỏa mãn bất phương trình
thỏa mãn bất phương trình 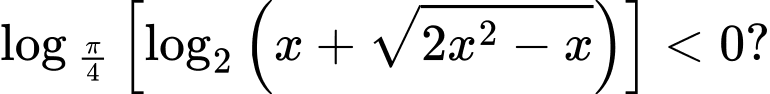
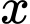 trong đoạn
trong đoạn 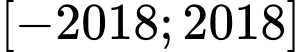 thỏa mãn bất phương trình
thỏa mãn bất phương trình 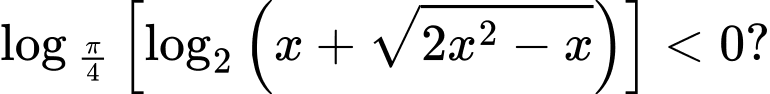
A, 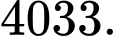
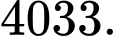
B, 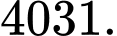
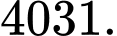
C, 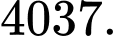
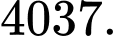
D, 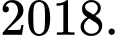
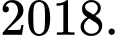
Điều kiện: 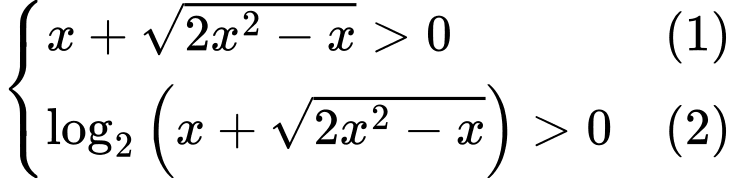 .
.
Bất phương trình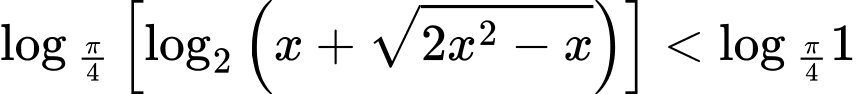
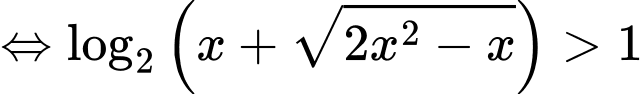 (thỏa
(thỏa  )
)
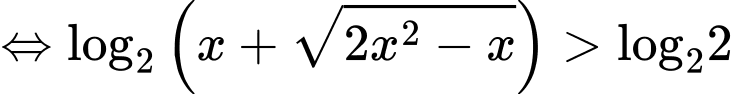
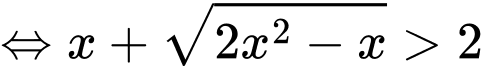 (thỏa
(thỏa  )
)
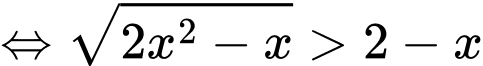
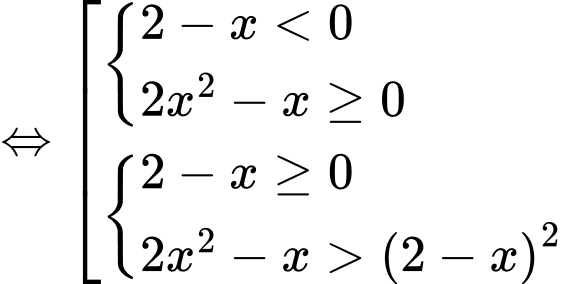
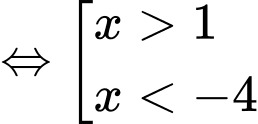
có giá trị nguyên của
giá trị nguyên của 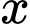 thỏa mãn. Đáp án: B
thỏa mãn. Đáp án: B
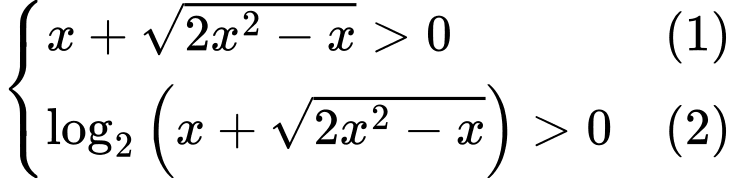 .
.Bất phương trình
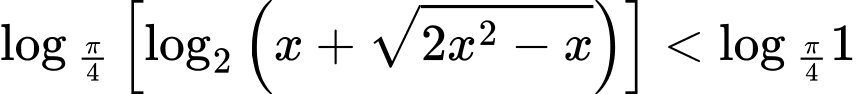
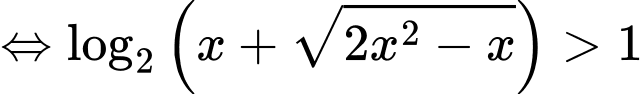 (thỏa
(thỏa  )
)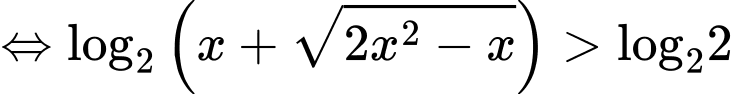
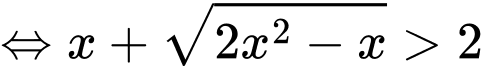 (thỏa
(thỏa  )
)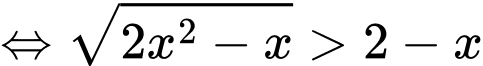
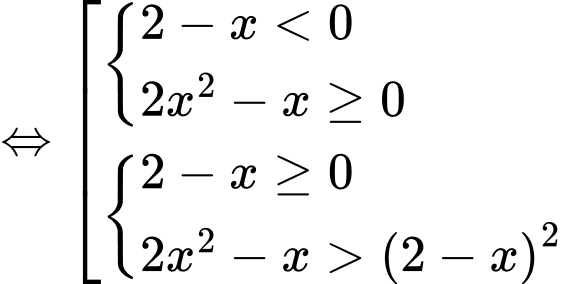
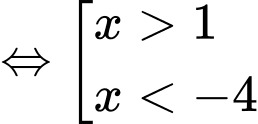
có
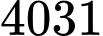 giá trị nguyên của
giá trị nguyên của 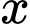 thỏa mãn. Đáp án: B
thỏa mãn. Đáp án: B
Câu 15 [582227]: Cho phương trình 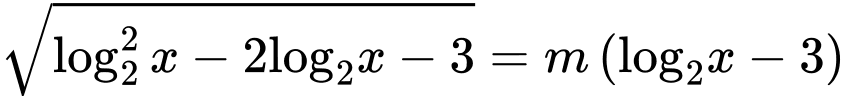 với
với 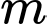 là tham số thực. Tìm tất cả các giá trị của
là tham số thực. Tìm tất cả các giá trị của 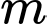 để phương trình có nghiệm thuộc
để phương trình có nghiệm thuộc 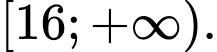
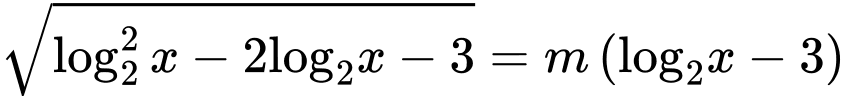 với
với 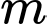 là tham số thực. Tìm tất cả các giá trị của
là tham số thực. Tìm tất cả các giá trị của 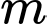 để phương trình có nghiệm thuộc
để phương trình có nghiệm thuộc 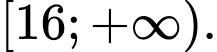
A, 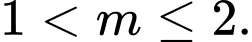
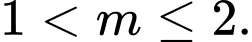
B, 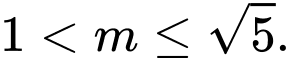
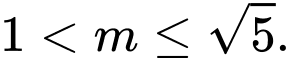
C, 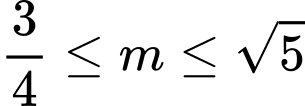 .
.
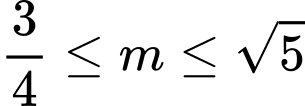 .
.D, 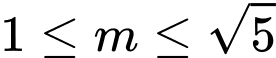 .
.
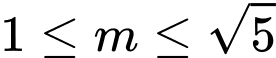 .
.
Đặt 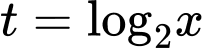 , với
, với 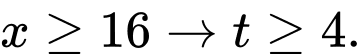
Phương trình trở thành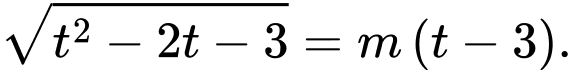

● Với thì phương trình vô nghiệm, do
thì phương trình vô nghiệm, do 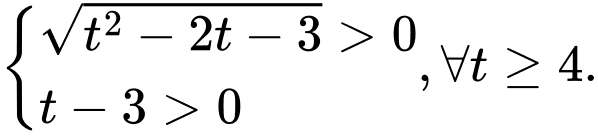
● Với thì
thì 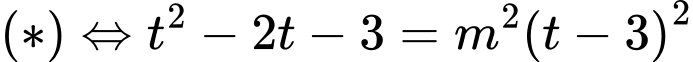

Nếu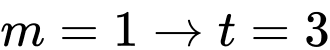 : không thỏa mãn.
: không thỏa mãn.
Nếu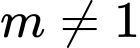 , ta nhẩm được một nghiệm
, ta nhẩm được một nghiệm 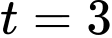 (không thỏa mãn), suy ra nghiệm còn lại
(không thỏa mãn), suy ra nghiệm còn lại 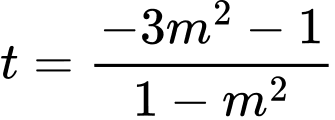 .
.
Do đó để phương trình đã cho có nghiệm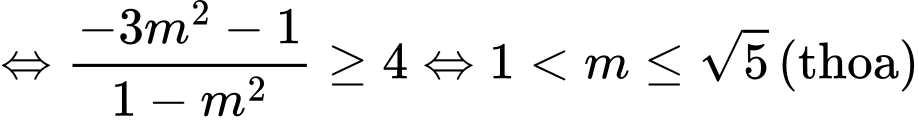 . Đáp án: B
. Đáp án: B
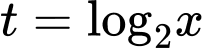 , với
, với 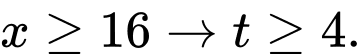
Phương trình trở thành
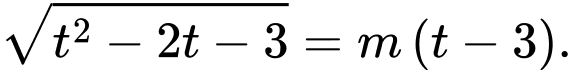

● Với
 thì phương trình vô nghiệm, do
thì phương trình vô nghiệm, do 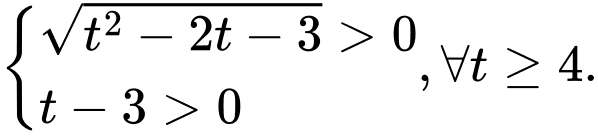
● Với
 thì
thì 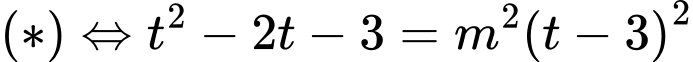

Nếu
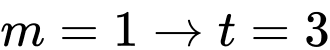 : không thỏa mãn.
: không thỏa mãn.Nếu
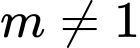 , ta nhẩm được một nghiệm
, ta nhẩm được một nghiệm 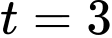 (không thỏa mãn), suy ra nghiệm còn lại
(không thỏa mãn), suy ra nghiệm còn lại 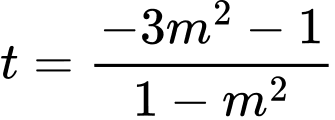 .
.Do đó để phương trình đã cho có nghiệm
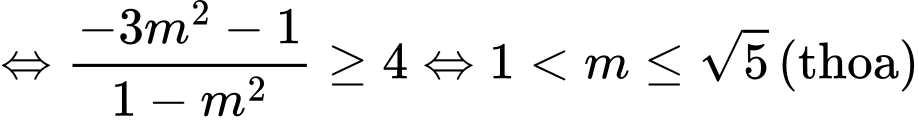 . Đáp án: B
. Đáp án: B Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời từ câu 16,17. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 16 [582228]: Cho hàm số 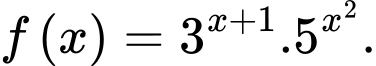 Xác định tính đúng – sai của các mệnh đề sau:
Xác định tính đúng – sai của các mệnh đề sau:
a)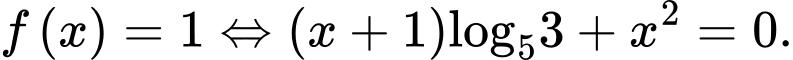
b)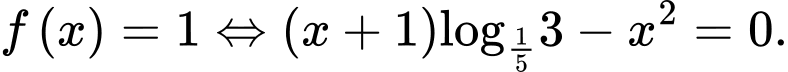
c)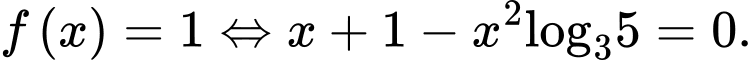
d)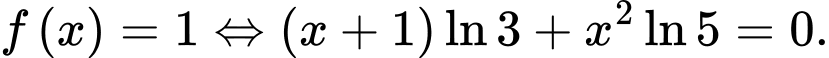
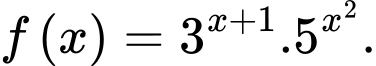 Xác định tính đúng – sai của các mệnh đề sau:
Xác định tính đúng – sai của các mệnh đề sau:a)
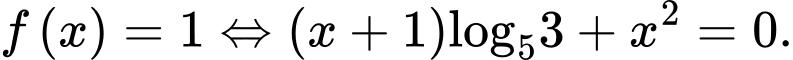
b)
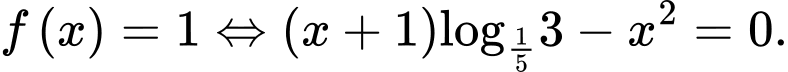
c)
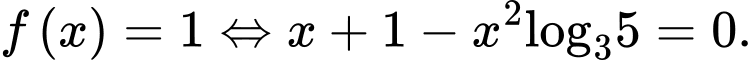
d)
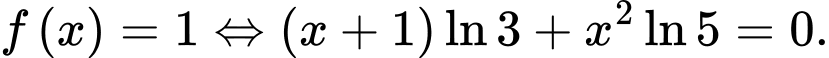
Ta có 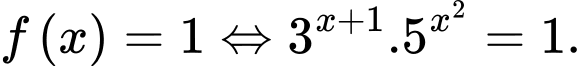

Lấy logarit cơ số 5 hai vế của ta được
ta được 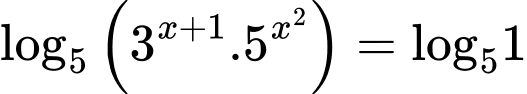
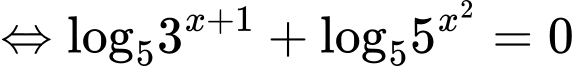
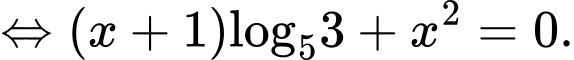 Do đó a) đúng.
Do đó a) đúng.
Lấy logarit cơ số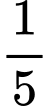 hai vế của
hai vế của  ta được
ta được 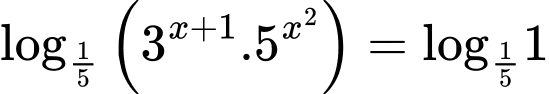
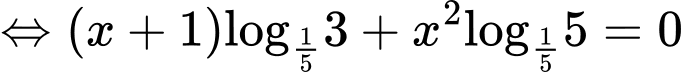
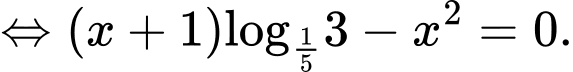 Do đó b) đúng.
Do đó b) đúng.
Lấy logarit cơ số 3 hai vế của ta được
ta được 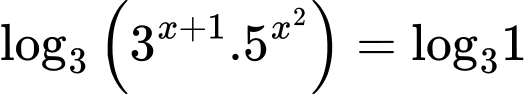
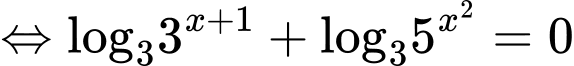
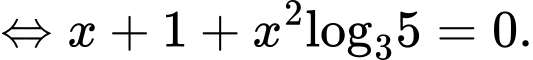 Do đó c) sai.
Do đó c) sai.
Lấy ln hai vế của ta được
ta được 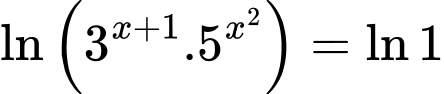

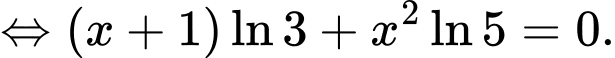 Do đó d) đúng.
Do đó d) đúng.
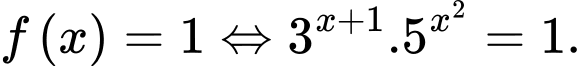

Lấy logarit cơ số 5 hai vế của
 ta được
ta được 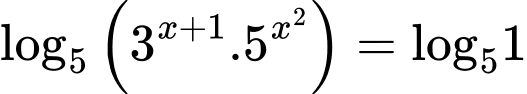
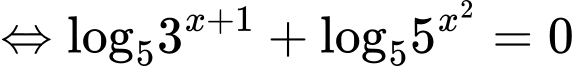
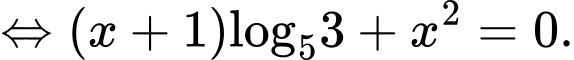 Do đó a) đúng.
Do đó a) đúng.Lấy logarit cơ số
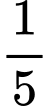 hai vế của
hai vế của  ta được
ta được 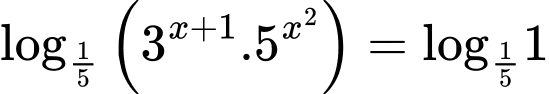
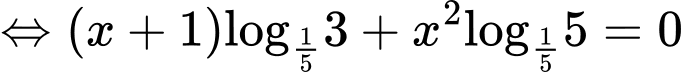
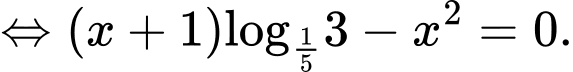 Do đó b) đúng.
Do đó b) đúng.Lấy logarit cơ số 3 hai vế của
 ta được
ta được 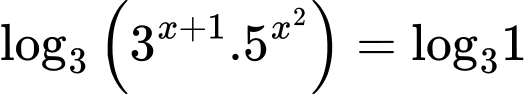
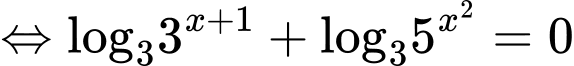
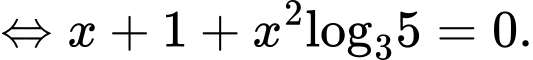 Do đó c) sai.
Do đó c) sai.Lấy ln hai vế của
 ta được
ta được 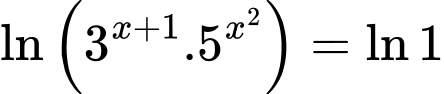

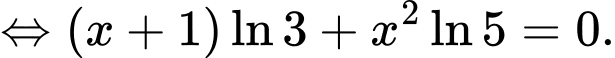 Do đó d) đúng.
Do đó d) đúng.
Câu 17 [582229]: Cho phương trình 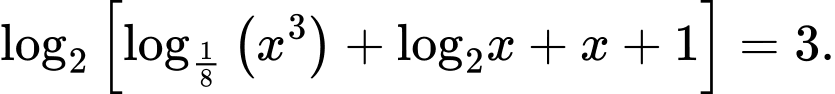 Xác định tính đúng – sai của các mệnh đề sau:
Xác định tính đúng – sai của các mệnh đề sau:
a) Nghiệm của phương trình là số nguyên.
b) Nghiệm của phương trình là số chính phương.
c) Nghiệm của phương trình là số nguyên tố.
d) Nghiệm của phương trình là số vô tỉ.
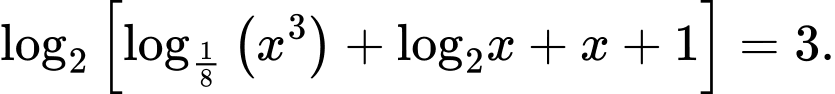 Xác định tính đúng – sai của các mệnh đề sau:
Xác định tính đúng – sai của các mệnh đề sau: a) Nghiệm của phương trình là số nguyên.
b) Nghiệm của phương trình là số chính phương.
c) Nghiệm của phương trình là số nguyên tố.
d) Nghiệm của phương trình là số vô tỉ.
Điều kiện: 
Phương trình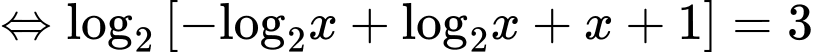
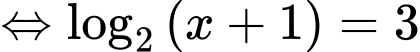


Vậy a) và c) đúng, b) và d) sai.

Phương trình
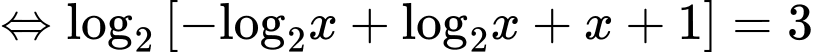
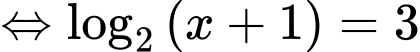


Vậy a) và c) đúng, b) và d) sai.
Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [582230]: Cho phương trình 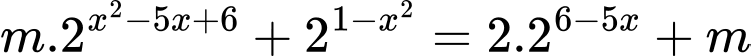 với
với 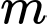 là tham số thực. Có tất cả bao nhiêu giá trị của
là tham số thực. Có tất cả bao nhiêu giá trị của 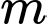 để phương trình có đúng ba nghiệm phân biệt.
để phương trình có đúng ba nghiệm phân biệt.
TRẢ LỜI: ……………………….
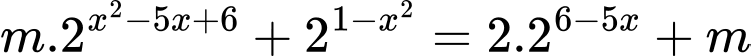 với
với 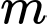 là tham số thực. Có tất cả bao nhiêu giá trị của
là tham số thực. Có tất cả bao nhiêu giá trị của 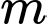 để phương trình có đúng ba nghiệm phân biệt.
để phương trình có đúng ba nghiệm phân biệt.TRẢ LỜI: ……………………….
Ta có 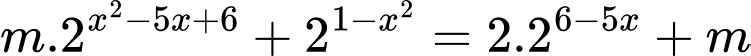
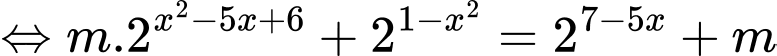
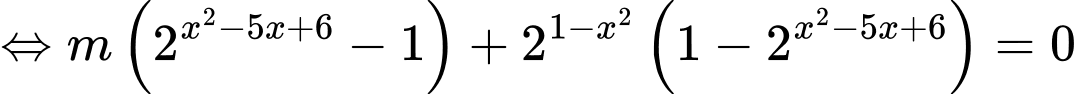
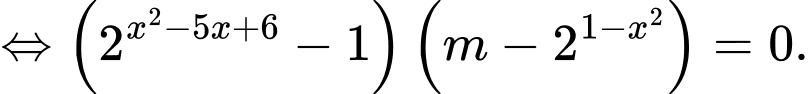
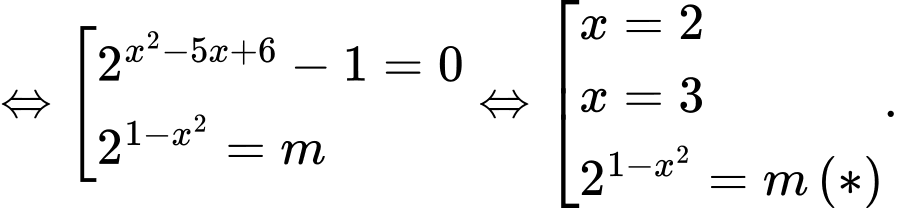
Yêu cầu bài toán tương đương với
TH1: Phương trình có nghiệm duy nhất
có nghiệm duy nhất 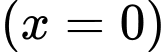 , suy ra
, suy ra 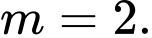
TH2: Phương trình có hai nghiệm phân biệt, trong đó có một nghiệm là
có hai nghiệm phân biệt, trong đó có một nghiệm là 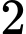 và nghiệm còn lại khác
và nghiệm còn lại khác 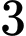
TH3: Phương trình có hai nghiệm phân biệt, trong đó có một nghiệm là
có hai nghiệm phân biệt, trong đó có một nghiệm là 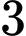 và nghiệm còn lại khác
và nghiệm còn lại khác 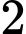
Vậy có tất cả ba giá trị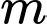 thỏa mãn.
thỏa mãn.
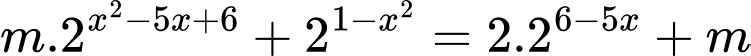
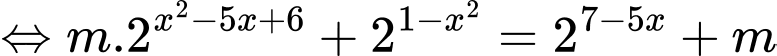
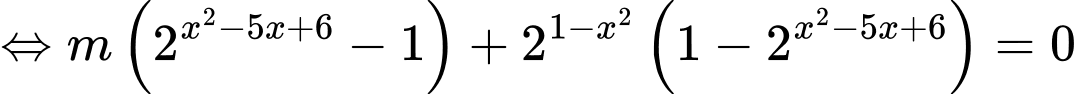
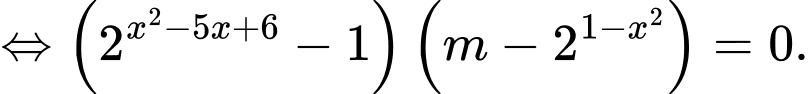
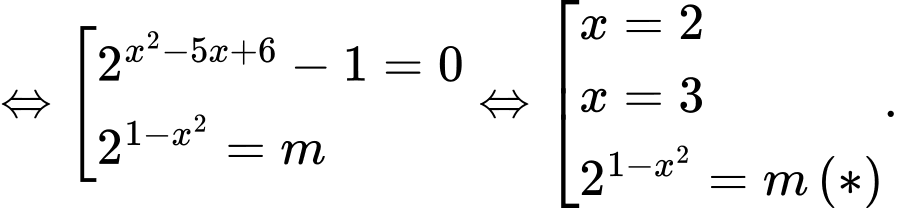
Yêu cầu bài toán tương đương với
TH1: Phương trình
 có nghiệm duy nhất
có nghiệm duy nhất 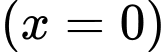 , suy ra
, suy ra 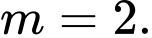
TH2: Phương trình
 có hai nghiệm phân biệt, trong đó có một nghiệm là
có hai nghiệm phân biệt, trong đó có một nghiệm là 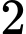 và nghiệm còn lại khác
và nghiệm còn lại khác 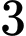
TH3: Phương trình
 có hai nghiệm phân biệt, trong đó có một nghiệm là
có hai nghiệm phân biệt, trong đó có một nghiệm là 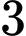 và nghiệm còn lại khác
và nghiệm còn lại khác 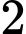
Vậy có tất cả ba giá trị
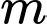 thỏa mãn.
thỏa mãn.
Câu 19 [582231]: Hỏi có bao nhiêu giá trị 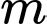 nguyên trong
nguyên trong 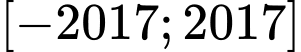 để phương trình
để phương trình 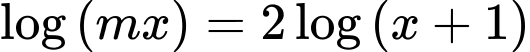 có nghiệm duy nhất?
có nghiệm duy nhất?
TRẢ LỜI: ……………………….
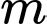 nguyên trong
nguyên trong 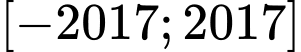 để phương trình
để phương trình 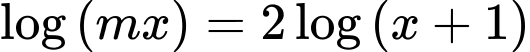 có nghiệm duy nhất?
có nghiệm duy nhất? TRẢ LỜI: ……………………….
Điều kiện: 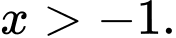
Phương trình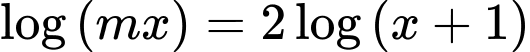
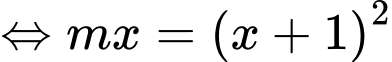
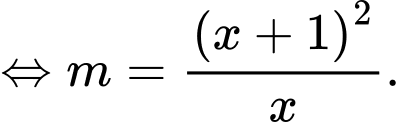
Xét hàm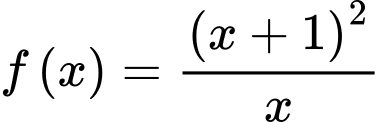 trên
trên 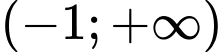 .
.
Đạo hàm và lập bảng biến thiên, ta được
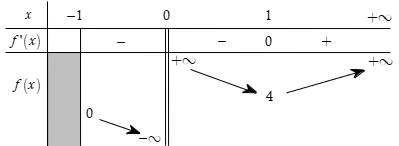
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm duy nhất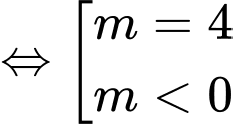
có giá trị
giá trị 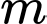 nguyên.
nguyên.
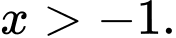
Phương trình
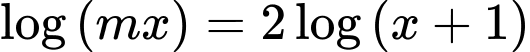
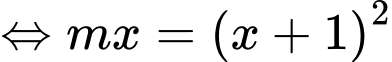
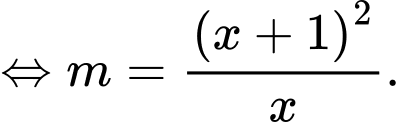
Xét hàm
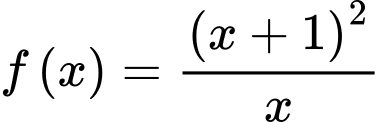 trên
trên 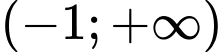 .
.Đạo hàm và lập bảng biến thiên, ta được

Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm duy nhất
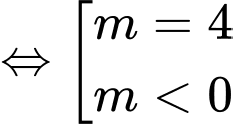
có
 giá trị
giá trị 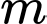 nguyên.
nguyên.
Câu 20 [582232]: Cho phương trình 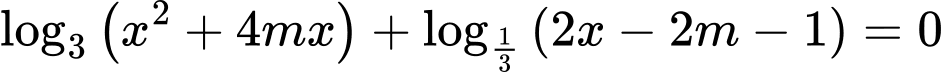 với
với 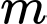 là tham số thực. Gọi
là tham số thực. Gọi 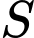 là tập tất cả các giá trị của
là tập tất cả các giá trị của 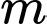 để phương trình có nghiệm duy nhất, khi đó
để phương trình có nghiệm duy nhất, khi đó 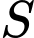 có dạng
có dạng 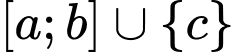 với
với 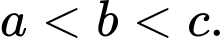 Tính
Tính 
TRẢ LỜI: ……………………….
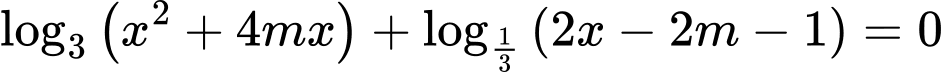 với
với 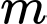 là tham số thực. Gọi
là tham số thực. Gọi 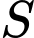 là tập tất cả các giá trị của
là tập tất cả các giá trị của 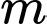 để phương trình có nghiệm duy nhất, khi đó
để phương trình có nghiệm duy nhất, khi đó 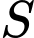 có dạng
có dạng 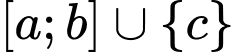 với
với 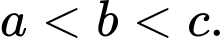 Tính
Tính 
TRẢ LỜI: ……………………….
Phương trình 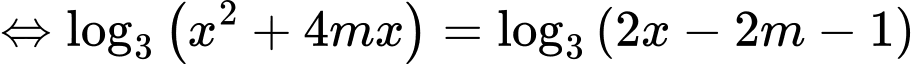
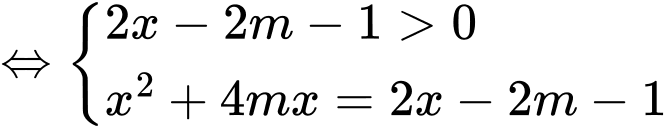
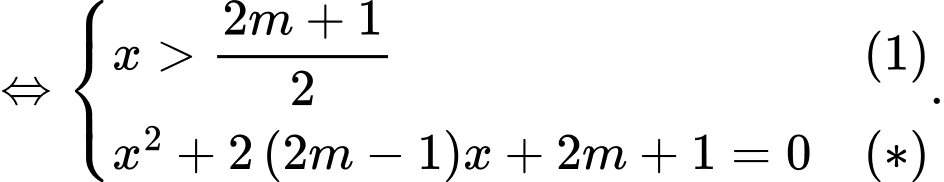
Yêu cầu bài toán phương trình
phương trình  có một nghiệm thỏa mãn
có một nghiệm thỏa mãn  .
.
● TH1: có nghiệm kép thỏa
có nghiệm kép thỏa
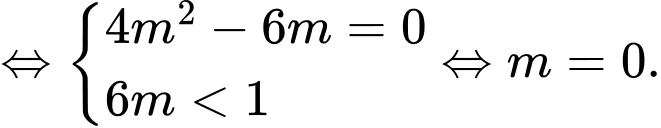
● TH2: có hai nghiệm
có hai nghiệm 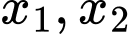 thỏa
thỏa 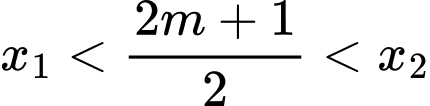
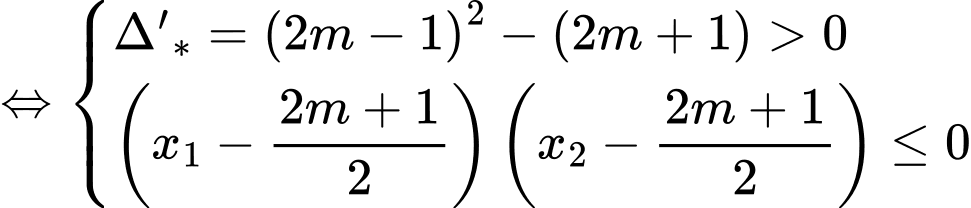
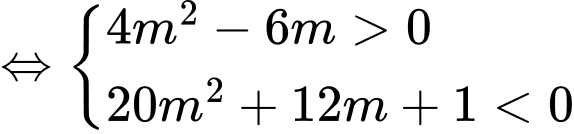
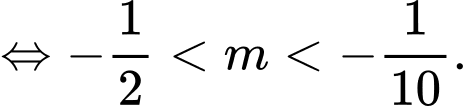
● TH3: có nghiệm
có nghiệm 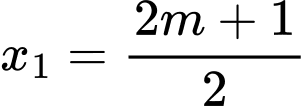 và nghiệm
và nghiệm 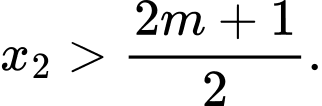
Thay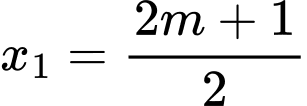 vào phương trình
vào phương trình  ta nhận được
ta nhận được 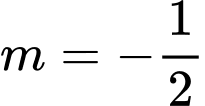 hoặc
hoặc 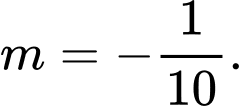
Thử lại ta thấy thỏa mãn.
Kết hợp các trường hợp, ta được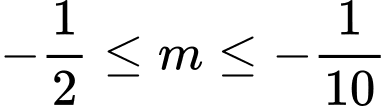 hoặc
hoặc 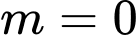 thỏa mãn yctb.
thỏa mãn yctb.
Vậy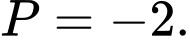
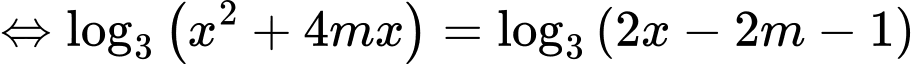
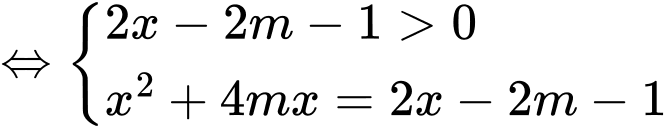
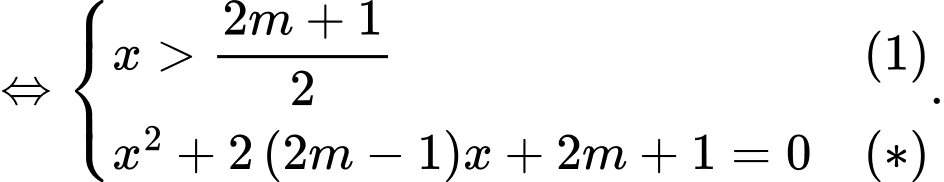
Yêu cầu bài toán
 phương trình
phương trình  có một nghiệm thỏa mãn
có một nghiệm thỏa mãn  .
.● TH1:
 có nghiệm kép thỏa
có nghiệm kép thỏa 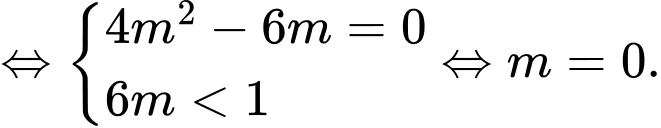
● TH2:
 có hai nghiệm
có hai nghiệm 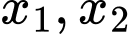 thỏa
thỏa 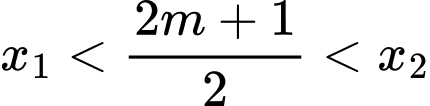
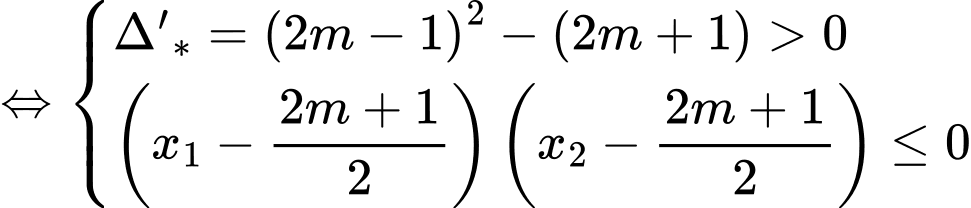
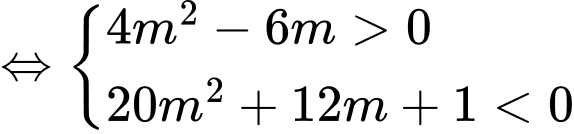
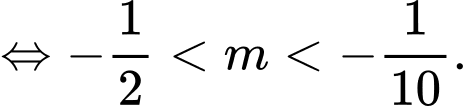
● TH3:
 có nghiệm
có nghiệm 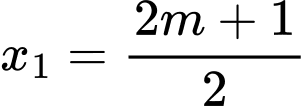 và nghiệm
và nghiệm 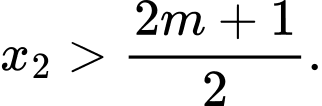
Thay
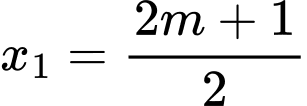 vào phương trình
vào phương trình  ta nhận được
ta nhận được 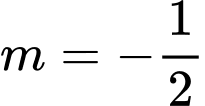 hoặc
hoặc 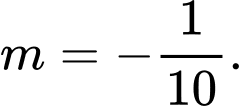
Thử lại ta thấy thỏa mãn.
Kết hợp các trường hợp, ta được
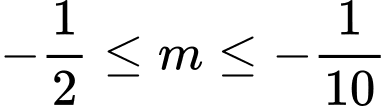 hoặc
hoặc 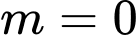 thỏa mãn yctb.
thỏa mãn yctb.Vậy
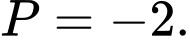
Dạng câu hỏi: Câu hỏi kéo thả.
Câu 21 [582233]: Xét các số thực 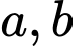 thỏa mãn điều kiện
thỏa mãn điều kiện 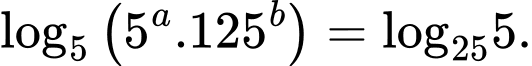
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Nếu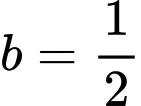 thì giá trị của số thực
thì giá trị của số thực 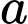 bằng _______.
bằng _______.
Mối liên hệ giữa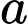 và
và 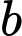 là
là 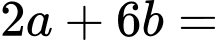 _______.
_______.
Nếu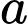 là số nguyên âm thuộc
là số nguyên âm thuộc 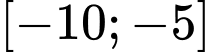 thì có _______ giá trị nguyên dương của
thì có _______ giá trị nguyên dương của 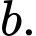
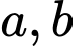 thỏa mãn điều kiện
thỏa mãn điều kiện 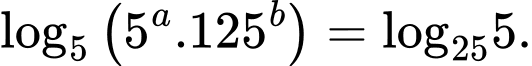
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Nếu
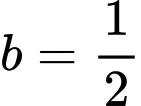 thì giá trị của số thực
thì giá trị của số thực 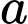 bằng _______.
bằng _______.Mối liên hệ giữa
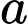 và
và 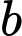 là
là 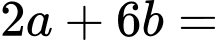 _______.
_______.Nếu
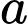 là số nguyên âm thuộc
là số nguyên âm thuộc 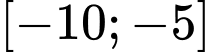 thì có _______ giá trị nguyên dương của
thì có _______ giá trị nguyên dương của 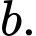
Nếu 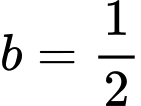 thì giá trị của số thực
thì giá trị của số thực 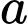 bằng
bằng 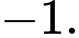
Mối liên hệ giữa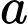 và
và 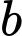 là
là 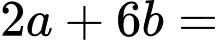 1.
1.
Nếu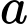 là số nguyên âm thuộc
là số nguyên âm thuộc 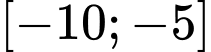 thì có 0 giá trị nguyên dương của
thì có 0 giá trị nguyên dương của 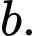
Lời giải
Ta có: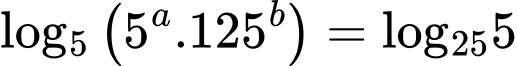
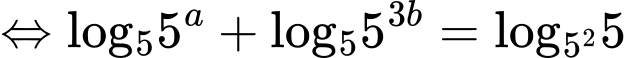

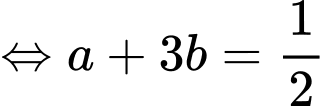
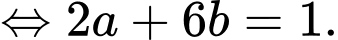
Nếu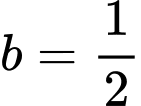 thì
thì 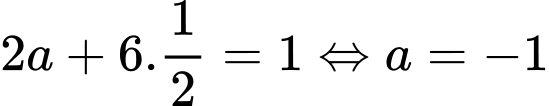 .
.
Vì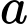 là số nguyên âm thuộc
là số nguyên âm thuộc 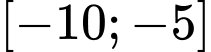 nên ta có bảng sau:
nên ta có bảng sau:
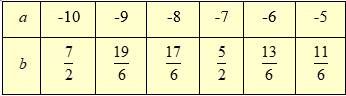
Vậy không có giá trị nguyên dương của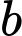 thỏa mãn.
thỏa mãn.
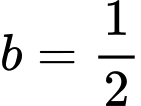 thì giá trị của số thực
thì giá trị của số thực 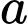 bằng
bằng 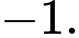
Mối liên hệ giữa
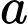 và
và 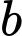 là
là 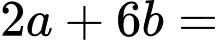 1.
1.Nếu
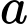 là số nguyên âm thuộc
là số nguyên âm thuộc 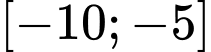 thì có 0 giá trị nguyên dương của
thì có 0 giá trị nguyên dương của 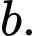
Lời giải
Ta có:
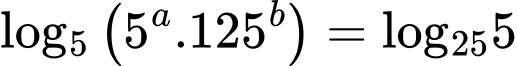
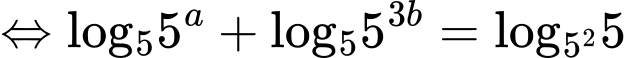

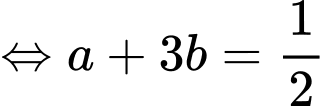
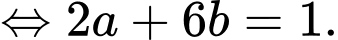
Nếu
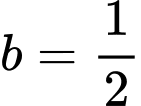 thì
thì 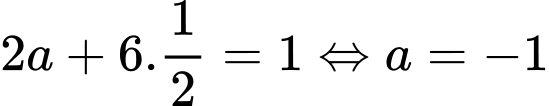 .
.Vì
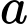 là số nguyên âm thuộc
là số nguyên âm thuộc 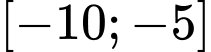 nên ta có bảng sau:
nên ta có bảng sau:
Vậy không có giá trị nguyên dương của
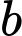 thỏa mãn.
thỏa mãn.