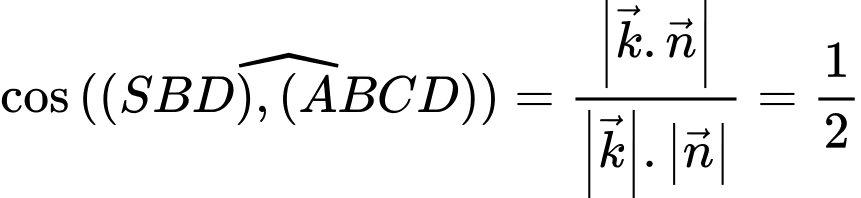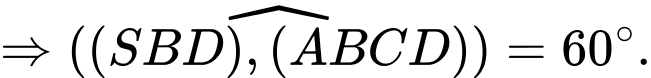Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 15. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
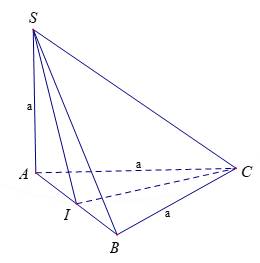
Câu 1 [585909]: Cho một hình thoi 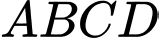 cạnh
cạnh 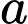 và một điểm
và một điểm 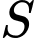 nằm ngoài mặt phẳng chứa hình thoi sao cho
nằm ngoài mặt phẳng chứa hình thoi sao cho  và vuông góc với
và vuông góc với 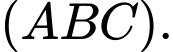 Tính góc giữa
Tính góc giữa 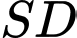 và
và 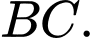
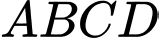 cạnh
cạnh 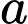 và một điểm
và một điểm 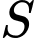 nằm ngoài mặt phẳng chứa hình thoi sao cho
nằm ngoài mặt phẳng chứa hình thoi sao cho  và vuông góc với
và vuông góc với 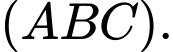 Tính góc giữa
Tính góc giữa 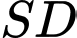 và
và 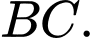
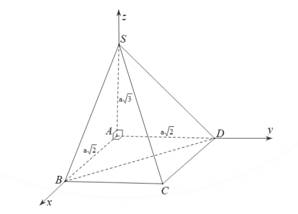
A, 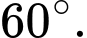
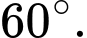
B, 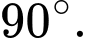
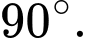
C, 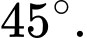
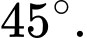
D, 
Ta có:
 Đáp án: C
Đáp án: C
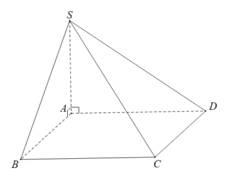
Câu 2 [585910]: Cho hình chóp 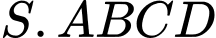 có đáy
có đáy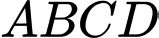 là hình bình hành với
là hình bình hành với 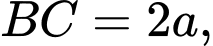
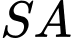 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 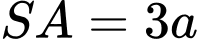 (minh họa như hình vẽ). Góc giữa hai đường thẳng
(minh họa như hình vẽ). Góc giữa hai đường thẳng 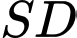 và
và 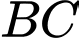 nằm trong khoảng nào?
nằm trong khoảng nào?
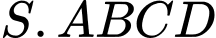 có đáy
có đáy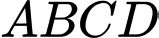 là hình bình hành với
là hình bình hành với 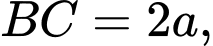
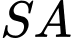 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 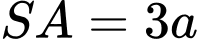 (minh họa như hình vẽ). Góc giữa hai đường thẳng
(minh họa như hình vẽ). Góc giữa hai đường thẳng 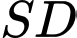 và
và 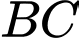 nằm trong khoảng nào?
nằm trong khoảng nào?
A, 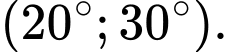
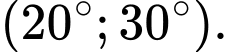
B, 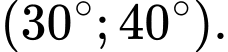
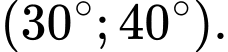
C, 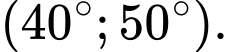
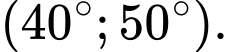
D, 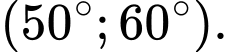
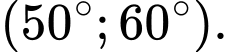
Chọn D
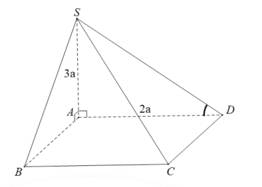
Ta có: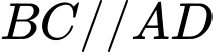
 ( Do
( Do 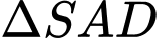 vuông tại
vuông tại 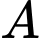 nên
nên 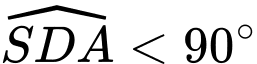 )
)
Xét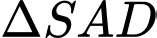 vuông tại
vuông tại 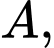 ta có:
ta có: 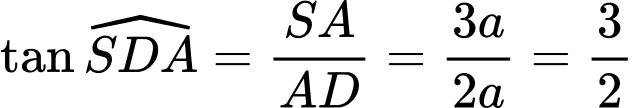
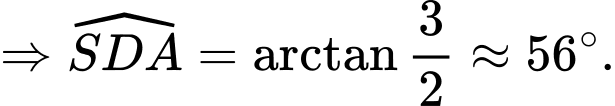 Đáp án: D
Đáp án: D

Ta có:
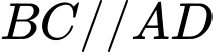
 ( Do
( Do 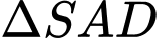 vuông tại
vuông tại 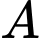 nên
nên 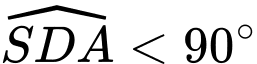 )
) Xét
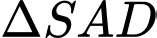 vuông tại
vuông tại 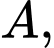 ta có:
ta có: 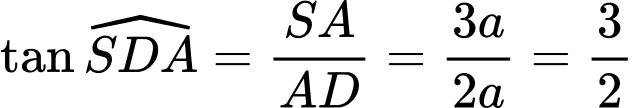
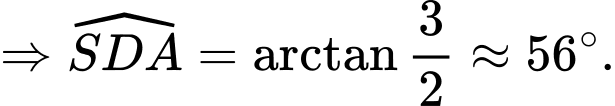 Đáp án: D
Đáp án: D
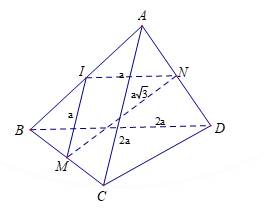
Câu 3 [585911]: Cho tứ diện 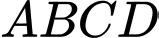 có
có 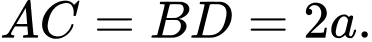 Gọi
Gọi 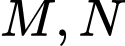 lần lượt là trung điểm
lần lượt là trung điểm 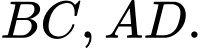 Biết rằng
Biết rằng 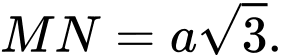 Tính góc của
Tính góc của 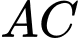 và
và 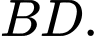
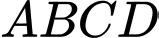 có
có 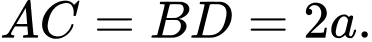 Gọi
Gọi 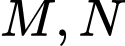 lần lượt là trung điểm
lần lượt là trung điểm 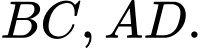 Biết rằng
Biết rằng 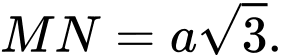 Tính góc của
Tính góc của 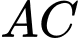 và
và 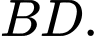
A, 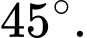
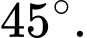
B, 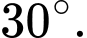
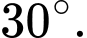
C, 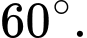
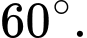
D, 
Chọn C
Gọi là trung điểm của
là trung điểm của 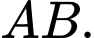 Ta có
Ta có 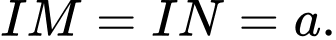
Áp dụng định lý cosin cho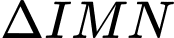 ta có:
ta có:
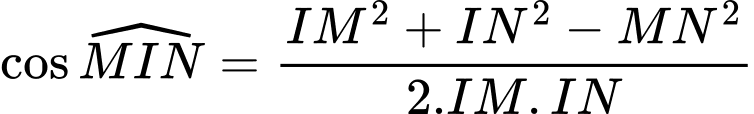
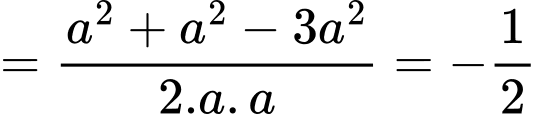
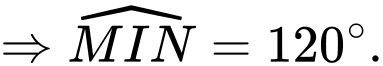
Vì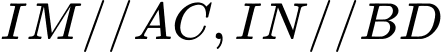
 Đáp án: C
Đáp án: C

Gọi
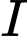 là trung điểm của
là trung điểm của 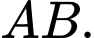 Ta có
Ta có 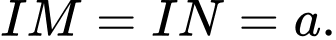
Áp dụng định lý cosin cho
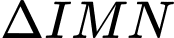 ta có:
ta có: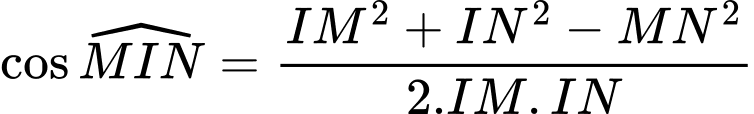
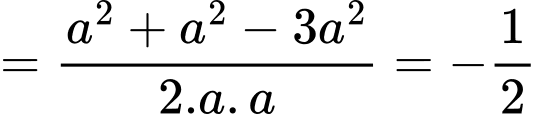
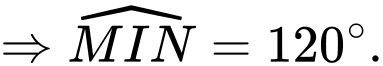
Vì
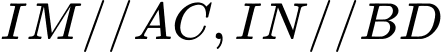
 Đáp án: C
Đáp án: C
Câu 4 [585912]: Cho tứ diện đều 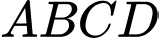 cạnh
cạnh 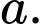 Gọi
Gọi  là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 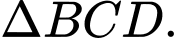 Gọi
Gọi 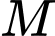 là trung điểm
là trung điểm 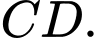 Tính cosin góc của
Tính cosin góc của 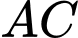 và
và 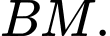
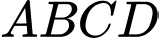 cạnh
cạnh 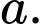 Gọi
Gọi  là tâm đường tròn ngoại tiếp
là tâm đường tròn ngoại tiếp 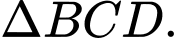 Gọi
Gọi 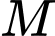 là trung điểm
là trung điểm 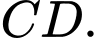 Tính cosin góc của
Tính cosin góc của 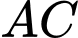 và
và 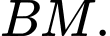
A, 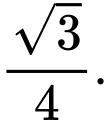
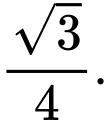
B, 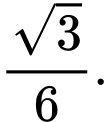
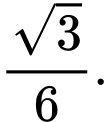
C, 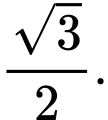
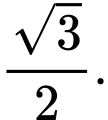
D, 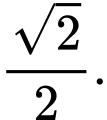
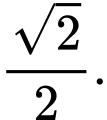
Chọn B
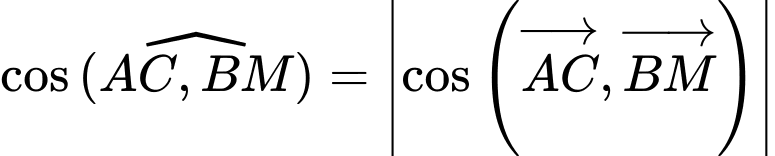
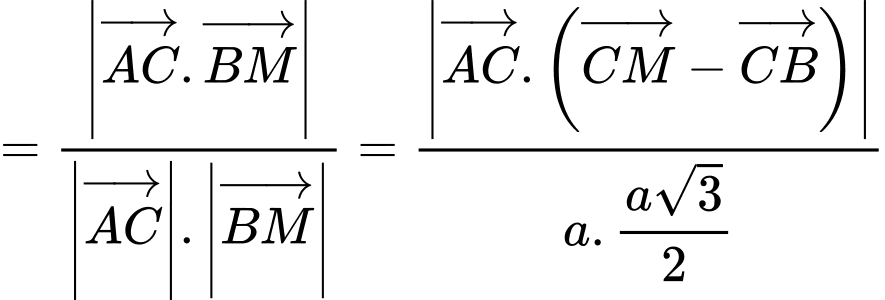
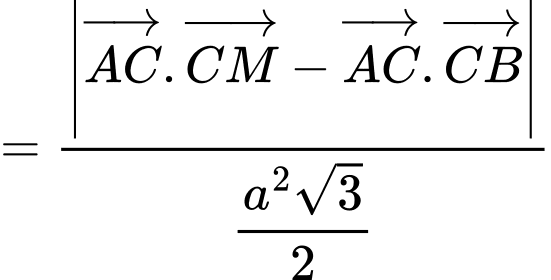
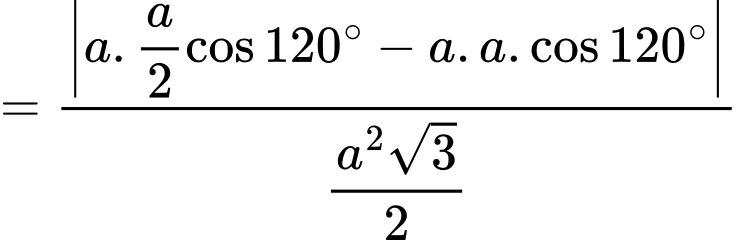
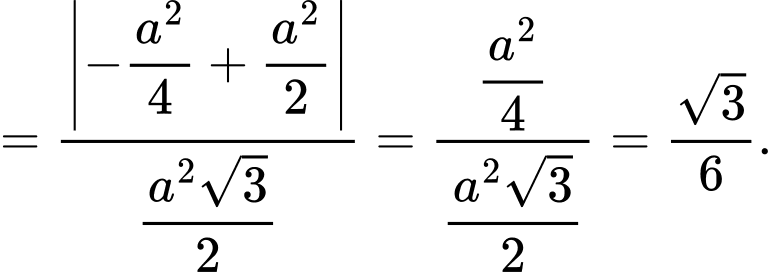 Đáp án: B
Đáp án: B
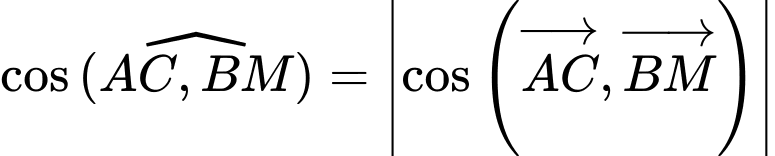
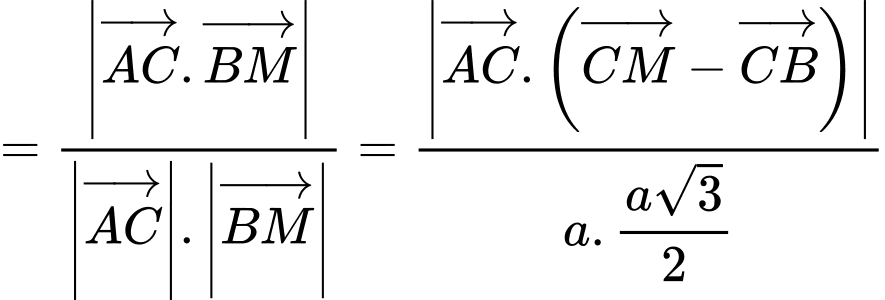
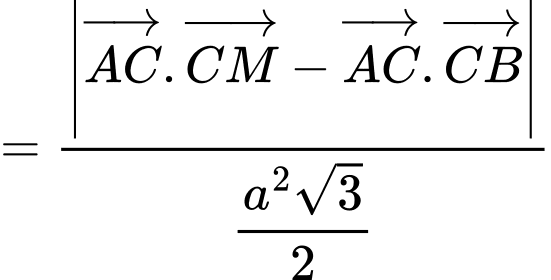
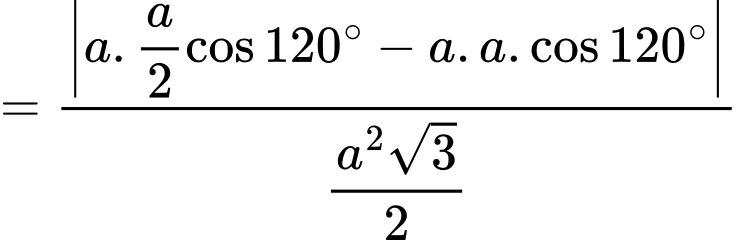
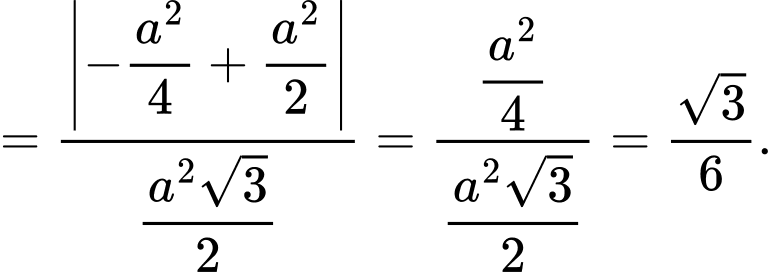 Đáp án: B
Đáp án: B
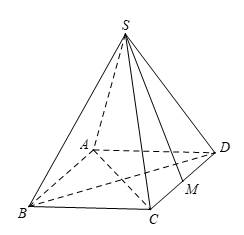
Câu 5 [585913]: Cho hình chóp 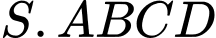 có đáy
có đáy 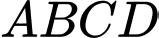 là hình chữ nhật với
là hình chữ nhật với 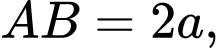
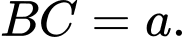 Các cạnh bên của hình chóp cùng bằng
Các cạnh bên của hình chóp cùng bằng 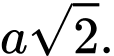 Khi đó, góc giữa hai đường thẳng
Khi đó, góc giữa hai đường thẳng  và
và 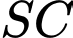 bằng:
bằng:
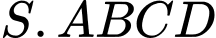 có đáy
có đáy 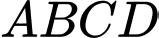 là hình chữ nhật với
là hình chữ nhật với 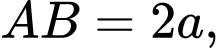
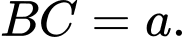 Các cạnh bên của hình chóp cùng bằng
Các cạnh bên của hình chóp cùng bằng 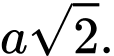 Khi đó, góc giữa hai đường thẳng
Khi đó, góc giữa hai đường thẳng  và
và 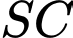 bằng:
bằng: A, 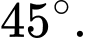
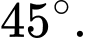
B, 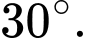
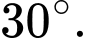
C, 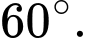
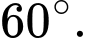
D, 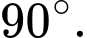
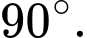
Chọn A
Ta có: nên
nên 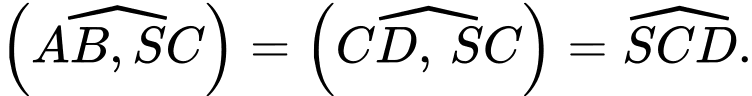
Gọi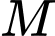 là trung điểm của
là trung điểm của 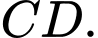
Tam giác vuông tại
vuông tại 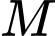 và có
và có 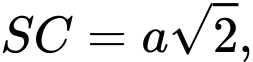
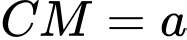 nên là tam giác vuông cân tại
nên là tam giác vuông cân tại 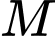 nên
nên 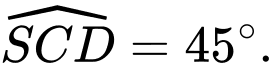
Vậy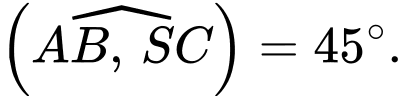 Đáp án: A
Đáp án: A

Ta có:
 nên
nên 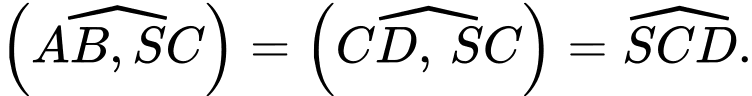
Gọi
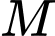 là trung điểm của
là trung điểm của 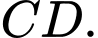
Tam giác
 vuông tại
vuông tại 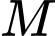 và có
và có 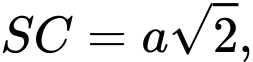
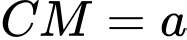 nên là tam giác vuông cân tại
nên là tam giác vuông cân tại 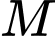 nên
nên 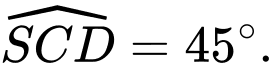
Vậy
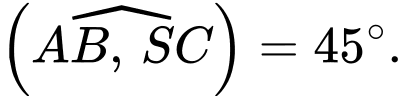 Đáp án: A
Đáp án: A
Câu 6 [585914]: Cho tứ diện 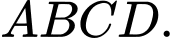 Gọi
Gọi 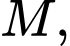
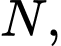
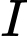 lần lượt là trung điểm của
lần lượt là trung điểm của 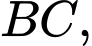
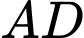 và
và 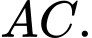 Cho
Cho 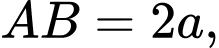
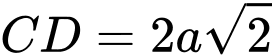 và
và 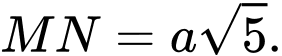 Tính góc
Tính góc 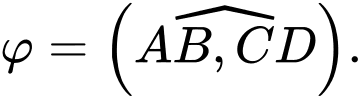
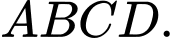 Gọi
Gọi 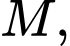
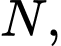
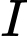 lần lượt là trung điểm của
lần lượt là trung điểm của 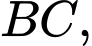
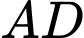 và
và 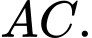 Cho
Cho 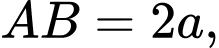
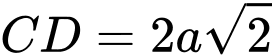 và
và 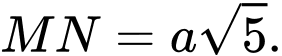 Tính góc
Tính góc 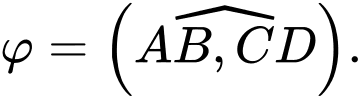
A, 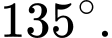
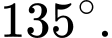
B, 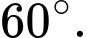
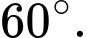
C, 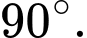
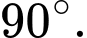
D, 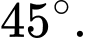
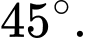
Chọn D
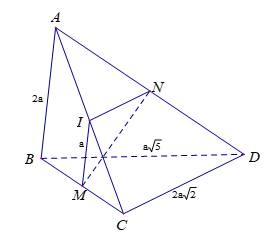
Theo tính chất đường trung bình trong tam giác: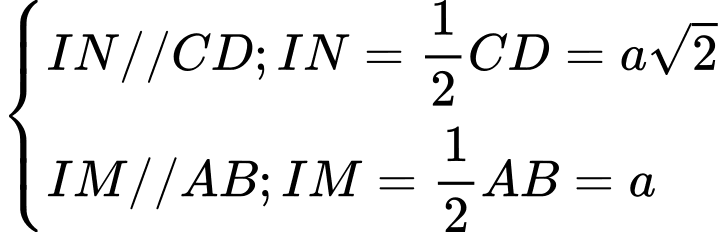
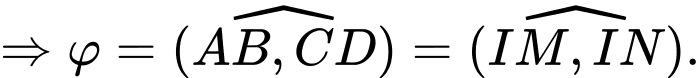
Áp dụng định lý cosin ta có:
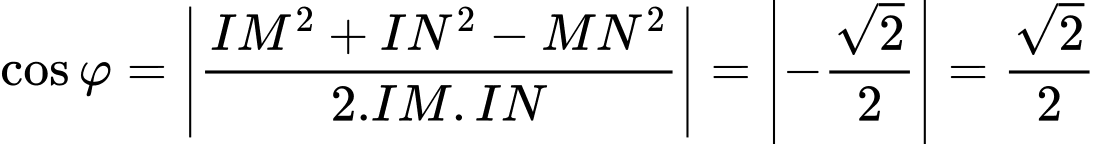
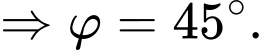 Đáp án: D
Đáp án: D

Theo tính chất đường trung bình trong tam giác:
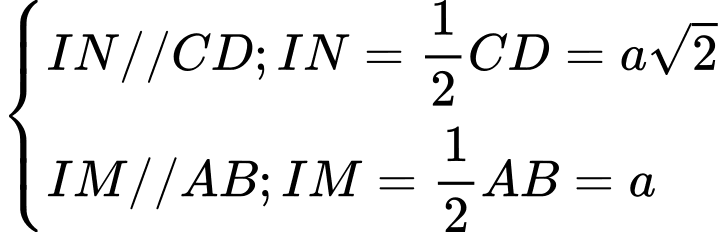
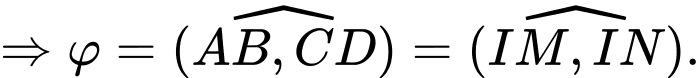
Áp dụng định lý cosin ta có:
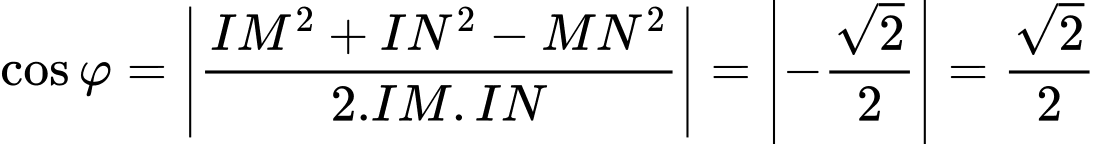
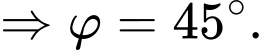 Đáp án: D
Đáp án: D
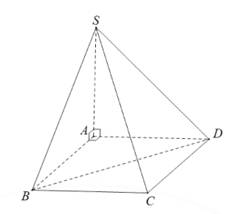
Câu 7 [585915]: Cho hình chóp 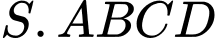 có đáy
có đáy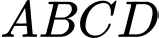 là hình chữ nhật với
là hình chữ nhật với 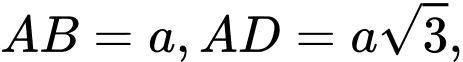
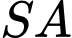 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 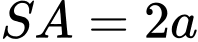 (minh họa như hình vẽ). Góc giữa hai đường thẳng
(minh họa như hình vẽ). Góc giữa hai đường thẳng 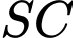 và
và 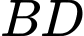 nằm trong khoảng nào?
nằm trong khoảng nào?
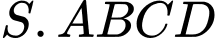 có đáy
có đáy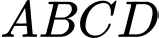 là hình chữ nhật với
là hình chữ nhật với 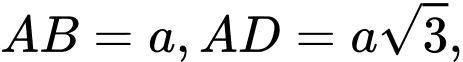
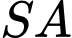 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 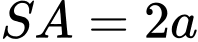 (minh họa như hình vẽ). Góc giữa hai đường thẳng
(minh họa như hình vẽ). Góc giữa hai đường thẳng 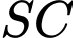 và
và 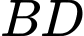 nằm trong khoảng nào?
nằm trong khoảng nào?
A, 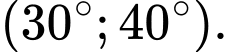
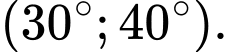
B, 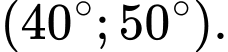
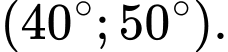
C, 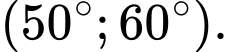
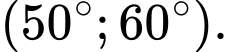
D, 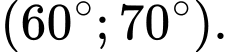
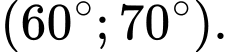
Chọn D
Gọi và
và  là trung điểm
là trung điểm 
Xét hình chữ nhật ta có:
ta có: 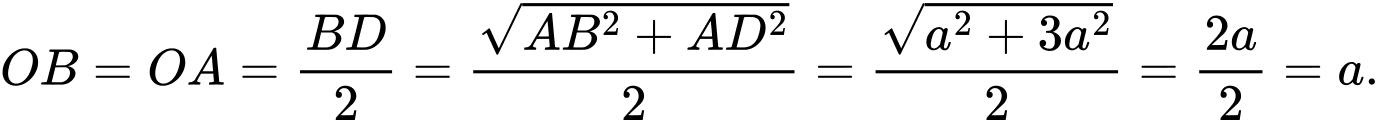
Xét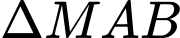 vuông tại
vuông tại 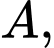 ta có:
ta có: 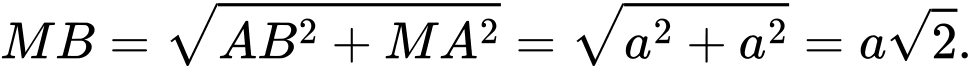
Xét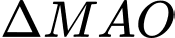 vuông tại
vuông tại 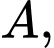 ta có:
ta có: 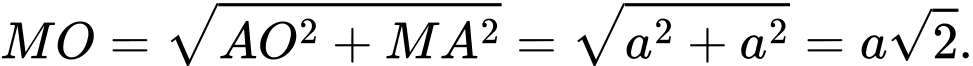
Xét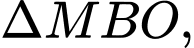 ta có:
ta có: 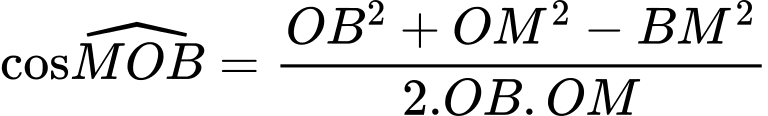
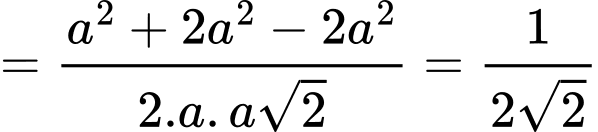
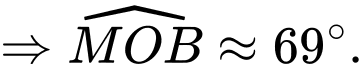
Ta có: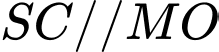
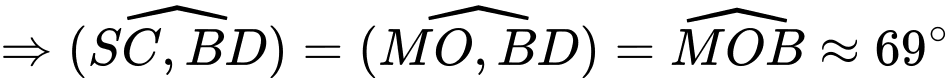 ( Do
( Do 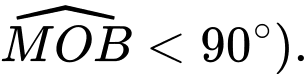
Cách khác: Sử dụng phương pháp tọa độ
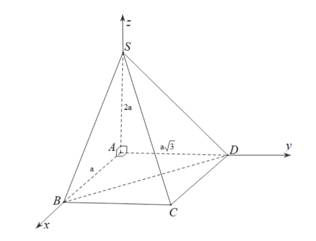
Chọn hệ trục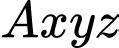 như hình vẽ với
như hình vẽ với 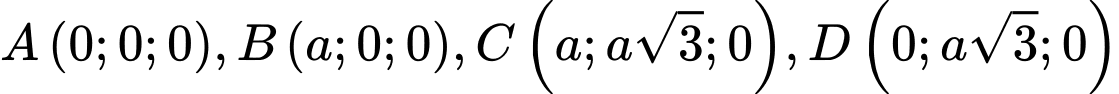 và
và 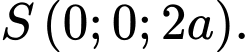
Ta có: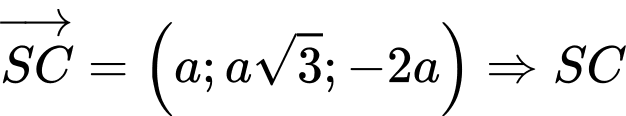 có một vectơ chỉ phương là
có một vectơ chỉ phương là 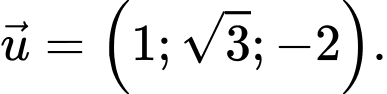
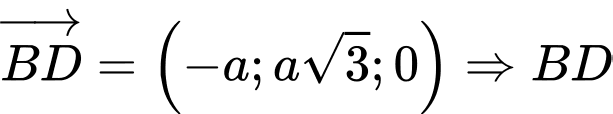 có một vectơ chỉ phương là
có một vectơ chỉ phương là 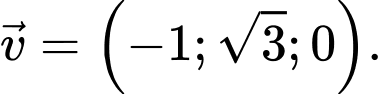
Suy ra: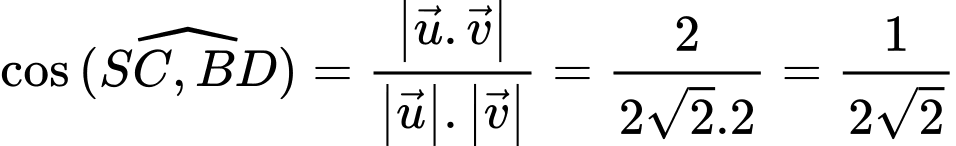
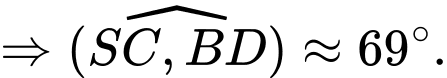 Đáp án: D
Đáp án: D

Gọi
 và
và 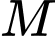 là trung điểm
là trung điểm 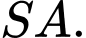
Xét hình chữ nhật
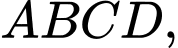 ta có:
ta có: 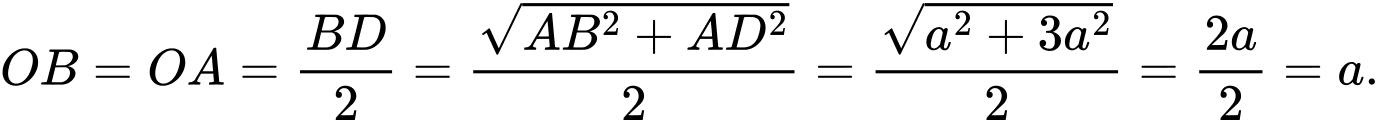
Xét
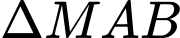 vuông tại
vuông tại 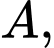 ta có:
ta có: 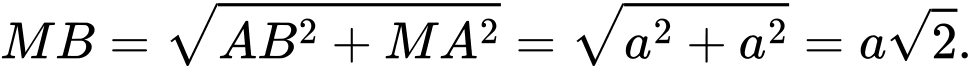
Xét
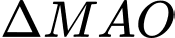 vuông tại
vuông tại 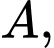 ta có:
ta có: 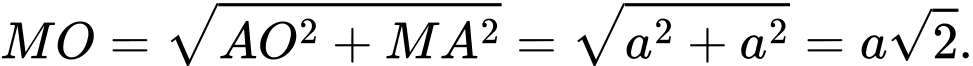
Xét
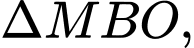 ta có:
ta có: 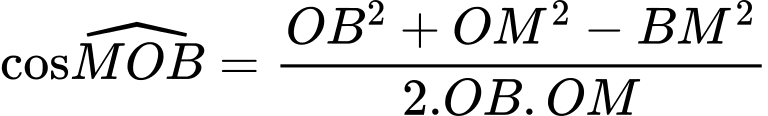
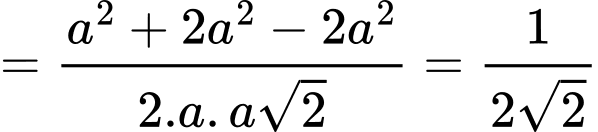
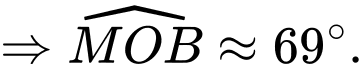
Ta có:
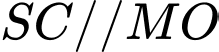
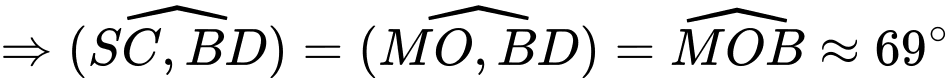 ( Do
( Do 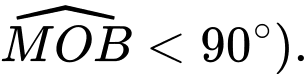
Cách khác: Sử dụng phương pháp tọa độ

Chọn hệ trục
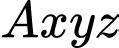 như hình vẽ với
như hình vẽ với 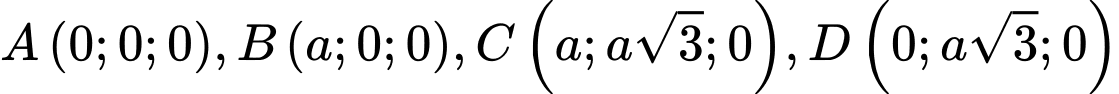 và
và 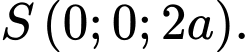
Ta có:
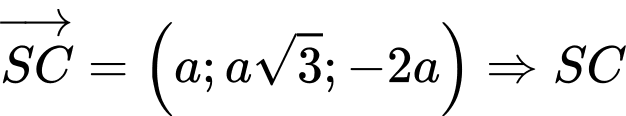 có một vectơ chỉ phương là
có một vectơ chỉ phương là 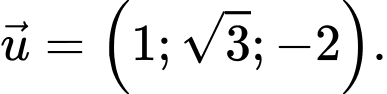
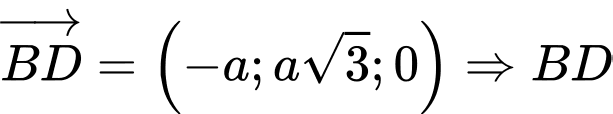 có một vectơ chỉ phương là
có một vectơ chỉ phương là 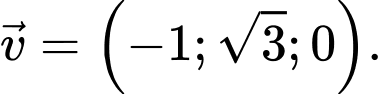
Suy ra:
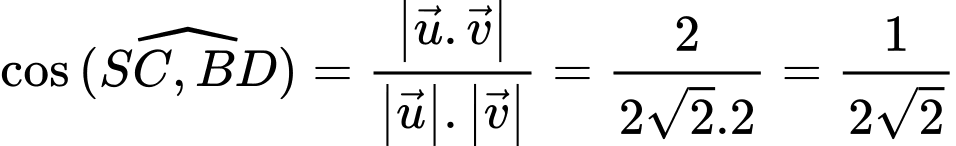
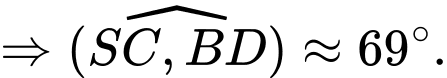 Đáp án: D
Đáp án: D
Câu 8 [585916]: Cho hình chóp 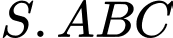 có các
có các 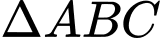 và
và 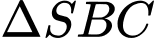 là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Góc giữa đường thẳng
là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Góc giữa đường thẳng 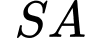 và
và 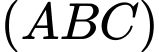 bằng
bằng
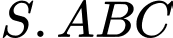 có các
có các 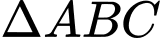 và
và 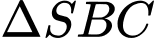 là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Góc giữa đường thẳng
là các tam giác đều và nằm trong hai mặt phẳng vuông góc với nhau. Góc giữa đường thẳng 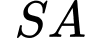 và
và 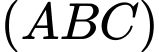 bằng
bằng A, 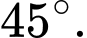
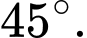
B, 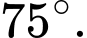
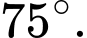
C, 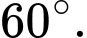
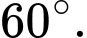
D, 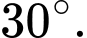
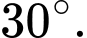
Chọn A
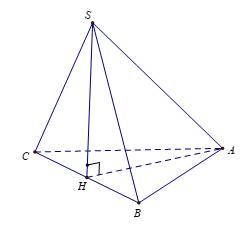
Theo giả thiết ta có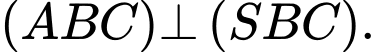
Trong mặt phẳng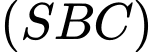 kẻ
kẻ 
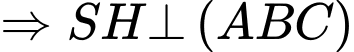 nên
nên 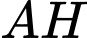 là hình chiếu của
là hình chiếu của 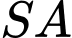 trên
trên 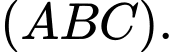 Do đó,
Do đó, 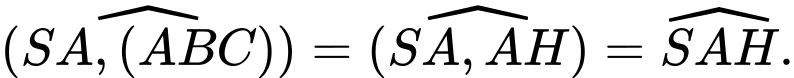
Giả sử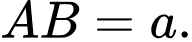
Ta có: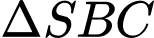 và
và 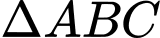 là tam giác đều nên
là tam giác đều nên 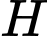 là trung điểm của
là trung điểm của 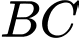 và
và 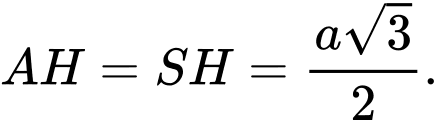
Xét tam giác vuông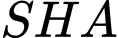 ta có
ta có 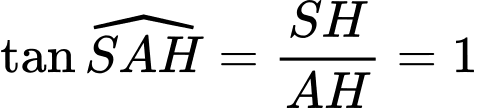
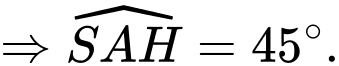
Vậy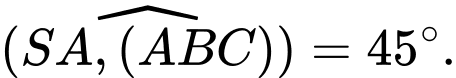 Đáp án: A
Đáp án: A

Theo giả thiết ta có
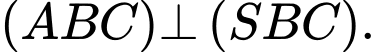
Trong mặt phẳng
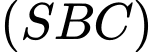 kẻ
kẻ 
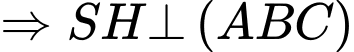 nên
nên 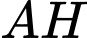 là hình chiếu của
là hình chiếu của 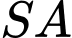 trên
trên 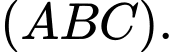 Do đó,
Do đó, 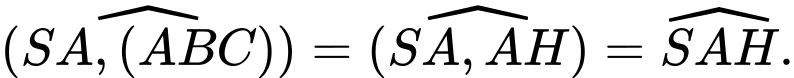
Giả sử
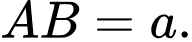
Ta có:
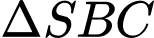 và
và 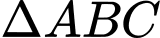 là tam giác đều nên
là tam giác đều nên 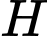 là trung điểm của
là trung điểm của 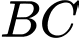 và
và 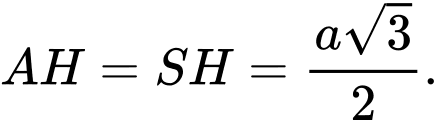
Xét tam giác vuông
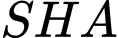 ta có
ta có 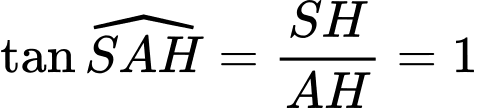
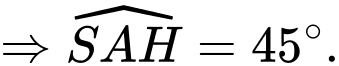
Vậy
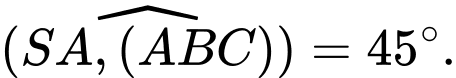 Đáp án: A
Đáp án: A
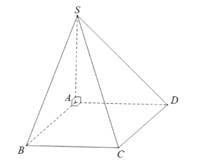
Câu 9 [585917]: Cho hình chóp 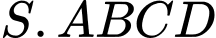 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 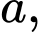
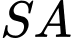 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 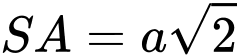 (minh họa như hình vẽ). Góc giữa đường thẳng
(minh họa như hình vẽ). Góc giữa đường thẳng 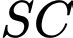 và mặt phẳng
và mặt phẳng 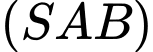 bằng:
bằng:
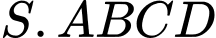 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 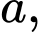
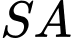 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 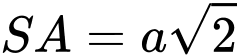 (minh họa như hình vẽ). Góc giữa đường thẳng
(minh họa như hình vẽ). Góc giữa đường thẳng 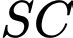 và mặt phẳng
và mặt phẳng 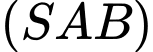 bằng:
bằng:
A, 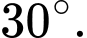
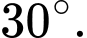
B, 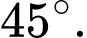
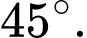
C, 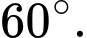
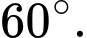
D, 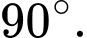
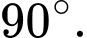
Chọn A
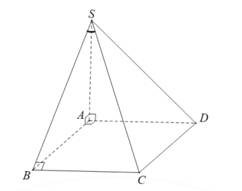
Ta có: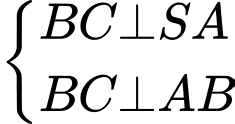
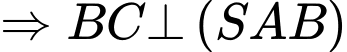 nên
nên 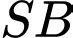 là hình chiếu của
là hình chiếu của 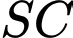 trên mặt phẳng
trên mặt phẳng 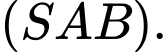
Do đó:
Xét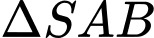 vuông tại
vuông tại 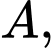 ta có:
ta có: 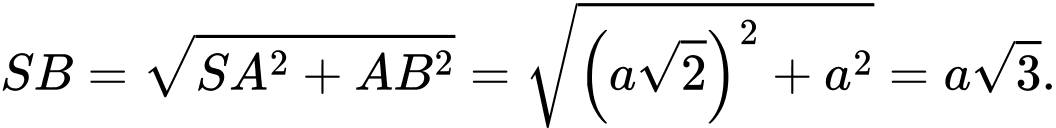
Xét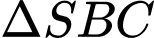 vuông tại
vuông tại 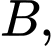 ta có:
ta có: 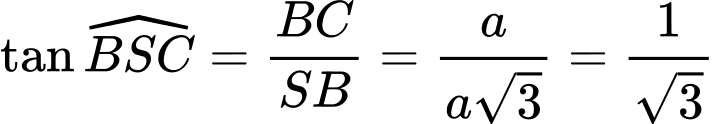
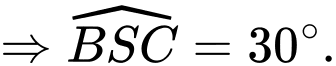
Cách khác: Sử dụng phương pháp tọa độ
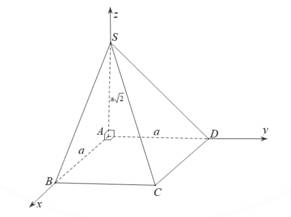
Chọn hệ trục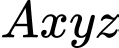 như hình vẽ với
như hình vẽ với 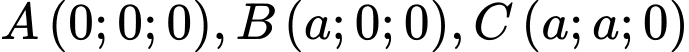 và
và 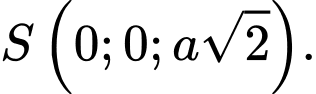
Ta có: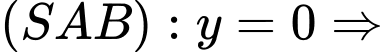 vectơ pháp tuyến của
vectơ pháp tuyến của 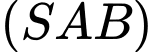 là
là 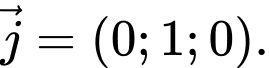
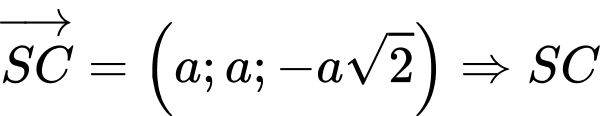 có một vectơ chỉ phương là
có một vectơ chỉ phương là 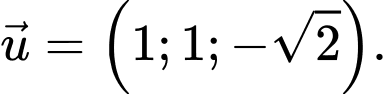
Suy ra: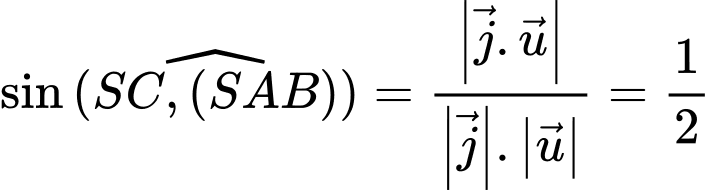
 Đáp án: A
Đáp án: A

Ta có:
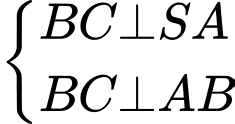
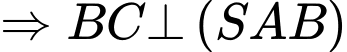 nên
nên 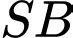 là hình chiếu của
là hình chiếu của 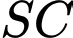 trên mặt phẳng
trên mặt phẳng 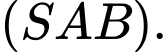
Do đó:

Xét
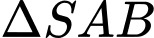 vuông tại
vuông tại 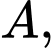 ta có:
ta có: 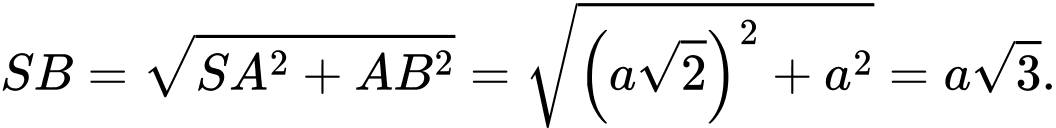
Xét
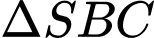 vuông tại
vuông tại  ta có:
ta có: 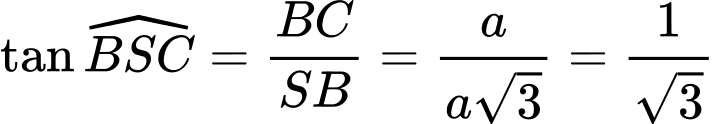
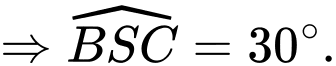
Cách khác: Sử dụng phương pháp tọa độ

Chọn hệ trục
 như hình vẽ với
như hình vẽ với 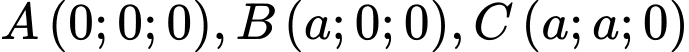 và
và 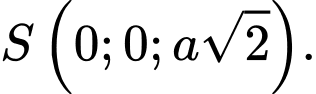
Ta có:
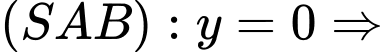 vectơ pháp tuyến của
vectơ pháp tuyến của 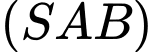 là
là 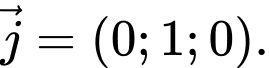
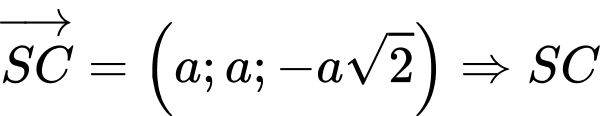 có một vectơ chỉ phương là
có một vectơ chỉ phương là 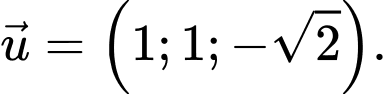
Suy ra:
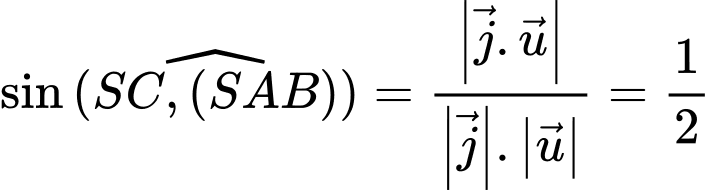
 Đáp án: A
Đáp án: A
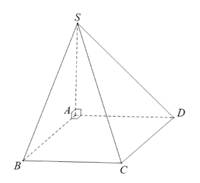
Câu 10 [585918]: Cho hình chóp 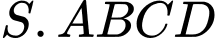 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 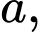
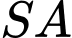 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy,  (minh họa như hình vẽ). Góc giữa đường thẳng
(minh họa như hình vẽ). Góc giữa đường thẳng 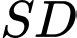 và mặt phẳng
và mặt phẳng 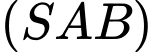 bằng:
bằng:
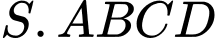 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 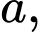
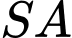 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy,  (minh họa như hình vẽ). Góc giữa đường thẳng
(minh họa như hình vẽ). Góc giữa đường thẳng 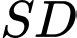 và mặt phẳng
và mặt phẳng 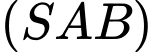 bằng:
bằng:
A, 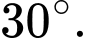
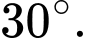
B, 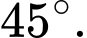
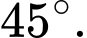
C, 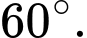
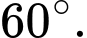
D, 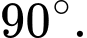
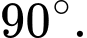
Chọn A
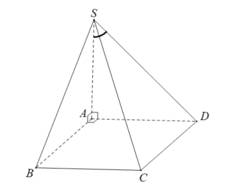
Ta có: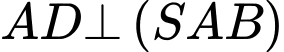 nên
nên 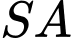 là hình chiếu của
là hình chiếu của 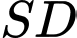 trên mặt phẳng
trên mặt phẳng 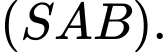
Do đó: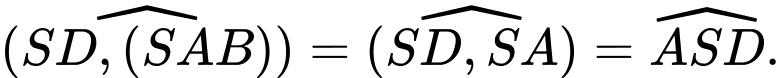
Xét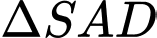 vuông tại
vuông tại 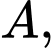 ta có:
ta có: 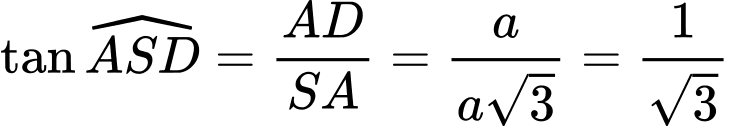
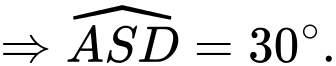
Cách khác: Sử dụng phương pháp tọa độ
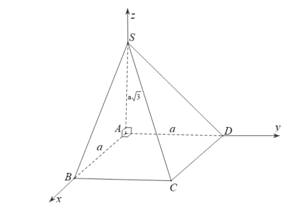
Chọn hệ trục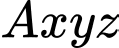 như hình vẽ với
như hình vẽ với 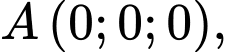
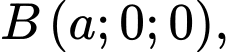
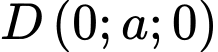 và
và 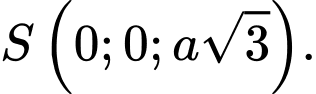
Ta có: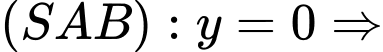 vectơ pháp tuyến của
vectơ pháp tuyến của 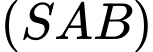 là
là 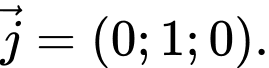
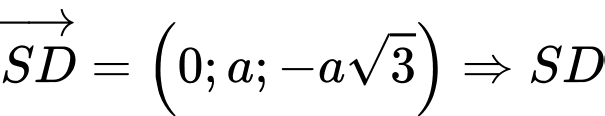 có một vectơ chỉ phương là
có một vectơ chỉ phương là 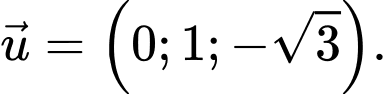
Suy ra: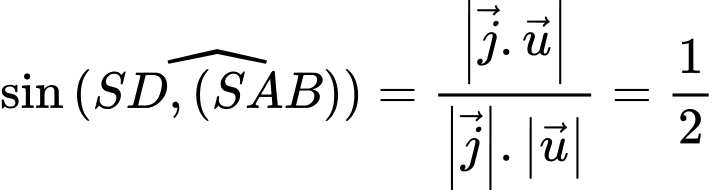
 Đáp án: A
Đáp án: A

Ta có:
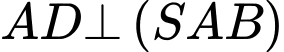 nên
nên 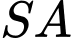 là hình chiếu của
là hình chiếu của 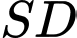 trên mặt phẳng
trên mặt phẳng 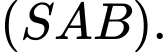
Do đó:
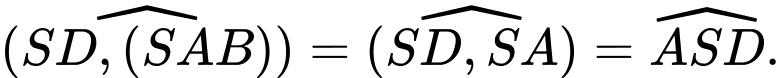
Xét
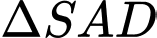 vuông tại
vuông tại 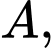 ta có:
ta có: 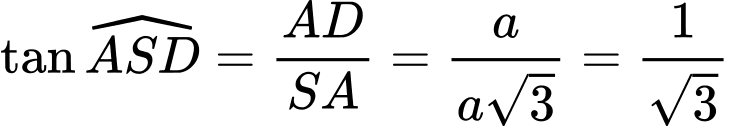
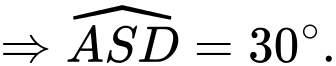
Cách khác: Sử dụng phương pháp tọa độ

Chọn hệ trục
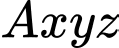 như hình vẽ với
như hình vẽ với 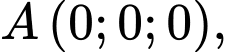
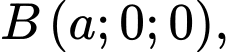
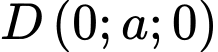 và
và 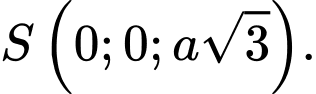
Ta có:
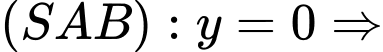 vectơ pháp tuyến của
vectơ pháp tuyến của 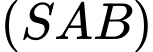 là
là 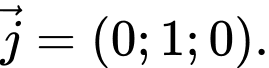
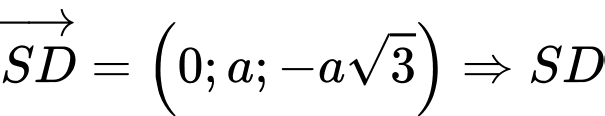 có một vectơ chỉ phương là
có một vectơ chỉ phương là 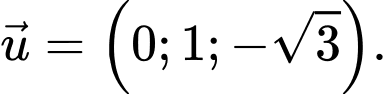
Suy ra:
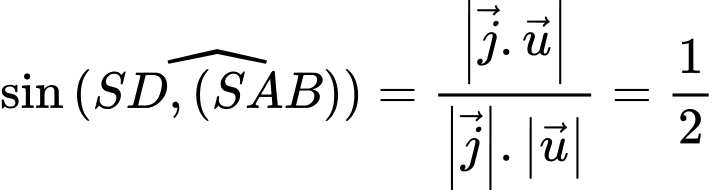
 Đáp án: A
Đáp án: A
Câu 11 [585919]: Cho hình chóp 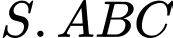 có
có 
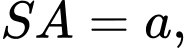
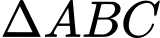 đều cạnh
đều cạnh 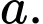 Tính góc giữa
Tính góc giữa 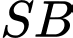 và
và 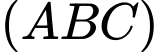
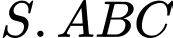 có
có 
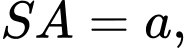
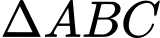 đều cạnh
đều cạnh 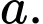 Tính góc giữa
Tính góc giữa 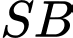 và
và 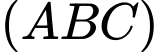
A, 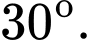
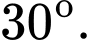
B, 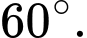
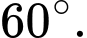
C, 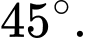
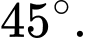
D, 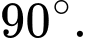
Chọn C
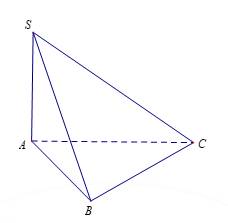
Ta có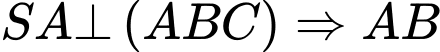 là hình chiếu của
là hình chiếu của 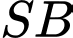 trên mặt phẳng
trên mặt phẳng 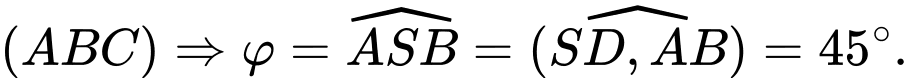 Đáp án: C
Đáp án: C

Ta có
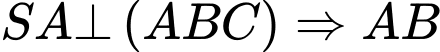 là hình chiếu của
là hình chiếu của 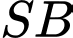 trên mặt phẳng
trên mặt phẳng 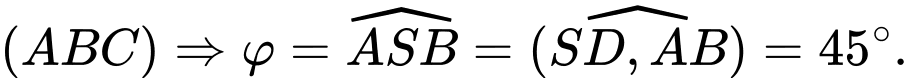 Đáp án: C
Đáp án: C
Câu 12 [585920]: Cho hình chóp 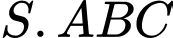 có
có 
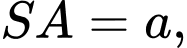
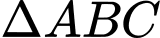 đều cạnh
đều cạnh 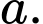 Gọi
Gọi 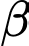 là góc giữa
là góc giữa 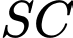 và mặt phẳng
và mặt phẳng 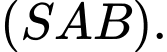 Khi đó,
Khi đó, 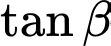 bằng
bằng
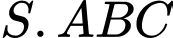 có
có 
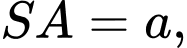
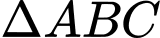 đều cạnh
đều cạnh 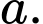 Gọi
Gọi 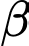 là góc giữa
là góc giữa 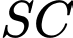 và mặt phẳng
và mặt phẳng 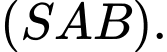 Khi đó,
Khi đó, 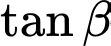 bằng
bằng A, 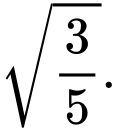
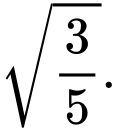
B, 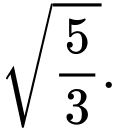
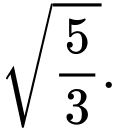
C, 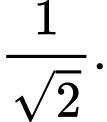
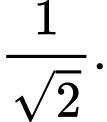
D, 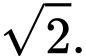
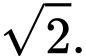
Chọn A
Gọi là trung điểm của
là trung điểm của 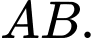 Ta có:
Ta có:
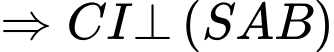
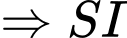 là hình chiếu của
là hình chiếu của 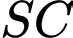 trên mặt phẳng
trên mặt phẳng 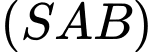
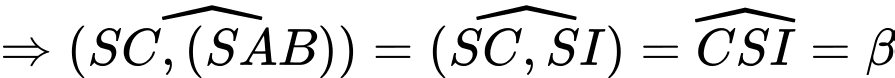
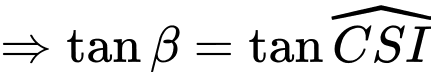

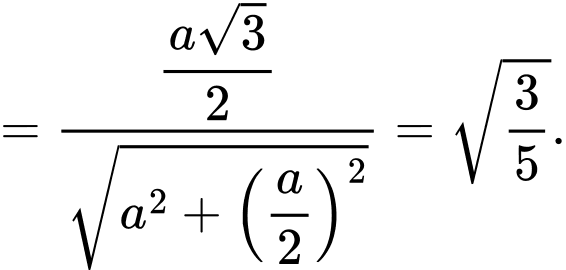 Đáp án: A
Đáp án: A

Gọi
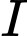 là trung điểm của
là trung điểm của 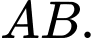 Ta có:
Ta có: 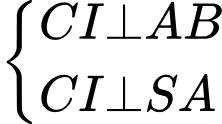
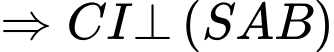
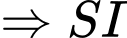 là hình chiếu của
là hình chiếu của 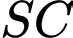 trên mặt phẳng
trên mặt phẳng 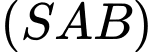
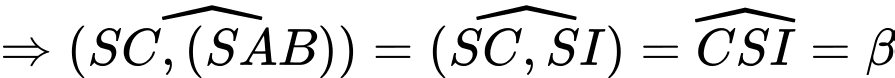
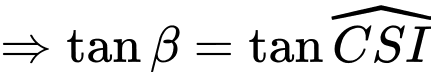

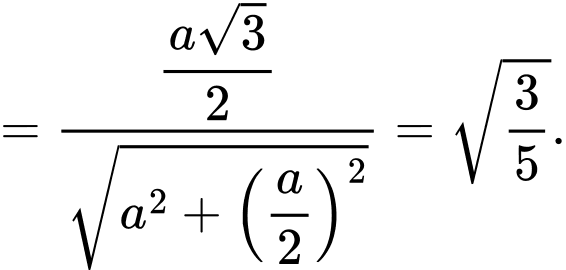 Đáp án: A
Đáp án: A
Câu 13 [585921]: Cho hình chóp 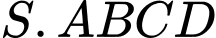 có đáy
có đáy 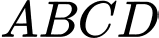 là hình vuông cạnh
là hình vuông cạnh 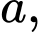
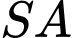 vuông góc với
vuông góc với 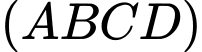 và
và 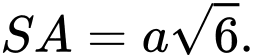 Tính sin của góc tạo bởi
Tính sin của góc tạo bởi 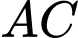 và mặt phẳng
và mặt phẳng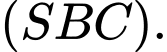
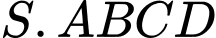 có đáy
có đáy 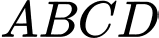 là hình vuông cạnh
là hình vuông cạnh 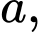
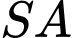 vuông góc với
vuông góc với 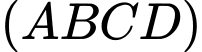 và
và 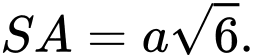 Tính sin của góc tạo bởi
Tính sin của góc tạo bởi 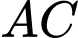 và mặt phẳng
và mặt phẳng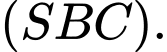
A, 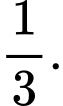
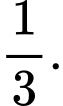
B, 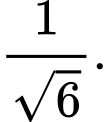
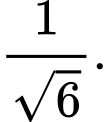
C, 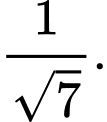
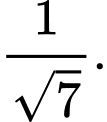
D, 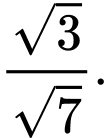
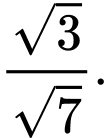
Chọn D
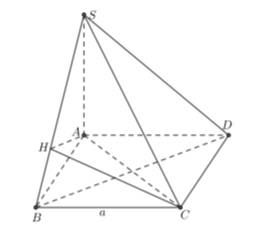
Kẻ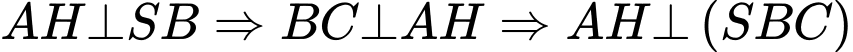
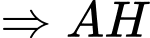 là hình chiếu của
là hình chiếu của 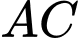 lên mặt phẳng
lên mặt phẳng 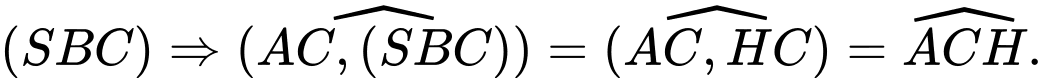
Tam giác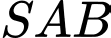 vuông
vuông 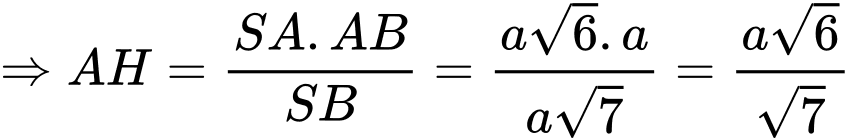
Vì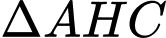 vuông tại
vuông tại 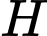
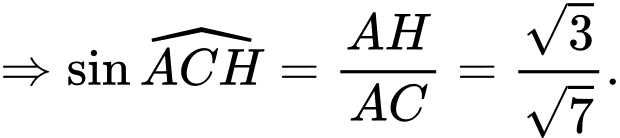 Đáp án: D
Đáp án: D

Kẻ
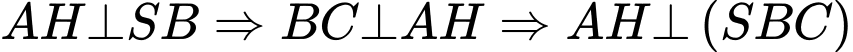
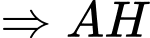 là hình chiếu của
là hình chiếu của 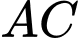 lên mặt phẳng
lên mặt phẳng 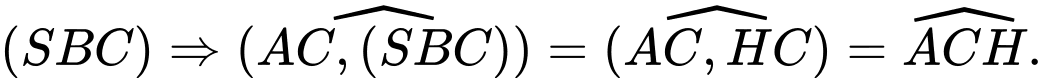
Tam giác
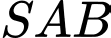 vuông
vuông 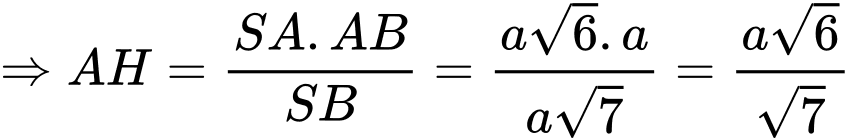
Vì
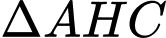 vuông tại
vuông tại 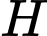
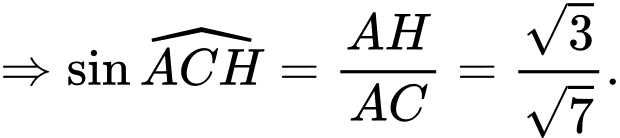 Đáp án: D
Đáp án: D
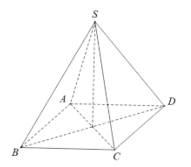
Câu 14 [585922]: Cho hình chóp đều 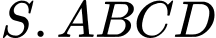 có cạnh đáy
có cạnh đáy 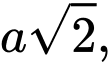 cạnh bên
cạnh bên 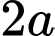 (minh họa như hình vẽ). Góc giữa cạnh bên và mặt đáy bằng:
(minh họa như hình vẽ). Góc giữa cạnh bên và mặt đáy bằng:
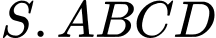 có cạnh đáy
có cạnh đáy 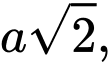 cạnh bên
cạnh bên 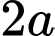 (minh họa như hình vẽ). Góc giữa cạnh bên và mặt đáy bằng:
(minh họa như hình vẽ). Góc giữa cạnh bên và mặt đáy bằng:
A, 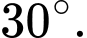
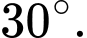
B, 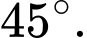
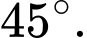
C, 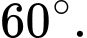
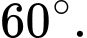
D, 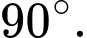
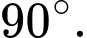
Chọn C
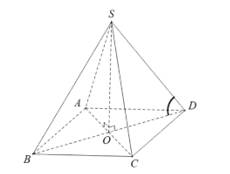
Ta có: góc giữa cạnh bên và mặt đáy là góc giữa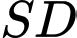 và
và 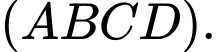
Gọi Vì
Vì 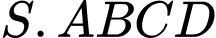 là hình chóp đều nên
là hình chóp đều nên 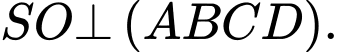
 là hình chiếu của
là hình chiếu của 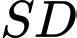 trên
trên 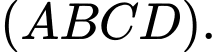
Do đó: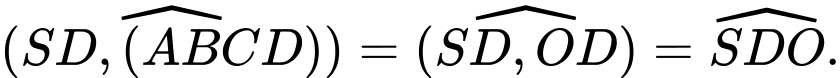
Xét hình vuông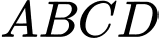 ta có:
ta có: 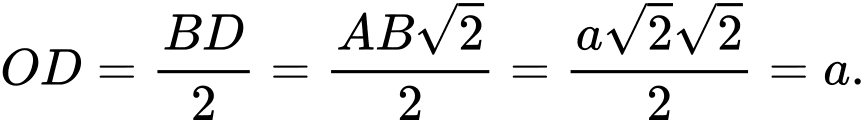
Xét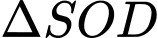 vuông tại
vuông tại  ta có:
ta có: 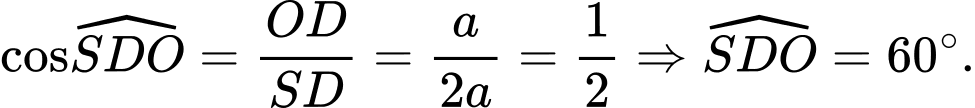
Cách khác: Sử dụng phương pháp tọa độ
Gọi
Vì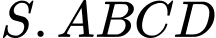 là hình chóp đều nên
là hình chóp đều nên 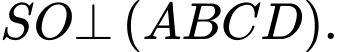
Ta có: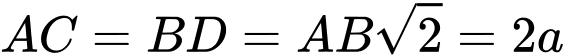 và
và 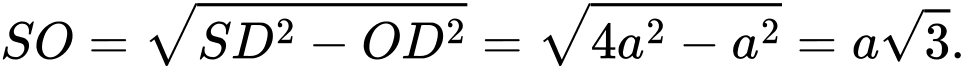
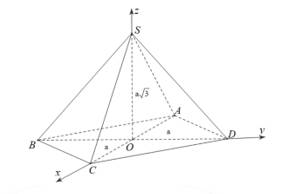
Chọn hệ trục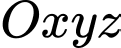 như hình vẽ với
như hình vẽ với 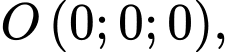
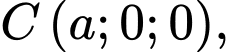
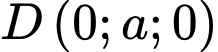 và
và 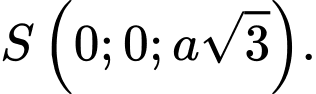
Ta có: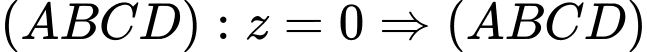 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 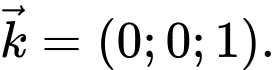
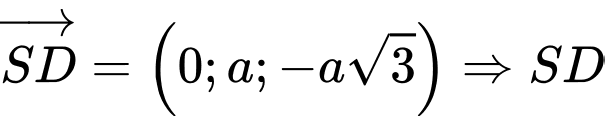 có một vectơ chỉ phương là
có một vectơ chỉ phương là 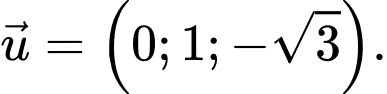
Suy ra: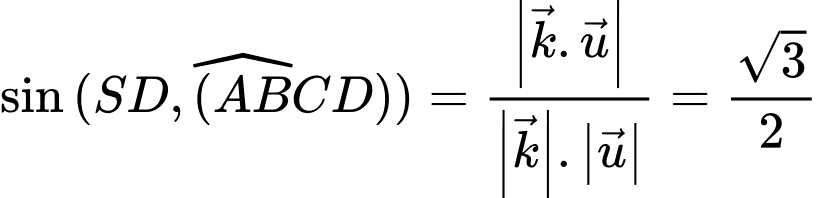
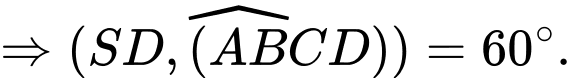 Đáp án: C
Đáp án: C

Ta có: góc giữa cạnh bên và mặt đáy là góc giữa
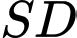 và
và 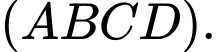
Gọi
 Vì
Vì 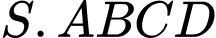 là hình chóp đều nên
là hình chóp đều nên 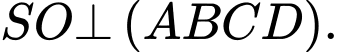
 là hình chiếu của
là hình chiếu của 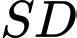 trên
trên 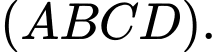
Do đó:
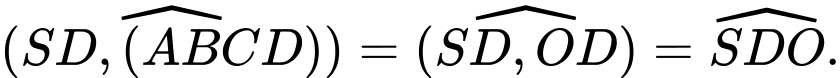
Xét hình vuông
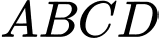 ta có:
ta có: 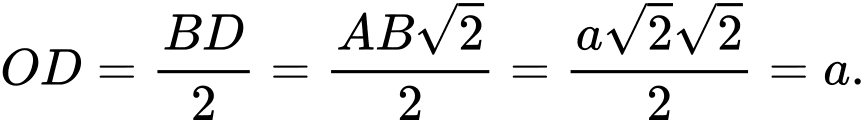
Xét
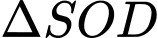 vuông tại
vuông tại  ta có:
ta có: 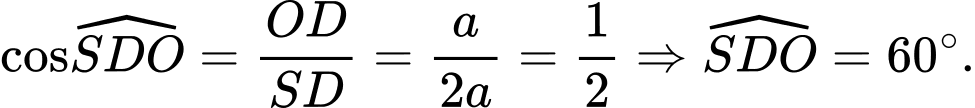
Cách khác: Sử dụng phương pháp tọa độ
Gọi

Vì
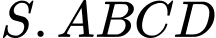 là hình chóp đều nên
là hình chóp đều nên 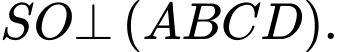
Ta có:
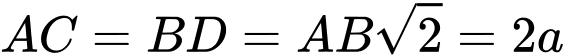 và
và 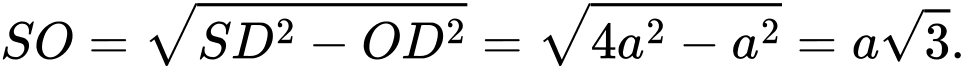

Chọn hệ trục
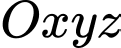 như hình vẽ với
như hình vẽ với 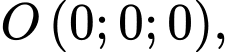
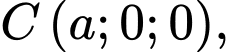
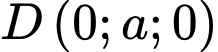 và
và 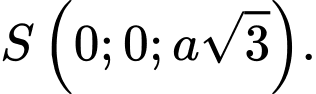
Ta có:
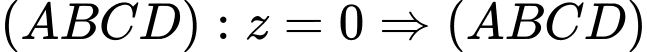 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 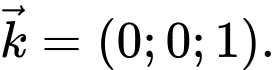
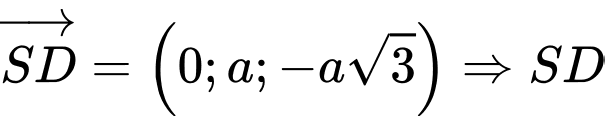 có một vectơ chỉ phương là
có một vectơ chỉ phương là 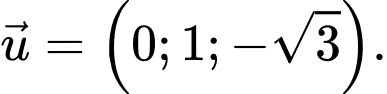
Suy ra:
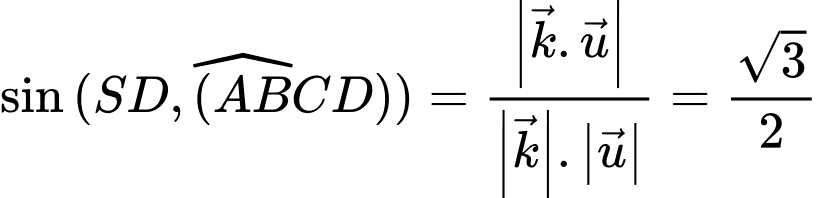
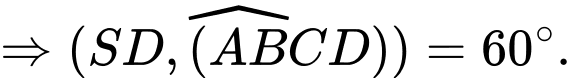 Đáp án: C
Đáp án: C
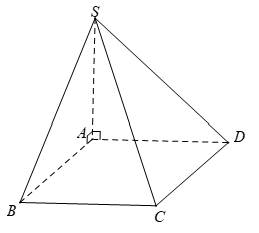
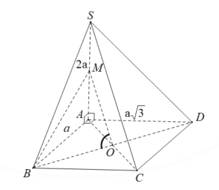
Câu 15 [585923]: Cho hình chóp 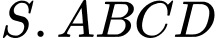 có đáy
có đáy 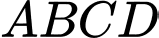 là hình thang vuông tại
là hình thang vuông tại 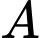 và
và 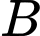 với
với 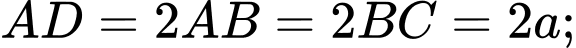
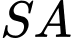 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 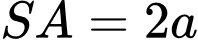 (minh họa như hình vẽ). Góc giữa đường thẳng
(minh họa như hình vẽ). Góc giữa đường thẳng 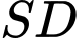 và mặt phẳng
và mặt phẳng 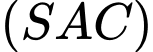 bằng:
bằng:
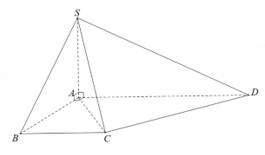
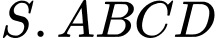 có đáy
có đáy 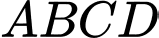 là hình thang vuông tại
là hình thang vuông tại 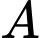 và
và 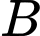 với
với 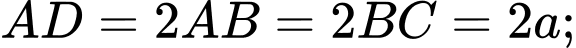
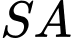 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 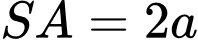 (minh họa như hình vẽ). Góc giữa đường thẳng
(minh họa như hình vẽ). Góc giữa đường thẳng 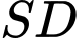 và mặt phẳng
và mặt phẳng 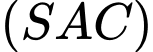 bằng:
bằng:
A, 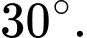
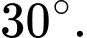
B, 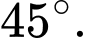
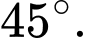
C, 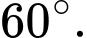
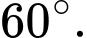
D, 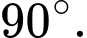
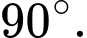
Chọn A
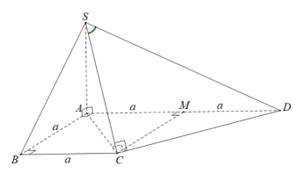
Gọi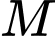 là trung điểm
là trung điểm 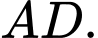 Ta có:
Ta có:
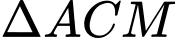 và
và 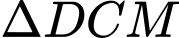 vuông cân tại
vuông cân tại 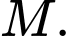

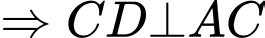 mà
mà  nên
nên 
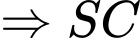 là hình chiếu của
là hình chiếu của 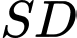 trên mặt phẳng
trên mặt phẳng 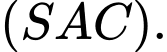
Do đó:
Xét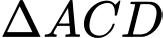 vuông cân tại
vuông cân tại 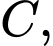 ta có:
ta có: 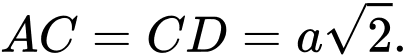
Xét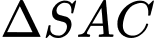 vuông tại
vuông tại 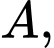 ta có:
ta có: 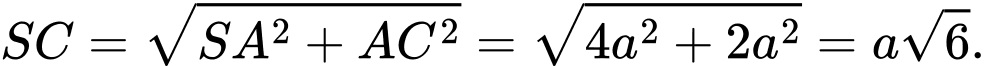
Xét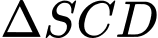 vuông tại
vuông tại 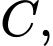 ta có:
ta có: 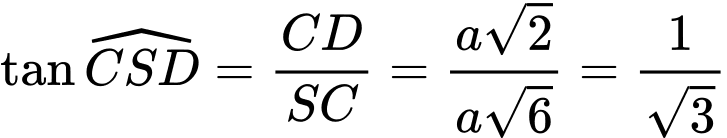
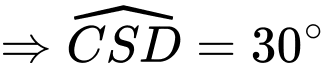
Cách khác: Sử dụng phương pháp tọa độ
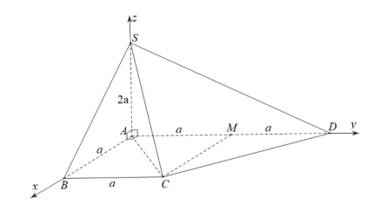
Chọn hệ trục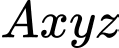 như hình vẽ với
như hình vẽ với 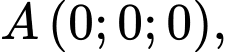
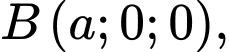
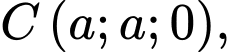
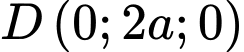 và
và 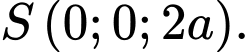
Ta có: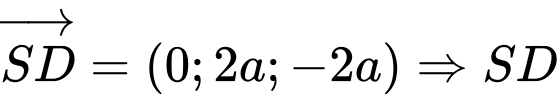 có một vectơ chỉ phương là
có một vectơ chỉ phương là 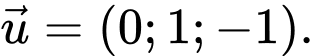
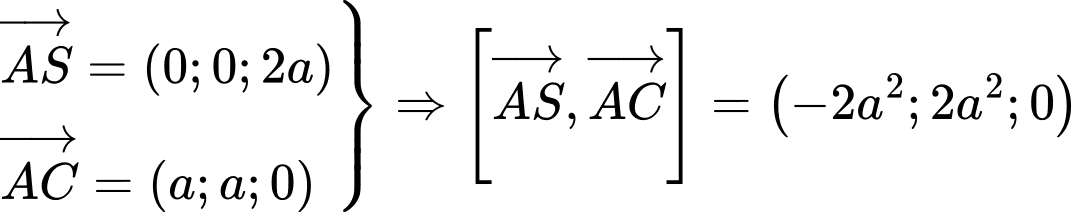
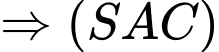 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 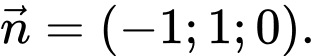
Suy ra: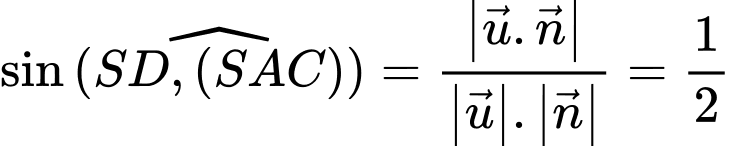
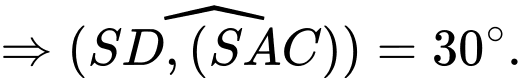 Đáp án: A
Đáp án: A

Gọi
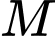 là trung điểm
là trung điểm 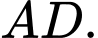 Ta có:
Ta có: 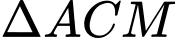 và
và 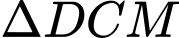 vuông cân tại
vuông cân tại 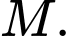

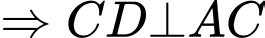 mà
mà  nên
nên 
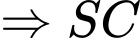 là hình chiếu của
là hình chiếu của 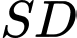 trên mặt phẳng
trên mặt phẳng 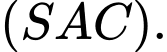
Do đó:

Xét
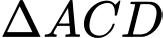 vuông cân tại
vuông cân tại 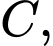 ta có:
ta có: 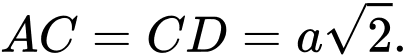
Xét
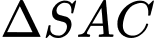 vuông tại
vuông tại 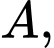 ta có:
ta có: 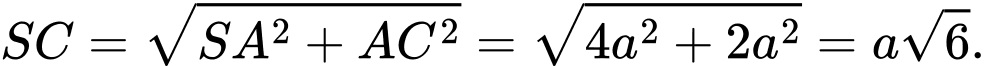
Xét
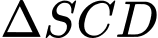 vuông tại
vuông tại 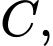 ta có:
ta có: 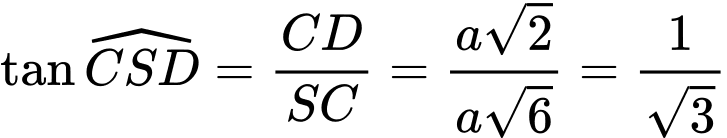
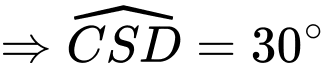
Cách khác: Sử dụng phương pháp tọa độ

Chọn hệ trục
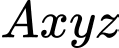 như hình vẽ với
như hình vẽ với 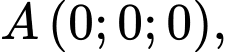
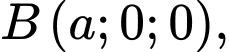
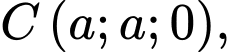
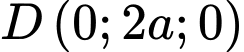 và
và 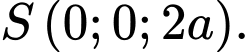
Ta có:
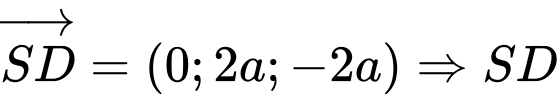 có một vectơ chỉ phương là
có một vectơ chỉ phương là 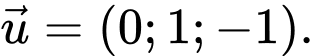
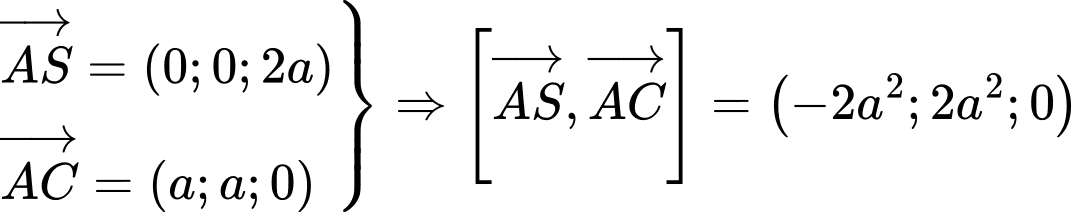
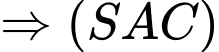 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 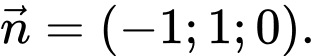
Suy ra:
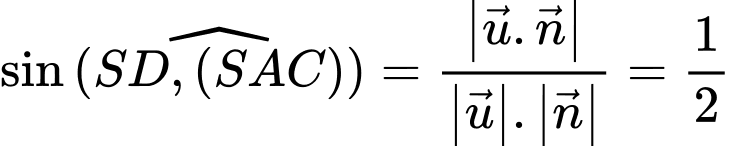
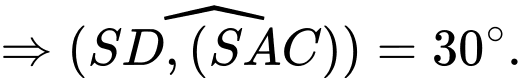 Đáp án: A
Đáp án: A Dạng câu hỏi: Câu trắc nghiệm đúng sai.
(Thí sinh trả lời đáp án từ câu 16 đến câu 17. Đáp án là Đúng hoặc Sai)
Câu 16 [585965]: Cho hình chóp 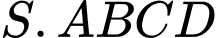 có đáy là hình chữ nhật có cạnh
có đáy là hình chữ nhật có cạnh 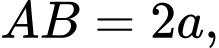
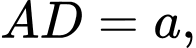 tam giác
tam giác 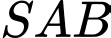 đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi  lần lượt là trung điểm
lần lượt là trung điểm  và
và 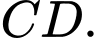 Khi đó:
Khi đó:
a)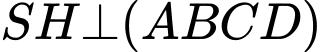
b) Góc phẳng nhị diện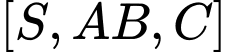 bằng
bằng 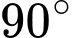
c)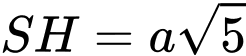
d) Góc phẳng nhị diện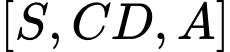 bằng
bằng 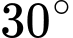
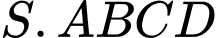 có đáy là hình chữ nhật có cạnh
có đáy là hình chữ nhật có cạnh 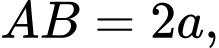
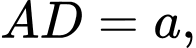 tam giác
tam giác 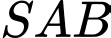 đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi  lần lượt là trung điểm
lần lượt là trung điểm  và
và 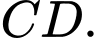 Khi đó:
Khi đó:a)
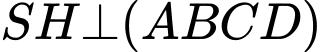
b) Góc phẳng nhị diện
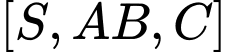 bằng
bằng 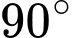
c)
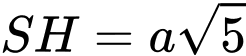
d) Góc phẳng nhị diện
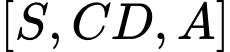 bằng
bằng 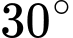
a) Đúng
b) Đúng
c) Sai
d) Sai
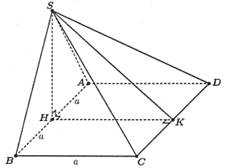
Gọi lần lượt là trung điểm
lần lượt là trung điểm  và
và 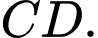 Ta có
Ta có  và
và 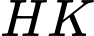 là đường trung bình của hình chữ nhật
là đường trung bình của hình chữ nhật 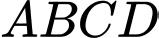 nên
nên
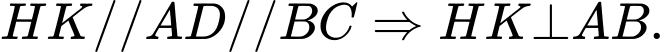 (1)
(1)
Ta lại có tam giác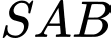 đều nên
đều nên  (2)
(2)
Mặt khác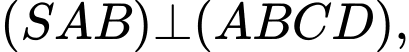 suy ra
suy ra 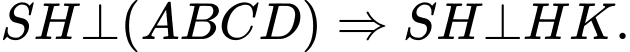
Từ (1) và (2) suy ra là góc phẳng nhị diện
là góc phẳng nhị diện 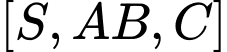 và
và 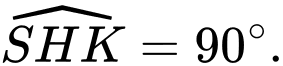
Theo câu a), ta có: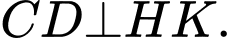 (3)
(3)
Mặt khác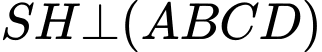 nên
nên 
Suy ra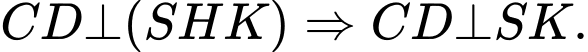 (4)
(4)
Từ (3) và (4) suy ra là góc phẳng nhị diện
là góc phẳng nhị diện 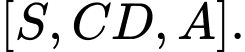
Tam giác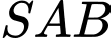 đều cạnh
đều cạnh 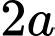 nên đường cao
nên đường cao 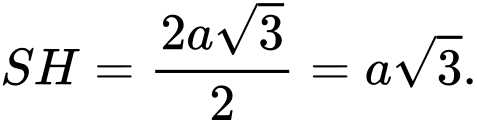
Từ câu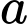 ), ta có
), ta có 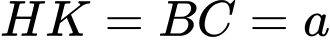 (tính chất đường trung bình của hình chữ nhật).
(tính chất đường trung bình của hình chữ nhật).
Do đó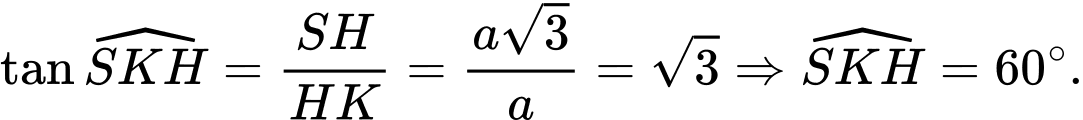
b) Đúng
c) Sai
d) Sai

Gọi
 lần lượt là trung điểm
lần lượt là trung điểm  và
và 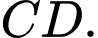 Ta có
Ta có  và
và 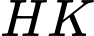 là đường trung bình của hình chữ nhật
là đường trung bình của hình chữ nhật 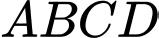 nên
nên 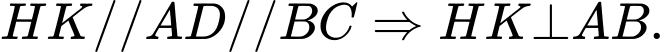 (1)
(1) Ta lại có tam giác
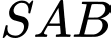 đều nên
đều nên  (2)
(2) Mặt khác
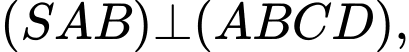 suy ra
suy ra 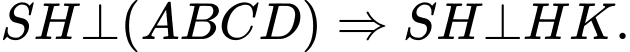
Từ (1) và (2) suy ra
 là góc phẳng nhị diện
là góc phẳng nhị diện 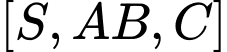 và
và 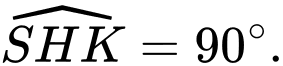
Theo câu a), ta có:
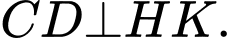 (3)
(3)Mặt khác
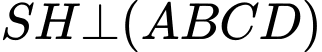 nên
nên 
Suy ra
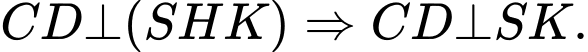 (4)
(4)Từ (3) và (4) suy ra
 là góc phẳng nhị diện
là góc phẳng nhị diện 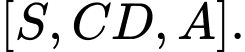
Tam giác
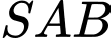 đều cạnh
đều cạnh 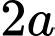 nên đường cao
nên đường cao 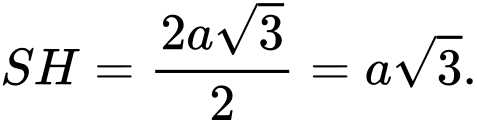
Từ câu
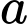 ), ta có
), ta có 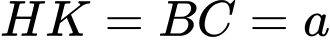 (tính chất đường trung bình của hình chữ nhật).
(tính chất đường trung bình của hình chữ nhật).Do đó
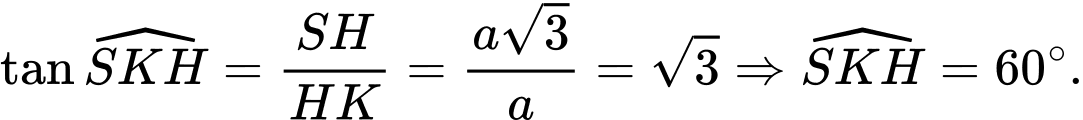
Câu 17 [585966]: Cho hình chóp 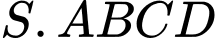 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 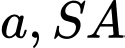 vuông góc với đáy và
vuông góc với đáy và  Khi đó:
Khi đó:
a)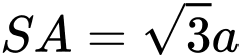
b)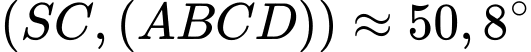
c)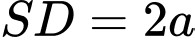
d)
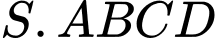 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 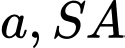 vuông góc với đáy và
vuông góc với đáy và  Khi đó:
Khi đó:a)
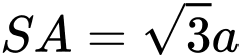
b)
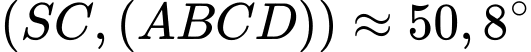
c)
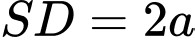
d)

a) Đúng
b) Đúng
c) Đúng
d) Sai
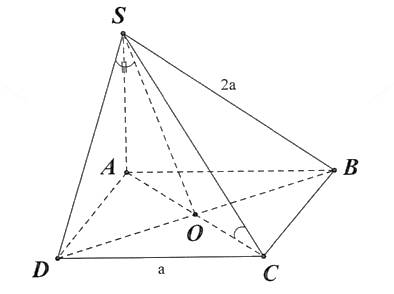
Ta có: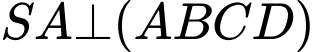 tại
tại 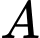 và
và 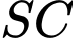 cắt mp
cắt mp 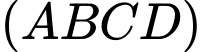 tại
tại 
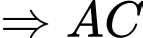 là hình chiếu của
là hình chiếu của 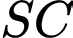 trên mp
trên mp 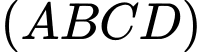
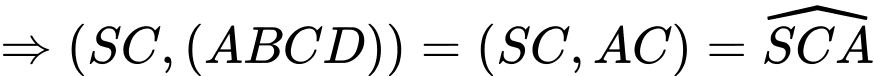
Ta có: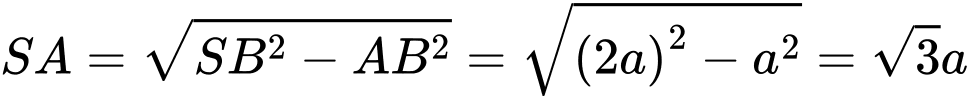
Xét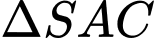 vuông tại
vuông tại 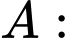
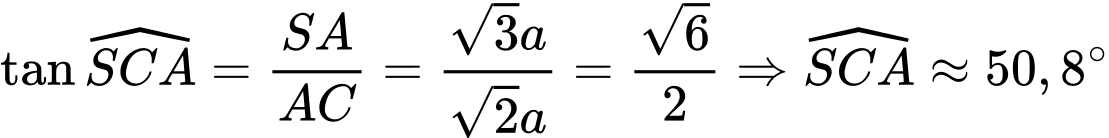
Vậy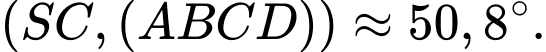
Ta có: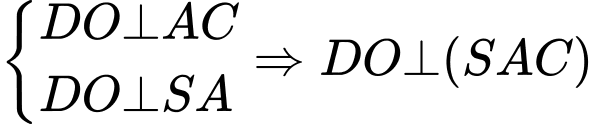 tại
tại  và
và 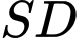 cắt mp
cắt mp 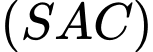 tại
tại 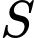
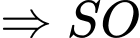 là hình chiếu của
là hình chiếu của 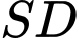 trên mp
trên mp 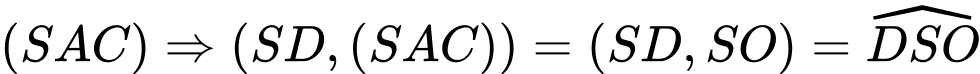
Ta có: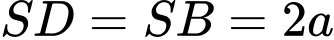 (vì
(vì 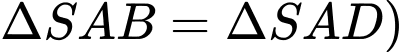
Xét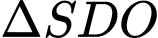 vuông tại O:
vuông tại O: 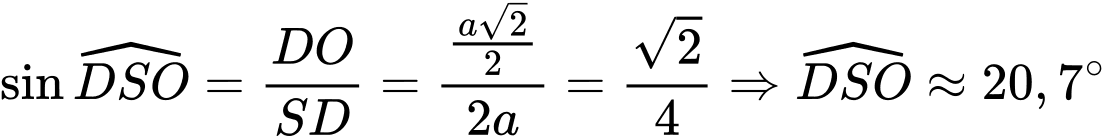
Vậy
b) Đúng
c) Đúng
d) Sai

Ta có:
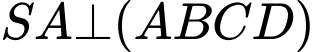 tại
tại 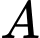 và
và 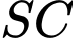 cắt mp
cắt mp 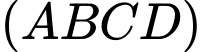 tại
tại 
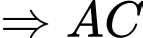 là hình chiếu của
là hình chiếu của 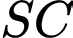 trên mp
trên mp 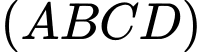
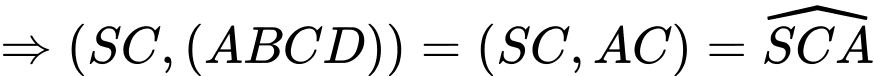
Ta có:
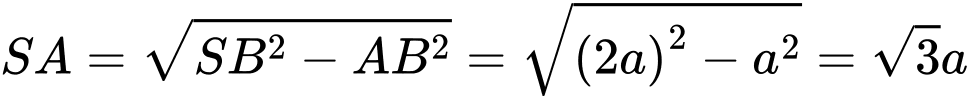
Xét
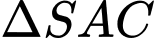 vuông tại
vuông tại 
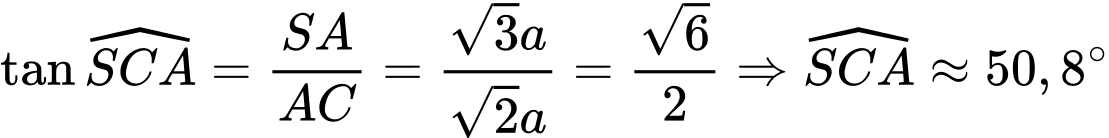
Vậy
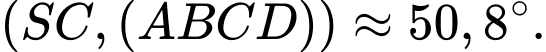
Ta có:
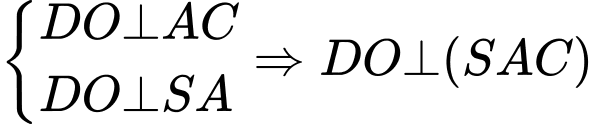 tại
tại  và
và 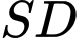 cắt mp
cắt mp 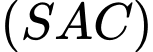 tại
tại 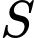
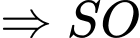 là hình chiếu của
là hình chiếu của 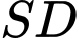 trên mp
trên mp 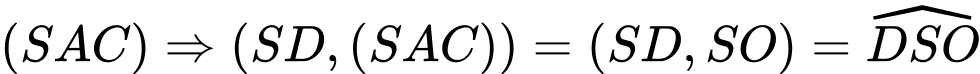
Ta có:
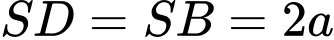 (vì
(vì 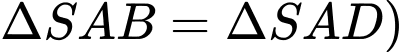
Xét
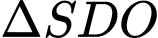 vuông tại O:
vuông tại O: 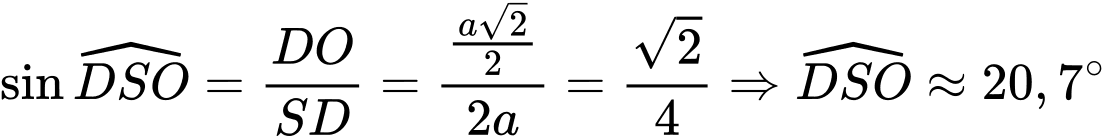
Vậy

Dạng câu hỏi: Câu trả lời ngắn.
(Thí sinh trả lời đáp án từ câu 18 đến câu 20. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 18 [585924]: Cho hình chóp tứ giác đều 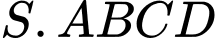 cạnh đáy bằng
cạnh đáy bằng 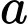 và
và 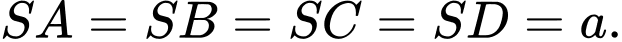 Khi đó, cosin góc giữa hai mặt phẳng
Khi đó, cosin góc giữa hai mặt phẳng 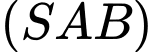 và
và 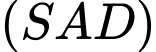 bằng
bằng
TRẢ LỜI: ……………………….
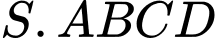 cạnh đáy bằng
cạnh đáy bằng 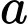 và
và 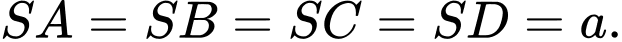 Khi đó, cosin góc giữa hai mặt phẳng
Khi đó, cosin góc giữa hai mặt phẳng 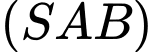 và
và 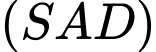 bằng
bằngTRẢ LỜI: ……………………….
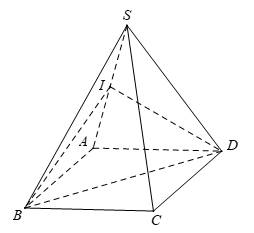
Gọi
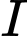 là trung điểm
là trung điểm 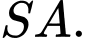
Do tam giác
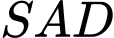 và
và 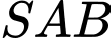 đều nên
đều nên 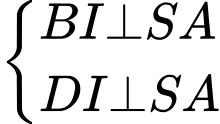
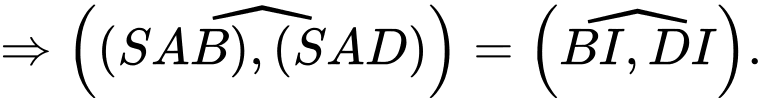
Áp dụng định lý cosin cho tam giác
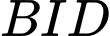 ta có:
ta có: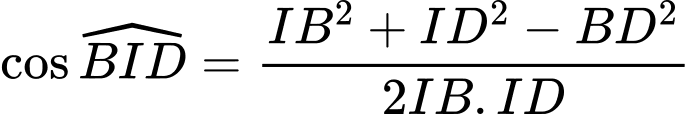
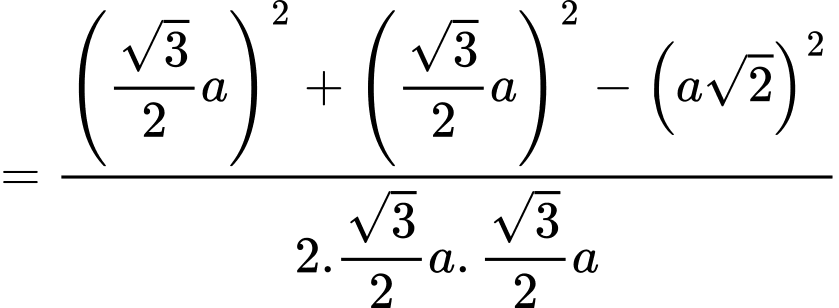
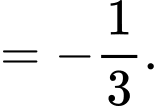
Vậy
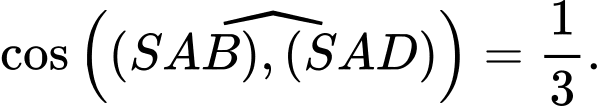
Câu 19 [585925]: Cho hình chóp đều 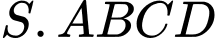 có cạnh
có cạnh 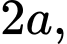 cạnh bên
cạnh bên 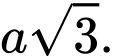 Góc giữa mặt bên và mặt đáy bằng:
Góc giữa mặt bên và mặt đáy bằng:
TRẢ LỜI: ……………………….
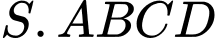 có cạnh
có cạnh 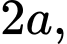 cạnh bên
cạnh bên 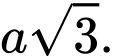 Góc giữa mặt bên và mặt đáy bằng:
Góc giữa mặt bên và mặt đáy bằng:TRẢ LỜI: ……………………….
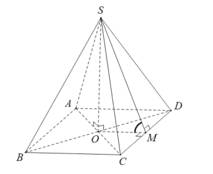
Ta có: góc giữa mặt bên và mặt đáy là góc giữa
 và
và 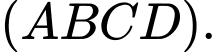
Gọi
 Vì
Vì 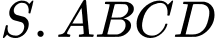 là hình chóp đều nên
là hình chóp đều nên 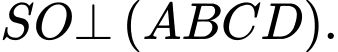
Gọi
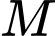 là trung điểm
là trung điểm 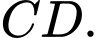 Ta có:
Ta có: 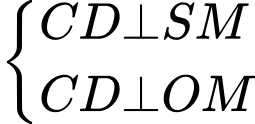
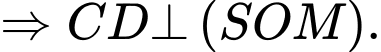
Do đó:
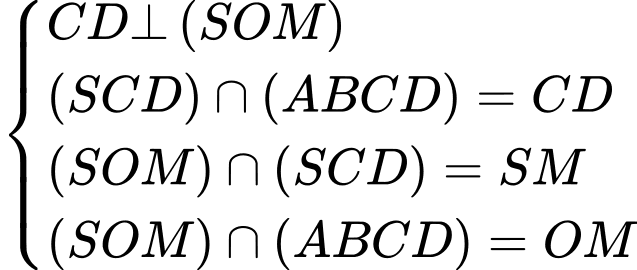
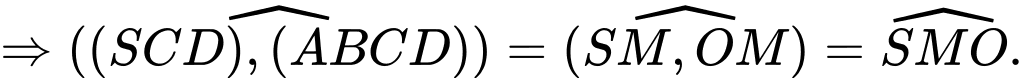
Xét hình vuông
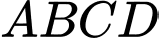 ta có:
ta có: 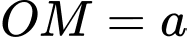 và
và 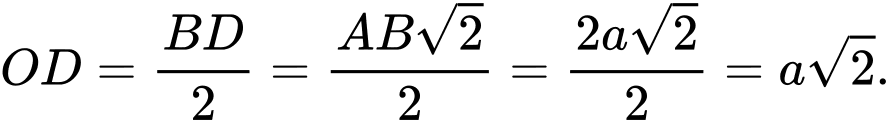
Xét
 vuông tại
vuông tại  ta có:
ta có: 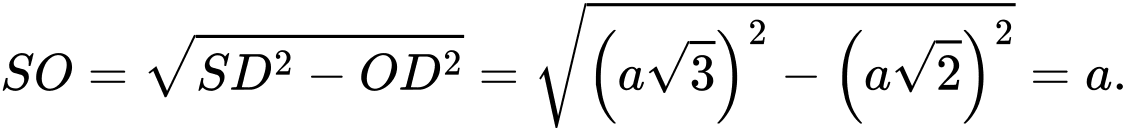
Xét
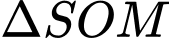 vuông tại
vuông tại  ta có:
ta có: 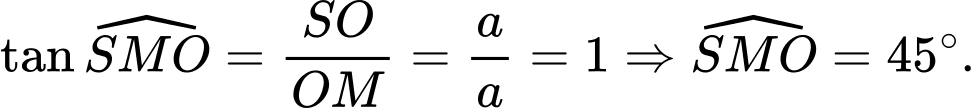
Cách khác: Sử dụng phương pháp tọa độ
Gọi
 Vì
Vì 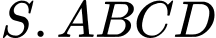 là hình chóp đều nên
là hình chóp đều nên 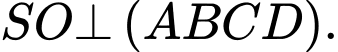
Ta có:
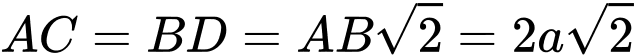 và
và 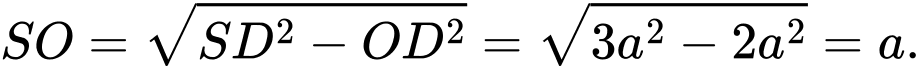
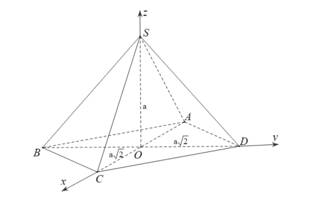
Chọn hệ trục
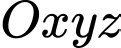 như hình vẽ với
như hình vẽ với 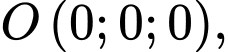
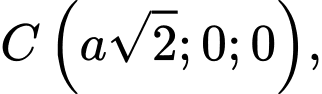
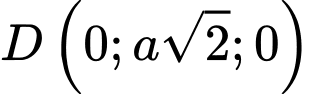 và
và 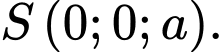
Ta có:
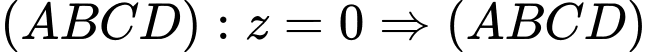 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 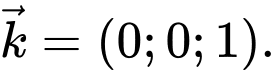
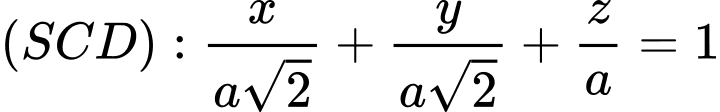
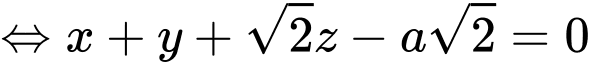
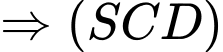 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 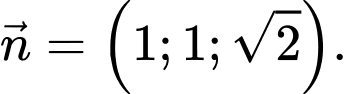
Suy ra:
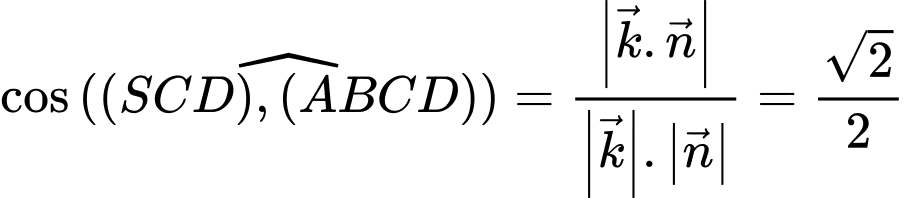
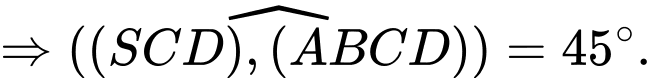
Câu 20 [585926]: Cho hình chóp 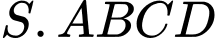 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 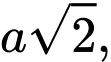
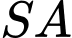 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 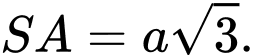 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 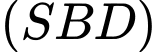 và
và 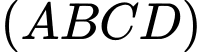 bằng:
bằng:
TRẢ LỜI: ……………………….
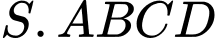 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 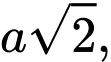
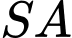 vuông góc với mặt phẳng đáy,
vuông góc với mặt phẳng đáy, 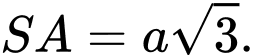 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 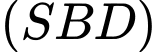 và
và 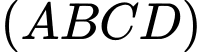 bằng:
bằng:TRẢ LỜI: ……………………….
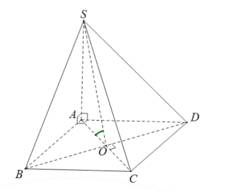
Gọi
 Ta có:
Ta có: 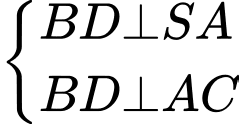
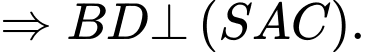
Do đó:
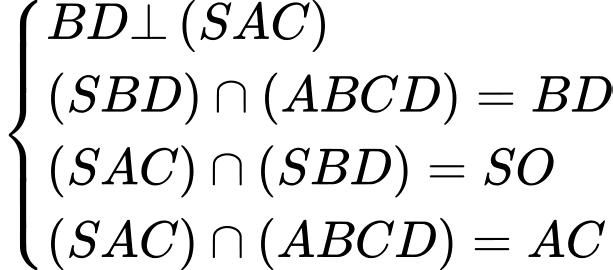
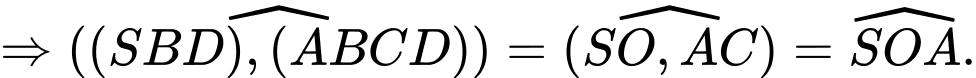
Xét hình vuông
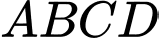 ta có:
ta có: 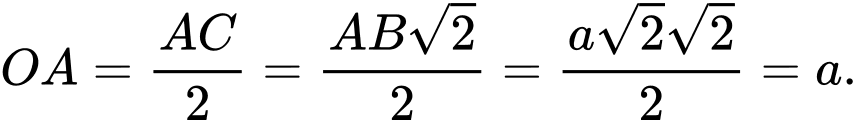
Xét
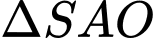 vuông tại
vuông tại 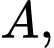 ta có:
ta có: 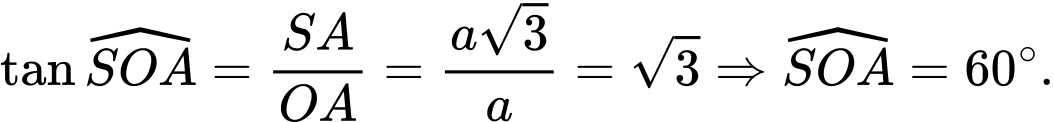
Cách khác: Sử dụng phương pháp tọa độ
Chọn hệ trục
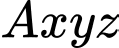 như hình vẽ với
như hình vẽ với 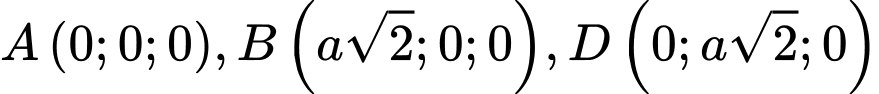 và
và 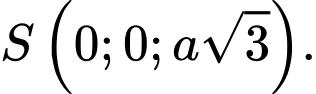
Ta có:
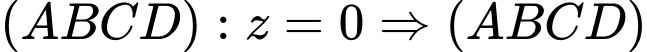 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 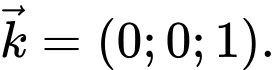
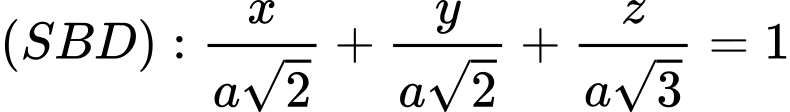
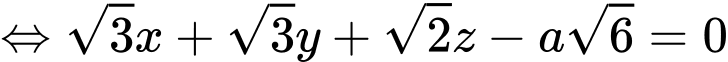
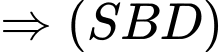 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 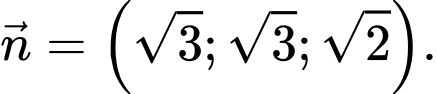
Suy ra: