DẠNG 1. NHẬN BIẾT SỐ CHÍNH PHƯƠNG
Câu 1 [582659]: Cho số tự nhiên 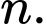 Chứng minh rằng
Chứng minh rằng 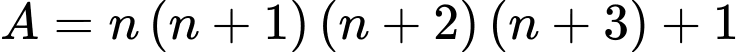 là một số chính phương.
là một số chính phương.
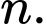 Chứng minh rằng
Chứng minh rằng 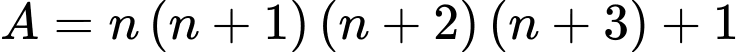 là một số chính phương.
là một số chính phương. 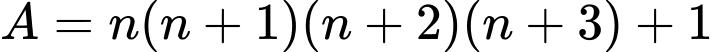
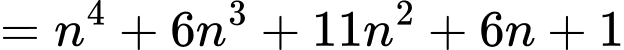
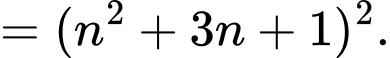 Vậy
Vậy 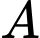 là số chính phương.
là số chính phương.
Câu 2 [582660]: Cho số tự nhiên 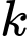 và biểu thức
và biểu thức 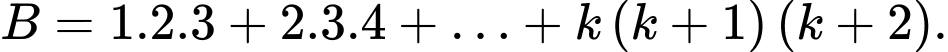 Chứng minh
Chứng minh 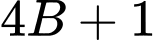 là số chính phương.
là số chính phương.
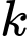 và biểu thức
và biểu thức 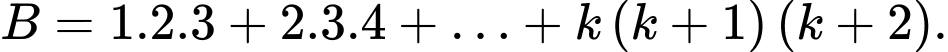 Chứng minh
Chứng minh 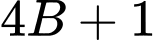 là số chính phương.
là số chính phương.
Ta có:
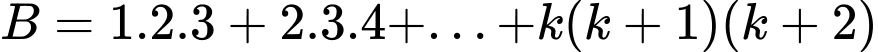
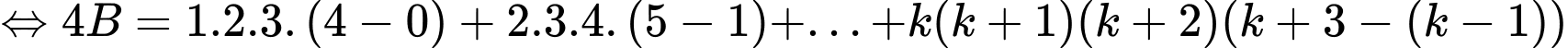
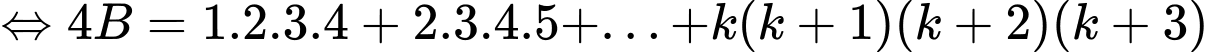
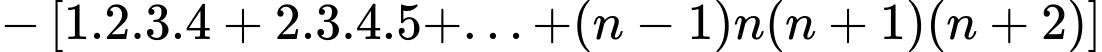
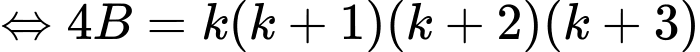
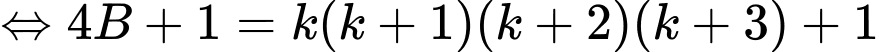
Theo VD1, suy ra đpcm.
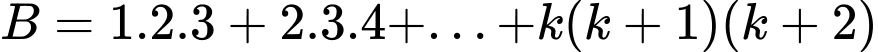
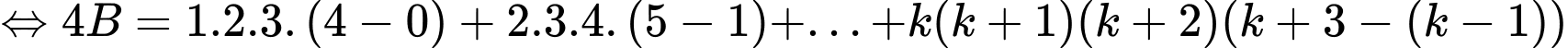
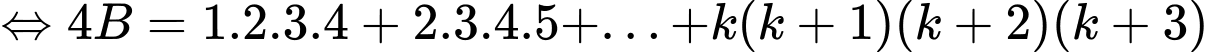
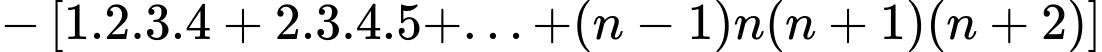
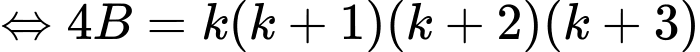
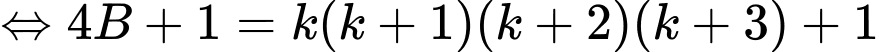
Theo VD1, suy ra đpcm.
Câu 3 [582662]: Số 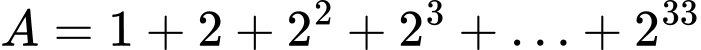 có phải một số chính phương hay không?
có phải một số chính phương hay không?
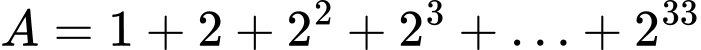 có phải một số chính phương hay không?
có phải một số chính phương hay không?
Ta có: 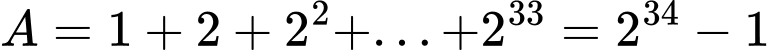
Vì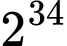 có tận cùng là
có tận cùng là 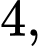 nên
nên 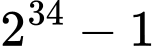 có tận cùng là
có tận cùng là 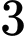
Vậy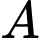 không phải là số chính phương.
không phải là số chính phương.
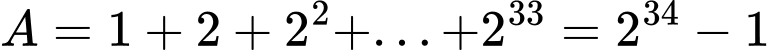
Vì
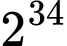 có tận cùng là
có tận cùng là 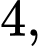 nên
nên 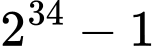 có tận cùng là
có tận cùng là 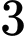
Vậy
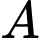 không phải là số chính phương.
không phải là số chính phương.
Câu 4 [582663]: Chứng minh rằng tổng bình phương của hai số lẻ bất kì không phải là một số chính phương?
Gọi 2 số lẻ đó là 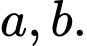 Giả sử
Giả sử  là số chính phương, ta có:
là số chính phương, ta có:
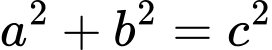
Do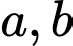 lẻ nên
lẻ nên 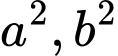 lẻ
lẻ  chẵn
chẵn chẵn.
chẵn.
Đặt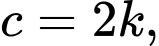 ta có:
ta có: 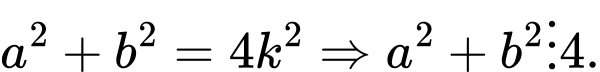
Vì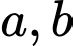 lẻ, đặt
lẻ, đặt 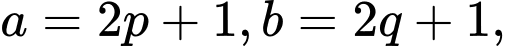 ta có:
ta có: 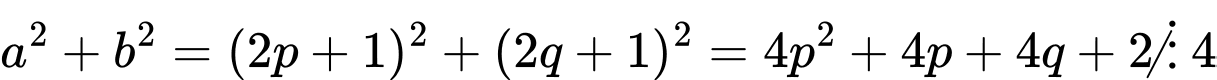
Mâu thẫn, suy ra đpcm
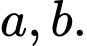 Giả sử
Giả sử  là số chính phương, ta có:
là số chính phương, ta có: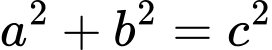
Do
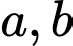 lẻ nên
lẻ nên 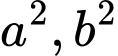 lẻ
lẻ  chẵn
chẵn chẵn.
chẵn.Đặt
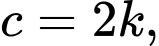 ta có:
ta có: 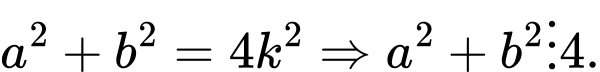
Vì
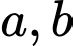 lẻ, đặt
lẻ, đặt 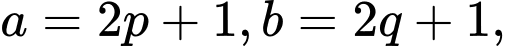 ta có:
ta có: 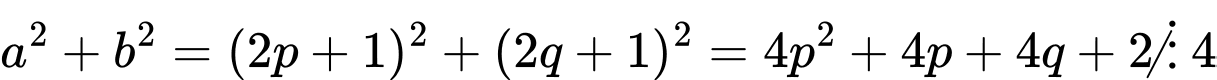
Mâu thẫn, suy ra đpcm
DẠNG 2: TÌM ĐIỀU KIỆN ĐỂ MỘT SỐ LÀ SỐ CHÍNH PHƯƠNG
Câu 5 [582665]: Tìm số nguyên dương 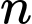 sao cho
sao cho 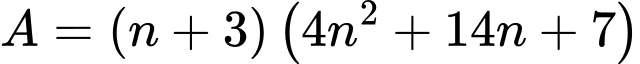 là số một chính phương.
là số một chính phương.
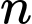 sao cho
sao cho 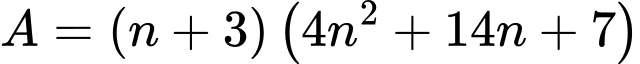 là số một chính phương.
là số một chính phương.
Dễ thấy 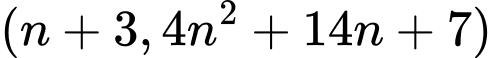 nguyên tố cùng nhau.
nguyên tố cùng nhau.
Khi đó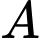 là số chính phương
là số chính phương 
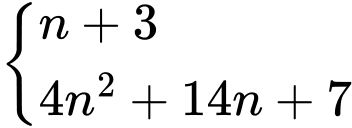 đều là số chính phương
đều là số chính phương
Ta có: do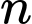 nguyên dương nên:
nguyên dương nên: 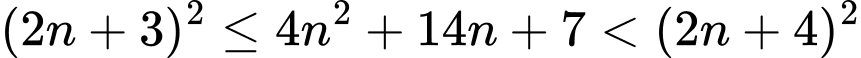
Khi đó: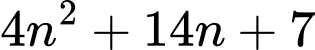 là số chính phương
là số chính phương 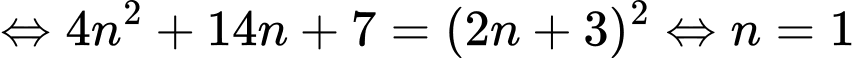 ;
;
Thử lại, ta cũng thấy là số chính phương.
là số chính phương.
Vậy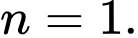
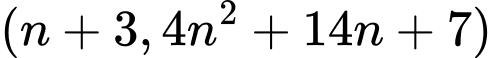 nguyên tố cùng nhau.
nguyên tố cùng nhau.Khi đó
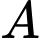 là số chính phương
là số chính phương 
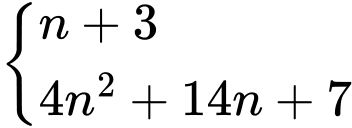 đều là số chính phương
đều là số chính phươngTa có: do
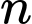 nguyên dương nên:
nguyên dương nên: 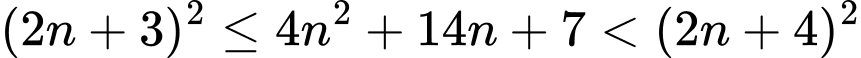
Khi đó:
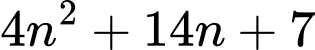 là số chính phương
là số chính phương 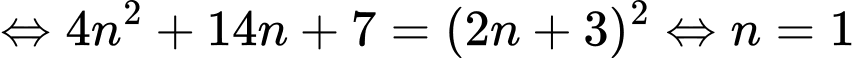 ;
;Thử lại, ta cũng thấy
 là số chính phương.
là số chính phương.Vậy
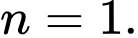
Câu 6 [582666]: Tìm số tự nhiên 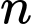 sao cho
sao cho  là số chính phương.
là số chính phương.
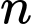 sao cho
sao cho  là số chính phương.
là số chính phương.
Theo lý thuyết thặng dư bậc 2, tồn tại số nguyên 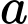 thỏa mãn
thỏa mãn 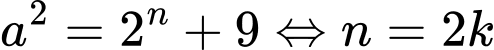 (xem bài phương trình đồng dư bậc 2).
(xem bài phương trình đồng dư bậc 2).
Từ đó, ta có: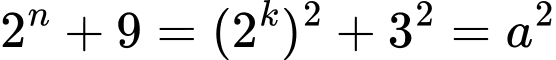
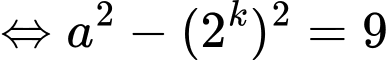
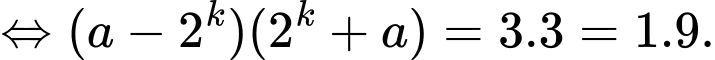

Vậy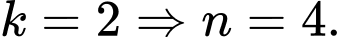
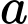 thỏa mãn
thỏa mãn 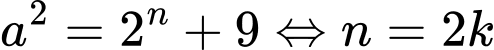 (xem bài phương trình đồng dư bậc 2).
(xem bài phương trình đồng dư bậc 2).Từ đó, ta có:
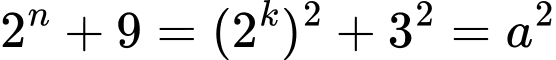
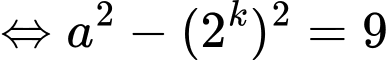
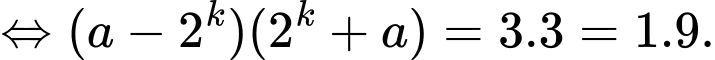

Vậy
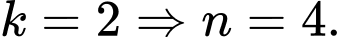
DẠNG 3. TÌM SỐ CHÍNH PHƯƠNG THỎA MÃN YÊU CẦU
Câu 7 [582667]: Tìm số chính phương 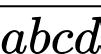 biết
biết 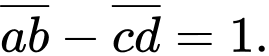
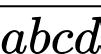 biết
biết 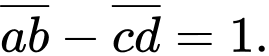
Ta có: 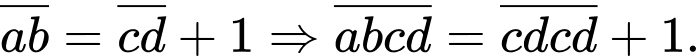
TH1: là số chính phương
là số chính phương 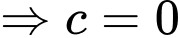 (loại)
(loại)
TH2: là số chính phương
là số chính phương 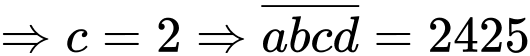 không là số chính phương (loại)
không là số chính phương (loại)
TH3: là số chính phương
là số chính phương 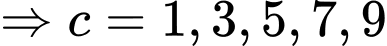 (thử ra không có giá trị
(thử ra không có giá trị  thỏa mãn)
thỏa mãn)
TH4: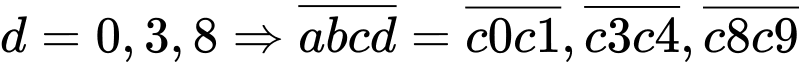 là số chính phương
là số chính phương 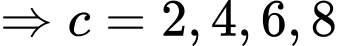
Thử hết các khả năng, không thu được nào thỏa mãn.
nào thỏa mãn.
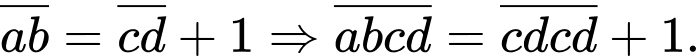
TH1:
 là số chính phương
là số chính phương 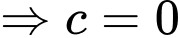 (loại)
(loại)
TH2:
 là số chính phương
là số chính phương 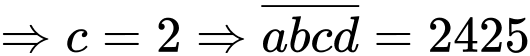 không là số chính phương (loại)
không là số chính phương (loại)
TH3:
 là số chính phương
là số chính phương 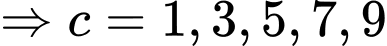 (thử ra không có giá trị
(thử ra không có giá trị  thỏa mãn)
thỏa mãn)
TH4:
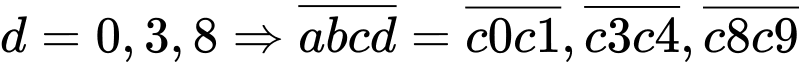 là số chính phương
là số chính phương 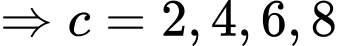
Thử hết các khả năng, không thu được
 nào thỏa mãn.
nào thỏa mãn.
Câu 8 [582668]: Tìm một số chính phương gồm 4 chữ số sao cho chữ số cuối là số nguyên tố, căn bậc hai của số đó có tổng các chữ số là một số chính phương.
Gọi số đó là 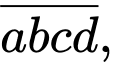 hiển nhiên
hiển nhiên 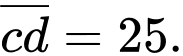
Do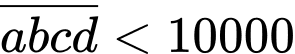 nên
nên 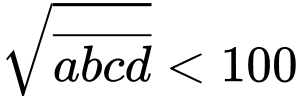 là số có hai chữ số.
là số có hai chữ số.
Gọi nó là: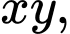 hiển nhiên
hiển nhiên 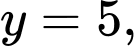 ta có:
ta có:  là số chính phương
là số chính phương 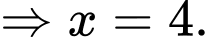
Khi đó: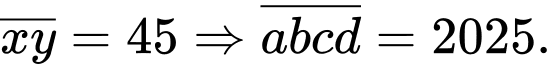
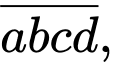 hiển nhiên
hiển nhiên 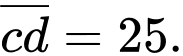
Do
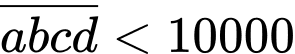 nên
nên 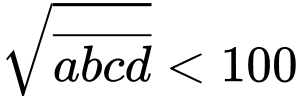 là số có hai chữ số.
là số có hai chữ số.
Gọi nó là:
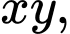 hiển nhiên
hiển nhiên 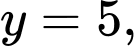 ta có:
ta có:  là số chính phương
là số chính phương 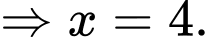
Khi đó: