Xét tính chia hết và không chia hết
Câu 1 [585462]: Khi chia số tự nhiên 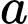 cho 36 ta được số dư là 12. Hỏi
cho 36 ta được số dư là 12. Hỏi 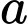 có chia hết cho 4, cho 9 không?
có chia hết cho 4, cho 9 không?
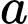 cho 36 ta được số dư là 12. Hỏi
cho 36 ta được số dư là 12. Hỏi 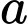 có chia hết cho 4, cho 9 không?
có chia hết cho 4, cho 9 không?
Ta có:  sao cho:
sao cho: 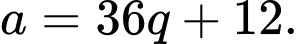
Do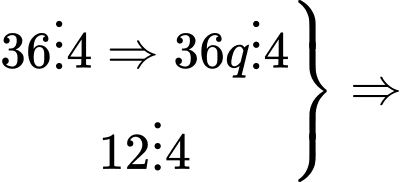
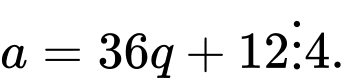
Do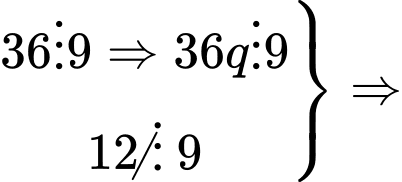
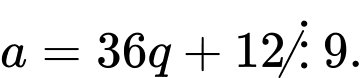
 sao cho:
sao cho: 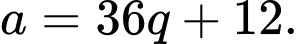
Do
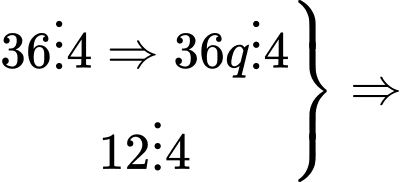
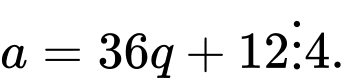
Do
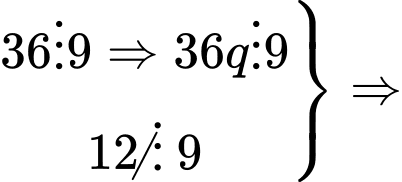
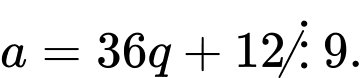
Câu 2 [585463]: Chứng minh tích của 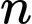 số tự nhiên liên tiếp luôn chia hết cho
số tự nhiên liên tiếp luôn chia hết cho 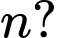
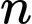 số tự nhiên liên tiếp luôn chia hết cho
số tự nhiên liên tiếp luôn chia hết cho 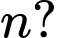
Gọi thừa số đầu tiên là 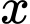
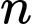 sẽ có
sẽ có 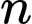 số dư là
số dư là 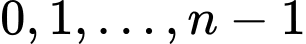
Ta có: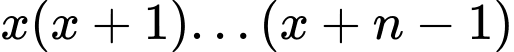 là tích của
là tích của 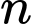 thừa số liên tiếp, tức là không có hai thừa số nào chia cho
thừa số liên tiếp, tức là không có hai thừa số nào chia cho 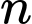 ra cùng một số dư.
ra cùng một số dư.
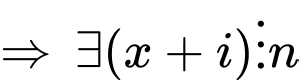 với
với 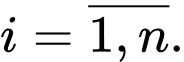

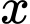
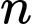 sẽ có
sẽ có 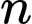 số dư là
số dư là 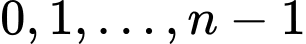
Ta có:
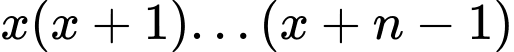 là tích của
là tích của 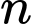 thừa số liên tiếp, tức là không có hai thừa số nào chia cho
thừa số liên tiếp, tức là không có hai thừa số nào chia cho 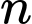 ra cùng một số dư.
ra cùng một số dư.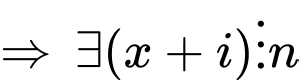 với
với 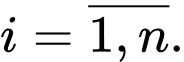

Câu 3 [585464]: Chứng minh nếu 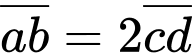 thì
thì 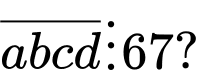
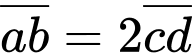 thì
thì 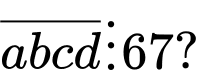
Ta có: 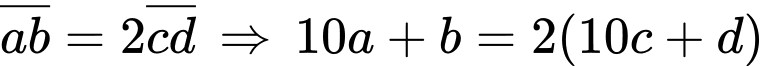
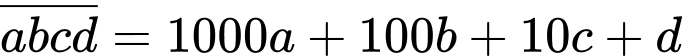
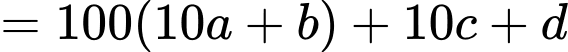
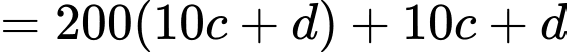
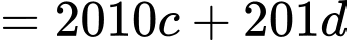
Do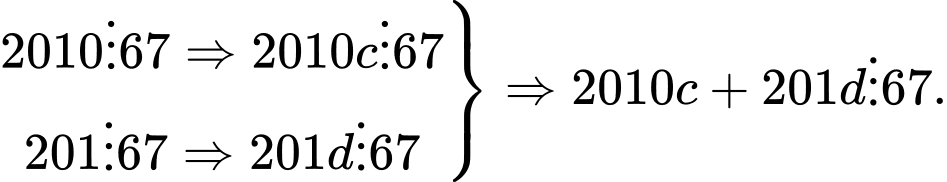
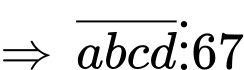
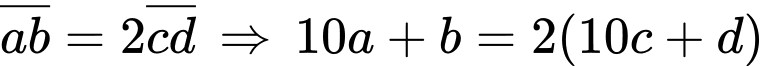
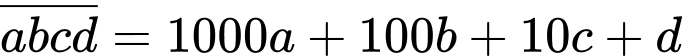
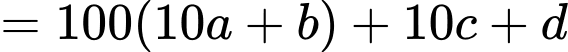
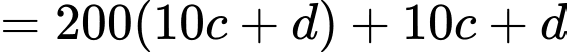
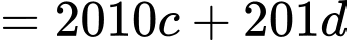
Do
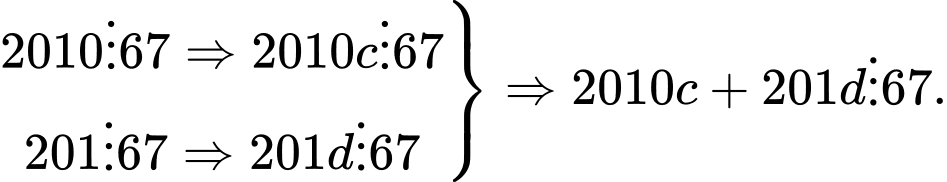
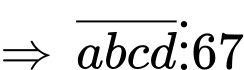
Câu 4 [585465]: Cho 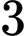 số nguyên dương
số nguyên dương 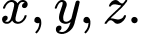 Chứng minh rằng:
Chứng minh rằng: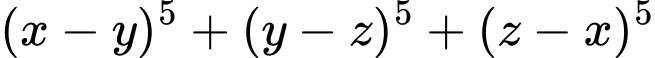 chia hết cho
chia hết cho 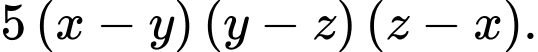
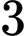 số nguyên dương
số nguyên dương 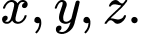 Chứng minh rằng:
Chứng minh rằng: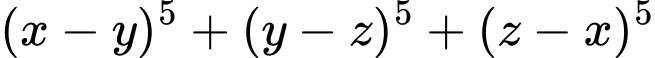 chia hết cho
chia hết cho 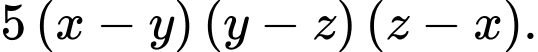
• Ta sẽ chứng minh kết quả sau: Nếu  thì
thì 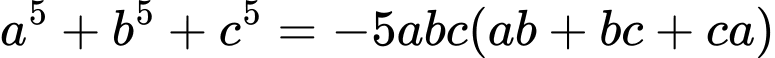
Ta có: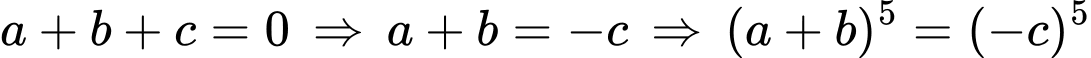
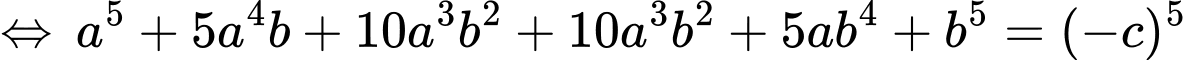
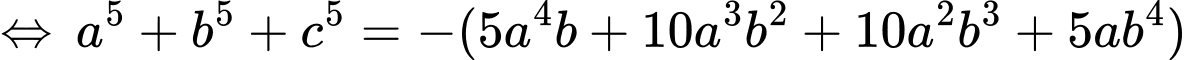
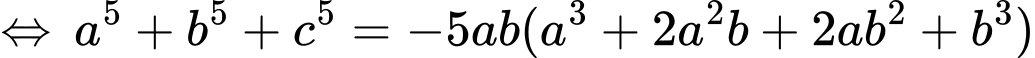
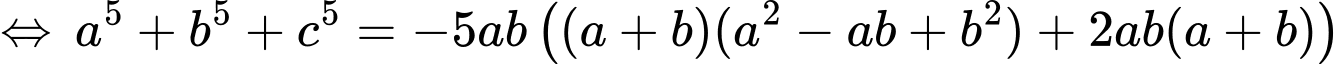
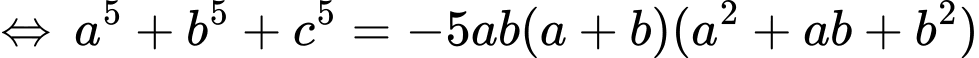
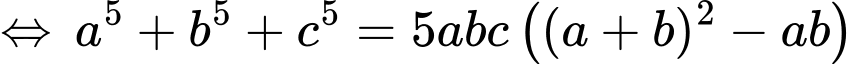
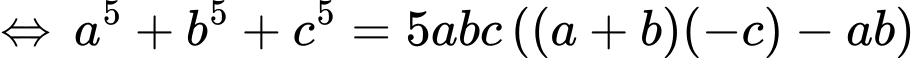
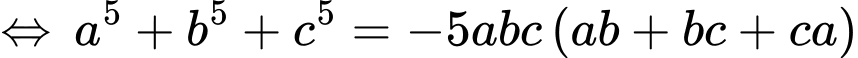
• Áp dụng: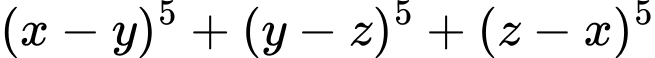
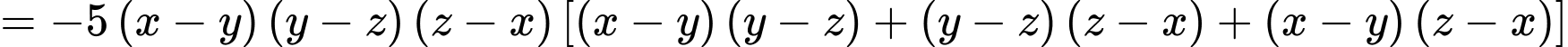 chia hết cho
chia hết cho 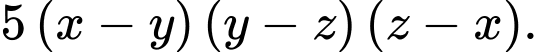
Vậy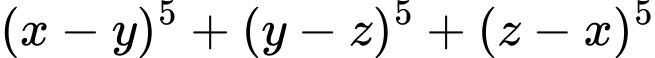 chia hết cho
chia hết cho 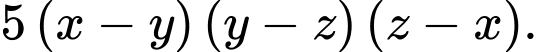
 thì
thì 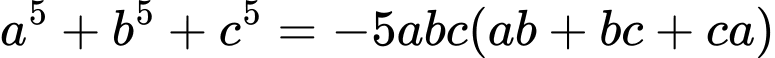
Ta có:
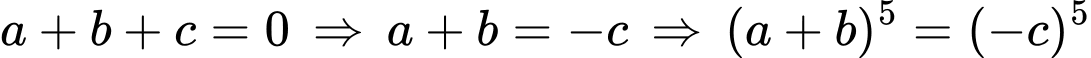
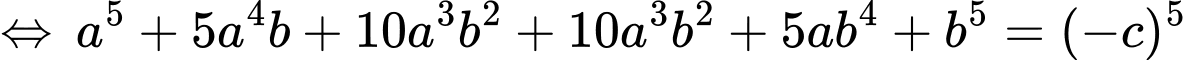
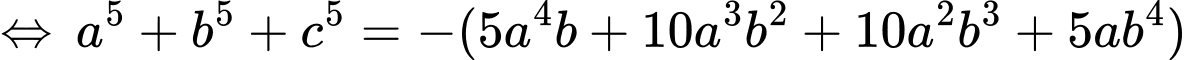
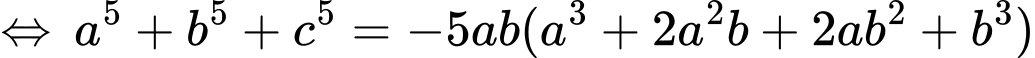
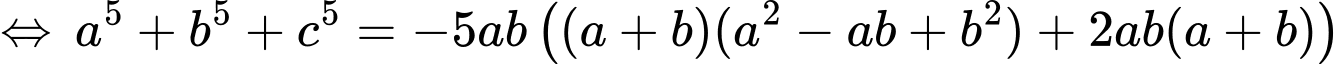
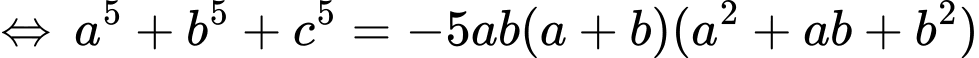
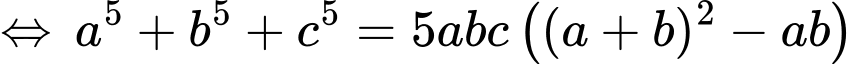
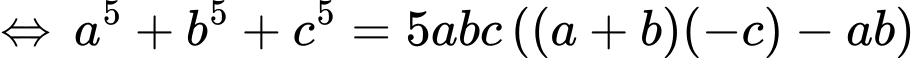
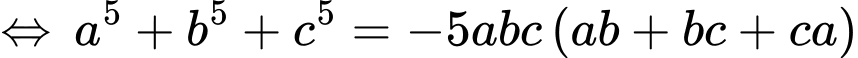
• Áp dụng:
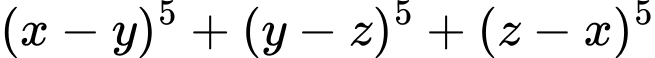
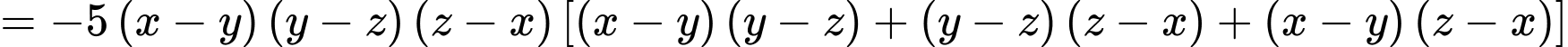 chia hết cho
chia hết cho 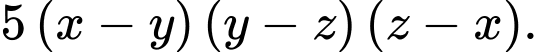
Vậy
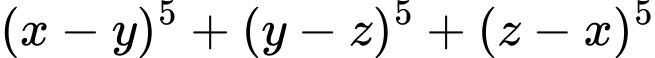 chia hết cho
chia hết cho 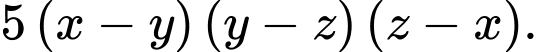
Tìm điều kiện để chia hết
Câu 5 [582487]: Cho một số tự nhiên có 4 chữ số 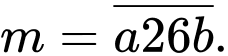 Biết
Biết 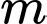 chia hết cho cả
chia hết cho cả 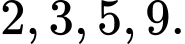 Tìm
Tìm 
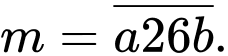 Biết
Biết 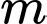 chia hết cho cả
chia hết cho cả 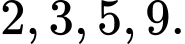 Tìm
Tìm 
Hiển nhiên: 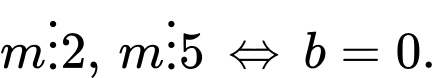
 và
và 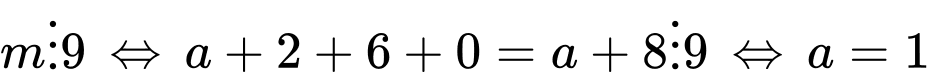
Vậy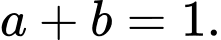
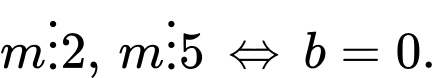
 và
và 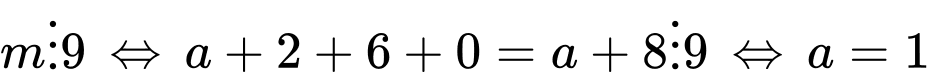
Vậy
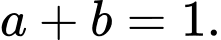
Câu 6 [582489]: Tìm số tự nhiên 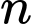 để
để  chia hết cho
chia hết cho 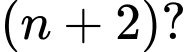
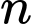 để
để  chia hết cho
chia hết cho 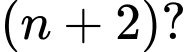
Xét thương: 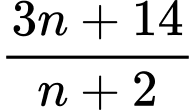
Khi đó: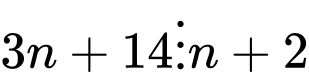
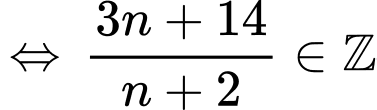
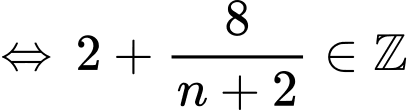
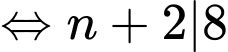
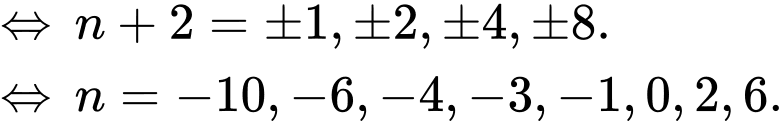
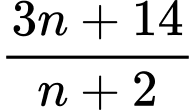
Khi đó:
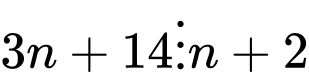
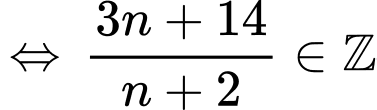
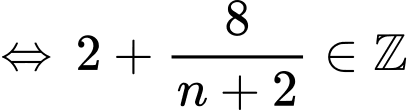
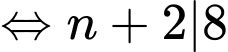
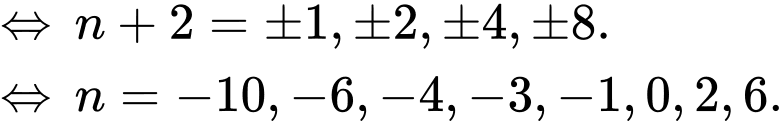
Câu 7 [582492]: Tìm điều kiện của số nguyên dương 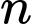 sao cho
sao cho 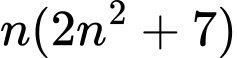 chia hết cho 3?
chia hết cho 3?
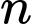 sao cho
sao cho 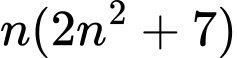 chia hết cho 3?
chia hết cho 3?
Xét:
+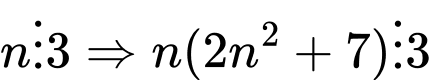
+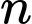 chia 3 dư 1, tức là
chia 3 dư 1, tức là  sao cho
sao cho 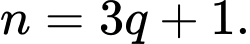
Ta có: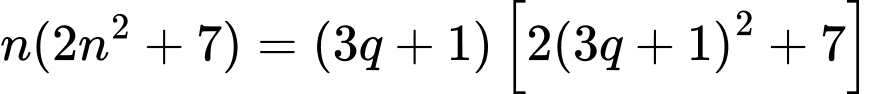
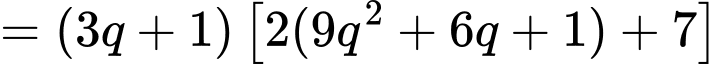
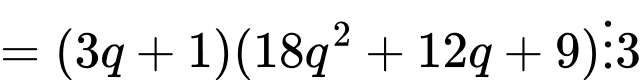
+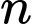 chia 3 dư
chia 3 dư 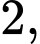 tức là
tức là  sao cho
sao cho 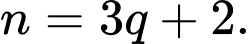
Ta có: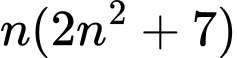
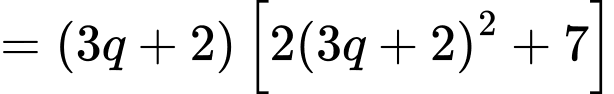
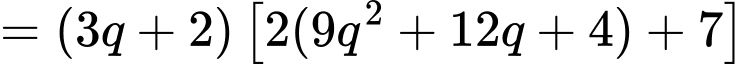
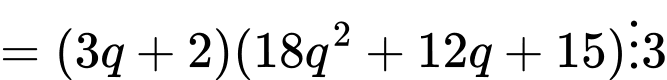
Vậy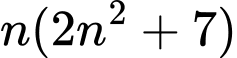 chia hết cho 3 với mọi
chia hết cho 3 với mọi 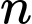
+
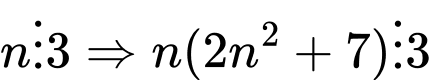
+
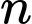 chia 3 dư 1, tức là
chia 3 dư 1, tức là  sao cho
sao cho 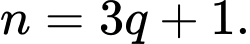
Ta có:
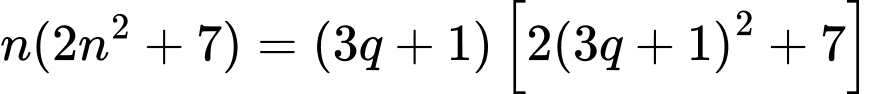
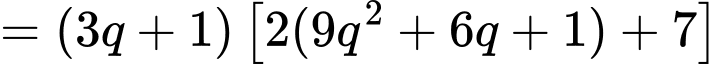
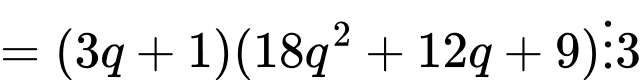
+
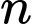 chia 3 dư
chia 3 dư 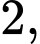 tức là
tức là  sao cho
sao cho 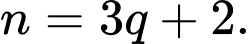
Ta có:
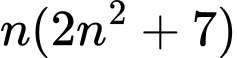
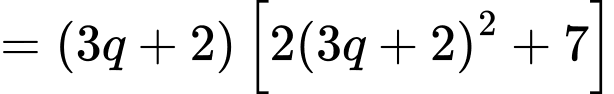
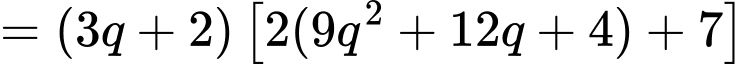
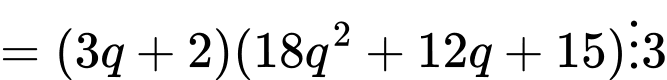
Vậy
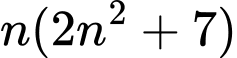 chia hết cho 3 với mọi
chia hết cho 3 với mọi 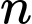
Tìm ưcln, bcnn, chứng minh các tính chất liên quan
Câu 8 [585487]: Tìm 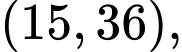
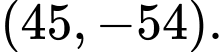
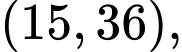
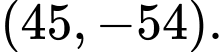
Ta có:
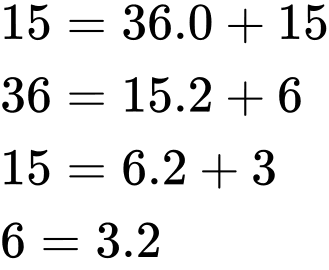
Vậy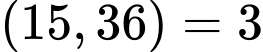
Ta có:
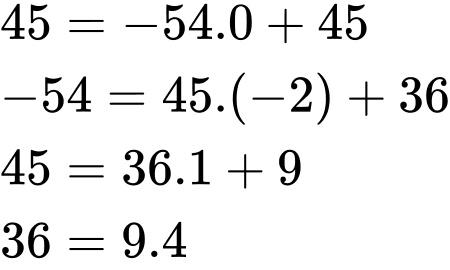
Vậy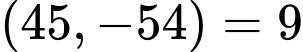
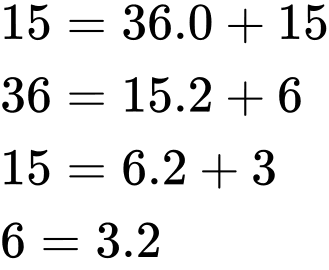
Vậy
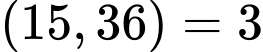
Ta có:
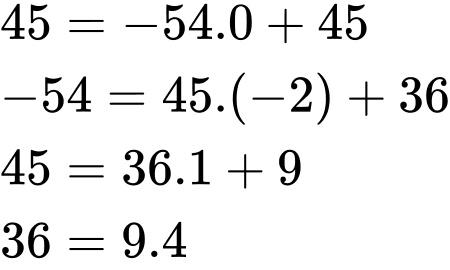
Vậy
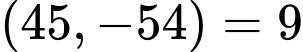
Câu 9 [585488]: Cho 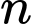 là một số tự nhiên lẻ. Tìm
là một số tự nhiên lẻ. Tìm 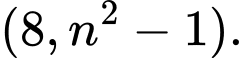
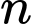 là một số tự nhiên lẻ. Tìm
là một số tự nhiên lẻ. Tìm 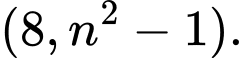
Ta có 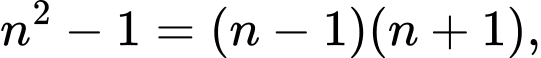 do
do 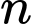 là một số tự nhiên lẻ nên
là một số tự nhiên lẻ nên 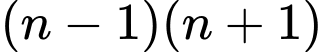 là tích của 2 số chẵn liên tiếp
là tích của 2 số chẵn liên tiếp
Trong 2 số chẵn liên tiếp phải có một số chia hết cho 4, như vậy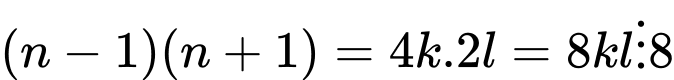
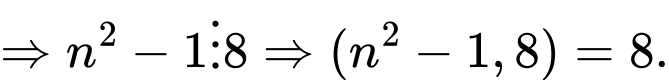
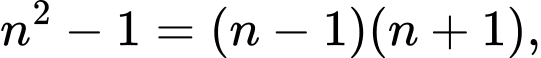 do
do 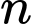 là một số tự nhiên lẻ nên
là một số tự nhiên lẻ nên 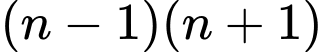 là tích của 2 số chẵn liên tiếp
là tích của 2 số chẵn liên tiếpTrong 2 số chẵn liên tiếp phải có một số chia hết cho 4, như vậy
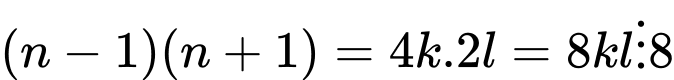
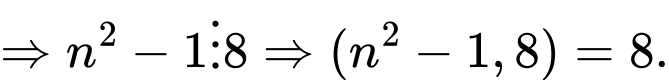
Câu 10 [585489]: Cho các số nguyên 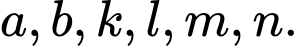 Chứng minh rằng:
Chứng minh rằng:
i)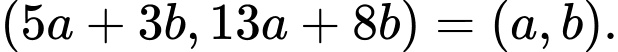
ii) Nếu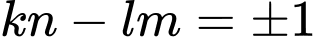 thì
thì 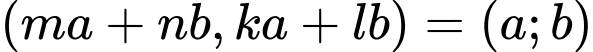
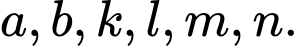 Chứng minh rằng:
Chứng minh rằng:i)
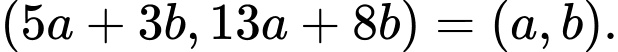
ii) Nếu
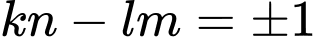 thì
thì 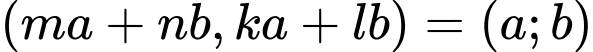
i) Ta có:

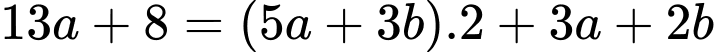

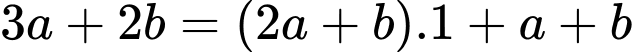
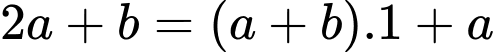
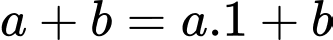
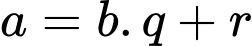

Vậy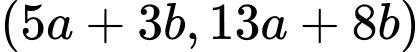
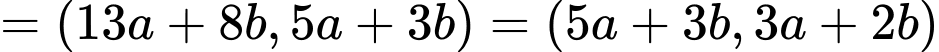
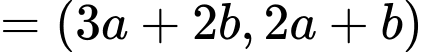
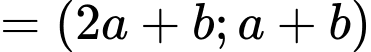

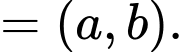
ii) Đặt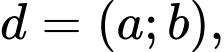
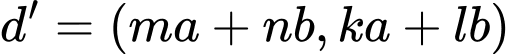
Do: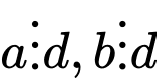 nên
nên 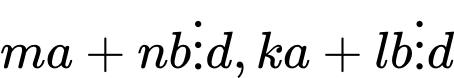
 là ước chung của
là ước chung của 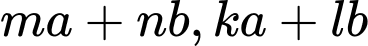
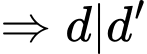
Do: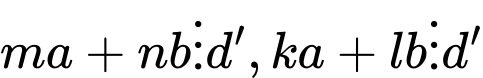 nên:
nên:
+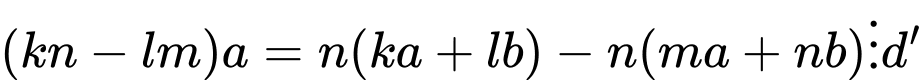
+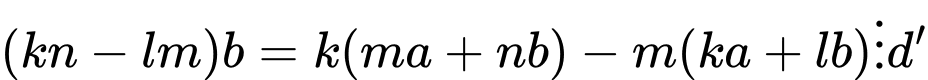
Lai có: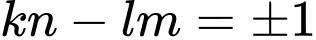
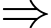
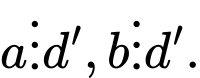
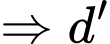 là ước chung của
là ước chung của 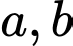
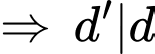
Vậy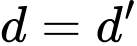

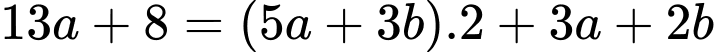

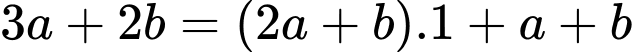
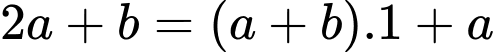
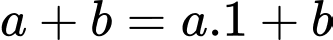
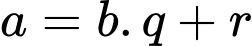

Vậy
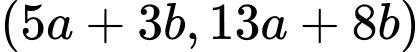
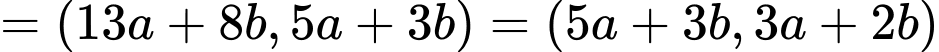
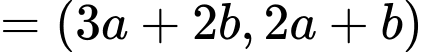
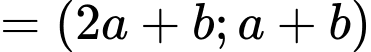

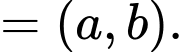
ii) Đặt
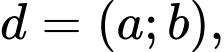
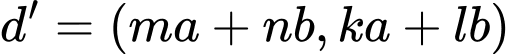
Do:
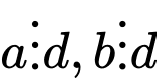 nên
nên 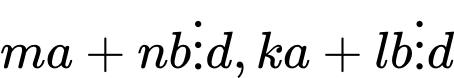
 là ước chung của
là ước chung của 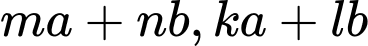
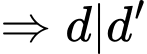
Do:
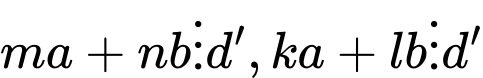 nên:
nên:+
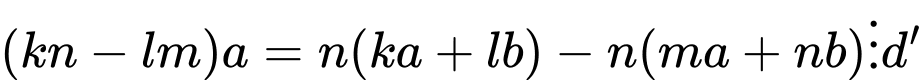
+
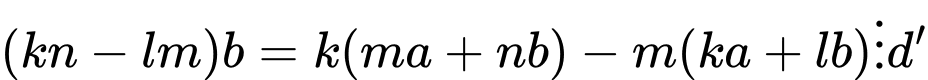
Lai có:
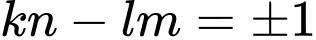
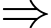
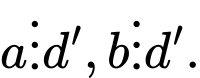
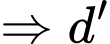 là ước chung của
là ước chung của 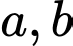
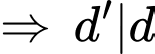
Vậy
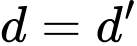
Giải phương trình nghiệm nguyên, tìm điều kiện để phương trình nghiệm nguyên có nghiệm, biện luận số nghiệm
Câu 11 [585490]: Giải phương trình nghiệm nguyên: 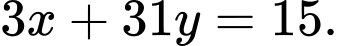
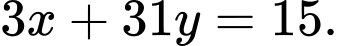
Ta có:
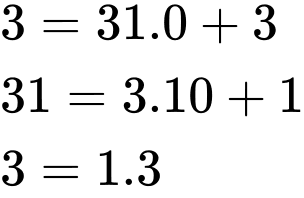
Vậy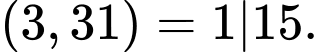 Phương trình có nghiệm
Phương trình có nghiệm
Đảo ngược:
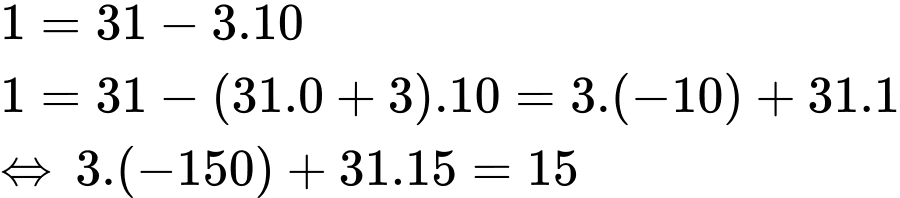
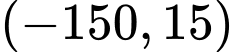 là một nghiệm riêng của phương trình.
là một nghiệm riêng của phương trình.
Nghiệm tổng quát của phương trình là:
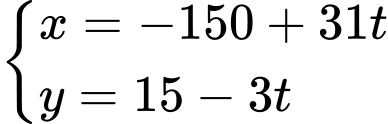
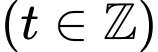
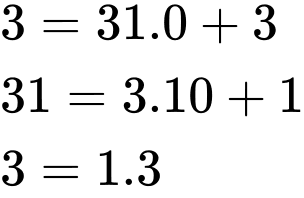
Vậy
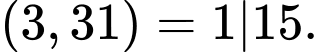 Phương trình có nghiệm
Phương trình có nghiệm
Đảo ngược:
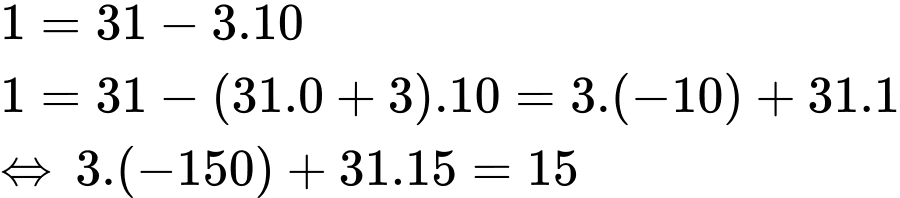
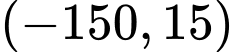 là một nghiệm riêng của phương trình.
là một nghiệm riêng của phương trình.
Nghiệm tổng quát của phương trình là:
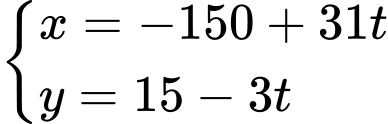
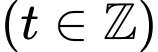
Câu 12 [585491]: Giải và biện luận số nghiệm của phương trình Diophante sau: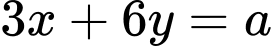
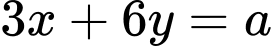
Ta có: 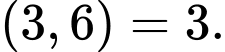 Phương trình có nghiệm
Phương trình có nghiệm 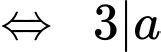
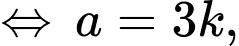
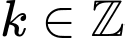
Phương trình trở thành:
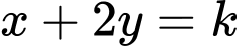
Ta có: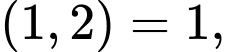 phương trình có nghiệm riêng:
phương trình có nghiệm riêng: 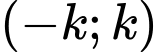
Nghiệm tổng quát của phương trình là:
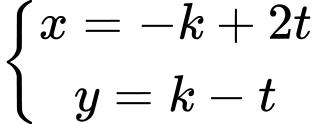

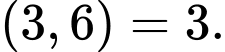 Phương trình có nghiệm
Phương trình có nghiệm 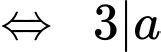
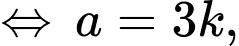
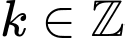
Phương trình trở thành:
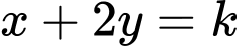
Ta có:
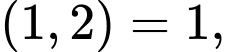 phương trình có nghiệm riêng:
phương trình có nghiệm riêng: 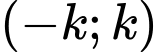
Nghiệm tổng quát của phương trình là: