Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn
(Thí sinh trả lời từ câu 1 đến câu 14. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [582496]: Cho 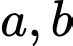 là các số tự nhiên. Trong các số sau số nào chắc chắn chia hết cho
là các số tự nhiên. Trong các số sau số nào chắc chắn chia hết cho 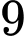 ?
?
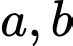 là các số tự nhiên. Trong các số sau số nào chắc chắn chia hết cho
là các số tự nhiên. Trong các số sau số nào chắc chắn chia hết cho 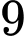 ?
? A, 123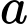 + 9
+ 9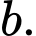
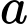 + 9
+ 9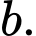
B, 414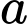 + 558
+ 558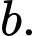
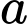 + 558
+ 558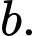
C, 99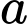 +
+ 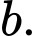
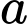 +
+ 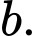
D, 991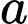 + 8
+ 8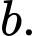
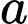 + 8
+ 8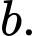
Ta có 414 và 558 có tổng các chữ số của nó lần lượt là 9 và 18 nên 414 và 558 đều chia hết cho 9 nên  chia hết cho 9.
chia hết cho 9.
Dễ thấy các biểu thức còn lại khi thay các giá trị cụ thể của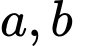 thì không chắc chắn chia hết cho 9
Đáp án: B
thì không chắc chắn chia hết cho 9
Đáp án: B
 chia hết cho 9.
chia hết cho 9.Dễ thấy các biểu thức còn lại khi thay các giá trị cụ thể của
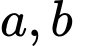 thì không chắc chắn chia hết cho 9
Đáp án: B
thì không chắc chắn chia hết cho 9
Đáp án: B
Câu 2 [582497]: Khẳng định nào sau đây là đúng?
A, Nếu 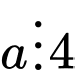 và
và 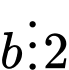 thì
thì 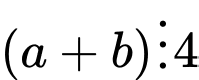 .
.
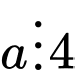 và
và 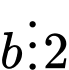 thì
thì 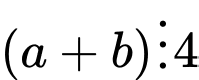 .
.B, Nếu 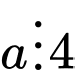 và
và 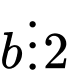 thì
thì 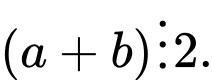
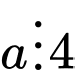 và
và 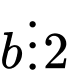 thì
thì 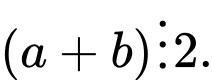
C, Nếu 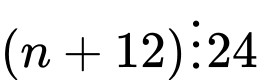 thì
thì 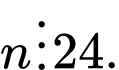
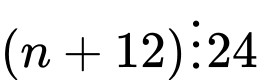 thì
thì 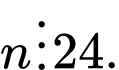
D, Nếu 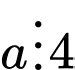 và
và 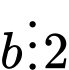 và
và  thì
thì 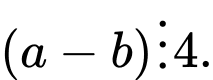
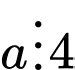 và
và 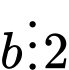 và
và  thì
thì 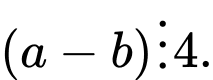
A sai với 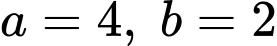
B đúng vì và
và 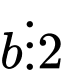 nên
nên 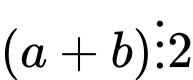
C sai với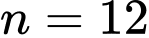
D sai với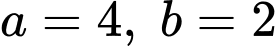 Đáp án: B
Đáp án: B
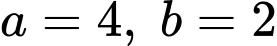
B đúng vì
 và
và 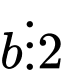 nên
nên 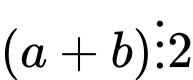
C sai với
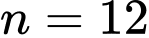
D sai với
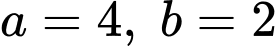 Đáp án: B
Đáp án: B
Câu 3 [582498]: Khi chia số tự nhiên 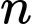 cho
cho 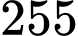 ta được số dư là
ta được số dư là 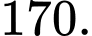 Số
Số 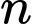 có chia hết cho
có chia hết cho 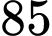 không?
không?
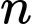 cho
cho 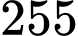 ta được số dư là
ta được số dư là 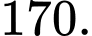 Số
Số 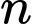 có chia hết cho
có chia hết cho 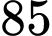 không?
không? A, Có.
B, Không.
C, Có khi và chỉ khi 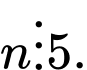
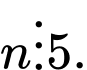
D, Chưa thể kết luận.
Ta có 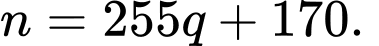
Mà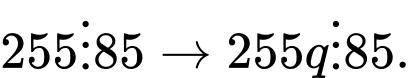
Mặt khác
Do đó n luôn chia hết cho 85 Đáp án: A
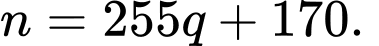
Mà
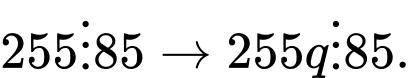
Mặt khác

Do đó n luôn chia hết cho 85 Đáp án: A
Câu 4 [582500]: Cho 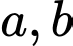 là các số tự nhiên và đều chia hết cho
là các số tự nhiên và đều chia hết cho 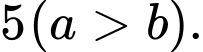 Trong các biểu thức dưới đây, biểu thức nào chắc chắn chia hết cho
Trong các biểu thức dưới đây, biểu thức nào chắc chắn chia hết cho  ?
?
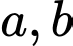 là các số tự nhiên và đều chia hết cho
là các số tự nhiên và đều chia hết cho 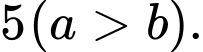 Trong các biểu thức dưới đây, biểu thức nào chắc chắn chia hết cho
Trong các biểu thức dưới đây, biểu thức nào chắc chắn chia hết cho  ?
? A, 

B, 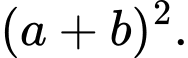
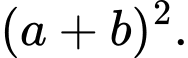
C, 

D, Không có biểu thức nào thỏa mãn.
Thử với 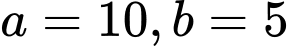 tất cả các biểu thức trên đều không chia hết cho
tất cả các biểu thức trên đều không chia hết cho  Đáp án: D
Đáp án: D
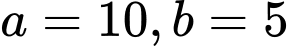 tất cả các biểu thức trên đều không chia hết cho
tất cả các biểu thức trên đều không chia hết cho  Đáp án: D
Đáp án: D
Câu 5 [582503]: Cho 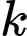 là một số tự nhiên. Tích của
là một số tự nhiên. Tích của 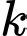 số nguyên liên tiếp luôn chia hết cho
số nguyên liên tiếp luôn chia hết cho 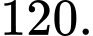 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của 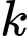 để khẳng định trên luôn đúng?
để khẳng định trên luôn đúng?
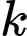 là một số tự nhiên. Tích của
là một số tự nhiên. Tích của 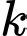 số nguyên liên tiếp luôn chia hết cho
số nguyên liên tiếp luôn chia hết cho 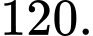 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của 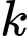 để khẳng định trên luôn đúng?
để khẳng định trên luôn đúng? A, 

B, 

C, 

D, 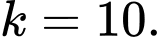
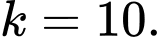
Ta lấy tích 4 số 1.2.3.4 = 24 không thể chia hết cho 120 nên loại 
Ta xét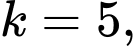 ta chứng minh: Tích của 5 số nguyên liên tiếp luôn chia hết cho 120.
ta chứng minh: Tích của 5 số nguyên liên tiếp luôn chia hết cho 120.
+) Tích của 3 số nguyên liên tiếp luôn chia hết cho 6 vì trong 3 số nguyên liên tiếp có một số chia hết cho 3 và một số chia hết cho 2 nên tích của 3 số nguyên liên tiếp chia hết cho 6 (do (2, 3) = 1).
+) Tích của 2 số chẵn liên tiếp luôn chia hết cho 8 vì:
Giả sử 2 số chẵn liên tiếp là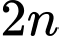 và
và  Tích của chúng là
Tích của chúng là 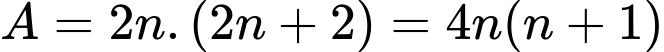
Trong 2 số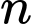 và
và  chắc chắn có 1 số chẵn, do đó
chắc chắn có 1 số chẵn, do đó 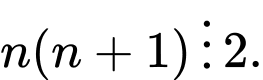
Vậy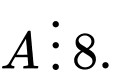
+) Ta có 120 = 3.5.8
Do 5 số nguyên liên tiếp có 3 số liên tiếp nên theo trên ta có tích 5 số nguyên liên tiếp chiahết cho 6.
Do 5 số nguyên liên tiếp có 2 số chẵn liên tiếp nên theo trên ta có tích 5 số nguyên liên tiếp chia hết cho 8.
Mặt khác 5 số nguyên liên tiếp luôn có một số chia hết cho 5 nên tích chúng cũng chia hết cho 5.
Vậy tích của 5 số nguyên liên tiếp luôn chia hết cho 120. Đáp án: B

Ta xét
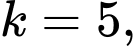 ta chứng minh: Tích của 5 số nguyên liên tiếp luôn chia hết cho 120.
ta chứng minh: Tích của 5 số nguyên liên tiếp luôn chia hết cho 120. +) Tích của 3 số nguyên liên tiếp luôn chia hết cho 6 vì trong 3 số nguyên liên tiếp có một số chia hết cho 3 và một số chia hết cho 2 nên tích của 3 số nguyên liên tiếp chia hết cho 6 (do (2, 3) = 1).
+) Tích của 2 số chẵn liên tiếp luôn chia hết cho 8 vì:
Giả sử 2 số chẵn liên tiếp là
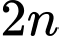 và
và  Tích của chúng là
Tích của chúng là 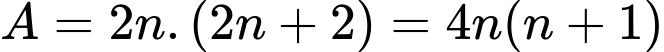
Trong 2 số
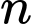 và
và  chắc chắn có 1 số chẵn, do đó
chắc chắn có 1 số chẵn, do đó 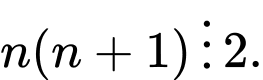
Vậy
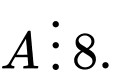
+) Ta có 120 = 3.5.8
Do 5 số nguyên liên tiếp có 3 số liên tiếp nên theo trên ta có tích 5 số nguyên liên tiếp chiahết cho 6.
Do 5 số nguyên liên tiếp có 2 số chẵn liên tiếp nên theo trên ta có tích 5 số nguyên liên tiếp chia hết cho 8.
Mặt khác 5 số nguyên liên tiếp luôn có một số chia hết cho 5 nên tích chúng cũng chia hết cho 5.
Vậy tích của 5 số nguyên liên tiếp luôn chia hết cho 120. Đáp án: B
Câu 6 [582504]: Cho 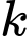 là một số tự nhiên. Tích của
là một số tự nhiên. Tích của 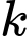 số chẵn liên tiếp luôn chia hết cho
số chẵn liên tiếp luôn chia hết cho 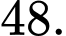 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của 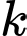 để khẳng định trên luôn đúng?
để khẳng định trên luôn đúng?
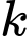 là một số tự nhiên. Tích của
là một số tự nhiên. Tích của 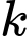 số chẵn liên tiếp luôn chia hết cho
số chẵn liên tiếp luôn chia hết cho 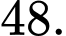 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của 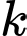 để khẳng định trên luôn đúng?
để khẳng định trên luôn đúng? A, 

B, 

C, 

D, 

Với 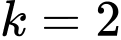 ta xét 2.4 = 8 không chia hết cho 48.
ta xét 2.4 = 8 không chia hết cho 48.
Ta xét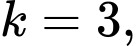 ta chứng minh: Tích của 3 số chẵn liên tiếp luôn chia hết cho 48.
ta chứng minh: Tích của 3 số chẵn liên tiếp luôn chia hết cho 48.
Ba số chẵn liên tiếp có dạng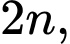
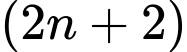 và
và 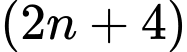 với
với 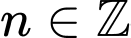
Do đó tích 3 số chẵn liên tiếp có dạng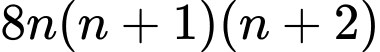
Do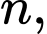
 và
và  là 3 số nguyên liên tiếp (mà tích của 3 số nguyên liên tiếp luôn chia hết cho 6 vì trong 3 số nguyên liên tiếp có một số chia hết cho 3 và một số chia hết cho 2 nên tích của 3 số nguyên liên tiếp chia hết cho 6 (do (2, 3) = 1).)
là 3 số nguyên liên tiếp (mà tích của 3 số nguyên liên tiếp luôn chia hết cho 6 vì trong 3 số nguyên liên tiếp có một số chia hết cho 3 và một số chia hết cho 2 nên tích của 3 số nguyên liên tiếp chia hết cho 6 (do (2, 3) = 1).)
Nên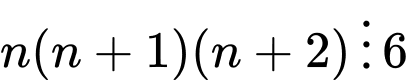
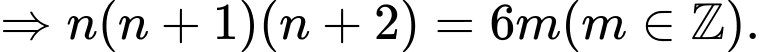
Do đó tích của 3 số chẵn liên tiếp là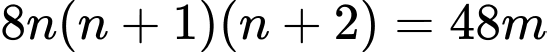 luôn chia hết 48.
luôn chia hết 48.
Vậy B là chính xác. Đáp án: B
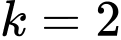 ta xét 2.4 = 8 không chia hết cho 48.
ta xét 2.4 = 8 không chia hết cho 48. Ta xét
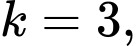 ta chứng minh: Tích của 3 số chẵn liên tiếp luôn chia hết cho 48.
ta chứng minh: Tích của 3 số chẵn liên tiếp luôn chia hết cho 48. Ba số chẵn liên tiếp có dạng
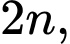
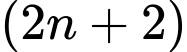 và
và 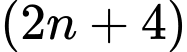 với
với 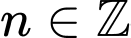
Do đó tích 3 số chẵn liên tiếp có dạng
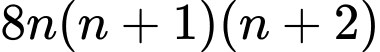
Do
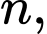
 và
và  là 3 số nguyên liên tiếp (mà tích của 3 số nguyên liên tiếp luôn chia hết cho 6 vì trong 3 số nguyên liên tiếp có một số chia hết cho 3 và một số chia hết cho 2 nên tích của 3 số nguyên liên tiếp chia hết cho 6 (do (2, 3) = 1).)
là 3 số nguyên liên tiếp (mà tích của 3 số nguyên liên tiếp luôn chia hết cho 6 vì trong 3 số nguyên liên tiếp có một số chia hết cho 3 và một số chia hết cho 2 nên tích của 3 số nguyên liên tiếp chia hết cho 6 (do (2, 3) = 1).) Nên
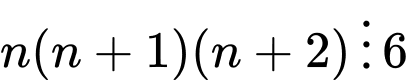
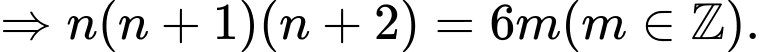
Do đó tích của 3 số chẵn liên tiếp là
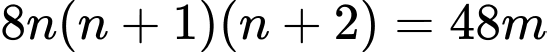 luôn chia hết 48.
luôn chia hết 48. Vậy B là chính xác. Đáp án: B
Câu 7 [582505]: Cho 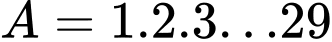 và
và 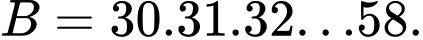 Biểu thức nào sau đây chia hết cho
Biểu thức nào sau đây chia hết cho 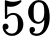 ?
?
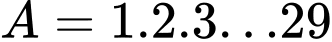 và
và 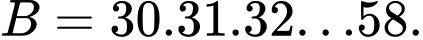 Biểu thức nào sau đây chia hết cho
Biểu thức nào sau đây chia hết cho 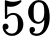 ?
? A, 

B, 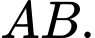
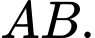
C, 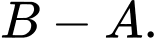
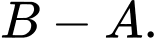
D, 

Ta có 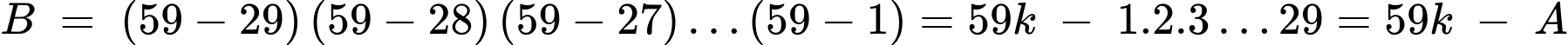
Nên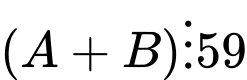
Biểu thức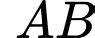 dễ thấy không có thừa số nguyên tố là 59 nên không chia hết cho 59
dễ thấy không có thừa số nguyên tố là 59 nên không chia hết cho 59
Hai biểu thức còn lại có thể dùng đồng dư để chứng minh chúng không chia hết cho 59.
Trong trường hợp bài tập 1 đáp án, chỉ cần giải ra biểu thức là đủ, biểu thức này cũng có thể chứng minh chia hết cho 59 bằng phép đồng dư. Đáp án: A
là đủ, biểu thức này cũng có thể chứng minh chia hết cho 59 bằng phép đồng dư. Đáp án: A
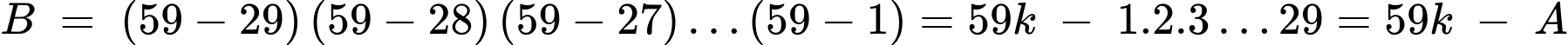
Nên
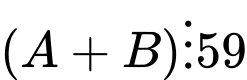
Biểu thức
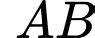 dễ thấy không có thừa số nguyên tố là 59 nên không chia hết cho 59
dễ thấy không có thừa số nguyên tố là 59 nên không chia hết cho 59Hai biểu thức còn lại có thể dùng đồng dư để chứng minh chúng không chia hết cho 59.
Trong trường hợp bài tập 1 đáp án, chỉ cần giải ra biểu thức
 là đủ, biểu thức này cũng có thể chứng minh chia hết cho 59 bằng phép đồng dư. Đáp án: A
là đủ, biểu thức này cũng có thể chứng minh chia hết cho 59 bằng phép đồng dư. Đáp án: A
Câu 8 [582506]: Có bao nhiêu số nguyên dương 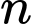 thỏa mãn
thỏa mãn 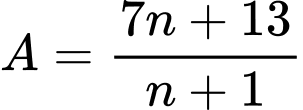 là một số tự nhiên?
là một số tự nhiên?
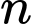 thỏa mãn
thỏa mãn 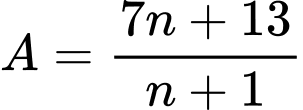 là một số tự nhiên?
là một số tự nhiên? A, 2.
B, 3.
C, 4.
D, 5.
Ta có 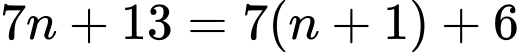
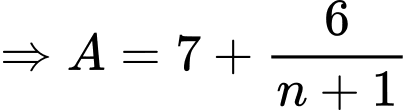
Để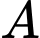 là một số tự nhiên thì
là một số tự nhiên thì 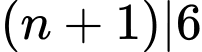
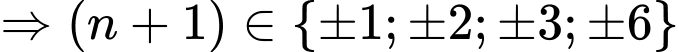
Do nên dễ thấy chỉ có các giá trị {1,2,5} là thỏa mãn. Đáp án: B
nên dễ thấy chỉ có các giá trị {1,2,5} là thỏa mãn. Đáp án: B
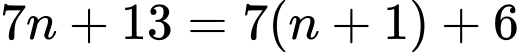
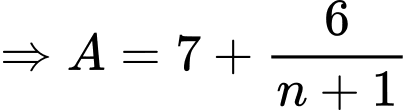
Để
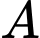 là một số tự nhiên thì
là một số tự nhiên thì 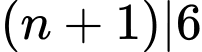
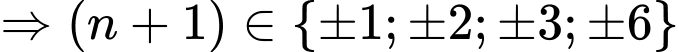
Do
 nên dễ thấy chỉ có các giá trị {1,2,5} là thỏa mãn. Đáp án: B
nên dễ thấy chỉ có các giá trị {1,2,5} là thỏa mãn. Đáp án: B
Câu 9 [582507]: Cho số nguyên  Giá trị nhỏ nhất của
Giá trị nhỏ nhất của 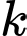 để
để 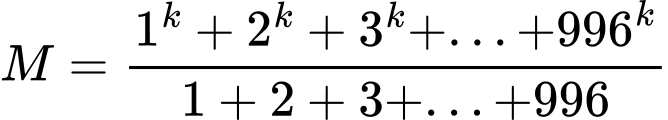 là một số nguyên?
là một số nguyên?
 Giá trị nhỏ nhất của
Giá trị nhỏ nhất của 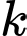 để
để 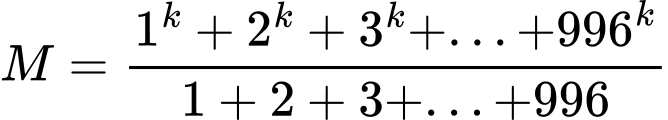 là một số nguyên?
là một số nguyên? A, 

B, 

C, 

D, 

Cách 1
Ta đặt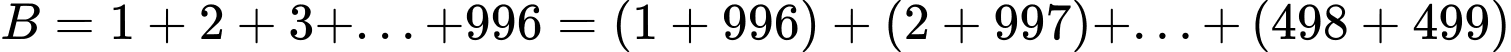
Nên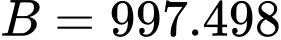
Ta đặt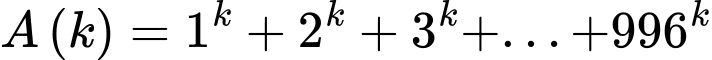
Xét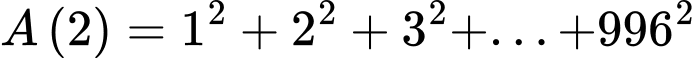
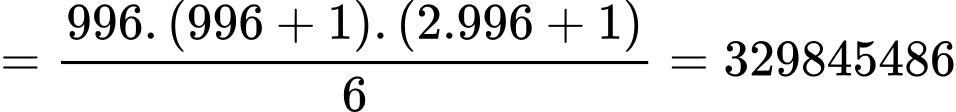 không chia hết cho
không chia hết cho 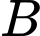
Xét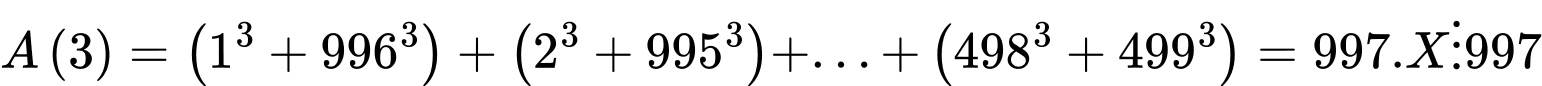
Lại có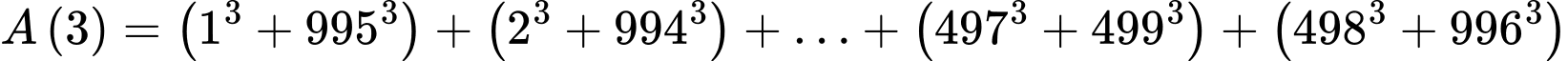
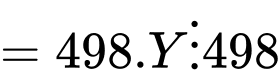
Mặt khác gcd(498,997) = 1.
Nên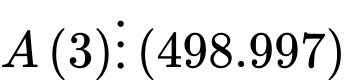 hay
hay 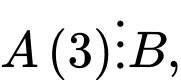 khi đó
khi đó 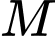 là một số nguyên.
là một số nguyên.
Vậy
Cách 2:
Theo định lý Nicomachus, ta biết rằng với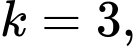 từ số = bình phương mẫu số.
từ số = bình phương mẫu số.
Vậy ít nhất với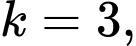
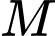 là một số nguyên.
là một số nguyên.
Ta xét thử với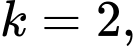 tính như cách 1 hoặc bấm máy, ta có tử số không chia hết cho mẫu số.
tính như cách 1 hoặc bấm máy, ta có tử số không chia hết cho mẫu số.
Vậy Đáp án: B
Đáp án: B
Ta đặt
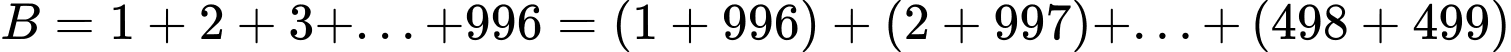
Nên
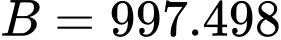
Ta đặt
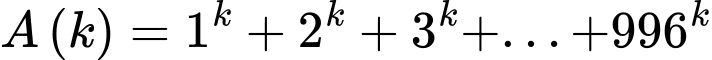
Xét
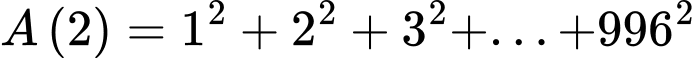
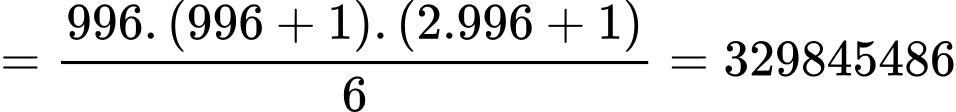 không chia hết cho
không chia hết cho 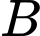
Xét
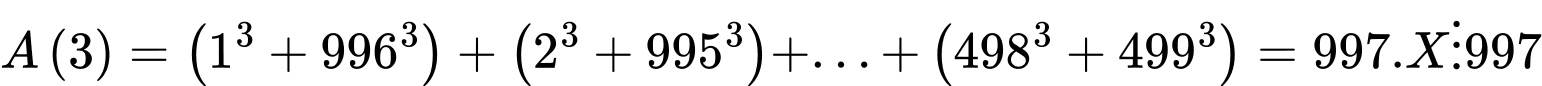
Lại có
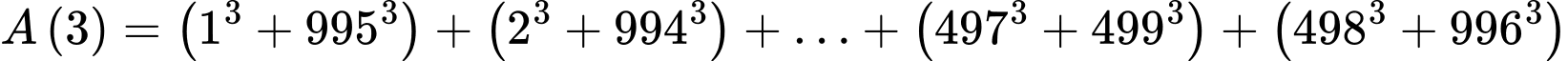
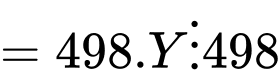
Mặt khác gcd(498,997) = 1.
Nên
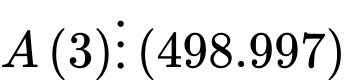 hay
hay 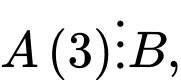 khi đó
khi đó 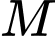 là một số nguyên.
là một số nguyên. Vậy

Cách 2:
Theo định lý Nicomachus, ta biết rằng với
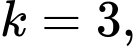 từ số = bình phương mẫu số.
từ số = bình phương mẫu số. Vậy ít nhất với
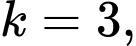
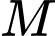 là một số nguyên.
là một số nguyên. Ta xét thử với
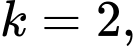 tính như cách 1 hoặc bấm máy, ta có tử số không chia hết cho mẫu số.
tính như cách 1 hoặc bấm máy, ta có tử số không chia hết cho mẫu số. Vậy
 Đáp án: B
Đáp án: B
Câu 10 [582508]: Số 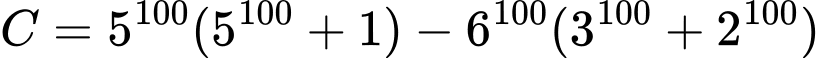 không chia hết cho số nào sau đây?
không chia hết cho số nào sau đây?
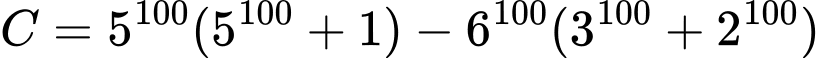 không chia hết cho số nào sau đây?
không chia hết cho số nào sau đây? A, 13.
B, 7.
C, 5.
D, 2.
Ta có 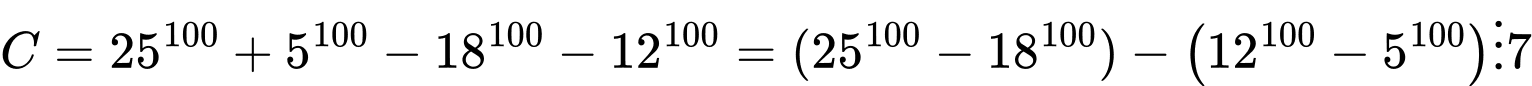
Mặt khác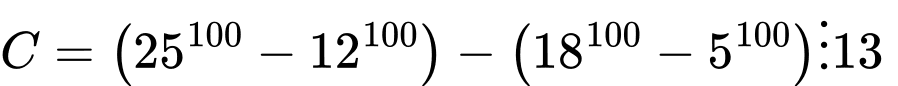
Lại có là số chẵn nên chia hết cho 2
là số chẵn nên chia hết cho 2
Đến đây có thể mạnh dạn khoanh giá trị 5, tuy nhiên có thể chứng minh thêm không chia hết cho 5.
không chia hết cho 5.
Có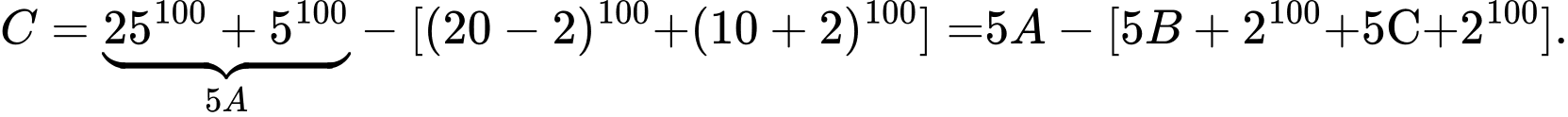
Nên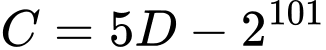 không chia hết cho 5 (Dùng chứng minh đồng dư sẽ thuận lợi hơn) Đáp án: C
không chia hết cho 5 (Dùng chứng minh đồng dư sẽ thuận lợi hơn) Đáp án: C
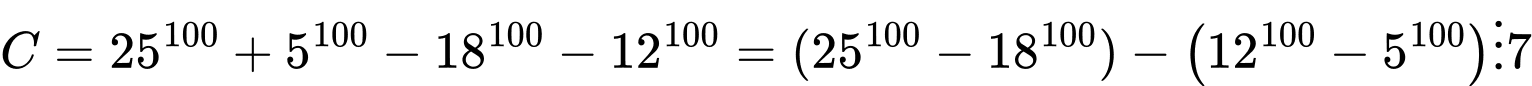
Mặt khác
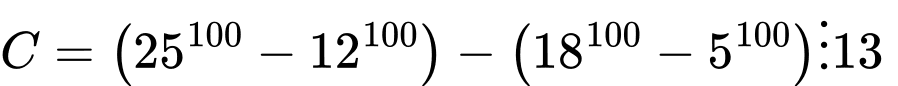
Lại có
 là số chẵn nên chia hết cho 2
là số chẵn nên chia hết cho 2Đến đây có thể mạnh dạn khoanh giá trị 5, tuy nhiên có thể chứng minh thêm
 không chia hết cho 5.
không chia hết cho 5. Có
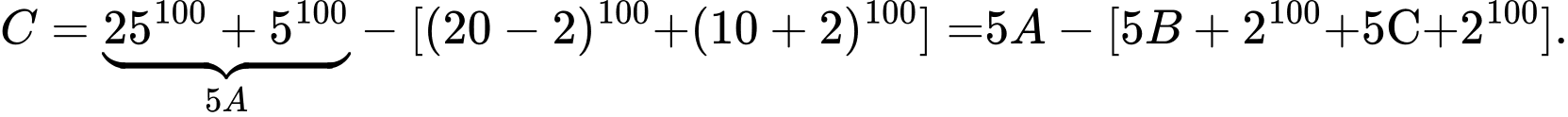
Nên
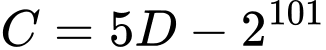 không chia hết cho 5 (Dùng chứng minh đồng dư sẽ thuận lợi hơn) Đáp án: C
không chia hết cho 5 (Dùng chứng minh đồng dư sẽ thuận lợi hơn) Đáp án: C
Câu 11 [582514]: Các số có dạng  luôn chia hết cho số tự nhiên nào?
luôn chia hết cho số tự nhiên nào?
 luôn chia hết cho số tự nhiên nào?
luôn chia hết cho số tự nhiên nào? A, 3.
B, 7.
C, 11.
D, 13.
Ta lấy cụ thể một số, giả sử là 1234321 thấy số này chia hết cho 11 nhưng không chia hết cho 3, 7, 13 nên mạnh dạn khoanh 11.
Để chứng minh các số có dạng trên luôn chia hết cho 11, ta chỉ cần dựa vào dấu hiệu chia hết cho 11. Đáp án: C
Để chứng minh các số có dạng trên luôn chia hết cho 11, ta chỉ cần dựa vào dấu hiệu chia hết cho 11. Đáp án: C
Câu 12 [582515]: Cho 2 số 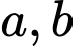 nguyên thỏa mãn
nguyên thỏa mãn 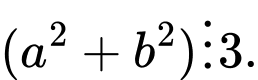 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
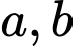 nguyên thỏa mãn
nguyên thỏa mãn 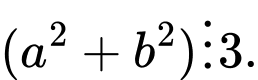 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, Tích 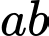 luôn chia hết cho
luôn chia hết cho 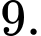
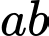 luôn chia hết cho
luôn chia hết cho 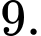
B, 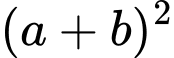 không chia hết cho
không chia hết cho 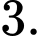
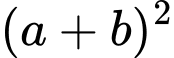 không chia hết cho
không chia hết cho 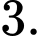
C, 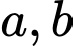 chưa chắc cùng chia hết cho
chưa chắc cùng chia hết cho 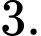
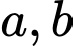 chưa chắc cùng chia hết cho
chưa chắc cùng chia hết cho 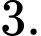
D, Ba khẳng định trên đều sai.
Với một số tự nhiên 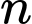 không chia hết cho 3 thì
không chia hết cho 3 thì 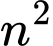 chia 3 luôn có số dư là 1.
chia 3 luôn có số dư là 1.
Nếu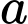 hoặc
hoặc 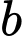 hoặc cả
hoặc cả 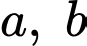 không chia hết cho 3 thì
không chia hết cho 3 thì 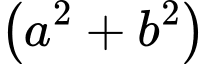 không thể chia hết cho 3.
không thể chia hết cho 3.
Do đó cả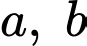 đều chia hết cho 3.
đều chia hết cho 3.
Vậy tích của chúng luôn chia hết cho 9. Đáp án: A
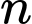 không chia hết cho 3 thì
không chia hết cho 3 thì 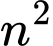 chia 3 luôn có số dư là 1.
chia 3 luôn có số dư là 1. Nếu
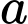 hoặc
hoặc 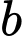 hoặc cả
hoặc cả 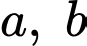 không chia hết cho 3 thì
không chia hết cho 3 thì 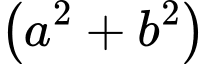 không thể chia hết cho 3.
không thể chia hết cho 3. Do đó cả
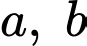 đều chia hết cho 3.
đều chia hết cho 3.Vậy tích của chúng luôn chia hết cho 9. Đáp án: A
Câu 13 [582510]: Có bao nhiêu số tự nhiên 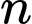 để
để 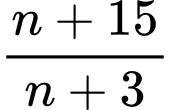 là số tự nhiên?
là số tự nhiên?
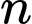 để
để 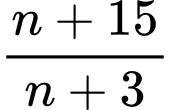 là số tự nhiên?
là số tự nhiên? A, 2.
B, 3.
C, 4.
D, 5.
Để 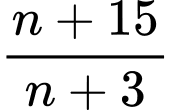 là số tự nhiên thì
là số tự nhiên thì  chia hết cho
chia hết cho 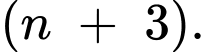
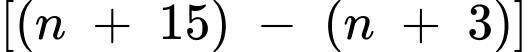 chia hết cho
chia hết cho 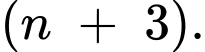
 12 chia hết cho
12 chia hết cho 

 là Ư(12)
là Ư(12) 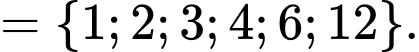

Vậy với 4 giá trị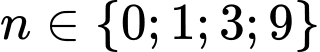 thì
thì 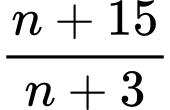 là số tự nhiên. Đáp án: C
là số tự nhiên. Đáp án: C
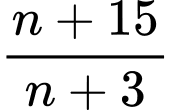 là số tự nhiên thì
là số tự nhiên thì  chia hết cho
chia hết cho 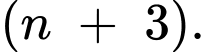
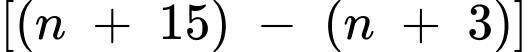 chia hết cho
chia hết cho 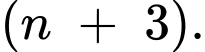
 12 chia hết cho
12 chia hết cho 

 là Ư(12)
là Ư(12) 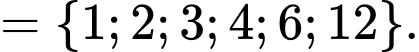

Vậy với 4 giá trị
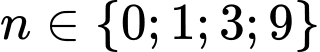 thì
thì 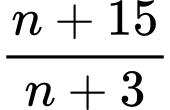 là số tự nhiên. Đáp án: C
là số tự nhiên. Đáp án: C
Câu 14 [582511]: Có bao nhiêu giá trị của 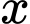 để
để 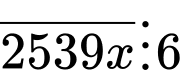 ?
?
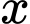 để
để 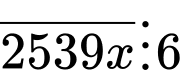 ?
? A, 1.
B, 2.
C, 3.
D, 4.
Ta có: 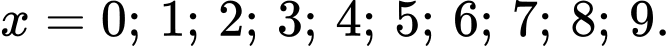
Ta xét tính chia hết của cho 2 và 3.
cho 2 và 3.
- Vì chia hết cho 2 nên
chia hết cho 2 nên 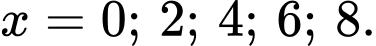
- Vì chia hết cho 3 nên
chia hết cho 3 nên 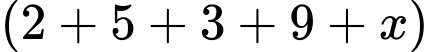 chia hết cho 3.
chia hết cho 3.
Suy ra: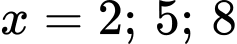
Do đó để chia hết cho cả 2 và 3 thì
chia hết cho cả 2 và 3 thì 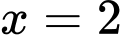 hoặc
hoặc 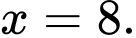 Đáp án: B
Đáp án: B
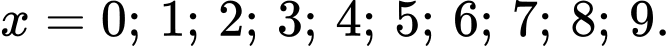
Ta xét tính chia hết của
 cho 2 và 3.
cho 2 và 3. - Vì
 chia hết cho 2 nên
chia hết cho 2 nên 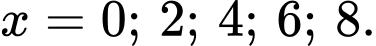
- Vì
 chia hết cho 3 nên
chia hết cho 3 nên 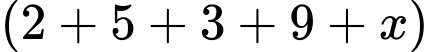 chia hết cho 3.
chia hết cho 3. Suy ra:
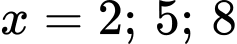
Do đó để
 chia hết cho cả 2 và 3 thì
chia hết cho cả 2 và 3 thì 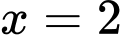 hoặc
hoặc 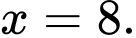 Đáp án: B
Đáp án: B Dạng câu hỏi: Trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 15, 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 15 [582502]: Mỗi phát biểu sau là đúng hay sai?
a) Tổng của 2 số tự nhiên liên tiếp luôn chia hết cho 2.
b) Tổng của 3 số tự nhiên liên tiếp luôn chia hết cho 3.
c) Tổng của 4 số tự nhiên liên tiếp luôn chia hết cho 4.
d) Tích của 2 số tự nhiên liên tiếp luôn chia hết cho 4.
e) Tích của 2 số chẵn liên tiếp luôn chia hết cho 8.
a) Tổng của 2 số tự nhiên liên tiếp luôn chia hết cho 2.
b) Tổng của 3 số tự nhiên liên tiếp luôn chia hết cho 3.
c) Tổng của 4 số tự nhiên liên tiếp luôn chia hết cho 4.
d) Tích của 2 số tự nhiên liên tiếp luôn chia hết cho 4.
e) Tích của 2 số chẵn liên tiếp luôn chia hết cho 8.
a) Sai
b) Đúng
c) Sai
d) Sai
e) Đúng
Phát biểu 1: Tổng 2 số tự nhiên liên tiếp luôn là 1 số lẻ nên không chia hết cho 2.
Phát biểu 2: Giả sử xét 3 số tự nhiên liên tiếp là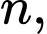
 và
và  Khi đó tổng của chúng là
Khi đó tổng của chúng là 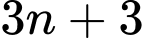 nên luôn chia hết cho 3 với mọi số tự nhiên
nên luôn chia hết cho 3 với mọi số tự nhiên 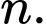
Phát biểu 3: Phản chứng: (1+2+3+4) = 10 không chia hết cho 4.
Phát biểu 4: Phản chứng: 5.6 = 30 không chia hết cho 4.
Phát biểu 5: Giả sử 2 số chẵn liên tiếp là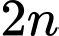 và
và  Tích của chúng là
Tích của chúng là 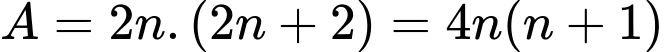
Trong 2 số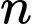 và
và  chắc chắn có 1 số chẵn, do đó
chắc chắn có 1 số chẵn, do đó 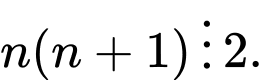 Vậy
Vậy 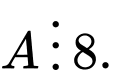
b) Đúng
c) Sai
d) Sai
e) Đúng
Phát biểu 1: Tổng 2 số tự nhiên liên tiếp luôn là 1 số lẻ nên không chia hết cho 2.
Phát biểu 2: Giả sử xét 3 số tự nhiên liên tiếp là
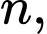
 và
và  Khi đó tổng của chúng là
Khi đó tổng của chúng là 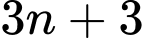 nên luôn chia hết cho 3 với mọi số tự nhiên
nên luôn chia hết cho 3 với mọi số tự nhiên 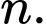
Phát biểu 3: Phản chứng: (1+2+3+4) = 10 không chia hết cho 4.
Phát biểu 4: Phản chứng: 5.6 = 30 không chia hết cho 4.
Phát biểu 5: Giả sử 2 số chẵn liên tiếp là
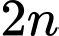 và
và  Tích của chúng là
Tích của chúng là 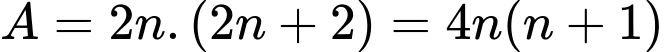
Trong 2 số
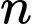 và
và  chắc chắn có 1 số chẵn, do đó
chắc chắn có 1 số chẵn, do đó 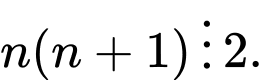 Vậy
Vậy 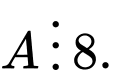
Câu 16 [582509]: Mỗi phát biểu sau là đúng hay sai?
a)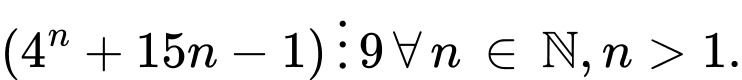
b)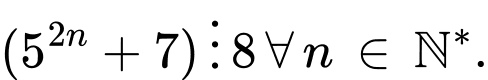
a)
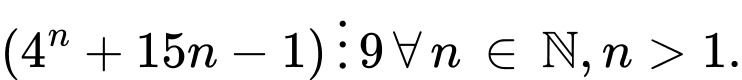
b)
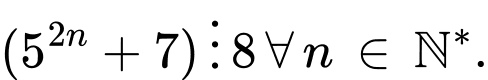
a) Đúng
b) Đúng
Cả hai phát biểu đều đúng, ta dùng quy nạp để chứng minh.
+)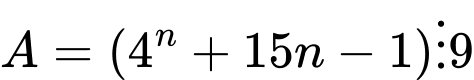
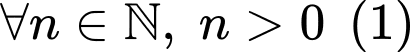
Với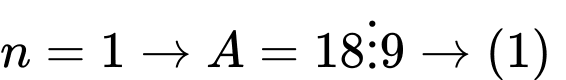 đúng với
đúng với 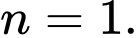
Giả sử (1) đúng đến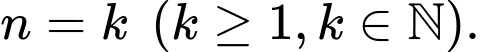
Khi đó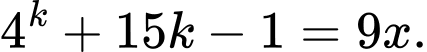
Với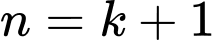
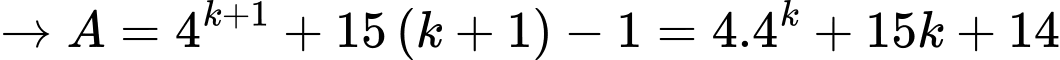
Nên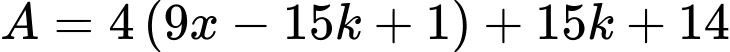
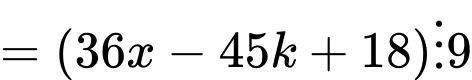
Theo quy nạp (1) luôn đúng
+)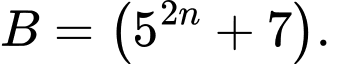
Ta chứng minh tương tự với lưu ý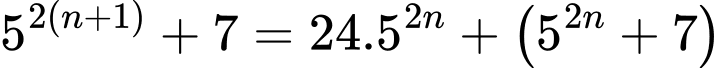
b) Đúng
Cả hai phát biểu đều đúng, ta dùng quy nạp để chứng minh.
+)
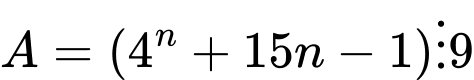
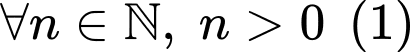
Với
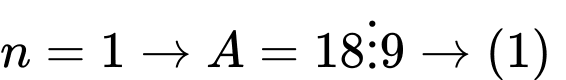 đúng với
đúng với 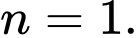
Giả sử (1) đúng đến
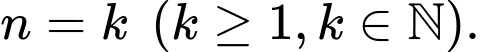
Khi đó
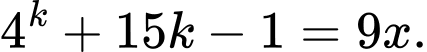
Với
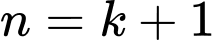
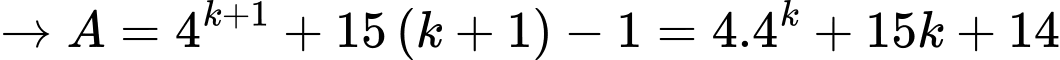
Nên
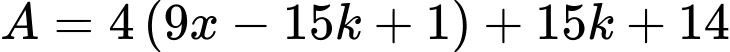
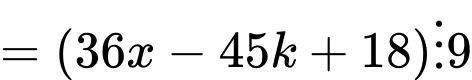
Theo quy nạp (1) luôn đúng
+)
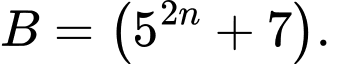
Ta chứng minh tương tự với lưu ý
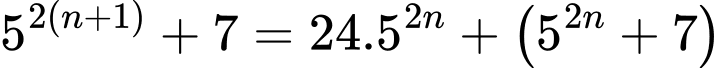
Dạng câu hỏi: Câu trả lời ngắn
(Thí sinh trả lời đáp án từ câu 17 đến câu 18. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 17 [582501]: Cho số tự nhiên 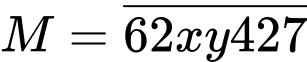 chia hết cho
chia hết cho 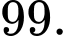
Khi lấy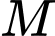 chia cho
chia cho 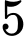 ta được số dư là __________
ta được số dư là __________
Khi lấy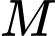 chia cho
chia cho  ta được số dư là __________
ta được số dư là __________
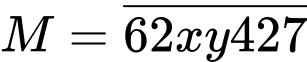 chia hết cho
chia hết cho 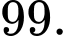
Khi lấy
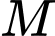 chia cho
chia cho 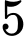 ta được số dư là __________
ta được số dư là __________Khi lấy
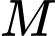 chia cho
chia cho  ta được số dư là __________
ta được số dư là __________
Cho số tự nhiên 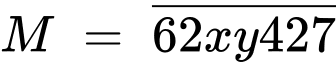 chia hết cho 99.
chia hết cho 99.
Khi lấy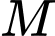 chia cho 5 ta được số dư là 2, khi lấy
chia cho 5 ta được số dư là 2, khi lấy 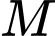 chia cho 13 ta được số dư là 1.
chia cho 13 ta được số dư là 1.
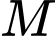 chia hết cho 9
chia hết cho 9 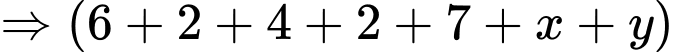 chia hết cho 9
chia hết cho 9 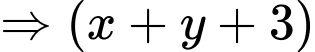 chia hết cho 9
chia hết cho 9
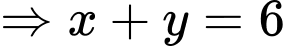 hoặc
hoặc 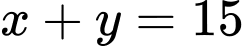
 chia hết cho 11
chia hết cho 11 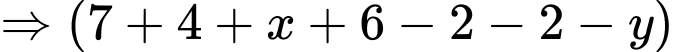 chia hết cho 11
chia hết cho 11  chia hết cho 11
chia hết cho 11
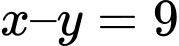 (loại) hoặc
(loại) hoặc 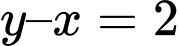
+ Với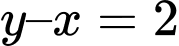 và
và 
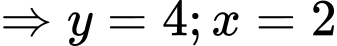
+ Với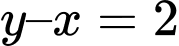 và
và 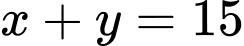 (loại)
(loại)
vậy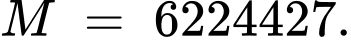
Ta lấy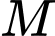 lần lượt chia 5 và 13 để có được các số dư.
lần lượt chia 5 và 13 để có được các số dư.
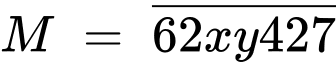 chia hết cho 99.
chia hết cho 99. Khi lấy
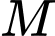 chia cho 5 ta được số dư là 2, khi lấy
chia cho 5 ta được số dư là 2, khi lấy 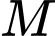 chia cho 13 ta được số dư là 1.
chia cho 13 ta được số dư là 1. 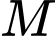 chia hết cho 9
chia hết cho 9 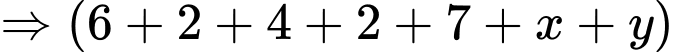 chia hết cho 9
chia hết cho 9 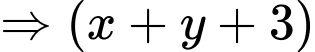 chia hết cho 9
chia hết cho 9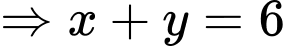 hoặc
hoặc 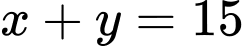
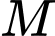 chia hết cho 11
chia hết cho 11 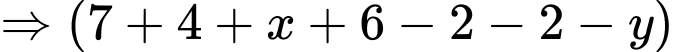 chia hết cho 11
chia hết cho 11  chia hết cho 11
chia hết cho 11 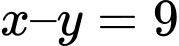 (loại) hoặc
(loại) hoặc 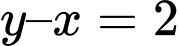
+ Với
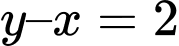 và
và 
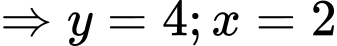
+ Với
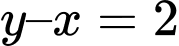 và
và 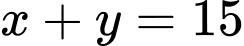 (loại)
(loại) vậy
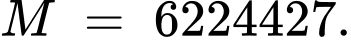
Ta lấy
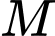 lần lượt chia 5 và 13 để có được các số dư.
lần lượt chia 5 và 13 để có được các số dư.
Câu 18 [582513]: Có __________, cặp chữ số 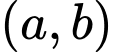 sao cho
sao cho 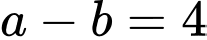 và
và 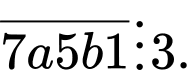
Trong các cặp chữ số đó, giá trị của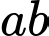 lớn nhất có thể là __________
lớn nhất có thể là __________
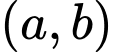 sao cho
sao cho 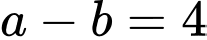 và
và 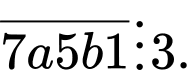
Trong các cặp chữ số đó, giá trị của
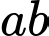 lớn nhất có thể là __________
lớn nhất có thể là __________
Có 2 cặp chữ số 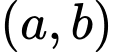 sao cho
sao cho 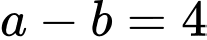 và
và 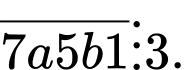
Trong các cặp chữ số đó, giá trị của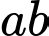 lớn nhất có thể là 45.
lớn nhất có thể là 45.
Ta có: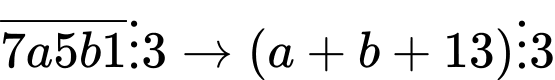 nên
nên  chia 3 dư 2 (1)
chia 3 dư 2 (1)
+)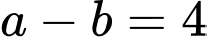
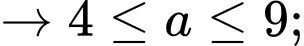
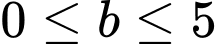
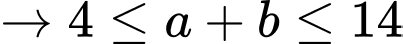 (2)
(2)
Mà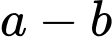 chẵn nên
chẵn nên  cũng là số chẵn (3)
cũng là số chẵn (3)
Từ (1), (2), (3) suy ra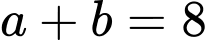 hoặc
hoặc 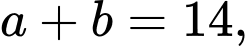 kết hơp cùng
kết hơp cùng 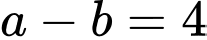 giải ra 2 cặp thỏa mãn là (6; 2) và (9; 5).
giải ra 2 cặp thỏa mãn là (6; 2) và (9; 5).
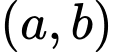 sao cho
sao cho 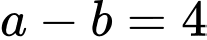 và
và 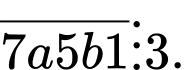
Trong các cặp chữ số đó, giá trị của
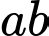 lớn nhất có thể là 45.
lớn nhất có thể là 45. Ta có:
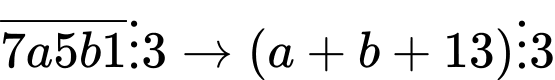 nên
nên  chia 3 dư 2 (1)
chia 3 dư 2 (1) +)
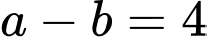
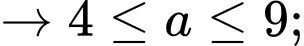
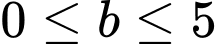
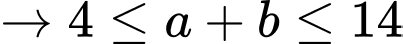 (2)
(2) Mà
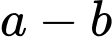 chẵn nên
chẵn nên  cũng là số chẵn (3)
cũng là số chẵn (3) Từ (1), (2), (3) suy ra
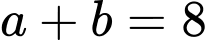 hoặc
hoặc 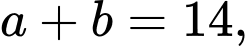 kết hơp cùng
kết hơp cùng 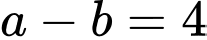 giải ra 2 cặp thỏa mãn là (6; 2) và (9; 5).
giải ra 2 cặp thỏa mãn là (6; 2) và (9; 5). Dạng câu hỏi: Câu hỏi kéo thả
Câu 19 [582499]: Cho số tự nhiên 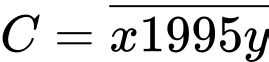 chia hết cho
chia hết cho 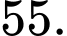
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
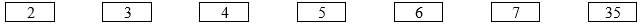
Có tất cả __________ cặp chữ số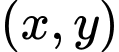 thỏa mãn.
thỏa mãn.
Giá trị lớn nhất có thể của là __________
là __________
Giá trị lớn nhất có thể của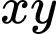 là __________
là __________
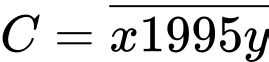 chia hết cho
chia hết cho 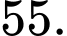
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Có tất cả __________ cặp chữ số
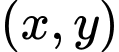 thỏa mãn.
thỏa mãn.Giá trị lớn nhất có thể của
 là __________
là __________Giá trị lớn nhất có thể của
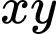 là __________
là __________
Có tất cả 2 cặp chữ số 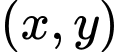 thỏa mãn.
thỏa mãn.
Giá trị lớn nhất có thể của là 7
là 7
Giá trị lớn nhất có thể của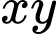 là 5
là 5
Ta có 55 =5.11 mà (5;1) = 1
Do đó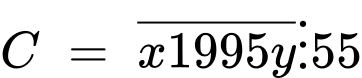 nên
nên 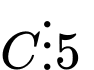 và
và 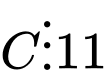
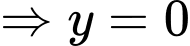 hoặc
hoặc 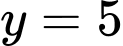
+)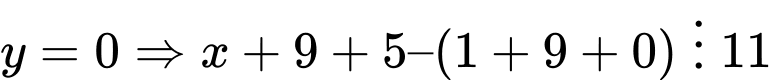
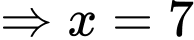
+)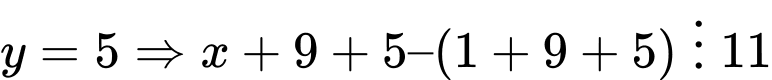
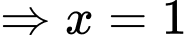
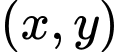 thỏa mãn.
thỏa mãn.Giá trị lớn nhất có thể của
 là 7
là 7Giá trị lớn nhất có thể của
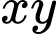 là 5
là 5Ta có 55 =5.11 mà (5;1) = 1
Do đó
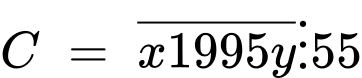 nên
nên 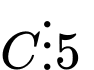 và
và 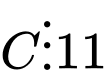
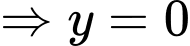 hoặc
hoặc 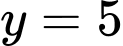
+)
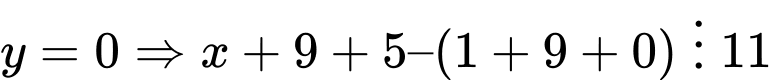
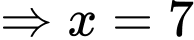
+)
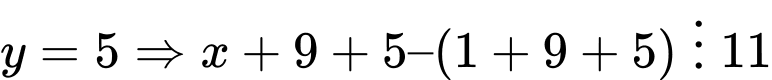
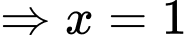
Câu 20 [582512]: Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Có __________, số tự nhiên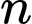 để
để 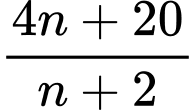 là một số nguyên.
là một số nguyên.
Có __________, số nguyên dương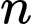 để
để 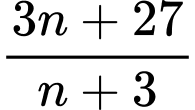 là một số nguyên không âm.
là một số nguyên không âm.
Có __________, số tự nhiên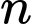 để cả
để cả 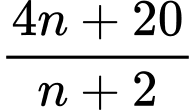 và
và 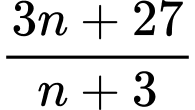 đều là các số nguyên.
đều là các số nguyên.

Có __________, số tự nhiên
 để
để 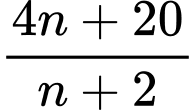 là một số nguyên.
là một số nguyên.Có __________, số nguyên dương
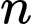 để
để 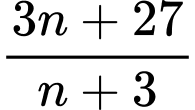 là một số nguyên không âm.
là một số nguyên không âm.Có __________, số tự nhiên
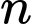 để cả
để cả 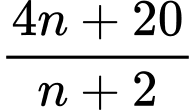 và
và 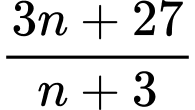 đều là các số nguyên.
đều là các số nguyên.
Có 5 số tự nhiên 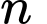 để
để 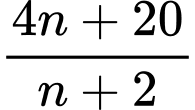 là một số nguyên.
là một số nguyên.
Có 3 số nguyên dương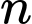 để
để 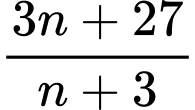 là một số nguyên không âm.
là một số nguyên không âm.
Có 1 số tự nhiên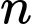 để cả
để cả 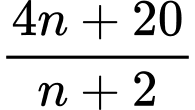 và
và 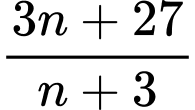 đều là các số nguyên dương.
đều là các số nguyên dương.
+) Ta có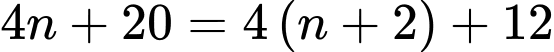 nên để
nên để 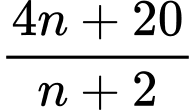 là một số nguyên thì
là một số nguyên thì  phải là ước của 12.
phải là ước của 12.
Từ đó giải ra các giá trị của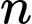 thỏa mãn là: 0; 1; 2; 4; 10.
thỏa mãn là: 0; 1; 2; 4; 10.
+) Ta có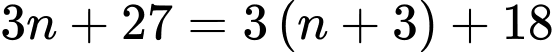 nên để
nên để 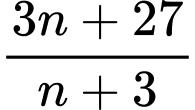 là một số nguyên thì
là một số nguyên thì  phải là ước nguyên không âm của 18.
phải là ước nguyên không âm của 18.
Từ đó giải ra các giá trị của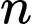 thỏa mã là: 3; 6; 15.
thỏa mã là: 3; 6; 15.
+) Chỉ có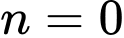 là số tự nhiên duy nhất làm cho cả
là số tự nhiên duy nhất làm cho cả 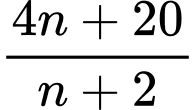 và
và 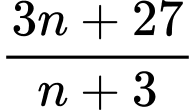 đều là các số nguyên dương.
đều là các số nguyên dương.
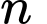 để
để 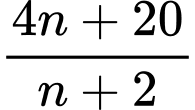 là một số nguyên.
là một số nguyên. Có 3 số nguyên dương
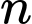 để
để 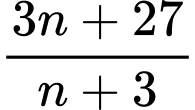 là một số nguyên không âm.
là một số nguyên không âm. Có 1 số tự nhiên
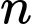 để cả
để cả 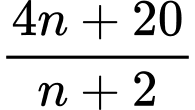 và
và 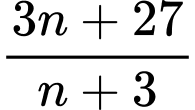 đều là các số nguyên dương.
đều là các số nguyên dương. +) Ta có
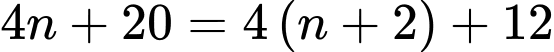 nên để
nên để 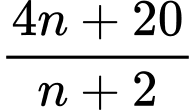 là một số nguyên thì
là một số nguyên thì  phải là ước của 12.
phải là ước của 12. Từ đó giải ra các giá trị của
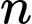 thỏa mãn là: 0; 1; 2; 4; 10.
thỏa mãn là: 0; 1; 2; 4; 10. +) Ta có
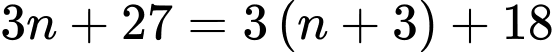 nên để
nên để 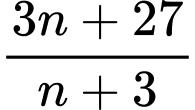 là một số nguyên thì
là một số nguyên thì  phải là ước nguyên không âm của 18.
phải là ước nguyên không âm của 18. Từ đó giải ra các giá trị của
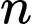 thỏa mã là: 3; 6; 15.
thỏa mã là: 3; 6; 15. +) Chỉ có
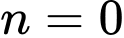 là số tự nhiên duy nhất làm cho cả
là số tự nhiên duy nhất làm cho cả 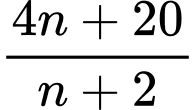 và
và 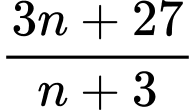 đều là các số nguyên dương.
đều là các số nguyên dương.