Dạng câu hỏi: Câu trắc nghiệm nhiều phương án
(Thí sinh trả lời từ câu 1 đến câu 14. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [582598]: Trong các khẳng định sau, khẳng định nào là đúng?
A, 

B, 

C, 

D, 

Ta có 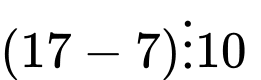 nên A đúng
nên A đúng
Tương tự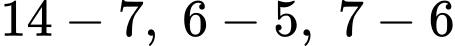 theo thứ tự không chia hết cho
theo thứ tự không chia hết cho 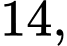
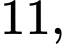
 nên B, C, D sai. Đáp án: A
nên B, C, D sai. Đáp án: A
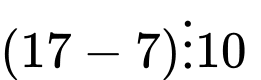 nên A đúng
nên A đúngTương tự
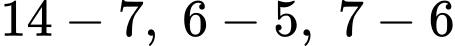 theo thứ tự không chia hết cho
theo thứ tự không chia hết cho 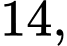
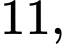
 nên B, C, D sai. Đáp án: A
nên B, C, D sai. Đáp án: A
Câu 2 [582599]: Cho  Ta không thể suy ra được điều nào sau đây?
Ta không thể suy ra được điều nào sau đây?
 Ta không thể suy ra được điều nào sau đây?
Ta không thể suy ra được điều nào sau đây? A, 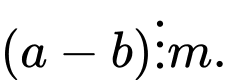
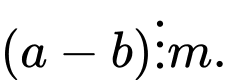
B, 

C, 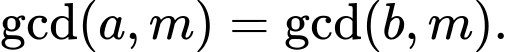
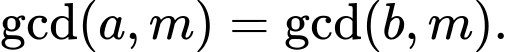
D, 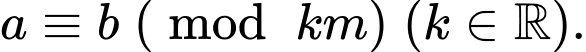
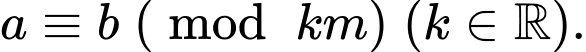
Theo cơ sở lý thuyết, A, B, C là đúng. D là sai, ví dụ  không thể suy ra
không thể suy ra 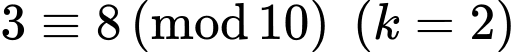 Đáp án: D
Đáp án: D
 không thể suy ra
không thể suy ra 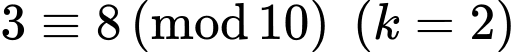 Đáp án: D
Đáp án: D
Câu 3 [582601]: Tìm số dư của 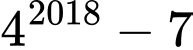 khi chia cho 9?
khi chia cho 9?
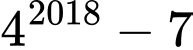 khi chia cho 9?
khi chia cho 9? A, dư 0.
B, dư 1.
C, dư 2.
D, dư 3.
Ta có 43 = 64  1 (mod 9)
1 (mod 9)  42016 =
42016 = 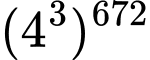
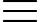 1(mod 9)
1(mod 9)
Mặt khác 42 = 16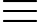 7(mod 9)
7(mod 9) 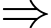 42018 = 42016 . 42
42018 = 42016 . 42  1. 7 (mod 9)
1. 7 (mod 9)
Vậy 42018 – 7 0 (mod 9) hay
0 (mod 9) hay 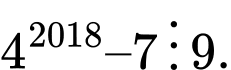 Đáp án: A
Đáp án: A
 1 (mod 9)
1 (mod 9) 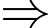 42016 =
42016 = 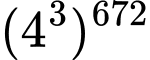
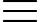 1(mod 9)
1(mod 9)Mặt khác 42 = 16
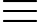 7(mod 9)
7(mod 9) 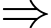 42018 = 42016 . 42
42018 = 42016 . 42 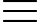 1. 7 (mod 9)
1. 7 (mod 9)Vậy 42018 – 7
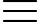 0 (mod 9) hay
0 (mod 9) hay 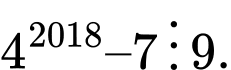 Đáp án: A
Đáp án: A
Câu 4 [582602]: Với mọi số nguyên dương  biểu thức
biểu thức 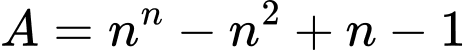 luôn chia hết cho biểu thức nào dưới đây?
luôn chia hết cho biểu thức nào dưới đây?
 biểu thức
biểu thức 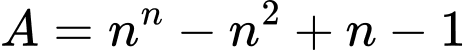 luôn chia hết cho biểu thức nào dưới đây?
luôn chia hết cho biểu thức nào dưới đây? A, 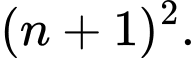
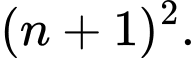
B, 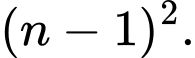
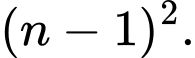
C, 

D, 

Xét 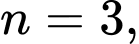
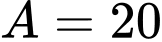 nên không chia hết cho
nên không chia hết cho 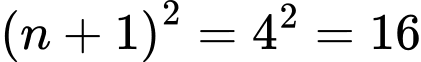
Xét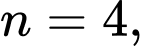
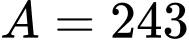 nên không chia hết cho
nên không chia hết cho 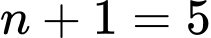 và
và 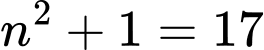
Ta chứng minh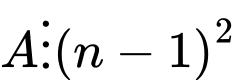 với mọi số nguyên dương
với mọi số nguyên dương 
Với
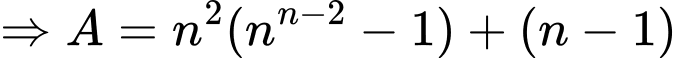
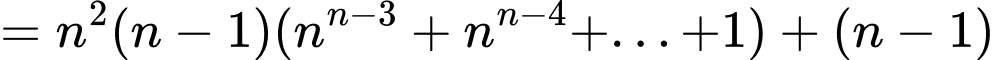
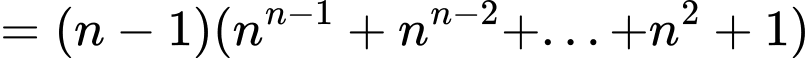
Mặt khác


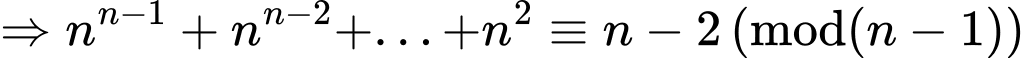
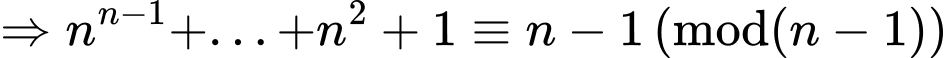
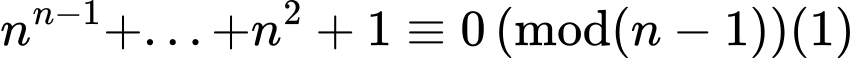
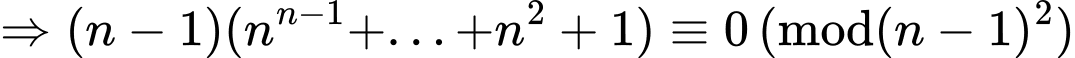
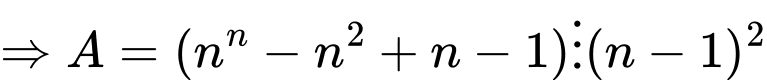 Đáp án: B
Đáp án: B
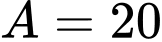 nên không chia hết cho
nên không chia hết cho 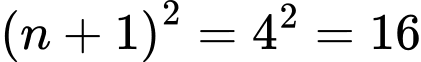
Xét
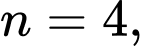
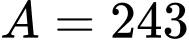 nên không chia hết cho
nên không chia hết cho 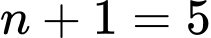 và
và 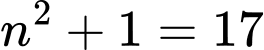
Ta chứng minh
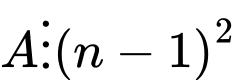 với mọi số nguyên dương
với mọi số nguyên dương 
Với

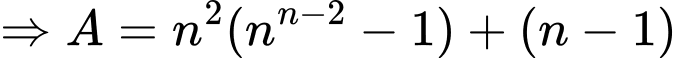
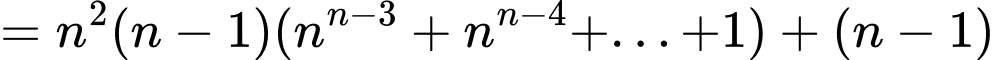
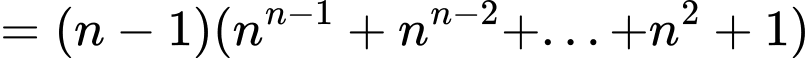
Mặt khác


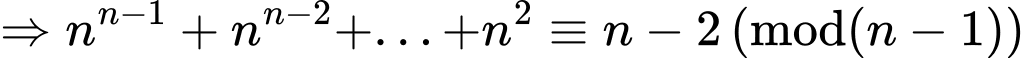
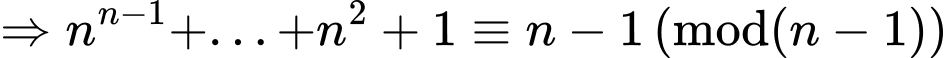
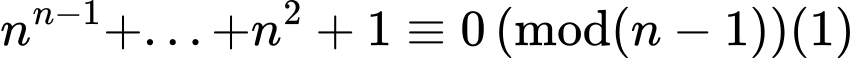
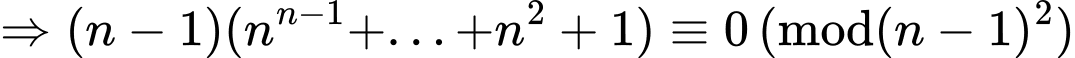
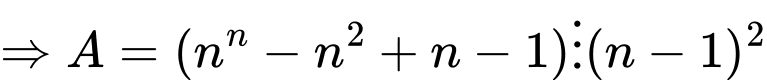 Đáp án: B
Đáp án: B
Câu 5 [582604]: Tìm số dư trong phép chia 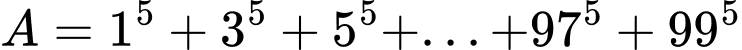 cho 4?
cho 4?
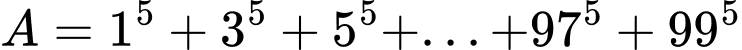 cho 4?
cho 4? A, dư 0.
B, dư 1.
C, dư 2.
D, dư 3.
15  1 (mod 4); 35
1 (mod 4); 35  – 1 (mod 4) ; 55
– 1 (mod 4) ; 55 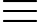 1 (mod 4) ; ...;
1 (mod 4) ; ...;
975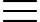 1 (mod 4); 995
1 (mod 4); 995 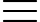 – 1 (mod 4).
– 1 (mod 4).
Đáp số: Dư 0. Đáp án: A
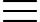 1 (mod 4); 35
1 (mod 4); 35 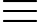 – 1 (mod 4) ; 55
– 1 (mod 4) ; 55 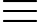 1 (mod 4) ; ...;
1 (mod 4) ; ...; 975
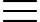 1 (mod 4); 995
1 (mod 4); 995 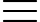 – 1 (mod 4).
– 1 (mod 4). Đáp số: Dư 0. Đáp án: A
Câu 6 [582605]: Với mọi số tự nhiên 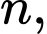 biểu thức
biểu thức  có luôn chia hết cho 100 hay không?
có luôn chia hết cho 100 hay không?
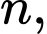 biểu thức
biểu thức  có luôn chia hết cho 100 hay không?
có luôn chia hết cho 100 hay không? A, Có, luôn chia hết.
B, Không, 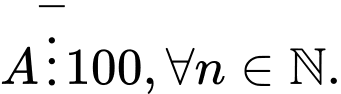
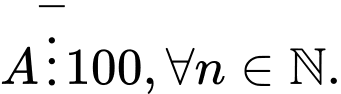
C, Có nhưng khi và chỉ khi 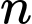 lẻ.
lẻ.
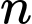 lẻ.
lẻ.D, Không thể kết luận.
Với 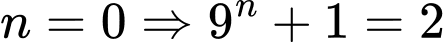 không chia hết cho 100. ⇨ A sai
không chia hết cho 100. ⇨ A sai
Với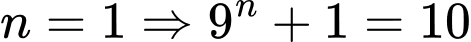 không chia hết cho 100. ⇨ C sai
không chia hết cho 100. ⇨ C sai
Với ta đi xét 2 khả năng sau:
ta đi xét 2 khả năng sau:
Khả năng 1:
Với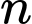 chẵn
chẵn 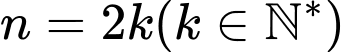
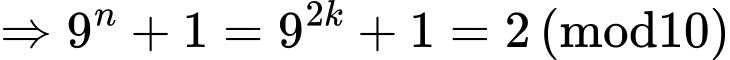
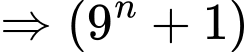 không chia hết cho 10.
không chia hết cho 10.
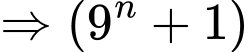 không chia hết cho 100.
không chia hết cho 100.
Khả năng 2:
Với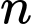 lẻ
lẻ 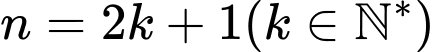
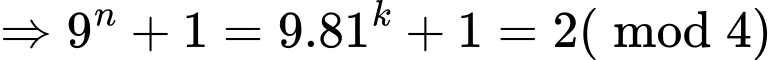
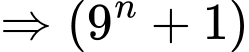 không chia hết cho 4.
không chia hết cho 4.
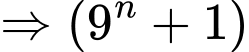 không chia hết cho 100.
không chia hết cho 100.
Vậy B là chính xác. Đáp án: B
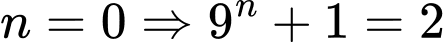 không chia hết cho 100. ⇨ A sai
không chia hết cho 100. ⇨ A saiVới
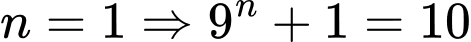 không chia hết cho 100. ⇨ C sai
không chia hết cho 100. ⇨ C saiVới
 ta đi xét 2 khả năng sau:
ta đi xét 2 khả năng sau:Khả năng 1:
Với
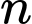 chẵn
chẵn 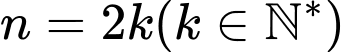
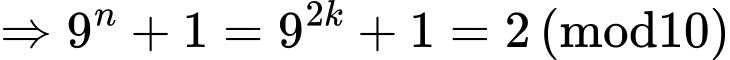
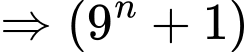 không chia hết cho 10.
không chia hết cho 10. 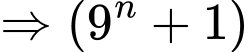 không chia hết cho 100.
không chia hết cho 100.Khả năng 2:
Với
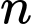 lẻ
lẻ 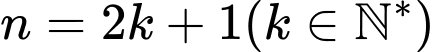
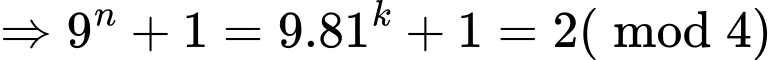
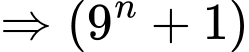 không chia hết cho 4.
không chia hết cho 4.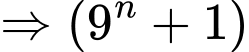 không chia hết cho 100.
không chia hết cho 100.Vậy B là chính xác. Đáp án: B
Câu 7 [582607]: Biểu thức nào sau đây không chia hết cho 7?
A, 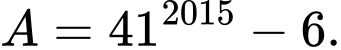
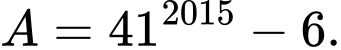
B, 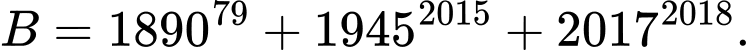
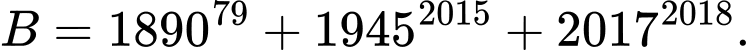
C, 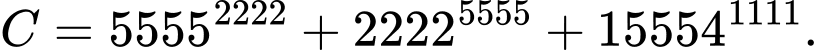
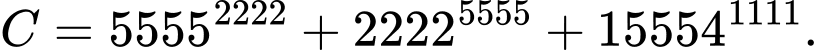
D, 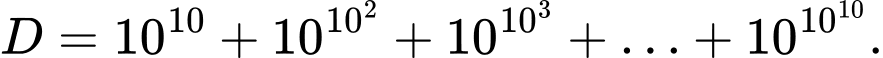
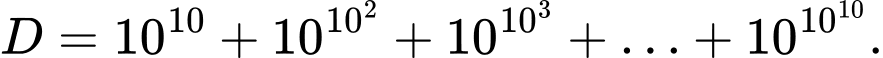
+) Với biểu thức  ta có
ta có 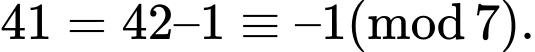
Do đó
Hay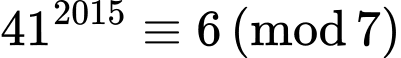
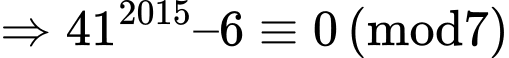
 chia hết cho 7.
chia hết cho 7.
+) Với biểu thức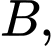
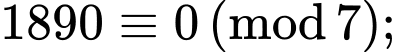
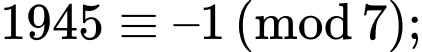
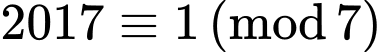
Nên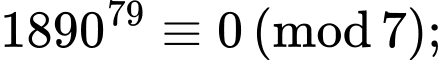
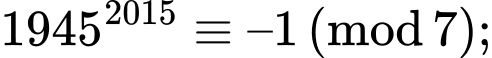
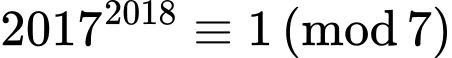
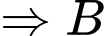 chia hết cho 7.
chia hết cho 7.
+) Với biểu thức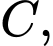 ta có
ta có 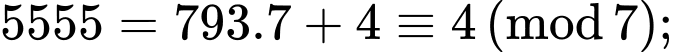
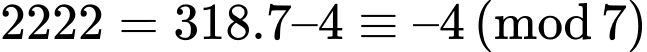
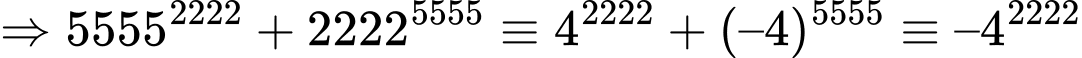
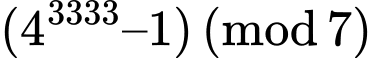
Do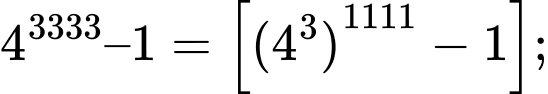
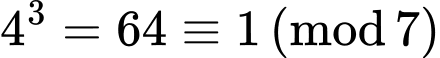 nên
nên 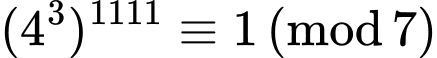
Hay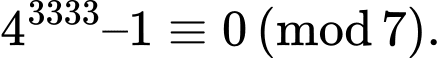
Do đó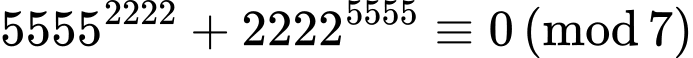 và
và
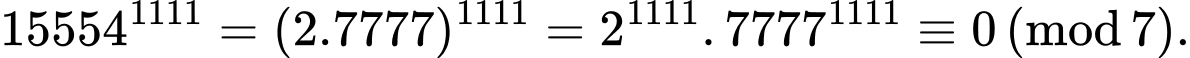
Vậy chia hết cho 7.
chia hết cho 7.
+) Với biểu thức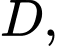 ta có
ta có 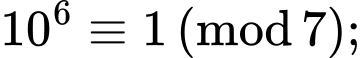
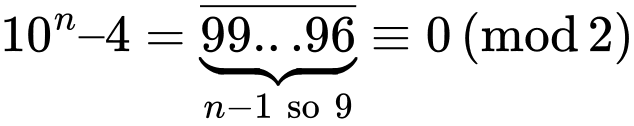 và
và 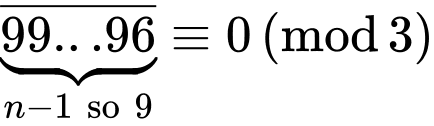
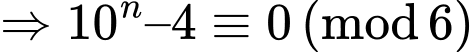
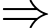
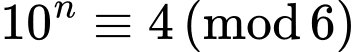 và
và 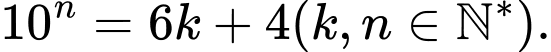
Do đó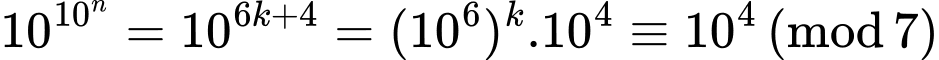
Vậy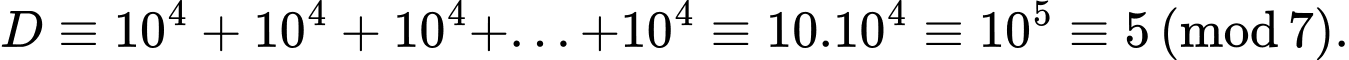
Vậy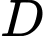 không chia hết cho 7. Đáp án: D
không chia hết cho 7. Đáp án: D
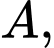 ta có
ta có 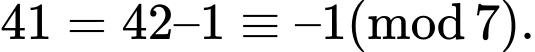
Do đó

Hay
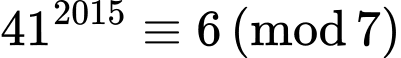
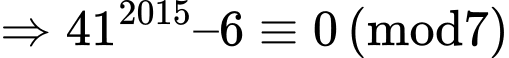
 chia hết cho 7.
chia hết cho 7.+) Với biểu thức
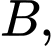
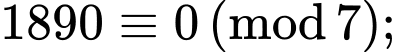
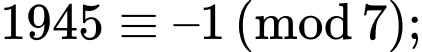
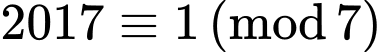
Nên
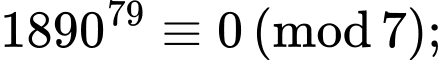
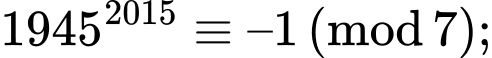
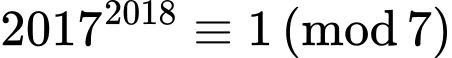
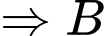 chia hết cho 7.
chia hết cho 7.+) Với biểu thức
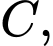 ta có
ta có 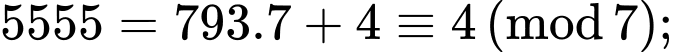
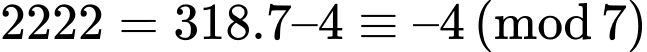
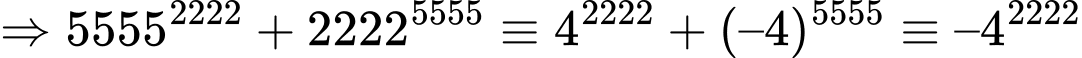
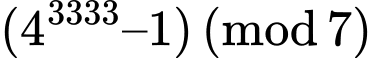
Do
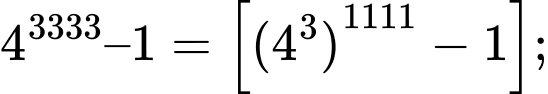
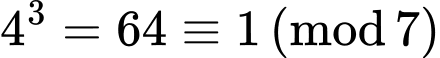 nên
nên 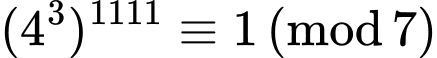
Hay
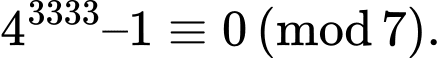
Do đó
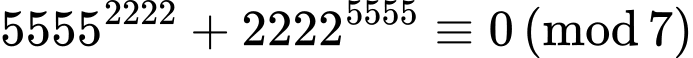 và
và 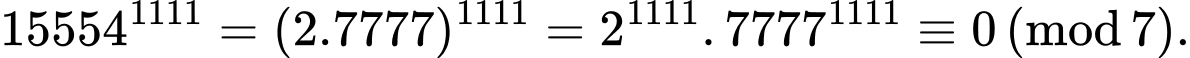
Vậy
 chia hết cho 7.
chia hết cho 7.+) Với biểu thức
 ta có
ta có 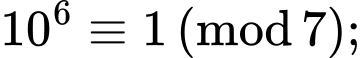
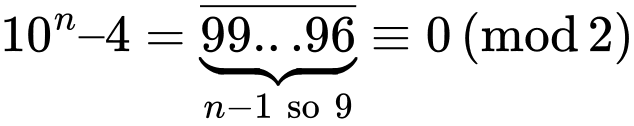 và
và 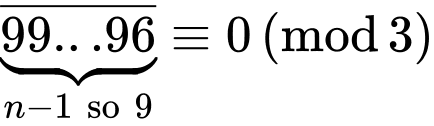
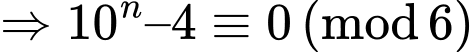
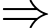
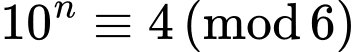 và
và 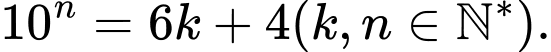
Do đó
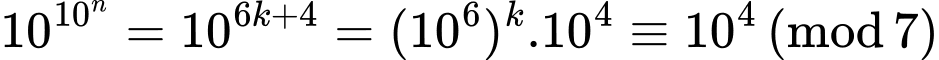
Vậy
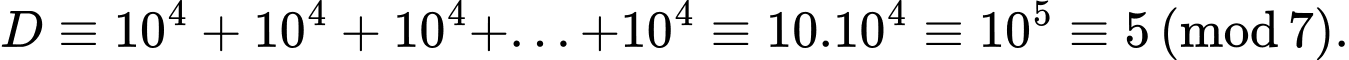
Vậy
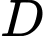 không chia hết cho 7. Đáp án: D
không chia hết cho 7. Đáp án: D
Câu 8 [582608]: Cho 2 số tự nhiên 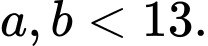 Ta có
Ta có 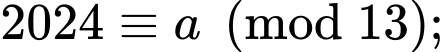
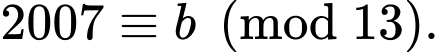 Tính giá trị của
Tính giá trị của 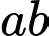 ?
?
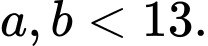 Ta có
Ta có 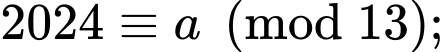
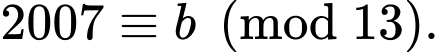 Tính giá trị của
Tính giá trị của 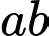 ?
? A, 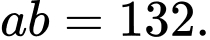
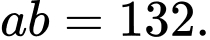
B, 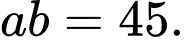
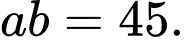
C, 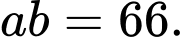
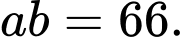
D, 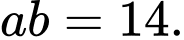
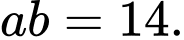

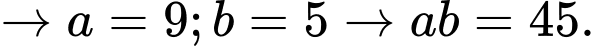 Đáp án: B
Đáp án: B
Câu 9 [582609]: Điều kiện của số tự nhiên 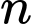 để
để 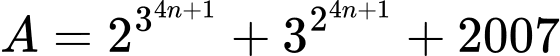 chia hết cho 22?
chia hết cho 22?
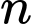 để
để 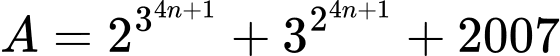 chia hết cho 22?
chia hết cho 22? A, Không có giá trị nào của 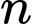 thỏa mãn.
thỏa mãn.
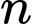 thỏa mãn.
thỏa mãn.B, Chỉ có duy nhất giá trị 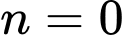 thỏa mãn.
thỏa mãn.
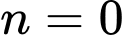 thỏa mãn.
thỏa mãn.C, Chỉ có 2 giá trị thỏa mãn là 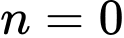 và
và 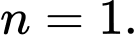
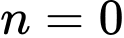 và
và 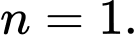
D, Mọi số tự nhiên 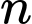 đều thỏa mãn.
đều thỏa mãn.
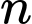 đều thỏa mãn.
đều thỏa mãn.
Ta có 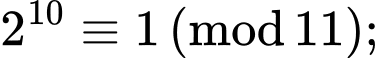
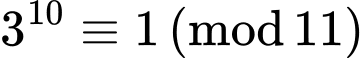
Ta có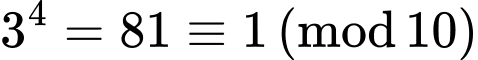
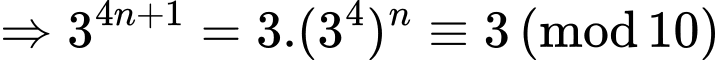
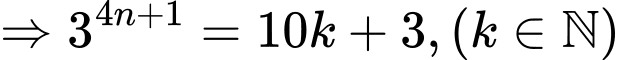
Mặt khác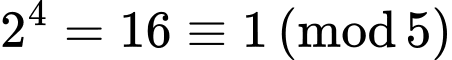
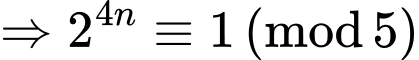
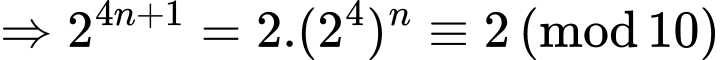
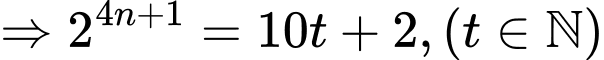
Do đó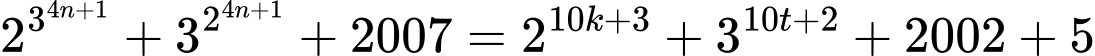
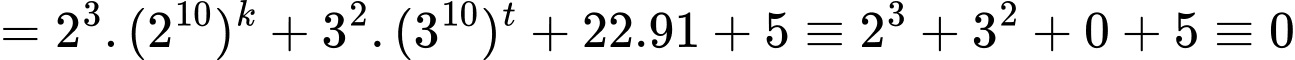 (mod 11)
(mod 11)
Mà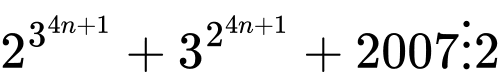 (vì
(vì 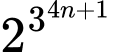 là số chẵn
là số chẵn 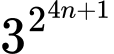 là số lẻ
là số lẻ  là số lẻ). Đáp án: D
là số lẻ). Đáp án: D
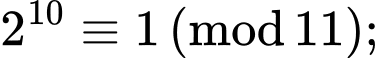
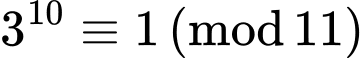
Ta có
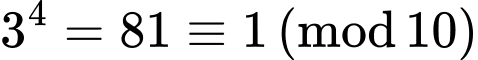
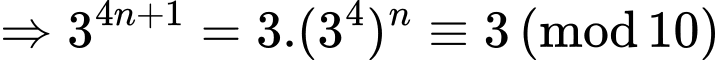
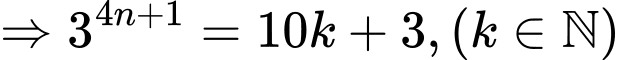
Mặt khác
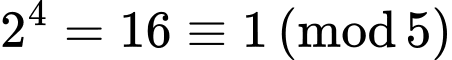
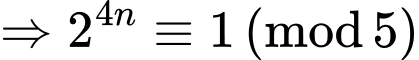
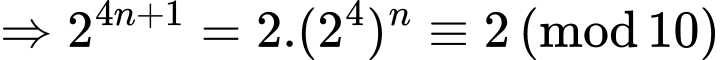
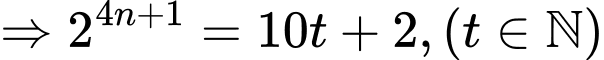
Do đó
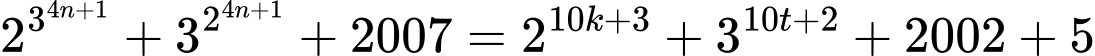
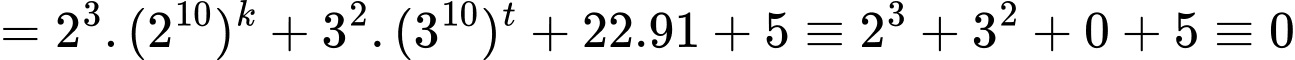 (mod 11)
(mod 11)Mà
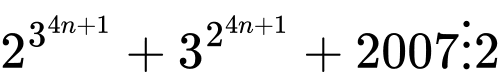 (vì
(vì 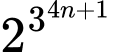 là số chẵn
là số chẵn 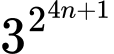 là số lẻ
là số lẻ  là số lẻ). Đáp án: D
là số lẻ). Đáp án: D
Câu 10 [582611]: Tìm số dư trong phép chia  cho 12?
cho 12?
 cho 12?
cho 12? A, Dư 0.
B, Dư 1.
C, Dư 3.
D, Dư 5.
Có 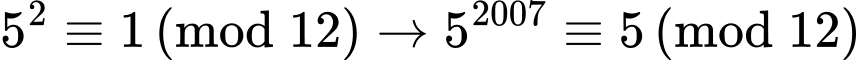 Đáp án: D
Đáp án: D
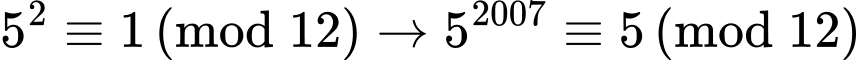 Đáp án: D
Đáp án: D
Câu 11 [582613]: Cho 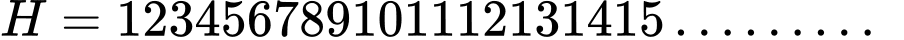 được viết bởi các số tự nhiên liên tiếp và có 121 chữ số. Số
được viết bởi các số tự nhiên liên tiếp và có 121 chữ số. Số 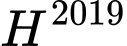 có chữ số tận cùng là chữ số nào?
có chữ số tận cùng là chữ số nào?
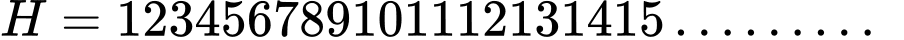 được viết bởi các số tự nhiên liên tiếp và có 121 chữ số. Số
được viết bởi các số tự nhiên liên tiếp và có 121 chữ số. Số 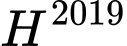 có chữ số tận cùng là chữ số nào?
có chữ số tận cùng là chữ số nào? A, 1.
B, 3.
C, 5.
D, 7.
Trước hết ta phải tìm được chữ số tận cùng của 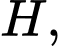 muốn vậy ta phải tính xem với
muốn vậy ta phải tính xem với 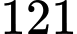 chữ số thì chữ số cuối cùng được viết là chữ số nào.
chữ số thì chữ số cuối cùng được viết là chữ số nào.
Ta dựa vào bài toán ngược của bài toán “Đánh số trang sách”.
Ta có từ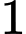 đến
đến 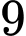 có
có 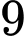 số, mỗi số gồm
số, mỗi số gồm 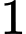 chữ số.
chữ số.
Từ đến
đến 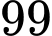 có
có 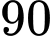 số, mỗi số gồm
số, mỗi số gồm 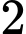 chữ số nên khi viết chúng liên tiếp ta có
chữ số nên khi viết chúng liên tiếp ta có 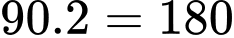 (chữ số).
(chữ số).
Mà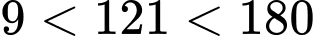 nên chữ số tận cùng của
nên chữ số tận cùng của  phải ở số có hai chữ số.
phải ở số có hai chữ số.
Số chữ số của các số có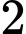 chữ số viết ở
chữ số viết ở 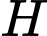 là:
là: 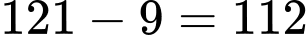 (chữ số)
(chữ số)
Số các số có chữ số viết viết ở
chữ số viết viết ở 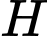 là
là 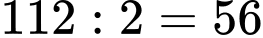
Số thứ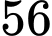 kể từ
kể từ  có
có 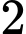 chữ số là:
chữ số là: 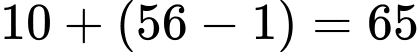 suy ra chữ số tận cùng của
suy ra chữ số tận cùng của  là chữ số
là chữ số 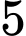 (là chữ số hàng đơn vị của số
(là chữ số hàng đơn vị của số 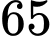 ).
).
Mặt khác, có tận cùng là
có tận cùng là 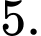
Vậy chữ số tận cùng của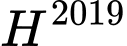 là chữ số
là chữ số 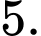 Đáp án: C
Đáp án: C
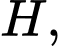 muốn vậy ta phải tính xem với
muốn vậy ta phải tính xem với 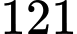 chữ số thì chữ số cuối cùng được viết là chữ số nào.
chữ số thì chữ số cuối cùng được viết là chữ số nào. Ta dựa vào bài toán ngược của bài toán “Đánh số trang sách”.
Ta có từ
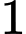 đến
đến 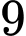 có
có 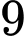 số, mỗi số gồm
số, mỗi số gồm 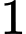 chữ số.
chữ số.Từ
 đến
đến 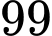 có
có 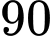 số, mỗi số gồm
số, mỗi số gồm 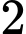 chữ số nên khi viết chúng liên tiếp ta có
chữ số nên khi viết chúng liên tiếp ta có 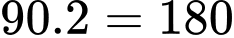 (chữ số).
(chữ số).Mà
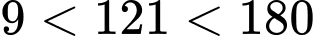 nên chữ số tận cùng của
nên chữ số tận cùng của  phải ở số có hai chữ số.
phải ở số có hai chữ số.Số chữ số của các số có
 chữ số viết ở
chữ số viết ở 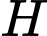 là:
là: 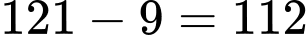 (chữ số)
(chữ số)Số các số có
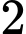 chữ số viết viết ở
chữ số viết viết ở 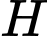 là
là 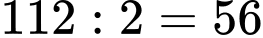
Số thứ
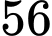 kể từ
kể từ  có
có 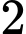 chữ số là:
chữ số là: 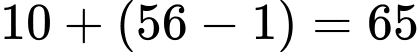 suy ra chữ số tận cùng của
suy ra chữ số tận cùng của 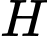 là chữ số
là chữ số 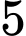 (là chữ số hàng đơn vị của số
(là chữ số hàng đơn vị của số 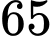 ).
). Mặt khác,
 có tận cùng là
có tận cùng là 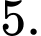
Vậy chữ số tận cùng của
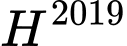 là chữ số
là chữ số 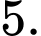 Đáp án: C
Đáp án: C
Câu 12 [582614]: Tìm hai chữ số tận cùng của 

A, 67.
B, 43.
C, 25.
D, 49.
Ta có 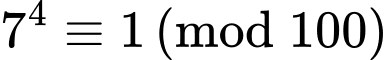
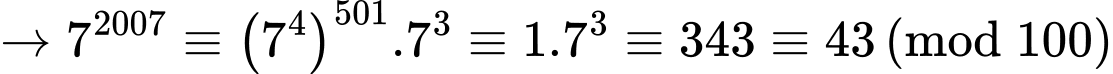
Do đó 2 chữ số tận cùng là 43. Đáp án: B
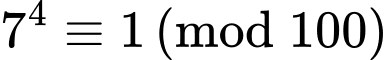
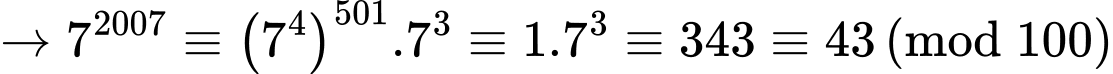
Do đó 2 chữ số tận cùng là 43. Đáp án: B
Câu 13 [582615]: Tìm hai chữ số tận cùng của 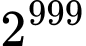 ?
?
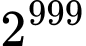 ?
? A, 88.
B, 38.
C, 76.
D, 26.
Ta có thể sử dụng đồng dư thức hoặc cách suy luận như sau:
Ta có: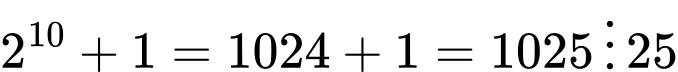 suy ra
suy ra 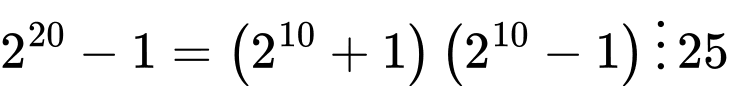
Ta lại có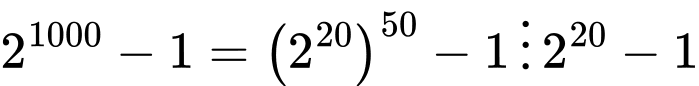 suy ra
suy ra 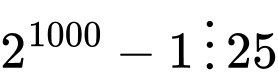
Do đó có thể có chữ số tận cùng là
có thể có chữ số tận cùng là 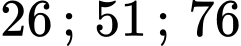
Tuy nhiên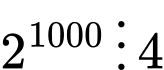 suy ra
suy ra  tận cùng là 76
tận cùng là 76
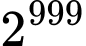 tận cùng là 38 hoặc 88
tận cùng là 38 hoặc 88
Mà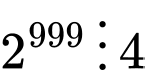 nên
nên 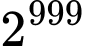 tận cùng là 88
tận cùng là 88
Vậy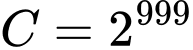 có hai chữ số tận cùng là 88. Đáp án: A
có hai chữ số tận cùng là 88. Đáp án: A
Ta có:
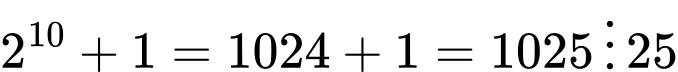 suy ra
suy ra 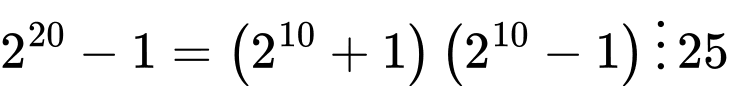
Ta lại có
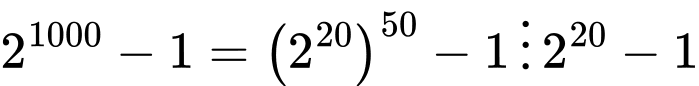 suy ra
suy ra 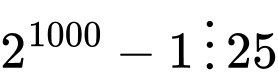
Do đó
 có thể có chữ số tận cùng là
có thể có chữ số tận cùng là 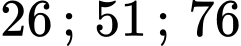
Tuy nhiên
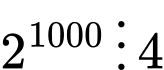 suy ra
suy ra  tận cùng là 76
tận cùng là 76 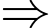
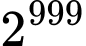 tận cùng là 38 hoặc 88
tận cùng là 38 hoặc 88 Mà
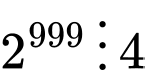 nên
nên 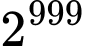 tận cùng là 88
tận cùng là 88Vậy
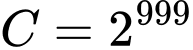 có hai chữ số tận cùng là 88. Đáp án: A
có hai chữ số tận cùng là 88. Đáp án: A
Câu 14 [582616]: Tìm 3 chữ số tận cùng của 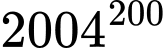 ?
?
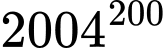 ?
? A, 626.
B, 126.
C, 088.
D, 376.
Ta dễ dàng chứng minh được chia hết cho 8, khi đó ta sẽ tìm 3 chữ số tận cùng bằng cách gián tiếp: tìm dư phép chia số đó cho 125 từ đó suy ra các khả năng 3 chữ số tận cùng, cuối cùng kiểm tra điều kiện chia hết cho 8
Ta lại có (2004,5) = 1 nên theo Định lý Euler:
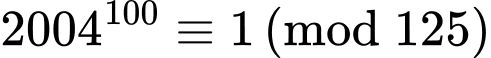
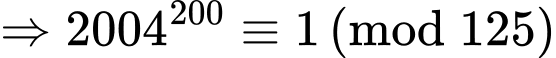
Hay (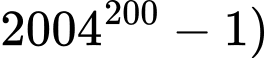 chia hết cho 125 khi đó số
chia hết cho 125 khi đó số 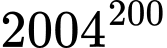 có các khả năng 3 chữ số tận cùng là 126; 251; 376; 501; 626; 751; 876
có các khả năng 3 chữ số tận cùng là 126; 251; 376; 501; 626; 751; 876
Vì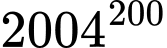 chia hết cho 8 nên số đó có chữ số tận cùng là 376 Đáp án: D
chia hết cho 8 nên số đó có chữ số tận cùng là 376 Đáp án: D
Ta lại có (2004,5) = 1 nên theo Định lý Euler:
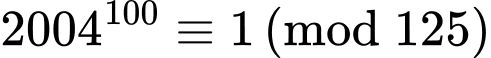
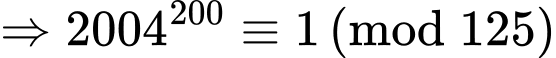
Hay (
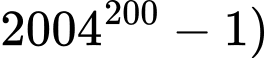 chia hết cho 125 khi đó số
chia hết cho 125 khi đó số 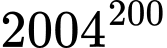 có các khả năng 3 chữ số tận cùng là 126; 251; 376; 501; 626; 751; 876
có các khả năng 3 chữ số tận cùng là 126; 251; 376; 501; 626; 751; 876Vì
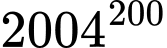 chia hết cho 8 nên số đó có chữ số tận cùng là 376 Đáp án: D
chia hết cho 8 nên số đó có chữ số tận cùng là 376 Đáp án: D Dạng câu hỏi: Câu trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 15, 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 15 [582600]: Cho  và
và  Mỗi phát biểu sau đúng hay sai?
Mỗi phát biểu sau đúng hay sai?
a)
b)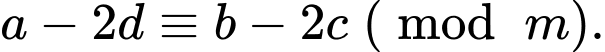
c)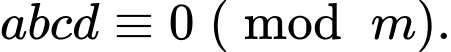
d)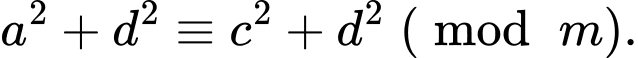
 và
và  Mỗi phát biểu sau đúng hay sai?
Mỗi phát biểu sau đúng hay sai?a)

b)
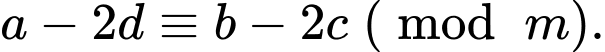
c)
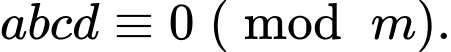
d)
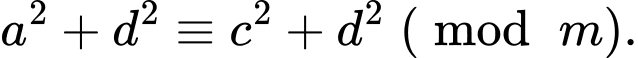
a) Đúng
b) Đúng
c) Sai
d) Sai
Theo lý thuyết, các ý a, b là đúng.
Ý c là sai, ví dụ và
và  nhưng kết luận
nhưng kết luận 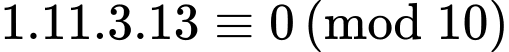 là sai.
là sai.
b) Đúng
c) Sai
d) Sai
Theo lý thuyết, các ý a, b là đúng.
Ý c là sai, ví dụ
 và
và  nhưng kết luận
nhưng kết luận 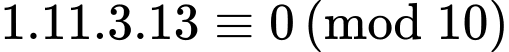 là sai.
là sai.
Câu 16 [582612]: Cho số 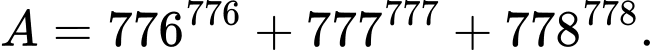 Số dư của
Số dư của 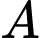 khi chia cho 3 là
khi chia cho 3 là 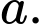 Số dư của
Số dư của 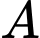 khi chia cho 5 là
khi chia cho 5 là 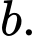 Mỗi phát biểu sau là đúng hay sai?
Mỗi phát biểu sau là đúng hay sai?
a)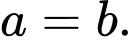
b)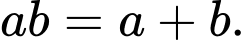
c)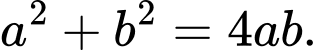
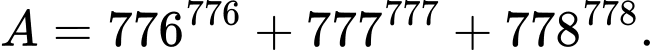 Số dư của
Số dư của 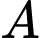 khi chia cho 3 là
khi chia cho 3 là 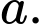 Số dư của
Số dư của 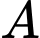 khi chia cho 5 là
khi chia cho 5 là 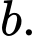 Mỗi phát biểu sau là đúng hay sai?
Mỗi phát biểu sau là đúng hay sai?a)
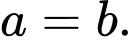
b)
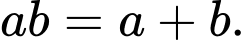
c)
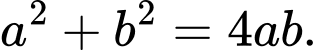
a) Đúng
b) Đúng
c) Sai
+)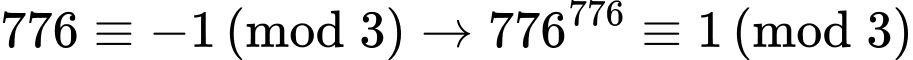
+)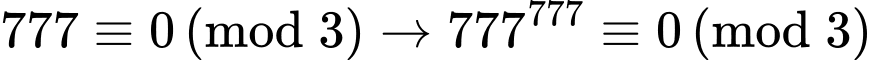
+)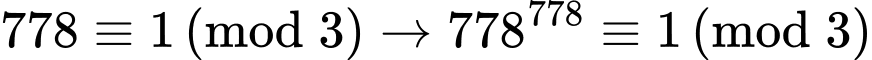
Do đó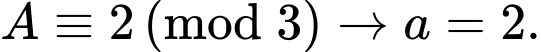
+)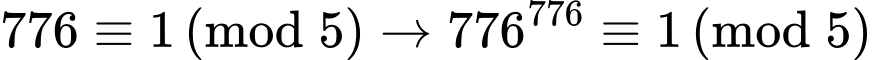
+)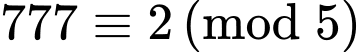
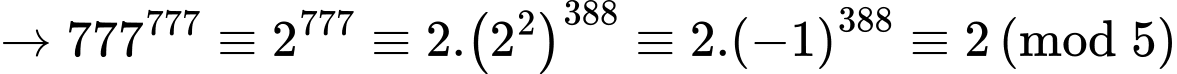
+)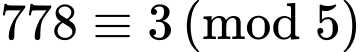
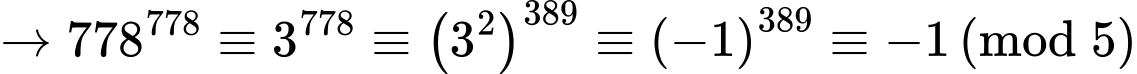
Do đó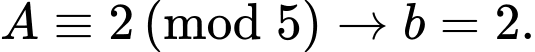
b) Đúng
c) Sai
+)
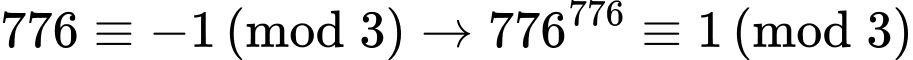
+)
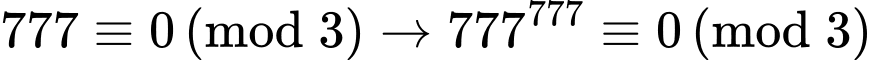
+)
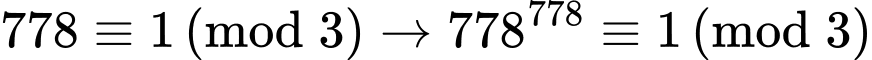
Do đó
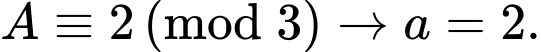
+)
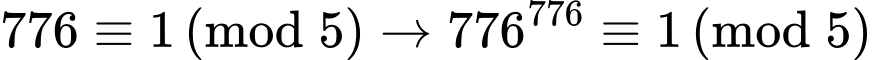
+)
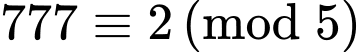
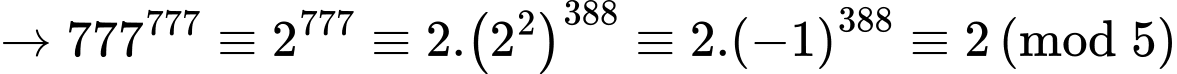
+)
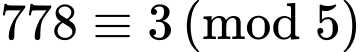
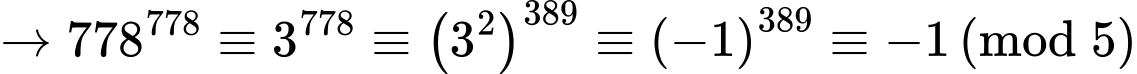
Do đó
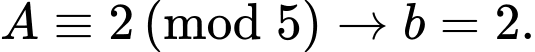
Dạng câu hỏi: Câu trả lời ngắn
(Thí sinh trả lời đáp án từ câu 17 đến câu 18. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 17 [582603]: Điền vào ô trống để hoàn thiện các câu sau:
Chữ số tận cùng của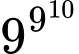 là: __________
là: __________
Hai chữ số tận cùng của là: __________
là: __________
Chữ số tận cùng của
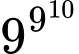 là: __________
là: __________Hai chữ số tận cùng của
 là: __________
là: __________
Chữ số tận cùng của 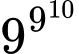 là: 9
là: 9
Hai chữ số tận cùng của là: 01
là: 01
1. Tìm chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 10.
Vì 92n + 1 = 9.81n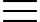 9 (mod 10). Do 910 là số lẻ nên số
9 (mod 10). Do 910 là số lẻ nên số 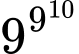 có chữ số tận cùng là 9.
có chữ số tận cùng là 9.
2. Tìm hai chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 100.
Ta có 34 = 81 – 19 (mod 100)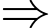 38
38 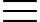 (– 19)2 (mod 100)
(– 19)2 (mod 100)
Mà (– 19)2 = 361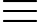 61 (mod 100)
61 (mod 100)
Vậy 38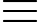 61 (mod 100)
61 (mod 100)
310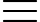 61.9
61.9 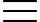 549
549 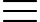 49 (mod 100)
49 (mod 100)
320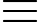 492
492 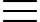 01 (mod 100) (do 492 = 2401 = 24.100 + 1)
01 (mod 100) (do 492 = 2401 = 24.100 + 1)
Do đó 31000 01 (mod 100) nghĩa là hai chữ số sau cùng của 31000 là 01.
01 (mod 100) nghĩa là hai chữ số sau cùng của 31000 là 01.
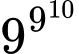 là: 9
là: 9Hai chữ số tận cùng của
 là: 01
là: 011. Tìm chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 10.
Vì 92n + 1 = 9.81n
 9 (mod 10). Do 910 là số lẻ nên số
9 (mod 10). Do 910 là số lẻ nên số 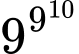 có chữ số tận cùng là 9.
có chữ số tận cùng là 9.2. Tìm hai chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 100.
Ta có 34 = 81 – 19 (mod 100)
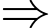 38
38 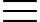 (– 19)2 (mod 100)
(– 19)2 (mod 100) Mà (– 19)2 = 361
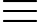 61 (mod 100)
61 (mod 100) Vậy 38
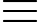 61 (mod 100)
61 (mod 100)310
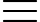 61.9
61.9 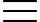 549
549 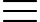 49 (mod 100)
49 (mod 100)320
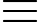 492
492  01 (mod 100) (do 492 = 2401 = 24.100 + 1)
01 (mod 100) (do 492 = 2401 = 24.100 + 1)Do đó 31000
 01 (mod 100) nghĩa là hai chữ số sau cùng của 31000 là 01.
01 (mod 100) nghĩa là hai chữ số sau cùng của 31000 là 01.
Câu 18 [582610]: Cho số nguyên 
Số dư của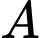 khi chia cho 11 là __________
khi chia cho 11 là __________
Số dư của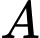 khi chia cho 13 là __________
khi chia cho 13 là __________
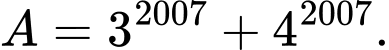
Số dư của
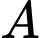 khi chia cho 11 là __________
khi chia cho 11 là __________Số dư của
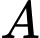 khi chia cho 13 là __________
khi chia cho 13 là __________
Cho số nguyên 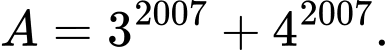
Số dư của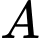 khi chia cho 11 là 3.
khi chia cho 11 là 3.
Số dư của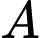 khi chia cho 13 là 0.
khi chia cho 13 là 0.
+)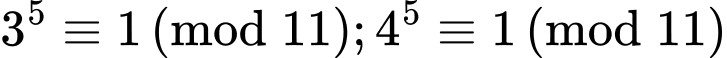
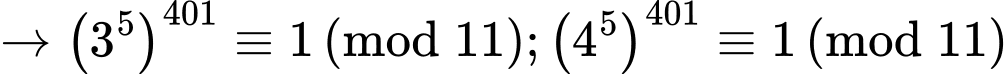
Do đó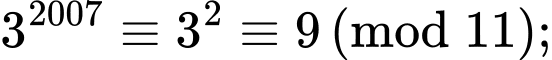
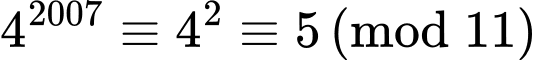
Nên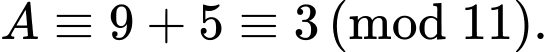
Vậy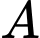 chia 11 dư 3.
chia 11 dư 3.
+)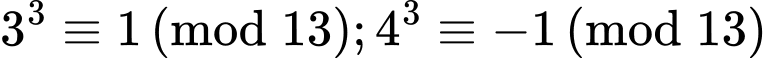
Do đó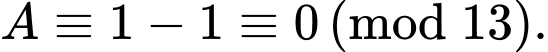
Vậy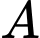 chia 13 dư 0.
chia 13 dư 0.
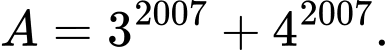
Số dư của
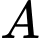 khi chia cho 11 là 3.
khi chia cho 11 là 3. Số dư của
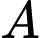 khi chia cho 13 là 0.
khi chia cho 13 là 0.+)
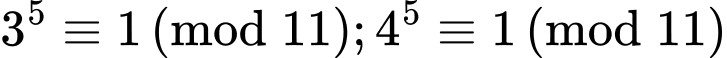
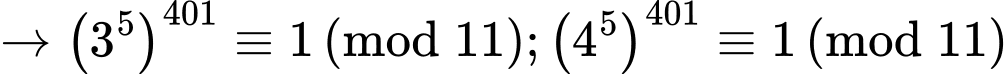
Do đó
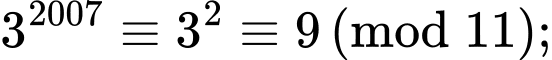
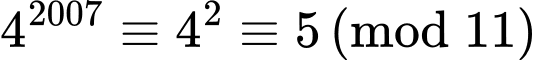
Nên
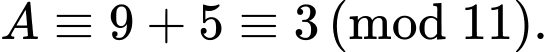
Vậy
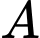 chia 11 dư 3.
chia 11 dư 3.+)
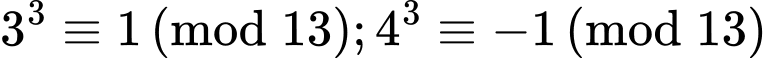
Do đó
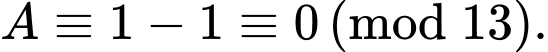
Vậy
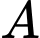 chia 13 dư 0.
chia 13 dư 0. Dạng câu hỏi: Câu hỏi kéo thả
Câu 19 [582606]: Kéo số ở các ô vuông thả vào vị trí thích hợp?

1.
2.
3. (

1.

2.

3. (

1. 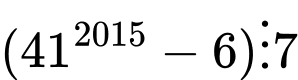
2.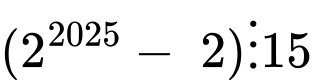
3. (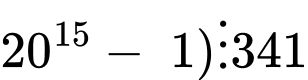
+)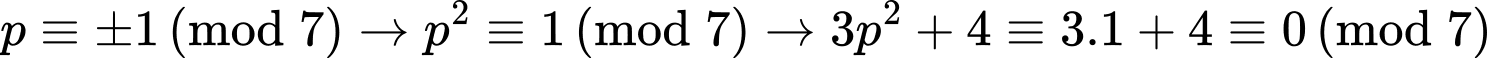
Do đó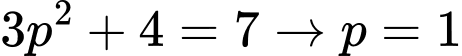 (vô lý).
(vô lý).
+)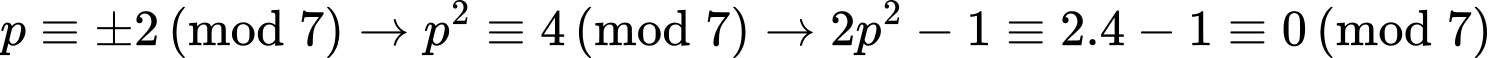
Do đó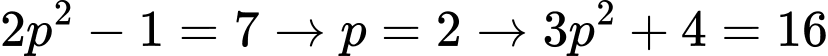 không phải số nguyên tố.
không phải số nguyên tố.
+)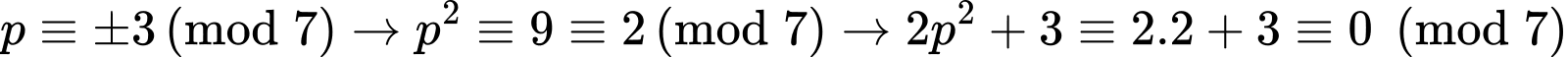
Do đó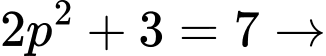 Không tồn tại
Không tồn tại 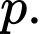
+)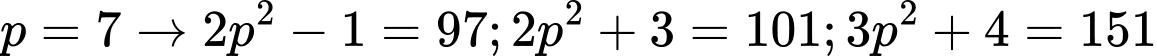 đều là các số nguyên tố.
đều là các số nguyên tố.
Vậy tồn tại duy nhất một số nguyên tố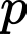 thỏa mãn yêu cầu.
thỏa mãn yêu cầu.
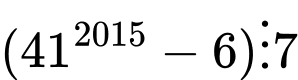
2.
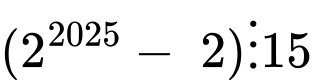
3. (
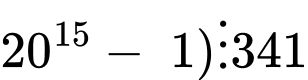
+)
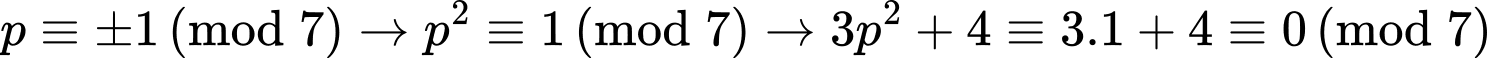
Do đó
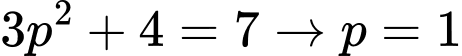 (vô lý).
(vô lý).+)
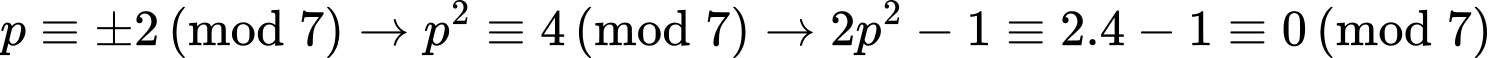
Do đó
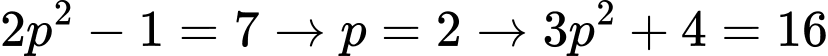 không phải số nguyên tố.
không phải số nguyên tố.+)
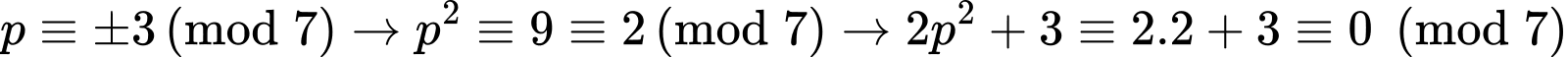
Do đó
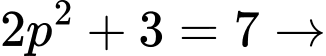 Không tồn tại
Không tồn tại 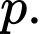
+)
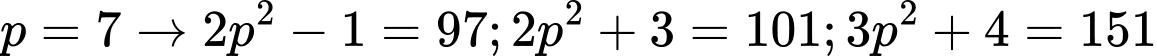 đều là các số nguyên tố.
đều là các số nguyên tố.Vậy tồn tại duy nhất một số nguyên tố
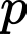 thỏa mãn yêu cầu.
thỏa mãn yêu cầu.
Câu 20 [582617]: Kéo số ở các ô vuông thả vào vị trí thích hợp?

Chữ số tận cùng của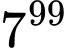 là …….
là …….
Chữ số tận cùng của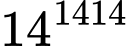 là ……...
là ……...
Chữ số tận cùng của là …………
là …………

Chữ số tận cùng của
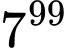 là …….
là …….Chữ số tận cùng của
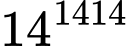 là ……...
là ……...Chữ số tận cùng của
 là …………
là …………
Chữ số tận cùng của 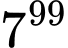 là 3.
là 3.
Chữ số tận cùng của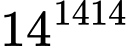 là 6.
là 6.
Chữ số tận cùng của là 4.
là 4.
Ta có: p q, là số nguyên tố nên pq +11 là số nguyên tố lớn hơn 11
 pq + 11 là số lẻ suy ra pq là số chẵn.
pq + 11 là số lẻ suy ra pq là số chẵn.
Do 7p + q là số nguyên tố lớn hơn 7 nên p và q không thể cùng tính chẵn lẻ.
*) TH1: p = 2 thì 7p + q =14 + q. Ta thấy 14 chia 3 dư 2
+) Nếu q chia hết cho 3, do q là số nguyên tố nên q = 3.
7p + q = 17; pq + 11 = 17 (T/m)
+) Nếu q chia cho 3 dư 1 thì 14 + q chia hết cho 3 7p + q là hợp số
7p + q là hợp số
+) Nếu q chia cho 3 dư 2 thì 2q chia cho 3 dư 1 nên pq + 11 = 2q +11 chia hết cho 3
 pq +11 là hợp số.
pq +11 là hợp số.
*) TH2: q = 2 thì 7p + q = 7p + 2
Nếu 7p chia hết cho 3 thì p chia hết cho 3 nên p = 3 7p+q=23; pq+11=17 (Thỏa mãn)
7p+q=23; pq+11=17 (Thỏa mãn)
+) Nếu 7 p chia cho 3 dư 1 chia hết cho 3 7p + 2 là hợp số
7p + 2 là hợp số
+) Nếu 7 p chia cho 3 dư 2 thì p chia cho 3 dư 2 nên 2p chia cho 3 dư 1
⇒ pq + 11 = 2p + 11 chia hết cho 3 nên là hợp số.
Vậy p = 2, q = 3 hoặc p = 3, q = 2.
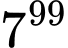 là 3.
là 3.Chữ số tận cùng của
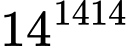 là 6.
là 6.Chữ số tận cùng của
 là 4.
là 4.Ta có: p q, là số nguyên tố nên pq +11 là số nguyên tố lớn hơn 11
 pq + 11 là số lẻ suy ra pq là số chẵn.
pq + 11 là số lẻ suy ra pq là số chẵn. Do 7p + q là số nguyên tố lớn hơn 7 nên p và q không thể cùng tính chẵn lẻ.
*) TH1: p = 2 thì 7p + q =14 + q. Ta thấy 14 chia 3 dư 2
+) Nếu q chia hết cho 3, do q là số nguyên tố nên q = 3.
7p + q = 17; pq + 11 = 17 (T/m)
+) Nếu q chia cho 3 dư 1 thì 14 + q chia hết cho 3
 7p + q là hợp số
7p + q là hợp số +) Nếu q chia cho 3 dư 2 thì 2q chia cho 3 dư 1 nên pq + 11 = 2q +11 chia hết cho 3
 pq +11 là hợp số.
pq +11 là hợp số. *) TH2: q = 2 thì 7p + q = 7p + 2
Nếu 7p chia hết cho 3 thì p chia hết cho 3 nên p = 3
 7p+q=23; pq+11=17 (Thỏa mãn)
7p+q=23; pq+11=17 (Thỏa mãn) +) Nếu 7 p chia cho 3 dư 1 chia hết cho 3
 7p + 2 là hợp số
7p + 2 là hợp số +) Nếu 7 p chia cho 3 dư 2 thì p chia cho 3 dư 2 nên 2p chia cho 3 dư 1
⇒ pq + 11 = 2p + 11 chia hết cho 3 nên là hợp số.
Vậy p = 2, q = 3 hoặc p = 3, q = 2.