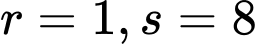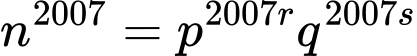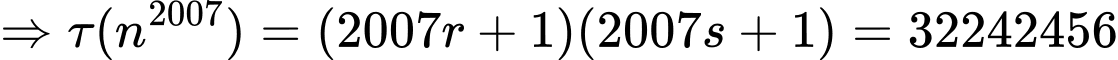DẠNG 1. NHẬN BIẾT SỐ NGUYÊN TỐ, HỢP SỐ
Câu 1 [582618]: Các số sau là số nguyên tố hay hợp số?
312 ; 213 ; 435 ; 417 ; 3311 ; 67.
312 ; 213 ; 435 ; 417 ; 3311 ; 67.
Các số 312, 213, 435 và 417 là hợp số
Số 3311 là hợp số; Số 67 là số nguyên tố
Số 3311 là hợp số; Số 67 là số nguyên tố
Câu 2 [582619]: Gọi 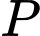 là tập các số nguyên tố. Điền kí hiệu
là tập các số nguyên tố. Điền kí hiệu 
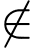 hoặc
hoặc  vào chỗ trống cho đúng:
vào chỗ trống cho đúng:
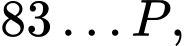
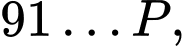
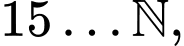

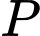 là tập các số nguyên tố. Điền kí hiệu
là tập các số nguyên tố. Điền kí hiệu 
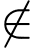 hoặc
hoặc  vào chỗ trống cho đúng:
vào chỗ trống cho đúng: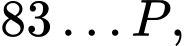
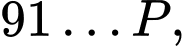
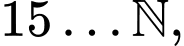





Câu 3 [582621]: Ta biết rằng có 25 số nguyên tố nhỏ hơn 100. Tổng của 25 số nguyên tố là số chẵn hay số lẻ.
Tổng của 25 số nguyên tố nhỏ hơn 100 bao gồm số 2 và 24 số nguyên tố lẻ, nên tổng của chúng là một số chẵn
Câu 4 [582622]: Có thể tìm được 2025 số tự nhiên liên tiếp là hợp số hay không?
Có, bởi trong khoảng (2025;4050) sẽ có ít nhất một số nguyên tố.
DẠNG 2: TÌM SỐ NGUYÊN TỐ, HỢP SỐ THỎA MÃN ĐIỀU KIỆN
Câu 5 [582623]: Tổng của 3 số nguyên tố bằng 1012. Tìm số nguyên tố nhỏ nhất trong ba số nguyên tố đó.
Tổng của 3 số này là một số chẵn, thế thì phải có một trong 3 số là số chẵn và số đó phải bằng 2.
Hiển nhiên 2 là số nguyên tố bé nhất nên 2 là số cần tìm.
Hiển nhiên 2 là số nguyên tố bé nhất nên 2 là số cần tìm.
Câu 6 [582626]: Tìm số nguyên tố, biết rằng số đó bằng tổng của hai số nguyên tố và bằng hiệu của hai số nguyên tố.
Hiển nhiên 2 không phải là số ta cần tìm
Vì số cần tìm là số nguyên tố lẻ, nên tổng của hai số nguyên tố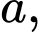
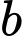 kia phải có một số chẵn và một số lẻ
kia phải có một số chẵn và một số lẻ
Không mất tính tổng quát, giả sử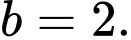
Vì số cần tìm là số nguyên tố lẻ, nên hiệu của hai số nguyên tố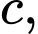
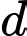 kia phải có một số chẵn và một số lẻ
kia phải có một số chẵn và một số lẻ
Không mất tính tổng quát, giả sử
Ta có: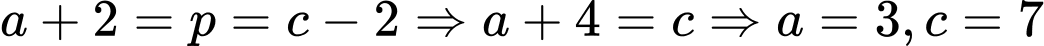
Vậy số cần tìm là 5.
Vì số cần tìm là số nguyên tố lẻ, nên tổng của hai số nguyên tố
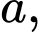
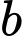 kia phải có một số chẵn và một số lẻ
kia phải có một số chẵn và một số lẻKhông mất tính tổng quát, giả sử
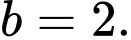
Vì số cần tìm là số nguyên tố lẻ, nên hiệu của hai số nguyên tố
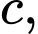
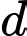 kia phải có một số chẵn và một số lẻ
kia phải có một số chẵn và một số lẻKhông mất tính tổng quát, giả sử

Ta có:
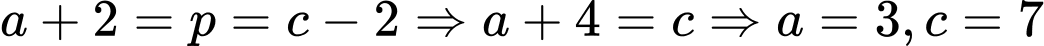
Vậy số cần tìm là 5.
Câu 7 [582627]: Tìm tất cả các số nguyên tố 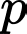 sao cho
sao cho  là một số nguyên tố?
là một số nguyên tố?
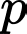 sao cho
sao cho  là một số nguyên tố?
là một số nguyên tố?
Ta có: 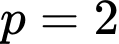 không thỏa mãn
không thỏa mãn
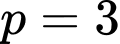 thỏa mãn
thỏa mãn
 ta xét:
ta xét:
+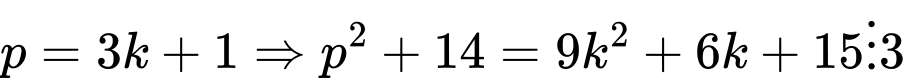
+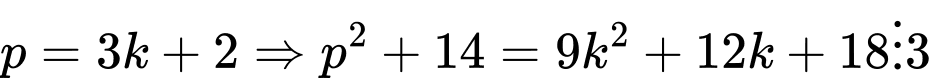
Vậy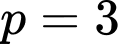
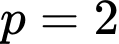 không thỏa mãn
không thỏa mãn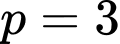 thỏa mãn
thỏa mãn ta xét:
ta xét:+
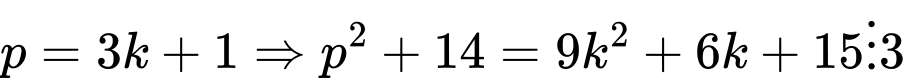
+
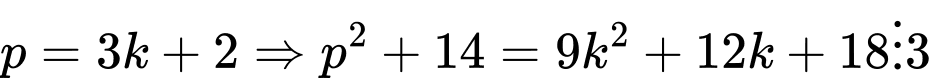
Vậy
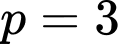
Câu 8 [582629]: Tìm tất cả các số nguyên tố 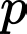 để
để  cũng là số nguyên tố.
cũng là số nguyên tố.
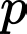 để
để  cũng là số nguyên tố.
cũng là số nguyên tố.
Ta có: 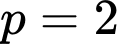 không thỏa mãn
không thỏa mãn
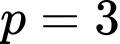 thỏa mãn
thỏa mãn
 ta xét:
ta xét:
+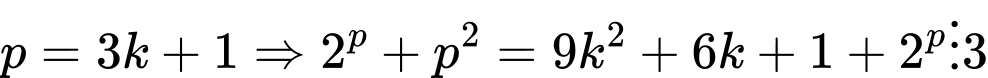 (do
(do 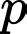 lẻ)
lẻ)
+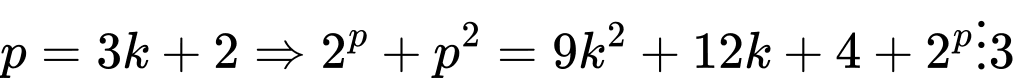 (do
(do 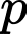 lẻ)
lẻ)
Vậy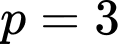
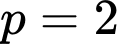 không thỏa mãn
không thỏa mãn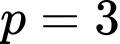 thỏa mãn
thỏa mãn ta xét:
ta xét:+
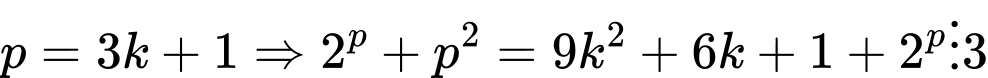 (do
(do 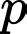 lẻ)
lẻ)+
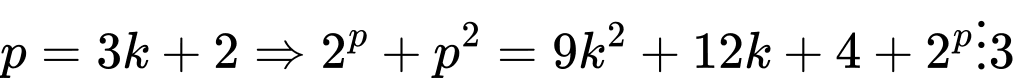 (do
(do 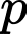 lẻ)
lẻ)Vậy
DẠNG 3. CÁC BÀI TOÁN CHỨNG MINH
Câu 9 [582633]: Chứng minh rằng: Nếu 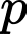 và
và 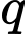 là hai số nguyên tố lớn hơn 3 thì
là hai số nguyên tố lớn hơn 3 thì 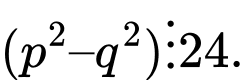
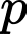 và
và 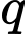 là hai số nguyên tố lớn hơn 3 thì
là hai số nguyên tố lớn hơn 3 thì 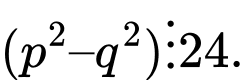
TH1: 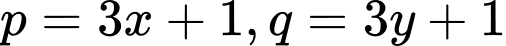
Ta có: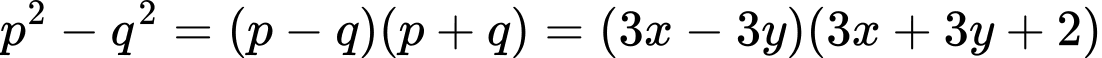
Hiển nhiên tích trên chia hết cho 3
Do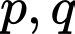 lẻ nên
lẻ nên 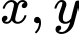 lẻ, trong 2 số
lẻ, trong 2 số 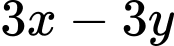 và
và 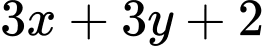 sẽ có một số chia 4 dư 2 và một số chia hết cho 4 nên
sẽ có một số chia 4 dư 2 và một số chia hết cho 4 nên 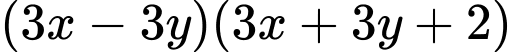 chia hết cho 8.
chia hết cho 8.
Do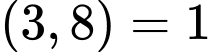 nên tích chia hết cho
nên tích chia hết cho 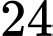
TH2, 3, 4: tương tự.
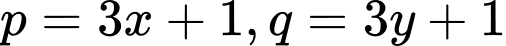
Ta có:
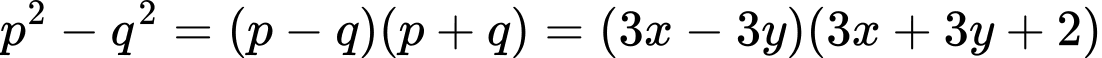
Hiển nhiên tích trên chia hết cho 3
Do
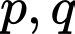 lẻ nên
lẻ nên 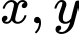 lẻ, trong 2 số
lẻ, trong 2 số 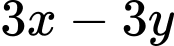 và
và 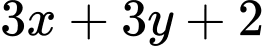 sẽ có một số chia 4 dư 2 và một số chia hết cho 4 nên
sẽ có một số chia 4 dư 2 và một số chia hết cho 4 nên 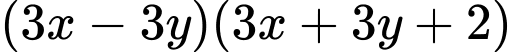 chia hết cho 8.
chia hết cho 8.Do
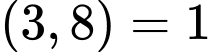 nên tích chia hết cho
nên tích chia hết cho 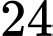
TH2, 3, 4: tương tự.
Câu 10 [582634]: Chứng minh mọi ước nguyên tố của 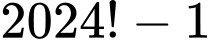 đều lớn hơn
đều lớn hơn 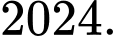
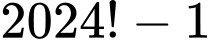 đều lớn hơn
đều lớn hơn 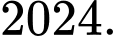
Giả sử tồn tại một ước nguyên tố 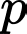 nhỏ hơn
nhỏ hơn 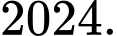 Ta có:
Ta có:
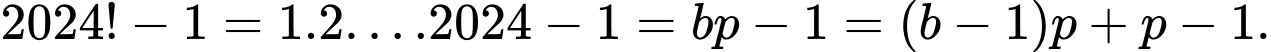
Do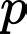 là ước của
là ước của 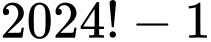 nên
nên 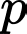 là ước của
là ước của  (vô lý, vì 2 số tự nhiên liên tiếp lớn hơn 1 luôn nguyên tố cùng nhau).
(vô lý, vì 2 số tự nhiên liên tiếp lớn hơn 1 luôn nguyên tố cùng nhau).
Ta có đpcm.
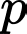 nhỏ hơn
nhỏ hơn 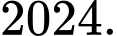 Ta có:
Ta có: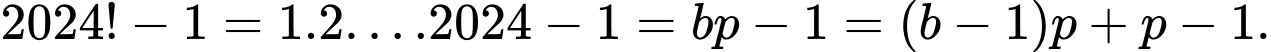
Do
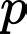 là ước của
là ước của 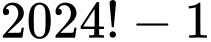 nên
nên 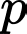 là ước của
là ước của  (vô lý, vì 2 số tự nhiên liên tiếp lớn hơn 1 luôn nguyên tố cùng nhau).
(vô lý, vì 2 số tự nhiên liên tiếp lớn hơn 1 luôn nguyên tố cùng nhau).Ta có đpcm.
Câu 11 [582635]: Cho 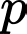 và
và 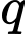 là các số nguyên tố lớn hơn 3 và thỏa mãn
là các số nguyên tố lớn hơn 3 và thỏa mãn 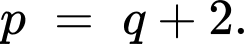 Chứng minh rằng
Chứng minh rằng 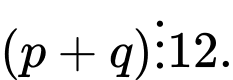
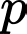 và
và 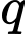 là các số nguyên tố lớn hơn 3 và thỏa mãn
là các số nguyên tố lớn hơn 3 và thỏa mãn 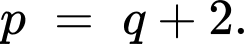 Chứng minh rằng
Chứng minh rằng 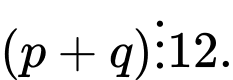
Xét trường hợp tương tự VD1
Câu 12 [582637]: Cho 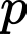 là số nguyên tố lớn hơn 7. Chứng minh rằng
là số nguyên tố lớn hơn 7. Chứng minh rằng 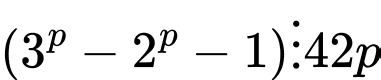
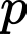 là số nguyên tố lớn hơn 7. Chứng minh rằng
là số nguyên tố lớn hơn 7. Chứng minh rằng 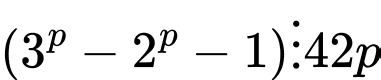
Theo Fermat nhỏ:
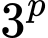 chia
chia 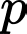 dư 3
dư 3
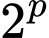 chia
chia 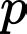 dư 2
dư 2
nên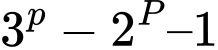 chia hết cho
chia hết cho 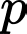
Ta có:
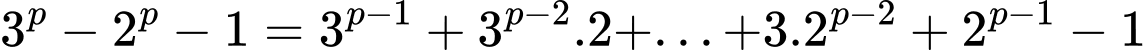
Dễ thấy: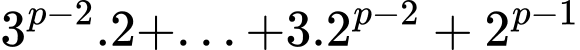 chia hết cho
chia hết cho 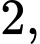 mà
mà 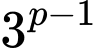 lẻ, nên:
lẻ, nên:
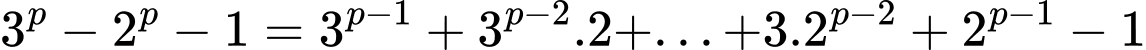 chia hết cho 2
chia hết cho 2
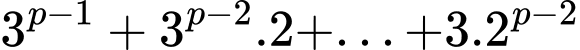 chia hết cho 3, mà
chia hết cho 3, mà 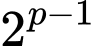 chia
chia 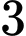 dư
dư 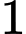 (do
(do 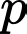 lẻ), nên:
lẻ), nên:
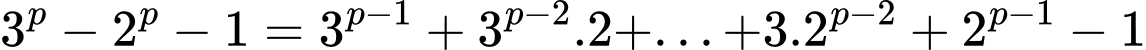 chia hết cho 3
chia hết cho 3
Xét theo lý thuyết đồng dư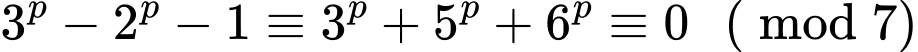 (Xem bài lý thuyết đồng dư)
(Xem bài lý thuyết đồng dư)
Nên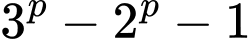 chia hết cho 7
chia hết cho 7
Do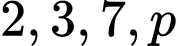 đôi một nguyên tố cùng nhau nên
đôi một nguyên tố cùng nhau nên 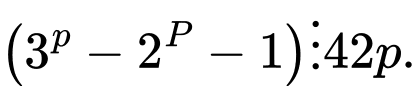
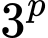 chia
chia 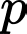 dư 3
dư 3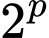 chia
chia 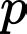 dư 2
dư 2nên
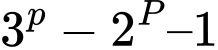 chia hết cho
chia hết cho 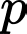
Ta có:
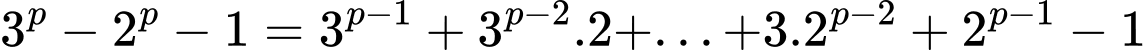
Dễ thấy:
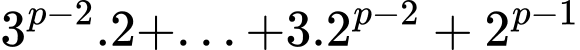 chia hết cho
chia hết cho 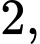 mà
mà 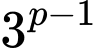 lẻ, nên:
lẻ, nên: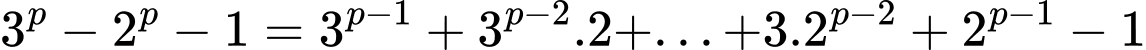 chia hết cho 2
chia hết cho 2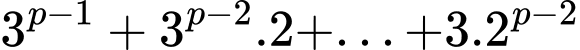 chia hết cho 3, mà
chia hết cho 3, mà 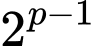 chia
chia 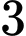 dư
dư 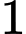 (do
(do 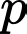 lẻ), nên:
lẻ), nên: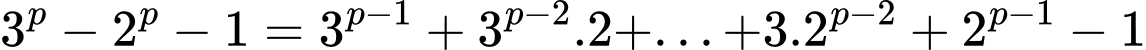 chia hết cho 3
chia hết cho 3Xét theo lý thuyết đồng dư
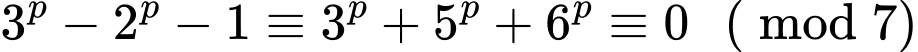 (Xem bài lý thuyết đồng dư)
(Xem bài lý thuyết đồng dư)Nên
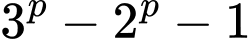 chia hết cho 7
chia hết cho 7Do
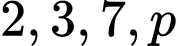 đôi một nguyên tố cùng nhau nên
đôi một nguyên tố cùng nhau nên 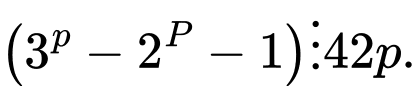
DẠNG 4. BÀI TẬP LIÊN QUAN TỚI CÁC HÀM SỐ HỌC
Câu 13 [585492]: Tìm giá trị của 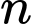 biết:
biết:
i)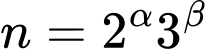 và
và 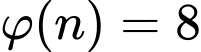
ii)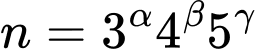 và
và 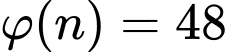
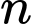 biết:
biết:i)
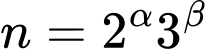 và
và 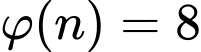
ii)
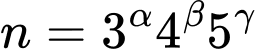 và
và 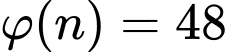
i) Do 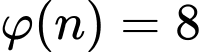 nên
nên 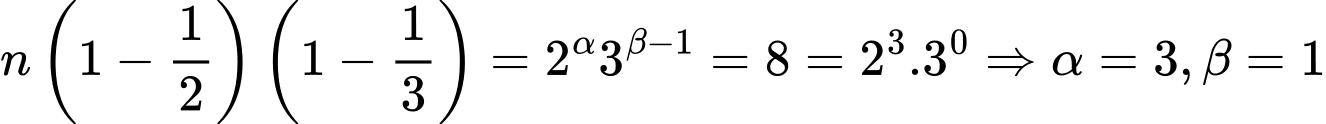
Vậy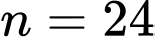
ii) Do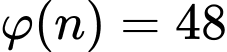 nên
nên 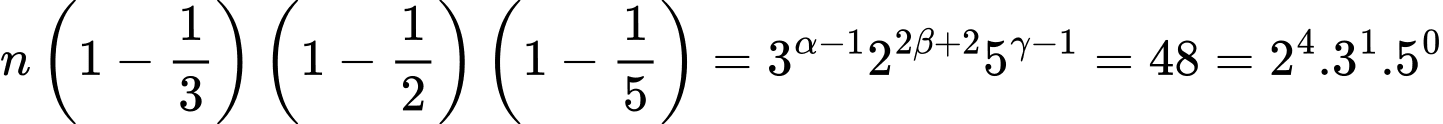
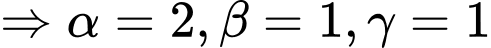
Vậy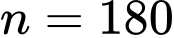
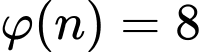 nên
nên 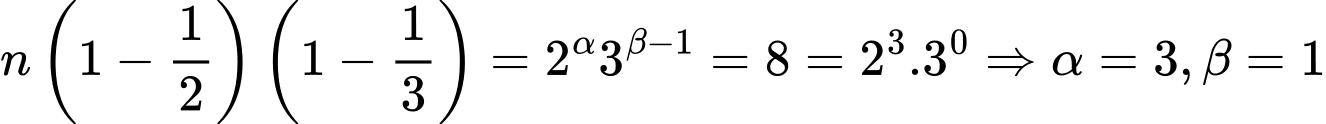
Vậy
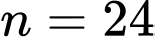
ii) Do
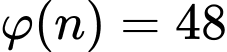 nên
nên 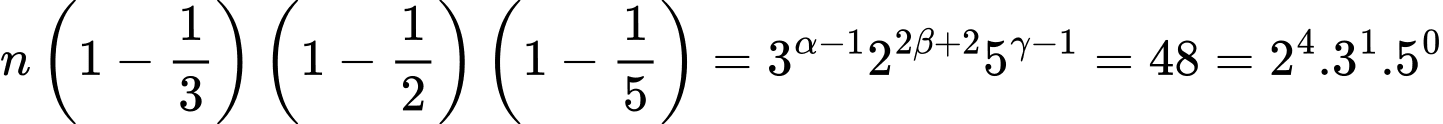
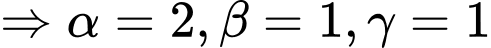
Vậy
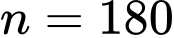
Câu 14 [585493]: Tìm các số tự nhiên 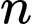 biết phân tích
biết phân tích 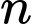 ra thừa số nguyên tố có dạng
ra thừa số nguyên tố có dạng 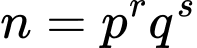 và
và 
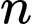 biết phân tích
biết phân tích 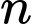 ra thừa số nguyên tố có dạng
ra thừa số nguyên tố có dạng 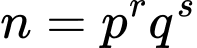 và
và 
Do:  (Không thể là
(Không thể là  vì
vì 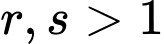 )
)
Không mất tính tổng quát, giả sử: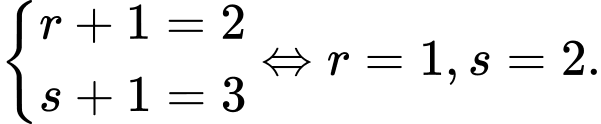
Khi đó,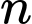 có dạng
có dạng 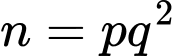
Mà: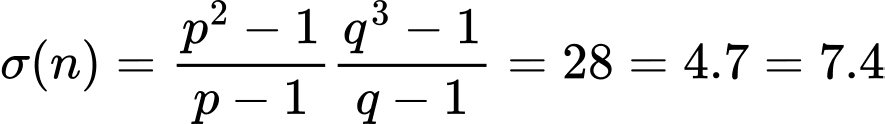 (Do
(Do 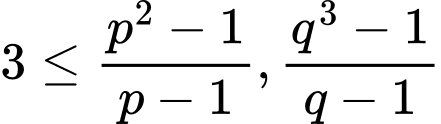 )
)
TH1: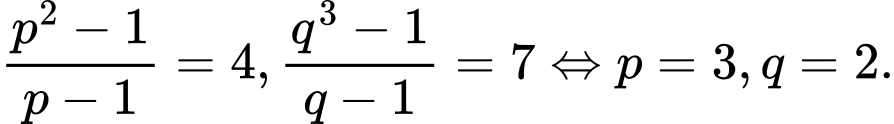
TH2: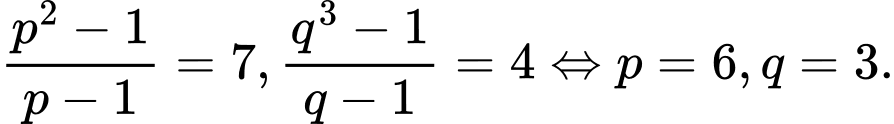 (Loại do
(Loại do 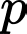 nguyên tố).
nguyên tố).
Vậy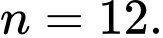
 (Không thể là
(Không thể là  vì
vì 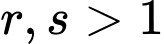 )
)
Không mất tính tổng quát, giả sử:
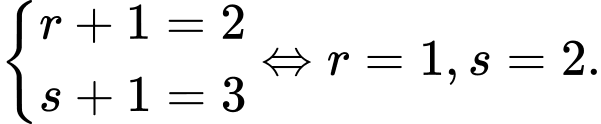
Khi đó,
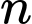 có dạng
có dạng 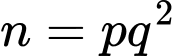
Mà:
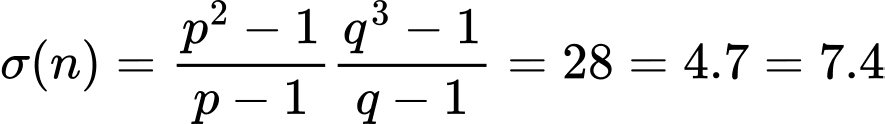 (Do
(Do 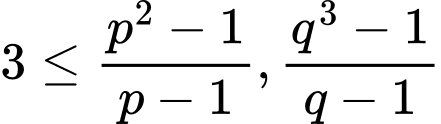 )
)
TH1:
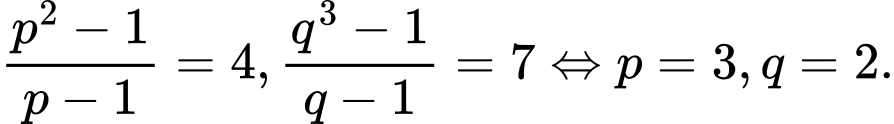
TH2:
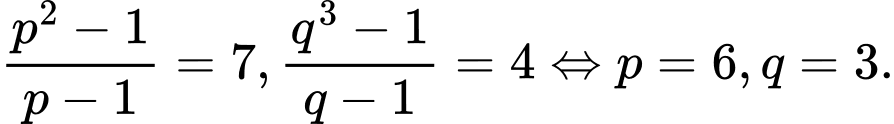 (Loại do
(Loại do 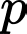 nguyên tố).
nguyên tố).
Vậy
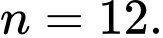
Câu 15 [585494]: Biết phân tích 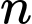 ra thừa số nguyên tố có dạng
ra thừa số nguyên tố có dạng 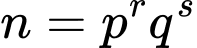 và
và 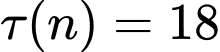 . Tính
. Tính 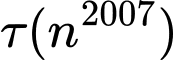 .
.
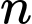 ra thừa số nguyên tố có dạng
ra thừa số nguyên tố có dạng 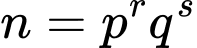 và
và 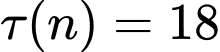 . Tính
. Tính 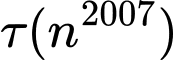 .
.
Do: 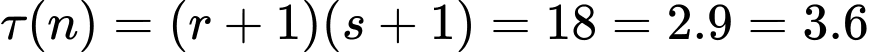
Không mất tính tổng quát, giả sử: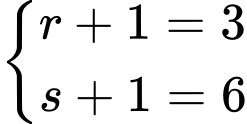
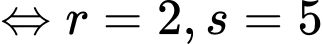 hoặc
hoặc 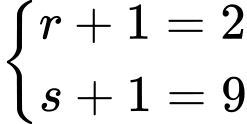
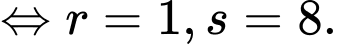
TH1: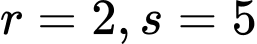
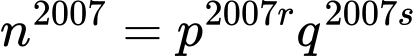
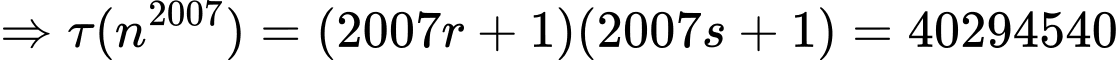
TH2: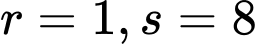
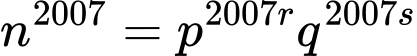
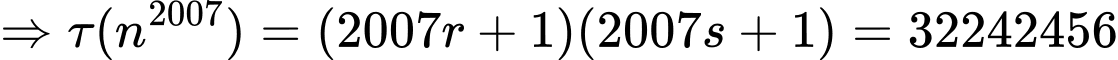
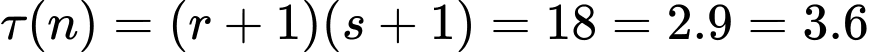
Không mất tính tổng quát, giả sử:
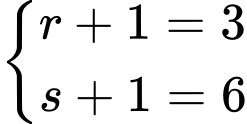
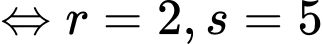 hoặc
hoặc 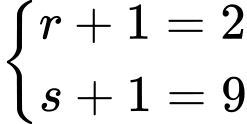
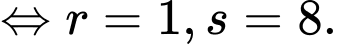
TH1:
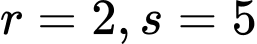
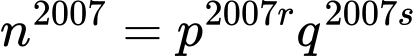
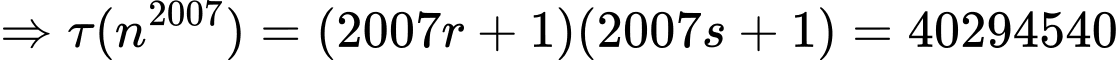
TH2: