Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn
(Thí sinh trả lời từ câu 1 đến câu 16. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất)
Câu 1 [582638]: Cho số nguyên tố 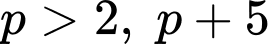 có thể là một số nguyên tố được không?
có thể là một số nguyên tố được không?
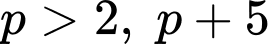 có thể là một số nguyên tố được không?
có thể là một số nguyên tố được không? A, Có vô số trường hợp như vậy.
B, Có hữu hạn trường hợp như vậy.
C, Không có trường hợp nào như vậy.
D, Không thể kết luận.
Ta có 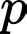 là một số nguyên tố lớn hơn 2 nên
là một số nguyên tố lớn hơn 2 nên 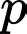 là một số lẻ
là một số lẻ 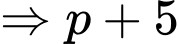 là một số chẵn nên
là một số chẵn nên  không thể là một số nguyên tố Đáp án: C
không thể là một số nguyên tố Đáp án: C
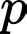 là một số nguyên tố lớn hơn 2 nên
là một số nguyên tố lớn hơn 2 nên 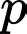 là một số lẻ
là một số lẻ 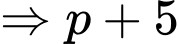 là một số chẵn nên
là một số chẵn nên  không thể là một số nguyên tố Đáp án: C
không thể là một số nguyên tố Đáp án: C
Câu 2 [582639]: Cho 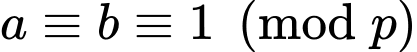 (
(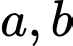 là các số nguyên,
là các số nguyên, 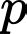 là số nguyên lẻ). Kết luận nào sau đây là đúng?
là số nguyên lẻ). Kết luận nào sau đây là đúng?
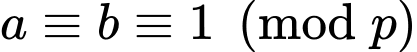 (
(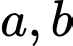 là các số nguyên,
là các số nguyên, 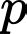 là số nguyên lẻ). Kết luận nào sau đây là đúng?
là số nguyên lẻ). Kết luận nào sau đây là đúng? A, 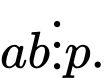
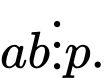
B, 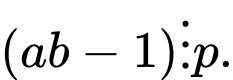
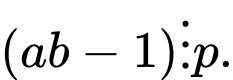
C, 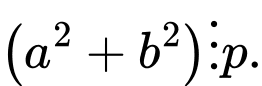
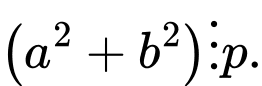
D, 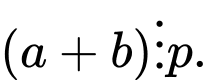
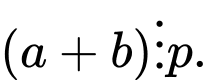
+) 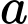 và
và 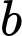 đều không chia hết cho
đều không chia hết cho 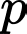 nên
nên 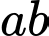 không chia hết cho
không chia hết cho 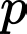
+)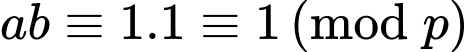 nên
nên 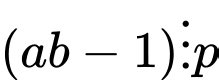
+)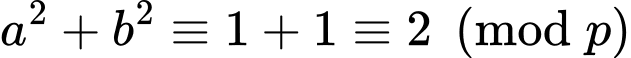 mà
mà 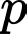 lẻ nên
lẻ nên  không chia hết cho
không chia hết cho 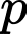
+) Tương tự vì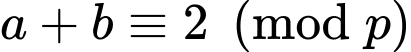 Đáp án: B
Đáp án: B
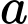 và
và 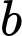 đều không chia hết cho
đều không chia hết cho 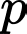 nên
nên 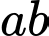 không chia hết cho
không chia hết cho 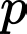
+)
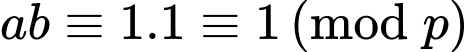 nên
nên 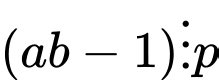
+)
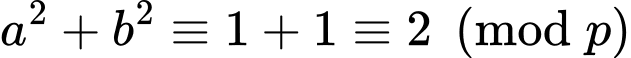 mà
mà 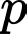 lẻ nên
lẻ nên  không chia hết cho
không chia hết cho 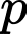
+) Tương tự vì
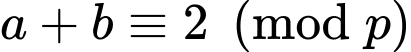 Đáp án: B
Đáp án: B
Câu 3 [582640]: Có bao nhiêu số nguyên dương 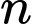 để
để 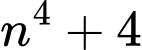 là số nguyên tố?
là số nguyên tố?
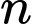 để
để 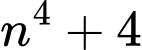 là số nguyên tố?
là số nguyên tố? A, 0.
B, 1.
C, 2.
D, 3.
Ta có:
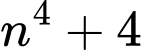
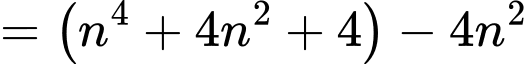
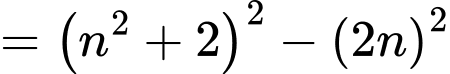
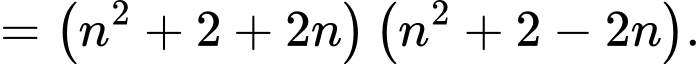
Nếu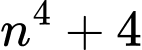 là số nguyên tố thì
là số nguyên tố thì 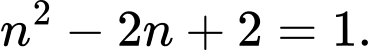
Suy ra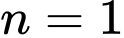
Thử lại: Với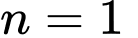 thì
thì 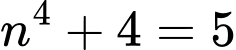 là số nguyên tố.
là số nguyên tố.
Vậy có một số nguyên dương thỏa mãn. Đáp án: B
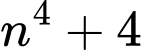
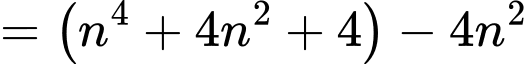
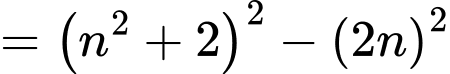
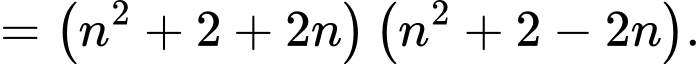
Nếu
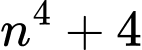 là số nguyên tố thì
là số nguyên tố thì 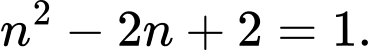
Suy ra
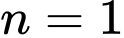
Thử lại: Với
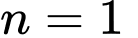 thì
thì 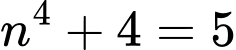 là số nguyên tố.
là số nguyên tố. Vậy có một số nguyên dương thỏa mãn. Đáp án: B
Câu 4 [582641]: Cho 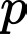 là số nguyên tố nhỏ nhất thỏa mãn
là số nguyên tố nhỏ nhất thỏa mãn 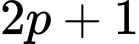 là lập phương của một số tự nhiên
là lập phương của một số tự nhiên 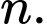 Tính giá trị
Tính giá trị  ?
?
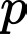 là số nguyên tố nhỏ nhất thỏa mãn
là số nguyên tố nhỏ nhất thỏa mãn 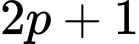 là lập phương của một số tự nhiên
là lập phương của một số tự nhiên 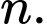 Tính giá trị
Tính giá trị  ?
? A, 30.
B, 40.
C, 35.
D, 45.
Ta có 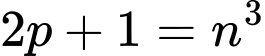 (với
(với 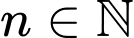 ).
).
Dễ thấy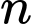 là số lẻ nên đặt
là số lẻ nên đặt 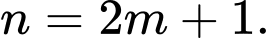
Do đó,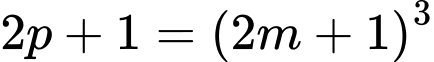
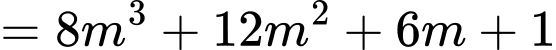
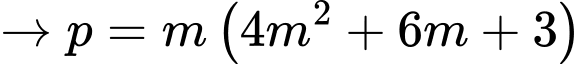
Suy ra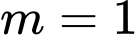
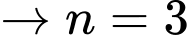
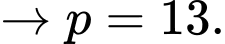
Vậy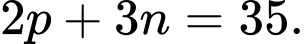 Đáp án: C
Đáp án: C
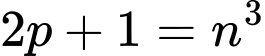 (với
(với 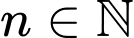 ).
). Dễ thấy
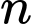 là số lẻ nên đặt
là số lẻ nên đặt 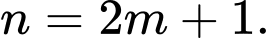
Do đó,
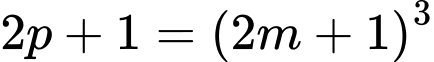
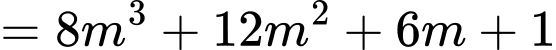
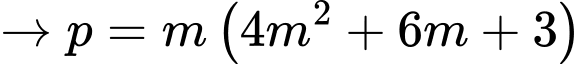
Suy ra
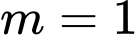
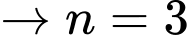
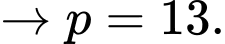
Vậy
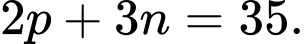 Đáp án: C
Đáp án: C
Câu 5 [582646]: Có bao nhiêu số nguyên tố 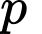 sao cho các số
sao cho các số 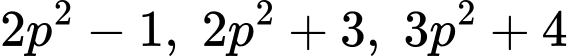 đều là số nguyên tố?
đều là số nguyên tố?
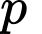 sao cho các số
sao cho các số 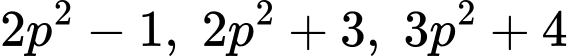 đều là số nguyên tố?
đều là số nguyên tố? A, Có vô số số nguyên tố 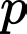 thỏa mãn.
thỏa mãn.
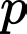 thỏa mãn.
thỏa mãn.B, Có ba số nguyên tố 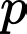 thỏa mãn.
thỏa mãn.
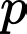 thỏa mãn.
thỏa mãn.C, Có duy nhất một số nguyên tố 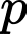 thỏa mãn.
thỏa mãn.
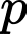 thỏa mãn.
thỏa mãn.D, Không có số nguyên tố 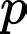 thỏa mãn.
thỏa mãn.
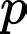 thỏa mãn.
thỏa mãn.
+) 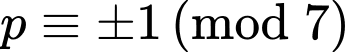
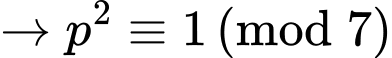
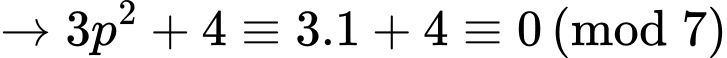
Do đó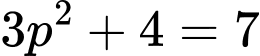
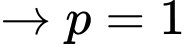 (vô lý).
(vô lý).
+)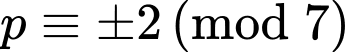
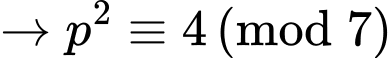
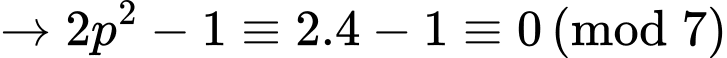
Do đó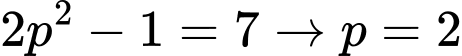
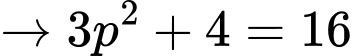 không phải số nguyên tố.
không phải số nguyên tố.
+)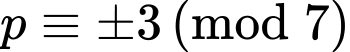

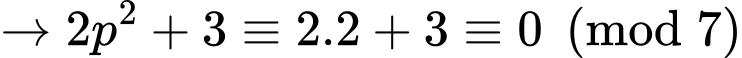
Do đó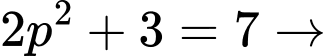 Không tồn tại
Không tồn tại 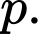
+)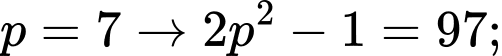
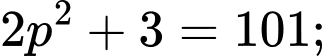
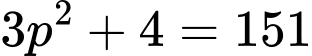 đều là các số nguyên tố.
đều là các số nguyên tố.
Vậy tồn tại duy nhất một số nguyên tố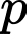 thỏa mãn yêu cầu. Đáp án: C
thỏa mãn yêu cầu. Đáp án: C
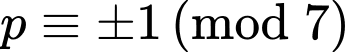
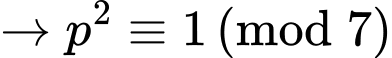
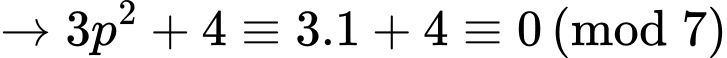
Do đó
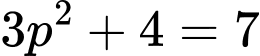
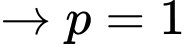 (vô lý).
(vô lý).+)
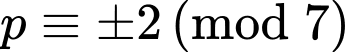
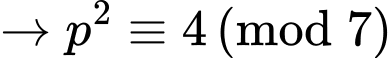
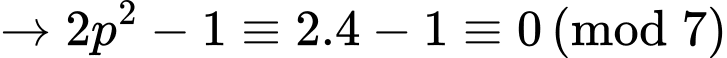
Do đó
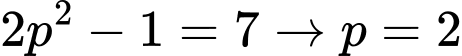
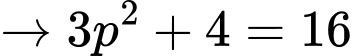 không phải số nguyên tố.
không phải số nguyên tố.+)
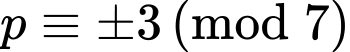

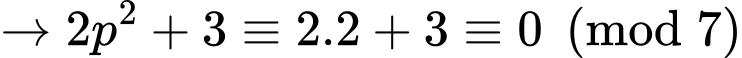
Do đó
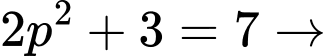 Không tồn tại
Không tồn tại 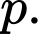
+)
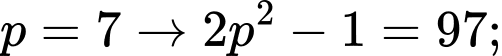
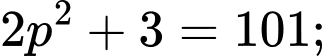
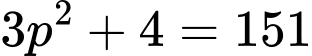 đều là các số nguyên tố.
đều là các số nguyên tố.Vậy tồn tại duy nhất một số nguyên tố
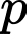 thỏa mãn yêu cầu. Đáp án: C
thỏa mãn yêu cầu. Đáp án: C
Câu 6 [582647]: Trong các cặp số tự nhiên 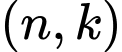 sao cho
sao cho 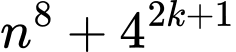 là số nguyên tố,
là số nguyên tố, 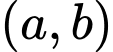 cặp số có tổng lớn nhất. Tìm giá trị của
cặp số có tổng lớn nhất. Tìm giá trị của 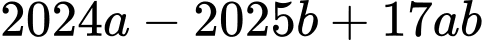 ?
?
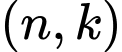 sao cho
sao cho 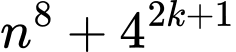 là số nguyên tố,
là số nguyên tố, 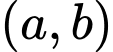 cặp số có tổng lớn nhất. Tìm giá trị của
cặp số có tổng lớn nhất. Tìm giá trị của 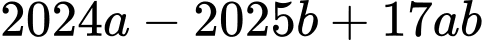 ?
? A, 2016.
B, 2024.
C, 2025.
D, 4037.
+) 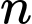 chẵn thì
chẵn thì 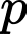 chẵn lớn hơn 2 nên không thể là số nguyên tố
chẵn lớn hơn 2 nên không thể là số nguyên tố
+)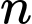 lẻ:
lẻ:
TH1: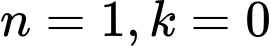 thì
thì 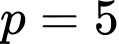 thỏa mãn.
thỏa mãn.
TH2: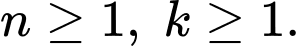 Ta có
Ta có 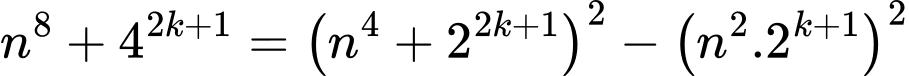
Nên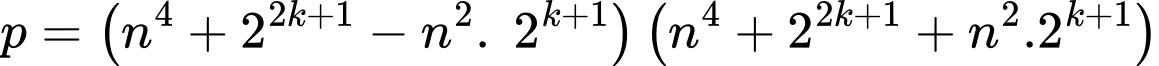
Mà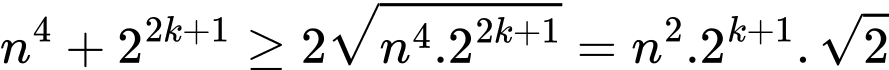
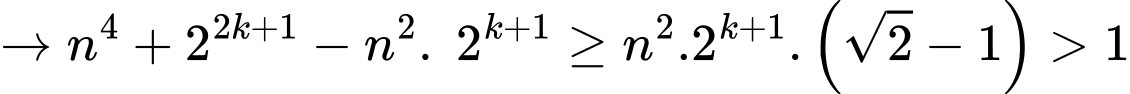
Và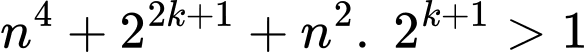 nên
nên 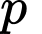 là hợp số (mẫu thuẫn giả thiết).
là hợp số (mẫu thuẫn giả thiết).
Vậy tồn tại duy nhất một bộ thỏa mãn nên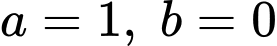
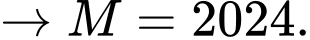 Đáp án: B
Đáp án: B
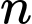 chẵn thì
chẵn thì 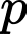 chẵn lớn hơn 2 nên không thể là số nguyên tố
chẵn lớn hơn 2 nên không thể là số nguyên tố+)
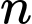 lẻ:
lẻ:TH1:
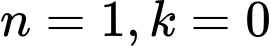 thì
thì 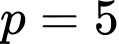 thỏa mãn.
thỏa mãn.TH2:
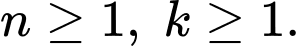 Ta có
Ta có 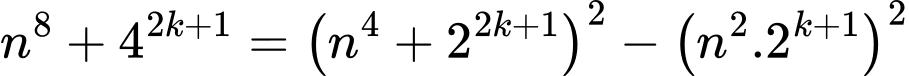
Nên
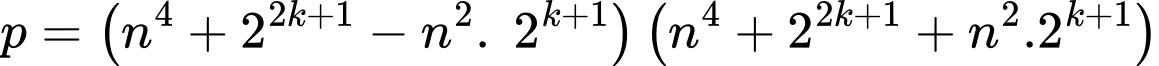
Mà
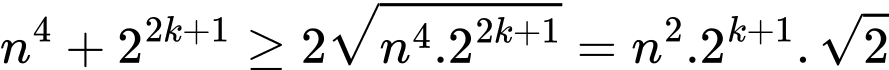
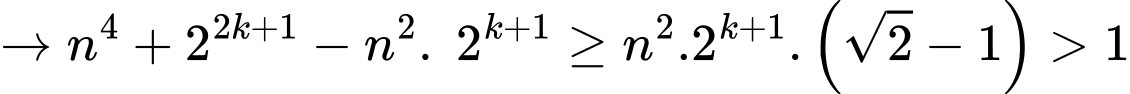
Và
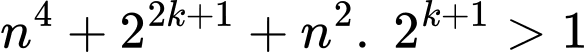 nên
nên 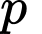 là hợp số (mẫu thuẫn giả thiết).
là hợp số (mẫu thuẫn giả thiết).Vậy tồn tại duy nhất một bộ thỏa mãn nên
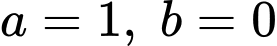
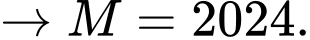 Đáp án: B
Đáp án: B
Câu 7 [582649]: Trong các số sau, số nào là hợp số?
A, 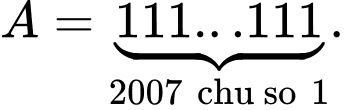
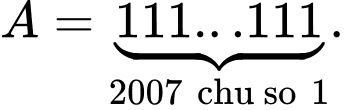
B, 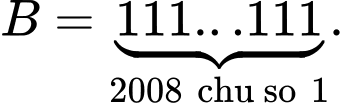
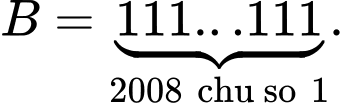
C, 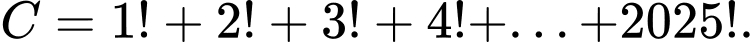
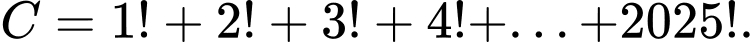
D, Tất cả đều là hợp số.
+) 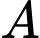 có tổng các chữ số là 2007 chia hết cho 3 nên
có tổng các chữ số là 2007 chia hết cho 3 nên 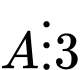
 là hợp số.
là hợp số.
+)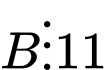 dựa vào dấu hiệu chia hết cho 11.
dựa vào dấu hiệu chia hết cho 11.
+)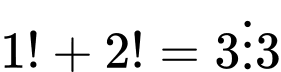 và
và 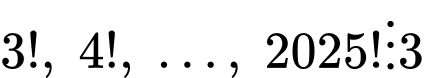

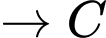 là hợp số. Đáp án: D
là hợp số. Đáp án: D
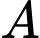 có tổng các chữ số là 2007 chia hết cho 3 nên
có tổng các chữ số là 2007 chia hết cho 3 nên 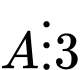
 là hợp số.
là hợp số.+)
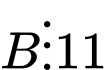 dựa vào dấu hiệu chia hết cho 11.
dựa vào dấu hiệu chia hết cho 11.+)
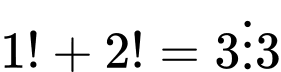 và
và 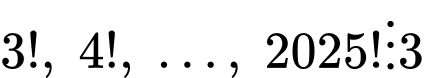

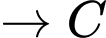 là hợp số. Đáp án: D
là hợp số. Đáp án: D
Câu 8 [582650]: Có bao nhiêu cặp số nguyên tố 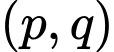 thỏa mãn
thỏa mãn 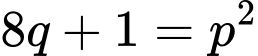 ?
?
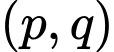 thỏa mãn
thỏa mãn 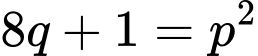 ?
? A, 0.
B, 1.
C, 2.
D, 3.
+) 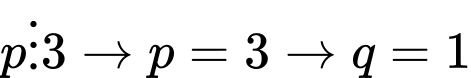 (không thỏa).
(không thỏa).
+)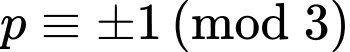
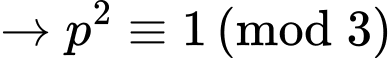
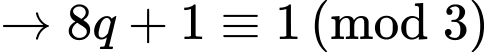
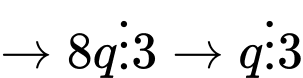
Do đó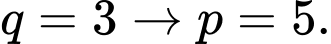 Vậy có duy nhất một cặp số nguyên tố thỏa mãn yêu cầu. Đáp án: B
Vậy có duy nhất một cặp số nguyên tố thỏa mãn yêu cầu. Đáp án: B
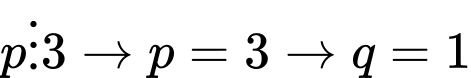 (không thỏa).
(không thỏa).+)
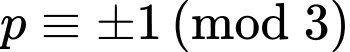
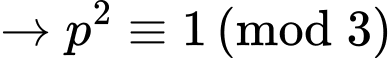
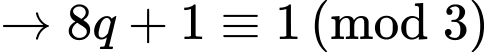
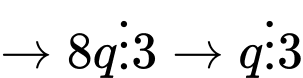
Do đó
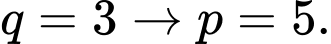 Vậy có duy nhất một cặp số nguyên tố thỏa mãn yêu cầu. Đáp án: B
Vậy có duy nhất một cặp số nguyên tố thỏa mãn yêu cầu. Đáp án: B
Câu 9 [582651]: Cho 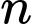 là số tự nhiên lớn nhất để
là số tự nhiên lớn nhất để  là một số nguyên tố. Phát biểu nào sau đây là chính xác về
là một số nguyên tố. Phát biểu nào sau đây là chính xác về 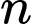 ?
?
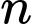 là số tự nhiên lớn nhất để
là số tự nhiên lớn nhất để  là một số nguyên tố. Phát biểu nào sau đây là chính xác về
là một số nguyên tố. Phát biểu nào sau đây là chính xác về 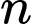 ?
? A, Tổng các chữ số của 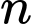 bằng 10.
bằng 10.
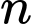 bằng 10.
bằng 10.B, 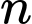 là một số lẻ.
là một số lẻ.
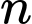 là một số lẻ.
là một số lẻ.C, 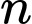 là một số nguyên tố.
là một số nguyên tố.
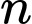 là một số nguyên tố.
là một số nguyên tố.D, Tất cả phát biểu trên đều sai.
+) 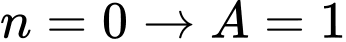 không phải số nguyên tố.
không phải số nguyên tố.
+)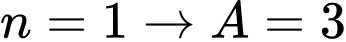 là một số nguyên tố.
là một số nguyên tố.
+)
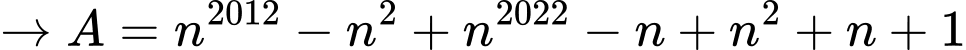
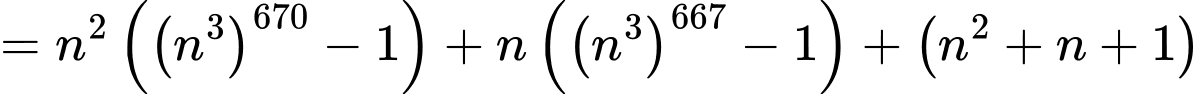
Có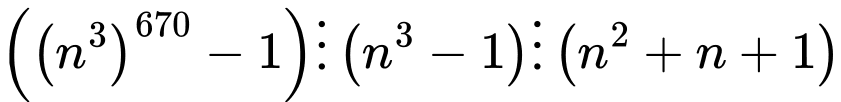
Tương tự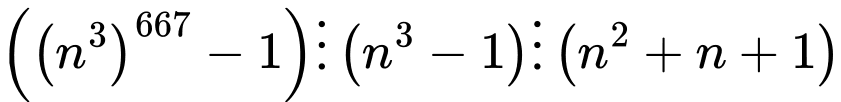
Do đó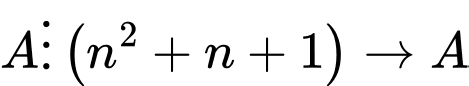 là hợp số.
là hợp số.
Vậy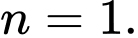 Đáp án: B
Đáp án: B
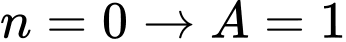 không phải số nguyên tố.
không phải số nguyên tố.+)
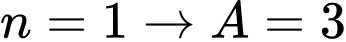 là một số nguyên tố.
là một số nguyên tố.+)

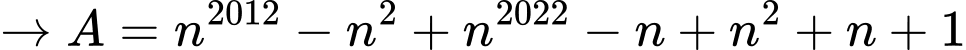
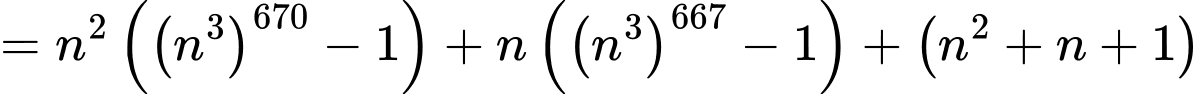
Có
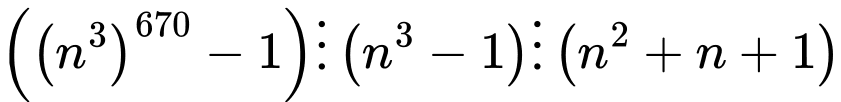
Tương tự
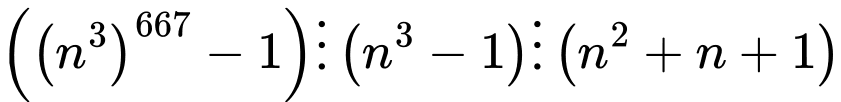
Do đó
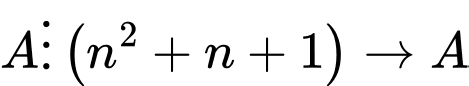 là hợp số.
là hợp số. Vậy
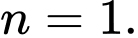 Đáp án: B
Đáp án: B
Câu 10 [582652]: Có bao nhiêu cặp số nguyên tố 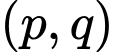 thỏa mãn 2 điều kiện
thỏa mãn 2 điều kiện 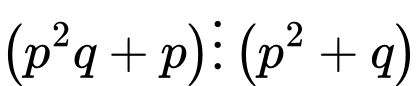 và
và 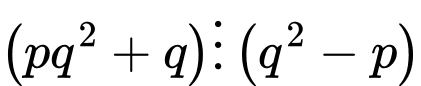 ?
?
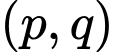 thỏa mãn 2 điều kiện
thỏa mãn 2 điều kiện 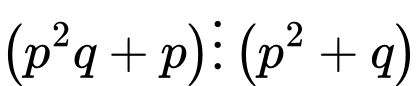 và
và 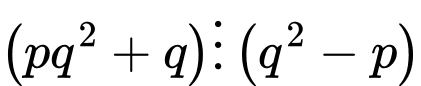 ?
? A, 0.
B, 1.
C, 2.
D, 3.
+) 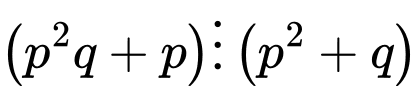
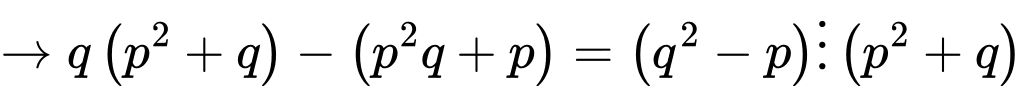
+)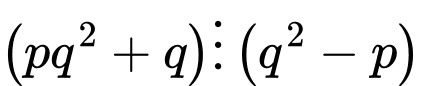
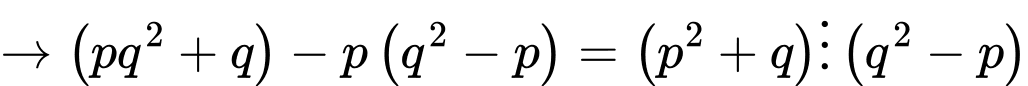
TH1: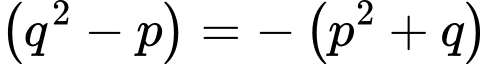
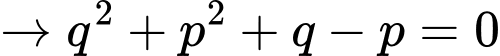 (Vô lý do thấy rõ VT>VP).
(Vô lý do thấy rõ VT>VP).
TH2: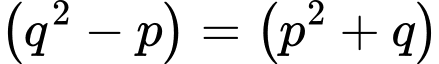
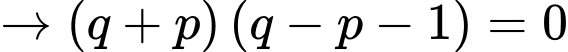
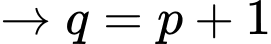
Vậy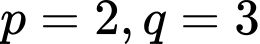 nên có duy nhất 1 cặp số nguyên tố thỏa mãn. Đáp án: B
nên có duy nhất 1 cặp số nguyên tố thỏa mãn. Đáp án: B
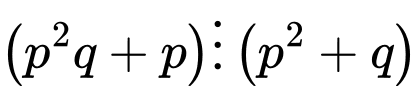
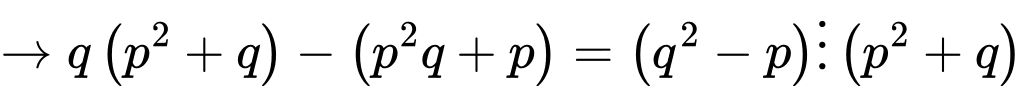
+)
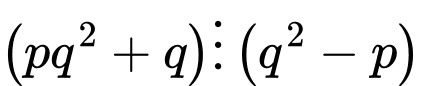
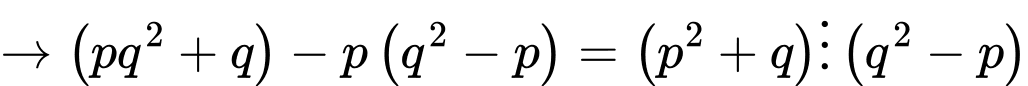
TH1:
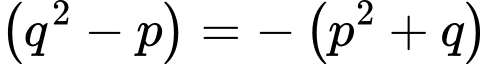
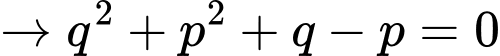 (Vô lý do thấy rõ VT>VP).
(Vô lý do thấy rõ VT>VP).TH2:
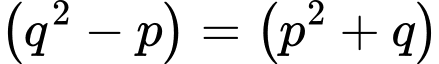
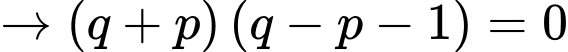
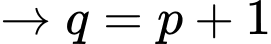
Vậy
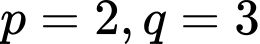 nên có duy nhất 1 cặp số nguyên tố thỏa mãn. Đáp án: B
nên có duy nhất 1 cặp số nguyên tố thỏa mãn. Đáp án: B
Câu 11 [582653]: Có bao nhiêu số tự nhiên 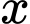 để
để 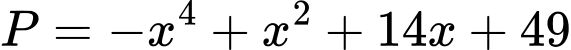 là một số nguyên tố?
là một số nguyên tố?
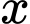 để
để 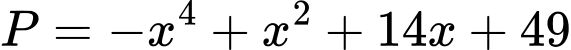 là một số nguyên tố?
là một số nguyên tố? A, 0.
B, 1.
C, 2.
D, 3.
+) 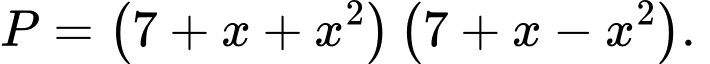
Mà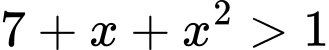 nên
nên 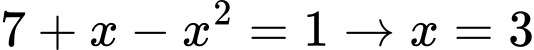
Thử lại thấy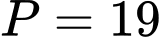 thỏa mãn là một số nguyên tố. Đáp án: B
thỏa mãn là một số nguyên tố. Đáp án: B
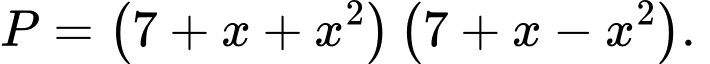
Mà
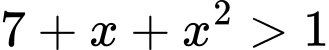 nên
nên 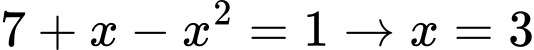
Thử lại thấy
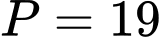 thỏa mãn là một số nguyên tố. Đáp án: B
thỏa mãn là một số nguyên tố. Đáp án: B
Câu 12 [582654]: Cho 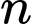 là số tự nhiên lớn nhất để
là số tự nhiên lớn nhất để 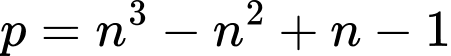 là một số nguyên tố. Giá trị biểu thức
là một số nguyên tố. Giá trị biểu thức 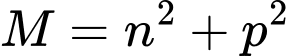 bằng bao nhiêu?
bằng bao nhiêu?
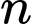 là số tự nhiên lớn nhất để
là số tự nhiên lớn nhất để 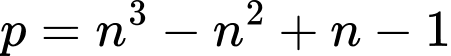 là một số nguyên tố. Giá trị biểu thức
là một số nguyên tố. Giá trị biểu thức 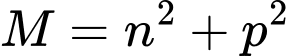 bằng bao nhiêu?
bằng bao nhiêu? A, 29.
B, 221.
C, 1404.
D, 3107.
+) 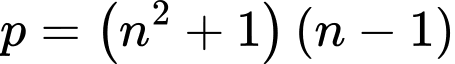
Xét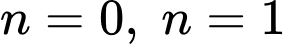 không thỏa mãn.
không thỏa mãn.
Xét là một số nguyên tố.
là một số nguyên tố.
Với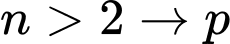 là tích của 2 số tự nhiên > 1 nên
là tích của 2 số tự nhiên > 1 nên 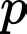 là hợp số. Đáp án: A
là hợp số. Đáp án: A
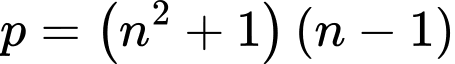
Xét
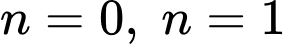 không thỏa mãn.
không thỏa mãn. Xét
 là một số nguyên tố.
là một số nguyên tố.Với
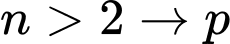 là tích của 2 số tự nhiên > 1 nên
là tích của 2 số tự nhiên > 1 nên 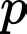 là hợp số. Đáp án: A
là hợp số. Đáp án: A
Câu 13 [582655]: Với điều kiện nào của số nguyên dương 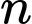 thì
thì 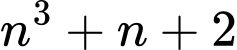 là hợp số?
là hợp số?
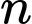 thì
thì 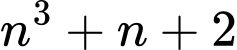 là hợp số?
là hợp số? A, 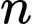 là số chẵn.
là số chẵn.
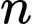 là số chẵn.
là số chẵn.B, 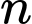 là số lẻ.
là số lẻ.
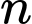 là số lẻ.
là số lẻ.C, 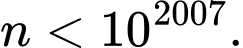
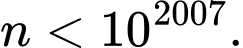
D, 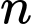 chỉ cần là số nguyên dương.
chỉ cần là số nguyên dương.
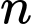 chỉ cần là số nguyên dương.
chỉ cần là số nguyên dương.
+) 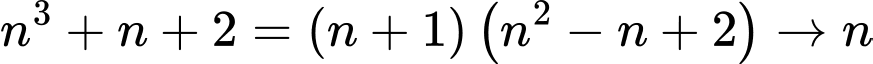 chỉ cần là số nguyên dương Đáp án: D
chỉ cần là số nguyên dương Đáp án: D
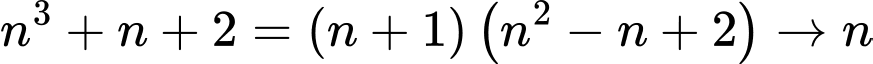 chỉ cần là số nguyên dương Đáp án: D
chỉ cần là số nguyên dương Đáp án: D
Câu 14 [582656]: Một số nguyên tố p khi chia cho 42 được số dư r là hợp số. Tổng các chữ số của r là
A, 5.
B, 6.
C, 7.
D, 8.
Vì p chia cho 42 có số dư là r nên: p = 42k + r (0 < r < 42, k, r tự nhiên)
Hay p = 2.3.7k + r.
Vì p là số nguyên tố nên r không chia hết cho 2; 3; 7 => r là hợp số không chia hết cho 2; 3; 7 và r < 42.
Chỉ ra được r = 25.
Vậy hợp số r = 25 Đáp án: C
Hay p = 2.3.7k + r.
Vì p là số nguyên tố nên r không chia hết cho 2; 3; 7 => r là hợp số không chia hết cho 2; 3; 7 và r < 42.
Chỉ ra được r = 25.
Vậy hợp số r = 25 Đáp án: C
Câu 15 [582657]: Có bao nhiêu cặp số nguyên tố (p, q) sao cho 7p + q và pq + 11 đều là các số nguyên tố?
A, 0.
B, 1.
C, 2.
D, 3.
Ta có: pq, là số nguyên tố nên pq +11 là số nguyên tố lớn hơn 11
 pq + 11 là số lẻ suy ra pq là số chẵn.
pq + 11 là số lẻ suy ra pq là số chẵn.
Do 7p + q là số nguyên tố lớn hơn 7 nên p và q không thể cùng tính chẵn lẻ.
*) TH1: p = 2 thì 7p + q =14 + q. Ta thấy 14 chia 3 dư 2
+) Nếu q chia hết cho 3, do q là số nguyên tố nên q = 3.
7p + q = 17; pq + 11 = 17 (T/m)
+) Nếu q chia cho 3 dư 1 thì 14 + q chia hết cho 3 7p + q là hợp số
7p + q là hợp số
+) Nếu q chia cho 3 dư 2 thì 2q chia cho 3 dư 1 nên pq + 11 = 2q +11 chia hết cho 3
 pq +11 là hợp số.
pq +11 là hợp số.
*) TH2: q = 2 thì 7p + q = 7p + 2
Nếu 7p chia hết cho 3 thì p chia hết cho 3 nên p = 3 7p+q=23; pq+11=17 (Thỏa mãn)
7p+q=23; pq+11=17 (Thỏa mãn)
+) Nếu 7 p chia cho 3 dư 1 chia hết cho 3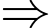 7p + 2 là hợp số
7p + 2 là hợp số
+) Nếu 7 p chia cho 3 dư 2 thì p chia cho 3 dư 2 nên 2p chia cho 3 dư 1
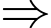 pq + 11 = 2p + 11 chia hết cho 3 nên là hợp số.
pq + 11 = 2p + 11 chia hết cho 3 nên là hợp số.
Vậy p = 2, q = 3 hoặc p = 3, q = 2. Đáp án: C
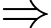 pq + 11 là số lẻ suy ra pq là số chẵn.
pq + 11 là số lẻ suy ra pq là số chẵn. Do 7p + q là số nguyên tố lớn hơn 7 nên p và q không thể cùng tính chẵn lẻ.
*) TH1: p = 2 thì 7p + q =14 + q. Ta thấy 14 chia 3 dư 2
+) Nếu q chia hết cho 3, do q là số nguyên tố nên q = 3.
7p + q = 17; pq + 11 = 17 (T/m)
+) Nếu q chia cho 3 dư 1 thì 14 + q chia hết cho 3
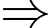 7p + q là hợp số
7p + q là hợp số +) Nếu q chia cho 3 dư 2 thì 2q chia cho 3 dư 1 nên pq + 11 = 2q +11 chia hết cho 3
 pq +11 là hợp số.
pq +11 là hợp số. *) TH2: q = 2 thì 7p + q = 7p + 2
Nếu 7p chia hết cho 3 thì p chia hết cho 3 nên p = 3
 7p+q=23; pq+11=17 (Thỏa mãn)
7p+q=23; pq+11=17 (Thỏa mãn) +) Nếu 7 p chia cho 3 dư 1 chia hết cho 3
 7p + 2 là hợp số
7p + 2 là hợp số +) Nếu 7 p chia cho 3 dư 2 thì p chia cho 3 dư 2 nên 2p chia cho 3 dư 1
 pq + 11 = 2p + 11 chia hết cho 3 nên là hợp số.
pq + 11 = 2p + 11 chia hết cho 3 nên là hợp số. Vậy p = 2, q = 3 hoặc p = 3, q = 2. Đáp án: C
Câu 16 [582645]: Số số nguyên tố nhiều nhất có thể trong 10 số tự nhiên liên tiếp là bao nhiêu?
A, 3.
B, 4.
C, 5.
D, 6.
+) Xét với 10 số tự nhiên liên tiếp bắt đầu từ 6 trở đi nếu là số nguyên tố phải là số lẻ và không chia hết cho 5 nên chỉ có tối đa là 4 số
+) trong các trường hợp 10 số liên tiếp bắt đầu từ một số nhỏ hơn 6, ta dễ dàng nhẩm ra được tối đa sẽ có 5 số nguyên tố. Cụ thể 10 số liên tiếp từ 2 đến 11 có 5 số nguyên tố là 2, 3, 5, 7, 11. Đáp án: C
+) trong các trường hợp 10 số liên tiếp bắt đầu từ một số nhỏ hơn 6, ta dễ dàng nhẩm ra được tối đa sẽ có 5 số nguyên tố. Cụ thể 10 số liên tiếp từ 2 đến 11 có 5 số nguyên tố là 2, 3, 5, 7, 11. Đáp án: C
Dạng câu hỏi: Câu trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 17, 18. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 17 [582643]: Mỗi phát biểu sau đúng hay sai?
a) Mọi số nguyên tố lớn hơn 2 đều có dạng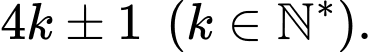
b) Tồn tại 4 số lẻ liên tiếp đều là các số nguyên tố.
c) Nếu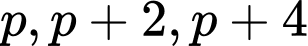 là các số nguyên tố thì
là các số nguyên tố thì 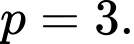
d) Với mọi số nguyên giữa
giữa 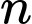 và
và 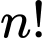 có ít nhất một số nguyên tố.
có ít nhất một số nguyên tố.
a) Mọi số nguyên tố lớn hơn 2 đều có dạng
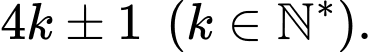
b) Tồn tại 4 số lẻ liên tiếp đều là các số nguyên tố.
c) Nếu
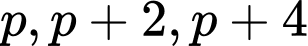 là các số nguyên tố thì
là các số nguyên tố thì 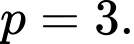
d) Với mọi số nguyên
 giữa
giữa 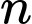 và
và 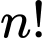 có ít nhất một số nguyên tố.
có ít nhất một số nguyên tố.
a) Đúng
b) Sai
c) Đúng
d) Sai
+) Ý a đúng theo lý thuyết
+) Xét ý c trước. Nếu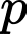 chia 3 dư 1 thì
chia 3 dư 1 thì  chia hết cho 3 (vô lý). Nếu
chia hết cho 3 (vô lý). Nếu 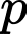 chia 3 dư 2 thì
chia 3 dư 2 thì  chia hết cho 3 (vô lý). Vậy
chia hết cho 3 (vô lý). Vậy 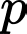 chia hết cho 3 nên
chia hết cho 3 nên 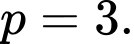 Chỉ có 3 số lẻ liên tiếp là 3 số nguyên tố là 3, 5, 7.
Chỉ có 3 số lẻ liên tiếp là 3 số nguyên tố là 3, 5, 7.
+) Nếu xét 4 số lẻ liên tiếp, dễ thấy không tồn tại trường hợp chúng đều là số nguyên tố.
+) Có thể áp dụng định lý Chebyshev. Hoặc:
Vì nên
nên 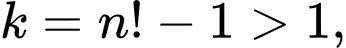 do đó
do đó 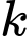 có ít nhất một ước số nguyên tố
có ít nhất một ước số nguyên tố 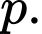
Ta chứng minh
Thật vậy, nếu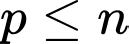 thì
thì 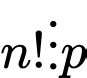
Mà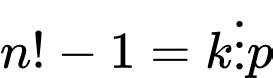 nên
nên 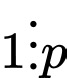 (Vô lý).
(Vô lý).
b) Sai
c) Đúng
d) Sai
+) Ý a đúng theo lý thuyết
+) Xét ý c trước. Nếu
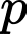 chia 3 dư 1 thì
chia 3 dư 1 thì  chia hết cho 3 (vô lý). Nếu
chia hết cho 3 (vô lý). Nếu 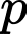 chia 3 dư 2 thì
chia 3 dư 2 thì  chia hết cho 3 (vô lý). Vậy
chia hết cho 3 (vô lý). Vậy 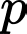 chia hết cho 3 nên
chia hết cho 3 nên 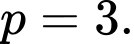 Chỉ có 3 số lẻ liên tiếp là 3 số nguyên tố là 3, 5, 7.
Chỉ có 3 số lẻ liên tiếp là 3 số nguyên tố là 3, 5, 7. +) Nếu xét 4 số lẻ liên tiếp, dễ thấy không tồn tại trường hợp chúng đều là số nguyên tố.
+) Có thể áp dụng định lý Chebyshev. Hoặc:
Vì
 nên
nên 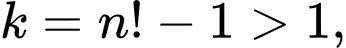 do đó
do đó 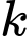 có ít nhất một ước số nguyên tố
có ít nhất một ước số nguyên tố 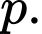
Ta chứng minh

Thật vậy, nếu
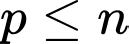 thì
thì 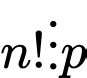
Mà
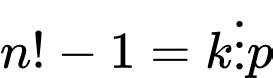 nên
nên 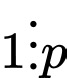 (Vô lý).
(Vô lý).
Câu 18 [582648]: Cho 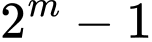 là một số nguyên tố. Mỗi phát biểu sau đúng hay sai?
là một số nguyên tố. Mỗi phát biểu sau đúng hay sai?
a)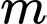 chia hết cho 2.
chia hết cho 2.
b)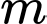 chia hết cho 5.
chia hết cho 5.
c)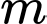 là một số nguyên tố.
là một số nguyên tố.
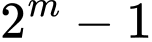 là một số nguyên tố. Mỗi phát biểu sau đúng hay sai?
là một số nguyên tố. Mỗi phát biểu sau đúng hay sai?a)
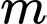 chia hết cho 2.
chia hết cho 2.b)
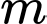 chia hết cho 5.
chia hết cho 5.c)
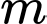 là một số nguyên tố.
là một số nguyên tố.
a) Sai
b) Sai
c) Đúng
Giả sử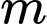 là hợp số thì
là hợp số thì 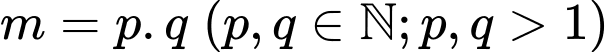
Khi đó
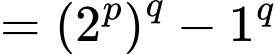
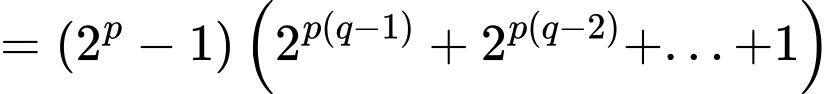
Vì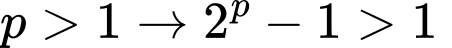 và
và 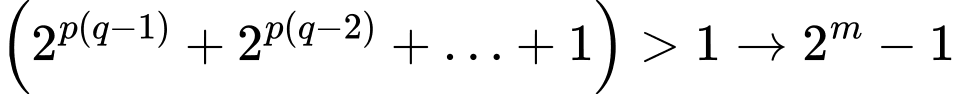 là hợp số
là hợp số
Vậy giả sử sai nên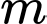 là một số nguyên tố.
là một số nguyên tố.
b) Sai
c) Đúng
Giả sử
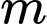 là hợp số thì
là hợp số thì 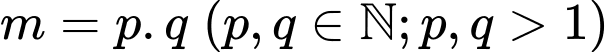
Khi đó

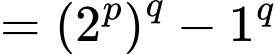
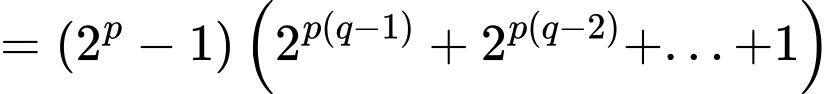
Vì
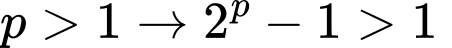 và
và 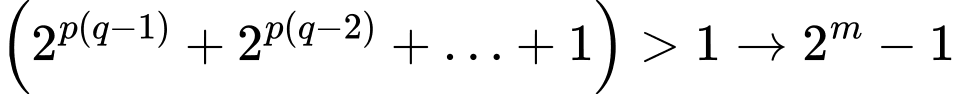 là hợp số
là hợp sốVậy giả sử sai nên
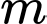 là một số nguyên tố.
là một số nguyên tố. Dạng câu hỏi: Câu trả lời ngắn
(Thí sinh trả lời đáp án câu 19. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 19 [582642]: Cho 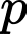 và
và 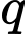 lần lượt là số nguyên tố lớn nhất và nhỏ nhất thỏa mãn
lần lượt là số nguyên tố lớn nhất và nhỏ nhất thỏa mãn 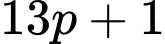 là lập phương của một số tự nhiên. Tổng
là lập phương của một số tự nhiên. Tổng  nhận giá trị là.............., hiệu
nhận giá trị là.............., hiệu 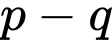 nhận giá trị là...............
nhận giá trị là...............
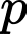 và
và 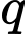 lần lượt là số nguyên tố lớn nhất và nhỏ nhất thỏa mãn
lần lượt là số nguyên tố lớn nhất và nhỏ nhất thỏa mãn 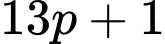 là lập phương của một số tự nhiên. Tổng
là lập phương của một số tự nhiên. Tổng  nhận giá trị là.............., hiệu
nhận giá trị là.............., hiệu 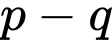 nhận giá trị là...............
nhận giá trị là...............
Xét 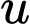 là số nguyên tố:
là số nguyên tố: 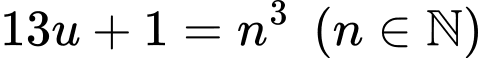
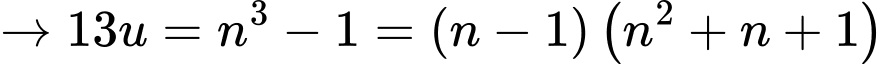
Dễ thấy
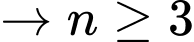 nên
nên 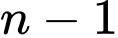 và
và 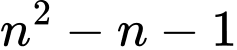 đều lớn hơn
đều lớn hơn 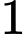
Mặt khác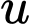 và
và  đều là các số nguyên tố nên có 2 trường hợp:
đều là các số nguyên tố nên có 2 trường hợp:
+)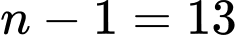
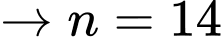
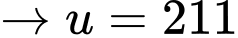 là một số nguyên tố.
là một số nguyên tố.
+)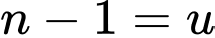 thì
thì 
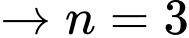
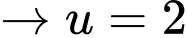 là một số nguyên tố.
là một số nguyên tố.
Theo giả thiết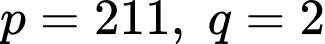
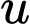 là số nguyên tố:
là số nguyên tố: 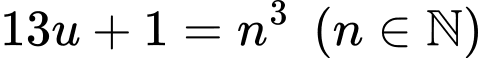
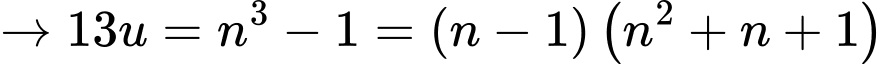
Dễ thấy

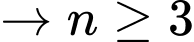 nên
nên 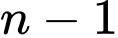 và
và 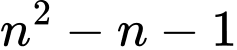 đều lớn hơn
đều lớn hơn 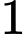
Mặt khác
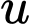 và
và  đều là các số nguyên tố nên có 2 trường hợp:
đều là các số nguyên tố nên có 2 trường hợp:+)
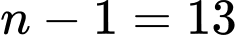
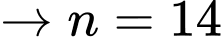
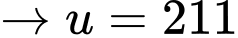 là một số nguyên tố.
là một số nguyên tố.+)
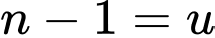 thì
thì 
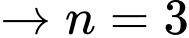
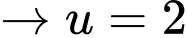 là một số nguyên tố.
là một số nguyên tố.Theo giả thiết
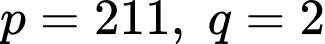
Dạng câu hỏi: Câu hỏi kéo thả
Câu 20 [582644]: Kéo số ở các ô vuông thả vào vị trí thích hợp?

Có ............ bộ 3 số nguyên tố sao cho tích của chúng gấp 5 lần tổng của chúng. Giả sử bộ 3 số nguyên tố (a, b, c) là bộ ba có tổng các số nguyên tố trong bộ là nhỏ nhất. Giá trị nhỏ nhất trong 3 số a, b, c là..........., tổng của bộ số này là...........

Có ............ bộ 3 số nguyên tố sao cho tích của chúng gấp 5 lần tổng của chúng. Giả sử bộ 3 số nguyên tố (a, b, c) là bộ ba có tổng các số nguyên tố trong bộ là nhỏ nhất. Giá trị nhỏ nhất trong 3 số a, b, c là..........., tổng của bộ số này là...........
Có 1 bộ 3 số nguyên tố sao cho tích của chúng gấp 5 lần tổng của chúng. Giả sử bộ 3 số nguyên tố (a, b, c) là bộ ba có tổng các số nguyên tố trong bộ là nhỏ nhất. Giá trị nhỏ nhất trong 3 số a, b, c là 2, tổng của bộ số này là 14
Giả sử bộ 3 số cần tìm là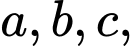 ta có
ta có 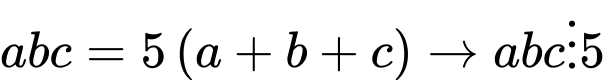
Không mất tổng quát giả sử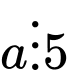 nên
nên 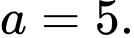
Khi đó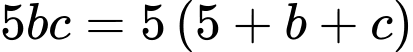
Nên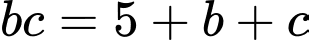
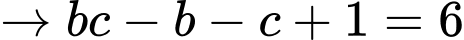
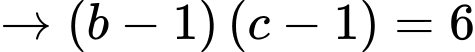
+)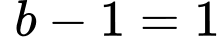 và
và 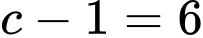 suy ra
suy ra 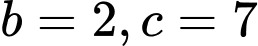
+)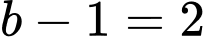 và
và 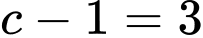 suy ra
suy ra 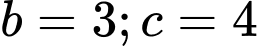 (không phải số chính phương)
(không phải số chính phương)
+) 2 trường hợp còn lại là đổi vai trò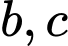
Tóm lại chỉ có 1 bộ số duy nhất thỏa mãn là (2; 5; 7)
Giả sử bộ 3 số cần tìm là
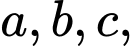 ta có
ta có 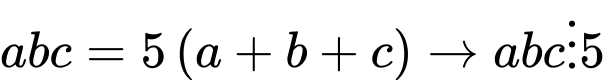
Không mất tổng quát giả sử
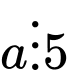 nên
nên 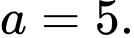
Khi đó
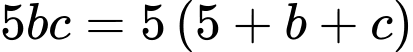
Nên
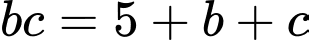
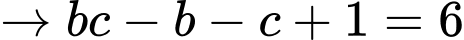
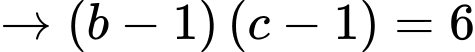
+)
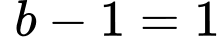 và
và 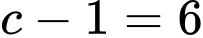 suy ra
suy ra 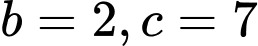
+)
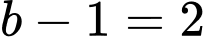 và
và 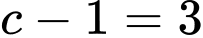 suy ra
suy ra 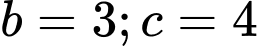 (không phải số chính phương)
(không phải số chính phương)+) 2 trường hợp còn lại là đổi vai trò
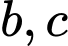
Tóm lại chỉ có 1 bộ số duy nhất thỏa mãn là (2; 5; 7)