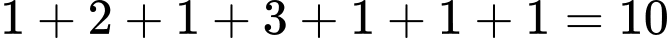Dạng câu hỏi: Câu trắc nghiệm nhiều phương án chọn.
(Thí sinh trả lời từ câu 1 đến câu 10. Mỗi câu hỏi thí sinh chỉ chọn một phương án
đúng nhất)
đúng nhất)
Câu 1 [582525]: Cho 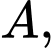
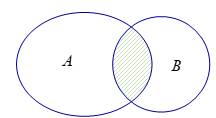
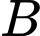 là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?
là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?
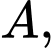
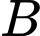 là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?
là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?
A, 

B, 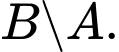
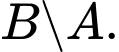
C, 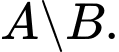
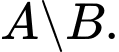
D, 

Theo biểu đồ Ven thì phần gạch sọc trong hình vẽ là tập hợp  . Đáp án: D
. Đáp án: D
 . Đáp án: D
. Đáp án: D
Câu 2 [582526]: Cho hai tập hợp 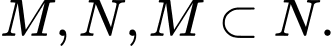 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
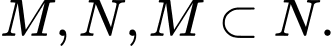 Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng? A, 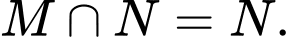
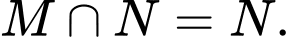
B, 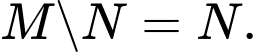
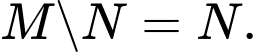
C, 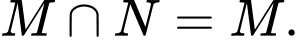
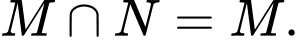
D, 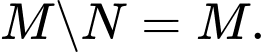
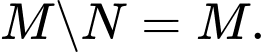
Theo giả thiết ta có  Ta có sơ đồ Ven
Ta có sơ đồ Ven
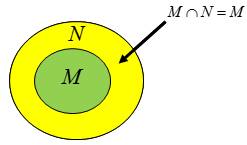 Đáp án: C
Đáp án: C
 Ta có sơ đồ Ven
Ta có sơ đồ Ven Đáp án: C
Đáp án: C
Câu 3 [582527]: Cho các tập hợp 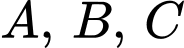 được minh họa bằng biểu đồ Ven như hình vẽ.
được minh họa bằng biểu đồ Ven như hình vẽ.
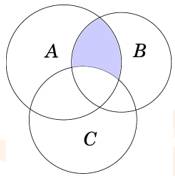
Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
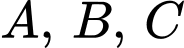 được minh họa bằng biểu đồ Ven như hình vẽ.
được minh họa bằng biểu đồ Ven như hình vẽ. 
Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
A, 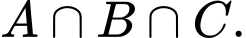
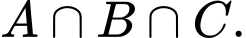
B, 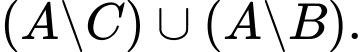
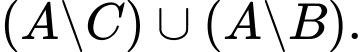
C, 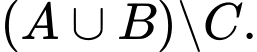
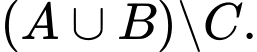
D, 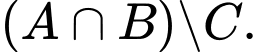
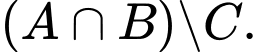
Phần tô xám trong hình là biểu diễn tập hợp các điểm vừa thuộc 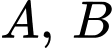 mà không thuộc
mà không thuộc  Chính là tập
Chính là tập 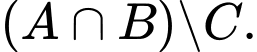 Đáp án: D
Đáp án: D
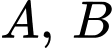 mà không thuộc
mà không thuộc  Chính là tập
Chính là tập 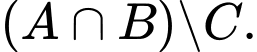 Đáp án: D
Đáp án: D
Câu 4 [582528]: Lớp 10A có 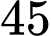 học sinh, trong đó có
học sinh, trong đó có  học sinh được xếp loại học lực giỏi,
học sinh được xếp loại học lực giỏi, 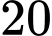 học sinh được xếp loại hạnh kiểm tốt,
học sinh được xếp loại hạnh kiểm tốt,  em vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt?
em vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt?
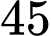 học sinh, trong đó có
học sinh, trong đó có  học sinh được xếp loại học lực giỏi,
học sinh được xếp loại học lực giỏi, 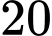 học sinh được xếp loại hạnh kiểm tốt,
học sinh được xếp loại hạnh kiểm tốt,  em vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt?
em vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt? A, 25.
B, 20.
C, 15.
D, 10.
Gọi 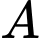 là tập hợp học sinh được xếp loại học lực giỏi.
là tập hợp học sinh được xếp loại học lực giỏi.
Gọi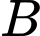 là tập hợp học sinh được xếp loại hạnh kiểm tốt.
là tập hợp học sinh được xếp loại hạnh kiểm tốt.
Khi đó là tập hợp học sinh vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt.
là tập hợp học sinh vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt.
 là tập hợp học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt.
là tập hợp học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt.
Ta có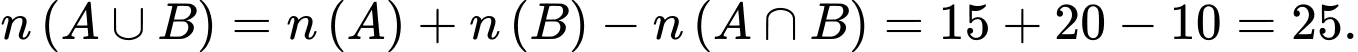 Đáp án: A
Đáp án: A
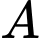 là tập hợp học sinh được xếp loại học lực giỏi.
là tập hợp học sinh được xếp loại học lực giỏi.Gọi
 là tập hợp học sinh được xếp loại hạnh kiểm tốt.
là tập hợp học sinh được xếp loại hạnh kiểm tốt.Khi đó
 là tập hợp học sinh vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt.
là tập hợp học sinh vừa được xếp loại học lực giỏi, vừa có hạnh kiểm tốt. là tập hợp học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt.
là tập hợp học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt.Ta có
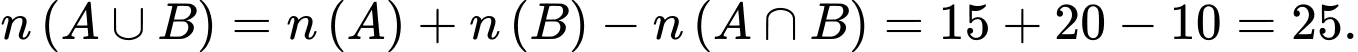 Đáp án: A
Đáp án: A
Câu 5 [582529]: Lớp 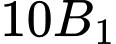 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Vậy số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là
có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Vậy số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là
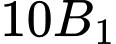 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Vậy số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là
có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Vậy số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là A, 7.
B, 6.
C, 9.
D, 10.
Ta thực hiện biểu đồ Ven như hình bên.
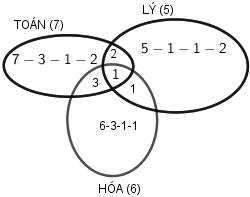
Số học sinh chỉ giỏi môn Toán: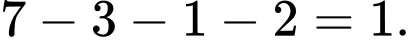
Số học sinh chỉ giỏi môn Lý: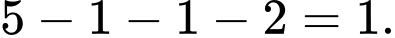
Số học sinh chỉ giỏi môn Hóa: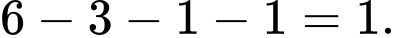
Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là: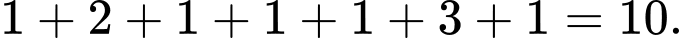 Đáp án: D
Đáp án: D

Số học sinh chỉ giỏi môn Toán:
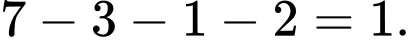
Số học sinh chỉ giỏi môn Lý:
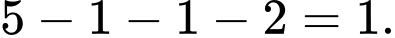
Số học sinh chỉ giỏi môn Hóa:
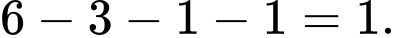
Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là:
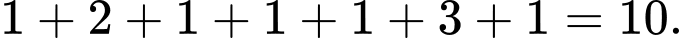 Đáp án: D
Đáp án: D
Câu 6 [582530]: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn, 6 học sinh không chơi môn nào. Tìm số học sinh chỉ chơi một môn thể thao.
A, 23.
B, 15.
C, 20.
D, 10.
Gọi 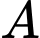 là tập hợp các học sinh chơi bóng đá,
là tập hợp các học sinh chơi bóng đá, 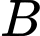 là tập hợp các học sinh chơi bóng bàn,
là tập hợp các học sinh chơi bóng bàn,
 là tập hợp các học sinh không chơi môn thể thao nào.
là tập hợp các học sinh không chơi môn thể thao nào.
Ta có: : là số học sinh chơi bóng đá;
: là số học sinh chơi bóng đá;  : là số học sinh chơi bóng bàn;
: là số học sinh chơi bóng bàn;  : là số học sinh không chơi môn thể thao nào.
: là số học sinh không chơi môn thể thao nào.
Khi đó số học sinh chỉ chơi một môn thể thao là: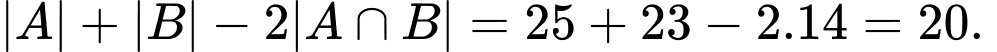 Đáp án: C
Đáp án: C
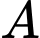 là tập hợp các học sinh chơi bóng đá,
là tập hợp các học sinh chơi bóng đá, 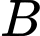 là tập hợp các học sinh chơi bóng bàn,
là tập hợp các học sinh chơi bóng bàn, là tập hợp các học sinh không chơi môn thể thao nào.
là tập hợp các học sinh không chơi môn thể thao nào.Ta có:
 : là số học sinh chơi bóng đá;
: là số học sinh chơi bóng đá;  : là số học sinh chơi bóng bàn;
: là số học sinh chơi bóng bàn;  : là số học sinh không chơi môn thể thao nào.
: là số học sinh không chơi môn thể thao nào.Khi đó số học sinh chỉ chơi một môn thể thao là:
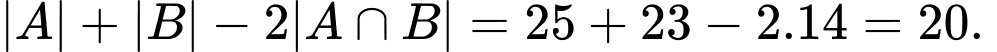 Đáp án: C
Đáp án: C
Câu 7 [582531]: Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu 30 em biết chơi cầu lông, 15 em biết chơi cả hai . Hỏi lớp 10A1 sĩ số lớp là bao nhiêu?
A, 40.
B, 30.
C, 20.
D, 35.
Dựa vào biểu đồ ven ta suy ra số học sinh chỉ biết đá cầu là 
Số học sinh chỉ biết đánh cầu lông là
Do đó ta có sĩ số học sinh của lớp 10A1 là
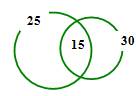 Đáp án: A
Đáp án: A

Số học sinh chỉ biết đánh cầu lông là

Do đó ta có sĩ số học sinh của lớp 10A1 là

 Đáp án: A
Đáp án: A
Câu 8 [582532]: Bạn A Súa thống kê số ngày có mưa, có sương mù ở bản mình trong tháng 3 vào một thời điểm nhất định và được kết quả như sau: 14 ngày có mưa, 15 ngày có sương mù, trong đó 10 ngày có cả mưa và sương mù. Hỏi trong tháng 3 đó có bao nhiêu ngày không có mưa và không có sương mù?
A, 12.
B, 10.
C, 19.
D, 15.
Gọi 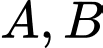 lần lượt là tập hợp các ngày có mưa, có sương mù. Khi đó,
lần lượt là tập hợp các ngày có mưa, có sương mù. Khi đó,  là tập hợp các ngày có cả mưa và sương mù,
là tập hợp các ngày có cả mưa và sương mù,  là tập hợp các ngày hoặc có mưa hoặc có sương mù.
là tập hợp các ngày hoặc có mưa hoặc có sương mù.
Ta có: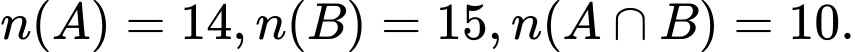
Số ngày hoặc có mưa hoặc có sương mù là:
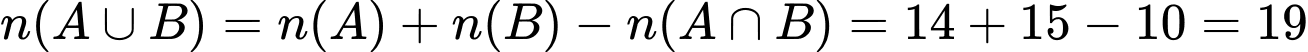 (ngày).
(ngày).
Tháng 3 có 31 ngày nên số ngày không có mưa và không có sương mù trong tháng 3 đó là: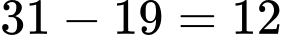 (ngày). Đáp án: A
(ngày). Đáp án: A
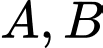 lần lượt là tập hợp các ngày có mưa, có sương mù. Khi đó,
lần lượt là tập hợp các ngày có mưa, có sương mù. Khi đó,  là tập hợp các ngày có cả mưa và sương mù,
là tập hợp các ngày có cả mưa và sương mù,  là tập hợp các ngày hoặc có mưa hoặc có sương mù.
là tập hợp các ngày hoặc có mưa hoặc có sương mù.Ta có:
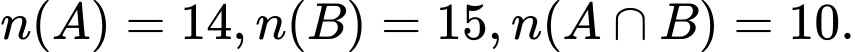
Số ngày hoặc có mưa hoặc có sương mù là:
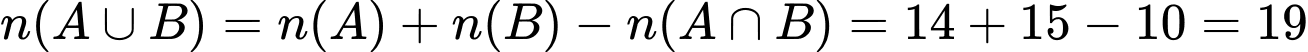 (ngày).
(ngày).Tháng 3 có 31 ngày nên số ngày không có mưa và không có sương mù trong tháng 3 đó là:
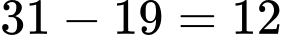 (ngày). Đáp án: A
(ngày). Đáp án: A
Câu 9 [582533]: Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu có thể sử dụng ít nhất một trong ba thứ tiếng: Nga, Trung Quốc và Anh. Biết rằng có 30 đại biểu chỉ nói được tiếng Anh, 40 đại biểu nói được tiếng Nga, 45 đại biểu nói được tiếng Trung Quốc và 10 đại biểu chỉ nói được hai thứ tiếng Nga và Trung Quốc. Hỏi có bao nhiêu đại biểu nói được cả ba thứ tiếng?
A, 5.
B, 7.
C, 15
D, 10.
Số đại biểu nói được tiếng Nga hoặc tiếng Trung Quốc là:
100 – 30 = 70 (đại biểu)
Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Trung Quốc là:
70 – 45 = 25 (đại biểu)
Số đại biểu nói được tiếng Trung Quốc nhưng không nói được tiếng Nga là:
70 – 40 = 30 (đại biểu)
Số đại biểu nói được tiếng Nga và tiếng Trung Quốc là:
70 – (25 + 30) = 15 (đại biểu)
Số đại biểu nói được cả ba thứ tiếng là:
15 – 10 = 5 (đại biểu) Đáp án: A
100 – 30 = 70 (đại biểu)
Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Trung Quốc là:
70 – 45 = 25 (đại biểu)
Số đại biểu nói được tiếng Trung Quốc nhưng không nói được tiếng Nga là:
70 – 40 = 30 (đại biểu)
Số đại biểu nói được tiếng Nga và tiếng Trung Quốc là:
70 – (25 + 30) = 15 (đại biểu)
Số đại biểu nói được cả ba thứ tiếng là:
15 – 10 = 5 (đại biểu) Đáp án: A
Câu 10 [582534]: Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết rằng có 4 học sinh của nhóm không tham gia tiết mục nào.
A, 5.
B, 6.
C, 7.
D, 8.
Kí hiệu 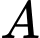 là tập hợp học sinh tham gia tiết mục múa,
là tập hợp học sinh tham gia tiết mục múa, 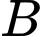 là tập hợp học sinh tham gia tiết mục hát,
là tập hợp học sinh tham gia tiết mục hát, 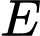 là tập hợp nhóm học sinh. Ta có thể biểu diễn ba tập hợp đó bằng biểu đồ Ven (Hình 2).
là tập hợp nhóm học sinh. Ta có thể biểu diễn ba tập hợp đó bằng biểu đồ Ven (Hình 2).
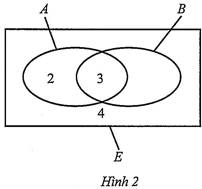
Khi đó, là tập hợp học sinh tham gia cả hai tiêt mục.
là tập hợp học sinh tham gia cả hai tiêt mục.
Số phần tử của tậ̀p hợp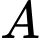 là 5, số phần tử của tập hợp
là 5, số phần tử của tập hợp  là 3, số phần tử của tập hợp
là 3, số phần tử của tập hợp 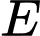 là 12.
là 12.
Số học sinh tham gia ít nhất một trong hai tiết mục là: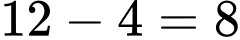 (học sinh).
(học sinh).
Số học sinh tham gia tiết mục hát mà không tham gia tiết mục múa là: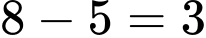 (học sinh).
(học sinh).
Số học sinh tham gia tiết mục hát là: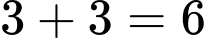 (học sinh). Đáp án: B
(học sinh). Đáp án: B
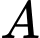 là tập hợp học sinh tham gia tiết mục múa,
là tập hợp học sinh tham gia tiết mục múa, 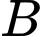 là tập hợp học sinh tham gia tiết mục hát,
là tập hợp học sinh tham gia tiết mục hát, 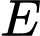 là tập hợp nhóm học sinh. Ta có thể biểu diễn ba tập hợp đó bằng biểu đồ Ven (Hình 2).
là tập hợp nhóm học sinh. Ta có thể biểu diễn ba tập hợp đó bằng biểu đồ Ven (Hình 2). 
Khi đó,
 là tập hợp học sinh tham gia cả hai tiêt mục.
là tập hợp học sinh tham gia cả hai tiêt mục. Số phần tử của tậ̀p hợp
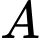 là 5, số phần tử của tập hợp
là 5, số phần tử của tập hợp  là 3, số phần tử của tập hợp
là 3, số phần tử của tập hợp 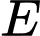 là 12.
là 12.Số học sinh tham gia ít nhất một trong hai tiết mục là:
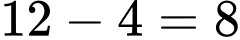 (học sinh).
(học sinh). Số học sinh tham gia tiết mục hát mà không tham gia tiết mục múa là:
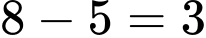 (học sinh).
(học sinh). Số học sinh tham gia tiết mục hát là:
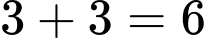 (học sinh). Đáp án: B
(học sinh). Đáp án: B Dạng câu hỏi: Câu trắc nghiệm đúng sai
(Thí sinh trả lời từ câu 11, 12. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai)
Câu 11 [582535]: Cho hai tập hợp 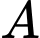 và
và 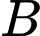 biết
biết 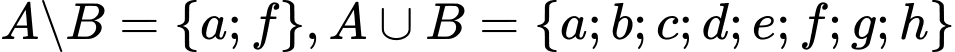 ,
,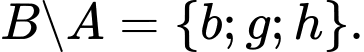 Khi đó
Khi đó
a)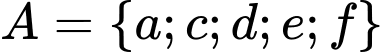
b)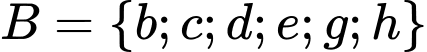
c)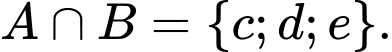
d)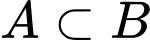
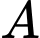 và
và 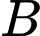 biết
biết 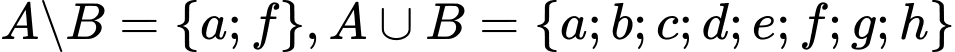 ,
,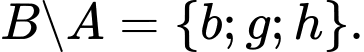 Khi đó
Khi đóa)
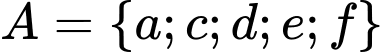
b)
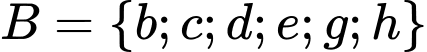
c)
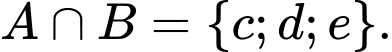
d)
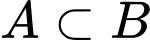
a) Đúng b) Đúng c) Đúng d) Sai
Thực hiện biểu đồ Ven như hình bên.
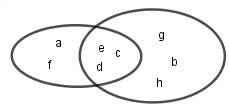
Ta có: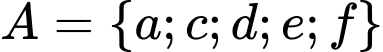 ,
,
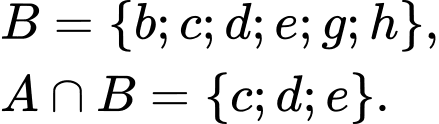
Thực hiện biểu đồ Ven như hình bên.

Ta có:
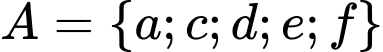 ,
,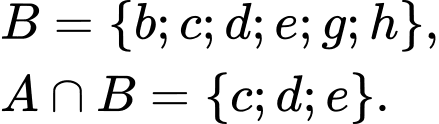
Câu 12 [582536]: Lớp 10C6 có 18 học sinh tham gia câu lạc bộ bóng đá và 15 học sinh tham gia câu lạc bộ bóng rổ. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên. Khi đó:
a) Có 8 học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ?
b) Có 23 học sinh tham gia ít nhất một trong hai câu lạc bộ trên?
c) Biết lớp 10C6 có 45 học sinh. Có 25 học sinh không tham gia câu lạc bộ bóng đá?
d) Biết lớp 10C6 có 45 học sinh. Có 24 học sinh không tham gia cả hai câu lạc bộ?
a) Có 8 học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ?
b) Có 23 học sinh tham gia ít nhất một trong hai câu lạc bộ trên?
c) Biết lớp 10C6 có 45 học sinh. Có 25 học sinh không tham gia câu lạc bộ bóng đá?
d) Biết lớp 10C6 có 45 học sinh. Có 24 học sinh không tham gia cả hai câu lạc bộ?
a) Đúng
b) Đúng
c) Sai
d) Sai
Kí hiệu:
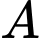 là tập hợp học sinh tham gia câu lạc bộ bóng đá.
là tập hợp học sinh tham gia câu lạc bộ bóng đá.
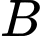 là tập hợp học sinh tham gia câu lạc bộ bóng rổ.
là tập hợp học sinh tham gia câu lạc bộ bóng rổ.
 là tập hợp học sinh của lớp 10C6. Ta có thể biểu diễn ba tập hợp trên bằng biểu đồ Ven như hình sau:
là tập hợp học sinh của lớp 10C6. Ta có thể biểu diễn ba tập hợp trên bằng biểu đồ Ven như hình sau:
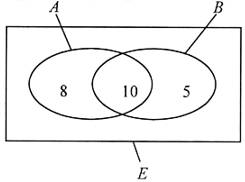
Khi đó, là tập hợp học sinh tham gia cả hai câu lạc bộ trên. Số phần tử của
là tập hợp học sinh tham gia cả hai câu lạc bộ trên. Số phần tử của  là 18, số phần tử của
là 18, số phần tử của  là 15, số phần tử của tập hợp
là 15, số phần tử của tập hợp  là 10.
là 10.
a) Tập hợp các học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ là tập hợp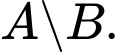 Số phần tử của
Số phần tử của 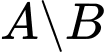 chính là số phần tử của
chính là số phần tử của 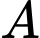 trừ đi số phần tử của
trừ đi số phần tử của 
Vậy số học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ là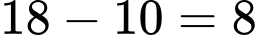 (học sinh).
(học sinh).
b) Tập hợp các học sinh tham gia ít nhất một trong hai câu lạc bộ trên chính là tập hợp Do khi đếm số học sinh tham gia câu lạc bộ bóng đá là 18, số học sinh tham gia câu lạc bộ bóng rổ là 15 thì số học sinh tham gia cả hai câu lạc bộ là 10 được tính hai lần.
Do khi đếm số học sinh tham gia câu lạc bộ bóng đá là 18, số học sinh tham gia câu lạc bộ bóng rổ là 15 thì số học sinh tham gia cả hai câu lạc bộ là 10 được tính hai lần.
Vậy số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là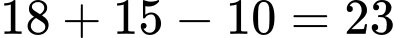 (học sinh).
(học sinh).
c) Số phần tử của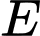 là 45. Tập hợp các học sinh không tham gia câu lạc bộ bóng đá là phần bù của
là 45. Tập hợp các học sinh không tham gia câu lạc bộ bóng đá là phần bù của 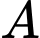 trong
trong 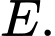
Vậy số học sinh không tham gia câu lạc bộ bóng đá là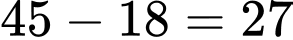 (học sinh).
(học sinh).
d) Tập hợp các học sinh không tham gia cả hai câu lạc bộ là phần bù của trong
trong 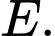
Vậy số học sinh không tham gia cả hai câu lạc bộ là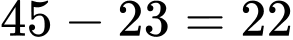 (học sinh).
(học sinh).
b) Đúng
c) Sai
d) Sai
Kí hiệu:
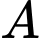 là tập hợp học sinh tham gia câu lạc bộ bóng đá.
là tập hợp học sinh tham gia câu lạc bộ bóng đá.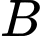 là tập hợp học sinh tham gia câu lạc bộ bóng rổ.
là tập hợp học sinh tham gia câu lạc bộ bóng rổ.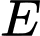 là tập hợp học sinh của lớp 10C6. Ta có thể biểu diễn ba tập hợp trên bằng biểu đồ Ven như hình sau:
là tập hợp học sinh của lớp 10C6. Ta có thể biểu diễn ba tập hợp trên bằng biểu đồ Ven như hình sau:
Khi đó,
 là tập hợp học sinh tham gia cả hai câu lạc bộ trên. Số phần tử của
là tập hợp học sinh tham gia cả hai câu lạc bộ trên. Số phần tử của 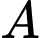 là 18, số phần tử của
là 18, số phần tử của 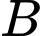 là 15, số phần tử của tập hợp
là 15, số phần tử của tập hợp  là 10.
là 10.a) Tập hợp các học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ là tập hợp
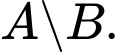 Số phần tử của
Số phần tử của 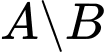 chính là số phần tử của
chính là số phần tử của 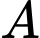 trừ đi số phần tử của
trừ đi số phần tử của 
Vậy số học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ là
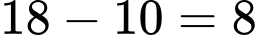 (học sinh).
(học sinh).b) Tập hợp các học sinh tham gia ít nhất một trong hai câu lạc bộ trên chính là tập hợp
 Do khi đếm số học sinh tham gia câu lạc bộ bóng đá là 18, số học sinh tham gia câu lạc bộ bóng rổ là 15 thì số học sinh tham gia cả hai câu lạc bộ là 10 được tính hai lần.
Do khi đếm số học sinh tham gia câu lạc bộ bóng đá là 18, số học sinh tham gia câu lạc bộ bóng rổ là 15 thì số học sinh tham gia cả hai câu lạc bộ là 10 được tính hai lần. Vậy số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là
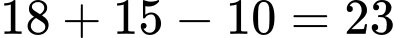 (học sinh).
(học sinh).c) Số phần tử của
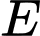 là 45. Tập hợp các học sinh không tham gia câu lạc bộ bóng đá là phần bù của
là 45. Tập hợp các học sinh không tham gia câu lạc bộ bóng đá là phần bù của 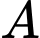 trong
trong 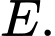
Vậy số học sinh không tham gia câu lạc bộ bóng đá là
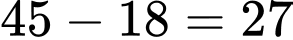 (học sinh).
(học sinh).d) Tập hợp các học sinh không tham gia cả hai câu lạc bộ là phần bù của
 trong
trong 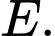
Vậy số học sinh không tham gia cả hai câu lạc bộ là
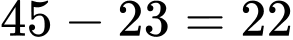 (học sinh).
(học sinh). Dạng câu hỏi: Câu trả lời ngắn
(Thí sinh trả lời đáp án từ câu 13 đến câu 15. Đáp án là số nguyên hoặc phân số tối giản nếu có)
Câu 13 [582537]: Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên.
Trả lời: 20
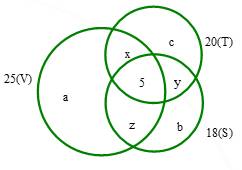
Gọi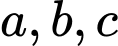 theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
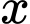 là số học sinh chỉ thích hai môn là Văn và Toán
là số học sinh chỉ thích hai môn là Văn và Toán
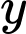 là số học sinh chỉ thích hai môn là Sử và Toán
là số học sinh chỉ thích hai môn là Sử và Toán
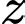 là số học sinh chỉ thích hai môn là Văn và Sử
là số học sinh chỉ thích hai môn là Văn và Sử
Ta có số em thích ít nhất một môn là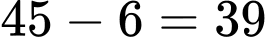
Dựa vào biểu đồ Ven ta có hệ phương trình
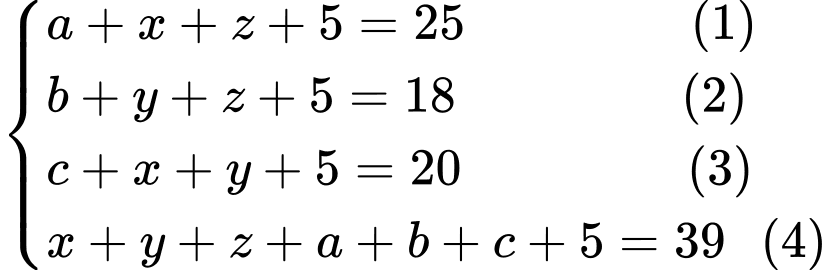
Cộng vế với vế (1), (2), (3) ta có
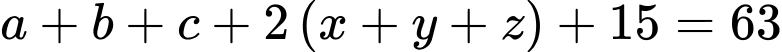 (5)
(5)
Từ (4) và (5) ta có

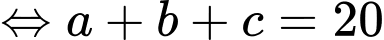
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.

Gọi
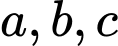 theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán; 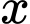 là số học sinh chỉ thích hai môn là Văn và Toán
là số học sinh chỉ thích hai môn là Văn và Toán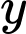 là số học sinh chỉ thích hai môn là Sử và Toán
là số học sinh chỉ thích hai môn là Sử và Toán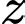 là số học sinh chỉ thích hai môn là Văn và Sử
là số học sinh chỉ thích hai môn là Văn và SửTa có số em thích ít nhất một môn là
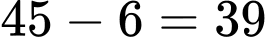
Dựa vào biểu đồ Ven ta có hệ phương trình
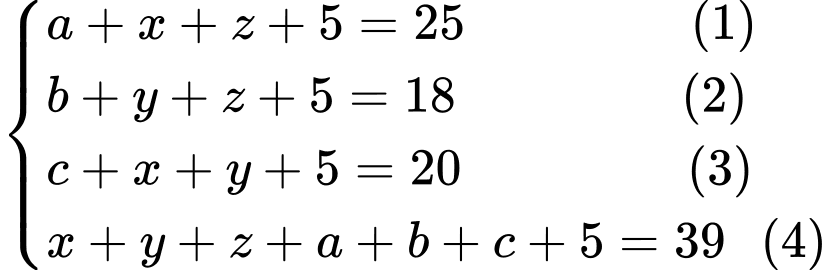
Cộng vế với vế (1), (2), (3) ta có
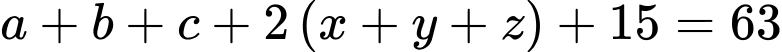 (5)
(5)Từ (4) và (5) ta có

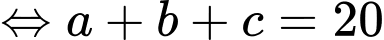
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
Câu 14 [582538]: Trong đột khảo sát nghề, giáo viên chủ nhiệm lớp 10D đưa ra ba nhóm ngành cho học sinh lựa chọn, đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có 6 học sinh chọn nhóm ngành Giáo dục, 9 học sinh chọn nhóm ngành Y tế, 10 học sinh chọn nhóm ngành Công nghệ thông tin, 22 học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có 3 học sinh chọn hai nhóm ngành Giáo dục và Y tế, 2 học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, 3 học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Hỏi có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết ló́p 10D có 40 học sinh?
Trả lời: 1
Gọi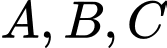 lần lượt là tập hợp học sinh chọn nhóm ngành Giáo dục, Y tế, Công nghệ thông tin. Khi đó,
lần lượt là tập hợp học sinh chọn nhóm ngành Giáo dục, Y tế, Công nghệ thông tin. Khi đó,
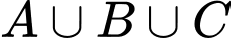 là tập hợp các học sinh chọn ít nhất một trong ba nhóm ngành trên.
là tập hợp các học sinh chọn ít nhất một trong ba nhóm ngành trên.
Do lớp 10D có 40 học sinh và 22 học sinh không chọn nhóm ngành trong ba nhóm ngành trên nên số học sinh chọn ít nhất một trong ba nhóm ngành trên là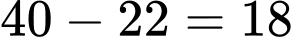
Ta có: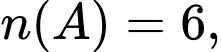
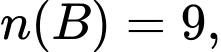
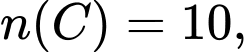

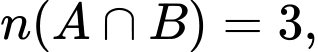
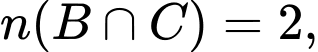
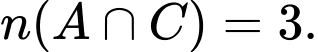
Áp dụng công thức:
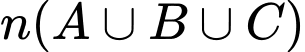
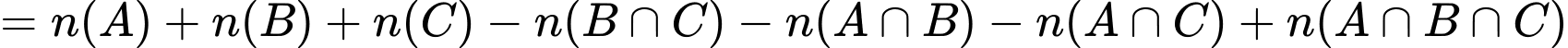
Ta có số học sinh chọn cả ba nhóm ngành nêu trên là:
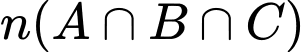
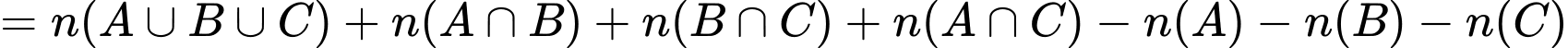
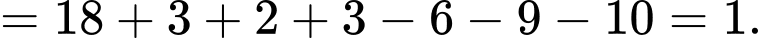
Gọi
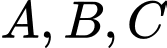 lần lượt là tập hợp học sinh chọn nhóm ngành Giáo dục, Y tế, Công nghệ thông tin. Khi đó,
lần lượt là tập hợp học sinh chọn nhóm ngành Giáo dục, Y tế, Công nghệ thông tin. Khi đó, 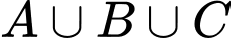 là tập hợp các học sinh chọn ít nhất một trong ba nhóm ngành trên.
là tập hợp các học sinh chọn ít nhất một trong ba nhóm ngành trên.Do lớp 10D có 40 học sinh và 22 học sinh không chọn nhóm ngành trong ba nhóm ngành trên nên số học sinh chọn ít nhất một trong ba nhóm ngành trên là
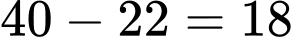
Ta có:
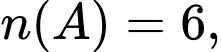
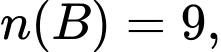
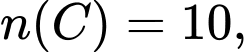

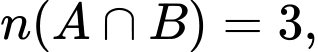
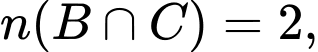
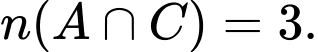
Áp dụng công thức:
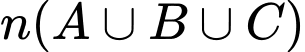
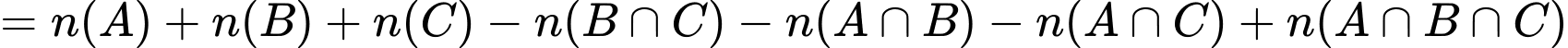
Ta có số học sinh chọn cả ba nhóm ngành nêu trên là:
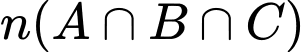
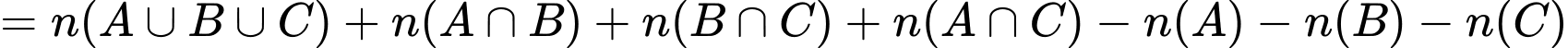
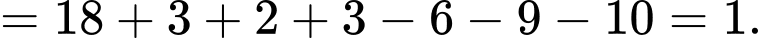
Câu 15 [582539]: Lớp 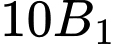 có
có 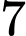 học sinh giỏi Toán,
học sinh giỏi Toán, 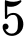 học sinh giỏi Lý,
học sinh giỏi Lý, 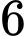 học sinh giỏi Hóa,
học sinh giỏi Hóa, 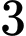 học sinh giỏi cả Toán và Lý,
học sinh giỏi cả Toán và Lý, 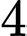 học sinh giỏi cả Toán và Hóa,
học sinh giỏi cả Toán và Hóa, 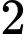 học sinh giỏi cả Lý và Hóa,
học sinh giỏi cả Lý và Hóa, 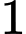 học sinh giỏi cả
học sinh giỏi cả 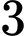 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp
môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp 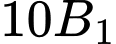 là:
là:
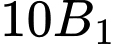 có
có 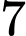 học sinh giỏi Toán,
học sinh giỏi Toán, 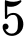 học sinh giỏi Lý,
học sinh giỏi Lý, 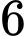 học sinh giỏi Hóa,
học sinh giỏi Hóa, 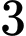 học sinh giỏi cả Toán và Lý,
học sinh giỏi cả Toán và Lý, 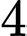 học sinh giỏi cả Toán và Hóa,
học sinh giỏi cả Toán và Hóa, 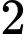 học sinh giỏi cả Lý và Hóa,
học sinh giỏi cả Lý và Hóa, 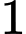 học sinh giỏi cả
học sinh giỏi cả 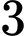 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp
môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp 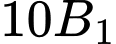 là:
là:
Trả lời: 10
Ta dùng biểu đồ Ven để giải:
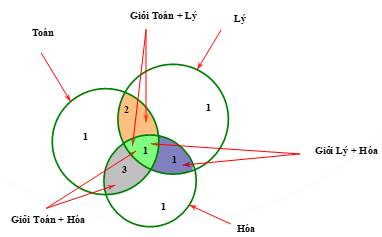
Nhìn vào biểu đồ, số học sinh giỏi ít nhất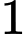 trong
trong 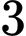 môn là:
môn là: 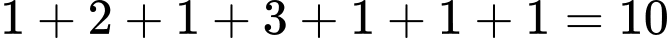
Ta dùng biểu đồ Ven để giải:

Nhìn vào biểu đồ, số học sinh giỏi ít nhất
 trong
trong  môn là:
môn là: