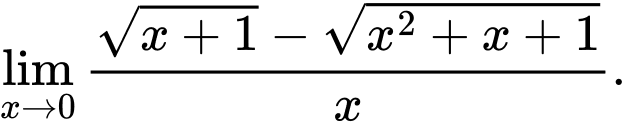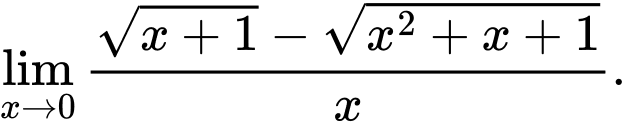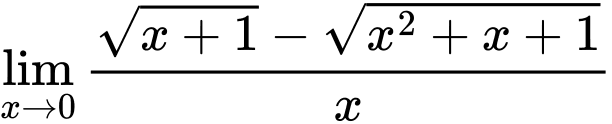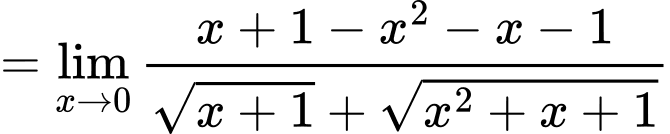Dạng toán: Giới hạn hữu tỉ
Câu 1 [582887]: Giá trị của 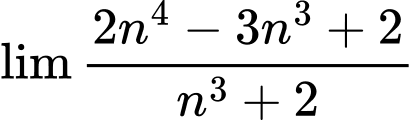 là
là
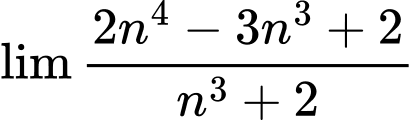 là
là A, 
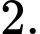
B, 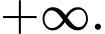
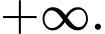
C, Không tồn tại.
D, 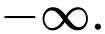
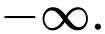
Chọn B
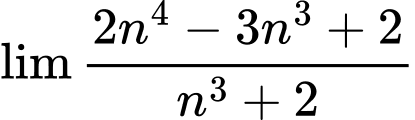
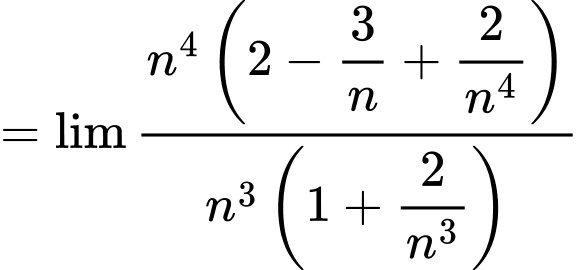
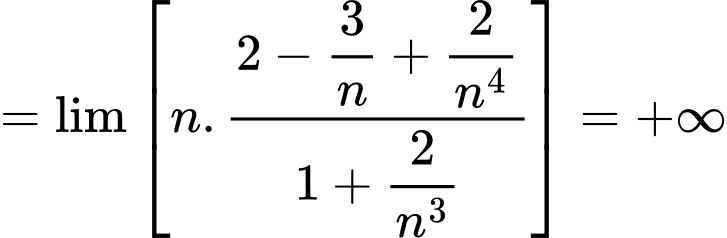
Vì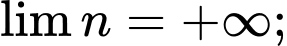
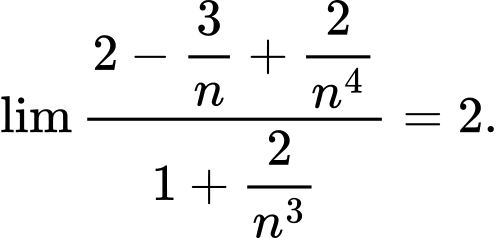 Đáp án: B
Đáp án: B
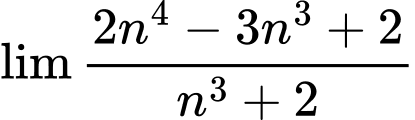
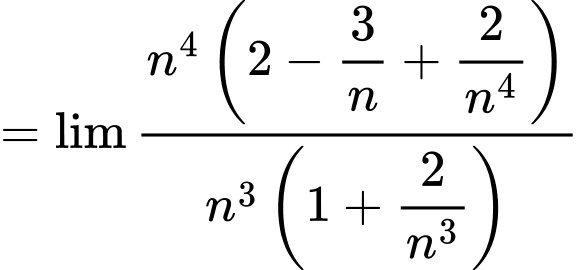
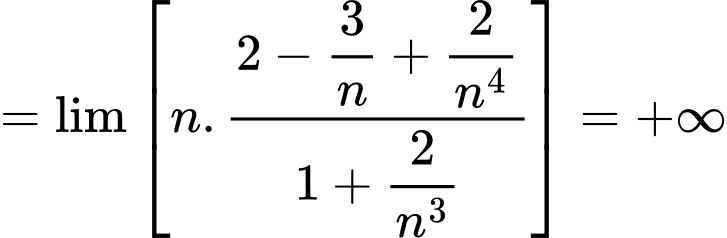
Vì
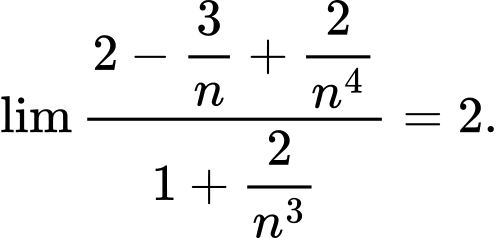 Đáp án: B
Đáp án: B
Câu 2 [582888]: Tính 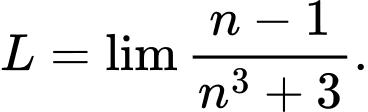
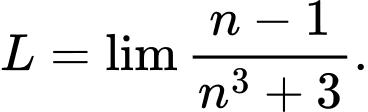
A, 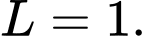
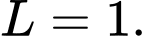
B, 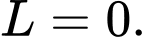
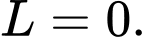
C, 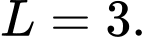
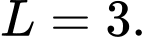
D, 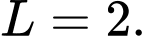
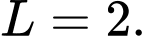
Chọn B
Ta có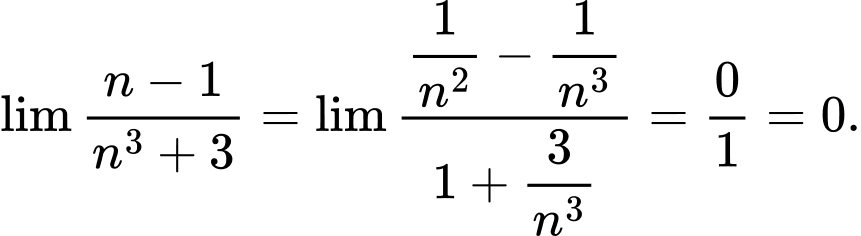 Đáp án: B
Đáp án: B
Ta có
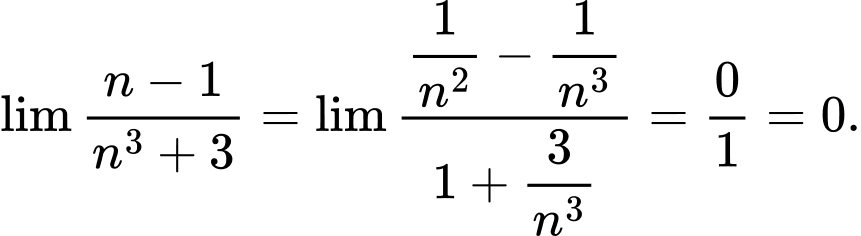 Đáp án: B
Đáp án: B
Câu 3 [582889]: Tính 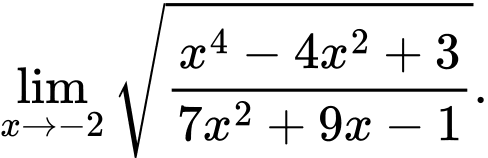
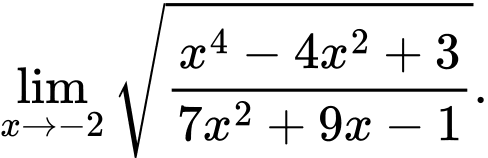
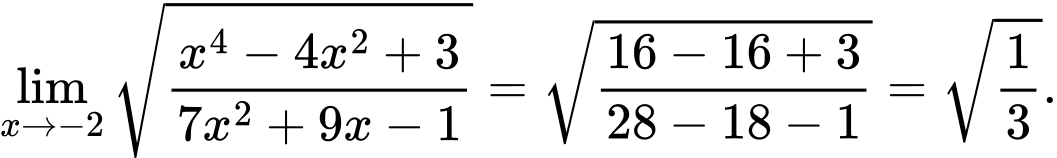
Dạng toán: Giới hạn của dãy số chứa hàm mũ
Câu 4 [582890]: Kết quả của giới hạn 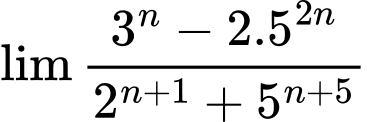 bằng:
bằng:
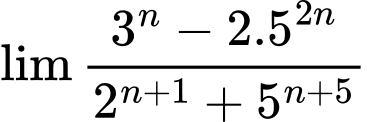 bằng:
bằng: A, 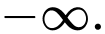
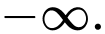
B, 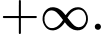
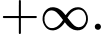
C, 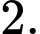
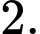
D, 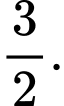
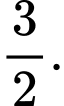
Chọn A
Ta có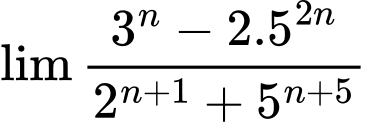
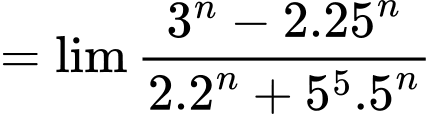
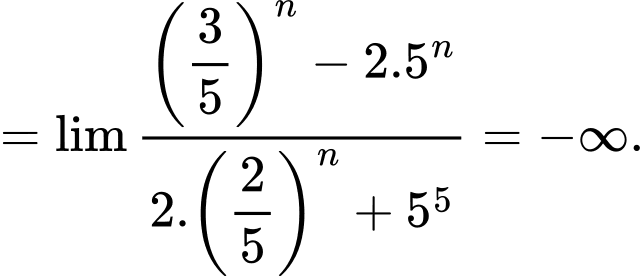 Đáp án: A
Đáp án: A
Ta có
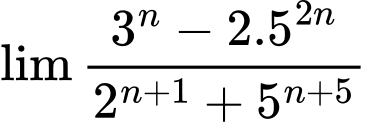
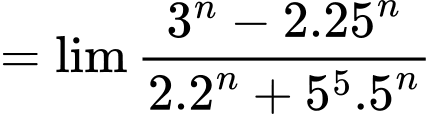
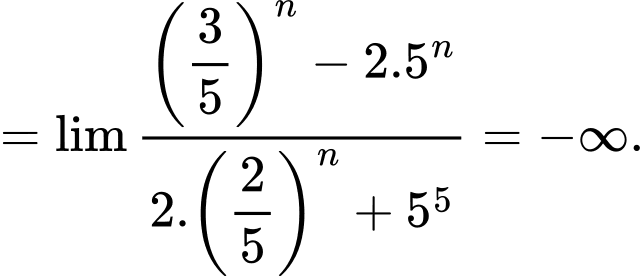 Đáp án: A
Đáp án: A
Câu 5 [582891]: Tính 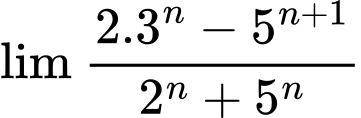 bằng:
bằng:
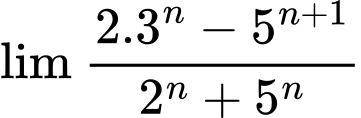 bằng:
bằng: A, 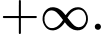
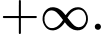
B, 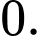
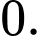
C, 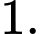
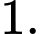
D, 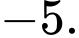
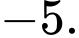
Chọn D
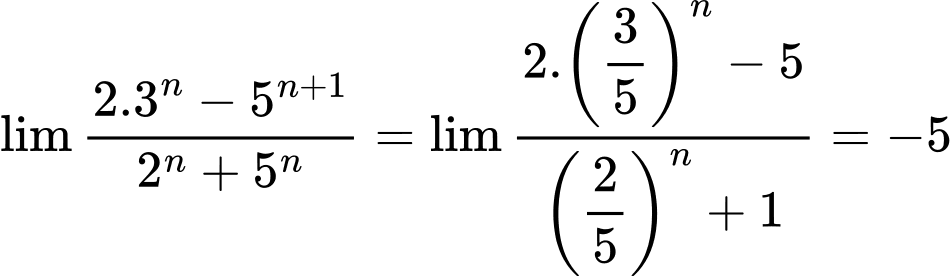
Theo nhận xét trên thì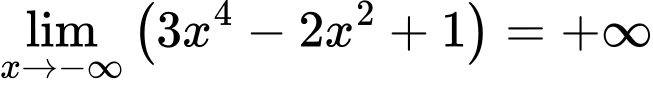 (
( chẵn và
chẵn và 
Thật vậy, ta có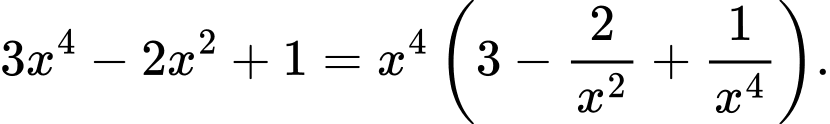 Đáp án: D
Đáp án: D
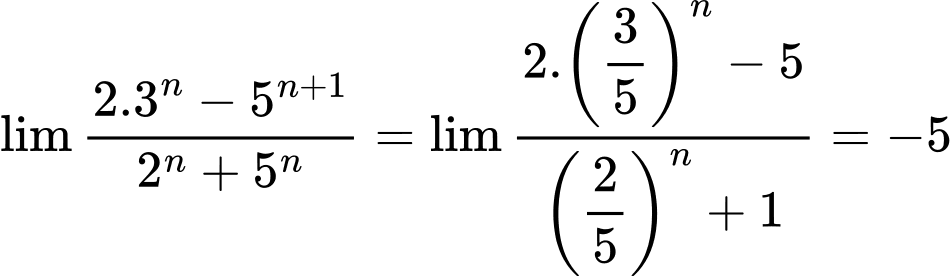
Theo nhận xét trên thì
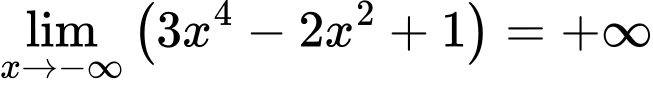 (
( chẵn và
chẵn và 
Thật vậy, ta có
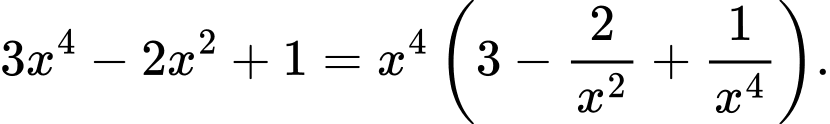 Đáp án: D
Đáp án: D
Câu 6 [582892]: Dãy số nào sau đây có giới hạn bằng 0?
A, 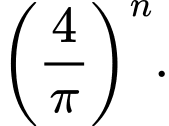
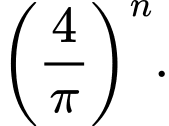
B, 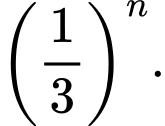
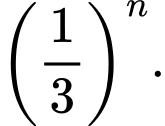
C, 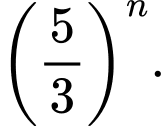
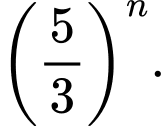
D, 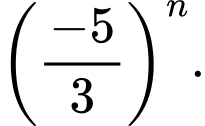
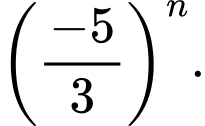
Chọn B
Ta có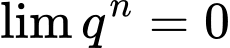 nếu
nếu 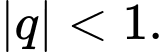
Mặt khác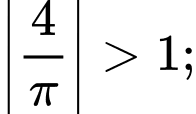

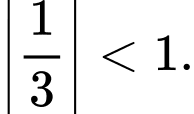
Vậy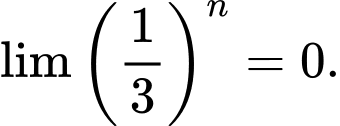 Đáp án: B
Đáp án: B
Ta có
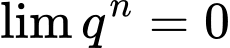 nếu
nếu 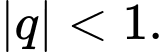
Mặt khác
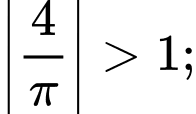

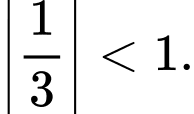
Vậy
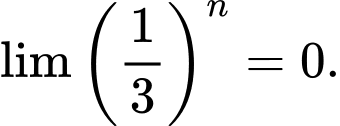 Đáp án: B
Đáp án: B Dạng toán: Tổng của cấp số nhân lùi vô hạn
Câu 7 [582893]: Cho 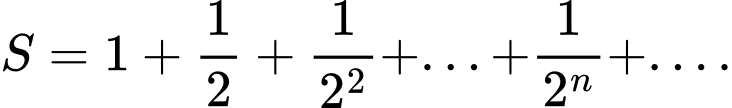 Chọn đáp án đúng.
Chọn đáp án đúng.
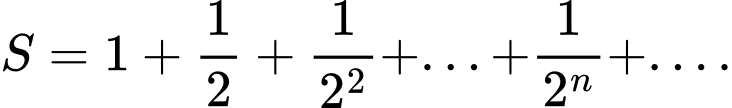 Chọn đáp án đúng.
Chọn đáp án đúng. A, 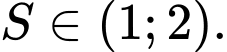
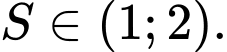
B, 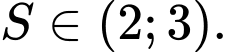
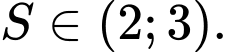
C, 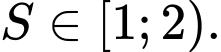
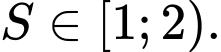
D, 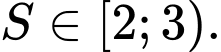
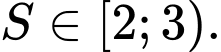
Chọn D.
Ta thấy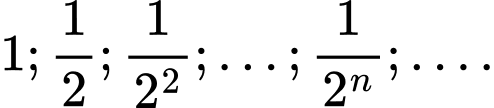 là một cấp số nhân lùi vô hạn với công bội
là một cấp số nhân lùi vô hạn với công bội 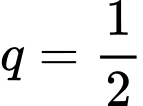 và số hạng đầu
và số hạng đầu 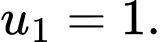
Do đó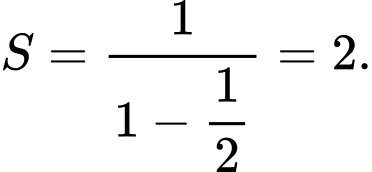
Vậy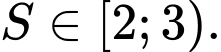 Đáp án: D
Đáp án: D
Ta thấy
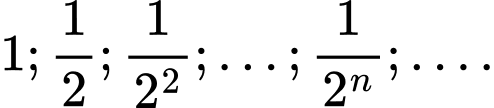 là một cấp số nhân lùi vô hạn với công bội
là một cấp số nhân lùi vô hạn với công bội 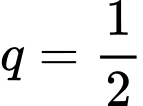 và số hạng đầu
và số hạng đầu 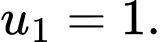
Do đó
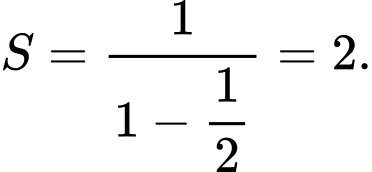
Vậy
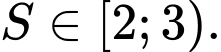 Đáp án: D
Đáp án: D
Câu 8 [582894]: Tìm giá trị đúng của 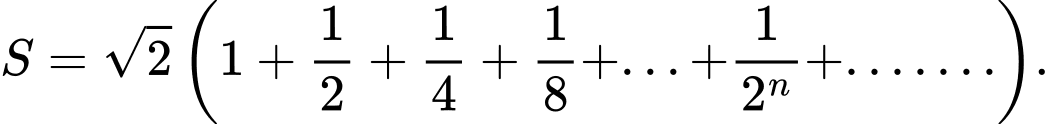
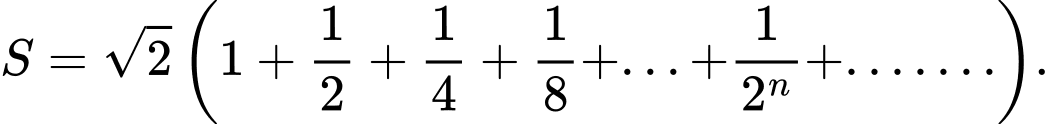
A, 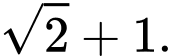
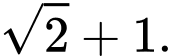
B, 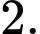
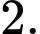
C, 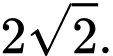
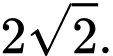
D, 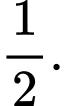
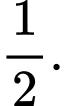
Chọn C
Ta có :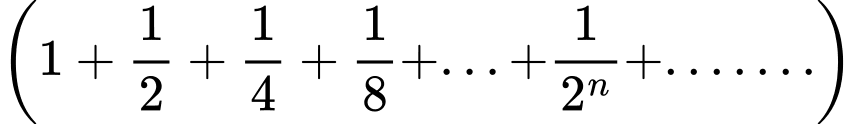 là tổng của cấp số nhân lùi vô hạn có
là tổng của cấp số nhân lùi vô hạn có 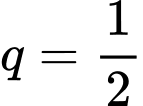 nên
nên
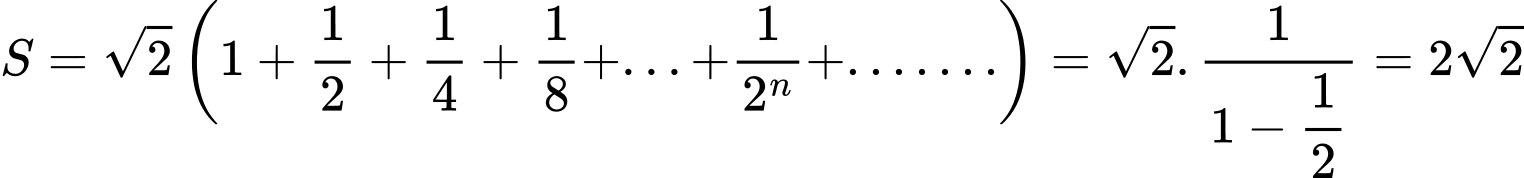 Đáp án: C
Đáp án: C
Ta có :
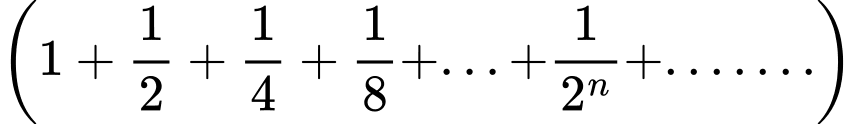 là tổng của cấp số nhân lùi vô hạn có
là tổng của cấp số nhân lùi vô hạn có 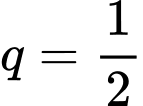 nên
nên 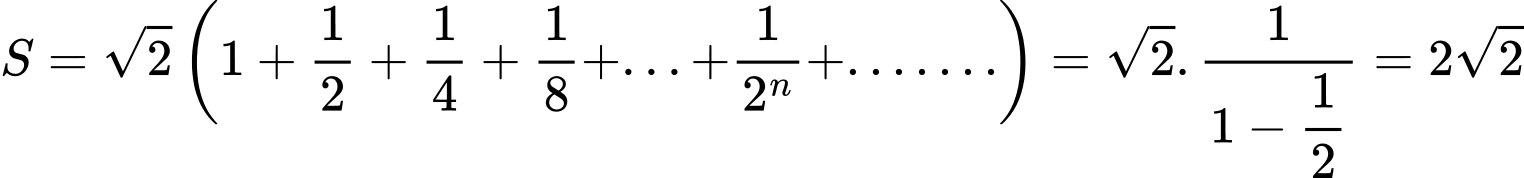 Đáp án: C
Đáp án: C
Câu 9 [582895]: Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Nó tô màu xám các hình vuông nhỏ được đánh số lần lượt là 1, 2, 3, 4, …n,… trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó.Giả sử quy trình tô màu của chuột Mickey có thể tiến ra vô hạn (như hình vẽ dưới đây). Tính tổng diện tích mà chuột Mickey phải tô màu.
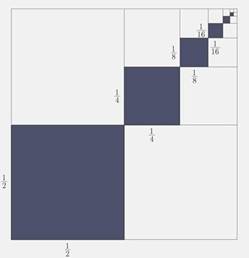

Ta có cạnh của hình vuông thứ nhất là 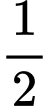 nên diện tích
nên diện tích 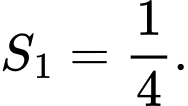
Cạnh hình vuông thứ hai là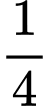 nên diện tích
nên diện tích 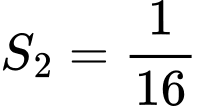 ,…
,…
Cứ tiếp tục như vậy thì ta có được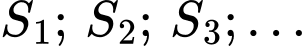 lập thành cấp số nhân lùi vô hạn có
lập thành cấp số nhân lùi vô hạn có 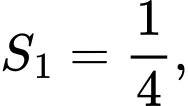
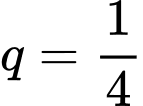 nên ta có tổng diện tích chuột Mickey cần tô màu là
nên ta có tổng diện tích chuột Mickey cần tô màu là 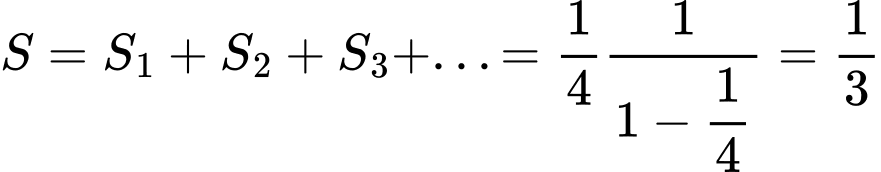 (đvdt).
(đvdt).
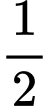 nên diện tích
nên diện tích 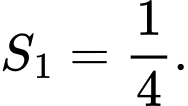
Cạnh hình vuông thứ hai là
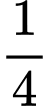 nên diện tích
nên diện tích 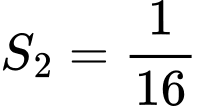 ,…
,…Cứ tiếp tục như vậy thì ta có được
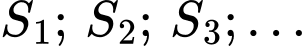 lập thành cấp số nhân lùi vô hạn có
lập thành cấp số nhân lùi vô hạn có 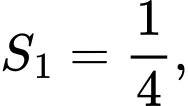
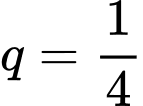 nên ta có tổng diện tích chuột Mickey cần tô màu là
nên ta có tổng diện tích chuột Mickey cần tô màu là 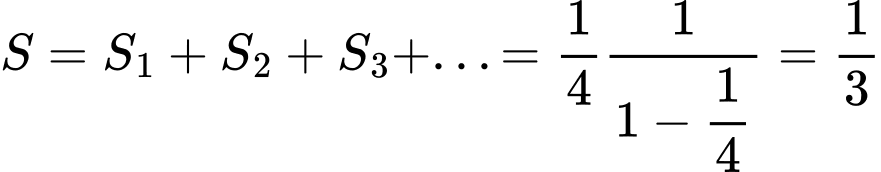 (đvdt).
(đvdt). Dạng toán: Phương pháp sai phân và quy nạp tính giới hạn
Câu 10 [582896]: Giới hạn 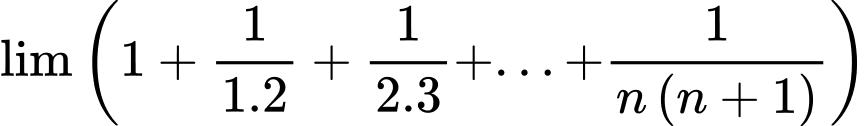 bằng
bằng
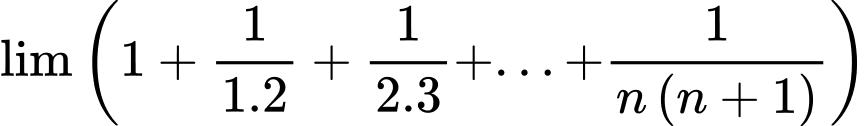 bằng
bằng A, 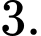
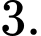
B, 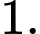
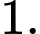
C, 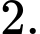
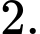
D, 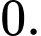
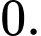
Chọn C
Ta có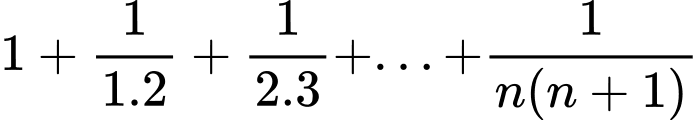
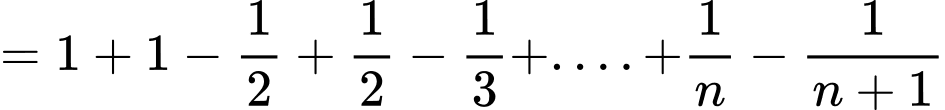
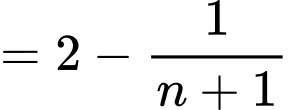
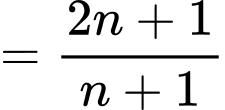
Nên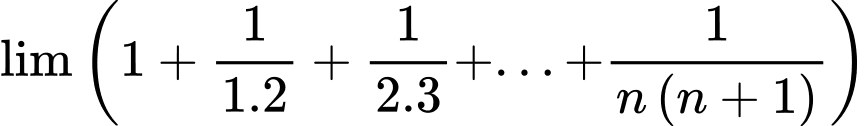
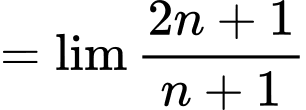
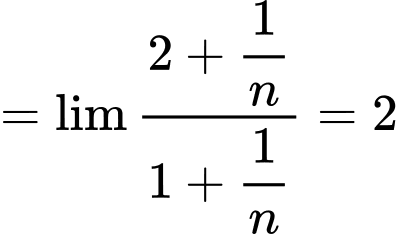 Đáp án: C
Đáp án: C
Ta có
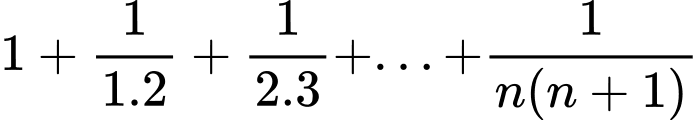
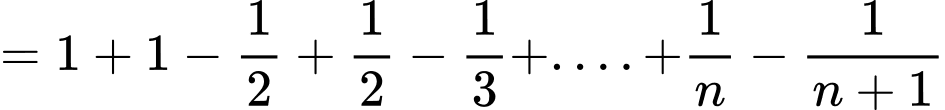
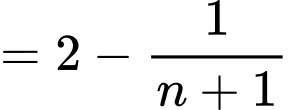
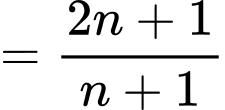
Nên
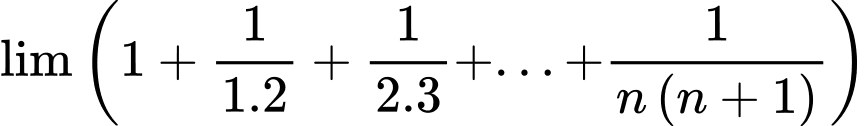
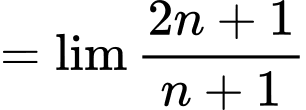
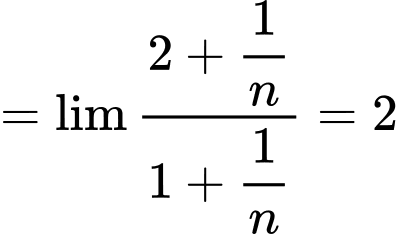 Đáp án: C
Đáp án: C
Câu 11 [582897]: Tính giới hạn: 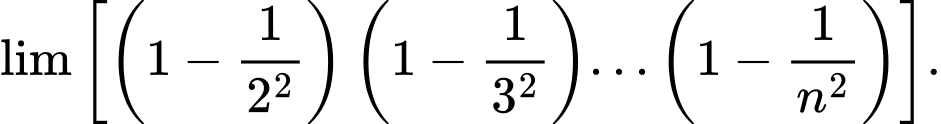
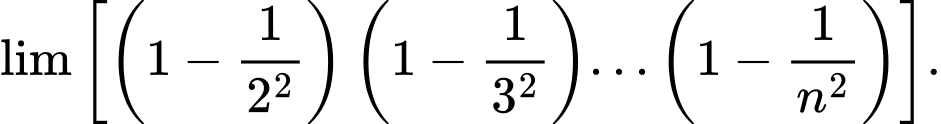
A, 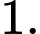
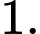
B, 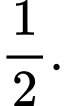
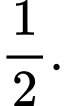
C, 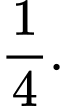
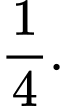
D, 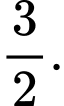
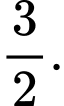
Chọn B
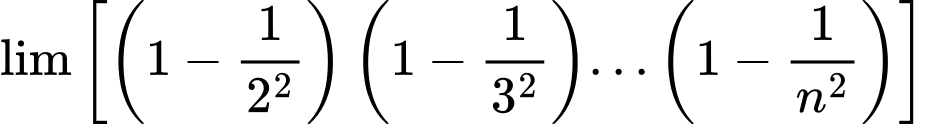
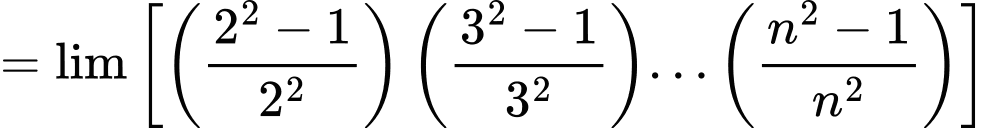

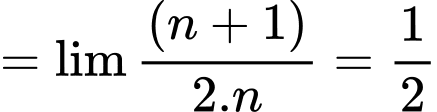 Đáp án: B
Đáp án: B
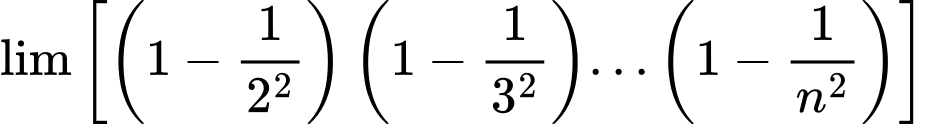
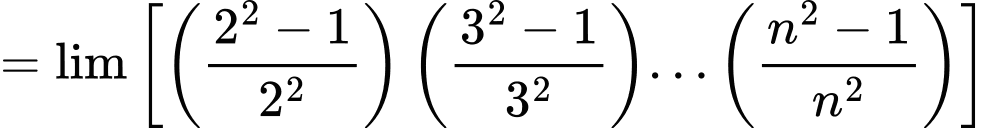

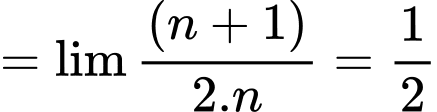 Đáp án: B
Đáp án: B
Câu 12 [582898]: Cho dãy số 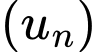 xác định bởi :
xác định bởi : 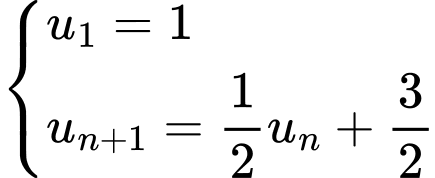

Tính giới hạn của dãy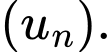
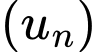 xác định bởi :
xác định bởi : 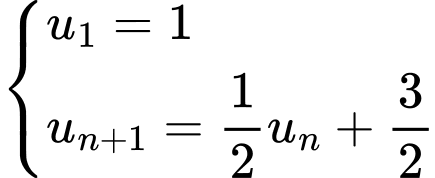

Tính giới hạn của dãy
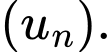
Đặt 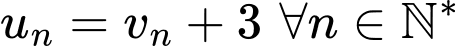 thì
thì 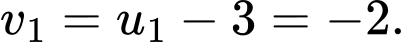
Khi đó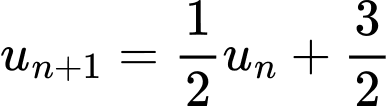
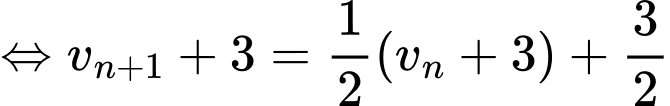
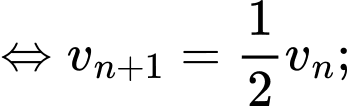
 nên dãy
nên dãy 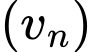 là một cấp số nhân với
là một cấp số nhân với 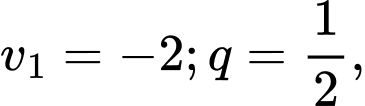 suy ra
suy ra 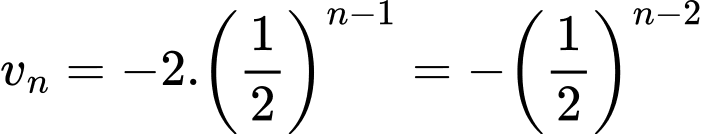
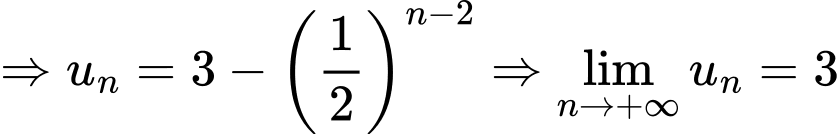
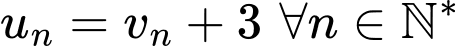 thì
thì 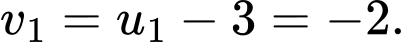
Khi đó
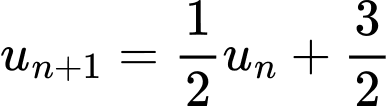
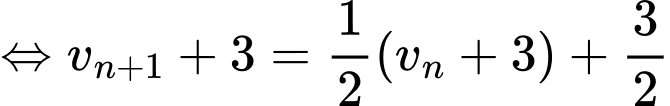
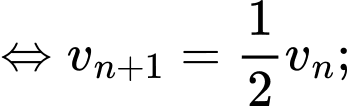
 nên dãy
nên dãy 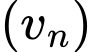 là một cấp số nhân với
là một cấp số nhân với 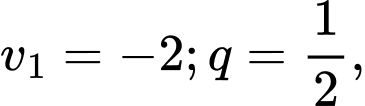 suy ra
suy ra 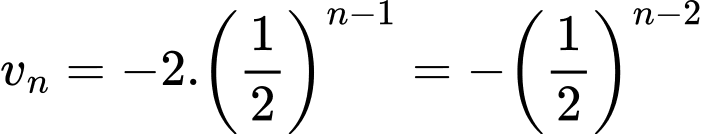
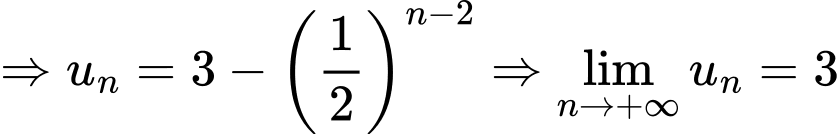
Dạng toán: Dãy số có giới hạn hữu hạn
Câu 13 [582899]: Tính 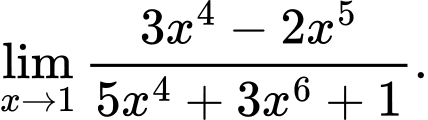
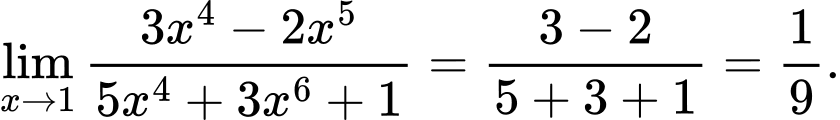
Câu 14 [582900]: Tính 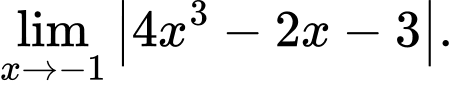
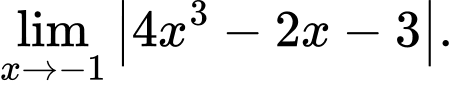
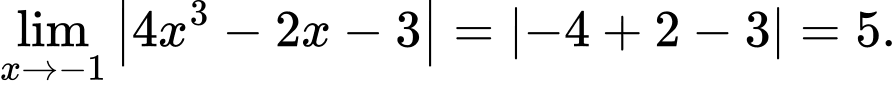
Câu 15 [582901]: Tính 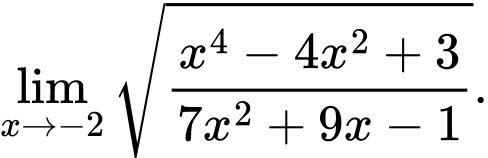
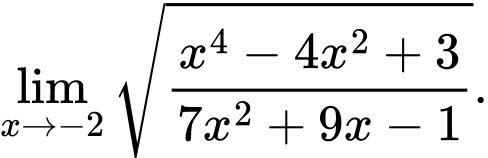
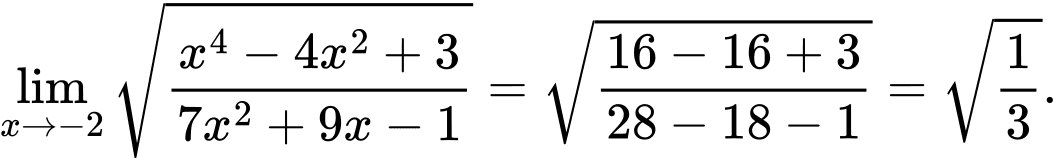
Dạng toán: Giới hạn tại vô cực
Câu 16 [582902]: Tính 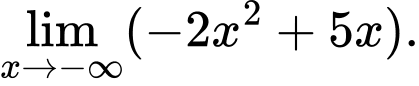
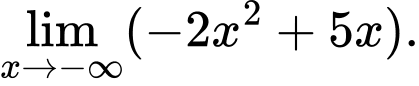
Cách 1: Ta có 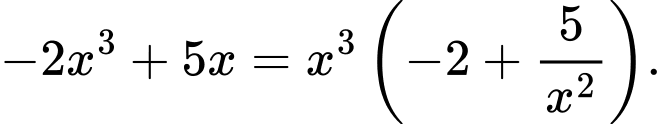
Vì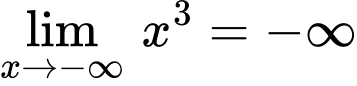 và
và 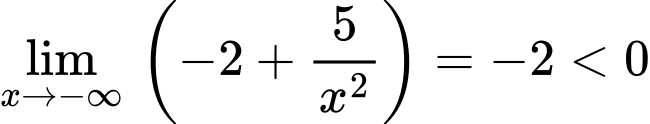 nên
nên 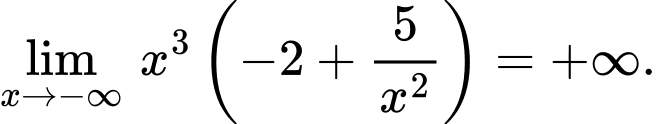
Vậy theo Quy tắc 1,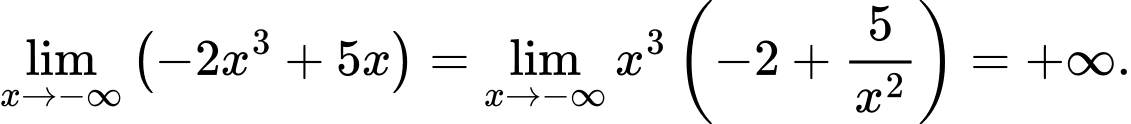
Cách 2: Sử dụng MTCT tính giá trị của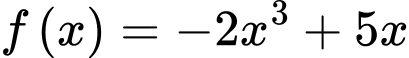 tại một điểm có giá trị âm rất nhỏ (do ta đang xét giới hạn của hàm số khi
tại một điểm có giá trị âm rất nhỏ (do ta đang xét giới hạn của hàm số khi 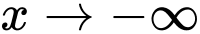 ), chẳng hạn tại
), chẳng hạn tại 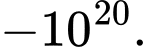
Máy hiển thị kết quả như hình:

Đó là một giá trị dương rất lớn. Vậy chọn đáp án C, tức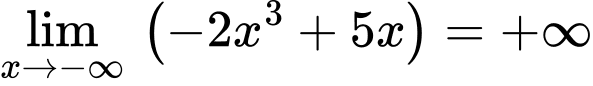
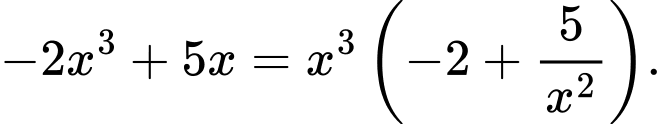
Vì
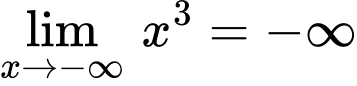 và
và 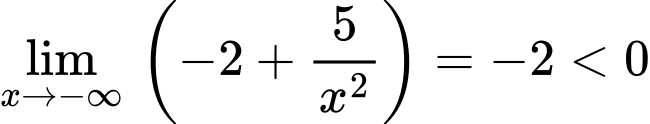 nên
nên 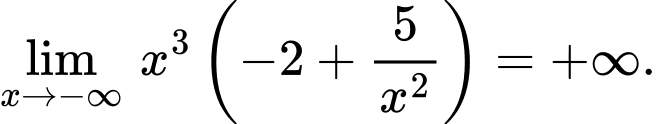
Vậy theo Quy tắc 1,
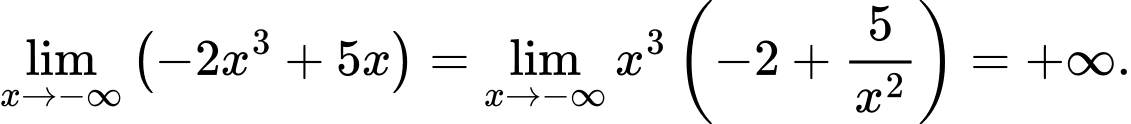
Cách 2: Sử dụng MTCT tính giá trị của
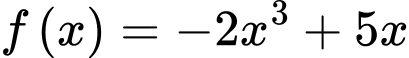 tại một điểm có giá trị âm rất nhỏ (do ta đang xét giới hạn của hàm số khi
tại một điểm có giá trị âm rất nhỏ (do ta đang xét giới hạn của hàm số khi 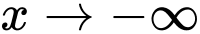 ), chẳng hạn tại
), chẳng hạn tại 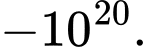
Máy hiển thị kết quả như hình:

Đó là một giá trị dương rất lớn. Vậy chọn đáp án C, tức
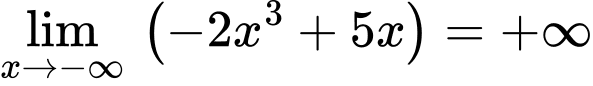
Câu 17 [582903]: Tính 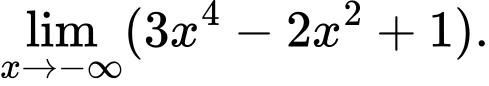
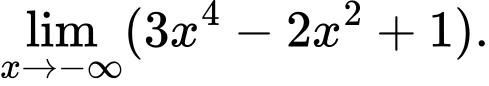
Theo nhận xét trên thì 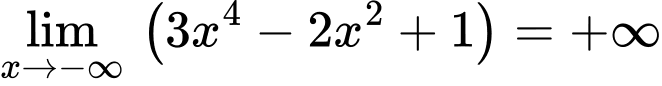
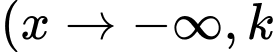 chẵn và
chẵn và  Thật vậy, ta có
Thật vậy, ta có 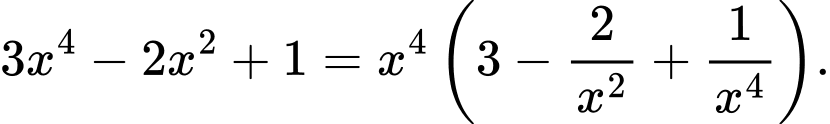
Vì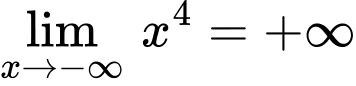 và
và 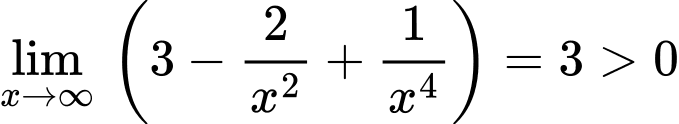 nên
nên 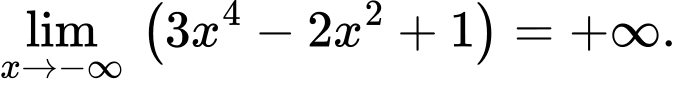
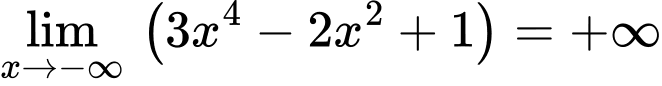
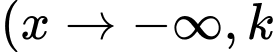 chẵn và
chẵn và  Thật vậy, ta có
Thật vậy, ta có 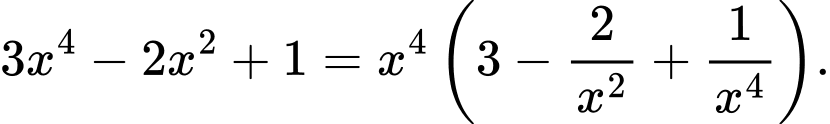
Vì
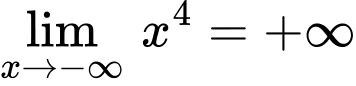 và
và 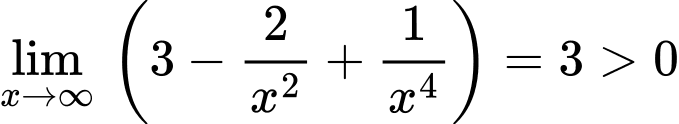 nên
nên 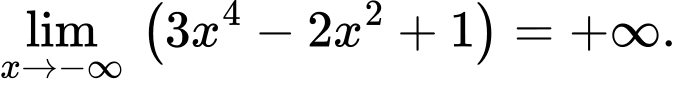
Câu 18 [582904]: 

Ta có: 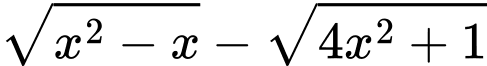
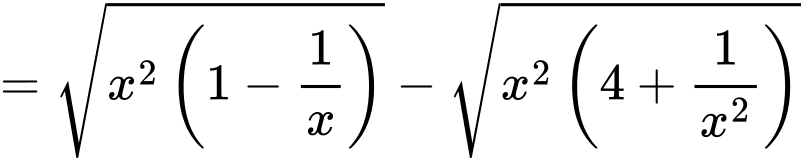
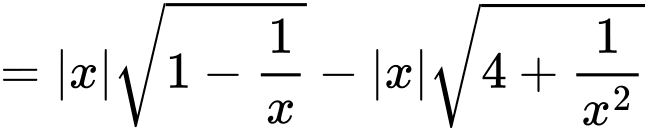
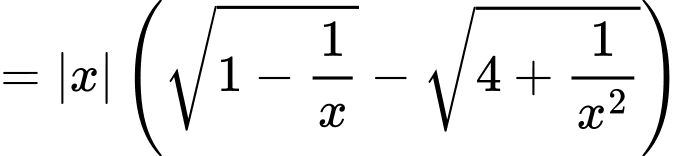
Mà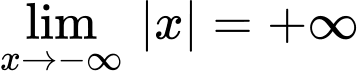 và
và 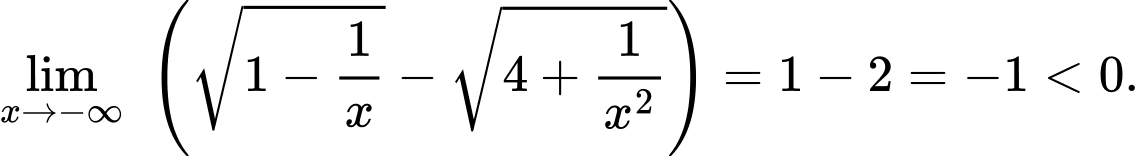
Vậy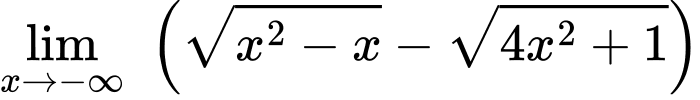
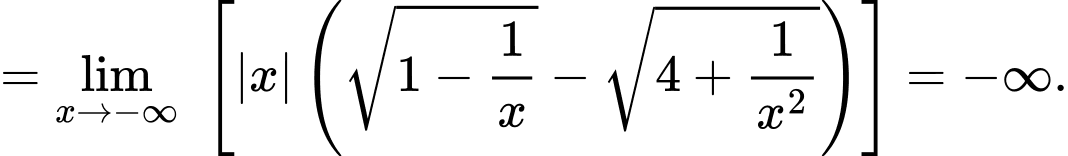
Lưu ý: Có thể thấy như sau:
Vì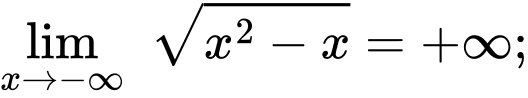
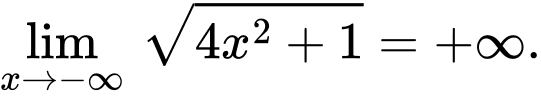
Mà hệ số của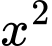 trong
trong 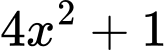 lớn hơn hệ số của
lớn hơn hệ số của 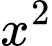 trong
trong 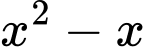 nên suy ra
nên suy ra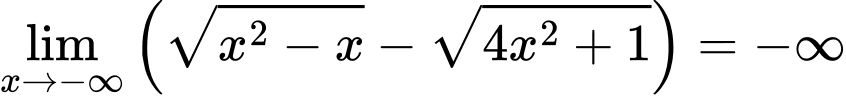
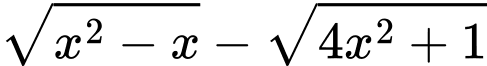
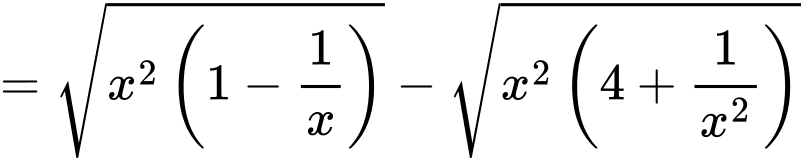
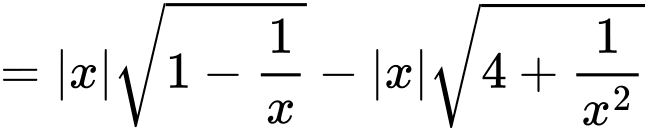
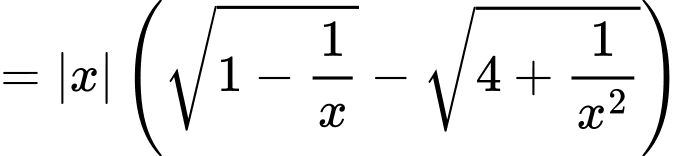
Mà
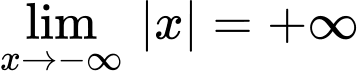 và
và 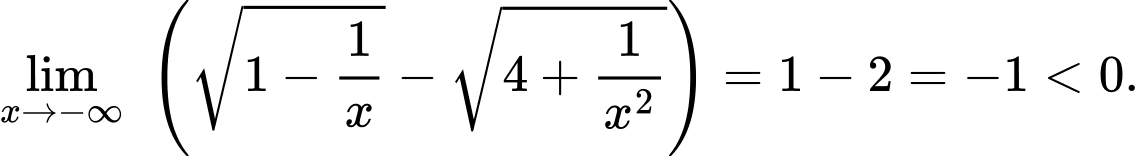
Vậy
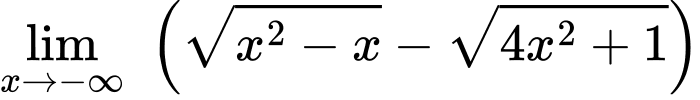
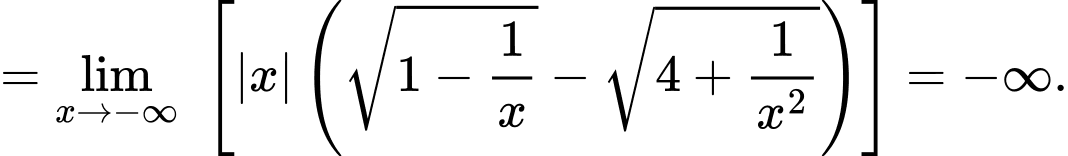
Lưu ý: Có thể thấy như sau:
Vì
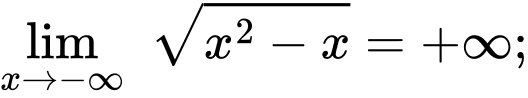
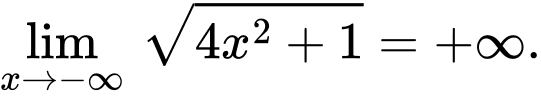
Mà hệ số của
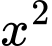 trong
trong 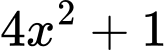 lớn hơn hệ số của
lớn hơn hệ số của 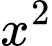 trong
trong 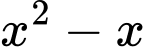 nên suy ra
nên suy ra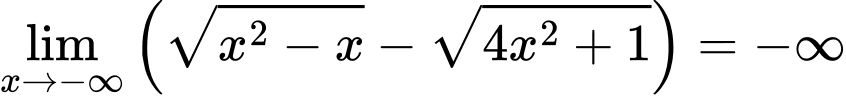
Dạng toán: Giới hạn một bên
Câu 19 [582905]: Tính 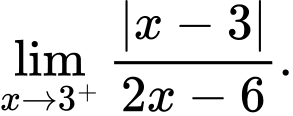
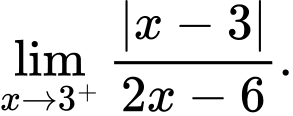
Cách 1: Giải bằng tự luận
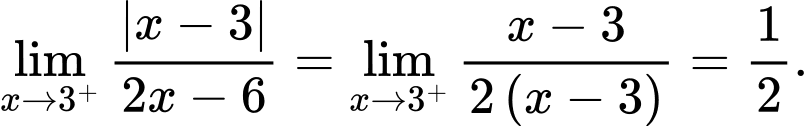
Cách 2: Giải nhanh bằng MTCT
Nhập vào màn hình và ấn CALC
và ấn CALC  ta được kết quả
ta được kết quả

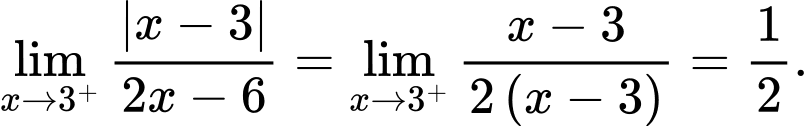
Cách 2: Giải nhanh bằng MTCT
Nhập vào màn hình
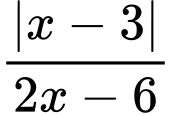 và ấn CALC
và ấn CALC 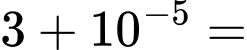 ta được kết quả
ta được kết quả
Câu 20 [582906]: Tính 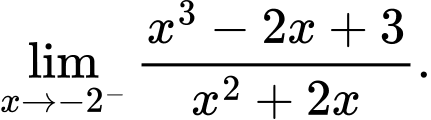
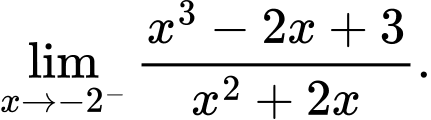
Tử số có giới hạn là 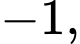 mẫu số có giới hạn 0 và khi
mẫu số có giới hạn 0 và khi  thì
thì 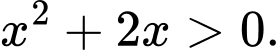
Do đó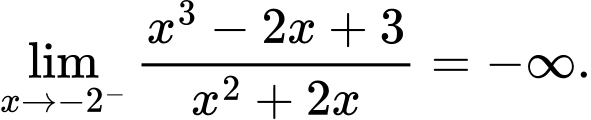
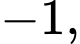 mẫu số có giới hạn 0 và khi
mẫu số có giới hạn 0 và khi  thì
thì 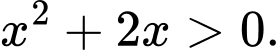
Do đó
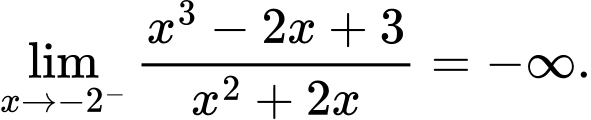
Câu 21 [582907]: Tính 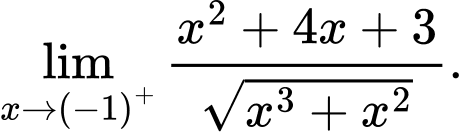
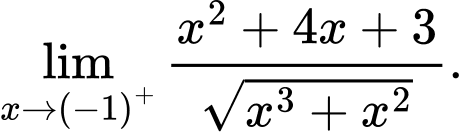
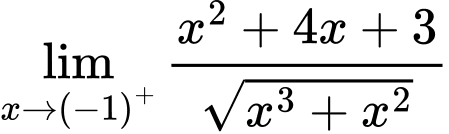
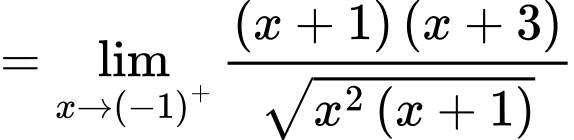
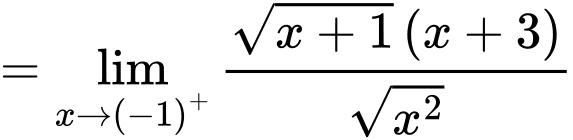
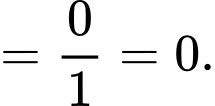
Câu 22 [582908]: Cho hàm số 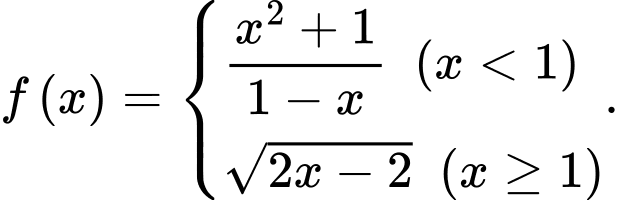
Khi đó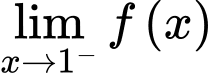 bằng bao nhiêu?
bằng bao nhiêu?
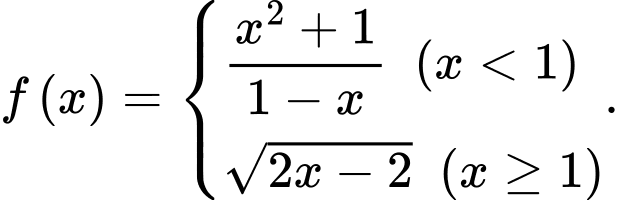
Khi đó
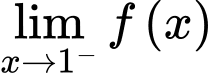 bằng bao nhiêu?
bằng bao nhiêu? 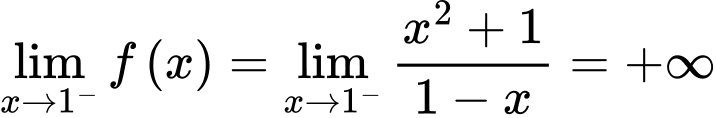 vì tử số có giới hạn là 2, mẫu số có giới hạn 0 và
vì tử số có giới hạn là 2, mẫu số có giới hạn 0 và 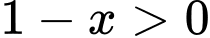 với
với 
Dạng toán: Dạng vô định 0/0
Câu 23 [582909]: Tính 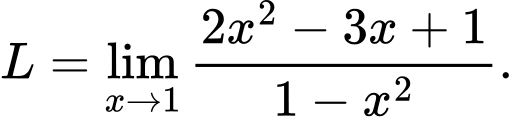
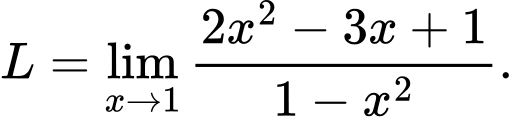
Cách 1: Giải bằng tự luận
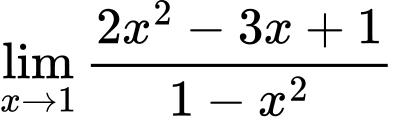
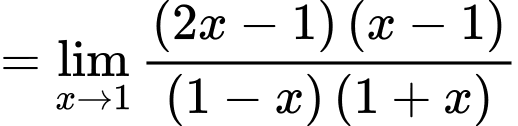
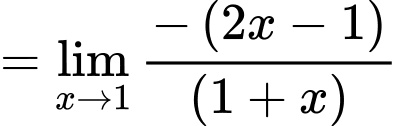
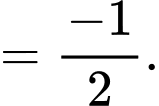
Cách 2: Giải nhanh bằng máy tính
Nhập vào màn hình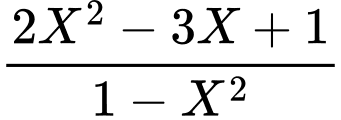 ấn CALC
ấn CALC 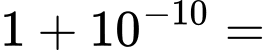 ta được kết quả
ta được kết quả
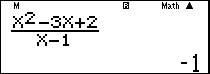
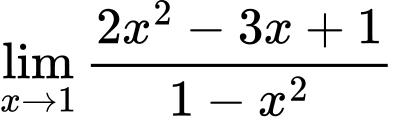
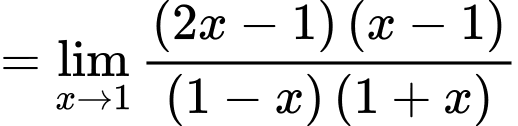
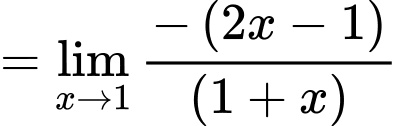
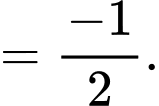
Cách 2: Giải nhanh bằng máy tính
Nhập vào màn hình
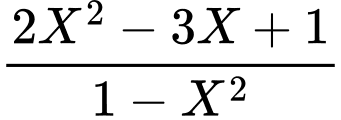 ấn CALC
ấn CALC 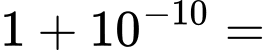 ta được kết quả
ta được kết quả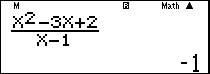
Câu 24 [582910]: Tính 

Cách 1: Giải bằng tự luận
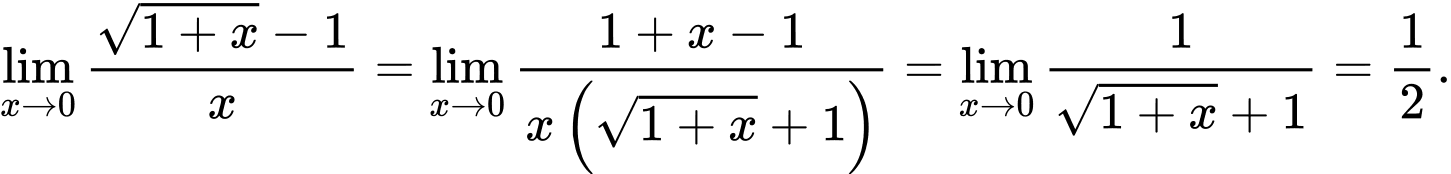
Cách 2: Giải nhanh bằng máy tính
Để ra kết quả chính xác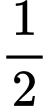 ta có thể tính theo quy tắc Lô-pi-tan như sau:
ta có thể tính theo quy tắc Lô-pi-tan như sau:
Nhập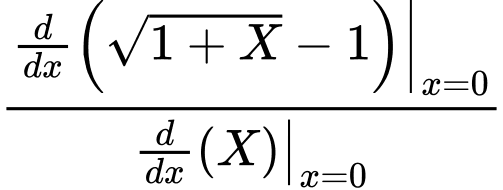 rồi ấn phím = ta được kết quả chính xác
rồi ấn phím = ta được kết quả chính xác 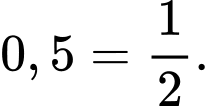
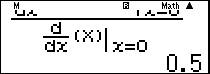
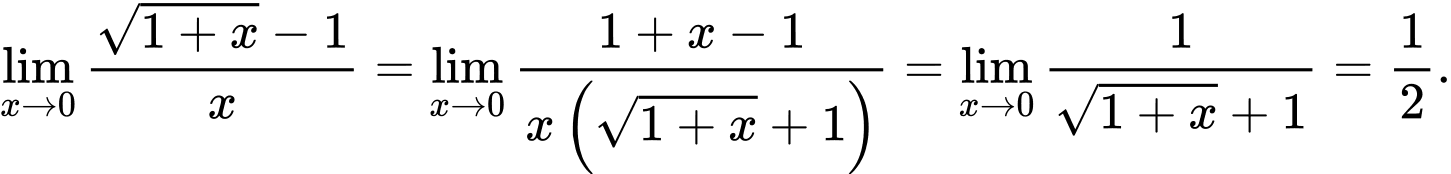
Cách 2: Giải nhanh bằng máy tính
Để ra kết quả chính xác
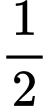 ta có thể tính theo quy tắc Lô-pi-tan như sau:
ta có thể tính theo quy tắc Lô-pi-tan như sau:Nhập
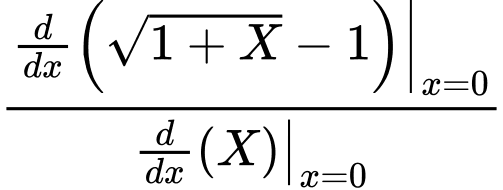 rồi ấn phím = ta được kết quả chính xác
rồi ấn phím = ta được kết quả chính xác 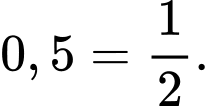
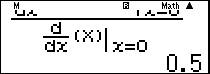
Câu 25 [582911]: Tính 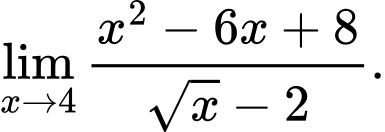
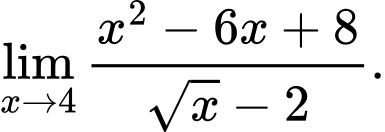
Cách 1: Giải bằng tự luận
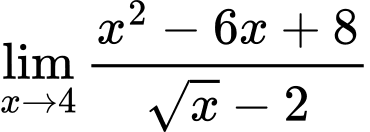
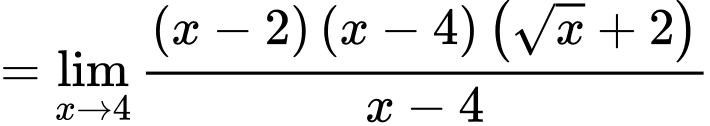
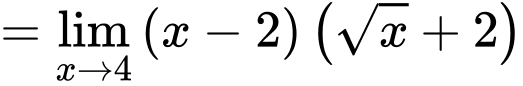
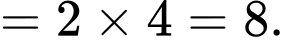
Cách 2: Giải nhanh bằng máy tính
Nhập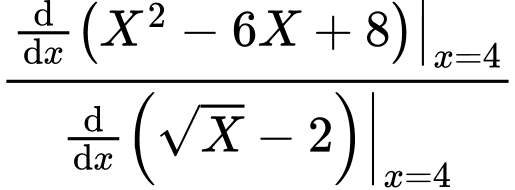 rồi ấn phím = ta được kết quả chính xác 8.
rồi ấn phím = ta được kết quả chính xác 8.
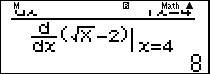
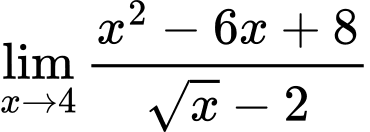
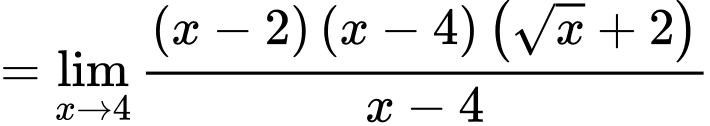
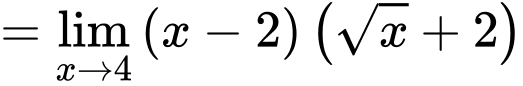
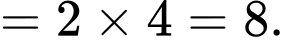
Cách 2: Giải nhanh bằng máy tính
Nhập
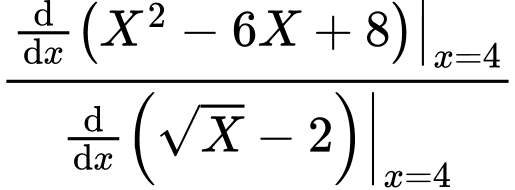 rồi ấn phím = ta được kết quả chính xác 8.
rồi ấn phím = ta được kết quả chính xác 8.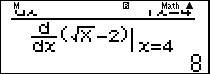
Dạng toán: Dạng vô định ∞/∞
Câu 26 [582912]: Tính 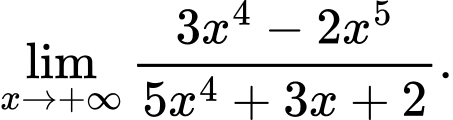
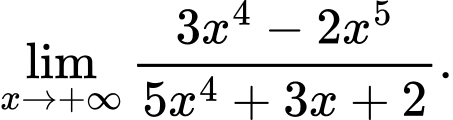
Cách 1: Giải bằng tự luận
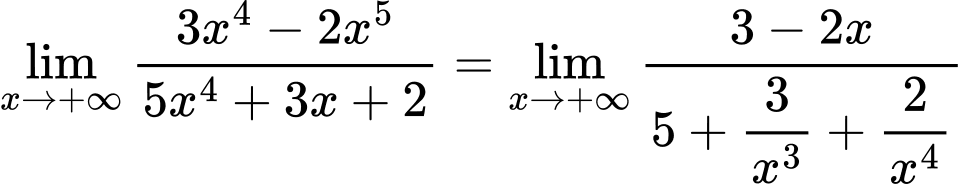
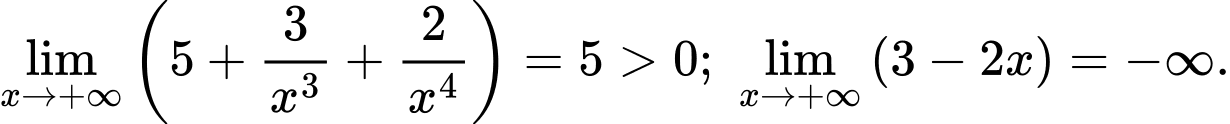
Do đó: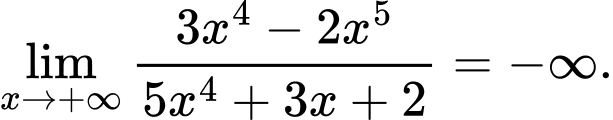
Cách 2: Mẹo giải nhanh
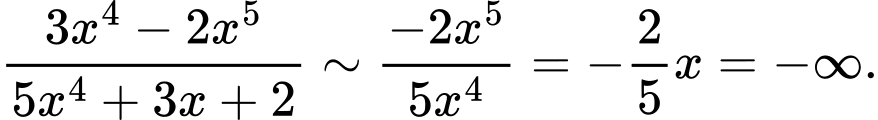
Lời bình: Bậc tử lớn hơn bậc mẫu nên kết quả là
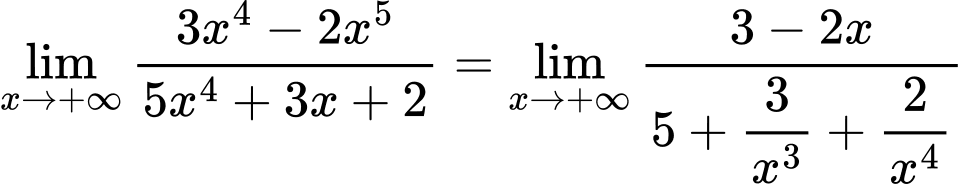
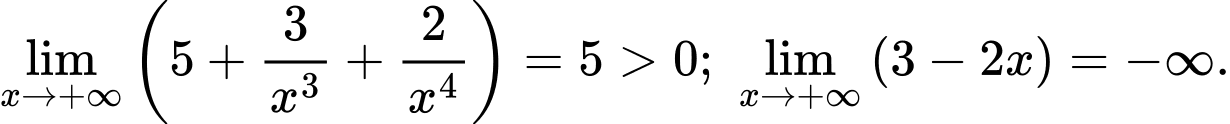
Do đó:
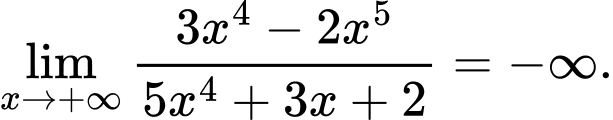
Cách 2: Mẹo giải nhanh
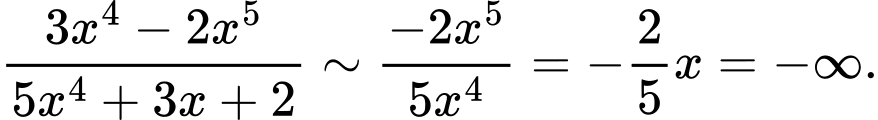
Lời bình: Bậc tử lớn hơn bậc mẫu nên kết quả là

Câu 27 [582913]: Tính 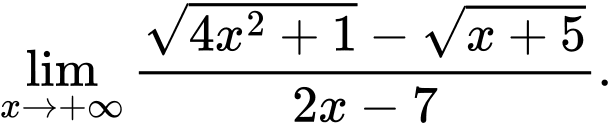
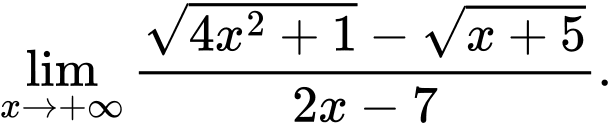
Ta có:
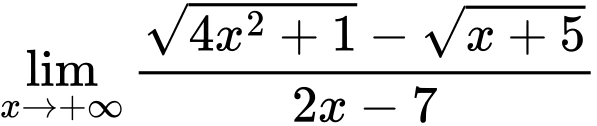
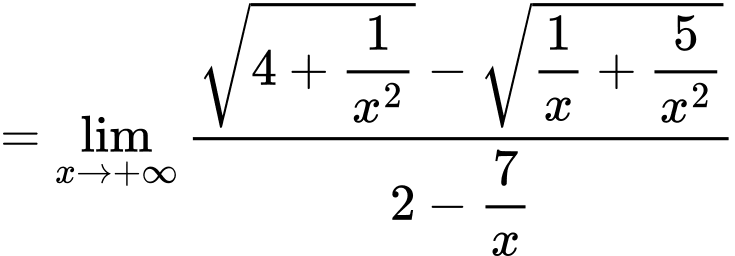
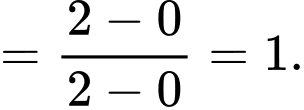
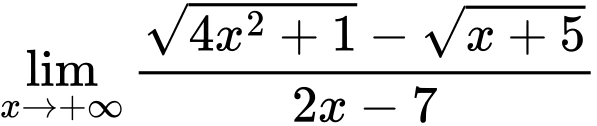
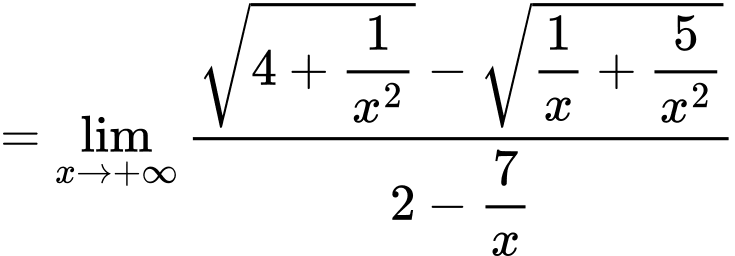
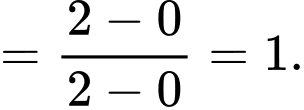
Câu 28 [582914]: Tính 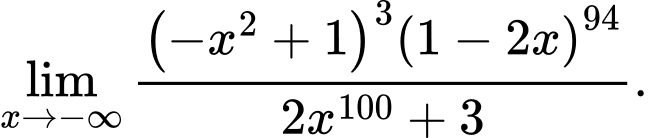
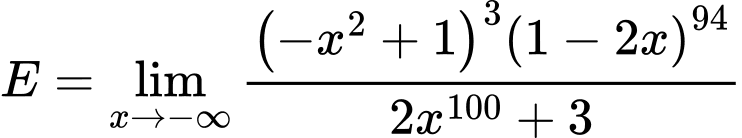
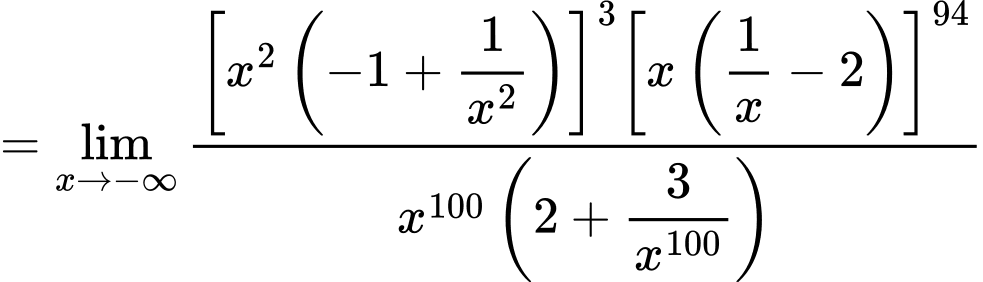
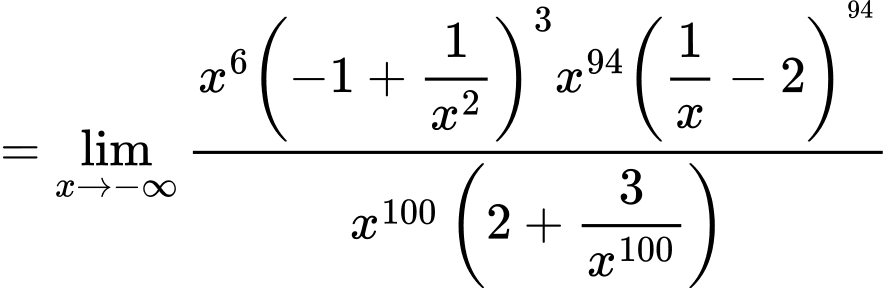
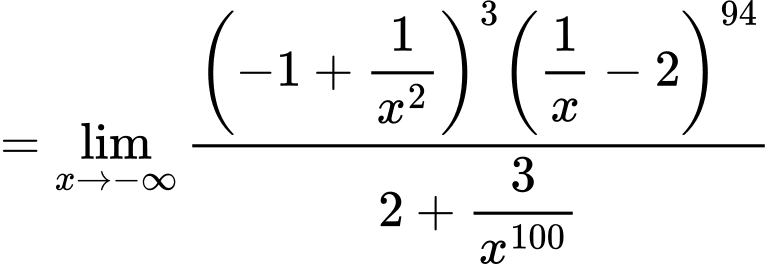
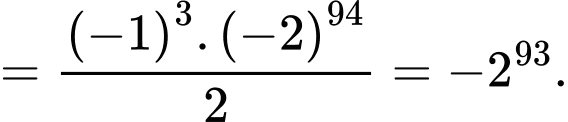
Dạng toán: Dạng vô định ∞ - ∞, 0.∞
Câu 29 [582915]: Tính 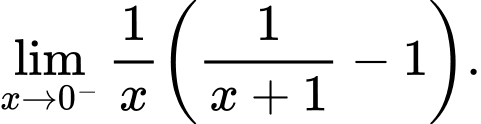
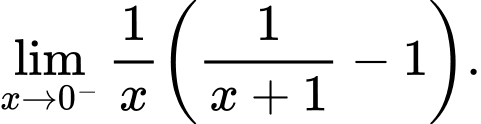
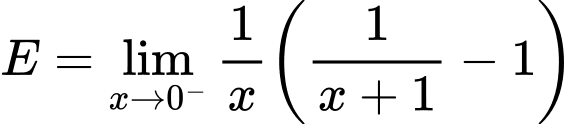 (Dạng vô định
(Dạng vô định  )
)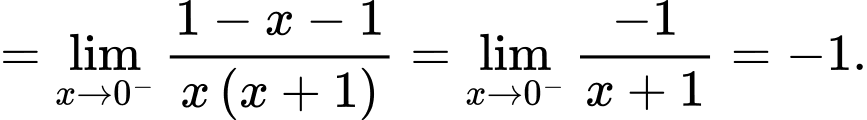
Câu 30 [582916]: Tính 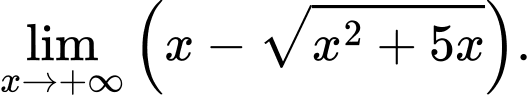
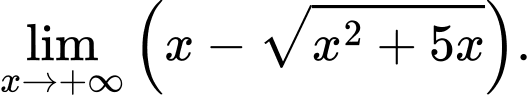
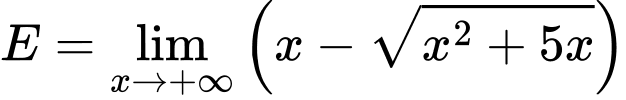
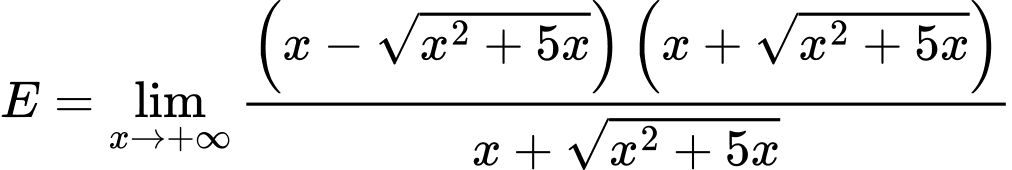
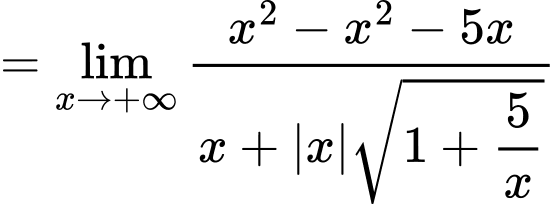
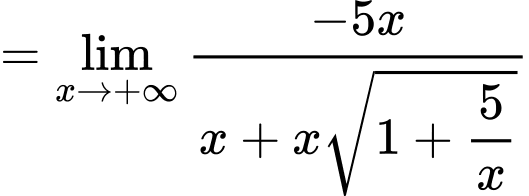 (Vì
(Vì 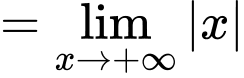
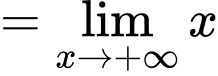 )
)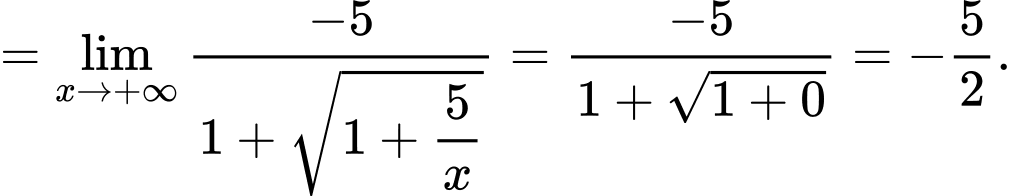
Câu 31 [582917]: Tính